Механическая работа (А) | |
Физическая величина, характеризующая результат действия силы и численно равная скалярному произведению вектора силы и вектора перемещения, совершенного под действием этой силы. | |
A=Fscosα | A=Fscosα |
Работа не совершается, если: 1.Сила действует, а тело не перемещается. Например: мы действуем с силой на шкаф, но не можем сдвинуть. | |
2.Тело перемещается, а сила равна нулю или все силы скомпенсированы. Например: при движении по инерции работа не совершается. | |
3. Например: центростремительная сила работу не совершает. | |
Если вектора силы и перемещения сонаправлены (α=00, cos0=1), то A=Fs | |
Если вектора силы и перемещения направлены противоположно (α=1800, cos1800 = -1), то A= -Fs (например, работа силы сопротивления, трения). | |
Если угол между векторами силы и перемещения 00 < α < 1800, то работа положительна. | |
Если угол между векторами силы и перемещения 00 < α < 180 0, то работа положительна. | |
Если на тело действует несколько сил, то полная работа (работа всех сил) равна работе результирующей силы. |
|
Если тело движется не по прямой, то можно разбить все движение на бесконечно малые участки, которые можно считать прямолинейными, и просуммировать работы. | |
Графическое представление работы. |
|
Рассмотрим движение тела под действием постоянной силы вдоль прямой Ох. График зависимости силы от координаты изображен на рисунке. Площадь заштрихованного прямоугольника на рисунке численно равна работе силы
| |
Если сила меняется с расстоянием (координатой), то необходимо разбить все движение на такие малые участки, на которых силу можно считать неизменной, сосчитать работы на каждом элементарном участке пути, и сложить все элементарные работы. | |
Единицы работы. |
|
В международной системе единиц (СИ): [А] = Дж = Н • м Механическая работа равна одному джоулю, если под действием силы в 1 Н оно перемещается на 1 м в направлении действия этой силы. | 1Дж = 1Н • 1м |
Мощность | |
Мощность – физическая величина, характеризующая скорость совершения работы и численно равная отношению работы к интервалу времени, за который эта работа совершена. Мощность показывает, какая работа совершается за единицу времени. | |
| |
Единицы мощности В международной системе единиц (СИ): Мощность равна одному ватту, если за 1 с совершается работа 1 Дж. | 1 л.с. (лошадиная сила) ≈ 735 Вт |
формула, мгновенный и средний расчет силы.
Термин «мощность» в физике имеет специфический смысл. Механическая работа может выполняться с различной скоростью. А механическая мощность обозначает, как быстро совершается эта работа. Способность правильно измерить мощность имеет важное значение для использования энергетических ресурсов.
Физический смысл мощности
Разные виды мощности
Для формулы механической мощности применяется следующее выражение:
N = ΔA/Δt.
В числителе формулы затраченная работа, в знаменателе – временной промежуток ее совершения. Это отношение и называется мощностью.
Существует три величины, которыми можно выразить мощность: мгновенная, средняя и пиковая:
- Мгновенная мощность – мощностной показатель, измеренный в данный момент времени. Если рассмотреть уравнение для мощности N = ΔA/Δt , то мгновенная мощность представляет собой ту, которая берется в чрезвычайно малый промежуток времени Δt. Если имеется построенная графическая зависимость мощности от времени, то мгновенная мощность – это просто считываемое с графика значение в любой взятый момент времени. Другая запись выражения для мгновенной мощности:
N = dA/dt.
- Средняя мощность – мощностная величина, измеренная за относительно большой временной отрезок Δt;
- Пиковая мощность – максимальное значение, которое мгновенная мощность может иметь в конкретной системе в течение определенного временного промежутка.
 Стереосистемы и двигатели автомобилей – примеры устройств, способных обеспечить максимальную мощность, намного выше их средней номинальной мощности. Однако поддерживать эту мощностную величину можно в течение короткого времени. Хотя для эксплуатационных характеристик устройств она может быть более важной, чем средняя мощность.
Стереосистемы и двигатели автомобилей – примеры устройств, способных обеспечить максимальную мощность, намного выше их средней номинальной мощности. Однако поддерживать эту мощностную величину можно в течение короткого времени. Хотя для эксплуатационных характеристик устройств она может быть более важной, чем средняя мощность.
Важно! Дифференциальная форма уравнения N = dA/dt универсальна. Если механическая работа выполняется равномерно в течение времени t, то средняя мощность будет равна мгновенной.
Из общего уравнения получается запись:
N = A/t,
где A будет общая работа за заданное время t. Тогда при равномерной работе вычисленный показатель равен мгновенной мощности, а при неравномерной –средней.
Формулы для механической мощности
В каких единицах измеряют мощность
Стандартной единицей для измерения мощности служит Ватт (Вт), названный в честь шотландского изобретателя и промышленника Джеймса Ватта. Согласно формуле, Вт = Дж/с.
Согласно формуле, Вт = Дж/с.
Существует еще одна единица мощности, до сих пор широко используемая, – лошадиная сила (л. с.).
Интересно. Термин «лошадиная сила» берет свое начало в 17-м веке, когда лошадей использовали для поднятия груза из шахты. Одна л. с. равна мощности для поднятия 75 кг на 1 м за 1 с. Это эквивалентно 735,5 Вт.
Мощность силы
Уравнение для мощности соединяет выполненную работу и время. Поскольку известно, что работа выполняется силами, а силы могут перемещать объекты, можно получить другое выражение для мгновенной мощности:
- Работа, проделанная силой при перемещении:
A = F x S x cos φ.
- Если поставить А в универсальную формулу для N, определяется мощность силы:
N = (F x S x cos φ)/t = F x V x cos φ, так как V = S/t.
- Если сила параллельна скорости частицы, то формула принимает вид:
N = F x V.
Мощность вращающихся объектов
Процессы, связанные с вращением объектов, могут быть описаны аналогичными уравнениями. Эквивалентом силы для вращения является крутящий момент М, эквивалент скорости V – угловая скорость ω.
Если заменить соответствующие величины, то получается формула:
N = M x ω.
M = F x r, где r – радиус вращения.
Для расчета мощности вала, вращающегося против силы, применяется формула:
N = 2π x M x n,
где n – скорость в об/с (n = ω/2π).
Отсюда получается то же упрощенное выражение:
N = M x ω.
Таким образом, двигатель может достичь высокой мощности либо при высокой скорости, либо, обладая большим крутящим моментом. Если угловая скорость ω равна нулю, то мощность тоже равна нулю, независимо от крутящего момента.
Видео
Оцените статью:формула, мгновенный и средний расчет силы
В общем смысле этим термином обозначают энергетические изменения определенной системы.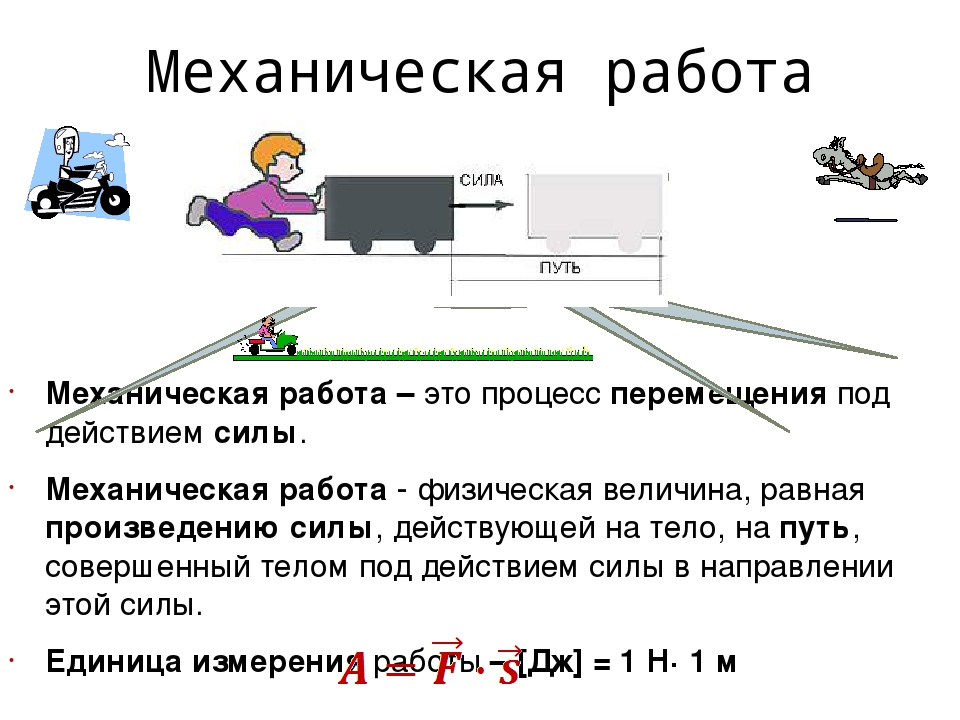 Классическая формула механической мощности устанавливает связь между работой и временем, которое понадобилось на завершение соответствующего процесса. В этой публикации дополнительно рассмотрены электрические и гидравлические параметры энергии, методики вычислений, измерительные приборы.
Классическая формула механической мощности устанавливает связь между работой и временем, которое понадобилось на завершение соответствующего процесса. В этой публикации дополнительно рассмотрены электрические и гидравлические параметры энергии, методики вычислений, измерительные приборы.
Механическая мощность характеризует скорость выполнения работы
Используемые обозначенияВ стандартных формулах мощность часто обозначают буквой N без уточнения происхождения. Достаточно часто применяют P. В этом варианте понятен исходный смысл: от латинского слова potestas – действие, мощь, сила. В электротехнике часто применяют W (watt – англ., ватт). Дополнительными символами отмечают специфическое назначение NH – гидравлическая мощность от hydraulics.
Основные формулыКогда рассчитывается средняя мощность формула содержит значения для определенных промежутков: ΔА (работа) и Δt (время). Мгновенные показатели обозначают dA и dt, соответственно. Чтобы узнать количество потребленной энергии, берут интеграл за необходимый временной интервал.
Чтобы узнать количество потребленной энергии, берут интеграл за необходимый временной интервал.
В действующей системе единиц «СИ», утвержденной на международном уровне, мощность предлагается указывать в ваттах (один Вт = работе 1 Джоуль, сделанной за 1 секунду). Устаревшее обозначение «лошадиная сила» рекомендовано изъять из оборота. Для удобства применяют производные значения с определенными приставками (один киловатт (1кВт) = 10 в третьей степени ватт = 1 000 Вт).
- килограмм-сила-метр в секунду (кгс*м/с) – 0,102;
- эрг в секунду (эрг/с) – 107;
- лошадиная сила (л.с.) метрическая/ английская – 1,36*10-3/ 1,34*10-3.
Мощность в механикеК сведению. Если в описании автомобиля указано 125 кВт, это равнозначно 170 л.с. (125*1,36=169,95).
В ходе исследования механических процессов необходимо учитывать точку приложения усилия и направление действия.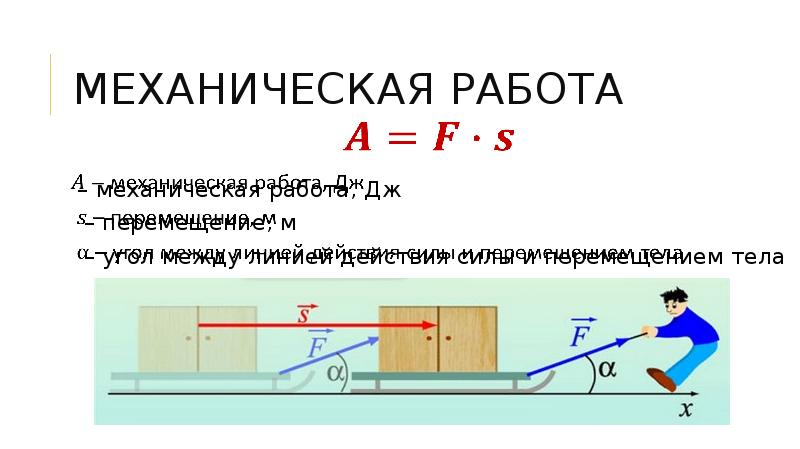 Рассчитать мощность можно по формуле (N=F*v) с учетом скорости движения (v) определенного тела. Если направления не совпадают, добавляют корректирующий множитель (cosα).
Рассчитать мощность можно по формуле (N=F*v) с учетом скорости движения (v) определенного тела. Если направления не совпадают, добавляют корректирующий множитель (cosα).
В этой области не важны тяжесть предметов, сила трения, другие механические термины и определения. Тем не менее, суть рассматриваемой физической величины остается неизменной, подобны принципы отдельных вычислений.
Можно применить для расчета мгновенной мощности формулу:
P(a-b) = А/ Δt,
где:
- (a-b) – обозначают энергию, затраченную на перемещение заряда (q) из одной в другую точку;
- А – выполненная в ходе этого процесса работа.
Если взять все заряды (Q), напряжение в контрольных точках (U), нетрудно вычислить суммарную мощность:
P = (U/ Δt) * Q = U * Q/ Δt = U *I.
Последнее преобразование основано на классическом определении тока (количество зарядов, протекающих по соответствующему проводнику за определенное время).
Для пассивных цепей можно пользоваться законом Ома и соответствующими формулами без дополнительных коррекций. Учитывают (при наличии) источник электродвижущей силы (направление движения токов).
Формулы для расчета мощности и других параметров
При подключении техники к источникам переменного тока вычисления усложняются. Приходится интегрировать мгновенные значения с учетом определенных периодов, частоты и формы сигналов. На практике часто решают задачи по вычислению мощности потребителей, подключенных к источнику питания с синусоидальным током (напряжением).
Активная составляющая энергии в этом случае будет зависеть от фазового сдвига. Значение вычисляют по формуле:
Pa = U * I * cosϕ (для 220V).
При работе с трехфазными источниками пользуются измененным вариантом выражения:
Pa = √3 * U * I * cosϕ = 1,732 * U * I * cosϕ.
Реактивная переменная потребляется и возвращается в источник питания. Для расчета берут следующую зависимость базовых параметров:
Pq = U * I * sinϕ.
Полная мощность:
Ps = √( Pa2 + Pq2).
Приборы для измерения электрической мощностиС учетом основных компонентов формулы несложно понять, что значения необходимых параметров (ток и напряжение) можно узнать с помощью обычного мультиметра. По необходимому уровню точности выбирают методику и класс измерительного прибора.
Современный ваттметр может передавать информацию в режиме онлайн для удаленного контроля телеметрии
Специализированные изделия (ваттметры) способны отображать результаты исследований при работе в сетях постоянного и переменного тока. Специальные модификации (варметры) замеряют реактивную составляющую.
Гидравлическая мощностьУзнать производительность асинхронного электродвигателя насоса можно косвенным методом, по выполненной работе. Для этого умножают перепад измеренных (вход/ выход) давлений (ΔP) на количество перекачанной жидкости (V) в м куб. за секунду.
Пример:
- напор по манометрам – 220 кгс/ см кв.

- производительность – 65 л/мин. = 3,9 куб. м/ час = 0,001083 куб. м /с.;
- мощность NH = ΔP * V = 220 * 100 (перевод см в м) * 0,001083 = 23,83 кВт.
Для решения практических задач меняют рассмотренные выражения необходимым образом. Расчет энергетических изменений отображает пример с падающим предметом:
- в исходных данных известны высота и масса тела;
- требуется установить мощность силы формула которой отображает результат на половине пути при свободном падении;
- подставляют вместо базовых компонентов известные величины:
- F = m *g;
- V (скорость в определенной точке) = Vn (начальная скорость) + g*t.
- после завершения преобразований получают:
P = m*√(g3*h).
Мощность вращающихся объектовДля расчета подобной системы применяют формулу:
N = M * w = (2π * M* n)/60,
где:
- M – момент силы;
- w – угловая скорость, характеризующая вращение;
- n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.

Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.
В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.
ВидеоМеханическая работа и мощность
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа – мера воздействия силы.
Определение механической работы
Определение 1Работа А, совершаемая постоянной силой F→, – это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F→ и перемещением s→.
Данное определение рассматривается на рисунке 1.
Формула работы записывается как,
A=Fs cos α.
Работа – это скалярная величина. Единица измерения работы по системе СИ – Джоуль (Дж).
Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.
Рисунок 1. Работа силы F→: A=Fs cos α=Fss
При проекции Fs→ силы F→ на направление перемещения s→ сила не остается постоянной, а вычисление работы для малых перемещений Δsiсуммируется и производится по формуле:
A=∑∆Ai=∑Fsi∆si.
Данная сумма работы вычисляется из предела (Δsi→0), после чего переходит в интеграл.
Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком Fs(x)рисунка 2.
Рисунок 2. Графическое определение работы ΔAi=FsiΔsi.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеПримером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F→, модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.
Рисунок 3. Растянутая пружина. Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.
Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.
F→упр=-F→
Зависимость модуля внешней силы от координат x можно изобразить на графике с помощью прямой линии.
Рисунок 4. Зависимость модуля внешней силы от координаты при растяжении пружины.
Из выше указанного рисунка возможно нахождение работы над внешней силой правого свободного конца пружины, задействовав площадь треугольника. Формула примет вид
A=kx22.
Данная формула применима для выражения работы, совершаемой внешней силой при сжатии пружины. Оба случая показывают, что сила упругости F→упр равняется работе внешней силы F→, но с противоположным знаком.
Определение 2Если на тело действует несколько сил, то их общая работа равняется сумме всех работ, совершаемых над телом. Когда тело движется поступательно, точки приложения сил перемещаются одинаково, то есть общая работа всех сил будет равна работе равнодействующей приложенных сил.
Мощность
Определение 3Мощностью называют работу силы, совершаемую в единицу времени.
Запись физической величины мощности, обозначаемой N, принимает вид отношения работы А к промежутку времени t совершаемой работы, то есть:
N=At.
Определение 4Система СИ использует в качестве единицы мощности ватт (Вт). 1 Ватт – это мощность, которую совершает работу в 1 Дж за время 1 с.
Помимо Ватта, существуют и внесистемные единицы измерения мощности. Например, 1 лошадиная сила примерна равна 745 Ваттам.
Физика механическая мощность. Мощность — физическая величина, формула мощности
Здравствуйте! Для вычисления физической величины, называемой мощностью, пользуются формулой, где физическую величину — работу делят на время, за которое эта работа производилась.
Выглядит она так:
P, W, N=A/t, (Вт=Дж/с).
В зависимости от учебников и разделов физики, мощность в формуле может обозначаться буквами P, W или N.
Чаще всего мощность применяется, в таких разделах физики и науки, как механика, электродинамика и электротехника. В каждом случае, мощность имеет свою формулу для вычисления. Для переменного и постоянного тока она тоже различна. Для измерения мощности используют ваттметры.
Теперь вы знаете, что мощность измеряется в ваттах. По-английски ватт — watt, международное обозначение — W, русское сокращение — Вт. Это важно запомнить, потому что во всех бытовых приборах есть такой параметр.
Мощность — скалярная величина, она не вектор, в отличие от силы, которая может иметь направление. В механике, общий вид формулы мощности можно записать так:
P=F*s/t, где F=А*s,
v=s/t,
Р=F*v.
Из формул видно, как мы вместо А подставляем силу F умноженную на путь s. В итоге мощность в механике, можно записать, как силу умноженную на скорость. К примеру, автомобиль имея определенную мощность, вынужден снижать скорость при движении в гору, так как это требует большей силы.
К примеру, автомобиль имея определенную мощность, вынужден снижать скорость при движении в гору, так как это требует большей силы.
Средняя мощность человека принята за 70-80 Вт. Мощность автомобилей, самолетов, кораблей, ракет и промышленных установок, часто, измеряют в лошадиных силах. Лошадиные силы применяли еще задолго до внедрения ватт. Одна лошадиная сила равна 745,7Вт. Причем в России принято что л. с. равна 735,5 Вт.
Если вас вдруг случайно спросят через 20 лет в интервью среди прохожих о мощности, а вы запомнили, что мощность — это отношение работы А, совершенной в единицу времени t. Если сможете так сказать, приятно удивите толпу. Ведь в этом определении, главное запомнить, что делитель здесь работа А, а делимое время t. В итоге, имея работу и время, и разделив первое на второе, мы получим долгожданную мощность.
При выборе в магазинах, важно обращать внимание на мощность прибора. Чем мощнее чайник, тем быстрее он погреет воду. Мощность кондиционера определяет, какой величины пространство он сможет охлаждать без экстремальной нагрузки на двигатель. Чем больше мощность электроприбора, тем больше тока он потребляет, тем больше электроэнергии потратит, тем больше будет плата за электричество.
Мощность кондиционера определяет, какой величины пространство он сможет охлаждать без экстремальной нагрузки на двигатель. Чем больше мощность электроприбора, тем больше тока он потребляет, тем больше электроэнергии потратит, тем больше будет плата за электричество.
В общем случае электрическая мощность определяется формулой:
W=I*U,
где I — сила тока, U-напряжение
Иногда даже ее так и измеряют в вольт-амперах, записывая, как В*А. В вольт-амперах меряют полную мощность, а чтобы вычислить активную мощность нужно полную мощность умножить на коэффициент полезного действия(КПД) прибора, тогда получим активную мощность в ваттах.
Часто такие приборы, как кондиционер, холодильник, утюг работают циклически, включаясь и отключаясь от термостата, и их средняя мощность за общее время работы может быть небольшой.
В цепях переменного тока, помимо понятия мгновенной мощности, совпадающей с общефизической, существуют активная, реактивная и полная мощности. Полная мощность равна сумме активной и реактивной мощностей.
Полная мощность равна сумме активной и реактивной мощностей.
Для измерения мощности используют электронные приборы — Ваттметры. Единица измерения Ватт, получила свое название в честь изобретателя усовершенствованной паровой машины, которая произвела революцию среди энергетических установок того времени. Благодаря этому изобретению развитие индустриального общества ускорилось, появились поезда, пароходы, заводы, использующие силу паровой машины для передвижения и производства изделий.
Если вам нужно единицы измерения мощности привести в одну систему, вам пригодится наш перевод мощности – конвертер онлайн. А ниже вы сможете почитать, в чем измеряется мощность.
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
В чем измеряется мощность?
Единицы измерения мощности, которые известны каждому школьнику и являются принятыми в международном сообществе – ватты.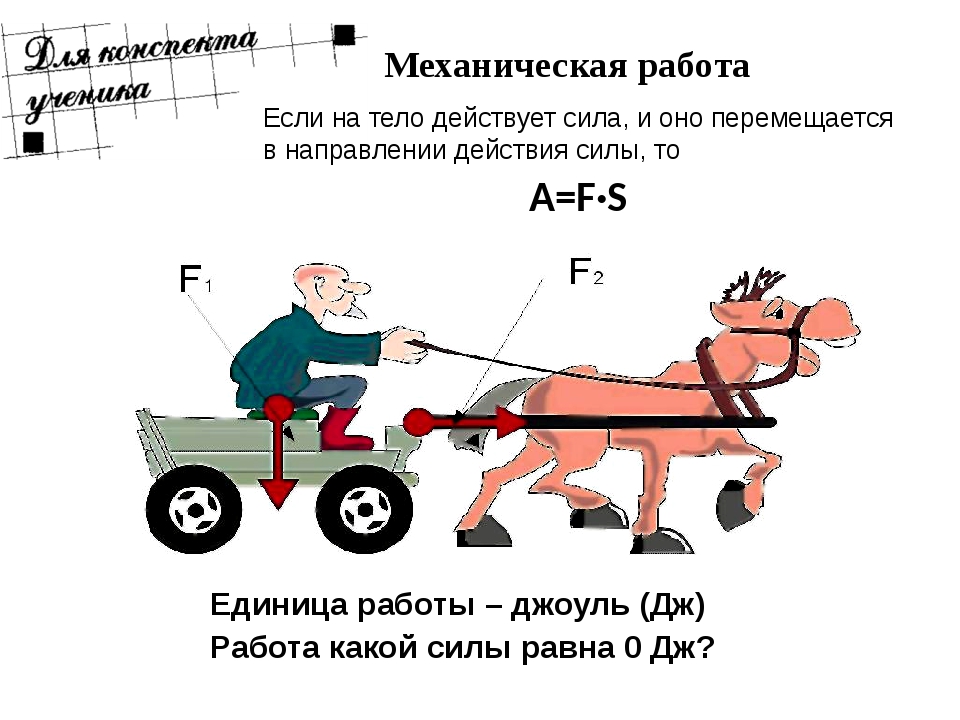 Названы так в честь ученого Дж. Уатта. Обозначаются латинской W или вт.
Названы так в честь ученого Дж. Уатта. Обозначаются латинской W или вт.
1 Ватт – единица измерения мощности, при которой за секунду происходит работа, равная 1 джоулю. Ватт равен мощности тока, сила которого 1 ампер, а напряжение – 1 вольт. В технике, как правило, применяются мегаватты и киловатты. 1 киловатт равен 1000 ватт.
Измеряется мощность и в эрг в секунду. 1 эрг в сек. Равен 10 в минус седьмой степени ватт. Соответственно, 1 ватт равен 10 в седьмой степени эрг/сек.
А еще единицей измерения мощности считается внесистемная «лошадиная сила». Она была введена в оборот еще в восемнадцатом веке и продолжает до сих пор применяться в автомобилестроении. Обозначается она так:
- Л.С. (в русском),
- HP (в английском).
- PS (в немецком),
- CV (во французском).
При переводе мощности помните, что в рунете существует невообразимая путаница при конверте лошадиных сил в ватты. В России, странах СНГ и некоторых других государствах 1 л. с. равняется 735, 5 ватт. В Англии и Америке 1 hp равняется 745, 7 ватт.
с. равняется 735, 5 ватт. В Англии и Америке 1 hp равняется 745, 7 ватт.
Механическая работа и мощность
Определение 1
Механическая работа $A$— это величина, равная произведению проекции силы $F_s$ на направление пути перемещения $S$, который проходит точка, подвергаемая действию силы $F$.
$A=F_S \cdot S \left(1\right)$
Данное равенство позволяет вычислять механическую работу только в случае если значение проекции силы $F_S$ является константой, то есть, тело движется прямолинейно и угол $α$ между силой, прикладываемой к телу, и направлением движения является неизменным.
Из определения косинуса следует, что проекция силы на направление движения равна $F_S=cosα \cdot F_S$, это значение можно подставить в формулу $(1)$:
$A=F \cdot S cosα\left(2\right).$
Значение механической работы в зависимости от угла
Работа может быть как положительной, так и отрицательной, её знак зависит от угла между векторами силы и направления движения. Если угол острый, то $cosα$ принимает положительное значение, а если тупой — то отрицательное, то есть именно угол определяет знак перед работой.
Если угол острый, то $cosα$ принимает положительное значение, а если тупой — то отрицательное, то есть именно угол определяет знак перед работой.
Полное значение механической работы
В случае если значение угла между направлением движения и силой не является постоянным, прибегают к разбиению пути на элементарные отрезки $ΔS$, на протяжении которых можно было бы считать величину проекции силы $F_S$ постоянной. Работа на каждом таком элементарном участке будет равна:
$ΔA≈F_S \cdot ΔS$,
Тогда работу на всём пути можно найти по формуле:
$A=\lim\limits_{ΔS_i\to 0}\sum F_{S_i}ΔS_i=\int F_S dS\left(3\right)$
Пример 1
Рисунок 1. Совершаемая работа для перемещения точки
Рассмотрим рисунок 1. На нём представлен график зависимости $F_s$ от положения точки, к которой прикладывается сила на траектории движения. Полная длина всего пути — это расстояние между точками $1$ и $2$. Работа, совершаемая при перемещении точки на $ΔS_i$ равна площади заштрихованной фигуры, а работа по перемещению из точки $1$ в точку $2$ равна всей площади фигуры, ограниченной линиями $1$ и $2$ и графиком.
Готовые работы на аналогичную тему
Работа измеряется в джоулях.
Определение 2
1 Джоуль — это работа, совершаемая силой в 1 ньютон на пути в 1 метр.
Мощность
Определение 3
Мощность $W$ — это величина, характеризующая количество работы, совершаемой за единицу времени.
Мощность в частности используется для характеристики различных двигательных устройств и механизмов, предназначенных для совершения работы.
Из определения мощности следует, что:
$W=\frac{ΔA}{Δt}\left(4\right)$
Если же мощность является величиной непостоянной, используется мгновенное значение мощности:
$W=\lim\limits_ {Δt\to 0} \frac{dA}{dt}$
Работу, необходимую для перемещения точки на расстояние $ds$ можно описать так:
$dA=F\cdot dS$, соответственно, мощность тогда составит:
$W=\frac{dA}{dt}=F\frac{dS}{dt}.$
Часть $\frac{dS}{dt}$ есть не что иное, как скорость, следовательно, мощность равна
$W=Fv$
Определение 4
Единица измерения мощности — ватты. 1 Ватт — это количество работы, измеряемое в джоулях и совершаемое за единицу времени, равную секунде.
1 Ватт — это количество работы, измеряемое в джоулях и совершаемое за единицу времени, равную секунде.
Механическая работа. Мощность
В данной теме речь пойдёт о механической работе и мощности.
Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы. Под действием постоянной силы тело двигается прямолинейно и совершает перемещение в направлении действия силы, то сила совершает работу, равную произведению модуля этой силы и модуля перемещения.
Из определения следует единица измерения работы в метрической системе единиц
Эта единица названа в честь английского ученого Джеймса Прескотта Джоуля, впервые экспериментально обосновавшего эквивалентность работы и теплоты.
Это самый простой случай,
когда перемещение тела и сила, действующая на него, совпадают по направлению.
Теперь рассмотрим, как вычисляется работа, когда направление действия силы не совпадает с направлением перемещения тела. Для этого рассмотрим следующий опыт. Через блок перекинута нить на которой висит брусок некоторой массы. На брусок действуют две силы — сила тяжести и сила натяжения нити.
Если равномерно тянуть за нить, то тело будет равномерно двигаться, и, следовательно, результирующая сила, действующая на тело, будет равна нулю.
Значит, при некотором перемещении тела работа результирующей силы тоже будет равна нулю.
Однако сила натяжения нити совершает работу.
Поскольку при равномерном движении сила натяжения нити по модулю равна силе тяжести тела, то можно предположить, что сила тяжести совершает такую же работу по величине, но отрицательную.
Отсюда можно сделать вывод: работа
силы может быть положительной, отрицательной или равной нулю.
Заметим, что сила тяжести по направлению противоположна перемещению тела. Это обстоятельство и другие соображения позволяют предложить общую формулу для работы постоянной силы при равномерном прямолинейном движении. Если вектор силы и перемещения составляют между собой угол a, то работа этой силы равна произведению модуля силы на модуль перемещения и на косинус угла между ними.
Это и есть общее выражение для работы постоянной силы.
Из этой формулы видно, что в случае, когда угол между направлением вектора силы и вектора перемещения острый, то косинус этого угла будет больше нуля и, следовательно, больше нуля будет работа силы.
Если вектор силы и вектор перемещения составляют между собой тупой угол, то значение косинуса этого угла меньше нуля. Значит и работа этой силы будет отрицательна.
И, наконец, если вектор
силы перпендикулярен вектору перемещения, то работа не
совершается (вернее, работа этой силы равна нулю).
Если к движущемуся телу приложено несколько сил, то каждая из них совершает работу, а общая работа равна алгебраической сумме работ, совершаемых отдельными силами.
Работу, совершенную силой, можно найти и графически. Так, если действие силы на тело не меняется с течением времени и совпадает по направлению с перемещением, то работа этой силы численно равна площади заштрихованного прямоугольника.
Если же сила изменяется в процессе движения, то работа этой силы тоже будет численно равна площади под кривой. В частности, на рисунке представлен график силы, которая линейно уменьшается с пройденным расстоянием до нуля. Очевидно, что работа этой силы на пройденном пути, численно равна площади треугольника.
Ранее говорилось, что
основными силами в механике являются гравитационные силы (в частности сила
тяжести), силы упругости и силы трения.
Проанализируем более подробно работы, совершаемые каждой из этих сил. Начнем с работы силы тяжести. Будем ее рассматривать считая, что тело находится на небольших расстояниях от поверхности Земли. В этом случае сила тяжести будет постоянной по модулю равной
Пусть тело массой m падает с некоторой высоты h1 до высоты h2. Тогда модуль перемещения тела равен разности этих высот
Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна произведению модуля силы тяжести и разности высот.
Следует помнить, что высоты, на которых находится тело, можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола или поверхности стола. Высоту выбранного уровня принимают равной нулю. Поэтому этот уровень называют нулевым. Так, если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна
Теперь выясним, какую работу
совершает сила тяжести, если тело движется не по вертикали. Для этого
рассмотрим движение тела по наклонной плоскости.
Для этого
рассмотрим движение тела по наклонной плоскости.
Пусть тело некоторой массы m совершило перемещение, равное по модулю длине наклонной плоскости. Работа силы тяжести в этом случае равна
Из рисунка видно, что
Поэтому работа силы тяжести в этом случае также равна
Таким образом, получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали. Отсюда следует главный вывод о том, что работа силы тяжести не зависит от того, по какой траектории движется тело и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела.
Тогда очевидно, что если
тело движется по замкнутой траектории, где начальное и конечное положения
тела совпадают, то работа силы тяжести равна нулю. Напомним, что такие
силы, работа которых не зависит от формы траектории, а определяется только
начальным и конечным положениями тела в пространстве, называются потенциальными
или консервативными. Следовательно, сила тяжести — это консервативная
сила.
Следовательно, сила тяжести — это консервативная
сила.
Теперь проанализируем работу, совершаемую силой упругости. Сила упругости — это сила, возникающая при деформации тела внешними воздействиями.
Рассмотрим систему, состоящую из пружины и тела некоторой массы, лежащего на достаточно гладкой горизонтальной поверхности. Левый конец пружины прикреплен к стене, а правый — к телу. Направим ось икс так, как показано на рисунке.
Если тело сместить на некоторое расстояние от положения равновесия, то пружина будет действовать на него с силой упругости, направленной вправо. Модуль проекции этой силы на ось Ox будет определяться на основании закона Гука.
Теперь отпустим тело. Тогда под действием силы упругости пружины тело будет смещаться вправо.
При этом сила упругости будет
совершать работу. Предположим, что тело переместилось так, что расстояние от
положения равновесия стало х2. Очевидно, что тогда модуль
перемещения тела равен разности между начальной и конечной координатой тела.
Очевидно, что тогда модуль
перемещения тела равен разности между начальной и конечной координатой тела.
Для нахождения работы, совершенной пружиной по перемещению тела, необходимо учесть, что сила упругости меняется, так как ее величина зависит от удлинения пружины. Воспользуемся графиком зависимости модуля силы упругости от удлинения пружины.
Известно, что работа силы численно равна площади под графиком силы. В рассматриваемом случае это площадь трапеции, основаниями которой являются силы упругости пружины в положении один и два, а высота — это перемещение тела.
Из полученной формулы следует,
что работа силы упругости пружины зависит только от координат начального и
конечного положений. Из рисунка видно, что х1 и х2
— это и удлинение пружины, и координаты ее конца в выбранной системе координат.
Следовательно, работа силы упругости не зависит от формы траектории. А если
траектория замкнута, то работа равна нулю. Таким образом, сила упругости
является потенциальной силой.
А если
траектория замкнута, то работа равна нулю. Таким образом, сила упругости
является потенциальной силой.
И проанализируем работу, совершаемую силой трения. Рассмотрим тело, находящееся на некоторой поверхности (например, брусок на поверхности стола).
Если толкнуть брусок, то он придет в движение, однако, через некоторое время, остановится. В процессе движения бруска на него действуют: сила тяжести, сила нормальной реакции опоры и сила трения скольжения. Под действием этих трех сил и движется брусок. Поскольку сила тяжести компенсируется силой нормальной реакции стола, то равнодействующая сила равна действующей на брусок силе трения. А так как сила трения направлена противоположна перемещению, то работа этой силы будет отрицательной (так как косинус ста восьмидесяти градусов равен минус единице).
Из формулы следует, что работа
силы трения зависит от модуля перемещения тела. И даже если тело
вернется в исходную точку, то работа силы трения не будет равна нулю.
Такие силы, работа которых зависит от формы траектории движения тела и на
замкнутой траектории отличны от нуля, называются непотенциальными или диссипативными
(от латинского — рассеяние).
И даже если тело
вернется в исходную точку, то работа силы трения не будет равна нулю.
Такие силы, работа которых зависит от формы траектории движения тела и на
замкнутой траектории отличны от нуля, называются непотенциальными или диссипативными
(от латинского — рассеяние).
Однако не надо думать, что работа сил трения всегда отрицательна. Ведь именно благодаря силе трения покоя человек и различные машины движутся по Земле. Действительно, при ходьбе человек действует на поверхность Земли с некоторой силой F1 (кроме силы нормальной реакции), а по третьему закону Ньютона Земля действует на ногу человека с силой трения покоя, равной по модулю силе воздействия человека, но противоположно направленной. Благодаря этой силе человек движется. Сила трения покоя направлена также, как и скорость человека, и, следовательно, работа этой силы положительна.
Таки образом, были рассмотрены
работы основных трех сил, с которыми чаще всего мы сталкиваемся в механике.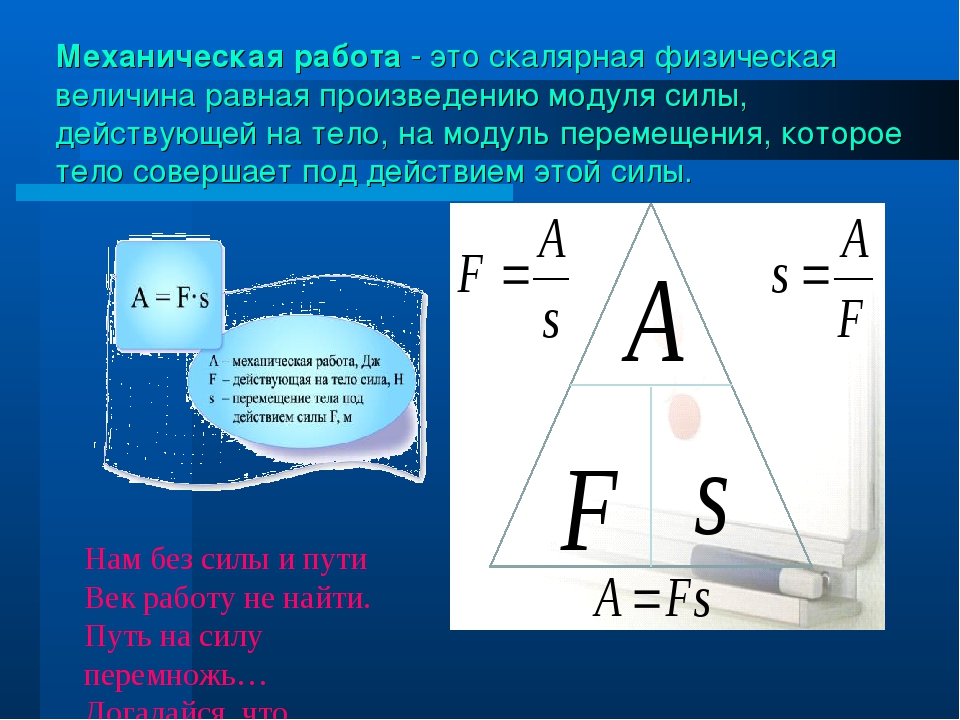 Однако, одна и та же работа в разных случаях может быть выполнена за различные
промежутки времени, то есть она может совершаться неодинаково быстро. Очевидно,
что чем меньшее времени требуется для выполнения данной работы, тем эффективнее
работает машина, механизм и прочее.
Однако, одна и та же работа в разных случаях может быть выполнена за различные
промежутки времени, то есть она может совершаться неодинаково быстро. Очевидно,
что чем меньшее времени требуется для выполнения данной работы, тем эффективнее
работает машина, механизм и прочее.
Величина, характеризующая быстроту совершения работы, и равная отношению работы, совершаемой силой, к промежутку времени, в течение которого она совершается, называется мощностью.
Исходя из определения видим, что единицей измерения мощности является
Эта единица получила название Ватт, в честь английского ученого Джеймса Уатта — изобретателя универсального парового двигателя.
При движении любого тела на него в общем случае действует несколько сил, каждая из которых совершает работу и, следовательно, для каждой силы можно вычислить мощность. Так, если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу, равную
Тогда мощность силы равна
отношению работы этой силы к промежутку времени.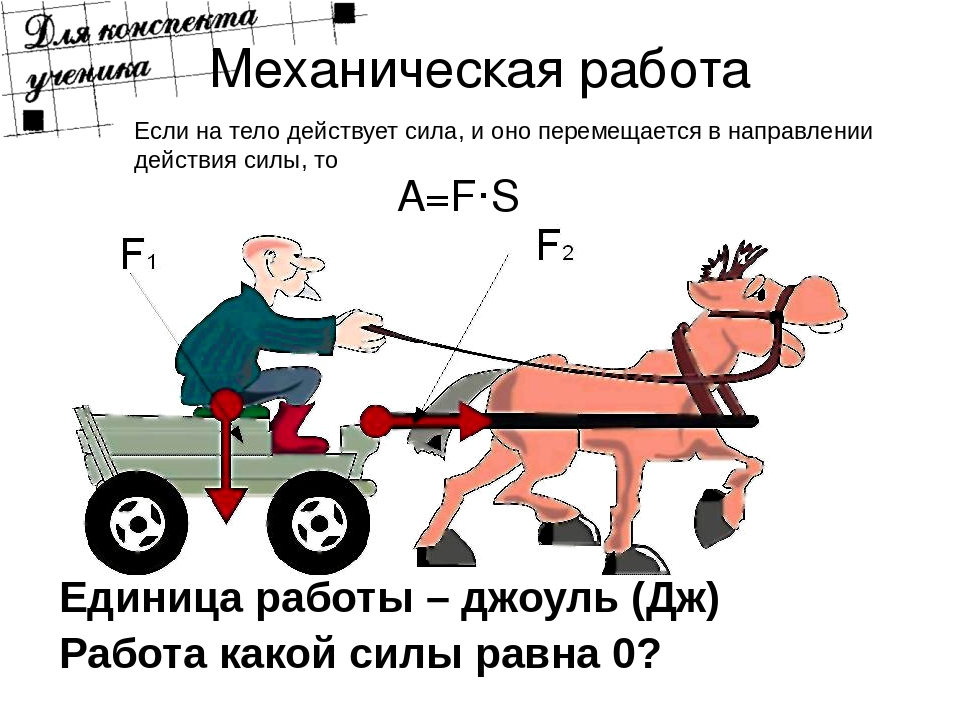
Мощность силы также равна произведению модуля силы на модуль скорости и на косинус угла между направлениями вектора силы и вектора скорости.
По записанной формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значение средней или мгновенной скорости.
Из полученной формулы следует, что при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения. Вот почему водители автомобилей при подъеме в гору, когда нужна наибольшая сила тяги, переключают двигатель на пониженную передачу.
И так, любой двигатель или механическое устройство предназначены для выполнения определенной механической работы. Эта работа называется полезной работой. Для двигателя автомобиля — это работа по его перемещению, для токарного станка — работа по вытачиванию детали.
Однако в любой машине, в
любом двигателе полезная работа всегда меньше той энергии, которая
затрачивается для приведения их в действие, потому что всегда существуют
силы трения, работа которых приводит к нагреванию каких-либо частей устройства. А нагревание нельзя считать полезным результатом действия машины. Поэтому
каждое устройство характеризуется особой величиной, которая показывает,
насколько эффективно используется подводимая к нему энергия. Эта величина
называется коэффициентом полезного действия и обычно обозначается
греческой буквой h.
А нагревание нельзя считать полезным результатом действия машины. Поэтому
каждое устройство характеризуется особой величиной, которая показывает,
насколько эффективно используется подводимая к нему энергия. Эта величина
называется коэффициентом полезного действия и обычно обозначается
греческой буквой h.
И так, коэффициентом полезного действия называется отношение полезной работы, совершенной машиной за некоторый промежуток времени, ко всей затраченной работе (или подведенной энергии) за тот же промежуток времени.
Коэффициент полезного действия обычно выражается в процентах. Поскольку и полезную, и затраченную работы можно представить, как произведение мощности на промежуток времени в течение которого работала машина, то
Основные выводы:
Рассмотрели важную физическую величины
– работу. Рассмотрели работы наиболее
часто встречающихся сил — силы тяжести, упругости и силы трения. Повторили
понятие мощности, а также вспомнили, что называют коэффициентом полезного
действия механизма.
Повторили
понятие мощности, а также вспомнили, что называют коэффициентом полезного
действия механизма.
Механическая мощность – Energy Education
Рис. 1. Потребляемая мощность в тепловом двигателе измеряется в МВт, а выходная мощность, полученная в виде электричества, измеряется в МВт. [1] Отношение выходной мощности к входящей – это КПД. Рис. 2. Реактивная турбина может выполнять большой объем работы за короткий промежуток времени, поэтому имеет высокую механическую мощность. [2] Механическая мощность означает скорость, с которой может выполняться работа. Это выходная мощность, а не входная мощность (см. Рисунок 1).Потребляемая мощность относится к тому, насколько быстро энергия топлива преобразуется в энергию для использования в автомобиле. Напротив, выходная мощность – это скорость, с которой двигатель может работать, получая энергию от топлива. Скорость, с которой двигатель использует топливо, – это тепловая мощность. Механическая мощность – это скорость, с которой механическая энергия может быть доставлена в систему. Напомним, что мощность – это передача энергии за определенный промежуток времени.
Механическая мощность – это скорость, с которой механическая энергия может быть доставлена в систему. Напомним, что мощность – это передача энергии за определенный промежуток времени.
Механическая мощность часто измеряется в лошадиных силах, хотя иногда она измеряется в ваттах.Некоторые примеры:
- Двигатель авто
- Двигатель самолета (см. Рисунок 2)
- Использование крана для подъема тяжелых предметов
Если механическая мощность исходит от теплового двигателя, такого как электростанция, она ограничена вторым законом термодинамики, а максимальное количество механической мощности определяется КПД Карно. [3] Механическая мощность ветряной турбины также ограничена, хотя и в совершенно другом аспекте, пределом Беца. [4]
Простые машины идеализированы как без потерь. Это означает, что они не теряют энергии при манипулировании силами. Следовательно, механическая мощность сохраняется на протяжении всего срока ее вывода, и это позволяет легко анализировать их с точки зрения механического преимущества. [5]
[5]
Посетите Hyperphysics для получения дополнительной информации о работе и власти.
Для дальнейшего чтения
Список литературы
- ↑ Сделано внутри команды энциклопедии
- ↑ Марк Хиллари, Flickr [Online], Доступно: https: // www.flickr.com/photos/markhillary/2427920269/in/photostream/
- ↑ Р. Д. Найт, «Пределы эффективности» в книге Физика для ученых и инженеров: стратегический подход, 3-е изд. Сан-Франциско, США: Pearson Addison-Wesley, 2008, глава 19, раздел 5, стр. 540-542
- ↑ WindPower Program, The Betz limit [Online], Доступно: http://www.wind-power-program.com/betz.htm
- ↑ Объясни это !, Tools and Simple Machines [Online], доступно: http: // www.exploainthatstuff.com/toolsmachines.html
Как рассчитать механическую мощность
Обновлено 22 декабря 2020 г.
Кенрик Везина
Вы можете найти механическую мощность , которые используются повсюду в современном мире. Вы сегодня ездили на машине? Он использовал энергию, получаемую либо от топлива, либо от батареи, для перемещения взаимосвязанного ряда механических компонентов – осей, шестерен, ремней и так далее – до тех пор, пока, наконец, эта энергия не использовалась для вращения колес и движения транспортного средства вперед.
Степень в физике – это мера скорости , с которой работа выполняется с течением времени. Слово «механический» носит чисто описательный характер; он говорит вам, что мощность связана с машиной и движением различных компонентов, таких как трансмиссия автомобиля или шестеренки часов.
Формула механической силы использует те же фундаментальные законы физики, которые используются для других форм силы.
TL; DR (слишком долго; не читал)
Мощность P определяется как работа Вт более раз т по следующей формуле.Примечание по единицам измерения: мощность должна быть в ваттах (Вт), работа – в джоулях (Дж), а время – в секундах (с) – всегда перепроверяйте, прежде чем вводить свои значения.
Механическая мощность подчиняется тем же законам, которые регулируют другие типы энергии, такие как химическая или тепловая. Механическая мощность – это просто мощность, связанная с движущимися компонентами механической системы, например шестернями, колесами и шкивами внутри старинного Часы.
Энергия, сила, работа и мощность
Чтобы понять выражение для механической силы, полезно выделить четыре взаимосвязанных термина: энергия , сила , работа И мощность .
- Энергия E , которую содержит объект, является мерой того, сколько работы он может выполнить; другими словами, сколько движения оно может создать. Он измеряется в джоулях (Дж).
- A force F , по сути, толкает или толкает. Силы передают энергию между объектами. Как и скорость, сила имеет величину и направление . Он измеряется в Ньютонах (Н).
- Если сила перемещает объект в том же направлении , в котором она действует, она выполняет работу .По определению, одна единица энергии необходима для выполнения одной единицы работы. Поскольку энергия и работа определяются друг с другом, они оба измеряются в джоулях (Дж).
- Мощность – это мера скорости , при которой выполняется работа или используется энергия с течением времени. Стандартная единица мощности – ватт (Вт).
Уравнение для механической мощности
Из-за взаимосвязи между энергией и работой существует два распространенных способа выражения мощности математически.Первый – работы Вт и время t :
P = \ frac {W} {t}
Мощность при линейном движении
Если вы имеете дело с линейным движением, вы можете предположить, что любая приложенная сила перемещает объект вперед или назад по прямому пути в соответствии с действием силы – подумайте о поездах на рельсах. Поскольку компонент направления в основном заботится о себе сам, вы также можете выразить мощность в терминах простой формулы, используя силы , расстояния и скорости .
В этих ситуациях работа W может быть определена как усилие F × расстояние d . Подключите это к основному уравнению, приведенному выше, и вы получите:
P = \ frac {Fd} {t}
Заметили что-нибудь знакомое? При линейном движении расстояние , деленное на время – это определение для скорости ( v ), поэтому мы также можем выразить мощность как:
P = F \ frac {d } {t} = Fv
Пример расчета: перевозка белья
Хорошо, это было много абстрактной математики, но давайте приступим к работе сейчас, чтобы решить примерную задачу:
Родители просят вас нести 10-килограммовая загрузка чистого белья наверху.Если обычно вам требуется 30 секунд, чтобы подняться по лестнице, а высота лестницы составляет 3 метра, оцените, сколько энергии вам потребуется, чтобы перенести одежду с нижней части лестницы наверх.
На основании подсказки мы знаем, что время t будет 30 секунд, но у нас нет значения для работы Вт . Однако мы можем упростить сценарий для оценки. Вместо того, чтобы беспокоиться о перемещении белья вверх и вперед на каждом отдельном этапе, давайте предположим, что вы просто поднимаете его по прямой с начальной высоты.Теперь мы можем использовать выражение механической мощности P = F × d / t , но нам все еще нужно выяснить задействованную силу.
Чтобы переносить белье, необходимо противодействовать действию силы тяжести на него. Поскольку сила тяжести составляет F = мг в направлении вниз, вы должны приложить ту же силу в направлении вверх. Обратите внимание, что g – это ускорение свободного падения, которое на Земле составляет 9,8 м / с 2 .Имея это в виду, мы можем создать расширенную версию стандартной формулы мощности:
P = mg \ frac {d} {t}
И мы можем подставить наши значения массы, ускорения, расстояния и времени:
P = (10 \ times 9,8) \ frac {3} {30} = 9,08 \ text {ватт}
Таким образом, вам нужно потратить около 9,08 ватт на переноску белья.
Последнее замечание о сложности
Наше обсуждение ограничилось довольно простыми сценариями и относительно простой математикой.В продвинутой физике сложные формы уравнения механической мощности могут потребовать использования расчетов и более длинных, более сложных формул, которые учитывают множественные силы, криволинейное движение и другие усложняющие факторы.
Если вам нужна более подробная информация, база данных HyperPhysics, размещенная в Университете штата Джорджия, является отличным ресурсом.
Эпизод 218: Механическая сила | IOPSpark
Вт = Fd
Силы и движение
Эпизод 218: Механическая сила
Практическая деятельность для 16-19
- Время активности 60 минут
- Уровень Продвинутый
Мощность – это скорость выполнения работы, т.е.е. скорость, с которой энергия передается силой. Вероятно, ваши ученики будут знакомы с этим определением. Возможно, они также изучали власть в электрическом контексте.
Краткое содержание урока
- Обсуждение: Значение силы (10 минут)
- Рабочий пример: Пример расчета; мощность = сила × скорость (10 минут)
- Студенческий эксперимент: Простые измерения силы человека (20 минут)
- Вопросы студентов: Практические расчеты (20 минут)
Многие практические действия, предложенные ранее в этом разделе, можно легко адаптировать для работы с властью; просто измерьте время, в течение которого действует сила, и вычислите: мощность = проделанная работа, затраченное время.
Обсуждение: Значение мощности
Дайте определение власти – вероятно, это будет пересмотр для ваших учеников. Спросите единицу измерения (ватт, Вт) и ее отношение к базовым единицам СИ
(1 Вт = 1 кг · м 2 с -3 ).
Рабочие примеры: Пример расчета; мощность = сила × скорость.
Двигатель автомобиля обеспечивает поступательное усилие в 1000 Н. Если автомобиль движется, какая мощность развивается?
За 1 с машина проезжает 20 м.Отсюда мы можем рассчитать:
работа за 1 с = сила × расстояние
выполненных работ = 1000 Н × 20 м
выполненных работ = 20 кДж
мощность = выполненная работа, затраченное время
мощность = 20 кДж1 с
мощность = 20 кВт
Из этого примера вы можете указать, что мы также могли бы использовать альтернативную форму уравнения для мощности:
мощность = сила × скорость
например мощность = выполненная работа, затраченное время
мощность = сила × расстояние (в направлении силы) затраченное время,
, так что мощность = сила × скорость.
(Однако это работает только в том случае, если скорость постоянна, то есть сила
равна , а не результирующей силе, действующей на движущийся объект.)
Студенческий эксперимент: простые измерения силы человека
Учащиеся могут выполнять различные физические упражнения, например поднимать отмеренные веса, и определять свою полезную выходную мощность с помощью секундомера. (Обратите внимание, что человеческое тело не очень эффективно в этих действиях, поэтому фактическая мощность, рассеиваемая учеником, будет значительно больше, чем предполагалось здесь.)
Это включено, поскольку возможно, что некоторые из ваших учеников менее чем уверены в этой области. Ожидается, что большинство студентов уже пройдут этот путь.
Эпизод 218-1: Сила ученика – бег по лестнице (Word, 39 КБ)
Вопросы студентов: Практические расчеты
Первые вопросы – это упражнения для разминки, которые должны вселить в учеников уверенность. Обратите внимание, что первый вопрос устанавливает связь между мощностью, силой и скоростью (мощность = сила × скорость).
Эпизод 218-2: Механическая сила (Word, 26 КБ)
Эпизод 218-3: Тренировка с циклом (Word, 114 КБ)
Механическая энергия
В предыдущей части Урока 1 было сказано, что работа выполняется над объектом всякий раз, когда на него действует сила, заставляющая его смещаться. Работа включает в себя силу, действующую на объект, вызывающую смещение. Во всех случаях, когда выполняется работа, есть объект, который обеспечивает силу для выполнения работы.Если книгу World Civilization поднять на верхнюю полку шкафчика ученика, тогда ученик предоставит силы для работы с книгой. Если плуг перемещается по полю, то какое-либо сельскохозяйственное оборудование (обычно трактор или лошадь) дает силу для работы на плуге. Если питчер разворачивается и ускоряет бейсбольный мяч по направлению к своей тарелке, то питчер предоставляет силу для выполнения работы с бейсбольным мячом. Если автомобиль с американскими горками перемещается с уровня земли на вершину первого падения американских горок, то цепь, приводимая в движение двигателем, обеспечивает силу, необходимую для работы с автомобилем.Если штанга перемещается с уровня земли на высоту над головой штангиста, то штангист прилагает усилия для выполнения работы со штангой. Во всех случаях объект, обладающий некоторой формой энергии, обеспечивает силу для выполнения работы. В описанных здесь случаях объекты, выполняющие работу (ученик, трактор, кувшин, двигатель / цепь), обладают химической потенциальной энергией , хранящейся в пище или топливе, которая превращается в работу. В процессе выполнения работы объект, выполняющий работу, обменивается энергией с объектом, над которым выполняется работа.Когда над объектом выполняется работа, этот объект получает энергию. Энергия, приобретаемая объектами, над которыми выполняется работа, известна как механическая энергия .Механическая энергия – это энергия, которой обладает объект в результате его движения или положения. Механическая энергия может быть кинетической (энергия движения) или потенциальной энергией (запасенная энергия положения). Объекты обладают механической энергией, если они находятся в движении и / или если они находятся в некотором положении относительно положения с нулевой потенциальной энергией (например, кирпич, удерживаемый в вертикальном положении над землей или в положении с нулевой высотой).Движущийся автомобиль обладает механической энергией за счет своего движения (кинетическая энергия). Движущийся бейсбольный мяч обладает механической энергией благодаря своей высокой скорости (кинетическая энергия) и вертикальному положению над землей (потенциальная энергия гравитации). Книга Мировой цивилизации, покоящаяся на верхней полке шкафчика, обладает механической энергией из-за своего вертикального положения над землей (потенциальная энергия гравитации). Штанга, поднятая высоко над головой штангиста, обладает механической энергией благодаря своему вертикальному положению над землей (потенциальная энергия гравитации).Натянутый лук обладает механической энергией из-за своего растянутого положения (упругая потенциальная энергия).
Механическая энергия как способность выполнять работуОбъект, обладающий механической энергией, способен совершать работу. Фактически, механическая энергия часто определяется как способность выполнять работу. Любой объект, обладающий механической энергией – будь то в форме потенциальной или кинетической энергии – способен выполнять работу. То есть его механическая энергия позволяет этому объекту применять силу к другому объекту, чтобы вызвать его смещение.
Можно привести множество примеров того, как объект с механической энергией может использовать эту энергию, чтобы приложить силу, чтобы вызвать смещение другого объекта. Классический пример – это огромный шар, разрушающий машину для сноса зданий. Мяч для разрушения представляет собой массивный объект, который отклоняется назад в высокое положение и позволяет качаться вперед в строительную конструкцию или другой объект, чтобы разрушить его. При попадании в конструкцию разрушающий шар прикладывает к нему силу, чтобы вызвать смещение стены конструкции.На приведенной ниже диаграмме показан процесс, с помощью которого механическая энергия разрушающего шара может быть использована для выполнения работы.
Молоток – это инструмент, использующий механическую энергию для выполнения работы. Механическая энергия молотка дает ему возможность приложить силу к гвоздю, чтобы вызвать его смещение. Поскольку молоток обладает механической энергией (в форме кинетической энергии), он способен воздействовать на гвоздь. Механическая энергия – это способность выполнять работу.
Другой пример, показывающий, как механическая энергия – это способность объекта выполнять работу, можно увидеть в любой вечер в вашем местном боулинге. Механическая энергия шара для боулинга дает ему возможность приложить силу к кегле, чтобы заставить его сместиться. Поскольку массивный шар обладает механической энергией (в форме кинетической энергии), он может работать со штифтом. Механическая энергия – это способность выполнять работу.
Дротик – еще один пример того, как механическая энергия одного объекта может воздействовать на другой объект.Когда дротик заряжен и пружины сжаты, он обладает механической энергией. Механическая энергия сжатых пружин дает им возможность прикладывать силу к дротику, чтобы вызвать его смещение. Поскольку пружины обладают механической энергией (в форме упругой потенциальной энергии), они способны работать над дротиком. Механическая энергия – это способность выполнять работу.
Обычная сцена в некоторых частях сельской местности – это «ветряная электростанция».«Высокоскоростной ветер используется для работы с лопастями турбины на так называемой ветряной электростанции. Механическая энергия движущегося воздуха дает воздушным частицам возможность прикладывать силу и вызывать смещение лопастей. лопасти вращаются, их энергия впоследствии преобразуется в электрическую энергию (немеханическую форму энергии) и подается в дома и промышленные предприятия для работы электроприборов. Поскольку движущийся ветер обладает механической энергией (в форме кинетической энергии), он может работать с лезвиями.Еще раз, механическая энергия – это способность совершать работу.
Общая механическая энергияКак уже упоминалось, механическая энергия объекта может быть результатом его движения (т. Е. Кинетической энергией) и / или результатом накопленной им энергии положения (т. Е. Потенциальной энергии). Общее количество механической энергии – это просто сумма потенциальной энергии и кинетической энергии. Эта сумма просто называется полной механической энергией (сокращенно TME).
TME = PE + KEКак обсуждалось ранее, в нашем курсе обсуждаются две формы потенциальной энергии – гравитационная потенциальная энергия и упругая потенциальная энергия. Учитывая этот факт, приведенное выше уравнение можно переписать:
TME = PE грав + PE пружина + KEНа диаграмме ниже изображено движение Ли Бена Фардеста (уважаемого американского прыгуна с трамплина), когда он спускается с холма и делает один из своих рекордных прыжков.
Полная механическая энергия Ли Бена Фардеста представляет собой сумму потенциальной и кинетической энергии. Сумма двух форм энергии составляет 50 000 Джоулей. Также обратите внимание, что общая механическая энергия Ли Бена Фардеста является постоянной величиной на протяжении всего его движения. Существуют условия, при которых общая механическая энергия будет постоянной величиной, и условия, при которых она будет изменяться. Это тема Урока 2 – отношения работы и энергии.На данный момент просто запомните, что полная механическая энергия – это энергия, которой обладает объект из-за его движения или накопленной энергии позиции . Общее количество механической энергии – это просто сумма этих двух форм энергии. И, наконец, объект с механической энергией может работать с другим объектом.
Краткий обзор механической мощности: простой заменитель вентиляции с регулируемым объемом | Экспериментальная интенсивная терапия
Acute Respiratory Distress Syndrome N, Brower RG, Matthay MA, Morris A, Schoenfeld D, Thompson BT, Wheeler A (2000) Вентиляция с меньшими дыхательными объемами по сравнению с традиционными дыхательными объемами при остром повреждении легких и синдроме острого респираторного дистресс-синдрома. N Engl J Med 342: 1301–1308
Статья Google ученый
Dreyfuss D, Soler P, Basset G, Saumon G (1988) Отек легких с высоким давлением инфляции. Соответствующие эффекты высокого давления в дыхательных путях, большого дыхательного объема и положительного давления в конце выдоха.Am Rev Respir Dis 137: 1159–1164
CAS Статья Google ученый
Amato MB, Meade MO, Slutsky AS, Brochard L, Costa EL, Schoenfeld DA, Stewart TE, Briel M, Talmor D, Mercat A, Richard JC, Carvalho CR, Brower RG (2015) Управляющее давление и выживаемость при остром респираторном дистресс-синдроме. N Engl J Med 372: 747–755
CAS Статья Google ученый
Protti A, Maraffi T, Milesi M, Votta E, Santini A, Pugni P, Andreis DT, Nicosia F, Zannin E, Gatti S, Vaira V, Ferrero S, Gattinoni L (2016) Роль скорости деформации в патогенезе отек легких, вызванный вентилятором. Crit Care Med 44: e838 – e845
Статья Google ученый
Collino F, Rapetti F, Vasques F, Maiolo G, Tonetti T, Romitti F, Niewenhuys J, Behnemann T., Camporota L, Hahn G, Reupke V, Holke K, Herrmann P, Duscio E, Cipulli F , Moerer O, Marini JJ, Quintel M, Gattinoni L (2019) Положительное давление в конце выдоха и механическая мощность.Анестезиология 130: 119–130
Статья Google ученый
Gattinoni L, Tonetti T, Cressoni M, Cadringher P, Herrmann P, Moerer O, Protti A, Gotti M, Chiurazzi C, Carlesso E, Chiumello D, Quintel M (2016) Причины легких, связанные с ИВЛ травма: механическая сила. Intensive Care Med 42: 1567–1575
CAS Статья Google ученый
Becher T, van der Staay M, Schadler D, Frerichs I., Weiler N (2019) Расчет механической мощности для вентиляции с регулируемым давлением.Intensive Care Med
van der Meijden S, Molenaar M, Somhorst P, Schoe A (2019) Расчет механической мощности для вентиляции с контролируемым давлением. Intensive Care Med
Serpa Neto A, Deliberato RO, Johnson AEW, Bos LD, Amorim P, Pereira SM, Cazati DC, Cordioli RL, Correa TD, Pollard TJ, Schettino GPP, Timenetsky KT, Celi LA, Pelosi P, Gama de Abreu M, Schultz MJ, Investigators PN (2018) Механическая мощность вентиляции связана со смертностью у тяжелобольных пациентов: анализ пациентов в двух наблюдательных когортах.Intensive Care Med 44: 1914–1922
CAS Статья Google ученый
Cressoni M, Chiumello D, Chiurazzi C, Brioni M, Algieri I, Gotti M, Nikolla K, Massari D, Cammaroto A, Colombo A, Cadringher P, Carlesso E, Benti R, Casati R, Zito F , Gattinoni L (2016) Неоднородности легких, инфляция и скорость поглощения [18F] 2-фтор-2-дезокси-D-глюкозы при остром респираторном дистресс-синдроме. Eur Respir J 47: 233–242
CAS Статья Google ученый
Gattinoni L, Caironi P, Cressoni M, Chiumello D, Ranieri VM, Quintel M, Russo S, Patroniti N, Cornejo R, Bugedo G (2006) Рекрутмент легких у пациентов с острым респираторным дистресс-синдромом. N Engl J Med 354: 1775–1786
CAS Статья Google ученый
Cressoni M, Chiumello D, Algieri I, Brioni M, Chiurazzi C, Colombo A, Colombo A, Crimella F, Guanziroli M, Tomic I, Tonetti T, Luca Vergani G, Carlesso E, Gasparovic V, Gattinoni L (2017) Давление открытия и ателектравма при остром респираторном дистресс-синдроме.Intensive Care Med 43: 603–611
Статья Google ученый
Chiumello D, Cressoni M, Carlesso E, Caspani ML, Marino A, Gallazzi E, Caironi P, Lazzerini M, Moerer O, Quintel M, Gattinoni L (2014) Выбор положительного давления в конце выдоха у постели больного. острый респираторный дистресс-синдром легкой, средней и тяжелой степени. Crit Care Med 42: 252–264
Статья Google ученый
Chiumello D, Marino A, Brioni M, Cigada I, Menga F, Colombo A, Crimella F, Algieri I, Cressoni M, Carlesso E, Gattinoni L (2016) Рекрутмент легких оценивается с помощью респираторной механики и компьютерной томографии у пациентов с острым респираторным заболеванием дистресс-синдром. Какие отношения? Am J Respir Crit Care Med 193: 1254–1263
CAS Статья Google ученый
Chiumello D, Mongodi S, Algieri I, Vergani GL, Orlando A, Via G, Crimella F, Cressoni M, Mojoli F (2018) Оценка аэрации и рекрутмента легких с помощью компьютерной томографии и УЗИ при остром респираторном дистресс-синдроме синдром больных.Crit Care Med 46: 1761–1768
Статья Google ученый
Chiumello D, Marino A, Cressoni M, Mietto C, Berto V, Gallazzi E, Chiurazzi C, Lazzerini M, Cadringher P, Quintel M, Gattinoni L (2013) Плевральный выпот у пациентов с острым повреждением легких: исследование компьютерной томографии. Crit Care Med 41: 935–944
Статья Google ученый
Guglielminotti J, Desmonts JM, Dureuil B (1998) Влияние аспирации трахеи на респираторное сопротивление у пациентов с механической вентиляцией легких.Сундук 113: 1335–1338
CAS Статья Google ученый
Polese G, Rossi A, Appendini L, Brandi G, Bates JH, Brandolese R (1991) Разделение дыхательной механики у пациентов с механической вентиляцией легких. J Appl Physiol 71: 2425–2433
CAS Статья Google ученый
Бернаскони М., Плойсонгсанг И., Готфрид С.Б., Милич-Эмили Дж., Росси А. (1988) Податливость и сопротивление дыхательной системы у пациентов с острой дыхательной недостаточностью на ИВЛ.Intensive Care Med 14: 547–553
CAS Статья Google ученый
Имз В.О., Рук Г.А., Ву Р.С., Бишоп М.Дж. (1996) Сравнение эффектов этомидата, пропофола и тиопентала на респираторное сопротивление после интубации трахеи. Анестезиология 84: 1307–1311
CAS Статья Google ученый
Gattinoni L, Carlesso E, Cadringher P, Valenza F, Vagginelli F, Chiumello D (2003) Физические и биологические триггеры повреждения легких, вызванного вентилятором, и его профилактика.Euro Respir J Suppl 47: 15–25 с
CAS Статья Google ученый
Gattinoni L, Giosa L, Bonifazi M, Pasticci I, Busana M, Macri M, Romitti F, Vassalli F, Quintel M (2019) Нацеливание на транспульмональное давление для предотвращения повреждения легких, вызванного вентилятором. Expert Rev Respir Med 13: 737–746
CAS Статья Google ученый
Беллани Дж., Лаффи Дж. Г., Фам Т., Фан Э, Брошард Л., Эстебан А., Гаттинони Л., ван Харен Ф., Ларссон А., Маколи Д. Ф., Раньери М., Рубенфельд Дж., Томпсон Б. Т., Ригге Х, Слуцкий AS, Pesenti A, Investigators LS, Group ET (2016) Эпидемиология, схемы оказания помощи и смертность пациентов с острым респираторным дистресс-синдромом в отделениях интенсивной терапии в 50 странах.Jama 315: 788–800
Статья Google ученый
Тобин М.Дж. (2000) Кульминация эпохи исследований острого респираторного дистресс-синдрома. N Engl J Med 342: 1360–1361
CAS Статья Google ученый
Cressoni M, Gotti M, Chiurazzi C, Massari D, Algieri I, Amini M, Cammaroto A, Brioni M, Montaruli C, Nikolla K, Guanziroli M, Dondossola D, Gatti S, Valerio V, Vergani GL , Pugni P, Cadringher P, Gagliano N, Gattinoni L (2016) Механическая сила и развитие повреждения легких, вызванного вентилятором.Анестезиология 124: 1100–1108
Статья Google ученый
Zhang Z, Zheng B, Liu N, Ge H, Hong Y (2019) Механическая мощность, нормализованная к прогнозируемой массе тела, как предиктор смертности у пациентов с острым респираторным дистресс-синдромом. Intensive Care Med 45: 856–864
Статья Google ученый
Schumann S, Goebel U, Haberstroh J, Vimlati L, Schneider M, Lichtwarck-Aschoff M, Guttmann J (2014) Определение механики дыхательной системы во время вдоха и выдоха с помощью выдоха с контролируемым потоком (FLEX): a пилотное исследование на анестезированных свиньях.Минерва Анестезиол 80: 19–28
CAS PubMed Google ученый
Maiolo G, Collino F, Vasques F, Rapetti F, Tonetti T, Romitti F, Cressoni M, Chiumello D, Moerer O, Herrmann P, Friede T, Quintel M, Gattinoni L (2018) Реклассификация острых респираторных заболеваний дистресс-синдром. Am J Respir Crit Care Med 197: 1586–1595
CAS Статья Google ученый
Tonetti T, Vasques F, Rapetti F, Maiolo G, Collino F, Romitti F, Camporota L, Cressoni M, Cadringher P, Quintel M, Gattinoni L (2017) Давление и механическая сила: новые цели для профилактики ВИЛИ. Ann Transl Med 5: 286
Статья Google ученый
Мид Дж, Такисима Т., Лейт Д. (1970) Распределение напряжения в легких: модель легочной эластичности. J Appl Physiol 28: 596–608
CAS Статья Google ученый
Cressoni M, Cadringher P, Chiurazzi C, Amini M, Gallazzi E, Marino A, Brioni M, Carlesso E, Chiumello D, Quintel M, Bugedo G, Gattinoni L (2014) Неоднородность легких у пациентов с острым респираторным дистресс-синдромом. Am J Respir Crit Care Med 189: 149–158
CAS PubMed Google ученый
Видеоурок: Механическая сила | Нагва
Стенограмма видео
В этом видео мы говорим о механическая сила.Это термин, который мы используем справедливо довольно часто. Мы могли бы говорить о силе тяжелоатлет, или молния, или сила в чьем-то голосе. Мы увидим это в В мире физики этот термин механическая мощность имеет очень специфическое значение.
Мы определяем этот термин механический власть таким образом. Это равно количеству энергии передано в процессе, разделенное на время, которое занимает процесс. Если мы запишем все это как уравнение, мы бы сказали, что энергетический капитал равен переданной энергии 𝐸 деленное на время, необходимое для выполнения этой передачи 𝑡.Когда мы говорим о власти в физика, вот что мы подразумеваем под этим термином. Это энергия, передаваемая на единицу время.
Чтобы понять, что это уравнение означает, что представьте, что человек стоит у подножия лестница. Теперь, если человек забирается на это лестница, мы можем сказать, что они потратили немного энергии, чтобы сделать это. Это потому, что, взбираясь наверх, они работают против силы тяжести, которая тянет их вниз.Итак, требуется энергия, чтобы выйти из низ лестницы наверх, на эту новую возвышенность. И это количество энергии должно сделать с высотой лестницы, насколько она высока.
Теперь предположим, что для того, чтобы подняться по лестнице, этому человеку потребовалось 10 секунд, чтобы пройти весь путь снизу на верхнюю ступеньку. Теперь представьте, что они возвращаются спуститесь вниз, а затем поднимитесь по лестнице во второй раз.Но в данном случае вместо им нужно 10 секунд, чтобы добраться до вершины, им требуется 20, в два раза дольше. Мы видим, что в обоих случаях человек использует такое же количество энергии, чтобы пройти снизу вверх. Это потому, что высота лестница не меняется, и масса человека не меняется. Довести столько массы до вершины лестницы такой высоты требует одинакового количества энергии, независимо от того, восхождение длится долго.Но чем отличается 10-секундный и 20-секундный период набора высоты – это выходная мощность этого человека.
Оглядываясь на наше уравнение для силы, так как этот человек использовал одинаковое количество энергии, чтобы подняться на вершину в обоих случаев, но второй раз потребовалось в два раза дольше, чем в первый раз, мы можем сказать, что при сравнении первого набора высоты, который занял 10 секунд, со вторым набором высоты, который занял 20, оба подъема требовали одинакового количества энергии, но второе восхождение потребовало половина мощности как первая.
Итак, если подниматься по лестнице очень медленно, или в нормальном темпе, или вы перепрыгиваете их по два-три за раз, всего В этих случаях для перехода снизу вверх используется одинаковое количество энергии. Топ. Но разница в мощности использовал. Это то, сколько времени нужно, чтобы потратить столько энергии.
Из этого уравнения видно, что сила, которая, если мы знаем две из этих трех переменных, мощность, энергию и время, мы возможность использовать это уравнение для решения третьего.И, на самом деле, можно сделайте замену в это уравнение, чтобы сделать его еще более полезным. Эта замена включает в себя это термин здесь, энергия. Вспоминая нашего подъемника по лестнице, мы сказали, что этому альпинисту нужно приложить некоторое количество энергии, чтобы добраться до вершины лестница. Другой способ сказать то же самое означает, что альпинисту нужно было работать. Им нужно приложить силу некоторое расстояние, чтобы добраться до вершины.
Два термина работа и энергия, мы можно сокращать их 𝑊 и 𝐸, очень тесно связаны друг с другом. Оба они выражаются в те же научные единицы джоули. А энергия фактически определяется в с точки зрения способности чего-то выполнять работу. Мы можем сказать, что всякий раз, когда что-то расходует энергию или расходует ее, она каким-то образом выполняет работу. Эта связь между работой и энергия настолько близка, что иногда мы можем увидеть уравнение для мощности, записанное как это.Мощность равна проделанной работе, разделенной по времени.
Итак, мы снова видим, что сила равна скорости изменения некоторой величины, в данном случае работы, а затем, ранее энергия. Но здесь мы используем работу и энергия взаимозаменяемы, как и обычно.
Мы уже говорили, что когда это доходит до единиц, единицы работы – джоули, обозначенные заглавной буквой J. что базовая единица времени – секунды.Итак, это подводит нас к базовая единица мощности. Если есть процесс, в котором выполнен джоуль работы или, что эквивалентно, один джоуль энергии передается за время одной секунды, то количество энергии, переданное за это время, называется равняться одному ватту. Это единица мощности. И ватт сокращенно обозначается капитал W.
Обратите внимание, что мы должны быть немного осторожно, чтобы не перепутать аббревиатуру единицы мощности с символ работы.Оба написаны с большой буквы. К счастью, контекст обычно дает понять, с какой из них мы работаем. Так что часто это не проблема.
Итак, если кто-нибудь подойдет к вам и говорит, что ватт – это единица мощности, правильный ответ – да. Теперь ватт действительно является базовой единицей СИ. для мощности, но вы, возможно, слышали о другой единице, называемой лошадиными силами. Теперь, что интересно, лошадиные силы, которая является реальной единицей мощности, но не в системе СИ, была изобретена человек, который в итоге получил единицу СИ для мощности, названную в его честь Джеймс Ватт.
Во времена Ватта именно лошади поставляла большую часть энергии для механических и промышленных процессов. Как Ватт, который был инженером, работал над разработкой и усовершенствованием паровых двигателей, ему нужен был практический способ оценки мощность его двигателей. Итак, он придумал единицу мощности основанный на наиболее распространенном в то время источнике энергии. Ватт определил одну лошадиную силу как количество энергии, необходимое для поднятия 550-фунтовой массы на расстояние в один фут в время одной секунды.Итак, это одна лошадиная сила.
А если сравнивать одиночный лошадиных сил на единицу, которая получила название в честь Ватта, мы находим, что одна лошадиная сила примерно равна 750 Вт. Итак, всякий раз, когда у нас есть сила, единиц лошадиных сил, вот что это значит. Но в большинстве случаев потому что мы работаем в СИ или международной системе единиц, единиц мощности мы встретим ватт, где один ватт равен одному джоулю энергии. переносится за одну секунду.Зная все это о механике power, давайте теперь немного попрактикуемся на примере.
Какая из следующих формул правильно показывает соотношение между временем, затраченным на выполнение объема работы, и мощность, необходимая для работы? А) Мощность равна времени, деленному на Работа. Б) Мощность равна времени работы время. C) Мощность равна работе минус время. D) Мощность равна работе, деленной на время.E) Мощность равна работе плюс время.
Нам сказали, что эти пять вариантов все кандидаты на правильную формулу, показывающую взаимосвязь между временем взятый для выполнения объем работы и мощность, необходимая для ее выполнения. Мы работаем с этими тремя конкретные количества, мощность, работа и время. Теперь, даже если у нас нет точного отношения между этими тремя терминами, запомненными, если мы можем вспомнить единиц этих трех терминов, мы сможем сузить наши варианты ответов.
Начиная снизу, СИ базовая единица времени – секунда, сокращенно с. Единицей работы является джоуль, сокращенно заглавная J. И заметьте, что это то же самое как единица измерения энергии. И, наконец, единица СИ для мощность – ватт, сокращенно заглавная буква W.
Рассматривая варианты ответа, мы знаем, что в зависимости от того, какой из них правильный, будут одинаковые единицы по обе стороны от знак равенства.Это часть того, что делает его уравнение. А поскольку мы знаем, что единица СИ мощности – это ватт, мы понимаем, что во всех пяти вариантах этот блок будет включен. левая часть равенства, что означает, что какой бы вариант ответа ни был У правильного должна быть такая же единица измерения, ватт, с правой стороны.
Рассматривая варианты ответов C и E, мы видим, что в правой части этих двух единиц не будет. выбор.Для этих двух вариантов у нас есть с правой стороны – смесь единиц. В произведении есть единицы джоулей и время измеряется секундами. В каждом из этих случаев мы не может выполнить операцию с правой стороны. Мы не сравниваем количество похожего типа друг на друга. Таким образом, с точки зрения юнитов, мы можно сказать, что варианты C и E вышли из употребления. Последний блок справа сторона этих выражений не может быть ваттами.Итак, это не может быть правильным формула.
Остались A, B и D. На этом этапе будет полезно напомним определение власти. Мощность определяется как энергия переносится в единицу времени. Другими словами, это количество энергия в джоулях, деленная на количество времени в секундах. И обратите внимание, что эта передача энергии может происходить благодаря работе, проделанной какой-либо сущностью. Мы могли бы одинаково хорошо определить власть как проделанная работа за единицу времени.
Итак, единицей работы, как мы видели, является джоуль. А базовая единица времени – это второй. И наше определение власти: сообщая нам, что мощность – это количество энергии в джоулях на количество времени в секунд. Чтобы ответить на наш вопрос, мы пройдите по вариантам ответа A, B и D и посмотрите, какой из них содержит единицы джоулей на второй справа.
Начнем с проверки ответа вариант А.В правой части этого уравнение, у нас есть время в секундах, разделенное на работу, которая имеет единицы измерения джоули. Это не общая единица джоулей в секунду. Итак, мы вычеркнем вариант А. Перейдем к варианту Б, это в правой части – работа, выполненная в джоулях, умноженная на время в единицах секунд. Единица здесь – джоуль-раз. секунду, а не джоуль в секунду, поэтому вариант B также не рассматривается.
Наконец, мы переходим к варианту D, где у нас есть проделанная работа в джоулях, разделенная на время в секундах. Здесь у нас есть совпадение для единиц мы искали, совпадение по единицам мощности. Тогда мы можем сказать, что джоуль на секунда равна ватту, единице мощности. И это делает вариант D правильным выбор. Мощность равна работе, деленной на время.
Давайте посмотрим еще на один пример с механической мощностью.
Предположим, что 260 джоулей работы сделано за 40 секунд. Какая мощность требуется для этого объем работы?
Хорошо, в данном случае у нас это данный объем работы, выполненной предположительно над каким-то процессом. Чтобы понять пример Что может происходить, представьте себе этот 25-килограммовый блок, стоящий на земле. Теперь, если бы мы взяли этот блок и поднимите его на один метр по вертикали, и если нам потребовалось 40 секунд, чтобы переместите блок на расстояние в один метр, тогда это даст представление о власть участвует в этом процессе.260 джоулей примерно столько работы потребуется, чтобы поднять блок такого размера на высоту один метр, а затем проделать это на промежуток времени 40 секунд, на самом деле довольно много времени. У нас будет процесс, который примерно сравнимо с описанным здесь процессом.
В любом случае, мы ищем мощность, необходимая для выполнения такого объема работы за такое количество времени. И для начала вычислить, что Давайте вспомним математическое уравнение для мощности в терминах работы и времени.Мощность 𝑃, необходимая для выполнения определенный объем работы 𝑊 за определенный промежуток времени 𝑡 равен этому количеству работа, разделенная на количество времени.
Итак, когда мы перейдем к вычислению необходимая мощность, назовем ее 𝑃, в данном конкретном процессе мы знаем, что она равна проделанной работы, которая измеряется в джоулях, и 260 из этих джоулей работы, разделенное на время, которое занимает процесс, что составляет 40 секунд.
Теперь обратите внимание, что единицы, которые у нас есть в этом выражении – джоули в секунду. Это базовые единицы энергии и время соответственно. И если бы мы разделили один джоуль энергии на одну секунду времени, тогда это будет равняться одному ватту, сокращенно заглавной Вт, мощности. Другими словами, ответ мы получить при вычислении этой дроби будут единицы ватт. Когда мы вычисляем этот результат, мы найти ответ 6.5 Вт. Это необходимая механическая мощность выполнить такой объем работы за это количество времени.
Давайте сейчас займемся обобщите то, что мы узнали о механической энергии. Первое, что мы увидели, это то, что механическая мощность равна энергии, переданной в процессе, деленной на время этот процесс занимает. Записывая это в виде уравнения выглядит вот так. Мощность 𝑃 равна энергии 𝐸 делить на время 𝑡.
Мы также видели, что во многих случаях работа и энергия – взаимозаменяемые термины. И в результате мы изменили наш уравнение для мощности так, чтобы оно читалось как произведение 𝑊, деленное на время 𝑡. Кроме того, единица работы, который равен единице энергии, является джоуль. Базовая единица времени – это второй. А базовая единица мощности в системе СИ – ватт.
Мы отметили, что ватт часто бывает сокращенно с заглавной буквы W.Итак, нам нужно быть осторожными, чтобы не путайте его с аббревиатурой рабочего капитала 𝑊. И на последок привязка всех агрегатов вместе мы увидели, что один ватт мощности равен одному джоулю энергии, разделенному на одну секунду времени.
механическая мощность Определение | Law Insider
Относится к механической мощности
Рабочее давление означает давление, при котором детали ирригационной системы рассчитаны на работу производителем.
Газификация означает субстехиометрическое окисление или преобразование паром вещества с образованием газовой смеси, содержащей два или все из следующих элементов: оксиды углерода, метана и водорода;
Электрооборудование означает подземное оборудование, которое содержит диэлектрическую жидкость, необходимую для работы такого оборудования, как трансформаторы и подземный электрический кабель.
Дизельное топливо со сверхнизким содержанием серы означает дизельное топливо с содержанием серы не более пятнадцати частей на
Соединительный элемент означает оборудование, используемое для соединения электрической системы штата с электрическими системами за пределами штата;
Заливная наполняющая труба означает любую заправочную трубу с полностью погруженным выпускным отверстием, когда уровень жидкости на шесть дюймов выше дна резервуара; или применительно к резервуару, загружаемому сбоку, означает любую наливную трубу с полностью погруженным сливным отверстием, когда уровень жидкости находится на восемнадцати дюймах выше дна резервуара.
На ископаемом топливе означает сжигание ископаемого топлива или любых производных ископаемых видов топлива, отдельно или в сочетании с любым другим топливом, независимо от процента ископаемого топлива, потребленного в течение любого календарного года (выраженного в миллиметрах БТЕ).
Энергетический бойлер означает бойлер, в котором пар или другой пар генерируется под давлением более 15 фунтов на кв. / или температуры, превышающие 250 градусов по Фаренгейту, за счет прямого применения энергии от сжигания топлива или электричества, солнечной или ядерной энергии.
Терминалы означает физическое местоположение, в котором бизнес-деятельность (операции) автотранспортной компании осуществляется на регулярной основе. Терминалы обычно включают погрузочные или отгрузочные доки, складские помещения, диспетчерские пункты, а также могут включать административные помещения.
Разъем означает устройство, обеспечивающее механическое подключение и отключение электрических проводов высокого напряжения к подходящему сопряженному компоненту, включая его корпус.
Системы означает трубопроводы природного газа, сжиженного природного газа, сжиженного природного газа, сырой нефти и других трубопроводов. , боковые линии, насосы, насосные станции, складские помещения, терминалы, перерабатывающие предприятия и другие связанные операции, активы, машины и оборудование, которые принадлежат Партнерству или любой из его Дочерних компаний и используются для ведения бизнеса Партнерства и Средний бизнес в текущем состоянии.
Турбина внутреннего сгорания означает замкнутое устройство, работающее на ископаемом или другом топливе, которое состоит из компрессора, камеры сгорания и турбины, и в котором дымовой газ, образующийся при сгорании топлива в камере сгорания, проходит через турбину. вращая турбину.
Подвод тепла означает произведение (выраженное в ммБТЕ / время) высшей теплотворной способности топлива (выраженное в британских тепловых единицах / фунт) на скорость подачи топлива в устройство сгорания (выраженную в массе топлива / времени) и не включает тепло, полученное от предварительно нагретого воздуха для горения, рециркулирующих дымовых газов или выхлопных газов из других источников.
Телекоммуникационная система означает систему для передачи визуальных изображений, звуков или другой информации с помощью электронных средств;
пожарный гидрант означает пожарную заглушку или пожарный гидрант с неподвижной опорой;
ветрогенератор означает конструкцию, состоящую из башни, ротора с тремя лопастями, соединенными в ступице, гондолы и вспомогательного электрического и другого оборудования, которое может включать в себя J-образную трубу (и), переходную деталь, платформы для доступа и отдыха, лестницы для доступа. системы доступа к лодкам, системы защиты от коррозии, кранцы и оборудование для обслуживания, посадочные площадки для вертолетов и другое сопутствующее оборудование, закрепленное на фундаменте; и
Промышленное ремонтное покрытие означает архитектурное покрытие с высокими эксплуатационными характеристиками, включая грунтовки, герметики, грунтовочные покрытия, промежуточные покрытия и верхние покрытия, разработанные для нанесения на основания, включая полы, подверженные одному или нескольким из следующих экстремальных условий окружающей среды, перечисленных ниже, и с пометкой «Только для промышленного использования»; «Только для профессионального использования»; «Не для использования в жилых помещениях»; или «Не предназначено для использования в жилых помещениях.
Охлаждающая вода означает воду, сбрасываемую при любом использовании, таком как кондиционирование воздуха, охлаждение или охлаждение, или к которой добавляется только тепло.
Трубопроводы означает Трубопроводную систему Малага, Трубопровод Roadrunner, Трубопроводы Талсы, Соединительные трубопроводы Талсы и Линии доставки Эльдорадо, а также любой другой трубопровод, включенный в Применимые активы.
СПГ означает сжиженный природный газ.
Пулемет означает любое огнестрельное оружие, известное как пулемет, механическая винтовка, пистолет-пулемет или любой другой механизм или инструмент, не требующий нажатия спускового крючка для каждого выстрела и имеющий складную обойму, диск, барабан, ремень или другое отделяемое механическое устройство для хранения, переноски или подачи боеприпасов, которые могут быть загружены в огнестрельное оружие, механизм или инструмент и произведены из них со скоростью пять или более выстрелов в секунду.


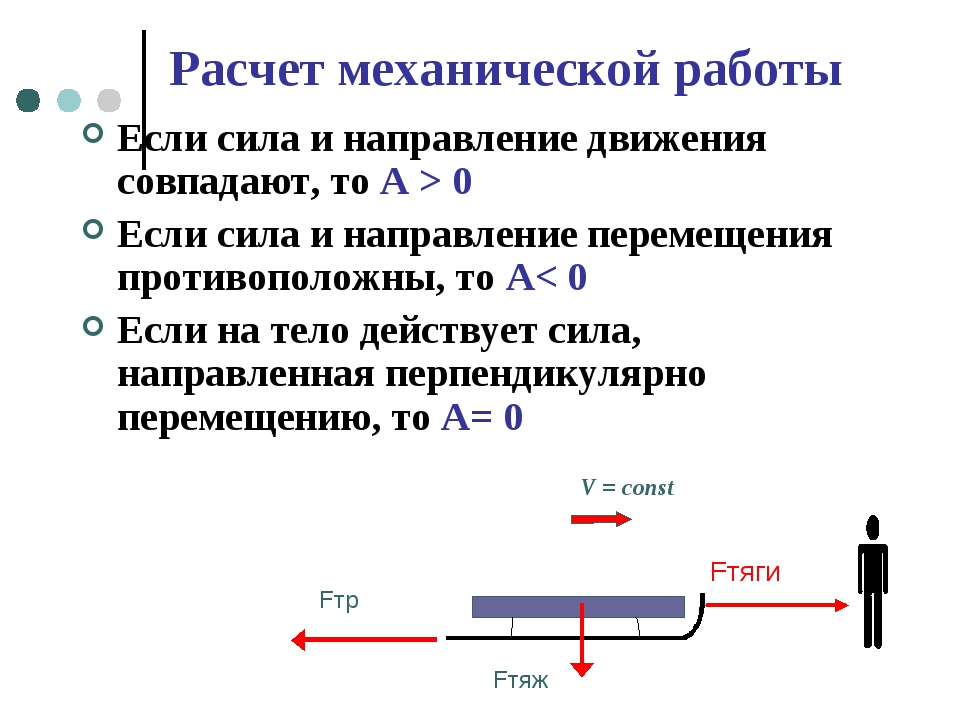

 Таким образом: работа численно равна площади фигуры под графиком зависимости силы от координаты F(x).
Таким образом: работа численно равна площади фигуры под графиком зависимости силы от координаты F(x).
