Почему делить на ноль нельзя? – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)
Все математические действия равны, но некоторые равнее других
Начнём с того, что четыре арифметических действия — сложение, вычитание, умножение и деление — не являются равноправными. И разговор идёт не о порядке выполнения действий при решении какого-нибудь примера или уравнения. Нет, имеется в виду само понятие числа. И согласно ему, наиболее важными являются сложение и умножение. А уже вычитание и деление «вытекают» из них тем или иным образом.
Сложение и вычитание
Например, разберём простую операцию: «3 – 1». Что это означает? Школьник легко объяснит эту задачку: это означает, что было три предмета (например, три апельсина), один вычли, оставшееся количество предметов и есть верный ответ. Верно описано? Верно. Мы и сами объяснили бы точно так же. Но математики рассматривают процесс вычитания иначе.
Операция «3 – 1» рассматривается не с позиции вычитания, а только со стороны сложения.
Умножение и деление
Аналогичные метаморфозы происходят с таким действием, как деление. Задачу «6 : 3» математики отказываются воспринимать как некие шесть предметов, разбитых на три части. «Шесть разделить на три» не что иное, как «неизвестное число, умноженное на три, в результате чего получилось шесть»: «х · 3».
Делим на ноль
Выяснив принцип математических действий по отношению к задачам с вычитанием и делением, рассмотрим наше деление на ноль.
Задача «4 : 0» превращается в «х · 0». Получается, нам нужно найти такое число, умножение с которым даст нам 4.
Больше интересных материалов:
- Почему минус на минус всегда даёт плюс?
- Типичные ошибки учителей при проведении уроков математики в начальной школе
- Методическая помощь учителю математики
- Внеурочная деятельность по математике в начальной школе
- Формирование математической грамотности в начальной школе
А что получится, если ноль разделить на ноль?
Представим такое уравнение: «0 · x = 0». С одной стороны, выглядит вполне справедливо. Представляем вместо неизвестного числа ноль и получаем готовое решение: «0 · 0 = 0». Из этого вполне логично вывести, что «0 : 0 = 0».
С одной стороны, выглядит вполне справедливо. Представляем вместо неизвестного числа ноль и получаем готовое решение: «0 · 0 = 0». Из этого вполне логично вывести, что «0 : 0 = 0».
Однако теперь давайте в это же уравнение с неизвестным вместо «x = 0» подставим любое другое число, например «x = 7». Получившееся выражение выглядит теперь как «0 · 7 = 0». Вроде бы, всё верно. Делаем обратную операцию и получаем «0 : 0 = 7». Но тогда, получается, что можно взять абсолютно любое число и вывести 0 : 0 = 1, 0 : 0 = 2… 0 : 0 = 145… — и так до бесконечности.
Если при любом числе х уравнение будет справедливо, то мы не имеем права выбрать лишь одно, исключив остальные. Значит, мы так и не можем ответить, какому числу соответствует выражение «0 : 0». Снова оказавшись в тупике, мы признаём, что и эта операция тоже бессмысленна. Получается, что ноль нельзя делить даже на самого себя.
Оговоримся, что в математическом анализе иногда бывают специальные условия задачи — так называемое «раскрытие неопределенности». В подобных случаях разрешается отдавать предпочтение одному из возможных решений уравнения «0 · x = 0». Однако в арифметике таких «допусков» не происходит.
В подобных случаях разрешается отдавать предпочтение одному из возможных решений уравнения «0 · x = 0». Однако в арифметике таких «допусков» не происходит.
Почему нельзя делить на ноль, даже если очень хочется? / Хабр
Недавно на Хабре появилась удивительная статья «Папа, а почему на ноль делить нельзя?», которая собрала массу не менее удивительных комментариев.
Детские вопросы обычно очень сложны («Почему небо ночью темное?», «Почему яблоки падают на землю?») и у взрослых обычно не хватает времени, чтобы их доходчиво объяснить. Да и не всегда взрослые знают ответ на эти вопросы.
Однако, вопрос о делении на ноль ни разу не относится к числу сложных вопросов, и для меня остается загадкой, почему с ним возникает столько проблем. Наверное, виной тому какие-то изъяны в методике преподавания математики в средней школе, в трудностях перехода от изучения арифметики к изучению буквенной алгебры и свойств элементарных функций.
Самые серьезные сомнения появляются, я думаю, после изучения рациональных чисел, когда для любого числа x, кроме нуля, вводится понятие обратного числа 1/x, и графика гиперболы y(x)=1/x.
Очевидно, что при делении 1 на очень маленькие числа появляются очень большие числа, и чем меньше мы берем x, тем больше становится 1/x. Почему же мы не можем сказать, что 1/x=∞ — есть некоторое число?
Алгебраическое возражение против этого состоит в следующем. Предположим, что ∞=1/x является числом. Тогда на это число должны распространяться все правила, которые имеют место быть для обычных чисел. В частности, с одной стороны должно быть верно соотношение 0⋅∞=1, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅∞=1⋅∞−1⋅∞=0. Таким образом, имеем 1=0, а из этого уже следует, что все числа равны между собой и равны нулю. В самом деле, поскольку для любого числа x верно 1⋅x=x, то 1⋅x=0⋅x=0.
«Ну разве это не полная чушь?» — спросим себя, добравшись до этого места.
Разумеется, это полная чушь, если мы говорим об обычных числах. Но я недаром подчеркнул выше слово «правила». К ним мы вернемся чуть позже, после рассмотрения арифметического возражения против деления на ноль, и поможет нам в этом фасоль.
Вернемся в те времена, когда не было ни компьютеров, ни калькуляторов, ни логарифмических линеек, и поставим перед собой задачу разделить некоторое случайное число, например, на 5.
Для этого берем чашу с фасолью, символизирующую натуральный ряд, и высыпаем из нее какое-то количество зерен на разлинованный лист бумаги:
Тем самым, мы установили делимое на нашем бобовом калькуляторе.
Задача состоит в том, чтобы разложить эти зерна на пять рядов. Чтобы не запутаться отмечаем эти ряды, то есть, устанавливаем делитель:
Теперь раскладываем зерна из кучи на пять рядов в столбик. Это значительно дольше, чем на обычном калькуляторе, зато позволяет почувствовать всю прелесть арифметики до изобретения позиционной системы счисления.
Алгоритм завершается, когда мы получаем некоторое прямоугольное число и (возможно) остаток:
В данном примере осталось 2 зерна, а рядов по 5 зерен образовалось 18. Получается, что случайное число было 18⋅5+2=92.
Ясно, что мы можем выполнить этот алгоритм для любого натурального делимого и любого натурального делителя, отличного от нуля; если же делитель равен 0, то этот алгоритм выполнить попросту невозможно.
«Подождите!» — скажет внимательный читатель. — «В рассмотренном примере мы получили остаток 2, что с ним делать?»
Это, на самом деле, очень важное замечание. Вообще говоря, мы не можем делить фасолины, не испортив наш бобовый калькулятор — мало того, что разделить 2 фасолины на 5 одинаковых частей проблематично, даже если мы их раздробим подобающим образом, мы уже не сможем их собрать.
Поэтому достаточно долго люди старались обходиться без дробей. Например, в анонимной арабской рукописи XII века описана следующая задача: «разделить 100 фунтов между 11 человеками». Поскольку 100=11⋅9+1, средневековый математик предлагает сначала раздать каждому по 9 фунтов, а затем обменять оставшийся фунт на яйца, которых, как оказывается по курсу обмена, получается ровно 91. Но 91=11⋅8+3, поэтому арабский ученый предлагает раздать каждому по 8 яиц, а три оставшихся яйца отдать тому, кто производит раздел, или же обменять на соль к яйцам.
Говоря современным математическим языком, деление проводилось в полукольце натуральных чисел. Впрочем, с таким же успехом, используя красную и белую фасоль, мы могли бы определить деление с остатком и в кольце целых чисел — в изложенном алгоритме появились бы дополнительные правила для выбора цветов используемых для вычислений зерен фасоли, но точно так же остались бы бессмысленными операции вида x/0 и 5/2.
Очевидно, что для того, чтобы придать символу 5/2 конкретный смысл, нужно изменить правила игры, и перейти к полю рациональных дробей, пополнив множество целых чисел всевозможными выражениями m/n, где m — целое, а n — натуральное.
Важно заметить, что сделать это можно не единственным способом, однако в классической арифметике рассматривается такое пополнение, в котором символ 1/n означает долю от деления 1 на n, т. е. такое число, для которого верно выражение n⋅1/n=1; при чем доли имеют смысл не при подсчете штучных предметов (например, зерен фасоли), а при измерении величин, которые предполагаются непрерывными (или хотя бы неограниченно делимыми) — длин отрезков, площадей фигур и т. д.
д.
В поле рациональных дробей уже нет смысла рассматривать неполное частное и остатки, так как частное от любого ненулевого делителя является какой-то рациональной дробью. Более того, как и в случае с натуральными числами, мы можем использовать для деления фасоль без изменения алгоритма.
В самом деле, пусть требуется разделить рациональное число α=p/q на β=r/s. Это равносильно выполнению следующих действий:
α:β=p/q:r/s=p⋅s/q⋅r
и задача при любых рациональных α и β свелась к уже известной процедуре деления целых чисел. Это еще раз показывает, что деление на ноль не имеет никакого арифметического смысла.
«Получается, делить на ноль нельзя, даже если очень хочется?» — увы, ответ на этот вопрос положительный: мы не можем определить операцию деления на ноль исходя их естественных потребностей счета и измерений. Правда, есть две лазейки.
Первая: вместо «обычных» чисел (т.е. кольца натуральных и поля рациональных, а также поля действительных чисел, о котором я, кстати, до сих пор не сказал ни слова и расскажу как-нибудь в другой раз) рассмотреть вырожденный случай — тривиальное кольцо {0}, и положить по определению 0/0=0. В этом случае, когда нам говорят: «Все числа равны между собой и равны нулю!» — мы можем сказать невозмутимым тоном: «Ну и что? Это всегда было так».
В этом случае, когда нам говорят: «Все числа равны между собой и равны нулю!» — мы можем сказать невозмутимым тоном: «Ну и что? Это всегда было так».
Вторая: отказаться от некоторых привычных правил умножения. В частности, от аксиомы 0⋅x=0. Говорят, что это возможно (см. http://en.wikipedia.org/wiki/Wheel_theory). Разумеется, этот вариант гораздо интереснее первого, но и он представляет собой такое изменение правил игры, которое сразу выводит нас за рамки классической арифметики.
В заключение этой заметки хочу привести список литературы для тех, кто заинтересовался числовыми системами:
— И.В. Арнольд «Теоретическая арифметика», М, ОГИЗ 1938 — очень подробная и детальная книга, в которой можно найти описания классических числовых систем, включая кватернионы.
— Е. Г. Гонин «Теоретическая арифметика», М, 1959 — эта книга покороче и посовременнее, и тоже очень хороша, хотя не так подробна, как книга И.В. Арнольда.
— С. Феферман «Числовые системы» — классическая монография, местами достаточно сложная; в ней изложены некоторые частные вопросы, которых нет в двух других книгах по теоретической арифметике.
— А. А. Кириллов «Что такое число?» (1993) — небольшая брошюра, рассчитанная на подготовленного читателя.
— Е. Б. Дынкин, В. А. Успенский «Математические беседы» — популярная книга, рассчитанная на школьников. Содержит массу информации и задач по такой «нестандартной» теме, как p-адические числа.
Определениев кембриджском словаре английского языка
Примеры нуля
нуля
Получение нулевой -процентной налоговой ставки, несмотря на получение прибыли, требует творческого учета, но не нарушения закона.
От ThinkProgress
И они уже настолько близки к ноль , насколько это вообще возможно.
Из ВРЕМЕНИ
Идеальный пробег для одного из этих электрических велосипедов — это пересечение финишной черты с ноль заряд остался.
С грани
Когда остаток на первом счете достигает ноль , высвобожденные деньги затем направляются на погашение долга со следующей по величине процентной ставкой и так далее.
Из Сиэтл Таймс
В 1985 году это число составляло 10 девочек и ноль мальчиков.
Из новостей ABC
Далее,
От Хаффингтон Пост
Недавний опыт и некоторые расширяющиеся исследования показывают, что ноль на самом деле не является обязательным нижним пределом процентных ставок.
От CNBC
Например, если ваш единственный интерес — это зарабатывание денег, вы можете присвоить максимальный вес 5 «доходу» и ноль всему остальному.
Из Атлантики
По словам официальных лиц, температура в этой части самолета падает примерно на 58 градусов ниже нуля во время полета.
Из Нью-Йорк Дейли Ньюс
Он держал ставки около ноль с конца 2008 года.
От Блумберга
У фирмы было ровно ноль опыта такой работы.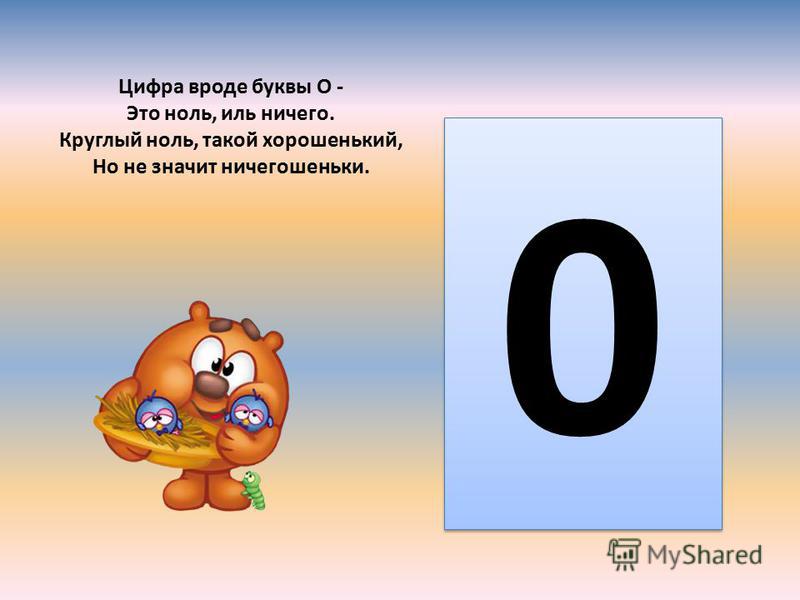
Из хроники Сан-Франциско
На этом сайте должна быть опция “ ноль “.
Из Phys.Org
Есть несколько ноль
сред ошибок, в которых вы бы не хотели, чтобы все принимали неудачи, например авиационная отрасль, военные или атомные электростанции.Из Fast Company
Другими словами, когда кубит измеряется, его суперпозиция коллапсирует в одно из доступных состояний (в данном случае ноль или единица).
Из Арс Техника
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Переводы zero
на китайский (традиционный)
(數字)零, 沒有,全無, 零(攝氏)度…
См. больше
на китайском (упрощенном)
(数字)零, 没有,全无, 零(摄氏)度…
Подробнее
на испанском языке
cero, cero [мужской род, единственное число]…
Подробнее
на португальском
ноль, ноль [мужской род]…
Увидеть больше
на других языкахна японском
на турецком
на французском языке
в каталонском языке
на голландском
на арабском языке
в чешском
на датских
на индонезийском языке
в Thai
на
в политике
в политике
в политике
в политике
в поли малайский
немецкий
норвежский
корейский
украинский
итальянский
русский
(数字の)ゼロ, (温度)零度, 氷点…
См. больше
См. больше
больше
См. больше
zero [мужской род], zéro, l’heure H…
Подробнее
ноль…
Подробнее
nul, nulinstelling…
Увидеть больше
صِفْر…
Подробнее
nula, nultá hodina…
Подробнее
nul, nulpunkt, affyring…
Подробнее
nol, sisa waktu…
См. Больше
เลข ศูนย์, ระดับ ศูนย์, เวลา ที่ ถูก กำหนด แน่นอน สำหรับ การ เกิด เหตุการณ์ บาง สิ่ง…
Узнать больше Подробнее
ноль, годзина ноль…
Подробнее
сифар, маса пеланкаран…
Подробнее
die Null, der Nullpunkt…
Увидеть больше
null [мужской род], nullpunkt [средний род], null…
Узнать больше
숫자 영, 0, 영도…
Подробнее
нуль, ніщо, нульва точка…
Подробнее
ноль, нулевой градиент…
Узнать больше
ноль…
Узнать больше
Нужен переводчик?
Получите быстрый бесплатный перевод!
Как произносится ноль ?
Обзор
зенит
цеолит
зефир
дирижабль
ноль
облигация с нулевым купоном
ноль дефектов
делитель нуля БЕТА
нулевая гравитация
Проверьте свой словарный запас с помощью наших веселых викторин по картинкам
- {{randomImageQuizHook.
 copyright1}}
copyright1}} - {{randomImageQuizHook.copyright2}}
Авторы изображений
Попробуйте пройти викторину прямо сейчас
Слово дня
член
Великобритания
Ваш браузер не поддерживает аудио HTML5
/ˈmem.bər/
НАС
Ваш браузер не поддерживает аудио HTML5
/ˈmem.bɚ/
человек, животное или вещь, входящие в группу
Об этом
Блог
Причудливый и новый: способы сказать, что что-то необычное (1)
Подробнее
Новые слова
frauxmage
В список добавлено больше новых слов
Наверх
Содержание
EnglishIntermediateBusinessExamplesTranslations
Ноль — определение, значение и синонимы
ПЕРЕЙТИ К СОДЕРЖАНИЮ
Другие формы: нули; обнулено; нули; обнуление
Ноль ничего не значит. Если к единице прибавить ноль , получится единица. И если кто-то получает ноль на тесте, это означает, что они пропустили все вопросы.
Возможно, вы знаете ноль как 0, zilch, zip, ничего или нет. Хотя это число не имеет значения, без него мы не смогли бы считать дальше 9. На числовой прямой все числа ниже нуля отрицательны. А температура, при которой вода замерзает, равна нулю градусов Цельсия. Время от времени вы можете услышать, как кто-то описывает человека как ноль — это не очень хороший способ сказать, что у человека нет ничего интересного.
На числовой прямой все числа ниже нуля отрицательны. А температура, при которой вода замерзает, равна нулю градусов Цельсия. Время от времени вы можете услышать, как кто-то описывает человека как ноль — это не очень хороший способ сказать, что у человека нет ничего интересного.
Определения нуля
существительное
математический элемент, который при добавлении к другому числу дает то же самое число
- синонимы: 0, шифр, шифр, ничего
существительное
количество не имеет значения
- синонимы: что-то, шифр, шифр, гусиное яйцо, нада, ничего, ноль, никс, ничего, ноль, пшик, почтовый индекс, зиппо
прилагательное
не имеющее измеримой или иным образом определяемой ценности
«цель ноль прирост населения»
- Синонимы:
- нет
квантификатор
; используется либо с массовыми существительными, либо с исчисляемыми существительными во множественном числе для обозначения полного или почти полного отсутствия или нулевого количества
- нет
квантификатор
прилагательное
из нулевого набора или относящегося к нему (набор без элементов)
прилагательное
указание на отсутствие какой-либо или всех рассматриваемых единиц
«а ноль балл»
- синонимы: 0
- кардинал
является или обозначает числовое количество, но не заказ
- кардинал
существительное
точка на шкале, от которой можно измерить положительные или отрицательные числовые величины
- синонимы: нулевая точка
глагол
настроить (прибор или устройство) на нулевое значение
прилагательное
указание начальной точки или источника
- Синонимы:
- порядковый номер
является или обозначает порядковый номер в серии
- порядковый номер
существительное
настройка прицела, при которой снаряд попадает в центр мишени без порыва ветра
глагол
отрегулировать (как при стрельбе в условиях испытаний) ноль (ружья)
«Он пристрелял из своей винтовки на 200 ярдов»
- синонимы: ноль в
ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ: Эти примеры предложений появляются в различных источниках новостей и книгах, чтобы отразить использование слова «ноль» .


