Нулевой проводник это: Нулевой защитный и нулевой рабочий проводники

Нулевой защитный и нулевой рабочий проводники

11.05.201804.01.2023 Админ.

Нулевой защитный и нулевой рабочий проводники различаются по назначению, способу подключения и функциональной нагрузки в электрических сетях.

Нулевой рабочий проводник

Нулевой рабочий проводник это проводник сети, подключенный к глухозаземленной нейтрали трансформатора трехфазного или нулевому выводу трансформатора однофазного. По нулевому рабочему проводнику протекает нагрузочный ток. На схеме нулевой рабочий проводник, обозначается буквой «N».

Нулевой защитный проводник

В системах TN-C, TN-S, TN-C-S, где нулевой вывод трансформатора глухозаземлен, нулевой защитный проводник соединяет нулевую точку питающего трансформатора и токопроводящие части электро приемников, которые могут оказаться под напряжением в аварийной ситуации (косвенное прикосновение). Нулевой защитный проводник несет, по названию понятно, защитные функции. Защитный проводник участвует в защите, как самой электросети, так и человека.

Нулевой защитный проводник это один из видов защитных проводников электросети и относится он к электросетям до 1кВ с глухозаземленной нейтралью трансформатора или генератора.

Согласно ПУЭ 1.7.76. подлежат защите от косвенного прикосновения следующие элементы электросети:

• Металлические корпуса светильников, электромашин, трансформаторов;
• Металлические корпуса распределительных щитов, квартирные и этажные щитки;
• Металлические корпуса распределительных устройств, лотков, муфт кабелей и металлические конструкции с электрооборудованием;
• Металлические корпуса переносных и передвижных устройств.

В качестве защитной меры применяется соединение этих устройств с глухозаземленной нейтралью ТП (трансформатора питания) в системах TN или заземление в системах TT и IT.

На схемах нулевой защитный проводник обозначается двумя латинскими буквами «PE».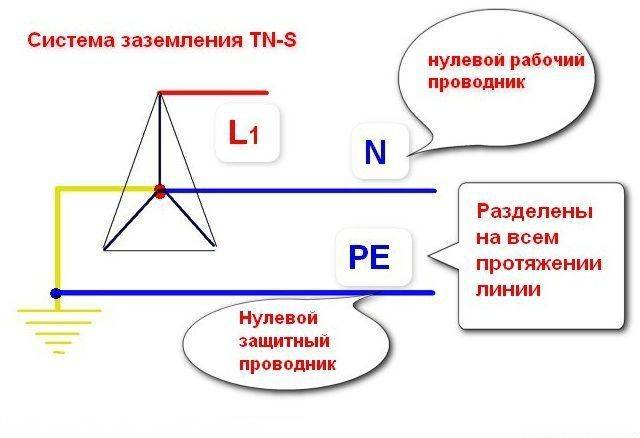 В нормальном режиме работы электросети по нулевому защитному проводнику электрический ток не течет.

На схемах буквами PE обозначаются не только нулевой защитный проводник, но и все защитные проводники сети: заземляющие проводники, защитный проводник в системе уравнивания потенциалов, отдельные жилы в кабелях, отдельно проложенные проводники и шины.

Разделение защитного и рабочего нулей электросети

В электросети с глухозаземленной нейтралью TN, нулевой рабочий проводник N и защитный проводник PN, до определенной точки в электросети объединены в один проводник и обозначается этот проводник буквами PEN.

Разделение PEN проводника, обычно, производится на ГЗШ-главной заземляющей шине, которая устанавливается на вводе электроустановки.

А именно:

• Для жилого дома ГЗШ стоит на вводном устройстве в дом;
• Для частного дома ГЗШ монтируется во вводном устройстве (ВУ) рядом с ответвлением к дому (на столбе) или в доме во вводно-распределительном устройстве (ВРУ).

Нулевой защитный и нулевой рабочий проводники – выводы

• Нулевой рабочий проводник (нейтральный) вместе с фазным проводником участвует в электропитании устройств. По нему течет рабочий ток;
• Нулевой защитный проводник не участвует в электропитании и предназначен для защиты от косвенного прикосновения в сетях с глухозаземленной нейтралью.

©Ehto.ru

Другие статьи радела “УЗО”

УЗОзащитный автомат, к электросети подключение дома, нулевой провод что это такое, проводник электрического тока, рабочий проводник, трансформатор электрического тока, устройство электрики

Нулевой рабочий проводник

Пример HTML-страницы

Нулевой рабочий проводник также называют нейтралью. Большинство бытовых приборов питаются от сети переменного напряжения 220 В. Для того чтобы подать на них это напряжение, используется один фазный провод, а второй нулевой. Фаза имеет потенциал 220 В, а нулевой провод имеет потенциал 0 относительно источника питания и фазного провода.

Нулевой обозначается как N, а его изоляция должна быть голубого цвета или бело-голубого, в соответствии с цветовой маркировкой кабеля. Часто функции нулевого рабочего провода и защитного совмещаются (для систем заземления TN-C). Такой совместный проводник обозначается PEN и имеет жёлто-зелёную изоляцию с голубыми маркерами (метками) на концах. Аналогичные цветовые обозначения применяются в Европе. В США нулевой рабочий провод может обозначаться белым или серым цветом.

В разных линиях электропередач и сетях могут использоваться различные нейтрали (изолированная, глухозаземлённая, эффективно-заземлённая). Выбор того или иного варианта определяется функциональным назначением сети.

В настоящий момент практически все жилые дома в России имеют системы заземления с глухозаземлённой нейтралью. В этом случае электроэнергия поставляется от трёхфазных генераторов по 3 фазам с потенциалом, а также от генератора идёт четвёртый провод — нейтральный (рабочий ноль). Три фазы в конце линии соединяются звездой: таким образом получается конец нейтрали, которая соединяется с нейтралью питающего генератора. Провод, соединяющий эти две нейтрали и называется рабочим нулевым проводником сети.

В случае симметричной нагрузки на все фазы ток в рабочем нуле отсутствует. Если же нагрузка распределена неравномерно, то по нулевому рабочему проводнику протекает ток небаланса. Использование такой схемы позволяет добиться саморегулирования всех трёх фаз, при этом напряжение на них почти равно между собой.

Для повышения безопасности рабочий ноль заземляется в конце линии, а также часто применяются дополнительные заземления: в начале линии и в разных её точках. В домах нулевой рабочий провод подводится к распределительному устройству, от которого уже отходят отдельные нулевые проводники к непосредственным потребителям электроэнергии (например, в квартиры).

Помимо сетей с глухозаземлённой нейтралью, также используются электросети с изолированной нейтралью. В таких сетях отсутствует нулевой рабочий провод. Вместо него при необходимости может использоваться нулевой заземляемый провод.

При использовании трёхфазных линий питания в здании, сечение нулевого рабочего проводника должно быть не меньше сечения фазных проводников, при размерах последних до 25 мм2 (алюминий). Если сечение фазных проводников больше 25 мм2, то площадь сечения рабочего нуля должна быть не менее 50% их сечения. Если сеть использует заземляющий рабочий ноль, то при подключении провода к главной заземляющей шине должен присутствовать опознавательный знак «земля».

Даже если на РУ защитный и рабочий нули соединены, дальнейшее их объединение у потребителей не допускается. Т. е. дальше по квартирам пускается два отдельных провода PE и N. Их нельзя соединять потому, что при КЗ фаза замыкается на нулевой рабочий проводник, и все устройства, подключённые к защитному проводнику PE (в случае объединения PE и N), окажутся под фазным напряжением, из-за чего возникает большая вероятность поражения человека током.

электромагнетизм – Почему в электростатике электрическое поле внутри проводника равно нулю?

$\begingroup$

В книгах по электромагнетизму, таких как Гриффитс и им подобных, когда говорят о свойствах проводников в случае электростатики, говорят, что электрическое поле внутри проводника равно нулю.

У меня 2 вопроса:

1. Мы знаем, что в проводниках (металлических) есть свободные электроны, которые беспорядочно движутся во всех направлениях, так как же мы можем говорить об электростатике, которая по определению означает стационарные заряды?

2. Когда в учебниках пытаются объяснить, почему электрическое поле внутри проводника равно нулю, они говорят, что давайте поместим наш проводник в электрическое поле. Тогда произойдет то, что будет индуцированная поверхностная плотность заряда, которая, следовательно, индуцирует электрическое поле внутри проводника, так что полное электрическое поле внутри проводника будет равно нулю. Это прекрасно понятно, но моя проблема заключается в следующем: изначально утверждалось, что электрическое поле внутри проводника равно 0, а не электрическое поле после помещения проводника во внешнее электрическое поле стало равным нулю. Я не понимаю логики!

• электромагнетизм
• электростатика
• электрические поля
• металлы

$\endgroup$

2

$\begingroup$

Проводники определяются свободой некоторых зарядов внутри перемещаться с небольшим сопротивлением.

Итак, если бы было ненулевое поле, что бы произошло? Ответ: некоторые из свободных зарядов перемещаются на , пока поле снова не станет равным нулю

.

---

Вам может быть интересно, есть ли пределы этому утверждению, но вводная книга такого рода не беспокоится об экстремальных ситуациях. В любом случае попробуйте выбрать простую геометрию, оцените долю свободно перемещающихся зарядов и рассчитайте поле насыщения.

$\endgroup$

5

$\begingroup$

В электростатике свободные заряды в хорошем проводнике находятся только на поверхности.

Это можно понять как минимум двумя способами

• Итак, свободный заряд внутри проводника равен нулю. Так что поле в нем обусловлено зарядами на поверхности. Поскольку заряды имеют одинаковую природу, а их распределение ОДНОРОДНО, электрические поля компенсируют друг друга.

• Рассмотрим поверхность Гаусса внутри проводника. Заключенный в нем заряд равен нулю (заряд находится только на поверхности). Следовательно, электрический поток =0 Кроме того, электрический поток = электрическое поле * площадь. Поскольку площадь не может быть равна нулю, электрическое поле равно нулю

$\endgroup$

3

$\begingroup$

Закон Гаусса гласит, что поток электрического поля через замкнутую поверхность равен отношению нагрузки внутри поверхности к $ \epsilon_0$.

Драйвер характеризуется тем, что носители заряда могут свободно перемещаться внутри него. Если заряды в проводнике находятся в равновесии в состоянии покоя, то напряженность электрического поля во всех внутренних точках же должна быть равна нулю, иначе движение нагрузки вызывалось бы электрическим током.

Внутри проводника произвольно нарисуйте замкнутую поверхность $S$, откуда следует, что:

Электрическое поле равно нулю, $E = 0$ во всех точках указанной поверхности.

Поток через замкнутую поверхность $S$ равен нулю.

Суммарный заряд q на внутренней стороне указанной поверхности равен нулю. В качестве замкнутой поверхности S мы можем сделать ее сколь угодно малой, поскольку заключаем, что в любой точке P внутри проводника нет избыточной нагрузки, поэтому ее следует разместить на поверхности проводника. это должно ответить на ваш вопрос.

$\endgroup$

$\begingroup$

Так как ответы меня не устраивают и кажется, что люди до сих пор натыкаются на этот вопрос гугля, попробую ответить на него.

Сначала нам нужно понять, каковы некоторые основные положения классической электродинамики. Как и любая другая область науки, она использует модели для описания природы. Некоторыми хорошо известными моделями являются точечная масса, точечный заряд, континуум и т. д.

Электродинамика использует модели заряда континуума и точечного заряда для описания зарядов в реальном мире. Континуум заряда задается одной основной величиной, а именно плотностью заряда.

Плотность заряда в точке $A$ определяется усреднением всех зарядов в малом объеме пространства $\Delta V$ вокруг точки $A$. Также мы усредняем плотность заряда по некоторому малому интервалу времени $\Delta t$. Сейчас я не буду вдаваться в подробности того, что такое $\Delta V$ и $\Delta t$ на самом деле, но вы можете прочитать о физически бесконечно малых объемах и временных интервалах. Дело в том, что $\rho(A)$ – это не “точная” плотность заряда в этой точке, а усредненное значение.

Теперь вернемся к вопросу:

Мы знаем, что в проводниках (металлических) есть свободные электроны, которые беспорядочно движутся во всех направлениях, так почему же мы можем говорить об электростатике, которая по определению означает стационарные заряды?

Да, они хаотично движутся во всех направлениях и это точка. При усреднении по небольшим промежуткам пространства и времени (учитывая, что электроны обычно не пересекают большие расстояния и не имеют большой скорости) – вы получите нулевую плотность заряда. Ключом является случайность теплового движения, которое в среднем равно нулю. На жаргоне вы бы сказали, что классическая электродинамика не видит квантовых и тепловых эффектов из-за уменьшенного масштаба.

Это прекрасно понятно, но моя проблема в следующем: изначально утверждалось, что электрическое поле внутри проводника равно 0, а не электрическое поле после помещения проводника во внешнее электрическое поле стало равным нулю. Я не понимаю логики!

Ответ на второй вопрос уже дан выше. Авторы обычно считают тривиальным вопрос о поле внутри проводника с внешним полем $E_{ext}=0$, поэтому сразу переходят к $E_{ext}\not=0$

$\endgroup$

$\begingroup$

Вопрос 1: В игре две космические шкалы: Микроскопическая шкала: Каждый рассматривает электроны по отдельности. Их движение и генерируемое ими электромагнитное поле широко варьируются как в пространстве, так и во времени. Макроскопический масштаб: Как движение отдельных электронов, так и электромагнитные поля невозможно измерить с помощью стандартных лабораторных приборов. В нашем масштабе можно наблюдать только среднее пространственно-временное. В кинетической теории плазмы используется метод расчета этих средних значений и их изменения в пространстве и времени.

Электростатика занимается только макроскопическими полями. Он не исключает микроскопического движения электронов, но предполагает, что среднее движение равно нулю.

Доказательство вашего второго вопроса не сложно. Сначала докажем, что любой свободный заряд диффундирует к поверхности за короткое время.

Комбинируя закон сохранения заряда, закон Ома и второе уравнение Максвелла, получаем:

$$\begin{case} \frac{\partial \rho }{\partial t} + \overrightarrow{ \nabla }. \overrightarrow{j} =0 \\\overrightarrow{j}= \sigma \overrightarrow{E} \\\overrightarrow{ \nabla }.\overrightarrow{E} = \frac{ \rho }{ \varepsilon _{0} } \end{case} ~~\Rightarrow ~~ \ frac {\ partial \ rho {\ partial t} + \ frac { \ sigma \ rho }{ \ varepsilon _ {0}} = 0 ~ ~ \ Rightarrow ~~ \ rho (t) = \ rho (0) e ^{-\frac{ \sigma}{\varepsilon _{0}}t}$$ 9{-3} s$$

Таким образом, для любой физической задачи, связанной с масштабом времени больше миллисекунды, можно считать, что в проводниках нет объемных зарядов.

На втором этапе применим закон Гаусса к любому объему внутри проводника: $$ \int_ \Sigma \overrightarrow{E}. \overrightarrow{d \Sigma } = \frac{Q_{en}}{ \varepsilon _{0}} =0 $$ Поскольку это верно для любого $\Sigma$, необходимо иметь: $\overrightarrow{E}=\overrightarrow{0}$

$\endgroup$

Почему электрическое поле внутри заряженного проводника равно нулю в электростатическом случае?

Задавать вопрос

спросил 7 лет, 10 месяцев назад

Изменено 6 лет, 7 месяцев назад

Просмотрено 20 тысяч раз

$\begingroup$

Я пытаюсь понять идею (или тот факт), что в большинстве книг рассказывается об электрическом поле внутри заряженного 9-10 кул) внутри твердого проводника радиуса 1.

Согласно представлению о заряде на поверхности и вследствие симметрии заряды будут распределяться следующим образом:

Я начертил электрический потенциал (V=Q/(4πε0r)) и электрическое поле (E=-∇V) с использованием принципа суперпозиции и графика:

Очевидно, что электрический потенциал внутри проводника непостоянен, а электрическое поле не равно нулю.

Как можно объяснить эту проблему?

• электростатика
• электрические поля
• проводники

$\endgroup$

$\begingroup$

Вы проигнорировали подвижные заряды в проводнике. На вашем графике линии поля не перпендикулярны поверхности, особенно вблизи зарядов. Это заставит электроны проводимости двигаться. Положительные заряды будут притягивать электроны до тех пор, пока поле внутри проводника не станет равным нулю. Это означает, что весь проводник, включая внутреннюю поверхность, является эквипотенциалом.