Величины | |
Наименование | Обозначение |
Механические величины | |
| Вес | G, P, W |
| Время | t |
| Высота | h |
| Давление | p |
| Диаметр | d |
| Длина | l |
| Длина пути | s |
| Импульс (количество движения) | p |
| Количество вещества | ν, n |
| Коэффицент жесткости (жесткость) | Ʀ |
| Коэффицент запаса прочности | Ʀ, n |
| Коэффицент полезного действия | η |
| Коэффицент трения качения | Ʀ |
| Коэффицент трения скольжения | μ, f |
| Масса | m |
| Масса атома | ma |
| Масса электрона | me |
| Механическое напряжение | σ |
| Модуль упругости (модуль Юнга) | E |
| Момент силы | M |
| Мощность | P, N |
| Объем, вместимость | V, ϑ |
| Период колебания | T |
| Плотность | ϱ |
| Площадь | A, S |
| Поверхностное натяжение | σ, γ |
| Постоянная гравитационная | G |
| Предел прочности | σпч |
| Работа | W, A, L |
| Радиус | r, R |
| Сила, сила тяжести | F, Q, R |
| Скорость линейная | ϑ |
| Скорость угловая | ώ |
| Толщина | d, δ |
| Ускорение линейное | a |
| Ускорение свободного падения | g |
| Частота | ν, f |
| Частота вращения | n |
| Ширина | b |
| Энергия | E, W |
| Энергия кинетитеская | EƦ |
| Энергия потенциальная | Ep |
Акустические величины | |
| Длина волны | λ |
| Звуковая мощность | P |
| Звуковая энергия | W |
| Интенсивность звука | I |
| Скорость звука | c |
| Частота | ν, f |
Тепловые величины и величины молекулярной физики | |
| Абсолютная влажность | a |
| Газовая постоянная (молярная) | R |
| Количество теплоты | Q |
| Коэффицент полезного действия | η |
| Относительная влажность | ϕ |
| Относительная молекулярная масса | Mr |
| Постоянная (число) Авогадро | NA |
| Постоянная Больцмана | Ʀ |
| Постоянная (число) Лошмидта | NL |
| Температура Кюри | TC |
| Температура па шкале Цельсия | t, ϴ |
| Температура термодинамическая (абсолютная температура) | T |
| Температурный коэффицент линейного расширения | a, ai |
| Температурный коффицент объемного расширения | β, av |
| Удельная теплоемкость | c |
| Удельная теплота парообразования | r |
| Удельная теплота плавления | λ |
| Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива) | q |
| Число молекул | N |
| Энергия внутренняя | U |
Электрические и магнитные величины | |
| Диэлектрическая проницаемость вакуума (электрическая постоянная) | Ԑo |
| Индуктивность | L |
| Коэффицент самоиндукции | L |
| Коэффицент трансформации | K |
| Магнитная индукция | B |
| Магнитная проницаемость вакуума (магнитная постоянная) | μo |
| Магнитный поток | Ф |
| Мощность электрической цепи | P |
| Напряженность магнитного поля | H |
| Напряженность электрического поля | E |
| Объемная плотность электрического заряда | ϱ |
| Относительная диэлектрическая проницаемость | Ԑr |
| Относительная магнитная проницаемость | μr |
| Плотность эенгии магнитного поля удельная | ωm |
| Плотность энергии электрического поля удельная | ωэ |
| Плотность заряда поверхностная | σ |
| Плотность электрического тока | J |
| Постоянная (число) Фарадея | F |
| Проницаемость диэлектрическая | ԑ |
| Работа выхода электрона | ϕ |
| Разность потенциалов | U |
| Сила тока | I |
| Температурный коэффицент электрического сопротивления | a |
| Удельная электрическая проводимость | γ |
| Удельное электрическое сопротивление | ϱ |
| Частота электрического тока | f, ν |
| Число виток обмотки | N, ω |
| Электрическая емкость | C |
| Электрическая индукция | D |
| Электрическая проводимость | G |
| Электрический момент диполя молекулы | p |
| Электрический заряд (количество электричества) | Q, q |
| Электрический потенциал | V, ω |
| Электрическое напряжение | U |
| Электрическое сопротивление | R, r |
| Электродвижущая сила | E, Ԑ |
| Электрохимический эквивалент | Ʀ |
| Энергия магнитного поля | Wm |
| Энергия электрического поля | Wэ |
| Энергия Электромагнитная | W |
Оптические величины | |
| Длина волны | λ |
| Освещенность | E |
| Период колебания | T |
| Плотность потока излучения | Ф |
| Показатель (коэффицент) преломления | n |
| Световой поток | Ф |
| Светасила объектива | f |
| Сила света | I |
| Скорость света | c |
| Увеличение линейное | β |
| Увеличение окуляра, микроскопа, лупы | Ѓ |
| Угол отражения луча | έ |
| Угол падения луча | ԑ |
| Фокусное расстояние | F |
| Частота колебаний | ν, f |
| Энергия излучения | Q, W |
| Энергия световая | Q |
Величины атомной физики | |
| Атомная масса относительная | Ar |
| Время полураспада | T1/2 |
| Дефект массы | Δ |
| Заряд электрона | e |
| Масса атома | ma |
| Масса нейтрона | mn |
| Масса протона | mp |
| Масса электрона | me |
| Постоянная Планка | h, ħ |
| Радиус электрона | re |
Величины ионизирующих излучений | |
| Поглощеная доза излучения (доза излучения) | D |
| Мощность поглощенной дозы излучения | Ď |
| Активность нуклида в радиоактивном источнике | A |
| Символ | Значение и происхождение |
|---|---|
| Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число | |
Ускорение (лат.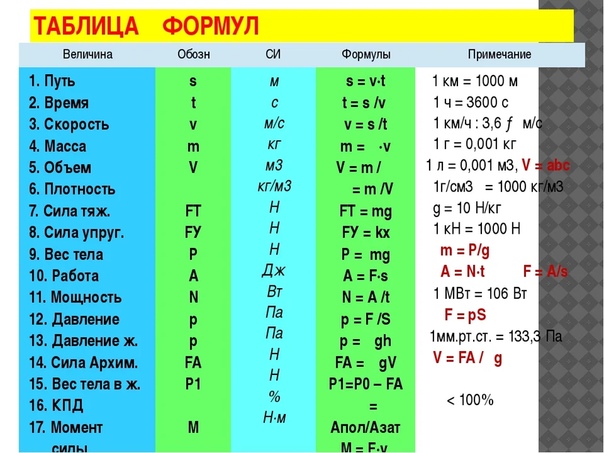 acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора | |
| Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы | |
| Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина (нем. Breite) | |
электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ.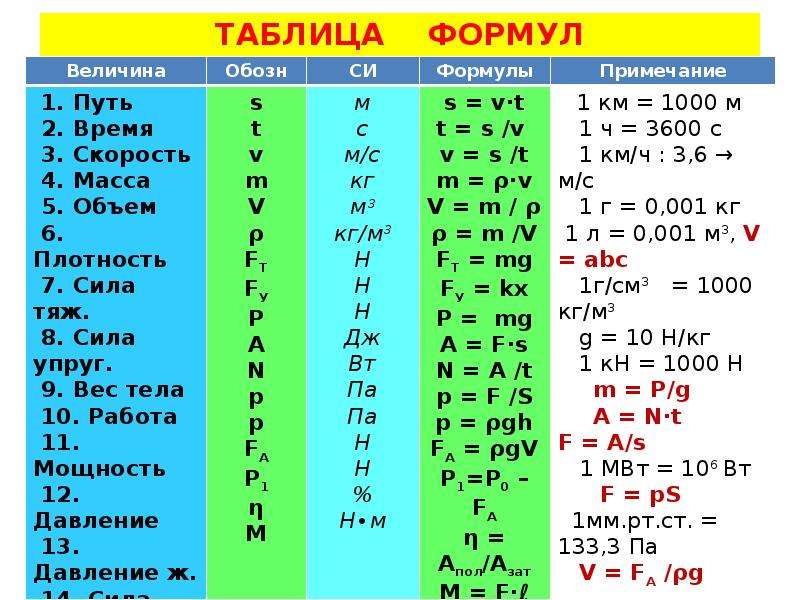 charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) | |
| Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоемкость (англ. heat capacity), волшебный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, Вторая радиационная постоянная | |
Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) | |
| Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) | |
| Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга | |
| 2.71828…, электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия | |
Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига | |
| Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения | |
| Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) | |
Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия | |
| Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) | |
| Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) | |
cила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат.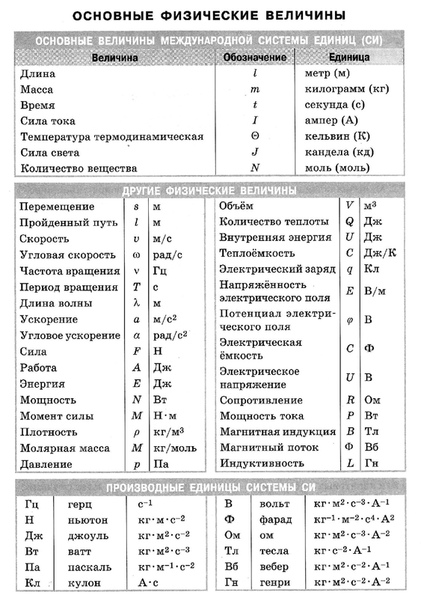 intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности | |
| Мнимая единица (лат. imaginarius), единичный вектор | |
| Плотность тока, момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, внутреннее квантовое число, вращательное квантовое число, сила света, J/ψ-мезон | |
| Мнимая единица, плотность тока, единичный вектор, внутреннее квантовое число, 4-вектор плотности тока | |
| Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона | |
| Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор | |
Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) | |
| Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина | |
| Момент силы, вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса | |
| Масса (лат. massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка | |
| Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность | |
Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ.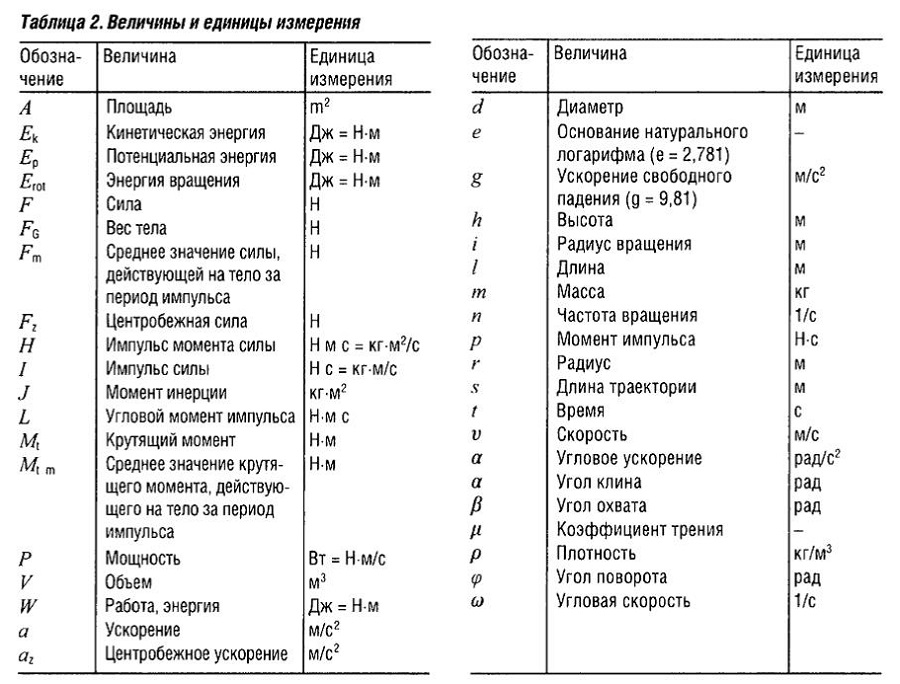 neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта | |
| Начало координат (лат. origo) | |
| Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, 4-импульс | |
| Импульс (лат. petere), протон (англ. proton), дипольный момент, волновой параметр | |
| Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции | |
Электрический заряд, обобщенная координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность quantity of heat), эффективный заряд, добротность | |
| Электрическое сопротивление (англ. resistance), газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние | |
| Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние | |
| Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга | |
Перемещение (итал. ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути | |
| Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин | |
| Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время | |
| Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение | |
| Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость | |
Объём (фр. volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) Verdet constant) | |
| Скорость (лат. vēlōcitās), фазовая скорость, удельный объём | |
| Механическая работа (англ. work), работа выхода, W бозон, энергия, энергия связи атомного ядра, мощность | |
| Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение | |
| Реактивное сопротивление, продольное увеличение | |
| Переменная, перемещение, декартова координата, молярная концентрация, постоянная ангармоничности, расстояние | |
| Гиперзаряд, силовая функция, линейное увеличение, сферические функции | |
| декартова координата | |
| Импеданс, Z бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума | |
| декартова координата | |
| Символ | Значение |
| Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения, поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, натуральный показатель поглощения света, степень черноты тела, постоянная затухания | |
| Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение | |
| Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня | |
| Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты | |
Изменение величины (напр. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект | |
| Небольшое перемещение, дельта-функция Дирака, дельта Кронекера | |
| Электрическая постоянная, угловое ускорение, единичный антисимметричной тензор, энергия | |
| Дзета-функция Римана | |
| КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон | |
| Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда | |
| Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга | |
| Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость | |
| Космологическая постоянная, Барион, оператор Лежандра, лямбда-гиперон, лямбда-плюс-гиперон | |
| Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновского длина волны, собственное значение оператора, матрицы Гелл-Мана | |
| Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон , возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон | |
| Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число | |
| Большой канонический ансамбль, кси-нуль-гиперон, кси-минус-гиперон | |
| Длина когерентности, коэффициент Дарси | |
| Произведение, коэффициент Пельтье, вектор Пойнтинга | |
3. 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон | |
| Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности | |
| Оператор суммирование, сигма-плюс-гиперон, сигма-нуль-гиперон, сигма-минус-гиперон | |
| Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана-Больцмана, поверхностная плотность, поперечное сечение реакции, сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина | |
| Время жизни, тау-лептон, интервал времени, время жизни, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули, тангенциальный вектор | |
| Y-бозон | |
| Магнитный поток, поток электрического смещения, работа выхода, язь, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока | |
| Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил | |
| X-бозон | |
| Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция | |
| Волновая функция, апертура интерференции | |
| Волновая функция, функция, функция тока | |
| Ом, телесный угол, количество возможных состояний статистической системы, омега-минус-гиперон, угловая скорость прецессии, молекулярная рефракция, циклическая частота | |
| Угловая частота, мезон, вероятность состояния, ларморова частота прецессии, Боровская частота, телесный угол, скорость течения |
| Символ | Значение и происхождение |
|---|---|
Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число | |
| Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора | |
| Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы | |
| Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина (нем. Breite) | |
электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) | |
| Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоемкость (англ. heat capacity), волшебный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, Вторая радиационная постоянная | |
Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) | |
| Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) | |
| Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга | |
| 2.71828…, электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия | |
Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига | |
| Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения | |
| Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) | |
Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия | |
| Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) | |
| Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) | |
cила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности | |
| Мнимая единица (лат. imaginarius), единичный вектор | |
| Плотность тока, момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, внутреннее квантовое число, вращательное квантовое число, сила света, J/ψ-мезон | |
| Мнимая единица, плотность тока, единичный вектор, внутреннее квантовое число, 4-вектор плотности тока | |
| Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона | |
| Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор | |
Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) | |
| Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина | |
| Момент силы, вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса | |
| Масса (лат. massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка | |
| Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность | |
Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта | |
| Начало координат (лат. origo) | |
| Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, 4-импульс | |
| Импульс (лат. petere), протон (англ. proton), дипольный момент, волновой параметр | |
| Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции | |
Электрический заряд, обобщенная координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность quantity of heat), эффективный заряд, добротность | |
| Электрическое сопротивление (англ. resistance), газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние | |
| Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние | |
| Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга | |
Перемещение (итал. ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути | |
| Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин | |
| Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время | |
| Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение | |
| Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость | |
Объём (фр. volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) Verdet constant) | |
| Скорость (лат. vēlōcitās), фазовая скорость, удельный объём | |
| Механическая работа (англ. work), работа выхода, W бозон, энергия, энергия связи атомного ядра, мощность | |
| Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение | |
| Реактивное сопротивление, продольное увеличение | |
| Переменная, перемещение, декартова координата, молярная концентрация, постоянная ангармоничности, расстояние | |
| Гиперзаряд, силовая функция, линейное увеличение, сферические функции | |
| декартова координата | |
| Импеданс, Z бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума | |
| декартова координата | |
| Символ | Значение |
| Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения, поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, натуральный показатель поглощения света, степень черноты тела, постоянная затухания | |
| Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение | |
| Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня | |
| Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты | |
Изменение величины (напр. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект | |
| Небольшое перемещение, дельта-функция Дирака, дельта Кронекера | |
| Электрическая постоянная, угловое ускорение, единичный антисимметричной тензор, энергия | |
| Дзета-функция Римана | |
| КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон | |
| Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда | |
| Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга | |
| Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость | |
| Космологическая постоянная, Барион, оператор Лежандра, лямбда-гиперон, лямбда-плюс-гиперон | |
| Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновского длина волны, собственное значение оператора, матрицы Гелл-Мана | |
| Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон , возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон | |
| Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число | |
| Большой канонический ансамбль, кси-нуль-гиперон, кси-минус-гиперон | |
| Длина когерентности, коэффициент Дарси | |
| Произведение, коэффициент Пельтье, вектор Пойнтинга | |
3. 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон | |
| Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности | |
| Оператор суммирование, сигма-плюс-гиперон, сигма-нуль-гиперон, сигма-минус-гиперон | |
| Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана-Больцмана, поверхностная плотность, поперечное сечение реакции, сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина | |
| Время жизни, тау-лептон, интервал времени, время жизни, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули, тангенциальный вектор | |
| Y-бозон | |
| Магнитный поток, поток электрического смещения, работа выхода, язь, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока | |
| Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил | |
| X-бозон | |
| Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция | |
| Волновая функция, апертура интерференции | |
| Волновая функция, функция, функция тока | |
| Ом, телесный угол, количество возможных состояний статистической системы, омега-минус-гиперон, угловая скорость прецессии, молекулярная рефракция, циклическая частота | |
| Угловая частота, мезон, вероятность состояния, ларморова частота прецессии, Боровская частота, телесный угол, скорость течения |
| Символ | Значение и происхождение |
|---|---|
Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число | |
| Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора | |
| Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы | |
| Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина (нем. Breite) | |
электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) | |
| Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоемкость (англ. heat capacity), волшебный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, Вторая радиационная постоянная | |
Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) | |
| Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) | |
| Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга | |
| 2.71828…, электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия | |
Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига | |
| Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения | |
| Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) | |
| Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия | |
| Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) | |
| Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) | |
| cила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности | |
| Мнимая единица (лат. imaginarius), единичный вектор | |
| Плотность тока, момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, внутреннее квантовое число, вращательное квантовое число, сила света, J/ψ-мезон | |
| Мнимая единица, плотность тока, единичный вектор, внутреннее квантовое число, 4-вектор плотности тока | |
| Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона | |
| Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор | |
| Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) | |
| Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина | |
| Момент силы, вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса | |
| Масса (лат. massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка | |
| Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность | |
| Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта | |
| Начало координат (лат. origo) | |
| Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, 4-импульс | |
| Импульс (лат. petere), протон (англ. proton), дипольный момент, волновой параметр | |
| Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции | |
| Электрический заряд, обобщенная координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность | |
| Электрическое сопротивление (англ. resistance), газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние | |
| Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние | |
| Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга | |
| Перемещение (итал. ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути | |
| Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин | |
| Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время | |
| Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение | |
| Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость | |
| Объём (фр. volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) | |
| Скорость (лат. vēlōcitās), фазовая скорость, удельный объём | |
| Механическая работа (англ. work), работа выхода, W бозон, энергия, энергия связи атомного ядра, мощность | |
| Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение | |
| Реактивное сопротивление, продольное увеличение | |
| Переменная, перемещение, декартова координата, молярная концентрация, постоянная ангармоничности, расстояние | |
| Гиперзаряд, силовая функция, линейное увеличение, сферические функции | |
| декартова координата | |
| Импеданс, Z бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума | |
| декартова координата | |
| Символ | Значение |
| Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения, поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, натуральный показатель поглощения света, степень черноты тела, постоянная затухания | |
| Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение | |
| Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня | |
| Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты | |
| Изменение величины (напр. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект | |
| Небольшое перемещение, дельта-функция Дирака, дельта Кронекера | |
| Электрическая постоянная, угловое ускорение, единичный антисимметричной тензор, энергия | |
| Дзета-функция Римана | |
| КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон | |
| Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда | |
| Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга | |
| Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость | |
| Космологическая постоянная, Барион, оператор Лежандра, лямбда-гиперон, лямбда-плюс-гиперон | |
| Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновского длина волны, собственное значение оператора, матрицы Гелл-Мана | |
| Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон , возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон | |
| Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число | |
| Большой канонический ансамбль, кси-нуль-гиперон, кси-минус-гиперон | |
| Длина когерентности, коэффициент Дарси | |
| Произведение, коэффициент Пельтье, вектор Пойнтинга | |
| 3.14159…, пи-связь, пи-плюс мезон, пи-ноль мезон | |
| Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности | |
| Оператор суммирование, сигма-плюс-гиперон, сигма-нуль-гиперон, сигма-минус-гиперон | |
| Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана-Больцмана, поверхностная плотность, поперечное сечение реакции, сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина | |
| Время жизни, тау-лептон, интервал времени, время жизни, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули, тангенциальный вектор | |
| Y-бозон | |
| Магнитный поток, поток электрического смещения, работа выхода, язь, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока | |
| Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил | |
| X-бозон | |
| Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция | |
| Волновая функция, апертура интерференции | |
| Волновая функция, функция, функция тока | |
| Ом, телесный угол, количество возможных состояний статистической системы, омега-минус-гиперон, угловая скорость прецессии, молекулярная рефракция, циклическая частота | |
| Угловая частота, мезон, вероятность состояния, ларморова частота прецессии, Боровская частота, телесный угол, скорость течения |
| Символ | Значение и происхождение |
|---|---|
| Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число | |
| Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора | |
| Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы | |
| Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина (нем. Breite) | |
| электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) | |
| Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоемкость (англ. heat capacity), волшебный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, Вторая радиационная постоянная | |
| Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) | |
| Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) | |
| Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга | |
| 2.71828…, электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия | |
| Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига | |
| Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения | |
| Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) | |
| Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия | |
| Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) | |
| Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) | |
| cила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности | |
| Мнимая единица (лат. imaginarius), единичный вектор | |
| Плотность тока, момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, внутреннее квантовое число, вращательное квантовое число, сила света, J/ψ-мезон | |
| Мнимая единица, плотность тока, единичный вектор, внутреннее квантовое число, 4-вектор плотности тока | |
| Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона | |
| Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор | |
| Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) | |
| Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина | |
| Момент силы, вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса | |
| Масса (лат. massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка | |
| Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность | |
| Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта | |
| Начало координат (лат. origo) | |
| Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, 4-импульс | |
| Импульс (лат. petere), протон (англ. proton), дипольный момент, волновой параметр | |
| Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции | |
| Электрический заряд, обобщенная координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность | |
| Электрическое сопротивление (англ. resistance), газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние | |
| Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние | |
| Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга | |
| Перемещение (итал. ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути | |
| Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин | |
| Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время | |
| Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение | |
| Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость | |
| Объём (фр. volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) | |
| Скорость (лат. vēlōcitās), фазовая скорость, удельный объём | |
| Механическая работа (англ. work), работа выхода, W бозон, энергия, энергия связи атомного ядра, мощность | |
| Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение | |
| Реактивное сопротивление, продольное увеличение | |
| Переменная, перемещение, декартова координата, молярная концентрация, постоянная ангармоничности, расстояние | |
| Гиперзаряд, силовая функция, линейное увеличение, сферические функции | |
| декартова координата | |
| Импеданс, Z бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума | |
| декартова координата | |
| Символ | Значение |
| Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения, поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, натуральный показатель поглощения света, степень черноты тела, постоянная затухания | |
| Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение | |
| Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня | |
| Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты | |
| Изменение величины (напр. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект | |
| Небольшое перемещение, дельта-функция Дирака, дельта Кронекера | |
| Электрическая постоянная, угловое ускорение, единичный антисимметричной тензор, энергия | |
| Дзета-функция Римана | |
| КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон | |
| Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда | |
| Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга | |
| Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость | |
| Космологическая постоянная, Барион, оператор Лежандра, лямбда-гиперон, лямбда-плюс-гиперон | |
| Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновского длина волны, собственное значение оператора, матрицы Гелл-Мана | |
| Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон , возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон | |
| Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число | |
| Большой канонический ансамбль, кси-нуль-гиперон, кси-минус-гиперон | |
| Длина когерентности, коэффициент Дарси | |
| Произведение, коэффициент Пельтье, вектор Пойнтинга | |
| 3.14159…, пи-связь, пи-плюс мезон, пи-ноль мезон | |
| Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности | |
| Оператор суммирование, сигма-плюс-гиперон, сигма-нуль-гиперон, сигма-минус-гиперон | |
| Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана-Больцмана, поверхностная плотность, поперечное сечение реакции, сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина | |
| Время жизни, тау-лептон, интервал времени, время жизни, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули, тангенциальный вектор | |
| Y-бозон | |
| Магнитный поток, поток электрического смещения, работа выхода, язь, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока | |
| Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил | |
| X-бозон | |
| Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция | |
| Волновая функция, апертура интерференции | |
| Волновая функция, функция, функция тока | |
| Ом, телесный угол, количество возможных состояний статистической системы, омега-минус-гиперон, угловая скорость прецессии, молекулярная рефракция, циклическая частота | |
| Угловая частота, мезон, вероятность состояния, ларморова частота прецессии, Боровская частота, телесный угол, скорость течения |
| Символ | Значение и происхождение |
|---|---|
| Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число | |
| Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора | |
| Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы | |
| Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина (нем. Breite) | |
| электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) | |
| Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоемкость (англ. heat capacity), волшебный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, Вторая радиационная постоянная | |
| Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ. Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) | |
| Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) | |
| Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга | |
| 2.71828…, электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия | |
| Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига | |
| Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения | |
| Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) | |
| Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия | |
| Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) | |
| Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) | |
| cила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности | |
| Мнимая единица (лат. imaginarius), единичный вектор | |
| Плотность тока, момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, внутреннее квантовое число, вращательное квантовое число, сила света, J/ψ-мезон | |
| Мнимая единица, плотность тока, единичный вектор, внутреннее квантовое число, 4-вектор плотности тока | |
| Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона | |
| Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор | |
| Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) | |
| Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина | |
| Момент силы, вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса | |
| Масса (лат. massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка | |
| Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность | |
| Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта | |
| Начало координат (лат. origo) | |
| Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, 4-импульс | |
| Импульс (лат. petere), протон (англ. proton), дипольный момент, волновой параметр | |
| Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции | |
| Электрический заряд, обобщенная координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность | |
| Электрическое сопротивление (англ. resistance), газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние | |
| Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние | |
| Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга | |
| Перемещение (итал. ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути | |
| Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин | |
| Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время | |
| Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение | |
| Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость | |
| Объём (фр. volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) | |
| Скорость (лат. vēlōcitās), фазовая скорость, удельный объём | |
| Механическая работа (англ. work), работа выхода, W бозон, энергия, энергия связи атомного ядра, мощность | |
| Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение | |
| Реактивное сопротивление, продольное увеличение | |
| Переменная, перемещение, декартова координата, молярная концентрация, постоянная ангармоничности, расстояние | |
| Гиперзаряд, силовая функция, линейное увеличение, сферические функции | |
| декартова координата | |
| Импеданс, Z бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума | |
| декартова координата | |
| Символ | Значение |
| Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения, поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, натуральный показатель поглощения света, степень черноты тела, постоянная затухания | |
| Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение | |
| Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня | |
| Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты | |
| Изменение величины (напр. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект | |
| Небольшое перемещение, дельта-функция Дирака, дельта Кронекера | |
| Электрическая постоянная, угловое ускорение, единичный антисимметричной тензор, энергия | |
| Дзета-функция Римана | |
| КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон | |
| Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда | |
| Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга | |
| Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость | |
| Космологическая постоянная, Барион, оператор Лежандра, лямбда-гиперон, лямбда-плюс-гиперон | |
| Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновского длина волны, собственное значение оператора, матрицы Гелл-Мана | |
| Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон , возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон | |
| Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число | |
| Большой канонический ансамбль, кси-нуль-гиперон, кси-минус-гиперон | |
| Длина когерентности, коэффициент Дарси | |
| Произведение, коэффициент Пельтье, вектор Пойнтинга | |
| 3.14159…, пи-связь, пи-плюс мезон, пи-ноль мезон | |
| Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности | |
| Оператор суммирование, сигма-плюс-гиперон, сигма-нуль-гиперон, сигма-минус-гиперон | |
| Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана-Больцмана, поверхностная плотность, поперечное сечение реакции, сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина | |
| Время жизни, тау-лептон, интервал времени, время жизни, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули, тангенциальный вектор | |
| Y-бозон | |
| Магнитный поток, поток электрического смещения, работа выхода, язь, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока | |
| Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил | |
| X-бозон | |
| Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция | |
| Волновая функция, апертура интерференции | |
| Волновая функция, функция, функция тока | |
| Ом, телесный угол, количество возможных состояний статистической системы, омега-минус-гиперон, угловая скорость прецессии, молекулярная рефракция, циклическая частота | |
| Угловая частота, мезон, вероятность состояния, ларморова частота прецессии, Боровская частота, телесный угол, скорость течения |
Обозначения физических величин, система СИ – Физика – Теория, тесты, формулы и задачи
Обозначения физических величин и другие сведения о системе СИ приводятся здесь в качестве справочного материала, так как они требуются при решении многих задач по физике. И хотя на большинстве экзаменов, в том числе и на ЦТ или ЕГЭ, все физические величины указываются вместе со своими единицами измерения, тем не менее очень важно всегда точно знать и хорошо уметь переводить любые единицы измерения любых физических величин в систему СИ, так как в большинстве задач корректно рассчитать ответ можно только выполняя расчеты именно в системе СИ.
Изучать обозначения физических величин и систему СИ онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
2.12: Химические символы и формулы
- Последнее обновление
- Сохранить как PDF
- Химические символы и формулы
- Резюме
- Узнать больше
- Авторы и авторство
Предположим, вы шли и заметили на земле лист бумаги с отметками.Вы берете его и видите бумагу на картинке ниже.
Игра в шахматы.
Для большинства людей эти заметки бессмысленны (возможно, это секретный шпионский код). Но для шахматиста эти символы рассказывают историю шахматной партии. Каждая аббревиатура описывает шахматную фигуру или ход во время игры. Использование специальных символов позволяет шахматистам «видеть» игру, не читая многословного и, возможно, неполного описания того, что произошло.
Химические символы и формулы
Для иллюстрации химических реакций и элементов и соединений, участвующих в них, химики используют символы и формулы.Химический знак – это одно- или двухбуквенное обозначение элемента. Некоторые примеры химических символов: \ (\ ce {O} \) для кислорода, \ (\ ce {Zn} \) для цинка и \ (\ ce {Fe} \) для железа. Первая буква символа всегда заглавная. Если символ состоит из двух букв, вторая буква – строчная. Большинство элементов имеют символы, основанные на их английских названиях. Однако некоторые из элементов, которые были известны с древних времен, сохранили символы, основанные на их латинских названиях, как показано ниже.
| Химический символ | Имя | Латинское имя |
|---|---|---|
| \ (\ ce {Na} \) | Натрий | Натриум |
| \ (\ ce {K} \) | Калий | Калиум |
| \ (\ ce {Fe} \) | Утюг | Феррум |
| \ (\ ce {Cu} \) | Медь | Медь |
| \ (\ ce {Ag} \) | Серебро | Аргентум |
| \ (\ ce {Sn} \) | Олово | Stannum |
| \ (\ ce {Sb} \) | Сурьма | Стибиум |
| \ (\ ce {Au} \) | Золото | Aurum |
| \ (\ ce {Pb} \) | Свинец | отвес |
Соединения – это комбинации двух или более элементов.Химическая формула – это выражение, которое показывает элементы в соединении и относительные пропорции этих элементов. Вода состоит из водорода и кислорода в соотношении два к одному. Химическая формула воды \ (\ ce {H_2O} \). Серная кислота является одним из наиболее широко производимых химических веществ в Соединенных Штатах и состоит из элементов водорода, серы и кислорода. Химическая формула серной кислоты \ (\ ce {H_2SO_4} \).
Сводка
- Химический символ – это одно- или двухбуквенное обозначение элемента.
- Соединения – это комбинации двух или более элементов.
- Химическая формула – это выражение, которое показывает элементы в соединении и относительные пропорции этих элементов.
- Некоторые элементы имеют символы, происходящие от латинского названия элемента.
Узнать больше
Воспользуйтесь ссылкой ниже, чтобы ответить на следующие вопросы:
1. Что такое химическая формула?
2. Какова химическая формула глюкозы? Что означает эта формула?
3.Какова химическая формула кофеина?
4. Какова химическая формула сахара?
Авторы и авторство
Фонд CK-12 Шэрон Бьюик, Ричард Парсонс, Тереза Форсайт, Шонна Робинсон и Жан Дюпон.
| # 1 Общий | Только единицы СИ и единицы, признанные для использования с СИ используются для выражения значений величин.Эквивалентные значения в других единицах даны в скобках следующие значения в допустимых единиц только тогда, когда это считается необходимым для целевой аудитории. | ||||||||||||||||||||||||||||
| # 2 Сокращения | Сокращения, такие как sec, cc или mps, не используются и используются только в стандартных символы единиц измерения, символы префикса, названия единиц и названия префиксов являются использовал. | ||||||||||||||||||||||||||||
| собственно: | с или секунда; см 3 или кубический сантиметр; м / с или метр в секунду | ||||||||||||||||||||||||||||
| неправильное: | сек; cc; mps | ||||||||||||||||||||||||||||
| # 3 Множественное число | Символы единиц во множественном числе не изменяются. | ||||||||||||||||||||||||||||
собственно: | л = 75 см | ||||||||||||||||||||||||||||
ненадлежащее: | л = 75 см | ||||||||||||||||||||||||||||
| # 4 Пунктуация | Символы единиц не имеют точки, если только она не находится в конце предложение. | ||||||||||||||||||||||||||||
собственно: | Длина штанги 75 см. Планка длиной 75 см. | ||||||||||||||||||||||||||||
ненадлежащее: | Штанга 75 см. длинная. | ||||||||||||||||||||||||||||
| # 5 Умножение И отдел | Пробел или полувысокая точка используется для обозначения умножения единиц. Солидус (, т.е. косая черта), горизонтальная линия или минус экспонента используется для обозначения деления единиц.Солидус не должен повторяться на та же строка, если не используются круглые скобки. | ||||||||||||||||||||||||||||
собственно: | Скорость звука составляет около 344 м · с -1 (метров в секунду) Скорость затухания 113 Cs составляет около 21 мс -1 (обратные миллисекунды) м / с, м · с -2 , м · кг / (с 3 · A), м · кг · с -3 · A -1 м / с, м с -2 , м кг / (с 3 A), м кг с -3 A -1 | ||||||||||||||||||||||||||||
ненадлежащее: | Скорость звука составляет около 344 мс -1 (обратные миллисекунды) Скорость затухания 113 Cs составляет около 21 м · с -1 (метров в секунду) м ÷ с, м / с / с, м · кг / с 3 / A | ||||||||||||||||||||||||||||
| # 6 Гарнитура | Переменные и символы количества выделены курсивом.Символы единиц набраны римским шрифтом. Цифры, как правило, следует писать латинскими буквами. тип. Эти правила применяются независимо от шрифта, используемого в окружающий текст. Подробнее см. Гарнитуры символов в научных рукописях | .||||||||||||||||||||||||||||
собственно: | Она воскликнула: « Эта собака весит 10 кг ! » t = 3 с, где t – время, а с – секунда T = 22 K, где T термодинамическая температура, а K – | Кельвина.||||||||||||||||||||||||||||
ненадлежащее: | Он воскликнул: « Эта собака весит 10 кг! t = 3 с, где t – время, а s – секунда T = 22 K, где T – термодинамическая температура, а K – | Кельвина.||||||||||||||||||||||||||||
| # 7 Гарнитура | Верхние и нижние индексы набираются курсивом, если они представляют переменные, количества или текущие числа.Они написаны римским шрифтом если они описательные. | ||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
| # 8 Сокращения | Комбинации букв “ppm”, “ppb” и “ppt”, а также термины часть на миллион, часть на миллиард и часть на триллион, и и т.п. не используются для выражения значений количеств. | ||||||||||||||||||||||||||||
| собственно: | 2,0 мкл / л; 2,0 x 10 -6 В; 4,3 нм / м; 4,3 x 10 -9 л; 7 пс / с; 7 x 10 -12 т , где V , l и t – символы количества для объема, длины и времени. | ||||||||||||||||||||||||||||
| неправильное: | «частей на миллион», «частей на миллиард» и «частей на миллион», а также термины часть на миллион, часть на миллиард, и часть на триллион и т. п. | ||||||||||||||||||||||||||||
| # 9 Установка модификации | Символы (или названия) единиц не изменяются добавлением нижних индексов или другая информация.Например, используются следующие формы вместо. | ||||||||||||||||||||||||||||
| собственно: | В макс = 1000 В массовая доля 10% | ||||||||||||||||||||||||||||
| неправильное: | В = 1000 В макс 10% ( м / м ) или 10% (по весу) | ||||||||||||||||||||||||||||
| # 10 Процент | Символ% используется для представляют собой просто число 0.01. | ||||||||||||||||||||||||||||
| собственно: | л 1 = л 2 (1 + 0,2%), или D = 0,2%, где D определяется соотношением D = ( l 1 – l 2 ) / l 2 . | ||||||||||||||||||||||||||||
| неправильное: | длина l 1 превышает длину l 2 на 0.2% | ||||||||||||||||||||||||||||
| # 11 Информация и единицы | Информация не смешана с символами или названиями единиц. | ||||||||||||||||||||||||||||
| собственно: | содержание воды 20 мл / кг | ||||||||||||||||||||||||||||
| неправильное: | 20 мл H 2 O / кг 20 мл воды / кг | ||||||||||||||||||||||||||||
| # 12 Математика обозначение | Понятно, к какому символу единицы принадлежит числовое значение и какая математическая операция применяется к значению количества. | ||||||||||||||||||||||||||||
| собственно: | 35 см x 48 см От 1 МГц до 10 МГц или (от 1 до 10) МГц От 20 ° C до 30 ° C или (от 20 до 30) ° C 123 г ± 2 г или (123 ± 2) г 70% ± 5% или (70 ± 5)% 240 x (1 ± 10%) В | ||||||||||||||||||||||||||||
| неправильное: | 35 x 48 см От 1 МГц до 10 МГц или от 1 до 10 МГц От 20 ° C до 30 ° C или от 20 до 30 ° C 123 ± 2 г 70 ± 5% 240 В ± 10% (нельзя складывать 240 В и 10%) | ||||||||||||||||||||||||||||
| # 13 Единица символа И имена | Символы единиц измерения и названия единиц измерения не являются смешанными математическими операциями. не применяются к названиям юнитов. | ||||||||||||||||||||||||||||
| собственно: | кг / м 3 , кг · м -3 , или килограмм на кубический метр | ||||||||||||||||||||||||||||
| неправильное: | килограмм / м 3 , кг / кубический метр, килограмм / кубический метр, кг на м 3 , или килограмм на метр 3 . | ||||||||||||||||||||||||||||
| # 14 Цифры и единица символа | Значения количеств выражены в допустимых единицах арабского языка. цифры и символы для единиц. | ||||||||||||||||||||||||||||
| собственно: | м = 5 кг ток был 15 А | ||||||||||||||||||||||||||||
| неправильное: | м = пять килограммов m = пять кг ток был 15 ампер | ||||||||||||||||||||||||||||
| # 15 Установка шаг | Между числовым значением и обозначением единицы есть пробел, даже когда значение используется в смысле прилагательного, за исключением случай верхних индексов единиц для плоского угла. | ||||||||||||||||||||||||||||
| собственно: | сфера 25 кг угол 2 ° 3 ‘ 4 “ Если используется полное название подразделения, обычные правила По английски применяют: «рулон 35-миллиметровой пленки». | ||||||||||||||||||||||||||||
| неправильное: | сфера 25 кг угол 2 ° 3 ‘ 4 “ | ||||||||||||||||||||||||||||
| # 16 Цифра шаг | Цифры числовых значений, состоящие более чем из четырех цифр на обе стороны десятичного маркера разделены на группы три, используя тонкое фиксированное пространство, считая как слева, так и справа от десятичного маркера.Запятые не разделяют цифры на группы по три человека. | ||||||||||||||||||||||||||||
собственно: | 15 739.012 53 | ||||||||||||||||||||||||||||
ненадлежащее: | 15739.01253 15739.012 53 | ||||||||||||||||||||||||||||
| # 17 Кол-во уравнения | Уравнения между величинами используются вместо уравнений между числовыми значениями и символами, представляющими числовые значения отличаются от символов, обозначающих соответствующие величины.Когда используется числовое уравнение, оно правильно записывается и соответствующее количественное уравнение приводится там, где это возможно. | ||||||||||||||||||||||||||||
| собственно : | ( л / м) = 3,6 -1 [ v / (км / ч)] ( т / с) | ||||||||||||||||||||||||||||
| неправильное: | л = 3,6 -1 vt ,
сопровождается текстом, говорящим: “ ” “где l в метрах, v в километрах в час, и t в секундах “ | ||||||||||||||||||||||||||||
| # 18 Стандартные символа | Используются стандартные символы количества.Точно так же стандартизированные используются математические знаки и символы. В частности, база «журнала» в уравнениях указывается при необходимости записью log a x (что означает журнал до основания a из x ), фунт x (что означает журнал 2 x ), ln x (что означает журнал e x ) или lg x (что означает журнал 10 x ). | ||||||||||||||||||||||||||||
| собственно: | желто-коричневый x R для сопротивления A r для относительной атомной массы | ||||||||||||||||||||||||||||
| неправильное: | tg x по касательной к x слова, акронимы или специальные группы букв | ||||||||||||||||||||||||||||
| # 19 Вес по сравнению с масса | Когда используется слово «вес», подразумеваемое значение ясно. (В науке и технике вес – это сила, для которой СИ единица – ньютон; в торговле и повседневном использовании вес обычно составляет синоним массы, единицей СИ является килограмм.) | ||||||||||||||||||||||||||||
| # 20 Частное количество | Частное количество записывается явно. | ||||||||||||||||||||||||||||
| собственно: | масса деленная на объем | ||||||||||||||||||||||||||||
| неправильное: | масса на единицу объема | ||||||||||||||||||||||||||||
| # 21 Объект и количество | Различают объект и любую величину, описывающую объект.(Обратите внимание на разницу между “поверхностью” и “площадью”, “телом” и «масса», «резистор» и «сопротивление», «катушка» и «индуктивность».) | ||||||||||||||||||||||||||||
| собственно: | Тело массой 5 г | ||||||||||||||||||||||||||||
| неправильное: | Масса 5 г | ||||||||||||||||||||||||||||
| # 22 Устарело Условия | Устаревшие термины нормальность, молярность и молярность и их символы N, M и m не используются. | ||||||||||||||||||||||||||||
| собственно: | количество вещества с концентрацией B (чаще
называется концентрацией B), и его символ c B и единица СИ моль / м 3 (или соответствующая приемлемая единица) | ||||||||||||||||||||||||||||
| неправильное: | нормальность и символ N , молярность и символ M моляль и символ m | ||||||||||||||||||||||||||||
Физические обозначения букв и формул.Обозначение: высота, ширина, длина
Построение чертежей – задача не из легких, но без нее в современном мире никуда. Ведь для того, чтобы изготовить даже самый обычный предмет (крохотный болт или гайку, полку для книг, новый дизайн платья и т. Д.), Нужно предварительно провести соответствующие расчеты и нарисовать чертеж будущего изделия. Однако часто его изготавливает один человек, а изготовлением чего-либо занимается другой человек по этой схеме.
Во избежание путаницы в понимании изображаемого объекта и его параметров, во всем мире принята длина легенды, ширина, высота и другие значения, используемые в дизайне.Кто они такие? Давайте разберемся.
Величины
Площадь, высота и другие обозначения аналогичного характера являются не только физическими, но и математическими величинами.
Их однобуквенное обозначение (используется во всех странах) было введено в середине двадцатого века Международной системой единиц (СИ) и используется по сей день. Именно по этой причине все такие параметры указываются латиницей, а не кириллическими буквами или арабским шрифтом. Чтобы не создавать отдельных сложностей, при разработке стандартов конструкторской документации в большинстве современных стран было решено использовать практически те же условные обозначения, которые используются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, изображена на чертеже двухмерная или трехмерная фигура (изделие), она имеет набор основных параметров. Если есть два измерения – это ширина и длина, если их три – также добавляется высота.
Итак, сначала разберемся, как правильно обозначать на чертежах длину, ширину, высоту.
Ширина
Как упоминалось выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта при условии, что его измерения производятся в поперечном направлении.Так чем же известна ширина? Имеет обозначение буквой «Б». Об этом знают во всем мире. Причем согласно ГОСТу допускается использование как прописных, так и строчных латинских букв. Часто возникает вопрос, почему была выбрана именно такая буква. Ведь обычно сокращение производится по первому греческому или английскому названию количества. В этом случае ширина на английском языке будет иметь вид «width».
Наверное, дело в том, что изначально этот параметр наиболее широко использовался в геометрии.В этой науке при описании фигур часто длина, ширина, высота обозначаются буквами «а», «б», «в». Согласно этой традиции, при выборе буква «B» (или «b») была заимствована системой СИ (хотя для двух других измерений стали использовать символы, отличные от геометрических).
Большинство считает, что это было сделано для того, чтобы не путать ширину (обозначенную буквой «B» / «b») с весом. Дело в том, что последнее иногда называют «W» (сокращение от английского веса имени), хотя использование других букв («G» и «P») также допустимо.Согласно международным стандартам системы СИ ширина измеряется в метрах или кратных (долях) их единиц. Следует отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и других точных науках это обозначение, как правило, не используется.
Длина
Как уже упоминалось, в математике длина, высота и ширина – это три пространственных измерения. Причем, если ширина является линейным размером в поперечном направлении, то длина в продольном направлении.Рассматривая это как масштаб физики, можно понять, что это слово означает числовую характеристику длины линий.
В английском языке этот термин называется длиной. Именно поэтому это значение обозначается заглавной или строчной начальной буквой этого слова – «L». Как и ширина, длина измеряется в метрах или кратных (дольных) единицах.
Высота
Наличие этого значения говорит о том, что приходится иметь дело с более сложным – трехмерным пространством.В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском это пишется как «высота». Поэтому по международным стандартам он обозначается латинской буквой «H» / «h». Помимо высоты, на чертежах иногда эта буква выступает еще и в качестве обозначения глубины. Высота, ширина и длина – все эти параметры измеряются в метрах и их кратных и кратных единицах (километрах, сантиметрах, миллиметрах и т. Д.).).
Радиус и диаметр
Помимо рассматриваемых параметров, при составлении чертежей приходится иметь дело с другими.
Например, при работе с кругами возникает необходимость определения их радиуса. Это название линии, соединяющей две точки. Первый – центр. Второй находится прямо на самом круге. На латыни это слово выглядит как «радиус». Отсюда строчные или прописные буквы «R» / «r».
При рисовании окружностей, помимо радиуса, часто приходится иметь дело с близким к нему явлением – диаметром.Это также отрезок прямой, соединяющий две точки на окружности. Причем обязательно проходит через центр.
Численно диаметр равен двум радиусам. В английском это слово пишется так: «диаметр». Отсюда и аббревиатура – большая или строчная латинская буква «D» / «d». Часто диаметр на чертежах обозначается перечеркнутым кружком – «Ø».
Хотя это общепринятая аббревиатура, следует учитывать, что ГОСТ предусматривает использование только латинского «D» / «d».
Толщина
Большинство из нас помнят школьные уроки математики. Уже тогда учителя говорили, что латинской буквой «s» принято обозначать такое значение, как площадь. Однако по общепринятым нормам на чертежах таким способом фиксируется совсем другой параметр – толщина.
Почему? Известно, что в случае высоты, ширины, длины обозначение буквами могло быть объяснено их написанием или традицией. Но толщина на английском языке выглядит как «толщина», а в латинском варианте – как «грубость».Также непонятно, почему, в отличие от других значений, толщину можно указывать только строчными буквами. Обозначение «s» также используется для обозначения толщины страниц, сторон, краев и т. Д.
Периметр и площадь
В отличие от всех вышеперечисленных значений, слово «периметр» произошло не из латинского или английского, а из греческого … Оно образовано от «περιμετρέο» (для измерения окружности). И сегодня этот термин сохранил свое значение (общая длина границ рисунка).Впоследствии слово попало в английский язык («периметр») и закрепилось в системе СИ в виде сокращения с буквой «П».
Площадь – это величина, которая показывает количественную характеристическую геометрическую форму с двумя измерениями (длиной и шириной). В отличие от всего вышеперечисленного, он измеряется в квадратных метрах (а также в дробных и кратных их единицах). Что касается буквенного обозначения местности, то в разных областях оно разное. Например, в математике это знакомая каждому с детства латинская буква «S».Почему так – информации нет.
Некоторые неосознанно думают, что это происходит из-за английского написания слова «квадрат». Однако в нем математическая область – это «площадь», а «квадрат» – это площадь в архитектурном смысле. Кстати, стоит помнить, что «квадрат» – это название геометрической формы «квадрат». Так что будьте осторожны при изучении чертежей на английском языке. Из-за того, что в некоторых дисциплинах переводится как «площадь», в качестве обозначения используется буква «А». В редких случаях также используется буква «F», но в физике эта буква означает величину, называемую «сила» («фортис»).
Другие общепринятые сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра наиболее часто используются при составлении чертежей. Однако есть и другие количества, которые также часто в них присутствуют. Например, строчная буква «т». В физике это означает «температура», однако по ГОСТу Единой системы конструкторской документации эта буква представляет собой ступеньку (винтовых пружин и т.п.). Однако, когда речь идет о зацеплении и резьбе, он не используется.
Заглавная и строчная буквы «А» / «а» (по всем тем же стандартам) на чертежах используются для обозначения не площади, а межцентрового расстояния и межцентрового расстояния. Помимо различных значений, на чертежах часто приходится указывать углы. разные размеры … Для этого принято использовать строчные буквы греческого алфавита. Чаще всего используются «α», «β», «γ» и «δ». Однако можно использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как упоминалось выше, чтобы не было недопонимания при чтении чертежа, представители разных стран приняли общие стандарты надписи.Другими словами, если вы сомневаетесь в толковании той или иной аббревиатуры, взгляните на ГОСТы. Таким образом вы узнаете, как правильно указаны высота, ширина, длина, диаметр, радиус и так далее.
Изучение физики в школе длится несколько лет. При этом студенты сталкиваются с проблемой, что одни и те же буквы означают совершенно разные размеры … Чаще всего это касается латинских букв. Как же тогда решать проблемы?
Не стоит бояться такого повторения.Ученые постарались ввести их в обозначение, чтобы одни и те же буквы не встречались в одной формуле. Чаще всего студенты сталкиваются с латинским n. Это может быть нижний или верхний регистр. Поэтому логично возникает вопрос, что такое n в физике, то есть в определенной формуле, с которой сталкивается школьник.
Что обозначает в физике заглавная буква N?
Чаще всего в школьном курсе встречается при изучении механики. Ведь там может быть сразу в духе смыслов – сила и сила нормальной реакции опоры.Естественно, эти понятия не пересекаются, потому что они используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определять, что такое n в физике.
Мощность – это скорость изменения энергии системы. Это скалярное значение, то есть просто число. Его единица измерения – ватт (Вт).
Сила нормальной реакции опоры – это сила, действующая на тело со стороны опоры или подвески. Помимо числового значения, оно имеет направление, то есть является векторным значением.Причем всегда перпендикулярно поверхности, на которую производится внешнее воздействие. Единицей этого N является Ньютон (N).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
номер Дебая;
Суммарная мощность излучения.
Что может означать строчная буква n в физике?
Список имен, которые могут скрываться за ним, довольно обширен.Обозначение n в физике используется для таких понятий:
показатель преломления, и он может быть абсолютным или относительным;
нейтрон – нейтральная элементарная частица с массой немного больше массы протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «ве») – количество повторений оборотов в единицу времени, измеряемое в герцах (Гц).
Что в физике означает n помимо уже указанных величин? Оказывается, главное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика).Кстати, при расчете концентрации вещества нужно знать значение, которое также пишется на латыни «en». Об этом и пойдет речь ниже.
Какая физическая величина может быть обозначена n и N?
Его название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что означает n в физике, довольно прост. Это количество любых объектов, тел, частиц – всего, что обсуждается в той или иной задаче.
Более того, «количество» – одна из немногих физических величин, не имеющих единицы измерения. Это просто номер, а не имя. Например, если проблема составляет около 10 частиц, тогда n будет всего 10. Но если окажется, что строчная «en» уже занята, тогда вам придется использовать прописную букву.
Формулы с прописными буквами N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике существует такое понятие, как химическое количество вещества.Обозначается греческой буквой «ню». Для его расчета необходимо количество частиц разделить на число Авогадро:
Кстати, последнее значение также обозначается столь популярной буквой N. Только у него всегда есть нижний индекс – A.
Для определения электрического заряда , вам нужна формула:
Еще одна формула с N в физике – частота вибрации. Для его подсчета нужно разделить их количество на время:
Буква «en» фигурирует в формуле для периода обращения:
Формулы, содержащие строчные буквы n
В школьном курсе физики чаще всего встречается эта буква. связанный с показателем преломления вещества.Поэтому важно знать формулы при ее применении.
Итак, для абсолютного показателя преломления формула записывается следующим образом:
Здесь c – скорость света в вакууме, v – его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1,
где n 1 и n 2 – абсолютные показатели преломления первой и второй среды. , v 1 и v 2 – скорость световой волны в этих веществах.
Как найти в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Что такое в физике, если это показатель преломления?
Обычно в таблицах приводятся значения абсолютных показателей преломления различных веществ. Не забывайте, что это значение зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления приведены для оптического диапазона.
Итак, стало понятно, что такое физика. Чтобы не осталось вопросов, стоит рассмотреть несколько примеров.
Энергетический вызов
№1. Во время вспашки трактор равномерно тянет плуг. При этом он прикладывает силу 10 кН. Этим движением за 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ. Можно начать с силы, 10 Н равно 10000 Н.Тогда расстояние: 1,2 × 1000 = 1200 м. Остается время – 10 × 60 = 600 с.
Выбор формул. Как упоминалось выше, N = A: t. Но для работы задача не имеет смысла. Для его вычисления полезна другая формула: A = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S): t.
Решение. Рассчитаем сначала работу, а потом мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 ватт.
Ответ. Мощность трактора 20 000 Вт.
Проблемы с показателем преломления
№2. Стекло имеет абсолютный показатель преломления 1,5. Скорость распространения света в стекле ниже, чем в вакууме. Требуется определить сколько раз.
Переводить данные в СИ не требуется.
При выборе формул нужно остановиться на этой: n = c: v.
Решение. Из приведенной выше формулы видно, что v = c: n.Это означает, что скорость распространения света в стекле равна скорости света в вакууме, деленной на показатель преломления. То есть уменьшается в полтора раза.
Ответ. Скорость распространения света в стекле в 1,5 раза меньше, чем в вакууме.
№3. Есть два прозрачных носителя. Скорость света в первом из них составляет 225 000 км / с, во втором – на 25 000 км / с меньше. Луч света идет из первой среды во вторую.Угол падения α равен 30º. Рассчитайте значение угла преломления.
Надо ли переводить в СИ? Скорости даны в внесистемных единицах. Однако при замене в формулы они будут сокращены. Следовательно, нет необходимости переводить скорость в м / с.
Выбор формул, необходимых для решения задачи. Вам нужно будет использовать закон преломления света: n 21 = sin α: sin γ. А также: n = c: v.
Решение. В первой формуле n 21 – это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1. Если мы запишем вторую указанную формулу для предлагаемых сред, мы получим следующее: n 1 = c: v 1 и n 2 = c: v 2. Если составить соотношение двух последних выражений, то окажется, что n 21 = v 1: v 2. Подставив его в формулу для закона преломления, вы можете получить следующее выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляя значения указанных скоростей и синуса 30º (равного 0,5) в формулу, получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ. Значение угла преломления 26º.
Задачи на время лечения
№4. Лопасти ветряка вращаются с периодом 5 секунд. Посчитайте количество оборотов этих лопастей за 1 час.
Необходимо перевести в единицы СИ только время 1 часа. Он будет равен 3600 секундам.
Выбор формул … Период вращения и количество оборотов связаны формулой T = t: N.
Решение. По этой формуле количество оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ. Число оборотов лопастей фрезы 720.
№5. Винт самолета вращается с частотой 25 Гц. За сколько времени пропеллер совершит 3000 оборотов?
Все данные приведены в СИ, поэтому переводить ничего не нужно.
Требуемая формула : частота ν = N: t. Нужно только вывести из него формулу для неизвестного времени. Это делитель, поэтому предполагается, что его можно найти, разделив N на ν.
Решение. В результате деления 3000 на 25 получается число 120.Он будет измеряться в секундах.
Ответ. Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда студент, решающий физическую задачу, встречает формулу, содержащую n или N, ему нужно разобраться с двумя пунктами. Первый – из какой области физики дано равенство. Это может быть ясно из названия в учебнике, справочнике или слов учителя. Затем следует определиться, что скрывается за многогранным «ан». Причем помогает в этом название единицы измерения, если, конечно, указано ее значение.Допускается и другой вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в вопросе, который необходимо решить.
Ни для кого не секрет, что в любой науке существуют специальные обозначения величин. Буквенные обозначения в физике доказывают, что эта наука не является исключением в плане определения величин с помощью специальных символов. Существует множество основных величин, а также их производных, каждая из которых имеет свой символ.Итак, буквенные обозначения в физике подробно рассматриваются в этой статье.
Физика и основные физические величины
Благодаря Аристотелю слово физика стало использоваться, так как именно он первым применил этот термин, который в то время считался синонимом термина философия. Это связано с общностью объекта исследования – законов Вселенной, а точнее – того, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена как самостоятельная наука.
Михаил Васильевич Ломоносов ввел слово физика в русский язык благодаря изданию учебника в переводе с немецкого – первого учебника физики в России.
Итак, физика – это раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движения и строения. Базовых физических величин не так много, как может показаться на первый взгляд – их всего 7: длина
- , масса
- , время
- , сила тока
- , температура
- , количество вещества
- сила света.
Конечно, в физике у них есть свои буквенные обозначения. Например, символ m выбран для массы, а символ T – для температуры. Также у всех величин есть своя единица измерения: сила света – кандела (кд), а единицей измерения количества вещества – моль.
Производные физические величины
Производных физических величин гораздо больше, чем базовых. Их 26, и часто некоторые из них относят к основным.
Итак, площадь является производной от длины, объем – также длины, скорость – времени, длины, а ускорение, в свою очередь, характеризует скорость изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество тепла, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент количества движения, момент силы – все это зависит от массы.Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол определяются длиной.
Какая буква обозначает напряжение в физике? Напряжение, являющееся скалярной величиной, обозначается буквой U. Для скорости обозначение в виде буквы v, для механической работы – A, а для энергии – E. Электрический заряд принято обозначать буквой V. буква q, а магнитный поток – F.
SI: общая информация
Международная система единиц (SI) – это система физических единиц, основанная на Международной системе единиц, включая названия и обозначения физических величин. Он был принят Генеральной конференцией по мерам и весам. Именно эта система регулирует буквенные обозначения в физике, а также их размеры и единицы измерения. Для обозначения используются буквы латинского алфавита, в некоторых случаях – греческого.Также возможно использование специальных символов в качестве обозначения.
Заключение
Итак, в любой научной дисциплине есть специальные обозначения для разного рода величин. Естественно, физика не исключение. Буквенных обозначений довольно много: сила, площадь, масса, ускорение, натяжение и т. Д. У них есть свои обозначения. Существует особая система, называемая Международной системой единиц. Считается, что базовые единицы не могут быть математически выведены из других.Производные величины получаются путем умножения и деления основных.
Переходя к физическим приложениям производной, мы будем использовать несколько другие обозначения, принятые в физике.
Во-первых, меняется обозначение функций. Действительно, какие функции мы будем различать? Эти функции являются физическими величинами, зависящими от времени. Например, координата тела x (t) и его скорость v (t) могут быть заданы формулами:
(читать ix с точкой).
Существует еще одно обозначение производной, очень распространенное как в математике, так и в физике:
производная функции x (t) обозначена | ||
(читать ¾de iks on de te¿).
Остановимся подробнее на значении обозначения (1.16). Математик понимает это двояко: либо как предел:
, либо как дробь, знаменателем которой является приращение времени dt, а в числителе – так называемый дифференциал dx функции x (t).Дифференциал несложен, но мы не будем его сейчас обсуждать; он ждет вас в первый год.
Физик, не ограниченный требованиями математической строгости, понимает обозначение (1.16) более неформально. Пусть dx будет изменением координаты за время dt. Возьмем интервал dt настолько малым, чтобы отношение dx = dt было близко к его пределу (1.17) с подходящей для нас точностью.
И тогда, скажет физик, производная координаты по времени – это просто дробь, в числителе которой есть довольно небольшое изменение координаты dx, а в знаменателе – довольно малое время интервал dt, в течение которого произошло это изменение координаты.
Такое расплывчатое понимание производной характерно для рассуждений в физике. Отныне мы будем придерживаться именно этого физического уровня строгости.
Производная x (t) физическая величина x (t) снова является функцией времени, и эту функцию снова можно дифференцировать, чтобы найти производную производной или вторую производную функции x (t). Вот одно обозначение второй производной:
вторая производная функции x (t) обозначается x (t)
(читается как ix с двумя точками), но кое-что еще:
вторая производная функции Функция x (t) обозначается dt 2
(она читается как de two x согласно de te square¿ или de two x согласно de te two¿).
Вернемся к исходному примеру (1.13) и вычислим производную координаты, и заодно посмотрим на совместное использование обозначений (1.15) и (1.16):
x (t) = 1 + 12t 3t2)
x (t) = dt d (1 + 12t 3t2) = 12 6t:
(Символ дифференциации dt d перед скобкой такой же, как тире над скобкой в предыдущем обозначении .)
Отметим, что производная координаты оказалась равной скорости (1.14). Это не случайно. Связь между производной координаты и скоростью тела будет разъяснена в следующем разделе «Механическое движение».
1.1.7 Предел вектора
Физические величины не только скалярные, но и векторные. Соответственно, нас часто интересует скорость изменения векторной величины, то есть производная вектора. Однако, прежде чем говорить о производной, вам необходимо понять концепцию предела векторной величины.
Рассмотрим последовательность векторов ~ u1; ~ u2; ~ u3; ::: Сделав при необходимости параллельный перенос, сведем их начала в одну точку О (рис. 1.5):
Рис.1.5. lim ~ un = ~ v | |||||||||
Концы векторов обозначим A1; A2; A3; ::: Таким образом, имеем: | |||||||||
Предположим последовательность точек A1; A2; A3; ::: ¾потоки¿2 в точку B:
lim An = B:
Обозначим ~ v = OB.Мы говорим тогда, что последовательность синих векторов ~ un стремится к красному вектору ~ v, или что вектор ~ v является пределом последовательности векторов ~ un:
~ v = lim ~ un:
2 Интуитивно понятный понимания этого «перетекания» вполне достаточно, но, может быть, вас интересует более строгое объяснение? Тогда вот оно.
Пусть будет в самолете. «Приток» последовательности A1; A2; A3; ::: в точку B означает следующее: независимо от того, насколько маленьким мы возьмем круг с центром в точке B, все точки последовательности, начиная с какой-то одной, попадут внутрь этого круга.Другими словами, вне любой окружности с центром B в нашей последовательности есть только конечное число точек.
А если в космосе? Немного изменено определение «плавный»: вам просто нужно заменить слово «круг» словом «шар».
Предположим теперь, что концы синих векторов на рис. 1.5 проходят не через дискретный набор значений, а через непрерывную кривую (например, обозначенную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~ un, а с вектором ~ u (t), который изменяется со временем.Это как раз то, что нам нужно в физике!
Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0. Если
к тому же концы векторов ~ u (t) «перетекают» в некоторую точку B, то мы говорим, что вектор
~ v = OB является пределом значения вектора ~ u (t):
т! t0
1.1.8 Дифференцирование векторов
Выяснив, каков предел векторной величины, мы готовы сделать следующий шаг, чтобы ввести понятие векторной производной.
Предположим, что существует некоторый вектор ~ u (t), зависящий от времени. Это означает, что длина данного вектора и его направление могут изменяться со временем.
По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~ u за время t является векторной величиной:
~ u = ~ u (t + t) ~ u (t):
Обратите внимание, что разность векторов находится справа от этого отношения. Изменение вектора ~ u показано на рис.1.6 (напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и «зажимаем» стрелкой вектор, из которого производится вычитание).
~ u (t) ~ u
Рис. 1.6. Изменение вектора
Если временной интервал t достаточно мал, то вектор ~ u мало изменяется в течение этого времени (в физике, по крайней мере, согласно, поэтому он всегда считается). Соответственно, если при t! 0 отношение ~ u = t стремится к определенному пределу, тогда этот предел называется производной вектора ~ u:
При обозначении производной вектора мы не будем использовать точку выше (поскольку символ ~ u_ выглядит не очень хорошо) и ограничимся обозначениями (1.18). Но для производной от скаляра мы, естественно, свободно используем оба обозначения.
Напомним, что d ~ u = dt – это символ производной. Также ее можно понимать как дробь, в числителе которой стоит дифференциал вектора ~ u, соответствующий временному интервалу dt. Выше мы не обсуждали понятие дифференциала, так как оно не передается в школе; мы также не будем обсуждать дифференциал.
Однако на физическом уровне строгости производную d ~ u = dt можно считать дробью, в знаменателе которой находится очень малый интервал времени dt, а в числителе есть соответствующее небольшое изменение d ~ u вектора ~ u.При достаточно малом dt значение этой доли отличается от
, предел в правой части (1.18) настолько мал, что с учетом имеющейся точности измерения этой разницей можно пренебречь.
Этого (не совсем строгого) физического понимания производной нам будет вполне достаточно.
Правила дифференцирования для векторных выражений очень похожи на правила для скаляров. Нам нужны только самые простые правила.
1.Постоянный скалярный множитель выносится за знак производной: если c = const, то
d (c ~ u) = cd ~ u: dt dt
Мы используем это правило в разделе “ Импульс ”, когда Второй закон Ньютона
2. Постоянный векторный множитель выносится за знак производной: если ~ c = const, то dt d (x (t) ~ c) = x (t) ~ c:
3. Производная суммы векторов равна сумме их производных:
dt d (~ u + ~ v) = d ~ u dt + d ~ v dt:
Мы будем использовать последние два правила более одного раза .Посмотрим, как они работают в важнейшей ситуации векторного дифференцирования при наличии прямоугольной системы координат OXY Z в пространстве (рис. 1.7).
Рис. 1.7. Разложение вектора в базис
Как известно, любой вектор ~ u можно однозначно разложить в базисе блока
векторов ~, ~, ~: ijk
~ u = ux i + uy j + uz k:
Здесь ux, uy, uz – проекции вектора ~ u на оси координат … Они – координаты вектора ~ u в этом базисе.
Вектор ~ u в нашем случае зависит от времени, а это значит, что его координаты ux, uy, uz являются функциями времени:
~ u (t) = ux (t) i | Uy (т) j | Уз (т) к: |
Различаем это равенство. Сначала воспользуемся правилом дифференцирования суммы:
ux (t) ~ i + | uy (t) ~ j | уз (т) ~ к: | ||||||||||||
Затем выносим постоянные векторы за знак производной: | ||||||||||||||
Ux (t) i + uy (t) j + uz (t) k: | ||||||||||||||
Таким образом, если вектор ~ u имеет координаты (ux; uy; uz), то координаты производной d ~ u = dt являются производными от координат вектора ~ u, а именно (ux; uy; uz) .
Ввиду особой важности формулы (1.20) дадим ее более прямой вывод. В момент t + t согласно (1.19) имеем:
~ u (t + t) = ux (t + t) i + uy (t + t) j + uz (t + t) k:
Запишем изменение вектора ~ u:
~ u = ~ u (t + t) ~ u (t) =
Ux (t + t) i + uy (t + t) j + uz ( t + t) k ux (t) i + uy (t) j + uz (t) k =
= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k = | ||||||||||
Ux i + uy j + uz k: | ||||||||||
Разделим обе части полученного равенства на t: | ||||||||||
Тел. + | т j + | |||||||||
В пределе при t! 0 дроби ux = t, uy = t, uz = t переходят соответственно в производные ux, uy, uz и снова получаем соотношение (1.20):
Ux i + uy j + uz k.
Поделитесь статьей с друзьями:
Похожие статьи
Все буквы в физике и их обозначения. Обозначение: высота, ширина, длина
Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения, принятые в физике.
Во-первых, меняется обозначение функций. Действительно, какие функции мы будем различать? Эти функции являются физическими величинами, зависящими от времени. Например, координата тела x (t) и его скорость v (t) могут быть заданы формулами:
(читать ix с точкой).
Существует еще одно обозначение производной, очень распространенное как в математике, так и в физике:
производная функции x (t) обозначена | ||
(читать ¾de iks on de te¿).
Остановимся подробнее на значении обозначения (1.16). Математик понимает это двояко: либо как предел:
, либо как дробь, знаменателем которой является приращение времени dt, а в числителе – так называемый дифференциал dx функции x (t). Дифференциал несложен, но мы не будем его сейчас обсуждать; он ждет вас в первый год.
Физик, не ограниченный требованиями математической строгости, понимает обозначение (1.16) более неформально. Пусть dx будет изменением координаты за время dt. Возьмем интервал dt настолько малым, чтобы отношение dx = dt было близко к своему пределу (1.17) с подходящей для нас точностью.
И тогда, скажет физик, производная координаты по времени – это просто дробь, в числителе которой есть довольно небольшое изменение координаты dx, а в знаменателе – довольно малое время интервал dt, в течение которого произошло это изменение координаты.
Такое расплывчатое понимание производной характерно для рассуждений в физике. В дальнейшем мы будем придерживаться этого физического уровня строгости.
Производная x (t) физической величины x (t) снова является функцией времени, и эту функцию снова можно дифференцировать, чтобы найти производную производной или вторую производную функции x (t). Вот одно обозначение второй производной:
вторая производная функции x (t) обозначается x (t)
(читается как ix с двумя точками), но вот другое:
вторая производная функции Функция x (t) обозначается dt 2
(она читается как de two x in de te square¿ или de two x in de te two).
Вернемся к исходному примеру (1.13) и вычислим производную координаты, а заодно посмотрим на совместное использование обозначений (1.15) и (1.16):
x (t) \ u003d 1 + 12t 3t2)
x (t) = dt d (1 + 12t 3t2) = 12 6t:
(Символ дифференциации dt d перед скобкой такой же, как тире над скобкой в предыдущие обозначения.)
Отметим, что производная координаты оказалась равной скорости (1.14). Это не совпадение. Связь между производной координаты и скоростью тела будет разъяснена в следующем разделе «Механическое движение».
1.1.7 Предел вектора
Физические величины не только скалярные, но и векторные. Соответственно, нас часто интересует скорость изменения векторной величины, то есть производная вектора. Однако, прежде чем говорить о производной, вам необходимо понять концепцию предела векторной величины.
Рассмотрим последовательность векторов ~ u1; ~ u2; ~ u3; ::: Сделав при необходимости параллельный перенос, сведем их начала в одну точку О (рис. 1.5):
Рисунок: 1.5. lim ~ un = ~ v | |||||||||
Концы векторов обозначим A1; A2; A3; ::: Таким образом, имеем: | |||||||||
Предположим последовательность точек A1; A2; A3; ::: ¾потоки¿2 в точку B:
lim An = B:
Обозначим ~ v = OB.Мы говорим тогда, что последовательность синих векторов ~ un стремится к красному вектору ~ v, или что вектор ~ v является пределом последовательности векторов ~ un:
~ v = lim ~ un:
2 интуитивного понимания этого «перетекания» вполне достаточно, но, может быть, вас интересует более строгое объяснение? Тогда вот оно.
Пусть будет в самолете. «Приток» последовательности A1; A2; A3; ::: в точку B означает следующее: независимо от того, насколько маленьким мы возьмем круг с центром в точке B, все точки последовательности, начиная с какой-то одной, попадут внутрь этого круга.Другими словами, вне любой окружности с центром B в нашей последовательности есть только конечное число точек.
А если в космосе? Немного изменено определение «плавный»: вам просто нужно заменить слово «круг» словом «шар».
Теперь предположим, что концы синих векторов на рис. 1.5 проходят не через дискретный набор значений, а через непрерывную кривую (например, обозначенную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~ un, а с вектором ~ u (t), который изменяется со временем.Это как раз то, что нам нужно в физике!
Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0. Если a
к тому же концы векторов ~ u (t) “ перетекают ” в некоторую точку B, то мы говорим, что вектор
~ v = OB является пределом значения вектора ~ u (t ):
т! t0
1.1.8 Дифференцирование векторов
Выяснив, каков предел векторной величины, мы готовы сделать следующий шаг, чтобы ввести понятие векторной производной.
Предположим, что существует некоторый вектор ~ u (t), зависящий от времени. Это означает, что длина данного вектора и его направление могут изменяться со временем.
По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~ u за время t – это векторная величина:
~ u = ~ u (t + t) ~ u (t):
Обратите внимание, что в правой части этого отношения находится векторная разность . Изменение вектора ~ u показано на рис.1.6 (напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и «зажимаем» стрелкой вектор, из которого производится вычитание).
~ u (t) ~ u
Рисунок 1.6. Изменение вектора
Если интервал времени t достаточно мал, то вектор ~ u также мало изменяется за это время (по крайней мере, в физике так всегда считается). Соответственно, если при t! 0 отношение ~ u = t стремится к определенному пределу, тогда этот предел называется производной вектора ~ u:
При обозначении производной вектора мы не будем использовать точку выше (так как ~ u_ выглядит не очень хорошо) и ограничимся обозначениями (1.18). Но для производной скаляра мы, естественно, свободно используем оба обозначения.
Напомним, что d ~ u = dt – символ производной. Также ее можно понимать как дробь, в числителе которой стоит дифференциал вектора ~ u, соответствующий временному интервалу dt. Выше мы не обсуждали понятие дифференциала, так как оно не проходит в школе; мы также не будем обсуждать дифференциал.
Однако на физическом уровне строгости производную d ~ u = dt можно считать дробью, в знаменателе которой находится очень малый интервал времени dt, а в числителе – соответствующее небольшое изменение d ~ u вектора ~ u.При достаточно малом dt значение этой доли отличается от
, предел в правой части (1.18) настолько мал, что с учетом имеющейся точности измерения этой разницей можно пренебречь.
Этого (не совсем строгого) физического понимания производной нам будет достаточно.
Правила дифференцирования векторных выражений во многом аналогичны правилам скалярного дифференцирования. Нам нужны только самые простые правила.
1. Постоянный скалярный множитель вынесен за знак производной: если c = const, то
d (c ~ u) = cd ~ u: dt dt
Воспользуемся этим правилом в разделе «Импульс» при втором законе Ньютона
2. Постоянный векторный множитель выносится за знак производной: если ~ c = const, то dt d (x (t) ~ c) = x (t) ~ c:
3. Производная суммы векторов равна сумме их производных:
dt d (~ u + ~ v) = d ~ u dt + d ~ v dt:
Будем использовать последние два правила более одного раза.Посмотрим, как они работают в важнейшей ситуации векторного дифференцирования при наличии прямоугольной системы координат OXY Z в пространстве (рис. 1.7).
Рисунок: 1.7. Разложение вектора в базис
Как известно, любой вектор ~ u можно однозначно разложить в базисе блока
векторов ~, ~, ~: ijk
~ u = ux i + uy j + uz k:
Здесь ux, uy, uz – проекции вектора ~ u на оси координат. Это координаты вектора ~ u в данном базисе.
Вектор ~ u в нашем случае зависит от времени, а это значит, что его координаты ux, uy, uz являются функциями времени:
~ u (t) = ux (t) i | Uy (т) j | Уз (т) к: |
Различаем это равенство. Сначала воспользуемся правилом дифференцирования суммы:
ux (t) ~ i + | uy (t) ~ j | уз (т) ~ к: | ||||||||||||
Затем выносим постоянные векторы за знак производной: | ||||||||||||||
Ux (t) i + uy (t) j + uz (t) k: | ||||||||||||||
Таким образом, если вектор ~ u имеет координаты (ux; uy; uz), то координаты производной d ~ u = dt являются производными от координат вектора ~ u, а именно (ux; uy; uz ).
Ввиду особой важности формулы (1.20) дадим ее более прямой вывод. В момент времени t + t согласно (1.19) имеем:
~ u (t + t) = ux (t + t) i + uy (t + t) j + uz (t + t) k :
Запишем изменение вектора ~ u:
~ u = ~ u (t + t) ~ u (t) =
Ux (t + t) i + uy (t + t) j + uz (t + t) k ux (t) i + uy (t) j + uz (t) k =
= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k = | ||||||||||
Ux i + uy j + uz k: | ||||||||||
Разделим обе части полученного равенства на t: | ||||||||||
Тел. + | т j + | |||||||||
В пределе при t! 0 дроби ux = t, uy = t, uz = t переходят соответственно в производные ux, uy, uz, и мы снова получаем соотношение (1.20):
Ux i + uy j + uz k.
Построение чертежей – задача не из легких, но в современном мире без нее нет ничего. Ведь для того, чтобы изготовить даже самый обычный предмет (крохотный болт или гайку, полку для книг, новый дизайн платья и т. Д.), Нужно предварительно провести соответствующие расчеты и нарисовать чертеж будущего изделия. Однако часто ее составляет один человек, а изготовление чего-либо по этой схеме занимается другой человек.
Во избежание путаницы в понимании изображаемого объекта и его параметров во всем мире приняты обозначения длины, ширины, высоты и других величин, используемые в дизайне. Кто они такие? Давайте разберемся.
Величины
Площадь, высота и другие обозначения аналогичного характера являются не только физическими, но и математическими величинами.
Их однобуквенное обозначение (используется во всех странах) было введено в середине двадцатого века Международной системой единиц (СИ) и используется по сей день.Именно по этой причине все такие параметры указываются латиницей, а не кириллическими буквами или арабским шрифтом. Чтобы не создавать отдельных сложностей, при разработке стандартов конструкторской документации в большинстве современных стран было решено использовать практически те же условные обозначения, которые используются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, изображена на чертеже двухмерная или трехмерная фигура (изделие), она имеет набор основных параметров.Если есть два измерения – это ширина и длина, если их три – также добавляется высота.
Итак, сначала разберемся, как правильно обозначать на чертежах длину, ширину, высоту.
Ширина
Как упоминалось выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта при условии, что его измерения производятся в поперечном направлении. Так чем же известна ширина? Имеет обозначение буквой «Б».Об этом знают во всем мире. Причем согласно ГОСТу допускается использование как прописных, так и строчных латинских букв. Часто возникает вопрос, почему была выбрана именно такая буква. Ведь обычно сокращение производится по первому греческому или английскому названию количества. Ширина на английском языке будет иметь вид «width».
Наверное, дело в том, что изначально этот параметр наиболее широко использовался в геометрии. В этой науке при описании фигур часто длина, ширина, высота обозначаются буквами «а», «б», «с».Согласно этой традиции, при выборе буква «B» (или «b») была заимствована системой СИ (хотя для двух других измерений стали использовать символы, отличные от геометрических).
Большинство считает, что это было сделано для того, чтобы не путать ширину (обозначенную буквой «B» / «b») с весом. Дело в том, что последнее иногда называют «W» (аббревиатура английского названия веса), хотя допустимы и другие буквы («G» и «P»). Согласно международным стандартам системы СИ ширина измеряется в метрах или кратных (долях) их единиц.Стоит отметить, что в геометрии иногда также допустимо использовать букву «w» для обозначения ширины, но в физике и других точных науках это обозначение обычно не используется.
Длина
Как уже упоминалось, в математике длина, высота и ширина – это три пространственных измерения. Более того, если ширина является линейным размером в поперечном направлении, то длина находится в продольном направлении. Рассматривая это как масштаб физики, можно понять, что это слово означает числовую характеристику длины линий.
В английском языке этот термин называется длиной. Именно поэтому это значение обозначается заглавной или строчной начальной буквой этого слова – «L». Как и ширина, длина измеряется в метрах или кратных (дольных) единицах.
Высота
Наличие этого значения указывает на то, что приходится иметь дело с более сложным трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском это пишется как «высота».Поэтому по международным стандартам он обозначается латинской буквой «H» / «h». Помимо высоты, на чертежах иногда эта буква выступает еще и в качестве обозначения глубины. Высота, ширина и длина – все эти параметры измеряются в метрах и их кратных и кратных единицах (километрах, сантиметрах, миллиметрах и т. Д.).
Радиус и диаметр
Помимо рассматриваемых параметров, при составлении чертежей приходится иметь дело с другими.
Например, при работе с кругами возникает необходимость определения их радиуса.Это название линии, соединяющей две точки. Первый – центр. Второй находится прямо на самом круге. На латыни это слово выглядит как «радиус». Отсюда строчные или прописные буквы «R» / «r».
При рисовании окружностей, помимо радиуса, часто приходится иметь дело с близким к нему явлением – диаметром. Это также отрезок прямой, соединяющий две точки на окружности. Причем обязательно проходит через центр.
Численно диаметр равен двум радиусам.В английском это слово пишется так: «диаметр». Отсюда и аббревиатура – большая или строчная латинская буква «Д» / «д». Часто диаметр на чертежах обозначается перечеркнутым кружком – «Ø».
Хотя это общепринятая аббревиатура, следует учитывать, что ГОСТ предусматривает использование только латинского «D» / «d».
Толщина
Большинство из нас помнят школьные уроки математики. Уже тогда учителя говорили, что латинской буквой «s» принято обозначать такое значение, как площадь.Однако по общепринятым нормам на чертежах таким способом фиксируется совсем другой параметр – толщина.
Почему? Известно, что в случае высоты, ширины, длины обозначение буквами могло быть объяснено их написанием или традицией. Но толщина на английском языке выглядит как «толщина», а в латинском варианте – как «грубость». Также непонятно, почему, в отличие от других значений, толщину можно указывать только строчными буквами.Обозначение «s» также используется для обозначения толщины страниц, стен, краев и т. Д.
Периметр и площадь
В отличие от всех значений, перечисленных выше, слово «периметр» пришло не из латинского или английского, а из греческого языка. Это производное от «περιμετρέο» (для измерения окружности). И сегодня этот термин сохранил свое значение (общая длина границ рисунка). Впоследствии слово попало в английский язык («периметр») и закрепилось в системе СИ в виде сокращения с буквой «П».
Площадь – это величина, которая показывает количественные характеристики геометрической фигуры с двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, он измеряется в квадратных метрах (а также в дробных и кратных их единицах). Что касается буквенного обозначения местности, то в разных областях она различается. Например, в математике это знакомая каждому с детства латинская буква «S». Почему так – информации нет.
Некоторые люди неосознанно думают, что это происходит из-за английского написания слова «квадрат».Однако в нем математическая область – это «площадь», а «квадрат» – это площадь в архитектурном смысле. Кстати, стоит помнить, что «квадрат» – это название геометрической формы «квадрат». Так что будьте внимательны при изучении чертежей на английском языке. Из-за того, что в некоторых дисциплинах переводится как «площадь», в качестве обозначения используется буква «А». В редких случаях также используется буква «F», но в физике эта буква означает величину, называемую «силой» («фортис»).
Другие общепринятые сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра наиболее часто используются при составлении чертежей.Однако есть и другие количества, которые также часто в них присутствуют. Например, строчная буква «т». В физике это означает «температура», однако по ГОСТу Единой системы конструкторской документации эта буква представляет собой ступеньку (пружины винтовые и тому подобное). Однако, когда речь идет о зацеплении и резьбе, он не используется.
Заглавная и строчная буквы «А» / «а» (по всем тем же стандартам) на чертежах используются для обозначения не площади, а межцентрового расстояния и межцентрового расстояния.Помимо разных значений, на чертежах часто указываются углы разных размеров. Для этого принято использовать строчные буквы греческого алфавита. Чаще всего используются «α», «β», «γ» и «δ». Однако допустимо использование других.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недоразумений при чтении чертежа, представители разных народов приняли единые стандарты буквенного обозначения.Другими словами, если вы сомневаетесь в толковании той или иной аббревиатуры, взгляните на ГОСТы. Таким образом вы узнаете, как правильно указаны высота, ширина, длина, диаметр, радиус и так далее.
Ни для кого не секрет, что в любой науке существуют специальные обозначения величин. Буквенные обозначения в физике доказывают, что эта наука не является исключением в плане определения величин с помощью специальных символов. Существует множество основных величин, а также их производных, каждая из которых имеет свой символ.Итак, буквенные обозначения в физике подробно рассматриваются в этой статье.
Физика и основные физические величины
Благодаря Аристотелю слово физика стало использоваться, так как именно он первым применил этот термин, который в то время считался синонимом термина философия. Это связано с общностью объекта исследования – законов Вселенной, а точнее – того, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, благодаря которой физика была выделена как самостоятельная наука.
Михаил Васильевич Ломоносов ввел слово «физика» в русский язык, издав учебник в переводе с немецкого – первый в России учебник по физике.
Итак, физика – это раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движения и строения. Базовых физических величин не так много, как может показаться на первый взгляд – их всего 7: длина
- , масса
- , время
- , сила тока
- , температура
- , количество вещества
- сила света.
Конечно, в физике у них есть свои буквенные обозначения. Например, символ m выбран для массы, а T выбран для температуры. Также у всех величин есть своя единица измерения: сила света – кандела (кд), а единицей измерения количества вещества – моль.
Производные физические величины
Производных физических величин гораздо больше, чем базовых. Их 26, и часто некоторые из них относят к основным.
Итак, площадь является производной от длины, объем – также длины, скорость – времени, длины, а ускорение, в свою очередь, характеризует скорость изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество тепла, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент количества движения, момент силы – все это зависит от массы.Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол определяются длиной.
Какая буква обозначает напряжение в физике? Напряжение, являющееся скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – A, а для энергии – E. Электрический заряд обычно обозначают буквой q, а магнитный поток – F.
SI: общая информация
Международная система единиц (СИ) – это система физических единиц, основанная на Международной системе единиц, включая названия и обозначения физических величин.Он был принят Генеральной конференцией по мерам и весам. Именно эта система регулирует буквенные обозначения в физике, а также их размеры и единицы измерения. Для обозначения используются буквы латинского алфавита, в некоторых случаях – греческого. Также возможно использование специальных символов в качестве обозначения.
Заключение
Итак, в любой научной дисциплине есть специальные обозначения для разного рода величин. Естественно, физика не исключение.Буквенных обозначений очень много: сила, площадь, масса, ускорение, натяжение и т. Д. У них есть свои обозначения. Существует особая система, называемая Международной системой единиц. Считается, что базовые единицы не могут быть математически выведены из других. Производные величины получаются путем умножения и деления основных.
Расстояние и смещение в физике: определение и примеры – стенограмма видео и урока
Расстояние и смещение
Давайте начнем с определения этих двух терминов, начиная с более простого.
Расстояние – это то, сколько земли покрывает объект, независимо от его начальной или конечной позиции. В измерении расстояния нет направленного компонента, что делает его скалярной величиной. Итак, за мои 5 км я пробежал всего 5 километров. Неважно, где была линия старта или финиша или в каком направлении я бежал. Имеет значение только то, что, если вы проследите и измерите мой путь, я преодолел расстояние в 5 км по земле. Итак, когда мы спросили других бегунов, как далеко я проехал, все они правильно ответили, измеряя расстояние в 5 километров.
Давайте на минутку посмотрим на наш другой термин: смещение , который представляет собой изменение положения объекта с учетом его начального и конечного положения. При измерении смещения не учитывается, по какому маршруту следовал объект, чтобы изменить положение, а учитывается только то, где он начался и где закончился. Легче всего изобразить смещение, указав место начала объекта и нарисовав прямую стрелку от этой точки к точке, где объект перестал двигаться. Помните, в физике эта стрелка называется вектором.Его длина соответствует величине или размеру движения, а стрелка указывает направление движения. Это делает смещение векторной величиной, поскольку оно включает в себя движение, величину и направление.
В сокращении физики смещение записывается как Δs . «Дельта» – это греческая буква в форме треугольника, обозначающая «изменение». ‘S’ обозначает пространственное расположение. Итак, Δs означает изменение пространственного положения. Вам следует освоиться с использованием этого сокращения на тот случай, если вы увидите вопросы, требующие решения для Δs , которые на самом деле не требуют смещения по имени.
Расчет смещения
Теперь, прежде чем мы посмотрим на мое смещение во время моих 5 км, я хочу попытаться проиллюстрировать концепцию смещения. Если я пойду на 3 метра на запад, затем поверну и пойду на 4 метра на север, вы легко сможете рассчитать пройденное расстояние: 3 м + 4 м = 7 метров. Поскольку это расстояние, не нужно беспокоиться о направлении движения. Теперь давайте определим мое перемещение. Я могу нарисовать стрелку, которая начинается там, где я начал ходить, и продолжается до точки, где я остановился.2.
Δs = √ {(3 * 3) + (4 * 4)}
Δs = √ (9 + 16)
Δs = 5 метров к северо-западу
Выполнение математических вычислений дает значение 5 метров. Но это не смещение. Помните, нам тоже нужно направление. В данном случае я оказался на северо-западе от того места, откуда начал, поэтому мое смещение составляет 5 метров к северо-западу. Обратите внимание, что я проехал всего 7 м, но сместился только на 5 метров к северо-западу.
А теперь вернемся к моей 5К.Возможно, вы уже сможете понять, что здесь происходит. Как я могу проехать 5 км, но иметь водоизмещение 0? Уловка здесь в том, что трасса гонки представляла собой большой круг; линия старта и линия финиша находились в одном месте. Итак, если мы нарисуем маршрут гонки и проследим мой прогресс по кругу, вы увидите, что я действительно пробежал 5 километров по маршруту гонки. Но попробуйте нарисовать вектор, напрямую соединяющий мою начальную позицию и мою конечную позицию, не принимая во внимание мой маршрут.У вас есть только одна точка, поэтому вы не можете нарисовать вектор. Итак, мое смещение было 0.
Итоги урока
Давайте быстро рассмотрим расстояние и смещение.
Расстояние – это то, сколько земли покрывает объект, независимо от его начальной или конечной позиции. Чтобы определить пройденное расстояние, вы должны измерить длину всего пути, пройденного объектом. Если вы пробежите 5 км по круговой трассе, пройденное расстояние составит 5 километров, независимо от того, где вы начали и где закончили.Расстояние – это скалярная величина.
Смещение – это изменение положения объекта, только измерение от его начального положения до конечного положения. Смещение учитывает только изменение вашего положения от начала до конца, а не точный путь, по которому вы туда пришли. Чтобы рассчитать смещение, просто нарисуйте вектор от начальной точки до конечной позиции и найдите длину этой линии. Если ваша начальная и конечная позиции совпадают, например, ваш круговой маршрут 5 км, то ваше смещение равно 0.В физике смещение представлено как Δs .
Результаты обучения
Завершив этот урок, вы можете усилить свои способности:
- Сравнить расстояние и смещение и различать два
- Вспомните значение Δs
- Расчет смещения
Площадь цилиндра
Поскольку цилиндр тесно связан с призма , формулы для их площади поверхности относятся к.
Помните, что формулы для площади боковой поверхности призмы п час а общая площадь поверхности равна п час + 2 B . Поскольку основание цилиндра – окружность, подставим 2 π р за п и π р 2 за B где р – радиус основания цилиндра.
Итак, формула для площадь боковой поверхности цилиндра L . S . А . знак равно 2 π р час .
Пример 1:
Найдите площадь боковой поверхности цилиндра с радиусом основания 3 дюймов и высотой 9 дюймы.
L . S . А . знак равно 2 π ( 3 ) ( 9 ) знак равно 54 π дюймы 2
≈ 169.64 дюймы 2
Общая формула для общая площадь поверхности цилиндра Т . S . А . знак равно 2 π р час + 2 π р 2 .
Пример 2:
Найдите общую площадь поверхности цилиндра с радиусом основания 5 дюймов и высотой 7 дюймы.
Т . S . А .знак равно 2 π ( 5 ) ( 7 ) + 2 π ( 5 ) 2 знак равно 120 π дюймы 2 ≈ 376.99 дюймы 2
Использование математики в физических науках, Рон Куртус
SfC Home> Физические науки>
Рон Куртус
Математика используется в Physical Science для расчета измерений объектов и их характеристик, а также для отображения взаимосвязи между различными функциями и свойствами.Могут использоваться арифметика, алгебра и высшая математика.
Арифметика и алгебра используются для определения значений и решения простых уравнений или формул.
В классической или повседневной физике и химии для решения уравнений используются нормальные значения. В астрономии расстояния, размеры и массы очень велики. Для представления этих значений требуется специальная номенклатура. В атомной физике и некоторых областях химии размеры и массы невелики, хотя количества могут быть большими.
Арифметика состоит из простых операций с числами и значениями.Алгебра используется для отображения взаимосвязей до того, как измеренные числа используются для расчетов. Высшая математика используется для сложных отношений между свойствами.
Вопросы, которые могут у вас возникнуть:
- Как арифметика используется в физических науках?
- Как используется алгебра?
- Как используется высшая математика?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц
Арифметические соглашения
Используя арифметику, мы можем складывать, вычитать, умножать и делить числа.Мы также используем дроби и десятичные дроби.
Сложение и вычитание
Мы используем символ « + » для обозначения сложения двух чисел и символ « – » для вычитания. Символ « = » означает равенство и является результатом. Таким образом, 5 + 2 = 7 равно 5 плюс 2 равно 7 , а 6-4 = 2 равно 6 минус 4 равно 2 .
Вы выполняете операции в том порядке, в котором они перечислены: 5 + 2 – 3 выполняется как 5 + 2 = 7, а затем 7 – 3 = 4.
Умножение и деление
Мы обычно используем символ «x» для обозначения умножения в арифметике: 2 x 3 = 6. Но обратите внимание, что «x» также может быть переменной в алгебре и означать что-то еще, поэтому следует проявлять осторожность. Часто люди используют * для обозначения умножения: 2 * 3 = 6.
На веб-страницах сложно написать символ деления, который встречается в ваших учебниках, поэтому для обозначения деления используется “/”: 8/4 = 2.
Заказ внесен в список
Операции умножения и деления выполняются в указанном порядке.Таким образом: 6 * 2/3 = 4 выполняется как 6 * 2 = 12 и 12/3 = 4.
Использование скобок
Когда вы объединяете сложение и вычитание с умножением и делением, это может стать сложным. Вы по-прежнему делаете это в указанном порядке, но необходимо использовать круглые скобки для объединения вместе взятых вместе терминов сложения и вычитания. Операции, заключенные в круглые скобки, выполняются в первую очередь.
5 * 3 + 7 отличается от 5 * (3 + 7). С 5 * 3 + 7 операции идут по порядку, поэтому мы имеем 5 * 3 = 15, а затем 15 + 7 = 22.С 5 * (3 + 7) вы сначала объединяете те, которые указаны в круглых скобках. (3 + 7) = 10 и затем 5 * 10 = 50.
Дроби и десятичные знаки
3/5 – это 3, разделенное на 5, но, поскольку это неудобно, мы можем обозначить это как дробь и написать 3/5.
Если вы все же разделите его, вы можете записать результат в виде десятичной дроби 0,6. Обратите внимание, что рекомендуется ставить 0 перед десятичной запятой, чтобы избежать путаницы. Написание .6 легко спутать с числом 6, если человек не замечает крошечный “.”символ.
Алгебра
Алгебра использует буквы для обозначения взаимосвязи между характеристиками. Обычно это просто аббревиатуры характеристики. Например, энергия обозначается E , а скорость v .
Обратите внимание, что мы обычно выделяем переменную жирным шрифтом , чтобы ее было легче отличить от других элементов, особенно на веб-страницах. Во многих учебниках физики векторы выделяются жирным шрифтом.
Умножение
Хотя вы можете умножать числа с помощью x или *, например 2 x 3 или 5 * 7, буквы часто используются для обозначения того, что еще не имеет присвоенного значения.Большая проблема в алгебре, буква x часто присваивается переменной или неизвестному значению. Но также используя x для умножения, вы можете получить 2 x x , что сбивает с толку. Даже использовать 2 * x громоздко. Итак, алгебраический стандарт – это просто сложить буквы вместе. 2x – это 2 раза x . xyz равно x раз y раз z . Но этот способ написания не соответствует числам. 23x – это , а не 2 раза 3 раза x .Это 23 умноженное на x .
Отношения
Ньютон предложил соотношение между силой, массой и ускорением. Его уравнение гласит, что сила равна массе объекта, умноженное на его ускорение. Чтобы не писать это предложение, мы используем символы F для силы, м, для массы и a для ускорения. Таким образом, уравнение можно записать: F = ma .
Это позволяет нам подставить значения для двух элементов и получить значение для третьего.Если м = 3 килограмма и = 2 метра в секунду в секунду, F = 3 * 2 = 6 ньютонов.
Обратите внимание, что в учебниках часто можно встретить уравнение, записанное как F = ma . Они пытаются сократить, используя символ умножения, просто помещая переменные рядом друг с другом, предполагая, что вы знаете, что они умножаются. В некоторых книгах между символами используется «. ». Чтобы избежать путаницы, мы продолжим использовать « * » в качестве умножения.
Индексы
Иногда вы сравниваете два или более элемента с одинаковой характеристикой. В таких случаях можно добавить индексный номер или букву, чтобы отделить друг от друга. Нижний индекс – это маленькая цифра или буква после и под переменной.
Если вы сравниваете несколько сил, вы можете назвать одну F 1 , другую F 2 и так далее. Также мы вызываем силу трения F r , чтобы отделить ее от другой силы.2 – это x в квадрате.
x²
Чаще всего квадрат числа записывается с помощью надстрочного индекса 2 : 3² = 3 * 3 = 9 и x² = x * x .
Возведено в степень
Вы можете возвести число в более высокую степень, но не во многих обычных физических уравнениях это используется: x 4 = x * x * x * x. Число 10 в более высокой степени – удобный способ обозначать большие числа: 10 6 – это 1, за которой следуют 6 нулей = 1 000 000.
Квадратный корень
Квадратный корень – это просто величина, обратная квадрату числа. Если 3² = 9, то квадратный корень из 9 – это число, которое при умножении само на себя равно 9. Другими словами, 3 – это квадратный корень из 9.
Большинство чисел не имеют простого квадратного корня, поэтому большинство чисел необходимо определять с помощью калькулятора. Например, квадратный корень из 25 равен 5, а квадратный корень из 24 равен 4,898979 …
.Символ квадратного корня, используемый в учебниках, не работает на веб-страницах, поэтому вместо этого мы используем SQRT для обозначения операции.Таким образом, SQRT (25) – это квадратный корень из 25, а SQRT ( v / g ) – квадратный корень из результата v , деленного на g .
Высшая математика
Исчисление, дифференциальные уравнения и другая передовая математика используются в сложных физических расчетах и уравнения. Они выходят за рамки наших уроков.
Один из примеров того, где и почему должна использоваться продвинутая математика, можно увидеть в простых уравнениях гравитации. F = m * g – это уравнение силы тяжести.Но это уравнение является лишь приближением для предметов, падающих близко к Земле. Фактическое уравнение изменяется обратно пропорционально квадрату расстояния друг от друга и связано с массами тел.
Сводка
Математика используется в физических науках для измерений и отображения взаимосвязей. Арифметика состоит из простых операций с числами, а алгебра показывает отношения – часто без чисел. Высшая математика используется для сложных отношений между свойствами.
Обучение помогает расти
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Ресурсы по физическим наукам
Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги по физике и математике с самым высоким рейтингом
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
math.htm
Пожалуйста, включите это как ссылку на свой веб-сайт или как ссылку в своем отчете, документе или тезисе.


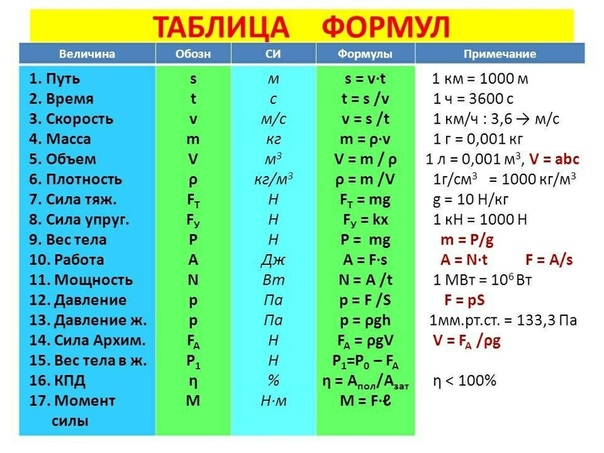 .. Что такое Список обозначений в физике?
.. Что такое Список обозначений в физике?
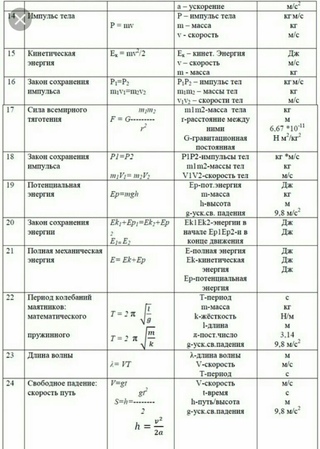 Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
 Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.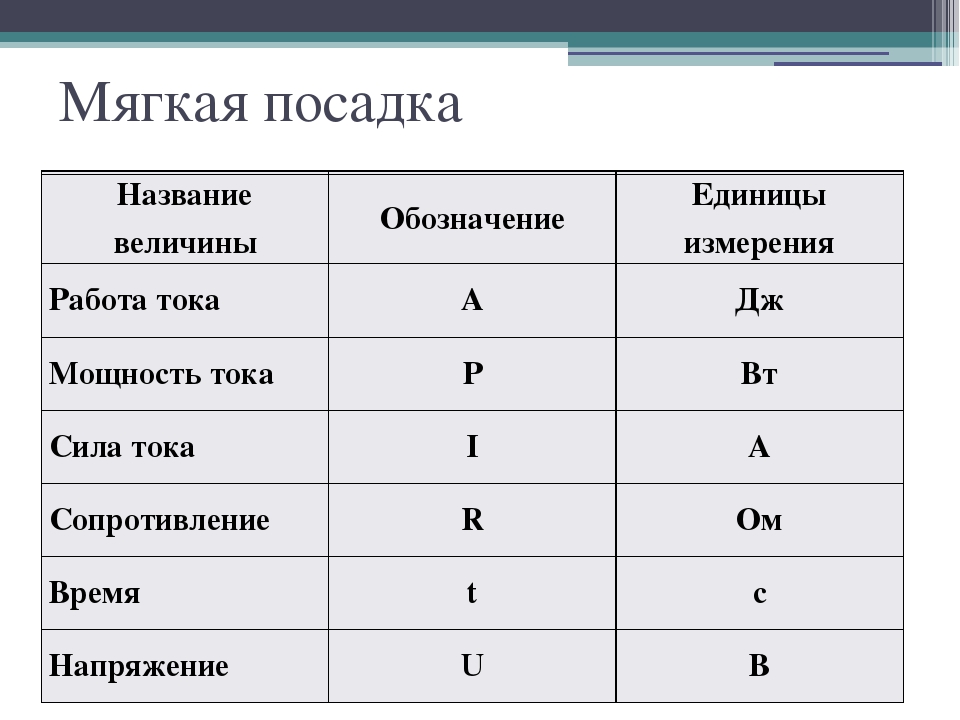 Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.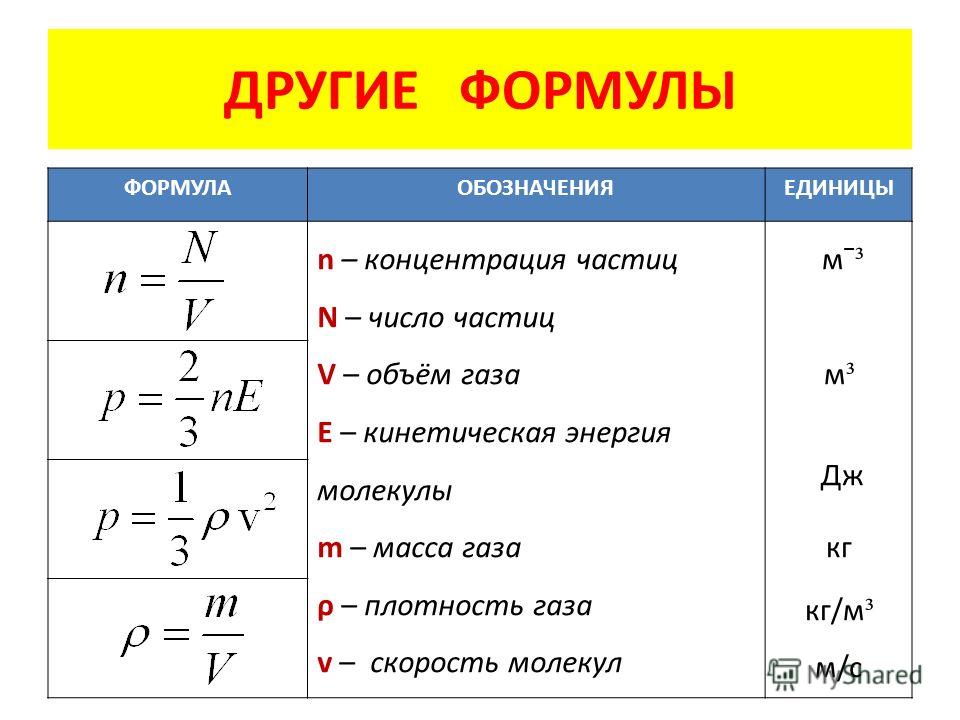
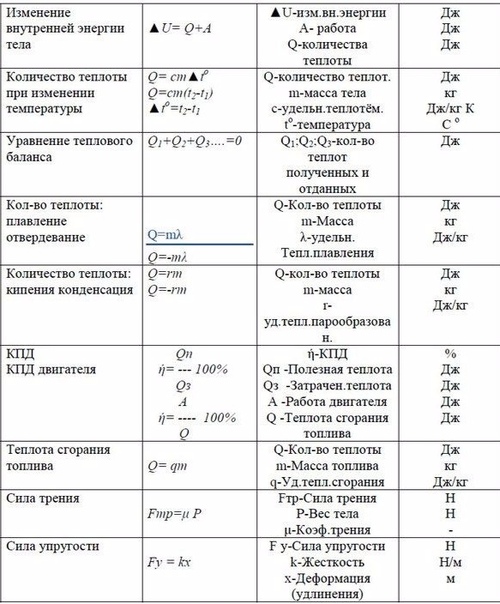 Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.