Определите емкость конденсатора сопротивление: Определите емкость конденсатора,сопротивление которого в цепи переменного тока частотой 50Гц равно 800 Ом…

404 Not Found

404 Not Found

Как определить емкость конденсатора без маркировки?

09. 03.2023

Конденсатор — распространенный компонент, использующийся во многих электрических устройствах. Их уникальная способность заключается в способности накапливать энергию и моментально ее отдавать. Эта функция востребована в работе многих устройств, но при выборе модели необходимо знать, как определить емкость конденсатора без маркировки — эта главная характеристика не всегда обозначается на корпусе из-за малых размеров элемента.

Где используются конденсаторы

Конденсатор — это двухполюсный накопитель пассивного типа, который накапливает и отдает энергию, но не меняет ее величину. Он состоит из двух деталей с разным зарядом, изолированных друг от друга диэлектрической прокладкой. При прохождении электрического тока емкость конденсатора постепенно заполняется и повышается его напряжение.

С помощью конденсаторов обеспечивают различные возможности электрических цепей:

• накопление и отдача заряда для моментального мгновенного импульса высокой силы, например, для фотографической вспышки;
• конденсаторы используются для поддержки работы устройств, снабженных устройствами памяти, для сохранения данных после отключения от источника питания;
• элементы могут снижать пульсации и помехи в цепях переменного тока, выравнивая напряжение;
• применяются для увеличения емкости устройств.

Также существует отдельный класс пусковых конденсаторов, функция которых заключается в снятии нагрузки на двигатели и другие устройства в момент запуска системы, когда напряжение максимально. Такие конденсаторы задействуются буквально на несколько секунд и затем отключаются. От обычного рабочего конденсатора он отличается большей емкостью.

Как определить номинал конденсатора без маркировки

Важно уметь определять емкость конденсатора для подбора оптимального устройства под параметры сети, а также для того, чтобы отличать рабочие модели от пусковых. Они не взаимозаменяемы: рабочий при высоких нагрузках, предназначенных для пускового, быстро выйдет из строя, а пусковой рассчитан на кратковременные циклы работы и при постоянном напряжении также перегорают.

Есть два способа определения емкости, если на конденсаторе нет маркировки.

• С помощью мультиметра. Для этого мультиметр нужно перевести в режим «Cx» и подключить к устройству с учетом полярности контактов.
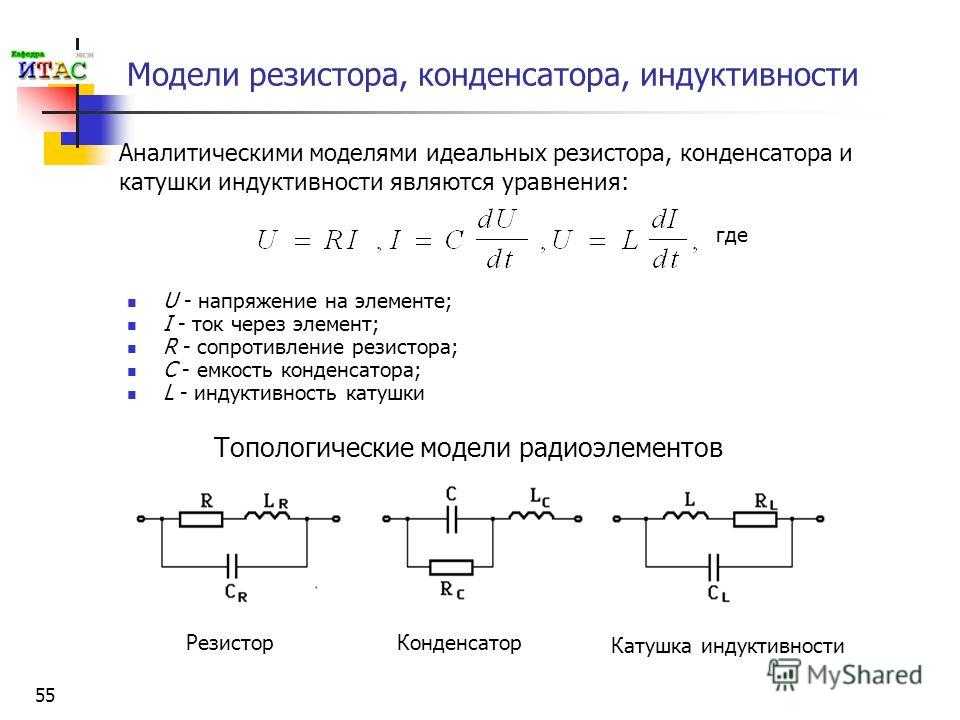
• С помощью мультиметра и резистора. Это способ пригодится на случай, если режим «Cx» на мультиметре не предусмотрен. Замерив показания напряжения, нужно подключить резистор и замкнуть конденсатор, например, обычной отверткой. Подключаем RC-цепь из резистора и конденсатора с устройству и снова замеряем напряжение. Конденсатор при прохождении тока стремится достигнуть напряжения самой цепи, и 95 % напряжения он достигает за время 3*RC. Вычисляем 95 % от напряжения цепи, размыкаем конденсатор и замеряем, за какое время он достигнет полученного значения — это параметр 3*RC. По формуле 3*t = 3*RC делим время на сопротивление и на три — это и будет напряжение конденсатора.

При заказе конденсаторов в нашем магазине емкость и другие технические характеристики можно уточнить в карточке товара или у наших менеджеров. Свяжитесь с нами по телефону, указанному вверху страницы.

домашнее задание и упражнения – Найти емкость конденсатора

спросил 6 лет, 6 месяцев назад

Изменено 2 года, 10 месяцев назад

Просмотрено 1к раз

$\begingroup$

Дано: Рассмотрим конденсатор, подключенный к батарее напряжением V . Пусть конденсатор имеет площадь А и расстояние между пластинами L. Предположим, что конденсатор имеет слой линейного диэлектрика (с диэлектрической проницаемостью κ, так что ε = κε0) толщиной L/2 на нижней пластине.

Я обнаружил, что емкость равна $C=\frac{2\kappa\epsilon_0 A}{L}$. Я был прав насчет разделительного расстояния? В более распространенных примерах конденсатора они утверждают, что пластины плоские, между ними ничего нет. В этом случае высота линейного диэлектрика равна половине общего расстояния между пластинами. Правильно ли я использую оставшееся свободное пространство, а именно $L/2$, в качестве разделительного расстояния в уравнении? Для справки:

$$C=\frac{\kappa \epsilon_0 A}{d}$$

• домашние задания и упражнения
• емкость
• напряжение

$\endgroup$

$\begingroup$

Мгновенная проверка, показывающая, что ваш ответ неверен: установите $\kappa = 1$, как если бы диэлектрика не было, и вы не восстановите формулу для параллельных пластин для зазора $L$.

Как решить эту задачу:

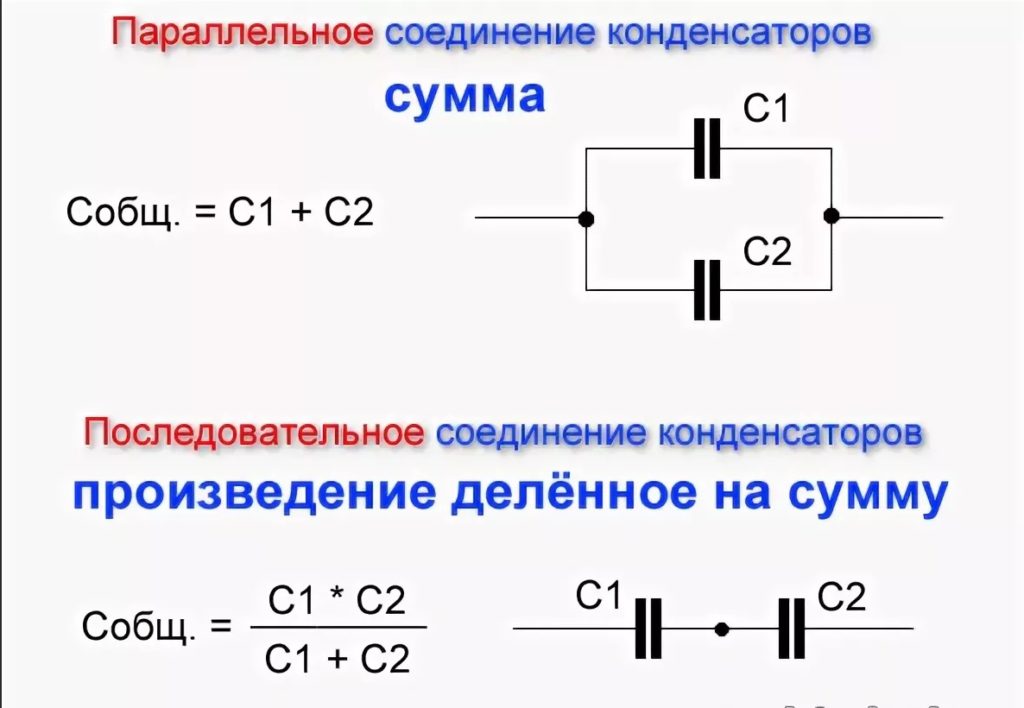
Пусть напряжение на конденсаторе равно $V$, а напряжение сверху и снизу равно $V_t$ и $V_b$ соответственно, тогда $$V=V_t+V_b,$$ что подразумевает, что $$1/C=1/C_t+1/C_b$$, поскольку $V=Q/C$.

Таким образом, эта система состоит из двух последовательных конденсаторов. Один конденсатор — это верхний зазор, а другой — нижняя часть. Используйте формулу для пластинчатых конденсаторов дважды, с расстоянием $L/2$ в обоих случаях, затем получите общую емкость, используя формулу для двух последовательно соединенных конденсаторов. Задействована некоторая алгебра.

Вы можете снова проверить полученный ответ, установив $\kappa=1$ и посмотрев, восстановите ли вы обычную формулу тарелки.

$\endgroup$

5

$\begingroup$

Поле $\mathbf{D}$ между пластинами (как обычно, без учета эффекта интерференции) однородно и нормально к плоскости пластин (для простоты предположим, что в направлении z) и определяется выражением

$$\ mathbf{D} = \frac{Q}{A}\hat{\mathbf{z}}$$

, где пластины имеют заряд $Q$ и $-Q$ соответственно. Электрическое поле (между пластинами) внутри диэлектрика равно

$$\mathbf{E_\kappa} = \frac{\mathbf{D}}{\kappa \epsilon_0}$$

а электрическое поле (между пластинами) в воздухе равно

$$\mathbf{ E} = \frac{\mathbf{D}}{\epsilon_0}$$

Таким образом, разность потенциалов между пластинами равна

$$V = \left(\frac{L}{2}\mathbf{E_ \ kappa} + \ frac {L} {2} \ mathbf {E} \ right) \ cdot \ hat {\ mathbf {z}} = \ left (\ frac {L} {2} \ frac {\ mathbf {D }}{\каппа\epsilon_0} + \frac{L}{2}\frac{\mathbf{D}}{\epsilon_0}\right)\cdot\hat{\mathbf{z}} = \left(\frac {L}{2}\frac{Q}{A\kappa\epsilon_0} + \frac{L}{2}\frac{Q}{A\epsilon_0} \right)$$

Тогда емкость равна

$$C = \frac{Q}{V} = \frac{1}{\frac{L/2}{A\kappa\epsilon_0} + \frac{L/2}{ A\epsilon_0}} = \frac{1}{\frac{1}{C_1}+ \frac{1}{C_2}}$$

, что является формулой для последовательно соединенных конденсаторов.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Конденсаторы и диэлектрики | Физика

Цели обучения

К концу этого раздела вы сможете:

• Описать действие конденсатора и дать определение емкости.
• Расскажите о конденсаторах с плоскими пластинами и их емкостях.
• Обсудите процесс увеличения емкости диэлектрика.
• Определить емкость при данных заряде и напряжении.

Конденсатор — это устройство, используемое для накопления электрического заряда. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы аккумулятора подключены к изначально незаряженному конденсатору, равному положительному и отрицательному заряду, + Q и – Q , разделены на две пластины. Конденсатор в целом остается нейтральным, но в этом случае мы называем его запасающим заряд Q .

Рис. 1. Оба показанных здесь конденсатора были изначально разряжены перед подключением к аккумулятору. Теперь у них есть отдельные заряды + Q и – Q на две половинки. а) Конденсатор с плоскими пластинами. (b) Свернутый конденсатор с изоляционным материалом между двумя его проводящими листами.

Конденсатор

Конденсатор — это устройство, используемое для накопления электрического заряда.

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Количество заряда

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Рисунок 2. Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.

Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как показано на рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для плоского конденсатора, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поле будет больше. линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна В .

Поле пропорционально заряду:

E ∝ Q ,

, где символ ∝ означает «пропорционально». Из обсуждения электрического потенциала в однородном электрическом поле мы знаем, что напряжение на параллельных пластинах равно

В = Эд .

Таким образом, V ∝ E . Отсюда следует, что В ∝ В и, наоборот,

В ∝ В .

В общем случае это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.

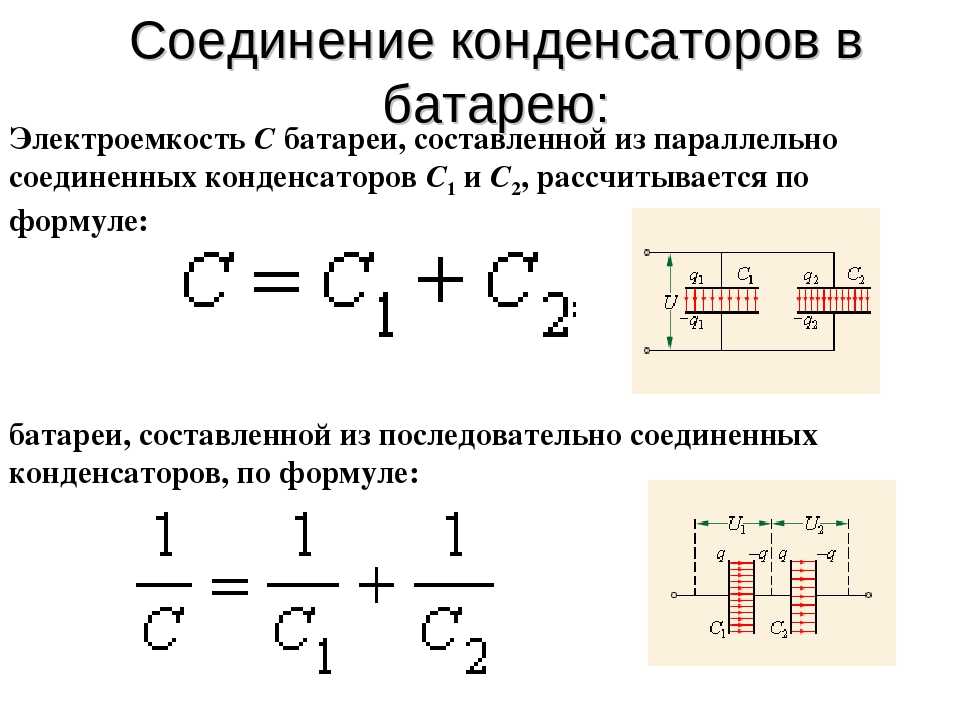
Различные конденсаторы сохраняют разный заряд при одном и том же приложенном напряжении в зависимости от их физических характеристик. Мы определяем их емкость C так, что заряд Q , хранящийся в конденсаторе, пропорционален C . Заряд, хранящийся в конденсаторе, равен

Q =  CV .

Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Преобразовывая уравнение, мы видим, что емкость C — это количество заряда, накопленного на вольт, или

[латекс]С=\frac{Q}{V}\\[/латекс].

Емкость

Емкость C количество заряда, хранимого на вольт, или

[latex]C=\frac{Q}{V}\\[/latex]

Единицей измерения емкости является фарад (F), названный в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или

[латекс]1\текст{ F}=\frac{1\text{ C}}{1\text{ V}} \\[/латекс].

Конденсатор емкостью 1 фарад может хранить 1 кулон (очень большое количество заряда) при подаче всего 1 вольта. Таким образом, один фарад — это очень большая емкость. Типичные конденсаторы варьируются от долей пикофарад (1 пФ = 10 ⁻¹² Ф) в миллифарад (1 мФ = 10 ⁻³ Ф).

На рис. 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.

Рисунок 3. Некоторые типовые конденсаторы. Размер и значение емкости не обязательно связаны. (кредит: Windell Oskay)

Конденсатор с параллельными пластинами

Рис. 4. Конденсатор с параллельными пластинами, пластины которого расположены на расстоянии d. Каждая пластина имеет площадь A.

Конденсатор с параллельными пластинами, показанный на рисунке 4 , состоит из двух идентичных проводящих пластин, каждая из которых имеет площадь поверхности 90 117 A 90 118 , разделенных расстоянием 90 117 d 90 118 (без материала между пластинами). Когда к конденсатору прикладывается напряжение В , он накапливает заряд Q , как показано на рисунке. Мы можем видеть, как его емкость зависит от A и d , рассматривая характеристики кулоновской силы.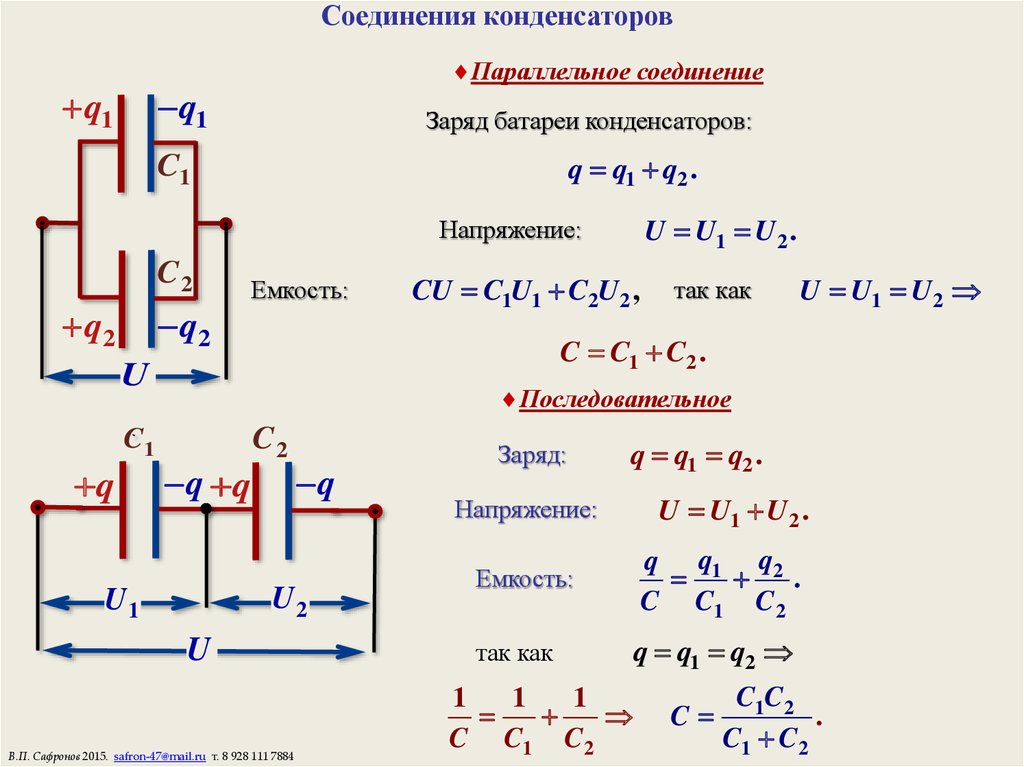 Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом C должен быть больше для более крупного A . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Таким образом, C должно быть больше для меньшего d .

Можно показать, что для конденсатора с плоскими пластинами есть только два фактора ( A и d ), которые влияют на его емкость C . Емкость конденсатора с плоскими пластинами в виде уравнения определяется как

[латекс] C=\epsilon_{o}\frac{A}{d}\\[/latex].

Емкость конденсатора с параллельными пластинами

[latex]C=\epsilon_{o}\frac{A}{d}\\[/latex]

A — площадь одной пластины в квадратных метрах, а d – расстояние между плитами в метрах. Постоянная ε ₀ — диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε ₀ = 8,85 × 10 ⁻¹² Ф/м. Единицы Ф/м эквивалентны C ² / Н·м ² . Небольшое числовое значение ε ₀ связано с большим размером фарада. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.)

Пример 1. Емкость и накопленный заряд в Конденсатор с параллельными пластинами

1. Какова емкость конденсатора с плоскими пластинами с металлическими пластинами площадью 1,00 м каждая ² , через 1,00 мм?
2. Какой заряд накапливается в этом конденсаторе, если к нему приложено напряжение 3,00 × 10 ³ В ?

Стратегия

Нахождение емкости C является прямым применением уравнения [латекс]С=\epsilon_{o}\frac{A}{d}\\[/latex]. {-9{3}\text{ V}\right)\\\text{ }&=&26.6\mu\text{C}\end{array}\\[/latex]

Обсуждение части 2

Эта плата лишь немного больше, чем в обычном статическом электричестве. Поскольку воздух разрушается примерно при 3,00 × 10 90 239 6 90 240 В/м, на этом конденсаторе невозможно накопить больше заряда за счет увеличения напряжения.

Еще один интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам избирательно входить и выходить из клетки. Разность потенциалов на мембране около -70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженного натрия (Na 9{6}\text{ В/м}\\[/latex]

Этого электрического поля достаточно, чтобы вызвать пробой воздуха.

Диэлектрик

В предыдущем примере подчеркивается сложность накопления большого количества заряда в конденсаторах. Если d уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]E=\frac{V}{d}\\[/latex]).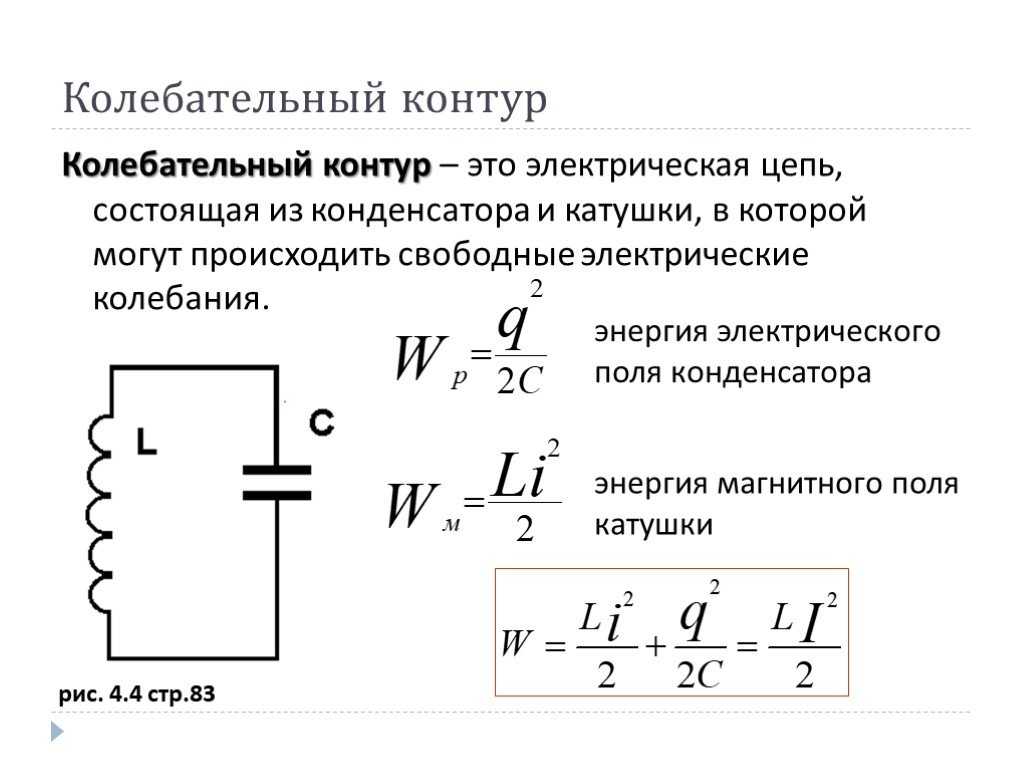 Важным решением этой проблемы является размещение изоляционного материала, называемого 9.0117 диэлектрик , между обкладками конденсатора и пусть будет как можно меньше. Мало того, что d меньшего размера увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, до разрушения.

Использование диэлектрика в конденсаторе имеет еще одно преимущество. В зависимости от используемого материала емкость больше, чем указанная уравнением [латекс]C=\kappa\epsilon_{0}\frac{A}{d}\\[/latex] в 9 раз.0117 κ , называемая диэлектрической проницаемостью . Емкость конденсатора с параллельными пластинами с диэлектриком между пластинами определяется формулой [латекс]C=\kappa\epsilon_{0}\frac{A}{d}\\[/латекс] (конденсатор с параллельными пластинами с диэлектриком).

Значения диэлектрической проницаемости κ для различных материалов приведены в таблице 1. Обратите внимание, что κ для вакуума точно равно 1, поэтому приведенное выше уравнение справедливо и в этом случае. Если использовать диэлектрик, возможно, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в 9 раз.0117 κ , что для тефлона составляет 2,1.

Самостоятельный эксперимент: изготовление конденсатора

Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут алюминиевой фольгой, а перегородка (диэлектрик) между ними будет бумагой.

Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность различных материалов при 20ºC
Материал	Диэлектрическая проницаемость κ	Диэлектрическая прочность (В/м)
Пылесос	1.00000	—
Воздух	1.00059	3 × 10 6
Бакелит	4,9	24 × 10 6
Плавленый кварц	3,78	8 × 10 6
Неопреновый каучук	6,7	12 × 10 6
Нейлон	3,4	14 × 10 6
Бумага	3,7	16 × 10 6
Полистирол	2,56	24 × 10 6
Стекло пирекс	5,6	14 × 10 6
Силиконовое масло	2,5	15 × 10 6
Титанат стронция	233	8 × 10 6
Тефлон	2. 1	60 × 10 6
Вода	80	—

Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением того, что воздух может стать проводящим, если напряженность электрического поля становится слишком большой. (Напомним, что [latex]E=\frac{V}{d}\\[/latex] для конденсатора с плоскими пластинами.) В таблице 1 также показаны максимальные значения напряженности электрического поля в В/м, называемые 9{-3}\text{ m}\right)\\\text{ }&=&3000\text{ V}\end{array}\\[/latex]

Тефлон составляет 60 000 В, так как диэлектрическая прочность тефлона составляет 60 × 10 ⁶ В/м. Так тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для заполненного воздухом конденсатора с плоскими пластинами, мы находим, что конденсатор с тефлоновым наполнением может хранить максимальный заряд 94\text{ V})\\\text{ }&=&1. 1\text{ mC}\end{array}\\[/latex]

Это в 42 раза больше заряда того же конденсатора, заполненного воздухом.

Диэлектрическая прочность

Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.

Каким образом диэлектрик увеличивает емкость под микроскопом? В этом виновата поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость к . Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рисунке 5 схематически показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии д прочь.

Рис. 5. (а) Молекулы изоляционного материала между пластинами конденсатора поляризуются заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (b) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к меньшему напряжению между пластинами при том же заряде. Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.

Другой способ понять, как диэлектрик увеличивает емкость, — рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5(b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно В = Эд , так что диэлектрик также уменьшает его. Таким образом, имеется меньшее напряжение В для того же заряда Q ; так как [latex]C=\frac{Q}{V}\\[/latex], емкость C больше.

Диэлектрическая проницаемость обычно определяется как [латекс]\каппа=\фрак{Е_0}{Е}\\[/латекс] или отношение электрического поля в вакууме к полю в диэлектрическом материале и составляет тесно связано с поляризуемостью материала.

Вещи большие и малые: субмикроскопическое происхождение поляризации

Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет усовершенствована в другом месте, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.

Рисунок 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.

В атомной физике мы найдем, что орбиты электронов правильнее рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных местоположений и траекторий планет в их обращается вокруг Солнца). Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.

Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому их называют полярными молекулами. На рисунке 7 показано разделение заряда в молекуле воды, которая имеет два атома водорода и один атом кислорода (H ₂ O). Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость. Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков.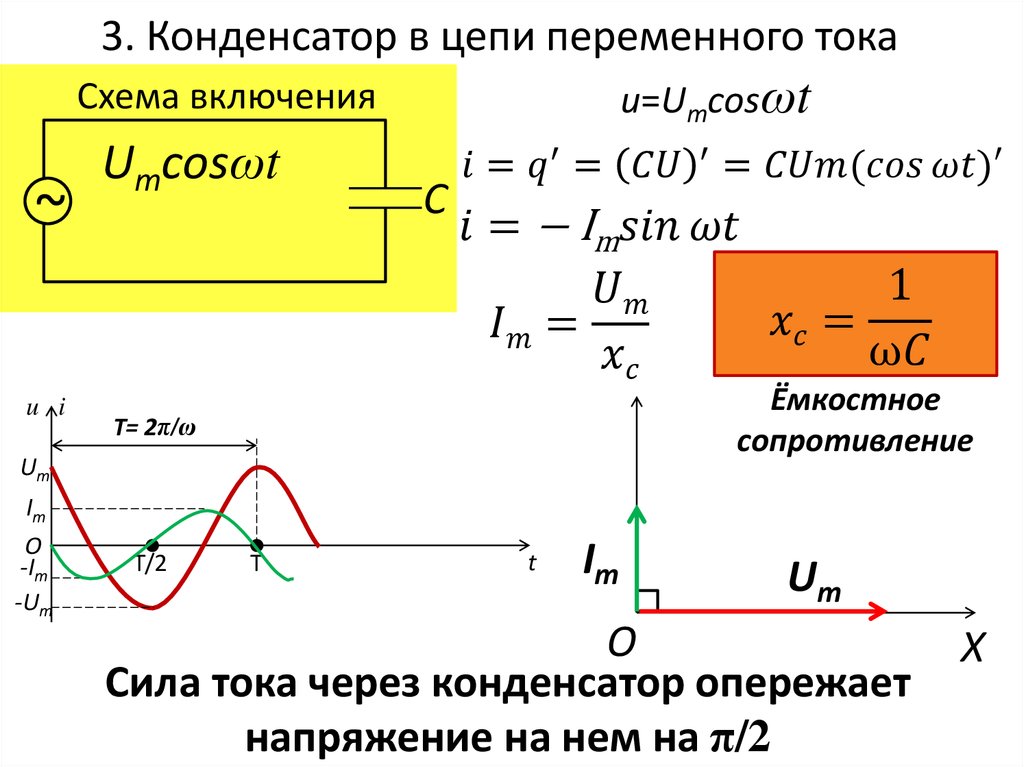 Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

Рис. 7. Представление художника о молекуле воды. Существует неотъемлемое разделение зарядов, поэтому вода является полярной молекулой. Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда вблизи двух ядер водорода. (Обратите внимание, что схема справа представляет собой грубую иллюстрацию распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)

PhET Explorations: Capacitor Lab

Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость. Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java.

Резюме раздела

• Конденсатор — это устройство, используемое для накопления заряда.
• Количество заряда  Q  , которое может хранить конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
• Емкость C  является количеством накопленного заряда на вольт, или [latex]C=\frac{Q}{V}\\[/latex].
• Емкость конденсатора с параллельными пластинами равна [латекс]C={\epsilon}_{0}\frac{A}{d}\\[/latex] , когда пластины разделены воздухом или свободным пространством. [latex]{\epsilon}_{\text{0}}[/latex] называется диэлектрической проницаемостью свободного пространства.
• Емкость плоскопараллельного конденсатора с диэлектриком между пластинами определяется как [латекс]C=\kappa\epsilon_{0}\frac{A}{d}\\[/latex], где κ — диэлектрическая проницаемость материала.
• Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.

Концептуальные вопросы

1. Зависит ли емкость устройства от приложенного напряжения? А заряд, хранящийся в нем?
2. Используйте характеристики силы Кулона, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора. Точно так же объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
3. Объясните, почему диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора. Какова независимая причина того, что диэлектрический материал также позволяет прикладывать большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C  и допускает большее В .)
4. Как полярный характер молекул воды помогает объяснить относительно большую диэлектрическую проницаемость воды? (См. рис. 7.)
5. Искры будут возникать между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем при сухом. Объясните почему, учитывая полярность молекул воды.
6. Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
7. Мембраны живых клеток, в том числе клеток человека, характеризуются разделением заряда поперек мембраны. Таким образом, мембраны представляют собой заряженные конденсаторы с важными функциями, связанными с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизация энергии пищи или какой-либо другой источник?

Рис. 8. Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K ⁺ (калий) и Cl ^– (хлорид) в указанных направлениях до тех пор, пока кулоновская сила не остановит дальнейший перенос. Это приводит к образованию слоя положительного заряда снаружи, слоя отрицательного заряда внутри и, таким образом, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na ⁺ (ионы натрия).

Задачи и упражнения

1. Какой заряд накапливается в конденсаторе емкостью 180 мкФ при приложении к нему напряжения 120 В?
2. Найдите заряд, накопленный при подаче 5,50 В на конденсатор емкостью 8,00 пФ.
3. Какой заряд хранится в конденсаторе в примере 1?
4. Рассчитайте напряжение, прикладываемое к конденсатору емкостью 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
5. Какое напряжение необходимо приложить к конденсатору емкостью 8,00 нФ, чтобы накопить заряд 0,160 мКл?
6. Какая емкость необходима для накопления заряда 3,00 мкКл при напряжении 120 В?
7. Какова емкость вывода большого генератора Ван де Граафа, если он хранит 8,00 мКл заряда при напряжении 12,0 МВ?
8. Найдите емкость плоского конденсатора с пластинами площадью 5,00 м ² , разделенными тефлоновым слоем толщиной 0,100 мм.
9. (a) Какова емкость плоского конденсатора с пластинами площадью 1,50 м ² , разделенными 0,0200 мм неопреновой резины? б) Какой заряд он имеет, когда 9. 00 В подается на него?
10. Интегрированные концепции. Шутник подает 450 В на конденсатор емкостью 80,0 мкФ, а затем бросает его ничего не подозревающей жертве. Палец пострадавшего обожжен разрядом конденсатора через 0,200 г плоти. Что такое повышение температуры тела? Разумно ли предположить отсутствие фазового перехода?
11. Необоснованные результаты.  (a) Некоторый конденсатор с параллельными пластинами имеет пластины площадью 4,00 м ² , разделенные нейлоном толщиной 0,0100 мм, и сохраняет заряд 0,170 Кл. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие предположения ответственны или непоследовательны?

Глоссарий

конденсатор: устройство, накапливающее электрический заряд материал

диэлектрическая прочность: максимальное электрическое поле, выше которого изоляционный материал начинает разрушаться и проводить

плоскопараллельный конденсатор: две одинаковые проводящие пластины, разделенные расстоянием

полярная молекула:  молекула с присущим разделением зарядов

Избранные решения задач и упражнений

1.