Power Electronics • Просмотр темы
Dizel1 писал(а):
только емкость у него разбита на 2 части – емкости эти разные – соответственно разные и напряжения и энергия накапливаемая в этих емкостях – напряжения разные и каждое напряжение нагружено на свое сопротивление
Это понятно. Теоретически абсолютное значение емкостей не важно, важно их соотношение. Но проблема в том, что ВК в режиме С накачивает в емкость не синусоидальный сигнал, а колокол с паузами. То есть сигнал с большим спектром гармоник, следовательно сам ВК слегка шунтирует П-контур и гробит добротность. Для того чтобы выйти на Q=3 расчеты пророчат емкости 200-500 пФ.. А это нереально много для УКВ частот. Реактивные токи многократно выше полезных. Вот эта проблема как раз и решилась установкой малой емкости последовательно с L. При этом оставшиеся бОльшие емкости так же выполняют функции согласования, только их номинал в 10 раз меньше чем в оригинальном п-контуре c Q=3.
Dizel1 писал(а):
ЗЫ а зачем Вам диполь?? сделайте чвертьволновый штырь и противовесы.
а диполь широкополосным трансиком согласовать можно.. но еще нужен переход с несимметричного выхода транзисторного ум на диполь..
можно сделать на колечке с феррита с проницаемостью 10-20 ..
или выход передатчика нагрузить на контур – а на контур катушку связи симметричную мотнуть…
Мне не нужна круговая направленность потому что придется вкачивать больше дури. В идеале мне надо передать телеметрию на дистанцию 10 км пучком с углом расхождения 30 градусов. Но даже диаграмма направленности горизонтального диполя меня вполне устраивает. А то что он малозаметный и малогабаритный очень плюс.
На счет симметрирования. Просто цеплял противовесную часть диполя к земле схемы, на провода подводящие питание и сигнал к передатчику надел ферритовое кольцо. Замерил напряженность поля на конце штыря и противовеса, она оказалось идентичной. Размер платки маленький. Так что можно забить… А сейчас я заложил двухтактный симметричный выход, так что будут два равнозначных противофазных штыря и “холодная” земля, без этих проблем.
Dizel1 писал(а):
посмотрите комнатную антенну к ТВ типа “телескопических усов” .. там такое есть…
или погуглите такую штуку как “Балун”
но лучше штырь – мороки меньше…
Спасибо, приму к сведению, когда плата передатчика и антенна будут связываться коаксиалом.
Dizel1 писал(а):
ЗЫ – если подавить гармоники – то фильтр на выход надо… не П контур… но Вы его в принципе сделали..
что не ясно – спросите..
Да я уже погрузился в ностальгию, копаю всякую схемотехнику. Приемник то тоже надо делать, это же по сути радиомодуль получается.
Пока думаю взять готовую платку на TDA7021 и ей на входе внешний гетеродин-смеситель мутить. Можно конечно МС3362, но боюсь что не найду всех фильтров. Да и особая избирательность и защита от помех не нужна. Принимающая сторона сама отличит полезное и лишнее. Я уже даже на сверхрегенератор соглашусь. Есть у меня некие наработки с контуром включенным частично. Избирательность не хуже радиовещательных приемников.
контур – не лучший вариант согласования для коротких антенн
Я решил провести несколько экспериментов, чтобы увидеть, как разные значения индуктивности и емкости в параллельной согласующей цепи LC-контура повлияют на величину выходного радиочастотного сигнала.
Для своего первого теста я хотел использовать только индуктивность без параллельной емкости, поскольку, согласно предыдущей теории, она должна давать наибольшую излучаемую мощность. У меня была в наличии переменная индуктивность с диапазоном регулировки 40–120 мкГн, чего было бы недостаточно для согласования с антенной на частоте 1000 кГц. Итак, я пробовал разные катушки индуктивности с фиксированным значением последовательно с переменной индуктивностью, пока индуктивность не была достаточной для настройки антенны на резонанс.
Благодаря такому расположению я смог достичь пика антенны без дополнительной параллельной емкости, и поэтому весь циркулирующий ток в резервуаре протекает через антенну.
Это должно обеспечить наиболее эффективное соединение с антенной.
Я установил передатчик, как показано на схеме выше, используя фиксированную индуктивность 330мкГн, последовательно с переменной индуктивностью 40–120 мкГн, и разместил пассивный измеритель мощности сигнала на фиксированном расстоянии от антенны. Для первого теста индуктивность была отрегулирована на пиковый выход, который имел место, когда общая индуктивность составляла 446 мкГн. (Это отличается от более ранних расчетов, которые предсказывали требуемую индуктивность в 1054 мкГн, но это объясняется дополнительной паразитной емкостью антенны.) Затем была зафиксирована мощность сигнала на измерителе.
Для следующего теста я удалил дроссель серии 330мкГн, чтобы в цепи была только переменная дроссель. К этому времени я подсчитал, что емкость антенны составляет примерно 50 пФ, поэтому для достижения пика антенны с переменной индуктивностью, установленной около ее максимальной индуктивности, потребуются дополнительные 220 пФ параллельной емкости.
Я подключил конденсатор 220 пФ параллельно переменной индуктивности, а затем настроил антенну, снова записав силу сигнала.
Я повторил эксперимент с различными конденсаторами фиксированной емкости и записал мощность сигнала с помощью переменной индуктивности, настроенной на лучший пик. Результаты представлены в таблице ниже:
L – это фактическое измеренное значение индуктивности, когда цепь находилась в резонансе.
C-net – это рассчитанная общая емкость резервуара на основе измеренной индуктивности с использованием стандартной формулы резонанса LC на частоте 1000 кГц.
C-parallel – это измеренное значение параллельного конденсатора фиксированной емкости, который был добавлен в схему (номинальные значения были 220, 270, 330 и 560 пФ соответственно).
C-антенна – это емкость антенны, рассчитанная путем вычитания C-параллели из C-net. Среднее значение составляет 52 пФ. Таким образом, считается, что емкость антенны составляет 52 пФ.
Уровень записанного сигнала определяется измерителем мощности сигнала, имеющим шкалу от 0 до 10.
Я понятия не имею, должна ли эта шкала от 0 до 10 быть линейной. Я подозреваю, что нет. Итак, хотя мы можем сказать, что 7 определенно лучше 3,5, мы не можем сказать, что значение 7 вдвое лучше, чем значение 3,5. (Он может быть более чем в два раза лучше, а может быть и не вдвое лучше.)
Видно, что экспериментальные результаты подтверждают теорию. Максимальный уровень сигнала был самым высоким, когда использовалась только индуктивность, заставляющая весь резонансный ток проходить через антенну. Также, как и предполагалось, при добавлении параллельной емкости для усиления антенны наименьшая емкость давала наибольшую мощность выходного сигнала.
После выполнения этих тестов мне было любопытно, как ранее упомянутій П-контур будет сравниваться с параллельной сетью согласования LC.
Итак, я повторил эксперимент еще раз, используя П-контур. В этом случае переменный конденсатор на правой стороне П-цепи был опущен, потому что он будет эффективно работать параллельно с емкостью антенны и приведет к той же проблеме разделения тока, которая возникает с добавленным конденсатором в параллельной цепи LC.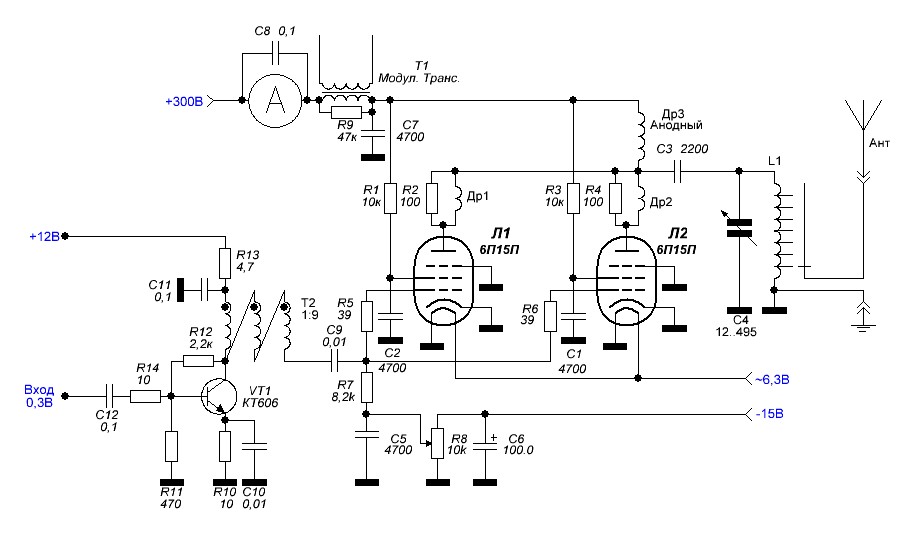
При настройке П-цепи на максимальный выходной сигнал уровень сигнала составил всего 1,4 – худшее из всех экспериментальных устройств. Хотя, как упоминалось ранее, П-контур будет лучшим выбором для минимизации гармоник сигнала.
Заключительные примечания
Простейшая и наиболее эффективная согласующая сеть для электрически малой антенны вещательного диапазона – это не что иное, как вариометр надлежащего размера или параллельный индуктор / конденсаторный бак с минимально возможной емкостью.
Было указано, что из-за чрезвычайно низкой радиационной стойкости антенны другие потери должны быть ниже того же порядка величины, чтобы получить любое разумное количество радиочастотного излучения.
Никакого упоминания о резистивной составляющей согласующей катушки индуктивности L1 не было. Конечно, он должен быть как можно ниже, потому что в конечном итоге он идет последовательно с другими потерями. Для имеющихся в продаже катушек индуктивности будет указано их сопротивление постоянному току.
Для самой антенны следует выбирать проводник наибольшего практического диаметра, чтобы минимизировать резистивные потери антенны. Медь – лучший проводящий материал из-за ее низкого удельного сопротивления.
Что такое «отклонение частоты» (1) ｜Методы оценки колебательного контура｜Продукция｜NDK
Что такое «отклонение частоты» (1) <Обзор>
На этот раз мы хотели бы представить обзор девиации частоты.
１．Основы
Основная девиация частоты (символ “dF”) представляет собой разницу между измеряемой частотой и опорной частотой.
Чтобы уточнить степень отклонения, отношение dF к опорной частоте обычно называют «отклонением частоты» (символ «dF/F»).
Общая формула для «dF/F» представляет собой следующее уравнение [1]
(* ИУ: тестируемое устройство)
Концепция уравнения [1] также используется в спецификациях кварцевых блоков.
Допуск по частоте, описанный в спецификациях кварцевых блоков, рассчитывается по следующему уравнению [2].
Если вы рассчитываете наименьшую и наибольшую частоту, ожидаемую для кварцевых блоков, подставьте наименьшее и наибольшее значения допустимой частоты в dF/F в приведенной ниже формуле (3), которая является вариантом приведенной выше формулы (2), чтобы получить их.
Например, в спецификации определенного кристалла указано
Номинальная частота: 20 000 МГц
Допуск по частоте: макс. ±50 ppm.
Емкость нагрузки: 8 пФ
Самая низкая и самая высокая частота кварцевого блока определяется следующим образом.
Минимальная частота: при CL=8 пФ: 20,000 МГц×(1-50×10-6)＝19,999000 МГц
２．Отклонение частоты при анализе цепи
Частота, подлежащая измерению при анализе цепи, представляет собой рабочую частоту тестируемой цепи.
Как правило, номинальная частота используется в качестве опорной частоты, но номинальная частота не используется в качестве опорной частоты при анализе цепи.
Причина этого в том, что кварцевые блоки имеют допуск по частоте.
Ниже приводится объяснение, основанное на конкретном примере.
Для удобства пояснений мы будем называть произведение минимальной частоты кварцевого генератора с номинальной частотой 20 000 МГц, описанного в «Основах», и произведение максимальной частоты следующим образом.
Кристалл A: произведение минимальной частоты (19,999000 МГц при CL=8 пФ)
Кристалл B: произведение максимальной частоты (20,001000 МГц при CL=8 пФ)
Предположим, что частота цепи составляет 19,999100 МГц, когда кварц A установлен в цепи.
Когда кварц B установлен в той же цепи, частота в цепи отличается от частоты, когда кварц A установлен. Частота простым расчетом составляет 20,001100 МГц.
Предположим, что кварц B колеблется с частотой 20,001100 МГц, как рассчитано выше.
Если вычислить dF/F, предполагая, что опорная частота является номинальной, результат будет следующим.
Вариант 1: использование кристалла A
Вариант 2: использование кристалла B
Как только что было сказано выше, полученные значения сильно различаются, даже если они оцениваются для одной и той же схемы.
Чтобы устранить эту разницу, dF/F выводится с использованием следующего уравнения [4] при анализе цепей.
| F ном. | ：Номинальная частота кристалла |
| F Класс ※2 | ：Частота кристалла при CL= x пФ (x : значение, указанное в спецификации кварцевых блоков) |
| F-контур ※2 | ：Частота цепи при установке экспериментального кристалла |
*1: «Символ почти равного в [4]» имеет место, потому что разница между F nom и F CL составляет сотни частей на миллион, независимо от того, насколько она велика.
*2：Этот символ не является общим (в этом отчете он предоставлен для удобства).
Результаты применения уравнения [4] к предыдущему примеру следующие.
Корпус: с использованием кристалла A
Случай: с использованием кристалла B
Получается такое же значение.
Вкратце, уравнение [4] используется для dF/F в случае анализа схемы, чтобы исключить влияние допуска по частоте, которое имеет любой кварцевый блок.
３．Точность частоты с учетом допустимого отклонения частоты кристаллических блоков
При учете изменения частоты среди произведений кристаллических блоков, т. е. допустимого отклонения частоты при комнатной температуре (+25°C), следующее уравнение может использоваться для определения допустимой частоты кварцевого блока.
Если вы хотите узнать, какова будет точность частоты колебаний (опорная частота является номинальной частотой), добавьте допуск частоты отдельного кварцевого блока к значению, полученному в уравнении (4), чтобы получить значение.
Точность частоты схемы с учетом допуска частоты кварцевого блока определяется по следующему уравнению [5].
Пример:
·dF/F согласно уравнению [4]: +10ppm
·Допуск по частоте кварцевого блока: в пределах ±30 ppm (при +25°C).
В приведенном выше случае Точность частоты = +10 ppm ± 30 ppm = от -20 ppm до +40 ppm
４．Погрешность частоты при учете допусков по частоте и частотно-температурных характеристик кварцевых блоков
Если вы хотите знать, какой будет точность частоты колебаний (опорная частота – номинальная частота) при учете отклонений частоты между изделиями и колебаний температуры, значение можно получить, прибавив к полученному значению частотно-температурную характеристику монокристаллического блока уравнение ⑤. Другими словами, получается следующее уравнение (6).
Точность частоты колебаний = Точность частоты колебаний по формуле (5) + Частотно-температурные характеристики монокристаллического блока … ⑥. Пример показан ниже.
Пример:
·dF/F согласно уравнению [4]: -10ppm
·Допуск частоты кристалла: в пределах ±40 ppm (при +25°C).
·Частотно-температурная характеристика кварцевого блока: в пределах ±50 ppm (в диапазоне рабочих температур)
В указанном случае точность частоты колебаний = -10 ppm ± 40 ppm ± 50 ppm = от -100 ppm до +80 ppm
５．В случае изменения характеристик нагрузочной емкости кварцевого блока
В отчете об анализе схемы может быть предложено изменить характеристики нагрузочной емкости кварцевого блока. Как получить dF/F в этом случае, описано ниже.
Принцип такой же, как описано в разделе 2.
Единственная разница заключается в том, «какая емкость нагрузки используется для измерения F CL».
Вот пример.
Пример:
Номинальная частота экспериментального кварцевого блока: 10 000 МГц (емкость нагрузки указана в спецификации: 8 пФ)
F (CL=8 пФ)=10,000028 МГц
F (CL=6 пФ)=10,000388 МГц
F контур=10,000400 МГц =8 пФ
Ф ( CL=6pF) ※3 ：F CL, измеренная с емкостью нагрузки = 6pF
F Circuit ※3 ：Частота в цепи, когда экспериментальный кварцевый блок установлен в измеряемой цепи.
※3：Этот символ не является общим (предоставлен для удобства
В приведенном выше случае девиация частоты колебаний определяется следующим образом.
(A): Когда опорная частота F (CL=8pF):
(B): Когда опорная частота F (CL=6pF):
Калькулятор частоты среза
Created by Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 02 февраля 2023 г.
Содержание:- Что такое частота среза? — определение частоты среза
- Что такое схема фильтра?
- Формула для частоты среза цепи RC-фильтра
- Формула для частоты среза схемы фильтра RL
- Как рассчитать частоту среза?
- Как пользоваться калькулятором частоты среза?
- Часто задаваемые вопросы
Калькулятор частоты среза Omni позволяет рассчитать частоту среза различных схем фильтра . Если вы не знаете, что такое частота среза или как ее рассчитать, не волнуйтесь! Прочтите эту статью, чтобы понять определение и формулу частоты среза.
Вы также найдете пример как определить частоту среза схемы RC-фильтра нижних частот .
Что такое частота среза? — определение частоты среза
Частота среза или угловая частота электронной схемы — это частота , при которой выходной сигнал системы начинает снижаться . Точнее, на частоте среза отношение (Выходная мощность)/(Входная мощность) ослабляет в 1/2 раза или коэффициент усиления по напряжению (Выходное напряжение)/(Входное напряжение) ослабляется в 1/√2 раз.
Чтобы понять это, давайте рассмотрим рисунок 1, на котором показано усиление цепи по напряжению в широком диапазоне частот. Мы можем выразить усиление схемы в децибелах следующим образом:
Усиление (дБ) = 20 log10Выходное напряжениеВходное напряжение\квадратный \скриптсайз \text{Усиление (дБ)} = 20\ \text{log}_{10} \frac{\text{Выходное напряжение}}{\text{Входное напряжение}}Усиление (дБ)=20 log10Входное напряжениеВыходное напряжение
Первоначально, когда Выходное напряжение=Входное напряжение\текст{Выходное напряжение} = \text{Входное напряжение}Выходное напряжение=Входное напряжение:
Коэффициент усиления (дБ)=20 log10(1)\quad \скриптсайз \text{Усиление (дБ)} = 20\ \text{log}_{10} (1)Усиление (дБ)=20 log10(1)
Так как log10(1)=0\text{log}_{ 10}(1) = 0log10(1)=0, мы можем написать:
Усиление (дБ)=0\quad \скриптсайз \text{Усиление (дБ)} = 0Усиление (дБ)=0
На частоте среза:
Выходное напряжениеВходное напряжение=12Усиление (дБ)=20 log10(0,707)=−3 дБ\quad \скриптсайз \начать{выравнивать*} \frac{\text{Выходное напряжение}}{\text{Входное напряжение}} &= \frac{1}{\sqrt{2}} \\ \\ \text{Усиление (дБ)} & = 20\ \text{log}_{10} (0,707) \\ &= -3\ \text{дБ} \end{align*}Входное напряжениеВыходное напряжениеУсиление (дБ)=2 1=20 log10(0,707)=−3 дБ Как видите, на частоте среза усиление схемы составляет -3 дБ .
Следовательно, частота среза также иногда известна как частота -3 дБ .
Частоты среза являются важными характеристиками любой схемы фильтра . Прежде чем идти дальше, давайте сначала попробуем понять, что такое схема фильтра.
Что такое контур фильтра?
Фильтры представляют собой электронные схемы, пропускающие через себя определенные частоты и блокирующие другие частоты . Две наиболее часто используемые схемы фильтров:
- Фильтр нижних частот; и
- Фильтр верхних частот.
Как следует из названия, фильтр нижних частот пропускает низкочастотные сигналы (от 0 Гц до частоты среза), а ослабляет высокочастотные сигналы . Фильтр верхних частот пропускает высокочастотные сигналы (выше частоты среза), а препятствует низкочастотным сигналам .
Чтобы узнать больше об этих двух схемах фильтров, воспользуйтесь нашим калькулятором фильтра верхних частот и калькулятором фильтра нижних частот.
Стоит отметить, что выходной сигнал не блокируется полностью на частоте среза, но становится все более и более ослабленным по мере продвижения к более высоким частотным областям (см. рис. 1).
В следующих разделах мы обсудим формулу угловой частоты для этих двух типов схем фильтров.
Формула для частоты среза цепи RC-фильтра
Цепь RC-фильтра состоит из резистора (RRR) и конденсатора (CCC). На рис. 2 показана принципиальная схема простого RC-фильтра нижних частот.
Мы знаем, что емкостное реактивное сопротивление (т. е. сопротивление конденсатора протекающему через него току) обратно пропорционально частоте . Следовательно, он будет иметь очень высокий импеданс на низких частотах, и мы можем считать цепь конденсатора разомкнутой. Это означает, что VoutV_{out}Vout равно VinV_{in}Vin на низких частотах. На более высоких частотах емкостное сопротивление очень низкое, что приводит к более низкому выходному напряжению по сравнению с входным напряжением.
Формула для расчета частоты среза для схемы RC-фильтра :
fc=12πRC\quad \скриптсайз f_c = \frac{1}{2 \pi R C}fc=2πRC1
Рисунок 2: Принципиальная схема RC-фильтра нижних частот. (Источник: wikimedia.org).Посетите наш калькулятор цепи RLC, если вы хотите рассчитать характеристическую частоту цепи RLC.
Формула для частоты среза схемы RL-фильтра
На рис. 3 показана простая схема RL-фильтра верхних частот, состоящая из резистора (RRR) и катушки индуктивности (LLL). Эта схема пропускает только высокочастотные сигналы. индуктивное реактивное сопротивление (т. е. сопротивление, оказываемое катушкой индуктивности протекающему через нее току) прямо пропорционально частоте сигнала . Цепь катушки индуктивности обеспечивает высокое сопротивление высокочастотным сигналам и, следовательно, может рассматриваться как разомкнутая цепь. Это означает, что VoutV_{out}Vout равно VinV_{in}Vin на высоких частотах.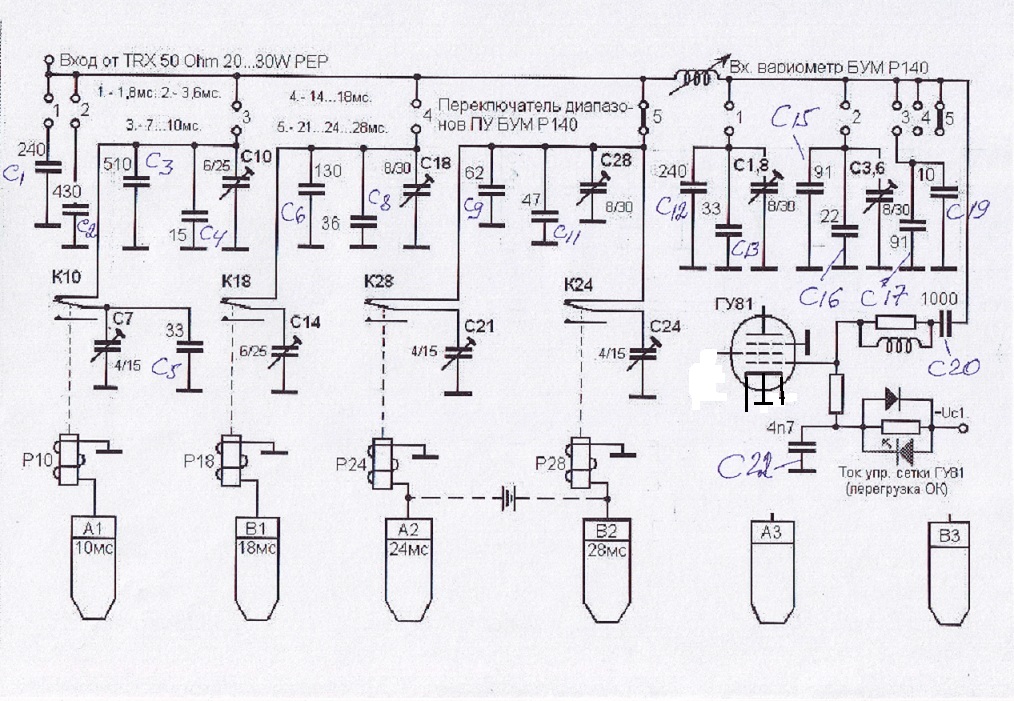
Для низкочастотных сигналов сопротивление практически отсутствует, поэтому падение напряжения на нем незначительно, что приводит к низкому выходному напряжению.
Формула для расчета частоты среза для схемы RL-фильтра :
fc=R2πL\quad \скриптсайз f_c = \frac{R}{2 \pi L}fc=2πLR
Рисунок 3: Принципиальная схема высокочастотного RL-фильтра.Формула угловой частоты для цепей фильтра верхних частот и цепей фильтра нижних частот одинакова.
Как рассчитать частоту среза?
Рассчитаем частоту среза схемы RC-фильтра нижних частот , состоящей из 10 кОм 9{-9} \ \rm F}fc=2π×10×103 Ом×25×10−9 F1
fc=636,6 Гцf_c = 636,6\ \text{Гц} fc=636,6 Гц.
Как пользоваться калькулятором частоты среза?
Теперь давайте решим ту же задачу, используя наш калькулятор частоты среза:
В раскрывающемся меню выберите схему фильтра типа в качестве RC.
Введите значение сопротивления как
10 кОм.
Введите значение емкость как
25 нФ.Калькулятор отобразит частоту среза (fcf_cfc), т. е.
636,6 Гц.Поскольку формула частоты среза RC-фильтра верхних частот такая же, как и у RC-фильтра нижних частот , вы можете использовать этот калькулятор для обоих.
Часто задаваемые вопросы
Что такое частота среза фильтра нижних частот?
Частота среза фильтра — это частота, при которой величина сигнала выходного напряжения падает на 70% . Фильтр нижних частот пропускает частоты между 0 Гц и частотой среза и ослабляет более высокие частоты.
Почему частота среза берется на уровне -3 дБ?
Децибел — это логарифмическая шкала, выраженная как 20 log(Выходная мощность/Входная мощность) . Усиление -3 дБ соответствует соотношению (выходная мощность/входная мощность) 0,5 , т.
