Петлевое усиление: Отрицательная обратная связь, часть 4: понятие устойчивости

Содержание

Отрицательная обратная связь, часть 4: понятие устойчивости

Добавлено 13 октября 2019 в 18:51

Сохранить или поделиться

Почему усилители с отрицательной обратной связью подвержены возбуждению? Каков основной критерий устойчивости? Давайте разберемся.

Вспомогательная информация

Чтобы вам не приходилось переключаться между страницами каждый раз, когда вы хотите обдумать общую структуру обратной связи, вот схема, представленная в первой статье:

Рисунок 1 – Абстрактный усилитель с отрицательной обратной связью

Бесплатного обеда не бывает…

Предыдущие статьи данной серии продемонстрировали, что отрицательная обратная связь – это простая недорогая методика, которая позволяет нам значительно улучшить характеристики схем усилителя. Сначала, кажется, что мы получаем что-то практически даром, пока мы не вспомним, что все эти выгоды достигаются за счет снижения коэффициента усиления. Однако этот дополнительный коэффициент усиления легко доступен у обычных полупроводниковых устройств, и, кроме того, нам обычно не требуется, или даже мы не хотим получить весь этот коэффициент усиления полностью. Итак, мы снова, кажется, получаем что-то почти даром; и поэтому все, кроме самых ярых оптимистов, могут что-то заподозрить. Возможно, вы скажете, должно же быть еще какое-то преимущество, которое мы теряем, когда добавляем эту, казалось бы, несущую только пользу схему отрицательной обратной связи. Что ж, интуиция вам не подвела, потому что, если мы не будем осторожны, мы потеряем что-то действительно важное: устойчивость.

Многие преимущества отрицательной обратной связи будут быстро забыты и отброшены, когда вы заметите, что ваш усилитель превратился в генератор. В каком-то смысле катастрофическое возбуждение колебаний не так уж и плохо, потому что проблема очевидна. Граничная устойчивость (marginal stability), приводящая к звону во временной области и появлению пиков в частотной области, может быть неуловимым источником проблем. Что еще хуже, схема в состоянии граничной устойчивости может работать во время тестирования, но будет бесполезна, когда усилитель будет подвергаться воздействию различных условий эксплуатации или окружающей среды. Таким образом, очень важно, чтобы мы хорошо понимали, почему отрицательная обратная связь может привести к возбуждению колебаний, и как обеспечить, чтобы усилитель усиливал, а не создавал колебания.

Когда отрицательная становится положительной

Неудивительно, что положительная обратная связь может привести к колебаниям: 1) подаем сигнал на вход 2) усиливаем этот входной сигнал 3) подаем усиленный выходной сигнал обратно и складываем его с входным сигналом 4) входной сигнал теперь больше, и этот больший входной усиливается 5) усиленный выходной сигнал снова подается обратно и складывается с входным сигналом 6) входной сигнал снова увеличивается, снова усиливается, снова получает положительный результат с выхода и т. д. Понятно, что это «неустойчивая» (нестабильная) ситуация – выходной сигнал будет быстро увеличиваться, пока он не будет ограничен какими-либо внешними условиями (обычно напряжениями питания).

Но почему отрицательная обратная связь вызывает возбуждение колебаний? Вычитая выходной сигнал из входного, мы обеспечиваем, чтобы увеличение входного сигнала всегда приводило через обратную связь к уравновешивающему уменьшению. Есть только одна ловушка: если сигнал переменного тока сдвигается по фазе на 180°, а затем подается обратно и вычитается, то наша отрицательная обратная связь становится положительной.

Рисунок 2 – Сдвиг фазы на 180° превращает отрицательную обратную связь в положительную

На левой диаграмме мы вычитаем положительное число из положительного числа и отрицательное число из отрицательного числа. Это действительно вычитание. На диаграмме справа мы вычитаем отрицательное число из положительного числа и положительное число из отрицательного числа. Это уже не отрицательная обратная связь – величина как положительных, так и отрицательных чисел увеличивается.

Петлевое усиление

Величина, которая непосредственно определяет, является ли цепь отрицательной обратной связи устойчивой, – это не коэффициент усиления с обратной связью или коэффициент усиления без обратной связи, а скорее петлевой коэффициент усиления (петлевое усиление), определяемый как Aβ.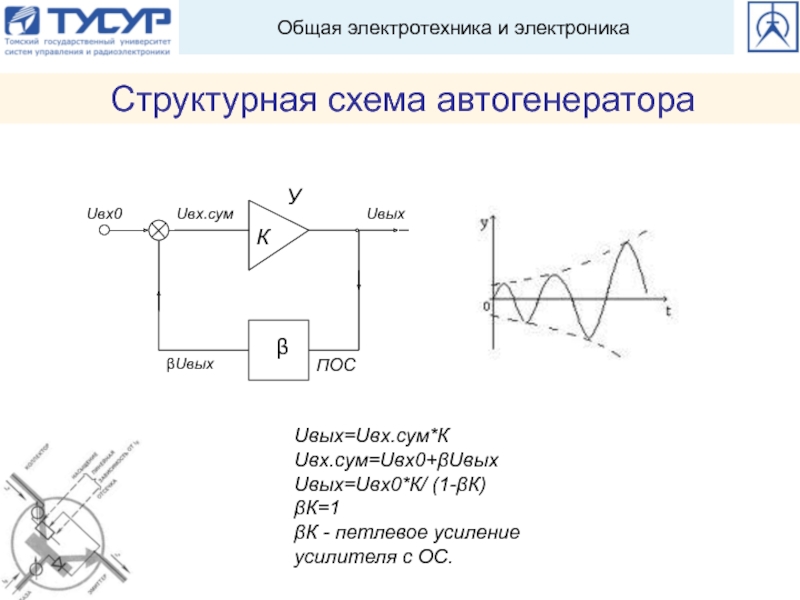 Напомним нашу формулу для коэффициента усиления усилителя с обратной связью:

\[G_{ОС}=\frac{A}{1+A\beta}\]

Эта формула предполагает, что Aβ является положительным числом (потому что положительный Aβ означает, что обратная связь отрицательна). Что происходит, когда Aβ не является положительным? Рассмотрим случай, когда Aβ = -1:

\[G_{ОС}=\frac{A}{1+\left(-1\right)}=\frac{A}{0}=\infty\]

В этом контексте коэффициент усиления усилителя с обратной связи, равный бесконечности, соответствует автогенератору – даже при нулевом входе выход насыщен. Таким образом, критической величиной в анализе устойчивости является петлевое усиление.

Важно выработать четкое понимание идеи того, почему возникают проблемы с устойчивостью, и как их предотвратить. Эта последовательность вопросов и ответов должна помочь решить некоторые из наиболее заметных проблем.

Вопрос: Откуда взялся этот сдвиг фазы? Я не просил никакого сдвига фазы в моем усилителе.

Ответ: Вспомните, что все усилители в конечном итоге будут демонстрировать спад усиления на высоких частотах. Усиление у операционных усилителей с внутренней компенсацией начинает спадать на очень низких частотах. В любом случае этот спад вызван полюсами где-то в цепи, а полюсы всегда приносят сдвиг фазы, а также уменьшают усиление.

Вопрос: Хорошо, у меня есть сдвиг фазы. Но все мои схемы на ОУ предназначены для применения либо для постоянного напряжения, либо для низкочастотных сигналов. Для моих сигналов не будет большого сдвига фазы, поэтому мне не нужно беспокоиться об устойчивости, верно?

Ответ: Хороший вопрос. К сожалению, частота интересующего вас сигнала, по сути, не имеет значения. Реальные сигналы всегда содержат шум, и часть этого шума будет находиться на высоких частотах. Кроме того, любой случайный скачок напряжения содержит высокочастотную составляющую. Помните, что при достаточном сдвиге фаз мы имеем дело с положительной, т. е. регенеративной, обратной связью. Даже когда эти неизбежные высокочастотные компоненты имеют очень низкую амплитуду, если ваша схема не является устойчивой по своей природе, регенеративный характер положительной обратной связи будет увеличивать их амплитуду до тех пор, пока колебания не станут заметными.

Вопрос: Тогда всё безнадежно! Усилители всегда демонстрируют сдвиг фазы на высоких частотах, а сигналы всегда зависят от высокочастотных составляющих – так как же схема может быть устойчивой?

Ответ: Не отчаивайтесь – здесь вступает в игру петлевое усиление. Подумайте об общей структуре обратной связи: любые сигналы, проходящие по петле обратной связи, умножаются на A, а затем на β. Вот почему мы называем Aβ «петлевым» усилением. Если на высоких частотах, где сдвиг фазы достигает 180°, Aβ меньше единицы, высокочастотные сдвинутые по фазе сигналы будут постепенно исчезать, вместо того, чтобы постепенно вырастать в основные колебания.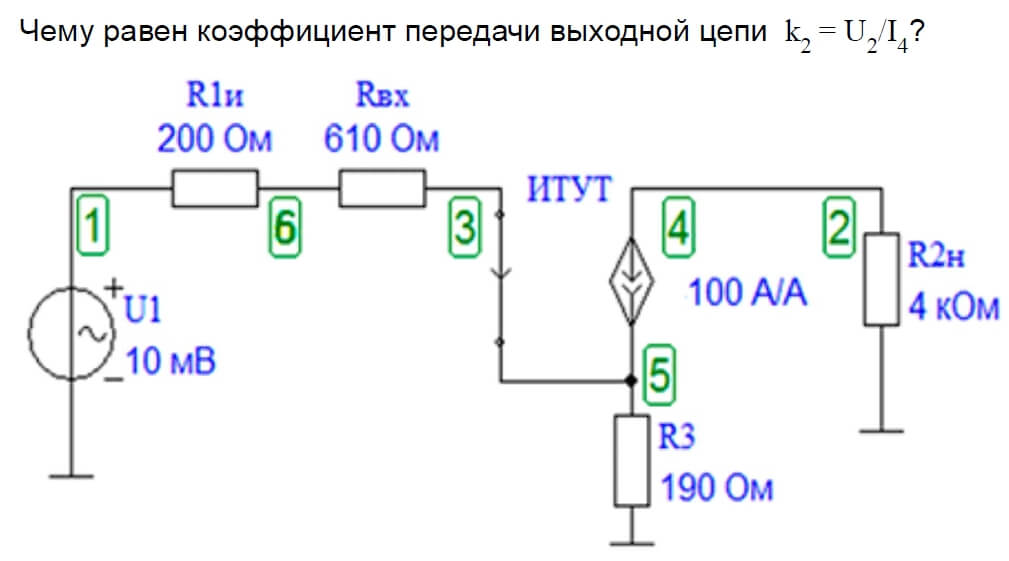 Убедитесь, что вы понимаете это. Представьте маленькие синусоидальные сигналы, проходящие через петлю Aβ: если Aβ больше единицы, синусоидальные сигналы будут увеличивать друг друга каждый раз, когда они проходят через петлю обратной связи, и их амплитуда будет постепенно увеличиваться, поскольку Aβ усиливает их. Если Aβ меньше единицы, сигналы будут постепенно ослабляться до незначительной величины, несмотря на то, что они усиливают друг друга в узле «вычитания».

Рисунок 3 – Отсутствие возбуждения колебаний на высоких частотах при Aβ < 1

Критерий устойчивости

Теперь мы можем явным образом сформулировать теоретический критерий устойчивости, где «петлевой коэффициент усиления» равен частотной характеристике коэффициента усиления усилителя без обратной связи, умноженной на частотную характеристику коэффициента передачи цепи обратной связи, (то есть равен петлевому коэффициенту усиления, Aβ, анализируемому как функция от частоты): если величина петлевого усиления меньше единицы на частоте, на которой сдвиг фазы петлевого усиления равен 180°, схема устойчива. На практике петлевое усиление на этой частоте должно быть значительно меньше единицы, чтобы избежать состояния граничной устойчивости.

Заключение

Теперь мы знаем, почему усилители с отрицательной обратной связью подвержены возбуждению колебаний, и какие условия должны быть соблюдены для обеспечения устойчивости. Но история устойчивости гораздо шире, что и будет показано в следующих статьях. Для большего понимания петлевого усиления в следующей статье мы используем моделирование в частотной области. Мы также обсудим запас по усилению и запас по фазе, два тесно связанных параметра, используемых для оценки степени устойчивости усилителя.

Оригинал статьи:

Отрицательная обратная связь, часть 9: разрыв петли

Добавлено 16 октября 2019 в 21:23

Сохранить или поделиться

Простая методика моделирования «с разрывом петли обратной связи» обеспечивает удобный анализ устойчивости, особенно в случае сложных схем. Рассмотрим ее.

Вспомогательная информация

Неуловимое петлевое усиление

Вы, возможно, уже поняли, что в анализе устойчивости есть что-то слегка неприятное – почему-то он не так прост, как должен быть. После некоторого размышления вы, вероятно, определили источник этого неудобства: петлевое усиление. Как мы теперь хорошо знаем, устойчивость в основном зависит от частотной характеристики петлевого усиления Aβ; проблема заключается в том, что петлевое усиление не является измеримой или даже интуитивно понятной величиной в реальных схемах. Коэффициент усиления без обратной связи A является интуитивно понятной и измеримой величиной: подайте тестовый сигнал на сам усилитель без обратной связи и измерьте выходной сигнал. Аналогично, коэффициент усиления с обратной связью интуитивно понятен и измерим: соберите (или смоделируйте) схему и измерьте выходной сигнал относительно входного. Петлевое усиление, напротив, «скрыто» внутри наблюдаемых извне напряжений и токов.

Так что же происходит, когда вам нужно исследовать устойчивость сложного усилителя с обратной связью? Или что, если вам просто не нравится некий «ручной» подход, принятый в предыдущих статьях, где мы рассматривали цепь обратной связи как частично отдельную цепь и объединяли напряжение обратной связи с амплитудно-частотной характеристикой усилителя без обратной связи для создания необходимых графиков для анализа устойчивости? Что ж, оказывается, что существует четко определенный метод извлечения петлевого усиления из существующей схемы.

Разорванная петля

На следующей диаграмме показана общая структура обратной связи, представленная в первой статье, но с одним важным изменением: цепь обратной связи была оторвана от выхода, и в точку разрыва подан тестовый сигнал.

Рисунок 1 – Усилитель с разорванной петлей отрицательной обратной связи

Если вы удалите (т. е. установите на ноль) входной сигнал из всей системы (здесь обозначен как элемент управление), а затем проанализируете поток сигналов через эту новую структуру, вы увидите, что в игру вступают следующие отношения:

\[\text{входной_сигнал}=0-\beta\times\text{тестовый_сигнал} \Rightarrow\\ \Rightarrow\ \text{выходной_сигнал}=-A\beta\times\text{тестовый_сигнал} \Rightarrow\\ \Rightarrow\ \ \frac{\text{выходной_сигнал}}{\text{тестовый_сигнал}}=-A\beta\]

В наших симуляциях мы всегда будем использовать тестовое напряжение 1 В, поэтому мы можем упростить это выражение следующим образом:

\[A\beta=-\text{выходной_сигнал}\]

Таким образом, когда мы разрываем петлю обратной связи и вводим тестовый сигнал 1 В в цепь обратной связи, выходной сигнал усилителя, умноженный на минус 1, представляет собой петлевой коэффициент усиления. Теоретически этот подход может быть использован для исследования петлевого усиления с помощью математического анализа, моделирования или даже реальной схемы вместе с тестовым сигналом с изменяющейся частотой. Но с математическим и измерительным подходами возникают практические трудности, прежде всего потому, что теоретически необходимо нагрузить разорванную петлю импедансом, эквивалентным импедансу, существовавшему до разрыва петли. Поэтому без дальнейших церемоний мы перейдем к использованию этого метода на основе моделирования. На самом деле, в данном контексте моделирование обычно (если не всегда) это наименее утомительный и наиболее информативный подход.

Еще один полюс, о котором стоит побеспокоиться

Из предыдущих статей мы знаем, что полюсы могут создавать проблемы тем, кому нужны устойчивые усилители. Операционные усилители с внутренней компенсацией имеют один полюс, доминирующий на частотной характеристике, что обеспечивает устойчивость в большинстве ситуаций. Но полюс в цепи обратной связи, созданный емкостью, параллельной резистору обратной связи, может обеспечить дополнительный сдвиг фазы, достаточный, чтобы ухудшить устойчивость. К сожалению, есть другое место, где (часто непреднамеренная) емкость может вызывать колебания, а именно – в выходном узле операционного усилителя:

Рисунок 2 – Емкость нагрузки

Как видите, любая емкость нагрузки, подключенная непосредственно к выходу, в сочетании с выходным сопротивлением операционного усилителя (небольшим, но ненулевым) образует RC-цепь – иными словами, однополюсный фильтр нижних частот, который дает дополнительные 90° сдвига фазы к частотной характеристике петлевого усиления.

Конечно, всегда есть хотя бы небольшое количество паразитной емкости. Сколько емкости нагрузки потребуется, чтобы реально сделать схему неустойчивой? Самый простой способ определить это – проверить техническое описание, в котором должно быть указано, какую емкость нагрузки можно безопасно использовать для конкретного операционного усилителя. Техническое описание может предоставить для этого числовую спецификацию или график, показывающий процент перерегулирования (выбросов) для различных значений емкости нагрузки. Вот пример последнего, взятый из технического описания операционного усилителя AD8505 производства Analog Devices:

Рисунок 3 – Зависимость амплитуды выбросов от емкости нагрузки для малых сигналов

Перерегулирование (амплитуда выбросов), превышающее приблизительно 20%, указывает на недостаточный запас по фазе, поэтому для AD8505 настолько маленькая емкость нагрузки, как 30 пФ, будет уже достаточной, чтобы вызывать беспокойство.

Методика

Давайте предположим, что мы используем ОУ для обеспечения опорного напряжения, равного V_DD/2, следующим образом:

Рисунок 4 – Тестовая схема в LTSpice

Текущее значение C_нагр представляет собой паразитную емкость. Давайте проверим устойчивость этой схемы, используя подход «разрыв петли». Мы должны убедиться, что симулятор может установить правильные условия смещения по постоянному напряжению, поэтому мы разрываем петлю, не разрывая цепь, с помощью очень большой индуктивности (1 ГГн). Эта нереально большая индуктивность с теоретическим импедансом, равным нулю при постоянном токе, обеспечивает правильное смещение по постоянному напряжению, одновременно эффективно блокируя все представляющие интерес сигналы переменного тока. Точно так же мы подаем тестовый сигнал 1 В переменного напряжения через большой конденсатор, который блокирует постоянный ток, но, по сути, не представляет импеданса для сигналов переменного тока.

Рисунок 5 – Организация разрыва петли обратной связи и подача тестового сигнала в LTSpice

Мы еще не закончили… нам еще нужно нагрузить цепь обратной связи импедансом, который был до того, как мы разорвали петлю. Для этого есть простой, хотя и не элегантный способ: скопировать и вставить всю схему и использовать этот дубликат в качестве фиктивной нагрузки; поскольку это та же схема, она обеспечит правильный нагрузочный импеданс.

Рисунок 6 – Нагружаем разрыв петли обратной связи

Как видите, исходный узел обратной связи подключен к узлу разрыва через другой большой конденсатор, чтобы обеспечить взаимодействие по переменному току при сохранении условий смещения по постоянному напряжению.

Теперь мы готовы к моделированию. Всё, что нам нужно сделать, это вывести V_выход.

Рисунок 7 – Полученная зависимость петлевого усиления от частоты

Напомним, что метод разрыва петли приводит к Aβ = -выходной_сигнал. Знак минуса соответствует сдвигу фазы на 180°, и это оказывается очень удобным: фаза начинается при 180° и приближается к нулю, что означает, что запас по фазе измеряется относительно 0°, а не 180°. Следовательно, на этом графике V_выход, если вы переместите курсор на частоту с единичным усилением, значение, указанное в поле «Phase» (фаза), представляет собой запас по фазе:

Рисунок 8 – Определение запаса по фазе

Как и ожидалось, этот операционный усилитель с внутренней компенсацией при такой небольшой емкости нагрузки полностью устойчив. Но, в конечном счете, мы решили, что нашему источнику опорного напряжения необходим дополнительный блокировочный конденсатор, поэтому мы добавим 1 нФ конденсатор на выход ОУ (не забудьте изменить конденсатор нагрузки в дублирующей схеме). Вот новый график –Aβ.

Рисунок 9 – Зависимость петлевого усиления от частоты после включения дополнительного конденсатора на выходе ОУ

Теперь у нас есть проблема. Запас по фазе уменьшился ниже 0°, что означает, что схема теперь совершенно устойчива (а не просто не достаточно устойчива). Существуют различные методы повышения устойчивости схем на операционных усилителях с большой емкостной нагрузкой; эта обширная тема выходит за рамки этой статьи. Здесь мы фокусируемся на анализе устойчивости, поэтому мы просто продемонстрируем эффект от одного простого, распространенного средства: установки последовательного резистора между выходом операционного усилителя и конденсатором нагрузки. Резистор создает ноль в передаточной функции обратной связи, и сдвиг фазы от этого нуля несколько компенсирует проблемный сдвиг фазы, создаваемый полюсом. Резистор должен иметь такой номинал, чтобы частота нуля была достаточно низкой, чтобы обеспечить адекватное восстановление фазы. Для этой схемы мы можем выбрать резистор в соответствии с информацией, приведенной в техническом описании для LTC6240:

Рисунок 10 – Выбор последовательного резистора для повышения устойчивости

Эти значения для перерегулирования (выбросов) 30%, но нам нужно что-то ближе к перерегулированию на 20%, поэтому мы попробуем 90 Ом:

Рисунок 11 – Добавляем на выход операционного усилителя резистор, включенный последовательно емкости нагрузкиРисунок 12 – Зависимость петлевого усиления от частоты после добавления последовательного резистора на выходе ОУ

Теперь у нас есть запас по фазе 34°, немного низковат, но, вероятно, достаточен. Чтобы довести запас по фазе до 45°, потребуется последовательное сопротивление около 130 Ом.

Заключение

Теперь в вашем аналитическом наборе инструментов есть метод моделирования, который может предоставить точную и удобную информацию об устойчивости для широкого спектра схем с отрицательной обратной связью, от простых буферов на операционных усилителях до сложных топологий усилителей на дискретных транзисторах. В следующей статье мы завершим эту серию исследованием устойчивости посредством моделирования во временной области, а не в частотной области.

Оригинал статьи:

LTspiceЕмкостная нагрузкаЗапас по фазеОбратная связьОтрицательная обратная связьОУ (операционный усилитель)Петлевое усилениеУсилитель с обратной связьюУстойчивость

Сохранить или поделиться

петлевое усиление – это… Что такое петлевое усиление?

петлевое усиление: Information technology: loop gain

петлевое уплотнение
петлевое устройство

Смотреть что такое “петлевое усиление” в других словарях:

Обратная связь — обратное воздействие результатов процесса на его протекание или управляемого процесса на управляющий орган. О. с. характеризует системы регулирования и управления в живой природе, обществе и технике. Различают положительную и… … Большая советская энциклопедия
Электронный генератор — Электронные генераторы большое множество устройств в радиотехнике и электронике (радиоэлектронике). Генератор представляет собой электронный усилитель охваченный цепью положительной обратной связи с фильтром. Содержание 1 Виды электронных… … Википедия

Генератор сигналов — Генератор сигналов это устройство, позволяющее получать сигнал определённой природы (электрический, акустический или другой), имеющий заданные характеристики (форму, энергетические или статистические характеристики и т.

t e(t)\mathrm{d}t.$$

Такой регулятор называется пропорционально-интегральным или ПИ-регулятором. Интегратор выдает сигнал, пропорциональный накопленной ошибке, поэтому переходный процесс несколько замедляется. Однако за счет интегрального канала обеспечивается нулевая ошибка в установившемся состоянии при ступенчатом возмущении и ступенчатом изменении задающего сигнала-уставки.

На рисунке ниже показаны переходные характеристики замкнутой системы с И-регулятором и объектом второго порядка вида

Реакция на скачок замкнутой системы с объектом 2-го порядка с И-регулятором.

При больших постоянных интегрирования переходная характеристика имеет вид, сходный с характеристикой апериодического звена. С уменьшением постоянных интегрирования растет усиление регулятора и когда петлевое усиление контура с обратной связью приближается к 1, в системе появляются колебания.

ПИ-регулятор имеет два существенных положительных отличия от И-регулятора: во-первых, его усиление на всех частотах не может стать меньше $K$, следовательно, увеличивается динамическая точность регулирования, во-вторых, по сравнению с И-регулятором, он вносит дополнительный сдвиг фаз только в области низких частот, что увеличивает запас устойчивости замкнутой системы. Оба фактора дают дополнительные степени свободы для оптимизации качества регулирования. В то же время, как и в И-регуляторе, модуль коэффициента передачи регулятора с уменьшением частоты стремится к бесконечности, обеспечивая тем самым нулевую ошибку в установившемся режиме. Отсутствие сдвига фаз на высоких частотах позволяет увеличить скорость нарастания управляемой переменной (по сравнению с И-регулятором) без снижения запаса устойчивости. Однако это справедливо до тех пор, пока пропорциональный коэффициент не станет настолько большой, что увеличит усиление контура до единицы.

Переходный процесс в ПИ-регуляторе показан на рисунке ниже.

Реакция замкнутой системы с ПИ регулятором на скачок .

С ростом пропорционального коэффициента появляется дополнительная ошибка во время переходного процесса, которая уменьшается с ростом $K$, однако при этом снижается запас устойчивости системы, поскольку с ростом $K$ увеличивается усиление на частоте . Это приводит к появлению затухающих колебаний в начале переходного процесса. Когда величина становится достаточно большой для компенсации ослабления сигнала в объекте, в системе появляются незатухающие колебания.

Следует отметить, что в отличие от П-регулятора, в котором ошибка остается в установившемся режиме, наличие интегрального члена в ПИ-регуляторе сводит эту ошибку в идеальном регуляторе до нуля, как в И-регуляторе.

Однако появление пропорционального коэффициента приводит к затягиванию переходного процесса по сравнению с И-регулятором. Объясняется это тем, что в ПИ-регуляторе сигнал ошибки, поступающий на вход интегратора, меньше, чем в И-регуляторе (он уменьшается благодаря пропорциональному коэффициенту), поэтому сигнал, компенсирующий ошибку нарастает медленнее, чем в И-регуляторе.

При работе прибора в режиме ПИ-регулятора величина выходного сигнала $Y_i$ зависит как от величины отклонения $E_i$, так и от суммы предыдущих рассогласований:

$$Y_i=\frac{1}{X_p}·\left(E_i+\frac{1}{τ_и}·\sum_{i=0}^n E_i·∆t_{изм}\right)·100%.

n E_i·∆t_{изм}$ – накопленная в i-й момент времени сумма рассогласований (интегральная сумма).

Из рисунка видно, что в первый момент времени, когда нет отклонения ($E_i=0$), нет и выходного сигнала ($Y_i=0$). С появлением отклонения $E_i$ появляются импульсы, длительность которых постепенно увеличивается. В импульсах присутствует пропорциональная составляющая, которая зависит от величины $E$ (незаштрихованная часть импульсов) и интегральная составляющая (заштрихованная часть). Увеличение длительности импульсов происходит за счет роста интегральной составляющей, которая зависит от рассогласования $E_i$ и коэффициента $τ_и$.

Выходной сигнал ПИ-регулятора и длительность управляющих импульсов при различных значениях $τ_и$ и $E=10$.

Вопросы проектирования усилителей с общей ООС

   В последнее время наблюдается очередной всплеск дискуссий на тему, которую можно условно назвать – “за” или “против” отрицательной обратной связи в усилителях. К сожалению, эти обсуждения редко содержат сколько-нибудь рациональную аргументацию, одновременно демонстрируя явный недостаток знаний о “мелочах” работы и проектирования систем с ООС. Положение осложняется тем, что в большинстве случаев в качестве оправдания возражений против применения обратной связи приводятся устройства, на поверку оказывающиеся примером неграмотного или неудачного ее использования. А затем в худших традициях школьной логики делается вывод: “обратная связь – это плохо!”.
   В то же время примеры правильного использования ООС, похоже, становятся все большей редкостью, и, скорее всего, по причине фактического отсутствия современной литературы, посвященной данному вопросу.
   Именно поэтому нам представляется особенно целесообразной публикация нескольких материалов, посвященных малоизвестным особенностям проектирования высоколинейных усилителей с обратной связью.

Напомним, что основной причиной изобретения усилителей с ООС Харольдом Блэком в 1927 г. была именно необходимость повышения линейности усилителей, используемых в системах многоканальной телефонной связи по одной паре проводов.

Проблема была в том, что требования к линейности этих усилителей по мере увеличения числа каналов очень резко растут. Причин тому две. Первая – количество возможных продуктов интермодуляции, создающих помехи.

Вторая причина состоит в том, что при росте полосы сигнала растут и потери в кабелях, из-за чего усилители приходится размещать на меньшем расстоянии (и сильнее корректировать их АЧХ), а на трассе 2500 км их число увеличивается до трех тысяч. Так как продукты искажений в линии связи суммируются, соответственно жестче требования к каждому отдельному усилителю.

Чтобы было понятно, сколь высок класс этой аппаратуры, отметим, что усилители для систем на 10800 каналов имеют уровень интермодуляционных искажений третьего порядка на конце полосы пропускания (60 МГц) не более -120…-126 дБ и величину разностного тона не более -130. ..-135 дБ. Интермодуляционные искажения высших порядков еще ниже. АЧХ тракта, содержащего две-три тысячи (!) усилителей, в течение срока службы (примерно 30 лет круглосуточной работы) изменяется не более чем на единицы децибел, в основном из-за старения кабеля. По меркам обычной аппаратуры – это фантастика, а на самом деле – лишь результат грамотного применения ООС.

Проблемой повышения линейности усилителей X. Блэк занимался в Bell Labs еще с 1921 г. Именно он разработал практически все известные способы компенсации искажений, в частности, коррекцию искажений так называемой прямой связью, а также компенсацию искажений путем суммирования искаженного выходного сигнала с выделенным противофазным сигналом искажений. Эти меры, конечно, давали эффект, но их было недостаточно.

Кардинальным решением проблемы линейности стало именно изобретение усилителей с ООС и, главное, их корректная практическая реализация, что было невозможно без создания соответствующей теории (“нет ничего практичнее хорошей теории!”). Первый шаг в построении теории был сделан Гарри Найквистом, нашедшим применяемый и поныне метод определения устойчивости еще до замыкания петли ООС исходя из вида АЧХ и ФЧХ разомкнутой системы (годограф Найквиста).

Однако не все так просто. Несмотря на простоту и кажущуюся очевидность принципа работы ООС, для реального получения тех преимуществ, которые можно достичь с ее использованием, пришлось создать весьма обширную теорию обратной связи, отнюдь не сводящуюся к обеспечению устойчивости (отсутствия генерации). Ее построение было практически завершено выдающимся американским математиком голландского происхождения Хендриком Ваде Боде только к 1945 г. [1]. Чтобы была понятна реальная сложность задач, отметим, что даже первый патент Блэка на усилитель с ООС, в котором описаны далеко не все проблемы, имеет объем небольшой книги – в нем 87 страниц. Кстати, всего X. Блэк получил 347 патентов, значительная часть которых связана именно с реализацией усилителей с ООС. В сравнении с таким объемом работ все претензии современных “ниспровергателей основ”, не создавших ничего и близкого по уровню, и зачастую даже ни разу не читавших (или не понявших) работ Блэка, Найквиста и Боде, выглядят по меньшей мере чрезмерно самоуверенными. Поэтому вопрос не в использовании ООС (реально она есть всегда, просто не всегда в явном виде), а в том, чтобы это использование было грамотным и приносило желаемый результат.

Итак, на что из “не описанного в учебниках” нужно обращать внимание при проектировании и оценке схемотехники усилителей с ООС?

Вначале напомним, что в формуле коэффициента передачи (передаточной функции) системы с обратной связью

H(s) = K(s)/[1+b(s)K(s)]

фигурируют комплексные числа и функции, а именно:
b(s) – комплексный коэффициент передачи (передаточная функция) цепи ОС;
K(s) – комплексный коэффициент передачи (передаточная функция) исходного усилителя.

Для получения корректных результатов вычисления нужно вести по правилам арифметики комплексных чисел [2], о чем нередко забывают даже авторы учебников. Например, при фазовом угле петлевого усиления, близком к ±90°, ±270°, амплитудные нелинейности исходного усилителя практически полностью конвертируются в фазовые (т. е. в паразитную фазовую модуляцию, пусть и ослабленную в |bК| раз). При этом паразитная модуляция амплитуды практически исчезает, и получаемые результаты измерений интермодуляционных искажений могут быть на 20…30 дБ более оптимистичными, чем на самом деле покажет анализатор спектра (и слух в случае УМЗЧ). К сожалению, именно так и обстоят дела с большинством ОУ и многими УМЗЧ.

Хорошим примером может служить усилитель с токовой обратной связью, описанный Марком Александером [3]. Реальный уровень интермодуляционных искажений (в англоязычной аббревиатуре – IMD) этого усилителя на двухтоновом сигнале с частотами 14 и 15 кГц по анализатору спектра составляет примерно 0,01 %, что хорошо согласуется с графиком зависимости коэффициента гармоник от частоты (примерно 0,007 % на частоте 15 кГц). Если интермодуляционные искажения этого усилителя измерить по стандартной (учитывающей только модуляцию амплитуды) методике, то получаемые значения IMD окажутся намного меньшими. На частоте 7 кГц мы получим только ничтожные 0,0002 %, а на 15 кГц – около 0,0015 %, что существенно ниже реальных значений (около 0,005 и 0,01 % соответственно). Этот эффект вскользь отмечен и в работе Матти Оталы [4].

Следующий момент. Важно понимать, что ООС не может снизить абсолютную величину приведенных к входу продуктов искажений и шумов по сравнению с ситуацией, когда петля ООС разомкнута, а уровни сигнала на выходе в обоих случаях одинаковы. На достаточно высоких частотах усиление у любого усилителя падает; как следствие, увеличивается и разностный сигнал в усилителе с ООС. Поэтому в области более высоких частот входной и последующий каскады неизбежно начнут проявлять свою нелинейность, поскольку возрастание разностного сигнала в усилителе с ООС возможно почти до удвоенной величины входного [5] из-за сдвига фаз. Отметим также, что при замкнутой петле ООС продукты искажений, особенно высокого порядка, типа “зубцов” переключения плеч выходного каскада, аналогичны высокочастотным входным сигналам и входной ФНЧ тут помочь не может. Именно поэтому для предотвращения катастрофического расширения спектра интермодуляционных искажений при введении ООС крайне желательно обеспечить более быстрый спад огибающей спектра продуктов искажений без ООС, чем скорость спада петлевого усиления. Условие это, к сожалению, не только малоизвестно (Боде на него лишь намекает, считая очевидным), но и крайне редко выполняется.

По той же причине вводимая для устойчивости частотная коррекция не должна приводить к ухудшению линейности усилителя во всем диапазоне частот, вплоть до частоты единичного усиления и даже несколько выше. Наиболее очевидный способ достичь этого – выполнить коррекцию так, чтобы уменьшать непосредственно величину входного сигнала, как это и было сделано в известном усилителе М. Оталы (рис. 1). Отметим, что используемое здесь “гашение” разностного сигнала на входе цепочкой R6C1 дает в итоге гораздо лучший результат, чем шаблонная схема частотной коррекции по типу ОУ, несмотря на наличие в эмиттерных цепях дифференциальных каскадов форсирующих конденсаторов С2, С4, С6, которые сильно увеличивают динамическую нелинейность.

Рис.1. Принципиальная схема усилителя М.Оталы

Сказанное объясняет желательность большого запаса линейности в каскадах, предшествующих тем, где формируется основной спад АЧХ – в усилителях с ООС это нужно в первую очередь для того, чтобы предотвратить существенное расширение спектра продуктов искажений.

С целью повышения линейности входных каскадов часто рекомендуют применение в них полевых транзисторов, однако эта рекомендация имеет определенный смысл только при использовании дискретных полевых транзисторов с большим напряжением отсечки (более 5 В) и задании соответствующего режима (около половины начального тока, правда, усиление такого каскада невелико). Усилительные каскады на биполярных транзисторах при введении местной ООС, обеспечивающей ту же эффективную крутизну и работающие при том же токе, что и каскады на полевых транзисторах, всегда обеспечивают значительно лучшую линейность, особенно на высоких частотах, за счет лучшего отношения проходной емкости к крутизне [6]. Использование стандартных ОУ с “полевым” входом, у которых входные транзисторы для достижения термостабильности работают в режиме, отстоящем от отсечки примерно на 0,6…0,7 В, дает выигрыш по линейности только при сравнении с дифференциальным каскадом на биполярных транзисторах, в котором на эмиттерных резисторах падает не более 0,1. ..0,2 В. В быстродействующих ОУ с “биполярным” входом падение напряжения на эмиттерных резисторах обычно не ниже 300…500 мВ, так что линейность их входных каскадов выше, а входная емкость у них меньше. Именно по этим причинам высоколинейные и быстродействующие ОУ с “полевым” входом (например, ОРА655 и AD843) обычно строятся как комбинация каскадов на биполярных транзисторах с входными истоковыми повторителями.

Для повышения линейности входных каскадов наиболее эффективно использование местных частотно-зависимых ООС, обеспечивающих одновременно необходимый спад АЧХ и рост линейности (например, с катушками индуктивности в эмиттерных цепях входных каскадов [7]). Частотно-зависимая местная ООС позволяет уменьшить потери глубины общей ООС в рабочей полосе частот; она применима как в каскадах усиления напряжения (например, в ОУ LM101, LM318, NE5534 [8]), так и в выходных каскадах (например, в ОУ ОР275, LM12 и в микросхемах УМЗЧ TDA729x и LM3876/3886).

Таким образом, при разработке усилителя с ООС необходимо обеспечить приемлемую (во всяком случае, не хуже нескольких процентов) линейность и лучшую стабильность характеристик без ООС именно в области частот, где петлевое усиление мало, а не на низких частотах, где петлевое усиление велико. Ряд мер по улучшению линейности на низких и средних частотах (например, введение так называемой следящей связи в каскодный усилитель) одновременно приводит к ухудшению стабильности характеристик и (или) снижению линейности на ВЧ. Поэтому их введение в усилители с ООС нецелесообразно.

В случае использования местных ООС для получения хороших результатов надо производить оптимизацию их частотных характеристик, так как каждая из них не только повышает линейность данного каскада, но и снижает петлевое усиление в цепи общей ООС. Задача эта нетривиальная, без очень аккуратного компьютерного моделирования и оптимизации тут не обойтись. В качестве правила первого приближения можно считать, что близким к оптимальному вариантом является тот, при котором вклад всех каскадов в результирующие искажения усилителя с ООС (при замкнутой петле ООС!) примерно одинаков. Далее, для усилителей с общей обратной связью критически важно отсутствие динамических срывов слежения в цепи ООС. Это означает, что недопустимы динамические нелинейности, приводящие к скачкообразным изменениям характеристик, например, из-за запирания или насыщения (квазинасыщения) транзисторов или же из-за появления сеточных токов у ламп при подаче сигнала через разделительный конденсатор. Если же подобные явления по каким-либо причинам нельзя исключить, необходимо принять меры по нивелированию их влияния в областях частот, где петлевое усиление невелико (особенно в области частоты единичного усиления), используя, например, местные ООС.

Отличный пример – двухтактный выходной каскад NE5534 [8] на транзисторах одинаковой структуры проводимости. Казалось бы, каскад весьма нелинейный: верхнее плечо – эмиттерный повторитель, нижнее – транзистор с общим эмиттером. Тем не менее в ОУ за счет роста глубины местной ООС с частотой отсутствуют даже следы “ступенек” (конечно, при условии правильной разводки платы). Поэтому основным источником искажений в данном усилителе чаще всего оказывается именно перегрузка входного каскада, не содержащего (с целью минимизации шума) эмиттерных резисторов! Как бы то ни было, рост искажений в полосе звуковых частот у этого ОУ отсутствует даже при усилении с ООС 40 дБ (Р = 0,01), когда глубина общей ООС на 20 кГц не превышает 30 дБ. Искажения при этом не превышают 0,005 % (и это при размахе выходного сигнала 20 В от пика до пика), а спектр их практически ограничен третьей гармоникой. При этом подключение нагрузки вплоть до 500 Ом на искажения почти не влияет.

Из других схемотехнических дефектов особенно опасны динамический гистерезис (создаваемый большинством схем, предназначенных для “плавного” переключения плеч двухтактных выходных каскадов), а также возникающая на высоких частотах “центральная отсечка” – ступенька (стандартная болезнь выходных каскадов на составных транзисторах по схеме Шиклаи или на основе “параллельного” усилителя). С точки зрения устойчивости эти дефекты эквивалентны появлению дополнительного фазового сдвига, доходящего до 80°… 100°. В ряде ОУ и некоторых моделях мощных усилителей для преодоления этих недостатков используются цепи обхода нелинейных элементов по ВЧ (многоканальная ОС).

Вопрос выбора вида АЧХ петлевого усиления довольно хорошо освещен в классической литературе, например в [1]. Выбор оптимального числа каскадов усиления с учетом их относительного быстродействия и проектирование систем с многоканальной ООС подробно рассмотрены в [9], поэтому ниже приведем лишь краткие сведения.

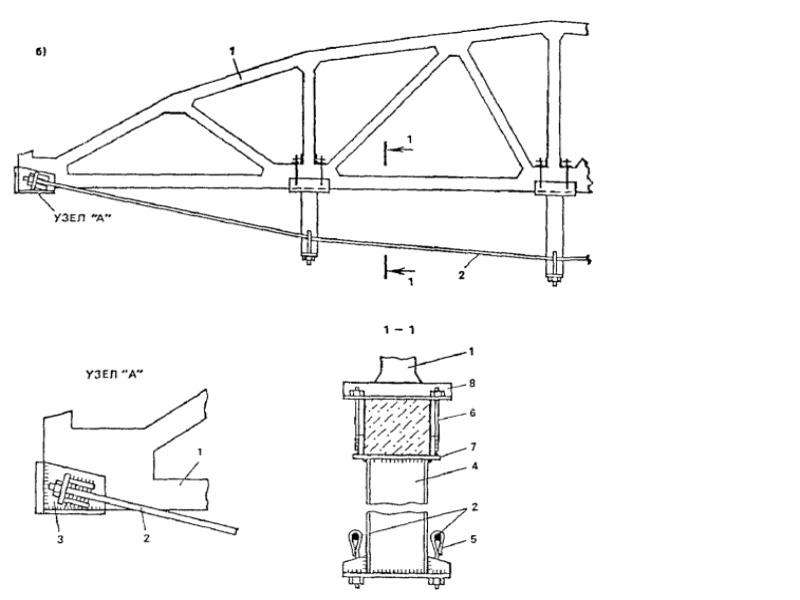
Так как самым “медленным” узлом УМЗЧ чаще всего является мощный выходной каскад, то оптимальное с точки зрения линейности и глубины ООС число каскадов в УМЗЧ заведомо не ниже трех (как установил еще Боде, при примерно равном быстродействии каскадов оптимален трехкаскадный усилитель). В случае выполнения коррекции с цепями обхода каскадов по ВЧ число каскадов ограничено лишь усложнением устройства.

Пропагандируемое рядом авторов разбиение общей петли ООС на несколько местных петель, несмотря на упрощение проектирования, нецелесообразно. Охват “местной” обратной связью более чем одного каскада в составе усилителя, как показано еще Боде, приводит к потере потенциально достижимой линейности. Например, последовательно включенные два каскада с местной ООС по 30 дБ будут иметь заведомо худшую линейность, чем эти же два каскада, охваченные общей ООС глубиной 60 дБ в той же полосе частот.

Конечно, из этого правила есть некоторые исключения. Так, для формирования АЧХ петлевого усиления полезно применение частотно-зависимых местных ООС, когда в области рабочих частот усилителя они практически выключены и не уменьшают достижимую глубину общей ООС. 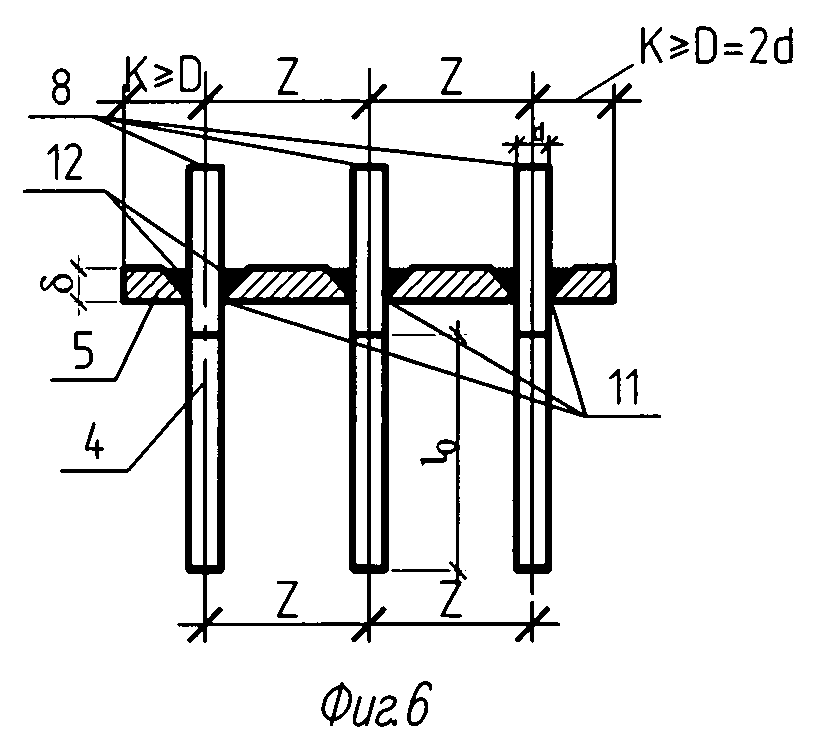Другой пример – в усилителях диапазона СВЧ, выполненных на дискретных компонентах, избыточный сдвиг фазы, вносимый активными элементами и пассивными цепями, начинает превосходить естественный, определяемый спадом АЧХ, и достижимая глубина общей ООС невелика. В этом случае вместо общей ООС оказывается практичнее использовать цепочки переплетенных местных ООС.

Запас устойчивости по фазе на высоких частотах для УМЗЧ не следует выбирать меньше 20°…25° (ниже – ненадежно) и невыгодно повышать более 50°…70° (заметные потери в площади усиления, т. е. в быстродействии и глубине ООС). Для увеличения глубины ООС в рабочей полосе частот целесообразно введение в АЧХ петлевого усиления участка с крутизной около 12 дБ на октаву. Еще лучше сформировать АЧХ петлевого усиления типа среза Боде или устойчивую по Найквисту (с заходомфазы за 180°), однако их корректная реализация довольно сложна и потому далеко не всегда оправдана. Именно поэтому УМЗЧ с АЧХ петлевого усиления “по Найквисту”, насколько известно, серийно не производятся. Описанные же в литературе конструкции имеют существенные эксплуатационные ограничения (в частности, недопустимость попадания на вход высокочастотных сигналов, плохой выход из “клиппирования” по выходному напряжению). Устранение указанных ограничений возможно, но громоздко.

Еще один часто упускаемый очень важный фактор реализуемости – конструктивное исполнение каскадов, охваченных обратной связью. Оно должно обеспечивать отсутствие паразитных резонансных пиков на спаде АЧХ и за полосой пропускания, вынуждающих для обеспечения устойчивости искусственно занижать быстродействие усилителя в целом (см. приведенные на рис. 2 примеры АЧХ усилителей с разомкнутой ООС). Наличие паразитных пиков на АЧХ резко снижает и достижимую без самовозбуждения глубину ООС. Кривая 1 демонстрирует возможность обеспечения большого (10 дБ) запаса устойчивости при частоте единичного усиления около 2 МГц. Глубина ООС на 20 кГц при этом не менее 40 дБ. Кривая 2 имеет паразитный пик, добротность которого составляет около 20 (реально бывает и больше). Чтобы усилитель с такой АЧХ не возбуждался (при запасе устойчивости всего 2…3 дБ), петлевое усиление и полосу действия ООС у такого усилителя придется снизить в 20 раз по сравнению с кривой 1, причем частота вероятного самовозбуждения окажется раз в сто выше номинальной частоты единичного усиления!

Рис.2. Примеры АЧХ усилителей с разомкнутой ООС

Подводя итог краткого обзора, заметим, что любое проектирование – это набор компромиссов, поэтому очень важно, чтобы применяемые решения были взаимно увязаны между собой, а конструкция представляла собой единое целое. Применительно к УМЗЧ, например, нет особого резона специально добиваться глубины ООС выше 80…90 дБ в звуковой полосе частот, так как основным источником продуктов искажений при этом будут уже не активные элементы, а конструктивные, например, наводки от двухтактных выходных каскадов. Ясно, что в подобном случае важнее тщательная отработка конструктивного исполнения, как это сделано в одной из конструкций автора [10] или в зарубежных усилителях марок Halcro и Dynamic Precision.

Источники

Боде Г. В. Теория цепей и проектирование усилителей с обратной связью. – М.: ГИИЛ, 1948.
Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. – М.: ГИТТЛ, 1953.
Alexander M. A Current Feedback Audio Power Amplifier. – 88-th Convention of the Audio Eng. Society, reprint #2902, March 1990.
Otala M. Feedback-generated Phase Nonlineatity in Audio Amplifiers. – London AES convention, March 1980, preprint 1976.
W. Marshall Leach, Jr. An Amplifier Input stage Design Criterion for the Suppression of Dynamic Dishtortion. – JAES, Vol. 29, No. 4, April 1981.
Self D. FETs vs BJTs – the linearity competition. – Electronics & Wireless World, May 1995, p. 387.
Витушкин А., Телеснин В. Устойчивость усилителя и естественность звучания. – Радио, 1980, № 7, с. 36, 37.
Лурье Б. Я. Максимизация глубины обратной связи в усилителях. – М.: Связь, 1973.
Агеев С. Сверхлинейный УМЗЧ с глубокой ООС. – Радио, 1999, № 10-12; 2000, № 1,2,4-6.

Автор: С.Агеев, г. Москва

Устойчивость усилителей с О.О.С. и коррекция их характеристик

Введение О.С. может привести к потере устойчивости и возникновению автоколебаний, ᴛ.ᴇ. к самовозбуждению усилителя.

При введении цепи О.О.С. сигнал обратной связи должен находиться в противофазе с входным сигналом и вычитаться из него. При этом на самом деле с ростом частоты в усилителе нарастает дополнительный фазовый сдвиг, и на некоторой частоте он достигает ^__180^° и обратная связь становится положительной:

В случае если петлевое усиление на этой частоте близко к единице, то общее усиление K_u.о.с ® ¥, и усилитель самовозбуждается.

При исследовании устойчивости рассматривается прохождение сигнала по участку усилитель ^__ цепь обратной связи в полосе частот от w, равной нулю, до w ® ¥ и анализируется параметр cK_u.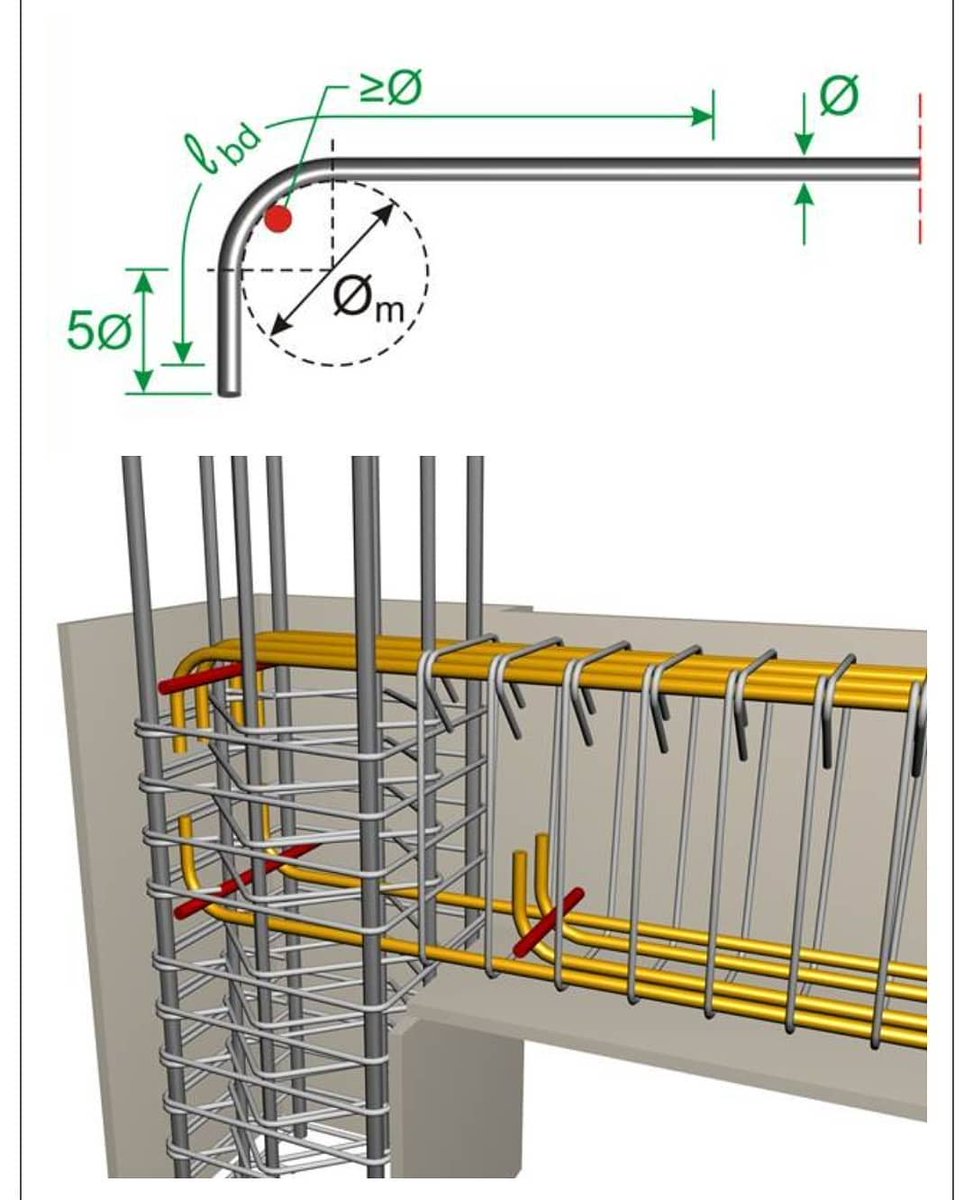 В случае если на частоте, где дополнительный фазовый сдвиг равен ^__180^°, cK_u< 1, то усилитель устойчив.

Для оценки устойчивости крайне важно построить амплитудно- и фазо-частотные характеристики петлевого усиления cK_u. Удобно пользоваться логарифмическими характеристиками ЛАЧХ и ЛФЧХ.

Для однокаскадного усилителя

;

В логарифмическом масштабе АЧХ строится как ломаная линия. На частоте среза усиление падает на 3дБ и фазовый сдвиг равен . А на частотах выше w_ср усиление падает со скоростью ^__20дБ/дек. Фазовый сдвиг в окрестности w_сризменяется со скоростью ^__45град/дек., на частотах выше w_срсдвиг достигает .

Логарифмические АЧХ и ФЧХ наглядны и удобны для анализа многокаскадных усилителей. По ЛАЧХ и ЛФЧХ отдельных каскадов легко построить логарифмические характеристики всего усилителя, геометрически складывая частотные характеристики отдельных каскадов.

Частотный коэффициент передачи двухкаскадного усилителя

где t₁и t₂ – постоянные времени каскадов. Им соответствуют частоты сопряжения

и .

Логарифмические АЧХ и ФЧХ имеют вид:

На частоте w₂ пересекаются асимптоты, одна из которых имеет наклон ^__20дБ/дек., а другая ^__40дБ/дек. В окрестности w₂ дополнительный фазовый ^__45^° к фазовому сдвигу низкочастотной части характеристики (^__90^° ). С ростом частоты общий фазовый сдвиг достигает ^__180^°. В случае если частоты w₁ и w₂отличаются больше, чем на две декады, на ФЧХ имеется плоский участок с задержкой ^__ 90^°.

В случае если ОУ не имеет цепей О.С., то вид АЧХ и ФЧХ никакого влияния на устойчивость усилителя не имеет. При введении цепи О.О.С. могут возникнуть условия самовозбуждения. При исследовании устойчивости крайне важно узнать частотные свойства петли О.С. Для этого разрывают цепь О.С. у точки усилителя, в которую вводится сигнал обратной связи. А для того, чтобы при этом не изменить параметры усилителя, к разорванной цепи О.С. подключается эквивалентное сопротивление, равное сопротивлению той цепи, из которой вводится сигнал О.С. до разрыва обратной связи.

При исследовании устойчивости анализируется коэффициент усиления разомкнутой петли О.С. cK_u. Для оценки устойчивости строят графики ЛАЧХ и ЛФЧХ петли О.С. путем геометрического сложения ординат логарифмических характеристик ОУ и цепи обратной связи.

Пример усилителя со слабой О.С.

В логарифмическом масштабе

На частоте w¢, где cK_u=1, ᴛ.ᴇ. 0дБ, фазовый сдвиг меньше ^__180^°, ᴛ.ᴇ. еще есть запас по фазе:

На частоте w², где j= –180,^° петлевое усиление меньше единицы, ᴛ.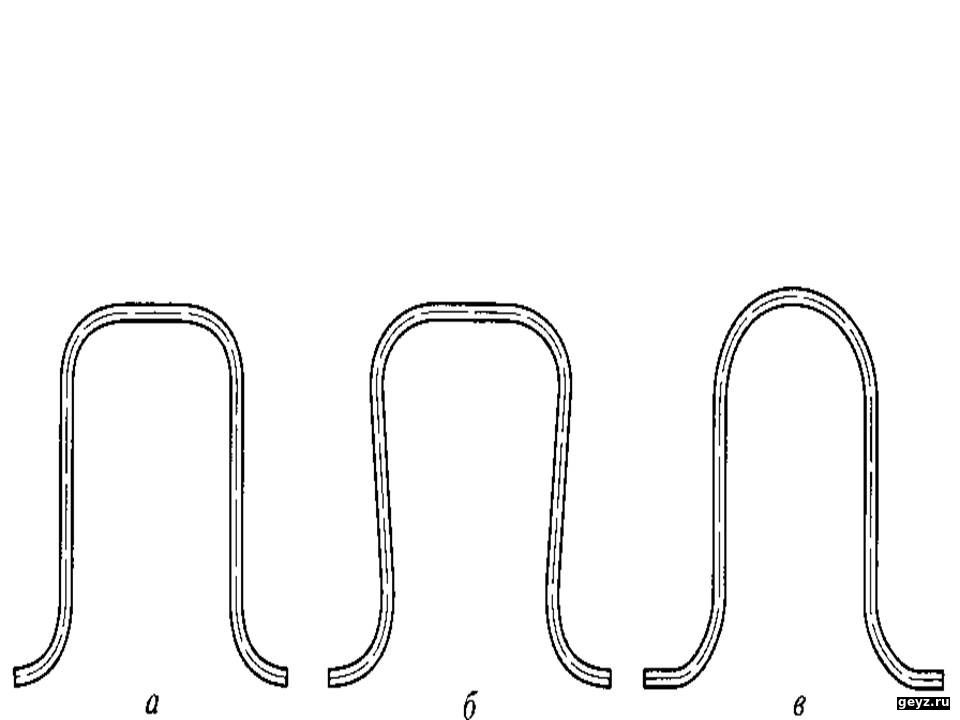 ᴇ. есть запас по усилению К_зап.

Этот усилитель с О.О.С. устойчив. Чтобы на АЧХ усилителя с О.О.С. не было подъема на частоте w², запас по фазе на частоте w¢ должен быть не менее 60^°, а запас по амплитуде на частоте w² ^__ не менее 3дБ, ᴛ.ᴇ. в Ö2 раз.

В случае глубокой О.О.С. усилитель может оказаться неустойчивым.

На частоте w¢, где ЛАЧХ петли О.О.С. пересекает ось частот со скоростью

^__40дБ/дек., ᴛ.ᴇ. w¢>w₂, нет запаса по фазе. На этой частоте наблюдается увеличение коэффициента усиления до ¥, и возникает самовозбуждние ОУ, так как cK_u > 1.

Чтобы устранить самовозбуждение, нужно сдвинуть частоту w₂ вправо путем уменьшения соответствующей постоянной времени.

Итак, для устойчивой работы усилителя с О.О.С. крайне важно , чтобы ЛАЧХ петлевого усиления пересекала ось частот с наклоном ^__20дБ/дек. Для этого нужно, чтобы в АЧХ ОУ преобладала одна постоянная времени t₁, ᴛ.ᴇ. w₂>>w₁.

Рассмотренный поход позволяет оценить устойчивость и найти границы допустимого коэффициента обратной связи c, при котором усилитель работает устойчиво.

В случае если усилитель неустойчив, крайне важно вводить корректирующие цепи, изменяющие его фазовую и амплитудно-частотную характеристики. Обычно используют пассивные цепи. Реактивные компоненты (обычно ^__ конденсаторы ) создают в определенной области частот отставание или опережение по фазе.

Простой способ улучшить динамический диапазон АЦП

Рассмотрим особенности подключения трансформатора ко входу малошумящего широкополосного усилителя с обратной связью по напряжению. Когда частота сигнала намного меньше частоты единичного усиления, предлагаемый подход позволяет сократить энергопотребление по сравнению со стандартной схемой на усилительных радиочастотных блоках. Уменьшение шума позволит измерять малые по величине сигналы за счет чего возрастет динамический диапазон.

Рассмотрим простой неинвертирующий усилитель. Для согласования на неинвертирующем входе установлен резистор, подключенный к земле. Резистор в контуре обратной связи подобран так, чтобы он не сильно увеличивал шум и в то же время обеспечивал отсутствие паразитных связей.

В ОУ с очень низким входным шумом, таких как ISL55190 со спектральной плотностью шумового напряжения и тока 1,06 нВ/√Гц и 5 пА/√Гц соответственно, шум резистора может представлять собой заметную величину. Следовательно, лучше заменить резистор на трансформатор. Коэффициент шума NF1 для простого неинвертирующего усилителя с резистором, подключенным к общей шине (согласование на 50 Ом), вычисляется по формуле:

(1)

Числитель дроби представляет собой общую спектральную мощность шума приведенного ко входу усилителя, в знаменателе – шум резистора R

s. Единственными параметрами, которые можно менять в выражении (1), являются коэффициент усиления и R_f. Так, при R_f = 332 Ом и коэффициенте усиления по напряжению 10, NF1 = 10,23 дБ для усилителя ISL55190.

При проектировании схемы важно проверить общую полосу пропускания и коэффициент передачи обратной связи. Для усилителя ISL55190 произведение коэффициента усиления на полосу пропускания равно 1150 МГц при токе потребления 16 мА и напряжении питания +5 В. Если коэффициент усиления равен 10, полоса пропускания с замкнутой ОС составляет 115 МГц. В подобных случаях не имеет смысла обеспечивать выходной сигнал с малыми искажениями до точки F_-3_dB, поскольку к этому моменту коэффициент передачи ОС уже спадет до 0 дБ.

Преимущества использования трансформатора

Рассмотрим пример. Трансформатор MiniCircuits ADT4-1WT имеет коэффициент передачи 12 дБ на полосе 29 МГц. Коэффициент усиления по напряжению 10, согласование на 50 Ом.

Рис. 1. Согласующий трансформатор подключен к неинвертирующему входу ОУ

Подключим к его неинвертирующему входу (см. рис. 1). При коэффициенте трансформации n согласование с Rs сохраняется до тех пор, пока сопротивление резистора не превышает n2R_s. Входное сопротивление трансформатора должно составлять 200 Ом.

Коэффициент шума вычисляется следующим образом:

(2)

Таким образом, за счет трансформатора суммарное приведенное ко входу шумовое напряжение уменьшается в n раз, а ток – увеличивается в n раз. Величина e_n включает в себя все слагаемые в числителе (3), кроме I_ni.

Отсюда оптимальный коэффициент трансформации, при котором коэффициент шума минимален, имеет следующий вид:

(3)

В зависимости от коэффициента преобразования трансформатора изменяют коэффициент усиления ОУ, чтобы общее усиление входного не менялось. Пусть коэффициент преобразования равен 2, а коэффициент усиления ОУ равен 5. При увеличении коэффициента усиления до 5 номинальная частота F

-3дБ увеличивается до 230 МГц, а коэффициент передачи ОС превышает 12 дБ на частоте выше 58 МГц. Полезная полоса частот увеличивается почти вдвое за счет того, что сигнал усиливается не только ОУ, но и трансформатором. При этом выходной шум в схеме с трансформатором меньше.

Подключение к инвертирующему входу

Рис. 2. Трансформатор подключен к инвертирующему входу ОУ

Еще более интересный результат получается, если трансформатор подключить к инвертирующему входу (см. рис. 2). Пусть коэффициент преобразования остается равным 2. Поскольку на инвертирующем входе ОУ виртуальный ноль, R2 = 200 Ом согласовано с сопротивлением 50 Ом на входе трансформатора и вместе с резистором 1 кОм обеспечивает коэффициент усиления -5.

При полосе пропускания больше 1 ГГц важно учесть паразитные связи, обусловленные резистором. В схеме на рисунке 2 для этого параллельно резистору включен конденсатор 200 фФ. Преимуществом данной схемы является то, что к неинвертирующему входу не подключены резисторы. Во-вторых, уменьшен коэффициент усиления шумового напряжения. Коэффициент усиления на неинвертирущем входе зависит от R2 + n2R

S. Соответственно, коэффициент усиления уменьшается до 3,5, в то время как общий коэффициент усиления остается равным -10. Коэффициент шума для данной схемы имеет следующий вид:

(4)

где

Оптимальный коэффициент преобразования равен

(5)

Для рассматриваемого примера NF3 = 6,99 дБ, практически так же, как и в предыдущем случае. За счет малого коэффициента усиления шума (3,5) коэффициент передачи обратной связи уменьшается до нуля при более высокой частоте, 328 МГц. Петлевое усиление превышает 12 дБ на полосе 82 МГц.

Сравнение схем

В таблице 1 сведены характеристики рассмотренных схем. В схемах с трансформаторами приведенный ко входу шум от Rs в точке подключения равен 1,4 нВ/√Гц. Для первой схемы он меньше, 1,03 нВ/√Гц. В то же время при использовании трансформатора расширяется частотный диапазон, на котором петлевое усиление превышает 12 дБ. Трансформатор не увеличивает потребление. Таким образом, динамический диапазон схемы увеличивается.

Табл. 1. Характеристики схем

	Коэффициент усиления ОУ	Сопротивление Rf, Ом	n_opt	opt	n	Расчетный NF, дБ	Макс. частота при коэффициенте передачи больше 12 дБ, МГц	F_-3dB, МГц
1 прямое подключение	10	332	—	—	—	10,23	29	131
2 трансформатор на неинвертирующем входе	5	332	3,33	6,12	2	6,98	58	276
3 трансформатор на инвертирующем входе	-5	1000	1,64	6,85	2	6,99	82	143

Промоделируем схемы с помощью открытого инструмента iSimPE для ОУ Intersil и сравним F_–3_dB. Полоса пропускания в инвертирующей схеме меньше, чем ожидалось, за счет паразитных эффектов. Тем не менее, в схеме 3 сигнал искажается меньше, чем в остальных. Уменьшение коэффициента усиления шума с 5 до 3,5 позволяет увеличить петлевое усиление на 3 дБ.

Дифференциальная схема

Трансформатор можно использовать для получения дифференциального выхода. Для этого следует воспользоваться дифференциальным усилителем ISL55290.

Для получения инвертированного сигнала можно воспользоваться полностью дифференциальными усилителями, например ISL55210. В этом случае более предпочтительно использовать усилитель с обратной связью по напряжению, поскольку номинал резистора в цепи ОС полностью определяется требованиями к импедансу и коэффициенту усиления. В полностью дифференциальных усилителях с токовой ОС номинал резистора в цепи ОС сильно зависит от динамических характеристик. Они имеют очень широкую полосу, если резистор Rf подобран правильно.

Loop Gain – обзор

13.3 Роль датчика

Датчик системы управления с обратной связью обычно не рассматривается в формальных рамках устойчивости. Однако датчик играет огромную роль в работе любой системы обратной связи и поэтому заслуживает особого внимания. Мы можем интуитивно утверждать, что производительность системы управления с обратной связью никогда не может быть лучше, чем производительность ее датчика. Например, если датчику не хватает точности, то и контролируемая переменная также не будет точной.Если система управления с обратной связью полагается на один датчик, отказ датчика неизменно вызывает отказ всей системы.

Любой датчик может иметь несколько недостатков, некоторым из которых можно противодействовать подходящей конструкцией. В этом аспекте конструкция датчика явно соответствует более широкому определению надежности. Например, неточности можно нейтрализовать подходящей калибровкой. Низкая точность, означающая, что повторное измерение одного и того же значения не дает одинаковый выходной сигнал датчика, часто может быть смоделирована и обработана как шум.Однако медленный дрейф устранить труднее, чем некоррелированный аддитивный шум. Шум был кратко упомянут во введении (см. Рис. 1.4), а шум датчика как представление некоторых форм низкой точности требует более внимательного изучения.

Общая блок-схема контура обратной связи с аддитивным шумом датчика N (s) показана на рис. 13.6. Модель предполагает, что выходной сигнал датчика отклоняется от идеализированного выходного сигнала на небольшую случайную величину n . Часто можно предположить, что шумовой сигнал n (t) имеет нулевое среднее значение, потому что ненулевое среднее значение может быть интерпретировано как смещение датчика и устранено калибровкой.Управляемая переменная зависит от уставки R (s), возмущения D (s) и шума датчика N (s):

Рисунок 13.6. Контур управления с обратной связью с передаточной функцией датчика G _с ( с ) и аддитивным шумом датчика N ( с ).

(13,17) Y (s) = G (s) H (s) 1 + L (s) R (s) + G (s) 1 + L (s) D (s) −L (s) 1+ L (s) N (s),

, где L (s) = G (s) Gs (s) H (s) – коэффициент усиления контура. В предыдущих главах мы уже обнаружили, что большое усиление контура (в частности, когда реализовано через большое усиление регулятора) приводит к улучшенному подавлению помех и лучшему отслеживанию уставки.Кроме того, увеличение коэффициента усиления контура улучшает устойчивость к неопределенности процесса (уравнение (13.4)). Это согласуется с определением функции чувствительности:

(13,18) S (s) = 11 + L (s).

Чувствительность S (s) уменьшается с увеличением коэффициента усиления контура. То же самое не верно для шумового члена, передаточная функция которого равна

(13,19) L (s) 1 + L (s) = 1-S (s).

Таким образом, высокое усиление контура увеличивает влияние шума измерения, и инженеру-проектировщику необходимо найти баланс между динамическим поведением системы и ее чувствительностью к шуму.Если это невозможно, необходимо найти другие подходы к обеспечению устойчивости системы управления к шуму. Существуют разные типы шума, каждый из которых требует отдельного подхода:

•: Широкополосный шум (белый шум, хорошим примером является радиостатический). Значительная часть его спектральной энергии превышает частотную характеристику процесса, а частотно-зависимое усиление может ослабить влияние широкополосного шума.
•: Коррелированный шум (цветной шум), спектральная энергия которого уменьшается с увеличением частоты.Этот тип шума трудно ослабить, но на практике он встречается нечасто.
•: Шум оцифровки, вызванный округлением до ближайшего целого числа в цифровых системах. На стороне цифро-аналогового преобразования можно использовать фильтр нижних частот, чтобы обеспечить плавный переход между ступенями. На аналогово-цифровой стороне более высокое разрешение по битам лучше всего подходит для уменьшения шума оцифровки, хотя усреднение нескольких последовательных выборок может создать допустимое псевдорешение.

Широкополосный шум, вероятно, является наиболее распространенной формой шума сенсора.Часто этому типу шума датчика уделяется мало внимания, потому что многие формы систем низкого порядка устойчивы к широкополосному шуму из-за своей инерции. Эта ситуация меняется при использовании ПИД- или ПИД-регулятора или ЧР-компенсатора. В частотной области операция первой производной соответствует умножению на jω , то есть любая частотная составляющая усиливается пропорционально своей частоте. Спектральная энергия широкополосного шума резко возрастает на более высоких частотах, и влияние на систему управления может быть пагубным.

Рассмотрим систему обратной связи, которая соответствует рис. 13.6. Процесс для этого примера представляет собой систему с недостаточным демпфированием, аналогичную системе чтения / записи DVD, и используется контроллер PD:

(13.20) G (s) = 50s2 + 4s + 50, H (s) = kp (τds + 1), Gc (s) = 1.

Мы можем выбрать, например, kp = 15 и τd = 0,2, чтобы получить пару полюсов замкнутого контура, которая близка к действительной оси (ζ = 0,87), а идеализированная система замкнутого контура в отсутствие шума показывает переходная характеристика, показанная на рис. 13.7A, с временем установления диапазона 95%, равным 0.52 секунды. Ситуация кардинально меняется при наличии даже небольшого количества шума. В этом примере к входу датчика был добавлен гауссовский шум с нулевым средним со стандартным отклонением 0,002 (т. Е. 0,2% от конечного входного значения датчика). Интересно, что влияние на регулируемую переменную не заметно, но на выходе контроллера наблюдаются резкие колебания на выходе, которые в основном вызваны усиленной первой производной сигнала датчика (рис. 13.7B). Такие флуктуации (даже если они ограничены насыщением, как показано серыми пунктирными линиями на рис.13.7B) может оказывать неблагоприятное воздействие на драйвер либо из-за большой нагрузки на систему механического привода, либо из-за быстрого переключения полярности при высоких токах для электронного драйвера. В крайнем случае может выйти из строя драйверный каскад контроллера, несмотря на то, что на выходе шум не виден. Иногда шум, присутствующий на уровне привода, действительно слышен. Например, серводвигатель, который приводится в действие зашумленным выходом контроллера, может издавать скрежет, хотя он почти не двигается.Иногда присутствие шума проявляется в необычном нагревании каскада драйвера (например, H-образного моста). Неожиданное поведение, подобное описанным здесь эффектам, следует исследовать, например, отслеживая сигналы с помощью осциллографа и выборочно отключая чувствительные к шуму компоненты (датчик, производный компонент) в конфигурации с разомкнутым контуром.

Рисунок 13.7. Влияние шума датчика на систему управления. (А) идеализированная бесшумная система. Сильное управляющее воздействие, в котором преобладает P-компонента, создает начальный импульс; управляющее воздействие быстро уменьшается из-за D-составляющей, и выходной сигнал устанавливается в диапазоне 95% в пределах 0.5 с без звонка. (B) Та же система в присутствии гауссовского шума датчика с нулевым средним значением со стандартным отклонением 0,2% от конечного значения. Инерция процесса предотвращает значительные колебания выходного сигнала, но выходной сигнал контроллера, в основном управляемый производной, демонстрирует экстремальные колебания, которые могут ухудшить или разрушить силовой каскад. (C) Та же система после добавления фильтра нижних частот первого порядка с ωc = 50 с − 1 в тракте датчика. Шум все еще присутствует, но колебания выходного сигнала контроллера уменьшаются как минимум на порядок.Так как полюс lowpass имеет гораздо более короткий переходной компонент, чем процесс, на динамический отклик не влияет ощутимо, хотя контроллер показывает небольшую тенденцию к колебаниям.

Широкополосный шум можно ослабить несколькими способами:

•

Фильтрация нижних частот: ширина полосы шумового сигнала может быть значительно уменьшена, если тракт датчика включает запаздывающий элемент (фильтр нижних частот). В простейшем виде он имеет передаточную функцию Gs (s) = ωf / (s + ωf).Недостаток фильтра нижних частот в том, что он вводит дополнительный полюс и, следовательно, фазовую задержку, что снижает относительную стабильность. Расположение полюсов ωf в идеале должно быть расположено намного левее в плоскости s , чем полюса технологического процесса, но при большем | ωf | снижает эффективность фильтра. Необходимо найти компромисс, который зависит от общей стабильности и уровня шума сигнала датчика. Этот подход показан в примере на рис. 13.7C, в котором фильтр нижних частот значительно снижает шумовую составляющую без значительного влияния на динамический отклик.

•

Полосовая фильтрация: Расширение подхода с использованием фильтра нижних частот заключается в добавлении нуля к передаточной функции Gs на еще более высокой частоте, так что

(13,21) Gs (s) = ωfωzs + ωzs + ωf

с | ωz |> | ωf | (компенсатор запаздывания). Частотная характеристика уменьшается на 20 дБ / декаду только между ωf и ωz, а снижение шума менее эффективно, чем у фильтра нижних частот. Однако фазовая асимптота увеличивается на 90 ° при ωz, и вводится дополнительный нуль без обратной связи.Система второго порядка, например, превращается в систему третьего порядка с чистым проходом нижних частот, и корневое геометрическое место будет иметь асимптоты, входящие в правую полуплоскость. Дополнительный ноль полосы пропускания восстанавливает исходную конфигурацию асимптоты.

•

Использование интегратора: Если система управления допускает использование интегратора, то его размещение на тракте датчика значительно уменьшит спектр шума. В частотной области интегрирование соответствует умножению амплитуды частоты на ω-1, а интегратор ослабляет высокочастотные компоненты пропорционально их частоте.Это решение возможно только в том случае, если система с обратной связью в первую очередь требует интегратора, но это очень эффективно для снижения шума.

•

Несколько датчиков: свойство шума с нулевым средним позволяет уменьшить шум путем усреднения показаний нескольких одинаковых датчиков. Как показывает опыт, отношение сигнал / шум n усредненных датчиков улучшается на n для гауссовского аддитивного шума. Усреднение датчика также эффективно для низкочастотного коррелированного шума, пока сохраняется свойство нулевого среднего.Более того, в отличие от фильтрации нижних частот, усреднение датчика не приводит к запаздыванию фазы и, следовательно, не влияет на стабильность или динамический отклик системы управления.

В цифровых системах, в зависимости от времени, необходимого для считывания показаний датчика, несколько показаний датчика могут быть получены последовательно и усреднены. Таким образом может быть достигнуто умеренное увеличение отношения сигнал / шум. Более того, быстрое повторное считывание датчика можно использовать для уменьшения шума оцифровки в цифровой системе.Однако процесс усреднения приводит к запаздыванию, которое необходимо поддерживать небольшим по сравнению с общими постоянными времени системы.

В дополнение к предыдущим соображениям подходящая конструкция датчика может значительно повысить надежность. Например, система управления многих самобалансирующихся транспортных средств регулирует угол по отношению к вертикальной ориентации, и цель управления состоит в том, чтобы поддерживать этот угол равным нулю градусов, то есть в идеально вертикальном положении. Существуют интегральные схемы, которые измеряют ускорение по одной, двум или трем осям.В современных акселерометрах используются микроэлектромеханические системы (МЭМС), которые образуют массив конденсаторов. Ускорение, включая статическое ускорение, такое как сила тяжести, перемещает один набор пластин конденсатора и изменяет емкость. Электроника обработки сигналов для преобразования емкости в напряжение предусмотрена на кристалле, но малейшие изменения емкости требуют значительного усиления. В одном примере, то есть двухосном датчике ADXL203, рекомендуется фильтрация нижних частот 60 Гц, чтобы поддерживать шум на уровне -60 дБ по отношению к силе тяжести.Одно стандартное отклонение сигнала аддитивного шума соответствует углу наклона 0,06 °.

Поскольку измеряется только угол по отношению к вертикальному положению, можно использовать обе оси, повернув акселерометр на 45 °, как показано на рис. 13.8. Хотя проекция вектора силы тяжести на оси приводит к уменьшению сигнала на 1/2, комбинированный сигнал больше, чем у одиночной оси. Вращение системы координат дает для угла θ ,

Рисунок 13.8. С помощью двухкоординатного акселерометра определить отклонение θ от вертикальной ориентации. (A) В своей простейшей конфигурации ось x используется для измерения, потому что x = gsin⁡θ≈gθ, тогда как y = gcos⁡θ≈1. (B) Если акселерометр повернут на 45 ° относительно вертикального направления, то сигнал на каждой оси уменьшается на 1/2 по оси x в (A), но комбинация обоих сигналов больше чем у одной оси сигнала, и SNR улучшается.

(13.22) θ≈sin⁡θ = 12− (Sxg) (Syg),

, где Sx / g и Sy / g – выходные сигналы каждой оси, нормированные на единицу для гипотетической вертикальной ориентации. Малоугловое приближение sin⁡θ≈θ справедливо для одноосного случая и для комбинированных осей. Арифметика, необходимая для объединения обеих осей, явно диктует необходимость использования решения цифрового управления, потому что аналоговое умножение и аналоговый квадратный корень потребуют несколько экзотических схем; однако объединение обеих осей не только улучшает отношение сигнал / шум, но также снижает шум оцифровки.

Мы можем пойти еще дальше в этом примере. Система управления самобалансирующимся транспортным средством требует некоторой формы PD-управления, и в какой-то момент необходимо вычислить первую производную θ˙ управляемой переменной. Как упоминалось ранее, взятие первой производной вызывает значительное усиление шумовой составляющей в θ˙, что требует дополнительной фильтрации нижних частот. В качестве альтернативы сенсорная система может быть дополнена гироскопом MEMS. Как и акселерометр MEMS, гироскоп основан на измерении емкости, но в этом случае колеблющаяся масса смещается с места под действием внешней угловой скорости.Подобно акселерометру, существуют одно- или многоосные гироскопы с выходным напряжением, пропорциональным угловой скорости. Кроме того, существуют встроенные комбинации 2- или 3-осевого акселерометра / гироскопа с аналоговыми или цифровыми выходами. Вместо использования первой производной в традиционной схеме управления ЧР комбинация датчиков позволяет нам вычислить корректирующее действие c (t) напрямую как

(13,23) c (t) = kpSθ (t) + kDSθ˙ (t) ,

где Sθ (t) – выходной сигнал акселерометра (одна ось или объединенная двойная ось), а Sθ˙ (t) – выходной сигнал гироскопа.Никакая производная не задействована, и, следовательно, не происходит усиление шума акселерометра. Однако гироскоп вносит свой собственный шумовой компонент. В частности, для этой формы объединения датчиков выгодно использовать фильтр Калмана (см. Раздел 7.4), который взвешивает два датчика таким образом, чтобы минимизировать шум в отфильтрованных сигналах θ и θ˙. В качестве альтернативы можно рассмотреть возможность интегрирования θ˙ для получения сигнала с очень низким уровнем шума для θ . Однако небольшие ошибки могут привести к медленно растущему смещению интеграции, и для сброса этого смещения необходимо использовать акселерометр.

Основная цель этого примера – показать, как выбор подходящего датчика может улучшить общие характеристики датчика. Ясно, что выбор выгодного или даже оптимального решения датчика очень сильно зависит от задачи управления, и нельзя предложить общего решения.

Отрицательная обратная связь и усиление

Изучив этот раздел, вы сможете:
Поймите основные принципы NFB применительно к усилителям.
• Коэффициент усиления без обратной связи.
• Коэффициент усиления с обратной связью.
• Связь между β и усилением.
• Причины использования отрицательной обратной связи.

Зачем нужен NFB в усилителях

Транзисторы не могут быть изготовлены так, чтобы иметь строго контролируемое значение коэффициента усиления по току h _fe, поэтому не должно быть возможности построить несколько примеров одной и той же схемы усилителя, все с одинаковым коэффициентом усиления.Кроме того, коэффициент усиления транзистора зависит от температуры и даже имеет разное усиление на разных частотах. Все эти факторы сделали бы транзисторные усилители совершенно ненадежными и невозможными в массовом производстве. Основная причина того, что такой ситуации не существует, а транзисторные усилители стали основой электронной промышленности, – это появление на очень ранней стадии истории транзисторов отрицательной обратной связи.

Принцип NFB

Принцип отрицательной обратной связи заключается в том, что часть выходного сигнала возвращается на вход и комбинируется с входным сигналом таким образом, чтобы уменьшить его.Это снижает общий коэффициент усиления усилителя, но также дает ряд преимуществ, таких как уменьшение искажений и шума, а также расширение полосы пропускания усилителя.

Проблемы с NFB

Введение обратной связи в систему также может привести к нестабильности; в усилителях сигнал обычно претерпевает изменение фазы на 180 градусов между входом и выходом, но реактивные компоненты, такие как конденсаторы и катушки индуктивности, будь то фактические компоненты или «паразитная» емкость и индуктивность, могут вызывать нежелательные фазовые изменения на определенных (обычно высоких) частотах.Если эти дополнительные изменения в сумме составляют еще 180 градусов на любой частоте, где транзистор имеет усиление более 1, применение отрицательной обратной связи может стать положительной обратной связью. Вместо уменьшения усиления это увеличит его до такой степени, что усилитель станет генератором и будет генерировать нежелательные сигналы. Следовательно, отрицательная обратная связь должна быть разработана таким образом, чтобы максимизировать упомянутые выше преимущества без создания нежелательных проблем.

Рис. 3.1.1 Режим разомкнутого контура

Усилитель в режиме разомкнутого контура

Рис.3.1.1 показан усилитель напряжения с обращением фазы с коэффициентом усиления в режиме разомкнутого контура, то есть без обратной связи, который можно обозначить как A _или (усиление A в режиме контура ручки o ). Предположим, что подается входной сигнал 1 мВ, тогда на выходе будет инвертированный (противофазный) сигнал с амплитудой 1 мВ x A _o = A _o (мВ).

Рис. 3.1.2 Режим замкнутого контура

Усилитель отрицательной обратной связи в режиме замкнутого контура

Базовая схема отрицательной обратной связи показана на рис.3.1.2, где фазовращающий усилитель имеет часть своего выхода (V _из), возвращаемую и добавляемую ко входу (V _в), чтобы уменьшить амплитуду входного сигнала. Стрелки показывают относительную полярность сигналов, и можно видеть, что выходной сигнал и сигналы обратной связи находятся в противофазе по отношению к входному сигналу. Доля возвращаемого выходного сигнала контролируется делителем потенциала (β), и эта часть добавляется к входному сигналу в противофазе, так что это фактически вычитается из входного сигнала (V _в ) для получения комбинированного сигнала (V _c), амплитуда которого уменьшается перед подачей на фактический вход усилителя.

Коэффициент усиления усилителя, исключая любую обратную связь, составляет _– A, так что, например, каждый 1 мВ, приложенный к входным клеммам схемы, усилитель будет выдавать на выходе сигнал с обратной фазой A _– x 1 мВ. терминалы.

Цепь обратной связи, содержащая R1 и R2, будет возвращать часть (β) выходного сигнала V _из, что = A _o, так что A _o x β мВ (Aβ) будет добавлено в противофазе к 1 мВ. сигнал для создания пониженного входного сигнала V _c.

Источник сигнала V _в, управляющий усилителем, должен, следовательно, выдавать не 1 мВ, а 1 + AβmV для получения той же амплитуды выходного сигнала. Поэтому общее усиление усилителя с отрицательной обратной связью уменьшается и теперь называется усилением с обратной связью (A _c).

Формула отрицательной обратной связи

Коэффициент усиления по напряжению любого усилителя можно описать формулой:

Поскольку в замкнутом усилителе отрицательной обратной связи (рис.3.1.2):

В

_выход = A _или

В

_дюйм = 1 + A _o β

коэффициент усиления с обратной связью (A _c) также может быть описан стандартной формулой NFB:

Усилители с отрицательной обратной связью спроектированы таким образом, что коэффициент усиления разомкнутого контура A _– (без применения обратной связи) усилителя намного больше 1, и поэтому 1 в формуле становится несущественной. Таким образом, коэффициент усиления с обратной связью (A _c) может быть приблизительно равен:

Влияние NFB на усиление усилителя

Это имеет большое значение, потому что это означает, что после применения отрицательной обратной связи коэффициент усиления замкнутого контура A _c зависит почти исключительно от β, который, в свою очередь, зависит от отношения делителя потенциалов R1, R2.

Пример:

В усилителе на рис. 3.1.2 используются следующие резисторы обратной связи:

R1 = 1 кОм

R2 = 10 кОм

Следовательно:

β = R1 / (R1 + R2) = 0,0909 = 1/11

и в качестве коэффициента усиления замкнутого контура A _c = 1 / β, тогда:

A _c 1 / 0,0909 = 11

Проверка этого приблизительного результата по полной формуле для коэффициента усиления замкнутого контура:

Предполагая усиление разомкнутого контура 1000 и β = 1/11, усиление замкнутого контура A _c должно быть 11

Сравните этот результат с полной формулой для коэффициента усиления с обратной связью, введя в свой калькулятор следующие данные:

1000 / (1+ 1000 * 11 ^-1) = 10.88

Таким образом, коэффициент усиления усилителя с обратной связью на самом деле составляет 10,88, но коэффициент усиления 11 достаточно близок к этому значению для любых практических целей.

Как изменение коэффициента усиления разомкнутого контура усилителя повлияет на усиление замкнутого контура при такой же отрицательной обратной связи?

Чтобы увидеть эффект больших изменений в усилении разомкнутого контура, попробуйте тот же расчет, но на этот раз сделайте усиление разомкнутого контура A _o = 5000

Введите эти данные в свой калькулятор: 5000 / (1+ 5000 * 11 ^-1) = 10.97

Таким образом, для увеличения коэффициента усиления разомкнутого контура на 400% коэффициент усиления замкнутого контура изменился только на 0,8%

Это означает, что усиление больше не зависит от переменных, температурно-зависимых и нелинейных характеристик усиления транзистора, а от минимальной схемы из двух резисторов, которая имеет линейный температурный коэффициент и легко предсказуемое значение β.

Начало страницы

Минимальная цель усиления контура – MATLAB и Simulink

Описание

Minimum Loop Gain Goal обеспечивает минимальное усиление контура в конкретном диапазон частот.Эта цель настройки полезна, например, для улучшения подавление помех в определенном месте.

Цель

Minimum Loop Gain Goal устанавливает минимальное усиление для разомкнутого контура. частотная характеристика ( L ) в указанном месте в вашей системе управления. Вы указываете минимальное усиление разомкнутого контура как функция частоты (минимальный профиль усиления ). Для контуров обратной связи MIMO интерпретируется указанный профиль усиления. как нижнюю границу наименьшего сингулярного значения L .

Когда вы настраиваете систему управления, минимальный профиль усиления преобразовано в ограничение на минимальное усиление, обратное чувствительности функция inv ( S ) = ( I + L ).

На следующем рисунке показано типичное указанное минимальное усиление. профиль (пунктирная линия) и результирующее усиление настроенного контура, L (синий линия). Зеленая область представляет значения профиля усиления, которые запрещены. этим требованием. На рисунке показано, что при L намного больше 1, что дает минимальный выигрыш по inv ( S ) – хороший прокси для минимального усиления разомкнутого контура.

Минимальная цель усиления контура – это ограничение на усиление разомкнутого контура. указанного контура управления. Таким образом, коэффициент усиления контура вычисляется с помощью петля открывается в указанном месте. Чтобы вычислить усиление с помощью открытия петель в других точках системы управления, используйте Compute ответ со следующими циклами открывает опцию в разомкнутом цикле Раздел Response Selection диалогового окна.

Указываются только минимальные и максимальные значения контурного усиления. ограничения с низким или высоким коэффициентом усиления в определенных частотных диапазонах.Когда вы используете эти требования, программа определяет лучший цикл форма возле кроссовера. Когда форма петли около кроссовера проста или хорошо понимаемый (например, интегральное действие), вы можете использовать цель формы петли, чтобы указать эту цель форма петли.

Создание

На вкладке Tuning в Control System Tuner выберите New Goal > Minimum gain for open-loop response to create a Minimum Gain Goal.

Эквивалент командной строки

При настройке систем управления из командной строки используйте TuningGoal.MinLoopGain к укажите минимальное целевое значение усиления контура.

Алгоритмы

Оценка целей настройки

Когда вы настраиваете систему управления, программное обеспечение преобразует каждую настройку цель в нормированное скалярное значение f ( x ). Здесь x – вектор свободных (настраиваемых) параметров. в системе управления. Затем программное обеспечение регулирует значения параметров. для минимизации f ( x ) или для управления f ( x ) ниже 1, если цель настройки является жестким ограничением.

Для цели Минимальное усиление контура , f ( x ) определяется выражением:

f (x) = ‖WS (D − 1SD) ‖∞.

D – диагональное масштабирование (для петель MIMO). S это функция чувствительности в Местоположение . Вт _S есть частотно-весовая функция, полученная из минимального коэффициента усиления контура профиль, который вы указываете. Коэффициент усиления этой функции примерно соответствует указанное усиление контура для значений от –20 дБ до 60 дБ.По числовым причинам весовая функция выравнивается за пределами этого диапазон, если указанный профиль усиления не изменит крутизну за пределами этого диапазона. диапазон. Эта корректировка называется регуляризацией . Потому что полюса W _S закрываются до с = 0 или с = Inf может приводят к плохой числовой обработке для настройки, не рекомендуется для задания профилей усиления с очень низкими или очень высокими частотами динамика. Для получения дополнительной информации о регуляризации и ее последствиях, см. «Визуализация целей настройки».

Хотя S является передаточной функцией с обратной связью, вождение f ( x ) <1 эквивалентно для обеспечения нижней границы передаточной функции без обратной связи, L , в полосе частот, где усиление L больше чем 1. Чтобы понять, почему, обратите внимание, что S = 1 / (1 + L ). Для петель SISO, когда | L | >> 1, | S | ≈ 1 / | L |. Следовательно, соблюдение требования минимального усиления разомкнутого контура, | L | > | Вт _S |, примерно эквивалентно принудительному | W _s S | <1.Для циклов MIMO применимы аналогичные рассуждения, с || S || ≈ 1/ σ _мин ( L ), где σ _мин – наименьшее сингулярное значение.

Неявные ограничения

Эта цель настройки накладывает неявное ограничение стабильности на функция чувствительности замкнутого контура, измеренная в заданных, оцененных с петлями, открытыми в указанных местах открытия петель. Динамика этим неявным ограничением подвержены стабилизированные динамика для этой цели тюнинга.Минимальный распад скорость и Максимальная собственная частота настройки параметры контролируют нижнюю и верхнюю границы этих неявно ограниченных динамика. Если оптимизация не соответствует границам по умолчанию, или если границы по умолчанию конфликтуют с другими требованиями, на вкладке Tuning , используйте параметры настройки , чтобы изменить значения по умолчанию.

Ридли Инжиниринг | – [077] Интерпретация измерений усиления контура

Как считывать критические области измерения коэффициента усиления и фазы контура.

Введение

За последние 20 лет в разработке источников питания произошло много кардинальных изменений, но измерение коэффициента усиления контура остается ключом к устойчивой и агрессивной производительности системы. Понимание того, как считывать усиление контура, важно.

Измерение коэффициента усиления контура в современных системах управления

Несколько лет назад я закончил колледж и начал заниматься проектированием коммерческих источников питания. Я изучил микропроцессоры, теорию оптимального управления, обратную связь с несколькими состояниями, и я был готов взяться за реальное оборудование и применить все, что, как мне казалось, я знал, на практике.Это было время, когда управление текущим режимом только начинало использоваться, и я мог видеть, что текущий режим был классическим примером обратной связи с несколькими состояниями. Все, что нам нужно было сделать, это определить правильные значения прироста от каждого состояния, и мы могли размещать полюса замкнутого контура там, где мы хотели, – прямо как в колледже!

Но возникла проблема. Никто на работе не знал, о чем я говорю. И, в отличие от набора задач в курсах колледжа, никто не мог сказать мне, где они хотели, чтобы полюса замкнутого контура были.Все они говорили странными терминами, такими как выходное сопротивление, усиление контура, чувствительность к звуку, и было непонятно, что делать дальше.

Я ясно помню три вещи из знаменитого курса аналоговой электроники Миддлбрука: как работает Cuk с нулевой пульсацией, новый способ решения квадратного уравнения и необходимость измерения коэффициента усиления контура в источниках питания.

Затем я посетил знаменитый курс Миддлбрука по проектированию аналоговых схем. Это было давно, но из этого курса я отчетливо помню три вещи:

Во-первых, он измерил коэффициенты усиления контура для всех своих источников питания и других аналоговых примеров и ввел в контур с помощью токового пробника, выведенного в обратном направлении от генератора.Очень изящный трюк, все, что вам нужно было сделать, это вставить петлю провода в тракт обратной связи и закрепить токовый пробник.

Второе, что я запомнил, это преобразователь Cuk с нулевой пульсацией. Была прозрачность (дни до Powerpoint!), Где он вращал изображение связанных сердечников, и когда зазор на сердечнике изменялся, ток пульсаций на входе и выходе выравнивался до нуля. Это был отличный визуальный ряд, который действительно убедил нас в этом.

И, наконец, он показал, что классическое решение квадратного уравнения с использованием обычного радикала b2 – 4ac численно неточно, и дал гораздо лучшее решение.

С тех пор я не использовал его квадратичное решение и не проектировал преобразователь Cuk со связанной индуктивностью. Но как только я покинул его курс, я начал измерять и понимать коэффициенты усиления контура и обнаружил, что они никогда не выходили из моды для импульсных источников питания. Хотя в то время они казались мне архаичными, они просто лучший способ оптимизировать обратную связь с вашим источником питания. Даже если вы используете цифровой контроллер, аналоговое усиление контура – просто лучший способ убедиться, что система обратной связи спроектирована и работает должным образом.

Если вы знаете, как правильно интерпретировать петли, они – все, что вам нужно для анализа устойчивости. В учебниках рассказывается о графиках Найквиста и характеристических уравнениях, но в реальном мире нам нужно использовать невероятно мощный инструмент для инженеров, который дал нам мистер Боде. Это удивительно – с помощью пары штрихов на бумаге, показывающих усиление и фазу контура, мы можем определить стабильность систем практически любого порядка. Какой мощный инженерный инструмент, без математики, без расчетов, только лабораторные измерения! Это был большой вклад Боде.

Большой вклад Боде состоял в том, что он позволил инженерам нарисовать пару линий на листе бумаги и объявить, является ли очень сложная нелинейная система высокого порядка стабильной или нет! Нет совпадений, никаких расчетов не требуется. Чего еще мы могли желать?

Мир аэрокосмического дизайна, вероятно, наиболее строг в создании полных наборов графиков Боде для входного импеданса, выходного импеданса, аудиовосприимчивости и петлевого усиления. За пределами аэрокосмического мира выполнение этого полного набора измерений менее распространено.Большинство опытных проектировщиков будут проводить измерения коэффициента усиления контура, поскольку они обнаруживают, что это очень чувствительное измерение практически всего в силовом каскаде и тракте обратной связи. Если какой-то компонент имеет неправильное значение или что-то построено неправильно, усиление контура, скорее всего, покажет, что есть проблема.

Критические области измерения коэффициента усиления контура в режиме напряжения

Говоря о коэффициентах усиления контура, большинство статей ссылаются только на частоту кроссовера и запас по фазе на этой частоте.На самом деле петлевое усиление – это гораздо больше, и если вы хотите получить максимальную выгоду от проведения этих измерений, важно понимать, где искать.

На рисунке 1 показано типичное усиление контура для источника питания в режиме напряжения. График на Рисунке 1 начинается с 10 Гц. Это рекомендуется всегда, независимо от частоты переключения вашей энергосистемы. Очень часто в первое десятилетие измерений наблюдается значительный шум (люди, работающие со звуком, болезненно осознают это в отношении гула), и вы должны иметь возможность убедиться, что у вас высокое усиление в низкочастотных областях, чтобы отклонить линию и другие низкочастотные помехи. частотный шум.Эта область показана на рис.1 заштрихованной синим цветом. Анализатор частотной характеристики AP300 [2, 3] может измерять усиление, превышающее 90 дБ, в присутствии высокого шума, и это имеет решающее значение для правильного определения характеристик высокопроизводительных систем.

Рисунок 1: Коэффициент усиления и фаза контура в режиме напряжения с указанием основных областей измерения.

Контурное усиление рефлексов, контролирующих положение человека, измеренное с использованием постуральных и вестибулярных нарушений

1.В этом исследовании мы измерили петлевое усиление постуральных рефлексов у стоящих людей. Рефлекторная активность обычно описывается в терминах мышечной активации, возникающей в результате возмущения, но в этом исследовании также измерялась способность вызванной мышечной активности корректировать возмущение и описывается поведение всей петли обратной связи. 2. Слабое непрерывное случайное возмущение применялось на уровне талии к стоящим испытуемым. Влияние возмущения на раскачивание тела и электромиограмму камбаловидной мышцы (ЭМГ) было выявлено с помощью взаимной корреляции, а спектральный анализ был использован для оценки характеристик передачи рефлекса разомкнутого контура (т.э., качание на ЭМГ). В тех же условиях активность в мышцах ног вызывали гальванической вестибулярной стимуляцией с использованием непрерывного произвольно меняющегося тока. Влияние на ЭМГ камбаловидной мышцы и последующее колебание тела определяли путем взаимной корреляции. Это позволило рассчитать мышцы с разомкнутым контуром и поведение нагрузки (т. Е. Колебание ЭМГ). На основе этих функций рефлекса разомкнутого контура, мышц и передачи нагрузки были рассчитаны коэффициент усиления и фаза контура. 3. В дополнение к усилению петли обратной связи, исследование описывает характеристики передачи рефлекторных ответов в мышцах ног, связанных с раскачиванием тела, и эффекты исключения визуального и проприоцептивного вкладов в реакцию; передаточная функция камбаловидной мышцы человека со стимулом, который сохраняет нормальный набор мотонейронов, включая влияние различных условий нагрузки на мышцу; и характеристики передачи вестибулярных путей, которые вызывают реакции в мышцах ног во время стояния в ситуациях, которые могут изменять рефлексы.4. В положении стоя усиление петли рефлекторной обратной связи приблизительно равно единице и не изменяется при закрытии глаза и устойчивости опоры. Рефлекторная передача привела к заметному сдвигу фазы, и это помогло компенсировать большую часть задержки фазы, вызванной мышцами и нагрузкой. Остаточная фаза отставания может объяснить частоту тремора, наблюдаемого при стоянии (6-8 Гц). 5. Коэффициент усиления обратной связи (приблизительно 1) выше, чем предполагалось как предыдущими оценками, так и теоретическими соображениями, но все же недостаточен для объяснения стабильности нормального положения человека.Это означает, что, хотя сенсорная информация используется для управления позой, это происходит не только с помощью процесса управления с отрицательной обратной связью. Экспериментальные данные согласуются с рефлекторной реакцией, основанной на процессе прямой связи, и это может привести к предсказанию реакции, необходимой для противодействия нарушению осанки.

Франк Видманн – Моделирование усиления контура

Коэффициент усиления контура или коэффициент возврата?

Когда я говорю о петлевом усилении на этой странице, это означает то же самое, что и термин «коэффициент возврата», который предпочитают использовать некоторые другие люди.Коэффициент возврата – это первоначальный термин, определенный Хендриком В. Боде в его книге «Сетевой анализ и конструкция усилителя обратной связи», опубликованной в 1945 году, но сегодня он не используется очень многими людьми. Вместо этого я использую термин «петлевое усиление», как Р. Дэвид Миддлбрук и, вероятно, большинство инженеров-электронщиков.

Некоторые люди делают разницу между коэффициентом возврата и усилением контура и определяют термин усиление контура по-другому. Например, Майкл Тиан и его коллеги определяют усиление контура как отрицательный коэффициент отдачи в своей статье «Стремление к стабильности слабого сигнала».Пол Дж. Херст использует термин усиление контура для результата двухпортового анализа в своих статьях «Точное моделирование параметров цепи обратной связи» и «Сравнение двух подходов к анализу цепи обратной связи» и в книге «Анализ и проектирование цепей обратной связи». Аналоговые интегральные схемы ».

Анализ линеаризованной схемы

Методы, представленные на этой странице, используют анализ слабого сигнала переменного тока SPICE и аналогичных имитаторов схем. Важно помнить, что для этого анализа схема линеаризуется вокруг своей рабочей точки.Это означает, что результаты действительны только в том случае, если линеаризованная схема является хорошим приближением к реальной схеме. Всегда рекомендуется проверять результаты моделирования усиления контура с переходным анализом переходной характеристики. Следует проверить ступеньки как вверх, так и вниз, ступенька на входе должна иметь максимальную амплитуду и скорость нарастания, с которыми схема может столкнуться в своем приложении, и в ответе схемы не должно быть нежелательных колебаний или звона.

Для цепей с несколькими различными состояниями, таких как цепи с переключаемыми конденсаторами или импульсные источники питания, анализ переменного тока недействителен.Метод, основанный на анализе переходных процессов, который можно использовать для этих схем, представлен в справочнике FRA учебных примеров в дистрибутиве LTspice. SIMPLIS имеет специальный анализ переменного тока для импульсных источников питания. Примеры для этих двух симуляторов показывают, как имитировать усиление контура напряжения. Третья возможность для моделирования усиления контура этих схем – анализ pstb SpectreRF от Cadence Design Systems, который использует расширенную версию метода Тиана.

Почему размыкание контура – плохая идея

Если вы разомкнете контур, чтобы имитировать усиление контура, вы создадите две проблемы:

Первая проблема часто решается повторным замыканием контура с помощью большой индуктивности и вводом сигнал с большим конденсатором.Ко второй проблеме можно подойти, добавив копию схемы с другой стороны проема. Однако во многих случаях это дает только приближение к фактическому импедансу замкнутого контура. В общем, открытие контура для имитации усиления контура – довольно неточный и подверженный ошибкам метод.

Из-за этих проблем были разработаны альтернативные методы моделирования усиления контура. С помощью этих методов идеальные источники переменного напряжения и тока вставляются в схему таким образом, что ни рабочие точки постоянного тока, ни импедансы переменного тока слабого сигнала не меняются.Чтобы получить окончательный результат, эти методы объединяют результаты двух или трех прогонов моделирования, в которых активны разные источники. Некоторые из этих методов также напрямую доступны в симуляторах схем, таких как SmartSpice, HSPICE, Eldo (анализ LSTB) и Spectre (анализ stb). Я представлю эти методы в следующих разделах. (При определенных условиях усиление контура напряжения, которое требует только одного прогона моделирования, также даст очень похожие результаты.)

Метод, широко известный как «Метод Миддлбрука», был опубликован Р.Дэвид Миддлбрук в 1975 году в своей статье «Измерение коэффициента усиления контура в системах с обратной связью», опубликованной в International Journal of Electronics (том 38, № 4, страницы 485-512, апрель 1975 года).

Миддлбрук разработал этот метод, используя упрощенную модель, которая не учитывала обратную передачу через контур. Позже это ограничение было снято двумя другими способами. Тем не менее, этот метод обычно дает довольно точные результаты и, как и два других метода, всегда правильно скажет вам, устойчива схема для небольших возмущений или нет (в случае сомнений используйте критерий устойчивости Найквиста).

Лучшее описание этого метода, доступное в настоящее время в сети, – в информационном бюллетене от Spectrum Software. Этот метод также представлен в учебном примере LoopGain, который поставляется с бесплатным симулятором схем LTspice.

Этот метод был разработан Майклом Тианом и его коллегами из Cadence Design Systems и был опубликован в 2001 году в их статье «Стремление к стабильности слабых сигналов», опубликованной в журнале IEEE Circuits and Devices Magazine (том 17, вып. .1, страницы 31-41, январь 2001 г.).

Этот метод используется компанией Cadence (с несколько необычным условным обозначением) в анализе устойчивости (stb) их симулятора цепей Spectre и, в более широком смысле, в периодическом анализе устойчивости (pstb) SpectreRF. Его преимущество перед двумя другими методами, представленными здесь, состоит в том, что он симметричен, так что ориентация компонентов зонда относительно петли не имеет значения.

Моя реализация этого метода для LTspice IV доступна в архиве LoopGain_Probe.zip. Он также содержит пример, показывающий, как измерить запас по фазе и запас по усилению. Документация включена в виде комментария в принципиальную электрическую схему. Дополнительное обсуждение этой реализации, которое первоначально началось на http://tech.groups.yahoo.com/group/LTspice/message/2482, теперь можно найти на https://groups.io/g/LTspice/topic/50145678. Обучающий пример LoopGain2 из дистрибутива LTspice представляет упрощенную версию этой реализации.

С 16.05.18 г. первый.размер шага всегда изменяется на увеличивающийся в LTspice XVII. Это потребовало некоторых обновлений, которые можно найти в архиве LoopGain_Probe_XVII.zip.

Коэффициент усиления контура дифференциальных схем

Как и два других метода, представленных здесь, метод Тиана может применяться только к схемам с ровно одним несимметричным контуром (подробности см. В упомянутой выше статье Тиана). Чтобы распространить этот метод на дифференциальные схемы, соедините два идеальных балуна друг за другом с их дифференциальными и синфазными портами и вставьте эту комбинацию в свою схему.Теперь вы можете вставить компоненты пробника в путь между портами дифференциального режима, чтобы имитировать усиление контура дифференциального режима, или между портами синфазного режима, чтобы имитировать усиление контура регулирования синфазного режима. В симуляторе цепи Spectre от Cadence ячейка diffstbprobe из библиотеки analogLib упрощает эту настройку.

Общая теорема Миддлбрука об обратной связи

Общая теорема об обратной связи (GFT), разработанная Р. Дэвидом Миддлбруком, позволяет более полный анализ цепи обратной связи, которая также включает коэффициент усиления с обратной связью.Его статья «Общая теорема обратной связи: окончательное решение для систем обратной связи» была опубликована в 2006 г. в журнале IEEE Microwave Magazine (том 7, № 2, страницы 50-63, апрель 2006 г.). Более подробное описание доступно в «Руководстве пользователя шаблона GFT», которое он написал для реализации метода симулятора цепей ICAP / 4 от Intusoft. Он также записал видеолекцию об общей теореме обратной связи. Основой для развития общей теоремы обратной связи была теорема о двух дополнительных элементах (2EET).Более обширную справочную информацию можно найти в «Правилах и инструментах анализа, ориентированном на дизайн» Миддлбрука и в его видеокурсе «Техническая терапия».

GFT показывает, что для общей цепи обратной связи обычно существует дополнительный путь H ₀ в эквивалентной схеме, который обходит контур и идет непосредственно от входа к выходу. Для некоторых цепей этот обходной путь может значительно изменить передаточную функцию с обратной связью. Например, это может вызвать пик передаточной функции замкнутого контура, хотя коэффициент усиления контура имеет очень большой запас по фазе.Один из таких случаев представлен в примере 1 «Руководства пользователя шаблона GFT».

GFT очень тесно связан с моделью из статьи в Википедии об асимптотической модели усиления. Новые аспекты GFT по отношению к этой модели описаны в ответе Р. Дэвида Миддлбрука на мой вопрос об этой взаимосвязи.

Моя реализация GFT для LTspice IV доступна в архиве GFT_LTspice.zip (необходимые обновления для LTspice XVII можно найти в архиве GFT_LTspice_XVII.zip). Он намного менее сложен, чем для ICAP / 4, и, как и моя реализация метода Тиана, может быть адаптирован для любого симулятора SPICE, который поддерживает пошаговое изменение параметров с последующими вычислениями с использованием результатов разных шагов. Если симулятор не поддерживает это, вы все равно можете использовать эти методы, сделав две или три идентичные копии вашей схемы (по одной для каждого шага). Расширяя мою реализацию GFT, группа INTEC_design в Гентском университете реализовала реализацию общей сетевой теоремы в Cadence Virtuoso.Теорию, лежащую в основе этой реализации, которая также применима для схем с несколькими контурами, можно найти в Приложении B к докторской диссертации Барта Моенекли.

Документация по моей реализации GFT находится в файле readme.txt из архива, который для вашего удобства также представлен в следующем разделе этой страницы. Вы можете найти дополнительную информацию о GFT и усилении цикла в целом в моем обсуждении с Р. Дэвидом Миддлбруком, которое начинается на http://groups.yahoo.com/group/Design-Oriented_Analysis_D-OA/message/40.

Что показывают эти примеры?

Эти примеры показывают, как в LTspice можно моделировать величины из общей теоремы обратной связи (GFT), разработанной Р. Дэвидом Миддлбруком. GFT объясняется в руководстве GFT, которое доступно по адресу http://www.intusoft.com/gft.htm, и в статье «Общая теорема обратной связи: окончательное решение для систем обратной связи», опубликованной в журнале IEEE Microwave Magazine. и доступен по адресу http://resolver.caltech.edu/CaltechAUTHORS:MIDieeemm06.Примеры в этом архиве взяты из этих двух документов. Дополнительную информацию о GFT можно также найти на веб-сайте Р. Дэвида Миддлбрука http://www.ardem.com.

Каковы преимущества общей теоремы об обратной связи?

В отличие от других методов расчета коэффициента усиления контура (см. Ниже), GFT также дает вам информацию об усилении контура с обратной связью. Это может быть особенно полезно, когда есть значительная прямая передача от входа к выходу схемы, минуя петлю.В этом случае только петлевое усиление часто не может объяснить поведение схемы.

Такую ситуацию можно найти в примере 1 руководства GFT (см. Соответствующую схему в файле manual1.asc). Здесь коэффициент усиления H в замкнутом контуре показывает значительный пик, хотя коэффициент усиления T в замкнутом контуре имеет очень большой запас по фазе 87 градусов и поэтому не может вызывать такое поведение. В таком случае расчет передаточных функций GFT может помочь вам лучше понять схему, а также показать возможные способы ее улучшения.

Как запустить эти примеры?

Прежде всего, установите LTspice, если вы еще этого не сделали. LTspice (также называемый SwitcherCAD III) можно бесплатно загрузить с http://www.linear.com/designtools/software/. Это полнофункциональный симулятор SPICE с очень хорошей производительностью и без произвольных ограничений. Также существует группа очень активных и полезных пользователей по адресу http://tech.groups.yahoo.com/group/LTspice/.

После установки LTspice скопируйте файл plot.defs из этого архива в каталог, где находится исполняемый файл scad3 LTspice.exe был установлен. (Если в этом каталоге уже есть файл plot.defs, добавьте в него его содержимое.) Файл plot.defs содержит формулы, используемые для оценки результатов моделирования.

Затем откройте один из файлов .asc и нажмите кнопку «Выполнить». После завершения моделирования окно графика откроется автоматически. Конфигурация графика хранится в файле .plt с тем же базовым именем, что и у файла .asc. Для некоторых примеров существуют дополнительные файлы .plt, которые соответствуют рисункам в руководстве GFT или в документе.Их можно загрузить с помощью «Параметры графика -> Открыть файл параметров графика». (Окно графика должно быть активным, чтобы было видно меню параметров графика.)

Как работают эти примеры?

Выполняется три моделирования с разными активными источниками. Это контролируется переменной z, которая принимает значения 1, 0 и -1. (Пошаговое изменение параметров в LTspice должно быть монотонным, поэтому порядок 0, 1 и -1 невозможен.) При z = 1 активен только источник ввода напряжения Vz, при z = 0 только источник ввода Vi (или Ii) активен, а для z = -1 активен только текущий источник инжекции Iz.(Если вы хотите выполнять только обычное моделирование с обратной связью без GFT, вы можете закомментировать команду .step и установить z = 0.)

Результаты трех прогонов моделирования объединяются уравнениями, заданными на графике. defs файл. Вы можете посмотреть файл plot.defs, выбрав «Параметры графика -> Редактировать файл определения графика» или открыв его в любом текстовом редакторе. Суффикс @ 1 в уравнениях относится к первому запуску с z = 1 (Vz активен), суффикс @ 2 относится ко второму запуску с z = 0 (Vi или Ii активен), а суффикс @ 3 относится к третьему. запустить с z = -1 (Iz активен).

Как были получены эти уравнения?

Основная идея для вывода этих уравнений заключалась в явном определении относительных амплитуд источников, необходимых для удовлетворения различных условий обнуления, а затем суммировании их вкладов в результаты. Конечно, это совершенно неправильный подход, если вы выполняете символьные вычисления в схеме, чтобы получить выражения с низкой энтропией. Однако здесь этот подход привел к удивительно компактным формулам для числовой оценки, которые, хотя и не являются низкоэнтропийными, также имеют определенную эстетическую ценность.Подробный вывод доступен в файле GFT_SPICE.doc в этом архиве благодаря Альберто Петрини, который взял мои рукописные вычисления и преобразовал их в понятную презентацию.

В чем преимущества этого метода?

Самым большим преимуществом этого метода является то, что вам нужно всего три моделирования для получения результатов. Его можно реализовать в любом симуляторе SPICE, который поддерживает пошаговое изменение параметров с последующими вычислениями с использованием результатов разных этапов.Если симулятор не поддерживает это, вы все равно можете использовать этот метод, сделав три идентичных копии вашей схемы (по одной для каждого из источников).

Как создать собственное моделирование?

При настройке собственных симуляций GFT необходимо учитывать ряд моментов. Источник напряжения Ey, управляемый напряжением, который измеряет напряжение Vy, и источник напряжения Viy, который измеряет ток Iy, должны быть размещены в обратном направлении от точки инжекции относительно направления передачи контура.Ориентация источников инжекции Vz и Iz должна быть такой, чтобы положительное напряжение Vz вызывало положительное напряжение V (y), а положительный ток Iz вызывал положительный ток на клемме «+» источника напряжения Viy (соответствующей положительный ток I (Вий)).

Имена источника напряжения Viy, узла y для Vy и выходного узла o используются в уравнениях и не должны изменяться (если вы также не измените уравнения соответствующим образом). Чтобы упростить уравнения, я использовал тот факт, что амплитуды источников равны ровно 1, когда они активны, поэтому это тоже не должно изменяться.

Конечно, вы также должны выбрать правильную точку впрыска, чтобы результаты были значимыми. Вы всегда должны сначала проверять Hinf (), чтобы узнать, имеет ли он ожидаемое значение. Для получения дополнительной информации, пожалуйста, обратитесь к руководству GFT и статье.

Доступные количества определены в файле plot.defs. Это H (), Hinf (), H0 (), T (), Tn (), Tp (), Dd (), Dn (), D0 () и Dp (). Я не мог использовать D () для фактора расхождения D, потому что функция D () уже используется LTspice для производной, поэтому вместо этого я выбрал Dd ().Величины, оканчивающиеся на _1, относятся к конфигурации с одним впрыском, как в примерах manual3a.asc и manual3b.asc.

Если у вас есть выходное напряжение, которое не имеет общего заземления в качестве опорного, вы можете использовать идеальный источник напряжения, управляемый напряжением (элемент E), например Vy, для измерения напряжения. Если у вас есть выходной ток, вы можете использовать идеальный источник напряжения с регулируемым током (элемент H) для его измерения, так что вам не придется изменять уравнения. Аналогичным образом могут быть реализованы более экзотические конфигурации впрыска, такие как двойная инжекция напряжения или двойная инжекция тока.

А как насчет других определений петлевого усиления?

Другой метод моделирования усиления контура был описан в статье Майкла Тиана и других авторов «Стремление к стабильности слабого сигнала», опубликованной в журнале IEEE Circuits & Devices Magazine и доступной по адресу http: //www.kenkundert .com / docs / cd2001-01.pdf. Различия между усилением контура GFT и усилением контура Тиана проще всего объяснить, взглянув на рисунок 7 и уравнение (3) из этой статьи.

На рисунке 7 показан контур обратной связи с подачей напряжения и тока.Вы можете заметить, что параметры компонента соответствуют параметрам Y цепи, если она разомкнута в точке впрыска, с Ye = Y11, k3 = Y12, k1 = Y21 и Yf = Y22. Для большей ясности я буду использовать параметры Y в следующем обсуждении.

Коэффициент усиления контура T (Тиан называет это коэффициентом возврата) определяется уравнением (20) как (Y12 + Y21) / (Y11 + Y22). Если вы вычислите усиление контура GFT для схемы на рисунке 7, вы обнаружите, что это Y21 / (Y11 + Y22 + Y12). Итак, кто виноват? Оказывается, ни один из них не ошибается.В этом можно убедиться, посмотрев на уравнение (3). Определитель Дельта для этой схемы – Y11 + Y12 + Y21 + Y22. Это означает, что оба определения удовлетворяют уравнению (3) с x = Y21 для коэффициента усиления контура GFT и x = Y21 + Y12 для усиления контура Tian.

Переменная x относится к управляемому источнику контура. Это означает, что усиление контура GFT является более физическим и напрямую связано с усилением замкнутого контура уравнениями GFT. С другой стороны, усиление контура Тиан симметрично, что означает, что оно не зависит от ориентации контура.Поскольку оба определения удовлетворяют уравнению (3), оба правильно скажут вам, устойчива схема или нет.

На практике результаты обоих определений в целом очень похожи. Я определил функцию Tt () для усиления цикла Тиана и файлы .plt … t.plt для сравнения. Реальную разницу можно наблюдать только для схемы article2.asc. Даже здесь различия проявляются только на очень высоких частотах, где усиление контура намного ниже 0 дБ.

В статье, опубликованной в 1975 году, Р.Дэвид Миддлбрук представил один из первых методов измерения усиления контура. Для своей разработки он использовал схемную модель с Y12 = 0. Хотя этот метод был заменен GFT и методом Тиана, он по-прежнему широко известен как «метод Миддлбрука» среди инженеров (большинство из которых, вероятно, никогда не слышали о более поздних методах) и рассматривается как продвинутый метод моделирования цикла. прирост.

Если применить этот метод к схеме на рис. 7, получится (Y21-Y12) / (Y11 + Y22 + 2 * Y12) для усиления контура.Сравнивая это выражение с уравнением (3), можно обнаружить, что оно также удовлетворяет этому уравнению с x = Y21-Y12. Итак, хорошая новость заключается в том, что даже старый метод даст правильный результат для стабильности схемы. В общем, усиление контура, вычисленное этим методом, также очень похоже на усиление контура GFT.

Можно показать, что усиление контура не зависит от выбора точки впрыска для всех трех обсуждаемых до сих пор методов (пока существует только один контур и размыкание контура в точке впрыска полностью разрывает контур, что означает что нет параллельных путей).Если Y12 = 0 (случай без обратной передачи), все три метода дают одинаковое усиление контура Y21 / (Y11 + Y22).

В некоторых простых схемах моделирования используется только коэффициент усиления контура напряжения Tv = Vy / Vx для ввода напряжения или коэффициент усиления контура тока Ti = Iy / Ix для ввода тока. Интересно отметить, что эти простые определения также удовлетворяют уравнению (3) с x = Y21 + Y11 для Tv и x = Y21 + Y22 для Ti. Таким образом, они также правильно скажут вам, стабильна схема или нет. Однако оба этих определения зависят от точки впрыска и могут сильно отличаться от коэффициента усиления контура GFT, поэтому следует проявлять большую осторожность, когда кто-то хочет оценить такие свойства, как запас по фазе, из этих определений.

При выводе хорошо известных соотношений между запасом по фазе и частотной характеристикой или переходной характеристикой в качестве отправной точки используется уравнение H = Hinf * T / (1 + T). Дополнительные условия заключаются в том, что Hinf постоянна и что T имеет два широко разделенных полюса и не имеет нулей. Уравнению всегда удовлетворяет коэффициент усиления псевдопетли Tp, потому что по определению H = Hinf * Tp / (1 + Tp). Коэффициент усиления псевдопетли Tp равен коэффициенту усиления T цикла GFT, если нет передачи по прямому пути, который обходит петлю, что эквивалентно H0 = 0, Dn = 1 или Tn = бесконечность.

Некоторое время назад я реализовал усиление петли Тиана в примере LTspice, который также содержит более старый метод Миддлбрука. Он доступен по адресу http://tech.groups.yahoo.com/group/LTspice/files/%20Examples/Educational/LoopGain_Probe/LoopGain_Probe.zip. Некоторые обсуждения этой схемы можно найти в группе пользователей LTspice в ветке, начинающейся с сообщения 2482 по адресу http://tech.groups.yahoo.com/group/LTspice/message/2482. Урезанная версия примера доступна как обучающий пример LoopGain2 из дистрибутива LTspice.

Если у вас есть вопросы, замечания, предложения по улучшению и т. Д., Вы можете связаться со мной (Фрэнк Видманн), используя контактную форму на http://sites.google.com/site/frankwiedmann/contact. Я извиняюсь за то, что не предоставил вам здесь свой адрес электронной почты, но я уже получил достаточно сообщений со спамом и не хочу, чтобы это число увеличивалось дальше.

Самый быстрый словарь в мире: Vocabulary.com

Контурное усиление (телекоммуникации) усиление усилителя или системы с обратной связью в зависимости от того, какой выходной сигнал подается обратно на вход
лепрекон озорной эльф в ирландском фольклоре
сделка о признании вины (уголовное право) переговоры, в которых обвиняемый соглашается признать себя виновным по менее серьезному обвинению, а прокурор соглашается снять более серьезное обвинение
Lepechinia род двудольных из семейства Labiatae
сделка о признании вины соглашается признать себя виновным в обмен на меньшее обвинение
Петлевой заболел острым вирусным заболеванием нервной системы овец
длинная цепь молекул с относительно длинными цепочками атомов в молекуле
длинная цепь (химия) относительно длинная цепь атомов в молекуле
цикл (информатика), выполнение одного и того же набора инструкций заданное количество раз или до тех пор, пока не будет получен заданный результат
кольцевая линия железнодорожной ветки, которая ответвляется от магистральной линии, а затем присоединяется к ней позже по
договор договор между сторонами, фиксирующий обязательства каждой
Боль при родах боль и дискомфорт, связанные с сокращениями матки во время родов
открытая цепь: цепь атомов в молекуле, концы которой не соединены с образованием кольца
открытая цепь со структурой открытой цепи
каллипигийские ягодицы или имеющие хорошо развитые ягодицы
узел петля любой из различных узлов, используемых для создания фиксированной петли на веревке
смотрите на наблюдайте внимательно
бумажная цепочка Цепочка из петель из цветной бумаги
пиперокаин соединение, используемое в форме его гидрохлорида в качестве местного или спинномозгового анестетика
Больше новостей

Петлевое усиление: Отрицательная обратная связь, часть 4: понятие устойчивости

Отрицательная обратная связь, часть 4: понятие устойчивости

Вспомогательная информация

Бесплатного обеда не бывает…

Когда отрицательная становится положительной

Петлевое усиление

Критерий устойчивости

Заключение

Теги

Отрицательная обратная связь, часть 9: разрыв петли

Вспомогательная информация

Неуловимое петлевое усиление

Разорванная петля

Еще один полюс, о котором стоит побеспокоиться

Методика

Заключение

Теги

петлевое усиление – это… Что такое петлевое усиление?

Смотреть что такое “петлевое усиление” в других словарях:

Вопросы проектирования усилителей с общей ООС

Устойчивость усилителей с О.О.С. и коррекция их характеристик

Простой способ улучшить динамический диапазон АЦП

Loop Gain – обзор

13.3 Роль датчика

Отрицательная обратная связь и усиление

Зачем нужен NFB в усилителях

Принцип NFB

Проблемы с NFB

Рис. 3.1.1 Режим разомкнутого контура

Усилитель в режиме разомкнутого контура

Рис. 3.1.2 Режим замкнутого контура

Усилитель отрицательной обратной связи в режиме замкнутого контура

Формула отрицательной обратной связи

В

В

Влияние NFB на усиление усилителя

Пример:

β = R1 / (R1 + R2) = 0,0909 = 1/11

Минимальная цель усиления контура – MATLAB и Simulink

Описание

Создание

Эквивалент командной строки

Алгоритмы

Оценка целей настройки

Неявные ограничения

Ридли Инжиниринг | – [077] Интерпретация измерений усиления контура

Введение

Измерение коэффициента усиления контура в современных системах управления

Критические области измерения коэффициента усиления контура в режиме напряжения

Контурное усиление рефлексов, контролирующих положение человека, измеренное с использованием постуральных и вестибулярных нарушений

Франк Видманн – Моделирование усиления контура

Коэффициент усиления контура или коэффициент возврата?

Анализ линеаризованной схемы

Почему размыкание контура – плохая идея

Коэффициент усиления контура дифференциальных схем

Общая теорема Миддлбрука об обратной связи

Что показывают эти примеры?

Каковы преимущества общей теоремы об обратной связи?

Как запустить эти примеры?

Как работают эти примеры?

Как были получены эти уравнения?

В чем преимущества этого метода?

Как создать собственное моделирование?

А как насчет других определений петлевого усиления?

Самый быстрый словарь в мире: Vocabulary.com

Больше новостей

Добавить комментарий Отменить ответ