Универсальный внешний накопитель для всех iOS-устройств, совместим с PC/Mac, Android
Header Banner
8 800 100 5771 | +7 495 540 4266
c 9:00 до 24:00 пн-пт | c 10:00 до 18:00 сб

Пид регулятор это – ПИД-регулятор — Википедия

0 Comments

Содержание

ПИД-регулятор — Википедия

Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации.

Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.

Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.

Пропорциональная составляющая[править | править код]

Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если

входной сигнал равен заданному значению, то выходной равен нулю.

Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.

Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.

Интегрирующая составляющая[править | править код]

Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.

Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.

Дифференцирующая составляющая[править | править код]

Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.

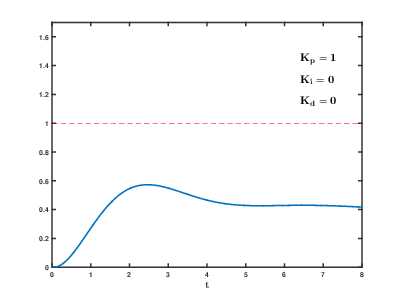Система управления с обратной связью с участием ПИД-регулятора. Система управляет величиной y(t), то есть выводит величину y(t) на заданное извне значение r(t). На вход ПИД-регулятора подаётся ошибка e(t), выход ПИД-регулятора является управляющим воздействием для некоторого процесса (для объекта управления), управляющего величиной y(t). Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.

Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением

(или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.

Выходной сигнал регулятора u определяется тремя слагаемыми:

u(t)=P+I+D=Kpe(t)+Ki∫0te(τ)dτ+Kddedt{\displaystyle u(t)=P+I+D=K_{p}\,{e(t)}+K_{i}\int \limits _{0}^{t}{e(\tau )}\,{d\tau }+K_{d}{\frac {de}{dt}}},

где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.

Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:

u(t)=Kp(e(t)+Kip∫0te(τ)dτ+Kdpdedt){\displaystyle u(t)=K_{p}\left(\,{e(t)}+K_{ip}\int \limits _{0}^{t}{e(\tau )}\,{d\tau }+K_{dp}{\frac {de}{dt}}\right)}

В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:

U(n)=KpE(n)+KpKipT∑k=0nE(k)+KpKdpT(E(n)−E(n−1)){\displaystyle U(n)=K_{p}E(n)+K_{p}K_{ip}T\sum _{k=0}^{n}{E(k)}+{\frac {K_{p}K_{dp}}{T}}(E(n)-E(n-1))},

где T{\displaystyle T} — время дискретизации. Используя замену Kidiscr=KpKipT,Kddiscr=KpKdpT{\displaystyle K_{i}^{discr}=K_{p}K_{ip}T,K_{d}^{discr}={\frac {K_{p}K_{dp}}{T}}} можно записать:

U(n)=KpE(n)+Kidiscr∑k=0nE(k)+Kddiscr(E(n)−E(n−1)){\displaystyle U(n)=K_{p}E(n)+K_{i}^{discr}\sum _{k=0}^{n}{E(k)}+K_{d}^{discr}(E(n)-E(n-1))}

В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:

U(n)=U(n−1)+Kp(E(n)−E(n−1))+KidiscrE(n)+Kddiscr(E(n)−2E(n−1)+E(n−2)){\displaystyle U(n)=U(n-1)+K_{p}(E(n)-E(n-1))+K_{i}^{discr}{E(n)}+K_{d}^{discr}(E(n)-2E(n-1)+E(n-2))}

Часто в качестве параметров ПИД-регулятора используются:

  • относительный диапазон
Pb=1Kp{\displaystyle P_{b}={\frac {1}{K_{p}}}}
  • постоянные интегрирования и дифференцирования, имеющие размерность времени
Ti=1Kip{\displaystyle T_{i}={\frac {1}{K_{ip}}}}
Td=Kdp{\displaystyle T_{d}={K_{dp}}\;}

Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.

Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции.

В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.

ru.wikipedia.org

что это такое, регулирование температуры ПИД регулятором

Дифференциальный пропорционально-интегральный регулятор – устройство, которое устанавливают в автоматизированных системах для поддержания заданного параметра, способного к изменениям.

На первый взгляд все запутанно, но можно объяснить ПИД регулирование и для чайников, т.е. людей, не совсем знакомых с электронными системами и приборами.

Что такое ПИД регулятор?

ПИД регулятор – прибор, встроенный в управляющий контур, с обязательной обратной связью. Он предназначен для поддержания установленных уровней задаваемых величин, например, температуры воздуха.

Устройство подает управляющий или выходной сигнал на устройство регулирования, на основании полученных данных от датчиков или сенсоров. Контроллеры обладают высокими показателями точности переходных процессов и качеством выполнения поставленной задачи.

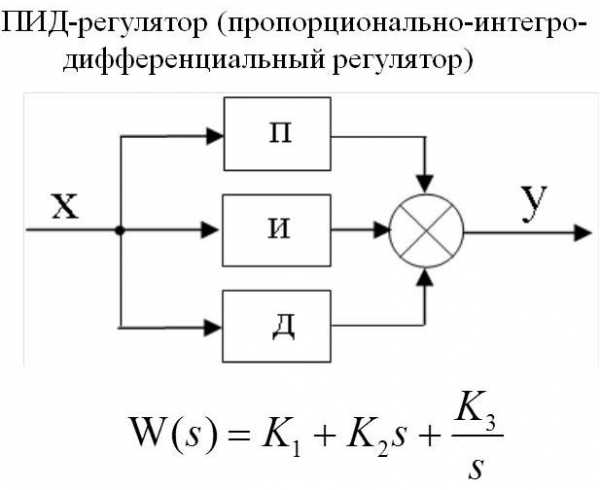
Три коэффициента ПИД регулятора и принцип работы

Работа ПИД-регулятора заключается в подаче выходного сигнала о силе мощности, необходимой для поддержания регулируемого параметра на заданном уровне. Для вычисления показателя используют сложную математическую формулу, в составе которой есть 3 коэффициента – пропорциональный, интегральный, дифференциальный.

Возьмем в качестве объекта регулирования ёмкость с водой, в которой необходимо поддерживать температуру на заданном уровне с помощью регулирования степени открытия клапана с паром.

Пропорциональная составляющая появляется в момент рассогласования с вводными данными. Простыми словами это звучит так – берется разница между фактической температурой и желаемой, умножается на настраиваемый коэффициент и получается выходной сигнал, который должен подаваться на клапан. Т.е. как только градусы упали, запускается процесс нагрева, поднялись выше желаемой отметки – происходит выключение или даже охлаждение.

Дальше вступает интегральная составляющая, которая предназначена для того, чтобы компенсировать воздействие окружающей среды или других возмущающих воздействий на поддержание нашей температуры на заданном уровне. Поскольку всегда присутствуют дополнительные факторы, влияющие на управляемые приборы, в момент поступления данных для вычисления пропорциональной составляющей, цифра уже меняется. И чем больше внешнее воздействие, тем сильнее происходят колебания показателя. Происходят скачки подаваемой мощности.

Интегральная составляющая пытается на основе прошлых значений температуры, вернуть её значение, если оно поменялось. Подробнее процесс описан в видео ниже.

А дальше выходной сигнал регулятора, согласно коэффициенту, подается для повышения или понижения температуры. Со временем подбирается та величина, которая компенсирует внешние факторы, и скачки исчезают.

Интеграл используется для исключения ошибок путем расчета статической погрешности. Главное в этом процессе – подобрать правильный коэффициент, иначе ошибка (рассогласование) будет влиять и на интегральную составляющую.

Третий компонент ПИД – дифференцирующий. Он предназначен для компенсации влияния задержек, возникающих между воздействием на систему и обратной реакцией. Пропорциональный регулятор подает мощность до тех пор, пока температура не достигнет нужной отметки, но при прохождении информации к прибору, особенно при больших значениях, ошибки всегда возникают. Это может привести к перегреву. Дифференциал прогнозирует отклонения, вызванные задержками или воздействием внешней среды, и снижает подаваемую мощность заранее.

Настройка ПИД регулятора

Настройка ПИД-регулятора осуществляется 2 методами:

  1. Синтез подразумевает вычисление параметров на основании модели системы. Такая настройка получается точной, но требует глубоких познаний теории автоматического управления. Она подвластна только инженерам и ученым. Так как необходимо снимать расходные характеристики и производить кучу расчетов.
  2. Ручной способ основывается на методе проб и ошибок. Для этого за основу берутся данные уже готовой системы, вносятся некоторые коррективы в один или несколько коэффициентов регулятора. После включения и наблюдений за конечным результатом проводится изменение параметров в нужном направлении. И так до тех пор, пока не будет достигнут нужный уровень работоспособности.

Теоретический метод анализа и настройки на практике применяются крайне редко, что связано с незнанием характеристик объекта управления и кучей возможных возмущающих воздействий. Более распространены экспериментальные методы на основе наблюдения за системой.

Современные автоматизированные процессы реализуются как специализированные модули под управлением программ для настройки коэффициентов регулятора.

Назначение ПИД регулятора

ПИД регулятор предназначен для поддержания на требуемом уровне некой величины – температуры, давления, уровня в резервуаре, расхода в трубопроводе, концентрации чего-либо и т.д., изменением управляющего воздействия на исполнительные механизмы, такие как автоматические регулирующие клапана, используя для этого пропорциональную, интегрирующую, дифференцирующую величины для своей настройки.

Целью использования является получение точного управляющего сигнала, который способен контролировать большие производства и даже реакторы электростанций.

Пример схемы регулирования температуры

Часто ПИД регуляторы используются при регулировке температуры, давайте на простом примере подогрева воды в ёмкости рассмотрим данный автоматический процесс.

В емкости налита жидкость, которую нужно подогреть до нужной температуры и поддерживать её на заданном уровне. Внутри бака установлен датчик измерения температуры – термопара или термометр сопротивления и напрямую связан с ПИД-регулятором.

Для подогрева жидкости будем подавать пар, как показано ниже на рисунке, с клапаном автоматического регулирования. Сам клапан получает сигнал от регулятора. Оператор вводит значение температурной уставки в ПИД-регуляторе, которую необходимо поддерживать в ёмкости.

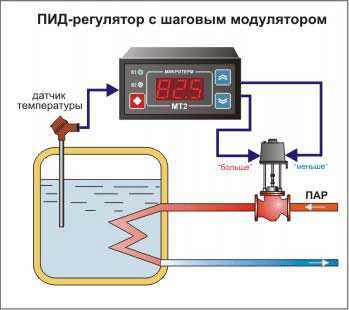
Если настройки коэффициентов регулятора неверны, будут происходить скачки температуры воды, при этом клапан будет то полностью открыт, то полностью закрыт. В этом случае необходимо рассчитать коэффициенты ПИД регулятора и ввести их заново. Если все сделано правильно, через небольшой промежуток времени система выровняет процесс и температура в ёмкости будет поддерживаться на заданной отметке, при этом степень открытия регулирующего клапана будет находиться в среднем положении.

odinelectric.ru

ПИД-регулятор своими руками / Habr

; PID управление
CalcMainEnd:
	; Вычисления, Go-Go.
CalcPid:
	;	1. Eo = E				 | 16bit
Pid1:
	MOV Err0H, ErrH
	MOV Err0L, ErrL
	;	2. E = Y-X				 | 16bit
Pid2:
	CLR C
	MOV A, SettingL
	SUBB A, ThermoL
	MOV ErrL, A
	MOV A, SettingH
	SUBB A, ThermoH
	MOV ErrH, A
	JNB  OV, Pid2Ov
	JB	ACC.7, Pid2Max
Pid2Min:
	MOV ErrL, #LOW(-500*32)
	MOV ErrH, #HIGH(-500*32)
	SJMP Pid2End
Pid2Max:
	MOV ErrL, #LOW(500*32)
	MOV ErrH, #HIGH(500*32)
	SJMP Pid2End
Pid2Ov:
	JNB ACC.7, Pid2OvP
Pid2OvN: ; Проверим на ограничение вниз
	CLR C
	MOV A, ErrL
	SUBB A, #LOW(-500*32)
	MOV A, ErrH
	SUBB A, #HIGH(-500*32)
	JNC Pid2End ; Если > -500 => всё ок
	SJMP Pid2Min
Pid2OvP:
	CLR C
	MOV A, ErrL
	SUBB A, #LOW(500*32)
	MOV A, ErrH
	SUBB A, #HIGH(500*32)
	JNC Pid2Max ; Если < 500 => всё ок
Pid2End:

	;	3. Int = Int + (E+Eo)/2  | 32bit+16bit
Pid3:
	JNB PowerReady, Pid3End ; Если нет сети -- интегральную часть не копим
	MOV A, ErrL
	ADD A, Err0L
	MOV R0, A ; временно
	MOV A, ErrH
	ADDC A, Err0H
	MOV C, ACC.7 ; Полусумма всегда влезает в 16 бит, поэтому при сдвиге надо сохранить знак
	RRC A	; Поделим без потери знака
	XCH A, R0 ; A= младшая часть, R0 - старшая часть полусуммы
	RRC A	; Доделили
	JNB  IntS, Pid3IntPos
	; Int отрицательный, изменим знак для R0:A, тем самым можно будет просто сложить с Int
	CLR C
	CPL A
	ADD A, #1
	XCH A, R0
	CPL A
	ADDC A, #0
	XCH A, R0
Pid3IntPos:
	; У Int и R0:A сейчас согласованы знаки, поэтому складываем обычным образом
	ADD A, IntLL
	MOV IntLL, A
	MOV A, IntLH
	ADDC A, R0
	MOV IntLH, A
	MOV A, R0
	JB	ACC.7, Pid3Neg ; Прибавляли отрицательную разность?
	; Если разность положительная, просто распространим перенос
	JNC jPid3End  ; Если прибавили слово и переноса небыло -- делать нам ничего не требуется.
	INC IntHL ; Распространяем перенос выше
	MOV A, IntHL
	JNZ Pid3End  ; Если перенос не ушел в 4й байт -- всё нормально
	INC IntHH ; Распространяем перенос на САМЫЙ старший байт
	MOV A, IntHH
	JNZ Pid3End  ; Если перенос не ушел еще выше -- всё нормально
	MOV IntHH, #0FFh ; Если перенс был выше -- ограничиваем интеграл потолком
	MOV IntHL, #0FFh
	MOV IntLH, #0FFh
	MOV IntLL, #0FFh
jPid3End:
	SJMP Pid3End
Pid3Neg: ; Если разность отрицательная, то надо продолжать добавлять оба раза, но FFh
	MOV A, IntHL
	ADDC A, #0FFh
	MOV IntHL, A
	MOV A, IntHH
	ADDC A, #0FFh
	MOV IntHH, A
	JC	Pid3End  ; Если тут был перенос, значит знак интеграла не изменился
	CPL IntS ; Если переноса небыло, значит у интеграла изменился знак
	CPL C		 ; Обратим знак получившегося числа
	MOV A, #0
	SUBB A, IntLL
	MOV IntLL, A
	MOV A, #0
	SUBB A, IntLH
	MOV IntLH, A
	MOV A, #0
	SUBB A, IntHL
	MOV IntHL, A
	MOV A, #0
	SUBB A, IntHH
	MOV IntHH, A
	; так как оно стало отрицательным -- то перенос тут будет всегда
Pid3End:

	;	5. cI = Int*(1/Ti)		 | 32*32=>32bit
Pid5: ; R3:R2:R1:R0 = Int*(1/Ti)
	JB Ti_sh2, Pid5Calc ; если Ti_sh2=0, то 1/Ti=1 или Ti=0. и ничего делать не надо
	MOV A, Ti_mLL
	ORL A, Ti_mLH
	ORL A, Ti_mHL
	ORL A, Ti_mHH
	JZ	Pid5Zero
	MOV R0, IntLL
	MOV R1, IntLH
	MOV R2, IntHL
	MOV R3, IntHH
	AJMP Pid5End
Pid5Zero:
	MOV A, #0
	MOV R0, A
	MOV R1, A
	MOV R2, A
	MOV R3, A
	MOV IntLL, A
	MOV IntLH, A
	MOV IntHL, A
	MOV IntHH, A
	AJMP Pid5End
Pid5Calc:
	; R7:R6:R5:R4[:R3] = MULUH(Int*Ti_m) // R3 считаем как часть для округления
	MOV R2, #0
	;; R7:R6 = IntHH*Ti_mHH
	MOV A, IntHH
	MOV B, Ti_mHH
	MUL AB
	MOV R7, B
	MOV R6, A
	; R6:R5 += IntHL*Ti_mHH
	MOV A, IntHL
	MOV B, Ti_mHH
	MUL AB
	MOV R5, A
	MOV A, R6
	ADD A, B
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R5:R4 += IntLH*Ti_mHH
	MOV A, IntLH
	MOV B, Ti_mHH
	MUL AB
	MOV R4, A
	MOV A, R5
	ADD A, B
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R4:R3 += IntLL*Ti_mHH
	MOV A, IntLL
	MOV B, Ti_mHH
	MUL AB
	MOV R3, A
	MOV A, R4
	ADD A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;; R6:R5 += IntHH*Ti_mHL
	MOV A, IntHH
	MOV B, Ti_mHL
	MUL AB
	ADD A, R5
	MOV R5, A
	MOV A, R6
	ADDC A, B
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R5:R4 += IntHL*Ti_mHL
	MOV A, IntHL
	MOV B, Ti_mHL
	MUL AB
	ADD A, R4
	MOV R4, A
	MOV A, R5
	ADDC A, B
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R4:R3 += IntLH*Ti_mHL
	MOV A, IntLH
	MOV B, Ti_mHL
	MUL AB
	MOV A, R3
	MOV R3, A
	MOV A, R4
	ADDC A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;; R5:R4 += IntHH*Ti_mLH
	MOV A, IntHH
	MOV B, Ti_mLH
	MUL AB
	ADD A, R4
	MOV R4, A
	MOV A, R5
	ADDC A, B
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	; R4:R3 += IntHL*Ti_mLH
	MOV A, IntHL
	MOV B, Ti_mLH
	MUL AB
	ADD A, R3
	MOV R3, A
	MOV A, R4
	ADDC A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;; R4:R3 += IntHH*Ti_mLL
	MOV A, IntHH
	MOV B, Ti_mLL
	MUL AB
	ADD A, R3
	MOV R3, A
	MOV A, R4
	ADDC A, B
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	;;; Если R3 > 7F --
	MOV A, R3
	JNB ACC.7, Pid5Shift ; Если R3<80 -- округление не надо
	ANL A, #7Fh
	JZ	Pid5Round ; Если = 80 -- округляем до нечетного
	MOV A, #1
	ADD A, R4
	MOV R4, A
	MOV A, R2 ; A=0
	ADDC A, R5
	MOV R5, A
	MOV A, R2 ; A=0
	ADDC A, R6
	MOV R6, A
	MOV A, R2 ; A=0
	ADDC A, R7
	MOV R7, A
	SJMP Pid5Shift
Pid5Round:
	MOV A, R4
	ORL A, #01h
	MOV R4, A
	;JMP Pid5Shift

Pid5Shift:
	; R3:R2:R1:R0 = (Int-R7:R6:R5:R4) >> 1
	CLR C
	MOV A, IntLL
	SUBB A, R4
	MOV R0, A
	MOV A, IntLH
	SUBB A, R5
	MOV R1, A
	MOV A, IntHL
	SUBB A, R6
	MOV R2, A
	MOV A, IntHH
	SUBB A, R7
	RRC A ; >>1 без потери переноса
	MOV R3, A
	MOV A, R2
	RRC A
	MOV R2, A
	MOV A, R1
	RRC A
	MOV R1, A
	MOV A, R0
	RRC A
	;MOV R0, A
	; R3:R2:R1:R0 += R7:R6:R5:R4
	;MOV A, R0
	ADD A, R4
	MOV R0, A
	MOV A, R1
	ADDC A, R5
	MOV R1, A
	MOV A, R2
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	ADDC A, R7
	MOV R7, A
	; Теперь сдвинуть вправо на sh3.
	; sh3 может быть до 16 (так как у нас Ti 16разрядный; проверим необходимость сдвига на 16 бит)
	MOV A, Ti_sh3
	JNB ACC.4, Pid5ShiftUnder16
	; Надо сдвинуть >=16 -- 2 байта сдвинем mov'ами
	MOV R0, 18h+2; R2, bank 3
	MOV R1, 18h+3; R3, bank 3
	MOV R2, #0
	MOV R3, #0
Pid5ShiftUnder16:
	JNB ACC.3, Pid5ShiftUnder8
	; Надо сдвинуть на >=8 -- 1 байт сдвигаем mov'ами
	MOV R0, 18h+1; R1, bank 3
	MOV R1, 18h+2; R2, bank 3
	MOV R2, 18h+3; R3, bank 3
	MOV R3, #0
Pid5ShiftUnder8:
	ANL A, #07h
	JZ Pid5End ; Если внутри байта двигать не надо -- всё
	MOV R4, A
	SJMP Pid5ShiftRight
Pid5NextShift:
	CLR C
	; К этому моменту C у нас еще возможнозначимый старший бит!
Pid5ShiftRight:
	MOV A, R3
	RRC A
	MOV R3, A
	MOV A, R2
	RRC A
	MOV R2, A
	MOV A, R1
	RRC A
	MOV R1, A
	MOV A, R0
	RRC A
	MOV R0, A
	DJNZ R4, Pid5NextShift
	; Всё, после всех сдвигов получили результат
	; Не забываем, что у вычисленного в R3:R2:R1:R0
	; сейчас число положительное, а знак его в IntS
Pid5End:

	;	4. PID += [ cD = Td * (E-Eo) ]		| 16*16=>32bit
Pid4: ; cD = R7:R6:R5:R4; ErrD = E-Eo
	CLR C
	MOV A, ErrL
	SUBB A, Err0L
	MOV DiffL, A
	MOV A, ErrH
	SUBB A, Err0H
	MOV DiffH, A
	MOV C, ACC.7 ; Берём знак результата
	MOV DiffS, C ; Сохраним знак E-Eo
	JNC Pid4Mul
	; Diff -- орицательный, обратим знак
	MOV A, DiffL
	CPL A
	ADD A, #1
	MOV DiffL, A
	MOV A, DiffH
	CPL A
	ADDC A, #0
	MOV DiffH, A
Pid4Mul:
	; R7:R6 = DiffH*TdH
	; MOV A, DiffH = в любом случае A=DiffH
	MOV B, TdH
	MUL AB
	MOV R6, A
	MOV R7, B
	; R5:R4 = DiffL*TdL
	MOV A, DiffL
	MOV B, TdL
	MUL AB
	MOV R4, A
	MOV R5, B
	; R6:R5 += DiffH*TdL
	MOV A, DiffH
	MOV B, TdL
	MUL AB
	ADD A, R5
	MOV R5, A
	MOV A, R6
	ADD A, B
	MOV R6, A
	MOV A, R7
	ADDC A, #0
	MOV R7, A
	; R6:R5 += DiffL*TdH
	MOV A, DiffL
	MOV B, TdH
	MUL AB
	ADD A, R5
	MOV R5, A
	MOV A, R6
	ADD A, B
	MOV R6, A
	MOV A, R7
	ADDC A, #0
	MOV R7, A

	;	6. PID = E + cI + cD	 | 32bit
Pid6:	; R3:R2:R1:R0 равно cI, знак в IntS;
	; R7:R6:R5:R4 = cD; знак в DiffS
	; E в обратном дополнительном коде

	JB IntS, ChkDiffN
	JNB DiffS, Pid6Add ; Int>0, Diff>0 => Add
	SJMP Pid6Sub ; Int>0, Diff<0 => Sub
ChkDiffN:
	JNB DiffS, Pid6Sub ; Int<0, Diff>0 => Sub
	; Int<0, Diff<0 => Add
Pid6Add:
	; Одинаковый знак => складываем их с проверкой на переполнение
	MOV A, R0
	ADD A, R4
	MOV R0, A
	MOV A, R1
	ADDC A, R5
	MOV R1, A
	MOV A, R2
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	ADDC A, R7
	MOV R3, A
	JNC Pid6Err ; Если нет переноса - в результате сложения переполнения небыло
	MOV R3, #0FFh
	MOV R2, #0FFh
	MOV R1, #0FFh
	MOV R0, #0FFh
	SJMP Pid6Err
Pid6Sub:
	; Знаки разные -- вычтем одно из другого и проверим знак результата
	CLR C
	MOV A, R4
	SUBB A, R0
	MOV R0, A
	MOV A, R5
	SUBB A, R1
	MOV R1, A
	MOV A, R6
	SUBB A, R2
	MOV R2, A
	MOV A, R7
	SUBB A, R3
	MOV R3, A
	JNC Pid6Err ; Если нет заимствования -- знак результата равен знаку DiffS
	CPL DiffS ; Если заимствование было, у DiffS и результата надо обратить знак
	MOV R6, #0 ; R6=0
	MOV A, R0
	CPL A
	ADDC A, R6 ; R6=0, C=1 => действие +1
	MOV R0, A
	MOV A, R1
	CPL A
	ADDC A, R6 ; +перенос
	MOV R1, A
	MOV A, R2
	CPL A
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	CPL A
	ADDC A, R6
	MOV R3, A

Pid6Err:
	MOV R6, #0 ; R6=0
	; В R3:R2:R1:R0 -- лежит cI+cD; знак суммы в DiffS
	; надо прибавить/отнять Err, записанное в обратном коде
	; Приведём знак Err к DiffS
	MOV R4, ErrL
	MOV A, ErrH
	JB ACC.7, Pid6ChkDiffS
	JNB DiffS, Pid6SumErrNoInv ; Err>0, Diff>0 => NoInv
	SJMP Pid6SumErrInv
Pid6ChkDiffS:
	JNB DiffS, Pid6SumErrNoInv ; Err<0, Diff>0 => NoInv
Pid6SumErrInv:
	; У Err знак отличается от DiffS -- инвертируем
	SETB C ; Не уверен в состоянии C
	MOV A, ErrL
	CPL A
	ADDC A, R6 ; A+=R6+C, R6=0	C=1 => A+=1
	MOV R4, A ; R4=ErrL
	MOV A, ErrH
	CPL A
	ADDC A, R6
Pid6SumErrNoInv:
	MOV R5, A ; ErrH
Pid6SumErr:
	; Итак, в R5:R4 лежит Err, знак которого согласован с DiffS; но в обратно-дополнительном коде
	MOV A, R0
	ADD A, R4
	MOV R0, A
	MOV A, R5
	CLR F0
	JNB ACC.7, Pid6SubErrPos
	SETB F0
	MOV R6, #0FFh ; Добавляем отрицательное => дополняем FFами
Pid6SubErrPos:
	ADDC A, R1
	MOV R1, A
	MOV A, R2
	ADDC A, R6 ; +расширение
	MOV R2, A
	MOV A, R3
	ADDC A, R6 ; +расширение
	MOV R3, A
	MOV R6, #0
	; Надо проверить нет ли смены знака итоговой суммы
	JNC Pid6ChkF0
	JB F0, Pid7 ; Err<0, был перенос => Знак не сменился, переполнения нет
	SJMP Pid6SumOv ; Err>0, был перенос => переполнение
Pid6ChkF0:
	JNB F0, Pid7 ; Err>0, небыло переноса => нет переполнения
	;SJMP Pid6SumUf ; Err<0, небыло переноса => сменился знак
Pid6SumUf:
	; Если Err<0 и небыло переноса => сменился знак
	CPL DiffS
	MOV A, R0
	CPL A
	ADD A, #1 ; C=?, поэтому прибавляем 1 обычным методом
	MOV R0, A
	MOV A, R1
	CPL A
	ADDC A, R6
	MOV R1, A
	MOV A, R2
	CPL A
	ADDC A, R6
	MOV R2, A
	MOV A, R3
	CPL A
	ADDC A, R6
	MOV R3, A
	SJMP Pid7 ; Знак у результата и DiffS приведены в норму
Pid6SumOv:
	; Было переполнение => округляем до максимума
	MOV R0, #0FFh
	MOV R1, #0FFh
	MOV R2, #0FFh
	MOV R3, #0FFh

	;	7. U = K*PID/256		 | 32bit*16bit/8bit => 40bit,
	;					 | которые усекаются до 10bit
	;					 | при вычислениях
Pid7: ; В R3:R2:R1:R0 лежит результат PID, в DiffS его знак
	  ; Нужно вычислить K*PID/256, ограничив результат до 10бит
	  ; K всегда положительно, поэтому если PID < 0 => минимум
	JB DiffS, Pid7Umin
	; поскольку мы можем жестко ограничить сверху 16ю битами,
	; то если R3 != 0 => ставим максимум в любом случае
	MOV A, R3
	JNZ Pid7Umax
	; [R2:R1:R0 * KH:HL] = [R7:R6:R5:R4:R3]
	; вычисляем, учитывая что должно получиться R7=0 R6=0,
	; иначе переполнение, поэтому R7 и R6 вообще не трогаем
	; но проверяем результат
	; R7:R6 = R2*KH
	MOV A, R2
	JZ Pid7S1
	MOV A, KH
	JNZ Pid7Umax ; Если R2!=0 и KH!=0 => R7:R6>0 => переполнение
Pid7S1:
	; R6:R5 = R2*KL
	MOV A, R2
	MOV B, KL
	MUL AB
	MOV R5, A
	MOV A, B
	JNZ Pid7Umax ; Если R6 > 0 => переполнение
	; R6:R5 = R1*KH
	MOV A, R1
	MOV B, KH
	MUL AB
	ADD A, R5
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	MOV A, B
	JNZ Pid7Umax ; Если R6 > 0 => переполнение
	; R5:R4 = R0*KH
	MOV A, R0
	MOV B, KH
	MUL AB
	MOV R4, A
	MOV A, R5
	ADD A, B
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	; R5:R4 = R1*KL
	MOV A, R1
	MOV B, KL
	MUL AB
	ADD A, R4
	MOV R4, A
	MOV A, R5
	ADDC A, B
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	; R4:R3 = R0*KL
	MOV A, R0
	MOV B, KL
	MUL AB
	RLC A ; C = R3>=0x80, Z=R3>0x80
	MOV R3, #0FFh ; R3<>0x80 => ничего
	JNZ Pid7S2
	MOV R3, #0FEh ; R3==0x80 => округление до четного
Pid7S2:
	MOV A, R4
	ADDC A, B ; Складываем умножение, регистр, и перенос-округление
	ANL A, R3 ; А так же если округление до четного -- отбрасываем после младший бит
	MOV R4, A
	MOV A, R5
	ADDC A, R6 ; R6=0 у нас с давних пор, хоть мы туда и не складывали ничего во время перемножения
	JC	Pid7Umax ; Если R6 > 0 => переполнение
	MOV R5, A
	; R5:R4 => ограниченный в 16 бит результат
	; Теперь надо ограничить R5:R4 до Umax/Umin
	MOV A, UmaxL
	SUBB A, R4 ; C=0 на текущий момент
	MOV A, UmaxH
	SUBB A, R5
	JC Pid7Umax ; Если R5:R4>Umax => R5:R4 = Umax
	MOV A, UminL
	SUBB A, R4 ; C=0 на текущий момент
	MOV A, UminH
	SUBB A, R5
	JNC Pid7Umin ; Если R5:R4<Umin => R5:R4 = Umin
	; Мощность вычислена
	MOV UH, R5
	MOV UL, R4
	SETB UReady
	AJMP CalcExit
Pid7Umax: ; Установить максимальную мощность
	MOV UH, UmaxH
	MOV UL, UmaxL
	SETB UReady
	AJMP CalcExit
Pid7Umin: ; Установить минимальную мощность
	MOV UH, UminH
	MOV UL, UminL
	SETB UReady
	AJMP CalcExit

habr.com

Принцип работы ПИД-регуляторов

Принцип работы

Регуляторы процесса

Регуляторы процесса (Process Controllers) – это параметрируемые цифровые контроллеры со встроенным набором стандартных функций для регулирования технологических переменных (температуры, давления и т.п.).

В качестве сигналов задания (Reference) могут использоваться как фиксированные уставки (Fixed Setpoints), так и внешние (External).

Аналоговые входы используются для подключения датчиков обратной связи (термометров сопротивления, термопар, манометров и т.п.).

Дискретные входы используются для задания фиксированных уставок и переключения между режимами.

Дискретные выходы используются для сигнализации: готовности, аварий, состояния.

Релейные выходы используются для дискретного управления, а аналоговые выходы – для непрерывного управления.

Дискретное управление
  • 2-х позиционный регулятор использует только 2 состояния:
    • включено (открыто)
    • выключено (закрыто)
      • Пример: управление нагреванием или охлаждением.
  • 3-х позиционный регулятор использует 3 состояния:
    • выключено
    • вращение по часовой стрелке
    • вращение против часовой стрелки (реверс)
      • Пример: управление реверсивным электродвигателем.
  • 5-и позиционный регулятор использует 5 состояний:
    • выключено
    • вращение на первой скорости по часовой стрелке
    • вращение на второй скорости по часовой стрелке
    • вращение на первой скорости против часовой стрелки
    • вращение на второй скорости против часовой стрелки
      • Пример: управление 2-скоростным реверсивным двигателем.
Непрерывное управление

Для непрерывного управления используются ПИД-регуляторы. Возможна реализация каскадного (подчинённого) управления.

Замкнутая система управления


Переходный процесс

Переходный процесс – это реакция системы на внешнее воздействие (задание, возмущение).

Неустойчивый (расходящийся) переходный процесс
Устойчивый (сходящийся) переходный процесс
КолебательныйАпериодическийМонотонный

ПИД-регулятор

С помощью настройки ПИД-регулятора (PID-controller) мы можем скорректировать переходный процесс так, как нам нужно для решения своей задачи.

Хзад – заданное (желаемое) значение выходной переменной
Xmax – верхний допустимый предел выходной переменной
Xmin – нижний допустимый предел выходной переменной
Т – период колебаний
Тн – время нарастания
Тр – время переходного процесса (последняя точка пересечения кривой с Xmin или Xmax)
А1 – первое перерегулирование
А2 – второе перерегулирование
d=А1/A2 – степень (декремент) затухания переходного процесса (отношение первого перерегулирования ко второму)

Рассогласование, перерегулирование, время нарастания, время переходного процесса, степень затухания характеризуют качество регулирования.

Пример

ПИД-регулятор открывает и закрывает регулирующий вентиль на горячей трубе так, чтобы из крана текла вода с температурой +40°С с погрешностью плюс-минус 2 градуса. Регулятор вычисляет рассогласование (ошибку) – отклонение реальной температуры (например, +20°С) от заданного значения (+40°С) и решает – когда и насколько необходимо приоткрыть горячий вентиль, чтобы температура повысилась на 20С. Реальную (фактическую) температуру регулятор узнаёт с помощью датчика температуры (обратная связь), а заданную температуру (уставку) ему сообщает оператор, например, набирая число «40» на своём ПК.

Чтобы настроить ПИД-регулятор, необходимо подобрать правильную комбинацию трёх коэффициентов:

  • Пропорционального – Kp
  • Интегрального – Ki
  • Дифференциального – Kd

Могут использоваться и более простые – П и ПИ-регуляторы.

Формула ПИД-регулятора

где e(t) – ошибка (рассогласование), u(t) – выходной сигнал регулятора (управляющее воздействие).

Чем больше Пропорциональный коэффициент, тем выше быстродействие, но меньше запас устойчивости. Но! простой П-регулятор не может полностью отработать рассогласование, т.е. всегда работает с ошибкой.

ПИ-регулятор позволяет избавиться от статической (установившейся) ошибки, но, чем больше Интегральный коэффициент, тем больше перерегулирование (динамическая ошибка).

ПИД-регулятор позволяет нам уменьшить перерегулирование, но, чем больше Дифференциальный коэффициент, тем больше погрешность из-за влияния шумов.

Если шумы идут по каналу обратной связи, то мы можем их отфильтровать с помощью фильтра низкой частоты, но чем больше постоянная этого фильтра, тем медленнее регулятор будет отрабатывать возмущения.


Настройка ПИД-регулятора по методу Циглера-Николса

Циглер и Николс предложили свой вариант быстрой настройки ПИД-регулятора для периодического переходного процесса, в котором затухание примерно равно 4.

  • Обнуляем Ki и Kd
  • Постепенно увеличиваем Kp до критического значения Kc, при котором возникают автоколебания
  • Измеряем период автоколебаний Т
  • Вычисляем значения Kp, Ki и Kd по разным формулам для разных регуляторов:
    • для П-регулятора: Kp=0,50*Kc
    • для ПИ-регулятора: Kp=0,45*Kc, Ki=1,2*Kp/T
    • для ПИД-регулятора: Kp=0,60*Kc, Ki=2,0*Kp/T, Kd=Kp*T/8

Каскадный регулятор (подчинённое управление)

Продолжение примера

Теперь нам захотелось добавить комфорта и сделать так, чтобы уставка задания температуры воды менялась в зависимости от температуры воздуха на улице (на улице мороз – вода горячая, на улице жара – вода прохладная). Можно установить ещё один регулятор комфортной температуры, который по показаниям термометра узнаёт фактическую температура наружного воздуха и решает, что комфортная температура воды должна быть, например, +40°С, поэтому он выдаёт задание регулятору температуры воды – поддерживать температуру на уровне +40С (см. пример выше). Здесь мы имеем каскадное регулирование: контур регулирования температуры воды подчинён контуру регулирования комфортной температуры воды.

С помощью регуляторов процесса мы можем реализовать и более сложные связи. Например, поддерживать постоянный расход и температуру воды, независимо от давления и температуры горячего и холодного трубопроводов.

Упреждающее регулирование (Feedforward Control)

Не всегда простой ПИД-регулятор в системе с обратной связью может обеспечить требуемое быстродействие из-за возникновения нежелательных колебаний или недопустимо большого перерегулирования. Для улучшения характеристик регулирования применяют комбинированное управление – с обратной связью (closed-loop) и без обратной связи (open-loop). К управляющему воздействию (выходу регулятора) добавляется сигнал упреждающего воздействия, который не зависит от рассогласования, а значит, не может вызвать автоколебания в системе.

Продолжение примера
Если мы доверяем прогнозу погоды, то вместо каскадного управления мы можем реализовать упреждающее регулирование без измерения уличной температуры: читаем прогноз на завтра, задаём уставку +40°С по таймеру времени на завтра на 7 утра.

Если измерить возмущение, то можно подать упреждающее воздействие, которое компенсирует влияние этого возмущения на процесс до того, как начнёт изменяться регулируемый параметр.


www.maxplant.ru

ПИД-регулятор — Википедия

Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации.

Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.

Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д.

Общие сведения

Пропорциональная составляющая

Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.

Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.

Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.

Интегрирующая составляющая

Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.

Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.

Дифференцирующая составляющая

Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.

Теория

Система управления с обратной связью с участием ПИД-регулятора. Система управляет величиной y(t), то есть выводит величину y(t) на заданное извне значение u(t). На вход ПИД-регулятора подаётся ошибка e(t), выход ПИД-регулятора является управляющим воздействием для некоторого процесса (для объекта управления), управляющего величиной y(t).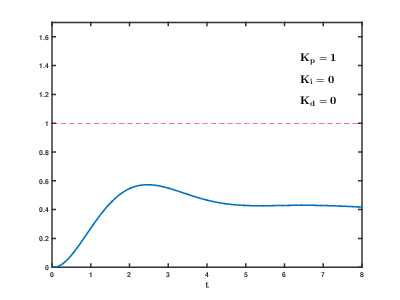 Влияние изменения параметров PID (Kp,Ki,Kd) на переходную характеристику системы.

Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением (или уставкой, в технике), а разность e = (x0 − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике.

Выходной сигнал регулятора u определяется тремя слагаемыми:

u(t)=P+I+D=Kpe(t)+Ki∫0te(τ)dτ+Kddedt{\displaystyle u(t)=P+I+D=K_{p}\,{e(t)}+K_{i}\int \limits _{0}^{t}{e(\tau )}\,{d\tau }+K_{d}{\frac {de}{dt}}},

где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно.

Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:

u(t)=Kp(e(t)+Kip∫0te(τ)dτ+Kdpdedt){\displaystyle u(t)=K_{p}\left(\,{e(t)}+K_{ip}\int \limits _{0}^{t}{e(\tau )}\,{d\tau }+K_{dp}{\frac {de}{dt}}\right)}

В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:

U(n)=KpE(n)+KpKipT∑k=0nE(k)+KpKdpT(E(n)−E(n−1)){\displaystyle U(n)=K_{p}E(n)+K_{p}K_{ip}T\sum _{k=0}^{n}{E(k)}+{\frac {K_{p}K_{dp}}{T}}(E(n)-E(n-1))},

где T{\displaystyle T} — время дискретизации. Используя замену Kidiscr=KpKipT,Kddiscr=KpKdpT{\displaystyle K_{i}^{discr}=K_{p}K_{ip}T,K_{d}^{discr}={\frac {K_{p}K_{dp}}{T}}} можно записать:

U(n)=KpE(n)+Kidiscr∑k=0nE(k)+Kddiscr(E(n)−E(n−1)){\displaystyle U(n)=K_{p}E(n)+K_{i}^{discr}\sum _{k=0}^{n}{E(k)}+K_{d}^{discr}(E(n)-E(n-1))}

В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:

U(n)=U(n−1)+Kp(E(n)−E(n−1))+KidiscrE(n)+Kddiscr(E(n)−2E(n−1)+E(n−2)){\displaystyle U(n)=U(n-1)+K_{p}(E(n)-E(n-1))+K_{i}^{discr}{E(n)}+K_{d}^{discr}(E(n)-2E(n-1)+E(n-2))}

Часто в качестве параметров ПИД-регулятора используются:

  • относительный диапазон
Pb=1Kp{\displaystyle P_{b}={\frac {1}{K_{p}}}}
  • постоянные интегрирования и дифференцирования, имеющие размерность времени
Ti=1Kip{\displaystyle T_{i}={\frac {1}{K_{ip}}}}
Td=Kdp{\displaystyle T_{d}={K_{dp}}\;}

Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.

Практика применения

Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции.

В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора.

Ссылки

См. также

wikipedia.green

регулятор – это… Что такое ПИД-регулятор?

Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации.

Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.

Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п.

Общие сведения

Пропорциональная составляющая

Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.

Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.

Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.

Интегральная составляющая

Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.

Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям.

Дифференциальная составляющая

Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.

Теория

Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением, а разность e = (x0 − x) — невязкой, рассогласованием или отклонением величины от заданной.

Выходной сигнал регулятора u определяется тремя слагаемыми:

,

где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно.

Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие:

В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:

,

где  — время дискретизации. Используя замену можно записать:

В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:

Система управления с обратной связью с участием ПИД-регулятора. Система управляет величиной y(t), т.е. выводит величину y(t) на заданное извне значение u(t). На вход ПИД-регулятора подаётся ошибка e(t), выход ПИД-регулятора является управляющим воздействием для некоторого процесса (для объекта управления), управляющего величиной y(t).

Часто в качестве параметров ПИД-регулятора используются:

  • относительный диапазон
  • постоянные интегрирования и дифференцирования, имеющие размерность времени

Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.

Ссылки

dic.academic.ru

Корректная реализация разностной схемы ПИД регулятора / Habr

ПИД-регулятор является простейшим регулятором, имеющим эффективные аппаратные аналоговые реализации, и потому применяемый наиболее широко. Для своей работы требует настройки 3х коэффициентов под конкретный объект, позволяющие подобрать процесс регулирования согласно требованиям. Обладая простым физическим смыслом и простой математической записью, применяется широко и часто в регуляторах температуры, регуляторах расхода газа и других системах, где требуется поддерживать некий параметр на заданном уровне, с возможными переходами между разными заданными уровнями. Разумеется, существуют более сложные регуляторы, позволяющие более точно и быстро и с меньшими перерегулированиями выходить на заданные параметры, а так же учитывающие нелинейность или гистерезис регулируемого объекта, однако они обладают большей вычислительной сложностью и сложнее в настройке.

Несмотря на свою простоту как физического смысла, так и математической записи:

при програмной реализаци ПИД регулятора очень часто допускают ошибки, которые встречаются даже в поверенных приборах автоматики.

Причем проверить качество реализации ПИД регулятора крайне легко.

Рассмотрим простейший пример: терморегулятор. Для проверки его качестве лучше всего подходит быстрый, малоинерциальный, маломощный объект. Классика жанра: обычная лампочка на 100Вт с прикрученной к ней тонкой термопарой (ХА). И первое, на чем следует проверять ПИД регулятор — деградация ПИД до просто П-регулятора. То есть коэффициенты интегральной и дифференциальной ставим в ноль, а пропорциональную ставим в максимум.

Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит. Начинаем начинаем увеличивать уставку: 16.1, 16.3, 16.7, 18… 19… лампочка загорелась. Как?! Откуда?! Останавливаемся — выключилась. Итак, мы встретились с первой классической ошибкой реализации ПИД регулятора.

Небольшое математическое отступление: вспомним еще раз интегральную запись указанную выше. Мы реализуем её програмно, а значит — дискретно. То есть с завидной регулярностью производим измерение входной величины, сравниваем её с уставкой, вычисляем воздействие, выдаём, повторить. А значит, надо из интегральной формы перейти в конечно-разностную схему. При переходе обычно используется переход «в лоб»:

где E(n) = X(n) - X0(n) — то есть величина рассогласования между текущим и заданным значением регулируемого параметра.

Использование прямой формулы потребует во-1х считать и хранить интеграл рассогласований за большой период, во-2х требует работы с плавающей точкой высокой точности (так как интегральный коэффициент Ki всегда < 1), либо операции деления (представляя коэффициент в форме 1/Ki) большой разрядности. Всё это требует вычислительных ресурсов, коих в embedded как правило сильно ограничено… Поэтому, вместо реализации прямой схемы, реализуют рекуррентную формулу:

использование рекуррентной формулы позволяет сократить объём вычислений и разрядность промежуточных значений.

Итак, вернёмся к нашему регулятору. Итак, есть регулируемый объект: лампочка. Для управления подаваемой на неё мощностью, используют простой подход: сеть питания (220В 50Гц) подаётся через симистор на нагрузку. Симистор в момент перехода полуволны через ноль выключается, и остаётся выключен до тех пор, пока не будет подан сигнал на управляющий электрод. Таким образом, чем раньше после начала полуволны мы подадим управляющий сигнал, тем больше энергии от этой полуволны достигнет управляемого объекта. Правильно расчитав время для линейности площади части полуволны с момента времени X до конца полуволны, мы получаем возможность выдавать мощность от 0 до 100% с точностью, с которой расчитали таблицу линеаризации.

Итак, мы можем выдавать мощность от 0 до 100%. В реальных объектах, часто нельзя выдавать 100% мощности — например, это черевато перегоранием нагревательного элемента. Поэтому, все приборы имеют настройку минимальной и максимальной выдаваемой мощности на объект.

Итак, после вычисления U(n) по вышестоящей формуле, добавляется еще ограничение результата:
if Un < Umin then Un := Umin; if Un>Umax then Un := Umax;
После чего, вычисленное Un и есть требуемая выходная мощность на текущий момент. Та-дам! Именно вот эта реализация и создаёт ошибку, о которой написано выше.

Причина банальна: в момент перехода от дикретной к конечно-разностной схеме, мы «выносим за скобки» операцию вычисления интеграла, и на каждом шаге мы прибавляем производную к накопленной сумме U(n-1). Наложив же на неё ограничение, мы весь вычисленный интеграл фактически обнуляем. (Ну не сколько обнуляем, сколько приводим к диапазону 0-100, что в данном случае несущественно). Таким образом, мы дифференциурем ПИД регулятор, и остаётся дифференциально-ускорительный. Что в реальности выглядит как просто дифференциальный регулятор — мощность при этом подаётся пропорционально изменению уставки или регулируемой величины, а не пропорционально разности между уставкой и регулируемой величиной.

Вывод №1: вычисление U(n) нельзя ограничивать. Для ограничения мощности подаваемой на выходное устройство следует заводить отдельную переменную.

Теперь, когда мы завели Urn, для ограниченной мощности, перезаливаем, продолжаем тестировать.
Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит.
Начинаем прибавлять уставку: 16.1, 16.4, 17, 18, 20, 22, 24 (опа! засветилось! ура!), 28, 30, 40, 60… Красота! Работает!
Наблюдаем за процессом — вышло примерно на 60, болтается чуток туда-сюда, но держит. Вроде, всё красиво. Выдыхаем, проверяем управление с ПК: задаём 600 градусов. И… Лампочка выключается. Как так? Уставка 600, текущая 60, а лампочка не горит?

Пока ждём и медленно осознаём, что мы явно напоролись на какой-то «Классический Косяк №2» ™ лампочка медленно разгорается, выходит на 100% мощности, и так и остаётся — 600-то градусов она выдать ну никак не может.

Возвращаемся снова к нашей разностной схеме. U(n) = U(n-1) + Kp*(dE + ...). К текущему расчетному значению воздействия прибавляется разность невязки помноженная на коэффициент пропорциональности. У нас была уставка 60, температура 60, то есть невязка нулевая. Выходная мощность так же была нулевая. И тут разом, скачком, уставку увеличили до 600 градусов. невязка резко стала 540 градусов, помножили еще и на коэффициент пропорциональности… и вылетели за разрядность хранения U(n). Не смейтесь, использование математики с фиксированной точки, вместо плавающей точки. При разнице в 540 градусов и работе через 1/16, при коэффициенте пропорциональности 20, получаем… 540*20*16=172800, а если у нас 16тиразрядный U(n), да еще и знаковый, то фактически, в результате вычисления мы получили A300h = −8960. Опачки. Вместо большого плюса — ощутимый такой минус.

Вывод №2: вычисления должны проводиться с корректной поддержкой переполнения. Переполнилось? Ограничь предельным числом, уж никак не заворачивать.

Итак, нарастили разрядность U(n), перетранслировали, зашили, запускаем. Лампочка еще не совсем остыла, там 80 градусов, уставка всё те же 600. Лампочка зажигается… и тухнет. Зажигается и тухнет. Как так? Уставка 600, лампочка 80 — и поддерживает вполне себе свои 80! Как так-то?! Явно у нас вылез Жучок №3.

И снова лирически-математическое отступление. Итак, есть наша разностная схема: U(n) = G(U(n-1), dE(n)). Еще раз: новое значение воздействия есть сумма прошлого воздействия и некого воздействия, зависящего от разности невязки в текущий момент и предыдущий. А что такое предыдущий момент? А какой момент предыдущий у предыдущего? Ну-ка, вспомнили школу. Доказательство по индукции. Если можно построить доказательство для K+1, считая что доказательство для K верно, И доказать отдельно что верно для K=0, тогда доказательство истинно. Итак, а как мы считаем U(0)?

Часто встречающееся решение: всё обнуляем, уставку считываем из флешпамяи уставки, ждём 1 цикл опроса, и считываем X(0). Вот, ноль готов, теперь работаем. И… И не правильно. Почему? Потому что рекурентная формула отталкивается от изменений в невязке. А проинициализировав нулём и загрузив текущие значения мы потеряли стартовые условия. Всё — вместо поддержания абсолютного значения температуры на уровне равном абсолютной уставке регулятор начинает держать температуру равную стартовой плюс разнице уставки. То есть было 80 градусов и уставка 200, включили прибор — он держет 80. Сменили уставку на 240 — он начал держать 120.

Правильная инициализация разностной схемы: обнулить _вообще всё_. То есть
X(0) = 0, X0(0) = 0. U(0) = 0. E(0)=X(0)-X0(0)=0.
И на первом же цикле вычислений у нас как бы скачком появляются уставке и текущее значение:
X(1) = 80. X0(1)=200. U(1) = U(0)+Kp*(E(1)-E(0)) = U(0)+Kp*(X(1)-X0(1)-E(0)) = 0 + 20*(200 - 80 - 0) = 2400
Вот теперь схема работает правильно.

Вывод №3: корректно инициализируй стартовые условия.

Правильно ли? Hу-ка, ну-ка… Еще раз… Ставим уставку 20. Ждём охлаждения… Выключаем. Включаем. Итак, красота: текущая 20, уставка 20. Ставим скачком 600. Поехало греться. 100, 120… ставим уставку 20. Отключилось, пошло охлаждаться. Ждём чуток (120… 110… 100… 90… 80…) и ставим уставку 100. Поехало греться… 105 градусов, отключилось. Стоп. А почему оно держит 105? У нас же сейчас работает только пропорциональная составляющая. При правильной реализации из физического смысла процесса колебательный процесс не может держать уставку выше чем задано. Строго ниже. А держит на 5 градусов больше чем попросили. Это наблюдается Прикол №4.

Итак, вспоминаем что у нас было выше: Вывод№2: U(n) нельзя ограничивать. И Вывод№3: при переполнении ограничить всё-таки придётся. Да-да. Иначе «рабочая точка» смещается на ограниченный момент. Что же делать? Увеличить разрядость? Хорошо, если хватает вычислительной мощности. А надо ли? Собственно, что плохого, что у нас U(n) = 9999.99, а не 29999.99? В общем-то только то, что мы потеряли 20000. Но сейчас-то для работы нам так и так надо вваливать просто 100% мощности, правильно? Правильно. Значит, проблемы с ограничением в полку нет, до тех пор, пока мы не отходим от предела. Таким образом, в случае переполнения надо ставить флаг, и по достижении, например, половины диапазона (то есть как U(n) после 9999.9 опустилось ниже 5000.00), заново реинициализировать схему. То есть отбрасывать историю, сказать что n=0 и см. выше Вывод №3. Пытливый ум уже сообразил, что в случае полной схемы, когда все три компоненты не равны нулю, обнуляя в процессе итеративный процесс, мы в том числе обнуляем накопленный интеграл интегральной составляющей. Однако, в связи с тем, что обнуляем мы значительно заранее, он успеет подкопиться за время довырабатывания остатка. Да и не совсем корректно копить интеграл на «больших» перегонах, так как цель интегральной составляющей — «выбрать» невязку, которую не может отработать пропорциональная составляющая отдельно.

Вывод №4: если по какой-то причине U(n) было ограничено, схему следует переинициализировать как только создалось впечатление, что схема вернулась в нормальное состояние.

В следующем выпуске: а так ли надо реализовывать разностную схему? Подробная реализация прямой дискретной схемы, обладающей простыми и понятными настраиваемыми коэффициентами, с прямым физическим смыслом, которая без проблем вычисляет управляющее воздействие с частотой 25Гц на процессоре ADuC847 (быстрый 8-битный контроллер, с ядром 8051), оставляя еще море процессорного времени для других процессов.

(Картинки с изображением формул взяты из статьи ПИД-Регулятор в Wikipedia)

habr.com

Больше новостей

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *