Пилообразная последовательность: Подробные данные об ошибке IIS 8.5 – 404.0

Содержание

Задача 20. Пилообразная последовательность | Тренер по программированию

Интересная задача с парой тонких моментов. Давайте читать условие:

Условие задачи с сайта acmp.ru

Первое, на что стоит обратить внимание, это размер входных данных. Количество чисел до одного миллиона, и это обычно требует быстрого ввода (особенно на acmp), а удобные способы считывания данных не укладываются. Одним из способов быстрого считывания может быть считывание всей строки целиком одной операцией, а потом уже её разбор в коде и оперативной памяти. В C++ это можно реализовать с помощью stringstream, например. А в Python’е это стандартный способ ввода данных, поэтому давайте писать на нём:

Ввод данных

Решать будем за один проход по массиву, поддерживая размер текущей пилообразной и размер максимальной. Тогда для очередного элемента надо будет проверить, продолжает ли он пилообразность и обновить наши значения. И тут мы встречаем второй тонкий момент – это одинаковые элементы, стоящие рядом. Например, если текущий элемент не продолжает текущую пилообразную последовательность, то возможны два варианта:

1 2 3 или 3 2 1 – текущий элемент продолжает возрастающее или нисходящее движение, тогда можно говорить он начале другой пилообразной последовательности длины 2: 2 3 или 2 1 соответственно;
1 2 2 – текущий элемент равен предыдущему, тогда только он является началом новой пилообразной последовательности длины 1.

Это необходимо учесть и при инициализации стартовых значений:

Инициализация стартовых значений

И при обработке каждого элемента:

Решение за один проход по массиву

Заметим, что благодаря множественным операциям сравнения в Python’е нет необходимости нагромождать сложное условие или делать его плохочитаемым с помощью арифметических операций:

Условие пилообразности

Выбираем язык под задачу и получаем красивое решение.

Предыдущий выпуск: Задача 193. Поиск прямоугольников

Я очень хочу, чтобы мои советы были полезны вам, а для того, чтобы быстрее всех получать новые статьи можно подписаться на мой канал.

تحميل Разбор задачи 794 acmp ru Ролевая игра Решение на c mp3 – mp4

Разбор задачи 794 Acmp Ru Ролевая игра Решение на C

Задача 794 Ролевая игра Acmp Ru C

Разбор задачи 644 Acmp Ru Временной ключ 2 Решение на C

Задача 763 Игра с ладьей Acmp Ru C

Разбор задачи 156 Acmp Ru Шахматы 2 Решение на Python

Разбор задачи 854 Acmp Ru Кондиционер Решение на C

Разбор задачи 1035 Acmp Ru Кондиционеры Решение на C

Разбор задачи 474 Acmp Ru Последовательность Кеане Решение на Java Python C

Задача 839 Всем известно Acmp Ru C

Разбор задачи 712 Acmp Ru Дипломы Решение на C

Разбор задачи 929 Acmp Ru Игральные кубики Решение на C

Задача 912 Одежда Acmp Ru C

Разбор задачи 796 Acmp Ru Форматирование текста Решение на C

Разбор задачи 350 Acmp Ru Перестановки Решение на C Python Java

Разбор задачи 127 Acmp Ru Путь Решение на C

ACMP Разбор задачи 933 ТЕЛЕФОН C

Разбор задачи 1009 Acmp Ru Прыжки в длину Решение на C

55 Сложная задача с сайта ACMP Зайчик

Разбор задачи 1651 Acmp Ru Интервальные тренировки Решение на C

Разбор задачи 850 Acmp Ru Цапли Решение на C

Всё, что вы хотели знать о динамическом программировании, но боялись спросить

Я был крайне удивлён, найдя мало статей про динамическое программирование (далее просто динамика) на хабре. Мне всегда казалось, что эта парадигма довольно сильно распространена, в том числе и за пределами олимпиад по программированию. Поэтому я постараюсь закрыть этот пробел своей статьёй.

# Весь код в статье написан на языке Python

Основы

Пожалуй, лучшее описание динамики в одно предложение, которое я когда либо слышал:

Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А. Кумок.

Чтобы успешно решить задачу динамикой нужно:

1) Состояние динамики: параметр(ы), однозначно задающие подзадачу.

2) Значения начальных состояний.

3) Переходы между состояниями: формула пересчёта.

4) Порядок пересчёта.

5) Положение ответа на задачу: иногда это сумма или, например, максимум из значений нескольких состояний.

Порядок пересчёта

Существует три порядка пересчёта:

1) Прямой порядок:

Состояния последовательно пересчитывается исходя из уже посчитанных.

2) Обратный порядок:
Обновляются все состояния, зависящие от текущего состояния.

3) Ленивая динамика:
Рекурсивная мемоизированная функция пересчёта динамики. Это что-то вроде поиска в глубину по ацикличному графу состояний, где рёбра — это зависимости между ними.

Элементарный пример: числа Фибоначчи. Состояние — номер числа.

Прямой порядок:

fib[1] = 1  # Начальные значения
fib[2] = 1  # Начальные значения
for i in range(3, n + 1):
    fib[i] = fib[i - 1] + fib[i - 2]  # Пересчёт состояния i

Обратный порядок:

fib[1] = 1  # Начальные значения
for i in range(1, n):
    fib[i + 1] += fib[i]  # Обновление состояния i + 1
    fib[i + 2] += fib[i]  # Обновление состояния i + 2

Ленивая динамика:

def get_fib(i):
    if (i <= 2):  # Начальные значения
        return 1
    if (fib[i] != -1):  # Ленивость
        return fib[i]
    fib[i] = get_fib(i - 1) + get_fib(i - 2)  # Пересчёт
    return fib[i]

Все три варианта имеют права на жизнь. Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.

Многомерная динамика

Пример одномерной динамики приведён выше, в «порядке пересчёта», так что я сразу начну с многомерной. Она отличается от одномерной, как вы уже наверно догадались, количеством измерений, то есть количеством параметров в состоянии. Классификация по этому признаку обычно строится по схеме «один-два-много» и не особо принципиальна, на самом деле.

Многомерная динамика не сильно отличается от одномерной, в чём вы можете убедиться взглянув на пару примеров:

Пример №1: Количество СМСок

Раньше, когда у телефонов были кнопки, их клавиатуры выглядели примерно так:

Требуется подсчитать, сколько различных текстовых сообщений множно написать используя не более k нажатий на такой клавиатуре.

Решение

1) Состояние динамики:

dp[n][m]

— количество различных сообщений длины

n

, использующих

m

нажатий.

2) Начальное состояние: есть одно сообщение длины ноль, использующее ноль нажатий — пустое.

3) Формулы пересчёта: есть по восемь букв, для написания которых нужно одно, два и три нажатия, а так же две буквы требующие 4 нажатия.

Прямой пересчёт:

dp[n][m] = (dp[n - 1][m - 1] + dp[n - 1][m - 2] + dp[n - 1][m - 3]) * 8 + dp[n - 1][m - 4] * 2

Обратный пересчёт:

dp[n + 1][m + 1] += dp[n][m] * 8
dp[n + 1][m + 2] += dp[n][m] * 8
dp[n + 1][m + 3] += dp[n][m] * 8
dp[n + 1][m + 4] += dp[n][m] * 2

4) Порядок пересчёта:

Если писать прямым методом, то надо отдельно подумать о выходе за границу динамики, к примеру, когда мы обращаемся к

dp[n - 1][m - 4]

, которого может не существовать при малых

m

. Для обхода этого можно или ставить проверки в пересчёте или записать туда нейтральные элементы (не изменяющие ответа).

При использовании обратного пересчёта всё проще: мы всегда обращаемся вперёд, так что в отрицательные элементы мы не уйдём.

5) Ответ — это сумма всех состояний.

UPD:
К сожалению, я допустил ошибку — задачу можно решить и одномерно, просто убрав из состояния длину сообщения

n.
1) Состояние: dp[m] — количество различных собщений, которые можно набрать за m нажатий.
2) Начальное состояние: dp[0] = 1.
3) Формула пересчёта:

dp[m] = (dp[m - 1] + dp[m - 2] + dp[m - 3]) * 8 + dp[m - 4] * 2

4) Порядок: все три варианта можно использовать.

5) Ответ — это сумма всех состояний.

Пример №2: Конь

Шахматный конь стоит в клетке

(1, 1)

на доске размера

N

M

. Требуется подсчитать количество способов добраться до клетки

(N, M)

передвигаясь четырьмя типами шагов:

Решение

1) Состояние динамики:

dp[i][j]

— количество способов добраться до

(i, j)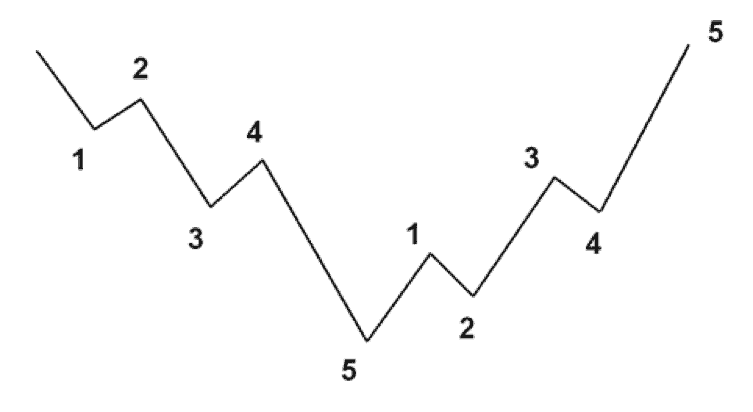

2) Начальное значение: В клетку

(1, 1)

можно добраться одним способом — ничего не делать.

3) Формула пересчёта:

Для прямого порядка:

dp[i][j] = dp[i - 2][j - 1] + dp[i - 2][j + 1] + dp[i - 1][j - 2] + dp[i + 1][j - 2]

Для обратного порядка:

dp[i + 1][j + 2] += dp[i][j]
dp[i + 2][j + 1] += dp[i][j]
dp[i - 1][j + 2] += dp[i][j]
dp[i + 2][j - 1] += dp[i][j]

4) А теперь самое интересное в этой задаче: порядок. Здесь нельзя просто взять и пройтись по строкам или по столбцам. Потому что иначе мы будем обращаться к ещё не пересчитанным состояниям при прямом порядке, и будем брать ещё недоделанные состояния при обратном подходе.

Есть два пути:
1) Придумать хороший обход.
2) Запустить ленивую динамику, пусть сама разберётся.

Если лень думать — запускаем ленивую динамику, она отлично справится с задачей.
Если не лень, то можно придумать обход наподобие такого:

Этот порядок гарантирует обработанность всех требуемых на каждом шаге клеток при прямом обходе, и обработанность текущего состояния при обратном.

5) Ответ просто лежит в dp[n][m].

Динамика и матрица переходов

Если никогда не умножали матрицы, но хотите понять этот заголовок, то стоит прочитать хотя бы

вики

Допустим, есть задача, которую мы уже решили динамическим программированием, например, извечные числа Фибоначчи.
Давайте немного переформулируем её. Пусть у нас есть вектор , из которого мы хотим получить вектор . Чуть-чуть раскроем формулы: . Можно заметить, что из вектора можно получить вектор путем умножения на какую-то матрицу, ведь в итоговом векторе фигурируют только сложенные переменные из первого вектора. Эту матрицу легко вывести, вот она: . Назовём её матрицей перехода.

Это значит, что если взять вектор и умножить его на матрицу перехода

n - 1 раз, то получим вектор , в котором лежит fib[n] — ответ на задачу.

А теперь, зачем всё это надо. Умножение матриц обладает свойством ассоциативности, то есть (но при этом не обладает коммутативностью, что по-моему удивительно). Это свойство даёт нам право сделать так: .

Это хорошо тем, что теперь можно применить метод быстрого возведения в степень, который работает за . Итого мы сумели посчитать N-ое число Фибоначчи за логарифм арифметических операций.

А теперь пример посерьёзнее:

Пример №3: Пилообразная последовательность

Обозначим пилообразную последовательность длины

N

как последовательность, у которой для каждого не крайнего элемента выполняется условие: он или меньше обоих своих соседей или больше. Требуется посчитать количество пилообразных последовательностей из цифр длины

N

. Выглядит это как-то так:

Решение

Для начала решение без матрицы перехода:

1) Состояние динамики: dp[n][last][less] — количество пилообразных последовательностей длины n, заканчивающихся на цифру last. Причём если less == 0, то последняя цифра меньше предпоследней, а если less == 1, значит больше.
2) Начальные значения:

for last in range(10):
    dp[2][last][0] = 9 - last
    dp[2][last][1] = last

3) Пересчёт динамики:

for prev in range(10):
    if prev > last:
        dp[n][last][0] += dp[n - 1][prev][1]
    if prev < last:
        dp[n][last][1] += dp[n - 1][pref][0]

4) Порядок пересчёта: мы всегда обращаемся к предыдущей длине, так что просто пара вложенных

for

‘ов.

5) Ответ — это сумма

dp[N][0..9][0..1]

Теперь надо придумать начальный вектор и матрицу перехода к нему. Вектор, кажется, придумывается быстро: все состояния, обозначающие длину последовательности N. Ну а матрица перехода выводится, смотря на формулы пересчёта.

Вектор и матрица перехода

Динамика по подотрезкам

Это класс динамики, в котором состояние — это границы подотрезка какого-нибудь массива. Суть в том, чтобы подсчитать ответы для подзадач, основывающихся на всех возможных подотрезках нашего массива. Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.

Пример №4: Запаковка строки

Вот

Развернутое условие

. Я вкратце его перескажу:

Определим сжатую строку:
1) Строка состоящая только из букв — это сжатая строка. Разжимается она в саму себя.
2) Строка, являющаяся конкатенацией двух сжатых строк A и B. Разжимается она в конкатенацию разжатых строк A и B.
3) Строка D(X), где D — целое число, большее 1, а X — сжатая строка. Разжимается она в конкатенацию D строк, разжатых из X.
Пример: “3(2(A)2(B))C” разжимается в “AABBAABBAABBC”.

Необходимо по строке s узнать длину самой короткой сжатой строки, разжимающийся в неё.

Решение

Решается эта задача, как вы уже наверняка догадались, динамикой по подотрезкам.

1) Состояние динамики: d[l][r] — сжатая строка минимальной длины, разжимающаяся в строку s[l:r]
2) Начальные состояния: все подстроки длины один можно сжать только в них самих.
3) Пересчёт динамики:
У лучшего ответа есть какая-то последняя операция сжатия: либо это просто строка из заглавных букв, или это конкатенация двух строк, или само сжатие. Так давайте переберём все варианты и выберем лучший.

dp_len = r - l
dp[l][r] = dp_len  # Первый вариант сжатия - просто строка.

for i in range(l + 1, r):
    dp[l][r] = min(dp[l][r], dp[l][i] + dp[i][r])  # Попробовать разделить на две сжатые подстроки

for cnt in range(2, dp_len):
    if (dp_len % cnt == 0):  # Если не делится, то нет смысла пытаться разделить
        good = True
        for j in range(1, (dp_len / cnt) + 1):  # Проверка на то, что все cnt подстрок одинаковы
            good &= s[l:l + dp_len / cnt] == s[l + (dp_len / cnt) * j:l + (dp_len / cnt) * (j + 1)]
        if good:  # Попробовать разделить на cnt одинаковых подстрок и сжать
            dp[l][r] = min(dp[l][r], len(str(cnt)) + 1 + dp[l][l + dp_len / cnt] + 1)

4) Порядок пересчёта: прямой по возрастанию длины подстроки или ленивая динамика.

5) Ответ лежит в

d[0][len(s)]

Пример №5: Дубы

Динамика по поддеревьям

Параметром состояния динамики по поддеревьям обычно бывает вершина, обозначающая поддерево, в котором эта вершина — корень. Для получения значения текущего состояния обычно нужно знать результаты всех своих детей. Чаще всего реализуют лениво — просто пишут поиск в глубину из корня дерева.

Пример №6: Логическое дерево

Дано подвешенное дерево, в листьях которого записаны однобитовые числа —

0

или

1

. Во всех внутренних вершинах так же записаны числа, но по следующему правилу: для каждой вершины выбрана одна из логических операций: «И» или «ИЛИ». Если это «И», то значение вершины — это логическое «И» от значений всех её детей. Если же «ИЛИ», то значение вершины — это логическое «ИЛИ» от значений всех её детей.

Требуется найти минимальное количество изменений логических операций во внутренних вершинах, такое, чтобы изменилось значение в корне или сообщить, что это невозможно.

Решение

1) Состояние динамики:

d[v][x]

— количество операций, требуемых для получения значения

x

в вершине

v

. Если это невозможно, то значение состояния —

+inf

2) Начальные значения: для листьев, очевидно, что своё значение можно получить за ноль изменений, изменить же значение невозможно, то есть возможно, но только за

+inf

операций.

3) Формула пересчёта:

Если в этой вершине уже значение

x

, то ноль. Если нет, то есть два варианта: изменить в текущей вершине операцию или нет. Для обоих нужно найти оптимальный вариант и выбрать наилучший.

Если операция «И» и нужно получить «0», то ответ это минимум из значений d[i][0], где i — сын v.
Если операция «И» и нужно получить «1», то ответ это сумма всех значений d[i][1], где i — сын v.
Если операция «ИЛИ» и нужно получить «0», то ответ это сумма всех значений d[i][0], где i — сын v.
Если операция «ИЛИ» и нужно получить «1», то ответ это минимум из значений d[i][1], где i — сын v.

4) Порядок пересчёта: легче всего реализуется лениво — в виде поиска в глубину из корня.
5) Ответ — d[root][value[root] xor 1].

Динамика по подмножествам

В динамике по подмножествам обычно в состояние входит маска заданного множества. Перебираются чаще всего в порядке увеличения количества единиц в этой маске и пересчитываются, соответственно, из состояний, меньших по включению. Обычно используется ленивая динамика, чтобы специально не думать о порядке обхода, который иногда бывает не совсем тривиальным.

Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера

Задан взвешенный (веса рёбер неотрицательны) граф

G

размера

N

. Найти

гамильтонов цикл

(цикл, проходящий по всем вершинам без самопересечений) минимального веса.

Решение

Так как мы ищем цикл, проходящий через все вершины, то можно выбрать за «начальную» вершину любую. Пусть это будет вершина с номером

0

1) Состояние динамики: dp[mask][v] — путь минимального веса из вершины 0 в вершину v, проходящий по всем вершинам, лежащим в mask и только по ним.
2) Начальные значения: dp[1][0] = 0, все остальные состояния изначально — +inf.
3) Формула пересчёта: Если i-й бит в mask равен 1 и есть ребро из i в v, то:

dp[mask][v] = min(dp[mask][v], dp[mask - (1 << i)][i] + w[i][v])

Где

w[i][v]

— вес ребра из

i

v

4) Порядок пересчёта: самый простой и удобный способ — это написать ленивую динамику, но можно поизвращаться и написать перебор масок в порядке увеличения количества единичных битов в ней.

5) Ответ лежит в

d[(1 << N) - 1][0]

Динамика по профилю

Классическими задачами, решающимися динамикой по профилю, являются задачи на замощение поля какими-нибудь фигурами. Причём спрашиваться могут разные вещи, например, количество способов замощения или замощение минимальным количеством фигур.

Эти задачи можно решить полным перебором за , где a — количество вариантов замощения одной клетки. Динамика по профилю же оптимизирует время по одной из размерностей до линейной, оставив от себя в экспоненте только коэффициент. Получится что-то такое: .

Профиль — это k (зачастую один) столбцов, являющиеся границей между уже замощённой частью и ещё не замощённой. Эта граница заполнена только частично. Очень часто является частью состояния динамики.

Почти всегда состояние — это профиль и то, где этот профиль. А переход увеличивает это местоположение на один. Узнать, можно ли перейти из одного профиля в другой можно за линейное от размера профиля время. Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив can[mask][next_mask] — можно ли от одной маски перейти к другой, положив несколько фигурок, увеличив положение профиля на один. Если предподсчитывать, то времени на выполнение потребуется меньше, а памяти — больше.

Пример №8: Замощение доминошками

Найти количество способов замостить таблицу

N

M

с помощью доминошек размерами

1

2

1

Решение

Здесь профиль — это один столбец. Хранить его удобно в виде двоичной маски:

0

— не замощенная клетка столбца,

1

— замощенная. То есть всего профилей

0) Предподсчёт (опционально): перебрать все пары профилей и проверить, что из одного можно перейти в другой. В этой задаче это проверяется так:

Если в первом профиле на очередном месте стоит 1, значит во втором обязательно должен стоять 0, так как мы не сможем замостить эту клетку никакой фигуркой.

Если в первом профиле на очередном месте стоит 0, то есть два варианта — или во втором 0 или 1.
Если 0, это значит, что мы обязаны положить вертикальную доминошку, а значит следующую клетку можно рассматривать как 1. Если 1, то мы ставим вертикальную доминошку и переходим к следующей клетке.

Примеры переходов (из верхнего профиля можно перейти в нижние и только в них):

После этого сохранить всё в массив can[mask][next_mask] — 1, если можно перейти, 0 — если нельзя.
1) Состояние динамики: dp[pos][mask] — количество полных замощений первых pos - 1 столбцов с профилем mask.
2) Начальное состояние: dp[0][0] = 1 — левая граница поля — прямая стенка.
3) Формула пересчёта:

dp[pos][mask] += dp[pos - 1][next_mask] * can[mask][next_mask]

4) Порядок обхода — в порядке увеличения

pos

5) Ответ лежит в dp[pos][0].

Полученная асимптотика — .

Динамика по изломанному профилю

Это очень сильная оптимизация динамики по профилю. Здесь профиль — это не только маска, но ещё и место излома. Выглядит это так:

Теперь, после добавления излома в профиль, можно переходить к следующему состоянию, добавляя всего одну фигурку, накрывающую левую клетку излома. То есть увеличением числа состояний в N раз (надо помнить, где место излома) мы сократили число переходов из одного состояния в другое с до . Асимптотика улучшилась с до .

Переходы в динамике по изломанному профилю на примере задачи про замощение доминошками (пример №8):

Восстановление ответа

Иногда бывает, что просто знать какую-то характеристику лучшего ответа недостаточно. Например, в задаче «Запаковка строки» (пример №4) мы в итоге получаем только длину самой короткой сжатой строки, но, скорее всего, нам нужна не её длина, а сама строка.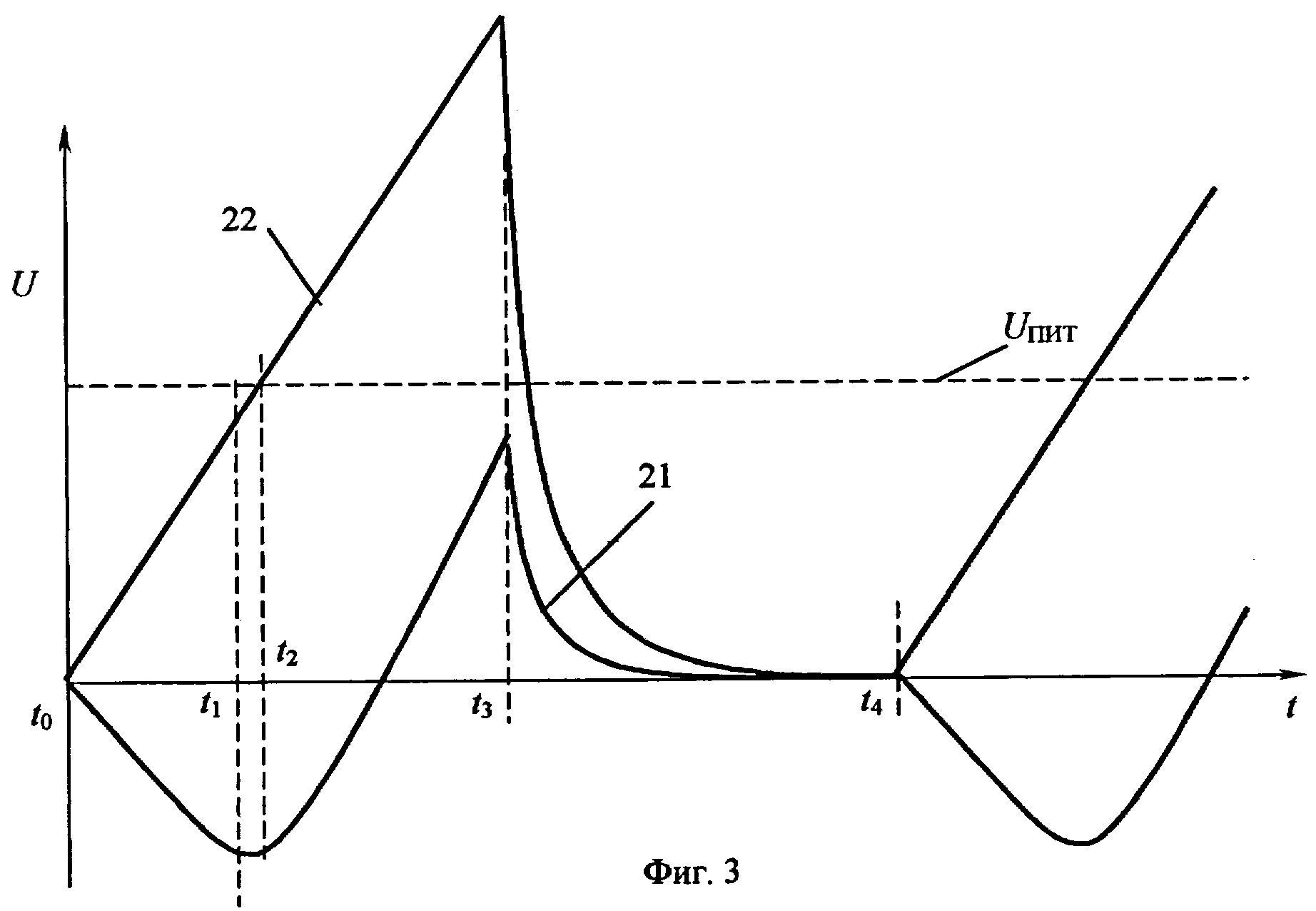 В таком случае надо восстановить ответ.

В каждой задаче свой способ восстановления ответа, но самые распространенные:

Рядом со значением состояния динамики хранить полный ответ на подзадачу. Если ответ — это что-то большое, то может понадобиться чересчур много памяти, поэтому если можно воспользоваться другим методом, обычно так и делают.
Восстанавливать ответ, зная предка(ов) данного состояния. Зачастую можно восстановить ответ, зная только как он был получен. В той самой «Запаковке строки» можно для восстановления ответа хранить только вид последнего действия и то, из каких состояний оно было получено.
Есть способ, вообще не использующий дополнительную память — после пересчёта динамики пойти с конца по лучшему пути и по дороге составлять ответ.

Небольшие оптимизации

Память

Зачастую в динамике можно встретить задачу, в которой состояние требует быть посчитанными не очень большое количество других состояний. Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.

Время

Иногда бывает так, что можно улучшить асимптотическое время, используя какую-нибудь структуру данных. К примеру, в

алгоритме Дейкстры

можно воспользоваться

очередью с приоритетами

для изменения асимптотического времени.

Замена состояния

В решениях динамикой обязательно фигурирует состояние — параметры, однозначно задающие подзадачу, но это состояние не обязательно одно единственное. Иногда можно придумать другие параметры и получить с этого выгоду в виде снижения асимптотического времени или памяти.

Пример №9: Разложение числа

Требуется найти количество разложений числа

N

на различные слагаемые. Например, если

N = 7

, то таких разложений

5

7
3 + 4
2 + 5
1 + 7
1 + 2 + 4

Два решения с различными состояниями

Решение №1:

1) Состояние динамики:

dp[n][k]

— количество разложений числа

n

на числа, меньшие или равные

k

. Параметр

k

нужен, чтобы брать всегда только большие числа, чем уже имеющиеся.

2) Начальные значения:

dp[1][1] = 1

dp[1][i] = 0

3) Формула пересчёта:

for last_summand in range(1, k + 1):
    dp[n][k] += dp[n - last_summand][last_summand]

4) Порядок: прямой, в порядке увеличения

n

5) Ответ — сумма

dp[N][1..N]

Состояний: , переходов: . Асимптотика: .

Решение №2:

1) Поменяем состояние. Теперь dp[n][k] — это количество разложений числа

n

на

k

различных чисел. Казалось бы незачем, но сейчас будет понятно.

2) Начальные значения:

dp[1][1] = 1

dp[1][i] = 0

3) Формула пересчёта:

dp[n][k] = dp[n - k][k] + dp[n - k][k - 1]

Теперь надо пояснить, что значит эта формула. Все состояния можно получить (причём единственным способом) делая поочерёдно два действия:

Все уже имеющиеся числа увеличить на 1.
Все уже имеющиеся числа увеличить на 1. Добавить число 1 в разложение.

Чтобы понять, почему это так можно посмотреть на

диаграммы Юнга

Строки здесь обозначают слагаемые.

Первое решение последовательно добавляет по одной строчке внизу таблицы, а второе — по одному столбцу слева таблицы. Вариантов размера следующей строчки много — главное, чтобы она была больше предыдущей, а столбцов — только два: такой же как предыдущий и на единичку больше.

4) Порядок пересчёта: прямой, в порядке увеличения n.

Невооруженным взглядом кажется, что у этого решения асимптотика , ведь есть два измерения в состоянии и переходов. Но это не так, ведь второй параметр — k ограничен сверху не числом N, а формулой (сумма чисел от 1 до k меньше или равна разлагаемого числа). Из этой формулы видно, что количество состояний .

5) Ответ — это сумма dp[N][1..k_max].

Асимптотика: .

Заключение

Основным источником была голова, а туда информация попала с лекций в

Летней Компьютерной Школе

(для школьников), а также кружка Андрея Станкевича и спецкурса Михаила Дворкина (

darnley

Спасибо за внимание, надеюсь эта статья кому-нибудь пригодится! Хотя мне уже пригодилась — оказывается, написание статьи это хороший способ всё вспомнить.

Волна пилообразная – Энциклопедия по машиностроению XXL

Следует также отметить, что в области стабилизации волны парциальный коэффициент поглощения (например, для первой гармоники) практически мало отличается от интегрального коэффициента ослабления волны пилообразной формы. [c.66]

Особенности нелинейных искажений формы профиля волны и взаимодействия волн в существенной мере зависят от вязкости среды, точнее, от отношения инерционных сил к вязким, т. е. от числа Рейнольдса. При больших числах Рейнольдса среда может рассматриваться как невязкая (за исключением таких вопросов, как ширина фронта волны, поглощение волн и некоторые другие). В невязкой среде волна рано или поздно, в зависимости от акустического числа Маха, перейдет к волне пилообразной формы даже в таких неблагоприятных для образования, разрыва условиях, как условия сферической расходимости. При малых числах Рейнольдса, когда вязкость среды играет существенную роль, диссипативные процессы препятствуют искажению формы профиля волны. При очень малых числах Рейнольдса с нелинейными искажениями практически можно не считаться. [c.53]

До сих пор рассматривалось течение, вызываемое волной монохроматической или, во всяком случае, близкой к монохроматической, причем интенсивность волны сравнительно мала, малы акустические числа Re. Вместе с тем интенсивные ультразвуковые волны могут искажаться так, что в результате образуется волна пилообразной формы (см. гл. 3). Естественно, что скорость течения в этом случае будет отличаться от скорости течения, вызванного [c.233]

Для упрощения расчета можно принять, что волна пилообразна на всей [c.127]

Оценим пределы применимости формулы (20). Эта формула справедлива для сферически расходящихся волн пилообразной формы. Следовательно, при использовании плоского излучателя диаметром В должно выполняться неравенство [c.365]

Точки профиля, соответствующие большему сжатию, движутся быстрее, чем точки, соответствующие меньшей плотности. В результате крутизна волновых фронтов увеличивается, что может привести к возникновению разрыва на каждом периоде волны и образованию волны пилообразной формы. [c.9]

Как видно, затухание импульса происходит медленнее, чем затухание пилообразной волны. Причину этого различия можно пояснить следующим образом. Как уже указывалось, поглощение волны пилообразной формы можно формально рассматривать как процесс срезания вершин зубцов ее профиля в результате того, что задние точки профиля волны догоняют ее фронт (см. рис. 2). Ясно, что эффективность этого процесса срезания зависит от того, насколько быстро точки профиля догоняют фронт волны, т. е. от соотношения скоростей точек профиля и скорости фронта. Но скорость фронта слабого разрыва равна [1] [c.35]

Далее отметим еще одну особенность распространения волн пилообразной формы. Как видно из (100) — (102) (см. также описание рис. 10), амплитуда пилообразной волны в области а 1 не зависит уже от амплитуды колебаний излучателя вследствие роста поглощения с увеличением интенсивности волны. Иными словами, как бы ни была велика интенсивность излучаемой волны, ее интенсивность в заданной точке пространства [c.35]

Учитывая, что интенсивность Т волны пилообразной формы связана с пиковым значением колебательной скорости соотношением [c.38]

Это волна пилообразной формы с периодическими разрывами, расположенными на расстоянии К один от другого, и на каждом разрыве с скачком меняется от —К/ 2 ) до К1 21). Данный результат согласуется с формулой (2.56). [c.112]

Рис. 4.6. Схематичное изображение синусоидальной и пилообразной волн

Для реальных двигателей эта погрешность всегда менее 0,1%. В более сложном случае, когда момент нагружения задан в виде пилообразной волны, имеем для одного периода [c.10]

Следовательно, пиковое значение пилообразной волны определяется выражением [c.64]

Коэффициент ослабления пилообразной волны конечной амплитуды (на участке стабилизации) можно также проанализировать исходя из термодинамических представлений для слабых разрывов [26]. [c.65]

Rea 3p //, где p-m — амплитуда звукового давления в МПа, / — п МГц, поэтому для наблюдения нелинейного эффекта на У 3-частотах 1 МГц должно быть Дт S 1 МПа. При 1 искажения формы волны становятся столь сильными, что образуется пилообразная волна (рис. 1). Профиль одного периода волны описывается точным решением ур-ния (1) [c.289]

Для исследования механизма образования возмущений в струе под действием звуковых волн были использованы газоструйные излучатели большой интенсивности (L = 170 дБ), что позволило при теневой съемке дозвуковой турбулентной струи (число Маха истечения Mq = 0,75) наблюдать не только вихри, образующиеся под действием звука, но и порождающие их звуковые волны [4.3,4.8]. При этом число Рейнольдса, определенное по диаметру сопла и скорости истечения, составило Re = 10 . Использование газоструйных излучателей большой интенсивности привело к тому, что периодическое возбуждение уже не было во времени гармоническим, а приобретало пилообразную форму (рис.4.6). [c.134]

Эффективность воздействия внешнего излучения на сверхзвуковые струи при увеличении l/h падает. Это иллюстрируется зависимостями на рис.7.6 для плоской струи (ро = 3,4 атм, / = 18,7 кГц). Этот вывод согласуется с данными работы [7.11], согласно которой воздействие поперечного акустического облучения сверхзвуковой струи становится особенно ощутимым при акустическом облучении кромки сопла. В этой же работе указывается, что при воздействии на сверхзвуковую струю пилообразных звуковых волн ее ударно-волновая структура может разрушиться, что приводит к значительным изменениям в излучении шума. Так, показано, что при этом (М = 2, п = 0,8, fs = 8,5 кГц и /а = 11,8 кГц) в направлении максимального излучения в области частот вблизи максимума спектра излучаемой акустической мощности наблюдается снижение широкополосного шума на величину до 10 дБ. [c.183]

Др. особенность У.—возможность получения большой интенсивности даже при сравнительно небольших амплитудах колебаний, т. к. при данной амплитуде плотность потока энергии пропори, квадрату частоты, УЗ-волны большой интенсивности сопровождаются рядом нелинейных эффектов. Так, для интенсивных плоских УЗ-волн при малом поглощении среды (особенно в жидкостях, твёрдых телах) синусоидальная у излучателя волна превращается по мере её распространения в слабую периодич. ударную волну (пилообразной формы) поглощение таких волн оказывается значительно больше (т. н. нелинейное поглощение), чем волн малой амплитуды. Распространению УЗ-волн в газах и жидкостях сопутствует движение среды, т. н. акустическое течение, скорость к-рого зависит от вязкости среды, интенсивности У. и его частоты вообще говоря, она мала и составляет долго % от скорости У. К числу важных нелинейных явлений, возникающих при распространении интенсивного У. в жидкостях, относится акустич. кавито1(ия. Интенсивность, соответствующая порогу кавитации, зависит от рода жидкости и степени её чистоты, частоты звука, темп-ры и др. факторов в водопроводной воде, содержащей пузырьки воздуха, на частоте 20 кГц она составляет доли Вт/см . На частотах диапазона У. средних частот в УЗ-поле с интенсивностью начиная с неск. Вт/см могут возникнуть фонтанирование жидкости и распыление её с образованием весьма мелкодисперсного тумана. Акустич, кавитация широко применяется в технол. процессах при этом пользуются У. низких частот. [c.215]

При условии 2eooRe > 1 (это условие может расс матри-ваться как условие образования разрыва в расходящейся волне) пилообразная циллндрическая волна имеет вид [c.128]

Рассмотрим теперь случай а > 1, когда в процессе распространения возникает волна пилообразной формы, которая затем дифрагирует на отверстии в экране. Этот процесс удобно описать с помощью интеграла Кирхгофа (3,4) (см., например, [Харкевич, 1950] ). Рассеянное поле представляет собой последовательность положительных импульсов, находящихся на отрицательном пьедестале [Островский, Сутин, 1976]. В прожекторной зоне возникают импульсы сжатия с разрьшными фронтами, их амплитуда приближенно равна 2pjy, где р – амплитуда падающей на экран пилообразной волны, и не меняется с расстоянием. Длительность импульсов равна а (2сг и уменьшается с увеличением расстояния г от центра отверстия в экране. [c.114]

В случае волп большой интенсивности аффект изменеиия фзрмы первоначально синусоидальной волны может привести к такому увеличению крутизны отдельных участков ео профиля, что на каждом периоде ее появятся разрывы и образуется периодич. ударная волна пилообразной формы (рис.). Расстояние В, на к-ром происходит переход от синусоидальной волны к пилообразной, зависит от алгали-туды колебательной скорости V и частоты ш волиы для плоской волны [c.408]

Предположим, что мы убрали стенки, разъединяющие оба сосуда. Вода на граничной поверхности (когда были стенки) не имела горизонтальной составляющей движения. Когда мы убрали стенки, горизонтальная составляющая (в месте, где были стенки) не появится вследствие симметрии движения воды в двух сосудах. Движение будет продолжаться, как будто бы ничего не произошло При желании к такой системе можно присоединить другие сосуды. В сосуде мы получили стоячую волну пилообразной формы, которую можно аппроксимировать синусоидальной волной. Заметим, что длина одного сосуда равна одной полуволне. (Замечание. Если сделать фурье-анализ этой периодической функции от г, то первый (и основной) член разложения Фурье будет соответствовать нашей аппроксимирующей синусоидальной функции.) Используйте это приблим ение в формуле, которая определяет частоту моды омывания (см. опыт 1.24). Покажите, что имеет место равенство [c.101]

В предыдущем параграфе мы нашли приближенные квазистационарные решения, на основе которых с учетом законов нелинейного искажения сконструируем профиль сферической и цилиндрической волн по аналогии с плоскими волнами. Для этого необходимо ударный фронт бесконечной крутизны в волне пилообразной формы заменить узкой областью конечных размеров и определенной структуры в соответствии с квазистационарпыми решениями. Строго говоря, в цилиндрически-симметричной волне следовало бы область фронта построить на основе решений (III.4.2) и (111.4.3) или хотя бы на основе формулы (III.4.5). И то, что мы этого не будем делать, продиктовано исключительно соображениями физической наглядности и укоренившимся в литературе единым подходом, несомненно, весьма полезным с методической точки зрения. [c.76]

Если В следующей, второй области распространения волн выполняются условия применимости квазистацио-нарных решений, то структура разрывов в сферической и цилиндрической волнах пилообразного профиля может быть описана с помощью квазистационарных решений [c.77]

Покажем, что требованию (VIII.3.16) удовлетворяет сила 2 , вызванная поглощ ением сферической волны пилообразного профиля. Используя в качестве исходных выражения (III.2.7), (III.2.9), получим аналог формулы (1.5.18) для а затем (с помощью выражения (VIII.1.10)) для F, записанного в сферической системе координат [c.211]

Амплитудный коэф. поглощения первой гармовики волны, а, в области пилообразной волны определяется ф-лой [c.289]

Пилообразную волну можно рассматривать как ударную волну, толщина сжатия к-рой, согласно (2), определяется ф-лой б/Х, ж (2Лец) . На начальной стадии образования пилообразной волны, когда Rea = Reg, 1, ЫК 1 и величину 6 мож-иой амплитуды. ио представить в виде б — [c.289]

Поглощение волн большой интенсивности происходит по неэкспоненц. закону. Уменьшение пикового значения колебат. скорости Гд плоской пилообразной волны описывается ф-лой [c.289]

Звуковые пучки большой интенсивности. В звуковых пучках высокой интенсивности изменение формы волны при распространении происходит не только вследствие различия в скоростях перемещения разл. точек профиля волны, но и в результате дифракц. эффектов. Если расстояние I от излучателя звука до области образования волны не выходит за пределы ближней зоны (см. Звуковое поле), т. е. I меньше длины т. и. прожекторной зоны излучателя I синусоидальной волны успевает образоваться пилообразная волна, к-рая затем в результате сферич. расхождения в дальней зоне преобразуется в периодич. последовательность импульсов (рис. 4). Если же интепеивность волны недостаточно велика и пилообразная волна не успевает образоваться в прожекторной зоне излучателя, то вначале развиваются дифракц. эффекты сферич. расхождения и лишь в дальней зоне, в расходящейся волне происходит увеличение крутизны профиля волны с расстоянием до логарифмич. закону. [c.289]

При больших интенсивностях волны накачки она трансформируется в пилообразную волну, возрастает её поглощение и работа параметрич. излучателя переходит в нелинейный режим. Длина пробега волны накачки определяется теперь нелинейным поглощением звука и равна = (еАгрн/рс ) . Если взаимодействие пилообразных волн происходит в основном в ближней зоне (цилиндрич. антенна, рис. 1), то амплитуда излучаемой НЧ-волны в дальней зоне выражается ф-лой [c.536]

Переходные процессы в рассматриваемом случае показаны на рис. 4.9 (первая 3ona7V = 1) и рис.4.10 (вторая 3ona7V=2). В первой зоне синусоидальное начальное возмущение j(z) с течением времени трансформируется в пилообразную волну (рис. 4.9,а) и, следовательно, в ее спектре появляются высокочастотные составляющие. Характерно, что максимальное значение волны смещения j (z) остается неизменным и процесс ее деформации напоминает эволюцию волн Римана в нелинейной среде. Производная же от бегущей волны dy dz представляет собой последовательность однополярных импульсов (рис. 4.9,6), амплитуда которых нарастает по закону, близкому к экспоненциальному. Колебания фиксированном сечении [c.163]

Например, конкретным объектом, исследуемым в системе, показанной на рис. 21, является громкоговоритель диаметром 7,6 см, приводимый в действие синусоидальным электрическим сигналом. Если объект освещают и рассматривают вдоль направления колебаний, то отраженный объектом свет оказывается модулированным по фазе. Колебания малой амплитуды можно обнаружить путем преобразования частоты опорной волны на величину, равную частоте электрического сигнала, подаваемого на громкоговоритель. Опорная волна преобразуется электрооптическим модулятором (ЭОМ), в котором пилообразная фазовая модуляция создает модуляцию ОМПН. [c.355]

Эшелле представляет собой решетку с глубоко прочерченными штрихами пилообразной формы, лежащими на большом расстоянии друг от друга. Эшелле используется при больших порядках интерференции (т — 500) и соответственно имеет малую дисперсионную область. Чтобы разделить различные порядки, необходима вспомогательная система с поперечной дисперсией. При этом можно получить двумерное распределение по длинам волн, У такого устройства имеется то важное [c.343]

Проблема взаимодействия звука со звуком и вообще проблема распространения нелинейных волн, интерес к которой за последнее время бурно растет в связи с тем, что мощности как 5 Льтразвуковых, так и когерентных электромагнитных волн в настоящее время уже достигли тех уровней, при которых линейное приближение во многих случаях не дает удовлетворительных результатов, является одной из основных в нелинейной акустике. Она весьма обширна, включает в себя ряд вопросов (искажение и взаимодействие волн, особенности распространения пилообразных волн нелинейное поглощение и т. д. ), и ей отведено значительное место в предлагаемой вниманию читателей книге. Однако этим не исчерпывается круг вопросов, который должен рассматриваться в нелинейной акустике. В первую очередь это относится к эффектам, вызываемым мощными звуковыми волнами, которые могли бы быть названы вторичными. Из вторичных эффектов в книге основное внимание уделяется акустическим течениям — постоянным вихревым потокам, возникающим в звуковых полях, и звуковой кавитации — образованию в жидкостях полостей под действием отрицательного давления волны. Эти вторичные явления ответственны за ряд эффектов, наблюдающихся в поле мощных звуковых волн часть из этих эффектов играет существенную роль в области технологического использования мощных ультразвуковых волн. [c.11]

Каталог радиолюбительских схем. Автоматическое цветомузыкальное устройство.

Автоматическое цветомузыкальное устройство.

Да-да, именно цветомузыкальное, а не светомузыкальное, как оказалось в конце разработки. Принцип работы устройства основан на учете изменения частот в наиболее интенсивном спектре звучания, а не на частотной выборке из общей гаммы звука. Да, наворочено, аж 20 ИМС (но оно того стоит) и всего 1 транзистор (хе-хе).

Управление данным устройством заключается в нажатии кнопки “Вкл.”. Все остальное оно делает само по себе.

И уж простите мне скудное описание работы схемы, но понять меня тоже можно – было это где-то году в 1994, всего ведь не упомнишь. Собственно, глядя на схему, и так все понятно. Единственное, что может вызывать вопросы – это номиналы резисторов в некоторых каскадах. Да просто нет объяснения – подобрано экспериментально по тому, как лучше выглядит цветовая картина. В качестве исполнительного устройства на период испытаний, использовались клубные 4-цветные софиты, с излучением на потолок. Даже в этом виде наблюдались такие цветосочетания, которых на обычных мигалках никогда не достигнуть. А если применить более-менее приличный экран? Кроме того, при относительно постоянном уровне освещенности глаза практически не устают. При отсутствии музыкального сигнала, в качестве фона, горят все 4 лампы.

Следует отметить, что схема и описание работы выполнено по принципу “As is…”. И рассматривать эту конструкцию следует как шаг для дальнейшей разработки. Можно применить оптосимисторы, в конце концов применить микроконтроллеры, но это уже Вам виднее. Итак:

Основная часть схемы представлена на рис. 1.

Рис. 1.

Входной сигнал поступает на ограничитель уровня VD1-VD2. Это сделано для исключения перегрузки входного компаратора DA1. Опорное напряжение для него формируется цепочкой делителя напряжения R1,R2. Емкости С1 и С2 предназначены для увеличения помехоустойчивости устройства. Для доработки устройства в целом, можно сказать, что на входе лучше установить еще и микрофонный усилитель – с проводами возни меньше.

Прямоугольные импульсы с выхода компаратора поступают на делитель f/10, выполненный на D1. Кроме того с выхода компаратора цепочкой C3R6 формируется сигнал сброса (можно сказать и остановки) для схемы в целом при отсутствии сигнала на входе.

Далее, деленный сигнал, через D4A и D4B с учетом сигнала остановки поступает на счетчик D6, который своими выходами благодаря матрице R2R на резисторах R29-R48 формирует пилообразный сигнал, который для дальнейшей схемы является сигналом для сравнения со средней частотой, который вырабатывает каскад на D2, D5.

Кроме того деленный D1 сигнал поступает на вход счетчика D2, который обеспечивает деление входного сигнала на 3. Сигнал с выхода 0 заполняется частотой 32768 Гц с генератора на D3B,D3C и поступает на вход D5, работающий аналогично каскаду на D6. Появление на выходе 3 уровня лог. 1 приводит к сбросу через D3D,D4D счетчика D5. Кроме того сброс при окончании сигнала производится через D4D. В целом пилообразная последовательность на выходе матрицы R2R является усредненным сигналом с счетчика D1. Задержка составляет 3 цикла счетчика D1. Этот сигнал и является как бы средней частотой звукового сигнала (относительно, конечно, так как звука там естессно нету) для сравнения с сигналом с матрицы счетчика D6.

Далее сигналы с матриц счетчиков подаются на схему сравнения, выполненную на компараторах DA2 типа К1401СА2 ( компараторы с однополярным питанием). Причем сигнал с матрицы счетчика D5 подается в середину резистивного делителя R49-R53 (формирователей опорных напряжений) для того чтобы засечь изменение звукового сигнала как в положительную, так и в отрицательную сторону. Сигнал с выхода матрицы R2R счетчика D6 подается непосредственно на вторые входа компараторов. Поскольку К1401СА2 компараторы с “открытым коллектором”, то необходимы нагрузочные резисторы R54-R57.

Далее сигналы с выходов компараторов поступают на схему взаимоисключения выполненную на элементах D7. По выходам элементов D7 установлены RC-фильтры для исключения пиковых сигналов (“тычков”) при переходе из состояния 1 в 0 одного компаратора, и соответственно наоборот его ближайшего соседа.

Следует отметить, что измерение изменения частоты производится в небольших пределах (порядка десятков – единиц сотен герц). Изменение этих пределов осуществляется изменением номиналов R49-R53. Но на мой взгляд, существующие в схеме номиналы – оптимальны. Голос певца или какого-либо инструмента не может резко измениться на килогерцы в единицу времени. Сигналы с выходов фильтров схемы исключения подаются на накопительные счетчики второй части схемы, которая представлена на рис. 2.

Рис. 2.

Как видно из схемы, она состоит из 4 аналогичных частей. Предназначение данной части схемы в том что бы формировать симметричный пилообразный сигнал подаваемого на вход широтно-импульсного модулятора. Это сделано для того, что бы нарастание и угасание ламп накаливания происходило как можно плавней. Хотя не стоит думать, что это схема для оформления симфоний. Для “тяжёлого” она еще как подходит. И не “краснотой долбит” как в мигалках, а всеми цветами сразу.

Рассмотрим работу одной ячейки.

Счетные импульсы поступают на вход СК D8. При отсутствии сигнала Reset на выходах реверсивного D8 начинают появляться импульсы последовательности, которые формируют на все той же пресловутой матрице R2R на R62-R69 нарастание пилы. Далее по достижении значения 16, на выходе СО (переполнение) появляется импульс, опрокидывающий делитель f/2 D10A в состояние 1, который дает команду на обратный счет для D8. Происходит плавное падение “пилы” на выходе матрицы. Конечно, насколько будет плавным нарастание и падение “пилы” полностью зависит от музыкального сигнала.

Резистор R70 предназначен для создания смещения относительно + питания, для более четкого срабатывания схемы ШИМ.

Широтно-импульсные модуляторы описаны в огромном количестве литературы, поэтому описывать как работают компараторы DA3 не буду. Резисторы R98-R101 нагрузки для открытых коллекторов DA3. Сигналы с них подаются на входы включенных параллельно элементов D15 и D16. Они являются инверторами и усилителями тока для светодиодов оптронов. Силовая часть схемы представлена на рис. 3.

Рис. 3.

Эта часть схемы и может вызвать наибольшее количество споров. Выполнена она из расчета, что в случае чего, тиристор поменять куда как проще по деньгам, чем скажем оптосимистор. Хотя с другой стороны, этого “в случае чего” в течении нескольких лет, как-то не наблюдалось. И все равно, “в нашей местности” данное решение дешевле, чем искать другие опто-каскады. Каскад на D17 вкупе с VT1 (пресловутым и единственным) формирует “пилу” с частотой сетевого напряжения. Хотя впрочем если еще немного подумать, то и от транзистора так же можно избавиться.

Стабилизатор на 142ЕН8Е (В) если и требует радиатора, то минимального, так как основное токопотребление устраивают только светодиоды оптронов. Соответственно и трансформатор может быть минимальной габаритной емкости, 25 Вт вполне достаточно.

R134 – выполняет роль впаянного предохранителя для логической части схемы. Он куда как более быстродействующий чем обычные проволочные, хотя можно и не ставить вовсе. Величина FU1 – на Ваше усмотрение, только нужно определиться с суммарной мощностью ламп.

Если применять более мощные лампы, то мосты КЦ405А лучше заменить на что-либо более мощное, или на самом деле применить оптосимисторы.

Успехов!

akali.github.io/list.html at master · akali/akali.github.io · GitHub

akali.github.io/list.html at master · akali/akali.github.io · GitHub Permalink

Cannot retrieve contributors at this time This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

	<meta charset=”utf-8″>
	<style>
	table, th, td {border: 1px solid black;border-collapse: collapse;}</style>
	<br>
	<table><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=6″>Шахматы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=10″>Уравнение</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=12″>Дачники</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=17″>Поле чудес</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=19″>Ферзь, ладья и конь</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=20″>Пилообразная последовательность</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=24″>Вырубка деревьев</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=27″>Художник</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=37″>Сжимающий оператор</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=38″>Игра – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=45″>Произведение цифр</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=55″>Фонарики</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=57″>Компьютерная сеть</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=67″>Маска подсетей</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=69″>N-угольное колесо</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=74″>Прыжки с шестом</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=76″>Музей</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=82″>Пересечение множеств</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=84″>Выпуклая оболочка</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=89″>Быстрый поезд</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=90″>Треугольные страны</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=91″>Две последовательности</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=96″>Винни-пух</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=97″>Заповедники</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=99″>Лабиринт</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=107″>Красивые номера</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=117″>Опасная зона</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=137″>Существование пути</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=151″>Банкет</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=153″>Монетки – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=155″>Резисторы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=162″>Манхэттенский полицейский</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=164″>Счастливый билет – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=169″>Магазин</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=175″>Наручные часы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=182″>Прямоугольник – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=184″>Рабочее время</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=186″>Субботник</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=190″>По размещению!</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=199″>Римские числа</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=200″>Марсианские факториалы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=205″>Таймер</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=206″>Домой на электричках</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=209″>Целые точки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=210″>Степень</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=215″>Водостоки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=216″>Коллекционирование этикеток</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=217″>Еловая аллея</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=218″>Шашки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=223″>Анаграммер</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=228″>Валютные махинации</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=235″>Робот К-79</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=236″>Многочлен</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=241″>Праздники</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=244″>Билетики</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=245″>Сплоченная команда</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=252″>Сортировка масс</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=253″>Часы с боем</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=256″>Гексагон</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=258″>Скорая помощь</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=260″>Олимпиада по алхимии</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=262″>Коммерческий калькулятор</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=265″>Шахматная доска</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=268″>Почти палиндром</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=269″>Тормозной механизм</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=273″>Вычеркивание</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=276″>Разбиение на части</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=277″>Школьная алгебра</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=279″>Скобочки – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=282″>Прямоугольники</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=285″>Костер</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=288″>Комментарии</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=293″>Налоги</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=298″>Стрелок</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=299″>Волейбол</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=300″>Радар</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=301″>Код</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=302″>Города</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=304″>Волейбол – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=306″>Танец</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=310″>Рамка из клеток</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=313″>Ежеминутные автобусы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=314″>Лексикографический порядок чисел</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=316″>Телеграфный перевод</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=319″>Точки отрезка</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=321″>Разные цифры</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=326″>Преобразование последовательности – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=334″>Китайские часы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=339″>Мероприятие</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=341″>Числовая последовательность</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=343″>Укладка плиток</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=344″>Ближайшие точки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=345″>Рекурсия</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=349″>Простые числа</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=353″>Треугольники</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=356″>Копилка</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=358″>Забор в парке</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=359″>Змейка – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=369″>Гангстеры</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=373″>Маршрут – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=374″>Выпуклая оболочка – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=375″>Системы счисления</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=376″>День рождения – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=379″>Игра с датой</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=380″>Площадь прямоугольников</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=382″>Покраска лабиринта</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=388″>Седловые точки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=389″>К коду Грея</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=390″>Треугольная область</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=399″>Жук</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=401″>Шары и коробки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=404″>Игра с камнями</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=406″>Криптография</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=408″>Письмо</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=409″>Железная дорога</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=411″>Квадратное уравнение</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=414″>Расследование</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=417″>Даты</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=418″>Редактор</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=419″>Палиндром</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=421″>Треугольники – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=424″>Игра умножения</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=425″>Прямая и квадраты</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=427″>Несоставляемое число</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=430″>Дуга на сфере</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=433″>Школа танцев</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=436″>Счастливые цифры</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=440″>Биатлон</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=443″>Хеш-функция</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=444″>Список</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=448″>Простые гири</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=449″>Плавающие числа</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=450″>Бутылки – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=452″>Система счисления Фибоначчи</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=453″>Раз-два, раз-два</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=454″>Оставшееся число</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=458″>Шифровка – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=461″>Выборы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=463″>Остаток</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=470″>Земельный комитет</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=472″>Подарки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=473″>Автомобильные пробки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=474″>Последовательность Кеане</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=480″>Игра с монетами</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=483″>Двоичная машина</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=485″>Рыбаки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=486″>Рыбаки – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=487″>Игра “Баше”</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=489″>Монеты</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=490″>Дни рождения</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=492″>Сближение с целью</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=495″>Двойственная ломаная</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=497″>Индикатор</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=499″>Турист</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=501″>Строение</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=502″>Лягушонок</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=507″>Адронный коллайдер</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=511″>Очередь</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=515″>Ловушки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=517″>Боулинг</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=520″>Оптовая покупка</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=521″>Пасьянс старухи Шапокляк</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=523″>Роман в томах</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=524″>Слон</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=527″>Алгоритм Евклида</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=531″>Газон</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=535″>Неправильное сложение</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=536″>Числа – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=540″>Таблица</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=541″>Две строки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=543″>Монеты – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=546″>Печать буклета</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=547″>Период дроби</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=548″>Минимальное число</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=551″>Заяц и дерево</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=553″>Объединение блоков</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=557″>Матрицы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=564″>Забор – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=566″>Халява</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=570″>Квадрат</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=574″>Анаграммы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=575″>Строительство</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=576″>Гадание – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=578″>Система счисления</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=580″>Поднос</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=581″>Атака летающих тарелок</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=588″>Число</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=590″>Зазеркалье</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=593″>Башни – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=594″>Треугольник – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=595″>Слова</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=596″>Сотовая связь в большом городе</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=598″>Друзья – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=601″>Цветной лабиринт</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=602″>Точки на прямой</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=605″>Дартс</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=606″>Треугольник – 3</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=625″>SMS – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=626″>Преобразователь строк</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=630″>Охрана</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=633″>ACM World Finals</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=635″>Интернет-олимпиады</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=637″>NEERC</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=638″>Всероссийская олимпиада по информатике</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=641″>Странная лотерея</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=642″>Кризисный бизнес</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=645″>Красивая стена</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=648″>Азартный Шрэк</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=649″>Защищенный пароль</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=651″>Преобразование моноклеточных</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=664″>Котлеты</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=666″>Абракадабра</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=667″>Автобусы – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=668″>Змей Горыныч</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=669″>Произведение цифр – 3</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=671″>Счастливые числа</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=672″>N-значные числа</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=674″>Выбор приборов</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=675″>Детали</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=677″>Количество участников олимпиады</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=678″>Напёрстки</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=679″>Просто простые числа</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=682″>Сумма n-значных чисел</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=684″>Шашки – 2</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=686″>Колокол</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=689″>Упрощение номеров</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=691″>Номера автобусов</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=694″>Лентяй</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=695″>Мифические шахматы</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=696″>Сон</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=697″>Ремонт</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=698″>Игра в дурака</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=699″>Грибной дождь</a></td><td>-</td></tr><tr><td><a href=”http://acmp.ru/index.asp?main=task&id_task=700”>Мёд</a></td><td>-</td></tr></table>

You can’t perform that action at this time. You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session.

Расширенное секвенирование – документация Qblox Instruments 0.5.2

В этом руководстве мы продемонстрируем расширенные операции на основе секвенсора, при этом мы сосредоточимся на параметризации формы волны (см. Раздел «Секвенсор»). Мы продемонстрируем это, создав последовательность, которая покажет различные функции секвенсора, включая сложные конструкции циклов, динамическое управление усилением, аппаратную модуляцию и управление выходом разметки.

Сама последовательность будет использовать четыре огибающих формы волны длительностью 1 мкс каждая; гауссиан, синус, пила и блок.У нас будет несколько вложенных циклов в последовательности. Первый цикл увеличит период ожидания между началом итерации и воспроизведением огибающей формы сигнала, а также увеличит усиление огибающей формы сигнала на каждой итерации. В конце этого цикла второй цикл выполнит обратные операции. Третий цикл будет проходить по первому и второму циклам, чтобы перебрать четыре огибающих сигнала. И, наконец, четвертый цикл будет функционировать как бесконечный цикл над третьим. В то же время последовательность будет также управлять выходом маркера 1 и создавать точку срабатывания в начале каждой итерации первого и второго циклов, а также «разрешение» во время воспроизведения.Наконец, каждая огибающая формы сигнала будет модулирована на частоте 10 МГц.

Результатом этой последовательности при наблюдении на осциллографе будет итерация огибающих формы сигнала, которые будут скользить по частоте модуляции с изменяющимся усилением, инкапсулированное «включением» на выходе маркера. Мы настоятельно рекомендуем вам взглянуть на него, чтобы получить представление о возможностях секвенсоров.

Это руководство разработано с учетом Pulsar QCM, но может быть легко использовано и с Pulsar QRM.Измените любую ссылку Pulsar QCM на Pulsar QRM и используйте только один секвенсор.

Настройка

Сначала мы импортируем необходимые пакеты и подключимся к прибору.

# Настройте окружающую среду.
импортный отпечаток
импорт ОС
импорт scipy.signal
импортная математика
импортировать json
импортировать matplotlib.pyplot
import numpy

из pulsar_qcm.pulsar_qcm импорт pulsar_qcm

# Закройте все существующие подключения к любому pulsar_qcm
pulsar_qcm.close_all ()

# Подключитесь к Pulsar QCM с IP-адресом по умолчанию.pulsar = pulsar_qcm ("qcm", "192.168.0.2")

# Перезагрузите инструмент для точного измерения.
pulsar.reset ()
print ("Статус:")
печать (pulsar.get_system_status ())

Положение дел:
{'status': 'OKAY', 'flags': []}

Генерация сигналов

Затем нам нужно создать огибающие гауссова, синусоидального, пилообразного и блочного сигналов для последовательности.

# Параметры формы волны
waveform_length = 1000 # наносекунды

# Словарь сигналов (данные будут содержать образцы, а индекс будет использоваться для выбора форм сигналов в приборе).waveforms = {
                "гауссовский": {"данные": [], "индекс": 0},
                "синус": {"данные": [], "индекс": 1},
                "sawtooth": {"data": [], "index": 2},
                "блок": {"данные": [], "индекс": 3}
            }

# Создать гауссовский сигнал
если "гауссовский" в осциллограммах:
    waveforms ["gaussian"] ["data"] = scipy.signal.gaussian (waveform_length, std = 0,12 * waveform_length)

# Создать синусоидальную форму волны
если "синусоида" в осциллограммах:
    waveforms ["синус"] ["данные"] = [math.sin ((2 * math.pi / waveform_length) * i) для i в диапазоне (0, waveform_length)]

# Создать пилообразную форму волны
если "пилообразный" в осциллограммах:
    waveforms ["sawtooth"] ["data"] = [(1.0 / (waveform_length)) * i для i в диапазоне (0, waveform_length)]

#Create block waveform
если "блок" в осциллограммах:
    waveforms ["block"] ["data"] = [1.0 для i в диапазоне (0, waveform_length)]

Давайте построим кривые, чтобы увидеть, что мы создали.

time = numpy.arange (0, max (map (lambda d: len (d ["data"]), waveforms.значения ())), 1)
fig, ax = matplotlib.pyplot.subplots (1,1, figsize = (10, 10 / 1.61))

ax.set_ylabel ("Амплитуда примитивной формы волны")
ax.set_xlabel ("Время (нс)")

для wf, d в waveforms.items ():
    ax.plot (время [: len (d ["данные"])], d ["данные"], ".-", ширина линии = 0,5, метка = wf)

ax.legend (loc = 4)
ax.yaxis.grid ()
ax.xaxis.grid ()

matplotlib.pyplot.draw ()
matplotlib.pyplot.show () # добавьте это в EOF, чтобы предотвратить остановку выполнения

Создать программу Q1ASM

Теперь, когда у нас есть формы сигналов для последовательности, нам нужна программа Q1ASM, которая упорядочивает формы сигналов, как описано ранее.

# Последовательная программа.
seq_prog = "" "
                  wait_sync 4 # Ждать синхронизации
                  reset_ph # Сбросить абсолютную фазу
                  upd_param 4 # Обновить все параметры и подождать 4нс
start: move 4, R0 # Введите количество сигналов
                  move 0, R1 # Начальный индекс формы сигнала

mult_wave_loop: move 166, R2 #Init количество одиночных волновых петель (возрастающее ожидание)
                  move 166, R3 # Начальное количество петель с одной волной (уменьшение ожидания)
                  move 24, R4 #Init количество динамического времени ожидания (всего 4us)
                  move 3976, R5 #Init номер динамического остатка времени ожидания
                  move 32768, R6 # Начальное усиление (максимальное усиление)

sngl_wave_loop_0: move 800, R7 #Init количество длинных циклов ожидания (всего 40 мс)
                  set_mrk 15 # Установить маркер на 0xF
                  upd_param 4 # Обновить все параметры и подождать 4нс
                  set_mrk 0 # Установить маркер на 0
                  upd_param 96 # Обновить все параметры и подождать 96нс

                  wait R4 # динамическое ожидание
                  add R4,24, R4 # Увеличить ожидание

                  set_mrk 1 # Установить маркер на 1
                  play R1, R1,996 # Play waveform и подождать 996ns
                  set_mrk 0 # Установить маркер на 0
                  upd_param 4 # Обновить все параметры и подождать 4нс

                  wait R5 # Компенсировать предыдущее динамическое ожидание
                  sub R5,24, R5 # Уменьшение ожидания

                  sub R6,98, R6 # Уменьшить усиление
                  нет
                  set_awg_gain R6, R6 # Установить усиление

long_wait_loop_0: wait 50000 # wait 50 us
                  loop R7, @ long_wait_loop_0 # Ждать всего 40 мс
                  loop R2, @ sngl_wave_loop_0 # Повторить одиночный волновой цикл

sngl_wave_loop_1: move 800, R7 #Init количество длинных циклов ожидания (всего 40 мс)
                  set_mrk 15 # Установить маркер на 0xF
                  upd_param 8 # Обновить все параметры и подождать 8нс
                  set_mrk 0 # Установить маркер на 0
                  upd_param 92 # Обновляем все параметры и ждем 92нс

                  wait R4 # динамическое ожидание
                  sub R4,24, R4 # Уменьшение ожидания

                  set_mrk 1 # Установить маркер на 1
                  play R1, R1,996 # Play waveform и подождать 996ns
                  set_mrk 0 # Установить маркер на 0
                  upd_param 4 # Обновить все параметры и подождать 4нс

                  wait R5 # Компенсировать предыдущее динамическое ожидание
                  add R5,24, R5 # Увеличить ожидание

                  sub R6,98, R6 # Уменьшить усиление
                  нет
                  set_awg_gain R6, R6 # Установить усиление

long_wait_loop_1: wait 50000 # ждать 50 мкс
                  loop R7, @ long_wait_loop_1 # Ждать всего 40 мс
                  loop R3, @ sngl_wave_loop_1 # Повторить одиночный волновой цикл

                  add R1,1, R1 # Настроить индекс сигнала
                  loop R0, @ mult_wave_loop # Повторить со следующей огибающей сигнала
                  jmp @start # Повторить всю последовательность
"" "

Последовательность загрузки

Теперь, когда у нас есть формы сигналов и программа Q1ASM, мы можем объединить их в последовательность, сохраненную в файле JSON.

# При необходимости преобразовать формы сигналов в списки. для имени в формах волны: if str (type (waveforms [name] ["data"]) .__ name__) == "ndarray": waveforms [name] ["data"] = waveforms [name] ["data"]. tolist () # JSON поддерживает только списки # Добавить программу последовательности и формы сигналов в один словарь и записать в файл JSON. wave_and_prog_dict = {"waveforms": формы сигналов, "веса": {}, "сборы": {}, "program": seq_prog} с open ("sequence.json", 'w', encoding = 'utf-8') как файл: json.dump (wave_and_prog_dict, файл, отступ = 4) файл.{[3-4]} \) соответственно.

# Загрузить формы сигналов и программы.
pulsar.sequencer0_waveforms_and_program (os.path.join (os.getcwd (), "sequence.json"))
pulsar.sequencer1_waveforms_and_program (os.path.join (os.getcwd (), "sequence.json"))

Последовательность воспроизведения

Последовательность загружена в прибор. Теперь нам нужно настроить секвенсоры в приборе для использования инструкции wait_sync в начале программы Q1ASM для синхронизации и включения аппаратной модуляции на частоте 10 МГц.

# Настройте секвенсоры для синхронизации и включения модуляции на частоте 10 МГц.
pulsar.sequencer0_sync_en (Верно)
pulsar.sequencer0_mod_en_awg (Верно)
pulsar.sequencer0_nco_freq (10e6)
pulsar.sequencer1_sync_en (Верно)
pulsar.sequencer1_mod_en_awg (Верно)
pulsar.sequencer1_nco_freq (10e6)

# Сопоставьте секвенсоры с определенными выходами (но сначала отключите все соединения секвенсора)
для секвенсора в диапазоне (0, 6):
    для вне диапазона (0, 4):
        pulsar.set ("секвенсор {} _ channel_map_path {} _ out {} _ en" .format (секвенсор, выход% 2, выход), ложь)
пульсар.sequencecer0_channel_map_path0_out0_en (Истина)
pulsar.sequencer0_channel_map_path2_out1_en (Истина)
pulsar.sequencer1_channel_map_path0_out2_en (Истина)
pulsar.sequencer1_channel_map_path2_out3_en (Истина)

А теперь давайте начнем последовательность. Если вы хотите наблюдать за последовательностью, пора подключить осциллограф к выходу маркера 1 и одному или нескольким из четырех выходов. Настройте осциллограф на запуск по выходу маркера 1.

# Включите и запустите оба секвенсора.
pulsar.arm_sequencer (0)
пульсар.arm_sequencer (1)
pulsar.start_sequencer ()

# Распечатать статус обоих секвенсоров.
print ("Статус:")
печать (pulsar.get_sequencer_state (0))
печать (pulsar.get_sequencer_state (1))

Положение дел:
{'status': 'РАБОТАЕТ', 'flags': []}
{'status': 'РАБОТАЕТ', 'flags': []}

Прежде чем мы продолжим, вы смотрели в осциллограф? Довольно изящно, правда? Это всего лишь пример. Представьте себе, что еще вы можете сделать с помощью секвенсоров для управления и / или ускорения ваших экспериментов.

Остановка

Наконец, давайте остановим секвенсоры, если они еще этого не сделали, и закроем соединение с прибором.

# Остановите оба секвенсора.
pulsar.stop_sequencer ()

# Распечатать статус обоих секвенсоров (теперь должно быть сказано, что он остановлен).
print ("Статус:")
печать (pulsar.get_sequencer_state (0))
печать (pulsar.get_sequencer_state (1))
Распечатать()

# Распечатать обзор параметров инструмента.
print ("Снимок:")
pulsar.print_readable_snapshot (update = True)

# Закройте приборное соединение.
pulsar.close ()

Положение дел:
{'status': 'STOPPED', 'flags': ['FORCED STOP']}
{'status': 'STOPPED', 'flags': ['FORCED STOP']}

Снимок:
qcm:
        значение параметра
-------------------------------------------------- ------------------------------
IDN: {'производитель': 'Qblox', 'режим...
out0_offset: 0 (В)
out1_offset: 0 (В)
out2_offset: 0 (В)
out3_offset: 0 (В)
reference_source: внутренний
sequencecer0_channel_map_path0_out0_en: Истина
sequencecer0_channel_map_path0_out2_en: Ложь
sequencecer0_channel_map_path2_out1_en: Истина
sequencecer0_channel_map_path2_out3_en: Ложь
Sequencer0_cont_mode_en_awg_path0: Ложь
Sequencer0_cont_mode_en_awg_path2: Ложь
секвенсор0_cont_mode_waveform_idx_awg_path0: 0
секвенсор0_cont_mode_waveform_idx_awg_path2: 0
секвенсор0_gain_awg_path0: 1
секвенсор0_gain_awg_path2: 1
Sequencer0_marker_ovr_en: Ложь
секвенсор0_marker_ovr_value: 0
секвенсор0_mixer_corr_gain_ratio: 1
секвенсор0_mixer_corr_phase_offset_degree: -0
Sequencer0_mod_en_awg: Верно
секвенсор0_nco_freq: 1e + 07 (Гц)
Sequencer0_nco_phase_offs: 0 (Градусы)
секвенсор0_offset_awg_path0: 0
секвенсор0_offset_awg_path2: 0
sequencecer0_sync_en: Верно
секвенсор0_upsample_rate_awg_path0: 0
секвенсор0_upsample_rate_awg_path2: 0
Sequencer0_waveforms_and_program: C: \ Users \ Damaz \ PycharmProjects \...
sequencecer1_channel_map_path0_out0_en: Ложь
sequencecer1_channel_map_path0_out2_en: Истина
sequencecer1_channel_map_path2_out1_en: Ложь
sequencecer1_channel_map_path2_out3_en: Истина
sequencecer1_cont_mode_en_awg_path0: Ложь
sequencecer1_cont_mode_en_awg_path2: Ложь
секвенсор1_cont_mode_waveform_idx_awg_path0: 0
sequencecer1_cont_mode_waveform_idx_awg_path2: 0
секвенсор1_gain_awg_path0: 1
секвенсор1_gain_awg_path2: 1
sequencecer1_marker_ovr_en: Ложь
sequencecer1_marker_ovr_value: 0
секвенсор1_mixer_corr_gain_ratio: 1
Sequencer1_mixer_corr_phase_offset_degree: -0
Sequencer1_mod_en_awg: Верно
Sequencer1_nco_freq: 1e + 07 (Гц)
Sequencer1_nco_phase_offs: 0 (Градусы)
секвенсор1_offset_awg_path0: 0
sequencecer1_offset_awg_path2: 0
sequencecer1_sync_en: Верно
секвенсор1_upsample_rate_awg_path0: 0
секвенсор1_upsample_rate_awg_path2: 0
Sequencer1_waveforms_and_program: C: \ Users \ Damaz \ PycharmProjects \...
sequencecer2_channel_map_path0_out0_en: Ложь
sequencecer2_channel_map_path0_out2_en: Ложь
sequencecer2_channel_map_path2_out1_en: Ложь
sequencecer2_channel_map_path2_out3_en: Ложь
sequencecer2_cont_mode_en_awg_path0: Ложь
sequencecer2_cont_mode_en_awg_path2: Ложь
секвенсор2_cont_mode_waveform_idx_awg_path0: 0
секвенсор2_cont_mode_waveform_idx_awg_path2: 0
секвенсор2_gain_awg_path0: 1
секвенсор2_gain_awg_path2: 1
Sequencer2_marker_ovr_en: Ложь
sequencecer2_marker_ovr_value: 0
секвенсор2_mixer_corr_gain_ratio: 1
секвенсор2_mixer_corr_phase_offset_degree: -0
Sequencer2_mod_en_awg: Ложь
Sequencer2_nco_freq: 0 (Гц)
Sequencer2_nco_phase_offs: 0 (Градусы)
секвенсор2_offset_awg_path0: 0
секвенсор2_offset_awg_path2: 0
sequencecer2_sync_en: Ложь
секвенсор2_upsample_rate_awg_path0: 0
секвенсор2_upsample_rate_awg_path2: 0
Sequencer2_waveforms_and_program: Нет
sequencecer3_channel_map_path0_out0_en: Ложь
sequencecer3_channel_map_path0_out2_en: Ложь
sequencecer3_channel_map_path2_out1_en: Ложь
sequencecer3_channel_map_path2_out3_en: Ложь
sequencecer3_cont_mode_en_awg_path0: Ложь
sequencecer3_cont_mode_en_awg_path2: Ложь
секвенсор3_cont_mode_waveform_idx_awg_path0: 0
секвенсор3_cont_mode_waveform_idx_awg_path2: 0
секвенсор3_gain_awg_path0: 1
секвенсор3_gain_awg_path2: 1
Sequencer3_marker_ovr_en: Ложь
sequencecer3_marker_ovr_value: 0
секвенсор3_mixer_corr_gain_ratio: 1
секвенсор3_mixer_corr_phase_offset_degree: -0
Sequencer3_mod_en_awg: Ложь
sequencecer3_nco_freq: 0 (Гц)
Sequencer3_nco_phase_offs: 0 (градусы)
секвенсор3_offset_awg_path0: 0
секвенсор3_offset_awg_path2: 0
Sequencer3_sync_en: Ложь
секвенсор3_upsample_rate_awg_path0: 0
секвенсор3_upsample_rate_awg_path2: 0
Sequencer3_waveforms_and_program: Нет
sequencecer4_channel_map_path0_out0_en: Ложь
sequencecer4_channel_map_path0_out2_en: Ложь
sequencecer4_channel_map_path2_out1_en: Ложь
sequencecer4_channel_map_path2_out3_en: Ложь
sequencecer4_cont_mode_en_awg_path0: Ложь
sequencecer4_cont_mode_en_awg_path2: Ложь
секвенсор4_cont_mode_waveform_idx_awg_path0: 0
секвенсор4_cont_mode_waveform_idx_awg_path2: 0
секвенсор4_gain_awg_path0: 1
секвенсор4_gain_awg_path2: 1
Sequencer4_marker_ovr_en: Ложь
sequencecer4_marker_ovr_value: 0
секвенсор4_mixer_corr_gain_ratio: 1
Sequencer4_mixer_corr_phase_offset_degree: -0
Sequencer4_mod_en_awg: Ложь
Sequencer4_nco_freq: 0 (Гц)
Sequencer4_nco_phase_offs: 0 (Градусы)
секвенсор4_offset_awg_path0: 0
sequencecer4_offset_awg_path2: 0
Sequencer4_sync_en: Ложь
секвенсор4_upsample_rate_awg_path0: 0
секвенсор4_upsample_rate_awg_path2: 0
Sequencer4_waveforms_and_program: Нет
sequencecer5_channel_map_path0_out0_en: Ложь
sequencecer5_channel_map_path0_out2_en: Ложь
sequencecer5_channel_map_path2_out1_en: Ложь
sequencecer5_channel_map_path2_out3_en: Ложь
sequencecer5_cont_mode_en_awg_path0: Ложь
sequencecer5_cont_mode_en_awg_path2: Ложь
секвенсор5_cont_mode_waveform_idx_awg_path0: 0
секвенсор5_cont_mode_waveform_idx_awg_path2: 0
секвенсор5_gain_awg_path0: 1
секвенсор5_gain_awg_path2: 1
sequencecer5_marker_ovr_en: Ложь
sequencecer5_marker_ovr_value: 0
секвенсор5_mixer_corr_gain_ratio: 1
секвенсор5_mixer_corr_phase_offset_degree: -0
sequencecer5_mod_en_awg: Ложь
sequencecer5_nco_freq: 0 (Гц)
sequencecer5_nco_phase_offs: 0 (Градусы)
секвенсор5_offset_awg_path0: 0
sequencecer5_offset_awg_path2: 0
sequencecer5_sync_en: Ложь
секвенсор5_upsample_rate_awg_path0: 0
секвенсор5_upsample_rate_awg_path2: 0
Sequencer5_waveforms_and_program: Нет

фундаментальных ограничений, оптимальных последовательностей переключения и ограниченного времени до встречи в JSTOR

Абстрактный

Одна из фундаментальных проблем в сети когнитивного радио, известная как проблема многоканального рандеву, состоит в том, чтобы два вторичных пользователя находили общий канал, который не блокируется первичными пользователями.Основная идея решения такой проблемы в большинстве работ в литературе состоит в том, чтобы два пользователя выбирали свои собственные последовательности переключения каналов, а затем встречались, когда они оба одновременно переключаются на общий разблокированный канал. В этой статье мы сосредотачиваемся на фундаментальных ограничениях проблемы многоканального рандеву и формулируем такую задачу как задачу оптимизации с ограничениями, где выбор случайных последовательностей переключения двух вторичных пользователей должен удовлетворять определенным ограничениям. Мы выводим различные нижние оценки ожидаемого (соответственно максимального) времени до встречи при определенных ограничениях.Для некоторых из этих нижних границ мы также можем построить оптимальные последовательности переключения каналов, которые достигают нижних границ. Вдохновленные конструкциями систем кворумов и наборов относительных разностей, наши конструкции последовательностей переключения каналов основаны на математических теориях конечных проективных плоскостей, ортогональных латинских квадратов и последовательностей пилообразных зубцов. Использование таких теорий при построении последовательностей переключения каналов кажется новым и лучше, чем другие существующие схемы, с точки зрения минимизации ожидаемого (соответственно максимального) времени до встречи.

Информация о журнале

Mathematics of Operations Research публикует статьи, касающиеся математических и вычислительных основ исследования операций, включая оптимизацию, математическое и динамическое программирование, случайные процессы и модели, моделирование, управление и адаптацию, сети, теорию игр и теорию принятия решений.

Информация об издателе

INFORMS, насчитывающая более 12 500 членов со всего мира, является ведущей международной ассоциацией профессионалов в области операционных исследований и аналитики.INFORMS продвигает передовой опыт и достижения в области исследования операций, науки об управлении и аналитики для улучшения операционных процессов, принятия решений и результатов посредством множества высоко цитируемых публикаций, конференций, конкурсов, сетевых сообществ и услуг по профессиональному развитию.

О роли тяжелых ионов в пилообразных событиях: анализ наложенных эпох на данные in situ

Абстрактные

Моделирование показало, что пилообразные события, особенно события, вызванные выбросами корональной массы (CME), основаны на механизме обратной связи, посредством которого O +, поступающий из ночной авроральной области в результате процесса суббури, помогает управлять последующими инжекциями в пилообразной последовательности [1, 2].Однако недавнее исследование [3] предполагает, что большая часть O +, наблюдаемая в области хвоста, происходит вместо этого из куспида, независимо от драйвера. Поскольку отток каспа вызывается непосредственно солнечным ветром, а не внутренними процессами магнитосферы, он не может быть частью механизма обратной связи. В этом исследовании мы исследуем этот вопрос дополнительно с наложенным эпохальным анализом данных in situ из области хвоста (-8 ≥ X _GSM ≥ -20) во время пилообразных событий. Мы обнаружили, что впрыскивание зубьев пилы связано с падением плотности хвоста H ⁺, в то время как плотность O ⁺ мало изменяется; однако парциальное давление из-за обоих видов уменьшается, что позволяет предположить, что O ⁺, наблюдаемые после закачки, холоднее, чем популяция до закачки.Мы исследуем следующие вопросы: (1) существует ли какое-либо систематическое различие между первоначальной и последующей инъекцией, как предсказывает гипотеза обратной связи; (2) существенно ли отличается поведение в событиях, управляемых CME, от событий, управляемых областями потокового взаимодействия; и (3) существенно ли отличается поведение в доле (к которой отток каспа имеет прямой доступ), чем в центральном и граничном плазменном слое (к которому ночной отток имеет прямой доступ, но ионы каспа могут достигать только с помощью конвекции) .

[1] О. J. Brambles et al. (2011), Science 332, 1183, DOI: 10.1126 / science.1202869. [2] О. J. Brambles et al. (2013), JGR 118, 6026, DOI: 10.1002 / jgra.50522. [3] Э. J. Lund et al. (2018), JGR 123, 665, DOI: 10.1002 / 2017JA024378.

Разработка защиты для числовых последовательностей, сгенерированных с помощью хаотической карты пилообразной формы

ПОКАЗ 1-10 ИЗ 30 ССЫЛОК

СОРТИРОВАТЬ ПО РелевантностиСамые влиятельные статьи Недавность

Период последовательностей, генерируемых картами типа палатки

Вкратце, мы опишем, как использовать знания о периоде последовательности, генерируемые линейным мультипликативным конгруэнтным генератором псевдослучайных числовых последовательностей, чтобы определить период последовательности… Развернуть

Просмотреть 1 отрывок, справочная информация

Секретные линейные конгруэнтные генераторы не являются криптографически безопасными

J.Stern
Математика, информатика
28-й ежегодный симпозиум по основам информатики (sfcs 1987)
1987

В этой статье обсуждается предсказуемость последовательности, полученной путем вывода постоянной пропорции α старших бит чисел, полученных с помощью линейный конгруэнтный генератор и доказывает, что значительная часть битов может быть предсказана из предыдущих. Развернуть

Просмотреть 3 выдержки, справочная информация

Как прогнозировать конгруэнтные генераторы

H.Krawczyk
Математика, информатика
J. Алгоритмы
1992

Доказано, что генераторы многомерных полиномов, т.е. генераторы, где si ≡ P (si - n,…, si +1) (mod m), для полинометрические P известной степени от n переменных, эффективно предсказуемы. Развернуть

Просмотреть 4 выдержки, справочная информация

Моделирование хаотического поведения с помощью конечных автоматов.

Binder, Jensen
Physics, Medicine
Physical Review.A, Общая физика
1986

Хотя этот результат ставит под сомнение достоверность цифрового компьютерного моделирования хаоса, обнаружено, что статистические свойства непрерывного уравнения, такие как инвариантное распределение вероятностей и показатель Ляпунова, сохраняются в этих циклах. . Развернуть

Просмотр 1 отрывок, справочная информация

Статистика хаотических двоичных последовательностей

Простое достаточное условие для того, чтобы такой класс карт произвел справедливую последовательность Бернулли, то есть последовательность независимых и одинаково распределенных (т.i.d.) двоичные случайные величины. Развернуть

Хаотическая карта пилообразной формы

Хаотическая пилообразная карта На удивление очень простые 1D карты дают хорошую модель хаотических систем.

Карта пилообразной формы определяется как
x _{n + 1} = 2x _n (мод. 1)
, где x (mod 1) - дробная часть x . В двоичном умножение системы счисления на 2 соответствует сдвигу влево на однобитный сайт и взяв дробный часть соответствует верхнему биту усечение.Следовательно, x _{n + 1} - это сдвиг Бернулли x _n
x _o = 0,01011 ...
x ₁ = 0,1011 ...
x ₂ = 0,011 ...
и так далее ... Последовательность (x _o, x ₁ ...) называется орбитой точки x _o .

Если n -я цифра после двоичной точки в x _o является 0 ( 1 ), то x _n лежит слева (справа) полуинтервал [0,1] .Таким образом, для карта любая орбита определяется уникально по его (s _o, s ₁ ...) символической последовательности σ посещений этих интервалов. Для случайной символической последовательности точки соответствующей орбиты будут посещать левый или правый полуинтервал случайно. Существование континуума комплекса орбиты - это признак хаоса.

Для непрерывная необратимая карта палатки (слева) для любого x _n всегда можно найти предшествующие x _n-1 ценить лежа в левом или правом полуинтервале.Таким образом, и в этом случае можно сделать орбиту для любой символической последовательности обратными итерациями карты. В общем случае разрешены не все символьные последовательности. Например. 11 подпоследовательность не рекомендуется для карты на рисунке 3 справа. Если x _o и y _o имеют k равные сначала двоичные цифры, затем для пилообразной карты, в то время как n
y _n - x _n = 2 ⁿ (y _o - x _o) = (y _o - x _o) e ^{n журнал 2} .
где Λ = log 2 - показатель Ляпунова для карты. Таким образом, расстояние между двумя близкими орбитами экспоненциально расходится с увеличение n . Это становится примерно 1 после k итераций. Это свойство называется чувствительностью к начальным условиям . Это означает, что все периодические орбиты тоже нестабильны. Для пилообразной карты известно, что орбита с рациональным x _o = p / q является периодическим для нечетных q .Например. 1/3 орбита период 2
1/3 → 2/3 → 1/3 ...
и 1/7 орбита имеет период 3
1/7 → 2/7 → 4/7 → 1/7 ...
Даже для q орбита со временем становится периодической, например
1/6 → 1/3 → 2/3 → 1/3 ... или 1/8 → 1/4 → 1/2 → 1 → 1 ...
Следовательно существует бесконечное (счетное) множество неустойчивых периодических орбит и эти орбиты находятся в [0,1] .
На рис.4 вторая итерация карты и две точки периода-2 показаны орбиты. Орбита периода 2 получается из символической последовательности σ = (01) (смотри Приложение)
x ₀ = 0,0101 ... = 0. (01) = 1/11 ₂ = 1/3,
x ₁ = 0,1010 ... = 0. (10) = 10 ₂/11 ₂ = 2/3
Еще две комбинации x ₂ = 0.(00) = 0 и x ₃ = 0. (11) = 1 - фиксированные точки карты. Две орбиты периода-3
x ₀ = 0,001001 ... = 0. (001) = 1 ₂/111 ₂ = 1/7,
x ₁ = 0. (010) = 2/7, x ₂ = 0. (100) = 4/7
и x ₃ = 0. (110) = 6/7, х ₄ = 0. (101) = 5/7, х ₅ = 0.(011) = 3/7 . Мы можно рассматривать пилообразную карту, чтобы представить два шага: (1) равномерный растяжение интервала [0,1] вдвое больше исходная длина и (2) левый сдвиг его правой половины в исходное положение. Растяжение свойство приводит к экспоненциальному разделение ближайших точек и, следовательно, чувствительная зависимость от начальных условий. Свойство shift сохраняет сгенерированный последовательность ограничена, но также делает карту необратимой, так как это вызывает два разных x _n точек быть отображенным в один x _{n + 1} точек.Экспоненциальный рост ошибок итерации хаотической динамической системы влечет что компьютер сгенерировал траекторию для некоторого начального состояния будет быстро отклоняются от истинной орбиты из-за ошибок округления, так что после относительно короткое время компьютер сгенерировал орбита (называемая псевдотраектория ) не будет иметь корреляции с истинной орбитой.
Однако для данного x _n псевдотраектории мы можем представьте, что вы выполняете итерацию в обратном направлении, чтобы найти прообраз этой точки.Поскольку карта договор при обратных итерациях ошибка уменьшается в обратном направлении. орбиты, а траектория остается близкой к обратной итерации из истинная траектория. Существование истинной траектории, которая остается близко к псевдотраектории называется затенение . В физических и компьютерных экспериментах мы можем задать начальные условия Только примерно. Но при любой конечной точности исходных данных хаотичность динамика предсказуема только с точностью до конечного количество шагов! Для таких "турбулентные" движения статистическое описание может быть более полезным, чем фактическое знание истинного орбиты.Следовательно, мы должны проследить эволюцию плотности репрезентативных точек.
Для пилообразной карты после каждого итерационное расстояние между близкими точками увеличивается в два раза, таким образом, гладкая плотность также увеличивается равномерно в два раза. В качестве поскольку все точки лежат в ограниченном интервале [0,1] , мы получить равномерное распределение точек в п → ∞ предел. Эту плотность не меняет пилообразная карта (она называется стационарный или инвариантный плотность ).Обратите внимание, что точки неустойчивой периодической орбиты образуют особую инвариантную плотность.
Если мы возьмем случайный x _o = 0.a ₁ a ₂ a ₃ ... тогда для любой s = 0.b ₁ b ₂ b ₃ ... b _k всегда можно найти где-нибудь в x _o совпадающая подпоследовательность, то есть x _n будет приближаться к s и вероятность этого "пересечение" делает не зависит от s .Таким образом, каждая случайная орбита будет идти произвольно близко к любой точке в [0,1] и покрыть этот интервал равномерно (забавное доказательство, основанное на загадочных свойствах случайности 🙂
Этот факт можно использовать для замены "временного" среднего к "ансамблевое" среднее (эргодичность , )
= ∑ _n A (x _n) = ∫ А (х) дх .
Общий случай для хаотической карты
= ∑ _n A (x _n) знак равно A (x) dμ = ∫ A (x) ρ (x) dx ,
, где μ - инвариантная мера и ρ (x) инвариантно плотность для карты.Вырожденная карта круга
x _n = x _n-1 + Δ (mod 1) = x _o + nΔ (mod 1)
"накручивает" регулярно x _n точек около интервала [0,1] (если соединить 0 и 1 точек, чтобы получился круг). Для рационально Δ = p / q все орбиты периодические с периодом q . Для иррационального Δ каждый орбита покрывает интервал [0,1] равномерно и, следовательно, можно снова ввести постоянную инвариантную плотность (для расчета средних значений).
Обратите внимание, однако, что все точки окружности [0,1] смещены на карта на том же расстояние Δ . Следовательно, расстояние между две орбиты постоянны и плотность любого ансамбля точек сохраняется его форма. У нас однородная инвариантная плотность без перемешивания!
В среднем корреляционная функция C (m) для последовательности x _k
C (м) = lim _{n → ∞} 1 / n _{k = 1, n} (x _k - ) (x _{k + m} - ), = lim _{n → ∞} 1 / п ∑ _к x _к .
Если известна инвариантная мера карты, то
C (м) = lim _{n → ∞} 1 / п ∑ _k (x _k - ) (f ^om (x _k) ) = ∫ (x - ) (f ^ом (х) ) dμ
Например. для вырожденного отображения окружности имеем
С (м) = 1/12 - δ (1 - δ) / 2 ,
, где δ = mΔ (mod 1) . Эта корреляционная функция колеблется с увеличением м .
Для функция корреляции карты пилообразной формы
C (м) = 2 ^-м/12 .
Таким образом, смешивание приводит к экспоненциальное затухание корреляций для больших м .
Приложение : двоичный преобразование кода к рациональной дроби
Сначала рассмотрим десятичную дробь
0. (3) = 0,333 ... = 3 (10 ^-1 + 10 ^-2 + 10 ^-3 +...) = 3 / [10 (1–1 / 10)] = 3/9 = 1/3
(формула для суммы геометрического ряда используется). Аналогично для двоичного кода 0. (101) = 101 ₂/111 ₂ = 5/7 (индекс 2 указывает двоичную систему).
Содержание Предыдущий: Хаос на простых картах Далее: Карта палатки
обновлено 12 июля 06
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}
Заявка на патент США на ПИЛЬНЫЙ ИНСТРУМЕНТ ДЛЯ МАШИНОСТРОЕНИЯ Заявка на патент (Заявка № 20120230788 от 13 сентября 2012 г.)
Изобретение относится к пильному инструменту для станка, в частности переносного электроинструмента, согласно ограничительной части пункта 1 .
Уровень техники
В ЕР 1228 829 А1 описана кольцевая пила, имеющая цилиндрический корпус сверла и центральное сверло, которое направляется в корпусе сверла и с помощью которого можно выпилить сверлильный стержень из обрабатываемой детали. Цилиндрический корпус сверла с торцевой стороны имеет режущие зубья, некоторые из которых снабжены набором, а некоторые - нет. В окружном направлении корпуса сверла три режущих зуба или зуба пилы, которые следуют непосредственно друг за другом, без набора, и два смежных режущих зуба, имеющих установленный угол в противоположном направлении, образуют непрерывную последовательность зубьев пилы.Множество таких пилообразных последовательностей, каждая из которых сформирована одинаково, расположено по окружности торцевой стороны.
Из-за установленных зубьев пилы в каждом случае имеется небольшой зазор между внутренней и внешней боковыми поверхностями цилиндрического корпуса сверла и выпиленным буровым стержнем, с одной стороны, и внутренней поверхностью просверленного отверстия, с другой стороны, указанный зазор облегчает извлечение корпуса сверла из отверстия и удаление бурового керна изнутри корпуса сверла.
РАСКРЫТИЕ ИЗОБРЕТЕНИЯ
В основе изобретения лежит задача создания пильного инструмента для станка с помощью простых мер, таких как чистая кромка пилы на обрабатываемой детали, а также захват режущего инструмента. в заготовке во время обработки противодействует.
Эта цель достигается согласно изобретению посредством признаков пункта 1 формулы изобретения. В зависимых пунктах формулы указываются целесообразные разработки.
Пильный инструмент согласно изобретению используется в станках, в частности в ручных станках, предпочтительно в моторизованных станках, которые имеют, например, электродвигатель в качестве приводного двигателя.На стороне механической обработки пильный инструмент имеет режущие зубья или зубья пилы, при этом возможны различные виды пильных инструментов в зависимости от цели использования. Пильный инструмент представляет собой, например, цилиндрический корпус сверла, который используется в кольцевой пиле. Однако в принципе возможна конфигурация пильного инструмента в виде пильного полотна, которое используется, например, в качающихся режущих или пильных станках, и которое представляет собой, например, полотно лобзиковой пилы или полотно для сабельной пилы.
Пильный инструмент в соответствии с изобретением имеет по меньшей мере две последовательности зубьев пилы, каждая из которых имеет множество зубцов пилы на стороне обработки, при этом последовательности зубьев пилы построены идентично друг другу.Между двумя последовательными последовательностями зубьев пилы имеется свободное от зубьев пространство для стружки, которое служит для приема или удаления стружки или стружки, образующейся во время обработки детали. Пространство для стружки увеличивает прямое удаление стружки из области резания и, как следствие, уменьшает засорение ряда зубьев.
Удаление стружки также улучшено тем, что первый зуб пилы в последовательности зубьев пилы, указанный первый зуб пилы непосредственно примыкает к пространству для стружки и расположен спереди в последовательности зубьев пилы в направлении обработки, имеет геометрию зуба, которая отличается от других зубьев пилы. в этой пилообразной последовательности.Различная геометрия зуба первой пилы от последующих зубьев пилы на последовательность зубьев пилы может иметь отношение, с одной стороны, к постановке, но, с другой стороны, также к форме зуба, а также положению зубьев пилы относительно друг друга или относительно друг друга. в сторону обработки. В этом случае, в частности, предусмотрено, что первый зуб пилы не расставлен, а следующие зубья пилы смещены. Неустановленный первый зуб также улучшает удаление стружки из области резания, тем самым снижая риск засорения ряда зубьев.Эти меры противодействуют застреванию пильного инструмента в заготовке, которая обычно состоит из металла.
Этот вариант осуществления с множеством циклов или последовательностей зубьев, имеющих пространство для стружки между ними, в сочетании с неустановленным первым зубцом пилы и последующим набором зубьев пилы на последовательность зубьев пилы, также имеет эффект улучшения процесса резания в комбинированных применениях, которые включают в себя механическую обработку различные материалы заготовок, такие как дерево, металл или гипс, или обработка гипсокартона.
Согласно предпочтительному варианту осуществления предусмотрено, что поверхность зуба первого зуба пилы имеет отрицательный передний угол, по крайней мере, на участках, в частности на участке, прилегающем к впадине зуба, тогда как поверхность зуба первого зуба пилы в часть, которая простирается до вершины зуба, может иметь положительный передний угол. Этот вариант выполнения первой пилообразной формы на последовательность пилообразных зубцов имеет то преимущество, что во время обработки листового металла край листового металла отклоняется от пространства для стружки и, таким образом, не может проходить в пространство для стружки или наклоняться в нем.В результате снижается риск защемления кромки листового металла в пространстве для стружки и связанного с этим заклинивания станка. Этот эффект также подтверждается тем фактом, что, в отличие от первой пилы, каждая из следующих пил имеет конфигурацию без отрицательного переднего угла, а скорее имеет положительный передний угол от вершины зуба до впадины зуба.
Может быть полезным снабдить поверхность зуба первого зуба пилы двумя разными участками, которые ориентированы под углом друг к другу в области впадины зуба, причем указанные разные участки имеют отрицательный передний угол, величина из которых, однако, отличается.
Кроме того, согласно предпочтительному варианту осуществления предусмотрено, что в последовательности зубьев пилы первый зуб пилы отличается от остальных зубьев пилы своим положением относительно стороны обработки или параллельно стороне обработки. В частности, первая пила расположена ниже, чем следующая, следующая за пилообразным зубом в ее последовательности зубцов, в результате чего также снижается риск захвата.
Что касается набора зубьев пилы в последовательности зубьев пилы, в соответствии с целесообразным вариантом осуществления предусмотрено, что зубья пилы, следующие за первым зубцом пилы, имеют набор в противоположном направлении.
В варианте реализации пильного инструмента в виде цилиндрического корпуса сверла для кольцевой пилы может оказаться целесообразным предусмотреть на внутренней стороне корпуса сверла дополнительный режущий элемент, имеющий режущую кромку, при этом режущая кромка смещена радиально внутрь относительно внутренней стороны или внутренней стенки корпуса сверла. Этот вариант осуществления имеет то преимущество, что внешний диаметр выпиленного сверла меньше внутреннего диаметра цилиндрического корпуса сверла, так что после обработки заготовки между боковой поверхностью сверла остается воздушный зазор. а внутреннюю сторону корпуса сверла и выпиленный буровой керн можно без проблем извлечь из внутренней части корпуса сверла.
Дополнительные преимущества и целесообразные варианты осуществления можно понять из дополнительных пунктов формулы изобретения, описания фигур и чертежей, на которых:
ФИГ. 1 показывает пильный инструмент для станка, который имеет множество зубьев пилы на стороне обработки, указанные зубья пилы объединены для образования последовательностей зубьев пилы, при этом пространство для стружки расположено между соседними последовательностями зубцов пилы,
Фиг. 2 показывает увеличенное изображение пилообразного зуба, который находится спереди в направлении обработки и примыкает к пространству для стружки,
ФИГ.3 показан вид сверху пилообразной последовательности,
; фиг. 4 показывает увеличенное изображение пространства для микросхемы,
фиг. 5 показан вид в перспективе цилиндрического корпуса сверла кольцевой пилы, причем указанный корпус сверла снабжен на своей стороне свободного конца зубьями для выпиливания сверлильного стержня и имеет на внутренней стороне проходящий в осевом направлении режущий элемент, имеющий режущую кромку, которая смещение радиально внутрь.
На рисунках идентичные компоненты снабжены одинаковыми ссылочными позициями.
РИС. 1 показан пильный инструмент 1 , который выполнен, например, как цилиндрический корпус сверла для кольцевой пилы или как пильный диск. Пильный инструмент 1 имеет обрабатывающую сторону 2 , на которой расположены режущие зубья или зубья пилы 3 . Зубья пилы 3 объединены для образования последовательностей зубьев пилы 20 , которые расположены последовательно и каждая из них содержит множество отдельных зубьев пилы 3 , при этом в примерном варианте осуществления имеется четыре зуба пилы 3 a от до 3 d на последовательность зубцов 20 .В каждом случае между двумя последовательными последовательностями 20, зубьев пилы имеется пространство для стружки для приема или отвода стружки или стружки, которая возникает (ют) во время обработки заготовки. Зубья пилы 3 a от до 3 d в пределах каждой последовательности зубьев пилы 20 имеют определенную геометрию зуба, которая улучшает удаление стружки и схему резания. Первая пила 3 a, , которая находится спереди в направлении обработки и расположена непосредственно рядом с предыдущим пространством для стружки 21 , отличается от следующей пилы 3 b до 3 d с точки зрения геометрии зуба.
РИС. 2 показан увеличенный фрагмент первой пилы 3, , , , непосредственно следующей за пространством для стружки 21 , а также следующей, второй пилы 3 b общей последовательности зубцов. Относительно стороны обработки или плоскости, параллельной стороне обработки, первый зубец пилы 3 a расположен ниже следующего зубца пилы 3 b на величину a, и, следовательно, вершина первого зуба пилы 3 a выступает менее далеко наружу, чем кончик следующей пилы 3 b. Преимущественно концы всех зубьев пилы, следующих за первым зубцом пилы, находятся на одинаковой высоте, так что только первый зуб пилы располагается ниже.
Кроме того, поверхность зуба первой пилы 3, , и имеет другую конфигурацию, чем остальные зубья пилы. На поверхности первого зуба пилы 3 a между вершиной зуба и переходом в пространство для стружки 21 имеется три, по меньшей мере, приблизительно прямых части или кромки A, B и C, каждая из которых имеет различный передний угол. γ ₁, γ ₂ и γ ₃, соответственно, относительно вертикали 22 к стороне обработки или к направлению обработки.Самая верхняя кромка A, которая проходит от вершины зуба в направлении впадины зуба или пространства для стружки 21 , имеет положительный передний угол γ ₁, который целесообразно находится в диапазоне значений до 20 ° и предназначен для пример 10 °. Прилегающие дополнительные кромки B и C, напротив, имеют отрицательный передний угол γ ₂ и γ ₃, соответственно, при этом передний угол γ ₂ центральной кромки B целесообразно также в диапазоне значений выше до 20 ° и предпочтительно составляет 5 °, тогда как передний угол γ ₃ самой нижней кромки C больше, чем γ ₂, и составляет, например, 45 °.
Острие первой пилы 3 a расположено ниже вершины следующей пилы 3 b и всех следующих зубьев пилы в этой последовательности зубьев на величину a. Протяженность краев A, B и C по вертикали обозначается буквами b, c и d соответственно; спроецировано на вертикаль 22 , экстенты b, c и d имеют, по крайней мере, примерно одинаковый размер. Нижнее положение первой пилы 3 a на величину a имеет порядок величины до 0.5 мм и составляет, например, 0,3 мм.
Длина в вертикальном направлении первой кромки A, а также второй, центральной кромки B также в каждом случае находится в диапазоне значений до 0,5 мм и составляет, например, 0,3 мм. Длина d в проекции на вертикаль самого нижнего края C находится в диапазоне значений до 0,8 мм и составляет, например, 0,4 мм.
РИС. 3 показан вид сверху обрабатывающей стороны пильного инструмента 1 , имеющего последовательность зубьев пилы 20 , состоящую из четырех зубцов пилы 3 a от до 3 d. Первая пила 3 a прямая, т. Е. Имеет конфигурацию без набора, тогда как остальные зубья пилы 3 b, 3 c и 3 d имеют набор, в частности чередующийся в противоположных направлениях.
В отличие от первой пилы 3 a, следующие зубья пилы имеют исключительно положительный передний угол, но не имеют отрицательного переднего угла. Это проиллюстрировано в качестве примера на фиг.2 на основе второй пилы 3 b, с положительным передним углом γ ₄, который простирается от вершины зуба до перехода в пищевод 23 по прямой кромке лица зуба. Все зубья пилы, следующие за первой пилой в последовательности зубьев, могут иметь одинаковый положительный передний угол, при этом, в принципе, также возможны разные положительные передние углы. Передний угол γ ₄ следующих зубьев может быть либо того же размера, что и положительный передний угол γ ₁ первой пилы 3 a , либо отличаться от него, т.е.е. быть меньше или больше положительного переднего угла первой пилы.
РИС. 4 показано только пространство для стружки 21 с прилегающими зубьями 3 a следующей последовательности зубьев и 3 d предыдущей последовательности зубцов. Как показано пунктирной линией, первый зубец 3 a следующей последовательности зубьев расположен немного ниже, чем последний зубец 3 d предыдущей последовательности зубцов.
РИС. 5 показан корпус сверла 1 цилиндрической или чашеобразной формы в качестве пильного инструмента, который используется в кольцевой пиле для выпиливания сверлильного стержня. На своей стороне свободного конца 2 корпус сверла 1 имеет ряд только частично проиллюстрированных режущих зубьев или зубьев пилы 3 , которые выполнены описанным выше образом с последовательностями зубьев пилы, имеющими пространство для стружки между ними. На внутренней стороне 6 цилиндрического корпуса сверла 1 находится режущее тело 4 , которое проходит по осевой длине корпуса сверла и снабжено режущей кромкой 5 , направленной радиально внутрь.Режущее тело 4 имеет треугольное поперечное сечение, при этом вершина треугольника, направленная радиально внутрь, образует режущую кромку 5 . Режущая кромка 5 проходит в осевом направлении до стороны свободного конца 2 корпуса сверла 1 , но режущее тело 4 целесообразно не выступает в осевом направлении до режущих зубцов 3 .

Пилообразная последовательность: Подробные данные об ошибке IIS 8.5 – 404.0

Задача 20. Пилообразная последовательность | Тренер по программированию

تحميل Разбор задачи 794 acmp ru Ролевая игра Решение на c mp3 – mp4

Всё, что вы хотели знать о динамическом программировании, но боялись спросить

Основы

Порядок пересчёта

Многомерная динамика

Пример №1: Количество СМСок

Пример №2: Конь

Динамика и матрица переходов

Пример №3: Пилообразная последовательность

Динамика по подотрезкам

Пример №4: Запаковка строки

Пример №5: Дубы

Динамика по поддеревьям

Пример №6: Логическое дерево

Динамика по подмножествам

Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера

Динамика по профилю

Пример №8: Замощение доминошками

Динамика по изломанному профилю

Восстановление ответа

Небольшие оптимизации

Память

Время

Замена состояния

Пример №9: Разложение числа

Решение №1:

Решение №2:

Заключение

Волна пилообразная – Энциклопедия по машиностроению XXL

Каталог радиолюбительских схем. Автоматическое цветомузыкальное устройство.

akali.github.io/list.html at master · akali/akali.github.io · GitHub

Расширенное секвенирование – документация Qblox Instruments 0.5.2

Настройка

Генерация сигналов

Создать программу Q1ASM

Последовательность загрузки

Последовательность воспроизведения

Остановка

фундаментальных ограничений, оптимальных последовательностей переключения и ограниченного времени до встречи в JSTOR

О роли тяжелых ионов в пилообразных событиях: анализ наложенных эпох на данные in situ

Абстрактные

Разработка защиты для числовых последовательностей, сгенерированных с помощью хаотической карты пилообразной формы

Хаотическая карта пилообразной формы

Мы не можем найти эту страницу

Заявка на патент США на ПИЛЬНЫЙ ИНСТРУМЕНТ ДЛЯ МАШИНОСТРОЕНИЯ Заявка на патент (Заявка № 20120230788 от 13 сентября 2012 г.)

Больше новостей

Добавить комментарий Отменить ответ