Площадь сечения: Площадь сечения проводов. Формулы и таблицы – СамЭлектрик.ру

особенности величины, как найти её для круга

В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.

• Определение величины
• Область применения
• Способы расчета

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой.

Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

1. Определение объемов емкостей.
2. Решение задач по сопротивлению материалов и электротехнике.
3. Расчет количества материалов при проектировании, строительстве и ремонте.
4. Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью.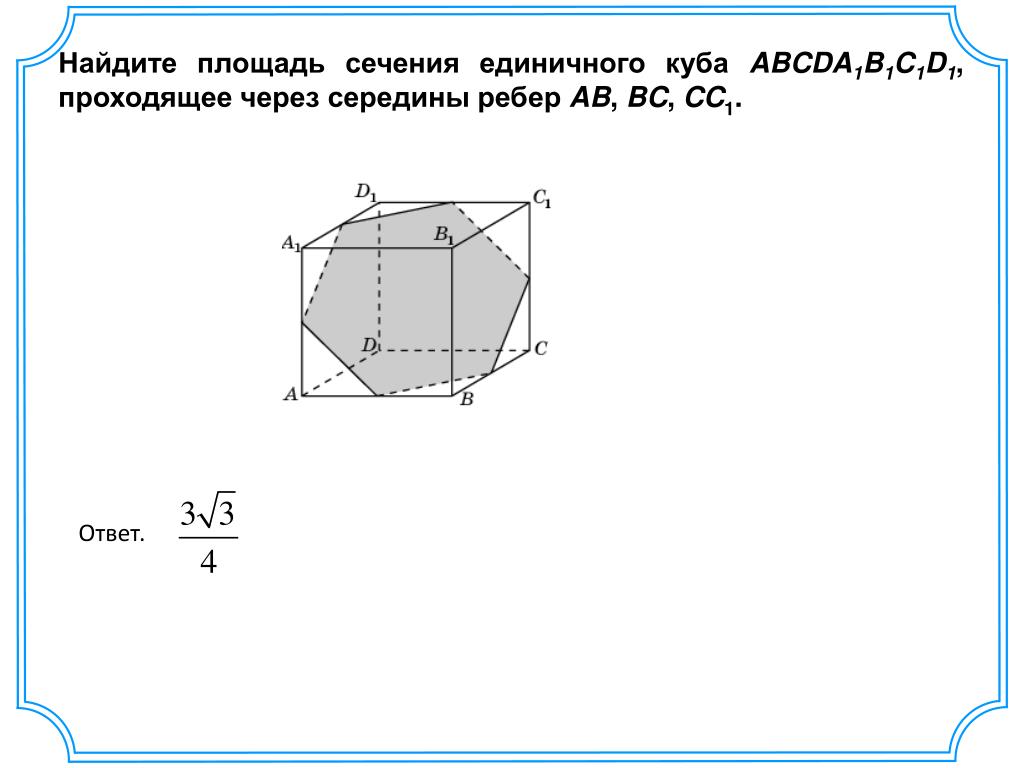 Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

• радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
• диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
• длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

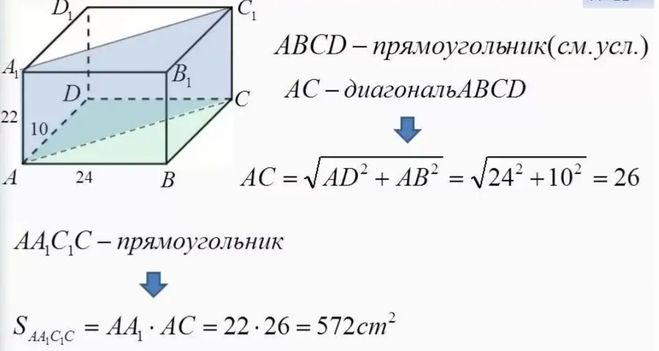
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Площадь сечения конуса

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2014-12-10

Площадь сечения конуса. Для вас представлена очередная статья с конусами. На момент написания этой статьи на блоге решены все примеры (прототипы) заданий с конусами, которые возможны на экзамене. Процесс решения несложен (1-2 действия), при определённой практике решаются устно. Нужно знать понятие образующей, об этом информация в этой статье. Так же необходимо понимать как образуются сечения конуса.

1. Если плоскость проходит через вершину конуса, то сечением является треугольник.

*Если плоскость проходит через ось конуса, то сечением является равнобедренный треугольник, высота которого равна высоте конуса, а основание на которое опущена эта высота равна диаметру основания конуса.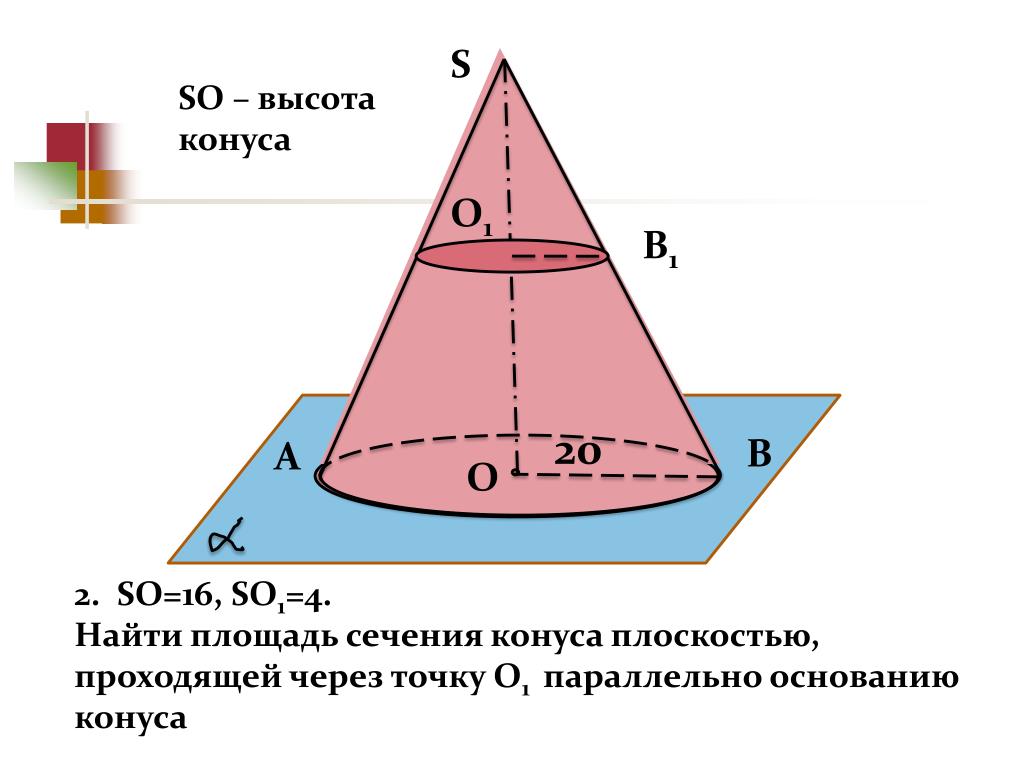

2. Если плоскость проходит перпендикулярно оси конуса, то сечением является круг.

Особенностью данных заданий является то, что применяется формула площади треугольника, здесь она первая. Формулы периодически повторяйте. Рассмотрим задачи:

324453. Площадь основания конуса равна 16Пи, высота равна 6. Найдите площадь осевого сечения конуса.

 

Осевым сечением конуса является треугольник с основанием равным диаметру основания конуса и высотой равной высоте конуса. Обозначим диаметр как D, высоту как Н, запишем формулу площади треугольника:

Высота известна, вычислим диаметр. Используем формулу площади круга:

Значит диаметр будет равен 8. Вычисляем площадь сечения:

Ответ: 24

324454. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Сечением является круг. Необходимо найти площадь этого круга.

Построим осевое сечение:

Рассмотрим треугольники AKL и AOC – они подобны. Известно, что в подобных фигурах отношения соответствующих элементов равны. Мы рассмотрим отношения высот и катетов (радиусов):

OC  это радиус основания, его можно найти:

Значит

Теперь можем вычислить площадь сечения:

*Это алгебраический способ вычисления без использования свойства подобных тел, касающегося их площади. Можно было рассудить так:

Два конуса (исходный и отсечённый) подобны, значит пощади их оснований являются подобными фигурами. Для площадей подобных фигур существует зависимость:

Коэффициент подобия в данном случае равен 1/3 (высота исходного конуса равна 9, отсечённого 3), 3/9=1/3.

Таким образом, площадь основания полученного конуса равна:

Ответ: 2

323455. Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.

Пусть образующая это L, высота это H, радиус основания это R.

Найдём диаметр основания и используя формулу площади треугольника вычислим площадь. По теореме Пифагора:

Вычисляем площадь сечения:

Ответ: 48

 

Диаметр основания конуса равен 40, а длина образующей — 25. Найдите площадь осевого сечения этого конуса.

Пусть образующая это L, высота это H, радиус основания это R. 

 

Радиус основания равен половине диаметра, то есть 20.

Вычислим высоту и далее используя формулу площади треугольника найдём искомую площадь. По теореме Пифагора:

Вычисляем площадь сечения:

Ответ: 300

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2Площадь

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Как рассчитать площадь поперечного сечения

Обновлено 7 февраля 2020 г.

Кевин Бек

Вы можете столкнуться с ситуациями, когда у вас есть трехмерная твердотельная фигура и вам нужно вычислить площадь воображаемой плоскости, вставленной через фигуру и имеющей границы, определяемые границами твердого тела.

Например, если под вашим домом проходит цилиндрическая труба длиной 20 метров (м) и диаметром 0,15 м, вам может понадобиться узнать площадь поперечного сечения трубы.

Поперечные сечения могут быть перпендикулярны оси твердого тела, если таковые существуют. В случае сферы любая секущая плоскость, проходящая через сферу, независимо от ориентации, приведет к диску определенного размера.

Площадь поперечного сечения зависит от формы твердого тела, определяющей границы поперечного сечения, и угла между осью симметрии твердого тела (если она есть) и плоскостью, создающей поперечное сечение.

Площадь поперечного сечения прямоугольного тела

Объем любого прямоугольного тела, включая куб, равен площади его основания (длина, умноженная на ширину), умноженной на его высоту: V = l × w × h.

Следовательно, если поперечное сечение параллельно верхней или нижней части твердого тела, площадь поперечного сечения равна l × w. Если секущая плоскость параллельна одному из двух наборов сторон, площадь поперечного сечения вместо этого определяется как l × h или w × h.

Если поперечное сечение не перпендикулярно какой-либо оси симметрии, созданная форма может быть треугольником (если провести через угол тела) или даже шестиугольником.

Пример: Вычислить площадь поперечного сечения плоскости, перпендикулярной основанию куба объемом 27 м ³ .

• Так как для куба l = w = h, длина любого ребра куба должна быть 3 м (поскольку 3

  × 3

  × 3 = 27). Таким образом, поперечное сечение описанного типа представляет собой квадрат со стороной 3 м, что дает площадь 9 м ² .

Площадь поперечного сечения цилиндра

Цилиндр представляет собой твердое тело, образованное путем вытягивания окружности через пространство перпендикулярно ее диаметру. Площадь круга находится по формуле πr ² , где r — радиус. Поэтому имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.

Если поперечное сечение параллельно оси симметрии, то площадь поперечного сечения представляет собой просто круг площадью πr ² . Если секущая плоскость вставляется под другим углом, создается эллипс. Для площади используется соответствующая формула: πab (где a — самое большое расстояние от центра эллипса до края, а b — самое короткое).

Пример: Какова площадь поперечного сечения трубы под вашим домом, описанной во введении?

Площадь поперечного сечения сферы

Любая теоретическая плоскость, проведенная через сферу, даст круг (подумайте об этом несколько минут). Если вы знаете диаметр или длину окружности, образуемой поперечным сечением, вы можете использовать соотношения C = 2πr и A = πr ² для получения решения.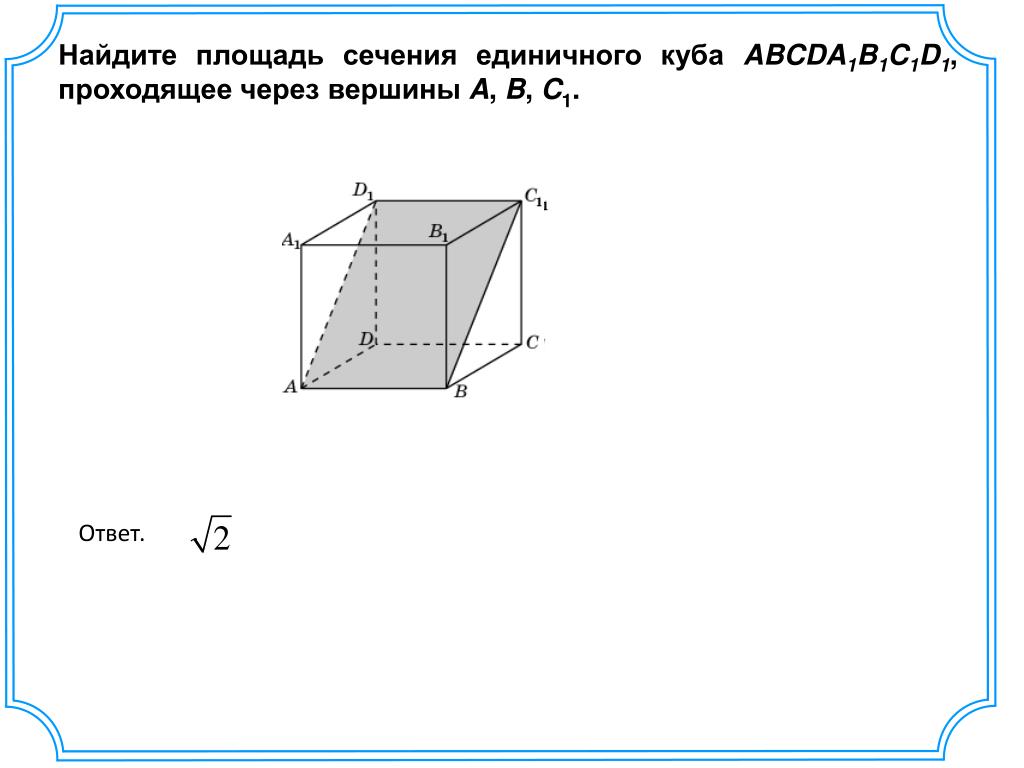

Пример 900:12: Самолет грубо вставлен в Землю очень близко к Северному полюсу, удаляя часть планеты в 10 м вокруг. Какова площадь поперечного сечения этого холодного куска Земли?

• Поскольку C = 2πr = 10 м, r = 10/2π = 1,59 м; A = πr ² = π(1,59) ² = 7,96 м ² .

Калькулятор площади поперечного сечения

Создано Рахулом Дхари

Отредактировано Стивеном Вудингом

Последнее обновление: 11 февраля 2023 г.

Содержание:

• Что такое поперечное сечение и как рассчитать площадь поперечного сечения?
• Как найти площадь поперечного сечения?
• Пример: Использование калькулятора площади поперечного сечения.
• Применение форм поперечного сечения
• Часто задаваемые вопросы

Калькулятор площади поперечного сечения определяет площадь для различных типов балок. Брус – очень важный элемент в строительстве. Несущие элементы мостов, крыш и полов в зданиях доступны в различных поперечных сечениях. Читайте дальше, чтобы понять, как рассчитать площадь поперечного сечения 9Профиль 0101 I , профиль T , балка C , балка L , круглый стержень, труба и балки с прямоугольным и треугольным поперечным сечением.

Что такое поперечное сечение и как рассчитать площадь поперечного сечения?

Поперечное сечение определяется как общая область, полученная в результате пересечения плоскости с трехмерным объектом. Например, рассмотрим длинную круглую трубу, вырезанную (пересеченную) плоскостью. Вы увидите пару концентрических кругов. Концентрические окружности – это поперечное сечение трубы. Аналогично балки — L , I , C и T — названы по форме поперечного сечения.

Разрез трубы

Чтобы рассчитать площадь поперечного сечения, вам нужно рассматривать их как основные формы. Например, трубка представляет собой концентрический круг. Следовательно, для трубы с внутренним и внешним диаметром ( d и D ) и толщиной t площадь поперечного сечения может быть записана как:

AC=π×(D2−d2)/4A_ {C} = \pi \times (D^2-d^2)/4AC​=π×(D2−d2)/4 92)/4AC​=π×(D2−(D−2t)2)/4

Аналогично, площадь поперечного сечения для всех других форм, имеющих ширину W , высоту H и толщину t₁ и t₂ приведены в таблице ниже.

Различные поперечные сечения17 (H.) – WS) – WS) – Holdangle

(H.) (Hlownsh Writangle

(H.) (2) (2) (2).1111179.

. H – t) × t

Раздел	Площадь
– Hollow Rectangle
Rectangle	W × H
I	2 × W × t₁ + (H – 2 × t₁) × t₂
C	2 × W × T₁ + (H – 2 × T₁) × T₂
T	W × T₁ + (H – T₁) × T₂
11111179. 9000 3
Равнобедренный треугольник	0.5 × B × H
Equilateral Triangle	0. 4330 × L²
Circle	0.25 × π × D²
Tube	0,25 × π × (D² – (D – 2 × t)²)

Как найти площадь поперечного сечения?

Выполните следующие действия, чтобы найти площадь поперечного сечения.

• Шаг 1: Выберите
  форма поперечного сечения из списка, скажем, Полый прямоугольник . Теперь будет видна иллюстрация поперечного сечения и связанных с ним полей.
• Шаг 2: Введите ширину полого прямоугольника, W .
• Шаг 3: Заполните высоту поперечного сечения, H .
• Шаг 4: Вставьте толщину полого прямоугольника, t .
• Шаг 5: Калькулятор вернет площадь поперечного сечения .

Пример: Использование калькулятора площади поперечного сечения.

Найдите площадь поперечного сечения трубы, имеющей внешний диаметр 10 мм и толщину 1 мм .

• Шаг 1: Выберите из списка форму поперечного сечения , т. е. Труба .

• Шаг 2: Введите наружный диаметр трубы, D = 10 мм .

92AC​=π×(102−(10−2×1)2)/4=28,274 мм2

Применение форм поперечного сечения

Знаете ли вы?

• Балка I или H широко используется на железнодорожных путях.
• Балки T используются в ранних мостах и ​​используются для усиления конструкций, чтобы выдерживать большие нагрузки на перекрытия мостов и опор. См. наш калькулятор нагрузки на балку , чтобы узнать больше!

FAQ

Как рассчитать площадь поперечного сечения трубы?

Для расчета поперечного сечения трубы:

1. Вычесть квадратов внутреннего диаметра из наружного диаметра.