Подключение конденсаторов для увеличения емкости: Последовательное и параллельное соединение.

Содержание

Последовательное и параллельное соединение.

Иногда нужно увеличить ёмкость или сопротивление, а подходящих деталей на нужное сопротивление нет, или размеры конструкции не позволяют вставить один большой конденсатор на 3000 мкф.

В этом случае можно набрать необходимые ёмкость или сопротивление из нескольких деталей, а вместо конденсатора на 3000 микрофарад вставить 3 штуки по 1000 микрофарад.

Для увеличения ёмкости конденсаторы соединяются параллельно.

Для увеличения сопротивления резисторы соединяются последовательно.
Вода через трубу с двумя валенками течёт хуже, чем через трубу с одним валенком.

Последовательное соединение – когда детали стоят друг за дружкой, “в очереди”, будто за колбасой, потому оно так и называется.

Не путайте эти соединения, для увеличения ёмкости конденсаторы соединяются параллельно, а резисторы для увеличения сопротивления последовательно

Со сложением ёмкостей и сопротивлений всё легко.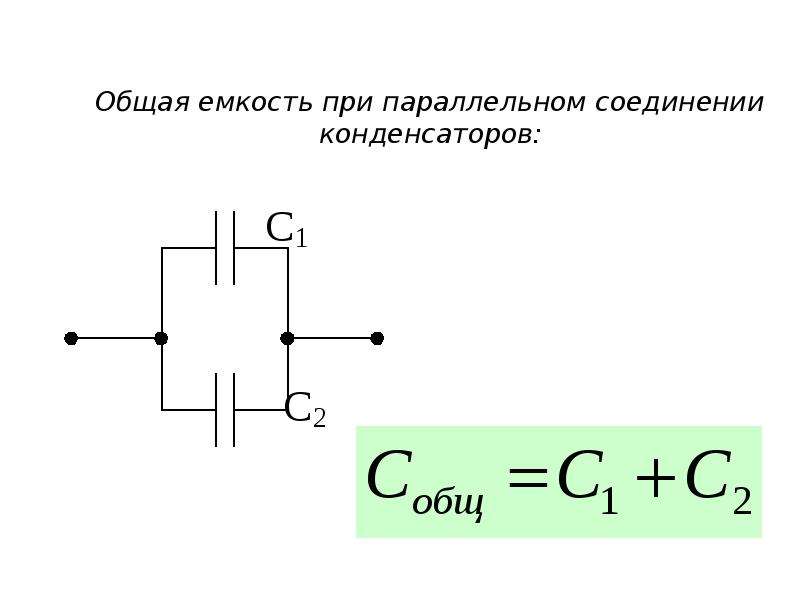

С параллельным соединением резисторов и последовательным соединением конденсаторов слегка посложнее, но к нашему счастью конденсаторы довольно редко соединяют последовательно, а резисторы параллельно.
Последовательное соединение конденсаторов может понадобиться например в сборке гаусс-гана (электромагнитной стрелялки), когда под рукой конденсаторы только на 400 вольт, а нам нужен 800-вольтовый конденсатор, а их редко где найдёшь и они дорогие.

Параллельное соединение резисторов считается вот по какой формуле:

Через три трубы, в которых в каждой по валенку, вода лучше потечёт, чем через одну трубу с одним валенком. Или если в бочке проковырять три дырки, то вода быстрее выльется, чем если бы мы проковыряли одну дырку.

Последовательное соединение конденсаторов считается по той же формуле.

Если два одинаковых конденсатора по 680uF с максимальным напряжением 400В поставить последовательно, то получится конденсатор на 340 uF с напряжением 800 вольт.
Ёмкость уменьшается, зато вырастает максимальное допустимое напряжение, а запасаемая в обеих конденсаторах энергия остаётся та же самая.

Последовательное и параллельное соединение конденсаторов

Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели. При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов.
Емкость набора при последовательном соединении конденсаторов будет вычисляться по формуле:

	1	=	1	+	1	+	1	+ . ..
	C		C1		C2		C3

А общее напряжение будет равняться сумме напряжений всех конденсаторов.
Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый. При их последовательном соединении общий конденсатор будет иметь следующие данные: 10 мкФ x 300 В.

При параллельном соединении общая емкость конденсаторов складывается, а допустимое напряжение всего набора будет равно напряжению конденсатора, имеющего самое низкое значение допустимого напряжения из всего набора.

C = C1 + C2 + C3 + C4 + …

Например: мы имеем три конденсатора 30 мкФ x 100 В, соединённые параллельно. Параметры всего набора конденсаторов в этом случае будут следующие: 90 мкФ x 100 В.

Соединение более двух конденсаторов последовательно редко встречается в реальных схемах.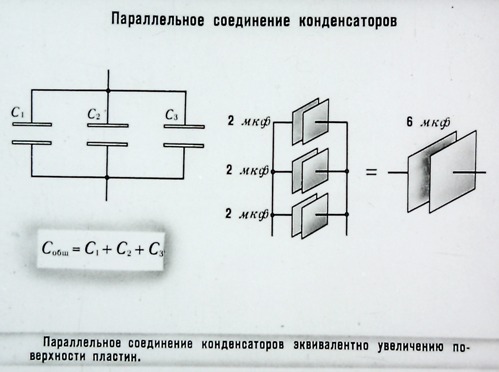 Хотя для увеличения общего напряжения такой набор может встретиться в высоковольтных источниках питания. А вот в низковольтных источниках довольно часто встречается параллельное соединение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах потребления.

Обратите внимание, формулы вычисления емкости последовательного и параллельного соединения конденсаторов в точности обратны формулам вычисления сопротивления при последовательном и параллельном соединении резисторов.

Как увеличить вольтаж конденсатора — MOREREMONTA

1	=	1	+	1	+	1	+ .
C		C1		C2		C3

C = C1 + C2 + C3 + C4 + .

Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

С₁ – ёмкость первого;

С₂ – ёмкость второго;

С₃ – ёмкость третьего;

С_N – ёмкость N-ого конденсатора;

C_общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость

C₁, C₂ в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт.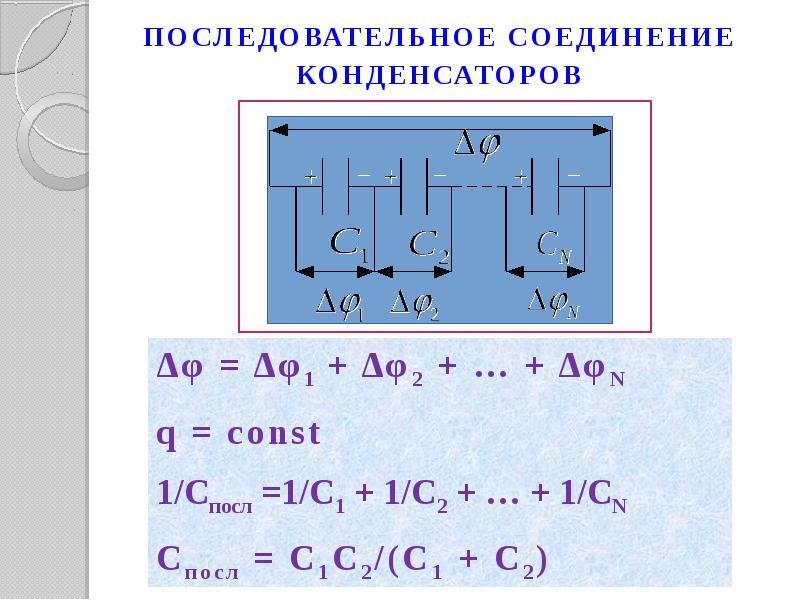 Подробнее об этом читайте здесь.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C₁ – его ёмкость.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.

Параллельное соединение электролитов

Схема параллельного соединения

В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Если нужно срочно отремонтировать технику, а нужного конденсатора нет, то можно увеличить емкость конденсатора, как известно из школьной программы, соединив несколько приборов в одну цепь.

Такая проблема может также возникнуть, если, например, нужного номинала нет в продаже, то есть для нестандартных подключений, например, в радиотехнических опытах.

Электрическая емкость

При соединении приборов для конденсации заряда, как правило, техника интересует электрическая емкость, которая получится в итоге.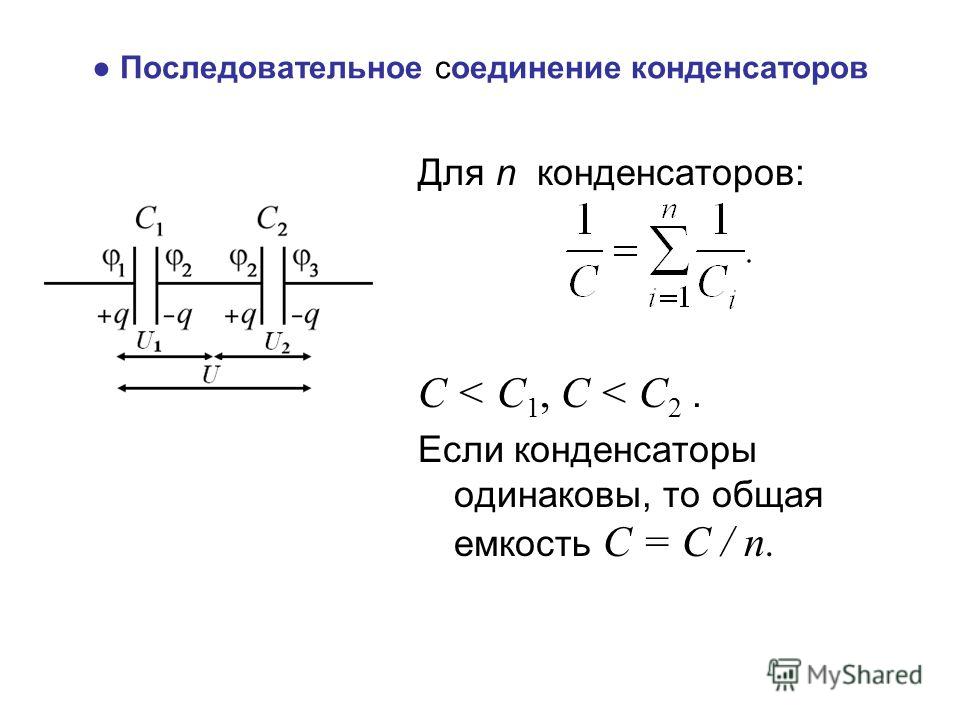

Электроемкость показывает способность двухполюсника накапливать в себе заряд и измеряется в фарадах. Может показаться, что чем выше это значение, тем лучше, но на практике не существует возможности создать все возможные на свете емкости, более того, часто это и не нужно, так как во всех приборах, использующихся повседневно, применяются стандартные приборы для конденсации.

Можно соединить несколько приборов для конденсации в цепь, создав одну конденсирующую емкость, при этом значение характерной величины будет зависеть от типа подключения, и для его расчета есть давно известные формулы.

Параллельное соединение

Существует два типа подключения приборов в цепь: последовательное и параллельное. Каждый из них обладает своими свойствами, но, как правило, используется параллельное соединение конденсаторов.

Параллельное соединение обладает такими свойствами:

Емкость составного двухполюсника увеличивается по сравнению с каждым отдельным прибором.
Напряжение в сети не изменяется.

Соединить конденсаторы для увеличения емкости, как показывают свойства, лучше этим способом. Для этого нужно соединить выводы с каждого двухполюсника по группам: у каждого из них два вывода. Нужно создать две группы: в одну соединить все конденсаторы с одного вывода, а во вторую с оставшегося.

При таком соединении приборы для конденсации образуют одну емкость, поэтому верна такая формула: С=С1+С2+…СN, где N — количество конденсаторов в цепи.

Например, если имеются номинальные значения 50мкф, 100мкф и 150мкф, то при последовательном подключении общее значение в цепи будет 300мкф.

В жизни это подключение используют довольно часто, например, если при расчетах оказалось, что требуется такой двухполюсник, которого в продаже точно не найти. С помощью этого способа можно варьировать емкость конденсатора так, как это потребуется, при этом не изменяя напряжение в сети.

Последовательное включение конденсаторов

Свойства последовательного включения конденсаторов:

Емкость последовательно соединенных приборов для конденсации заряда в отличие от емкости параллельно соединенных конденсаторов уменьшается.
Напряжение на приборах растет.

Для такого подключения нужно просто соединять выводы двухполюсников один с другим, образуя цепочку: вывод первого будет соединен с выводом второго, оставшийся вывод второго с выводом третьего и так далее.

Формула подключения: 1/(1/С1+1/С2+…+1/СN), где N — это количество приборов в соединении.

Например, есть три конденсатора по 100мкф. 1/100+1/100+1/100=0,03мкф. 1/0,03=33мкф.

Заряды распределятся с чередующимся знаком, а емкостное значение будет ограничено только им же для самого слабого звена в цепи. Как только он получит свой заряд, передача тока в цепи прекратится.

Для чего тогда нужен подобный способ подключения? Такая цепь более устойчива и может выдержать большее напряжение при подключении в схему при меньшем емкостном номинале конденсатора. Однако в продаже имеются приборы, которые и без того обладают нужными свойствами, поэтому-то такое подключение в жизни практически не используется, а если используется, то для специфических задач.

Смешанный способ

Сочетает в себе параллельное и последовательное подключения.

При этом для участков с последовательным соединением характерны свойства последовательного соединения, а для участков с параллельным — свойства параллельного.

Оно используется, когда ни электроемкость, ни номинальное напряжение приборов, имеющихся в продаже, не подходят для задачи. Обычно такая проблема возникает в радиотехнике.

Чтобы определить общее значение электроемкости, нужно будет сначала определить это же значение для параллельно соединенных двухполюсников, а потом для их последовательного соединения.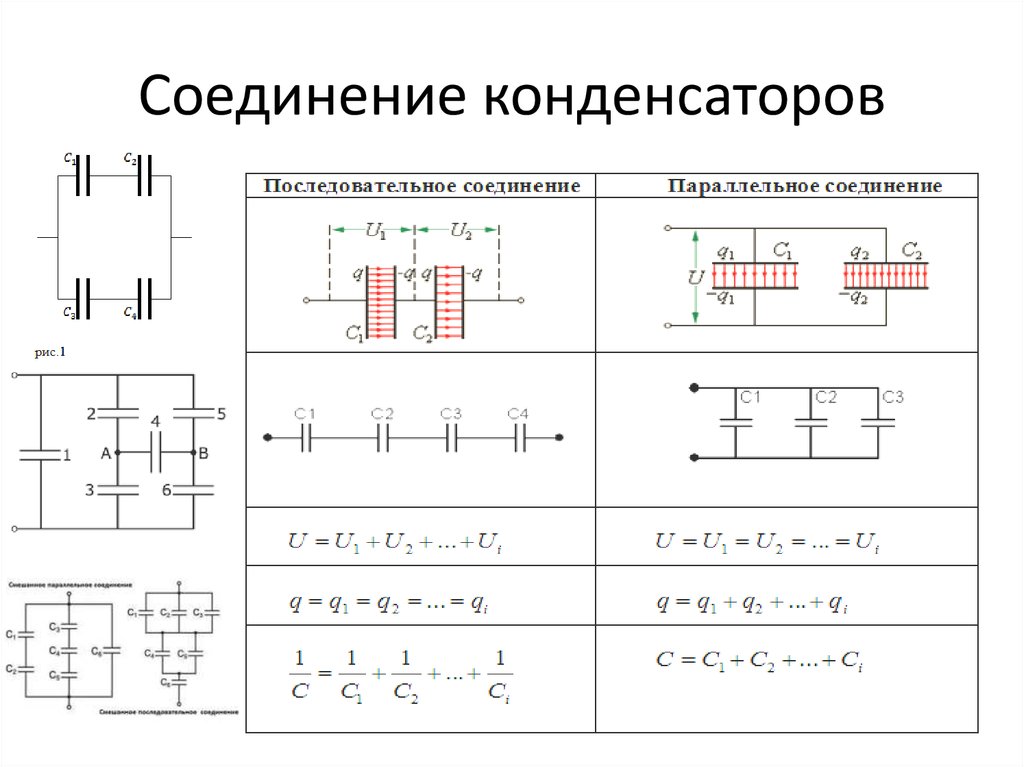

Сравнение различных вариантов

Емкость	Напряжение
Параллельное	Увеличивается	Не изменяется
Последовательное	Уменьшается	Увеличивается
Смешанное	Изменяется	Увеличивается

Для выбора соединения можно воспользоваться такой таблицей. Слева тип соединения приборов, сверху свойства прибора для конденсации заряда.

Если требуется увеличить емкость, то нужно использовать параллельное соединение, а если увеличить напряжение — то последовательное. Если же требуется и то, и то, то нужно будет рассчитывать смешанное подключение конденсаторов в цепь.

Как соединить электролитические конденсаторы для увеличения напряжения. Последовательное и параллельное соединение конденсаторов

Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.

Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.

При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.

Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах . Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.

Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.

На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.

При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.

Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле

Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.

При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.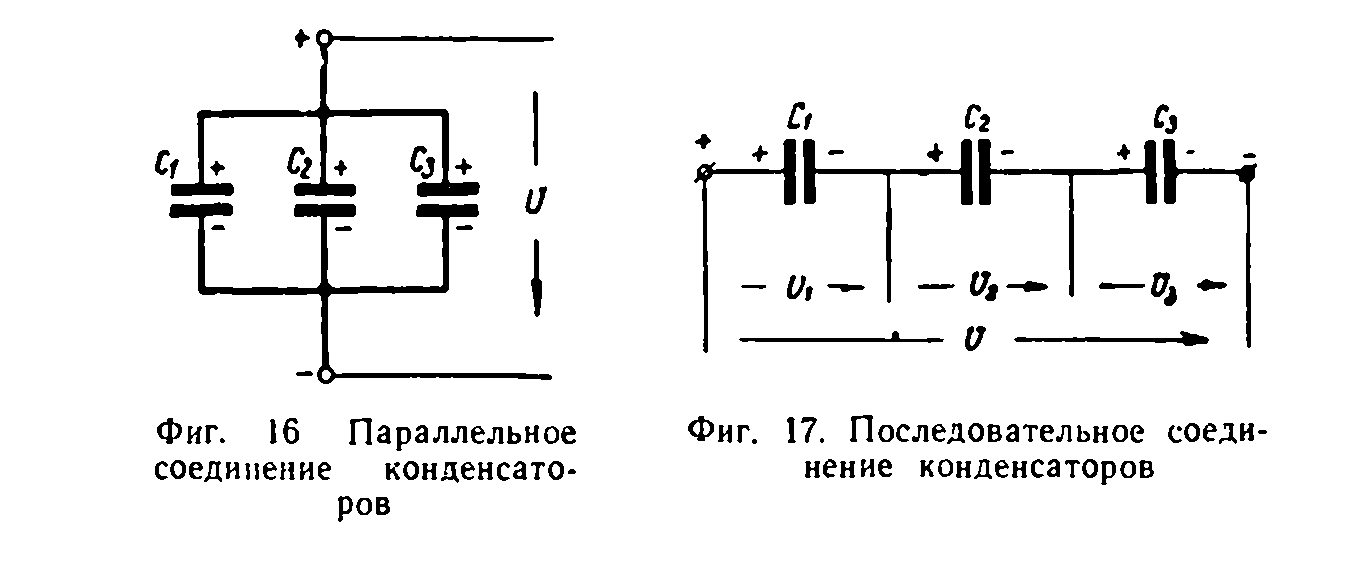

Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения .

Смешанное соединение конденсаторов

Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.

В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.

Параллельное соединение

Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии

Схема параллельного крепления

Емкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме.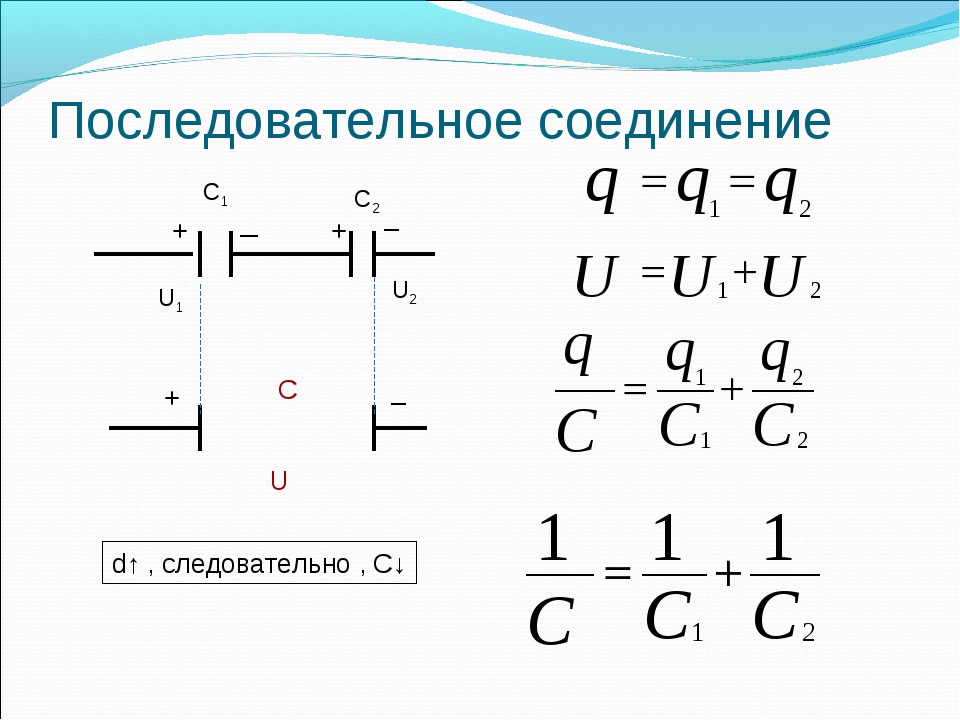 При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.

C общ = C 1 + C 2 + C 3

Схема – напряжение на накопителях

В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:

V AB = V C1 = V C2 = V C3 = 20 Вольт

Последовательное соединение

Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.

Схема – схема последовательного соединения

Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.

Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:

i = i c 1 = i c 2 = i c 3 = i c 4 , то есть токи проходящие через каждый конденсатор равны между собой.

Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:

Q общ = Q 1 = Q 2 = Q 3

А так определяется общая суммарная емкость конденсаторов при последовательном соединении:

1/C общ = 1/C 1 + 1/C 2 + 1/C 3

Видео: как соединять конденсаторы параллельным и последовательным методом

Смешанное подключение

Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента.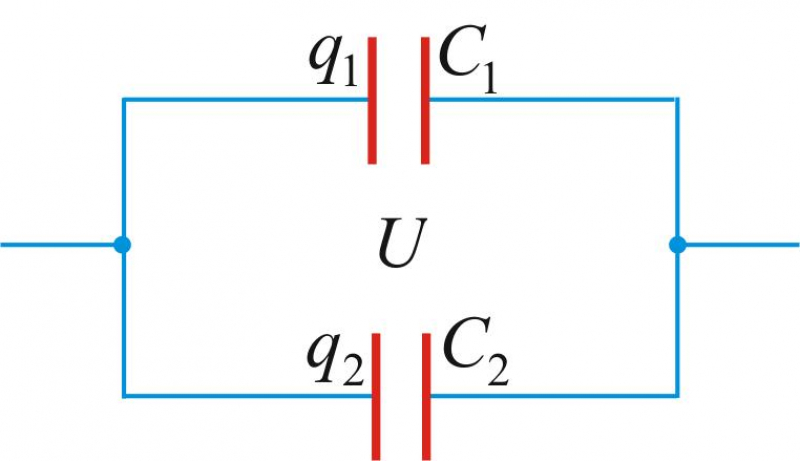 Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.

Схема: смешанное соединение конденсаторов

Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:

Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.

Содержание:

В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.

Последовательное соединение

При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = i c1 = i c2 = i c3 = i c4 .

В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Q общ = Q 1 = Q 2 = Q 3 .

Если рассмотреть три конденсатора С 1 , С 2 и С 3 , соединенные в последовательную цепь, то выясняется, что средний конденсатор С 2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.

Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.

Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/C общ = 1/C 1 + 1/C 2 + 1/C 3 .

Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.

Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.

Смешанное соединение

Параллельное соединение конденсаторов

Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.

Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно.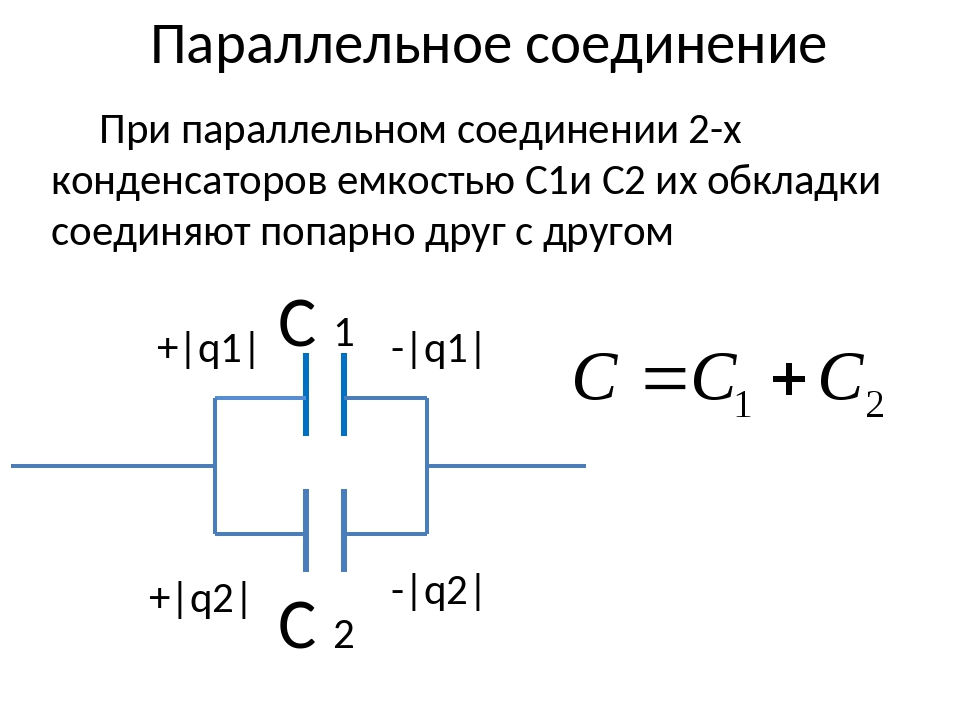 То есть, С общ = С 1 + С 2 + С 3 .

Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов применяется для увеличения емкости.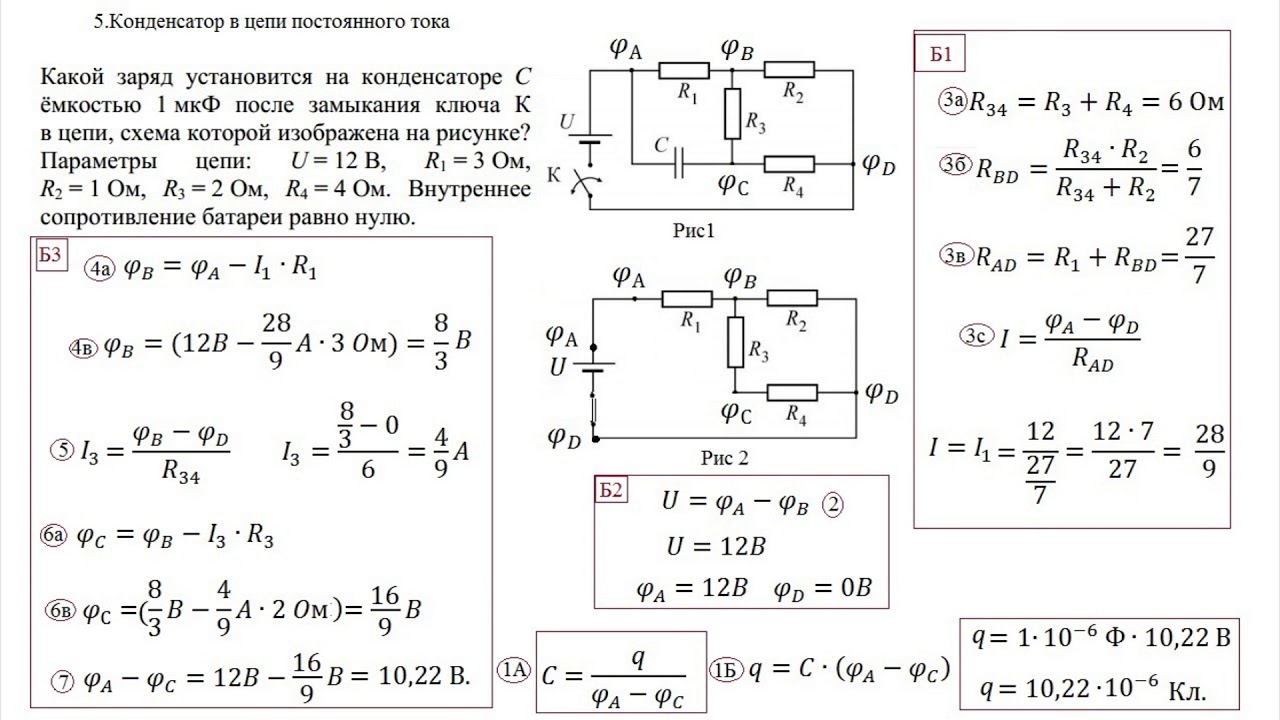

4)Если параллельно включены т одинаковых конденсаторов емкостью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис.3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденсаторов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих конденсаторов.

При последовательном включении двух конденсаторов их общая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конденсаторов емкостью С каждый, то общая емкость этих конденсаторов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. последовательное включение конденсаторов приводит к уменьшению общей емкости батареи конденсаторов.

На практике может оказаться, что допустимое рабочее напряжение U p конденсатора меньше напряжения, на которое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить несколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется меньше его допустимого рабочего U p . Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) конденсаторов применяют тогда, когда необходимо увеличить емкость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на нижеприведенных примерах.

Энергия конденсаторов

где Q – заряд конденсатора или конденсаторов, к которым приложено напряжение U ; С – электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .

Таким образом, конденсаторы служат для накопления и сохранения электрического поля и его энергии.

15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего сопротивления в расчет вводится внутренняя проводимостьg =1/ r .

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r – I ,

где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K – ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

Вопрос о том, как соединить конденсаторы может возникнуть у любого человека, интересующегося электроникой и пайкой . Чаще всего, необходимость в этом возникает в случаях отсутствия под рукой устройства подходящего номинала при сборке или ремонте какого-либо прибора.

К примеру, человеку нужно отремонтировать устройство, заменив в нем электролитический конденсатор ёмкостью 1000 микрофарад или больше, на руках подходящие по номиналу детали отсутствуют, но есть несколько изделий с меньшими параметрами. В этом случае есть три варианта выхода из сложившейся ситуации:

Поставить вместо конденсатора на 1000 микрофарад устройство с меньшим номиналом.
Поехать в ближайший магазин или радио-рынок для покупки подходящего варианта.
Соединить несколько элементов вместе для получения необходимой ёмкости.

От установки радиоэлемента меньшего номинала лучше отказаться, так как подобные эксперименты не всегда заканчиваются успешно. Можно съездить на рынок или в магазин, но это требует немало времени. Потому в сложившейся ситуации чаще соединяют несколько конденсаторов и получают необходимую емкость.

Параллельное соединение конденсаторов

Параллельная схема подключения конденсаторов предполагает соединение в две группы всех обкладок приборов. В одну группу соединяются первые выводы, а в другую группу – вторые выводы. На рисунке ниже представлен пример.

Конденсаторы, соединенные параллельно между собой, подключаются к одному источнику напряжения, поэтому на них существует две точки напряжения или разности потенциалов . Следует учитывать, что на всех выводах подключенных параллельно конденсаторов напряжение будет иметь одинаковую величину.

Параллельная схема образует из элементов единую ёмкость, величина которой равняется сумме ёмкостей всех подключенных в группу конденсаторов. При этом через конденсаторы в процессе работы устройства будет протекать ток разной величины. Параметры проходящего через изделия тока зависят от индивидуальной ёмкости устройства. Чем выше ёмкость, тем больший по величине ток пройдет через него. Формула, характеризующее параллельное соединение, имеет следующий вид:

Параллельная схема чаще всего используется в быту, она позволяет собрать необходимую ёмкость из любого числа отдельных, различных по номиналу элементов.

Последовательное соединение конденсаторов

Схема последовательного подключения представляет собой цепочку, в которой первая обкладка конденсатора соединяется со второй обкладкой предыдущего устройства, а вторая обкладка – с первой обкладкой следующего прибора. Первый вывод первого конденсатора и второй вывод последней детали в цепи соединяются с источником электрического тока, благодаря чему между ними осуществляется перераспределение электрических зарядов. Все промежуточные обкладки имеют одинаковые по величине заряды, чередующиеся по знаку.

На рисунке ниже представлен пример последовательного подключения.

Через соединенные в группу конденсаторы протекает ток одинаковой величины. Общая мощность ограничивается площадью обкладок устройства с наименьшим номиналом, так как после зарядки наименьшего по ёмкости устройства, вся цепь перестанет пропускать ток.

Несмотря на явные недостатки, данный способ обеспечивает увеличение изоляции между отдельными обкладками до суммы расстояний между выводами на всех последовательно соединенных конденсаторах. То есть, при последовательном соединении двух элементов с рабочим напряжением 200 В, изоляция между их выводами сможет выдерживать напряжение до 1000 В. Ёмкость по формуле:

Данный способ позволяет получить эквивалент меньшего по ёмкости конденсатора в группе, способной работать при высоких напряжениях. Всего этого можно достичь путем покупки одного единственного элемента подходящего номинала, потому на практике последовательные соединения практически не встречаются.

Эта формула актуальна для расчета общей ёмкости цепи последовательно соединенных двух конденсаторов. Для определения общей ёмкости цепи с большим числом приборов необходимо воспользоваться формулой:

Смешанная схема

Пример смешанной схемы подключения представлен ниже.

Чтобы определить общую ёмкость нескольких устройств, всю схему необходимо разделить на имеющиеся группы последовательного и параллельного соединения и рассчитать параметры ёмкости для каждой из них.

На практике данный способ встречаются на различных платах, с которыми приходиться работать радиолюбителям.

Соединение конденсаторов – Основы электроники

В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.

Рисунок 1. Способы соединения конденсаторов.

Параллельное соединение конденсаторов.

Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.

При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор.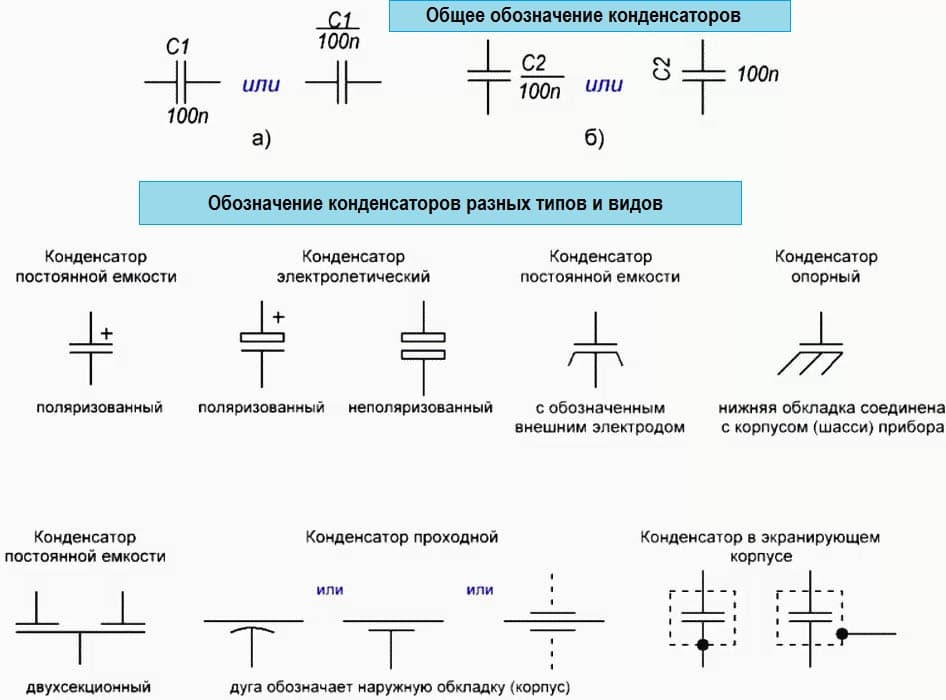 Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.

Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:

Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.

Последовательное соединение конденсаторов.

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.

При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.

Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.

Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.

Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.

Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.

Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:

Последовательно-параллельное (смешанное) соединение конденсаторов

Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.

На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.

Рисунок 4. Последовательно-параллельное соединение конденсаторов.

При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:

1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.

2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.

3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.

4. Рассчитывают емкость полученной схемы.

Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.

Рисунок 5. Пример расчета последовательно-параллельного соединения конденсаторов.

Подробнее о расчетах соединения конденсаторов можно узнать в мультимедийном учебнике по основам электротехники и электроники:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Параллельное и последовательное соединение конденсаторов

В предыдущих статьях были рассмотрены вопросы работы и характеристики конденсаторов. Сейчас Я расскажу о всех методах соединения конденсаторов для подключения в схему. Сразу скажу, что в жизни практически везде, за исключением редких случаев используется только параллельная схема подключения.

Следует знать, что в цепи переменного тока конденсатор выступает еще как емкостное сопротивление. При чем с увеличением величины емкости конденсатора- уменьшается сопротивление в цепи переменного тока.

Параллельное соединение конденсаторов

При параллельной схеме подключения все обкладки конденсаторов соединяются в две группы, причем один вывод с каждого конденсатора соединяется в одну группу с другими, а второй — в другую. Наглядный пример параллельного соединения и схема на картинке.
Все параллельно соединенные конденсаторы подключаются к одному источнику напряжения, поэтому существует на них две точки разности потенциалов или напряжения. На всех выводах конденсаторов будет абсолютно одинаковое напряжение.

При подключении параллельно все конденсаторы вместе, образуют принципиально одну емкость, величина которой будет равняться сумме всех емкостей подключенных в цепи конденсаторов.При параллельном подключении через каждый из конденсаторов потечет разный ток, который будет зависеть от величины емкости каждого из них. Чем выше емкость, тем больший ток потечет через неё.

Параллельное соединение очень часто встречается в жизни. С его помощью можно из группы конденсаторов собрать любую необходимую емкость. Например, для запуска 3 фазного электродвигателя в однофазной сети 220 Вольт в результате расчетов Вы получили что необходима рабочая емкость 125 мкФ. Такой емкости конденсаторов Вы не найдете в продаже. Для того, что бы получить необходимую емкость придется купить и соединить параллельно 3 конденсатора один на 100 мкФ, второй- на 20, и третий на 5 мкФ.

Соединение конденсаторов последовательно

При последовательном соединении конденсаторов каждая из обкладок соединяется только в одной точке с одной обкладкой другого конденсатора. Получается цепочка конденсаторов. Крайние два вывода подключаются к источнику тока, в результате чего происходит перераспределение между ними электрических зарядов. Заряды на всех промежуточных обкладках одинаковые величине с чередованием по знаку.

Через все соединенные конденсаторы последовательно протекает одинаковой величины ток, потому что у него нет другого пути прохождения.
Общая же емкость будет ограничиваться площадью обкладок самого маленького по величине, потому что как только зарядится полностью конденсатор с самой маленькой емкостью- вся цепочка перестанет пропускать ток и заряд остальных прервется. Высчитывается же емкость по этой формуле:Но при последовательном соединении увеличивается расстояние (или изоляция) между обкладками до величины равной сумме расстояний между обкладками всех последовательно подключенных конденсаторов. Например, если взять два конденсатора с рабочим напряжением 200 Вольт и соединить последовательно, то изоляция между их обкладками сможет выдержать 1000 Вольт при подключении в схему.

Из выше сказанного можно сделать вывод, что последовательно соединять необходимо:

Для получения эквивалентного меньшего по емкости конденсатора.
Если необходима емкость, работающая на более высоких напряжениях.
Для создания емкостного делителя напряжения, который позволяет получить меньшей величины напряжение из более высокого.

Практически, для получения первого и второго достаточно просто купить один конденсатор с необходимой величиной емкости или рабочим напряжением. Поэтому данный метод соединения в жизни не встречается.

Смешанное соединение конденсаторов

Встречается смешанное соединение только на различных платах. Для него характерно наличие в одной цепи параллельного и последовательного соединения конденсаторов. При чем смешанное соединение может быть как последовательного, так параллельного характера.

В жизни подробные знания о смешанном соединении могут только пригодится радиолюбителям, поэтому не буду на этом подробно останавливаться.

Из следующей статьи Вы узнаете как правильно проверить и определить емкость конденсатора.

Последовательное и параллельное соединение конденсаторов (ёмкостей)

Практически ни одно электронное устройство не обходится без конденсатора. Он может стоять на входе или выходе устройства, перед или после некоторых элементов. Применяется последовательное и параллельное соединение конденсаторов. Как и для чего их подключать тем или иным способом и будем обсуждать.

Содержание статьи

Что такое конденсатор и его основные характеристики

Конденсатор — это радиодеталь, которая работает как накопитель электрической энергии. Чтобы понятнее было, как он работает, его можно представить как своего рода небольшой аккумулятор. Обозначается двумя параллельными чёрточками.

Обозначения различных типов конденсаторов на схемах. Чаще всего из строя выходят электролитические конденсаторы, так что стоит запомнить их обозначение

Основная характеристика конденсатора любого типа — ёмкость. Это то количество заряда, которое он в состоянии накопить. Измеряется в Фарадах (сокращенно просто буква F или Ф), а вернее, в более «мелких» единицах:

микрофарадах — мкФ это 10^-6 фарада,
нанофарадах — нФ это 10^-9 фарада;
пикофарадах — пФ это 10^-12 фарада.

Вторая важная характеристика — номинальное напряжение. Это то напряжение, при котором гарантирована длительная безотказная работа. Например, 4700 мкФ 35 В, где 35 В — это номинальное напряжение 35 вольт.

У крупных по размеру конденсаторов, ёмкость и напряжение указаны на корпусе

Нельзя ставить конденсатор в цепь с более высоким напряжением чем то, которое на нём указано. В противном случае он быстро выйдет из строя.

Можно использовать конденсаторы на 50 вольт вместо конденсаторов на 25 вольт. Но это порой нецелесообразно, так как те, которые рассчитаны на более высокое напряжение, дороже, да и габариты у них больше.

Что он из себя представляет и как работает

В самом простейшем случае конденсатор состоит из двух токопроводящих пластин (обкладок), разделённых слоем диэлектрика.

Между обкладками находится слой диэлектрика — материала плохо проводящего электрический ток

На пластины подаётся постоянный или переменный ток. Вначале, пока энергия накапливается, потребление энергии конденсатором высокое. По мере «наполнения» ёмкости оно снижается. Когда заряд набран полностью, токопотребления вообще нет, источник питания как бы отключается. В это время конденсатор сам начинает отдавать накопленный заряд. То есть, он на время становится своеобразным источником питания. Поэтому его и сравнивают с аккумулятором.

Где и для чего используются

Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:

Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом.
Часто можно увидеть электролитические цилиндрические конденсаторы
Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец. Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.

Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.

Как подключать конденсаторы

В электротехнике есть два основных вида соединения деталей — параллельное и последовательное. Конденсаторы также можно подключать по любому из указанных способов. Есть ещё особая — мостовая схема. Она имеет собственную область использования.

В схеме может быть последовательное и параллельное соединение конденсаторов

Параллельное подключение конденсаторов

При параллельном соединении все конденсаторы объединены двумя узлами. Чтобы параллельно подключить конденсаторы, скручиваем попарно их ножки, обжимаем пассатижами, потом пропаиваем. У некоторых конденсаторов большие корпуса (банки), а выводы маленькие. В таком случае используем провода (как на рисунке ниже).

Так физически выглядит параллельное подключение конденсаторов

Если конденсаторы электролитические, следите за полярностью. На них должны стоять «+» или «-«. При их параллельном подключении соединяем одноимённые выводы — плюс к плюсу, минус — к минусу.

Расчёт суммарной ёмкости

При параллельном подключении конденсаторов их номинальная ёмкость складывается. Просто суммируете номиналы всех подключённых элементов, сколько бы их ни было. Два, три, пять, тридцать. Просто складываем. Но следите, чтобы размерность совпадала. Например, складывать будем в микрофарадах. Значит, все значения переводим в микрофарады и только после этого суммируем.

Расчёт ёмкости при параллельном подключении конденсаторов

Когда на практике применяют параллельное соединение конденсаторов? Например, тогда, когда надо заменить «пересохший» или сгоревший, а нужного номинала нет и бежать в магазин некогда или нет возможности. В таком случае подбираем из имеющихся в наличии. В сумме они должны дать требуемое значение. Все их проверяем на работоспособность и соединяем по приведенному выше принципу.

Пример расчёта

Например, включили параллельно два конденсатора — 8 мкФ и 12 мкФ. Следуя формуле, их номиналы просто складываем. Получаем 8 мкФ + 12 мкФ = 20 мкФ. Это и будет суммарная ёмкость в данном случае.

Пример расчёта конденсаторов при параллельном подключении

Последовательное соединение

Последовательным называется соединение, когда выход одного элемента соединяется со входом другого. Сравнить можно с вагонами или цепочкой из лампочек. По такому же принципу последовательно соединяют и конденсаторы.

Вот что значит последовательно соединить конденсаторы

При подключении полярных электролитических «кондеров» надо следить за соблюдением полярности. Плюс первого конденсатора подаете на минус второго и так далее. Выстраиваете цепочку.

Существуют неполярные (биполярные) электролитические конденсаторы. При их соединении нет необходимости соблюдать полярность.

Как определить ёмкость последовательно соединенных конденсаторов

При последовательном соединении конденсаторов суммарная ёмкость элементов будет меньше самого маленького номинала в цепочке. То есть, ёмкость последовательно соединённых конденсаторов уменьшается. Это также может пригодиться при ремонте техники — замена конденсатора требуется часто.

Последовательно соединённые конденсаторы

Использовать формулу расчёта приведённую выше не очень удобно, поэтому её обычно используют в преобразованном виде:

Формула расчёта ёмкости при последовательном соединении

Это формула для двух элементов. При увеличении их количества она становится значительно сложнее. Хотя, редко можно встретить больше двух последовательных конденсаторов.

Пример расчёта

Какая суммарная ёмкость будет если конденсаторы на 12 мкФ и 8 мкФ соединить последовательно? Считаем: 12*8 / (12+8) = 96 / 20 = 4,8 мкФ. То есть, такая цепочка соответствует номиналу 4,8 мкФ.

Пример расчета ёмкости при последовательном подключении конденсаторов

Как видите, значение меньше чем самый маленький номинал в последовательности. А если подключить таким образом два одинаковых конденсатора, то результат будет вполовину меньше номинала. Например, рассчитаем для двух ёмкостей по 12 мкФ. Получим: 12*12 / (12 + 12) = 144 / 24 = 6 мкФ. Проверим для 8 мкФ. Считаем: 8*8 / (8+8) = 64 / 16 = 4 мкФ. Закономерность подтвердилась. Это правило можно использовать при подборе номинала.

Почему электролитические конденсаторы выходят из строя и что делать

Зачастую, чтобы отремонтировать вышедшую из строя электронную технику, достаточно найти и заменить вздувшиеся конденсаторы. Дело в том, что срок жизни их небольшой — 1000-2000 тысячи рабочих часов. Потом он обычно выходит из строя и требуется его замена. И это при нормальном напряжении не выше номинального. Так происходит потому, что диэлектрик в конденсаторах, чаще всего, жидкий. Жидкость понемногу испаряется, меняются параметры и, рано или поздно, конденсатор вздувается.

Электролитические конденсаторы имеют специальные насечки на верхушке корпуса, чтобы при выходе из строя избежать взрыва

Высыхает электролит не только во время работы. Даже просто «от времени». Это конструктивная особенность электролитических конденсаторов. Поэтому не стоит ставить выпаянные из старых схем конденсаторы или те, которые несколько лет (или десятков лет) хранятся в мастерской. Лучше купить «свежий», но проверьте дату производства.

Можно ли продлить срок эксплуатации конденсаторов? Можно. Надо улучшить теплоотвод. Чем меньше греется электролит, тем медленнее высыхает. Поэтому не стоит ставить аппаратуру вблизи отопительных приборов.

Для улучшения отвода тепла ставят радиаторы

Второе — надо следить за тем, чтобы хорошо работали кулера. Третье — если рядом стоят детали, которые активно греются во время работы, надо конденсаторы каким-то образом от температуры защитить.

Как подобрать замену

Если часто приходится менять один и тот же конденсатор, его лучше заменить на более «мощный» — той же ёмкости, но на большее напряжение. Например, вместо конденсатора на 25 вольт, поставить конденсатор на 35 вольт. Только надо иметь в виду, что более мощные конденсаторы имеют большие размеры. Не всякая плата позволяет сделать такую замену.

Конденсатор той же ёмкости, но рассчитанный на большее напряжение, имеет больший размер

Можно поставить параллельно несколько конденсаторов с тем же напряжением, подобрав номиналы так, чтобы получить требуемую ёмкость. Что это даст? Лучшую переносимость пульсаций тока, меньший нагрев и, как следствие, более продолжительный срок службы.

Что будет, если поставить конденсатор большей ёмкости?

Часто приходит в голову идея поставить вместо сгоревшего или вздувшегося конденсатор большей ёмкости. Ведь он должен меньше греться. Так, во всяком случае, кажется. Ёмкость практически никак не связана со степенью нагрева корпуса. И в этом выигрыша не будет.

Устройство электролитического конденсатора

По нормативным документам отклонение номинала конденсаторов допускается в пределах 20%. Вот на эту цифру можете спокойно ставить больше/меньше. Но это может привести к изменениям в работе устройства. Так что лучше найти «родной» номинал. И учтите, что не всегда можно ставить большую ёмкость. Можно если конденсатор стоит на входе и сглаживает скачки питания. Вот тут большая ёмкость уместна, если для её установки достаточно места. Это точно нельзя делать там, где конденсатор работает как фильтр, отсекающий заданные частоты.

Можно менять на ту же ёмкость, но чуть более высокое напряжение. Это имеет смысл. Но размеры такого конденсатора будут намного больше. Не в любую плату получится его установить. И учтите, что корпус его не должен соприкасаться с другими деталями.

При параллельном подключении конденсаторов у них одинаковые

Когда конденсаторы подключены параллельно, имеют ли они одно и то же?

Последовательные конденсаторы имеют одинаковый заряд, а конденсаторы, подключенные параллельно, имеют одинаковое напряжение. Три одинаковых конденсатора соединены последовательно с батареей.

Кстати, при параллельном подключении конденсаторов у них одно и то же?

разница заключается в заряде двух конденсаторов.(Другими словами, конденсаторы, подключенные параллельно, подключаются к одним и тем же начальным и конечным точкам входа и выхода, поэтому все они имеют одинаковую разность потенциалов.

Тогда возникает вопрос: что происходит, когда конденсаторы соединяются параллельно?

При параллельном подключении конденсаторов общая емкость складывается из емкостей отдельных конденсаторов. Когда два или более конденсатора соединены параллельно, общая мощность равна мощности одного эквивалентного конденсатора, который имеет сумму площадей якоря отдельных конденсаторов.

Также можно спросить: а параллельно ли конденсаторы имеют одинаковую нагрузку?

Параллельные конденсаторы Параллельно подключенные конденсаторы увеличивают емкость. Параллельное соединение – самый удобный способ увеличить общее накопление электрического заряда. Общее значение напряжения не меняется. На каждом конденсаторе будет одинаковое напряжение.

Что верно для конденсаторов, соединенных параллельно?

(a.) Заряд каждого конденсатора равен заряду соответствующего конденсатора.Разность напряжений на отдельных конденсаторах равна разнице напряжений на соответствующем конденсаторе.

Что делать, если два или более конденсатора подключены параллельно через разность потенциалов?

: два или более конденсатора соединены параллельно через разность потенциалов, разность потенциалов на каждом конденсаторе одинакова. каждый конденсатор несет одинаковое количество заряда. соответствующая емкость комбинации меньше емкости некоторых конденсаторов.

Как рассчитываются параллельные конденсаторы?

Общая ставка Q – это сумма индивидуальных затрат: Q = Q1 + Q2 + Q3. Рисунок 2. (а) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, поэтому общая параллельная емкость – это просто сумма отдельных емкостей.

Конденсаторы накапливают больше энергии последовательно или параллельно?

Три конденсатора, соединенные параллельно с другой стороны, имеют падение напряжения V, поэтому общая накопленная энергия составляет 3/2 C V2, что в девять раз больше энергии в трех соединенных последовательно.Чтобы ответить на ваш вопрос, конденсаторы, подключенные параллельно, хранят больше энергии, чем конденсаторы, подключенные последовательно.

Зачем добавлять конденсаторы параллельно?

Когда вы подключаете конденсаторы параллельно, вы в основном подключаете пластины к каждому конденсатору. Таким образом, параллельное соединение двух идентичных конденсаторов существенно увеличивает размер пластин вдвое, что существенно удваивает емкость.

Что является символом мастерства?

Одно и то же напряжение на резисторах, включенных параллельно?

Напряжение на каждом резисторе в параллельной комбинации точно такое же, но ток, протекающий через него, не такой, как он определяется значением его сопротивления и законом Ома.Итак, параллельные цепи – это делители мощности.

Могут ли конденсаторы повышать напряжение?

Ни один конденсатор не увеличивает напряжение. Однако их можно использовать во многих схемах, которые создают более высокое выходное напряжение на входе. Конденсаторы – это запасы энергии. Если вы зарядите два конденсатора параллельно, а затем соедините их последовательно, вы получите удвоенное входное напряжение.

Будет ли напряжение параллельно уменьшаться вдвое?

При параллельном подключении разность электрических потенциалов на каждом резисторе (ΔV) одинакова.При параллельном подключении напряжение на каждой ветви уменьшается по мере увеличения напряжения на батарее. Таким образом, падение напряжения на каждом из этих резисторов одинаковое.

Как рассчитать заряд конденсатора?

Электрический заряд Q, накопленный в конденсаторе (в кулонах, сокращенно C), равен произведению емкости C конденсатора (в фарадах, сокращенно F) и напряжения V (в вольтах, сокращенно V) на нем.

То есть Q = C?

В.

Если, например, C = 33 мкФ и V = 20 В, то Q = (33?

106)?

(20) = 660 ° С.

Когда два конденсатора подключены параллельно к батарее?

Как мне добавить индукторы параллельно?

Параллельные вспомогательные катушки

Какова эквивалентная емкость двух параллельно соединенных конденсаторов?

Соответствующая емкость для двух конденсаторов, соединенных параллельно, является суммой индивидуальных емкостей. Рисунок 16: Два конденсатора, подключенных последовательно.он общий для всех трех конденсаторов.

Можно ли подключить конденсаторы последовательно?

Конденсаторы серии

. Когда конденсаторы подключаются последовательно, это называется последовательным подключением. В случае последовательных конденсаторов общую емкость можно определить путем сложения взаимности отдельных емкостей и суммы взаимностей.

Что происходит, когда конденсатор подключен к источнику постоянного тока?

Когда конденсаторы переключаются с помощью постоянного напряжения, они заряжаются до значения приложенного напряжения и действуют как буфер и удерживают этот заряд в течение неопределенного периода времени, пока не будет подано напряжение питания.

Как подключить конденсатор?

Что происходит, когда конденсатор подключен к батарее?

Цепь конденсатора. Пластина конденсатора, прикрепленная к отрицательному полюсу батареи, поглощает электроны, генерируемые батареей. Пластина конденсатора, прикрепленная к положительному полюсу батареи, теряет электроны в батарее.

Для чего нужен конденсатор?

При параллельном подключении конденсаторов у них одинаковые Конденсатор

Основные расчеты – Инженерное мышление

Конденсаторы

используются во многих схемах для разных целей, поэтому мы собираемся изучить некоторые основные вычисления конденсаторов для цепей постоянного тока.

Прокрутите вниз, чтобы просмотреть обучающее видео на YouTube.

Конденсаторы в цепях постоянного тока

Конденсаторы

обычно выглядят так. У нас есть конденсатор электролитического и керамического типа. Электролитик поляризован, что означает, что одна сторона должна быть подключена к плюсу, а другая – к минусу источника питания. Керамический тип обычно может быть подключен любым способом. На стороне электролитического конденсатора мы находим пунктирную линию, указывающую отрицательную сторону, длинный вывод также указывает на положительную сторону нового конденсатора.Но обычно они обрезаются во время установки, поэтому не полагайтесь только на это. Эти два конденсатора представлены подобными символами, обратите внимание, что у поляризованного конденсатора есть маленький символ плюса, указывающий на положительную сторону.

При подключении к источнику постоянного тока напряжение аккумулятора подталкивает электроны к конденсатору, поэтому конденсатор заряжается до того же напряжения, что и аккумулятор. Конденсаторы заряжаются почти мгновенно при подключении напрямую к батарее, но мы почти всегда используем резистор, это задерживает время зарядки, и позже в этой статье мы увидим, как это рассчитать.

Внутри конденсатора скопилось много электронов с одной стороны, и им препятствует перемещение поперек из-за изоляционного материала между двумя сторонами. Поскольку электроны заряжены отрицательно, у нас есть накопление заряда на одной стороне по сравнению с другой, поэтому у нас есть разница напряжений между двумя выводами.

Эти электроны удерживаются на месте, и конденсатор может удерживать этот заряд в течение длительных периодов времени. Получив путь, они будут разряжаться до тех пор, пока не опустеют.Электроны не проходят через конденсатор; они просто накапливаются внутри, а затем высвобождаются.

Количество заряда, накопленного в конденсаторе, рассчитывается по формуле «Заряд = емкость (в фарадах), умноженная на напряжение». Итак, для этого конденсатора микрофарад на 12 В 100 мкФ мы преобразуем микрофарады в фарады (100 / 1,000,000 = 0,0001F), затем умножаем это на 12 В, чтобы увидеть, что он хранит заряд 0,0012 кулонов.

Если нам нужно сохранить заряд, скажем, в 0,0002 кулонов, мы просто разделим его на напряжение, в данном случае 12 В, чтобы увидеть, что нам нужен 0.2
= 0,5 x 0,0001F x 144
= 0,0072 Дж

Мы знаем, что конденсатор будет заряжаться до напряжения батареи. Итак, если мы подключим такой конденсатор, какое будет напряжение на конденсаторе? Будет 1,5В. Если мы подключим вот так конденсатор, какое на нем будет напряжение? Тоже будет 1,5В. Это два разных способа соединения конденсаторов в цепях, последовательно или параллельно. Это заставит конденсаторы работать по-другому.

Параллельные конденсаторы

Если мы разместим конденсатор параллельно с лампой, когда батарея будет удалена, конденсатор начнет питать лампу, он медленно тускнеет по мере разряда конденсатора.Если мы используем два конденсатора, мы сможем запитать лампу дольше.

Допустим, конденсатор 1 = 10 мкФ и конденсатор 2 = 220 мкФ. Как рассчитать общую емкость? Это очень просто, ответ – 230 мкФ. Конденсаторы соединяются параллельно. Итак, 10 мкФ + 220 мкФ = 230 мкФ. Мы можем добавлять больше, например конденсатор емкостью 100 мкФ, и общая сумма будет просто суммой всех конденсаторов. Помещая их параллельно, мы, по сути, объединяем их, чтобы сформировать конденсатор большего размера. Это очень полезно, потому что если, например, нам нужен большой конденсатор на 2000 мкФ, но у нас его не было, мы можем просто использовать более мелкие конденсаторы, такие как 2 x 1000 мкФ по 4 x 500 мкФ и т. Д.Он также часто используется для фильтрации шума и обеспечения большего тока в цепях с высокими требованиями.

Общий заряд, накопленный в параллельных конденсаторах, равен: заряд = общая емкость, умноженная на напряжение. Итак, у нас есть батарея на 9 В и два конденсатора общей емкостью 230 мкФ. Поскольку он параллелен, этот провод составляет 9 В, а это 0 В, поэтому оба конденсатора заряжены до 9 В. Следовательно, 0,00023 F, умноженное на 9V = 0,00207 кулонов. И с тремя конденсаторами у нас есть 330 мкФ (0.00033 F), умноженное на 9V = 0,00297 кулонов.

Мы также можем рассчитать заряд каждого конденсатора индивидуально. Мы просто используем одну и ту же формулу для каждого конденсатора, ответы на этот вопрос вы можете увидеть на экране.
Конденсатор 1 = 0,00001 F x 9 В = 0,00009 Кулонов
Конденсатор 2 = 0,00022 F x 9 В = 0,00198 Кулонов
Конденсатор 3 = 0,0001 F x 9 В = 0,0009 Кулонов
Всего = 0,00009 + 0,00198 + 0,0009 = 0,00297 Кулонов

Конденсаторы серии

Если мы поместим конденсатор последовательно с лампой, когда мы нажмем переключатель, он загорится, но затем станет тусклее, когда конденсатор достигнет уровня напряжения батареи, и как только он достигнет этого уровня, лампа выключится.Помните, что электроны не могут проходить через конденсатор из-за изоляционного материала внутри. Электроны просто накапливаются внутри на одной пластине, и по мере накопления они отбрасывают равное количество от противоположной пластины. Таким образом, ток может течь только тогда, когда конденсатор заряжается или разряжается. В настоящее время, когда батарея снята, конденсатор не может разрядиться, поэтому он будет поддерживать напряжение на одном уровне. Неважно, подключим мы или отключим аккумулятор, лампа не загорится.Однако, если мы предоставим другой путь, при нажатии переключателя конденсатор может теперь разрядиться, поэтому электроны могут проходить через лампу и освещать ее. По мере разряда конденсатора он станет более тусклым.

Что, если бы у нас было 2 конденсатора, соединенных последовательно, опять же, конденсатор 1 – 10 мкФ, а конденсатор 2 – 220 мкФ. Как найти общую емкость? Для этого мы используем эту формулу, она может показаться сложной, но на самом деле она очень проста. Все, что нам нужно сделать, это ввести наши конденсаторы емкостью 10 и 220 мкФ.Мы можем ввести это так на наших калькуляторах или в Excel. Но при ручном вычислении мы делим 1 на 10, что равно 0,1, и 1, деленное на 220, что составляет 0,00454. Мы складываем их вместе, чтобы получить 0,10454, а затем 1, разделенное на это, дает в сумме 9,56 мкФ. Обратите внимание, что общая емкость теперь меньше, чем конденсатор с наименьшим значением.

Если мы добавим в схему третий конденсатор емкостью 100 мкФ, мы получим общую емкость 8,73 мкФ. Так что уменьшилось еще больше. Это потому, что, комбинируя их последовательно, мы существенно увеличиваем толщину изоляционного материала, поэтому притяжение отрицательно заряженных электронов к положительно заряженным дыркам на противоположной пластине становится слабее.

Общий заряд последовательных конденсаторов определяется по формуле заряд = емкость (в фарадах), умноженная на напряжение. Итак, если мы использовали батарею 9 В, мы конвертируем микрофарады в фарады и видим, что общий заряд равен 0,00008604 кулонов
(0,00000956F x 9V = 0,00008604 кулонов)

Общий заряд конденсаторной цепи из 3-х рядов составляет 0,00007857 кулонов
(0,00000873 x 9 В = 0,00007857 кулонов)

Заряд, удерживаемый каждым конденсатором в отдельности, очень легко вычислить в последовательных цепях.Это то же самое, что и общая. Каждый конденсатор содержит одинаковое количество электронов, когда они подключены последовательно. Это потому, что когда мы заряжали конденсаторы, ток был одинаковым во всех частях цепи. То же количество электронов, которые были вытолкнуты в одну пластину, вытолкнулось из противоположной пластины, поэтому каждый последовательный конденсатор может быть заряжен только до одного и того же уровня. Таким образом, наименьший конденсатор будет ограничивающим фактором.

Однако, поскольку каждый конденсатор может иметь разную емкость, напряжение каждого конденсатора будет разным.Мы находим напряжение каждого конденсатора по формуле напряжение = заряд (в кулонах), деленное на емкость (в фарадах).

Итак, для этой схемы мы видим, что конденсатор 1 – 7,8 В, конденсатор 2 – 0,35 В, а конденсатор 3 – 0,78 В. Они складываются в общее напряжение батареи, которое составляет 9 В.

Конденсатор 1: 0,00007857 C / 0,00001 F = 7,857 В
Конденсатор 2: 0,00007857 C / 0,00022 F = 0,357 В
Конденсатор 3: 0,00007857 C / 0,0001 F = 0,786 В
Общее напряжение = 7,857 В + 0,357 В + 0.786 В = 9 В

Время заряда конденсатора

Допустим, у нас есть батарея на 9 В, конденсатор емкостью 100 мкФ, резистор на 10 кОм и переключатель, соединенные последовательно. Конденсатор полностью разряжен, и мы читаем 0 В на двух выводах.

Когда мы замыкаем выключатель, конденсатор заряжается. Напряжение будет увеличиваться до тех пор, пока не сравняется с уровнем заряда батареи. Повышение напряжения не мгновенное, оно имеет экспоненциальную кривую. Сначала напряжение быстро увеличивается, а затем замедляется, пока не достигнет того же уровня напряжения, что и аккумулятор.

Мы разделили эту кривую на 6 сегментов, но нас интересуют только первые 5, потому что на отметке 5 мы в основном находимся на полном напряжении, поэтому мы можем игнорировать все, что выходит за рамки этого. Каждый сегмент представляет собой нечто, называемое постоянной времени. Следовательно, поскольку у нас есть 5 сегментов, у нас есть 5 постоянных времени, поэтому для заряда конденсатора от 0 до чуть менее 100% потребуется 5 постоянных времени. Все, что нам нужно сделать, это вычислить длину одной постоянной времени, а затем умножить ее на 5.

Для вычисления одной постоянной времени мы используем эту формулу.

Постоянная времени (в секундах) = сопротивление (в Ом), умноженное на емкость (в фарадах). Итак, мы конвертируем наш резистор в Ом, а емкость конденсатора в фарады и видим, что 10 000 Ом, умноженные на 0,0001 Фарад, равны 1. Итак, в этом примере постоянная времени равна 1 секунде. Следовательно, 5 из них составляют 5 секунд. Это означает, что для полной зарядки этого конденсатора до 9В требуется 5 секунд.

Если бы сопротивление резистора было всего 1000 Ом, постоянная времени была бы 0,1 секунды, так что это заняло бы 0.5 секунд, чтобы достичь 9 В. Если бы емкость конденсатора была 1000 микрофарад, это заняло бы всего 50 секунд. Так что с увеличением размера конденсатора время увеличивается. При увеличении номинала резистора увеличивается и время.

Возвращаясь к нашей исходной схеме. Поэтому мы можем рассчитать уровень напряжения для каждой постоянной времени. В точке 1 напряжение всегда 63,2%, в точке 2 – 86,5%, в точке 3 – 95%, в точке 4 – 98,2% и в точке 5 – 99,3%.

Итак, в этом примере через 1 секунду напряжение конденсатора равно 5.68 В, через 2 секунды – 7,78 В, через 3 секунды – 8,55 В, через 4 секунды – 8,83 В и через 5 секунд – 8,94 В

Если вам нужен более точный ответ, мы можем вычислить каждую точку следующим образом.

Точка 1 = 9V-0V) x0.632 = 5.6880V
Point 2 = ((9V – 5.688V) x0.632) + 5.68V = 7.7812V
Point 3 = ((9V-7.7812V) x0.632) + 7,7812 В = 8,5515 В
Точка 4 = ((9–8,55 В) x0,632) + 8,5515 В = 8,8349 В
Точка 5 = ((9–8,8349 В) x0,632) + 8,8349 В = 8,9393 В

Помните, поскольку это последовательно, ток в цепи уменьшается, а напряжение конденсатора увеличивается.После достижения полного напряжения в цепи не будет протекать ток. Если бы резистор был лампой, он бы мгновенно достиг полной яркости, когда переключатель был замкнут, но затем стал бы более тусклым, когда конденсатор достигал полного напряжения.

Время разряда конденсатора

Когда мы обеспечиваем путь для разряда конденсатора, электроны покидают конденсатор, и напряжение на конденсаторе уменьшается. Он не разряжается мгновенно, а следует экспоненциальной кривой. Мы разбиваем эту кривую на 6 сегментов, но нас интересуют только первые 5.В точке 1 напряжение всегда 36,8%, в точке 2 будет 13,5%, в точке 3 будет 5%, в точке 4 будет 1,8% и в точке 5 будет 0,7%.

Например, если бы у нас была батарея 9 В, лампа с сопротивлением 500 Ом и конденсатор 2000 мкФ, наша постоянная времени была бы 500 Ом, умноженная на 0,002 Фарад, что составляет 1 секунду.
Итак, в тот момент, когда аккумулятор отключен, конденсатор будет на 9 В, и, поскольку он питает цепь, лампа также будет. Через 1 постоянную времени, в данном случае через 1 секунду, напряжение будет 36.8%, что составляет 3,312 В, через 2 секунды – 1,215 В, через 3 секунды – 0,45 В, через 4 секунды – 0,162 В и через 5 секунд – 0,063 В. Таким образом, лампа будет гореть чуть менее 3 секунд. Очевидно становится тусклее.

Конденсаторы в последовательной и параллельной комбинациях с примерами

Конденсатор является накопителем энергии. Они классифицируются как электролитические и неэлектролитические конденсаторы в зависимости от диэлектриков и полярностей. Он должен быть включен в схему таким образом, чтобы получить необходимое значение емкости.Существуют и другие комбинации конденсаторов, используемых при его включении в схему. Среди которых ряд и параллель являются основными.

Несколько подключенных конденсаторов действуют как «один эквивалентный конденсатор». Общая емкость в цепи зависит от количества отдельных конденсаторов, соединенных последовательно в цепи, и будет меньше, чем у любого из конденсаторов в цепи. Расстояние между пластинами конденсатора также влияет на емкость конденсатора.

В системах распределения электроэнергии, где уровень напряжения падает ниже указанного уровня. Эти компоненты, называемые конденсаторами, используются для поддержания линии напряжения. Эти компоненты могут минимизировать потерю мощности. С помощью базовых последовательных и параллельных комбинаций можно получить более сложные соединения.

Что такое последовательный конденсатор?

Соединение между конденсаторами, помещенными в одну линию, можно определить как конденсаторы, соединенные последовательно.Пластина положительных зарядов одного конденсатора соединена с пластиной отрицательного заряда другого конденсатора. В этом типе подключения каждый конденсатор имеет одинаковую величину заряда и зарядный ток.

Хотя зарядный ток такой же, но отличается падением напряжения. На каждом конденсаторе разное падение напряжения. Но общее падение напряжения, которое применяется между входной и выходной линиями, равно сумме напряжений отдельных падений.

Последовательные конденсаторы, работа и уравнение

Конденсатор, подключенный последовательно, обычно имеет меньшую емкость. Когда эти соединения выполнены, ток, протекающий по цепи, будет одинаковым. Следовательно, заряд, накопленный вокруг каждого из конденсаторов, также одинаков.

Конденсаторы, подключаемые последовательно

Обычно конденсаторы подключаются по схеме «гирляндной цепи». В таких схемах ток для зарядки будет одинаковым.Это потому, что путь устанавливается таким же.

Общий ток = Ток на C1 = Ток на C2

Вместо емкости заряд в каждом конденсаторе одинаков. Потому что обкладки каждого конденсатора соединены смежным образом.

Общий заряд = Заряд на C1 = Заряд на C2

Когда конденсаторы следуют последовательному соединению и подключено более трех конденсаторов. C1 обеспечивается источником питания, а C3 подключается к выходному концу.В то время как C2 в середине изолирован от прямого взаимодействия источника напряжения (DC). Из-за этого падения напряжения на каждом конденсаторе разные. Это зависит от индивидуальных емкостей каждого конденсатора.

Обычно заряд, емкость и падение напряжения связаны как

Q = CV

Формулу можно переписать как

C = Q / V

Напряжение на конденсаторах можно рассчитать как

Общее напряжение = Напряжение на C1 + напряжение на C2

Общее напряжение (Q / C) = Q1 / C1 + Q2 / C2

Последовательный заряд будет равен Q1 = Q2

Наконец, разделив уравнение на Q с обеих сторон

1 / C = 1 / C1 + 1 / C2

Следовательно, приведенное выше уравнение предназначено для расчета емкости для последовательного соединения конденсаторов.

Пример

Два последовательно соединенных конденсатора номиналом 10 мкФ и 20 мкФ. Найти значение емкости в цепи?

раствор : дано C1 = 10 мкФ

C2 = 20 мкФ

Общая емкость может быть рассчитана как обратная величина для отдельных емкостей.

1 / C = 1/10 +1/20

1 / C = 0,15 мкФ

Какой конденсатор подключен параллельно?

Поскольку в конденсаторах две пластины, первая пластина конденсатора соединена с первой пластиной второго конденсатора.Это называется параллельным подключением конденсаторов. Следовательно, конденсаторы при параллельном соединении имеют одинаковое количество значений напряжения. Общее значение емкости – это сумма отдельных емкостей.

Конденсаторы при параллельной работе и уравнении

При параллельном подключении конденсаторов. Каждый из конденсаторов в цепи имеет прямое взаимодействие с проводником. Это приводит к тому, что потенциал конденсатора остается прежним. Заряд будет таким же, как и у каждого конденсатора, имеющего индивидуальное соединение с предоставленным источником питания.

Общая стоимость может быть рассчитана как сумма отдельных платежей.

Общая сумма начислений (Q) = Q1 + Q2 + …….

Если два конденсатора подключены параллельно.

Тогда Q = Q1 + Q2. Где Q = CV

CV = C1V1 + C2V2

В параллельной комбинации V = V1 = V2

CV = (C1 + C2) V

Следовательно, C = C1 + C2

Пример

Найдите значение итога емкость, если в цепь включены два конденсатора по 10 мкФ и 20 мкФ?

Решение:

При C1 = 10 мкФ

C2 = 20 мкФ

В параллельной комбинации общую емкость можно рассчитать как

C = C1 + C2

C = 10 + 20 = 30 мкФ

На основании приведенных выше формул можно рассчитать значение емкости.

Конденсаторы можно подключать последовательно и параллельно. В таких ситуациях соединение должно быть идентифицировано. На основе идентификации используются подходящие формулы последовательного и параллельного совмещения.

Пример

Найдите значение емкости, при котором в цепь включены три конденсатора по 10 мкФ?

Конденсаторы, соединенные последовательно и параллельно

Решение:

Данная схема состоит из конденсаторов C1, C2 и C3.

Из анализа схемы конденсаторы C1 и C2 соединены последовательно.

Эквивалентную емкость C1 и C2 можно рассчитать по формуле

1 / C = 1 / C1 + 1 / C2

1 / C = 1/10 + 1/10

1 / C = 2/10

Наконец, C = 10/2 = 5 мкФ.

Далее этот C подключен параллельно конденсатору C3.

Эквивалентную емкость схемы можно найти по формуле

C (Всего) = C + C3 = 5 + 10 = 15 микрофарад

Пожалуйста, обратитесь по этой ссылке, чтобы узнать больше о конденсаторах MCQ

Следовательно, значение емкости может реализовываться на основе последовательного и параллельного анализа.Отмечается, что значение емкости уменьшается при последовательном соединении. В параллельной комбинации увеличивается значение емкости. Но в случае сопротивления все наоборот. Из приведенного выше анализа можете ли вы определить, если вам нужно хранить огромное количество энергии, то какая комбинация подключения предпочтительнее?

8.3: Последовательные и параллельные конденсаторы

Несколько конденсаторов могут быть соединены вместе для использования в различных приложениях.Несколько подключений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения. Конденсаторы могут быть организованы в два простых и распространенных типа соединений, известных как серия и параллельно , для которых мы можем легко вычислить общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серия конденсаторов

На рисунке \ (\ PageIndex {1} \) показано последовательное сочетание трех конденсаторов, расположенных в ряд внутри схемы.Как и в случае любого конденсатора, емкость комбинации связана как с зарядом, так и с напряжением:

\ [C = \ dfrac {Q} {V}. \]

Когда эта последовательная комбинация подключена к батарее с напряжением В , каждый из конденсаторов получает идентичный заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен \ (+ Q \), а заряд на пластине, подключенной к отрицательной клемме, равен \ (- Q \). Затем на других пластинах индуцируются заряды, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю.Однако падение потенциала \ (V_1 = Q / C_1 \) на одном конденсаторе может отличаться от падения потенциала \ (V_2 = Q / C_2 \) на другом конденсаторе, потому что, как правило, конденсаторы могут иметь разные емкости. Последовательная комбинация двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентной емкостью ) меньше наименьшей из емкостей в последовательной комбинации.Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательной комбинации: то есть , все конденсаторы последовательной комбинации имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи удаляется с пластины первого конденсатора (который мы обозначаем как \ (- Q \)), он должен быть помещен на пластину второго конденсатора (который мы обозначаем как \ ( + Q \)) и т. Д.

Рисунок \ (\ PageIndex {1} \): (a) Три конденсатора соединены последовательно.Величина заряда на каждой пластине равна Q. (b) Сеть конденсаторов на (a) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей на (a), а заряд на его пластинах равен Q.

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны, соответственно, \ (V_1 = Q / C_1 \), \ (V_2 = Q / C_2 \) и \ (V_3 = Q / C_3 \). Эти потенциалы должны суммироваться с напряжением батареи, давая следующий баланс потенциалов:

\ [V = V_1 + V_2 + V_3.\]

Потенциал \ (V \) измеряется на эквивалентном конденсаторе, который держит заряд \ (Q \) и имеет эквивалентную емкость \ (C_S \). Вводя выражения для \ (V_1 \), \ (V_2 \) и \ (V_3 \), получаем

\ [\ dfrac {Q} {C_S} = \ dfrac {Q} {C_1} + \ dfrac {Q} {C_2} + \ dfrac {Q} {C_3}. \]

Отменяя заряд Q , мы получаем выражение, содержащее эквивалентную емкость \ (C_S \) трех последовательно соединенных конденсаторов:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3}.\]

Это выражение можно обобщить на любое количество конденсаторов в последовательной сети.

Комбинация серии

Для конденсаторов, соединенных последовательно, эквивалентная емкость, обратная величине, является суммой обратных величин индивидуальных емкостей:

\ [\ dfrac {1} {C_S} = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} + \ dots \ label {capseries} \]

Пример \ (\ PageIndex {1} \): эквивалентная емкость последовательной сети

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их отдельные емкости равны \ (1.000 мкФ \), \ (5.000 мкФ \) и \ (8.000 мкФ \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capseries} с тремя членами.

Решение

Вводим данные емкости в уравнение \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} + \ dfrac {1} {C_3} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} + \ dfrac {1} {8.000 \ mu F} \\ [4pt] & = \ dfrac {1.325} {\ mu F}. \ End {align *} \]

Теперь инвертируем этот результат и получаем

\ [\ begin {align *} C_S & = \ dfrac {\ mu F} {1.325} \\ [4pt] & = 0.755 \ mu F. \ end {align *} \ nonumber \]

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация из трех конденсаторов, одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рисунке \ (\ PageIndex {2a} \).Поскольку конденсаторы подключены параллельно, , все они имеют одинаковое напряжение V на своих пластинах . Однако каждый конденсатор в параллельной сети может накапливать свой заряд. Чтобы найти эквивалентную емкость \ (C_p \) параллельной сети, отметим, что общий заряд Q , хранящийся в сети, является суммой всех отдельных зарядов:

\ [Q = Q_1 + Q_2 + Q_3. \]

В левой части этого уравнения используется соотношение \ (Q = C_pV \), которое выполняется для всей сети.В правой части уравнения мы используем соотношения \ (Q_1 = C_1 V \), \ (Q_2 = C_2V \) и \ (Q_3 = C_3V \) для трех конденсаторов в сети. Таким образом получаем

\ [C_pV = C_1V + C_2V + C_3V. \]

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

\ [C_p = C_1 + C_2 + C_3. \]

Это выражение легко обобщается на любое количество конденсаторов, включенных параллельно в сеть.

Параллельная комбинация

Для конденсаторов, соединенных параллельно, эквивалентная (полезная) емкость представляет собой сумму всех индивидуальных емкостей в сети,

\ [C_p = C_1 + C_2 + C_3 + … \ label {capparallel} \]

Рисунок \ (\ PageIndex {2} \): (a) Три конденсатора подключены параллельно. Каждый конденсатор подключен напрямую к батарее. (b) Заряд эквивалентного конденсатора представляет собой сумму зарядов отдельных конденсаторов.

Пример \ (\ PageIndex {2} \): эквивалентная емкость параллельной сети

Найдите полезную емкость для трех конденсаторов, соединенных параллельно, учитывая, что их индивидуальные емкости равны \ (1.0 \ mu F \), \ (5.0 \ mu F \) и \ (8.0 \ mu F \).

Стратегия

Поскольку в этой сети всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение \ ref {capparallel} с тремя членами.

Решение

Ввод заданных емкостей в уравнение \ ref {capparallel} дает

\ [\ begin {align *} C_p & = C_1 + C_2 + C_3 \\ [4pt] & = 1.0 \ mu F + 5.0 \ mu F + 8.0 \ mu F \\ [4pt] & = 14.0 \ mu F.\ end {align *} \]

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Конденсаторные сети обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на рисунке \ (\ PageIndex {3} \). Чтобы найти чистую емкость таких комбинаций, мы определяем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости.Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

Рисунок \ (\ PageIndex {3} \): (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. (б) \ (C_1 \) и \ (C_2 \) идут последовательно; их эквивалентная емкость \ (C_S \) c) Эквивалентная емкость \ (C_S \) подключена параллельно с \ (C_3 \). Таким образом, эквивалентная емкость всей сети является суммой \ (C_S \) и \ (C_3 \).

Пример \ (\ PageIndex {3} \): эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {3} \). Предположим, что емкости известны с точностью до трех десятичных знаков (\ (C_1 = 1.000 мкФ, C_2 = 5.000 мкФ, C_3 = 8.000 мкФ \)). Округлите ответ до трех десятичных знаков.

Стратегия

Сначала мы определяем, какие конденсаторы включены последовательно, а какие – параллельно. Конденсаторы \ (C_1 \) и \ (C_2 \) включены последовательно.Их комбинация, обозначенная \ (C_S \), параллельна \ (C_3 \).

Решение

Поскольку \ (C_1 \) и \ (C_2 \) включены последовательно, их эквивалентная емкость \ (C_S \) получается с помощью уравнения \ ref {capseries}:

\ [\ begin {align *} \ dfrac {1} {C_S} & = \ dfrac {1} {C_1} + \ dfrac {1} {C_2} \\ [4pt] & = \ dfrac {1} {1.000 \ mu F} + \ dfrac {1} {5.000 \ mu F} \\ [4pt] & = \ dfrac {1.200} {\ mu F} \ end {align *} \]

Для этого

\ [C_S = 0,833 \ mu F. \ nonumber \]

Емкость \ (C_S \) соединена параллельно с третьей емкостью \ (C_3 \), поэтому мы используем уравнение \ ref {capparallel}, чтобы найти эквивалентную емкость C всей сети:

\ [\ begin {align *} C & = C_S + C_3 \\ [4pt] & = 0.833 \ mu F + 8.000 \ mu F \\ [4pt] & = 8.833 \ mu F. \ end {align *} \]

Сеть конденсаторов

Определите чистую емкость C комбинации конденсаторов, показанной на рисунке \ (\ PageIndex {4} \), когда емкости равны \ (C_1 = 12,0 мкФ, C_2 = 2,0 мкФ \) и \ (C_3 = 4,0 мкФ \). Когда на комбинации поддерживается разность потенциалов 12,0 В, найдите заряд и напряжение на каждом конденсаторе.

Рисунок \ (\ PageIndex {4} \): (a) Комбинация конденсаторов.(b) Эквивалентная комбинация из двух конденсаторов. Стратегия

Сначала мы вычисляем чистую емкость \ (C_ {23} \) параллельного соединения \ (C_2 \) и \ (C_3 \). Тогда C – это чистая емкость последовательного соединения \ (C_1 \) и \ (C_ {23} \). Мы используем соотношение \ (C = Q / V \), чтобы найти заряды \ (Q_1, Q_2 \) и \ (Q_3 \), а также напряжения \ (V_1, V_2 \) и \ (V_3 \) на конденсаторы 1, 2 и 3 соответственно.

Решение Эквивалентная емкость для \ (C_2 \) и \ (C_3 \) составляет

\ [C_ {23} = C_2 + C_3 = 2.0 мк F + 4,0 мк F = 6,0 мк F. \]

Вся комбинация из трех конденсаторов эквивалентна двум последовательно включенным конденсаторам,

\ [\ dfrac {1} {C} = \ dfrac {1} {12.0 \ mu F} + \ dfrac {1} {6.0 \ mu F} = \ dfrac {1} {4.0 \ mu F} \ Rightarrow C = 4,0 мкм F. \]

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рисунке \ (\ PageIndex {2b} \). Поскольку конденсаторы включены последовательно, они имеют одинаковый заряд, \ (Q_1 = Q_ {23} \). Кроме того, конденсаторы разделяют разность потенциалов 12,0 В, поэтому

\ [12.0 V = V_1 + V_ {23} = \ dfrac {Q_1} {C_1} + \ dfrac {Q_ {23}} {C_ {23}} = \ dfrac {Q_1} {12.0 \ mu F} + \ dfrac {Q_1 } {6.0 \ mu F} \ Rightarrow Q_1 = 48.0 \ mu C. \]

Теперь разность потенциалов на конденсаторе 1 равна

\ [V_1 = \ dfrac {Q_1} {C_1} = \ dfrac {48.0 \ mu C} {12.0 \ mu F} = 4.0 V. \]

Поскольку конденсаторы 2 и 3 подключены параллельно, они имеют одинаковую разность потенциалов:

\ [V_2 = V_3 = 12,0 В – 4,0 В = 8,0 В. \]

Следовательно, заряды на этих двух конденсаторах равны, соответственно,

\ [Q_2 = C_2V_2 = (2.0 мкФ) (8,0 В) = 16,0 мкФ, \]

\ [Q_3 = C_3V_3 = (4,0 мкФ) (8,0 В) = 32,0 мкФ \]

Значимость Как и ожидалось, чистая плата за параллельную комбинацию \ (C_2 \) и \ (C_3 \) составляет \ (Q_ {23} = Q_2 + Q_3 = 48,0 \ mu C. \)

Упражнение \ (\ PageIndex {1} \)

Определите чистую емкость C каждой сети конденсаторов, показанной ниже. Предположим, что \ (C_1 = 1,0 пФ, C_2 = 2,0 пФ, C_3 = 4,0 пФ \) и \ (C_4 = 5,0 пФ \). Найдите заряд на каждом конденсаторе, предполагая, что разность потенциалов равна 12.0 В в каждой сети.

Ответьте на: \ (C = 0,86 пФ, Q_1 = 10 пКл, Q_2 = 3,4 пКл, Q_3 = 6,8 пКл \)
Ответ б: \ (C = 2,3 пФ, Q_1 = 12 пКл, Q_2 = Q_3 = 16 пКл \)
Ответ c: \ (C = 2,3 пФ, Q_1 = 9,0 пКл, Q_2 = 18 пКл, Q_3 = 12 пКл, Q_4 = 15 пКл \)

Емкость | Electronics Club

Емкость | Клуб электроники

Следующая страница: Импеданс и реактивное сопротивление

См. Также: Конденсаторы | Блоки питания

Емкость

(символ C) – это мера способности конденсатора накапливать заряд .Большая емкость означает, что можно сохранить больше заряда. Емкость измеряется в фарадах, символ F, но 1F очень большой, поэтому для отображения меньших значений используются префиксы (множители):

мкФ (микро) означает 10 ^-6 (миллионная), поэтому 1000000 мкФ = 1F
n (нано) означает 10 ^-9 (миллиардная), поэтому 1000 нФ = 1 мкФ
p (пико) означает 10 ^-12 (миллионно-миллионная), поэтому 1000 пФ = 1 нФ

неполяризованный конденсатор

поляризованный конденсатор

Rapid Electronics: Конденсаторы

Заряд и накопленная энергия

Количество заряда (Q), сохраняемого конденсатором, определяется как:

Заряд, Q = C × V

Когда они накапливают заряд, конденсаторы также накапливают энергию (E):

Энергия, E = ½QV = ½CV²

Q = заряд в кулонах (Кл)
C = емкость в фарадах (Ф)
V = напряжение в вольтах (В)
E = энергия в джоулях (Дж) )

Конденсаторы возвращают накопленную энергию в цепь

Обратите внимание, что конденсаторы возвращают накопленную энергию в цепь.Они не «расходуют» электрическую энергию преобразовывая его в тепло, как это делает резистор.

Энергия, запасаемая конденсатором, намного меньше, чем энергия, хранящаяся в батарее, поэтому они не могут использоваться в качестве источника энергии для большинства целей.

Емкостное реактивное сопротивление Xc

Емкостное реактивное сопротивление (Xc) – это мера сопротивления конденсатора переменному току. Как и сопротивление, он измеряется в Ом () но реактивное сопротивление сложнее, чем сопротивление, потому что его значение зависит от частоты (f) электрического сигнала, проходящего через конденсатор, а также емкости (C).

Емкостное реактивное сопротивление, Xc =	1
	2fC

Xc = реактивное сопротивление в Ом ()
f = частота в герцах (Гц)
C = емкость в фарадах (F)

Реактивное сопротивление велико на низких частотах и мало на высоких частотах. Для постоянного постоянного тока, который является нулевой частотой, Xc бесконечно (полное противодействие), отсюда правило, что Конденсаторы пропускают переменный ток, но блокируют постоянный ток .

Например, конденсатор 1 мкФ имеет реактивное сопротивление 3,2 кГц для сигнала 50 Гц, но когда частота выше 10 кГц, его реактивное сопротивление составляет только 16.

Емкостное и индуктивное сопротивление

Символ Xc используется для отличия емкостного реактивного сопротивления от индуктивного X _L что является свойством индукторов.

Различие важно, потому что X _L увеличивается с частотой (противоположность Xc) и если в цепи присутствуют оба X _L и Xc, объединенное реактивное сопротивление (X) равно разнице между ними.

Для получения дополнительной информации см. Страницу Импеданс.

Последовательные и параллельные конденсаторы

Суммарная емкость (C) конденсаторов, подключенных в серии , определяется по формуле:

1	=	1	+	1	+	1	+…
C		C1		C2		C3

Суммарная емкость (C) конденсаторов, подключенных параллельно , составляет:

C = C1 + C2 + C3 + …

Два или более конденсатора редко намеренно соединяются последовательно в реальных цепях, но может быть полезно подключить конденсаторы параллельно, чтобы получить очень большую емкость, например, чтобы сгладить питание.

Обратите внимание, что эти уравнения обратны для резисторы последовательно и параллельно.

Зарядка конденсатора

Конденсатор (C) на принципиальной схеме заряжается от напряжения питания (Vs) с током проходящий через резистор (R). Напряжение на конденсаторе (Vc) изначально равно нулю, но увеличивается. по мере заряда конденсатора. Конденсатор полностью заряжен, когда Vc = Vs.

Зарядный ток (I) определяется напряжением на резисторе (Vs – Vc):

Зарядный ток, I = (Vs – Vc) / R

Сначала Vc = 0V, поэтому:

Начальный ток, Io = Vs / R

Vc увеличивается, как только заряд (Q) начинает накапливаться (Vc = Q / C), это снижает напряжение на резисторе и, следовательно, снижает ток зарядки.Это означает, что скорость зарядки постепенно снижается.

Постоянная времени (RC)

Постоянная времени – это мера того, насколько медленно конденсатор заряжается током, протекающим через резистор. Большая постоянная времени означает, что конденсатор заряжается медленно. Обратите внимание, что постоянная времени является свойством цепь , содержащая конденсатор и резистор, не является свойством только конденсатора.

Постоянная времени (RC) – это время, необходимое для того, чтобы зарядный (или разрядный) ток (I) упал до ¹ / е его начального значения (Io).’е’ – важное число в математике (нравиться ). e = 2,71828 (до 6 значащих цифр), поэтому мы можем грубо сказать, что постоянная времени – это время, необходимое для того, чтобы ток упал до ¹/₃ от его начального значения.

После каждой постоянной времени ток падает на ¹ / e (около ¹/₃). После 5 постоянных времени (5RC) ток упал до менее 1% от своего начального значения, и мы можем разумно говорят, что конденсатор полностью заряжен , а на самом деле конденсатор нужно навсегда зарядить полностью!

Нижний график показывает, как напряжение (В) увеличивается по мере заряда конденсатора.Сначала напряжение быстро меняется из-за большого тока; но по мере уменьшения тока заряд нарастает медленнее, а напряжение увеличивается медленнее.

9019 9019

Время	Напряжение	Заряд
0RC	0,0 В	0%
1RC	5,714		5,714	В	86%
3RC	8.6V	95%
4RC	8,8V	98%
5RC	8,9V	99%

Зарядка конденсатора
постоянная времени = RC

После 5 постоянных времени (5RC) конденсатор почти полностью заряжен, а его напряжение почти равно напряжение питания. Можно с полным основанием сказать, что конденсатор полностью заряжен после 5RC, хотя реально заряжается продолжается вечно (или пока схема не будет изменена).

Разряд конденсатора

Верхний график показывает, как ток (I) уменьшается по мере разряда конденсатора. Начальный ток (Io) определяется начальным напряжением на конденсаторе (Vo) и сопротивлением (R):

Начальный ток, Io = Vs / R

Обратите внимание, что графики тока имеют одинаковую форму как для зарядки, так и для разрядки конденсатора. Этот тип графика является примером экспоненциального убывания.

Нижний график показывает, как напряжение (В) уменьшается по мере разряда конденсатора.

9019 906 В

Время	Напряжение	Заряд
0RC	9,0 В	100%
1RC	3,314		3,314	14%
3RC	0,4 В	5%
4RC	0.2 В	2%
5RC	0,1 В	1%

Разрядка конденсатора
постоянная времени = RC

Сначала ток большой, потому что напряжение велико, поэтому заряд быстро теряется и напряжение быстро уменьшается. По мере того, как заряд теряется, напряжение уменьшается, уменьшая ток, поэтому скорость разрядки становится все медленнее.

После 5 постоянных времени (5RC) напряжение на конденсаторе почти равно нулю, и мы можем с полным основанием сказать, что конденсатор полностью разряжен, хотя реально разряд продолжается вечно (или пока не поменяют схему).

Применение конденсаторов

Конденсаторы используются в нескольких целях:

Конденсаторная муфта (CR-муфта)

Секции электронных схем могут быть связаны с конденсатором, потому что конденсаторы проходят переменный ток (изменяющиеся) сигналы, но блокируют постоянный ток (постоянные) сигналы. Это называется конденсаторной связью или соединением CR .

Он используется между ступенями аудиосистемы для передачи аудиосигнала (переменного тока) без постоянного напряжения (постоянного тока). которые могут присутствовать, например, для подключения громкоговорителя.Он также используется для установки переключателя «AC» на осциллографе.

Точное поведение конденсаторной связи определяется ее постоянной времени (RC). Обратите внимание, что сопротивление (R) может быть внутри следующего участка цепи, а не отдельного резистора.

Для успешной связи конденсаторов в аудиосистеме сигналы должны проходить через с небольшим искажением или без него. Это достигается, если постоянная времени (RC) больше, чем период времени (T) аудиосигналов самой низкой частоты требуется (обычно 20 Гц, T = 50 мс).

Выход при RC >> T
Когда постоянная времени намного больше, чем период времени входного сигнала конденсатор не успевает существенно зарядиться или разрядиться, поэтому сигнал проходит с незначительными искажениями.
Выход при RC = T
Когда постоянная времени равна периоду времени, вы можете видеть, что конденсатор успевает частично зарядиться и разрядиться до изменения сигнала. В результате есть значительное искажение сигнала при прохождении через CR-муфту.Обратите внимание, как внезапные изменения входного сигнала проходят прямо через конденсатор на выход.
Выход при RC << T
Когда постоянная времени намного меньше периода времени, конденсатор успевает для полной зарядки или разрядки после каждого резкого изменения входного сигнала. Фактически только внезапные изменения передаются на выходе, и они выглядят как «всплески», попеременно положительный и отрицательный. Это может быть полезно в системе, которая должна определять, когда сигнал меняется внезапно, но игнорируйте медленные изменения.

Следующая страница: Импеданс и реактивное сопротивление | Исследование

Политика конфиденциальности и файлы cookie

Этот сайт не собирает личную информацию. Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет используется только для ответа на ваше сообщение, оно не будет передано никому. На этом веб-сайте отображается реклама, если вы нажмете на рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден. Рекламодателям не передается никакая личная информация.Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации. Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов. (включая этот), как объяснил Google. Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста, посетите AboutCookies.org.

Как рассчитать конденсаторы, подключенные последовательно и параллельно – Kitronik Ltd

Параллельные конденсаторы

Когда конденсаторы подключаются друг к другу (бок о бок), это называется параллельным подключением.Это показано ниже. Чтобы рассчитать общую общую емкость ряда конденсаторов, подключенных таким образом, вы складываете отдельные емкости по следующей формуле: CTotal = C1 + C2 + C3 и т. Д. Пример: Чтобы рассчитать общую емкость для этих трех конденсаторов, подключенных параллельно. Cобщ = C1 + C2 + C3 = 10F + 22F + 47F = 79F

Задача 1:

Рассчитайте общую емкость следующих конденсаторов, включенных параллельно.

Конденсаторы серии

Когда конденсаторы подключаются друг за другом, это называется последовательным соединением.Это показано ниже. Чтобы рассчитать общую общую емкость двух подключенных таким образом конденсаторов, вы можете использовать следующую формулу:

Cобщ. =	C1 x C2	и так далее
	C1 + C2

Пример: чтобы рассчитать общую емкость для этих двух последовательно соединенных конденсаторов.

Задача 2:

Рассчитайте общую емкость следующих последовательно включенных конденсаторов.

Три или более конденсатора последовательно

Чтобы рассчитать общую общую емкость трех или более конденсаторов, подключенных таким образом, вы можете использовать следующую формулу: и так далее.Пример: чтобы рассчитать общую емкость для этих трех последовательно соединенных конденсаторов.

Задача 3:

Рассчитайте общую емкость следующих последовательно включенных конденсаторов.

ответы

Задача 1

1 = 232,2 ° F 2 = 169,0 ° F 3 = 7,0 ° F

Задача 2

1 = 2,48F 2 = 14,99F 3 = 4,11F

Задача 3

1 = 3,33F 2 = 1,167F 3 = 0,35F Примечание Значения конденсаторов в этом листе поддерживаются высокими (близкими к единице или больше). Это сделано для упрощения процесса обучения.На самом деле типичные значения конденсаторов намного меньше единицы. Загрузите PDF-версию этой страницы здесь. Узнать больше об авторе подробнее »Если вы нашли эту статью полезной и хотели бы получать от нас обновления продуктов и бесплатные электронные ресурсы, зарегистрируйтесь здесь. Мы тоже ненавидим спам и обещаем никогда не продавать и не сообщать свой адрес электронной почты, и вы можете отказаться от подписки в любое время.

Как будет влиять на емкость конденсатора с параллельными пластинами, если все пространство будет? – Mvorganizing.org

Как будет влиять на емкость конденсатора с параллельными пластинами, если все пространство будет?

Полное заполнение пространства между пластинами конденсатора диэлектриком увеличивает емкость в разы диэлектрической постоянной: C = KCo, где Co – емкость без диэлектрика между пластинами.

Как увеличить емкость конденсатора с параллельными пластинами?

Емкость конденсатора увеличивается при увеличении площади пластины.

Что происходит, когда между пластинами конденсатора помещается проводящая плита?

Если пластины конденсатора соединить с идеальной батареей, то напряжение, а не заряд, останется постоянным, а запасенная энергия уменьшится. Металлическая пластина создает два новых конденсатора, каждый с таким же исходным зарядом и меньшим расстоянием между пластинами.

Что произойдет, если конденсатор с параллельными пластинами заполнить проводящей пластиной?

Емкость – это способность пластин удерживать заряд.Но здесь, если мы подключим пластины конденсатора к клеммам батареи, ток будет течь через проводящую пластину, через пластины. Заряды на пластинах не накапливаются. Разность потенциалов на пластинах равна нулю.

Что произойдет с емкостью конденсатора с параллельными пластинами, если мы поместим металлическую пластину между пластинами конденсатора?

Следовательно, общая емкость будет ниже, чем емкость любого отдельного конденсатора в устройстве.Расстояние между пластинами также влияет на общую емкость.

Что из перечисленного блокируется конденсатором?

Когда конденсатор подключен к источнику постоянного напряжения, сначала положительный вывод источника постоянного тока отводит электроны от одного вывода и подталкивает электроны ко второму выводу.

Что происходит, если в конденсатор вставить металл?

Металлическая пластина, вставленная между пластинами конденсатора с параллельными пластинами, создает частичные заряды на каждой стороне металлической пластины.положительно заряженная пластина, создавая частичный заряд на этой стороне пластины, равный отрицательному заряду на положительной стороне конденсатора.

Что происходит с емкостью при увеличении заряда?

Когда на конденсатор подается напряжение, на двух проводниках накапливается определенное количество заряда. Увеличение напряжения приведет к большему накоплению заряда, что вызовет большее притяжение между пластинами, что приведет к дальнейшему сжатию пружин, что приведет к увеличению емкости.

Что из следующего увеличивает емкость конденсатора?

Уменьшение площади пластин увеличивает емкость конденсатора с параллельными пластинами. Уменьшение расстояния между пластинами увеличит емкость конденсатора с параллельными пластинами. Увеличение расстояния между пластинами увеличит емкость конденсатора с параллельными пластинами.

Какое из следующих изменений приведет к уменьшению емкости конденсатора с параллельными пластинами?

Емкость обратно пропорциональна расстоянию между пластинами.Следовательно, емкость конденсатора уменьшается, когда пластины находятся дальше друг от друга.

Когда два или более конденсатора соединены последовательно?

Когда конденсаторы соединены последовательно, общая емкость меньше, чем любая из отдельных емкостей последовательных конденсаторов. Если два или более конденсатора соединены последовательно, общий эффект будет таким, как у одиночного (эквивалентного) конденсатора, имеющего сумму расстояний между пластинами отдельных конденсаторов.

Что из следующего увеличивает емкость конденсатора, выберите два ответа?

Выберите два ответа.Пояснение: B, C Размещение диэлектрика (изолятора) между пластинами конденсатора всегда увеличивает емкость.

Что из следующего не влияет на емкость конденсатора с параллельными пластинами, выберите один?

Где C – емкость конденсатора, ε0 – диэлектрическая проницаемость пластин, A – площадь параллельных пластин, а d – расстояние между двумя параллельными пластинами. Таким образом, тип материала пластин является единственным фактором, не влияющим на емкость конденсатора.

Какие факторы влияют на емкость конденсатора?

На емкость влияют три фактора: размер проводников, размер зазора между ними и материал между ними (диэлектрик). Чем больше проводники, тем больше емкость.

Что относится к конденсаторам, включенным параллельно?

Что верно для конденсаторов, соединенных параллельно? Заряд каждого конденсатора такой же и такой же, как заряд эквивалентного конденсатора.Разность напряжений на отдельных конденсаторах одинакова и равна разнице напряжений на эквивалентном конденсаторе. (б.)

Влияет ли материал пластин на емкость?

На емкость конденсатора влияет площадь пластин, расстояние между пластинами и способность диэлектрика выдерживать электростатические силы. Пластины большего размера обеспечивают большую емкость для хранения электрического заряда. Следовательно, с увеличением площади пластин увеличивается емкость.

Подключение конденсаторов для увеличения емкости: Последовательное и параллельное соединение.

Последовательное и параллельное соединение.

Последовательное и параллельное соединение конденсаторов

Как увеличить вольтаж конденсатора — MOREREMONTA

Как правильно соединять конденсаторы?

Как рассчитать общую ёмкость соединённых конденсаторов?

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Для электролитических конденсаторов.

Электрическая емкость

Параллельное соединение

Последовательное включение конденсаторов

Смешанный способ

Сравнение различных вариантов

Как соединить электролитические конденсаторы для увеличения напряжения. Последовательное и параллельное соединение конденсаторов

Смешанное соединение конденсаторов

Параллельное соединение

Последовательное соединение

Смешанное подключение

Последовательное соединение

Смешанное соединение

Параллельное соединение конденсаторов

Последовательное соединение конденсаторов

Смешанное соединение конденсаторов

Параллельное соединение конденсаторов

Последовательное соединение конденсаторов

Смешанная схема

Соединение конденсаторов – Основы электроники

Параллельное соединение конденсаторов.

Последовательное соединение конденсаторов.

Последовательно-параллельное (смешанное) соединение конденсаторов

Похожие материалы:

Добавить комментарий

Параллельное и последовательное соединение конденсаторов

Параллельное соединение конденсаторов

Соединение конденсаторов последовательно

Смешанное соединение конденсаторов

Последовательное и параллельное соединение конденсаторов (ёмкостей)

Что такое конденсатор и его основные характеристики

Что он из себя представляет и как работает

Где и для чего используются

Как подключать конденсаторы

Параллельное подключение конденсаторов

Расчёт суммарной ёмкости

Пример расчёта

Последовательное соединение

Как определить ёмкость последовательно соединенных конденсаторов

Пример расчёта

Почему электролитические конденсаторы выходят из строя и что делать

Как подобрать замену

Что будет, если поставить конденсатор большей ёмкости?

При параллельном подключении конденсаторов у них одинаковые

При параллельном подключении конденсаторов у них одинаковые

Когда конденсаторы подключены параллельно, имеют ли они одно и то же?

Кстати, при параллельном подключении конденсаторов у них одно и то же?

Тогда возникает вопрос: что происходит, когда конденсаторы соединяются параллельно?

Также можно спросить: а параллельно ли конденсаторы имеют одинаковую нагрузку?

Что верно для конденсаторов, соединенных параллельно?

Что делать, если два или более конденсатора подключены параллельно через разность потенциалов?

Как рассчитываются параллельные конденсаторы?

Конденсаторы накапливают больше энергии последовательно или параллельно?

Зачем добавлять конденсаторы параллельно?

Что является символом мастерства?

Одно и то же напряжение на резисторах, включенных параллельно?

Могут ли конденсаторы повышать напряжение?

Будет ли напряжение параллельно уменьшаться вдвое?

Как рассчитать заряд конденсатора?

То есть Q = C?

Если, например, C = 33 мкФ и V = 20 В, то Q = (33?

106)?

Когда два конденсатора подключены параллельно к батарее?

Как мне добавить индукторы параллельно?

Какова эквивалентная емкость двух параллельно соединенных конденсаторов?

Можно ли подключить конденсаторы последовательно?

Что происходит, когда конденсатор подключен к источнику постоянного тока?

Как подключить конденсатор?

Что происходит, когда конденсатор подключен к батарее?

Для чего нужен конденсатор?

Основные расчеты – Инженерное мышление

Конденсаторы в цепях постоянного тока

Параллельные конденсаторы