При последовательном соединении напряжение: Сопротивление при последовательном соединении резисторов равно сумме всех резисторов

Сопротивление при последовательном соединении резисторов равно сумме всех резисторов

Часто надо посчитать общее сопротивление при последовательном соединении резисторов. Внешний участок электрической цепи часто образуется не од­ним приемником с определенным сопротивлением, а нескольки­ми, соединенными последовательно, параллельно или смешанно.

Если несколько сопротивлений электрической цепи соедине­ны, как указано на рисунке ниже, одно за другим без разветвлений и по ним проходит один и тот же ток, то такое соединение называ­ется последовательным соединением сопротив­лений.

Последовательное соединение сопротивлений показано на рисунке.

По закону Ома напряжения на отдельных участках цепи (со­противлениях) или падения напряжения

U₁ = IR₁;
U₂ = IR₂;
U₃ = IR₃;
U₄ = IR₄.

Так как ток во всех участках имеет одинаковое значение, то напряжения на участках пропорциональны их сопротивлениям,

т. е.

U₁ : U₂ = R₁ : R₂;
U₂ : U₃ = R₂ : R₃;
U₃ : U₄ = R₃ : R₄.
Мощности отдельных участков соответственно равны:

P₁ = U₁I;
P₂ = U₂I;
P₃ = U₃I;
P₄ = U₄I,

а мощность всей цепи, по закону сохранения энергии равная сумме мощностей отдельных участков,

P = P₁ + P₂ + P₃ + P₃ = I(U₁ + U₂ + U₃ + U₄) = IU,

откуда следует, что напряжение на зажимах цепи

U равно сум­ме напряжений на отдельных участках:

U = U₁ + U₂ + U₃ + U₄

Разделив правую и левую части этого выражения  на ток, получим:
U : I = U₁ : I + U₂ : I + U₃ : I + U₄ : I
или

R = R₁ + R₂ + R₃ + R₄

где R — общее сопротивление при последовательном соединении в цепи, т. е. такое равно­ценное (эквивалентное) сопротивление, заменяя которым все со­противления цепи (R₁, R₂, R₃ и R₄) при неизменном напряжении на ее зажимах, получим то же самое значение тока.

Или

Общее сопротивление при последовательном соединении проводников (сопротивлений) равно сумме всех сопротивлений в цепи.

Например:

Последовательно с постоянным сопротивлением, имеющей сопротивление R₁ = 2 ком (2000 ом), включен реостат R₂ (переменное сопротивление), сопротив­ление которого можно изменять от 0 до 10 ком (10000 ом). Определить, в каких пре­делах можно регулировать ток в цепи при напряжении, подведенным к этой цепи, равным 120 В.

При последовательном соединении сопротивление равно:

R = R₁ + R₂

При сопротивлении реостата, равным нулю:
I = U : ( R₁ + R₂ ) = 120 : (2000 + 0) = 0,06 а

При введенном реостате на максимальное значение

I = U : ( R₁ + R₂ ) = 120 : (2000 + 10000) = 0,01 а

Таким образом, ток можно регулировать в пределах от 0,01 а до 0,06 а.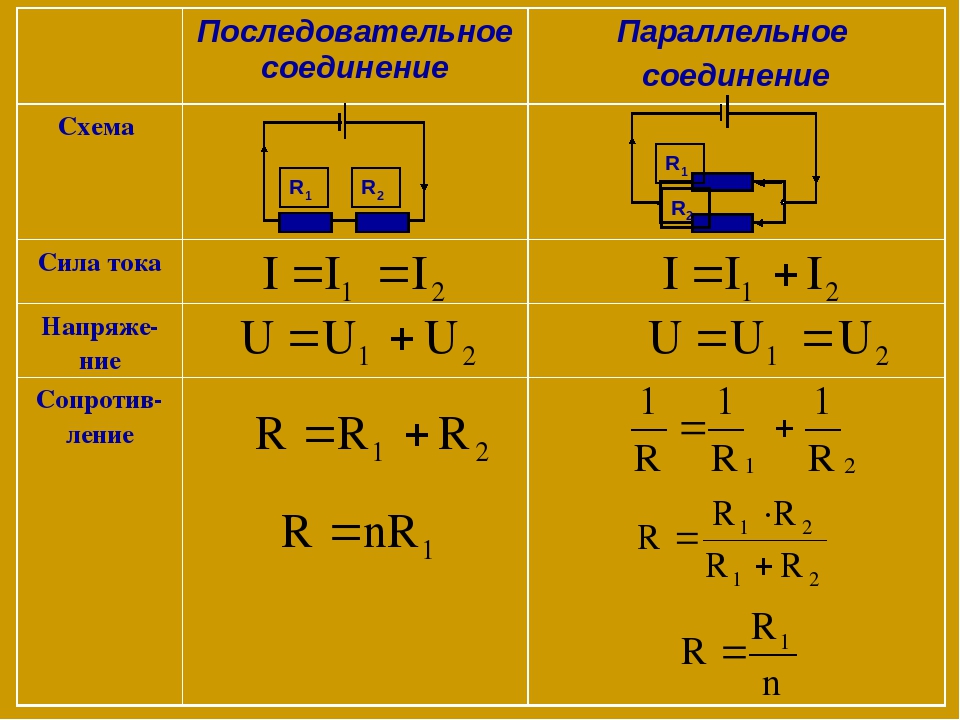

При последовательном подключении приборы соединены подобно вагонам поезда. (Так подключается, например, амперметр.) Можно представить себе, что ток последовательно «проходит» один прибор за другим. В результате во всех приборах наблюдается

одна и та же сила тока. Общее напряжение делится, на каждом приборе падает часть общего напряжения. Сопротивление приборов при этом складывается.
При параллельном подключении приборы соединены подобно параллельным железнодорожным путям на сортировочной станции. Так подключается вольтметр. Ток разветвляется, делится на части (ветви). Напряжение на всех приборах одинаково, а общее сопротивление уменьшается.

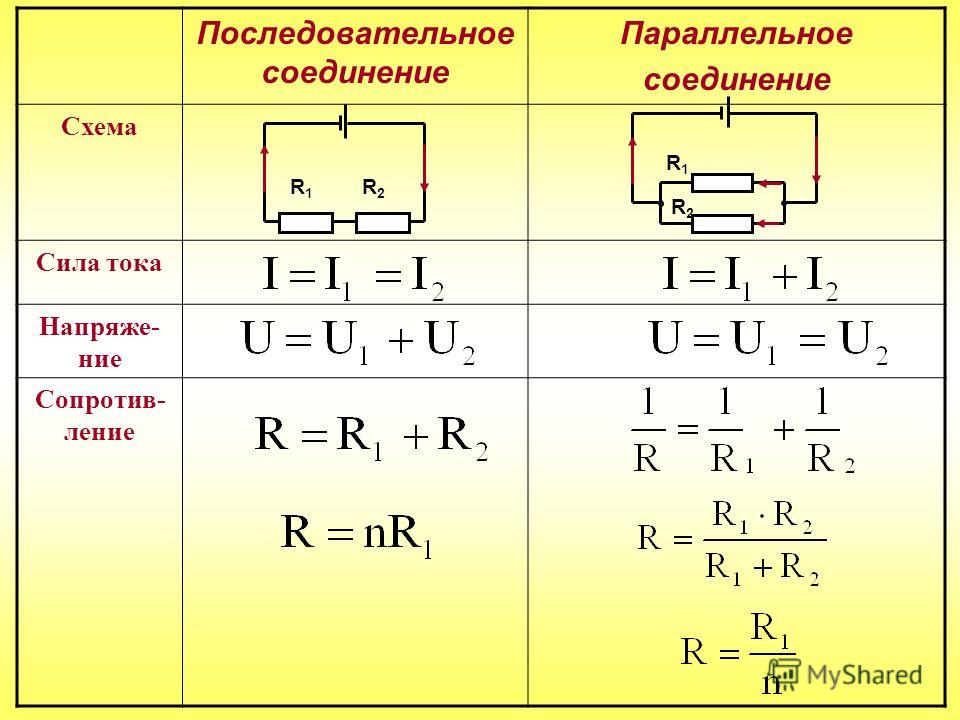
Последовательное соединение	Параллельное соединение
Сила тока одинакова: Iобщ = I1 = I2	Сила тока складывается: Iобщ = I1 + I2
Напряжение складывается: Uобщ = U1 + U2	Напряжение одинаково: Uобщ = U1 = U2
Сопротивление складывается: Rобщ = R1 + R2	Сопротивление уменьшается: Rобщ = R1 R2/(R1 + R2)

 

Физика 8 класс.

Последовательное и параллельное соединение проводников :: Класс!ная физика

Физика 8 класс. ПАРАЛЛЕЛЬНОЕ И ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ

Включим в электрическую цепь в качестве нагузки ( потребителей тока) две лампы накаливания,
каждая из которых обладает каким-то определенным сопротивлением, и каждую из которых

можно заменить проводником с таким же сопротивлением.

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ

Расчет параметров электрической цепи
при последовательном соединении сопротивлений:

1. сила тока во всех последовательно соединенных участках цепи одинакова

2. напряжение в цепи, состоящей из нескольких последовательно соединенных участков,
равно сумме напряжений на каждом участке

3. сопротивление цепи, состоящей из нескольких последовательно соединенных участков,
равно сумме сопротивлений каждого участка

4. работа электрического тока в цепи, состоящей из последовательно соединенных участков,
равна сумме работ на отдельных участках

А = А1 + А2

5. мощность электрического тока в цепи, состоящей из последовательно соединенных участков,

равна сумме мощностей на отдельных участка

Р = Р1 + Р2

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

 

Расчет параметров электрической цепи
при параллельном соединении сопротивлений:

1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках

2. напряжение на всех параллельно соединенных участках цепи одинаково

3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :

( R – сопротивление проводника,
1/R – электрическая проводимость проводника)

Устали? – Отдыхаем!

Последовательное и параллельное соединение резисторов.

Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.

Последовательное соединение резисторов.

Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

Здесь у нас классический случай последовательного соединения — два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

I = I_1 = I_2

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

U = U_1 + U_2

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

U_1 = I_1R_1 = IR_1

U_2 = I_2R_2 = IR_2

Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)

Но для общего напряжение также справедлив закон Ома:

U = IR_0

Здесь R_0 — это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

R_0 = R_1 + R_2

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.

Например для следующей цепи:

Общее сопротивление будет равно:

R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном  соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:

R_0 = nR

В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.

Параллельное соединение резисторов.

При параллельном соединении напряжения на проводниках равны:

U_1 = U_2 = U

А для токов справедливо следующее выражение:

I = I_1 + I_2

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}

I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}

Подставим эти выражения в формулу общего тока:

I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})

А по закону Ома ток:

I = \frac{U}{R_0}

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}

Данную формулу можно записать и несколько иначе:

R_0 = \frac{R_1R_2}{R_1 + R_2}

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}

Смешанное соединение резисторов.

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 — они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:

R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1

Теперь у нас образовались две группы последовательно соединенных резисторов:

Заменим эти две группы двумя резисторами, сопротивление которых равно:

R_{1-2-3} = R_{1-2} + R_3 = 5

R_{4-5} = R_4 + R_5 = 24

Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5}  одним резистором R_{1-2-3-4-5}:

R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4. 14

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

Общее сопротивление цепи получилось равным:

R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!

Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление — для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!

Чему равна сила тока в параллельном соединении. Мощность при параллельном и последовательном соединении резисторов

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова.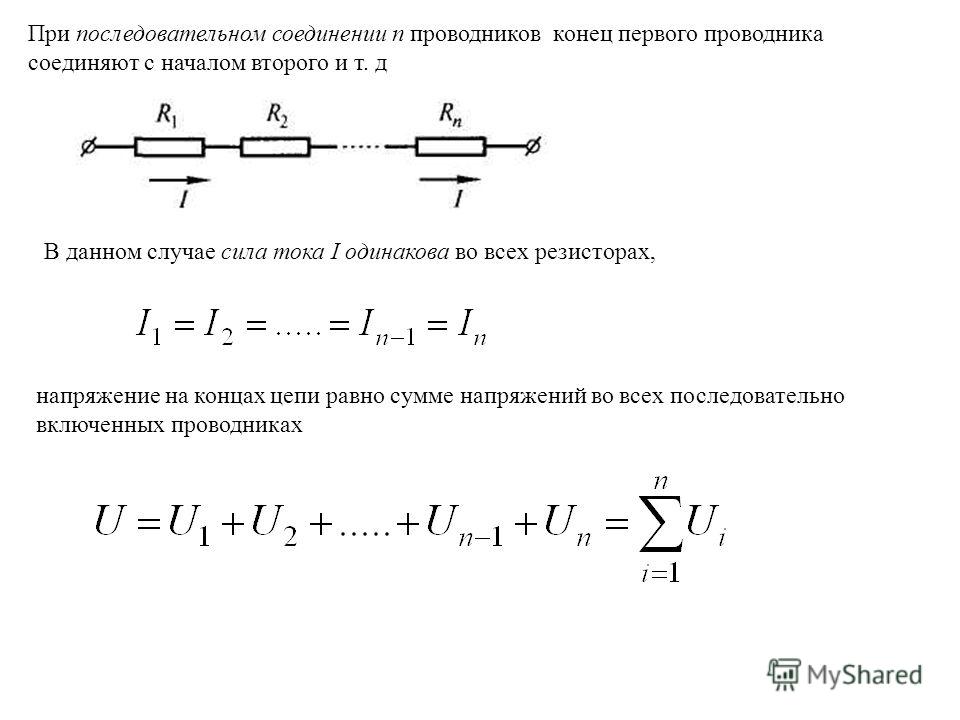 Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

\(~I = I_1 = I_2 .\)

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A → 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам Μ и N напряжение U . Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:

\(~U = U_1 + U_2 . \qquad (1)\)

Применяя закон Ома для каждого участка цепи, получим:

\(~U = IR ; \ U_1 = IR_1 ; \ U_2 = IR_2 ,\)

где R – общее сопротивление последовательно соединенной цепи. Подставляя U , U 1 , U 2 в формулу (1), имеем

\(~IR = IR_1 + IR_2 \Rightarrow R = R_1 + R_2 .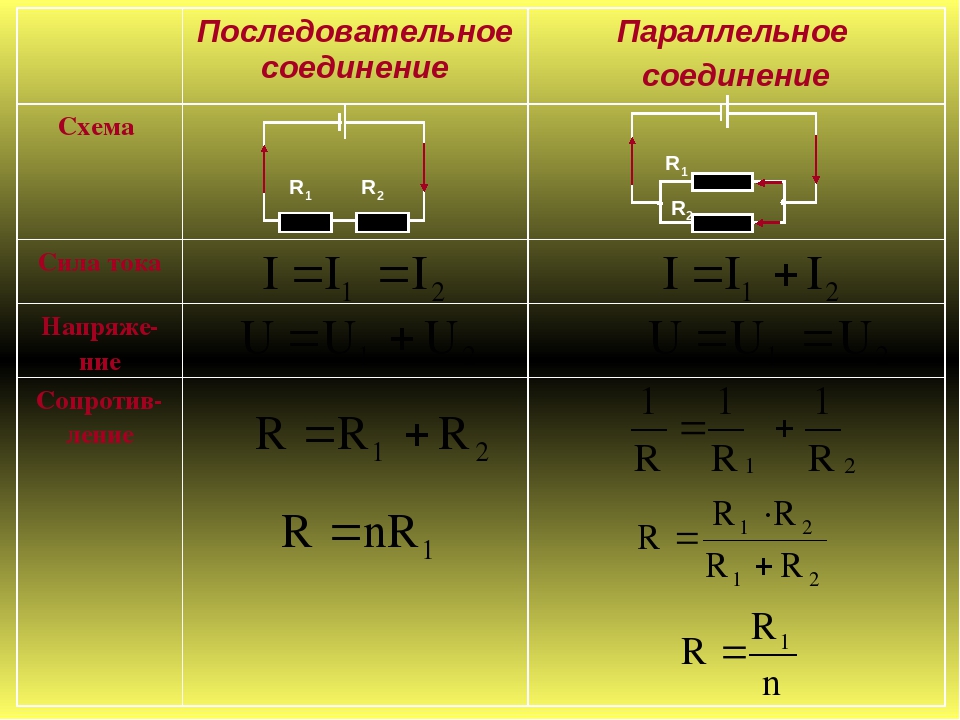 n R_i .\)

Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы – в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

\(~U = U_1 = U_2 .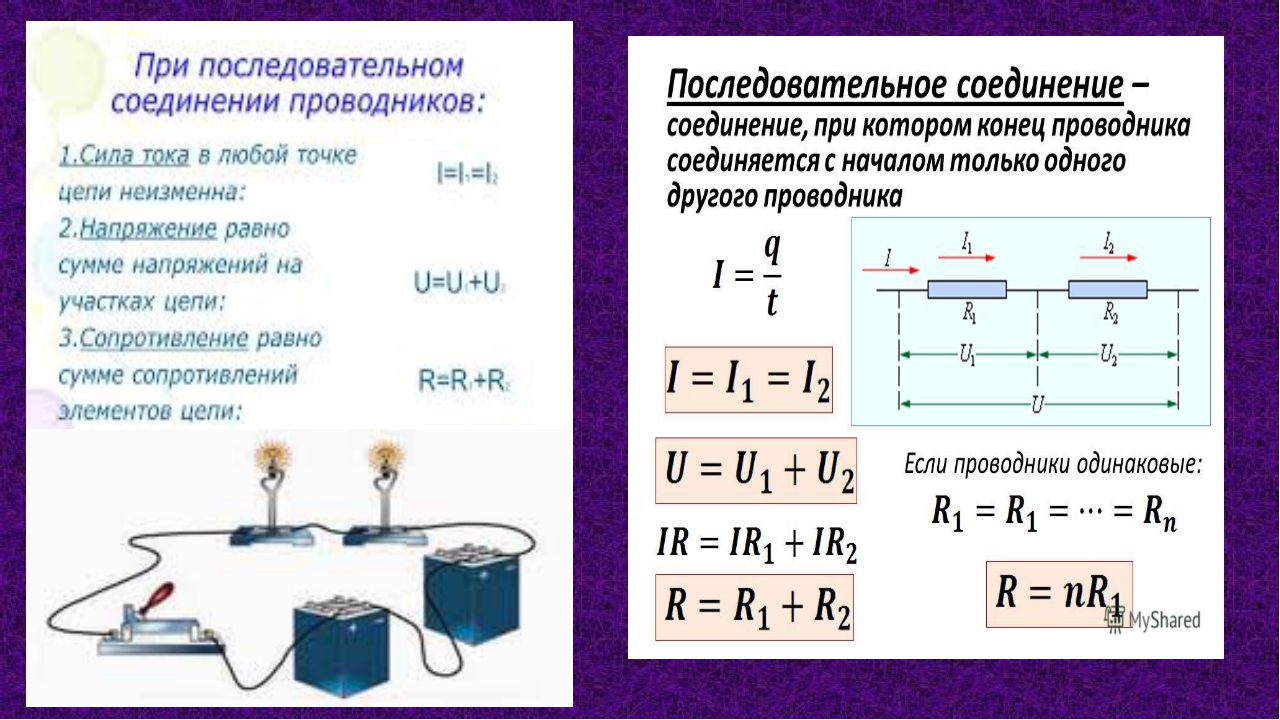 n \frac{1}{R_i} .\)

Если сопротивления всех n параллельно соединенных резисторов одинаковы и равны R 1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .

Сопротивление цепи, состоящей из n одинаковых параллельно соединенных резисторов, в n раз меньше сопротивления каждого из них.

При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C. 257-259.

В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R . Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).

Закон Ома для участка цепи : сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).

Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д ва основных типа соединения проводников : последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.

Последовательное соединение проводников

При последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец – с началом третьего и т. д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.

Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I 1 = I 2 = I .

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений : R 1 + R 2 = R . Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

По закону Ома напряжение на каждом проводнике равно: U 1 = I* R 1 , U 2 = I*R 2 . В таком случае общее напряжение равно U = I ( R 1 + R 2) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике : U = U 1 + U 2 .

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

Для последовательного соединения проводников справедливы законы :

1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Параллельное соединение проводников

Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U .

При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть – через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I 1 + I 2 .

В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2 . Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2 , U = U 1 = U 2 , 1/R = 1/R 1 + 1/R 2 Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г , то их общее сопротивление равно: R = г/2 . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.

Для параллельного соединения проводников справедливы законы:

1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

Содержание:

Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов – параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким – параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения.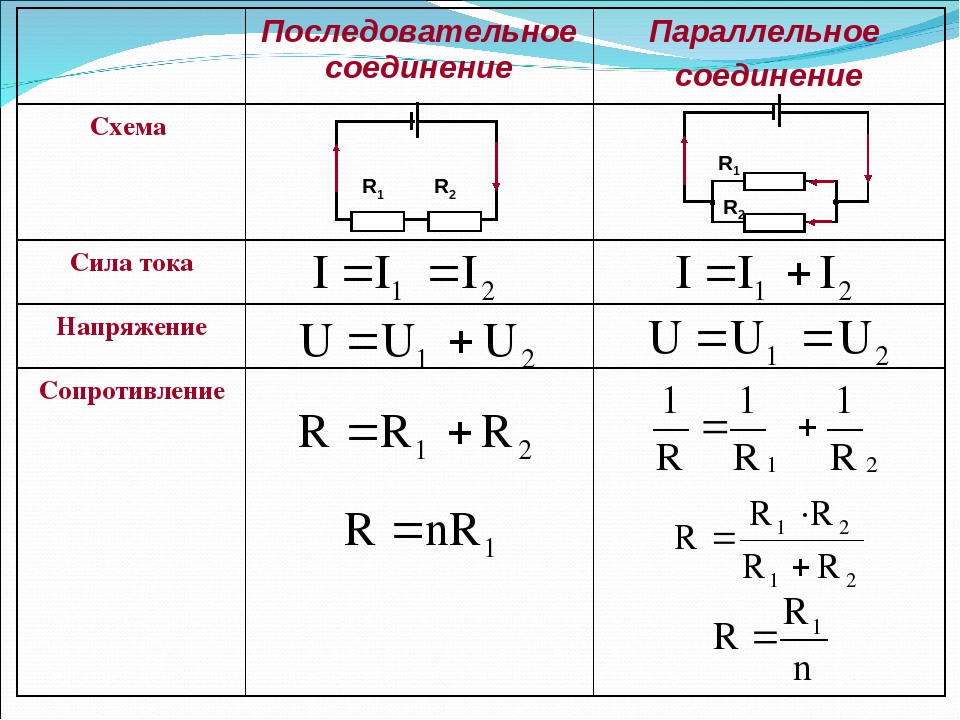 Начать следует с определений и правил.

Способы подключения и их особенности

Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.

Последовательное соединение

Последовательное подключение – это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом – это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает – все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.

Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.

Параллельное соединение

Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы – во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.

Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.

Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.

Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.

Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.

Последовательно-параллельное соединение

Последовательно-параллельное соединение – это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.

Подведем итог

Подводя итог всему вышеизложенному можно сделать следующие выводы:

1. При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов – сумма и будет общим сопротивлением.
2. При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
3. Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
4. Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
5. Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.

В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому – внимательность и скрупулезность в расчетах – залог правильной работы схемы.

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R – общее сопротивление, R1 – сопротивление одного элемента, а n – количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов.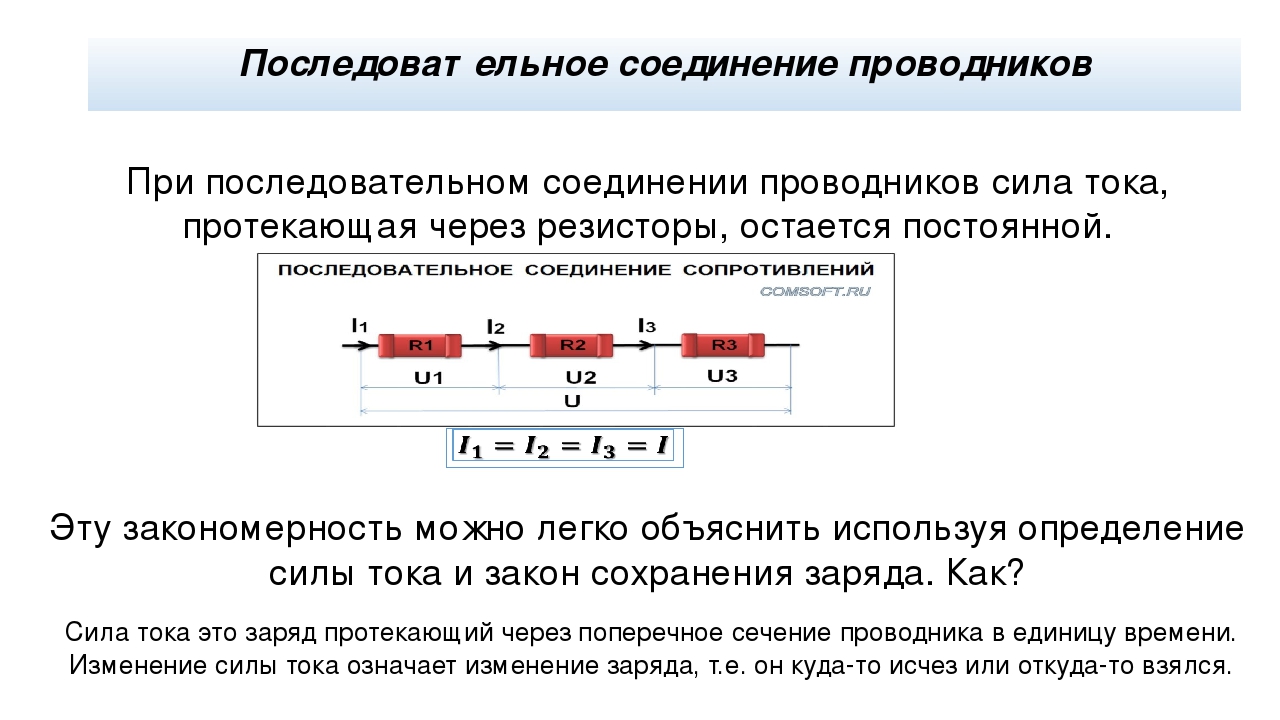 Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 – сопротивления обеих лампочек, U = U1 = U2 – значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях – увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.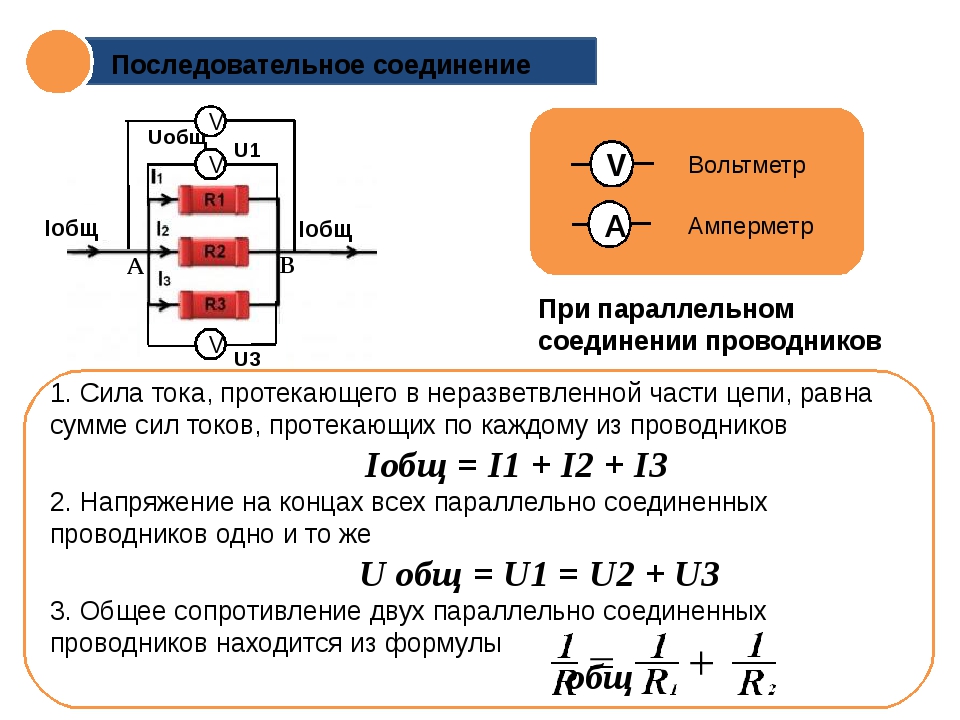

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения.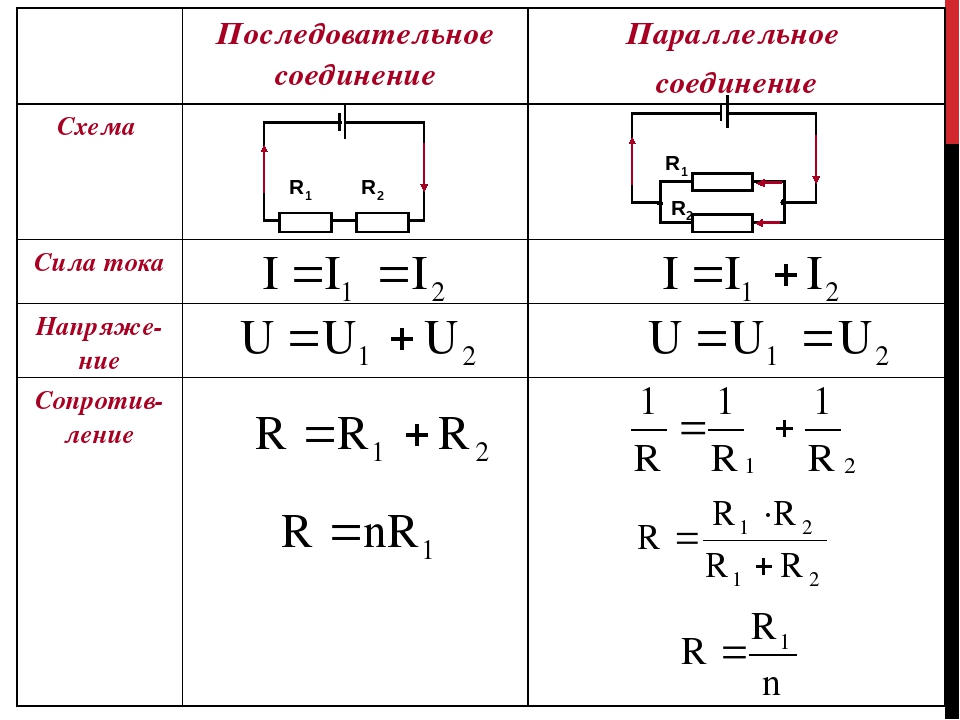 Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.

Электричество начинается с закона Ома.

А уж если рассматривать дилемму в контексте параллельного или последовательного соединений – считая одно соединение курицей, а другое – яйцом, то сомнений вообще нет никаких.

Потому что закон Ома – это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.

Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.

И это обычно рисуют на схеме вот так:

По закону Ома I=U/R

Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится

R = 1/U , где R = 1 Ом

А мощность будет выделяться P = I * U , то есть P=2,25 Вm

В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, – все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое – ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки.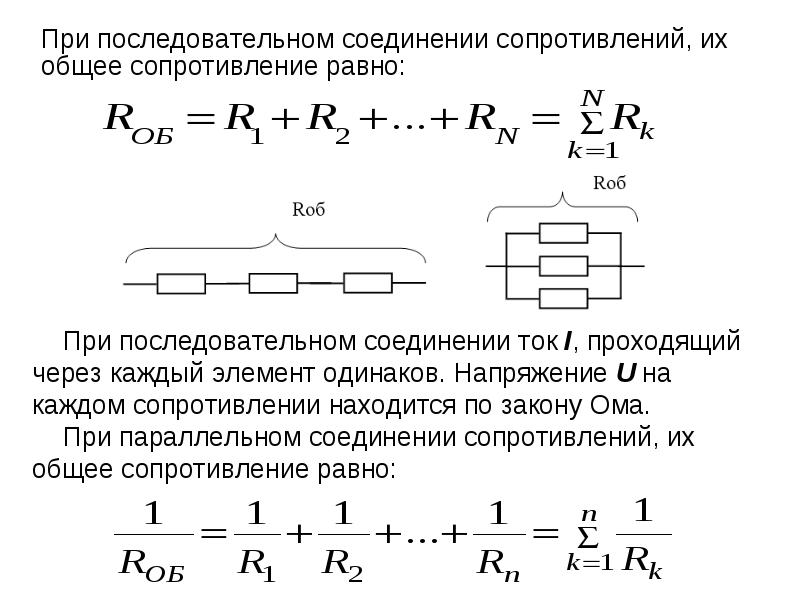 Новый ток вычисляем опять по закону Ома.

Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.

В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек – они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R – сопротивление одной лампочки. Логика безупречная.

А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.

Делаем вывод:

• При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.

Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).

То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине – то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.

Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.

Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе – 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А – ток «полного накала».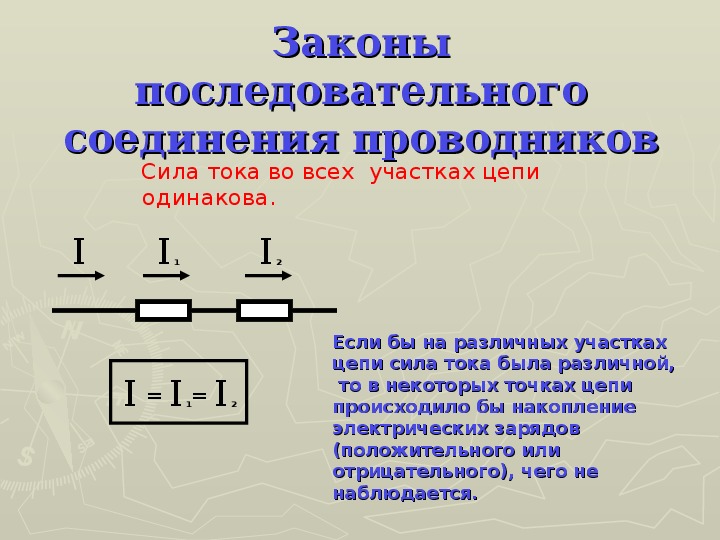

Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.

В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.

Тогда ток был 0,75 А, а теперь он стал сразу 3 А.

Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?

А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.

Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G , по аналогии с сопротивлением R и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.

Ну и вот она

Закон Ома тогда будет выглядеть

I = U * G &

И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.

Замена элементов цепи общим эквивалентным элементом

Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.

Самое первое что, напрашивается – это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.

Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».

Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая – которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.

Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.

Вот это и есть полный расчет электрической сети.

Примеры

Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.

На ее входные клеммы подано напряжение в 60 В.

Значения сопротивлений для всех элементов следующие:

Найти все неизвестные токи и напряжения.

Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.

Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 .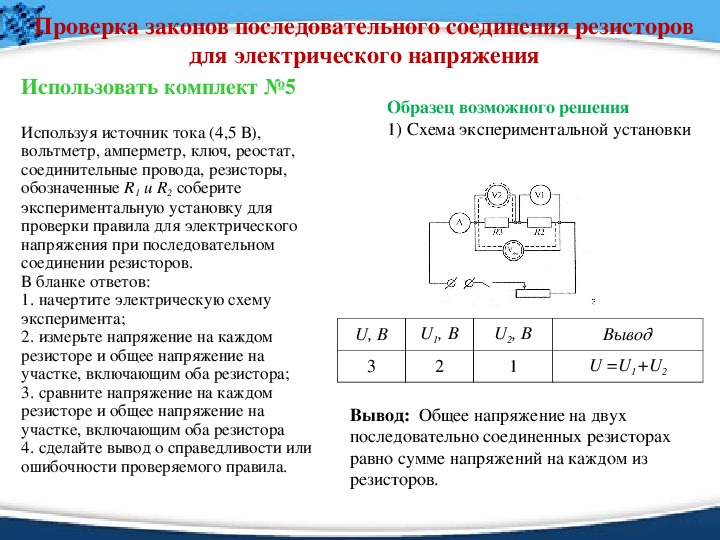 Только при параллельном соединении проводников, складывать придется проводимости.

Проводимость измеряется в единицах, называемых сименсами, обратных омам.

Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом

Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.

Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.

Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом

На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений

R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом

Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I

Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.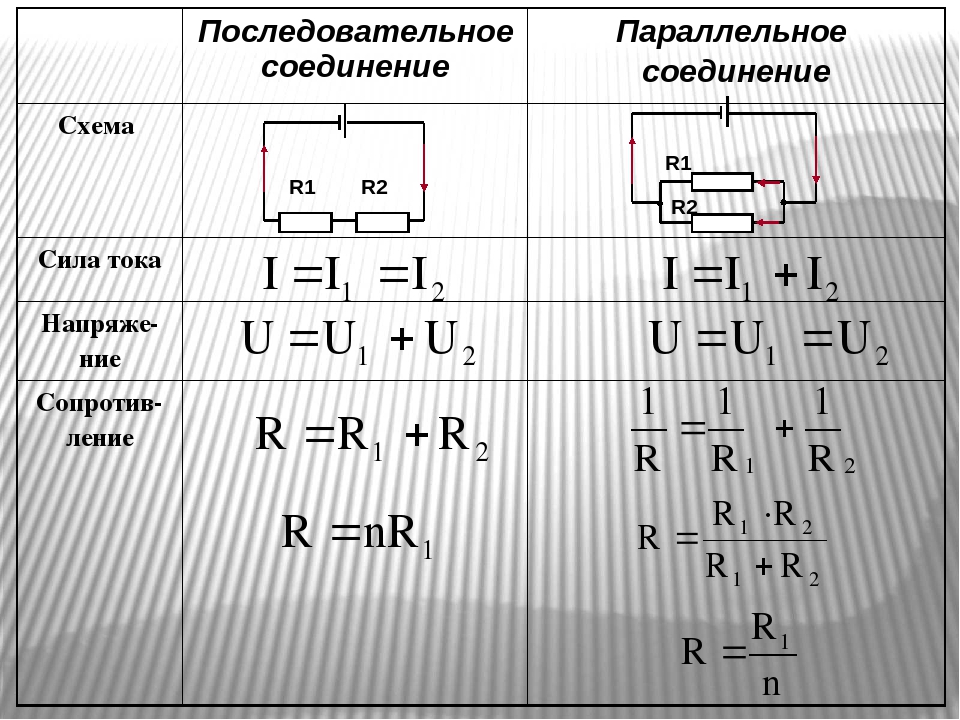

Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.

Предыстория: наука, инженерия, концепции: серия и параллель [PEN wiki]

версия для печати в формате pdf

Помните, что ток вызывается перемещающимися зарядами по проводам и компонентам. Ток , сколько зарядов движется по проводу – огромный поток или крошечная струйка.

Количество имеющегося у вас тока обычно зависит от сопротивления вашей цепи – низкое сопротивление означает большой ток.

Напряжение измеряет, сколько энергии имеет ток.Он определяется напряжением аккумулятора.

Последовательное и параллельное соединение

Компоненты схемы могут быть подключены последовательно или параллельно, как показано ниже:

Последовательно все компоненты находятся в одной «петле», а параллельно они находятся на разных ветвях схемы.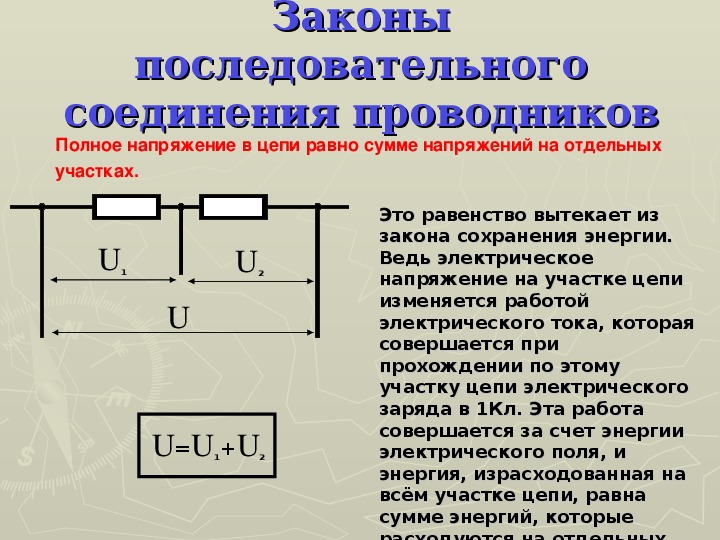

Ток и напряжение

В параллельном ток делится между двумя секциями. Например, это как если бы труба, соединенная с резервуаром с водой, была разделена – вода отделилась и стекала по обеим секциям трубы.Сила тока в каждой секции складывается с общим током до разделения.

Однако напряжение на двух секциях остается неизменным. Это как если бы обе трубы находились на одинаковой высоте от земли – вода имеет одинаковое расстояние, чтобы падать в обе ветви.

В «серии» одинаковый ток проходит через все компоненты – это как если бы они были подключены к одной и той же «трубе», и через все они протекало одинаковое количество воды.

Однако * падение напряжения * на каждом компоненте разное. Это как если бы разные секции трубы падали на разную высоту – падение высоты представляет собой изменение потенциальной энергии, как падение напряжения.

Падения напряжения на каждом из компонентов складываются в падение напряжения во всей цепи.

Сопротивления

Последовательно

Когда резисторы соединены последовательно, все они имеют одинаковый ток, и падение напряжения на каждом из них в сумме приводит к падению напряжения во всей цепи.

Поскольку напряжение равно току, умноженному на сопротивление, а ток во всем одинаков, последовательно добавляются сопротивления. Сумма каждого резистора – это полное сопротивление последовательной цепи.

Сопротивление можно рассматривать как засорение труб – чем выше сопротивление, тем сильнее забивается труба, пропускающая меньше воды. Если трубы соединены последовательно, очень засоренная труба означает очень небольшой поток воды, даже если другие менее засоренные трубы подключены в соответствии с ней.

Параллельно

Параллельно резисторы складывают немного иначе. Все они имеют одинаковое напряжение на них, но их * токи * складываются в общий ток цепи. Снова используя V = IR:

Опять же, резисторы можно рассматривать как трубы – вода разделяется между разными трубами, а это означает, что через них может протекать больше воды, чем если бы они были подключены последовательно.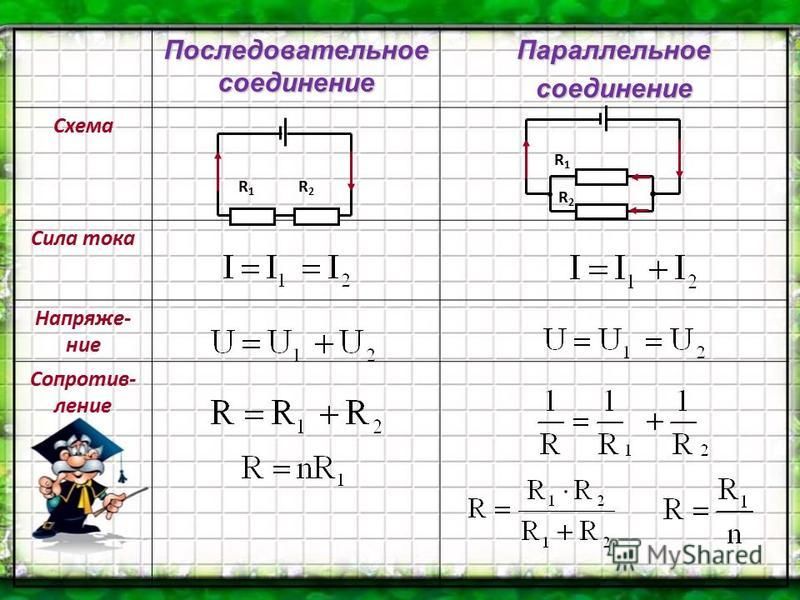 Вот почему общее сопротивление компонентов, соединенных последовательно, на самом деле ниже, чем сопротивление самих компонентов – у «воды» больше мест, куда она может пойти, поэтому ее может течь больше.

Использование последовательного / параллельного

серии

Поскольку резисторы добавляются последовательно, такое соединение хорошо, если вам нужно большое сопротивление, например, для ограничения тока.

Если у вас есть компоненты, требующие высокого тока, их последовательное соединение потребляет меньший ток для системы в целом.

Параллельный

Если у вас есть компоненты, которым требуется высокое напряжение, но низкий ток, их параллельное соединение означает, что все компоненты будут иметь одинаковое напряжение на них, а добавление большего количества просто уменьшит ток.

Если вы подключите их последовательно, вам понадобится источник большего напряжения, так как их напряжения будут складываться.

Параллельные соединения также хороши для построения надежных цепей, которые могут быть повреждены. Если одна ветвь параллельной цепи разорвана, остальная часть цепи все еще будет работать, поскольку это все еще полная цепь.

Однако при последовательном подключении, если часть цепи разорвана, вся цепь перестанет работать, поскольку нет альтернативных путей для прохождения тока.

Отдел цепей и напряжений серии

Отдел цепей и напряжений серии

---

Пример 1: Найдите полное эквивалентное сопротивление в следующей цепи

---

Пример 2: Для следующей цепи:

1. Найдите полное сопротивление
2. Найти текущий i
3. Найдите напряжение на резисторе 10 Ом

Решение Общее сопротивление Ток можно рассчитать как Напряжение на резисторе 10 Ом

---

Пример 3: Для следующей цепи:

1. Найдите общее значение сопротивления R _T
2. Найти текущий i
3. Найдите напряжение на отдельных резисторах
4. Проверить закон напряжения Кирхгофа

---

Пример 4: Для следующей цепи:

1. Найти V ₁
2. Найти V ₂
3. Проверить закон напряжения Кирхгофа вокруг замкнутого контура

---

Отдел напряжения :

В следующей схеме ток через все последовательно включенные резисторы равен . Эквивалентный резистор R eq является суммой номинала резистора. Чтобы найти падение напряжения v i на резисторе R i , мы используем ток и значение резистора . Правая часть уравнения дает нам уравнение деления напряжения.

---

Примеры:

Пример 5: Для следующей схемы

1. Найдите общее значение сопротивления R _T
2. Найти текущий i
3. Найти напряжение на резисторах
4. Проверить закон напряжения Кирхгофа

---

Пример 6: Найдите ток для следующей цепи

---

Практические задачи :

(Щелкните изображение, чтобы просмотреть решение)

Задача 1: Найдите следующую схему.

Просмотреть решение

Решение: Применить закон Кирхгофа о напряжении

---

Задача 2: Рассчитайте напряжения для следующей цепи.

Просмотреть решение

Решение: текущее, Применение закона Кирхгофа:

---

Проблема 3: Найдите приложенное напряжение к следующей цепи, используя предоставленную информацию

Просмотреть решение

---

Задача 4: Найдите значение резистора R , используя предоставленную информацию

Просмотреть решение

---

Задача 5 : Найти V _x

Просмотреть решение

---

Операции:

Ресурсы

Последовательная цепь

Глобусы, соединенные последовательно

В последовательной цепи одна за другой подключены две или более нагрузки.

У тока есть только один путь, по которому оно может течь.

Примером последовательной схемы является набор огней на елку. Все шары ставятся один за другим.

Путь только один, поэтому ток будет одинаковым в любой точке цепи.

Принципиальная схема, показывающая три последовательно включенных резистора

Общее сопротивление в последовательной цепи будет равно сумме каждого отдельного сопротивления в цепи.

Чем больше нагрузок помещено в цепь, тем больше сопротивление.

Общее сопротивление для последовательной цепи рассчитывается по следующей формуле:

R _T = R ₁ + R ₂ + R ₃

Закон напряжения Кирхгофа

Вольтметр на каждом резисторе в последовательной цепи t

Закон Кирхгофа расширяет закон Ома в отношении напряжений на сопротивлениях в последовательной цепи. Общее напряжение питания будет равно сумме падений напряжения на каждом резисторе.

Общее падение напряжения (В _T ) рассчитывается по формуле:

V _T = V ₁ + V ₂ + V ₃

Если известны как ток, так и каждое значение сопротивления, то можно использовать закон Ома для расчета падения напряжения на каждом резисторе.

Например:

В ₁ = IR ₁

Рассеиваемая мощность

Мощность, рассеиваемая в последовательной цепи, зависит от напряжения питания, приложенного к цепи, и тока, протекающего в цепи.Ток зависит от общего сопротивления цепи.

Из раздела о мощности вы знаете формулу рассеиваемой мощности:

P = VI

Мощность, рассеиваемая в каждом отдельном компоненте, зависит от сопротивления компонента. Общая рассеиваемая мощность будет равна сумме мощности, рассеиваемой каждым отдельным сопротивлением. В зависимости от известных значений комбинации формулы мощности, а также закона Ома могут использоваться для расчета рассеиваемой мощности (или любого другого неизвестного значения).

Пример

На приведенной выше принципиальной схеме, если значения:

В _Т = 20 В

R ₁ = 50 Ом

R ₂ = 20 Ом

R ₃ = 100 Ом

Общее сопротивление можно рассчитать следующим образом:

R _T = R ₁ + R ₂ + R ₃

R _T = 50 + 20 + 100

R _T = 170 Ом

Какая общая рассеиваемая мощность?

Вы можете рассчитать текущий расход, а затем рассчитать мощность.Вместо этого вы можете использовать подстановку, чтобы получить формулу.

В формуле P = VI замените I на V _T / R _T , чтобы получить формулу

P _T = V _T x V _T / R _T , что совпадает с

P _T = V _T ² / R _T

P _T = 20 ² /170

P _T = 0,235 Вт или 235 мВт

Введение в последовательные, параллельные и последовательно-параллельные соединения

Серия

, параллельные и последовательно-параллельные схемы, их сравнение и применения
Почему параллельное соединение предпочтительнее последовательного?

Сегодня невозможно переоценить использование, применение и важность последовательного и параллельного соединения цепей. Применение последовательного и параллельного подключения цепей можно увидеть в наших домах, школьных залах и в наших уличных фонарях. Одним нажатием кнопки включаются все качели в наших гостиных. некоторые говорят, что у бобов в их домах должны быть разные переключатели.

Что ж, это не волшебство, когда одним переключателем управляет более трех электрических бобов или нагрузок. Нагрузка – это что угодно, то есть это могут быть приборы, электрические качалки или даже потолочные вентиляторы, которые потребляют электроэнергию при подключении к источнику питания.Электрические бобы, телевизоры, холодильники и т. Д. Можно назвать грузом. Бобы преобразуют электрическую энергию в световую и тепловую форму энергии. Вентиляторы преобразуют электрическую энергию в механическую.

Тип подключения наших потолочных вентиляторов и электрических бобов определит, будут ли они иметь общий выключатель или нет. Последовательное соединение цепи дает нам возможность подключить более двух нагрузок к общему выключателю. Уличные фонари – очень хороший тому пример. Параллельное соединение цепи позволяет нам подключать нагрузки к их индивидуальному переключателю.Подходит как последовательное, так и параллельное соединение, но одно предпочтительнее другого по той или иной причине. Прежде чем мы поговорим о том, почему параллельное соединение предпочтительнее последовательного, давайте вспомним, какие последовательные и параллельные соединения являются первыми.

Последовательная цепь


Последовательная цепь – это цепь, в которой резисторы или нагрузки подключены встык, так что в цепи будет только один путь, по которому протекает электрический ток.Таким образом, когда несколько резисторов соединены последовательно, эффективное сопротивление (общее сопротивление в цепи) получается путем алгебраического сложения отдельных сопротивлений. То есть, если у нас есть резисторы с сопротивлением R1, R2, R3… Rn , соединенные последовательно , то;

R _eff = R _T = R ₁ + R ₂ + R ₃ +… R _n .

При последовательном соединении один и тот же ток течет по всем ветвям цепи, но разное напряжение на нем, что заставляет резисторы иметь разное напряжение на них.На каждом резисторе или нагрузке будет падение напряжения. Приложенное напряжение равно сумме падений напряжения на разных частях цепи. Падение напряжения пропорционально тому, что ток сопротивления одинаков во всей цепи. Когда нагрузки подключаются последовательно, они, как правило, имеют общий выключатель. Такой вид подключения используется в школьных залах, уличных фонарях.

Как подключить фары последовательно?
Использование и применение последовательного соединения

Некоторые люди подключают сигнальные огни в своих домах последовательно, что позволяет использовать общий выключатель.Проблема с таким типом подключения заключается в том, что при возникновении проблемы с нагрузкой другая подключенная система выйдет из строя. Это тип подключения по схеме “все или ничего”. Пока нагрузка не получит энергию до того, как она передаст ее другой, и одна из них не выйдет из строя, будет отключение электроэнергии.

Последовательные соединения схем распространены и широко используются в электрическом оборудовании. Нити трубки в небольших радиоприемниках обычно идут последовательно. Устройства управления током всегда подключаются последовательно с устройством, которое они защищают.Предохранители соединены последовательно с устройством, которое они защищают. Автоматическое отопительное оборудование имеет термостат, электромагнитные катушки и предохранительные выключатели, соединенные последовательно с источником напряжения и т. Д.

Недостатки последовательной цепи
• Разрыв в проводе отказ или удаление любой отдельной лампы приведет к разрыву цепи и приведению к прекращению работы всех остальных, поскольку в цепи протекает только один единственный путь тока.
• Если добавить в цепь последовательного освещения больше ламп, их яркость уменьшится.потому что напряжение распределяется по последовательной цепи. Если мы добавим больше нагрузок в последовательную цепь, падение напряжения возрастет, что не является хорошим признаком для защиты электроприборов.
Проводка серии
• представляет собой проводку типа «ВСЕ или НЕТ», что означает, что все устройства будут работать одновременно или все они отключатся, если произойдет сбой в любом из подключенных устройств в последовательной цепи.
• Высокое напряжение питания необходимо, если нам нужно добавить дополнительную нагрузку (лампочки, электрические обогреватели, кондиционер и т. Д.) В последовательную цепь.Например, если пять ламп 220 В должны быть подключены последовательно, то напряжение питания должно быть: 5 x 220 В = 1,1 кВ.
• Общее сопротивление последовательной цепи увеличивается (а ток уменьшается), когда в цепь добавляется дополнительная нагрузка.
• В соответствии с будущими потребностями, в последовательную цепь тока следует добавлять только те электроприборы, если они имеют тот же номинальный ток, что и ток, одинаковый в каждой точке последовательной цепи. Однако мы знаем, что электрические приборы и устройства i.е. лампочки, вентилятор, обогреватель, кондиционер и т. д. имеют разные номинальные токи, поэтому их нельзя подключать последовательно для бесперебойной и эффективной работы. Фары, подключенные последовательно
Преимущества последовательного подключения
• Меньше размер провода кабеля требуется при последовательном подключении.
• Мы используем для защиты цепи для последовательного подключения предохранителей и автоматических выключателей с другими приборами.
• Последовательная цепь не может легко получить накладные расходы из-за высокого сопротивления, когда в цепь добавляется дополнительная нагрузка.
• Срок службы батареи в последовательной цепи больше, чем в параллельной.
• Это самый простой метод подключения электропроводки, который позволяет легко обнаружить и устранить неисправность по сравнению с параллельным или последовательно-параллельным подключением.
Параллельная схема


Резисторы, нагрузки считаются подключенными параллельно, когда конец каждого из резисторов или нагрузок имеет общую точку или соединение, а другие концы также подключены к общей точке или переходу.Такие схемы известны как параллельные схемы.

Лампочки, подключенные параллельно

В отличие от последовательного подключения, при нахождении общего (эффективного) сопротивления в параллельной цепи берется величина, обратная отдельному сопротивлению. Таким образом, когда несколько сопротивлений соединены параллельно, величина, обратная величине эффективного сопротивления, определяется арифметической или алгебраической суммой величины, обратной величине отдельного сопротивления.

1 / R _eff или 1 / R _T = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ … 1 / R _n .

Параллельное соединение цепи имеет одинаковое напряжение, протекающее по всем ветвям цепи. У разных резисторов свои токи.

Использование и применение параллельного соединения

Параллельное соединение используется очень часто. Различные лампы и электроприборы в наших домах подключаются параллельно, так что каждая из ламп или бобышек и приборов может работать независимо. Чтобы мы могли управлять отдельными лампами или нагрузками, они должны быть подключены параллельно.

Преимущества параллельной схемы
• Каждое подключенное электрическое устройство и устройство не зависят от других. Таким образом, включение / выключение устройства не повлияет на другие устройства и их работу.
• В случае обрыва кабеля или удаления какой-либо лампы все цепи и подключенные нагрузки не разорвутся, другими словами, другие светильники / лампы и электроприборы по-прежнему будут работать без сбоев.
• Если добавить больше ламп в параллельные цепи освещения, их яркость не будет уменьшена (как это происходит только в цепях последовательного освещения).Потому что напряжение одинаково в каждой точке параллельной цепи. Короче говоря, они получают то же напряжение, что и напряжение источника.
• Можно добавить дополнительные осветительные приборы и точки нагрузки в параллельных цепях в соответствии с будущими потребностями, если цепь не будет перегружена.
• Добавление дополнительных устройств и компонентов не приведет к увеличению сопротивления, но уменьшит общее сопротивление цепи, особенно когда используются устройства с высоким номинальным током, такие как кондиционер и электрические нагреватели.
• параллельная проводка более надежна, безопасна и проста в использовании. Неисправности в параллельных цепях освещения.
• При добавлении дополнительной лампочки в параллельную цепь требуется больше тока.
• Батарея разряжается быстрее при установке постоянного тока.
• Схема параллельного подключения более сложна по сравнению с последовательным подключением.

Связанное сообщение: Какая лампа светится ярче при последовательном и параллельном подключении и почему?

Последовательно-параллельные соединения и схемы

Схема не является последовательной или параллельной на следующем рисунке, т.е. это последовательно-параллельная схема. Первые три лампы (B ₁ , B ₂ и B ₃ ) подключены параллельно, а переключатели (S ₁ , S ₂ и S ₃ ) подключены последовательно соответственно.B ₇ , B ₈ , B ₉ и B ₁₀ соединены последовательно друг с другом, в то время как они параллельны первым трем лампочкам (B ₁ , B ₂ и B ₃ ) в то время как переключатели (S5 и S6) подключены параллельно к лампе (B ₁₀ ). Кроме того, лампы (B ₄ , B ₅ и B ₆ ) и выключатель (S ₇ ) включены последовательно друг с другом, в то время как они параллельны (B ₁ , B ₂ и B ₃ ) и так далее.

Поскольку схема является комбинацией последовательной и параллельной, мы не можем упростить ток, напряжение, сопротивление и мощность с помощью простого закона Ома. Мы должны применить различные теоремы, такие как теоремы Нортона, Тевенина, теоремы о максимальной передаче мощности и т. Д., Или упростим схему в основных последовательных и параллельных схемах, чтобы найти все эти величины.

Наиболее распространенная в настоящее время установка бытовой электропроводки с использованием этого метода электропроводки.

Последовательная параллельная световая цепь и соединение
Сравнение последовательного и параллельного подключения

Ниже в данной таблице показаны основные различия между последовательным и параллельным подключением.

9 0128 Чтобы найти электрическую мощность (P)

S №	Последовательная цепь	Параллельная цепь
Ток (I)	Ток одинаковый в каждой точке последовательной цепи 9016 = 10002 I 2 = I 3 =…. I n	Ток аддитивен в последовательной цепи: I 1 + I 2 + I 3 +…. I n
Напряжение (В)	Напряжение складывается в последовательной цепи: В 1 + V 2 + V 3 +….V n	Напряжения одинаковы в каждой точке параллельной цепи: V 1 = V 2 = V 3 =…. V n
Сопротивление (R) и найти (R)	Сопротивления складываются в последовательной цепи: R 1 + R 2 + R 3 +… R n = R eff = R T	Сопротивление делится при увеличении нагрузки в цепи. 1 / R T = 1 / R 1 + 1 / R 2 + 1 / R 3 … 1 / R n или I = G 1 + G 2 + G 3 +… G n
Найти ток (I)	I = V 1 / R 1 = V 2 / R 2 = V 3 / R 3 = V n / R n	I = V 1 / R 1 + V 2 / R 2 + V 3 / R 3 + V n / R n
Найти напряжение (В)	V = I 1 R 1 + I 2 R 2 + I 3 R 3 +… I n R n	V = I 1 R 1 = I 2 R 2 = I 3 R 3 =… I n R n
P = I 2 R 1 + I 2 R 2 +… I 2 R n или P = V 1 2 / R 1 + V 2 2 / R 2 +… V n 2/ R n	P = V 2 1 + V 2 / R 2 +… V 2/ R n или P = I 1 2 R 1 + I 2 2 2 R 2 +… I n 2 R n
Правило делителя тока и напряжения	V 1 = V T (R 16 1 901 901 901 901 901 901 ), V 2 = V T (R 2 / R T )	I 1 = I T (G 1 / G T 901 70), I 2 = I T (G 2 / G T )
Пути прохождения электрического тока	Только один путь	Два или более пути
Яркость лампы	Диммер, если добавлено больше ламп (P = V x I)	Ярче из-за того же напряжения
При обрыве в цепи	Вся цепь бесполезна	Остальное цепь будет по-прежнему работать
Состояние батареи	Медленная разрядка батареи (Ач-номинал батареи)	Быстрая разрядка батареи (время работы и токи в ампер-часах)
Приложения	Используется для защиты цепи во время подключение предохранителей и автоматических выключателей последовательно с подключенными приборами	Используется в большинстве бытовых электропроводок

Преимущества параллельного соединения по сравнению с последовательным соединением

Последовательное соединение – это соединение всех или отсутствующих схем.Это означает, что если одно из устройств выйдет из строя, все другие устройства также выйдут из строя, поэтому этот тип подключения хорош только тогда, когда мы хотим защитить устройство. Когда плавкий предохранитель сгорает, например, из-за высокого тока, тогда устройство подключается к нему. защита не будет повреждена, потому что ток больше не будет достигать ее. В то время как последовательное соединение является полным или нулевым, параллельное соединение дает вам возможность дать нагрузкам и приборам их индивидуальный переключатель. Параллельное соединение обеспечивает сопротивление протеканию тока по сравнению с последовательным соединением.

Недостатки последовательной схемы освещения

Резисторы сопротивлением 100 Ом и 150 Ом, подключенные параллельно, будут иметь меньшее влияние на электрический ток по сравнению с резисторами 50 Ом и 40 Ом, подключенными последовательно. В электронных устройствах параллельное соединение имеет первостепенное значение. Все элементы в блоке питания подключены параллельно. Параллельное соединение продлевает срок службы электроэнергии. Сами элементы имеют свое внутреннее сопротивление, поэтому, если они были соединены последовательно, часть энергии будет потеряна, преодолевая внутреннее сопротивление, поскольку его влияние выше при последовательном подключении, чем при параллельном.

Связанные сообщения:


Цепь серии

– принцип работы, характеристики, применение, преимущество

Два типа цепей, которые обычно используются для подачи электроэнергии, – это последовательные цепи и параллельные цепи. Главный принцип любой электрической схемы – подача электричества на электрическое устройство. Эта статья дает вам представление о последовательной схеме, принципе работы, характеристиках последовательной схемы, приложениях, преимуществах и недостатках.

Что такое последовательная цепь

Цепь, в которой электричество должно проходить через все компоненты в цепи и не имеет альтернативного пути, называется последовательной цепью.

В этой схеме все компоненты соединены в один контур. Наиболее распространенный пример последовательной схемы – это необычные светильники или струнные светильники.




Рис. 1 – Пример последовательной схемы

Как построена последовательная схема (принцип работы)

Путь для потока электронов (электричества) называется схемой.Назначение любой электрической цепи – подавать электричество для прибора или любого другого электрического устройства. Эти устройства называются нагрузками. Прежде чем нагрузка сработает, электричество должно пройти определенный путь от источника к нагрузке и обратно к источнику.

На рисунке ниже показана типичная последовательная цепь, в которой резисторы (R1, R2, R3) последовательно подключаются, а конец одного резистора соединяется с другим концом следующего резистора, образуя петлю. Ток течет от отрицательной клеммы. батареи через резисторы, и, следовательно, ток одинаков во всех компонентах в последовательной цепи.

Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений. Напряжение на разных резисторах разное, а сумма падений напряжения на каждом компоненте (резисторе) равна приложенному напряжению. Разрыв в последовательной цепи остановит ток через цепь.

Рис. 2 – Схематическое изображение последовательной цепи

Характеристики последовательной цепи

Ниже приведены важные характеристики последовательных схем:

Сопротивление

R _T = R1 + R2 + R3 +…..R _n

Где R _T = общее сопротивление

Если R1 = 10 Ом, R2 = 20 Ом, R3 = 40 Ом

R _T = 10 + 20 + 40

R _T = 70 Ом

Ток

Предположим, что приложенное напряжение (В) = 10 В, тогда ток (I) можно рассчитать по формуле:

I = V / R = 10/70 = 1/7 Ампер = 0,1428 Ампер = 142,8 мА

I = 142,8 мА

Напряжение

Поскольку значения сопротивления и тока известны, напряжение можно рассчитать по формуле:

В = IR

Назовем напряжение на резисторе 1, 2, 3 как E _R1, E _R2 и E _R3 соответственно.

E _R1 = IxR1 = 0,142 x 10 = 1,42 В

E _R2 = IxR2 = 0,142 x 20 = 2,84 В

E _R3 = IxR42 = 0,18 v

Падение напряжения

Поскольку мы знаем, что сумма падений напряжения на каждом резисторе равна приложенному напряжению,

E _T = E _R1 + E _R2 + E _R3 = 1,42 + 2,84 + 5,68

= 9,94 В (с ошибкой округления) ≈ 10 В (приложенное напряжение)

Применения последовательной цепи

Применения последовательных схем включают:

• Последовательные резистивные цепи используются в маломощных схемы.
Цепи серии
• используются в схемах делителя напряжения.
Преимущества последовательной схемы

К преимуществам последовательной схемы относятся:

• Простота проектирования и изготовления схемы.
• Если компонент выходит из строя, ток прекращается.
• Он действует как регулятор тока.
• Стоимость построения последовательной цепи меньше по сравнению с параллельной схемой.
Недостатки последовательной цепи

К недостаткам последовательной схемы относятся:

• Если одна последовательная лампа перегорела, то в цепи не будет протекать ток.
• При увеличении нагрузки, т.е. при подключении большего количества лампочек, свет становится тусклее.

  Также прочтите:  
  Что такое цифровой вольтметр - как он работает, типы, применения, преимущества  
  Что такое технология Li-Fi - как это работает, приложения и преимущества  

Серия

и параллельные электрические соединения

Серия и параллельная

Есть 2 способа подключить несколько устройств к источнику питания (например,грамм. динамики к усилителю), последовательно и параллельно. Ну … Хорошо, есть еще последовательный / параллельный. Но мы расскажем об этом на следующей странице.

---

---

Серийные динамики

В последовательной цепи (как в двух вышеупомянутых) ток должен протекать через одно устройство, чтобы добраться до следующего устройства. Это означает, что скорость протекания тока через все устройства одинакова. Напряжение на каждом устройстве зависит от его полного сопротивления / сопротивления каждого устройства и тока, протекающего по цепи. При добавлении дополнительных компонентов в последовательную цепь ток уменьшается, если приложенное напряжение остается постоянным.

---

---

Параллельные динамики

В параллельной схеме (как в двух приведенных выше примерах) каждое устройство напрямую подключается к источнику питания. Это означает, что каждое устройство получает одинаковое напряжение. Величина тока, протекающего через каждое устройство, зависит от импеданса / сопротивления этого конкретного устройства. Если устройства добавляются к источнику питания в параллельной конфигурации, ток потребления / потока от источника питания увеличивается.

На 2 диаграммах ниже вы можете увидеть взаимосвязь между током, выходящим из усилителя, и количеством динамиков.Вы можете видеть, что четыре динамика потребляют от усилителя в два раза больше тока, чем конфигурация с двумя динамиками.


---

При подключении к любому источнику питания вы должны знать пределы источника, чтобы предотвратить повреждение источника. Это означает, что если вы подключите слишком много динамиков с параллельной проводкой к усилителю (в данном случае источнику питания), он может выйти из строя и не подлежит ремонту. Я видел, как это происходило, особенно когда усилитель был неправильно вставлен.


---

Для тех, кто хочет заниматься математикой …

На диаграммах / тексте выше у нас были либо последовательные ИЛИ параллельные цепи. В этом разделе показано, что происходит с напряжением, током и рассеиваемой мощностью в последовательной / параллельной цепи. Как было сказано ранее, в последовательной цепи «ток» в каждом устройстве одинаков. В параллельной цепи «напряжение» одинаково на каждом устройстве. На следующей схеме вы можете видеть, что два резистора на 1000 Ом последовательно соединены с одним резистором на 400 Ом.Мы знаем, что напряжение на двух резисторах 1000 Ом будет одинаковым (потому что они подключены параллельно). Мы также знаем, что общий ток, протекающий через два параллельно соединенных резистора, будет равен току, протекающему через резистор 400 Ом.

Чтобы рассчитать полный ток, сначала следует упростить схему. Это означает, что нам нужно найти полное сопротивление параллельной сети. Для простой схемы с двумя резисторами равного номинала мы можем просто разделить сопротивление отдельного компонента на общее количество компонентов.Для этой параллельной сети у нас есть два резистора по 1000 Ом.

Общее сопротивление параллельных резисторов = сопротивление отдельного компонента / количество резисторов
Общее сопротивление параллельных резисторов = 1000/2
Общее сопротивление параллельных резисторов = 500 Ом

Если бы у нас было 3 параллельных резистора, мы бы разделили 1000 на 3, чтобы найти общее сопротивление параллельных резисторов.

Общее сопротивление параллельных резисторов = 1000/3
Общее сопротивление параллельных резисторов = 333.33 …. Ом

Теперь, когда мы знаем, что параллельные резисторы равны одному резистору на 500 Ом. Теперь, когда у нас есть, по сути, один резистор на 500 Ом, соединенный последовательно с резистором на 400 Ом, мы можем рассчитать полный ток в цепи. Мы знаем, что у нас есть источник питания на 12 вольт. Мы также знаем, что резистор на 500 Ом, включенный последовательно с резистором на 400 Ом, равен резистору на 900 Ом.

Ток через цепь = напряжение в цепи / общее сопротивление цепи
Прохождение тока через цепь = 12/900
Прохождение тока через цепь = 0.0133 ампер


Теперь мы можем найти напряжение на отдельных компонентах. Чтобы избежать путаницы, сначала рассчитайте напряжение на единственном резисторе.

Напряжение на резисторе = сопротивление резистора * ток, протекающий через резистор
Напряжение на резисторе = 400 * 0,0133
Напряжение на резисторе = 5,333 вольт

В последовательной цепи все напряжения на всех отдельных компонентах серии будут равны напряжению источника питания.Если у нас есть источник 12 В, а напряжение на резисторе 400 Ом составляет 5,333 В, мы знаем, что напряжение на параллельной паре резисторов будет 6,67 В (12-5,333 = 6,67). Чтобы вычислить ток через параллельные компоненты …

Ток через один резистор 1000 Ом = напряжение на резисторе / сопротивление
Ток через один резистор 1000 Ом = 6,67 / 1000
Ток через один резистор 1000 Ом = 0,0067 ампера

Теперь, когда мы знаем напряжение на каждом из компонентов и ток через на каждом из компонентов, мы можем рассчитать рассеиваемую мощность для каждого компонента.На самом деле мы могли бы это сделать, как только узнали бы напряжение на компонентах, но я решил пойти по «живописному» маршруту.

Рассеиваемая мощность на резисторе 400 Ом = напряжение на компоненте * ток через компонент
Рассеиваемая мощность на резисторе 400 Ом = 5,33 * 0,013
Рассеиваемая мощность на резисторе 400 Ом = 0,071 Вт

Рассеиваемая мощность на каждом резисторе 1000 Ом = напряжение на компоненте * ток на компоненте
Рассеиваемая мощность на каждом резисторе 1000 Ом = 6.67 * .0067
Рассеиваемая мощность на каждом резисторе 1000 Ом = 0,045 Вт

В этом примере использовались резисторы, но те же вычисления будут работать для любого резистивного устройства. Хотя громкоговорители не являются чисто резистивными при работе с переменным напряжением, приведенные здесь расчеты можно использовать для грубых расчетов напряжения, тока и рассеиваемой мощности в громкоговорителях.

Последовательные и параллельные резисторы

Введение

Цепи постоянного тока (DC) характеризуются величинами тока, напряжения и сопротивления.Ток – это скорость потока заряда. Единица СИ – ампер (А). Условно направление тока – это направление потока заряда, хотя в металлических проводниках ток возникает из-за потока отрицательного заряда (электронов) в противоположном направлении. Из-за сохранения заряда ток одинаков во всех точках однопетлевой цепи. В точке ветвления в цепи, где проводящий путь разделяется на два или более, общий ток в точке ветвления равен полному току из этой точки.Обычно ток течет от положительной клеммы батареи или источника питания к отрицательной клемме. Для поддержания тока в цепи должен быть полный проводящий путь. Напряжение – это мера разности электрических потенциалов между двумя точками в цепи. Единица СИ – вольт (В). Поскольку электрическая сила является консервативной, сумма напряжений увеличивается и уменьшается вокруг любого замкнутого контура, она равна нулю. Сопротивление – это свойство элемента схемы (проводника) препятствовать прохождению тока.Сопротивление определяется где В, – напряжение на элементе схемы, а I, – ток, протекающий через него. Если R постоянно, то же самое для всех V , то элемент схемы подчиняется закону Ома. Единицей измерения сопротивления в системе СИ является ом (Ом). Сопротивление резистивного элемента цепи изменяется в зависимости от температуры. Два резистора R ₁ и R ₂ соединены последовательно, если весь ток, который проходит через R ₁ , также проходит через R ₂ .Следовательно, для двух последовательно соединенных резисторов ток от I ₁ до R ₁ совпадает с током от I ₂ до R ₂ , и этот ток такой же, как ток ток, I , который входит в последовательную сеть:

I = I ₁ = I ₂ .

Общее напряжение В в последовательной сети представляет собой сумму напряжений В ₁ и В ₂ на каждом резисторе.То есть

V = V ₁ + V ₂ .

Эквивалентное сопротивление, R _с , R ₁ и R ₂ последовательно определяется как Два резистора R ₁ и R ₂ подключены параллельно, если напряжения В ₁ и В ₂ на каждом из них одинаковы и равны напряжению В , через параллельную сеть.То есть

V = V ₁ = V ₂ .

Токи I ₁ и I ₂ через каждый из резисторов складываются, чтобы получить общий ток, I , текущий в сеть и из нее:

I = I ₁ + I ₂ .

Эквивалентное сопротивление R _p из R ₁ и R ₂ параллельно определяется выражением Это также можно записать как Амперметры используются для измерения тока.Амперметр подключается последовательно к цепи, так что весь измеряемый ток течет через амперметр. Следовательно, амперметры должны иметь очень маленькое сопротивление, чтобы не изменять ток в цепи. Вольтметры используются для измерения напряжений. Вольтметр подключается параллельно в двух точках, между которыми должна быть измерена разность потенциалов. Следовательно, вольтметр должен иметь большое сопротивление, чтобы через него проходил очень небольшой ток.

Цель

В этой лаборатории мы будем измерять и анализировать токи и напряжения для цепей, содержащих один резистор, а также для двух последовательно включенных резисторов и двух параллельно.

Аппарат

• Источник питания постоянного тока 0-40 вольт
• Лампочка на 12 вольт и розетка
• Резисторы 150 и 700 Ом
• Цифровой мультиметр

Процедура

Распечатайте лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.

Измерение напряжения

1

Блок питания является источником разности потенциалов (напряжения).Найдите источник питания постоянного тока за столом. Нажмите кнопку POWER ON / OFF в положение ON. Затем нажмите кнопку RANGE в положение IN (0,85 A). Это устанавливает источник питания в диапазоне 0-35 В / 0-0,85 А. Поверните ручку регулировки напряжения и тока ADJUST против часовой стрелки. Затем установите максимальный выходной ток для этого эксперимента, нажав кнопку CC Set и, удерживая ее, поверните текущую ручку ADJUST по часовой стрелке, пока на дисплее AMPS не появится 0.30 A. Отпустите кнопку CC Set . Не перемещайте ручку текущей настройки ( CC Set ) в любой момент во время эксперимента.

2

Мультиметр – это измерительное устройство, которое используется для измерения разности напряжений, электрических токов и электрических сопротивлений. Он также может измерять другие электрические свойства. См. Рис. 1. Вверху измерителя находится ЖК-дисплей (жидкокристаллический дисплей), в центре – переключатель функций / диапазонов (диск), а внизу – четыре входных разъема.

Примечание. Измеритель особенно чувствителен (и склонен к перегоранию предохранителя) при использовании входного разъема 200 мА (см. I в обозначении на Рисунке 1).

Ключ для рисунка 1:

• А

  3-1 / 2-разрядный ЖК-дисплей с сигнализаторами.

• В

  Кнопка ВКЛ / ВЫКЛ: включает и выключает питание измерителя.

• С

  Кнопка HI / LO: выбирает высокий или низкий уровень запуска для измерения частоты.

• D

  Кнопка MAX: выбирает функцию удержания максимального показания.

• E

  Кнопка DC / AC: выбирает напряжение постоянного или переменного тока.

• Ф

  Переключатель функции / диапазона: выбирает желаемую функцию и диапазон.

• G

  Входной разъем V Ω: входной разъем для напряжения, сопротивления, проверки диодов, целостности цепи, частоты и логики.

• H

  Входной разъем COM: входной разъем заземления.

• Я

  Входной разъем 200 мА: входной разъем для тока до 200 мА, L _x (индуктивность), C _x (емкость).

• Дж

  Входной разъем на 10 А: входной разъем для тока до 10 А.
Чтобы измерить заданное количество, циферблат должен находиться в соответствующем положении и должны использоваться соответствующие два входных разъема.Таким образом, при повороте шкалы для перехода от одного типа измерения к другому (например, от разности напряжений к электрическому току) вам, возможно, также придется изменить входные разъемы. При перегрузке предохранитель может перегореть.

Осторожно:
Для защиты счетчик гудит при перегрузке; если гудит, немедленно отсоедините провода счетчика!

Чтобы защитить измеритель от перегрузки при измерении неизвестного напряжения или тока, сначала необходимо установить измеритель на самый высокий масштаб для этой функции.Если показания недостаточно велики, чтобы дать по крайней мере три значащих цифры, шкалу следует переключить (если возможно) на такую, которая позволяет проводить точное измерение.

3

Чтобы включить мультиметр, нажимайте верхнюю левую кнопку на измерителе, пока на его циферблате не появится дисплей. Чтобы настроить мультиметр на измерение постоянного напряжения, В, , переключите верхнюю правую кнопку на постоянный ток. Убедитесь, что на дисплее глюкометра отображается постоянный ток. Установите переключатель функций / диапазонов в положение напряжения (В) и установите значение 20.Теперь измеритель настроен на считывание напряжений до 20 вольт постоянного тока. Подключите банан к банановым выводам к общему разъему (COM) и к разъему напряжения (V).

4

Подключите выводы мультиметра к клеммам + и – источника питания. См. Рисунок 2. На блоке питания поверните ручку регулировки напряжения ADJUST по часовой стрелке до тех пор, пока на дисплее вольт не отобразится 5,0 вольт. Сравните показания напряжения на мультиметре и на измерителе блока питания. Эти два показания могут не совпадать.Ожидается, что мультиметр будет точнее.

Ток и напряжение для одиночного резистора

1

Уменьшите напряжение источника питания (против часовой стрелки) до нуля вольт. Подключите блок питания к резистору на печатной плате с маркировкой 700 Ом. (Не перенастраивайте и не изменяйте настройку тока на источнике питания.) Мы будем использовать мультиметр для измерения постоянного тока через резистор 700 Ом в зависимости от приложенного напряжения. Для этого мы должны соединить мультиметр серии с резистором, чтобы одинаковый ток проходил через оба. Так как предохранитель легко перегорит, когда мультиметр настроен на текущую настройку, внимательно следуйте инструкциям. Установите шкалу мультиметра на шкалу тока 20 мА и подключите банановые штекеры к гнездам COM и мА на измерителе.

Осторожно:
Не повышайте напряжение на блоке питания, пока ТА не проверит вашу цепь.

2

После того, как ваш ТА даст добро, установите источник питания на 1 В и запишите в Таблице 1 ток через резистор, как показано на мультиметре.Повторите то же самое с источником питания, установленным на 2, 3, 4 и 5 вольт.

3

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Инструкции по построению графиков в Excel см. В приложении к интерактивному руководству лаборатории. Если вы получите ожидаемые результаты, данные будут располагаться близко к прямой линии, проходящей через начало координат. Используйте Excel, чтобы найти наклон прямой, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.

4

Используйте закон Ома и наклон графика, чтобы рассчитать сопротивление резистора R в единицах Ом (Ом). Запишите свой результат.

Ток и напряжение для лампочки

1

УСТАНОВИТЕ НАПРЯЖЕНИЕ ПИТАНИЯ НА НУЛЬ, но не выключайте питание. Не изменяйте текущую настройку источника питания ( CC Set ). Мы будем использовать мультиметр для измерения постоянного тока через лампочку в зависимости от приложенного напряжения.Для этого мы должны соединить мультиметр серии с лампочкой, чтобы одинаковый ток проходил через оба. Так как предохранитель легко перегорит, когда мультиметр настроен на текущую настройку, внимательно следуйте инструкциям.

2

Установите шкалу мультиметра на шкалу постоянного тока 10 А. Используйте входные гнезда COM и 10 A. Подключите схему, как показано на рисунке 3.

Осторожно:
Не повышайте напряжение на блоке питания, пока ТА не проверит вашу цепь.

3

После того, как ваш ТА даст добро, переключите напряжение питания на 2 вольта. В таблице 2 запишите текущие показания мультиметра. Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.

4

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Ожидается, что ваши данные не будут приближаться к прямой. Определите и вычислите R для каждого набора значений V и I в таблице 2 и запишите в третий столбец таблицы 2.Увеличивается ли R , уменьшается или остается на том же уровне, что и ток, I , через лампочку увеличивается?

Два резистора в серии

1

Подключите на печатной плате два резистора с маркировкой 150 Ом и 700 Ом, как показано на рисунке 4. Говорят, что они подключены последовательно, потому что весь ток, проходящий через один, также проходит через другой. Убедитесь, что напряжение источника питания установлено на ноль. Подключите источник питания к комбинации последовательных резисторов, как показано на рисунке 4.Установите блок питания на 5 вольт. Установите шкалу мультиметра на диапазон 20 В и используйте гнезда COM и V. С помощью мультиметра измерьте и запишите разности потенциалов (напряжение) В ₁₅₀ и В ₇₀₀ на каждом резисторе и напряжение В на комбинации из двух резисторов.

2

Когда вы закончите эти измерения, установите напряжение источника питания на ноль и отключите мультиметр от цепи.Что из следующего лучше отражает ваши результаты?

• •

  В = В ₁₅₀ + В ₇₀₀

• •

  В = В ₁₅₀ = В ₇₀₀

3

Когда напряжение источника питания установлено на ноль, подключите мультиметр последовательно с резисторами, как показано на рисунке 5. Установите мультиметр на диапазон постоянного тока 200 мА и подключите выводы мультиметра к правильным гнездам.

Осторожно:
Перед тем, как продолжить, попросите инструктора лаборатории проверить правильность настройки: предохранитель может перегореть, если измеритель не подключен к нужным точкам в цепи.

Получив добро от ТА, включите источник питания и установите его на 5 вольт. Измерьте ток в проводе между двумя резисторами, проводе между резистором 700 Ом и источником питания и проводе между резистором 150 Ом и источником питания.Убедитесь, что эти три тока равны.

4

Продолжая схему, показанную на рисунке 5, установите напряжение источника питания на 2 вольта. В таблице 3 запишите текущее показание мультиметра. Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.

5

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Используйте Excel, чтобы найти наклон прямой, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.

6

Используйте закон Ома и наклон графика, чтобы вычислить эквивалентное сопротивление, R _s , двух последовательно соединенных резисторов в единицах Ом (Ом). Запишите свой результат.

Два параллельных резистора

1

Подключите на печатной плате два резистора с маркировкой 150 Ом и 700 Ом, как показано на Рисунке 6a. Они считаются параллельными, поскольку напряжение на каждом резисторе равно напряжению источника питания, а резисторы обеспечивают параллельные пути для прохождения тока.

2

Убедитесь, что напряжение источника питания установлено на ноль. Подключите источник питания к комбинации параллельных резисторов, как показано на рисунке 6b. Установите блок питания на 5 вольт. С помощью мультиметра измерьте и запишите токи I ₁₅₀ и I ₇₀₀ , протекающие через каждый резистор, и общий ток, I , протекающий через источник питания.

3

Когда вы закончите эти измерения, установите напряжение источника питания на ноль и отключите мультиметр от цепи.

4

Что из следующего лучше отражает ваши результаты?

• •

  Я = Я ₁₅₀ + Я ₇₀₀

• •

  Я = Я ₁₅₀ = Я ₇₀₀

5

Продолжите параллельную сеть резисторов. Когда напряжение источника питания установлено на ноль, подключите мультиметр для измерения полного тока, I , протекающего через источник питания.Установите мультиметр на диапазон постоянного тока 200 мА.

Осторожно:
Перед тем, как продолжить, попросите инструктора лаборатории проверить правильность настройки: предохранитель может перегореть, если измеритель не подключен к нужным точкам в цепи.

Получив добро от ТА, включите источник питания и установите его на 2 вольта.

6

В таблице 4 запишите текущие показания мультиметра.Повторите эти действия для напряжений источника питания 4, 6, 8, 10 и 12 вольт.

7

Используйте Excel для построения графика данных с током по вертикальной оси и напряжением по горизонтальной оси. Используйте Excel, чтобы найти наклон прямой, который лучше всего соответствует вашим данным, и запишите результат, включая единицы измерения.

8

Используйте закон Ома и наклон графика, чтобы рассчитать эквивалентное сопротивление R _p двух параллельно включенных резисторов в единицах Ом (Ом).