Электрический конденсатор — Википедия
Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик
Слева — конденсаторы для поверхностного монтажа; справа — конденсаторы для объёмного монтажа; сверху — керамические; снизу — электролитические. На танталовых конденсаторах (слева) полоской обозначен «+», на алюминиевых (справа) маркируют «-».
SMD-конденсатор на плате, макрофотография 
Различные конденсаторы для объёмного монтажаКонденса́тор (от лат. condensare — «уплотнять», «сгущать» или от лат. condensatio — «накопление») — двухполюсник с постоянным или переменным значением ёмкости[1] и малой проводимостью; устройство для накопления заряда и энергии электрического поля.
Конденсатор является пассивным электронным компонентом. Ёмкость конденсатора измеряется в фарадах.
В 1745 году в Лейдене немецкий каноник Эвальд Юрген фон Клейст и независимо от него голландский физик Питер ван Мушенбрук изобрели конструкцию-прототип электрического конденсатора — «лейденскую банку»
Конденсатор является пассивным электронным компонентом[4]. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).
Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит зарядка или перезарядка конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.
В методе гидравлических аналогий конденсатор — это гибкая мембрана, вставленная в трубу. Анимация демонстрирует мембрану, которая растягивается и сокращается под действием потока воды, что аналогично заряду и разряду конденсатора под действием электрического токаС точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом
Z^C=1jωC=−jωC=−j2πfC,{\displaystyle {\hat {Z}}_{C}={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}=-{\frac {j}{2\pi fC}},}
где j{\displaystyle j} — мнимая единица, ω{\displaystyle \omega } — циклическая частота (радиан/с) протекающего синусоидального тока, f{\displaystyle f} — частота в герцах, C{\displaystyle C} — ёмкость конденсатора (фарад). Отсюда также следует, что реактивное сопротивление конденсатора равно XC=1ωC.{\displaystyle \scriptstyle X_{C}={\tfrac {1}{\omega C}}.} Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью C{\displaystyle C}, собственной индуктивностью Lc{\displaystyle L_{c}} и сопротивлением потерь Rn{\displaystyle R_{n}}.
Резонансная частота конденсатора равна
fp=12πLcC{\displaystyle f_{p}={\frac {1}{2\pi {\sqrt {L_{c}C}}}}}
При f>fp{\displaystyle f>f_{p}} конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f<fp{\displaystyle f<f_{p}}, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.
Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
W=CU22=qU2=q22C{\displaystyle W={CU^{2} \over 2}={qU \over 2}={q^{2} \over 2C}}
где U{\displaystyle U} — напряжение (разность потенциалов), до которого заряжен конденсатор, q{\displaystyle q} — электрический заряд на одной из обкладок.
Обозначение конденсаторов на схемах[править | править код]
В России для условных графических обозначений конденсаторов на схемах рекомендуется использовать ГОСТ 2.728-74[5] либо стандарт международной ассоциации IEEE 315—1975:
На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 1·106 пФ = 1·10−6 Ф) и пикофарадах (1 пФ = 1·10−12 Ф), но нередко и в нанофарадах (1 нФ = 1·10−9 Ф). При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения. Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мкФ × 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10—180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, то есть на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.
Характеристики[править | править код]
Ёмкость[править | править код]
Основной характеристикой конденсатора является его ёмкость, характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.
Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга, в системе СИ выражается формулой C=εε0Sd{\displaystyle C={\tfrac {\varepsilon \varepsilon _{0}S}{d}}}, где ε{\displaystyle \varepsilon } — диэлектрическая проницаемость среды, заполняющая пространство между пластинами (в вакууме равна единице), ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная, численно равная 8,854187817⋅10−12 Ф/м. Эта формула справедлива, лишь когда d намного меньше линейных размеров пластин.
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
C=∑i=1nCi{\displaystyle C=\sum _{i=1}^{n}C_{i}} или C=C1+C2+…+Cn.{\displaystyle C=C_{1}+C_{2}+\ldots +C_{n}.}
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.
При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна
1C=∑i=1n1Ci⇒C=(∑i=1n1Ci)−1{\displaystyle {\tfrac {1}{C}}=\sum _{i=1}^{n}{\tfrac {1}{C_{i}}}\Rightarrow C={\begin{pmatrix}\sum _{i=1}^{n}{\tfrac {1}{C_{i}}}\end{pmatrix}}^{-1}} или 1C=1C1+1C2+…+1Cn.{\displaystyle {\tfrac {1}{C}}={\tfrac {1}{C_{1}}}+{\tfrac {1}{C_{2}}}+\ldots +{\tfrac {1}{C_{n}}}.}
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.
Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.
Удельная ёмкость[править | править код]
Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
Плотность энергии[править | править код]
Плотность энергии электролитического конденсатора зависит от конструктивного исполнения. Максимальная плотность достигается у больших конденсаторов, где масса корпуса невелика по сравнению с массой обкладок и электролита. Например, у конденсатора EPCOS B4345 с ёмкостью 12 000 мкФ, максимально допустимым напряжением 450 В и массой 1,9 кг плотность энергии при максимальном напряжении составляет 639 Дж/кг или 845 Дж/л. Особенно важен этот параметр при использовании конденсатора в качестве накопителя энергии, с последующим мгновенным её высвобождением, например, в пушке Гаусса.
Номинальное напряжение[править | править код]
Другой не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах.
Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. Эксплуатационное напряжение на конденсаторе должно быть не выше номинального.
Полярность[править | править код]
Современные конденсаторы, разрушившиеся без взрыва благодаря специальной разрывающейся конструкции верхней крышки. Разрушение возможно из-за нарушения режима эксплуатации (температуры, напряжения, полярности) или старения. Конденсаторы с разорванной крышкой практически неработоспособны и требуют замены, а если она просто вздувшаяся, но ещё не разорвана, то, скорее всего, скоро он выйдет из строя или сильно изменятся параметры, что сделает его использование невозможным.Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.
Опасность разрушения (взрыва)[править | править код]
Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). В современных компьютерах перегрев конденсаторов — частая причина выхода их из строя вследствие близкого расположения с источниками тепла, например, рядом с радиатором охлаждения.
Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают вышибной предохранительный клапан или выполняют надсечку корпуса (часто её можно заметить в виде креста или в форме букв X, K или Т на торце цилиндрического корпуса, иногда, на больших конденсаторах, она покрыта пластиком). При повышении внутреннего давления вышибается пробка клапана или корпус разрушается по насечке, пары электролита выходят в виде едкого газа и, даже, брызг жидкости. При этом разрушение корпуса конденсатора происходит без взрыва, разбрасывания обкладок и сепаратора.
Взорвавшийся электролитический конденсатор на печатной плате жидкокристаллического монитора. Видны волокна бумажного сепаратора обкладок и развернувшиеся фольговые алюминиевые обкладки.Старые электролитические конденсаторы выпускались в герметичных корпусах и в конструкции их корпусов не предусматривалась взрывобезопасность. Скорость разлёта осколков при взрыве корпуса устаревших конденсаторов может быть достаточной для того, чтобы травмировать человека.
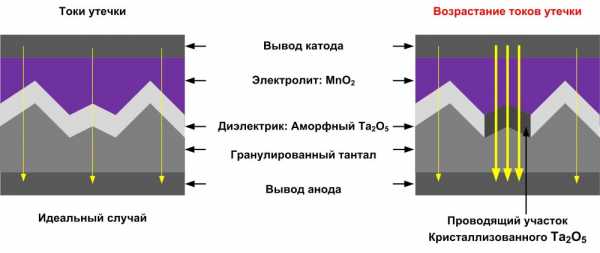
В отличие от электролитических, взрывоопасность оксиднополупроводниковых (танталовых) конденсаторов связана с тем, что такой конденсатор фактически представляет собой взрывчатую смесь: в качестве горючего служит тантал, а в качестве окислителя — двуокись марганца, и оба этих компонента в конструкции конденсатора перемешаны в виде тонкого порошка. При пробое конденсатора или при его случайной переполюсовке выделившееся при протекании тока тепло инициирует реакцию между данными компонентами, протекающую в виде сильной вспышки с хлопком, что сопровождается разбрасыванием искр и осколков корпуса. Сила такого взрыва довольно велика, особенно у крупных конденсаторов, и способна повредить не только соседние радиоэлементы, но и плату. При тесном расположении нескольких конденсаторов возможен прожог корпусов соседних конденсаторов, что приводит к одновременному взрыву всей группы.
Паразитные параметры[править | править код]
Реальные конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлением и индуктивностью. С достаточной для практики точностью, эквивалентную схему реального конденсатора можно представить как показано на рисунке, где все двухполюсники подразумеваются идеальными.
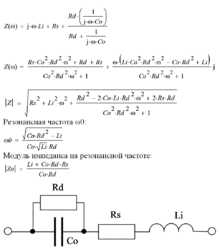Эквивалентная схема реального конденсатора и некоторые формулы.C0 — собственная ёмкость конденсатора;
Rd — сопротивление изоляции конденсатора;
Rs — эквивалентное последовательное сопротивление;
Li — эквивалентная последовательная индуктивность. Зависимость модуля импеданса реального конденсатора от частоты и формула импеданса.
Электрическое сопротивление изоляции диэлектрика конденсатора, поверхностные утечки и саморазряд[править | править код]
Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением Rd = U / Iут, где U — напряжение, приложенное к конденсатору, Iут — ток утечки.
Из-за тока утечки, протекающего через слой диэлектрика между обкладками и по поверхности диэлектрика, предварительно заряженный конденсатор с течением времени теряет заряд (саморазряд конденсатора). Часто, в спецификациях на конденсаторы, сопротивление утечки определяют через постоянную времени T саморазряда конденсатора, которая численно равна произведению ёмкости на сопротивление утечки:
- T=RdC0{\displaystyle T=R_{d}C_{0}}
T — это время, за которое начальное напряжение на конденсаторе, неподключенном ко внешней цепи уменьшится в e раз.
Хорошие конденсаторы с полимерными и керамическими диэлектриками имеют постоянные времени саморазряда достигающие многих сотен тысяч часов.
Эквивалентное последовательное сопротивление — Rs[править | править код]
Эквивалентное последовательное сопротивление (англ. Equivalent series resistance; ESR, ЭПС, внутреннее сопротивление) обусловлено, главным образом, электрическим сопротивлением материала обкладок и выводов конденсатора и контактов между ними, а также учитывает потери в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор, вследствие поверхностного эффекта.
В большинстве практических случаев этим параметром можно пренебречь, но, иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания), достаточно малое его значение существенно для надёжности и устойчивости работы устройства. В электролитических конденсаторах, где один из электродов является электролитом, этот параметр при эксплуатации со временем деградирует, вследствие испарения растворителя из жидкого электролита и изменения его химического состава, вызванного взаимодействием с металлическими обкладками, что происходит относительно быстро в низкокачественных изделиях («конденсаторная чума» [en]).
Некоторые схемы (например, стабилизаторы напряжения) критичны к диапазону изменения ЭПС конденсаторов в своих цепях. Это связано с тем, что при проектировании таких устройств инженеры учитывают этот параметр в фазочастотной характеристике (ФЧХ) обратной связи стабилизатора. Существенное изменение со временем ЭПС применённых конденсаторов изменяет ФЧХ, что может привести к снижению запаса устойчивости контуров авторегулирования, и, даже, к самовозбуждению.
Существуют специальные приборы (ESR-метр (англ.)) для измерения этого достаточно важного параметра конденсатора, по которому можно часто определить пригодность его дальнейшего использования в определённых целях. Этот параметр, кроме собственно ёмкости (ёмкость — это основной параметр) — часто имеет решающее значение в исследовании состояния старого конденсатора и принятия решения, стоит ли использовать его в определённой схеме, или он прогнозируемо выйдет за пределы допустимых отклонений.
Эквивалентная последовательная индуктивность — Li[править | править код]
Эквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. Результатом этой распределенной паразитной индуктивности является превращение конденсатора в колебательный контур с характерной собственной частотой резонанса. Эта частота может быть измерена и обычно указывается в параметрах конденсатора либо в явном виде либо в виде рекомендованной максимальной рабочей частоты.
Саморазряд[править | править код]
Предварительно заряженный конденсатор с течением времени теряет запасённую энергию за счёт тока утечки, протекающего через слой диэлектрика между обкладками. Часто в справочниках на конденсаторы приводится постоянная времени саморазряда конденсатора, численно равная произведению ёмкости на сопротивление утечки. Это время, за которое начальное напряжение на отключенном конденсаторе уменьшится в e раз.
Тангенс угла диэлектрических потерь[править | править код]
Тангенс угла диэлектрических потерь — отношение мнимой и вещественной части комплексной диэлектрической проницаемости. tgδ=εimεre=σωεa.{\displaystyle {\rm {{tg}\,\delta ={\frac {\varepsilon _{im}}{\varepsilon _{re}}}={\frac {\sigma }{\omega \varepsilon _{a}}}.}}}
Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол φ=π2−δ,{\displaystyle \scriptstyle \varphi ={\tfrac {\pi }{2}}-\delta ,} где δ — угол диэлектрических потерь. При отсутствии потерь δ = 0. Тангенс угла потерь определяется отношением активной мощности
Температурный коэффициент ёмкости (ТКЕ)[править | править код]
ТКЕ — относительное изменение ёмкости при изменении температуры окружающей среды на один градус Цельсия (кельвин). ТКЕ определяется так:
- TKE=ΔCCΔT{\displaystyle TKE={\frac {\Delta C}{C\Delta T}}}.
где
ru.wikipedia.org
Напряжение пробоя конденсатора
Адрес: Москва, Сокольническая пл. Пробивное и рабочее напряжения конденсатора. Если напряжение между пластинами конденсатора превысит этот предел, произойдет пробой диэлектрика, помещенного между пластинами. При пробое диэлектрика через него проскакивает искра, которая разрушает диэлектрик, обугливая его. А так как уголь является проводником, пластины конденсатора оказываются соединенными между собой и конденсатор выходит из строя.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Конденсатор в цепи переменного токаИзмеритель емкости конденсаторов
Мастера, ремонтирующие радиоаппаратуру, чаще всего сталкиваются с пробоем конденсаторов либо со снижением емкости.
Чтобы узнать, исправна деталь или нет, надо измерить емкость конденсатора. Для этого существуют различные приборы. Конденсатор содержит две обкладки из металла, между которыми помещается диэлектрик. Для диэлектрика используются воздух, пластик, слюда, картон, керамические материалы. В более современных деталях вместо металла применяется фольга, которую сворачивают в рулоны. Таким образом, при меньших габаритах конденсатора можно повысить его емкость.
Конденсаторы классифицируются по диэлектрическому материалу, способам монтажа, форме обкладок и т. По полярности они делятся на:. Электролитические конденсаторные элементы требуют обязательного соблюдения полярности при включении. Диэлектриком в них служит оксидный слой, формирующийся на танталовом алюминиевом аноде. Катод — электролит в виде жидкости или геля.
Измерение емкости конденсатора такого типа должно проводиться, учитывая маркировку полюсов детали. Основное свойство конденсатора — накопление электрического заряда, благодаря которому он широко используется в различных фильтрах. С его помощью можно передавать сигнал между каскадами усиления, разделять высокие и низкие частоты и т. Различают несколько видов неисправностей конденсаторов, влияющих на работу электрической схемы:.
В большинстве случаев детали выходят из строя по причине продолжительной работы в условиях перегрева. Всегда важно обеспечить оптимальный режим температур для работы аппаратуры. На первом этапе надо сделать визуальный осмотр детали на наличие механических повреждений, деформации корпуса, изменения цвета. У электролитических элементов это разбухание в верхней части, которое может быть небольшим, но заметным в сравнении с исправными аналогами.
Зачастую деталь внешне выглядит нормально. Тогда для ее проверки потребуются специальные приборы:. Используя мультиметр, иногда трудно сделать вывод о неисправности, так как емкость поврежденного конденсаторного элемента снижается на очень малые величины. С помощью LC-метров или специальных приборов определить ее значение можно точнее. Причем замеры производятся без выпаивания деталей из схемы.
Если нет специального прибора, то емкостные замеры неполярных элементов можно производить мультиметром, измеряющим сопротивление. При этом они выпаиваются из платы. У конденсаторов с малой емкостью процесс изменения сопротивления ускорен так, что можно его не зафиксировать. Плавное нарастание сопротивления наблюдается из-за зарядки детали от батареи мультиметра.
Можно применить для емкостных замеров и старые аналоговые тестеры. При этом наблюдения ведутся за движениями стрелки. Она должна сразу отклониться вправо со скоростью, зависящей от конденсаторной емкости, продолжая свое медленное движение до пределов шкалы. Если она не дергается или, отклонившись, останавливается, это говорит о повреждении. О том же сигнализирует резкий бросок до предельных цифр.
Проверке мультиметром можно подвергнуть конденсаторные элементы емкостью до 0,25 мкФ. Для меньших параметров проверка ведется на LC-метрах. Вышеописанным способом невозможно определить количественные емкостные значения, можно только сделать вывод об исправности конденсаторного элемента. По приборам, измеряющим емкость в фарадах, сразу определяется ее отклонение от номинального параметра. Нулевое значение говорит о пробое, сниженное — тоже сигнализирует о том, что деталь нужно заменить.
Опосредованно о величине емкости можно судить по скорости нарастания сопротивления в момент подключения к мультиметру. Чем она ниже, тем больше емкость. Вывод делается на основании сравнения с испытываемым конденсаторным элементом.
Вместо них могут присутствовать обыкновенные щупы. Для измерения конденсаторные элементы вставляются в эти разъемы с обязательным соблюдением полярности у электролитических деталей. Маркировка присутствует и на самих конденсаторах. Для неполярных элементов это не имеет значения. Предельное значение шкалы измеряемой емкости надо выставлять, исходя из конденсаторных параметров. Перед подсоединением к прибору необходимо снять остаточный заряд с конденсатора.
ESR означает эквивалентное последовательное сопротивление, параметр очень важный для электролитического конденсатора. Когда это сопротивление увеличивается, зарядный ток уменьшается, что вызывает сбои в работе электрической цепи. Причем емкость, измеренная традиционными способами, может не выходить из границ нормы.
Особенно влияние эквивалентного сопротивления заметно у деталей емкостью больше 5 мкФ. Для стабильной работы параметр не должен превышать 1 Ом. При проверке конденсаторных элементов без выпаивания из платы такой аппарат дает более точные результаты.
Попытки аналогично замерить параметры детали мультиметром не дадут достоверной картины. Рядом с конденсатором существуют другие элементы: индуктивности, сопротивления и т. Обычно делают вывод об исправности конденсаторного элемента с помощью косвенных измерений либо параллельно ему припаивают другой с идентичными характеристиками.
Это возможно только в низковольтных цепях. Мастерам-радиолюбителям может встретиться случай, когда все характеристики конденсатора в норме при замере мультиметром, но при работе в схеме наблюдаются признаки его пробоя. Это происходит при снижении напряжения пробоя ниже номинальной величины. Если деталь рассчитана на напряжение 25 В, а пробой наступает при 15 В, то при измерении мультиметром не будет выявлена неисправность конденсаторного элемента, так как пробой имеет обратимый характер.
Для определения такой неисправности надо использовать источник постоянного тока с возможностью регулировать уровень напряжения. Подключив к нему деталь и постепенно увеличивая подводимое напряжение, выясняется наличие повреждения, заметное по резкому возрастанию тока вплоть до срабатывания защитного отключения ИП. Измерения конденсаторной емкости можно проводить разными способами. Просто обнаружить неисправный элемент можно омметром, более точные результаты получаются при использовании LC-метров и приборов ESR.
RU – интернет-энциклопедия про всё, что связано с домашней электрикой: выключатели, розетки, лампочки, люстры, проводка. Советы, инструкции и наглядные примеры.
Вы точно человек?
Рассмотрены возможные неисправности конденсаторов, способы проверки при помощи подручных средств и приборов. Как показывает практика ремонта за последние годы, наибольшее число отказов аппаратуры происходит по вине электролитических конденсаторов. При этом наблюдается снижение числа отказов по вине других компонентов. Здесь будут перечислены основные виды неисправностей конденсаторов, и способы их выявления.
Какое напряжение у этих конденсаторов? . во время проверки он, скорее всего, просто пробьётся, хотя и покажет напряжения пробоя.
Керамические конденсаторы MLCC: особенности применения
Как это делается? Мы принимаем формат Sprint-Layout 6! Экспорт в Gerber из Sprint-Layout 6. Обозначений напряжения на конденсаторах нет. Верхняя буква у последних трех, судя по таблице, никак не может быть напряжением, а буква после номинала – допуск. Конденсаторы Panasonic. Часть 4.
Научный форум dxdy
Пробой конденсатора может произойти не только через толщину диэлектрика, но и по поверхности закраин перекрытие ; поэтому необходимо рассмотреть вопрос о поверхностном пробое. Пробой конденсатора может быть вызван перенапряжением, в результате которого происходит пробой изоляции и закорачивание обкладок конденсатора между собой. Замыкание пластин, чаще всего встречающееся в переменных конденсаторах, может произойти в результате механических воздействий на них. Утечка конденсаторов появляется вследствие повышенного их нагрева, из-за чего сопротивление изоляции снижается и конденсатор начинает пропускать постоянный ток. Изменение номинального значения емкости может произойти в результате длительной работы конденсатора и пребывания его в различных температурных условиях.
На страницу Пред. Мне непонятно, почему емкость равна , а точнее, почему она зависит от расстояния.
Территория электротехнической информации WEBSOR
Последний раз редактировалось Nikolay1 В моем школьном учебнике написано: “При большей напряженности диэлектрик становится проводящим”. Электроемкость конденсатора высчитывается по формуле: Но напряженность, создаваемая двумя пластинами, однородна. В чем смысл тогда этой формулы. В том, что эти вещи пробой диэлектрика, определение ёмкости, однородность поля никак не связаны. Потом, однородным будет поле между двумя бесконечными равномерно заряжеными пластинами, а между конечными — только приближённо, и тем дальше от однородного, чем меньше отношение их размера к расстоянию между ними.
Как проверить конденсатор, неисправности конденсаторов и их устранение
В основу классификации конденсаторов положено деление их на группы по виду применяемого диэлектрика и по конструктивным особенностям. Сокращенное обозначение конденсатора состоит из букв и цифр. Первый элемент обозначения – буква или сочетание букв – обозначает подкласс конденсатора: К – постоянной емкости, КТ – подстроечные, КП – переменной емкости. Второй элемент означает группу конденсаторов в зависимости от вида диэлектрика табл. Третий элемент пишется через дефис и соответствует порядковому номеру разработки. В состав второго и третьего элементов могут входить буквы. Таблица 2.
Большинство отказов конденсаторов происходит из-за пробоя и перекрытия , пробой конденсатора, если он происходит при рабочем напряжении.
Удивительный конденсатор SMD 1206 10мкФ / 50В
По сути ремонт любой радиоэлектронной аппаратуры сводится к поиску и замене неисправных деталей. И, возможно, вы удивитесь тому, насколько часто выходят из строя такие, казалось бы, простые компоненты как конденсаторы. В то время как нежные диоды, чувствительные транзисторы и сложные микросхемы остаются целыми и невредимыми.
Дневники Файлы Справка Социальные группы Все разделы прочитаны. Увеличение напряжения пробоя конденсатора, путем последовательного подключения. Оценка 0. Крупнейшее в Китае предприятие по производству прототипов печатных плат, более , клиентов и более 10, онлайн-заказов ежедневно. Литиевые батарейки Fanso для систем телеметрии и дистанционного контроля. Системы телеметрии находят все более широкое применение во многих отраслях на промышленных и коммунальных объектах.
Пробивное напряжение конденсатора составляет В.
Однако не многие знают компанию DUCATI Energia, изготавливающую современные пленочные конденсаторы, используемые в силовой электронике. В обзоре приведены сведения о технологии производства полипропиленовых конденсаторов, их основные технические параметры, номенклатура и области применения. Это означает, что они способны восстановить свои электрические свойства после короткого замыкания внутри диэлектрика. К этой категории относятся конденсаторы серий GP, GP рис. Максимально допустимое значение скорости нарастания периодически изменяющегося рабочего напряжения. Справедливо следующее соотношение:. Соответствующая внешняя схема защиты, которая должна быть предусмотрена пользователем, немедленно отключает конденсатор.
Мастера, ремонтирующие радиоаппаратуру, чаще всего сталкиваются с пробоем конденсаторов либо со снижением емкости. Чтобы узнать, исправна деталь или нет, надо измерить емкость конденсатора. Для этого существуют различные приборы. Конденсатор содержит две обкладки из металла, между которыми помещается диэлектрик.
all-audio.pro
Пробивное и рабочее напряжения конденсатора. Сопротивление утечки конденсатора
Deprecated: Non-static method Date_TimeZone::isValidID() should not be called statically, assuming $this from incompatible context in /home/carkey/hitech/hardtech/kernel/pear/date/Date.php on line 576
Notice: Undefined offset: 1 in /home/carkey/hitech/hardtech/kernel/common/common/common.class.php on line 343
Notice: Undefined offset: 1 in /home/carkey/hitech/hardtech/kernel/common/common/common.class.php on line 343
Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
Deprecated: mysql_escape_string(): This function is deprecated; use mysql_real_escape_string() instead. in /home/carkey/hitech/hardtech/kernel/common/db/mysql.class.php on line 135
Для каждого конденсатора существует предельное напряжение, до которого его можно зарядить. Если напряжение между пластинами конденсатора превысит этот предел, произойдет пробой диэлектрика, помещенного между пластинами. При пробое диэлектрика через него проскакивает искра, которая разрушает диэлектрик, обугливая его. А так как уголь является проводником, пластины конденсатора оказываются соединенными между собой и конденсатор выходит из строя. Напряжение, при котором происходит пробой диэлектрика, называется пробивным напряжением конденсатора. Пробивное напряжение конденсатора зависит от свойств диэлектрика и от его толщины. Чем больше толщина диэлектрика, тем большее напряжение он может выдержать. Зависимость пробивного напряжения от свойств диэлектрика характеризуется электрической прочностью диэлектрика. Электрической прочностью называют такое напряжение, при котором происходит пробой слоя данного диэлектрика толщиной 1 мм. Электрическую прочность выражают в киловольтах на миллиметр.
Конденсаторы, в которых изолятором между пластинами является воздух, не портятся после пробоя, поэтому их часто используют в поселениях, далеко от города, примером может послужить коттеджный поселок в Подмосковье. Наибольшее напряжение, которое кратковременно выдерживает конденсатор, не пробиваясь, называется испытательным напряжением конденсатора. Под таким напряжением конденсаторы испытывают после изготовления на заводе. Испытательное напряжение иногда указывается на корпусе конденсатора. На каждом конденсаторе указывается его рабочее напряжение. Рабочим напряжением конденсатора называется такое напряжение, при котором конденсатор может длительное время надежно работать не пробиваясь. Рабочее напряжение устанавливается обычно в 2-3 раза меньше испытательного, чтобы случайные броски напряжения, которые всегда могут быть, не вывели конденсатор из строя. Пробой диэлектрика может произойти не только между пластинами конденсатора, но и между любыми двумя проводниками, если между ними действует высокое напряжение. Чем выше напряжение, тем труднее предотвратить пробой. Нашим ученым и инженерам пришлось разрешить целый ряд сложных вопросов для предотвращения пробоя изоляторов на строящихся линиях передачи электрической энергии между Куйбышевом, Сталинградом и Москвой, где напряжение будет 400 000 е. Провода будут подвешены на стальных мачтах при помощи гирлянд изоляторов длиной 6 м.
Сопротивление утечки конденсатора. Как уже упоминалось, не существует в природе таких изоляторов, которые бы совершенно не пропускали тока. Поэтому, если конденсатор зарядить, то в диэлектрике будет проходить очень малый ток, разряжающий конденсатор. Этот ток называется токомутечки. Сопротивление, которое оказывает конденсатор току утечки, называется сопротивлением утечки. Сопротивление утечки конденсатора должно иметь очень большую величину. Чем больше сопротивление утечки, тем лучше конденсатор. Обычно сопротивление утечки имеет величину в несколько сотен или даже тысяч мегом. Сопротивление утечки измеряют приборами, предназначенными для измерения больших сопротивлений. Такие приборы называются мегомметрами.
Наша продукция
…
Warning: Unknown: Failed to write session data (files). Please verify that the current setting of session.save_path is correct (/opt/alt/php56/var/lib/php/session) in Unknown on line 0
www.hardtech.ru
Конденсатор | Класс робототехники
Электрический конденсатор (англ. capacitor) — это устройство, которое может накапливать электрический заряд и хранить его некоторое время. Конденсаторы можно найти практически в любом электронном устройстве. Они бывают разных типов и размеров.
На электрических схемах конденсаторы обозначают двумя параллельными черточками. При этом, у полярных конденсаторов около положительного электрода дополнительно ставится плюсик.Для чего нужен конденсатор?
У этого прибора есть множество применений. Мы не будем перечислять их все, отметим лишь некоторые. 1) Фильтрация пульсаций в цепях питания. Конденсаторы часто ставят на входе и выходе преобразователей напряжения, на входе питания микросхем. В этом случае конденсаторы служат своего рода амортизаторами, которые могут сгладить неровности напряжения, подобно амортизаторам автомобиля, сглаживающим неровности дороги. 2) Времязадающие электрические цепи. Конденсаторы разной ёмкости заряжаются и разряжаются за разное время. Эту особенность используют в устройствах, где необходимо отсчитывать определенные промежутки времени. Например, с помощью резистора и конденсатора задается период и скважность импульса в микросхеме таймера 555 (урок про таймер 555). 3) Датчики прикосновения. В роли одной из обкладок конденсатора может выступить человек. Эту особенность нашего тела используют в своей работе сенсорные кнопки, тачскрины и тачпады некоторых видов. 4) Хранение данных. Конденсаторы применяются для хранения данных в оперативной памяти — ОЗУ (SRAM). Каждый модуль такой памяти содержит миллиарды отдельных конденсаторов, которые могут быть заряжены или разряжены, что интерпретируется как единица или ноль. И это далеко не все варианты применения этого незаменимого прибора. Попробуем разобраться, как устройство конденсатора позволяет ему выполнять столько полезных функций!Устройство простейшего конденсатора
Конденсатор состоит их двух металлических пластин — электродов, называемых также обкладками, между которыми находится тонкий слой диэлектрика. Собственно, все конденсаторы устроены именно таким (или почти таким) образом, разве что меняется материал обкладок и диэлектрика. Чтобы увеличить ёмкость конденсатора, не увеличивая его размеры, применяют разные хитрости. Например, если мы возьмем две обкладки в виде длинных полосок фольги, проложим между ними хотя бы тот же полиэтилен и свернем все это как рулет, то получится очень компактный прибор с большой ёмкостью. Именно так устроены плёночные конденсаторы. Если вместо полиэтилена взять бумагу и пропитать её электролитом, то на поверхности фольги образуется тонкий слой оксида, который не проводит ток. Такой конденсатор будет называться электролитическим.
Существует много разных видов конденсаторов: бумажные, плёночные, оксидные алюминиевые и танталовые, вакуумные и т.п. В нашем уроке мы будем использовать оксидные электролитические конденсаторы из-за их большой ёмкости и доступности.Полярные и неполярные конденсаторы
Очень важным является разделение конденсаторов на полярные и неполярные. Приборы на основе оксидов: электролитические алюминиевые и танталовые обычно являются полярными, а значит если перепутать их полярность — они выйдут из строя. Причём этот выход из строя будет сопровождаться бурной электрохимической реакций вплоть до взрыва конденсатора.
На полярных конденсаторах всегда имеется маркировка. Как правило на электролитических конденсаторах на корпусе контрастной полосой отмечается отрицательный вывод (катод), у танталовых (в желтых прямоугольных корпусах) полоской помечается положительный вывод (анод). Если есть сомнения в маркировке, то лучше найти документацию на этот конденсатор и убедиться. Неполярные же конденсаторы можно включать в цепь какой угодно стороной. К примеру, многослойные керамические конденсаторы — неполярные.Ёмкость и напряжение конденсатора
Теперь обратим внимание на две важные характеристики конденсатора: ёмкость и номинальное напряжение. Ёмкость конденсатора характеризует способность конденсатора накапливать заряд. Это как ёмкость банки, в которой хранится, к примеру, вода. Кстати, не зря одним из первых электрических конденсаторов была так называемая Лейденская банка. Она представляла собой обыкновенную стеклянную посуду, снаружи обмотанную фольгой. В банку была налита токопроводящая жидкость — электролит. Фольга и электролит играли роль обкладок, а стекло банки служило тем самым диэлектрическим барьером. Ёмкость электрического конденсатора измеряют в фарадах. В схемах ёмкость обозначают латинской буквой C. Как правило, ёмкость классических конденсаторов варьируется от нескольких пикофарад (пФ) до нескольких тысяч микрофарад (мкФ). Ёмкость указывается на корпусе конденсатора. Если единицы не указаны — то это пикофарады. Микрофарады часто обозначают как uF — так как буква u внешне похожа на греческую букву мю, которую используют вместо приставки микро. Существует и особый вид конденсаторов, называемых ионисторами (англ. supercapacitor), которые имеют ёмкость в несколько фарад! Чем больше ёмкость конденсатора, тем больше энергии в нём может храниться и тем дольше он заряжается, при прочих равных условиях. Номинальное напряжение — второй важный параметр. Это такое напряжение, при котором конденсатор будет работать весь срок службы без критичного изменения своих параметров. Нельзя применять в 12-вольтовой цепи конденсатор на 6 вольт — он быстро выйдет из строя. Именно эти два параметра обычно наносят на поверхность корпуса конденсатора. На фотографии ниже изображён электролитический конденсатор ёмкостью 470 мкФ и номинальным напряжением 16 Вольт.
А вот на керамических конденсаторах часто указывают только ёмкость. На картинке ниже конденсатор имеет маркировку 104. Что бы это значило? 
Последняя цифра в этом коде — количество нулей после двухзначного числа в начале. 104 = 10 0000 пФ = 100 нФ = 0,1 мкФПараллельное и последовательное подключение конденсаторов
Как и в случае резисторов, конденсаторы можно составлять в цепочки. Это бывает нужно, когда в схеме необходима какая-то конкретная ёмкость, а у вас нет такого конденсатора. Параллельное подключение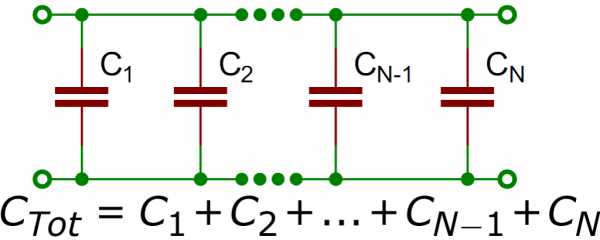
В отличие от резисторов, при параллельном подключении конденсаторов их ёмкости складываются. Например, если нам нужно получить ёмкость 3000 мкФ, а у нас есть два конденсатора по 1000 мкФ, и 10 штук по 100 мкФ, смело ставим их параллельно и получаем: 1000*2+100*10 = 2000 + 1000 = 3000 мкФ Последовательно подключение При последовательном подключении конденсаторы ведут себя как резисторы, соединённые параллельно. Например, посчитаем суммарную ёмкость двух конденсаторов на 100 мкФ, соединённых последовательно: Суммарная ёмкость Ctot = 50 мкФ.Заряд и разряд конденсатора — RC-цепочка
Теперь разберёмся с процессами, происходящими внутри конденсатора во время заряда и разряда. Для этого рассмотрим самую простую электрическую цепь с конденсатором. С левой стороны схемы подключим источник питания. Сверху разместим ключ и резистор, а справа сам конденсатор. Участок цепи, на котором есть конденсатор и резистор называют RC-цепью.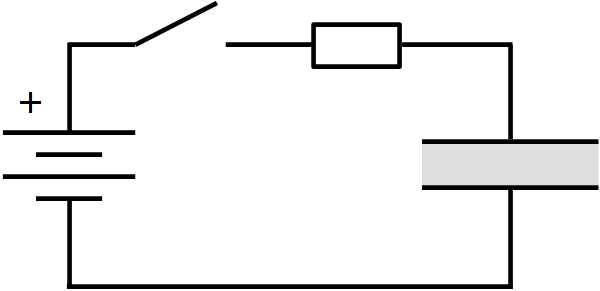
При замыкании ключа, в такой цепи образуется электрический ток, сила которого зависит от сопротивления резистора и внутреннего сопротивления самого конденсатора. Заряженные частицы устремятся к конденсатору, но не смогут преодолеть слой диэлектрика (по крайней мере все разом). Вследствие чего, с одной стороны конденсатора накопятся отрицательно заряженные частицы, а с другой стороны — положительно заряженные. Концентрация заряженных частиц на обкладках создаст мощное электрическое поле между ними. 
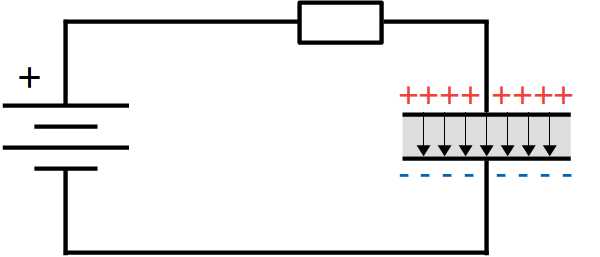С течением времени, напряжение на конденсаторе растет, а сила тока падает. После завершения процесса заряда, ток в цепи упадет почти до нуля. Останется только очень маленький ток утечки, который образуется благодаря тому, что некоторым заряженным частицам всё же удается проскочить через слой диэлектрика. Напряжение, напротив, станет практически равным напряжению источника. Когда мы отключим конденсатор от источника питания, этот самый ток утечки постепенно разрядит конденсатор. Эта особенность электрических конденсаторов не даёт нам сделать из них контейнер для длительного хранения энергии. Хотя частично эту проблему решают ионисторы.Резистор и время заряда конденсатора
Зачем в цепи нужен резистор? Что на мешает подключить его напрямую к источнику? Тому есть две причины. Резистор ограничивает ток, протекающий через конденсатор. Чем меньше заряженных частиц за единицу времени прибывает в конденсатор, тем больше времени для заряда ему потребуется. Конденсатор заряжается и разряжается по экспоненциальному закону. Зная это, мы можем легко рассчитать время заряда/разряда в зависимости от его ёмкости и от сопротивления резистора.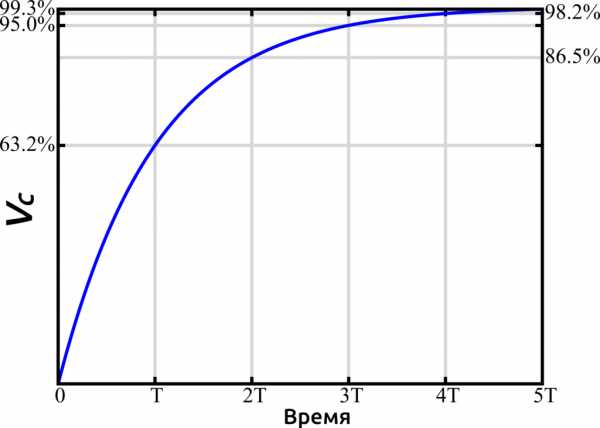
По картинке можно понять, что за время T конденсатор заряжается на 63,2%. А вот за время 3T уже на 95%. Время T здесь равно произведению ёмкости конденсатора C на сопротивление R, последовательно соединенного резистора: Например, у нас есть конденсатор ёмкостью 100 мкФ, соединенный с резистором 1 кОм. Посчитаем за сколько секунд он зарядится хотя бы до 95%: Теперь умножаем это на 3 и получаем 3T = 0,3 секунды — за такое время конденсатор почти полностью будет заряжен. Таким образом, меняя ёмкость конденсатора и резистора мы можем управлять временем его заряда, что нам ещё пригодится в будущем. Вторая важная причина, по которой в цепи присутствует резистор — защита источника питания. Дело в том, что разряженные конденсаторы имеют очень низкое внутреннее сопротивление, которое составляет доли Ома. По сути, их можно рассматривать как обычные проводники. А что будет, если замкнуть выводы питания проводником? Будет короткое замыкание! Такой режим работы цепи является аварийным для источника питания, и его нужно всячески избегать.Плавное выключение светодиода при помощи конденсатора
Проведем небольшой опыт. Для этого соберем на макетной плате цепь с кнопкой, конденсатором и светодиодом. В качестве источника питания используем контакты питания Ардуино Уно. Принципиальная схема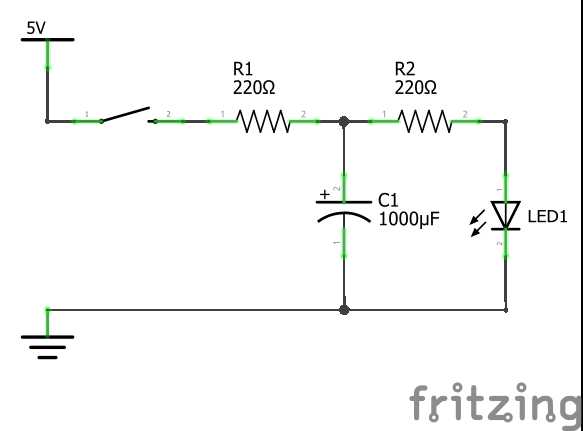
Внешний вид макета 
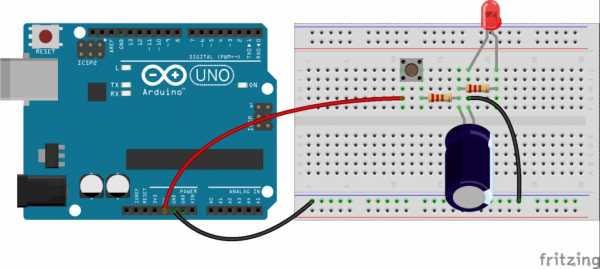Подключим Ардуино к питанию. Затем, нажмем кнопку и светодиод практически мгновенно загорится. Отпустим кнопку — светодиод медленно начнет гаснуть. Почему так происходит? Сразу после подключения нашей схемы к источнику питания, в ней начинают происходит интересные процессы. Как уже говорилось ранее, пока конденсатор пустой, ток через него максимален. Следовательно, конденсатор начинает стремительно набирать заряд. При этом светодиоду, который подключен параллельно, ничего не достается 🙁 Напряжение на нем близко к нулю. С течением времени конденсатор насыщается, благодаря чему ток начинает постепенно переходить в параллельную цепь — через светодиод. Напряжение на светодиоде начинает расти. Наступает момент, когда напряжение на светодиоде принимает критическое значение (для красного светодиода около 1,8 В), при котором он стремительно отбирает остатки тока у конденсатора и вспыхивает! Когда мы отпускаем кнопку, ситуация становится гораздо проще. Конденсатор становится источником питания для светодиода с резистором. Светодиод начинает медленно высасывать заряд из конденсатора, пока тот не разрядится. Тут мы и наблюдаем медленно угасание. Меняя сопротивление R1, мы можем влиять на скорость вспыхивания светодиода. Однако, следует учитывать, что увеличивая R1 мы будем снижать ток в цепи, тем самым уменьшая максимальный заряд конденсатора и яркость светодиода. Увеличивая C1, мы получим более длительное время работы светодиода после выключения источника. Это как поставить более ёмкую батарейку. Наконец, меняя R2 можно регулировать яркость светодиода, и соответственно, время его работы. Ведь чем меньше тока мы забираем из конденсатора, тем на большее время его хватит.Заключение
Итак, мы познакомились с конденсатором — интересным и порой опасным жителем любой электронной платы. В следующих уроках уделим внимание резистору и индуктивности, а также более сложному их собрату — транзистору.Вконтакте
robotclass.ru
Конденсатор
Конденсатор состоит из двух пластин (или обкладок), находящихся одна перед другой и сделанных из проводящего материала. Между пластинами находится изолирующий материал, называемый диэлектриком (рис. 4.1). Простейшими диэлектриками являются воздух, бумага, слюда и т. д.
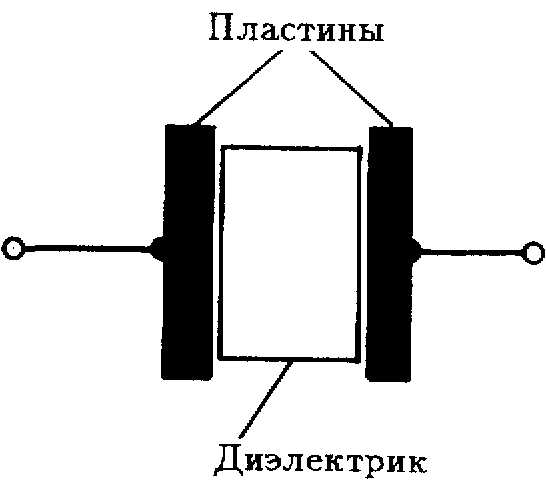
Рис. 4.1. Конденсатор
Зарядка конденсатора
Основным свойством конденсатора является его способность запасать электрическую энергию в виде электрического заряда.
На рис. 4.2(а) изображена схема, в которой конденсатор соединяется через ключ с источником питания. Когда ключ замкнут (рис. 4.2(б)), положительный полюс источника «откачивает» электроны с обкладки А, и она приобретает положительный заряд. Отрицательный полюс источника питания тем временем «поставляет» электроны на обкладку В, в результате чего она приобретает отрицательный заряд, по абсолютной величине равный положительному заряду обкладки А. Такой поток электронов называется током заряда. Он продолжает течь до тех пор, пока напряжение на конденсаторе не сравняется с ЭДС источника питания. В этом случае говорят, что конденсатор полностью заряжен. Электрический заряд обозначается буквой Q, а его величина измеряется в кулонах (Кл).
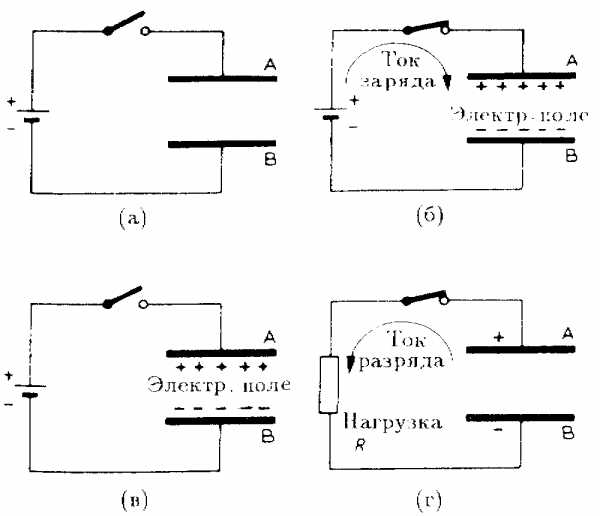
Рис. 4.2. Заряд и разряд конденсатора
Когда конденсатор заряжен, между его обкладками возникает разность потенциалов, а следовательно, и электрическое поле.
Если в момент, когда конденсатор уже зарядился, разомкнуть ключ (рис. 4.2(в)), конденсатор будет хранить заряд. В этом случае внутри диэлектрика между обкладками возникает электрическое поле. При разряде конденсатора через сопротивление нагрузки (рис. 4.2(г)) электрическое ноле исчезает.
Емкость конденсатора
Способность конденсатора накапливать электрический заряд называется емкостью, а величина этой емкости обозначается буквой С и измеряется в фарадах (Ф). Фарада — очень большая единица емкости, и поэтому она практически не используется. Чаще используются дробные единицы:
1 микрофарада (мкФ) = Ф = 10-6 Ф,
1 пикофарада (пФ) = мкФ = 10-6 мкФ = 10-12 Ф.
Емкость конденсатора возрастает с увеличением площади обкладок и убывает с увеличением расстояния между ними.
Например, при возрастании площади обкладок вдвое емкость также увеличивается в два раза. Если же увеличить вдвое расстояние между обкладками, емкость станет вдвое меньше.
Связь заряда, емкости и напряжения
Если конденсатор заряжен до разности потенциалов V , его заряд определяется формулой Q=CV
где С выражается в фарадах, V – в вольтах, а Q – в кулонах. Преобразовав эту формулу, получим:
Энергия заряженного конденсатора
Энергия W, запасенная конденсатором, определяется формулой
где W выражается в джоулях, С – в фарадах, а V — в вольтах.
Параллельное и последовательное соединение конденсаторов
Если два конденсатора, С1 и С2, соединены параллельно (рис. 4.3(а)), результирующая емкость СТ такого соединения равна сумме емкостей этих конденсаторов:
Если конденсаторы соединены последовательно (рис. 4.3(б)), результирующая емкость СТ оказывается меньше емкости любого из конденсаторов я выражается формулой
Например, если С1 = С2, то результирующая емкость СТ последовательного соединения равна половине емкости любого из конденсаторов:
Напряжение на последовательно соединенных конденсаторах
На схеме, показанной на рис. 4.4, конденсаторы С1 и С2 соединены последовательно и подключены к источнику постоянного напряжения VТ. Полное напряжение VТ будет поделено между С1 и С2 таким образом, что на конденсаторе меньшей емкости установится большее напряжение,
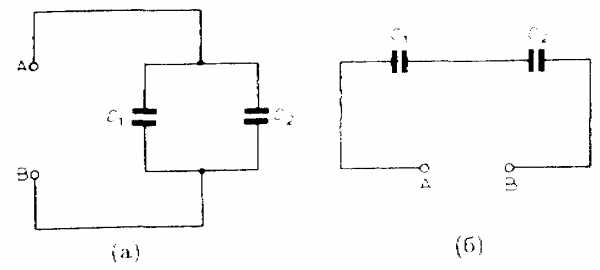
Рис. 4.3. Параллельное (а) и последовательное (б) соединение конденсаторов.
Рис. 4.4. Напряжение на конденсаторах при их последовательном соединении
и наоборот.
Сумма V1 (напряжения на С1) и V2 (напряжения на С2) всегда равна полному напряжению VТ.
В общем случае, когда несколько конденсаторов, соединенных последовательно, подключено к источнику постоянного тока, напряжение на каждом из конденсаторов обратно пропорционально его емкости. При последовательном соединении двух конденсаторов напряжения на С1 и С2 соответственно равны
Пример 1
Определим результирующую емкость цепи, изображенной на рис. 4.5. Результирующая емкость параллельного соединения равна
С2 + С3 = 10 + 20 = 30 пФ
Поскольку емкость С1 также равна 30 пФ, то результирующая емкость всей цепи равна ½*30 = 15 пФ.
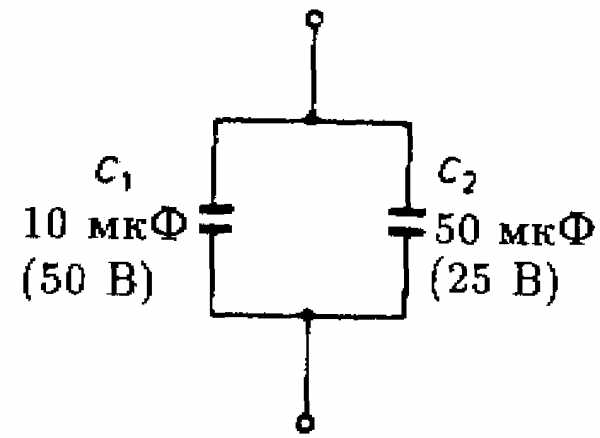
Рис. 4.6. Рис. 4.7.
Пример 2
На рис. 4.6 напряжение на конденсаторе С1 равно
откуда напряжение на С2 равно 30 – 20 = 10 В.
Рабочее напряжение
Любой конденсатор характеризуется некоторым максимальным напряжением, при превышении которого наступает пробой диэлектрика. Это напряжение называется рабочим, или номинальным, напряжением конденсатора, и подаваемое на конденсатор напряжение ни в коем случае не должно его превышать. При использовании конденсатора в цепях переменного тока амплитудное значение напряжения в цепи также не должно превышать рабочего напряжения конденсатора. Рабочим напряжением для батареи конденсаторов, соединенных параллельно, является наименьшее из рабочих напряжений конденсаторов, входящих в схему, Например, рабочее напряжение для цепи, изображенной на рис. 4.7, равно 25 В.
Для конденсаторов, соединенных последовательно, рабочее напряжение подбирать труднее. Рассмотрим схему на рис. 4.8. Конденсатор С1 (1 мкФ, рабочее напряжение Vраб = 25 В) соединен последовательно с конденсатором С2 (10 мкФ, Vраб = 10 В). Поскольку на конденсаторе С1, обладающем меньшей емкостью, установится большее напряжение, чем на С2, то при расчетах следует прежде всего иметь в виду рабочее напряжение конденсатора С1, равное 25 В. Таким образом, V1 = 25 В. соотношения V1/ V2 = С1/ С2 следует, что
Поскольку рабочее напряжение конденсатора С2 выше, чем V2, рабочее напряжение данной батареи конденсаторов равно 25 + 2,5 = 27,5 В.
Следует заметить, что если бы рабочее напряжение конденсатора было равно, например, 2 В, как показано на рис. 4.9, то он зарядился бы
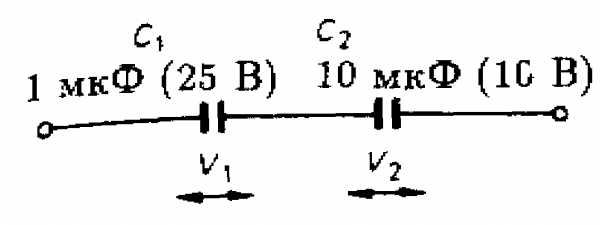
Рис. 4.8. Рис. 4.9.
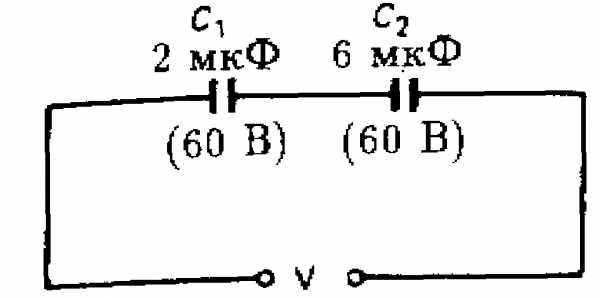
Рис. 4.10. Рис. 4.11. Катушка индуктивности
до уровня рабочего напряжения прежде, чем напряжение на конденсаторе С1 достигло бы 25 В. Вот расчет для этого случая:
V2 = 2 В, тогда.
Следовательно, рабочее напряжение такой батареи будет составлять 20 + 2 = 22 В.
Пример 3
Конденсаторы С1 и С2, изображенные на рис. 4.10, имеют каждый рабочее напряжение 60 В. Какое максимальное напряжение может быть приложено к этой схеме?
Решение
Поскольку на конденсаторе С1 установится более высокое напряжение, чем на конденсаторе С2, то напряжение на нем раньше достигнет уровня рабочего напряжения. При V1 = 60 В
Максимальное напряжение, которое может быть подано на данную схему, составляет 60 + 20 = 80 В.
В этом видео рассказывается о понятии конденсатора:
Добавить комментарий
radiolubitel.net
Конденсатор и RC цепочка | Электроника для всех
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.
О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:
Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Ток через резистор определяется законом ома — I=U/R, где U напряжение на выводах резистора, R — его сопротивление.
Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику. Получается интересная зависимость — есть ток, нет напряжения, есть напряжение — нет тока.
Чтобы визуализировать себе этот процесс, представь ган… эмм.. воздушный шарик который наполняется водой. Поток воды — это ток. Давление воды на упругие стенки — эквивалент напряжения. Теперь смотри, когда шарик пуст — вода втекает свободно, большой ток, а давления еще почти нет — напряжение мало. Потом, когда шарик наполнится и начнет сопротивляться давлению, за счет упругости стенок, то скорость потока замедлится, а потом и вовсе остановится — силы сравнялись, конденсатор зарядился. Есть напряжение натянутых стенок, но нет тока!
 |
Теперь, если снять или уменьшить внешнее давление, убрать источник питания, то вода под действием упругости хлынет обратно. Также и ток из конденсатора потечет обратно если цепь будет замкнута, а напряжение источника ниже чем напряжение в конденсаторе.
Емкость конденсатора. Что это?
Теоретически, в любой идеальный конденсатор можно закачать заряд бесконечного размера. Просто наш шарик сильней растянется и стенки создадут большее давление, бесконечно большое давление.
А что же тогда насчет Фарад, что пишут на боку конденсатора в качестве показателя емкости? А это всего лишь зависимость напряжения от заряда (q = CU). У конденсатора малой емкости рост напряжения от заряда будет выше.
Представь два стакана с бесконечно высокими стенками. Один узкий, как пробирка, другой широкий, как тазик. Уровень воды в них — это напряжение. Площадь дна — емкость. И в тот и в другой можно набузолить один и тот же литр воды — равный заряд. Но в пробирке уровень подскочит на несколько метров, А в тазике будет плескаться у самого дна. Также и в конденсаторах с малой и большой емкостью.
Залить то можно сколько угодно, но напряжение будет разным.
Плюс в реале у конденсаторов есть пробивное напряжение, после которого он перестает быть конденсатором, а превращается в годный проводник 🙂
А как быстро заряжается конденсатор?
В идеальных условиях, когда у нас бесконечно мощный источник напряжения с нулевым внутренним сопротивлением, идеальные сверхпроводящие провода и абсолютно безупречный конденсатор — этот процесс будет происходить мгновенно, с временем равным 0, равно как и разряд.
Но в реальности всегда существуют сопротивления, явные — вроде банального резистора или неявные, такие как сопротивление проводов или внутреннее сопротивление источника напряжения.
В этом случае скорость заряда конденсатора будет зависить от сопротивлений в цепи и емкости кондера, а сам заряд будет идти по экспоненциальному закону.
 |
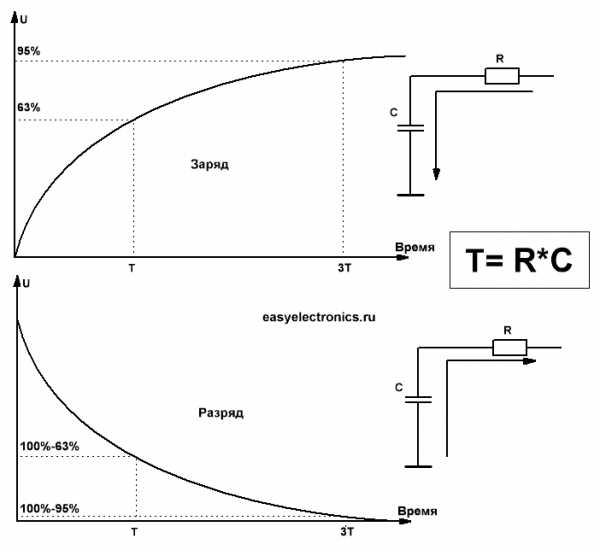А у этого закона есть пара характерных величин:
- Т — постоянная времени, это время при котором величина достигнет 63% от своего максимума. 63% тут взялись не случайно, тут прямая завязка на такую формулу VALUET=max—1/e*max.
- 3T — а при троекратной постоянной значение достигнет 95% своего максимума.
Постоянная времени для RC цепи Т=R*C.
Чем меньше сопротивление и меньше емкость, тем быстрей конденсатор заряжается. Если сопротивление равно нулю, то и время заряда равно нулю.
Рассчитаем за сколько зарядится на 95% конденсатор емкостью 1uF через резистор в 1кОм:
T= C*R = 10-6 * 103 = 0.001c
3T = 0.003c через такое время напряжение на конденсаторе достигнет 95% от напряжения источника.
Разряд пойдет по тому же закону, только вверх ногами. Т.е. через Твремени в на конденсаторе остаенется всего лишь 100% — 63% = 37% от первоначального напряжения, а через 3T и того меньше — жалкие 5%.
Ну с подачей и снятием напряжения все ясно. А если напряжение подали, а потом еще ступенчато подняли, а разряжали также ступеньками? Ситуация тут практически не изменится — поднялось напряжение, конденсатор дозарядился до него по тому же закону, с той же постоянной времени — через время 3Т его напряжение будет на 95% от нового максимума.
Чуть понизилось — подразрядился и через время 3Т напряжение на нем будет на 5% выше нового минимума.
Да что я тебе говорю, лучше показать. Сварганил тут в мультисиме хитровыдрюченный генератор ступечнатого сигнала и подал на интегрирующую RC цепочку:
 |
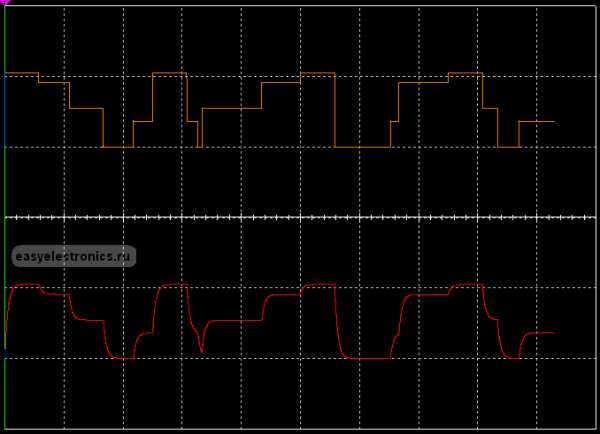Видишь как колбасится 🙂 Обрати внимание, что и заряд и разряд, вне зависимости от высоты ступеньки, всегда одной длительности!!!
А до какой величины конденсатор можно зарядить?
В теории до бесконечности, этакий шарик с бесконечно тянущимися стенками. В реале же шарик рано или поздно лопнет, а конденсатор пробьет и закоротит. Вот поэтому у всех конденсаторов есть важный параметр — предельное напряжение. На электролитах его часто пишут сбоку, а на керамических его надо смотреть в справочниках. Но там оно обычно от 50 вольт. В общем, выбирая кондер надо следить, чтобы его предельное напряжение было не ниже того которое в цепи. Добавлю что при расчете конденсатора на переменное напряжение следует выбирать предельное напряжение в 1.4 раза выше. Т.к. на переменном напряжении указывают действующее значение, а мгновенное значение в своем максимуме превышает его в 1.4 раза.
Что следует из вышеперечисленного? А то что если на конденсатор подать постоянное напряжение, то он просто зарядится и все. На этом веселье закончится.
А если подать переменное? То очевидно, что он будет то заряжаться, то разряжаться, а в цепи будет туда и обратно гулять ток. Движуха! Ток есть!
Выходит, несмотря на физический обрыв цепи между обкладками, через конденсатор легко протекает переменный ток, а вот постоянному слабо.
Что нам это дает? А то что конденсатор может служить своего рода сепаратором, для разделения переменного тока и постоянного на соответствующие составляющие.
Любой изменяющийся во времени сигнал можно представить как сумму двух составляющих — переменной и постоянной.
 |
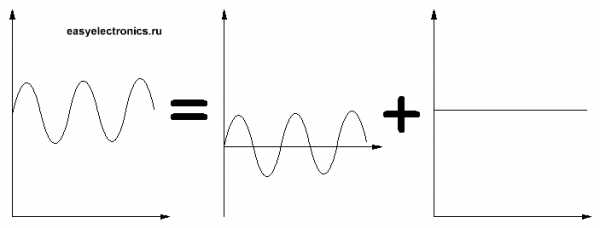Например, у классической синусоиды есть только переменная часть, а постоянная равна нулю. У постоянного же тока наоборот. А если у нас сдвинутая синусоида? Или постоянная с помехами?
Переменная и постоянная составляющие сигнала легко разделяются!
Чуть выше я тебе показал как конденсатор дозаряжается и подразряжается при изменениях напряжения. Так что переменная составляющая сквозь кондер пройдет на ура, т.к. только она заставляет конденсатор активно менять свой заряд. Постоянная же как была так и останется и застрянет на конденсаторе.
Но чтобы конденсатор эффективно разделял переменную составляющую от постоянной частота переменной составляющей должна быть не ниже чем 1/T
Возможны два вида включения RC цепочки:
Интегрирующая и дифференцирующая. Они же фильтр низких частот и фильтр высоких частот.
Фильтр низких частот без изменений пропускает постоянную составляющую (т.к. ее частота равна нулю, ниже некуда) и подавляет все что выше чем 1/T. Постоянная составляющая проходит напрямую, а переменная составляющая через конденсатор гасится на землю.
Такой фильтр еще называют интегрирующей цепочкой потому, что сигнал на выходе как бы интегрируется. Помнишь что такое интеграл? Площадь под кривой! Вот тут она и получается на выходе.
Как здесь вычисляется постоянная составляющая? А с виду и не скажешь, но надо помнить, что любой периодически сигнал раскладывается в ряд Фурье, превращаясь в сумму из постоянной составляющей и пачки синусоид разной частоты и амплитуды.
Фильтр высоких частот работает наоборот. Он не пускает постоянную составляющую (т.к. ее частота слишком низка — 0) — ведь конденсатор для нее равносилен обрыву, а вот переменная пролазит через кондер без проблем.
А дифференцирующей цепью ее называют потому, что на выходе у нас получается дифференциал входной функции, который есть не что иное как скорость изменения этой функции.
- На участке 1 происходит заряд конденсатора, а значит через него идет ток и на резисторе будет падение напряжения.
- На участке 2 происходит резкое увеличение скорости заряда, а значит и ток резко возрастет, а за ним и падение напряжения на резисторе.
- На участке 3 конденсатор просто удерживает уже имеющийся потенциал. Ток через него не идет, а значит на резисторе напряжение тоже равно нулю.
- Ну и на 4м участке конденсатор начал разряжаться, т.к. входной сигнал стал ниже чем его напряжение. Ток пошел в обратную сторону и на резисторе уже отрицательное падение напряжения.
А если подать на вход прямоугольнй импульс, с очень крутыми фронтами и сделать емкость конденсатора помельче, то увидим вот такие иголки:
 |
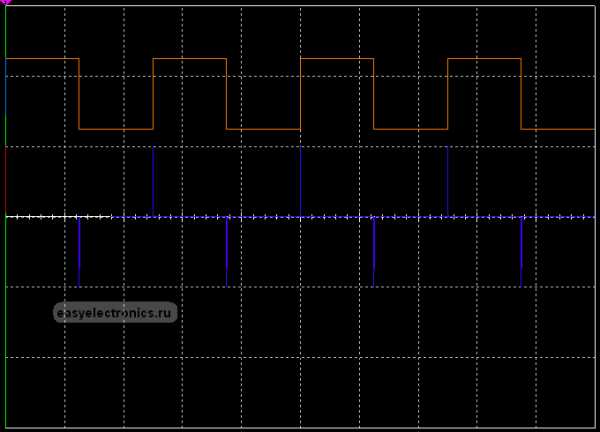Вверху идет осциллограма того что на входе, внизу то что на выходе дифференциальной цепи.
Как видишь, тут мощные всплески на фронтах. Оно и понятно, в этом месте функция меняется резко, а значит производная (скорость изменения) этой функции велика, на пологих участках сигнал константа и его производная, скорость изменения, равна нулю — на графике ноль.
А если загнать в дифференциатор пилу, то на выходе получим…
 |
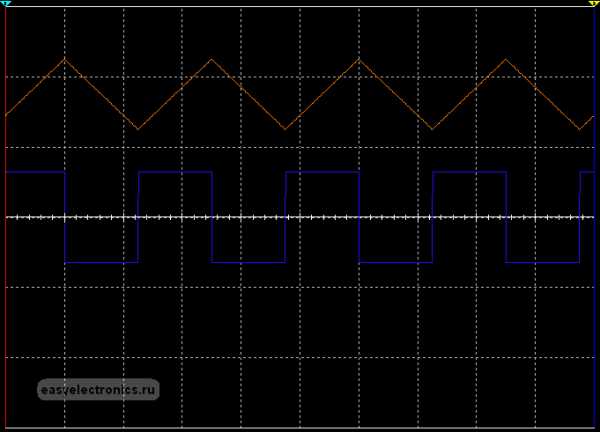прямоугольник. Ну, а чо? Правильно — производная от линейной функции есть константа, наклон этой функции определяет знак константы.
Короче, если у тебя сейчас идет курс матана, то можешь забить на богомерзкий Mathcad, отвратный Maple, выбросить из головы матричную ересь Матлаба и, достав из загашников горсть аналоговой рассыпухи, спаять себе истинно ТРУЪ аналоговый компьютер 🙂 Препод будет в шоке 🙂
Правда на одних только резисторах кондерах интеграторы и диффернциаторы обычно не делают, тут юзают операционные усилители. Можешь пока погуглить на предмет этих штуковин, любопытная вещь 🙂
А вот тут я подал обычный приямоугольный сигнал на два фильтра высоких и низких частот. А выходы с них на осциллограф:
И вот что получилось на осциллографе:
 |
Вот, чуть покрупней один участок:
 | >
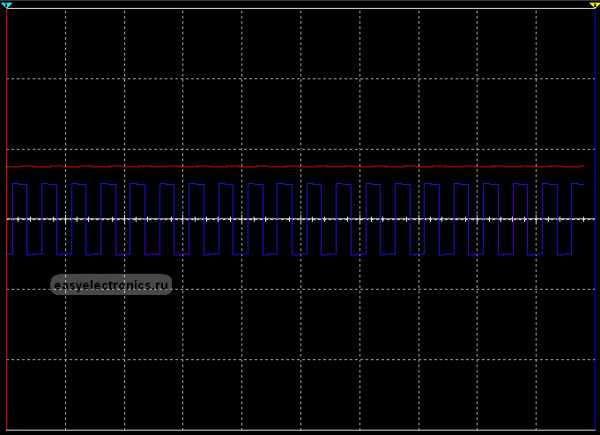Как видишь, на одном срезало постоянную составляющую, на другом переменную.
Ладно, что то мы отвлеклись от темы.
Как еще можно применить RC цепь?
Да способов много. Часто ее используют не только в качестве фильтров, но и как формирователи импульсов. Например, на сбросе контроллера AVR, если надо чтобы МК стартанул не сразу после включения питания, а с некоторой выдержкой:
 |
При старте кондер разряжен, ток через него вваливат на полную, а напряжение на нем мизерное — на входе RESET сигнал сброса. Но вскоре конденсатор зарядится и через время Т его напряжение будет уже на уровне логической единицы и на RESET перестанет подаваться сигнал сброса — МК стартанет.
А для AT89C51 надо с точностью наоборот RESET организовать — вначале подать единицу, а потом ноль. Тут ситуация обратная — пока кондер не заряжен, то ток через него течет большой, Uc — падение напряжения на нем мизерное Uc=0. А значит на RESET подается напряжение немногим меньше напряжения питания Uпит-Uc=Uпит.
Но когда кондер зарядится и напряжение на нем достигнет напряжения питания (Uпит=Uс), то на выводе RESET уже будет Uпит-Uc=0
Аналоговые измерения
Но фиг сними с цепочками сброса, куда прикольней использовать возможность RC цепи для замера аналоговых величин микроконтроллерами в которых нет АЦП.
Тут используется тот факт, что напряжение на конденсаторе растет строго по одному и тому же закону — экспоненте. В зависимости от кондера, резистора и питающего напряжения. А значит его можно использовать как опорное напряжение с заранее известными параметрами.
Работает просто, мы подаем напряжение с конденсатора на аналоговый компаратор, а на второй вход компаратора заводим измеряемое напряжение. И когда хотим замерить напряжение, то просто вначале дергаем вывод вниз, чтобы разрядить конденсатор. Потом возвращем его в режим Hi-Z, cбрасываем и запускаем таймер. А дальше кондер начинает заряжаться через резистор и как только компаратор доложит, что напряжение с RC догнало измеряемое, то останавливаем таймер.
Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также зная сколько натикал таймер, мы можем довольно точно узнать чему было равно измеряемое напряжение на момент сработки компаратора. Причем, тут не обязательно считать экспоненты. На начальном этапе зарядки кондера можно предположить, что зависимость там линейная. Или, если хочется большей точности, аппроксимировать экспоненту кусочно линейными функциями, а по русски — отрисовать ее примерную форму несколькими прямыми или сварганить таблицу зависимости величины от времени, короче, способов вагон просто.
Если надо заиметь аналоговую крутилку, а АЦП нету, то можно даже компаратор не юзать. Дрыгать ножкой на которой висит конденсатор и давать ему заряжаться через перменный резистор.
По изменению Т, которая, напомню T=R*C и зная что у нас С = const, можно вычислить значение R. Причем, опять же необязательно подключать тут математический аппарат, в большинстве случаев достаточно сделать замер в каких-нибудь условных попугаях, вроде тиков таймера. А можно пойти другим путем, не менять резистор, а менять емкость, например, подсоединяя к ней емкость своего тела… что получится? Правильно — сенсорные кнопки!
Если что то непонятно, то не парься скоро напишу статью про то как прикрутить к микроконтроллеру аналоговую фиговину не используя АЦП. Там подробно все разжую.
Теперь, думаю, ты понял за что я так люблю RC цепочки и почему на моей отладочной плате PinBoard их несколько и с разными параметрами 🙂
easyelectronics.ru
Как проверить конденсатор | soundbass
При конструировании и ремонте электронной техники часто возникает необходимость в проверке радиоэлементов, в том числе и конденсаторов. О том, как с достоверной точностью проверить исправность конденсаторов перед их использованием и пойдёт речь.
Самым доступным и распространённым прибором, с помощью которого можно проверить практически любой конденсатор, является цифровой мультиметр, включенный в режим омметра.
Наиболее важным является проверка конденсатора на пробой.
Пробой конденсатора – это неисправность, связанная с изменением сопротивления диэлектрика между обкладками конденсатора вследствие превышения допустимого рабочего напряжения на обкладках конденсатора.
При значительном превышении рабочего напряжения на конденсаторе, между его обкладками происходит электрический пробой. На корпусе пробитых конденсаторов можно обнаружить потемнения, вздутия, тёмные пятна и другие внешние признаки неисправности элемента.
Поскольку конденсатор не пропускает постоянный ток, то сопротивление между его выводами (обкладками) должно быть очень большим и ограничиваться лишь так называемым сопротивлением утечки. В реальных конденсаторах диэлектрик, несмотря на то, что он является, по сути, изолятором, пропускает незначительный ток. Этот ток для исправного конденсатора очень мал и не учитывается. Он называется током утечки.
Проверка конденсаторов с помощью омметра
Данный способ подходит для проверки неполярных конденсаторов. В неполярных конденсаторах, в которых диэлектриком является слюда, керамика, бумага, стекло, воздух, сопротивление утечки бесконечно большое и если измерить сопротивление между выводами такого конденсатора цифровым мультиметром, то прибор зафиксирует бесконечно большое сопротивление.
Обычно, если у конденсатора присутствует электрический пробой, то сопротивление между его обкладками составляет довольно малую величину – несколько единиц или десятки Ом. Пробитый конденсатор, по сути, является обычным проводником.
На практике проверить на пробой любой неполярный конденсатор можно так:
Переключаем цифровой мультиметр в режим измерения сопротивления и устанавливаем самый большой из возможных пределов измерения сопротивления. Для цифровых мультитестеров серий DT-83x, MAS83x, M83x это будет предел 2M (2000k), то бишь, 2 Мегаома.
Далее подключаем измерительные щупы к выводам проверяемого конденсатора. При исправном конденсаторе прибор не покажет никакого значения и на дисплее засветиться единичка. Это свидетельствует о том, что сопротивление утечки конденсатора более 2 Мегаом. Этого достаточно, чтобы в большинстве случаев судить об исправности конденсатора. Если цифровой мультиметр чётко зафиксирует какое-либо сопротивление, меньшее 2 Мегаом, то, скорее всего, конденсатор неисправен.
Следует учесть, что держаться обеими руками выводов и щупов мультиметра при измерении нельзя. Так как в таком случае прибор зафиксирует сопротивление Вашего тела, а не сопротивление утечки конденсатора. Поскольку сопротивление тела человека меньше сопротивления утечки, то ток потечёт по пути наименьшего сопротивления, то есть через ваше тело по пути рука – рука. Поэтому не стоит забывать о правилах при проведении измерения сопротивления.
Проверка полярных электролитических конденсаторов с помощью омметра несколько отличается от проверки неполярных.
Сопротивление утечки полярных конденсаторов обычно составляет не менее 100 килоОм. Для более качественных полярных конденсаторов это значение не менее 1 Мегаом. При проверке таких конденсаторов омметром следует сначала разрядить конденсатор, замкнув выводы накоротко.
Далее необходимо установить предел измерения сопротивления не ниже 100 килоОм. Для упомянутых выше конденсаторов это будет предел 200k (200.000 Ом). Далее соблюдая полярность подключения щупов, измеряют сопротивление утечки конденсатора. Так как электролитические конденсаторы имеют довольно высокую емкость, то при проверке конденсатор начнёт заряжаться. Этот процесс занимает несколько секунд, в течение которых сопротивление на цифровом дисплее будет расти, и будет расти до тех пор, пока конденсатор не зарядится. Если значение измеряемого сопротивления перевалило за 100 килоОм, то в большинстве случаев можно с достаточной уверенностью судить об исправности конденсатора.
Ранее, когда среди радиолюбителей были распространены стрелочные омметры, проверка конденсаторов проводилась аналогичным образом. При этом конденсатор заряжался от батареи омметра и сопротивление, показываемое стрелочным прибором росло, в конечном итоге достигая значения сопротивления утечки.
По скорости отклонения стрелки измерительного прибора от нуля и до конечного значения оценивали емкость электролитического конденсатора. Чем дольше проходила зарядка (дольше отклонялась стрелка прибора), тем соответственно, была больше ёмкость конденсатора. Для конденсаторов с небольшой ёмкостью (1 – 100 мкф) стрелка измерительного прибора отклонялась достаточно быстро, что свидетельствовало о небольшой ёмкости конденсатора, а вот при проверке конденсаторов с большой ёмкостью (1000 мкф и более), стрелка отклонялась значительно медленнее.
Проверка конденсаторов с помощью омметра является косвенным методом. Более точную и правдивую оценку об исправности конденсатора и его параметрах позволяет получить мультиметр с возможностью измерения ёмкости конденсатора.
При проверке электролитических конденсаторов необходимо перед проведением измерения ёмкости полностью разрядить проверяемый конденсатор. Особенно этого правила стоит придерживаться при проверке полярных конденсаторов, имеющих большую ёмкость и высокое рабочее напряжение. Если этого не сделать, то можно испортить измерительный прибор.
Например, часто приходиться проверять исправность конденсаторов, которые выполняют роль фильтрующих, и применяются в импульсных блоках питания. Их ёмкость и рабочее напряжение достаточно велики и при неполном разряде могут привести к порче измерительного прибора.
Поэтому такие конденсаторы перед проверкой следует разрядить, закоротив выводы накоротко (для низковольтных конденсаторов с малой ёмкостью), либо подсоединив к выводам резистор, сопротивлением 5-10 килоОм (для высоковольтных конденсаторов).
При проведении данной операции не стоит касаться руками выводов конденсатора, иначе можно получить неприятный удар током при разряде обкладок. При закорачивании выводов заряженного электролитического конденсатора проскакивает искра. Чтобы исключить появление искры, выводы высоковольтных конденсаторов и закорачивают через резистор.
Одной из существенных неисправностей электролитических конденсаторов является частичная потеря ёмкости, вызванная повышенной утечкой. В таких случаях ёмкость конденсатора заметно меньше, чем указанная на корпусе. Определить такую неисправность при помощи омметра довольно сложно. Для точного обнаружения такой неисправности, как потеря ёмкости потребуется измеритель ёмкости, который есть не в каждом мультиметре.
Также с помощью омметра трудно обнаружить такую неисправность конденсатора как обрыв. При обрыве конденсатор электрически представляет собой два изолированных проводника не имеющих никакой ёмкости.
Для полярных электролитических конденсатором косвенным признаком обрыва может служить отсутствие изменения показаний на дисплее мультиметра при замере сопротивления. Для неполярных конденсаторов малой ёмкости обнаружить обрыв практически невозможно, поскольку исправный конденсатор также имеет очень высокое сопротивление.
Обнаружить обрыв в конденсаторе возможно лишь с помощью приборов для измерения ёмкости конденсатора.
На практике обрыв в конденсаторах встречается довольно редко, в основном при механических повреждениях. Куда чаще при ремонте аппаратуры приходиться заменять конденсаторы, имеющие электрический пробой либо частичную потерю ёмкости.
Например, люминесцентные компактные лампы частенько выходят из строя по причине электрического пробоя конденсаторов в электронной схеме преобразователя.
Причиной неисправности телевизора может служить потеря ёмкости электролитического конденсатора в схеме источника питания.
Потеря ёмкости электролитическими конденсаторами легко обнаруживается при замере ёмкости таких конденсаторов с помощью мультиметров с функцией измерения ёмкости. К таким мультиметрам относиться мультиметр Victor VC9805A+, который имеет 5 пределов измерения ёмкости:
20 нФ (20nF)
200 нФ (200nF)
2 мкФ (2uF)
20 мкФ (20uF)
200 мкФ (200uF)
Данный прибор способен измерять ёмкость в диапазоне от 20 нанофарад (20 нФ) до 200 микрофарад (мкФ). Как видно, с помощью этого прибора есть возможность замерить ёмкость, как обычных неполярных конденсаторов, так и полярных электролитических. Правда, максимальный предел измерения ограничен значением в 200 микрофарад (мкФ).
Измерительные щупы прибора подключаются к гнёздам измерения ёмкости (обозначается как Cx). При этом нужно соблюдать полярность подключения щупов. Как уже упоминалось, перед измерением ёмкости следует в обязательном порядке полностью разрядить проверяемый конденсатор. Несоблюдение этого правила может привести к порче прибора.
Неисправность конденсатора можно определить при внешнем осмотре, например, корпус электролитических конденсаторов имеет разрыв насечки в верхней части корпуса. Это свидетельствует о том, что на конденсатор действовало завышенное напряжение, вследствие чего и произошёл, так называемый «взрыв” конденсатора. Корпуса неполярных конденсаторов при значительном превышении рабочего напряжения имеют свойство раскалываться, на поверхности образуются расколы и трещины.
Такие дефекты конденсаторов появляются, например, при воздействии мощного электрического разряда на электронный прибор во время грозовых разрядов и сильных скачков напряжения электроосветительной сети.
Источник: go-radio.ru
soundbass.org.ua
