Пробивное напряжение конденсатора: Пробивное и рабочее напряжения конденсатора. Сопротивление утечки конденсатора

Электрическая прочность конденсаторов — Студопедия

Электрическая прочность – это способность изоляции противостоять пробою. При нарушении электрической прочности происходит пробой диэлектрика, между обкладками конденсатора возникает короткое замыкание и конденсатор отказывает в работе. Электрическая прочность конденсатора зависит от толщины и качества диэлектрика, от площади обкладок, условий теплоотдачи и т.д.

Электрическая прочность характеризуется величиной пробивной напряженности, которая равна отношению пробивного напряжения 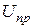к толщине диэлектрика h: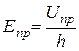 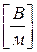[144]

Если напряженность поля в диэлектрике достигает значения равного 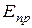, то происходит пробой диэлектрика конденсатора.

В газообразных диэлектриках пробой носит чисто электрический характер и может быть объяснен теорией ударной ионизации. Пробой газа происходит тогда, когда кинетическая энергия свободных ионов будет достаточной, чтобы ионизировать молекулы при соударении, то есть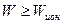

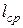, образуется ионная лавина, проводимость газа растет. Энергия, приобретенная частицей на длине свободного пробега равна:

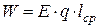, [145]

где Е – электрическая прочность;

q – заряд частицы,

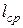– длина свободного пробега.

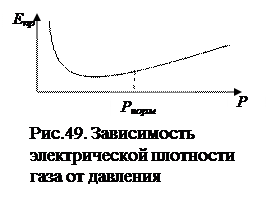Электрическая прочность газов зависит от давления (рис. 49). С увеличением давления газа величина 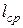уменьшается и электрическая прочность растет пропорционально росту давления так как при меньших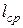

требуется более высокая напряженность поля, чтобы накопить энергию, необходимую для ионизации. При переходе в область высокого вакуума, электрическая прочность газа резко возрастает. Это объясняется тем, что количество молекул в единице объема резко снижается и уменьшается вероятность столкновения ионов с молекулами.

Применяя повышенное давление можно повысить электрическую прочность газовой изоляции в 10 – 20 раз, еще более высокие значения пробивной напряженности можно получить, применяя вакуум. Особенностью газообразной изоляции является полная ее восстанавливаемость после пробоя.

Пробивная напряженность зависит от расстояния между электродами (рис. 50).

В случае твердых диэлектриков внутри его или у краев обкладок могут встретиться воздушные включения, которые разрушаются электрическим полем раньше, чем может произойти пробой твердого диэлектрика. Кроме того, возможен поверхностный разряд на границе раздела между воздухом и твердым диэлектриком по поверхности выводных изоляторов или по поверхности изоляционного корпуса.

В случае очень чистых жидких диэлектриков явление пробоя можно объяснить тоже с точки зрения ионизационной теории. Жидкий диэлектрик имеет большую плотность, чем газы, поэтому 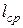у них меньше и электрическая прочность значительно выше.

Для жидких диэлектриков технической очисткипробивная напряженность ниже, что связано с наличием пузырьков воздуха, влаги и механических примесей. Под действием поля они выстраиваются в цепочки от электрода к электроду по которым происходит пробой. С увеличением примесей пробивная напряженность уменьшается (рис. 51). Восстанавливаемость электрической прочности жидкости после пробоя хуже, чем газов, так как происходит загрязнение жидкости продуктами ее разложения, образующиеся в момент пробоя.

Для твердых диэлектриков различают: электрический пробой, ионизационный пробой, электротепловой пробой, электрохимический пробой.

С чисто электрическим пробоем конденсаторов с однородным диэлектриком можно встретиться в редких случаях, в основном при воздействии кратковременных единичных импульсов напряжения.

Для конденсаторов с воздушными включениями в порах диэлектрика или у краев обкладок характерен электрический пробой неоднородных диэлектриков, связанный с ионизацией.

При электротепловом пробое нарушается тепловое равновесие между теплом 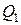, выделяющимся в диэлектрике и теплом, отводимым от него в окружающую среду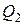

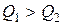. Если , то происходит нагрев диэлектрика. При этом растет его проводимость, что способствует дальнейшему росту 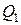, что ведет к тепловому разрушению диэлектрика. Тепло выделяемое в диэлектрике можно рассчитать по формуле:

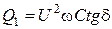, [146]

где 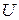– приложенное напряжение;

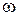– угловая частота;

– емкость конденсатора;

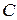
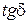– тангенс угла диэлектрических потерь.

Тепло, отведенное в окружающую среду, описывается выражением:

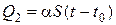[147]

где 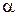– коэффициент теплоотдачи с поверхности конденсатора в окружающую среду;

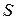– поверхность с которой происходит теплоотдача;

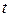– температура конденсатора;

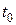– температура окружающей среды.

Зависимость 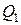от температуры определяется характером зависимости угла потерь от температуры (рис. 52)

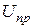– пробивное напряжение, которое выводит конденсатор из строя.

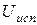– испытательное напряжение которое конденсатор должен выдержать не пробиваясь в течении определенного промежутка времени (по ГОСТу). Воздействию 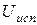подвергается каждый конденсатор.

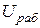– рабочее напряжение при котором конденсатор может надежно работать длительное время. 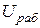указывается в маркировке конденсатора и его называют номинальным .

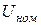Отношение 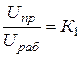– характеризует запас электрической прочности при работе конденсатора, а отношение 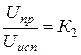– запас электрической прочности при испытании конденсатора.

Для конденсаторов с органическим диэлектриком, заметно снижающим свою электрическую прочность с течением времени, применяют большие запасы электрической прочност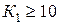и и .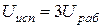

Для конденсаторов с газообразным и твердым неорганическим диэлектриком, в которых явление старения диэлектрика отсутствует или выражено слабее, значения 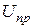, 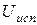и 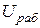сближаются. .

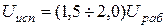В конденсаторах с металлизированным диэлектриком в связи с их способностью к самовосстановлению при пробое значение 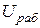лежит ближе к 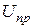, чем у конденсаторов с обкладками из фольги. Для них .

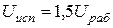Для электролитического конденсаторов испытания на пробой не применяют, так как оксидные слои в этих конденсаторах используются на пределе.

Конденсаторы для «чайников» / Хабр

Если вы регулярно занимаетесь созданием электрических схем, вы наверняка использовали конденсаторы. Это стандартный компонент схем, такой же, как сопротивление, который вы просто берёте с полки без раздумий. Мы используем конденсаторы для сглаживания пульсаций напряжения/тока, для согласования нагрузок, в качестве источника энергии для маломощных устройств, и других применений.

Но конденсатор – это не просто пузырёк с двумя проводочками и парой параметров – рабочее напряжение и ёмкость. Существует огромный массив технологий и материалов с разными свойствами, применяемых для создания конденсаторов. И хотя в большинстве случаев для любой задачи сгодится практически любой конденсатор подходящей ёмкости, хорошее понимание работы этих устройств может помочь вам выбрать не просто нечто подходящее, а подходящее наилучшим образом. Если у вас когда-нибудь была проблема с температурной стабильностью или задача поиска источника дополнительных шумов – вы оцените информацию из этой статьи.

Начнём с простого

Лучше начать с простого и описать основные принципы работы конденсаторов, прежде чем переходить к настоящим устройствам. Идеальный конденсатор состоит из двух проводящих пластинок, разделённых диэлектриком. Заряд собирается на пластинах, но не может перетекать между ними – диэлектрик обладает изолирующими свойствами. Так конденсатор накапливает заряд.

Ёмкость измеряется в фарадах: конденсатор в один фарад выдаёт напряжение в один вольт, если в нём находится заряд в один кулон. Как и у многих других единиц системы СИ, у неё непрактичный размер, поэтому, если не брать в расчёт суперконденсаторы, о которых мы здесь говорить не будем, вы скорее всего встретитесь с микро-, нано- и пикофарадами. Ёмкость любого конденсатора можно вывести из его размеров и свойств диэлектрика – если интересно, формулу для этого можно посмотреть в Википедии. Запоминать её не нужно, если только вы не готовитесь к экзамену – но в ней содержится один полезный факт. Ёмкость пропорциональна диэлектрической проницаемости ε_r использованного диэлектрика, что в результате привело к появлению в продаже различных конденсаторов, использующих разные диэлектрические материалы для достижения больших ёмкостей или улучшения характеристик напряжения.

Паразитные индуктивность и сопротивление реального конденсатора

С использованием диэлектриков в конденсаторах есть одна проблемка, наряду с тем, что диэлектрик с нужными характеристиками обладает неприятными побочными эффектами. У всех конденсаторов есть небольшие паразитные сопротивление и индуктивность, которые иногда могут влиять на его работу. Электрические постоянные меняются от температуры и напряжения, пьезоэлектричества или шума. Некоторые конденсаторы стоят слишком дорого, у некоторых существуют состояния отказа. И вот мы подошли к основной части статьи, в которой расскажем о разных типах конденсаторов, и об их свойствах, полезных и вредных. Мы не будем освещать все возможные технологии, хотя большинство обычных мы опишем.

Алюминиевые электролитические

Алюминиевые электролитические конденсаторы используют анодно-оксидированный слой на алюминиевом листе в качестве одной пластины-диэлектрика, и электролит из электрохимической ячейки в качестве другой пластины. Наличие электрохимической ячейки делает их полярными, то есть напряжение постоянного тока должно прикладываться в одном направлении, и анодированная пластина должна быть анодом, или плюсом.

На практике их пластины выполнены в виде сэндвича из алюминиевой фольги, завёрнутой в цилиндр и расположенной в алюминиевой банке. Рабочее напряжение зависит от глубины анодированного слоя.

У электролитических конденсаторов наибольшая среди распространённых ёмкость, от 0,1 до тысяч мкФ. Из-за плотной упаковки электрохимической ячейки у них наблюдается большая эквивалентная последовательная индуктивность (equivalent series inductance, ESI, или эффективная индуктивность), из-за чего их нельзя использовать на высоких частотах. Обычно они используются для сглаживания питания и развязывания, а также связывания на аудиочастотах.

Танталовые электролитические

Танталовый конденсатор поверхностного размещения

Танталовые электролитические конденсаторы изготавливаются в виде спечённого танталового анода с большой площадью поверхности, на которой выращивается толстый слой оксида, а затем в качестве катода размещается электролит из диоксида марганца. Комбинация большой площади поверхности и диэлектрических свойств оксида тантала приводит к высокой ёмкости в пересчёте на объём. В результате такие конденсаторы выходят гораздо меньше алюминиевых конденсаторов сравнимой ёмкости. Как и у последних, у танталовых конденсаторов есть полярность, поэтому постоянный ток должен идти в строго одном направлении.

Их доступная ёмкостью варьируется от 0,1 до нескольких сотен мкФ. У них гораздо меньше сопротивление утечки и эквивалентное последовательное сопротивление (ESR), в связи с чем они используются в тестировании, измерительных приборах и высококачественных аудиоустройствах – там, где эти свойства полезны.

В случае танталовых конденсаторов необходимо особенно следить за тем, чтобы они не вышли из строя — бывает, что в таком случае они загораются. Аморфный оксид тантала – хороший диэлектрик, а в кристаллической форме он становится хорошим проводником. Неправильное использование танталового конденсатора – например, подача слишком большого пускового тока может привести к переходу диэлектрика в другую форму, что увеличит проходящий через него ток. Правда, репутация, связанная с возгораниями, появилась у более ранних поколений танталовых конденсаторов, и улучшенные методы производства привели к созданию более надёжной продукции.

Полимерные плёнки

Целое семейство конденсаторов использует полимерные плёнки в качестве диэлектриков, а плёнка либо находится между витыми или перемежающимися слоями металлической фольги, либо имеет металлизированный слой на поверхности. Их рабочее напряжение может доходить до 1000 В, но высокими ёмкостями они не обладают – это обычно от 100 пФ до единиц мкФ. У каждого вида плёнки есть свои плюсы и минусы, но в целом всё семейство отличается более низкими ёмкостью и индуктивностью, чем у электролитических. Посему они используются в высокочастотных устройствах и для развязывания в электрически шумных системах, а также в системах общего назначения.

Полипропиленовые конденсаторы используются в схемах, требующих хорошей тепловой и частотной стабильности. Также они используются в системах питания, для подавления ЭМП, в системах, использующих переменные токи высокого напряжения.

Полиэстеровые конденсаторы, хотя и не обладают такими температурными и частотными характеристиками, получаются дешёвыми и выдерживают большие температуры при пайке для поверхностного монтажа. В связи с этим они используются в схемах, предназначенных для использования в некритичных приложениях.

Полиэтилен-нафталатовые конденсаторы. Не обладают стабильными температурными и частотными характеристиками, но могут выдерживать гораздо большие температуры и напряжения по сравнению с полиэстеровыми.

Полиэтилен-сульфидовые конденсаторы обладают температурными и частотными характеристиками полипропиленовых, и в дополнение выдерживают высокие температуры.

В старом оборудовании можно наткнуться на поликарбонатные и полистиреновые конденсаторы, но сейчас они уже не используются.

Керамика

История керамических конденсаторов довольно длинная – они использовались с первых десятилетий прошлого века и по сей день. Ранние конденсаторы представляли собою один слой керамики, металлизированной с обеих сторон. Более поздние бывают и многослойными, где пластины с металлизацией и керамика перемежаются. В зависимости от диэлектрика их ёмкости варьируются от 1 пФ до десятков мкФ, а напряжения достигают киловольт. Во всех отраслях электроники, где требуется малая ёмкость, можно встретить как однослойные керамические диски, так и многослойные пакетные конденсаторы поверхностного монтажа.

Проще всего классифицировать керамические конденсаторы по диэлектрикам, поскольку именно они придают конденсатором все свойства. Диэлектрики классифицируют по трёхбуквенным кодам, где зашифрована их рабочая температура и стабильность.

C0G лучшая стабильность в ёмкости по отношению к температуре, частоте и напряжению. Используются в высокочастотных схемах и других контурах высокого быстродействия.

X7R не обладают такими хорошими характеристиками по температуре и напряжению, посему используются в менее критичных случаях. Обычно это развязывание и различные универсальные приложения.

Y5V обладают гораздо большей ёмкостью, но характеристики температуры и напряжения у них ещё ниже. Также используются для развязывания и в различных универсальных приложениях.

Поскольку керамика часто обладает и пьезоэлектрическими свойствами, некоторые керамические конденсаторы демонстрируют и микрофонный эффект. Если вы работали с высокими напряжениями и частотами в аудиодиапазоне, например, в случае ламповых усилителей или электростатики, вы могли услышать, как «поют» конденсаторы. Если вы использовали пьезоэлектрический конденсатор для обеспечения частотной стабилизации, вы могли обнаружить, что его звук модулируется вибрацией его окружения.

Как мы уже упоминали, статья не ставит целью охватить все технологии конденсаторов. Взглянув в каталог электроники вы обнаружите, что некоторые технологии, имеющиеся в наличии, здесь не освещены. Некоторые предложения из каталогов уже устарели, или же имеют такую узкую нишу, что с ними чаще всего и не встретишься. Мы надеялись лишь развеять некоторые тайны по поводу популярных моделей конденсаторов, и помочь вам в выборе подходящих компонентов при разработке собственных устройств. Если мы разогрели ваш аппетит, вы можете изучить нашу статью по катушкам индуктивности.

Об обнаруженных вами неточностях и ошибках прошу писать через личные сообщения сайта. Спасибо.

Конденсатор | Класс робототехники

Электрический конденсатор (англ. capacitor) — это устройство, которое может накапливать электрический заряд и хранить его некоторое время. Конденсаторы можно найти практически в любом электронном устройстве. Они бывают разных типов и размеров. На электрических схемах конденсаторы обозначают двумя параллельными черточками. При этом, у полярных конденсаторов около положительного электрода дополнительно ставится плюсик.

Для чего нужен конденсатор?

У этого прибора есть множество применений. Мы не будем перечислять их все, отметим лишь некоторые. 1) Фильтрация пульсаций в цепях питания. Конденсаторы часто ставят на входе и выходе преобразователей напряжения, на входе питания микросхем. В этом случае конденсаторы служат своего рода амортизаторами, которые могут сгладить неровности напряжения, подобно амортизаторам автомобиля, сглаживающим неровности дороги. 2) Времязадающие электрические цепи. Конденсаторы разной ёмкости заряжаются и разряжаются за разное время. Эту особенность используют в устройствах, где необходимо отсчитывать определенные промежутки времени. Например, с помощью резистора и конденсатора задается период и скважность импульса в микросхеме таймера 555 (урок про таймер 555). 3) Датчики прикосновения. В роли одной из обкладок конденсатора может выступить человек. Эту особенность нашего тела используют в своей работе сенсорные кнопки, тачскрины и тачпады некоторых видов. 4) Хранение данных. Конденсаторы применяются для хранения данных в оперативной памяти — ОЗУ (SRAM). Каждый модуль такой памяти содержит миллиарды отдельных конденсаторов, которые могут быть заряжены или разряжены, что интерпретируется как единица или ноль. И это далеко не все варианты применения этого незаменимого прибора. Попробуем разобраться, как устройство конденсатора позволяет ему выполнять столько полезных функций!

Устройство простейшего конденсатора

Конденсатор состоит их двух металлических пластин — электродов, называемых также обкладками, между которыми находится тонкий слой диэлектрика. Собственно, все конденсаторы устроены именно таким (или почти таким) образом, разве что меняется материал обкладок и диэлектрика. Чтобы увеличить ёмкость конденсатора, не увеличивая его размеры, применяют разные хитрости. Например, если мы возьмем две обкладки в виде длинных полосок фольги, проложим между ними хотя бы тот же полиэтилен и свернем все это как рулет, то получится очень компактный прибор с большой ёмкостью. Именно так устроены плёночные конденсаторы. Если вместо полиэтилена взять бумагу и пропитать её электролитом, то на поверхности фольги образуется тонкий слой оксида, который не проводит ток. Такой конденсатор будет называться электролитическим. Существует много разных видов конденсаторов: бумажные, плёночные, оксидные алюминиевые и танталовые, вакуумные и т.п. В нашем уроке мы будем использовать оксидные электролитические конденсаторы из-за их большой ёмкости и доступности.

Полярные и неполярные конденсаторы

Очень важным является разделение конденсаторов на полярные и неполярные. Приборы на основе оксидов: электролитические алюминиевые и танталовые обычно являются полярными, а значит если перепутать их полярность — они выйдут из строя. Причём этот выход из строя будет сопровождаться бурной электрохимической реакций вплоть до взрыва конденсатора. На полярных конденсаторах всегда имеется маркировка. Как правило на электролитических конденсаторах на корпусе контрастной полосой отмечается отрицательный вывод (катод), у танталовых (в желтых прямоугольных корпусах) полоской помечается положительный вывод (анод). Если есть сомнения в маркировке, то лучше найти документацию на этот конденсатор и убедиться. Неполярные же конденсаторы можно включать в цепь какой угодно стороной. К примеру, многослойные керамические конденсаторы — неполярные.

Ёмкость и напряжение конденсатора

Теперь обратим внимание на две важные характеристики конденсатора: ёмкость и номинальное напряжение. Ёмкость конденсатора характеризует способность конденсатора накапливать заряд. Это как ёмкость банки, в которой хранится, к примеру, вода. Кстати, не зря одним из первых электрических конденсаторов была так называемая Лейденская банка. Она представляла собой обыкновенную стеклянную посуду, снаружи обмотанную фольгой. В банку была налита токопроводящая жидкость — электролит. Фольга и электролит играли роль обкладок, а стекло банки служило тем самым диэлектрическим барьером. Ёмкость электрического конденсатора измеряют в фарадах. В схемах ёмкость обозначают латинской буквой C. Как правило, ёмкость классических конденсаторов варьируется от нескольких пикофарад (пФ) до нескольких тысяч микрофарад (мкФ). Ёмкость указывается на корпусе конденсатора. Если единицы не указаны — то это пикофарады. Микрофарады часто обозначают как uF — так как буква u внешне похожа на греческую букву мю, которую используют вместо приставки микро. Существует и особый вид конденсаторов, называемых ионисторами (англ. supercapacitor), которые имеют ёмкость в несколько фарад!  Чем больше ёмкость конденсатора, тем больше энергии в нём может храниться и тем дольше он заряжается, при прочих равных условиях. Номинальное напряжение — второй важный параметр. Это такое напряжение, при котором конденсатор будет работать весь срок службы без критичного изменения своих параметров. Нельзя применять в 12-вольтовой цепи конденсатор на 6 вольт — он быстро выйдет из строя. Именно эти два параметра обычно наносят на поверхность корпуса конденсатора. На фотографии ниже изображён электролитический конденсатор ёмкостью 470 мкФ и номинальным напряжением 16 Вольт. А вот на керамических конденсаторах часто указывают только ёмкость. На картинке ниже конденсатор имеет маркировку 104. Что бы это значило? Последняя цифра в этом коде — количество нулей после двухзначного числа в начале. 104 = 10 0000 пФ = 100 нФ = 0,1 мкФ

Параллельное и последовательное подключение конденсаторов

Как и в случае резисторов, конденсаторы можно составлять в цепочки. Это бывает нужно, когда в схеме необходима какая-то конкретная ёмкость, а у вас нет такого конденсатора. Параллельное подключение В отличие от резисторов, при параллельном подключении конденсаторов их ёмкости складываются. Например, если нам нужно получить ёмкость 3000 мкФ, а у нас есть два конденсатора по 1000 мкФ, и 10 штук по 100 мкФ, смело ставим их параллельно и получаем: 1000*2+100*10 = 2000 + 1000 = 3000 мкФ Последовательно подключение При последовательном подключении конденсаторы ведут себя как резисторы, соединённые параллельно. Например, посчитаем суммарную ёмкость двух конденсаторов на 100 мкФ, соединённых последовательно: Суммарная ёмкость Ctot = 50 мкФ.

Заряд и разряд конденсатора — RC-цепочка

Теперь разберёмся с процессами, происходящими внутри конденсатора во время заряда и разряда. Для этого рассмотрим самую простую электрическую цепь с конденсатором. С левой стороны схемы подключим источник питания. Сверху разместим ключ и резистор, а справа сам конденсатор. Участок цепи, на котором есть конденсатор и резистор называют RC-цепью. При замыкании ключа, в такой цепи образуется электрический ток, сила которого зависит от сопротивления резистора и внутреннего сопротивления самого конденсатора. Заряженные частицы устремятся к конденсатору, но не смогут преодолеть слой диэлектрика (по крайней мере все разом). Вследствие чего, с одной стороны конденсатора накопятся отрицательно заряженные частицы, а с другой стороны — положительно заряженные. Концентрация заряженных частиц на обкладках создаст мощное электрическое поле между ними. С течением времени, напряжение на конденсаторе растет, а сила тока падает. После завершения процесса заряда, ток в цепи упадет почти до нуля. Останется только очень маленький ток утечки, который образуется благодаря тому, что некоторым заряженным частицам всё же удается проскочить через слой диэлектрика. Напряжение, напротив, станет практически равным напряжению источника. Когда мы отключим конденсатор от источника питания, этот самый ток утечки постепенно разрядит конденсатор. Эта особенность электрических конденсаторов не даёт нам сделать из них контейнер для длительного хранения энергии. Хотя частично эту проблему решают ионисторы.

Резистор и время заряда конденсатора

Зачем в цепи нужен резистор? Что на мешает подключить его напрямую к источнику? Тому есть две причины. Резистор ограничивает ток, протекающий через конденсатор. Чем меньше заряженных частиц за единицу времени прибывает в конденсатор, тем больше времени для заряда ему потребуется. Конденсатор заряжается и разряжается по экспоненциальному закону. Зная это, мы можем легко рассчитать время заряда/разряда в зависимости от его ёмкости и от сопротивления резистора. По картинке можно понять, что за время T конденсатор заряжается на 63,2%. А вот за время 3T уже на 95%. Время T здесь равно произведению ёмкости конденсатора C на сопротивление R, последовательно соединенного резистора: Например, у нас есть конденсатор ёмкостью 100 мкФ, соединенный с резистором 1 кОм. Посчитаем за сколько секунд он зарядится хотя бы до 95%: Теперь умножаем это на 3 и получаем 3T = 0,3 секунды — за такое время конденсатор почти полностью будет заряжен. Таким образом, меняя ёмкость конденсатора и резистора мы можем управлять временем его заряда, что нам ещё пригодится в будущем. Вторая важная причина, по которой в цепи присутствует резистор — защита источника питания. Дело в том, что разряженные конденсаторы имеют очень низкое внутреннее сопротивление, которое составляет доли Ома. По сути, их можно рассматривать как обычные проводники. А что будет, если замкнуть выводы питания проводником? Будет короткое замыкание! Такой режим работы цепи является аварийным для источника питания, и его нужно всячески избегать.

Плавное выключение светодиода при помощи конденсатора

Проведем небольшой опыт. Для этого соберем на макетной плате цепь с кнопкой, конденсатором и светодиодом. В качестве источника питания используем контакты питания Ардуино Уно. Принципиальная схема Внешний вид макета Подключим Ардуино  к питанию. Затем, нажмем кнопку и светодиод практически мгновенно загорится. Отпустим кнопку — светодиод медленно начнет гаснуть. Почему так происходит? Сразу после подключения нашей схемы к источнику питания, в ней начинают происходит интересные процессы. Как уже говорилось ранее, пока конденсатор пустой, ток через него максимален. Следовательно, конденсатор начинает стремительно набирать заряд. При этом светодиоду, который подключен параллельно, ничего не достается 🙁 Напряжение на нем близко к нулю. С течением времени конденсатор насыщается, благодаря чему ток начинает постепенно переходить в параллельную цепь — через светодиод. Напряжение на светодиоде начинает расти. Наступает момент, когда напряжение на светодиоде принимает критическое значение (для красного светодиода около 1,8 В), при котором он стремительно отбирает остатки тока у конденсатора и вспыхивает! Когда мы отпускаем кнопку, ситуация становится гораздо проще. Конденсатор становится источником питания для светодиода с резистором. Светодиод начинает медленно высасывать заряд из конденсатора, пока тот не разрядится. Тут мы и наблюдаем медленно угасание. Меняя сопротивление R1, мы можем влиять на скорость вспыхивания светодиода. Однако, следует учитывать, что увеличивая R1 мы будем снижать ток в цепи, тем самым уменьшая максимальный заряд конденсатора и яркость светодиода. Увеличивая C1, мы получим более длительное время работы светодиода после выключения источника. Это как поставить более ёмкую батарейку. Наконец, меняя R2 можно регулировать яркость светодиода, и соответственно, время его работы. Ведь чем меньше тока мы забираем из конденсатора, тем на большее время его хватит.

Заключение

Итак, мы познакомились с конденсатором — интересным и порой опасным жителем любой электронной платы. В следующих уроках уделим внимание резистору и индуктивности, а также более сложному их собрату — транзистору.

Вконтакте

Facebook

Twitter

Конденсатор

Конденсатор состоит из двух пластин (или обкладок), находящихся одна перед другой и сделанных из проводящего материала. Между пластинами находится изолирующий материал, называемый диэлектриком (рис. 4.1). Простейшими диэлектриками являются воздух, бумага, слюда и т. д.

Рис. 4.1. Конденсатор

 

Зарядка конденсатора

Основным свойством конденсатора является его способность запасать электрическую энергию в виде электрического заряда.
На рис. 4.2(а) изображена схема, в которой конденсатор соединяется через ключ с источником питания. Когда ключ замкнут (рис. 4.2(б)), положительный полюс источника «откачивает» электроны с обкладки А, и она приобретает положительный заряд. Отрицательный полюс источника питания тем временем «поставляет» электроны на обкладку В, в результате чего она приобретает отрицательный заряд, по абсолютной величине равный положительному заряду обкладки А. Такой поток электронов называется током заряда. Он продолжает течь до тех пор, пока напряжение на конденсаторе не сравняется с ЭДС источника питания. В этом случае говорят, что конденсатор полностью заряжен. Электрический заряд обозначается буквой Q, а его величина измеряется в кулонах (Кл).

 

 

Рис. 4.2. Заряд и разряд конденсатора

 

Когда конденсатор заряжен, между его обкладками возникает разность потенциалов, а следовательно, и электрическое поле.
Если в момент, когда конденсатор уже зарядился, разомкнуть ключ (рис. 4.2(в)), конденсатор будет хранить заряд. В этом случае внутри диэлектрика между обкладками возникает электрическое поле. При разряде конденсатора через сопротивление нагрузки (рис. 4.2(г)) электрическое ноле исчезает.

 

Емкость конденсатора

Способность конденсатора накапливать электрический заряд называется емкостью, а величина этой емкости обозначается буквой С и измеряется в фарадах (Ф). Фарада — очень большая единица емкости, и поэтому она практически не используется. Чаще используются дробные единицы:

                         1 микрофарада (мкФ) =  Ф = 10^-6 Ф,

                         1 пикофарада (пФ) =   мкФ = 10^-6 мкФ = 10^-12 Ф.

 

Емкость конденсатора возрастает с увеличением площади обкладок и убывает с увеличением расстояния между ними.
Например, при возрастании площади обкладок вдвое емкость также увеличивается в два раза. Если же увеличить вдвое расстояние между обкладками, емкость станет вдвое меньше.

 

Связь заряда, емкости и напряжения

Если конденсатор заряжен до разности потенциалов V , его заряд определяется формулой Q=CV

где С выражается в фарадах, V – в вольтах, а Q – в кулонах. Преобразовав эту формулу, получим:

 

Энергия заряженного конденсатора

Энергия W, запасенная конденсатором, определяется формулой

где W выражается в джоулях, С – в фарадах, а V — в вольтах.

 

Параллельное и последовательное соединение конденсаторов

Если два конденсатора, С1 и С2, соединены параллельно (рис. 4.3(а)), результирующая емкость СТ такого соединения равна сумме емкостей этих конденсаторов:

Если конденсаторы соединены последовательно (рис. 4.3(б)), результирующая емкость СТ оказывается меньше емкости любого из конденсаторов я выражается формулой

Например, если С1 = С2, то результирующая емкость СТ последовательного соединения равна половине емкости любого из конденсаторов:

 

Напряжение на последовательно соединенных конденсаторах

На схеме, показанной на рис. 4.4, конденсаторы С1 и С2 соединены последовательно и подключены к источнику постоянного напряжения VТ. Полное напряжение VТ будет поделено между С1 и С2 таким образом, что на конденсаторе меньшей емкости установится большее напряжение,

Рис. 4.3. Параллельное (а) и последовательное (б) соединение конденсаторов.

Рис. 4.4. Напряжение на конденсаторах при их последовательном соединении

и наоборот.

Сумма V1 (напряжения на С1) и V2 (напряжения на С2) всегда равна полному напряжению VТ.
В общем случае, когда несколько конденсаторов, соединенных последовательно, подключено к источнику постоянного тока, напряжение на каждом из конденсаторов обратно пропорционально его емкости. При последовательном соединении двух конденсаторов напряжения на С1 и С2 соответственно равны

 

Пример 1

Определим результирующую емкость цепи, изображенной на рис. 4.5. Результирующая емкость параллельного соединения равна

С2 + С3 = 10 + 20 = 30 пФ

Поскольку емкость С1 также равна 30 пФ, то результирующая емкость всей цепи равна ½*30 = 15 пФ.

Рис. 4.6.                                                                                                   Рис. 4.7.

 

Пример 2

На рис. 4.6 напряжение на конденсаторе С1 равно

откуда напряжение на С2 равно 30 – 20 = 10 В.

 

Рабочее напряжение

Любой конденсатор характеризуется некоторым максимальным напряжением, при превышении которого наступает пробой диэлектрика. Это напряжение называется рабочим, или номинальным, напряжением конденсатора, и подаваемое на конденсатор напряжение ни в коем случае не должно его превышать. При использовании конденсатора в цепях переменного тока амплитудное значение напряжения в цепи также не должно превышать рабочего напряжения конденсатора. Рабочим напряжением для батареи конденсаторов, соединенных параллельно, является наименьшее из рабочих напряжений конденсаторов, входящих в схему, Например, рабочее напряжение для цепи, изображенной на рис. 4.7, равно 25 В.
Для конденсаторов, соединенных последовательно, рабочее напряжение подбирать труднее. Рассмотрим схему на рис. 4.8. Конденсатор С1 (1 мкФ, рабочее напряжение Vраб = 25 В) соединен последовательно с конденсатором С2 (10 мкФ, Vраб = 10 В). Поскольку на конденсаторе С1, обладающем меньшей емкостью, установится большее напряжение, чем на С2, то при расчетах следует прежде всего иметь в виду рабочее напряжение конденсатора С1, равное 25 В. Таким образом, V1 = 25 В. соотношения V1/ V2 = С1/ С2 следует, что

Поскольку рабочее напряжение конденсатора С2 выше, чем V2, рабочее напряжение данной батареи конденсаторов равно 25 + 2,5 = 27,5 В.
Следует заметить, что если бы рабочее напряжение конденсатора было равно, например, 2 В, как показано на рис. 4.9, то он зарядился бы

 

                      Рис. 4.8.                                                                          Рис. 4.9.

                           Рис. 4.10.                                     Рис. 4.11. Катушка индуктивности

 

до уровня рабочего напряжения прежде, чем напряжение на конденсаторе С1 достигло бы 25 В. Вот расчет для этого случая:
V2 = 2 В, тогда.

Следовательно, рабочее напряжение такой батареи будет составлять 20 + 2 = 22 В.

 

Пример 3

Конденсаторы С1 и С2, изображенные на рис. 4.10, имеют каждый рабочее напряжение 60 В. Какое максимальное напряжение может быть приложено к этой схеме?

 

Решение
Поскольку на конденсаторе С1 установится более высокое напряжение, чем на конденсаторе С2, то напряжение на нем раньше достигнет уровня рабочего напряжения. При V1 = 60 В

Максимальное напряжение, которое может быть подано на данную схему, составляет 60 + 20 = 80 В.

 

В этом видео рассказывается о понятии конденсатора:

Добавить комментарий

как определить напряжение, вольтаж конденсаторов

Конденсатор – один из самых важных элементов электрической цепи. Он накапливает внутри себя электрический заряд и передает его другим элементам электрической цепи. О том, что представляет собой конденсатор и как определить на нём напряжение, рассказывается ниже.

Что такое конденсатор

Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.

Конденсатор

Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический –  из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).

Термин из учебного пособия

Характеристики конденсаторов

Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.

Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.

Емкость

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.

В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.

В чем измеряется напряжение конденсаторов

Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.

Измерение силы заряда двухполюсника

Что влияет на напряжение конденсаторов

Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.

Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.

Описание влияния на показатель

Как вычислить напряжение и вольтаж

Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.

Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.

Вычисление мультиметром

Формулы измерения напряжения конденсаторов

Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.

Основные формулы для расчета

В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.

Характеристики конденсаторов ⋆ diodov.net

Ранее мы уже рассмотрели принцип работы и маркировку многих типов конденсаторов. Однако настоящий электронщик должен знать следующие характеристики конденсаторов: допустимое напряжение, классы точности, температурный коэффициент емкости и тангенс угла потерь. Понимание указанных характеристик позволяет сделать выбор и применить лучший из имеющихся накопителей, что благоприятно скажется в целом на работе электронного устройства.

Основные характеристики конденсаторов

Допустимое напряжение является очень важным параметром любого конденсатора и его нельзя превышать, иначе произойдет пробой диэлектрика и накопитель придет в непригодность. На корпусе указывается всегда величина максимального допустимого напряжения. Поэтому начинающих радиолюбителей такое обозначение вводит в заблуждения, поскольку в розетке напряжение 230 В, то казалось бы, что напряжения накопителя 300 В вполне достаточно. Однако это не так. Так как 230 В – это действующее напряжение, а диэлектрик может пробиться от мгновенного амплитудного значения, которое в 1,41 раза больше действующего и равно 230×1,41 = 324 В плюс допуск отклонения 10 % от номинального значения в сторону увеличения, нормированный ГОСТом, и того получим 324×0,1+324 = 356 В. Поэтому допустимое напряжение должно быть не ниже 360 В.

Стандартные значения емкости конденсаторов

Если взять любой радиоэлектронный прибор, например, резистор, диод, транзистор, стабилитрон и снять его характеристики либо измерить параметры высокоточным измерительным прибором, то они будут иметь некоторые отклонения от заявленных номинальных значений. Такое отклонение от указанных параметров вызвано технологическим процессом и нормируется производителем. Дело в том, что на изготовление любого устройства или его отдельного компонента влияет много факторов, которые невозможно учесть и скомпенсировать. Даже лист бумаги, формата А4, имеет некоторые отклонения от заданных размеров, но тем не менее это никак не сказывается на их применении.

Аналогично обстоят дела и с емкостью. Если измерить ее в нескольких накопителей одинакового номинала, то можно заметить небольшую разницу. Эта разница строго нормирована и называется допустимым отклонением емкости от номинального значения. Она измеряется в процентах, значения которых соответствуют классам точности.

В зависимости от класса точности и допустимого отклонения производятся стандартные значения емкости, то есть стандартные номиналы конденсаторов. Емкость в приведенной ниже таблице исчисляется пикофарадоми. Любое значение из таблицы может быть умножено на 0,1 или 1 или 10 и т.д.

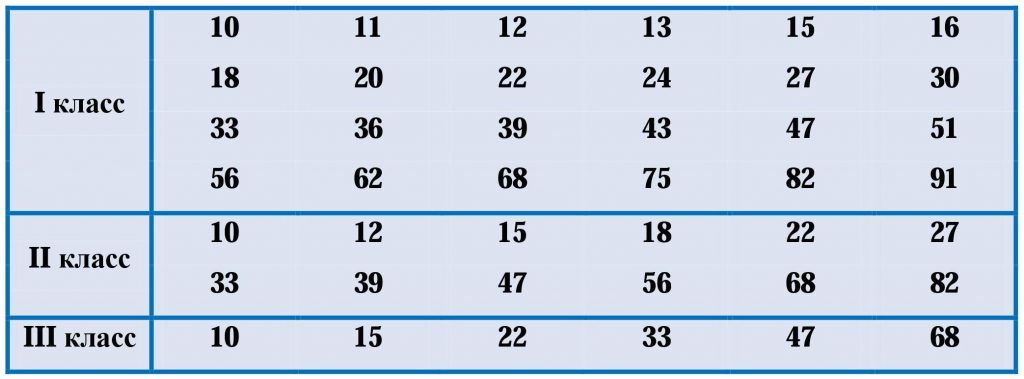
Температурный коэффициент емкости

Протекание электрического тока через любой радиоэлектронный элемент вызывает его нагрев, ввиду неизбежного наличия сопротивления. Чем больше ток и выше сопротивление, тем интенсивнее нагревается прибор. Такое явление в большинстве случаев является вредным и может привести к изменению параметров схемы, а соответственно и нарушить режим работы всего устройства. Поэтому нагрев радиоэлектронных элементов всегда учитывается при проектировании изделия. Характеристики конденсаторов также склонны изменятся с изменением температуры и с этим обязательно нужно считаться. Для этого введен температурный коэффициент емкости, сокращенно ТКЕ.

ТКЕ показывает, насколько отклоняется емкость конденсатора от номинального значения с ростом температуры. Номинальное значение емкости накопителя приводится для температуры окружающей среды +20 С.

Рост температуры может вызвать как рост емкости, так и ее уменьшение. В зависимости от этого различают конденсаторы с положительным и отрицательным температурным коэффициентом емкости.

Следует знать, чем меньше значение ТКЕ, тем более стабильными характеристиками обладает конденсатор. Особое внимание уделяют ТКЕ разработчик измерительного оборудования высокого класса точности, где критичны значительные отклонения характеристик любого радиоэлектронного элемента.

Тангенс угла потерь

Потери, неизбежно возникающие при работе конденсатора, главным образом определяются свойствами диэлектрика, расположенного между обкладками накопителя, и характеризуются тангенсом угла потерь tg δ. Производители стремятся снизить значение угла tg δ и за счет этого улучшить характеристики конденсаторов. Поэтому наибольшее применение получила специальная керамика, обладающая минимальным тангенсом угла потерь. Обратной величиной тангенса угла потерь конденсатора является добротность, равная Q_C=1/tgδ. Конденсаторы высокого качества обладают добротностью свыше тысячи единиц.

Еще статьи по данной теме

90000 Capacitance Of a Capacitor Formula 90001 90002 90003 The capacitance of a capacitor is the ability of a capacitor to store an electric charge per unit of 90004 voltage 90005 across its plates of a capacitor. Capacitance is found by dividing electric charge with voltage by the formula C = Q / V. Its unit is Farad. 90006 90007 Formula 90008 90002 Its formula is given as: 90006 90002 C = Q / V 90006 90002 Where C is capacitance, Q is voltage, and V is voltage. We can also find charge Q and voltage V by rearranging the above formula as: 90006 90002 Q = CV 90006 90002 V = Q / C 90006 90002 90004 Farad 90005 is the unit of capacitance.One Farad is the amount of capacitance when one coulomb of charge is stored with one volt across its plates. 90006 90002 Most capacitors that are used in electronics work have capacitance values ​​that are specified in microfarad (μF) and picofarads (pF). A microfarad is one-millionth of a farad, and a picofarad is one-trillionth of a farad. 90006 90007 What are the factors that effect the capacitance of capacitor? 90008 90002 It depends on the following factors: 90006 90029 Area of ​​plates 90030 90002 90032 90006 90002 Capacitance is directly proportional to the physical size of the plates as determined by the plate area, A.A larger plate area produces a larger capacitance and a smaller capacitance.Fig (a) shows that the plate area of ​​a parallel plate capacitor is the area of ​​one of the plates. If the plates are moved in relation to each other, as shown in fig (b), the overlapping area determines the effective plate area. This variation in the effective plate area is basic for a certain type of variable capacitor. 90006 90029 Plates seperation 90030 90002 90039 90006 90002 `Capacitance is inversely proportional to the distance between the plates.The plate separation is designated d, as shown in fig (a). Greater separation of the plates produces a smaller capacitance, as illustrated in fig (b). As previously discussed, the breakdown voltage is directly proportional to the plate separation. The further the plates are separated, the greater the 90004 breakdown voltage 90005. 90006 90029 Dielectric Constant of material 90030 90002 As you know, the insulating material between the plates of a capacitor is called the dielectric. Dielectric materials tend to reduce the voltage between plates for a given charge and thus increase the capacitance.If the voltage is fixed, more charge can be stored due to the presence of a dielectric than can be stored without a dielectric. The measure of a material’s ability to establish an 90004 electric field 90005 is called dielectric constant or relative permittivity, symbolized by ∈ 90050 r 90051. 90006 90002 Capacitance is directly proportional to the dielectric constant. The dielectric constant of a vacuum is defined as 1 and that of air is very close to 1. These values ​​are used as a reference, and all other materials have values ​​of ∈r specified with respect to that of a vacuum or air.For example, a material with ∈r = 8 can result in a capacitance eight times greater than that of air with all other factors being equal. 90006 90002 The dielectric constant ∈r is dimensionless because it is a relative measure. It is a ratio of the absolute permittivity of a material, ∈r, to the absolute permittivity of a vacuum, ∈ 90050 0 90051, as expressed by the following formula: 90006 90002 ∈ 90050 r 90051 = ∈ / ∈ 90050 0 90051 90006 90002 Below given some common dielectric materials and typical dielectric constants for each.Values ​​can vary because they depend on the specific composition of the material. 90006 90002 Material Typical ∈r values ​​90006 90069 90070 Air 1.0 90071 90070 Teflon 2.0 90071 90070 Paper 2.5 90071 90070 Oil 4.0 90071 90070 Mica 5.0 90071 90070 Glass 7.5 90071 90070 Ceramic 1200 90071 90084 90002 The dielectric constant ∈r is dimensionless because it is a relative measure.It is a ratio of the absolute permittivity of a material, ∈r, to the absolute permittivity of a vacuum, ∈0, as expressed by the following formula: 90006 90002 ∈r = ∈ / ∈0 90006 90002 The value of ∈0 is 8.85 × 10-12 F / m. 90006 90029 Formula of capacitance in terms of physical parameters 90030 90002 You have seen how capacitance is directly related to plate area, A, and the dielectric constant, ∈r, and inversely related to plate separation, d. An exact formula for calculating the capacitance in terms of these three quantities is: 90006 90002 C = A ∈ 90050 r 90051 ∈ / d 90006 90002 where ∈ = ∈ 90050 r 90051 ∈ 90050 0 90051 = ∈r (8.85 × 10-12F / m) 90006 90007 Capacitance of parallel plate capacitor derivation 90008 90002 Consider a parallel plate capacitor. The size of the plate is large and the distance between the plates is very small, so the electric field between the plates is uniform. 90006 90002 90110 90006 90002 The electric field ‘E’ between the parallel plate capacitor is: 90006 90002 90115 90006 90007 Capacitance of cylindrical capacitors physics 90008 90002 Consider a cylindrical capacitor of length L, formed by two coaxial cylinders of radii ‘a’ and ‘ b ‘.Suppose L >> b, such that there is no fringing field at the ends of cylinders. 90006 90002 90122 90006 90002 Let ‘q’ is the charge in the capacitor and ‘V’ is the potential difference between plates. The inner cylinder is positively charged while the outer cylinder is negatively charged. We want to find out the expression of capacitance for the cylindrical capacitor. For this, we consider a cylindrical Gaussian surface of radius ‘r’ such that a << b. 90006 90002 If 'E' is the electric field intensity on any point of the cylindrical Gaussian surface, then by Gauss's law: 90006 90002 If 'V' is the potential difference between plates, then 90006 90002 90131 90006 90002 This is the relation for the capacitance of a cylindrical capacitor.90006 90007 Capacitance of a spherical capacitor 90008 90002 90138 90006 90007 Capacitance of an isolated spherical capacitor 90008 90002 90143 90006 90002 90146 90147 90006 90002 External source 90150 https://en.wikipedia.org/wiki/Capacitance 90006.90000 How to find out the breakdown voltage? 90001 90002 90003 90004 90005 Physics 90006 Science 90007 90002 90003 Anatomy & Physiology 90004 90003 Astronomy 90004 90003 Astrophysics 90004 90003 Biology 90004 90003 Chemistry 90004 90003 Earth Science 90004 90003 Environmental Science 90004 90003 Organic Chemistry 90004 90003 Physics 90004 90005 90006 Math 90007 90002 90003 Algebra 90004 90003 Calculus 90004 90003 Geometry 90004 90005.