Журнал «Программирование» РАН
Журнал основан в 1975 году и публикует статьи по всем проблемам, связанным с теоретическим и практическим программированием: операционные системы, технологии программирования, языки программирования и компиляторы, параллельное программирование, верификация и тестирование программ, машинная графика, компьютерная алгебра и т.п. Журнал предназначен для исследователей, практиков и студентов. Периодичность выпуска – 6 номеров в год. Журнал внесен в список ВАК. Журнал выпускается ФГУП «Издательство «Наука».
Главный редактор журнала
А.И. Аветисян, академик РАН, доктор физ.-мат. наук. Институт системного программирования РАН, Москва, Россия.
Заместитель главного редактора
А. К. Петренко, доктор физ.-мат. наук, профессор. Институт системного программирования РАН, Москва, Россия.
Ответственный секретарь
Л. Е. Карпов, доктор техн. наук. Институт системного программирования РАН, Москва, Россия.
Редакционная коллегия
С. А. Абрамов, доктор физ.-мат. наук, профессор. Вычислительный центр им. А. А. Дородницына Федерального исследовательского центра «Информатика и управление», РАН, Москва, Россия;
И. Б. Вирбицкайте, доктор физ.-мат. наук, профессор. Институт систем информатики им. А. П. Ершова, СО РАН, Новосибирск, Россия;
К. В. Воронцов, доктор физ.-мат. наук, профессор. Вычислительный центр им. А. А. Дородницына РАН Федерального исследовательского центра «Информатика и управление», РАН, Москва, Россия.
В. А. Галактионов, доктор физ.-мат. наук, профессор. Институт прикладной математики им. М. В. Келдыша, РАН, Москва, Россия;
Ф. Я. Дзержинский. ТехноСофт, Москва, Россия;
С. В. Клименко, доктор физ.-мат. наук, профессор. Нижегородский государственный архитектурно-строительный университет, Нижний Новгород, Россия;
М. Р. Когаловский, кандидат техн. наук. Институт проблем рынка РАН, Москва, Россия;
А. С. Косачев, кандидат физ.-мат. наук. Институт системного программирования РАН, Москва, Россия;
И. В. Машечкин, доктор физ.
А. Абрамов, доктор физ.-мат. наук, профессор. Вычислительный центр им. А. А. Дородницына Федерального исследовательского центра «Информатика и управление», РАН, Москва, Россия;
И. Б. Вирбицкайте, доктор физ.-мат. наук, профессор. Институт систем информатики им. А. П. Ершова, СО РАН, Новосибирск, Россия;
К. В. Воронцов, доктор физ.-мат. наук, профессор. Вычислительный центр им. А. А. Дородницына РАН Федерального исследовательского центра «Информатика и управление», РАН, Москва, Россия.
В. А. Галактионов, доктор физ.-мат. наук, профессор. Институт прикладной математики им. М. В. Келдыша, РАН, Москва, Россия;
Ф. Я. Дзержинский. ТехноСофт, Москва, Россия;
С. В. Клименко, доктор физ.-мат. наук, профессор. Нижегородский государственный архитектурно-строительный университет, Нижний Новгород, Россия;
М. Р. Когаловский, кандидат техн. наук. Институт проблем рынка РАН, Москва, Россия;
А. С. Косачев, кандидат физ.-мат. наук. Институт системного программирования РАН, Москва, Россия;
И. В. Машечкин, доктор физ.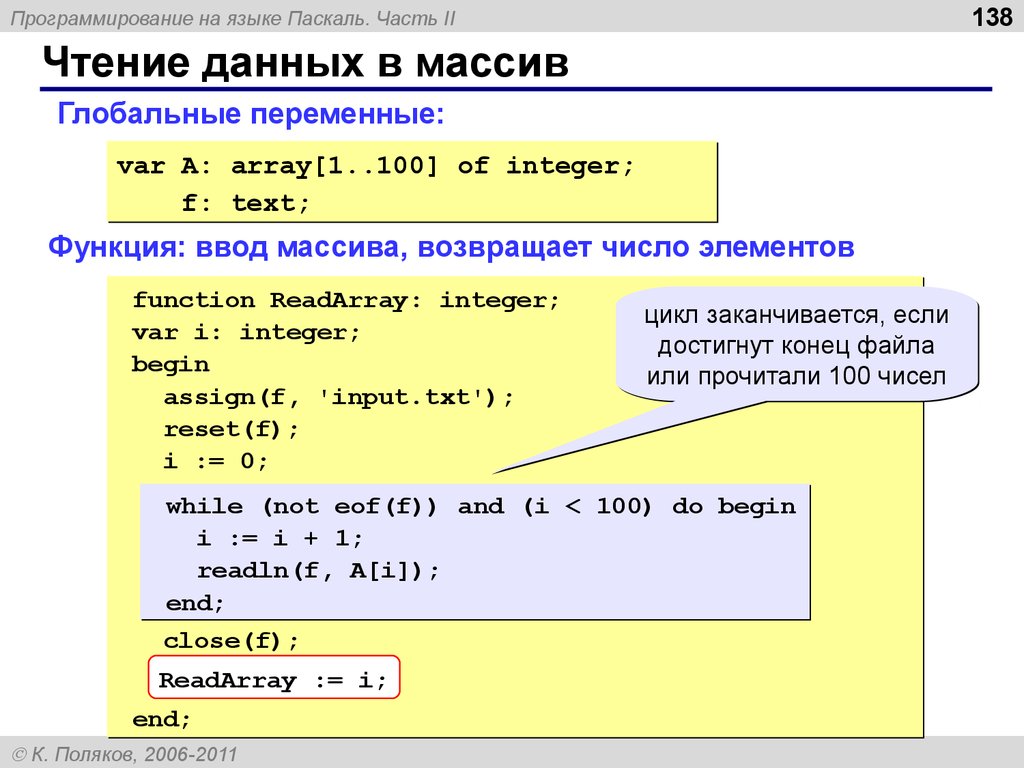
Зав. редакцией журнала
Т.А. Оловянникова. ФГУП Академиздатцентр “Наука” РАН, Москва, Россия.
Журнал реферируется и индексируется
Научные статьи, опубликованные в журнале «Программирование», полностью переводятся на английский язык группой издательств Pleiades Publishing и печатаются издательством Springer в журнале «Programming and Computer Software», сведения о котором можно найти здесь и здесь.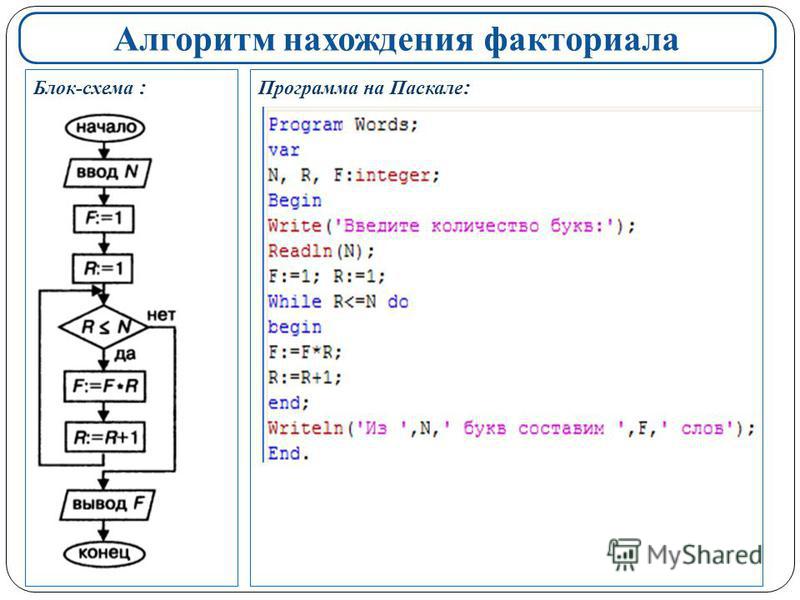 Там же можно найти сведения об импакт-факторе переводного журнала и международных системах, индексирующих его.
Там же можно найти сведения об импакт-факторе переводного журнала и международных системах, индексирующих его.
Программирование это так просто программирование это так сложно (3 изд.) (м) Андреева (Елена Андреева)
220 ₽
+ до 33 баллов
Бонусная программа
Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.
Купить
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Последний экземпляр
В наличии в 2 магазинах. Смотреть на карте
1
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Книга представляет собой практический курс для обучения программированию, основную часть которого составляет подборка около 200 задач.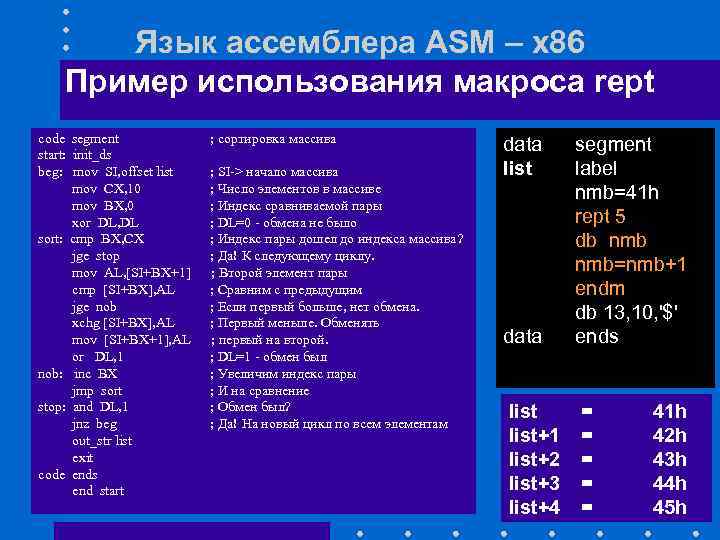 В ней делается попытка показать, как обучить программированию в школе за 16 уроков. Рассмотрены все алгоритмы из перечня, входящего в “Требования к уровню подготовки выпускников” согласно нормативным документам ЕГЭ. Большинство приведенных задач предполагают проверку их решений на системе тестов.
В ней делается попытка показать, как обучить программированию в школе за 16 уроков. Рассмотрены все алгоритмы из перечня, входящего в “Требования к уровню подготовки выпускников” согласно нормативным документам ЕГЭ. Большинство приведенных задач предполагают проверку их решений на системе тестов.
Описание
Характеристики
Книга представляет собой практический курс для обучения программированию, основную часть которого составляет подборка около 200 задач. В ней делается попытка показать, как обучить программированию в школе за 16 уроков. Рассмотрены все алгоритмы из перечня, входящего в “Требования к уровню подготовки выпускников” согласно нормативным документам ЕГЭ.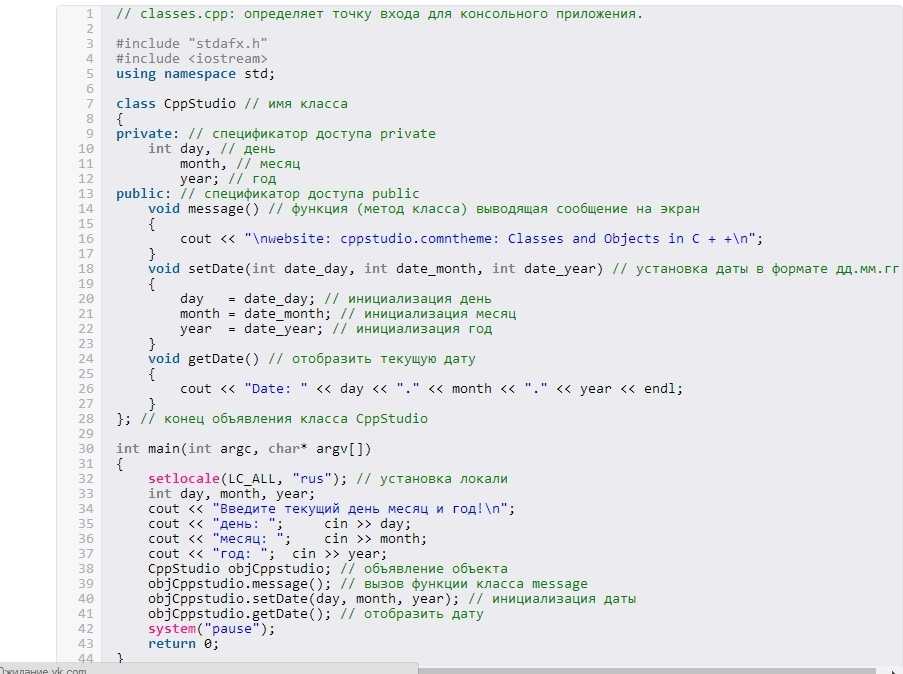 Большинство приведенных задач предполагают проверку их решений на системе тестов.
Большинство приведенных задач предполагают проверку их решений на системе тестов.
Абрис Д
На товар пока нет отзывов
Поделитесь своим мнением раньше всех
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине
2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили
3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя.
Правила начисления бонусов
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов
Книга «Программирование это так просто программирование это так сложно (3 изд.) (м) Андреева» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Елена Андреева
«Программирование это так просто программирование это так сложно (3 изд.
Введение в программирование на M · Лагерь разработчиков Power BI
- Дом
- Сессии в лагере
- Сессия 08: Введение в М-программирование
Это учебное занятие послужит базовым курсом по написанию логики запросов Power BI с использованием языка программирования M. Цель этого занятия — дать участникам более прочную основу для работы непосредственно с кодом M в расширенном редакторе при разработке запросов для наборов данных в Power BI Desktop, а также для потоков данных в браузере. Участники узнают, как создавать эффективные запросы, используя свертывание запросов, а также как очищать текстовые значения с помощью функции Text.Select. Студенты познакомятся с написанием запросов с использованием сложных типов данных M, включая списки, записи, таблицы, функции и пользовательские типы, а также с оптимизацией логики запросов с использованием свертывания запросов.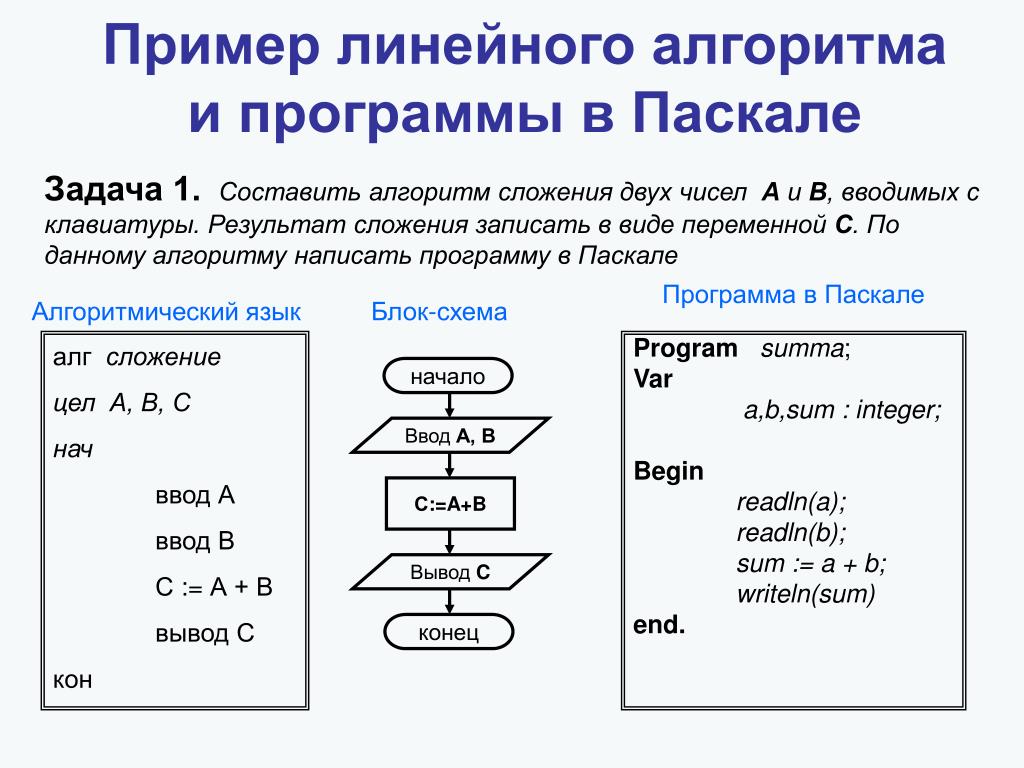
Участники лагеря должны иметь предыдущий опыт работы с Power Query в Power BI Desktop. Рекомендуется (но не обязательно), чтобы участники лагеря имели опыт работы непосредственно с M-кодом в расширенном редакторе.
Смотреть видео от 25 марта 2021 г. Ссылки на сеансы и ресурсыСлайды PowerPoint для введения в программирование на M
Это набор слайдов PowerPoint, использованный в презентации 25 марта 2021 г.
Образец PBIX – Введение в программирование на M.pbix
Образец PBIX — демо дизайна запроса.pbix
Пример проекта PBIX, который показывает, как писать и структурировать запросы в расширенном сценарии.
Образец PBIT — состав команды НФЛ.pbit
Эти файлы шаблонов Power BI Desktop позволяют выбрать команду НФЛ, а затем импортировать данные об игроках этой команды из списка на их общедоступном веб-сайте.
Система типа Power Query M — PowerQuery M
- Статья
- 8 минут на чтение
Язык формул Power Query M — это полезный и выразительный язык гибридных данных. Но у него есть некоторые ограничения. Например, нет строгого соблюдения системы типов. В некоторых случаях требуется более строгая проверка. К счастью, M предоставляет встроенную библиотеку с поддержкой типов, позволяющую сделать возможной более строгую проверку.
Разработчики должны иметь полное представление о системе типов, чтобы делать это с любой универсальностью. И хотя спецификация языка Power Query M хорошо объясняет систему типов, она оставляет несколько сюрпризов. Например, для проверки экземпляров функций требуется способ сравнения типов на совместимость.
При более тщательном изучении системы типа М многие из этих вопросов могут быть прояснены, а разработчики получат возможность создавать необходимые им решения.
Знание исчисления предикатов и наивной теории множеств должно быть достаточным для понимания используемых обозначений.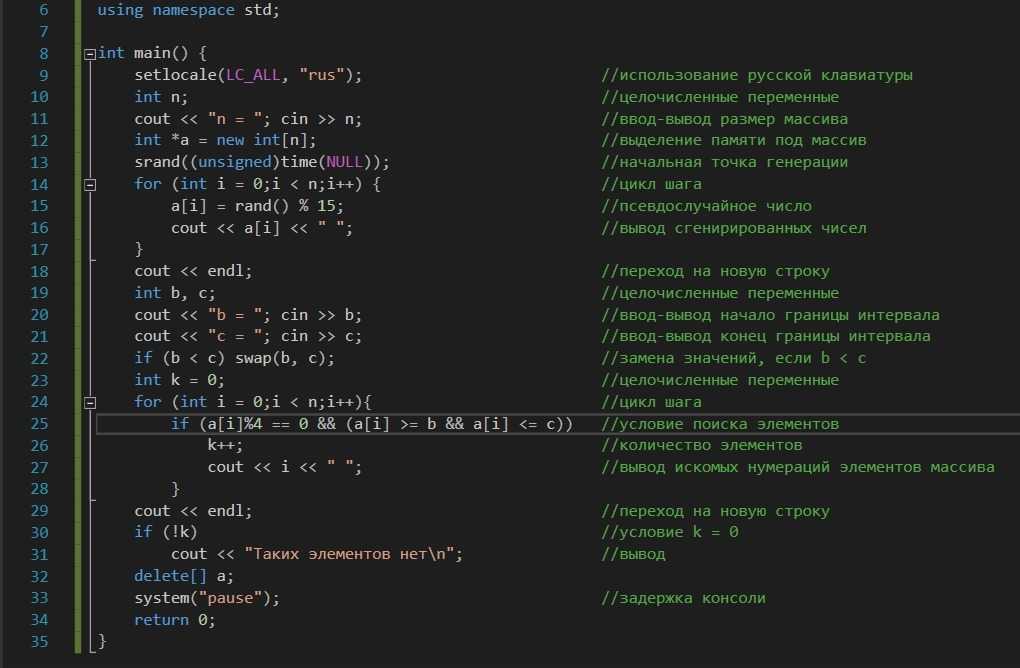
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
(1) B := { true ; false }
B — типичный набор логических значений
(2) N := { допустимые идентификаторы M }
N — набор всех допустимых имен в M. Это определено в другом месте.
(3) P := ⟨ B , T ⟩
P — набор параметров функции. Каждый из них, возможно, является необязательным и имеет тип. Имена параметров не имеют значения.
(4) P N : = ⋃ 0≤IN ⟨ I , P I ⟩ P IS . последовательности из n параметров функции.
(5) P * := ⋃ 0≤i≤∞ P i
P * — набор всех возможных последовательностей параметров функций, начиная с длины 0 и выше.
(6) F := ⟨ B , N , T ⟩
F множество всех полей записи. Каждое поле, возможно, является необязательным, имеет имя и тип.
Каждое поле, возможно, является необязательным, имеет имя и тип.
(7) F N : = ∏ 0≤i≤n F
F N – это сет.
(8) F * := ( ⋃ 0≤i≤∞ F i { 07 F ) ⟨ b 1 , n 1 , t 1 ⟩, ⟨ b 2 , n 2 , t 2 ⟩ ∈ F ⋀ n 1 = n 2 }
F * — множество всех наборов (любой длины) полей записи, за исключением наборов, в которых несколько полей имеют одинаковое имя.
(9) C := ⟨ N , T ⟩
C — набор типов столбцов для таблиц. Каждый столбец имеет имя и тип.
(10) C N ⊂ ⋃ 0≤i≤n ⟨ I , C ⟩
C , C ⟩
C , C ⟩
C , C . типы.
типы.
(11) C * := ( ⋃ 0≤i≤∞ C i ) ∖ { C м | ⟨ a , ⟨ n 1 , t 1 ⟩⟩, ⟨ b , ⟨ n 2 , t 2 ⟩⟩ ∈ C m ⋀ n 1 = n 2 }
C * — множество всех комбинаций (любой длины) типов столбцов, за исключением тех, где несколько столбцов имеют одно и то же имя.
M Типы
(12) T F : = ⟨ P , P * ⟩
Тип функции. или более параметров функции.
(13) T L :=〖 T 〗
Тип списка обозначается заданным типом (называемым «типом элемента»), заключенным в фигурные скобки.
Поскольку в метаязыке используются фигурные скобки, 〖 〗 В этом документе используются скобки .
(14) T R := ⟨ B , F * ⟩ * ⟩
A поля записи.
(15) T R o := ⟨ true , F ⟩
(16) T R • := ⟨ false , F ⟩
T R o и T R • являются сокращенными обозначениями для открытых и закрытых типов записей соответственно.
(17) T T := C *
Тип таблицы — это упорядоченная последовательность нулевого или более типов столбцов, где нет конфликтов имен.
(18) T P := { любой; никто; нулевой; логический; число; время; дата; дата-время; дата и время; продолжительность; текст; двоичный; тип; список; записывать; стол; функция; любой ненулевой }
Примитивный тип является одним из этого списка M ключевых слов.
(19) T N := { t n , u ∈ T | t n = u+null } = nullable t
Любой тип может быть дополнительно помечен как допускающий значение NULL с помощью ключевого слова “nullable” .
(20) T := T F ∪ T L ∪ T R ∪ T T ∪ T P ∪ T N
Набор всех типов – это союз из этих шести сетов:
. Типы записей, типы таблиц, примитивные типы и типы, допускающие значение NULL.
ФУНКЦИИ
Необходимо определить одну функцию: NonNullable : T ← T
Эта функция принимает тип и возвращает эквивалентный тип, за исключением того, что он не соответствует нулевому значению.
ИДЕНТИФИКАЦИИ
Некоторые идентичности необходимы для определения некоторых особых случаев, а также могут помочь прояснить вышеизложенное.
(21) nullable any = any
(22) nullable anynonnull = any
(23) nullable null = null
(24) nullable none = null
(25) nullable nullable t ∈ T = nullable t
(26) NonNullable (nullable t ∈ T ) = NonNullable ( t )
(27) Необнуляемый (любой) = anynonnull
СОВМЕСТИМОСТЬ ТИПОВ
Как определено в другом месте, М-тип совместим с другим М-типом тогда и только тогда, когда все значения, соответствующие первому типу, также соответствуют второму типу.
Здесь определяется отношение совместимости, которое не зависит от соответствующих значений и основано на свойствах самих типов. Предполагается, что это отношение, как определено в этом документе, полностью эквивалентно исходному семантическому определению.
Отношение «совместимо с» : ≤ : B ← T × T
В приведенном ниже разделе строчные буквы t всегда будут представлять M-тип, элемент T .
A Φ будет представлять подмножество F * или C * .
(28) t ≤ t
Это отношение рефлексивно.
(29) т а ≤ T B ∧ T B ≤ T C → T A ≤ T C
74.
(30) нет ≤ t ≤ любой
M типов образуют решетку над этим отношением; none — нижняя, any — верхняя.
(31) t a , t b ∈ T N ∧ T A ≤ T A → NONLULABLE ( T A ) ≤ НЕВЕСТНЫЙ ( T B
10 70075,,,, 70070 70070 7007. также совместимы. (32) null ≤ t ∈ T N
Примитивный тип null совместим со всеми типами, допускающими значение NULL.
(33) т ∉ т N ≤ anynonnull
Все ненулевые типы совместимы с anynonnull.
(34) NonNullable ( t ) ≤ t
Тип NonNullible совместим с эквивалентом, допускающим значение NULL.
(35) t ∈ T F → t ≤ функция
Все типы функций совместимы с функцией .
(36) t ∈ T L → t ≤ список
Все типы списков совместимы со списком .
(37) t ∈ T R → t ≤ запись
Все типы записей совместимы с записью .
(38) t ∈ T T → t ≤ стол
Все типы столов совместимы со столом .
(39) t a ≤ t b ↔ 〖 t a 〗≤〖 t b 〗
Тип списка совместим с другим типом списка, если типы элементов совместимы, и наоборот.
(40) t a ∈ T F = ⟨ p a , p * ⟩, t b ∈ T F = ⟨ p b , p * ⟩ ∧ p a ≤ p b → t a ≤ t b
Тип функции совместим с другим типом функции, если совместимы возвращаемые типы и списки параметров идентичны.
(41) t a ∈ T R o , t b ∈ T R • → t a ≰ т б
Тип открытой записи никогда не совместим с типом закрытой записи.
(42) t a ∈ T R • = ⟨ false , Φ ⟩, t b ∈ T R o = ⟨ true , Φ ⟩ → t a ≤ t b
В противном случае закрытый идентичный тип записи совместим с открытым типом записи.
(43) t a ∈ T R o = ⟨ true , ( Φ , ⟨ true , n , any⟩)⟩, t b ∈ T R o = ⟨ true , Φ ⟩ → t a ≤ t b ∧ t b ≤ t a
Необязательное поле с типом любой может быть проигнорирован при сравнении двух типов открытых записей.
(44) t a ∈ T R = ⟨ b , (Φ, ⟨ β , n , u a ⟩)⟩, t b ∈ T R = ⟨ b , (Φ, ⟨ β , n , u b ⟩)⟩ ∧ u a ≤ u b → т а ≤ t b
Два типа записей, отличающихся только одним полем, совместимы, если имя и необязательность поля идентичны, а типы указанного поля совместимы.
(45) t a ∈ T R = ⟨ b , (Φ, ⟨ false , n , u ⟩)⟩, t b ∈ T R = ⟨ b , (Φ, ⟨ истинно , n , u ⟩)⟩ → t a ≤ t b
Тип записи с необязательным полем совместим с идентичным типом записи, но для этого поля является необязательным.
(46) T A ∈ T R O = ⟨ True , ( φ , ⟨, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . , т б ∈ Т Р O = ⟨ True , φ ⟩ → T A ≤ T B
(47) T A ∈ T T = ( φ , ⟨ I , ⟨ N , U A .


