Простой фильтр низких частот: Фильтр для сабвуфера своими руками. Фильтр низких частот для саба

Фильтр для сабвуфера своими руками. Фильтр низких частот для саба

Автор admin На чтение 5 мин Просмотров 9.9к. Опубликовано 14.12.2018

Низкочастотная акустическая система предназначена для воспроизведения определённого участка звукового диапазона. Этот участок находится ближе к нижним границам зоны слышимости и составляет интервал от 20 до 100-200 Гц. Басовая колонка представляет собой прочный ящик, в котором установлены один или два мощных динамика. Благодаря особенностям воспроизведения низких частот диффузоры имеют большой диаметр, а подвес обеспечивает сильную амплитуду качания звуковой катушки и диффузора. Для того чтобы на катушку низкочастотного громкоговорителя не попадали лишние частоты, на входе системы ставится пассивный или активный фильтр-кроссовер. Фильтр для сабвуфера можно купить или сделать своими руками.

Содержание

1. Фильтр низких частот для сабвуфера своими руками
2. Пассивный фильтр НЧ для сабвуфера схема
3. Активный фильтр для сабвуфера своими руками

Фильтр низких частот для сабвуфера своими руками

Фильтр низких частот для сабвуфера представляет собой простую схему, которую можно сделать самостоятельно. Это устройство, в самом простом варианте, содержит катушку индуктивности и конденсатор, поэтому конструкция называется LC-фильтром. Индуктивности и ёмкостиявляются реактивными элементами, поэтому изменяют своё сопротивление в зависимости от частоты сигнала. Конденсатор меняет своё сопротивление обратно пропорционально частоте. При включении ёмкости параллельно нагрузке, высокочастотная составляющая сигнала, закорачивается на землю, а низкие частоты будут беспрепятственно проходить на динамик. Частота, на которой начинается подавление сигнала, называется частотой среза.

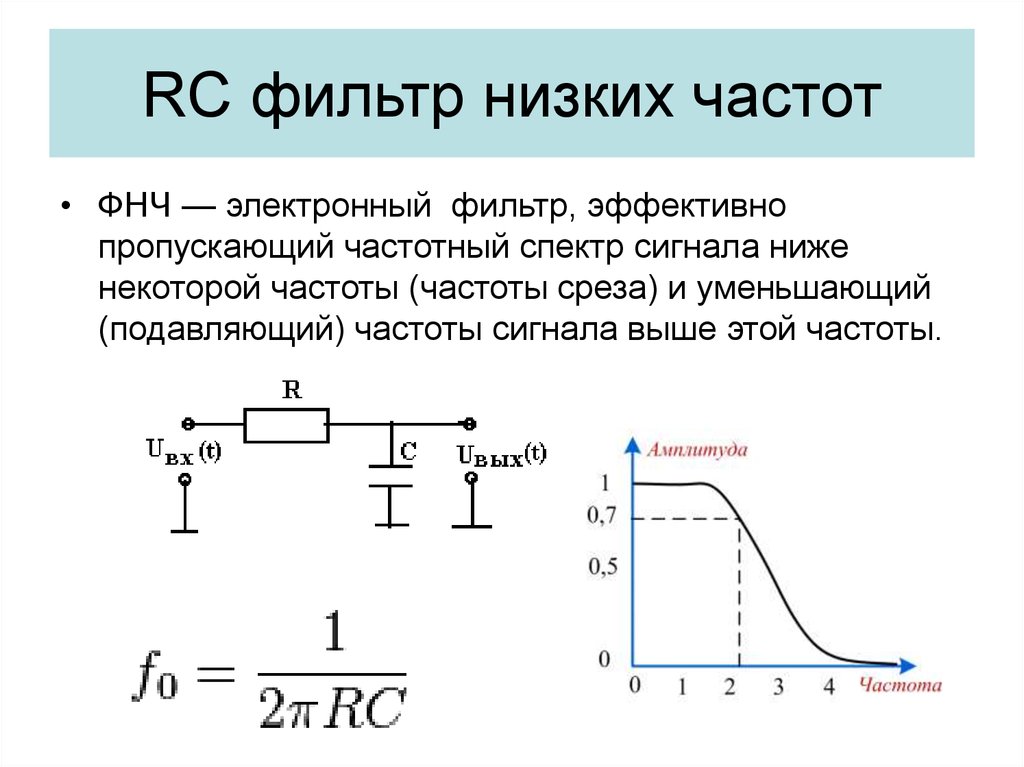
Идеальный низкочастотный фильтр для сабвуфера должен мгновенно «гасить» определённые частот. На снимке это показано жёлтой линией. Реальная схема фильтра для сабвуфера отличается тем, что спад происходит плавно. Простейшее устройство из двух элементов называется фильтр первого порядка. Он обеспечивает подавление частот выше порога среза в 6 dBна октаву. Схема второго порядка с дополнительными элементами увеличивает крутизну подавления до 12 dBна октаву, а каждое последующее звено добавляет по 6 dB.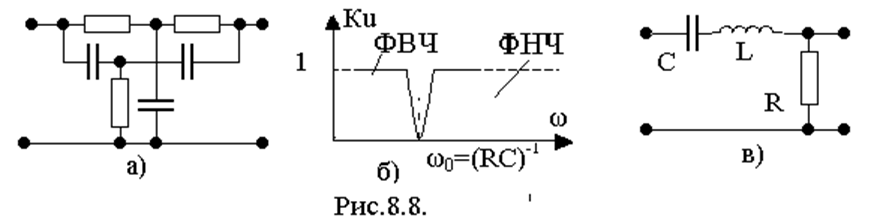

Чем больше звеньев, тем круче происходит подавление лишней полосы звукового диапазона.

Схема фильтра для сабвуфера сделанного своими руками, может включать в себя любое число звеньев. Устройство может быть пассивным или активным.

Пассивный фильтр НЧ для сабвуфера схема

Пассивный фильтр НЧ для сабвуфера своими руками можно сделать за короткое время. Схема не содержит дефицитных деталей и правильно собранная не требует настройки. Простой фильтр низких частот для сабвуфера состоит всего из двух деталей. Это катушка индуктивности и конденсатор. Для того чтобы определить электрические величины этих элементов лучше всего воспользоваться онлайн калькулятором. Для этого нужно набрать в строке поиска «Расчёт LC-фильтров. Онлайн калькулятор». Далее в окне нужно найти следующую таблицу.

Здесь достаточно указать нужную частоту среза, сопротивление нагрузки и нажать «Вычислить». Например, при сопротивлении динамика 4 Ома и частоте среза 220 Гц калькулятор выдаст ёмкость конденсатора в 255,7 микрофарад, а индуктивность 4,09 миллигенри.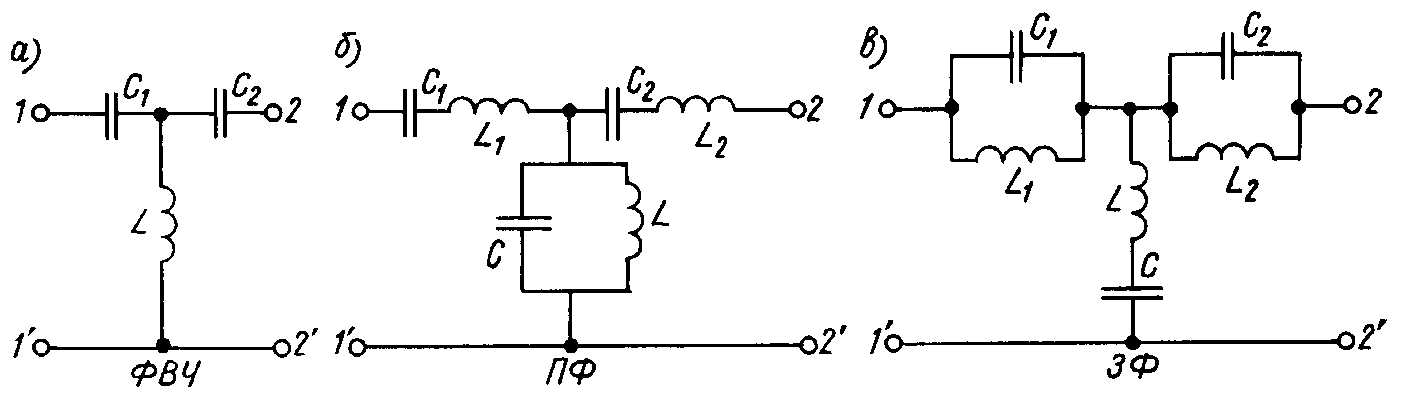 При сопротивлении головки 8 ом и подавлении «верхов» начиная с 250 Гц, данные будут 112,5 мкф и 7,2 мГн. Сделать фильтр низких частот для сабвуфера можно на простой печатной плате или использовать пластину из текстолита с контактными площадками.

В качестве конденсаторов используется ёмкость ближайшая по номиналу. В фильтре частот для сабвуфера можно использовать электролитические конденсаторы, но лучше поставить бумажные типа «МБГО», К73-16 или специально предназначенные для акустических систем полипропиленовые ёмкости К78-34. Для получения нужного номинала конденсаторы можно соединять параллельно. Катушки индуктивности можно купить готовые или намотать самостоятельно.

Активный фильтр для сабвуфера своими руками

По сравнению с пассивными конструкциями, активные схемы выравнивают амплитудно- частотную характеристику низкочастотного сигнала, корректируя пики и спады, негативно влияющие на прослушивание музыки. Простой фильтр для сабвуфера своими руками можно сделать на малошумящем операционном усилителе.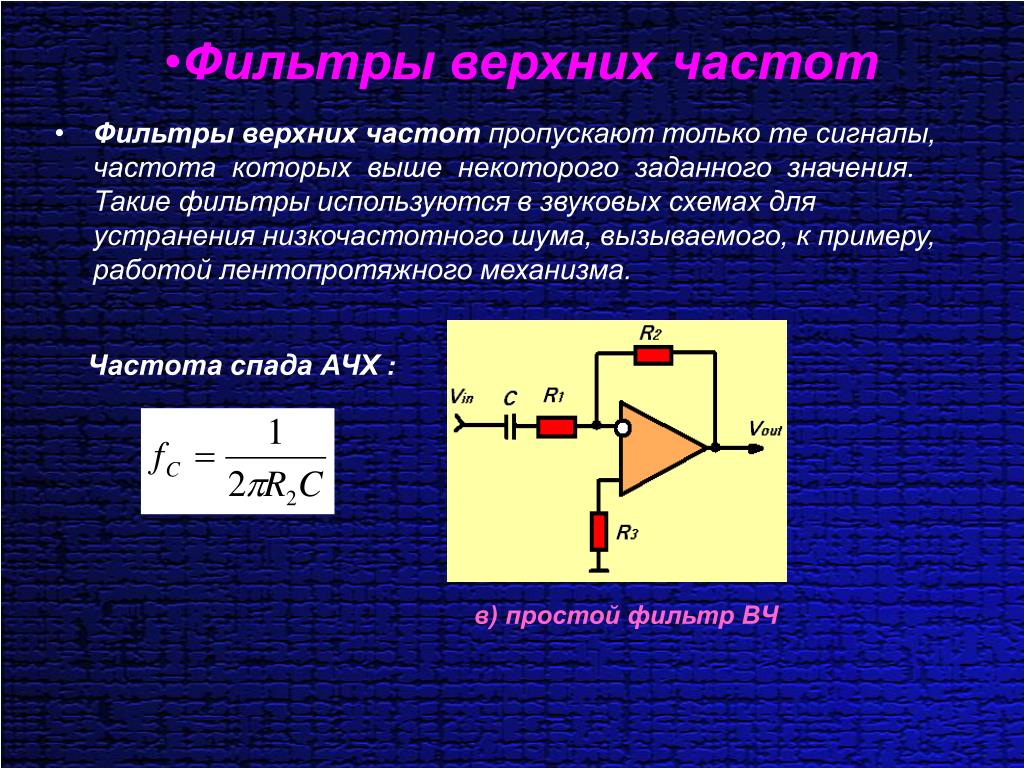

Схема фильтра НЧ для сабвуфера, сделанного своими руками, состоит из двух операционных усилителей и небольшого числа дискретных элементов. В качестве основного элемента используется интегральная микросхема LM324, которая содержит четыре операционных усилителя с однополярным питанием, что особенно удобно, если сабвуфер будет использоваться в автомобиле. Активное устройство обеспечивает подавление высокочастотной части звукового диапазона, начиная с 120 Гц. Существует много схем разного уровня сложности, которые сделаны на микросхемах или транзисторах. Интегральные схемы требуют меньшего количества деталей и не критичны к изменению напряжения питания.

Более качественную схему можно сделать на специализированной микросхеме РТ2351. Сигналы с выходов стереофонического усилителя поступают на входные каскады, микшируются и поступают на активный блок подавления низких частот. Точка начала подавления высокочастотной части спектра определяется величиной конденсаторов С3 и С7. Буферный каскад позволяет подключать устройство непосредственно к акустической системе.

Сигнал с двух каналов стереофонического усилителя через RCцепочки поступает на соответствующие входы интегральной микросхемы. Благодаря стабилизатору микросхему можно питать от любого однополярного источника постоянного тока напряжением до 20 вольт. Порог среза активного устройства составляет примерно 70 Гц. Для некоторых акустических систем эта величина подавления может быть слишком низкой. Для величины подавления 200 Гц номиналы конденсаторов должны быть следующими:

• С1 – 0,47 мкф
• С2 – 0,47 мкф
• С3 – 0,047 мкф
• С7 – 0, 068 мкф

Активный блок ограничения высокочастотной части звукового диапазонаможет использоваться как для домашнего звукового комплекса, так и в автомобиле. Недостатком данной схемы можно считать отсутствие плавной регулировки полосы пропускания, но для работы звукового комплекса это не так важно.

Простейший фильтр низких частот

Фильтры частот — это простейшие электрические цепи, АЧХ которых нелинейная.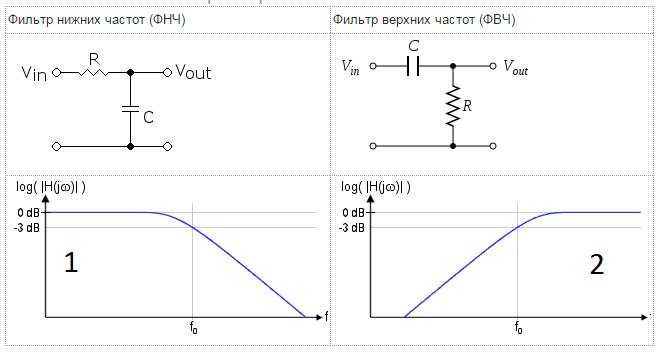 Сопротивление в таких цепях изменяется при изменении частоты сигнала. Состоять такая цепь может из одного или нескольких элементов цепи. Пассивный фильтр состоит только из резисторов или конденсаторов. Они не требуют энергии для выполнения возложенных на них задач.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Простой фильтр низких частот своими руками
• 1.19. RC-фильтры
• Фильтры нижних частот
• Фильтры нижних частот типа k
• Простой фильтр низких частот своими руками
• Аналоговые измерительные устройства
• Фильтр нижних частот
• Простейший пассивный фильтр низких частот
• Фильтр нижних частот
• Фильтры высоких и низких частот (частотный фильтр)

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Простой способ увеличения НИЗКИХ ЧАСТОТ/БАССА прокачай свой усилитель за копейки

Простой фильтр низких частот своими руками

Фильтры частот — это простейшие электрические цепи, АЧХ которых нелинейная. Сопротивление в таких цепях изменяется при изменении частоты сигнала. Состоять такая цепь может из одного или нескольких элементов цепи. Пассивный фильтр состоит только из резисторов или конденсаторов. Они не требуют энергии для выполнения возложенных на них задач. Почти все пассивные фильтры обладают линейной характеристикой.

Активный фильтр включает в свою конструкцию транзистор или операционный усилитель. АЧХ такого фильтра благоприятнее чем у пассивного. Спрашивается, зачем и где они применяются? У фильтров принцип действия следующий: поступающий на них сигнал фильтруется, и остаются только те сигналы, которые необходимы.

Одной из областей применения таких устройств является электронная цветомузыка. Частота, при которой понижается амплитуда выходного сигнала, до значения 0,7 от входного, называется частотой среза.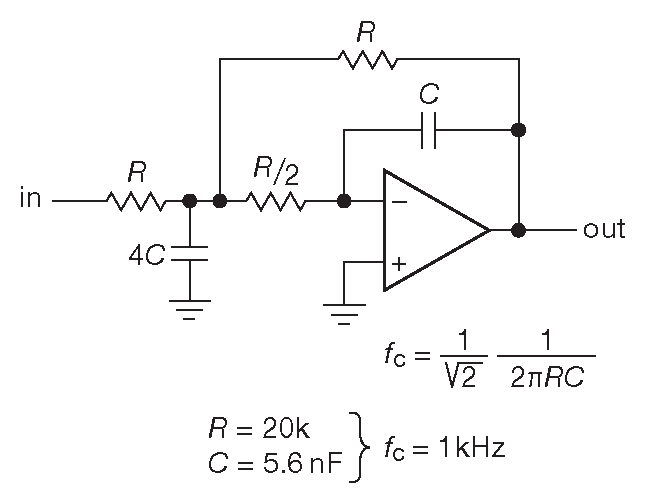

Крутизна частотной характеристики фильтра. Она показывает, как резко меняется сигнал после того, как прошел фильтр. Чем больше будет угол, тем лучше. В домашних условиях вполне можно изготовить данное устройство и по качеству оно будет не сильно уступать магазинному аналогу.

К тому же, дешевизна и простота конструкции окупит все вложенные усилия. В схеме включающей в себя резистор R11, конденсатор С6, и стабилизатор VD1 собран блок, который стабилизирует входящее напряжение.

Если подаваемое напряжение меньше 15 В резистор нужно удалить из схемы. Элементы R1, R2, С1, С2 являются сумматорами входящих сигналов. Если на фильтр подается моносигнал, сумматор можно удалить. После этого необходимо подключить источник сигнала напрямую к следующему второму контакту. Далее фильтром входного сигнала служит R7, а R9, R10, С8 является регулятором звука.

Его можно отключать, при этом С7 будет снят со звуковой дорожки. Мы описали схему, которую нужно использовать, теперь изготовим важнейший элемент, а именно печатную плату.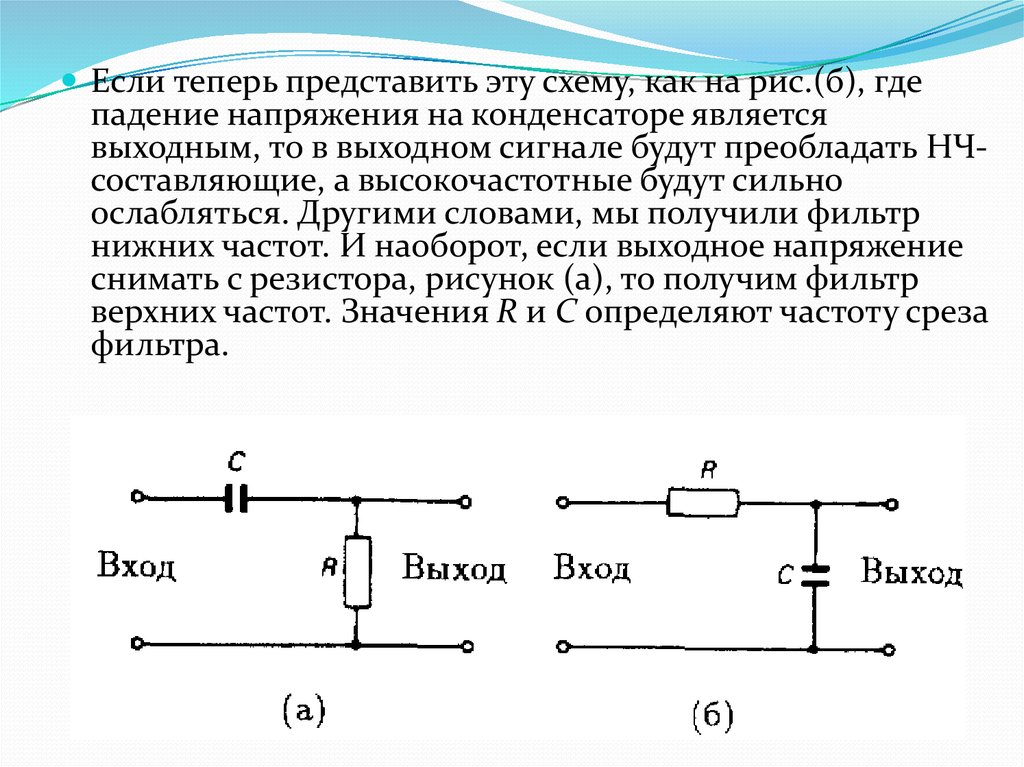

Необходимо взять стеклотекстолит, ширина которого должна быть 2 см, а длина 4 см. Для начала обезжирьте поверхность и тщательно ее отшлифуйте. Затем распечатав представленную ниже схему, перенесите ее на кусочек стеклотекстолита, соблюдая габариты.

Рекомендуется использовать метод ЛУТ. Рисунок должен полностью отпечататься на поверхности заготовки, если не получилось сделать это с первого раза, можно дорисовать прерванные дорожки о руки. Нужно поместить приготовленную заготовку с начертанными дорожками прямо в полученный раствор. Перед погружением убедитесь, что рисунок дорожки хорошо прорисован, иначе вы испортите поверхность.

Подождав немного убедитесь, что весь лишний медный слой растворился. Затем необходимо достать заготовку из емкости и промыть ее в проточной воде. При помощи ацетона удаляем чернила с платы. Для того, чтобы не ошибиться во время спаивания желательно использовать схему. Последовательно и аккуратно припаивайте все элементы.

Описанная выше схема должна заработать после первого включения.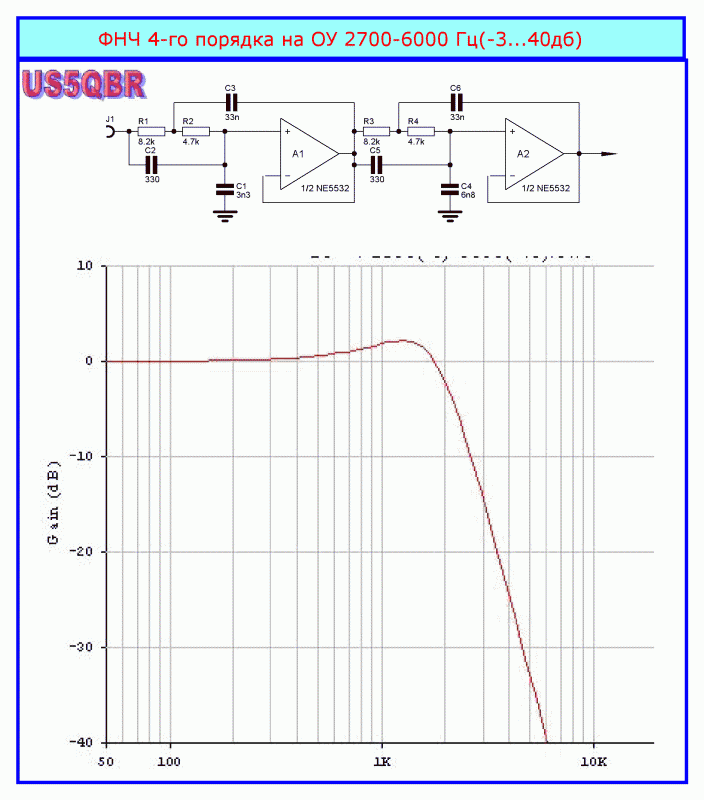 Никаких настроек фильтр не требует. Основные проблемы, которые могут возникнуть при запуске, связанны с некачественной сборкой или спайкой, в редких случаях с неисправностью применяемых элементов схемы. В некоторых случаях звук не идет после включения фильтра. Чтобы исправить проблему требуется покрутить ручку переменного резистора. Если не помогло, проверьте все соединения в местах спайки. Сделать самому фильтр для сабвуфера не так сложно, как кажется на первый взгляд.

Решение изготовить его самостоятельно, приходит не просто. Рано или поздно, все любители автозвука становятся профессионалами и стараются всеми способами усовершенствовать аудиосистему.

Простейший нч фильтр для сабвуфера и его изготовление, как раз и станет одним из решений по модернизации. Фильтр или кроссовер см. Самодельные кроссоверы для акустики и их предназначение , как его еще называют, сегодня выполняет важнейшую функцию. Дело в том, что практически все современные динамики, включая и сабвуфер, воспроизводят эффективно только определенную долю частот.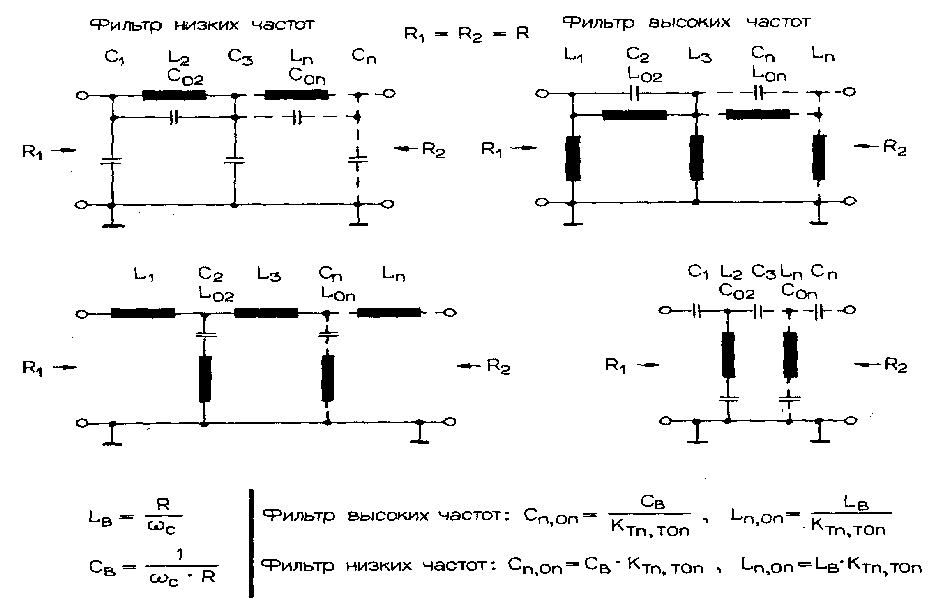

К примеру, тот же басовик воспроизводить хорошо в состоянии только низкие басы. Объяснить такую ограниченность современных динамиков очень просто. Снизу этому мешает резонансная частота подвижной системы, а сверху — масса самого диффузора.

В таком случае говорить о каком-то качестве звука просто глупо и следовательно, чтобы решить проблему, приходится использовать в аудиосистеме несколько динамиков см. Как выбрать динамики для автомагнитолы своими силами. Касательно автомобильной акустики хотелось бы выделить две типичные схемы построения системы звука, с которыми знакомы, наверное, все, кто много мало знаком с автозвуком.

Речь идет о следующих схемах:. Такая схема используется в большинстве своем любителями и в любом автомобиле, где грамотно задействована акустическая схема, ее можно встретить.

Несмотря на существенные отличия, обе схемы подчиняются единому правилу: каждый динамик в ответе за воспроизведение своей полосы частот и другие он не затрагивает. Фильтры см.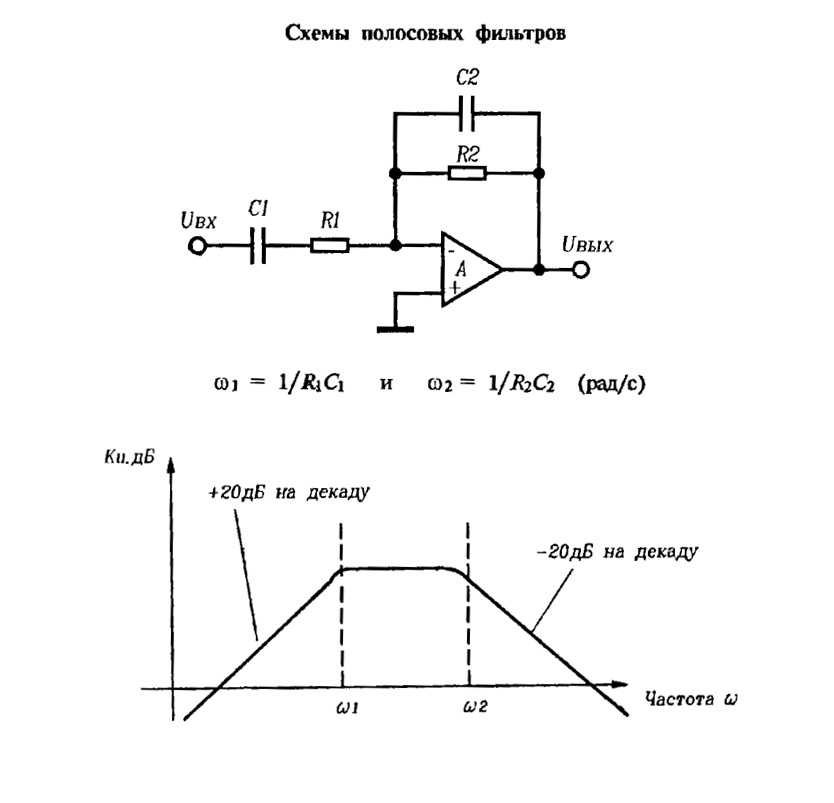 Как сделать самому фильтр для автомагнитолы частот различаются по типам. Принято выделять следующие варианты:. Кроме типов фильтров, принято разделять и их параметры.

К примеру такой параметр, как порядок, свидетельствует о количестве катушек и конденсаторов реактивных элементов :. В принципе, любой фильтр, в том числе и этот, представляет собой сочетание нескольких элементов. Обладают компоненты эти свойством избирательно пропускать сигналы определенных частот. Принято разделять три популярные схемы этого разделителя для басовика. Каким бы ни был разделитель, простейшим или сложным, он должен иметь следующие технические характеристики.

Этот разделитель не нуждается в особенной настройке и собрать его проще простого. Выполнен он на доступных ОУ. У этой схемы фильтра есть одно небольшое преимущество перед остальными.

Процесс изготовления фильтра своими руками потребует ознакомления с тематическим видео обзором. Кроме того, будет полезно изучить подробные фото — материалы, схемы, другие инструкции и многое другое. Цена самостоятельного изготовления и установки фильтра минимальна, ведь никаких расходов делать практически не нужно.

Он особенно полезен при расширении стереофонической звуковой системы на дополнительный динамик воспроизводящий только самые низкие частоты. Данный проект состоит из активного фильтра второго порядка с регулируемой граничной частотой 50 — Гц, входного усилителя с регулировкой усиления 0. Конструкция обеспечивает прямое подключение к усилителю с мостовой схемой, так как сигналы сдвинуты относительно друг друга по фазе на градусов. Благодаря встроенному источнику питания, стабилизатору на плате, можно обеспечить питание фильтра симметричным напряжением от усилители мощности — как правило это двухполярка 20 — 70 В.

Фильтр НЧ идеально подходит для совместной работы с промышленными и самодельными усилителями и предусилителями. Схема фильтра для сабвуфера показана на рисунке.

Работает он на основе двух операционных усилителей U1-U2 NE Первый из них отвечает за суммирование и фильтрацию сигнала, в то время как второй обеспечивает его кэширование.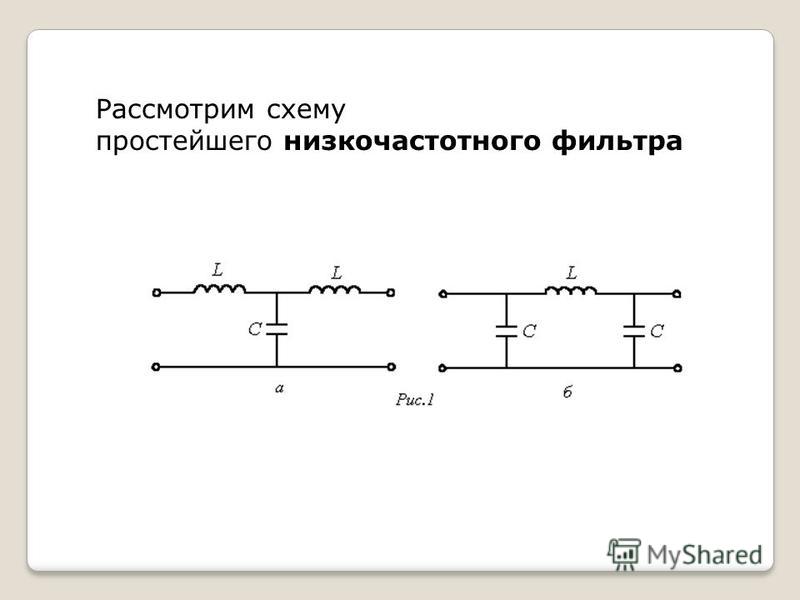 На этом элементе реализован сумматор сигнала с регулируемым коэффициентом усиления, собранный по классической схеме. Резистор R6 27k вместе с P1 50k позволяют провести регулировку усиления в диапазоне от 0. Резистор R9 k улучшает стабильность работы усилителя U1A и обеспечивает его хорошую поляризацию в случае отсутствия входного сигнала.

Сигнал с выхода усилителя попадает на активный фильтр нижних частот второго порядка, построенный U1B. Это типичная архитектура Sallen-Key, которая позволяет получить фильтры с разной крутизной и амплитудной. Логарифмическая шкала потенциометра позволяет добиться линейного изменения граничной частоты во время вращения ручки.

Широкий диапазон частот до Гц достигается при крайнем левом положении потенциометра P2, поворачивая вправо вызываем сужения полосы частот до 50 Гц.

На рисунке далее показана измеренная амплитудная характеристика всей схемы для двух крайних и среднего положения потенциометра P2. В каждом из случаев потенциометр P1 был установлен в среднем положении, обеспечивающим усиление 1 0 дб. Сигнал с выхода фильтра обрабатывается с помощью усилителя U2. Резисторы R2 4,7k и R8 4,7k представляют собой ограничители тока стабилитронов, и были подобраны таким образом, чтобы при минимальном напряжении питания ток составлял около 1 мА, а при максимальном был безопасен для D1 и D2.

Разъем питания — GP2. Стоит отметить, что модуль фильтра для сабвуфера должен быть присоединен к выходу предварительного усилителя после регулятора громкости, что позволит улучшить регулировку громкости всей системы. Потенциометром усиления можно отрегулировать соотношение громкости сабвуфера к громкости всего сигнального тракта.

К выходу модуля необходимо подключить любой усилитель мощности, работающий в классической конфигурации, например такой. При необходимости используйте только один из выходных сигналов, сдвинутых по фазе на градусов относительно друг друга.

Оба выходные сигнала можно использовать, если нужно построить усилитель в мостовой конфигурации.

1.19. RC-фильтры

Фильтр верхних частот – это схема, которая передает без изменений сигналы высоких частот, а на низких частотах обеспечивает затухание сигналов и опережение их по фазе относительно входных сигналов.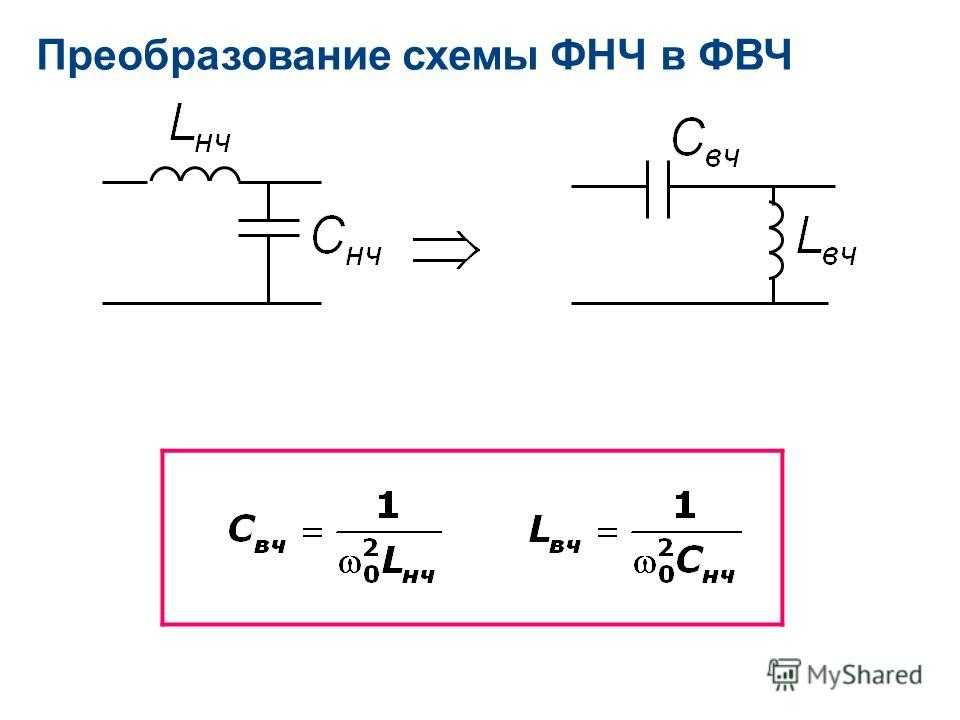 Схема простого RC-фильтра верхних частот приведена на рис. Рис 2. Простой фильтр верхних частот. Амплитудно-частотные и фазо-частотные характеристики опять получим из формулы для отношения напряжений: Отсюда находим Обе кривые представлены на рис.

Активный фильтр низких частот усиливает низкие частоты. Схема простейшего фильтра низких частот представлена на рис

Фильтры нижних частот

Степень подавления каждой частоты зависит от вида фильтра. В отличие от фильтра нижних частот НЧ , фильтр верхних частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты. В схемах пассивных аналоговых фильтров используют реактивные элементы , такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя такие элементы, можно добиться усиления или ослабления гармоник с нужными частотами. Идеальный фильтр нижних частот sinc-фильтр полностью подавляет все частоты входного сигнала выше частоты среза и пропускает без изменений все частоты ниже частоты среза. Переходной зоны между частотами полосы подавления и полосы пропускания не существует. Однако такой фильтр практически нереализуем для большинства сигналов, так как sinc-функция имеет ненулевые значения для всех моментов времени вплоть до бесконечности. Его можно использовать только для уже записанных цифровых сигналов либо для идеально периодических сигналов. Реальные фильтры для приложений реального времени могут лишь приближаться к идеальному фильтру. Один из наиболее распространённых типов линейных фильтров , отличительной особенностью которого является максимально гладкая групповая задержка линейная фазо-частотная характеристика.

Фильтры нижних частот типа k

Парни, я в акустике не силён, и поэтому решил задать необычный для данного сообщества вопрос. Подскажите простейший RC-фильтр для срезания басов, который можно подвесить на скрутках между проводами динамика. Чего там париться. Емкость указал условно.

Простейший фильтр нижних частот содержит всего два элемента рис.

Простой фильтр низких частот своими руками

Фильтры частот — это простейшие электрические цепи, АЧХ которых нелинейная. Сопротивление в таких цепях изменяется при изменении частоты сигнала. Состоять такая цепь может из одного или нескольких элементов цепи. Пассивный фильтр состоит только из резисторов или конденсаторов. Они не требуют энергии для выполнения возложенных на них задач. Почти все пассивные фильтры обладают линейной характеристикой.

Аналоговые измерительные устройства

В воздушном, водяном, масляном и других видах фильтров происходит очистка от посторонних частиц и примесей. Но что же фильтрует электрический фильтр? Ответ простой: частоту. Для остальных частот, которые не входят в полосу пропускания , фильтр создает большое затухание, вплоть до полного их исчезновения. Ниже пример идеального фильтра, который пропускает частоты до какого-то определенного значения частоты среза.

В этом разделе вы познакомитесь с примерами простейших RС-фильтров, к которым . Рис. Частотная характеристика фильтра низких частот.

Фильтр нижних частот

Фильтры — это схемы, которые пропускают без затухания ослабления определенную полосу частот и подавляют все остальные частоты. Частота, на которой начинается подавление, называется частотой среза f с рис. Частотная характеристика фильтра нижних а и верхних б частот. Влияние фильтра на прямоугольный сигнал.

Простейший пассивный фильтр низких частот

ВИДЕО ПО ТЕМЕ: Как улучшить любые колонки, повысить громкость, устранить пердёж на высокой громкости.

Конденсатор пропускает лишь переменный ток, а выходное напряжение снимается с резистора. Что это за показатель. Чем быстрее происходит спад АЧХ тем лучше. Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала.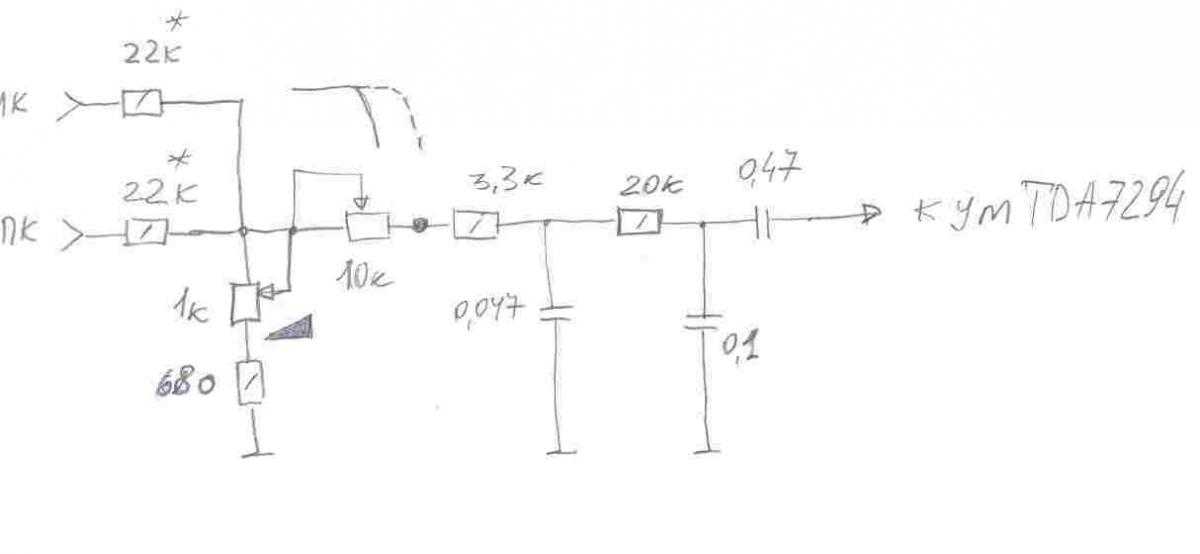 То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты. В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов фильтры с катушками индуктивности трогать не будем.

Фильтр нч для сабвуфера своими руками схема фото К примеру такой параметр, как порядок, свидетельствует о количестве катушек и конденсаторов реактивных элементов : 1-ый порядок содержит только один элемент; 2-ой порядок два элемента и т.

Фильтр нижних частот

А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания? А как насчёт расчёта активных полиномиальных фильтров второго порядка на звеньях Рауха, Сален-Ки и биквадратного звена? А кривую изменения реактивного сопротивления ёмкости в зависимости от частоты – не изобразить ли? И действительно.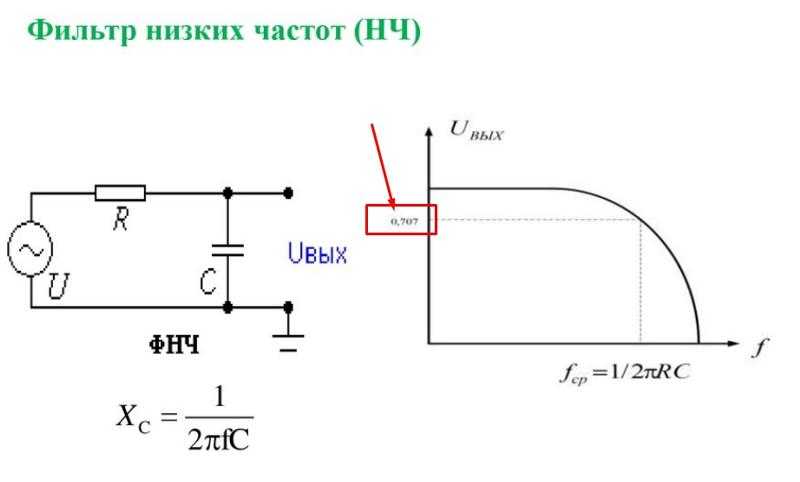 Здесь мне не тут! Базар надо фильтровать, а не безобразия нарушать! Итак, приступим.

Фильтры высоких и низких частот (частотный фильтр)

В данной статье поговорим о фильтре высоких и низких частот, как характеризуются и их разновидностях. Фильтры высоких и низких частот — это электрические цепи, состоящие из элементов, обладающих нелинейной АЧХ — имеющих разное сопротивление на разных частотах. Частотные фильтры можно поделить на фильтры верхних высоких частот и фильтры нижних низких частот.

Простой фильтр нижних частот

---

Введение

Фильтр нижних частот снижает содержание высоких частот в сигнале, пропуская более низкие частоты.

Существует много причин, по которым может потребоваться ослабление или удаление высоких частот. В процессе аналого-цифрового преобразования (АЦП) оцифровки электрического сигнала важно удалить частоты, превышающие частоту Найквиста (т. е. превышающие 1/2 частоты дискретизации), чтобы они не были искажены в цифровой сигнал.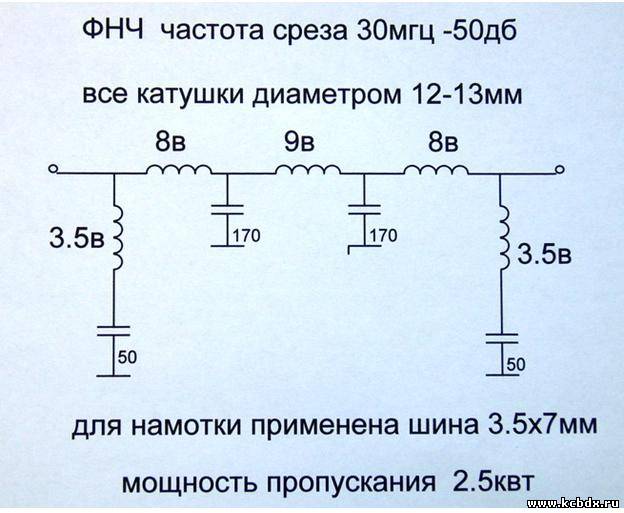 Фильтр нижних частот, используемый для этой цели, называется фильтр сглаживания . В цифровом сигнале, полученном от датчика (например, детектора движения), данные могут быть зашумленными и дрожащими или могут содержать случайные ложные неверные значения. Сглаживающий фильтр нижних частот может сгладить эти несоответствия. А в случае звукового сигнала фильтр нижних частот часто используется для уменьшения высокочастотного шипения в записи или для уменьшения амплитуды верхних частот в самом звуке, чтобы изменить тембр звука.

Во всех случаях уменьшение содержания высоких частот в сигнале приводит к несколько более гладкой форме волны во временной области.

---

Простейший фильтр нижних частот

Большинство фильтров нижних частот сглаживают входной сигнал, взвешивая комбинацию текущей входной выборки и одной или нескольких предыдущих выборок для расчета взвешенного скользящего среднего. Простейшим примером этого может быть фильтр, который выводит среднее значение (среднее) текущей входной выборки и предыдущей входной выборки.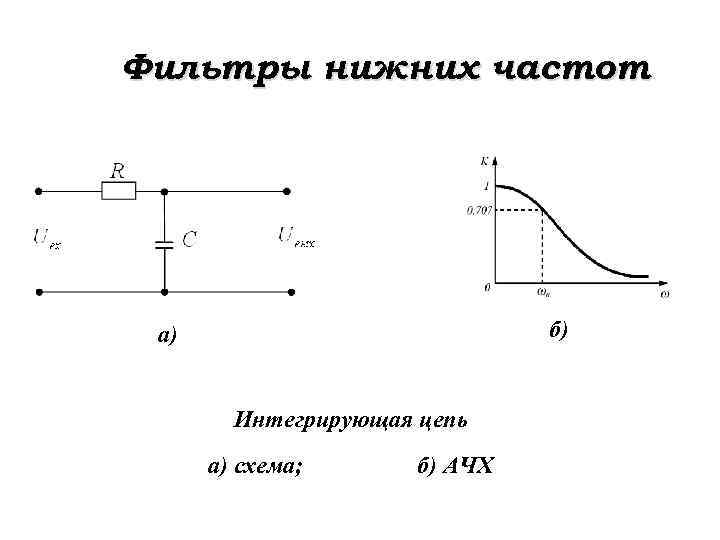 Уравнение разности для этого фильтра нижних частот будет следующим:

Y _N = (x _N +x _N-1 )/2

Где x _N является значением текущего входного образца, x _N- является значением текущего входного образца, x _N- . — предыдущая входная выборка, а y _n — текущая выходная выборка.

Этот вид усреднения вообще не изменит входной сигнал, если сигнал меняется очень постепенно от одной выборки к другой, но значительно сгладит сигнал, если входные данные резко меняются от выборки к выборке. Таким образом, высокие частоты, вызывающие более быстрое и радикальное изменение сигнала, немного сглаживаются, уменьшая высокочастотную энергию.

Если вам это интуитивно не очевидно, давайте рассмотрим пару примеров. Если входной поток чисел равен 0,0,1 0,2 0,4 0,5 0,3 0,1 0, — и мы предполагаем, что исходное число равно x _n-1 со значением 0, — на выходе будет 0,0,05 0,15 0,3 0,45 0,4 0,2 0,05, который имеет прогрессию и форму, очень похожую на ввод.

Гладкий вход лишь слегка сглаживается фильтром нижних частот

В то время как с зубчатым входным потоком (содержащим высокочастотную энергию) сглаживающий фильтр будет иметь более заметный эффект. С входным потоком типа 0,8 0,7 -0,1 0,9-0,9 0,1 -0,4 0,4, на выходе будет 0,4 0,75 0,3 0,4 0, -0,4 0,15 0, что существенно отличается по форме и амплитуде (особенно зубчатых высокочастотных фронтов) от входного.

Зубчатый вход более заметно сглаживается фильтром нижних частот

Точно так же в звуковых сигналах звук без большого количества высокочастотной энергии, такой как синусоидальный тон 1000 Гц, показанный ниже, не сильно подвержен этому простому воздействию. фильтр нижних частот.

Синусоидальный тон частотой 1 кГц, практически не затронутый фильтром нижних частот

В то время как шумовой сигнал покажет более значительное изменение из-за затухания его высоких частот.

Шумовой вход более сильно изменен фильтром нижних частот

Ниже вы можете увидеть плавно наклонную амплитудную характеристику этого фильтра нижних частот, представленную в виде графика зависимости амплитуды от частоты.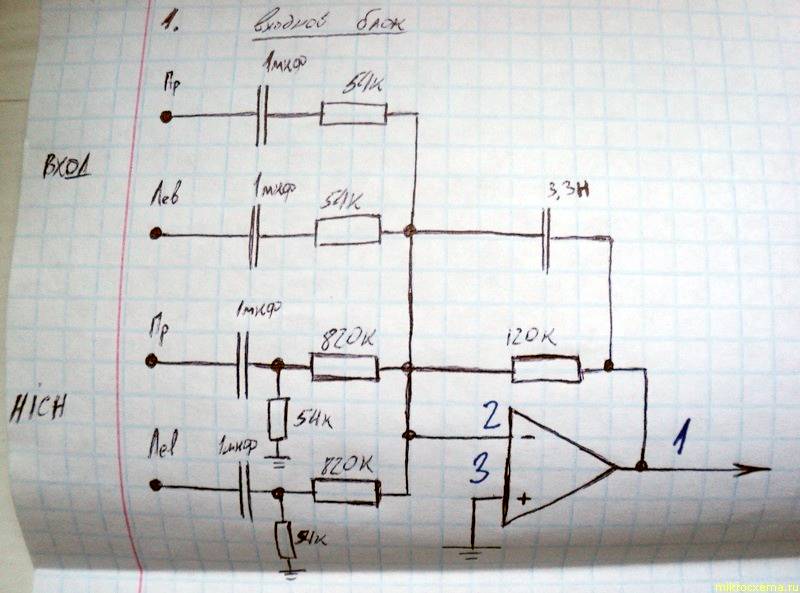

Влияние фильтра нижних частот y _n = (x _n +x _n-1 )/2

---

Регулируемый фильтр нижних частот

Стоит отметить, что фильтр усреднения, описанный выше, является лишь одним из экземпляров немного более общего фильтра, который допускает любой баланс между текущим входным сэмплом и предыдущим входным сэмплом. Приведенное выше уравнение в среднем может быть пересмотрено эквивалентно как

Y _N = 0,5x _N +0,5x _N-1

, и это конкретный случай уравнения

Y _N = AX. _п +(1-а))х _n-1

, в котором текущее входное значение умножается на коэффициент a , а предыдущее входное значение умножается на (1-a) . Когда значение коэффициента a равно 1, не будет изменений на входе (задержанная входная выборка будет умножена на 0), тогда как когда значение коэффициента a равно 0,5, 1-a также будет равно 0,5, что дает среднее значение двух последних входных выборок.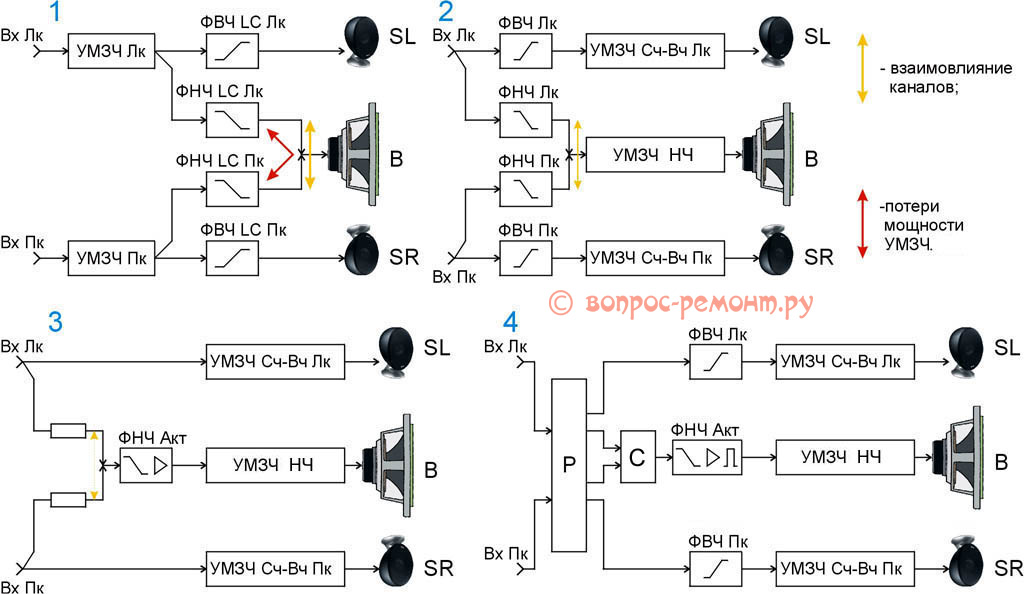 Любое значение и между 1 и 0 обеспечат различное взвешивание между двумя выборками.

В случае, если это поможет увидеть графическое представление этого, вот способ, которым алгоритмы фильтрации часто изображаются схематически. Символ z _-1 означает задержку на один отсчет, а треугольные значки обозначают усиление (умножение) на указанный коэффициент.

КИХ-фильтр первого порядка

(Стоит отметить, что эффект фильтра становится наиболее сильным при и приближаются к 0,5. Когда a опускается ниже 0,5 к 0, эффект фильтра становится слабее, пока, когда a = 0, выход не будет таким же, как и ввод, только с задержкой на одну выборку.)

Интересно, если мы изменим оператор + до -оператор в вышеуказанном уравнении,

Y _N = AX _N -(1 -A)) x _{N -1}

или

Y _N = AX _N +(a-1))x _n-1

фильтр становится фильтром высоких частот.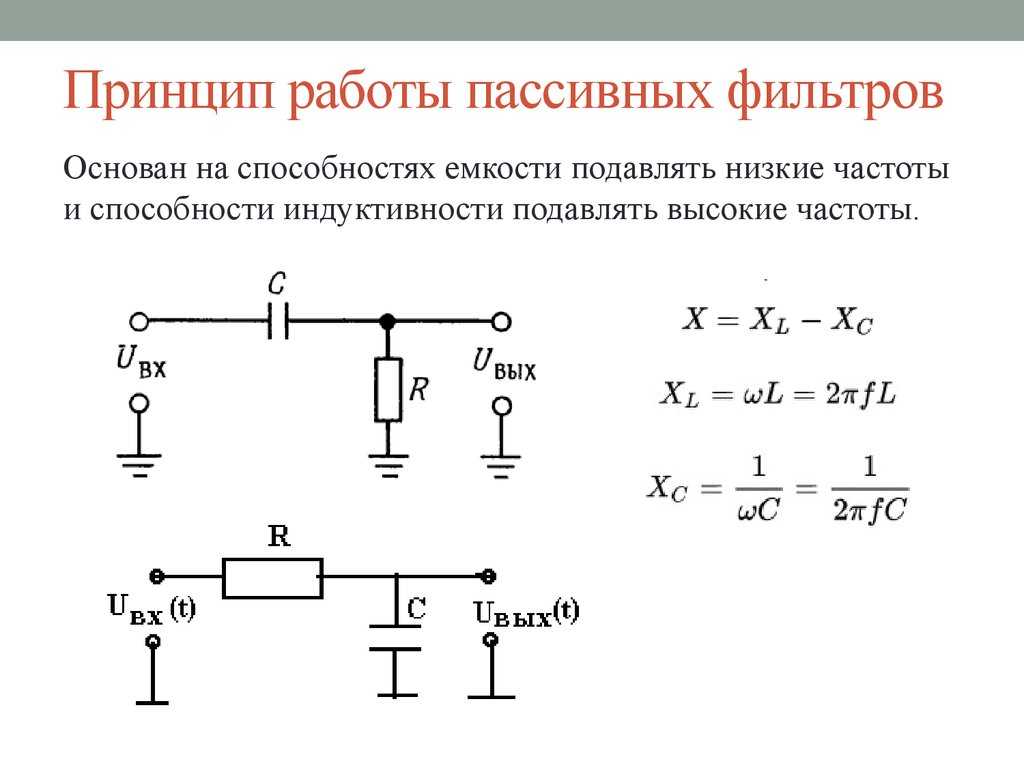

Эффект фильтра верхних частот y _n = (x _n -x _n-1 )/2

---

КИХ-фильтр N-го порядка, показанный выше

, КИХ-фильтр нижних частот, показанный выше

, 9000 коэффициент задержанной выборки всегда равен единице минус коэффициент текущей входной выборки. Если бы мы сделали два коэффициента независимыми друг от друга, мы могли бы написать немного более общее уравнение:

Y _N = A ₀ x _N +A ₁ x _N-1

, в котором A ₀ и A ₁ 9009 может быть любыми значениями. -1 и 1). И на самом деле, вы можете экстраполировать это еще более общее уравнение, которое даст взвешенную сумму любых числа непосредственно предшествующих выборок,

y _n = a ₀ x _n +a ₁ x _n-1 +a ₂ x _n-2 + … a _N x _n-N

Другой способ записи той же самой формулы — в форме так называемой записи суммирования или сигма-записи.

Уравнение КИХ-фильтра в сигма-нотации

Упорядоченный набор коэффициентов в этом уравнении называется его импульсной характеристикой . В цифровом аудио термин «импульс» используется для обозначения одной выборки со значением 1 (окруженной нулями до и после нее). Если бы вы подавали в это уравнение звуковой сигнал, состоящий из 1, за которым следуют N 0 (и предположили, что все предыдущие выборки также были 0), выходным результатом был бы сигнал, равный импульсной характеристике, коэффициенты уравнения. Приведенное выше уравнение описывает то, что называется фильтром с конечной импульсной характеристикой (КИХ). Для любого конечного сигнала, который помещается в него, результирующий вывод также будет конечным, в конечном итоге возвращаясь к 0 N выборкам позже. Уравнение фильтра, состоящее из текущей входной выборки плюс N предыдущих входных выборок, называется КИХ-фильтром N-го порядка.

КИХ-фильтр, в котором все коэффициенты находятся в диапазоне от -1 до 1, приводит к затуханию (уменьшению амплитуды) сигнала только на определенных частотах. Он не будет резонировать (увеличивать) энергию на любой частоте.

Словарь

• Фильтр нижних частот
• Разностное уравнение
• Коэффициенты фильтра
• Импульсная характеристика
• Обозначение суммирования (сигма-обозначение)
• Фильтр с конечной импульсной характеристикой (КИХ)

Самопроверка

1. Фильтр нижних частот подавляет низкие или высокие частоты?
2. На что указывают острые углы в звуковой волне?
3. Какой термин используется для уравнения, объединяющего взвешенные задержанные выборки цифрового сигнала?
4. Что такое импульс?
5. Как мы называем уравнение фильтра, состоящее только из текущей входной выборки плюс N предыдущих входных выборок?
6. Что подразумевается под «импульсной характеристикой» КИХ-фильтра?

Дополнительные ресурсы

• Введение в цифровые фильтры с аудиоприложениями Джулиуса О. Смита

Как создать простой фильтр нижних частот

Резюме: В этой статье показано, как создать простой фильтр нижних частот, начиная с частоты среза \(f_c\) и полосы пропускания перехода \(b\). Эта статья дополнена Инструмент проектирования фильтров , который позволяет создавать собственные пользовательские версии примера фильтра, показанного ниже, и загружать полученные коэффициенты фильтра.

Как создать простой фильтр нижних частот? Фильтр нижних частот предназначен для того, чтобы пропускать низкие частоты, но задерживать высокие частоты. Теоретически фильтр нижних частот perfect (т. е. perfect ) является фильтром sinc . Функция sinc ( нормализовано , следовательно, \(\pi\), как это принято в обработке сигналов), определяется как

\[\mathrm{sinc}(x)=\frac{\sin(\pi x)}{\pi x}.\]

Фильтр sinc представляет собой масштабированную версию этого, которую я определю ниже.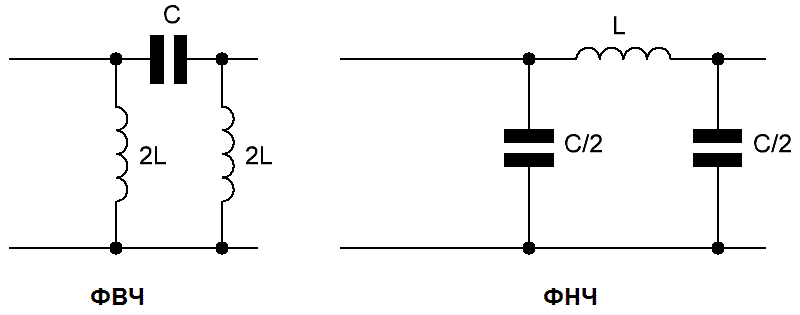 При свертывании с входным сигналом sinc-фильтр приводит к выходному сигналу, в который включены все частоты до частоты среза , а все более высокие частоты заблокированы. Это связано с тем, что функция sinc является обратным преобразованием Фурье прямоугольной функции . Умножение частотного представления сигнала на прямоугольную функцию можно использовать для генерации идеально подходит для АЧХ, так как полностью убирает частоты выше точки отсечки. И, поскольку умножение в частотной области эквивалентно свертке во временной области, фильтр sinc имеет точно такой же эффект.

Фильтр windowed-sinc , описанный в этой статье, является примером фильтра с конечной импульсной характеристикой ( FIR ).

Sinc Filter

Функция sinc должна быть масштабирована и семплирована, чтобы создать последовательность и превратить ее в (цифровой) фильтр. Импульсная характеристика фильтра sinc определяется как

\[h[n]=2f_c\mathrm{sinc}(2f_cn),\]

где \(f_c\) — частота среза.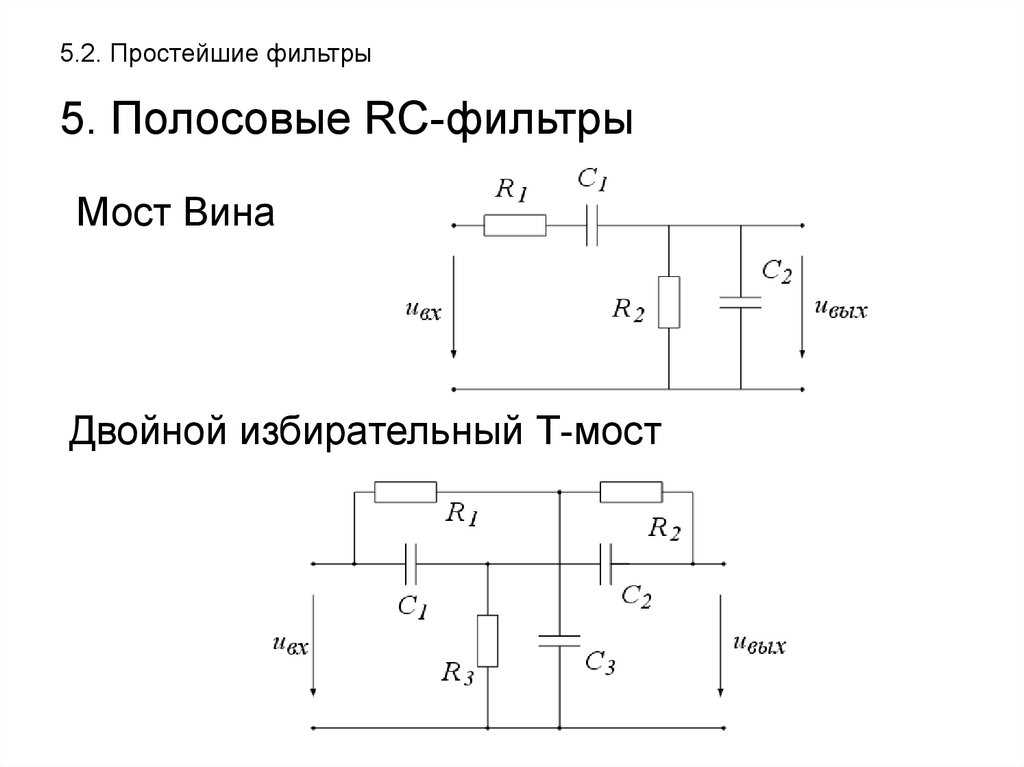 Частота среза должна быть указана как часть частоты дискретизации. Например, если частота дискретизации составляет 10 кГц, то \(f_c=0,1\) приведет к удалению частот выше 1 кГц. Центральная часть sinc-фильтра с \(f_c=0,1\) показана на рисунке 1.

Рисунок 1. Sinc-фильтр.

Проблема с фильтром sinc заключается в том, что он имеет бесконечную длину в том смысле, что его значения не падают до нуля. Это означает, что задержка фильтра также будет бесконечной, что делает этот фильтр нереализуемый . Простое решение состоит в том, чтобы просто прекратить вычисления в определенный момент (фактически усекая фильтр), но это приводит к чрезмерной пульсации . Лучшим решением является window фильтр sinc, в результате чего, как вы уже догадались, получается windowed-sinc filter .

Окно

Оконная функция — это функция, которая равна нулю за пределами некоторого интервала. Существует великое множество этих функций, настроенных на разные свойства, но я просто воспользуюсь известными Окно Blackman здесь, что является хорошим выбором для общего использования.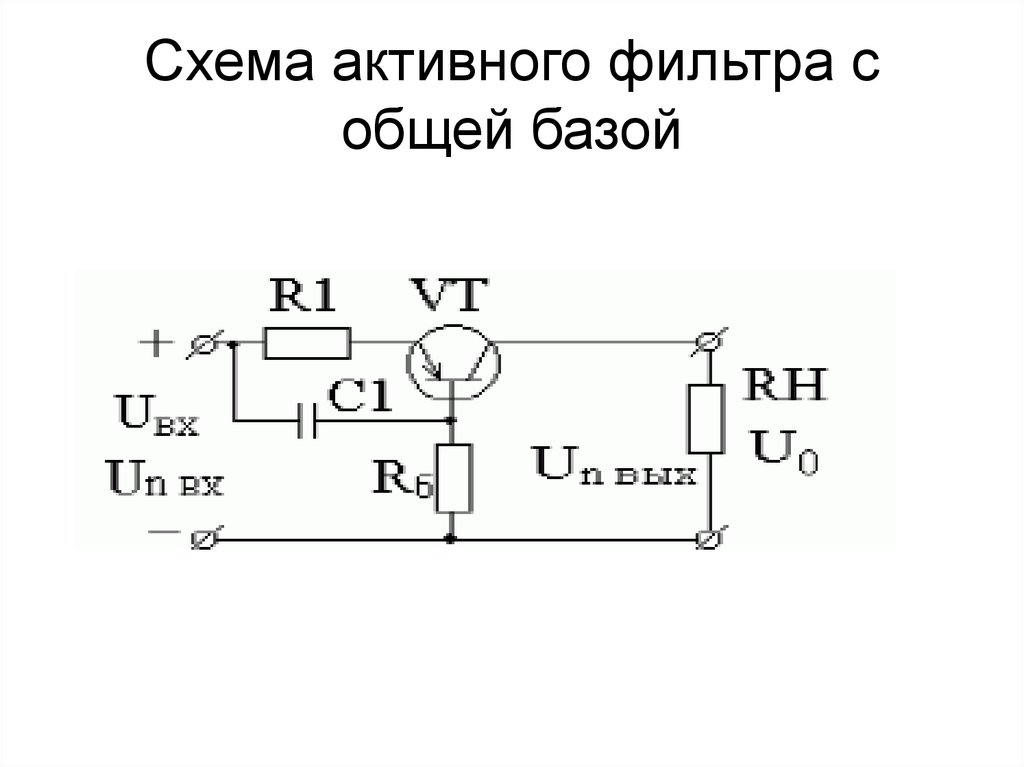 Он определяется как (для \(N\) точек)

\[w[n]=0,42-0,5\cos\left({\frac{2\pi n}{N-1}}\right)+0,08 \cos\left({\frac{4\pi n}{N-1}}\right),\]

с \(n\in[0,\,N-1]\). Это показано на рисунке 2 для \(N=51\).

Рис. 2. Окно Блэкмана.

Фильтр Windowed-Sinc

Окончательный фильтр Windowed-Sinc является просто произведением двух предыдущих выражений следующим образом (с фильтром sinc, сдвинутым в диапазон \([0,\,N-1]\)) .

\[h[n]=\mathrm{sinc}\left(2f_c\left(n-\frac{N-1}{2}\right)\right)\left(0.42-0.5\cos\left( {\ frac {2 \ pi n} {N-1}} \ right) + 0,08 \ cos \ left ({\ frac {4 \ pi n} {N-1}} \ right) \ right), \]

с \(h[n]=0\) для \(n\notin[0,\,N-1]\). Я исключил множитель \(2f_c\) из фильтра sinc, так как гораздо проще сначала игнорировать константы, а в самом конце нормализовать весь фильтр, просто убедившись, что сумма всех коэффициентов равна единице, что дает коэффициент усиления фильтра, с

9{N-1}h[i]. \]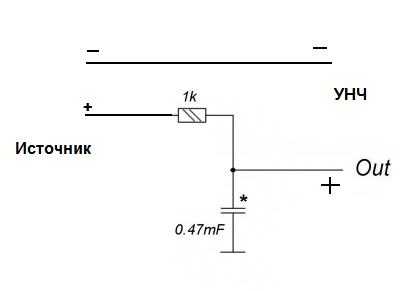

В результате получается нормализованный оконный фильтр sinc, показанный на рисунке 3.

Рисунок 3. Нормализованный оконный фильтр sinc.

Полоса пропускания перехода

Последняя задача состоит в том, чтобы включить желаемую полосу пропускания перехода (или спада ) фильтра. Для простоты можно использовать следующую аппроксимацию отношения между пропускной способностью перехода \(b\) и длиной фильтра \(N\),

\[b\приблизительно\frac{4}{N},\ ]

с дополнительным условием, что лучше всего сделать \(N\) нечетным. На самом деле это не требуется, но симметричный КИХ-фильтр нечетной длины имеет задержку, которая представляет собой целое число отсчетов, что упрощает сравнение отфильтрованного сигнала с исходным. Установка \(N=51\) выше была достигнута установкой \(b=0,08\). Что касается \(f_c\), параметр \(b\) должен быть указан как часть частоты дискретизации. Следовательно, для частоты дискретизации 10 кГц установка \(b=0,08\) приводит к переходной полосе около 800 Гц, что означает, что фильтр переходит от пропуска частот к их блокировке в диапазоне примерно 800 Гц.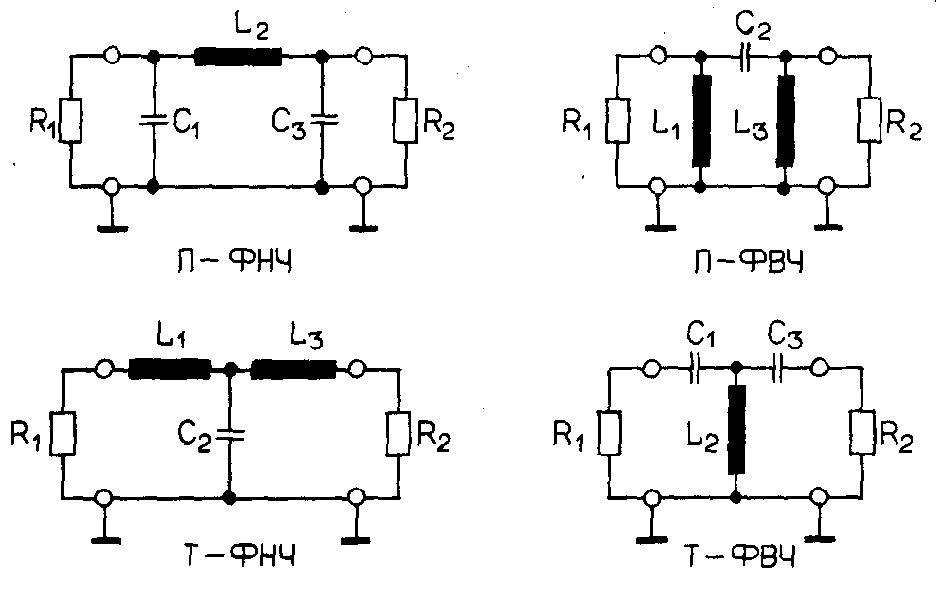 Значения для \(f_c\) и \(b\) в этой статье были выбраны, чтобы сделать цифры максимально понятными. Частотная характеристика окончательного фильтра (при \(f_c=0,1\) и \(b=0,08\)) показана на рисунке 4.

Рис. 4. Частотная характеристика в линейной (слева) и логарифмической (справа) шкале.

Код Python

В Python все эти формулы могут быть реализованы лаконично.

 
 из отдела импорта __future__  импортировать numpy как np  fc = 0,1 # Частота среза как часть частоты дискретизации (в (0, 0,5)).
b = 0,08 # Полоса перехода как доля частоты дискретизации (в (0, 0,5)).
N = int(np.ceil((4/b)))
если не N % 2: N += 1 # Убедитесь, что N нечетно.
n = np.arange (N)  # Вычислить фильтр sinc.
ч = np.sinc (2 * fc * (n - (N - 1) / 2))  # Вычислить окно Блэкмана.
w = 0,42 - 0,5 * np.cos (2 * np.pi * n / (N - 1)) + \
 0,08 * np.cos (4 * np.pi * n / (N - 1))  # Умножить фильтр sinc на окно.
ч = ч * ш  # Нормализация для получения единичного усиления.