Расчет катушки индуктивности без сердечника: Расчет катушки индуктивности | Онлайн калькулятор

Как рассчитать индуктивность катушек на разомкнутых сердечниках?

Всем доброго времени суток! В прошлой статье я рассказал о катушках индуктивности на сердечниках с малым магнитным зазором (длина зазора δ меньше любого линейного размера сердечника). Кроме сердечников с малым зазором существует сердечники, имеющие воздушный зазор сопоставимый с линейными размерами самого сердечника. Такие сердечники называются разомкнутыми. Данная статья описывает расчёт и параметры стержневых сердечников, являющихся разомкнутыми.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Факторы, влияющие на индуктивность катушки на разомкнутом сердечнике

В сердечниках с малым воздушным зазором магнитное поле практически всё сосредоточенно в сердечнике, и в воздушном зазоре рассеивание магнитного поля незначительно. Другая картина возникает, если магнитное поле возникает в сердечнике, имеющем воздушный зазор l_з сопоставимый с длиной магнитной силовой линии в сердечнике l_c.

Магнитное поле в разомкнутом сердечнике.

Таким образом, магнитные сопротивления сердечника и воздушного зазора становятся соизмеримыми, что приводит к усложнению расчётных выражений для индуктивности катушек на таких сердечниках. В этом случае расчёт параметров ведут с учётом того, что в разомкнутых сердечниках на торцах сосредотачиваются противоположно ориентированные магнитные частицы, то есть частицы с положительным доменом смещаются в направлении внешнего поля, а отрицательные навстречу ему. В результате возникает размагничивающее поле, противоположное основному. Данное поле характеризуется размагничивающим фактором N или коэффициентом размагничивания. Данный фактор зависит от формы и размеров самого сердечника. Влияние размагничивающего фактора на магнитное поле сердечника описывается следующим выражением

где Н – напряженность магнитного поля в сердечнике,

Н₀ – напряженность внешнего магнитного поля, то есть поля создаваемого катушкой, намотанной на разомкнутый сердечник,

Н_Р – размагничивающее поле сердечника,

N – размагничивающий фактор,

J – вектор намагничивания сердечника.

Точное значение размагничивающего фактора, возможно, рассчитать только для однородно намагниченных тел, например, эллипсоидов вращения, шаров, дисков. Для учёта размагничивающего фактора на магнитные свойства сердечника ввели понятие эффективной магнитной проницаемости сердечника μ_е, которая зависит от магнитной проницаемости вещества сердечника μ_r и размагничивающим фактором N. Значение эффективной магнитной проницаемости сердечника для однородно намагниченных тел определяется следующим выражением

Однако в практике, используются неоднородно намагниченные тела – цилиндры, призмы, поэтому для расчёта эффективной магнитной проницаемости таких сердечников применяются эмпирически выведенные выражения.

Вследствие того, что значение размагничивающего фактора в неоднородно намагничиваемых телах различно по длине, то необходимо учитывать и расположение катушки индуктивности относительно сердечника и длину данной катушки относительно длины сердечника.

Таким образом, индуктивность катушки, выполненной на разомкнутом сердечнике можно определить по следующему выражению

где L₀ – индуктивность катушки без сердечника, расчет смотреть (Часть 1, Часть 2, Часть 3),

μ_е – эквивалентная магнитная проницаемость разомкнутого сердечника,

k– коэффициент зависящий от отношения длины катушки к длине сердечника,

p_l – коэффициент зависящий от расположения катушки относительно середины длины сердечника.

Рассмотри более подробно зависимость индуктивности от различных факторов.

Расчёт размагничивающего фактора

Как я уже говорил, размагничивающий фактор N зависит от размеров сердечника

Катушка индуктивности с разомкнутым сердечником

Для его определения введём коэффициент λ, зависящий от отношения длины сердечника l_c к его диаметру d_c

Тогда в интервале 2 ≤ λ ≤ 50 с точностью 10 % размагничивающий фактор данного сердечника можно определить по следующему выражению

где λ – отношение длины сердечника к диаметру сердечника

Тогда эффективная магнитная проницаемость разомкнутого сердечника можно рассчитать по следующей формуле

где μ_r – относительная магнитная проницаемость вещества сердечника,

l_c – длина сердечника,

d_c – диаметр сердечника.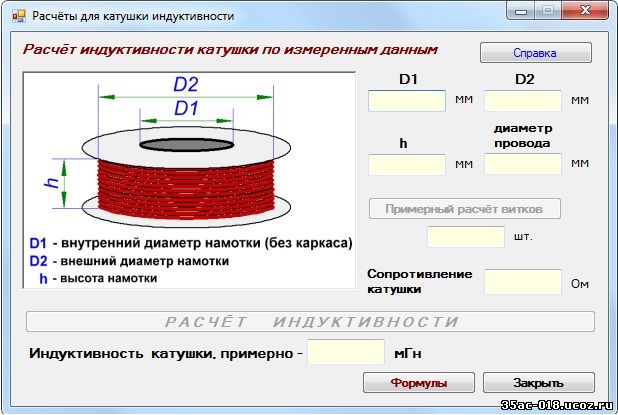

Как влияет форма сердечника на магнитную проницаемость?

Эмпирическая формула вычисления эквивалентной магнитной проницаемости сердечников предполагает, что сечение сердечника представляет собой круг, но существует большое количество сердечников с не круглым сечением (прямоугольные, трубчатые).

Вычисление эквивалентных диаметров сердечника.

Для упрощения расчётов все сердечники необходимо приводить к эквивалентному круговому сечению согласно следующим выражениям:

для прямоугольного сечения

где с – ширина сердечника,

h – высота сердечника.

для трубчатого сечения

где d_нар – наружный диаметр сердечника,

d_вн – внутренний диаметр сердечника.

Влияние расположение катушки индуктивности относительно сердечника

Довольно часто стержневые сердечники используют для точной настройки индуктивности или подстройки в небольших пределах, также длинные стержневые сердечники используют в магнитных антеннах радиоприёмников на средне- и длинноволновом диапазоне. Их объединяет то, что катушка индуктивности зачастую расположена не на средине сердечника. Ниже представлена катушка индуктивности на разомкнутом сердечнике, используемая в качестве магнитной антенны

Расположение катушки индуктивности на сердечнике в магнитной антенне.

Как я уже говорил, размагничивающий фактор не равномерно распределён по длине разомкнутого сердечника. Его значение увеличивается от середины сердечника к его краям, а магнитная проницаемость, а соответственно уменьшается от центра сердечника к его краям. Чтобы не усложнять выражение для размагничивающего фактора введем корректирующий коэффициент p_l, зависящий от расположения катушки на сердечнике

где х – расстояние от середины сердечника до середины катушки,

l – длина сердечника,

β – коэффициент, зависящий от расположения катушки на сердечнике.

Влияние размеров катушки относительно размеров сердечника

Как я писал выше, размагничивающий фактор неравномерен по длине сердечника, то необходимо учитывать любое различие в относительных размерах катушки индуктивности и сердечника.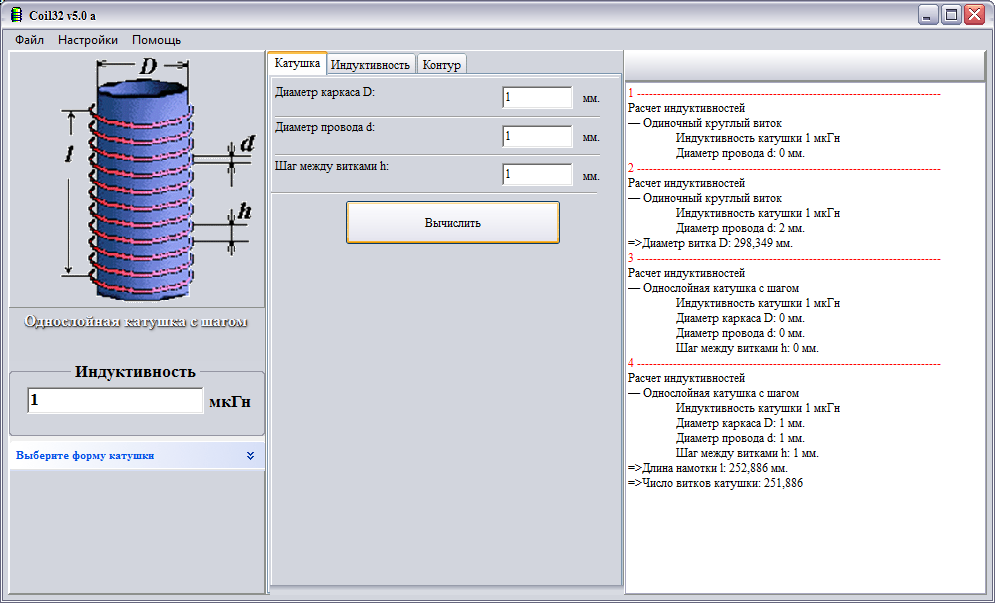

Ещё одним существенным фактором при расчёте индуктивности является различие в длине катушки и длине сердечнике. Данное различие можно описать коэффициентом k, зависящем от отношения длины сердечника к длине катушки

где а – длина катушки индуктивности,

l – длина сердечника,

γ – коэффициент, зависящий от отношения длины катушки к длине сердечника.

Пример расчёта индуктивности катушки на разомкнутом сердечнике

В качестве примера рассчитаем катушку индуктивности на разомкнутом сердечнике круглого сечения со следующими параметрами: диаметр сердечника d_c = 6 мм, длина сердечника l_c = 30 мм, катушка состоит из 30 витков провода диаметром d_p = 1 мм, намотанных плотно виток к витку в один ряд, магнитная проницаемость материала сердечника μ_r = 600.

1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит l_k = 30*1 = 30 мм, а диаметр катушки d_k = d_cp = 30,5 мм.

2.Вычислим эффективную магнитную проницаемость сердечника

3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Так как длина катушки совпадает с длинной сердечника и смещение катушки относительно сердечника отсутствует, то поправочные коэффициенты будут равны 1, тогда индуктивность данной катушки составит

В качестве второго примера рассчитаем индуктивность магнитной антенны выполненной на сердечнике из феррита марки 600НН, размерами l_c = 160 мм, d_с = 8 мм, количество витков провода w = 60, диаметр провода d_р = 0,15 мм. Катушка смещена на 30 мм относительно середины сердечника.

1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит l_k = 60*0,15 = 9 мм, а диаметр катушки d_k = d_cp = 8,075 мм.

2.Вычислим эффективную магнитную проницаемость сердечника

3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Коэффициент, учитывающий расположение катушки на сердечнике составит

Коэффициент, учитывающий отношение длины катушки по отношению к длине сердечника составит

4.Рассчитаем индуктивность катушки индуктивности на разомкнутом сердечнике

Данная статья заканчивает цикл расчётов индуктивности катушек с различными конструктивными параметрами.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

Расчёт катушки индуктивности под динамик

Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.

На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению.

Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.

высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.

Пример расчета

Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.

Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.

1. откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
2. далее имеем:
   h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
3. длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
4. количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
5. диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
6. масса намотки: m = (h³ х 10^-3) / 21,4 = (26,96³ х 10^-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.

Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.

Итак имеем данные, которые понадобятся для расчета будущей катушки:

1. высота намотки h = 26,96 мм;
2. значит внутренний диаметр a = 53,92 мм;
3. соответственно внешний: b = 107,84 мм;
4. длинна жилы: 34,3 м;
5. количество витков: 135;
6. диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).

Статья специально подготовлена для сайта ldsound.info

• Найти:

• МД-57 «Октава»

  Микрофон типа МД-57 является динамическим микрофоном. Изготавливался на заводе Октава, в г. Тула, с 1958 …

  Эквилайзер Феникс-005-стерео

  Эквалайзер “Феникс-005” изготавливался малой тиражом на заводе телеграфной аппаратуры, в г. Львов (Львовское ПО им …

Значение AL [Encyclopedia Magnetica]

Содержание

• Значение AL

  • Единицы и уравнения

  • Расчет индуктивности по значению AL и количеству витков

  • Практическое использование

  • Пример технического паспорта

  • См. также

  • Каталожные номера

Стэн Зурек, AL value, Encyclopedia Magnetica, E-Magnetica.pl

A _L ^{, A _L value , AL factor , inductance factor , inductance coefficient , inductance per turn , inductance per square turn а также удельная индуктивность – значение удельной индуктивности (измеряется с 1 витка), характерное для данного магнитопровода (типа, размера, воздушного зазора и т.}

п.), часто предоставляемое изготовителем, для простоты расчетов.

A Ferrite Corerm8, заполненный производителем, так что коэффициент индуктивности A _L = 250NH/ Turn ² (примечание A25/ In Inscription, 3h7h7 3h7h, A25/ . тип ферритового материала)



Значение A _L обычно используется при проектировании электронных трансформаторов на основе ферритовых сердечников, для которых значение часто указывается в наногенри.

Значение A _L широко используется в отношении магнитопроводов из мягкого феррита.

Название магнитной проводимости физически и математически синонимично значению

A _L , но является более общим термином, относящимся к свойству данной магнитной цепи. Постоянная величина обратна магнитному сопротивлению

→ → → Полезная страница? Поддержите нас! → → →

PayPal

← ← ← Помогите нам с всего за $0,10 в месяц? Давай… ← ← ←

Единицы и уравнения

Математически A _L имеет единицу СИ генри ( H ), но связь с индуктивностью нелинейна, и практическая единица измерения – наногенри на квадратный виток или нГн/виток ² .

Следовательно, для расчета индуктивности 92 $$ (Н)

A _L значение = (nH/t²)(µH/t²)(mH/t²)(H/t²) количество витков Н = (безразмерно)

л = (нГн)(мкГн)(мГн)(Гн)



Примечание: значение AL обычно указывается только в единицах индуктивности, т.е. (nH), без квадратных витков. В этом случае просто выберите соответствующую единицу измерения, например. (нН/т ² ).

---

(См. также калькулятор Значение AL от индуктивности и числа витков ).

Практическое использование

При разработке трансформаторов и катушек индуктивности для импульсных источников питания параметры переключения и уровень мощности определяют значения индуктивности, необходимые для такого компонента.

Следовательно, значение индуктивности известно для следующего шага проектирования. Использование значения A _L позволяет быстро рассчитать необходимое количество витков для данного размера сердечника.

Следует отметить, что значение A _L часто дается в единицах (нГн) или подобных, подразумевая «на квадратный оборот». Важно помнить, что связь между значением A _L и индуктивностью не пропорциональна из-за возведения в квадрат витков.

Значение A _L особенно полезно при проектировании с сердечниками с зазором, например, для катушек индуктивности с зазором или трансформаторов обратного хода. В нормальных условиях воздушный зазор аккумулирует всю энергию и определяет эффективную магнитную проницаемость магнитопровода. 92 ⋅ \mu_0 ⋅ \mu_r ⋅ A}{l} $$ ( H )

где: Н – число витков, мк ₀ – магнитная проницаемость свободного пространства ( Гн/м ), мк

r – относительная магнитная проницаемость материала (безразмерная), – А площадь поперечного сечения ( м ² ), l – длина магнитного пути ( м ).

Приведенное выше уравнение можно переписать как: 92 ⋅ x $$ ( H )

где:

$$ x = \frac{\mu_0 ⋅ \mu_r ⋅ A}{l} $$

(W)

И, сравнивая уравнения, можно увидеть, что значение $x = A_L$ и является константой для данного магнитного сердечника с фиксированными параметрами, пока это не влияет на эффективную магнитную проницаемость (например, предотвращается насыщение).

Поэтому, если производитель предоставляет A _L это упрощает расчеты.

Типичное обозначение A _L =160 нГн ±3% означает, что сердечник имеет такой воздушный зазор, что A _L = 160 нГн (на квадратный оборот). Для сердечника ER14,5-3-7 это синоним воздушного зазора 150 мкм.

Жесткий допуск ±3% можно получить для пропорционально больших зазоров. В приведенном выше примере 150 мкм — это относительно большое значение для магнитного пути сердечника, которое составляет 19мм. Это снижает эффективную проницаемость с более чем 1000 до примерно 137 (см. также калькулятор эффективной проницаемости).

Для меньших зазоров влияние сердечника увеличивается, и допуск может достигать ±25%. То же самое относится и к неразрывным жилам.

Пример технического паспорта

Пример листа технических данных со значением A _L .

Файл	Описание
	Спецификация: ER14.5-3-7, Сердечники Planar ER и аксессуары, Ferroxcube ER14.5-3-7, Сердечники Planar ER и аксессуары, Ferroxcube

См. также

• Проницаемость

• Индуктивность

• Проницаемость

Каталожные номера

---

^{1) , 1) , 1)} Спецификация, ER14.5-3-7, Ferroxcube.pdf

^{2) , 2)} W.G.Hurley, W.H. Вольфле, Трансформаторы и катушки индуктивности для силовой электроники: теория, конструкция и применение, John Wiley & Sons, 2013, ISBN 9781118544662, с. 63

^{3) , 3) , 3)} Конструкция индуктора и обратноходового трансформатора, Texas Instruments Inc., 2001, с. 5-7, {по состоянию на 24 июня 2013 г.}

⁴⁾ Ferrite, Summary, Ferrites, TDK, 2014, 001-01 / 20140308 / ferrite_summary_en.fm, {по состоянию на 2021-09 гг.-12}

⁵⁾ Патент US7117583, T.E. Динан и др., Метод и устройство, использующие затравочный слой с предварительно нанесенным рисунком для обеспечения выровненной катушки для конструкции индуктивной головки, 2006

^{6) , 6)} Венцислав Чеков Валчев, Алекс Ван ден Босше, Катушки индуктивности и трансформаторы для силовой электроники, CRC Press, 2005, ISBN 9781420027280, с. 17

⁷⁾ Симус О’Дрисколл, Питер Мини, Джон Флэннери и Джордж Янг, Проектирование магнитных компонентов для оптимальной работы недорогих преобразователей переменного тока в постоянный, 2010–2011 Семинар по проектированию источников питания, тема 5 , Texas Instruments, {по состоянию на 27 июня 2013 г. }

⁸⁾ T. Brander, A. Gerfer, B. Rall, H. Zenker, Trilogy of Magnetics, Руководство по проектированию фильтров электромагнитных помех, SMPS и RF схемы, Wurth Elektronik, 2001, ISBN 9783899291575

^{6 6 6 6 6 6 6 6 9) Джон Клейтон Роулинз, Основные схемы переменного тока, Newnes, 2000, ISBN 9780750671736, с. 264}

Магнитопроводы, Магнитные свойства, Калькуляторы, Счетчик

Конструкция индуктора с магнитными порошковыми сердечниками


Чтобы получить помощь в выборе сердечника(ов) Magnetics для использования в конкретных конструкциях индукторов, загрузите наш инструмент для проектирования индукторов или свяжитесь с Magnetics, отправив запрос на индивидуальную конструкцию индуктора.

Для выбора сердечника для дросселя с ограничением по току необходимо знать только два параметра приложения для проектирования; индуктивность, необходимая при смещении постоянного тока и постоянном токе. Используйте следующую процедуру, чтобы определить размер сердечника и количество витков.

1. Вычислить произведение LI ²  где: 

  L = требуемая индуктивность при смещении постоянного тока (мГн) 
I = постоянный ток (А)
l _e  = длина магнитного пути сердечника (мм) 
N = количество витков
H = напряженность магнитного поля (А•Тл/см)

2. Найдите значение LI ² на диаграмме выбора основных компонентов. Следуйте по этой координате до пересечения с первым размером керна, лежащим выше диагональной линии проницаемости. Это наименьший размер ядра, который можно использовать.

3. Линия проницаемости разделена на стандартные доступные проницаемости керна. Выбор указанной проницаемости, как правило, является лучшим компромиссом между A _L и смещение постоянного тока.

4. Теперь известны индуктивность, размер сердечника и проницаемость. Рассчитайте количество витков, используя следующую процедуру: 

     (a) Коэффициент индуктивности (A _L  в нГн/Тл ² ) для сердечника получен из паспорта сердечника. Определите минимум A _L  , используя отрицательный допуск для наихудшего случая (обычно -8%). Имея эту информацию, рассчитайте количество витков, необходимое для получения требуемой индуктивности из:

    

Где L требуется индуктивность (мкГн)

     (b) Рассчитайте смещение в A•T/см из:  

    

     (c) По кривым зависимости проницаемости от смещения постоянного тока определите спад в единицах начальной проницаемости для ранее рассчитанного уровня смещения. Уравнения подгонки кривой, представленные в каталоге, могут упростить этот шаг.

     (d) Умножьте требуемую индуктивность на единичный спад, чтобы найти индуктивность при подаче тока смещения.

     (e) Увеличьте количество витков, разделив начальное количество витков (из шага 4 (a)) на начальное значение проницаемости на единицу. Это даст индуктивность, близкую к требуемому значению, после повторения шагов 4 (b), (c) и (d).

     (f) При необходимости повторите шаги 4 (b), (c) и (d), чтобы отрегулировать смещенную индуктивность вверх или вниз, пока она не будет удовлетворительно близка к целевому значению.

5. Выберите правильный размер провода, используя Таблицу проводов. Рабочие циклы ниже 100% допускают меньшие размеры проводов и меньшие коэффициенты намотки, но не позволяют меньшие размеры сердечника.

6. Чтобы рассчитать коэффициент намотки, умножьте количество витков на площадь провода, указанную в таблице проводов, чтобы найти общую площадь провода. Разделите общую площадь провода на площадь окна сердечника, чтобы получить коэффициент намотки конструкции. Убедитесь, что коэффициент намотки является приемлемым, сославшись на различные способы намотки, описанные здесь . (Область ядра и площадь окна можно найти в техническом описании ядра или на странице каталога. )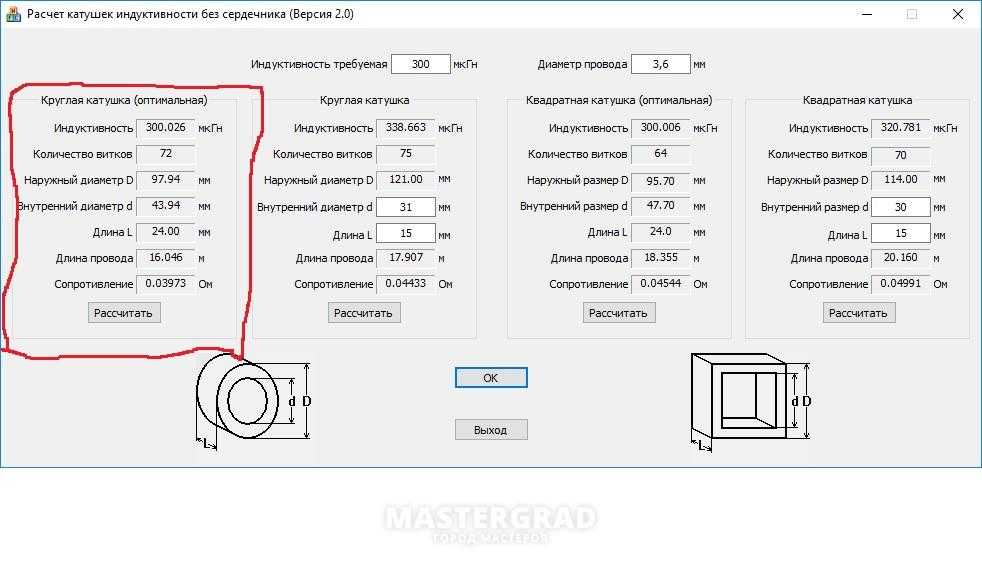

7. Если будет присутствовать значительный пульсирующий ток, оцените потери в сердечнике, используя процедуру расчета потерь в сердечнике. Если потери в сердечнике переменного тока приведут к слишком сильному нагреву или кпд ниже требований, тогда индуктор может быть ограничен по потерям, а не по насыщению. Варианты конструкции для этого сердечника включают более крупный сердечник, материал с более низкой проницаемостью, материал с меньшими потерями или некоторую комбинацию этих трех.

Пример выбора сердечника 

Определите размер сердечника и количество витков, чтобы выполнить следующее требование: 

     (a) Минимальная индуктивность при постоянном смещении 0,6 мГн (600 мкГн) 

     (b) Постоянный ток 5,0 А 

1. LI ² = 0,6 X 5,0 ² = 15,0 мГн•А ² 

2. С помощью таблицы Kool Mμ Toroids LI ² найдите 15 мГн•А ²  на нижней оси. Следование этой координате по вертикали приводит к выбору 0077083A7 в качестве ядра, подходящего для вышеуказанных требований.

3. Исходя из данных сердечника 0077083A7, коэффициент индуктивности (A _L ) этого сердечника составляет 81 нГн/Тл ² ± 8%. Минимум A _L  этого ядра составляет 74,6 нГн/Тл ² .

4. Количество витков, необходимых для получения 600 мкГн без нагрузки, составляет 90 витков. Чтобы рассчитать количество витков, необходимых при полной нагрузке, определите уровень смещения постоянного тока: H= N•I/l _e = A•T/см, где l _e — длина пути в см. Смещение постоянного тока составляет 45,7 А•Тл/см, что дает 71% начальной проницаемости по кривой смещения постоянного тока 60 мкм Kool Mµ. Скорректированные обороты составляют 90/0,71 = 127 оборотов.

5. Пересчитайте уровень смещения постоянного тока в А•Тл/см: Кривая зависимости проницаемости от смещения постоянного тока показывает 57% начальной проницаемости при 64,5 А•Тл/см.