Расчет lc фильтра низких частот: Автоматизированный расчет пассивных LC-фильтров

Содержание

1.3. Описание lc-фильтров

Фильтры более высокого качества реализуются на основе катушек индуктивности и конденсаторов. В LC-фильтр могут входить также и резисторы. Связь входной и выходной цепей большинства LC-фильтров соответственно с источником сигнала и с нагрузкой производится таким образом, чтобы значения их реактивных или полных сопротивлений были равны.

На рис. 4 приведена схема и амплитудно-частотная характеристика типового Г – образного LC-фильтра нижних частот.

Рис. 4. Схема и АЧХ Г – образного низкочастотного фильтра.

Расчет такого фильтра производится по следующим формулам:

Все LC-фильтры обладают тем преимуществом, что на переменном токе конденсаторы и катушки индуктивности работают взаимообратно, т.е. при увеличении частоты сигнала индуктивное сопротивление возрастает, а емкостное падает.

Таким образом, в LC-фильтре нижних частот реактивное сопротивление параллельного элемента при увеличении частоты сигнала уменьшается и этот элемент шунтирует высокочастотные сигналы. На низких частотах реактивное сопротивление параллельного элемента достаточно высокое. Последовательный элемент обеспечивает прохождение низкочастотных сигналов, а для сигналов высоких частот его реактивное сопротивление велико.

Простой Г – образный фильтр не обеспечивает достаточную крутизну амплитудно-частотной характеристики. Для увеличения крутизны в основную Г-образную структуру вводят дополнительную катушку индуктивности, как показано на рис. 5. Такой фильтр называется Т-образным.

Рис. 5. Т – образный НЧ LC-фильтр.

В Т – образном фильтре значение конденсатора С такое же, как и в исходной Г-образной структуре, и все ее расчетные формулы сохраняются. Суммарная индуктивность катушек L

1 и L₂ должна быть эквивалентна индуктивности единственной катушки исходной Г-образной структуры.

Обычно требуемая общая индуктивность распределяется между двумя этими катушками поровну таким образом, чтобы каждая из катушек в Т – образном фильтре нижних частот имела индуктивность в два раза меньше, чем катушка в Г – образном фильтре.

Крутизну амплитудно-частотной характеристики можно увеличить также путем введения в цепь дополнительного конденсатора. Такой фильтр называется П-образным (рис. 6.).

Рис. 6. П-образный низкочастотный LC-фильтр.

В П – образном фильтре значение индуктивности L такое же, как и в исходной Г-образной структуре, тогда как суммарная емкость конденсаторов С₁

и С₂ должна быть эквивалентна емкости конденсатора исходной Г – образной структуры. Обычно требуемая общая емкость распределяется между двумя этими конденсаторами поровну таким образом, чтобы каждый из конденсаторов в П – образном фильтре имел емкость, равную половине емкости конденсатора в Г – образном фильтре.

На рис.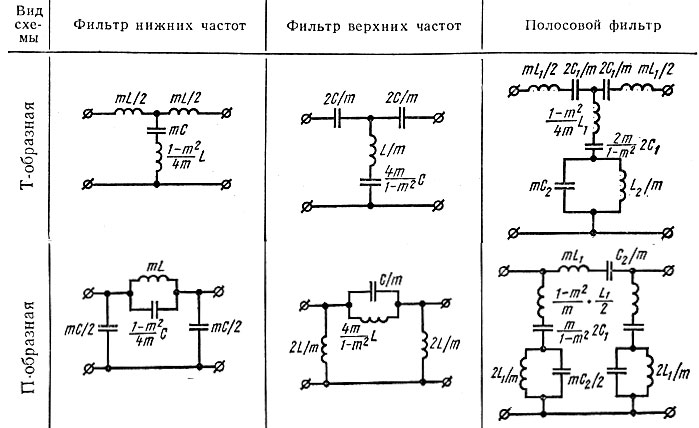 7 приведена схема и амплитудно-частотная характеристика типового Г – образногоLС-фильтра верхних частот.

Рис. 7. Схема и АЧХ высокочастотного Г-образного LC-фильтра.

Расчет Г – образного LС-фильтра верхних частот производится по следующим формулам:

В этом фильтре при увеличении частоты сопротивление последовательного элемента уменьшается. Он пропускает высокочастотные сигналы, а для сигналов низких частот его реактивное сопротивление велико. Параллельный элемент оказывает шунтирующее влияние на сигналы низких частот, а для высокочастотных сигналов его реактивное сопротивление велико.

Для увеличения крутизны амплитудно-частотной характеристики в Г – образную структуру можно ввести дополнительный конденсатор, как показано на рис. 8.

Рис. 8. Т – образный высокочастотный LC-фильтр.

Такой фильтр имеет Т – образную структуру. В Т – образном фильтре значение индуктивности L не отличается от ее значения в исходной Г – образной структуре и все расчетные формулы остаются такими же. Суммарная емкость конденсаторов С₁ и С₂ должна быть эквивалентна емкости одиночного конденсатора исходной Г-образной структуры. Обычно эта требуемая общая емкость распределяется поровну между двумя конденсаторами так, что Т – образном фильтре верхних частот каждый конденсатор имеет емкость, равную удвоенному значению емкости в Г – образной структуре.

Крутизну амплитудно-частотной характеристики фильтра можно также повысить путем введения в схему дополнительной катушки индуктивности, как показано на рис. 9, образуя П – образный фильтр.

Рис. 9. П-образный высокочастотный LC-фильтр.

В П – образном LC-фильтре значение емкости конденсатора не изменяется, а суммарная индуктивность катушек L₁ и L₂ должна быть эквивалентна индуктивности одиночной катушки исходной Г-образной структуры. Обычно требуемая общая индуктивность распределяется поровну между двумя катушками так, что каждая из них имеет индуктивность, равную удвоенному значению индуктивности Г – образной структуры.

Работа полосно-заграждающего (режекторного) фильтра основана на различии зависимостей полных сопротивлений параллельной и последовательной резонансных цепей от частоты. Полное сопротивление параллельной LC-цепи на резонансной частоте максимально, тогда как у последовательной цепи оно минимально. Эти две LC-цепи, соединенные определенным образом (рис. 10), образуют Г – образный режекторный фильтр.

Рис. 10. Г – образный режекторный LC-фильтр.

На центральной частоте требуемого диапазона полное сопротивление последовательной LC-цепи (она включена параллельно нагрузке) минимально, и она оказывает шунтирующее воздействие и ослабляет сигналы. Полное сопротивление параллельной LC-цепи (которая включена последовательно с нагрузкой) на центральной частоте требуемого диапазона максимально, и она препятствует прохождению сигналов.

Т-образные и П-образные полосно-пропускающие фильтры (рис. 11) обладают более высокой крутизной амплитудно-частотной характеристики.

Расчет полосно-пропускающих LC-фильтров производится по следующим формулам:

Рис.11. Полосовые П- и Т-образные LC – фильтры.

Расчет фильтра нижних частот (Курсовая работа)

Содержание

Введение

1 Физические основы и принцип действия широкополосных фильтров

2 Пример расчета фильтра нижних частот на заданные параметры

Заключение

Список использованной литературы

Введение

Во многих радиотехнических устройствах часто возникает необходимость выделения заданных частотных диапазонов из имеющегося спектра частот. Выделение требуемой полосы частот с очень малым затуханием осуществляется фильтрами.

В начале нашего столетия электрические фильтры, составленные из ряда катушек индуктивности и конденсаторов, получили широкое применение в технике.

Благодаря их применению оказалось возможным осуществление многих магистралей дальней телефонной, телеграфной и других видов связи.

Известный интерес представляют пассивные цепочные, или лестничные фильтры, состоящие из комбинаций элементов L и C и не требующие источника питания. Пассивные фильтры могут обладать как широкими полосами пропускания, так и очень узкими.

При расчете фильтра, с одной стороны, необходимо определить, с какими допустимыми искажениями передается входной сигнал, являющийся функцией частоты или времени, на выход фильтра, и, с другой стороны, из каких конкретных элементов должен состоять этот фильтр. Получение наивыгоднейших выходных характеристик с минимальными искажениями и создание принципиальной схемы фильтра с минимальным числом элементов, осуществляющей требуемую передачу сигнала, является содержанием расчета фильтров.

1 Физические основы и принцип действия широкополосных фильтров

В электрических, радиотехнических и телемеханических установках часто решается задача: из совокупного сигнала, занимающего широкую полосу частот, выделить один или несколько составляющих сигналов с более узкой полосой. Сигналы заданной полосы выделяют при помощи частотных электрических фильтров.

К частотным электрическим фильтрам различной аппаратуры предъявляются разные, порой противоречивые требования. В одной области частот, которая называется полосой пропускания, сигналы не должны ослабляться, а в другой, называемой полосой задерживания, ослабление сигналов не должно быть меньше определенного значения. Фильтр считают идеальным, если в полосе пропускания отсутствует ослабление сигналов и фазо-частотная характеристика линейна (нет искажения формы сигналов), а вне полосы пропускания сигналы на выходе фильтра отсутствуют.

Фильтры могут быть однозвенные (первого порядка), двухзвенные (второго порядка) и многозвенные (n- го). Чем выше порядок фильтра, тем круче его амплитудно-частотная характеристика и тем более она похожа на его идеальную характеристику. Фильтр любого порядка можно построить путем каскадного соединения фильтров первого и второго порядков.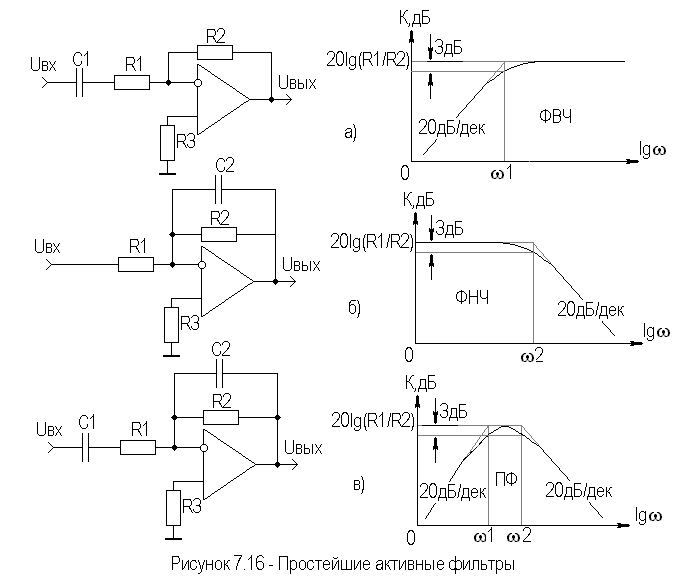

Электрический фильтр представляет собой четырехполюсник, предназначенный для выделения из состава сложного электрического колебания частотных составляющих, расположенных в заданной полосе частот, и подавления тех составляющих, которые расположены в других полосах частот. Первая из названных полос представляет собой полосу пропускания, а вторая – полосу задерживания.

По взаимному расположению полос пропускания и полос задерживания различают фильтры нижних частот, фильтры верхних частот, полосовые и режекторные фильтры.

Фильтры нижних частот (ФНЧ) пропускают сигналы частот от 0 до и задерживающей колебания любых белее высоких частот (рис.1).

LC–фильтр нижних частот (рис. 6.3,а) пропускает электрические колебания в полосе частот от 0 до

Это объясняется тем, что на низких частотах сопротивление индуктивного элемента XL фильтра мало, а емкостного XC – велико и электрические колебания проходят со входа на выход почти без ослабления. С увеличением частоты сопротивление индуктивного элемента возрастает, а емкостного – снижается и коэффициент передачи фильтра уменьшается (рисунок 1–б).

Фильтры верхних частот (ФВЧ), напротив, пропускают сигналы, частоты которых простираются от до , и задерживают сигналы более низких частот(рис.2).

Полосовые фильтры (ПФ) пропускают сигналы в полосе частот от до (рис.3).

Режекторные (заграждающие) фильтры (РФ) задерживают сигналы в полосе частот от до (рис.4).

(а)

(б)

Рисунок – 1 Фильтры нижних частот (а) и его АЧХ (б).

Рисунок – 2 Фильтры верхних частот

Рисунок – 3 Полосовые фильтры

Рисунок – 4 Заграждающие фильтры

Широкополосный фильтр состоит из звеньев, включающих в себя только элементарные контуры.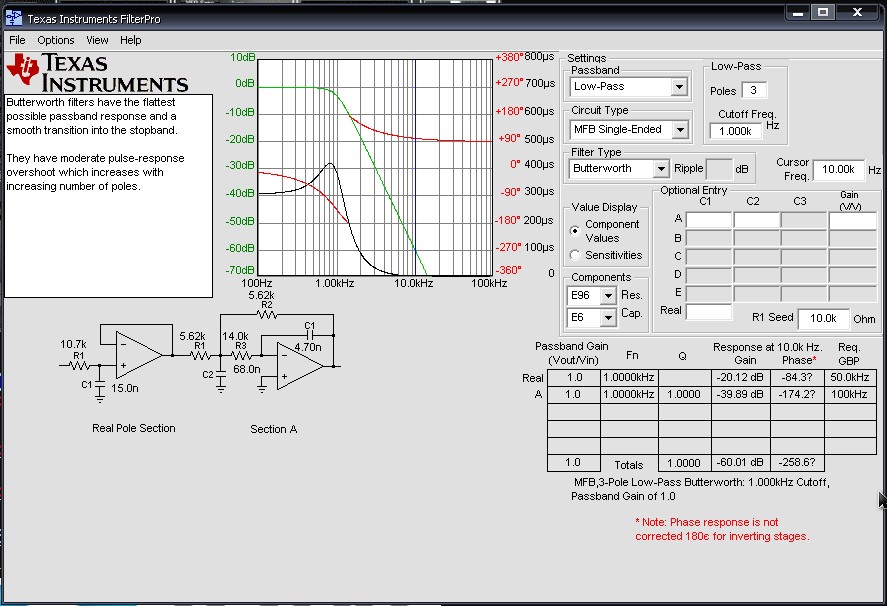 Поэтому механизм фильтрации в широкополосных фильтрах определяется в основном процессами, происходящими в элементарны контурах, т. е. в двухэлементных двухполюсниках, имеющих одну резонансную частоту.

Полное сопротивление Z любого элементарного контура состоит из активной R и реактивной X составляющих:

Z = R + jX (1)

или

Y = G + jB (2)

где Y – полная проводимость

G – активная составляющая полной проводимости

B – реактивная составляющая поной проводимости

Реактивное сопротивление последовательного контура на частоте = равно нулю, активное сопротивление при этом мало, так как оно определяется только потерями в контуре; полное сопротивление контура близко к нулю. Поэтому последовательные контуры применяются в параллельных плечах Т-образных звеньев фильтров верхних частот (рис.5)., так как они оказывают сильное шунтирующее действие на частотах, близких к резонансной.

Рисунок – 5 Схема звена ФВЧ и резонансные характеристики последовательного контура

Реактивная проводимость = равна нулю. Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот (рис.6). Резонансные частоты элементарных контуров равны частотам бесконечного затухания соответствующих звеньев =. Резонансные частоты контуров, или частоты бесконечного затухания, для ФНЧ располагаются выше частот полосы пропускания ( >), а для ФВЧ – ниже (<). Параллельные плечи фильтра шунтируют частоты полосы задерживания в то время, как последовательные являются для них пробкой. В полосе пропускания сопротивление параллельных плеч фильтра , напротив, велико, а сопротивление последовательных плеч близко к нулю.

автореферат диссертации по радиотехнике и связи, 05.12.04, диссертация на тему:Анализ и расчет LC фильтров в совершенствовании избирательности судового радиооборудования

Библиография Бессонова, Елена Анатольевна, диссертация по теме Радиотехника, в том числе системы и устройства телевидения

1. Автоматизация проектирования радиоэлектронных средств: Учеб. Пособие для вузов / О.В. Алексеев, A.A. Головков, И.Ю. Пивоваров и др.; Под ред. О.В. Алексеева. – М.:Высшая школа, 2000. – 479 с.

2. Автоматизированная связь с судами / Под ред. К.А. Семенова. JI.Судостроение, 1989. 334 с.

3. Акулынин П.К., Кульбацкий И.А., Кощеев К.Е. Теория связи по проводам. М.: Связьиздат, 1940. – 568 с.

4. Альбац М.Е. Справочник по расчету фильтров и линий задержки. -М.:ГТИ, 1963.-200 с.

5. Байрашевский A.M., Ничипоренко Н.Т. Судовые радиолокационные системы. М.:Транспорт, 1982. – 317 с.

6. Белецкий А.Ф. Теория линейных электрических цепей. М.:Радио и связь, 1986. – 544 с.

7. Босый Н.Д. Электрические фильтры. УССР.ТИТЛ, 1957. – 516 с.

8. Брауде Г.В. Коррекция телевизионных и импульсных сигналов. -М.: Связь, 1967.

9. Буга H.H., Фалько А.И., Чистяков Н.И. Радиоприемные устройства. М.:Радио и связь, 1986. 320 с.121

10. Васильев В.Я. Графоаналитический метод анализа характеристических параметров электрических фильтров с применением машинной графики.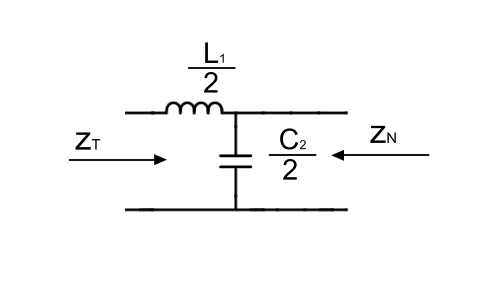 : Дис.кан.техн.наук. Л.:ЛВИМУ, 1986. – 128 с.

11. Великин Я.И., Гельмонт З.Я., Зелях Э.В. Пьезоэлектрические фильтры.- М.:Связь, 1966.-396 с.

12. Венскаускас К.К., Ильин A.A. Принципы построения глобальной морской связи при бедствии и для обеспечения безопасности мореплавания.- М.:ВЮ “Мортехинформреклама”, 1988. 104 с.

13. Витков М.Г., Виткова A.A. Численная обусловленность характеристики ослабления некоторых разновидностей фильтров // Электросвязь. -2000. №5.-С. 36-37.

14. Витков М.Г., Виткова A.A., Горштейн JI.B. Обобщенные полиноминальные полосовые фильтры // Электросвязь. 1999. – №2. – С. 40-42.

15. Гауси М., Лакер К. Активные фильтры с переключаемыми конденсаторами. Пер. с англ. / Под ред. В.И. Капустина. М.:Радио и связь, 1986. -166 с.

16. Гехер К. Теория чувствительности и допусков электронных цепей. / Пер. с англ. Под ред. Ю.Х. Хотунцева. М.:Советское радио, 1973. -200 с.

17. Глобальная морская система связи при бедствии и для обеспечения безопасности. / Под ред. Ю.С. Ацерова. М.:Транспорт, 1989. – 62 с.

18. Головин О.В. Радиоприемные устройства. М.: Высшая школа, 1997. -384 с.

19. Голубев В.И., Окогот В.А., Полищук Я.В. Схемы дискретной перестройки резонансной частоты колебательного контура // Электросвязь.- 1969. -№5.-С. 41-46.

20. Голубев В.Н. Эффективная избирательность радиоприемных устройств. М.:Связь, 1978. – 240 с.

21. Зааль Р. Справочник по расчету фильтров. / Пер. с нем. Под ред. H.H. Слепова. М.:Радио и связь, 1983. – 752 с.122

22. Знаменский А. Е., Попов Е.С. Перестраиваемые электрические фильтры. М.:Связь, 1979.- 129 с.

23. Знаменский А.Е., Теплюк И.Н. Активные RC фильтры. – М.:Связь, 1970.

24. Карлащук И.К. Электронная лаборатория на IBM PC. Программа Electronics Workbench и ее применение. М.:Солон-Р, 2000. – 512 с.

25. Кильдишева О.Э., Лондон С.Е., Раутиан В.Г. Высокоселективные LC фильтры гармоник радиопередающих устройств // Электросвязь. -2000. №5. – С. 33-35.

26. Коган С.С. Теория и расчет фильтров для установок дальней связи. -М.:Связьиздат, 1950. 170 с.

27. Короткое A.C. Микроэлектронные аналоговые фильтры на преобразователях импеданса. СПб.:Наука, 1999.- 416 с.

28. Коротков A.C. Синтез полосовых фильтров на переключаемых конденсаторах // Радиотехника. 1999. – №8. – С. 17-21.

29. Лабутин В.К. Частотно-избирательные цепи с электронной настройкой. М.:Энергия, 1966.

30. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.:Гостехиздат, 1951. 607 с.

31. Ланнэ A.A. Оптимальный синтез линейных электронных схем. -М.:Связь, 1978.-336 с.

32. Лапшин Б.А. Новая теория и расчет фильтров и трансформаторов на отрезках передающих линий. СПб.:Наука, 1998. – 179 с.

33. Ларионов О.М. Исследование и разработка выходных трактов ключевых гираторов с улучшенным спектральным составом выходного напряжения. / Автореф.дис.кан.техн.наук. СПб.:СПбГУТ, 2000. – 17 с.

34. Лосев А.К. Теория и расчет электромеханических фильтров. М.:Связь, 1965.-264 с.

35. Лосев А.К. Теория линейных электрических цепей: Учеб. Для вузов. -М.:Высшая школа, 1987. 512 с.123

36. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.- М.:Высшая школа, 1990.

37. Моле Дж. X. Расчет электрических фильтров для аппаратуры связи. -М.:Госэнергоиздат, 1963. 332 с.

38. Никанкин В.К, Никанкин К.В. Техническое обслуживание радиооборудования ГМССБ: Учебное пособие для учебно-тренажерных центров Глобальной морской системы связи при бедствии (ГМССБ GMDSS).- СПб.:ГМА им. адм. С.О. Макарова, 2000. 144 с.

39. Обломов А.Ф., Токарев JT.A., Момот Е.Г. Вопросы избирательности радиопремников. М.:Энергия, 1965. – 140 с.

40. Общесоюзные нормы на ширину полосы частот и внеполосные спектры излучений радиопередающих устройств гражданского назначения. -М.:Связь, 1976.-64 с.

41. Орлов B.C., Бондаренко B.C. Фильтры на поверхностных акустических волнах. М.:Радио и связь, 1984, 273 с.

42. Попов В.П. Основы теории цепей. М.:Высшая школа, 2000. – 576 с.

43. Правила по оборудованию морских судов. СПб.¡Морской регистр судоходства, 1999.

44. Применение пакета программ Microwave Harmonica: Методические указания. / Сост.: A.A. Головков, В.Ю.Приходько. СПб.:СПбГЭТУ, 1998.-32 с.

45. Проектирование радиопередающих устройств с применением ЭВМ. / Под ред. О.В. Алексеева. М.:Радио и связь, 1987. – 392 с.

46. Проектрирование радиопередатчиков. / Под ред. В.В. Шахгильдяна. -М.:Радио и связь, 2000. 654 с.

47. Пшесмыцкий О. Проектирование электрических лестничных фильтров. Пер. с польского. М.:Связь, 1968.

48. Радиоприемное устройство: Техническое описание, инструкция по эксплуатации, схемы электрические принципиальные. Cn6.:MCS, 2000.124

49. Самарский A.A., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. М. .Наука. Физматлит, 1997. – 320 с.

50. Семенов К.А. Анализ линейных электрических цепей методом круговых диаграмм. Л.:Энергия, 1979. – 112 с.

51. Семенов К.А. Критическая добротности и оптимизация параметров фильтров верхних частот типа ш // Радиотехника. 1994. – №11. – С. 9394.

52. Семенов К.А. Круговые диаграммы для расчета собственного затухания электрических фильтров. М.:Морской транспорт, 1958. – 195 с.

53. Семенов К.А. О затухании фильтров нижних и верхних частот типа т на частоте среза // Электросвязь. 1956. – №7. – С. 59-61.

54. Семенов К.А., Бессонова Е.А. Анализ затухания фильтров нижних и верхних частот типа m // Радиотехника. 1999. – №12. – С. 87-89.

55. Семенов К.А., Бессонова Е.А. Полосовой фильтр, обеспечивающий наибольшую избирательность в системах радиосвязи. / Морские информационные технологии: Сб. Научн. Статей. Выпуск 1. Под ред. А.Е. Сазонова. -СПб.:РГПУ им. А.И. Герцена, 2001. С. 94-100.

56. Семенов К.А., Васильев В.Я. Обобщенный графоаналитический расчет фильтров с применением машинной графики // Радиотехника. 1985. -№12.

57. Семенов К.А., Каплин Е.А., Кузьмин Б.И., Рябышкин В.Н. Состояние и перспективы развития морской радиосвязи // Электросвязь. 1998. -№8.-С. 9-12.125

58. Семенов К.А., Кузьмин Б.И., Бессонова Е.А. Системы и средства морской радиосвязи на выставке “Нева-99” // Электросвязь. 1999. – №12. -С. 67.

59. Семенов К.А., Рябышкин В.Н., Кузьмин Б.И. Современная судовая радиосвязь на морском флоте // Электросвязь. 1998. – №8. – С. 12-15.

60. Сергеев В.В Развитие теории энергетических функций реактивных четырехполюсников и ее приложение к анализу и синтезу LC-фильтров. / Автореферат дис.докт.техн.наук. СПб.:СПбГУТ, 2000. – 31 с.

61. Симонов Ю.Л. Усилители промежуточной частоты. М.:Советское радио, 1973.-383 с.

62. Смит Ф. Круговые диаграммы в радиоэлектронике. / Пер. с англ. М.Н. Бергера, Б.Ю. Капилевича. М.:Связь, 1976. – 144 с.

63. Собенин Я.А. Расчет полиномиальных фильтров. М.Связьиздат, 1963.-208 с.

64. Справочник по расчету фильтров с учетом потерь / Пер. с нем. под ред. К.А.Сильвинской М.:Связь, 1972. 200 с.

65. Справочник по судовому оборудованию радиосвязи и радионавигации. / Под ред. К.А. Семенова. Л.Судостроение, 1979. – 336 с.

66. Судовые радиоприемные устройства / К.А. Семенов, Г.М. Крылов, Б.И. Кузьмин, В.А. Марков. М.:Транспорт, 1984. – 382 с.

67. Ханзел Г. Справочник по расчету фильтров. / Пер. с англ. Под ред. А.Е. Знаменского. М.Советское радио, 1974. – 288 с.

68. Христиан Э., Эйзенман Е. Таблицы и графики по расчету фильтров. / Пер. с англ. Под ред. А.Ф. Белецкого. М.Связь, 1975. -408 с.

69. Хьюлсман Л.П. Активные фильтры: Пер. с англ. / Под ред. И.Н. Теп-люка. М.:Мир, 1972. – 516 с.

70. Шенберг М.М. Графики для расчета фильтров по характеристическим параметрам // Радиотехника. 1956. – т. 11. – №11.

71. Ши Т.Е. Четырехполюсники и электрические фильтры. М.Связьтехиздат, 1934. 367 с.126

72. Balakrishnan A.V. Matched filters for multiple processes // JRE Trans Inform Theory. -1961. V. 7. – №1.

73. Cauer W. Theorie der linearen Wechselstromschattungen, 2 Aulf, Akademie-Verlag, Berlin, 1954.

74. Epprecht G.W. A new circle-diagram for transformation in line technique // Arch. Electr. Übertragung. June. – 1958. – V. 12. – №6.

75. Gordon J.P. A circle diagram for optical resonators // Bell system Technical J.-V. 43.- 1964.-July. №4.

76. Have R.G., Lightfoot F.M. Matced filter for low and medium date rate communications // JREE. V. 7. 1963. – Oct. – №9.

77. IMO GMDSS Handbook. IMO, London, 1995.

78. Jones W.L. Design of tunable filters of near constant bandwidth // Electronic Letters. 1965. – V. 1. – №6.

79. Kurzrok R.M. Additional consideration in comb-line band-pass filters interstage coupling // IEEE Trans. 1967. – V. MTT-15. – April. – P. 262-263.

80. Levy R.A. A comb-line band-pass elliptic filters// IEEE Trans. 1971. – V. MTT-19. – №1. – P. 26-29.

81. Lichtenfeld K. Method for simplifying filter design // Electronics. 1960. – V. 33. -№21.

82. Nicolson B.F. The practical design of interdigital and comb-line filters // The Radio and Electronic Engineer. 1967. – July. – P. 39-52.

83. Schumacher T. Direct coupled ganged tuned band-pass filters // The Microwave Journal. 1964. – July. – №7. – P. 48-52.

84. Serenade Design Environment. Ansoft New Jersy, USA, 1999.

85. Thungwist D. Circle diagram applied to monopulse // JRE. Trans. Commun. Syst. V. GS-10. – 1962. – September. – №3.

86. Zobel O.J. Extensions to the theory and design of electric wave-filters, Bell Syst. Techn. Journ., Vol. 10.11, April 1931.

87. Zverev A.J. Handbook of filter synthesis. John Wiley. New-York, 1967. -521 p.127

Lc фильтр для шим – Вэб-шпаргалка для интернет предпринимателей!

В статье речь пойдёт про расчёт простейших фильтрующих цепей для сглаживания широтно-импульсной модуляции. Что такое ШИМ, где он применяется и как его реализовать читайте в отдельной статье.

Первое, на чём следует заострить внимание — это назначение цепи, для которой вы собрались строить фильтр. Немного упрощая схемы с ШИМ можно поделить на два типа:

Сигнальные цепи с ШИМ
Силовые цепи с ШИМ

Примером сигнального ШИМ служит, например, простейший ЦАП, под силовым ШИМ чаще всего имеется ввиду ШИМ-сигнал на выходе силовых ключей, например в импульсных источниках питания (ИИП). Строго говоря, в источниках питания сам сигнал ШИМ тоже используется в сигнальной цепи (управление транзисторами) и на выходе таких источников сигнал повторяет форму управляющих сигналов, однако имеет более высокую мощность, потому они требуют фильтров позволяющих пропускать большие мощности.

Фильтрация ШИМ в сигнальных цепях

Рис.1. Простейший фильтр нижних частот — интегрирующая RC-цепь и её АЧХ.

Основная характеристика фильтра это частота среза (на рисунке 1 обозначена угловая частота среза — ω_с) — амплитуда колебаний данной данной частоты на выходе фильтра ослабляется до уровня

0.707 (-3 Дб) от входного значения. Частота среза определяется по следующей формуле:

Тут R и С — сопротивление резистора в омах и ёмкость конденсатора в фарадах. Необходимо помнить, что для корректной работы сглаживающего фильтра постоянная времени RC-цепочки (τ = R · C) должна быть как можно меньше периода ШИМа, тогда за один период не будет происходить полный заряд-разряд конденсатора.

Следующий важный параметр, позволяющий расчитать ослабление колебаний на заданной частоте это коэффициент передачи фильтра — это отношение K = U_вых/U_вх. Для данной RC-цепочки коэффициент передачи рассчитывается следующим образом:

Зная эти формулы и учтя постоянное падение напряжения на резисторе можно приближённо рассчитать фильтр с нужными характеристиками — например, задавшись имеющейся ёмкостью, либо необходимым уровнем пульсаций.

Калькулятор ШИМ-фильтра на RC-цепочке

Входные данные:	Расчётные значения:

Частота ШИМ	Гц
Коэффициент заполнения ШИМ (duty cycle)	%
Напряжение на входе	В
Сопротивление резистора фильтра	Ом
Сопротивление нагрузки R_н	Ом
Ёмкость конденсатора	мкФ

Частота среза RC-фильтра— ГцАмплитуда пульсаций на частоте ШИМ— ВКоэффициент пульсаций на выходе— %Напряжение на выходе
(с учётом потерь на резисторе фильтра)— В

Постоянная времени RC-цепи

Постоянная времени цепи (R · C) не должна быть сильно меньше периода ШИМ!

Потери на резисторе фильтра
(не менее)— Вт

Обратите внимание — если вы хотите получать из ШИМ-сигнала сглаженный синусоидальный сигнал, необходимо чтобы частота среза фильтра была выше максимальной частоты сигнала, а значит частота ШИМ должна быть ещё выше.

Фильтрация ШИМ в силовых цепях

Рис.2. Фильтр нижних частот на LC-контуре и его АЧХ.

LC-фильтр представляет из себя элементарный колебательный контур, который имеет собственную частоту резонанса, поэтому его реальная АЧХ будет несколько отличаться от АЧХ, приведённой на рисунке 2.

Поскольку речь в данной статье идёт о фильтре для силовых цепей, при расчёте фильтра нужно учитывать, что основная гармоника входящего напряжения тоже должна ослабляться фильтром, следовательно, его резонансная частота должна быть ниже частоты ШИМ.

Формула для расчёта частоты резонанса LC-контура:

f = 1/(2 · π · (L · C) 0.5 )

Если частота резонанса контура совпадёт с частотой ШИМ, LC-контур может перейти в режим генерации, тогда на выходе может случиться конфуз, посему предлагаю вам данного недоразумения тщательно избегать. Кроме того, при проектировании данного фильтра есть ещё несколько нюансов, которые неплохо бы соблюдать для получения желаемого результата, а именно:

Для исключения резонансных явлений на одной из высокочастотных гармонических составляющих ёмкость конденсатора желательно находить из условия равенства волнового сопротивления фильтра сопротивлению нагрузки:

Для сглаживания пульсаций таким фильтром желательно, чтобы ёмкостное сопротивление конденсатора для низшей частоты пульсации было как можно меньше сопротивления нагрузки, а также много меньше индуктивного сопротивления дросселя для первой гармоники.

Комплексный коэффициент передачи LC-фильтра рассчитывается по следующей формуле:

где n — номер гармонической составляющей входного сигнала, i — мнимая единица, ω = 2πf, L — индуктивность дросселя (Гн), C — ёмкость конденсатора (Ф), R — сопротивление нагрузки (Ом).

Из формулы очевидно, что чем выше гармоника, тем лучше она подавляется фильтром, следовательно, достаточно рассчитывать уровень только для первой гармоники.

Чтобы перейти от комплексного представления коэффициента передачи к показательному, нужно найти модуль комплексного числа. Для тех, кто (как и я) спал на парах матана в институте, напомню, модуль комплексного числа считается очень просто:

r = |Z| = (x 2 + y 2 ) 0.5

Так как у нас в формуле коэффициента дробь, просто так сходу посчитать модуль не получится и проще всего посчитать это всё, например в MathCad’е. А для тех, кому лень делать всё самим, я запилил весь расчёт в этот прекрасный калькулятор. Пользуйтесь:

Калькулятор силового ШИМ-фильтра на LC-контуре

Частота ШИМ	Гц
Коэффициент заполнения ШИМ (duty cycle)	%
Напряжение на входе	В
Сопротивление нагрузки	Ом
Индуктивность катушки	мГн
Ёмкость конденсатора	мкФ
Амплитуда пульсаций на частоте ШИМ	В
Резонансная частота контура	Гц
Напряжение на выходе (потери не учитываются)	В

Обратите внимание — при использовании LC-фильтра следует помнить, что из-за наличия в цепи индуктивности, на выходе могут появляться выбросы обратной полярности. Если полярность импульсов на входе не изменяется (например для изменения направления вращения двигателя) для ограничения амлитуды отрицательных выбросов параллельно конденсатору (?) можно включать диод Шоттки.

Захаров Александр Александрович

Аннотация. Разработана методика расчёта параметров выходного фильтра на заданный коэффициент гармоник напряжения на нагрузке. Приведён пример расчета Г-образного LC-фильтра мостового инвертора, реализующего равномерную многократную однополярную широтно-импульсную модуляцию (ШИМ) по синусоидальной функции построения, с применением необходимых формул и иллюстрацией характерных графиков и диаграмм.

В наше время — время бурного роста силовой преобразовательной техники трудно себе представить линейный блок питания у современного бытового прибора. Например, в отличие от предшественника, имеющего несколько килограммовый вторичный источник питания (ВИП), современный телевизор получает питание от импульсного многоканально источника несравнимо меньших массы и габаритов, обладающего большими функциями и возможностями. Причём частоты преобразования энергии стали намного выше стандартных пятидесяти герц обычной сети и с развитием элементной базы постоянно повышаются. Конечно, нельзя утверждать, что импульсная силовая электроника полностью вытеснила линейную (например, высококачественные усилители звуковой частоты комплектуются только линейными источниками питания, так как импульсные ВИПы являются источниками, недопустимых для устройств данного класса, помех), но что в настоящее время заняла доминирующее положение — несомненно. Причём это характерно для большого класса устройств преобразующих электрическую энергию: преобразователи тока и напряжения, преобразователи частоты, приводы электрических машин.

Вот и современные DC/AC-преобразователи, или в терминологии преобразовательной техники — инверторы, строятся с применением высокочастотных импульсных схем, что позволяет более точно воспроизводить требуемый вид напряжения на выходе, с возможностью регулирования уровня и частоты, а так же формы сигнала при помощи только системы управления. Данные принципы построения DC/AC-преобразователей применяют практически повсеместно где требуется преобразовать энергию постоянного тока в энергию переменного тока, например для питания обычных бытовых приборов от химических источников питания постоянного тока на автономных транспортных средствах, или как часть источников бесперебойного питания для обслуживания особо критичных компьютерных, телерадиокоммуникационных систем, медицинской техники, или для создания приводов управления электрическими двигателями. Да и мало ли еще, какие задачи ставит жизнь перед разработчиками преобразовательной техники, где необходимо использование устройств подобного класса.

Инверторы в своей массе строятся на основе самых разнообразных схемных решений, в зависимости от конкретного назначения. Нас же, исходя из темы разговора, интересуют в основном автономные инверторы напряжения с какой-то формой выходного сигнала, в частном случае, как наиболее часто востребованной, синусоидальной формой. Обычно форма сигнала формируется по средствам ШИМ, то есть при помощи изменения ширины импульса на отрезке квантования, на которые разбивается весь период сигнала, что в конечном итоге изменяет амплитуду выходного напряжения, в пределах данного интервала, после фильтрации. Но из-за дискретности преобразования, сигнал получается не идеально сглаженным, в нём присутствуют высокочастотные гармонические составляющие, да и диапазон регулирования уровня сигнала на выходе вносит свою отрицательную лепту в коэффициент гармоник, увеличивая их действующее значение. Вот здесь и встаёт вопрос о фильтрации этих высокочастотных гармонических составляющих на выходе инверторов для того, что бы они ни как не сказывались на работе потребителя. Зачем скажете вы, такие тонкости как расчёт выходного фильтра на заданный коэффициент гармоник инвертора привода для питания, например, асинхронного двигателя? И, наверное, будете правы, так как сам двигатель является отличным индуктивным фильтром. Но, несомненно, существуют применения, где выходное синусоидальное напряжение просто необходимо, не какое-нибудь больше похожее на меандр с кучей высокочастотных гармонических составляющих, которые вызывают дополнительные потери мощности, помехи и риск возникновения резонансных процессов, а именно синусоидальное. Например, источники бесперебойного питания, серьёзных и уже давно зарекомендовавших себя фирм-производителей, для критичных применений на выходе имеют именно синусоидальное напряжение. Да и множество приборов и устройств рассчитано именно на синусоидальное питающее напряжение, допуская некоторые отклонения по нелинейности. Поэтому то вопрос расчёта фильтра на заданный коэффициент гармоник столь важен в современной преобразовательной технике, так как является необходимым условием нормального функционирования приборов и устройств потребителей, задавая ограничение по нелинейности выходного синусоидального сигнала.

В настоящее время в технической литературе достаточно широко и полно описываются алгоритмы расчёта выходных фильтров выпрямителей на заданный коэффициент пульсаций напряжения на нагрузке, с приведением необходимых формул и соотношений к ним. А вот с методикой расчёта выходных фильтров инверторов на заданный коэффициент гармоник напряжения на нагрузке познакомиться довольно сложно, если не сказать, что практически невозможно. И в основном, разработчики электронной техники, сталкиваясь с такой проблемой, решают её опытным путём. Хотя экспериментальные данные наиболее правдиво отражают сложившуюся ситуацию, но все со мной согласятся, что постановка и проведение эксперимента трудоёмкий и кропотливый процесс, требующий, кроме того, и дополнительных финансовых затрат. Как этого избежать? Можно попытаться решить эту проблему аналитически, но это тоже довольно трудоёмкая задача, требующая много времени и ни кто не поручится за то, что вы сможете получить положительный результат. Что же делать? Я предлагаю воспользоваться вторым путём — решить эту проблему аналитически с некоторыми упрощениями и допущениями, перекладывая все сложные математические расчёты на “плечи” электронно-вычислительных машин (ЭВМ), а первый способ применить как проверку выдвинутому методу.

В чём же суть предложенного метода? Суть метода заключается в раскладывании формы напряжения на выходе инвертора с помощью прямого быстрого преобразования Фурье (ПБПФ) в спектр амплитуд гармонических составляющих, “пропускания” через фильтр каждой гармонической составляющей в отдельности и последующего восстановления сигнала на выходе фильтра по средствам обратного быстрого преобразования Фурье (ОБПФ). Что же мы получаем? Мы получаем простую идею, основанную только на БПФ, результат применения которой хоть и не будет сверхточным применительно к реальным устройствам, причём точность будет в большей степени зависеть от применённых упрощений и допущений, нежели от точности вычислительного процесса, но тем ни менее сможет дать представление об основных параметрах фильтра. Причем, можно получить не только вид кривой напряжения на нагрузке, а, следовательно, определить коэффициент гармоник, действующие значения напряжений первой и высших гармонических составляющих, но и вычислить фазовый сдвиг, обусловленный влиянием фильтра. И всё же, каким бы простым не казалось решение поставленной задачи, данный метод имеет свои нюансы применения. Для его реализации необходимо хотя бы представлять форму выходного напряжения инвертора и получить коэффициент передачи фильтра по напряжению от номера гармонической составляющей. Второе условие, как мне кажется, имеет довольно тривиальное решение, причём вид коэффициента передачи будет различен в каждом конкретном случае, и зависеть не только от типа применяемого фильтра, от тех упрощений, которые будут допущены разработчиком, но и от конкретных условий технического задания на разрабатываемое устройство. А вот первое условие требует более детального изучения непосредственно алгоритма работы самого инвертора и его структуры.

Рассмотрим подробнее, на конкретном примере, предлагаемый способ расчёта выходного фильтра инвертора на заданный коэффициент гармоник синусоидального напряжения на нагрузке. Пусть имеется мостовой инвертор (рисунок 1) реализующий равномерную многократную однополярную ШИМ по синусоидальной функции построения с частотой выходного сигнала Гц, частотой квантования кГц и требуется рассчитать параметры выходного Г-образного LC-фильтра, обеспечивающего на активной нагрузке Ом коэффициент гармоник синусоидального напряжения не более %. Данный тип фильтра мы выбрали исходя из его оптимальных массогобаритных показателей и большей эффективности по сравнению с обычными L- или C-фильтрами. Хотелось бы отметить, что в каждом конкретном случае выбор типа фильтра определяется только параметрами технического задания на проектируемое устройство и фантазией разработчика. Данный метод лишь помогает рассчитать основные параметры фильтра на основе той передаточной функции, которую разработчик выведет, основываясь на своих предпочтениях и умозаключениях по его типу и синтезированной структуре.

Для расчёта необходимо, как мы уже отметили выше, получить форму выходного напряжения инвертора. Поэтому сначала рассмотрим именно эту проблему. Примем для простоты все элементы в схеме идеальными, а все процессы, протекающие в инверторе, будем рассматривать на периоде выходного напряжения в установившемся режиме. Это допущение вполне оправдано, так как разработчики всегда пытаются минимизировать паразитные явления, которые оказывают негативное влияние на работу устройства. Все математические расчёты, построение графиков и диаграмм работы будем реализовывать на персональном компьютере с использованием пакета математических вычислений Mathcad [1]. Управляющие импульсы по синусоидальной функции построения получаем, как показано на рисунке 2, путём сравнения управляющего выпрямленного синусоидального сигнала с пилообразным развёртывающим напряжением. Имеем в результате широтномодулированную импульсную последовательность по синусоидальной функции построения, которую перераспределяем между ключами инвертора в соответствии с рисунком 3, причём логическая единица соответствует замкнутому состоянию ключа, а логический ноль — разомкнутому. В соответствии с полученным алгоритмом управления, принимая уровень постоянного напряжения на входе равным 10В, строим диаграмму напряжения на выходе (рисунок 4). Как видим, из постоянного напряжения на входе инвертора с помощью ШИМ получили двухполярное модулированное по синусоидальной функции построения напряжение на выходе инвертора. Раскладываем полученную функцию с помощью БПФ и определяем её спектр амплитуд гармонических составляющих (рисунок 5). Замечаем, что спектр состоит из первой гармонической составляющей (50Гц) и массивов более высокочастотных гармоник, сконцентрированных возле частот кратных частоте квантования (1.2кГц, 2.4кГц и т.д.). То есть данный спектр не содержит относительно низкочастотных гармонических составляющих (кроме первой), а только высокочастотные и, следовательно, обычным LC-фильтром можно легко их отфильтровать, оставив только первую гармонику. Причём чем больше будет частота квантования, тем в более высоком частотном диапазоне окажутся массивы высокочастотных гармонических составляющих. Определим так же действующее значение выходного напряжения 7.955В, действующее значение первой гармонической составляющей 7.071В и рассчитаем коэффициент гармоник, который составит 51.525%.

Теперь найдём функцию коэффициента передачи выходного фильтра от номера гармонической составляющей. Для этого составляем по эквивалентной схеме выходного фильтра (рисунок 6) систему уравнений с использованием законов Кирхгофа и, производя простейшие математические преобразования, находим искомую функцию (1).

где
n — номер гармонической составляющей;
i — мнимая единица;
— круговая частота выходного напряжения;
L — индуктивность дросселя фильтра;
С — ёмкость конденсатора фильтра;
R — сопротивление нагрузки.

Для дальнейших вычислений нам необходимо задаться начальными параметрами фильтра. Индуктивность дросселя принимаем равной мГн, а ёмкость конденсатора находим из условия равенства волнового сопротивления фильтра сопротивлению нагрузки (2) для исключения резонансных явлений на одной из высокочастотных гармонических составляющих.

Перемножаем каждую гармоническую составляющую выходного напряжения инвертора на коэффициент передачи фильтра (рисунок 7). Применяя БПФ, находим диаграмму напряжения на нагрузке, изображённую на рисунке 8 на фоне идеального синусоидального напряжения имеющего такие же амплитуду и фазовый сдвиг. Видим, что напряжение на нагрузке имеет синусоидальный характер с некоторыми искажениями из-за наличия высокочастотных гармонических составляющих не полностью подавленных фильтром и фазовым сдвигом по первой гармонике, величиной 5.549 электрических градусов. Коэффициент гармоник напряжения на нагрузке составляет 9.739%. То есть фильтр с данными параметрами не достаточен для обеспечения на выходе коэффициента гармоник напряжения, требующегося в условии, при заданной выходной частоте и частоте квантования.

Поэтому рассчитываем по данному алгоритму коэффициент гармоник напряжения на нагрузке, при различных параметрах фильтра, с учётом выражений (1) и (2), от начального значения индуктивности дросселя равного мГн с шагом мГн для тридцати значений. Получаем зависимость коэффициента гармоник выходного напряжения от индуктивности дросселя фильтра, график которой изображён на рисунке 9. Производя расчёты при разных частотах квантования или выходных частотах инвертора можно получить семейства подобных характеристик.

Теперь, исходя из зависимости представленной на рисунке 9, принимаем индуктивность дросселя фильтра равной мГн, ёмкость конденсатора фильтра находим, с учётом выражения 2, равной мкФ и, основываясь на приведённой выше методике, находим диаграмму напряжения на нагрузке изображённую на рисунке 10. Видим, что напряжение на нагрузке имеет синусоидальный характер с некоторыми незначительными искажениями, причём фазовый сдвиг, обусловленный влиянием фильтра, увеличился до 11.176 электрических градусов. Коэффициент гармоник напряжения на нагрузке составляет всего 2.283%, что вполне удовлетворяет требуемому в условии значению. То есть мы нашли необходимые основные параметры фильтра, при заданных выходной частоте и частоте квантования.

Данная методика расчёта фильтров применялась при разработке универсального лабораторного макета одно/трёхфазного инвертора ШИМ (УМИШИМ-3/1) [2] и показала свою эффективность. На рисунке 10 приведена осциллограмма напряжения на нагрузке при работе инвертора в режиме многократной равномерной двухполярной трёхфазной ШИМ. Причём, затраты времени на расчет были минимальны и составили порядка нескольких десятков минут, а сам расчёт проводился на персональном компьютере, имеющем невысокую вычислительную мощность.

Литература

Mathcad 6.0 PLUS. Финансовые, инженерные и научные расчёты в среде Windows 95. Издание 2-е, стереотипное — М.: Информационно-издательский дом “Филинъ”, 1997. — 712с.
Семёнов В. Д., Матвеев К. Ф., Захаров А. А. Универсальный макет одно/трёхфазного инвертора для проведения лабораторных работ по курсу преобразовательная техника. Материалы Всероссийской научно-методической конференции “Совершенствование систем управления качеством подготовки специалистов”. 20-21 марта 2003 года, Красноярск, Россия. В двух частях. Часть вторая, стр. 23-24.

Обзор продукции: синусный фильтр для преобразователя частоты

Синусные фильтры и моторные дроссели открытого типа

Синусные фильтры в корпусе

Сетевые (входные) дроссели открытого исполнения

Входные дроссели (линеаторы) в корпусе

Сазонов А.С. (канд.техн.наук), Лебедев Д.Ю. (инж.)
АО «СПИК СЗМА», Санкт-Петербург

Назначение синусного фильтра

Для регулирования частоты вращения многих механизмов, в частности, электрических погружных насосов (ЭПН) с асинхронными двигателями (АД), используются частотно-регулируемые приводы (ЧРП) на основе трехфазных ШИМ-инверторов напряжения с синусоидальным выходным напряжением. Формирование трехфазного синусоидального выходного напряжения ШИМ — инвертора напряжения осуществляется с помощью различных фильтров, наиболее распространенным из которых является однозвенный трехфазный LC- фильтр. В виду сложности аналитического расчета выбор параметров фильтра обычно производится либо экспериментальным путем, что представляет собой трудоемкий и кропотливый процесс, либо путем компьютерного моделирования, что также вызывает определенные трудности.

Проще говоря, синусные фильтры предназначены для устранения гармонических искажений напряжения на выходе частотного преобразователя (ПЧ) до допустимых значений (не более 5% по ГОСТ Р 52776-2007). Таким образом, из ШИМ-формы получается синусоидальная форма выходного напряжения ПЧ. Наши синусные фильтры подходят для частотников любого производителя с существенно более низкой ценой. Это могут быть частотники ABB ACS, Danfoss VLT FC, Vacon, DELTA VFD, Веспер E, Siemens SINAMICS, Hyundai N700, Schneider Electric Altivar ATV, Omron, Lovato, INVT, Mitsubishi Electric FR, ОВЕН ПЧВ, Toshiba VF, SEW, EATON.

Схема подключения синусного фильтра

В настоящей статье рассмотрены основные положения для упрощенного расчета и выбора параметров синусного фильтра c требуемым качеством выходного напряжения, характеризуемым коэффициентом гармоник выходного напряжения фильтра.

Расчет и выбор параметров синусного фильтра для конкретного типоисполнения ЧРП (частотного преобразователя) осуществляются при следующих исходных данных:

напряжение питающей сети на входе ЧРП;
спектр гармоник входного напряжения фильтра;
кратность несущей и модулирующей частот инвертора;
диапазон регулирования выходной частоты;
характеристика нагрузки;
принятый критерий оптимальности для рассчитываемого фильтра.

Расчёт и выбор выходного фильтра инвертора производится при имеющемся частотном спектре напряжения на входе фильтра и требуемом коэффициенте гармоник выходного напряжения, регламентируемым ГОСТ Р 52776-2007 для электрических машин.

Для расчёта параметров фильтра в [1] предлагается критерий подобия для однозвенного LC-фильтра нижних частот, связанный с определением минимума суммарной относительной установленной мощности фильтра. По этому критерию можно провести выбор параметров элементов фильтра при коэффициенте гармоник входного напряжения фильтра, зависящего от диапазона регулирования амплитуды первой гармоники напряжения инвертора и величины нагрузки, при заданном качестве выходного напряжения фильтра.

При анализе фильтров инверторов на первом этапе и в практических приложениях учитывают только мощность по основной гармонике, т.к. суммарная реактивная мощность, создаваемая высшими гармониками, существенно меньше реактивной мощности, создаваемой основной гармоникой в том же элементе фильтра.

При заданной выходной мощности ЧРП массо-габаритные показатели однозвенного LC-фильтра определяются заданным коэффициентом гармоник выходного напряжения фильтра и коэффициентом гармоник входного напряжения фильтра.

Формулы расчета синусного фильтра

Коэффициент подобия фильтра m 2 для однозвенного LC-фильтра нижних частот связан с коэффициентом гармоник входного и выходного напряжений k_Гвх, k_Гвых и параметрами фильтра соотношением [2]:

где N- кратность несущей и модулирующей частот

Квадрат волнового сопротивления фильтра рассчитывается по формуле

где Z_H — полное сопротивление нагрузки.

Из соотношений (1) и (2) определяются параметры фильтра. Резонансную частоты фильтра вычисляют по уравнению

Связь между выходным напряжением выпрямителя и трехфазной системой выходного напряжения инвертора с трехфазной нагрузкой можно установить с помощью обобщенного (результирующего) вектора напряжения для трехфазных систем.

Амплитуда основной гармоники напряжения на выходе инвертора (на входе фильтра) U_m1зависит от коэффициента регулирования k_p , а амплитуда основной гармоники напряжения на выходе фильтра определяется соотношением

— коэффициент передачи фильтра по первой гармонике при работе на активно-индуктивную нагрузку, определяемый из [3].

При питании насосных установок мощность на валу приводного двигателя в зависимости от частоты вращения изменяется по закону

где — текущая и номинальная (базовая) частоты вращения; — текущая и номинальная (базовая) активные мощности нагрузки.

Тогда полная мощность нагрузки

Для определения коэффициента гармоник входного напряжения фильтра необходимо учесть спектральный состав напряжения на выходе инвертора, зависящего от способа формирования многоимпульсного напряжения инвертора.

В [2] проанализированы различные алгоритмы работы инверторов напряжения и спектральный состав их выходного напряжения. Анализ показывает, что, например, спектральный состав напряжения с однополярной ШИМ, полученный синусоидальной модуляцией длительности импульсов, при достаточно большом отношении несущей и модулирующей частот- , практически неизменен.

Установлено, что для однополярной ШИМ типовой спектральный состав с учётом первой группы учитываемых гармонических составляющих, необходимых для расчёта силового однозвенного LC-фильтра, состоит из четырёх гармонических составляющих, имеющих кратности N-3, N-1, N+1, N+3. При этом амплитуды гармонических составляющих практически не зависят от кратности частот, а определяются величиной коэффициента регулирования k_p.

Приведены относительные значения учитываемых гармонических составляющих для различных значений кратности частот в зависимости от коэффициента регулирования, которые можно использовать для практических расчётов при любых кратностях частот.

Анализ гармонического состава импульсного напряжения на выходе инвертора в заданном диапазоне регулирования амплитуды первой гармоники напряжения инвертора и величины нагрузки при различных видах модуляции (ШИМ, ШИМ-КД) показывает, что гармоники выходного напряжения имеют наихудший состав при минимальном коэффициенте регулирования [1]. Поэтому величина коэффициента гармоник выходного напряжения фильтра в значительной части диапазона регулирования оказывается меньше заданного.

Следует иметь в виду, что при практических измерениях коэффициента гармоник напряжения на выходе фильтра для правильных замеров необходимо использовать измерительный прибор, фиксирующий максимальные гармоники порядка не менее (N+3).

а)
б)

Рис.1 – Входные (а) и выходные (б) фазные токи и напряжения

Порядок выбора параметров элементов синусного фильтра

Для определения расчетных значений индуктивности и емкости фильтра необходимо проводить вычисления на максимальной и минимальной частотах в следующей последовательности:

определяем коэффициент гармоник входного напряжения k_Гвх1 для заданных значений k_p и N;
критерии подобия при требуемом и вычисленном коэффициенте гармоник соответственно выходного k_г.вых и входного k_г.вх1 напряжений
коэффициент передачи фильтра по первой гармонике при активно- индуктивной нагрузке;
амплитуду напряжения на выходе фильтра;

Далее по критерию подобия и полному сопротивлению нагрузки, исходя из полной мощности нагрузки, находят емкость и индуктивность фильтра. Из рассчитанных в двух режимах работы значений отбираем наибольшие для удовлетворения качества выходного напряжения во всем диапазоне регулирования частоты. Затем выбираем значения емкости и индуктивности фильтра из стандартного ряда и для них проверяем коэффициент гармоник выходного напряжения фильтра. После этого определяем резонансную частоту фильтра.

Все вычисления можно производить на персональном компьютере с использованием пакета математических вычислений Mathcad.

а)
б)

Рис.2 – Спектры входного (а) и выходного (б) фазных напряжений

Практическая реализация синусных фильтров

Синусные фильтры конструктивно могут быть размещены в шкафу с частотным преобразователем (ЧРП) или в отдельном шкафу, причем элемент индуктивности может быть выполнен в виде дросселя с магнитопроводом, или в виде воздушного реактора. Использование воздушного реактора в отдельно стоящем шкафу с экономической точки зрения более выгодно, чем дросселя с магнитопроводом. Заводом АО «СПИК СЗМА» выпускаются оба типоисполнения синусных фильтров на токи до 1600А.

По разработанной методике был рассчитан и изготовлен синусный фильтр для работы совместно с частотным преобразователем (ЧРП) с диапазоном регулирования выходной частоты (30-70) Гц и с несущей частотой ШИМ-инвертора напряжения 3кГц при требуемом коэффициенте гармоник выходного напряжения не более 5% на заданном диапазоне регулирования при квадратичной зависимости момента на валу асинхронного двигателя от частоты вращения.

Список литературы

Малышков Г.М., Крючков В.В., Соловьев И.Н. и др. Выбор параметров фильтров инверторов. — ЭТВА/ Под ред. Ю.И.Конева. – М.: Радио и связь,1986, вып. 17, с. 148-168.
Крючков В.В., Малышков Г.М., Соловьев И.Н. Кодовое широтно-импульсное регулирование для инверторов.
Бедфорд Б., Хофт Р. Теория автономных инверторов, пер. с англ. под ред. И.В.Антика. М., «Энергия», 1969.-280 с.

Промышленная Энергетика №2, 2012

PDF версия

Сервисный центр

Расчет фильтра нижних частот

Название: Расчет фильтра нижних частот

Вид работы: курсовая работа

Рубрика: Коммуникации и связь

Размер файла: 777,63 Kb

Скачать файл: referat.me-170615.docx

Краткое описание работы: Содержание Введение 1 Физические основы и принцип действия широкополосных фильтров 2 Пример расчета фильтра нижних частот на заданные параметры Заключение

Содержание

Введение

1 Физические основы и принцип действия широкополосных фильтров

2 Пример расчета фильтра нижних частот на заданные параметры

Заключение

Список использованной литературы

Введение

В начале нашего столетия электрические фильтры, составленные из ряда катушек индуктивности и конденсаторов, получили широкое применение в технике. Благодаря их применению оказалось возможным осуществление многих магистралей дальней телефонной, телеграфной и других видов связи.

1 Физические основы и принцип действия широкополосных фильтров

LC–фильтр нижних частот (рис. 6.3,а) пропускает электрические колебания в полосе частот от 0 до

Полосовые фильтры (ПФ) пропускают сигналы в полосе частот от до (рис.3).

Режекторные (заграждающие) фильтры (РФ) задерживают сигналы в полосе частот от до (рис.4).

(а)

(б)

Рисунок – 1 Фильтры нижних частот (а) и его АЧХ (б).

Рисунок – 2 Фильтры верхних частот

Рисунок – 3 Полосовые фильтры

Рисунок – 4 Заграждающие фильтры

Полное сопротивление Z любого элементарного контура состоит из активной R и реактивной Xсоставляющих:

Z = R + jX(1)

или

Y = G + jB(2)

где Y – полная проводимость

G – активная составляющая полной проводимости

B – реактивная составляющая поной проводимости

Рисунок – 5 Схема звена ФВЧ и резонансные характеристики последовательного контура

Рисунок – 6 Схема звена ФНЧ и резонансные характеристики параллельного контура

Благодаря этому через фильтр беспрепятственно проходят частоты полосы пропускания. В этой связи становится понятным, почему в широкополосных фильтрах все звенья настраиваются на частоты полосы задерживания.

Крутизна частотной характеристики фильтра в переходной области зависит от числа звеньев. Широкополосный фильтр всегда состоит из фильтра нижних частот и фильтра верхних частот. Полоса пропускания широкополосный фильтра – образуется благодаря перекрытию полос пропускания ФНЧ (0 -) и ФИЧ (- ) – (рис.7)

Рисунок – 7 Образование полосы пропускания широкополосного фильтра

2 Пример расчета фильтра нижних частот на заданные параметры

Аналитический метод расчета цепочных фильтров основан на нахождении оптимальных параметров фильтра по заданной характеристике собственного или рабочего затухания. При этом реализуется фильтр, удовлетворяющий заданным условиям, при минимальном числе элементов, что гарантирует минимальное искажение в полосе пропускания. Отметим, что, так как последовательно и параллельно-производные звенья фильтров являются дуальными, т.е. взаимообратными, а свойства таких схем в отношении передачи энергии аналогичны, то количество расчетных формул, используемых для расчета фильтров, будет вдвое уменьшено. Поэтому ведется единый расчет фильтра.

Требуется рассчитать фильтр, удовлетворяющий следующим техническим требованиям:

1. Полоса пропускания

= 50 кГц, = 100 кГц,

где и соответственно нижняя и верхняя граничные полосы пропускания.

2. Полоса задерживания

От = 115 кГц и выше

где и соответственно верхняя и нижняя граничные полосы задерживания.

3. Рабочее затухание в полосе пропускания

7дБ = =0,805 неп

4. Рабочее затухание в полосе задерживания

50 дБ = =5,75 неп

5.Фильтр включается между сопротивлением нагрузок

= 1000 Ом

6.Отклонение характеристического сопротивления от номинального в полосе пропускания (коэффициент несогласованности)

= 10 % =0,1

7. Амплитуда входного сигнала

= 5 В

9. Коэффициент использования полосы пропускания.

8. Рекомендуется выполнить катушки индуктивностей на альсиферовых сердечниках.

Прежде чем приступить к расчету фильтра, необходимо определить критерий полосности

Так как n < 2, рассчитываем фильтр как полосовой.

Зная вычислим ,затем определим затухание несогласованности

Выбрав класс фильтра по сопротивлению (обычно 2-ой), т.е. =2, найти параметр

Далее определить расчетный параметр полосы пропускания

и затем расчетный параметр

Найдем коэффициент использования полосы пропускания

И только потом можно определить коэффициент использования полосы задерживания и теоретическую частоту среза. Для реальных фильтров . Заданные параметры и = 100 кГц, определим теоретическую частоту среза

Так как теоретическая частота среза лежит в пределах переходной области, она удовлетворяет предъявленным условиям. Исходя из этого, определяем предварительный коэффициент использования полосы пропускания

Поскольку величина не превышает предельно достижимого в реальных фильтрах значения 0,98, останавливаемся на этих значениях и . Определяем коэффициент использования полосы задерживания и расчетные параметры – расчетный параметр и – расчетный параметр полосы задерживания:

Зная , определяем затухание одного звена фильтра с учетом потерь в полосе задерживания

Далее находим минимальное собственное затухание всего фильтра в полосе задерживания, которое необходимо для обеспечения гарантируемого минимума затухания

По найденным значениям и определяем число звеньев N (или, что то же самое, класс фильтра по затуханию)

Для выбранного округленного числа звеньев N=4 пересчитываем величины , , , а также . Уточнив все эти параметры проверяем отклонение характеристического сопротивления от номинального.

Зная , пересчитываем коэффициент использования полосы задерживания

используя который, определяем уточненную верхнюю теоретическую частоту среза

Полученное значение теоретической частоты среза удовлетворяет исходным требованиям, так как находится в переходной области. Далее определяем уточненный коэффициент использования полосы пропускания

Теперь по сути дела возвращаемся в начало расчета. Для проверки отклонения характеристического сопротивления фильтра от номинального сопротивления нагрузки в полосе пропускания рассчитываем параметры , и (по данным полосы пропускания):

Выбираем заранее фильтр 2-го класса по сопротивлению и определяем затухание несогласованности в полосе пропускания

и затухание эха

После определяем величину отклонения характеристического сопротивления от номинального в полосе пропускания

Что удовлетворяет исходным техническим требованиям. Таким образом, на основании проведенного расчета выбран фильтр 2-го класса по сопротивлению с числом звеньев N=4. Отклонение характеристического сопротивления от номинального в полосе пропускания составляет 3,558 %, коэффициент использования полосы пропускания =0,885, теоретическая частота среза =113,016 кгц.

Расчетные параметры необходимые в дальнейшем,

=0,43 =0,4659=113,016 кгц.

Так как фильтр состоит из четырех звеньев, то для каждого звена рассчитываем коэффициент и соответственно расчетный параметр m.

где

=1,2,3,4 – № звена

N= 4 – число звена

Таким образом

Проверкой правильности расчета при четном числе звеньев служит соблюдение следующих соотношений:

, и т.д.

т.е. в рассматриваемом примере и т.д.

Для расчета коэффициентов m полагаем, что =0,43, тогда

Затем определяем

Для получения наилучшего согласования фильтра с нагрузкой начинаем и оканчиваем фильтр полузвеньями, у которых значение коэффициента m ближе к . В рассматриваемом примере этому требованию удовлетворяет коэффициент .

Внутри фильтра звенья с различными коэффициентами могут соединяться в произвольном порядке, но при условии соблюдения согласования.

Затем приступаем к выбору конкретной схемы фильтра нижних частот. При этом нужно стремиться к выбору звеньев с наименьшим числом катушек индуктивности, поскольку именно эти элементы наиболее усложняют производство и настройку фильтра. Так как класс фильтра определяется классом конечных полузвеньев, то для них выбираем звено типа 2А1н (звено Т-образного вида, 2-го класса по сопротивлению, с одной стороной среза фильтра нижних частот) и делим его пополам, для того, чтобы не увеличивать общее число звеньев. При этом получаются оконечные полузвенья Г-образного вида. В качестве промежуточных звеньев используем звенья типа 1В1н (звено П-образного вида, первого класса по сопротивлению, с одной частотой среза, фильтра нижних частот). Далее составляем полную принципиальную схему всего фильтра нижних частот рисунок 8.

звена 2А1н 1В1н 1В1н1В1нзвена 2А1н

Рисунок 8 – Полная принципиальная схема фильтра нижних частот

Первый этап расчета заканчиваем вычислением частот минимального затухания, лежащих в полосе задерживания.

соответственно

Формула для расчета частот минимального затухания

Аналогично формуле для расчета с той лишь разницей, что вместо параметра подставляется . Коэффициент , аналогичный коэффициенту , рассчитывается по формуле

где=1,2,3,4 – № звена

N= 4 – число звеньев

=0,3986 – ранее определенный параметр

Таким образом

Проверка правильности расчета коэффициентов :

, и т.д.

где

т.е. в рассматриваемом примере и т.д.

Далее для каждого звена определяем параметр и частоту минимального затухания:

Частота последнего минимума затухания должна совпадать с верхней граничной частотой полосы задерживания. Кроме того должно соблюдаться строгое чередование частот бесконечного и минимального затухания. Правильность расчета подтверждается в рассматриваемом примере равенством и таблицей 1.

Таблица 1

Заметим, что наибольшему значению m соответствует наиболее удаленная от полосы пропускания частота бесконечного затухания, а наименьшему значению m соответствует ближайшая к переходной области частота бесконечного затухания. Все частоты и находятся в полосе задерживания. Не допускается расположение частот и в полосе пропускания.

Определив частоты бесконечного и минимального затухания, а так же значения коэффициентов для всех звеньев и составив полную принципиальную схему фильтра нижних частот (ФНЧ состоит из трех звеньев типа 1В1н и двух полузвеньев типа 2А1н), приступаем к расчету номинальных значений элементы схемы ФНЧ. Начинаем с определения величины расчетного сопротивления , а затем единичной индуктивности и единичной емкости .

Коэффициент нагрузки рассчитывается графоаналитическим способом. Суть расчета сводится к тому, что выбирается такое соотношение между сопротивлением нагрузки и номинальным характеристическим сопротивлением, при котором в заданной полосе частот обеспечивается наилучшее согласование. Расчет характеристического сопротивления ведется только для оконечного полузвена, ибо если выполняются условия согласования характеристического сопротивления с сопротивлением нагрузки для оконечного полузвена на всех частотах полосы пропускания, то они выполняются и для всех промежуточных звеньев (данные расчета приведены в таблице 2).

Таблица 2

Оконечное полузвено Ом =113,016 кгц.
f, кгц
50	0,4424	0,8968	0,87128	1,02929	1029,29	1,03592
55	0,4867	0,8736	0,84421	1,0348	1034,8	1,0415
60	0,5309	0,8474	0,8146	1,04027	1040,27	1,04697
65	0,5751	0,81805	0,7825	1,0454	1045,4	1,0521
70	0,6194	0,7851	0,7477	1,0500	1050,0	1,0568
75	0,6636	0,7481	0,71037	1,05311	1053,11	1,053865
80	0,7079	0,7064	0,6704	1,05369	1053,69	1,0605
85	0,7521	0,6590	0,62797	1,0494	1049,4	1,0562
90	0,7964	0,6048	0,58285	1,03766	1037,66	1,0443
95	0,8406	0,5417	0,53526	1,01203	1012,03	1,01855
100	0,8848	0,4659	0,48511	0,9604	960,4	0,9666

Коэффициент согласования – это отношение характеристического сопротивления к сопротивлению нагрузки, т.е. . Чем меньше коэффициент согласования отличается от единицы, тем лучше согласованы характеристическое сопротивление и сопротивление нагрузки. Графоаналитический метод заключается в симметрировании кривой относительно значения (т.е. уравнивания наибольшего и наименьшего значений в полосе пропускания).

Исходя из этого, определяется коэффициент нагрузки , позволяющий затем вычислить как оптимальное номинальное характеристическое сопротивление. Проводя симметрирование, перемещаем кривую вдоль оси ординат относительно значения (в рассматриваемом примере вниз) так, чтобы максимальное положительное и максимальное отрицательное отклонения функции от значения были приблизительно равны.

Рисунок 9 – График симметрирования характеристического сопротивления ФНЧ

В рассматриваемом примере экспериментальное значение функции соответствует значениям и . На частоте коэффициент согласования . На частоте коэффициент согласования .

Из этого обобщенного графика можно сделать заключение о форме характеристики затухания фильтра нижних частот. Положительное отклонение от значения свидетельствует об обеспечении неискаженной передачи частот полосы пропускания в диапазоне частот и ; отрицательное отклонение свидетельствует о наличие искажений для некоторых частот полосы пропускания (наблюдается так называемый завал фронтов амплитудно-частотной характеристики).

Максимально положительное и максимально отрицательное отклонение на этих частотах составляют соответственно ()

Разность отклонений

Среднее отклонение

Новое значение коэффициента согласования на частоте с учетом среднего отклонения

Коэффициент несогласованности и коэффициент нагрузки на частоте соответственно равны

Полагая коэффициент нагрузки на частотах и одинаковым, находим коэффициент согласования и коэффициент несогласованности на частоте :

Так как значения и ничтожно мало отличаются друг от друга, коэффициент нагрузки выбираем окончательно .

Определяем расчетное характеристическое сопротивление

Ом

Следует отметить, что, так как и мало отличается от , можно было бы пренебречь несогласованностью при расчете и полагать Ом.

Вычисляем величины единичной индуктивности и единичной емкости исходного звена типа .

, ,

Рисунок 10 – Расчетные соотношения для П-образного звена типа 1В1н фильтра нижних частот.

Учитывая составленную полную принципиальную схему фильтра нижних частот (см. рисунок 8), рассчитываем номинальные величины элементов каждого звена схемы. Звено типа 1В1н рассчитывается следующим образом:

Зная коэффициенты и можно рассчитать элементы всех звеньев (рисунок 10), учитывая при этом, что для каждого звена требуются свои значения m, а значения и постоянны для всех звеньев. Расчет дается для одного типового промежуточного звена и оконечного полузвена. Значения элементов остальных звеньев сведены в таблице 3.

Расчет промежуточного полузвена

,,,

Сразу же проверяем резонансную частоту контура, значение которой должно совпадать со значением частоты бесконечного затухания при том же значении m.

()

Таблица 3

№

звена

Расчетный

коэффициент

кГц

0,31642

1,4099

0,63284

0,8974

1973,8

442,97

119,65

0,19862

2,4181

0,39742

0,56329

3385,22

278,06

115,31

Расчет оконечного полузвена.

Четвертое звено состоит из двух полузвеньев, включенных на входе и на выходе фильтра. Для того, чтобы рассчитать номинальные величины Г-образных полузвеньев по приведенным формулам, необходимо пересчитать величину , так как оконечные полузвенья образуются путем деления пополам Т-образного звена типа 2А1н (линия а-а на рисунке 11).

Рисунок 11 – Преобразование звена типа 2А1н в оконечные полузвенья ФНЧ и расчетные соотношения.

Проверяем резонансную частоту контура

()

Имея полную схему фильтра (см. рисунок 8), можно составить его приведенную схему, отличающуюся от полной тем, что параллельно соединенные элементы заменим одним эквивалентным элементом (см.рисунок 12). Это внесет упрощение в изготовление фильтра и также удешевит его. В приведенной схеме изменены обозначения. Поэтому приведем нумерацию и расчет эквивалентных элементов (обозначения полной схемы в скобках):

, ,

Рисунок 12 – Приведенная схема фильтра нижних частот

Построение полной характеристики затухания ФНЧ. Необходимо рассчитать затухание в полосе задерживания и в полосе пропуская. Так же учтем, что общее собственное затухание как в полосе задерживания, так и в полосе пропускания равняется сумме затуханий всех звеньев . Поэтому рассчитаем затухания отдельно для каждого звена, и затем просуммируем их.

Расчет характеристики затухания фильтра нижних частот начинаем с расчета собственного затухания каждого звена на частотах , где учитываем что Q – добротность катушек индуктивности (для выбранных мною альсиферовых сердечников она обычно берется равной 60) и – рассчитанные ранее коэффициенты звеньев.

Таким образом

Далее считаем собственное затухание в полосе задерживания без учета потерь, так как потери в полосе задерживания не сказываются существенно на затухании.

где

Рассчитываем собственное затухание в полосе задерживания на всех частотах и , кроме частоты бесконечного затухания данного звена, так как оно рассчитано ранее. Полный расчет для звена I () приведен в таблице 4. Для всех остальных звеньев в таблице 5 приведены расчетные значения частот и и величины соответствующих им затуханий, там же приводится собственное затухание всего ФНЧ в полосе задерживания.

Таблица 4

I звено
f,кГц
115,00	1,0176	5,4001	6,0296	4,0296	0,40301
115,313	1,0203	5,0385	5,6928	3,0928	0,43282
116,419	1,0301	4,1056	4,8239	2,8239	0,5346
119,137	1,0542	3,1594	3,9426	1,9426	0,7048
125,179	1,1076	2,3259	3,1663	1,1663	0,9987
139,356	1,2331	1,7091	2,5918	0,5918	1,4769
176,369	1,5606	1,3026	2,2132	0,2132	2,3399

Таблица 5

f,кГц	I звено	II звено	III звено	IV звено
310,442	9,381	1,47681	0,7077	0,4333	11,99881
176,369	2,3399	2,00241	0,8765	0,5294	5,74821
139,356	1,4769	5,247	1,21056	0,7071	8,64156
125,179	0,9987	1,87846	1,8832	0,9997	5,76006
119,137	0,7078	1,21113	2,328	1,4738	5,72073
116,419	0,53546	0,88646	2,0395	2,2865	5,74792
115,313	0,43282	0,70645	1,4737	3,39	6,00297
115	0,40301	0,6556	1,34079	1,04941	3,44881

Для получения рабочего затухания в полосе задерживания рассчитаем затухание задерживания , так как оно существенно влияет в этой области частот на рабочее затухание.

где

Затухание отражения считаем только для оконечного полузвена со значением , так как затухание отражения получается за счет несогласованности характеристического сопротивления с сопротивлением нагрузки. Окончательные результаты сведены в таблице 6.

Таблица 6


f, кГц	, неп	f, кГц	, неп
115,000	–0,5637	125,179	–0,3235
115,3013	–0,5972	139,356	7,45
116,419	–0,674	176,369	–0,467
119,137	–0,6806	310,442	–0,602

Далее находим рабочее затухание всего фильтра в полосе задерживания (таблица 7).

Таблица 7

f, кГц					, дБ	, неп
115,00	1,0176	3,44881	–0,5637	2,88511	28,14	2,89
115,313	1,0203	6,00297	–0,5972	5,40577	47,07	5,41
116,419	1,0301	5,74792	–0,674	5,07392	44,11	5,07
119,137	1,0542	5,72073	–0,6806	5,04013	43,85	5,04
125,179	1,1076	5,76006	–0,3235	5,43656	47,33	5,44
139,356	1,2331	8,64156	7,45	16,0916	139,98	16,09
176,369	1,5606	5,74821	–0,467	5,28121	45,94	5,28
310,442	2,75	11,99881	–0,602	11,3968	99,15	11,39

Рассчитываем фазовый сдвиг, вносимый одним звеном ФНЧ.

где – фазовый сдвиг, вносимый каждым звеном;

= 1,2,3,4 – № звена

Общий фазовый сдвиг представляет собой сумму фазовых сдвигов звеньев. Расчеты фазового сдвига каждого звена и всего фильтра приведены в таблицах 8 и 9. Как видно из таблицы 9 фазовый сдвиг вырастает при приближении к частоте среза. Для ФНЧ эта частотой является наивысшей частотой полосы пропускания.

Для получения полной характеристики затухания ФНЧ рассчитываем для каждого звена в отдельности затухание в полосе пропускания с учетом потерь по следующей формуле:

Таблица 8

I звено
f, кГц			f, кГц
50	0,4424	0,4595	80	0,7079	0,9334
55	0,4867	0,5189	85	0,7521	1,0629
60	0,5309	0,5835	90	0,7964	1,2264
65	0,5751	0,6548	95	0,8406	1,4453
70	0,6194	0,7348	100	0,8848	1,7688
75	0,6636	0,8262

Расчет собственного затухания в полосе пропускания, вносимого I звеном, отражен в таблице 10. Окончательные результаты аналогичных расчетов затухания полосы пропускания для остальных звеньев сведены в таблице 11. В этой же таблице приведено суммарное собственное затухание фильтра в полосе пропускания .

Таблица 9

Таблица10

I звено Q=60
f, кГц					, неп	, дБ
50	0,4424	0,21114	1,21114	0,37939	0,002797	0,02433
55	0,4867	0,26926	1,6926	0,30657	0,002487	0,02164
60	0,5309	0,34047	1,3047	0,44723	0,003957	0,03443
65	0,5751	0,42876	1,42876	0,45829	0,004393	0,03822
70	0,6194	0,53993	1,53993	0,47716	0,004926	0,04286
75	0,6636	0,68261	1,68261	0,49102	0,005431	0,04725
80	0,7079	0,87124	1,87124	0,49881	0,005885	0,05120
85	0,7521	1,12976	2,12976	0,49907	0,006256	0,05443
90	0,7964	1,50406	2,50406	0,48976	0,006501	0,05657
95	0,8406	2,08889	3,08889	0,46790	0,006555	0,05703
100	0,8848	3,12865	4,12865	0,42842	0,063178	0,05496

За счет потерь энергии в катушках индуктивности и конденсаторах собственное затухание фильтра не равно нулю, а имеет некоторое конечное значение, возрастающее по мере приближения к предельной частоте.

На основании ранее полученных данных о затухании фильтра составляем таблицу для расчета выходного напряжения в полосе пропускания и полосе задерживания фильтра нижних частот, помня, что и (таблица 12).

Рисунок 13 – Фазовая характеристика ФНЧ с полосой

пропускания 50–100 кГц

Таблица 12


f, кГц	, дБ	, В	f, кГц	, дБ	, В
50	0,057409	4,967	100	0,217759	4,876
55	0,062213	4,964	115,00	28,14	0,196
60	0,083417	4,952	115,313	47,07	0,0222
65	0,096649	4,945	116,419	44,11	0,03115
70	0,111872	4,936	119,137	43,85	0,0321
75	0,128068	4,927	125,179	47,33	0,0215
80	0,145215	4,917	139,356	139,98	0
85	0,163141	4,907	176,369	45,94	0,0252
90	0,181667	4,896	310,442	99,15	0,000055
95	0,200216	4,886

Таблица 11

f, кГц	I звено		II звено		III звено		IV звено		, неп	, дБ
f, кГц	, неп	, дБ	, неп	, дБ	, неп	, дБ	, неп	, дБ	, неп	, дБ
50	0,002797	0,02433	0,001964	0,01709	0,001124	0,009775	0,000714	0,006214	0,006599	0,057409
55	0,002487	0,02164	0,00239	0,020792	0,001387	0,012067	0,000887	0,007714	0,007151	0,062213
60	0,003957	0,03443	0,002859	0,024873	0,001687	0,014681	0,001084	0,009433	0,009587	0,083417
65	0,004393	0,03822	0,003372	0,029336	0,002031	0,017672	0,001313	0,011421	0,011109	0,096649
70	0,004926	0,04286	0,003928	0,034175	0,002426	0,021102	0,001579	0,013735	0,012859	0,111872
75	0,005431	0,04725	0,004522	0,039338	0,002878	0,025037	0,00189	0,016443	0,014721	0,128068
80	0,005885	0,05120	0,005148	0,044789	0,003399	0,029574	0,002259	0,019652	0,016691	0,145215
85	0,006256	0,05443	0,005789	0,050363	0,004004	0,034836	0,002703	0,023512	0,018752	0,163141
90	0,006501	0,05657	0,006419	0,055829	0,004713	0,041	0,003249	0,028268	0,020882	0,181667
95	0,006555	0,05703	0,006973	0,060658	0,005543	0,048221	0,003943	0,034307	0,023014	0,200216
100	0,063178	0,05496	0,007332	0,063794	0,00651	0,05664	0,00487	0,042365	0,08189	0,217759

Рисунок – 14 Амплитудно-частотная характеристика ФНЧ с полосой пропускания 50–100 кГц

Окончательной проверкой правильности расчета фильтра является близкое совпадение расчетной характеристики с экспериментальной (рисунок 15).

1–теоретическая характеристика; 2– расчетная характеристика

Рисунок – 15 Амплитудно-частотная характеристика ФНЧ с полосой пропускания 50–100 кГц

В заключении расчета приведем общую схему фильтра нижних частот, сопротивление нагрузки ставим в конце схемы.

; ; ; ;

; ; ; ; ; ; ; ; ;

Рисунок –16 Общая схема ФНЧ с рассчитанными значениями емкостей и индуктивностей

Так как в расчете использованы катушки индуктивности с альсиферовыми тороидальными сердечниками, то рекомендуется расположение всех катушек на общей оси и воспользоваться изолирующими прокладками между ними. Монтаж конденсатора может быть осуществлен подобно монтажу сопротивлений, на общей плате. Кожух фильтра выполняется из алюминия, дюраля либо пермаллоя, или другого материала, играющего роль электрического экрана (рисунок 17). Выводы осуществляются через разъемы, которые могут быть и герметичными. Если требуется герметичность всего фильтра, можно рекомендовать заливку компаундами, например эпоксидной смолой. При этом катушки индуктивности должны пройти предварительную пропитку церезином.

При монтаже всех деталей требуется тщательная и надежная пайка, потому что в большинстве случаев неисправности фильтре связаны с плохой пайкой контактов.

Рисунок 17 – Наружный вид фильтра нижних частот 120 80 60

Заключение

В результате выполнения курсового проекта был рассчитан фильтр нижних частот 2-го порядка по сопротивлению, с полосой пропускания 50–100кГц. Характеристики затуханий, построенные по рассчитанным частотам, отвечают требованиям к полосам задержания и пропускания. Проведенное моделирование показало, что характеристики рассчитанных фильтров близки к идеальным, что подтверждает точность расчёта и возможность использования этого фильтра на практике. Преобразование общей схемы фильтра, т.е. уменьшение общего количества необходимых емкостей и индуктивностей позволило удешевить и уменьшить вес конструкции фильтра.

Следует отметить, чторассчитанный мною фильтр может использоваться как все L C -фильтры: в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя; в каскадах радиоэлектронной аппаратуры, включенный на входе средневолнового радиоприёмника обеспечивая настройку на определённую радиостанцию; в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ; для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах; в схемах частотной коррекции магнитофонов и др.

Список использованной литературы

1. Богданов Н.Г. Расчёт электрических фильтров. – Пособие по курсовому и дипломному проектированию – М.: ВИПС, 2000 г.,352 с.

2. Зааль Р., Справочник по расчетам фильтров – М.: Радио и связь, 1983 г., 753 с.

3. Куцко Т. Ю. Расчет полосовых фильтров – М.: Энергия 1985 г., 193 с.

4. Босый К. Д. Электрические фильтры – М.: Гостехиздат 1960 г., 350 с.

Lc последовательный фильтр с трансформаторной связью выход

Наиболее известными пассивными фильтрами являются LC фильтры, названные так потому, что строятся при помощи индуктивностей L и емкостей C. В настоящее время наиболее распространены сетевые фильтры или антенные фильтры.

Простейшим LC фильтром является колебательный контур, в котором могут возникать затухающие колебания, но нас интересует то его свойство, что LC-контур обладает частотной зависимостью коэффициента передачи. Колебательный контур может быть использован для реализации полосового фильтра. На рисунке 1 приведена схема параллельного колебательного контура, реализующая простейший пассивный LC фильтр.

Рисунок 1. Схема пассивного полосового фильтра на параллельном колебательном контуре

Пример амплитудно-частотной характеристики приведенной на рисунке 1 схемы LC фильтра приведен на рисунке 2.

Рисунок 2. Амплитудно-частотная характеристика схемы пассивного фильтра на параллельном контуре

По графику амплитудно-частотной характеристики данного LC фильтра можно определить, что его схема обладает одним полюсом и двумя нулями коэффициента передачи. Один ноль АЧХ соответствует нулевой частоте (постоянному току). Он определяется нулевым сопротивлением индуктивности на нулевой частоте. Второй ноль АЧХ приходится на частоту, равную бесконечности. Этот ноль соответствует нулевому сопротивлению конденсатора на бесконечной частоте. Именно наличием нулей объясняется несимметричность амплитудно-частотной характеристики полосовых LC фильтров. Во всех рассуждениях принимается, что конденсаторы и индуктивности идеальны, в реальных схемах LC фильтров придется учитывать паразитные составляющие элементов схемы.

На графике амплитудно-частотной характеристики пассивного фильтра, приведенной на рисунке 2, отчетливо видна несимметричность, которую приходится учитывать при переходе от полосового фильтра к ФНЧ-прототипу. Еще одна особенность, которая бросается в глаза на данном графике, это коэффициент передачи, больший единицы. В приведенном примере более 50 дБ. Выходной сигнал больше входного почти в тысячу раз! Пассивный LC фильтр обладает усилением? Нет и еще раз нет! Увеличено выходное напряжение, но ток при этом уменьшен. Просто этот фильтр трансформирует сопротивление. Его входное сопротивление меньше выходного. Параллельный контур нельзя шунтировать малым сопротивлением. LC фильтр, показанный на рисунке 1, работает подобно обычному трансформатору напряжения.

Полюс в схеме пассивного фильтра, приведенной на рисунке 1, реализуется параллельным LC контуром. Поэтому остановимся на свойствах параллельного контура подробнее. Известно, что в параллельном контуре возникает резонанс на частоте, определяемой следующей формулой:

(1),

Именно эта резонансная частота LC контура определяет частоту полюса пассивного фильтра. Следующим важным параметром параллельного LC контура (и полюса передачи разрабатываемого LC фильтра) является добротность. Добротность параллельного LC контура определяется как отношение его резонансной частоты к полосе пропускания амплитудно-частотной характеристики по уровню 3 дБ:

(2),

В схеме пассивного LC фильтра, приведенной на рисунке 1, добротность контура определяет, насколько напряжение на выходе схемы будет больше напряжения, поданного на его вход. Одновременно на выходе схемы уменьшится ток, отдаваемый в нагрузку.

Добротность параллельного LC контура зависит от многих факторов. Различают конструктивную добротность контура и нагруженную добротность. Конструктивная добротность зависит от качества исполнения элементов контура (индуктивностей и конденсаторов), а нагруженная добротность LC контура учитывает влияние сопротивления нагрузки.

(3),

Следует отметить, что схема пассивного LC фильтра, приведенная на рисунке 1, реализует не только полюс амплитудно-частотной характеристики, но и два нуля. Конденсатор C1 обеспечивает нулевой коэффициент передачи на частоте, стремящейся к бесконечности. Индуктивность L1 обеспечивает нулевой коэффициент передачи фильтра на нулевой частоте (постоянном токе). Подобная схема LC фильтра подходит для реализации полосовых фильтров Баттерворта и фильтров Чебышева.

Подобным же образом может работать и последовательный LC контур. Для этого он должен быть подключен между источником сигнала и нагрузкой. Пример включения последовательного LC контура для реализации полюса передачи амплитудно-частотной характеристики приведен на рисунке 3.

Рисунок 3. Схема LC фильтра на последовательном колебательном контуре

Особенность данной схемы пассивного фильтра заключается в том, что сопротивление источника сигнала R1 и нагрузки R2 должны быть как можно меньше при реализации полюса большей добротности. Это связано с тем, что в схеме LC фильтра, реализованной на последовательном контуре, используется резонанс токов.

Амплитудно-частотная характеристика пассивного фильтра, реализованного на последовательном LC контуре, ничем не отличается от АЧХ фильтра, реализованного на параллельном LC контуре. Амплитудно-частотная характеристика, приведенная на рисунке 2, может быть получена и схемой LC фильтра, приведенной на рисунке 3.

Для реализации фильтра низких частот LC контур в схеме пассивного фильтра можно включить немного по-другому. Например, так, как показано на рисунке 4.

Рисунок 4. Схема пассивного фильтра на LC контуре

В этом случае нули функции передачи, формируемые индуктивностью L1, и ёмкостью C1, совпадут и будут расположены на частоте, равной бесконечности. Амплитудно-частотная характеристика при этом преобразуется к виду, приведенному на рисунке 5.

Рисунок 5. Амплитудно-частотная характеристика схемы пассивного НЧ фильтра на LC контуре

Подобная схема пассивного фильтра подходит для реализации фильтра низких частот с аппроксимацией АЧХ по Баттерворту или Чебышеву. Тем не менее, LC фильтр c АЧХ, показанной на рисунке 5 (очень высокая добротность контура), может использоваться как полосовой фильтр, приводящий сопротивление нагрузки к сопротивлению источника сигнала.

Аналогичным образом может быть реализована схема LC фильтра высоких частот. Для реализации фильтра высоких частот в схеме пассивного фильтра необходимо оба нуля фунции передачи передвинуть на нулевую частоту (постоянный ток). Для этого схему LC контура включают следующим образом:

Рисунок 6. Схема пассивного фильтра высоких частот на LC контуре

Амплитудно-частотная характеристика данной схемы LC фильтра приобретает вид, показанный на рисунке 7. Естественно, для фильтра высоких частот обычно добротность выбирается меньше показанной на рисунке, и тогда она приобретает вид АЧХ фильтра Чебышева или Баттерворта.

Рисунок 7. Амплитудно-частотная характеристика схемы пассивного ВЧ фильтра на LC контуре

Наличия полюсов достаточно для реализации фильтров Чебышева, Баттерворта и Бесселя. Все рассмотренные выше схемы являются цепями второго порядка. Для реализации LC фильтров более высокого порядка их можно соединять последовательно. В качестве примера на рисунке 7 приведены схемы пассивных LC фильтров низкой частоты.

Рисунок 8. Схемы пассивных LC фильтров низкой частоты

Точно так же реализуются и фильтры Чебышева, Баттерворта и Бесселя высокой частоты. Отличие заключается в том, что индуктивность пересчитывается в емкость, а емкость пересчитывается в индуктивность. Полученные схемы пассивных фильтров высокой частоты приведены на рисунке 9.

Рисунок 9. Схемы пассивных LC фильтров высокой частоты

Применение расчета фильтров через ФНЧ-прототип позволяет рассчитать и полосовые фильтры. Преобразование фильтра низких частот в полосовой фильтр осуществляется заменой емкостей ФНЧ прототипа параллельными контурами, а индуктивностей — последовательными. Пример полосовых фильтров приведен на рисунке 10.

Рисунок 10. Схемы пассивных полосовых LC фильтров

В настоящее время пассивные LC фильтры рассчитываются при помощи специализированных программ, наиболее известные из которых входят в состав программных пакетов MicroCAP и AWR Office. Однако продолжают сохранять актуальность справочники по расчету фильтров такие как Ханзел Г. Е. Справочник по расчету фильтров [2] и Зааль Р. Справочник по расчету фильтров [1].

Следует отметить, что фильтры, рассчитываемые в MicroCAP и у Ханзела имеют одинаковое входное и выходное сопротивления, а фильтры, расчитываемые в AWR Office и у Зааля позволяют одновременно осуществлять трансформацию сопротивлений. Это свойство пассивных LC фильтров очень полезно при разработке высокочастотных усилителей (УВЧ).

Что касается полосовых LC фильтров, то в настоящее время они практически вытеснены кварцевыми или ПАВ-фильтрами, в области относительно низких частот (сотни килогерц) пьезокерамическими фильтрами. Исключение составляют перестраиваемые LC фильтры.

Это связано с достаточно высокой стоимостью изготовления индуктивностей, которые наматываются на ферритовых сердечниках. В случае сетевых фильтров, где широко применяются кольцевые ферритовые сердечники стоимость дополнительно повышается из-за сложности намотки обмотки индуктивности.

Вместе со статьёй “Схемы пассивных фильтров” читают:

LC-фильтр предназначен для подавления высокочастотных помех (частотой 100 Гц — 100 МГц), которые искажают синусоиду переменного напряжения в сети и отрицательно ск азываются на работе электрооборудования. Эффективность работы LC-фильтра в различных диапазонах частот измеряется в дБ. Источниками ВЧ-помех являются различные электрические устройства: электродвигатели, генераторы, сварочные аппараты и т. п.

На рисунке показан пример простейшего LC-фильтра нижних частот: при подаче сигнала определённой частоты на вход фильтра (слева), напряжение на выходе фильтра (справа) определяется отношением реактивных сопротивлений катушки индуктивности (XL = щL) и конденсатора (XC = 1 / щC).

Коэффициент передачи ФНЧ можно вычислить, рассматривая делитель напряжения, образованный частотно-зависимыми сопротивлениями. Комплексное (с учетом сдвига фаз между напряжением и током) сопротивление катушки индуктивности есть ZL = jщL = jXL и конденсатора ZC = 1 / (jщC) = ? jXC, где , поэтому, для ненагруженного LC-фильтра.

Подставляя значения сопротивлений, получим для частотно-зависимого коэффициента передачи:

Как видно, коэффициент передачи ненагруженного идеального ФНЧ неограниченно растет с приближением к частоте , и затем убывает. На очень низких частотах коэффициент передачи ФНЧ близок к единице, на очень высоких — к нулю. Вообще, зависимость модуля комплексного коэффицента передачи фильтра от частоты называют амлитудно-частотной характеристикой (АЧХ), а зависимость фазы — фазо-частотной характеристикой (ФЧХ).

В реальных схемах к выходу фильтра подключается активная нагрузка, которая понижает добротность фильтра и предотвращает острый резонанс АЧХ вблизи частоты щ0. Величину называют характеристическим сопротивлением фильтра. ФНЧ, нагруженный на сопротивление, равное характеристическому, имеет нерезонансную АЧХ, примерно постоянную для частот щ

Аналогичным образом строится и LC-фильтр верхних частот. В схеме ФВЧ меняются местами катушка индуктивности и конденсатор. Для ненагруженного ФВЧ получается следующий коэффициент передачи:

На очень низких частотах модуль коэффициента передачи ФВЧ близок к нулю. На очень высоких — к единице.

2.1.1.3 .1 Применение

LC-фильтры используются в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя. В каскадах радиоэлектронной аппаратуры часто применяются перестраиваемые LC-фильтры, например, простейший LC-контур, включенный на входе средневолнового радиоприёмника обеспечивает настройку на определённую радиостанцию.

Фильтры используются в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ, для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах, в схемах частотной коррекции магнитофонов и др.

Разделительный трансформатор

Разделительный трансформатор — это трансформатор, первичная обмотка которого изолирована от вторичных обмоток при помощи защитного электрического разделения цепей с помощью двойной или усиленной изоляции, т.е. между обмотками имеется заземленный металлический защитный экран.

Трансформатор будет являться разделительным, если его вторичная обмотка не заземлена. Обычно используются трансформаторы с коэффициентом трансформации 1. Допускается подключение к одному трансформатору только одного потребителя. Применение такого подключения электроприемника существенно снижает вероятность поражения электрическим током, так как токи, возникающие в случае пробоя изоляции, имеют небольшое значение, что обусловлено гальванической изоляцией вторичных цепей трансформатора от цепей заземления.

Разделительные трансформаторы предназначены для повышения безопасности электросетей, при случайных одновременных прикасаний к земле и токоведущим частям или нетоковедущим частям, которые могут оказаться под напряжением в случае повреждения изоляции. Они также могут обеспечивать гальваническую развязку электрических цепей. Для повышения электробезопасности, увеличения надежности и срока службы электрооборудования рекомендуется включение его в сеть через разделительный трансформатор.

Например, согласно “Правилам технической эксплуатации электроустановок” ванные комнаты входят в категорию особо опасных помещений из-за наличия повышенной влажности, текущей воды и обилия изделий из металла, имеющих неустойчивое заземление. В таких помещениях не должно быть розеток на 220 В, или же эти розетки должны быть включены через разделительный трансформатор.

Выбор разделительных трансформаторов по параметрам

— входное напряжение и силу тока (на первичной обмотке)

— выходное напряжение и силу тока (на вторичной обмотке)

— предельно допустимое напряжение между выходными зажимами и землёй

— тип и конфигурацию выводов

— способ монтажа (на плату, на DIN-рейку, навесной)

Из чего состоит LC-фильтр и как он работает, формулы для расчетов, принципиальные схемы LC-фильтров, статья для начинающих радиолюбителей. Во многих электронных устройствах применяются LC-фильтры, как видно по названию, эти фильтры состоят из индуктивности (L) и емкости (С).

Самый простой LC-фильтр

Самый простой LC-фильтр — это колебательный контур, включенный так как показано на рис. 1. Входное переменное напряжение поступает на контур через резистор R1, а выходное снимается с самого контура.

Вообще это очень похоже на делитель напряжения на двух резисторах, но вместо одного из резисторов здесь контур. В сущности дела оно так и есть.

На резонансной частоте реактивное сопротивление контура сильно возрастает, а значит, коэффициент деления такого делителя уменьшается.

Эта схема (рис.1) действует как узкополосной полосовой фильтр, центральную частоту кото-рого можно рассчитать по известной формуле:

, где частота в Гц, индуктивность в Гн, емкость в Ф. Сопротивление контура на резонансной частоте:

где р — характеристическое сопротивление, равное реактивному сопротивлению катушки и конденсатора. Величину р можно рассчитать по формуле:

А вот рассчитать добротность Q значительно сложнее. Эта величина зависит от потерь в контуре. Так как конденсатор обычно вносит минимум потерь, то добротность контура чаще всего практически равна добротности индуктивности, входящей в состав этого контура.

Резонансную частоту и добротность можно определить измерениями. Нужно собрать схему по рисунку 2. Это практически такая же схема как на рис.1.

Переменное напряжение, соответствующее по частоте расчетному значению подают от генератора «Г» на контур через сопротивление R1. Подстраивая генератор нахо-дят такую частоту, при которой возникает резонанс, то есть, при которой вольтметр переменного тока Р1 показывает наибольшую величину.

Рис. 1. Схема LC-фильтра.

Рис. 2. Схема для измерения резонансной частоты и добротности.

Эта частота и будет реальной резонансной частотой. Она может отличаться от расчетной из-за погрешностей величин емкости и индуктивности. В идеале -равна расчетной.

На частоте резонанса R1 и резонансное сопротивление контура Ro образуют делитель напряжения, поэтому выходное напряжение Uвых = Uвх * Ro / (R1+Ro).

Измерив входное напряжение Uвх и выходное Uвых из этой формулы можно найти резонансное сопротивление контура Ro, ну а потом, зная величину характеристического сопротивления (из формулы

можно из формулы Ro=pQ найти добротность Q. Другой параметр LC-фильтра — это полоса пропускания

где — это отклонение частоты входного напряжения от резонанса в ту или другую сторону, при которой выходное напряжение, соответствующее резонансу (Uвых), уменьшается до 0,7Uвых. Зная величину полосы пропуская можно найти добротность по формуле Q=Fo/(2*дельтаF).

Таким образом становится ясно, что полоса пропускания LC-фильтра прежде всего зависит от добротности контура. При этом нужно учесть, что таким образом будет определена не собственная добротность контура, а величина меньше, из-за шунтирующего действия резистора R1.

Недостаток фильтра по рисунку 1 в том, что на него оказывает сильное влияние величина выходного сопротивления источника входного переменного напряжения.2.

На контур может оказывать шунтирующее влияние не только выходное сопротивление источника Uвх, но и входное сопротивление каскада, на который с контура поступает выходное напряжение Uвых (R2 на рис. 6). Особенно если входное сопротивление каскада (R2) невелико (сопоставимо или даже меньше Ro).

Рис. 6. Схема фильтра.

В этом случае необходимо сначала вычислить новое значение Ro, уменьшенное параллельным включением сопротивления R2. Расчет производить по известной формуле параллельных сопротивлений: R = (RoR1) / (Ro+R2). А потом уже рассчитывать согласование (взяв полученную величину R как Ro в формулах).

Контуры с индуктивной и емкостной связью

Параметры узкополосного фильтра можно существенно улучшить, используя в нем несколько контуров. Связь между этими контурами может быть индуктивной (рис. 7) или емкостной (рис. 8).

Рис. 7. Контуры с индуктивной связью.

При индуктивной связи коэффициент взаимной индукции выбирается в Q раз меньше индуктивности катушек, а емкость конденсатора связи — в Q раз меньше емкостей контурных конденсаторов.

Рис. 8. Контуры с емкостной связью.

Подача сигнала последовательно

Сигнал на контур можно подавать не только параллельно, но и последовательно, как показано на рис. 9. При этом, в отличие от схемы на рис. 6, сопротивление R1 (сопротивление источника сигнала) для получения острой характеристики нужно выбирать как можно меньше, а вот входное сопротивление каскада (R2) должно быть как и на рис. 6, как можно больше.

Рис. 9. Последовательная подача сигнала на контур.

Если в схеме на рис. 9 соблюсти зависимость: R1 = R2 = p, то получается согласованный ФНЧ (фильтр нижних частот), коэффициент передачи которого постоянен на всех частотах от нуля, до резонансной частоты контура, и равен -6dB, но выше частоты резонанса коэффициент передачи начинает резко падать по 12 dB на октаву. Это соответствует фильтру второго порядка.

Т-образный и П-образный фильтры

Для получения более крутых скатов характеристики можно два таких фильтра, как на рис. 9 («Г»-образных) соединить и получить «Т»-образный фильтр (рис. 10).

Рис. 10. Т-образный фильтр.

Обратите внимание, — конденсатор должен быть двойной емкости по сравнению с рис.9. Либо сделать «П»-образный фильтр (рис. 11), в котором двойное значение должна иметь индуктивность. Это будет уже ФНЧ третьего порядка.

Рис. 11. П-образный фильтр.

Возможно и дальнейшее наращивание, например, на рисунке 12 показан ФНЧ пятого порядка обладающий спадом характеристики на частотах выше резонансной 30 dB на октаву.

Рис. 12. Схема ФНЧ пятого порядка.

Фильтры высших частот ФВЧ отличаются тем, что ослабляют частоты ниже частоты резонанса. ФВЧ можно сделать, если в показанных на рисунках 9-12 индуктивности и емкости поменять местами.

Электротехника: On-line расчет сглаживающего LC-фильтра.

Для сглаживания пульсаций напряжения и тока в нагрузке может быть применён LC-фильтр нижних частот. Простейший LC-фильтр нижних частот приведён на рисунке 1:

Рисунок 1 – Сглаживающий LC-фильтр

E – источник напряжения какой либо формы. RE – резистор имитирующий внутреннее сопротивление источника питания (или внутреннее сопротивление + дополнительное сопротивление фильтра). C – конденсатор LC-фильтра, L – катушка индуктивности фильтра, RH – нагрузка. Такой фильтр может называться Г-фильтром. Помимо Г-фильтров существуют и другие например: Т-фильтр, П-фильтр, двойной Т-фильтр и т.д. (расположение катушек и конденсаторов в П-фильтре напоминает букву “П”, в Т-фильтре букву “Т” и т.д.). Достоинством LC-фильтра приведённого на рисунке 1, по сравнению с ёмкостным фильтром, является то что ток источника питания ограничивается катушкой, поэтому в момент подключения питания не будет резкого “скачка” тока. Размеры LC-фильтра могут быть меньше чем ёмкостного или индуктивного при одинаковых амплитудах ненужных высших гармоник в нагрузке. Расчёт Г-образного LC-фильтра (рисунок 1) более сложен чем расчёт ёмкостного или индуктивного и при неправильном подборе ёмкости конденсатора или индуктивности катушки вместо сглаживания, в нагрузке, могут возникнуть колебания. Для расчёта формы напряжения на нагрузке (оно же Uc-напряжение на конденсаторе)(форма тока в нагрузке повторяет форму напряжения на ней т.к. считается что нагрузка активная) и тока катушки IL можно воспользоваться программой приведённой ниже. Для нормальной работы необходимо чтобы браузер поддерживал HTML5. Нажатие на кнопку “Открыть график в виде картинки” приводит к открытию окна с картинкой на которой будут рассчитанные графики (если перед этим была нажата кнопка “Рассчитать и показать график”) остальные инструкции те же что и к программе из предыдущей статьи. Если график неправильно рассчитывается то можно попробовать увеличить число точек и уменьшить шаг интегрирования.
HTML5 не поддерживается браузером.

Руководство по цепям LC – ФИЛЬТРЫ

Наряду с простыми настроенными схемами наиболее широко используются LC-схемы. фильтры; и хотя активные (усилительные) фильтры сейчас широко используются, остаются приложения, для которых предпочтительнее использовать LC-фильтр, часто потому, что ему не нужен источник питания, и обычно потому, что приложение не требует бесступенчатая настройка и малый размер твердотельного активного фильтра. Тип LC по-прежнему доминирует в фильтрации источников питания и довольно часто используется при фильтрации помех.

Фильтры

удобно классифицировать как волновые фильтры (те, которые обрабатывают сигналы). и фильтры питания (те, которые устраняют пульсации на выходе деактивации). выпрямитель). В этом разделе описывается каждый тип и предлагаются простые проектные данные. применимо к ним.

3,1 ОСНОВНЫЕ СВОЙСТВА ФИЛЬТРАЦИИ L И C

Катушка индуктивности и конденсатор в основном являются фильтрами. Поскольку их реактивное сопротивление изменяется с частотой, каждый передает частоты неравномерно, стремясь разделить одни от других.

Это действие показано для катушки индуктивности на рис. 1 и для конденсатора на рис. Рис. 2.

В этих примерах в целях иллюстрации предполагается, что катушка индуктивности и конденсатор являются чистым реактивным сопротивлением, т. е. не имеют сопротивления. Таким образом, на рис. 1А a на катушку индуктивности L подается постоянное напряжение переменной частоты и ток метр М последовательно. Результирующий ток I = E / XL. Но XL увеличивается с частотой, поэтому I уменьшается с увеличением частоты, и наоборот, как показано на рис.1Б. (Если E = 1 В и L = 1 Гн, ток I составляет 1,59 мА при 100 Гц, 0,159 мА при 1000 Гц. Гц и 159 а.е., А при 10 кГц.) Аналогично, на рис. 2А постоянное напряжение переменной частоты подается последовательно на конденсатор C и измеритель тока M. Здесь результирующий ток I = E / X, .. Но X уменьшается с частотой, поэтому I увеличивается с увеличением частоты и наоборот, как показано на фиг. 2B. (Здесь, для сравнения, если E = 1 В и C = 1 мкФ, ток I составляет 0,628 мА при 100 Гц, 6,28 мА при 1000 Гц и 62.8 мА при 10 кГц.)

Рис. 1. Основное фильтрующее действие индуктора. (А) Цепь. (B) Производительность график.

Рис. 2. Основное фильтрующее действие конденсатора (А) Схема. (B) Производительность график.

Из рис. 1B и 2B соответственно видно, что индуктор стремится для передачи низких частот и ослабления высоких частот, в то время как конденсатор имеет тенденцию ослаблять низкие частоты и передавать высокие частоты. Сейчас, пока это простое действие фильтрации полезно, оно ограничено, поскольку нет единого точка (частота среза, f_c), по одну сторону от которой передаются частоты с небольшими потерями, с другой стороны которого ослаблены частоты.Действие в каждом случае непрерывное и равномерное (рис. 1B и 2B). Когда катушки индуктивности и конденсаторы объединены в секции фильтров, каждая из которых усиливает фильтрующее действие другого. Секции фильтра можно использовать по отдельности. или каскадно.

Рис. 3. Идеальное действие фильтра. (A) Низкий проход. (B) Высокий проход. (C) Bandpass. (D) Остановка полосы движения.

Рис. 4. Базовые конфигурации фильтров. (A) L-образный. (B) Т-образный. (C) Пи-тип.

3,2 СЕКЦИИ ФИЛЬТРА

Раздел фильтра назван в соответствии с назначением: ФНЧ, ФВЧ, полосовой, или блокировка полосы пропускания (последний тип также называется подавлением полосы или исключением полосы).На рис. 3 показано идеальное действие этих секций. Что касается конфигурации, то раздел назван в соответствии с греческой или римской буквой, которая на схеме напоминает : L, T или пи. Рис. 4 иллюстрирует эти основные конфигурации.

Фиг. С 5 по 15 приведены схемы и данные для L-типа ФНЧ, ФВЧ, полосы пропускания, и секции полосового фильтра. Для каждого из этих классов показаны два типа: постоянные – k и m – производные (как последовательного, так и шунтирующего типа). Постоянный тип k является более простым, но производительность типа m ближе к идеалу.Тип постоянного k называется так потому, что произведение импеданса (Z1) его последовательного плеча и импеданса (Z2) его шунтирующего плеча равны константе: Z1Z2 = k2.

В типе m коэффициент m определяет отношение частоты среза f. к заданная частота с высоким затуханием (например, частота, на которой передача стремится к нулю) и обычно имеет выбранное значение 0,6.

Рис. 5. Фильтр нижних частот (тип постоянного k). А) Схема. (B) Типичная производительность график.

3,3 ВОЛНОВЫЕ ФИЛЬТРЫ

Это в основном сигнальные фильтры и считаются сетями без рассеяния. (хотя это идеальное состояние недостижимо, к нему можно подойти, используя высокодобротные катушки индуктивности и конденсаторы).

Во всех показанных разделах оконечное сопротивление принимается как сопротивление (R в уравнениях), и входной импеданс фильтра предполагает такое же значение сопротивления на большей части выбранной полосы частот. Частоты среза выбираются дизайнером в соответствии с его требованиями к фильтру.Во всех уравнения, индуктивность L в генри, емкость C в фарадах, сопротивление R в омах, а частота f в герцах.

Low-Pass, тип Constant-k См. Рис. 5. Уравнения 3-1 и 3-2 описывают это фильтр.

R L1 =

пи ф, 1 C1 =

pi упал низкочастотный, последовательный m-тип См. Рис. 6. Уравнения с 3-3 по 3-6 опишите этот фильтр.

(3-1) (3-2)

(3-3) (3-4) (3-5)

Рис. 6. ФНЧ (последовательный m-тип).(А) Цепь. (B) Типичная производительность график.

(3-6)

Низкочастотный, шунтирующий m-тип См. Рис. 7. Уравнения с 3-7 по 3-10 описывают этот фильтр.

Рис. 7. ФНЧ (шунтирующий m-тип). (А) Цепь. (B) Типичная производительность.

(3-7) (3-8) (3-9) (3-10)

Высокочастотный, Constant-k Тип

См. Рис. 8. Уравнения 3-11 и 3-12 описывают этот фильтр.

(3-11)

Фиг.8. Фильтр высоких частот (тип постоянного k). (А) Цепь. (B) Типичная производительность график.

High-Pass, последовательное соединение m-типа См. Рис. 9. Уравнения с 3-13 по 3-16 описывают этот фильтр.

Рис. 9. Фильтр верхних частот (последовательный m-тип). (А) Цепь. (B) Типичный график производительности.

(3-16)

High-Pass, шунтирующий m-тип См. Рис. 10. Уравнения с 3-17 по 3-20 описывают этот фильтр.

Рис. 10. Фильтр верхних частот (шунтирующий m-тип).(А) Цепь. (B) Типичный график производительности.

(3-17) (3-18) (3-19) (3-20)

Bandpass, Тип Constant-k См. Рис. 11. Это описывается уравнениями с 3-21 по 3-24. фильтр.

(3-21) (3-22)

Рис. 11. Полосовой фильтр (тип постоянного k). (А) Цепь. (B) Типичная производительность график.

(3-24) (3-23)

Bandpass, последовательное соединение m-типа См. Рис. 12. Уравнения с 3-25 по 3-34 описывают этот фильтр.

(3-25) (3-26)

Фиг.12. Полосовой фильтр (последовательный m-тип). А) Схема. (B) Типичный график производительности.

(3-27) (3-28) (3-29) (3-30) (3-31) (3-32) (3-33)

(3-34)

Bandpass, шунтирующий тип m

См. Рис. 13. Уравнения с 3-35 по 3-40 описывают этот фильтр.

(Для x, y, z и m см. Уравнения 3-25, 3-27 и 3-28. Чтобы определить все fe, см. рис. 13B.)

(3-35) (3-36) (3-37) (3-38) (3-39)

Фиг.13. Полосовой фильтр (шунтирующий m-тип). (А) Цепь. (B) Типичный график производительности.

(3-40)

Ограничитель полосы пропускания, тип Constant-k См. Рис. 14. Уравнения с 3-41 по 3-45 описывают это фильтр. (В уравнении 3-41 и на рис. 14B, fm – центральная частота полоса заглушки.)

(3-41) (3-42) (3-43) (3-44) (3-45)

Ленточный ограничитель, серийный тип m

Рис. 14. Полосовой фильтр (тип с постоянным k). (А) Цепь. (B) Типичная производительность график.

См. Рис. 15. Уравнения с 3-46 по 3-54 описывают этот фильтр.

(3-46)

(3-47)

(3-48)

Рис. 15. Полосовой фильтр (последовательный m-тип). (А) Цепь. (B) Типичный график производительности.

(3-49) (3-50) (3-51) (3-52) (3-53) (3-54)

Ограничитель полосы пропускания, шунтирующий m-тип См. Рис. 16. Уравнения с 3-55 по 3-60 описывают этот фильтр.

(Для m, x и y см. Уравнения 3-46, 3-47 и 3-48. Чтобы определить все fe, см. рис.16Б.)

(3-55) (3-56) (3-57) (3-58) (3-59)

Рис. 16. Полосовой фильтр (шунтирующий m-тип). (А) Цепь. (B) Типичная производительность график

(3-60)

Таблица 3-1. Частота пульсаций для обычных источников питания

4. ФИЛЬТРЫ ПИТАНИЯ

Фильтр блока питания предназначен для удаления пульсации на выходе постоянного тока выпрямителя. В таком фильтре индуктор – это последовательное плечо, а конденсатор – это шунтирующее плечо.Дроссель блокирует поток пульсации, отсюда и его привычное название – дроссельная катушка; конденсатор закорачивает пульсацию (которая является составляющей переменного тока) на землю, следовательно, ее знакомое название обхода.

В этом действии дроссель не может заблокировать компонент де, и конденсатор не может закоротить компонент постоянного тока.

Рис. 17. Типовые односекционные фильтры питания. (A) Вход конденсатора. (B) Вход дросселя.

Фильтр источника питания представляет собой схему нижних частот, как правило, с конфигурацией «пи» или «L».Для достижения наилучших результатов он должен быть рассчитан на значительную частоту среза. ниже, чем частота пульсаций (см. Таблицу 3-1), чтобы пульсации и все его гармоники будут сильно ослаблены. Дроссель должен быть способным управления максимальной нагрузкой постоянного тока источника питания и конденсатора (а) должны быть способны безопасно работать при пиковом выходном напряжении выпрямителя.

На рис. 17 показаны два основных типа односекционных фильтров источника питания. Тип конденсаторного входа (рис.17A) обеспечивает более высокое выходное напряжение постоянного тока, который при низком уровне выходного тока (высокое сопротивление нагрузки) может приближаться к пиковое значение переменного напряжения на входе выпрямителя (т. е. Ed = 1,41, но имеет худшее регулирование напряжения. Тип дроссельного ввода (рис. 17Б) обеспечивает более низкую постоянного напряжения (Ede = приблизительно 0,9E ,,), но имеет улучшенную стабилизацию выходного напряжения.

Обратите внимание, что в каждом случае требуется выходной конденсатор (C2 на рис. 17A, C1 на рис. 17B). На рис.18 показаны типичные двухсекционные фильтры для увеличенной сглаживание выхода постоянного тока.В фильтрах питания конденсаторы работают не только как частотно-избирательные элементы, а также как накопители энергии: во время нарастание импульса выпрямленного напряжения от нуля до максимума, конденсатор заряжается при подаче тока на выходную нагрузку постоянного тока; затем, как впоследствии напряжение снижается до нуля, конденсатор разряжается, обеспечивая свою энергию к выходной нагрузке и, таким образом, поддерживая выходное напряжение фильтра постоянный.

Беглый просмотр рис.17 и 18 показывает, что все фильтры низкочастотный, постоянного типа. Соответственно, их дизайн может быть выполнен с с помощью уравнений 3-1 и 3-2. (Загрузить R в этих формулах будет фактическим сопротивление, на которое блок питания подает энергию, или будет частным E / I, где E – напряжение снятия нагрузки в вольтах, а I – постоянный ток нагрузки. в амперах.) Для некоторых приложений процедура расчета полностью игнорируется. Вместо этого имеющиеся в наличии дроссели с высокой индуктивностью и конденсаторы с большой емкостью просто объединились.Результирующая частота среза обычно настолько мала, что фильтр эффективен в большом количестве возможных приложений. Такое расположение обычно называют фильтром грубой силы.

Рис. 18. Типовые каскадные фильтры. (A) Вход конденсатора. (B) Вход дросселя.

Рис. 19. Резонансные одночастотные фильтры. (A) Тип шунта. (B) Тип серии.

Иногда бывает, что одна частота – например, мешающая гармоника в сети переменного тока. частоту – необходимо снять с выхода выпрямителя.Простые комбинации LC для выполнения этой задачи показаны на рис. 19. На рис. 19А шунт L1C1 схема улавливает сигнал; на рис. 19В, цепь L1C1 последовательно замкнута накоротко. сигнал на землю. Эти меры редко бывают удовлетворительными, поскольку полный фильтра для источника питания, поскольку они удаляют только одну частоту (в лучшем случае очень узкая полоса частот), но они очень эффективны при использовании в в сочетании с обычным фильтром питания. Оба сразу узнаются как простые волновые ловушки, описанные в разделе 2.12, Раздел 2.

EMC Filters Comparison Part I: CL and LC Filters

В этом столбце обсуждаются фильтры ЭМС нижних частот второго и третьего порядка. Сначала определяются вносимые потери для общего фильтра, а затем исследуется влияние импеданса источника и нагрузки на вносимые потери. При моделировании и измерениях основное внимание уделяется фильтрам CL и LC. В Части II (которая будет опубликована в следующем выпуске) оценивается эффективность фильтров Pi и T и сравнивается с характеристиками фильтров CL и LC.

Вносимые потери и основные конфигурации фильтра ЭМС Фильтры ЭМС

описаны с точки зрения вносимых потерь, определенных как [1],

(1а)

, где V _L – величина комплексного напряжения _L . Рисунок 1 иллюстрирует это определение.

Рисунок 1: Иллюстрация вносимых потерь фильтра

Начиная с V _L, _{без фильтра} > V _L, _{с фильтром} вносимые потери, определяемые уравнением.(1a) – положительное число в дБ. Вносимые потери в качестве альтернативы можно определить как

(1б)

В этом случае вносимые потери в дБ являются отрицательными значениями потерь, определенных в формуле. (1б). Мы будем использовать это определение при построении графика результатов моделирования и сравнении результатов моделирования с измерениями ВАЦ.

Типичный фильтр нижних частот ЭМС 2 ^и состоит из последовательно соединенных индуктивности и шунтирующей емкости [2]. На рисунке 2 показаны две разные конфигурации фильтров.

Рисунок 2: Фильтры нижних частот CL и LC

3 ^rd – фильтры порядка π и T показаны на рисунке 3.

Рисунок 3: π- и T-фильтры нижних частот

Влияние импеданса источника и нагрузки

Обратите внимание, что для каждого порядка фильтра у нас есть две разные конфигурации. Какой из них будет работать лучше, то есть какая конфигурация имеет больше вносимых потерь (в отрицательном смысле)? Как мы увидим, в большинстве случаев это зависит от импеданса источника и нагрузки.

Общее правило состоит в том, что катушка индуктивности должна быть на стороне с низким сопротивлением, а конденсатор – на стороне с высоким сопротивлением [2, 3].

Таким образом, когда полное сопротивление источника и нагрузки низкое, подходящей конфигурацией из показанных выше является Т-фильтр, показанный на рисунке 4.

Когда импеданс источника и нагрузки высокие, подходящей конфигурацией является π-фильтр, показанный на рисунке 5.

На рисунке 6 показаны соответствующие конфигурации, когда полное сопротивление источника низкое, а сопротивление нагрузки высокое.

Наконец, на рисунке 7 показаны соответствующие конфигурации, когда полное сопротивление источника высокое, а сопротивление нагрузки низкое.

Рисунок 4: Конфигурация фильтра при низком импедансе источника и нагрузки

Рисунок 5: Конфигурации фильтра при высоком импедансе источника и нагрузки

Рисунок 6: Конфигурации фильтра при низком импедансе источника и высоком импедансе нагрузки

Рисунок 7: Конфигурации фильтра при высоком импедансе источника и низком сопротивлении нагрузки

Проверка с помощью моделирования и измерений (фильтры CL и LC)

Давайте проверим некоторые из приведенных выше утверждений, исследуя фильтры CL и LC второго порядка.Во-первых, давайте сосредоточимся на конфигурациях, показанных на рисунке 6, где полное сопротивление источника низкое, а сопротивление нагрузки высокое.

На рисунке 8 показана схема моделирования LT-специй. Импеданс источника 50 Ом обеспечивается анализатором цепей на Порте 1. Измерение, выполняемое анализатором цепей на Порте 2, проводится по его внутреннему сопротивлению 50 Ом. Это показано на Рисунке 8 (а). Для изменения импеданса в источнике или нагрузке линейное сопротивление может быть вставлено с одной или обеих сторон.На рисунках 8 (b) и (c) показана конфигурация, в которой на стороне нагрузки вводится импеданс 1 кОм.

Рисунок 8: Конфигурации фильтров – источник с низким импедансом, нагрузка с высоким импедансом: (a) без фильтра, (b) фильтр с индуктором на стороне низкого импеданса, конденсатор на стороне высокого импеданса (c) фильтр с индуктором на стороне высокого импеданса, конденсатор на стороне низкого сопротивления

На рисунке 9 показаны вносимые потери (согласно уравнению (1b)) двух конфигураций фильтров.

Рисунок 9: Вносимые потери двух конфигураций, показанных на рисунке 8

Как видно из рисунка 9, фильтр LC явно превосходит фильтр CL.Вносимые потери LC-фильтра на частоте 10 МГц примерно на 15 дБ выше, чем у CL-фильтра. Это соответствует общему правилу, согласно которому катушка индуктивности должна располагаться на стороне с низким импедансом, а конденсатор – на стороне с высоким импедансом.

Для проверки результатов моделирования использовалась измерительная установка, показанная на Рисунке 10.

Рисунок 10: Схема измерения ВАЦ фильтра ЭМС

Рисунок 11: LC-структура фильтра ЭМС с C на стороне высокого импеданса

Поскольку использовался четырехканальный анализатор цепей, мы могли одновременно оценивать две различные конфигурации фильтров.На рисунке 11 показан крупный план платы фильтра печатной платы, используемой в измерениях.

На рисунке 12 показаны результаты измерений для двух конфигураций, показанных на рисунке 8 и смоделированных на рисунке 9.

Рисунок 12: Измерения вносимых потерь (s ₂₁ и s ₃₄) для двух конфигураций, показанных на рисунке 8

Очевидно, что фильтр LC превосходит фильтр CL, что согласуется с результатами моделирования. В диапазоне частот 100 кГц – 10 МГц результаты моделирования и измерений очень близки, как показано в таблицах 1 и 2.

Фильтр CL	f = 100 кГц	f = 1 МГц	f = 10 МГц
Имитация вносимых потерь	21,2 дБ	30,8 дБ	50,7 дБ
Измеренная вносимая потеря	21,3 дБ	30 дБ	49 дБ

Таблица 1: Моделируемые и измеренные вносимые потери для фильтра CL

Фильтр LC	f = 100 кГц	f = 1 МГц	f = 10 МГц
Имитация вносимых потерь	21.2 дБ	30,8 дБ	65,8 дБ
Измеренная вносимая потеря	21,3 дБ	30 дБ	65,7 дБ

Таблица 2: Моделируемые и измеренные вносимые потери для LC-фильтра

На частоте 10 МГц разница между смоделированными вносимыми потерями двух фильтров составляет 15,1 дБ, что близко к измеренной разнице в 16,7 дБ.

Результаты измерений показывают частоту собственного резонанса 30 МГц с вносимыми потерями 84.9 дБ для фильтра CL и 115 дБ для фильтра LC. Второй резонанс возникает на частоте 60 МГц с вносимыми потерями 83 дБ для фильтра CL и 95,5 дБ для фильтра LC. Эти резонансы не были предсказаны имитационными моделями, поскольку в этих моделях предполагались идеальные компоненты и не учитывались паразиты платы.

Результаты измерений ясно показывают, что во всем частотном диапазоне LC-фильтр (катушка индуктивности на стороне низкого импеданса и конденсатор на стороне высокого импеданса) имеет более высокие вносимые потери, чем фильтр CL (конденсатор на стороне низкого импеданса и катушка индуктивности. на стороне высокого импеданса).

Список литературы

Клейтон Р. Пол, Введение в электромагнитную совместимость , Wiley, 2006.
Богдан Адамчик, Основы электромагнитной совместимости с практическими приложениями , Wiley, 2017.
https://link.springer.com/content/pdf/10.1007%2F978-3-642-27326-1_90.pdf

Д-р Богдан Адамчик – профессор и директор Центра EMC в Государственном университете Гранд-Вэлли (http: // www.gvsu.edu/emccenter/), где он разрабатывает учебные материалы EMC и ведет курсы с сертификатами EMC для промышленности. Он является сертифицированным инженером-проектировщиком EMC, сертифицированным iNARTE. Профессор Адамчик является автором учебника «Основы электромагнитной совместимости с практическими приложениями» (Wiley, 2017). С ним можно связаться по адресу [email protected].

Димитри Херинг получил степень магистра в области электротехники и вычислительной техники в Государственном университете Гранд-Вэлли в 2019 году, где он работал с проф.Адамчик в Центре EMC. В настоящее время работает инженером-конструктором РФ. Его дальнейшие интересы – Интернет вещей и программирование встраиваемых систем.

Правильный выбор ВЧ-фильтра низких частот

Если вы каким-либо образом связаны с радио, вы столкнулись с фильтром нижних частот как средством удаления нежелательных гармоник с выхода ваших передатчиков. Это сеть конденсаторов и катушек индуктивности, которую обычно называют пи-сетью из-за грубого сходства схемы с заглавной греческой буквой Пи, и их правильное построение традиционно было чем-то вроде черного искусства.Существуют таблицы и формулы, но даже после впечатляющих вычислений результат часто может не соответствовать ожиданиям.

Фильтр нижних частот 30 МГц, как его поставил QUCS.

К счастью, как и во многих других областях, в последние десятилетия появление доступных мощных вычислений принесло с собой возможность избавиться от тяжелой работы по проектированию фильтров. Просто сообщите некоторому программному обеспечению, каковы характеристики желаемого фильтра, и он сделает все остальное. Результаты хорошие, и каждый может стать дизайнером фильтров, но, как это часто бывает, остается загвоздка.Программное обеспечение вычисляет идеальные индуктивности и емкости для желаемых значений отсечки и импеданса, и при выборе ближайших предпочтительных значений мы изменяем характеристики результата и, возможно, даже разрушаем наш окончательный фильтр. Так что стоит взглянуть на процесс здесь и изучить эффект от настройки значений компонентов таким образом.

Идеализированный график, созданный QUCS для нашего фильтра.

Фильтр, который мы разрабатываем, достаточно прост, фильтр Бесселя 5-го порядка, а программное обеспечение представляет собой простой в использовании пакет QUCS на машине Ubuntu Linux.Подключите необходимые цифры, и он выдаст принципиальную схему, которую мы затем можем смоделировать, чтобы показать красивую кривую с точкой 3 дБ прямо на 30 МГц. Это чрезвычайно идеализированный график, и опыт научил меня, что в реальных фильтрах, использующих эти конструкции, есть точка отсечки более низкой частоты, но для наших целей здесь это достаточно хорошее начало.

Как упоминалось ранее, значения компонентов не являются предпочтительными из серийно выпускаемых серий, поэтому я не могу купить их с полки. Я могу намотать свои собственные катушки индуктивности, но в этом заключается целый мир собственной боли, и я бы предпочел не идти туда.RS, Mouser, Digikey, Farnell и др. существуют, чтобы спасти меня от такой ямы электронной гибели, с какой стати мне делать что-то еще, кроме как покупать готовые?

Моя переработанная схема фильтра с готовыми значениями компонентов.

Таким образом, каждый из компонентов на приведенной выше схеме требует небольшого перемещения вверх или вниз до желаемого значения. Как это повлияет на работу моего фильтра? Изменение каждого значения и повторный запуск моделирования показывает нам, что график каждый раз тонко меняется, и иногда бывает сложно настроить их, не разрушая полностью фильтр.В частности, с фильтрами более высокого порядка с большим количеством компонентов в сети вы можете наблюдать влияние отдельных компонентов на градиент в разных частях графика, но, как правило, увеличение значений снижает частоту среза и делает их более низкими. увеличивает его. В моем случае я всегда выбираю более высокие значения по этой причине: моя ближайшая гармоника, которую я хочу отфильтровать, имеет двойную частоту, поэтому у меня есть некоторый запас, с которым можно поиграть.

Исправленная кривая из фильтра с предпочтительными значениями.

Заменив значения моих компонентов на предпочтительные, я могу снова запустить моделирование, и из полученного графика я вижу, что мне очень повезло, что я не слишком сильно повредил его характеристики. Как и ожидалось, частота среза немного увеличилась, но сохранилась та же форма кривой, без появления ряби или уменьшения глубины.

Если бы я использовал этот фильтр с настоящим передатчиком, я бы удостоверился, что я спроектировал его с отсечкой по крайней мере на четверть выше, чем частота передачи.На практике я считаю, что отсечка более резкая и ниже, чем можно было бы ожидать, исходя из результатов моделирования, и, например, если бы я использовал ее с передатчиком 30 МГц, я бы обнаружил, что он ослабляет несущую больше, чем я считаю приемлемым. Также следует признать, что изменение значений компонентов таким образом также приведет к изменению импеданса фильтра по сравнению с рассчитанными 50 Ом, однако на практике это не кажется достаточно значительным, чтобы вызвать проблему, пока изменения значений незначительны. .

Мы не делали этот фильтр, но в прошлом мы использовали другой фильтр, который я сделал, и по совпадению он находился в том же частотном диапазоне. Когда я писал функцию автоматизации считывания показаний осциллографа, в качестве примера я использовал характеристику фильтра нижних частот 7-го порядка 30 МГц. Это может быть даже один из тех, что изображены в заголовке, извлеченный из моего случайного пакета фильтровальных картонов по этому случаю.

Фильтр | RC фильтр | Low High Pass | RC Notch | LC фильтр | Roll-off

Что такое фильтр?

Фильтр – это частотно-избирательная схема.Фильтры предназначены для пропускания одних частот и отклонения других. Последовательные и параллельные резонансные цепи, рассмотренные в разделе 2-2, являются примерами фильтров. Существует множество способов реализации схем фильтров.

Простые фильтры, созданные с использованием резисторов и конденсаторов или катушек индуктивности и конденсаторов, называются пассивными фильтрами, потому что в них используются пассивные компоненты, которые не усиливают. В коммуникационной работе многие фильтры относятся к разновидности пассивных LC, хотя используются многие другие типы.

Некоторые специальные типы фильтров представляют собой активные фильтры, в которых используются RC-цепи с обратной связью в схемах операционных усилителей, фильтры с переключаемыми конденсаторами, кварцевые и керамические фильтры, фильтры на поверхностных акустических волнах (SAW) и цифровые фильтры, реализованные с цифровой обработкой сигналов (DSP). ) техники.Пять основных типов схем фильтрации следующие:

Фильтр нижних частот . Пропускает частоты ниже критической частоты, называемой частотой среза, и значительно ослабляет частоты выше частоты среза.
Фильтр высоких частот. Передает частоты выше границы среза, но отклоняет частоты ниже нее.
Полосовой фильтр. Передает частоты в узком диапазоне между нижними и верхними частотами среза.
Фильтр отклонения полосы. Отклоняет или останавливает частоты в узком диапазоне, но пропускает частоты выше и ниже. Всепроходный фильтр. Одинаково хорошо передает все частоты во всем своем расчетном диапазоне, но имеет фиксированную или предсказуемую характеристику фазового сдвига.

RC фильтр

Фильтр нижних частот позволяет низкочастотным компонентам приложенного напряжения создавать выходное напряжение на сопротивлении нагрузки, тогда как высокочастотные компоненты ослабляются или уменьшаются на выходе.Фильтр высоких частот делает обратное, позволяя высокочастотным компонентам приложенного напряжения создавать напряжение на выходном сопротивлении нагрузки.

Случай RC-цепи связи является примером фильтра верхних частот, поскольку переменная составляющая входного напряжения возникает через резистор R, а постоянное напряжение блокируется последовательным конденсатором. Кроме того, с более высокими частотами в компоненте переменного тока возникает большее напряжение переменного тока. Любой фильтр нижних или верхних частот можно рассматривать как частотно-зависимый делитель напряжения, поскольку величина выходного напряжения зависит от частоты.

В фильтрах

RC используются комбинации резисторов и конденсаторов для достижения желаемого отклика. Большинство RC-фильтров относятся к фильтрам нижних или верхних частот. Некоторые режекторные или режекторные фильтры также изготавливаются с использованием RC-цепей. Полосовые фильтры можно создать, комбинируя RC-секции нижних и верхних частот, но это делается редко.

Фильтр низких частот

Фильтр нижних частот – это схема, которая не вводит ослабления на частотах ниже частоты среза, но полностью устраняет все сигналы с частотами выше частоты среза.Фильтры низких частот иногда называют фильтрами высоких частот. Кривая идеального отклика для фильтра нижних частот показана на рис. 2-23. Такую кривую отклика невозможно реализовать на практике. В практических схемах вместо резкого перехода на частоте среза существует более постепенный переход от небольшого или нулевого затухания к максимальному затуханию.

Простейшей формой фильтра нижних частот является RC-схема, показанная на рис. 2-24 (a). Схема представляет собой простой делитель напряжения с одним частотно-чувствительным компонентом, в данном случае конденсатором.На очень низких частотах конденсатор имеет очень высокое реактивное сопротивление по сравнению с сопротивлением, поэтому затухание минимально. С увеличением частоты емкостное реактивное сопротивление уменьшается. Когда реактивное сопротивление становится меньше сопротивления, затухание быстро увеличивается.

Частотная характеристика базовой схемы показана на Рис. 2-24 (b). Частота среза этого фильтра – это точка, в которой R и XC равны. Частота среза, также известная как критическая частота, определяется выражением.

Пример 2-23 Какова частота среза односекционного RC-фильтра нижних частот с R = 8,2 кВ
и C = 0,0033 мкФ?

На частоте среза выходная амплитуда составляет 70,7% входной амплитуды на более низких частотах. Это так называемая нижняя точка на 3 дБ. Другими словами, этот фильтр имеет усиление по напряжению 23 дБ на частоте среза. На частотах выше частоты среза амплитуда уменьшается линейно на 6 дБ на октаву или 20 дБ на декаду.

Октава определяется как удвоение или уменьшение частоты вдвое, а декада представляет собой соотношение в одну десятую или умноженное на 10. Предположим, что фильтр имеет отсечку 600 Гц. Если частота удвоится до 1200 Гц, затухание увеличится на 6 дБ или с 3 дБ на срезе до 9 дБ при 1200 Гц. Если частота увеличится в 10 раз с 600 Гц до 6 кГц, затухание увеличится в 20 дБ с 3 дБ на срезе до 23 дБ на 6 кГц.

Если требуется более высокая скорость затухания, можно использовать две RC-секции, настроенные на одинаковую частоту среза.Такая схема показана на рис. 2-25 (а). В этой схеме коэффициент затухания составляет 12 дБ на октаву или 40 дБ на декаду. Используются две идентичные RC-цепи, но между ними используется изоляционный или буферный усилитель, такой как эмиттер-повторитель (коэффициент усиления <1), чтобы вторая секция не загружала первую. Каскадирование двух RC-цепочек без изоляции даст коэффициент затухания меньше теоретически идеальной октавы 12 дБ из-за эффектов нагрузки.

Если частота среза каждой RC-секции одинакова, общая частота среза для всего фильтра несколько меньше.Это вызвано дополнительным затуханием второй секции. С более крутой кривой затухания схема считается более избирательной.

Недостатком каскадирования таких секций является то, что большее затухание значительно снижает выходной сигнал. Это затухание сигнала в полосе пропускания фильтра называется вносимыми потерями. Фильтр нижних частот также может быть реализован с помощью катушки индуктивности и резистора, как показано на рис. 2-26. Кривая отклика для этого фильтра RL такая же, как на рис.2-24 (б).

Частота среза определяется по формуле. Фильтры нижних частот RL не так широко используются, как фильтры RC, потому что катушки индуктивности обычно больше, тяжелее и дороже, чем конденсаторы. Катушки индуктивности также имеют большие потери, чем конденсаторы, из-за собственного сопротивления обмотки.

Фильтр высоких частот

Фильтр верхних частот пропускает частоты выше частоты среза с небольшим ослаблением или без него, но значительно ослабляет те сигналы, которые находятся ниже частоты среза.Идеальная кривая отклика верхних частот показана на рис. 2-27 (а). Аппроксимация идеальной кривой отклика, показанной на рис. 2-27 (b), может быть получена с помощью различных RC- и LC-фильтров. Базовый RC-фильтр верхних частот показан на рис. 2-28 (a). Опять же, это не что иное, как делитель напряжения с конденсатором, выступающим в качестве частотно-чувствительного компонента в делителе напряжения. На низких частотах XC очень высок.

Когда XC намного выше, чем R, эффект делителя напряжения обеспечивает сильное затухание низкочастотных сигналов.С увеличением частоты емкостное реактивное сопротивление уменьшается. Когда емкостное реактивное сопротивление равно или меньше сопротивления, делитель напряжения дает очень небольшое затухание. Следовательно, высокие частоты проходят относительно без ослабления. Частота среза для этого фильтра такая же, как и для схемы нижних частот, и получается путем установки XC равным R и решения для частоты:

Скорость спада составляет 6 дБ на октаву или 20 дБ на декаду. Фильтр верхних частот также может быть реализован с катушкой и резистором, как показано на рис.2-28 (б). Частота среза –

Кривая отклика для этого фильтра такая же, как на рис. 2-27 (b). Скорость затухания составляет 6 дБ на октаву или 20 дБ на декаду, как в случае с фильтром нижних частот. Опять же, улучшенное затухание может быть получено путем каскадирования секций фильтров.

Пример 2-24 Какое наиболее близкое значение стандартного резистора EIA обеспечивает частоту среза
3,4 кГц с конденсатором 0,047 мкФ в RC-фильтре верхних частот?

Режекторный фильтр RC

Notch-фильтры также называются полосовыми или режекторными фильтрами.Фильтры отклонения полосы используются для значительного ослабления узкого диапазона частот вокруг центральной точки. Режекторные фильтры служат для той же цели, но для одной частоты. Простой режекторный фильтр, который реализован с помощью резисторов и конденсаторов, как показано на рис. 2-29 (a), называется режекторным фильтром с параллельной Т-образной или двойной Т-образной схемой.

Этот фильтр представляет собой разновидность мостовой схемы. Напомним, что в мостовой схеме выход равен нулю, если мост сбалансирован. Если значения компонентов точно совпадают, схема будет сбалансирована и произведет ослабление входного сигнала на проектной частоте от 30 до 40 дБ.Типичная кривая отклика показана на рис. 2-29 (b). Центральная режекторная частота вычисляется по формуле

Например, если значения сопротивления и емкости равны 100 кВ и 0,02 мкФ, частота режекции будет

. Режекторные фильтры

Twin-T используются в основном на низких частотах, аудио и ниже. Обычно используется для устранения гула линии электропередачи с частотой 60 Гц из аудиосхем и усилителей низкочастотного медицинского оборудования. Ключом к высокому затуханию на частоте режекции являются точные значения компонентов.Значения резистора и конденсатора должны быть согласованы для достижения высокого затухания.

Пример 2-25 Конденсаторы каких номиналов вы бы использовали в режекторном фильтре RC twin-T для удаления 120 Гц, если R 5 220 кВ?

Фильтр LC Фильтры

RC используются в основном на низких частотах. Они очень распространены на звуковых частотах, но редко используются выше 100 кГц. На радиочастотах их затухание в полосе пропускания слишком велико, а крутизна среза слишком плавная.Чаще встречаются LC-фильтры с катушками индуктивности и конденсаторами. Катушки индуктивности для низких частот большие, громоздкие и дорогие, но те, которые используются для высоких частот, очень маленькие, легкие и недорогие. За прошедшие годы было разработано множество типов фильтров. Методы проектирования фильтров также изменились с годами благодаря компьютерному дизайну.

Терминология фильтра

При работе с фильтрами вы услышите множество терминов, описывающих работу и характеристики фильтров.Следующие определения помогут вам понять характеристики и работу фильтра.

Полоса пропускания

Это частотный диапазон, в котором фильтр пропускает сигналы. Это частотный диапазон между частотами среза или между частотой среза и нулем (для низких частот) или между частотой среза и бесконечностью (для высоких частот).

Ограничительная лента

Это диапазон частот вне полосы пропускания, т.е.е., диапазон частот, который сильно ослабляется фильтром. Частоты в этом диапазоне отклоняются.

Затухание

Это величина, на которую снижаются нежелательные частоты в полосе задерживания. Это может быть выражено как отношение мощностей или отношение выходного напряжения к входному. Затухание обычно указывается в децибелах.

Вносимые потери

Вносимые потери – это потери, которые фильтр вносит в сигналы в полосе пропускания.Пассивные фильтры вносят ослабление из-за резистивных потерь в компонентах. Вносимые потери обычно указываются в децибелах.

Импеданс

Импеданс – это значение сопротивления нагрузки и истока нагрузки фильтра. Фильтры обычно разрабатываются для конкретного источника возбуждения и сопротивления нагрузки, которые должны присутствовать для правильной работы.

Пульсация

Изменение амплитуды с частотой в полосе пропускания или повторяющееся повышение и понижение уровня сигнала в полосе пропускания некоторых типов фильтров известно как пульсация.Обычно указывается в децибелах. В некоторых типах фильтров также может наблюдаться колебание полосы пропускания.

Коэффициент формы

Коэффициент формы, также известный как коэффициент пропускной способности, представляет собой отношение полосы пропускания полосы пропускания к полосе пропускания полосового фильтра. Он сравнивает полосу пропускания при минимальном затухании, обычно в точках 23 дБ или частотах отсечки, с полосой максимального затухания и, таким образом, дает относительную индикацию скорости затухания или избирательности.Чем меньше коэффициент, тем выше избирательность. Идеальным является отношение 1, которое, как правило, невозможно получить с помощью практических фильтров. Фильтр на рис. 2-30 имеет полосу пропускания 6 кГц в точке затухания 23 дБ и полосу пропускания 14 кГц в точке затухания 240 дБ. Тогда коэффициент формы составляет 14 кГц / 6 кГц = 2,333. Точки сравнения различаются в зависимости от фильтров и производителей. Точки сравнения могут находиться в точках на 6 дБ и 60 дБ или на любых других назначенных двух уровнях.

Полюс

Полюс – это частота, при которой в цепи высокий импеданс. Он также используется для описания одной RC-секции фильтра. Простой RC-фильтр нижних частот, такой как на рис. 2-24 (a), имеет один полюс. Двухсекционный фильтр на рис. 2-25 имеет два полюса. Для ЖК-фильтров нижних и верхних частот количество полюсов равно количеству реактивных компонентов в фильтре. Для полосовых и режекторных фильтров обычно предполагается, что количество полюсов составляет половину количества используемых реактивных компонентов.

Ноль

Этот термин относится к частоте, при которой в цепи отсутствует полное сопротивление.

Задержка конверта

Также известная как временная задержка, задержка огибающей – это время, необходимое для прохождения определенной точки входного сигнала через фильтр.

Отвал

Также называется скоростью затухания, спад – это скорость изменения амплитуды с частотой в фильтре. Чем быстрее спад или чем выше коэффициент затухания, тем более избирательным является фильтр, т.е.е., тем лучше он способен различать два близко расположенных сигнала, один желательный, а другой нет.

Любой из четырех основных типов фильтров можно легко реализовать с помощью катушек индуктивности и конденсаторов. Такие фильтры могут быть созданы для частот до нескольких сотен мегагерц, прежде чем значения компонентов станут слишком малы, чтобы их можно было применить на практике. На частотах выше этой частоты используются специальные фильтры, изготовленные с использованием микрополосковых технологий на печатных платах, фильтры поверхностных акустических волн и объемные резонаторы.Поскольку используются два типа реактивных сопротивлений, индуктивный в сочетании с емкостным, скорость спада затухания больше у LC-фильтров, чем у RC-фильтров. Катушки индуктивности делают такие фильтры больше и дороже, но необходимость в лучшей селективности делает их необходимыми.

ЖХ фильтры нижних и верхних частот

На рис. 2-31 показаны основные конфигурации фильтра нижних частот. Базовая двухполюсная схема на рис. 2-31 (a) обеспечивает коэффициент затухания 12 дБ на октаву или 20 дБ на декаду.Эти секции могут быть соединены каскадом для обеспечения еще большей скорости спада. На диаграмме на рис. 2-32 показаны коэффициенты затухания для фильтров нижних частот с двумя-семью полюсами. Горизонтальная ось f / FC представляет собой отношение любой заданной частоты к частоте среза фильтра Fc.

Значение n – это количество полюсов в фильтре. Предположим, что частота среза равна 20 МГц. Соотношение для частоты 40 МГц будет 40/20 = 2. Это означает удвоение частоты или одну октаву.Затухание на кривой с двумя полюсами составляет 12 дБ. Π- и T-фильтры на рис. 2-31 (b) и (c) с тремя полюсами дают коэффициент затухания 18 дБ для отношения частот 2: 1. На рис. 2-33 показаны основные конфигурации фильтра верхних частот. Кривая, аналогичная кривой на рис. 2-32, также используется для определения затухания для фильтров с несколькими полюсами. Каскадирование этих секций обеспечивает больший коэффициент затухания. Те конфигурации фильтров, в которых используется наименьшее количество катушек индуктивности, предпочтительнее из-за меньшей стоимости и меньшего пространства.

Посмотреть видео Для большего понимания

Нажмите здесь, чтобы загрузить приложение WhatsWho

Смещения транзистора

Нравится:

Нравится Загрузка …

ФНЧ

НОВИНКА! ‣ – Пакеты электронных компонентов Amazon. Посетите страницу Amazon Electronic Component Packs.

Что такое фильтры нижних частот?

Мы начнем с фильтров нижних частот (ФНЧ), потому что они являются основой других конструкций фильтров. Фильтры верхних частот или полосовые фильтры часто являются просто преобразованием конструкций фильтров нижних частот.

Возможно, самый простой фильтр нижних частот – это классическая схема схемы Пи Баттуорта, в которой реактивные элементы имеют постоянный импеданс e.грамм. 50 Ом и конструкция Q = 1.

Рисунок 1 – Схема фильтра нижних частот сети Пи Баттерворта

Этот пример наиболее часто используется на выходе передатчика для минимизации выходных гармоник и устранения QRM. Как и в случае со всеми простыми конструкциями, выгода, которую можно получить, имеет предел. Если бы такой фильтр был разработан с отсечкой (Fc) 7,5 МГц, ослабление становится значительным только далеко от этой частоты.

Фильтр нижних частот состоит из двух L-цепей

Это просто две L-сети, сложенные вместе таким образом, чтобы сформировать сетевой фильтр низких частот с ПИ:

Рисунок 2 – два сетевых фильтра нижних частот L

Где реактивные сопротивления C1 = C2 = 50 Ом каждое и L1a = L2a = 50 Ом каждое или всего 100 Ом.

Затухание этого конкретного фильтра определяется уравнением:

A _дБ = 10 log [1 + (W / W _c ) ²ⁿ]
W = частота желаемого затухания
W _c = частота среза ( W _3db ) фильтра
n = количество элементов в фильтре

Для нашего трехэлементного фильтра ( n ) выше с W _c из 7.5 МГц и проверка первой гармоники ( Вт, ) на частоте 15 МГц мы находим, что затухание на частоте 15 МГц составляет всего 18,13 дБ .

Очевидно, это число вас не слишком взволнует, но это факт жизни. Кто из вас думал, что такой LPF даст потрясающие результаты?

Хорошим примером для исследования является тот же фильтр, который используется на входе приемника с ПЧ 455 кГц. Наш гетеродин работает на частоте 7500 кГц + 455 кГц или 7955 кГц. Частота изображения будет 8410 кГц.Хотите верьте, хотите нет, но я видел серьезные попытки создания приемника с использованием такого очень случайного подхода.

Размещение изображения с частотой 8,410 МГц в приведенном выше уравнении дает ослабление на этой частоте всего 4,75 дБ . Если вы мне не верите, проверьте это сами (что, кстати, вам все равно следует делать). С другой стороны, никакой фильтр ПЧ никогда не устранит помехи на изображении.

O.K. ну какая польза от такого фильтра нижних частот ?. Во-первых, если вы решите уменьшить помехи в низком диапазоне УКВ ТВ, вы можете получить приемлемую производительность.Сделайте расчет затухания на частоте 50 МГц. Во-вторых, фильтр превосходен (по моему скромному мнению) как преобразователь импеданса или согласующее устройство. В этом случае я считаю, что любые преимущества от ослабления полностью являются бонусом.

Снова вернемся к простому 3-полюсному фильтру нижних частот, который мы использовали выше. При любой расчетной частоте реактивные сопротивления при входном / выходном сопротивлении 50 Ом всегда остаются 50 Ом. L1 составляет 100 Ом, а C1 и C2 также 50 Ом. В 7.На 5 МГц эти реактивные сопротивления становятся C1 = C2 = 424 пФ и L1 = 2,12 мкГн.

Теорема Бартлетта о делении пополам, примененная к фильтрам нижних частот

А вот и очень хитрый трюк, Теорема Бартлетта о делении пополам . Я понятия не имею, кем был мистер Бартетт, откуда он и когда обнаружил этот трюк. Все, что я знаю, это то, что я читал об этом где-то очень давно, и я был так впечатлен, что с тех пор это запомнилось мне.

В приведенном выше примере Zin = Zout = 50 Ом, а реактивные сопротивления: C1 = C2 = 50 Ом и L1 = 100 Ом.Это то же самое, что:

Рисунок 3 – Теорема Бартлетта о делении пополам, примененная к фильтрам нижних частот

Где мы просто разделили верхнее реактивное сопротивление пополам, то есть L1 становится 1/2 L1 + 1/2 L1 или 50 Ом + 50 Ом. Логично, а! Мы вернулись к двум L-сетям, расположенным вплотную друг к другу.

Предположим, вы хотите согласовать 50 Ом с 200 Ом . Хорошо, сторона L / H остается статичной при 50 Ом, и преобразуйте сторону R / H в 200 Ом, умножив реактивные сопротивления на 200/50. В результате индуктивности R / H умножаются на 4, а емкости R / H делятся на 4.

В нашем примере C1 осталось 50 Ом, C2 теперь 200 Ом, а L1 стало 250 Ом. На 7,5 МГц С1 осталось 424 пФ, С2 стало 106 пФ, а L1 = 5,3 мкГн. Поэтому у нас есть согласующие цепи и с некоторым затуханием гармоник.

Помните, что эти фильтры ЯВЛЯЮТСЯ двусторонними, это означает, что любая сторона может использоваться как вход или выход в соответствии с вашими требованиями.

Также помните, что вышеупомянутая конструкция двух стыковых L-сетей имела конструкцию Q, равную 1. Вы скоро обнаружите, что это несколько ограничивает.Лучше всего, чтобы обе L-сети соответствовали мифическому центру или невидимому сопротивлению, которое называется «виртуальным сопротивлением» или творчески R .

Переход от сетевых фильтров нижних частот с двойной L к Pi

Для наших целей мы будем использовать загруженный Q или QL, который соответствует:

Q = SQRT [ (Rh / R) -1]

Где Rh – это максимальное из наших сопротивлений R _S или R _L, а R – виртуальное сопротивление. Термин SQRT означает «квадратный корень из».Хотя это не совсем правильно, этого достаточно для практических целей в реальном мире. Вышеупомянутая формула также может быть переписана как:

R = R _h / (Q ² + 1)

НО Q должен превышать SQRT [(_{рэндов самый высокий} / ранд _{самый низкий}) -1]

Предположим, что в нашем предыдущем примере Q = 1 и R _s = 50 Ом, а R _L = 200 Ом.

Здесь Q ДОЛЖНО превышать 1,732, что является квадратным корнем из трех, полученным из [(200/50) – 1], поэтому вместо этого мы будем использовать типичное более высокое, но номинальное значение Q, равное 3.Тогда R станет R _h / (Q ² + 1) или 200 / 10 или 20, т.е. R = 20 и:

для Zin = 50 Ом и Z out = 200 Ом

Рисунок 4 – Теорема Бартлетта о бисекторе применительно к фильтрам нижних частот

Для правой стороны или со стороны нагрузки

Xp2 = Rp / Qp = R _L / Q = 200/3 = 66,6 Ом
Xs2 = Q * R _серия = 3 * 20 = 60 Ом

Для стороны L / H или источника

Q ₁ здесь – отношение Rs к R или;

Q ₁ = SQRT & nbsp [(Rs / R) -1]

Q ₁ = SQRT [(50/20) -1]

Q ₁ = 1.2247 И;

Xp1 = Rs / Q ₁ = 50 / 1,2247 = 40,83 Ом
Xs1 = Q ₁ * R _серии = 1,2247 * 20 = 24,494 Ом

Рисунок 5 – Вычисления по теореме Бартлетта, фильтры нижних частот

Насколько полезна вся эта информация для фильтров нижних частот?

Каждое из четырех рассчитанных нами реактивных сопротивлений может быть катушкой индуктивности. ИЛИ конденсатор. Единственный аспект, который вы должны запомнить , это то, что X _{p имеет} и X _{s имеют противоположные типы или знаки и добавляют или вычитают
соответственно.}

Отсюда мы можем получить четыре разные сети. Все показано как реактивные сопротивления, и я опустил импедансы источника и нагрузки.

Рисунок 6 – Сетевые вычисления по теореме Бартлетта о делении пополам

Обратите внимание, как складываются подобные реактивные сопротивления. Но емкостные реактивные сопротивления отрицательны, а индуктивные реактивные сопротивления положительны. Если чистое реактивное сопротивление заканчивается отрицательным, то это конденсатор, чистое положительное – это катушка индуктивности.

Первая сеть, очевидно, представляет собой фильтр нижних частот.Второй становится фильтром высоких частот, два других демонстрируют характеристики высоких или низких частот. Вы используете конфигурацию слева или конфигурацию справа?

Это будет полностью зависеть от индивидуальных обстоятельств, наличия компонентов и т. Д. И, в частности, от необходимости иногда включать переменный элемент в вашу схему. В других случаях вы можете включить катушку индуктивности в коллектор вашей схемы и вам понадобится блокирующий конденсатор для следующего каскада. Однако этот сценарий должен учитывать влияние паразитных искажений схемы и емкости транзистора на вашу конструкцию и ее последующее отклик.

Информация [Исправление] в следующем абзаце была изменена для включения исправления – 27/11/03

Чтобы применить его в реальном мире, вы просто преобразуете свое реактивное сопротивление в интересующую частоту. Рассмотрим фильтр нижних частот. У нас есть два емкостных реактивных сопротивления по 40,83 Ом. и 66,6 Ом. При частоте среза 7,5 МГц они будут 520 пФ и 318 пФ соответственно (используйте 330 пФ + 180 пФ для 520 пФ и используйте конденсатор 330 пФ для другого). Реактивное сопротивление индуктора 84.5 Ом – это индуктор 1,79 мкГн.

Если бы этот фильтр использовался в каком-либо низкоуровневом приложении, таком как выход усилителя 200 Ом на нагрузку 50 Ом, я бы подумал о том, чтобы сделать катушку индуктивности переменной для достижения улучшенных характеристик усилителя путем регулировки индуктивности, наблюдая выход усилителя в известном Резистивная нагрузка 50 Ом.

Пользовательский поиск Google

Есть вопросы по этой теме?

Если вы занимаетесь электроникой, подумайте о том, чтобы присоединиться к нашей группе новостей «Электроника Вопросы и ответы», чтобы задать там свой вопрос, а также поделиться своими тернистыми вопросами и ответами.Помогите своим коллегам !.

Абсолютно самый быстрый способ получить ответ на свой вопрос, и да, я DO прочитал большинство сообщений.

Это группа взаимопомощи с очень профессиональной атмосферой. Я ничего не узнал. Это отличный обучающий ресурс как для скрытых, так и для активных участников.

СВЯЗАННЫЕ ТЕМЫ, КАСАЮЩИЕСЯ НИЗКОПРОХОДНЫХ ФИЛЬТРОВ

полосовые фильтры
фильтра верхних частот
Фильтры усилителя ПЧ
фильтры для улавливания гармоник
реактивное сопротивление
присоединяйтесь к нашей “дискуссионной группе по электронике”

Ссылка на эту страницу

НОВИНКА! – Как перейти по прямой ссылке на эту страницу

Хотите создать ссылку на мою страницу со своего сайта? Нет ничего проще.Знания HTML не требуются; даже технофобы могут это сделать. Все, что вам нужно сделать, это скопировать и вставить следующий код. Все ссылки приветствуются; Искренне благодарю вас за вашу поддержку.

Скопируйте и вставьте следующий код для текстовой ссылки :

<а href = "https://www.electronics-tutorials.com/filters/low-pass-filters.htm" target = "_ top"> посетите страницу Ian Purdie VK2TIP "LC Low Pass Filters"

, и он должен выглядеть так:
посетите Ян Пурди VK2TIP “LC Low Pass Filters” Страница

ВЫ ЗДЕСЬ: ГЛАВНАЯ> ФИЛЬТРЫ> ФИЛЬТРЫ НИЗКОГО ПРОХОДА

автор Ян К.Purdie, VK2TIP www.electronics-tutorials.com заявляет о моральном праве называться автором этого веб-сайта и всего его содержимого. Copyright © 2000, все права защищены. См. Копирование и ссылки. Эти электронные учебные пособия предназначены для индивидуального частного использования, и автор не несет никакой ответственности за применение, использование, неправильное использование любого из этих проектов или учебных пособий по электронике, которое может привести к прямому или косвенному ущербу или убыткам, связанным с этими проектами или учебными пособиями. .Все материалы предоставляются для бесплатного частного и общественного использования.
Коммерческое использование запрещено без предварительного письменного разрешения www.electronics-tutorials.com.

Обновлено 27 ноября 2003 г.

Связаться ВК2ТИП

Фильтр нижних частот для синусоидальных инверторов

Пожалуйста, дайте нам в зоне комментариев любые предложения, которые, по вашему мнению, улучшат статью!

Если вам понравился артикул , нажмите кнопку «Подписаться» , чтобы оставаться на связи с нами!

Если в предыдущих сообщениях я разработал метод для генерации управляющего сигнала для получения чистой синусоидальной волны и H-моста, чтобы использовать этот сигнал в различных приложениях, таких как чистый синусоидальный инвертор; В этом посте я разработал фильтр нижних частот для этого инвертора, который установлен на выходе моста на 12 вольт.

Должен признать, что создать этот фильтр было немного сложно, и я до сих пор не знаю, хорош ли мой дизайн. Я использовал этот фильтр в разных тестах и приложениях, и для меня он достаточно хорош, как вы можете видеть на изображениях, снятых с моего осциллографа (в конце этого поста). Я начну с небольшой теории о передаточных функциях, а затем я реализую дизайн и, наконец, некоторые тесты.

1. передаточная функция

Большинство фильтров нижних частот, описанных в Интернете, представляют собой RC-фильтры нижних частот, но установка резистора таким образом – не такая уж и хорошая вещь.Итак, я сделал фильтр нижних частот из трех частей: R, L и C.
Первый компонент – это катушка индуктивности, а затем конденсатор, включенный параллельно резистору. На низких частотах ток будет проходить через катушку индуктивности намного легче, но на более высоких частотах он будет действовать как высокий импеданс, потому что, как мы знаем, XL = L x Omega, где omega – частота в радианах. Конденсатор действует противоположным образом: на низкой частоте он ведет себя как неповрежденная цепь, а на более высоких частотах как короткое замыкание.
Резистор предназначен для демпфирования, поскольку внутреннее сопротивление L незначительно и могут появиться нежелательные режимы.

Передаточная функция необходима для расчета частоты среза, коэффициента демпфирования и отклика фильтра.
Передаточная функция, представленная ниже, предназначена только для компонентов L C, чтобы сравнить и обосновать наличие резистора в цепи.

Недостатком этого фильтра является то, что вблизи частоты среза могут появиться нежелательные режимы, потому что дзета равна нулю, и он вносит некоторый шум на этой частоте, как на рисунке ниже.5 из графика:

для:

дзета = 0, система не демпфируется;

дзета = 0,707 <1, система сброшена;

дзета = 1, система критически сброшена и нет пика.

Итак, чтобы сделать дзета ≠ равным нулю, я включил резистор параллельно конденсатору.
Перед тем, как показать вам новую передаточную функцию, я должен сказать, что я не получил желаемой дзеты, потому что, когда я вычислил желаемую омегу, выбранные значения для L и C дали очень маленькое значение для дзеты.Итак, передаточная функция схемы с демпфирующим резистором равна:

Хорошо, как вы можете видеть на этой схеме, дзета (коэффициент демпфирования) отличен от нуля, поэтому мы можем управлять им.

2. Параметры R, L, C

На практике для фильтра нижних частот вы можете выбрать частоту среза между 10 раз большей, чем основная частота (в нашем случае 50 Гц для инвертора), и в 10 раз меньшей, чем частота ШИМ (в нашем случае приблизительно 3100 Гц). Я попытался выбрать частоту среза около 2 кГц, поэтому я выбрал керамический конденсатор на 20 мкФ, индуктор на 200 мкГн (других значений у меня нет :)) и резистор на 50 Ом.

При этих значениях частота среза (в Гц) составляет f = 2055,724, а коэффициент демпфирования zeta = 0,0224.

Как я уже сказал, коэффициент затухания дзета очень низкий по сравнению с 0,707. Чтобы улучшить этот коэффициент, я мог бы уменьшить значение R, но небольшое значение напряжения означает потерю мощности или большую катушку индуктивности. Проблема с индуктором большего размера заключается в том, что наименьшие импульсы ШИМ (на крайнем уровне половины рабочего цикла) исчезают, поэтому между половиной рабочего цикла синусоидальной волны есть период при нулевом напряжении, что недопустимо.

Хорошо, но вы можете сказать, если дзета очень мала, зачем вы вставляете резистор…?

Что ж, если вы посмотрите на изображения ниже, то увидите большую разницу между схемами без резистора и с резистором на диаграмме частотной характеристики, полученной из передаточной функции.

Без резистора:

С резистором:

Как вы можете видеть, без резистора усиление составляет около 50 дБ, а с резистором около 25 дБ, так что даже небольшой сброс, уменьшение усиления вдвое – это хорошо.

3. Тесты

Прежде чем начать испытания с фильтром из R, L, C, определенным выше, я должен сказать, что на изображении ниже осциллограф повторно использует тот же фильтр, но с более высокой индуктивностью L = 15 мГн, и вы можете увидеть, как ШИМ пропадают импульсы с малой скважностью. По этой причине мне не удалось улучшить коэффициент демпфирования с помощью индуктивности.

Чтобы понять, что такое индуктор на 200 мкГн, вы можете увидеть ниже (он сделан из старого блока питания для ПК, и я измерил его с помощью мультиметра, способного измерять индуктивность):

Затем тесты с фильтром будут выполнены с некоторыми потребителями непосредственно на выходе напряжения 12, а другие тесты с двумя типами трансформаторов, трансформатором с железным сердечником и трансформатором с феритовым сердечником, чтобы увидеть различия между этими двумя.

с резистором 8,2 Ом 10Вт

с резистором 8,2 Ом последовательно с катушкой индуктивности 62 мГн (z = омега x L = 2 x pi x f x L = 19,46 Ом (при 50 Гц))

с галогенным пятном на 12 В, 16 Вт

со светодиодной подсветкой 12 В, 5,5 Вт

в этом случае синусоида имеет низкий уровень шума по сравнению с другими нагрузками, и это похоже на случай с фильтром без нагрузки.

Трансформатор с железным сердечником без нагрузки (пиковое напряжение будет составлять 12 вольт на стороне низкого напряжения, поэтому на стороне высокого напряжения 220 вольт представляют пиковое значение)

-на стороне 12 вольт

– на стороне 220 вольт

Трансформатор пикового напряжения 220 В с железным сердечником и зарядное устройство для телефона (оно принимает напряжение от 100 до 240 В, поэтому должно работать нормально)

Надо сказать, телефон заряжается без проблем.

без нагрузки

Как видите, между этими типами трансформаторов нет различий

и зарядным устройством для телефона

Также в этом случае нет отличий.

Заключительные испытания проводятся с двумя двигателями переменного тока мощностью 15 Вт и 50 Вт с обоими вентиляторами. Один с меньшей мощностью – со шпилем короткого замыкания в статоре, а другой – с конденсатором.

На рисунке ниже представлен полностью синусоидальный инвертор (извините за аспект 🙂):

Два видео с моторами:

Калькулятор ЖК-фильтра нижних частот 2-го порядка. RC фильтр низких частот

Evowars hack

Фильтр высоких частот предотвращает прохождение частот ниже его частоты среза и пропускает сигналы выше него.В этой статье вы узнаете, как рассчитать различные пассивные фильтры верхних частот.

Кроме того, у вас будет доступ к онлайн-калькулятору фильтра верхних частот. Схема фильтра верхних частот обозначает схему в электротехнике с целью ослабления или блокировки низких частот.

Однако высокие частоты должны быть как можно более беспрепятственными. Также широко используется термин фильтр высоких частот. Высокочастотный фильтр пассивен, если не используется усилительный элемент. В противном случае он считается активным.Высокочастотный фильтр используется там, где низкие частоты нежелательны и поэтому должны быть отфильтрованы. Примеры включают конструкцию твитеров или передачу высокочастотного сигнала по линиям электропередачи. Низкие частоты в этих случаях делают сигнал практически непригодным для дальнейшей обработки и должны быть устранены.

Электрики различают высокие частоты 1-го порядка и 2-го порядка. Высокие проходы высокого порядка достигаются последовательным переключением более низких порядков. Мы объясняем, как работает фильтр высоких частот и как его можно рассчитать.Кроме того, для простоты мы предлагаем калькулятор высоких частот.

Простой фильтр верхних частот 1-го порядка состоит из последовательно соединенных конденсатора и резистора. Ниже приведены аспекты схемы фильтра высоких частот. CR high pass также часто называют, но обозначают ту же схему. Когда на вход подается высокая частота, на конденсаторе падает незаметно небольшое напряжение.

Однако, если присутствует низкая частота, часть напряжения на конденсаторе упадет.В результате выходное напряжение падает параллельно резистору с задержкой по времени.

Это связано с тем, что конденсатор пропускает измененное напряжение в течение короткого времени. С увеличением частоты падение напряжения на конденсаторе уменьшается. Следовательно, выходное напряжение увеличивается. Высокочастотный фильтр RL также является фильтром 1-го порядка.

Однако вместо конденсатора используется катушка индуктивности, и выходное напряжение отводится параллельно ей. Структура идентична фильтру верхних частот 1-го порядка, за исключением того, что омическое сопротивление заменено на индуктивность.Следовательно, в фильтре верхних частот 2-го порядка катушка последовательно соединена с конденсатором. Поэтому широко используется термин LC high pass.

Фильтр верхних частот 2-го порядка фильтрует низкие частоты вдвое эффективнее, чем фильтр верхних частот 1-го порядка. Кромка в два раза круче. Разница заключается в катушке, которая, в отличие от конденсатора, быстро реагирует на высокие частоты.

Функция конденсатора остается без изменений. Однако при подаче синусоидального напряжения катушка выполняет свое предназначение.Конденсатор образует резистор на низких частотах и пропускает высокие частоты. Этот калькулятор кроссовера динамиков поможет вам создать набор динамиков с потрясающим звучанием.

Он расскажет, какие конденсаторы и катушки индуктивности вам понадобятся для создания конструкции пассивного кроссовера для двух динамиков (двухполосный пассивный кроссовер) или трех динамиков (трехполосный пассивный кроссовер). В 2-полосном режиме калькулятор использует импеданс высокочастотного и низкочастотного динамиков для создания кроссовера двухполосного динамика.

Если вы выберете три динамика, он станет трехполосным калькулятором кроссовера на тот случай, если вы также захотите включить в свой дизайн среднечастотный динамик. Также есть пара дополнительных схем для одного динамика. Один для стабилизации импеданса динамика при изменении частоты Zobel, а другой – для уменьшения громкости L-pad.

В конце концов, вы узнаете кроссовер низких частот от кроссовера высоких частот. Если вы новичок в области дизайна акустических систем Hi-Fi, вам может быть интересно, почему мы не можем использовать только одну акустическую систему?

Sportstake propick tips

В конце концов, вы, вероятно, найдете в своем доме устройства, в которых есть только один динамик, например, небольшой портативный радиоприемник или ваш мобильный телефон.Но отлично ли они звучат на всех частотах?

Распространенная жалоба на конструкции с одним динамиком – отсутствие низких частот. Это означает низкую громкость и искажения звука на низких частотах, например басовый инструмент в музыкальной дорожке. Чтобы решить эту проблему, вы можете увеличить громкоговоритель, но тогда громкость высоких частот будет низкой. Для дизайна Hi-Fi динамиков мы стремимся к одинаковой громкости звука в максимально широком диапазоне частот.

Решение состоит в том, чтобы иметь два или три, может быть, больше, но это менее распространенные специальные динамики внутри каждого динамика.Громкоговоритель, который выводит высокие частоты, называется высокочастотным, а динамик, воспроизводящий низкие частоты, называется низкочастотным динамиком. Для настройки с тремя динамиками вам также понадобится среднечастотный динамик для покрытия диапазона частот между высокочастотным и низкочастотным динамиками более высокого качества.

ФНЧ второго порядка – LIC –

Однако при подключении нашего решения с несколькими динамиками к усилителю возникает проблема. Кабель динамика содержит все частоты в виде электронных сигналов, поэтому низкочастотный динамик по-прежнему будет получать высокие частоты, а твитер – низкие частоты.Это несоответствие частот приведет к искажению звука и даже может повредить динамик, если он получит достаточно громкий сигнал на неправильной частоте.

Одним из решений этой проблемы является разделение сигнала, поступающего от усилителя, в соответствии с частотой сигнала. Тогда, например, низкочастотные сигналы пойдут на низкочастотный динамик, а высокочастотные сигналы – на высокочастотный динамик.

Комбинация правильных конденсаторов и катушек индуктивности создает фильтры, которые позволяют передавать только правильный диапазон частот на правильный динамик или драйвер.Когда задействованы два динамика, это называется двухполосным пассивным кроссовером. Для трех водителей это известно как пассивный кроссовер с 3 путями.

Он называется «пассивным», так как динамик не требует дополнительного источника питания. Еще одно решение, с которым вы можете столкнуться, – это конструкция активного кроссовера, которая включает разделение сигнала перед усилением, при этом каждая специализированная акустическая система имеет усилитель, требующий включения динамиков.

Обратите внимание, что этот калькулятор применим только к конструкциям пассивного кроссовера.Для двухполосного кроссовера у вас есть фильтр кроссовера низких частот и фильтр кроссовера высоких частот.

Фильтр нижних частот пропускает частоты меньше определенного значения, в то время как фильтр верхних частот пропускает только более высокие частоты. Частота кроссовера – это то место, где фильтр нижних частот начинает затухать, а фильтр верхних частот начинает увеличивать амплитуду сигнала.

Типичное значение для частоты 2-полосного кроссовера – Гц. Фильтр типа Чебышева назван в честь Пафнутия Чебышева, потому что их математические характеристики получены из полиномов Чебышева.Фильтр PI – это фильтр, который состоит из последовательного элемента и двух параллельных элементов, соединенных в форме греческой буквы PI.

Фильтры Чебышева – это аналоговые или цифровые фильтры, имеющие более крутой спад и большую пульсацию полосы пропускания или пульсацию полосы задерживания, чем фильтры Баттерворта. Фильтры Чебышева обладают тем свойством, что они минимизируют ошибку между идеализированной характеристикой фильтра и фактической во всем диапазоне фильтра, но с колебаниями в полосе пропускания.

Фильтры Чебышева обеспечивают более резкое затухание за пределами точки -3 дБ.

Калькулятор фильтра нижних частот

Фильтры Чебышева более чувствительны к допускам компонентов, чем фильтры Баттерворта. Для фильтров четного порядка вся пульсация превышает нормированный по постоянному току отклик усиления полосы пропускания, поэтому отсечка составляет 0 дБ.

Для фильтров нечетного порядка вся пульсация ниже нормированного по постоянному току отклика усиления полосы пропускания, поэтому отсечка составляет – пульсация дБ. Фильтр нижних частот – это фильтр, который пропускает низкочастотные сигналы, но ослабляет сигналы с частотами выше частоты среза.

Введите значение, выберите единицу измерения и нажмите «Рассчитать». Результат будет отображен. Введите свои значения :. Частота среза :. Импеданс Z 0:. Частотная характеристика Пульсация :.

Количество компонентов :. Введите условия поиска. Отправить форму поиска. Фильтр нижних частот пропускает только сигналы ниже своей частоты среза и ослабляет компоненты над ним. В дополнение к формулам вам могут помочь несколько калькуляторов низких частот.

Инструмент для проектирования фильтров нижних частот RLC

Низкочастотный фильтр обозначает компонент в электротехнике, который ослабляет или блокирует высокие частоты и позволяет низким частотам проходить в значительной степени беспрепятственно.Также широко используется термин фильтр нижних частот. Термин пассивный просто означает, что схема фильтра нижних частот построена без усилительного элемента.

При использовании операционного усилителя имеем активный НЧ. Фильтр нижних частот используется, когда нежелательны быстрые и резкие изменения напряжения на выходе. Он используется, например, в конструкции низкочастотных динамиков для улучшения их акустики.

Специалисты различают ФНЧ 1-го порядка и ФНЧ 2-го порядка.Мы объясняем элементы каждого фильтра нижних частот, как он работает и как рассчитать фильтр нижних частот. Поскольку это очень сложные вычисления, мы также предоставляем калькулятор фильтра нижних частот.

Фильтр нижних частот первого порядка состоит из последовательно соединенных резистора и конденсатора. Это важно, потому что в противном случае это фильтр высоких частот. В следующем разделе мы хотим рассчитать RC-фильтр нижних частот и пролить свет на передаточную функцию фильтра нижних частот первого порядка.

Это связано с тем, что измененное входное напряжение на короткое время проходит через конденсатор, потому что сначала нарастает емкостное сопротивление конденсатора.Как только емкостное реактивное сопротивление достигает нового значения, выходное напряжение больше не изменяется. С другой стороны, при синусоидальном входном напряжении мы получаем ослабленное выходное напряжение. Затухание сильно зависит от частоты из-за медленно развивающегося емкостного реактивного сопротивления конденсатора.

По мере увеличения входной частоты увеличивается и разница между входным и выходным напряжениями. При работе с частотой среза расчет частоты среза для RC-фильтра нижних частот выполняется по следующей формуле:С помощью онлайн-калькулятора вы можете рассчитать необходимые компоненты для желаемой частоты среза.

Если вместо конденсатора используется катушка, можно также построить фильтр нижних частот первого порядка. Однако для этого выходное напряжение должно быть отведено параллельно резистору. Принцип работы прямо противоположный: чем выше частота, тем большая доля напряжения падает на катушке. Онлайн-калькулятор помогает рассчитать необходимые элементы конструкции для соответствующей частоты среза.

Низкочастотный фильтр второго порядка также состоит из двух компонентов. В фильтре нижних частот 2-го порядка катушка последовательно соединена с конденсатором, поэтому этот фильтр нижних частот также называется LC-фильтром нижних частот.

Used gtx 1080 ftw

Таким образом, структура идентична низкочастотному фильтру 1-го порядка, это только омическое сопротивление, замененное на катушку. Низкочастотный проход 2-го порядка в основном выполняет ту же функцию, что и его аналог 1-го порядка, но имеет вдвое больший наклон. Так низкие частоты могут возникать, в то время как высокие частоты фильтруются вдвое эффективнее.Фильтр типа Баттерворта впервые описал британский инженер Стивен Баттерворт.

Тройниковый фильтр – это фильтр, который имеет два последовательных элемента и параллельный элемент, соединенные в форме буквы T. Фильтр Баттерворта характеризуется плоской характеристикой постоянного усиления в средней полосе цепи и спадом 20 дБ на декаду. скорость для каждого полюса, содержащегося в цепи. Фильтры Баттерворта называются фильтрами с максимально плоской характеристикой амплитуды, оптимизированными для равномерности усиления в полосе пропускания.

Затухание составляет -3 дБ на частоте среза. Выше частоты среза затухание составляет дБ. Фильтр Баттерворта – единственный фильтр, который сохраняет ту же форму для более высоких порядков, в то время как другие разновидности фильтров Бесселя, Чебышева, эллиптического имеют разные формы для более высоких порядков. Фильтр нижних частот – это фильтр, который пропускает низкочастотные сигналы, но ослабляет сигналы с частотами выше частоты среза.

Введите значение, выберите единицу измерения и нажмите «Рассчитать». Результат будет отображен.Введите свои значения :. Частота среза :. Импеданс Z 0:. Количество компонентов :.

Введите условия поиска. Заполните форму поиска. Но как убедить клиентов оставить отзыв о вашей компании? Большое значение имеет высокий уровень обслуживания клиентов. Счастливые клиенты оставят лучшие отзывы. Эти обзоры послужат социальным подтверждением концепции.

Расширение их возможностей увеличит шансы, что они оставят отзыв. Ваш веб-сайт не должен быть единственным местом, где покупатели могут оставлять отзывы о ваших товарах.Сделайте себя доступным на платформах, которые, как вы знаете, люди используют ежедневно. Обзоры в Facebook могут сделать ваш бизнес более привлекательным из-за его популярности. Это позволяет добиться двух вещей. Обзор увидят другие пользователи Facebook. Это может побудить потенциальных клиентов щелкнуть ваш профиль.

Привлечь потенциальных потребителей на вашу страницу – это половина дела. С вашей стороны потребовалось совсем немного усилий и почти ничего не стоило. Привлечение большего количества людей на вашу страницу в Facebook также может увеличить посещаемость вашего сайта.С учетом сказанного, вам все равно нужно присутствовать на этих других платформах.

Не все из них актуальны для каждого бизнеса. Однако местному ресторану потребуется присутствие на этой платформе. Попросите клиентов оставить отзыв о ваших продуктах.

Amazon делает то же самое. Их платформа немного отличается. Спросите их также прямо в вашем магазине. Это отличная стратегия для владельцев малого бизнеса и ресторанов. Клиенты, у которых был негативный опыт, скорее всего, изо всех сил будут высказывать свое мнение.

Итак, как заставить клиентов, у которых был хороший опыт, поделиться своим мнением. Вам нужно сделать это как можно проще. Разместите на своем веб-сайте ссылку, по которой клиенты будут напрямую переходить на платформу для обзора. Вашему клиенту придется перейти на веб-сайт TripAdvisor в отдельном окне просмотра. Найдите свой бизнес. Независимо от того, рассматриваете ли вы NSX или опытного пользователя, в этом сеансе есть что-то для вас.

Проводка топливного насоса Gmc sierra 3500

Он является признанным специалистом по программно-определяемым центрам обработки данных и VMware с ключевыми сертификатами, включая VCAP для нескольких дорожек и VCIX-NV.Джон обладает более чем 19-летним опытом работы в сфере технологий, и его специальности включают виртуализацию сети и серверов, облачные вычисления, сети и корпоративное хранилище.

Мы также обсудим подходы к устранению неполадок, которые помогут вам выявить, решить и избежать проблем во время установки и обновления. Мы предоставим обзор функции vCenter Server Appliance Migration в vSphere 6. Мы также поделимся основными проблемами, с которыми вы можете столкнуться, способами их выявления и решения, а также поделимся советами о том, как их избежать во время миграции.

Вы получите общее представление о функциях vSphere 6. Мы также обсудим последнюю версию vSphere 6. Это практическое занятие, призванное помочь вам и вашей организации реализовать все преимущества обновления существующей инфраструктуры vSphere до vSphere. 6. Присоединяйтесь к нам для ознакомления с новыми функциями, включая ярлыки приложений и выделенную поддержку мгновенного клонирования.

Вы также узнаете, как Site Recovery Manger выполняет аутентификацию с помощью Platform Services Controller и vCenter Server.Правильный подход к подготовке повысит ваши шансы сдать экзамен с первой попытки. Присоединяйтесь к Полу Соренсену, чтобы получить советы, рекомендации и ресурсы, которые сэкономят вам время и силы во время учебы, практики и подготовки, включая несколько шагов, которые вы никогда не должны пропустить, когда будете готовиться к следующему экзамену.

Какова роль каждого компонента vRealize Automation. Какие инструменты доступны для устранения неполадок vRealize Automation. Советы по поиску и устранению неисправностей Как отслеживать машинный запрос с помощью журналов vRealize Automation.Распространенные проблемы vRealize Automation и способы их решения. Мы также расскажем, как идентифицировать эти проблемы по их симптомам и на основе анализа сообщений журнала.

А также объясните, как решить эти проблемы, а в некоторых случаях как их обойти, если решение недоступно. Мы рассмотрим конкретные области, такие как PSOD, база данных, установка, обновление, миграция и многое другое. Докладчик выделит основные компоненты решения и предложит несколько сценариев развертывания.Кроме того, он обсудит передовой опыт и предложит некоторые способы устранения некоторых проблем интеграции.

Присоединяйтесь к нам, чтобы получить обзор интерфейса командной строки (CLI) с шагами и командами, которые вы можете использовать в процессе устранения неполадок. Мы поделимся советами по устранению неполадок в критических областях вашей среды NSX. Кроме того, мы обсудим последнюю версию vSphere 6. Этот практический курс разработан, чтобы помочь вам и вашей организации реализовать все преимущества обновления существующей инфраструктуры vSphere до vSphere 6.Мы также выделим методы устранения неполадок, обзоры архитектуры, совместимость и совместимость с VMware, обеспечивающие оптимальную настройку кластеров VSAN с точки зрения емкости и производительности, что можно ожидать увидеть при возникновении проблем в кластере Virtual SAN, а также способы их решения. как обновления и создание группы дисков.

Расчет lc фильтра низких частот: Автоматизированный расчет пассивных LC-фильтров

1.3. Описание lc-фильтров

Расчет фильтра нижних частот (Курсовая работа)

Библиография Бессонова, Елена Анатольевна, диссертация по теме Радиотехника, в том числе системы и устройства телевидения

Lc фильтр для шим – Вэб-шпаргалка для интернет предпринимателей!

Фильтрация ШИМ в сигнальных цепях

Калькулятор ШИМ-фильтра на RC-цепочке

Фильтрация ШИМ в силовых цепях

Калькулятор силового ШИМ-фильтра на LC-контуре

Обзор продукции: синусный фильтр для преобразователя частоты

Синусные фильтры и моторные дроссели открытого типа

Синусные фильтры в корпусе

Сетевые (входные) дроссели открытого исполнения

Входные дроссели (линеаторы) в корпусе

Назначение синусного фильтра

Формулы расчета синусного фильтра

Порядок выбора параметров элементов синусного фильтра

Практическая реализация синусных фильтров

Список литературы

Рекомендуем к прочтению

Расчет фильтра нижних частот

Lc последовательный фильтр с трансформаторной связью выход

Самый простой LC-фильтр

Контуры с индуктивной и емкостной связью

Подача сигнала последовательно

Т-образный и П-образный фильтры

Электротехника: On-line расчет сглаживающего LC-фильтра.

Руководство по цепям LC – ФИЛЬТРЫ

EMC Filters Comparison Part I: CL and LC Filters

Таблица 1: Моделируемые и измеренные вносимые потери для фильтра CL

Таблица 2: Моделируемые и измеренные вносимые потери для LC-фильтра

Правильный выбор ВЧ-фильтра низких частот

Фильтр | RC фильтр | Low High Pass | RC Notch | LC фильтр | Roll-off

Нравится:

ФНЧ

Что такое фильтры нижних частот?

Фильтр нижних частот состоит из двух L-цепей

Теорема Бартлетта о делении пополам, примененная к фильтрам нижних частот

Переход от сетевых фильтров нижних частот с двойной L к Pi

Насколько полезна вся эта информация для фильтров нижних частот?

Пользовательский поиск Google

Есть вопросы по этой теме?

СВЯЗАННЫЕ ТЕМЫ, КАСАЮЩИЕСЯ НИЗКОПРОХОДНЫХ ФИЛЬТРОВ

Ссылка на эту страницу

Фильтр нижних частот для синусоидальных инверторов

1. передаточная функция

2. Параметры R, L, C

3. Тесты

Калькулятор ЖК-фильтра нижних частот 2-го порядка. RC фильтр низких частот

Калькулятор фильтра нижних частот

Инструмент для проектирования фильтров нижних частот RLC

Больше новостей

Добавить комментарий Отменить ответ