Магнитек – Пример простейшего расчёта электромагнита
Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь. Магнитная цепь характеризуется величиной магнитной индукции — В, которая зависит от напряженности поля и магнитной проницаемости материала. Именно поэтому сердечники электромагнитов делают из железа, обладающего высокой магнитной проницаемостью.
При конструировании электромагнитов весьма желательно получить большой силовой поток. Добиться этого можно, если уменьшить магнитное сопротивление. Для этого надо выбрать магнитопровод с наименьшей длиной пути силовых линий и с наибольшим поперечным сечением, а в качестве материала — железоматериал с большой магнитной проницаемостью.
Другой путь увеличения силового потока путем увеличения ампервитков не является приемлемым, так как в целях экономии проволоки и питания следует стремиться к уменьшению ампервитков.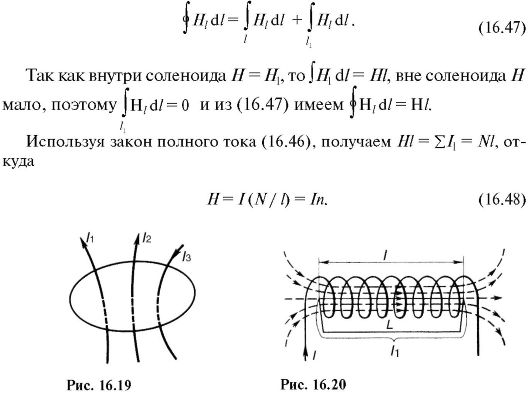
Обычно расчеты электромагнитов делаются по специальным графикам. В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ам-первитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке 4,а и сделанного из железа самого низкого качества.
Рассматривая график намагничивания железа, нетрудно убедиться, что наиболее выгодной является магнитная индукция в пределах от 10 000 до 14 000 силовых линий на 1 см2, что соответствует от 2 до 7 ампервиткам на 1 см. Для намотки катушек с наименьшим числом витков и более экономичных в смысле питания для расчетов надо принимать именно эту величину (10 000 силовых линий на 1 см2 при 2 ампервитках на 1 см длины). В этом случае расчет может быть произведен следующим образом. Так, при длине магнитопровода Z=/1-)-/2, равной 20 см -f- 10 см = 30 см, потребуется 2×30=60 ампервитков.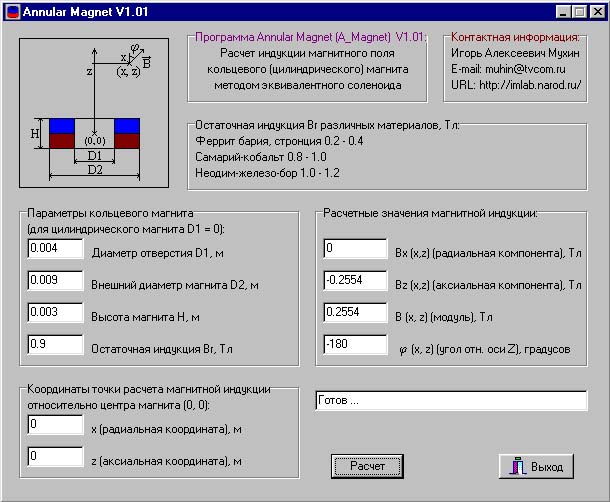 25 кг. При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но, и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы.
25 кг. При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но, и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы.
Далее производится расчет катушки электромагнита. В нашем примере подъемная сила в 25 кг обеспечивается 60 ампервитками. Рассмотрим, какими средствами можно получить произведение N-J—60 ампервиткам.
Очевидно, этого можно добиться либо путем использования большого тока при малом количестве витков катушки, например 2 а и 30 витков, либо путем увеличения числа витков катушки при уменьшении, тока, например 0,25 а и 240 витков. Таким обра-1 зом, чтобы электромагнит имел подъемную силу в 25 кг, на его сердечник можно намотать, и 30 витков и 240 витков, но при этом изменить величину питающего тока. Конечно, можно выбрать и другое соотношение.
Однако изменение величины тока в больших пределах не всегда возможно, так как оно обязательно потребует изменения диаметра применяемой проволоки. Так, при кратковременной работе (несколько минут) для проводов диаметром до 1. мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной 5 A/мм2. В нашем примере проволока должна быть следующего сечения: для тока в 2A — 0,4 мм2, а для тока в 0,25A – 0,05 мм2.
Так, при кратковременной работе (несколько минут) для проводов диаметром до 1. мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной 5 A/мм2. В нашем примере проволока должна быть следующего сечения: для тока в 2A — 0,4 мм2, а для тока в 0,25A – 0,05 мм2.
Каким же из этих проводов следует производить обмотку?
С одной стороны, выбор диаметра провода может определяться имеющимся у руководителя ассортиментом проволоки, с другой — возможностями источников питания как по току, так и по напряжению. Действительно, две катушки, одна из которых изготовлена из толстой проволоки в 0,7 мм и с небольшим числом витков — 30, а другая — из проволоки в 0,2 мм и числом витков 240, будут иметь резко различное сопротивление.
Зная диаметр проволоки и ее длину, можно легко определить сопротивление. Длина проволоки равна произведению общего числа витков на длину одного из них (среднюю): l=Nxlt где lt — длина одного витка, равная 3,14 x Д.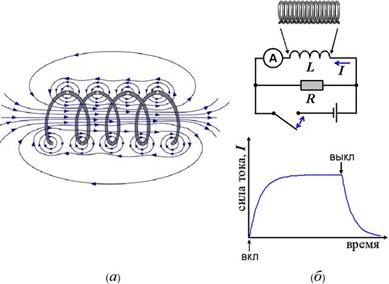 В нашем примере Д = 2 см, и 1г x 6,3 см. Следовательно, для первой катушки длина провода будет 30 x 6,3 = 190 см, а для второй — 240 X 6,3 = 1 512 см. Сопротивления обмоток будут также различными.
В нашем примере Д = 2 см, и 1г x 6,3 см. Следовательно, для первой катушки длина провода будет 30 x 6,3 = 190 см, а для второй — 240 X 6,3 = 1 512 см. Сопротивления обмоток будут также различными.
Пользуясь законом Ома, нетрудно вычислить необходимое напряжение. Так, для создания в обмотках тока в 2A необходимое напряжение равно 0,2B, а для тока в 0,25A — 2,5B.
Таким образом, для питания первой катушки достаточно одного элемента или аккумулятора, причем для понижения напряжения приходится включать реостат; для питания второй катушки необходимо взять два элемента, соединяя их последовательно. Ясно, что во втором случае имеется меньше потерь электроэнергии и обмотка получается более выгодной.
Анализ полученных результатов позволяет сделать еще такой вывод: диаметр проволоки подбирается так, чтобы питание катушки можно было производить только от одного элемента (или аккумулятора) без каких-либо реостатов, где энергия тратится непроизвольно. Нетрудно заметить, что при диаметре проволоки приблизительно 0,4 мм и силе тока около 0,4 а нужное напряжение для питания катушки составит 1,3-г-1,4 в,-то-есть как раз напряжение одного элемента.
Таков элементарный расчет электромагнитов.
Все своими руками Электромагниты | Все своими руками
Однажды, в очередной раз, перелистывая книгу, которую нашел у мусорного бачка, обратил внимание на простой, приблизительный расчет электромагнитов. Титульный лист книги показан на фото1.
Вообще их расчет это сложный процесс, но для радиолюбителей, расчет, приведенный в этой книге, вполне подойдет. Электромагнит применяется во многих электротехнических приборах. Он представляет собой катушку из проволоки, намотанной на железный сердечник, форма которого может быть различной. Железный сердечник является одной частью магнитопровода, а другой частью, с помощью которой замыкается путь магнитных силовых линий, служит якорь. Магнитная цепь характеризуется величиной магнитной индукции — В, которая зависит от напряженности поля и магнитной проницаемости материала. Именно поэтому сердечники электромагнитов делают из железа, обладающего высокой магнитной проницаемостью.
Ф = магнитодвижущая сила (Ем) • магнитное сопротивление (Rм)
Здесь Ем = 1,3•I•N, где N — число витков катушки, а I — сила текущего по катушке тока в амперах. Другая составляющая:
Rм = L/M•S, где L — средняя длина пути силовых магнитных линий, М — магнитная проницаемость, a S — поперечное сечение магнитопровода. При конструировании электромагнитов весьма желательно получить большой силовой поток. Добиться этого можно, если уменьшить магнитное сопротивление. Для этого надо выбрать магнитопровод с наименьшей длиной пути силовых линий и с наибольшим поперечным сечением, а в качестве материала — железоматериал с большой магнитной проницаемостью.
 Другой путь увеличения силового потока путем увеличения ампервитков не является приемлемым, так как в целях экономии проволоки и питания следует стремиться к уменьшению ампервитков. Обычно расчеты электромагнитов делаются по специальным графикам. В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ампервитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке 1,а и сделанного из железа самого низкого качества.
Другой путь увеличения силового потока путем увеличения ампервитков не является приемлемым, так как в целях экономии проволоки и питания следует стремиться к уменьшению ампервитков. Обычно расчеты электромагнитов делаются по специальным графикам. В целях упрощения в расчетах мы будем также пользоваться некоторыми выводами из графиков. Предположим, требуется определить ампервитки и силовой поток замкнутого железного магнитопровода, изображенного на рисунке 1,а и сделанного из железа самого низкого качества. Рассматривая график (к сожалению я его в приложении не нашел) намагничивания железа, нетрудно убедиться, что наиболее выгодной является магнитная индукция в пределах от 10 000 до 14 000 силовых линий на 1 см2, что соответствует от 2 до 7 ампервиткам на 1 см. Для намотки катушек с наименьшим числом витков и более экономичных в смысле питания для расчетов надо принимать именно эту величину (10 000 силовых линий на 1 см2 при 2 ампервитках на 1 см длины). В этом случае расчет может быть произведен следующим образом.
Если диаметр D сердечника (Рис.1,в)примем равным 2 см, то его площадь будет равна: S = 3,14xD2/4 = 3,14 см2. 0тсюда возбуждаемый магнитный поток будет равен: Ф = B х S= 10000 x 3,14=31400 силовых линий. Можно приближенно вычислить и подъемную силу электромагнита (P). P = B2 • S/25 • 1000000 = 12,4 кг. Для двухполюсного магнита этот результат следует удвоить. Следовательно, Р=24,8 кг = 25 кг. При определении подъемной силы необходимо помнить, что она зависит не только от длины магнитопровода, но и от площади соприкосновения якоря и сердечника. Поэтому якорь должен точно прилегать к полюсным наконечникам, иначе даже малейшие воздушные прослойки вызовут сильное уменьшение подъемной силы. Далее производится расчет катушки электромагнита. В нашем примере подъемная сила в 25 кг обеспечивается 60 ампервитками. Рассмотрим, какими средствами можно получить произведение N•J = 60 ампервиткам.

Очевидно, этого можно добиться либо путем использования большого тока при малом количестве витков катушки, например 2 А и 30 витков, либо путем увеличения числа витков катушки при уменьшении тока, например 0,25 А и 240 витков. Таким образом, чтобы электромагнит имел подъемную силу в 25 кг, на его сердечник можно намотать и 30 витков и 240 витков, но при этом изменить величину питающего тока. Конечно, можно выбрать и другое соотношение. Однако изменение величины тока в больших пределах не всегда возможно, так как оно обязательно потребует изменения диаметра применяемой проволоки. Так, при кратковременной работе (несколько минут) для проводов диаметром до 1 мм допустимую плотность тока, при которой не происходит сильного перегревания провода, можно принять равной 5 а/мм2. В нашем примере проволока должна быть следующего сечения: для тока в 2 а — 0,4 мм2, а для тока в 0,25 а — 0,05 мм2, диаметр проволоки будет 0,7 мм или 0,2 мм соответственно. Каким же из этих проводов следует производить обмотку? С одной стороны, выбор диаметра провода может определяться имеющимся ассортиментом проволоки, с другой — возможностями источников питания, как по току, так и по напряжению.
Таков элементарный расчет электромагнитов. Конструируя электромагниты, надо не только производить указанный расчет, но и уметь выбрать материал для сердечника, его форму, продумать технологию изготовления.
 Удовлетворительными материалами для изготовления сердечников в кружках являются прутковое железо (круглое и полосовое) и различные. железные изделия: болты, проволока, гвозди, шурупы и т. д. Чтобы избежать больших потерь на токах Фуко, сердечники для приборов переменного тока необходимо собирать из изолированных друг от друга тонких листов железа или проволоки. Для придания железу «мягкости» его необходимо подвергать отжигу. Большое значение имеет и правильный выбор формы сердечника. Наиболее рациональные из них кольцевые и П-образные. Некоторые из распространенных сердечников показаны на рисунке 1.
Удовлетворительными материалами для изготовления сердечников в кружках являются прутковое железо (круглое и полосовое) и различные. железные изделия: болты, проволока, гвозди, шурупы и т. д. Чтобы избежать больших потерь на токах Фуко, сердечники для приборов переменного тока необходимо собирать из изолированных друг от друга тонких листов железа или проволоки. Для придания железу «мягкости» его необходимо подвергать отжигу. Большое значение имеет и правильный выбор формы сердечника. Наиболее рациональные из них кольцевые и П-образные. Некоторые из распространенных сердечников показаны на рисунке 1.Просмотров:38 984
Расчёт электромагнитов постоянного тока |
Электромагниты получили широкое распространение в различных областях промышленности. В настоящее время существуют электромагниты массой от нескольких десятков грамм до нескольких тонн.
Применение информационных технологий в расчётах электрических магнитов постоянного тока позволяет быстро и качественно производить необходимые расчёты с минимальными затратами интеллектуального труда и времени инженерного персонала и дает возможность инженерному персоналу сосредоточиться на решении более сложных задач.
Разработанная программа предназначена для расчёта электромагнитов постоянного тока броневого типа. Исходными данными для работы программы являются: напряжение питания, сила тяги электромагнита, его геометрические параметры, марка стали и обмоточного провода, а также величины воздушного и паразитного зазоров.
В результате работы программы производятся выбор и расчёт обмотки электромагнита, определяются число витков и диаметр провода в зависимости от его марки и способа укладки, а также рассчитываются мощность, потребляемая этой обмоткой, и температура её нагрева, делается вывод о работоспособности электромагнита.
Программа позволяет производить расчёт магнитных цепей для наиболее широко используемых марок сталей с учётом их аппроксимированных кривых намагничивания.
Компьютерная программа позволяет также протестировать обмотку, предложенную пользователем, определить температуру ее нагрева и допустимое время включения в сеть.
Программа разработана на языке программирования Delphi—5. 5 для операционной системы Windows 98 и выше, имеет удобный графический интерфейс и оригинальный дизайн.
5 для операционной системы Windows 98 и выше, имеет удобный графический интерфейс и оригинальный дизайн.
Разработанная программа позволяет, в случае если исходные данные заданы корректно, смоделировать работу электромагнита и продемонстрировать процесс притяжения якоря после подачи напряжения на его обмотку. Если расчёт магнитной цепи или обмотки не корректен, то появится сообщение о необходимости скорректировать исходные данные. Программа предназначена для сотрудников научно-исследовательских и проектных институтов, а также инженеров, занимающихся расчетами электромагнитов.
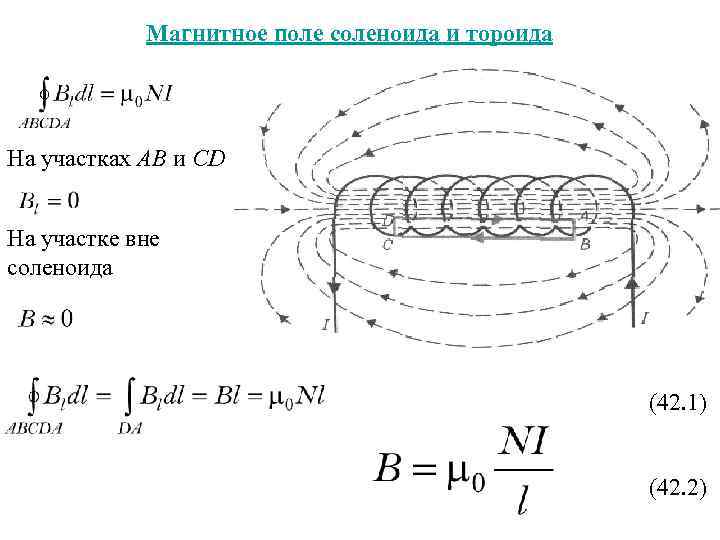
Статьи по теме10-б. Соленоид и электромагнит
§ 10-б. Соленоид и электромагнит
В предыдущем параграфе мы изучали магнитные поля прямых проводников. Рассмотрим теперь проводник, свёрнутый в виде спирали, по которому идёт ток – соленоид (греч. «солен» – трубка). Расположим вдоль его оси лист картона и посыплем его железными опилками. На рисунке отчётливо видно, что опилки выстроились в виде замкнутых линий, наиболее часто расположенных внутри витков соленоида. Следовательно, магнитное поле внутри соленоида сильнее, чем вне его.
Следовательно, магнитное поле внутри соленоида сильнее, чем вне его.
Намотаем теперь проволочную спираль на каркасе, располагая витки вплотную друг к другу – мы получим катушку (см. рисунки ниже). Включим ток и поднесём к катушке мелкие гвоздики – часть из них примагнитится. Если в неё вставить железный или стальной стержень – сердечник, то примагнитится заметно больше гвоздиков. Другими словами, происходит усиление магнитного поля.
Катушка из изолированной проволоки с железным сердечником внутри называется электромагнитом. При прочих равных условиях магнитное поле электромагнита всегда сильнее магнитного поля соленоида или катушки без сердечника.
Объясним усиление магнитного поля. Сначала ток намагничивает сердечник. Намагнитившись, он создаёт собственное поле, которое, складываясь с полем соленоида, образует новое, более сильное поле. Об этом мы судим по количеству притянувшихся гвоздиков.
Рассмотрим другие причины, влияющие на силу магнитного действия электромагнита.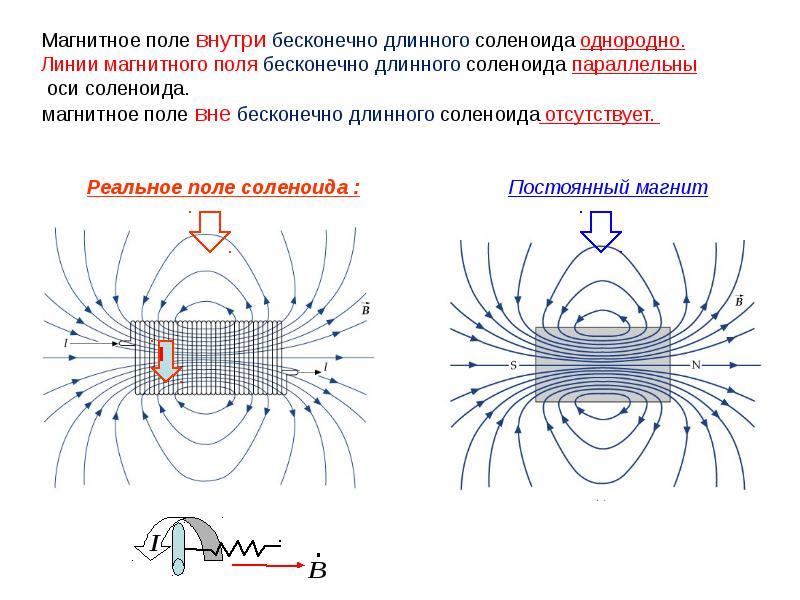 Вспомним, что для наблюдения силовых линий поля прямого проводника (см. § 10-а) мы использовали ток силой 5–10 А. При меньшей силе тока опилки будут плохо намагничиваться, и картинка получится нечёткой. Следовательно, магнитное поле электромагнита усиливается при увеличении силы тока в его проводнике.
Вспомним, что для наблюдения силовых линий поля прямого проводника (см. § 10-а) мы использовали ток силой 5–10 А. При меньшей силе тока опилки будут плохо намагничиваться, и картинка получится нечёткой. Следовательно, магнитное поле электромагнита усиливается при увеличении силы тока в его проводнике.
Кроме того, при одной и той же силе тока поле электромагнита можно усилить, увеличив число витков проводника в его обмотке. Это объясняется тем, что магнитные поля, создаваемые каждым из витков, накладываются друг на друга и тем самым образуют новое, более сильное магнитное поле.
Познакомимся с ещё одним свойством электромагнита или соленоида – запасать электроэнергию. Проделаем опыт (см. схему). Две одинаковые лампы подключены параллельно к источнику тока. Верхняя лампа – через реостат, а нижняя – через электромагнит или соленоид. У них есть общее название – катушка индуктивности.
При замыкании выключателя лампа, соединённая с катушкой индуктивности, загорается позже, чем лампа, соединённая с реостатом (левый рисунок).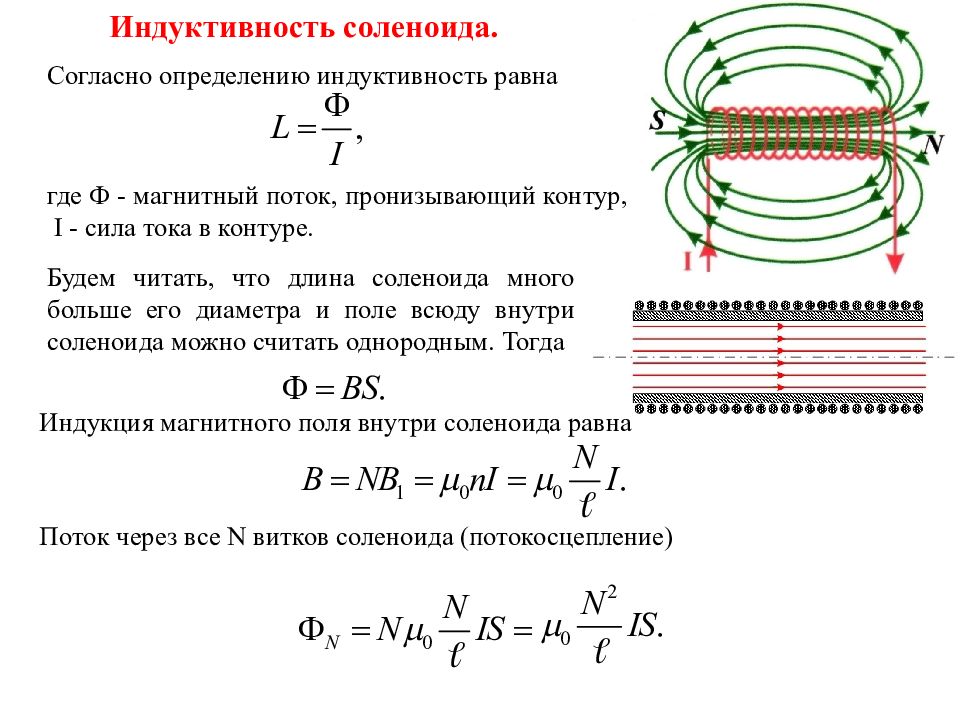 Теперь разомкнём выключатель. В этот момент обе лампы не погаснут, а вспыхнут ещё ярче, правда, на очень короткое время (правый рисунок).
Теперь разомкнём выключатель. В этот момент обе лампы не погаснут, а вспыхнут ещё ярче, правда, на очень короткое время (правый рисунок).
Более позднее загорание ближней к нам лампы объясняется так. При включении тока его энергия идёт не только на нагревание спирали лампы, но и на создание магнитного поля вокруг электромагнита. Однако по прошествии некоторого времени энергия тока будет целиком превращаться в теплоту, разогревая спираль лампочки настолько, что она начинает светиться.
При размыкании цепи ток в нижнем её проводе прекращается, и с этого момента реостат, катушка индуктивности и обе лампочки оказываются соединёнными друг с другом последовательно (мы это показали красным цветом на схеме). Поскольку лампочки кратковременно ярко вспыхнули, значит, в красной части цепи ненадолго возник источник тока. В его роли выступила катушка индуктивности. Магнитное поле вокруг неё стало исчезать, передавая свою энергию электронам в проводе, поэтому они приходят в движение. Это значит, что катушка становится источником тока.
Это значит, что катушка становится источником тока.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxКак спроектировать катушку соленоида постоянного тока?
Электромагнитный клапан становится важным элементом комплектного оборудования и бытового электроприбора. Электромагнитный клапан превращается в серию электротехнической продукции. Согласно системе питания, электромагнитный клапан можно разделить на электромагнитный клапан переменного тока, электромагнитный клапан постоянного тока, электромагнитный клапан с фиксацией; согласно заявкам, есть пневматический электромагнитный клапан и электромагнитный клапан для регулирования расхода, электромагнитный клапан для холодильного оборудования, паровой электромагнитный клапан, импульсный электромагнитный клапан; в зависимости от окружающей среды бывают электромагнитные клапаны общего типа, наружного типа и взрывозащищенные. Эта статья дает решение, как быстро спроектировать катушку соленоида? Катушка соленоида играет основную роль в электромагнитном клапане, в основном, качество соленоидной катушки определяет качество электромагнитного клапана. Конкретные шаги проектирования катушки соленоида, как показано ниже.
Эта статья дает решение, как быстро спроектировать катушку соленоида? Катушка соленоида играет основную роль в электромагнитном клапане, в основном, качество соленоидной катушки определяет качество электромагнитного клапана. Конкретные шаги проектирования катушки соленоида, как показано ниже.
Подтвердите проектные требования
На основе соответствия двум основным свойствам, а также без изменений диаметра сердечника, размера затеняющей катушки, хода сердечника, только расчетных витков на катушку и диаметра проволоки. При номинальном рабочем напряжении, оригинальном формирователе катушки, нам необходимо подтвердить основные свойства, которых должна достичь катушка соленоида.
Конструкция и расчет
Оборотов на катушку, расчет
Расчет катушки соленоида: при изменении тока через катушку соленоида, чтобы электромагнитная сила оставалась неизменной, ампер-витки (IW) должны быть зафиксированы таким образом, чтобы количество витков на катушку составляло:
Вт 2 = Вт 1 × I1 / I2
Расчет плотности тока
Выберите две существующие электромагнитные катушки, которые в основном соответствуют требованиям. Например, есть катушка соленоида переменного тока 220 В, нагружающая постоянный ток и измеряющая его минимальное напряжение, нагрузка 1.1-кратное номинальное напряжение и измерьте повышение температуры, разница между минимальным рабочим напряжением и расчетным минимальным рабочим напряжением составляет более 30%, его повышение температуры составляет менее 30% по сравнению с расчетным. Расчет плотности тока формулируется следующим образом:
Например, есть катушка соленоида переменного тока 220 В, нагружающая постоянный ток и измеряющая его минимальное напряжение, нагрузка 1.1-кратное номинальное напряжение и измерьте повышение температуры, разница между минимальным рабочим напряжением и расчетным минимальным рабочим напряжением составляет более 30%, его повышение температуры составляет менее 30% по сравнению с расчетным. Расчет плотности тока формулируется следующим образом:
I Дж = I / πr 2
r: радиус токоподвода; I: рабочий ток при номинальном напряжении.
Расчет силы постоянного тока на соленоиде
F = 62,8 × (IW) 2 [πr 2 / δ 2 + g / μ o (z / l c ) 2 ] × 10 -8 [2]
В соответствии с требованиями дизайна, мы можем получить, что значение в скобках является константой, поэтому мы устанавливаем его как k, окончательная формулировка показана ниже:
F = k (IW) 2
Из приведенной выше формулировки мы можем знать, что для сохранения катушки соленоида необходимо поддерживать значение IW.
- Если минимальное рабочее напряжение двух выбранных катушек меньше проектных требований, превышение температуры также меньше проектных требований, мы выбираем существующую соленоидную катушку;
- Если минимальное рабочее напряжение двух выбранных катушек больше проектных требований, повышение температуры также больше проектных требований, поэтому разработанная соленоидная катушка должна увеличивать значение диаметра провода и уменьшать количество витков на катушку;
- Если минимальное рабочее напряжение одной выбранной катушки меньше проектных требований, повышение температуры больше проектных требований, а другая катушка противоположна, для диаметра проволоки следует использовать значение между значениями диаметра проволоки двух выбранных катушек; количество витков на катушку определяется таким же образом.
Тест основных свойств продукта
В связи с практической необходимостью конструкции катушки соленоида, для проверки параметров конструкции катушки соленоида необходимо провести некоторые испытания основных свойств.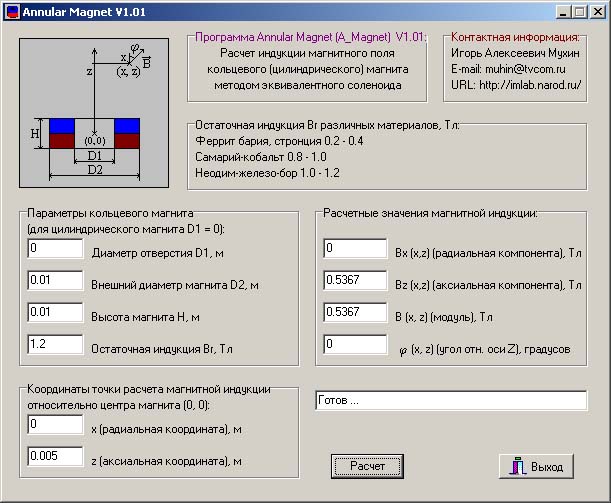 После того, как основные свойства достигают требований и каждое свойство катушки должно соответствовать промышленным стандартам.
После того, как основные свойства достигают требований и каждое свойство катушки должно соответствовать промышленным стандартам.
Заключение
Благодаря конструкции, которую мы сделали выше, мы получаем быстрый способ конструировать соленоидную катушку. Новый тип конструкции соленоидной катушки отличается быстротой и удобством, а также высокой надежностью.Эта новая конструкция соленоидной катушки не только в основном сокращает время от проектирования до производства, но и снижает стоимость испытаний продукта. По результатам теста мы можем убедиться, что новый дизайн соответствует требованиям быстрого проектирования и параметризации.
Kaidi специализируется на производстве соленоидных катушек более 40 лет. Мы производим технологии и современное производственное оборудование. Соленоиды Rexroth, Yuken и Vickers – наши популярные продукты. Кроме того, мы также предоставляем индивидуальные соленоиды в соответствии с потребностями клиентов.
Часто задаваемые вопросы о соленоиде постоянного тока| TDS Co.
 LTD./Top Page Соленоид работает под напряжением, а плунжер притягивается и намагничивается.
LTD./Top Page Соленоид работает под напряжением, а плунжер притягивается и намагничивается. Плунжер возвращается в исходное положение с помощью внешней нагрузки, такой как возвратная пружина.
Элементы, которые необходимо учитывать для освобождения плунжера, следующие.
(1) Ток
(2) Ход
(3) Остаточная удерживающая сила (остаточный магнетизм)
(4) Возвратная нагрузка
Ниже приводятся подробные пояснения.
(1) Ток
1 、 Убедитесь, что ток не течет.
Независимо от направления тока (+ или -), даже при небольшом токе, тяговое усилие соленоида может стать больше, чем обратная нагрузка.
2 、 Даже после отключения питания катушка генерирует противоэлектродвижущую силу из-за изменения тока, вызывая переходное явление.
Таким образом, текущий поток не будет нулевым в течение от нескольких до нескольких десятков миллисекунд.
В это время соленоид является магнитным и не возвращается, если обратная нагрузка меньше тягового усилия.
(2) Ход
Плунжер должен вернуться в исходное положение через некоторое время.
Когда ток для следующего рывка течет во время обратного движения, плунжер не может полностью вернуться, но будет вытянут.
(3) Остаточная удерживающая сила (остаточный магнетизм)
Магнетизм остается в металлических частях соленоидов даже после того, как протекающий ток становится равным нулю, что является остаточным магнетизмом, создающим удерживающую силу.
Когда остаточная удерживающая сила превышает возвратную нагрузку, плунжер не возвращается.
Если монтажная часть соленоида сделана из железа, остаточная удерживающая сила станет еще больше из-за его остаточного магнетизма.
(4) Возвратная нагрузка
Возвратная нагрузка должна быть больше, чем (1) и (3), и особое внимание требуется для сценариев и ② ниже.
① Если ожидается трение между плунжером и его направляющей трубой или механическое трение, в зависимости от ориентации соленоида при работе в горизонтальном направлении.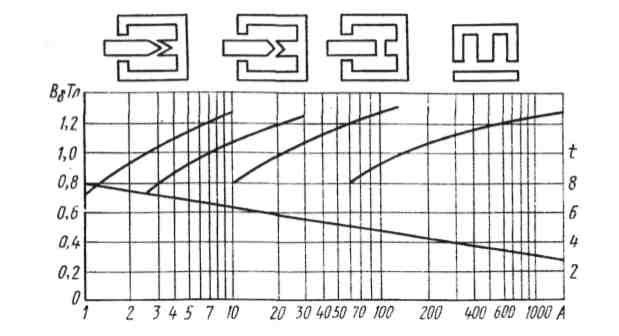
② Если соленоид установлен в приложении таким образом, чтобы его обратная нагрузка была меньше из-за того, что направление силы тяжести плунжера и направление обратной нагрузки различны.
Анализ влияния магнитного поля соленоида в системе передачи азимута
Согласно анализу факторов, влияющих на точность магнитооптической модуляции, описанной в принципе системы, известно, что решение статической Магнитное поле заключается в изучении магнитного поля в соленоиде.В этом разделе в основном описывается изучение размера, направления и распределения компонентов магнитного поля. Основываясь на исследовании статического магнитного поля соленоида, можно продолжить изучение магнитного поля соленоида, возбуждаемого переменным током.
Теоретический вывод магнитного поля
Устанавливается однослойный соленоид с тонкой плотно намотанной проволокой. Его радиус \ (a \), длина \ (2b \), количество витков \ (N \), приложен ток \ (I \), а плотность катушки определяется как \ (n = N / 2b \).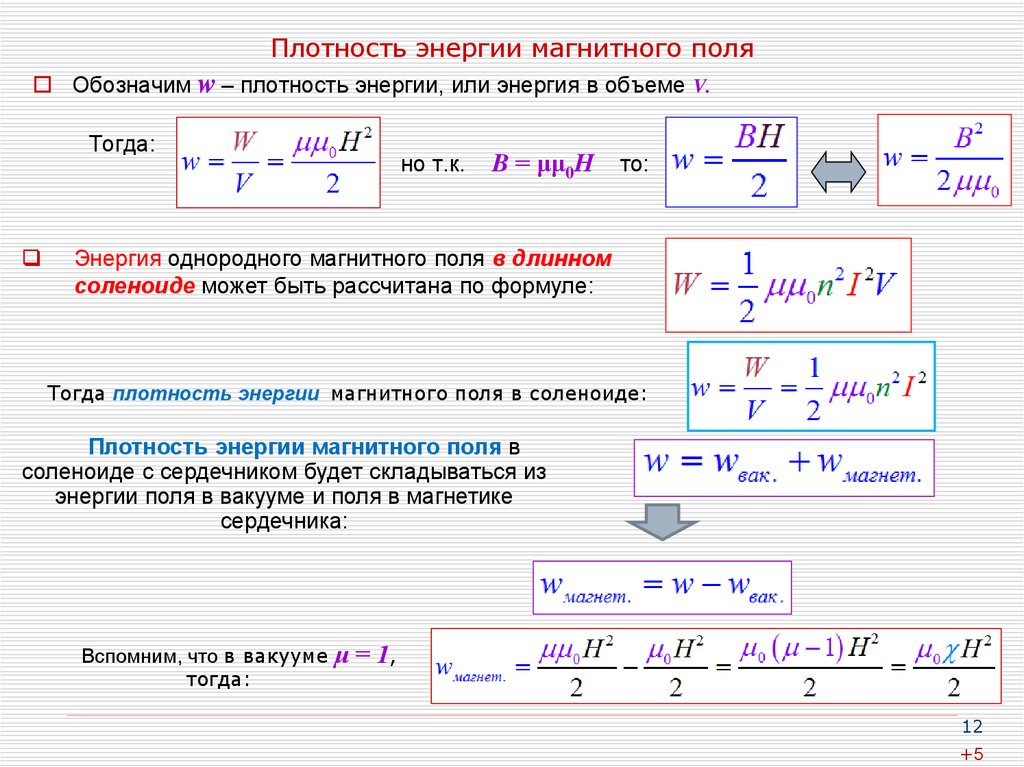 Центр соленоида берется за начало координат, а центральная ось берется за ось \ (z \), чтобы установить цилиндрическую систему координат \ (\ left ({r, \ varphi, z} \ right) \), как показано на рис. 2. Положительное направление оси \ (z \) и направление тока в катушке удовлетворяют соотношению правой спирали. Учитывая замкнутую обмотку, линейный ток эквивалентен поверхностному току по цилиндрической поверхности.
Центр соленоида берется за начало координат, а центральная ось берется за ось \ (z \), чтобы установить цилиндрическую систему координат \ (\ left ({r, \ varphi, z} \ right) \), как показано на рис. 2. Положительное направление оси \ (z \) и направление тока в катушке удовлетворяют соотношению правой спирали. Учитывая замкнутую обмотку, линейный ток эквивалентен поверхностному току по цилиндрической поверхности.
Принципиальная схема катушки соленоида.{\ prime} {\ mathbf {z}}}}}}}} \ right]. \\ \ end {собрано} $$
(10)
где \ (D \) – модуль векторной траектории, \ (\ mu_ {0} \) – проницаемость вакуума. На основании уравнения. Используя уравнение (10), можно получить компоненты магнитного поля соленоида в трех направлениях.
- 1.
Осевой компонент
Осевая составляющая магнитного поля соленоида
$$ B_ {z} \ left ({r, \ varphi, z} \ right) = \ frac {{\ mu_ {0} nIa}} {4 \ pi } \ int_ {- \ pi} ^ {\ pi} {\ text {d}} \ theta \ int _ {{z_ {1}}} ^ {{z_ {2}}} {\ frac {a – \ cos \ theta} {{D ^ {3}}} {\ text {d}} z ^ {\ prime}} = \ frac {{\ mu_ {0} nI}} {2 \ pi} \ left [{f_ {z } \ left ({r, z – z_ {2}} \ right) – f_ {z} \ left ({r, z – z_ {1}} \ right)} \ right], $$
(11)
где, \ (f_ {z} \ left ({r, t} \ right) = \ frac {t} {{\ sqrt {\ left ({r + a} \ right) ^ {2} + t ^ {2}}}} \ left [{\ frac {r – a} {{r + a}} \ prod \ left ({h, g} \ right) – {\ text {K}} \ left (g \ right)} \ right] \) и \ (g = \ sqrt {\ frac {4ar} {{\ left ({r + a} \ right) ^ {2} + t ^ {2}}}} \), и \ (h = – \ frac {4ar} {{\ left ({a + r} \ right) ^ {2}}} \). {2}}}} \).{\ prime} = 0, $$
{2}}}} \).{\ prime} = 0, $$
(13)
Это видно из Ур. (11) и (12) что выражения осевой составляющей \ (B_ {z} \) и радиальной составляющей \ (B_ {r} \) являются независимыми функциями от \ (\ varphi \). поэтому их также можно записать как \ (B_ {z} \ left ({r, z} \ right) \) и \ (B_ {r} \ left ({r, z} \ right) \), что полностью отражает цилиндрическую симметрию соленоида. Как видно из уравнения. Согласно формуле (13), в магнитном поле соленоида отсутствует окружная составляющая, поскольку в модели используется эквивалент однородного цилиндрического поверхностного тока, который эквивалентен наложению множественных кольцевых токов в осевом направлении.У тока есть составляющая в окружном направлении \ (\ varphi \), но не в осевом направлении \ (z \). Окружное магнитное поле, создаваемое осевой составляющей тока, следует учитывать, когда шаг соленоида очевиден, но применение такого соленоида редко.
Характеристики распределения магнитного поля в приосевой области
Помимо расчета величины точечного магнитного поля, иногда необходимо учитывать распределение общего магнитного поля в определенном пространстве. Например, в системе магнитооптической модуляции, когда установлен магнитооптический материал, требуется, чтобы он был сначала соосен с соленоидом, а затем в центре соленоида. В это время свет, излучаемый лазером, распространяется вдоль центральной оси, проходит через магнитооптическое стекло и образует тонкую оптическую колонну длиной в стекло. Диапазон действия оптической колонны – это эффективная область взаимодействия магнитного поля и света, которая называется параксиальной областью.При исследовании магнитного поля в параксиальной области его размер и распределение анализируются на основе осевой и радиальной составляющих.
Например, в системе магнитооптической модуляции, когда установлен магнитооптический материал, требуется, чтобы он был сначала соосен с соленоидом, а затем в центре соленоида. В это время свет, излучаемый лазером, распространяется вдоль центральной оси, проходит через магнитооптическое стекло и образует тонкую оптическую колонну длиной в стекло. Диапазон действия оптической колонны – это эффективная область взаимодействия магнитного поля и света, которая называется параксиальной областью.При исследовании магнитного поля в параксиальной области его размер и распределение анализируются на основе осевой и радиальной составляющих.
- 1.
Осевое магнитное поле
Установка \ (r = {0} \), основанная на симметрии соленоида, можно увидеть, что радиальная составляющая магнитного поля на оси равна нулю, то есть \ (B_ {r} \ left ({0, z} \ right) = 0 \), и учитывается только осевая составляющая. {2}}}}} \ right), $$
{2}}}}} \ right), $$
(14)
Уравнение (14) представляет собой выражение магнитного поля на оси соленоида, которое распределено по оси \ (z \), имеет только компоненты \ (z \) и связано с радиусом \ ( a \) и полудлины \ (b \) соленоида. Когда выполняется \ (b \ gg a \), уравнение (14) сокращается до
$$ B_ {z} \ left ({0, z} \ right) \ приблизительно \ mu_ {0} nI = B _ {\ infty}. $$
(15)
Уравнение (15) является выражением магнитного поля бесконечного соленоида.Здесь магнитное поле на центральной оси связано только с плотностью катушки и током, а магнитное поле равно \ (\ mu_ {0} nI \). Следует отметить, что бесконечной длины не существует, но для длинного прямого соленоида с \ (b> {10} a \) очень удобно анализировать магнитное поле бесконечной длины.
Для удобства обсуждения соотношение сторон \ (m \) определено как \ (m = b / a \). Ток \ (I = {2} {A} \), плотность катушки \ (n = {1000} \), длина соленоида \ ({2} b = {\ text {10 см}} \) и радиус \ ( а = {0} {\ текст {.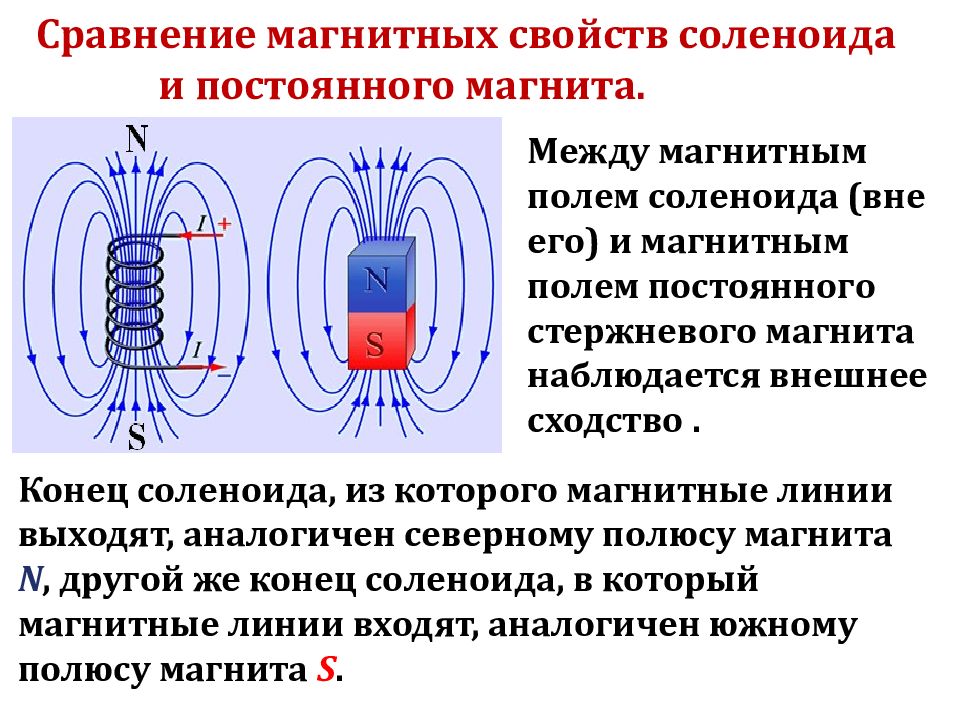 5 см}} \), \ ({1} {\ text {.0 cm}} \), \ ({2} {\ text {.0 cm}} \) и \ ({4} {\ text {.0 cm}} \) взяты, а \ (r = {0} \) установлено. Размер и распределение \ (B_ {z} \) показаны на рис. 3.
5 см}} \), \ ({1} {\ text {.0 cm}} \), \ ({2} {\ text {.0 cm}} \) и \ ({4} {\ text {.0 cm}} \) взяты, а \ (r = {0} \) установлено. Размер и распределение \ (B_ {z} \) показаны на рис. 3.
Распределение компоненты \ (B_ {z} \) на оси, когда \ (b \) постоянна и \ (а \) меняется.
Из рис. 3 видно, что при постоянной длине соленоида \ (b \) осевое магнитное поле \ (B_ {z} \) внутри соленоида увеличивается с уменьшением радиуса \ (a \) , а магнитное поле вне соленоида уменьшается.Чем меньше радиус \ (a \), тем стабильнее магнитное поле в среднем сечении \ (\ left ({- L / 2
- 2.
Радиальное магнитное поле
Радиус соленоида \ (a = {\ text {1 см}} \), полудлина \ (b = {5} \, {\ text {cm}} \), плотность катушки \ ( n = {1000} \), текущий \ (I = {\ text {2 A}} \) и компоненты \ (z_ {1} \) и \ (z_ {2} \) уравнения. (12) с \ (- b \) и \ (b \) взяты отдельно.Берутся разные значения \ (r (r Как видно из рис. 4, когда \ (r = {0} \), составляющая \ (B_ {r} \) на центральной оси равна нулю. Когда \ (r \) не равно нулю, есть составляющая \ (B_ {r} \), а в пределах радиуса соленоида радиальная составляющая \ (B_ {r} \) увеличивается с увеличением расстояние \ (г \). Характеристики распределения в направлении \ (z \) следующие.С увеличением координат \ (z \) значение \ (B_ {r} \) сначала увеличивается от нуля, а затем уменьшается до нуля, и есть максимум на обоих концах соленоида \ (z = \ pm b \), но значение \ (B_ {r} \) намного меньше, чем значение \ (B_ {z} \), особенно для диапазона внутренней средней части \ (\ left ({- L / 2 < z Распределение \ (B_ {r} \) для различных условий \ (r \). Можно сделать вывод, что радиальной составляющей магнитного поля часто пренебрегают и при анализе магнитного поля в соленоиде учитывают только осевую составляющую. Этот вывод может принести большое удобство для реального анализа и расчета, а ошибку, вызванную упрощением, можно не учитывать. В практических приложениях для увеличения магнитного поля и получения большего угла фарадеевского вращения часто используются многослойные соленоиды без увеличения выходной мощности сигнала модуляции и объема соленоид.Согласно закону Био – Савара и принципу суперпозиции магнитных полей, магнитное поле многослойного соленоида можно рассматривать как суперпозицию магнитных полей нескольких однослойных соленоидов, но толщина многослойной катушки не может здесь можно проигнорировать. Итак, эквивалентный радиус должен быть введен для замены предыдущего радиуса. (16) где \ (N_ {c} \) – количество слоев катушки, а \ (a _ {{\ text {d}}} = (a_ {2} – a_ {1}) / \ ln (a_ {2} / a_ {1}) \) – эквивалентный радиус, где \ (a _ {{1}} \) – внутренний диаметр катушки, а \ (a _ {{2}} \) – внешний диаметр катушки. Фактически, магнитное поле многослойного соленоида похоже на магнитное поле однослойного соленоида. Для анализа магнитного поля вблизи оси существует только множественная связь. В «Принципе системы» магнитооптическая система модуляции, представленная в принципе системы, использует многослойный соленоид, и его основные параметры: длина соленоида \ ({2} b = {\ text {10 см} } \), внутренний диаметр катушки \ (a _ {{1}} = {3} {\ text {.5 см}} \), внешний диаметр \ (a _ {{2}} = {4} {\ text {. 0 см}} \), количество слоев \ (N_ {c} = {5} \) и плотность катушки \ (n = {1000} \). Генератор сигналов подключен к усилителю мощности для вывода возбуждения постоянного тока (DC); напряжение возбуждения равно \ ({\ text {5 V}} \), а магнитное поле в каждой позиции на оси соленоида измеряется гауссметром, чтобы обеспечить точность измерения и позиционирования, деревянная линейка используется для точного измерения, как показано в таблице 1. Положение в таблице 1 представляет собой расстояние между точкой измерения и центром соленоида, а положительное и отрицательное значение означает, что положение измерения находится с обеих сторон и симметрично относительно центра. Измерения 1, 2 и 3 представляют собой три цикла измерения. Порядок точек измерения – от нуля вправо (положительное направление) до тех пор, пока координата не станет положением \ (13 \, {см} \), а затем от отрицательного направления нуля.Конкретное место и значение измерения показаны в Таблице 1. Наконец, в качестве окончательного результата измерения берется среднее значение трех измерений. Согласно формуле. (16) и данные в таблице 1, расчет показан на рис. 5. Магнитное поле на центральной оси. Сплошная синяя линия на рис. 5 представляет кривую, полученную из теоретической модели, а маленький красный треугольник – измеренное значение в нескольких точках в таблице 1. Следовательно, без учета других факторов, обычно сначала можно изучить однослойный соленоид, а затем можно рассчитать магнитное поле многослойного соленоида с помощью принципа суперпозиции и метода эквивалентного радиуса, что может упростить решение. магнитного поля и подходит для большинства случаев. Предполагая, что диаметр кабеля
электромагнитного клапана 2,5 мм2, максимальное сопротивление кабеля постоянному току
7,41 Ом / км, расстояние передачи по кабелю составляет 650 м, а номинальная мощность
выбранного электромагнитного клапана составляет 10 Вт (максимальное сопротивление постоянному току
кабель и данные о номинальной мощности электромагнитного клапана можно найти по продукту
руководство по эксплуатации). 1.Расчет рабочего тока электромагнитного клапана См. Формулу 2. Расчет падения напряжения на кабеле См. В формуле Таким образом, напряжение питания электромагнитного клапана составляет Пока минимальное рабочее напряжение электромагнитного клапана составляет не менее 20,0 В, электромагнитный клапан может нормально работать. 3. Колебания напряжения в блоке питания Следует отметить, что в этом случае напряжение питания блока питания
напряжение питания 24 В и находится в идеальном состоянии. Предполагая, что колебания
выход устройства питания постоянного тока (нерегулируемый источник питания)
± 5%, в случае -5% он пересчитывается следующим образом. В Smin = 24 × (1 – 5%) = 22,8 В См. В формуле Итак, наименьшее напряжение питания для электромагнитного клапана: В это время минимальное рабочее напряжение электромагнитного клапана должно быть не менее
чем 18,58 В, чтобы электромагнитный клапан мог нормально работать. Иногда катушка электромагнитного клапана может перегореть из-за дефекта при ее изготовлении. Контрольный список для электромагнитных клапанов переменного тока 1. Катушка не соответствует рабочему напряжению Испытание низкого напряжения должно проводиться путем измерения напряжения непосредственно на проводах катушки, когда соленоид находится под напряжением и его якорь заблокирован в открытом состоянии, поэтому он потребляет пусковой ток. Подайте питание на соленоид на время, достаточное для снятия показаний напряжения. Также снимите показания холостого хода, когда соленоид отключен от питающих проводов.Разница более чем на 5% между этими двумя показаниями указывает на чрезмерное сопротивление в цепи проводки или недостаточную вольт-амперную емкость управляющего трансформатора, если он используется. 2.Перекрытие подачи питания Соленоид может сгореть, если оба соленоида находятся под напряжением Состояние перегорания, описанное выше, возникает только на двойных соленоидных клапанах, где два соленоида соединены ярмом с противоположными концами общего золотника, как показано на рисунке. Если каждый соленоид может немедленно закрыть свой магнитный зазор, ни один из них не сгорит при одновременном включении питания. Особое внимание следует уделить конструкции электрической цепи, чтобы оператор из-за несчастного случая не мог подать питание на оба соленоида одновременно. Даже при правильной конструкции схемы и схемах блокировки реле с заедающими контактами или медленным срабатыванием может быть ответственным за кратковременное перекрытие подачи питания в каждом цикле и возможное сгорание катушки.Простое устройство для обнаружения этого состояния описано в техническом описании конструкции 18 . 3. Слишком быстрое переключение между циклами Приложения с высокой цикличностью можно грубо определить как те, в которых соленоид должен быть запитан более 5-10 раз в минуту.В этих случаях следует использовать конструкции соленоидов, погруженных в масло. Проведение тепла через масло, окружающее обмотку, позволяет катушке работать при более низкой температуре. На предприятиях, где имеется контрольно-измерительная аппаратура, термопара может быть размещена на поверхности обмотки в двух идентичных клапанах того типа, который будет использоваться. Один клапан может непрерывно работать в течение нескольких часов с предложенной частотой цикла, в то время как другой постоянно находится под напряжением. Разница в температуре поверхности двух катушек более чем на несколько градусов указывает на необходимость использования соленоидов, погруженных в масло. 4. Высокие электрические переходные процессы 5.Грязь в масле или в атмосфере Мелкие частицы грязи в масле могут оседать на поверхности катушки, приклеенные «лаком», циркулирующим в масле, или сам лак может вызвать чрезмерное сопротивление катушки и чрезмерный ток катушки. 6. Условия окружающей среды 7. Тупиковое обслуживание 8. Атмосферная влажность Замена на формованные катушки или соленоиды, погруженные в масло. Держите защитные крышки соленоидов плотно на месте и, возможно, закройте отверстия электрических проводов после установки проводки. 9. Чрезмерный поток через клапан При проектировании схемы будьте очень осторожны, чтобы не перегрузить такой клапан, если он превышает номинальный расход, указанный производителем. Его следует снизить при использовании жидкостей с высокой вязкостью или жидкостей с высоким удельным весом (огнестойкие жидкости и т. Д.). Контрольный список для электромагнитных клапанов постоянного тока Конденсатор, подключенный к контактам переключателя на соленоидах переменного или постоянного тока, помогает поглощать выделяемую энергию. Наилучшее значение емкости может быть определено опытным путем, либо путем наблюдения за интенсивностью дуги, либо путем измерения скачка напряжения с помощью осциллографа при испытании различных конденсаторов. Чтобы уменьшить искрение переключателя, конденсатор может быть подключен к контактам © 1990, компания Womack Machine Supply Co . Эта компания не несет ответственности за ошибки в данных, а также за безопасную и / или удовлетворительную работу оборудования, разработанного на основе этой информации. Назначение катушки соленоида – преобразование электрической энергии в поступательное движение. Электромагнитный клапан – это устройство с электрическим управлением. Клапан состоит из медной проволоки, намотанной вокруг полой формы, которая представляет собой электрическую катушку с подвижным ферромагнитным сердечником, также называемым плунжером, расположенным в ее центре. В исходном положении поршень закрывает небольшое отверстие. Пропуская ток через катушку, линии магнитного потока превращают поршень в электромагнит. Генерируемое магнитное поле оказывает направленное вверх усилие на поршень, открывающий отверстие. На следующем изображении показаны различные части электромагнитного клапана. Электромагнитные клапаны доступны с двумя типами мощности. Срок службы соленоида постоянного тока в значительной степени зависит от степени механического износа между подвижным железным сердечником и направляющей (трубой). Скользящая часть или секция направляющей проходят специальную обработку для продления срока службы. С соленоидом постоянного тока сила притяжения, идентичная действительной нагрузке, может быть обеспечена путем изменения формы сопрягаемой части подвижного и неподвижного стальных сердечников. Автор: Р. Джаган Мохан Рао Читать дальше: Clark-Cooper использует различные соленоиды или «катушки» для удовлетворения требований к рабочим характеристикам наших клапанов во всех областях применения.Критерии для соленоида включают источник питания переменного или постоянного тока, напряжение, перепад давления на клапане (требуемое тяговое усилие), рейтинг NEMA, рабочий цикл, специальные соединения, температуру жидкости и окружающей среды и даже длину проводов. Рабочий цикл: Инкапсулированный: Полярность и подключение: Установка: Катушки легко снимаются с клапанов. Катушку можно повернуть наверху любого клапана, чтобы при необходимости расположить провода отведений. Потребляемая мощность: «Полная мощность» измеряется в вольтах * амперах. Он используется для определения размеров проводов, автоматических выключателей, предохранителей и т. Д.для схемы. Для цепей постоянного тока расчет снова прост: V * A = VDC * I DC. Для цепей переменного тока: ВА = В СКЗ x I СКЗ «Коэффициент мощности» = Вт / (В * А). От нуля до 1.0. Мощность, потребляемая устройством, всегда меньше или равна вольт-амперам. Это происходит из-за емкости или индуктивности устройства, делающего цепь «реактивной». Устройство может потреблять значительный вольт * ампер и не работать и не нагреваться. «Гудение» или болтовня: Магнитное поле многослойного соленоида
 {2}}}}} \ right) \ cdot N_ {c}.$$
{2}}}}} \ right) \ cdot N_ {c}.$$
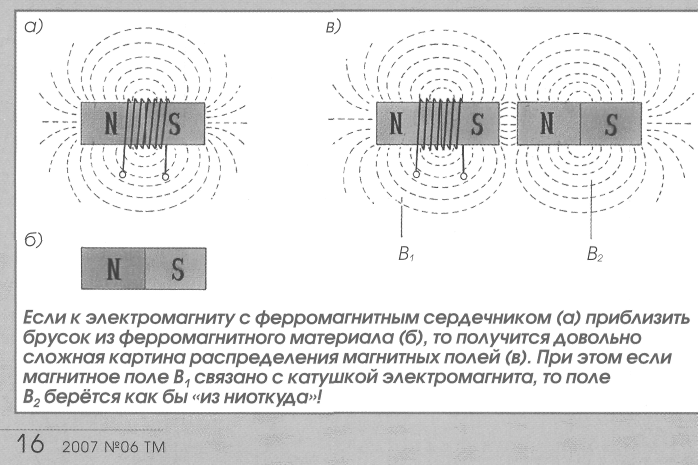
 Наблюдая за данными и числовыми кривыми в таблице, можно увидеть, что напряженность магнитного поля в центре является наибольшей. По мере удаления от центра магнитное поле становится меньше. Когда положение равно \ (z = \ pm {\ text {5 cm}} \) на обоих концах соленоида, амплитуда магнитного поля составляет почти половину от центрального значения, а когда положение равно \ (z = \ pm {\ text {15 см}} \) на конце соленоида магнитное поле почти равно нулю. Измеренные точки данных хорошо согласуются с теоретической кривой, которая показывает возможность использования этого метода для расчета магнитного поля многослойного соленоида.
Наблюдая за данными и числовыми кривыми в таблице, можно увидеть, что напряженность магнитного поля в центре является наибольшей. По мере удаления от центра магнитное поле становится меньше. Когда положение равно \ (z = \ pm {\ text {5 cm}} \) на обоих концах соленоида, амплитуда магнитного поля составляет почти половину от центрального значения, а когда положение равно \ (z = \ pm {\ text {15 см}} \) на конце соленоида магнитное поле почти равно нулю. Измеренные точки данных хорошо согласуются с теоретической кривой, которая показывает возможность использования этого метода для расчета магнитного поля многослойного соленоида. Электромагнитные клапаны переменного или постоянного тока
На практике и применении существует два основных типа общих
источник питания для электромагнитных клапанов: переменного тока (например, 110 В, 220 В) и постоянного тока (например, 12 В,
24 В).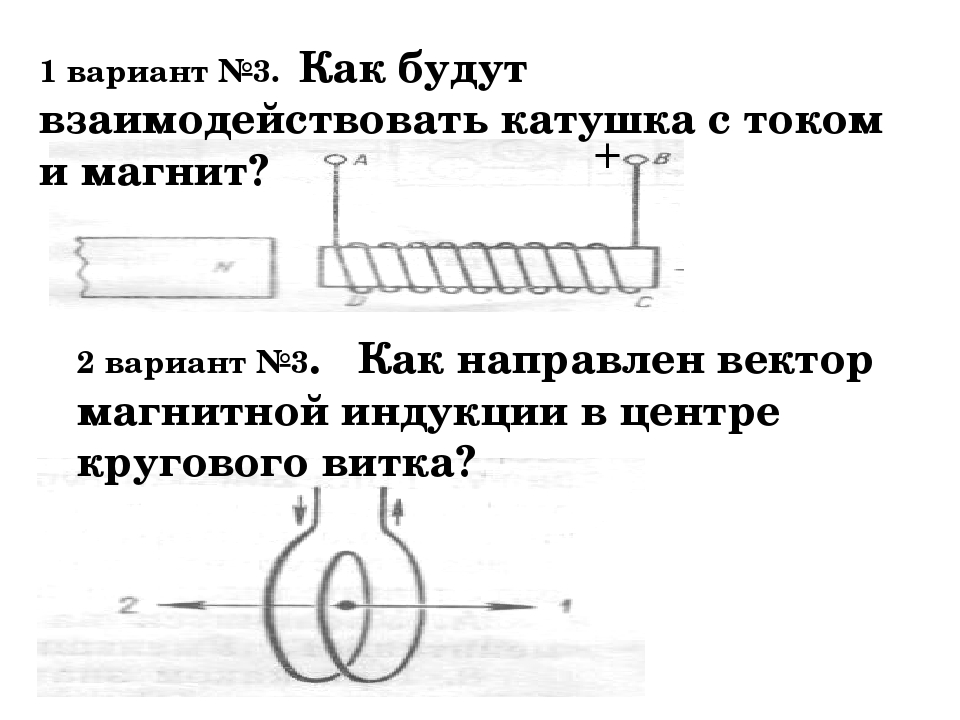 Из-за высокого напряжения питания и небольших потерь напряжения в кабеле
сопротивление в процессе передачи, блок питания переменного тока почти не будет
причиной недостаточного напряжения привода электромагнитного клапана, так что
электромагнитный клапан не может работать. Но кабель 220 В переменного тока нельзя путать с
сигнальные кабели других инструментов, которые необходимо прокладывать отдельно,
доставляет массу неудобств при проектировании и строительстве. 24 В постоянного тока
кабель питания отдельно прокладывать не нужно, а лучше
рассчитайте напряжение питания соленоида, прежде чем принимать решение об использовании 24 В постоянного тока.
электромагнитный клапан, особенно при большом расстоянии от источника питания.Ниже приведен пример расчета напряжения питания электромагнитного клапана 24 В постоянного тока.
Из-за высокого напряжения питания и небольших потерь напряжения в кабеле
сопротивление в процессе передачи, блок питания переменного тока почти не будет
причиной недостаточного напряжения привода электромагнитного клапана, так что
электромагнитный клапан не может работать. Но кабель 220 В переменного тока нельзя путать с
сигнальные кабели других инструментов, которые необходимо прокладывать отдельно,
доставляет массу неудобств при проектировании и строительстве. 24 В постоянного тока
кабель питания отдельно прокладывать не нужно, а лучше
рассчитайте напряжение питания соленоида, прежде чем принимать решение об использовании 24 В постоянного тока.
электромагнитный клапан, особенно при большом расстоянии от источника питания.Ниже приведен пример расчета напряжения питания электромагнитного клапана 24 В постоянного тока.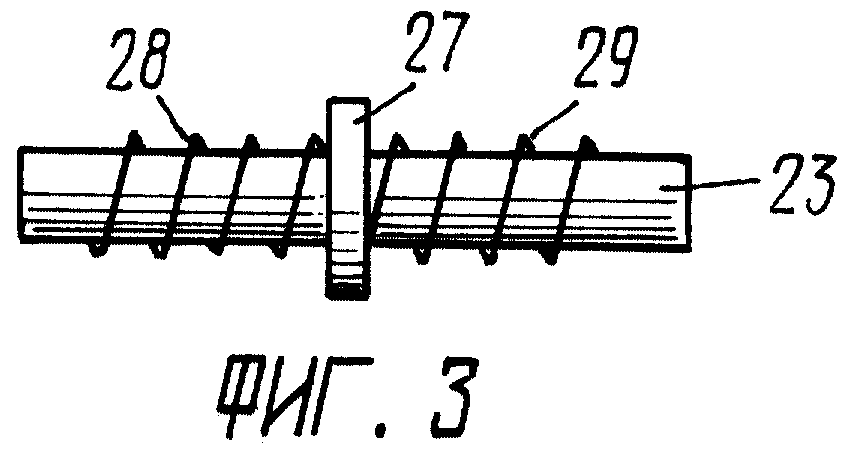 Шаги расчета следующие.
Шаги расчета следующие.
P = IV S
I = P / V S = 10/24 = 0,416 A
I – Рабочий ток электромагнитного клапана (А)
P – Номинальная мощность электромагнитного клапана (Вт)
В S – Напряжение источника питания (В)
L = 650 м × 2 = 1,3 км
R = 1,3 × 7,41 = 9,63 Ом
V = IR = 0,416 × 9.63 = 4. 0V
L – Длина кабеля туда и обратно (м)
R – Сопротивление кабеля (Ом)
V – Падение напряжения на кабеле (В)
V S – V = 24 – 4,0 = 20,0 В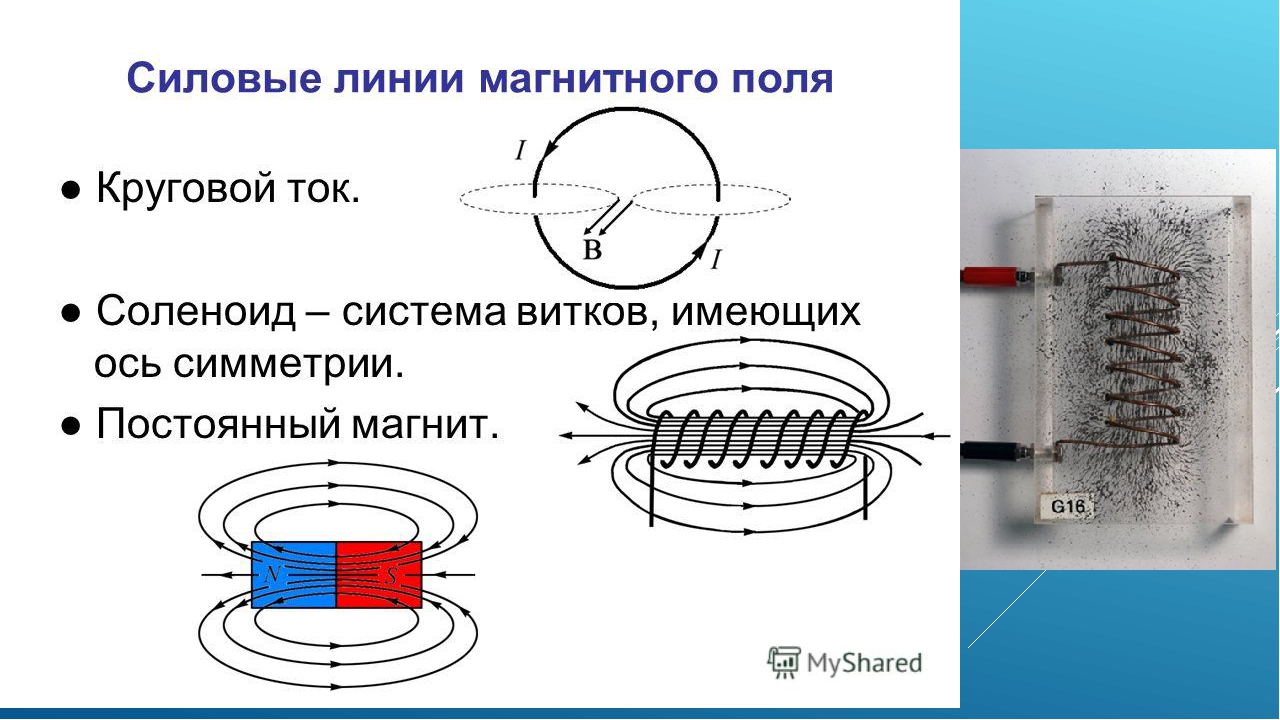 Собственно, на выходе
устройство источника питания постоянного тока будет в определенной степени колебаться. Если это
коэффициент учитывается, напряжение питания электромагнитного клапана
будет меньше 20,0 В.
Собственно, на выходе
устройство источника питания постоянного тока будет в определенной степени колебаться. Если это
коэффициент учитывается, напряжение питания электромагнитного клапана
будет меньше 20,0 В.
I = 10 / 22,8 = 0,438 А
V = IR = 0.438 × 9,63 = 4,22 В
V Smin – наименьшее напряжение питания (В)
V Smin – V = 22,8 – 4,22 = 18,58 В Поиск причины перегорания катушки соленоида
 Но обычно причина может быть связана с каким-либо ненормальным состоянием либо в условиях эксплуатации машины, на которой установлен клапан, либо в необычных условиях окружающей среды. Это становится очевидным, если выгорание должно произойти более одного раза в одном и том же месте змеевика.
Но обычно причина может быть связана с каким-либо ненормальным состоянием либо в условиях эксплуатации машины, на которой установлен клапан, либо в необычных условиях окружающей среды. Это становится очевидным, если выгорание должно произойти более одного раза в одном и том же месте змеевика.
Перегорание чаще встречается на клапанах с катушками переменного тока, чем на клапанах с катушками постоянного тока, из-за высокого пускового тока. До тех пор, пока якорь на соленоиде не сможет втянуть и закрыть воздушный зазор в магнитной петле, ток часто в 5 раз превышает установившийся или удерживающий ток после установки якоря.Бросок тока примерно такой же, как ток удержания на электромагнитном клапане постоянного тока.
Неправильное соответствие между источником электрического тока и номинальными характеристиками катушки иногда является причиной ее сгорания: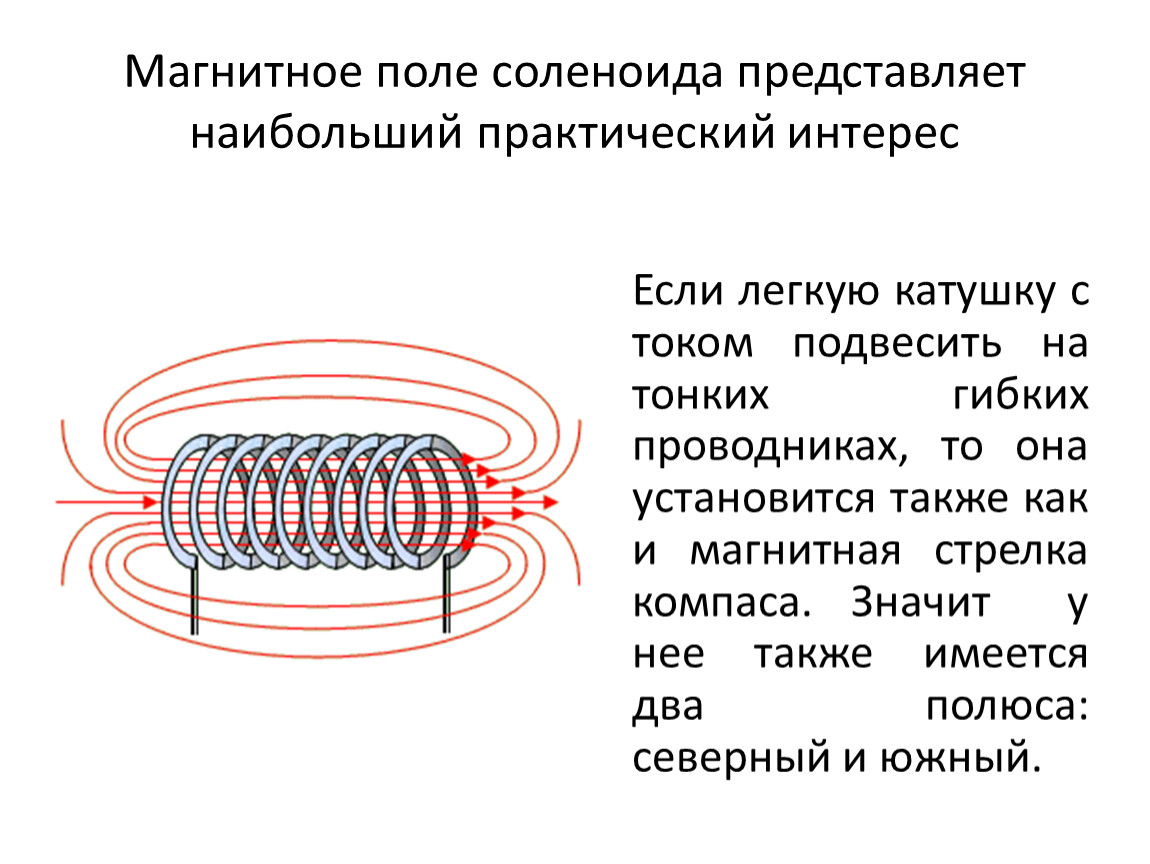 Рабочее напряжение не должно быть более чем на 10% выше номинального напряжения катушки. Чрезмерное напряжение вызывает чрезмерный ток катушки, что приводит к ее перегреву.
Рабочее напряжение не должно быть более чем на 10% выше номинального напряжения катушки. Чрезмерное напряжение вызывает чрезмерный ток катушки, что приводит к ее перегреву.
На некоторых двойных электромагнитных клапанах, если оба соленоида находятся под напряжением одновременно и удерживаются в этом состоянии в течение короткого времени, последняя катушка, на которую будет подаваться напряжение, сгорит из-за чрезмерного пускового тока, что примерно в 5 раз. удерживающий ток.
одновременно на двойном соленоидном клапане, построенном
как этот, в котором соленоиды механически
соединены с противоположными концами общего золотника.
Поскольку пусковой ток может в 5 раз превышать ток удержания, стандартная катушка переменного тока на соленоиде с воздушным зазором может перегреться и сгореть, если потребуется слишком частое переключение. Избыточное тепло, выделяемое во время пусковых периодов, не может уйти достаточно быстро. Постепенное нагревание внутри обмотки катушки может со временем повредить изоляцию катушки.
Избыточное тепло, выделяемое во время пусковых периодов, не может уйти достаточно быстро. Постепенное нагревание внутри обмотки катушки может со временем повредить изоляцию катушки.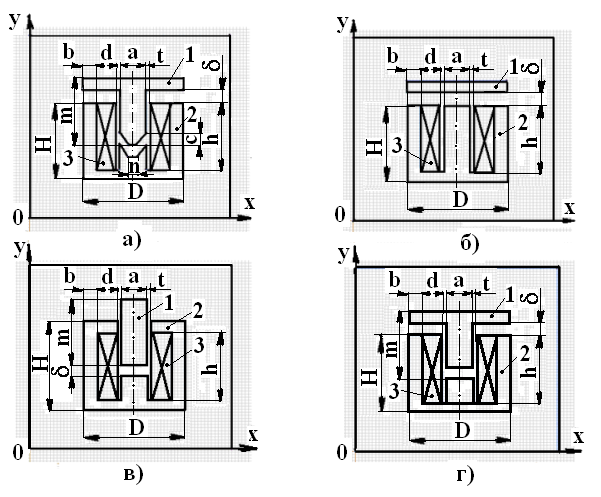
Если ток для электромагнитных клапанов берется непосредственно из линии питания, питающей большие индуктивные устройства, такие как электродвигатели, переключение этих двигателей может вызвать переходные процессы высокого напряжения, которые могут нарушить изоляцию. катушек электромагнитного клапана. Для «короткого замыкания» этих переходных процессов поперек каждой катушки должен быть установлен «тиреектор». Тиректоры доступны в промышленных предприятиях электроснабжения.
Небольшие твердые частицы, застрявшие под якорем соленоида, могут помешать ему полностью прижаться к сердечнику, в результате чего ток катушки останется выше обычного в течение периода выдержки. Убедитесь, что пылезащитные колпачки соленоидов плотно прилегают к месту для защиты от пыли, оседающей из воздуха. «Лак» образуется в системах, в которых допускается нагревание масла до слишком высокой температуры. Тепло ускоряет нежелательные химические реакции. Снизьте температуру масла с помощью теплообменника.
«Лак» образуется в системах, в которых допускается нагревание масла до слишком высокой температуры. Тепло ускоряет нежелательные химические реакции. Снизьте температуру масла с помощью теплообменника.
Чрезмерно высокие или аномально низкие температуры окружающей среды, воздействию которых соленоид подвергается продолжительное время, могут вызвать его перегорание. Пункт 9). Механические части клапана или конструкции соленоида могут деформироваться, что приведет к заеданию золотника клапана и сгоранию катушки соленоида. Используйте масло, более подходящее для низких температур, или используйте масляный или высокотемпературный змеевик, чтобы выдерживать большую нагрузку, вызванную аномально низкой температурой окружающей среды.
Пункт 9). Механические части клапана или конструкции соленоида могут деформироваться, что приведет к заеданию золотника клапана и сгоранию катушки соленоида. Используйте масло, более подходящее для низких температур, или используйте масляный или высокотемпературный змеевик, чтобы выдерживать большую нагрузку, вызванную аномально низкой температурой окружающей среды.
Циркуляция жидкости через электромагнитный клапан помогает отводить электрическое тепло. Некоторые клапаны зависят от потока жидкости, чтобы предотвратить накопление чрезмерного тепла, и если они используются в тупике, когда соленоид остается под напряжением в течение длительного времени без потока жидкости, катушка может сгореть из-за этого эффекта, возможно, в сочетании с другими проблемами.
Высокая влажность в сочетании с часто меняющейся температурой окружающей среды может вызвать коррозию металлических частей конструкции соленоида, в результате чего якорь будет тянуть или заедать катушку. Влажность также имеет тенденцию к повреждению стандартных соленоидных катушек, вызывая короткое замыкание в обмотке.
Влажность также имеет тенденцию к повреждению стандартных соленоидных катушек, вызывая короткое замыкание в обмотке.
Падение давления через золотник соленоидного клапана прямого действия, вызванное потоком жидкости, создает дисбаланс сил, который заставляет золотник двигаться в осевом направлении.Этот феномен описан в техническом паспорте № 18 .
Электромагнитные клапаны переменного тока гораздо чаще используются в промышленных установках, но в некоторых случаях соленоиды постоянного тока могут иметь особое преимущество. Переменный ток можно пропускать через двухполупериодный выпрямитель для получения постоянного тока. Возможно, потребуется добавить фильтрующий конденсатор, чтобы устранить дребезг или гудение.
Переменный ток можно пропускать через двухполупериодный выпрямитель для получения постоянного тока. Возможно, потребуется добавить фильтрующий конденсатор, чтобы устранить дребезг или гудение. Соленоиды постоянного тока обычно сгорают контакты переключателя быстрее, чем соленоиды переменного тока. Энергия, накопленная в индуктивности катушки, должна рассеиваться при отключении катушки, вызывая дугу на контактах переключателя при их размыкании.Большую часть этой энергии можно безопасно рассеять, подключив диод через катушку, при этом положительный диод подключен к положительной стороне напряжения катушки. Диод должен быть рассчитан как минимум на 2–3-кратное напряжение питания постоянного тока.
Соленоиды постоянного тока обычно сгорают контакты переключателя быстрее, чем соленоиды переменного тока. Энергия, накопленная в индуктивности катушки, должна рассеиваться при отключении катушки, вызывая дугу на контактах переключателя при их размыкании.Большую часть этой энергии можно безопасно рассеять, подключив диод через катушку, при этом положительный диод подключен к положительной стороне напряжения катушки. Диод должен быть рассчитан как минимум на 2–3-кратное напряжение питания постоянного тока.
, или диод может быть подключен к катушке.
Разница между электромагнитными клапанами постоянного и переменного тока
Принцип

Типы соленоидов
Соленоид переменного тока в сравнении с соленоидом постоянного тока
Рабочий шум
 Следовательно, между подвижным и неподвижным стальными сердечниками может быть предусмотрен амортизирующий материал, чтобы минимизировать рабочие шумы.
Следовательно, между подвижным и неподвижным стальными сердечниками может быть предусмотрен амортизирующий материал, чтобы минимизировать рабочие шумы. Требования к питанию
Жужжащий шум
Возбуждающий ток
Время работы

Срок службы
Желаемая сила притяжения
Электромагнитные клапаны и клапаны высокого давления Clark Cooper
Общая информация о катушках
Наши клапаны спроектированы с катушками, которые могут находиться под напряжением неограниченное время без перегрева. Однако соленоиды с питанием от переменного тока имеют ограничения по частоте подачи питания на них из-за высоких пусковых токов.Слишком частое открытие и закрытие клапана с помощью соленоида переменного тока может привести к перегреву змеевика, особенно при высокой температуре жидкости / газа. Некоторые версии наших соленоидов имеют цепи, которые принимают питание переменного тока и преобразуют его в постоянный ток. Их можно часто менять, не рискуя перегореть. Обязательно обсудите частоту открытия / закрытия вашего клапана при покупке.
Наши соленоиды обладают отличной устойчивостью к влаге и проникновению твердых частиц.Имеются сертификаты.
Соленоиды, поставляемые Clark Cooper, не требуют подключения проводов с соблюдением определенной полярности. К любому проводу можно подавать линейное напряжение. Если есть 3 провода, зеленый провод заземлен.
К любому проводу можно подавать линейное напряжение. Если есть 3 провода, зеленый провод заземлен.
Выключатель всегда должен быть установлен в горячей ноге цепей на 120 вольт. Когда обе ножки горячие, например, цепи на 240 или 480 вольт, предпочтительнее использовать двухполюсный переключатель.Если используется однополюсный переключатель, проводка должна иметь высококачественную изоляцию, поскольку даже незначительные токи утечки могут вызвать проблемы с заеданием. При подключении двигателя к пускателю со ступенчатым управлением на обмотку должно быть немедленно подано полное напряжение.
«Реальная мощность», измеряемая в ваттах, – это фактические потери работы и тепла.Если умножить на время, получится количество энергии, за которое вам выставляет счет ваша коммунальная компания. Для цепей постоянного тока активная мощность = В постоянного тока * I постоянного тока. Для цепей переменного тока это:
Для цепей постоянного тока активная мощность = В постоянного тока * I постоянного тока. Для цепей переменного тока это:
Типичный мультиметр не может измерять ватт, если напряжение и сила тока не равны постоянному току. Мультиметр измеряет среднеквадратичное напряжение и среднеквадратичный ток. Когда вы подключаетесь к стене, чтобы получить 120 В переменного тока, это RMS. Коэффициент мощности, близкий к значению 1,0, указывает на эффективную настройку.
Коэффициент мощности, близкий к значению 1,0, указывает на эффективную настройку.
Дребезжание часто является признаком того, что плунжер (якорь) не находится в полном контакте с полюсным наконечником в магнитном поле, создаваемом соленоидом переменного напряжения. Такая простая вещь, как кусок тефлоновой ленты, застрявшей внутри клапана, может вызвать вибрацию с частотой, равной подаваемой мощности переменного тока (60 Гц). Соленоид в этом случае будет тянуть более высокую силу тока, чем разрешено для использования в установившемся режиме, и в конечном итоге сгорит.Другие физические повреждения деталей также могут возникать из-за гудения, гудения или стука. Если вы слышите гудение клапана, отключите питание и обратитесь в Clark-Cooper за технической помощью. Решение может быть таким простым, как очистка клапана.


