Расчет усилительного каскада на транзисторе по схеме с общим эмиттером
Электроника и схемотехника
Тема:
Расчет усилительного каскада на
транзисторе по схеме с общим
эмиттером.
2. 1. Условие задачи.
Для схемы усилительного каскада с общим эмиттером, представленной нарисунке ниже, определить основные параметры усилителя при следующих
значениях номиналов элементов схемы: транзистор КТ375Б, входные и
выходные характеристики которого представлены ниже; источник питания
усилительного каскада EK = 20 В; сопротивление в цепи коллектора Rк=400
Ом; амплитуда входного синусоидального сигнала низкой частоты,
подлежащего усилению Umвх = 10 мВ.
Схема усилительного каскада с
общим эмиттером
Упрощенная эквивалентная электрическая схема каскада с общим эмиттером для области средних частот.
Входные и выходные статические характеристики транзистора КТ375Б(2N3904)
4. 2. Расчет параметров.
Параметры усилительного каскада, подлежащие определению:1.
Положение рабочей точки на входных и выходных характеристикахтранзистора.
2. h – параметры транзистора в районе рабочей точки.
3. Входное сопротивление усилительного каскада, RВХ.
4. Выходное сопротивление усилительного каскада, RВЫХ.
5. Коэффициент усиления каскада по напряжению, KU.
6. Коэффициент усиления каскада по току, KI.
7. Коэффициент усиления каскада по мощности, KP.
8. Величина выходного напряжения усилительного каскада.
2. Расчет параметров.
1. Режим покоя усилительного каскада, при котором UВХ = 0, определяет
положение рабочей точки на семействе входных и выходных характеристик.
Положение рабочей точки (точка А) определяется значениями сопротивлений
базовых резисторов R1, R2, коллекторного резистора RK при заданном
значении напряжения питания ЕК.
Начертим линию нагрузки, на выходных статических характеристиках.
Сопротивление Rк=400 Ом. Учтем то, что по второму закону Кирхгофа для
выходной цепи в режиме покоя имеем:
где UКЭ – напряжение между коллектором и эмиттером в режиме покоя.
Данное уравнение изображается на выходной статической характеристике
транзистора в виде прямой линии (линии нагрузки), построение которой
проходит путем нахождения двух характерных точек: в режиме холостого хода,
когда IК = 0, имеем UКЭ = EК; и в режиме короткого замыкания – UКЭ = 0, имеем
IК = EК/RК.
Определим эти точки: в режиме холостого хода, когда IК = 0, имеем UКЭ = EК=
20 В; и в режиме короткого замыкания – UКЭ = 0, имеем IК = EК/RК = 20/400 =
0,05 А = 50 mА. Проведем линию нагрузки.
Линия нагрузки на выходных статических характеристиках
Если мы зададим на оси Uкэ значение 0,5 Ек и проведем перпендикулярную
линию до пересечения с линией нагрузки, то определим положение рабочей
точки на выходных статических характеристиках.
Линия нагрузки и положение рабочей точки на выходных
статических характеристиках
Получается, что в рабочей точке линия нагрузки пересекается с
характеристикой IK = f(UКЭ), при IБ0 = 0,135 mА. Определим значение Iк в
рабочей точке.
Линия нагрузки и положение рабочей точки на выходных
статических характеристиках
Получаем Iк= 25 мА, Uкэ=10В, при IБ0 = 0,135 mА.
Линия нагрузки и положение рабочей точки на выходных
статических характеристиках
Положение рабочей точки на входных статических характеристиках
получается при пересечении линии IБ0 = 0,135 mА, параллельной оси Uбэ, с
характеристикой IБ = f(UБЭ), при Uкэ = 10 В. Определим в рабочей точке
напряжение Uбэ.
Положение рабочей точки
на входных статических
характеристиках
Напряжение в рабочей точке Uбэ0=1,06В.
Положение рабочей точки на
входных статических
характеристиках
Резисторы R1, R2 создают на входе усилительного каскада в режиме покоя
напряжение смещения. Рассчитаем значения R1 и R2 по формулам:
Получим:
2. При работе транзисторов в качестве усилителей малых электрических
сигналов, свойства транзисторов определяются с помощью, так называемых, h
– параметров. Всего h – параметров четыре: h21, h22, h31 и h32.
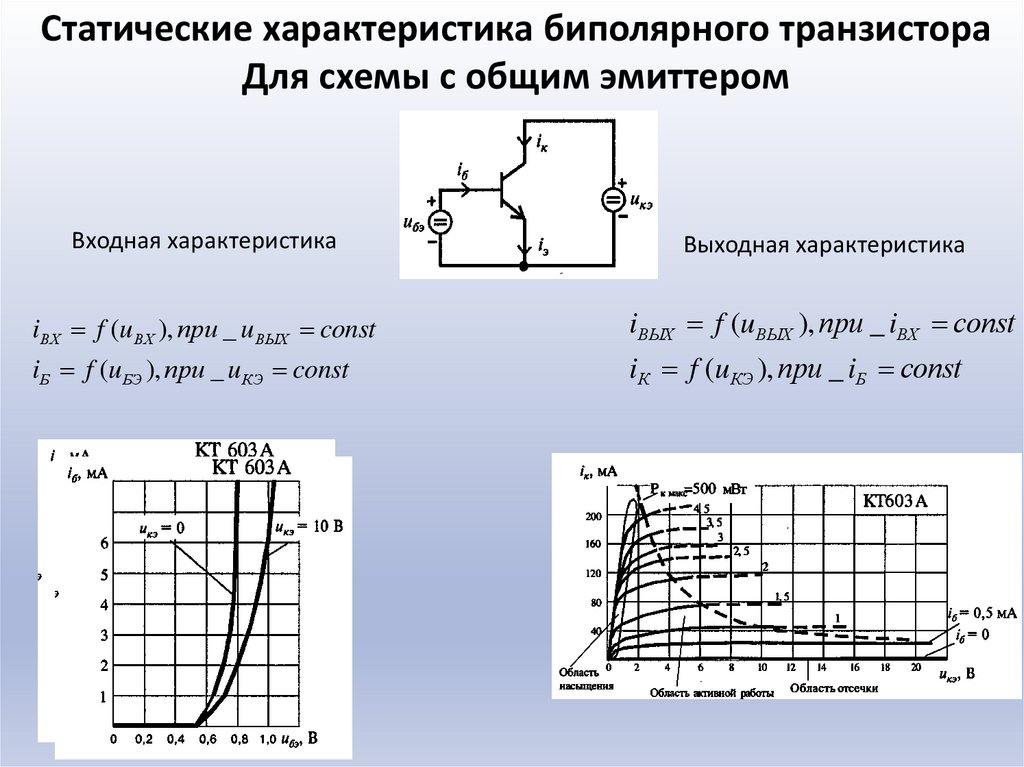Они связываютвходные и выходные токи и напряжения транзистора и определяются для
схемы ОЭ,
по следующим выражениям:
h21э = ∆UВХ/∆IВХ = ∆UБЭ/∆IБ
при неизменном напряжении
UВЫХ = UКЭ = const.
Параметр h21э численно равен входному сопротивления схемы с ОЭ. Знак ∆
обозначает приращение соответствующей величины тока или напряжения.
h22э = ∆UВХ/∆UВЫХ = ∆UБЭ/∆UКЭ при IБ = const.
Параметр h22э равен коэффициенту обратной связи по напряжению.
h31э = ∆IВЫХ/∆IВХ = ∆IК/∆IБ при UКЭ = const.
Параметр h31э равен коэффициенту передачи по току.
h32э = ∆IВЫХ/ ∆UВЫХ = ∆IК/∆UКЭ при IБ = const.
Параметр h32э равен выходной проводимости транзистора.
Значения h – параметров можно найти с помощью входных и выходных
статических характеристик транзистора.
Параметры входной цепи h21 и h22 определяют по входным характеристикам
транзистора.
Определим параметр h21э.
Для определения параметра h21 в рабочей точке задаем приращение тока
базы ∆IБ при постоянном напряжении коллектора UКЭ = 10 В и находим
получающееся, при этом, приращение напряжения базы ∆UБЭ.
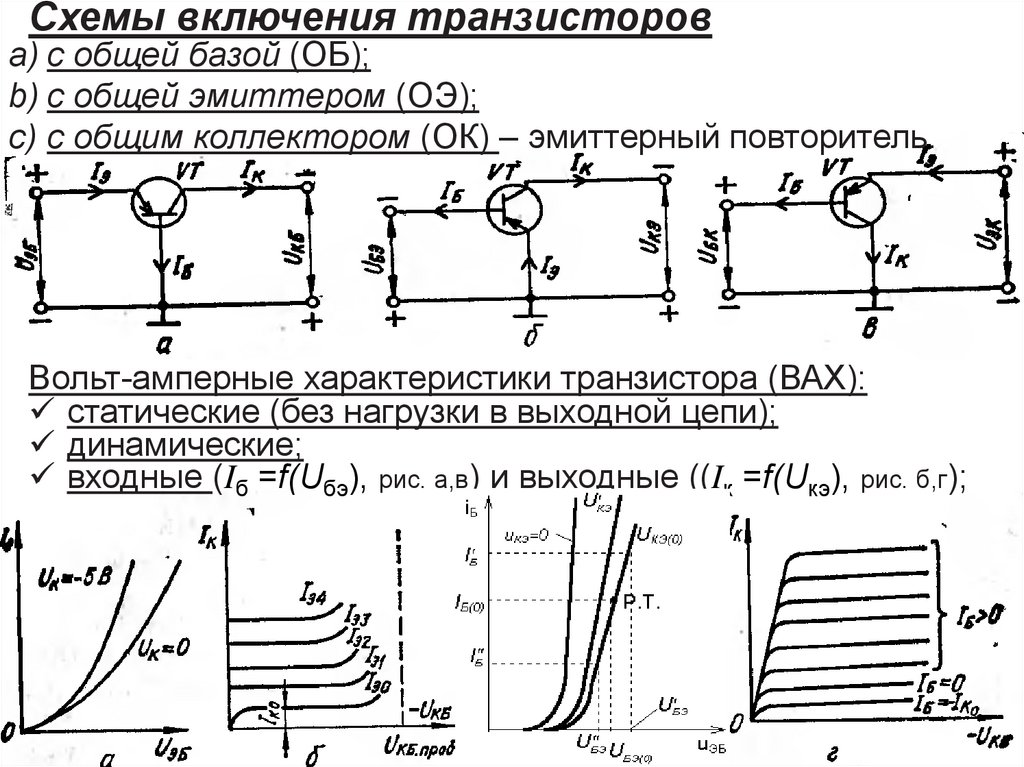Тогда входноесопротивление транзистора равно:
Определение приращений тока
Iб и напряжения Uбэ
Вычислим приращения.
Значения приращений для
определения параметра h21э
Тогда входное сопротивление транзистора можно вычислить по формуле:
h21э = ∆UБЭ/∆IБ . Вычисляем.
h21э = ∆UБЭ/∆IБ = 0,1 В/ 0,34 mА = 294 Ом.
Определим параметр h22э.
При постоянном токе базы IБ = 0,135 mА определяем приращение
напряжения на базе ∆UБЭ и приращение напряжения на коллекторе ∆UКЭ.
Порядок определения приращений
Uбэ и Uкэ
Определение значений приращений
для вычисления параметра h22э
Приращение напряжения коллектора ∆UКЭ = 10 В приращение напряжения
базы ∆UБЭ= 0,085 В. Тогда коэффициент обратной связи по напряжению равен
h22э = ∆UБЭ/∆UКЭ= 0,085 /10 = 0,0085.
Параметры h31э и h32э определяют по выходным характеристикам
транзистора. В районе рабочей точки А (IK0 = 25 mА и UКЭ0 = 10 В) на
выходной характеристике, при постоянном напряжении коллектора UКЭ= 10 В.
Определим параметр h31э.
Проводим через рабочую точку, на выходных характеристиках, линию
постоянного Uкэ, до пересечения двух соседних выходных характеристик.
Берем приращение тока базы ∆IБ (по точкам пересечения двух соседних
выходных характеристик) и определяем, получающееся при этом, приращение
тока коллектора ∆IК.
Порядок определения приращений Iб и Iк
Берем приращение тока базы ∆IБ = 0,06 mА и определяем приращение тока
коллектора ∆IК = 12,6 mА. Тогда коэффициент передачи по току равен
h31э = ∆IК/∆IБ = 12,6 mА / 0,06 mА = 210.
Определение значений приращений для вычисления
параметра h31э
Определим параметр h32э.
Параметр h32э также определяют по выходным статическим характеристикам
транзистора.
В районе рабочей точки А (IK0 = 25 mА и UКЭ0 = 10 В), на статической
выходной характеристике, при постоянном токе базы IБ = 0,135 mА, задаем
приращение коллекторного напряжения ∆UКЭ и находим приращение тока
коллектора ∆IК.
Порядок определения приращений Uкэ и Iк
Примем приращение напряжения ∆UКЭ = 4 В и получим приращение тока
коллектора ∆IК = 0,6 mА. Тогда выходная проводимость транзистора равна
h32э = ∆IК/∆UКЭ = 0,6 mА /4 В = 0,15 мСм.
Определение значений приращений для вычисления
параметра h32э
3. Определим входное сопротивление усилительного каскада, RВХ
Входное сопротивление усилительного каскада равно:
Упрощенная эквивалентная электрическая схема каскада с общим эмиттером для области средних частот.
Получим результат:
4. Определим выходное сопротивление усилительного каскада.
Выходное сопротивление усилительного каскада равно:
Упрощенная эквивалентная электрическая схема каскада с общим эмиттером для области средних частот.
Получим результат:
5. Определим коэффициент усиления по напряжению.
Коэффициент усиления по напряжению равен:
Получим результат:
6. Определим коэффициент усиления по току.
Коэффициент усиления по току равен:
Получим результат:
7.
Определим коэффициент усиления по мощности.Получим результат:
8. Определим величину выходного напряжения усилительного каскада.
Получим результат:
Расчет окончен.
39. 3. Расчет параметров Rэ, Сэ.
Усилительный каскад по схеме с ОЭ с цепью Rэ, Сэ.Рассчет Rэ.
Rэ (0,1…0,2)Eк/IЭ0 сопротивление резистора Rэ в цепи эмиттера, где IЭ0 IК0
– ток коллектора в рабочей точке.
Подставим исходные данные – IЭ0 IК0 0,025 А – ток коллектора в рабочей
точке, Ек=20В, получим:
Rэ (0,1…0,2)Eк/IЭ0 = 0,1 20/0,025 = 80 Ом.
Емкость Сэ выбирается из условия, чтобы при подаче входного переменного
сигнала выполнялось неравенство:
Отсюда:
где min = 2
Каскад с общим коллектором эмиттерный повторитель
Схему рис. 1.23а называют каскадом с общим коллектором (ОК), потому что коллекторный вывод транзистора
по переменному току является общим электродом для входной и выходной цепей каскада. Схема также
называется эмиттерным повторителем, т.
к. выходное напряжение, снимаемое с эмиттера транзистора
близко по величине входному напряжению ( Uвых = Uвх + Uбэ Uвх ) и совпадает с ним по фазе.
Рисунок 1.23 – Схема усилительного каскада ОК (а) и его схема замещения (б)
Расчет каскада по постоянному току проводят аналогично со схемой ОЭ. Резистор Rэ в
схеме выполняет ту же функцию, что и резистор Rк в схеме ОЭ – создание
изменяющегося напряжения в выходной цепи за счет протекания в ней тока,
по цепи базы. Конденсаторы С
Входное сопротивление каскада ОК определяется параллельно включенными сопротивлениями R1, R2 и сопротивлением входной цепи транзистора rвх:
Rвх = R1 || R2 || rвх
Из эквивалентной схемы замещения рис.
1.23б можно найти:
Uвх = Iб [rб + (1 + )(rэ + R э || Rн)]
а разделив левую и правую часть уравнения на Iб получим:
rвх = rб + (1 + )(rэ + Rэ || Rн)
Если принять, что rэ и rб значительно меньше других составляющих полученного выражения, то входное сопротивление транзистора , включенного по схеме ОЭ
rвх (1 + )(Rэ || Rн),
а входное сопротивление каскада ОК:
Rвх R1 || R2 || (1 + )(Rэ || Rн)
При достаточно высокоомном входном делителе и транзисторе с высоким
входное сопротивление каскада может достигать десятков-сотен кОм, что является одним из важнейших достоинств каскада ОК.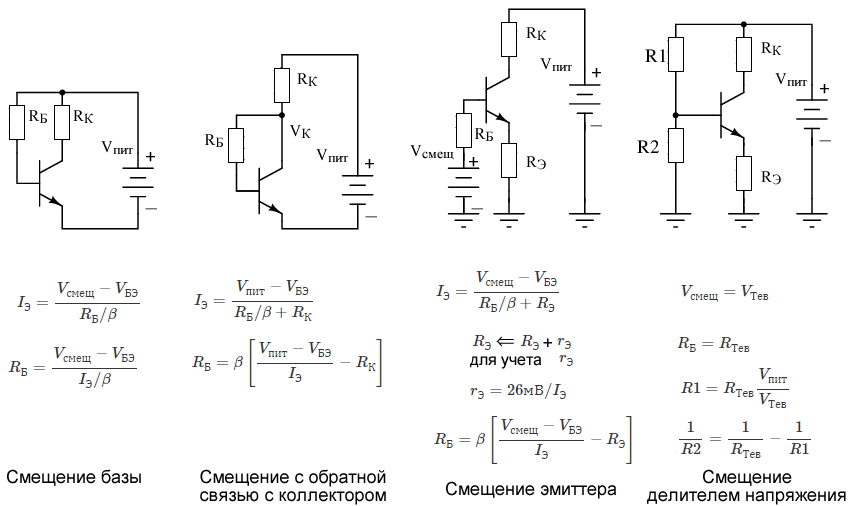
Коэффициент усиления по току можно определить , используя эквивалентную схему замещения, аналогично каскаду ОК
Ток нагрузки является частью эмиттерного тока транзистора, поэтому:
откуда:
Выразив аналогично схеме ОЭ ток базы через входной ток каскада получаем:
Разделив левую и правую часть уравнения на Iвх имеем:
т.е. коэффициент усиления каскада ОК зависит от соотношений Rвх и rвх, а также Rэ и R н. Если предположить, что Rвх rвх, имеем;
Таким образом, каскад ОК обеспечивает усиление по току, причем при Rэ = Rк и одинаковых значениях Rн
коэффициенты усиления по току в схемах ОК и ОЭ примерно одинаковы.
Коэффициент усиления по напряжению аналогично схеме ОЭ может быть определен как:
После подстановки значения КI:
Для оценки коэффициента усиления каскада ОК по напряжению примем Rвх >> Rг и считаем делитель в цепи базы достаточно высокоомным. Это позволяет принять и получить КU 1. Точный расчет дает КU
Выходное сопротивление каскада ОК представляет собой сопротивление со стороны эмиттера, которое из эквивалентной схемы замещения определяется как:
Выходное сопротивление каскада ОК мало и составляет 10 – 50 Ом, поэтому каскад ОК целесообразно использовать при необходимости согласования выходной цепи усилителя с низкоомным сопротивлением нагрузки.
Нравится
Твитнуть
BJT Усилитель с общим коллектором | mbedded.
ninjaСодержание
Обзор
Усилитель BJT с общим коллектором является одной из трех основных топологий однокаскадных усилителей BJT. Топология усилителя с общим коллектором также известна как усилитель эмиттерного повторителя или повторитель напряжения . Он имеет высокий входной импеданс, низкий выходной импеданс и неинвертирующий коэффициент усиления около 1. Он НЕ обеспечивает усиление по напряжению, но может обеспечить усиление по току и, следовательно, общее усиление по мощности. Из-за своих «буферных» возможностей он часто используется между входами с высоким импедансом и выходами с низким импедансом (т. е. он хорош для управления энергоемкими нагрузками) 1 .
Аналог MOSFET усилителя с общим коллектором на биполярных транзисторах представляет собой усилитель с общим стоком .
Свойства:
| Коэффициент усиления по напряжению | Низкий |
| Коэффициент усиления по току | Высокий |
| 8 | Средний |
| Входной импеданс | Высокий |
| Выходной импеданс | Низкий |
| Фазовый сдвиг | 0° |
Строчные буквы, используемые ниже, обозначают изменения количества, например, \(V_C\) – это напряжение на коллекторе, а \(v_c\) – изменение напряжения на коллекторе, \(\Delta V_C\) .
Базовый усилитель с общим коллектором
Ниже показана схема базового усилителя с общим коллектором:
Базовая схема усилителя с общим коллектором.
Выходное напряжение почти равно входному напряжению, за исключением приблизительно \(0,7В\) Падение на диоде на переходе база-эмиттер. Это означает, что усилитель имеет усиление по напряжению почти единицу (1), или \(0dB\) .
\begin{align} v_{выход} = v_{вход} – 0,7 В \\ \end{align}
Вот график \(v_{in}\) по сравнению с \(v_{out}\)
\(R1=1k\Omega\) : \(V_{out}\) по сравнению с \(V_{in}\) для базового BJT-усилителя с общим коллектором.
(файл моделирования Micro-Cap: Circuit.cir)
Усилитель с общим коллектором моделируется в схеме, приведенной ниже:
(полностраничная версия)
Усилитель с общим коллектором со связью по переменному току и смещением по постоянному току точка смещения постоянного тока в основании биполярного транзистора.
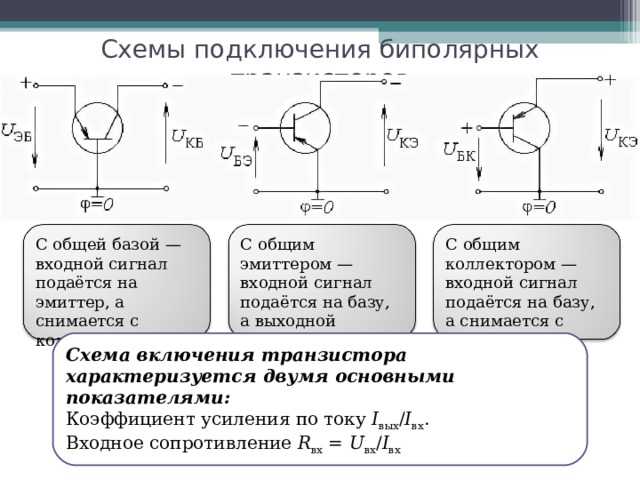Ниже приведена схема усилителя, построенного на транзисторе NPN:Схема усилителя BJT NPN с общим коллектором, связанного по переменному току.
Модель слабого сигнала переменного тока для этой цепи показана ниже. Шины постоянного напряжения и конденсаторы закорочены.
Модель переменного тока со слабым сигналом для BJT-усилителя с общим коллектором, связанного по переменному току.
\(r_e\) – сопротивление эмиттера слабого сигнала, которое является внутренним для биполярного транзистора.
Коэффициент усиления по напряжению без нагрузки
Коэффициент усиления по напряжению слабого сигнала без нагрузки усилителя с общим коллектором находится путем игнорирования \(R_L\) в модели переменного тока слабого сигнала схемы с общим коллектором. По определению выигрыш равен:
\begin{align} A_V = \frac{v_{out}}{v_{in}} \\ \end{выравнивание}
Помните, что \(v_{in}\) и \(v_{out}\) написаны строчными буквами и представляют изменения в сигнале (т.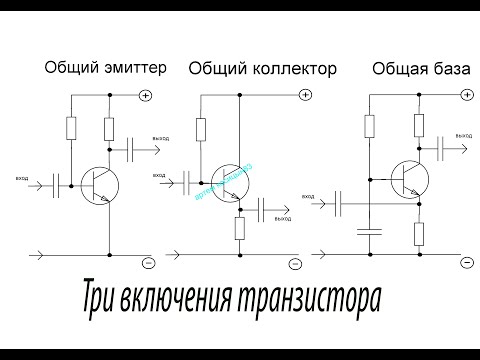
е. дельты, и игнорируют их уровни постоянного тока). Таким образом, изменение \(v_{in}\) – это просто изменение базового напряжения. Мы также можем применить закон Ома, чтобы получить:
\begin{align} A_V &= \frac{v_e}{v_b} \nonumber \\ &= \frac{i_c R_E}{i_c(r_e + R_E)} \nonumber \\ &= \frac{R_E}{r_e + R_E} \\ \end{выравнивание}
Входное сопротивление
Входное сопротивление базы транзистора:
\begin{align} Z_{in(base)} &= \beta (r_e + R_E) \nonumber \\ \end{align}
Тогда общее входное сопротивление равно базовому входному сопротивлению, включенному параллельно с обоими базовыми резисторами:
\begin{align} Z_{in} &= Z_{in(база)} || Р_{В1} || R_{B2} \номер\\ \end{align}
Дополнительная литература
Проект усилителя с общим коллектором Кеннет А. Кун подробно описывает конструкцию усилителя с точными уравнениями и соображениями 2 .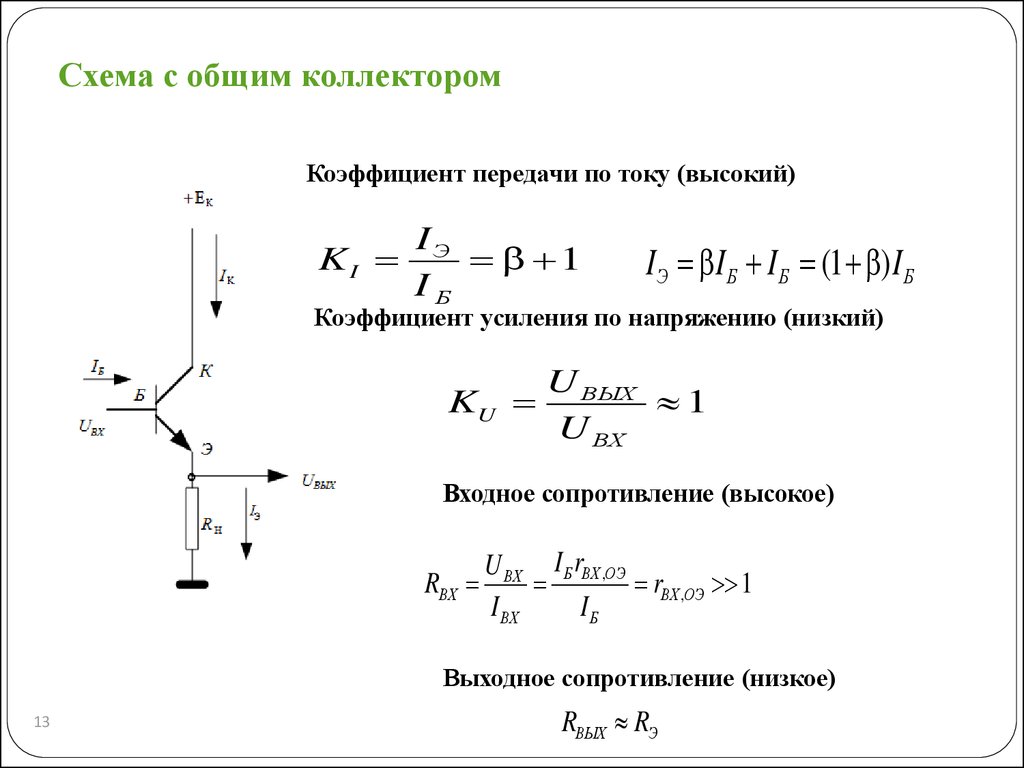
Это намного лучше, чем то, что у меня есть здесь!
Только один пример графика из превосходной схемы усилителя с общим коллектором Кеннета Куна 2 .
Ссылки
Джеймс М. Фиоре (2022, 23 мая). Усилитель с общим коллектором . LibreTexts: Инженерия. Получено 11 августа 2022 г. с https://eng.libretexts.org/Bookshelves/Electrical_Engineering/Electronics/Book%3A_Semiconductor_Devices_-_Theory_and_Application_(Fiore)/07%3A_BJT_Small_Signal_Amplifiers/7.4%3A_Common_Collector_Amplifier. ↩︎
Кеннет А. Кун. Конструкция усилителя с общим коллектором . Получено 03 сентября 2022 г. с https://www.kennethkuhn.com/students/ee351/bjt_cc_amplifier_design.pdf. ↩︎ ↩︎
транзисторы – Проблемы с пониманием выходного импеданса общего коллектора
Анализ KCL без интуиции
Давайте начнем с того, что на мгновение отвлечемся от интуиции и просто проработаем проблему. Для начала схема:
смоделируйте эту схему — Схема создана с помощью CircuitLab
(Для тех, кто заинтересован, я предоставил более полный контекст OP в конце ниже.
Обычно, для целей слабого сигнала, вы также можете вставить \$r_e\$ в приведенную выше схему прямо на кончике . эмитента \$Q_1\$. Но учебник игнорирует его значение до раздела 2.3 и считает его отсутствующим на данный момент.
Вы знаете, что \$V_\text{B}-V_\text{E}=V_\text{BE}\$ и что для слабых сигналов, при отсутствии \$r_e\$, это фиксированная разность напряжений. Это позволяет нам заменить одно на другое. Также обратите внимание, что \$I_\text{E}=\frac{V_\text{E}}{R_\text{E}}\$.
Если предположить, что \$I_x\$ является произвольной текущей нагрузкой приемника, которая будет либо \$0\:\text{A}\$ (без нагрузки), либо \$1\:\text{A}\$ (загружена), тогда KCL:
$$\begin{align*} \frac{V_\text{E}+V_\text{BE}}{R_1}+\frac{V_\text{E}+V_\text{BE}}{R_2}+\frac{V_\text{E }+V_\text{BE}}{Z_\text{IN}}+\frac{\frac{V_\text{E}}{R_\text{E}}+I_x}{\beta+1}&= \frac{V_\text{CC}}{R_1}+\frac{0\:\text{V}}{R_2}+\frac{V_\text{IN}}{Z_\text{IN}}+\ гидроразрыва {\ гидроразрыва {0 \: \ текст {V}} {R_ \ текст {E}}} {\ бета + 1} \end{выравнивание*}$$
(В приведенном выше примере я поместил исходящие токи с левой стороны и входящие токи с правой стороны.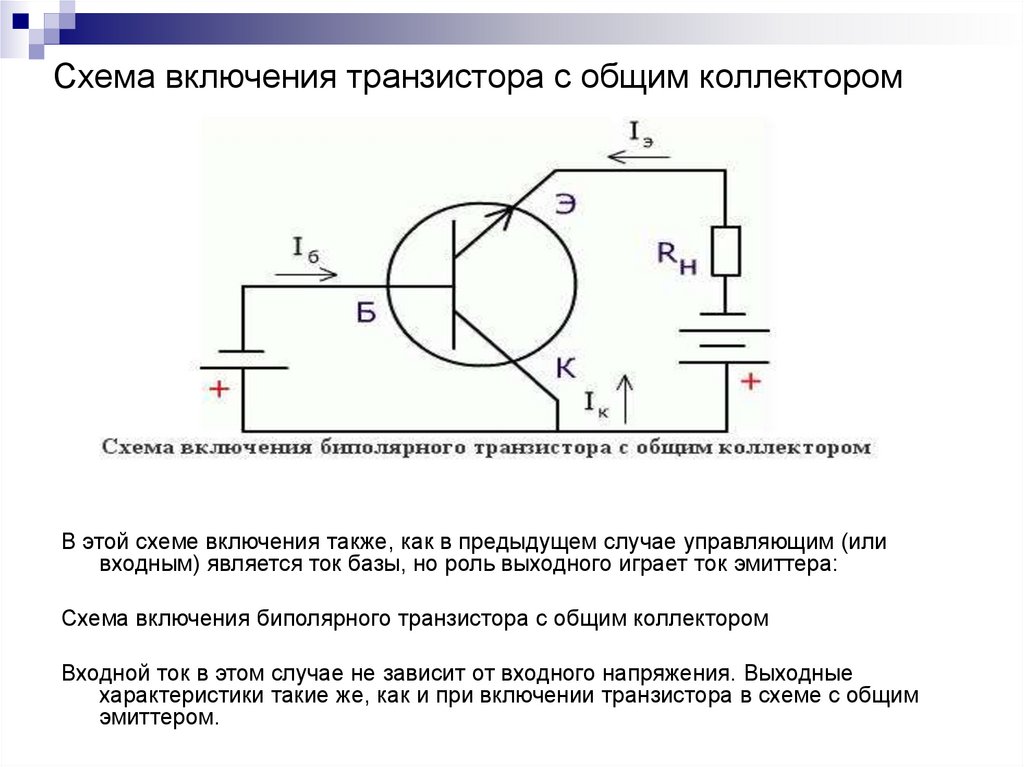
Хотя я много раз писал об этом новом подходе к KCL, показан более свежий пример. здесь.)
Таким образом, приведенное выше уравнение говорит
“Ток, вытекающий из базового узла через \$R_1\$, плюс ток, вытекающий из базового узла через \$R_2\$, плюс ток, вытекающий из базового узла через \$Z_\text{IN}\$, плюс ток, вытекающий из узла-эмиттера через \$R_\text{E}\$ с точки зрения базового узла равно току, втекающему в базовый узел от \$V_\text{CC}\$ до \$R_1\$, плюс текущий течет в базовый узел из земли через \$R_2\$, плюс ток, протекающий в базовый узел из \$V_\text{IN}\$ через \$Z_\text{IN}\$ плюс ток, втекающий в эмиттерный узел из заземление через \$R_\text{E}\$ с точки зрения базового узла .”
Если вы решите приведенное выше для \$V_{\text{E}\left(I_x\right)}\$, то вы можете получить: \$Z_\text{OUT}=\frac{\Delta \, V_\text{E}}{\Delta\,I_\text{E}}=\frac{V_{\text{E}\left(I_x=0\right)}-V_{\text{E}\left (I_x=1\right)}}{1\:\text{A}-0\:\text{A}}\$:
$$Z_\text{OUT}= \frac{\frac1{\beta+1}\left(\beta+1\right)R_\text{E}\,R_1\, R_2\,Z_\text{ IN}}{\left(\beta+1\right)R_\text{E}\,R_1\, R_2+\left(\beta+1\right)R_\text{E}\,R_1\,Z_\text {IN}+\left(\beta+1\right)R_\text{E}\, R_2\,Z_\text{IN}+R_1\, R_2\,Z_\text{IN}}$$
Это точно такой же результат, который вы получили бы, если бы взяли \$\frac1{\beta+1}\left[R_1\mid\mid R_2\mid\mid Z_\text{IN}\mid\mid \left(\beta+ 1\right)R_\text{E} \right]\$ или, умножая \$\frac1{\beta+1}\$ на:
$$Z_\text{OUT}=\left[\left(\ frac{R_1\mid\mid R_2\mid\mid Z_\text{IN}}{\beta+1}\right)\mid\mid R_\text{E} \right]$$
Единственное отличие здесь от учебника в том, что авторы решили использовать \$\beta\$ в качестве приближения для \$\beta+1\$.
Интуиция
Посмотрите на оригинальную схему. Там вы можете легко увидеть, что \$R_1\$, \$R_2\$ и \$Z_\text{IN}\$ связаны от источника напряжения (предположительно идеального) к общему узлу на базе BJT. С точки зрения базы, глядя на эти три импеданса с точки зрения переменного тока, все они фактически «заземлены» и, следовательно, «параллельны» друг другу.
Теперь, поскольку крошечные вариации тока в базе подразумевают гораздо большие вариации тока в эмиттере, параллельное сопротивление, видимое на базе, будет выглядеть в \$\beta+1\$ раз меньше на эмиттере. Затем это выполняется параллельно с \$R_\text{E}\$.
Вот откуда берется интуитивное представление.
Искусство электроники, 3-е издание, стр. 84
Упомянутая вами рабочая проблема имеет \$V_\text{CC}=+15\:\text{V}\$, \$R_1=130\:\text {k}\Omega\$, \$R_2=150\:\text{k}\Omega\$, \$Z_\text{IN}=10\:\text{k}\Omega\$, \$R_ \text{E}=7,5\:\text{k}\Omega\$ и \$\beta=100\$. С этими значениями вы должны найти, что \$Z_\text{OUT}\ приблизительно 85,59\:\Omega\$ и \$A_v\приблизительно 0,86446\$.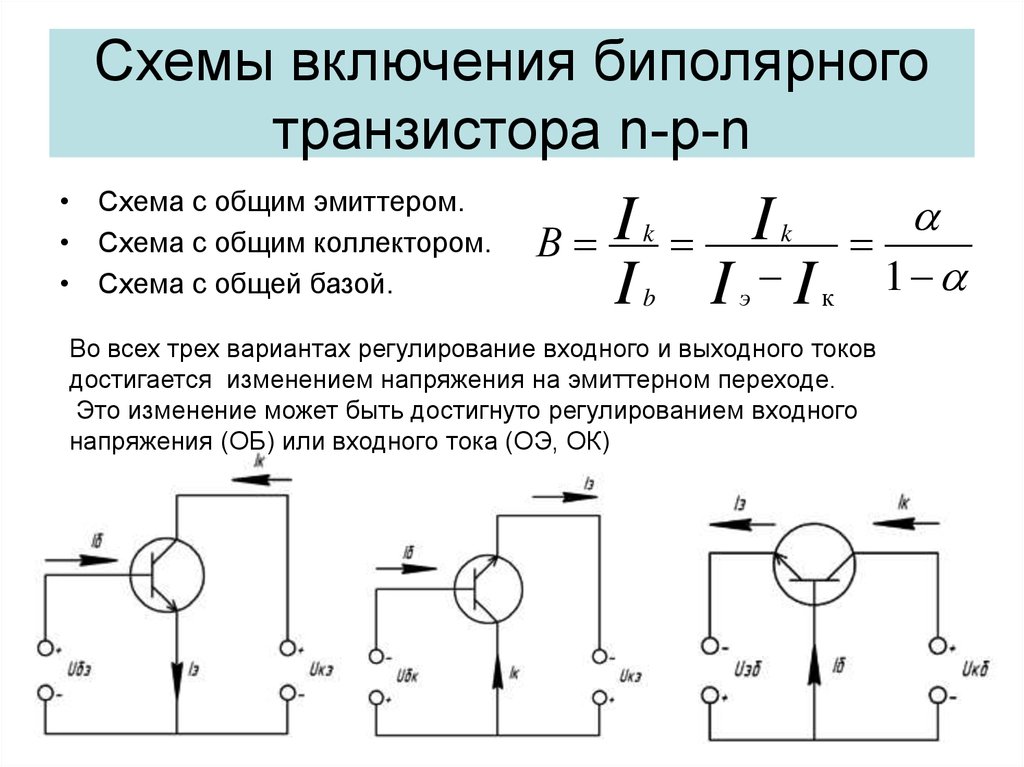
В книге написано, что \$Z_\text{OUT}\приблизительно 87\:\Omega\$, что достаточно близко.
Как указано в книге, поскольку расчет рассчитан на \$I_\text{E}\приблизительно 1\:\text{мА}\$, динамическое значение импеданса переменного тока Эберса-Молла будет обсуждаться позже (\ $r_e\$) будет примерно \$26\:\Omega\$. (Они говорят \$r_e\примерно 25\:\Omega\$.) Это добавляется последовательно и увеличивает \$Z_\text{OUT}\$ до \$Z_\text{OUT}\приблизительно 112\: \Омега\$. (В книге это написано как \$110\:\Omega\$, используя их немного меньшее значение.)
Превышать точность бессмысленно, поэтому учебник обрабатывает это так, как вы должны: показывает не более двух цифр точности.
Полный контекст, взятый из The Art of Electronics, 3-е издание:
ОП не смог предоставить рабочий пример, о котором шла речь, я думаю:
Они полагаются на более простую модель BJT, которая еще НЕ включает \ $g_m\$ и после предыдущих дискуссий о \$Z_\text{IN}\$ и \$Z_\text{OUT}\$, которые также помогают сформулировать приведенное выше обсуждение в учебнике.
