Ряд E24 номиналов резисторов – RadioLibrary
Ряд E24 номиналов резисторов – RadioLibrary
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Номиналы резисторов, ряды резисторов, ряд Е24
ОТ КАТОДА ДО АНОДА
Поиск по сайту Новости Токоизмерительные клещи с мультиметром СМР-1006 | ГЛАВНАЯ » РЕЗИСТОРЫ » Номиналы резисторов Номиналы резисторов представлены так называемыми рядами резисторов (например ряд Е24). Номиналы резисторов соответствуют числам в приведенных ниже таблицах или числам, полученным умножением или делением этих чисел на 10n (где n – целое положительное или отрицательное число). Например, по ряду Е6 номиналы резисторов в каждой декаде должны соответствовать числам 1; 1,5; 2,2; 3,3; 4,7; 6,8 или числам, полученным умножением или делением этих чисел на 10n, где n — целое положительное или отрицательное число. Например 10, 100, 15, 150 или 0.1, 0.01, 0.15, 0.015 и т.д. Принцип построения рядов Е48, Е96 и Е192 аналогичен приведенному с той лишь разницей, что увеличивается число промежуточных значений номиналов. Номиналы резисторов по ряду Е3, Е6, Е12, Е24
Номиналы резисторов по ряду Е48, Е96, Е192
|
Резисторы последовательно | Вращающиеся числа
Компоненты входят в серию , если они соединены таким образом,
Мы показываем свойства последовательного соединения с использованием резисторов.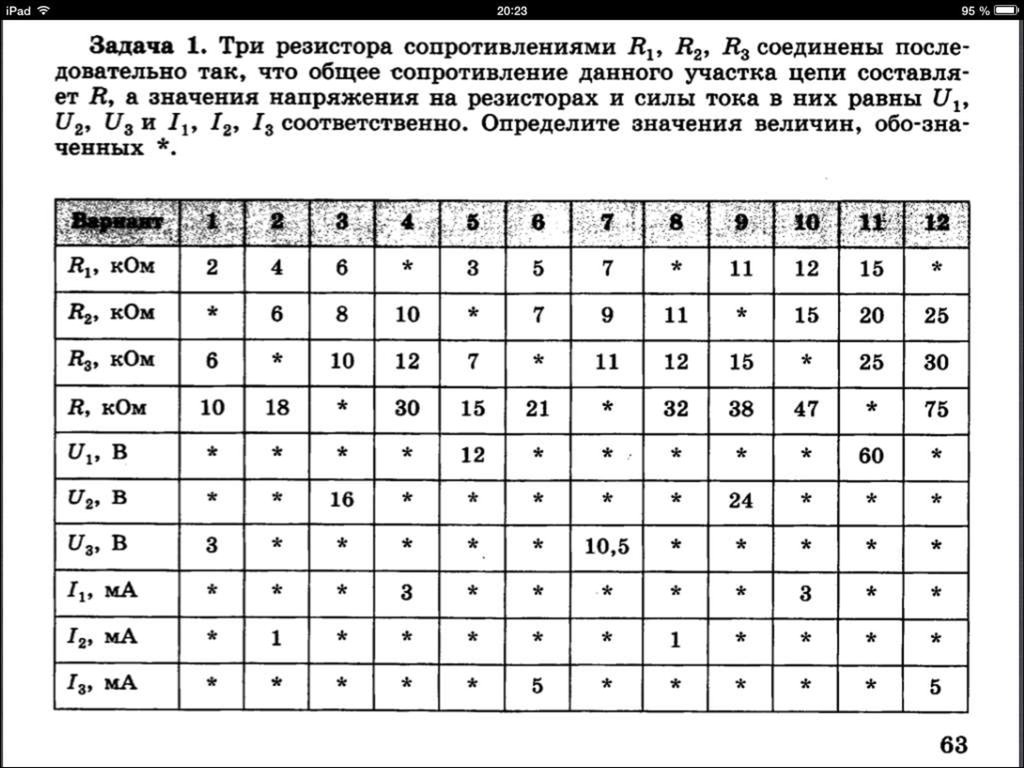
Автор Вилли Макаллистер.
Содержимое
- Последовательное соединение
- Резисторы серии
- Эквивалентный последовательный резистор
- Напряжение распределяется между последовательными резисторами
- Проверка концепции
Последовательное соединение
Резисторы соединены последовательно, когда они соединены «голова к хвосту» и нет других проводов, ответвляющихся от узлов между компонентами. $\text{R1}$, $\text{R2}$ и $\text{R3}$ включены последовательно,
При последовательном соединении через каждый резистор течет одинаковый ток. Весь ток, идущий на передний конец, вытекает на другой конец. Ток одинаков по всей цепи.
Резисторы на следующем изображении имеют последовательное соединение , а не . Дополнительные ответвления отходят от узлов между резисторами. Если эти ветви имеют ток (оранжевые стрелки), то $\text{R1}$, $\text{R2}$ и $\text{R3}$ не имеют одного и того же тока и, следовательно, не являются последовательными.
Резисторы последовательно
Вот схема с последовательно соединенными резисторами. Источник напряжения $\text V_{\text{S}}$ подключен к цепочке резисторов. Резисторы соединены встречно, поэтому мы знаем, что они последовательно.
Вот что мы знаем,
- Напряжение $v_\text S$ — некоторая известная постоянная величина $\text V_\text S$.
- Резисторы соединены последовательно, поэтому мы знаем, что через все три протекает одинаковый ток $i$.
- Сумма отдельных напряжений на резисторах должна составлять $v_{\text S}$.
С этим небольшим знанием и Законом Ома мы можем вычислить неизвестные. Вот то, чего мы не знаем:
- Мы не знаем текущий $i$.
- Нам неизвестны напряжения на отдельных резисторах.
Запишите сумму напряжений,
$v_{\text S} = v_{\text R1} + v_{\text R2} + v_{\text R3}$
Напряжение на каждом резисторе может быть записано через сопротивление и ток,
$v_{\text R1} = i\,\text R1 \qquad v_{\text R2} = i\,\text R2 \qquad v_{\text R3} = i \,\text R3$
Подставьте эти выражения обратно в сумму напряжений,
$v_{\text{S}} = i\, \text R1 \,+\, i\, \text R2 \,+ \, я\, \текст R3$
Умножьте ток и сгруппируйте резисторы вместе,
$v_{\text{S}} = i\,\, (\text R1 + \text R2 + \text R3)$
Найдите неизвестное $ i$,
$i = \dfrac{v_{\text{S}}} {\text R1 + \text R2 + \text R3}$
Взгляните на это уравнение. Это похоже на закон Ома для одного резистора, $i = v/\text R$, за исключением того, что знаменатель представляет собой сумму последовательных резисторов. Делаем вывод,
Это похоже на закон Ома для одного резистора, $i = v/\text R$, за исключением того, что знаменатель представляет собой сумму последовательных резисторов. Делаем вывод,
При последовательном соединении общее сопротивление равно сумме сопротивлений отдельных резисторов.
Эквивалентный последовательный резистор
Мы можем представить новый больший эквивалентный резистор, равный сумме последовательных резисторов. Это эквивалентно в том смысле, что для данного $\text V_\text S$ течет один и тот же ток $i$.
$\text R_{\text{серия}} = \text{R1} + \text{R2} + \text{R3}$
Вы можете услышать это сленговое выражение: С «точки зрения» источника напряжения, три последовательных резистора «выглядят» как один эквивалентный резистор большего размера. Ток $i$, обеспечиваемый источником напряжения, в обоих случаях одинаков.
Как источник напряжения может иметь «точку зрения»?В инженерных дискуссиях очень часто говорят что-то вроде
.
«С точки зрения источника напряжения… бла-бла-бла».
Мы говорим об источнике напряжения, как если бы это был человек.
У людей богатый словарный запас, чтобы говорить о себе, поэтому мы часто используем слова людей в других ситуациях. Но вы должны быть осторожны. Ведь электронные компоненты и электроны не люди. Источники напряжения на самом деле не имеют «точки зрения» и не могут «смотреть» на то, к чему они подключены.
Один из моих любимых вопросов о схемах: «Как электроны решают, куда им двигаться?» Ну, электроны на самом деле ничего не «решают». Электроны реагируют на электрическую силу, описываемую законом Кулона, и текут в резисторах согласно закону Ома.
Если вы оказались в запутанном разговоре о том, как работает схема, причиной проблемы могут быть сленговые выражения. Если вы чувствуете, что это происходит, вернитесь к первым принципам электроники: напряжению, току и закону Ома.
Если последовательно подключено много резисторов, общая форма эквивалентного последовательного сопротивления будет следующей:
$\text R_{\text{серия}} = \text{R1} + \text{R2} + \ldots + \text {R}_\text N$
Напряжение распределяется между последовательно соединенными резисторами
Рассмотрим напряжение на каждом резисторе в последовательной цепи. Мы применяем закон Ома к отдельным резисторам по одному. Ток $i$ в каждом резисторе одинаков.
Мы применяем закон Ома к отдельным резисторам по одному. Ток $i$ в каждом резисторе одинаков.
$v_{\text R1} = i\,\text R1 \qquad v_{\text R2} = i\,\text R2 \quad \ldots \quad v_{\text {RN}} = i\,\ текст R_\текст N$
Это имеет больше смысла, если мы сделаем пример с действительными числами. Я призываю вас попробовать это самостоятельно, прежде чем заглянуть в ответ.
Проверка концепции
ПРОБЛЕМА 1
a. Каков текущий $\blueD i$ ?
б. Каково напряжение на трех резисторах?
в. Покажите, что напряжение отдельных резисторов в сумме составляет $\text V_\text S$.
Ступени,
- Найдите эквивалентное последовательное сопротивление $\text R_{\text{серии}}$.
- Используйте $v_\text S$ и $\text R_\text{series}$, чтобы найти $i$ по закону Ома.
- Найдите напряжения отдельных резисторов, снова используя закон Ома.

- Убедитесь, что сумма напряжений соответствует норме.
а. Эквивалент $\text R_{\text{серии}}$ – это сумма трех сопротивлений.
$\text R_{\text{ряд}} = 300\,\Омега + 500\,\Омега + 1200\,\Омега = 2000\,\Омега$
Текущее значение $i$ определяется законом Ома,
$i = \dfrac{v_\text S}{\text R_{\text{серия}}} = 10\,\text V / 2000\,\Omega = 0,005\,\text A = 5\,\text {мА} $
б. Зная $i$, вычисляем напряжения отдельных резисторов,
$v_{\text{R1}} = i\, \text R_{300} = 5\,\text{мА} \cdot 300\,\Omega = 1,5\,\text V$
$v_{\text{R2}} = i\, \text R_{500} = 5\,\text{мА} \cdot 500\,\Omega = 2,5\,\text V$
$v_{\text{R3}} = i\, \text R_{1200} = 5\,\text{мА} \cdot 1200\,\Omega = 6,0\,\text V$
Вот полное решение,
г. Проверьте: сумма напряжений резисторов соответствует напряжению источника?
$1,5\,\text V + 2,5\,\text V + 6,0\,\text V \stackrel{\checkmark}{=} 10\,\text V\qquad$ Да!
ЗАДАЧА 2
Основываясь на напряжениях резисторов, которые вы только что вычислили,
Какой резистор имеет наибольшее или наименьшее напряжение?
Показать ответ Наибольшее напряжение.
Наименьший резистор имеет наибольшее или наименьшее напряжение?
Показать ответНаименьшее напряжение.
Какой резистор имеет наибольший ток?
Показать ответВопрос с подвохом. Все резисторы имеют одинаковый ток при последовательном соединении.
Резюме
Резисторы последовательно добавить,
$\text R_{\text{серия}} = \text{R1} + \text{R2} + \ldots + \text{R}_\text N$
Резисторы, включенные последовательно, имеют одинаковый ток.
Напряжение распределяется между последовательными резисторами. Наибольшее напряжение появляется на самом большом резисторе.
Резисторы в серии – Справочник по электронике
Резисторы можно найти практически в каждой цепи на планете. Это не зря; резисторы дают нам возможность контролировать поток тока, ограничивая поток электричества, и устанавливать опорные напряжения для подсхем.
Резисторы являются одними из наиболее важных электрических компонентов.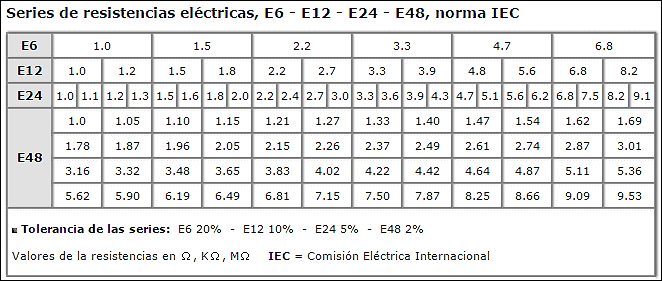 Резисторы — это компоненты, которые используются для увеличения сопротивления электрических цепей. При последовательном соединении резисторов общее сопротивление равно сумме вкладов каждого резистора.
Резисторы — это компоненты, которые используются для увеличения сопротивления электрических цепей. При последовательном соединении резисторов общее сопротивление равно сумме вкладов каждого резистора.
Они часто используются последовательно и параллельно по разным причинам. Понимание того, как резисторы работают последовательно, является важным шагом к более сложным конфигурациям резисторов и других компонентов. Этот урок также укрепит вашу способность читать электрические схемы и закрепит понятия, которые были введены в Модуле 1 и Модуле 2. Это поможет вам анализировать более сложные схемы, ведущие к законам тока и напряжения Кирхгофа.
Содержание – Резисторы серии
Обзор резисторов
Резисторы – это электрические компоненты, которые пропускают электрический ток, но не так легко, как обычный провод или проводник. Вместо этого они уменьшают ток, протекающий через них, на величину, пропорциональную сопротивлению в омах:
I = \frac{V}{R} Допустим, у нас есть 12-вольтовая батарея, подключенная к резистору на 1 Ом. Закон Ома гласит, что ток (I) равен напряжению батареи (V) относительно номинала резистора (R):
Закон Ома гласит, что ток (I) равен напряжению батареи (V) относительно номинала резистора (R):
I = \frac{V_{battery}}{R} = \frac{12V}{1\Omega}=12\ Amps Для обзора этой темы ознакомьтесь с нашим уроком по закону Ома!
Если бы мы использовали больший резистор, скажем, 15 Ом, то мы уменьшили бы ток намного больше:
I = \frac{V_{battery}}{R} = \frac{12V}{15 \Омега}=0,8\ Ампер Резисторы уменьшают ток, а резисторы большего размера уменьшают ток сильнее.
Они также вызывают падение напряжения, которое также пропорционально сопротивлению:
В = I R
В последних двух случаях мы знаем, что падение напряжения должно быть равно напряжению батареи. Это потому, что по обе стороны от клемм батареи мы будем всегда измерять разность потенциалов, обеспечиваемую батареей. Батареи не были бы очень хорошими источниками напряжения, если бы это было не так.
Однако, если два резистора соединены последовательно, общее падение напряжения будет равно напряжению батареи.
Резисторы полезны 92R
Резисторы преобразуют электрическую энергию в тепловую (тепло) при прохождении через них тока. Это основная функция резистора. Это рассеивание мощности также известно в просторечии как «потери R в квадрате».
Поскольку резисторы плохо проводят ток, они преобразуют часть нашего электричества в тепло.
Зачем нам это?
На самом деле есть несколько причин:
- Сопротивление не просто тратит энергию; это также уменьшает текущий поток. Некоторое сопротивление всегда необходимо для предотвращения короткого замыкания. Несмотря на то, что проводники имеют небольшое сопротивление, обычно требуется более высокий уровень сопротивления, чтобы ограничить ток до безопасного уровня. Вот почему важно всегда использовать один резистор последовательно или в каждой ветви параллельной цепи.
- Когда мы используем определенные значения и конфигурации резисторов, мы можем настроить нашу схему, чтобы взять заданный источник питания и выдать определенный ток или уровни напряжения по мере необходимости.

Гораздо проще использовать резисторы для регулировки тока, который нам нужен, чем добавлять новую, очень специфичную батарею каждый раз, когда нам нужен новый ток.
Вернуться к… Сопротивлению!
Вернемся ненадолго к концепции электрического сопротивления. Сопротивление — это в основном то, насколько что-то проводит.
Важно помнить, что все в цепи (кроме сверхпроводника) имеет некоторое сопротивление. Каждый элемент (резисторы, катушки индуктивности, диоды, транзисторы) имеет сопротивление. Сами провода имеют сопротивление. Даже провода из серебра, обладающего самой высокой электропроводностью среди всех металлов, обладают некоторым сопротивлением. Это низкое сопротивление, но оно все же есть.
Таким образом, сопротивление является постоянным фактором в любой цепи.
Резисторы серии
Чтобы получить общее сопротивление в последовательной цепи (или отдельной ветви параллельной цепи), вы просто складываете сопротивления всех элементов цепи (или ветви).
R_T = R_1 +R_2+R_3+...+R_N
Очень удобно, что сопротивление так легко добавляется. Кроме того, сопротивление, добавляемое такими вещами, как провода и переключатели, достаточно низкое, поэтому мы обычно его игнорируем.
Концепция последовательного добавления сопротивлений интуитивно понятна. Поскольку каждый проводник имеет сопротивление, чем длиннее проводящий путь, тем выше будет сопротивление. Резисторы просто облегчают получение надежного сопротивления, поэтому вам не нужно добавлять 50 футов дополнительного провода, когда вы хотите увеличить сопротивление.
Нежелательное сопротивление может быть плохой вещью
Если мы не используем сопротивление для определенной функции в цепи, сопротивление, как правило, плохо. Тот факт, что сопротивление увеличивается при последовательном соединении проводников (или резисторов), может сделать эти проблемы значительными.
Например, сопротивление может быть важным фактором, который следует учитывать при установке новой проводки. Провод длиной более нескольких футов часто требует учета сопротивления провода. К счастью, сопротивление уменьшается по мере увеличения размера провода. Это означает, что провода определенной длины могут иметь рекомендуемый «калибр», чтобы предотвратить влияние резистивных потерь на систему. Ознакомьтесь с нашей статьей о проводке для получения дополнительной информации.
Провод длиной более нескольких футов часто требует учета сопротивления провода. К счастью, сопротивление уменьшается по мере увеличения размера провода. Это означает, что провода определенной длины могут иметь рекомендуемый «калибр», чтобы предотвратить влияние резистивных потерь на систему. Ознакомьтесь с нашей статьей о проводке для получения дополнительной информации.
Другой отличный пример — передача энергии. Когда мы передаем электричество на большие расстояния, сопротивление проводов становится очень важным. На самом деле это был решающий момент между мощностью постоянного тока Эдисона и мощностью переменного тока Вестингауза. По этой причине, когда вы подключаете шнур питания к настенной розетке, вы подключаетесь к сети переменного тока (а не постоянного тока!), чтобы обеспечить необходимое электричество. Мы рассмотрим питание переменного тока и электронику в Модуле 4. Однако изучение переменного тока не очень важно для начала работы с электроникой. Помогает. (Просто к вашему сведению. )
)
Хорошо, давайте начнем последовательно ставить резисторы и посмотрим, что получится!
Соединение резисторов последовательно
Понять, как резисторы работают последовательно, просто: значение сопротивления R (в Омах) просто складывается.
Рассмотрим следующую схему: Общее сопротивление равно 5 + 12 = 17 Ом.
Эта схема имеет источники питания 1,5 В и два резистора; R1 с сопротивлением 5 Ом и R2 с сопротивлением 12 Ом. Значения сопротивления последовательно складываются, так что в сумме получается:
R_T = R_1 + R_2 = 5\Omega + 12\Omega = 17\Omega
Вы не заметите, что мы используем обозначение R T для описания полного сопротивления цепи. Иногда вы также можете увидеть использование R eq для обозначения эквивалентного сопротивления цепи или параллельной ветви цепи.
Эквивалентное сопротивление просто означает, что мы притворяемся, что некоторое количество резисторов является одним резистором. Их можно расположить последовательно, параллельно или в какой-то сумасшедшей комбинации. Мы всегда можем проанализировать цепь и выяснить, какое общее сопротивление имеет цепь. Суммарная величина сопротивления называется эквивалентным сопротивлением, обозначаемым R экв. .
Их можно расположить последовательно, параллельно или в какой-то сумасшедшей комбинации. Мы всегда можем проанализировать цепь и выяснить, какое общее сопротивление имеет цепь. Суммарная величина сопротивления называется эквивалентным сопротивлением, обозначаемым R экв. .
Имейте в виду, что (не считая сверхпроводников) каждый провод или компонент имеет определенное сопротивление. Таким образом, точное эквивалентное сопротивление в реальной жизни должно включать сопротивление каждого компонента и провода. В электронике иногда мы используем «ручные» аппроксимации, которые работают очень хорошо. Игнорирование сопротивления всего, кроме резисторов, работает просто отлично.
Анализ последовательно соединенных резисторов
Мы говорили о том, что происходит с сопротивлением при последовательном соединении резисторов, но как насчет тока, напряжения и мощности?
Ток резисторов в серии
Начнем с тока. Добавление резистора или нескольких последовательно соединенных резисторов оказывает такое же влияние на ток, как и использование более крупного резистора.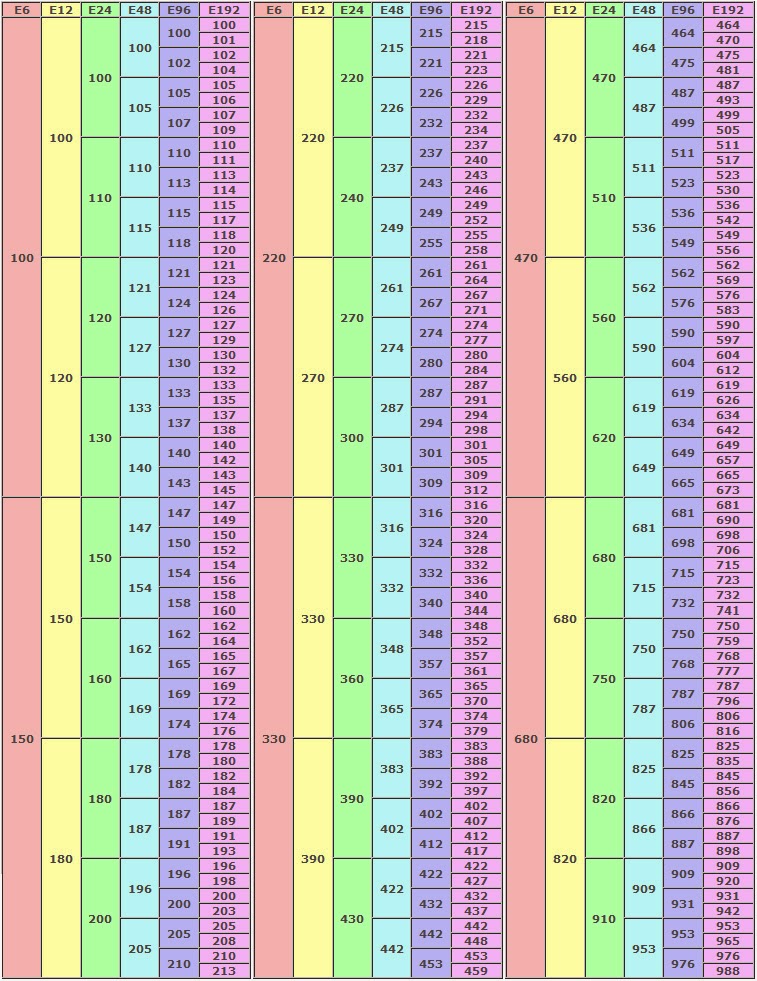 Чем больше общее сопротивление, тем меньше ток. Это точно так же, как пример закона Ома, который мы видели выше.
Чем больше общее сопротивление, тем меньше ток. Это точно так же, как пример закона Ома, который мы видели выше.
Вот (слегка) сложная часть: ток не «падает» на каждом резисторе, как напряжение. Ток во всей цепи, через каждый резистор, абсолютно одинаков. Добавление резистора уменьшает ток через все резистора.
Один приятный побочный эффект заключается в том, что нам нужно отслеживать только один ток. Это везде одинаково. Давайте рассмотрим пример или два.
Для сравнения рассмотрим эту простую схему с резистором 2 Ом, подключенным к батарее 1,5 В. Ток будет просто следовать закону Ома, используя напряжение батареи и сопротивление одного резистора (R 1 ).
I = \frac{V_{батарея}}{R_1} = \frac{1,5V}{2\Omega}=0,75\ A Сила тока в цепи составляет 0,75 ампер.
Теперь добавим в схему второй резистор.
На этот раз ток будет зависеть от сопротивления как R 1 , так и R 2 . Обозначим общее сопротивление как R T :
I = \frac{V_{battery}}{R_T} = \frac{V_{battery}}{R_1+R_2} = \frac{1,5V}{ 2\Omega + 4\Omega}= \frac{1. 5V}{6\Omega}=.25A
5V}{6\Omega}=.25A Добавив второй резистор, мы уменьшили ток с 0,75 до 0,25 ампер. Новый ток одинаков во всей цепи. У нас есть 0,25 ампер, проходящих через резистор R 1 и 0,25 А через резистор R 2 .
Теперь мы можем видеть, что добавление резистора имеет функцию уменьшения тока во всей последовательной цепи. На следующем уроке (параллельные резисторы) мы обнаружим, что каждая ветвь имеет разное сопротивление.
Напряжение для последовательно соединенных резисторов
При рассмотрении последовательно соединенных резисторов необходимо помнить о двух вещах:
- Общее напряжение во всей цепи одинаково (напряжение батареи или напряжение питания).
- Теперь «падение» напряжения, т. е. разность потенциалов на каждом отдельном резисторе, отличается. Другими словами, теперь у нас есть V 1 , что соответствует R 1 , V 2 , что соответствует R 2 и т. д. Суммарное напряжение V T на всех резисторах одинаково.
 как батарея или напряжение питания (см. пункт №1).
как батарея или напряжение питания (см. пункт №1).
Давайте еще раз посмотрим на две цепи, которые мы только что проанализировали на ток, чтобы увидеть, как добавление резистора изменяет напряжение в разных точках цепи.
С одним резистором напряжение на резисторе такое же, как и напряжение батареи, 1,5 вольта. Это то, что мы ожидаем, потому что, если вы измерите напряжение на аккумуляторе без цепи, мы измерим 1,5 вольта.
Добавим R 2 :
Со вторым резистором напряжение батареи 1,5 В теперь падает на оба резистора. Каждый из них вносит свой вклад в общее напряжение. Теперь у нас есть V 1 , что является напряжением между R 1 и V 9.0347 2 , напряжение на R 2 . Сумма V 1 и V 2 будет равна V T , то есть напряжению аккумулятора. Давайте рассчитаем V1 и V2, используя ток 0,25 А, который мы рассчитали выше. Помните, ток I через оба резистора одинаков!
В_1 = IR_1=(.25А)(2\Омега)=.5В \\ V_2 = IR_2 = (.25A)(4\Omega)=1V
Давайте проверим, правильно ли мы это сделали. Если мы рассчитали правильно, общее напряжение должно составить напряжение батареи (1,5 В).
V_T = V_1 + V_2 = 0,5 В + 1 В = 1,5 В
Как мы видим, V T , представляющее собой сумму падений напряжения на обоих резисторах, совпадает с напряжением батареи. Это обеспечивает хорошую двойную проверку.
Мощность резисторов в серии
Получается, что чем больше сопротивление, тем меньше рассеиваемая мощность в цепи. Один из способов думать об этом таков: разомкнутая цепь (то есть отключенная) не приведет к рассеиванию или подаче мощности. С другой стороны, короткое замыкание (подключение к источнику напряжения без сопротивления) приведет к подаче и рассеиванию огромной мощности. Если вы случайно соедините две клеммы батареи без какого-либо сопротивления, батарея разрядится очень быстро. 92(2\Омега) = (0,5625)(2) = 1,125 Вт
Мощность, рассеиваемая резистором, составляет 1,125 Вт. Какая мощность обеспечивается (P s ) аккумулятором?
Какая мощность обеспечивается (P s ) аккумулятором?
P_s = IV = (0,75 А)(1,5 В)=1,125 Вт
Мощность, выдаваемая батареей, идентична мощности, рассеиваемой резистором. Этот расчет служит двойной проверкой правильности расчета рассеиваемой мощности.
Давайте добавим наш второй резистор и посмотрим, что произойдет с питанием!
На этот раз резистор R2 уменьшает ток, потребляемый схемой. Наши два резистора, R 92(4\Омега)=.25Вт\\ P_T=P_1+P_2=0,125 Вт+0,25 Вт=0,375 Вт
Мы видим, что добавление второго резистора уменьшило мощность с 1,125 Вт до 0,375 Вт.
Давайте подтвердим, что мы правильно рассчитали, дважды сверив наш результат с мощностью, подаваемой батареей.
P_s = IV = (0,25 А) (1,5 В) = 0,375 Вт
Отличная работа!
Теперь, когда мы увидели, что происходит с сопротивлением, током, напряжением и мощностью при последовательном соединении резисторов, давайте рассмотрим несколько примеров.
Примеры проблем
Пример 1.
 Одиночный резистор
Одиночный резисторВернемся к примеру с одним резистором, чтобы продолжить практику и развить нашу интуицию. В следующей схеме мы видим, что у нас есть один резистор 5 Ом, подключенный к батарее 1,5 В:
Попробуйте ответить на следующие вопросы. Ответы чуть ниже на случай, если у вас возникнут трудности или вы захотите подтвердить.
1) Каково общее сопротивление цепи?
2) Какова сила тока в цепи?
3) Каково падение напряжения на резисторе?
4) Какая мощность обеспечивается цепью?
5) Какова рассеиваемая мощность (потери) резистора?
Ответы на пример 1
1) Каково общее сопротивление цепи?
R_T = R_1 = 5\Омега
2) Какова сила тока в цепи?
I = \frac{V}{R} = \frac{1,5V}{5\Omega} = .3A 3) Каково падение напряжения на резисторе?
В = IR = (.3A)(5\Омега) = 1,5 В 92(5\Омега) = 0,45 Вт
В качестве двойной проверки общая подводимая мощность должна равняться рассеиваемой мощности. Это энергия, подводимая к цепи в единицу времени.
Это энергия, подводимая к цепи в единицу времени.
Давайте сравним это с двумя последовательными резисторами, чтобы увидеть, как меняются наши результаты.
Пример 2. Два последовательно соединенных резистора
В этом случае последовательно соединены два резистора: R1 номиналом 5 Ом и R2 номиналом 10 Ом.
Попробуйте ответить на следующие вопросы:
1) Каково общее сопротивление цепи?
2) Какова сила тока в цепи?
3) Каково падение напряжения на каждом резисторе?
4) Какая мощность обеспечивается цепью?
5) Какова мощность, рассеиваемая каждым резистором?
Ответы на пример 2
1) Каково общее сопротивление цепи?
R_T = R_1 + R_2 = 5\Омега + 10\Омега = 15\Омега
Мы видим, что сопротивление увеличилось на величину второго резистора.
2) Какова сила тока в цепи?
I = \frac{1,5V}{15\Omega} = 0,1A Ток уменьшился из-за увеличения сопротивления в цепи.
3) Каково падение напряжения на каждом резисторе?
Помните: ток через каждый резистор одинаков в последовательной цепи.


 3 МОм
3 МОм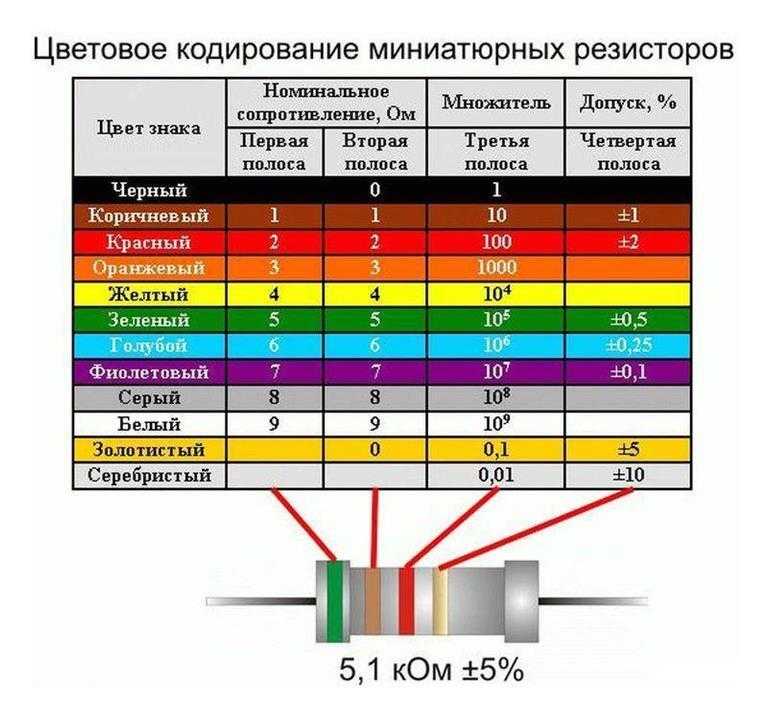 2 МОм
2 МОм Ряды резисторов являются результатом стандартизации номинальных значений резисторов. Для постоянных резисторов существует шесть, так называемых, рядов: Е6, Е12, Е24, Е48, Е96 и Е192, а для переменных резисторов установлен один ряд – Е6. Кроме того существует дополнительный ряд Е3. Цифра после буквы E обозначает число номинальных значений сопротивлений резисторов в каждом десятичном интервале.
Ряды резисторов являются результатом стандартизации номинальных значений резисторов. Для постоянных резисторов существует шесть, так называемых, рядов: Е6, Е12, Е24, Е48, Е96 и Е192, а для переменных резисторов установлен один ряд – Е6. Кроме того существует дополнительный ряд Е3. Цифра после буквы E обозначает число номинальных значений сопротивлений резисторов в каждом десятичном интервале.
