Сигма-дельта АЦП / Теория, измерения и расчеты / Сообщество EasyElectronics.ru
Сигма-дельта АЦП
Сигма-дельта АЦП состоит из двух частей: модулятор и цифровой ФНЧ.
Модулятор преобразует входное напряжение Uвх в последовательность импульсов, а ФНЧ формирует выходной код.
Uвх подается на вычитатель, где из него вычитается опорное напряжение +Uоп или -Uоп, в зависимости от того, был ли превышен порог компаратора на предыдущем шаге.
Интегратор формирует пилообразное напряжение, наклон пилы зависит от напряжения на выходе вычитателя. Как только пила пересекает уровень нуля, срабатывает компаратор и на следующем такте пила развернется в направлении нуля. Вообще говоря, уровень компаратора может быть любым, главное чтобы пила не подходила близко к уровням Uоп.
С выхода компаратора сигнал поступает на тактируемый триггер. Частота тактирования определяет время шага работы модулятора и минимальное время «1» или «0» на выходе модулятора.

Далее сигнал поступает на аналоговый ключ, который коммутируя +Uоп и –Uоп замыкает обратную связь.
На вход ФНЧ поступает последовательность нулей и единиц, при этом количество «1» в единицу времени пропорционально Uвх. Так при Uвх=-Uоп будут одни нули, при Uвх = +Uоп – одни единицы. Нулевому уровню Uвх будет соответствовать равное количество нулей и единиц. Остается только их сосчитать и вычесть уровень нуля равный (+Uоп – -Uоп)/2.
Для примера Uоп = 2В; Uвх = 1В.
Напряжение на выходе интегратора принимает значения:
0+(1-2) =-1; => 0
-1+(1+2) = 2; => 1
2+(1-2) = 1; => 1
1+(1-2) = 0; => 1
0+(1-2) =-1; => 0
-1+(1+2) = 2; => 1
2+(1-2) = 1; => 1
Здесь постоянная времени интегратора такая, что за 1 такт напряжение на его выходе становится равным напряжению на его входе. При другой постоянной времени изменится крутизна пилы, но соотношение нулей и единиц останется то же.

Интерактивный сигма-дельта модулятор от Analog Devices
Возьмем 8 импульсов 0,1,1,1,0,1,1,1. Сумма равна 6. Это и будет выходной код АЦП. 6/8=0.75. А весь диапазон -2…+2 равен 4В.
4*0.75=3; И минус уровень нуля 3-2 = +1В. Максимальный код для 8 импульсов равен 8, а это уже 4 разряда, но он будет достигнут только если Uвх>=Uоп. Поэтому проще всего ограничить счет по максимальному значению счетчика и сделать его равным 7, тогда для 8 тактов хватит 3разрядов. И маскимальный код будет соответствовать 7/8 = 1.5В
Теперь как это можно сделать. На рисунке ниже схема нарисованная в Proteus.
U1:A — вычитатель;
U1:B — интегратор. Так, как интегратор инвертирующий, у вычитателя входы поменяны местами — входное напряжение вычитается из опорного.
U1:D — повторитель, чтобы входное сопротивление вычитателя не подсаживало Uоп. Можно и без него.
U5 — ключ. Переключает +Uоп и -Uоп.
Сверху U10 — счетчик задает 2048 тактов для счета (2^11).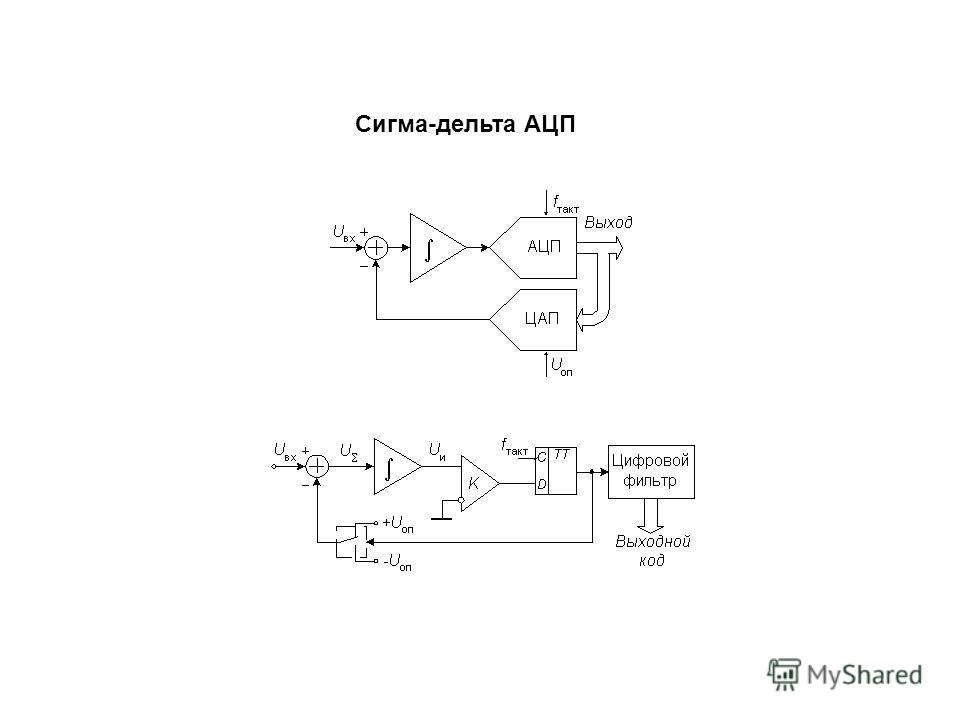 11 в случае использования накапливающего регистра и счетчика на 11бит, а при использовании фильтров (скользящее среднее, экспоненциальное сглаживание, КИХ, БИХ) останется равной Fclk.
11 в случае использования накапливающего регистра и счетчика на 11бит, а при использовании фильтров (скользящее среднее, экспоненциальное сглаживание, КИХ, БИХ) останется равной Fclk.
В современных АЦП используют частоты тактирования десятки МГц, такая частота выдачи отсчетов избыточна (код то меняется максимум на +-1), поэтому код прореживается и на выход подается лишь каждый 2048 или 65536 или еще какой с порядком кратным двойке. Прореживание кода называют децимацией (в римской империи так называли наказание, когда отбирали каждого десятого из подразделения для казни). В результате частота отчетов на выходе будет уже Fclk/N, где N- это коэффициент децимации.
Схему можно упростить, вместо подключения GND и +Uоп запитать триггер от +Uоп. Убрать буферный каскад U1:D. Можно даже выкинуть компаратор U1:C. Уровень порога будет определяться порогом «1» триггера. Это немного снизит точность, но уже потребуется только 2ОУ. А можно ли совсем без операционников?
МОЖНО! на интегрирующей RC-цепи и компараторе.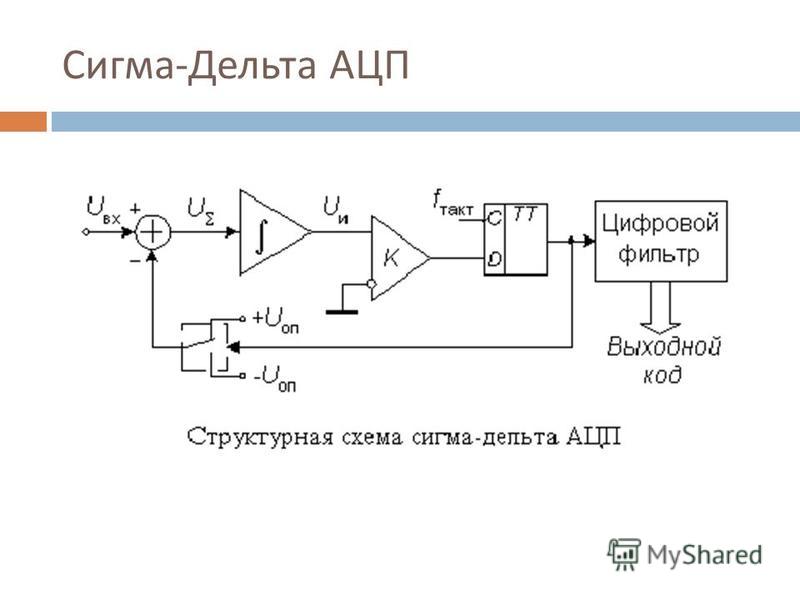
графики (для Uвх=1.5В):
и результаты работы схемы:
Uвх=500мВ
Uвх=1000мВ
Uвх=2000мВ
Как же это работает? RC цепочка заряжается и разряжается в зависимости от предыдущего такта работы (был превышен порог или нет). Крутизна заряда-разряда меняется в зависимости от напряжения. Так вблизи нуля скорость заряда больше скорости разряда, в середине равны, вблизи +Uоп заряд медленнее разряда.
Если в МК есть компаратор, то потребуется лишь внешняя RC цепочка.
Постоянная времени должна быть выбрана в соответствии с временем такта.
Пример программы для контроллера MSP430
mov #04096,R15 ; 12- бит
; предварительный заряд конденсатора;
Pre_ADC
bis.b #DAC_Out,&P2OUT ; Заряд конденсатора
C1 bit.b #CAOUT,&CACTL2 ; На выходе компаратора высокий или низкий сигнал?
jz C1 ;
; Настройка и накопление импульсов ЦАП ;
Test_DAC
bit.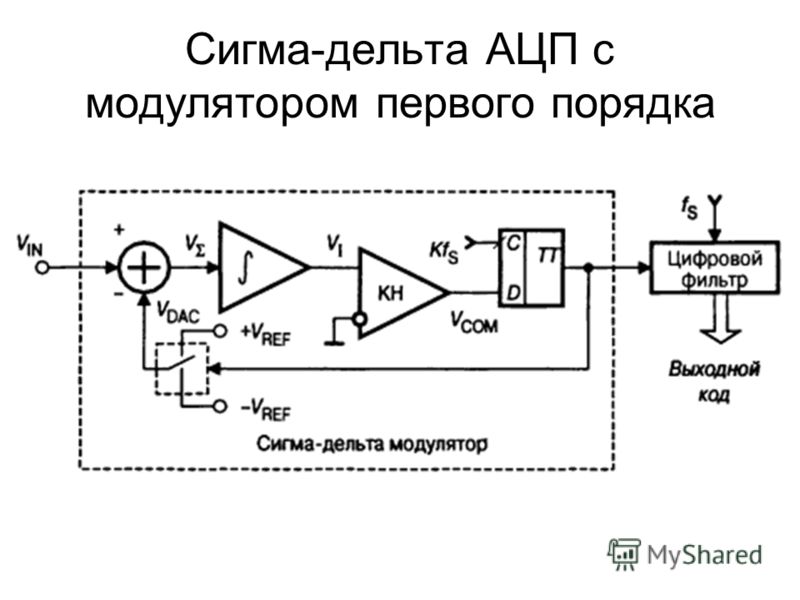 b #CAOUT,&CACTL2 ; На выходе компаратора высокий или низкий сигнал?
jnc Low1 ;
High
bic.b #DAC_Out,&P2OUT ; Разряд конденсатора
jmp Meas_ ;
Low1
bis.b #DAC_Out,&P2OUT ; Заряд конденсатора
nop ;
inc ADCData ; Увеличение ADCData
Meas_
dec R15 ; Уменьшение счетчика цикла слежения
jnz Test_DAC ; Цикл слежения закончен?
bic.b #DAC_Out,&P2OUT ; Разряд конденсатора
xor.b #CAEX,&CACTL1 ; Инвертирование выводов компаратора
ret ; Выход из подпрограммы
b #CAOUT,&CACTL2 ; На выходе компаратора высокий или низкий сигнал?
jnc Low1 ;
High
bic.b #DAC_Out,&P2OUT ; Разряд конденсатора
jmp Meas_ ;
Low1
bis.b #DAC_Out,&P2OUT ; Заряд конденсатора
nop ;
inc ADCData ; Увеличение ADCData
Meas_
dec R15 ; Уменьшение счетчика цикла слежения
jnz Test_DAC ; Цикл слежения закончен?
bic.b #DAC_Out,&P2OUT ; Разряд конденсатора
xor.b #CAEX,&CACTL1 ; Инвертирование выводов компаратора
ret ; Выход из подпрограммы
Пример взят отсюда:
Милливольтметр сигма-дельта типа на MSP430F11x1
Аналого-цифровое преобразование для начинающих / Хабр
В этой статье рассмотрены основные вопросы, касающиеся принципа действия АЦП различных типов. При этом некоторые важные теоретические выкладки, касающиеся математического описания аналого-цифрового преобразования остались за рамками статьи, но приведены ссылки, по которым заинтересованный читатель сможет найти более глубокое рассмотрение теоретических аспектов работы АЦП.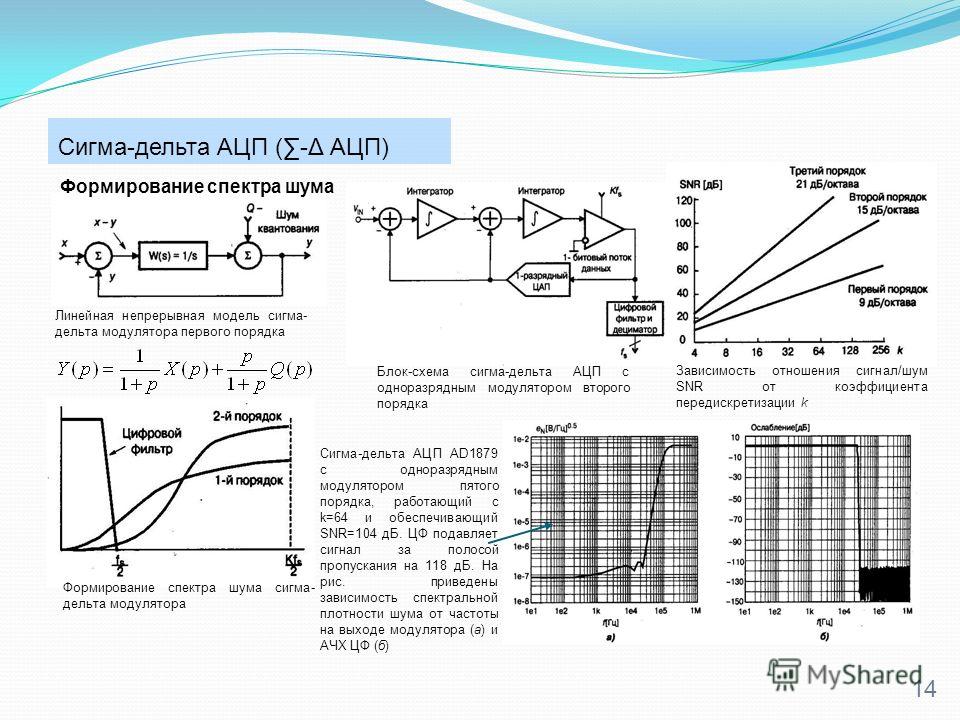 Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.
Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.
”
Введение
В качестве отправной точки дадим определение аналого-цифровому преобразованию. Аналого-цифровое преобразование – это процесс преобразования входной физической величины в ее числовое представление. Аналого-цифровой преобразователь – устройство, выполняющее такое преобразование. Формально, входной величиной АЦП может быть любая физическая величина – напряжение, ток, сопротивление, емкость, частота следования импульсов, угол поворота вала и т.п. Однако, для определенности, в дальнейшем под АЦП мы будем понимать исключительно преобразователи напряжение-код.
Понятие аналого-цифрового преобразования тесно связано с понятием измерения. Под измерением понимается процесс сравнения измеряемой величины с некоторым эталоном, при аналого-цифровом преобразовании происходит сравнение входной величины с некоторой опорной величиной (как правило, с опорным напряжением).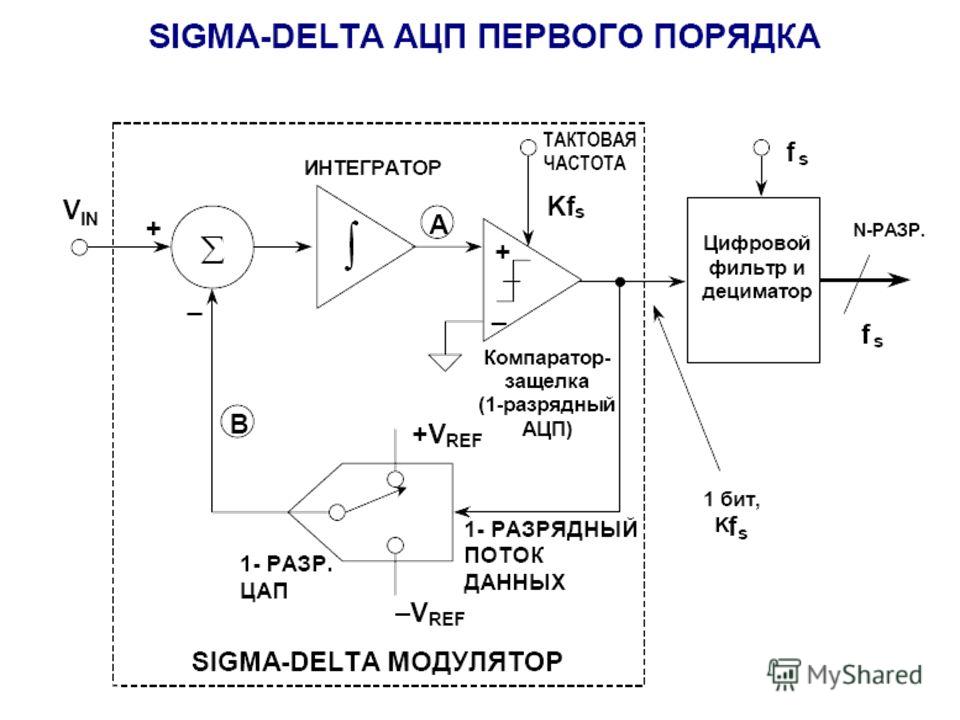 Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.
Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.
Основные характеристики АЦП
АЦП имеет множество характеристик, из которых основными можно назвать частоту преобразования и разрядность. Частота преобразования обычно выражается в отсчетах в секунду (samples per second, SPS), разрядность – в битах. Современные АЦП могут иметь разрядность до 24 бит и скорость преобразования до единиц GSPS (конечно, не одновременно). Чем выше скорость и разрядность, тем труднее получить требуемые характеристики, тем дороже и сложнее преобразователь. Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.
Типы АЦП
Существует множество типов АЦП, однако в рамках данной статьи мы ограничимся рассмотрением только следующих типов:
- АЦП параллельного преобразования (прямого преобразования, flash ADC)
- АЦП последовательного приближения (SAR ADC)
- дельта-сигма АЦП (АЦП с балансировкой заряда)
Существуют также и другие типы АЦП, в том числе конвейерные и комбинированные типы, состоящие из нескольких АЦП с (в общем случае) различной архитектурой.
Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Здесь можно отметить, что еще большим быстродействием обладают конвейерные АЦП (pipelined ADC), однако они являются комбинацией нескольких АЦП с меньшим быстродействием и их рассмотрение выходит за рамки данной статьи.
Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100KSPS-1MSPS.
Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до единиц KSPS.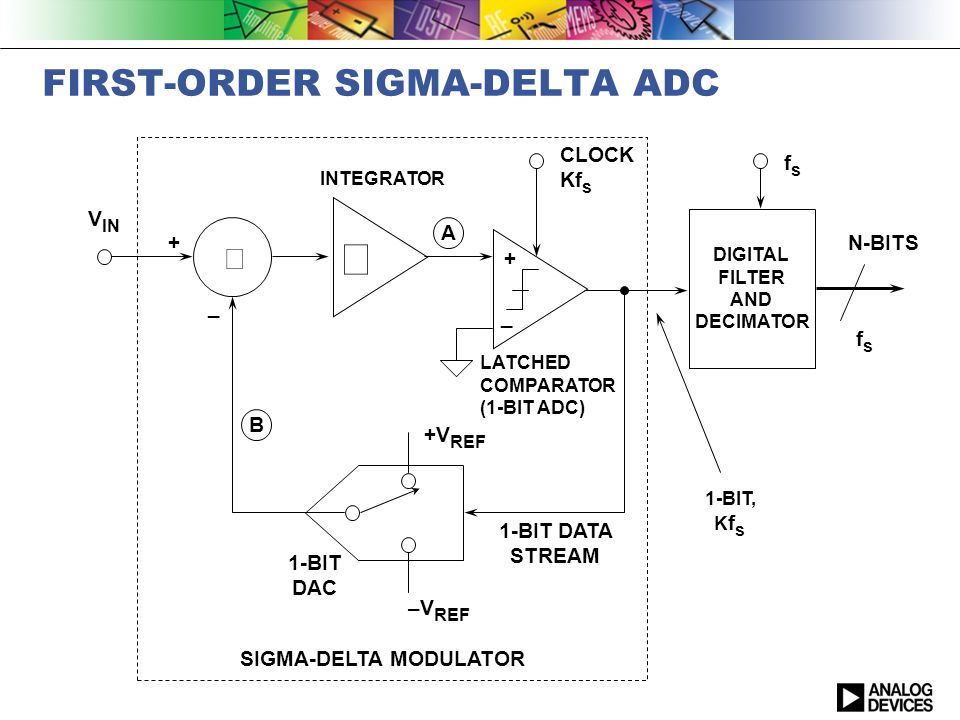
Еще одним типом АЦП, который находил применение в недавнем прошлом, является интегрирующий АЦП. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в старых измерительных приборах.
АЦП прямого преобразования
АЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.
Архитектура АЦП прямого преобразования изображена на рис. 1
Рис. 1. Структурная схема АЦП прямого преобразования
Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений, получаемых из опорного путем деления резисторами R. Для схемы на рис. 1 этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.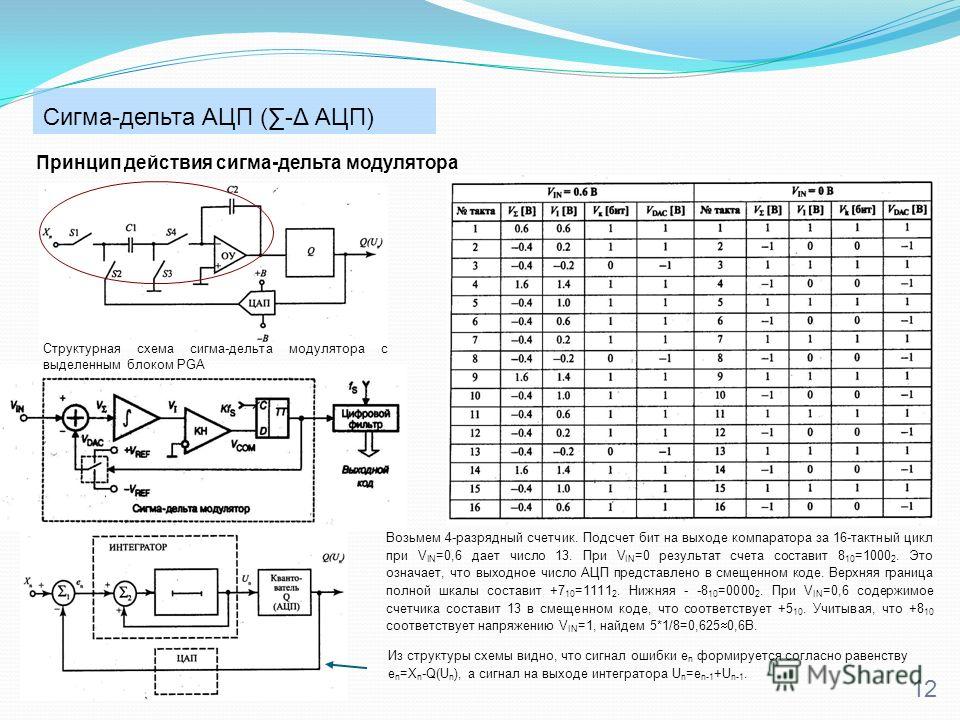
АЦП последовательного приближения
АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь: http://www.goldenmuseum.com/2015AMT_rus.html.
Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом:
1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).
на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).
2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref).
3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.
Рис. 2. Структурная схема АЦП последовательного приближения.
Таким образом, АЦП последовательного приближения состоит из следующих узлов:
1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником).
2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.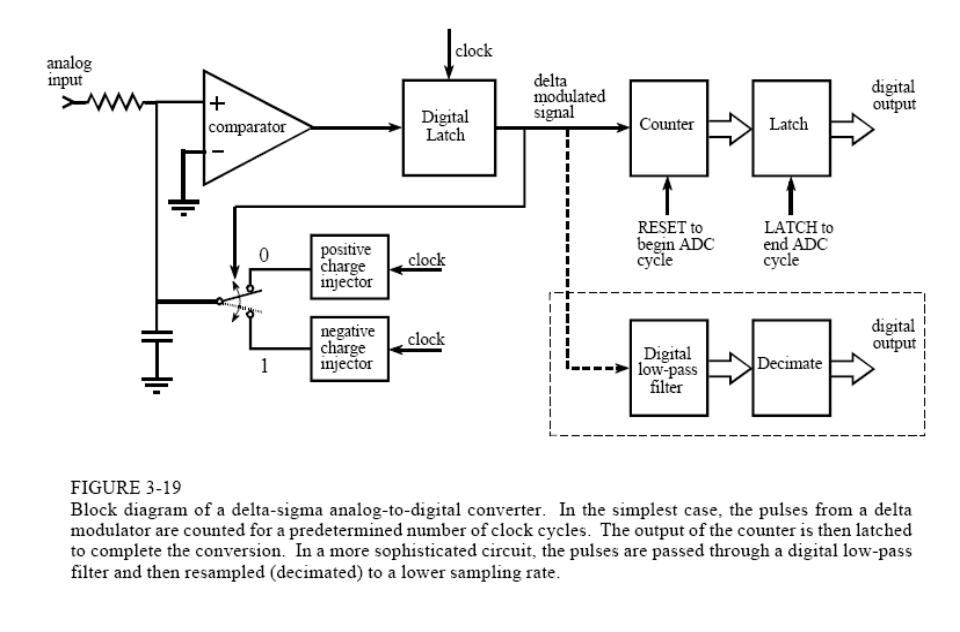
3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.
4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.
Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).
Дельта-сигма АЦП
И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда.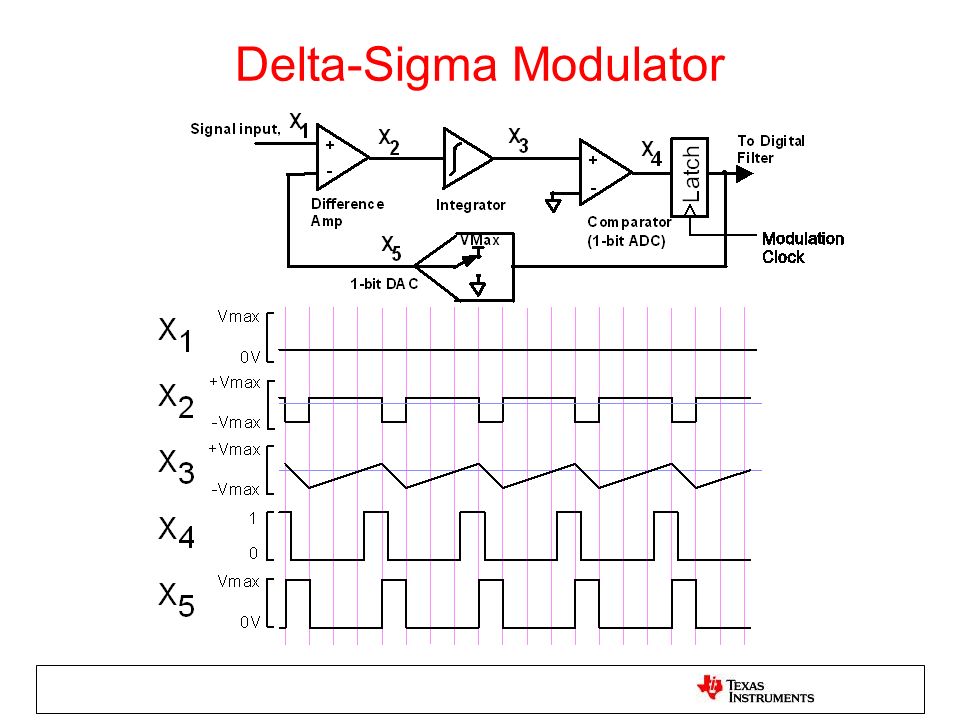 Структурная схема сигма-дельта АЦП приведена на рис. 3.
Структурная схема сигма-дельта АЦП приведена на рис. 3.
Рис.3. Структурная схема сигма-дельта АЦП.
Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания».
Рис. 4. Сигма-дельта АЦП как следящая система
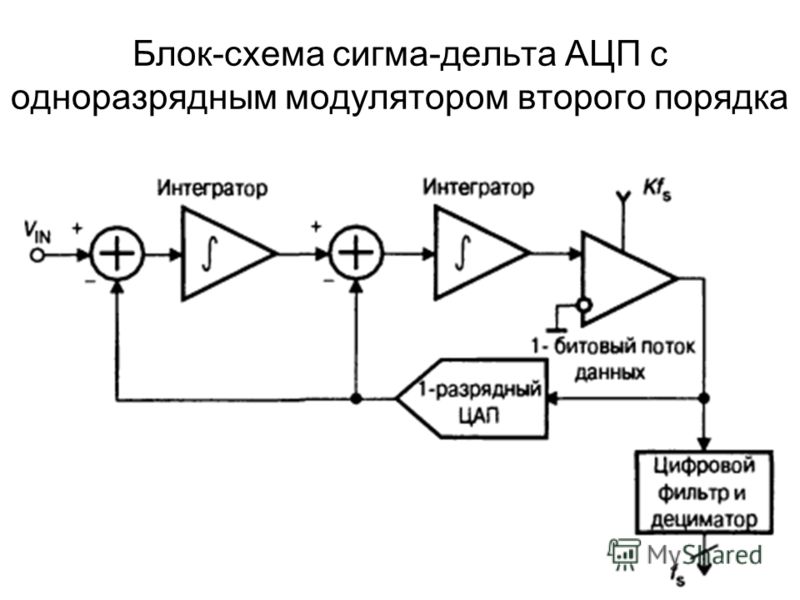
Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка.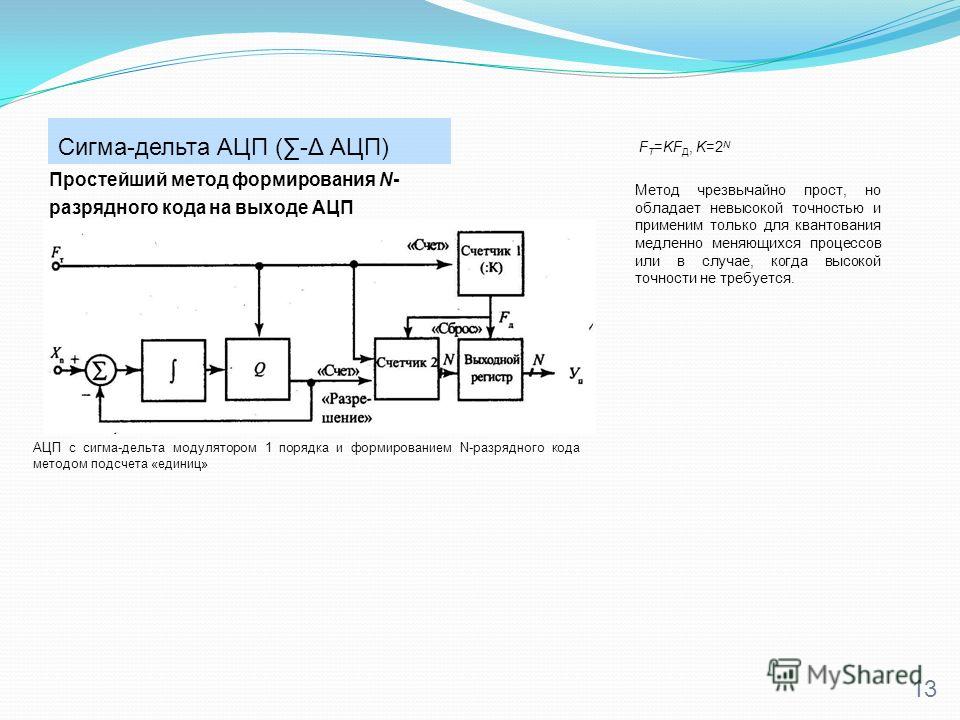 Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].
Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].
На рис. 5 показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).
Рис. 5. Сигналы в АЦП при разных уровнях сигнала на входе.
Более наглядно работу сигма-дельта АЦП демонстрирует небольшая программа, находящаяся тут: http://designtools.analog.com/dt/sdtutorial/sdtutorial.html.
Теперь, не углубляясь в сложный математический анализ, попробуем понять, почему сигма-дельта АЦП обладают очень низким уровнем собственных шумов.
Рассмотрим структурную схему сигма-дельта модулятора, изображенную на рис. 3, и представим ее в таком виде (рис. 6):
Рис. 6. Структурная схема сигма-дельта модулятора
Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал и шум квантования.
Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:
Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:
Y(s) = X(s)/(s+1) + E(s)s/(s+1)
То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.
Рис. 7. Явление «вытеснения» шума в высокочастотную часть спектра
Однако следует понимать, что это чрезвычайно упрощенное объяснение явления вытеснения шума (noise shaping) в сигма-дельта АЦП.
Итак, основным достоинством сигма-дельта АЦП является высокая точность, обусловленная крайне низким уровнем собственного шума. Однако для достижения высокой точности нужно, чтобы частота среза цифрового фильтра была как можно ниже, во много раз меньше частоты работы сигма-дельта модулятора.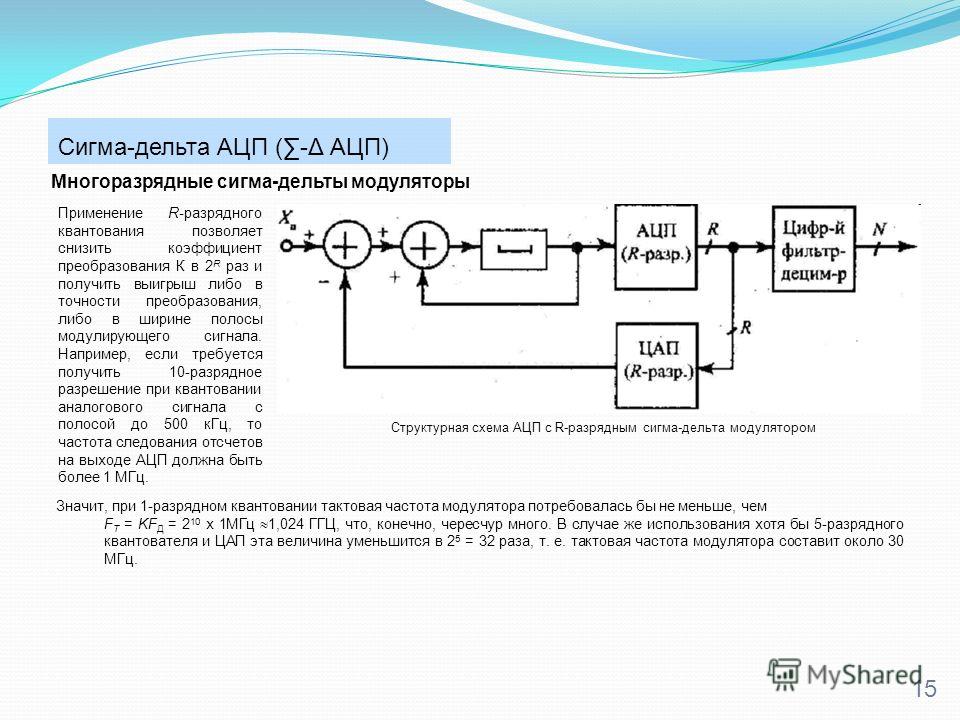 Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.
Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.
Они могут использоваться в аудиотехнике, однако основное применение находят в промышленной автоматике для преобразования сигналов датчиков, в измерительных приборах, и в других приложениях, где требуется высокая точность. но не требуется высокой скорости.
Немного истории
Самым старым упоминанием АЦП в истории является, вероятно, патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования.
Рис. 8. Первый патент на АЦП
Рис. 9. АЦП прямого преобразования (1975 г.)
Устройство, изображенное на рисунке, представляет собой АЦП прямого преобразования MOD-4100 производства Computer Labs, 1975 года выпуска, собранный на основе дискретных компараторов. Компараторов 16 штук (они расположены полукругом, для того, чтобы уравнять задержку распространения сигнала до каждого компаратора), следовательно, АЦП имеет разрядность всего 4 бита.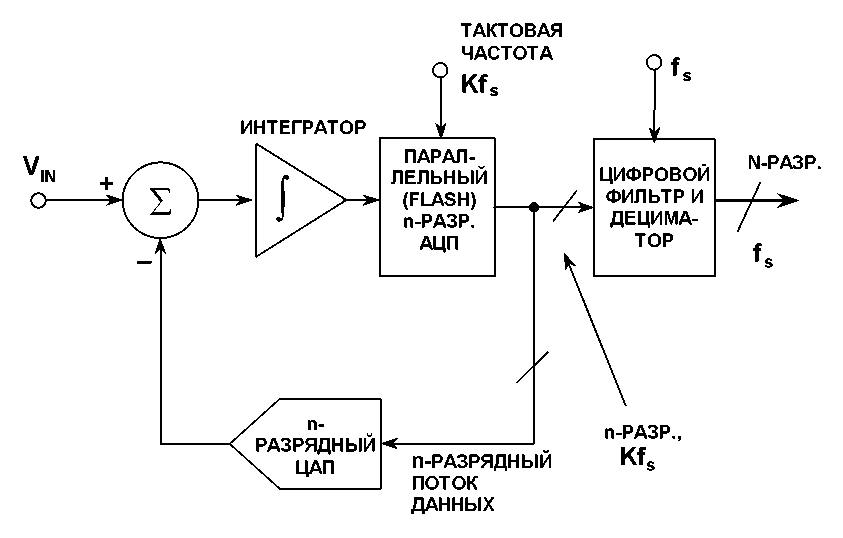 Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.
Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.
На следующем рисунке изображена продвинутая версия АЦП прямого преобразования.
Рис. 10. АЦП прямого преобразования (1970 г.)
Устройство VHS-630 1970 года выпуска, произведенное фирмой Computer Labs, содержало 64 компаратора, имело разрядность 6 бит, скорость 30MSPS и потребляло 100 ватт (версия 1975 года VHS-675 имела скорость 75 MSPS и потребление 130 ватт).
Литература
W. Kester. ADC Architectures I: The Flash Converter. Analog Devices, MT-020 Tutorial. www.analog.com/static/imported-files/tutorials/MT-020.pdf
W. Kester. ADC Architectures II: Successive Approximation ADC. Analog Devices, MT-021 Tutorial. www.analog.com/static/imported-files/tutorials/MT-021.pdf
W. Kester. ADC Architectures III: Sigma-Delta ADC Basics. Analog Devices, MT-022 Tutorial. www.analog.com/static/imported-files/tutorials/MT-022.pdf
W. Kester. ADC Architectures IV: Sigma-Delta ADC Advanced Concepts and Applications.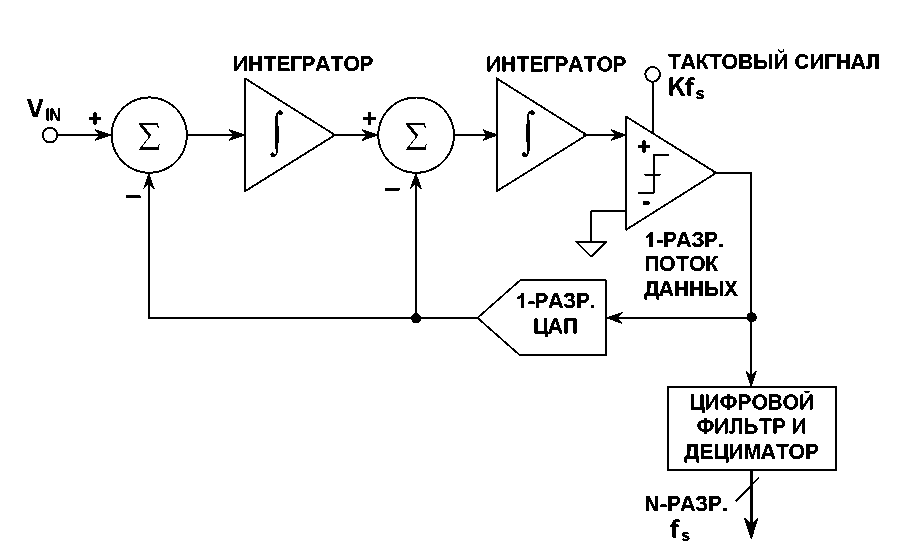 Analog Devices, MT-023 Tutorial. www.analog.com/static/imported-files/tutorials/MT-023.pdf
Analog Devices, MT-023 Tutorial. www.analog.com/static/imported-files/tutorials/MT-023.pdf
Модуляция delta-sigma (ΔΣ, или sigma-delta ΣΔ) это метод кодирования аналоговых сигналов с преобразованием их в цифровую форму, что обычно делают аналого-цифровые преобразователи, АЦП (analog-to-digital converter, ADC). Принцип delta-sigma также используют для преобразования высокоразрядных, низкочастотных цифровых сигналов в высокочастотные, низкоразрядные – как часть преобразования цифровых сигналов в аналоговые, что применяется в цифро-аналоговых преобразователях, ЦАП (digital-to-analog converter, DAC). В обычных АЦП аналоговый сигнал оцифровывается на частоте дискретизации, и далее квантуется по нескольким уровням, в результате чего получается цифровой сигнал. Этот процесс вводит так называемый шум ошибки квантования (quantization error noise). И АЦП, и ЦАП, оба могут использовать delta-sigma модуляцию. Сначала delta-sigma АЦП кодирует аналоговый сигнал с помощью высокочастотной delta-sigma модуляции, затем применяется цифровой фильтр для формирования цифрового потока данных с высоким разрешением, но низкочастотного. Delta-sigma ЦАП кодирует входной цифровой сигнал высокого разрешения в сигнал низкого разрешения, но на высокой частоте выборок, который отображается на напряжения, и затем сглаживается аналоговым ФНЧ. Прежде всего из-за своей ценовой эффективности и снижения сложности схем эта техника находит все большее применение в современных электронных компонентах, таких как ЦАП, АЦП, синтезаторах частоты, импульсных источниках питания и контроллерах двигателей. Грубо квантованный выход delta-sigma модулятора иногда используется в цифровой обработки сигналов или как представление сигнала для его хранения на носителе памяти. Например, формат Super Audio CD (SACD) сохраняет выходной поток данных delta-sigma модулятора прямо на диск. Почему преобразуют аналоговый сигнал в поток импульсов? Если кратко, то причина в том, что очень просто восстановить импульсы в приемнике в идеальную форму, которая была при передаче. Единственная часть переданной формы сигнала, требуемая в приемнике, это время, в котором произошел импульс. Каждый импульс составляется из перепада вверх, следующего после короткого интервала перепада вниз. Можно даже в присутствии шума электроники реконструировать интервалы этих шагов, и восстановить переданный поток импульсов почти без всякого шума. Тогда точность процесса передачи снижается до точности, с которой переданный поток импульсов представляет входную форму сигнала. Почему используется delta-sigma модуляция? Модуляция delta-sigma преобразует аналоговое напряжение в частоту импульсов, и её можно понимать как модуляцию плотности импульсов или импульсно-частотную модуляцию – в зависимости от реализации. Обычно частота может меняться гладко по бесконечно малым шагам, как может меняться напряжение, и оба могут служить аналогом бесконечно мало меняющейся физической переменной, такой как акустическое давление, интенсивность освещения, и т. Почему используется delta-sigma модуляция в АЦП? АЦП преобразуют значение аналоговое напряжение в значение частоты импульсов, и подсчитывают количество импульсов в известном интервале времени так, чтобы количество импульсов, поделенное на интервал, давало точное цифровое представление значения аналогового напряжения во время этого интервала. Интервал может быть выбиран для получения нужной разрешающей способности или точности. Этот метод дешево реализуется современными технологиями, и широко используется. [АЦП, анализ] АЦП генерирует поток импульсов частотой f, где импульсы в поток пропорциональны входному аналоговому напряжению v, так что f = k * v, где k это константа для конкретной реализации. Счетчик суммирует количество импульсов, произошедших в заранее определенный период времени P, так что эта сумма Σ равна P * f = k * P. В зависимости от реализации k * P выбирается так, чтобы цифровое отображение счетчика Σ, отображает v с заранее определенным коэффициентом масштабирования. Поскольку P может получить разработанное значение, оно может быть сделано достаточно большим, чтобы получить любое желаемое разрешение или точность. Ниже на рис. 1 показана диаграмма схемы вместе с формами сигнала, обозначенными цифрами от 1 до 5, для входного уровня 0. Рис. 1. Диаграммы сигналов sigma delta АЦП. В наиболее практических применениях выбирается большой интервал суммирования по сравнению с длительностью импульса, и это применяется для сигналов, у которых доля переменной составляющей от полного диапазона уровней достаточно мала на интервале суммирования. Теорема оцифровки сигала Найквиста-Шеннона (Котельникова) требует двух выборок для восстановления изменения входного сигнала. Выборки, подходящие к этому критерию, относятся к двум последовательным Σ, взятым на двух следующих друг за другом интервалах суммирования. Интервал суммирования, который должен принять больше значение счетчика, чтобы достичь адекватной точности, неизбежно становится достаточно длинным, чтобы можно было воссоздать относительно низкие частоты сигнала. Следовательно, будет удобным и справедливым представлять входное напряжение (1) как постоянное во время нескольких импульсов. Рассмотрим сначала замкнутую петлю обратной связи, состоящую из аналогового сумматора/вычитателя, интегратора, детектора пересечения порога и генератора импульсов. Слева на входе 1 показано, что на коротком интервале времени сигнал постоянный, на уровне 0.2V. Поток из импульсов изменения (delta) генерируется по каждому пересечению порога, как показано в точке 2, и разница между 1 и 2 показана в точке 3. Эта разница интегрируется, чтобы получить форму сигнала 4. Детектор порога генерирует импульс 5, который начинается в момент, когда 4 пересекает порог, и импульс переходит в 0, когда 4 падает ниже порога. Обратная связь 5 вызывает срабатывание генератора для генерации импульса фиксированной мощности. Справа показано, как входной уровень 0.4V и сумма во время импульса -0.6V отличается от суммы -0.8V на картинке слева. Из-за этого интервал отрицательной части импульса на диаграмме справа меньше, чем на диаграмме слева. Также сравните сумму 0.4V справа с суммой 0.2V слева. Таким образом, положительная часть импульса больше справа, чем слева. В результате получается, что интеграл (4) пересекает порог быстрее справа, чем слева. Получающиеся формы сигнала 4 следуют концепции, связанной с delta-функцией Дирака, по которой все импульсы одинаковой мощности продуцируют по определению тот же шаг для их интеграла. Тогда 4 конструируется с помощью промежуточного шага (6), на котором каждый интегрированный импульс представлен шагом установленной мощности, который спадает до 0 со скоростью, определяемой входным напряжением. Теперь рассмотрим схему за петлей обратной связи. Интервал времени суммирования это префиксное время, и по его истечении значение счетчика стробируется в буфер, и счетчик сбрасывается. Это необходимо, чтобы соотношение между интервалом импульса и интервалом суммирования был равен максимальному значению счетчика (полная шкала). Тогда возможно формировать длительность импульса и интервал суммирования теми же тактами, с подходящей конфигурацией логики и счетчиков. Преимущество такого решения в том, что никакой интервал не должен быть определен с абсолютной точностью, важно только лишь соотношение. Тогда для достижения общей точности требуется только формирование точной амплитуды импульсов. На рис. 1 упрощенная блок-диаграмма delta-sigma АЦП показана с отдельными функциональными элементами, и таким способом сделана попытка показать принцип, независимый от конкретной реализации. Рис. 1a. Эффект от импульсов тактирования. [Практическая реализация] Пример схемы показан на рис. 1b, и её формы сигнала показаны на рис. 1c. Эта схема составлена главным образом для иллюстрации, подробности по отдельным реализациям можно получить из даташитов производителей микросхем АЦП. Преимущество альтернативной схемы 1b в том, что напряжение на контактах ключа относительно постоянное, и близко к 0. Рис. 1b. Схема примера практической реализации дельта-сигма АЦП. Формы сигнала, показанные на рис. 1c, необычно сложные, потому что они предназначены иллюстрировать поведение петли обратной связи в предельных условиях, Vin насыщается на полной шкале 1.0V, и насыщение вниз происходит при нуле. Также показано промежуточное состояние Vin = 0.4V, и обычные рабочие условия входного сигнала от 0 до 1.0v очень похожи на работу блок-диаграммы рис. 1. Рис. 1c. Формы сигнала схемы. На рис. 1c показаны формы сигнала, помеченные следующими метками: Clock, тактовый сигнал. (a), Vin. На этой диаграмме показано изменение входного сигнала от 0.4V до 1.0V, и затем к 0V, чтобы показать эффект работы петли обратной связи. (b), осциллограмма импульса, соответствует осциллограмме 5 рис. 1. (c), ток в конденсатор, Ic. этот ток формируется линейной суммой импульсного напряжения после R2 и Vin через R1. График показывает эту сумму как напряжение результата умножения R * Ic. Входное сопротивление усилителя считается достаточно высоким, чтобы входным током можно было пренебречь. Емкость подключена между инвертирующим входом усилителя и его выходом. Этим соединением обеспечивается отрицательная обратная связь для усилителя и формируется интегратор. Изменение входного напряжения равно изменению выходного напряжения, поделенному на коэффициент усиления усилителя. Когда этот коэффициент усиления очень большой, можно пренебречь изменением входного напряжения на инвертирующем входе усилителя (можно считать его замкнутым на землю), потому что обратная связь принуждает усилитель поддерживать на инвертирующем входе напряжение, близкое к напряжению на неинвертирующем входе (это следует из теории работы операционных усилителей []), который в нашем случае замкнут на землю. (d), инверсный интеграл Ic. Эта инверсия стандартна для реализации интегратора на основе операционного усилителя, и появляется потому, что ток в конденсатор на входе усилителя равен току из конденсатора на выходе усилителя, и выходное напряжение будет интегралом тока, поделенного на емкость C. (e), выход компаратора. Компаратор это усилитель с чрезвычайно большим коэффициентом усиления. У него неинвертирующий вход (опорное напряжение сравнения) также подключен к земле. Всякий раз, когда инвертирующий вход компаратора получает отрицательное напряжение относительно не инвертирующего входа, на выходе компаратора появляется положительный максимальный уровень, и наоборот, когда напряжение на инвертирующем входе компаратора становится положительным относительно не инвертирующего входа, на выходе компаратора появляется отрицательный максимальный уровень (происходит насыщение выхода компаратора). (f), выход импульсного таймера. В качестве импульсного таймера работает D-триггер, срабатывающий по положительному перепаду тактов clock. Входная информация, подаваемая на D, передается на выход триггера Q, когда происходит положительный перепад импульса clock. Таким образом, когда выход компаратора (e) положительный, то на выходе Q сигнал остается положительным до следующего положительного перепада тактов. Подобным образом, когда уровень (e) станет отрицательным, выход Q станет отрицательным на следующем положительном перепаде clock. Q управляет электронным ключом для генерации импульса тока в интегратор. Показана форма (e) во время начального периода, когда Vin = 0.4 V, (e) пересекает порог перед положительным перепадом clock, так что здесь есть заметная задержка перед запуском импульса. Иногда Vin (a) переходит в 0, что означает, что сумма токов (c) станет полностью отрицательным, и уровень на выходе интегратора будет повышаться. На короткое время порог будет пересечен, и в результате переключения Q, импульсный ток будет выключен на короткое время. Ток конденсатора (c) теперь нулевой, так что уровень интегратора направляется к нулю, оставаясь постоянным на величине, которая была определена на окончании импульса. (g), выходной поток бит. Это поток импульсов, который генерируется с помощью управления вентиля тактов отрицательным выходом импульсного таймера. После всех действий интервал суммирования, sigma-счетчик и буфер счетчика реализуются подходящими счетчиками и регистрами. Дополнительные замечания. В этой секции мы главным образом имели дело с аналого-цифровым преобразователем на основе интегратора и отдельными простыми и дешевыми узлами схемы, которые позволяют при этом добиться удивительной точности. Изначально конфигурация Delta-Sigma была создана INOSE и другими разработчиками, чтобы решить проблемы точной передачи аналоговых сигналов. Известно, что техника анализа Фурье может представить приходящую форму сигнала на интервале суммирования как сумму константы и базовых гармоник, у каждой из которых есть точное целое число периодов на интервале оцифровки. Также хорошо известно, что интеграл от синусоидальной или косинусоидальной волны от целого числа её периодов равен 0. Тогда интеграл от приходящего сигнала по интервалу суммирования уменьшается до интеграла от константы, и когда этот интеграл поделен на интервал суммирования, то он становится средним значением за этот интервал. Интервал между импульсами пропорционален инверсии среднего значения входного напряжения на этом интервал, так что по этому интервалу ts выборка среднего значения входного напряжения пропорциональна V/ts. К сожалению, анализ передаваемого потока импульсов во многих случаях был не критически перенесен на АЦП. Как было показано в секции “АЦП, анализ”, эффект ошибки ограничения импульса происходит на границах тактов и вводит шум при ожидании следующего перепада тактов. Это окажет самое вредное влияние на высокочастотные компоненты сложного сигнала. Был показан способ устранения одного из источников ошибки на примере работы ЦАП, путем изменения соотношения между длительностью импульса тактов и интервала суммирования, все еще далеко не ясно, почему полезна синхронизация в среде одноканальной передачи, так как это лишняя сложность и лишний источник шума. Однако возможно, что такой принцип обработки полезен в среде TDM (time division multiplex, передача информации по разным каналам с разделением времени). Очень точная система передачи информации с постоянной частотой дискретизации может быть сформирована по полному принципу, показанному здесь, когда передача выборок из буфера осуществляется с защитой кодами коррекции ошибок на основе избыточности (redundancy error correction). Все выше приведенное описание показывает, почему импульс называется delta. Шаг это интеграл импульса. Может быть применен 1-битный ЦАП для генерации шага, и также должно быть соединение импульса и интегрирования. Анализ, который рассматривает импульс как выход 1-битного АЦП, скрывает структуру за именем (sigma delta), что вносит путаницу и усложняет интерпретацию имени, показывающего функцию работы системы. Этот анализ распространен очень широко, но он устарел. Современный альтернативный метод преобразования напряжения в частоту обсуждается в описании синхронного преобразователя напряжение/частота (synchronous voltage to frequency converter, SVFC), за которым может идти счетчик, чтобы получить такое же цифровое представление сигнала, как показано выше. [ЦАП] Каждый импульс в потоке имеет известную, постоянную амплитуду V и длительность dt, что известно как интеграл от V по dt, но с переменным разделяющим интервалом. В формальном анализе импульс, такой как интеграл от V по dt, рассматривается как δ (дельта) функция Дирака, определенная на шаге интегрирования. Здесь мы покажем этот шаг как следующее выражение: Между импульсами склон интеграла пропорционален v, так что для некоторого A справедливо: Откуда: Delta-sigma модуляторы часто используются в преобразователях цифра-аналог, или ЦАП. В общем случае ЦАП преобразует цифровое представление аналогового сигнала в соответствующий физический уровень этого аналогового сигнала. Например, уровень аналогового напряжения, подаваемого на динамик акустической системы, может быть представлен 20-битным цифровым значением, и ЦАП преобразует это значение в нужное напряжение. Можно использовать delta-sigma модулятор в УНЧ класса D (Class D Amplifier). В этом случае многобитное цифровое число подается на вход delta-sigma модулятора, который преобразует его в быструю последовательность ноликов и единичек (0 и 1). Эти 0 и 1 преобразуются в аналоговые напряжения. Это преобразование обычно осуществляется мощными драйверами MOSFET, что очень эффективно в контексте затрат энергии, потому что эти драйверы либо полностью открыты (пропускают ток), либо полностью закрыты (ток через не проходит), так что энергия тратится главным образом только на перезарядку емкостей при переключении драйвера из одного состояния в другое, и также есть небольшие потери, связанные с ненулевым сопротивлением каналов транзисторов MOSFET, когда они находятся в режиме насыщения (открыты). В результате на выходе получается сигнал двух уровней, похожий на исходный, но более мощный, однако в нем присутствуют высокочастотная компонента, связанная с быстрыми переключениями между двумя уровнями. Сама схема относительно недорогая. Цифровая часть схемы маленькая, и силовая часть схемы проста. Это контрастирует с многобитным ЦАП, у которого могут быть очень строгие условия дизайна, чтобы точно представлять цифровые значения большими количествами бит. Для использования delta-sigma модулятора в цифро-аналоговом преобразовании решение может быть эффективным по цене, с малым потреблением и высокой производительностью. Взаимосвязь с дельта-модуляцией. Сигма-дельта модуляция (SDM) была инспирирована дельта-модуляцией (DM), как показано на рис. 2. Если квантование гомогенно (т. е. если оно линейно), то тогда могут быть следующие преобразования при переходе от DM к эквивалентной SDM, см. Рис. 2. Как из Δ-модуляции перешли к ΔΣ-модуляции. (1). Начнем с блок-диаграммы, состоящей из дельта-модулятора и демодулятора. (2). Линейное свойство интегрирования (интеграл(а) + интеграл(b) = интеграл(a + b)) делает возможным переместить интегратор, который реконструирует аналоговый сигнал в секции демодулятора, в место перед дельта-модулятором. (3). И снова по свойству линейности интегрирования можно скомбинировать друг с другом два интегратора, и получить один блок дельта-сигма модулятора/демодулятора. Однако квантователь не гомогенный, так что такое объяснение некорректно. Правда, что дельта-сигма инспирирована дельта-модуляцией, но они отличаются в работе. Из первой блок-диаграммы на рис. 2 интегратор в петле обратной связи может быть удален, если обратная связь будет взята напрямую со входа ФНЧ. Следовательно, для входного сигнала дельта-модуляции u фильтр низкой частоты видит сигнал: Однако сигма-дельта модуляция помещает тот же входной сигнал на фильтр низкой частоты: Другими словами, SDM и DM переставляют положение интегратора и квантователя. Изначально, когда запускается последовательность преобразования, схема будет иметь произвольное состояние, которое зависит от интеграла всей предыдущей истории. На математическом языке это соответствует произвольной интегральной константе неопределенного интервала. Это следует из факта, что основа метода это интегратор, который может иметь произвольное состояние в зависимости от предыдущего состояния входа, см. рис. 1c (d). Начиная с появления первого импульса частота потока импульсов пропорциональна преобразуемому входному напряжению. Доступен демонстрационный онлайн-апплет [5] для симуляции всей архитектуры. Дополнительно квантователь (т. е. компаратор), используемый в DM, имеет выходной сигнал с малым шагом вверх и вниз при квантованной аппроксимации входа, в то время как квантователь, используемый в SDM, должен принимать значения вне диапазона входного сигнала, как показано на рис. 3. Рис. 3. Пример SDM из 100 выборок для одного периода синусоидального сигнала. 1-битные выборки (на выходе компаратора) наложены на диаграмму синусоидального сигнала, где лог. 1 (т. е. +VCC) показана синим цветом, и лог. 0 (т. е. -VCC) показан белым. В общем, ΔΣ-модуляция имеет несколько достоинств по сравнению с Δ-модуляцией: • Вся структура проще: – Нужен только 1 интегратор. • Квантованное значение это интеграл от изменений сигнала, что делает его менее чувствительным к скорости изменения сигнала. Есть несколько видов АЦП, которые построены на структуре преобразования delta-sigma. Показанный ниже анализ сфокусирован на простейшем АЦП 1-го порядка, 2-уровневом, со стандартной децимацией. Многие АЦП используют sigma-delta структуру 2-го порядка и фильтр sinc3. Модуляторы 2-го и более высокого порядка. Количество интеграторов, и соответственно количество петель обратной связи дает порядок ΔΣ модулятора. Модулятор ΔΣ второго порядка показан на рис. 4. Модуляторы 1-го порядка стабильны, но для модуляторов более высокого порядка должен быть произведен анализ стабильности. Рис. 4. Блок-диаграмма ΔΣ модулятора 2-го порядка. Квантователь 3-го и более высокого уровня. Модулятор также может быть классифицирован по количеству бит на выходе, что непосредственно зависит от выхода квантователя. Квантователь может быть реализован в виде N-уровневого компаратора, чтобы модулятор имел на выходе log2N бит. Структуры децимации. Концептуально простейшая структура децимации это счетчик, который сбрасывается в 0 в начале каждого периода интегрирования, и затем считывается по окончании периода интегрирования. Структура многоступенчатого сглаживания шума (multi-stage noise shaping, MASH) обладает свойством подавления шума, что обычно используется в цифровых синтезаторах звука и дробно-частотных синтезаторах. MASH состоит из двух или большего количества переполняющихся аккумуляторов, каждый из которых эквивалентен сигма-дельта модулятору первого порядка. Передача выходов комбинируется через сумматоры и задержки, чтобы получить двоичный выход, разрядность которого зависит от количества стадий (порядка) MASH. Помимо функции шумоподавления, MASH обладает еще двумя привлекательными свойствами: • Простая аппаратная реализация, содержащая только общие цифровые блоки, такие как аккумуляторы, сумматоры и D-триггеры. Очень популярна структура децимации в виде sinc-фильтра. Для модуляторов 2-го порядка фильтр sinc3 близок к оптимальному. Пример децимации. Предположим, что имеется фильтр децимации 8:1 и 1-разрядный поток бит; если у нас есть поток бит наподобие 10010110, то при подсчете его единиц получим 4. Тогда результатом децимации будет 4/8 = 0.5. Это значение можно представить 3-разрядным числом 100 (в двоичном виде), что даст половину от самого большого возможного числа. Другими словами, • частота выборки снижается в 8 раз Когда сигнал квантуется, результирующий сигнал приблизительно имеет статистику второго порядка с независимым добавлением белого шума в сигнал (так называемый шум квантования). Предполагая, что значение сигнала находится в пределах одного шага значения квантования с равномерным распределением, среднеквадратическое значение (root mean square, RMS) значение этого шума квантования: Конечно, в реальной жизни шум квантования не зависит от входного сигнала; он зависит от холостых тонов и шаблонных шумов преобразователей Sigma-Delta. Коэффициент передискретизации (over-sampling ratio, OSR), где fs это частота выборки, и 2f0 это частота Найквиста, определяется по формуле: Напряжение RMS шума в интересующем диапазоне частот может быть выражен в терминах OSR: Подробнее см. [6]. Передискретизация. Рассмотрим сигнал на частоте f0, и частоту оцифровки fs, которая намного выше частоты Найквиста (см. рис. 5). ΔΣ модуляция основана на технике передискретизации, чтобы уменьшить шум в интересующем диапазоне частот (показан зеленым), что также позволяет избежать высокоточных аналоговых схем для антиалиасингового фильтра. Шум квантования остается такой же и в конвертере Найквиста, и в конвертере передискретиации (показано синим), но он распространен по широкому спектру. В ΔΣ конвертерах шум еще больше уменьшается, поскольку спектр шума перемещается в сторону более высоких частот, где его проще фильтровать. Рис. 5. Кривые сглаживания шума и спектр шума в ΔΣ модуляторе. Для дельта-сигма модулятора первого порядка шум сглаживается фильтром с передаточной функцией Hn(z) = [1 – z-1]. Если предположить, что частота fs много больше f0, шум квантования в желаемом диапазоне частот может быть аппроксимирован: Подобным образом для дельта-сигма модулятора второго порядка шум сглаживается передаточной функцией Hn(z) = [1 – z-1]2. Этот шум квантования в рабочем диапазоне может быть аппроксимирован как: Для общего случая с ΔΣ модулятором порядка N, вариантность шума квантования в рабочем диапазоне определяется формулой: Когда частота выборок удваивается, шум квантования может быть ослаблен на 10log10(2)(2N+1) dB для ΔΣ модулятора порядка N. Другой ключевой аспект передискретизации – выбор компромисса скорость/разрешающая способность. Фактически фильтры децимации, помещаемый после модулятора, не только фильтрует весь оцифрованный сигнал в интересующем диапазоне (вырезая шум на более высоких частотах), но также уменьшает частоту сигнала, повышая разрешающую способность. Это получается за счет некого усреднения высокоскоростного потока бит. См. также [7, 8]. [Ссылки] 1. Delta-sigma modulation site:wikipedia.org. |
| Центр дизайна
Инструкции | Связанная информация
Инструкции
На схеме внутри апплета показан базовый сигма-дельта модулятор первого порядка. Более сложные детали могут иметь несколько модуляторов и интеграторов, однако они, как правило, затемняют лежащий в основе принцип сигма-дельта.
Работа сигма-дельта модулятора
Входное напряжение V IN сначала суммируется с выходным сигналом ЦАП с обратной связью. Это суммирование может быть выполнено с помощью схемы переключаемого конденсатора, которая накапливает заряд в узле суммирования конденсаторов.
Затем интегратор добавляет результат этого суммирующего узла к значению, которое он сохранил с предыдущего шага интегрирования.
Компаратор выдает логическую 1, если выход интегратора больше или равен нулю вольт, и логический 0 в противном случае.
1-битный ЦАП возвращает выходной сигнал компаратора в суммирующий узел: + V REF для логической 1 и -V REF для логического 0.Эта обратная связь пытается удерживать выход интегратора на нуле, делая выходные единицы и нули компаратора равными аналоговому входу.
Это суммирование может быть выполнено с помощью схемы переключаемого конденсатора, которая накапливает заряд в узле суммирования конденсаторов.
Затем интегратор добавляет результат этого суммирующего узла к значению, которое он сохранил с предыдущего шага интегрирования.
Компаратор выдает логическую 1, если выход интегратора больше или равен нулю вольт, и логический 0 в противном случае.
1-битный ЦАП возвращает выходной сигнал компаратора в суммирующий узел: + V REF для логической 1 и -V REF для логического 0.Эта обратная связь пытается удерживать выход интегратора на нуле, делая выходные единицы и нули компаратора равными аналоговому входу.
Поток единиц и нулей впоследствии подвергается цифровой фильтрации (не показан) для получения более медленного потока многобитовых выборок.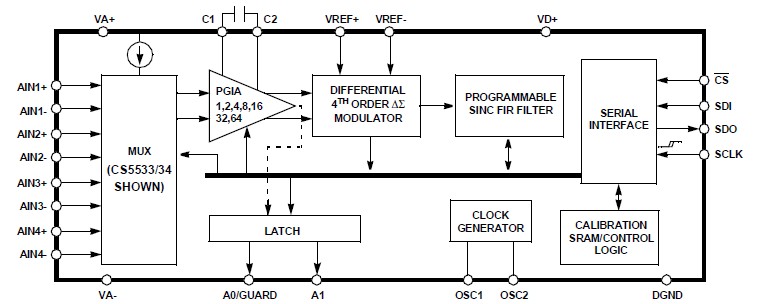 Контур сигма-дельта модулятора обычно работает на гораздо более высокой частоте, чем конечная скорость вывода цифрового фильтра.Например, преобразователь с частотой выходных данных 2 кГц может иметь частоту контура модулятора более 2,5 МГц.
Контур сигма-дельта модулятора обычно работает на гораздо более высокой частоте, чем конечная скорость вывода цифрового фильтра.Например, преобразователь с частотой выходных данных 2 кГц может иметь частоту контура модулятора более 2,5 МГц.
Как пользоваться этим инструментом
Введите опорное напряжение АЦП в нижнее поле ввода.
АЦП преобразует входные напряжения в диапазоне +/- В REF .Демонстрация выведет все единицы для входа + V REF и все нули.
для -V REF . Вход. Однако настоящий АЦП будет использовать внутреннее масштабирование.
чтобы ограничить допустимую плотность единиц и нулей примерно до 10% минимум.
Введите напряжение, которое нужно преобразовать, в поле V IN . Примечание: V IN и V REF можно изменить только при запуске. руководства, поэтому вам, возможно, придется нажать кнопку Start , чтобы ввести новые значения.
Нажмите кнопку Next Step , чтобы переместить руководство на шаг вперед. На каждом шаге диаграмма обновляется, чтобы показать текущий вывод каждого блока.
Чтобы увидеть результаты на предыдущем шаге руководства, нажмите кнопку Предыдущий шаг .
Чтобы продвинуться вперед на 512 полных циклов модулятора, нажмите кнопку Next 512 Loops .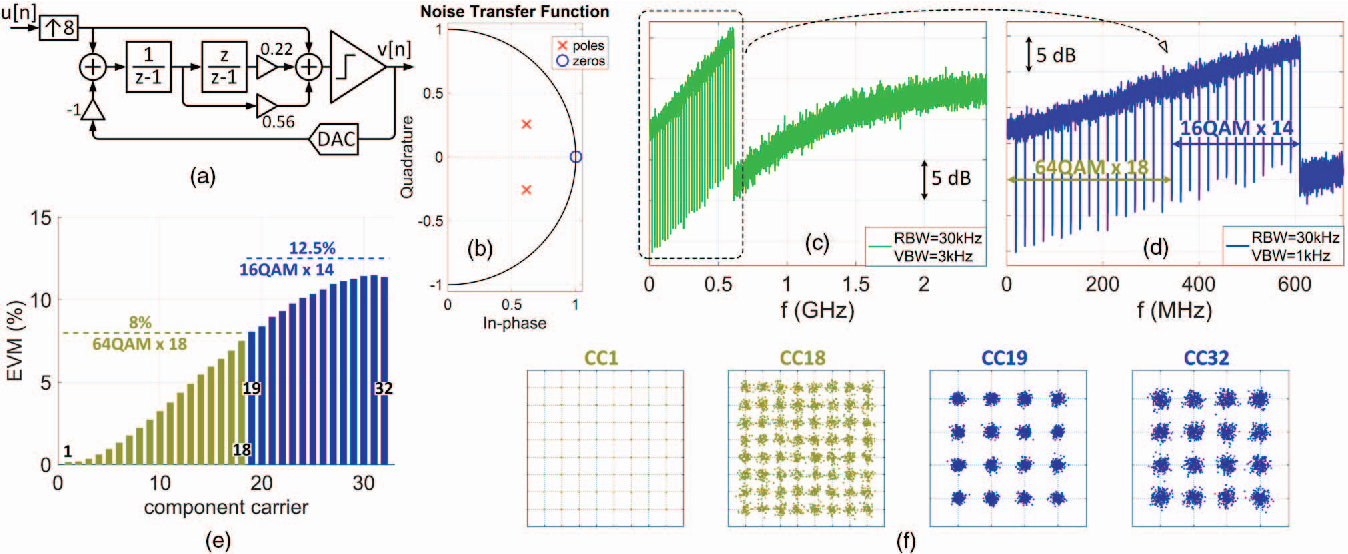
Выходы компаратора будут: 1, 0, 1, 1, 1, 0, 1, 1.
Это означает, что 6 из 8 выходов были равны 1; т.е. выход составляет 75% от полной шкалы.
Допустимый диапазон ввода -2.От 5 до +2,5 (+/- V REF ), поэтому диапазон составляет от -2,5 до +2,5.
При входном напряжении 1,0 В входное напряжение на 3,5 В выше нижней границы диапазона 5,0 В или 70% от полной шкалы.
Если мы продолжим цикл, плотность единиц вышеприведенного выходного потока будет приближаться к 70%.
Цифровой фильтр обнаруживает эту тенденцию гораздо лучше, чем наш простой метод подсчета.
Сигма-дельта-преобразователь – обзор
7.5.4 Сигма-дельта-преобразователи или преобразователи с избыточной дискретизацией
Сигма-дельта-преобразователь берет свое начало в методе модуляции или кодирования сигнала, при котором учитываются только изменения формы сигнала. передан.В аналого-цифровом преобразователе отслеживаются изменения на аналоговом входе и создается последовательность выходных импульсов. Среднее значение напряжения выходных импульсов пропорционально или представляет собой величину входного сигнала. Следовательно, исходный входной сигнал может быть восстановлен линейной фильтрацией нижних частот.
Среднее значение напряжения выходных импульсов пропорционально или представляет собой величину входного сигнала. Следовательно, исходный входной сигнал может быть восстановлен линейной фильтрацией нижних частот.
В простейшем случае сигма-дельта модулятор можно представить себе как схему, показанную на рис. 7.12. Аналоговый вход, отрицательное напряжение, подается на один вход суммирующего интегратора (см. Раздел 4.5). Положительные импульсы можно подавать на другой вход, подключив его либо к опорному напряжению В, ref , либо к земле в соответствии с настройкой переключателя, которая, в свою очередь, определяется выходом компаратора. Если выход интегратора более положительный, чем ноль, как обнаруживает компаратор, положительное опорное напряжение подключается, чтобы управлять интегратором в отрицательном направлении. Когда выход становится более отрицательным, чем ноль, компаратор меняет состояние, и переключатель подключает вход интегратора к нулю.Можно видеть, что схема действует как система управления с обратной связью, предназначенная для поддержания выходного сигнала интегратора при нулевом напряжении.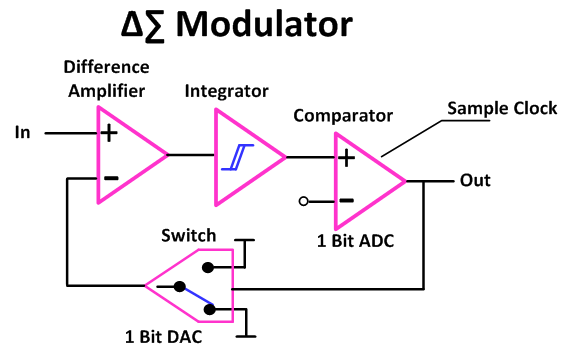 Для этого требуется, чтобы среднее значение входного сигнала, подаваемого на один вход, было равно среднему значению импульсов подавления, подаваемых на другой вход. Таким образом, выход аналого-цифрового преобразователя представляет собой поток импульсов постоянной длительности, среднее количество которых и, следовательно, величина их среднего значения представляют величину аналогового входного сигнала.
Для этого требуется, чтобы среднее значение входного сигнала, подаваемого на один вход, было равно среднему значению импульсов подавления, подаваемых на другой вход. Таким образом, выход аналого-цифрового преобразователя представляет собой поток импульсов постоянной длительности, среднее количество которых и, следовательно, величина их среднего значения представляют величину аналогового входного сигнала.
Фиг.7.12. Схема простого сигма-дельта аналого-цифрового преобразователя.
Разрешение аналого-цифрового преобразователя определяется количеством импульсов, используемых для представления одной выборки. Следовательно, частота подавляющих импульсов должна быть выше, а иногда и намного выше, чем требуется по теореме выборки (см. Раздел 7.3), то есть в два раза шире полосы пропускания аналогового входного сигнала. Вот почему эти преобразователи также называются преобразователями с передискретизацией . Отношение двух частот называется коэффициентом передискретизации.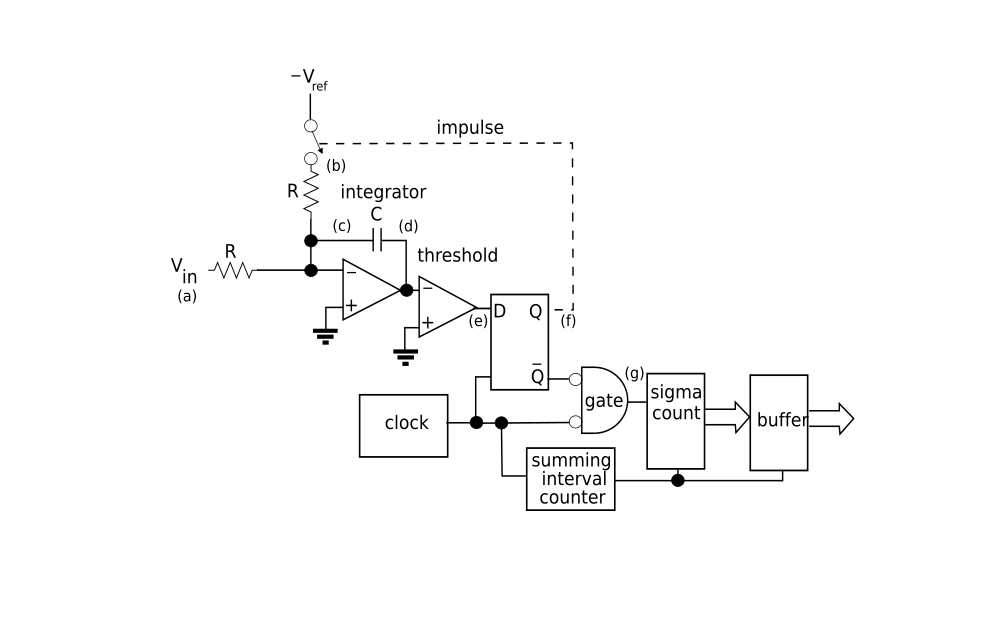 Типичные значения коэффициента передискретизации составляют от 64 до 256. Разрешение и линейность ранее описанных аналого-цифровых преобразователей, таких как вспышка или типы последовательного приближения, определяются характеристиками их компонентов в терминах амплитуды. В сигма-дельта преобразователях используются простые однобитовые элементы, а разрешение определяется производительностью во времени. Это представляет собой обмен производительности в амплитудной области для одного во временной области.
Типичные значения коэффициента передискретизации составляют от 64 до 256. Разрешение и линейность ранее описанных аналого-цифровых преобразователей, таких как вспышка или типы последовательного приближения, определяются характеристиками их компонентов в терминах амплитуды. В сигма-дельта преобразователях используются простые однобитовые элементы, а разрешение определяется производительностью во времени. Это представляет собой обмен производительности в амплитудной области для одного во временной области.
Частотные составляющие шума квантования возникают со скоростью подавляющих импульсов и их гармоник.Они намного выше частотных составляющих входного сигнала (на коэффициент, равный коэффициенту передискретизации). Хотя однобитовое преобразование приводит к высоким уровням шума квантования, его можно подавить относительно простыми фильтрами из-за большого разделения частот. Приемлемые шумовые характеристики могут быть обеспечены с помощью более сложных структур преобразователя даже для высокого разрешения (16-20 бит), достигаемого с их помощью. Вот почему термин аналого-цифровые преобразователи с формированием шума передискретизации (OSNA) также применяется к этим преобразователям.На входе этих преобразователей требуются только очень простые фильтры сглаживания из-за высокого коэффициента передискретизации. Часто достаточно простого фильтра R – C .
Вот почему термин аналого-цифровые преобразователи с формированием шума передискретизации (OSNA) также применяется к этим преобразователям.На входе этих преобразователей требуются только очень простые фильтры сглаживания из-за высокого коэффициента передискретизации. Часто достаточно простого фильтра R – C .
Максимальная частота импульсов подавления определяется максимальной скоростью схемы. Его можно разделить на коэффициент передискретизации, чтобы определить максимальную частоту входного аналогового сигнала.
Основные принципы этой системы могут быть распространены на более общие структуры.Переключатель, часть опорного напряжения может рассматриваться как однобитовый цифро-аналоговый преобразователь, поскольку он прикладывает аналоговое напряжение в соответствии с цифровым входом, а компаратор – как однобитный аналого-цифровой преобразователь. Блок-схема этой обобщенной структуры показана на рисунке 7.13. Это приводит к идее использования более одного битового A – D и D – A элементов. Хотя это возможно, это не всегда так, поскольку высокая линейность системы зависит от превосходной линейности, стабильности и т. Д. Простых однобитовых элементов по сравнению с элементами с более высоким разрешением.Однобитовые устройства также проще в изготовлении и не требуют подрезки после изготовления.
Хотя это возможно, это не всегда так, поскольку высокая линейность системы зависит от превосходной линейности, стабильности и т. Д. Простых однобитовых элементов по сравнению с элементами с более высоким разрешением.Однобитовые устройства также проще в изготовлении и не требуют подрезки после изготовления.
Рис. 7.13. Обобщенная структура сигма-дельта аналого-цифрового преобразователя.
Цифровой фильтр, называемый прореживающим фильтром, может использоваться на выходе для уменьшения кажущейся частоты дискретизации для эффективной передачи или хранения. Затем сигнал может быть восстановлен в исходной форме с помощью другой формы цифровой обработки сигнала, называемой интерполятором. В этой форме проще выполнить цифро-аналоговое преобразование.
Могут быть построены и более сложные конструкции. Они содержат более одного интегратора на прямом пути и несколько контуров обратной связи. Они также могут состоять из каскадных подсистем. К этим структурам применяются все правила, относящиеся к системам обратной связи с обратной связью.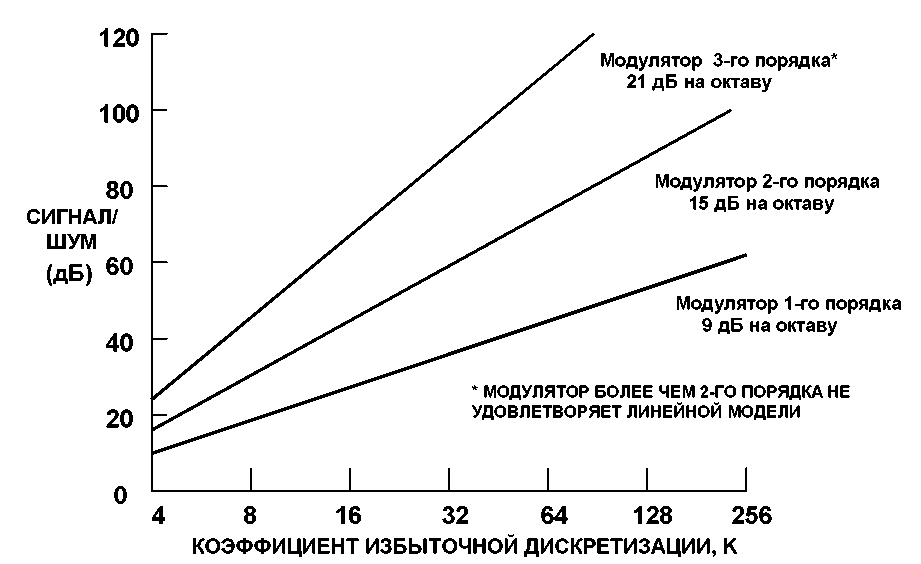 Поэтому на этапе проектирования необходимо тщательно учитывать устойчивость.
Поэтому на этапе проектирования необходимо тщательно учитывать устойчивость.
Достижения в технологии СБИС теперь позволяют изготавливать относительно сложные схемы по разумной цене. Эти схемы не требуют сложной калибровки или подстройки, а влияние неточности элементов схемы на линейность и разрешение сводится к минимуму.Поэтому они набирают популярность для использования в таких приложениях, как приборостроение и обработка аудиосигналов, где требуется высокое разрешение и динамический диапазон (до 20 бит) и хорошая линейность (общее гармоническое искажение -100 дБ или лучше), но где частоты входного сигнала не превышают нескольких десятков килогерц.
Сигма-дельта АЦП в сравнении с АЦП последовательного приближения
Эта страница поможет вам понять работу модуля SAM C21 сигма-дельта АЦП , сравнив его работу с методом аналого-цифрового преобразования (АЦП) регистра последовательного приближения (SAR).
Конвертер SAR берет выборку аналогового входа во время запроса преобразования. Образец сравнивается с выходом цифро-аналогового преобразователя (ЦАП). ЦАП инициализируется старшим битом, а все остальные биты низкими, затем выход компаратора определяет, является ли аналоговый отсчет или ЦАП выше. Если аналоговая выборка выше, MSB остается высоким, если DAC выше, то MSB устанавливается на низкий уровень. Затем устанавливается следующий младший бит, и выход компаратора снова определяет, остается ли этот бит установленным или очищенным.После n сравнений доступен n-битный результат, представляющий числовой эквивалент аналогового входа. Поскольку каждое сравнение выполняется в разный момент времени, очень важно, чтобы аналоговая выборка не изменялась за это время, иначе полученное число будет недействительным. Это цель схемы выборки и удержания, которая по сути является переключателем и конденсатором для хранения аналогового напряжения. Переключатель разомкнут во время преобразования, поэтому конденсатор сохраняет аналоговое значение, присутствующее при запуске преобразования.
Образец сравнивается с выходом цифро-аналогового преобразователя (ЦАП). ЦАП инициализируется старшим битом, а все остальные биты низкими, затем выход компаратора определяет, является ли аналоговый отсчет или ЦАП выше. Если аналоговая выборка выше, MSB остается высоким, если DAC выше, то MSB устанавливается на низкий уровень. Затем устанавливается следующий младший бит, и выход компаратора снова определяет, остается ли этот бит установленным или очищенным.После n сравнений доступен n-битный результат, представляющий числовой эквивалент аналогового входа. Поскольку каждое сравнение выполняется в разный момент времени, очень важно, чтобы аналоговая выборка не изменялась за это время, иначе полученное число будет недействительным. Это цель схемы выборки и удержания, которая по сути является переключателем и конденсатором для хранения аналогового напряжения. Переключатель разомкнут во время преобразования, поэтому конденсатор сохраняет аналоговое значение, присутствующее при запуске преобразования.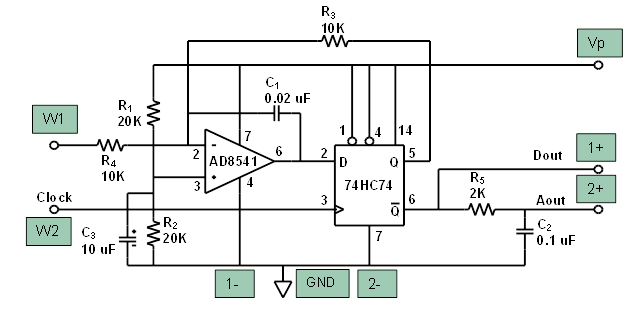
Сигма-дельта АЦП работает совершенно иначе. Вместо дискретных выборок аналогового сигнала входной сигнал преобразуется в непрерывный процесс. Разница между входом и 1-битным ЦАП подается на интегратор. Выход интегратора сравнивается с опорным напряжением, и в результате этого сравнения устанавливается следующее значение ЦАП:
.
Зачем нужен 1-битный ЦАП? Во-первых, это действительно просто, и в основном это просто переход на V ref или -V ref .Другой причиной является недостаток многобитовых ЦАП, используемых в преобразователях SAR. Эти ЦАП обычно построены с помощью резистивной лестницы, и, поскольку для каждого бита используются разные компоненты, для каждого бита существует допуск, поэтому каждый бит может иметь немного другой размер, что влияет на точность результата. 1-битный ЦАП в преобразователе сигма-дельта гарантирует, что каждый бит имеет точно такой же размер. Вес каждого бита в конечном результате определяется количеством времени, в течение которого бит применяется к интегратору. В преобразователе SAR часы, применяемые к модулю, влияют только на количество времени, которое занимает преобразование – в преобразователе сигма-дельта часы выборки определяют размер бит. В преобразователе сигма-дельта нет функции выборки и хранения из-за непрерывной работы, но все же важно, чтобы входной сигнал не изменялся быстрее, чем преобразователь может обработать изменения, поэтому частота дискретизации должна быть намного выше, чем любая присутствующая частота. в аналоговом входном сигнале.
В преобразователе SAR часы, применяемые к модулю, влияют только на количество времени, которое занимает преобразование – в преобразователе сигма-дельта часы выборки определяют размер бит. В преобразователе сигма-дельта нет функции выборки и хранения из-за непрерывной работы, но все же важно, чтобы входной сигнал не изменялся быстрее, чем преобразователь может обработать изменения, поэтому частота дискретизации должна быть намного выше, чем любая присутствующая частота. в аналоговом входном сигнале.
Выходной сигнал сигма-дельта модулятора представляет собой поток одиночных битов, и отношение единиц к нулю в этом потоке основывается на значении аналогового входа.Чтобы получить многобитовый результат от модуля, поток битов пропускается через цифровой фильтр. Затем выходной сигнал фильтра прореживается, что приводит к меньшему количеству отсчетов с большим количеством битов. Прореживание контролируется коэффициентом передискретизации (OSR), который в модуле SAM C21 SDADC составляет степень 2 между 64 и 1024:

Почему вход фильтра прореживания имеет ширину 2 бита? Модуль сигма-дельта АЦП SAM C21 является дифференциальным, поэтому выходной сигнал может быть положительным или отрицательным.Из-за этого поток битов из сигма-дельта модулятора фактически составляет 2 бита на выборку, поскольку необходим знаковый бит.
Переключение входных каналов
Поскольку поток битов из преобразователя сигма-дельта является непрерывным, а не дискретной временной выборкой, как у преобразователя SAR, вы не можете просто переключить мультиплексор на определенный канал и сделать разовую выборку, как вы можете с SAR. Когда вы начинаете преобразование, вы должны прогнать достаточно отсчетов, чтобы интегратор установил свое конечное значение (22 отсчета через сигма-дельта модулятор в SAM C21), затем вы должны отбросить несколько отсчетов из фильтра децимации, пока он установится. его значению (три отсчета из вывода после OSR на SAM C21).
Корректировка выходного значения
Хотя размеры битов в преобразователе сигма-дельта одинаковы, есть несколько источников ошибок, о которых следует беспокоиться. Во-первых, это ошибка смещения, из-за смещения в дифференциаторе и компараторе нулевой вход может давать ненулевой выход. Во-вторых, это ошибка усиления, потому что размер битов и время выборки могут не точно соответствовать полномасштабному выходному сигналу. Чтобы исправить эти ошибки, вы должны выбрать нулевой вход и полномасштабный вход и применить поправочные коэффициенты к выходному значению, чтобы получить правильный выход.
Во-первых, это ошибка смещения, из-за смещения в дифференциаторе и компараторе нулевой вход может давать ненулевой выход. Во-вторых, это ошибка усиления, потому что размер битов и время выборки могут не точно соответствовать полномасштабному выходному сигналу. Чтобы исправить эти ошибки, вы должны выбрать нулевой вход и полномасштабный вход и применить поправочные коэффициенты к выходному значению, чтобы получить правильный выход.
В SAM C21 поправки применяются автоматически аппаратно. К результату добавляется поправка смещения, а затем это значение умножается на поправку усиления. Выходной регистр составляет 24 бита, поэтому поправки можно применять к максимальному разрешению 16 бит, не беспокоясь о переполнении в процессе коррекции. Программное обеспечение должно взять образцы на нулевом и полномасштабном входах, чтобы определить соответствующие поправочные коэффициенты, а затем установить эти поправочные коэффициенты в соответствующие регистры в модуле сигма-дельта АЦП.
Planet Analog – что лучше: SAR или дельта-сигма АЦП?
Высокопроизводительные сигнальные цепи сбора данных, используемые в промышленном, контрольно-измерительном и медицинском оборудовании, требуют высокого динамического диапазона и точных измерений сигналов, одновременно решая проблемы жестких пространственных ограничений, тепловых и силовых расчетов.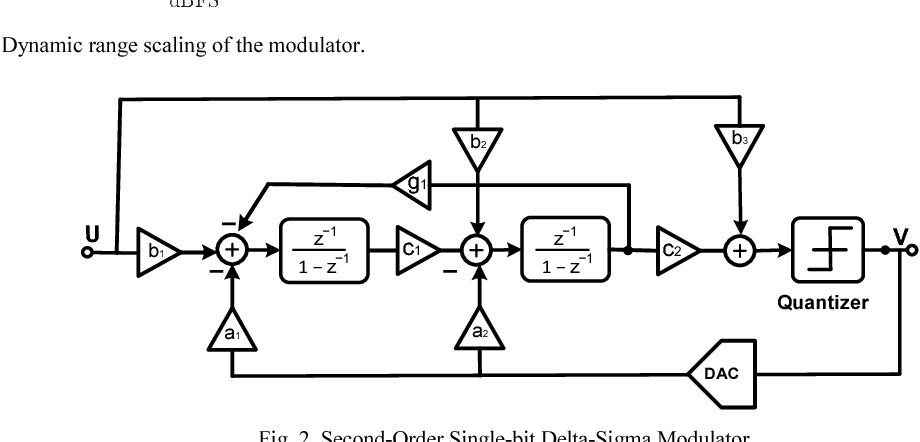 Одним из способов достижения более высокого динамического диапазона является передискретизация преобразователя для точного отслеживания и измерения как малых, так и больших входных сигналов от датчиков.
Одним из способов достижения более высокого динамического диапазона является передискретизация преобразователя для точного отслеживания и измерения как малых, так и больших входных сигналов от датчиков.
Передискретизация – это рентабельный процесс дискретизации входного сигнала с гораздо более высокой частотой, чем частота Найквиста, для увеличения отношения сигнал / шум (SNR) и разрешения или эффективного числа битов (ENOB). Как правило, передискретизация АЦП в четыре раза обеспечивает один дополнительный бит разрешения или увеличение динамического диапазона (DR) на 6 дБ. Улучшение DR из-за передискретизации определяется следующим образом:
ΔDR = log 2 (OSR) × 3 дБ
Во многих случаях передискретизация по своей природе хорошо реализована в дельта-сигма (Δ-Σ) АЦП со встроенной функцией цифровой фильтрации, где тактовая частота модулятора обычно в 32–256 раз превышает ширину полосы сигнала.Но передискретизация сложнее реализовать, когда требуется быстрое переключение между входными каналами.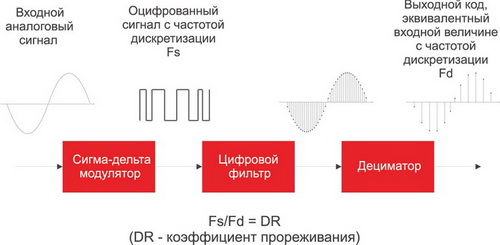
SAR (регистр последовательного приближения) также популярны для архитектуры, основанной на мультиплексировании каналов, которая требует быстрого отклика на ступенчатый вход, близкого к полной амплитуде (наихудший случай), без каких-либо проблем со временем установления. Однако это накладывает дополнительную нагрузку на требования к усилителю драйвера. Чтобы компенсировать отдачу, исходящую от массива ЦАП с переключаемыми конденсаторами на входе SAR, усилитель должен иметь очень хорошие характеристики с точки зрения полосы пропускания, скорости нарастания и выходной мощности.Если этого не произойдет, в выходной реакции проявятся нелинейные эффекты.
Высокая пропускная способность АЦП последовательного приближения допускает передискретизацию. В этом случае критически важным является низкий уровень шума (достигаемый за счет сочетания низкого среднеквадратичного шума и высокой пропускной способности) с линейностью. Некоторые из высокопроизводительных АЦП последовательного приближения обеспечивают увеличенную полосу пропускания, высокую точность и дискретную выборку за небольшой временной интервал, необходимый для приложений быстрого управления и измерения. Высокая пропускная способность и низкое энергопотребление при небольшом размере корпуса помогают разработчикам решать проблемы, связанные с пространством, температурой, питанием и другими ключевыми задачами проектирования, характерными для систем с высокой плотностью каналов.
Хотя обе топологии АЦП могут точно измерять сигналы, простирающиеся до постоянного тока, архитектура SAR обычно позволяет масштабировать мощность ядра АЦП в зависимости от пропускной способности. Это минимизирует энергопотребление как минимум на 50 процентов, что помогает удовлетворить тепловые ограничения. Для сравнения, Δ-Σ АЦП обычно имеет фиксированную потребляемую мощность. Пример высокой пропускной способности вместе с масштабированием мощности можно найти в 18-разрядном АЦП AD7960 SAR ADI 5MSPS.
Передискретизация с помощью АЦП SAR может улучшить сглаживание и уменьшить шум.Фильтр нижних частот, расположенный перед АЦП, предназначен для минимизации наложения спектров; но он также снижает шум за счет ограничения полосы пропускания. Высокий коэффициент передискретизации и профиль цифрового фильтра Δ-Σ АЦП минимизируют требования к сглаживанию на их аналоговых входах. Передискретизация модулятора АЦП снижает общий шум.
АрхитектураSAR без задержки или задержки конвейера обеспечивает быстрое проектирование контуров управления. АЦП последовательного приближения, такой как AD7960, обеспечивает самый низкий уровень шума относительно полномасштабного минимального уровня входного сигнала, что приводит к более высокому SNR и отличным характеристикам линейности.Даже в этом случае он не может отклонять шум 1 / f, близкий к содержанию постоянного тока (50/60 Гц), в отличие от Δ-Σ АЦП. Существует ряд других способов увеличения динамического диапазона АЦП, например, параллельное добавление АЦП и их чередование во времени. Однако некоторые разработчики могут посчитать этот метод громоздким или непрактичным для реализации в своей системе в основном из-за проблем с питанием, пространством и стоимостью.
Вы проектировали с использованием АЦП SAR и Δ-Σ? Какие проблемы у вас были с ними и как вы их обходили?
Похожие сообщения:
Основы аналого-цифровых преобразователей сигма-дельта
Для разработчиков программного и аппаратного обеспечения, которые имеют опыт работы в основном в цифровой области, мы предлагаем обзор основ сигма-дельта (SD) аналого-цифровых преобразователей (АЦП).Это будет полезно для дизайнера в качестве обзора, независимо от того, реализует ли ADC на плате для работы с соответствующими цифровыми компонентами или в более сложной среде SoC. Мы объясняем функционирование всех компонентов на примере аналогового входа. Также объясняется множество различных параметров, используемых в сигма-дельта-АЦП. (Эта статья предназначена для чтения в качестве дополнения к «Проверка смешанных сигналов сигма-дельта-АЦП в среде SoC ».
SD-ADC имеет модулятор и цифровой фильтр (также известный как децимационный фильтр), как показано на рис. 1 .Модулятор преобразует входной аналоговый сигнал в цифровые битовые потоки (единицы и нули). Можно наблюдать бит, 1’b1 или 1’b0, поступающий на каждом фронте тактового сигнала модулятора.
Децимационный фильтр принимает входные потоки битов и, в зависимости от значения коэффициента передискретизации (OSR), выдает один N-битный цифровой выход на каждый фронт тактовой частоты OSR. Например, если мы считаем OSR равным 64, то фильтр дает один N-битный выход для каждых 64 фронтов тактовой частоты (64 выхода данных модулятора). Здесь N – разрешение SD-АЦП.
Нажмите на картинку для увеличения.
Рисунок 1: Схема прохождения сигналов в сигма-дельта АЦП первого порядка
Как работает модулятор
Работу модулятора можно пояснить на примере преобразования. В таблице 1 заголовки X, B, C, D и W соответствуют точкам пути прохождения сигнала на блок-схеме на фиг. 2 , . В этом примере вход X – это вход постоянного тока 3/8. Результирующий сигнал в каждой точке пути прохождения сигнала для каждой выборки сигнала показан в Таблица 1 .
Обратите внимание, что повторяющийся шаблон развивается каждые шестнадцать выборок, и что среднее значение сигнала W по выборкам с 1 по 16 составляет 3/8, таким образом показывая, что контур обратной связи заставляет среднее значение сигнала обратной связи W быть равным входному X
Рисунок 2: Блок-схема сигма-дельта первого порядка
Таблица 1
Данные D принимаются децимационным фильтром, который генерирует N-битный выходной сигнал.В приведенном выше примере, если усреднение (или OSR) меньше 16, то будет ошибка квантования. Это связано с тем, что контур обратной связи не дает достаточно времени для того, чтобы выход достиг значения входа. Следовательно, точность / SNR сигма-дельта АЦП улучшается с увеличением значения OSR, при условии, что входная частота очень низкая. Кроме того, даже если OSR больше 16, если разрешение SDADC (значение N) меньше 8, то будет конечный шум квантования, причина в том, что разрешение АЦП меньше, чем степень детализации Сигнал.
С точки зрения частотной области, когда входной сигнал проходит через модулятор, белый шум смещается в высокочастотный шум в частотной области, как показано на Рис. 3 , но частота сигнала не смещается. Децимационный фильтр, будучи фильтром нижних частот, отсекает высокочастотные составляющие.
Рисунок 3: Отображение того, как шум квантования преобразуется в форму фильтра верхних частот
Как работает прореживающий фильтр
Существует два типа цифровых фильтров – КИХ (конечная импульсная характеристика) и БИХ (бесконечная импульсная характеристика). Фильтр, наиболее часто используемый для задней части преобразователя сигмадельта, – это КИХ из-за его стабильности и простоты. реализации, линейной фазовой характеристики и того факта, что децимация может быть включена в сам фильтр.Схема прохождения сигналов фильтра децимации показана на рис. 4 .
Рисунок 4: Схема прохождения сигналов децимационного фильтра
Пример передаточной функции децимационного БИХ-фильтра:
Формула 1
Пример передаточной функции децимационного КИХ-фильтра с его блок-схемой показан на рис. 5 .
Рисунок 5: Блок-схема КИХ-фильтра
Процесс прореживания используется в сигма-дельта-преобразователе для удаления избыточных данных на выходе.Теорема выборки говорит нам, что частота дискретизации должна быть только в два раза больше ширины полосы входного сигнала, чтобы надежно восстановить входной сигнал без искажений.
Нажмите на картинку для увеличения.
Рисунок 6: Децимационный фильтр, отсекающий высокочастотные компоненты
Однако входной сигнал был сильно передискретизирован сигма-дельта-модулятором, чтобы уменьшить шум квантования. Следовательно, есть избыточные данные, которые можно удалить без искажения результата преобразования.Процесс прореживания показан в частотной области на рис. 6 . Это показывает, что процесс прореживания просто снижает частоту дискретизации выходного сигнала, сохраняя при этом необходимую информацию.
Ссылки
1. Краткое введение в сигма-дельта-преобразование от Дэвид Джарман
Сидди Джай Пракаш – инженер по архитектуре смешанных сигналов в Freescale Semiconductor, занимающийся архитектурой и проверкой измерительной SoC и автомобильной SoC для радарных приложений.
Kushal Kamal в течение последних трех лет участвовал в проверке SoC со смешанными сигналами в Freescale Semiconductor. Он специализируется на HDL-моделировании, моделировании смешанных сигналов на уровнях SoC / IP и полномасштабном SPICE-моделировании.
Кумар Абхишек (Kumar Abhishek ) – руководитель службы смешанной архитектуры сигналов и проверки в Freescale. Последние 8 лет он работал в области архитектуры и верификации смешанных сигналов
Продолжить чтение
Многокаскадный сигма-дельта-модулятор, основанный на методах шумовой связи и цифровой прямой связи
Моргадо, А., дель Рио, Р., и де ла Роса, Дж. (2008). Каскадный Σ∆-модулятор на основе резонанса для широкополосного аналого-цифрового преобразования низкого напряжения. Electronics Letters, 44 (2), 97–99
Статья Google ученый
Влейгельс, К., Рабии, С., и Вули, Б.А. (2001). Сигма-дельта модулятор 2,5 В для приложений широкополосной связи. IEEE Journal of Solid-State Circuits, 36 (12), 1887–1899
Статья Google ученый
Ван Рурмунд, Х. М., Касье, Х., и Стеяерт, М. (2006). Проектирование аналоговых схем . Springer.
Книга Google ученый
Пэн Дж., Ван Дж. И Тан С. (2014). Оптимальная конструкция КИХ-фильтра на основе аппроксимации кривой для неопределенного сигма-дельта модулятора 2–1. Система цепей и обработка сигналов, 33 (3), 885–894
Статья Google ученый
Линг, Б. В., Хо, К. Ю., Дай, К., и Рейсс, Дж. Д. (2014). Снижение шума квантования с помощью периодического кода для входных сигналов с избыточной дискретизацией и соответствующего оптимального дизайна кода. Цифровая обработка сигналов, 24 , 209–222
Артикул Google ученый
Ян Ф., Гани М. и Робаст Х. (2007). подход к цифровой коррекции каскадного сигма-дельта модулятора. Circuits System and Signal Processing, 26 (4), 607–618
MathSciNet Статья Google ученый
Ли, К., Чае, Дж., Ания, М., Хамашита, К., Такасука, К., Такеучи, С., и Темес, Г. К. (2008). Дельта-сигма АЦП с шумоподавлением и временным чередованием с полосой пропускания 4,2 МГц, КНИ 98 дБ и SNDR 79 дБ. IEEE Journal of Solid-State Circuits, 43 (12), 2601–2612
Статья Google ученый
Ли К., Миллер М. Р. и Темес Г. К. (2009). Дельта-сигма АЦП 8,1 мВт, 82 дБ, полоса пропускания 1,9 МГц и коэффициент нелинейных искажений 98 дБ. IEEE Journal of Solid-State Circuits, 44 (8), 2202–2211
Статья Google ученый
Temes GC (2008) Новые архитектуры для маломощного аналого-цифрового преобразователя дельта-сигма. Азиатско-Тихоокеанская конференция IEEE по схемам и системам , стр. 1–6
Силва, Дж., Мун, Ю., Стинсгаард, Дж., И Темес, Г. К. (2001). Топология широкополосного дельта-сигма АЦП с низким уровнем искажений. Electronics Letters, 37 (12), 737–738
Артикул Google ученый
Q Liang, Sai-Weng, U Seng-Pan et al (2017) SNDR 4,2 мВт, 77,1 дБ, 5 МГц BW DT 2–1 MASH Σ∆-модулятор с совместным использованием многоскоростных операционных усилителей. IEEE (TCAS1) 64: 1549–8328
Пакаш Дж., Хосе Б., Мэтью Дж. И др. (2017). Модулятор обратной связи по ошибке на основе дифференциального квантователя для аналого-цифровых преобразователей. IEEE Transactions Circuit System II: Express Briefs, 99 , 1
Google ученый
Gutierrez E, Hernandez L, Cardes F (2017) Прочная архитектура MASH ADC на основе VCO. Electronics Letters 5th , 53, 1, 14–16
Джамшиди П. и Майманди-Неджад М. (2018). Анализ влияния источников помех на дельта-сигма модуляторы непрерывного времени на основе VCO Elsevier B.V. Интеграция, 1–10 , 0167–9260
Google ученый
Шахгасеми М., Явари М. (2016). ΣΔ Модуляторы МАШ с шумоформирующим двухступенчатым АЦП во втором каскаде. Интеграция , Журнал СБИС , 7 октября.
Khazaeili, B., & Yavari, M. (2017). Простая структура модуляторов MASH Σ∆ с сильно уменьшенным внутриполосным шумом квантования. Springer Journal of Circuits, Systems, and Signal Processing, 36 , 2125–2153
Article Google ученый
Себастьян Р., Пракаш Дж, Хосе Б.Р. и др. (2016) Многорежимный Σ∆-модулятор MASH для маломощных широкополосных приложений. Шестой международный симпозиум по встроенным вычислениям и проектированию систем (ISED) , 15–17: 87–90
Себастьян Р., Пракаш Дж., Хосе Б. Р. и др. (2017). Σ∆-модулятор с многоступенчатым шумоподавлением с улучшенным шумоподавлением для маломощных широкополосных приложений. Journal of Low Power Electron, 13 (4), 661–668
Статья Google ученый
Kwak, Y. S., et al. (2018). SNDR 72,9 дБ, полоса пропускания 2–2, 20 МГц, надежный дельта-сигма-модулятор MASH с дискретным временным разрешением и повышенным разрешением, использующий интеграторы на основе повторителя источника. IEEE Journal of Solid-State Circuits, 53 (10), 2772–2782
Статья Google ученый
Шрайер Р. и Темес Г. К. (2005). Что такое преобразователи дельта-сигма данных . Wiley / IEEE Press.
Google ученый
Hamoui AA, Martin KW (2004) Многобитовые модуляторы высокого порядка и взвешенное по псевдоданным усреднение в Σ∆ АЦП с низкой передискретизацией для широкополосных приложений. IEEE Transactions on Circuits Syst ems I 51 (1), 72–85.
Нам, К. Ю., Ли, С. М., Су, Д. К., и Вулли, Б. А. (2005). Низковольтный маломощный сигма-дельта-модулятор для широкополосного аналого-цифрового преобразования. IEEE Journal of Solid State Circuits, 40 (9), 1855–1864
Статья Google ученый
Hamoui A, Sukhon M, Maloberti F (2008) Цифровой ΣΔ-модулятор 2-го порядка с передаточной функцией сигнала с единичным усилением . Международный симпозиум IEEE. Схемы Syst ems 1664–1667.
Хамуи А., Сухон М., Малоберти Ф. (2008) Цифровые модуляторы Σ∆ высокого порядка. IEEE International. Conference Electronics Circuits Syst ems 161–170
Квон С., Малоберти Ф. (2006) Многобитовый ΔΣ-модулятор мощностью 14 мВт с соотношением сигнал / шум 82 дБ и DR 86 дБ для ADSL2 +. Сборник технических документов ISSCC , 161–170.
Wang Y, Temes GC (2009) SD-АЦП с улучшением формирования шума второго порядка. Международный симпозиум IEEE по схемам и системам на Среднем Западе , 345–348, август.
Wei, R., & Yu, J. (2016). Многокаскадный сигма-дельта АЦП с технологией шумоподавления. IEICE Electronics Express, 13 (23), 1–9
Артикул Google ученый
Бэрд Р. и Физ Т. (1995). Повышение линейности многоразрядных дельта-сигма аналого-цифровых и цифро-аналоговых преобразователей с использованием взвешенного усреднения. IEEE Transactions on Circuits and Systems II, 42 (12), 753–762
Статья Google ученый
Kwon S, Moon UK (2007) Высокоскоростной дельта-сигма-модулятор с ослабленным требованием синхронизации DEM. Международный симпозиум IEEE по схемам и системам , 733–736.
Санднер, К., Клара, М., Сантнер, А., Хартиг, Т., и Каттнер, Ф. (2005). 6-битный маломощный флэш-АЦП 1,2 Гвыб / с в цифровой КМОП-матрице 0,13 мкм. IEEE Journal of Solid-State Circuits, 40 (7), 1499–1505
Статья Google ученый
Харун, М. А. Н. (2014). Маломощные высокоскоростные дельта-сигма модуляторы высокого разрешения для цифровых ТВ-приемников в нанометровой КМОП-матрице [диссертация] .Канада, факультет электротехники и вычислительной техники Университета Макгилла.
Google ученый
Грегориан Р. (1999). Введение в операционные усилители и компараторы CMOS . Вайли.
Google ученый
Разави Б. (1995). Принципы построения систем преобразования данных . IEEE Press.
Google ученый
Кобаяси Т., Ногами К., Широтори Т. и Фудзимото Ю. (1993). Управляемый током усилитель с фиксацией фиксации и статический энергосберегающий входной буфер для маломощной архитектуры. IEEE Journal of Solid-State Circuit, 28 (4), 863–867
Статья Google ученый
Haroun M, Hamoui A (2013) Операционный усилитель с токовым зеркалом и переключаемыми крутизнами для маломощных интеграторов с переключаемыми конденсаторами.in Proceedings IEEE International Symposium Circuits Systems 393–396.
Lancioni W, Dualibe F (2018). Непрерывная архитектура MASH 2–2 с полной прямой связью для сигма-дельта модуляторов. IEEE 9-й латиноамериканский симпозиум по схемам и системам (LASCAS).
Dessouky, M., & Kaiser, A. (2001). ΣΔ-модулятор с очень низким напряжением и динамическим диапазоном 88 дБ с использованием локального переключателя. IEEE Journal of Solid-State Circuits, 36 (3), 349–355
Статья Google ученый
Преимущества аналого-цифрового преобразования дельта-сигма
Отличительными особенностями дельта-сигма АЦП являются использование передискретизации в сочетании с децимационной фильтрацией и формированием шума квантования.
Передискретизация
Дельта-сигма АЦПиспользуют частоты дискретизации, которые в несколько раз превышают частоту дискретизации, достаточную для данного сигнала, например, в 128 раз. Например, для дискретизации сигнала 25 кГц будет достаточно частоты дискретизации, превышающей частоту Найквиста (то есть> 50 кГц). Однако дельта-сигма АЦП, использующий коэффициент передискретизации 128, выбирает сигнал на частоте 6 МГц. Этот подход имеет несколько преимуществ, таких как лучшее сглаживание и более высокое разрешение.
В частотной области выборка сигнала эффективно модулирует спектр входного сигнала несущими частотами, которые кратны частоте дискретизации F с (то есть 0, F с , 2F с , 3 F с , и так далее).Чтобы гарантировать, что эти модулированные версии спектра входного сигнала не перекрываются, вызывая наложение спектров, частота дискретизации должна быть более чем в два раза больше максимальной частотной составляющей сигнала (то есть 2F max ), частоты Найквиста. И наоборот, если входной сигнал имеет частотные компоненты выше F s /2, также называемые частотой Найквиста, эти компоненты могут накладываться на частотный диапазон суб-Найквиста, что затрудняет обнаружение представляющих интерес сигналов среди псевдонимов.Этот эффект наложения спектров проявляется в виде шума и искажения сигнала.
Для предотвращения наложения спектров аналоговый интерфейс устройства сбора данных часто использует аналоговый фильтр нижних частот, который ослабляет частотные составляющие, превышающие частоту Найквиста, перед дискретизацией АЦП. К таким фильтрам предъявляются строгие требования, поскольку ожидается, что они будут иметь характеристики, напоминающие кирпичную стену, включая резкий спад, плоскую полосу пропускания и т. Д. При таких жестких ограничениях и том факте, что они должны быть реализованы в виде аналоговых схем, эти фильтры сложны в конструкции и дороги в производстве.
Рис. 2. Передискретизация снижает требования к аналоговому фильтру сглаживания.
Дельта-сигма АЦПослабляют требования к аналоговым фильтрам сглаживания за счет передискретизации входного сигнала, как показано на рисунке 2. Благодаря передискретизации модулированные версии спектра входного сигнала дополнительно разделяются в частотной области, что позволяет получить характеристики фильтра с постепенным спадом. , что значительно упрощает конструкцию аналогового фильтра антиалиасинга.Дельта-сигма АЦП состоят в основном из цифровых компонентов, что делает их еще более привлекательными. Имея преимущественно цифровую конструкцию, они могут быть реализованы на кремнии и, таким образом, использовать преимущества крупномасштабной интеграционной технологии СБИС.
Цифровая децимационная фильтрация
Битовый поток из дельта-сигма модулятора выводится на цифровой децимационный фильтр, который усредняет и понижает дискретизацию, создавая, таким образом, n-битную выборку с желаемой частотой дискретизации Fs. Этот процесс усреднения имеет эффект фильтрации нижних частот сигнала в частотной области, что ослабляет шум квантования и удаляет псевдонимы из интересующей полосы.Этот децимационный фильтр обычно построен для чрезвычайно плоской частотной характеристики в полосе пропускания и отсутствия фазовой ошибки, резкого спада около частоты среза (примерно в 0,49 раза больше частоты дискретизации Fs) и отличного подавления в полосе заграждения, что делает его очень эффективным. при сглаживании. Цифровой фильтр прореживания обычно реализуется как фильтр с конечной импульсной характеристикой (FIR), такой как гребенчатый фильтр, который является экономичным способом реализации прореживания.
Формирование шума квантования
Преобразование аналогового сигнала в цифровой приводит к появлению шума в сигнале, который называется шумом квантования.Для одного цифрового отсчета шум составляет просто ± 1/2 младшего значащего разряда. Чем меньше LSB, тем выше будет разрешение АЦП. Более высокое разрешение подразумевает более низкий шум квантования или более высокое отношение сигнал / шум (SNR). Классическое уравнение, которое отражает связь между разрешением АЦП и SNR, показано в Уравнении 1, где N – эффективное количество бит разрешения АЦП.
SNR = 6,02N + 1,76 дБ (Уравнение 1)
Однако это не конец истории.Дельта-сигма-модулятор ведет себя как фильтр нижних частот для сигнала и фильтр верхних частот для шума квантования, тем самым продвигая шум в области более высоких частот, как показано на рисунке 3. Это явление называется формированием шума квантования и используется в своих интересах. за счет использования цифрового прореживания, которое эффективно фильтрует нижние частоты выходного сигнала модулятора и удаляет шум квантования. Снижение мощности шума в интересующей полосе частот означает более высокое отношение сигнал / шум или больший динамический диапазон, так как минимальный уровень шума был значительно снижен.
Это улучшение отношения сигнал / шум из-за передискретизации можно увидеть в уравнении 2, где F s – частота дискретизации, K – коэффициент передискретизации, а BW – ширина полосы входного сигнала.


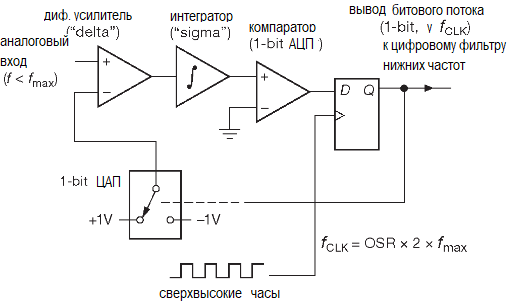 Первый шаг в модуляции delta-sigma это модуляция delta. В ней delta-модуляции кодируется изменение в сигнале (delta), вместо кодирования абсолютного значения. В результате получается поток импульсов, в противоположность потоку чисел, как это происходит в импульсно-кодовой модуляции (pulse code modulation, PCM). В delta-sigma модуляции точность модуляции улучшается путем пропускания цифрового вывода через 1-битный ЦАП и добавлением (sigma) полученного аналогового сигнала к входному сигналу (тому, который имеется перед delta-модуляцией), тем самым уменьшая ошибку, которая вводится delta-модуляцией.
Первый шаг в модуляции delta-sigma это модуляция delta. В ней delta-модуляции кодируется изменение в сигнале (delta), вместо кодирования абсолютного значения. В результате получается поток импульсов, в противоположность потоку чисел, как это происходит в импульсно-кодовой модуляции (pulse code modulation, PCM). В delta-sigma модуляции точность модуляции улучшается путем пропускания цифрового вывода через 1-битный ЦАП и добавлением (sigma) полученного аналогового сигнала к входному сигналу (тому, который имеется перед delta-модуляцией), тем самым уменьшая ошибку, которая вводится delta-модуляцией.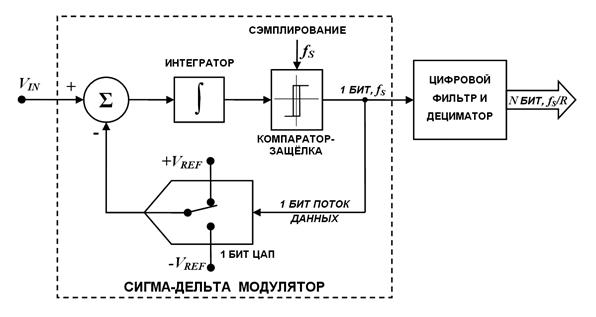 В обоих случаях временное использование сигнала низкого разрешения упрощает проектирование схем и повышает эффективность.
В обоих случаях временное использование сигнала низкого разрешения упрощает проектирование схем и повышает эффективность. Учитывая информацию времени, переданная форма сигнала может быть электрически распознана большой точностью. И напротив, без преобразования в поток импульсов, с простой передачей аналогового сигнала напрямую, к аналоговому сигналу добавляется весь шум системы, непосредственно снижая его качество.
Учитывая информацию времени, переданная форма сигнала может быть электрически распознана большой точностью. И напротив, без преобразования в поток импульсов, с простой передачей аналогового сигнала напрямую, к аналоговому сигналу добавляется весь шум системы, непосредственно снижая его качество.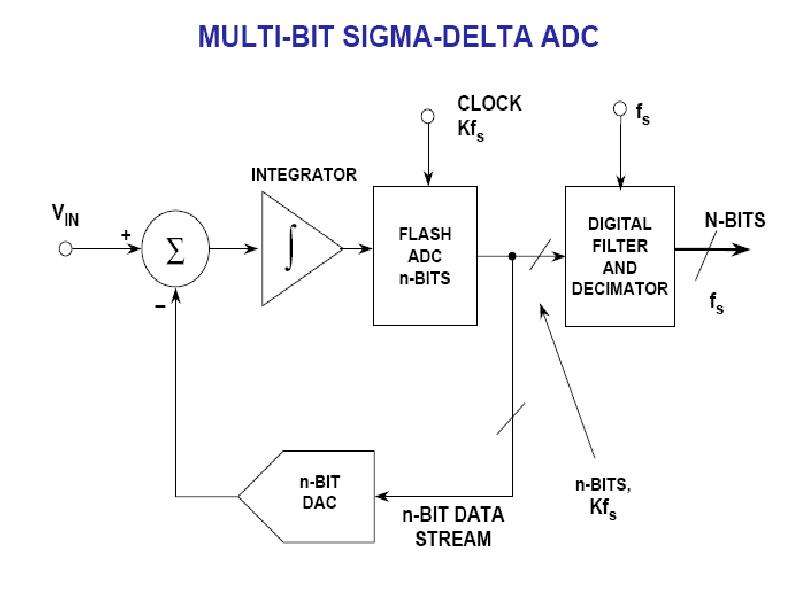 д. Таким образом, замена частотой напряжения происходит совершенно естественно, и используется вместе с достоинством и простотой передачи потока импульсов.
д. Таким образом, замена частотой напряжения происходит совершенно естественно, и используется вместе с достоинством и простотой передачи потока импульсов.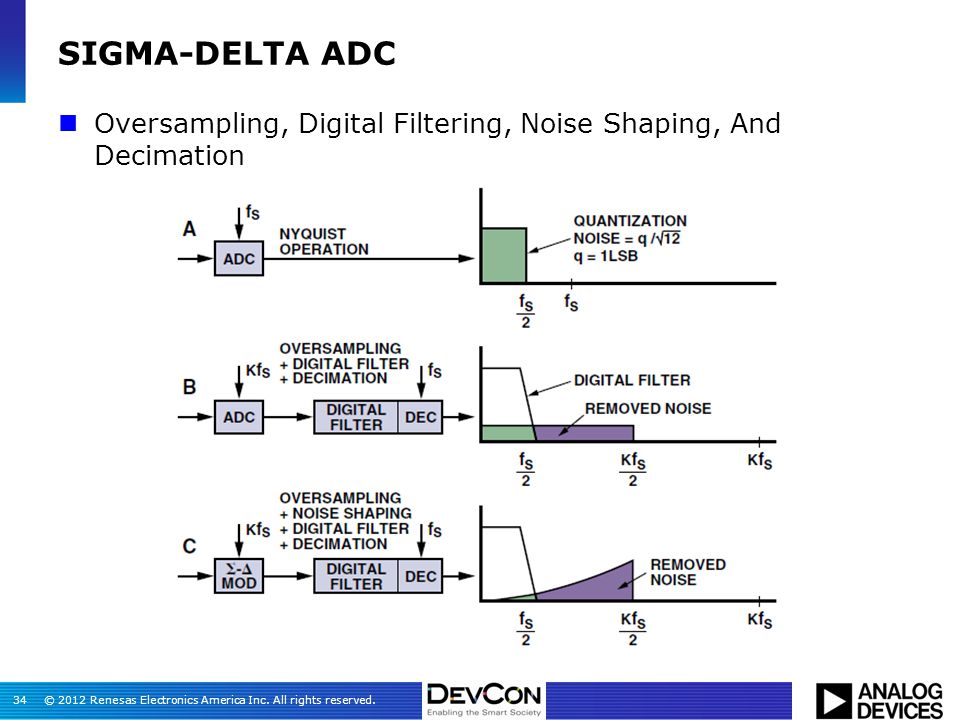 Интервал между импульсами p определяется петлей обратной связи, p = 1/f = 1/(k * v). Действие петли обратной связи служит для мониторинга интеграла v, и затем этот интеграл инкрементируется на Δ, что показывается порогом пересечения интегрированной формы сигнала T. Затем Δ вычитается интеграла v так, чтобы объединенная форма сигнала пилы между T и T – ΔΣ. На каждом шаге импульс добавляется к потоку импульсов.
Интервал между импульсами p определяется петлей обратной связи, p = 1/f = 1/(k * v). Действие петли обратной связи служит для мониторинга интеграла v, и затем этот интеграл инкрементируется на Δ, что показывается порогом пересечения интегрированной формы сигнала T. Затем Δ вычитается интеграла v так, чтобы объединенная форма сигнала пилы между T и T – ΔΣ. На каждом шаге импульс добавляется к потоку импульсов.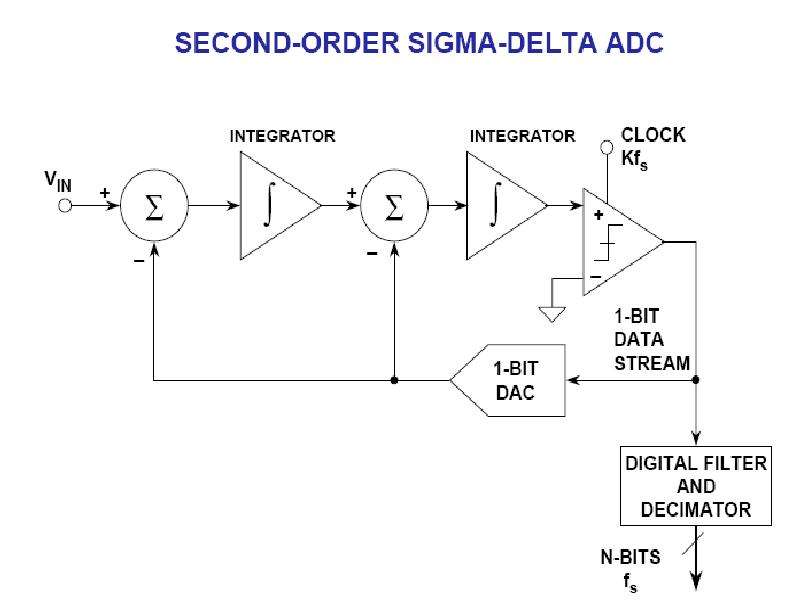 2V слева и 0.4V справа.
2V слева и 0.4V справа.
 Полный анализ показал бы, что фактически интервал между пересечениями порога справа составляет половину от интервала между пересечениями порога слева. Т. е. частота импульсов удваивается. Счетчик инкрементируется в 2 раза быстрее, что адекватно изменению в 2 раза входного напряжения. Общий эффект петли отрицательной обратной связи состоит в поддержке работающего интеграла последовательности импульсов таким образом, чтобы он соответствовал входному аналоговому сигналу. Также частота последовательности импульсов пропорциональна ограниченной амплитуде полосы пропускания входного сигнала. Ограничение полосы пропускания происходит из-за того, что теорема Найквиста-Шеннона требует 2 импульса на период, чтобы определить самую высокую пропускаемую частоту.
Полный анализ показал бы, что фактически интервал между пересечениями порога справа составляет половину от интервала между пересечениями порога слева. Т. е. частота импульсов удваивается. Счетчик инкрементируется в 2 раза быстрее, что адекватно изменению в 2 раза входного напряжения. Общий эффект петли отрицательной обратной связи состоит в поддержке работающего интеграла последовательности импульсов таким образом, чтобы он соответствовал входному аналоговому сигналу. Также частота последовательности импульсов пропорциональна ограниченной амплитуде полосы пропускания входного сигнала. Ограничение полосы пропускания происходит из-за того, что теорема Найквиста-Шеннона требует 2 импульса на период, чтобы определить самую высокую пропускаемую частоту.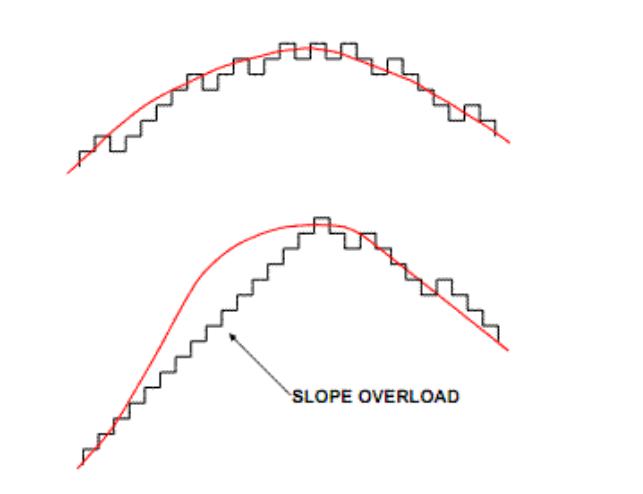 Эффект конечной длительности импульса, сконструированного в (4) происходит от формирования линии от базы на 0V до пересечения с линией затухания из (6) на полной длительности импульса.
Эффект конечной длительности импульса, сконструированного в (4) происходит от формирования линии от базы на 0V до пересечения с линией затухания из (6) на полной длительности импульса.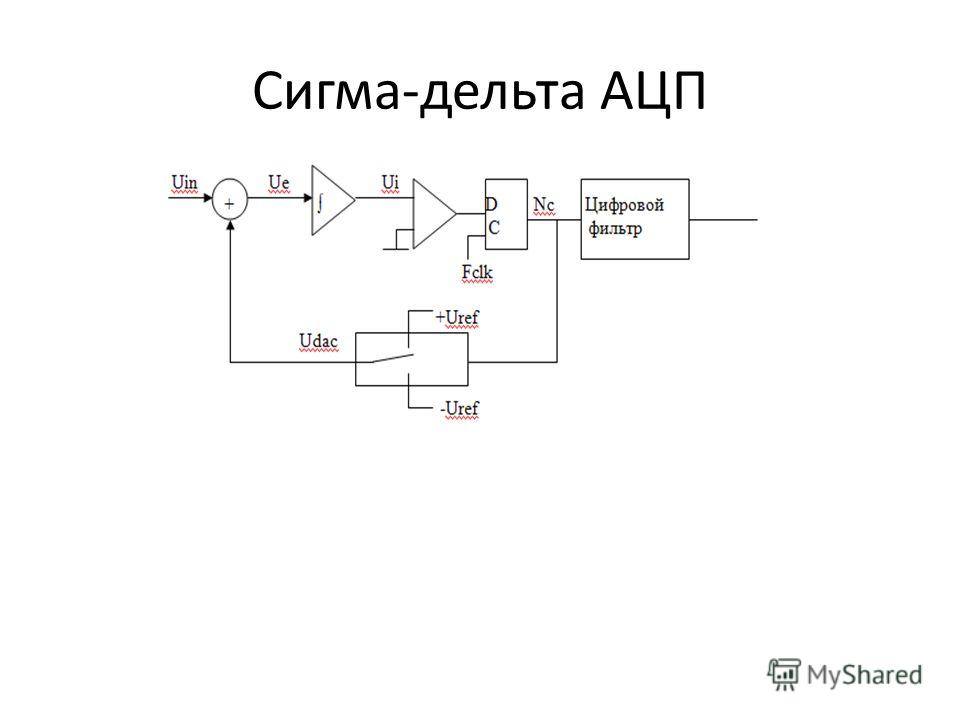 Многие частные реализации стремятся определить длительность импульса и интервал суммирования от той же самой частоты, о которой говорилось выше, но при таком способе начало импульса задерживается до следующей подходящей границы импульса. Эффект такой задержки показан на рис. 1a для последовательности импульсов с номинальными интервалами 2.5 такта – сначала для импульсов, генерируемых сразу при пересечении порога, как было описано ранее, и затем с импульсами, задержанными из-за тактирования. Эффект от этой задержки, во-первых, проявляется в том, что полка продолжается до начала импульса, и во-вторых, что импульс генерирует фиксированный шаг амплитуды, чтобы интеграл сохраняет избыток, полученный за время задержки импульса, и полка стартует снова с верхней точки, и находится теперь на той же точке, что и свободно работающий интеграл. Получаемый эффект для этого примера в том, что не задержанные импульсы в точках такта 0, 2.5, 5, 7.5, 10 и т. д. и импульсы тактирования произойдут в моменты 0, 3, 5, 8, 10 и т.
Многие частные реализации стремятся определить длительность импульса и интервал суммирования от той же самой частоты, о которой говорилось выше, но при таком способе начало импульса задерживается до следующей подходящей границы импульса. Эффект такой задержки показан на рис. 1a для последовательности импульсов с номинальными интервалами 2.5 такта – сначала для импульсов, генерируемых сразу при пересечении порога, как было описано ранее, и затем с импульсами, задержанными из-за тактирования. Эффект от этой задержки, во-первых, проявляется в том, что полка продолжается до начала импульса, и во-вторых, что импульс генерирует фиксированный шаг амплитуды, чтобы интеграл сохраняет избыток, полученный за время задержки импульса, и полка стартует снова с верхней точки, и находится теперь на той же точке, что и свободно работающий интеграл. Получаемый эффект для этого примера в том, что не задержанные импульсы в точках такта 0, 2.5, 5, 7.5, 10 и т. д. и импульсы тактирования произойдут в моменты 0, 3, 5, 8, 10 и т. д. Максимальная ошибка, которая может произойти из-за тактирования немного меньше одного отсчета. Хотя преобразователь Sigma-Delta обычно реализуется с общей тактовой частотой, чтобы определить длительность импульса, и интервал суммирования не является абсолютно необходимым, реализации, где длительности определены независимо, избегают одного из источников шума, генерируемого ожиданием следующей общей границы такта. Там, где шум является главным фактором, переопределяющим важность абсолютной точности по амплитуде, например при передаче сигнала в ограниченной полосе пропускания, могут быть реализованы раздельно определенные интервалы.
д. Максимальная ошибка, которая может произойти из-за тактирования немного меньше одного отсчета. Хотя преобразователь Sigma-Delta обычно реализуется с общей тактовой частотой, чтобы определить длительность импульса, и интервал суммирования не является абсолютно необходимым, реализации, где длительности определены независимо, избегают одного из источников шума, генерируемого ожиданием следующей общей границы такта. Там, где шум является главным фактором, переопределяющим важность абсолютной точности по амплитуде, например при передаче сигнала в ограниченной полосе пропускания, могут быть реализованы раздельно определенные интервалы.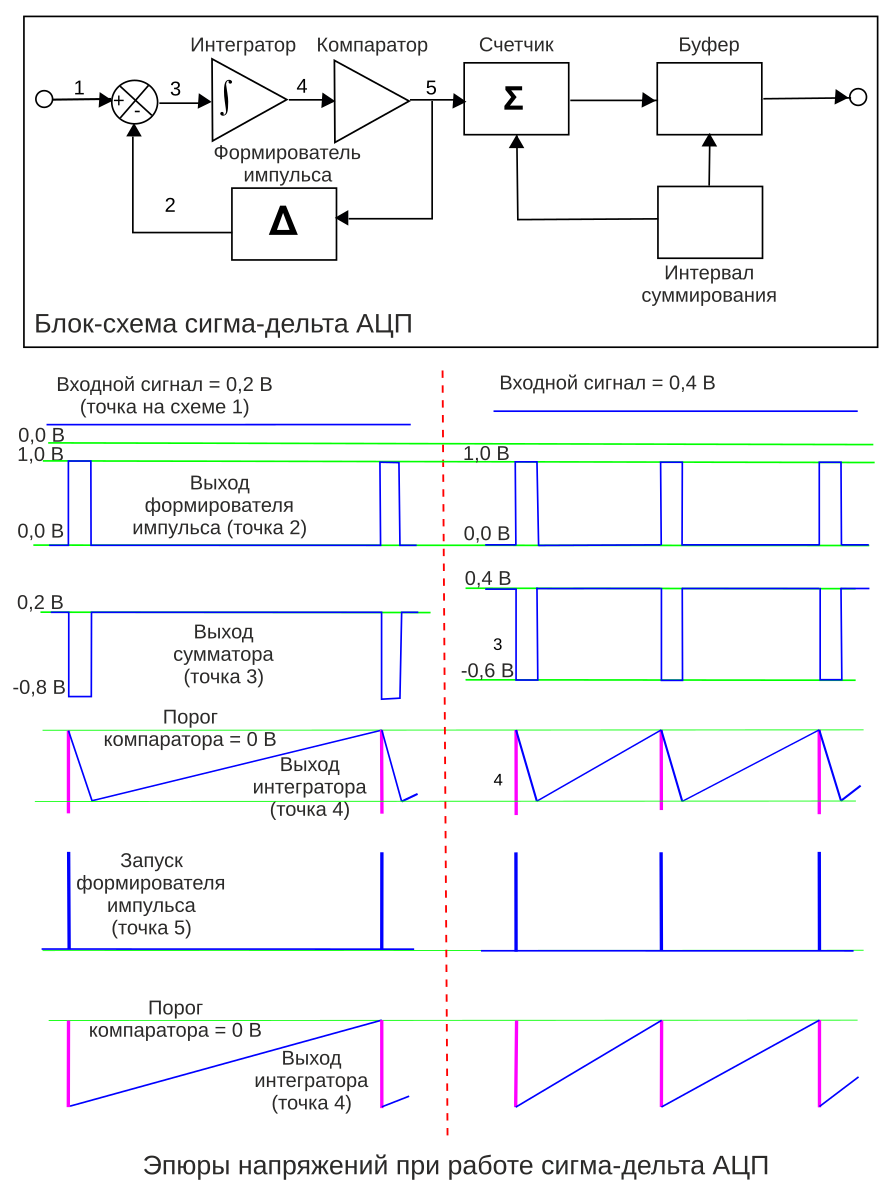 0V. Также ток, генерирумый через R опорным напряжением -Vref, постоянный на уровне -Vref/R, что генерирует намного меньше шума на соседних частях схемы. Это было бы предпочтительной схемой на практике, но чтобы показать импульс как импульс напряжения (для согласования с предыдущим описанием), на этой схеме используется электрический эквивалент.
0V. Также ток, генерирумый через R опорным напряжением -Vref, постоянный на уровне -Vref/R, что генерирует намного меньше шума на соседних частях схемы. Это было бы предпочтительной схемой на практике, но чтобы показать импульс как импульс напряжения (для согласования с предыдущим описанием), на этой схеме используется электрический эквивалент.
 Из-за того, что на инвертирующем входе усилителя (на правом выводе R1) напряжение равно 0V, то напряжение на R1 просто равно Vin, таким образом ток в конденсатор равен входному напряжению, поделенному на сопротивление R1.
Из-за того, что на инвертирующем входе усилителя (на правом выводе R1) напряжение равно 0V, то напряжение на R1 просто равно Vin, таким образом ток в конденсатор равен входному напряжению, поделенному на сопротивление R1.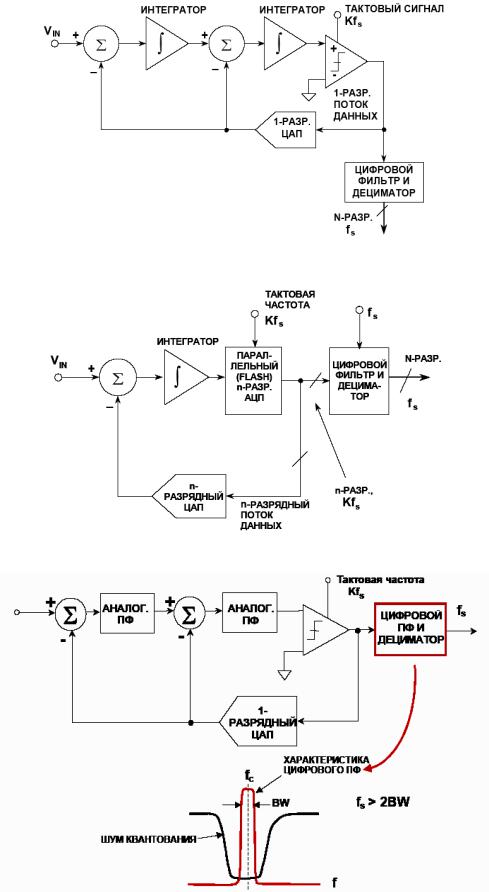 Таким образом, выход получает положительное насыщение всякий раз, когда интеграл (d) переходит на уровень ниже 0V опорного уровня, и остается там, пока (d) не станет положительным.
Таким образом, выход получает положительное насыщение всякий раз, когда интеграл (d) переходит на уровень ниже 0V опорного уровня, и остается там, пока (d) не станет положительным.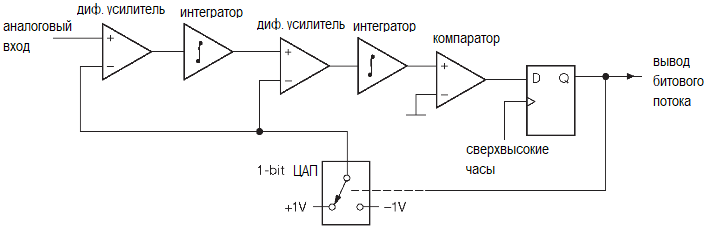 После запуска импульса еще одна задержка происходит, когда (e) поднимается обратно через порог. Из-за этого выход компаратора остается в высоком уровне, но перейдет в низкий на следующем перепаде тактов триггера. На следующем перепаде выход импульсного таймера перейдет в 0, отслеживая уровень на выходе компаратора. Таким образом, период тактов определяет длительность импульса. Для следующего импульса порог пересекается сразу перед перепадом тактов триггера, так на выходе компаратора высокий уровень останется только на короткое время. Vin (a) переходит на уровень полного диапазона +Vref, коротко перед окончанием следующего импульса. Остаток импульсного тока через конденсатор (c) перейдет в 0, и следовательно наклон интегратора кратко перейдет к нулю. После этого импульса течет положительный ток полной шкалы (c), и интегратор переходит на свой максимальный уровень, и пересечение порога произойдет на следующем тактовом перепаде триггера. На этом перепаде запускается импульс, и ток Vin теперь соответствует опорному току, так как левая обкладка конденсатора (c) заземлена благодаря активности операционного усилителя интегратора.
После запуска импульса еще одна задержка происходит, когда (e) поднимается обратно через порог. Из-за этого выход компаратора остается в высоком уровне, но перейдет в низкий на следующем перепаде тактов триггера. На следующем перепаде выход импульсного таймера перейдет в 0, отслеживая уровень на выходе компаратора. Таким образом, период тактов определяет длительность импульса. Для следующего импульса порог пересекается сразу перед перепадом тактов триггера, так на выходе компаратора высокий уровень останется только на короткое время. Vin (a) переходит на уровень полного диапазона +Vref, коротко перед окончанием следующего импульса. Остаток импульсного тока через конденсатор (c) перейдет в 0, и следовательно наклон интегратора кратко перейдет к нулю. После этого импульса течет положительный ток полной шкалы (c), и интегратор переходит на свой максимальный уровень, и пересечение порога произойдет на следующем тактовом перепаде триггера. На этом перепаде запускается импульс, и ток Vin теперь соответствует опорному току, так как левая обкладка конденсатора (c) заземлена благодаря активности операционного усилителя интегратора.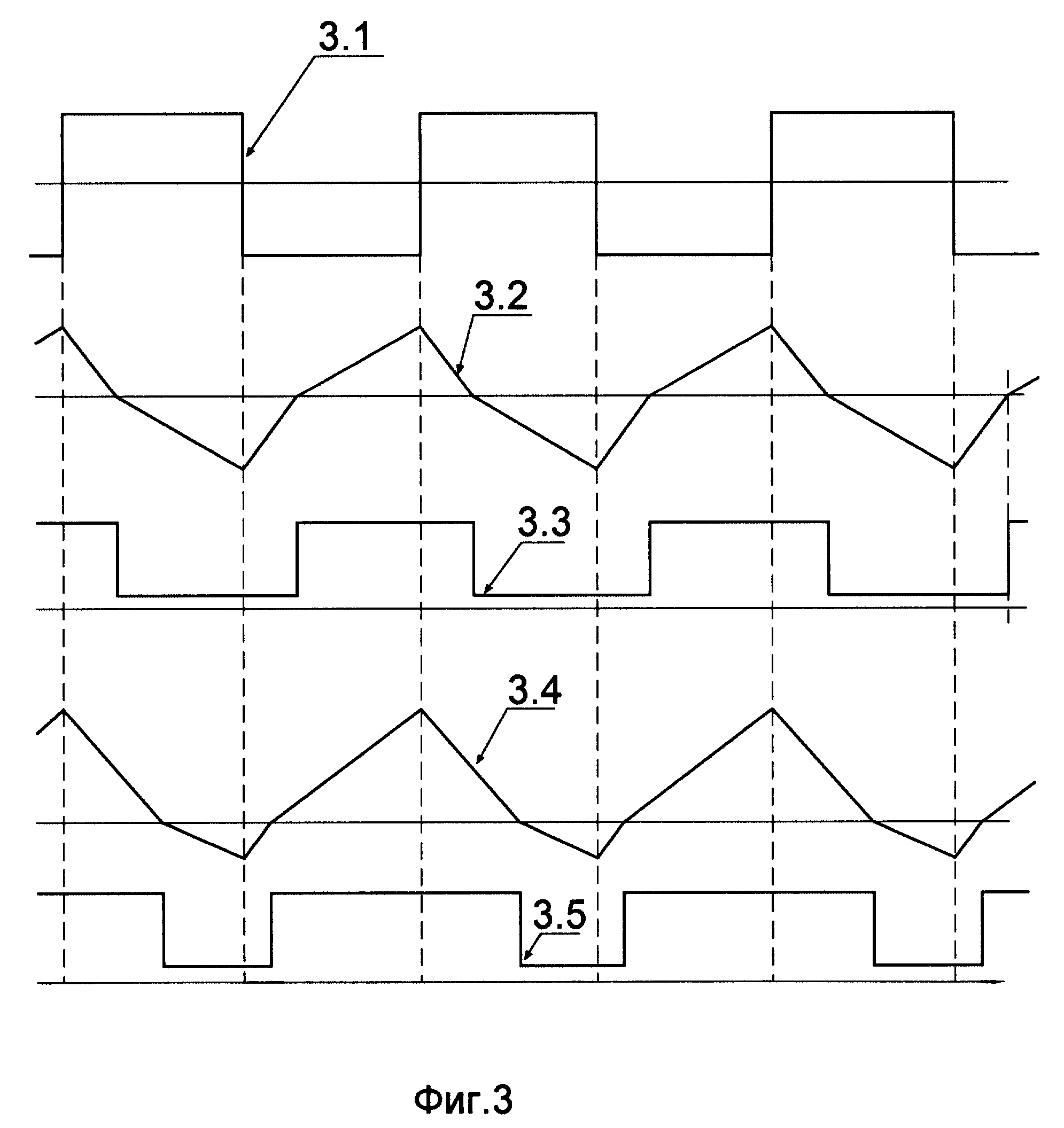 Тогда интегрирование идет по наклону к нулю, и остается на отрицательном значении, которое было в начале импульса. В результате получается, что импульсный ток остается включенным, потому что Q на высоком уровне на каждом перепаде сигнала тактов.
Тогда интегрирование идет по наклону к нулю, и остается на отрицательном значении, которое было в начале импульса. В результате получается, что импульсный ток остается включенным, потому что Q на высоком уровне на каждом перепаде сигнала тактов.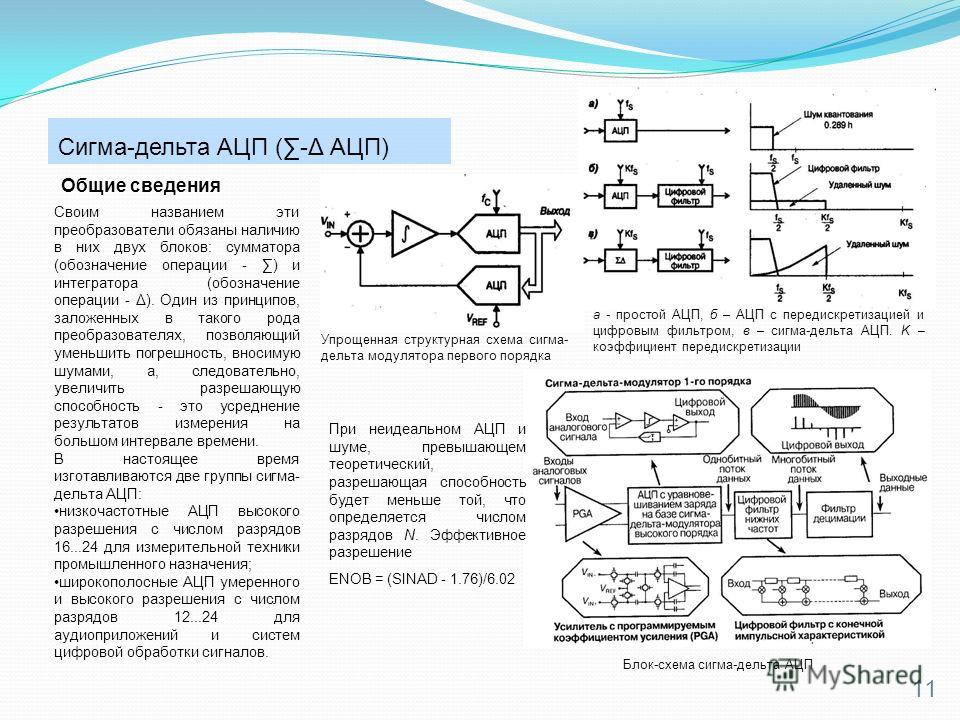 Форма сигнала на входе Vin аппроксимируется путем передачи потока импульсов (g) в фильтр низкой частоты, однако в результате получится дефект, обсуждаемый в контексте рис. 1a. Одна из возможностей уменьшить эту ошибку – снизить вдвое период тактов, и удвоить его амплитуду путем уменьшения в два раза резистор R2; благодаря этому мощность импульса останется такой же, и она не будет влияет на соседние импульсы. Тогда здесь будет переход порога для каждого импульса. По такому изменению моностабильный триггер, управляемый компаратором по порогу пересечения будет точнее отслеживать эти пересечения, что устранит один из источников ошибки, как в ЦАП, так и в sigma-delta модуляторе.
Форма сигнала на входе Vin аппроксимируется путем передачи потока импульсов (g) в фильтр низкой частоты, однако в результате получится дефект, обсуждаемый в контексте рис. 1a. Одна из возможностей уменьшить эту ошибку – снизить вдвое период тактов, и удвоить его амплитуду путем уменьшения в два раза резистор R2; благодаря этому мощность импульса останется такой же, и она не будет влияет на соседние импульсы. Тогда здесь будет переход порога для каждого импульса. По такому изменению моностабильный триггер, управляемый компаратором по порогу пересечения будет точнее отслеживать эти пересечения, что устранит один из источников ошибки, как в ЦАП, так и в sigma-delta модуляторе. В таком приложении аналоговый сигнал преобразовывался в поток импульсов, который передавался, и на месте приема оригинальный сигнал восстанавливался с помощью восстановителя импульсов и ФНЧ. Этот ФНЧ выполнял функцию суммирования, связанную с Σ. Математическая обработка учитывает ошибки, возникающие при передаче сигнала по каналу связи, так что эти ошибки уничтожаются на приемнике в процессе накопления, связанного с операцией Σ.
В таком приложении аналоговый сигнал преобразовывался в поток импульсов, который передавался, и на месте приема оригинальный сигнал восстанавливался с помощью восстановителя импульсов и ФНЧ. Этот ФНЧ выполнял функцию суммирования, связанную с Σ. Математическая обработка учитывает ошибки, возникающие при передаче сигнала по каналу связи, так что эти ошибки уничтожаются на приемнике в процессе накопления, связанного с операцией Σ.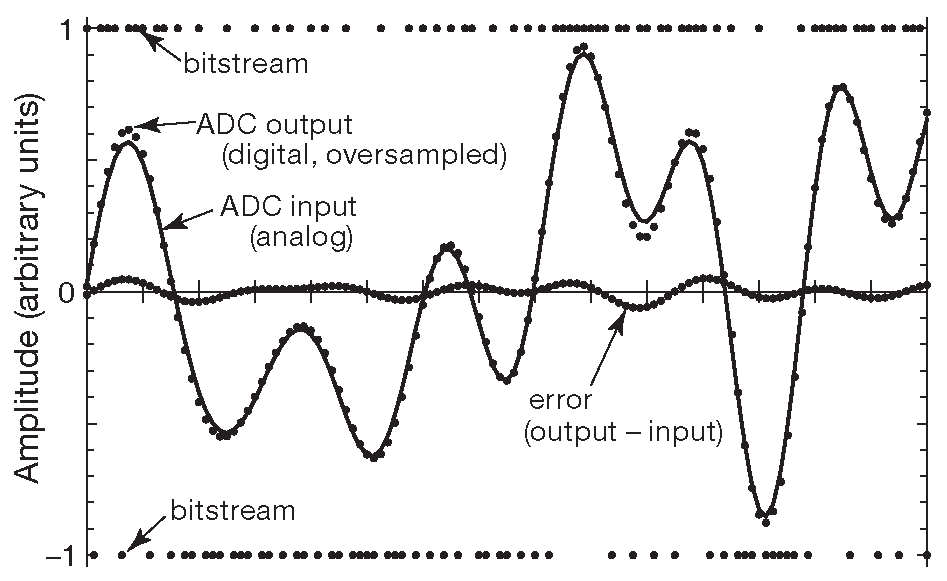 Таким образом, усреднение входного напряжения по периоду суммирования отражает значение входного сигнала, и будет подвергнуто незначительным вариациям.
Таким образом, усреднение входного напряжения по периоду суммирования отражает значение входного сигнала, и будет подвергнуто незначительным вариациям. В этом случае выбирается компромисс между полосой пропускания и размером буфера N. Система восстановления сигналов потребует проверку и коррекцию ошибок на канале передачи, преобразование из цифровой формы в аналоговую (ЦАП) и схему выборки-хранения. Возможные дальнейшие улучшения включают некую форму восстановления перепадов сигнала. Это может быть реализовано на PCM (pulse code modulation, импульсно-кодовая модуляция) о оцифровкой на основе sigma-delta АЦП.
В этом случае выбирается компромисс между полосой пропускания и размером буфера N. Система восстановления сигналов потребует проверку и коррекцию ошибок на канале передачи, преобразование из цифровой формы в аналоговую (ЦАП) и схему выборки-хранения. Возможные дальнейшие улучшения включают некую форму восстановления перепадов сигнала. Это может быть реализовано на PCM (pulse code modulation, импульсно-кодовая модуляция) о оцифровкой на основе sigma-delta АЦП.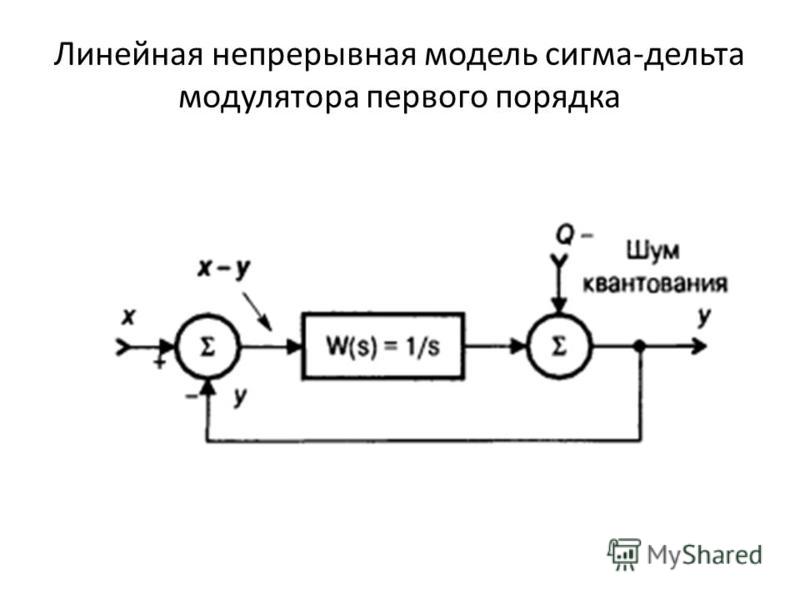
 Для реального питания нагрузки (наподобие динамика) выход ЦАП обычно соединяется со входом электронного усилителя, или интегрируется в усилитель.
Для реального питания нагрузки (наподобие динамика) выход ЦАП обычно соединяется со входом электронного усилителя, или интегрируется в усилитель.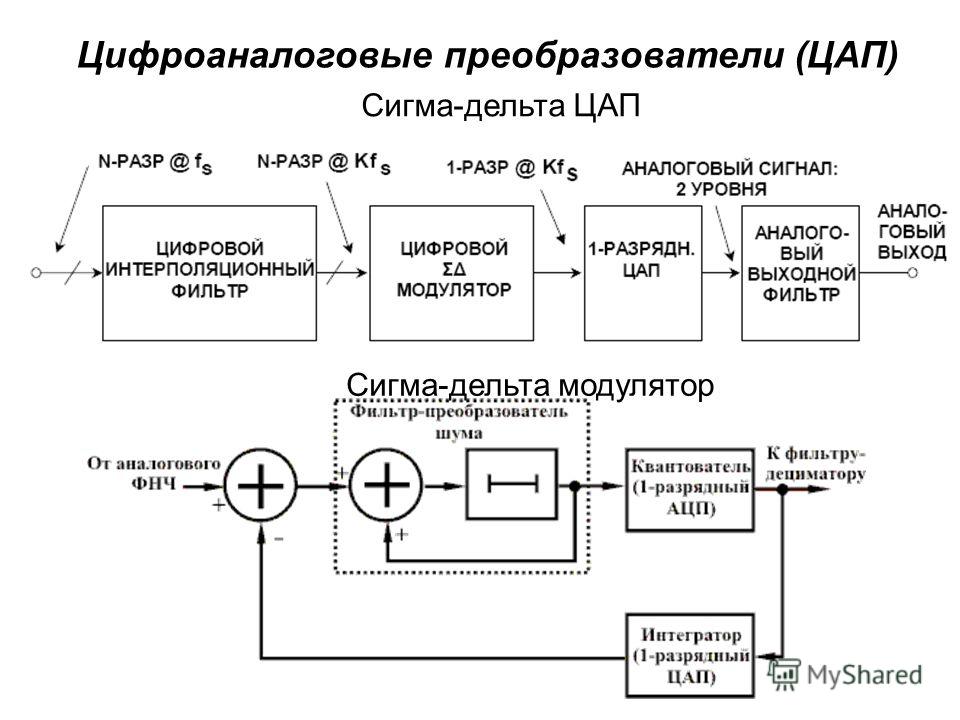 Эти добавленные частотные компоненты также содержат в себе ошибку квантования delta-sigma модулятора, но они могут быть отфильтрованы с помощью ФНЧ. В результате получится оригинальный аналоговый сигнал, синтезированный из цифровых значений.
Эти добавленные частотные компоненты также содержат в себе ошибку квантования delta-sigma модулятора, но они могут быть отфильтрованы с помощью ФНЧ. В результате получится оригинальный аналоговый сигнал, синтезированный из цифровых значений.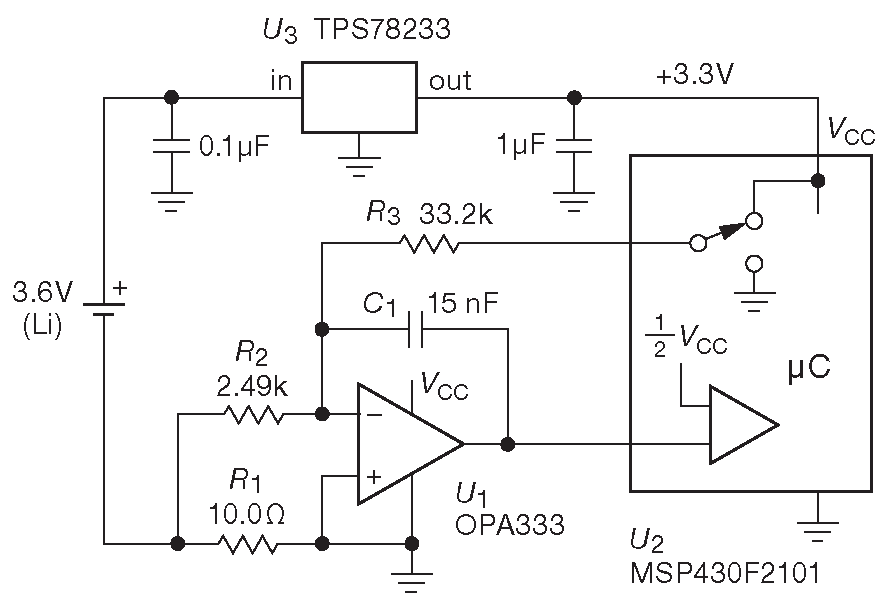 диаграммы (1)..(3) на рис. 2:
диаграммы (1)..(3) на рис. 2: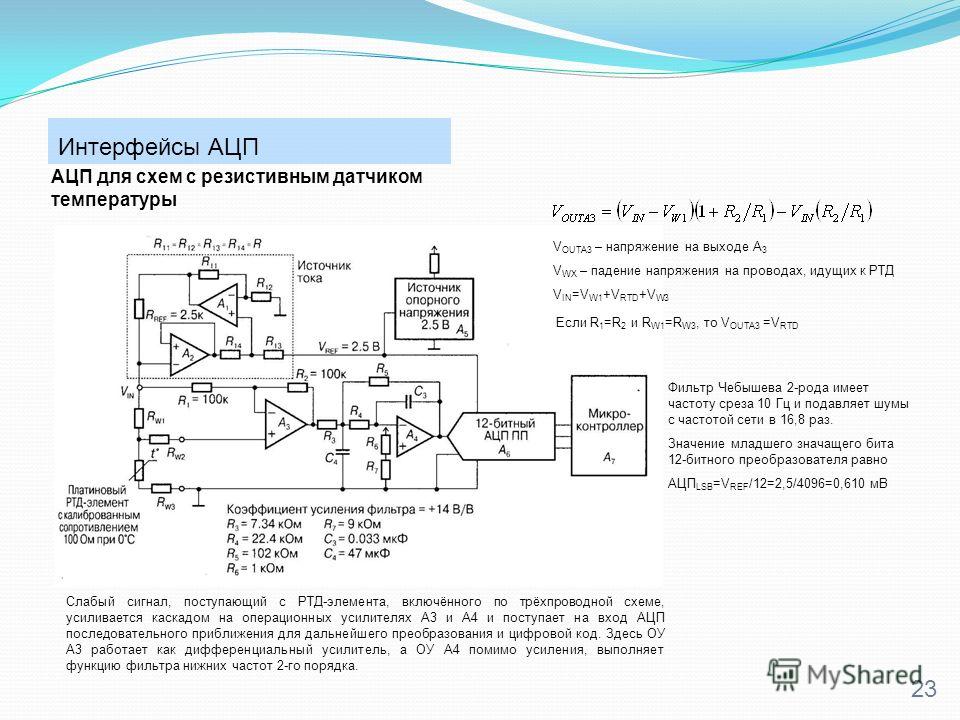 В результате получается проще реализация, которая добавляет выгоду вырезания шума квантования из интересующих сигналов (т. е. интересующие сигналы фильтруются ФНЧ, в то время как шум квантования фильтруется ФВЧ). Этот эффект увеличивается с повышением передискретизации, что позволяет управлять шумом квантования. С другой стороны, дельта-модуляция одинаково формирует как шум, так и сигнал.
В результате получается проще реализация, которая добавляет выгоду вырезания шума квантования из интересующих сигналов (т. е. интересующие сигналы фильтруются ФНЧ, в то время как шум квантования фильтруется ФВЧ). Этот эффект увеличивается с повышением передискретизации, что позволяет управлять шумом квантования. С другой стороны, дельта-модуляция одинаково формирует как шум, так и сигнал.
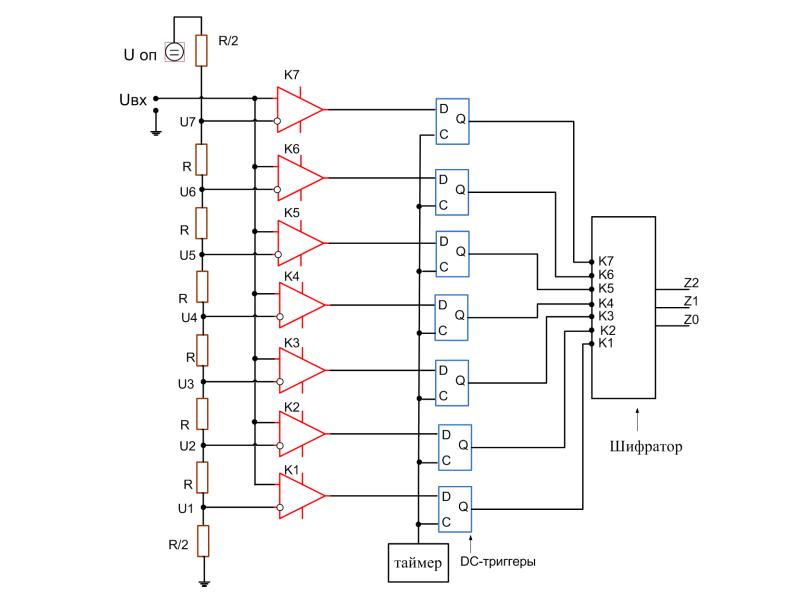
 Простой компаратор имеет 2 уровня, и таким образом является 1-битным квантователем; 3-уровневый квантователь называется квантователем “1.5 bit”; 4-уровневый квантователь является 2-разрядным; 5-уровеневый квантователь называется “2.5 bit”.
Простой компаратор имеет 2 уровня, и таким образом является 1-битным квантователем; 3-уровневый квантователь называется квантователем “1.5 bit”; 4-уровневый квантователь является 2-разрядным; 5-уровеневый квантователь называется “2.5 bit”.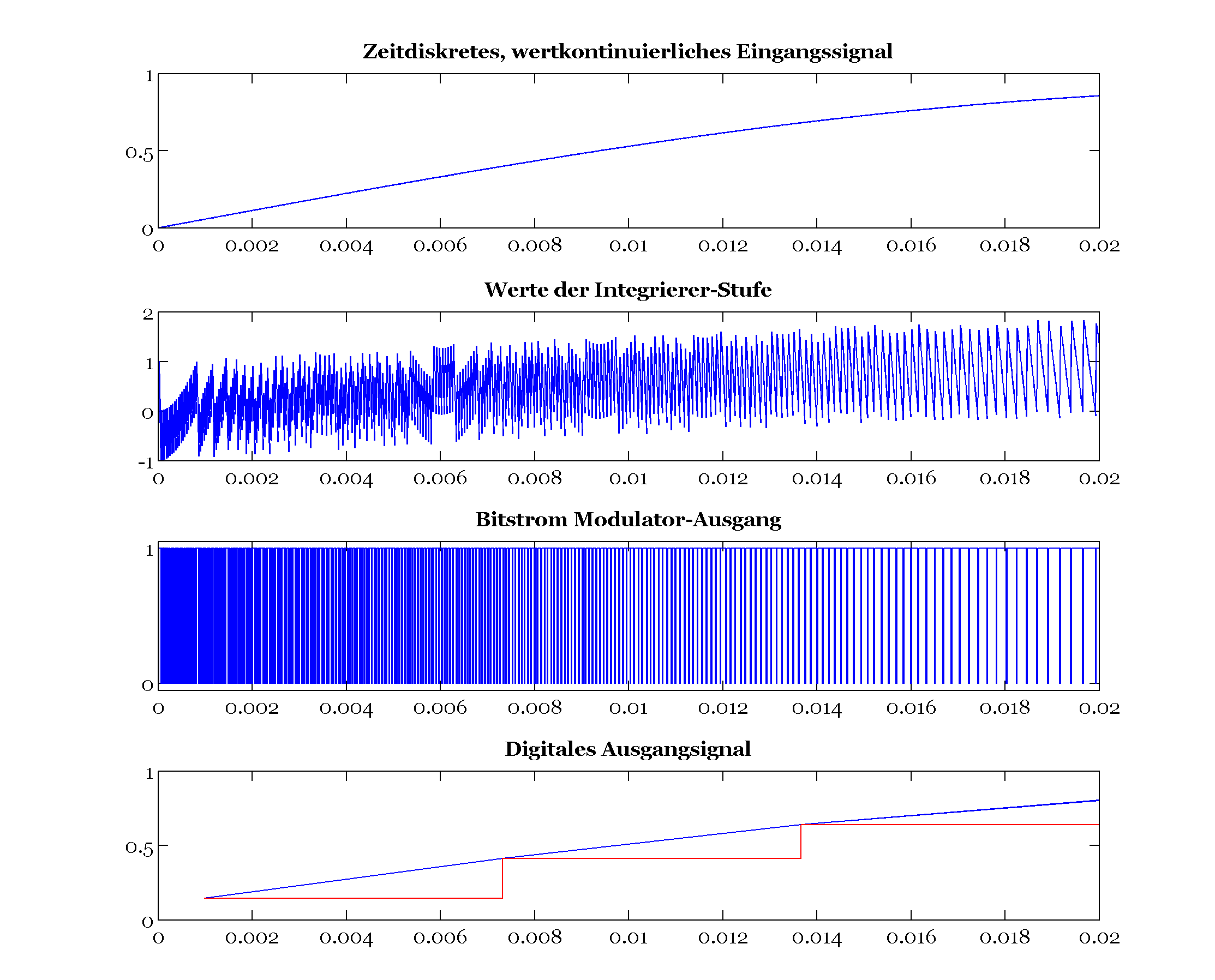
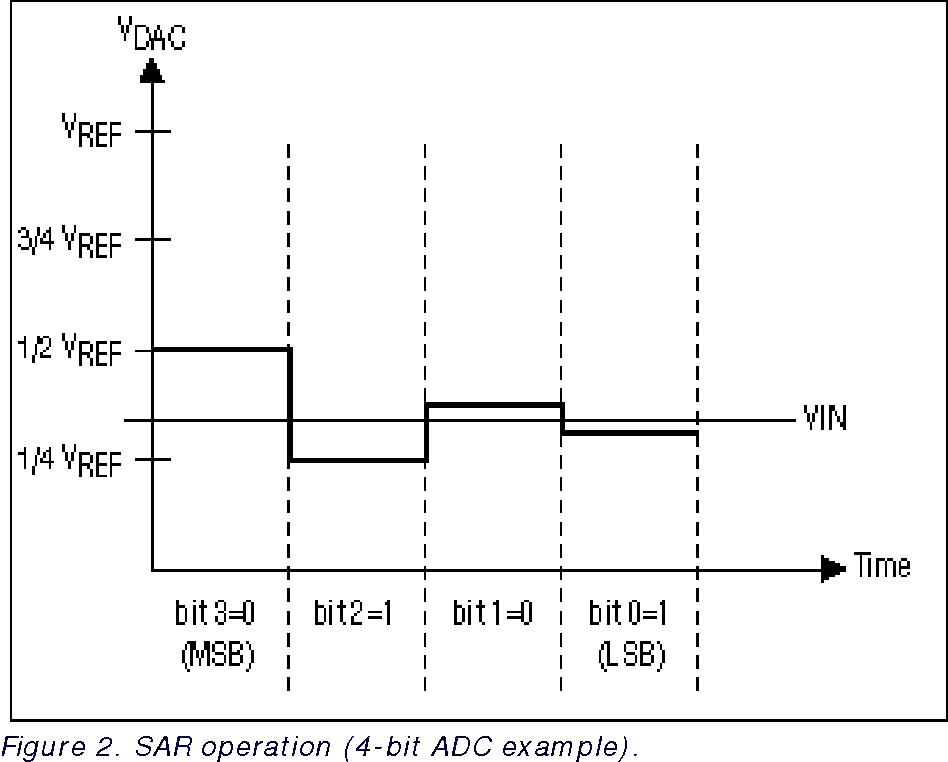
 Эта техника называется noise shaping (сглаживание шума).
Эта техника называется noise shaping (сглаживание шума). Чем выше коэффициент передискретизации, тем выше соотношение сигнал/шум, и выше разрешающая способность в битах.
Чем выше коэффициент передискретизации, тем выше соотношение сигнал/шум, и выше разрешающая способность в битах. org.
org.