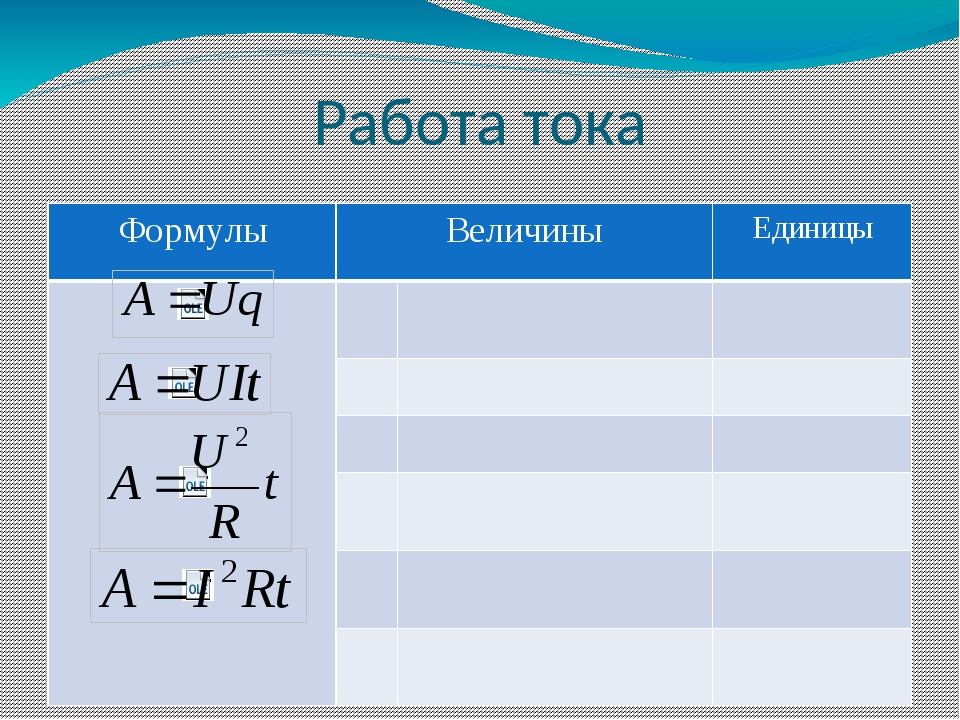
Сила напряжения формула: Ошибка 404 – документ не найден

Содержание

формулы расчета мощности в проводнике

Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.

Электрический ток в проводнике

В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.

От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:

Зависимость силы тока от электрического заряда

Входящие в формулу величины:

I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си. Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах. Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
Время в секундах.

Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:

I = (qnv)cosαS.

Также используется интегрирование по площади поверхности и сечению проводника.

Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.

Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:

Сила тока участка цепи и цепи с источником тока

Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.

В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.

При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.

Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:

RC = 1/ FC.

Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.

Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:

Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.

Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.

I = I1 + I2 + I3

Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.

Видео

Оцените статью:

Основные расчетные электротехнические формулы

Электрическое сопротивление материала определяется по формулам:

Электрическое сопротивление, Ом, материала

R = U/I, где U — напряжение, В; I — сила тока, А.

Удельное электрическое сопротивление, Ом·м,

ρ=Rs/l. S – сечение проводника, м² ; l – длина проводника, м.

Под удельным электрическим сопротивлением материала понимают сопротивление проводника длиной 1 м и сечением 1 м² при 20°С.

Величина, обратная удельному сопротивлению, называется проводимостью:

v=1/ρ.

Если вместо сечения проводника S задан его диаметр D, то сечение, м², находят по формуле

S= πD²/4, где π =3,14.

Сопротивление материала зависит от температуры. Если материал нагрет до температуры t°С, то его сопротивление, Ом, при этой температуре равно:

Rt= R0[1 + α (t – t0)],

где R0 – сопротивление при начальной температуре t0°С, Ом; α – температурный коэффициент.

Далее приводятся значения α для различных материалов.

Медь, алюминий, вольфрам	0,004
Сталь	0,006
Латунь	0,002

Сопротивление нескольких проводников зависит от способа их соединения. Например, при параллельном соединении сопротивление трех проводников определяется по формуле:

Rоб=R1*R2*R3/(R1R2+R2R3+R3R1)

При последовательном соединении:

Rоб=R1+R2+R3.

Постоянный ток

Постоянный ток применяют для питания устройств связи, транзисторных приборов, стартеров автомобилей, электрокар, а также, для зарядки аккумуляторов.

В качестве источников постоянного тока используют гальванические элементы, солнечные батареи, термоэлектрогенераторы, генераторы постоянного тока.

При параллельном соединении нескольких проводников с током с равными напряжениями:

Iоб = I1+I2+…+In Uоб=U1=U2=…=Un

При последовательном соединении: Iоб = Imin; – где Imin, ток наименьшего по мощности источника тока (генератора, аккумуляторной батареи).

Uоб = U1+U2+…+Un

Основные параметры цепей однофазного переменного тока

Однофазный переменный ток промышленной частоты имеет 50 периодов колебаний в секунду, или 50 Гц. Его применяют для питания небольших вентиляторов, электробытовых приборов, электроинструмента, при электросварке и для питания большинства осветительных приборов.

Частота переменного тока, Гц:

f= 1/T = np/60, где п — частота вращения генератора, мин ^-1; р – число пар полюсов генератора.

Мощность однофазного переменного тока:

активная, Вт, Ра = IUcosφ;

реактивная, вар, Q = IUsinφ;

кажущаяся, В А, S = IU =√ (P ²α+Q ²)

Если в цепь переменного однофазного тока включено только активное сопротивление (например, нагревательные элементы или электрические лампы), то значение силы тока и мощности в каждый момент времени определяют по закону Ома:

I=U/R; Рa = IU = I²R=U²/R.

Коэффициент мощности в цепи с индуктивной нагрузкой

Cosφ= Рa/IU= Рa/S.

Основные параметры цепей трехфазного переменного тока

Трехфазный переменный ток используют для питания большинства промышленных электроприемников.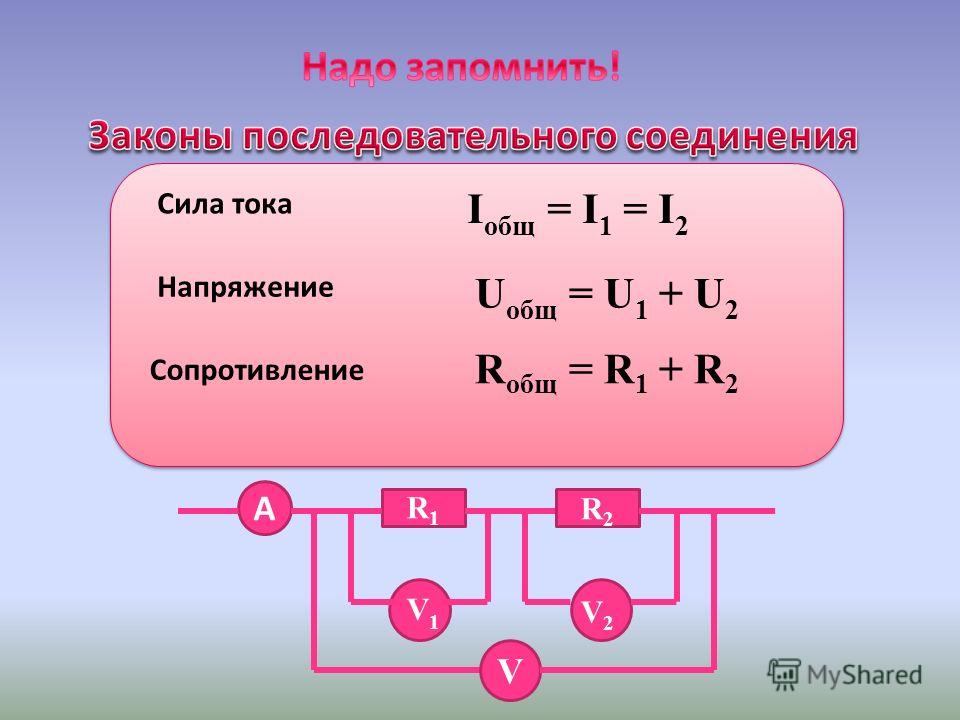 Частота трехфазного переменного тока 50 Гц.

В трехфазных системах обмотки генератора и электроприемника соединяют по схемам «звезда» или «треугольник». При соединении в звезду концы всех трех обмоток генератора (или электроприемника) объединяют в общую точку, называемую нулевой или нейтралью (рис. 5а).

При соединении в треугольник начало первой обмотки соединяют с концом второй, начало второй обмотки — с концом третьей и начало третьей — с концом первой обмотки (рис. 5б).

Если от генератора отходят только три провода, то такая система называется трехфазной трехпроводной; если от него отходит еще и четвертый нулевой провод, то систему называют трехфазной четырехпроводной.

Трехфазные трехпроводные сети используют для питания трехфазных силовых потребителей, а четырехпроводные сети – для питания преимущественно осветительных и бытовых нагрузок.

В трехфазных системах различают фазные и линейные токи и напряжения. При соединении фаз звездой линейный I и фазный Iφ токи равны:

а напряжение U =√3Uφ

При соединении треугольником

I =√3Iφ

а напряжение U = Uφ.

Мощность переменного трехфазного тока:

генератора:

активная, Вт, Рг =√3IUcosφ ,
реактивная, вар, Q=√3IUsinφ
полная, ВА, S = √3IU.

где φ – угол сдвига фаз между фазным напряжением генератора и током в той же фазе приемника, который равен току в линии при соединении обмоток генератора звездой.

приемника:

активная, Вт, Рп =3UφIcosφп=√3 IUcosφп ,
реактивная, вар, Q=√3 UφIsinφп=√3 UIsinφ
полная, ВА, S = √3UI.

где φ – угол сдвига фаз между фазным напряжением приемника и током в той же фазе приемника, который равен току линейному только при соединении звездой.

Подсчет количества теплоты, выделяемой при протекании электрического тока по проводнику.

Количество теплоты, Дж, выделяемой электрическим током в проводнике,

Q=I²Rt где t — время, с.

При определении теплового действия электрического тока учитывают, что 1 кВт·ч выделяет 864 ккал (3617 кДж).

Если у Вас остались вопросы – обращайтесь к нам, в авторизованный сервисный центр “Эл Ко-сервис” Мы всегда рады помочь Вам в решении возникших у Вас проблем.

Инженерно-технический отдел авторизованного сервисного центра “Эл Ко-сервис”

Ток, напряжение, сопротивление. Закон Ома.

Мы начинаем публикацию материалов новой рубрики «Основы электроники«, и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление 🙂 Кроме того, мы не обойдем стороной закон Ома, который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно.

Итак, давайте начнем с понятия напряжения.

Напряжение.

По определению напряжение — это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля — это скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду. Давайте рассмотрим небольшой пример:

В пространстве действует постоянное электрическое поле, напряженность которого равна E. Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:

U = \phi_1\medspace-\medspace \phi_2

В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:

\phi_1\medspace-\medspace \phi_2 = Ed

И в итоге получаем формулу, связывающую напряжение и напряженность:

U = Ed

В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками. Соответственно, становится понятно, что напряжение в цепи — это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, «напряжение в резисторе» — не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и «землей». Вот так плавно мы вышли к еще одному важнейшему понятию при изучении электроники, а именно к понятию «земля» 🙂 Так вот «землей» в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).

Давайте еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения. Единицей измерения является Вольт (В). Глядя на определение понятия напряжения мы можем легко понять, что для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт, необходимо совершить работу, равную 1 Джоулю. С этим вроде бы все понятно и можно двигаться дальше 🙂

А на очереди у нас еще одно понятие, а именно ток.

Ток, сила тока в цепи.

Что же такое электрический ток?

Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны… Рассмотрим проводник, к которому приложено определенное напряжение:

Из направления напряженности электрического поля (E) мы можем сделать вывод о том, что \phi_1 > \phi_2 (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:

F = Ee

где e − это заряд электрона.

И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток 🙂

Ток — это упорядоченное движение заряженных частиц под воздействием электрического поля.

Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.

Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E. И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы 🙂

Для того, чтобы оценить ток в цепи придумали такую величину как сила тока. Итак, сила тока (I) — это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер. Сила тока в проводнике равна 1 Амперу, если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон.

Мы уже рассмотрели понятия силы тока и напряжения, теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника.

Сопротивление проводника/цепи.

Термин «сопротивление» уже говорит сам за себя 🙂

Итак, сопротивление — физическая величина, характеризующая свойства проводника препятствовать (сопротивляться) прохождению электрического тока.

Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S:

Сопротивление проводника зависит от нескольких факторов:

удельного сопротивления проводника \rho
длины проводника l
площади поперечного сечения проводника S

Удельное сопротивление — это табличная величина. Формула, с помощью которой можно вычислить сопротивление проводника выглядит следующим образом:

R = \rho\medspace \frac{l}{S}

Для нашего случая \rho будет равно 0,0175 (Ом * кв. мм / м) — удельное сопротивление меди. Пусть длина проводника составляет 0.5 м, а площадь поперечного сечения равна 0.2 кв. мм. Тогда:

R =0,0175 \cdot \frac{0.5}{0.2} = 0.04375\medspace Ом

Как вы уже поняли из примера, единицей измерения сопротивления является Ом 🙂

С сопротивлением проводника все ясно, настало время изучить взаимосвязь напряжения, силы тока и сопротивления цепи.

Закон Ома.

И тут на помощь нам приходит основополагающий закон всей электроники — закон Ома:

Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.

Рассмотрим простейшую электрическую цепь:Как следует из закона Ома напряжение и сила тока в цепи связаны следующим образом:

I = \frac{U}{R}

Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:

I = \frac{10}{200} = 0.05 = 50\medspaceмА

Как видите, все несложно 🙂 Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч!

Закон Ома – физика процесса на примере движения воды.

Формулы зависимости сопротивления, напряжения, силы тока и мощности

Существует всего 2 базовых формулы которые помогут вам понять взаимосвязь между силой тока(Амер), напряжением(Вольт), сопротивлением (Ом) и мощностью (Ватт).
Зная хотя бы два из перечисленных параметра вы всегда можете рассчитать два других.

ЗАКОН ОМА

Базовая формула	P=I*E	E=I*R
Расчет напряжения	E=P/I	E=I*R	E=SQR(P*R)
Расчет силы тока	I=P/E	I=E/R	I=SQR(P/R)
Расчет мощности	P=I*E	P=E ² /R	P=I ² *R
Расчет сопротивления	R=E ² /P	R=E/I	R=P/I ²

P – Мощность (Ватт)
E – Напряжение (Вольт)
I – Сила тока (Ампер)
R – Электрическое сопротивление (Ом)
SQR – квадратный корень

Для справки:

Мы используем переменную E для обозначения напряжения, иногда вы можете встретить обозначение V для напряжения. Не дайте себя запутать названиям переменных.

Изменение сопротивления:

На следующей схеме вы видите разность сопротивлений между системами изображенными на правой и левой стороне рисунка. Сопротивление давлению воды в кране противодействует задвижка, в зависимости от степени открытия задвижки изменяется сопротивление.

Сопротивление в проводнике изображено в виде сужения проводника, чем более узкий проводник тем больше он противодействует прохождению тока.

Вы можете заметить что на правой и на левой стороне схемы напряжение и давление воды одинаково.

Вам необходимо обратить внимание на самый важный факт.

В зависимости от сопротивления увеличивается и уменьшается сила тока.

Слева при полностью открытой задвижке мы видим самый большой поток воды. И при самом низком сопротивлении, видим самый большой поток электронов (Ампераж) в проводнике.

Справа задвижка закрыта намного больше и поток воды тоже стал намного больше.

ужение проводника тоже уменьшилось вдвое, я значит вдвое увеличилось сопротивление протеканию тока. Как мы видим через проводник из за выского сопротивления протекает в два раза меньше электронов.

Для справки

Обратите внимание что сужение проводника изображенное на схеме используется только для примера сопротивления протеканию тока. В реальных условиях сужения проводника не сильно влияет на протекающий ток. Значительно большее сопротивление могут оказывать полупроводники и диэлектрики.

Сужающийся проводник на схеме изображен лишь для примера, для понимания сути происходящего процесса.

Формула закона Ома – зависимость сопротивления и силы тока

I = E/R

Как вы видите из формулы, сила тока обратнапропорциональна сопротивлению цепи.

Больше сопротивление = Меньше ток

* при условии что напряжение постоянно.

Изменение напряжения.

На изображенной схеме во всех системах сопротивление имеет одинаковую величину.
В этот раз на картинке изменяется сопротивление/давление.

Вы можете увидеть что при увеличении напряжения приводит к увеличению протекающего тока даже при постоянном сопротивлении.

Формула закона Ома – зависимость напряжения и силы тока

I = E/R

Обратите внимание что сила тока протекающего в проводнике прямопропорциональна напряжению.

Больше напряжение = Больше сила тока

* при условии что сопротивление постоянно.

Математический рассчет

Рассмотрим пример.
У нас есть аккумуляторная батарея с напряжением питания 12 Вольт. К ней напрямую подключен резистор (сопротивление) 10 Ом. Для того что бы рассчитать какая мощность приложена к нашему резистору, можно воспользоваться формулой.

P = E2/R
P = 122/10
P = 144/10.
P = 14.4 watts

Мощность рассеиваемая на резисторе состовляет 14,4 Ватта.

Если вы хотите определить величину тока протекающего через проводник, мы используем другую формулу

I = E/R
I = 12/10
I = 1.2 amps

Сила тока протекающего через цепь составляет 1,2 Ампера
—————-
Калькуляторы зависимости напряжения, силы тока и сопротивления.

1. Калькулятор рассеиваемой мощности и протекающей силы тока в зависимости от сопротивления и приложенного напряжения.

Демо закона Ома в реальном времени.

Для справки
В данном примере вы можете увеличивать напряжение и сопротивление цепи. Данные изменения в реальном времени будут изменять силу тока протекающего в цепи и мощность рассеиваемую на сопротивлении.

Если рассматривать аудио системы – вы должны помнить что усилитель выдает определенное напряжение на определенную нагрузку (сопротивление). Соотношение двух этих величин определяет мощность.
Усилитель может выдать ограниченную величину напряжения в зависимости от внутреннего блока питания и источника тока. Так же точно ограничена и мощность которую может подать усилитель на определенную нагрузку (к примеру 4 Ома).
Для того что бы получить больше мощности, вы можете подключить к усилителю нагрузку с меньшим сопротивлением (к примеру 2 Ома). Учтите что при использовании нагрузки с меньшим сопротивлением – скажем в два раза (было 4 Ома, стало 2 Ома) – мощность тоже возрастет в два раза.(при условии что данную мощность может обеспечить внутренний блок питания и источник тока).
Если мы возьмем для примера моно усилитель мощностью 100 Ватт на нагрузку 4 Ома, зная что он может выдать напряжение не более 20 Вольт на нагрузку.
Если вы поставите на нашем калькуляторе бегунки
Напряжение 20 Вольт
Сопротивление 4 Ома
Вы получите
Мощность 100 Ватт

Если вы сдвинете бегунок сопротивления на величину 2 Ома, вы увидите как мощность удвоится и составит 200 Ватт.

В общем примере источником тока является аккумуляторная батарея (а не усилитель звука) но зависимости силы тока, напряжения, сопротивления и сопротивления одинаковы во всех цепях.

Закона Ома для участка цепи

В природе существует два основных вида материалов, проводящие ток и непроводящие (диэлектрики). Отличаются эти материалы наличием условий для перемещения в них электрического тока (электронов).

Из токопроводящих материалов (медь, алюминий, графит, и многие другие), делают электрические проводники, в них электроны не связаны и могут свободно перемещаться.

В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может. Из них делают изоляцию для проводов, детали электроприборов.

Для того чтобы электроны начали перемещаться в проводнике (по участку цепи пошел ток), им нужно создать условия. Для этого в начале участка цепи должен быть избыток электронов, а в конце – недостаток. Для создания таких условий используют источники напряжения – аккумуляторы, батарейки, электростанции.

Формула Закона Ома

В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.

Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.

Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.

где: I – сила тока, измеряется в амперах и обозначается буквой А;; U – напряжение, измеряется в вольтах и обозначается буквой В;; R – сопротивление, измеряется в омах и обозначается Oм.

Если известны напряжение питания U и сопротивление электроприбора R, то с помощью вышеприведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I.

С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.

Применение закона Ома на практике

На практике часто приходится определять не силу тока I, а величину сопротивления R. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.

Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.

Формула Закона Джоуля-Ленца

Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.

Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.

где: P – мощность, измеряется в ваттах и обозначается Вт;; U – напряжение, измеряется в вольтах и обозначается буквой В;; I – сила ток, измеряется в амперах и обозначается буквой А.

Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.

Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.

Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.

Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.

Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.

Преобразованные формулы Закона Ома и Джоуля-Ленца

Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения

По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.

А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.

Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.

формула, как найти, куда направлена

Сила натяжения нити — формулировка

Определение

Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.

Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:

создание строительного отвеса;
установка растяжек для фиксации радиоантенн;
поведение арматуры внутри напряженного бетона;
устройство корабельного такелажа.

Как определить силу, формулы

Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.

С неподвижно закрепленным верхним концом

Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:

\(F=F_{тяж}=m*g\)

где m – это масса тела, а g представляет собой ускорение свободного падения.

Если нить под углом

В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.

\(F_n=m*g*cos(a)\)

где а равен углу отклонения.

Формула с учетом ускорения и массы

В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:

\(F=F_{тяж}+m*a\)

Сила натяжения во вращающейся системе

Описание

Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели.{2}}\)

Примеры решения задач

Задание 1

На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.

Решение

Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.

Источник: webmath.ru

\(\bar{T}+m\bar{g}=m\bar{a}\)

\(\bar{T}\) является силой натяжения нити.

Проекция уравнения будет иметь следующий вид:

\(T – mg = ma\)

Данное выражение позволяет рассчитать ускорение:

\(a=\frac{T-mg}{m}\)

Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления

\(a=\frac{4400-4*9,8}{400}\)

Ответ: a = 1.2\)

Задание 2

На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.

Решение

Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:

\(\bar{T}+m\bar{g}=m\bar{a}\)

Источник: webmath.ru

Проекции данной формулы по осям определяются следующим образом:

X: \(T sin α = ma = mω2R\)

Y: \(-mg + T cos α = 0\)

Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:

\(T=\frac{mg}{\cos \alpha }\)

Анализ рисунка позволяет вывести следующее уравнение:

\(\sin \alpha = \frac{R}{l}\rightarrow \cos \alpha = \sqrt{1-\left(\frac{R}{l} \right)^{2}}\)

Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:

\(T=\frac{mg}{\sqrt{1-\left(\frac{R}{l} \right)^{2}}}= \frac{mgl}{\sqrt{l^{2}-R^{2}}}\)

Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:

\(T=\frac{0,1*9,8*5}{\sqrt{5^{2}-3^{2}}}=1,225\left(H \right)\)

Ответ: Т=1,225 H

Мощность переменного тока. Мощность тока через катушку, резистор, конденсатор

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Напряжение (механика) – Простая английская Википедия, бесплатная энциклопедия

Рис. 1.1 Напряжение в нагруженном деформируемом материальном теле, принимаемое как континуум. Рисунок 1.2 Осевое напряжение в призматическом стержне, нагруженном в осевом направлении. Рисунок 1.3 Нормальное напряжение в призматическом (прямолинейном элементе с однородной площадью поперечного сечения) стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Однако можно использовать среднее нормальное напряжение σavg {\ displaystyle \ sigma _ {\ mathrm {avg}} \, \!}.Рисунок 1.4 Напряжение сдвига в призматическом стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Тем не менее, среднее напряжение сдвига τavg {\ displaystyle \ tau _ {\ mathrm {avg}} \, \!} Является разумным приближением. ^[1]

Напряжение – это сила, приходящаяся на единицу площади тела, которая вызывает изменение формы. ^[2]

Напряжение – это мера внутренних сил в теле между его частицами. ^[2] Эти внутренние силы являются реакцией на внешние силы, приложенные к телу, которые заставляют его разделяться, сжиматься или скользить.^[2] Внешние силы – это поверхностные или объемные силы. Напряжение – это средняя сила на единицу площади, которую частица тела оказывает на соседнюю частицу через воображаемую поверхность, которая их разделяет.

Формула одноосного нормального напряжения:

σ = FA {\ displaystyle {\ sigma} = {\ frac {F} {A}}}

где σ – напряжение, F – сила, а A – площадь поверхности.

В единицах СИ сила измеряется в ньютонах, а площадь – в квадратных метрах.Это означает, что напряжение составляет ньютоны на квадратный метр или Н / м ². Однако у стресса есть своя собственная единица СИ, называемая паскаль. 1 паскаль (символ Па) равен 1 Н / м ². В британских единицах измерения напряжение измеряется в фунтах силы на квадратный дюйм, что часто сокращается до «фунт / кв. Дюйм». Размер напряжения такой же, как и у давления.

В механике сплошных сред нагруженное деформируемое тело ведет себя как сплошная среда. Таким образом, эти внутренние силы непрерывно распределяются в объеме материального тела.(Это означает, что распределение напряжений в теле выражается как кусочно-непрерывная функция пространства и времени.) Силы вызывают деформацию формы тела. Деформация может привести к необратимому изменению формы или разрушению конструкции, если материал недостаточно прочен.

Некоторые модели механики сплошных сред рассматривают силу как нечто, что может изменяться. Другие модели рассматривают деформацию материи и твердых тел, потому что характеристики материи и твердых тел трехмерны.Каждый подход может дать разные результаты. Классические модели механики сплошных сред предполагают среднюю силу и не включают должным образом «геометрические факторы». (Геометрия тела может иметь значение для распределения стресса и накопления энергии во время приложения внешней силы.)

В некоторых ситуациях напряжение внутри объекта можно описать одним числом или одним вектором (числом и направлением). Тремя такими ситуациями простого напряжения являются одноосное нормальное напряжение , простое напряжение сдвига и изотропное нормальное напряжение .^[3]

Одноосное нормальное напряжение [изменение | изменить источник]

Напряжение растяжения (или растяжение) – это напряженное состояние, приводящее к расширению; то есть длина материала имеет тенденцию к увеличению в направлении растяжения. Объем материала остается постоянным. Когда к телу прилагаются равные и противоположные силы, то напряжение, создаваемое этой силой, называется растягивающим напряжением.

Следовательно, в одноосном материале длина увеличивается в направлении растягивающего напряжения, а в двух других направлениях уменьшается размер.При одноосном растяжении растягивающее напряжение вызывается растягивающими силами. Напряжение растяжения противоположно напряжению сжатия.

Конструктивными элементами, находящимися на прямом растяжении, являются канаты, грунтовые анкеры и гвозди, болты и т. Д. Балки, подверженные действию изгибающих моментов, могут включать в себя растягивающее напряжение, а также напряжение сжатия и / или напряжение сдвига.

Растягивающее напряжение может увеличиваться до достижения предела прочности на разрыв , а именно предельного состояния напряжения.

Все реальные объекты занимают трехмерное пространство.Однако, если два измерения очень большие или очень маленькие по сравнению с другими, объект может быть смоделирован как одномерный. Это упрощает математическое моделирование объекта. Одномерные объекты включают кусок проволоки, загруженный на концах и просматриваемый сбоку, и металлический лист, загруженный на лицевую сторону и просматриваемый вблизи и через поперечное сечение.

↑ Уолтер Д. Пилки, Оррин Х. Пилки (1974). Механика твердого тела . п. 292.
↑ ^2.0 ^2,1 ^2,2 Дейнтит, Джон, изд. (2005). Физический словарь (Пятое изд.). Издательство Оксфордского университета. п. 509. ISBN 978-0-19-280628-4 .
↑ Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжений в инженерном проектировании». 3-е издание, CRC Press, 634 страницы. ISBN 9781574447132

Амин, Мохаммед (2005). Вычислительная упругость: теория упругости, методы конечных и граничных элементов .Alpha Science Int’l Ltd. стр. 33–66. ISBN 184265201X . CS1 maint: ref = harv (ссылка)
Atanackovic, Teodor M .; Гуран, Ардешир (2000). Теория упругости для ученых и инженеров . Springer. С. 1–46. ISBN 081764072X . CS1 maint: ref = harv (ссылка)
Чедвик, Питер (1999). Механика сплошной среды: краткая теория и проблемы . Дуврские книги по физике (2-е изд.). Dover Publications. С. 90–106. ISBN 0486401804 . CS1 maint: ref = harv (ссылка)
Чакрабарти, Дж. (2006). Теория пластичности (3-е изд.). Баттерворт-Хайнеманн. С. 17–32. ISBN 0750666382 . CS1 maint: ref = harv (ссылка)
Чаттерджи, Рабиндранат (1999). Математическая теория механики сплошной среды . Alpha Science Int’l Ltd. стр. 111–157. ISBN 8173192448 . CS1 maint: ref = harv (ссылка)
Чен, Вай-Фах; Хан, Да-Цзянь (2007). Пластичность для инженеров-строителей .Издательство Дж. Росс. С. 46–71. ISBN 1932159754 . CS1 maint: ref = harv (ссылка)
Fung, Yuan-cheng; Тонг, Пин (2001). Классическая и вычислительная механика твердого тела . Том 1 серии Advanced по техническим наукам. World Scientific. С. 66–96. ISBN 9810241240 . CS1 maint: ref = harv (ссылка)
Хэмрок, Бернард (2005). Основы элементов машин . Макгроу-Хилл. С. 58–59. ISBN 0072976829 . CS1 maint: ref = harv (ссылка)
Хьельмстад, Кейт Д. (2005). Основы строительной механики . Международная серия Prentice-Hall по гражданскому строительству и инженерной механике (2-е изд.). Springer. С. 103–130. ISBN 038723330X . CS1 maint: ref = harv (ссылка)
Иргенс, Фритьов (2008). Механика сплошной среды . Springer. С. 42–81. ISBN 3540742972 . CS1 maint: ref = harv (ссылка)
Джегер, Джон Конрад; Кук, Н.Г.У. и Циммерман Р.В. (2007). Основы механики горных пород (Четвертое изд.). Вили-Блэквелл. С. 9–41. ISBN 0632057599 . CS1 maint: несколько имен: список авторов (ссылка) CS1 maint: ref = harv (ссылка)
Люблинер, Якоб (2008). Теория пластичности (переработанное издание) (PDF). Dover Publications. ISBN 0486462900 . Архивировано из оригинального (PDF) 31 марта 2010 года. Проверено 24 июля 2011. CS1 maint: ref = harv (ссылка)
Мейс, Джордж Э.(1970). Механика сплошной среды . Макгроу-Хилл. С. 44–76. ISBN 0070406634 . CS1 maint: ref = harv (ссылка)
Mase, G. Thomas; Джордж Э. Мейс (1999). Механика сплошной среды для инженеров (Второе изд.). CRC Press. С. 47–102. ISBN 0-8493-1855-6 . CS1 maint: ref = harv (ссылка)
Прагер, Уильям (2004). Введение в механику сплошных сред . Dover Publications. С. 43–61. ISBN 0486438090 . CS1 maint: ref = harv (ссылка)
Смит, Дональд Рэй; Трусделл, Клиффорд (1993). Введение в механику сплошных сред – после Трусделла и Нолла . Springer. ISBN 0792324544 . CS1 maint: ref = harv (ссылка)
Ву, Хан-Чин (2005). Механика сплошной среды и пластичность . CRC Press. С. 45–78. ISBN 1584883634 . CS1 maint: ref = harv (ссылка)

Stress (механика) – Простая английская Википедия, бесплатная энциклопедия

Рисунок 1.1 Напряжение в нагруженном деформируемом материальном теле, принимаемое как сплошная среда. Рисунок 1.2 Осевое напряжение в призматическом стержне, нагруженном в осевом направлении. Рисунок 1.3 Нормальное напряжение в призматическом (прямолинейном элементе с однородной площадью поперечного сечения) стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Однако можно использовать среднее нормальное напряжение σavg {\ displaystyle \ sigma _ {\ mathrm {avg}} \, \!}. Рисунок 1.4 Напряжение сдвига в призматическом стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным.Тем не менее, среднее напряжение сдвига τavg {\ displaystyle \ tau _ {\ mathrm {avg}} \, \!} Является разумным приближением. ^[1]

Напряжение – это сила, приходящаяся на единицу площади тела, которая вызывает изменение формы. ^[2]

Напряжение – это мера внутренних сил в теле между его частицами. ^[2] Эти внутренние силы являются реакцией на внешние силы, приложенные к телу, которые заставляют его разделяться, сжиматься или скользить. ^[2] Внешние силы – это поверхностные или объемные силы.Напряжение – это средняя сила на единицу площади, которую частица тела оказывает на соседнюю частицу через воображаемую поверхность, которая их разделяет.

Формула одноосного нормального напряжения:

σ = FA {\ displaystyle {\ sigma} = {\ frac {F} {A}}}

где σ – напряжение, F – сила, а A – площадь поверхности.

В единицах СИ сила измеряется в ньютонах, а площадь – в квадратных метрах. Это означает, что напряжение составляет ньютоны на квадратный метр или Н / м ².Однако у стресса есть своя собственная единица СИ, называемая паскаль. 1 паскаль (символ Па) равен 1 Н / м ². В британских единицах измерения напряжение измеряется в фунтах силы на квадратный дюйм, что часто сокращается до «фунт / кв. Дюйм». Размер напряжения такой же, как и у давления.

В механике сплошных сред нагруженное деформируемое тело ведет себя как сплошная среда. Таким образом, эти внутренние силы непрерывно распределяются в объеме материального тела. (Это означает, что распределение напряжений в теле выражается как кусочно-непрерывная функция пространства и времени.) Силы вызывают деформацию формы тела. Деформация может привести к необратимому изменению формы или разрушению конструкции, если материал недостаточно прочен.

Некоторые модели механики сплошных сред рассматривают силу как нечто, что может изменяться. Другие модели рассматривают деформацию материи и твердых тел, потому что характеристики материи и твердых тел трехмерны. Каждый подход может дать разные результаты. Классические модели механики сплошных сред предполагают среднюю силу и не включают должным образом «геометрические факторы».(Геометрия тела может иметь значение для распределения стресса и накопления энергии во время приложения внешней силы.)

Одноосное нормальное напряжение [изменение | изменить источник]

Напряжение растяжения (или растяжение) – это напряженное состояние, приводящее к расширению; то есть длина материала имеет тенденцию к увеличению в направлении растяжения.Объем материала остается постоянным. Когда к телу прилагаются равные и противоположные силы, то напряжение, создаваемое этой силой, называется растягивающим напряжением.

Следовательно, в одноосном материале длина увеличивается в направлении растягивающего напряжения, а в двух других направлениях уменьшается размер. При одноосном растяжении растягивающее напряжение вызывается растягивающими силами. Напряжение растяжения противоположно напряжению сжатия.

Конструктивные элементы, находящиеся на прямом растяжении: канаты, грунтовые анкеры и гвозди, болты и т. Д.Балки, подверженные изгибающим моментам, могут включать в себя напряжение растяжения, а также напряжение сжатия и / или напряжение сдвига.

Все реальные объекты занимают трехмерное пространство. Однако, если два измерения очень большие или очень маленькие по сравнению с другими, объект может быть смоделирован как одномерный. Это упрощает математическое моделирование объекта. Одномерные объекты включают кусок проволоки, загруженный на концах и просматриваемый сбоку, и металлический лист, загруженный на лицевую сторону и просматриваемый вблизи и через поперечное сечение.

↑ Уолтер Д. Пилки, Оррин Х. Пилки (1974). Механика твердого тела . п. 292.
↑ ^2,0 ^2,1 ^2,2 Дейнтит, Джон, изд. (2005). Физический словарь (Пятое изд.). Издательство Оксфордского университета. п. 509. ISBN 978-0-19-280628-4 .
↑ Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжений в инженерном проектировании». 3-е издание, CRC Press, 634 страницы.ISBN 9781574447132

Амин, Мохаммед (2005). Вычислительная упругость: теория упругости, методы конечных и граничных элементов . Alpha Science Int’l Ltd. стр. 33–66. ISBN 184265201X . CS1 maint: ref = harv (ссылка)
Atanackovic, Teodor M .; Гуран, Ардешир (2000). Теория упругости для ученых и инженеров . Springer. С. 1–46. ISBN 081764072X . CS1 maint: ref = harv (ссылка)
Чедвик, Питер (1999). Механика сплошной среды: краткая теория и проблемы . Дуврские книги по физике (2-е изд.). Dover Publications. С. 90–106. ISBN 0486401804 . CS1 maint: ref = harv (ссылка)
Чакрабарти, Дж. (2006). Теория пластичности (3-е изд.). Баттерворт-Хайнеманн. С. 17–32. ISBN 0750666382 . CS1 maint: ref = harv (ссылка)
Чаттерджи, Рабиндранат (1999). Математическая теория механики сплошной среды . Alpha Science Int’l Ltd.С. 111–157. ISBN 8173192448 . CS1 maint: ref = harv (ссылка)
Чен, Вай-Фах; Хан, Да-Цзянь (2007). Пластичность для инженеров-строителей . Издательство Дж. Росс. С. 46–71. ISBN 1932159754 . CS1 maint: ref = harv (ссылка)
Fung, Yuan-cheng; Тонг, Пин (2001). Классическая и вычислительная механика твердого тела . Том 1 серии Advanced по техническим наукам. World Scientific. С. 66–96. ISBN 9810241240 . CS1 maint: ref = harv (ссылка)
Хэмрок, Бернард (2005). Основы элементов машин . Макгроу-Хилл. С. 58–59. ISBN 0072976829 . CS1 maint: ref = harv (ссылка)
Хьельмстад, Кейт Д. (2005). Основы строительной механики . Международная серия Prentice-Hall по гражданскому строительству и инженерной механике (2-е изд.). Springer. С. 103–130. ISBN 038723330X . CS1 maint: ref = harv (ссылка)
Иргенс, Фритьов (2008). Механика сплошной среды . Springer. С. 42–81. ISBN 3540742972 . CS1 maint: ref = harv (ссылка)
Джегер, Джон Конрад; Кук, Н. Г. У. и Циммерман, Р. В. (2007). Основы механики горных пород (Четвертое изд.). Вили-Блэквелл. С. 9–41. ISBN 0632057599 . CS1 maint: несколько имен: список авторов (ссылка) CS1 maint: ref = harv (ссылка)
Люблинер, Якоб (2008). Теория пластичности (переработанное издание) (PDF).Dover Publications. ISBN 0486462900 . Архивировано из оригинального (PDF) 31 марта 2010 года. Проверено 24 июля 2011. CS1 maint: ref = harv (ссылка)
Мейс, Джордж Э. (1970). Механика сплошной среды . Макгроу-Хилл. С. 44–76. ISBN 0070406634 . CS1 maint: ref = harv (ссылка)
Mase, G. Thomas; Джордж Э. Мейс (1999). Механика сплошной среды для инженеров (Второе изд.). CRC Press. С. 47–102. ISBN 0-8493-1855-6 . CS1 maint: ref = harv (ссылка)
Прагер, Уильям (2004). Введение в механику сплошных сред . Dover Publications. С. 43–61. ISBN 0486438090 . CS1 maint: ref = harv (ссылка)
Смит, Дональд Рэй; Трусделл, Клиффорд (1993). Введение в механику сплошных сред – после Трусделла и Нолла . Springer. ISBN 0792324544 . CS1 maint: ref = harv (ссылка)
Ву, Хан-Чин (2005). Механика сплошной среды и пластичность .CRC Press. С. 45–78. ISBN 1584883634 . CS1 maint: ref = harv (ссылка)

Напряжение (механика) – Простая английская Википедия, бесплатная энциклопедия

Рис. 1.1 Напряжение в нагруженном деформируемом материальном теле, принимаемое как континуум. Рисунок 1.2 Осевое напряжение в призматическом стержне, нагруженном в осевом направлении. Рисунок 1.3 Нормальное напряжение в призматическом (прямолинейном элементе с однородной площадью поперечного сечения) стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным.Однако можно использовать среднее нормальное напряжение σavg {\ displaystyle \ sigma _ {\ mathrm {avg}} \, \!}. Рисунок 1.4 Напряжение сдвига в призматическом стержне. Распределение напряжения или силы в поперечном сечении стержня не обязательно является равномерным. Тем не менее, среднее напряжение сдвига τavg {\ displaystyle \ tau _ {\ mathrm {avg}} \, \!} Является разумным приближением. ^[1]

Напряжение – это сила, приходящаяся на единицу площади тела, которая вызывает изменение формы. ^[2]

Напряжение – это мера внутренних сил в теле между его частицами.^[2] Эти внутренние силы являются реакцией на внешние силы, приложенные к телу, которые заставляют его разделяться, сжиматься или скользить. ^[2] Внешние силы – это поверхностные или объемные силы. Напряжение – это средняя сила на единицу площади, которую частица тела оказывает на соседнюю частицу через воображаемую поверхность, которая их разделяет.

Формула одноосного нормального напряжения:

σ = FA {\ displaystyle {\ sigma} = {\ frac {F} {A}}}

где σ – напряжение, F – сила, а A – площадь поверхности.

В единицах СИ сила измеряется в ньютонах, а площадь – в квадратных метрах. Это означает, что напряжение составляет ньютоны на квадратный метр или Н / м ². Однако у стресса есть своя собственная единица СИ, называемая паскаль. 1 паскаль (символ Па) равен 1 Н / м ². В британских единицах измерения напряжение измеряется в фунтах силы на квадратный дюйм, что часто сокращается до «фунт / кв. Дюйм». Размер напряжения такой же, как и у давления.

В механике сплошных сред нагруженное деформируемое тело ведет себя как сплошная среда.Таким образом, эти внутренние силы непрерывно распределяются в объеме материального тела. (Это означает, что распределение напряжений в теле выражается как кусочно-непрерывная функция пространства и времени.) Силы вызывают деформацию формы тела. Деформация может привести к необратимому изменению формы или разрушению конструкции, если материал недостаточно прочен.

Одноосное нормальное напряжение [изменение | изменить источник]

↑ Уолтер Д. Пилки, Оррин Х. Пилки (1974). Механика твердого тела . п. 292.
↑ ^2.0 ^2,1 ^2,2 Дейнтит, Джон, изд. (2005). Физический словарь (Пятое изд.). Издательство Оксфордского университета. п. 509. ISBN 978-0-19-280628-4 .
↑ Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжений в инженерном проектировании». 3-е издание, CRC Press, 634 страницы. ISBN 9781574447132

Амин, Мохаммед (2005). Вычислительная упругость: теория упругости, методы конечных и граничных элементов .Alpha Science Int’l Ltd. стр. 33–66. ISBN 184265201X . CS1 maint: ref = harv (ссылка)
Atanackovic, Teodor M .; Гуран, Ардешир (2000). Теория упругости для ученых и инженеров . Springer. С. 1–46. ISBN 081764072X . CS1 maint: ref = harv (ссылка)
Чедвик, Питер (1999). Механика сплошной среды: краткая теория и проблемы . Дуврские книги по физике (2-е изд.). Dover Publications. С. 90–106. ISBN 0486401804 . CS1 maint: ref = harv (ссылка)
Чакрабарти, Дж. (2006). Теория пластичности (3-е изд.). Баттерворт-Хайнеманн. С. 17–32. ISBN 0750666382 . CS1 maint: ref = harv (ссылка)
Чаттерджи, Рабиндранат (1999). Математическая теория механики сплошной среды . Alpha Science Int’l Ltd. стр. 111–157. ISBN 8173192448 . CS1 maint: ref = harv (ссылка)
Чен, Вай-Фах; Хан, Да-Цзянь (2007). Пластичность для инженеров-строителей .Издательство Дж. Росс. С. 46–71. ISBN 1932159754 . CS1 maint: ref = harv (ссылка)
Fung, Yuan-cheng; Тонг, Пин (2001). Классическая и вычислительная механика твердого тела . Том 1 серии Advanced по техническим наукам. World Scientific. С. 66–96. ISBN 9810241240 . CS1 maint: ref = harv (ссылка)
Хэмрок, Бернард (2005). Основы элементов машин . Макгроу-Хилл. С. 58–59. ISBN 0072976829 . CS1 maint: ref = harv (ссылка)
Хьельмстад, Кейт Д. (2005). Основы строительной механики . Международная серия Prentice-Hall по гражданскому строительству и инженерной механике (2-е изд.). Springer. С. 103–130. ISBN 038723330X . CS1 maint: ref = harv (ссылка)
Иргенс, Фритьов (2008). Механика сплошной среды . Springer. С. 42–81. ISBN 3540742972 . CS1 maint: ref = harv (ссылка)
Джегер, Джон Конрад; Кук, Н.Г.У. и Циммерман Р.В. (2007). Основы механики горных пород (Четвертое изд.). Вили-Блэквелл. С. 9–41. ISBN 0632057599 . CS1 maint: несколько имен: список авторов (ссылка) CS1 maint: ref = harv (ссылка)
Люблинер, Якоб (2008). Теория пластичности (переработанное издание) (PDF). Dover Publications. ISBN 0486462900 . Архивировано из оригинального (PDF) 31 марта 2010 года. Проверено 24 июля 2011. CS1 maint: ref = harv (ссылка)
Мейс, Джордж Э.(1970). Механика сплошной среды . Макгроу-Хилл. С. 44–76. ISBN 0070406634 . CS1 maint: ref = harv (ссылка)
Mase, G. Thomas; Джордж Э. Мейс (1999). Механика сплошной среды для инженеров (Второе изд.). CRC Press. С. 47–102. ISBN 0-8493-1855-6 . CS1 maint: ref = harv (ссылка)
Прагер, Уильям (2004). Введение в механику сплошных сред . Dover Publications. С. 43–61. ISBN 0486438090 . CS1 maint: ref = harv (ссылка)
Смит, Дональд Рэй; Трусделл, Клиффорд (1993). Введение в механику сплошных сред – после Трусделла и Нолла . Springer. ISBN 0792324544 . CS1 maint: ref = harv (ссылка)
Ву, Хан-Чин (2005). Механика сплошной среды и пластичность . CRC Press. С. 45–78. ISBN 1584883634 . CS1 maint: ref = harv (ссылка)

Напряжение и деформация – растягивающее напряжение, деформация растяжения, энергия упругой деформации, разрывное напряжение, пластичность, хрупкость

Напряжение

Напряжение, приложенное к материалу, – это сила, приложенная к материалу на единицу площади.Максимальное напряжение, которое может выдержать материал до разрушения, называется разрывным напряжением или пределом прочности при растяжении.

Растяжение означает, что материал находится под напряжением. Действующие на него силы пытаются растянуть материал. Сжатие – это когда силы, действующие на объект, пытаются его раздавить.

Уравнение ниже используется для расчета напряжения.

напряжение = напряжение, измеренное в Нм ^-2 или паскалях (Па)
F = сила в ньютонах (Н)
A = площадь поперечного сечения в м ²

Штамм

Отношение удлинения к исходной длине называется деформацией. Он не имеет единиц измерения, так как представляет собой отношение двух длин, измеренных в метрах.

деформация = деформация не имеет единиц
DL = удлинение, измеренное в метрах
L = исходная длина, измеренная в метрах

График напряжение-деформация для пластичного материала (например, меди)

L = предел пропорциональности, до этого момента действует закон Гука.
E = предел упругости, за пределами этой точки материал постоянно растягивается и не возвращается к своей исходной длине. Упругое поведение – это когда материал возвращается к своей исходной длине, пластическое поведение – это когда растянутый материал не возвращается к своей исходной длине.
Y = предел текучести, за пределами этой точки небольшое увеличение силы приводит к значительному увеличению длины.
B = предел разрушения / разрывное напряжение, в этой точке материал разрушается.

График напряжение-деформация для хрупкого материала (например, стекла)

Энергия упругой деформации (энергия, запасенная в растянутой проволоке или пружине)

Энергия, запасенная в растягивающейся проволоке или пружине, – это площадь под графиком «сила-растяжение», как мы можем видеть в уравнении ниже.

E = энергия упругой деформации в джоулях (Дж)
F = сила в ньютонах (Н)
DL = изменение длины в метрах (м)

Резина растяжка

Когда резина растягивается и выделяется энергия, теряется в виде тепла, и это называется гистерезисом. Площадь между двумя линиями – это потеря энергии на единицу объема.

Механика материалов: напряжение »Механика тонких конструкций

Добро пожаловать в Механику материалов.Этот курс основан непосредственно на основах, которые мы изучили в статике, – вычислении статического равновесия различных конструкций при различных нагрузках. В статике мы рассматриваем внешних сил , действующих на твердых тел . В действительности все тела деформируемы , и эти внешние силы создают внутренних напряжений . Ну тогда что за стресс?

Напряжение – это мера внешней силы , действующей на площадь поперечного сечения объекта.Напряжение имеет единицы силы на площадь: Н / м ² (СИ) или фунт / дюйм ² (США). Единицы СИ обычно называют паскалями, сокращенно Па . Поскольку 1 Па является неудобно малым по сравнению с напряжениями, которые испытывает большинство конструкций, мы часто будем сталкиваться с 10 ³ Па = 1 кПа (килопаскаль), 10 ⁶ Па = МПа (мегапаскаль) или 10 ^9. Па = ГПа (гигапаскаль).

Есть два типа стресса, который может испытывать конструкция: 1. Нормальное напряжение и 2. Напряжение сдвига . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она вызывает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.

Рассмотрим светильник, подвешенный к потолку на веревке. Веревка имеет круглое поперечное сечение, а свет тянет вниз перпендикулярно веревке. Эта сила создает нормальное напряжение внутри каната.

Хорошо, как мы пришли к этому уравнению. За кадром существует множество предположений. На протяжении всего этого курса мы будем предполагать, что все материалы однородны, изотропны и эластичны. Мы также предположим, что объект является «призматическим» – это означает, что поперечные сечения одинаковы по всей его длине (например, огурец является призматическим, а тыквенный орех – нет). Все эти предположения позволяют утверждать, что объект будет деформировать равномерно в каждой точке своего поперечного сечения.Нормальное напряжение в точке поперечного сечения определяется как (с аналогичными уравнениями в направлениях x и y ). :

На каждый небольшой участок поперечного сечения действует одинаковая сила, и сумма всех этих сил должна равняться внутренней равнодействующей силе P . Если мы позволим ΔA перейти к dA, а ΔF перейти к dF, то мы сможем просто проинтегрировать обе части уравнения, и мы придем к нашему соотношению для нормального напряжения.

Это соотношение для нормального напряжения более точно соответствует среднему нормальному напряжению , поскольку мы усреднили внутренние силы по всему поперечному сечению.

Понятие стресса часто бывает трудно понять, потому что его нелегко заметить. Оказывается, размещение прозрачного объекта через кросс-поляризованный свет позволяет непосредственно наблюдать напряжение внутри материала на основе концепции, называемой фотоупругостью:

Напряжение действительно может существовать в материале при отсутствии приложенной нагрузки. Это называется остаточным напряжением, и его можно использовать как способ упрочнения материалов, например, при изготовлении японского меча катана.И наоборот, нежелательные остаточные напряжения могут стимулировать рост трещин и привести к разрушению, как, например, при обрушении Серебряного моста в Западной Вирджинии в 1967 году. Возможно, самый яркий пример остаточного напряжения связан с быстрым охлаждением расплавленного стекла, известным как « Капля принца Руперта »:

Давайте посмотрим на другой пример. Рассмотрим болт, соединяющий две прямоугольные пластины, и растягивающее усилие, перпендикулярное болту. Из диаграммы свободного тела мы видим, что приложенная извне сила оказывает силу, параллельную круглому поперечному сечению болта.Эта внешняя сила приводит к напряжению сдвига внутри болта.

Теперь формальные определения напряжения сдвига принимают форму, аналогичную описанным выше. Рассмотрим напряжение сдвига, действующее на z -грань элемента:

Напряжение сдвига – это касательное напряжение, действующее по касательной к поперечному сечению, и оно принимает среднее значение:

Важно отметить, что напряжения, которые мы только что описали, составляют средних напряжений .Мы предположили, что вся внешняя сила была равномерно распределена по площади поперечного сечения конструкции – это не всегда так, и мы будем пересматривать это предположение на протяжении всего курса.

Когда вы смотрите на элемент при сдвиге, все кажется немного сложнее. Рассмотрим небольшой кубический элемент внутри конструкции при сдвиге, как показано ниже.

Теперь равновесие требует, чтобы напряжение сдвига, действующее на τ _zy, сопровождалось напряжениями сдвига в других плоскостях.Но давайте рассмотрим равновесие сил в направлении y . Зная, что силу можно записать как напряжение (тау), умноженное на площадь (ΔxΔy), мы можем записать это силовое равновесие как:

Поскольку площади куба по определению одинаковы, это означает, что τ _zy = τ ‘_zy. Подобное равновесие сил в направлении z приводит к τ _yz = τ ‘_yz. Рассмотрим моментное равновесие относительно оси x . Зная, что мы можем записать силу, как и раньше, и плечо момента будет Δz, этот баланс моментов станет:

Это простое соотношение говорит нам, что τ _zy = τ _yz, и, следовательно, все четыре касательных напряжения имеют равные величины и должны указывать навстречу или от друг друга на противоположных краях элемента.Это соотношение известно как «чистый сдвиг».

1,2 Фактор безопасности

Инженеры используют стресс при проектировании конструкций. Внешняя нагрузка и геометрия конструкции говорят нам, какое напряжение действует в материале, но ничего не говорят нам о самом материале. У каждого материала есть предельное напряжение – мера того, какое напряжение может выдержать материал перед разрушением. Чтобы правильно спроектировать безопасную конструкцию, нам необходимо убедиться, что приложенное напряжение от внешней нагрузки никогда не превышает предельное напряжение материала. Отчасти сложность этой задачи заключается в том, что мы не всегда точно знаем, какова внешняя нагрузка – она может изменяться непредсказуемо, и конструкции, возможно, придется выдерживать неожиданно высокие нагрузки. Чтобы учесть эту неопределенность, мы включили в нашу конструкцию коэффициент безопасности . Коэффициент безопасности – это просто отношение разрушающей нагрузки или напряжения к допустимой нагрузке или напряжению. Разрушение или предельное значение – это свойство материала , в то время как допустимое значение определяется внешней силой и геометрией конструкции.

Сводка

В этой лекции мы представили понятие стресса. Напряжение – это мера того, что материал ощущает от приложенных извне сил. Это просто отношение внешних сил к площади поперечного сечения материала. Силы, приложенные перпендикулярно поперечному сечению, составляют нормальных напряжений , в то время как силы, приложенные параллельно поперечному сечению, составляют касательных напряжений .Хотя представленные здесь концепции не слишком чужды, большая часть трудностей с этим материалом связана с проблемой правильного расчета статического равновесия . Расчет статического равновесия скажет нам величину и направление приложенных сил, которые мы затем можем использовать для расчета напряжений. Если следующие примеры видео и домашнее задание вызывают у вас затруднения, сейчас самое время вернуться и просмотреть некоторые концепции из вашего курса статики.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта No.1454153. Любые мнения, выводы, заключения или рекомендации, выраженные в этом материале, принадлежат автору (авторам) и не обязательно отражают точку зрения Национального научного фонда.

Приложение «Напряжение и деформация – сопротивление материалов для энергетики»

напряжение-деформация

Цели обучения

После завершения этой главы вы сможете:

Определите нормальное напряжение и напряжение сдвига и деформацию и обсудите взаимосвязь между расчетным напряжением, пределом текучести и предельным напряжением
Расчетные элементы при нагрузках на растяжение, сжатие и сдвиг
Определение деформации элементов при растяжении и сжатии

Механическое напряжение

В этом разделе обсуждается влияние механических нагрузок (сил), действующих на элементы.В следующей главе будут рассмотрены эффекты тепловых нагрузок (тепловое расширение).

Нормальные, растягивающие и сжимающие напряжения

Растяжение или сжатие в элементе создают нормальные напряжения; они называются «нормальными», потому что поперечное сечение, которое выдерживает нагрузку, перпендикулярно (перпендикулярно) направлению приложенных сил. И растягивающие, и сжимающие напряжения рассчитываются по формуле:

Если элемент имеет переменное поперечное сечение, площадь, которая должна использоваться в расчетах, является минимальной площадью поперечного сечения; это даст вам максимальное напряжение в элементе, что в конечном итоге будет определять дизайн.

При сдвиге площадь поперечного сечения, выдерживающая нагрузку, параллельна направлению приложенных сил. В дополнение к этому, при оценке площади сдвига вы должны учитывать, сколько поперечных сечений вносит вклад в общую прочность сборки.

Например, если вы считаете, что штифт дверной петли подвергается действию сдвигающей нагрузки, вы должны подсчитать, сколько поперечных сечений выдерживает эту нагрузку.

Формула для расчета напряжения сдвига та же:

При штамповке область, которая сопротивляется сдвигу, имеет форму цилиндра для круглого отверстия (представьте себе формочку для печенья).Следовательно, площадь сдвига будет найдена путем умножения длины окружности формы на толщину пластины.

Обратите внимание:

Глядя на цифры из учебника, вы заметите, что указаны две силы. Это не означает, что сила, которую вы используете в формуле, равна (2 × Сила P), но просто указывает, что одна сила – это сила действия, а вторая – реакция.

Деформация и модуль упругости

Элемент при растяжении или сжатии будет упруго деформироваться пропорционально, помимо других параметров, исходной длине.Деформация, также называемая единичной деформацией, представляет собой безразмерный параметр, выражаемый как:

Если вы решили использовать отрицательное значение для деформации сжатия (уменьшение длины), вы также должны выразить эквивалентное напряжение сжатия как отрицательное значение.

Модуль упругости

Кривая напряжение-деформация построена в результате испытания на растяжение. В упругой области графика деформация прямо пропорциональна нагрузке. Разделив нагрузку на площадь поперечного сечения (константу) и деформацию на исходную длину (константа), можно получить графическое представление зависимости деформации от деформации.Стресс. Постоянное соотношение напряжения и деформации – это модуль Юнга или модуль упругости, свойство каждого материала.

Упругая деформация

Объединение двух приведенных выше соотношений для деформации и модуля упругости приводит к единой формуле для упругой деформации при растяжении или сжатии.

Это соотношение применимо к элементам с однородным поперечным сечением из однородного материала, подверженным растягивающим или сжимающим нагрузкам, которые приводят к напряжениям ниже пропорционального предела (прямая линия на кривой σ-ε).

Расчетное напряжение и факторы безопасности

Эти темы были рассмотрены в 1 ^{-м году} года «Сопротивление материалов» и представлены здесь в виде краткого обзора.

Стержни, подвергающиеся чрезмерному напряжению, могут выйти из строя в результате разрушения, когда фактическое рабочее напряжение превышает предельное напряжение, или из-за чрезмерной деформации, которая в таком случае приводит к неработоспособности. Рассмотрим тяжелую линию конденсата, которая прогибается сверх допустимого предела, и, хотя она не ломается, во фланцевых соединениях на концах линий будут возникать утечки из-за углового перемещения.

Расчетное напряжение σ _d – это максимальный уровень фактического / рабочего напряжения, который считается приемлемым с точки зрения безопасности. Расчетное напряжение определяется по:

Коэффициент безопасности выбирается проектировщиком на основе опыта, суждений И руководящих принципов / правил соответствующих норм и стандартов, на основе нескольких критериев, таких как риск травм, точность проектных данных, вероятность, отраслевые стандарты и, что не менее важно, стоимость. . Стандарты коэффициентов безопасности были установлены инженерами-строителями на основе точных оценок и многолетнего опыта.Стандарты постоянно развиваются, отражая новую и улучшенную философию дизайна. Пример:

Дизайнерские шкафы

При решении задач ученики могут столкнуться с разными сценариями. Хотя теоретические концепции одинаковы, пути к окончательным ответам могут быть разными в зависимости от каждого подхода.

Оценка безопасности конструкции / конструкции
1. Дано: величина и распределение нагрузок, свойства материала, форма и размеры элемента
2. Найти: фактическое напряжение и сравнить с расчетным напряжением; в качестве альтернативы найдите коэффициент безопасности и решите, является ли он приемлемым в соответствии с применимыми стандартами
Выбор подходящего материала
1. Дано: величина и распределение нагрузок, форма и размеры стержня
2. Найдите: какой тип или марка материала обеспечит прочность (предел текучести или предельную) большую, чем требуется, с учетом выбранного или заданного запаса прочности.
Определение формы и размеров поперечного сечения элемента
1. Дано: величина и распределение нагрузок, свойства материала
2. Найдите: форму и размеры элемента таким образом, чтобы фактическая площадь поперечного сечения была больше требуемого минимума.
Оценка максимально допустимой нагрузки на компонент
1. Дано: тип и распределение нагрузки, свойства материала, форма и размеры элемента
2. Найти: максимальная величина нагрузки, которая приводит к приемлемому напряжению

Стержни из двух разных материалов

Бывают случаи, когда стержень при нормальных напряжениях изготавливается из двух (или более) материалов. Одна из целей таких задач – найти напряжение в каждом компоненте.

Например, у вас может быть короткая колонна, сделанная из стальной трубы, заполненной бетоном, как на рисунке. Учитывая общую нагрузку, свойства материалов и геометрические размеры, мы должны найти индивидуальное напряжение в каждом компоненте.

И стальная труба, и бетонный стержень работают вместе, поддерживая нагрузку, поэтому мы должны найти дополнительные отношения, которые объединяют две проблемы в одну. Обычно ищем:

соотношение, которое описывает распределение силы между двумя материалами
соотношение, которое коррелирует деформации каждого материала

Для этой конкретной задачи мы можем сказать, что:

Уравнение 1: Общая нагрузка P = нагрузка на сталь P _сталь + нагрузка на бетон P _бетон

, следовательно, P = Напряжение _{, сталь} × Площадь _{, сталь} + Напряжение _{, бетон} × Площадь _{, бетон}

Уравнение 2: деформации обоих материалов одинаковы

поэтому Деформация _сталь = Деформация _бетон

Учитывая, что модуль упругости = напряжение / деформация, уравнение (2) дает соотношение между напряжением и упругостью обоих материалов

Подстановка этого последнего соотношения в уравнение (1) и решение для Напряжения _бетон приводит к следующему соотношению

Далее можно найти Stress _{, сталь}.

Обратите внимание, что в зависимости от проблемы исходные два отношения могут отличаться, поэтому каждый раз может потребоваться полный пошаговый вывод.

Разумные ответы

При решении обычных задач «напряжение – деформация», особенно в системе СИ, вы должны суметь оценить, являются ли ваши ответы разумными или нет.

Пример: Пруток из углеродистой стали A 36 длиной 1 м и диаметром 20 мм (свойства материалов в приложении B, таблица B2) выдерживает нагрузку 6 тонн.Оцените напряжение и деформацию штанги.

Обратите внимание, что обычно нагрузки выражаются в кН, площади поперечного сечения 10 ^-3 м ² и результирующие напряжения в МПа.

Кроме того, поскольку модули упругости выражены в ГПа, деформация (безразмерная) будет в диапазоне 10 ^-3. Этот стержень будет растягиваться на 0,9 мм при данной нагрузке.

Назначенные задачи

При решении этих вопросов необходимо использовать приложения учебника.Это ценные справочные материалы по свойствам материалов, геометрическим размерам и т. Д.

Задача 1: Конденсатопровод номинальным диаметром 152 мм, изготовленный из трубы из углеродистой стали сортамента 40, поддерживается подвесами для стержней с резьбой, расположенными на расстоянии 2,5 м от центра к центру. Подвески из углеродистой стали, длиной 50 см, диаметром основания 12 мм. Рассчитайте напряжение и деформацию в подвесках. Для материала подвесов используйте E = 200 ГПа.

Проблема 2: Зажимная скоба со штифтом 1/2 дюйма используется в подъемной машине для магазинов.Если штифт изготовлен из стали A36, определите максимальную безопасную нагрузку, используя коэффициент безопасности 2,5, основанный на пределе текучести.

Проблема 3: Котел поддерживается на нескольких коротких стойках, как показано на рисунке, изготовленных из серого чугуна класса 35. Каждая колонна выдерживает нагрузку 50 тонн. Требуемый коэффициент запаса прочности для этой конструкции равен 3. Безопасны ли колонны?

Используйте следующие размеры: A = 30 мм, B = 80 мм, C = 50 мм, D = 140 мм

Проблема 4: Натяжной элемент в ферме крыши подвергается нагрузке в 25 тысяч фунтов.Конструкция требует использования уголка L2x2x1 / 4 с поперечным сечением 0,944 дюйма ². Для строительных конструкций Американский институт стальных конструкций рекомендует использовать расчетное напряжение 0,60 × S _y. Используя таблицу B2 приложения B, укажите подходящий стальной материал.

Задача 5: Гидравлический цилиндр со стяжной тягой, показанный на рисунке, изготовлен из 6-дюймовой трубы из нержавеющей стали Schedule 40 и длиной 15 дюймов. Шесть стяжных шпилек представляют собой шпильки с резьбой 1 / 2-13 UNC с диаметром впадины 0.4822 дюйма и шаг резьбы 13 TPI. При сборке цилиндра требуется усилие зажима, эквивалентное одному полному обороту гайки из положения затяжки вручную.

Определите напряжение в цилиндре и стяжных шпильках. Также рассчитайте деформацию в каждом компоненте, используя модуль упругости E _ss = 28 × 10 ⁶ фунтов на квадратный дюйм и стержень E = 30 × 10 ⁶ фунтов на квадратный дюйм.

Задача 6: Предложите одно улучшение для этой главы.

Эластичность: напряжение и деформация | Физика

Цели обучения

К концу этого раздела вы сможете:

Закон штата Гука.
Объясните закон Гука, используя графическое представление между деформацией и приложенной силой.
Обсудите три типа деформаций, такие как изменение длины, сдвиг в сторону и изменение объема.
Опишите на примерах модуль Юнга, модуль сдвига и модуль объемной упругости.
Определите изменение длины с учетом массы, длины и радиуса.

Теперь мы переходим от рассмотрения сил, влияющих на движение объекта (таких как трение и сопротивление), к тем, которые влияют на форму объекта. Если бульдозер втолкнет машину в стену, машина не двинется с места, но заметно изменит форму. Изменение формы из-за приложения силы – это деформация . Известно, что даже очень небольшие силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики.Во-первых, объект возвращается к своей исходной форме, когда сила снимается, то есть деформация является упругой для небольших деформаций. Во-вторых, размер деформации пропорционален силе, то есть при малых деформациях соблюдается закон Гука. В форме уравнения Закон Гука определяется как

F = k Δ L ,

, где Δ L – величина деформации (например, изменение длины), вызванная силой F , а k – константа пропорциональности, которая зависит от формы и состава объекта, а также направления движения. сила.Обратите внимание, что эта сила является функцией деформации Δ L – она не постоянна, как кинетическая сила трения. Переставляем это на

[латекс] \ displaystyle \ Delta {L} = \ frac {F} {k} [/ latex]

дает понять, что деформация пропорциональна приложенной силе. На рисунке 1 показано соотношение по закону Гука между удлинением Δ L пружины или человеческой кости. Для металлов или пружин область прямой линии, к которой относится закон Гука, намного больше.Кости хрупкие, эластичная область небольшая, а перелом резкий. В конце концов, достаточно большое напряжение материала приведет к его разрушению или разрушению.

Закон Гука

F = kΔL ,

[латекс] \ displaystyle \ Delta {L} = \ frac {F} {k} [/ latex]

Рис. 1. График деформации ΔL в зависимости от приложенной силы F. Прямой сегмент – это линейная область, где соблюдается закон Гука. Наклон прямой области [латекс] \ frac {1} {k} [/ latex]. Для больших сил график изогнут, но деформация остается упругой – ΔL вернется к нулю, если сила будет устранена. Еще большие силы деформируют объект до тех пор, пока он не сломается.Форма кривой возле трещины зависит от нескольких факторов, в том числе от того, как прикладывается сила F . Обратите внимание, что на этом графике наклон увеличивается непосредственно перед трещиной, указывая на то, что небольшое увеличение F дает большое увеличение L рядом с трещиной.

Константа пропорциональности k зависит от ряда факторов материала. Например, гитарная струна из нейлона растягивается при затягивании, а удлинение Δ L пропорционально приложенной силе (по крайней мере, для небольших деформаций).Более толстые нейлоновые струны и струны из стали меньше растягиваются при одной и той же приложенной силе, что означает, что у них больше k (см. Рисунок 2). Наконец, все три струны возвращаются к своей нормальной длине, когда сила снимается, при условии, что деформация мала. Большинство материалов будут вести себя таким образом, если деформация будет меньше примерно 0,1% или примерно 1 часть на 10 ³.

Рис. 2. Одна и та же сила, в данном случае груз (w), приложенная к трем различным гитарным струнам одинаковой длины, вызывает три различных деформации, показанные заштрихованными сегментами.Левая нить из тонкого нейлона, посередине – из более толстого нейлона, а правая – из стали.

Растянись немного

Как бы вы измерили константу пропорциональности k резиновой ленты? Если резинка растянулась на 3 см, когда к ней была прикреплена 100-граммовая масса, то насколько она растянулась бы, если бы две одинаковые резинки были прикреплены к одной и той же массе – даже если их соединить параллельно или, наоборот, если связать вместе последовательно?

Теперь мы рассмотрим три конкретных типа деформаций: изменение длины (растяжение и сжатие), сдвиг в сторону (напряжение) и изменения объема.Все деформации считаются небольшими, если не указано иное.

Изменения длины – растяжение и сжатие: модуль упругости

Изменение длины Δ L происходит, когда к проволоке или стержню прилагается сила, параллельная ее длине L ₀, либо растягивая (натяжение), либо сжимая. (См. Рисунок 3.)

Рис. 3. (а) Напряжение. Стержень растягивается на длину ΔL , когда сила прилагается параллельно его длине. (б) Сжатие.Тот же стержень сжимается силами той же величины в противоположном направлении. Для очень малых деформаций и однородных материалов ΔL примерно одинаково для одинаковой величины растяжения или сжатия. При больших деформациях площадь поперечного сечения изменяется при сжатии или растяжении стержня.

Эксперименты показали, что изменение длины (Δ L ) зависит только от нескольких переменных. Как уже отмечалось, Δ L пропорциональна силе F и зависит от вещества, из которого изготовлен объект.Кроме того, изменение длины пропорционально исходной длине L ₀ и обратно пропорционально площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растягивается больше, чем короткая, а толстая струна растягивается меньше, чем тонкая. Мы можем объединить все эти факторы в одно уравнение для Δ L :

[латекс] \ displaystyle \ Delta {L} = \ frac {1} {Y} \ text {} \ frac {F} {A} L_0 [/ latex],

, где Δ L – изменение длины, F – приложенная сила, Y – коэффициент, называемый модулем упругости или модулем Юнга, который зависит от вещества, A – площадь поперечного сечения, и L ₀ – исходная длина.В таблице 1 перечислены значения Y для нескольких материалов – те, которые имеют большой Y , как говорят, имеют большую прочность на разрыв , потому что они деформируются меньше при заданном растяжении или сжатии.

Таблица 1. Модули упругости
Материал	Модуль Юнга (растяжение – сжатие) Y (10 ⁹ Н / м ²)	Модуль сдвига S (10 ⁹ Н / м ²)	Модуль объемной упругости B (10 ⁹ Н / м ²)
Алюминий	70	25	75
Кость – напряжение	16	80	8
Кость – компрессия	9
Латунь	90	35	75
Кирпич	15
Бетон	20
Стекло	70	20	30
Гранит	45	20	45
Волосы (человеческие)	10
Твердая древесина	15	10
Чугун, литье	100	40	90
Свинец	16	5	50
Мрамор	60	20	70
Нейлон	5
Полистирол	3
Шелк	6
Паутинка	3
Сталь	210	80	130
Сухожилие	1
Ацетон			0.7
Этанол			0,9
Глицерин			4,5
Меркурий			25
Вода			2,2

Модули Юнга не указаны для жидкостей и газов в таблице 1, потому что они не могут быть растянуты или сжаты только в одном направлении. Обратите внимание, что предполагается, что объект не ускоряется, поэтому на самом деле существуют две приложенные силы величиной F , действующие в противоположных направлениях.Например, струны на Рисунке 3 тянут вниз силой величиной w и удерживаются за потолок, который также оказывает силу величиной w .

Пример 1. Растяжение длинного кабеля

Подвесные тросы используются для перевозки гондол на горнолыжных курортах. (См. Рис. 4). Рассмотрим подвесной трос, длина которого без опоры составляет 3 км. Рассчитайте степень растяжения стального троса. Предположим, что кабель имеет диаметр 5,6 см и максимальное натяжение, которое он может выдержать, равно 3.0 × 10 ⁶ Н.

Рис. 4. Гондолы перемещаются по подвесным тросам на горнолыжном курорте Гала Юдзава в Японии. (Источник: Руди Херман, Flickr)

Стратегия

Сила равна максимальному натяжению, или F = 3,0 × 10 ⁶ Н. Площадь поперечного сечения π r ² = 2,46 × 10 ^–3 м ². Уравнение [latex] \ displaystyle \ Delta {L} = \ frac {1} {Y} \ text {} \ frac {F} {A} L_0 [/ latex] можно использовать для определения изменения длины.{2}} \ right) \ left (\ text {3020 m} \ right) \\ & = & \ text {18 m}. \ End {array} [/ latex]

Обсуждение

Это довольно большое натяжение, но только около 0,6% от длины без опоры. В этих условиях влияние температуры на длину может быть важным.

Кости в целом не ломаются от растяжения или сжатия. Скорее они обычно ломаются из-за бокового удара или изгиба, что приводит к срезанию или разрыву кости. Поведение костей при растяжении и сжатии важно, потому что оно определяет нагрузку, которую кости могут нести.Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревья. Несущие конструкции обладают особенностями; колонны в здании имеют стальные арматурные стержни, а деревья и кости – волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости расположена в виде тонких пластин, разделенных костным мозгом, в то время как в других местах кости могут быть цилиндрическими и заполненными костным мозгом или просто твердыми.Люди с избыточным весом имеют тенденцию к повреждению костей из-за длительного сжатия костных суставов и сухожилий.

Другой биологический пример закона Гука встречается в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу для большего напряжения. На рисунке 5 показана зависимость напряжения от деформации человеческого сухожилия. Некоторые сухожилия имеют высокое содержание коллагена, поэтому деформация или изменение длины относительно невелико; другие, например, опорные сухожилия (например, в ноге), могут изменять длину до 10%.Обратите внимание, что эта кривая напряжения-деформации является нелинейной, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальца, волокна сухожилия начинают выравниваться в направлении напряжения – это называется , распрямление . В линейной области фибриллы будут растянуты, а в области разрушения отдельные волокна начнут разрываться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения.Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.

Рис. 5. Типичная кривая “напряжение-деформация” для сухожилия млекопитающих. Показаны три области: (1) область пальца ноги (2) линейная область и (3) область разрушения.

В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть легко растяжимыми. Эластичные свойства артерий важны для кровотока. Когда кровь выкачивается из сердца, давление в артериях увеличивается, и стенки артерий растягиваются.Когда аортальный клапан закрывается, давление в артериях падает, и артериальные стенки расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это – эластичное поведение артерий, когда кровь хлынет через каждый насос сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластичными свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но расслабляемся свободно и эластично, когда мы выдыхаем. Наша кожа особенно эластична, особенно для молодых.Молодой человек может подняться от 100 кг до 60 кг без видимого провисания кожи. С возрастом снижается эластичность всех органов. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-х годов.

Пример 2. Расчет деформации: насколько укорачивается нога, когда вы стоите на ней?

Рассчитайте изменение длины кости верхней части ноги (бедренной кости), когда мужчина весом 70,0 кг поддерживает на ней 62,0 кг своей массы, при условии, что кость эквивалентна стержню, равному 40.0 см в длину и 2,00 см в радиусе.

Стратегия

Сила равна поддерживаемому весу, или F = мг = (62,0 кг) (9,80 м / с ²) = 607,6 Н, а площадь поперечного сечения равна π r ² = 1,257 × 10 ^–3 м ². Уравнение [latex] \ displaystyle \ Delta {L} = \ frac {1} {Y} \ text {} \ frac {F} {A} L_0 [/ latex] можно использовать для определения изменения длины.

Решение

Все величины, кроме Δ L , известны.{-5} \ text {m.} \ End {array} [/ latex]

Обсуждение

Это небольшое изменение длины кажется разумным, поскольку мы знаем, что кости жесткие. Фактически, даже довольно большие силы, возникающие при напряженных физических нагрузках, не сжимают и не сгибают кости в больших количествах. Хотя кость более жесткая по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 1, имеют более высокие значения модуля Юнга Y . Другими словами, они более жесткие и обладают большей прочностью на разрыв.

Уравнение изменения длины по традиции перестраивается и записывается в следующем виде:

[латекс] \ displaystyle \ frac {F} {A} = Y \ frac {\ Delta {L}} {L_0} [/ latex].

Отношение силы к площади, [латекс] \ frac {F} {A} [/ latex], определяется как напряжение (измеряется в Н / м ²), а отношение изменения длины к длина, [латекс] \ frac {\ Delta {L}} {L_0} [/ latex], определяется как деформация (безразмерная величина). Другими словами, напряжение = Y × деформация.

В этой форме уравнение аналогично закону Гука с напряжением, аналогичным силе, и деформацией, аналогичной деформации. Если снова переписать это уравнение к виду

[латекс] \ displaystyle {F} = YA \ frac {\ Delta {L}} {L_0} [/ latex],

мы видим, что он совпадает с законом Гука с константой пропорциональности

[латекс] \ displaystyle {k} = \ frac {YA} {L_0} [/ latex].

Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны небольшим деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.

Напряжение

Отношение силы к площади, [латекс] \ frac {F} {A} [/ латекс], определяется как напряжение, измеренное в Н / м ².

Штамм

Отношение изменения длины к длине, [латекс] \ frac {\ Delta {L}} {L_0} [/ latex], определяется как деформация (безразмерная величина). Другими словами, напряжение = Y × деформация.

Боковое напряжение: модуль сдвига

На рисунке 6 показано, что подразумевается под боковым напряжением или срезающей силой .Здесь деформация называется Δ x , и она перпендикулярна L ₀, а не параллельна, как при растяжении и сжатии. Деформация сдвига аналогична растяжению и сжатию и может быть описана аналогичными уравнениями. Выражение для деформации сдвига : [latex] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex], где S – модуль сдвига ( см. Таблицу 1) и F – сила, приложенная перпендикулярно к L ₀ и параллельно площади поперечного сечения A .Опять же, чтобы объект не ускорялся, на самом деле есть две равные и противоположные силы F , приложенные к противоположным граням, как показано на рисунке 6. Уравнение логично – например, легче согнуть длинный тонкий карандаш (маленький A ), чем короткие и толстые, и оба гнутся легче, чем аналогичные стальные стержни (большие S ).

Рис. 6. Сила сдвига прикладывается перпендикулярно длине L ₀ и параллельно области A , создавая деформацию Δx.Вертикальные силы не показаны, но следует иметь в виду, что в дополнение к двум силам сдвига, F , должны существовать поддерживающие силы, препятствующие вращению объекта. Искажающие эффекты этих поддерживающих сил игнорируются при этом лечении. Вес объекта также не показан, поскольку он обычно незначителен по сравнению с силами, достаточно большими, чтобы вызвать значительные деформации.

Деформация сдвига

[латекс] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex],

, где S – модуль сдвига, а F – сила, приложенная перпендикулярно к L ₀ и параллельно площади поперечного сечения A .

Изучение модулей сдвига в таблице 1 выявляет некоторые характерные закономерности. Например, для большинства материалов модули сдвига меньше модулей Юнга. Кость – замечательное исключение. Его модуль сдвига не только больше, чем модуль Юнга, но и такой же, как у стали. Это одна из причин того, что кости могут быть длинными и относительно тонкими. Кости могут выдерживать нагрузки, сопоставимые с бетонными и стальными. Большинство переломов костей возникает не из-за сжатия, а из-за чрезмерного скручивания и изгиба.

Позвоночный столб (состоящий из 26 позвоночных сегментов, разделенных дисками) обеспечивает основную опору для головы и верхней части тела. Позвоночник имеет нормальную кривизну для стабильности, но это искривление может быть увеличено, что приведет к увеличению силы сдвига на нижних позвонках. Диски лучше выдерживают силы сжатия, чем силы сдвига. Поскольку позвоночник не вертикальный, вес верхней части тела влияет на обе части. Беременным женщинам и людям с избыточным весом (с большим животом) необходимо отвести плечи назад, чтобы поддерживать равновесие, тем самым увеличивая искривление позвоночника и тем самым увеличивая сдвигающий компонент напряжения.Увеличенный угол из-за большей кривизны увеличивает поперечные силы вдоль плоскости. Эти более высокие усилия сдвига увеличивают риск травмы спины из-за разрыва дисков. Пояснично-крестцовый диск (клиновидный диск под последними позвонками) особенно подвержен риску из-за своего расположения.

Модули сдвига для бетона и кирпича очень малы; они слишком изменчивы, чтобы их можно было перечислить. Бетон, используемый в зданиях, может выдерживать сжатие, как в колоннах и арках, но очень плохо противостоит сдвигу, который может возникнуть в сильно нагруженных полах или во время землетрясений.Современные конструкции стали возможны благодаря использованию стали и железобетона. Практически по определению жидкости и газы имеют модуль сдвига, близкий к нулю, потому что они текут в ответ на силы сдвига.

Пример 3. Расчет силы, необходимой для деформации: гвоздь не сильно изгибается под нагрузкой

Найдите массу картины, висящей на стальном гвозде, как показано на рисунке 7, учитывая, что гвоздь изгибается только на 1,80 мкм. (Предположим, что модуль сдвига известен с двумя значащими цифрами.)

Рис. 7. Гвоздь, вид сбоку, на котором висит изображение. Гвоздь очень слабо прогибается (показан намного больше, чем на самом деле) из-за срезающего воздействия поддерживаемого веса. Также показано направленное вверх усилие стенки на гвоздь, иллюстрирующее равные и противоположные силы, приложенные к противоположным поперечным сечениям гвоздя. См. Пример 3 для расчета массы изображения.

Стратегия

Сила F на гвоздь (без учета собственного веса гвоздя) – это вес изображения w .Если мы сможем найти w , то масса изображения будет просто [латекс] \ frac {w} {g} [/ latex]. Уравнение [латекс] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex] может быть решено для F .

Решение

Решая уравнение [латекс] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex] для F , мы видим, что все остальные величины могут быть найдены :

[латекс] \ displaystyle {F} = \ frac {SA} {L_0} \ Delta {x} [/ latex]

S находится в таблице 1 и составляет S = 80 × 10 ⁹ Н / м ².{-6} \ text {m} \ right) = 51 \ text {N} [/ latex]

Эта сила 51 Н составляет вес w изображения, поэтому масса изображения [латекс] m = \ frac {w} {g} = \ frac {F} {g} = 5.2 \ text {kg} [ /латекс].

Обсуждение

Это довольно массивное изображение, и впечатляет то, что гвоздь прогибается всего на 1,80 мкм – величину, невидимую невооруженным глазом.

Изменения объема: модуль объемной упругости

Объект будет сжиматься во всех направлениях, если внутренние силы приложены равномерно ко всем его поверхностям, как показано на рисунке 8.Относительно легко сжимать газы и чрезвычайно сложно сжимать жидкости и твердые тела. Например, воздух в винной бутылке сжимается, когда она закупорена. Но если вы попытаетесь закупорить бутылку с полными краями, вы не сможете сжать вино – некоторые из них необходимо удалить, чтобы вставить пробку. Причина такой разной сжимаемости заключается в том, что атомы и молекулы разделены большими пустыми пространствами в газах, но плотно упакованы в жидкостях и твердых телах. Чтобы сжать газ, вы должны сблизить его атомы и молекулы.Чтобы сжать жидкости и твердые тела, вы должны действительно сжать их атомы и молекулы, и очень сильные электромагнитные силы в них препятствуют этому сжатию.

Рис. 8. Внутренняя сила на всех поверхностях сжимает этот куб. Его изменение в объеме пропорционально силе на единицу площади и его первоначальному объему и связано со сжимаемостью вещества.

Мы можем описать сжатие или объемную деформацию объекта уравнением. Во-первых, отметим, что сила, «приложенная равномерно», определяется как имеющая одинаковое напряжение или отношение силы к площади [латекс] \ frac {F} {A} [/ латекс] на всех поверхностях.Произведенная деформация представляет собой изменение объема Δ V , которое, как было обнаружено, ведет себя очень аналогично сдвигу, растяжению и сжатию, рассмотренным ранее. (Это неудивительно, поскольку сжатие всего объекта эквивалентно сжатию каждого из его трех измерений.) Связь изменения объема с другими физическими величинами определяется выражением [latex] \ displaystyle \ Delta {V} = \ frac {1} {B} \ frac {F} {A} V_0 [/ latex], где B – объемный модуль упругости (см. Таблицу 1), V ₀ – исходный объем, а [латекс] \ frac {F} {A} [/ latex] – это сила на единицу площади, равномерно приложенная внутрь ко всем поверхностям.Обратите внимание, что объемные модули для газов не приводятся.

Какие есть примеры объемного сжатия твердых тел и жидкостей? Одним из практических примеров является производство алмазов промышленного качества путем сжатия углерода с чрезвычайно большой силой на единицу площади. Атомы углерода перестраивают свою кристаллическую структуру в более плотно упакованный узор алмазов. В природе аналогичный процесс происходит глубоко под землей, где чрезвычайно большие силы возникают из-за веса вышележащего материала. Еще один естественный источник больших сжимающих сил – давление, создаваемое весом воды, особенно в глубоких частях океанов.Вода воздействует на все поверхности погружаемого объекта и даже на саму воду. На больших глубинах вода ощутимо сжата, как показано в следующем примере.

Пример 4. Расчет изменения объема при деформации: насколько вода сжимается на глубинах огромного океана?

Рассчитайте частичное уменьшение объема [латекс] \ left (\ frac {\ Delta {V}} {V_0} \ right) [/ latex] для морской воды на глубине 5,00 км, где сила на единицу площади составляет 5,00 × 10 ⁷ Н / м ².

Стратегия

Уравнение [латекс] \ displaystyle \ Delta {V} = \ frac {1} {B} \ frac {F} {A} V_0 [/ latex] является правильным физическим соотношением. Все величины в уравнении, кроме [latex] \ frac {\ Delta {V}} {V_0} [/ latex], известны.

Решение

Решение для неизвестного [латекса] \ frac {\ Delta {V}} {V_0} [/ latex] дает [latex] \ displaystyle \ frac {\ Delta {V}} {V_0} = \ frac {1} {B } \ frac {F} {A} [/ латекс].

Замена известных значений значением модуля объемной упругости B из таблицы 1,

[латекс] \ begin {array} {lll} \ frac {\ Delta {V}} {V_0} & = & \ frac {5.2} \\ & = & 0.023 = 2.3 \% \ end {array} [/ latex]

Обсуждение

Хотя это можно измерить, это незначительное уменьшение объема, учитывая, что сила на единицу площади составляет около 500 атмосфер (1 миллион фунтов на квадратный фут). Жидкости и твердые вещества чрезвычайно трудно сжимать.

И наоборот, очень большие силы создаются жидкостями и твердыми телами, когда они пытаются расшириться, но не могут этого сделать, что эквивалентно их сжатию до меньшего, чем их нормальный объем.Это часто происходит, когда содержащийся в нем материал нагревается, поскольку большинство материалов расширяются при повышении их температуры. Если материалы сильно стеснены, они деформируют или ломают свой контейнер. Другой очень распространенный пример – замерзание воды. Вода, в отличие от большинства материалов, при замерзании расширяется, и она может легко сломать валун, разорвать биологическую клетку или сломать блок двигателя, который встанет у нее на пути.

Другие типы деформаций, такие как кручение или скручивание, ведут себя аналогично рассмотренным здесь деформациям растяжения, сдвига и объемной деформации.

Сводка раздела

Закон Гука определяется выражением [латекс] F = k \ Delta {L} [/ latex], где [латекс] \ Delta {L} [/ latex] – величина деформации (изменение длины), F – это приложенная сила, а k – константа пропорциональности, которая зависит от формы и состава объекта, а также направления силы. Связь между деформацией и приложенной силой также может быть записана как [latex] \ displaystyle \ Delta L = \ frac {1} {Y} \ frac {F} {A} {L} _ {0} [/ latex] , где Y – это модуль Юнга , , который зависит от вещества, A – площадь поперечного сечения, а [латекс] {L} _ {0} [/ latex] – исходная длина.
Отношение усилия к площади, [латекс] \ frac {F} {A} [/ латекс], определяется как напряжение , измеренное в Н / м ².
Отношение изменения длины к длине, [латекс] \ frac {\ Delta L} {{L} _ {0}} [/ latex], определяется как деформация (безразмерная величина). Другими словами, [латекс] \ текст {напряжение} = Y \ times \ text {напряжение} [/ латекс].
Выражение деформации сдвига [латекс] \ displaystyle \ Delta x = \ frac {1} {S} \ frac {F} {A} {L} _ {0} [/ latex], где S – модуль сдвига и F – это сила, приложенная перпендикулярно [латексу] {L} _ {\ text {0}} [/ latex] и параллельно площади поперечного сечения A .
Связь изменения объема с другими физическими величинами определяется выражением [latex] \ displaystyle \ Delta V = \ frac {1} {B} \ frac {F} {A} {V} _ {0} [/ latex ], где B – объемный модуль, [latex] {V} _ {\ text {0}} [/ latex] – исходный объем, а [latex] \ frac {F} {A} [/ latex] – сила на единицу площади, равномерно приложенная внутрь ко всем поверхностям.

Концептуальные вопросы

Эластичные свойства артерий важны для кровотока. Объясните важность этого с точки зрения характеристик кровотока (пульсирующий или непрерывный).
Что вы чувствуете, когда щупаете пульс? Измерьте частоту пульса в течение 10 с и 1 мин. Есть ли разница в 6 раз?
Изучите различные типы обуви, включая спортивную обувь и шлепанцы. С точки зрения физики, почему нижние поверхности устроены именно так? Какие различия будут иметь для этих поверхностей сухие и влажные условия?
Ожидаете ли вы, что ваш рост будет отличаться в зависимости от времени суток? Почему или почему нет?
Почему белка может спрыгнуть с ветки дерева на землю и убежать целой, а человек может сломать кость при таком падении?
Объясните, почему беременные женщины часто страдают растяжением спины на поздних сроках беременности.
Уловка старого плотника, чтобы не допустить сгибания гвоздей при забивании их в твердый материал, заключается в том, чтобы крепко удерживать центр гвоздя плоскогубцами. Почему это помогает?
Когда стеклянная бутылка, полная уксуса, нагревается, и уксус, и стекло расширяются, но уксус расширяется значительно больше с температурой, чем стекло. Бутылка разобьется, если наполнить ее до плотно закрытой крышки. Объясните, почему, а также объясните, как воздушный карман над уксусом предотвратит разрыв.(Это функция воздуха над жидкостями в стеклянных контейнерах.)

Задачи и упражнения

Во время циркового представления один артист качается вверх ногами, висит на трапеции, держа другого, также перевернутого, за ноги. Если восходящая сила, действующая на более низкую спортсменку, в три раза превышает ее вес, насколько растягиваются кости (бедра) в ее верхних конечностях? Вы можете предположить, что каждый из них эквивалентен одинаковому стержню длиной 35,0 см и радиусом 1,80 см. Ее масса 60.0 кг.
Во время схватки борец 150 кг ненадолго встает на одну руку во время маневра, призванного сбить с толку его и без того умирающего противника. Насколько укорачивается длина кости плеча? Кость может быть представлена однородным стержнем длиной 38,0 см и радиусом 2,10 см.
(a) «Грифель» в карандашах представляет собой состав графита с модулем Юнга примерно 1 × 10 ⁹ Н / м ². Вычислите изменение длины грифеля в автоматическом карандаше, если постучите им прямо по карандашу с силой 4.0 Н. Шнур диаметром 0,50 мм и длиной 60 мм. б) разумен ли ответ? То есть согласуется ли это с тем, что вы наблюдали при использовании карандашей?
– самые высокие искусственные сооружения на Земле. В 1987 году физик весом 72,0 кг разместил себя и 400 кг оборудования на вершине одной антенны высотой 610 м для проведения гравитационных экспериментов. Насколько была сжата антенна, если считать ее эквивалентом стального цилиндра радиусом 0,150 м?
(а) На сколько стоит 65.Альпинист весом 0 кг натягивает нейлоновую веревку диаметром 0,800 см, когда она висит на 35,0 м ниже скалы? б) Соответствует ли ответ тому, что вы наблюдали для нейлоновых веревок? Имел бы смысл, если бы веревка была на самом деле эластичным шнуром?
Полый алюминиевый флагшток высотой 20,0 м по жесткости эквивалентен твердому цилиндру диаметром 4,00 см. Сильный ветер изгибает полюс так же, как горизонтальная сила в 900 Н. Насколько далеко в сторону прогибается верхняя часть шеста?
По мере бурения нефтяной скважины каждая новая секция бурильной трубы выдерживает собственный вес, а также вес трубы и бурового долота под ней.Рассчитайте растяжение новой стальной трубы длиной 6,00 м, которая поддерживает 3,00 км трубы, имеющей массу 20,0 кг / м, и 100-килограммовое буровое долото. Труба эквивалентна по жесткости сплошному цилиндру диаметром 5 см.
Рассчитайте усилие, которое настройщик рояля применяет для растяжения стальной рояльной струны на 8,00 мм, если проволока изначально имеет диаметр 0,850 мм и длину 1,35 м.
Позвонок подвергается действию силы сдвига 500 Н. Найдите деформацию сдвига, принимая позвонок в виде цилиндра 3.00 см в высоту и 4,00 см в диаметре.
Диск между позвонками позвоночника подвергается действию силы сдвига 600 Н. Найдите его деформацию сдвига, принимая модуль сдвига 1 × 10 ⁹ Н / м ². Диск эквивалентен сплошному цилиндру высотой 0,700 см и диаметром 4,00 см.
При использовании ластика для карандашей вы прикладываете вертикальное усилие 6,00 Н на расстоянии 2,00 см от соединения ластика с твердой древесиной. Карандаш имеет диаметр 6,00 мм и держится под углом 20 °.0º к горизонтали. а) Насколько дерево прогибается перпендикулярно своей длине? б) Насколько он сжат в продольном направлении?
Чтобы рассмотреть влияние проводов, подвешенных на столбах, мы возьмем данные из рисунка 9, на котором были рассчитаны натяжения проводов, поддерживающих светофор. Левая проволока образовывала угол 30,0 ° ниже горизонтали с вершиной своего столба и выдерживала натяжение 108 Н. Полый алюминиевый столб высотой 12,0 м по жесткости эквивалентен твердому цилиндру диаметром 4,50 см.а) Насколько он наклонен в сторону? б) Насколько он сжат?
Рисунок 9. Светофор подвешен на двух тросах. (б) Некоторые из задействованных сил. (c) Здесь показаны только силы, действующие на систему. Также показана схема свободного движения светофора. (d) Силы, проецируемые на вертикальную ( x ) и горизонтальную ( x ) оси. Горизонтальные составляющие натяжения должны компенсироваться, а сумма вертикальных составляющих натяжений должна равняться весу светофора.{-2} [/ латекс]). Какую силу на единицу площади вода может оказывать на емкость при замерзании? (В этой задаче допустимо использовать объемный модуль упругости воды.) (B) Удивительно ли, что такие силы могут разрушать блоки двигателя, валуны и тому подобное?
Эта проблема возвращается к канатоходцу, изученному на рисунке 10, который создал натяжение 3,94 × 10 ³ Н в канате, образующем угол 5,0 ° ниже горизонтали с каждой опорной стойкой. Подсчитайте, насколько это натяжение растягивает стальную проволоку, если она изначально была длиной 15 м и равной 0.50 см в диаметре.
Рис. 10. Вес канатоходца вызывает провисание каната на 5,0 градуса. Интересующая здесь система – это точка на проволоке, на которой стоит канатоходец.
Полюс на Рисунке 11 находится под изгибом 90,0º в линии электропередачи и поэтому подвергается большей силе сдвига, чем полюса на прямых участках линии. Натяжение в каждой линии составляет 4,00 × 10 ⁴ Н при показанных углах. Шест 15,0 м в высоту, 18,0 см в диаметре и, как считается, имеет вдвое меньшую жесткость, чем древесина твердых пород.(а) Рассчитайте сжатие полюса. (б) Найдите, насколько он изгибается и в каком направлении. (c) Найдите натяжение троса, используемого для удержания вехи прямо, если она прикреплена к верхней части столба под углом 30,0 ° к вертикали. (Ясно, что растяжка должна быть в направлении, противоположном изгибу.)

Рис. 11. Этот телефонный столб находится под углом 90 ° к линии электропередачи. Оттяжка прикрепляется к вершине мачты под углом 30º к вертикали.

Глоссарий

сила сопротивления: F _D, как оказалось, пропорционально квадрату скорости объекта; математически

[латекс] \ begin {array} \\ F _ {\ text {D}} \ propto {v} ^ 2 \\ F _ {\ text {D}} = \ frac {1} {2} C \ rho {Av } ^ 2 \ end {array} [/ latex],

, где C – коэффициент сопротивления, A – площадь объекта, обращенная к жидкости, а ρ – плотность жидкости.