Сила тока через конденсатор: Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца | ЕГЭ по физике

Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца | ЕГЭ по физике

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.

Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения. 2}$

где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.

То есть $1$ Кл$= 1А·с$.

Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т.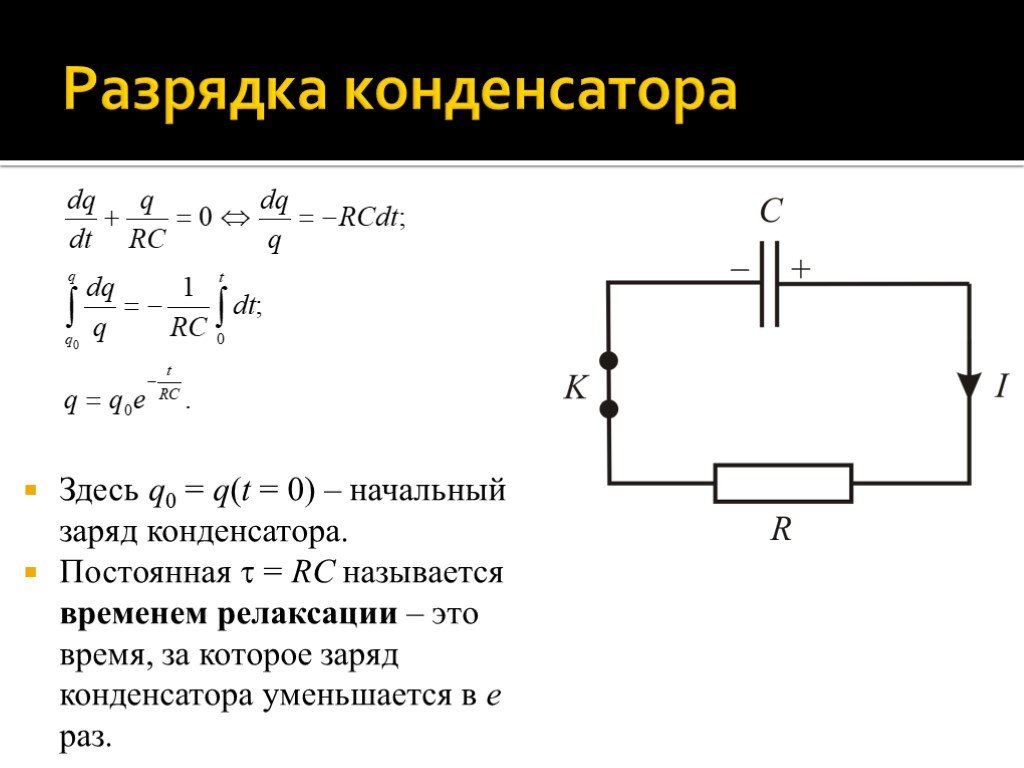 2$ – электрическая постоянная.

Электрическая емкость конденсатора

Электроемкость

Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:

$C={q}/{φ}$

Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.

Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.

Электрический конденсатор

Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.

Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. 2}/{2}$

где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.

Сила тока

Электрическим током называется упорядоченное (направленное) движение заряженных частиц.

Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:

$I={∆q}/{∆t}$

Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.

Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.

Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. 2$, дает весьма незначительную величину — $∼0.1$ мм/с.

Закон Ома для участка цепи

Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.

Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.

Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:

$I={U}/{R}$

Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.

Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I={U}/{R}$, и растворов электролитов.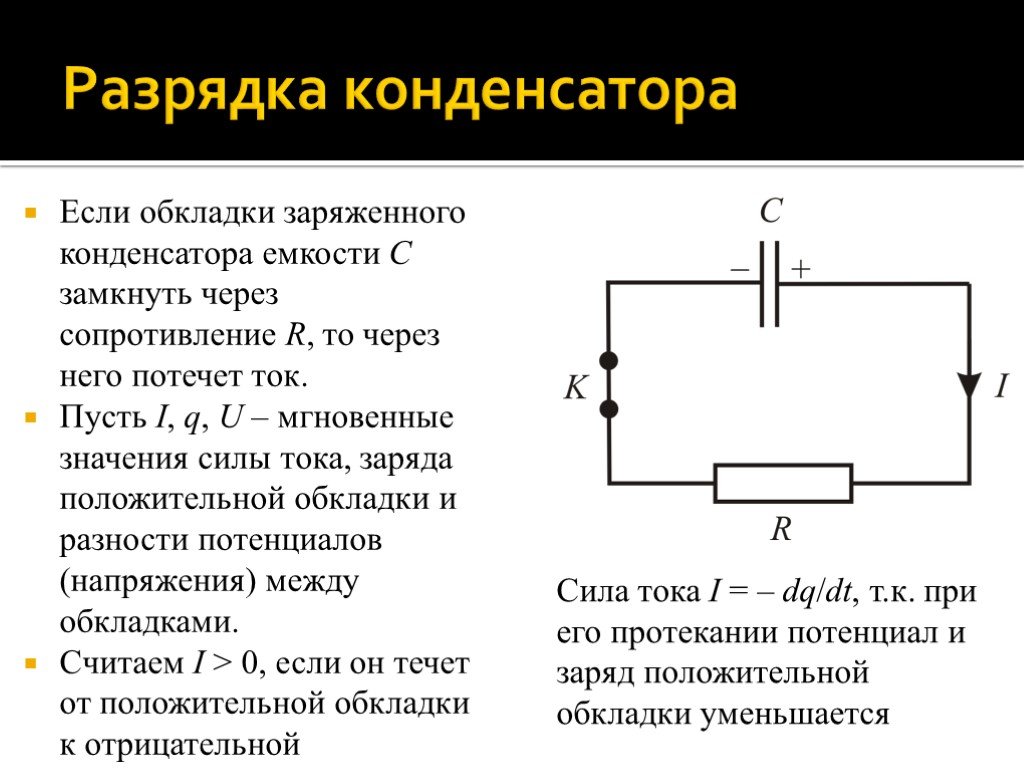

Знание ВАХ играет большую роль при изучении тока.

Закон Ома — это основа всей электротехники. Из закона Ома $I={U}/{R}$ следует:

1. сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
2. сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.

Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).

Электрическое сопротивление

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.

Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.

Удельное сопротивление

Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:

$R=ρ{l}/{S}$

где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.

Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.

Из формулы $R=ρ{l}/{S}$ следует, что

$ρ={RS}/{l}$

Величина, обратная $ρ$, называется удельной проводимостью $σ$:

$σ={1}/{ρ}$

Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. {-1}$. Для растворов электролитов $α

Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.

Параллельное и последовательное соединение проводников

Для параллельного соединения проводников справедливы следующие соотношения:

1) электрический ток, поступающий в точку $А$ разветвления проводников (она называется также узлом), равен сумме токов в каждом из элементов цепи:

$I=I_1+I_2;$

2) напряжение $U$ на концах проводников, соединенных параллельно, одно и то же:

$U=U_1=U_2;$

3) при параллельном соединении проводников складываются их обратные сопротивления:

${1}/{R}={1}/{R_1}+{1}/{R_2}, R={R_1·R_2}/{R_1+R_2};$

4) сила тока и сопротивление в проводниках связаны соотношением:

${I_1}/{I_2}={R_2}/{R_1}$

Для последовательного соединения проводников в цепи справедливы следующие соотношения:

1) для общего тока $I$:

$I=I_1=I_2,$

где $I_1$ и $I_2$ — ток в проводниках $1$ и $2$ соответственно; т.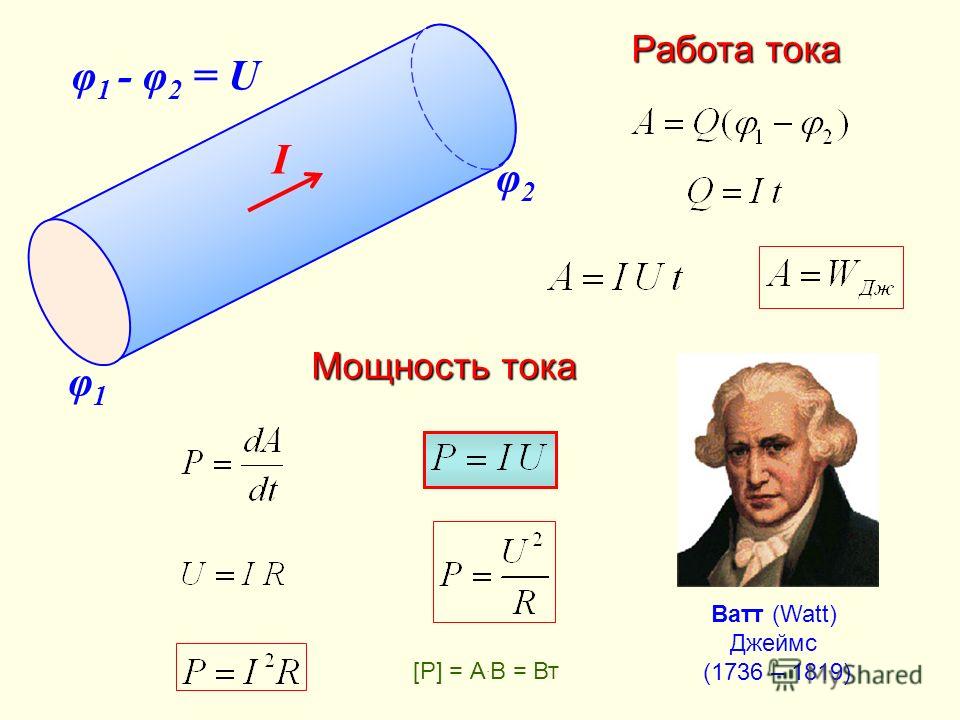 е. при последовательном соединении проводников сила тока на отдельных участках цепи одинакова;

2) общее напряжение $U$ на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:

$U=U_1+U_2;$

3) полное сопротивление $R$ всего участка цепи равно сумме последовательно соединенных сопротивлений:

$R=R_1+R_2;$

4) также справедливо соотношение:

${U_1}/{U_2}={R_1}/{R_2}$

Работа электрического тока. Закон Джоуля-Ленца

Работа, совершаемая током, проходящим по некоторому участку цепи, согласно ($U=φ_1-φ_2={A}/{q}$) равна:

$A=qU$

где $А$ — работа тока; $q$ — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство формулу $q=It$, получаем:

$A=IUt$

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Закон Джоуля-Ленца

Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:

$Q=I^2Rt$

Закон был установлен в 1841 г.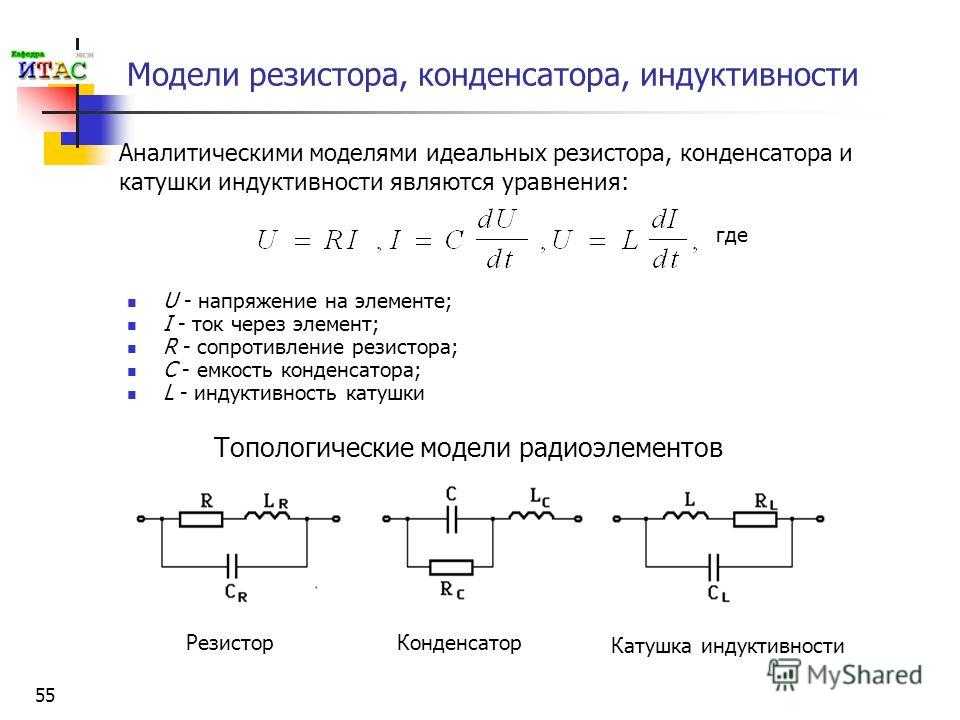 2}/{R}$

Из соотношения для ЭДС легко получить мощность источника тока:

$P_ε=εI$

В СИ работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время -в секундах (с). При этом

$1$Вт$=1$Дж/с, $1$Дж$=1$Вт$·$с.

Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать $I=10$А, то при напряжении $U=220$В соответствующая электрическая мощность оказывается равной:

$Р=10А·220В=2200Вт=2.2кВт.$

Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока, и потому недопустимо.

В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения прямо пропорциональна силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах ($кВт·ч$).

$1кВт·ч$ — это работа, совершаемая электрическим током мощностью $1кВт$ в течение $1ч$. Так как $1кВт=1000Вт$, а $1ч=3600с$, то $1кВт·ч=1000Вт·3600с=3600000 Дж$.

влияние на переменный и постоянный ток, формулы для расчета

Конденсатор используется в схемах для разделения переменной и постоянной составляющей напряжения, при этом он хорошо проводит высокочастотный сигнал, и плохо – низкочастотный. Находясь в цепи постоянного тока, его импеданс принимается бесконечно большим. Для переменного тока ёмкостное сопротивление конденсатора не имеет постоянной величиной. Поэтому расчёт этого значения крайне важен при проектировании различных радиоэлектронных приборов.

• Общее описание
• Характеристики прибора
• Импеданс элемента
  • Ёмкостное сопротивление
  • Индуктивная составляющая
• Пример расчёта

Общее описание

Физически электронное устройство – конденсатор – представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.

Слово “конденсатор” произошло от латинского “condensatio” – “накопление”. Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).

На схемах конденсатор изображается в виде двух прямых, соответствующих проводящим пластинам прибора, и перпендикулярно к их серединам нарисованными отрезками — выводами устройства.

Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом – отрицательного.

Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток – минимальным.

Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.

Характеристики прибора

Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:

C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.

Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:

• удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
• рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
• температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
• сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
• эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
• абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
• ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
• полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
• эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Импеданс элемента

Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.

Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.

Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) ² ) ^½, где

• Xl — индуктивность;
• Xс — ёмкость;
• R — активная составляющая.

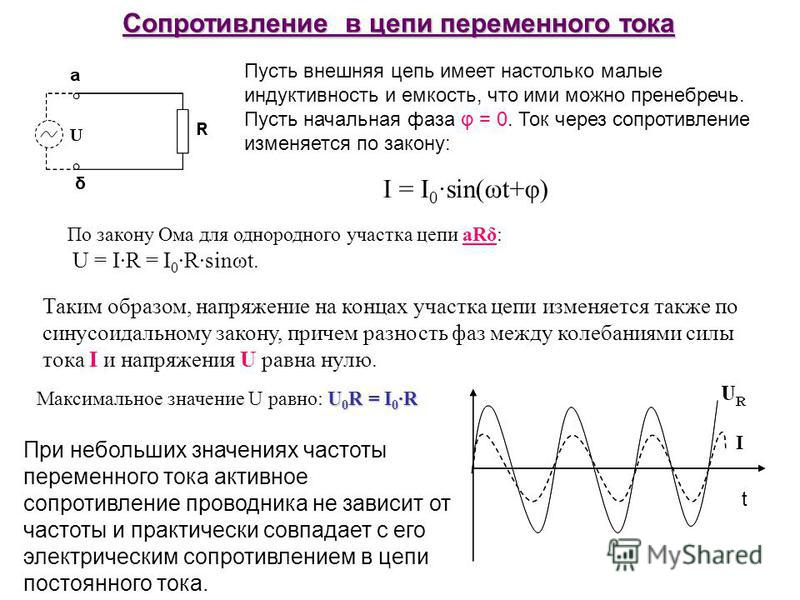
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.

Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:

• X > 0, в элементе проявляются индуктивные свойства;
• X = 0, в ёмкости присутствует только активная величина;
• X < 0, в элементе проявляется ёмкостное сопротивление.

Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.

Ёмкостное сопротивление

Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.

Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.

Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы,

можно будет получить следующее выражение:

• Xc = 1/w*C = ½*p*f*C. Единица измерения – ом.

Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.

На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит – из-за присутствия паразитной индуктивности и всё того же тока утечки.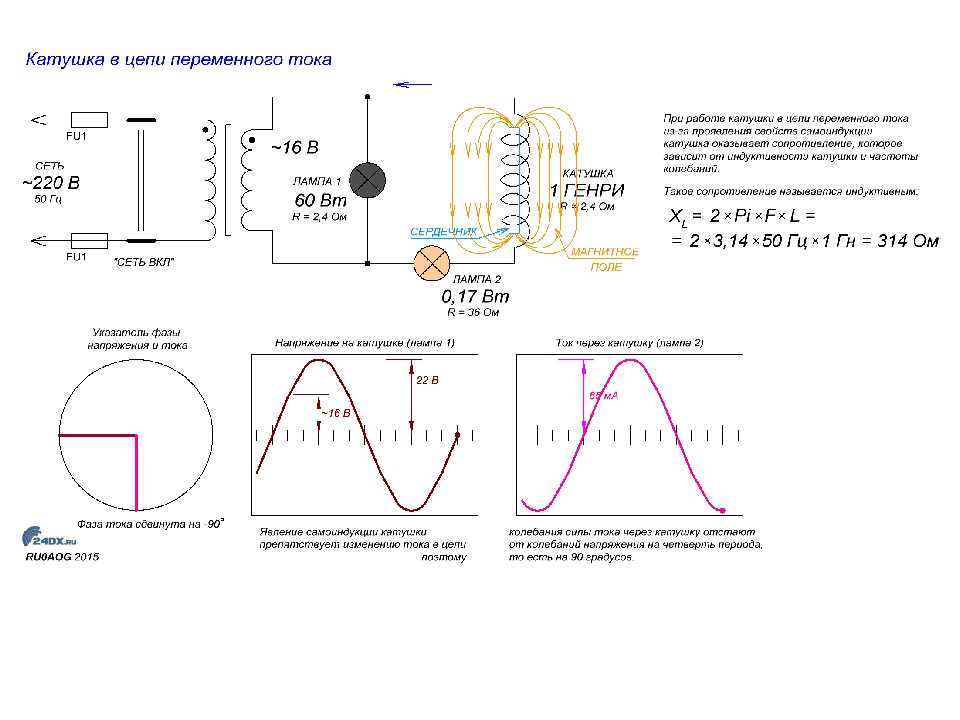

Индуктивная составляющая

При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .

Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность.

Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.

Таким образом, индуктивное сопротивление будет равно Xl = w * L, измеряется оно также в омах. Из полученного выражения видно, что чем больше частота сигнала, тем сильнее будет сопротивление прохождению тока.

Пример расчёта

Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R ² +Xc ² ) ^½.

Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.

В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет

Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 ⁻⁶ ) = 3,2 кОм.

По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.

Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 ⁻³ + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (5000²+3200²)½ = 5 936 Ом =5,9 кОм.

Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.

Электрическое сопротивление

– Как протекает ток в цепи с конденсатором?

спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 11 тысяч раз

$\begingroup$

Когда конденсатор подключен к батарее, в цепи начинает течь ток, который заряжает конденсатор до тех пор, пока напряжение между обкладками не станет равным напряжению батареи.

Так как между обкладками конденсатора находится изолятор/диэлектрик, как возможно, что в цепи с конденсатором течет ток, ведь по закону Ома ток обратно пропорционален сопротивлению, а изолятор по определению имеет большое сопротивление, так что у нас в основном разомкнутая цепь?

• электрические цепи
• электрическое сопротивление
• напряжение
• емкость
• диэлектрик

$\endgroup$

$\begingroup$

Так как это физика q и a, объяснение физики в порядке.

Есть два вида тока.

Ток проводимости представляет собой чистый поток зарядов. Это то, о чем люди обычно думают, когда используют слово «ток».

Ток смещения — еще одна форма тока, впервые обнаруженная Максвеллом. Ток смещения играет существенную роль в уравнениях Максвелла. Плотность тока смещения пропорциональна производной по времени от изменения плотности электрического потока.

Когда ток электронов течет в одну сторону конденсатора, электроны накапливаются, так как им некуда деваться. По мере накопления электронов плотность электрического потока изменяется. Это вызывает или, возможно, «является» током смещения.

На противоположной обкладке конденсатора происходит аналогичный процесс, но с противоположной электрической полярностью.

Ток смещения течет от одной пластины к другой через диэлектрик всякий раз, когда ток втекает или выходит из пластин конденсатора, и имеет точно такую ​​же величину, что и ток, протекающий через клеммы конденсатора.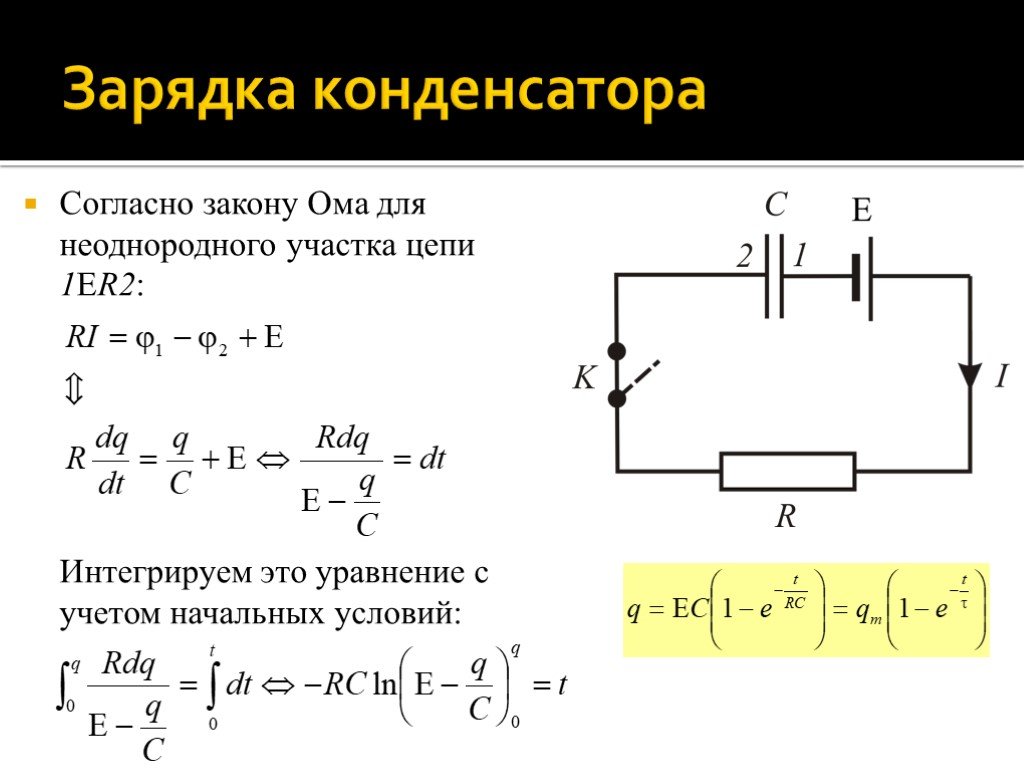

Можно предположить, что этот ток смещения не имеет никакого реального эффекта, кроме «сохранения» тока. Однако ток смещения создает магнитные поля так же, как и ток проводимости.

Этот ответ, возможно, больше, чем хотелось бы знать, но это часть истории электричества, которую стоит рассказать.

$\endgroup$

1

$\begingroup$

как возможно, что ток течет в цепи с конденсатором так как по закону Ома сила тока обратно пропорциональна сопротивление, а изолятор по определению имеет большое сопротивление, поэтому мы в основном есть разомкнутая цепь?

Короткий ответ заключается в том, что электроны могут течь к конденсатору и от него без необходимости прохождения электронов через изоляцию между пластинами. Предлагается следующее качественное объяснение:

Если предположить, что конденсатор изначально не заряжен, то перед его подключением к батарее каждая металлическая пластина имеет равное количество протонов (положительный заряд) и высокоподвижных электронов (отрицательный заряд), так что каждая пластина электрически нейтральна и между пластинами нет напряжения (разности потенциалов).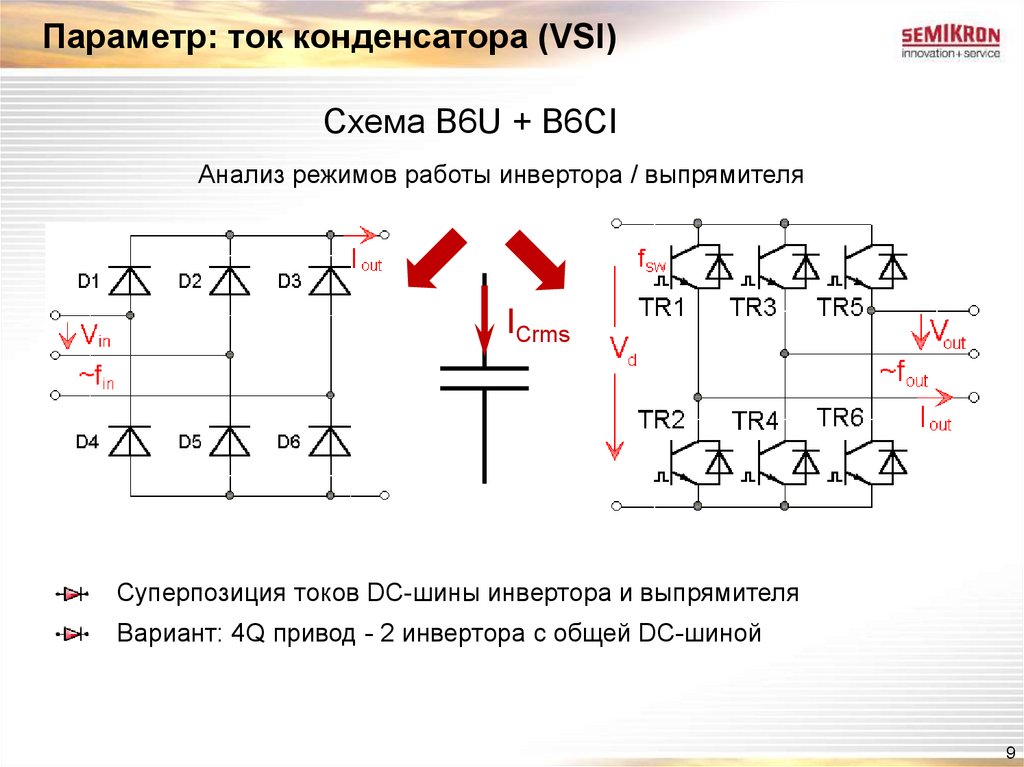

Когда конденсатор подключен к батарее, положительная клемма батареи притягивает электроны от пластины, соединенной с ним, перемещая их к положительной клемме батареи. Это оставляет дефицит электронов на этой пластине, что делает ее положительно заряженной.

В то же время отрицательный полюс батареи подает равное количество электронов на подсоединенную к нему пластину, создавая избыток электронов, делая пластину отрицательно заряженной.

Это перемещение электронов с одной пластины на положительную клемму батареи и с отрицательной клеммы батареи на другую пластину представляет собой ток конденсатора. Обратите внимание, что электроны не проходят через изоляционный материал (диэлектрик) между пластинами.

Вы можете представить себе это примерно как электроны, которые «стягиваются» с одной пластины и «выталкиваются» на другую силой электрического поля, создаваемого батареей, но заряды «застревают» на пластине. пластины, потому что они не могут пройти через изолирующий диэлектрик.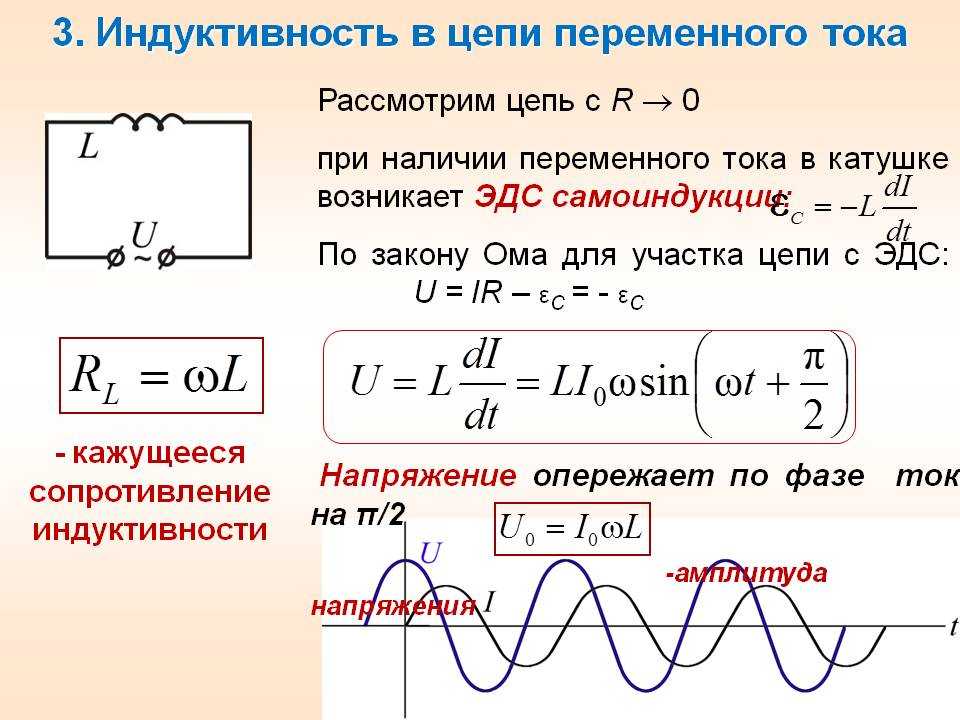

В конце концов, как вы, кажется, уже знаете, батарея перестает перемещать электроны между пластинами, когда разность потенциалов между пластинами становится равной разности потенциалов батареи.

Надеюсь, это поможет.

$\endgroup$

9

$\begingroup$

Удаление электронов с обкладки конденсатора, подключенной к клемме +, представляет собой ток. Поскольку эти электроны удаляются для этой пластины, происходит накопление электронов на другой пластине. Это движение электронов составляет ток.

Ток прекращается, когда потенциалы пластин конденсатора становятся равными потенциалам соответствующих клемм батареи. Это не происходит мгновенно, а скорее зависит от времени, потому что транспорт электронов из конденсатора и в него требует времени, а потенциалы зависят от дисбаланса заряда пластин.

$\endgroup$

$\begingroup$

Наличие плоского конденсатора означает, что в части цепи (лишь малая часть; конденсаторы редко имеют такой большой зазор как один миллиметр) нет движения электронов, только накопление поля (в сопровождении электронов, если конденсатор не вакуумный тип). Это проблематично, потому что есть простой способ обнаружения ток, который заключается в наблюдении за магнитным полем, создаваемым током, и ЧАСТЬ цепи больше не имеет тока.

Дело в том, что «поправка» на магнитное поле не существует. Соответствующее уравнение Максвелла для тока, создающего магнетизм имеет член, добавленный к текущему току смещения, который представляет собой скорость изменения электрическое поле (например, поле внутри диэлектрика конденсатора). Это дополнение к уравнению необходимо не только для цепей, у него есть дополнительный побочный эффект, заключающийся в том, что изменяющееся электрическое поле создает магнитное поле даже при отсутствии движущихся заряженных частиц.

Этот член уравнения объясняет, почему электромагнитные волны (свет) путешествует в вакууме. И, почему зарядка конденсатора (по-нашему измерений) неотличимы от непрерывного течения тока в цепь.

Буквально мы можем видеть, как светит солнце, потому что конденсатор в цепи не отличим от непрерывного тока в цепи.

$\endgroup$

2

$\begingroup$

Конденсатор действительно блокирует постоянный ток (DC). Однако значительный переменный ток (AC) может протекать, когда период колебаний меньше времени зарядки конденсатора.

$\endgroup$

3

$\begingroup$

Накачка электронов в одну пластину конденсатора приводит к тому, что свободные электроны на другой пластине отталкиваются, когда они «видят» входящие другие электроны. другая пластина. Для больших тарелок этот короткий импульс длинный, а для маленьких тарелок короткий импульс.

Это означает, что короткие импульсы переменного тока могут легко проходить через конденсатор, в то время как установившийся постоянный ток полностью блокируется.

$\endgroup$

$\begingroup$

Емкость (конденсатор) может первоначально заряжаться при кратковременном накоплении заряда на конденсаторе при замыкании цепи. Обычно:

$𝑡 = 𝑅.𝐶$

С:

$R$: Сопротивление цепи.

$C$: значение емкости.

На самом деле это и есть механизм способности емкости пропускать переменную во времени составляющую сигнала (ток, индуцированный изменением заряда на стенках емкости), блокируя при этом постоянную его компонент.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Конденсаторы – SparkFun Learn

Авторы: Джимблом

Избранное Любимый 82

Примечание : Материал на этой странице не является критически важным для понимания новичками в области электроники… и становится немного сложнее ближе к концу. Рекомендуем прочитать Как изготавливается конденсатор , другие, вероятно, можно пропустить, если они вызывают у вас головную боль.

Как изготавливается конденсатор

Схематичное обозначение конденсатора на самом деле очень похоже на способ его изготовления. Конденсатор состоит из двух металлических пластин и изоляционного материала, называемого диэлектриком . Металлические пластины расположены очень близко друг к другу, параллельно, но между ними находится диэлектрик, чтобы они не соприкасались.

Стандартный сэндвич-конденсатор: две металлические пластины, разделенные изолирующим диэлектриком.

Диэлектрик может быть изготовлен из любых изоляционных материалов: бумаги, стекла, резины, керамики, пластика или любого другого материала, препятствующего прохождению тока.

Пластины изготовлены из токопроводящего материала: алюминия, тантала, серебра или других металлов. Каждый из них подключен к терминальному проводу, который в конечном итоге соединяется с остальной частью схемы.

Емкость конденсатора — сколько у него фарад — зависит от его конструкции. Для большей емкости требуется больший конденсатор. Пластины с большей площадью перекрытия обеспечивают большую емкость, а большее расстояние между пластинами означает меньшую емкость. Материал диэлектрика даже влияет на то, сколько фарад имеет колпачок. Полную емкость конденсатора можно рассчитать по уравнению:

Где ε _r — относительная диэлектрическая проницаемость диэлектрика (постоянное значение, определяемое материалом диэлектрика), A — площадь, на которой пластины перекрывают друг друга, а d — расстояние между пластинами.

Как работает конденсатор

Электрический ток — это поток электрического заряда, который используется электрическими компонентами для освещения, вращения или других действий. Когда ток течет в конденсатор, заряды «застревают» на пластинах, потому что они не могут пройти через изолирующий диэлектрик. Электроны — отрицательно заряженные частицы — всасываются в одну из пластин, и в целом она становится отрицательно заряженной. Большая масса отрицательных зарядов на одной пластине отталкивает заряды другой пластины, делая ее положительно заряженной.

Положительные и отрицательные заряды на каждой из этих пластин притягиваются друг к другу, потому что это то, что делают противоположные заряды. Но с диэлектриком, сидящим между ними, как бы они ни хотели соединиться, заряды навсегда застрянут на пластине (пока им некуда будет деться). Постоянные заряды на этих пластинах создают электрическое поле, влияющее на электрическую потенциальную энергию и напряжение. Когда заряды группируются на таком конденсаторе, колпачок накапливает электрическую энергию так же, как батарея может накапливать химическую энергию.

Зарядка и разрядка

Когда положительные и отрицательные заряды сливаются на пластинах конденсатора, конденсатор становится заряженным . Конденсатор может сохранять свое электрическое поле — удерживать свой заряд — потому что положительные и отрицательные заряды на каждой из пластин притягиваются друг к другу, но никогда не достигают друг друга.

В какой-то момент пластины конденсатора будут настолько заряжены, что просто не смогут больше принимать. На одной пластине достаточно отрицательных зарядов, чтобы они могли оттолкнуть любые другие, пытающиеся присоединиться. Вот где емкость (фарад) конденсатора вступает в игру, что говорит вам о максимальном количестве заряда, который может хранить крышка.

Если в цепи создается путь, который позволяет зарядам найти другой путь друг к другу, они покинут конденсатор, и он разрядится .

Например, в приведенной ниже схеме можно использовать батарею для создания электрического потенциала на конденсаторе. Это приведет к тому, что на каждой из пластин будут накапливаться одинаковые, но противоположные заряды, пока они не будут настолько заполнены, что будут отражать дальнейшее протекание тока. Светодиод, включенный последовательно с крышкой, может обеспечить путь для тока, а энергия, накопленная в конденсаторе, может использоваться для кратковременного освещения светодиода.

Расчет заряда, напряжения и тока

Емкость конденсатора — сколько у него фарад — говорит вам, сколько заряда он может хранить. Сколько заряда конденсатора в настоящее время хранит , зависит от разности потенциалов (напряжения) между его пластинами. Эту взаимосвязь между зарядом, емкостью и напряжением можно смоделировать с помощью следующего уравнения:

Заряд (Q), накопленный в конденсаторе, является произведением его емкости (C) и приложенного к нему напряжения (V).

Емкость конденсатора всегда должна быть постоянной известной величиной. Таким образом, мы можем регулировать напряжение, чтобы увеличить или уменьшить заряд крышки. Большее напряжение означает больше заряда, меньше напряжения… меньше заряда.

Это уравнение также дает нам хороший способ определить стоимость одного фарада. Один фарад (Ф) — это способность хранить одну единицу энергии (кулон) на каждый вольт.

Вычисление тока

Мы можем развить уравнение заряд/напряжение/емкость еще на один шаг, чтобы выяснить, как емкость и напряжение влияют на ток, потому что ток – это ставка потока заряда. Суть отношения конденсатора к напряжению и току такова: величина тока через конденсатор зависит как от емкости, так и от того, насколько быстро повышается или падает напряжение. Если напряжение на конденсаторе быстро возрастает, через конденсатор индуцируется большой положительный ток. Более медленный рост напряжения на конденсаторе соответствует меньшему току через него. Если напряжение на конденсаторе постоянно и неизменно, то через него не будет проходить ток.

(Это уродливо и усложняет исчисление.