Скорость изменения магнитной индукции: «Как вычисляется скорость изменения индукции магнитного поля?» – Яндекс.Кью

Глава 23. Закон электромагнитной индукции

Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.

Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как

(23. 1)

где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м² однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.

Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока

(23.2)

Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле.

Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.

Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.

Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи

(23.3)

где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи.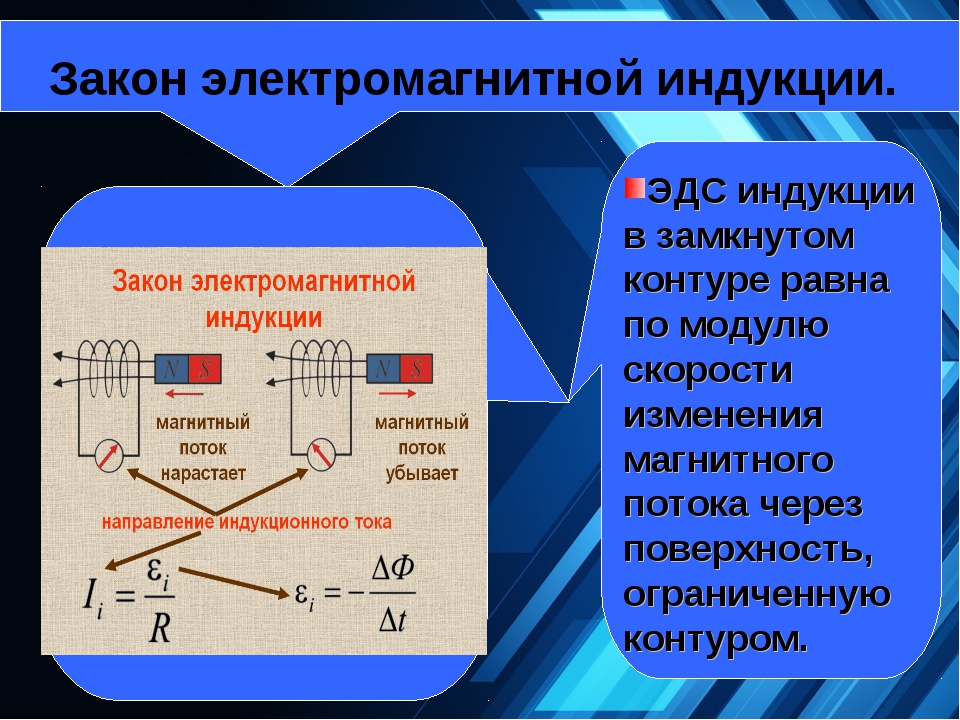 Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции

(23.4)

Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током

(23.5)

где — индуктивность контура, — сила тока в нем.

Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.

Рассмотрим теперь задачи.

Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.

Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).

Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).

Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в

задаче 23. 1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).

При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ

2).

В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется.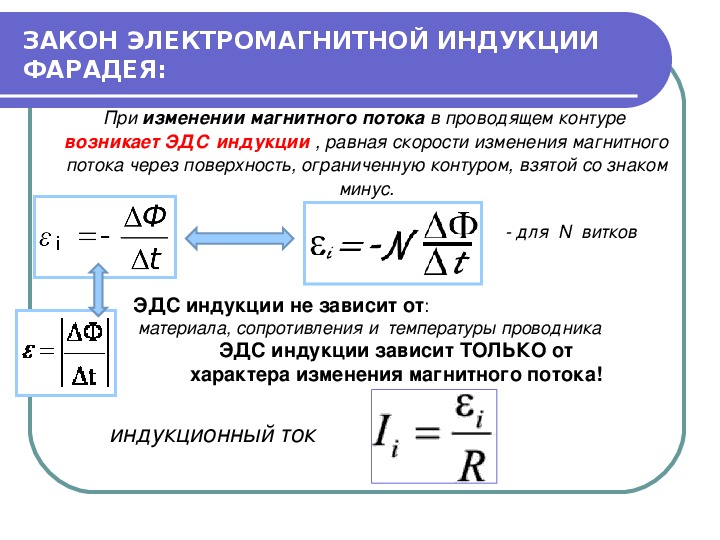 При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток

В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.

Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию

задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).

В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4). Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.

В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ

1).

При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 — ответ 3).

Используя формулу (23. 3) находим в задаче 32.2.3 Гн (ответ 4).

Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.

Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).

Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).

Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).

При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.

Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.

Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур . Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).

Репетитор-онлайн — подготовка к ЦТ

Пример 13. Проводящий контур, имеющий форму квадрата со стороной 20 см, помещен в однородное магнитное поле с индукцией 45 мТл. Плоскость контура составляет угол 30° с направлением силовых линий поля. За 0,15 с контур поворачивают таким образом, что его плоскость устанавливается перпендикулярно силовым линиям поля. Найти среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле.

Решение. Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость квадрата, при повороте контура в магнитном поле.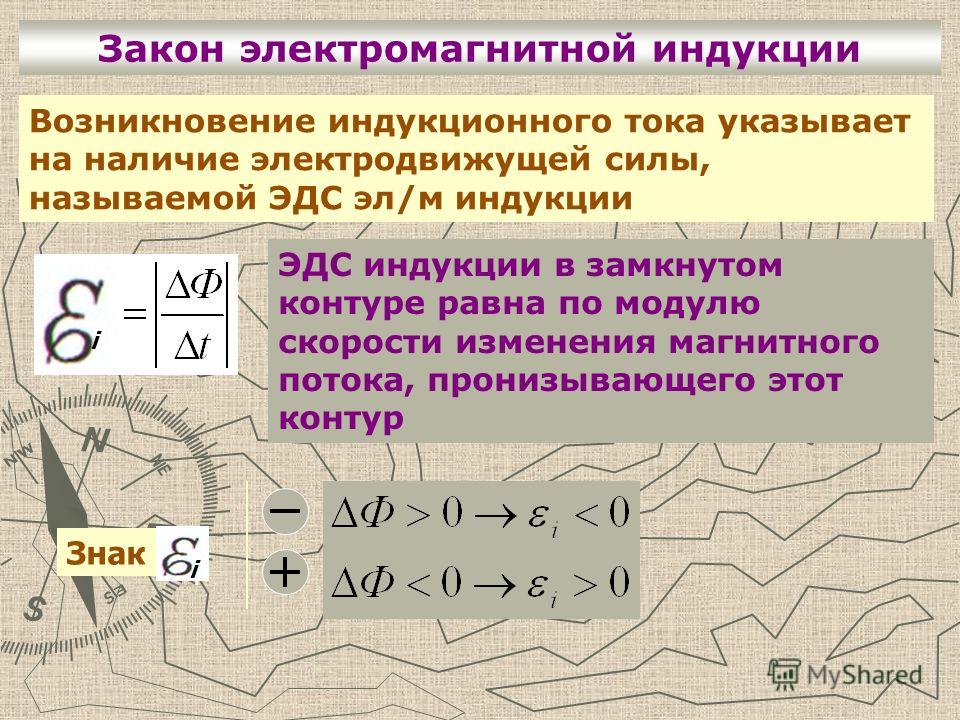

Поток индукции магнитного поля через площадь квадрата определяется формулами:

• в первом положении контура (до поворота)

Ф₁ = BS cos α₁,

где B — модуль индукции магнитного поля, B = 45 мТл; S — площадь квадрата, S = a ²; a — сторона квадрата, a = 20 см; α₁ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата в первом положении контура, α₁ = = 90° − 30° = 60°;

• во втором положении контура (после поворота)

Ф₂ = BS cos α₂,

где α₂ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата во втором положении контура, α₂ = 0°.

Изменение потока вектора индукции магнитного поля определяется разностью

ΔФ=Ф2−Ф1=BScos0°−BScos60°=BS2.

Среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле:

〈ℰi〉=|ΔФΔt|=−BS2Δt=Ba22Δt,

где ∆t — интервал времени, за который происходит поворот контура, ∆t = 0,15 с.

Расчет дает значение:

〈ℰi〉=45⋅10−3⋅(20⋅10−2)22⋅0,15=6,0⋅10−3 В=6,0 мВ.

При повороте контура в нем возникает ЭДС индукции, среднее значение которой равно 6,0 мВ.

явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца

9.5. Индукционный ток

9.5.1. Тепловое действие индукционного тока

Возникновение ЭДС приводит к появлению в проводящем контуре индукционного тока , сила которого определяется по формуле

I i = | ℰ i | R ,

где ℰ i – ЭДС индукции, возникающая в контуре; R – сопротивление контура.

При протекании индукционного тока в контуре выделяется теплота , количество которой определяется одним из выражений:

Q i = I i 2 R t , Q i = ℰ i 2 t R , Q i = I i | ℰ i | t ,

где I i – сила индукционного тока в контуре; R – сопротивление контура; t – время; ℰ i – ЭДС индукции, возникающая в контуре.

Мощность индукционного тока вычисляется по одной из формул:

P i = I i 2 R , P i = ℰ i 2 R , P i = I i | ℰ i | ,

где I i – сила индукционного тока в контуре; R – сопротивление контура; ℰ i – ЭДС индукции, возникающая в контуре.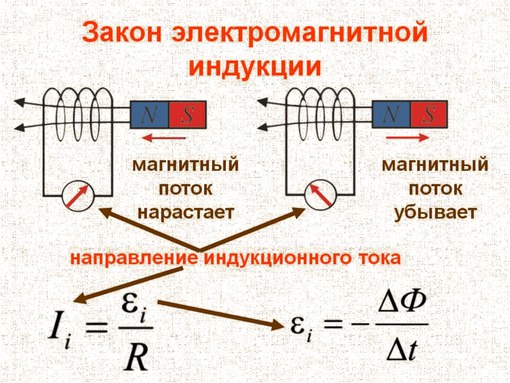

При протекании индукционного тока в проводящем контуре через площадь поперечного сечения проводника переносится заряд , величина которого вычисляется по формуле

q i = I i ∆t ,

где I i – сила индукционного тока в контуре; Δt – интервал времени, в течение которого по контуру течет индукционный ток.

Пример 21. Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10 −10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм 2 . Какой максимальный заряд пройдет по кольцу при выключении поля?

Решение . Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.

Поток индукции магнитного поля через площадь кольца определяется формулами:

• до выключения магнитного поля

Ф 1 = B 1 S  cos α,

где B 1 – первоначальное значение модуля индукции магнитного поля, B 1 = 250 мТл; S – площадь кольца; α – угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;

• после выключения магнитного поля

Ф 2 = B 2 S  cos α = 0,

где B 2 – значение модуля индукции после выключения магнитного поля, B 2 = 0.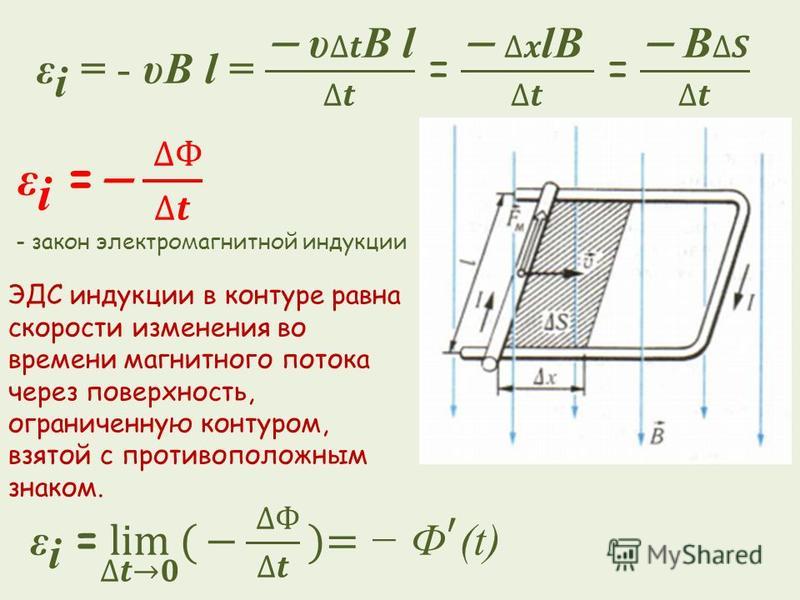

∆Ф = Ф 2 − Ф 1 = −Ф 1 ,

или, с учетом явного вида Ф 1 ,

∆Ф = −B 1 S  cos α.

Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,

| ℰ i | = | Δ Ф Δ t | = | − B 1 S cos α Δ t | = B 1 S | cos α | Δ t ,

где ∆t – интервал времени, за который происходит выключение поля.

Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = B 1 S | cos α | R Δ t ,

где R – сопротивление кольца.

При протекании индукционного тока по кольцу переносится индукционный заряд

q i = I i Δ t = B 1 S | cos α | R .

Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):

q i max = I i Δ t = B 1 S R .

Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.

Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.

Площадь кольца – площадь круга радиусом r , периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:

l = 2πr ,

где l – длина проволоки, l = 1,57 м.

Отсюда следует, что радиус кольца определяется отношением

r = l 2 π ,

а его площадь –

S = π r 2 = π l 2 4 π 2 = l 2 4 π .

Сопротивление кольца задается формулой

R = ρ l S 0 ,

где ρ – удельное сопротивление материала проволоки, ρ = 50,0 × × 10 −10 Ом ⋅ м; S 0 – площадь поперечного сечения проволоки, S 0 = = 0,100 мм 2 .

Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:

q i max = B 1 l 2 S 0 4 π ρ l = B 1 l S 0 4 π ρ .

Вычислим:

q i max = 250 ⋅ 10 − 3 ⋅ 1,57 ⋅ 0,100 ⋅ 10 − 6 4 ⋅ 3,14 ⋅ 50,0 ⋅ 10 − 10 = 0,625 Кл = 625 мКл.

При выключении поля по кольцу проходит заряд, равный 625 мКл.

Пример 22. Контур площадью 2,0 м 2 и сопротивлением 15 мОм находится в однородном магнитном поле, индукция которого возрастает на 0,30 мТл в секунду. Найти максимально возможную мощность индукционного тока в контуре.

Решение . Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость контура, при изменении индукции магнитного поля с течением времени.

Изменение потока вектора индукции магнитного поля определяется разностью

∆Ф = ∆BS  cos α,

где ∆B – изменение модуля индукции магнитного поля за выбранный интервал времени; S – площадь, ограниченная контуром, S = 2,0 м 2 ; α – угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости контура.

Среднее значение ЭДС индукции, возникающей в контуре, при изменении индукции магнитного поля:

| ℰ i | = | Δ Ф Δ t | = | Δ B S cos α Δ t | = Δ B S | cos α | Δ t ,

где ∆B /∆t – скорость изменения модуля вектора индукции магнитного поля с течением времени, ∆B /∆t = 0,30 мТл/с.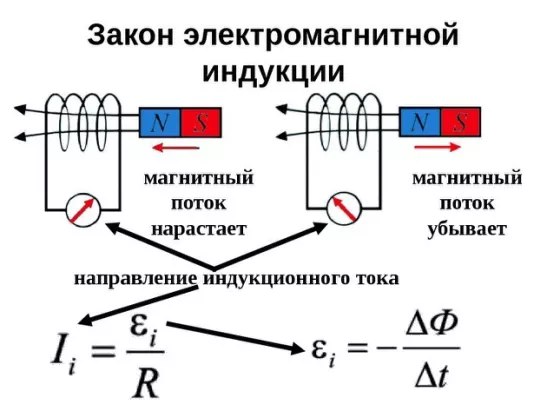

Появление ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:

I i = | ℰ i | R = Δ B S | cos α | R Δ t ,

где R – сопротивление контура.

Мощность индукционного тока

P i = I i 2 R = (Δ B Δ t) 2 S 2 R cos 2 α R 2 = (Δ B Δ t) 2 S 2 cos 2 α R .

Максимальному значению мощности индукционного тока соответствует максимальное значение функции косинус (cos α = 1):

P i max = (Δ B Δ t) 2 S 2 R .

Вычислим:

P i max = (0,30 ⋅ 10 − 3) 2 (2,0) 2 15 ⋅ 10 − 3 = 24 ⋅ 10 − 6 Вт = 24 мкВт.

Максимальная мощность индукционного тока в данном контуре равна 24 мкВт.

Взаимосвязь электрических и магнитных полей замечена очень давно. Данную связь еще в 19 веке обнаружил английский ученый-физик Фарадей и дал ему название . Она появляется в тот момент, когда магнитный поток пронизывает поверхность замкнутого контура.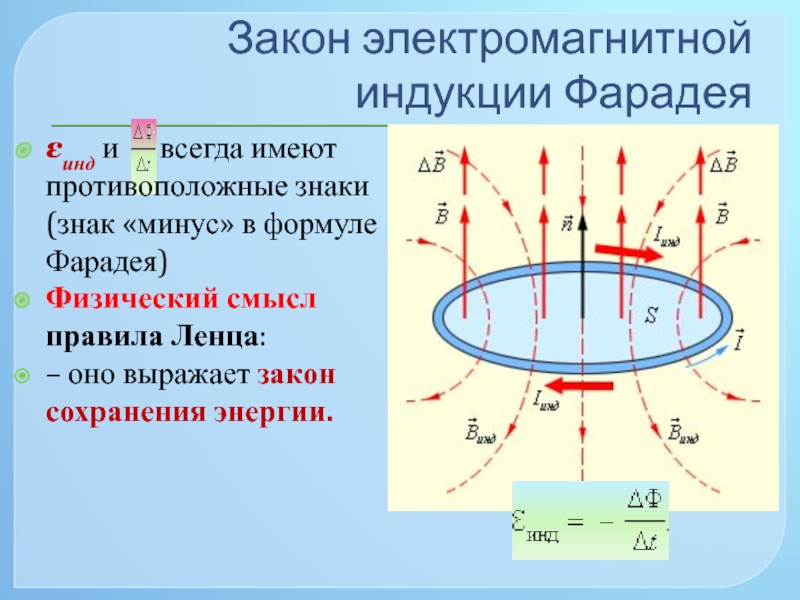 После того как происходит изменение магнитного потока в течение определенного времени, в этом контуре наблюдается появление электрического тока.

Взаимосвязь электромагнитной индукции и магнитного потока

Суть магнитного потока отображается известной формулой: Ф = BS cos α. В ней Ф является магнитным потоком, S – поверхность контура (площадь), В – вектор магнитной индукции. Угол α образуется за счет направления вектора магнитной индукции и нормали к поверхности контура. Отсюда следует, что максимального порога магнитный поток достигнет при cos α = 1, а минимального – при cos α = 0.

Во втором варианте вектор В будет перпендикулярен к нормали. Получается, что линии потока не пересекают контур, а лишь скользят по его плоскости. Следовательно, определять характеристики будут линии вектора В, пересекающие поверхность контура. Для расчета в качестве единицы измерения используется вебер: 1 вб = 1в х 1с (вольт-секунда). Еще одной, более мелкой единицей измерения служит максвелл (мкс). Он составляет: 1 вб = 108 мкс, то есть 1 мкс = 10-8 вб.

Для исследования Фарадеем были использованы две проволочные спирали, изолированные между собой и размещенные на катушке из дерева. Одна из них соединялась с источником энергии, а другая – с гальванометром, предназначенным для регистрации малых токов. В тот момент, когда цепь первоначальной спирали замыкалась и размыкалась, в другой цепи стрелка измерительного устройства отклонялась.

Проведение исследований явления индукции

В первой серии опытов Майкл Фарадей вставлял намагниченный металлический брусок в катушку, подключенную к току, а затем вынимал его наружу (рис. 1, 2).

1 2

В случае помещения магнита в катушку, подключенную к измерительному прибору, в цепи начинает протекать индукционный ток. Если магнитный брусок удаляется из катушки, индукционный ток все равно появляется, но его направление становится уже противоположным. Следовательно, параметры индукционного тока будут изменены по направлению движения бруска и в зависимости от полюса, которым он помещается в катушку. На силу тока оказывает влияние быстрота перемещения магнита.

Во второй серии опытов подтверждается явление, при котором изменяющийся ток в одной катушке, вызывает индукционный ток в другой катушке (рис. 3, 4, 5). Это происходит в моменты замыкания и размыкания цепи. От того, замыкается или размыкается электрическая цепь, будет зависеть и направление тока. Кроме того, эти действия есть ни что иное, как способы изменения магнитного потока. При замыкании цепи он будет увеличиваться, а при размыкании – уменьшаться, одновременно пронизывая первую катушку.

3 4

5

В результате опытов было установлено, что возникновение электрического тока внутри замкнутого проводящего контура возможно лишь в том случае, когда они помещаются в переменное магнитное поле. При этом, поток может изменяться во времени любыми способами.

Электрический ток, появляющийся под действием электромагнитной индукции, получил название индукционного, хотя это и не будет током в общепринятом понимании. Когда замкнутый контур оказывается в магнитном поле, происходит генерация ЭДС с точным значением, а не тока, зависящего от разных сопротивлений.

Данное явление получило название ЭДС индукции, которую отражает формула: Еинд = – ∆Ф/∆t. Ее значение совпадает с быстротой изменений магнитного потока, пронизывающего поверхность замкнутого контура, взятого с отрицательным значением. Минус, присутствующий в данном выражении, является отражением правила Ленца.

Правило Ленца в отношении магнитного потока

Известное правило было выведено после проведения цикла исследований в 30-х годах 19 века. Оно сформулировано в следующем виде:

Направление индукционного тока, возбуждаемого в замкнутом контуре изменяющимся магнитным потоком, оказывает влияние на создаваемое им магнитное поле таким образом, что оно в свою очередь создает препятствие магнитному потоку, вызывающему появление индукционного тока.

Когда магнитный поток увеличивается, то есть становится Ф > 0, а ЭДС индукции снижается и становится Еинд

Если поток снижается, то наступает обратный процесс, когда Ф 0, то есть действие магнитного поля индукционного тока, происходит увеличение магнитного потока, проходящего через контур.

Физический смысл правила Ленца заключается в отражении закона сохранения энергии, когда при уменьшении одной величины, другая увеличивается, и, наоборот, при увеличении одной величины другая будет уменьшаться. Различные факторы влияют и на ЭДС индукции. При вводе в катушку поочередно сильного и слабого магнита, прибор соответственно будет показывать в первом случае более высокое, а во втором – более низкое значение. То же самое происходит, когда изменяется скорость движения магнита.

На представленном рисунке видно, как определяется направление индукционного тока с применением правила Ленца. Синий цвет соответствует силовым линиям магнитных полей индукционного тока и постоянного магнита. Они расположены в направлении полюсов от севера к югу, которые имеются в каждом магните.

Изменяющийся магнитный поток приводит к возникновению индукционного электрического тока, направление которого вызывает противодействие со стороны его магнитного поля, препятствующее изменениям магнитного потока. В связи с этим, силовые линии магнитного поля катушки направлены в сторону, противоположную силовым линиям постоянного магнита, поскольку его движение происходит в сторону этой катушки.

Для определения направления тока используется с правой резьбой. Он должен ввинчиваться таким образом, чтобы направление его поступательного движения совпадало с направлением индукционных линий катушки. В этом случае направления индукционного тока и вращения рукоятки буравчика будут совпадать.

На рисунке показано направление индукционного тока,возникающего в короткозамкнутой проволочной катушке,когда относительно нее перемещают

магнит.Отметьте,какие из следующих утверждений правильные,а какие- неправильные.
А.Магнит и катушка притягиваются друг к другу.
Б. Внутри катушки магнитное поле индукционного тока направленно вверх.
В. Внутри катушки линии магнитной индукции поля магнита направлены вверх.
Г. Магнит удаляют от катушки.

1. Первый закон Ньютона?

2. Какие системы отсчета являются инерциальными и неинерциальными? Приведите примеры.
3. В чем состоит свойство тел, называемое инертностью? Какой величиной характеризуется инертность?
4. Какова связь между массами тел и модулями ускорений, которые они получают при взаимодействии?
5. Что такое сила и чем она характеризуется?
6. Формулировка 2 закона Ньютона? Какова его математическая запись?
7. Как формулируется 2 закон Ньютона в импульсной форме? Его математическая запись?
8. Что такое 1 Ньютон?
9. Как движется тело, если к нему приложена сила постоянная по модулю и направлению? Как направлено ускорение, вызванное действующей на него силой?
10. Как определяется равнодействующая сил?
11. Как формулируется и записывается 3 закон Ньютона?
12. Как направлены ускорения, взаимодействующих между собой тел?
13. Приведите примеры проявления 3 закона Ньютона.
14. Каковы границы применимости всех законов Ньютона?
15. Почему мы можем считать Землю инерциальной системой отсчета, если она двигается с центростремительным ускорением?
16. Что такое деформация, какие виды деформации вы знаете?
17. Какая сила называется силой упругости? Какова природа этой силы?
18. Каковы особенности силы упругости?
19. Как направлена сила упругости (сила реакции опоры, сила натяжения нити?)
20. Как формулируется и записывается закон Гука? Каковы его границы применимости? Постройте график, иллюстрирующий закон Гука.
21. Как формулируется и записывается закон Всемирного тяготения, когда он применим?
22. Опишите опыты, по определению значения гравитационной постоянной?
23. Чему равна гравитационная постоянная, каков ее физический смысл?
24. Зависит ли работа силы тяготения от формы траектории? Чему равна работа силы тяжести по замкнутому контуру?
25. Зависит ли работа силы упругости от формы траектории?
26. Что вы знаете о силе тяжести?
27. Как вычисляется ускорение свободного падения на Земле и других планетах?
28. Что такое первая космическая скорость? Как ее вычисляют?
29. Что называют свободным падением? Зависит ли ускорение свободного падения от массы тела?
30. Опишите опыт Галилео Галилея, доказывающий, что все тела в вакууме падают с одинаковым ускорением.
31. Какая сила называется силой трения? Виды сил трения?
32. Как вычисляют силу трения скольжения и качения?
33. Когда возникает сила трения покоя? Чему она равна?
34. Зависит ли сила трения скольжения от площади соприкасающихся поверхностей?
35. От каких параметров зависит сила трения скольжения?
36. От чего зависит сила сопротивления движению тела в жидкостях и газах?
37. Что называют весом тела? В чем заключается различие между весом тела и силой тяжести, действующей на тело?
38. В каком случае вес тела численно равен модулю силы тяжести?
39. Что такое невесомость? Что такое перегрузка?
40. Как вычислить вес тела при его ускоренном движении? Изменяется ли вес тела, если оно движется по неподвижной горизонтальной плоскости с ускорением?
41. как изменяется вес тела при его движении по выпуклой и вогнутой части окружности?
42. Каков алгоритм решения задач при движении тела под действием нескольких сил?
43. Какая сила называется Силой Архимеда или выталкивающей силой? От каких параметров зависит эта сила?
44. По каким формулам можно вычислить силу Архимеда?
45. При каких условиях тело, находящееся в жидкости плавает, тонет, всплывает?
46. Как зависит глубина погружения в жидкость плавающего тела от его плотности?
47. Почему воздушные шары наполняют водородом, гелием или горячим воздухом?
48. Объясните влияние вращения Земли вокруг своей оси на значение ускорения свободного падения.
49. Как изменяется значение силы тяжести при: а) удалении тела от поверхности Земли, Б) при движении тела вдоль меридиана, параллели

электрической цепи?

3. Каков физический смысл ЭДС? Дать определение вольту.

4. Соединить на короткое время вольтметри источником электрической энергии, соблюдая полярность. Сравнить его показания с вычислением по результатам опыта.

5. От чего зависит напряжение на зажимах источников тока?

6. Пользуясь результатами измерений, определить напряжение на внешней цепи (если работа выполнена I методом), сопротивление внешней цепи (если работа выполнена II методом).Свитый в катушку проводник замыкается на гальванометре (рис. 3.19). Если вдвигать в катушку постоянный магнит, то гальванометр покажет наличие тока в течение всего промежутка времени, пока магнит перемещается относительно катушки. При выдергивании магнита из катушки гальванометр показывает наличие тока противоположного направления. Изменения направления тока происходит при изменении вдвигаемого или выдвигаемого полюса магнита.

Аналогичные результаты наблюдались при замене постоянного магнита электромагнитом (катушкой с током). Если обе катушки закрепить неподвижно, но в одной из них менять значение тока, то в этот момент в другой катушке наблюдается индукционный ток.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ состоит в возникновении электродвижущей силы (э.д.с.) индукции в проводящем контуре, через который меняется поток вектора магнитной индукции. Если контур является замкнутым, то в нем возникает индукционный ток.

Открытие явления электромагнитной индукции:

1) показало взаимосвязь между электрическим и магнитным полем ;

2) предложило способ получения электрического тока с помощью магнитного поля.

Основные свойства индукционного тока :

1. Индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции.

2. Сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.

Опытами Фарадея было установлено, что величина электродвижущей силы индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур проводника (закон электромагнитной индукции Фарадея)

Или , (3.46)

где (dF) – изменение потока в течении времени (dt).МАГНИТНЫМ ПОТОКОМ или ПОТОКОМ МАГНИТНОЙ ИНДУКЦИИ называется величина, которая определяется на основе следующего соотношения: (магнитный поток через поверхность площадью S ): Ф=ВScosα, (3.45), угол a – угол между нормалью к рассматриваемой поверхности и направлением вектора индукции магнитного поля

единица магнитного потока в системе СИ носит название вебер – [Вб=Тл×м 2 ].

Знак «–» в формуле означает, что э.д.с. индукции вызывает индукционный ток, магнитное поле которого противодействует всякому изменению магнитного потока, т.е. при >0 э.д.с. индукции e И

э.д.с. индукции измеряется в вольтах

Для нахождения направления индукционного тока существует правило Ленца (правило установлено в 1833 г.): индукционный ток имеет такое направление, что создаваемое им магнитное поле стремится компенсировать изменение магнитного потока, вызвавшее этот индукционный ток.

Например, если вдвигать северный полюс магнита в катушку, т. е. увеличивать магнитный поток через его витки, в катушке возникает индукционный ток такого направления, что на ближайшем к магниту конце катушки возникает северный полюс (рис.3.20). Итак, магнитное поле индукционного тока стремится нейтрализовать вызвавшее его изменение магнитного потока.

Не только переменное магнитное поле порождает индукционный ток в замкнутом проводнике, но и при движении замкнутого проводника длиной l в постоянном магнитном поле (В) со скоростью v в проводнике возникает эдс:

a (B Ùv) (3.47)

Как вы уже знаете, электродвижущая сила в цепи– это результат действия сторонних сил. При движении проводника в магнитном поле роль сторонних сил выполняет сила Лоренца (которая действует со стороны магнитного поля на движущийся электрический заряд). Под действием этой силы происходит разделение зарядов и на концах проводника возникает разность потенциалов. Э.д.с. индукции в проводнике является работой по перемещению единичных зарядов вдоль проводника.

Направление индукционного тока можно определитьпо правилу правой руки: Вектор В входит в ладонь, отведенный большой палец совпадает с направлением скорости проводника, а 4 пальца укажут направление индукционного тока.

Таким образом переменное магнитное поле вызывает появление индуцированного электрического поля. Оно не потенциально (в отличие от электростатического), т.к. работа по перемещению единичного положительного заряда равна э.д.с. индукции , а не нулю.

Такие поля называются вихревыми. Силовые линии вихревого электрического поля – замкнуты сами на себя, в отличие от линий напряженности электростатического поля.

Э.д.с. индукции возникает не только в соседних проводниках, но и в самом проводнике при изменении магнитного поля тока, идущего по проводнику. Возникновение э.д.с. в каком-либо проводнике при изменении в нем самом силы тока (следовательно, магнитного потока в проводнике) называется самоиндукцией, а ток, индуцируемый в этом проводнике, – током самоиндукции.

Ток в замкнутом контуре создает в окружающем пространстве магнитное поле, напряженность которого пропорциональна силе тока I. Поэтому магнитный поток Ф, пронизывающий контур, пропорционален силе тока в контуре

Ф=L×I, (3.48).

L – коэффициент пропорциональности, который носит название коэффициента самоиндукции, или, просто, индуктивности. Индуктивность зависит от размеров и формы контура, а также от магнитной проницаемости среды, окружающей контур.

В этом смысле индуктивность контура – аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.

Единица индуктивности – генри (Гн) : 1Гн – индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1А равен 1Вб (1Гн=1Вб/А=1В·с/А).

Если L=const, то э.д.с. самоиндукции можно представить в следующем виде:

, или , (3.49)

где DI (dI) – изменение тока в цепи, содержащей катушку индуктивности (или контур) L, за время Dt (dt). Знак «–» в этом выражении означает, что э.д.с. самоиндукции препятствует изменению тока (т. е. если ток в замкнутом контуре уменьшается, то э.д.с. самоиндукции приводит к возникновению тока того же направления и наоборот).

Одним из проявлений электромагнитной индукции является возникновение замкнутых индукционных токов в сплошных проводящих средах: металлических телах, растворах электролитов, биологических органах и т.д. Такие токи носят название вихревых токов или токов Фуко. Эти токи возникают при перемещении проводящего тела в магнитном поле и/или при изменении со временем индукции поля, в которое помещены тела. Сила токов Фуко зависит от электрического сопротивления тел, а также от скорости изменения магнитного поля.

Токи Фуко также подчиняются правилу Ленца : их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующему вихревые токи.

Поэтому массивные проводники тормозятся в магнитном поле. В электрических машинах, для того чтобы минимизировать влияние токов Фуко, сердечники трансформаторов и магнитные цепи электрических машин собирают из тонких пластин, изолированных друг от друга специальным лаком или окалиной.

Вихревые токи вызывают сильное нагревание проводников. Джоулево тепло, выделяемое токами Фуко , используется в индукционных металлургических печах для плавки металлов, согласно закону Джоуля-Ленца .

Урок 5. электромагнитная индукция – Физика – 11 класс

Физика, 11 кл

Урок 5. Электромагнитная индукция

Перечень вопросов, рассматриваемых на этом уроке

1. Знакомство с явлением электромагнитной индукции.
2. Изучение законов, описывающих явление электромагнитной индукции.
3. Решение задач, практическое использование электромагнитной индукции.

Глоссарий по теме

Явление электромагнитной индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром, меняется со временем. Магнитный поток Ф – графически величина пропорциональная числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единица измерения магнитного потока: магнитный поток в один вебер создаётся однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции.

Правило Ленца: возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.

Сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

Основная и дополнительная литература по теме:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112

Рымкевич А.П. Сборник задач по физике. 10-11класс. – М.: Дрофа,2009. Стр. 28-29

ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.

Теоретический материал для самостоятельного изучения

Электрические и магнитные поля создаются одними и теми же источниками – электрическими зарядами. Отсюда естественнее было предположить, что между этими полями имеется связь. Экспериментально это предположение было доказано в 1831 г. английским учёным М. Фарадеем, открывшим явление электромагнитной индукции. Все опыты Фарадея по изучению явления электромагнитной индукции объединял один признак – магнитный поток пронизывающий замкнутый контур проводника менялся. При всяком изменении магнитного потока через замкнутый контур, в нем возникал индукционный ток.

Сила индукционного тока пропорциональна ЭДС индукции.

Направление индукционного тока менялось в зависимости от направления движения магнита относительно катушки. Это направление тока, можно найти используя правило Ленца.

М. Фарадеем экспериментально было установлено, что при изменении магнитного потока, в проводящем контуре возникает электродвижущая сила индукции, которая равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Знак минус в этой формуле отражает правило Ленца.

Закон электромагнитной индукции формулируется для ЭДС индукции.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

ЭДС индукции в движущихся проводниках:

Ɛ_i = Вlvsinα.

Джеймс Максвелл в 1860 году сделал вывод что переменное со временем магнитное поле всегда порождает вихревое электрическое поле, а переменное во времени электрическое поле в свою очередь порождает магнитное поле. Следовательно, существует единая теория электромагнитного поля.

Разбор типового контрольного задания

1.

На рисунке изображен момент демонстрационного эксперимента по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится внутри сплошного металлического кольца, но не касается его. Коромысло с металлическими кольцами может свободно вращаться вокруг вертикальной опоры. При выдвижении магнита из кольца влево кольцо будет

1) оставаться неподвижным

2) перемещаться вправо

3) совершать колебания

4) перемещаться вслед за магнитом

При выдвижении магнита из кольца влево магнитный поток от магнита через кольцо будет уменьшаться. В замкнутом кольце возникает индукционный ток. Направление этого тока по правилу Ленца такое, что создаваемое им магнитное поле препятствует изменению магнитного потока. Так как коромысло вокруг вертикальной оси может свободно вращаться, и магнитное поле магнита неоднородно, коромысло под действием сил Ампера начнёт двигаться так, чтобы препятствовать изменению магнитного потока. Следовательно, коромысло начнёт перемещаться вслед за магнитом.

Ответ:4) перемещаться вслед за магнитом.

2.

Проводник МN с длиной активной части 1м и сопротивлением 2 Ом находится в однородном магнитном поле индукцией 0,2 Тл. Проводник подключён к источнику тока с ЭДС 4 В (внутренним сопротивлением источника и сопротивлением подводящих проводников пренебречь). Какова сила тока в проводнике, если:

№1 проводник покоится;

№2 проводник движется в право со скоростью 6 м/с.

Дано:

ℓ= 1м

R = 2 Ом

В = 0,2 Тл

Ɛ = 4 В

I =?

Решение:

№1: Ток в неподвижном проводнике течёт от N к М

v = 0; Закон Ома для полной цепи I = Ɛ/R = 4В/2Ом = 2А

№2: Если проводник движется в право со скоростью 6 м/с, то по правилу правой руки индукционный ток потечёт от точки N к точке М:

Ответ: №1 2А

№2 2,6А

Электромагнитная индукция – материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.

Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.

Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?

Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.

1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».

Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.

При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.

Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.

При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.

Вывод.

Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.

Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.

Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.

Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.

Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).

2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.

Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.

3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.

Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.

Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.

Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».

Магнитный поток

Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.

Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .

Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

Рис. 1.

В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:

(1)

Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2).

Рис. 2.

Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем . Но , поэтому

(2)

Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.

А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.

Единицей измерения магнитного потока является вебер (Вб). Как видим,

Вб = Тл · м = В · с. (3)

Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!

Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.

Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.

ЭДС индукции

Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.

Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается .

Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.

Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.

Закон электромагнитной индукции Фарадея

Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.

Если за малое время изменение магнитного потока равно , то скорость изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).

Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:

Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.

Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:

(4)

ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:

(5)

Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.

Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.

Правило Ленца

Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.

Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.

Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.

Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.

Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .

Правило Ленца позволяет находить направление индукционного тока в любой ситуации.

Рассмотрим некоторые примеры применения правила Ленца.

Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.

Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.

Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).

Рис. 3. Магнитный поток возрастает

Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает

Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.

В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.

Взаимодействие магнита с контуром

Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?

Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.

1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.

Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.

Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .

Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1

Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.

Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.

Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .

Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.

Закон Фарадея + Правило Ленца = Снятие модуля

Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.

Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.

Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .

ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.

Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.

Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: .

Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).

Рис. 5. Магнитный поток возрастает

Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.

А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, (рис. 6).

Рис. 6. Магнитный поток возрастает

Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :

(6)

Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.

Вихревое электрическое поле

Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?

Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.

Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.

Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.

Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля

Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля

Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.

Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.

1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.

Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .

Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:

Следовательно, для ЭДС индукции получаем:

ЭДС индукции в движущемся проводнике

Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.

Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле . По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9).

Рис. 9. Движение проводника в магнитном поле

Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:

Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).

Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:

(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:

(7)

Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой . Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные — к точке .

Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к — и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).

Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:

Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень проходит путь и занимает положение (рис. 9). Площадь контура возрастает на величину площади прямоугольника :

Магнитный поток через контур увеличивается. Приращение магнитного потока равно:

Скорость изменения магнитного потока положительна и равна ЭДС индукции:

Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.

На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.

Закон электромагнитной индукции:магнитный поток и электродвижущая сила

 

После возникновения понятия о явлении электромагнитной индукции, интересно было бы узнать её количественные характеристики. Согласно опытам сила индукционного тока, которая возникнет в замкнутом контуре, будет пропорциональна изменению магнитного потока, который пронизывает этот контур.

Магнитный поток

Магнитный поток – это не что иное, как количество пронизывающих контур линий магнитной индукции. Чем больше их пронизывает контур, тем больше будет магнитный поток. Поэтому скорость изменения магнитного потока, можно представить как скорость изменения количество линий магнитной индукции, которые пронизывают контур.

За некоторое достаточно малое время ∆t магнитный поток изменится на некоторую величину ∆Ф. Следовательно, сила индукционного тока в замкнутом контуре будет пропорциональна скорости изменения магнитного потока, который пронизывает поверхность, ограниченную этим контуром.

Ii = ∆Ф/∆t.

Электродвижущая сила

Ток в цепи будет возникать при направленном движении заряженных частиц, под действием некоторых сторонних сил. Электродвижущая сила, величина численно равная работе сил по перемещению, единичного положительного заряда вдоль замкнутого контура, называется электродвижущей силой. 

При изменении магнитного потока в контуре возникает электрический ток, а следовательно, возникает электродвижущая сила, которая в этом случае называется ЭДС индукции. Для её обозначение используют прописную букву Е. Мы будем обозначать ЭДС индукции Ei.

Согласно закону Ома для замкнутой цепи, будет выполняться следующее равенство:

Ii = Ei/R.

Теперь сформулируем закон электромагнитной индукции. Он будет говорить об ЭДС индукции, так как сила тока, будет зависеть от свойств проводника, а ЭДС будет определяться только изменением магнитного потока, пронизывающего замкнутый контур.

Закон электромагнитной индукции

ЭДС индукции возникающая в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, которую ограничивает этот контур.

Ei = |∆Ф/∆t |.

Теперь необходимо учесть направление индукционного тока, который возникает в контуре. Для этого в формуле необходимо раскрыть модуль и поставить перед частным знак минус.

Ei = -∆Ф/∆t.

Индукционный ток должен быть направлен в направлении против положительного обхода контура. ЭДС индукции будет отрицательна.

Нужна помощь в учебе?

Предыдущая тема: Направление индукционного тока: правило Ленца и опыт
Следующая тема:&nbsp&nbsp&nbspСпособы определения ЭДС индукции в движущихся проводниках

«Двуликая» индукция

Подмена экспериментальной зависимости Фарадея «Основным законом электромагнитной индукции» Максвелла стало поворотным пунктом в развитии электродинамики. Из процесса взаимодействия магнитного поля с электрическими зарядами электромагнитная индукция (ЭМИ) превратилась в процесс взаимодействия полей. Это было самой большой мистификацией в электродинамике, определившей все ее развитие в 20-ом веке. В частности, исследования ЭМИ пошло по двум принципиально отличным путям.

Электромагнитная индукция в движущемся проводнике

Эксперименты показывают, что ЭДС индукции возникает в любом отрезке проводника, движущемся в магнитном поле и пересекающем линии магнитной индукции. ЭДС индукции в таком «микрогенераторе» можно рассчитать с помощью схемы, представленной на Рис.1. По параллельным металлическим «рельсам», замкнутым с одной стороны проводящей перемычкой AB, в однородном поле с магнитной индукцией B с постоянной скоростью v скользит проводящий «мостик» CD длиной l . За время dt магнитный поток, пронизывающий контур ABCD, возрастает на величину dФ = Bvl·dt, откуда

(1)

Согласно основному закону электромагнитной индукции ЭДС, индуктируемая в контуре, определяется соотношением

(2)

Так как все элементы контура, кроме «мостика», неподвижны относительно магнитного поля, то (2) — это и есть ЭДС, возникающая в движущемся проводнике.

Эта же ЭДС возникает и в незамкнутом проводящем отрезке, движущемся в магнитном поле (Рис. 2). Считается, что при перемещении проводящего отрезка в магнитном поле силой, «разделяющей» заряды q в проводнике и создающей на концах такого «микрогенератора» индукционную ЭДС, является магнитная составляющая силы Лоренца:

(3)

Если скорость движения проводника постоянна, то и ЭДС индукции остается постоянной. В момент остановки заряды в проводнике под действием кулоновских сил «схлопываются» и микрогенератор практически мгновенно разряжается.

ЭДС в таком индукционном микрогенераторе возникает вследствие того, что проводник пересекает линии магнитного поля с некоторой скоростью v. Назовем (для краткости) такой способ генерации ЭДС электромагнитной индукции «способом пересечения». Процесс электромагнитной индукции «с пересечением» можно схематически представить так:

пересечение → возникновение силы Лоренца → перемещение зарядов → образование ЭДС

Электромагнитная индукция в замкнутом контуре

В неподвижном недеформируемом контуре пересечение линий магнитного поля проводниками отсутствует. Изменение магнитного потока, пронизывающего контур, происходит вследствие изменения магнитной индукции В. Как же возникает индукционная ЭДС в этом случае? Вот как описан этот процесс в учебнике [1]: «В этом случае объяснение возникновения ЭДС оказывается в принципе (курсив мой — К.К.) другим. Изменяющееся со временем магнитное поле порождает вихревое электрическое поле Е… Под действием поля Е носители тока в проводнике приходят в движение — возникает индуцированный ток». Назовем такой способ генерация ЭДС «способом индукции».

Сравнивая «способ индукции» со «способом пересечения», автор [2] замечает, что «в результате изменения индукции на элементе проводника dl появляется ЭДС индукции Фарадея, которая не зависит от индукции B и скорости v движения этого элемента, а зависит только от dB/dt. Это и доказывает, что физическая природа ЭДС индукции в этих двух случаях различна». И даже так: «… оба эти явления (два механизма генерации ЭДС индукции — К.К.) … независимы друг от друга, и, тем не менее — что удивительно — ЭДС индукции в контуре всегда равна скорости изменения магнитного потока сквозь контур» [3].

Индукционный процесс по «способу индукции» можно представить так:

изменение магнитного потока → возникновение ЭДС → перемещение зарядов (индукционный ток)

Таким образом, сегодня электромагнитная индукция имеет «два лица», абсолютно непохожие друг на друга. Сравнив схематическое представление обоих процессов, можно заметить, что они в чем-то даже смотрятся «шиворот—навыворот»: в «способе пересечения» движение зарядов предшествует возникновению индукционной ЭДС, а по «способу индукции» — наоборот. Если вдуматься, то в «двуличии» индукционного процесса просматривается извечная проблема: «что первично — яйцо или курица», то есть — заряды или поля. Попробуем решить эту вечную проблему в одном частном случае.

Многочисленные эксперименты показывают, что ЭДС индукции в замкнутом контуре не зависит от того, каким способом изменяется пронизывающий его магнитный поток. Поскольку движение относительно, то во многих случаях возникновение ЭДС в замкнутом контуре можно свести к механизму пересечения проводниками магнитного потока. Этим механизмом можно объяснить возникновение в контуре индукционной ЭДС при приближении или удалении постоянного магнита, при вращении контура в однородном (или его поступательном движении — в неоднородном) магнитном поле, при деформации контура, приводящей к изменению его площади и/или ориентации, и во многих других случаях. И только один случай не удается описать этим механизмом — возникновение ЭДС в замкнутом неподвижном и недеформируемом контуре вследствие изменения магнитной индукции в потоке, пронизывающем контур.

Уже то обстоятельство, что только один экспериментальный факт не удается объяснить механизмом, безотказно работающим во всех остальных случаях (в том числе — и в замкнутом контуре), заставляет поискать другой способ описания процесса генерации ЭДС по «способу индукции».

Большинство авторов, по-видимому, представляет себе механизм изменения магнитного потока так: по мере увеличения магнитной индукции вновь появляющиеся линии магнитного поля как бы «расталкивают» уже существующие линии, увеличивая их плотность. Кстати, именно так представлял себе процесс возрастания магнитного потока в замкнутом контуре Максвелл: «… по мере возрастания… тока <в индукционной катушке> появляются новые линии и постепенно распространяются вовне, так что вся система развертывается изнутри» [4].

Представление магнитного поля совокупностью линий поля — это лишь модель непростого физического объекта, позволяющая дать его математическое описание. Предполагаемый механизм изменения магнитного поля — не единственный. Среди множества других вариантов описания этого процесса можно поискать и такой, который примирил бы оба способа генерации индукционной ЭДС.

На рис. 3 показан замкнутый проводящий контур в бесконечном однородном магнитном поле. Процесс увеличения магнитной индукции можно представить себе, как сгущение поля за счет поступления в поток, пронизывающий контур, новых линий поля извне — из окружающего пространства. При этом «вновь прибывающие» линии в своем движении «проникают» в контур, создавая в нем ЭДС индукции по «механизму пересечения». Такая модель сводит все случаи электромагнитной индукции к одному механизму — процессу пересечения магнитного потока проводником. Если, конечно, она не противоречит основному закону электромагнитной индукции. В этом еще нужно убедиться…

Разобьем замкнутый контур, представленный на рисунке 3, на n участков, изолированных друг от друга. При возрастании индукции в магнитном потоке по предлагаемому механизму магнитные линии, «проникая» в контур, пересекают его со скоростью v по направлению к центру. При этом выделенный на рисунке участок контура находится в тех же условиях, что и одиночный участок на рисунке 2. На каждый заряд в проводнике действует сила Лоренца F_L (3), с той лишь разницей, что скорость v — это скорость движения линий поля относительно неподвижного проводника. Как и на рисунке 2, сторонние силы «разносят» электрические заряды на концы участка, создавая на нем разность потенциалов Δφ_k = φ₁–φ₂. При этом на каждый заряд q действует кулоновская сила

(4)

где E_k — напряженность электрического поля на k-том участке контура. Эта сила равна по модулю и направлена навстречу силе Лоренца:

(5)

Полагая, что векторы v, B и элемент длины контура Δl_k взаимно перпендикулярны, соотношение (3) можно записать в скалярной форме:

(6)

Подставив (4) и (6) в (5), получаем

(7)

Если теперь соединить все участки в замкнутый контур, получим результирующую ЭДС в контуре

(8)

Разность потенциалов на участке определяется зависимостью

(9)

Подставляя (7) в (9) и далее в (8), получаем

(10)

В пределе (при n → ∞ и Δl_k→0) эта сумма переходит в интеграл

(11)

«Приток» линий магнитного поля в контур за время dt составляет, очевидно,

(12)

Сравнивая (12) и (2), получаем основной закон электромагнитной индукции.

Таким образом, предлагаемый механизм не противоречит основному закону электромагнитной индукции. Но он позволяет исключить «исключения» и свести все индукционные процессы к механизму пересечения.

Должен, однако, признаться, что идея описывать процесс возникновения индукционной ЭДС в замкнутом контуре способом пересечения принадлежит не мне. Меня опередил… Майкл Фарадей! Вот что писал по этому поводу ветеран электротехнического образования профессор МГУ С. Г. Калашников:

«… если проводник находится в покое, но изменяется магнитная индукция, то при усилении поля густота линий индукции будет увеличиваться, и они будут стягиваться друг к другу, а при ослаблении поля — расходиться друг от друга. И в этом случае произойдет пересечение некоторого числа линий индукции проводником. Поэтому Фарадей заключил, что индукционный ток возникает в проводнике в том случае, если проводник или какая-либо его часть пересекает линии магнитной индукции» [5].

Разрешение «парадоксов»

Таким образом, физическая природа электромагнитной индукции («способ пересечения») — едина:

Индукционная ЭДС возникает лишь в том случае, когда электрические заряды (проводник) пересекают линии магнитного поля.

Теперь можно вернуться к «парадоксам» электромагнитной индукции.

Расчёт, приведенный выше, сделан для того, чтобы показать, что возникновение индукционной ЭДС в замкнутом контуре по методу пересечения не противоречит и «максвелловской» формулировке закона электромагнитной индукции. Но «парадоксальные» схемы, приведенные здесь, ведут себя парадоксально лишь по отношению к «максвелловской» формулировке закона. Если же оценивать результаты этих экспериментов с точки зрения закона электромагнитной индукции Фарадея, то никаких парадоксов не возникает.

Начнём с того, что только при пересечении проводником линий поля на электрические заряды действует сила (сила Лоренца), способная совершить работу (создать ЭДС) (см. далее). Когда такое пересечение отсутствует, работа не совершается, не возникает индукционный ток и не создается ЭДС индукции.

Если обратиться к тем экспериментам (схемам), которые дают «парадоксальные» результаты, то во всех этих случаях пересечение проводниками линий магнитного поля отсутствует, в чем читатель может убедиться самостоятельно.

Наиболее трудным для понимания является сам «Парадокс Геринга». Хотя цепь гальванометра остается замкнутой, магнитное поле все-таки из нее «выскальзывает». Почему же гальванометр «молчит»? Причина в том, что магнитное поле «выскальзывает» из контура… вместе с электронами на этом участке цепи (металлическом «мостике» через магнитопровод). То есть и в этом случае электроны не пересекают линии магнитного поля. Поэтому ток в цепи и не возникает.

И еще один «парадокс»

В заключение этого раздела рассмотрим еще один — классический пример, который называют «Парадоксом Фарадея». Речь идет о так называемых «униполярных генераторах», которые уже много десятилетий используются в качестве сильноточных низковольтных электрогенераторов.

После открытия электромагнитной индукции М. Фарадей предложил несколько устройств с использованием этого явления. Одним из таких устройств был индукционный генератор, получивший название «Диск Фарадея». Устройство представляло вращающийся металлический диск 1 (см. Рис. 4), который пронизывал магнитный поток от постоянного магнита 2. Электрический контур, содержавший электроизмерительный прибор (3), подключался к диску двумя скользящими контактами — на оси диска (4) и на ободе (5). При вращении диска прибор показывал в цепи постоянный ток, зависящий от скорости вращения. Возникновение индукционной ЭДС в контуре объяснялось воздействием силы Лоренца на свободные электроны вращающегося диска при пересечении ими линий магнитного поля.

В XIX веке было опробовано много вариантов «машины Фарадея». Один из них озадачил исследователей. Оказалось, что ЭДС индукции возникает в контуре и в том случае, если магнит… вращается вместе с диском. Казалось бы, при этом сила Лоренца на электроны не действует, но прибор показывал ток в контуре. На рисунке 5 схематически представлен вариант такой модификация «машины Фарадея». Конструкция отличается от «Диска Фарадея» тем, что вместо диска вращается сам цилиндрический магнит.

Этот парадоксальный результат вызвал в XIX веке оживленную дискуссию по странному вопросу: а вращается ли магнитное поле вместе с его материальным носителем — магнитом? За полтора века ученые так и не пришли к единому мнению по этому вопросу. Сегодня эта тема активно обсуждается на Интернет-форумах. Один из участников этого форума привел простой аргумент, который (по моему мнению) дает логичный и исчерпывающий ответ на этот вопрос: «Ведь никто … не сомневается, что когда мы переносим магнит из комнаты в комнату, то с ним вместе перемещается и его магнитное поле. Почему же при вращении должно быть не так?!» [6].

Согласиться с этим простым и очевидным заключением, диктуемым здравым смыслом, мешает лишь… закон ЭМИ в максвелловской формулировке. Круг замкнулся…

История науки в XX веке изобилует примерами, когда, зайдя в тупик, «научная мысль» прибегала к услугам «палочки-выручалочки» — представлениям релятивизма. В 1929 году академик И. Е. Тамм, обсуждая принцип работы униполярного генератора, писал: «В движении силовых линий <магнитного поля — К. К.>, пересекающих неподвижный проводник … усматривалась причина возникновения в этом проводнике электродвижущих сил индукции. Нечего и говорить, что такая интерпретация не выдерживает никакой критики…» [7, §112]. Но если магнитное поле неподвижно, как возникает ЭДС в контуре? Объяснить работу униполярного генератора удалось лишь с помощью… представлений теории относительности. Такое объяснение уже тогда не встретило у специалистов ни восторга, ни понимания, ни согласия.

В 1956 году С. Г. Калашников снова привел описание работы униполярного генератора [5, с. 324]. В отличие от варианта, рассмотренного И. Е. Таммом, автор считал линии магнитной индукции вращающегося магнита направленными не вдоль оси магнита, а радиально («наподобие жестких спиц»). Но магнитное поле по-прежнему предполагалось неподвижным в пространстве. И хотя это — принципиально другая конструкция, тем не менее, теория относительности объяснила работу и такого устройства! Ну чем не «палочка-выручалочка»! Такое объяснение «униполярной индукции» сегодня доказательно оспаривается участниками Интернет-форумов.

Как же работает униполярный генератор? Если признать, что магнитное поле связано с магнитом, то очевидно, что в объеме магнита никакая ЭДС возникнуть не может. Это тот же механизм, который отвечает за «Парадокс Геринга»: в обоих случаях электроны магнита движутся вместе с его магнитным полем, отсутствует пересечение линий поля электрическими зарядами, а, следовательно, и индукционная ЭДС. Где же генерируется ток в контуре? Ответ очевиден: там, где линии поля пересекают контур, то есть в проводах на участке контура АС (см. рис. 5).

Так представления о механизме электромагнитной индукции по «способу пересечения» позволяют разрешить многие «парадоксы» электромагнитного взаимодействия, в том числе и классический «Парадокс Фарадея».

Таким образом, «парадокс» в том, что уже более 100 лет ошибочно трактуется физическая природа самого процесса электромагнитной индукции. Экспериментальная зависимость Фарадея заменена ее математически тождественным выражением Максвелла, из которого исчезли главные участники процесса — электрические заряды. Почему так произошло, почему этот «парадокс» больше века оставался не замеченным? На эти вопросы отвечать не физикам, а психологам…

Чтобы понять природу электромагнитных взаимодействий, познакомимся поближе с «участниками» этих взаимодействий – магнитным и электрическим полем.

Далее: Магнитное поле.

Ссылки

[1]	Савельев И. В. Курс общей физики. Т. 2. М.: Наука, 1978. С. 178.
[2]	Матвеев А. Н. Электричество и магнетизм. М.: Высш. школа, 1956. С. 317.
[3]	Иродов И. Е. Электромагнетизм. Основные законы. М.: Лаб. Базовых Знаний, 2001. С. 248.
[4]	Максвелл Д. К. Статьи и речи. М.: Наука, 1968. С. 59.
[5]	Калашников С. К. Электричество. М.: Физматлит, 2004. С. 194.
[6]	Мисюченко И. Последняя тайна Бога. СПб.: 2009. С. 106.
[7]	Тамм И. Е. Основы теории электричества. М.: Гос. изд-во техн.-теорет. лит., 1956.

Закон Фарадея

Концепция закона Фарадея заключается в том, что любое изменение магнитной среды катушки с проволокой вызывает в катушке «индуцированное» напряжение (ЭДС). Независимо от того, как производится изменение, напряжение будет генерироваться. Изменение может быть произведено изменением напряженности магнитного поля, перемещением магнита к катушке или от нее, перемещением катушки в магнитное поле или из него, вращением катушки относительно магнита и т. Д.

Слева вверху на иллюстрации две катушки пронизаны изменяющимся магнитным полем.Магнитный поток F определяется как F = BA, где B – магнитное поле или среднее магнитное поле, а A – площадь, перпендикулярная магнитному полю. Обратите внимание, что для данной скорости изменения потока через катушку генерируемое напряжение пропорционально количеству витков N, через которые проходит поток. Этот пример относится к работе трансформаторов, где магнитный поток обычно следует за железным сердечником от первичной катушки ко вторичной катушке и генерирует вторичное напряжение, пропорциональное количеству витков во вторичной катушке.

По часовой стрелке второй пример показывает напряжение, генерируемое при перемещении катушки в магнитное поле. Иногда это называют «ЭДС движения», и она пропорциональна скорости, с которой катушка перемещается в магнитное поле. Эта скорость может быть выражена через скорость изменения области, находящейся в магнитном поле.

Следующий пример – это стандартная геометрия генератора переменного тока, в которой катушка с проволокой вращается в магнитном поле. Вращение изменяет перпендикулярную площадь катушки по отношению к магнитному полю и генерирует напряжение, пропорциональное мгновенной скорости изменения магнитного потока.При постоянной скорости вращения генерируемое напряжение является синусоидальным.

Последний пример показывает, что напряжение можно генерировать, перемещая магнит к катушке с проволокой или от нее. При постоянной площади изменяющееся магнитное поле вызывает генерируемое напряжение. Направление или «смысл» генерируемого напряжения таковы, что любой результирующий ток создает магнитное поле, противодействующее изменению магнитного поля, которое его создало. Это значение знака минус в законе Фарадея, и это называется законом Ленца.

Магнитный поток, индукция и закон Фарадея

Индуцированные ЭДС и магнитный поток

Закон индукции Фарадея гласит, что электродвижущая сила индуцируется изменением магнитного потока.

Цели обучения

Объясните взаимосвязь между магнитным полем и электродвижущей силой

Основные выводы

Ключевые моменты

• Это изменение потока магнитного поля, которое приводит к возникновению электродвижущей силы (или напряжения).
• Магнитный поток (часто обозначаемый Φ или Φ _B ), проходящий через поверхность, является составляющей магнитного поля, проходящего через эту поверхность.
• В самом общем виде магнитный поток определяется как [латекс] \ Phi _ {\ text {B}} = \ iint _ {\ text {A}} \ mathbf {\ text {B}} \ cdot \ text {d} \ mathbf {\ text {A}} [/ latex]. Это интеграл (сумма) всего магнитного поля, проходящего через бесконечно малые элементы площади dA.

Ключевые термины

• векторная площадь : вектор, величина которого соответствует рассматриваемой области, а направление перпендикулярно площади поверхности.
• гальванометр : аналоговое измерительное устройство, обозначенное буквой G, которое измеряет ток, используя отклонение стрелки, вызванное силой магнитного поля, действующей на провод с током.

Индуцированная ЭДС

Аппарат, использованный Фарадеем для демонстрации того, что магнитные поля могут создавать токи, показан на следующем рисунке. Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается (или направляется) на катушку в нижней части кольца.Гальванометр используется для обнаружения любого тока, наведенного в отдельной катушке внизу.

Аппарат Фарадея : Это аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, вызывает ЭДС и, следовательно, ток в нижней катушке. Когда переключатель разомкнут и замкнут, гальванометр регистрирует токи в противоположных направлениях. Когда переключатель остается замкнутым или разомкнутым, через гальванометр не течет ток.

Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр обнаруживает ток в одном направлении в катушке внизу. Каждый раз при размыкании переключателя гальванометр обнаруживает ток в противоположном направлении. Интересно, что если переключатель остается замкнутым или разомкнутым в течение некоторого времени, через гальванометр нет тока. Замыкание и размыкание переключателя индуцирует ток. Это изменение магнитного поля, которое создает ток. Более важным, чем текущий ток, является вызывающая его электродвижущая сила (ЭДС).Ток является результатом ЭДС, индуцированной изменяющимся магнитным полем, независимо от того, есть ли путь для протекания тока.

Магнитный поток

Магнитный поток (часто обозначаемый Φ или Φ _B ), проходящий через поверхность, является составляющей магнитного поля, проходящего через эту поверхность. Магнитный поток через некоторую поверхность пропорционален количеству силовых линий, проходящих через эту поверхность. Магнитный поток, проходящий через поверхность с векторной площадью А, равен

.

[латекс] \ Phi_ \ text {B} = \ mathbf {\ text {B}} \ cdot \ mathbf {\ text {A}} = \ text {BA} \ cos \ theta [/ latex],

, где B – величина магнитного поля (в Тесла, Тл), A – площадь поверхности, а θ – угол между силовыми линиями магнитного поля и нормалью (перпендикулярно) к A.

Для переменного магнитного поля мы сначала рассмотрим магнитный поток [латекс] \ text {d} \ Phi _ \ text {B} [/ latex] через бесконечно малый элемент площади dA, где мы можем считать поле постоянным:

Изменяющееся магнитное поле : Каждая точка на поверхности связана с направлением, называемым нормалью к поверхности; магнитный поток, проходящий через точку, тогда является составляющей магнитного поля вдоль этого нормального направления.

[латекс] \ text {d} \ Phi_ \ text {B} = \ mathbf {\ text {B}} \ cdot \ text {d} \ mathbf {\ text {A}} [/ latex]

Общая поверхность A затем может быть разбита на бесконечно малые элементы, и тогда полный магнитный поток через поверхность равен интегралу поверхности

[латекс] \ Phi_ \ text {B} = \ iint_ \ text {A} \ mathbf {\ text {B}} \ cdot \ text {d} \ mathbf {\ text {A}} [/ latex].

Закон индукции Фарадея и закон Ленца

Закон индукции Фарадея гласит, что ЭДС, вызванная изменением магнитного потока, равна [латексу] \ text {EMF} = – \ text {N} \ frac {\ Delta \ Phi} {\ Delta \ text {t}} [ / латекс], когда поток изменяется на Δ за время Δt.

Цели обучения

Выразите закон индукции Фарадея в форме уравнения

Основные выводы

Ключевые моменты

• Минус в законе Фарадея означает, что ЭДС создает ток I и магнитное поле B, которые противодействуют изменению потока Δ, известному как закон Ленца.
• Закон индукции Фарадея является основным принципом работы трансформаторов, индукторов и многих типов электродвигателей, генераторов и соленоидов.
• Закон Фарадея гласит, что ЭДС, вызванная изменением магнитного потока, зависит от изменения магнитного потока Δ, времени Δt и числа витков катушек.

Ключевые термины

• электродвижущая сила : (ЭДС) – напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея.Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
• соленоид : Катушка с проволокой, которая действует как магнит, когда через нее протекает электрический ток.
• поток : Скорость передачи энергии (или другой физической величины) через данную поверхность, в частности электрического или магнитного потока.

Закон индукции Фарадея

Закон индукции Фарадея – это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).Это основной принцип работы трансформаторов, индукторов и многих типов электродвигателей, генераторов и соленоидов.

Эксперименты Фарадея показали, что ЭДС, вызванная изменением магнитного потока, зависит только от нескольких факторов. Во-первых, ЭДС прямо пропорциональна изменению потока Δ. Во-вторых, ЭДС является наибольшей, когда изменение во времени Δt наименьшее, то есть ЭДС обратно пропорциональна Δt. Наконец, если катушка имеет N витков, будет создаваться ЭДС, которая в N раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна N.Уравнение для ЭДС, вызванной изменением магнитного потока, равно

[латекс] \ text {EMF} = – \ text {N} \ frac {\ Delta \ Phi} {\ Delta \ text {t}} [/ latex].

Это соотношение известно как закон индукции Фарадея. Единицы измерения ЭДС, как обычно, – вольты.

Закон Ленца

Знак минус в законе индукции Фарадея очень важен. Минус означает, что ЭДС создает ток I и магнитное поле B, которые противодействуют изменению потока Δ, известному как закон Ленца. Направление (обозначенное знаком минус) ЭМП настолько важно, что оно названо законом Ленца в честь русского Генриха Ленца (1804–1865), который, подобно Фарадею и Генри, независимо исследовал аспекты индукции.Фарадей знал о направлении, но Ленц указал его, поэтому ему приписывают это открытие.

Закон Ленца : (a) Когда стержневой магнит вставляется в катушку, сила магнитного поля в катушке увеличивается. Ток, наведенный в катушке, создает другое поле в противоположном направлении от стержневого магнита, чтобы противодействовать увеличению. Это один из аспектов закона Ленца: индукция препятствует любому изменению потока. (b) и (c) – две другие ситуации. Убедитесь сами, что показанное направление индуцированной катушки B действительно противостоит изменению магнитного потока и что показанное направление тока согласуется с правилом правой руки.

Энергосбережение

Закон Ленца является проявлением сохранения энергии. Индуцированная ЭДС создает ток, который противодействует изменению потока, потому что изменение потока означает изменение энергии. Энергия может входить или уходить, но не мгновенно. Закон Ленца – это следствие. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. Фактически, если бы индуцированная ЭДС была в том же направлении, что и изменение потока, была бы положительная обратная связь, которая не давала бы нам бесплатную энергию из любого видимого источника – закон сохранения энергии был бы нарушен.

Движение ЭДС

Движение в магнитном поле, которое является стационарным относительно Земли, вызывает ЭДС движения (электродвижущую силу).

Цели обучения

Определить процесс, вызывающий двигательную электродвижущую силу

Основные выводы

Ключевые моменты

• Закон индукции Фарадея можно использовать для расчета ЭДС движения, когда изменение магнитного потока вызвано движущимся элементом в системе.
• То, что движущееся магнитное поле создает электрическое поле (и, наоборот, движущееся электрическое поле создает магнитное поле), является частью причины, по которой электрические и магнитные силы теперь рассматриваются как разные проявления одной и той же силы.
• Любое изменение магнитного потока индуцирует электродвижущую силу (ЭДС), противодействующую этому изменению – процесс, известный как индукция. Движение – одна из основных причин индукции.

Ключевые термины

• электродвижущая сила : (ЭДС) – напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
• магнитный поток : Мера силы магнитного поля в заданной области.
• индукция : Генерация электрического тока изменяющимся магнитным полем.

Как было замечено в предыдущих атомах, любое изменение магнитного потока индуцирует электродвижущую силу (ЭДС), противодействующую этому изменению – процесс, известный как индукция. Движение – одна из основных причин индукции. Например, магнит, перемещенный к катушке, индуцирует ЭДС, а катушка, перемещенная к магниту, создает аналогичную ЭДС. В этом атоме мы концентрируемся на движении в магнитном поле, которое является стационарным относительно Земли, производя то, что в общих чертах называется ЭДС движения.

ЭДС движения

Рассмотрим ситуацию, показанную на. Стержень перемещается со скоростью v по паре проводящих рельсов, разделенных расстоянием в однородном магнитном поле B. Рельсы неподвижны относительно B и соединены с неподвижным резистором R ( резистором может быть что угодно от лампочки до вольтметра). Учтите площадь, ограниченную подвижным стержнем, направляющими и резистором. B перпендикулярно этой области, и площадь увеличивается по мере перемещения стержня. Таким образом, магнитный поток между рельсами, стержнем и резистором увеличивается.Когда поток изменяется, ЭДС индуцируется согласно закону индукции Фарадея.

ЭДС движения : (a) ЭДС движения = Bℓv индуцируется между рельсами, когда этот стержень перемещается вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущемуся стержню и рельсам и, следовательно, к области, окружающей их. (б) Закон Ленца дает направление индуцированного поля и тока, а также полярность наведенной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или за пределы страницы.Правило правой руки дает указанное направление тока, и полярность стержня будет управлять таким током.

Чтобы найти величину ЭДС, индуцированной вдоль движущегося стержня, мы используем закон индукции Фарадея без знака:

[латекс] \ text {EMF} = \ text {N} \ frac {\ Delta \ Phi} {\ Delta \ text {t}} [/ latex].

В этом уравнении N = 1 и поток Φ = BAcosθ. Имеем θ = 0º и cosθ = 1, так как B перпендикулярно A. Теперь Δ = Δ (BA) = BΔA, поскольку B однородна. Отметим, что площадь, заметаемая стержнем, равна ΔA = ℓx.Ввод этих величин в выражение для ЭДС дает:

[латекс] \ text {EMF} = \ frac {\ text {B} \ Delta \ text {A}} {\ Delta \ text {t}} = \ text {B} \ frac {\ text {l} \ Дельта \ text {x}} {\ Delta \ text {t}} = \ text {Blv} [/ latex].

Чтобы найти направление индуцированного поля, направление тока и полярность наведенной ЭДС, мы применяем закон Ленца, как объяснено в Законе индукции Фарадея: Закон Ленца. Как видно на рис. 1 (b), уровень освещенности увеличивается, так как увеличивается закрытая площадь.Таким образом, индуцированное поле должно противостоять существующему и быть вне страницы. (Правило правой руки требует, чтобы я вращался против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано.)

Зависимость электрического поля от магнитного поля

Между электрической и магнитной силой существует множество связей. То, что движущееся магнитное поле создает электрическое поле (и, наоборот, движущееся электрическое поле создает магнитное поле), является частью причины, по которой электрические и магнитные силы теперь рассматриваются как различных проявлений одной и той же силы (впервые замечено Альбертом Эйнштейном) .Это классическое объединение электрических и магнитных сил в так называемую электромагнитную силу является источником вдохновения для современных усилий по объединению других основных сил.

Обратная ЭДС, вихревые токи и магнитное демпфирование

Обратная ЭДС, вихревые токи и магнитное затухание – все это происходит из-за наведенной ЭДС и может быть объяснено законом индукции Фарадея.

Цели обучения

Объясните взаимосвязь между двигательной электродвижущей силой, вихревыми токами и магнитным демпфированием

Основные выводы

Ключевые моменты

• Входной ЭДС, которая питает двигатель, может противодействовать самогенерируемая ЭДС двигателя, называемая обратной ЭДС двигателя.
• Если ЭДС движения может вызвать токовую петлю в проводнике, ток называется вихревым током.
• Вихревые токи могут вызывать значительное сопротивление движению, называемое магнитным затуханием.

Ключевые термины

• электродвижущая сила : (ЭДС) – напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
• Закон индукции Фарадея : основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).

Задняя ЭДС

Двигатели и генераторы очень похожи. (Прочтите наши атомы в разделах «Электрические генераторы» и «Электродвигатели».) Генераторы преобразуют механическую энергию в электрическую, а двигатели преобразуют электрическую энергию в механическую. Кроме того, двигатели и генераторы имеют одинаковую конструкцию. Когда катушка двигателя поворачивается, магнитный поток изменяется, и возникает электродвижущая сила (ЭДС), соответствующая закону индукции Фарадея. Таким образом, двигатель действует как генератор всякий раз, когда его катушка вращается.Это произойдет независимо от того, поворачивается ли вал под действием внешнего источника, например ременной передачи, или под действием самого двигателя. То есть, когда двигатель выполняет работу и его вал вращается, возникает ЭДС. Закон Ленца говорит нам, что наведенная ЭДС противодействует любому изменению, так что входной ЭДС, питающей двигатель, будет противодействовать самогенерируемая ЭДС двигателя, называемая обратной ЭДС двигателя.

Вихретоковый

Как обсуждалось в «ЭДС движения», ЭДС движения индуцируется, когда проводник движется в магнитном поле или когда магнитное поле движется относительно проводника.Если подвижная ЭДС может вызвать токовую петлю в проводнике, мы называем этот ток вихревым. Вихревые токи могут вызывать значительное сопротивление движению, называемое магнитным затуханием.

Рассмотрим устройство, показанное на рисунке, которое раскачивает маятник между полюсами сильного магнита. Если боб металлический, то при входе в поле и выходе из поля он испытывает значительное сопротивление, что быстро гасит движение. Однако, если боб представляет собой металлическую пластину с прорезями, как показано на (b), эффект от магнита будет гораздо меньше.Заметного воздействия на боб из изолятора не наблюдается.

Устройство для исследования вихревых токов и магнитного затухания : Обычное демонстрационное устройство для изучения вихревых токов и магнитного затухания. (а) Движение металлического маятника, раскачивающегося между полюсами магнита, быстро затухает под действием вихревых токов. (b) Имеется незначительное влияние на движение металлического боба с прорезями, что означает, что вихревые токи становятся менее эффективными. (c) На непроводящем бобе также отсутствует магнитное затухание, поскольку вихревые токи чрезвычайно малы.

показывает, что происходит с металлической пластиной, когда она входит в магнитное поле и выходит из него. В обоих случаях он испытывает силу, противодействующую его движению. Когда он входит слева, поток увеличивается, и поэтому возникает вихревой ток (закон Фарадея) в направлении против часовой стрелки (закон Ленца), как показано. Только правая сторона токовой петли находится в поле, так что слева на нее действует беспрепятственная сила (правило правой руки). Когда металлическая пластина полностью находится внутри поля, вихревой ток отсутствует, если поле однородно, поскольку поток остается постоянным в этой области.Но когда пластина покидает поле справа, поток уменьшается, вызывая вихревой ток по часовой стрелке, который, опять же, испытывает силу слева, еще больше замедляя движение. Аналогичный анализ того, что происходит, когда пластина поворачивается справа налево, показывает, что ее движение также затухает при входе в поле и выходе из него.

Проводящая пластина, проходящая между полюсами магнита : более подробный взгляд на проводящую пластину, проходящую между полюсами магнита.Когда он входит в поле и выходит из него, изменение потока создает вихревой ток. Магнитная сила на токовой петле препятствует движению. Когда пластина полностью находится внутри однородного поля, нет ни тока, ни магнитного сопротивления.

Когда металлическая пластина с прорезями входит в поле, как показано на, ЭДС индуцируется изменением магнитного потока, но это менее эффективно, поскольку прорези ограничивают размер токовых петель. Более того, в соседних контурах есть токи в противоположных направлениях, и их эффекты нейтрализуются.Когда используется изолирующий материал, вихревые токи чрезвычайно малы, поэтому магнитное затухание на изоляторах незначительно. Если необходимо избегать вихревых токов в проводниках, они могут быть выполнены с прорезями или состоять из тонких слоев проводящего материала, разделенных изоляционными листами.

Вихревые токи, индуцированные в металлической пластине с прорезями : Вихревые токи, индуцированные в металлической пластине с прорезями, входящие в магнитное поле, образуют небольшие петли, и силы на них имеют тенденцию нейтрализоваться, тем самым делая магнитное сопротивление почти нулевым.

Изменение магнитного потока создает электрическое поле

Закон индукции Фарадея гласит, что изменение магнитного поля создает электрическое поле: [latex] \ varepsilon = – \ frac {\ partial \ Phi_ \ text {B}} {\ partial \ text {t}} [/ latex].

Цели обучения

Опишите взаимосвязь между изменяющимся магнитным полем и электрическим полем

Основные выводы

Ключевые моменты

• Закон индукции Фарадея – это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу.
• Альтернативная дифференциальная форма закона индукции Фарадея выражается в уравнении [латекс] \ nabla \ times \ vec {\ text {E}} = – \ frac {\ partial \ vec {\ text {B}}} { \ partial \ text {t}} [/ latex].
• Закон индукции Фарадея – одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.

Ключевые термины

• векторная область : вектор, величина которого соответствует рассматриваемой области и направление которого перпендикулярно плоскости.
• Уравнения Максвелла : Набор уравнений, описывающих, как электрические и магнитные поля генерируются и изменяются друг другом, а также зарядами и токами.
• Теорема Стокса : утверждение об интегрировании дифференциальных форм на многообразиях, которое одновременно упрощает и обобщает несколько теорем векторного исчисления.

Мы изучили закон индукции Фарадея в предыдущих атомах. Мы узнали взаимосвязь между наведенной электродвижущей силой (ЭДС) и магнитным потоком.Вкратце, закон гласит, что изменение магнитного поля [латекс] (\ frac {\ text {d} \ Phi_ \ text {B}} {\ text {dt}}) [/ latex] создает электрическое поле [латекс] (\ varepsilon) [/ latex], закон индукции Фарадея выражается как [latex] \ varepsilon = – \ frac {\ partial \ Phi_ \ text {B}} {\ partial \ text {t}} [/ latex], где [латекс] \ varepsilon [/ latex] – это индуцированная ЭДС, а [latex] \ Phi_ \ text {B} [/ latex] – магнитный поток. («N» опущено из нашего предыдущего выражения. Число витков катушки может быть включено в магнитный поток, поэтому коэффициент не является обязательным.) Закон индукции Фарадея – это основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС). В этом Атоме мы узнаем об альтернативном математическом выражении закона.

Эксперимент Фарадея : эксперимент Фарадея, показывающий индукцию между витками проволоки: жидкая батарея (справа) обеспечивает ток, который течет через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется.Но когда малая катушка перемещается внутрь или из большой катушки (B), магнитный поток через большую катушку изменяется, вызывая ток, который регистрируется гальванометром (G).

Дифференциальная форма закона Фарадея

Магнитный поток [латекс] \ Phi_ \ text {B} = \ int_ \ text {S} \ vec {\ text {B}} \ cdot \ text {d} \ vec {\ text {A}} [/ латекс], где [латекс] \ vec {\ text {A}} [/ latex] – это векторная площадь над замкнутой поверхностью S. Устройство, которое может поддерживать разность потенциалов, несмотря на протекание тока, является источником электродвижущей силы. .(EMF) Математически определение [латекс] \ varepsilon = \ oint_ \ text {C} \ vec {\ text {E}} \ cdot \ text {d} \ vec {\ text {s}} [/ latex], где интеграл вычисляется по замкнутому циклу C.

Закон Фарадея теперь можно переписать [latex] \ oint_ \ text {C} \ vec {\ text {E}} \ cdot \ text {d} \ vec {\ text {s}} = – \ frac {\ partial} {\ partial \ text {t}} (\ int \ vec {\ text {B}} \ cdot \ text {d} \ vec {\ text {A}}) [/ latex]. Используя теорему Стокса в векторном исчислении, левая часть равна [latex] \ oint_ \ text {C} \ vec {\ text {E}} \ cdot \ text {d} \ vec {\ text {s}} = \ int_ \ text {S} (\ nabla \ times \ vec {\ text {E}}) \ cdot \ text {d} \ vec {\ text {A}} [/ latex].Также обратите внимание, что в правой части [latex] \ frac {\ partial} {\ partial \ text {t}} (\ int \ vec {\ text {B}} \ cdot \ text {d} \ vec {\ текст {A}}) = \ int \ frac {\ partial \ vec {\ text {B}}} {\ partial \ text {t}} \ cdot \ text {d} \ vec {\ text {A}} [ /латекс]. Таким образом, мы получаем альтернативную форму закона индукции Фарадея: [latex] \ nabla \ times \ vec {\ text {E}} = – \ frac {\ partial \ vec {\ text {B}}} {\ partial \ text {t}} [/ latex]. Это также называют дифференциальной формой закона Фарадея. Это одно из четырех уравнений Максвелла, управляющих всеми электромагнитными явлениями.

Электрогенераторы

Электрические генераторы преобразуют механическую энергию в электрическую; они индуцируют ЭДС, вращая катушку в магнитном поле.

Цели обучения

Объясните, как в электрогенераторах индуцируется электродвижущая сила.

Основные выводы

Ключевые моменты

• Электрический генератор вращает катушку в магнитном поле, индуцируя ЭДС, заданную как функцию времени величиной ε = NABw sinωt.
• Генераторы поставляют почти всю мощность для электрических сетей, которые обеспечивают большую часть мировой электроэнергии.
• Двигатель становится генератором, когда его вал вращается.

Ключевые термины

• электродвижущая сила : (ЭДС) – напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
• турбина : Любая из различных вращающихся машин, которые используют кинетическую энергию непрерывного потока жидкости (жидкости или газа) для вращения вала.

Электрические генераторы – это устройства, преобразующие механическую энергию в электрическую.Они индуцируют электродвижущую силу (ЭДС), вращая катушку в магнитном поле. Это устройство, преобразующее механическую энергию в электрическую. Генератор заставляет электрический заряд (обычно переносимый электронами) проходить через внешнюю электрическую цепь. Возможные источники механической энергии включают в себя поршневой или турбинный паровой двигатель, воду, падающую через турбину или водяное колесо, двигатель внутреннего сгорания, ветряную турбину, ручной кривошип, сжатый воздух или любой другой источник механической энергии.Генераторы поставляют почти всю мощность для электрических сетей, которые обеспечивают большую часть мировой электроэнергии.

Паровой турбогенератор : современный паротурбинный генератор.

Базовая настройка

Рассмотрим установку, показанную на. Заряды в проводах петли испытывают магнитную силу, потому что они движутся в магнитном поле. Заряды в вертикальных проводах испытывают силы, параллельные проводу, вызывая токи. Однако те, кто находится в верхнем и нижнем сегментах, ощущают силу, перпендикулярную проводу; эта сила не вызывает тока.Таким образом, мы можем найти наведенную ЭДС, рассматривая только боковые провода. ЭДС движения задается равной ЭДС = Bℓv, где скорость v перпендикулярна магнитному полю B (см. Наш Атом в «ЭДС движения»). Здесь скорость находится под углом θ к B, так что ее составляющая, перпендикулярная B, равна vsinθ.

Схема электрического генератора : Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, синусоидально изменяющуюся во времени.Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для выработки тока, а не наоборот.

Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС = Bℓvsinθ, и они направлены в одном направлении. Общая ЭДС [латекс] \ varepsilon [/ latex] вокруг петли тогда:

[латекс] \ varepsilon = 2 \ text {Blv} \ sin {\ theta} [/ latex].

Это выражение допустимо, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью ω.Угол θ связан с угловой скоростью соотношением θ = ωt, так что:

[латекс] \ varepsilon = 2 \ text {Blv} \ sin {\ omega \ text {t}} [/ latex].

Итак, линейная скорость v связана с угловой скоростью соотношением v = rω. Здесь r = w / 2, так что v = (w / 2) ω, и:

[латекс] \ varepsilon = 2 \ text {Bl} \ frac {\ text {w}} {2} \ omega \ sin {\ omega \ text {t}} = (\ text {lw}) \ text {B } \ omega \ sin {\ omega \ text {t}} [/ латекс].

Учитывая, что площадь петли A = ℓw, и учитывая N петель, мы находим, что:

[латекс] \ varepsilon = \ text {NABw} ~ \ sin {\ omega \ text {t}} [/ latex] – это ЭДС, индуцированная в катушке генератора N витков и площади A, вращающейся с постоянной угловой скоростью в однородное магнитное поле B.

Генераторы, показанные в этом Atom, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически, двигатель становится генератором, когда его вал вращается.

Электродвигатели

Электродвигатель – это устройство, преобразующее электрическую энергию в механическую.

Цели обучения

Объясните, как сила создается в электродвигателях

Основные выводы

Ключевые моменты

• Большинство электродвигателей используют взаимодействие магнитных полей и токопроводящих проводов для создания силы.
• Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца.
• В двигателе катушка с током в магнитном поле испытывает силу с обеих сторон катушки, которая создает крутящую силу (называемую крутящим моментом), заставляющую ее вращаться.

Ключевые термины

• Сила Лоренца : Сила, действующая на заряженную частицу в электромагнитном поле.
• крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)

Основные принципы работы двигателя такие же, как и у генератора, за исключением того, что двигатель преобразует электрическую энергию в механическую энергию (движение).(Сначала прочтите наш атом об электрических генераторах.) Большинство электродвигателей используют взаимодействие магнитных полей и проводников с током для создания силы. Электродвигатели находят применение в самых разных областях, таких как промышленные вентиляторы, нагнетатели и насосы, станки, бытовые приборы, электроинструменты и дисководы.

Lorentz Force

Если вы поместите движущуюся заряженную частицу в магнитное поле, на нее будет действовать сила, называемая силой Лоренца:

[латекс] \ text {F} = \ text {q} \ times \ text {v} \ times \ text {B} [/ latex]

Правило правой руки : Правило правой руки, показывающее направление силы Лоренца

, где v – скорость движущегося заряда, q – заряд, а B – магнитное поле.Ток в проводнике состоит из движущихся зарядов. Следовательно, катушка с током в магнитном поле также будет ощущать силу Лоренца. Для неподвижного прямолинейного токоведущего провода сила Лоренца составляет:

[латекс] \ text {F} = \ text {I} \ times \ text {L} \ times \ text {B} [/ latex]

где F – сила (в ньютонах, Н), I – ток в проводе (в амперах, А), L – длина провода, находящегося в магнитном поле (в м). , B, – напряженность магнитного поля (в теслах, Тл).Направление силы Лоренца перпендикулярно как направлению потока тока, так и магнитного поля, и его можно найти с помощью правила правой руки, показанного на рисунке. Используя правую руку, направьте большой палец в направлении тока, и укажите указательным пальцем в направлении магнитного поля. Ваш третий палец теперь будет указывать в направлении силы.

Момент : Сила на противоположных сторонах катушки будет в противоположных направлениях, потому что заряды движутся в противоположных направлениях.Это означает, что катушка будет вращаться.

Механика двигателя

И двигатели, и генераторы можно объяснить с помощью катушки, вращающейся в магнитном поле. В генераторе катушка подключена к внешней цепи, которая затем включается. Это приводит к изменению потока, который индуцирует электромагнитное поле. В двигателе катушка с током в магнитном поле испытывает силу с обеих сторон катушки, которая создает крутящую силу (называемую крутящим моментом), заставляющую ее вращаться.Любая катушка, по которой проходит ток, может чувствовать силу в магнитном поле. Эта сила является силой Лоренца, действующей на движущиеся заряды в проводнике. Сила на противоположных сторонах катушки будет в противоположных направлениях, потому что заряды движутся в противоположных направлениях. Это означает, что катушка будет вращаться.

Индуктивность

Индуктивность – это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве или на самом себе.

Цели обучения

Описание свойств катушки индуктивности с указанием взаимной индуктивности и самоиндукции

Основные выводы

Ключевые моменты

• Взаимная индуктивность – это влияние двух устройств, индуцирующих друг в друге ЭДС.Изменение тока ΔI ₁ / Δt в одном вызывает ЭДС ЭДС2 в секунду: ЭДС ₂ = -M ΔI ₁ / Δt, где M определяется как взаимная индуктивность между двумя устройствами.
• Самоиндуктивность – это эффект, который устройство вызывает само по себе.
• Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором, и ЭДС, индуцированная в нем изменением тока через него, равна ЭДС = −L ΔI / Δt.

Ключевые термины

• Закон индукции Фарадея : основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).
• Трансформатор : статическое устройство, передающее электрическую энергию от одной цепи к другой с помощью магнитной связи. Их основное назначение – передача энергии между различными уровнями напряжения, что позволяет выбирать наиболее подходящее напряжение для выработки, передачи и распределения электроэнергии по отдельности.

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными для создания желаемого напряжения и тока с очень небольшими потерями энергии в другие формы (см. Наш Atom в разделе «Трансформаторы.«) Есть ли полезная физическая величина, связанная с тем, насколько« эффективно »данное устройство? Ответ – да, и эта физическая величина называется индуктивностью.

Взаимная индуктивность

Взаимная индуктивность – это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.

Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор.Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы концентрируемся на скорости изменения тока, ΔI / Δt, как на причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1, индуцирует ЭДС ₂ в другом.Мы выражаем это в форме уравнения как

[латекс] \ text {EMF} _2 = – \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex],

, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M, тем эффективнее связь.

Природа здесь симметрична. Если мы изменим ток I2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, которая равна

[латекс] \ text {EMF} _1 = – \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex],

, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M.

Самоиндуктивность

Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство.Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается

[латекс] \ text {EMF} = – \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex],

где L – самоиндукция устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором. Опять же, знак минус является выражением закона Ленца, указывающего на то, что ЭДС препятствует изменению тока.

Количественная интерпретация ЭДС движения

A ЭДС движения – это электродвижущая сила (ЭДС), индуцированная движением относительно магнитного поля B.

Цели обучения

Сформулируйте две точки зрения, которые применяются для расчета электродвижущей силы

Основные выводы

Ключевые моменты

• Двигательная и наведенная ЭДС – это одно и то же явление, только наблюдаемое в разных системах отсчета. Эквивалентность этих двух явлений подтолкнула Эйнштейна к работе над специальной теорией относительности.
• ЭДС, возникающая из-за относительного движения петли и магнита, определяется как [latex] \ varepsilon _ {\ text {motion}} = \ text {vB} \ times \ text {L} [/ latex] (Eq.1), где L – длина объекта, движущегося со скоростью v относительно магнита.
• ЭДС можно рассчитать с двух разных точек зрения: 1) с точки зрения магнитной силы, действующей на движущиеся электроны в магнитном поле, и 2) с точки зрения скорости изменения магнитного потока. Оба дают одинаковый результат.

Ключевые термины

• специальная теория относительности : теория, которая (игнорируя эффекты гравитации) согласовывает принцип относительности с наблюдением, что скорость света постоянна во всех системах отсчета.
• магнитное поле : Состояние в пространстве вокруг магнита или электрического тока, в котором существует обнаруживаемая магнитная сила и где присутствуют два магнитных полюса.
• рамка отсчета : система координат или набор осей, в пределах которых можно измерить положение, ориентацию и другие свойства объектов в ней.

Электродвижущая сила (ЭДС), индуцированная движением относительно магнитного поля B, называется ЭДС движения. Вы могли заметить, что ЭДС движения очень похожа на ЭДС, вызванную изменением магнитного поля.В этом атоме мы видим, что это действительно одно и то же явление, показанное в разных системах отсчета.

ЭДС движения

В случае, когда проводящая петля перемещается в магнит, показанный на (а), магнитная сила, действующая на движущийся заряд в петле, определяется выражением [латекс] evB [/ латекс] (сила Лоренца, e: заряд электрона).

Петля проводника, движущаяся в магнит : (а) ЭДС движения. Токовая петля переходит в неподвижный магнит. Направление магнитного поля внутрь экрана.(б) Индуцированная ЭДС. Токовая петля неподвижна, а магнит движется.

Из-за силы электроны будут продолжать накапливаться на одной стороне (нижний конец на рисунке), пока на стержне не установится достаточное электрическое поле, препятствующее движению электронов, то есть [латекс] \ text {eE} [/ латекс]. Приравнивая две силы, получаем [латекс] \ text {E} = \ text {vB} [/ latex].

Следовательно, двигательная ЭДС на длине L стороны петли определяется как [latex] \ varepsilon _ {\ text {motion}} = \ text {vB} \ times \ text {L} [/ latex] (Eq .1), где L – длина объекта, движущегося со скоростью v относительно магнита.

Индуцированная ЭДС

Поскольку скорость изменения магнитного потока, проходящего через петлю, равна [latex] \ text {B} \ frac {\ text {dA}} {\ text {dt}} [/ latex] (A: площадь петли что магнитное поле проходит), индуцированная ЭДС [латекс] \ varepsilon _ {\ text {индуцированный}} = \ text {BLv} [/ latex] (уравнение 2).

Эквивалентность движущей и индуцированной ЭДС

Из уравнения. 1 и уравнение. 2 мы можем подтвердить, что двигательная и индуцированная ЭДС дают одинаковый результат.Фактически, эквивалентность двух явлений побудила Альберта Эйнштейна исследовать специальную теорию относительности. В своей основополагающей статье по специальной теории относительности, опубликованной в 1905 году, Эйнштейн начинает с упоминания эквивалентности двух явлений:

«…… например, взаимное электродинамическое действие магнита и проводника. Наблюдаемое явление здесь зависит только от относительного движения проводника и магнита, в то время как обычный взгляд проводит резкое различие между двумя случаями, когда одно или другое из этих тел находится в движении.Ведь если магнит находится в движении, а проводник находится в покое, в окрестности магнита возникает электрическое поле с определенной энергией , производящее ток в местах, где части проводника находятся расположенный. Но если магнит неподвижен, а проводник движется, электрическое поле поблизости от магнита не возникает. В проводнике, однако, мы находим электродвижущую силу, которой сама по себе не соответствует энергия, но которая порождает – при условии равенства относительного движения в двух рассмотренных случаях – электрические токи того же пути и силы, что и создаваемые электрическими силами в первом случае.«

Механические работы и электроэнергия

Механическая работа, совершаемая внешней силой для создания ЭДС движения, преобразуется в тепловую энергию; энергия сохраняется в процессе.

Цели обучения

Применить закон сохранения энергии для описания производственной двигательной электродвижущей силы с механической работой

Основные выводы

Ключевые моменты

• ЭДС движения, создаваемая движущимся проводником в однородном поле, задается следующим образом [latex] \ varepsilon = \ text {Blv} [/ latex].
• Чтобы стержень двигался с постоянной скоростью v, мы должны постоянно прикладывать внешнюю силу F _ext к стержню во время его движения.
• Закон Ленца гарантирует, что движение стержня противоположно, и, следовательно, закон сохранения энергии не нарушается.

Ключевые термины

• ЭДС движения : ЭДС (электродвижущая сила), индуцированная движением относительно магнитного поля.
• Закон индукции Фарадея : основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).

Мы узнали о двигательной ЭДС ранее (см. Наш Атом в «Двигательной ЭДС»). Для простой схемы, показанной ниже, ЭДС движения [латекс] (\ varepsilon) [/ латекс], создаваемая движущимся проводником (в однородном поле), задается следующим образом:

[латекс] \ varepsilon = \ text {Blv} [/ латекс]

, где B – магнитное поле, l – длина проводящего стержня, а v – (постоянная) скорость его движения. ( B , l и v все перпендикулярны друг другу, как показано на изображении ниже.)

ЭДС движения : (a) ЭДС движения = Bℓv индуцируется между рельсами, когда этот стержень перемещается вправо в однородном магнитном поле. Магнитное поле B направлено внутрь страницы, перпендикулярно движущемуся стержню и рельсам и, следовательно, к области, окружающей их. (б) Закон Ленца дает направление индуцированного поля и тока, а также полярность наведенной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или за пределы страницы. Правило правой руки дает указанное направление тока, и полярность стержня будет управлять таким током.

Сохранение энергии

В этом атоме мы рассмотрим систему с точки зрения энергии . Поскольку стержень движется и пропускает ток и , он ощущает силу Лоренца

.

[латекс] \ text {F} _ \ text {L} = \ text {iBL} [/ latex].

Чтобы стержень двигался с постоянной скоростью v , мы должны постоянно прикладывать внешнюю силу F _ext (равную величине F _L и противоположную по направлению) к стержню вдоль его движения. .Поскольку стержень движется под углом v , мощность P , передаваемая внешней силой, будет:

[латекс] \ text {P} = \ text {F} _ {\ text {ext}} \ text {v} = (\ text {iBL}) \ times \ text {v} = \ text {i} \ варепсилон [/ латекс].

На последнем этапе мы использовали первое уравнение, о котором мы говорили. Обратите внимание, что это в точности мощность, рассеиваемая в контуре (= ток [латекс] \ умноженное на [/ латекс] напряжение). Таким образом, мы заключаем, что механическая работа, совершаемая внешней силой, чтобы стержень двигался с постоянной скоростью, преобразуется в тепловую энергию в контуре.В более общем смысле, механическая работа, совершаемая внешней силой для создания ЭДС движения, преобразуется в тепловую энергию. Энергия сохраняется в процессе.

Закон Ленца

Из «Закона индукции Фарадея и закона Ленца» мы узнали, что закон Ленца является проявлением сохранения энергии. Как мы видим в примере с этим атомом, закон Ленца гарантирует, что движение стержня противодействует из-за склонности природы противодействовать изменению магнитного поля. Если бы индуцированная ЭДС была в том же направлении, что и изменение потока, возникла бы положительная обратная связь, заставляющая стержень улетать от малейшего возмущения.

Энергия в магнитном поле

Магнитное поле накапливает энергию. Плотность энергии задается как [латекс] \ text {u} = \ frac {\ mathbf {\ text {B}} \ cdot \ mathbf {\ text {B}}} {2 \ mu} [/ latex].

Цели обучения

Выразите плотность энергии магнитного поля в форме уравнения

Основные выводы

Ключевые моменты

• Энергия необходима для создания магнитного поля как для работы против электрического поля, создаваемого изменяющимся магнитным полем, так и для изменения намагниченности любого материала в магнитном поле.2 [/ латекс].

Ключевые термины

• проницаемость : Количественная мера степени намагничивания материала в присутствии приложенного магнитного поля (измеряется в ньютонах на квадратный ампер в единицах СИ).
• индуктор : пассивное устройство, которое вводит индуктивность в электрическую цепь.
• ферромагнетик : Материалы, обладающие постоянными магнитными свойствами.

Энергия необходима для создания магнитного поля как для работы против электрического поля, создаваемого изменяющимся магнитным полем, так и для изменения намагниченности любого материала в магнитном поле.Для недисперсионных материалов эта же энергия высвобождается при разрушении магнитного поля. Следовательно, эту энергию можно смоделировать как «хранящуюся» в магнитном поле.

Магнитное поле, создаваемое соленоидом : Магнитное поле, создаваемое соленоидом (вид в разрезе), описанное с использованием силовых линий. Энергия «хранится» в магнитном поле.

Энергия, запасенная в магнитном поле

Для линейных недисперсионных материалов (таких, что B = мкм, H, где мкм, называемая проницаемостью, не зависит от частоты), плотность энергии составляет:

[латекс] \ text {u} = \ frac {\ mathbf {\ text {B}} \ cdot \ mathbf {\ text {B}}} {2 \ mu} = \ frac {\ mu \ mathbf {\ text {H}} \ cdot \ mathbf {\ text {H}}} {2} [/ latex].

Плотность энергии – это количество энергии, хранящейся в данной системе или области пространства на единицу объема. Если поблизости нет магнитных материалов, μ можно заменить на μ ₀ . Однако приведенное выше уравнение нельзя использовать для нелинейных материалов; необходимо использовать более общее выражение (приведенное ниже).

В общем, дополнительная работа на единицу объема δW , необходимая для того, чтобы вызвать небольшое изменение магнитного поля δ B, составляет:

[латекс] \ delta \ text {W} = \ mathbf {\ text {H}} \ cdot \ delta \ mathbf {\ text {B}} [/ latex].

Когда связь между H и B известна, это уравнение используется для определения работы, необходимой для достижения заданного магнитного состояния. Для гистерезисных материалов, таких как ферромагнетики и сверхпроводники, необходимая работа также зависит от того, как создается магнитное поле. Однако для линейных недисперсионных материалов общее уравнение приводит непосредственно к более простому уравнению плотности энергии, приведенному выше.

Энергия, запасенная в поле соленоида

Энергия, запасаемая индуктором, равна количеству работы, необходимой для установления тока через индуктор и, следовательно, магнитного поля.2 [/ латекс].

Трансформаторы

Трансформаторы преобразуют напряжения из одного значения в другое; его функция определяется уравнением трансформатора.

Цели обучения

Примените уравнение трансформатора для сравнения вторичного и первичного напряжений

Основные выводы

Ключевые моменты

• Трансформаторы часто используются в нескольких точках систем распределения электроэнергии, а также во многих бытовых адаптерах питания.
Уравнение трансформатора
• гласит, что отношение вторичного напряжения к первичному в трансформаторе равно отношению количества витков в их катушках: [латекс] \ frac {\ text {V} _ \ text {s}} {\ text { V} _ \ text {p}} = \ frac {\ text {N} _ \ text {s}} {\ text {N} _ \ text {p}} [/ latex].
• Если предположить, что сопротивление незначительно, выходная электрическая мощность трансформатора равна его входной. Это приводит нас к другому полезному вопросу: [latex] \ frac {\ text {I} _ \ text {s}} {\ text {I} _ \ text {p}} = \ frac {\ text {N} _ \ текст {p}} {\ text {N} _ \ text {s}} [/ latex]. Если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.

Ключевые термины

• магнитный поток : мера силы магнитного поля в заданной области.
• Закон индукции Фарадея : основной закон электромагнетизма, который предсказывает, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС).

Трансформаторы изменяют напряжение с одного значения на другое. Например, такие устройства, как сотовые телефоны, ноутбуки, видеоигры, электроинструменты и небольшая бытовая техника, имеют трансформатор (встроенный в их съемный блок), который преобразует 120 В в напряжение, соответствующее устройству.Трансформаторы также используются в нескольких точках в системах распределения электроэнергии, как показано на рисунке. Мощность передается на большие расстояния при высоком напряжении, поскольку для данного количества мощности требуется меньший ток (это означает меньшие потери в линии). Поскольку высокое напряжение представляет большую опасность, трансформаторы используются для получения более низкого напряжения в месте нахождения пользователя.

Настройка трансформатора : Трансформаторы изменяют напряжение в нескольких точках в системе распределения электроэнергии. Электроэнергия обычно вырабатывается при напряжении более 10 кВ и передается на большие расстояния при напряжениях более 200 кВ, иногда даже 700 кВ, для ограничения потерь энергии.Распределение электроэнергии по районам или промышленным предприятиям осуществляется через подстанцию ​​и передается на короткие расстояния с напряжением от 5 до 13 кВ. Оно снижено до 120, 240 или 480 В для безопасности на месте отдельного пользователя.

Тип трансформатора, рассматриваемого здесь, основан на законе индукции Фарадея и очень похож по конструкции на устройство, которое Фарадей использовал для демонстрации того, что магнитные поля могут создавать токи (показано на рисунке). Две катушки называются первичной и вторичной катушками.При нормальном использовании входное напряжение подается на первичную обмотку, а вторичная обмотка создает преобразованное выходное напряжение. Мало того, что железный сердечник улавливает магнитное поле, создаваемое первичной катушкой, его намагниченность увеличивает напряженность поля. Поскольку входное напряжение переменного тока, изменяющийся во времени магнитный поток направляется во вторичную обмотку, вызывая ее выходное переменное напряжение.

Простой трансформатор : Типичная конструкция простого трансформатора имеет две катушки, намотанные на ферромагнитный сердечник, ламинированный для минимизации вихревых токов.Магнитное поле, создаваемое первичной обмоткой, в основном ограничивается и увеличивается сердечником, который передает его вторичной обмотке. Любое изменение тока в первичной обмотке вызывает ток во вторичной. На рисунке показан простой трансформатор с двумя катушками, намотанными с обеих сторон многослойного ферромагнитного сердечника. Набор катушек на левой стороне сердечника обозначен как первичный, и его номер указан как N p. Напряжение на первичной обмотке равно V p. Набор катушек на правой стороне сердечника обозначен как вторичный, и его номер представлен как N s.Напряжение на вторичной обмотке равно В с. Символ трансформатора также показан под диаграммой. Он состоит из двух катушек индуктивности, разделенных двумя равными параллельными линиями, представляющими сердечник.

Уравнение трансформатора

Для простого трансформатора, показанного на, выходное напряжение V _s почти полностью зависит от входного напряжения V _p и соотношения количества петель в первичной и вторичной обмотках. Закон индукции Фарадея для вторичной обмотки дает ее индуцированное выходное напряжение V _с как:

[латекс] \ text {V} _ \ text {s} = – \ text {N} _ \ text {s} \ frac {\ Delta \ Phi} {\ Delta \ text {t}} [/ latex],

, где N _s – количество витков вторичной катушки, а Δ / Δt – скорость изменения магнитного потока.Обратите внимание, что выходное напряжение равно индуцированной ЭДС (В _с = ЭДС _с ), при условии, что сопротивление катушки невелико. Площадь поперечного сечения катушек одинакова с обеих сторон, как и напряженность магнитного поля, поэтому / Δt одинаково с обеих сторон. Входное первичное напряжение V _p также связано с изменением магнитного потока:

[латекс] \ text {V} _ \ text {p} = – \ text {N} _ \ text {p} \ frac {\ Delta \ Phi} {\ Delta \ text {t}} [/ latex].

Соотношение этих двух последних уравнений дает полезное соотношение:

[латекс] \ frac {\ text {V} _ \ text {s}} {\ text {V} _ \ text {p}} = \ frac {\ text {N} _ \ text {s}} {\ текст {N} _ \ text {p}} [/ latex].

Это известно как уравнение трансформатора , которое просто устанавливает, что отношение вторичного напряжения к первичному в трансформаторе равно отношению количества петель в их катушках. Выходное напряжение трансформатора может быть меньше, больше или равно входному напряжению, в зависимости от соотношения количества витков в их катушках. Некоторые трансформаторы даже обеспечивают переменный выход, позволяя выполнять подключение в разных точках вторичной обмотки.Повышающий трансформатор – это трансформатор, который увеличивает напряжение, тогда как понижающий трансформатор снижает напряжение.

Если предположить, что сопротивление незначительно, выходная электрическая мощность трансформатора равна его входной. Уравнивание входной и выходной мощности,

[латекс] \ text {P} _ \ text {p} = \ text {I} _ \ text {p} \ text {V} _ \ text {p} = \ text {I} _ \ text {s} \ text {V} _ \ text {s} = \ text {P} _ \ text {s} [/ latex].

Комбинируя эти результаты с уравнением трансформатора, находим:

[латекс] \ frac {\ text {I} _ \ text {s}} {\ text {I} _ \ text {p}} = \ frac {\ text {N} _ \ text {p}} {\ текст {N} _ \ text {s}} [/ latex].

Значит, если напряжение увеличивается, ток уменьшается. И наоборот, если напряжение уменьшается, ток увеличивается.

Видео с вопросом: Скорость изменения наведенного тока

Стенограмма видео

Ток индуцируется в круговой петле радиусом 1,5 см между двумя полюсами подковообразного электромагнита, когда ток в электромагните изменяется. Магнитное поле в области петли перпендикулярно петле и имеет одинаковую величину.Если скорость изменения магнитного поля составляет 10 тесла в секунду, найдите величину индуцированного тока, если сопротивление контура составляет 25 Ом.

В этом утверждении нам сообщается скорость изменения магнитного поля, 10 тесла в секунду, которую мы назовем 𝑑𝐵 𝑑𝑡. Нам также сообщили, что сопротивление круговой петли составляет 25 Ом, что мы будем называть заглавной. Нам сказали, что радиус этой петли составляет 1,5 сантиметра, что мы будем называть строчными буквами 𝑟. Мы хотим найти величину тока, индуцируемого в контуре.Мы можем назвать это 𝐼.

Начнем с эскиза нашей петли в магните. У нас есть круглая проволочная петля с радиусом в нижнем регистре 𝑟 и электрическим сопротивлением большой буквы, 25 Ом. Наша петля помещена между полюсами подковообразного магнита, который представляет собой электромагнит, магнетизм которого создается пропусканием тока через петли, окружающие магнит.

Создается магнитное поле, которое проходит через круговую петлю. И сила этого магнитного поля со временем меняется.Нам сказали, что изменение 𝐵 по составляет 10 тесла в секунду. Чтобы вычислить ток, который индуцируется в круговой петле из-за этого изменения магнитного поля, мы можем вспомнить закон Фарадея. Этот закон гласит, что ЭДС, обозначенная здесь символом, индуцированная в проводе, равна изменению магнитного потока, который проходит через этот замкнутый контур за единицу времени, умноженному на количество витков в проводе.

И в подтверждение этого закона мы можем далее напомнить, что магнитный поток sub равен напряженности магнитного поля, умноженной на площадь, через которую это поле движется.Когда мы применяем закон Фарадея к нашему сценарию, первое, что мы замечаем, – это то, что 𝑁 равно единице. У нас есть только одна петля. Следующий элемент, который мы хотим рассмотреть, – это магнитный поток 𝜙 sub. Когда мы смотрим на отношения для этого, мы хотим увидеть, какие из 𝐵 или 𝐴 или оба меняются по мере развития этой проблемы.

Когда мы смотрим на круговую проволочную петлю, через которую проходят силовые линии магнитного поля, мы видим, что площадь этой петли не меняется на протяжении всей этой задачи. Однако магнитное поле со временем меняется.И нам сообщают скорость этого изменения в постановке задачи. Это указывает на то, что изменение количества 𝐵 раз 𝐴 за изменение времени равно 𝐴 раз 𝑑𝐵 𝑑𝐵, поскольку 𝐴 является постоянной величиной на всем протяжении.

Мы уже знаем 𝑑𝐵 𝑑𝑡, потому что он указан в формулировке задачи. И мы можем найти 𝐴, зная радиус нашей круговой петли в нижнем регистре 𝑟. Вспомнив, что площадь круга равна 𝜋, умноженному на квадрат его радиуса, мы можем написать, что наведенная ЭДС или напряжение в кольцевой проволочной петле равно 𝜋 умноженному на 0.015 квадратных метров, умноженных на 10 тесла в секунду.

Если бы мы вычислили это значение, оно дало бы нам ответ в единицах вольт. Но мы хотим получить ответ тока, который индуцируется в этом контуре, а не разности потенциалов. Вспоминая закон Ома, мы видим, что разность потенциалов равна произведению тока на сопротивление 𝑅.

Итак, чтобы найти ток, мы можем разделить наведенную ЭДС на сопротивление 𝑅, которое, как нам сказали, составляет 25 Ом. Когда мы вводим эти значения на нашем калькуляторе, мы видим, что до двух значащих цифр 𝐼 равно 2.8 раз по 10 в отрицательную четвертую ампер. Это ток, который индуцируется в кольцевой проволочной петле.

(PDF) О методе связи ЭДС и скорости изменения магнитного потока

Биография

Д-р Виджаякумар Х. Доддамани

Профессор

Физический факультет

Бангалорский университет

Джнанабхарати

Кампус Майнанабхарати

, Майнкрафт,

-56

Штат Карнатака

Индия

Доктор В.Х. Доддамани обучал аспирантов и докторантов последние 20 лет.Его исследования

областей включают активные галактические ядра, радиоастрономию, физику плазмы и т. Д. Под его руководством на докторскую степень работают несколько ученых

. Он опубликовал исследовательские работы в известных журналах и представил статьи на

национальных и международных конференциях. Он является членом нескольких ассоциаций и академических комитетов

, вносящих свой вклад в разработку лучших методик обучения и учебных программ. В настоящее время он участвует в разработке

экспериментов, связанных с радиоастрономией.

Равиша К.Х.

Факультет

Кафедра физики

Технологический институт CMR

IT Park Road

Кундалахалли

Бангалор-37

Штат Карнатака

Индию

студентов инженерного факультета Равеисха Кундалахалли преподавал в штате Карнатака. последние 18 лет. В настоящее время он

занимается разработкой лабораторных экспериментов для студентов бакалавриата.Он проводит исследования в области радиоастрономии

в Бангалорском университете и Индийском институте астрофизики в Бангалоре. Его интересы

включают разработку экспериментов, связанных с электромагнетизмом.

Ссылки

[1] Майкл Фарадей, Фил. Пер. R. Soc. Лондон. 1832, 122, 125-162

[2] Оливер Хевисайд, Электромагнитная теория, Лондон, Челси, 1897

[3] Дэвид Дж. Гриффитс, Введение в электродинамику (3-е издание), Нью-Дели, Прентис

Зал Индии , 2004

[4] D.Ченг, Полевая и волновая электромагнетизм (2-е издание), Нью-Дели, Пирсон

Education (Индия), 2002

[5] Натан Ида, Engineering Electromagnetics (2-е издание), Нью-Дели, Спрингер (Индия),

1998

[6] D. Chattopadyay et al., Electricity and Magnetism, Calcutta, Central, 2006,

[7] Джон Д. Краус, Electromagnetics (3-е издание), Нью-Йорк, McGraw-Hill, 2001

[8] Дж. Д. Джексон, Классическая электродинамика (3-е издание), Нью-Дели, Wiley India Edition,

2000

International Letters of Chemistry, Physics and Astronomy Vol.44 55

Демонстрационное оборудование

Набор индукционной первичной вторичной катушки (Science First item # 10-140) Аккумулятор 4,5 В Гальвонометр Переключатель Зажимы Алигатора (4) Скрепки

Студенты могут задаться вопросом, как работают трансформаторы и генераторы. Здесь описана потенциальная лаборатория или демонстрация принципа электромагнитной индукции Фарадея.Поскольку медные катушки (называемые петлей) содержат изменяющийся электрический заряд, объект, помещенный в электрическое поле, станет заряженным (намагниченным). Когда стержень вставляется и выходит из катушек, магнитное поле вокруг катушки заменены. Это, в свою очередь, заставляет электроны (ток) в катушка двигаться. Это можно наблюдать по чередующемуся (+) и (-) движениям. на гальванометре. Альтернативно или дополнительно устройство можно переконфигурировать так, чтобы электрический ток, генерируемый батареей, проходил через катушку.Стержень обеспечивает направление тока и стабилизирует его. Кроме того, стержень намагничивается, и его можно использовать для захвата небольших металлических предметов, например скрепок. Справочная информация: Закон индукции Фарадея Прописью: Индуцированная ЭДС (напряжение или разность потенциалов) вокруг замкнутого контура равна мгновенной скорости изменения (производной) магнитного потока через контур. В форме уравнения: Есть три способа изменить магнитный поток через петлю: Изменение напряженности магнитного поля (увеличение, уменьшение) по площади поверхности Изменить площадь петли (увеличить за счет расширения петли, уменьшить за счет сжатия петли) Измените угол между поверхностью, определяемой петлей, и вектором магнитного поля.Помните, что поток – это интеграл скалярного произведения между B и dA . Следовательно, изменение угла либо увеличивает, либо уменьшает поток, потому что скалярное произведение зависит от синуса угла между векторами B и dA . Так работает генератор. Генератор вращает петлю (фактически несколько витков) провода через фиксированное магнитное поле и индуцирует напряжение вокруг петли, быстро изменяя поток через петлю при ее вращении.Это индуцированное напряжение вокруг контуров заставляет ток течь через провод, и это выходной ток генератора. Знак минус указывает на то, что индуцированное напряжение направлено в направлении, которое создает ток, противодействующий изменению магнитного потока в контуре. Это соотношение зафиксировано в Законе Ленца. Закон Ленца : Индуцированный ток в проволочной петле будет в направлении, противоположном изменению потока через петлю.Другими словами, если поток через контур увеличивается, то индуцированный ток создаст свой собственный поток, который будет пытаться компенсировать увеличение потока. Если поток через петлю уменьшается, то индуцированный ток будет в направлении, которое пытается увеличить поток через петлю.

Процедура : Соберите материалы Подключите первичную (большую) катушку к гальванометру с помощью алигатора. зажимы Вводите стержень в катушку и вынимайте из нее и наблюдайте, как гальванометр движется в направлении движения Измените конфигурацию проводов и зажимов так, чтобы батарея замыкала цепь с большой катушкой. Продемонстрируйте, что стержень, помещенный в катушку, теперь намагничен и будет захватывать канцелярские скрепки, тактильные кнопки и скобы. Используйте то же расположение с батареей, на этот раз используя катушку меньшего диаметра. Обратите внимание, что с большим количеством витков катушка меньшего диаметра будет производить более сильный магнатизм, чем катушка большего размера. Стержень в меньшей катушке захватит больше зажимов. Записать результаты в таблицу данных Попросите учащихся ответить на вопросы Проведите мозговой штурм “реальных” приложений электромагнитных индукция

Индуктивность – Гипертекст по физике

Обсуждение

введение

Готовы? Вот так.

Пуск с соленоидом. Пропустите через него ток, и вы получите электромагнит. Поле внутри задается формулой…

B = μ 0 nI = μ 0	N	я
	ℓ

В то же время соленоид – это еще и устройство для улавливания магнитного потока.

Φ _B = NBA

Статическая ситуация, безусловно, достаточно интересна, но когда дело доходит до потока, то, что нас действительно волнует, – это скорость изменения во времени.Это то, что дает нам электромагнитную индукцию или индуцированную электродвижущую силу, или как вы хотите это называть. Эта ситуация описывается законом Фарадея.

Давайте еще раз рассмотрим эти уравнения, но с изменяющимся во времени поворотом. Соленоид с изменяющимся током, проходящим через него, будет генерировать изменяющееся магнитное поле.

дБ	= мк 0	N		dI
дт		ℓ		дт

Это изменяющееся магнитное поле затем улавливается тем самым соленоидом, который его создал.Захваченное поле называется потоком, а изменяющийся поток генерирует ЭДС – в данном случае самоиндуцированную или обратную ЭДС.

ℰ = –	d Φ B	= – N	⎛ ⎜	мкм 0	N		dI	⎞ ⎟	А
	дт				ℓ		дт

Немного изменив порядок вещей, мы получим это уравнение…

ℰ = –	мкм 0 AN 2		dI
	ℓ		дт

, который может показаться не таким уж большим, пока вы не поймете, что члены первой дроби в значительной степени определяются геометрией соленоида.Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.

Самоиндуцированная ЭДС в цепи прямо пропорциональна скорости изменения тока во времени ( dI / dt ), умноженной на константу ( L ). Эта постоянная называется индуктивностью (точнее, самоиндуктивностью ) и определяется геометрией схемы (или, чаще, геометрией отдельных элементов схемы).Например, индуктивность соленоида (как определено выше) определяется формулой…

Символ L для обозначения индуктивности был выбран в честь Генриха Ленца (1804–1865), чья новаторская работа в области электромагнитной индукции сыграла важную роль в развитии окончательной теории. Если вы помните, закон Ленца гласит, что индуцированный ток в цепи всегда действует таким образом, чтобы противодействовать изменению, которое в первую очередь его вызвало. Это наблюдение является причиной того, почему во всех версиях закона Фарадея стоит знак минус.Ленц поставил нам знак минус, и мы чествуем его символом L .

Индуктивность лучше всего определяется по ее роли в уравнении, выведенном из закона индукции Фарадея. Некоторым это не нравится, и они предпочитают определения, написанные в форме простого предложения субъект-глагол-объект.

На английском языке мы бы прочитали это как «самоиндуктивность ( L ) – это отношение обратной ЭДС () к временной скорости изменения тока, производящего ее ( dI / dt ).«Как я уже сказал, мне не очень нравится такое определение, но оно помогает нам определить подходящие единицы измерения.

⎡ ⎢ ⎣	H =	В	=	Дж / К	=	(кг · м 2 / с 2 ) / (A · с)	=	кг м 2	⎤ ⎥
		А / с		А / с		А / с		A 2 с 2

Единицей индуктивности является генри , названный в честь Джозефа Генри (1797–1878), американского ученого, открывшего электромагнитную индукцию независимо и примерно в то же время, что и Майкл Фарадей (1791–1867) в Англии.Первым свои открытия опубликовал Фарадей, поэтому ему заслуга в большей степени. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое легло в основу телеграфа). Схема с собственной индуктивностью в один генри будет испытывать противоэдс в один вольт, когда ток изменяется со скоростью один ампер в секунду.

Индуктивность – это что-то. Индуктивность – это сопротивление элемента схемы изменениям тока.Индуктивность в цепи – это аналог массы в механической системе.

ℰ = – л	dI	⇔	причина изменения	=	сопротивление изменить	×	ставка сдача	⇔	F = м	d v
	дт									дт

индуктивный датчик петли

Движение на некоторых перекрестках контролируется с помощью индуктивных петлевых детекторов (ILD).ILD – это петля из проводящего провода, проложенная всего на несколько сантиметров ниже тротуара. Когда автомобиль проходит через поле, он действует как проводник, изменяя индуктивность контура. Изменение индуктивности контура указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, отслеживания транспортного потока или автоматического цитирования.

примеры

индуктивность зависит от геометрии

Соленоид ( A площадь поперечного сечения, N количество витков, длина ℓ, n количество витков на длину)

Φ B	= N	Б		А
Φ B	= N	мкм 0 NI		А
		ℓ
Φ B	=	мкм 0 AN 2		я
		ℓ
d Φ B	=	мкм 0 AN 2		dI
дт		ℓ		дт
л	=	мкм 0 AN 2		=	мкм 0 Aℓn 2
		ℓ

коаксиальных проводников ( a внутренний радиус, b внешний радиус, длина)

Φ B	=	⌠	В	·	d A
		б						б
Φ B	=	⌠	мкм 0 I		ℓ др	=	мкм 0 Iℓ	⌠	др
			2π r				2π		r
		a						a
Φ B	=		мкм 0 ℓ		пер.	⎛ ⎜	a	⎞ ⎟	я
			2π				б
d Φ B	=		мкм 0 ℓ		пер.	⎛ ⎜	a	⎞ ⎟	dI
дт			2π				б		дт
л	=		мкм 0 ℓ		пер.	⎛ ⎜	a	⎞ ⎟
			2π				б

тороид ( A площадь поперечного сечения, R радиус вращения, N число витков)

Φ B	=	N	Б		А
Φ B	≈	N	мкм 0 NI		А
			2π R
Φ B	≈	N	мкм 0 NA		я
			2π R
d Φ B	≈		мкм 0 AN 2		dI
дт			2π R		дт
л	≈		мкм 0 AN 2
			2π R

прямоугольная петля ( w ширина, h высота, a радиус провода )

Φ B

=

N

Φ B

=

N

⎡ ⎢ x w x w ⎤ ⎥ мкм 0 NI ⌠ г др + ⌠ x др + ⌠ г др + ⌠ x др 2π r r r r a a a a

Φ B

=

2

мкм 0 N 2

⎡ ⎢

y ln

⎛ ⎜

x

⎞ ⎟

+

x дюйм

⎛ ⎜

y

⎞ ⎟

⎤ ⎥

я

2π

a

a

d Φ B

=

мкм 0 N 2

⎡ ⎢

y ln

⎛ ⎜

x

⎞ ⎟

+

x дюйм

⎛ ⎜

y

⎞ ⎟

⎤ ⎥

dI

дт

π

a

a

дт

л

=

мкм 0 N 2

⎡ ⎢

y ln

⎛ ⎜

x

⎞ ⎟

+

x дюйм

⎛ ⎜

y

⎞ ⎟

⎤ ⎥

π

a

a

Эта формула не совсем работает, поскольку игнорирует краевые эффекты.Вы можете найти точную формулу (а также скрипты, которые будут рассчитывать индуктивность для вас) в Интернете на нескольких веб-сайтах по электротехнике.

Что такое закон индукции Фарадея?

Закон индукции Фарадея описывает, как электрический ток создает магнитное поле и, наоборот, как изменяющееся магнитное поле генерирует электрический ток в проводнике. Английский физик Майкл Фарадей получил признание за открытие магнитной индукции в 1830 году; однако, по данным Техасского университета, американский физик Джозеф Генри, независимо друг от друга, сделал то же открытие примерно в то же время.

Значение открытия Фарадея невозможно переоценить. Магнитная индукция позволяет создавать электродвигатели, генераторы и трансформаторы, которые составляют основу современных технологий. Понимая и используя индукцию, мы получаем электрическую сеть и многие вещи, которые мы к ней подключаем.

Позже закон Фарадея был включен в более полные уравнения Максвелла, по словам Майкла Дабсона, профессора физики из Университета Колорадо в Боулдере.Уравнения Максвелла были разработаны шотландским физиком Джеймсом Клерком Максвеллом, чтобы объяснить взаимосвязь между электричеством и магнетизмом, по сути объединив их в единую электромагнитную силу и описав электромагнитные волны, из которых состоят радиоволны, видимый свет и рентгеновские лучи.

Электричество

Согласно Рочестерскому технологическому институту, электрический заряд является фундаментальным свойством материи. Хотя трудно описать, что это на самом деле, мы хорошо знакомы с тем, как он ведет себя и взаимодействует с другими зарядами и полями.По словам Серифа Урана, профессора физики в Питтсбургском государственном университете, электрическое поле от локализованного точечного заряда относительно просто. Он описывает ее как излучающую одинаково во всех направлениях, как свет от голой лампочки, и уменьшающуюся в силе как обратный квадрат расстояния (1/ r ² ) в соответствии с законом Кулона. Когда вы отодвигаетесь вдвое дальше, напряженность поля уменьшается до одной четвертой, а когда вы удаляетесь в три раза дальше, она уменьшается до одной девятой.

Протоны имеют положительный заряд, а электроны – отрицательный. Однако протоны в основном иммобилизованы внутри атомных ядер, поэтому перенос заряда из одного места в другое выполняют электроны. Электроны в проводящем материале, таком как металл, в значительной степени могут свободно перемещаться от одного атома к другому по своим зонам проводимости, которые являются высшими электронными орбитами. Достаточная электродвижущая сила (ЭДС) или напряжение вызывает дисбаланс заряда, который может заставить электроны перемещаться по проводнику из области с более отрицательным зарядом в область с более положительным зарядом.Это движение мы называем электрическим током.

Магнетизм

Чтобы понять закон индукции Фарадея, важно иметь базовые представления о магнитных полях. По сравнению с электрическим полем магнитное поле более сложное. По данным Государственного университета Сан-Хосе, хотя положительные и отрицательные электрические заряды могут существовать отдельно, магнитные полюса всегда приходят парами – северный и южный. Обычно магниты всех размеров – от субатомных частиц до магнитов промышленных размеров до планет и звезд – являются диполями, то есть каждый из них имеет два полюса.Мы называем эти полюса северным и южным по направлению, в котором указывают стрелки компаса. Интересно, что поскольку противоположные полюса притягиваются и, как полюса, отталкиваются, северный магнитный полюс Земли на самом деле является южным магнитным полюсом, потому что он притягивает северные полюса стрелок компаса.

Магнитное поле часто изображают в виде линий магнитного потока. В случае стержневого магнита силовые линии выходят из северного полюса и изгибаются, чтобы снова войти в южный полюс. В этой модели количество силовых линий, проходящих через заданную поверхность в пространстве, представляет собой плотность потока или напряженность поля.Однако следует отметить, что это всего лишь модель. Магнитное поле гладкое и непрерывное и на самом деле не состоит из дискретных линий.

Силовые линии магнитного поля от стержневого магнита. (Изображение предоставлено snapgalleria Shutterstock)

Магнитное поле Земли создает огромный магнитный поток, но он рассеивается в огромном объеме космоса. Следовательно, только небольшое количество потока проходит через данную область, что приводит к относительно слабому полю. Для сравнения, магнитный поток от магнита-холодильника крошечный по сравнению с магнитным потоком Земли, но его сила поля во много раз сильнее на близком расстоянии, где его силовые линии гораздо более плотно упакованы.Однако по мере удаления поле быстро становится намного слабее.

Индукция

Если пропустить через провод электрический ток, вокруг него возникнет магнитное поле. Направление этого магнитного поля можно определить по правилу правой руки. По данным физического факультета Университета штата Нью-Йорк Буффало, если вы вытянете большой палец и согнете пальцы правой руки, ваш большой палец будет указывать в положительном направлении тока, а пальцы согнуты в северном направлении магнитного поля. .

Правило левой и правой руки для магнитного поля, вызванного током в прямом проводе. (Изображение предоставлено Фуадом А. Саадом Shutterstock)

Если вы согнете провод в петлю, силовые линии магнитного поля согнутся вместе с ним, образуя тороид или форму пончика. В этом случае ваш большой палец указывает в северном направлении магнитного поля, выходящего из центра петли, а ваши пальцы будут указывать в положительном направлении тока в петле.

В круговой петле с током (а) правило правой руки определяет направление магнитного поля внутри и вне петли.(б) Более подробное отображение поля, подобное полю стержневого магнита. (Изображение предоставлено OpenStax)

Если мы пропустим ток через проволочную петлю в магнитном поле, взаимодействие этих магнитных полей будет оказывать скручивающую силу или крутящий момент в петле, заставляя ее вращаться, согласно данным Рочестерского института. Технологии. Однако он будет вращаться только до тех пор, пока магнитные поля не выровняются. Если мы хотим, чтобы петля продолжала вращаться, мы должны изменить направление тока, что изменит направление магнитного поля петли.Затем петля повернется на 180 градусов, пока ее поле не выровняется в другом направлении. Это основа электродвигателя.

И наоборот, если мы вращаем проволочную петлю в магнитном поле, поле будет индуцировать электрический ток в проводе. Направление тока меняется каждые пол-оборота, создавая переменный ток. Это основа электрогенератора. Здесь следует отметить, что это не движение провода, а скорее размыкание и замыкание петли по отношению к направлению поля, которое индуцирует ток.Когда петля обращена лицом к полю, через петлю проходит максимальное количество магнитного потока. Однако, когда петля повернута ребром к полю, силовые линии не проходят через петлю. Именно это изменение количества потока, проходящего через контур, вызывает ток.

Другой эксперимент, который мы можем провести, – сформировать из провода петлю и подключить концы к чувствительному измерителю тока или гальванометру. Если затем протолкнуть стержневой магнит через петлю, стрелка гальванометра переместится, указывая на индуцированный ток.Однако, как только мы останавливаем движение магнита, ток возвращается к нулю. Поле от магнита будет индуцировать ток только тогда, когда он увеличивается или уменьшается. Если мы вытащим магнит обратно, он снова вызовет ток в проводе, но на этот раз он будет в противоположном направлении.

Магнит в проволочной петле, подключенной к гальванометру. (Изображение предоставлено: Фуад А. Саад Shutterstock)

Если бы мы включили в цепь электрическую лампочку, она рассеивала бы электрическую энергию в виде света и тепла, и мы бы почувствовали сопротивление движению магнита при движении. это внутри и вне цикла.Чтобы переместить магнит, мы должны совершить работу, эквивалентную энергии, используемой лампочкой.

В еще одном эксперименте мы могли бы построить две проволочные петли, соединить концы одной с батареей с помощью переключателя и подключить концы другой петли к гальванометру. Если мы поместим две петли близко друг к другу лицом к лицу и включим питание первой петли, гальванометр, подключенный ко второй петле, покажет индуцированный ток, а затем быстро вернется к нулю.

Здесь происходит то, что ток в первом контуре создает магнитное поле, которое, в свою очередь, индуцирует ток во втором контуре, но только на мгновение, когда магнитное поле изменяется. Когда вы выключаете переключатель, счетчик на мгновение отклоняется в противоположном направлении. Это еще один признак того, что ток индуцирует изменение интенсивности магнитного поля, а не его сила или движение.

Объяснение этому состоит в том, что магнитное поле заставляет электроны в проводнике двигаться.Это движение мы называем электрическим током. В конце концов, однако, электроны достигают точки, в которой они находятся в равновесии с полем, и в этой точке они перестают двигаться. Затем, когда поле снимается или выключается, электроны возвращаются в свое исходное положение, создавая ток в противоположном направлении.

В отличие от гравитационного или электрического поля, магнитное дипольное поле представляет собой более сложную трехмерную структуру, сила и направление которой различаются в зависимости от места измерения, поэтому для ее полного описания требуется расчет.Однако мы можем описать упрощенный случай однородного магнитного поля – например, очень маленький участок очень большого поля – как Φ B = BA , где Φ B – абсолютное значение магнитного потока. , B, – это напряженность поля, а A – это определенная область, через которую проходит поле. И наоборот, в этом случае напряженность магнитного поля – это поток на единицу площади, или B = Φ B / A .

Закон Фарадея

Теперь, когда у нас есть базовое представление о магнитном поле, мы готовы определить закон индукции Фарадея.Он утверждает, что индуцированное напряжение в цепи пропорционально скорости изменения во времени магнитного потока, проходящего через эту цепь. Другими словами, чем быстрее изменяется магнитное поле, тем больше будет напряжение в цепи. Направление изменения магнитного поля определяет направление тока.

Увеличить напряжение можно за счет увеличения количества витков в цепи. Индуцированное напряжение в катушке с двумя петлями будет вдвое больше, чем с одной петлей, а с тремя петлями – втрое.Вот почему настоящие двигатели и генераторы обычно имеют большое количество катушек.

Теоретически моторы и генераторы одинаковы. Если вы включите двигатель, он будет вырабатывать электричество, а подача напряжения на генератор заставит его вращаться. Однако большинство реальных двигателей и генераторов оптимизированы только для одной функции.

Трансформаторы

Еще одним важным приложением закона индукции Фарадея является трансформатор, изобретенный Николой Тесла. В этом устройстве переменный ток, который меняет направление много раз в секунду, проходит через катушку, намотанную вокруг магнитного сердечника.Это создает изменяющееся магнитное поле в сердечнике, которое, в свою очередь, индуцирует ток во второй катушке, намотанной вокруг другой части того же магнитного сердечника.

Схема трансформатора (Изображение предоставлено photoiconix Shutterstock)

Отношение числа витков в катушках определяет соотношение напряжения между входным и выходным током. Например, если мы возьмем трансформатор со 100 витками на входе и 50 витками на выходе, и введем переменный ток 220 вольт, выход будет 110 вольт.Согласно Hyperphysics, трансформатор не может увеличивать мощность, которая является произведением напряжения и тока, поэтому, если напряжение повышается, ток пропорционально понижается, и наоборот. В нашем примере входное напряжение 220 В при 10 А или 2200 Вт даст на выходе 110 В при 20 А, опять же 2200 Вт. На практике трансформаторы никогда не бывают идеально эффективными, но, по данным Техасского университета, потери мощности хорошо спроектированного трансформатора обычно составляют всего несколько процентов.

Трансформаторы делают возможной электрическую сеть, от которой мы зависим для нашего промышленного и технологического общества. Линии передачи по пересеченной местности работают под напряжением в сотни тысяч вольт, чтобы передавать больше энергии в пределах допустимого для проводов тока.