Онлайн калькулятор для расчета электромагнитной силы
В процессе эксплуатации электрического оборудования львиная доля логических схем используют в своей работе в качестве исполнительного органа катушку с магнитным сердечником. Принцип работы данного устройства заключается в появлении магнитной силы внутри витков, которая притягивает соленоид и совершает механическую работу.
За счет такого воздействия происходит перемещение контактов реле, открытие или закрытие клапанов, механическое включение кнопок и прочие манипуляции. Возможность перемещения того или иного ферромагнитного сердечника определяется параметрами катушки, которые и обуславливают величину электромагнитной силы.
Катушка с сердечникомЧтобы рассчитать электромагнитную силу катушки, с которой та воздействует на соленоид, используется онлайн калькулятор. Для расчета силы введите данные в соответствующие поля калькулятора:
- Укажите величину тока в амперах;
- Внесите площадь сечения сердечника в квадратных метрах;
- Проставьте значение количества витков в катушке;
- Укажите величину зазора между магнитопроводом и соленоидом катушки;
- Нажмите кнопку «Рассчитать» и в графе электромагнитной силы появится результат вычислений.
Если в результате расчета вы получили недостаточную величину силы и необходимо подобрать другие параметры для катушки, то просто сбросьте данные. Для этого используйте кнопку «Сбросить», которая обнулит нынешнее значение.
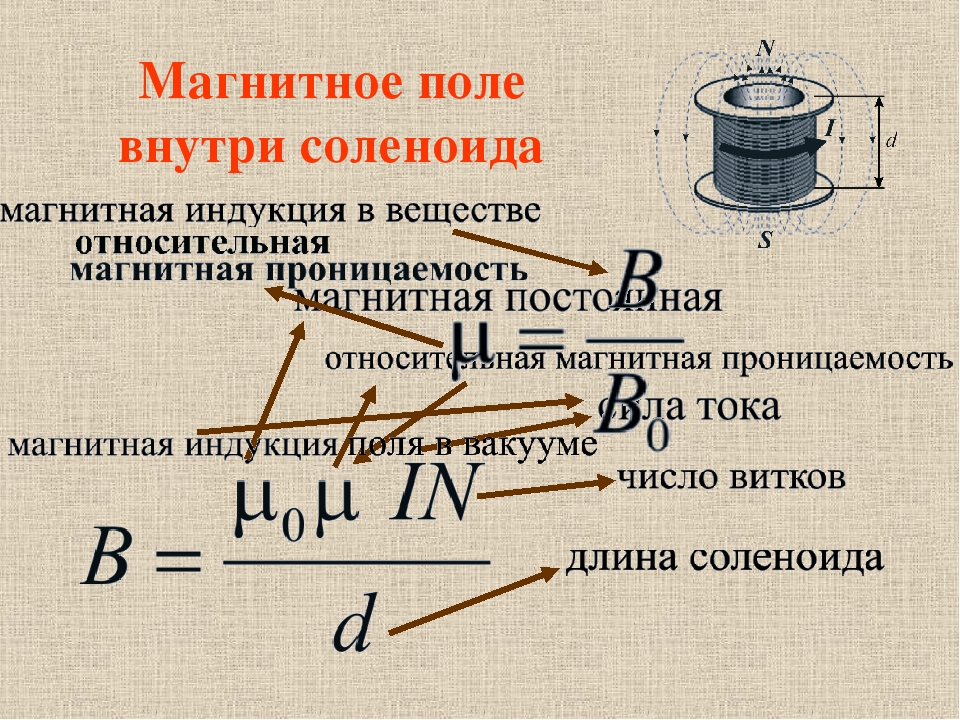
В калькуляторе для расчета электромагнитной силы используется такая формула:
Где
- F – величина электромагнитной силы, создаваемой катушкой;
- n – количество витков в этой катушке;
- I – сила тока, протекающего по катушке;
- m – магнитная постоянная;
- S – величина площади поперечного сечения магнитопровода;
- lср – величина зазора между элементами магнитной цепи.
Вышеприведенные расчеты применяются в случае выхода со строя катушки с магнитным сердечником, выполнявшей роль исполнительного органа какой-либо логической цепи, когда возникает вопрос о необходимости замены катушки или намотки новой. Калькулятор для расчета электромагнитной силы позволяет подбирать оптимальные параметры индуктивного элемента путем изменения каких-либо ее характеристик.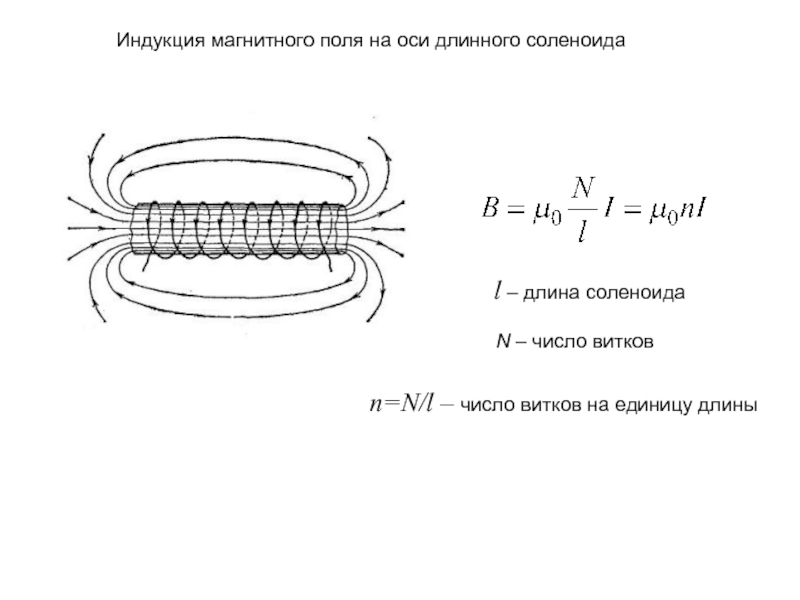
Калькулятор магнитной индукции соленоида • Магнитостатика, магнетизм и электродинамика • Онлайн-конвертеры единиц измерения
Определения и формулы
Соленоид представляет собой намотанную виток к витку катушку, длина которой значительно больше ее диаметра. Если через катушку соленоида протекает электрический ток, в ней образуется однородное магнитное поле. Соленоиды с ферромагнитными сердечниками часто используются в качестве исполнительных механизмов для преобразования электрической энергии в линейное перемещение сердечника. Самым привычным примером такого соленоида является реле стартера, которое выполняет две функции: подает напряжение на двигатель стартера и вводит шестерню двигателя стартера в зацепление с маховиком коленвала двигателя на время запуска.
Модуль магнитной индукции B длинного соленоида в воздухе без сердечника рассчитывается по формуле
где μ₀=4π × 10⁻⁷ Гн/м — магнитная постоянная, N число витков катушки соленоида, I протекающий через катушку ток и L — длина соленоида.
Соленоиды и ферромагнитные жидкости
Соленоидные исполнительные механизмы — довольно шумные устройства, поэтому иногда в зазор между сердечником и каркасом катушки вводят ферромагнитную жидкость. Она уменьшает или даже полностью устраняет шум при срабатывании соленоида, а также увеличивает силу притяжения, что позволяет уменьшить размеры соленоидных исполнительных устройств при сохранении их характеристик. Ферромагнитные жидкости также позволяют уменьшить утечку магнитного поля в магнитопроводе, а также улучшают охлаждение соленоида.
Еще одно применение ферромагнитных жидкостей в соленоидах — в качестве эластичного сердечника. Это позволяет изготовить эластичные соленоиды, которые можно использовать в современных гибких электронных устройствах, например, в носимых компьютерах и устройствах биомедицинского контроля.
Общие сведения
Синий и зеленый лазерные лучи хорошо видны через коллоидную смесь благодаря эффекту Тиндаля
В этой статье поговорим о занимательных и необычных ферромагнитных жидкостях. Если их намагнитить, воздействуя на них магнитным полем, то эти жидкости формируют интересные складки на поверхности. Ферромагнитные жидкости — это коллоидные системы, состоящие из наночастиц
Если их намагнитить, воздействуя на них магнитным полем, то эти жидкости формируют интересные складки на поверхности. Ферромагнитные жидкости — это коллоидные системы, состоящие из наночастиц
Пронаблюдать ван-дер-ваальсовы силы в действии можно, когда гекконы, ящерицы анолисы, сцинковые и некоторые насекомые перемещаются по вертикальным поверхностям стен, или даже по потолку
Зеленая ящерица анолис
Молекулы поверхностно-активного вещества присоединяются к наночастицам и окружают каждую частицу, создавая, таким образом, буфер вокруг частицы. Притяжение между наночастицами регулируется ван-дер-ваальсовыми силами, которые ослабевают при увеличении расстояния между этими частицами. Поэтому, когда расстояние между наночастицами увеличивается благодаря поверхностно-активному веществу, притяжение между этими частицами ослабевает.
Магнетит
В некоторых случаях поверхностно-активные вещества работают по-другому. Их молекулы присоединяются к наночастице так, что их наружная полярность одинакова по всей наружной поверхности (например, наружная оболочка приобретает положительный заряд). Таким образом, вокруг каждой наночастицы образуется оболочка с определенным зарядом.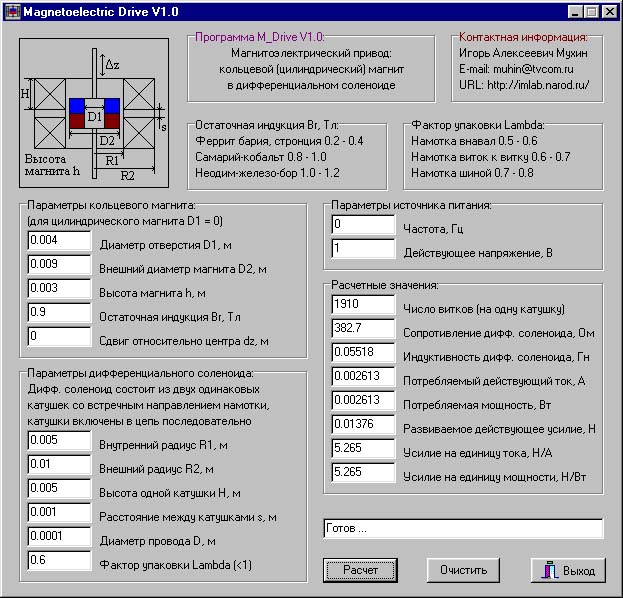
Магнетит, как естественный магнит
Мы немного поговорили о жидкостях-носителях. Но из чего же состоят сами наночастицы? Иногда для этого используют частицы магнетита — минерала с магнитными свойствами. Магнетит — минерал, встречающийся в природе, который легко намагнитить. Стоит заметить, что в некоторых особых случаях магнетит имеет свойства постоянного магнита, то есть в обычных условиях его магнитные свойства постоянны и неизменны. Частицы магнетита в ферромагнитных жидкостях не являются постоянным магнитом, то есть их можно намагнитить с помощью магнитного поля, но это намагничивание пропадает, как только магнитное поле перестает на них действовать. Также для изготовления ферромагнитных жидкостей используют высокодисперсные порошки металлов, обладающих магнитными свойствами и некоторые ферримагнитные материалы.
Свойства
Ферромагнитные жидкости под действием магнитного поля — завораживающее зрелище. На поверхности образуются складки похожие на конусы, и при перемещении магнитного поля эти складки движутся за полем. Они располагаются по силовым линиям, и их высота зависит от силы магнитного поля. Сила магнитного поля, в свою очередь, зависит от того, как близко расположен магнит относительно жидкости. Ниже мы обсудим различные применения ферромагнитных жидкостей. Все эти применения основываются на этом свойстве ферромагнитной жидкости двигаться за магнитным полем.
На поверхности образуются складки похожие на конусы, и при перемещении магнитного поля эти складки движутся за полем. Они располагаются по силовым линиям, и их высота зависит от силы магнитного поля. Сила магнитного поля, в свою очередь, зависит от того, как близко расположен магнит относительно жидкости. Ниже мы обсудим различные применения ферромагнитных жидкостей. Все эти применения основываются на этом свойстве ферромагнитной жидкости двигаться за магнитным полем.
Разобранный гидродинамический подшипник накопителя на жестких магнитных дисках
Свойства ферромагнитных жидкостей изменяются с температурой. При очень высоких температурах, известных как температура или точка Кюри, наночастицы теряют магнитные свойства и ферромагнитная жидкость превращается в обычную жидкость. Также, со временем поверхностно-активное вещество теряет отталкивающие свойства, и наночастицы слипаются, так что при этом свойства ферромагнитной жидкости пропадают.
Использование ферромагнитных жидкостей
Ферромагнитные жидкости реагируют на магнит и следуют за ним, поэтому с помощью магнита их можно либо перемещать с места на место, либо удерживать в нужном месте. Благодаря этому они нашли широкое применение в науке, технике и медицине.
Благодаря этому они нашли широкое применение в науке, технике и медицине.
Как смазочные вещества
Ферромагнитные жидкости используют как смазки во вращающихся механизмах. Как и традиционные смазки, они помогают уменьшить трение между механическими деталями, но при этом их главное преимущество в том, что с помощью магнита или магнитного поля ферромагнитные жидкости легко удерживать в нужном положении.
Ферромагнитная жидкость под действием сильного магнита
В герметизирующих уплотнениях
В некоторых случаях герметизирующие уплотнения могут быть в виде жидкости — в этой ситуации очень удобно использовать именно ферромагнитные жидкости. Их используют, к примеру, чтобы герметизировать внутреннюю часть накопителя на жестком магнитном диске, в которой находятся электропривод шпинделя, сами жесткие диски и сервопривод блока головок. Магниты удерживают ферромагнитную жидкость в нужном месте, а она, в свою очередь, не пропускает пыль извне в гермозону жесткого диска, и помогает предотвратить повреждение дисков.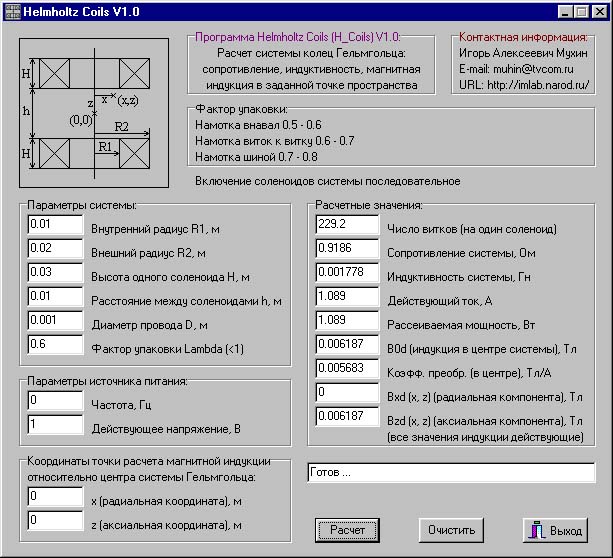 Некоторые производители ферромагнитных жидкостей продают для этих целей саму жидкость, а некоторые разрабатывают и выпускают полный комплект магнитожидкостных уплотнений, и не продают саму жидкость отдельно, чтобы предотвратить ее неправильное использование.
Некоторые производители ферромагнитных жидкостей продают для этих целей саму жидкость, а некоторые разрабатывают и выпускают полный комплект магнитожидкостных уплотнений, и не продают саму жидкость отдельно, чтобы предотвратить ее неправильное использование.
В искусстве
Некоторые скульпторы и художники используют ферромагнитную жидкость для создания современных произведений искусства. Кроме объемных и подвижных скульптур, которые демонстрируют во всей красе игру складок ферромагнитной жидкости под действием магнита, художники создают также плоские картины из этой жидкости. Ферромагнитные жидкости не смешиваются с водой и красками на водной основе, поэтому такие краски и пигменты (например, люминесцентные) добавляют в ферромагнитную жидкость, а потом двигают ее магнитом для создания красочных форм. На сайте YouTube много интересных примеров картин и скульптур из ферромагнитной жидкости.
Ферромагнитная жидкость под действием сильного магнита
В системах звуковоспроизведения
В электродинамических громкоговорителях систем звуковоспроизведения ферромагнитную жидкость используют для охлаждения звуковой катушки.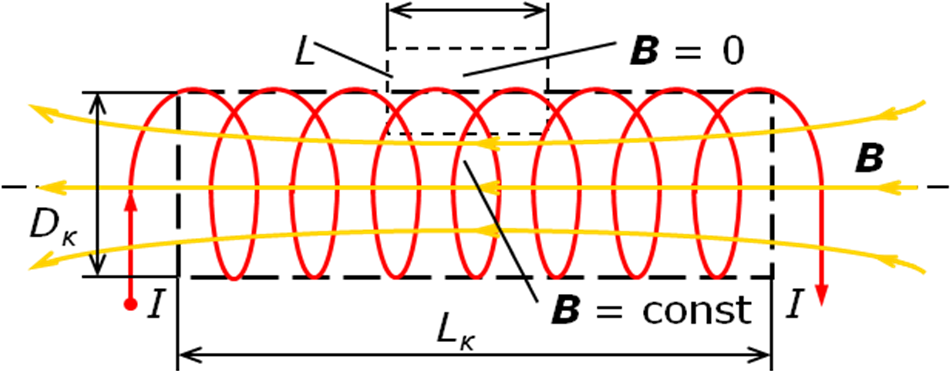 Из-за низкой энергетической эффективности звуковоспроизводящих систем, во время их работы большая часть электрической энергии преобразуется в тепловую, и это тепло может привести к выводу из строя звуковой катушки, если ее не охладить. Ферромагнитные жидкости отводят это тепло от звуковой катушки, а в зазоре их удерживает магнит, так же как и в других системах, описанных выше.
Из-за низкой энергетической эффективности звуковоспроизводящих систем, во время их работы большая часть электрической энергии преобразуется в тепловую, и это тепло может привести к выводу из строя звуковой катушки, если ее не охладить. Ферромагнитные жидкости отводят это тепло от звуковой катушки, а в зазоре их удерживает магнит, так же как и в других системах, описанных выше.
Ферромагнитные жидкости используют, также, для демпфирования диффузора с катушкой на резонансных частотах. Это сглаживает амплитудно-частотную характеристику динамика. Для этого ферромагнитные жидкости помещают в зазор между звуковой катушкой и магнитом.
При выборе ферромагнитной жидкости руководствуются знаниями о том, в какой среде ее будут использовать. Так, например, выбирая жидкость-носитель или при выборе вязкости ферромагнитной жидкости, учитывают такие факторы как влажность окружающей среды, в которой эта жидкость будет использоваться, или будет ли устройство, в котором используется ферромагнитная жидкость, соприкасаться с водой.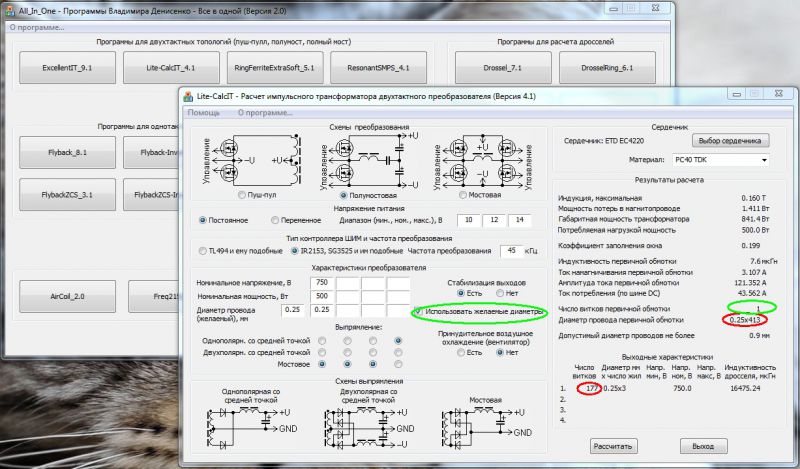
В медицине
В медицине у ферромагнитных жидкостей несколько применений. На данный момент ученые проводят исследования по использованию ферромагнитных жидкостей как носителей лекарств и других необходимых больным препаратов. С помощью магнита эти лекарственные препараты перемещают в определенный участок организма. Обычно в этом случае наночастицы покрывают слоем препарата, после чего ферромагнитную жидкость вводят в организм (чаще всего путем инъекции) и удерживают на месте с помощью магнита, пока препарат не окажет нужное действие. Существует ряд других методов локализированного введения лечебных препаратов, но ученные надеются, что этот метод обеспечит наибольшую точность.
Еще одно интересное применение ферромагнитных жидкостей в медицине — теплотерапия определенных участков тела. Чаще всего она используется для уничтожения раковых клеток. Для этого ферромагнитную жидкость вводят в организм, а после этого заставляют ферромагнитные частицы колебаться с высокой частотой, используя электромагниты.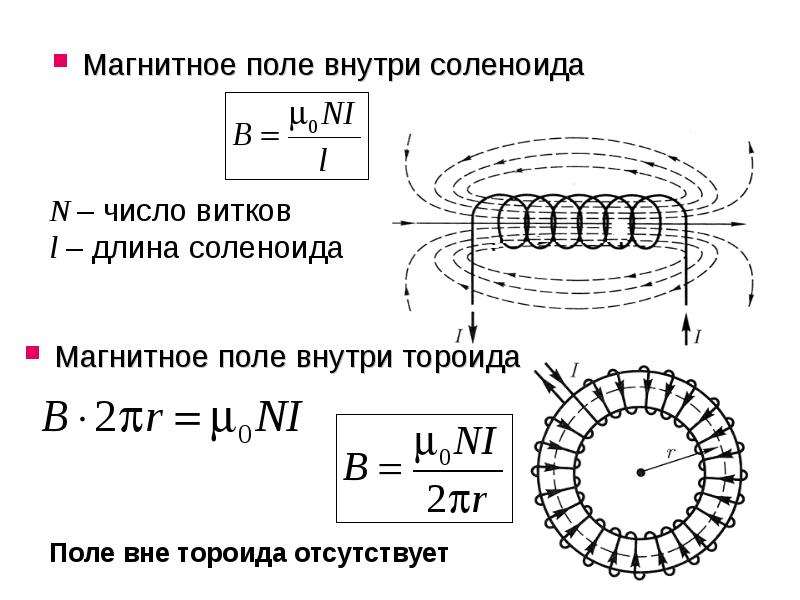 При этом выделяется большое количество тепла, и высокие температуры разрушают ткани на этом участке, убивая раковые клетки.
При этом выделяется большое количество тепла, и высокие температуры разрушают ткани на этом участке, убивая раковые клетки.
В диагностике магнитных носителей
Ферромагнитные жидкости используют для определения структуры магнитных доменов различных магнитных носителей, таких как накопители на магнитной ленте, жесткие диски и кредитные карты. Также с их помощью проверяют дефекты на поверхности материалов, не имеющих отношения к магнитным носителям, например сварочных швов, а также природных минералов и металлов. Это применяется, например, в производстве миниатюрных компонентов. Для этого поверхность материала покрывают ферромагнитной жидкостью, и она распределяется по этой поверхности в соответствии с магнитным полем материала. После того, как жидкость-носитель испарилась, на поверхности остаются ферромагнитные частицы, по которым и определяют структуру магнитного поля поверхности. Обычно для этого нужен микроскоп. Этот метод используют не только для проверки поверхности магнитных носителей и материалов, описанных выше, но и в судебно-медицинской экспертизе. Например, с помощью ферромагнитной жидкости можно определить удаленные в домашних условиях заводские номера на огнестрельном оружии.
Например, с помощью ферромагнитной жидкости можно определить удаленные в домашних условиях заводские номера на огнестрельном оружии.
В теплообменниках
Перегрев — широко распространенная проблема в радиоэлектронике. Чтобы избежать поломки, электронные приборы необходимо охлаждать. Ферромагнитные жидкости иногда используют в этих целях, например в громкоговорителях и некоторых микроэлектронных приборах. В начале этой статьи, когда мы обсуждали свойства ферромагнитных жидкостей, мы уже упоминали, что при высоких температурах (температурах Кюри) ферромагнитные жидкости теряют магнитные свойства. Эту особенность ферромагнитных жидкостей используют в системах охлаждения. Во время охлаждения ферромагнитная жидкость, удерживаемая возле детали, которую охлаждают, теряет свои магнитные свойства после того, как в ней достигнута температуры Кюри. Магнит перестает ее удерживать и ее замещает холодная ферромагнитная жидкость, у которой еще есть магнитные свойства. Новая жидкость нагревается, а нагретая — охлаждается, и процесс периодически повторяется. В этом случае магнит выступает в роли насоса, так как он помогает замещать менее намагниченную горячую жидкость более намагниченной холодной.
В заключение
В этой статье мы поговорили о том, что собой представляют ферромагнитные жидкости и о том, как их использовать. На них очень интересно смотреть, когда они под воздействием магнита, и мы очень советуем вам посмотреть примеры видео ферромагнитных жидкостей в интернете, например на сайте YouTube.
Автор статьи: Kateryna Yuri
Изготовление соленоида (электромагнитный возвратно-поступательный механизм) – Электроника
Кто изготавливал лично соленоиды? Столкнулся с трудностями в расчетах и решил выложить вопросы с рассуждениями сюда, заодно пригодится может кому.
Соленоид это електромагнит с подвижным якорем. Якорь играет роль возвратно поступательного механизма. Используются в електрозамках дверей машин и других областях. В моем случае соленоид выполняет функцию плавного регулятора давления в системе: Дроссель, електромагнит и левый конец пружины статически зафиксированы, правый конец пружины и рычаг крана соеденены. При подачи тока в катушку якорь втягивается, соотвественно тянет за собой рычаг, рычаг тянет пружыну и осуществляется плавный ход если добавлять ток. Если ток сбросит – рычаг вернется в исходное положение, которое задает пружина и поток будет перекрыт.
При подачи тока в катушку якорь втягивается, соотвественно тянет за собой рычаг, рычаг тянет пружыну и осуществляется плавный ход если добавлять ток. Если ток сбросит – рычаг вернется в исходное положение, которое задает пружина и поток будет перекрыт.
Альтернативой есть актуатор, это електродвигатель + винтовая передача. Видео на ютубе ищите. Минус в том, что оно слишком медленное.
В общем перелопатил я весь интернет в поисках информации по соленоидам и електромагнитам нашел тонны знаний, но без особой конкретики, или это мне так тяжело собрать все в кучу. Тем не менее точных понятных доступных формул я так и не нашел. Даже строители гаусганов пользуются фиксироваными парамтерами и подбирают все методом проб.
Вот что есть на данный момент:
R=U\IR-требуемое сопротивление исходя из параметров источника питания
L=(SR)\g
L-длинна катушки
S-площадь проводника
g-удельное сопротивление меди 0,0175 ом*мм2/м
В нашем случае для примера источником питания является “крона”, 9 вольт напряжение и 500мАч емкость (I не указано на корпусе, взял стандарт с гугла)
Провод медный сечение 0.
8мм, значит радиус 0.4, площадь =piR2= 3.14*0.4*0.4 = 0.5024мм2
Ток в аккумуляторах высчитывается по формуле= емкость делено на 20 часов. Это значит, что полный расход произойдет за 20 часов с напряжением 9 вольт и током 0.025 А, I = 500\20=0.025A
Сопротивление системы равно = R=9\0.025=360Om
Значит длинна провода
L= (0.5024*360)\0,0175= 10335 мм = 10м
Надо так много провода на относительно маломощный соленоид. Что ж, попробуем.
В итоге получилась высота катушки 5см, внутренний диаметр 0.5см, внешний где-то 2см, и 6.5 слоев намотки провода. Витки не считал.
Результат вообще нулевой, вставив гвоздь в середину ели притянулась к гвоздю шайбочка маленькая. Отчаявшись решил сделать простой електромагнит – намотал 1 метр провода прямо на гвоздь в несколько слоев, так же результат мизерный.
Игорь Мухин сделал программу (http://imlab.narod.ru/M_Fields/Coil10/Coil10. htm ) для расчетов соленоида, исходные данные:
htm ) для расчетов соленоида, исходные данные:
R1 – внутренний радиус соленоида
R2 – внешний радиус соленоида
H – высота соленоида
D – диаметр обмоточного провода
и напряжение
Результативные данные: Ток, Индуктивность, Сопротивление, Количество витков, индукция то есть тяга
(в софте надо изменить точки на запятые что бы заработало)
Вот в моем случае внутренний внешний радиусы не существенны, главное ток и длинна на которую тянет. Ток же нельзя регулировать, надо его вписать в исходные значения, а в программе нельзя. Написал автору на почту с просьбой скинуть формулы – ответа пока что нету…
Тема интересная, думаю пригодится не только мне
Электричество и магнетизм
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
По условию эта разница мала: , то есть мало отношение диаметра соленоида к его длине: 2R/l << 1. Поэтому можно воспользоваться формулой разложения квадратного корня
Поэтому можно воспользоваться формулой разложения квадратного корня
Отсюда
или
Подставляя численное значение d, находим, что разница будет менее половины процента при выполнении соотношения
Иными словами, соленоид может рассматриваться как бесконечно длинный, если его длина в двадцать или более раз превышает радиус.
Пример 2. Найти магнитное поле Ве в крайней торцевой точке оси соленоида конечной длины l. Сравнить с результатом предыдущего примера.
Решение. Магнитное поле в торцевой точке оси соленоида конечной длины l дается тем же интегралом (6.19), но теперь пределы интегрирования будут выглядеть иначе
|
(6. |
Отношение полей в средней и крайней точках оси соленоида равно
Это отношение всегда меньше единицы (то есть поле на торце меньше поля в середине соленоида). При l >> R имеем
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.
Соленоиды – Справочник химика 21
В установках плазменного нагрева (плазмотронах) температуру дуги повышают до 2-10 К и более, воздействуя на дугу параллельным потоком газа, закручиванием потока газа и обжатием магнитным полем соленоида [13]. В этом случае объемная плотность мощности в дуге достигает десятков кВт/см . Дуговые плазмотроны подразделяют на высоковольтные (2-6 кВ, 50-500 А) и низковольтные (100-800 В, 2-10, к А).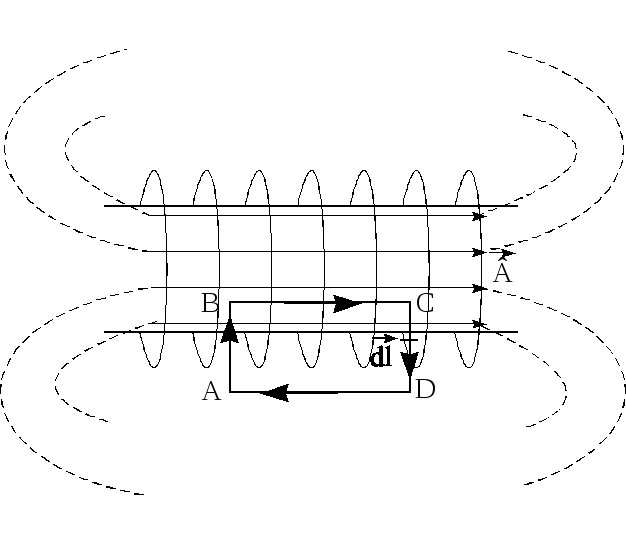 Подавляющее число плазмотронов работает на постоянном [c.81]
Подавляющее число плазмотронов работает на постоянном [c.81]
Индукционное нагревание слоя из металлических элементов соленоидом, окружающим рабочий участок. Тепловой поток определяется по нагреванию газа. Трудности осуществления этого метода связаны с необходимостью обеспечения равномерного тепловыделения в слое и определения средней температуры поверхности зерен, в которых циркулируют высокочастотные электрические токи. [c.144]
На рис. 118 приведена принципиальная схема блокировки быстросъемной крышки. На крышке установлен упор 8 для конечного выключателя, расположенного на запорно-поворотном кольце байонетного затвора так, что при повороте кольца во время закрепления крышки и плотном перекрытии зубьев кольца зубьями крышки конечный выключатель нажимает на упор и замыкает электрическую цепь, в которую включены сигнальная лампа и соленоид 3. Лампа горит до тех пор, пока крышка закрыта.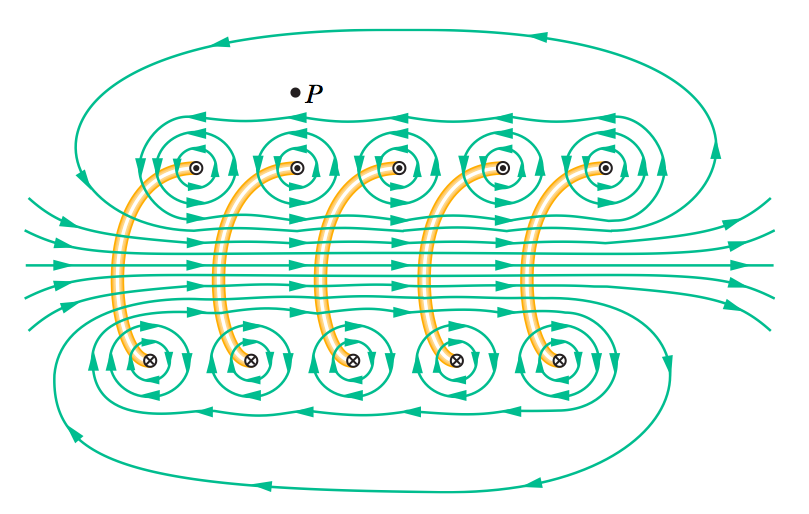 Соленоид смонтирован над рукояткой выпускного пробкового крана 5 [c.332]
Соленоид смонтирован над рукояткой выпускного пробкового крана 5 [c.332]
Если же крышка закреплена не полностью, то концевой выключатель не дойдет до упора и не сработает, цепь не замкнется, сигнальная лампа 7 не будет гореть и пробковый кран нельзя будет Открыть, так как запорная вилка соленоида не позволит повернуть рычаг крана. [c.333]
Размыкание и замыкание электрической цепи регулируется специальным пневматическим клапаном (рис. 119). Резиновая диафрагма 1 предохраняет клапан со штоком 2 и пружиной 4 от влаги, содержащейся в сжатом воздухе. Давление в сосуде, если оно более 100 кПа, передается через диафрагму на клапан, который, приподнимаясь, перемещает шток с контактной планкой 3. Электрическая цепь разрывается и обесточивает соленоид. В этот момент сердечник со стержнями опускается и фиксирует рукоятку воздухораспределительной коробки в положении закрытой крышки. [c.333]
Индукционная печь (рис. 5.4 ля с сливным носком, помещенного в индуктор в виде соленоида из медной трубки, охлаждаемой водой.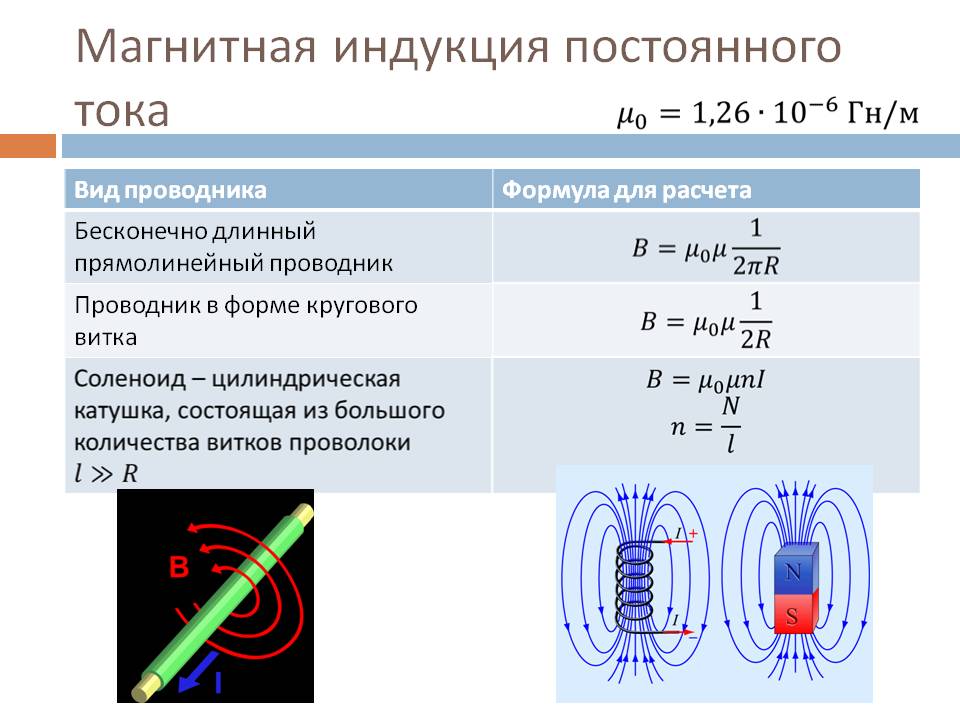 Печь заключена в металлический кожух, закрываемый сверху сводом. Для слива металла печь может наклоняться в сторону сливного носка. Процесс плавки в индукционных печах протекает весьма быстро. В качестве металлической шихты в них используется металлический лом известного состава, который точно рассчитан по содержанию углерода, серы, фосфора и легирующих элементов.Так как в индукционных печах отсутствуют электроды, выплавляемая в них сталь не загрязняется углеродом и продуктами их обжига, угар легирующих элементов весьма мал. Поэтому индукционные печи применяют для выплавки только высококачественных сталей и сплавов сложного химического состава. Расход энергии [c.89]
Печь заключена в металлический кожух, закрываемый сверху сводом. Для слива металла печь может наклоняться в сторону сливного носка. Процесс плавки в индукционных печах протекает весьма быстро. В качестве металлической шихты в них используется металлический лом известного состава, который точно рассчитан по содержанию углерода, серы, фосфора и легирующих элементов.Так как в индукционных печах отсутствуют электроды, выплавляемая в них сталь не загрязняется углеродом и продуктами их обжига, угар легирующих элементов весьма мал. Поэтому индукционные печи применяют для выплавки только высококачественных сталей и сплавов сложного химического состава. Расход энергии [c.89]
Электровакуумные приборы, провода, антенны, соленоиды [c.586]
В безэлектродном разряде разрядная трубка помещается внутри соленоида, через который пропускается электрический ток. Разряд произойдет тогда, когда сила и частота тока достигнут достаточных значений.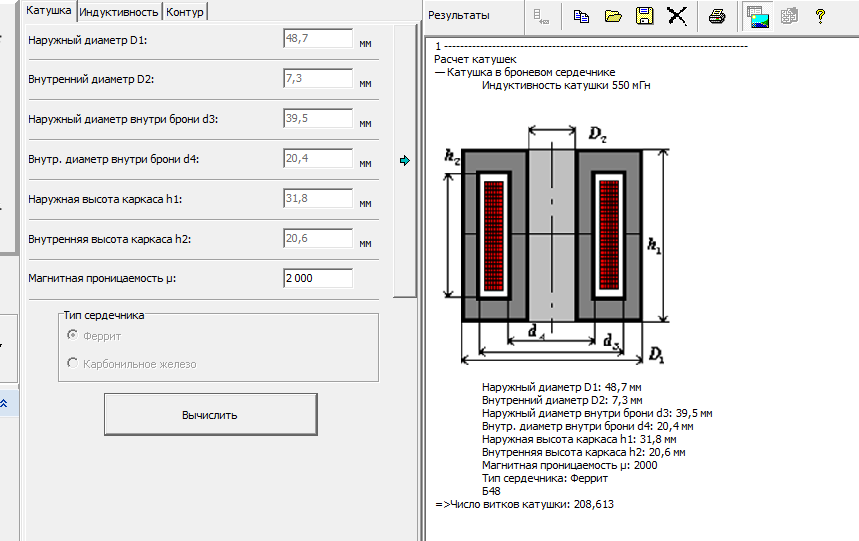 В безэлектродном разряде полимер осаждается на стенки ре- [c.77]
В безэлектродном разряде полимер осаждается на стенки ре- [c.77]
Полуавтоматический захват с магнитным приводом имеет пружину, запорный штифт, соленоид и рукоятку для ручного оттягивания запорного штифта (пальца) при строповке. Расстроповка осуществляется включением тока в линии, питающей соленоид. Аналогично устроен полуавтоматический захват с пневмоприводом. [c.275]
Преобразование заданных параметров в системе водопитателя контролируется датчиками и реле технологического контроля, а исполнительными механизмами являются электроприводы насосов и задвижек, соленоиды вентилей и т. п. Основная задача автоматики сводится в данном случае к пуску и отключению двигателей насосов или открыванию и закрыванию клапанов и задвижек. Для этого предусмотрена пуско-регулирующая аппаратура, работа которой задается автоматически в определенной последовательности. [c.156]
В импульсном электродинамическом излучателе (рис. 3.18) при протекании импульса тока от генератора 1 через обмотку (соленоид) 2, выполненную в виде плоской спирали, создается импульсное магнитное поле, наводящее в проводящей пластине (мембране) 4 вихревые токи. Взаимодействие поля с токами приводит к отталкиванию пластины. Для устранения электрического пробоя пластина 4 отделена от соленоида 2 тонкой изолирующей прокладкой 3 и основание 5 выполнено из изолирующего материала. Контакт мембраны с жидкостью приводит при ее импульсном движении к генерации в ней ударной волны. [c.72]
Взаимодействие поля с токами приводит к отталкиванию пластины. Для устранения электрического пробоя пластина 4 отделена от соленоида 2 тонкой изолирующей прокладкой 3 и основание 5 выполнено из изолирующего материала. Контакт мембраны с жидкостью приводит при ее импульсном движении к генерации в ней ударной волны. [c.72]
Аналогично в магнито-гидродинамическом сепараторе, основанном на разности магнитных проницаемостей (или поляризуемостей), можно выделять, например, газовые включения из парамагнитной среды. В работе [40] предложено в качестве такого МГД-сепаратора использовать соленоид. Для газовых включений радиусом около 5 мм в жидком кислороде дан расчет коэффициента сепарации в зависимости от скорости потока и магнитной индукции в интервале 0,1 Тл при скорости от 1 м/с и 1 Тл при скорости до 1 см/с. [c.139]
Автоматическая головка Коллинза—Ленца с делением парового потока 1 — термометр со стандартным шлифом 2 — соленоид 3 — дефлегматор [c.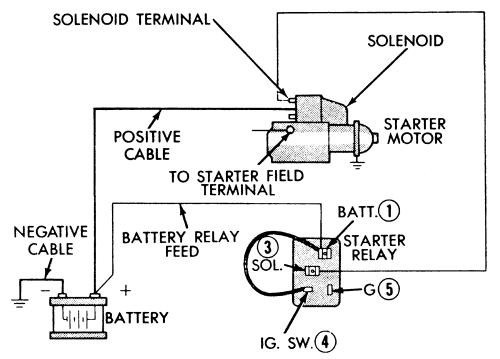 384]
384]
Модификация этой головки в имеет расходомер на Потоке орошения и автоматическое управление клапаном отбора с помощью соленоида. Расходомер орошения включает капилляр, рассчитанный на пропуск орошения в требуемых для данной колонны количествах и мерную трубку, высота уровня жидкости в которой определяет расход орошения. Предварительно расходомер тарируется. [c.99]
Электрические индукционные печи (рис. 7-11). Нагревание в этих печах осуществляется индукционными токами. Обогреваемый аппарат 1 является сердечником соленоида 2, охватывающего аппарат по соленоиду пропускается переменный ток, при этом вокруг соленоида возникает переменное магнитное поле, которое индуцирует в стенках обогреваемого аппарата электродвижущую силу. Под действием возникающего вторичного тока нагреваются стенки аппарата. Соленоид выполняется из медной или алюминиевой проволоки, имеющей малое омическое сопротивление. [c.173]
Магнитное поле может быть наведено пропусканием электрического тока непосредственно по деталям или через проводник, окружающий изделие или контактирующий с ним, либо с помощью соленоидов и магнитов.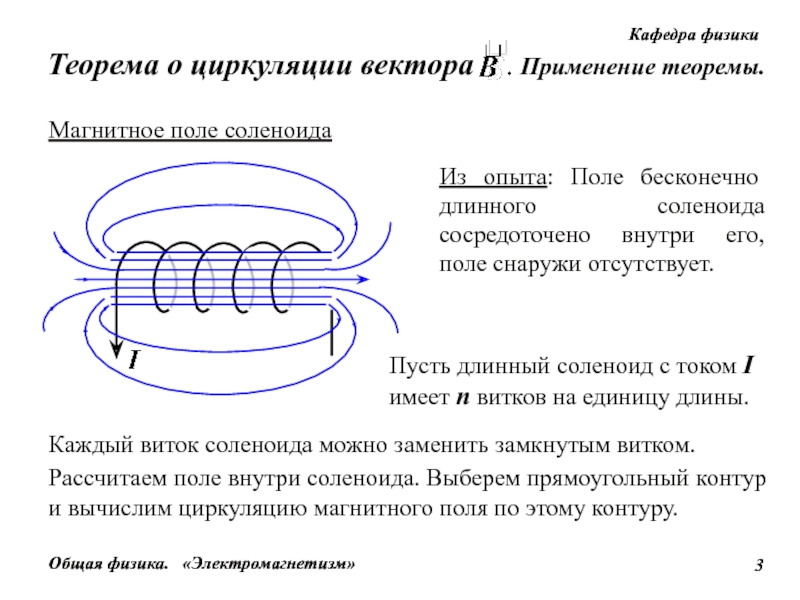 Наиболее рационально намагничивание с помощью соленоида или переносного электромагнита. [c.484]
Наиболее рационально намагничивание с помощью соленоида или переносного электромагнита. [c.484]
Смеситель высокого давления, в котором удобно приготовлять и хранить любые взрывчатые газовые смеси, представляет собой толстостенный стальной сосуд, способный выдержать давление, развивающееся при случайно произошедшем взрыве заключенной в него смеси. Смеситель снабжен электромагнитной мешалкой. Ее сердечник может совершать возвратно-поступательные движения внутри головки из немагнитной стали (она не препятствует проникновению силовых линий) при периодическом включении и выключении тока в соленоид, надетый на головку. [c.55]
Поле соленоида и тороида. Сила Лоренца. Движение заряженных частиц в электрическом и магнитном полях. Ускорители заряженных частиц – их применение в производстве. [c.165]
После падения первой капли неподвижный термоэлемент отключается я включаются подвижной термоэлемент (ПТЭ) 21 и электродвигатель 24 механизма задатчика скорости разгонки. Последний поднимает с постоянной скоростью подвижный термоэлемент предполагается, что скорость разгонки соответствует скорости подъема подвижного термоэлемента. В случае несовпадения этих скоростей срабатывает регулятор скорости разгонки (состоящий из электронного усилителя 20 и блока переключателя мощностей 18), изменяющий соответствующим образом нагрев колбы. В процессе разгонки механизм задатчика скорости разгонки производит замыкание специального микропереключателя, который включает соленоид отметки объемов (СОО) через каждые 10% изменения объема дистиллята. Включение соленоида (СОО) влечет за собой нанесение пером на картограмме очередной отметки объема дистиллята в виде вертикальной черточки. [c.180]
Последний поднимает с постоянной скоростью подвижный термоэлемент предполагается, что скорость разгонки соответствует скорости подъема подвижного термоэлемента. В случае несовпадения этих скоростей срабатывает регулятор скорости разгонки (состоящий из электронного усилителя 20 и блока переключателя мощностей 18), изменяющий соответствующим образом нагрев колбы. В процессе разгонки механизм задатчика скорости разгонки производит замыкание специального микропереключателя, который включает соленоид отметки объемов (СОО) через каждые 10% изменения объема дистиллята. Включение соленоида (СОО) влечет за собой нанесение пером на картограмме очередной отметки объема дистиллята в виде вертикальной черточки. [c.180]
Задача 5.1. Группа ученых под руководством П. Л. Капицы изучала поведение плазменного разрвда в гелии. Установка (точнее, интересующая нас часть установки) представляла собой бочку , положенную на бок.
 Внутри бочки находился газообразный гелий под давлением 3 атм. Под действием мощного электромагнитного излучения в гелии возникал плазменный шнуровой разряд, стягивающийся в сферический сгусток плазмы ( шаровую молнию ). Для удержания этого сгустка в центральной части бочки использовали соленоид, кольцом охватывающий бочку . В ходе опытов постелено наращивали мощность электромагнитного излучения. Плазма становилась все горячее и горячее. Но с повышением температуры уменьшалась плотность плазменного шара. Молния поднималась вверх. Мощности соленоидного кольца явно не хватало. Сотрудники Капицы предложили строить новую установку — с более сильной соленоидной системой. Но Петр Леонидович Капица нашел другое решение. Как Вы думаете, какое [c.73]
Внутри бочки находился газообразный гелий под давлением 3 атм. Под действием мощного электромагнитного излучения в гелии возникал плазменный шнуровой разряд, стягивающийся в сферический сгусток плазмы ( шаровую молнию ). Для удержания этого сгустка в центральной части бочки использовали соленоид, кольцом охватывающий бочку . В ходе опытов постелено наращивали мощность электромагнитного излучения. Плазма становилась все горячее и горячее. Но с повышением температуры уменьшалась плотность плазменного шара. Молния поднималась вверх. Мощности соленоидного кольца явно не хватало. Сотрудники Капицы предложили строить новую установку — с более сильной соленоидной системой. Но Петр Леонидович Капица нашел другое решение. Как Вы думаете, какое [c.73] На трубопроводе сжатого воздуха между выпускным краном и сосудом имеется специальный пневматический клапан 4 с контактным устройством, размыкающим электрическую цепь. К этой цепр подключен соленоид 3, установленный на пульте управления над воздухораспределительной коробкой 1.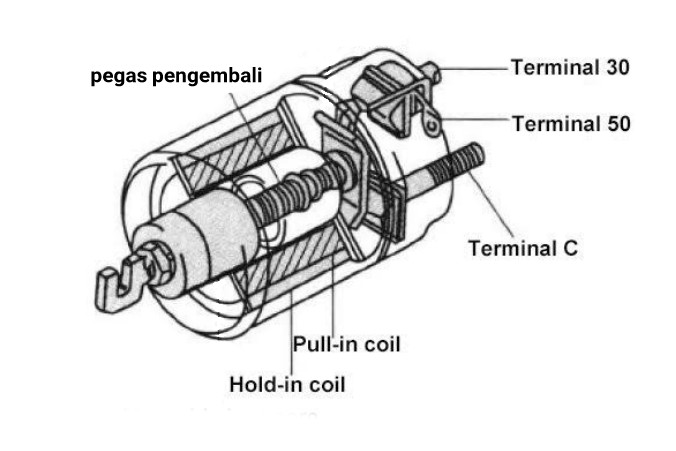 С помощью распределительной коробки включаются пневмотолкатели поворота запорного кольца байонетного затвора. [c.333]
С помощью распределительной коробки включаются пневмотолкатели поворота запорного кольца байонетного затвора. [c.333]
Укрепленный на сердечнике соленоида стержень 2 препятствует повороту рукоятки подачи воздуха к пневмотолкателям поворотного механизма кольца. Крышку невозможно открыть до тех пор, пока сердечник не втянется в соленоид и не поднимет стержень, который выйдет из зацепления с рукояткой воздухораспределительной коробки и освободит ее. [c.333]
I — соленоидиы вентиль 2 — защнтно-запальное устрой- , ство . 3 — штуцер для бегущего огня — трубопровод природного газа 5 — промежуточная труба б — трубо-провод природного газа с горелкой 7 — свеча печного газа. [c.229]
В проточно-циркуляционных установках для прокачки реагиру-юш,ей смеси часто используют стеклянные плунжерные циркуляционные насосы. Поршень насоса приводится в возвратно-поступательное движение с помощью соленоида. Прерывистое магнитное поле соленоида создается посредством релейной схемы. Магнитные плунжерные насосы не всегда удобны в применении, в частности при сильно экзотермических реакциях, когда требуется создавать большую циркуляцию газа, чтобы избежать неоднородного температурного поля в реакторе. Поэтому наряду с этими насосами применяют и другие конструкции, например, сильфонные или диафраг-менпые насосы, приводимые в движение от электродвигателя [14,151. Весьма целесообразно включать в схему центробежные газодувки высокой производительности. Здесь, однако, надо исключить утечки газа через сальники на оси ротора насоса. [c.410]
Магнитные плунжерные насосы не всегда удобны в применении, в частности при сильно экзотермических реакциях, когда требуется создавать большую циркуляцию газа, чтобы избежать неоднородного температурного поля в реакторе. Поэтому наряду с этими насосами применяют и другие конструкции, например, сильфонные или диафраг-менпые насосы, приводимые в движение от электродвигателя [14,151. Весьма целесообразно включать в схему центробежные газодувки высокой производительности. Здесь, однако, надо исключить утечки газа через сальники на оси ротора насоса. [c.410]
На рис. Х.12 приведена очень удобная конструкция металлической ампулы емкостью 30 мл с магнитной возвратно-по-ступательной мешалкой, в которой исключены холодные выступающие части запорных приспособлений и связанные с этим ошибки из-за наличия мертвого объема с пониженной температурой [22]. В верхней части ампулы находится уплотняющая головка 2 с размещенной в ней частью вентиля с запорной иглой Другая часть вентиля расположена в специальном выносном устройстве, служащем для заполнения ампулы газом до давления опыта. При необходимости работать с постоянной подачей газа головку с иглой замепют на головку с приваренным капилляром. Мешалка состоит из плунжера 5, выполненного из железа Армко и, если нужно, запущенного коррозионностойким покрытием, и лопастей 6. Всю ампулу вставляют в катушку соленоида, помещенную в жидкость термостата. При числе переключений соленоида 2—3 в 1 сек обеспечивается весьма интенсивное перемешивание содержимого ампулы. [c.416]
При необходимости работать с постоянной подачей газа головку с иглой замепют на головку с приваренным капилляром. Мешалка состоит из плунжера 5, выполненного из железа Армко и, если нужно, запущенного коррозионностойким покрытием, и лопастей 6. Всю ампулу вставляют в катушку соленоида, помещенную в жидкость термостата. При числе переключений соленоида 2—3 в 1 сек обеспечивается весьма интенсивное перемешивание содержимого ампулы. [c.416]
Источниками электростатического поля в окружающем пространстве служат тела – проводники (электроды) или диэлектрики различной геометрической конфигурации, несущие электрический заряд. Источниками магнитного поля являются намагниченные тела или системы проводников с токами (катушки, соленоиды), р асполагаемые на маг-нитопроводах. [c.75]
В тлеющем разряде также могут протекать разнообразные химические реакции. В 1920 г. американский физик Р. Вуд получил с помощью тлеющего разряда водород. В тлеющем разряде можно синтезировать различные вещества (Н2О2, О3, N0). Предложено использовать тлеющий разряд для получения напыленных полимерных мембран [8]. Плазменной полимеризации подвергаются различные органические соединения. Используется как электродная, так и безэлектродная форма разряда (разряд, протекающий в стеклянной трубке, помещенной внутри соленоида, питаемого от ВЧ-генератора). Образующийся полимер осаждается на пористой подложке в зоне тлеющего разряда. [c.175]
Предложено использовать тлеющий разряд для получения напыленных полимерных мембран [8]. Плазменной полимеризации подвергаются различные органические соединения. Используется как электродная, так и безэлектродная форма разряда (разряд, протекающий в стеклянной трубке, помещенной внутри соленоида, питаемого от ВЧ-генератора). Образующийся полимер осаждается на пористой подложке в зоне тлеющего разряда. [c.175]
Основной стандарт ASTM Ректификация сьфой нефти в колонне с 15-ю теоретическими тарелками (Д-2892 – 73) является аналогом отечественного ГОСТ 11011 – 64, хотя существенно отличается о него в аппаратурном отношении. В качестве ректификационной установки стандарт предусматривает использование одной из трех установок, выпускаемых различными фирмами и выполненных из термостойкого стекла. Схема одной из них показана на рис. 5.5. Колонна диаметром 50 мм и высотой не более 914 мм заполнена насадкой и помещена в обогреваемую снаружи вакуумную рубашку. Эффективность колонны при полном возврате флегмы – 14-17 теоретических тарелок. Стеклянный куб емкостью 5-6 л помещен в эластичный нагреватель и расположен над магнитной мешалкой. Конденсационная гоповка с двойным контуром охлаждения. Отбор фракций регулируют частотой открытия клапана, управляемого соленоидом. Для улавпивания газов j -С4 за головкой подключена ловушка, охлаждаемая сухим льдом, а между этой ловушкой и кубом расположен дифференциальный манометр. [c.85]
I – насадочная колонна 2 – вакуумная рубашка 3 – обогреваемый кожух 4 – клапан 5 – соленоид 6 – гоповка 7 – термопары 8 – трубка для отбора фракций 9 – приемник 4ракций 10 – куб [c.86]
Наиболее простой по конструкции является головка с делением сконденсированного потока флегмы с помощью клапана или крана (см. рис. 5.7). Управление иглой клапана осуществляется вручную как показано на рис. 5.2 или с помощью электромагнита (соленоида). В такой головке с выносным хоподильншсом тубус и паровой патрубок 7 являются дополнительными поверхностями конденсации и источниками неконтролируемого потока орошения. [c.99]
Автоклавы Вишневского и микроавтоклавы представляют собою жидкостные бессальниксвые реакторы высокого давления с внешним магнитным приводом. В первых из них создается вращающее магнитное поле, приводящее в движение установленный внутри автоклава винтовой циркуляционный насос, во-вторых устанавливается дисковая возвратно-поступательная мешалка, приводимая в движение внешним соленоидом. Расчет активности катализатора при работе с такими аппаратами проводится аналогично расчету для статических циркуляционных установок. [c.363]
Первая капля дистиллята, характеризующая начало кипения, падает на неподвижный термоэлемент (НТЭ) 19, представляющий собой термопару ХК) с приваренным к горячему спаю нихромовым подогревателем. Эта капля охлаждает горячий спай термоэлемента, в результате чего происходят шгновенное изменение э. д. с. и переключение элементов схемы выключается соленоид отметки (СОО), расположенный на каретке пера регистратора ПС1-01-АФР, перо опускается на картограмму и фиксирует начало кипения продукта. [c.180]
Протоны защищены от действия внешнего магнитного ноля окружающими электронами (эффект электронного экранирования). Поясним эффект электронного экранирования на примере молекулы бензола (рис. 27). Если молекула бензола находится в магнитном поле, то электроны бензольного ядра начинают вращаться вокруг силовых линий магнитного поля, образуя как бы круговой ток (подобие соленоида) внутри молекулы возникает свое магнитное поле, противоположно направлепное внешнему Таким образе . [c.40]
В индукционных печах тепло выделяется за счет возникновения в толще шихты индукционных токов. В основе действия индукционных печей лежит трансформаторный принцип пехю-дачи энергии от первичной цепи к вторичной. При этом первичной обмоткой — индуктором является соленоид, а вторичной — металлическая шихта. [c.87]
Магнитное поле однослойного соленоида
Соленоид – это цилиндрическая обмотка из провода по которой протекает постоянный или переменный электрический ток.{N} I_i.\]
(1)
Если пренебречь краевыми эффектами, то первое и третье слагаемые в (1) будут равны нулю, так как магнитное поле перпендикулярно контуру и $B_l=0$. Если контур выбрать так, что $AD$ будет лежать на большом расстоянии от соленоида, где поле стремиться к нулю, то и четвёртое слагаемое в (1) также превратиться в нуль. Тогда, учитывая приближение однородности поля получим:
где $L$ – длина соленоида, $N$ – количество витков. Если ввести понятие плотности витков (число витков на единицу длины) $n=N/L$, то индукцию магнитного поля внутри соленоида (2) можно записать в виде:
Рис. 2: Соленоид с произвольными размерами $L$ и $R$.
Чтобы получить точное выражение для индукции магнитного поля в любой точке на оси конечного соленоида необходимо воспользоваться законом Био-Савара-Лапласа (Рис. 2), который приводит к следующему выражению:
\[B=\frac12\mu_0 nI (\cos\alpha_2-\cos\alpha_1).2}},\](5)
где $R$ – радиус соленоида. А на краю полубесконечного соленоида:
\[B=\frac12 \mu_0 nI.\]
(6)
Калькулятор
Индукция магнитного поля бесконечного соленоида (3)
Индукция магнитного поля конечного соленоида (5)
Распределение индукция магнитного внутри конечного соленоида (4)
(PDF) Determination of mutual inductances and electrodynamic forces between the coil and the coaxial solenoid in a symmetrical arrangement
Труды Крыловского государственного научного центра. Т. 2, № 396. 2021
Transactions of the Krylov State Research Centre. Vol. 2, no. 396. 2021
103
где M1–22′ ≠ M1–22” – взаимная индуктивность между
катушкой и частью соленоида за торцевой плоско-
стью с противоположной стороны.
Список использованной литературы
1. Цицикян Г.Н., Антипов М.Ю. Электродинамические
силы в ошиновке электротехнического оборудования
автономных систем // Электротехника. 2018. № 4.
С. 53–57.
2. Цицикян Г.Н., Антипов М.Ю. Расчет индуктивностей
однослойного и двухслойного соленоида с учетом
особенностей практического применения // Электри-
чество. 2019. № 10. С. 48–53. DOI: 10.24160/0013-
5380-2019-10-48-53.
3. Накопители энергии / Д.А. Бут, Б.Л. Алиевский,
С.Р. Мизюрин, П.В. Васюкевич; под ред. Д.А. Бута.
Москва: Энергоатомиздат, 1991. 398, [1] с.
4. Калантаров П.А., Цейтлин Л.А. Расчет индуктив-
ностей: cправ. книга. Ленинград: Энергоатомиздат,
1986. 487, [1] c.
5. Цицикян Г.Н. Взаимные индуктивности и силы взаи-
модействия соосных контуров соленоидов и кату-
шек // Известия АН СССР. Энергетика и транспорт.
1985. № 6. С. 90–99.
6. Цицикян Г.Н., Бобровников П.В., Антипов М.Ю. Ру-
ководство по расчету индуктивностей и электроди-
намических сил в токоведущих частях электротехни-
ческих комплексов. Санкт-Петербург: Крыловский
гос. научный центр, 2020. 118 с.
7. Цицикян Г.Н., Антипов М.Ю. Строгие и аппрокси-
мирующие выражения для индуктивности солено-
идов круговой и квадратной формы // Электриче-
ство. 2020. № 2. С.35–41. DOI: 10.24160/0013-
5380-2020-2-35-41.
8. Цицикян Г.Н., Антипов М.Ю. Оценка сжимающих
сил, действующих на тонкослойные катушки (со-
леноиды) с током // Известия Российской академии
наук. Энергетика. 2018. № 5. С. 26–31. DOI:
10.31857/S000233100003212-7.
References
1. G.N. Tsitsikyan, M.Yu. Antipov. Electrodynamic forces
in the busbar of electrotechnical equipment of autono-
mous systems // Elektrotekhnika. 2018. No. 4. P. 53–57
(in Russian).
2. G.N. Tsitsikyan, M.Yu. Antipov. Calculation of inductivi-
ties for single-layer and two-layer solenoid taking into
account the features of practical application // Electricity.
2019. No. 10. P. 48–53. DOI: 10.24160/0013-5380-
2019-10-48-53 (in Russian).
3. Energy storage devices / D.A. Bout, B.L. Alievsky,
S.R. Mizyurin, P.V. Vasyukevich; ed. by D.A. Bout.
Moscow: Energoatomizdat, 1991. 398, [1] p.
(in Russian).
4. P.A. Kalantarov, L.A. Tseitlin. Calculation of in-
ductivities: reference book. Leningrad: Energoatom-
izdat, 1986. 487, [1] p. (in Russian).
5. G. Tsitsikyan. Mutual inductances and interaction forces
of coaxial circuits, solenoids and coils // USSR Academy
of Sciences. Izvestiya. Power engineering and transport.
1985. No. 6. P. 90–99 (in Russian).
6. G.N. Tsitsikyan, P.V. Bobrovnikov, M.Yu. Antipov.
Manual for calculating inductivities and electrodynamic
forces in conductive parts of electrical complexes.
St. Petersburg: Krylov State Research Centre, 2020.
118 p. (in Russian).
7. G.N. Tsitsikyan, M.Yu. Antipov. Strict and approxi-
mating expressions for the inductance of circular
and square shape solenoids // Electricity. 2020.
No. 2. P. 35–41. DOI: 10.24160/0013-5380-2020-2-
35-41 (in Russian).
8. G.N. Tsitsikyan, M.Yu. Antipov. Evaluation of com-
pressive forces acting on thin-layer coils (solenoids)
with current // A journal of the Russian Academy of
Sciences. Power engineering. 2018. No. 5. P. 26–31.
DOI: 10.31857/S000233100003212-7 (in Russian).
Сведения об авторах
Цицикян Георгий Николаевич, д.т.н., профессор, на-
чальник сектора – заместитель начальника отдела фи-
лиала «ЦНИИ СЭТ» ФГУП «Крыловский государствен-
ный научный центр». Адрес: 196128, Россия, Санкт-
Петербург, ул. Благодатная, д. 6. Тел.: +7 (812) 748-52-39.
E-mail: [email protected]. https://orcid.org/0000-
0002-8813-6003.
Антипов Михаил Юрьевич, инженер-конструктор 1 кате-
гории филиала «ЦНИИ СЭТ» ФГУП «Крыловский
государственный научный центр». Адрес: 196128, Рос-
сия, г. Санкт-Петербург, ул. Благодатная, д. 6. Тел.:
+7 (812) 369-94-91. E-mail: [email protected].
Ахмед Рифаат Абуэльфадл Махмуд, преподаватель
кафедры электротехники Инженерного факультета
Университета Порт-Саида. Адрес: 42526, Египет, Порт-
Саид, Порт-Фоад. E-mail: [email protected].
https://orcid.org/0000-0002-4865-9045.
About the authors
Georgy N. Tsitsikyan, Dr. Sci. (Eng.), Prof., Head of Sector –
Deputy Head of Department, TSNII SET branch of Krylov
State Research Centre. Address: 6, Blagodatnaya st., St. Pe-
tersburg, Russia, post code 196128. Tel.: +7 (812) 748-52-39.
E-mail: [email protected]. https://orcid.org/0000-
0002-8813-6003.
Калькулятор магнитного поля соленоида
Калькулятор магнитного поля соленоида помогает вычислить магнитное поле внутри длинного соленоида. Хотите узнать, что такое соленоид и как рассчитать магнитное поле соленоида? Просто продолжайте читать. Вы также узнаете об уравнении магнитного поля соленоида.
Что такое соленоид?
Если пропустить через провод ток, вокруг него возникнет магнитное поле. Соленоид – это провод, плотно намотанный в длинную тонкую катушку.Из-за его формы, если мы пропустим ток через соленоид, внутри него будет сильное магнитное поле, а снаружи – небольшое.
Соленоидыиспользуются во многих практических приложениях, когда необходимо создать магнитное поле. В отличие от магнитов, мы можем контролировать силу магнитного поля, просто регулируя электрический ток. Соленоиды и в целом катушки также являются основными индуктивными элементами в электрических цепях. Чтобы узнать больше, воспользуйтесь нашим калькулятором индуктивности соленоида, калькулятором цепи RLC и калькулятором индуктивного реактивного сопротивления.
Уравнение магнитного поля соленоида
Соленоид бесконечной длины описать проще всего. Магнитное поле бесконечного соленоида точно равно нулю снаружи и имеет постоянное значение внутри соленоида. Бесконечный соленоид часто является разумным приближением реального соленоида конечной длины, если мы можем принять, что вблизи концов магнитное поле будет немного отличаться от рассчитанного для бесконечного соленоида.
Магнитное поле внутри длинного соленоида правильно рассчитывается с помощью перекрестного произведения и, возможно, правила правой руки, но все это можно упростить до:
B = µ₀ * N * I / L
где
- В – магнитное поле,
-
µ₀ = 1.-6 Тл * м / А– вакуумная проницаемость, - N – количество витков в соленоиде,
- I – электрический ток,
- L – длина соленоида.
Как рассчитать магнитное поле соленоида?
Самый простой способ рассчитать магнитное поле соленоида – использовать наш калькулятор. Просто укажите
- количество витков,
- электрический ток,
- длина соленоида,
, чтобы внутри него было магнитное поле.Чтобы узнать о влиянии магнитного поля на заряженные частицы, воспользуйтесь нашим калькулятором силы Лоренца.
Как рассчитать соленоид
Обновлено 28 декабря 2020 г.
Дэвид Латчман
Соленоид – это катушка из проволоки, длина которой значительно превышает ее диаметр, которая создает магнитное поле, когда через него проходит ток. На практике эта катушка наматывается на металлический сердечник, и сила магнитного поля зависит от плотности катушки, тока, проходящего через катушку, и магнитных свойств сердечника.
Таким образом, соленоид представляет собой тип электромагнита, предназначенный для создания управляемого магнитного поля. Это поле может использоваться для различных целей в зависимости от устройства, от использования для создания магнитного поля в качестве электромагнита, для предотвращения изменений тока в качестве индуктора или для преобразования энергии, накопленной в магнитном поле, в кинетическую энергию в качестве электродвигателя. .
Магнитное поле производного соленоида
Магнитное поле производного соленоида можно найти с помощью закона Ампера .Получаем
Bl = \ mu_0 NI
, где B – плотность магнитного потока, l – длина соленоида, μ 0 – магнитная постоянная или магнитная проницаемость в вакууме. , N – количество витков в катушке, а I – ток через катушку.
Разделив на l , мы получим
B = \ mu_0 (N / l) I
, где N / l – плотность витков или количество витков на единицу. длина.Это уравнение применимо к соленоидам без магнитопроводов или в свободном пространстве. Магнитная постоянная 1,257 × 10 -6 Гн / м.
Магнитная проницаемость материала – это его способность поддерживать формирование магнитного поля. Некоторые материалы лучше других, поэтому проницаемость – это степень намагничивания, которое материал испытывает в ответ на магнитное поле. Относительная проницаемость мкм r говорит нам, насколько она увеличивается по отношению к свободному пространству или вакууму.
\ mu = \ mu_r \ mu_0
где μ – магнитная проницаемость, а μ r – относительность. Это говорит нам, насколько увеличивается магнитное поле, если через соленоид проходит материальный сердечник. Если мы поместим магнитный материал, например, железный стержень, и соленоид обернут вокруг него, железный стержень будет концентрировать магнитное поле и увеличивать плотность магнитного потока B . 2 A} {l}
Мы видим, что индуктивность L зависит от геометрии катушки – плотности витков и площади поперечного сечения – и магнитной проницаемости материала катушки. .
12.7: Соленоиды и тороиды – Physics LibreTexts
Два наиболее распространенных и полезных электромагнитных устройства называются соленоидами и тороидами. В той или иной форме они являются частью множества инструментов, больших и малых. В этом разделе мы исследуем типичное для этих устройств магнитное поле.
Соленоиды
Длинный провод, намотанный в виде спиральной катушки, известен как соленоид . Соленоиды обычно используются в экспериментальных исследованиях, требующих магнитных полей.Соленоид обычно легко наматывается, и вблизи его центра его магнитное поле довольно однородно и прямо пропорционально току в проводе.
На рисунке \ (\ PageIndex {1} \) показан соленоид, состоящий из N витков провода, плотно намотанного на длину L . По проводу соленоида течет ток – . Количество витков на единицу длины – N / L ; Следовательно, количество витков на бесконечно малой длине dy составляет ( N / L ) dy витков.Это дает текущий
\ [dI = \ frac {NI} {L} dy. \ label {12.24} \]
Сначала мы вычисляем магнитное поле в точке P на рисунке \ (\ PageIndex {1} \). Эта точка находится на центральной оси соленоида. По сути, мы разрезаем соленоид на тонкие кусочки толщиной dy и обрабатываем каждый как токовую петлю. Таким образом, dI – это ток через каждый слайс. Магнитное поле \ (d \ vec {B} \) из-за тока dI в dy можно найти с помощью уравнения 12.{\ theta_2} cos \, \ theta \, d \ theta = \ frac {\ mu_0 IN} {2L} (sin \, \ theta_2 – sin \, \ theta_1) \ hat {j}, \ label {12.27} \ ]
, которое представляет собой магнитное поле вдоль центральной оси конечного соленоида.
Особый интерес представляет бесконечно длинный соленоид, для которого \ (L \ rightarrow \ infty \). С практической точки зрения бесконечный соленоид – это соленоид, длина которого намного больше его радиуса \ ((L >> R) \). В этом случае \ (\ theta_1 = \ frac {- \ pi} {2} \) и \ (\ theta_2 = \ frac {\ pi} {2} \).Тогда из уравнения \ ref {12.27} магнитное поле вдоль центральной оси бесконечного соленоида равно
\ [\ vec {B} = \ frac {\ mu_0 IN} {2L} \ hat {j} [sin (\ pi / 2) – sin (- \ pi / 2)] = \ frac {\ mu_0 IN} {L} \ hat {j} \] или
\ [\ vec {B} = \ mu_0 n I \ hat {j}, \ label {12.28} \]
, где n – количество витков на единицу длины. Вы можете определить направление \ (\ vec {B} \) с помощью правила правой руки: согните пальцы в направлении тока, а большой палец указывает вдоль магнитного поля внутри соленоида.
Теперь мы используем эти свойства вместе с законом Ампера для вычисления величины магнитного поля в любом месте внутри бесконечного соленоида. Рассмотрим замкнутый путь на рисунке \ (\ PageIndex {2} \). Вдоль отрезка 1 \ (\ vec {B} \) равномерно и параллельно пути. Вдоль отрезков 2 и 4 \ (\ vec {B} \) перпендикулярна части пути и исчезает на остальной части. Следовательно, отрезки 2 и 4 не вносят вклад в линейный интеграл в законе Ампера. Вдоль сегмента 3 \ (\ vec {B} = 0 \), потому что магнитное поле вне соленоида равно нулю.Если вы рассмотрите петлю закона Ампера вне соленоида, ток течет в противоположных направлениях по разным сегментам провода. Следовательно, в соответствии с законом Ампера нет замкнутого тока и магнитного поля. Таким образом, вклад в линейный интеграл от отрезка 3 отсутствует. В результате находим
\ [\ oint \ vec {B} \ cdot d \ vec {l} = \ int_1 \ vec {B} \ cdot d \ vec {l} = Bl. \ label {12.29} \]
Рисунок \ (\ PageIndex {2} \): путь интегрирования, используемый в законе Ампера для оценки магнитного поля бесконечного соленоида.Соленоид имеет n витков на единицу длины, поэтому ток, который проходит через поверхность, ограниченную дорожкой, равен nlI . Следовательно, согласно закону Ампера,
\ [Bl = \ mu_0 n lI \] и
Примечание
\ [B = \ mu_0 n I \ label {12.30} \]
внутри соленоида. Это согласуется с тем, что мы обнаружили ранее для B на центральной оси соленоида. Однако здесь положение сегмента 1 произвольно, поэтому мы обнаружили, что это уравнение дает магнитное поле всюду внутри бесконечного соленоида.
За пределами соленоида можно провести петлю закона Ампера вокруг всего соленоида. Это закроет ток, текущий в обоих направлениях. Следовательно, чистый ток внутри контура равен нулю. Согласно закону Ампера, если чистый ток равен нулю, магнитное поле должно быть нулевым. Следовательно, за пределами радиуса соленоида магнитное поле равно нулю.
Когда пациенту проводят магнитно-резонансную томографию (МРТ), он ложится на стол, который перемещается в центр большого соленоида, который может генерировать очень сильные магнитные поля.Соленоид способен создавать эти высокие поля от сильных токов, протекающих по сверхпроводящим проводам. Сильное магнитное поле используется для изменения вращения протонов в теле пациента. Время, необходимое для выравнивания или расслабления спинов (возврата к исходной ориентации), является признаком различных тканей, который можно проанализировать, чтобы увидеть, нормальны ли структуры тканей (рисунок \ (\ PageIndex {3} \)).
Рисунок \ (\ PageIndex {3} \): . В аппарате МРТ большое магнитное поле создается цилиндрическим соленоидом, окружающим пациента.(кредит: Лиз Уэст)Пример \ (\ PageIndex {1} \): Магнитное поле внутри соленоида
Соленоид имеет 300 витков, намотанных на цилиндр диаметром 1,20 см и длиной 14,0 см. Если ток через катушки составляет 0,410 А, какова величина магнитного поля внутри и около середины соленоида?
Стратегия
Нам дано количество витков и длина соленоида, поэтому мы можем найти количество витков на единицу длины. Следовательно, магнитное поле внутри и около середины соленоида определяется уравнением \ ref {12.о \)? Соленоид имеет 1000 витков на 50 см с током 1,0 А, протекающим по катушкам
.- Решение
а. 1.00382; б. 1.00015
Тороиды
Тороид – это катушка в форме пончика, тесно намотанная одним непрерывным проводом, как показано в части (а) рисунка \ (\ PageIndex {4} \). Если тороид имеет обмотки N , а ток в проводе составляет I , каково магнитное поле внутри и снаружи тороида?
Рисунок \ (\ PageIndex {4} \): (a) Тороид – это катушка, намотанная на объект в форме пончика.(b) Тороид со слабой намоткой не имеет цилиндрической симметрии. (c) В тороиде с плотной намоткой цилиндрическая симметрия является очень хорошим приближением. d) несколько путей интеграции закона Ампера.Начнем с предположения цилиндрической симметрии вокруг оси OO ’. На самом деле это предположение не совсем верно, поскольку, как показано в части (b) рисунка \ (\ PageIndex {4} \), вид тороидальной катушки меняется от точки к точке (например, \ (P_1, \, P_2 \) и \ (P_3 \)) по круговой траектории с центром около OO ‘.Однако, если тороид плотно намотан, все точки на окружности становятся по существу эквивалентными [часть (c) рисунка \ (\ PageIndex {4} \)], а цилиндрическая симметрия является точным приближением.
При такой симметрии магнитное поле должно быть касательным и постоянным по величине на любом круговом пути с центром на OO ’. Это позволяет нам писать для каждого из путей \ (D_1, \, D_2 \) и \ (D_3 \), показанных в части (d) рисунка \ (\ PageIndex {4} \),
\ [\ oint \ vec {B} \ cdot d \ vec {l} = B (2 \ pi r).\ label {12.31} \]
Закон Ампера связывает этот интеграл с чистым током, проходящим через любую поверхность, ограниченную путем интегрирования. Для пути, который является внешним по отношению к тороиду, либо ток не проходит через ограничивающую поверхность (путь \ (D_1 \)), либо ток, проходящий через поверхность в одном направлении, точно уравновешивается током, проходящим через него в противоположном направлении. (путь \ (D_3 \)). В любом случае через поверхность не проходит чистый ток, поэтому
\ [\ oint B (2 \ pi r) = 0 \] и
\ [B = 0 \, (вне \, \, тороида).\ label {12.32} \]
Витки тороида образуют спираль, а не круговые петли. В результате снаружи катушки возникает небольшое поле; однако приведенный выше вывод верен, если катушки были круговыми.
Для кругового пути внутри тороида (путь \ (D_2 \)) ток в проводе разрезает поверхность N раз, в результате чего через поверхность возникает чистый ток NI . Теперь мы находим с помощью закона Ампера,
\ [B (2 \ pi r) = \ mu_0 NI \] и
Примечание
\ [B = \ frac {\ mu_0 NI} {2 \ pi r} \, (внутри \, \, тороида).\ label {12.33} \]
Магнитное поле для показанных обмоток направлено против часовой стрелки. Когда ток в катушках меняется на противоположное, направление магнитного поля также меняется на противоположное.
Магнитное поле внутри тороида неоднородно, так как оно изменяется обратно пропорционально расстоянию r от оси OO ’. Однако, если центральный радиус R (радиус на полпути между внутренним и внешним радиусами тороида) намного больше диаметра поперечного сечения катушек r , изменение будет довольно небольшим, и величина магнитное поле можно рассчитать по формуле \ ref {12.33} где \ (r = R \).
Видео с вопросом: Расчет количества витков токоведущего соленоида
Стенограмма видео
Провод, несущий постоянную ток 0,9 ампера формируется в соленоид длиной 310 миллиметров. Сила магнитного поля в центре соленоида измеряется как 7,7 умножить на 10 до четвертой отрицательной теслас.Рассчитайте количество используемых витков чтобы сформировать соленоид, дающий ответ с точностью до целого числа оборотов. Используйте значение четыре 𝜋 умножить на 10, чтобы отрицательные седьмые тесла-метры на ампер напрасно.
В этом примере у нас есть соленоид, который пропускает постоянный ток, мы можем назвать его заглавным 𝐼, 0,9 ампер и длина которого составляет 310 миллиметров. И мы назовем эту длину заглавной. 𝐿. Соленоид изготовлен из неизвестного количество ходов.Назовем это число заглавной, и это то, что мы хотим решить. Чтобы помочь нам сделать это вместе с тока 𝐼 и длины 𝐿, нам сообщают силу магнитного поля на соленоид в центре. Мы можем назвать это поле 𝐵, а его сила дается как 7,7 умножить на 10 отрицательной четвертой тесла. Чтобы рассчитать капитал 𝑁, общее количество витков в соленоиде, напомним, как эта переменная связанные с переменными напряженности магнитного поля, силы тока и длины.
Напряженность магнитного поля в центре соленоида равна нулю, эта константа называется проницаемость свободного пространства, умноженная на общее количество витков в соленоиде умноженный на ток, который существует в нем, деленный на длину соленоида вдоль его ось. В нашем случае это не 𝐵, что мы хотите решить, но количество витков, 𝑁. Для этого давайте умножим оба части уравнения на 𝐿 по 𝜇 нулю раз 𝐼.С правой стороны это означает, что все, 𝜇 ноль и 𝐼 сокращаются. И мы находим, что количество витков в соленоиде равна его длине, умноженной на напряженность магнитного поля на его центр делится на 𝜇 нулевое значение тока в соленоиде 𝐼.
Что касается факторов В левой части этого выражения нам даны все четыре из них. Мы знаем 𝐿, 𝐵 и 𝐼. И нам говорят использовать значение четыре 𝜋 умножить на 10 до отрицательной седьмой тесла-метра на ампер за ничего.Подставляя все эти значения в, находим это выражение для числа витков. Прежде чем рассчитать это значение тем не менее, давайте преобразуем эту длину нашего соленоида, которая в настоящее время измеряется в единицах миллиметры, в единицы метры. Чтобы помочь нам в этом, мы можем вспомнить что 1000 миллиметров равны одному метру, что означает, что для преобразования 310 миллиметров в метры, сдвинем десятичный разряд на одну, две, три точки влево, давая нам результат 0.310 метров.
А теперь давайте посмотрим на единицы в числитель и знаменатель этой дроби. Мы видим, прежде всего, что эти здесь единицы метров в числителе отменяются на метры. А также единица тесла компенсируется сверху и снизу, как и единица ампер, потому что ампер в числителе и знаменателе, можно сказать, нашего общего знаменателя. Так же, как мы и надеемся, этот результат будет безразмерным, потому что мы вычисляем чистое число.
Теперь, когда мы вводим эту дробь на наш калькулятор, мы обнаруживаем, что на самом деле не получаем результат целого числа. Это может произойти практически из-за конструкция соленоида, где, скажем, на концах соленоида, один полный очередь не может быть закончена. Итак, нет ничего обязательного неправильно, что 𝑁 не целое число. Но наша постановка вопроса скажите нам округлить наш результат до ближайшего целого числа.Когда мы это делаем, мы находим результат из 211. Это количество витков этого соленоид с точностью до целого числа.
Inductance – The Physics Hypertextbook
Обсуждение
введение
Готовы? Вот так.
Пуск с соленоидом. Пропустите через него ток, и вы получите электромагнит. Поле внутри задается формулой…
| B = μ 0 nI = μ 0 | N | Я |
| ℓ |
В то же время соленоид – это еще и устройство для улавливания магнитного потока.
Φ B = NBA
Статическая ситуация, безусловно, достаточно интересна, но когда дело доходит до потока, то, что нас действительно волнует, – это скорость изменения во времени. Это то, что дает нам электромагнитную индукцию или индуцированную электродвижущую силу, или как вы хотите это называть. Эта ситуация описывается законом Фарадея.
Давайте снова рассмотрим эти уравнения, но с изменяющимся во времени поворотом. Соленоид с изменяющимся током, проходящим через него, будет генерировать изменяющееся магнитное поле.
| дБ | = мк 0 | N | dI | |
| дт | ℓ | дт |
Это изменяющееся магнитное поле затем улавливается тем самым соленоидом, который его создал. Захваченное поле называется потоком, а изменяющийся поток генерирует ЭДС – в данном случае самоиндуцированную или обратную ЭДС.
| ℰ = – | d Φ B | = – N | ⎛ ⎜ ⎝ | мкм 0 | N | dI | ⎞ ⎟ ⎠ | А | |
| дт | ℓ | дт |
Немного изменив порядок вещей, мы получим это уравнение…
| ℰ = – | мкм 0 AN 2 | dI | |
| ℓ | дт |
, который может показаться не таким уж большим, пока вы не поймете, что члены первой дроби в значительной степени определяются геометрией соленоида.Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.
Самоиндуцированная ЭДС в цепи прямо пропорциональна скорости изменения тока ( dI / dt ), умноженной на константу ( L ). Эта постоянная называется индуктивностью (или, точнее, самоиндуктивностью ) и определяется геометрией схемы (или, чаще, геометрией отдельных элементов схемы).Например, индуктивность соленоида (как определено выше) определяется формулой…
Символ L для обозначения индуктивности был выбран в честь Генриха Ленца (1804–1865), чьи новаторские работы в области электромагнитной индукции сыграли важную роль в развитии окончательной теории. Если вы помните, Закон Ленца гласит, что индуцированный ток в цепи всегда действует таким образом, чтобы противодействовать изменению, которое в первую очередь его вызвало. Это наблюдение является причиной того, почему во всех версиях закона Фарадея стоит знак минус.Ленц поставил нам знак минус, и мы его чествуем символом L .
Индуктивность лучше всего определяется по ее роли в уравнении, полученном из закона индукции Фарадея. Некоторым это не нравится, и они предпочитают определения, написанные в форме простого предложения субъект-глагол-объект.
На английском языке мы читаем это как «собственная индуктивность ( L ) – это отношение обратной ЭДС () к скорости изменения тока, производящего ее ( dI / dt ).«Как я уже сказал, мне не очень нравится такое определение, но оно помогает нам определить подходящие единицы.
| ⎡ ⎢ ⎣ | H = | В | = | Дж / К | = | (кг · м 2 / с 2 ) / (А · с) | = | кг м 2 | ⎤ ⎥ ⎦ |
| А / с | А / с | А / с | A 2 с 2 |
Единицей индуктивности является генри , названный в честь Джозефа Генри (1797–1878), американского ученого, открывшего электромагнитную индукцию независимо и примерно в то же время, что и Майкл Фарадей (1791–1867) в Англии.Первым свои открытия опубликовал Фарадей, поэтому ему заслуга в большей степени. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое легло в основу телеграфа). Схема с собственной индуктивностью в один генри будет испытывать противоэдс в один вольт при изменении тока со скоростью один ампер в секунду.
Индуктивность это что-то. Индуктивность – это сопротивление элемента схемы изменениям тока.Индуктивность в цепи – это аналог массы в механической системе.
| ⇕ | |||||
| |||||
| ⇕ | |||||
детектор индуктивной петли
Движение на некоторых перекрестках контролируется с помощью индуктивных петлевых детекторов (ILD).ILD – это петля из проводящего провода, проложенная всего на несколько сантиметров ниже тротуара. Когда автомобиль проходит через поле, он действует как проводник, изменяя индуктивность контура. Изменение индуктивности контура указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, отслеживания транспортного потока или автоматического цитирования.
примеры
индуктивность зависит от геометрии
Соленоид ( A площадь поперечного сечения, N количество витков, ℓ длина, n количество витков на длину)
| Φ B | = N | B | А | ||
| Φ B | = N | мкм 0 NI | А | ||
| ℓ | |||||
| Φ B | = | мкм 0 AN 2 | Я | ||
| ℓ | |||||
| d Φ B | = | мкм 0 AN 2 | dI | ||
| дт | ℓ | дт | |||
| L | = | мкм 0 AN 2 | = | мкм 0 Aℓn 2 | |
| ℓ |
коаксиальных проводников ( a внутренний радиус , b внешний радиус , длина ℓ)
| Φ B | = | ⌠ | B | · | d A | ||||
| б | б | ||||||||
| Φ B | = | ⌠ ⌡ | мкм 0 I | ℓ др | = | мкм 0 Iℓ | ⌠ ⌡ | др | |
| 2π r | 2π | r | |||||||
| a | a | ||||||||
| Φ B | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ | a | ⎞ ⎟ ⎠ | Я | ||
| 2π | б | ||||||||
| d Φ B | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ | a | ⎞ ⎟ ⎠ | dI | ||
| дт | 2π | б | дт | ||||||
| L | = | мкм 0 ℓ | пер. | ⎛ ⎜ ⎝ | a | ⎞ ⎟ ⎠ | |||
| 2π | б | ||||||||
тороид ( A площадь поперечного сечения, R радиус вращения, N количество витков)
| Φ B | = | N | B | А | |
| Φ B | ≈ | N | мкм 0 NI | А | |
| 2π R | |||||
| Φ B | ≈ | N | мкм 0 NA | Я | |
| 2π R | |||||
| d Φ B | ≈ | мкм 0 AN 2 | dI | ||
| дт | 2π R | дт | |||
| L | ≈ | мкм 0 AN 2 | |||
| 2π R | |||||
прямоугольная петля ( w ширина, h высота, a радиус провода )
| Φ B | = | N | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | N |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ B | = | 2 | мкм 0 N 2 | ⎡ ⎢ ⎣ | y ln | ⎛ ⎜ ⎝ | x | ⎞ ⎟ ⎠ | + | x дюйм | ⎛ ⎜ ⎝ | y | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | Я | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2π | a | a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| d Φ B | = | мкм 0 N 2 | ⎡ ⎢ ⎣ | y ln | ⎛ ⎜ ⎝ | x | ⎞ ⎟ ⎠ | + | x дюйм | ⎛ ⎜ ⎝ | y | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | dI | ||||||||||||||||||||||||||||||||||||||||||||||||||
| дт | π | a | a | дт | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| L | = | мкм 0 N 2 | ⎡ ⎢ ⎣ | y ln | ⎛ ⎜ ⎝ | x | ⎞ ⎟ ⎠ | + | x дюйм | ⎛ ⎜ ⎝ | y | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | |||||||||||||||||||||||||||||||||||||||||||||||||||
| π | a | a | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эта формула не совсем работает, поскольку игнорирует краевые эффекты.Вы можете найти точную формулу (а также скрипты, которые будут рассчитывать индуктивность для вас) в Интернете на нескольких веб-сайтах по электротехнике.
Магнитное поле в формуле соленоида
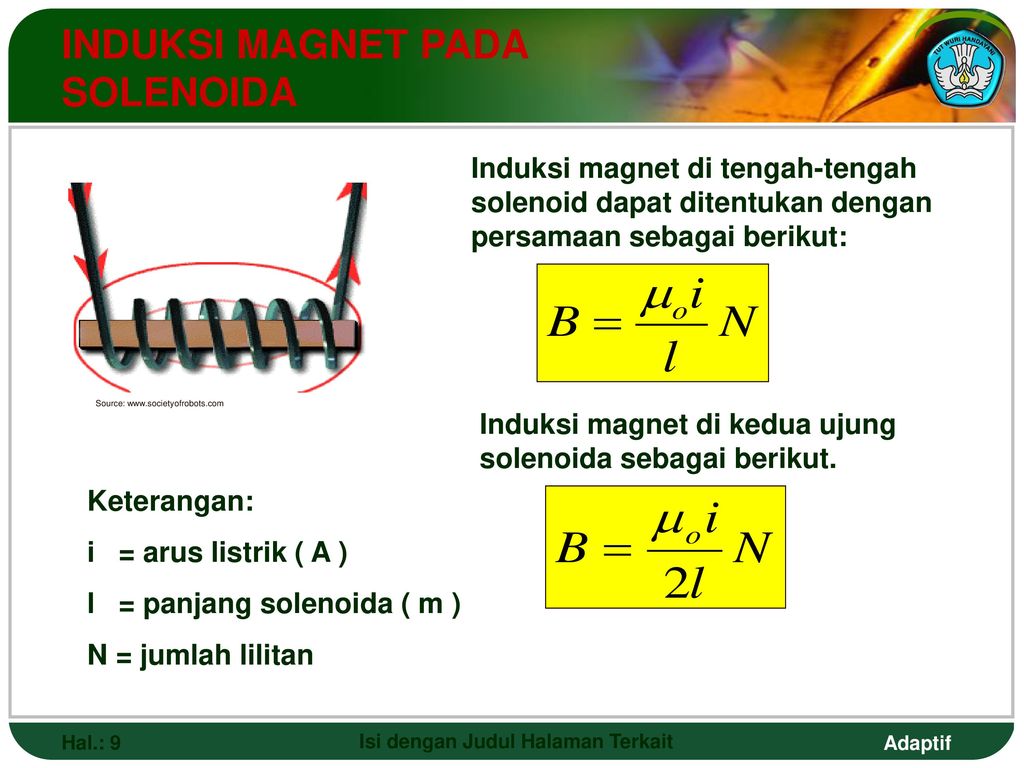
Термин «соленоид» по-гречески означает «трубчатый». Это тип электромагнита, его цель – генерировать контролируемое магнитное поле через катушку, намотанную в плотно упакованную спираль. Катушка может быть устроена так, чтобы создавать однородное магнитное поле в объеме пространства, когда через нее пропускается электрический ток.Согласно исследованию электромагнетизма, соленоид – это катушка, длина которой больше ее диаметра; это означает, что он имеет форму стержня. Спиральная катушка соленоида не обязательно должна вращаться вокруг прямой оси, например, электромагнит Уильяма Стерджена 1824 года состоял из соленоида, изогнутого в форме подковы. Следовательно, формула магнитного поля уравнения соленоида имеет следующий вид:
B = \ [\ mu_ {0} \] \ [\ frac {NI} {l} \]
Здесь B представляет собой плотность магнитного потока, \ [\ mu_ {0} \] – магнитная постоянная, значение которой равно 4π x 10 \ [^ {- 7} \] Hm \ [^ {- 1} \] или 12.{-1} \], N – количество витков, I – ток, протекающий через соленоид, а l – длина соленоида.
[Изображение будет загружено в ближайшее время]
Магнитное поле внутри соленоида, формула
Магнитное поле внутри бесконечно длинного соленоида однородно, и его сила не зависит ни от расстояния от оси, ни от площади поперечного сечения соленоида.
Определение плотности магнитного потока, окружающей соленоид, достаточно длительное, чтобы можно было пренебречь краевыми эффектами.Мы сразу знаем, что из рисунка плотность потока векторных точек находится в положительном z-направлении внутри соленоида, а вне соленоида – в отрицательном z-направлении. Мы можем подтвердить это, применив правило правого захвата или правило правого большого пальца для поля, которое присутствует вокруг провода. Если мы обернем правую руку вокруг провода, направив большой палец в направлении тока, изгиб пальцев будет отражать поведение поля. Поскольку мы имеем дело с длинным соленоидом, из-за симметрии все компоненты магнитного поля, которые не направлены вверх, могут компенсироваться.
[Изображение будет загружено в ближайшее время]
Теперь рассмотрим воображаемую петлю «c» на рисунке, она расположена внутри соленоида. По закону Ампера мы можем сказать, что линейный интеграл B, который представляет собой вектор плотности магнитного потока вокруг этой петли, равен нулю. Это происходит потому, что в нем нет электрического тока. Выше мы показали, что поле направлено вверх внутри соленоида, поэтому горизонтальные участки петли c не вносят никакого вклада в интеграл. Таким образом, интеграл верхней стороны фигуры, представляющей единицу, равен составной части второй стороны, которая движется вниз.Поскольку изменение размеров петли может производиться произвольно, чтобы получить тот же результат, подынтегральные выражения фактически равны. Это означает, что магнитное поле внутри соленоида радиально однородно.
Соленоид – это катушка из проволоки, по которой протекает ток, а магнитное поле внутри него определяется с помощью вклада каждой петли в соленоиде. Следовательно, общее магнитное поле зависит от количества витков катушки и длины соленоида.
Магнитное поле внутри соленоида максимальное, а магнитное поле внутри соленоида по формуле равно
B = \ [\ mu_ {0} \] nI, Здесь ‘n’ представляет количество витков, а ‘I’ – ток, протекающий через соленоид.
Формула магнитного поля вне соленоида
Аналогичный аргумент можно применить к контуру, чтобы сделать вывод о том, что поле вне соленоида является радиально однородным или постоянным. Также можно использовать интуитивный аргумент, чтобы показать, что плотность потока вне соленоида на самом деле равна нулю.Линии магнитного поля существуют только в форме петель, они не могут расходиться или сходиться в точку, как у силовых линий электрического поля. Силовые линии магнитного поля в соленоиде проходят по продольной траектории, поэтому вне соленоида эти силовые линии должны двигаться в противоположном направлении. Это происходит из-за линий, образующих петлю. Однако объем, который присутствует вне соленоида, намного больше, чем объем, присутствующий внутри. Таким образом, плотность силовых линий магнитного поля вне соленоида значительно снижается.Таким образом, можно сказать, что поле вне соленоида постоянно. Чтобы общее количество силовых линий было сохранено, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.
Уравнение магнитного поля соленоида вне его равно
B = \ [\ mu_ {0} \] nI, поскольку поле вне соленоида сравнительно меньше, чем то, что оно присутствует внутри, мы можем считать его равным нулю, так как длина соленоид увеличивается, и, таким образом, B = 0.
Магнитное поле вокруг соленоида с примерами
Магнитное поле вокруг соленоида
На рисунке ниже показан соленоид.Типичный соленоид ведет себя как стержневой магнит. Магнитное поле, создаваемое соленоидом, постоянно внутри соленоида и параллельно его оси.
Мы находим магнитное поле, создаваемое соленоидом, по следующей формуле;
Где: i – ток, N – количество витков, а l – длина соленоида.
Мы находим направление магнитного поля, снова используя правило правой руки. Возьмитесь за соленоид, пока ваши четыре пальца показывают направление тока, а большой палец показывает направление магнитного поля.
Пример: Найдите магнитное поле, создаваемое соленоидом, если количество витков равно 400, а ток, проходящий через него, равен 5 А. (Длина соленоида составляет 40 см, а k = 10 -7 Н / А 2 )
Н = 400, i = 5 А, l = 40 см = 0,4 м, k = 10 -7 Н / А 2 ,
Пример: Соленоид имеет диаметр 80 см, количество витков – 4, а магнитное поле внутри него – 1,2.10 -5 Н / А.м. Найдите ток, проходящий через каждую петлю провода.
Поскольку вопросы задают ток в каждой петле, мы принимаем каждую петлю как круг, таким образом, мы находим магнитное поле;
Пример: Ниже приведены два соленоида, они имеют одинаковую длину, i 1 = 4 А и i 2 = 3 А. Найти вектор магнитного поля в точке A.
i 1 ток создает магнитное поле B 1 , а ток i 2 создает магнитное поле B 2 .Мы суммируем эти векторы, используя свойства вектора, и получаем следующий вектор полного магнитного поля в точке A.
Экзамены на магнетизм и решения
| Магнитное поле вокруг круглой проволоки <Назад | Далее> Сила, действующая на движущуюся частицу и токопроводящий провод |
|---|


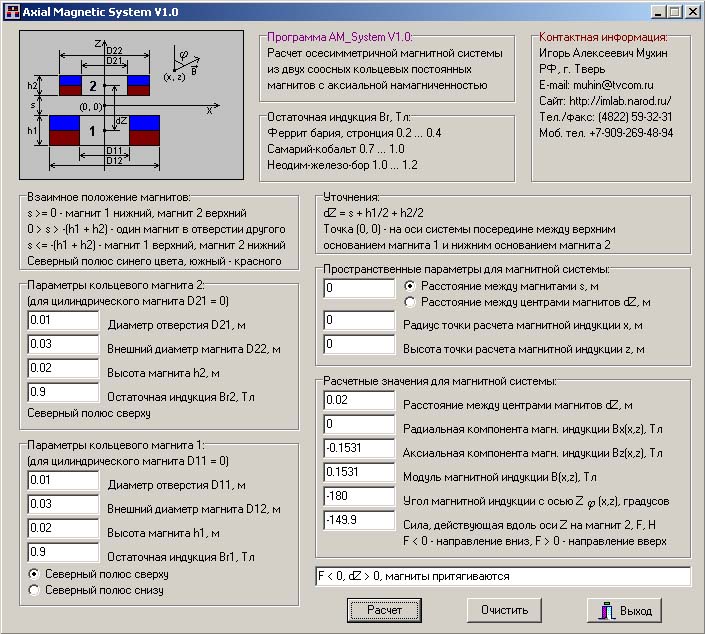 22)
22)