Сопротивление петли фаза ноль: Допустимое сопротивление петли «фаза-ноль»

Содержание

Допустимое сопротивление петли «фаза-ноль»

Чаще всего реальное сопротивление петли «фаза-ноль» достаточно невелико для надёжной защиты линии. Но бывают ситуации, когда токи КЗ не достигают требуемых значений. В самом деле, при значениях петли более 0,8 Ом величина тока КЗ не превышает 275А и, с учётом требований ПТЭЭП, прил. 3, табл. 28, п. 4, автомат с Iном=25А уже не гарантирует отключение в заданное время. А это очень распространённый номинал автомата для защиты групповых линий розеточной сети. Иногда это можно увидеть в сельской местности, в садоводческих обществах, когда линия 0,4 кВ имеет длину 1-2 км, а сечение проводов невелико.

На величину сопротивления петля «фаза-ноль» влияет площадь поперечного сечения жил кабеля и его длина. Эти параметры связаны между собой. При увеличении длины линии приходится увеличивать её сечение, чтобы обеспечить необходимую кратность токов КЗ. Больше всего это проявляется в осветительных и розеточных сетях, где линии протяженные, а сечение проводов небольшое. По тем же причинам увеличено сопротивление петли «фаза-ноль» линий электроснабжения на вводе в здание. При этом свою долю вносит сопротивление обмоток силового трансформатора на подстанции.

Конечно, устранение указанных причин, т.е. замена электропроводки или кабельных линий повлечет за собой немалые затраты и частичную остановку функционирования объекта. Такая ситуация встречается, в основном, там, где электромонтажные работы выполнялись без предварительных расчетов и разработки проекта. При разработке проекта, проектировщики, используя справочники и таблицы производят расчеты сопротивлений цепи «фаза-ноль» и учитывают полученные значения при выборе аппаратов защиты. Поэтому так важно, чтобы монтаж любой электроустановки производился на основе качественно подготовленной проектной документации.

Можно ли как-нибудь исправить сложившуюся ситуацию, не прибегая к радикальным мерам? Конечно можно! Если не получается убрать причину малых токов короткого замыкания, можно ужесточить требования к защитным аппаратам. В осветительных и розеточных сетях, в основном, применяются модульные автоматы бытового назначения с характеристиками «В», «С», «D». В таких случаях единственный выход – установить в качестве аппарата защиты автомат с характеристикой «В» расцепителя мгновенного действия. В отличие от распространенного автомата с характеристикой «С» у него срабатывание происходит при токе Iкз = 5хIном, т.е. в рассмотренном выше примере он уверенно отключит даже ещё меньший ток (137 А) при сопротивлении петли «фаза-ноль» до 1,6 Ом. Можно уменьшить номинал автомата, тогда будут автоматически отключаться ещё меньшие токи КЗ. При этом следует помнить, что номинал автомата не должен быть меньше расчетного тока на защищаемом участке. Для защиты кабельных или воздушных линий электроснабжения можно применить предохранители, выносные реле.

Петля фаза-ноль | Заметки электрика

Уважаемые, читатели!!!

Приветствую Вас на своем ресурсе «Заметки электрика».

На повестке сегодняшнего дня у нас статья на тему петля фаза-ноль.

Что же такое петля фаза-ноль?

Все об этом Вы узнаете, прочитав материал ниже.

Мы с Вами знаем, что все электрооборудование, будь то в квартире или на производстве, должно работать исправно и долговечно.

Во время повреждений (короткое замыкание, перегруз и др.) электрооборудования или же самой электропроводки, должны мгновенно срабатывать аппараты защиты, отключая поврежденный участок цепи.

Но мы забываем о том, что в процессе эксплуатации электрооборудования и электрических сетей необходимо заранее и заблаговременно обследовать и выявлять неисправности (отказы).

Чаще всего никто этого правила не придерживается, а обращаются к специалистам-электрикам уже при возникновении самой неисправности. А иногда бывает так, что обращаться уже поздно.

Нет, уважаемые, я Вас не пугаю. Так оно и есть.

Просто примите себе за правило, что для выявления, предупреждения и устранения всех неисправностей Ваших электрических сетей и электрооборудования необходимо с определенной периодичностью производить комплекс следующих электрических измерений:

Кто имеет право проведения вышеперечисленных измерений? Об этом читайте в статье про электролабораторию.

Что это такое «петля фаза-ноль»?

Мы уже с Вами знакомы с системами заземления электроустановок до 1000 (В) TN-C, TN-C-S, TN-S. Все они являются глухозаземленными.

Если соединить фазный проводник L на нулевой рабочий проводник N или защитный проводник PE, то образуется контур, называемый петля фаза-ноль.

Т.е. эта петля состоит из электрической цепи фазного проводника L и нулевого рабочего проводника N, либо из электрической цепи фазного проводника L и защитного проводника PE, которая обладает своим сопротивлением.

Можно, конечно, и самостоятельно рассчитать сопротивление петли фаза-ноль, но это достаточно сложно и проблематично из-за ряда следующих факторов:

переходные сопротивления всех коммутационных аппаратов (автоматических выключателей, предохранителей, рубильников, разъединителей, контакторов и др.)
точный путь тока в аварийном режиме (металлические конструкции, водопроводы, трубопроводы, контур заземления, повторное заземление)

При измерении сопротивления петли фаза-ноль специальным прибором, все вышеперечисленные факторы учитываются автоматически.

Причины и цель измерения

Причины проведения измерения петли Ф-О:

приемосдаточные испытания, т.е. вновь вводимая электроустановка (после монтажа или реконструкции)
по требованию службы Ростехнадзора или других контролирующих организаций
собственное желание

Целью проведения измерений заключаются в определении следующих параметров:

1. Величина сопротивления петли фаза-ноль

В это значение входит сопротивление обмоток питающего трансформатора, фазного проводника L и нулевого (защитного) проводника N (PE), переходных сопротивлений силовых контактов автоматических выключателей, рубильников, контакторов и др.

2. Величина тока короткого замыкания

Величина тока однофазного короткого замыкания может быть получена косвенным путем по нижеприведенной формуле, или же расчитана прибором автоматически.

Iк.з = Uном / Zп

Uном – номинальное напряжение питающей сети

Zп – полное сопротивление петли фаза-ноль

Расчитанный или измеренный ток короткого замыкания сравнивают с уставкой автоматического выключателя (либо тепловой, либо электромагнитной).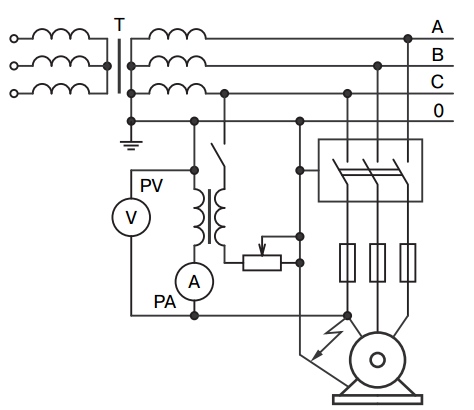

Заключение об измерении петли фазы-ноль делаем согласно нормативно-технических документов ПТЭЭП и ПУЭ.

Как проводить измерение петли фаза-ноль Вы можете узнать в моей следующей статье — измерение петли фаза-ноль.

В той же статье я наглядно покажу на примере, как сделать правильное заключение по полученным параметрам.

Если статья была Вам полезна, то поделитесь ей со своими друзьями:

Сопротивление цепи фаза – ноль

Таблица 1

Сечение фазных жил мм²	Сечение нулевой жилы мм²	Полное сопротивление цепи фаза – ноль, Ом/км при температуре жил кабеля +65 градусов
Сечение фазных жил мм²	Сечение нулевой жилы мм²	Материал жилы:
		Алюминий			Медь
		R фазы	R нуля	Z цепи (кабеля)	R фазы	R нуля	Z цепи (кабеля)
1,5	1,5	–	–	–	14,55	14,55	29,1
2,5	2,5	14,75	14,75	29,5	8,73	8,73	17,46
4	4	9,2	9,2	18,4	5,47	5,47	10,94
6	6	6,15	6,15	12,3	3,64	3,64	7,28
10	10	3,68	3,68	7,36	2,17	2,17	4,34
16	16	2,3	2,3	4,6	1,37	1,37	2,74
25	25	1,47	1,47	2,94	0,873	0,873	1,746
35	35	1,05	1,05	2,1	0,625	0,625	1,25
50	25	0,74	1,47	2,21	0,436	0,873	1,309
50	50	0,74	0,74	1,48	0,436	0,436	0,872
70	35	0,527	1,05	1,577	0,313	0,625	0,938
70	70	0,527	0,527	1,054	0,313	0,313	0,626
95	50	0,388	0,74	1,128	0,23	0,436	0,666
95	95	0,388	0,388	0,776	0,23	0,23	0,46
120	35	0,308	1,05	1,358	0,181	0,625	0,806
120	70	0,308	0,527	0,527	0,181	0,313	0,494
120	120	0,308	0,308	0,616	0,181	0,181	0,362
150	50	0,246	0,74	0,986	0,146	0,436	0,582
150	150	0,246	0,246	0,492	0,146	0,146	0,292
185	50	0,20	0,74	0,94	0,122	0,436	0,558
185	185	0. 20	0,20	0,40	0,122	0,122	0,244
240	240	0,153	0,153	0,306	0,090	0,090	0,18

Таблица 2

Мощность трансформатора, кВ∙А	25	40	69	100	160	250	400	630	1000
Сопротивление трансформатора, Zт/3, Ом (Δ/Υ)	0,30	0,19	0,12	0,075	0,047	0,03	0,019	0,014	0,009

Таблица 3

I ном. авт. выкл, А	1	2	6	10	13	16	20	25	32-40	50 и более
R авт., Ом	1,44	0,46	0,061	0,014	0,013	0,01	0,007	0,0056	0,004	0,001

Таблица 4

R цепи, Ом	0,05	0,1	0,2	0,3	0,4	0,5	0,6	0,8	1,0	1,5	2 и более
Rдуги, Ом	0,015	0,022	0,032	0,04	0,045	0,053	0,058	0,075	0,09	0,12	0,15

При проектировании групповой сети, если питающая и распределительная сеть уже проложены, целесообразно выполнить измерение сопротивления цепи фаза – ноль от трансформатора до шин группового щита. Это может значительно уменьшить вероятность ошибок при расчетах групповой сети. В этом случае сопротивление рассчитываем по формуле:

R_L_–_N= R_расп + R_пер.гр + R_авт.гр+ Rn_гр∙Ln_гр +Rдуги (2)

где, R_расп – измеренное сопротивление цепи фаза – ноль линии, подключаемой к вводному автоматическому выключателю группового щитка, Ом; R_пер.гр – сопротивление переходных контактов в групповой линии, Ом; R_авт.гр– суммарное сопротивление автоматических выключателей – вводного группового щита и отходящей групповой линии, Ом; Rn_гр– удельное сопротивление кабеля n-й групповой линии (по таблице 1), Ом/км; Ln_гр– длина n-й групповой линии, км.

Рассмотрим процесс вычисления сопротивления цепи фаза – ноль схемы, показанной на Рис.1 при однофазном коротком замыкании фазы на ноль в конце групповой линии.

Исходные данные:

– трансформатор мощностью 630 кВ∙А подключен по схеме «треугольник – звезда» – по таблице 2 находим Zт/3=0,014 Ом;

– питающая сеть – кабель с алюминиевыми жилами длиной 80 метров имеет фазный проводник 150 мм² и нулевой – 50 мм².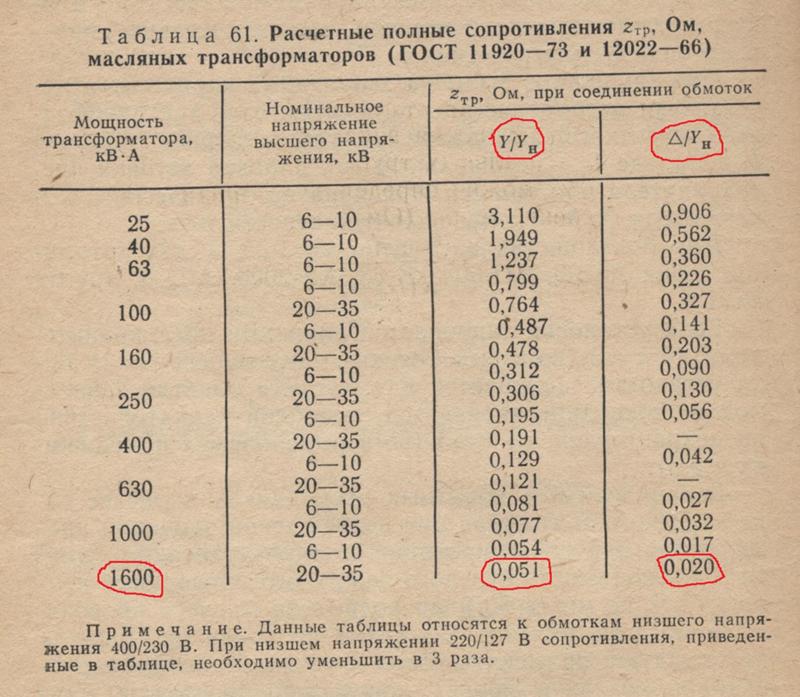 По таблице 1 находим удельное сопротивление кабеля 0,986 Ом/км. Вычисляем его сопротивление (длины кабелей выражаем в километрах): 0,986 Ом/км∙0,08 км=0,079 Ом;

– распределительная сеть – кабель с медными жилами длиной 50 метров и сечением жил 35 мм². По таблице 1 находим удельное сопротивление кабеля 1,25 Ом/км. Вычисляем его сопротивление:

1,25 Ом/км∙0,05 км=0,0625 Ом;

– групповая сеть – кабель с медными жилами длиной 35 метров и сечением жил 2,5 мм². По таблице 1 находим удельное сопротивление кабеля 17,46 Ом/км. Вычисляем его сопротивление:

17,46 Ом/км∙0,035 км=0,61 Ом;

– автоматический выключатель отходящий линии – 16 Ампер (с характеристикой срабатывания «С»), вводной автоматический выключатель группового щитка 32 Ампера, остальные автоматические выключатели в линии имеют номинальный ток более 50 Ампер. Вычисляем их сопротивление (по таблице 3) 0,01 Ом+0,004 Ом+3∙0,001 Ом=0,017 Ом;

– переходные сопротивления контактов учтем только в групповой линии (точки подключения кабеля групповой линии к щитку и к нагрузке). Получаем 2∙0,01 Ом=0,02 Ом.

Суммируем все полученные значения и получаем сопротивление цепи фаза – ноль без учета сопротивления дуги R_L_–_N=0,014+0,079+0,0625+0,61+0,017+0,02=0,80 Ом.

Из таблицы 4 берем сопротивление дуги 0,075 Ом, и получаем окончательное значение искомой величины R_L_–_N=0,80 Ом+0,075 Ом=0,875 Ом.

В Правилах устройства электроустановок (ПУЭ) задано наибольшее время отключения цепей при коротком замыкании в сетях с глухозаземленной нейтралью 0,2 секунды при напряжении 380 В и 0,4 секунды при напряжении 220В.

Для обеспечения заданного времени срабатывания защиты необходимо, что бы при коротком замыкании в защищаемой линии возникал ток, превышающий не менее чем в 3 раза номинальный ток плавкой вставки ближайшего предохранителя (для взрывоопасных помещений не менее чем в 4 раза) и не менее чем в 3 раза ток расцепителя автоматического выключателя, имеющего обратнозависимую от тока характеристику (для взрывоопасных помещений не менее чем в 6 раз). Для автоматических выключателей с комбинированным расцепителем (имеющим тепловой расцепитель для защиты от перегрузок и электромагнитный расцепитель для защиты от токов коротких замыканий) ток короткого замыкания должен превысить ток срабатывания электромагнитного расцепителя не менее, чем в 1,2 – 1,25 раза.

В настоящее время используются автоматические выключатели с различной кратностью токов срабатывания электромагнитного расцепителя к тепловому. Автоматические выключатели группы «В» имеют кратность в пределах от 3 до 5, группы «С» от 5 до 10, группы «D» от 10 до 20, группы «K» от 10 до 15 и группы «Z» от 2 до 3. При расчетах всегда берется максимальное значение кратности токов срабатывания расцепителей. Например для автоматического выключателя С16, ток короткого замыкания должен быть не менее 16 А∙10∙1,2=192 А (для автоматического выключателя С10 не менее10А∙10∙1,2=120 А и для С25 не менее 25 А∙10∙1,2=300 А). В приведенном выше примере мы получили сопротивление цепи фаза – ноль 0,875 Ом. При таком сопротивлении цепи ток короткого замыкания Iкз составит величину

U_ф/ R_L_–_N=220В/0,875 Ом=251 А. Следовательно групповая линия в приведенном примере защищена от токов коротких замыканий.

Максимальное сопротивление цепи фаза – ноль для автоматического выключателя С16 составит величину 220 В/192А=1,14 Ом. В приведенном примере сети (Рис. 1) сопротивление цепи от трансформатора до шин группового щита составит 0, 875 Ом – 0,61 Ом=0.265 Ом. Следовательно максимально возможное сопротивление кабеля групповой линии будет равно 1,14 Ом – 0, 265 Ом=0,875 Ом. Его максимальную длину L при сечении жил кабелей 2,5 мм²определим при помощи таблицы 1.

L, км=0,875 Ом/(17,46 Ом/км)=0,050 км.

Всегда, когда есть возможность, следует рассчитывать групповую сеть с максимальным запасом по сопротивлению цепи фаза – ноль, особенно розеточную сеть. Часто нагрузки (утюг, чайник и другие бытовые приборы), в которых часто происходят замыкания, подключают к розетке через удлинитель. Начиная с определенной длины провода удлинителя, нарушается согласование параметров цепи с характеристиками аппаратов защиты, то есть ток короткого замыкания оказывается недостаточным для мгновенного отключения сети. Отключение аварийного участка осуществится только тепловым расцепителем через сравнительно большой промежуток времени (несколько секунд), в результате чего кабели могут нагреться до недопустимо высоких температур вплоть до воспламенения изоляции.

Проект электропроводки должен быть выполнен таким образом, что бы даже в случае воспламенения изоляции кабеля при коротком замыкании это не приводило к пожару. Именно поэтому возникли требования к прокладке скрытой электропроводки в стальных трубах в зданиях со строительными конструкциями, выполненными из горючих материалов. Во взрывоопасных зданиях целесообразно использовать более сложную защиту кабелей от воздействия токов короткого замыкания.

9 марта 2013 г.

К ОГЛАВЛЕНИЮ

Чем измерить сопротивление петли «фаза-ноль»

Фирма Астро-УЗО специализируется на разработке, внедрении и тестировании электрозащитных устройств, в частности УЗО – устройств защитного отключения , которые предназначены для защиты людей от поражения электрическим током при прикосновении к неизолированным токоведущим частям электроустановок и для предотвращения пожаров, к которым могут привести токи утечки на землю из-за нарушения изоляции электропроводки (мы рассказывали о них в газете и в статьях на сайте).

Для тестирования их работоспособности фирма Астро-УЗО разработала приборы Астро-Тест (И4725) и Астро-Тест-М (И4700). Они проверяют наличие в схеме электроустановки защитного нулевого проводника и его целостность, исправность системы заземления. С их помощью определяется правильность выбора уставок УЗО, селективности действия устройства при многоступенчатой системе защиты (об этом мы также рассказывали).

Новая разработка фирмы – прибор Астро-профи (И4739) – предназначен для испытаний функциональных характеристик УЗО («Автоматы и замера некоторых параметров электроустановки.

Прибор позволяет измерить отключающий дифференциальный ток УЗО типов А и АС (уставки – 10, 30, 100, 300 mА с кратностью 1, 2, 5, 1.25), время его отключения, частоту и напряжение сети, малые сопротивления 0–199,9 Ом, напряжение встроенного источника питания.

Важная и наиболее существенная способность аппарата – измерение сопротивления петли «фаза-ноль», по которому определяются ток однофазного короткого замыкания и временные параметры срабатывания устройств защиты электрооборудования от сверхтоков при замыкании фазы на корпус. Астро-профи может также непосредственно измерять токи однофазных замыканий в диапазоне 10–550 А, тогда время срабатывания защитного аппарата вычисляется по измеренной величине этого тока.

Прибор оснащён микроконтроллером, который реализует алгоритм работы прибора, производит измерения и вычисления эффективного (действующего) значения несинусоидального тока и других параметров, выводит информацию на жидкокристаллический индикатор, а также на компьютер.

Прибор работает от сети 220 В или встроенного аккумулятора 6 В. Габаритные размеры 200x80x280 мм.

Измеритель сопротивления петли фаза-ноль ИФН-200 выпускает ижевская компания Радио-Сервис (И4740).

Прибор способен измерять полное, активное и реактивное сопротивление цепи фаза-ноль 0,01–200 Ом без отключения источника питания, сопротивление металлосвязи током до 250 мА для сопротивлений

Микропроцессорное управление позволяет автоматически выбирать диапазоны измерений, результаты выводятся на ЖК дисплей, имеется встроенная память на 35 измерений.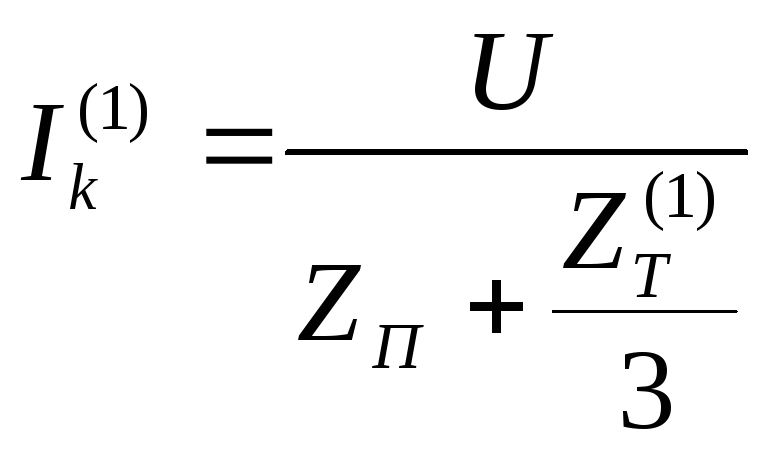

Питание от сети 220 В или аккумулятора 12 В. Корпус ударопрочный, пылевлагозащищенный IP42. Габариты 120x250x40 мм.

Петля фаза ноль. Для чего проверяют сопротивление петли фаза-ноль

Электричество в настоящее время – это не только удобство и качество проживания, но это и большая опасность для человека. И хорошо, если проводку в доме делают профессионалы. Ведь свою работу они обязательно проверяют на степень безопасности. Каким образом? Для этого используется метод, основанный на создании высокой нагрузки в электрической разводке. Этот метод электрики называют измерением сопротивления петля фаза ноль.

Что это такое, и как формируется проверочная схема

Начать надо с пути, который проходит электрический ток от подстанции до розетки в доме. Обращаем ваше внимание, что в старых домах в электрике чаще всего присутствует сеть без заземляющего контура (земля), то есть, к розетке подходит фазный провод и нулевой (фаза и ноль).

Итак, от подстанции до дома сеть может быть длиною в несколько сот метров, к тому же она разделена на несколько участков, где используются разного сечения кабели и несколько распределительных щитов. То есть, это достаточно сложная коммуникация. Но самое главное, весь участок имеет определенное сопротивление, которое приводит к потерям мощности и напряжения. И это независимо от того, качественно ли проведена сборка и монтаж или не очень. Этот факт известен специалистам, поэтому проект сети делается с учетом данных потерь.

Конечно, грамотно проведенный монтаж – это гарантия корректной работы сетевого участка. Если в процессе сборки и разводки были сделаны отклонения от норм и требований или просто сделаны ошибки, то это гарантия увеличения потерь, сбоя работы сети, аварий. Вот почему специалисты проводят измерения показателей сети и анализируют их.Что это такое, и как формируется проверочная схема.

Видео измерения петля фаза ноль

Необходимо отметить, что вся электрическая цепочка – это зацикленный контур, образованный фазным контуром и нулевым. По сути, это своеобразная петля. Поэтому ее так и называют петля фаза ноль.

Как измеряется сеть

Чтобы это понять, необходимо рассмотреть схему, в которой присутствует потребитель, подключенный через обычную розетку. Так вот к розетке, как уже было сказано выше, подводятся фаза и ноль. При этом до розетки происходит потеря напряжения за счет сопротивления магистральных кабелей и проводов. Это известно давно, описан данный процесс формулой Ома:

R=U/I.

Правда, эта формула описывает соотношение величин постоянного электрического тока. Чтобы перевести ее на ток переменный, придется учитывать некоторые показатели:

Активная составляющая сопротивления сети.
Реактивная, состоящая из емкостной и индуктивной части.

Что это значит?

Необходимо понять, что электродвижущая сила, которая появляется в обмотках трансформатора, образует электрический ток. Он теряет свое напряжение при прохождении через потребителя и подводящие провода. При этом сам ток преодолевает несколько видов сопротивления:

Активное – это потребитель и провода. Это самая большая часть сопротивления.
Индуктивное – это сопротивление встроенных обмоток.
Емкостное – это сопротивление отдельных элементов.

Как измерить сопротивление петля фаза ноль

Чтобы подсчитать полное сопротивление сети (петля фазы и ноля), необходимо определить электродвижущую силу, которая создается на обмотках трансформатора. Правда, на подстанцию без специального допуска не пустят, поэтому измерение петли фаза-ноль придется делать в самой розетке. При этом учитывайте, что розетка не должна быть нагружена. После чего необходимо замерить напряжение под нагрузкой. Для этого включается в розетку любой прибор, это может быть даже обычная лампочка накаливания. Замеряется напряжение и сила тока.

Внимание! Нагрузка на розетке должна быть стабильной в процессе проведения замеров. Это первое. Второе – оптимальным вариантом считается, если в схеме ток будет силой от 10 до 20 ампер. В противном случае дефекты сетевого участка могут не проявиться.

Теперь по закону Ома можно определить полное сопротивление петли. При этом придется учитывать, что напряжение (замеряемое) в розетке может отклоняться от номинального при нагрузке и без таковой. Поэтому сначала надо высчитать сопротивление при разных величинах напряжения. Понятно, что при нагрузке напряжение будет больше, поэтому полное сопротивление петли – это разница двух сопротивлений:

Rп=R2-R1, где R2 – это сопротивление петли при нагрузке, R1 – без таковой.

Что касается точно проведенных замеров. Самодельными приборами это можно сделать, никаких проблем здесь нет, но вот только точность замеров в данном случае будет очень низкой. Поэтому для этого процесса рекомендуется использовать вольтметры и амперметры с высокой точностью (класс 0,2).

Процесс измерения петля фаза ноль

Хотя надо отдать должное рынку, сегодня можно такие приборы приобрести в свободном доступе. Стоят они недешево, но для профессионала это необходимая вещь.

Где провести замер

Измерение петли фаза-ноль – розетки. Но опытные электрики знают, что это место не единственное. К примеру, дополнительное место – это клеммы в распределительном щите. Если в дом заводится трехфазная электрическая сеть, то проверять сопротивление петли фаза ноль надо на трех фазных клеммах. Ведь всегда есть вероятность, что контур одной из фаз был собран неправильно.

Цель проводимых замеров

Итак, цели две – определение качества эксплуатируемых сетей и оценка надежности защитных блоков и приборов.

Что касается первой позиции, то здесь придется сравнивать полученные замеры, а, точнее, сопротивление петли с проектной. В данном случае, если расчетный показатель оказался выше нормативного, то на поверку явно неправильно произведенный монтаж или другие дефекты магистрали. К примеру, грязь или коррозия контактов, малое сечение кабелей и проводов, неграмотно проведенные скрутки, плохая изоляция и так далее. Если проект электрической сети по каким-то причинам отсутствует, то для сравнения расчетного сопротивления петли с номинальным необходимо будет обратиться в проектную организацию. Чтобы разобраться в таблицах и расчетах самому, надо в первую очередь обладать инженерными знаниями по электрике.

Замер сопротивления петля фаза ноль

Что касается второй позиции. В принципе, здесь также необходимо провести некоторые расчеты, основанные на законе и формуле Ома. Основная задача определить силу тока короткого замыкания, ведь чаще всего от него и надо будет защищать электрическую сеть. Поэтому в данном случае используется формула:

Iкз=Uном/Rп.

Если считать, что сопротивление петли фаза к нулю равно, например, 1,47 Ом, то сила тока короткого замыкания будет равна 150 ампер. Под эту величину и придется подбирать прибор защиты, то есть, автомат. Правда, в правилах ПУЭ есть определенные нормы, которые создают некий запас прочности. Поэтому Iном увеличивают на коэффициент 1,1.

Подобрать автомат под все вышеуказанные величины можно, если сравнить их в таблицах ПУЭ. В нашем случае потребуется автомат класса «С» с Iном=16 А и кратностью 10. В итоге получаем:

I = 16 х 10 х 1,1 = 176 А. Расчетная сила тока короткого замыкания у нас составила – 150 А. о чем это говорит.

Во-первых, автомат был неправильно выбран и установлен. Его надо обязательно заменить.
Во-вторых, ток КЗ в сети меньше, чем автомата. Значит, он не отключится. А это может привести к пожару.

Будем рады, если подпишетесь на наш Блог!

[wysija_form id=»1″]

Измерение сопротивления петли фаза-нуль | Пусконаладочные работы при монтаже электроустановок | Архивы

Страница 53 из 56

§ 70. Измерение сопротивления петли фаза-нуль
В установках напряжением до 1000 В с глухим заземлением нейтрали необходимо измерять сопротивление петли фаза-нуль для наиболее удаленных и мощных приемников электроэнергии, но не менее 10% общего числа приемников электроэнергии, питаемых от одного трансформатора. Зная это сопротивление и напряжение сети, можно выбрать плавкие предохранители и уставки автоматов с тем, чтобы при замыкании фазных проводов электроустановки на части, соединенные с заземленным нулевым проводом, происходило автоматическое отключение поврежденного участка. Сопротивление петли фаза-нуль можно измерять методом амперметра и вольтметра при отключенном испытываемом оборудовании, а также с помощью специальных приборов без отключения испытываемого оборудования.
При измерении методом амперметра и вольтметра собирают схему (рис. 217). Питание на схему подают от понижающего трансформатора Тр2 (нагрузочного, сварочного или другого с соответствующим вторичным напряжением), который размещают вблизи силового трансформатора Tpl. Для образования петли фаза-нуль соответствующий фазовый провод А наиболее удаленного проверяемого электроприемника М соединяют с корпусом электроприемника перемычкой П, предварительно измерив сопротивление изоляции фазовых проводов и убедившись в хорошем ее состоянии, и включают соответствующий рубильник. Приборы выбирают класса 0,5 на пределы, соответствующие вторичному напряжению трансформатора Тр2 для вольтметра и 20—30 А для амперметра (или прибор 5 А с трансформатором тока 20—30/5 А).
Остальные электроприемники, питающиеся от той же линии, нужно отключить соответствующими коммутационными аппаратами. После этого включают рубильник Р и, установив силу тока в цепи 10—20 А, снимают показания приборов. Полное сопротивление петли фаза-нуль с учетом сопротивления обмоток питающего трансформатора .

где U — измеренное напряжение, В; 1 — измеренный ток, A; zT — полное сопротивление трансформатора, Ом (табл. 29).
Таблица 29 Расчетные сопротивления трансформаторов (ГОСТ 11920—66 и ГОСТ 12022—66)
при однофазном коротком замыкании на стороне 400/230 В

Мощность трансформатора, кВ-А	Первичное напряжение, кВ	Полное сопротивление трансформатора, Ом
25	6—10	1,04
40	6—10	0,65
63	6—ю	0,418
63	20	0 38
100	6—10	0 26
100	20-35	0,253 ~
160	6—10	0,162
160	20—35	0,159
250	6—10	0,104
250	20—35	0,102
400	6—10	0,065 0,064
400	20—85	0,065 0,064
630	6—10	0,043
630	20—35	0,04
1000	6—10	0,027
1000	20—35	0,026

Эти данные приведены для масляных трансформаторов ТМ со схемой соединения обмоток Y/Y0.

Рис. 217 Измерение сопротивления петли фаза-нуль
Зная сопротивление петли фаза-нуль и учитывая сопротивление трансформатора, а также возможность снижения фазового напряжения в процессе эксплуатации, ток однофазного замыкания на землю

Для обеспечения надежного отключения поврежденного участка электрической сети номинальный ток плавкой вставки или ток уставки расцепителя автомата выбирают из условия /8>/nК (А), где К — коэффициент, равный не менее 3 при защите предохранителями или автоматами с тепловыми расцепителями или 1,1КР (Кр — коэффициент разброса, заданный заводом), для автоматов с электромагнитным расцепителем. При отсутствии данных по коэффициенту разброса для автоматов с электромагнитным расцепителем на ток до 100 А К равен 1,4, а на ток более 100 А — 1,25.

§ 71. Проверка состояния пробивных предохранителей

В установках напряжением до 1000 В с изолированной нейтралью ставят пробивные предохранители, которые в случае пробоя с обмоток высшего напряжения на обмотки низшего напряжения в трансформаторах пробиваются, обеспечивая соединение последних с землей. Исправность пробивных предохранителей проверяют предварительным осмотром (целость фарфора, резьбовых соединений, качество заземления). Разрядные поверхности электродов должны быть чистыми и гладкими, без заусенцев и подгаров, слюдяная прокладка должна иметь общую толщину, указанную в табл. 30, причем отверстия в слоях многослойной прокладки должны совпадать. Сопротивление изоляции, измеренное мегомметром на напряжение 250 В у исправного предохранителя, должно быть не менее 5 МОм.
Таблица 30

Рис. 218. Схема измерения напряжения пробоя пробивного предохранителя
Основные данные пробивных предохранителей ПП-А/3

Номинальное напряжение защищаемой сети, В	Исполнение	Пробивное напряжение, В	Толщина слюдяной прокладки, ш
220—380 500—660	I II	351—500 701—1000	0,08—0,02 0,21—0,03

Для испытания пробивного предохранителя собирают схему (рис. 218) и поднимают напряжение до пробоя предохранителя. Балластное сопротивление выбирают величиной 5—10 кОм, чтобы ограничить ток при пробое предохранителя и избежать подгорания разрядных поверхностей. Если пробивное напряжение соответствует данным табл. 30, то после снижения подводимого напряжения его снова поднимают до 0,75 t/np. В случае отсутствия пробоя при этом напряжении испытание заканчивают и измеряют сопротивление изоляции пробивного предохранителя. При значительном снижении сопротивления изоляции (более чем на 30%) по сравнению с первым замером предохранитель нужно разобрать, прочистить подгоревшие разрядные поверхности и снова провести испытание в полном объеме.

Контрольные вопросы
Где используют заземляющие устройства и как их разделяют по назначению?
На каком принципе работают защитное заземление и зануление?
Дайте определение шаговому напряжению и напряжению прикосновения.
В чем опасность выноса потенциала от заземленного оборудования и подведения нулевого потенциала к этому оборудованию?
Почему недопустимо в одном помещении применять одновременно защитное заземление для одного оборудования и зануление для другого?
Какой объем работ необходимо выполнять при наладке заземляющего устройства?
Как измерить сопротивление заземлителя прибором МС-08 и методом амперметра и вольтметра?
Как проверяют сеть защитного заземления?
Для чего и как измеряют сопротивление петли фаза-нуль в сетях напряжением до 1000 В с глухозаземленной нейтралью?

Измерение петли фаза-ноль | Электролаборатория БЭТЛ Ярославль

Главная › Документация

Краткое содержание.

Петля Ф-Н — это измерение в электроустановках до 1000 В. Представляет из себя контур, соединяющий фазу и ноль.
Необходимо для проверки качества монтажа и соответствия защитной автоматики сечению проводов.
Периодичность — не реже 1 раза в 3 года.
Обычно проводится без снятия напряжения.
При помощи прибора ИФН или аналогичного измеряется ток короткого замыкания (КЗ) в самой отдаленной точке от распределительного щита.
Ток КЗ должен быть больше номинала защитного устройства не менее чем в 3 раза.
Протокол содержит номинал автомата, соответствующие измеренные значения и другие данные установленной формы.

1. Что такое петля фаза-ноль

В электрических установках напряжением до 1000 вольт с глухозаземленной нейтралью обязательна металлическая связь частей, подлежащих заземлению, с заземленной нейтралью электроустановки. Для таких установок должно быть измерено сопротивление петли, образованной при коротком замыкании фазы на корпус аппарата. Это сопротивление равно сумме полных сопротивлений фазового провода, фазы силового трансформатора и нулевого провода.

Цепь (петля) фаза-ноль в электроустановках с глухозаземленной нейтралью образуется при замыкании фазного провода с нулевым или корпусом электрооборудования. Обычно это происходит при повреждении изоляции электропроводки. В случае такой аварии устройства защиты (автоматические выключатели, предохранители) должны отключить электроустановку в кратчайшее время, обеспечивающее условия электробезопасности.

Петля фаза-ноль — это контур, состоящий из соединения фазного и нулевого проводника. Сопротивление петли фаза-ноль зависит от сечения жил кабеля, его протяженности, переходных сопротивлений в соединительных коробках данной линии. Измерения проводят на самом удаленном от аппарата защиты участке линии.

2. Зачем необходимо измерение

При повреждении электрооборудования или электропроводки от короткого замыкания, перегрузки, аппараты защиты должны мгновенно отключать поврежденный участок цепи.

Данное испытание необходимо для проверки соответствия уставки токовой отсечки автоматических выключателей, УЗО, дифавтоматов, реле и т.д. току короткого замыкания. То есть необходимо знать, отключит ли аппарат защиты поврежденную линию и за какое время. Это позволит проверить качество монтажа, подбор защитной автоматики и сечения проводов.

2.1. Периодичность проведения измерений

Замеры проводятся после выполнения монтажных и ремонтных работ. В дальнейшем профилактическая проверка производится не реже чем раз в 3 года.

По усмотрению ответственного за электрохозяйство испытания проводятся чаще.

3. Какие приборы используют?

М-417 — выпускался до 1985 года. Аналоговый прибор, время измерения устанавливается вручную. Измеряет сопротивление петли, ток короткого замыкания необходимо рассчитывать.
Щ 41160 – выпускался на замену М-417. Цифровой прибор, измеряет ток короткого замыкания. Время протекания измерительного тока не более 10 мс., перерыв до повторного включения не менее 15 минут.
MZC-300 – измеряет полное сопротивление петли фаза-ноль, автоматически вычисляет ток короткого замыкания. Время протекания тока 30 мс. Достоверность показаний гарантируется только при применении фирменных соединительных проводов.
ИФН-200 – имеет характеристики, аналогичные МZС-300. Дополнительно позволяет измерять переходное сопротивление контактных соединений. Можно применять провода произвольной длины. Встроенная память на 35 измерений.
ИФН-300 – выпускается на замену ИФН-200. Дополнительно измеряет сопротивление петли фаза-фаза. Встроенная память на 10 000 измерений.

4. Порядок измерения петли фаза-ноль

Измерение сопротивления цепи фаза-ноль может проводиться со снятием и без снятия напряжения. В большинстве случаев выполняются без снятия напряжения.

Измерения без снятия напряжения могут выполняться:

В режиме дополнительной нагрузки. Замыкание цепи фаза-ноль происходит через дополнительную нагрузку. При этом измеряются падение напряжение и ток, проходящий через нагрузку и вычисляется сопротивление петли.
В режиме кратковременного замыкания цепи. Время замыкания составляет несколько миллисекунд. Этот способ реализован в большинстве современных приборов.

4.1. Методика измерения

Измерение характеристик петли зависит от выбранной методики и используемого прибора. Наиболее часто применяются приборы, измеряющие непосредственно сопротивление петли фаза-ноль с дальнейшим вычислением прогнозируемого тока короткого замыкания. Например, с помощью ИФН-200.

Прибор подключается к рабочей цепи в наиболее отдаленной точке от вводного щита. При отсутствии возможности определить самую дальнюю точку линии, измерения выполняются по всем или нескольким точкам данной линии. Далее по полученным значениям производится сравнение тока возможного короткого замыкания с характеристиками аппарата защиты.

4.2. Выводы о результатах

Результаты измерений сопротивления петли фаза-ноль заносятся в протокол. Это позволяет сохранить результаты и использовать их для сравнения в будущем.

Согласно п. 28.4. прил. 3.1 ПТЭЭП ток короткого замыкания должен превышать не менее чем:

в 3 раза плавкую вставку ближайшего предохранителя;
в 3 раза номинальный ток нерегулируемого расцепителя или уставку тока регулируемого расцепителя автоматического выключателя, имеющего обратно зависимую характеристику.

4.3 Форма протокола

В отчете отражается:

Участок цепи (группа в распределительном щите).
Тип автомата защиты и номинальные токи ( в амперах) теплового и электромагнитного расцепителей.
Измеренное значение сопротивления петли (если прибор его измеряет) на линиях A (L1), B (L2), C (L3).
Измеренное значение тока короткого замыкания (если прибор его измеряет) на линиях A (L1), B (L2), C (L3).
Допустимые коэффициенты срабатывания защиты для теплового и электромагнитного расцепителя. Для автомата с характеристикой С это 3 и 10.
Фактический коэффициент срабатывания защиты. Отношение измеренного тока к номинальному току автомата.
Соответствие фактического коэффициента допустимым. Если рассчитанное в п. 6 значение больше 10 то автомат отключится меньше чем за 0,1 секунды. Если меньше 10 но больше 3, время отключения сложно определить. Оно будет в интервале 0,1 — 30 секунд.

Зная параметры автомата защиты конкретной линии, после проведения измерения, можно с уверенностью сказать, сможет ли автомат сработать при коротком замыкании или возможно возгорание проводов.

В конце составленной формы подводятся итоги испытания. При отсутствии замечаний в заключении указывается возможность дальнейшей эксплуатации сети без принятия дополнительных мер, а при наличии — список необходимых действий.

Своевременный поиск проблемных участков линий электропитания позволяет принимать профилактические меры. Это не только делает работу электроустановки более безопасной, но и увеличивает срок эксплуатации сети.

Коэффициент усиления контура и его влияние на аналоговые системы управления

Аннотация

В этой статье объединены идеи усиления разомкнутого контура, усиления замкнутого контура, усиления и запаса по фазе, стабильности минимального усиления и показано, как эти параметры взаимосвязаны в системе обратной связи . Он рассматривает усиление контура с точки зрения теоретической системы управления, а также практических электронных схем, включая линейные регуляторы.

В статье Боба Добкина 2014 г. Новые линейные регуляторы решают старые проблемы, в которой описывается революционный линейный стабилизатор LT3081 с малым падением напряжения, предполагается, что его постоянный коэффициент усиления контура улучшает переходные характеристики и абсолютную точность выходного напряжения по сравнению с другими решениями LDO.Это утверждение, хотя и впечатляющее и верное, делает важное предположение о понимании инженерами петлевого усиления и о том, что существует четкая связь между постоянным контурным усилением и преимуществами LT3081. К сожалению, усиление контура не так широко признано, как усиление замкнутого или разомкнутого контура.

Без понимания коэффициента усиления контура и его влияния на электронную схему нельзя по-настоящему оценить преимущества LT3081. Эта статья предназначена для инженеров по источникам питания, исследуя влияние коэффициента усиления контура на коэффициент усиления и запас по фазе и связывая их с теоретической системой управления и реальными аналоговыми цепями обратной связи.

Классическим аналоговым строительным блоком является операционный усилитель, и его поведение можно применить к большинству систем управления с обратной связью. Фактически, производительность многих устройств можно упростить, смоделировав их как операционные усилители. Мы можем применить теорию операционных усилителей, скажем, к линейным регуляторам с малым падением напряжения (LDO) и импульсным стабилизаторам, чтобы предсказать стабильность части. На рисунке 1 показана упрощенная схема операционного усилителя.

Рисунок 1. Упрощенная схема операционного усилителя

Входное напряжение подается на усилитель ошибки, который вычитает долю (β) выходного напряжения из V _IN для получения сигнала ошибки.Таким образом, ошибка

Этот сигнал ошибки подвергается усилению без обратной связи усилителя (A0) для получения выходного напряжения:

Это преобразовано, чтобы найти коэффициент усиления усилителя с обратной связью:

В большинстве схем операционных усилителей коэффициент усиления разомкнутого контура усилителя очень высок, то есть намного больше, чем «1» в знаменателе, что позволяет использовать приближение коэффициента усиления замкнутого контура:

На рисунке 2 показана традиционная схема операционного усилителя, предсказуемая работа которой зависит от этого приближения усиления.

Рисунок 2. Схема традиционного ОУ

Для любого заданного напряжения на выходе, если коэффициент усиления разомкнутого контура бесконечен, разность напряжений между двумя входными контактами (V _DIFF) равна нулю, и операционный усилитель регулируется, чтобы поддерживать оба своих входных контакта при одинаковом напряжении. Здесь выход подается обратно на вход через резистивный делитель R1-R2, поэтому доля обратной связи (β) составляет 0,1 (1 кОм / 10 кОм). Из приведенных выше уравнений, если коэффициент усиления разомкнутого контура высокий, коэффициент усиления замкнутого контура схемы приближается к обратной величине, поэтому коэффициент усиления замкнутого контура равен 10.

Эта упрощенная теория операционного усилителя полезна при моделировании множества схем, справедливо для низкочастотных входов, но эта простая модель теряет силу для высокочастотных входов.

Операционный усилитель LT1012 отличается классической зависимостью коэффициента усиления разомкнутого контура от частотной характеристики, показанной на рисунке 3.

Рисунок 3. Коэффициент усиления ОУ LT1012 в разомкнутом и замкнутом контурах в зависимости от частоты

На Рисунке 3 вы можете видеть, что усиление разомкнутого контура велико до входной частоты 0,3 Гц, а затем уменьшается со скоростью 20 дБ за декаду.Хотя коэффициент усиления остается очень высоким в широком диапазоне входных частот, наступает момент, когда коэффициент усиления без обратной связи нельзя считать относительно бесконечным. То есть, когда коэффициент усиления разомкнутого контура приближается к усилению замкнутого контура, идеальная модель операционного усилителя, описанная выше, и соответствующие предположения, которые мы сделали о ее характеристиках, начинают терять доверие.

Рассмотрим влияние конечного коэффициента усиления разомкнутого контура на усиление замкнутого контура схемы на рисунке 2. Доля обратной связи (β) равна 1/10, поэтому в идеальной модели операционного усилителя усиление замкнутого контура обратно пропорционально этому , или 10.Если наш операционный усилитель имеет коэффициент усиления без обратной связи 100, расчетное усиление с обратной связью составляет

Расчетное усиление замкнутого контура

Прирост по-прежнему составляет примерно 10, но с ошибкой 9%.

Теперь рассмотрите возможность использования того же усилителя, но с обратной связью с единичным усилением. Доля обратной связи (β) равна 1, поэтому идеальное усиление замкнутого контура операционного усилителя должно быть обратным этому, или 1. Если наш операционный усилитель имеет усиление разомкнутого контура, равное 100, это приводит к усилению замкнутого контура

Хотя коэффициенты усиления разомкнутого контура этих двух схем одинаковы, ошибка усиления снижается до 1% просто за счет уменьшения усиления замкнутого контура.

Приведенные выше уравнения показывают, что ошибка является функцией того, насколько велик βA ₀ по отношению к члену «1» в знаменателе. Обратите внимание, что одно только усиление разомкнутого контура не всегда определяет ошибку, но важно произведение коэффициента усиления разомкнутого контура (A ₀) и доли обратной связи (β). Для больших βA ₀ член «1» теряет значение; для βA ₀, близкого к единице, «1» становится значимой, увеличивая ошибку.

Так что же такое βA ₀? На рисунке 3 разница между кривой замкнутого контура (приблизительно 1 / β) и кривой разомкнутого контура (A ₀) в логарифмической шкале составляет

Таким образом, зазор между кривой усиления без обратной связи и кривой усиления с обратной связью составляет βA ₀ (около 105 дБ при постоянном токе).Ссылаясь на рисунок 1, мы видим, что A ₀ • β – это усиление, проходящее через усилитель и контур обратной связи, поэтому βA ₀ – это усиление контура и представляет собой избыточное усиление, доступное в системе. Хотя часто считается, что коэффициент усиления разомкнутого контура усилителя должен быть высоким, чтобы коэффициент усиления ОУ был точным, мы можем видеть, что это не обязательно усиление разомкнутого контура, а усиление контура, которое должно быть высоким. Другими словами, усиление разомкнутого контура должно быть высоким по сравнению с усилением замкнутого контура, чтобы получить точный коэффициент усиления схемы.

Итак, какое влияние конечное усиление разомкнутого контура оказывает на схему операционного усилителя? Базовая теория операционного усилителя утверждает, что два входных напряжения регулируются до одного и того же напряжения, что является подходящим предположением при очень высоких коэффициентах усиления разомкнутого контура, но что происходит, когда усиление разомкнутого контура уменьшается с увеличением частоты сигнала?

Рассмотрим схему на Рисунке 2: поскольку коэффициент усиления без обратной связи усилителя уменьшается с увеличением входной частоты, мы видим возрастающее напряжение переменного тока между двумя входными контактами, равное выходному напряжению, деленному на коэффициент усиления без обратной связи.Это не входное напряжение смещения, а небольшое напряжение переменного тока (V _DIFF), которое равно выходному напряжению, деленному на коэффициент усиления разомкнутого контура усилителя. Если коэффициент усиления разомкнутого контура равен одному миллиону и у нас есть 1 В на выходе, тогда V _DIFF составляет 1 мкВ на двух входных контактах. По мере увеличения входной частоты и уменьшения коэффициента усиления разомкнутого контура V _DIFF увеличивается. В крайнем случае, когда коэффициент усиления разомкнутого контура упал до 10, наш V _DIFF становится значительным 100 мВ.

Это то место, где многие неправильно понимают работу операционного усилителя на более высоких частотах переменного тока, когда два входных контакта больше не регулируются на одно и то же напряжение. Напряжение между двумя входными контактами состоит из входного напряжения смещения постоянного тока (которое для простоты мы здесь игнорируем) и V _DIFF. V _DIFF обычно можно игнорировать, но только не на высоких частотах.

Мы знаем, что коэффициент усиления разомкнутого контура представлен как

, и мы знаем, что β представлен

, где V ^– – напряжение на инвертирующем входе, поэтому коэффициент усиления контура определяется как

Коэффициент усиления контура сравнивает V ^– (который должен быть равен входному сигналу) с V _DIFF.

Также существует фазовый сдвиг, связанный с V _DIFF. Кривая усиления без обратной связи на рисунке 3 идентична отклику фильтра нижних частот. Частота прерывания составляет 0,3 Гц, после чего усиление снижается до 20 дБ за декаду, а затем – 1 МГц, после чего усиление снижается до 40 дБ за декаду. На рисунке 4 показан фильтр нижних частот с такими же частотами срыва.

Рисунок 4. Фильтр низких частот с частотной характеристикой, которая соответствует кривой усиления разомкнутого контура на рисунке 2

Передаточная функция фильтра нижних частот одинарного порядка (состоящего из R1 и C1) определяется как

Как показывает практика, для фильтра нижних частот одинарного порядка на одной десятой частоты излома фазовый сдвиг примерно равен нулю.На каждой частоте обрыва фаза сдвигается на –45 ° (фазовое отставание), а при десятикратной частоте обрыва фазовый сдвиг составляет примерно –90 °, оставаясь на более высоком уровне. Если вторая частота прерывания составляет 1 МГц, то при 100 кГц общий фазовый сдвиг фильтра составляет примерно –90 °, на 1 МГц общий фазовый сдвиг составляет –135 °, а на 10 МГц общий фазовый сдвиг составляет примерно –180 °.

Поскольку усиление без обратной связи усилителя ведет себя одинаково, хотя входное и выходное напряжения на Рисунке 2 синфазны, существует фазовый сдвиг между V _DIFF и V _OUT, связанный с фазовым сдвигом коэффициент усиления разомкнутого контура усилителя.Опять же, поскольку V _DIFF обычно невелик, мы можем игнорировать его, но по мере увеличения входной частоты увеличение V _DIFF, не совпадающее по фазе с входным напряжением, может привести к проблемам со стабильностью. Кривая усиления разомкнутого контура на Рисунке 3 не представляет проблем со стабильностью, но легко представить, что если бы вторая частота прерывания была на гораздо более низкой частоте, чем 1 МГц, наша схема теперь имела бы увеличивающийся V _DIFF, который имеет потенциал быть на 180 ° не в фазе с входным напряжением, что, безусловно, повлияет на стабильность.

LTspice – полезный инструмент для анализа эффектов фазового сдвига на различных частотах. На рисунке 5a показано отставание выходного напряжения V _DIFF на 90 ° на частоте 1 кГц.

Рисунок 5а. V _OUT Отставание V _DIFF по фазе на 90 ° при 1 кГц

Если входная частота увеличивается с 1 кГц до 10 кГц, V _DIFF увеличивается в 10 раз, но фазовая задержка остается 90 °, что указывает на то, что мы еще далеко не приблизились ко второй частоте прерывания коэффициента усиления разомкнутого контура.Это показано на рисунке 5b. Когда входная частота приближается к 1 МГц, фазовая задержка начинает увеличиваться выше 90 °, и V _DIFF соответственно увеличивается.

Рисунок 5б. V _OUT Отставание V _DIFF по фазе на 90 ° при 10 кГц

Таким образом, можно увидеть, что V _DIFF может иметь значение, сравнимое с входным напряжением и сдвигом на 180 ° по фазе с входным напряжением – для того, чтобы цепь колебалась, коэффициент усиления вокруг контура должен быть равен единице и фазовый сдвиг вокруг контура должен составлять 180 °.Если V _DIFF подвергается усилению без обратной связи усилителя (A ₀), то ослаблению цепи обратной связи, (β), мы можем видеть, что это усиление контура (βA ₀) и его фазы, которые определяют устойчивость системы.

Рассматривая схему на рисунке 2, операционный усилитель усиливает напряжение между своими входами (V _DIFF), и это подвергается усилению βA ₀, создавая напряжение на уровне V ^–. Если коэффициент усиления контура равен 1, это означает, что напряжение на V ^– такое же, как V _DIFF, таким образом, амплитуда V _DIFF не изменилась при прохождении через контур.Если он претерпел сдвиг фазы на 180 ° и V _DIFF не изменился по амплитуде, цепь будет колебаться. Пуристы могут возразить, что фазовый сдвиг должен составлять 360 °, и эти дополнительные 180 ° обеспечиваются инвертирующим входным контактом.

Кстати, если схема на Рисунке 2 имеет высокий коэффициент усиления, это означает, что резисторы обратной связи значительно ослабляют выходное напряжение. Большая часть фазового сдвига происходит в усилителе (поскольку резисторы обратной связи не имеют реактивных компонентов и, следовательно, не имеют фазового сдвига), поэтому чем ниже коэффициент усиления, тем большее «сдвинутое по фазе» выходное напряжение появляется на инвертирующем входе, что увеличивает вероятность нестабильности.Вот почему некоторые усилители имеют минимальную стабильность усиления. Если вы уменьшите коэффициент усиления ниже определенной точки, на инвертирующем выводе появится больше сдвинутого по фазе выходного напряжения, поэтому схема будет более подвержена колебаниям.

Стоит рассмотреть работу схемы на Рисунке 2 для различных коэффициентов усиления контура и фазовых сдвигов.

На низких частотах, когда усилитель имеет большое усиление контура, V _DIFF невелик и имеет фазовый сдвиг –90 ° по сравнению с напряжением на инвертирующем входе (V ^–).В этой ситуации напряжение на инвертирующем входе падает до V _DIFF, поэтому V _DIFF можно игнорировать. Однако, если фазовый сдвиг V _DIFF составляет –180 ° по отношению к V ^–, и есть усиление в контуре, мы можем видеть, что любое напряжение на V _DIFF усиливается при перемещении по контуру. и инвертированный, затем усиленный и инвертированный, поэтому цепь колеблется. Для поддержания колебаний в схеме должно быть только единичное усиление контура. Насколько близко V _DIFF приближается к –180 °, когда схема имеет единичный коэффициент усиления контура, является мерой запаса по фазе схемы и говорит нам, насколько близка к точке нестабильности фаза схемы.Схема с фазовым сдвигом –120 ° имеет запас по фазе 60 °.

Аналогично, если V _DIFF имеет фазовый сдвиг -180 ° по отношению к V ^–, но испытывает затухание при прохождении через контур, напряжение, возвращающееся к V ^–, будет меньше, поэтому любые потенциальные колебания останавливаются из-за отсутствия усиления контура. Сколько затухания V _DIFF испытывает при прохождении через контур (когда фазовый сдвиг составляет –180 °), является мерой запаса по усилению схемы и говорит нам, насколько ниже единицы коэффициент усиления контура схемы, когда фаза сдвиг –180 °.Схема с затуханием в контуре 10 дБ, когда V _DIFF составляет –180 °, имеет запас усиления 10 дБ.

Все вышеперечисленное может быть связано с теорией управления и блок-схемой на рисунке 1. Мы знаем, что коэффициент усиления замкнутого контура системы обратной связи равен

, где βA ₀ – контурное усиление системы. Если βA ₀ имеет фазовый сдвиг –180 ° и единичное усиление, знаменатель становится равным нулю на одной определенной частоте, и схема колеблется на этой частоте.Если βA ₀ большое, но не имеет фазового сдвига -180 °, знаменатель не равен нулю и цепь не колеблется – у нас есть достаточный запас по фазе. Точно так же, если βA ₀ меньше единицы, но имеет фазовый сдвиг -180 °, схема не колеблется – у нас есть достаточный запас по усилению.

Итак, теперь мы можем видеть, что мы связали усиление разомкнутого контура, усиление замкнутого контура, усиление контура, запас усиления и запас по фазе, а также объяснили это в области теории управления и области теории цепей.

Так как это относится к цепям питания? Большинство систем питания можно смоделировать как схему операционного усилителя. На рисунке 6 показан линейный регулятор LT1086. Мы видим, что в схеме есть два резистора обратной связи, которые обеспечивают часть выходного напряжения на выводе ADJ (который является инвертирующим входом внутреннего операционного усилителя). Неинвертирующий терминал привязан к внутреннему опорному напряжению.

Рисунок 6. Традиционный линейный регулятор (LT1086)

Как обсуждалось выше, точность усиления усилителя определяется контурным усилением усилителя: чем больше контурное усиление в усилителе, тем выше точность усиления.

Увеличение выходного напряжения LT1086 идентично увеличению коэффициента усиления с обратной связью операционного усилителя. На рисунке 7 показан эффект увеличения коэффициента усиления с обратной связью с 20 дБ до 80 дБ. Если усиление контура представлено разностью между кривой усиления разомкнутого контура и кривой усиления замкнутого контура, увеличение выходного напряжения LT1086 уменьшает усиление контура, уменьшая абсолютную точность выходного напряжения. Еще одним недостатком увеличения выходного напряжения является уменьшение частотной характеристики схемы (в данном случае от 100 кГц до 100 Гц), поэтому страдает переходная характеристика нагрузки.

Рисунок 7. Зависимость усиления напряжения от частоты

Семейство линейных регуляторов LT308x заменяет традиционную архитектуру LDO на ту, что показана на рисунке 8.

Рис. 8. Линейный регулятор LT3080 использует нетрадиционную архитектуру для повышения точности и переходных характеристик

LT3080 использует внутренний источник тока для создания напряжения на внешнем резисторе R _SET. Затем это напряжение подается на буфер с единичным усилением для получения выходного напряжения.Это имеет ряд последствий.

Внутренний операционный усилитель работает с постоянным единичным усилением с обратной связью, с выходным напряжением, установленным значением резистора R _SET на «входе» операционного усилителя.

Сравните LT3080, показанный на рисунке 7, с традиционной схемой операционного усилителя, показанной на рисунке 6. Выходное напряжение LT1086 на рисунке 6 изменяется путем изменения резисторов обратной связи (и, следовательно, коэффициента усиления с обратной связью) LT1086. Сравните это с LT3080, работающим с постоянным усилением замкнутого контура, где «входное» напряжение усилителя изменяется, задаваемое напряжением на R _SET.Если коэффициент усиления замкнутого контура остается неизменным, коэффициент усиления контура остается неизменным, поэтому схема обеспечивает хорошую абсолютную точность даже при высоких выходных напряжениях. Кстати, именно поэтому компоненты компенсации контура в преобразователе постоянного / постоянного тока всегда имеют последовательную емкость. Выход усилителя ошибки является источником тока, а последовательная емкость на постоянном токе имеет высокий импеданс, что обеспечивает высокий коэффициент усиления на постоянном токе в компенсационном контуре.

Еще одним следствием сохранения неизменного коэффициента усиления контура является то, что частотная характеристика остается неизменной и не приносится в жертву при высоких выходных напряжениях, поэтому компонент может быстро реагировать на переходные процессы нагрузки.

Еще одно преимущество, представляющее особый интерес в свете постоянно уменьшающегося напряжения питания, заключается в том, что компоненты LT308x могут выдавать выходное напряжение до 0 В. Традиционные LDO-стабилизаторы не могут устанавливать выходное напряжение ниже внутреннего опорного напряжения, тогда как путем замыкания RSET на части LT308x выходное напряжение может быть установлено на уровне 0 В.

Семейство LDO LT308x, благодаря их постоянному высокому коэффициенту усиления контура, отличается более высокой точностью выходного напряжения и переходной характеристикой, чем традиционные LDO.Их также можно использовать способами, недоступными для традиционных LDO, например, для установки выхода на 0 В или их параллельного подключения для работы с более высоким током.

KMSR-DS0252 | Menics |

Магазин не будет работать корректно, если куки отключены.

Похоже, в вашем браузере отключен JavaScript. Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.

SSR, 1 фаза, переход через нуль, вход 4-32 В постоянного тока, 25 А, напряжение нагрузки 90-240 В переменного тока

Дополнительная информация
Номер детали	KMSR-DS0252
Артикул	KMSR-DS0252
Управляющее напряжение	от 4 до 32 В постоянного тока
Номинальный ток	25 ампер
Тип реле	Реле Ice Cube
Переключение выхода	Zero Crossing
Рабочее напряжение	230 В переменного тока
Фаза	Однофазный
Рейтинги	IP20
Производитель	Menics
Наличие	Свяжитесь с нами
Масса – фунты.	0,350000
Базовая единица измерения	Каждый

Функции включают:

Номинальное входное управляющее напряжение: 4-32 В постоянного тока
Входной ток: 3-35 мА максимум
Номинальное выходное напряжение нагрузки: 90-240 В переменного тока
Пиковое выходное напряжение: 600 В
Сопротивление изоляции: 100 МОм / 500 В постоянного тока (между клеммами и корпусом)
Диэлектрическая прочность: 2500 В переменного тока (50/60 Гц, 1 минута)
Устойчивость к вибрации: 10-55 Гц, амплитуда: 1.5 мм, x, y, z по каждой оси 2 часа
Ударопрочность: 100 м / с², s, y, z по каждой оси 3 раза по
Светодиодный индикатор состояния управляющего входа
Зажим-крышка IP20 защиты от прикосновения

2021-06-26 13:05:22

Phase Zero Project: формирование конкурентного пространства

Программы

New America Local –

Нью-Америка, Калифорния

Нью-Америка Чикаго

Нью-Америка Индианаполис

Программы –

Лаборатория лучшей жизни

Центр образования и труда

Инициатива цифрового воздействия и управления

Политика в области образования

научных сотрудников

Земля и жилищное будущее

Будущее время

Международная безопасность

Новая практическая лаборатория

Институт открытых технологий

Политическая реформа

Технология, представляющая общественный интерес

Безопасность ресурсов

Инициатива ответственного распределителя активов

Публикации

Резьба

События

Около

Поддержка New America –

Мы посвящаем себя обновлению обещаний Америки, продолжая стремиться к реализации высших идеалов нашей страны, честно преодолевая проблемы, вызванные быстрыми технологическими и социальными изменениями, и используя возможности, которые эти изменения создают.

О компании –

Наша история

Наши люди

Наше финансирование

Пресс-комната

Работа и стипендии

New America исполняется 20 лет

Пожертвовать

Новая Америка

Наша история
Публикации
Программы
События
Наши люди
Работа и стипендии
Пресс
Свяжитесь с нами

Новая Америка

740 15th Street NW, Suite 900

Вашингтон, округ Колумбия 20005
Программы
События
Публикации
Подписаться
Creative Commons
Миссия
Люди
Финансирование
Политики и процедуры
Контакт
Работа и стипендии
Пресс
Пожертвовать
Тендер правительства Украины на услуги по измерению сопротивления изоляции, заземления, перехода
Главная> Тендеры> Европа> Украина> Услуги по измерению сопротивления изоляции, заземления, переходного сопротивления
ДОПОРОГОВІ ЗАКУПІВЛІ PROZORRO объявил тендер на оказание услуг по измерению сопротивления изоляции, заземления, переходного сопротивления и фазы-ноль контура 71630000-3 – Технический осмотр и испытания Услуги по измерению сопротивления изоляции, протяженности…. Месторасположение проекта – Украина, и тендер закрывается 21 марта 2018 года. Номер тендерного объявления -, а ссылочный номер TOT – 21520574. Участники торгов могут получить дополнительную информацию о тендере и запросить полную тендерную документацию, зарегистрировавшись на сайт.
Страна: Украина
Резюме: Услуги по измерению сопротивления изоляции, заземления, переходного сопротивления и шлейфа фаза-ноль 71630000-3 – Технический осмотр и испытание Услуги по измерению сопротивления изоляции, грунт…
Срок сдачи: 21 марта 2018 г.
Реквизиты покупателя
Заказчик: ДОПОРОГОВІ ЗАКУПІВЛІ ПРОЗОРРО
Украина, Відповідно до документации, 20.04.2018 00:04
Украина
Прочая информация
ТОТ Ссылка: 21520574
Номер документа.№:
Конкурс: ICB
Финансист: Самофинансируемый
Информация о тендере
Услуги по измерению сопротивления изоляции, заземления, переходного сопротивления и фазы-ноль контура 71630000-3 – Технический осмотр и испытания Услуги по измерению сопротивления изоляции, заземления, переходного сопротивления и фазы-ноль контура – 1 Услуга
Сумма покупки: 50000 руб.00
Конец подачи предложений: 21.03.18 17:00
% PDF-1.6 % 738 0 объект > эндобдж xref 738 154 0000000016 00000 н. 0000005661 00000 н. 0000005857 00000 н. 0000005901 00000 н. 0000006051 00000 н. 0000006185 00000 п. 0000006262 00000 н. 0000007154 00000 н. 0000007807 00000 н. 0000008985 00000 н. 0000010164 00000 п. 0000010410 00000 п. 0000010488 00000 п. 0000010687 00000 п. 0000011238 00000 п. 0000011490 00000 п. 0000042375 00000 п. 0000067473 00000 п. 0000078523 00000 п. 0000089603 00000 п. 0000089812 00000 п. 0000089870 00000 п. 00000
00000 н. 00000
00000 п. 00000 00000 п. 00000 00000 п. 00000 00000 п. 00000 00000 п. 00000 00000 п. 00000
00000 п. 00000
00000 п. 00000
00000 п. 00000
00000 п. 00000_{00000 п.
00000 00000 п.
00000 00000 п.
00000}
00000 п. 00000 00000 п. 00000 00000 п. 00000 00000 н. 0000092490 00000 н. 0000092652 00000 п. 0000092708 00000 п. 0000092896 00000 п. 0000093089 00000 п. 0000093239 00000 п. 0000093295 00000 п. 0000093431 00000 п. 0000093588 00000 п. 0000093644 00000 п. 0000093793 00000 п. 0000093849 00000 п. 0000093905 00000 п. 0000094044 00000 п. 0000094100 00000 п. 0000094291 00000 п. 0000094347 00000 п. 0000094494 00000 п. 0000094550 00000 п. 0000094717 00000 п. 0000094773 00000 п. 0000094948 00000 н. 0000095004 00000 п. 0000095060 00000 п. 0000095116 00000 п. 0000095325 00000 п. 0000095381 00000 п. 0000095548 00000 п. 0000095604 00000 п. 0000095845 00000 п. 0000095901 00000 п. 0000096072 00000 п. 0000096128 00000 п. 0000096339 00000 п. 0000096537 00000 п. 0000096593 00000 п. 0000096725 00000 п. 0000096882 00000 п. 0000096938 00000 п. 0000097117 00000 п. 0000097173 00000 п. 0000097229 00000 п. 0000097424 00000 п. 0000097480 00000 п. 0000097536 00000 п. 0000097592 00000 п. 0000097648 00000 п. 0000097811 00000 п. 0000097867 00000 п. 0000098026 00000 п. 0000098082 00000 п. 0000098138 00000 п. 0000098194 00000 п. 0000098381 00000 п. 0000098437 00000 п. 0000098493 00000 п. 0000098549 00000 п. 0000098760 00000 п. 0000098816 00000 п. 0000098967 00000 п. 0000099023 00000 н. 0000099190 00000 н. 0000099246 00000 п. 0000099417 00000 п. 0000099473 00000 п. 0000099648 00000 н. 0000099784 00000 п. 0000099840 00000 п. 0000100037 00000 н. 0000100236 00000 н. 0000100292 00000 н. 0000100519 00000 п. 0000100665 00000 н. 0000100721 00000 н. 0000100941 00000 п. 0000101102 00000 п. 0000101158 00000 н. 0000101214 00000 н. 0000101413 00000 н. 0000101469 00000 н. 0000101636 00000 н. 0000101692 00000 н. 0000101863 00000 н. 0000101919 00000 п. 0000102058 00000 н. 0000102114 00000 п. 0000102249 00000 п. 0000102305 00000 н. 0000102442 00000 н. 0000102498 00000 н. 0000102635 00000 н. 0000102691 00000 н. 0000102747 00000 н. 0000102803 00000 п. 0000102954 00000 н. 0000103010 00000 н. 0000103178 00000 п. 0000103234 00000 н. 0000103375 00000 п. 0000103431 00000 н. 0000103487 00000 н. 0000103543 00000 н. 0000103599 00000 н. 0000103719 00000 п. 0000103775 00000 п. 0000103933 00000 н. 0000103989 00000 н. 0000104136 00000 п. 0000104192 00000 п. 0000104337 00000 н. 0000104393 00000 п. 0000104544 00000 н. 0000104598 00000 п. 0000003376 00000 н. трейлер ] >> startxref 0 %% EOF 891 0 объект > поток xW {L [? ^ lecBy, u2 * a & TT۲TͦdTuZ’VD’YM [m6M ݚ? & m] sν6v $ ~} s
Цепи переменного тока серии
RLC | Физика
Цели обучения
К концу этого раздела вы сможете:
Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
Нарисуйте принципиальную схему последовательной цепи RLC.
Объясните значение резонансной частоты.
Когда один в цепи переменного тока, все катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом данного раздела.Суть анализа цепи RLC – это частотная зависимость X _L и X _C, а также их влияние на фазу зависимости напряжения от тока (установлено в предыдущий раздел). Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.
Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.
Комбинированный эффект сопротивления R , индуктивного реактивного сопротивления X _L и емкостного реактивного сопротивления X _C определяется как импеданс , аналог сопротивления в цепи постоянного тока по переменному току. Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex].
Здесь I ₀ – пиковый ток, В ₀ – пиковое напряжение источника, а Z – полное сопротивление цепи. Единицы измерения импеданса – омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для Z через R , X _L и X _C, мы теперь рассмотрим, как напряжения на различных компонентах связаны с источником. Напряжение.Эти напряжения обозначены V _R, V _L и V _C на рисунке 1. Для сохранения заряда ток должен быть одинаковым в каждой части цепи. всегда, так что мы можем сказать, что токи в R , L и C равны и синфазны. Но мы знаем из предыдущего раздела, что напряжение на катушке индуктивности В _L опережает ток на одну четверть цикла, напряжение на конденсаторе В _C следует за током на единицу. -четвертая часть цикла, и напряжение на резисторе В _R точно совпадает по фазе с током.На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение в цепи В = В _R + В _L + В _C, где все четыре напряжения – мгновенные значения. Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В также является напряжением источника. {2}} \\ [/ latex],
, который является сопротивлением цепи переменного тока серии RLC .Для схем без резистора принять R = 0; для тех, у кого нет индуктора, возьмите X _L = 0; а для тех, у кого нет конденсатора, возьмите X _C = 0.
Рис. 2. На этом графике показаны отношения напряжений в цепи RLC к току. Напряжения на элементах схемы складываются, чтобы равняться напряжению источника, которое, как видно, не совпадает по фазе с током.
Пример 1.Расчет импеданса и тока
Последовательная цепь RLC имеет резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из раздела Реактивное, индуктивное и емкостное. (b) Если источник напряжения имеет В _СКЗ = 120 В, что будет I _СКЗ на каждой частоте?
Стратегия
Для каждой частоты мы используем [latex] Z = \ sqrt {{R} ^ {2} + \ left ({X} _ {L} – {X} _ {C} \ right) ^ {2}} \ \ [/ latex], чтобы найти импеданс, а затем закон Ома, чтобы найти ток. { 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {kHz} \ end {array} \\ [/ latex]
Обсуждение для (а)
В обоих случаях результат почти такой же, как и наибольшее значение, а импеданс определенно не является суммой отдельных значений. Ясно, что X _L доминирует на высокой частоте, а X _C доминирует на низкой частоте.
Решение для (b)
Текущее значение I _{действующее значение} можно найти, используя версию закона Ома для переменного тока в уравнении I _{среднеквадратичное значение} = В _{среднеквадратичное значение}/ Z :
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {531 \ text { } \ Omega} = 0.226 \ text {A} \\ [/ latex] при 60,0 Гц
Наконец, на частоте 10,0 кГц мы находим
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {190 \ text { } \ Omega} = 0,633 \ text {A} \\ [/ latex] при 10,0 кГц
Обсуждение для (а)
Ток при 60,0 Гц такой же (до трех цифр), что и для одного конденсатора в примере 2 из раздела «Реактивное сопротивление, индуктивность и емкость». Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь немного отличается от того, который был обнаружен для одного индуктора в Примере 1 из раздела «Реактивное сопротивление, индуктивный и емкостной».{2}}} \\ [/ latex]
Реактивные сопротивления изменяются в зависимости от частоты: X _L большое на высоких частотах и X _C большое на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f ₀ реактивные сопротивления будут равны и отменены, давая Z = R – это минимальное значение для импеданса и максимальное значение для I _rms результаты .Мы можем получить выражение для f ₀, взяв
X _L = X _C.
Замена определений X _L и X _C,
[латекс] 2 \ pi f_ {0} L = \ frac {1} {2 \ pi f_ {0} C} \\ [/ latex].
Решение этого выражения для f ₀ дает
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex],
, где f ₀ – это резонансная частота цепи серии RLC .Это также собственная частота , на которой цепь будет колебаться, если не будет управляться источником напряжения. При f ₀ влияние катушки индуктивности и конденсатора компенсируется, так что Z = R , а I _rms является максимальным.
Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание – в данном случае вызываемое источником напряжения – на собственной частоте системы.Приемник в радиоприемнике представляет собой схему RLC , которая лучше всего колеблется на своем f ₀. Переменный конденсатор часто используется для настройки f ₀, чтобы получить желаемую частоту и отклонить другие. На рис. 3 представлен график зависимости тока от частоты, иллюстрирующий резонансный пик в I _{среднеквадратичное значение} при f ₀. Две кривые относятся к двум разным цепям, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.
Рис. 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f ₀, но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В ₀.
Пример 2. Расчет резонансной частоты и тока
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (b) Рассчитайте I _rms при резонансе, если V _rms составляет 120 В.
Стратегия
Резонансная частота находится с помощью выражения в [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex].{-6} \ text {F} \ right)}} = 1,30 \ text {кГц} \ end {array} \\ [/ latex]
Обсуждение для (а)
Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности – на высокой. Их эффекты такие же на этой промежуточной частоте.
Решение для (b)
Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,
[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40.0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].
Обсуждение для (б)
В резонансе ток больше, чем на более высоких и низких частотах, рассмотренных для той же цепи в предыдущем примере.
Питание в цепях переменного тока серии
RLC
Если ток изменяется с частотой в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты.Но средняя мощность – это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Имеется фазовый угол ϕ между напряжением источника В и током I , который можно найти из
.
[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex]
Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex] \ text {cos} \ varphi = 1 \\ [/ latex].Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I _{действующее значение} ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
Таким образом, cos ϕ называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте cos ϕ = 1.
Пример 3. Расчет коэффициента мощности и мощности
Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с В _{действующее значение} 120 В: (a) Рассчитайте коэффициент мощности и фазу угол для f = 60,0 Гц. (б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.
Стратегия и решение для (a)
Коэффициент мощности при 60,0 Гц находится из
.
[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex].
Мы знаем Z = 531 Ом из Пример 1: Расчет импеданса и тока , так что
[латекс] \ cos \ varphi = \ frac {40.0 \ text {} \ Omega} {531 \ text {} \ Omega} = 0,0753 \ text {at} 60.0 \ text {Hz} \\ [/ latex].
Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе.{-1} 0,0753 = \ text {85,7º} \ text {at} 60,0 \ text {Hz} \\ [/ latex].
Обсуждение для (а)
Фазовый угол близок к 90º, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая схема RC имеет напряжение и ток, сдвинутые по фазе на 90º).
Стратегия и решение для (b)
Средняя мощность при 60,0 Гц –
P _ср. = I _{среднеквадратичное значение} В _{среднеквадратичное значение} cos ϕ .
I _{среднеквадратичное значение} оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает
P _средн. = (0,226 A) (120 В) (0,0753) = 2,04 Вт при 60,0 Гц.
Стратегия и решение для (c)
На резонансной частоте мы знаем, что cos ϕ = 1, и I _{среднеквадратичное значение} оказалось равным 6,00 A в Пример 3: Расчет резонансной частоты и тока .Таким образом, P _ср = (3,00 A) (120 В) (1) = 360 Вт при резонансе (1,30 кГц)
Обсуждение
Как ток, так и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на высоких и низких частотах.
Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по рифленой дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.
Рис. 4. Вынужденное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC .Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.
Чистая цепь LC с незначительным сопротивлением колеблется с частотой f ₀, той же резонансной частотой, что и цепь RLC . Он может служить эталоном частоты или схемой часов – например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний.Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.
Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и без движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.
Исследования PhET: комплект для конструирования цепей (AC + DC), виртуальная лаборатория
Создавайте цепи с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
Аналогом сопротивления переменного тока является сопротивление Z , комбинированное действие резисторов, катушек индуктивности и конденсаторов, определяемое версией закона Ома для переменного тока:
[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex],
, где I _o – пиковый ток, а В _o – пиковое напряжение источника.{2}} \\ [/ латекс].
Резонансная частота f ₀, при которой X _L = X _C , составляет
[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex]
В цепи переменного тока существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из
[латекс] \ text {cos} \ varphi = \ frac {R} {Z} \\ [/ latex],
ϕ = 0º для чисто резистивной цепи или цепи RLC в резонансе.
Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением
[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],
cos ϕ называется коэффициентом мощности, который находится в диапазоне от 0 до 1.
Концептуальные вопросы
1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.
2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1.Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.
Задачи и упражнения
1. Схема RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (a) Найдите его полное сопротивление Z при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был конденсатор.
2. Схема RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.
3. Цепь LC состоит из катушки индуктивности 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.
4. Какова резонансная частота индуктора 0,500 мГн, подключенного к конденсатору 40,0 мкФ?
5. Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, подключенной к конденсатору переменной емкости. Какой диапазон емкости нужен?
6. Предположим, у вас есть запас индукторов от 1,00 нГн до 10,0Гн и конденсаторов от 1.От 00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одной катушки индуктивности и одного конденсатора?
7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?
8. Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?
9. Самая низкая частота в диапазоне FM-радио – 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?
10. Последовательная цепь RLC имеет резистор 2,50 Ом, индуктивность 100 мкГн и конденсатор 80,0 мкФ. (A) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В _{действующее значение} = 5,60 В, что будет I _{среднеквадратичное значение} на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I _RMS в резонансе?
11.Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В _СКЗ = 408 В, что будет I _СКЗ на каждой частоте? (г) Какова резонансная частота контура? (e) Что такое I _RMS в резонансе?
12. Схема серии RLC имеет 2.Резистор 50 Ом, катушка индуктивности 100 мкГн и конденсатор 80,0 мкФ. (а) Найдите коэффициент мощности при f = 120 Гц. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи.
13. Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (a) Найдите коэффициент мощности при f = 7,50 Гц. б) Каков фазовый угол на этой частоте? (c) Какая средняя мощность на этой частоте? (d) Найдите среднюю мощность на резонансной частоте цепи.
14. Последовательная цепь RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн. При 8000 Гц фазовый угол составляет 45,0 °. {2}} \\ [/ latex]
резонансная частота:
– частота, при которой полное сопротивление в цепи является минимальным, а также частота, с которой цепь будет колебаться, если не будет управляться источником напряжения; рассчитывается по [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} \\ [/ latex]
фазовый угол:
обозначается ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи
Коэффициент мощности:
– величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ
Избранные решения проблем и упражнения
1.(a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором, Z = 531 Ом, что в 13 раз больше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z = 190 Ом, примерно так же, как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.
3. (a) 529 Ом при 60,0 Гц, 185 Ом при 10,0 кГц (b) Эти значения близки к значениям, полученным в Пример 1: Расчет импеданса и тока , поскольку на низкой частоте преобладает конденсатор, а на высокой – индуктор. доминирует.Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.
5. От 9,30 нФ до 101 нФ
7. 3,17 пФ
9. (а) 1,31 мкГн (б) 1,66 пФ
11. (a) 12,8 кОм (b) 1,31 кОм (c) 31,9 мА при 500 Гц, 312 мА при 7,50 кГц (d) 82,2 кГц (e) 0,408 A
13. (а) 0,159 (б) 80,9º (в) 26,4 Вт (г) 166 Вт
15. 16.0 Вт
Энергонезависимый оптический переключатель сопротивления в туннельных фотоэлементах
1.
Струков Д. Б., Снайдер Г. С., Стюарт Д. Р. и Уильямс Р. С. Обнаружен пропавший мемристор. Nature 453 , 80–83 (2008).
ADS CAS PubMed Статья Google Scholar
2.
Ян Дж. Дж., Струков Д. Б. и Стюарт Д. Р. Мемристивные устройства для вычислений. Нац. Нанотех. 8 , 13 (2013).
ADS CAS Статья Google Scholar
3.
Wang, Z. et al. Мемристоры с диффузной динамикой как синаптические эмуляторы для нейроморфных вычислений. Нац. Матер. 16 , 101–108 (2017).
ADS CAS PubMed Статья Google Scholar
4.
От редакции. Снова о мемристоре. Нац. Электрон . 1 , 261 (2018).
5.
Garcia, V. et al. Гигантское туннельное электросопротивление для неразрушающего считывания сегнетоэлектрических состояний. Nature 460 , 81–84 (2009).
ADS CAS PubMed Статья Google Scholar
6.
Chanthbouala, A. et al. Твердотельная память на основе туннельных сегнетоэлектрических переходов. Нац. Нанотех. 7 , 101 (2012).
ADS CAS Статья Google Scholar
7.
Yin, Y. et al. Эффект усиленного туннельного электросопротивления из-за сегнетоэлектрического фазового перехода на границе раздела магнитного сложного оксида. Нац. Матер. 12 , 397–402 (2013).
ADS CAS PubMed Статья Google Scholar
8.
Boyn, S. et al. Высокопроизводительная сегнетоэлектрическая память на основе полностью структурированных туннельных переходов. заявл. Phys. Lett. 104 , 052909 (2014).
ADS Статья CAS Google Scholar
9.
Wang, L. et al.Преодоление фундаментальных ограничений толщины барьеров сегнетоэлектрических туннельных переходов с помощью композитных барьеров BaTiO ₃ / SrTiO ₃. Nano Lett. 16 , 3911–3918 (2016).
ADS CAS PubMed Статья Google Scholar
10.
Xi, Z. et al. Гигантское туннельное электросопротивление в туннельных переходах металл / сегнетоэлектрик / полупроводник путем создания барьера Шоттки. Нац.Commun. 8 , 15217 (2017).
ADS CAS PubMed PubMed Central Статья Google Scholar
11.
Xi, Z., Zheng, C. & Wen, Z. Комплементарные резистивные переключатели неразрушающего считывания на основе сегнетоэлектрических туннельных переходов. ACS Appl. Матер. Интерфейсы 10 , 6024–6030 (2018).
CAS PubMed Статья Google Scholar
12.
Цянь М., Фина И., Санчес Ф. и Фонкуберта Дж. Дополнительное резистивное переключение с использованием туннельных функций металл-сегнетоэлектрик-металл. Малый 15 , 1805042 (2019).
Артикул CAS Google Scholar
13.
Журавлев М.Ю., Сабирьянов Р.Ф., Ясвал С., Цымбал Е.Ю. Гигантское электросопротивление в туннельных сегнетоэлектрических переходах. Phys. Rev. Lett. 94 , 246802 (2005).
ADS Статья CAS Google Scholar
14.
Гарсиа В. и Бибес М. Сегнетоэлектрические туннельные переходы для хранения и обработки информации. Нац. Commun. 5 , 4289 (2014).
ADS CAS PubMed Статья Google Scholar
15.
Индивери Г. и Дуглас Р. Нейроморфные датчики зрения. Science 288 , 1189–1190 (2000).
PubMed Статья Google Scholar
16.
Ди Мартино Г. и Таппертцхофен С. Оптически доступные мемристивные устройства. Нанофотоника 8 , 1579–1589 (2019).
Артикул Google Scholar
17.
Kundys, B., Viret, M., Colson, D. & Kundys, D. Изменения размеров кристаллов BiFeO ₃ под действием света. Нац. Матер. 9 , 803–805 (2010).
ADS CAS PubMed Статья Google Scholar
18.
Чой, Т., Ли, С., Чой, Ю., Кирюхин, В., Чеонг, С.-В. Переключаемый сегнетоэлектрический диод и фотоэлектрический эффект в BiFeO ₃. Science 324 , 63–66 (2009).
ADS CAS PubMed Статья Google Scholar
19.
Иурчук В.В. и др. Оптическая запись магнитных свойств остаточной фотострикцией. Phys. Rev. Lett. 117 , 107403 (2016).
ADS CAS PubMed Статья Google Scholar
20.
Zhang, X. et al. Световая модуляция переключения намагниченности в гетероструктуре PMN-PT / Ni. заявл. Phys. Lett. 116 , 132405 (2020).
ADS CAS Статья Google Scholar
21.
Guo, R. et al. Энергонезависимая память на основе сегнетоэлектрического фотоэлектрического эффекта. Нац. Commun. 4 , 1990 (2013).
ADS PubMed PubMed Central Статья CAS Google Scholar
22.
Ху, У. Дж., Ван, З., Ю, У. и Ву, Т. Оптически контролируемое электросопротивление и электрически управляемое фотоэдс в сегнетоэлектрических туннельных переходах. Нац. Commun. 7 , 10808 (2016).
CAS Статья Google Scholar
23.
Ghising, P. & Hossain, Z. Контроль электрического поля фотоиндуцированного увеличения сопротивления в гетероструктуре La _0,7 Sr _0,3 MnO ₃ / LaTiO ₃ / SrTiO ₃. Phys. Ред. B 100 , 115119 (2019).
ADS CAS Статья Google Scholar
24.
Фридкин В. М. Фотоферроэлектрики (Springer-Verlag, Берлин, Гейдельберг, Нью-Йорк, 1979).
25.
Dimos, D., Warren, WL, Sinclair, MB, Tuttle, BA & Schwartz, RW Фотоиндуцированные изменения гистерезиса и оптическое хранение в (Pb, La) (Zr, Ti) O ₃ тонких пленок и керамика. J. Appl. Phys. 76 , 4305–4315 (1994).
ADS CAS Статья Google Scholar
26.
Димос Д., Поттер Б. Г., Синклер М. Б., Таттл Б. А. и Уоррен В. Л. Фотоиндуцированные и электрооптические свойства (Pb, La) (Zr, Ti) O ₃ пленок для оптической памяти. Интегр. Сегнетоэлектр. 5 , 47–58 (1994).
CAS Статья Google Scholar
27.
Liu, Y. et al. Легко-ферроидное взаимодействие в гибридных органо-неорганических перовскитах. Adv. Опт. Матер. 7 , 1_{1 (2019).}
CAS Статья Google Scholar
28.
Рубио-Маркос, Ф., Дель Кампо, А., Марше, П. и Фернандес, Дж. Ф. Движение сегнетоэлектрической доменной стенки, индуцированное поляризованным светом. Нац. Commun. 6 , 1–9 (2015).
Артикул CAS Google Scholar
29.
Rubio-Marcos, F. et al. Обратимое оптическое управление макроскопической поляризацией в сегнетоэлектриках. Нац. Фотоника 12 , 29–32 (2018).
ADS CAS Статья Google Scholar
30.
Akamatsu, H. et al. Светоактивированная динамика гигагерцовых сегнетоэлектрических доменов. Phys. Rev. Lett. 120 , 096101 (2018).
ADS PubMed Статья PubMed Central Google Scholar
31.
Li, T. et al. Оптический контроль поляризации в сегнетоэлектрических гетероструктурах. Нац. Commun. 9 , 1–8 (2018).
ADS Статья CAS Google Scholar
32.
Kundys, D. et al. Оптически перезаписываемая память в гетероструктуре графен / сегнетоэлектрик-фотоэлектрическая. Phys. Rev. Appl. 13 , 064034 (2020).
ADS CAS Статья Google Scholar
33.
Янг М. М. и Алексей М.Обратимое светоиндуцированное управление поляризацией сегнетоэлектрика в BiFeO _{3 900 18. Adv. Матер. 30 , 1704908 (2018).}
Артикул CAS Google Scholar
34.
Луо, З.-Д., Парк, Д.-С., Ян, М.-М. & Alexe, M. Контролируемая светом наноскопическая запись электронных воспоминаний с использованием объемного фотоэлектрического эффекта с усилением наконечника. ACS Appl. Матер. Интерфейсы 11 , 8276–8283 (2019).
CAS PubMed Статья PubMed Central Google Scholar
35.
Липатов А., Шарма П., Груверман А., Синицкий А. Оптоэлектрические сегнетоэлектрические накопители на основе дисульфида молибдена (MoS ₂). ACS Nano 9 , 8089–8098 (2015).
CAS PubMed Статья PubMed Central Google Scholar
36.
Luo, Z.-D. и другие. Искусственные оптоэлектронные синапсы, основанные на сегнетоэлектрическом полевом эффекте, позволили создать мемристивные транзисторы из двухмерных дихалькогенидов переходных металлов. ACS Nano 14 , 746–754 (2019).
ADS Статья CAS Google Scholar
37.
Ван, Дж., Лю, Дж., Сандо, Д., Нагараджан, В. и Зейдел, Дж. Морфологически зависимое восстановление поляризации в тонких сегнетоэлектрических пленках. заявл. Phys. Lett. 111 , 092902 (2017).
ADS Статья CAS Google Scholar
38.
Wang, P. et al. Фотоиндуцированное сегнетоэлектрическое переключение в пленках перовскита CH ₃ NH ₃ PbI ₃. Nanoscale 9 , 3806–3817 (2017).
CAS PubMed Статья Google Scholar
39.
Ван, Дж., Вилкин, Б.И Барретт Н. Экранирование сегнетоэлектрических доменов на поверхности BaTiO ₃ (001) с помощью ультрафиолетового фотоиндуцированного заряда и диссоциативной адсорбции воды. заявл. Phys. Lett. 101 , 092902 (2012).
ADS Статья CAS Google Scholar
40.
Liu, F. et al. Управление поляризацией сегнетоэлектрических конденсаторов одновременным действием света и адсорбатов. ACS Appl. Матер. Интерфейсы 10 , 23968–23975 (2018).
CAS PubMed Статья Google Scholar
41.
Wu, W., Wong, K. & Choy, C. Смещение напряжения, контролируемое потерей кислорода на границе раздела фаз в эпитаксиальном Pb (Zr _0,52 Ti _0,48) O _{3 Тонкопленочные конденсаторы} с электродами из La _0,7 Sr _0,3 MnO ₃. заявл. Phys. Lett. 85 , 5013–5015 (2004).
ADS CAS Статья Google Scholar
42.
Fong, D. et al. Стабилизация монодоменной поляризации в ультратонких пленках PbTiO ₃. Phys. Rev. Lett. 96 , 127601 (2006).
ADS CAS PubMed Статья Google Scholar
43.
Балке, Н., Рамеш, Р. и Ю, П. Манипулирование сегнетоэлектриками посредством изменения свойств поверхности и интерфейса. ACS Appl. Матер. Интерфейсы 9 , 39736–39746 (2017).
CAS PubMed Статья Google Scholar
44.
Lu, H. et al. Повышение стабильности поляризации сегнетоэлектриков с помощью инженерии интерфейсов. Adv. Матер. 24 , 1209–1216 (2012).
CAS PubMed Статья Google Scholar
45.
Solmaz, A. et al. Селективность доменов в тонких пленках BiFeO ₃ за счет модифицированного торцевания подложки. Adv. Функц. Матер. 26 , 2882–2889 (2016).
CAS Статья Google Scholar
46.
Хестанова Е. и др. Распутывание электростатических и деформационных эффектов на поляризацию сегнетоэлектрических сверхрешеток. Adv. Функц. Матер. 26 , 6446–6453 (2016).
CAS Статья Google Scholar
47.
Guan, Z.и другие. Определение собственного сегнетоэлектричества тонкой пленки с помощью силовой микроскопии пьезоотклика. AIP Adv. 7 , 095116 (2017).
ADS Статья CAS Google Scholar
48.
Ким, С., Сеол, Д., Лу, X., Алекс, М. и Ким, Ю. Силовая микроскопия пьезореактивного отклика без электростатического разряда. наук. Отчет 7 , 41657 (2017).
ADS CAS PubMed PubMed Central Статья Google Scholar
49.
Scott, J. et al. Пробой диэлектрика в пленках с высоким ε для ULSI DRAM. II. Керамика из титаната бария – стронция. Интегр. Сегнетоэлектр. 4 , 61–84 (1994).
CAS Статья Google Scholar
50.
Лю Ф., Фина И., Бертакко Р. и Фонкуберта Дж. Распознавание и управление скрытыми полями отпечатка в сегнетоэлектрических конденсаторах. наук. Отчет 6 , 2835 (2016).
Google Scholar
51.
Radaelli, G. et al. Деформационно-управляемая чувствительность подчиненного полулегированного манганита La _0,5 Sr _0,5 MnO ₃ слоев, вставленных в сегнетоэлектрические туннельные переходы BaTiO3. Adv. Электрон. Матер. 2 , 1600368 (2016).
Артикул CAS Google Scholar
52.
Qin, Q.H. et al. Резистивное переключение в полностью оксидных сегнетоэлектрических туннельных переходах с ионными интерфейсами. Adv.Матер. 28 , 6852–6859 (2016).
CAS PubMed Статья PubMed Central Google Scholar
53.
Цянь М., Фина И., Санчес Ф. и Фонткуберта Дж. Асимметричная резистивная динамика переключения в туннельных переходах BaTiO ₃. Adv. Электрон. Матер. 5 , 1800407 (2019).
Артикул CAS Google Scholar
54.
Yoo, H.-I., Chang, M.-W., Oh, T.-S., Lee, C.-E. И Беккер, К. Электроокрашивание и подвижность кислородных вакансий BaTiO _{3 900 18. J. Appl. Phys. 102 , 093701 (2007).}
ADS Статья CAS Google Scholar
55.
Эрор Н. и Смит Д. Нестехиометрический беспорядок в монокристаллическом BaTiO ₃ при повышенных температурах. J. Solid State Chem. 24 , 235–244 (1978).
ADS CAS Статья Google Scholar
56.
Чан Н. Х., Шарма Р. и Смит Д. М. Нестехиометрия нелегированного BaTiO _{3 900 18. J. Am. Ceram. Soc. 64 , 556–562 (1981).}
CAS Статья Google Scholar
57.
Waser, R. Объемная проводимость и химия дефектов акцепторно-легированного титаната стронция в закаленном состоянии. J. Am. Ceram. Soc. 74 , 1934–1940 (1991).
CAS Статья Google Scholar
58.
Zafar, S. et al. Механизм электронной проводимости в тонких пленках титаната бария-стронция. заявл. Phys. Lett. 73 , 3533–3535 (1998).
ADS CAS Статья Google Scholar
59.
Nian, Y., Strozier, J., Ву, Н., Чен, X. и Игнатьев, А. Доказательства модели диффузии кислорода для эффекта изменения сопротивления, индуцированного электрическим импульсом, в оксидах переходных металлов. Phys. Rev. Lett. 98 , 146403 (2007).
ADS CAS PubMed Статья Google Scholar
60.
Chanthbouala, A. et al. Сегнетоэлектрический мемристор. Нац. Матер. 11 , 860–864 (2012).
ADS CAS PubMed Статья Google Scholar
61.
Вемпл С. Флуктуации поляризации и край оптического поглощения в BaTiO ₃. Phys. Ред. B 2 , 2679 (1970).
ADS Статья Google Scholar
62.
Makhort, A., Chevrier, F., Kundys, D., Doudin, B. & Kundys, B. Фотоэлектрический эффект и фотополяризация в Pb [(Mg _1/3 Nb _2/3 ) _0,68 Ti _0,32] O ₃ кристалл. Phys.Rev. Mater. 2 , 012401 (2018).
Артикул Google Scholar
63.
Quattropani, A. et al. Настройка фотовольтаического отклика пленок Bi ₂ FeCrO ₆ методом сегнетоэлектрического полинга. Nanoscale 10 , 13761–13766 (2018).
CAS PubMed Статья Google Scholar
64.
Sulzbach, M.C. et al.Блокировка проводящих каналов расширяет окно для сегнетоэлектрической резистивной коммутации в интерфейсных устройствах Hf _0,5 Zr _0,5 O ₂ туннельных устройств. Adv. Функц. Матер. 30 , 2002638 (2020).
CAS Статья Google Scholar
65.
Windt, D. L. et al. Оптические постоянные для тонких пленок Ti, Zr, Nb, Mo, Ru, Rh, Pd, Ag, Hf, Ta, W, Re, Ir, Os, Pt и Au от 24 A до 1216 A. заявл. Опт.

Сопротивление петли фаза ноль: Допустимое сопротивление петли «фаза-ноль»

Допустимое сопротивление петли «фаза-ноль»

Петля фаза-ноль | Заметки электрика

Что это такое «петля фаза-ноль»?

Причины и цель измерения

Сопротивление цепи фаза – ноль

Чем измерить сопротивление петли «фаза-ноль»

Петля фаза ноль. Для чего проверяют сопротивление петли фаза-ноль

Что это такое, и как формируется проверочная схема

Видео измерения петля фаза ноль

Как измеряется сеть

Как измерить сопротивление петля фаза ноль

Процесс измерения петля фаза ноль

Где провести замер

Цель проводимых замеров

Замер сопротивления петля фаза ноль

Будем рады, если подпишетесь на наш Блог!

Измерение сопротивления петли фаза-нуль | Пусконаладочные работы при монтаже электроустановок | Архивы

§ 71. Проверка состояния пробивных предохранителей

Измерение петли фаза-ноль | Электролаборатория БЭТЛ Ярославль

1. Что такое петля фаза-ноль

2. Зачем необходимо измерение

2.1. Периодичность проведения измерений

3. Какие приборы используют?

4. Порядок измерения петли фаза-ноль

4.1. Методика измерения

4.2. Выводы о результатах

4.3 Форма протокола

Коэффициент усиления контура и его влияние на аналоговые системы управления

Аннотация

KMSR-DS0252 | Menics |

Phase Zero Project: формирование конкурентного пространства

Наша история

Наши люди

Наше финансирование

Пресс-комната

Работа и стипендии

New America исполняется 20 лет

Новая Америка

Наша история

Публикации

Программы

События

Наши люди

Работа и стипендии

Пресс

Свяжитесь с нами

Новая Америка

740 15th Street NW, Suite 900

Тендер правительства Украины на услуги по измерению сопротивления изоляции, заземления, перехода

RLC | Физика

Цели обучения

Пример 1.Расчет импеданса и тока

Пример 2. Расчет резонансной частоты и тока

Питание в цепях переменного тока серии

Пример 3. Расчет коэффициента мощности и мощности

Сводка раздела

Концептуальные вопросы

Задачи и упражнения

Избранные решения проблем и упражнения

Энергонезависимый оптический переключатель сопротивления в туннельных фотоэлементах

Больше новостей

Добавить комментарий Отменить ответ