Среднеквадратическое значение напряжения: Действующее значение переменного напряжения

Среднеквадратическое (действующее) значение напряжения – это… Что такое Среднеквадратическое (действующее) значение напряжения?

Среднеквадратическое (действующее) значение напряжения

Среднеквадратическое (действующее) значение напряжения

31

Смотри также родственные термины:

31 среднеквадратическое (действующее) значение напряжения (тока): Корень квадратный из среднего арифметического значения квадратов мгновенных значений напряжения (тока), измеренных в определенный интервал времени и в определенной полосе частот.

Примечание – Действующее значение напряжения (тока) является одним из используемых способов измерения и соответствует среднеквадратическому значению напряжения, если определяется как корень квадратный из среднего арифметического значения квадратов мгновенных значений, полученных в определенный интервал времени и в определенной полосе частот

de.

Mittelwertbedeutung

en. [r.m.s.] (root-mean-square) value

fr. Valeur de la moyenne quadratique de tension (courant)

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

• среднеквадратическая погрешность результата измерений среднеарифметического
• среднеквадратическое (действующее) значение напряжения (тока)

Полезное

Смотреть что такое “Среднеквадратическое (действующее) значение напряжения” в других словарях:

• среднеквадратическое (действующее) значение напряжения (тока) — 31 среднеквадратическое (действующее) значение напряжения (тока): Корень квадратный из среднего арифметического значения квадратов мгновенных значений напряжения (тока), измеренных в определенный интервал времени и в определенной полосе частот.… …   Словарь-справочник терминов нормативно-технической документации

• действующее значение тока

  — Среднеквадратичное значение периодического электрического тока за период. Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… …   Справочник технического переводчика

• ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ — электрической величины (ранее наз. эффективным значением) среднеквадратическое за период значение периодич. величины (силы тока, электрич. напряжения, эдс и т. д.). Для синусоидально изменяющихся величин Д. з. в корень из 2 раз меньше… …   Большой энциклопедический политехнический словарь

• ГОСТ Р 54130-2010: Качество электрической энергии. Термины и определения — Терминология ГОСТ Р 54130 2010: Качество электрической энергии. Термины и определения оригинал документа: Amplitude die schnelle VergroRerung der Spannung 87 Определения термина из разных документов: Amplitude die schnelle VergroRerung der… …   Словарь-справочник терминов нормативно-технической документации

• номинальное напряжение — 3. 17 номинальное напряжение (rated voltage): Напряжение, установленное для выключателя изготовителем. Источник: ГОСТ Р 51324.1 2005: Выкл …   Словарь-справочник терминов нормативно-технической документации

• Рабочее напряжение — 3а. Номинальная мощность светового прибора Суммарная номинальная мощность ламп, на которую рассчитан световой прибор Источник: ГОСТ 16703 79: Приборы и комплексы световые. Термины и определения оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• напряжение — 3.10 напряжение: Отношение растягивающего усилия к площади поперечного сечения звена при его номинальных размерах. Источник: ГОСТ 30188 97: Цепи грузоподъемные калиброванные высокопрочные. Технические условия …   Словарь-справочник терминов нормативно-технической документации

• ГОСТ Р 51317.3.2-2006: Совместимость технических средств электромагнитная. Эмиссия гармонических составляющих тока техническими средствами с потребляемым током не более 16 А (в одной фазе). Нормы и методы испытаний — Терминология ГОСТ Р 51317.3.2 2006: Совместимость технических средств электромагнитная. Эмиссия гармонических составляющих тока техническими средствами с потребляемым током не более 16 А (в одной фазе). Нормы и методы испытаний оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• среднее — 3.3 среднее (mean): Среднее значение для (выбранного) времени усреднения результатов измерений анемометром. Источник: ГОСТ Р ИСО 1 …   Словарь-справочник терминов нормативно-технической документации

• Воздушный автоматический выключатель — Содержание 1 ОПРЕДЕЛЕНИЯ 1.1 Ключевые определения 1.2 Требова …   Википедия

Действующее значение тока. Действующее значение напряжения

Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие

действующего тока.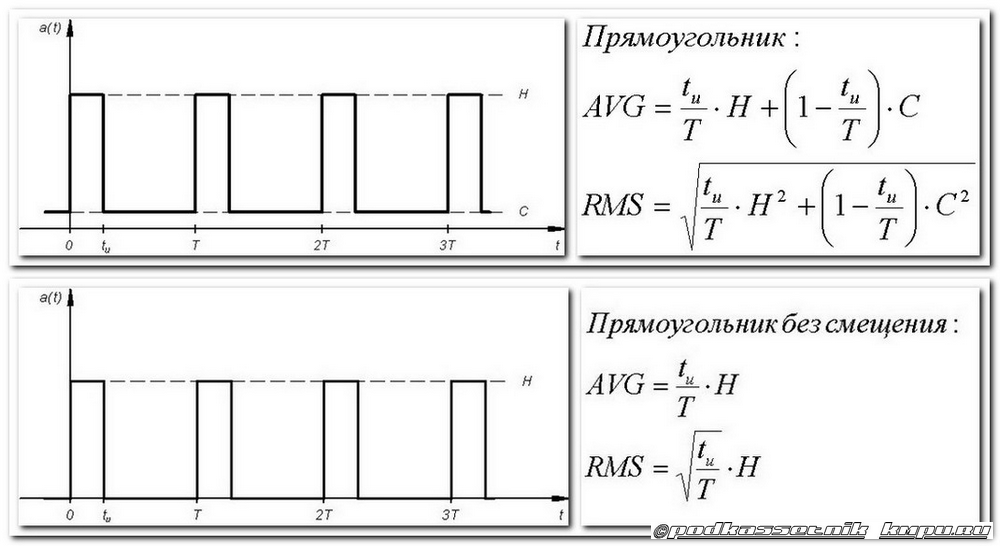

Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток.

Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда А_m и период T_период (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период T_период нашего синусоидального тока выделится вполне определенное количество джоулей энергии.

Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз. Допустим, мы насчитали, что за один период T_период синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время T_период выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики.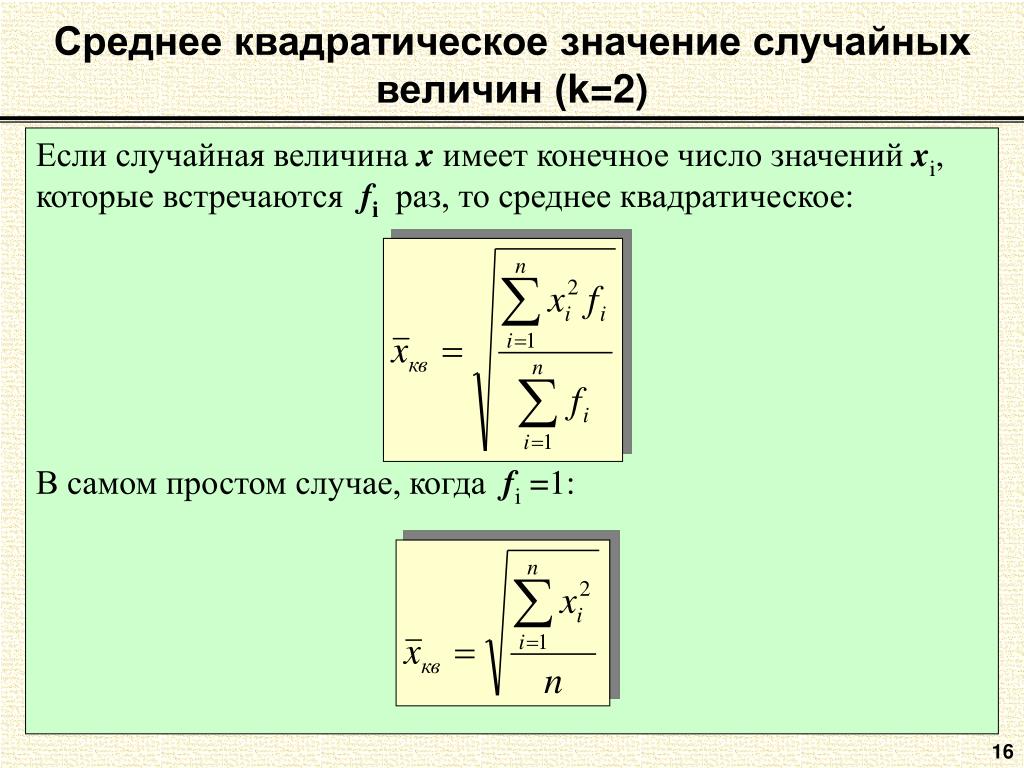 Как мы уже писали в прошлой статье, закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время T_период – соответственно, равно интегралу за время периода T_период:

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I_m² и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу

понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Погнали считать!

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Итак, имеем

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой I_m в течении периода T_период. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время T_период выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца. А мы тем временем выразим действующее значение тока I_{действ.} из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Отсюда получаем

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Действующее значение напряжения. Активное сопротивление. Действующие значения силы тока и напряжения — Гипермаркет знаний

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого , мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от (Im х sinωt ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √ 2 E= Em / √ 2

Действующие значения переменных величин обозначаются прописными буквами без индексов (I , U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.

Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.

Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.

В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.

Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.

Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э. д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.

Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает

а) б)

Рис. 3.4. Пример трехфазной системы переменного тока

а) генератор трёхфазного тока; б) с тремя генераторами;

изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.

Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.

Соединение звездой

Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы – X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).

Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.

Дополнительные сведения

В англоязычной технической литературе для обозначения действующего значения употребляется термин «effective value » – в дословном переводе «эффективная величина »

В электротехнике приборы электромагнитной, электродинамической и тепловой систем реагируют на действующее значение.

Источники

• «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
• Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
• «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10

Ссылки

См. также

• Список параметров напряжения и силы электрического тока

Wikimedia Foundation . 2010 .

Смотреть что такое “Действующее значение переменного тока” в других словарях:

действующее значение переменного тока

эффективное значение переменного тока – efektinė srovė statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas(ai) Grafinis formatas atitikmenys: angl. effective current; root mean square current vok. Effektivstrom, m rus. действующее значение… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

действующее значение тока – Среднеквадратичное значение периодического электрического тока за период. Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… …

В электротехнике среднее квадратичное за период значение переменного тока, напряжения, электродвижущей силы, магнитодвижущей силы, магнитного потока и т. п. Действующее значение синусоидального тока и напряжения в раз меньше их амплитудных… … Большой Энциклопедический словарь

– (электротехн.), среднее квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магнитного потока и т. п. Действующие значения синусоидального тока и напряжения в √2 раз меньше их амплитудных значений. * * *… … Энциклопедический словарь

Ср. квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магн. потока и т. п. Д. з. синусоидального тока и напряжения в кв. корень из 2 раз меньше их амплитудных значений … Естествознание. Энциклопедический словарь

ГОСТ Р МЭК 60252-2-2008: Конденсаторы для двигателей переменного тока. Часть 2. Пусковые конденсаторы – Терминология ГОСТ Р МЭК 60252 2 2008: Конденсаторы для двигателей переменного тока. Часть 2. Пусковые конденсаторы оригинал документа: 1.3.11 длительность рабочего цикла (duty cycle duration): Общее время одного нагружения (подачи напряжения) и… … Словарь-справочник терминов нормативно-технической документации

истинное действующее значение Справочник технического переводчика

истинное действующее значение – [Интент] Прибор, измеряющий несинусоидальный электрический сигнал, например, имеющий форму импульсов или отрезков синусоиды, с учетом всех гармоник этого сигнала, является прибором, определяющим истинное действующее значение этого сигнала. … … Справочник технического переводчика

истинное действующее значение – [Интент] Прибор, измеряющий несинусоидальный электрический сигнал, например, имеющий форму импульсов или отрезков синусоиды, с учетом всех гармоник этого сигнала, является прибором, определяющим истинное действующее значение этого сигнала.… … Справочник технического переводчика

Мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока . Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.

Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда А m и период T период (ну или частота f ). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период T период нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз . Допустим, мы насчитали, что за один период T период синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время T период выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока . А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье , закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время T период – соответственно, равно интегралу за время периода T период :

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I m 2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Итак, имеем

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой I m в течении периода T период . Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время T период выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца . А мы тем временем выразим действующее значение тока I действ . из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения . При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры , включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Отсюда получаем

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления , на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу

Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянном токеза время, определяется по формуле
. Переменный ток можно считать постоянным только в течение очень малых промежутков времени
. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

.

Сила тока в цепи изменяется по синусоидальному закону

,

.

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

.

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло
. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

(4.29)

Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

4.4.5. Мощность в цепи переменного тока

Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

,
.

Тогда мгновенное значение мощности, выделяемой на участке цепи,

Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

С использованием известной тригонометрической формулы

.

Величину
усреднять не нужно, так как она не зависит от времени, следовательно:

.

За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

, поэтому
(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то
и
. Если участок цепи содержит только индуктивность или только ёмкость, то
и
.

Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением
а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

.

В результате средняя расходуемая генератором мощность

.

Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

.

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Действующее значение напряжения в сети. SA Переменный ток

Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.

В современной литературе чаще используется математическое определение этой величины – среднеквадратичное значение переменного тока.

Иначе говоря, действующее значение переменного тока можно определить по формуле:

I = 1 T ∫ 0 T i 2 d t . {\displaystyle I={\sqrt {{\frac {1}{T}}\int _{0}^{T}i^{2}dt}}.}

Для синусоидального тока:

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}

I m {\displaystyle I_{m}} – амплитудное значение тока.

Для тока треугольной и пилообразной формы:

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}

Аналогичным образом определяются действующие значения ЭДС и напряжения.

Дополнительные сведения

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value – эффективное значение. Также применяется аббревиатура RMS (rms) – root mean square – среднеквадратичное (значение).

В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.

Источники

• «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
• Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
• «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10

Ссылки

• Действующие значения тока и напряжения
• Среднеквадратичное значение

Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока

Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p ).
Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е m , напряжения – U m , тока – I m .

Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.

Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.

Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.

По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:

E m = E · 1,41; U m = U · 1,41; I m = I · 1,41;

Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.

Под средним значением понимают среднеарифметическое ее значение за половину периода.

/ Среднее и действующие значения синусоидальных токов и напряжений

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока

т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,

Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током,

Выделенная за то же время постоянным током теплота равна Приравняем их:

Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.

Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,

		i 2r dt =		I m 2 sin2 ωt r dt. .

При неизменном во времени токе энергия

W = I 2rT

Приравняв правые части

I m

0,707I m .

Таким образом, действующее значение тока меньше амплитудного в √2 раз.

Аналогично определяют действующие значения ЭДС и напряжения:

Е = E m / √2, U = U m / √2.

Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значе­ниях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока

I m = √2I = 1,41 10 = 14,1 A,

и мгновенное значение тока

i = I m sin (ωt + ψ) = 14,1 sin (ωt + ψ).

При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):

		T 2
Е ср =			Е т sin ωt dt =			sin ωt d ωt =		|cos ωt | π 0 =		0,637Е т .

Аналогично можно найти средние значения тока и напряжения:

I ср = 2I т /π; U ср = 2U т /π.

Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока. Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M, Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени. Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется.

Список параметров напряжения и силы электрического тока

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)

Мгновенное значение

Мгновенное значение – это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}).{2}(t)dt}}}

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение

Среднее значение (смещение) – постоянная составляющая напряжения или силы тока

U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения).{T}\mid i(t)\mid dt}

На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

Коэффициенты пересчёта значений

• Коэффициент формы кривой переменного напряжения (тока) – величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .

• Коэффициент амплитуды кривой переменного напряжения (тока) – величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .

Параметры постоянного тока

• Размах пульсации напряжения (тока) – величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

• Коэффициент пульсации напряжения (тока) – величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
  • Коэффициент пульсации напряжения (тока) по действующему значению – величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
  • Коэффициент пульсации напряжения (тока) пo среднему значению – величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература и документация

Литература

• Справочник по радиоэлектронным устройствам : В 2-х т.; Под ред. Д. П. Линде – М.: Энергия, 1978
• Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989

Нормативно-техническая документация

• ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
• ГОСТ 23875-88 Качество электрической энергии. Термины и определения
• ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения

Ссылки

• Электрические цепи постоянного тока
• Переменный ток. Изображение синусоидальных переменных
• Амплитудное, среднее, эффективное
• Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
• Системы тока и номинальные напряжения электроустановок
• Электричество
• Проблемы высших гармоник в современных системах электропитания

Какой физический смысл имеет действующее значение напряжения и тока

Александр титов

Действующее значение силы ПЕРЕМЕННОГО тока – это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия.2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.

То же самое с действующим значением напряжения и ЭДС.

Vitas latish

можно грубо сказать
– напряжение – потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
– ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого , мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от (Im х sinωt ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √ 2 E= Em / √ 2

Действующие значения переменных величин обозначаются прописными буквами без индексов (I , U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.

Мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока . Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.

Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда А m и период T период (ну или частота f ). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период T период нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз . Допустим, мы насчитали, что за один период T период синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время T период выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока . А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье , закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время T период – соответственно, равно интегралу за время периода T период :

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I m 2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Итак, имеем

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой I m в течении периода T период . Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время T период выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца . А мы тем временем выразим действующее значение тока I действ . из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения . При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры , включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Отсюда получаем

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления , на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу

Рассмотрим следующую цепь.

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Активное сопротивление

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = Um*cos(ω*t).

Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.

I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).

Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.

Действующее значение силы тока

Амплитуда силы тока определяется по следующей формуле:

Среднее значение квадрата силы тока за период вычисляется по следующей формуле:

Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока.2) = Um/√2.

Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:

Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний – такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.

Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.

Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .

На шкалах измерительных приборов и технической документации также указываются действующие значения величин.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени

а за период переменного тока Т

Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:

Сократив общий множитель , получим действующее значение тока

Рис. 5-8. График переменного тока и квадрата тока.

На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока

Если ток изменяется по закону синуса, т. е.

Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:

Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.

Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.

Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.

Эффективные значения силы тока и напряжения. Действующее значение напряжения

При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.

Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .

На шкалах измерительных приборов и технической документации также указываются действующие значения величин.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени

а за период переменного тока Т

Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:

Сократив общий множитель , получим действующее значение тока

Рис. 5-8. График переменного тока и квадрата тока.

На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока

Если ток изменяется по закону синуса, т. е.

Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:

Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.

Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.

Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.

Рассмотрим следующую цепь.

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Активное сопротивление

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = Um*cos(ω*t).2) = Um/√2.

Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:

Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний – такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.

Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

>> Активное сопротивление. Действующие значения силы тока и напряжения

§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

P = i 2 R. (4.19)

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение

График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t

Средняя мощность равна, таким образом, первому члену в формуле (4.20):

Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем

Это закон Ома для участка цепи переменного тока с резистором.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:

P = I 2 R = UI.

Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!

Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. – 17-е изд., перераб. и доп. – М. : Просвещение, 2008. – 399 с: ил.

Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

Дополнительные сведения

В англоязычной технической литературе для обозначения действующего значения употребляется термин «effective value » – в дословном переводе «эффективная величина »

В электротехнике приборы электромагнитной, электродинамической и тепловой систем реагируют на действующее значение.

Источники

• «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
• Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
• «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10

Ссылки

См. также

• Список параметров напряжения и силы электрического тока

Wikimedia Foundation . 2010 .

Смотреть что такое “Действующее значение переменного тока” в других словарях:

действующее значение переменного тока

эффективное значение переменного тока – efektinė srovė statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas(ai) Grafinis formatas atitikmenys: angl. effective current; root mean square current vok. Effektivstrom, m rus. действующее значение… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

действующее значение тока – Среднеквадратичное значение периодического электрического тока за период. Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… …

В электротехнике среднее квадратичное за период значение переменного тока, напряжения, электродвижущей силы, магнитодвижущей силы, магнитного потока и т. п. Действующее значение синусоидального тока и напряжения в раз меньше их амплитудных… … Большой Энциклопедический словарь

– (электротехн.), среднее квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магнитного потока и т. п. Действующие значения синусоидального тока и напряжения в √2 раз меньше их амплитудных значений. * * *… … Энциклопедический словарь

Ср. квадратичное за период значение переменного тока, напряжения, эдс, магнитодвижущей силы, магн. потока и т. п. Д. з. синусоидального тока и напряжения в кв. корень из 2 раз меньше их амплитудных значений … Естествознание. Энциклопедический словарь

ГОСТ Р МЭК 60252-2-2008: Конденсаторы для двигателей переменного тока. Часть 2. Пусковые конденсаторы – Терминология ГОСТ Р МЭК 60252 2 2008: Конденсаторы для двигателей переменного тока. Часть 2. Пусковые конденсаторы оригинал документа: 1.3.11 длительность рабочего цикла (duty cycle duration): Общее время одного нагружения (подачи напряжения) и… … Словарь-справочник терминов нормативно-технической документации

истинное действующее значение Справочник технического переводчика

истинное действующее значение – [Интент] Прибор, измеряющий несинусоидальный электрический сигнал, например, имеющий форму импульсов или отрезков синусоиды, с учетом всех гармоник этого сигнала, является прибором, определяющим истинное действующее значение этого сигнала.… … Справочник технического переводчика

истинное действующее значение – [Интент] Прибор, измеряющий несинусоидальный электрический сигнал, например, имеющий форму импульсов или отрезков синусоиды, с учетом всех гармоник этого сигнала, является прибором, определяющим истинное действующее значение этого сигнала.… … Справочник технического переводчика

Мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока . Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.

Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда А m и период T период (ну или частота f ). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период T период нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз . Допустим, мы насчитали, что за один период T период синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время T период выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока . А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье , закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время T период – соответственно, равно интегралу за время периода T период :

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I m 2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Итак, имеем

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой I m в течении периода T период . Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время T период выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца . А мы тем временем выразим действующее значение тока I действ . из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения . При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры , включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Отсюда получаем

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления , на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу

Расчет среднего и среднеквадратичного значений тока/напряжения

.
.
Вот здесь есть расширенный и углубленный вариант данной заметки
.
.

Будучи в очень недавнем прошлом яростным разработчиком всевозможных импульсных источников питания, интересовался всяким по данной теме. В частности – вычислением среднего (AVG, Average) и среднеквадратичного (действующего, эффективного, RMS) значений напряжений и (особенно) токов, живущих в разрабатываемом источнике. Для тех, кто не помнит/не знает – напомню определение среднеквадратичного значения тока/напряжения из Википедии:

Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока

Посему, хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. И про выпрямители во вторичной цепи – та же песня. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.

Или, например, делаем могучий источник с высоким КПД. Чтобы оптимально спроектировать обмотку магнитного элемента требуются уже среднее значение тока и среднеквадратичное значение переменной составляющей. В общем – куда ни плюнь, везде фигурируют RMS и AVG (среднее значение, а не антивирус, это важно). Поэтому было принято решение сделать себе некий инструмент, упрощающий жизнь разработчика импульсных источников питания. Вот этим инструментом я и хочу поделиться с общественностью – вдруг кому пригодится.

Как нетрудно заметить, данный инструмент («программа») представляет собой обычный Экселовский файл, поскольку в «компьютерном» программировании я вообще ничего не понимаю. В задачу рассматриваемой «программы» входит отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период) и отрисовка формы переменной составляющей заданного сигнала. Также «программа» умеет вычислять среднее и среднеквадратичное значения заданного сигнала и RMS-значение его переменной составляющей. Исходные данные вводятся слева в ячейки, выделенные зеленым цветом (на рисунке обведены красным). Рассчитанные значения AVG и RMS, а также среднеквадратичное значение переменной составляющей заданного сигнала отображаются в правой стороне экрана (обведены синим). Ну а картинки рисуются в нижней части экрана: слева – исходный сигнал, справа – его переменная составляющая.

В нагрузку к «программе» идет короткая заметка, в которой выводятся (а не берутся невесть откуда) расчетные формулы для основных форм сигналов в импульсных источниках питания (трапеции, прямоугольника, треугольника, пилы). Также в этой короткой заметке рассмотрен пример расчета AVG и RMS значений сложного сигнала.

Почему в качестве основы взята именно трапеция? Потому, что из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник

и треугольник

А уж на основе этих базовых сигналов можно сляпать и пилу

и даже то, что творится на вторичке пушпула:

И еще много чего. Пример же расчета среднего и среднеквадратичных значений для сложных (т.е., составленных из простейших) сигналов, повторюсь, есть в короткой заметке-нагрузке. Хотя, если кого-то заинтересует данный аспект, могу впоследствие осветить его и в этом топике.

Вот, в принципе, и всё описание представленной «программы». Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!

Примечание: все вопросы лучше валить в камменты после заметки, так как не факт, что я смогу на них на все ответить. А вот шансы на то, что в сообществе найдется более прошаренный человек по твоей теме — довольно хорошие. Но уж если зарегистрироваться на сайте совсем никак — можно воспользоваться возможностями электрической почты: [email protected]

Содержание архива (также прилеплен к заметке):
AVG_RMS.zip:
Среднее_и_среднеквадратичное_Трапеция.xls – собственно, «программа» для расчета AVG и RMS в формате Microsoft Excel;
Среднее и среднеквадратичное.pdf – короткая заметка-нагрузка с выводом расчетных формул и с примером расчета AVG и RMS значений сложного сигнала.

Метод измерения действующего значения напряжения с применением МК / Хабр

    В данном посте речь пойдет об одном из вариантов измерения действующего значения напряжения и частоты сети на 8-ми битном микроконтроллере PIC18. При желании, можно метод перенести на любой другой МК, вплоть до всеми любимых ARDUINO (если они поддерживают реализацию прерываний по таймеру с частотой 5-10 кГц).

    Также, рассматриваемый метод позволяет измерять частоту сетевого напряжения без использования внешних дополнительных средств, таких как компараторы. Но, при этом приходится жертвовать либо временными ресурсами МК, либо точностью измерения частоты.

    Почему важно измерять действующее значение, а не какое либо другое, например, средневыпрямленное? Большинство “китайских” электронных вольтметров измеряют сетевое напряжение по средневыпрямленному значению. Методика измерения следующая: за период сетевого напряжения делается выборка из N значений амплитуды напряжения, результаты суммируются (без знака), делятся на N (усредняются), после чего полученный результат умножается на коэффициент

    Указанный коэффициент определяет зависимость действующего значения синусоидального (!) сигнала от средневыпрямленного.

    Такая методика измерения проста, не требует много ресурсов микроконтроллера (как временных, так и ресурсов памяти). Основным недостатком такой методики измерения является большая ошибка измерения на несинусоидальных сигналах.

    Как все знают, изменение сигнала сетевого напряжения подчиняется синусоидальному закону (вследствие применения синхронных генераторов на электростанции), с частотой изменения сигнала 50 Гц (60 Гц). Однако, на практике вследствие влияния сторонних факторов (в основном подключение к сети мощных нелинейных нагрузок), а также применения инверторов с квазисинусоидальным выходным напряжением (см. рисунок), синусоида напряжения либо значительно искажается, либо заменятся прямоугольными импульсами. В таких случаях указанный выше метод измерения даст очень большую погрешность (например, в квазисинусоидальных инверторах выходное напряжение, измеренное “китайским» вольтметром может быть равно 180-200В, в то время как действующее напряжение будет равно 220В ).

    Например, напряжение у меня дома

    Почему важно измерять именно действующее значение напряжения (тока)? Потому что именно действующие (еще называют его эффективными) значения напряжения и тока определяют работу электрической системы (грубо говоря, электронагреватель выделяет тепло в прямой зависимости от действующих значений напряжения и тока сети).
    Действующее значение измеряемой периодической величины рассчитывается по формуле

    Или после дискретизации получим

    Т.е. нам нужно делать выборку ряда значений за период сетевого напряжения, просуммировать значения квадратов точек выборки, поделить на количество точек за период (при определении количества точек выборки не забываем про теорему Котельникова-Шеннона), и взять квадратный корень из полученного результата.
    Вроде бы ничего сложного, если бы не но:
      1)  Каждый период точки выборки набираются заново, что увеличивает погрешность измерения;
      2)  В реальной сети, около нуля напряжения, могут встречаться как “нулевые полки”, так и повторные переходы через ноль напряжения, что значительно внесет погрешность в измерение.
    С первым пунктом будем бороться измерением измерением суммы квадратов точек выборки за каждый полупериод, после чего суммируя n-ую сумму квадратов с (n+1)-й и откидывая (n-1)-ую.
    Со вторым пунктом будем бороться введением зон нечувствительности по напряжению (введем границы напряжения перехода через ноль с положительной и отрицательной сторон) обычно 5-10 В в обе стороны, а также зон нечувствительности по частоте (ограничим допустимую частоту сигнала напряжения).

    Таким образом, мы получим рассчитанное значение действующего значения сетевого напряжения за период на каждом полупериоде сетевого напряжения.2/R) — чтобы не превышала допустимой мощности резисторов. Плечи дифференциального усилителя тоже делаем равными. Тогда, напряжение в точке 1 рассчитывается по формуле:

А напряжение в точке 1 будет иметь вид:

    Также, половина опорного напряжения подается на один из каналов АЦП. Это позволяет в постоянном режиме (например, один раз за период) определять положение уровня нуля измеряемого напряжения.
Т.е. мы обошлись операционным усилителем с однополярным питанием, и наш входной сигнал в точке 1 изменяется от 0 до Uоп. Такой способ дает достаточно точные результаты, по сравнению, например, с выпрямлением напряжения с помощью диодов.
    Расчет делителя и коэффициента АЦП сводится к следующему:

где A и В — замеры АЦП (за вычетом измеренного значения нуля сигнала — AN1) для текущего и предыдущего полупериодов; N1, N2 — число замеров для текущего и предыдущего полупериодов; Nadс — разрядность АЦП; U’оп — опорное напряжение за вычетом зон нелинейности (нечувствительности) операционного усилителя (обычно 0,6 В).
    Расчет делителя удобно проводить считая сигнал постоянным, приведенным к амплитуде синусоидального, а не синусоидальным. Тогда действующее значение сигнала равно амплитудному и равно значению каждого замера.
Например, нужно рассчитать делитель для измерения максимального значения 420В переменного тока:

Сопротивление Ra выбирается в диапазоне от 500 кОм до 1500 кОм. По выбранному сопротивлению Ra рассчитывается Rb.
    В итоге, алгоритм расчета действующего значения напряжения и частоты примет вид:

При этом часть затратных расчетов (деление, извлечение корня) можно перенести из прерывания в основную программу.

    При расчете действующих значений на 8-ми битном МК целесообразно пользоваться целочисленными методами (с использованием масштабных коэффициентов) не прибегая к расчетам с плавающей запятой, а также упрощать по возможности арифметические операции (деление, изъятие квадратного корня и проч.). Это значительно экономит ресурсы МК.

Объяснение действующего значения напряжения и тока

Переменный ток

Электричество и магнетизм

Объяснение действующего значения напряжения и тока

Учебное руководство для 14–16

Есть много способов объяснить среднеквадратичное (среднеквадратичное) напряжение и ток на разных уровнях сложности для студентов продвинутого уровня.

• Для простейшего уровня скажем, что вы измеряете ток (или разность потенциалов) через крошечные интервалы времени. Возведите каждое значение в квадрат, сложите квадраты (все положительные) и разделите на количество выборок, чтобы найти средний квадрат или средний квадрат. Затем извлеките из этого квадратный корень. Это среднеквадратичное значение (среднеквадратическое значение) (rms).
Например, предположим, что существует 8 временных интервалов, как показано на диаграмме выше:

Значения	7	10	7	0	-7	-10	-7	0
Квадраты	49	100	49	0	49	100	49	0

Сумма квадратов = 396 Среднее значение квадратов = 396/8 = почти 50 Квадратный корень ~ 7 При большем количестве интервалов среднеквадратичное значение оказывается равным (пиковое значение) √ 2 = пиковое значение 1.41 = 0,707 пиковое значение
• Для тех, кто знаком с графиками функций синуса и косинуса, можно попробовать следующий алгебраический метод.
• I = I ₀ sinω t и I ² = I ₀ ² sin ² ω t
• Эффект нагрева зависит от I ² R , поэтому требуется в среднем I ² , а не в среднем I .
• Чтобы найти среднеквадратичное значение, вам нужно среднее значение sin ² с течением времени.
• График sinω t и график cosω t выглядят одинаково, за исключением смещения начала координат. Поскольку это одна и та же модель, sin ² ω t и cos ² ω t имеют одинаковое среднее значение с течением времени.
• Но sin ² ω t + cos ² ω t = 1. Следовательно, средние значения любого из них должны быть 1/2.
• Следовательно, действующее значение I ₀ sinω t должно быть I ₀ √ 2
• Среднеквадратичное значение составляет 0,707 пикового значения, а пиковое значение – 1,41 раза больше значения, отображаемого вольтметром. Пиковое значение для сети 230 В составляет 325 В.
• В качестве альтернативы: Постройте график sin ² θ. Разрежьте график пополам и переверните одну половину вверх ногами или скопируйте на прозрачную пленку и совместите вместе. Две половины точно совпадают, показывая, что среднее значение равно 1/2.
• Обратите внимание, что при использовании несглаженного выпрямленного переменного тока от простого источника питания оценка мощности, полученная путем умножения показаний вольтметра постоянного тока с подвижной катушкой и амперметра с подвижной катушкой, вероятно, будет почти на 20% меньше. Это связано с тем, что каждый измеритель с подвижной катушкой измеряет простое среднее по времени горбов за полупериод, а не среднеквадратичное значение.
Умноженные действующие значения тока и напряжения дают фактическую мощность. Это жизненно важная часть при проведении количественных экспериментов с мощностью и энергией, таких как удельная теплоемкость.Значения в лучшем случае составляют только 80% от стоимости.

Калькулятор среднеквадратичного напряжения – от среднего значения, пика и пика к пиковому значению такие значения, как среднее значение (V

_AV ), пиковое или максимальное значение (V _P или V _MAX ) и значение от пика до пика (V _PP ).

Как рассчитать действующее значение напряжения?

Как уже говорилось ранее о среднеквадратичном (RMS) или V _RMS напряжении, это эквивалентное постоянное напряжение синусоидальной волны i.е. если среднеквадратичное значение напряжения составляет 230 В _AC , генерируя 60 Вт тепла при подключении к нагревательному элементу, например резистору, такое же количество тепла может генерироваться через источник постоянного напряжения 230 В _DC при подключении к тому же нагревательному элементу, что и ранее в цепи переменного тока.

Мы покажем различные уравнения для расчета среднеквадратичного напряжения с примененными формулами и решенными примерами, как показано ниже.

Связанный калькулятор: 3-, 4-, 5- и 6-полосный калькулятор значений резисторов

Уравнения для калькулятора среднеквадратичных значений

Поскольку калькулятор среднеквадратичного напряжения связан со средним значением (В _AV ), пиковым или максимальным значением (VP или V) _MAX ) и от пика до пика (V _PP ), следующие уравнения для вычислителя среднеквадратичного напряжения показаны на рис.2.

Пиковое значение: V _P или V _MAX

Максимальное положительное или отрицательное значение переменной величины (например, напряжения или тока) известно как ее амплитуда формы волны, максимальное значение или пик ценить. Обозначается V _P , I _P или E _MAX и I _MAX .

V _P = √2 x V _RMS

Используя приведенную выше формулу, мы можем найти значение RMS напряжения следующим образом:

V _RMS = 0.7071 x В _P

Пример:

Предположим, что значение пикового напряжения составляет 325 В переменного тока, значение среднеквадратичного напряжения будет:

В _RMS = 0,7071 x 325 В = 229,80 В _RMS

От пика до пика Значение (V _PP )

Сумма положительных и отрицательных пиковых значений в синусоиде называется величиной от пика до пика. Выражается как I _PP или V _PP .

В _PP = 2√2 x V _RMS

Используя приведенную выше формулу, мы можем найти значение RMS напряжения следующим образом:

V _RMS = 0,35355 x V _PP

Пример:

Предположим, что значение пик-пикового напряжения составляет 340 В переменного тока, значение RMS напряжения будет:

В _RMS = 0,35355 x 340 В = 120,2 В _RMS

Связанные калькуляторы:

Среднее напряжение Значение (В _AV )

Если мы преобразуем синусоидальную волну переменного тока в волну постоянного тока (DC) через выпрямители, то преобразованное значение в постоянное будет известное как среднее значение этой синусоидальной волны переменного тока.

Имейте в виду, что среднее значение напряжения полной синусоидальной волны переменного тока равно нулю, потому что площадь, покрытая положительными полупериодами, равна площади, покрытой отрицательными полупериодами, которые компенсируют друг друга. Вот почему мы не можем использовать переменный ток для хранения батарей.

Мы используем только полуволны для измерения среднего значения напряжения или тока переменного тока.

В _AV = (2√2) / π x V _RMS

Используя приведенную выше формулу, мы можем найти значение RMS напряжения следующим образом:

V _RMS = 1.11 x V _AV

Пример:

Предположим, что среднее значение напряжения равно 200VAC, значение RMS Voltage будет:

V _RMS = 1,11 x 200V = 222 V _RMS

Связанное сообщение:

Среднее и среднеквадратичное напряжение – Electronics-Lab.com

Введение

В режиме постоянного тока возможно только одно определение значения напряжения, это значение однозначно и определяется разницей между опорным значением 0 В и плоской линией сигнала постоянного тока.

Однако в режиме переменного тока может возникнуть путаница, если будет указано только одно значение напряжения. Из простого синусоидального сигнала мы можем, по крайней мере, перечислить четыре различных определения напряжения:

рис 1: Иллюстрация пикового, среднего и среднеквадратичного значений

Пиковое значение соответствует разнице между опорным значением (которое является значением, в котором колеблется сигнал переменного тока) и максимальным значением сигнала. Пиковое значение – это пиковое значение, умноженное на коэффициент 2, оно соответствует общей вертикальной ширине сигнала.

На рис. 1 мы также выделили красным цветом средние значения , и RMS, , на которых мы сосредоточимся в следующем уроке.

В двух разделах, разработанных в этой статье, будут отдельно представлены среднеквадратические значения и RMS , мы увидим, как они определены, как их определять, и, наконец, мы увидим, что особенного в среднеквадратичном значении.

Среднее напряжение

Для элементарной симметричной синусоидальной, треугольной, квадратной или пилообразной формы волны (см. , рис. 2, и руководство по форме волны переменного тока) неясно говорить о среднем значении напряжения, которое мы отметим A в дальнейшем.Действительно, эти типы сигналов в течение половины своего периода являются положительными, а в течение второй половины – отрицательными. Другими словами, сигналы 50% времени находятся над горизонтальной осью и 50% под ней.

Из этого наблюдения легко понять, что если мы рассмотрим среднее значение любого из этих сигналов за полный период, оно будет равно 0 , независимо от пикового значения, и, следовательно, не имеет значения.

Рис. 2: Элементарные синусоидальные, треугольные, квадратные и пилообразные формы сигналов

Мы можем продемонстрировать этот результат, объяснив, как вычислить среднее значение.Для конечного набора значений процесс усреднения состоит из суммирования всех значений (V ₁ , V ₂ , V ₃ …) и их деления на кардинальное число N набора (сколько значений имеется в комплекте):

Для аналогового сигнала, однако, невозможно суммировать все мгновенные значения, также называемые средними ординатами, которые принимает сигнал в течение периода, просто потому, что существует бесконечность. Вместо суммирования используем операцию интегрирования:

уравнение 1: Среднее значение сигнала переменного тока V (t) за полный период

Уравнение 1 представляет собой среднее значение сигнала V (t), взятого между моментами времени 0 и T, то есть за полный период.Член ∫V (t) dt дает значение площади между кривой V (t) и опорным значением 0 В. Поскольку операция интегрирования является линейной, этот член можно разделить на две части:

Для элементарной формы волны, такой как представлена ​​на рис. 1 , мы можем видеть, что первый и второй члены этой формулы равны, но имеют противоположные знаки, поэтому среднее значение равно 0.

Для того, чтобы среднее значение таких сигналов имело смысл, мы предпочитаем рассматривать отдельно полуположительные и отрицательные периоды, некоторые их значения соответственно выделены красным и зеленым цветом на следующем рисунке. Рисунок 3 :

рис 3: Некоторые мгновенные значения для положительного полупериода (красным) и отрицательного полупериода (зеленым) синусоидального сигнала

Аналогично уравнению , мы можем определить отдельно средние значения для положительного полупериода (A ₊ ) и отрицательного полупериода (A _– ):

уравнение 3: Средние значения переменного сигнала V (t), взятые для положительного (+) и отрицательного (-) полупериодов

Значение A ₊ и A _– зависит от сигнала, с которым мы имеем дело, и их соответствующие пиковые значения (V _p ) _. Ниже перечислены абсолютные значения | A | A + и A _– для наиболее распространенных элементарных и симметричных сигналов переменного тока :

• Форма синусоидального сигнала: | A | = 0,637 × V _p
• Треугольник: | A | = 0
• Прямоугольная форма сигнала: | A | = V _p
• Форма волны пилообразной формы: | A | = 0,5 × В _p

Мы можем завершить этот раздел, сказав, что когда мы хотим усреднить сигнал, нам нужно указать точность, если процесс выполняется на полном периоде или меньшем значении.Для элементарных и симметричных сигналов переменного тока усреднение за полный период всегда дает результат 0 В независимо от частоты, пикового значения или периода. По этой причине более целесообразно усреднять эти сигналы в течение их полупериодов.

RMS Напряжение

RMS обозначает среднеквадратическое значение, это операция, аналогичная представленной ранее усредненной величине, но вместо этого мгновенные значения возводятся в квадрат, а общая дробь определяется корнем:

По тем же причинам, что указывалось ранее, мы используем операцию интегрирования для определения V _RMS для аналогового сигнала:

уравнение 4: Среднеквадратичное значение сигнала переменного тока V (t) периода T

В отличие от среднего значения, среднеквадратичное значение всегда определяется для полного периода сигнала, действительно нет никакой путаницы при определении этого значения.

В качестве примера давайте определим среднеквадратичное значение синусоидального сигнала с пиковым значением V _p и угловой пульсацией ω V (t) = V _p × sin (ωt) . Отметим f частоту, которая удовлетворяет f = ω / 2π и T = 1 / f периоду.

Прежде всего, мы вычисляем интегральный член, который мы отмечаем I:

Мы используем тригонометрическую идентичность sin ² (x) = (1-cos (2x)) / 2 , чтобы продолжить:

Оценка члена в скобках между 0 и T дает 2π / ω = T .Следовательно, член интегрирования в конечном итоге равен (πV _p ² ) / ω . Из уравнения мы видим, что нам все еще нужно умножить на 1 / T, что приводит к [(πV _p ² ) / ω] × [ω / (2π)] = V _p ² /2 на срок под корень.

Наконец, после извлечения корня окончательное выражение для среднеквадратичного значения синусоидального сигнала дается следующим образом:

Ниже перечислены среднеквадратичные значения, которые можно вычислить тем же методом, что и в приведенном выше примере синуса для элементарных и симметричных сигналов, указанных в предыдущем разделе:

• Форма синусоидального сигнала: V _RMS = V _p / √2
• Треугольник и пилообразный сигнал: V _RMS = V _p / √3
• Прямоугольная форма сигнала: В _RMS = В _P

Важно отметить, что V _RMS > | A |, значение RMS всегда больше, чем абсолютное значение среднего.

Что важно для понимания значения RMS, так это то, что оно создает связь между режимами постоянного и переменного тока в соответствии со следующим Рисунок 4 :

рис 4: Сходство между режимами переменного и постоянного тока

Среднеквадратичные значения напряжения и тока – это значения, которые развивают ту же мощность на сопротивлении в режиме постоянного тока.

Заключение

Средние и среднеквадратичные значения можно легко измерить современными вольтметрами или осциллографами и предоставить информацию о сигнале переменного тока.

Численный подход к вычислению среднего состоит из суммирования всех значений сигнала и деления суммы на количество значений. Для реальных сигналов мы предпочитаем использовать операцию интегрирования, которая является расширением суммы для бесконечного набора значений.

Для среднего значения возможны два определения, в зависимости от того, выполняется ли усреднение за полный период или за полупериод. Симметричные сигналы характеризуются средним значением 0 за полный цикл . Среднее значение за полный цикл отличается от 0 только в том случае, если в сигнале присутствует составляющая постоянного тока или если сигнал не является симметричным относительно горизонтального эталона.Усреднение по полупериоду также может быть выполнено для характеристики различных симметричных сигналов.

Среднеквадратичное значение определяется аналогично среднему значению, но вместо этого каждое значение суммы возводится в квадрат, а окончательный результат коренится. Среднеквадратичное значение всегда выше абсолютного значения среднего и устанавливает связь между режимами переменного и постоянного тока, поэтому оно особенно используется инженерами.

Калькулятор RMS напряжения

– от среднего значения, пикового и пикового значения к пиковому значению

Введение

Что такое действующее напряжение? Среднеквадратичное (среднеквадратичное) напряжение синусоидального источника электродвижущей силы (Vrms) используется для характеристики источника.Это квадратный корень из среднего по времени квадрата напряжения в форме сигнала переменного тока.

Как рассчитать действующее значение напряжения?

Например, если в форме сигнала выбраны 100 значений напряжения, среднеквадратичное значение будет равно квадратному корню из всех напряжений, возведенных в квадрат, сложенных вместе и разделенных на 100.

Следующая формула показывает, как найти среднеквадратичное значение напряжения для выборки напряжений.

Для вычисления среднеквадратичного напряжения из пикового напряжения пиковое напряжение умножается на 0.7071 .
Для вычисления среднеквадратичного напряжения из размаха напряжения , размах напряжения умножается на 0,35355 .
Для вычисления среднеквадратичного напряжения из среднего напряжения среднее напряжение умножается на 1,1107 .

Используя приведенную выше формулу, мы можем легко найти значение RMS напряжения . А V _rms всегда больше, чем абсолютное значение V _avg .

Аналогичный анализ приводит к аналогичному уравнению для В _{среднеквадратичного значения} напряжения:
Чистая синусоида: В _{среднеквадратичного значения} = В _P / √2
Треугольная и пилообразная волны: В _{среднеквадратичное значение} = V _P / √3
Прямоугольная волна: V _rms = VP

Люди тоже спрашивают (Q&A)

1. Что означает RMS?
Среднеквадратичное значение
Среднеквадратичное значение (RMS) и пиковая мощность являются основными терминами, необходимыми для определения мощности…. В мире бытовой электроники вы часто слышите о ваттах, мощности и выходной мощности. Эти термины взаимозаменяемы для обозначения двух значений, а именно: среднеквадратичного значения (RMS) и пиковой мощности.

2. Что такое действующее значение напряжения?
Среднеквадратичное значение – это действующее значение переменного напряжения или тока. Это эквивалентное постоянное (постоянное) значение постоянного тока, которое дает такой же эффект. Например, лампа, подключенная к источнику переменного тока 6 В RMS, будет светить с такой же яркостью при подключении к стабильному источнику 6 В постоянного тока.

3. Как рассчитать среднеквадратичное значение напряжения?
Затем определяется среднеквадратичное значение напряжения (VRMS) синусоидальной формы волны путем умножения значения пикового напряжения на 0,7071, которое совпадает с делением единицы на квадратный корень из двух (1 / √2).

4. Что такое среднеквадратичное и пиковое напряжение?
Пиковые значения могут быть рассчитаны на основе значений RMS по приведенной выше формуле, которая подразумевает VP = VRMS × √2, при условии, что источником является чистая синусоида. Таким образом, пиковое значение сетевого напряжения в США составляет около 120 × √2, или около 170 вольт.Размах напряжения, увеличенный вдвое, составляет около 340 вольт.

5. RMS равно постоянному току?
«RMS» означает среднеквадратическое значение и представляет собой способ выражения величины переменного напряжения или тока в терминах, функционально эквивалентных постоянному току. … Также известно как «эквивалент» или «эквивалент постоянного тока» для переменного напряжения или тока. Для синусоидальной волны среднеквадратичное значение составляет примерно 0,707 от его пикового значения.

6. Что такое среднеквадратичное и среднее значение?
Среднеквадратичное значение – это квадратный корень из среднего (среднего) значения функции квадрата мгновенных значений.Поскольку переменное напряжение со временем повышается и падает, для получения заданного среднеквадратичного напряжения требуется больше переменного напряжения, чем для постоянного тока. Например, для достижения среднеквадратичного значения 120 вольт потребуется пиковое значение переменного тока 169 вольт.

7. Почему используется RMS?
Это видео знакомит с концепцией «среднеквадратичного значения», обычно называемой RMS. Это математический метод определения среднего постоянно меняющегося значения. В электронике RMS используется для расчета эффективной мощности переменного тока таким образом, чтобы ее можно было сравнить с эквивалентной теплотворной способностью системы постоянного тока.

8. Какое среднеквадратичное значение синусоидальной волны?
Среднеквадратичное значение или ROOT MEAN SQUARED – это значение эквивалентного постоянного (неизменяемого) напряжения или тока, которые будут обеспечивать такую ​​же энергию в цепи, что и измеренная синусоидальная волна. … Можно показать, что среднеквадратичное значение синусоидальной волны составляет 0,707 пикового значения.

9. Пиковое значение 120 В или среднеквадратичное значение?
120 В – это среднеквадратичное напряжение. И пиковое напряжение для этого на самом деле составляет 170 В. Таким образом, пиковое значение этого напряжения на самом деле намного больше, чем 120 В.И если вы посмотрите на это от пика до пика, то напряжение в розетке переменного тока на самом деле составляет 340 В от пика до пика.

10. Что такое допустимая среднеквадратичная ошибка?
Основываясь на практическом правиле, можно сказать, что значения RMSE от 0,2 до 0,5 показывают, что модель может относительно точно предсказывать данные. Кроме того, скорректированный R-квадрат более 0,75 является очень хорошим показателем точности. В некоторых случаях также допускается скорректированный R-квадрат 0,4 или более.

11. Как преобразовать среднеквадратичное напряжение в пиковое?
Пиковые значения могут быть рассчитаны на основе значений RMS по приведенной выше формуле, которая подразумевает VP = VRMS × √2, при условии, что источником является чистая синусоида.Таким образом, пиковое значение сетевого напряжения в США составляет около 120 × √2, или около 170 вольт.

12. Действующее значение напряжения переменного или постоянного тока?
«RMS» означает среднеквадратическое значение и представляет собой способ выражения величины переменного напряжения или тока в терминах, функционально эквивалентных постоянному току. Например, среднеквадратичное значение 10 вольт переменного тока – это величина напряжения, при которой через резистор заданного значения рассеивается такое же количество тепла, что и при источнике питания постоянного тока на 10 вольт.

13. Что означает 120 RMS?
Напряжение между горячим проводом и нейтральным проводом составляет от 110 до 120 вольт, среднеквадратичное значение (среднеквадратичное значение).Напряжение между двумя горячими проводами составляет от 220 до 240 вольт (среднеквадратичное значение). Более высокое напряжение используется для управления приборами, которым требуется больше энергии, такими как стиральные машины и кондиционеры.

14. Почему мы измеряем среднеквадратичное значение?
Попытки найти среднее значение переменного тока напрямую дадут вам нулевой ответ … Следовательно, используются значения RMS. Они помогают найти эффективное значение переменного тока (напряжения или тока). Это среднеквадратичное значение – математическая величина (используется во многих математических областях), используемая для сравнения как переменного, так и постоянного тока (или напряжения).

15. Какое среднеквадратичное значение напряжения 120 вольт?
120 В – это среднеквадратичное напряжение. И пиковое напряжение для этого на самом деле составляет 170 В. Таким образом, пиковое значение этого напряжения на самом деле намного больше, чем 120 В. И если вы посмотрите на это от пика до пика, то напряжение в розетке переменного тока на самом деле составляет 340 В от пика до пика.

16. Что означает 120 RMS?
Напряжение между горячим проводом и нейтральным проводом составляет от 110 до 120 вольт, среднеквадратичное значение (среднеквадратичное значение). Напряжение между двумя горячими проводами составляет от 220 до 240 вольт (среднеквадратичное значение).Более высокое напряжение используется для управления приборами, которым требуется больше энергии, такими как стиральные машины и кондиционеры.

Что такое истинное среднеквадратичное значение? | Fluke

Устройство с истинным среднеквадратичным значением (среднеквадратичное значение = среднеквадратичное значение) является одним из трех инструментов, которые могут измерять переменный ток (ac) или напряжение переменного тока:

1. Цифровые мультиметры с истинным среднеквадратичным значением (или токоизмерительные клещи)
2. Среднее значение – соответствующий цифровой мультиметр (или токоизмерительные клещи)
3. Осциллограф

Обычно используются только первые два инструмента, и оба могут точно измерять стандартные синусоидальные сигналы (чистый переменный ток).

Тем не менее, измеритель истинного среднеквадратичного значения является широко предпочтительным, потому что это единственный прибор, который может точно измерять как синусоидальные, так и несинусоидальные формы волны переменного тока.

• Синусоидальные (синусоидальные) волны : Чистые, без искажений, с симметричными переходами между пиками и впадинами.
• Несинусоидальные волны: Волны с искаженными, нерегулярными формами – пики, последовательности импульсов, квадраты, треугольники, пилообразные и любые другие неровные или угловатые волны.

Как рассчитать RMS

Как упоминалось ранее, RMS = среднеквадратичное значение. Хотя его формула может быть сложной для понимания, RMS по существу вычисляет эквивалентное значение постоянного тока (dc) формы волны переменного тока . С технической точки зрения, он определяет «эффективную» или постоянную теплотворную способность любой формы волны переменного тока.

Измеритель среднего отклика использует математические формулы усреднения для точного измерения чистых синусоидальных волн. Он может измерять несинусоидальные волны, но с неопределенной точностью.

Более совершенный измеритель истинного среднеквадратичного значения может точно измерять как чистые волны, так и более сложные несинусоидальные волны.Формы сигналов могут быть искажены нелинейными нагрузками, такими как приводы с регулируемой скоростью или компьютеры. Усредняющий измеритель, пытающийся измерить искаженные волны, может иметь в своих расчетах до 40% низкого или 10% высокого уровня.

Где измерять истинное среднеквадратичное значение

Потребность в измерителях истинного среднеквадратичного значения возросла, поскольку возможность несинусоидальных волн в схемах значительно возросла в последние годы. Некоторые примеры:

• Электроприводы с регулируемой скоростью
• Электронные балласты
• Компьютеры
• HVAC
• Твердотельные среды

В этих средах ток возникает короткими импульсами, а не гладкой синусоидальной волной, создаваемой стандартной индукцией мотор.Форма волны тока может существенно повлиять на показания токоизмерительных клещей. Кроме того, измеритель истинного среднеквадратичного значения – лучший выбор для измерений в линиях электропередач, где характеристики переменного тока неизвестны.

Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.

Статьи по теме

Синусоидальные напряжения – Vpk, Vpk-pk, Vavg, Vrms

Синусоида определяется тригонометрической функцией синуса. При построении графика зависимости напряжения (В) от фазы (θ) он похож на рисунок справа.Форма волны повторяется каждые 2p. радиан (360 °) и симметрично относительно оси напряжения (при отсутствии смещения постоянного тока). Выставление напряжения и тока циклическое поведение называется чередованием; то есть переменного тока (AC). Здесь показан один полный цикл. Базовый уравнение для синусоиды выглядит следующим образом:

Существует несколько способов определения амплитуды синусоиды, обычно как пикового напряжения (V _pk или V _p ), размах напряжения (V _pp или V _p-p или V _pkpk или V _pk-pk ), среднее напряжение (В _{среднеквадратичное значение} или В _{среднее значение} ) и среднеквадратичное напряжение (В _{среднеквадратичное значение} ).Пиковое напряжение и размах напряжения очевидны, глядя на приведенный выше график. Среднеквадратичное и среднее напряжение не так очевидный.

См. Также напряжения треугольной волны и Страницы напряжения прямоугольной волны.

Среднеквадратичное напряжение (В

_{действующее значение} )

В качестве название подразумевает, что V _rms рассчитывается путем извлечения квадратного корня из среднего среднего квадрата напряжение в правильно выбранном интервале.В случае симметричных сигналов, таких как синусоида, четверть цикла точно отображает все четыре четверти цикла сигнала. Поэтому приемлемо выбрать первую четверть. цикл, который идет от 0 радиан (0 °) до p / 2 радиан (90 °).

В _{среднеквадратичное значение} – это значение, отображаемое подавляющим большинством вольтметров переменного тока. Это значение, которое при применении через сопротивление, производит такое же количество тепла, что и напряжение постоянного тока той же величины. производить.Например, при подаче напряжения 1 В на резистор сопротивлением 1 Ом выделяется 1 Вт тепла. Применена синусоида 1 В _{среднеквадратичное значение} через резистор 1 Ом также выделяет 1 Вт тепла. Эта синусоида 1 В _rms имеет пиковое напряжение √2 В (≈1,414 В) и размахом напряжения 2√2 В (≈2,828 В).

Поскольку найти полный вывод формул для среднеквадратичного (V _rms ) напряжения затруднительно, здесь сделано для вас.

Итак, ≈ 0.707 В _pk , где = 0,70710678118654752440084436210485

Среднее напряжение (В

_avg )

Как следует из названия, V _avg рассчитывается путем взятия среднего значения напряжения в надлежащим образом выбранном интервал. В случае симметричных сигналов, таких как синусоида, четверть цикла точно соответствует всем четырем четвертям. циклы формы волны. Поэтому приемлемо выбрать цикл первой четверти, который начинается с 0 радиан (0 °). через p / 2 радиана (90 °).

Как и в случае формулы V _rms , здесь также приводится полный вывод формулы V _avg .

Итак, ≈ 0,636 В _pk, где = 0,63661977236758134307553505349006

* Я понятия не имею, почему мы пишем «Sinewave», а не «Trianglewave» и «Squarewave».” Калькулятор напряжения

RMS и формула синусоидальной кривой со смещением

Калькулятор и формула для расчета среднеквадратичного значения синусоидального напряжения со смещением

Рассчитайте среднеквадратичное значение

Эта функция вычисляет среднеквадратичное значение синусоидального напряжения с наложенным постоянным напряжением.

На картинке показано синусоидальное напряжение с пиковым значением ± 60 вольт. на которое накладывается постоянное напряжение (смещение) 20 вольт.

Формулы для синусоидального напряжения со смещением

Действующее значение синусоидального напряжения

Действующее значение определяется как значение постоянного напряжения с таким же тепловым эффектом, что и заданное напряжение переменного тока. При синусоидальном переменном токе это без смещения:

\ (\ Displaystyle U_ {eff} = \ гидроразрыва {U_s} {\ sqrt {2}} \)

Чтобы вычислить эффективное значение наложенного синусоидального напряжения, значение разности напряжений между максимальным и минимальным напряжением (U _ss ) необходимо сначала определить.

\ (\ Displaystyle U_ {ss} = U_ {макс} -U_ {мин} \)

Пиковое значение может быть получено из этого

\ (\ displaystyle U_s = \ frac {U_ {ss}} {2} = \ frac {U_ {max} -U_ {min}} {2} \)

Таким образом, формула для среднеквадратичного значения синусоидального напряжения без составляющей постоянного напряжения имеет следующий вид:

\ (\ displaystyle U_ {eff} = \ frac {U_s} {\ sqrt {2}} = \ frac {U_ {ss}} {2 · \ sqrt {2}} = \ frac {U_ {max} -U_ {min}} {2 · \ sqrt {2}} \)

Среднеквадратичное значение со смещением

Для расчета среднеквадратичного значения со смещением среднеквадратичное значение синусоидального напряжения добавляется к квадрат значения постоянного напряжения.2} \)

Среднее значение чистого синусоидального напряжения всегда равно 0 В. Если напряжение накладывается на напряжение постоянного тока, среднее значение идентично наложенному напряжению постоянного тока.

Легенда

\ (\ Displaystyle U_s \)	Пиковое напряжение
\ (\ Displaystyle U_ {ss} \)	Пиковое напряжение
\ (\ Displaystyle U_ {эфф} \)	Действующее значение переменного напряжения
\ (\ Displaystyle U2_ {эфф} \)	Действующее значение переменного напряжения с наложенным постоянным током
\ (\ Displaystyle U_O \)	Накладываемое постоянное напряжение (смещение)

Эта страница полезна? да Нет Спасибо за ваш отзыв! Извините за это Как мы можем это улучшить? послать

---

.