Среднеквадратическое значение: СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ – это… Что такое СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ?

СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ – это… Что такое СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ?

СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ

СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ, в математике – величина, получаемая определением СРЕДНЕГО ЗНАЧЕНИЯ множества возведенных в квадрат величин. Предоставляет значение периодически изменяющейся величины и была разработана в начале XX в. для точного измерения ГАЛЬВАНИЧЕСКОГО и ЭЛЕКТРИЧЕСКОГО ТОКА. Среднеквадратическая погрешность аппроксимации также используется в уравнениях, предназначенных для предсказания результатов, таких как прогнозы погоды.

Научно-технический энциклопедический словарь.

• СРЕДНЕЕ ЧИСЛО
• СРЕДНИЙ МОЗГ

Смотреть что такое “СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ” в других словарях:

• среднеквадратичное значение — 3. 4 среднеквадратичное значение: Эффективное значение тока. Источник: ГОСТ Р 52506 2005: Совместимость технических средств электромагнитная. Лифты, эскалаторы и пассажирские конв …   Словарь-справочник терминов нормативно-технической документации

• среднеквадратичное значение — vidutinė kvadratinė vertė statusas T sritis automatika atitikmenys: angl. root mean square value vok. Effektivwert, m; quadratischer Mittelwert, m rus. среднеквадратичное значение, n pranc. valeur moyenne quadratique, f …   Automatikos terminų žodynas

• среднеквадратичное значение — efektinis vidurkis statusas T sritis radioelektronika atitikmenys: angl. effective mean value; mean square value; root mean square value vok. quadratischer Mittelwert, m rus. среднеквадратичное значение, n pranc. valeur effective, f; valeur… …   Radioelektronikos terminų žodynas

• среднеквадратичное значение — kvadratinis vidurkis statusas T sritis fizika atitikmenys: angl.

  mean effective value; root mean square value vok. quadratischer Mittelwert, m; quadratisches Mittel, n rus. среднеквадратичное значение, n pranc. valeur moyenne quadratique, f …   Fizikos terminų žodynas

• Среднеквадратичное значение сигнала — 11. Среднеквадратичное значение сигнала Ндп. Среднеквадратичное значение. Действующее значение. Эффективное значение Корень квадратный из среднего значения квадрата сигнала Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины… …   Словарь-справочник терминов нормативно-технической документации

• среднеквадратичное значение корректированного ускорения a_w — 3.1.5.1 среднеквадратичное значение корректированного ускорения aw: Усредненная по времени поступательная или угловая вибрация, определяемая формулой                                                     (1) где aw(x) текущее значение… …   Словарь-справочник терминов нормативно-технической документации

• среднеквадратичное значение шума — efektinė triukšmo vertė statusas T sritis radioelektronika atitikmenys: angl. noise root mean square value vok. Mittelquadratrauschwert, m rus. среднеквадратичное значение шума, n pranc. valeur moyenne quadratique de bruit, f …   Radioelektronikos terminų žodynas

• Среднеквадратичное значение сигналя — 1. Корень квадратный из среднего значения квадрата сигнала Употребляется в документе: ГОСТ 16465 70 Сигналы радиотехнические измерительные. Термины и определения …   Телекоммуникационный словарь

• текущее среднеквадратичное значение корректированного ускорения a_w, — 3.1.5.3 текущее среднеквадратичное значение корректированного ускорения aw, q(t): Среднеквадратичное значение корректированного ускорения в момент времени t, определяемое формулой                                               (3) где aw(x)… …   Словарь-справочник терминов нормативно-технической документации

• максимальное кратковременное среднеквадратичное значение (корректированного ускорения) MTVV — 3. 1.5.4 максимальное кратковременное среднеквадратичное значение (корректированного ускорения) MTVV: Максимальное значение текущего среднеквадратичного значения корректированного ускорения для периода интегрирования q, равного 1 с. Источник: ГОСТ …   Словарь-справочник терминов нормативно-технической документации

Что такое истинные среднеквадратичное значение?

Устройства с измерением истинных СКЗ (СКЗ = среднеквадратичное значение) представлены тремя приборами, которые измеряют переменный ток или напряжение переменного тока:

1. цифровые мультиметры с измерением истинных среднеквадратичных значений (или токоизмерительные клещи)
2. цифровой мультиметр с усредненными показаниями (или токоизмерительные клещи)
3. осциллограф

Обычно используются приборы первых двух типов, которые могут точно измерять стандартные (чистые) синусоидальные сигналы переменного тока.

Специалисты предпочитают пользоваться устройствами с измерением истинных среднеквадратичных значений, поскольку только такие приборы способны точно измерять как синусоидальные, так и несинусоидальные сигналы переменного тока.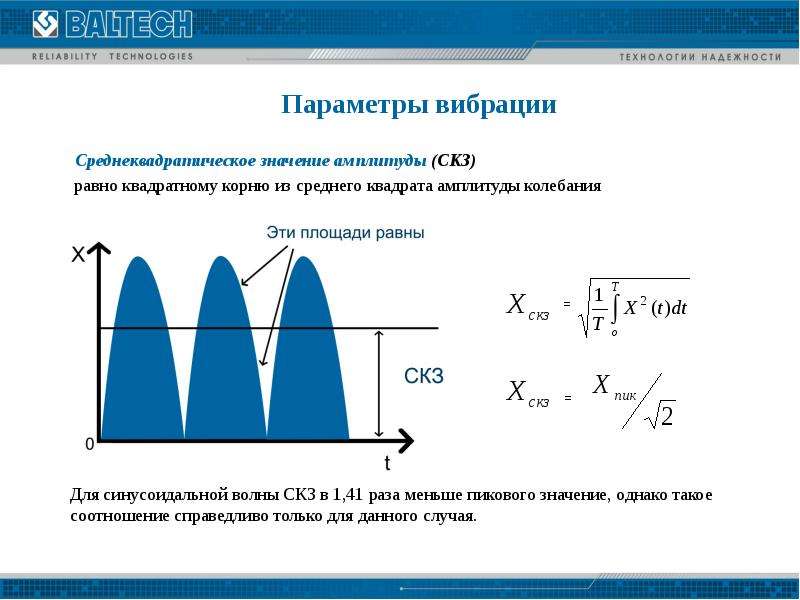 (См. рисунки в верхней части страницы).

• Синусоидальные сигналы: чистые, без искажений, сигналы с симметричными переходами между точками максимума и минимума.
• Несинусоидальные сигналы: сигналы нерегулярной формы с искажениями: импульсные выбросы, последовательности импульсов, квадратные, треугольные и пилообразные сигналы, а также любые другие сигналы неровной или угловатой формы.

Порядок расчета СКЗ

Как уже говорилось ранее, СКЗ расшифровывается как среднеквадратичное значение. Хотя формула среднеквадратичного значения может быть сложной для понимания, оно фактически соответствует эквивалентному значению постоянного тока для сигнала переменного тока. С технической точки зрения она определяет «эффективное» значение (значение нагрева постоянным током) для волны переменного тока любой формы.

В устройствах с усредненными показаниями для точного измерения чистых синусоидальных волн используются математические формулы усреднения.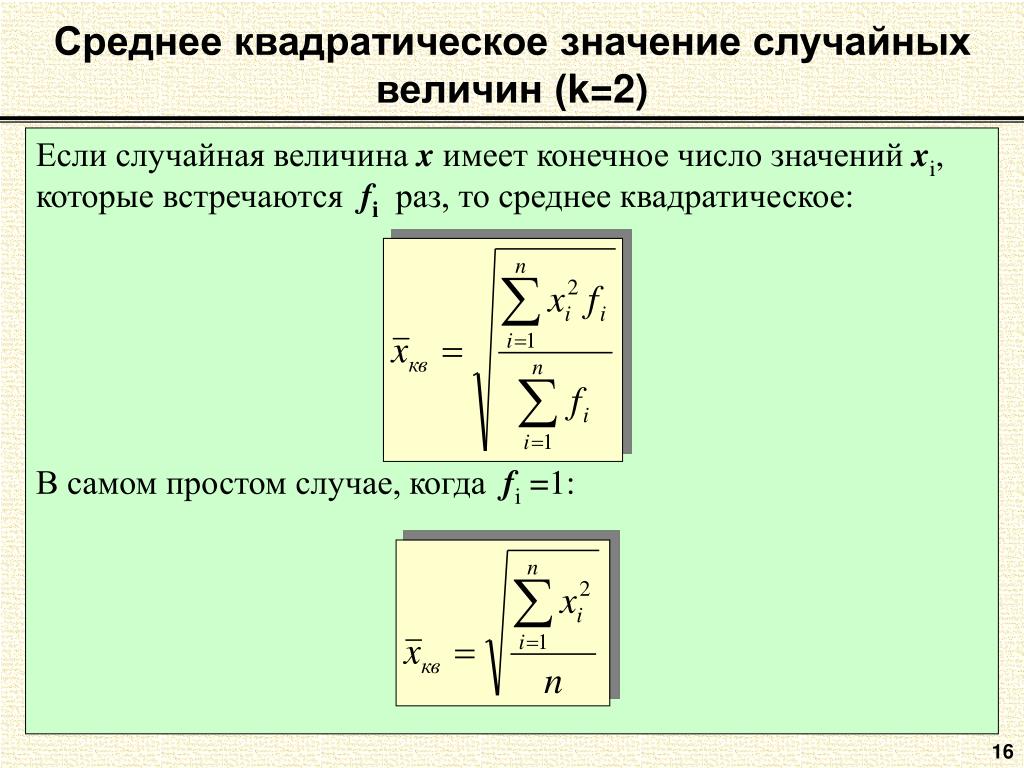 Такое устройство может измерять несинусоидальные волны, но с невысокой точностью.

Более совершенные устройства с измерением истинных среднеквадратичных значений могут точно измерять как чистые волны, так и более сложные несинусоидальные волны. Формы сигнала могут быть искажены из-за нелинейных нагрузок, например приводов с регулируемой частотой вращения или компьютеров. При измерении искаженной волны устройство с усредненными показаниями может показать результат на 40 % ниже или на 10 % выше фактических значений.

Где измеряются истинные среднеквадратичные значения?

Потребность в устройствах с измерением истинных среднеквадратичных значений возросла, поскольку за последние годы значительно увеличилась вероятность возникновения несинусоидальных сигналов в цепях. Некоторые примеры:

• Приводы двигателей с регулируемой частотой вращения
• Электронные балластное сопротивление
• Компьютеры
• Системы ОВКВ
• Твердотельные среды

В таких условиях ток возникает в форме коротких импульсов, а не в виде сглаженной синусоиды, как на стандартном асинхронном двигателе. Форма волны такого сигнала тока может значительно повлиять на показания токовых клещей. Кроме того, устройство с измерением истинных среднеквадратичных значений лучше всего подходит для измерений на линиях электропередач с неизвестными характеристиками переменного тока.

Ссылка: Digital Multimeter Principles by Glen A. Mazur, American Technical Publishers.

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s² – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А² раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А² D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y)

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

=СТАНДОТКЛОН.В()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. 

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Поделиться в социальных сетях:

Функция STDEVX.S (DAX) – DAX

• 08/31/2021
• Чтение занимает 2 мин

В этой статье

Возвращает среднеквадратичное отклонение выборки из совокупности.

Синтаксис

STDEVX.S(<table>, <expression>)  

Параметры

Термин	Определение
table	Любое выражение DAX, возвращающее одно скалярное значение, в котором выражение вычисляется несколько раз (для каждой строки или контекста).
expression	Любое выражение DAX, возвращающее одно скалярное значение, в котором выражение вычисляется несколько раз (для каждой строки или контекста).

Возвращаемое значение

Число со стандартным отклонением выборки из совокупности.

Исключения

Remarks

• Функция STDEVX.S вычисляет expression для каждой строки таблицы table и возвращает стандартное отклонение expression, предполагая, что эта таблица table ссылается на выборку из совокупности. Если table представляет собой полную совокупность, вычислите стандартное отклонение с помощью функции STDEVX.P.

• STDEVX.S использует следующую формулу:

  √[∑(x – x̃)²/(n–1)]

  где x̃ — среднее значение x для всей совокупности, а n — размер генеральной совокупности.

• Пустые строки отфильтровываются из columnName и не учитываются в вычислениях.

• Если columnName содержит менее двух непустых строк, возвращается ошибка.

• Эта функция не поддерживается для использования в режиме DirectQuery при использовании в вычисляемых столбцах или правилах безопасности на уровне строк (RLS).

Пример

В следующем примере показана формула для вычисляемого столбца, который оценивает стандартное отклонение цены за единицу для каждого продукта в выборке, когда формула используется в таблице продуктов.

= STDEVX.S(RELATEDTABLE(InternetSales_USD), InternetSales_USD[UnitPrice_USD] – (InternetSales_USD[DiscountAmount_USD]/InternetSales_USD[OrderQuantity]))  

Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор

Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор

03.04.18

Данный текст является расширенным и углубленным вариантом моей старой заметки на сайте we. easyelectronics.ru.

Введение

В рамках данной заметки рассмотрим способы вычисления среднего и среднеквадратичного значений тока и напряжения. При этом для простоты ограничимся формами сигнала, характерными для импульсных источников питания. Обращаю ваше внимание – все формулы, приводимые в заметке, даются без выводов, дабы не забивать головы читателей мутной и не особо нужной херней. С другой стороны, если кому-то интересно, откуда данные формулы взялись – можно скачать файл, в котором приведены все необходимые выводы с пояснениями.

Основные определения

Будучи в недавнем прошлом яростным разработчиком всевозможных импульсных источников питания (ИИП), интересовался всяким по данной теме (да и сейчас, бывает, трясу стариной). В частности, весьма важными мне всегда казались такие характеристики сигнала, как среднее и среднеквадратичное значение токов и напряжений в различных точках схемы, поскольку при расчетах ИИП данные параметры используются сплошь и рядом.

Естественно, существуют строгие «математические» определения как для среднего, так и для среднеквадратичного значений физических величин, периодически изменяющихся во времени по некоторому закону. Однако, больно уж они мутные и абстрактные, и, на мой взгляд, нужны только при выводе формул. Разработчику же гораздо важнее понимать физический смысл используемых в расчетах величин, поэтому приводимые ниже определения среднего и среднеквадратичного значений будут носить сугубо прикладной характер.

Среднее значение переменного тока или напряжения (во вражеских терминах AVG) – это просто их постоянная составляющая. Поэтому вполне очевидно, что среднее значение широко применяется при расчетах схем, выделяющих из переменного сигнала постоянный уровень. Простейший понижающий преобразователь (Step-Down) с LC-фильтром на выходе, RC-цепочка, призванная выделить постоянное напряжение из поступающего на вход ШИМ-сигнала – всё это примеры того, где без использования среднего значения физической величины ничего толком не посчитаешь.

Среднеквадратичное (действующее, эффективное) значение определяется немного сложнее. Как известно, любой переменный ток (напряжение), проходя через активную линейную нагрузку (например, резистор), выделяет на ней некоторое количество тепла. Но так поступает не только переменный сигнал – постоянный ток тоже будет греть резистор.

Так вот, среднеквадратичное значение

В общем, среднее и среднеквадратичное значения используются довольно часто. Поэтому неплохо было бы уметь их рассчитывать для любого сигнала, который может нам встретиться в импульсном источнике питания. При этом лично я разделяю токи и напряжения в ИИП на две большие группы: сигналы с простой формой (элементарные) и сигналы со сложной формой (т.е. те, которые могут быть представлены в виде суммы нескольких элементарных). И поскольку принципы расчета среднего и среднеквадратичного значений для этих двух групп немного отличаются, предлагаю рассмотреть их по отдельности.

Сигналы простой формы

У сигналов простой формы вычислить среднее и среднеквадратичное значение довольно легко – для этого надо всего лишь взять соответствующую формулу и подставить в нее нужные значения. Чтобы постоянно не шариться по различным справочникам, я завел себе специальную табличку, в которую свел расчетные формулы для наиболее часто встречающихся элементарных сигналов:

•  прямоугольника:

•  треугольника:

•  трапеции:

•  и пилы:

(данные формулы, кстати, взяты не с потолка – их вывод при желании можно посмотреть в специальной заметке-пояснении).

Здесь хотелось бы заострить внимание на нескольких моментах. Во-первых, на приведенных выше рисунках рассматривается по два варианта каждого из простейших сигналов: «в общем виде» и «без смещения». При этом с точки зрения разработчика импульсных источников питания наиболее интересным обычно является именно второй вариант, поэтому для него и даны отдельные формулы (чтобы постоянно не подставлять С=0 в «общие» выражения). Во-вторых, пилообразное напряжение, вообще говоря, является сложным сигналом, поскольку может быть представлено в виде суммы двух простых (либо трапеций, либо треугольников). Однако, пила настолько часто встречается при расчетах ИИП, а выражения AVG и RMS для нее настолько лаконичны и красивы, что я в результате включил-таки ее в список сигналов, среднее и среднеквадратичное значение которых вычисляется тупо всего по одной формуле. Ну и в-третьих, вышеприведенная таблица, в принципе, могла бы состоять всего из одной трапеции, ибо из нее легко получить как прямоугольник, так и треугольник, поставляя соответствующие значения «H», «L» и «C». Однако практика показала, что постоянно этим заниматься весьма муторно, ибо мы рассчитываем источник, а не тренируем математические навыки. Поэтому в итоге я себе выписал готовые формулы AVG и RMS для прямоугольника и треугольника, что оказалось весьма и весьма удобным. Ну а в целом – как ни странно, представленные выше формулы для элементарных сигналов покрывают, наверное, 75-80% всех потребностей разработчика импульсных источников питания, что весьма немало. Однако, всё многообразие токов и напряжений в ИИП отнюдь не ограничивается вышеупомянутыми четырьмя (и даже тремя, если не учитывать пилу) формами. Поэтому рано или поздно любой разработчик импульсников сталкивается с необходимостью вычисления среднего и среднеквадратичного значения сложного сигнала (яркий пример – расчет пуш-пула).

Сигналы сложной формы

Как было сказано выше, сигналы сложной формы – это такие, которые могут быть представлены в виде суммы нескольких элементарных сигналов. Применительно к импульсным источникам питания в качестве последних выступают прямоугольник, треугольник или трапеция, и значительно реже – синус, косинус и прочая «плавная» херня. Отметим, что в данном случае, в отличие от простейших форм, нахождение аналитических выражений для среднего и среднеквадратичного значений обычно превращается в неблагодарное занятие.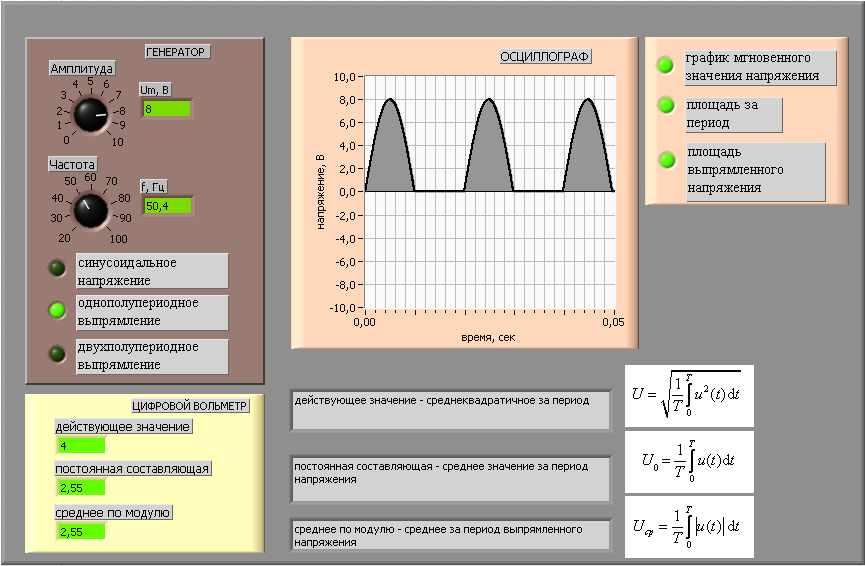 Например, для вывода «среднеквадратичной» формулы нам надо разбить сложный сигнал на несколько простейших, а затем извлечь квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений (думаю, даже понять, о чем говорится в данном предложении, у вас получится далеко не сразу). Найти среднее значение сложного сигнала немного проще (надо просто просуммировать средние «элементарные» значения), однако поверьте – сделать из этого удобоваримую формулу в подавляющем большинстве случаев не удается:

К счастью, готовая формула для нахождения AVG и RMS сложного сигнала обычно не требуется. Чаще всего нам надо просто узнать среднее или среднеквадратичное значение тока (напряжения) именно для нашего конкретного случая, а не вывести аналитическое выражение на все случаи жизни. А это существенно упрощает задачу, ибо посчитать числовое значение AVG или RMS для каждого элементарного сигнала на соответствующем временно́м интервале не так уж и сложно. В качестве примера можно рассмотреть нахождение среднего и среднеквадратичного значения напряжения, характерного для пушпульной, полумостовой и полномостовой схем (данный расчет есть и в специальной заметке-пояснении):

Как следует из предпоследнего рисунка, для начала нам надо разбить исходный сигнал на элементарные. Очевидно, что это будут три трапеции и один прямоугольник:

Дальше нам надо посчитать среднее и среднеквадратичное значение каждого из четырех элементарных сигналов, для чего воспользуемся формулами из вышеприведенной таблицы. Начнем с первого из них – трапеции №1. Как видно из последнего рисунка, это трапеция без смещения с параметрами

H₁=11;
L₁=9;
C₁=0;
t_И1=0,15∙T.

Поэтому в соответствии с формулами для трапеции, приведенными выше, будем иметь:

Сигнал №2 – это тоже трапеция без смещения. Параметры данной трапеции будут таковы:

H₂=21;
L₂=19;
C₂=0;
t_И2=0,50∙T – 0,15∙T = 0,35∙T.

Поэтому среднее и среднеквадратичное значение второго сигнала составят соответственно

Трапеция №3 полностью совпадает с трапецией №1, просто она сдвинута вправо на полпериода. Поэтому как параметры третьего сигнала, так и его среднее и среднеквадратичное значения будут равны соответствующим значениям первого сигнала:

H₃= H₁=11;
L₃= L₁=9;
C₃= C₁=0;
t_И3= t_И1= 0,65∙T – 0,50∙T = 0,15∙T.

Ну и остался сигнал №4. Данный сигнал представляет собой прямоугольник с параметрами

H₄=0,5;
C₄=0;
t_И4=1,00∙T – 0,65∙T = 0,35∙T.

И после использования формул для вычисления среднего и среднеквадратичного значения сигнала №4, получим следующее:

Теперь у нас есть все данные для нахождения AVG и RMS исходного сигнала. Как было сказано выше, среднее значение находится как сумма средних значений элементарных сигналов, на которые был разложен «исходник», а среднеквадратичное – как квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений. То есть в нашем случае будем иметь

Для проверки полученного результата используем широко распространенное бесплатное ПО LTSpice IV от компании Linear Technology Corporation (LTC). Сгенерировав сигнал с требуемыми параметрами, измерим в эмуляторе среднее и среднеквадратичное его значение за 5 периодов:

Как видим, результаты работы эмулятора полностью совпадают с расчетными AVG и RMS, т.е. предложенный способ вычисления среднего и среднеквадратичного значений для сложного сигнала вполне имеет право на жизнь. Более того, способ этот довольно прост и не требует от разработчика ИИП никаких особых математических навыков. С другой стороны, муторность рассмотренного алгоритма также налицо. Лично меня дичайше бесит постоянно считать на калькуляторе и выписывать на бумажку средние и среднеквадратичные значения для всех элементарных сигналов, на которые раскладывается исходный, а пото́м складывать их на том же калькуляторе (и это в лучшем случае, ибо если требуется RMS, всё становится еще волшебнее). Поэтому я принял решение сделать себе некий инструмент, упрощающий жизнь разработчика ИИП, которым и хотел бы поделиться с читателями.

Калькулятор

Данный инструмент – это такая специальная «программа» (cko4aTb бесплатно). «Программа» представляет собой обычный экселовский файл (т.к. программист я тот еще), поэтому для работы нам потребуется «Excel» (у меня вот такой: Microsoft® Excel 2002 (10.4302.2625)). Изначальная и основная задача рассматриваемой «программы» – отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период), а также вычисление среднего и среднеквадратичного значений для этого сигнала. Также «программа» умеет рисовать переменную составляющую заданной трапеции (она получается если из исходного сигнала вычесть постоянную составляющую) и вычислять ее RMS-значение (это уж так, чисто на всякий случай). Ну и еще предлагаемый софт позволяет быстро посчитать среднее и среднеквадратичное значения для сложного сигнала, состоящего максимум из 16-ти различных элементарных (большее количество в реальной жизни вряд ли потребуется):

Почему в качестве основы взята именно трапеция? Потому что, как было сказано выше, из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник и треугольник:

Ну а уж на основе этих базовых сигналов можно сляпать и пилу, и напряжение на стоке ключа во флайбэке, и то, что творится на вторичке пушпула и многое другое.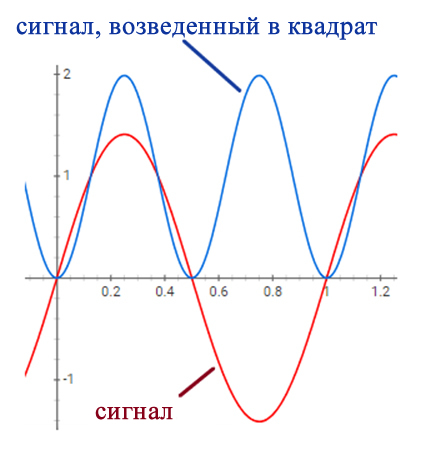

Пользоваться «программой» очень просто. Исходные данные для трапеции вводятся слева в ячейки, выделенные зеленым цветом. После этого чуть ниже можно посмотреть на форму сигнала с введенными параметрами, а еще ниже отобразятся рассчитанные среднее и среднеквадратичное значения этого сигнала. За переменную составляющую трапеции отвечает правый нижний угол экрана (здесь рисуется ее график и рассчитывается значение RMS). Ну а для работы со сложным сигналом предназначен правый верхний угол. Здесь в ячейки, выделенные зеленым цветом, вводятся средние и среднеквадратичные значения элементарных сигналов, из которых состоит «исходник», а ниже рассчитываются уже́ его собственные AVG и RMS.

Отмечу, что на всю «программу» наложена магическая защита, позволяющая редактировать только те ячейки, которые можно. При необходимости защита снимается элементарно («Сервис» => «Защита» => «Снять защиту листа»), однако делать это не рекомендую: можно по дури снести какую-нибудь нужную формулу, восстанавливать которую – лишний геморрой.

Вот, в принципе, и всё описание представленной «программы». Несмотря на свою простоту и очевидность, данный софт довольно существенно помогает и экономит время при расчетах ИИП (ну, во всяком случае, у меня происходит именно так). Например, на расчет среднего и среднеквадратичного значения сложного сигнала, приведенного в предыдущем пункте, понадобится менее минуты. Последовательность действий проста – вводим параметры первой трапеции, затем переписываем рассчитанные для нее значения AVG и RMS в ячейки секции сложного сигнала. Затем то же самое проделываем для остальных трех элементарных функций, из которых состоит «исходник». Всё, остальное «программа» сделает сама, не надо никаких шаманств с бумажками и калькуляторами:

Ну а у меня на сегодня всё. Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!

Обсудить эту заметку можно здесь

Ссылки по теме, документация

Заметка-пояснение с выводом формул и примером расчета среднего и среднеквадратичного значений сложного сигнала:

•  AVG_RMS. pdf;

Калькулятор для упрощения вычислений среднего и среднеквадратичного значений простых и сложных сигналов:

•  AVG_RMS_Calc.xls;

Среднеквадратическое значени – Энциклопедия по машиностроению XXL

Оценка ожидаемых погрешностей. Подсчитаем среднеквадратическое значение погрешности косвенного измерения объемного расхода Q , которое в соответствии с уравнением (9.10) определяется по формуле, аналогичной (5.21),  [c.128]

Для вычисления коэффициентов pk, при которых достигается минимум среднеквадратического значения взвешенной разности, надо составить систему уравнений (19.17), выполняя диф-  [c.374]

[c. 122]

В корреляционной хроматографии [3] среднеквадратическое значение помехи  [c.106]

Результаты, приведенные в табл. 3, и сравнение их с соответствующими средними и среднеквадратическими значениями приближаемой функции табл. 4 показывают, что в линейных приближениях ошибки весьма существенны и соизмеримы с соответствующими значениями приближаемых функций. Последующие нелинейные приближения не всегда достаточно для практических целей снижают ошибку. Кроме того, проекции исследуемой нелинейной функции (рис. 2) показывают, что зависимость от переменных состояния весьма сложная.  [c.84]

Среднеквадратическое значение функции  [c.85]

Оценка вибрации с помощью среднеквадратических значений исключает необходимость определения фазового угла между отдельными составляющими. Все это свидетельствует о целесообразности использования при контроле и нормировании вибрации ее среднеквадратического значения.  [c. 24]

Предположим, что корреляционная функция случайной возмущающей силы известна (найдена, задана) и требуется найти движение, вызываемое такой силой. Нужно отметить, что искомое движение в этих задачах также является случайной функцией времени, и поэтому определить движение — это значит найти характеристики такой случайной функции. Если речь идет о воздействии центрированной возмущающей силы, то главной целью расчета обычно служит определение среднеквадратического значения перемещения (скорости, ускорения, какого-либо внутреннего усилия и т. п.). Для решения такой задачи нужно прежде всего найти спектральную плотность возмущающей силы  [c.232]

Теория и практика показывают, что при технической реализации таких схем требуется тщательный подбор деталей высокого качества. В этом случае можно обеспечить удовлетворительные инструментальные точности, при которых среднеквадратическое значение нестабильности фазы составит 4—5°.  [c.138]

При статистическом исследовании колебательных систем выходной сигнал представляет собой случайную функцию и при его определении следует пользоваться понятием среднеквадратического значения случайной величины, которое определяется через соответствующую спектральную плотность с помощью выражения [2J  [c. 262]

Примечание, а — среднеквадратическое значение.  [c.14]

В задачах 9, 10, 11 решен вопрос оптимизации силовых, энергоемких механизмов, в которых скорость ведущего звена не может полагаться известной, а известны приложенные к механизму силы. В качестве критерия оптимальности принято среднеквадратическое значение динамической работы за период.  [c.17]

Что касается критериев оптимальности, то для систем рассматриваемого вида большое значение имеют энергетические характеристики динамического режима. Обобщенной характеристикой динамического режима является норма среднеквадратического значения динамической мощности механизма Л Ц.  [c.91]

Рациональным выбором параметра aj внутри полученной области можно получить наиболее сильный оптимум в данной задаче. Кроме передаточной функции и среднеквадратического значения динамической работы R представляет интерес определение величины потребного движущего момента Ми для которого преобразованием формулы (П1.47) получим выражение  [c.103]

Обозначим среднеквадратическое значение вибрации от дисбаланса а.х, а всех остальных вибраций изделия о, суммарная вибрация  [c.433]

В этом случае, пользуясь приближенной формулой (30), можно определить среднеквадратическое значение и дисперсию изменения обобщенного параметра.  [c.155]

Число испытуемых изделий можно найти, используя выражение для определения среднеквадратического значения средней наработки  [c. 116]

Если известны решения (27), можно вычислить среднеквадратические значения / Т 0,5  [c.159]

Рассматривая параметры как декартовы координаты s-мерного эвклидова пространства и приравнивая попарно среднеквадратические значения (28),  [c.159]

Здесь P — средний угол сдвига у. — коэффициент, зависящий от характера распределения сдвигов по сечению и способа определения среднего значения для угла сдвига. Если под Р понимают среднеквадратическое значение  [c.154]

Среднеквадратические значения виброускорений и йу составляют 30—40 % от соответствующих значений виброускорения а .  [c.370]

При значительных уровнях вибрации в диапазоне частот 4—10 Гц человек может испытывать болевые ощущения и дискомфорт вследствие резонансных колебаний системы грудь—живот Резонансы головы (8—27 Гц) вызывают снижение остроты зрения вследствие смещений изображения объекта относительно сетчатки глаза. На рис. 5 представлены предельные среднеквадратические значения виброускорения а , превышение которых вызывает заметное ухудшение остроты зрения [259].  [c.372]

Рис, 5. Предельные среднеквадратические значения виброускорения a f превышение которых вызывает ухудшение остроты зрения  [c.372]

Для обеспечения безопасности проводимых измерений среднеквадратические значения вибрационных воздействий не должны превышать максимальные величины, установленные гигиеническими нормами с учетом длительности вибрационных воздействий.  [c.401]

Международной организацией по стандартизации (ИСО) предложены нормы на допустимый уровень вибрации, действующей на человека [48]. Стандарт ИСО устанавливает допустимые среднеквадратические значения виброускорения в диапазоне  [c.404]

Среднеквадратическое значение виброскорости  [c.405]

Санитарные нормы допустимых вибраций в жилых домах Минздрав СССР. М.. 1975 Жилые помещении Среднеквадратические значения виброскорости (виброускорения вибро-перемещения) Октава 2—63 – X, у. г а 1975 оэ сп о  [c.406]

Среднеквадратические значения виброскорости,  [c.407]

Допустимые среднеквадратические значения виброскорости и виброускорений при длительности воздействия 480 мин (Для категории I)  [c.409]

Низкая помехоустойчивость аналоговых систем интенсивности и систем с амплитудной модуляцией [1] не позволяет применить их в рассматр.иваемон ИИС, где среднеквадратическое значение помехи моллинии связи ( an/i/m = 0,1). Согласно ГОСТ 16521-74 дополнительная погрешность от помех в этих условиях не должна превышать половины основной, что не обеспечивается при измерении мощности сигнала.  [c.53]

До опробования насоса отдельно пускается электродвигатель с целью проверки направления вращения, отсутствия ьибрацки, температуры подшипников, после чего полумуф-ты соединяются и опробуется совместная работа электро-дв 1гателя с насосом вначале на холостом ходу, а затем под нагрузкой. Колеса и роторы в сборе необходимо отбалансировать. Среднеквадратическое значение вибрационной скорости, измеренной на корпусах подшипников насоса, не должно быть более 7 мм/с при изготовлении и 11 мм/с — при эксплуатации, а температура металла и масла подшипников не должна быть более чем на 35—40 °С выше температуры окружающего поздуха  [c.214]

В более общей постановке задача может быть сформулнрована следующим образом. Пусть непараметрическая система с п степенями свободы, описываемая, вообще говоря, связанными обобщенными координатами х , х ,. .х , совершает вынужденную вибрацию под действием периодического возбуждения, которое описывается обобщенной силой, соответствующей одной из обобщенных координат. Пусть далее необходимо максимизировать интенсивность колебаний k-й координаты путем нахождения той из обобщенных координат, соответствие которой обобщенной силе обеспечивает названную максимизацию. Интенсивность колебаний может быть выражена, например, среднеквадратическим значением й-й координаты, отсчитываемой от ее среднего значения, а в случае линейной системы и синусоидальной обобщенной силы — амплитудным значением указанной координаты.  [c.158]

Для обеспечения безопасных условий труда человека с виброактивными машинами установлены методы контроля вибрационных характеристик этих машин, например среднеквадратических значений виброскорости или их уровней в октавных полосах, измеренных на рабочих местах в диапазонах частот, регламентированных соответствующими гигиеническими нормами (см. табл. 5).  [c.411]

Среднеквадратичное значение в excel. Как работает стандартное отклонение в Excel

Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?

Как посчитать отклонение в процентах в Excel

Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.

Обратите внимание! Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки .

Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2

Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.

Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.

Альтернативная формула для вычисления процента отклонения в Excel

В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.

Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.

Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.

Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.

Андрей Липов

Если говорить простым языком, то стандартное отклонение показывает насколько сильно цена инструмента колбасится во времени. То есть чем больше этот показатель, тем сильнее волатильность или изменчивость ряда значений.

Стандартное отклонение можно и нужно использовать для анализа наборов значений, так как два набора с, казалось бы, одинаковым средним могут оказаться совершенно разными по разбросу величин.

Пример

Возьмем два ряда чисел.

a) 1,2,3,4,5,6,7,8,9 . Среднее – 5. Ст. отклонение = 2,7386

б) 20,1,7,1,15,-1,-20,4,18,5 . Среднее – 5. Ст. отклонение = 12,2066

Если не держать перед глазами всего ряда чисел, то по показателю стандартного отклонения видно, что в случае «б» величины гораздо сильнее разбрасываются вокруг своего среднего значения.

Грубо говоря, в ряде «б» значение равно 5 плюс-минус 12 (в среднем) – не точно, но раскрывает смысл.

Как посчитать стандартное отклонение

Для расчета стандартного отклонения можно использовать формулу, позаимствованную из расчета стандартного отклонения доходности ПИФов :

Здесь N – количество величин,
ДОХсредн – среднее всех величин,
ДОХпериода – величина N.

В экселе соответствующая функция называется СТАНДОТКЛОН (или STDEV в английской версии программы).

Пошаговая инструкция такова:

1. Рассчитайте среднее значение для ряда чисел.
2. Для каждого значения определите разницу между средним и этим значением.
3. Вычислите сумму квадратов этих разниц.
4. Разделите получившуюся сумму на количество чисел в ряде.
5. Возьмите квадратный корень от получившегося в прошлом пункте числа.

Вашим друзьям будет полезна эта информация. Поделитесь с ними!

Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.

Сначала рассмотрим дисперсию , затем стандартное отклонение .

Дисперсия выборки

Дисперсия выборки (выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно .

Все 3 формулы математически эквивалентны.

Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1. 2)/ (СЧЁТ(Выборка)-1 ) –

Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.

Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье .

Дисперсия случайной величины

Чтобы вычислить дисперсию случайной величины, необходимо знать ее .

Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]

дисперсия вычисляется по формуле:

где x i – значение, которое может принимать случайная величина, а μ – среднее значение (), р(x) – вероятность, что случайная величина примет значение х.

Если случайная величина имеет , то дисперсия вычисляется по формуле:

Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .

Некоторые свойства дисперсии :

Var(Х+a)=Var(Х), где Х – случайная величина, а – константа.

Var(aХ)=a 2 Var(X)

Var(Х)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2 =E(X 2)-2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2

Это свойство дисперсии используется в статье про линейную регрессию .

Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y – случайные величины, Cov(Х;Y) – ковариация этих случайных величин.

Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе .

Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения .

Стандартное отклонение выборки

Стандартное отклонение выборки – это мера того, насколько широко разбросаны значения в выборке относительно их .

По определению, стандартное отклонение равно квадратному корню из дисперсии :

Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) – отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.2)/(СЧЁТ(Выборка)-1))

Другие меры разброса

Функция КВАДРОТКЛ() вычисляет сумму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г(Выборка )*СЧЁТ(Выборка ) , где Выборка – ссылка на диапазон, содержащий массив значений выборки (). Вычисления в функции КВАДРОТКЛ() производятся по формуле:

Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка – ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции СРОТКЛ () производятся по формуле:

Необходимо вмешательство менеджмента для выявления причин отклонений.

Для построения контрольной карты я использую исходные данные, среднее значение (μ) и стандартное отклонение (σ). В Excel: μ = СРЗНАЧ($F$3:$F$15), σ = СТАНДОТКЛОН($F$3:$F$15)

Сама контрольная карта включает: исходные данные, среднее значение (μ), нижнюю контрольную границу (μ – 2σ) и верхнюю контрольную границу (μ + 2σ):

Скачать заметку в формате , примеры в формате

Посмотрев на представленную карту, я заметил, что исходные данные демонстрируют вполне различимую линейную тенденцию к снижению доли накладных расходов:

Чтобы добавить линию тренду выделите на графике ряд с данными (в нашем примере – зеленые точки), кликните правой кнопкой мыши и выберите опцию «Добавить линию тренда». В открывшемся окне «Формат линии тренда», поэкспериментируйте с опциями. Я остановился на линейном тренде.

Если исходные данные не разбросаны в соответствии с вокруг среднего значения, то описывать их параметрами μ и σ не вполне корректно. Для описания вместо среднего значения лучше подойдет прямая линейного тренда и контрольные границы, равноудаленные от этой линии тренда.

Линию тренда Excel позволяет построить с помощью функции ПРЕДСКАЗ.2)/(СЧЁТЗ($F$3:$F$15)-1))

необходимо нажать не Enter, а Ctrl + Shift + Enter. Не пытайтесь ввести фигурные скобки с клавиатуры – формула массива не заработает. Если требуется отредактировать формулу массива, сделайте это так же, как и с обычной формулой, но опять же по окончании редактирования нажмите не Enter, а Ctrl + Shift + Enter.

Формулу массива, возвращающую одно значение, можно «протаскивать», как и обычную формулу.

В результате получили контрольную карту, построенную для данных, имеющих тенденцию к понижению

P.S. После того, как заметка была написана, я смог усовершенствовать формулы, используемые для вычисления стандартного отклонения для данных с тенденцией. Ознакомиться с ними вы можете в Excel-файле

В данной статье я расскажу о том, как найти среднеквадратическое отклонение . Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

• Определите среднее (простое среднее арифметическое ряда значений).
• Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности ).
• Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение . Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего :

Наконец, чтобы вычислить дисперсию , каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия мм 2 .

Таким образом, дисперсия составляет 21704 мм 2 .

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

Мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = мм 2 .

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

.

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

.

Для второго примера получится:

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал , Сергей Валерьевич

Среднеквадратичное значение – обзор

РАЗДЕЛ 2-12 Преобразователи среднеквадратичного значения в постоянный ток

Среднеквадратичное значение (СКЗ) является основным измерением величины сигнала переменного тока. С практической точки зрения, среднеквадратичное значение, присвоенное сигналу переменного тока, представляет собой количество постоянного тока, необходимое для выработки эквивалентного количества тепла при той же нагрузке. С математической точки зрения среднеквадратичное значение напряжения определяется как значение, полученное возведением сигнала в квадрат, взятием среднего и последующим извлечением квадратного корня. Время усреднения должно быть достаточно большим, чтобы обеспечить фильтрацию на самых низких желаемых рабочих частотах.Полное обсуждение преобразователей среднеквадратичного значения в постоянный ток можно найти в ссылке 13, но мы покажем несколько примеров того, насколько эффективно аналоговые схемы могут выполнять эту функцию.

Первый метод, называемый явным методом , показан на рис. 2-78. Входной сигнал сначала возводится в квадрат множителем. Затем берется среднее значение с использованием соответствующего фильтра, а квадратный корень извлекается с помощью операционного усилителя со вторым квадратором в контуре обратной связи. Эта схема имеет ограниченный динамический диапазон, потому что каскады, следующие за квадратором, должны пытаться иметь дело с сигналом, который сильно различается по амплитуде.Это ограничивает этот метод входами с максимальным динамическим диапазоном приблизительно 10: 1 (20 дБ). Однако отличная полоса пропускания (более 100 МГц) может быть достигнута с высокой точностью, если в качестве строительного блока использовать умножитель, такой как AD834 (см. Рисунок 2-79).

Рисунок 2-78 :. Явное вычисление RMS

Рисунок 2-79 :. Широкополосное среднеквадратичное измерение

На рисунке 2-80 показана схема для вычисления среднеквадратичного значения сигнала с использованием неявного метода . Здесь выходной сигнал возвращается на вход прямого деления умножителя, такого как AD734.В этой схеме выходной сигнал умножителя изменяется линейно (вместо квадрата) со среднеквадратичным значением входного сигнала. Это значительно увеличивает динамический диапазон неявной схемы по сравнению с явной схемой. Недостатком этого подхода является то, что он обычно имеет меньшую полосу пропускания, чем явное вычисление.

Рисунок 2-80 :. Неявный расчет RMS

Хотя можно построить такую ​​схему RMS из AD734, гораздо проще спроектировать выделенную схему RMS.Схема V _IN ² / V _Z может управляться током и должна быть только в одном квадранте, если вход сначала проходит через схему абсолютного значения.

На Рис. 2-81 показана упрощенная схема типичного монолитного преобразователя среднеквадратичного значения в постоянный ток, AD536A. Он разделен на четыре основные части: схема абсолютного значения (активный выпрямитель), квадрат / делитель, токовое зеркало и буферный усилитель. Входное напряжение V _IN , которое может быть переменным или постоянным, преобразуется в униполярный ток I ₁ схемой абсолютного значения A ₁ , A ₂ .I ₁ управляет одним входом квадрантного квадранта / делителя, который имеет передаточную функцию: I ₄ = I ₁ ² / I ₃ . Выходной ток I ₄ квадратора / делителя управляет зеркалом тока через фильтр нижних частот, образованный R ₁ и подключенным внешним конденсатором C _AV . Если постоянная времени R ₁ C _AV намного больше, чем самый длинный период входного сигнала, то I ₄ эффективно усредняется.Текущее зеркало возвращает ток I3, равный AVG [I ₄ ], обратно квадратору / делителю для завершения неявного вычисления RMS. Таким образом:

Рисунок 2-81 :. Монолитный преобразователь среднеквадратичного значения в постоянный ток AD536A

(2-21) I4 = AVG [I12 / I4] = I1 RMS

Токовое зеркало также вырабатывает выходной ток I _OUT , который равен 2I ₄ . I _OUT можно использовать напрямую или преобразовать в напряжение с помощью R ₂ и буферизовать с помощью A4 для обеспечения выходного напряжения с низким импедансом.Передаточная функция принимает следующий вид:

(2-22) VOUT = 2R2 × IRMS = VIN RMS

Выход в дБ выводится из эмиттера Q3, поскольку напряжение в этой точке пропорционально −log V _IN . Эмиттерный повторитель, Q5, буферизует и сдвигает это напряжение, так что выходное напряжение в дБ равно нулю, когда ток эмиттера, подаваемый извне (I _REF ) до Q5, приближается к I ₃ . Тем не менее, коэффициент усиления схемы дБ имеет TC примерно 3300 ppm / ° C и должен иметь температурную компенсацию.

Существует ряд коммерчески доступных преобразователей RMS / DC в монолитной форме, в которых используются эти принципы. AD536A – это настоящий преобразователь среднеквадратичного значения в постоянный ток с полосой пропускания приблизительно 450 кГц для V _RMS > 100 мВ _RMS и полосой пропускания 2 МГц для V _RMS > 1 В _RMS . AD636 обеспечивает полосу пропускания 1 МГц для сигналов низкого уровня до 200 мВ _RMS . AD637 имеет полосу пропускания 600 кГц для сигналов _RMS 100 мВ и полосу пропускания 800 МГц для сигналов RMS 1 В.Также доступны недорогие преобразователи среднеквадратичного значения в постоянный ток общего назначения, такие как AD736 и AD737 (опция отключения питания).

Формула среднеквадратичного значения – Изучение формулы для определения среднеквадратичного значения

Формула среднего квадрата дает квадратный корень из общей суммы квадратов всех данных в наблюдении. Среднеквадратичное значение, сокращенно RMS, представляет собой квадратный корень из среднего арифметического квадратов группы значений. Его также называют квадратичным средним. Среднеквадратичное значение функции также может быть определено для непрерывно изменяющейся функции в виде интеграла квадратов мгновенных значений в течение цикла.Здесь формула среднеквадратичного значения вычисляет квадратный корень из среднего арифметического квадрата функции, определяющей непрерывный сигнал.

Разбивайте сложные концепции с помощью простых изображений.

Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации с помощью Cuemath.

Забронируйте бесплатную пробную версию Класс

Что такое формула среднего квадрата?

Формула 1

Для группы значений «n», включающих \ ({x_1, x_2, x_3,….2 дт] \)

где \ (f_ {rms} \) = Среднеквадратичное значение данной функции f (t). 5 = \ dfrac {1} {3} \ left [\ dfrac {125} {3} – \ dfrac {8} {3} \ right] = \ dfrac {117} {9} = 13 \ end {уравнение *} \)

Ответ: Среднеквадратичное значение данной функции, f (t) = 13.

перейти к слайду

Среднеквадратичная ошибка (RMSE) или средняя абсолютная ошибка (MAE)? – Аргументы против избегания RMSE в литературе

Методы оценки моделей 30 июн 2014

Методы оценки моделей | 30 июн 2014

 (метрики)
rmse (данные $ фактические, данные $ прогнозируемые)
2,041241