Среднеквадратичное значение тока: Среднеквадратичное значение. RMS.

Что такое истинные среднеквадратичное значение?

Устройства с измерением истинных СКЗ (СКЗ = среднеквадратичное значение) представлены тремя приборами, которые измеряют переменный ток или напряжение переменного тока:

1. цифровые мультиметры с измерением истинных среднеквадратичных значений (или токоизмерительные клещи)
2. цифровой мультиметр с усредненными показаниями (или токоизмерительные клещи)
3. осциллограф

Обычно используются приборы первых двух типов, которые могут точно измерять стандартные (чистые) синусоидальные сигналы переменного тока.

Специалисты предпочитают пользоваться устройствами с измерением истинных среднеквадратичных значений, поскольку только такие приборы способны точно измерять как синусоидальные, так и несинусоидальные сигналы переменного тока. (См. рисунки в верхней части страницы).

• Синусоидальные сигналы: чистые, без искажений, сигналы с симметричными переходами между точками максимума и минимума.
• Несинусоидальные сигналы: сигналы нерегулярной формы с искажениями: импульсные выбросы, последовательности импульсов, квадратные, треугольные и пилообразные сигналы, а также любые другие сигналы неровной или угловатой формы.

 

Порядок расчета СКЗ

Как уже говорилось ранее, СКЗ расшифровывается как среднеквадратичное значение. Хотя формула среднеквадратичного значения может быть сложной для понимания, оно фактически соответствует эквивалентному значению постоянного тока для сигнала переменного тока. С технической точки зрения она определяет «эффективное» значение (значение нагрева постоянным током) для волны переменного тока любой формы.

В устройствах с усредненными показаниями для точного измерения чистых синусоидальных волн используются математические формулы усреднения. Такое устройство может измерять несинусоидальные волны, но с невысокой точностью.

Более совершенные устройства с измерением истинных среднеквадратичных значений могут точно измерять как чистые волны, так и более сложные несинусоидальные волны. Формы сигнала могут быть искажены из-за нелинейных нагрузок, например приводов с регулируемой частотой вращения или компьютеров. При измерении искаженной волны устройство с усредненными показаниями может показать результат на 40 % ниже или на 10 % выше фактических значений.

Где измеряются истинные среднеквадратичные значения?

Потребность в устройствах с измерением истинных среднеквадратичных значений возросла, поскольку за последние годы значительно увеличилась вероятность возникновения несинусоидальных сигналов в цепях. Некоторые примеры:

• Приводы двигателей с регулируемой частотой вращения
• Электронные балластное сопротивление
• Компьютеры
• Системы ОВКВ
• Твердотельные среды

В таких условиях ток возникает в форме коротких импульсов, а не в виде сглаженной синусоиды, как на стандартном асинхронном двигателе. Форма волны такого сигнала тока может значительно повлиять на показания токовых клещей. Кроме того, устройство с измерением истинных среднеквадратичных значений лучше всего подходит для измерений на линиях электропередач с неизвестными характеристиками переменного тока.

Ссылка: Digital Multimeter Principles by Glen A. Mazur, American Technical Publishers.

Действующее значение переменного синусоидального тока

Если в цепь переменного синусоидального тока включить прибор, который предназначен для измерения среднего значения тока в цепи, то этот прибор зафиксирует нулевое значение. Действительно, в каждый период ток протекает полпериода в одном направлении и полпериода — в другом.

В цепи такого тока не будет происходить электролиза, то есть осаждения металла на катоде в электролитической ванне. В то же время в сопротивлении, включенном в цепь переменного тока, идет непрерывный процесс выделения тепла независимо от направления тока: и в первый и во второй полупериоды. Поэтому, чтобы судить о силе переменного синусоидального тока, его сравнивают с постоянным током по одинаковому тепловому действию. Полученное путем такого сравнения значение силы переменного тока называют действующим.

Таким образом, действующее (эффективное) значение переменного тока численно равно эквивалентной по тепловому действию силе постоянного тока, то есть такому току, который за то же время,

на том же сопротивлении выделит такое же количество тепла, что и переменный ток одинаковой силы.

В цепи постоянного тока на сопротивлении R за время Т при силе тока I выделяется количество теплоты

Q_–= I² RT.                                    (6.6)

В подобном сопротивлении, включенном в цепь переменного тока, в каждый очень короткий отрезок времени ∆t, в течение которого мгновенное значение силы тока i можно считать практически неизменным, выделяется элементарное количество теплоты:

∆Q_~ = i²R∆t,

то есть количество теплоты, пропорциональное произведению i

2R. На рисунке 6.4 построены кривые i и i² для синусоидального переменного тока. Как видно из графика, несмотря на то, что ток i в течение периода меняется по значению и направлению, i² меняется только по значению и остается положительным независимо от направления тока i, то есть в первом полуперирде эта величина имеет положительное значение (+ i)•(+ i) = +i², во втором полупериоде она также остается положительной: (—i)•(—i)= +i².

Разделив площадь, ограниченную кривой i² и осью ωt, на время Т, получим среднюю ординату кривой i² за период, которую обозначим i²_ср. Тогда количество теплоты, которое выделится на сопротивлении в цепи переменного тока за время Т,

Q_~= i²_cр RT.                                (6.7)

Согласно приведенному выше определению действующего значения переменного тока,

Q_~= Q_– , то есть из формул (6.6) и (6.7) следует, что

I² RT=i²_сp RT,

откуда действующее значение переменного тока

I = √i²_сp.                                       (6.8).

Действующее значение переменного тока есть среднеквадратичное за период значение переменного тока.

Величину i², графически представленную на рисунке 6.4, можно определить аналитически через амплитудное значение I_m²:

.                                   1-cos2ωt         I_m² _Im²

i² = I_m² sin²ωt = I_m²—————— = ——— – —— cos2ωt ,

.                                       2                  2         2

где .

 

.             1-cos2ωt

sin²ωt = —————  ,

.                 2

Среднее значение cos2ωt за период Т равно нулю (соответствует сумме площадей, помеченных на рисунке 6.4 знаками + и —). Тогда среднее за период значение квадрата силы синусоидального переменного тока

i_ср² =I_m² /2

а действующее значение синусоидального переменного тока

 

I = √i_ср² = √I_m²/2 = I_m/2 = I_m/1.414 = 0,707 I_m.        (6.9)

Действующее значение переменного синусоидального напряжения может быть найдено из предыдущего как

.

       I_m

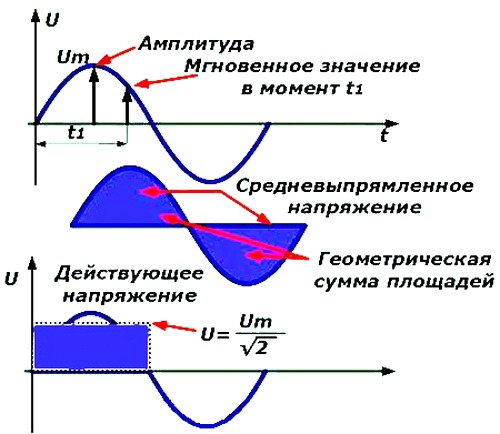
IR = ——— R

.       √²

или

.      U_m

U = —— = 0,707 U_m.

.      √²

Значит, если в сети напряжение U — 220 В, то его максимальное (амплитудное) значение

U_m = 220•1,414 = 311 В.

Амплитуда напряжения 380 В равна 380•1,414 = 538 В. То обстоятельство, что амплитуда значительно превышает действующее значение, дает преимущество переменному току при использовании люминесцентных или дуговых ламп, которые легче зажигаются на переменном токе.

< Предыдущая		Следующая >

%d0%b4%d0%b5%d0%b9%d1%81%d1%82%d0%b2%d1%83%d1%8e%d1%89%d0%b5%d0%b5%20%d0%b7%d0%bd%d0%b0%d1%87%d0%b5%d0%bd%d0%b8%d0%b5%20%d0%bf%d0%b5%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%bd%d0%be%d0%b3%d0%be%20%d1%82%d0%be%d0%ba%d0%b0 — с русского на все языки

Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАканАлтайскийАрагонскийАрабскийАстурийскийАймараАзербайджанскийБашкирскийБагобоБелорусскийБолгарскийТибетскийБурятскийКаталанскийЧеченскийШорскийЧерокиШайенскогоКриЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийВаллийскийДатскийНемецкийДолганскийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГэльскийГуараниКлингонскийЭльзасскийИвритХиндиХорватскийВерхнелужицкийГаитянскийВенгерскийАрмянскийИндонезийскийИнупиакИнгушскийИсландскийИтальянскийЯпонскийГрузинскийКарачаевскийЧеркесскийКазахскийКхмерскийКорейскийКумыкскийКурдскийКомиКиргизскийЛатинскийЛюксембургскийСефардскийЛингалаЛитовскийЛатышскийМаньчжурскийМикенскийМокшанскийМаориМарийскийМакедонскийКомиМонгольскийМалайскийМайяЭрзянскийНидерландскийНорвежскийНауатльОрокскийНогайскийОсетинскийОсманскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПортугальскийКечуаКвеньяРумынский, МолдавскийАрумынскийРусскийСанскритСеверносаамскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиШумерскийСилезскийТофаларскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийТувинскийТвиУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВьетнамскийВепсскийВарайскийЮпийскийИдишЙорубаКитайский

 

Все языкиАнглийскийНемецкийНорвежскийКитайскийИвритФранцузскийУкраинскийИтальянскийПортугальскийВенгерскийТурецкийПольскийДатскийЛатинскийИспанскийСловенскийГреческийЛатышскийФинскийПерсидскийНидерландскийШведскийЯпонскийЭстонскийТаджикскийАрабскийКазахскийТатарскийЧеченскийКарачаевскийСловацкийБелорусскийЧешскийАрмянскийАзербайджанскийУзбекскийШорскийРусскийЭсперантоКрымскотатарскийСуахилиЛитовскийТайскийОсетинскийАдыгейскийЯкутскийАйнский языкЦерковнославянский (Старославянский)ИсландскийИндонезийскийАварскийМонгольскийИдишИнгушскийЭрзянскийКорейскийИжорскийМарийскийМокшанскийУдмурдскийВодскийВепсскийАлтайскийЧувашскийКумыкскийТуркменскийУйгурскийУрумскийЭвенкийскийБашкирскийБаскский

действующее значение тока – это.

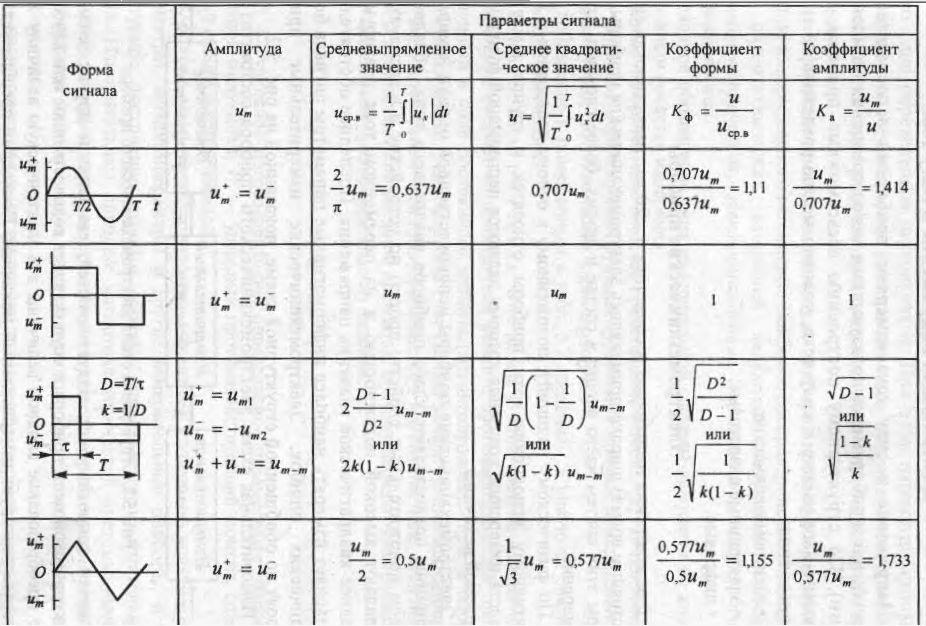.. Что такое действующее значение тока?

действующее значение тока

 

действующее значение тока

Среднеквадратичное значение периодического электрического тока за период.
Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д.
[ГОСТ Р 52002-2003]

Более понятные определения:

• Действующее значение переменного тока равно значению эквивалентного постоянного тока, который, проходя через одно и то же сопротивление, выделяет за период одинаковое количество тепла.
  [Словарь-справочник по электротехнике, промышленной электронике и автоматике. Бензарь В.К. 1985 г.]
   
• Действующее значение переменного тока это такая сила постоянного тока, которая выделяет в проводнике то же количество теплоты, что и данный переменный ток (т. е. такой постоянный ток, который по своему тепловому действию равен данному переменному току).

Раньше вместо термина действующее значение применялся термин “эффективное значение”.

Для синусоидального тока действующее значение тока I связано с амплитудным значением Im по формуле:
I = 0.707ImПараллельные тексты EN-RU

The r.m.s. value of a perfectly sinusoidal waveform is equal to:
Ir.m.s. = Imax / √2
(where Imax is the maximum value of the amplitude of the sinusoidal waveform).
[ABB]

Действующее значение синусоидального тока равно:
Ir.m.s. = Imax / √2,
где Imax – значение амплитуды синусоидального сигнала.
[Перевод Интент]

R.m.s. value of a sinusoidal quantity

The r. m.s. value is the parameter which relates alternating to direct current.

The r.m.s. value of an alternating current represents the direct current value which causes the same thermal effects in the same period of time;

for example, a direct current of 100A produces the same thermal effects of a sinusoidal alternating current with the maximum value of 141A.
[ABB]

Действующее значение синусоидального тока

Действующее значение тока является величиной, определяющей соотношение постоянного и переменного токов.

Действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за одинаковое время выделяет такое же количество теплоты.

Например, постоянный ток значением 100 А приводит к выделению такого же количества теплоты, что и синусоидальный ток с амплитудой 141 А.
[Перевод Интент]

Недопустимые, нерекомендуемые

• действующий ток
• среднеквадратический ток
• среднеквадратическое значение тока
• эффективное значение тока
• эффективный ток

Тематики

• электротехника, основные понятия

Синонимы

• действующее значение периодического электрического тока
• среднеквадратичное значение тока

EN

• Ir.m.s.
• root-mean-square current

Справочник технического переводчика. – Интент. 2009-2013.

• действующее значение полного тока КЗ, усреднённое по трём фазам
• действующее значение тока короткого замыкания в электроустановке

Смотреть что такое “действующее значение тока” в других словарях:

• действующее значение тока короткого замыкания в электроустановке — Среднее квадратическое значение тока короткого замыкания в электроустановке за период рабочей частоты, середина которого есть рассматриваемый момент времени [ГОСТ 26522 85] Тематики электробезопасность …   Справочник технического переводчика

• наибольшее действующее значение тока короткого замыкания — наибольшее действующее значение тока короткого замыкания; действующее значение ударного тока короткого замыкания Действующее значение тока короткого замыкания за первые полпериода основной частоты (с момента возникновения короткого замыкания) …   Политехнический терминологический толковый словарь

• комплексное действующее значение тока — Комплексная величина, модуль которой равен действующему значению синусоидального электрического тока и аргумент которой равен начальной фазе этого электрического тока. Примечание — Аналогично определяют комплексные действующие значения… …   Справочник технического переводчика

• максимальное действующее значение тока КЗ — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва] Тематики электротехника, основные понятия EN maximum effective short circuit current …   Справочник технического переводчика

• Среднеквадратическое (действующее) значение тока — 31 Источник: ГОСТ Р 54130 2010: Качество электрической энергии. Термины и определения оригинал документа …   Словарь-справочник терминов нормативно-технической документации

• Действующее значение переменного тока — Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В… …   Википедия

• действующее значение ударного тока короткого замыкания — наибольшее действующее значение тока короткого замыкания; действующее значение ударного тока короткого замыкания Действующее значение тока короткого замыкания за первые полпериода основной частоты (с момента возникновения короткого замыкания) …   Политехнический терминологический толковый словарь

• действующее значение периодической составляющей тока отключения выключателя — Iо.п Действующее значение периодической составляющей тока отключения в момент размыкания контактов [ГОСТ Р 52565 2006] Тематики выключатель, переключательвысоковольтный аппарат, оборудование …   Справочник технического переводчика

• ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЕ — в электротехнике среднее квадратичное за период значение переменного тока, напряжения, электродвижущей силы, магнитодвижущей силы, магнитного потока и т. п. Действующее значение синусоидального тока и напряжения в раз меньше их амплитудных… …   Большой Энциклопедический словарь

• действующее значение периодической составляющей тока короткого замыкания рабочей частоты в электроустановке — Среднее квадратическое значение периодической составляющей тока короткого замыкания рабочей частоты в электроустановке за период, середина которого есть рассматриваемый момент времени [ГОСТ 26522 85] Тематики электробезопасность …   Справочник технического переводчика

Максимальное КЗ и среднеквадратичное значение

Тип продуктаКабельные скобы (12)Кабельные вводы (106)

Правила монтажа оборудованияAS/NZS, для горнодобывающей отрасли (Группа I) (15)Зоны AS/NZS (48)Разделы класса CEC (20)Зоны класса CEC (26)CEC, не классифицировано (3)GOST Zones (36)IEC, для горнодобывающей отрасли (Группа I) (14)IEC, не классифицировано (45)Зоны IEC (49)Разделы класса NEC (19)Зоны класса NEC (19)NEC, не классифицировано (3)Зоны Norsok (11)Параллельная конструкция (8)Один кабель (8)Трехлистная компоновка кабелей (7)

Тип защиты1Ex d IIC Gb X (27)1Ex e IIC Gb X (36)2Ex nR IIC Gc X (27)Класс I, Разд. 1 (8)Класс I, Разд. 1, Группы A, B, C, D (8)Класс I, Разд. 2 (18)Класс I, Разд. 2, Группы A, B, C, D (17)Класс I, Группы A, B, C, D (6)Класс I, Группы B, C, D (2)Класс I, Зона 1 (19)Класс I, Зона 1, AEx d IIC Gb (10)Класс I, Зона 1, AEx e IIC Gb (19)Класс I, Зона 2 (19)Класс I, Зона 2, AEx d IIC Gb (10)Класс I, Зона 2, AEx e IIC Gb (12)Класс I, Зона 2, AEx nR IIC Gc (8)Класс I, Зона 20 (10)Класс I, Зона 20, AEx ta IIIC Da (10)Класс I, Зона 21 (10)Класс I, Зона 21, AEx tb IIIC Db (10)Класс I, Зона 22 (10)Класс I, Зона 22, AEx tc IIIC Dc (10)Класс II, Разд. 1 (10)Класс I, Разд. 1, Группы E, F, G (10)Класс II, Разд. 2 (18)Класс II, Разд. 2, Группы E, F, G (18)Класс III, Разд. 1 (15)Класс III, Разд. 2 (13)Ex d I Mb (20)Ex d IIC Gb (36)Ex db I Mb (1)Ex db IIC Gb (1)Ex e I Mb (20)Ex e IIC Gb (46)Ex eb I Mb (1)Ex eb IIC Gb (3)Ex nR IIC Gc (34)Ex nRc IIC Gc (1)Ex ta IIIC Da (43)Ex ta IIIC Da X (35)Ex tb IIIC Db (43)Ex tb IIIC Db X (35)Ex tc IIIC Dc (43)Ex tc IIIC Dc X (35)Ex tD A21 IP66 (2)Промышленного назначения (45)Стандартные среды (6)Одноболтовой (10)Двухболтовой (10)Влажные среды (6)

Тип кабеляАлюминиевая ленточная броня (ASA) (25)Алюминиевая ленточная броня (например, ATA) (24)Алюминиевая проволочная броня (AWA) (34)Оснащенные броней и оболочкой (24)Судовой кабель с броней в виде оплетки (24)Гофрированная металлическая броня, приваренная непрерывным швом (MC-HL) — алюминий (4)Гофрофольгированная броня, приваренная непрерывным швом (MC-HL) — сталь (4)Гофрированная и взаимосвязанная металлическая броня (MC) — алюминий (4)Гофрированная и взаимосвязанная металлическая броня (MC) — сталь (4)Сверхтвердый шнур (2)Небронированный кабель плоской формы (2)Гибкий шнур (5)Освинцованный кабель с алюминиевой проволочной броней (LC/AWA) (9)Освинцованный кабель с гибкой проволочной броней (LC/PWA) (8)Освинцованный кабель с однослойной проволочной броней (LC/SWA) (9)Освинцованный кабель со стальной ленточной броней (LC/STA) (8)Освинцованный кабель с ленточной броней (LC/ASA) (8)Освинцованный кабель с броней в виде проволочной оплетки (8)Освинцованный небронированный кабель (2)M10 (12)M12 (8)Морской судовой кабель с броней в виде оплетки (24)Морской судовой кабель (11)Небронированный морской судовой кабель (19)Гибкая проволочная броня (PWA) (27)Оплетка и алюминиевая проволочная броня (AWA) (4)Оплетка и однослойная проволочная броня (SWA) (4)Гибкая проволочная (EMC) оплетка (например, CY/SY) (42)Однослойная проволочная броня (SWA) (38)Стальная ленточная броня (STA) (24)TECK (4)TECK 90 (4)TECK 90-HL (4)Кабель, укладывающийся в короб (9)Без брони (27)Броня в виде проволочной оплетки (42)

Конфигурация уплотненияДвойное наружное уплотнение (3)Внутреннее и наружное уплотнения (28)Внутреннее защитное уплотнение и кабельный ввод (2)Внутреннее защитное уплотнение и наружное уплотнение (18)Внутреннее защитное уплотнение и наружное уплотнение/переходная муфта FRAS (1)Без уплотнения (4)Наружное уплотнение (46)Наружное уплотнение/кабельный ввод (3)Наружное уплотнение/переходная муфта FRAS (1)Очень высокая (12)

СертификатыABS (67)Алюминий (3)Алюминий/нержавеющая сталь (1)ATEX (61)BS 6121 (45)BV (40)c-CSA-us (19)CCO-PESO (44)CSA (11)DNV-GL (41)Алюминий, покрытый эпоксидным составом (2)ГОСТ К (74)ГОСТ Р (44)IEC 62444 (45)IECEX (61)INMETRO (30)KCC (27)Lloyds (70)LSF (2)Одобренный LUL (Лондонский метрополитен) полимер (2)NEPSI (34)Нейлон (2)RETIE (35)Нержавеющая сталь (6)TR-CU-EAC (38)UL (9)

Защита от влагиОсевая нагрузка (12)Горизонтальная нагрузка (12)Нет (68)Силы при коротком замыкании (8)Да (41)

Среднеквадратичное значение (СКЗ).

Действующее или эффективное значение. Root-mean-square (RMS)

Среднеквадратичное значение (СКЗ). Действующее или эффективное значение
Истинное среднеквадратичное значение (ИСКЗ)

Root-mean-square (RMS) − среднеквадратичное значение – англ.
True Root-Mean-Square (TRMS) − истинное среднеквадратичное значение – англ.

 

Для любой периодической функции (например, тока или напряжения) вида f = f(t) среднеквадратичное значение функции определяется как:

Если функция задана в виде суммы гармоник (как например в случае тока нелинейной нагрузки)

то действующее значение периодической несинусоидальной функции выражается формулой

Поскольку Fn − амплитуда n-ой гармоники, то Fn / √2 − действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.

Например если, несинусоидальный ток выражается формулой:

то среднеквадратичное значение тока равно:

 

Все приведённые выше соотношения используются при вычислении в тестерах измеряющих ИСКЗ, в цепях измерения тока ИБП, в анализаторах сети и в др. оборудовании.

 

Истинное среднеквадратичное значение (ИСКЗ), True Root-Mean-Square (TRMS)

Большинство простых тестеров не могут точно измерять среднеквадратичное значение несинусоидального сигнала (то есть сигнала с большими гармоническими искажениями, например, прямоугольной формы). Они правильно определяют СКЗ напряжения  только для синусоидальных сигналов. Если таким прибором измерить СКЗ напряжения прямоугольной формы, то показание будет ошибочным.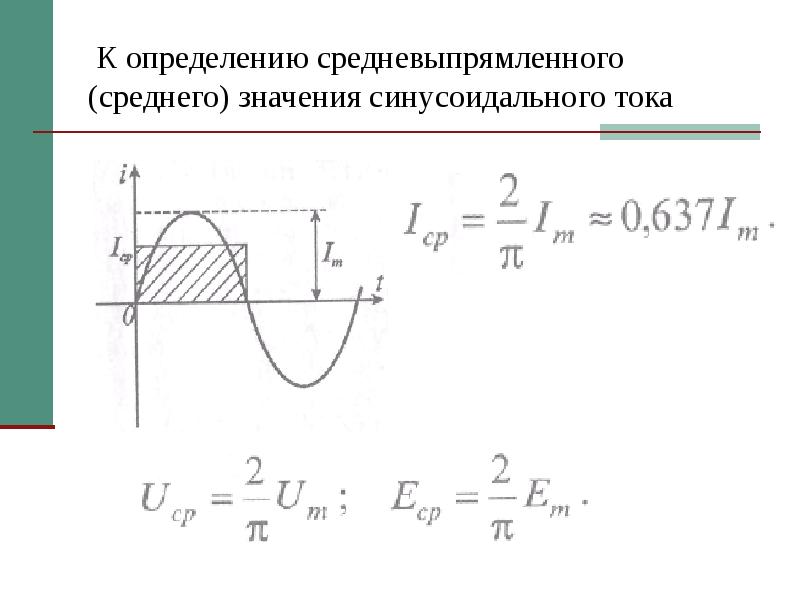 Причина ошибки – обычные тестеры при вычислении учитывают основную гармонику (для обычной сети – 50 Гц), но не берут в расчет высшие гармоники сигнала.

Для решения данной проблемы существуют особые приборы, точно измеряющие СКЗ с учётом высших гармоник (обычно до 30-50 гармоник). Они маркируются символом TRMS или ИСКЗ (true root-mean-square) – истинное среднеквадратичное значение, True RMS, истинное СКЗ.

Так, например, обычный тестер может измерить с ошибкой напряжение на выходе ИБП с аппроксимированной синусоидой, в то время как тестер «APPA 106 TRUE RMS MULTIMETER» измеряет напряжение (СКЗ) правильно.

 

Замечания

Для синусоидального сигнала, фазное напряжение в сети (нейтраль – фаза, phase voltage) равно:

UСКЗ_ф = Uмакс_ф / (√2)

 

Для синусоидального сигнала, линейное напряжение в сети (фаза – фаза, interlinear voltage) равно:

UСКЗ_л = Uмакс_л / (√2)

 

Соотношение между фазным и линейным напряжением:

UСКЗ_л = UСКЗ_ф * √3

 

Обозначения:

ф – линейное (напряжение)

л – фазное (напряжение)

СКЗ – среднеквадратичное значение

макс – максимальное или амплитудное значение (напряжения)

 

Примеры:

Фазному напряжению 220 В соответствует линейное напряжение 380 В

Фазному напряжению 230 В соответствует линейное напряжение 400 В

Фазному напряжению 240 В соответствует линейное напряжение 415 В

 

Фазное напряжение:

Напряжение в сети 220 В (СКЗ), – амплитудное значение напряжения около ±310 В

Напряжение в сети 230 В (СКЗ), – амплитудное значение напряжения около ±325 В

Напряжение в сети 240 В (СКЗ), – амплитудное значение напряжения около ±340 В

 

Линейное напряжение:

Напряжение в сети 380 В (СКЗ), – амплитудное значение напряжения около ±537 В

Напряжение в сети 400 В (СКЗ), – амплитудное значение напряжения около ±565 В

Напряжение в сети 415 В (СКЗ), – амплитудное значение напряжения около ±587 В

 

 

Ниже приведён обычный пример фазных напряжений в 3-фазной сети:

 

 

---

[1] Г. И. Атабеков Основы Теории Цепей с.176, 434 с.

Почему при расчете средней мощности используется среднеквадратичное значение, а не просто среднее значение напряжения / тока?

Чтобы мощность была средней, я должен быть средним током, поэтому я предполагаю, что эффективный ток – это средний ток.

Короче говоря, среднее напряжение х средний ток равен только средней мощности, когда напряжение и ток являются величинами постоянного тока. Подумайте о следующем примере:

Если вы подали 230 В переменного тока от электрической розетки к нагревательному элементу, он нагревается или даже нагревается. Это захват власти, за которую можно выставить счет. 230 В переменного тока – это синусоида, и все синусоиды имеют среднее значение ноль. Результирующий ток, протекающий через нагревательный элемент, также представляет собой синусоидальную волну со средним значением, равным нулю.

Таким образом, использование среднего напряжения х среднего тока дает нулевую среднюю мощность, и это явно не так. Это среднеквадратичное напряжение х среднеквадратичный ток, который даст значимый ответ (независимо от того, постоянный или переменный ток).

Вы должны вернуться к основам и спросить себя, что такое мощность – это напряжение х ток, и это мгновенные значения, умноженные вместе. Это приводит к такой форме волны мощности:

Из-за акта умножения форма волны мощности теперь имеет среднее значение, которое не равно нулю . Если продвинуться дальше, если нагрузочный резистор составлял 1 Ом, амплитуда тока будет равна амплитуде приложенного напряжения, поэтому мощность станет средним значением .v2v2

Это заставляет нас сказать, что мощность the mean of the square of voltage(или ток) и, учитывая, что мы выбрали 1 Ом в этом примере, мы также можем сказать, что эффективное напряжение, которое производит эту мощность, является значением square root of the mean of the voltage squaredили среднеквадратичным значением.

Таким образом, для синусоидальной волны максимальной амплитуды вершина волны мощности равна v 2 p k, и, поскольку волна мощности, создаваемая квадратом синусоиды, также является синусоидой (с удвоенной частотой), среднее значение (среднее) значение:vpkvpkv2pkvpk2

. Затем, взяв квадратный корень, чтобы получитьэффективноенапряжение, мы получаем√v2pk2vpk22 илиvpkv2pk2−−−√vpk22vpk2–√vpk2

В действительности, среднеквадратическое значение переменного напряжения (или тока) является эквивалентным значением постоянного напряжения (или тока), которое создает такой же эффект нагрева в резистивной нагрузке.

Так что нет, среднее напряжение или средний ток не имеет значения, но средняя мощность важна.

переменного тока | Безграничная физика

Фазоры

Фазоры используются для анализа электрических систем в синусоидальном устойчивом состоянии и с постоянной угловой частотой.

Цели обучения

Обсудить применение фазового вектора

Основные выводы

Ключевые моменты

• Вектор – это представление синусоидальной функции, амплитуда (A), частота (ω) и фаза (θ) не зависят от времени.Если ω используется всеми компонентами системы, его можно исключить, оставив только A и ω. Термин фазор обычно относится к двум последним факторам.
• Фазоры значительно упрощают выражение синусоидально изменяющихся сигналов.
• Фазоры могут использоваться для анализа поведения электрических систем, таких как цепи RLC, которые достигли своего рода равновесия, называемого синусоидальным устойчивым состоянием. В синусоидальном установившемся состоянии каждое напряжение и ток в системе являются синусоидальными с угловой частотой ω.
• Phasors позволяют нам применять методы, используемые для решения цепей постоянного тока, для решения цепей RC.

Ключевые термины

• синусоидальное установившееся состояние : Указывает, что все напряжение и ток в системе синусоидальны с одинаковой угловой частотой ω.
• комплексные числа : числа с мнимой частью. Обычно обозначается как i.
• phasor : представление комплексного числа в виде комплексной экспоненты.

Фазоры

Комплексные числа играют важную роль в физике. Обычно комплексные числа записываются в виде их действительной части плюс мнимая часть. Например, [latex] \ text {a} + \ text {bi} [/ latex], где a и b – действительные числа, а [latex] \ text {i} [/ latex] сигнализирует о мнимой части. Однако часто бывает удобно записывать комплексные числа в форме экспоненты, называемой фазором.

В физике фазовый вектор или фазор – это представление синусоидальной функции, амплитуда ( A ), частота ( ω ) и фаза ( θ ) не зависят от времени, как показано на диаграмме.Фазоры разделяют зависимости от A , ω и θ на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид. В таких ситуациях фазоры позволяют исключить эту общую характеристику, оставляя только функции A и θ . В результате тригонометрия сводится к алгебре, а линейные дифференциальные уравнения становятся алгебраическими.Поэтому термин фазор часто относится только к этим двум факторам.

Векторная диаграмма : Пример последовательной RLC-цепи и соответствующая векторная диаграмма для определенного ω. Инженеры-электрики, инженеры-электронщики, инженеры-электронщики и авиастроители – все используют векторные диаграммы для визуализации сложных констант и переменных (векторов). Как и векторы, стрелки, нарисованные на миллиметровой бумаге или компьютерных дисплеях, представляют собой векторы.

Фазоры часто используются в электрических системах при рассмотрении напряжений и токов, которые изменяются синусоидально во времени, например, в цепях RLC. {\ text {i} \ theta} [/ латекс]. В последнем случае это сокращенное обозначение, кодирующее амплитуду и фазу лежащей в основе синусоиды.

Фазорное представление сигналов

В основе векторного представления сигнала лежат две ключевые идеи:

1. реальный изменяющийся во времени сигнал может быть представлен сложным изменяющимся во времени сигналом; и
2. сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа, которое не зависит от времени, и сложного сигнала, который зависит от времени.

Сигнал:

[латекс] \ text {x} (\ text {t}) = \ text {Acos} (\ omega \ text {t} + \ theta) [/ latex]

, показанный на рисунке ниже, представляет собой косинусоидальный сигнал с амплитудой A , частотой и фазой θ . Амплитуда A характеризует размах размаха сигнала 2A от пика до пика, угловая частота ω характеризует период T = 2π / ω между отрицательными и положительными пересечениями нуля (или положительными пиками или отрицательными значениями). пиков), а фаза θ характеризует время τ = – θ / ω , когда сигнал достигает своего первого пика.С таким определением сигнал x (t) также может быть записан как

[латекс] \ text {x} (\ text {t}) = \ text {Acos} (\ text {t} – \ tau) [/ latex].

Косинусоидальный сигнал : Косинусоидальный сигнал.

Если значение τ положительно, тогда τ представляет собой «временную задержку», которая описывает время (больше нуля), когда достигается первый пик. Когда τ отрицательно, тогда τ – это «временной прогресс», который описывает время (меньше нуля), когда был достигнут последний пик.Подставив = 2π / T, мы получим третий способ записи x (t):

[латекс] \ text {x} (\ text {t}) = \ text {Acos} \ frac {2 \ pi} {\ text {T}} (\ text {t} – \ tau) [/ latex]

В этой форме сигнал легко построить.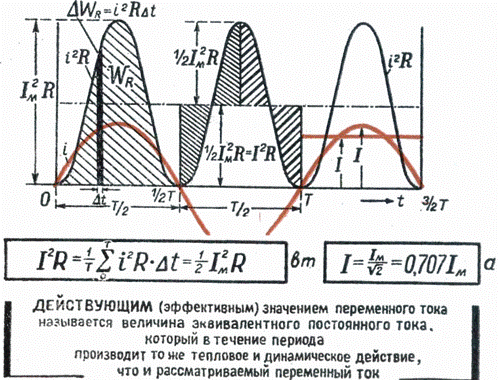 Просто нарисуйте косинусоидальную волну с амплитудой A и периодом T ; затем ударьте по началу координат (t = 0) так, чтобы сигнал достиг своего пика при τ . Таким образом, параметры, определяющие косинусоидальный сигнал, имеют следующие единицы:

• A , произвольно (e.g., вольт или метры / сек, в зависимости от применения)
• ω , в радианах / сек (рад / сек)
• T , в секундах (sec)
• θ , в радианах (рад)
• τ , в секундах (сек)

Синусоидальное установившееся состояние и последовательные схемы RLC CircuitPhasors могут использоваться для анализа поведения электрических и механических систем, которые достигли своего рода равновесия, называемого синусоидальным установившимся состоянием.

В синусоидальном установившемся состоянии каждое напряжение и ток (или сила и скорость) в системе синусоидальны с угловой частотой ω .Однако амплитуды и фазы этих синусоидальных напряжений и токов различны.

Например, напряжение на резисторе может опережать напряжение на конденсаторе на 90 ^∘ и отставать от напряжения на катушке индуктивности на 90 ^∘ . Чтобы конкретизировать наше применение векторов к электрическим системам, мы рассмотрим схему серии RLC , показанную на рисунке. Стрелка с надписью i (t) обозначает ток, который течет в ответ на приложенное напряжение.{\ text {i} \ theta} [/ латекс].

Затем мы описываем источник напряжения вектором В и помним, что мы всегда можем вычислить фактическое напряжение, умножив его на e ^iωt и взяв действительную часть.

Среднеквадратичные значения

Среднеквадратичное значение напряжения или тока – это усредненное по времени напряжение или ток в системе переменного тока.

Цели обучения

Связать среднеквадратичное напряжение и ток в цепи переменного тока с пиковым напряжением и током и средней мощностью.

Основные выводы

Ключевые моменты

• Напомним, что в отличие от постоянного тока и напряжения, которые постоянны, переменный ток и напряжение меняются со временем.Это называется переменным током, потому что его направление меняется.
• Среднеквадратичное значение (сокращенно RMS или RMS) – это статистическая мера величины изменяющейся величины. Мы используем среднеквадратическое значение для выражения среднего тока или напряжения в системе переменного тока.
• Среднеквадратичные значения тока и напряжения (для синусоидальных систем) представляют собой пиковый ток и напряжение, полученные квадратным корнем из двух.
• Средняя мощность в цепи переменного тока является произведением среднеквадратичного значения тока и среднеквадратичного напряжения.

Ключевые термины

• среднеквадратичное значение : Квадратный корень из среднего арифметического квадратов.
• среднеквадратичный ток : среднеквадратичное значение тока, Irms = I0 / √2, где I0 – пиковый ток, в системе переменного тока
• среднеквадратичное напряжение : среднеквадратичное значение напряжения, Vrms = V0 / √2, где V0 – пиковое напряжение, в системе переменного тока

Среднеквадратичные значения и переменный ток

Напомним, что в случае переменного тока (AC) поток электрического заряда периодически меняет направление.В отличие от постоянного тока (DC), где токи и напряжения постоянны, переменные токи и напряжения меняются со временем. Напомним, что в большинстве жилых и коммерческих источников питания используется переменный ток. Часто бывает так, что нам нужно знать среднее время , равное току или напряжению. Зная ток или напряжение как функцию времени, мы можем извлечь среднеквадратичное значение с течением времени, чтобы получить средние значения.

Определение

Среднеквадратичное значение (сокращенно RMS или rms), также известное как среднее квадратичное, является статистической мерой величины переменной величины.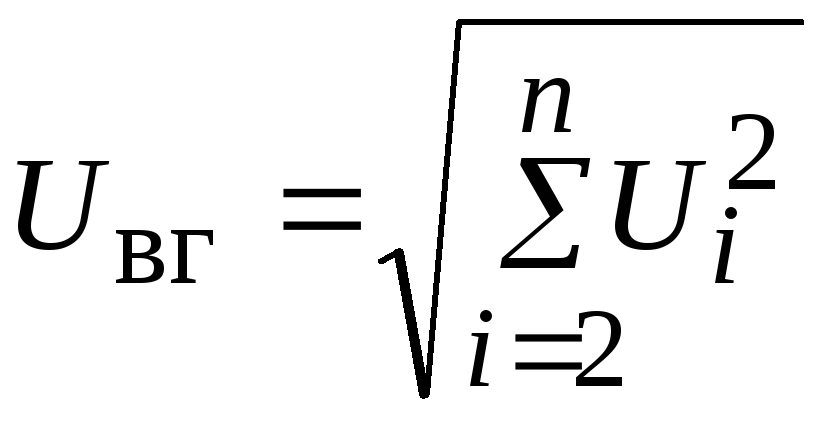 {2} \ text {dt}} [/ latex]

RMS для функции за все время ниже.{2} \ text {dt}} [/ latex]

RMS за все время периодической функции равно RMS одного периода функции. Среднеквадратичное значение непрерывной функции или сигнала можно приблизительно оценить, взяв среднеквадратичное значение серии равномерно распределенных отсчетов.

Применение к напряжению и току

Рассмотрим случай синусоидального изменения напряжения:

Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.

[латекс] \ text {V} = \ text {V} _ {0} \ text {sin} (2 \ pi \ text {ft}) [/ latex]

В – это напряжение в момент времени t , В, _0, – пиковое напряжение, а f – частота в герцах. Для этой простой цепи сопротивления I = V / R, поэтому переменный ток равен:

[латекс] \ text {I} = \ text {I} _ {0} \ text {sin} (2 \ pi \ text {ft}) [/ latex]

Здесь I – ток в момент времени t, а I ₀ = V ₀ / R – пиковый ток.{\ text {T} _ {2}}} = \ text {V} _ {0} \ sqrt {\ frac {1} {\ text {T} _ {2} – \ text {T} _ {1} } \ frac {\ text {T} _ {2} – \ text {T} _ {1}} {2}} [/ latex]

[латекс] = \ frac {\ text {V} _ {0}} {\ sqrt {2}} [/ латекс]

Точно так же вы можете обнаружить, что среднеквадратичный ток может быть выражен довольно просто:

[латекс] \ text {I} _ {\ text {rms}} = \ text {I} _0 / \ sqrt {2} [/ latex]

Обновленные уравнения цепи для AC

Многие из полученных нами уравнений для постоянного тока в равной степени применимы и к переменному току. Если нас интересует усредненный по времени результат, и соответствующие переменные выражаются как их среднеквадратичные значения.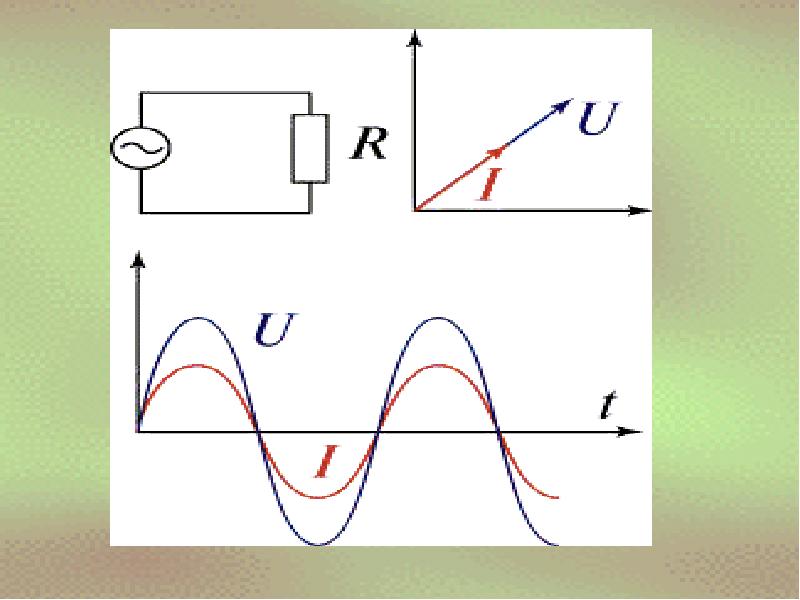 {2} \ text {R} [/ latex]

Из приведенных выше уравнений видно, что мы можем выразить среднюю мощность как функцию пикового напряжения и тока (в случае синусоидального изменения тока и напряжения):

Средняя мощность : мощность переменного тока как функция времени. Поскольку напряжение и ток здесь синфазны, их произведение неотрицательно и колеблется между нулем и I0V0. Средняя мощность (1/2) I0V0.

[латекс] \ text {P} _ {\ text {ave}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} = \ frac {\ text {I} _ {0}} {\ sqrt {2}} \ frac {\ text {V} _ {0}} {\ sqrt {2}} = \ frac {1} {2} \ text {V} _ {0} \ text {I} _ {0} [/ latex]

Среднеквадратичные значения также полезны, если напряжение изменяется в зависимости от формы волны, отличной от синусоиды, например прямоугольной, треугольной или пилообразной волны.

Формы сигналов : синусоидальные, квадратные, треугольные и пилообразные формы сигналов

Меры предосторожности в домашнем хозяйстве

Системы и устройства электробезопасности спроектированы и широко используются для снижения рисков теплового удара и поражения электрическим током.

Цели обучения

Определить основные риски, связанные с электрическими цепями, и стратегии снижения этих рисков

Основные выводы

Ключевые моменты

• Электрические цепи могут привести к перегреву и поражению электрическим током.
• Предохранители и автоматические выключатели используются для отключения токов, превышающих установленный предел безопасности, что предотвращает перегрев.
• Трехпроводная система защищает от термического воздействия и поражения электрическим током за счет использования проводов под напряжением, нейтрали и заземления, а также заземления нейтрального провода и токопроводящих корпусов приборов.
• Прежде чем вносить изменения в какую-либо схему, важно установить правильную схему цветовой кодировки для вашего региона (цвет проводов под напряжением / током, нейтрали и заземления).
• Переменный ток может вызвать ЭДС на корпусе устройства, что создает опасность поражения электрическим током, поэтому важно заземлить корпус.

Ключевые термины

• термическая опасность : опасность поражения электрическим током, вызванная перегревом (например, в резистивном элементе)
• опасность поражения электрическим током : опасность поражения электрическим током, при котором ток проходит через тело
• трехпроводная система : современная электромонтажная система с соблюдением техники безопасности; содержит провода под напряжением, нейтраль и заземление

Электробезопасность и бытовая техника

У электричества две опасности.Опасность термического воздействия возникает в случае электрического перегрева. Опасность поражения электрическим током возникает, когда через человека проходит электрический ток. Существует множество систем и устройств, предотвращающих опасность поражения электрическим током.

Цепь переменного тока, не имеющая средств безопасности. : Схема простой цепи переменного тока с источником напряжения и одним устройством, обозначенным сопротивлением R. В ней отсутствуют средства безопасности.

На практике простая цепь переменного тока без функций безопасности не является способом распределения мощности.Современная бытовая и промышленная электропроводка требует трехпроводной системы, которая имеет несколько функций безопасности. Первая функция безопасности – это знакомый автоматический выключатель (или предохранитель), предотвращающий тепловую перегрузку. Во-вторых, вокруг прибора есть защитный чехол, как у тостера или холодильника. Корпус предотвращает прикосновение людей к оголенным проводам и электрический контакт с цепью, помогая предотвратить удары.

Трехпроводная система : Трехпроводная система соединяет нейтральный провод с землей в источнике напряжения и в месте расположения пользователя.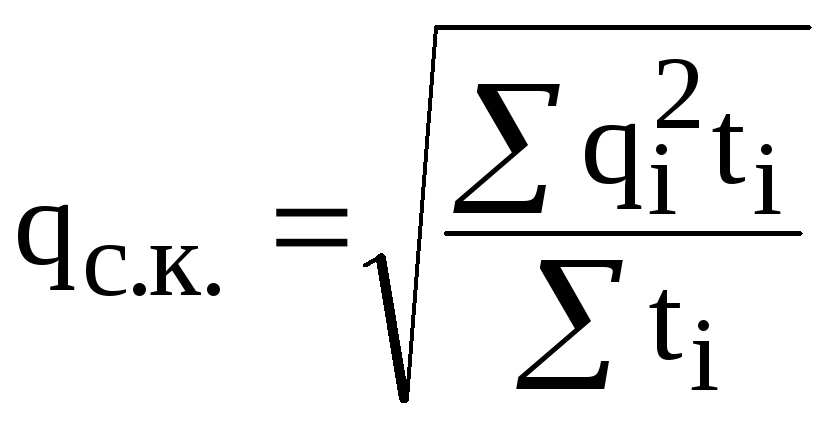 Он существует при нулевом напряжении и обеспечивает альтернативный обратный путь для тока через землю. Корпус прибора также заземлен до нуля вольт. Автоматический выключатель или предохранитель предотвращают тепловую перегрузку и находятся последовательно на активном (токоведущем / горячем) проводе. Цвет изоляции проводов зависит от региона. Важно проверить на месте, какие цветовые коды используются, даже если они использовались в одной конкретной установке.

Есть три соединения с землей или землей (земля / земля,).Заземление – это путь с низким сопротивлением непосредственно к земле. Два соединения “земля / земля” на нейтральном проводе заставляют его существовать при нулевом напряжении относительно земли, что и дало этому проводу свое название. Таким образом, к этому проводу безопасно прикасаться, даже если его изоляция отсутствует. Нейтральный провод – это обратный путь для тока, по которому следует замкнуть цепь.

Два соединения “земля / земля” обеспечивают альтернативный путь через землю для замыкания цепи, поскольку земля является хорошим проводником.Ближайшее к источнику питания соединение заземления может быть на электростанции, а другое – у пользователя. Третье соединение “земля / земля” связано с корпусом устройства через зеленый провод “земля / заземление”, заставляя корпус быть на нуле вольт. Провод под напряжением или под напряжением (под напряжением / под напряжением) подает напряжение и ток для работы прибора. Трехпроводная система подключается к прибору через трехконтактную вилку.

Трехконтактная вилка : Стандартная трехконтактная вилка может быть вставлена ​​только одним способом для обеспечения правильного функционирования трехпроводной системы.

Заглушка с тремя штырями

Трехпроводная система заменила старую двухпроводную систему, в которой отсутствует заземляющий провод. В обычных условиях изоляция на токоведущем / горячем и нейтральном проводах предотвращает размещение корпуса непосредственно внутри цепи, так что заземляющий провод может казаться двойной защитой. Однако заземление корпуса решает несколько проблем. Самая простая проблема – это износ изоляции на токоведущем / горячем проводе, который позволяет ему контактировать с корпусом.При отсутствии заземления (некоторые люди отрезают третий контакт вилки, потому что у них только устаревшие розетки с двумя отверстиями), возможно сильное поражение электрическим током. Это особенно опасно на кухне, где хорошее заземление обеспечивается за счет воды на полу или водопроводного крана.

При неповрежденном соединении “земля / земля” автоматический выключатель сработает, что потребует ремонта устройства. Некоторые приборы по-прежнему продаются с двухконтактными вилками. Эти приборы, в том числе электроинструменты с ударопрочными пластиковыми корпусами, имеют непроводящие корпуса и называются «с двойной изоляцией».«Современные двухконтактные вилки можно вставлять в асимметричную стандартную розетку только одним способом, обеспечивая правильное подключение токоведущих / горячих и нейтральных проводов.

Цветовое кодирование

Изоляционный пластик имеет цветовую кодировку для обозначения проводов под напряжением, нейтрали и заземления, но эти коды различаются во всем мире. Провода под напряжением / под напряжением могут быть коричневыми, красными, черными, синими или серыми. Нейтральные провода могут быть синими, черными или белыми. Поскольку один и тот же цвет может использоваться для токоведущих / горячих или нейтральных проводов в разных частях мира, важно подтвердить цветовую кодировку для любого данного местного региона.Единственное исключение – провод заземления, который часто бывает зеленого цвета, но может быть желтым или оголенным. «Полосатые покрытия иногда используются в интересах дальтоников.

Индукционный ток и ток утечки

Электромагнитная индукция вызывает более тонкую проблему, решаемую путем заземления корпуса. Переменный ток в приборах может вызвать на корпусе ЭДС. В случае заземления напряжение на корпусе поддерживается близким к нулю, но если корпус не заземлен, может произойти поражение электрическим током. Ток, который создается наведенной ЭДС корпуса, называется током утечки, хотя ток не обязательно проходит от резистора к корпусу.

Мощность

RMS в сравнении со средней мощностью

ВОПРОС:

Должен ли я использовать единицы среднеквадратичного значения мощности для определения или описания мощности переменного тока, связанной с моим сигналом, системой или устройством?

Ответ:

Это зависит от того, как вы определяете среднеквадратичную мощность.

Вы не хотите рассчитывать среднеквадратичное значение сигнала мощности переменного тока. Это приводит к физически бессмысленному результату.

Вы действительно используете среднеквадратичные значения напряжения и / или тока для расчета средней мощности, что дает значимые результаты.

Обсуждение:

Сколько мощности рассеивается при подаче синусоидального напряжения 1 В (среднеквадратичное значение) на резистор 1 Ом?

Это хорошо понятно ¹ , и здесь нет никаких противоречий.

Теперь давайте посмотрим, как это соотносится со значением, полученным при расчете среднеквадратичной мощности.

На рисунке 1 показан график синусоиды 1 В.Размах размаха составляет 1 В среднеквадратичное значение × 2 √2 = 2,828 В с изменением от +1,414 В до –1,414 В. ²

Рисунок 1. График синусоиды 1 В (среднеквадратичное значение).

Рисунок 2 представляет собой график мощности, рассеиваемой этой синусоидой 1 В (среднеквадратичное значение) на резисторе 1 Ом (P = V ² / R), который показывает:

Рис. 2. График мощности, рассеиваемой синусоидой 1 В (среднеквадратичное значение) на резисторе 1 Ом.

• Кривая мгновенной мощности имеет смещение на 1 Вт и колеблется от 0 Вт до 2 Вт.
• Среднеквадратичное значение этого сигнала мощности равно 1.225 Вт.
  • Одним из методов вычисления этого числа является уравнение 2 ³ :
  • Это можно проверить, используя более подробную формулу ⁴ в MATLAB ^® или Excel.
• Среднее значение этого сигнала мощности составляет 1 Вт. Это очевидно при осмотре; осциллограмма колеблется симметрично выше и ниже 1 Вт. Это же значение получается при вычислении среднего числового значения точек данных осциллограммы.
• Среднее значение мощности соответствует мощности, рассчитанной с использованием среднеквадратичного значения напряжения.

Мощность, рассеиваемая синусоидальным среднеквадратичным значением 1 В на резисторе 1 Ом, составляет 1 Вт, а не 1,225 Вт. Таким образом, именно средняя мощность дает правильное значение, и, следовательно, именно средняя мощность имеет физическое значение. Среднеквадратичная мощность (как определено здесь) не имеет очевидного полезного значения (не имеет очевидного физического / электрического значения), кроме как величина, которую можно рассчитать как упражнение.

Выполнение того же анализа с использованием синусоидального тока 1 А, действующего через резистор 1 Ом, является тривиальным упражнением.Результат тот же.

Источники питания для интегральных схем (ИС) обычно являются источниками постоянного тока, поэтому среднеквадратичная мощность не является проблемой для питания ИС. Для постоянного тока среднее и среднеквадратичное значение такие же, как и для постоянного тока. Важность использования средней мощности, в отличие от среднеквадратичной мощности, как определено в этом документе, относится к мощности, связанной с изменяющимися во времени напряжением и током, то есть шумом, радиочастотными сигналами и генераторами.

Используйте среднеквадратичное значение напряжения и / или среднеквадратичного значения тока для расчета средней мощности, что дает значимые значения мощности.

¹ Мощность, рассеиваемая напряжением на резисторе, является фундаментальным соотношением, которое легко выводится из закона Ома (V = IR) и основных определений напряжения (энергия / единица заряда) и тока (единица заряда / времени). Напряжение × ток = энергия / время = мощность

² Размах амплитуды синусоиды – это среднеквадратичное значение, умноженное на 2√2. Для синусоидального напряжения V p-p = V rms × 2√2, где V p-p – размах напряжения, а V rms – среднеквадратичное значение напряжения.Это хорошо известная связь, описанная в бесчисленных учебниках, а также здесь: en.wikipedia.org/wiki/Root_mean_square.

³ Это адаптировано из среднеквадратичного значения, рассчитанного из постоянного значения смещения постоянного тока плюс отдельное среднеквадратичное значение переменного тока, а также из примечания по применению «Улучшите измерения среднеквадратичного значения переменного тока с помощью цифрового мультиметра» от Keysight.

⁴ Стандартное определение в учебнике – это один из примеров более подробной формулы.

AMCI: Advanced Micro Controls Inc :: Драйверы шагового двигателя: среднеквадратичное значение или пиковый ток?

Драйверы шагового двигателя

определяют величину тока, который они выводят на шаговый двигатель, в виде RMS или пикового тока.Насколько они разные?

В этом руководстве вы познакомитесь с разницей между двумя типами тока, используемыми при указании шаговых приводов и двигателей. Вы узнаете о взаимосвязи между среднеквадратичным значением и пиковым током и о том, почему это соединение важно при настройке систем шагового управления.

Изучив технические преимущества среднеквадратичного значения по сравнению с пиковым током, вы поймете, почему производители шаговых двигателей указывают кривые крутящего момента и максимальные значения только в среднеквадратичном токе, а не в пиковых значениях тока, при этом также используя драйвер шагового двигателя, указанный в среднеквадратичном токе.Какая для вас польза? Это упрощает согласование шагового двигателя с драйвером шагового двигателя в любом приложении. Следующие несколько абзацев проливают свет на это утверждение.

RMS, что означает среднеквадратическое значение, является основным измерением величины сигнала переменного тока.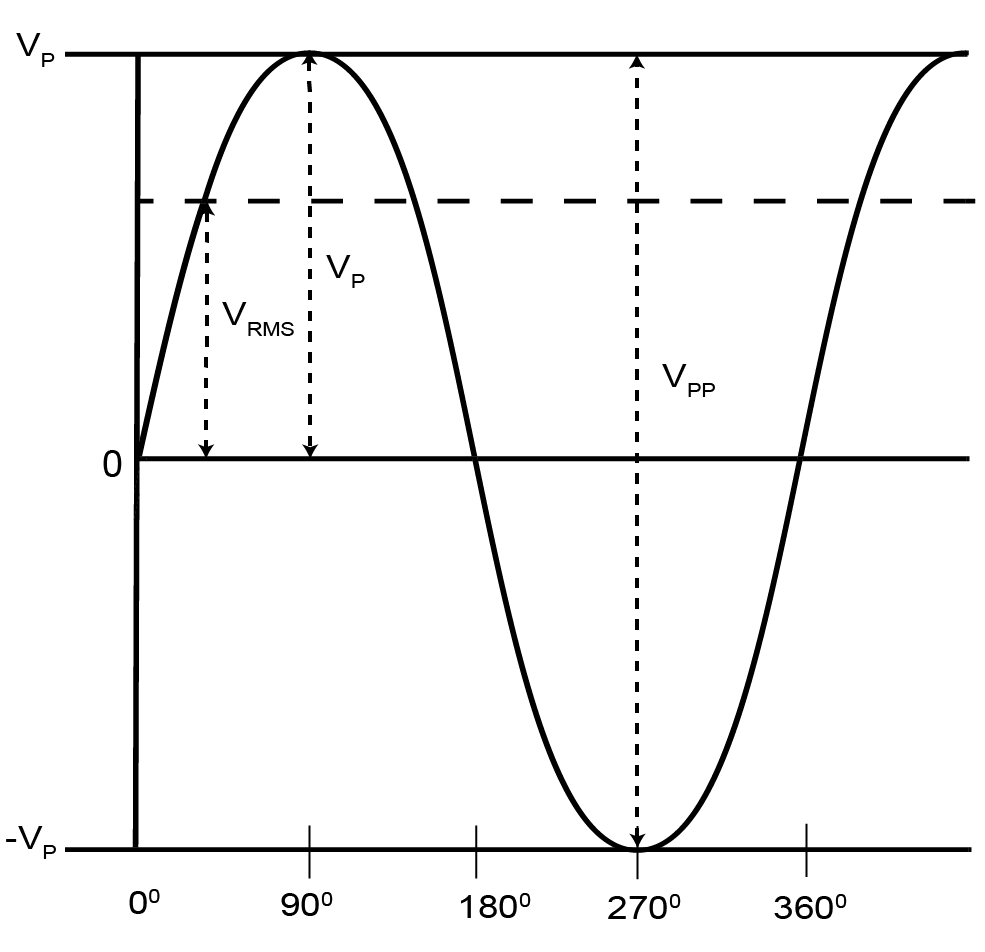 Среднеквадратичное значение равно количеству постоянного тока (DC), необходимого для выработки эквивалентного количества тепла при нагрузке того же размера. Форма волны переменного тока переменного тока не важна.Значения RMS упрощают расчет средней мощности и энергии. Однако пиковые значения, которые дают только максимальное значение сигнала переменного тока, требуют дополнительной информации и могут сравниваться со среднеквадратичными значениями, только если форма сигнала известна.

Например, когда форма волны переменного тока является идеальной синусоидой, соотношение между среднеквадратичным значением и пиковым током будет следующим:

RMS-ток = Пиковый ток x 0,707 или Пиковый ток = RMS-ток x 1,414.

Соотношение между среднеквадратичным значением и пиковым током шагового двигателя зависит от конфигурации драйвера.Три общих режима работы драйверов шаговых двигателей включают в себя полный шаг, полушаговый режим и микрошаговый режим. Если вы посмотрите на осциллограф формы сигналов тока этих трех режимов, все они будут выглядеть по-разному, представляя соотношение между среднеквадратичным значением и пиковым током:

• Идеальная форма сигнала с полным шагом (Рисунок A.)
• Идеальный полушаговый Форма волны (Рисунок B.)
• Идеальный микрошаговый форма волны (Рисунок C.)

Все шаговые двигатели рассчитаны на среднеквадратичный ток, и при полном шаге, 200 шагов / оборот, нет разницы между драйверами шаговых двигателей, которые выводят среднеквадратичный ток, и теми, которые выводят пиковый ток. Драйвер шагового двигателя просто выводит значение тока, которое требуется двигателю. В следующем примере предположим, что среднеквадратичное значение 1,0 А:

.

Рисунок A.

Однако при половинном шаге, 400 шагов / оборот, среднеквадратичный и пиковый ток не равны, как показано на рисунке B.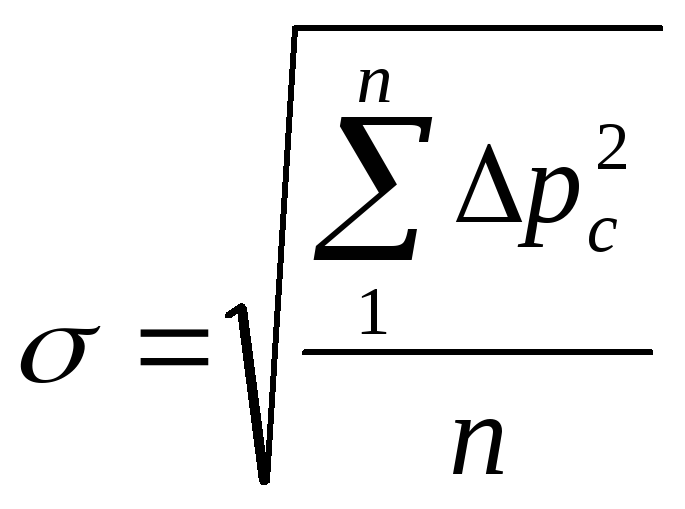 Если пиковый драйвер не увеличит свой выходной ток на 15% (как показано на рисунке B.), двигатель не получит свой номинальный среднеквадратичный ток 1,0 А и, следовательно, не будет генерировать весь крутящий момент, который он способен обеспечить.

Рисунок B.

Микрошаговый сигнал показывает еще большую разницу между среднеквадратичным значением и пиковым током. В этом случае значение пикового тока должно быть увеличено примерно на 41% (как показано на рисунке С.), чтобы равняться требуемому среднеквадратичному току двигателя 1,0 А.

Рисунок C.

RMS Приводы с управлением по току будут отправлять на двигатель выбранное среднеквадратичное значение тока независимо от формы сигнала тока. Это может быть не так с приводами, управляемыми пиковым током, которые выдают разные среднеквадратичные токи в зависимости от формы сигнала.

В заключение, поскольку шаговые двигатели определяют только кривые крутящего момента и максимальные номинальные значения в среднеквадратичном токе, использование шагового драйвера, который также указан в среднеквадратичном токе, вместо того, который указан в пиковом токе, упрощает согласование шагового двигателя с шаговым драйвером в любое приложение.

Для удобства AMCI указывает все свои шаговые приводы и двигатели как в среднеквадратических, так и в пиковых значениях тока (если применимо). Чистый результат = Гарантированная совместимость, производительность и надежность.

Среднеквадратичное значение переменного тока – определение, формула и расчет

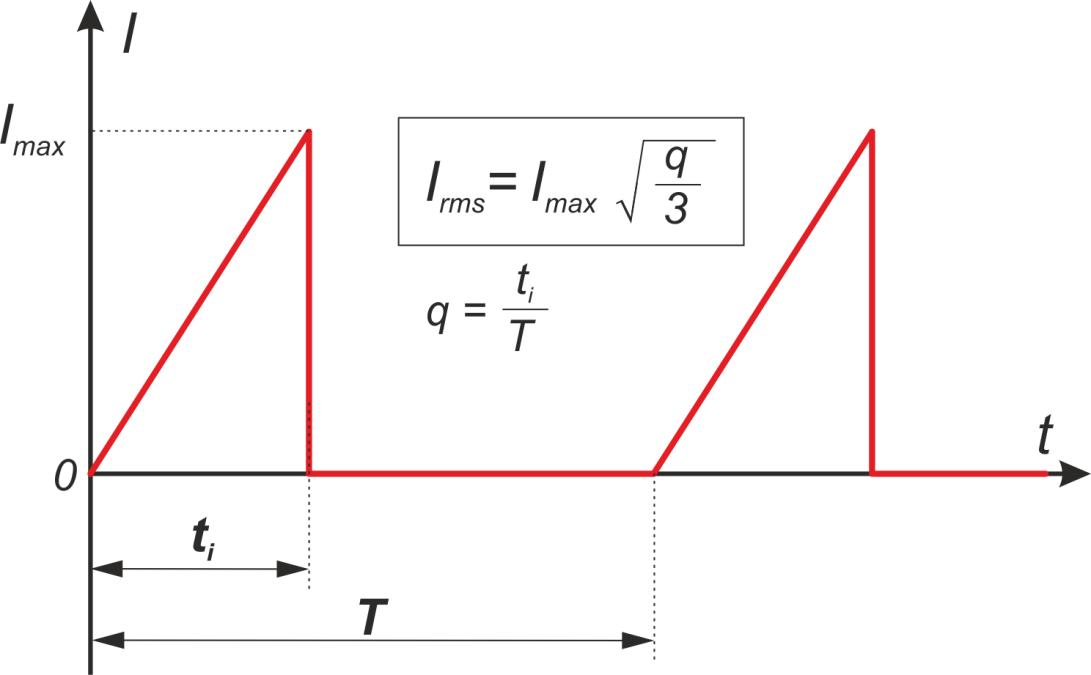
Определение

Среднеквадратичное значение (RMS) переменного тока определяется как установившийся или постоянный ток, который при протекании по цепи в течение заданного периода времени производит такое же тепло, как и ток переменного тока, протекающий по той же цепи в течение того же периода времени. .Среднеквадратичное значение также известно как действующее значение или виртуальное значение переменного тока.

Расчет среднеквадратичного значения

Предположим, что через цепь протекает переменный ток i = I _м Sinωt, и нас интересует вычисление среднеквадратичного или среднеквадратичного значения этого тока.

Среднеквадратичное или среднеквадратичное значение можно рассчитать двумя разными методами: методом средней ординаты и аналитическим методом .

Оба эти метода можно удобно использовать для вычисления среднеквадратичных значений симметричных или несимметричных синусоидальных или несинусоидальных сигналов.Метод средней ординаты очень удобен для симметричных несинусоидальных сигналов. Давайте обсудим каждый из методов по очереди.

Метод средней оси ординат:

В методе средней оси ординат временная развертка положительной половины сигнала переменного тока делится на n равных интервалов времени, каждый длительностью (T / n) секунд.

На приведенном выше рисунке весь положительный полупериод разделен на n равных интервалов времени. Вы можете спросить, почему мы учитывали только положительную половину.Это потому, что, поскольку мы собираемся вычислить тепло, выделяемое переменным током, нам нужно применить формулу I ² R. Возведение в квадрат тока (I ² ) уравняет положительный и отрицательный цикл симметричной формы волны. Поэтому будет разумным решением рассматривать только положительный цикл.

Давайте теперь продолжим, чтобы найти тепло, выделяемое в цепи из-за протекания переменного тока, форма волны, показанная на рисунке выше.

Тепло, произведенное за 1 ^{-й интервал времени} = i ₁ ² R (T / n) Джоуль

Тепло, произведенное во временном интервале 2 ^nd = i ₂ ² R (T / n) Джоуль

………………………………………………………. .

……………………………………………………… ..

Тепло, произведенное за n ^{-й интервал времени} = i _n ² R (T / n) Джоуль

Таким образом, общее количество тепла, произведенного этим током, равно

.

i ₁ ² R (T / n) + i ₂ ² R (T / n) + …… + i _n ² R (T / n) …………… (1)

Пусть среднеквадратичное значение этого тока равно I _{действующее значение} . Этот постоянный ток I _rms должен генерировать тепло Q, равное I _rms ² RT.Следовательно, согласно определению действующего значения тока,

Из приведенного выше выражения действующего значения ясно, что действующее значение переменного тока равно квадратному корню из среднего квадратов мгновенных значений тока. Хотя приведенная выше формула была получена для переменного тока, она также применима и для переменного напряжения. Единственная разница в том, что вместо мгновенных значений тока следует брать мгновенное значение напряжения.

Аналитический метод

Мне лично нравится этот метод расчета среднеквадратичного значения величин переменного тока. По сути, этот метод не отличается от метода средней ординаты. В методе средних ординат мы вычисляли действующее значение, рассматривая дискретные значения мгновенного тока в разном временном интервале. Но в аналитическом методе мы используем интегрирование для получения среднего квадрата мгновенных значений тока, а затем находим квадратный корень из него, чтобы получить среднеквадратичное значение.

Чтобы вычислить среднеквадратичное значение, нам нужно сначала вычислить среднее значение квадрата переменного тока / напряжения за один период времени. Затем находим квадратный корень из вычисленного среднего значения. Это дает среднеквадратичное значение (СКЗ). Это все, что нам нужно сделать.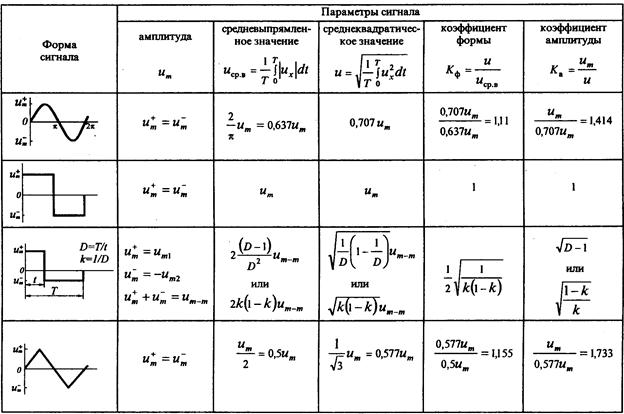

Так как среднее значение любой функции f (x), имеющей период времени T, равно

Следовательно, среднее значение квадрата f (x),

Следовательно, формула для среднеквадратичного значения

.

Эта формула для расчета среднеквадратичного значения очень важна и может применяться для сигналов любого типа.Я лично этим пользуюсь. Я никогда не использую метод средней оси ординат. Я рекомендую вам использовать эту формулу. Прочтите «Как найти среднеквадратичное значение любой функции», чтобы узнать, как эта формула может оказаться лучшим оружием для расчета среднеквадратичного значения.

Действующее значение стандартного синусоидального переменного тока

Ну, все мы знаем, что стандартный переменный синусоидальный ток записывается как i = I _m Sinωt. Нас просят найти действующее значение этого тока. Как вы рассчитываете? Я буду использовать аналитический метод или, откровенно говоря, формулу для среднеквадратичного значения.На рисунке ниже показана форма синусоидального сигнала переменного тока.

Шаг-1: Определите период времени T. сигнала.

Период времени T сигнала равен 2π, как видно из его формы сигнала.

Шаг 2: Используйте формулу.

В нашем примере мы положим в формулу T = 2π и f (x) = I _m Sinωt.

RMS Значение синусоидального переменного тока рассчитывается, как показано ниже.

Таким образом, действующее значение синусоидального переменного тока или напряжения равно пиковому значению тока / напряжения, деленному на √2.

Среднеквадратичное значение комплексной волны

Давайте рассмотрим сложную волну, чтобы проиллюстрировать метод или формулу для расчета среднеквадратичного значения. Предположим, что ток, имеющий уравнение i = A1Sinωt + A2Sin3ωt + A3Sin5ωt, протекает через сопротивление R. Поскольку этот ток состоит из основной составляющей тока вместе с гармонической составляющей 3 ^rd и 5 ^th , эффект нагрева такого сложного тока для один период времени T будет обусловлен индивидуальным тепловым эффектом основной гармоники, а также 3 ^-й -й и 5 ^-й гармонических составляющих.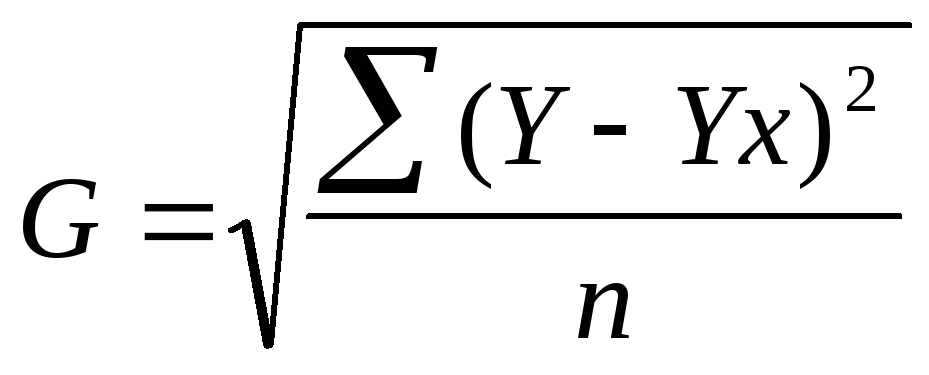

Нагрев за счет основного тока = (A1 / √2) ² RT

Нагрев из-за 3 ^rd Гармонический ток = (A2 / √2) ² RT

Нагрев из-за 5 ^th Гармонический ток = (A3 / √2) ² RT

Следовательно, общий нагрев комплексным током будет суммой отдельных тепловых эффектов основной и 3 ^-й и 5 ^-й гармонических составляющих тока.

Если I – среднеквадратичное значение комплексного тока, то эквивалентный эффект нагрева будет I ² RT.Но по определению это должно быть равно нагреву, фактически производимому комплексным током. Следовательно,

Следовательно, для сложной волны правило выглядит следующим образом:

«Действующее значение комплексной волны тока или напряжения равно квадратному корню из суммы квадратов действующего значения ее отдельных компонентов».

Формула среднеквадратичного значения

Формулы для среднеквадратичного значения приведены в таблице ниже.

Измерений амплитуды переменного тока | Базовая теория переменного тока

На данный момент мы знаем, что переменное напряжение меняется по полярности, а переменный ток – по направлению.Мы также знаем, что переменный ток может изменяться множеством различных способов, и, отслеживая изменение во времени, мы можем построить его в виде «формы волны».

Мы можем измерить скорость чередования, измерив время, необходимое для развития волны, прежде чем она повторится («период»), и выразить это как количество циклов в единицу времени или «частоту». В музыке частота такая же, как pitch , что является важным свойством, отличающим одну ноту от другой.

Однако мы сталкиваемся с проблемой измерения, если пытаемся выразить, насколько велика или мала величина переменного тока.С постоянным током, где величины напряжения и тока обычно стабильны, у нас нет проблем с выражением того, сколько напряжения или тока у нас есть в любой части цепи.

Но как дать единичное измерение величины чему-то, что постоянно меняется?

Способы выражения величины сигнала переменного тока

Один из способов выразить интенсивность или величину (также называемую амплитудой ) величины переменного тока – это измерить высоту его пика на графике формы сигнала.Это известно как значение пика или пика сигнала переменного тока: Рисунок ниже

Пиковое напряжение формы волны.

Другой способ – измерить общую высоту между противоположными вершинами. Это известно как размах сигнала (размах) (P-P) для сигнала переменного тока: Рисунок ниже

Размах напряжения формы волны.

К сожалению, любое из этих выражений амплитуды сигнала может вводить в заблуждение при сравнении двух разных типов волн.Например, прямоугольная волна с пиком 10 вольт, очевидно, представляет собой большее количество напряжения в течение большего количества времени, чем треугольная волна с пиком 10 вольт.

Эффекты этих двух напряжений переменного тока, питающих нагрузку, будут совершенно разными: Рисунок ниже

Прямоугольная волна дает больший эффект нагрева, чем такая же треугольная волна пикового напряжения.

Один из способов выразить амплитуду различных форм волны более эквивалентным способом – это математически усреднить значения всех точек на графике формы волны до единого совокупного числа.Это измерение амплитуды известно как среднее значение сигнала.

Если мы усредним все точки на осциллограмме алгебраически (то есть, чтобы рассмотреть их знак , положительный или отрицательный), среднее значение для большинства сигналов технически равно нулю, потому что все положительные точки компенсируют все отрицательные точки по полный цикл: рисунок ниже

Среднее значение синусоиды равно нулю.

Это, конечно, будет верно для любой формы волны, имеющей участки равной площади выше и ниже «нулевой» линии графика. Однако, как практическая мера совокупного значения формы сигнала , «среднее» обычно определяется как математическое среднее абсолютных значений всех точек за цикл.

Другими словами, мы вычисляем практическое среднее значение сигнала, рассматривая все точки на волне как положительные величины, как если бы форма сигнала выглядела следующим образом: Рисунок ниже

Форма сигнала, измеренная измерителем «среднего отклика» переменного тока.

Нечувствительные к полярности механические движения счетчика (счетчики, рассчитанные на одинаковую реакцию на положительные и отрицательные полупериоды переменного напряжения или тока) регистрируются пропорционально (практическому) среднему значению формы волны, потому что инерция стрелки по отношению к напряжению пружина естественным образом усредняет силу, создаваемую изменяющимися значениями напряжения / тока с течением времени.

И наоборот, чувствительные к полярности движения измерителя бесполезно вибрируют при воздействии переменного напряжения или тока, их стрелки быстро колеблются около нулевой отметки, указывая истинное (алгебраическое) среднее значение нуля для симметричной формы волны. Когда в этом тексте упоминается «среднее» значение формы сигнала, предполагается, что подразумевается «практическое» определение среднего значения, если не указано иное.

Другой метод получения совокупного значения амплитуды сигнала основан на способности сигнала выполнять полезную работу при приложении к сопротивлению нагрузки.К сожалению, измерение переменного тока, основанное на работе, выполняемой осциллограммой, не совпадает со «средним» значением этой формы сигнала, потому что мощность , рассеиваемая данной нагрузкой (работа, выполняемая в единицу времени), не прямо пропорциональна величине того и другого. приложенное к нему напряжение или ток.

Напротив, мощность пропорциональна квадрату напряжения или тока, приложенного к сопротивлению (P = E ² / R и P = I ² R).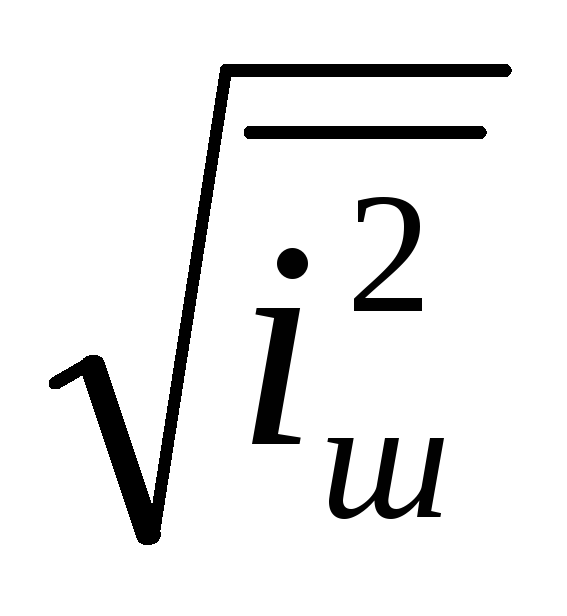 Хотя математика такого измерения амплитуды может быть непростой, польза от этого есть.

Рассмотрим ленточную пилу и лобзик, две части современного деревообрабатывающего оборудования. Пилы обоих типов режут дерево с помощью тонкого зубчатого металлического полотна с моторным приводом. Но в то время как ленточная пила использует непрерывное движение полотна для резки, лобзик использует возвратно-поступательное движение.

Сравнение переменного тока (AC) с постоянным током (DC) можно сравнить со сравнением этих двух типов пил: Рисунок ниже

Ленточно-лобзиковая аналогия постоянного и переменного тока.

Проблема попытки описать изменяющиеся величины переменного напряжения или тока в одном совокупном измерении также присутствует в этой аналогии с пилой: как бы мы могли выразить скорость полотна лобзика? Полотно ленточной пилы движется с постоянной скоростью, подобно тому, как проталкивается постоянное напряжение или постоянный ток с постоянной величиной. С другой стороны, полотно лобзика движется вперед и назад, скорость его вращения постоянно меняется. Более того, возвратно-поступательное движение любых двух лобзиков может быть неодинаковым, в зависимости от механической конструкции пил.

Один лобзик может перемещать лезвие синусоидально, а другой – треугольником. Оценка лобзика на основе его максимальной скорости пикового полотна может ввести в заблуждение при сравнении одного лобзика с другим (или лобзика с ленточной пилой!). Несмотря на то, что эти разные пилы перемещают свои полотна по-разному, они равны в одном отношении: все они режут древесину, и количественное сравнение этой общей функции может служить общей основой для оценки скорости полотна.

Представьте себе лобзик и ленточную пилу бок о бок, оснащенные одинаковыми лезвиями (одинаковым шагом зубьев, углом и т. Д.), Одинаково способными резать одинаковую толщину одного и того же вида древесины с одинаковой скоростью. Можно сказать, что эти две пилы были эквивалентны или равны по своей режущей способности. Можно ли использовать это сравнение, чтобы приписать «эквивалентную» скорость полотна ленточной пилы возвратно-поступательному движению полотна лобзика; связать эффективность лесозаготовки одного с другим?

Это общая идея, используемая для присвоения измерения «эквивалента постоянного тока» любому переменному напряжению или току: независимо от величины постоянного напряжения или тока, будет происходить такое же количество рассеивания тепловой энергии через равное сопротивление: Рисунок ниже

Среднеквадратичное напряжение вызывает такой же нагревательный эффект, как и такое же напряжение постоянного тока

Какое значение имеет среднеквадратичное значение (RMS) для переменного тока?

В двух схемах, приведенных выше, у нас одинаковое сопротивление нагрузки (2 Ом), рассеивающее одинаковое количество энергии в виде тепла (50 Вт), одна питается от переменного тока, а другая от постоянного тока.Поскольку изображенный выше источник переменного напряжения эквивалентен (с точки зрения мощности, подаваемой на нагрузку) 10-вольтовой батарее постоянного тока, мы бы назвали это «10-вольтовым» источником переменного тока.

Более конкретно, мы бы обозначили его значение напряжения как 10 вольт RMS . Квалификатор «RMS» означает Среднеквадратичное значение , алгоритм, используемый для получения значения эквивалента постоянного тока из точек на графике (по сути, процедура состоит из возведения в квадрат всех положительных и отрицательных точек на графике формы сигнала, усреднения этих квадратов значений. , а затем извлечение квадратного корня из этого среднего, чтобы получить окончательный ответ).

Иногда вместо «среднеквадратичного значения» используются альтернативные термины эквивалент или эквивалент постоянного тока , но количество и принцип одинаковы.

Измерение амплитуды

RMS – лучший способ связать величины переменного тока с величинами постоянного тока или другими величинами переменного тока с различной формой волны при измерении электрической мощности.

Из других соображений лучше всего использовать измерения от пика до пика. Например, при определении правильного размера провода (допустимой нагрузки) для передачи электроэнергии от источника к нагрузке лучше всего использовать измерение среднеквадратичного тока, потому что основной проблемой, связанной с током, является перегрев провода, который является функцией рассеивание мощности, вызванное током через сопротивление провода.

Однако при оценке изоляторов для работы в высоковольтных системах переменного тока измерения пикового напряжения являются наиболее подходящими, поскольку здесь основной проблемой является «пробой» изолятора, вызванный кратковременными скачками напряжения независимо от времени.

Инструменты, используемые для измерения амплитуды сигнала

Измерения пиков и размаха лучше всего выполнять с помощью осциллографа, который может захватывать пики формы сигнала с высокой степенью точности благодаря быстрому срабатыванию электронно-лучевой трубки в ответ на изменения напряжения.Для измерений RMS будут работать аналоговые измерительные приборы (D’Arsonval, Weston, железная лопасть, электродинамометр), если они были откалиброваны в значениях RMS.

Поскольку механическая инерция и демпфирующие эффекты движения электромеханического измерителя делают отклонение стрелки естественным образом пропорциональным среднему значению переменного тока, а не истинному среднеквадратичному значению, аналоговые измерители должны быть специально откалиброваны (или неправильно откалиброваны, в зависимости от от того, как вы на это смотрите), чтобы указать напряжение или ток в единицах RMS.

Точность этой калибровки зависит от предполагаемой формы волны, обычно синусоидальной.

Электронные счетчики, специально разработанные для измерения среднеквадратичных значений, лучше всего подходят для этой задачи. Некоторые производители инструментов разработали хитроумные методы определения среднеквадратичного значения любой формы волны. Один из таких производителей производит измерители True-RMS с крошечным резистивным нагревательным элементом, питаемым напряжением, пропорциональным измеряемому.

Эффект нагрева этого элемента сопротивления измеряется термически, чтобы получить истинное среднеквадратичное значение без каких-либо математических вычислений, только законы физики в действии в соответствии с определением среднеквадратичного значения.Точность этого типа измерения RMS не зависит от формы волны.

Взаимосвязь пика, размаха, среднего и среднеквадратичного значения

Для «чистых» сигналов существуют простые коэффициенты преобразования для приравнивания значений пикового, разностного, среднего (практического, а не алгебраического) и среднеквадратичного значений друг к другу:

Коэффициенты преобразования для распространенных сигналов.

В дополнение к измерениям RMS, среднего, пика (пика) и размаха сигнала переменного тока существуют соотношения, выражающие пропорциональность между некоторыми из этих основных измерений.Пик-фактор сигнала переменного тока, например, представляет собой отношение его пикового (пикового) значения, деленного на его среднеквадратичное значение.

Форм-фактор сигнала переменного тока – это отношение его среднеквадратичного значения к его среднему значению. Сигналы прямоугольной формы всегда имеют пик и коэффициент формы, равные 1, поскольку пик такой же, как среднеквадратичное и среднее значения. Синусоидальные сигналы имеют среднеквадратичное значение 0,707 (величина, обратная квадратному корню из 2) и форм-фактор 1,11 (0,707 / 0.636).

Сигналы треугольной и пилообразной формы имеют среднеквадратичные значения 0,577 (величина, обратная квадратному корню из 3) и форм-фактор 1,15 (0,577 / 0,5).

Имейте в виду, что константы преобразования, показанные здесь для пиковых, среднеквадратичных и средних амплитуд синусоидальных, прямоугольных и треугольных волн, верны только для чистых форм этих форм волны. Среднеквадратичные и средние значения искаженных форм волн не связаны одними и теми же соотношениями: Рисунок ниже

Сигналы произвольной формы не имеют простого преобразования.

Это очень важная концепция, которую необходимо понимать при использовании аналогового движения измерителя Д’Арсонваля для измерения переменного напряжения или тока. Аналоговый механизм Д’Арсонваля, откалиброванный для индикации среднеквадратичной амплитуды синусоидальной волны, будет точным только при измерении чистых синусоидальных волн.

Если форма сигнала измеряемого напряжения или тока не является чистой синусоидой, показание измерителя не будет истинным среднеквадратичным значением формы сигнала, поскольку степень отклонения стрелки в аналоговом перемещении измерителя Д’Арсонваля пропорционально среднему значению сигнала, а не среднеквадратичному значению.

Калибровка измерителя

RMS получается путем «перекоса» диапазона измерителя так, чтобы он отображал небольшое кратное среднему значению, которое будет равно среднеквадратичному значению для определенной формы волны, а – только для определенной формы волны .

Поскольку форма синусоидальной волны является наиболее распространенной в электрических измерениях, она является формой волны, принятой для калибровки аналогового измерителя, а малое кратное, используемое при калибровке измерителя, составляет 1,1107 (коэффициент формы: 0,707 / 0,636: отношение среднеквадратичных значений деленное на среднее значение для синусоидального сигнала).

Любая форма волны, кроме чистой синусоидальной волны, будет иметь другое соотношение среднеквадратичных и средних значений, и, таким образом, измеритель, откалиброванный для синусоидального напряжения или тока, не будет показывать истинное среднеквадратичное значение при считывании несинусоидальной волны. Имейте в виду, что это ограничение применяется только к простым аналоговым счетчикам переменного тока, не использующим технологию True-RMS.

ОБЗОР:

• Амплитуда сигнала переменного тока – это его высота, как показано на графике во времени.Измерение амплитуды может принимать форму пика, размаха, среднего или среднеквадратичного значения.
• Пиковая амплитуда – это высота сигнала переменного тока, измеренная от нулевой отметки до наивысшей положительной или самой низкой отрицательной точки на графике. Также известен как гребень амплитуда волны .
• Полная амплитуда – это общая высота сигнала переменного тока, измеренная от максимальных положительных до максимальных отрицательных пиков на графике. Часто обозначается как «П-П».
• Средняя амплитуда – это математическое «среднее» всех точек сигнала за период одного цикла. Технически, средняя амплитуда любой формы волны с участками равной площади выше и ниже «нулевой» линии на графике равна нулю. Однако в качестве практической меры амплитуды среднее значение сигнала часто рассчитывается как математическое среднее абсолютных значений всех точек (принимая все отрицательные значения и считая их положительными). Для синусоиды среднее значение, вычисленное таким образом, приблизительно равно 0.637 пикового значения.
• «Среднеквадратичное значение» означает среднеквадратическое значение и представляет собой способ выражения величины переменного напряжения или тока в терминах, функционально эквивалентных постоянному току. Например, среднеквадратичное значение 10 вольт переменного тока – это величина напряжения, при которой через резистор заданного значения рассеивается такое же количество тепла, как и у источника питания постоянного тока на 10 вольт. Также известен как «эквивалент» или «эквивалент постоянного тока» для переменного напряжения или тока. Для синусоидальной волны среднеквадратичное значение составляет примерно 0,707 от его пикового значения.
• Пик-фактор сигнала переменного тока – это отношение его пика (пика) к его среднеквадратичному значению.
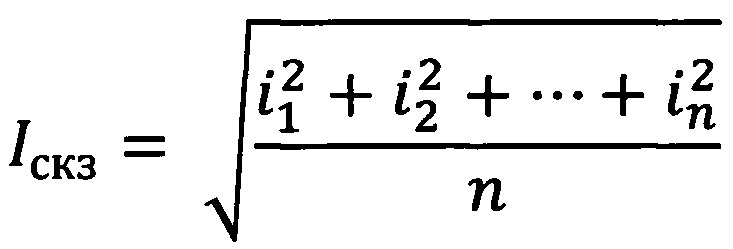
• Форм-фактор сигнала переменного тока – это отношение его среднеквадратичного значения к его среднему значению.
• Аналоговые, электромеханические движения счетчика реагируют пропорционально среднему значению переменного напряжения или тока. Когда требуется индикация среднеквадратичного значения, калибровка измерителя должна быть соответственно «искажена». Это означает, что точность показаний RMS электромеханического измерителя зависит от чистоты формы волны: от того, точно ли она совпадает с формой волны, используемой при калибровке.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Определение действующего значения тока в физике.

Примеры среднеквадратичного значения тока в следующих разделах:

• Цепь серии

  RLC: на больших и малых частотах; Фазорная диаграмма

  • Путем объединения закона Ома (Irms = Vrms / Z; Irms и Vrms равны rms ток и напряжение) и выражение для импеданса Z из:
  • Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при подаче синусоидального напряжения ток , , отстает от напряжения на 90º по фазе в цепи с катушкой индуктивности, в то время как ток , , опережает напряжение. на 90∘ в цепи с конденсатором.
  • Следовательно, rms ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
  • Следовательно, rms ток будет дан как Vrms / XC, а ток опережает напряжение почти на 90 °.

• Среднеквадратичное значение

  • В отличие от постоянного тока (DC), где токи и напряжения постоянны, ток переменного тока и напряжения меняются с течением времени.
  • Среднеквадратичное значение (сокращенно RMS или rms ), также известное как среднее квадратичное, является статистической мерой величины переменной величины.
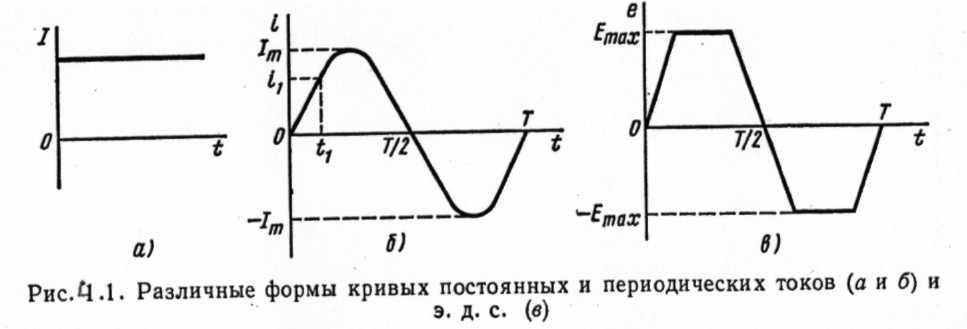
  • Здесь I – ток , в момент времени t, а I0 = V0 / R – пиковый ток , .
  • Теперь, используя приведенное выше определение, давайте вычислим напряжение среднеквадратическое значение и среднеквадратичное значение ток .
  • Если нас интересует усредненный по времени результат, и соответствующие переменные выражаются как их значения rms .
• Конденсаторы

  в цепях переменного тока: емкостное сопротивление и фазовые диаграммы

  • Напряжение на конденсаторе отстает от тока .
  • Мы говорим, что ток и напряжение совпадают по фазе.
  • Поскольку подается переменное напряжение, существует среднеквадратичных значений тока , но он ограничен конденсатором.
  • Считается, что это эффективное сопротивление конденсатора переменному току, и поэтому среднеквадратичное значение ток Irms в цепи, содержащей только конденсатор C, по другой версии закона Ома определяется как $ I_ { среднеквадратичное значение } = \ frac {V_ { rms }} {X_C} $, где Vrms – это напряжение rms .
  • Поскольку напряжение на конденсаторе отстает от тока , вектор, представляющий ток , и напряжение, будет иметь вид.

• Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы

  • График показывает напряжение и ток как функции времени.
  • Ток затем становится отрицательным, снова вслед за напряжением.
  • Ток отстает от напряжения, так как индукторы противодействуют изменению тока .
  • Изменение тока индуцирует ЭДС.
  • Среднеквадратичное значение ток Irms через катушку индуктивности L определяется версией закона Ома: $ I_ { rms } = \ frac {V_ { rms }} {X_L} $, где Vrms – это rms напряжение на катушке индуктивности и $ X_L = 2 \ pi \ nu L $ с $ \ nu $ частотой источника переменного напряжения в герцах.

• Резонанс в цепях RLC

  • , где Irms и Vrms равны rms ток и напряжение соответственно.
  • Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график тока как функции частоты, иллюстрирующий резонансный пик в Irms при $ \ nu_0 = f_0 $.
  • График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления.

• Люди и опасность поражения электрическим током

  • Опасность поражения электрическим током возникает, когда электрический ток проходит через человека.
  • Человек может ощущать не менее 1 мА ( среднеквадратичное значение ) переменного тока при 60 Гц и не менее 5 мА постоянного тока .
  • Ток , если он достаточно высок, может вызвать повреждение ткани или фибрилляцию, что приведет к остановке сердца. 60 мА переменного тока ( среднеквадратичное значение , 60 Гц) или 300-500 мА постоянного тока могут вызвать фибрилляцию. Потенциальная сила удара зависит от путей через тело, которые проходят токи и .
  • Current : чем выше значение current , тем больше вероятность летального исхода.
  • Поскольку ток пропорционален напряжению при фиксированном сопротивлении (закон Ома), высокое напряжение является косвенным риском для создания более высоких токов .

• Фазовый угол и коэффициент мощности

  • Импеданс – это переменный ток ( переменного тока, ), аналог сопротивления в цепи постоянного тока.
  • (Представим мгновенный ток как i (t).)
  • мы замечаем, что напряжение $ v (t) $ и ток $ $ i (t) $ имеют разность фаз $ \ phi $.
  • Поскольку напряжение и ток не совпадают по фазе, мощность, рассеиваемая схемой, не равна: (пиковое напряжение) умноженное на (пиковый ток , ).
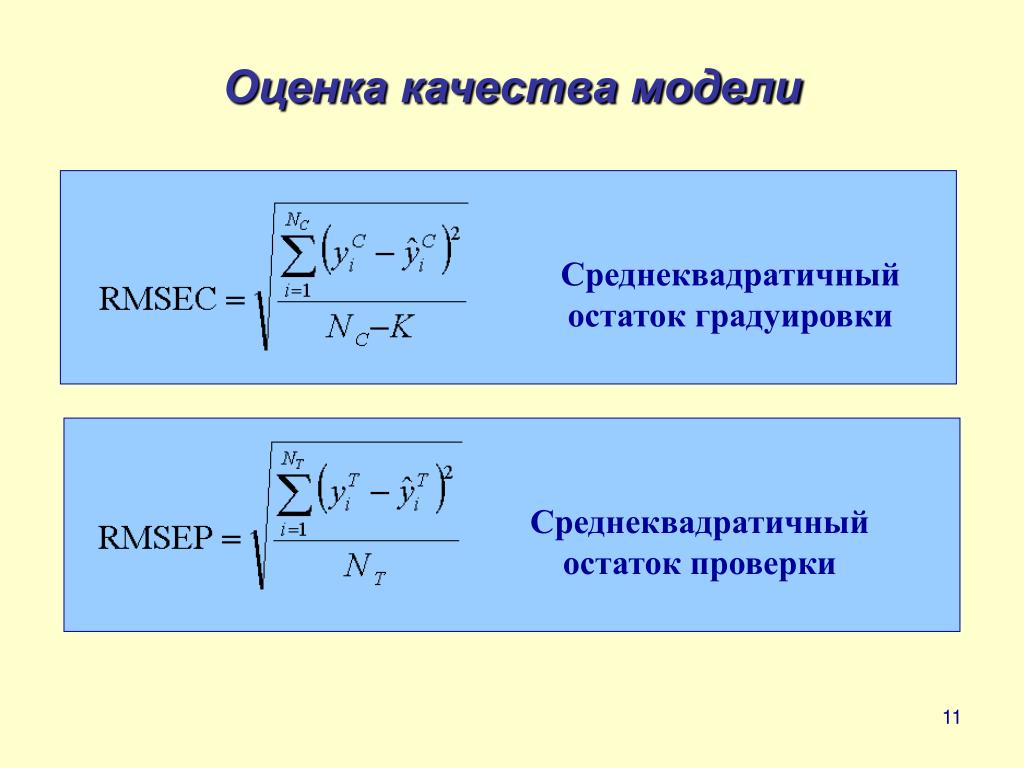
  • Можно показать, что средняя мощность равна IrmsVrmscosϕ, где Irms и Vrms – среднеквадратичные ( rms, ) средние значения тока, и напряжения, соответственно.

• Мощность

  • Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается на сопротивлении цепи и определяется как $ P_ {avg} = I_ { rms } V_ { rms } cos \ phi $.
  • Как видно из предыдущих Атомов, напряжение и ток не совпадают по фазе в цепи RLC.
  • Существует фазовый угол ϕ между напряжением источника V и током I, заданный как
  • I (t) и V (t) – это ток и напряжение в момент времени t).
  • \ phi – фазовый угол, равный разности фаз между напряжением и током .

• Распределение скорости молекул

  • Распределение имеет длинный хвост, потому что некоторые молекулы могут идти в несколько раз быстрее rms скорости.
  • Наиболее вероятная скорость vp (на пике кривой) меньше, чем rms speed vrms.
  • Наиболее вероятная скорость v_p меньше rms speed v_rms .
  • Хотя возможны очень высокие скорости, лишь небольшая часть молекул имеет скорости на порядок больше, чем v_rms .

• Число Авогадора

Питание переменного тока, среднеквадратичные и трехфазные цепи

Мощность в цепях переменного тока, использование величин RMS и трехфазного переменного тока – включая ответы на эти вопросы: Что такое среднеквадратичные значения? Как определить мощность, развиваемую в цепи переменного тока? Как можно получить 680 В постоянного тока от источника 240 В переменного тока, просто выпрямляя? Когда вам нужны три фазы и зачем вам четыре провода? Эта страница дает ответы на эти вопросы.Это страница ресурса от Physclips. Это вспомогательная страница для сайта главных цепей переменного тока. Отдельные страницы посвящены RC-фильтрам, интеграторам. и дифференциаторы, колебания LC и двигатели и генераторы. Значения мощности и среднеквадратического значения Мощность p, преобразованная в резистор (т. Е. Скорость преобразования электрического энергия для нагрева) p (t) = iv = v 2 / R = i 2 R. Мы используем строчные буквы p (t), потому что это выражение для мгновенного мощность в момент времени t.Обычно нас интересует средняя поставленная мощность, обычно пишется P. P – это полная энергия, преобразованная за один цикл, делится на период T цикла, поэтому: В последней строке мы использовали стандартное тригонометрическое тождество, которое cos (2A) = 1-2 sin 2 A. Теперь синусоидальный член усредняет к нулю за любое количество полных циклов, поэтому интеграл прост и мы получаем Этот последний набор уравнений полезен, потому что они точно такие же, как обычно. используется для резистора в электричестве постоянного тока.Однако следует помнить, что P – средняя мощность, а V = V м / √2 и I = I м / √2. Посмотрев на интеграл выше и разделив на R, мы увидим, что I равно к квадратному корню из среднего значения i 2 , поэтому I называется среднеквадратичное значение или RMS значение . Аналогично V = V м / √2 ~ 0,71 * В м – среднеквадратичное значение напряжения. Когда говорят о переменном токе, значения RMS используются настолько часто, что, если не иное заявлено, вы можете предположить, что среднеквадратичные значения предназначены *.Например, нормальный Внутренний переменный ток в Австралии составляет 240 вольт переменного тока с частотой 50 Гц. Среднеквадратичное значение напряжения составляет 240 вольт, поэтому пиковое значение V м = V.√2 = 340 вольт. Таким образом, активный провод идет от +340 вольт до -340 вольт и обратно снова 50 раз в секунду. (Это ответ на тизер-вопрос на сайте верх страницы: выпрямление сети 240 В может дать как + 340 Vdc и -340 Vdc.) * Исключение: производители и продавцы HiFi оборудования иногда используют пиковые значения, а не среднеквадратичные значения, из-за чего оборудование кажется более мощным чем есть. Мощность в резисторе. В резисторе R пиковая мощность (достигается мгновенно 100 раз в секунду для 50 Гц переменного тока) составляет В м 2 / R = i м 2 * R. Как обсуждалось выше, напряжение, ток и мощность проходят через ноль. 100 раз в секунду, поэтому средняя мощность меньше этой. Среднее точно как показано выше: P = V м 2 / 2R = V 2 / R. Мощность в катушках индуктивности и конденсаторах. В идеальных катушках индуктивности и конденсаторах, синусоидальный ток создает напряжения, которые соответственно на 90 опережают и за фазой тока. Таким образом, если i = I m sin wt, напряжения на катушке индуктивности и конденсаторе равны V m cos wt. и -V m cos мас. соответственно. Теперь интеграл cos * sin по целому количество циклов равно нулю. Следовательно, идеальные катушки индуктивности и конденсаторы в среднем не забирают мощность из цепи. Трехфазный переменный ток Однофазный переменный ток имеет то преимущество, что он только требует 2 провода.Его недостаток виден на графике вверху этой страницы: дважды каждый цикл V стремится к нулю. Если подключить фототранзистор цепи к осциллографу, вы увидите, что люминесцентные лампы включаются 100 раз в секунду (или 120, если вы работаете с частотой 60 Гц). Что делать, если вам нужно более равномерное электроснабжение? Можно хранить энергию в конденсаторах, конечно, но в цепях большой мощности это потребует большие, дорогие конденсаторы. Что делать? AC генератор может иметь более одной катушки.Если есть три катушки, установленные под относительными углами 120, то он будет производить три синусоидальных ЭДС с относительными фазами 120, как показано на верхнем рисунке справа. Мощность, подаваемая на резистивный нагрузка каждого из них пропорциональна V 2 . В сумма трех членов V 2 является константой. Мы видели выше этого среднего V 2 составляет половину пика значение, поэтому эта константа равна 1.В 5 раз больше пиковой амплитуды для любой цепи, как показано на нижнем рисунке справа. Вам нужно четыре провода? В принципе нет. Сумма трех Члены V равны нулю, поэтому при условии, что нагрузки на каждой фазе идентичны, токи, полученные от трех линий, складываются в ноль. На практике ток в нейтральном проводе обычно не совсем ноль. Далее, он должен быть того же калибра, что и другой. провода, потому что, если одна из нагрузок вышла из строя и образовала разомкнутая цепь, нейтраль будет пропускать ток, подобный что в оставшихся двух нагрузках. Напряжение (вверху) и квадрат напряжения (внизу) в трех активных линиях 3-х фазного питания. Перейти на сайт главных цепей переменного тока, RC фильтры, интеграторы и дифференциаторы LC колебания, или чтобы Двигатели и генераторы. Больше новостей Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт