Сдвиг фаз переменного тока и напряжения
Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.
Для этого случая формула мощности
остается справедливой.
На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.
При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.
О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.
Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.
Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.
Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.
Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.
При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).
Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.
Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т. е. формулы
в этом случае будут неверны
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Временная и векторная диаграммы напряжения и тока в идеальной катушке индуктивности представлены на рисунке
А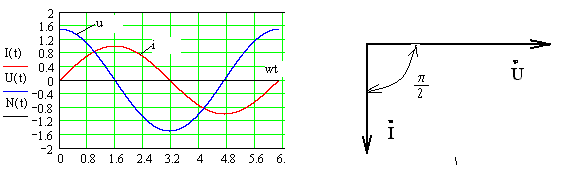
ктивная,
реактивная и полная мощности идеальной
катушки индуктивности
P = U I cos = 0 ( так как = 0 )
Q = U I sin = U I = I2 XL = U2 bL
S = U I = Q
В реальных катушках индуктивности часть электрической энергии преобразуется в тепло, т.е. катушка обладает не только индуктивностью L, но и активным сопротивлением Rk .
Эквивалентная схема замещения реальной катушки индуктивности представлена на рисунке.
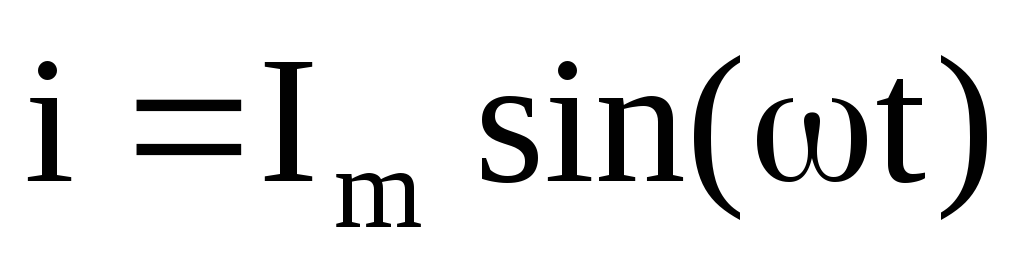
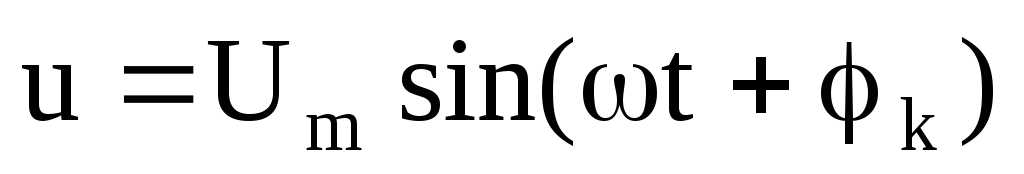
Um = Im Zk Zk =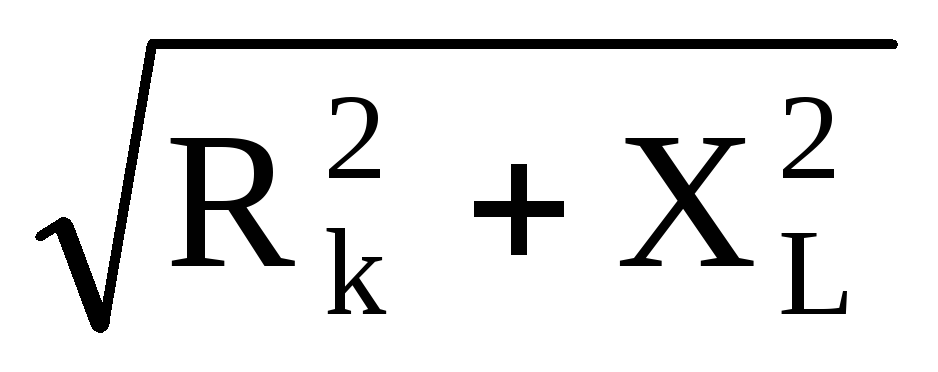 
XL=
L
= 2f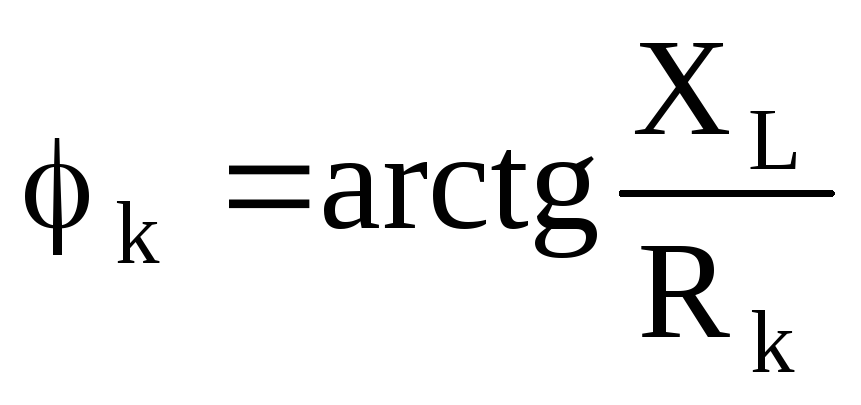 
В реальной индуктивности к < 900
Емкость с.
Емкостью С называается элемент электрической
цепи (конденсатор), в котором накапливается
энергия электрического поля. Количественно
емкость определяется выражением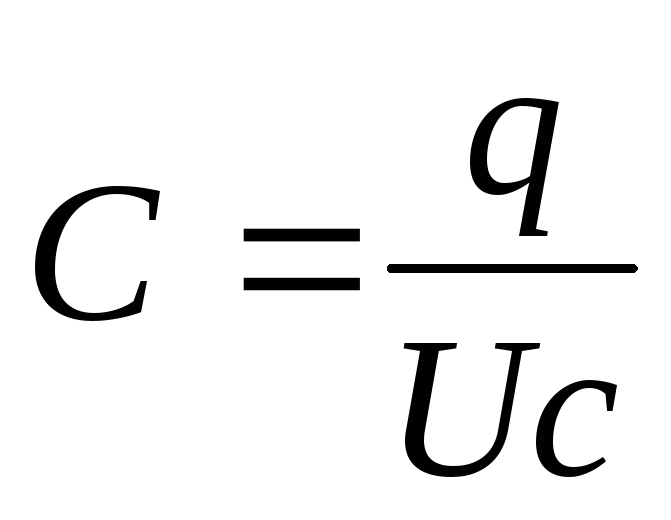 
.
Если q – количество электричества измеряется в кулонах,
Uc – в вольтах, то емкость С в фарадах.
, 
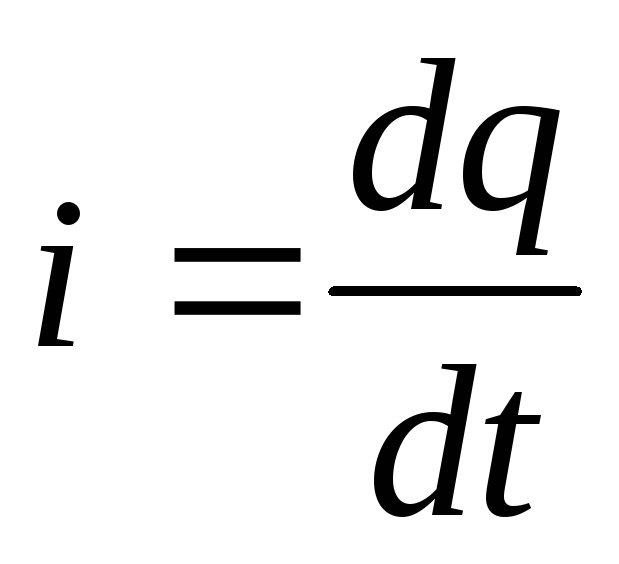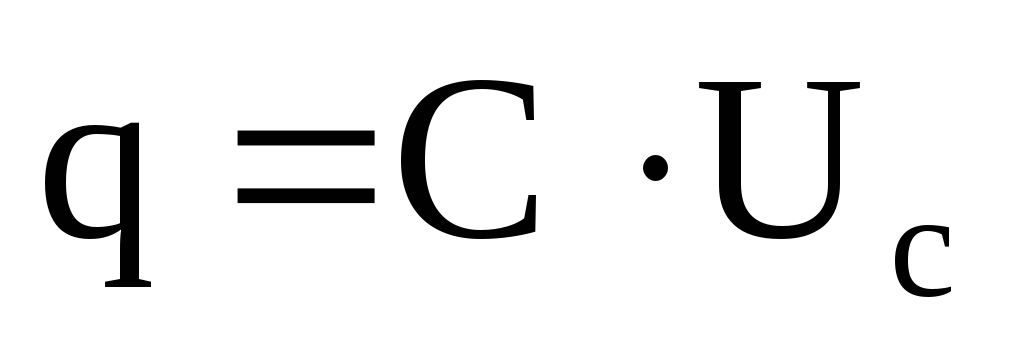
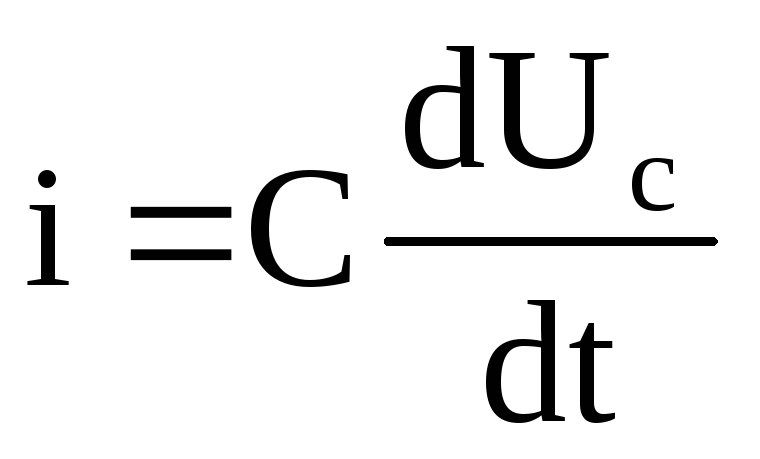
Если
напряжение возрастает, то 
>
0. Это значит, что ток и напряжение
совпадают по направлению, энергия
электрического поля в конденсаторе
возрастает.
При убывании напряжения ток также уменьшается, энергия возвращается обратно к источнику.
Если напряжение на емкости с меняется по закону синуса ,
то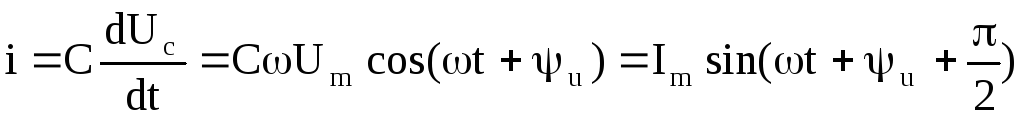 
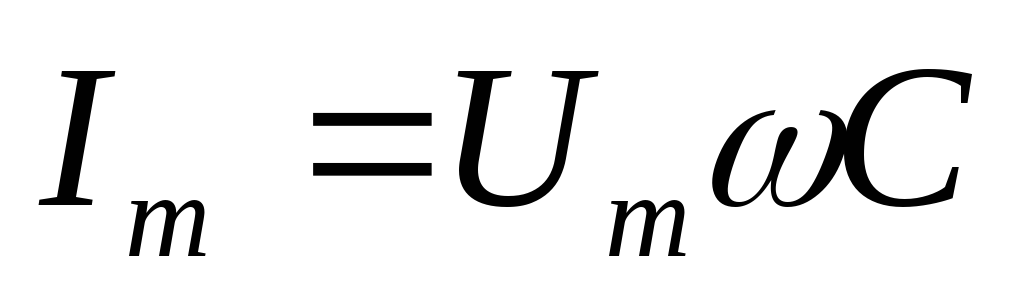
В идеальной емкости ток опережает напряжения на 90о.
Емкостное сопротивление зависит от частоты по гиперболическому закону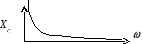
XС =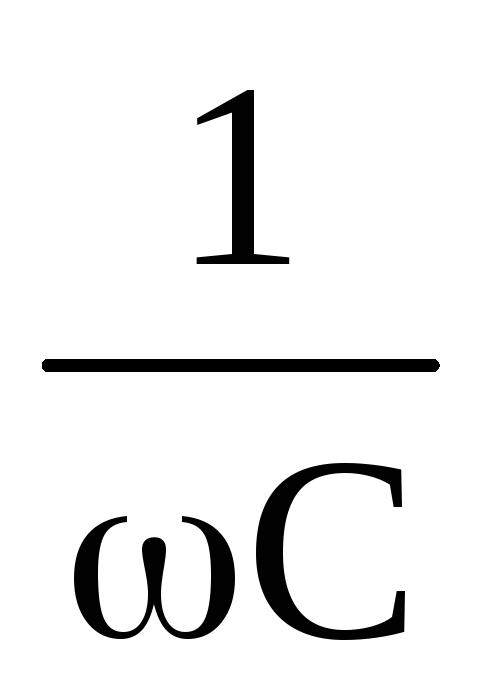 
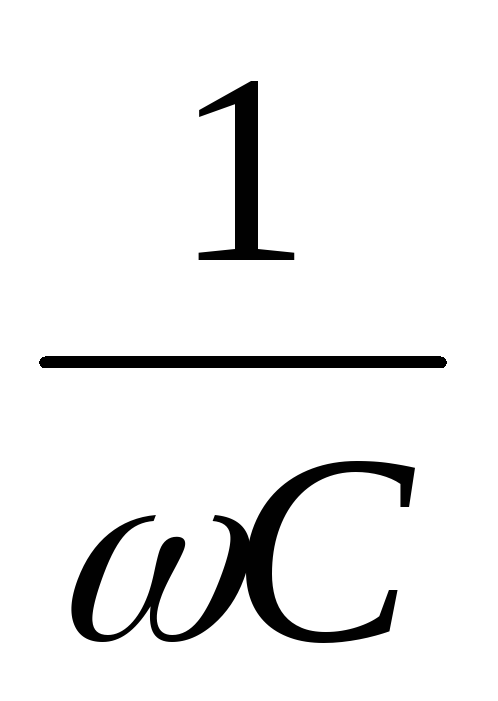
В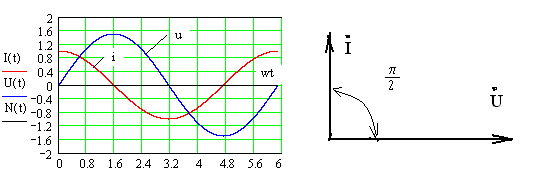
ременная
и векторная диаграммы напряжения и тока
в емкости представлены на рисунке
Активная, реактивная и полная мощности идеального конденсатора составляют соответственно
P = U I cos = 0 ( так как = – 0 )
Q = U I sin = U I = I2 XС
S = U I = Q
Реальные конденсаторы характеризуются не только емкостью С, но и активным сопротивлением RС или проводимостью gC , учитывающими потери энергии в диэлектрике.
Эквивалентная схема замещения реального конденсатора представлена на рисунке.
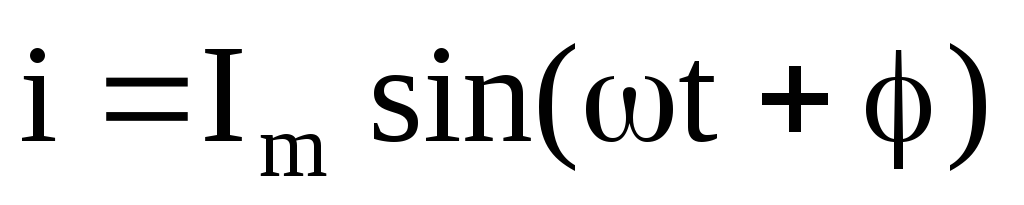
Im = Um YC YC =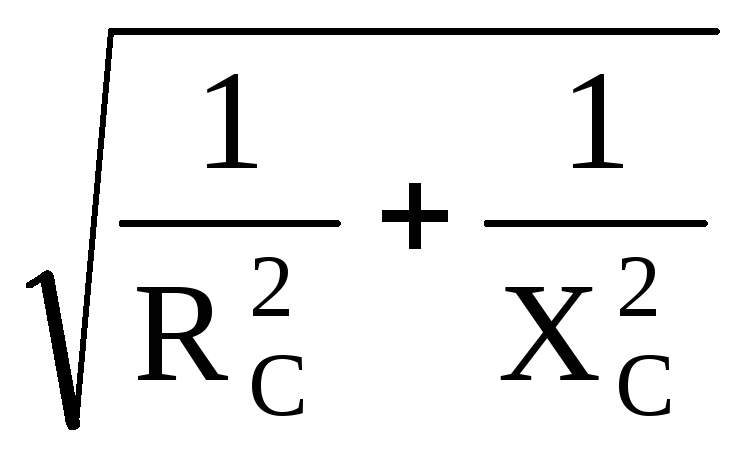 
XC =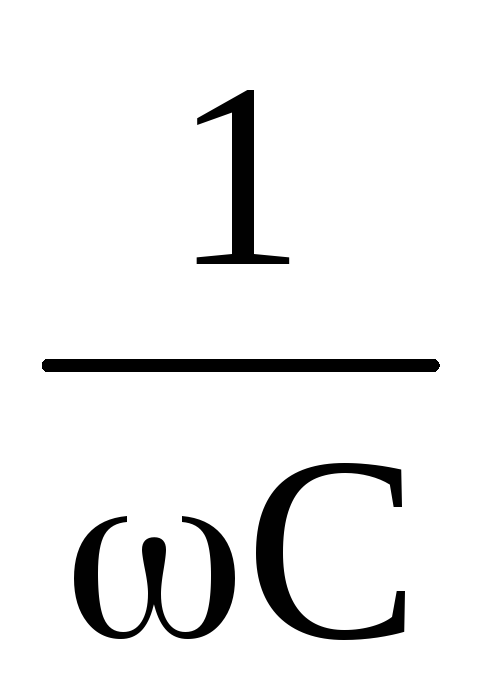 
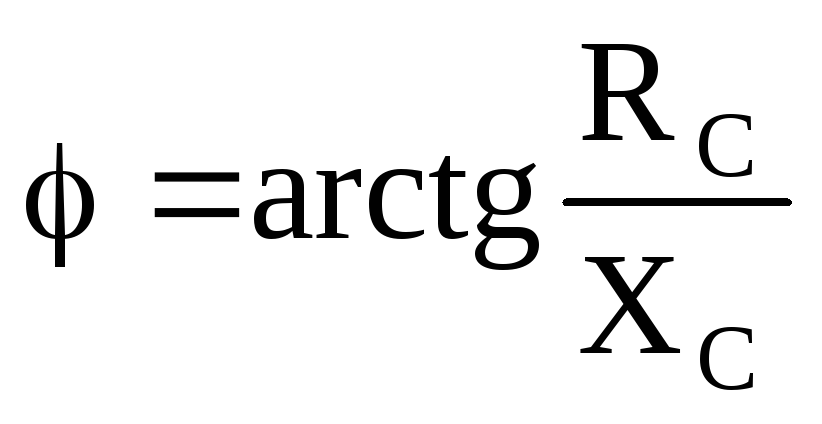
Порядок выполнения работы
Собрать схему, изображенную на рис.1.
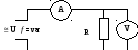
Рис.1.
Установить напряжение источника питания 4 В и записать показания приборов в табл.1 для ряда частот источника, начиная с f = 0.
Построить в Excel зависимость R = f() и поместить в отчет.
Включить осциллограф и поместить в отчет кривые напряжения и тока.
Таблица 1
№ | Гц | U B | I A | P Вт | R Ом | cos | град |
1 | 200 | ||||||
2 | 500 | ||||||
3 | 1000 | ||||||
4 | 2000 | ||||||
5 | 5000 | ||||||
6 | 11000 |
Собрать схему, изображенную на рис.2.
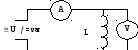
Рис.2.
Записать показания приборов в табл.2 для ряда частот источника, начиная с f = 0, произвести необходимые вычисления.
Построить в Excel зависимость XL = f() и поместить в отчет.
Включить осциллограф и поместить в отчет кривые напряжения и тока.
Таблица 2
№ | f Гц | U B | I A | P Вт | Zк Ом | Rк Ом | XL Ом | L Гн | cos | град |
1 | 200 | |||||||||
2 | 500 | |||||||||
3 | 1000 | |||||||||
4 | 2000 | |||||||||
5 | 5000 | |||||||||
6 | 11000 |
; 
; 
; 
; 
; 
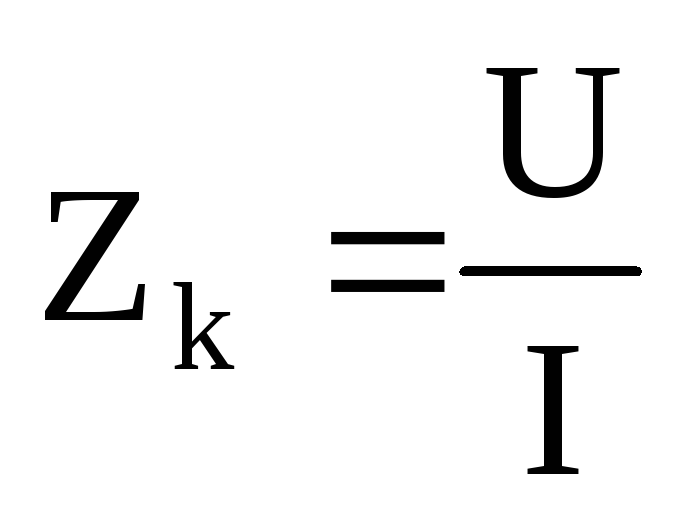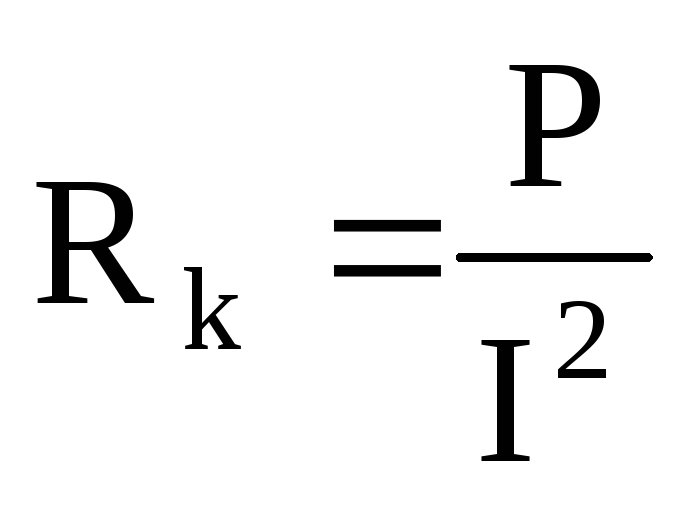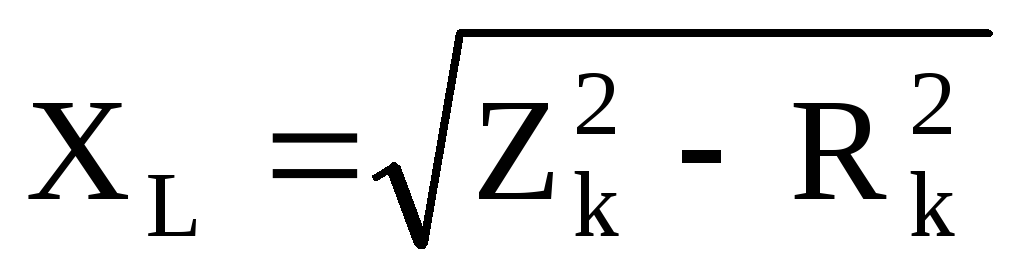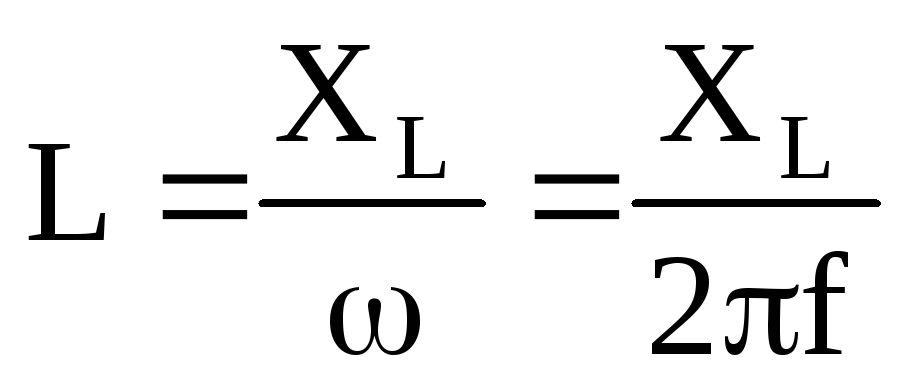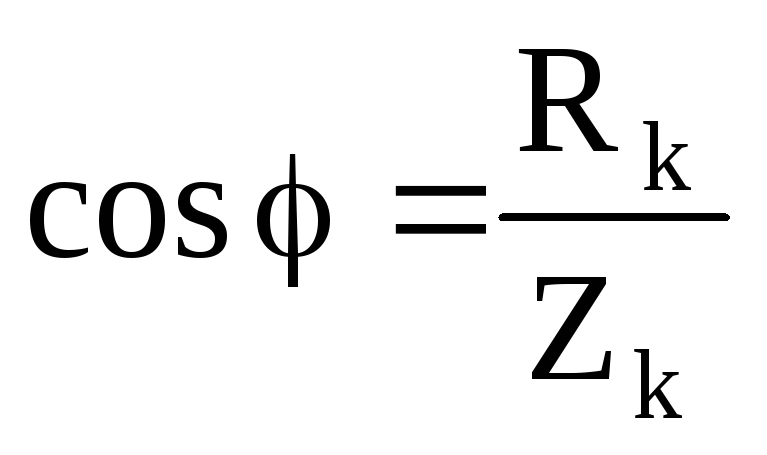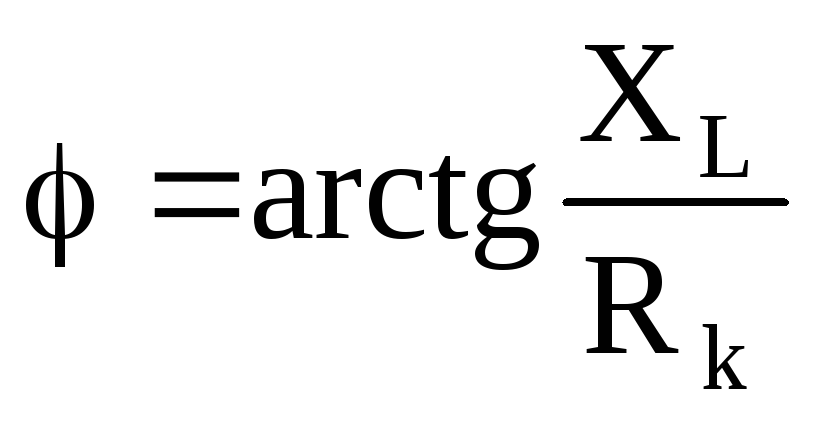
Собрать схему, изображенную на рис.3.
Рис.3.
Записать показания приборов в табл.3 для ряда частот источника, начиная с f = 0, произвести необходимые вычисления.
Построить в Excel зависимость XC = f() и поместить в отчет.
Включить осциллограф и поместить в отчет кривые напряжения и тока.
Таблица 3
№ | f Гц | U B | I A | P Вт | Yc 1/Ом | gc 1/Ом | RС Ом | XС Ом | C мкФ | cos | град |
1 | 200 | ||||||||||
2 | 500 | ||||||||||
3 | 1000 | ||||||||||
4 | 2000 | ||||||||||
5 | 5000 | ||||||||||
6 | 11000 |
; 
; 
; 
;
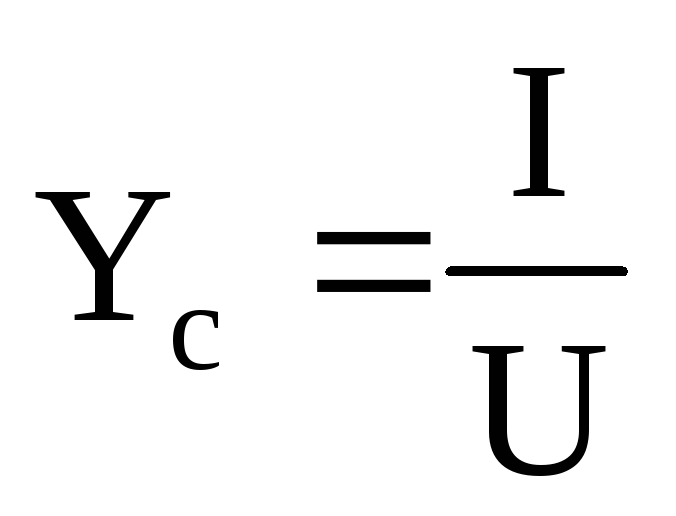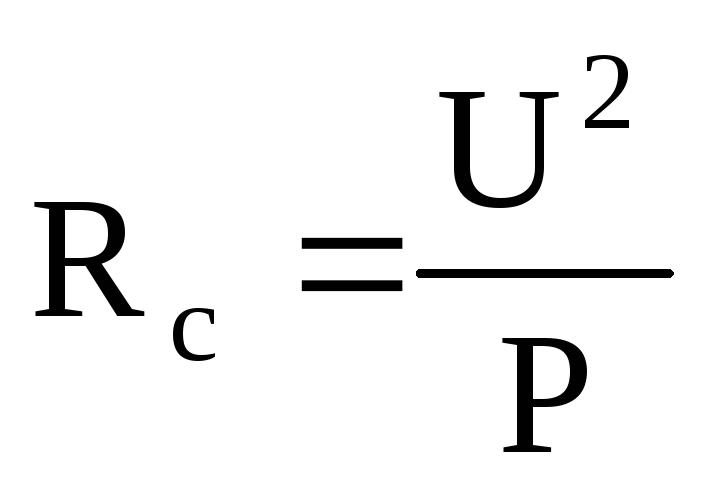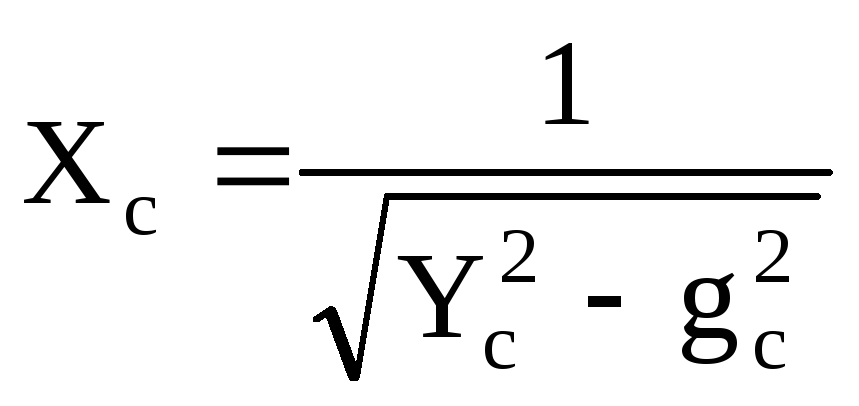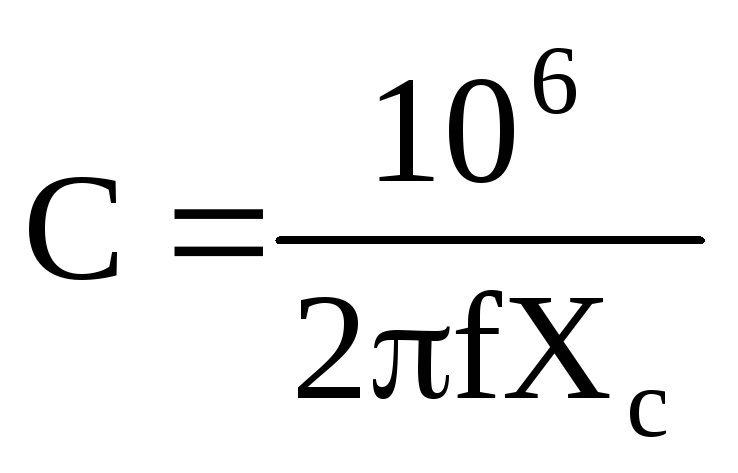мкФ;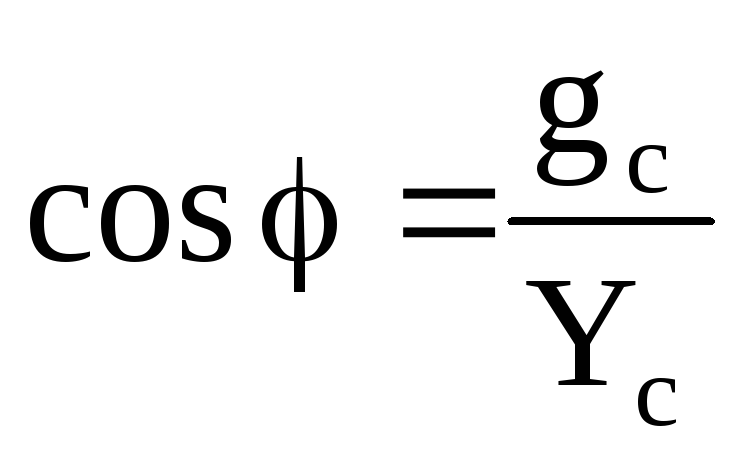 
; 
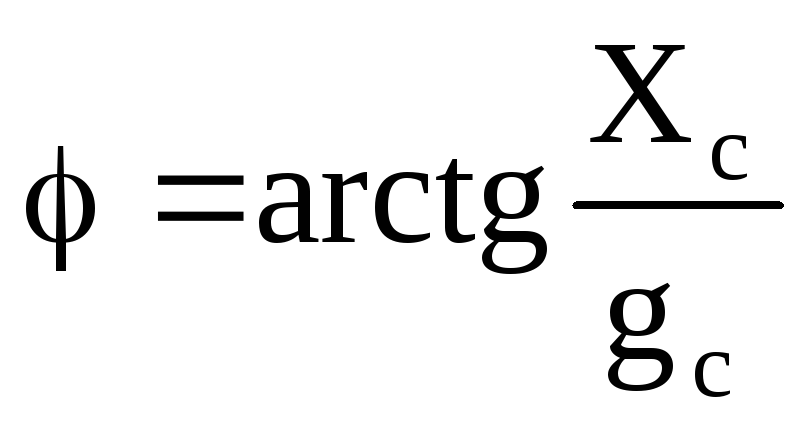
Закон Ома для переменного тока
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
где, U-напряжение на элементе цепи,
I – ток через элемент цепи
R – активное сопротивление элемента
Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
| (2) |
где, Um-амплитудное значение напряжения на элементе цепи,
Im – амплитудное значение тока через элемент цепи
R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
| (3) | |
| (4) |
где — UL-падение напряжение на чисто индуктивном сопротивлении ;
UС—падение напряжения на чисто емкостном сопротивлении;
I— значение тока в через реактивное сопротивление;
L— индуктивность реактивного элемента;
C— емкость реактивного элемента;
ω— циклическая частота.
Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
| (5) |
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Закон Ома для различных типовых цепей переменного тока
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)
Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
| (6) |
где —эффективное значение силы тока в А;
U—эффективное значение напряжения в В;
R—активное сопротивление в Ом;
ωL—индуктивное сопротивление в ом.
Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.
А закон Ома для такой цепи принимает вид:
| (7) |
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.
Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
| (8) |
где I-сила тока в А;
U-напряжение в В;
R-активное сопротивление в Ом;
ωL-индуктивное сопротивление в Ом;
1/ωС-емкостное сопротивление в Ом.
Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока .
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉
Осциллограмма силы тока на активном сопротивлении
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма – это напряжение с генератора Uген , а желтая осциллограмма – это напряжение с шунта Uш , в нашем случае – сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:
Частота 285 Герц:
Частота 30 Килогерц:
Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:
Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:
Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.
100 Герц
200 Герц
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:
где
Хс – реактивное сопротивление конденсатора, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
С – емкость конденсатора, Фарад
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка – это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле
где
ХL – реактивное сопротивление катушки, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
L – индуктивность, Генри
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность – это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком “плюс”, а напряжение со знаком “минус”. В итоге плюс на минус дает минус. Получается мощность со знаком “минус”. А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем “плющить” пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно – это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо – это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком “минус”. Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL – это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L – собственно сама индуктивность катушки
С – межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r – сопротивление диэлектрика и корпуса между обкладками
С – собственно сама емкость конденсатора
ESR – эквивалентное последовательное сопротивление
ESI (ESL) – эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Резюме
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.
Сопротивление катушки вычисляется по формуле
Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.
Почему мощность равна нулю (0) в чисто индуктивной, чисто емкостной или цепи, в которой ток и напряжение не совпадают по фазе?
Эти типы вопросов задаются в интервью по электротехнике или электронике. Итак, вернемся к основам, чтобы прояснить основные и важные понятия электротехники.
1. Почему мощность в цепи равна нулю (0), в которой ток и напряжение не совпадают по фазе на 90 °?
Если ток и напряжение не совпадают по фазе на 90 градусов, то мощность (P) будет равна нулю.Причина в следующем:
Мы знаем, что мощность в однофазных цепях переменного тока:
P = V I Cos θ
Где;
- P = мощность в ваттах
- V = напряжение в вольтах
- I = ток в амперах
- Cos θ = коэффициент мощности цепи, т. Е. Разность фаз между волнами тока и напряжения.
Если угол между током и напряжением равен 90 ° (θ = 90), то
Мощность = P = VI Cos (90 °) = 0… .. → [Cos (90 °) = 0]
Так что если мы ставим Cos 90 ° = 0, тогда общая мощность схемы будет равна нулю (т.е.е. В чисто индуктивной или емкостной цепи, где напряжение опережает ток на 90 °, а ток опережает напряжение на 90 ° соответственно).
2. Почему мощность в чистой индуктивной цепи равна нулю (0).
Мы знаем, что в чисто индуктивной цепи ток отстает на 90 градусов от напряжения (другими словами, напряжение опережает ток на 90 °), то есть разность фаз между током и напряжением составляет 90 градусов.
Как объяснено выше, если ток и напряжение не совпадают по фазе друг с другом, как в чисто индуктивной цепи, общая мощность схемы будет равна 0, как показано ниже.
P = VI Cos θ
, если угол между током и напряжением составляет 90 ° (θ = 90), то
Power P = VI Cos (90 °) = 0
[Обратите внимание, что Cos (90 °) = 0 ]
Это показывает, что для в случае чисто индуктивной цепи полная мощность схемы будет равна нулю при Cos 90 ° = 0.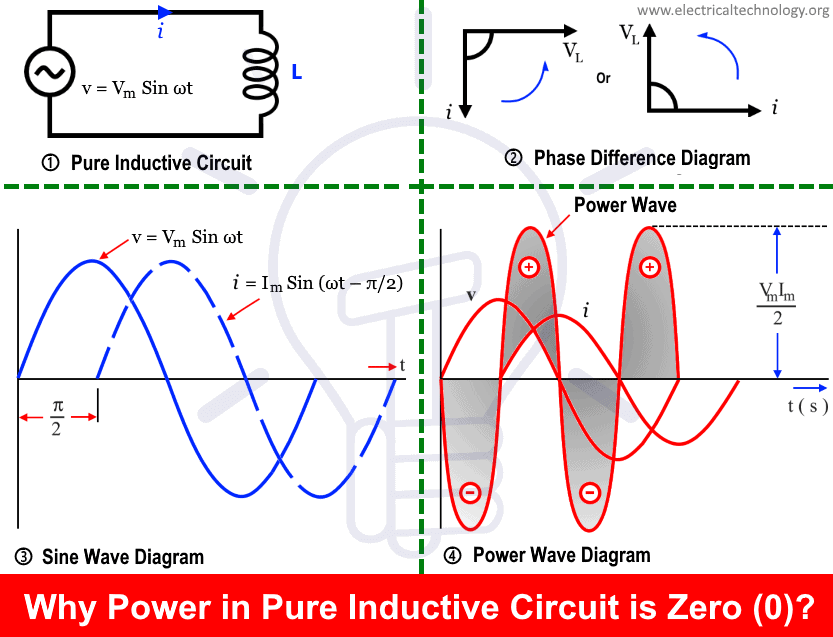 
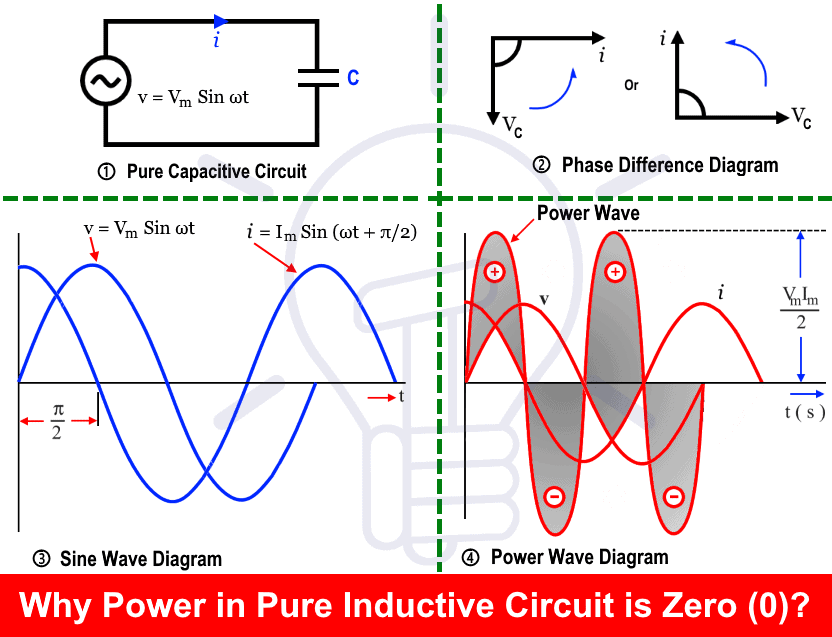
3. Почему мощность в чистой емкостной цепи равна нулю (0)?
Мы знаем, что в чисто емкостной цепи ток опережает напряжение на 90 ° (другими словами, напряжение отстает на 90 ° от тока) i.Разность фаз между током и напряжением составляет 90 градусов.
Как упомянуто выше, если ток и напряжение не совпадают по фазе друг с другом, как в чисто емкостной цепи, суммарная мощность схемы будет равна нулю, как указано ниже.
Мощность в цепи переменного тока
P = V I Cos θ
, если угол между током и напряжением составляет 90 (θ = 90) градусов. затем
Мощность P = V I Cos (90 °) = 0
[Обратите внимание, что Cos (90 °) = 0]
Это показывает то же, что и для чистой индуктивной цепи i.е. в случае чисто емкостной цепи, полная мощность цепи будет равна нулю , так как Cos 90 ° = 0.
Короче говоря, в цепи, где напряжение или ток опережают или отстают на 90 ° (разность фаз = 90 °) друг за другом, положительный цикл отменяет отрицательный, что приводит к нулевой средней мощности схемы, т.е. общий коэффициент мощности цепи переменного тока равен нулю, что приводит к нулевой средней мощности.
Похожие сообщения:
.Что такое чисто индуктивная цепь? – Phasor Diagram & Waveform
Цепь, которая содержит только индуктивность (L), а не любые другие величины, такие как сопротивление и емкость в цепи, называется Pure индуктивной цепью. В схеме этого типа ток отстает от напряжения на угол 90 градусов.
Содержание:
Катушка индуктивности – это тип катушки, которая запасает электрическую энергию в магнитном поле, когда через нее протекает ток.Индуктор состоит из провода, который намотан в виде катушки. Когда ток, протекающий через индуктор, изменяется, изменяющееся во времени магнитное поле вызывает ЭДС, которая препятствует протеканию тока. Индуктивность измеряется в Генри . Противостояние потока тока известно как индуктивное сопротивление .
Объяснение и вывод индуктивной схемы
Схема, содержащая чистую индуктивность, показана ниже:
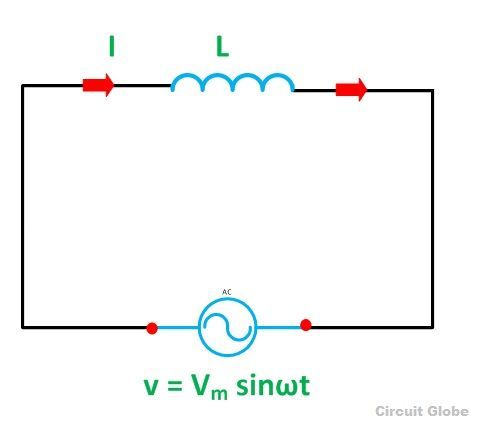Схемачистой индуктивной схемы
Пусть переменное напряжение, подаваемое на цепь, определяется уравнением:
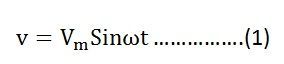
В результате переменный ток i протекает через индуктивность, которая индуцирует в нем ЭДС.Уравнение показано ниже:
ЭДС, которая индуцируется в цепи, равна и противоположна приложенному напряжению. Следовательно, уравнение становится,
Положив значение е в уравнении (2), получим уравнение как
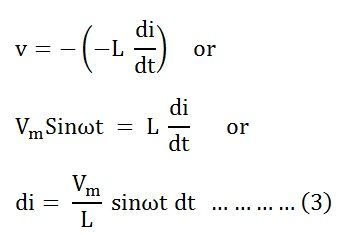
Интегрируя обе части уравнения (3), мы получим
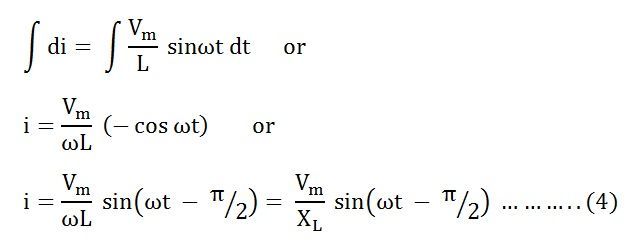, где X L = ω L – сопротивление, предлагаемое потоку переменного тока чистой индуктивностью и называемое индуктивным реактивным сопротивлением.
Значение тока будет максимальным, когда sin (ωt – π / 2) = 1
Следовательно,
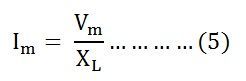
Подставив это значение в I м из уравнения (5) и поместив его в уравнение (4), получим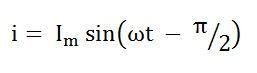 
Диаграмма вектора и кривая мощности индуктивной цепи
Ток в чистой индуктивной цепи переменного тока отстает от напряжения на 90 градусов. Форма волны, кривая мощности и фазовая диаграмма чисто индуктивного контура показаны ниже
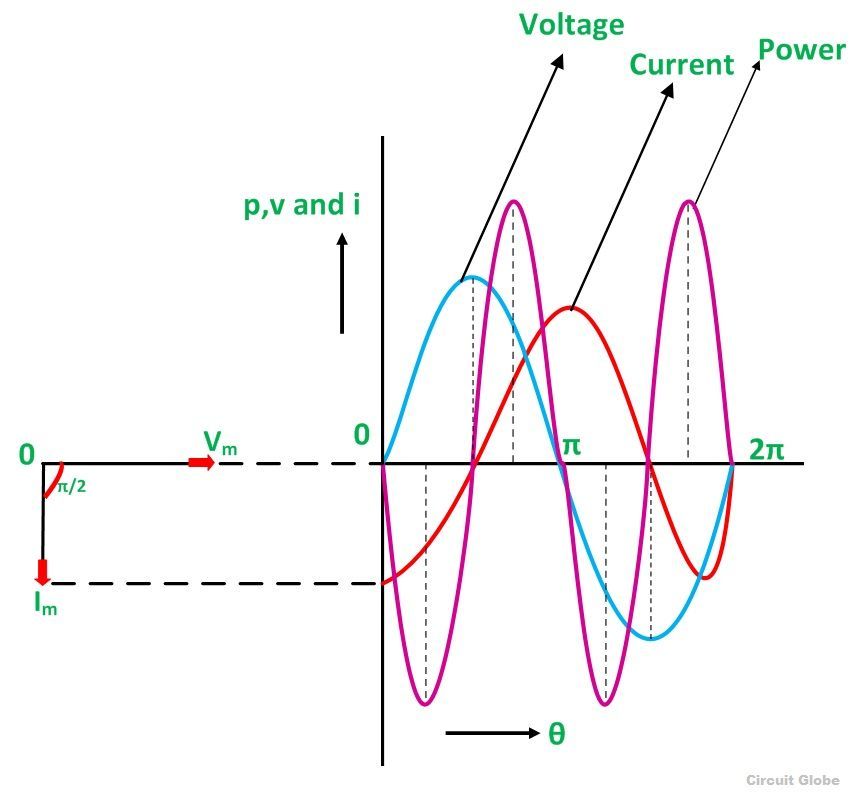
Диаграмма вектора и форма волны чистой индуктивной цепи
Форма волны напряжения, тока и мощности показана синим, красным и розовым цветами соответственно.Когда значения напряжения и тока находятся на своем пике в качестве положительного значения, мощность также является положительной, и аналогично, когда напряжение и ток дают отрицательный сигнал, мощность также станет отрицательной. Это из-за разности фаз между напряжением и током.
Когда напряжение падает, значение тока изменяется. Когда значение тока достигает своего максимального или пикового значения, напряжение в этот момент времени будет равно нулю, и, следовательно, напряжение и ток не совпадают по фазе друг с другом на угол 90 градусов.
Диаграмма вектора также показана на левой стороне формы сигнала, где текущее (I м ) запаздывающее напряжение (V м ) под углом π / 2.
Власть в чистой индуктивной цепи
Мгновенная мощность в индуктивной цепи задается
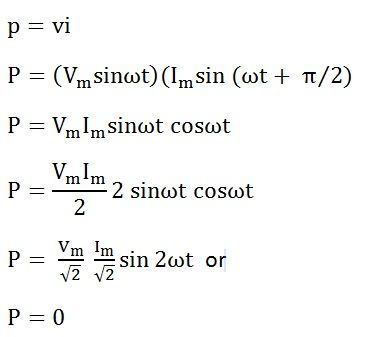
Следовательно, средняя мощность, потребляемая в чисто индуктивной цепи, равна нулю.
Средняя мощность в одном изменении, то есть в полупериоде, равна нулю, так как отрицательная и положительная петли находятся под кривой мощности, то же самое.
В чисто индуктивной цепи в течение первой четверти цикла мощность, подаваемая источником, сохраняется в магнитном поле, установленном вокруг катушки. В следующем цикле четверти магнитное поле уменьшается, и энергия, которая была сохранена в цикле первой четверти, возвращается источнику.
Этот процесс продолжается в каждом цикле, и, следовательно, в цепи не потребляется энергия
,Больше новостей
