Сдвиг фаз переменного тока и напряжения
Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.
Для этого случая формула мощности
остается справедливой.
На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.
При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.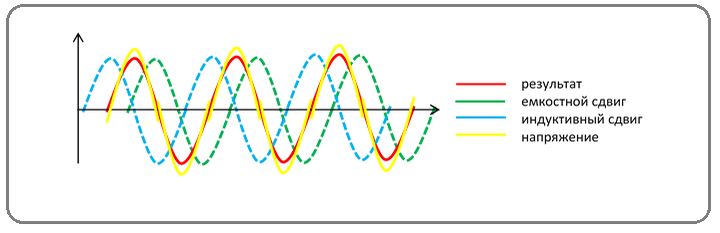
О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.
Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.
Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.
Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.
Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее.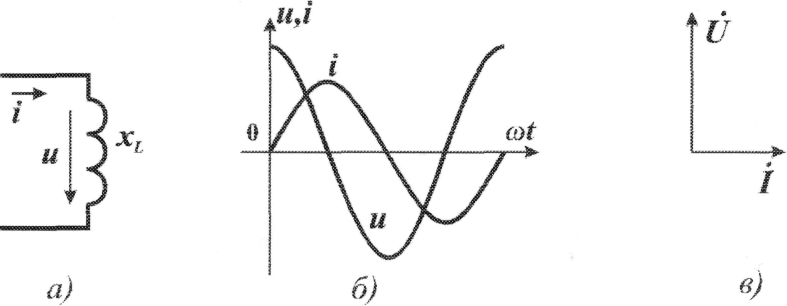 Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.
При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).
Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.
Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т.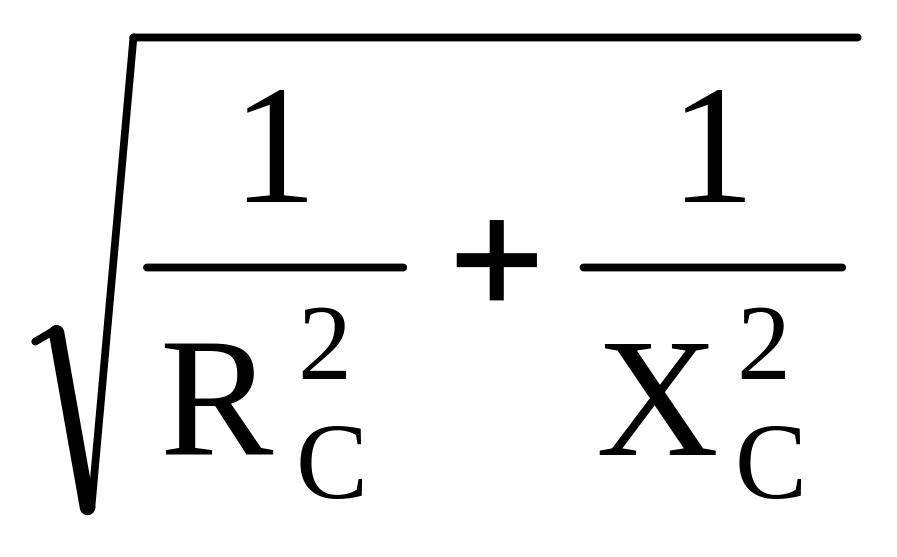 е. формулы
е. формулы
в этом случае будут неверны
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Почему конденсатор создает сдвиг фазы на 90 градусов по напряжению и току?
Ну, после 20 лет разработки цифровых схем, я думаю, что я все еще знаю ответ.
Как ваш источник напряжения движется за ноль градусов. у него 0 вольт на выходе. Тем не менее, напряжение быстро увеличивается. Таким образом, напряженность электрического поля в диэлектрике колпачка быстро меняется, и по мере того, как поле становится сильнее, оно выталкивает больше электронов из положительной боковой пластины (из-за увеличения электрической силы на них, создаваемой полем). Здесь важно понимать, что колпачок – это, по сути, разомкнутая цепь, просто особой формы. Поэтому ток течет не через конденсатор (идеальный здесь, мы можем поговорить об эффекте утечки позже, если хотите), а скорее к одной или другой пластине.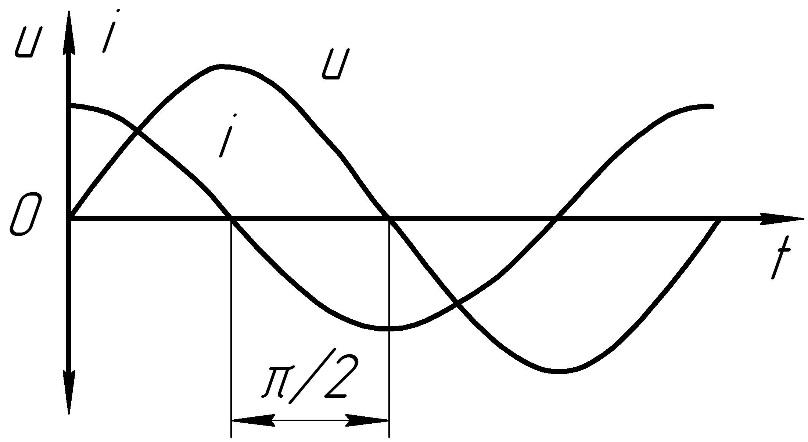 Это заставляет электрическое поле накапливаться в диэлектрике, который воздействует на свободные электроны на другой пластине посредством электрической силы. Чтобы объяснить всю эту физику, нам нужно войти в закон Гаусса и т. Д., Поэтому я не буду этого делать здесь.
Это заставляет электрическое поле накапливаться в диэлектрике, который воздействует на свободные электроны на другой пластине посредством электрической силы. Чтобы объяснить всю эту физику, нам нужно войти в закон Гаусса и т. Д., Поэтому я не буду этого делать здесь.
Каждая пластина представляет собой относительно большой кусок проводящего металла, поэтому в ней существует множество свободных электронов. Гораздо больше, чем просто участие в разумном уровне тока. Таким образом, разница напряжения между пластинами, генерируемая вашим источником, будет толкать свободные электроны с отрицательной стороны источника на пластину, к которой он подключен. Это создает электрическое поле в диэлектрике крышки, так что электроны выталкиваются электрической силой из противоположной пластины. Схема переносит их обратно к положительному участку вашего источника. По мере того, как все больше и больше заряда выталкивается в отрицательную пластину, поле становится сильнее, и все больше электронов выталкивается из другой пластины.
Однако, поскольку скорость изменения напряжения замедляется, когда мы достигаем максимального напряжения (при 90 градусах), наша напряженность поля все еще увеличивается, но все медленнее. По этой причине все меньше и меньше электронов выталкивается с положительной пластины в единицу времени (поэтому ток становится меньше). В точке максимального напряжения скорость изменения напряжения равна нулю, поэтому больше нуля электронов выталкивается с этой положительной пластины. В этот момент напряжение начинает падать, и поле ослабевает. Это позволяет некоторым вытесненным электронам из положительной пластины возвращаться в нее. Когда скорость изменения напряжения ускоряется и само напряжение падает обратно к нулю вольт, скорость, с которой электроны возвращаются на положительную пластину, увеличивается (ток увеличивается). Когда напряжение равно нулю, оно меняется с максимальной скоростью, поэтому в цепи протекает максимальный ток (электроны возвращаются к пластине так же быстро, как и когда-либо для этой цепи).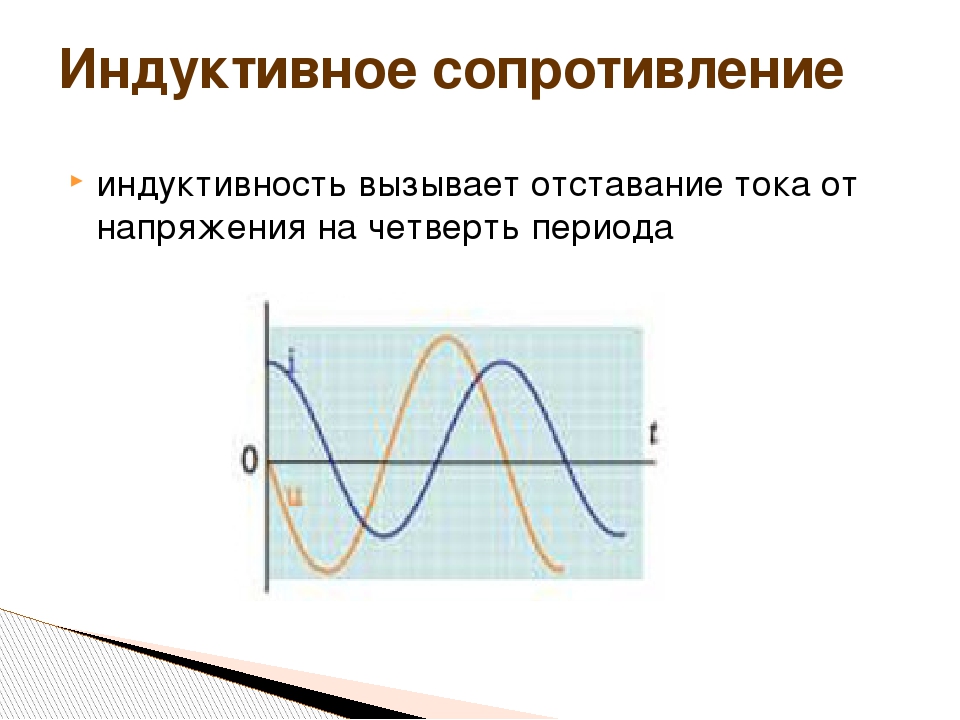 Другая половина формы сигнала (отрицательный лепесток синусоиды напряжения) такая же, но поменяйте местами пластины, которые я называю отрицательными и положительными, поскольку напряжение в этой точке меняется на противоположное (ток, конечно, не меняется на 90 °). и снова будет на 270).
Другая половина формы сигнала (отрицательный лепесток синусоиды напряжения) такая же, но поменяйте местами пластины, которые я называю отрицательными и положительными, поскольку напряжение в этой точке меняется на противоположное (ток, конечно, не меняется на 90 °). и снова будет на 270).
Я полагаю, что это может быть написано более элегантно, но вы понимаете мой смысл здесь? Можете ли вы представить себе влияние поля в диэлектрике колпачка и его связь с электронами, вытекающими из или в пластины? (положительные и отрицательные напряжения на самом деле не таковы, они просто указывают, что они связаны с векторами тока противоположного направления)
Активное и реактивное сопротивление | Практическая электроника
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением.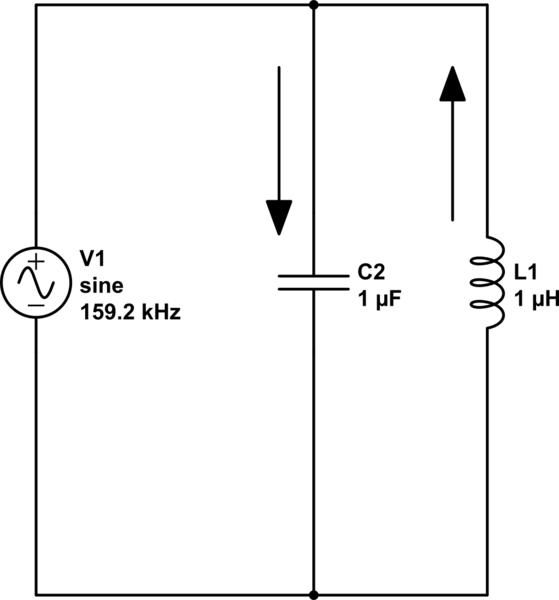 Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока .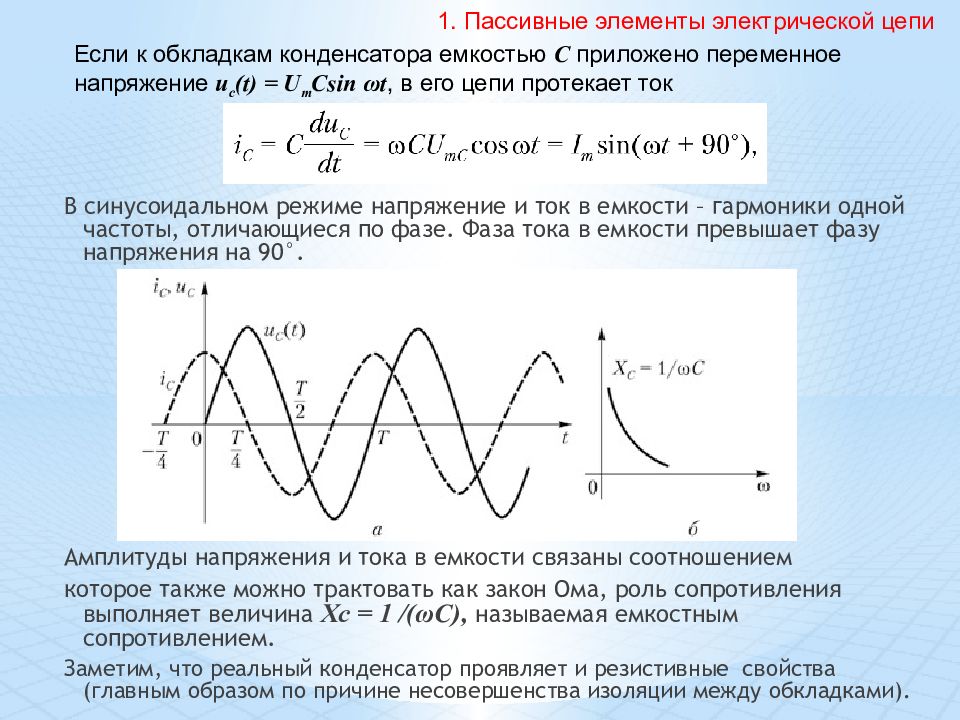
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉
[quads id=1]
Осциллограмма силы тока на активном сопротивлении
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
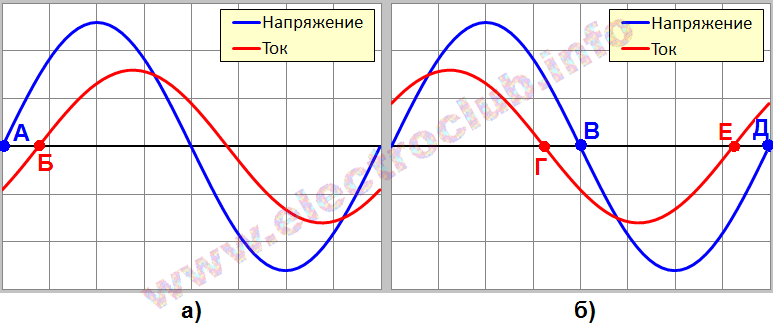
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма – это напряжение с генератора Uген , а желтая осциллограмма – это напряжение с шунта Uш , в нашем случае – сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:
Частота 285 Герц:
Частота 30 Килогерц:
Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:
Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:
Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.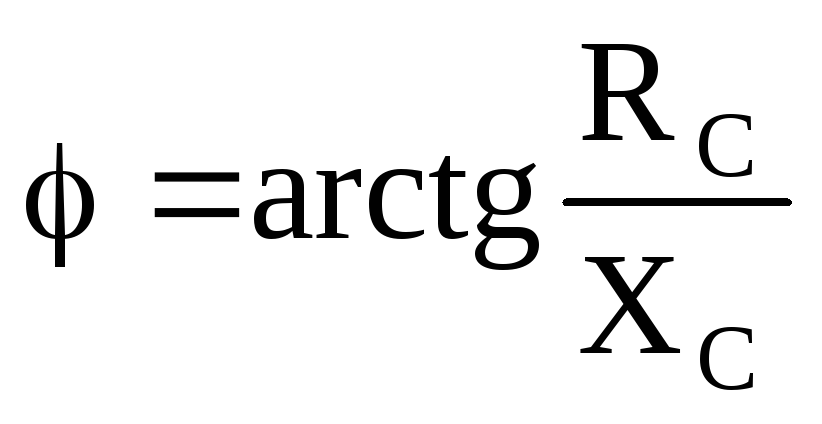
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.
100 Герц
200 Герц
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть.
где
Хс – реактивное сопротивление конденсатора, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
С – емкость конденсатора, Фарад
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.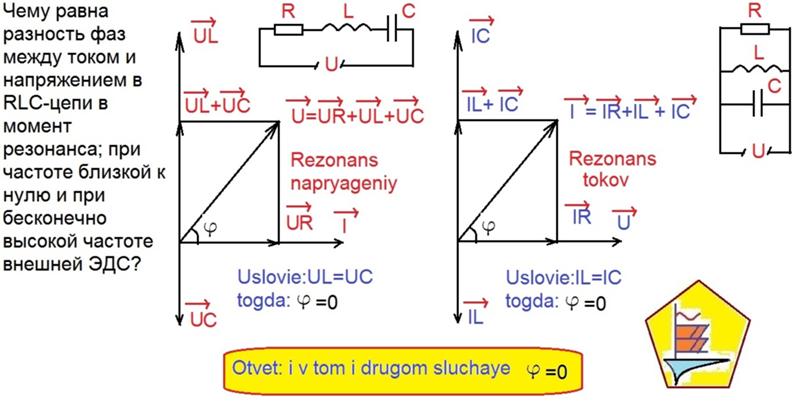
[quads id=1]
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка – это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле
где
ХL – реактивное сопротивление катушки, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
L – индуктивность, Генри
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность – это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком “плюс”, а напряжение со знаком “минус”. В итоге плюс на минус дает минус. Получается мощность со знаком “минус”. А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем “плющить” пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно – это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо – это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком “минус”. Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL – это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L – собственно сама индуктивность катушки
С – межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r – сопротивление диэлектрика и корпуса между обкладками
С – собственно сама емкость конденсатора
ESR – эквивалентное последовательное сопротивление
ESI (ESL) – эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Резюме
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.
Сопротивление катушки вычисляется по формуле
Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.
Глава 16. Индуктивные цепи переменного тока . Введение в электронику
ЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Описать фазовое соотношение между током и напряжением в индуктивной цепи переменного тока.
• Дать определение индуктивного сопротивления в цепи переменного тока.
• Дать определение импеданса и рассказать о его влиянии на индуктивные цепи.
• Описать, как индуктивно-резистивная цепь может быть использована для фильтрации и сдвига фаз.
• Объяснить, как работают фильтры верхних и нижних частот на индуктивных цепях.
Катушки индуктивности, как и конденсаторы, препятствуют прохождению тока в цепях переменного тока. Большое количество электронных цепей состоит из катушек индуктивности и резисторов.
Большое количество электронных цепей состоит из катушек индуктивности и резисторов.
16-1. ИНДУКТИВНОСТЬ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
Катушки индуктивности противодействуют протеканию тока в цепях переменного тока. Когда к катушке индуктивности приложено переменное напряжение, она создает магнитное поле. Изменение полярности приложенного напряжения приводит к расширению или сжатию магнитного поля. Магнитное поле в свою очередь индуцирует напряжение в витках катушки, которое называется электродвижущей силой (э.д.с.) самоиндукции. Чем больше индуктивность, тем больше э.д.с. самоиндукции. Э.д.с. самоиндукции сдвинута по фазе на 180 градусов относительно приложенного напряжения (рис. 16-1) и противодействует приложенному напряжению. Это противодействие так же эффективно уменьшает ток, как и резистор.
Рис. 16-1. В индуктивной цепи приложенное напряжение и индуцированное напряжение сдвинуты относительно друг друга по фазе на 180 градусов.
Величина напряжения, индуцируемого катушкой индуктивности, зависит от скорости изменения магнитного поля. Чем быстрее магнитное поле расширяется и сжимается, тем больше индуцируемое напряжение. Общее эффективное напряжение на катушке индуктивности равно разности приложенного и индуцированного напряжений.
Индуцированное напряжение всегда меньше, чем приложенное напряжение.
На рис. 16-2 показано фазовое соотношение между током и приложенным напряжением. Заметим, что в чисто индуктивной цепи ток отстает от приложенного напряжения на 90 градусов.
Рис. 16-2. В индуктивной цепи переменного тока ток отстает по фазе от приложенного напряжения.
Противодействие, которое оказывает катушка индуктивности току в цепи переменного тока, называется индуктивным сопротивлением. Индуктивное сопротивление измеряется в омах. Величина индуктивного сопротивления зависит от индуктивности и частоты приложенного напряжения. Чем больше индуктивность, тем больше создаваемое ею магнитное поле и тем больше противодействие току.
Чем больше индуктивность, тем больше создаваемое ею магнитное поле и тем больше противодействие току.
Аналогично, чем выше частота, тем больше противодействие току.
Индуктивное сопротивление обозначается символом XL.
Индуктивное сопротивление определяется формулой:
ХL = 2πfL
где π = 3,14, f — частота в герцах, L — индуктивность в генри.
ПРИМЕР: Чему равно индуктивное сопротивление катушки индуктивностью 0,15 генри на частоте 60 герц?
Дано:
π = 3,14; f = 60 Гц; L = 0,15 Гн
ХL =?
Решение:
ХL = 2πfL
ХL = (2)(3,14)(60)(0,15)
ХL = 56,52 Ом.
ПРИМЕР: Чему равно индуктивное сопротивление катушки индуктивностью 0,15 генри на частоте 400 герц?
Дано:
π = 3,14; f = 400 Гц; L = 0,15 Гн
ХL =?
Решение:
ХL = 2πfL
ХL = (2)(3,14)(400)(0,15)
ХL = 376,80 Ом.
Заметим, что индуктивное сопротивление увеличивается при увеличении частоты.
Закон Ома применяется к индуктивному сопротивлению в цепях переменного тока точно так же, как он применяется к резисторам. Индуктивное сопротивление в цепи переменного тока прямо пропорционально приложенному напряжению и обратно пропорционально току. Это соотношение выражается следующей формулой:
I = E/XL
ПРИМЕР: Какой ток течет через катушку индуктивности 250 миллигенри, когда к ней приложено напряжение 12 вольт с частотой 60 герц?
Дано:
π = 3,14; f = 60 Гц; L = 0,25 Гн; E = 12 B
I =?; ХL =?
Решение:
Сначала найдем индуктивное сопротивление (XL)
ХL = 2πfL
ХL = (2)(3,14)(60)(0,25)
ХL = 94,20 Ом
Используя XL, найдем ток (I).
I = E/ХL = 12/94,2
I = 0,127 А или 127 мА.
ПРИМЕР: Какое напряжение нужно приложить для того, чтобы через дроссель индуктивностью 15 миллигенри шел ток 10 миллиампер при частоте 400 герц?
Дано:
π = 3,14; f = 400 Гц; L = 0,015 Гн; I = 0,01 A
E =?; ХL =?
Решение:
Сначала найдем индуктивное сопротивление (XL)
ХL = 2πfL
ХL = (2)(3,14)(400)(0,015)
ХL = 37,68 Ом
Используя XL, найдем напряжение (Е).
I = E/ХL
0,01 = E/37,68
E = 0,38 B
ПРИМЕР: Чему равно индуктивное сопротивление катушки, по которой течет ток 120 миллиампер при приложенном напряжении 120 вольт?
Дано:
I = 0,12 A; E = 120 В
ХL =?
Решение:
I = E/ХL
0,12 = 120/ХL
ХL = 1000 Ом
Импедансом цепи, содержащей индуктивность и сопротивление, называется общее противодействие току, оказываемое и индуктивностью, и резистором. Вследствие наличия сдвига фаз, обусловленного наличием индуктивности, индуктивное сопротивление и сопротивление резистора нельзя просто сложить. Импеданс является векторной суммой индуктивного сопротивления и сопротивления резистора в цепи. Импеданс измеряется в омах и обозначается буквой Z. Импеданс можно определить с помощью закона Ома следующим образом:
Импеданс является векторной суммой индуктивного сопротивления и сопротивления резистора в цепи. Импеданс измеряется в омах и обозначается буквой Z. Импеданс можно определить с помощью закона Ома следующим образом:
I = E/Z
Наиболее распространенная индуктивная цепь состоит из резистора и катушки индуктивности, соединенных последовательно. Такая цепь называется RL цепью. Импеданс последовательной RL цепи равен корню квадратному из суммы квадратов индуктивного сопротивления и сопротивления резистора:
ПРИМЕР: Чему равен импеданс цепи, состоящей из дросселя индуктивностью 100 миллигенри и соединенного последовательно резистора 470 ом, при приложенном к ним напряжении 12 вольт с частотой 60 герц?
Дано:
π = 3,14; f = 60 Гц; L = 100 мГн = 0,1 Гн; R = 400 Ом
ХL =?; Z =?
Решение:
Сначала найдем индуктивное сопротивление (XL):
XL = 2πfL
XL = (2)(3,14)(60)(0,1)
XL = 37,68 Ома.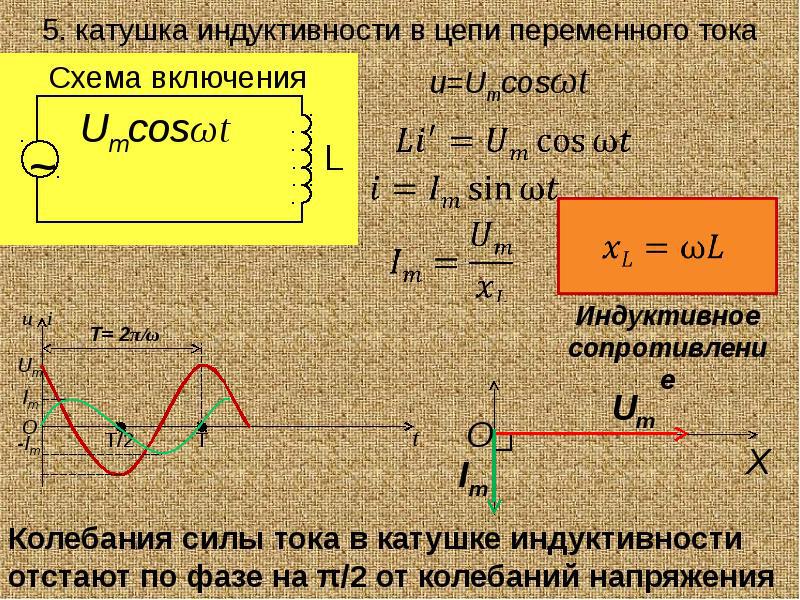
Используя XL, найдем импеданс (Z):
Z = √(R2 + XL2)
Z = √[(470)2 +(37,68)2]
Z = 471,51 Ом.
Когда катушки индуктивности соединены последова тельно, их общее индуктивное сопротивление равно сумме индуктивных сопротивлений отдельных катушек:
XLT = XL1 + XL2 + XL3 +… + XLn
Когда катушки индуктивности соединены параллельно, обратная величина их общего индуктивного сопротивления равна сумме обратных величин индуктивных сопротивлений отдельных катушек:
1/XLT = 1/XL1 + 1/XL2 + 1/XL3 +… + 1/XLn
16-1.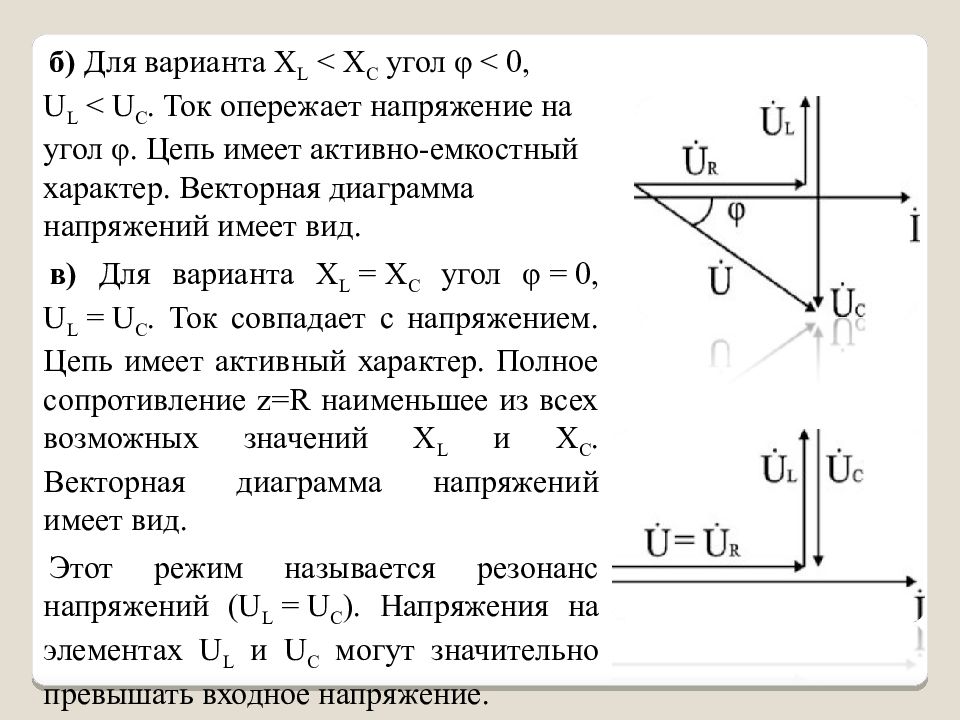 Вопросы
Вопросы
1. Как катушки индуктивности реагируют на приложенное переменное напряжение?
2. Каково фазовое соотношение между током и напряжением в индуктивной цепи?
3. Что такое индуктивное сопротивление?
4. Чему равно индуктивное сопротивление катушки индуктивностью 200 миллигенри на частоте 10000 герц?
5. Как определяется импеданс для индуктивно-резистивной цепи?
16-2. ПРИМЕНЕНИЯ ИНДУКТИВНЫХ ЦЕПЕЙ
Индуктивные цепи широко используются в электронике. Катушки индуктивности дополняют конденсаторы в цепях фильтрации и фазового сдвига. Поскольку катушки индуктивности больше, тяжелее и дороже, чем конденсаторы, они применяются реже. Однако преимущество катушек индуктивности в том, что они обеспечивают реактивное сопротивление и пропускают постоянный ток. Конденсаторы могут обеспечивать реактивное сопротивление, но при этом они блокируют прохождение постоянного тока.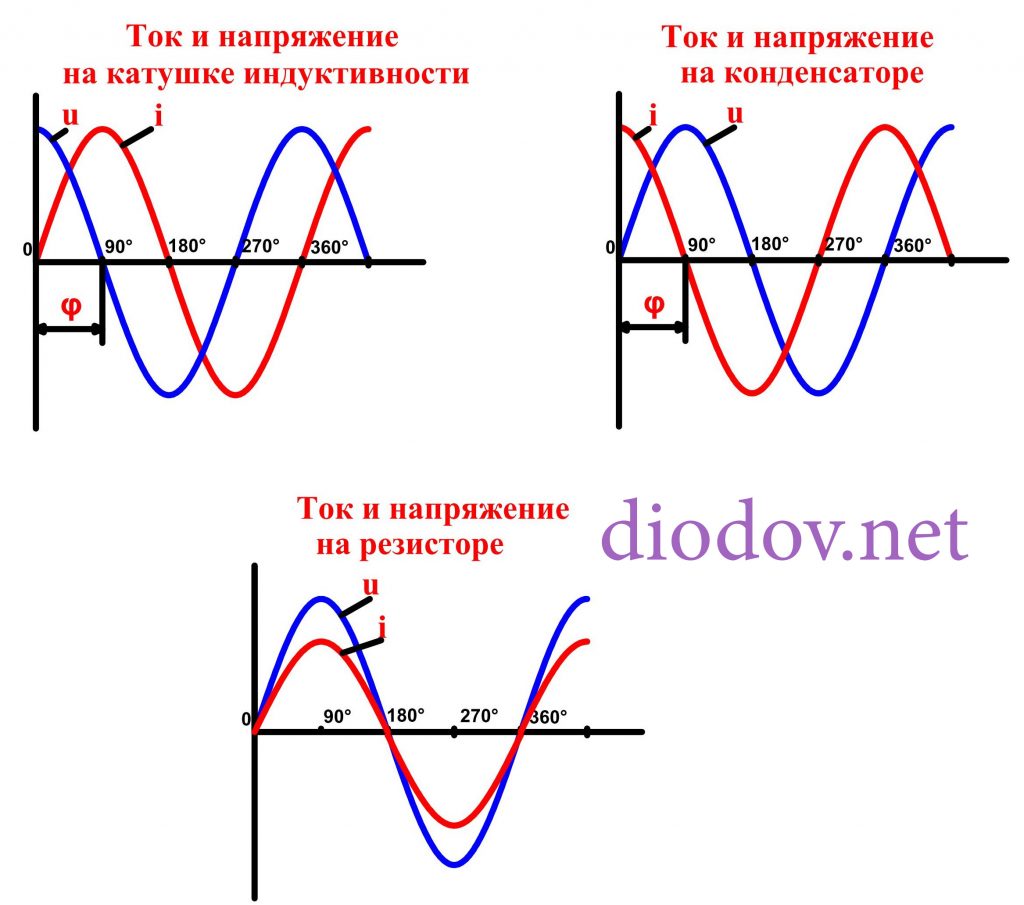
Катушки индуктивности иногда комбинируют с конденсаторами для улучшения характеристик цепи. В этом случае реактивный эффект конденсатора противоположен реактивному эффекту катушки индуктивности. Конечный результат состоит в том, что они взаимно дополняют друг друга в цепи.
Последовательные RL цепочки используются в качестве фильтров нижних и верхних частот. На рис. 16-3 показаны два основных типа фильтров. По существу эти цепи являются резистивно-индуктивными делителями напряжения. На рис. 16-3(А) изображен фильтр нижних частот.
Входное напряжение приложено к катушке индуктивности и резистору. Выходное напряжение снимается с резистора. На низких частотах реактивное сопротивление катушки низкое. Следовательно, она слабо противодействует току, и основная часть напряжения падает на резисторе.
При увеличении частоты входного напряжения индуктивное сопротивление увеличивается и оказывает большее противодействие току, так что большая часть приложенного напряжения падает на индуктивности. Чем больше падение напряжения на катушке индуктивности, тем меньше падение напряжения на резисторе, т. к. сумма падений напряжения в цепи равна приложенному напряжению. Увеличение частоты входного напряжения уменьшает выходное напряжение. Низкие частоты фильтр пропускает с небольшим уменьшением амплитуды, тогда как амплитуда напряжений высоких частот уменьшается значительно.
Чем больше падение напряжения на катушке индуктивности, тем меньше падение напряжения на резисторе, т. к. сумма падений напряжения в цепи равна приложенному напряжению. Увеличение частоты входного напряжения уменьшает выходное напряжение. Низкие частоты фильтр пропускает с небольшим уменьшением амплитуды, тогда как амплитуда напряжений высоких частот уменьшается значительно.
На рис. 16-3(Б) изображен фильтр верхних частот. Входное напряжение приложено к катушке индуктивности и резистору, а выходное напряжение снимается с катушки индуктивности. На высоких частотах индуктивное сопротивление катушки высокое, и большая часть приложенного напряжения падает на катушке. При уменьшении частоты индуктивное сопротивление уменьшается, оказывая меньшее противодействие току. Это приводит к уменьшению падения напряжения на катушке, и к увеличению падения напряжения на резисторе.
Рис. 16-3. RL фильтры.
Частота, выше или ниже которой фильтр пропускает или ослабляет сигналы, называется частотой среза.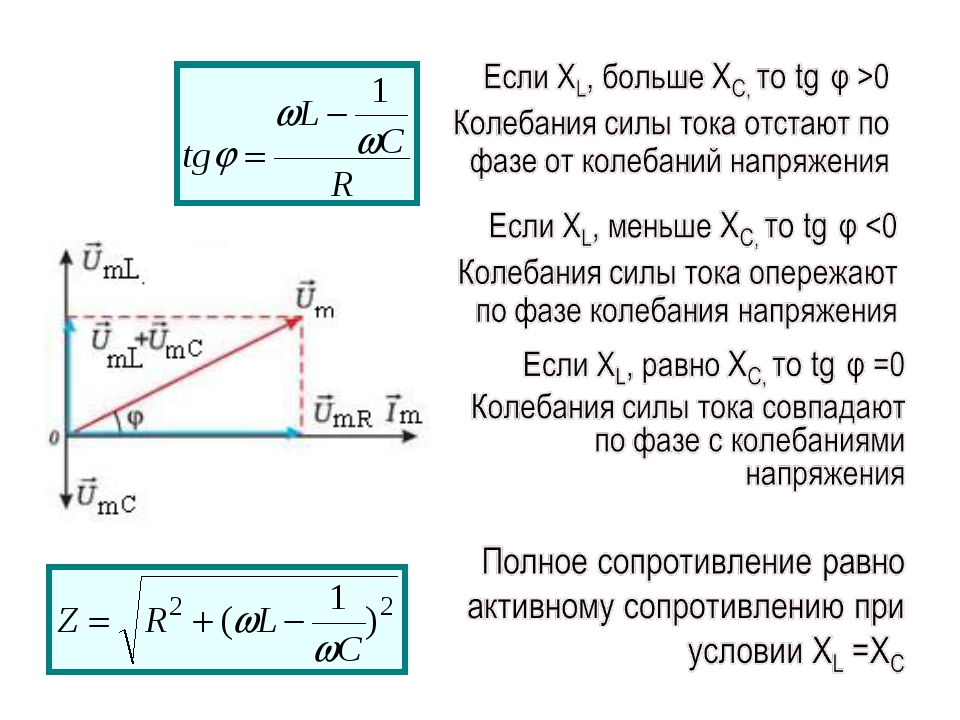 Частота среза обозначается символом fс. Частоту среза можно определить по формуле:
Частота среза обозначается символом fс. Частоту среза можно определить по формуле:
fc = R/2πfL
где fc — частота среза в герцах, R — сопротивление в омах, π = 3,14, f — частота в герцах, L — индуктивность в генри.
16-2. Вопросы
1. В чем неудобство использования катушек индуктивности в цепях?
2. В чем преимущество использования катушек индуктивности в цепях?
3. Нарисуйте амплитудно-частотную характеристику RL фильтра нижних частот и объясните, как он работает.
4. Нарисуйте амплитудно-частотную характеристику RL фильтра верхних частот и объясните, как он работает.
5. Как можно определить частоту среза RL цепи?
РЕЗЮМЕ
• В чисто индуктивной цепи ток отстает от приложенного напряжения на 90 градусов.
• Индуктивное сопротивление — это противодействие току, оказываемое катушкой индуктивности в цепи переменного тока.
• Индуктивное сопротивление обозначается символом XL.
• Индуктивное сопротивление измеряется в омах.
• Индуктивное сопротивление можно вычислить по формуле:
XL = 2πfL
• Импеданс — это векторная сумма индуктивного сопротивления и сопротивления резистора в цепи.
• Последовательные RL цепи используются в качестве фильтров верхних и нижних частот.
Глава 16. САМОПРОВЕРКА
1. Каково фазовое соотношение между током и приложенным напряжением в индуктивной цепи?
2. Какой фактор влияет на индуктивное сопротивление цепи?
3. Чему равно индуктивное сопротивление катушки индуктивностью 100 миллигенри на частоте 60 герц?
4. Какой ток будет течь через катушку, описанную в вопросе 3, если к ней приложить напряжение 24 вольта?
Какой ток будет течь через катушку, описанную в вопросе 3, если к ней приложить напряжение 24 вольта?
5. Как используются в цепях катушки индуктивности?
6. Что такое частота среза индуктивной цепи?
Мощность электрического тока: особенности и измерения
Мощность электрического тока – скорость выполняемой цепью работы. Простое определение, морока с пониманием. Мощность подразделяется на активную, реактивную. И начинается…
Работа электрического тока, мощность
При движении заряда по проводнику поле выполняет над ним работу. Величина характеризуется напряжением, в отличие от напряженности в свободном пространстве. Заряды двигаются в сторону убывания потенциалов, для поддержания процесса требуется источник энергии. Напряжение численно равно работе поля при перемещении на участке единичного заряда (1 Кл).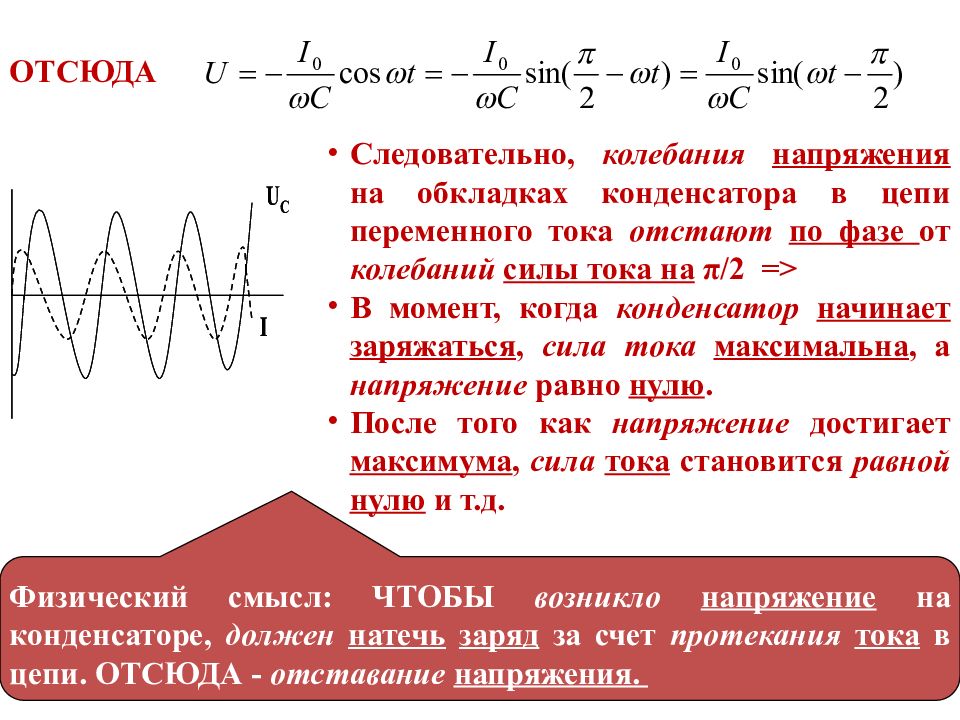 В ходе взаимодействий электрическая энергия переходит в другие виды. Поэтому необходим ввод универсальной единицы, физической свободно конвертируемой валюты. В организме мерой выступает АТФ, электричестве — работа поля.
В ходе взаимодействий электрическая энергия переходит в другие виды. Поэтому необходим ввод универсальной единицы, физической свободно конвертируемой валюты. В организме мерой выступает АТФ, электричестве — работа поля.
Электрическая дуга
На схеме момент превращения энергии отображается в виде источников ЭДС. Если у генераторов направлены в одну сторону, у потребителя – обязательно в другую. Наглядным фактом отражается процесс расхода мощности, отбора у источников энергии. ЭДС несет обратный знак, часто называется противо-ЭДС. Избегайте путать понятие с явлением, возникающим в индуктивностях при выключении питания. Противо-ЭДС означает переход электрической энергии в химическую, механическую, световую.
Потребитель хочет выполнить работу за некоторую единицу времени. Очевидно, газонокосильщик не намерен ждать зимы, надеется управиться к обеду. Мощность источника должна обеспечить заданную скорость выполнения. Работу осуществляет электрический ток, следовательно, понятие также относится. Мощность бывает активной, реактивной, полезной и мощностью потерь. Участки, обозначаемые физическими схемами сопротивлениями, на практике вредны, являются издержками. На резисторах проводников выделяется тепло, эффект Джоуля-Ленца ведет к лишнему расходу мощности. Исключением назовем нагревательные приборы, где явление желательно.
Мощность бывает активной, реактивной, полезной и мощностью потерь. Участки, обозначаемые физическими схемами сопротивлениями, на практике вредны, являются издержками. На резисторах проводников выделяется тепло, эффект Джоуля-Ленца ведет к лишнему расходу мощности. Исключением назовем нагревательные приборы, где явление желательно.
Полезная работа на физических схемах обозначается противо-ЭДС (обычный источник с обратным генератору направлением). Для мощности имеется несколько аналитических выражений. Иногда удобно использовать одно, в других случаях – иное (см. рис.):
Выражения мощности тока
- Мощность – скорость выполнения работы.
- Мощность равна произведению напряжения на ток.
- Мощность, затрачиваемая на тепловое действие, равна произведению сопротивления на квадрат тока.
- Мощность, затрачиваемая на тепловое действие, равна отношению квадрата напряжения к сопротивлению.
Запасшемуся токовыми клещами проще использовать вторую формулу.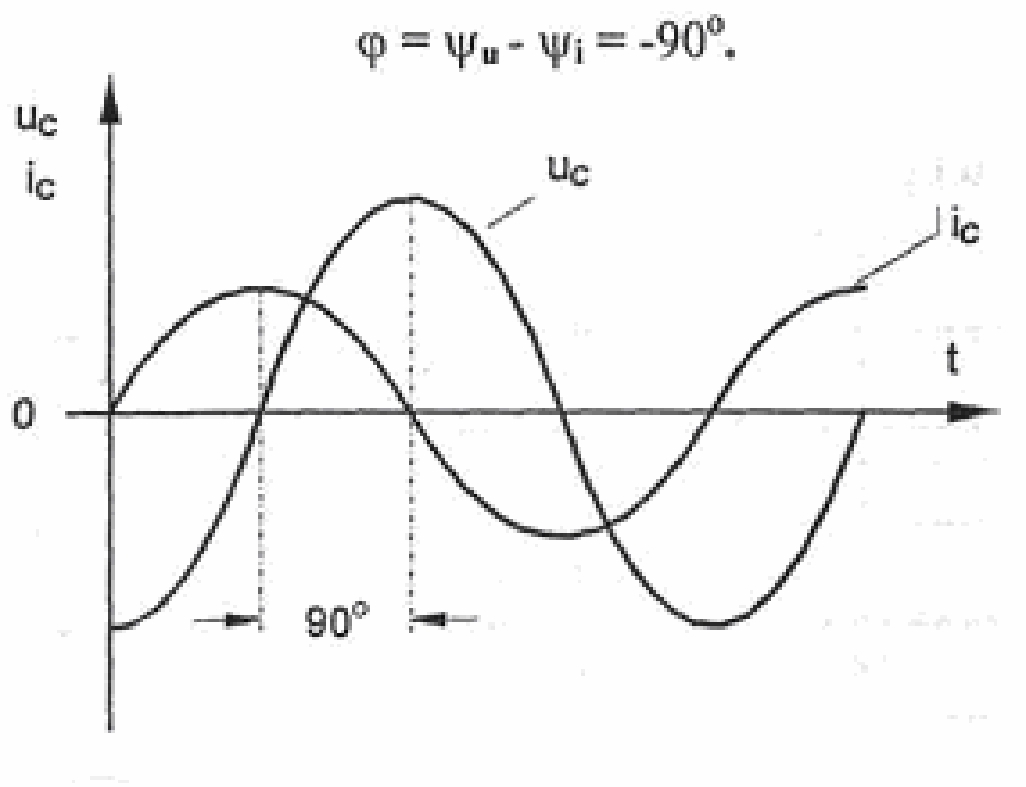 Вне зависимости от характера нагрузки посчитаем мощность. Только активную. Мощность определена многими факторами, включая температуру. Под номинальным для прибора значением понимаем, развиваемое в установившемся режиме. Для нагревателей следует применять третью, четвертую формулу. Мощность зависит целиком и полностью от параметров питающей сети. Предназначенные для работы со 110 вольт переменного тока в европейских условиях быстро сгорят.
Вне зависимости от характера нагрузки посчитаем мощность. Только активную. Мощность определена многими факторами, включая температуру. Под номинальным для прибора значением понимаем, развиваемое в установившемся режиме. Для нагревателей следует применять третью, четвертую формулу. Мощность зависит целиком и полностью от параметров питающей сети. Предназначенные для работы со 110 вольт переменного тока в европейских условиях быстро сгорят.
Трехфазные цепи
Новичкам трехфазные цепи представляются сложными, на деле это более элегантное техническое решение. Даже электричество домом поставляют тремя линиями. Внутри подъезда делят по квартирам. Больше смущает то, что некоторые приборы на три фазы лишены заземления, нулевого провода. Схемы с изолированной нейтралью. Нулевой провод не нужен, ток возвращается источнику по фазным линиям. Разумеется, нагрузка здесь на каждую жилу повышенная. Требования ПУЭ отдельно оговаривают род сети. Для трехфазных схем вводятся следующие понятия, о которых нужно иметь представление, чтобы правильно посчитать мощность:
Трехфазная цепь с изолированной нейтралью
- Фазным напряжением, током называют, соответственно, разницу потенциалов и скорость передвижения заряда меж фазой и нейтралью.
 Понятно, в оговоренном выше случае с полной изоляцией формулы будут недействительны. Поскольку нейтрали нет.
Понятно, в оговоренном выше случае с полной изоляцией формулы будут недействительны. Поскольку нейтрали нет. - Линейным напряжением, током называют, соответственно, разницу потенциалов или скорость перемещения заряда меж любыми двумя фазами. Номера понятны из контекста. Когда говорят о сетях 400 вольт, подразумевают три провода, разница потенциалов с нейтралью равна 230 вольт. Линейное напряжение выше фазного.
Меж напряжением и током существует сдвиг фаз. О чем умалчивает школьная физика. Фазы совпадают, если нагрузка 100% активная (простые резисторы). Иначе появляется сдвиг. В индуктивности ток отстает от напряжения на 90 градусов, в емкости – опережает. Простая истина легко запоминается следующим образом (плавно подходим к реактивной мощности). Мнимая часть сопротивления индуктивности составляет jωL, где ω – круговая частота, равная обычной (в Гц), помноженной на 2 числа Пи; j – оператор, обозначающий направление вектора. Теперь пишем закон Ома: U = I R = I jωL.
Из равенства видно: напряжение нужно отложить вверх на 90 градусов при построении диаграммы, ток останется на оси абсцисс (горизонтальная ось Х). Вращение по правилам радиотехники происходит против часовой стрелки. Теперь очевиден факт: ток отстает на 90 градусов. По аналогии проведем сравнение для конденсатора. Сопротивление переменному току в мнимой форме выглядит так: -j/ωL, знак указывает: откладывать напряжение нужно будет вниз, перпендикулярно оси абсцисс. Следовательно, ток опережает по фазе на 90 градусов.
Вращение по правилам радиотехники происходит против часовой стрелки. Теперь очевиден факт: ток отстает на 90 градусов. По аналогии проведем сравнение для конденсатора. Сопротивление переменному току в мнимой форме выглядит так: -j/ωL, знак указывает: откладывать напряжение нужно будет вниз, перпендикулярно оси абсцисс. Следовательно, ток опережает по фазе на 90 градусов.
В реальности параллельно с мнимой частью присутствует действительная – называют активным сопротивлением. Проволока катушки представлена резистором, будучи свитой, приобретает индуктивные свойства. Поэтому реальный угол фаз будет не 90 градусов, немного меньше.
А теперь можно переходить к формулам мощности тока трехфазных цепей. Здесь линия формирует сдвиг фаз. Меж напряжением и током, и относительно другой линии. Согласитесь, без заботливо изложенных авторами знания факт нельзя осознать. Меж линиями промышленной трехфазной сети сдвиг 120 градусов (полный оборот – 360 градусов). Обеспечит равномерность вращения поля в двигателях, для рядовых потребителей безразличен. Так удобнее генераторам ГЭС – нагрузка сбалансированная. Сдвиг идет меж линиями, в каждой ток опережает напряжение или отстает:
Так удобнее генераторам ГЭС – нагрузка сбалансированная. Сдвиг идет меж линиями, в каждой ток опережает напряжение или отстает:
- Если линия симметричная, сдвиги меж любыми фазами по току составляют 120 градусов, формула получается предельно простой. Но! Если нагрузка симметрична. Посмотрим изображение: фаза ф не 120 градусов, характеризует сдвиг меж напряжением и током каждой линии. Предполагается, включили двигатель с тремя равноценными обмотками, получается такой результат. Если нагрузка несимметрична, потрудитесь провести вычисления для каждой линии отдельно, затем сложить результаты воедино для получения общей мощности тока.
- Вторая группа формул приведена для трехфазных цепей с изолированной нейтралью. Предполагается, ток одной линии утекает по другой. Нейтраль отсутствует за ненадобностью. Поэтому напряжения берутся не фазные (не от чего отсчитывать), как предыдущей формулой, а линейные. Соответственно, цифры показывают, какой параметр следует взять. Повремените пугаться греческих букв – фазы меж двумя перемножаемыми параметрами.
 Цифры меняются местами (1,2 или 2,1), чтобы правильно учесть знак.
Цифры меняются местами (1,2 или 2,1), чтобы правильно учесть знак. - В асимметричной цепи вновь появляются фазные напряжение, ток. Здесь расчет ведется отдельно для каждой линии. Никаких вариантов нет.
Формулы мощности тока
На практике измерить мощность тока
Намекнули, можно воспользоваться токовыми клещами. Прибор позволит определить крейсерские параметры дрели. Разгон можно засечь только при многократных опытах, процесс чрезвычайно быстрый, частота смены индикации не выше 3-х раз в секунду. Токовые клещи демонстрируют погрешность. Практика показывает: достичь погрешности, указанной в паспорте, сложно.
Чаще для оценки мощности используют счетчики (для выплат компаниям-поставщикам), ваттметры (для личных и рабочих целей). Стрелочный прибор содержит пару неподвижных катушек, по которым течет ток цепи, подвижную рамку, для заведения напряжения путем параллельного включения нагрузки. Конструкция рассчитана сразу реализовать формулу полной мощности (см.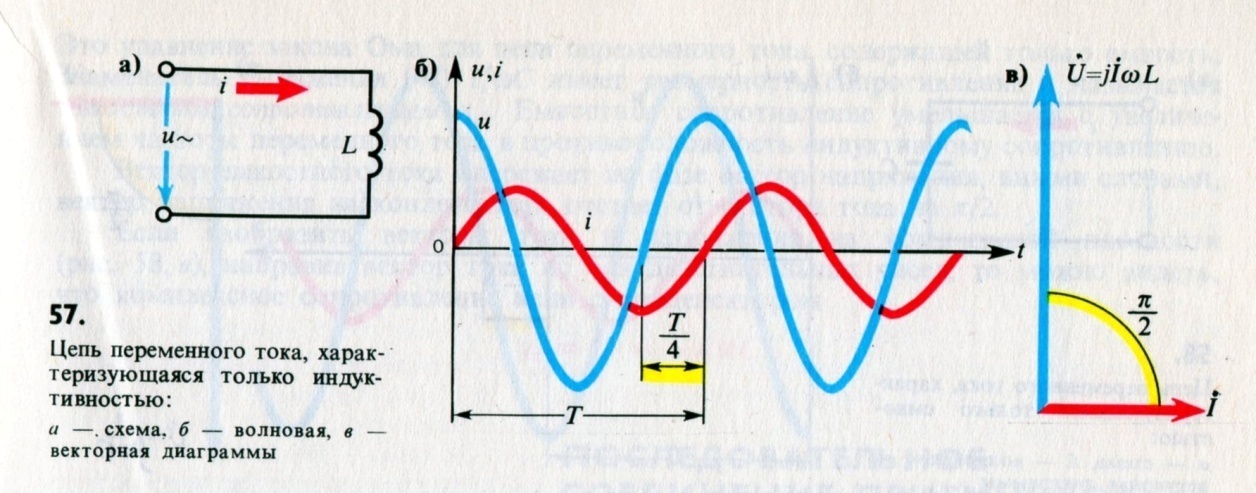 рис.). Ток умножается на напряжение и некий коэффициент, учитывающий градуировку шкалы, также на косинус сдвига фаз между параметрами. Как говорили выше, сдвиг умещается в пределах 90 – минус 90 градусов, следовательно, косинус положителен, крутящий момент стрелки направлен в одну сторону.
рис.). Ток умножается на напряжение и некий коэффициент, учитывающий градуировку шкалы, также на косинус сдвига фаз между параметрами. Как говорили выше, сдвиг умещается в пределах 90 – минус 90 градусов, следовательно, косинус положителен, крутящий момент стрелки направлен в одну сторону.
Отсутствует возможность сказать индуктивная ли нагрузка или емкостная. Зато при неправильном включении в цепь показания будут отрицательными (завал набок). Произойдет аналогичное событие, если потребитель вдруг станет отдавать мощность обратно нагрузке (бывает такое). В современных приборах происходит нечто подобное же, вычисления ведет электронный модуль, интегрирующий расход энергии, либо считывающий показания мощности. Вместо стрелки присутствует электронный индикатор и множество других полезных опций.
Особые проблемы вызывают измерения в асимметричных цепях с изолированной нейтралью, где нельзя прямо складывать мощности каждой линии. Ваттметры делятся принципом действия:
Ваттметры делятся принципом действия:
- Электродинамические. Описаны разделом. Состоят из одной подвижной, двух неподвижных катушек.
- Ферродинамические. Напоминает двигатель с расщепленным полюсом (shaded-pole motor).
- С квадратором. Используется амплитудно-частотная характеристика нелинейного элемента (например, диода), напоминающая параболу, для возведения электрической величины в квадрат (используется в вычислениях).
- С датчиком Холла. Если индукцию сделать при помощи катушки пропорциональной напряжению магнитного поля в сенсоре, подать ток, ЭДС будет результатом умножения двух величин. Искомая величина.
- Компараторы. Постепенно повышает опорный сигнал, пока не будет достигнуто равенство. Цифровые приборы достигают высокой точности.
В цепях с сильным сдвигом фаз для оценки потерь применяется синусный ваттметр. Конструкция схожа с рассмотренной, пространственное положение таково, что вычисляется реактивная мощность (см. рис.). В этом случае произведение тока и напряжения домножим на синус угла сдвига фаз. Реактивную мощность измерим обычным (активным) ваттметром. Имеется несколько методик. Например, в трехфазной симметричной цепи нужно последовательную обмотку включить в одну линию, параллельную – в две другие. Затем производятся вычисления: показания прибора умножаются на корень из трех (с учетом, что на индикаторе произведение тока, напряжения и синуса угла между ними).
Реактивную мощность измерим обычным (активным) ваттметром. Имеется несколько методик. Например, в трехфазной симметричной цепи нужно последовательную обмотку включить в одну линию, параллельную – в две другие. Затем производятся вычисления: показания прибора умножаются на корень из трех (с учетом, что на индикаторе произведение тока, напряжения и синуса угла между ними).
Методика двух ваттметров
Для трехфазной цепи с простой асимметрией задача усложняется. На рисунке показана методика двух ваттметров (ферродинамических или электродинамических). Начала обмоток указаны звездочками. Ток проходит через последовательные, напряжение с двух фаз подается на параллельную (одно через резистор). Алгебраическая сумма показаний обоих ваттметров складывается, умножается на корень из трех для получения значения реактивной мощности.
Формула реактивное сопротивление конденсатора
Реактивное сопротивление XL и XC
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока. При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении – положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt). Отсюда выразим синусоидальный ток .
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2). Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω. В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°). Для среднеквадратичных значений U и I в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Реактивное сопротивление конденсатора.
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt). Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2). Тогда для синусоидального напряжения u = Uampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2). Тогда для синусоидального напряжения u = Uampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
i = UampωCsin(ωt+π/2).
Отсюда выразим соотношение среднеквадратичных значений .
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.
Онлайн-калькулятор расчёта реактивного сопротивления
Необходимо вписать значения и кликнуть мышкой в таблице. При переключении множителей автоматически происходит пересчёт результата.
Реактивное сопротивление ёмкостиXC = 1 /(2πƒC) | Реактивное сопротивление индуктивностиXL = 2πƒL |
Расчитать ёмкость или индуктивность для реактивного сопротивления:
Расчёт ёмкости: C = 1 /(2πƒXC) | Расчёт индуктивности: L = XL /(2πƒ) |
Похожие страницы с расчётами:
Расcчитать импеданс.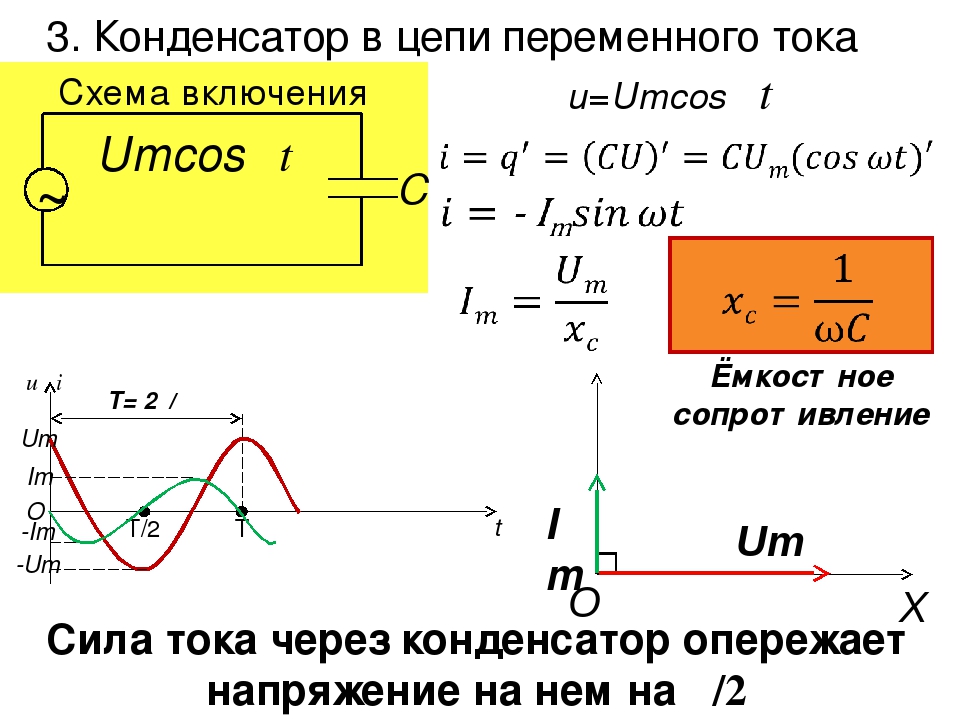
Реактивное сопротивление
Главная > Теория > Реактивное сопротивление
В цепь переменного электрического тока входят активные (содержащие внутренние источники энергии) и пассивные элементы (потребители энергии). К пассивным элементам относят резисторы и реактивные устройства.
Виды пассивных элементов
В электротехнике рассматривают два типа резисторов: активное и реактивное сопротивление. Активным – обладают приборы, в которых энергия электрического тока преобразуется в тепловую. В физике оно обозначается символом R. Единица измерения – Ом.
Рассчитать его можно, используя закон Ома:
R = U/I.
Этой формулой можно пользоваться для расчёта по мгновенным значениям тока и напряжения, максимальным или действующим.
Реактивные устройства энергию не рассеивают, а накапливают. К ним относятся:
- катушка индуктивности;
- конденсатор.

Реактивное сопротивление обозначается символом Х. Единица измерения – Ом.
Катушка индуктивности
Представляет собой проводник, выполненный в форме спирали, винта или винтоспирали. Благодаря высокой инерционности, прибор используют в схемах, которые применяются для уменьшения пульсаций в цепях переменного тока и колебательных контурах, для создания магнитного поля и т.д. Если она имеет большую длину при небольшом диаметре, то катушку называют соленоидом.
Для вычисления падения напряжения (U) на концах катушки используют формулу:
U = –L·DI/Dt, где:
- L – индуктивность прибора, измеряется в Гн (генри),
- DI – изменение силы тока (измеряется в амперах) за промежуток времени Dt (измеряется в секундах).
Внимание! При любом изменении тока в проводнике возникает ЭДС самоиндукции, которая препятствует этому изменению.
Вследствие этого в катушке возникает сопротивление, которое называется индуктивным.
В электротехнике обозначается ХL и рассчитывается по формуле:
ХL = w · L,
где w – угловая частота, измеряется в рад/с.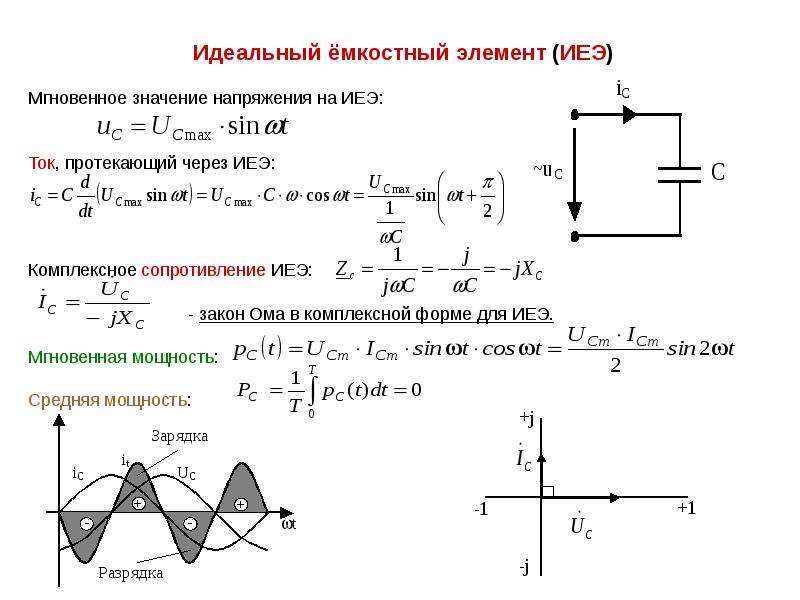
Угловая частота является характеристикой гармоничного колебания. Связана с частотой f (количество полных колебаний в секунду). Частота измеряется в колебаниях в секунду (1/с):
w = 2 · p · f.
Если в схеме используется несколько катушек, то при их последовательном соединении общее ХL для всей системы будет равно:
XL = XL1 + XL2 + …
В случае параллельного соединения:
1/XL = 1/XL1 + 1/XL2 + …
Закон Ома для такого соединения имеет вид:
XL=UL/I,
где UL – падение напряжения.
Помимо индуктивного, устройство обладает и активным R.
Электрический импеданс в этом случае равен:
Z = XL + R.
Емкостной элемент
В проводниках и обмотке катушки, кроме индуктивного и активного сопротивлений, присутствует и емкостное, которое обусловлено наличием ёмкости в этих приборах. Кроме резистора и катушки, в схему может быть включен конденсатор, который состоит из двух металлических пластин, между которыми размещён слой диэлектрика.
К сведению. Электрический ток протекает за счёт того, что в устройстве проходят процессы заряда и разряда пластин.
При максимальном заряде на пластинах прибора:
U = max, I = 0.
За счёт того, что резистивное устройство может накапливать энергию, его используют в приборах, которые стабилизируют напряжение в цепи.
Возможность накапливать заряд характеризуется ёмкостью.
Реактивное сопротивление конденсатора (ХС) можно рассчитать по формуле:
XC = 1/(w·C), где:
- w – угловая частота,
- С – ёмкость конденсатора.
Единица измерения ёмкости – Ф (фарада).
Учитывая, что угловая частота связана с циклической частотой, расчет значения реактивного сопротивления конденсатора можно выполнить по формуле:
XC=1/(2·p·f·C).
Если в цепи последовательно соединены несколько устройств, то общее XС системы будет равно:
XС = XС1 + XС2 + …
Если соединение объектов параллельное, то:
1/XC = 1/XC1 + 1/XC2+…
Закон Ома для этого случая записывается следующим образом:
XC = UC/I,
где UС – падение напряжения на конденсаторе.
Расчёт цепи
Эквивалентное сопротивлениеПри последовательном соединении I = const в любой точке и, согласно закону Ома, его можно рассчитать по формуле:
I = U/R,
где Z – электрический импеданс.
Последовательное соединение элементов
Напряжение на устройствах рассчитывается следующим образом:
UR = I · R, UL = I · XL, UC = I · XC.
Вектор индуктивной составляющей напряжения направлен в противоположную сторону от вектора емкостной составляющей, поэтому:
UX = UL – UC,
следовательно, согласно расчётам:
X = XL – XC.
Внимание! Для вычисления значения импеданса можно воспользоваться «треугольником сопротивлений», в котором гипотенузой является значение Z, а катетами – значения X и R.
Треугольник сопротивлений
Если в цепь подключены и конденсатор, и катушка индуктивности, то, согласно теореме Пифагора, гипотенуза (Z) будет равна:
Так как X = XL – XC, то:
При решении электротехнических задач часто импеданс записывают в виде комплексного числа, в котором действительная часть соответствует значению активной составляющей, а мнимая – реактивной.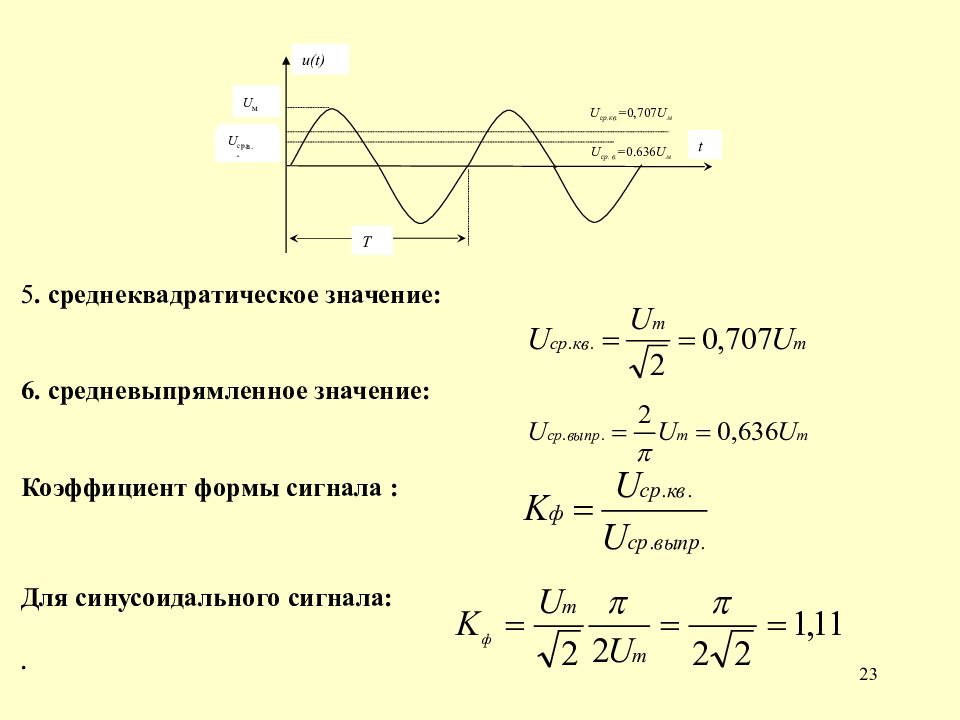 Таким образом, выражение для импеданса в общем виде имеет вид:
Таким образом, выражение для импеданса в общем виде имеет вид:
Z = R + X·i,
где i – мнимая единица.
Для онлайн расчёта реактивного сопротивления можно использовать программу – калькулятор, которую можно найти в сети Интернет. Подобных сервисов достаточно много, поэтому вам не составит труда подобрать удобный для вас калькулятор.
Онлайн калькулятор для расчёта емкостных и индуктивных характеристик
Благодаря таким Интернет сервисам, можно быстро выполнить нужный расчёт.
Видео
Активное и реактивное сопротивление
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента – резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, “активный – это деятельный, энергичный, проявляющий инициативу”. Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока .
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто).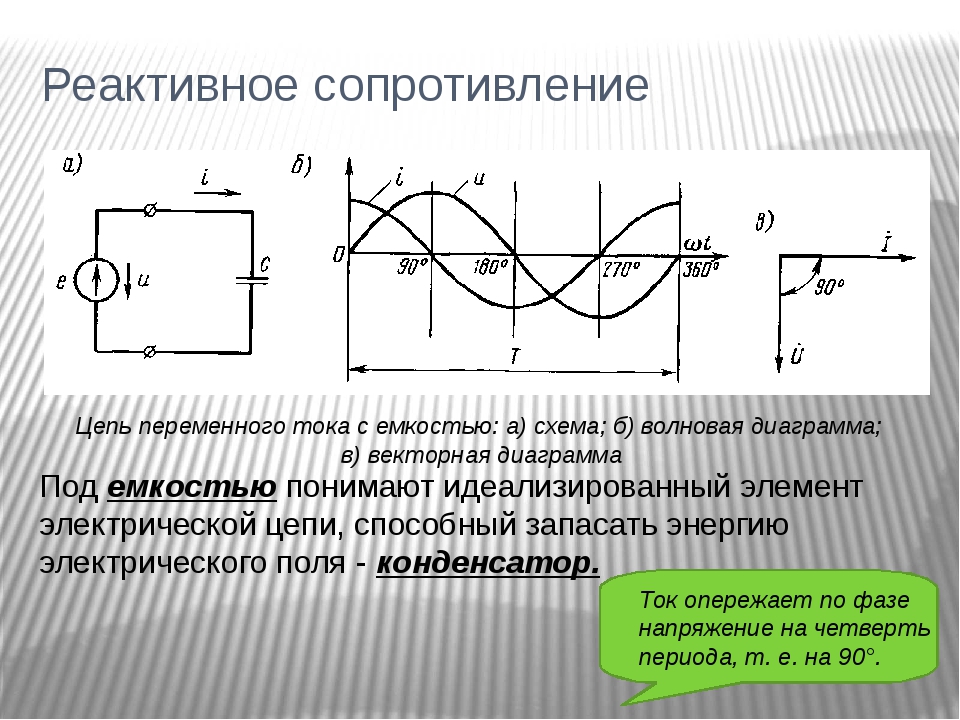 Для этого достаточно вспомнить правило шунта.
Для этого достаточно вспомнить правило шунта.
Кто не помнит – напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом.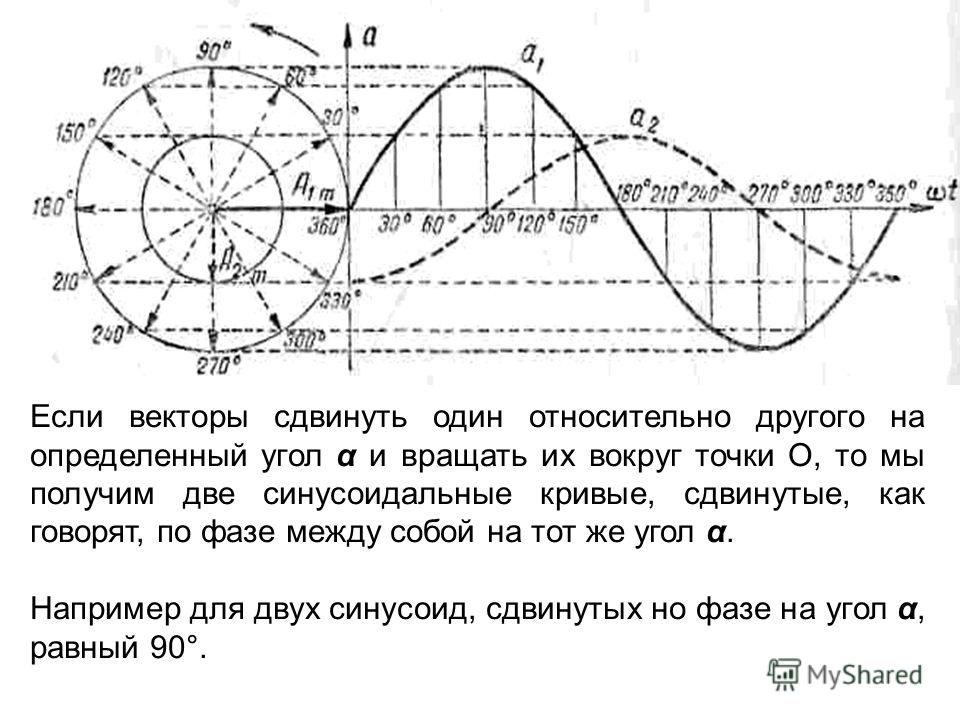 Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма – это напряжение с генератора Uген , а желтая осциллограмма – это напряжение с шунта Uш , в нашем случае – сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:
Частота 285 Герц:
Частота 30 Килогерц:
Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:
Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток.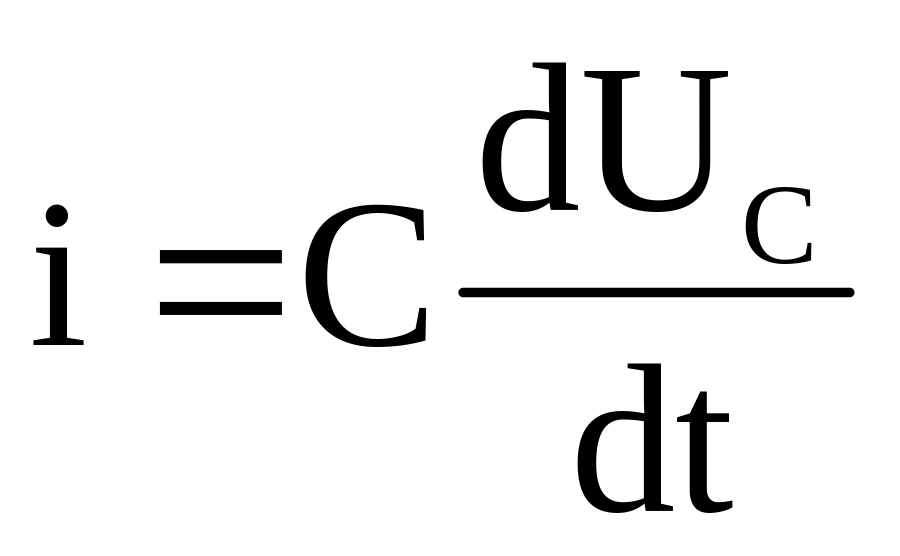 Они двигаются синфазно, то есть одновременно.
Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:
Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T – это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма – это напряжение, которое мы подаем на конденсатор, а желтая – это сила тока в цепи конденсатора.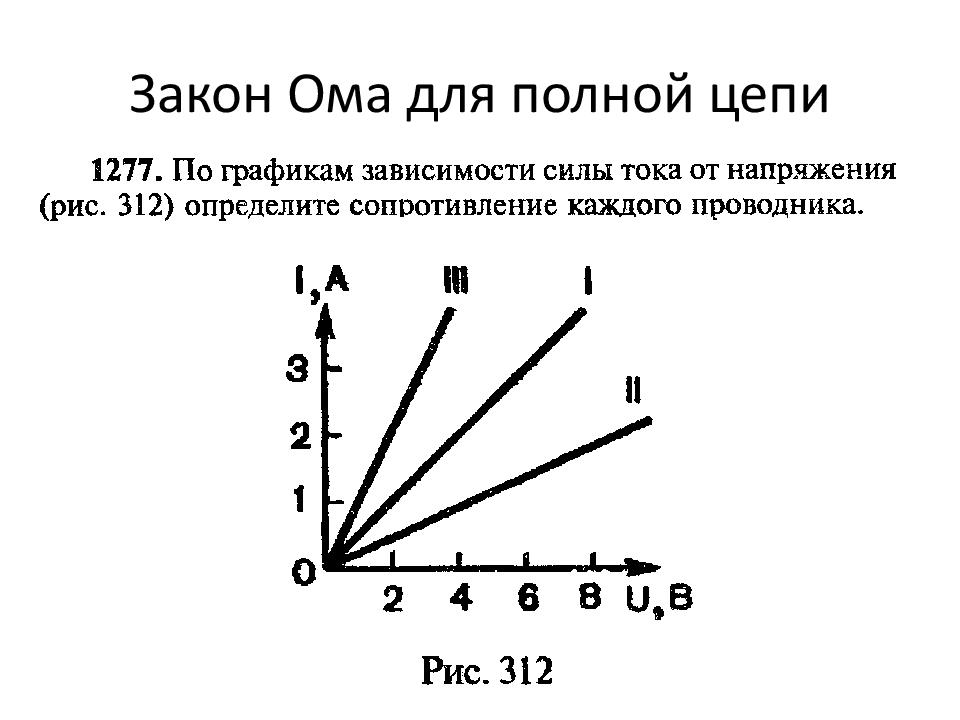 По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.
100 Герц
200 Герц
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:
где
Хс – реактивное сопротивление конденсатора, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
С – емкость конденсатора, Фарад
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка – это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле
где
ХL – реактивное сопротивление катушки, Ом
П – постоянная и приблизительно равна 3,14
F – частота, Гц
L – индуктивность, Генри
Почему не сгорает первичная обмотка трансформатора
Ну и теперь главный вопрос, который часто задают в личке: “Почему когда я меряю первичную обмотку трансформатора, у меня выдает от 10 Ом и больше в зависимости от трансформатора. На трансформаторных сварочных аппаратах вообще пару Ом! Ведь первичная обмотка трансформатора цепляется к 220 Вольтам! Почему не сгорает обмотка, ведь сопротивление обмотки всего то десятки или сотни Ом, и может случится короткое замыкание!
А ведь и вправду, мощность равна как напряжение помноженное на ток P=IU. То есть через пару секунд от первичной обмотки трансформатора должен остаться уголек.
То есть через пару секунд от первичной обмотки трансформатора должен остаться уголек.
Дело все в том, что парные обмотки трансформатора представляют из себя катушку индуктивности с какой-то индуктивностью. Получается, что реальное сопротивление обмотки будет выражаться через формулу
поставьте сюда индуктивность, которая в трансформаторах составляет от единицы Генри и получим что-то типа от 300 и более Ом. Но это еще цветочки, ягодки впереди;-)
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или П/2.
Мощность в цепи с реактивными радиоэлементами
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность – это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс.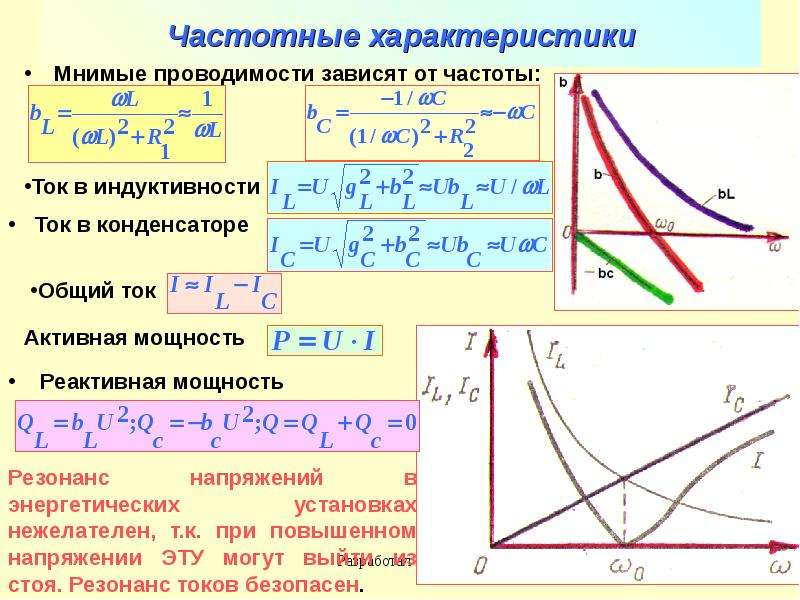 В эту четверть периода энергия поступает из источника в реактивное сопротивление.
В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком “плюс”, а напряжение со знаком “минус”. В итоге плюс на минус дает минус. Получается мощность со знаком “минус”. А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был салабоном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем “плющить” пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно – это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо – это уже другая история для полноценной статьи.
В третий промежуток времени t3 и ток и напряжение у нас со знаком “минус”. Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL – это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L – собственно сама индуктивность катушки
С – межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r – сопротивление диэлектрика и корпуса между обкладками
С – собственно сама емкость конденсатора
ESR – эквивалентное последовательное сопротивление
ESI (ESL) – эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Резюме
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.
Сопротивление катушки вычисляется по формуле
Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.
Реактивное сопротивление конденсатора
Реактивным называется сопротивление, препятствующее прохождению переменного электротока в цепи под действием конденсатора или катушки индуктивности, включенных в эту цепь.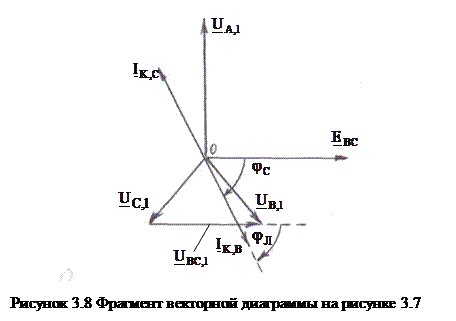 Это связано со свойствами индуктивности, которая выступает в качестве обычного проводника для постоянного тока с бесконечно малым сопротивлением. В тех же условиях конденсатор уже становится диэлектриком с возрастающим сопротивлением.
Это связано со свойствами индуктивности, которая выступает в качестве обычного проводника для постоянного тока с бесконечно малым сопротивлением. В тех же условиях конденсатор уже становится диэлектриком с возрастающим сопротивлением.
При переменном токе реактивное сопротивление конденсатора оказывает влияние на такие параметры, как частота самого тока, индуктивность катушки или емкость. Из-за этого свойства конденсатор получил наименование реактивного элемента или реактивного электронного компонента.
Свойства реактивного сопротивления конденсатора
В каждом заряженном конденсаторе присутствует электрический ток. В этих условиях он является составной частью процесса зарядки и разрядки, когда электрическое поле, образующееся между обкладками, накапливает или отдает энергию.
Установленный в цепь переменного тока, конденсатор будет накапливать энергию, то есть заряжаться, до определенного максимума, пока направление тока не изменится на противоположное. Поэтому при амплитудном значении напряжения, ток в конденсаторе будет иметь нулевое значение. В результате, ток и напряжение конденсатора будут постоянно расходиться во времени на четверть периода. Таким образом, падение напряжения на конденсаторе ограничивает ток во всей цепи, создавая реактивное сопротивление. Его значение обратно пропорционально частоте тока и емкости конденсатора.
Если к конденсатору подвести напряжение U, в этом случае начнется уменьшение тока от максимума до нуля. Одновременно, напряжение на его выводах будет возрастать от нулевого до максимального значения. В этом случае напряжение на обкладках конденсатора отстает по фазе от тока на угол, равный 90 градусам. Данное явление получило название отрицательного сдвига фаз.
Практическое использование реактивного сопротивления
С помощью конденсаторных установок осуществляется компенсация реактивной мощности. Через электрические сети высоковольтная электроэнергия передается на большие расстояния. В большинстве случаев она потребляется электродвигателями с резистивными элементами и значительным индуктивным сопротивлением.
Полная мощность, поступающая к потребителям, включает в себя активную составляющую Р, с помощью которой совершается полезная работа, и реактивную составляющую Q, приводящую к нагреву обмоток электродвигателей и трансформаторов. Качество электроэнергии существенно снижается под действием реактивной составляющей, возникающей на индуктивных сопротивлениях. Для того чтобы ликвидировать ее негативное воздействие, была разработана специальная схема компенсации. С этой целью подключались конденсаторные батареи, емкостное сопротивление которых способствовало понижению косинуса угла ф.
Установка таких конденсаторных батарей практиковалась в основном на подстанциях, осуществляющих непосредственную поставку электроэнергии проблемным потребителям. Данное мероприятие позволяло эффективно регулировать качество поставляемой энергии.
Снижение уровня реактивной компоненты способствует существенному уменьшению нагрузки на установленное оборудование, хотя активная мощность остается на одном и том же уровне. Используя реактивное сопротивление конденсатора, удалось добиться экономии электроэнергии на предприятиях промышленного производства и объектах жилищно-коммунального хозяйства, повысить надежность работы энергетических систем.
Расчет онлайн
Разность фаз напряжения и тока
Условимся под разностью фаз φ напряжения и тока всегда понимать разность начальных фаз напряжения и тока (а не наоборот):
Поэтому на векторной диаграмме угол φ отсчитывается в направлении от вектора I к вектору U (рис. 3.10). Именно при таком определении разности фаз угол φ равен аргументу комплексного сопротивления. Угол φ положителен при отстающем токе () и отрицателен при опережающем токе ().
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При имеем и ток отстает по фазе от напряжения, . При имеем , ток совпадает по фазе с напряжением, rLC-цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при имеем , ток опережает по фазе напряжение.
Векторные диаграммы для трех возможных соотношений даны на рис. 3.11. При построении этих диаграмм начальная фаза тока ; принята равной нулю. Поэтому равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3.8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при как последовательное соединение сопротивления и индуктивности (), при как сопротивление r и при как последовательное соединение сопротивления и емкости (). При заданных L и С соотношение между зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
Выше, в разделе, было принято, что задан ток, а определялись напряжения на элементах и на входных выводах цепи. Однако часто бывает задано напряжение на выводах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток
и тем самым действующий ток и начальную фазу тока.
Часто равной нулю принимается начальная фаза заданного напряжения: . В этом случае, как следует из раздела, начальная фаза тока ; равна и противоположна по знаку разности фаз φ, т. е .
Установленные выше соотношения между амплитудами и действующими токами и напряжениями, а также выражение для сдвига фаз ф позволяют вычислить ток и не прибегая к записи закона Ома в комплексной форме. Подробно этот путь решения показан в примере 3.4.
ac – Почему напряжение на конденсаторе отстает от напряжения источника в RC-цепи?
ac – Почему напряжение на конденсаторе отстает от напряжения источника в RC-цепи? – Обмен электротехнического стекаСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Electrical Engineering Stack Exchange – это сайт вопросов и ответов для профессионалов в области электроники и электротехники, студентов и энтузиастов.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 51 раз
\ $ \ begingroup \ $Как мы знаем, напряжение на конденсаторе отстает от тока через конденсатор.Но почему напряжение на конденсаторе отстает от напряжения источника в этой цепи? Аналогичным образом обнаружено, что напряжение на катушке индуктивности опережает напряжение источника в цепи RL.
Почему это происходит, когда резистор между источником и конденсатором в цепи RC и резистор между источником и индуктором в цепи RL не влияет на фазу напряжения и тока в этих цепях? Разве в этих случаях напряжение источника не должно появляться на конденсаторе и индукторе, хотя и с меньшей амплитудой, но с тем же фазовым углом на конденсаторе / катушке индуктивности?
задан 21 апр в 7:41
AlexAlex68022 золотых знака88 серебряных знаков1919 бронзовых знаков
\ $ \ endgroup \ $ \ $ \ begingroup \ $Представьте, что резистор настолько велик, что конденсатор почти не заряжается.Теперь рассмотрим, что происходит сразу после того, как напряжение источника достигает своего положительного пика. Напряжение конденсатора будет ниже напряжения источника еще почти на 90 градусов. Таким образом, напряжение конденсатора будет продолжать расти все это время.
В таких экстремальных условиях это легко увидеть. Очевидно, что если резистор или конденсатор меньше, напряжение на конденсаторе достигнет своего пика раньше. Но это всегда будет после напряжения источника, поскольку напряжение источника все равно будет немного выше, чем напряжение конденсатора, и напряжение конденсатора не может начать падать, пока напряжение источника не станет меньше, чем оно есть.
ответ дан 21 апр в 7:53
\ $ \ endgroup \ $ 5Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками ac phasor или задайте свой вопрос.
Электротехнический стек Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Может кто-нибудь объяснить, почему ток отстает от напряжения на 90 градусов в катушке индуктивности и опережает на 90 градусов в конденсаторе? : askscience
Я попытаюсь объяснить это, используя только интуитивно понятные термины.Во-первых, считайте напряжение мерой того, насколько сильно электрон хочет перейти из точки A в точку B. Затем ток – это измерение того, сколько электронов в настоящее время течет из точки A в точку B и с какой скоростью. Сопротивление – это то, насколько сложно перейти из точки A в точку B. Если вы разделите, насколько сильно электроны хотят перемещаться из точки A в точку B, на то, насколько трудно это сделать, то вы получите меру того, сколько электронов на самом деле переезжаем туда прямо сейчас. Интуитивно это закон Ома.
Теперь давайте помешаем индуктору.Текущие показатели вращающегося магнитного поля. Точно так же вращающийся магнит индуцирует ток. Это закон. Охлаждающий провод в одном направлении позволяет нескольким частям тока воздействовать на одно и то же магнитное поле вместе, усиливая эффект. Когда электроны начинают двигаться через индуктор, они запускают магнитное поле, теряя при этом скорость. Когда мы останавливаем электроны, магнитное поле на мгновение продолжает вращаться, продолжая толкать электроны. Поэтому вы можете думать о индукторе как о маховике.Обратите внимание, что это влияет только на скорость, с которой движутся электроны, а не на то, насколько сильно вы хотите добраться из точки A в точку B. Следовательно, индуктор маховика задерживает начало и остановку тока, не влияя на напряжение, поэтому мы говорим, что ток отстает от напряжения.
В качестве примечания, из-за такого поведения индукторы сглаживают нерегулярные токи, такие как пусковой ток.
Конденсатор похож на большое пустое пространство с двумя входами и забором посередине. По обе стороны движется несколько электронов.Теперь представьте, что то, что заставляет электрон хотеть быть где-то, – это ненависть к другим электронам. Он хочет побыть один. Это ворота в людные места. Внезапно через одну из дверей вливаются выходные. Электроны на другой стороне видят их, что очень неудобно, и начинают уходить. Поскольку некоторые электроны входят, а некоторые уходят, ток продолжает течь в обычном режиме. Но чем больше электронов собирается на первой стороне забора, тем меньше они хотят там находиться, но ток все равно течет.В очень большой комнате ток будет продолжать течь долгое время, а электроны будут чувствовать себя некомфортно. Таким образом, ток продолжает течь как обычно, но желание электронов двигаться уменьшается, и напряжение падает. Таким образом, напряжение «отстает» от тока. Или, чтобы перевернуть слова, ток опережает напряжение.
Уф, это заняло больше времени, чем ожидалось. Надеюсь, я не позволил себе слишком много вольностей, объясняя это. Не хочу обидеть физиков. Сообщите мне, что эти аналогии помогут вам, и если да, я постараюсь ответить на другие ваши вопросы.
Обязательно набирается на мобильном телефоне, возможны опечатки.
Почему ток через индуктор отстает от напряжения?
Чтобы понять причину, по которой ток через индуктор отстает от напряжения на индукторе, мы сначала рассмотрим математику, а затем разберемся с концепцией аналитически. Давайте рассмотрим чисто индуктивную цепь, как показано на рисунке ниже.
Как показано на рисунке выше, индуктор значения L Henray подключен к источнику питания переменного тока V = V м Sinωt.
Согласно закону петли Кирхгофа, напряжение, индуцированное на индукторе, будет равно напряжению питания, и поэтому мы можем написать, как показано ниже.
В м Sinωt = Напряжение, индуцированное на индукторе
Но наведенная ЭДС в индукторе равна Ldi / dt и, следовательно,
В м Sinωt = Ldi / dt
⇒ Ldi = V м Sinωtdt
Интегрируя обе стороны, получаем
i = (V м / wL) Cosωt + C
где C – некоторая постоянная.
Теперь, поскольку среднее значение Cosωt за один период времени равно нулю, а напряжение питания в нашем обсуждении синусоидальное, мы ожидаем, что ток также будет синусоидальным. Следовательно, в нашем случае значение константы C должно быть равно нулю.
⇒ i = (V м / ωL) Cosωt
⇒ i = (V м / ωL) Sin (ωt – π / 2)
Таким образом, из приведенного выше выражения мы видим, что разность фаз между приложенным напряжением V = V m Sinωt и током через индуктор i = (V m / ωL) Sin (ωt – π / 2) составляет π / 2 .Это означает, что ток через катушку индуктивности отстает от приложенного напряжения V на угол 90 °.
Это был математический расчет, показывающий, что ток через катушку индуктивности отстает от напряжения питания на угол 90 °. Но сейчас мы обсудим тот же аспект, но аналитически. Для аналитического обсуждения мы примем стационарное состояние.
Как мы знаем, когда ток течет через соленоид, магнитное поле создается соленоидом, которое остается ограниченным только внутри соленоида.Теперь предположим, что ток через соленоид изменяется со временем, это просто означает, что магнитный поток также изменится, что приведет к изменению магнитного потока. Поскольку катушка соленоида соединяется с этим изменяющимся магнитным потоком, в соленоиде будет индуцироваться ЭДС в таком направлении, чтобы противодействовать причине, возникшей в соответствии с законом Ленца. Здесь причиной является ток, протекающий через соленоид, поэтому ЭДС будет индуцироваться в таком направлении, чтобы противодействовать протеканию тока. Здесь соленоид – это индуктор.
Рассмотрим установившееся состояние, когда напряжение питания V становится положительным от нуля (точка P на рисунке ниже). В этом случае обратная ЭДС индуктивности также будет равна нулю и, следовательно, ток, протекающий по цепи, будет максимальным. Теперь, когда напряжение питания увеличивается в положительном направлении, обратная ЭДС индуктора также будет расти, но в противоположном направлении, из-за чего ток, протекающий через цепь, начнет уменьшаться и станет нулевым, когда обратная ЭДС индуктора станет максимально равной напряжению питания. поскольку в это время напряжение питания становится максимально положительным (точка Q на рисунке ниже).После этого напряжение питания начнет уменьшаться от своего максимального значения, но поскольку обратная ЭДС индуктивности максимальна, но противоположна по направлению, ток в цепи изменит свое направление. Поскольку ток в цепи течет в противоположном направлении, противоэдс индуктора начнет нарастать в противоположном направлении тока, и, следовательно, чистая противоэдс индуктора будет уменьшаться и достигнет нуля, когда напряжение питания достигнет нуля. В этот момент (R) через цепь будет протекать максимальный ток.
Таким образом, мы видим, что именно генерация обратной ЭДС в катушке индуктивности заставляет ток, протекающий через нее, отставать от приложенного напряжения.
цепей переменного тока | Безграничная физика
Индуктивность
Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока, например изменением тока в проводнике.
Цели обучения
Опишите свойства индуктора
Основные выводы
Ключевые моменты
- В случае электроники индуктивность – это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводе, называемое самоиндукцией, так и в любых соседних проводниках, называемое взаимной индуктивностью.
- Согласно закону Ленца, изменяющийся электрический ток в цепи с индуктивностью индуцирует пропорциональное напряжение, которое противодействует изменению тока.
- Взаимная индуктивность обозначена. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, вызывает эдс 2 в другом. Мы выражаем это в форме уравнения как [латекс] \ text {emf} _2 = – \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]. M то же самое для обратного процесса.
- Самоиндукция – это действие закона индукции Фарадея устройства на самого себя. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока, задаваемой [latex] \ text {emf} = – \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ латекс].
- Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
Ключевые термины
- взаимная индуктивность : отношение напряжения в цепи к изменению тока в соседней цепи.
- самоиндукция : Отношение напряжения к изменению тока в той же цепи.
- индуктор : Пассивное устройство, которое вводит индуктивность в электрическую цепь.
Индуктивность
ОБЗОР
Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. В частности, в случае электроники индуктивность – это свойство проводника, благодаря которому изменение тока в проводнике создает напряжение как в самом проводнике (самоиндукция), так и в любых соседних проводниках (взаимная индуктивность).Этот эффект основан на двух фундаментальных физических наблюдениях: во-первых, постоянный ток создает постоянное магнитное поле, а во-вторых, изменяющееся во времени магнитное поле индуцирует напряжение в соседнем проводнике (закон индукции Фарадея). Согласно закону Ленца, изменяющийся электрический ток через цепь, имеющую индуктивность, индуцирует пропорциональное напряжение, которое противодействует изменению тока (если бы это было не так, можно легко увидеть, что энергия не может быть сохранена, с изменяющимся током, усиливающим изменение тока). петля положительной обратной связи).
ВЗАИМНАЯ ИНДУКТИВНОСТЬ
Взаимная индуктивность – это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. Посмотрите, где простые катушки наводят друг на друга ЭДС.
Взаимная индуктивность катушек : Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает в катушке 2 ЭДС.(Обратите внимание, что «E2 индуцированная» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы сконцентрируемся на скорости изменения тока Δ I / Δ t как причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, вызывает эдс 2 в другом. Мы выражаем это в форме уравнения как
[латекс] \ text {emf} _2 = – \ text {M} \ frac {\ Delta \ text {I} _1} {\ Delta \ text {t}} [/ latex]
, где M определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Единицы измерения для M : (V⋅s) / A = Ωs, который назван генри (H) в честь Джозефа Генри (обнаружил самоиндукцию). То есть 1 H = 1 Ом.
Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, что равно
[латекс] \ text {emf} _1 = – \ text {M} \ frac {\ Delta \ text {I} _2} {\ Delta \ text {t}} [/ latex]
, где M то же, что и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью M.
Большая взаимная индуктивность M может быть или нежелательна. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(Видеть ).
Противоточная намотка : Нагревательные катушки электрической сушилки для белья могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.
САМОИНДУКЦИЯ
Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока ΔI через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
[латекс] \ text {emf} = – \ text {L} \ frac {\ Delta \ text {I}} {\ Delta \ text {t}} [/ latex]
, где L – собственная индуктивность устройства.Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначается символом в.
.Обозначение индуктора
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой L и не позволит току быстро меняться.Чтобы избежать этого эффекта, необходимо добиться небольшого L, например, за счет встречной намотки катушек, как в.
СОЛЕНОИДЫ
Можно рассчитать L для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Индуктивность L обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.{2} \ text {A}} {\ mathscr {\ text {l}}} [/ latex] (соленоид).
Поучительно вывести это уравнение, но это оставлено читателю в качестве упражнения. (Подсказка: начните с того, что отметьте, что индуцированная ЭДС определяется законом индукции Фарадея как ЭДС = −N (Δ / Δt), а по определению самоиндукции задается как ЭДС = −L (ΔI // Δt) и приравняем эти два выражения). Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением. {\ frac {- \ text {t }} {\ tau}} [/ латекс].В первом временном интервале τ ток падает в раз [латекс] \ frac {1} {\ text {e}} [/ latex] до [latex] 0,368 \ cdot \ text {I} _0 [/ latex].
Ключевые термины
- характеристическая постоянная времени : Обозначается $ \ tau $, в цепях RL она задается $ \ tau = \ frac {L} {R} $, где R – сопротивление, а L – индуктивность. Когда переключатель замкнут, это время, необходимое для того, чтобы сила тока уменьшилась с коэффициентом 1 / e.
- катушка индуктивности : Устройство или компонент схемы, который демонстрирует значительную самоиндукцию; устройство, которое хранит энергию в магнитном поле.
RL Схемы
Цепь резистор-индуктор (цепь RL) состоит из резистора и катушки индуктивности (последовательно или параллельно), приводимых в действие источником напряжения.
Обзор
Напомним, что индукция – это процесс, в котором ЭДС индуцируется изменением магнитного потока. Взаимная индуктивность – это действие закона индукции Фарадея одного устройства на другое, в то время как самоиндукция – это действие закона индукции Фарадея устройства на самого себя.Катушка индуктивности – это устройство или компонент схемы, который демонстрирует самоиндукцию.
Энергия индуктора
Мы знаем из закона Ленца, что индукторы противодействуют изменениям тока. Мы можем думать об этой ситуации с точки зрения энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, а также время, чтобы истощить ее; следовательно, есть противодействие быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства.{2} [/ латекс].
Катушки индуктивности в цепях
Мы знаем, что ток через катушку индуктивности L нельзя включить или выключить мгновенно. Изменение тока изменяет магнитный поток, вызывая противодействие изменению ЭДС (закон Ленца). Как долго длится противостояние? Текущий будет течь, а можно выключить , но сколько времени это займет? На следующем рисунке показана схема переключения, которую можно использовать для измерения тока через катушку индуктивности как функции времени.
Ток в цепи RL : (a) Цепь RL с переключателем для включения и выключения тока. В положении 1 батарея, резистор и катушка индуктивности включены последовательно, и устанавливается ток. В положении 2 аккумулятор извлекается, и ток в конечном итоге прекращается из-за потери энергии в резисторе. (b) График роста тока в зависимости от времени, когда переключатель перемещен в положение 1. (c) График уменьшения тока, когда переключатель перемещается в положение 2.
Когда переключатель сначала перемещается в положение 1 (при t = 0 ), ток равен нулю и в конечном итоге повышается до I 0 = В / R , где R – полное сопротивление цепи, а V – напряжение батареи.{\ frac {- \ text {t}} {\ tau}}) [/ latex]
– это ток в цепи RL при включении. (Обратите внимание на сходство с экспоненциальным поведением напряжения на зарядном конденсаторе.) Начальный ток равен нулю и приближается к I 0 = В / R с характеристической постоянной времени для цепи RL , задаваемой формулой :
[латекс] \ tau = \ frac {\ text {L}} {\ text {R}} [/ latex],
, где [latex] \ tau [/ latex] имеет единицы измерения в секундах, поскольку [latex] 1 \ text {H} = 1 \ Omega \ cdot \ text {s} [/ latex].В первый период времени [латекс] \ тау [/ латекс] ток возрастает от нуля до 0,632I 0 , поскольку I = I 0 (1 − e −1 ) = I 0 ( 1−0,368) = 0,632I 0 . В следующий раз ток составит 0,632 от остатка. Хорошо известным свойством экспоненциальной функции является то, что конечное значение никогда не достигается точно, но 0,632 остатка от этого значения достигается за каждое характерное время [латекс] \ тау [/ латекс]. Всего за несколько кратных [latex] \ tau [/ latex] времени, конечное значение почти достигнуто (см. Часть (b) на рисунке выше).
Характерное время [латекс] \ тау [/ латекс] зависит только от двух факторов: индуктивности L и сопротивления R . Чем больше индуктивность L , тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменению. Чем меньше сопротивление R, тем больше [латекс] \ тау [/ латекс]. Опять же, это имеет смысл, поскольку небольшое сопротивление означает большой конечный ток и большее изменение, чтобы достичь его. В обоих случаях (большой L и маленький R) больше энергии хранится в катушке индуктивности, и требуется больше времени для ее ввода и вывода.
Когда переключатель на (a) перемещается в положение 2 и отключает батарею из цепи, ток падает из-за рассеивания энергии резистором. Однако это также не происходит мгновенно, поскольку катушка индуктивности противодействует уменьшению тока, создавая ЭДС в том же направлении, что и батарея, управляющая током. Кроме того, в катушке индуктивности накапливается определенное количество энергии, (1/2) LI 0 2 , и она рассеивается с конечной скоростью. Когда ток приближается к нулю, скорость убывания замедляется, поскольку скорость рассеяния энергии составляет I 2 R.{\ frac {- \ text {t}} {\ tau}} [/ latex]
В (c), в первый период времени [latex] \ tau = \ text {L} / \ text {R} [/ latex] после того, как переключатель замкнут, ток падает до 0,368 от своего начального значения, поскольку I = I 0 e −1 = 0,368I 0 . В каждый последующий раз [латекс] \ тау [/ латекс] ток падает до 0,368 от предыдущего значения, а через несколько кратных [латекс] \ тау [/ латекс] ток становится очень близким к нулю.
Цепь серииRLC: на больших и малых частотах; Фазорная диаграмма
Отклик цепи RLC зависит от частоты возбуждения – на достаточно больших частотах преобладает индуктивный (емкостной) член.
Цели обучения
Различать поведение цепей серии RLC на больших и малых частотах
Основные выводы
Ключевые моменты
- Цепи RLC могут быть описаны (обобщенным) законом Ома. Что касается фазы, то при приложении синусоидального напряжения ток отстает от напряжения на 90 ° по фазе в цепи с индуктором, в то время как ток опережает напряжение на 90 ° в цепи с конденсатором.
- На достаточно больших частотах [латекс] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна цепи переменного тока только с индуктор.Следовательно, среднеквадратичный ток будет Vrms / XL, а ток отстает от напряжения почти на 90 °.
- На достаточно малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] схема почти эквивалентна схеме переменного тока с конденсатор. Следовательно, среднеквадратичный ток будет представлен как В / X C, , а ток опережает напряжение почти на 90 ∘ .
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- резонанс : Увеличение амплитуды колебаний системы под действием периодической силы, частота которой близка к собственной частоте системы.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущих версиях Atoms мы узнали, как последовательная цепь RLC, показанная на рисунке, реагирует на источник переменного напряжения. Объединив закон Ома (I среднеквадратичное значение = В действующее значение / Z; I среднеквадратичное значение и В среднеквадратичное значение являются среднеквадратичным значением тока и напряжения) и выражения для импеданса Z из:
Последовательная цепь RLC : Последовательная цепь RLC: резистор, катушка индуктивности и конденсатор (слева).2}} [/ латекс].
Из уравнения мы исследовали условия резонанса для контура. Мы также изучили фазовые соотношения между напряжениями на резисторе, конденсаторе и катушке индуктивности: при приложении синусоидального напряжения ток отстает от напряжения на фазу 90º в цепи с индуктором, в то время как ток опережает напряжение на 90 ∘ в цепи с конденсатором. Теперь мы исследуем отклик системы в пределах больших и малых частот.
на больших частотах
На достаточно больших частотах [latex] (\ nu \ gg \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex], X L намного больше, чем X C .Если частота достаточно высока, так что X L также намного больше, чем R, то в импедансе Z преобладает индуктивный член. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {L} [/ latex], схема почти эквивалентна цепи переменного тока с одним индуктором. Следовательно, среднеквадратичный ток будет составлять В, действующее значение / X L , а ток отстает от напряжения почти на 90 ∘ . Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление индуктора будет большим.
на малых частотах
В импедансе Z на малых частотах [латекс] (\ nu \ ll \ frac {1} {\ sqrt {2 \ pi \ text {LC}}}) [/ latex] преобладает емкостной член, предполагая, что частота достаточно высока, так что X C намного больше R. Когда [latex] \ text {Z} \ приблизительно \ text {X} _ \ text {C} [/ latex], схема почти эквивалентна AC схема только с конденсатором. Следовательно, среднеквадратичный ток будет представлен как В / X C, , а ток опережает напряжение почти на 90 ∘ .
Резисторы в цепях переменного тока
В цепи с резистором и источником питания переменного тока все еще действует закон Ома ( В = IR ).
Цели обучения
Применить закон Ома для определения силы тока и напряжения в цепи переменного тока
Основные выводы
Ключевые моменты
- При напряжении переменного тока, определяемом следующим образом: [latex] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex], ток в цепи определяется как : [latex] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex] Это выражение происходит от Ohm закон: [латекс] \ text {V} = \ text {IR} [/ latex].2} {2 \ text {R}} [/ латекс].
Ключевые термины
- Закон Ома : Согласно наблюдениям Ома, постоянный ток, протекающий в электрической цепи, состоящей только из сопротивлений, прямо пропорционален приложенному напряжению.
Постоянный ток (DC) – это поток электрического заряда только в одном направлении. Это установившееся состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) – это поток электрического заряда, который периодически меняет направление.Если источник периодически меняется, особенно синусоидально, цепь называется цепью переменного тока. Примеры включают коммерческую и бытовую энергетику, которая обслуживает так много наших потребностей. показывает графики зависимости напряжения и тока от времени для типичных источников постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.
Синусоидальное напряжение и ток : (a) Напряжение и ток постоянного тока постоянны во времени после установления тока.(б) График зависимости напряжения и тока от времени для сети переменного тока 60 Гц. Напряжение и ток синусоидальны и совпадают по фазе для простой цепи сопротивления. Частоты и пиковое напряжение источников переменного тока сильно различаются.
Мы изучили закон Ома:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R}} [/ latex]
, где I – ток, В, – напряжение, а R – сопротивление цепи. Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.Следовательно, с напряжением переменного тока, определяемым по формуле:
[латекс] \ text {V} = \ text {V} _0 \ sin (2 \ pi \ nu \ text {t}) [/ latex]
, где В 0 – пиковое напряжение, а [latex] \ nu [/ latex] – частота в герцах, ток в цепи задается как:
[латекс] \ text {I} = \ frac {\ text {V} _0} {\ text {R}} \ sin (2 \ pi \ nu \ text {t}) [/ latex]
В этом примере, в котором у нас есть резистор и источник напряжения в цепи, напряжение и ток считаются синфазными, как показано на (b). 2} {\ text {R}} \ cdot \ sin (2 \ pi \ nu \ text {t}) [/ latex]
Чтобы найти среднюю мощность, потребляемую этой схемой, нам нужно взять среднее значение функции по времени.2} {2 \ text {R}} [/ латекс]
Конденсаторы в цепях переменного тока: емкостное сопротивление и фазовые диаграммы
Напряжение на конденсаторе отстает от тока. Из-за разности фаз для описания этих схем полезно вводить векторы.
Цели обучения
Объясните преимущества использования векторного представления
Основные выводы
Ключевые моменты
- Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.
- Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно.
- Действующее значение тока в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}} {\ text {X} _ \ text {C}} [/ latex], где [latex] \ text {X} _ \ text {c} [/ latex] – это емкостное реактивное сопротивление.
Ключевые термины
- среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
В предыдущем Atom «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Там мы использовали закон Ома (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и катушки индуктивности. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.
Конденсаторы в цепях переменного тока с фазорами
Фазор
Ключевая идея представления вектора состоит в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), [latex] \ nu [/ latex] (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{\ text {i} \ theta} [/ латекс]. Поскольку векторы представлены величиной (или модулем) и углом, они графически представлены вращающейся стрелкой (или вектором) в плоскости x-y.
Рис. 3 : Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса – это проекция вектора на действительную ось. Его амплитуда – это модуль вектора, а его аргумент – полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0.
Конденсаторы в цепях переменного тока
Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются со временем. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе.
Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пика напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ». Это показано на.
Рис. 2 : Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению.
Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V max / I max является полезным и называется емкостным реактивным сопротивлением (X C ) компонента.Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), единицей измерения является ом. Значение X C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. [латекс] \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ latex].
Конденсатор влияет на ток, имея возможность полностью его отключить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором.Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I , действующее значение в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как [латекс] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text {rms}}} {\ text {X} _ \ text {C}} [/ latex], где V rms – это действующее значение напряжения. Обратите внимание, что X C заменяет R в версии закона Ома для постоянного тока.
Фазовое представление
Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид.На схеме стрелки вращаются против часовой стрелки с частотой [латекс] \ ню [/ латекс]. (Следовательно, ток ведет к напряжению.) В следующих атомах мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Рис. 4 : Фазорная диаграмма для цепи переменного тока с конденсатором
Индукторы в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы
В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца.
Цели обучения
Объясните, почему напряжение на катушке индуктивности «опережает» ток в цепи переменного тока с катушкой индуктивности
Основные выводы
Ключевые моменты
- С индуктором в цепи переменного тока напряжение опережает ток на одну четверть цикла или на фазовый угол 90º.
- Среднеквадратичный ток I среднеквадратичное значение через катушку индуктивности L определяется версией закона Ома: [latex] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ { \ text {rms}}} {\ text {X} _ \ text {L}} [/ latex].X L называется индуктивным реактивным сопротивлением, которое задается как [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex].
- Фазоры – это векторы, вращающиеся против часовой стрелки. Вектор для катушки индуктивности показывает, что напряжение опережает ток по фазе 90º.
Ключевые термины
- Закон Ленца : Закон электромагнитной индукции, который гласит, что электродвижущая сила, индуцированная в проводнике, всегда имеет такое направление, что возникающий ток будет противодействовать изменению, вызвавшему его; этот закон является формой закона сохранения энергии.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- фазор : представление комплексного числа в терминах комплексной экспоненты.
Предположим, что индуктор подключен непосредственно к источнику переменного напряжения, как показано на рисунке. Разумно предположить, что сопротивление пренебрежимо мало, потому что на практике мы можем сделать сопротивление индуктора настолько малым, что оно окажет незначительное влияние на схему. График показывает напряжение и ток как функции времени.(б) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля, затем повышается до своего пика после управляющего им напряжения (как показано в предыдущем разделе, когда было включено напряжение постоянного тока).
Источник переменного напряжения, подключенный последовательно с индуктором : (a) Источник переменного напряжения, подключенный последовательно с индуктором, имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.
Когда напряжение становится отрицательным в точке а, ток начинает уменьшаться; оно становится нулевым в точке b, где напряжение является самым отрицательным.Затем ток становится отрицательным, снова вслед за напряжением. Напряжение становится положительным в точке c, где оно начинает делать ток менее отрицательным. В точке d ток проходит через ноль, когда напряжение достигает своего положительного пика, чтобы начать следующий цикл. Следовательно, когда на катушку индуктивности подается синусоидальное напряжение, оно опережает ток на одну четверть цикла или на фазовый угол 90º.
Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает ЭДС.Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичный ток I RMS через катушку индуктивности L определяется версией закона Ома: [latex] \ text {I} _ {\ text {rms}} = \ frac {\ text {V} _ {\ text { rms}}} {\ text {X} _ \ text {L}} [/ latex] где V rms – среднеквадратичное напряжение на катушке индуктивности, а [латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L} [/ latex] с [latex] \ nu [/ latex] частота источника переменного напряжения в герцах. X L называется индуктивным реактивным сопротивлением. Поскольку катушка индуктивности препятствует прохождению тока, X L имеет единицы измерения Ом (1 Гн = 1 Ом · с, так что частота, умноженная на индуктивность, имеет единицы (циклов / с) (Ом · с) = Ом), что соответствует его роли в качестве эффективное сопротивление.
Представление фазора
Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца. Следовательно, вектор, представляющий ток и напряжение, будет иметь вид. Опять же, вектора – это векторы, вращающиеся против часовой стрелки с частотой [latex] \ nu [/ latex] (вы можете видеть, что напряжение опережает ток) . В последующих выпусках Atoms будет обсуждаться, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC.
Векторная диаграмма : Векторная диаграмма для цепи переменного тока с индуктором.
Фазоры для индукторов в цепях переменного тока
Резонанс в цепях RLC
Резонанс – это тенденция системы к колебаниям с большей амплитудой на некоторых частотах – в последовательной цепи RLC он возникает на [latex] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}} }[/латекс].
Цели обучения
Сравнить резонансные характеристики цепей с высоким и низким сопротивлением
Основные выводы
Ключевые моменты
- Условие резонанса последовательной цепи RLC может быть получено приравниванием X L и X C , так что два противоположных вектора компенсируют друг друга.
- В резонансе влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I среднеквадратичное значение является максимальным.
- Цепи с более высоким сопротивлением не так сильно резонируют по сравнению с цепями с более низким сопротивлением, и при этом они не будут такими избирательными, например, в радиоприемнике.
Ключевые термины
- реактивное сопротивление : Противодействие изменению протекания тока в цепи переменного тока из-за индуктивности и емкости; мнимая часть импеданса.
- rms : Среднеквадратичное значение: статистическая мера величины переменной величины.
- импеданс : мера сопротивления течению переменного тока в цепи; совокупность его сопротивления, индуктивного и емкостного сопротивления. Обозначается символом Z.
Резонанс – это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} [/ latex],
, где I rms и V rms – среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты [латекс] \ nu [/ latex], причем X L большое на высоких частотах и X C большое на низких частотах, представленных как:
[латекс] \ text {X} _ \ text {L} = 2 \ pi \ nu \ text {L}, \ text {X} _ \ text {C} = \ frac {1} {2 \ pi \ nu \ text {C}} [/ латекс].
На некоторой промежуточной частоте [latex] \ nu_0 [/ latex] реактивные сопротивления будут равны и погашены, давая Z = R – это минимальное значение для импеданса, а максимальное значение для I rms результатов.Мы можем получить выражение для [latex] \ nu_0 [/ latex], взяв X L = X C . Подстановка определений X L и X C дает:
[латекс] \ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} [/ латекс].
[латекс] \ nu_0 [/ latex] – это резонансная частота последовательной цепи RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. В [latex] \ nu_0 [/ latex] эффекты катушки индуктивности и конденсатора нейтрализуются, так что Z = R, а I rms является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.
Приемник в радиостанции – это RLC-цепь, которая лучше всего колеблется на своем [latex] \ nu_0 [/ latex]. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик I rms при [латексе] \ nu_0 = \ text {f} _0 [/ latex].Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.
Зависимость тока от частоты : График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.
Мощность
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается сопротивлением в цепи и задается как [латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms }} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ latex]. Здесь [latex] \ phi [/ latex] называется фазовым углом.
Цели обучения
Рассчитать мощность, подаваемую в цепь переменного тока серии RLC с учетом тока и напряжения.
Основные выводы
Ключевые моменты
- Фазовый угол ϕ – это разность фаз между напряжением источника V и током I.См. Векторную диаграмму в. .
- На резонансной частоте или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны.
- Среднюю мощность, рассеиваемую в цепи RLC, можно рассчитать, взяв среднее значение мощности по времени, P (t) = I (t) V (t), за период.
Ключевые термины
- среднеквадратичное значение : Среднеквадратичное значение: статистическая мера величины переменной величины.
Если ток изменяется в зависимости от частоты в цепи RLC, то мощность, подаваемая на него, также зависит от частоты.Однако средняя мощность – это не просто ток, умноженный на напряжение, как в случае чисто резистивных цепей. Как было замечено в предыдущих атомах, напряжение и ток в цепи RLC не совпадают по фазе. Между напряжением источника V и током I существует фазовый угол ϕ, равный
.[латекс] \ cos {\ phi} = \ frac {\ text {R}} {\ text {Z}} [/ latex], как показано на рисунке
Векторная диаграмма для последовательной цепи RLC : Векторная диаграмма для последовательной цепи RLC. \ phi – фазовый угол, равный разности фаз между напряжением и током.
Например, на резонансной частоте [латекс] (\ nu_0 = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}}) [/ latex] или в чисто резистивной цепи Z = R, так что cosϕ = 1. Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем в резонансе, потому что напряжение и ток не совпадают по фазе, а I rms ниже.
Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь.Можно показать, что средняя мощность
[латекс] \ text {P} _ {\ text {avg}} = \ text {I} _ {\ text {rms}} \ text {V} _ {\ text {rms}} \ cos {\ phi} [/ латекс]
(уравнение, полученное путем взятия среднего значения мощности по времени, P (t) = I (t) V (t), за период. I (t) и V (t) – это ток и напряжение в момент времени t). Таким образом, cosϕ называется коэффициентом мощности, который может находиться в диапазоне от 0 до 1. Коэффициенты мощности, близкие к 1, желательны, например, при проектировании эффективного двигателя. На резонансной частоте cosϕ = 1.
Мощность, подаваемая в цепь переменного тока серии RLC, рассеивается только за счет сопротивления.Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают энергию из цепи. Скорее, они передают энергию вперед и назад друг другу, а резистор рассеивает именно то количество, которое источник напряжения дает цепи. Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора (например, радиоволн).
Схема аналогична колесу автомобиля, движущегося по гофрированной дороге, как показано на рисунке. Равномерно расположенные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз.Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний. Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, запасенной в индукторе) и потенциальной энергией, запасенной в автомобильной пружине (аналогично отсутствию тока и энергии, запасенной в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.
Принудительное демпфированное движение колеса на автомобильной пружине : Принудительное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC.Амортизатор гасит движение и рассеивает энергию аналогично сопротивлению в цепи RLC. Масса и пружина определяют резонансную частоту.
ИндукторПочему ток отстает от напряжения на 90 градусов Математическое объяснение – Cute766
в индуктивности отстает по току, почему
Почему в индуктивной цепи ток отстает от напряжения на 90 градусов? Индуктор в своей основной форме представляет собой катушку с проволокой, намотанную вокруг некоторого материала сердечника.wh. Таким образом, из приведенного выше выражения мы видим, что разность фаз между приложенным напряжением v = vmsinωt и током через индуктор i = (vm ωl) sin (ωt – π 2) равна π 2. Это означает, что ток через индуктор отстает. за приложенным напряжением v на угол 90 °. это был математический расчет, чтобы показать этот ток. Если ваш источник представляет собой синусоидальную волну, напряжение будет составлять интеграл от тока или запаздывать на 90 градусов. но если вы подключите источник тока к катушке индуктивности. ну, вы не можете, потому что ток – это производная напряжения.а колебания тока – это то, что будет генерировать напряжение (или ЭДС электродвижущей силы). и если у вас синусовая волна. Следовательно, напряжение опережает ток на 90 градусов. но помните, что это относится только к анализу сигналов переменного тока. например, если вы приложили ступенчатое напряжение к катушке индуктивности, ток линейно возрастает со временем, потому что: $$ \ dfrac {di} {dt} = \ dfrac {v} {l} $$ основное уравнение описывает как переменные, так и переходные процессы. Хотя это объясняет, почему напряжение и ток сдвинуты по фазе на 90 градусов в конденсаторе или катушке индуктивности, это не объясняет, почему напряжение ведет ток в одном и противоположном – в другом.в любом из них, когда ток максимален (амплитуда), напряжение равно нулю, и аналогично, когда ток равен нулю, напряжение находится на максимуме (амплитуда).
в индуктивности отстает по току, почему
Индуктор: индукторы – это элементы хранения, которые хранят энергию в виде магнитных полей. ток, протекающий через катушку индуктивности, является причиной создания магнитного поля.Индуктор; вы подаете на него напряжение. ток начинает течь. нарастающий ток создает изменяющийся поток. изменение магнитного потока, в свою очередь, вызывает в проводе напряжение. Когда конденсаторы или катушки индуктивности включены в цепь переменного тока, ток и напряжение не достигают пика одновременно. доля разности периодов между пиками, выраженная в градусах, называется разностью фаз. разность фаз = 90 градусов. принято использовать угол, на который напряжение опережает ток.
в индуктивности отстает по току, почему
Индуктор | Почему ток отстает от напряжения на 90 градусов? (математическое объяснение)
почему в индуктивной цепи ток отстает от напряжения на 90 градусов? индуктор в своей основной форме представляет собой катушку с проволокой, намотанную на некоторый материал сердечника.Основное свойство индуктора – поддерживать постоянный ток – заставляет ток отставать от напряжения. если хотите узнать, как это происходит, посмотрите видео. В чисто резистивной цепи ток и напряжение находятся в фазе друг с другом. в чисто индуктивной цепи напряжение и ток сдвинуты по фазе на 90 градусов, а ток в чистой катушке индуктивности отстает от напряжения на ней на 90 градусов. когда переменное во времени напряжение (например, синусоидальная волна) прикладывается к чистой катушке индуктивности, давайте выясним, почему ток, проходящий через нее, отстает от напряжения на 90 градусов.Академия khan – это некоммерческая организация, задача которой – предоставить индукторы, индуктивность, задержку по току и противоэдс. Все это объясняется в одном видео. так как же работает индуктор? изменяющийся ток создает обратную ЭДС из-за того, почему в емкостной цепи переменного тока возникает напряжение на токопроводе. это видео представляет собой пошаговое объяснение того, почему. Название факультета: thotakura nsc sekhar. Посмотрите другие наши лекции и подпишитесь, чтобы получать уведомления о новых загрузках, на сайте я объясню, почему электрический ток в катушке индуктивности отстает от сдвига фазы на 90 градусов от напряжения в этом обучающем видео.концепция протекания электрического тока в катушке индуктивности объясняет, почему ток отстает от напряжения в индуктивной цепи. почему ток через дроссель отстает от напряжения? мы рассмотрим уравнения индуктивности i v в производной и интегральной форме.
Фазовый сдвиг
Цепи переменного тока> Фазовый сдвиг
Как правило, цепи переменного тока могут содержать резисторы, катушки индуктивности и (или) конденсаторы. Импеданс, обозначенный буквой «Z» и измеренный в омах, представляет собой полное сопротивление, которое цепь предлагает потоку переменного тока, это комбинация сопротивления R и реактивного сопротивления X, Z = R + jX, рисунок 1.
Рисунок 1: Диаграмма импеданса
В цепях переменного тока, поскольку наличие реактивных компонентов, напряжение и ток могут не достигать одинаковых пиков амплитуды в одно и то же время, они обычно имеют разницу во времени. Эта разница во времени называется фазовым сдвигом, f, 0 ≤ f ≤ 90, и измеряется в угловых градусах.
Цепь, содержащая только резисторы, называется резистивной цепью. Отсутствует фазовый сдвиг между напряжением и током в резистивной цепи, Φ = 0, рисунок 2a.Ток “синфазен” с напряжением.
Рисунок 2a: Взаимосвязь V-I контура R
Конденсаторы и катушки индуктивностиназываются реактивными компонентами, в которых напряжение и ток не совпадают по фазе друг с другом. В индукторе напряжение опережает ток на 90, Φ = 90, рис. 2b; в конденсаторе напряжение отстает от тока на 90, Φ = -90, рисунок 2c.
Рисунок 2b: Взаимосвязь V-I контура L
Рисунок 2c: Взаимосвязь V-I контура C
Цепь, содержащая индукторы и (или) конденсаторы, называется реактивной цепью, которую можно разделить на индуктивную цепь, X L > X C , и емкостную цепь, X C > X L .
На рис. 3а показана индуктивная цепь, состоящая из последовательно соединенных резисторов R и L. Поскольку индуктор противодействует изменению тока и накапливает энергию от источника питания в виде магнитного поля, напряжение индуктора v L опережает ток индуктора i L на 90 и опережает напряжение источника питания v на фазу. Угол Φ.
Рисунок 3a: Связь V-I цепи RL
На рисунке 3b показана емкостная цепь, состоящая из последовательно соединенных резисторов R и C.Поскольку конденсатор противодействует изменению напряжения и накапливает энергию от источника питания в виде электрического поля, напряжение конденсатора v C отстает от тока конденсатора i C на 90 и отстает от напряжения источника питания v на фазу. Угол Φ.
Рисунок 3b: Взаимосвязь V-I цепей RC
Цепи переменного тока> Фазовый сдвиг
Заключительная часть 13 лекции. Последовательный RLC в переменном токе Напряжение в конденсаторе отстает от тока на фазовый угол 90 градусов.
Презентация на тему: «Заключительная часть лекции 13. Серия RLC в переменном токе. Напряжение в конденсаторе отстает от тока на фазовый угол 90 градусов напряжения». – Расшифровка презентации:
ins [data-ad-slot = “4502451947”] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = “4502451947”]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]>1 Заключительная часть лекции 13
2 Последовательный RLC в переменном токе Напряжение в конденсаторе отстает от тока на фазовый угол 90 градусов Напряжение в конденсаторе отстает от тока на фазовый угол 90 градусов Ток синфазен с напряжением на резисторе Ток находится в фазе с напряжением на резисторе. Напряжение в катушке индуктивности опережает ток с фазовым углом 90 градусов.Напряжение в катушке индуктивности опережает ток на фазовый угол 90 градусов.
3 фазовый угол между током и общим напряжением Последовательный RLC в переменном токе
4 RLC НЕ в серии Z и φ НЕ такие, как в последовательном RLC. Цепь может быть решена с использованием правил Кирхгофа. Ограничивающее поведение: когда частота очень высокая или очень низкая
5 очень большая f, очень маленькая f
6 Xc = (открытый зазор) XL = 0 (ярлык) очень НИЗКАЯ частота XL = (открытый зазор) Xc = 0 (ярлык) очень ВЫСОКАЯ частота
7 Концептуальный пример 4 Предельное поведение конденсаторов и индукторов.


