Угловая скорость через частоту вращения: Конвертер угловой скорости и частоты вращения • Механика • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Конвертер угловой скорости и частоты вращения • Механика • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева

Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту

Общие сведения

Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.

Угловая скорость в спорте

Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.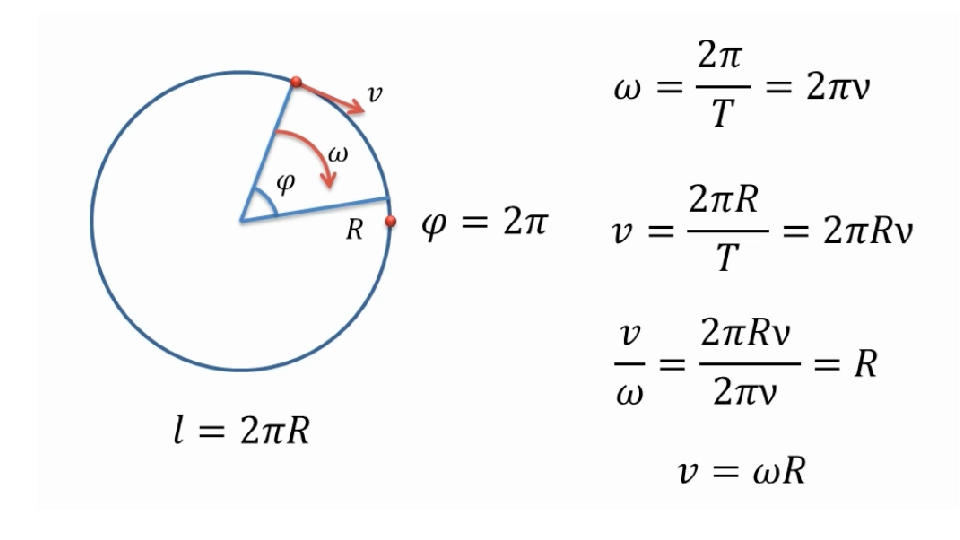

При первобытнообщинном строе главными охотниками были мужчины

Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости

У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.

В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.

Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.

Угловая скорость и хранение данных на оптических носителях

Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4&nbsp200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15&nbsp000 оборотов в минуту на высокоэффективных серверах

Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим

частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной. Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.

Угловая скорость в космосе

Геостационарная орбита

На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники.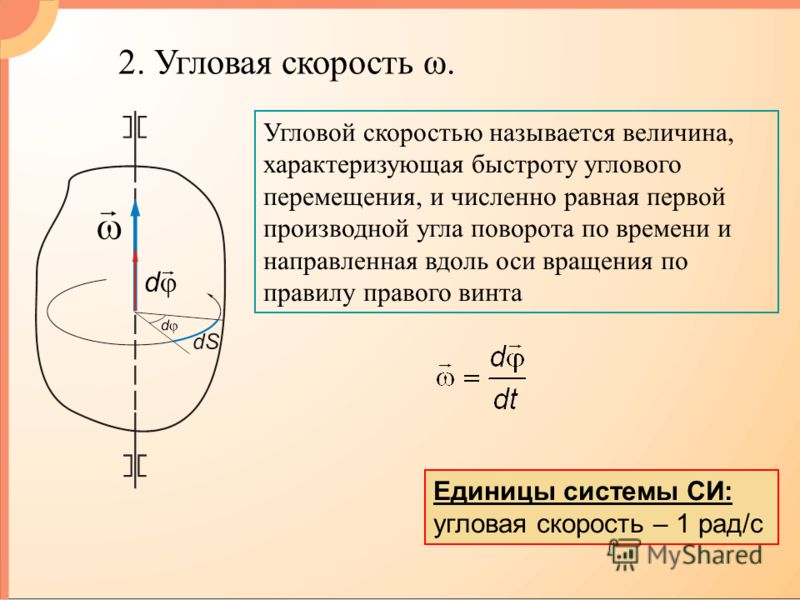 Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.

На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.

Спутниковые антенны

Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.

Литература

Автор статьи: Kateryna Yuri

Unit Converter articles were edited and illustrated by Анатолий Золотков

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.

Угловая скорость и ускорение. Определения и формулы для расчета

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

Размерности:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

ω=dφ/dt=φ’, рад/с; с^-1    (2. 3)

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω=1,5 с^-1=9,42 рад/с.

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Изменение угловой скорости характеризуется угловым ускорением:

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

В технике угловая скорость часто задается в оборотах в минуту

n [об/мин]. Один оборот – это 2π радиан:

ω=n2π/60=nπ/30 рад/с; с^-1.

1.9.2 Угловая и линейная скорости вращения

Вращательное движение вокруг неподвижной оси – еще один частный случай движения твердого тела. Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4). В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов. Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути. Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол – угол между осью ОХ и радиус-вектором , определяющим положение точки А (см. рис.2.5). Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое – на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел. Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению Угловая скорость выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска – около 140 рад/с1. Угловую скорость можно выразить через частоту вращения, т. е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде: Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1) Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2. 1) равен: Если , то , или . Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается. Тем самым мы можем описать положение точек вращающегося тела в любой момент времени. Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так: Так как , то Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли . Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: Следовательно, Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет. Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами , можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени. Знаем мы и направления и , a также форму траекторий точек.

Глава 7. Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел

(7.1)

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан – безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота – радиан), получим связь угловой скорости и периода вращения

(7.2)

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим

(7.3)

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т. е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна

(7.4)

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах

(7.5)

Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине

(7.6)

Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7. 1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем

(правильный ответ – 2).

Применяя определение угловой скорости к колесу (

задача 7.1.3), получаем

(правильный ответ 1).

Из формулы (7.2) имеем

(задача 7.1.4 – правильный ответ 4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска

А теперь по формуле (7.5) для второй точки получаем

(ответ 2).

Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ –

3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно

(ответ 4).

Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –

1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с², получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1

(ответ 1).

Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем

(ответ 3).

Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим

(7.5)

Поэтому

(ответ 1).

Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)

где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем

(ответ 2).

Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения

Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства

(ответ 4).

В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем

(ответ 3).

В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает

(1)

На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем

Подставляя в эту формулу силу из формулы (1), находим (ответ 2).

В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем

где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим

(ответ 3).

Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):

где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно

(задача 7. 2.9 – ответ 1).

Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).

Равномерное движение по окружности. Скорость, ускорение

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности – это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.

Период обращения – это время одного полного оборота. Для периода имеем очевидную формулу:

. (1)

Частота обращения – это величина, обратная периоду:

.

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.

 

Угловая скорость.

 

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

Рис. 1. Равномерное движение по окружности

 

Пусть – начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

. (2)

Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому

. (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

. (4)

 

Закон движения.

 

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

.

Но из формулы (2) имеем: . Следовательно,

. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

 

Центростремительное ускорение.

 

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

С учётом формул (5) имеем:

(6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

(7)

где – радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

(8)

Выразим угловую скорость из (4)

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

.

 

Асинхронные электродвигатели (страница 2)

1. Определить угловую скорость вращении ротора асинхронного электродвигателя, если обмотка статора четырехполюсная, частота напряжения сети, к которой присоединен электродвигатель, 50 Гц и скольжение ротора равно 3,5%.

Решение:
Частота токов, проходящих в обмотках статора, равна частоте напряжения сети:

Кроме того, известно, что обмотка статора четырехполюсная, т. е. число пар полюсов р = 2.
Скорость вращения магнитного потока, вызываемого трехфазной системой токов, проходящих в обмотках статора, зависит от частоты этих токов и числа пар полюсов обмотки р, так как , откуда число оборотов в минуту вращающегося синхронно магнитного потока

Угловая скорость вращения

Вращение ротора асинхронного электродвигателя возможно лишь при наличии отставания ротора от вращающегося магнитного потока. Величина, характеризующая это отставание, называется скольжением:

где — скорость вращения магнитного потока;
— скорость вращения ротора.
Подставив числовые значения, получим

откуда

Угловая скорость вращения ротора

2. На щитке асинхронного электродвигателя значится: 730 об/мин, 50 Гц.
Определить скольжение ротора, вращающегося с указанной скоростью, и число пар полюсов обмотки статора. Каким было скольжение ротора в первые мгновения пуска?

Решение:
В табл. 13 синхронных скоростей вращения при частоте 50 Гц ближайшей скоростью вращения (по отношению к скорости ) является скорость .
Следовательно, скольжение ротора

Число пар полюсов обмотки статора

Число полюсов

В момент пуска ротор неподвижен . Поэтому скольжение при пуске

Такое значение имеет скольжение ротора в момент пуска любого асинхронного электродвигателя.

Таблица 13

р пар полюсов	1	2	3	4	5
n, об/мин	3000	1500	1000	750	600

3. В разрыв провода линии, соединяющей контактные кольца ротора асинхронного электродвигателя с трехфазным реостатом, введен магнитоэлектрический амперметр, шкала которого имеет нулевое значение посередине (рис. 80). Разомкнув рубильник, шунтировавший амперметр во время разбега ротора, не поднимая щеток, наблюдали за отклонениями амперметра: оказалось, что за полминуты указательная стрелка прибора совершила 60 полных колебаний.
Определить скорость вращения ротора в течение указанного промежутка времени, если обмотка статора шестиполюсная и частота напряжения сети 50 Гц.

Решение:
Полное колебание указательной стрелки соответствует полному периоду тока в обмотке ротора. Если 60 полных колебаний (периодов) произошло за полминуты, то число полных колебаний (периодов) в секунду равно двум. Следовательно,

Магнитный поток в асинхронном электродвигателе вращается относительно ротора со скоростью, равной разности скоростей:

причем частота тока в роторе

Подставив числовые значения, получим

При шестиполюсной обмотке статора и частоте токов в цепи статора скорость вращения магнитного потока

Подставим в выражение для величины

откуда скорость вращения ротора

Скольжение ротора

4. Когда трехфазный асинхронный двигатель с фазным ротором присоединили к сети с линейным напряжением 220 В, напряжение между контактными кольцами при разомкнутой обмотке ротора составило 90 В.
Определить коэффициент трансформации, рассматривая этот электродвигатель как трансформатор в режиме холостого хода, если обмотки статора и ротора соединены звездой.

Решение:
Фазное напряжение на обмотке статора при схеме соединения звездой в раз меньше линейного напряжения. Следовательно,

Фазное напряжение на обмотке ротора

Коэффициент трансформации фазных напряжений

5. Асинхронный электродвигатель с короткозамкнутым ротором характеризуется отношением вращающих моментов соответственно при пуске и при номинальном режиме .
Можно ли осуществить пуск двигателя в случае полной его нагрузки на валу и понижения напряжения в сети на 5 и 10%? К сети присоединен статор.

Решение:
Вращающий момент асинхронного двигателя прямо пропорционален квадрату напряжения в сети:

Следовательно, если напряжение в сети понизится на 5% и составит , то вращающий момент

Отношение
Так как пусковой момент при номинальном напряжении , то при понижении напряжения в сети на 5% пусковой момент

Таким образом, пуск при этих условиях позволит электродвигателю развить вращающий момент больше номинального.
Если напряжение в сети понизится на 10% и составит , то вращающий момент

Пусковой момент при указанном понижении напряжения

Обозначим через долю, которую составляет пусковой вращающий момент от вращающего момента при номинальном напряжении. Тогда для возможности пуска электродвигателя при номинальной нагрузке должно быть выполнено равенство

Поэтому при пуске электродвигателя напряжение сети может составлять от номинального напряжения долю

Таким образом, при заданной кратности пускового момента от номинального понижение напряжения в сети может происходить на и пуск может быть осуществлен при номинальной нагрузке на валу электродвигателя.

6. Асинхронный электродвигатель с короткозамкнутым ротором типа А51-4 имеет следующие номинальные данные: ; кратность вращающих моментов .

Определить вращающие моменты: номинальный , максимальный и пусковой .

Решение:
Номинальный вращающий момент можно определить из основного соотношения

Вращающий момент измерен в и мощность Р — в Вт. При этом

Если подставить сюда в качестве Р мощность, измеренную в киловаттах, то число будет в 1000 раз меньше.
Таким образом, при тех же единицах измерения вращающего момента получим

Подставим величины номинального режима:

Используя известные кратности моментов, максимальный вращающий момент

пусковой вращающий момент

7. Асинхронный электродвигатель развивает номинальную мощность при номинальной скорости вращения ротора , имея перегрузочную способность 2,1.
Выразить зависимость между вращающим, моментом и скольжением ротора S электродвигателя.

Решение:
Номинальный вращающий момент

Перегрузочная способность l = 2,1 представляет собой отношение максимального вращающего момента к номинальному вращающему моменту . Следовательно,

Номинальному вращающему моменту соответствует и номинальное скольжение

где в качестве подставлена ближайшая большая (по отношению к ) синхронная скорость вращения магнитного потока статора.
Зависимость между вращающим моментом и скольжением ротора s в асинхронном двигателе выражается формулой

где означает критическое скольжение, а и s соответствуют одному и тому же режиму работы. Если в левую часть подставить , то в качестве s следует подставить . Тогда можно определить критическое скольжение , при котором имеет место момент . В этом случае получается квадратное уравнение, из которого берут большее значение корня.
Так как

Разделив на 0,238 левую и правую части равенства и сосредоточив все члены в одной стороне, получим

Корни полученного квадратного уравнения

Далее берется только больший из корней (при положительном знаке перед корнем):

Подставив в формулу, выражающую зависимость между вращающим моментом и скольжением ротора s, численные значения , получим требуемую зависимость

Угловые эффекты / Хабр

Добрый день, дорогой читатель! Это вторая переводная статья из цикла статей о создании физического движка авторства Chris Hecker. Если Вы ещё не ознакомились с первой, то рекомендую это сделать, т. к. всё сразу станет понятнее. Большое спасибо за поддержку первого перевода: это очень стимулирует работать дальше и больше! Приятного чтения!


Только что я захотел подпереть дверь чем-нибудь тяжёлым, чтобы ко мне не вошёл злоумышленник. Неужели я многого прошу? Я хочу, чтобы его машина перевернулась и взорвалась в определенным месте. Я хочу, чтобы огромные шестерни заело перед тем, как меня расплющит. И я хочу наспех построить штуку, похожую на качели, для того, чтобы катапультировать милый пылающий подарок через крепостную стену замка. Кто же может мне помешать воплотить это всё в реальность? Вы предположите, что мой соперник в игровом мире, но в действительности – программист физического движка, потому что в основе всего вышеперечисленного лежит угловой эффект. Можно пересчитать по пальцам те игры, где реализованы угловые эффекты, не говоря уж о том, чтобы найти хотя бы одну, в которой это сделано правильно.

Основная причина, почему угловые (или иначе вращательные) эффекты не реализованы в играх на сегодняшний день – это то, что программисты считают, что физика, описывающая вращательное движение, слишком сложная для понимания и воплощения в реальность. На уроках физики в старшей школе (где мы все узнали второй закон Ньютона) обычно не рассказывают о вращательных эффектах, и это не совсем очевидно, как перейти от силы, приложенной к объекту, ко вращению этого объекта. Конечно, динамика вращательного движения немного труднее для понимания, чем динамика линейного движения, но она проще, чем кажется. Любой, кто может создать физический движок в соответствии с тем материалом, что представлен в первой статье цикла, справится и с тем, чтобы включить в него угловые эффекты, описанные в этой статье. Есть надежда, что после публикации данной статьи мир наполнится играми, которые используют все возможности и преимущества угловых эффектов, или, по меньшей мере, вы сможете создать игру, в которой вы, выгнувшись, выстрелите в ногу вашего друга в смертельном бою.

Краткое повторение

Несмотря на то, что каждая моя статья на какую-то единственную тему, я всегда перечитываю то, что написал ранее, для того, чтобы понять, где закончил. Я только что посмотрел свою первую статью о физике, и я в восторге: мы успели выучить так много, и притом, ни разу не писали программный код и не читали дополнительную литературу! Прежде, чем начнем, давайте освежим в памяти материал из последней статьи.

Таблица 1 содержит важнейшие выводы для динамики твердых тел. Из Уравнения 1 следует, что вектор коодинаты ( r ), вектор скорости (v), и вектор ускорения (a) связаны производными (и интегралами, если читать в обратном порядке). Как напоминание – мы отмечаем дифференцирование по времени штрихом (r’). r’ – это то же самое, что dr/dt, а r’’ – это то же, что и вторая производная по времени. Из Уравнения 2 следует, что сила связана с линейным импульсом (произведение массы на скорость), массой, и ускорением. Определение центра масс можно почерпнуть из Уравнения 3 (это точка, где все массы и расстояния уравновешивают друг друга). Уравнение 4 гласит, что полный линейный импульс твердого тела – это сумма всех его импульсов, которые, к нашей удаче, просто равны импульсу центра масс (CM). Уравнение 5 – это настоящий драгоценный камень. В нем используется Уравнение 4 для демонстрации того, что ускорение центра масс объекта связано с полной силой (вектором суммы всех сил, действующих на объект в данное время) посредством скалярной величины, массы объекта.

Подведем итоги всему, что описано в первой статье: мы узнали, что общая сила, действующая на наш центр масс, равна сумме всех сил, приложенных к телу (включая силу гравитации, фуру злодея, взрыв неподалёку, импульс тяги нашего двигателя и т. д.). После мы разделили этот вектор суммы на массу тела для того, чтобы получить ускорение CM, и затем интегрировали ускорение по времени, чтобы получить скорость и координату тела.

Уравнение 5 – это просто шедевр! Вы увидите, что в нём нет понятия точек приложения сил к телу, а это является ключевым моментом для определения, как тело будет вращаться под их действием. Уравнение 5 правильное. В действительности, оно превосходно подходит для нахождения линейного ускорения. Мы упускаем половину дела. Но всё по порядку…

Каков твой угол?

В первой статье игнорировалось вращение, поэтому нам были необходимы лишь радиус-вектор и его производная для описания конфигурации нашего тела в 2D.A α$$display$$

Уравнение 14

Это уравнение – угловой эквивалент Уравнения 5; по факту, это F = ma для угловой динамики. Это уравнение связи полного момента силы и угловое ускорение тела посредством скалярного момента инерции. Если мы знаем момент силы, оказываемой на наше тело, мы можем найти его угловое ускорение, а дальше – угловую скорость и ориентацию в пространстве посредством интегрирования – поделив момент силы на момент инерции.

Алгоритм динамики

Он с трудом видится нам через этот вихрь уравнений, но все они – его составная часть. Мы вывели достаточно уравнений для того, чтобы получить великолепную динамику двумерного мира с произвольно заданными силами и моментами сил, перемещающими и вращающими наши объекты. Как же использовать эти уравнения? Ниже представлен базовый алгоритм:

1. Найти величину центра масс и момент инерции в центре масс.
2. Задать начальные координаты тела, его ориентацию в пространстве, его линейную и угловую скорости.
3. Учесть все силы, действующие на тело и точки их приложения.
4. Найти равнодействующую всех сил и разделить ее на массу тела для того, чтобы найти линейное ускорение центра масс (Уравнение 5).
5. Для каждой силы построить скалярное произведение с перпендикуляром между вектором, направленным из центра масс в точку приложения силы, и вектором приложенной силы, добавить эту величину в полный момент силы в уравнении центра масс (Уравнение 11).
6. Найти частное для полного момента силы и момента инерции в центре масс для нахождения углового ускорения (Уравнение 14).
7. Численно интегрировать линейное ускорение и угловое ускорение для обновления координаты, линейной скорости, ориентации в пространстве и угловой скорости (смотри последнюю статью).
8. Отрисовать объект в полученной координате, и перейти к Шагу 3.

В алгоритме выше есть лишь два шага, которые я не объяснил. Во-первых, как подсчитать момент инерции в Шаге 1 для сплошного объекта? Во-вторых, как решить проблему с силами из Шага 3? Ответ на первый вопрос может быть найден в простом примере кода, который я оставлю в приложении в конце этой статьи (вы выполните интегрирование объекта по его площади). Множество книг по динамике содержат рассчитанный момент инерции для часто встречающихся форм объектов в приложении в самом конце, поэтому вам не придется каждый раз выводить их самостоятельно.

Ответ на вопрос, как подсчитать силы из Шага 3, зависит от приложения, но немного общих рекомендаций я дам. Во-первых, такие силы, как гравитация, всегда направленные в одну сторону (вниз, в случае с гравитацией), не создают момент силы, т. к. они тянут все точки в одно и то же время в одном направлении, хотя мы и прикладываем эти силы напрямую к центру масс. Силы, подобные силе упругости, приложены к определенной точке объекта, они создадут момент силы, поэтому рассматриваем их в общем случае. Как мы увидели в первой статье, сила трения – это та же сила, направленная в противоположную от скорости тела сторону.

Вы можете сделать простую физическую модель, демонстрирующую силу трения, и просто приложить силу к центру масс, или вы можете выбрать, к каким частям объекта будут приложены силы трения, и сделать это, что может создать момент силы, действующий на объект. Силы, которые тела испытывают при столкновениях, немного труднее, и мы познакомимся с ними в следующей статье. Силы, подобные тяге ракетного двигателя, нужно рассматривать, как силы с точкой приложения (вы этом случае, если один из двигателей откажет, вы начнете крутиться вокруг своей оси до тех пор, пока не отрегулируете руль, чтобы обеспечить уравновешивание момента силы!). Если вы хотите что-то, похожее на гравитационные лучи из НЛО, то эта сила должна рассчитываться, как сила гравитации и не создавать момент силы, или она должна быть приложена к определенной точке объекта, и он будет вращаться вокруг этой точки, пока поднимается ввысь? Выбор за вами. Ключевой момент – не бояться экспериментировать с различными силами, рассчитанными разными способами, ведь уже сейчас у вас есть настоящий симулятор двумерной графики, попробуйте разные виды сил!

Я оставил весь необходимый вам код и ссылки на своем веб-сайте, потому что здесь закончилось свободное место. В своем простом приложении я воплотил в жизнь алгоритм динамики двумерного мира, а также добавил объекты, скрепленные пружиной; они вращаются вокруг своей оси, и иногда даже сталкиваются со стенами, крутсясь. Но об этом я расскажу в другой раз. Перейдите по ссылке за дополнительной литературой и простым приложением для Windows 32 и Macintosh.

Очень редко Chris Hecker испытывает на себе действие момента инерции, но обычно это проходит и довольно быстро. Силы можно прикладывать к [email protected].

Примечания переводчика: здесь представлена игра слов, обыгрывается тема статьи и ее содержание.

P.S. Обратная связь приветствуется. Ваши комментарии позволяют повысить качество работ. Спасибо!

P.P.S. Автор перевода выражает отдельную благодарность пользователям berez и Василий Терешков за правки перевода. Спасибо!

Угол поворота и угловая скорость

Цели обучения

К концу этого раздела вы сможете:

• Определите длину дуги, угол поворота, радиус кривизны и угловую скорость.
• Вычислить угловую скорость вращения колеса автомобиля.

В «Кинематике» мы изучали движение по прямой и ввели такие понятия, как смещение, скорость и ускорение. Двумерная кинематика имеет дело с движением в двух измерениях.Движение снаряда – это частный случай двумерной кинематики, в которой объект проецируется в воздух, находясь под действием силы тяжести, и приземляется на некотором расстоянии. В этой главе мы рассматриваем ситуации, когда объект не приземляется, а движется по кривой. Мы начинаем изучение равномерного кругового движения с определения двух угловых величин, необходимых для описания вращательного движения.

Угол поворота

Когда объекты вращаются вокруг некоторой оси – например, когда компакт-диск (компакт-диск) на рисунке 1 вращается вокруг своего центра – каждая точка в объекте движется по дуге окружности.Рассмотрим линию от центра компакт-диска до его края. Каждая лунка , , используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота – это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота Δ θ как отношение длины дуги к радиусу кривизны: [latex] \ displaystyle \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [ / латекс]

Рис. 1. Все точки на компакт-диске движутся по дугам окружности.Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δθ за время Δt .

Рис. 2. Радиус круга повернут на угол Δθ . Длина дуги Δs описана на окружности.

Длина дуги Δs – это расстояние, пройденное по круговой траектории, как показано на рисунке 2. Обратите внимание, что r – это радиус кривизны круговой траектории.

Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r . Окружность круга равна 2π r . Таким образом, за один полный оборот угол поворота составляет

°.

[латекс] \ displaystyle \ Delta \ theta = \ frac {2 \ pi {r}} {r} = 2 \ pi \\ [/ latex].

Этот результат является основой для определения единиц, используемых для измерения углов поворота, Δ θ как радиан, (рад), определенное таким образом, что 2π рад = 1 оборот.

Сравнение некоторых полезных углов, выраженных как в градусах, так и в радианах, показано в таблице 1.

Таблица 1. Сравнение угловых единиц
Градус меры	Мера радиана
30º	[латекс] \ displaystyle \ frac {\ pi} {6} \\ [/ latex]
60º	[латекс] \ displaystyle \ frac {\ pi} {3} \\ [/ latex]
90º	[латекс] \ displaystyle \ frac {\ pi} {2} \\ [/ latex]
120º	[латекс] \ displaystyle \ frac {2 \ pi} {3} \\ [/ latex]
135º	[латекс] \ displaystyle \ frac {3 \ pi} {4} \\ [/ latex]
180º	π

Рисунок 3. {\ circ}} {2 \ pi} \ приблизительно 57.{\ circ} \\ [/ латекс].

Угловая скорость

Насколько быстро вращается объект? Определим угловую скорость ω как скорость изменения угла. В символах это [латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta {t}} \\ [/ latex], где угловой поворот Δ θ происходит за время Δ t . Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости – радианы в секунду (рад / с).

Угловая скорость ω аналогична линейной скорости v . Чтобы получить точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги Δ с за время Δ t , поэтому она имеет линейную скорость [латекс] v = \ frac {\ Delta {s}} {\ Delta {t}} \\ [/ латекс].

Из [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex] мы видим, что Δ s = r Δ θ . Подстановка этого в выражение для v дает [latex] v = \ frac {r \ Delta \ theta} {\ Delta {t}} = r \ omega \\ [/ latex].

Мы записываем эту взаимосвязь двумя разными способами и получаем два разных вывода:

[латекс] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex].

Первое соотношение в [latex] v = r \ omega \ text {or} \ omega \ frac {v} {r} \\ [/ latex] утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, он является наибольшим для точки на ободе (наибольшее r ), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью .Вторую взаимосвязь в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] можно проиллюстрировать на примере шины движущегося автомобиля. Обратите внимание, что скорость точки на ободе шины такая же, как скорость v автомобиля. См. Рис. 4. Таким образом, чем быстрее движется автомобиль, тем быстрее вращается шина – большой v означает большой ω , потому что v = rω . Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ( ω ), будет создавать для автомобиля большую линейную скорость ( v ).

Рис. 4. Автомобиль, движущийся вправо со скоростью v , имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси составляет v , как если бы автомобиль был поднят. Таким образом, автомобиль движется вперед с линейной скоростью v = r ω, где r – радиус шины. Чем больше угловая скорость шины, тем больше скорость автомобиля.

Пример 1. Как быстро вращается автомобильная шина?

Рассчитайте угловую скорость 0.Автомобильная шина с радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 4.

Стратегия

Поскольку линейная скорость обода шины такая же, как и скорость автомобиля, мы имеем v = 15,0 м / с. Радиус шины задан равным r = 0,300 м. Зная v и r , мы можем использовать второе соотношение в [latex] v = r \ omega \ text {или} \ omega \ frac {v} {r} \\ [/ latex] для вычисления угловой скорости .

Решение

Для вычисления угловой скорости мы будем использовать следующее соотношение: [latex] \ omega \ frac {v} {r} \\ [/ latex].

Замена известных,

[латекс] \ omega = \ frac {15.0 \ text {m / s}} {0.300 \ text {m}} = 50.0 \ text {rad / s} \\ [/ latex].

Обсуждение

Когда мы отменяем единицы в приведенном выше вычислении, мы получаем 50,0 / с. Но угловая скорость должна иметь единицы рад / с. Поскольку радианы на самом деле безразмерны (радианы определяются как отношение расстояний), мы можем просто вставить их в ответ для угловой скорости. Также обратите внимание, что если землеройный комбайн с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его шины вращались медленнее. У них будет угловая скорость [latex] \ omega = \ frac {15.0 \ text {m / s}} {1.20 \ text {m}} = 12.5 \ text {rad / s} \\ [/ latex].

И ω , и v имеют направления (следовательно, это угловая и линейная скорости соответственно). Угловая скорость имеет только два направления относительно оси вращения – либо по часовой стрелке, либо против часовой стрелки. Линейная скорость касается пути, как показано на рисунке 5.

Эксперимент на вынос

Привяжите какой-либо предмет к концу веревки и поверните его по горизонтальному кругу над головой (взмахнув запястьем). Поддерживайте равномерную скорость при качании объекта и измеряйте угловую скорость движения. Какая примерная скорость объекта? Определите точку рядом с вашей рукой и выполните соответствующие измерения, чтобы рассчитать линейную скорость в этой точке. Определите другие круговые движения и измерьте их угловые скорости.

Рисунок 5.Когда объект движется по кругу, например, муха на краю старинной виниловой пластинки, его мгновенная скорость всегда касается круга. Направление угловой скорости в этом случае – по часовой стрелке.

Исследования PhET: Ladybug Revolution

Присоединяйтесь к божьей коровке в исследовании вращательного движения. Вращайте карусель, чтобы изменить ее угол, или выберите постоянную угловую скорость или угловое ускорение. Изучите, как круговое движение соотносится с положением, скоростью и ускорением жука x , y , используя векторы или графики.

Нажмите, чтобы загрузить. Запускать на Java.

Краткое содержание раздела

• Равномерное круговое движение – это движение по окружности с постоянной скоростью. Угол поворота [latex] \ Delta \ theta \\ [/ latex] определяется как отношение длины дуги к радиусу кривизны: [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r } \\ [/ latex], где длина дуги Δ s – это расстояние, пройденное по круговой траектории, а r – радиус кривизны круговой траектории. {\ circ} = 1 \ text { революция} \\ [/ латекс].{\ circ} \\ [/ латекс].
• Угловая скорость ω – это скорость изменения угла, [латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta {t}} \\ [/ latex], где вращение [латекс] \ Delta \ theta \\ [/ latex] имеет место во времени [latex] \ Delta {t} \\ [/ latex]. Единицы угловой скорости – радианы в секунду (рад / с). Линейная скорость v и угловая скорость ω связаны соотношением [latex] v = \ mathrm {r \ omega} \ text {или} \ omega = \ frac {v} {r} \ text {.} [/ Latex]

Концептуальные вопросы

1. Существует аналогия между вращательными и линейными физическими величинами.Какие вращательные величины аналогичны расстоянию и скорости?

Задачи и упражнения

1. Грузовики с полуприцепом имеют одометр на одной ступице колеса прицепа. Ступица утяжеляется таким образом, что она не вращается, но в ней есть шестерни для подсчета количества оборотов колеса – затем она вычисляет пройденное расстояние. Если колесо имеет диаметр 1,15 м и совершает 200 000 оборотов, сколько километров должен показывать одометр?
2. Микроволновые печи вращаются со скоростью около 6 об / мин.6 \ text {m} \\ [/ latex] на его экваторе, какова линейная скорость у поверхности Земли?
3. Бейсбольный питчер вытягивает руку вперед во время подачи, поворачивая предплечье вокруг локтя. Если скорость мяча в руке питчера составляет 35,0 м / с, а мяч находится на расстоянии 0,300 м от локтевого сустава, какова угловая скорость предплечья?
4. В лакроссе мяч выбрасывается из сетки на конец клюшки путем вращения клюшки и предплечья вокруг локтя. Если угловая скорость мяча около локтевого сустава 30.0 рад / с и мяч находится на расстоянии 1,30 м от локтевого сустава, какова скорость мяча?
5. Грузовик с шинами радиусом 0,420 м движется со скоростью 32,0 м / с. Какова угловая скорость вращающихся шин в радианах в секунду? Что это в об / мин?
6. Комплексные концепции. При ударе по футбольному мячу игрок, выполняющий удар, вращает ногой вокруг тазобедренного сустава. (a) Если скорость кончика ботинка кикера составляет 35,0 м / с, а тазобедренный сустав находится на расстоянии 1,05 м от кончика ботинка, какова угловая скорость кончика ботинка? (b) Башмак находится в контакте с изначально неподвижным 0.Футбол 500 кг за 20,0 мс. Какая средняя сила прилагается к футбольному мячу, чтобы придать ему скорость 20,0 м / с? (c) Найдите максимальную дальность действия футбольного мяча, пренебрегая сопротивлением воздуха.
7. Создайте свою проблему. Представьте аттракцион в парке развлечений, в котором участники вращаются вокруг вертикальной оси в цилиндре с вертикальными стенками. Как только угловая скорость достигает своего полного значения, пол опускается, и трение между стенами и пассажирами препятствует их скольжению.Постройте задачу, в которой вы вычисляете необходимую угловую скорость, которая гарантирует, что всадники не соскользнут со стены. Включите свободную схему тела одного всадника. Среди переменных, которые следует учитывать, – радиус цилиндра и коэффициенты трения между одеждой гонщика и стеной.

Глоссарий

длина дуги: Δ с , расстояние, пройденное объектом по круговой траектории

яма: крошечная выемка на спиральной дорожке, отформованная в верхней части слоя поликарбоната CD

угол поворота: отношение длины дуги к радиусу кривизны на круговой траектории: [latex] \ Delta \ theta = \ frac {\ Delta {s}} {r} \\ [/ latex]

радиус кривизны: радиус круговой траектории

радиан: единица измерения угла

угловая скорость: ω, скорость изменения угла, под которым объект движется по круговой траектории

Избранные решения проблем и упражнения

1.723 км

3. 5 × 10 ⁷ оборотов

5. 117 рад / с

7. 76,2 рад / с; 728 об / мин

8. (а) 33,3 рад / с; (б) 500 Н; (в) 40,8 м

6.1 Угол поворота и угловая скорость

Угловая скорость

Насколько быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Рассмотрим сначала угловую скорость (ω) (ω) – это скорость, с которой изменяется угол поворота. В форме уравнения угловая скорость равна

6.2ω = ΔθΔt, ω = ΔθΔt,

, что означает, что угловое вращение (Δθ) (Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота в данный момент времени, он имеет большую угловую скорость. Единицы измерения угловой скорости – радианы в секунду (рад / с).

Теперь давайте рассмотрим направление угловой скорости, а это значит, что теперь мы должны называть ее угловой скоростью. Направление угловой скорости – вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость указывает от вас вдоль оси вращения.Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.

Угловая скорость (ω) – это угловая версия линейной скорости v . Тангенциальная скорость – это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим углубление на вращающемся компакт-диске. Эта яма перемещается по длине дуги (Δs) (Δs) за короткий промежуток времени (Δt) (Δt), поэтому его тангенциальная скорость равна

Из определения угла поворота, Δθ = ΔsrΔθ = Δsr, мы видим, что Δs = rΔθΔs ​​= rΔθ.Подставляя это в выражение для v , получаем

v = rΔθΔt = rω. v = rΔθΔt = rω.

Уравнение v = rωv = rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем крае CD (с большим r ), чем для точки ближе к центру CD (с меньшим r ). Это имеет смысл, потому что точка, находящаяся дальше от центра, должна покрыть большую длину дуги за то же время, что и точка ближе к центру.Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.

Рисунок 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она дальше от центра вращения.

Теперь рассмотрим другой пример: шину движущегося автомобиля (см. Рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль – большое ωω означает большое v , потому что v = rωv = rω.Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет создавать для автомобиля большую линейную (тангенциальную) скорость v, . Это связано с тем, что больший радиус означает, что большая длина дуги должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.

Рисунок 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят домкратом, а колеса вращались, не касаясь дороги.Непосредственно под осью, где шина касается дороги, протектор шины движется назад по отношению к оси с тангенциальной скоростью v = rωv = rω, где r – радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.

Однако есть случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда автомобиль вращает свои колеса по льду.В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой движутся протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или на велотренажере; вы буквально никуда не денетесь.

Советы для успеха

Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны включить величину и направление.Направление угловой скорости – вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как вверх, вниз, влево, вправо, север, юг, восток или запад, как показано на рисунке 6.6.

Рис. 6.6. Поскольку муха на краю старинной виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена ​​по касательной к кругу.Направление угловой скорости в данном случае указано на странице.

Watch Physics

Взаимосвязь между угловой скоростью и скоростью

В этом видео рассматриваются определение и единицы угловой скорости и их связь с линейной скоростью. Здесь также показано, как преобразовать число оборотов в радианы.

Проверка захвата

Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса пути?

1. Да, потому что тангенциальная скорость не зависит от радиуса.
2. Да, потому что тангенциальная скорость зависит от радиуса.
3. Нет, поскольку тангенциальная скорость не зависит от радиуса.
4. Нет, потому что тангенциальная скорость зависит от радиуса.

об / мин в зависимости от угловой скорости | Sciencing

Число оборотов в минуту (об / мин) и угловая скорость, два показателя скорости вращения точки относительно другой точки, используются для решения задач физики, машиностроения и компьютерного программирования.Часто обороты и угловая скорость используются как взаимозаменяемые, чтобы моделировать вращение шкивов и качение колес в инженерных симуляторах и видеоиграх.

Использование угловой скорости

Угловая скорость используется для выражения скорости вращения круглого объекта, например колеса. Поскольку круг состоит из 360 градусов, колесо, которое совершает один полный оборот вокруг своего центра за одну секунду, будет иметь угловую скорость 360 градусов в секунду. Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 60 секунд, она имеет угловую скорость 360 градусов каждые 60 секунд или 6 градусов в секунду.

Число оборотов в минуту Использует

Число оборотов в минуту также используется для выражения скорости вращения круглого объекта, такого как колесо. Поскольку один оборот эквивалентен одному полному обороту или вращению вокруг центральной точки, говорят, что колесо, которое совершает один полный оборот вокруг своего центра за минуту, вращается вокруг своего центра со скоростью 1 оборот в минуту или 1 оборот в минуту. Поскольку секундная стрелка часов совершает один полный оборот вокруг своего центра за 1 минуту, ее скорость вращения составляет 1 оборот в минуту или 1 оборот в минуту.

Преобразование угловой скорости в число оборотов в минуту

Угловая скорость в градусах в секунду может быть преобразована в число оборотов в минуту путем умножения угловой скорости на 1/6, поскольку один оборот составляет 360 градусов, а это 60 секунд в минуту. Если угловая скорость задана как 6 градусов в секунду, число оборотов в минуту будет 1 оборот в минуту, поскольку 1/6, умноженное на 6, дает 1.

об / мин Преобразование угловой скорости

Оборотов в минуту можно преобразовать в угловую скорость в градусов в секунду, умножив число оборотов на 6, так как один оборот составляет 360 градусов и 60 секунд в минуту.Если частота вращения равна 1 об / мин, угловая скорость в градусах в секунду будет 6 градусов в секунду, так как 6 умноженное на 1 дает 6.

Калькулятор угловой скорости

Как найти угловую скорость Земли?

Как насчет того, чтобы использовать наш калькулятор угловой скорости? Оценим угловую скорость Земли! Во-первых, мы рассматриваем скорость вращения. Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что примерно равно 23.934 ч . Полное вращение составляет угол 2π рад , поэтому результирующая угловая скорость равна:

ω₁ = 2π рад / 23,934 h = 0,2625 рад / час = 0,00007292 рад / с ,

или 7,292 * 10⁻⁵ рад / с (в экспоненциальном представлении).

Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. Для этого нам нужен радиус Земли, который составляет примерно 6,371 км . Единственное, что нам нужно сделать, это вставить значения во вторую формулу угловой скорости:

v₁ = r₁ * ω₁ = 6,371 км * 7.292 * 10⁻⁵ рад / с = 0,4646 км / с = 464,6 м / с .

Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить полученный результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно запускаются с космодромов, расположенных вблизи экватора, а не с полюсов? Ну, почти 500 м / с ускорение в начале – это значительная часть его конечной скорости. Таким образом, перемещение начальной точки как можно ближе к экватору снижает количество топлива, необходимого для разгона ракеты. 2).Уравнение ниже определяет скорость изменения угловой скорости.

ω = угловая скорость в стандартной системе СИ, радиан в секунду (рад / сек), 1 радиан = 57,3 градуса

t = время разгона в секундах

π = 3,1416

n = скорость привода в оборотах в минуту об / мин

В следующем примере угловая скорость будет рассчитана для ускорения от 0 до 60 об / мин за одну секунду. Обратите внимание, что 2π радиан в секунду = 60 об / мин.

Этот расчет очень полезен при проектировании машин, поскольку угловое ускорение, умноженное на крутящий момент инерции, равняется крутящему моменту. Имейте в виду, что точный момент инерции может быть трудно вычислить на основе сложной геометрии реальных приводных линий, а другие переменные, такие как трение, не учитываются в следующем расчете. Тем не менее, он по-прежнему очень полезен при приближении требований к крутящему моменту или установлении базовых минимальных значений для определения размеров компонентов.

Дж = момент инерции в кг ∙ м ²

T = крутящий момент в Н ∙ м

Н = сила в Ньютонах

кг = масса в килограммах

м = радиус плеча рычага в метрах

В последнем примере ниже мы будем использовать угловое ускорение, которое мы нашли выше, для расчета крутящего момента на маховике с радиусом 1 метр и массой 1000 кг.

Как мы видим, если бы маховик с радиусом 1 метр и массой 1000 кг разогнался до 60 об / мин за одну секунду, это потребовало бы 3141.59 Ньютон-метров входного крутящего момента.

Надеюсь, этот обзор по вычислению углового ускорения оказался для вас полезным. Если у вас есть вопросы, касающиеся выбора размеров и применения муфт валов или предохранительных муфт, обращайтесь в наш технический отдел.

[email protected]

10.1 Вращательные переменные – University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Опишите физический смысл вращательных переменных применительно к вращению с фиксированной осью
• Объясните, как угловая скорость связана с тангенциальной скоростью
• Вычислить мгновенную угловую скорость с учетом функции углового положения
• Найдите угловую скорость и угловое ускорение во вращающейся системе
• Расчет среднего углового ускорения при изменении угловой скорости
• Вычислить мгновенное угловое ускорение по функции угловой скорости

До сих пор в этом тексте мы в основном изучали поступательное движение, включая переменные, которые его описывают: смещение, скорость и ускорение.Теперь мы расширим наше описание движения до вращения, в частности, вращательного движения вокруг фиксированной оси. Мы обнаружим, что вращательное движение описывается набором связанных переменных, аналогичных тем, которые мы использовали для поступательного движения.

Угловая скорость

Равномерное круговое движение (обсуждавшееся ранее в разделе «Движение в двух и трех измерениях») – это движение по кругу с постоянной скоростью. Хотя это простейший случай вращательного движения, он очень полезен во многих ситуациях, и мы используем его здесь, чтобы ввести вращательные переменные.

В (Рисунок) мы показываем частицу, движущуюся по кругу. Система координат является фиксированной и служит точкой отсчета для определения положения частицы. Его вектор положения от начала круга до частицы выметает угол

, который увеличивается в направлении против часовой стрелки, когда частица движется по круговой траектории. Угол

называется угловым положением частицы. Когда частица движется по круговой траектории, она также отслеживает длину дуги с .

Рис. 10.2 Частица движется по круговой траектории. Когда он движется против часовой стрелки, он выметает положительный угол

относительно оси x и определяет длину дуги s.

Угол связан с радиусом окружности и длиной дуги на

.

Уголок

, угловое положение частицы на ее пути, измеряется в радианах (рад). Есть

радиан в

Обратите внимание, что мера в радианах представляет собой отношение измерений длины и, следовательно, является безразмерной величиной.По мере движения частицы по круговой траектории ее угловое положение изменяется, и она претерпевает угловые смещения

Мы можем назначить векторы для величин (рисунок). Угол

– вектор вне страницы (рисунок). Вектор углового положения

и длина дуги

оба лежат в плоскости страницы. Эти три вектора связаны между собой соотношением

.

То есть длина дуги – это произведение вектора угла и вектора положения, как показано на (Рисунок).

Рис. 10.3 Вектор угла указывает на ось z, а вектор положения и вектор длины дуги лежат в плоскости xy. Мы видим, что

. Все три вектора перпендикулярны друг другу.

Величина угловой скорости , обозначенная цифрой

, – временная скорость изменения угла

, когда частица движется по круговой траектории. Мгновенная угловая скорость определяется как предел, при котором

при средней угловой скорости

:

где

– угол поворота ((рисунок)).Единицы угловой скорости – радианы в секунду (рад / с). Угловая скорость также может называться скоростью вращения в радианах в секунду. Во многих ситуациях нам задают скорость вращения в оборотах в секунду или циклах в секунду. Чтобы найти угловую скорость, мы должны умножить обороты / с на

.

, так как имеется

радиана за один полный оборот. Поскольку направление положительного угла в круге – против часовой стрелки, мы принимаем вращения против часовой стрелки как положительные, а вращения по часовой стрелке – как отрицательные.

Мы можем увидеть, как угловая скорость связана с тангенциальной скоростью частицы, дифференцируя (рисунок) по времени. Записываем (рисунок) как

Взяв производную по времени и отметив, что радиус r является константой, получаем

где

. Здесь

– это просто тангенциальная скорость частицы на (Рисунок).Таким образом, используя (рисунок), получаем

То есть тангенциальная скорость частицы равна ее угловой скорости, умноженной на радиус круга. Из рисунка видно, что тангенциальная скорость частицы увеличивается по мере удаления от оси вращения при постоянной угловой скорости. Этот эффект показан на (Рисунок). Две частицы размещены под разными радиусами на вращающемся диске с постоянной угловой скоростью. По мере вращения диска тангенциальная скорость увеличивается линейно с радиусом от оси вращения.На (рисунок) мы видим, что

и

. Но диск имеет постоянную угловую скорость, поэтому

. Это означает

или

. Таким образом, с

,

.

Рис. 10.4 Две частицы на вращающемся диске имеют разные тангенциальные скорости, в зависимости от их расстояния до оси вращения.

До сих пор мы обсуждали величину угловой скорости

– скалярная величина – изменение углового положения во времени. Вектор

– вектор, связанный с угловой скоростью, и указывает вдоль оси вращения. Это полезно, потому что, когда твердое тело вращается, мы хотим знать как ось вращения, так и направление, в котором тело вращается вокруг оси, по или против часовой стрелки.Угловая скорость

дает нам эту информацию. Угловая скорость

имеет направление, определяемое так называемым правилом правой руки. Правое правило таково, что если пальцы вашей правой руки сгибаются против часовой стрелки от оси x (направление, в котором

) по направлению к оси y- , ваш большой палец указывает в направлении положительной оси z ((Рисунок)).Угловая скорость

, который указывает вдоль положительной оси z , следовательно, соответствует вращению против часовой стрелки, тогда как угловая скорость

, который указывает на отрицательную ось z , соответствует вращению по часовой стрелке.

Рис. 10.5 Для вращения против часовой стрелки в показанной системе координат угловая скорость указывает в положительном направлении z по правилу правой руки.

Мы можем проверить правило правой руки, используя векторное выражение для длины дуги

, (рисунок).Если продифференцировать это уравнение по времени, находим

с

– константа, член

. С

– тангенциальная скорость,

– тангенциальная скорость.

– угловая скорость, имеем

То есть тангенциальная скорость – это векторное произведение угловой скорости и вектора положения, как показано на (Рисунок).Из части (а) этого рисунка мы видим, что при угловой скорости в положительном направлении z вращение в плоскости xy происходит против часовой стрелки. В части (b) угловая скорость находится в отрицательном направлении z-, что дает вращение по часовой стрелке в плоскости xy-.

Рисунок 10.6 Показаны векторы угловой скорости, положения и тангенциальной скорости. (а) Угловая скорость указывает в положительном направлении оси z, что дает вращение против часовой стрелки в плоскости xy.(b) Угловая скорость указывает в отрицательном направлении оси z, что дает вращение по часовой стрелке.

Пример

Вращение маховика

Маховик вращается так, что проходит под углом со скоростью

радиана. Колесо вращается против часовой стрелки, если смотреть в плоскости страницы. а) Какова угловая скорость маховика? (б) В каком направлении угловая скорость? (c) На сколько радиан проходит маховик за 30 с? (d) Какова тангенциальная скорость точки на маховике на расстоянии 10 см от оси вращения?

Стратегия

Функциональная форма углового положения маховика задана как

, поэтому, взяв производную по времени, мы можем найти угловую скорость.Мы используем правило правой руки, чтобы найти угловую скорость. Чтобы найти угловое смещение маховика за 30 с, ищем угловое смещение

, где изменение углового положения составляет от 0 до 30 с. Чтобы найти тангенциальную скорость точки на расстоянии от оси вращения, мы умножаем ее расстояние на угловую скорость маховика.

Решение

1. . Мы видим, что угловая скорость постоянна.

2. По правилу правой руки мы сгибаем пальцы в направлении вращения, которое находится против часовой стрелки в плоскости страницы, а большой палец указывает в направлении угловой скорости, которая выходит за пределы страницы.

3. .

4. .

Значение

За 30 с маховик совершил большое количество оборотов, около 215, если разделить угловое смещение на

.

.Таким образом можно использовать массивный маховик для хранения энергии, если потери на трение минимальны. В недавних исследованиях рассматривались сверхпроводящие подшипники, на которых покоится маховик, с нулевыми потерями энергии из-за трения.

Угловое ускорение

Мы только что обсудили угловую скорость для равномерного кругового движения, но не все движения однородны. Представьте себе фигуриста, вращающегося с вытянутыми руками – когда он втягивает руки внутрь, его угловая скорость увеличивается. Или представьте себе, как жесткий диск компьютера останавливается при уменьшении угловой скорости.Мы рассмотрим эти ситуации позже, но мы уже видим необходимость определения углового ускорения для описания ситуаций, когда

изменения. Чем быстрее смена

, тем больше угловое ускорение. Определяем мгновенное угловое ускорение

как производная угловой скорости по времени:

, где мы взяли предел среднего углового ускорения,

как

.

Единицы углового ускорения: (рад / с) / с, или

.

.

Точно так же, как мы определили вектор, связанный с угловой скоростью

, мы можем определить

, вектор, связанный с угловым ускорением ((Рисунок)). Если угловая скорость направлена ​​вдоль положительной оси z- , как на (Рисунок), и

положительный, то угловое ускорение

положительный и указывает на

ось.Аналогично, если угловая скорость

находится вдоль положительной оси z- и

отрицательно, тогда угловое ускорение отрицательно и указывает на

ось.

Рисунок 10.7 Вращение против часовой стрелки в (a) и (b) с угловой скоростью в одном направлении. (а) Угловое ускорение совпадает с направлением угловой скорости, что увеличивает скорость вращения.(b) Угловое ускорение противоположно угловой скорости, что снижает скорость вращения.

Мы можем выразить вектор тангенциального ускорения как произведение углового ускорения и вектора положения. Это выражение можно найти, взяв производную по времени от

и оставлен как упражнение:

Векторные зависимости углового и тангенциального ускорений показаны на (Рисунок).

Рис. 10.8 (a) Угловое ускорение является положительным по оси z и вызывает тангенциальное ускорение против часовой стрелки. (b) Угловое ускорение происходит в отрицательном направлении по оси z и вызывает тангенциальное ускорение по часовой стрелке.

Мы можем связать тангенциальное ускорение точки вращающегося тела на расстоянии от оси вращения таким же образом, как мы связали тангенциальную скорость с угловой скоростью. Если продифференцировать (рисунок) по времени, учитывая, что радиус r постоянен, мы получим

Таким образом, тангенциальное ускорение

– радиус, умноженный на угловое ускорение.(Рисунок) и (Рисунок) важны для обсуждения качения (см. Угловой момент).

Давайте применим эти идеи к анализу нескольких простых сценариев вращения с фиксированной осью. Прежде чем сделать это, мы представляем стратегию решения проблем, которая может быть применена к вращательной кинематике: описание вращательного движения.

Стратегия решения проблем: вращательная кинематика

1. Изучите ситуацию, чтобы определить, задействована ли кинематика вращения (вращательное движение).
2. Определите, что именно необходимо определить в проблеме (определите неизвестные). Набросок ситуации полезен.
3. Составьте полный список того, что дано или может быть выведено из указанной проблемы (укажите известные).
4. Решите соответствующее уравнение или уравнения для величины, которую необходимо определить (неизвестное). Может быть полезно думать в терминах поступательного аналога, потому что теперь вы знакомы с уравнениями поступательного движения.
5. Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения с указанием единиц. Обязательно используйте радианы для углов.
6. Проверьте свой ответ, чтобы узнать, разумен ли он: Имеет ли ваш ответ смысл?

Теперь давайте применим эту стратегию решения проблем к нескольким конкретным примерам.

Пример

A Колесо для спиннинга

Веломеханик устанавливает велосипед на ремонтный стенд и запускает вращение заднего колеса из состояния покоя до конечной угловой скорости 250 об / мин за 5 секунд.00 с. (а) Рассчитайте среднее угловое ускорение в

. (b) Если она сейчас нажимает на тормоза, вызывая угловое ускорение -87,3

, сколько времени нужно, чтобы колесо остановилось?

Стратегия

Среднее угловое ускорение можно найти непосредственно из его определения

, потому что даны окончательная угловая скорость и время. Мы видим, что

и

равно 5.00 с. Для части (b) нам известны угловое ускорение и начальная угловая скорость. Мы можем найти время остановки, используя определение среднего углового ускорения и решение для

, давая

Решение

1. Вводя известную информацию в определение углового ускорения, получаем

   Потому что

   выражается в оборотах в минуту (об / мин), и нам нужны стандартные единицы

   .

   для углового ускорения, нам нужно преобразовать из об / мин в рад / с:

   Ввод этого количества в выражение для

   , получаем

2. Здесь угловая скорость уменьшается с 26.2 рад / с (250 об / мин) до нуля, так что

   составляет −26,2 рад / с, а

   принимается равным –87,3

   . Таким образом,

Значение

Обратите внимание, что угловое ускорение, когда механик раскручивает колесо, небольшое и положительное; для получения заметной угловой скорости требуется 5 с. Когда она нажимает на тормоз, угловое ускорение велико и отрицательно. Угловая скорость быстро стремится к нулю.

Проверьте свое понимание

Лопасти вентилятора турбореактивного двухконтурного двигателя (показан ниже) ускоряются из состояния покоя до скорости вращения 40,0 об / с за 20 с. Увеличение угловой скорости вентилятора постоянно во времени. (Турбореактивный двухконтурный двигатель GE90-110B1, установленный на Боинг 777, как показано на рисунке, в настоящее время является самым большим турбовентиляторным двигателем в мире, способным развивать тягу 330–510 кН.)

(а) Какое среднее угловое ускорение?

(b) Какое мгновенное угловое ускорение в любой момент времени в течение первых 20 с?

Рисунок 10.9 (источник: «Bubinator» / Wikimedia Commons)

[показать-ответ q = ”821157 ″] Показать ответ [/ показать-ответ]
[скрытый-ответ a =” 821157 ″] a.

,

; б. Поскольку угловая скорость увеличивается линейно, в течение указанного времени должно быть постоянное ускорение. Следовательно, мгновенное угловое ускорение в любой момент является решением для

. [/ Hidden-answer]

Пример

Ветряная турбина

Ветряная турбина ((Рисунок)) в ветряной электростанции останавливается на техническое обслуживание.Турбине требуется 30 с, чтобы перейти от своей рабочей угловой скорости до полной остановки, при которой функция угловой скорости равна

.

. Если турбина вращается против часовой стрелки, глядя на страницу, (а) каковы направления векторов угловой скорости и ускорения? б) Что такое среднее угловое ускорение? (c) Какое мгновенное угловое ускорение при

?

Рис. 10.10 Ветряная турбина, вращающаяся против часовой стрелки, если смотреть спереди.

Стратегия

1. Нам дано направление вращения турбины против часовой стрелки в плоскости страницы. Используя правило правой руки ((Рисунок)), мы можем установить направления векторов угловой скорости и ускорения.
2. Рассчитываем начальную и конечную угловые скорости, чтобы получить среднее угловое ускорение. Мы устанавливаем знак углового ускорения из результатов в (а).
3. Нам дана функциональная форма угловой скорости, поэтому мы можем найти функциональную форму функции углового ускорения, взяв ее производную по времени.

Раствор

1. Поскольку турбина вращается против часовой стрелки, угловая скорость

   балла за страницу. Но поскольку угловая скорость уменьшается, угловое ускорение

   указывает на страницу в противоположном смысле угловой скорости.

2. Начальная угловая скорость турбины, уставка

   . Конечная угловая скорость равна нулю, поэтому среднее угловое ускорение равно

   .

3. Взяв производную угловой скорости по времени, получаем

Значение

Мы обнаружили из расчетов в (а) и (б), что угловое ускорение

и среднее угловое ускорение

отрицательны.Турбина имеет угловое ускорение, противоположное ее угловой скорости.

Теперь у нас есть базовый словарь для обсуждения кинематики вращения с фиксированной осью и взаимосвязей между переменными вращения. Мы обсудим больше определений и связей в следующем разделе.

Вращательное движение | Блог Гэри Гарбера

До сих пор в этом семестре нашего изучения классической механики мы изучали поступательное движение. Теперь мы приступим к изучению вращательного движения.

У каждой концепции, которую мы изучили до сих пор, есть вращательный аналог.

В начале года мы обсуждали, как объект может претерпеть смещение x . Мы также могли повернуть объект на угол θ.

Аналогично, скорость объекта или скорость изменения положения

имеет аналог вращения, скорость вращения, скорость изменения угла

ω = Δθ / Δt

Существует также угловое ускорение, которое представляет собой скорость изменения угловой скорости.Мы можем изучить крутящий момент, который представляет собой силу вращения. Момент инерции (или инерции вращения) – это тенденция объекта оставаться в состоянии покоя или оставаться в состоянии вращательного движения. Основываясь на этом, угловой момент – это инерция вращения в состоянии вращательного движения. У нас также может быть кинетическая энергия вращения!

Если мы предположим, что объект непрерывно вращается, то другой способ взглянуть на вращательное движение – это исследовать период вращения, T . Измеряемый в единицах времени ( миллисекунд, секунды, часы, годы, эоны …), период – это время, необходимое для одного полного оборота.Мы также могли бы описать, как часто объект вращается. Частота объекта, f , на самом деле обратно пропорциональна периоду вращения.

T = 1 / f

и

ф = 1 / т

Метрической единицей измерения частоты является герц ( Гц, ), где 1 Гц = 1 цикл / секунду . Вы, вероятно, знакомы с термином Герц по частотам на шкале радиоприемника, например, WBUR 90,9 МГц или WBZ 1030 кГц .

Пример

Представьте себе маленького мальчика, который пытается вызвать головокружение, быстро вращаясь.Если он вращается с частотой 0,8 Гц, сколько времени ему потребуется, чтобы сделать 1 оборот?

f = 0,8 Гц

T = 1 / f = 1 / 0,8 Гц = 1 / 0,8 циклов в секунду = 1,25 секунд

Другая традиционная единица измерения частоты – оборотов в минуту или оборотов в минуту . Вы можете увидеть это на старомодном проигрывателе, который мог вращаться со скоростью 33 или 45 об / мин на .

А пока рассмотрим двух маленьких человечков LEGO, стоящих на проигрывателе.Когда проигрыватель поворачивается, мы можем описать движение маленьких человечков LEGO с точки зрения их линейной скорости (метры в секунду) или скорости их вращения. Если мы установим проигрыватель на 45 об / мин, то оба LEGO-человечка будут иметь одинаковую скорость вращения. Однако у них разные линейные или тангенциальные скорости. Мы используем слово тангенциальный, потому что, если человек LEGO поскользнется и упадет, его собственная инерция заставит его отлететь от проигрывателя по линии, касающейся его кругового движения!

Мы можем рассчитать линейную скорость для каждого человека, используя уравнение

v = 2πr / Т

где r – радиус круга, а T – период вращения.Помните, что скорость – это расстояние во времени. В этом случае расстояние за один период вращения оказывается длиной окружности.

Если мужчины расположены на нашем проигрывателе на расстоянии 10 см и 4 см от центральной оси:

Пример

f = 45 об / мин

r = 12 см

Сначала вычисляем период. С 45 об / мин = 0,75 об / с

Таким образом, период вращения равен 1.33 секунд .

Таким образом, скорость будет

v = 2πr / T = 2π (10 см ) / 1,33 с = 47 см / с

Для маленького человечка, стоящего в радиусе 4 см, у него гораздо меньшая линейная скорость, хотя и такая же скорость вращения.

v = 2πr / T = 2π (4 см ) / 1,33 с = 19 см / с

Есть тонкая разница между скоростью вращения и скоростью вращения, которую мы представим позже.

Мы можем определить взаимосвязь между линейной скоростью и угловой скоростью с помощью следующего уравнения

v = ω r

Обратите внимание, что ω, угловая скорость, была определена ранее как изменение угла в единицу времени.

ω = Δθ / Δt

При рассмотрении приведенного выше уравнения возникает интересный вопрос об единицах измерения угловой скорости. До сих пор мы использовали такие термины, как обороты в минуту или обороты в секунду. Но революцию можно было бы определить как ПОЛНЫЙ поворот на 360 °.

Вы, наверное, изучали единицы измерения углов в градусах. Но когда мы обсуждаем угловую скорость, мы обычно не говорим об целом числе оборотов. Таким образом, мы могли бы использовать такие единицы измерения, как градусы в секунду. Однако градус не является метрической единицей вращения. Стандартная единица измерения – радиан.

2π радиан = 360 °

Если мы посмотрим на изображение единичного круга, мы сможем увидеть преобразование между радианами и градусами. Это действительно одно и то же, просто разные единицы.

В каком-то смысле единственная разница между частотой и угловой скоростью заключается в единицах измерения. Угловая скорость измеряется в радиан / секунду , а частота измеряется в Гц или оборотов в секунду . Таким образом, мы могли бы выразить алгебраическую связь между этими двумя терминами как

2πf = ω

Используя это, мы могли бы фактически найти угловую скорость нашего проигрывателя, который вращается со скоростью 45 об / мин .

ω = 2πf = 2π (0.75 об / с ) = 4,7 радиан / с

Пример

Давайте еще раз посмотрим на человечков LEGO на проигрывателе. Используя соотношение между линейной скоростью и угловой скоростью, находим

v = ω r

v = 4,7 радиан в секунду x 10 см = 47 см / с

и для человека ближе к центру

v = 4,7 радиан в секунду x 4 см = 19 см / с

Важно отметить, что линейная скорость увеличивается как с угловой скоростью, так и с радиусом

.