Увеличение емкости конденсатора: «Нужно ли изменять емкость конденсаторов, чтобы при неизменном напряжении между его пластинами заряд увеличился?» — Яндекс Кью

Увеличение – емкость – конденсатор

Cтраница 1

Схема трехкаскадного усилителя с емкостной связью, построенная на каскадах с общим эмиттером.  [1]

Увеличение емкости конденсатора С увеличивает коэффициент усиления усилителя и уменьшает величину фазового сдвига.  [2]

Увеличение емкости конденсатора на выходе источника питания выше некоторого значения не приводит к заметному улучшению качества выходного напряжения.  [3]

Увеличение емкости конденсаторов С12, С14 вызывает снижение чувствительности, а уменьшение – увеличение.  [4]

Увеличение емкости конденсатора увеличивает длительность.  [5]

Увеличение емкости конденсатора должно осуществляться в те моменты, когда напряжение на конденсаторе проходит через нуль. Поскольку в эти моменты энергия электрического поля контура равна нулю ( см.

§ 2.1), ее уменьшения не происходит.  [6]

Определение рабочей точки ре-зисторного усилителя по заданным ЯА.  [7]

Увеличение емкости конденсатора Сс связано с увеличением его геометрических размеров и вследствие этого увеличением емкости по отношению к другим проводникам. В результате увеличиваются наводки и появляется фон усилителя.  [8]

Для увеличения емкости конденсаторов С без сильного увеличения их линейных размеров конденсаторы соединяют параллельно в батарею.  [9]

Для увеличения емкости конденсаторов С без сильного увеличения их линейных размеров конденсаторы соединяют параллельно в батарею. Сп, а их заряды соответственно 7i 7z, 7n – Разность потенциалов U, приложенная между точками А и В, одинакова для всех конденсаторов.  [10]

Макроскопическое описание изменения разности потенциалов при введении диэлектрика между пластинами плоско параллельного конденсатора.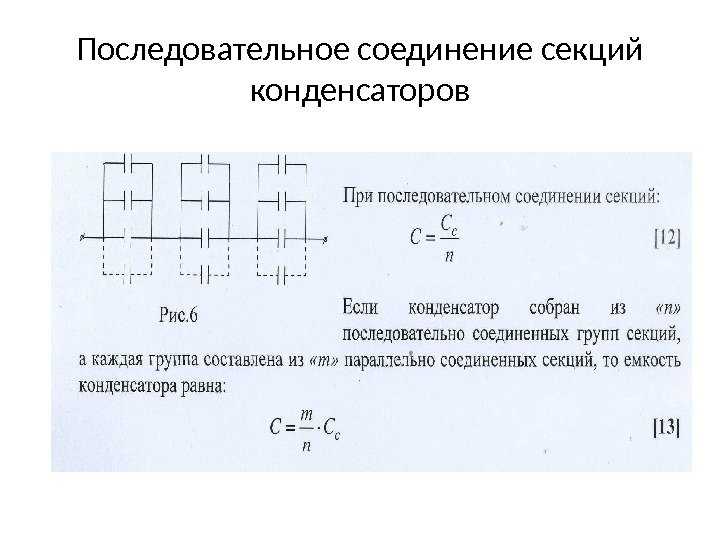  [11]

Причиной увеличения емкости конденсатора является поляризация диэлектрика под действием приложенного электрического поля.  [12]

Обобщенная эквивалентная схема заряда конденсатора ячейки.  [13]

С увеличением емкости конденсатора С2 увеличивается мощность потребляемая схемой, поэтому условие (3.72) в дальнейших расчетах используется только со знаком равенства.  [14]

С увеличением емкости конденсатора скорость нарастания напряжения С / ост уменьшается ( рис. 15, 6), а потому при небольших значениях времени т3 величина ka кажущимся образом снижается. При достаточно больших значениях т3 величина Аа от емкости не зависит.  [15]

Страницы:      1    2    3    4    5

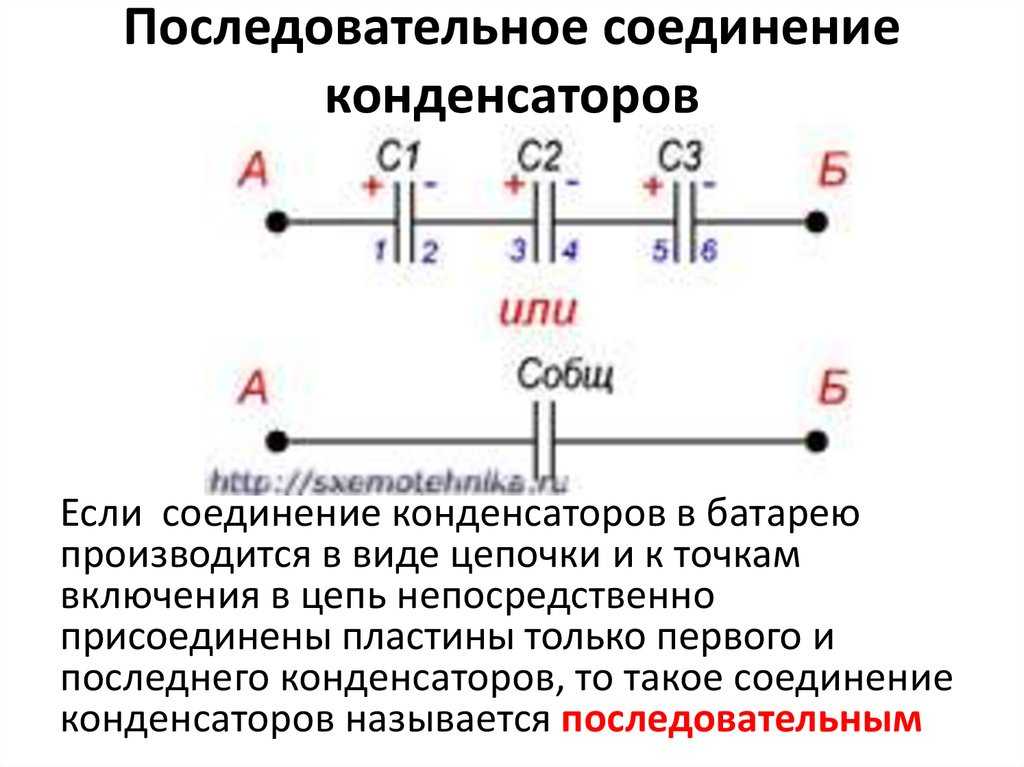
Сложение емкостей. Соединение конденсаторов

Рис.2 U=U 1 =U 2 =U 3

Общий заряд Q всех конденсаторов

Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов при­меняется для увеличения емкости.

4)Если параллельно включены т одинаковых конденсаторов ем­костью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис.3

На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U , появятся заряды одинаковые по величине с противоположными знаками.

Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденса­торов:

Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих кон­денсаторов.

При последовательном включении двух конденсаторов их об­щая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конден­саторов емкостью С каждый, то общая емкость этих конденса­торов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость

С, т. е. по­следовательное включение конденсаторов приводит к уменьше­нию общей емкости батареи конденсаторов.

На практике может оказаться, что допустимое ра­бочее напряжение U p конденсатора меньше напряжения, на кото­рое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить не­сколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется мень­ше его допустимого рабочего U p .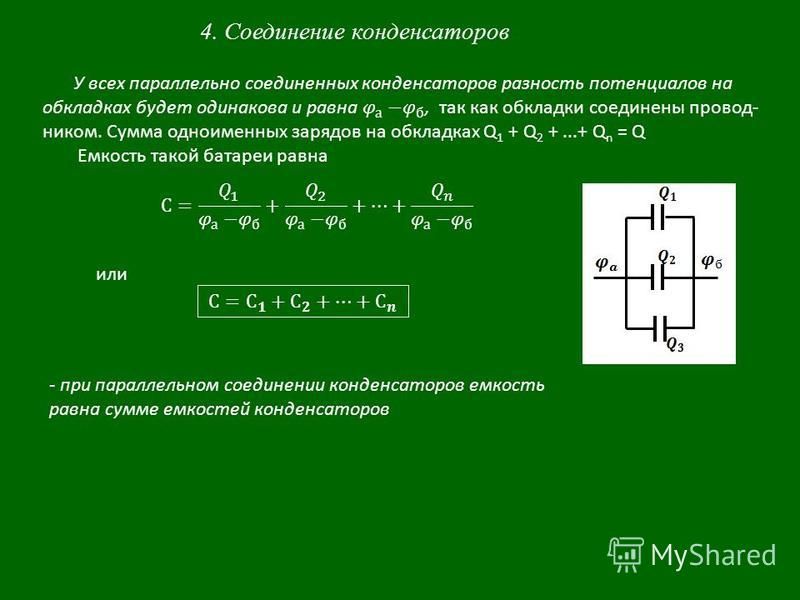 Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения U p .

Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) кон­денсаторов применяют тогда, когда необходимо увеличить ем­кость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на ниже­приведенных примерах.

Энергия конденсаторов

где Q – заряд конденсатора или конденсаторов, к которым при­ложено напряжение U ; С – электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U .

Таким образом, конденсаторы служат для накопления и сохра­нения электрического поля и его энергии.

15. Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений. Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U = E = const.

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис.

3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI K , а вместо внутреннего со­противления в расчет вводится внутренняя проводимостьg =1/ r .

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U / r = E / r – I ,

где U / r = Io -некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E / r = I K – ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I K = Io + I , которому удовлетворяет эквивалентная схема рис. 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

Для получения большего спектра емкостей конденсаторы часто соединяют между собой, получают, так называемые батареи конденсаторов. Соединение при этом может быть параллельным, последовательным или комбинированным (смешанным). Рассмотрим случай с двумя конденсаторами.

Последовательное соединение конденсаторов показано на рис. 1

Здесь (рис.1) обкладка одного конденсатора, имеющая отрицательный заряд соединяется с положительной обкладкой следующего конденсатора. При последовательном соединении средние пластины конденсаторов электризуются через влияние, следовательно, их заряды по величине равны и противоположны по знаку. Заряды на этих конденсаторах одинаковы. При этом соединении разности потенциалов складываются:

При этом имеем:

Получаем, что при последовательном соединении конденсаторов емкость соединения находят как:

Обобщив формулу (3) для N конденсаторов, получаем:

где – электрическая емкость i-го конденсатора.

Последовательное соединение конденсаторов используют тогда, когда для избегания пробоя конденсатора необходимо разность потенциалов распределить между несколькими конденсаторами.

Последовательное соединение конденсаторов показано на рис. 2

При параллельном соединении разности потенциалов между обкладками конденсаторов одинаковы. Суммарный заряд системы равен сумме зарядов на каждом из конденсаторов:

Из сказанного выше получим:

Для батареи из N параллельно соединенных конденсаторов имеем:

Параллельное соединение конденсаторов используют тогда, когда необходимо увеличить емкость конденсатора.

Примеры решения задач

ПРИМЕР 1

Задание	Получите формулу для расчета емкости слоистого конденсатора.
Решение	Конденсатор, который называют слоистым, состоит из двух параллельных металлических обкладок, разделенных несколькими плоскими слоями разных диэлектриков (рис.3). Обозначим диэлектрические проницаемости слоев диэлектриков как . Будем считать, что соответствующая толщина слоя диэлектрика при этом: . Допустим, что между слоями диэлектриков вставлены очень тонкие листы из проводника. От такой процедуры заряды на обкладках конденсатора и напряженности полей в солях диэлектриков останутся неизменными. Останутся без изменений разности потенциалов между обкладками, следовательно, не изменится емкость конденсатора. Но, наличие тонких листов проводника превратит слоистый конденсатор в последовательное соединение конденсаторов. Применим формулы емкости плоского конденсатора: и расчета емкости батареи последовательно соединенных конденсаторов: получаем:
Ответ

ПРИМЕР 2

Задание	Какой будет емкость соединения конденсаторов (рис.4), если батарея составлена из одинаковых конденсаторов, емкость каждого из них равна Ф.
Решение	Емкость параллельного соединения конденсаторов обозначим как Она равна:

Параллельное соединение конденсаторов – это батарея, в которой все конденсаторы находятся под одним и тем же напряжением, а суммарный ток равен полной алгебраической сумме токов этих элементов.

Основные тезисы

При параллельном включении конденсаторов их ёмкости складываются. Это позволяет быстро вычислить результат. Рабочее напряжение для всех конденсаторов одинаковое, а заряды из всех складываются воедино. Это следует из формулы, выведенной Вольтой ещё в XVIII веке:

C = q/U, тогда C1 + C2 + … = q1 + q2 + …/U.

Параллельное включение конденсаторов ведёт себя, как один конденсатор большой ёмкости.

Зачем нужно включать конденсаторы параллельно

• В радиоприёмниках подстройка под частоту волны осуществляется коммутацией блоков конденсаторов. Этим осуществляется ввод резонансного контура в резонанс.
• В фильтрах мощных блоков питания за каждый рабочий цикл нужно запасать много энергии. Строить его на индуктивностях экономически нецелесообразно. Поэтому применяют параллельный набор из больших электролитических конденсаторов.
• Параллельное включение конденсаторов можно встретить в измерительных схемах. Где эталоны ответвляют на себя часть тока, и по этой величине оценивается номинал. То есть размер ёмкости исследуемого конденсатора.
• Параллельно время от времени могут устанавливаться компенсаторы реактивной мощности. Это устройства, которые блокируют выход лишней энергии в питающую сеть. Что предотвращает образование помех, перегрузку генераторов, трансформаторов и избыточный нагрев проводки.

Реактивная мощность сети

Когда работает асинхронный двигатель, то происходит расхождение тока и напряжения по фазе. Это наблюдается вследствие наличия обмотки, которая имеет индуктивное сопротивление. Как результат, часть мощности отражается обратно в цепь. Этот эффект можно устранить, если индуктивное сопротивление компенсировать ёмкостным. Имеется и другой способ – использование синхронных двигателей. Он эффективен при напряжениях от 6 до 10 кВ.

По возможности предприятия должно потреблять всю произведённую им самим реактивную мощность. Но синхронные двигатели не всегда подходят условиям технологических процессов. Тогда и ставят конденсаторные установки. Их реактивное сопротивление должно быть равным индуктивностям двигателей. Конечно, в идеале, потому что на производстве условия постоянно меняются. В этом свете становится понятно, почему так сложно отыскать золотую середину.

Но если использовать параллельное соединение конденсаторов и коммутировать их при помощи реле должным образом, то задача достаточно просто решается. Сюда можно добавить, что некоторые предприятия за отражённую реактивную мощность тоже платят. И если её не использовать, то это будут чистой воды экономические потери. Поставщиков энергии тоже можно понять: реактивная мощность забивают линию ЛЭП, нагружает трансформаторы и тогда оборудование не может выдавать полную нагрузку. Если каждое предприятие станет загружать канал лишним током, то экономическое положение энергетиков немедленно пошатнётся.

В то же время реле реактивной мощности широко распространены и помогут определить, какую часть конденсаторов включить в работу. Пример графика расчёта затрат приведён на рисунке. Имеется некая оптимальная точка, перешагивать которую экономически нецелесообразно. Но можно это сделать из каких-либо иных мотивов.

Схема соединения компенсирующих установок

В трёхфазных сетях компенсирующие конденсаторы ставят тройками по двум общеизвестным схемам:

1. Звезда.
2. Треугольник.

Реактивная мощность в этих случаях вычисляется по формулам, представленным на рисунке. Через греческую омегу обозначена круговая частота сети (2 х Пи х 50 Гц). Из соотношений получается, что схема включения конденсаторов треугольником более выгодна: мощность выросла в 3 раза. Это происходит от того, что звезда использует фазное напряжение, а оно в 1,73 раза меньше линейного. Компенсируемая реактивная мощность же зависит от квадрата этого параметра.

Из этих соображений трёхфазные конденсаторы обычно всегда изготавливаются треугольником, а под звезду нужно выпросить индивидуальный заказ (фактически три однофазных конденсатора). Есть и другая сторона медали: на вольтаж 1,05; 3,15; 6,3; 10,5 кВ все конденсаторы однофазные. И можно соединять их так, как заблагорассудится. У звезды, например, меньше рабочее напряжение, а значит, и каждый конденсатор в отдельности выйдет дешевле. Ту и другую схему нельзя отнести к параллельным включениям, но такие тройки, в свою очередь, объединяются в:

• группы;
• секции;
• установки.

И внутри объединений однофазные конденсаторы могут включаться последовательно и параллельно, а трёхфазные – только параллельно. При этом рекомендуется номиналы всех отдельных элементов выбирать одинаковы. Это не только упрощает расчёт, но и уравнивает нагрузку по всем частям электрической схемы. Имеются и установки, где присутствует смешанное соединение по каждой фазе. Образуются параллельные ветви .

Установки выполняют однофазными или трёхфазными. В сетях с напряжением 380 В практически всегда применяется параллельное соединение конденсаторов. Исключением является случай использования оборудования с одной фазой как на 220 В (фазное), так и 380 В (линейное). Тогда под прибор ставится индивидуальная установка (или группа), компенсирующая реактивную мощность. В осветительных сетях конденсаторы по большей части ставят уже после выключателя по очевидным причинам. В прочих случаях – в зависимости от особенностей функционирования объекта.

Для напряжений 3, 6 и 10 кВ однофазные конденсаторы могут включаться обычной или двойной звездой (см. рис.). Один вывод здесь может быть заземлены (глухозаземленная нейтраль). По этой причине и допускается использование однофазных конденсаторов, в том числе и одним изолированным выводом. В последнем случае нужно убедиться, что нулевой проводник выходит на корпус изделия.

Обычно главный выключатель ставится в той или иной секции защищаемого оборудования (территориально) и управляет цепью компенсации в общем. То есть задействует или убирает вовсе дополнительное реактивное сопротивление. Если в данном секторе технологическое оборудование простаивает, то и главный выключатель разорвёт цепь компенсации. Конденсаторные установки обычно стоят в выделенном помещении вместе, электрически соединены параллельно. Перед каждой из них стоит выключатель цепи релейной регуляции для повышения или уменьшения общей ёмкости компенсаторов.

Таким образом, в зависимости от того, какое именно оборудование используется предприятием, объем реактивной мощности обусловливает помощь тех или иных конденсаторных установок, гибко подстраиваемых под имеющиеся нужды. В итоге:

1. Секции оборудования включены параллельно. Это легко понять, если представить бытовые приборы, питаемые одним удлинителем. Все включены параллельно. Но находятся, например, в разных цехах, секторах и пр. Встречаются и случаи, когда одна крупная энергетическая установка (например, генератор ГЭС) делится на сравнительно независимые секции.
2. Конденсаторные установки также включены параллельно, но находятся, как правило, в одном месте. Это сделано для того, чтобы можно было автоматически или вручную легко регулировать общую ёмкость посредством коммутации выключателей облегчённого типа. Один и тот же конденсатор может работать для компенсации реактивной мощности любой из секций или сразу обеих.

Особенности конденсаторной защиты

Главные выключатели, как правило, используются при авариях и вырубают сразу целую секцию оборудования. Конденсаторные установки также могут набираться в секции параллельным их включением. Тогда главный выключатель может сразу вырубать одну такую «батарею». Тогда как другие секции конденсаторных установок останутся в действии. Важно понять, что защитное оборудование, как и защищаемое можно группировать самыми разными методами. В зависимости от того, как это удобно и экономически обосновано.

Облегчённые выключатели применяются, как правило, в цепях регуляции. Управляются через реле и повышают или понижают общую ёмкость конденсаторных установок. В качестве главного выключателя обычно выбирается вакуумный или элегазовый.

Особенностью цепей выше 10 кВ является использование однофазных конденсаторов, собираемых по схеме звезды или треугольника, в каждой ветви которых стоит параллельно-последовательная группа ёмкостей (см. рис.). При наличии изделий с высоким рабочим напряжением можно делать и наоборот. То есть применять последовательно-параллельно включение. Тогда рабочие напряжения конденсаторов выбираются так, чтобы количество групп, включенных друг за другом было минимальным. Напряжение на каждом из элементов при этом, естественно, увеличивается. Для справки: .

Если сделать все так, как описано выше, то при выходе из строя любого элемента цепи компенсации реактивной мощности прочие будут работать в относительно щадящем режиме. Разумеется, параметры цепи нужно контролировать, а эксплуатирующий персонал согласно имеющимся методикам ведёт проверку конденсаторных установок на исправность. При проектировании нужно учесть одну небольшую особенность:

Чем больше в цепи компенсации последовательных групп конденсаторов, тем сложнее для каждой из них будет обеспечить равномерное распределение напряжения. В частности, возможны частые перегрузки того или иного сегмента.

Вдобавок ко всему сложные электрические соединения непросто проверять обслуживающему персоналу. Витиеватая схема плохо поддаётся монтажу, часты ошибки. Идеальным является параллельное соединение конденсаторных блоков по каждой фазе. Тогда и монтировать легко, и методика проверки упрощается максимально.

Разряд конденсаторов

Включенные параллельно конденсаторы обладают большой ёмкостью, вследствие чего при прекращении работы на них остаётся заряд. Это можно прочувствовать на себе, если коснуться штекера только что выключенной старенькой дрели. В новых моделях фильтр устроен так, что цепь разряжается через резистор, и ничего подобного, описанному выше, не наблюдается.

Для снижения напряжения можно также использовать и индуктивности, включенные параллельно конденсаторам. В этом случае сопротивление заземления переменному току весьма велико, а для постоянного – не сложно преодолеть этот участок. То есть, в период работы оборудования ток здесь весьма мал, и потери невелики. После останова технологической линии заряд понемногу сливается через высокоомный резистор или индуктивность. Разумеется, никто не запрещает поставить в цепи заземления реле, замыкающее контакты только после выключения всех устройств. Но это дороже и требует автоматизации.

Процесс разряда цепи важен с точки зрения обеспечения безопасности. Можно представить это так: конденсатор, заряжённый от розетки, ещё долго хранит разность потенциалов и представляет определённую опасность для окружающих. В однофазных сетях с напряжением 220 В разряд выполняется через входные фильтры при условии, что корпус правильно заземлён. Сопротивление в цепи, включенной параллельно конденсаторам, определяется по формуле, представленной ниже.

Под Q подразумевается реактивная мощность установки в варах (ВАР), а Uф – фазное напряжение. Можно легко показать, что формула дана из расчёта времени разряда. В самом деле: Q зависит линейно от ёмкости, будучи перенесена в левую часть формулы, она даст постоянную времени RC. За три таких периода батарея разряжается примерно на 97%. Исходя, из этих условий можно найти и параметры индуктивности. А ещё лучше – последовательно с нею включить резистор, как часто и делается в реальных схемах.

Содержание:

Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.

Параллельное включение конденсаторов в цепь

Параллельное соединение конденсаторов – это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.

Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.

Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.

При параллельном соединении конденсаторов емкость равняется:

Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.

Конденсаторы, соединенные параллельно, имеют напряжение:

Последовательное включение конденсаторов в цепь

Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.

Последовательное соединение конденсатора:

При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.

Формула нахождения заряда на конденсаторе, схема подключения конденсатора:

Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах – чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.

Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.

Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:

Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:

Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:

Смешанное включение емкостных накопителей в схему

Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.

Участок цепи подсоединенных смешанным включением накопителей емкости:

Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:

• разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
• вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
• проводим нахождение эквивалентной емкости на параллельном участке;
• когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
• рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.

Последовательное, параллельное и смешанное соединение конденсаторов, расчет емкости:

Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:

1. Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
2. Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
3. Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.

Вывод

Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс – с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.

Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.

Как увеличить емкость?

Подсказка: Способность системы накапливать электрический заряд известна как емкость. Емкость конденсатора с плоскими пластинами зависит от величины площади пластин, расстояния между пластинами и среды между пластинами. Следовательно, чтобы увеличить емкость, можно изменить одно или несколько из этих условий.

Полный ответ:
Устройство, образованное двумя изолированными друг от друга проводниками, называется конденсатором. Емкость — это, по сути, способность системы накапливать заряд, и технически она определяется как отношение заряда на проводнике к с к разности потенциалов между проводниками, которая математически выражается как 9{-2}$
$A$ = площадь двух параллельных пластин
$d$ = расстояние между параллельными пластинами

Обычно в пространстве между пластинами нет ничего, кроме вакуума, поэтому мы берем диэлектрическую проницаемость свободного пространства в уравнении емкости. Но, как мы знаем, этот вакуум неполяризуемый и, следовательно, переносит относительно меньше заряда. Следовательно, заменим все пространство между пластинами конденсатора поляризуемым диэлектрическим материалом, диэлектрическая проницаемость которого выражается как $\varepsilon$ . Следовательно, теперь емкость с диэлектрическим материалом выражается как
$C’=\dfrac{\varepsilon A}{d}$

Теперь отношение диэлектрической проницаемости диэлектрического материала к диэлектрической проницаемости вакуума определяется как диэлектрическая проницаемость среды, которая математически выражается как
$\ dfrac{\varepsilon }{{{\varepsilon }_{0}}}=K$
$\Rightarrow\varepsilon =K{{\varepsilon }_{0}}$
Мы можем подставить это значение в уравнение емкости as,
$C’=\dfrac{K{{\varepsilon}_{0}}A}{d}$
$\следовательно C’=KC$
Следовательно, емкость с диэлектрическим материалом составляет $K$ раз емкость со свободным пространством между пластинами. Экспериментально доказано, что значение $K$ всегда больше $1$. Следовательно, емкость с диэлектрическим материалом всегда будет больше, чем емкость со свободным пространством между пластинами.

Следовательно, мы можем увеличить емкость, вставив диэлектрический материал между пластинами.

Примечание: Из формулы емкости видно, что емкость также пропорциональна площади пластин и обратно пропорциональна расстоянию между пластинами. Следовательно, емкость также можно увеличить, либо увеличив площадь пластин, либо уменьшив расстояние между пластинами. Но из уравнения можно понять, что даже для увеличения емкости на $1\mu F$ площадь пластин нужно увеличить на несколько сотен метров или расстояние между пластинами уменьшить до нескольких микрометров. Оба условия практически невозможны. Следовательно, мы увеличиваем емкость только с использованием диэлектрического материала.

электростатика – Почему емкость диэлектрика увеличивается, а не уменьшается?

спросил 4 года, 1 месяц назад

Изменено 4 месяца назад

Просмотрено 6к раз

$\begingroup$

Итак, концептуально, если конденсатор подключен к источнику напряжения, и если вы уменьшите расстояние между двумя пластинами, электрическое поле между пластинами увеличится. Это означает, что вы можете удерживать больше заряда на каждой пластине, потому что теперь там больше силы, что увеличивает емкость. Таким образом, кажется, что более сильное электрическое поле между пластинами приведет к более высокой емкости, но тогда диэлектрики увеличивают емкость за счет уменьшения электрического поля.

Если электрическое поле уменьшить, разве пластины не смогут удерживать меньше заряда?

Единственным объяснением, которое я мог бы объяснить, было бы то, что, уменьшая эффективное электрическое поле, вы уменьшаете напряжение, и если вы подключены к источнику напряжения, вам нужно будет поддерживать это постоянное напряжение, поэтому вам придется увеличить количество заряда, которое вы держите, чтобы вернуться к этому постоянному напряжению. Увеличивая количество удерживаемого заряда, не увеличиваете ли вы также и электрическое поле, так что ваше эффективное электрическое поле станет таким же, как и без диэлектрика?

• электростатика
• емкость
• диэлектрик

$\endgroup$

3

$\begingroup$

Еще один полезный и немного более интуитивный способ представить это следующим образом: вставка пластины диэлектрического материала в существующий зазор между двумя пластинами конденсатора обманывает пластины, заставляя их думать, что они ближе друг к другу на коэффициент, равный относительной диэлектрической проницаемости плиты. Как указывалось выше, это увеличивает способность конденсатора накапливать электрический заряд.

Хорошим примером этого является электролитический конденсатор , в котором диэлектрик представляет собой очень тонкий слой оксида алюминия, сформированный на поверхности куска алюминиевой фольги, а другая «пластина» представляет собой химическую пасту, находящуюся в контакте с фольгой. Поскольку диэлектрическая проницаемость оксида алюминия удобно велика, а его толщина чрезвычайно мала, таким образом можно втиснуть много микрофарад емкости в физически компактный корпус.

$\endgroup$

$\begingroup$

если уменьшить расстояние между двумя пластинами, электрическое поле в между пластинами увеличивается.

…

Похоже, более сильное электрическое поле между пластинами приведет к более высокая емкость

Но более сильное электрическое поле , а не причина большей емкости $C$ в случае постоянного напряжения, большая емкость обусловлена ​​уменьшением расстояния $d$ между пластинами независимо от напряжения на них (рассмотрите увеличение в емкости в случае, когда напряжение $V$ на конденсаторе является постоянным $V = 0$).

Верно, что напряженность электрического поля $E$ увеличивается с уменьшением $d$, если $V \ne 0$ остается постоянным. Начните с фундаментального соотношения

$$Q = CV$$

, где $Q$ — заряд одной пластины, а $-Q$ — заряд другой пластины. Теперь соответствующие уравнения для идеального конденсатора с плоскими пластинами таковы:

$$C = \frac{\epsilon A}{d}$$ $$Q = \эпсилон AE$$ $$V = Ed$$

Так как $V \ne 0$ постоянна, то $\frac{C}{E} = \frac{\epsilon A}{Ed}$ постоянна и, следовательно, $C$ увеличивается с $E$ по мере уменьшения $d$.

Почему емкость диэлектрика увеличивается, а не уменьшается

Теперь пусть $d$ будет постоянным, а вместо этого пусть $\epsilon$ будет возрастать. $V \ne 0$ по-прежнему остается постоянным, но теперь константа $\frac{C}{\epsilon E} = \frac{A}{Ed}$, поэтому $C$ возрастает с ростом $\epsilon$, а $ E$ — это константа .

$\endgroup$

$\begingroup$

Когда проводились сравнения, очевидные противоречия были связаны с неспособностью указать, что происходит с зарядом/напряжением.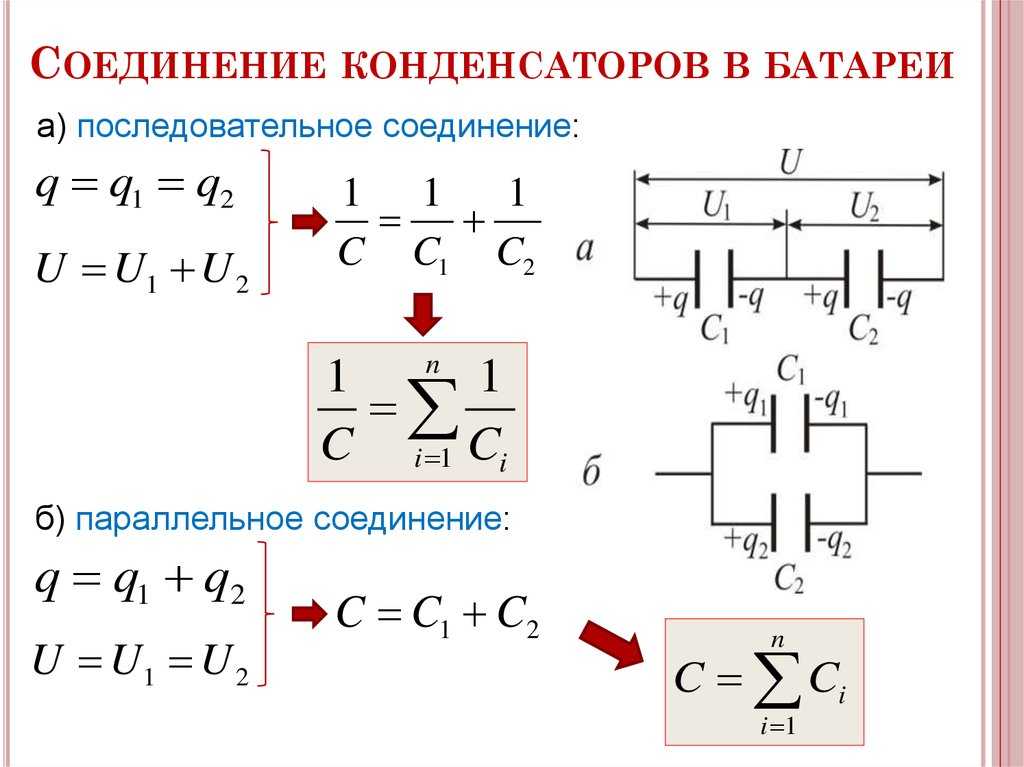

Емкость определяется как $C=\frac QV$.

Для идеального плоского конденсатора электрическое поле между пластинами равно $E=\frac Vd$, а емкость равна $C=\frac{\epsilon A}{d} \Rightarrow C\propto \epsilon$, если площадь $A$ и расстояние $d$ остаются постоянными.

Если $V$ поддерживается постоянным, то электрическое поле $E \propto \frac 1 d$, т.е. $E$ не зависит от $\epsilon$ и $Q$ изменяется при изменении $d$.

$E=\frac Vd \propto \frac Q \epsilon$ и если $Q$ остается постоянным $E \propto \frac 1 \epsilon$ т.е. $E$ не зависит от $d$ и $V$ изменяется если $\epsilon$ изменен.

$\endgroup$

$\begingroup$

Я могу сказать, как я это понимаю. Вы правы, что чистая Е внутри диэлектрика уменьшится из-за поляризации диэлектрика. Однако поляризация создаст поверхностный заряд на поверхностях (рядом с обкладками конденсатора) диэлектрика. Теперь этот поверхностный заряд будет иметь свое собственное электрическое поле внутри пластины конденсатора, которое будет положительно складываться с внешним E внутри пластины.