ХОЛЛА ЭФФЕКТ • Большая российская энциклопедия
Авторы: О. А. Котельникова
ХО́ЛЛА ЭФФЕ́КТ, возникновение в твёрдом проводнике с плотностью тока $\boldsymbol j$, помещённом в магнитное поле напряжённостью $\boldsymbol H$, электрич. поля напряжённостью $\boldsymbol E_H$ в направлении, перпендикулярном $\boldsymbol H$ и $\boldsymbol j$. Открыт Э. Г. Холлом в 1879 в тонких пластинках золота. Величина напряжённости электрич. поля (поля Холла) $E_H=RHj\sin α$, где $α$ – угол между $\boldsymbol H$ и $\boldsymbol j$ ($α < 180°$). Если $\boldsymbol H⊥\boldsymbol j$, то $E_H$ максимально: $E_H=RHj$. Коэф. $R$ называется постоянной Холла, которая полностью характеризует Х. э. Знак $R$ положителен, если $\boldsymbol j$, $\boldsymbol H$ и $\boldsymbol E_H$ образуют правовинтовую систему координат. Эдс Холла $U_H=E_Hb=RHI/d$ измеряют между электродами, расположенными на боковых гранях образца в виде прямоугольной пластины ($b$ – ширина, $d$ – толщина, которые намного меньше длины пластины), перпендикулярно току $I=jbd$.
Возникновение эдс Холла обусловлено взаимодействием носителей тока (электронов и дырок) с внешним магнитным полем. Сила Лоренца $\boldsymbol F=q[\boldsymbol v \boldsymbol H]$, действующая со стороны магнитного поля на движущиеся заряды ($q$ – заряд, $\boldsymbol v=\boldsymbol j/nq$ – ср. скорость направленного движения носителей заряда, $n$ – их концентрация), приводит к отклонению носителей в направлении, перпендикулярном $\boldsymbol H$ и $\boldsymbol j$, или к «закручиванию» их траектории. В результате возникает поле Холла, которое действует на заряды и уравновешивает силу Лоренца: $qE_H=qvH$, и, следовательно, $R=1/nq$. Знак $R$ совпадает со знаком носителей заряда. В металлах, где $n$≈1028 м–3, R имеет порядок величины 10–9 м3/Кл, в полупроводниках $R$≈10–5-10–1 м3/Кл.
Для металлов величина $R$ зависит от зонной структуры, степени чистоты образца, его ориентации относительно кристаллографич. осей, величины магнитного поля и темп-ры.
При описании Х. э. в магнетиках следует учитывать наличие в них собств. молекулярного поля, создаваемого упорядоченными магнитными моментами. Тогда поле Холла имеет вид: $E_y=RB_zj_x+R_s4πM_zj_x$ (индексы $x$, $y$, $z$ указывают соответствующую проекцию на координатную ось; $\boldsymbol B$, $\boldsymbol M$ – индукция магнитного поля и намагниченность магнетика соответственно; $R_s$ – постоянная аномального эффекта Холла). Вклад в поле Холла, пропорциональный $M$, называют спонтанным или аномальным Х. э., поскольку он реализуется в ферро-, антиферро- и ферримагнитных проводниках и полупроводниках. В ферромагнетиках $R_s$ может на порядок превышать величину $R$.
Постоянная $R_s$ имеет сложную температурную зависимость, причём знаки $R$ и $R_s$ могут не совпадать. За возникновение аномального Х. э. ответственно спин-орбитальное взаимодействие, которое приводит к асимметричному рассеянию носителей заряда в магнетиках. В сильных магнитных полях в плоских проводниках (квазидвумерных системах) проявляются квантовые особенности поведения носителей заряда (квазидвумерного электронного газа) – возникает квантовый эффект Холла. При дальнейшем увеличении магнитного поля перестройка электронной системы становится столь сильной, что приводит к т. н. дробному квантовому эффекту Холла.
Линейную зависимость поля Холла от $H$ используют для измерения напряжённости магнитного поля (датчики Холла). Х. э. применяется для умножения постоянных токов в аналоговых вычислит. машинах, в измерит.
технике и др.
2.Методика измерения постоянной Холла.
2.1.Определение постоянной Холла.
Рассмотрим величины, непосредственно измеряемые в эксперименте. Во время эксперимента измеряются не электрические поля и плотность тока, а разности потенциалов (напряжения) и сила тока
(34)
где а, b, d—длина, ширина и толщина образца (см. рис. 2).
Рис. 2. Образец для измерения эффекта Холла и проводимости
Перепишем формулы (5), (6), (9) и (10) с учетом (34)
, (35)
, (36)
(37)
. (38)
Кроме того, принимая во внимание (7), коэффициент Холла можно выразить в зависимости от приложенного к образцу напряжения и проводимости
(39)
Однако поскольку проводимость связана с током соотношением
(40)
Что касается подвижности, то она связана только с приложенным напряжением (продольного электрического поля), но не с током. Это явно видно из первого уравнения (12), которое можем переписать с учетом (34)
(41)
Проводя исследования эффекта Холла в примесных полупроводниках в зависимости от окружающих условий (например, от окружающей температуры), можно измерять э. д. с. Холла Vy в двух режимах: в режиме питания образца от источника тока и в режиме питания образца от источника напряжения . Тогда в соответствии с выражениями (37) и (35) и при в первом случае э. д. с. Холла будет функцией концентрации носителей, во втором – функцией подвижности носителей заряда.
Для исключения
влияния сопротивления токовых контактов
целесообразно продольное напряжение
измерять зондовым методом (контакты 4—5 на рис. 2). Измерив поперечное напряжения и индукцию магнитного поля (ВZ) для образца с данными размерами (рис.
2), можно определить три главных параметра
полупроводника:
(42)
(43)
(44)
2.2. Метод постоянного поля.
Первый эксперимент по измерению эффекта Холла, проведенный самим Е. X. Холлом в ноябре 1878г был выполнен методом постоянного магнитного поля и постоянного тока ( методом ). С тех пор благодаря относительной простоте реализации этот метод получил широкое распространение.
В методе уменьшение вклада посторонних поперечных э.д.с. в измеряемую э.д.с. Холла осуществляется усреднением результатов измерений общего поперечного напряжения для двух направлений тока Ix и двух направлений магнитного поля Bz.
(45)
Из (45) видно, что
усредненное напряжение кроме э.
д.с.
Холла, содержит э.д.с. Эттингсгаузена,
э.д.с. Нернста – Эттингсгаузена – Пельтье
и э.д.с. Риги – Ледюка – Пельтье. При
исследовании многих материалов, главным
образом высокоомных, вкладом дополнительных
э.д.с. можно пренебречь (см. табл. 2). Кроме
того, принимая во внимание зависимость
установления состояния термического
равновесия от времени, получаем
(46)
где – постоянная времени, определяемая теплопроводностью образца и теплоемкостью системы образец-держатель, t – время. Таким образом, вклад дополнительных э. д. с. можно уменьшить, сократив время измерений.
Часто усреднение Vy производят только по двум направлениям. В этом случае в соответствии с (45) среднее напряжение
(47)
Пренебречь последними э.д.с можно лишь при исследовании высокоомных материалов и при обеспечении изотермических условий измерений.
Измерения на эффекте Холла
Электрические характеристики материалов развивались на трех уровнях понимания.
В начале 1800-х годов сопротивление R и проводимость G считались измеримыми физическими величинами, которые можно получить из двухполюсных I-V измерений (т. е. ток I , напряжение V ). Позже стало очевидно, что одного только сопротивления недостаточно, поскольку разные формы образцов давали разные значения сопротивления. Это привело к пониманию (второй уровень), что требуется внутреннее свойство материала, такое как удельное сопротивление (или проводимость), на которое не влияет конкретная геометрия образца. Впервые это позволило ученым количественно оценить токопроводящую способность материала и провести значимые сравнения между различными образцами. Теории электропроводности строились с переменным успехом, но до появления квантовой механики не было выработано общеприемлемого решения проблемы электрического транспорта. Это привело к определению плотности носителей n и мобильность µ (третий уровень понимания), которые сегодня способны выполнять даже самые сложные электрические измерения.
Эффект Холла и сила Лоренца
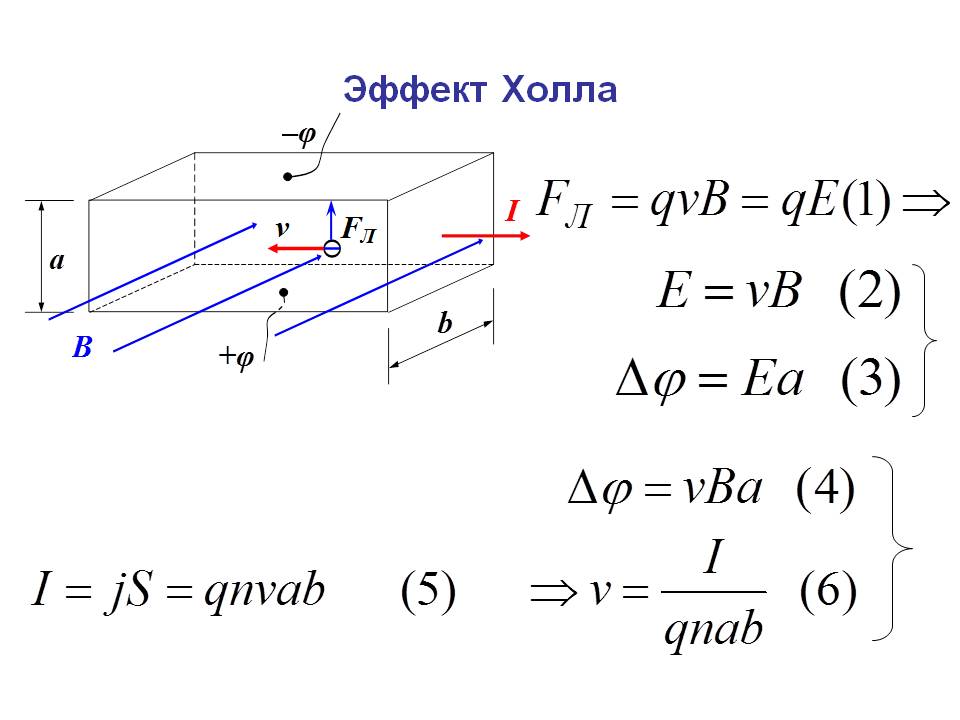
Основным физическим принципом, лежащим в основе эффекта Холла, является сила Лоренца. Когда электрон движется в направлении, перпендикулярном приложенному магнитному полю, на него действует сила, действующая по нормали к обоим направлениям, и он движется под действием этой силы и силы, действующей со стороны внутреннего электрического поля. Сила Лоренца равна
Эффект Холла показан на рис. 1 для образца в форме стержня, в котором заряд переносится электронами. Через стержень протекает постоянный ток I, и на весь стержень действует однородное магнитное поле B , которое направлено в экран перпендикулярно протеканию тока. Поскольку электроны движутся через магнитное поле, на них действует восходящая сила Лоренца, и поэтому они дрейфуют к вершине стержня, сохраняя при этом свое горизонтальное движение. Это приводит к накоплению отрицательного заряда на одной стороне стержня и положительного заряда на другой из-за отсутствия электронов.
Это приводит к разности потенциалов между двумя сторонами образца, которую можно измерить как напряжение Холла V Н . (Обратите внимание, что сила на отверстиях направлена в одну сторону из-за их противоположной скорости и положительного заряда.)
Рисунок 1: Иллюстрация эффекта Холла в стержне из проводящего материала.
Это поперечное напряжение представляет собой напряжение Холла В H и его величина равна IB/qnd , где I – ток, B – магнитное поле, d – толщина образца , и q (1,602 x 10 -19 С) — элементарный заряд. В некоторых случаях удобно использовать плотность слоя или листа ( n s = nd ) вместо насыпной плотности. Тогда получается уравнение
(1)
Таким образом, измерив напряжение Холла V H и по известным значениям I , B и q , можно определить листовая плотность n s носителей заряда в полупроводниках.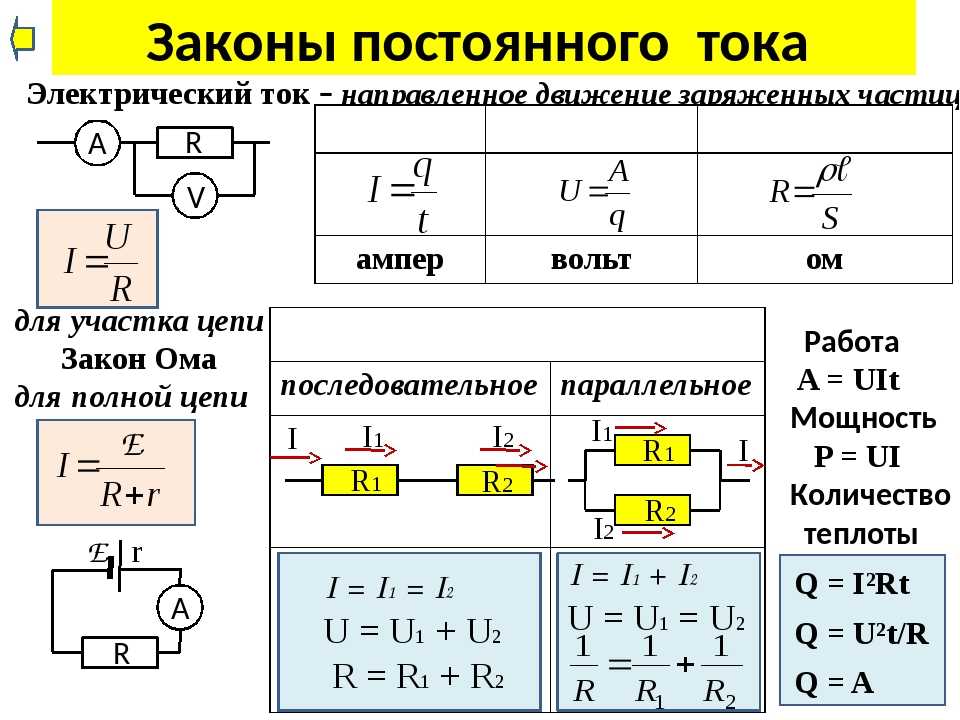
Если измерительный прибор настроен, как показано, напряжение Холла отрицательное в течение n полупроводники и положительный для полупроводников p типа. Поверхностное сопротивление R S полупроводника можно удобно определить с помощью метода измерения удельного сопротивления Ван дер Пау. Поскольку поверхностное сопротивление включает в себя как плотность, так и подвижность листа, подвижность Холла можно определить из уравнения
(2)
.0003 r = R S d ) и насыпной плотности ( n = n S / d ).
Метод Ван дер Пау
Чтобы определить подвижность µ и плотность листа n s , необходимо сочетание измерения удельного сопротивления и измерения Холла. Мы обсудим здесь метод Ван-дер-Пау, который благодаря своему удобству широко используется в полупроводниковой промышленности для определения удельного сопротивления однородных образцов (ссылки 3 и 4).
Первоначально разработанный Ван дер Пау, используется образец тонкой пластины произвольной формы (но просто соединенный, т. тарелка. Примеры конфигураций Ван-дер-Пау показаны на рис. 2.9.0017
Рис. 2. Примеры возможных конфигураций Ван-дер-Пау и их предпочтения [12]
Целью измерения удельного сопротивления является определение поверхностного сопротивления R S . Ван дер Пау продемонстрировал, что на самом деле существует два характеристических сопротивления R A и R B , связанных с соответствующими клеммами, показанными на рис. 2. R A и R B связаны с поверхностным сопротивлением R S уравнением Ван дер Пау
(3)
, которое можно решить численно для R S .
Общее удельное электрическое сопротивление r можно рассчитать, используя
(4)
Для получения двух характеристических сопротивлений подается постоянный ток I на контакт 1 и вне контакта 2 и измеряется напряжение В 43 от контакта 4 к контакту 3. 9 с можно рассчитать через n s = IB / q | В Н | по известным значениям I , B и q . Существуют практические аспекты, которые необходимо учитывать при проведении измерений Холла и удельного сопротивления. Основными проблемами являются (1) качество и размер омического контакта, (2) однородность образца и точное определение толщины, (3) термомагнитные эффекты из-за неоднородной температуры и (4) фотопроводящие и фотогальванические эффекты, которые можно свести к минимуму путем измерения в темноте. . Кроме того, поперечные размеры образца должны быть большими по сравнению с размером контактов и толщиной образца. Наконец, необходимо точно измерить температуру образца, напряженность магнитного поля, электрический ток и напряжение. Некоторая дополнительная информация о температурной зависимости измерений Холла и о том, как эту зависимость можно использовать, обсуждается на странице температурной зависимости Тип присутствующих носителей, то есть n- или p-тип, очень важен. Более подробное обсуждение этой области можно найти на странице типов перевозчиков Содержание Коэффициент Холла — это физическая константа, которая связывает величину магнитного поля с электрическим током, протекающим через материал. Он был открыт Эдвином Холлом в 1879 году и назван в его честь. Коэффициент Холла является мерой реакции материала на приложенное магнитное поле и выражается как отношение индуцированного электрического поля к приложенному магнитному полю. Эффект Холла связан с силой Лоренца, которая представляет собой силу, действующую на заряженную частицу, когда она помещена в магнитное поле. Сила Лоренца перпендикулярна направлению магнитного поля и заставляет ток течь в направлении, перпендикулярном как магнитному полю, так и току. Ток называется током Холла, а явление известно как эффект Холла. Коэффициент Холла определяется как отношение напряжения Холла (индуцированного электрического поля) к приложенному магнитному полю. Коэффициент Холла зависит от материала и обычно измеряется в единицах V/T (вольт на тесла). Коэффициент Холла является полезным инструментом для исследователей в области материаловедения и инженерии, поскольку он дает представление о транспортных свойствах материала. Это также полезно для идентификации различных материалов, поскольку разные материалы имеют разные коэффициенты Холла. Коэффициент Холла использовался для изучения широкого круга материалов, включая полупроводники, металлы и сверхпроводники. Коэффициент Холла является важным параметром во многих приложениях, таких как разработка магнитных датчиков, проектирование высокоскоростных электронных схем и оптимизация работы электродвигателей. Коэффициент Холла — это физическая константа, используемая для измерения величины эффекта Холла в материале. Он определяется как отношение индуцированного электрического поля к произведению плотности тока и магнитного поля. Это безразмерная величина и обозначается символом R_H. Коэффициент Холла является важным параметром при определении электрических свойств материала. Это указывает на тип носителей заряда, присутствующих в материале, и используется для изучения электронной структуры материалов. Его также можно использовать для идентификации различных типов полупроводников. Коэффициент Холла определяется экспериментально путем измерения напряжения Холла, которое представляет собой напряжение, возникающее на образце, когда к нему перпендикулярно приложено магнитное поле. Эффект Холла — это явление, при котором поперечное электрическое поле создается в проводнике при наличии тока и магнитном поле, приложенном перпендикулярно к току. Напряжение Холла пропорционально произведению плотности тока и приложенного магнитного поля и обратно пропорционально толщине образца. Коэффициент Холла можно рассчитать по измеренному напряжению Холла как R_H = \frac{\text{напряжение Холла}}{\text{плотность тока} \times \text{магнитное поле}} Единицей измерения коэффициента Холла является вольт -метры на Тесла (Vm/T). Это мера подвижности носителей заряда в материале, обычно выражаемая в см2/В-с. Он назван в честь американского физика Эдвина Холла, открывшего этот эффект в 1879 году.. Коэффициент Холла рассчитывается путем измерения поперечного напряжения (напряжения Холла), создаваемого электрическим током в магнитном поле вдоль направления тока. B: R_H = \frac{V_H}{IB} Коэффициент Холла положителен для полупроводников p-типа и отрицательно для полупроводников n-типа. В большинстве материалов величина коэффициента Холла относительно мала, и поэтому ее трудно точно измерить. По этой причине эффект Холла часто используется для измерения электропроводности материалов. Коэффициент Холла обычно измеряется с помощью устройства, называемого датчиком Холла, которое состоит из тонкой металлической полоски, через которую проходит небольшой ток. Полоску помещают между двумя электродами и прикладывают магнитное поле в направлении тока. Напряжение Холла, генерируемое током, затем измеряется между двумя электродами. Затем коэффициент Холла рассчитывается на основе измеренных значений напряжения и тока Холла. Коэффициент Холла также можно рассчитать по другим параметрам, таким как удельное сопротивление материала, концентрация носителей и их подвижность. Эффект Холла — это явление, при котором в материале индуцируется напряжение при приложении тока и при воздействии на материал магнитного поля. Эдвин Холл открыл этот эффект в 1879 году., и это наблюдалось в различных материалах, включая металлы, полупроводники и изоляторы. Коэффициент Холла является мерой чувствительности материала к магнитному полю и используется для характеристики свойств материала. Коэффициент Холла представляет собой безразмерную величину, определяемую как отношение индуцированного напряжения к произведению приложенного тока и напряженности магнитного поля. Единица измерения коэффициента Холла обычно выражается обратной величиной Тесла, которая известна как обратная Тесла (1T-1). Коэффициент Холла определяется путем измерения разности напряжений на образце материала при подаче тока и изменении магнитного поля. Коэффициент Холла является важным параметром при изучении электрических свойств материалов и используется для характеристики реакции материалов на приложенные магнитные поля. Коэффициент Холла является мерой восприимчивости материала к приложенному магнитному полю и используется для определения исследуемого материала. Например, металлы обычно имеют положительный коэффициент Холла, а изоляторы обычно имеют отрицательный коэффициент. Коэффициент Холла также используется для расчета подвижности носителей заряда в материале, который является мерой скорости, с которой носители заряда перемещаются в материале. Коэффициент Холла также используется при расчете коэффициента Зеебека, меры термоэлектрической способности материала. Коэффициент Холла является полезным параметром для характеристики электрических свойств материалов и используется для изучения влияния магнетизма на материал. Коэффициент Холла является важным параметром для изучения электронных материалов и используется для определения электрических свойств этих материалов. Коэффициент Холла — это безразмерная величина, используемая для измерения напряженности магнитного поля при пропускании через материал электрического тока. Он используется для характеристики свойств полупроводников, металлов и других материалов, взаимодействующих с магнитными полями. Коэффициент Холла чаще всего измеряется в инверсных метрах (1/м). Коэффициент Холла назван в честь Эдвина Холла, американского физика, впервые описавшего этот эффект в 1879 году. Коэффициент Холла рассчитывается на основе измеренной разницы напряжений между двумя точками в материале, когда магнитное поле приложено в одном направлении, а электрический ток — в другом. Коэффициент Холла рассчитывается путем деления разности напряжений на произведение напряженности магнитного поля и электрического тока. Коэффициент Холла используется в различных приложениях, включая характеристику электрических свойств материалов и анализ структуры магнитных полей. Его также можно использовать для измерения эффекта Холла, который представляет собой возникновение напряжения в материале, когда магнитное поле прикладывается перпендикулярно электрическому току. Это явление используется в самых разных областях, включая измерение магнитных полей в системах магнитно-резонансной томографии (МРТ) и разработку датчиков магнитного поля. Кроме того, коэффициент Холла можно использовать для характеристики свойств материалов при высоких температурах, таких как сверхпроводники. Коэффициент Холла также используется для изучения свойств полупроводников, таких как ширина запрещенной зоны, концентрация носителей и подвижность электронов. Его также можно использовать для определения типа полупроводникового материала, например, n-типа или p-типа, и для измерения холловской подвижности материала. Коэффициент Холла также можно использовать для изучения свойств металлов, в том числе их электропроводности и намагниченности. Соображения безопасности для единицы коэффициента Холла должны включать следующее: 1. 2. Убедитесь, что все электрические соединения надежны, а все оголенные провода должным образом изолированы. 3. Избегайте контакта с магнитным полем, создаваемым устройством на эффекте Холла. 4. Убедитесь, что для эксперимента используется соответствующий источник питания. 5. Убедитесь, что квалифицированный технический специалист поможет с любой настройкой или устранением неполадок. 6. Помните о любых опасностях, связанных с устройством. 7. Иметь общее представление о физике эксперимента и его принципах. 8. Примите соответствующие меры для обеспечения точности и надежности измерений. 9. Уберите все беспорядки и утилизируйте все опасные материалы надлежащим образом. 10. Перед выполнением любого технического обслуживания или ремонта отключите устройство от источника питания. Вывод блока по коэффициенту Холла состоит в том, что это важная величина для понимания свойств материала. Коэффициент Холла можно использовать для различения различных типов материалов и для измерения подвижности носителей заряда в материале. Коэффициент Холла также важен при изучении полупроводников, поскольку он может предоставить информацию о концентрации носителей в материале. Наконец, измерения эффекта Холла также можно использовать для измерения намагниченности материала, что может быть использовано для определения его магнитных свойств. Коэффициент Холла (R_H) — это физическая константа, которая описывает реакцию материала на магнитное поле. Коэффициент Холла является мерой сопротивления материала магнитному полю и используется для характеристики ряда материалов, от полупроводников до сверхпроводников. Коэффициент Холла был впервые открыт физиком Эдвином Холлом в 1879 году и назван в его честь.
Затем подается ток I на контакт 2 и вне контакта 3 при измерении напряжения В 14 от контакта 1 к контакту 4 с использованием показанной геометрии на рис. 3. R A и R B рассчитываются с помощью следующих выражений: методика заключается в определении плотности листового носителя n s путем измерения напряжения Холла В H . Измерение напряжения Холла состоит из серии измерений напряжения с постоянным током I и постоянным магнитным полем B , приложенным перпендикулярно плоскости образца. Удобно, что тот же образец, снова показанный на рис. 3, также можно использовать для измерения Холла. Для измерения напряжения Холла В H через противоположную пару контактов 1 и 3 нагнетают ток I и напряжение Холла В H (= В 24 ) измеряется на оставшейся паре контактов 2 и 4. После получения напряжения Холла В H плотность несущей пластины n
Ссылки
eeel.nist.gov/812/effe.htm
Единица коэффициента Холла 2023
Он также использовался для изучения влияния температуры, давления и других внешних факторов на транспортные свойства материала.
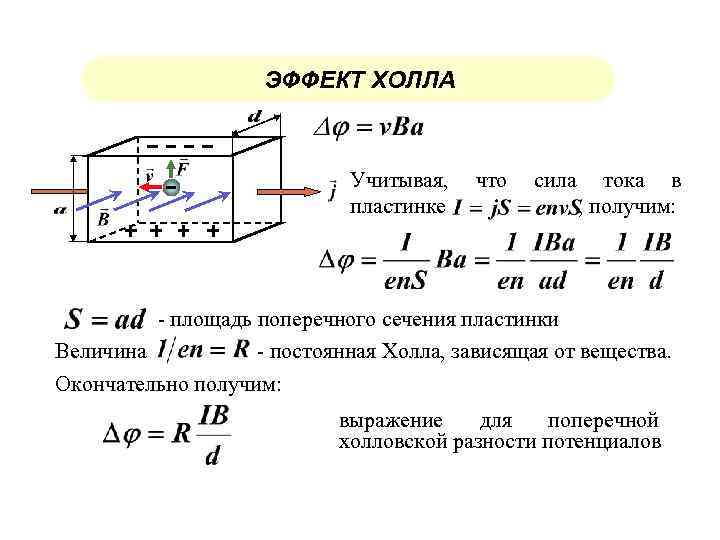
Коэффициент Холла определяется как отношение напряжения Холла VH к произведению тока I и приложенного магнитного поля
Все эти параметры могут быть измерены прямо или косвенно.
Носите средства индивидуальной защиты (СИЗ), такие как защита глаз, перчатки и лабораторный пальто при экспериментах.
Это мера отношения поперечного напряжения Холла к продольному току, протекающему через материал, когда к нему перпендикулярно приложено магнитное поле.
