Особенности работы выпрямителей, или как правильно рассчитать мощность силового трансформатора – Начинающим – Теория
Хороший и надёжный силовой трансформатор – это уже половина собираемой и разрабатываемой конструкции.
В настоящее время выбор силовых трансформаторов, предлагаемых рынком, для радиолюбителей довольно широк. Но не смотря на это, не все предлагаемые трансформаторы идеально подходят для нужд радиолюбителя (по току, напряжению, количеству обмоток и т.д.), и поэтому довольно часто ему приходится самостоятельно изготавливать силовые трансформаторы для своих разработок и собираемых конструкций.
В этой статье я попробую объяснить, как правильно выбрать, или рассчитать силовой трансформатор для своей конструкции.
Нового я здесь ничего не открою, и постараюсь как можно проще и на примерах, объяснить Вам то, что уже давно доказано и решено. Просто в силу каких либо обстоятельств, не все это могут знать.
В основном радиолюбителю приходится изготавливать силовые трансформаторы средней мощности 50 – 300 Вт.
КПД таких трансформаторов достигает 0,88 – 0,92. У более мощных промышленных трансформаторов, при мощностях более 1 кВт, КПД может достигать 0,97-0,98, так как обмотки их намотаны толстым проводом и потери в них на активное сопротивление минимальны.
Чтобы правильно рассчитать трансформатор, нужны довольно сложные вычисления, радиолюбители-же пользуются для этих целей упрощёнными формулами и радиолюбительскими программами, которые в принципе тоже довольно точно позволяют это сделать, поэтому я тоже постараюсь не отходить от этой традиции и всё попробую объяснить на практических примерах и готовых расчётах, используя по минимуму формулы и вычисления.
Как обычно производится расчёт силового трансформатора.
Зная напряжение и ток, который должна давать вторичная (или несколько вторичных) обмотка (U2 и I2), находим мощность вторичной цепи: При наличии нескольких вторичных обмоток мощность подсчитывают путем сложения мощностей отдельных обмоток.
Отсюда можно найти и мощность первичной обмотки, где для трансформаторов средней мощности к нашим расчётам мы берём КПД трансформатора 0,9 (90%). Для трансформаторов меньшей мощности соответственно и КПД берётся меньше (0,8).
Мощность первичной обмотки Р1 (мощность трансформатора) в этом случае будет равна;
То есть поясню, если расчётная мощность вторичной (вторичных) обмотки у нас получилась например 100 Вт, то общая мощность трансформатора будет равна 111,1 Вт (100/0,9). Это ещё не учитывая ток холостого хода, который тоже прибавляется к общей мощности трансформатора.
Как определить мощность первичной обмотки мы уяснили, теперь как правильно определить мощность вторичной обмотки?
Для этого у нас имеется какая либо нагрузка, которая потребляет определённый ток при определённом напряжении. Например имеется нагрузка, потребляющая ток 2 Ампера при напряжении 15 Вольт.
Если же вторичная обмотка нагружена на нагрузку через элементы выпрямителя, или выпрямителя и фильтра, то ситуация приобретает совсем другой оборот. Ток отдаваемый вторичной обмоткой будет больше тока, потребляемого нагрузкой!
Почему так, давайте попробуем вместе с этим разобраться.
Работа вторичной обмотки на активную нагрузку мы рассматривать не будем, здесь всё ясно, давайте пойдём дальше.
Работа выпрямителя на активную нагрузку.
Однополупериодный выпрямитель.
Поставим перед нагрузкой выпрямительный диод. То есть у нас получился однополупериодный выпрямитель.
Соберём такую же схемку. Трансформатор у меня тороидальный, мощностью 60 Вт, с напряжением ХХ вторичной обмотки около 20 вольт (номинальный ток нагрузки 3,8 А, номинальное напряжение 16,5 Вольт), ток ХХ трансформатора 7 мА.
В разрыв первичной обмотки, для измерения её тока, я поставил резистор, величиной 1,0 Ом, в разрыв вторичной (последовательно с нагрузкой) резистор, величиной 0,1 Ом. Для измерения в цепях переменного и пульсирующего тока и напряжения, я использовался среднеквадратичный (RMS) микровольтметр В3-57, ну и для измерения в цепях постоянного тока – цифровой мультиметр “Mastech MY64”.
Для безопасности измерений, вся эта конструкция подключалась через разделительный трансформатор. В качестве нагрузочных резисторов использовались проволочные переменные сопротивления различных величин, мощностью 25 Вт.
Действующий ток нагрузки был установлен 0,5 ампер (рисунок выше). Предел измерения 100 мВ, шунт во вторичной цепи 0,1 Ом.
Измерим ток, потребляемый первичной обмоткой.
Ток первичной обмотки получился 97 мА, минус 7 мА ХХ, итого 90 мА. Напряжение на первичной обмотке 215 вольт. Мощность потребляемая первичной обмоткой получилась 19,35 Вт, то есть в 4 (четыре) раза больше мощности потребляемой нагрузки. Почему так? Кому интересны все подробности происходящих процессов в трансформаторе, рекомендую почитать первоисточники, приведённые в конце статьи, кому лень читать, попробую объяснить по простому.
При установке диода последовательно с нагрузкой, у нас получается однополупериодный выпрямитель. На нагрузку подаётся импульс напряжения (тока) только в положительный полупериод, а в отрицательный ничего нет (пауза). В результате чего среднее напряжение на нагрузке уменьшается более, чем в два раза (точнее в 2,2) по сравнению с напряжением на вторичной обмотке. Средний ток через диод соответствует току нагрузки, а действующий ток диода и самой вторичной обмотки – больше тока нагрузки в 1,57 раза.
Ток нагрузи 0,5 А, умножаем на 1,57=0,785 (ток вторичной обмотки). Полученный ток умножаем на напряжение вторичной обмотки (19 Вольт) 0,785х19=14,9 Вт – это получается отдаваемая мощность вторичной обмотки, плюс сюда ещё добавляются и переходные процессы при работе диода (вентиля), плюс реактивные токи, которые просто нагревают обмотку, в итоге мощность трансформатора получается минимум в 3,5 раза больше мощности потребляемой нагрузкой.
Ещё при работе этой схемы во вторичной обмотке возникает постоянная составляющая (из-за того, что ток в обмотке протекает только в одном направлении в один полупериод), которая намагничивает сердечник трансформатора и тем больше, чем больше ток нагрузки. Из-за этого свойства сердечника ухудшаются и увеличивается ток ХХ, в последствии чего повышается потребляемая мощность трансформатора (у нас получилась мощность в 4 раза больше).
Например уже при токе нагрузки в 1,0 Ампер, напряжение на нагрузке получилось 9,0 Вольт, сопротивление нагрузки 9,0 Ом, мощность нагрузки 9,0 Вт. Ток первичной обмотки получился 230 мА (минус 7 мА) итого 223 и напряжение на первичной обмотке 210 вольт. Итоговая потребляемая мощность трансформатора 46,83 Вт, то есть больше мощности потребляемой нагрузкой уже в 5,2 раза. Сильно увеличился ток ХХ с увеличением тока нагрузки (от которого увеличилось намагничивание сердечника).
Двухполупериодный выпрямитель.
Ну, с однополупериодным выпрямителем разобрались, давайте пойдём дальше. Посмотрим как ведёт себя двухполупериодная схема.
Что из себя представляет двухполупериодная схема выпрямителя. Это два однополупериодных выпрямителя, которые работают на общую нагрузку. Каждый выпрямитель имеет свою обмотку, но в отличии от другого – противофазную, в результате чего выпрямляются (поступают в нагрузку) оба полупериода, за счёт чего эффективность такого выпрямителя, по сравнению с однополупериодным, повышается два раза.
Посмотрим, как он себя ведёт. Соберём схему двухполупериодного выпрямителя. Для этой схемы нужен трансформатор с отводом от средней точки вторичной обмотки. Трансформатор другой, вторичная обмотка имеет напряжение 193-193 Вольт, ток ХХ у него 36 мА (какой нашёл).
Проволочными резисторами выставил ток нагрузки 150 мА.
Нагрузочный резистор получился с сопротивлением 1,17 кОм, измеренное напряжение на нём 175 Вольт. Мощность потребляемая нагрузкой получилась 26,17 Вт. Смотрим ток первичной обмотки.
Ток первичной обмотки 210 мА, минус ток ХХ (36) итого 174 мА. Мощность потребляемая трансформатором получилась 38,28 Вт. Это больше мощности потребляемой нагрузкой в 1,46 раз.
Идём дальше.
Мостовая схема выпрямителя.
Проверим, как поведёт себя мостовая схема выпрямителя.
Для этого соберём следующую схему.
Трансформатор возьмём тот, что был и раньше, с одной вторичной обмоткой из первого рассматриваемого случая для однополупериодного выпрямителя.
Ток нагрузки я выставил 0,5 А, проволочное переменное сопротивление получилось величиной 32 Ома. Напряжение на нагрузке 16 Вольт. Мощность потребляемая нагрузкой получилась 8 Вт.
Смотрим ток потребляемый первичной обмоткой.
Ток первички 53 мА минус ток ХХ (7 мА) = 45 мА. Мощность потребляемая первичной обмоткой получилась 9,9 Вт. Это в 1,23 раза больше, чем мощность потребляемая нагрузкой.
Как видите, здесь показатели ещё лучше, чем у двухполупериодного выпрямителя, не говоря уже об однополупериодном.
Работа выпрямителя на нагрузку с ёмкостной реакцией.
В основном радиолюбители используют в своей практической деятельности выпрямители с сглаживающими фильтрами, начинающимися с ёмкости (конденсатора), то есть нагрузка с ёмкостной реакцией.
Переписывать учебники не имеет смысла, кому интересно, список литературы в конце статьи. Просто я здесь дальше кратко изложу основные схемы выпрямителей применяемых радиолюбителями, их особенности и приближённые электрические характеристики, и как они влияют на общую мощность трансформатора.
Однополупериодный выпрямитель.
Начнём как обычно с однополупериодного выпрямителя.
У такого выпрямителя конденсатор фильтра заряжается до амплитудного значения напряжения вторичной обмотки (при отсутствии нагрузки). То есть если напряжение вторички 10 Вольт, то конденсатор зарядится до 10х1,41=14,1 Вольта (это без падения напряжения на диоде).
Простота схемы, используется всего один вентиль (диод, кенотрон).
Недостатки;
Большая зависимость выходного напряжения от тока нагрузки, пониженная частота пульсаций по отношению с другими схемами, что требует применение конденсаторов в два раза большей ёмкости, плохое использование трансформатора (низкий КПД), присутствует вынужденное намагничивание сердечника. При пробое вентиля, переменное напряжение поступает на конденсатор, что ведёт его к выходу из строя и взрыву.
Особенности схемы;
Применяется радиолюбителями для питания слаботочных цепей. Обратное напряжение в этой схеме прикладываемое к вентилю, приблизительно в три раза больше напряжения вторичной обмотки (точнее в 2,82 раза), почему так происходит – попробуйте сами определить. То есть если у Вас вторичка имеет напряжение 100-110 Вольт, то диод необходимо ставить на обратное напряжение не менее 400 Вольт, на 300 Вольт может пробить.
Средний ток через вентиль здесь соответствует току нагрузки, а действующее значение тока через вентиль в два раза больше тока нагрузки.
Вторичная обмотка для однополупериодного выпрямителя выбирается в 1,8 -1,9 раз больше по току (лучше в 2 раза), чем ток потребления нагрузки. К общей расчётной мощности трансформатора, если есть ещё другие обмотки, добавьте мощность этой Вашей нагрузки умноженной на 2.
Двухполупериодный выпрямитель.
Двухполупериодный выпрямитель обладает гораздо лучшими параметрами, чем однополупериодный. Выходное напряжение этого выпрямителя (напряжение на конденсаторе) в 1,41 раз выше, чем напряжение вторичной обмотки (половины). Это при отсутствии нагрузки.
Достоинства выпрямителя;
Малое количество используемых вентилей (2). Среднее значение тока через вентиль почти в два раза меньше тока нагрузки. Уровень пульсаций у этой схемы в 2 раза меньше по сравнению с однополупериодной схемой выпрямления. Емкость конденсатора при одинаковом с однополупериодной схемой коэффициенте пульсаций, может быть в 2 раза меньше. Отсутствует вынужденное намагничивание сердечника, но это зависит от конструкции трансформатора и способа намотки обмоток, о чём будет сказано ниже.
Недостатки;
Сложная конструкция трансформатора, вторичная обмотка состоит из двух половин, откуда не рациональное использование меди. Обратное напряжение на один вентиль здесь также больше напряжения (половины) вторичной обмотки в 2,82 раза. Плохое использование трансформатора, так как общая расчётная мощность всей вторичной обмотки получается в 2,2 раза больше мощности потребляемой нагрузкой.
Особенности схемы;
Так как за один период, в этой схеме работают обе половины вторичной обмотки по очереди, соответственно и вентили (диоды) тоже работают по очереди, то среднее значение тока через один вентиль (за период) здесь получается почти в два раза меньше, чем ток нагрузки. То есть например, если поставить в эту схему диоды с допустимым постоянным током на 5 Ампер, то снять с этого выпрямителя можно будет 7-8 Ампер без особого риска выхода из строя диодов, естественно обеспечив им необходимое охлаждение. Действующий же ток через вентиль и вторичную обмотку здесь будут в 1,1 раза больше тока нагрузки.
Провод для вторичной обмотки в этой схеме, можно выбирать на 30-40% меньше по току (сечение), чем ток нагрузки, так как половины вторичной обмотки так же работают по очереди и среднее значение тока вторичной обмотки получается меньше тока нагрузки. Но лучше, если позволяют размеры трансформатора и возможности, мотать вторичку проводом соответствующего сечения с током нагрузки.
Насчёт вынужденного намагничивания сердечника. Если сердечник трансформатора Ш-образный, броневой, и все обмотки размещены на одном каркасе, то вынужденного намагничивания сердечника здесь не будет.
Если сердечник трансформатора стержневой и в конструкции трансформатора предусмотрены два каркаса, на которых размещены обмотки, и сетевая обмотка состоит из двух половин, размещённых на разных стержнях (ТС-180, ТС250), то вторичную обмотку в таких трансформаторах необходимо выполнять следующим образом;
Каждая половина вторичной обмотки делится ещё раз пополам и наматывается на разных стержнях, потом всё соединяется последовательно, сначала четверти одной половины, затем другой. Как ниже на рисунке. Иначе будет намагничивание сердечника.
Так как кенотроны обладают большим внутренним сопротивлением, то при выборе кенотронной схемы выпрямителя, напряжение вторичной обмотки (половины) выбирается в среднем примерно на 10-15% меньше планируемого выходного напряжения выпрямителя. Это ещё зависит от тока нагрузки. Чем больше ток нагрузки, тем меньше должна быть разница.
Ещё запомните, что во всех выпрямителях и с кенотронами и с диодами, конденсаторы фильтра при отсутствии нагрузки, всегда заряжаются до амплитудного напряжения вторичной обмотки (UC = U2 x 1,41). Это учитывайте при выборе напряжения конденсаторов фильтра.
Как примерно определить здесь, какая мощность добавится к общей мощности трансформатора? Не углубляясь глубоко в теорию, так как там очень много зависящих друг от друга факторов, можно поступить следующим образом;
Зная расчётный ток нагрузки, умножаем его на 1,7 (схема с кенотронами), или на 1,6 (схема с диодами), потом полученный результат умножаем на напряжение нагрузки. Это будет приблизительный результат полученной мощности, которая добавится к общей мощности трансформатора. Большой ошибки здесь не будет.
Мостовой выпрямитель.
Мостовой выпрямитель, так же как и двухполупериодный, обладает гораздо лучшими параметрами, чем однополупериодный и немного получше КПД, чем у двухполупериодного. Поэтому это наиболее распространённая схема.
Достоинства выпрямителя;
Среднее значение тока через вентиль почти в два раза меньше тока нагрузки. Уровень пульсаций у этой схемы в 2 раза меньше по сравнению с однополупериодной схемой выпрямления. Емкость конденсатора при одинаковом с однополупериодной схемой коэффициенте пульсаций, может быть в 2 раза меньше. Отсутствует вынужденное намагничивание сердечника. Используется всего одна вторичная обмотка.
Недостатки;
Плохое использование трансформатора, так как приходится увеличивать расчётную мощность вторичной обмотки на величину амплитудного значения напряжения вторичной обмотки, т.е. в 1,41 раз. Увеличенное число используемых вентилей (4) и необходимость их шунтирования резисторами, для выравнивания обратного напряжения на каждом их них. Хотя это уже не столь актуально при современном качестве их исполнения. Ещё в два раза большее падение напряжения, по сравнению с другими схемами, так как выпрямляемый ток проходит по двум вентилям последовательно. Но это заметно только при низком выходном напряжении и больших токах нагрузки.
Особенности схемы;
В этой схеме так же, как и в двухполупериодной, среднее значение тока через один вентиль (за период) получается почти в два раза меньше, чем ток нагрузки. То есть также можно использовать диоды с меньшим рабочим током (на 30-40%), чем ток нагрузки.
А вот действующий ток вторичной обмотки всегда будет выше, чем ток нагрузки, минимум на 1,41. Поэтому провод для вторичной обмотки в этой схеме нужно выбирать в 1,5 раза больше по току (сечение), чем ток нагрузки. Почему, потому что выпрямитель всегда будет заряжать конденсатор фильтра до амплитудного значения напряжения вторичной обмотки, и от величины этого напряжения и подсчитывается мощность. А так, как по закону сохранения энергии она никуда не пропадает, то вторичной обмотки ничего не остаётся, как постоянно восполнять эту разницу. То есть у нас например вторичная обмотка имеет напряжение 14 Вольт. На конденсаторе фильтра будет напряжение около 20-ти Вольт. Нагрузили мы её током 0,5 Ампер. Мощность получилась 10 Вт. Значит и вторичка должна отдавать 10 Вт, а при выходном напряжении 14 Вольт это будет ток примерно 0,71 Ампера, то есть больше тока нагрузки в 1,41 раз.
Вторичная обмотка в мостовой схеме выпрямителя, всегда будет отдавать энергию на заряд конденсатора до амплитудного значения напряжения, а нагрузка разряжать его. То есть это как повышающий преобразователь, где низковольтная часть – это вторичная обмотка, а высоковольтная – конденсатор фильтра. Поэтому и ток вторичной обмотки всегда будет выше тока нагрузки на эту разницу напряжений, то есть минимум в 1,41 раз.
Например нашли Вы трансформатор с выходным напряжением 24 Вольта и током нагрузки 5 Ампер (120 Вт). Собрали линейный регулируемый блок питания, подключили к нему нагрузку 12 Вольт и током потребления 5 Ампер (60 Вт). Вроде всё нормально должно быть. Погоняли с полчаса-час, запахло палёным, потрогали трансформатор – обожглись. Как так?
Давайте проверим что у нас было с трансформатором;
Ток нагрузки 5 Ампер, напряжение на конденсаторе фильтра в режиме ХХ будет 24х1,41=33,84 Вольта. Мощность потребляемая нагрузкой будет 33,84х5=169,2 Вт, притом это не зависит от выходного напряжения Вашего БП, хоть 5 Вольт, хоть 25. Остальная мощность просто потеряется на регулирующем транзисторе.
И вот оказывается, что в течении часа наш транс отдавал мощность нагрузке 170 Вт!!!, хотя его мощность 120.
Вывод; Для схемы мостового выпрямителя, сечение провода вторичной обмотки необходимо выбирать на 50% или в 1,5 раза больше планируемого тока нагрузки для обеспечения нормальных условий работы трансформатора, или же выбирать трансформатор для своей конструкции с током вторичной обмотки выше планируемого на такую же величину, так как ток нагрузки на трансформаторах указан для активной нагрузки.
Ну и соответственно мощность вторичной обмотки подсчитывается так: Ток нагрузки умножаем на напряжение вторичной обмотки и полученный результат умножаем на 1,5.
Схема удвоения напряжения.
Схема удвоения напряжения, тоже довольно часто применяется на практике. Схема состоит из двух однополупериодных выпрямителей, включенных последовательно и работающих на общую нагрузку. Особенностью данной схемы является то, что в одном полупериоде от вторичной обмотки “заряжается” один конденсатор, а во втором полупериоде от той же обмотки – другой. Поскольку конденсаторы включены последовательно, то результирующее напряжение на обоих конденсаторах (на нагрузке) в два раза выше, чем можно получить от той же вторичной обмотки в схеме с однополупериодным выпрямителем. То есть максимальное выходное напряжение ХХ выпрямителя равно U2 х 2,82 , почти в три раза больше напряжения вторичной обмотки.
Достоинства выпрямителя;
Вторичную обмотку трансформатора можно рассчитывать на значительно меньшее напряжение. Отсутствует вынужденное намагничивание сердечника. Используется всего одна вторичная обмотка.
Недостатки;
Большая зависимость выходного напряжения от тока нагрузки. Значительные токи через вентили выпрямителя и вторичную обмотку. Уровень пульсаций значительно выше, чем в схемах двухполупериодных выпрямителей.
Особенности схемы;
Схемы эти на практике применяются для получения высоких напряжений при малых токах нагрузки. Например вполне можно использовать такую схему для питания анодных цепей в маломощных ламповых усилителях, если нет подходящего трансформатора а перематывать лень, в предварительных каскадах мощных ламповых усилителях, сеточных цепей, и т.д.. Пульсации на нагрузке здесь такие же, как в мостовой или двухполупериодной схеме выпрямителей. Ток протекающий через вентиль соответствует току нагрузки. Обратное напряжение на вентиль равно амплитудному значению напряжения вторичной обмотки.
Действующий ток вторичной обмотки здесь больше тока нагрузки почти в три раза (2,82). Мощность вторичной обмотки подсчитывается так, ток нагрузки умножаем на 2,9 и полученный результат умножаем на напряжение вторичной обмотки. Сечение провода вторичной обмотки для этой схемы, выбирается по току в три раза больше, чем ток потребляемый нагрузкой.
Почему так, теперь Вы сами вполне сможете догадаться. Если напряжение ХХ вторичной обмотки например 10 Вольт, то при положительном полупериоде конденсатор С1 здесь зарядится до какого напряжения? Правильно, до 14,1 вольта (до амплитудного значения напряжения вторичной обмотки, которое больше действующего в 1,41 раз). При отрицательном полупериоде конденсатор С2 так же зарядится до 14,1 вольт. Какое будет итоговое напряжение на нагрузке (R), 28,2 Вольта, то есть в 2,82 раза больше напряжения вторичной обмотки. Отсюда и вторичке ничего не остаётся, как всё время компенсировать эту разницу.
Удачи Вам в конструировании!
Список литературы;
- Терентьев Б.П. “Электропитание радиоустройств” (1958).
- Белопольский И.И. “Электропитание радиоустройств” (1965).
- Рогинский В. “Электропитание радиоустройств” (1970).
vprl.ru
Что получается после выпрямления | Практическая электроника
Предисловие
Очень много вопросов задают по статье как получить из переменного напряжения постоянное. Напомню, что мы получали постоянное напряжение с помощью типичной схемы, которая используется во всей электронике:
Да, та статья получилась чуток сыровата, но суть преобразования переменного тока в постоянный мы постарались объяснить на пальцах. Но читатели все равно “не вкурили” ту статью, поэтому было решено написать еще одну статейку, но на этот раз разжевать все досконально.
Снова да ладом…
Придется возвращаться к истокам. Вместо трансформатора я возьму ЛАТР, который будет выдавать переменный ток:
Выставляем на ЛАТРе с помощью цифрового осциллографа напряжение амплитудой в 10 Вольт:

Как мы можем увидеть в нижнем левом углу, частота нашего сигнала 50 Герц. Это и есть частота сети. Длина одного кубика по вертикали равна 2 Вольтам.
Далее берем 4 кремниевых диода
И спаиваем из них диодный мост вот по такой схеме:
Подаем напряжение с ЛАТРа на диодный мост, а с других концов цепляем щуп осциллографа
Тыкаем щупом осциллографа в эти красные кружочки на схеме. Землю на один кружочек, а сигнальный на другой.
Смотрим, что получилось на дисплее осциллографа


Дело в том, что сопротивление щупа осциллографа обладает очень высоким входным сопротивлением, или иначе простыми словами: мы подцепили очень-очень высокоомный резистор к выходу диодного моста. Поэтому диодный мост в холостом режиме, то есть в режиме без нагрузки, не функционирует.
Для того, чтобы проверить диодный мост на работоспособность, нам надо его нагрузить. Это может быть резистор в несколько десятков или сотен Ом, лампочка, либо какая-нибудь электронная безделушка. В моем случае я взял лампочку накаливания на 12 Вольт от поворотника мотоцикла:
Цепляем ее к диодному мосту
Тыкаем щуп осциллографа в эти точки и смотрим осциллограмму

Как мы видим, напряжение с ЛАТРа чуть просело. Все зависит, конечно, от подключаемой нагрузки и мощности самого ЛАТРа. Про это я писал еще в статье работа трансформатора
Теперь тыкаем щупом в эти точки

Классика жанра! Превращаем отрицательную полуволну в положительную и получаем “горки” с частотой в 100 Герц ;-). Но ваш внимательный глаз ничего не заметил? Если даже мы и выпрямили напряжение с помощью диодного моста, то почему амплитуда каждой полуволны стала еще чуть меньше?
Дело все в том, что на PN-переходе диода в прямом смещении падает напряжение в 0,6-0,7 Вольт. Именно поэтому оно и вычитается с амплитуды напряжения, которое надо выпрямить.
Давайте теперь к диодному мосту запаяем конденсатор емкостью в 5000 мкФ и не будем цеплять никакую нагрузку
Тыкаем щупом сюда

Получили вот такую осциллограмму постоянного тока. Она в 1,41 раз больше, чем действующее (среднеквадратичное) значение сигнала с ЛАТРа (о действующем напряжении чуть ниже)
А теперь цепляем лампочку
Осциллограмма кардинально изменилась.

Как мы видим, напряжение просело и у нас получилась осциллограмма постоянного напряжения с небольшими пульсациями. Вот эти маленькие “холмики” и есть пульсации, в отличите от “гор” сразу после диодного моста с лампочкой-нагрузкой. Физический смысл здесь такой: конденсатор не успевает разряжаться на нагрузке, как снова приходит новая “горка” и снова заряжает конденсатор.
Правило диодного выпрямителя с конденсатором очень простое: чем больше емкость конденсатора и чем больше сопротивление нагрузки, тем меньше по амплитуде будут пульсации, и наоборот.
Но почему у нас просело напряжение? Ведь было уже 10 Вольт постоянного напряжения на конденсаторе без нагрузки?

А как цепанули лампочку стало намного меньше…

В чем же проблема? А проблема именно в законе сохранения энергии…
Среднеквадратичное значения напряжения
Итак, давайте еще раз вспомним: что такое среднеквадратичное значение напряжения?
Допустим, у нас есть лампочка накаливания. Я ее подцепил к источнику постоянного тока и она у меня загорелась с какой-то яркостью. Потом я цепляю эту лампу к источнику переменного тока и добиваюсь такого же свечения лампы. Форма сигнала постоянного и переменного напряжения разные, а мощность, выдаваемая в нагрузку, в данном случае лампочку, одинаковая. Можно сказать, что среднеквадратичное значение переменного тока равняется значению постоянного тока.
То есть если у нас лампочка на 12 Вольт, я могу подать на нее 12 Вольт с блока питания или 12 Вольт с ЛАТРа. Лампочка будет светить с такой же яркостью. Мультиметр в режиме измерения переменного тока показывает именно среднеквадратичное значение напряжения.
Итак, чему же равняется среднеквадратичное значение вот этого сигнала?
А давайте замеряем. Для этого я беру мой любимый прибор токоизмерительные клещи, в который встроен целый мультиметр с True RMS и начинаю замерять среднеквадратичное значение
Мультиметр показал 7,18 Вольт. Это и есть среднеквадратичное значение этого сигнала.
Для синусоидальных сигналов оно легко вычисляется по формуле:

где
Umax – максимальная амплитуда, В
UД – действующее (среднеквадратичное) значение напряжения, В
Если считать по формуле, то получим 10/√2=7,07 Вольт. Сходится с небольшой погрешностью.
Как мы подцепили нагрузку, у нас сразу просела амплитуда напряжения с ЛАТРа, а следовательно, и среднеквадратичное значение напряжения
6, 68 Вольт. Хотя по формуле получается 9/1,41=6,38. Спишем на погрешности измерения.
Среднеквадратичное значение сложных сигналов
Но чему же равняется среднеквадратичное значение напряжения после диодного моста с включенной нагрузкой-лампочкой?

Для определения среднеквадратичного значения такого сигнала:

нам понадобится формула и табличка.
Вот формула:

где Ka – это коэффициент амплитуды
Umax – максимальная амплитуда сигнала
U – действующее (среднеквадратичное) значение сигнала
А вот и табличка:

Теперь ищем по табличке наш пульсирующий сигнал с выпрямителя. Как мы видим, его коэффициент амплитуды равен 1,41 или, если быть точнее, √2. То есть точно такой же, как и у синусоидального сигнала.
Вычисляем по формуле и получаем:

После того, как мы поставили конденсатор, у нас почти получилась осциллограмма постоянного тока с значением в примерно в 6 Вольт, если полностью усреднить нашу кривую, то есть пренебречь небольшими пульсациями. Можно даже сказать, что это значение постоянного тока будет равняться среднеквадратичному значению переменного тока номиналом в 6 Вольт. Не забываем, что 0,6-0,7 Вольт у нас падают на диодах.

Заключение
Итак, какие выводы делаем из всего вышесказанного и показанного? Среднеквадратичное значение напряжения на выходе диодного выпрямителя чуточку меньше, чем до диодного моста. По 0,6-0,7 Вольт падает на диодах. Если бы мы поставили диоды Шоттки, то выиграли бы 0,3-0,4 Вольта, так как падения на Шоттках 0,2-0,3 Вольта. Схема двухполупериодного выпрямителя, с энергетической точки зрения является очень неплохой и поэтому используется в большинстве радиоэлектронных устройств.
www.ruselectronic.com
Пример расчета выпрямителя напряжения.
Требуется рассчитать выпрямитель для зарядного устройства по следующим данным: номинальное выпрямленное напряжение U0 = 15 В; номинальный выпрямленный ток I0 = 7 А; допустимый коэффициент пульсаций KП% = 1,5; напряжение питающей сети UС = 220 В; частота сети f = 50 Гц. В качестве исходной схемы возьмем мостовую схему, рис. 6.7, выполненную с использованием германиевых диодов..
1 .
Структурная схема вторичного источника
питания приведена на рис. Рядом с ней
приведено название и назначение всех
составных частей схемы.
.
Структурная схема вторичного источника
питания приведена на рис. Рядом с ней
приведено название и назначение всех
составных частей схемы.
2. Выбираем схему выпрямителя согласно номера варианта, приводим ее в отчет и поясняем назначение всех элементов схемы.
Схема выпрямителя напряжения приведена на рис.6.7 . В ней
Тр – трансформатор напряжения, служит для преобразования амплитуды переменного напряжения до необходимой величины;;
диоды VD1-VD4 образуют схему мостового выпрямителя ;
конденсатор С0 служит сглаживающим фильтром, уменьшая пульсации напряжения на нагрузке;
резистор Rн я является нагрузкой выпрямителя.
3. Выполнить расчет трансформатора (т.е. определить его мощность по вторичной обмотке, коэффициент трансформации, определить его типовую мощность).
3.1. Рассчитаем внутреннее сопротивление диода
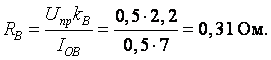
где Uпр – прямое падение напряжения на вентиле (0,4 – 0,5 В для германиевых диодов и 1,0 – 1,1 В для кремниевых диодов), kВ – коэффициент, учитывающий динамические свойства характеристики диода (2,0 – 2,2 для германиевых диодов и 2,2 – 2,4 для кремниевых диодов), IОВ – среднее значение тока вентиля выбирается по табл. 6.3 для соответствующей схемы выпрямления.
3.2. Рассчитаем активное сопротивление обмоток трансформатора.
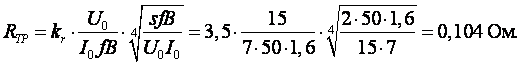
где kr – коэффициент, зависящий от схемы выпрямления, определяется по таблице 7; B – магнитная индукция в сердечнике, Т. Величину магнитной индукции В для трансформаторов мощностью до 1000 Вт можно предварительно принимать равной 1,2 – 1,6 Т для сети с частотой тока 50 Гц и 1,0 – 1,3 Т для сети с частотой тока 400 Гц; f – частота переменного тока питающей сети; s – число стержней сердечника трансформатора (s = 1 для броневой, s = 2 для стержневой и s = 3 для трехфазной конфигурации магнитопровода).
3.3.Активное сопротивление фазы выпрямителя
R = RB + RТР = 0,31 + 0,104 = 0,414 Ом.
Определим основной расчетный коэффициент выпрямителя А:
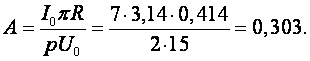
Определим вспомогательные коэффициенты В и D по графикам на рис. 6.11.
Получаем :В = 1,1; D = 2,1.
Определим параметры трансформатора (таблица 6.3)
Действующее напряжение вторичной обмотки
U2 = B·U0 = 1,1·15 = 16,5 В.
Действующий ток вторичной обмотки
I2 = 0,707 DI0 = 0,707·2,1·7 = 10,39 A.
Коэффициент трансформации km = U1/U2 . km = U1/U2=220/16,5=
Рассчитаем действующий ток первичной обмотки
I1 = 0,707 DI0/km,
I1 = 0,707·2,1·7·16,5/220 = 0,779 A.
Рассчитаем типовая мощность трансформатора
PТИП = 0,707 BDU0I0 = 0,707·1,1·2,1·15·7 = 171,48 Вт
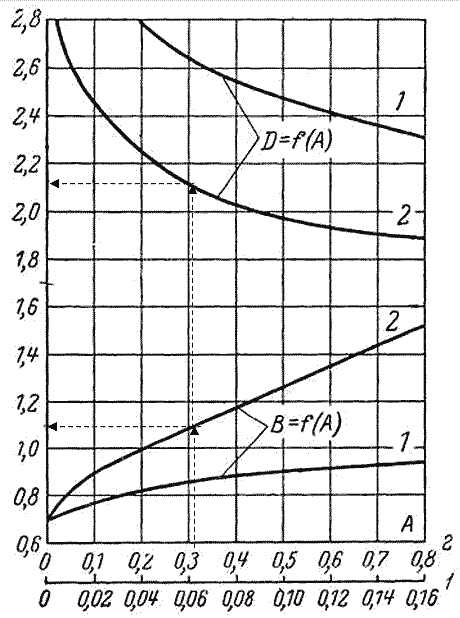 Рис.
6.11 – Зависимость параметров В и D от
параметра А
Рис.
6.11 – Зависимость параметров В и D от
параметра А
Определим вспомогательный коэффициент F по графику на рис. 6.12.
Получим F = 5,5.
 Рис.
6.12 – Зависимость параметра F от
параметра А
Рис.
6.12 – Зависимость параметра F от
параметра А
Определим вспомогательный коэффициент H по графику на рис. 6.13.
Получим H = 490.
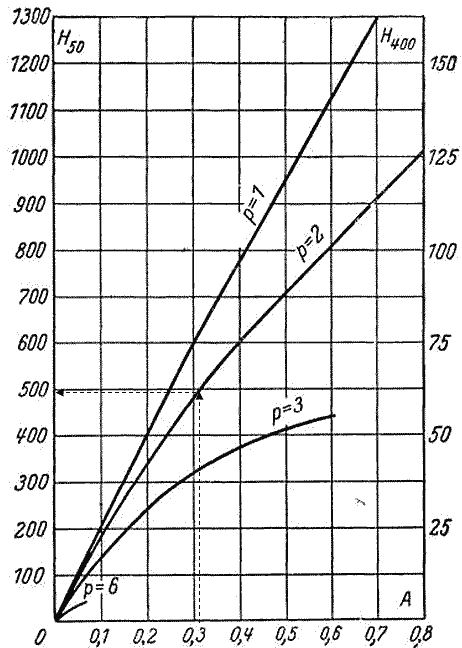 Рис.
6.13 – Зависимость параметра Н от параметра
А при частотах тока сети 50 и 400 гц
Рис.
6.13 – Зависимость параметра Н от параметра
А при частотах тока сети 50 и 400 гц
4. Выполнить расчет выпрямителя (исходя из выбранного типа выпрямителя и формул для выпрямителей такого типа, заданного типа диодов – определить количество диодов в схеме, выполнить проверку по току и по напряжению).
Определим токи и напряжения на диоде (табл. 6.3)
Обратное напряжение на диоде:
Uобр = 1,41·BU0 = 1,41·1,1·15 = 23,26 B.
Среднее значение тока диода
I0В = 0,5I0 = 0,5·7 = 3,5 A.
Действующее значение тока диода
IВ = 0,5DI0 = 0,5·2,1·7 = 7,35 A.
Амплитудное значение тока диода
IВ.макс = 0,5FI0 = 0,5·4·7 = 14 A.
Число диодов 4.
Для данного выпрямителя можно использовать диоды типа Д305, имеющие Uобр. макс.= 50 В, I0В = 10 А (справочные данные). Данные диоды имеют значительный запас по величине наибольшей амплитуды обратного напряжения и наибольшему выпрямленному среднему значению тока.
5. Выполнить расчет сглаживающего фильтра.
5.1. Предварительный
расчет выполнить из условия, что в
качестве фильтра используется единичный
конденсатор. Если емкость получится не
более 1 Ф, то этого достаточно и фильтр
будет простейшим. При расчете фильтра
следует учитывать, что коэффициент
сглаживания q=
εвх/εвых,
где εвх – коэффициент пульсаций на входе
фильтра, а εвых – коэффициент пульсаций на выходе
фильтра перед нагрузкой. При расчетах
необходимо, в соответствии со схемой
фильтра, использовать следующие формулы
: 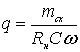 ,
где mсх – фазность выпрямителя (=1 для
однополупериодного и =2 для двухполупериодного
),Rн – нагрузка блока питания, С – емкость,
которую нужно установить после
выпрямителя, ω=2πf – угловая частота,
ƒ=50Гц-сетевая частота, определить
сопротивление нагрузки можно из требуемой
от блока питания мощности и параметров
напряжения по формуле:
,
где mсх – фазность выпрямителя (=1 для
однополупериодного и =2 для двухполупериодного
),Rн – нагрузка блока питания, С – емкость,
которую нужно установить после
выпрямителя, ω=2πf – угловая частота,
ƒ=50Гц-сетевая частота, определить
сопротивление нагрузки можно из требуемой
от блока питания мощности и параметров
напряжения по формуле: 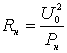 .
.
5.2. Если при расчете
окажется , что емкость конденсатора 1Ф
и более, то необходимо рассчитать
«Г»-образный LC или RC фильтр – тип на
усмотрение студента. Нужно использовать
формулы 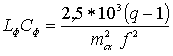 или
или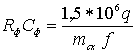 .
При этом за емкость фильтра принять
половинную емкость из предварительного
расчета.
.
При этом за емкость фильтра принять
половинную емкость из предварительного
расчета.
Расчет емкости конденсатора фильтра
 .
.
Выбираем электролитический конденсатор типа с рабочим напряжением 20 В и емкостью 8000 мкФ.
6.4. Биполярные транзисторы
Биполярный транзистор представляет собой полупроводниковый прибор, имеющий два p – n перехода, образованных в одном монокристалле полупроводника. В зависимости от чередования p и n областей различают транзисторы с p – n – p и n – p – n структурой, рис.6.14. Средний слой биполярного транзистора называется базой (Б), один крайний слой – коллектором (К), а другой крайний слой – эмиттером (Э). Каждый слой имеет вывод, с помощью которого транзистор включается в электрическую цепь. Транзистор называется биполярным потому, что физические процессы в нем связаны с движением носителей зарядов обоих знаков – свободных дырок и электронов.
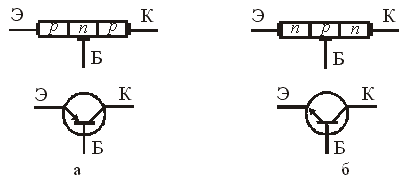 Рис.
6.14. Структура и графическое обозначение
биполярных транзисторов p – n – p типа (а) и n – p –
n типа (б)
Рис.
6.14. Структура и графическое обозначение
биполярных транзисторов p – n – p типа (а) и n – p –
n типа (б)
Электронно-дырочный переход, образованный эмиттером и базой, называется эмиттерным, коллектором и базой – коллекторным. Эмиттерный переход включается в прямом направлении, коллекторный переход – в обратном направлении. Общая точка эмиттерной и коллекторной цепей соединена с базовым электродом. Такое включение транзистора называется схемой с общей базой, рис.6.15,а. Схемы включения транзистора с общим эмиттером и общим коллектором приведены на рис.6.15, б, в.
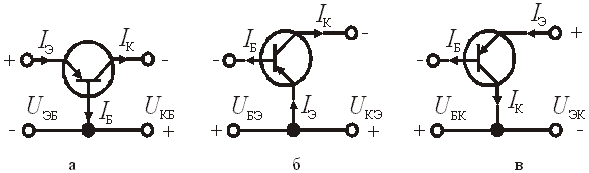 Рис.
6.15. Схемы включения транзистора: а – с
общей базой,
б – с общим эмиттером, в
– с общим коллектором
Рис.
6.15. Схемы включения транзистора: а – с
общей базой,
б – с общим эмиттером, в
– с общим коллектором
Толщина базы выбирается достаточно малой, чтобы дырки, двигаясь через базу, не успели рекомбинировать с электронами в области базы. Таким образом, основная часть дырок пролетает сквозь базу до коллекторного перехода. Здесь дырки увлекаются электрическим полем коллекторного перехода, включенного в обратном направлении, и создают в цепи коллектора ток, величина которого пропорциональна эмиттерному току IЭ:
IК ≈ α IЭ.
Коэффициент пропорциональности α называется коэффициентом передачи тока эмиттера. При достаточно тонкой базе, когда потери дырок за счет рекомбинации их в базе малы, коэффициент передачи тока может доходить до 0,99 и более.
Транзистор представляет собой управляемый прибор, его коллекторный ток зависит от тока эмиттера, который в свою очередь можно изменять напряжением эмиттер – база, UЭБ. Поскольку напряжение в цепи коллектора, включенного в обратном направлении, значительно больше, чем в цепи эмиттера, включенного в прямом направлении, а токи в этих цепях практически равны, мощность, создаваемая переменной составляющей коллекторного тока в нагрузке, включенной в цепи коллектора, может быть значительно больше мощности, затрачиваемой на управление тока в цепи эмиттера, т. е. транзистор обладает усилительным эффектом.
Для усиления электрических сигналов применяются схемы с общим коллектором (ОК) и общим эмиттером (ОЭ). Работу биполярного транзистора по схеме с ОЭ определяют статические входные и выходные характеристики.
Входные характеристики устанавливают зависимость тока базы IБ от напряжения эмиттер – база UЭБ при неизменном напряжении коллектор – эмиттер UКЭ. Входные (базовые) статические характеристики для схемы ОЭ германиевого транзистора p – n – p типа ГТ320А приведены на рис.6.16.
Так как эмиттерный переход включен в прямом направлении, повышение напряжения на нем приводит к увеличению тока, подобно характеристики полупроводникового диода.
Выходные (коллекторные) статические характеристики устанавливают связь между коллекторным током IК и напряжением коллектор – эмиттер UКЭ при постоянном токе базы IБ. Выходные характеристики транзистора ГТ320А, включенного по схеме ОЭ, приведены на рис.6.17.
В электронных устройствах широко используется схема усилителя с общим эмиттером, представленная на рис.6.18. В качестве усилительного элемента в данном случае используется транзистор ГТ320А. Сопротивление нагрузки усилительного каскада RК включено в коллекторную цепь транзистора. Входное усиливаемое напряжение UВХ подается на базу транзистора. Питание усилителя осуществляется от источника постоянного напряжения ЕК.
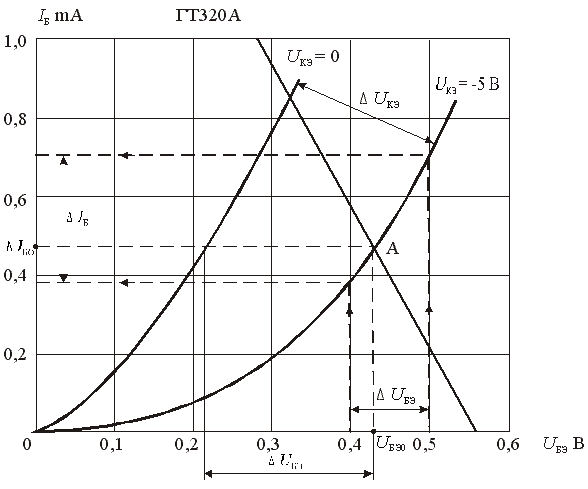 Рис.
6.16. Входные статические характеристики
транзистора ГТ320А
Рис.
6.16. Входные статические характеристики
транзистора ГТ320А
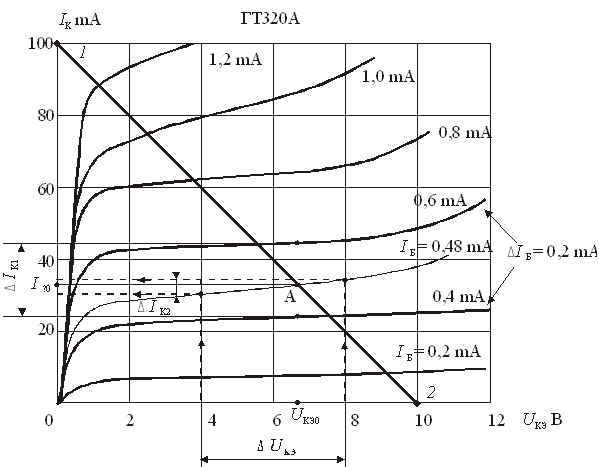 Рис.
6.17. Выходные характеристики транзистора
ГТ320А
Рис.
6.17. Выходные характеристики транзистора
ГТ320А
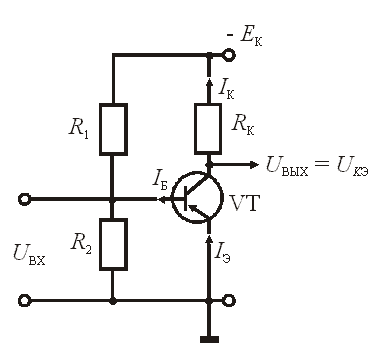 Рис.
6.18. Схема усилительного каскада с общим
эмиттером
Рис.
6.18. Схема усилительного каскада с общим
эмиттером
Данное уравнение является уравнением прямой, которое наносится
Режимы работы усилительного каскада находятся по уравнению нагрузки, которое определяется следующим образом. Напряжение коллектора UКЭ = UВЫХ при наличии нагрузки RК в его цепи, как следует из рис. 6.18, в соответствии со вторым законом Кирхгофа, равно
UКЭ = ЕК – RК·IК.
на семейство выходных (коллекторных) характеристик транзистора. Построение прямой (уравнения нагрузки) проводится путем нахождения двух точек, приравнивая поочередно нулю UКЭ и IК в уравнении нагрузки. При UКЭ = 0 имеем точку 1 линии нагрузки IК = ЕК /RК, точку 2 получаем при IК = 0, UКЭ = ЕК. Данный режим работы усилительного каскада выбран при RК = 100 Ом, ЕК = 10 В.
Пересечение линий нагрузки с коллекторными характеристиками определяет режим работы усилительного каскада при различных базовых токах.
6.5. Пример расчет параметров усилительного каскада на транзисторе по схеме с общим эмиттером
Для схемы усилительного каскада с общим эмиттером, представленной на рис. 6.18, определить основные параметры усилителя при следующих значениях номиналов элементов схемы: транзистор ГТ320А, входные и выходные характеристики которого представлены на рис. 6.16, 6.17; резисторы в цепи базы транзистора R1 = 500 Ом, R2 = 300 Ом; резистор в коллекторной цепи RK = 100 Ом; источник питания усилительного каскада EK = 10 В; амплитуда входного синусоидального сигнала низкой частоты, подлежащего усилению Um = 0,1 В.
Параметры усилительного каскада, подлежащие определению:
1. Положение рабочей точки на входных и выходных характеристиках транзистора (рис.6.16 и рис.6.17).
2. h – параметры транзистора в районе рабочей точки.
3. Входное сопротивление усилительного каскада, RВХ.
4. Выходное сопротивление усилительного каскада, RВЫХ.
5. Коэффициент усиления каскада по напряжению, KU.
6. Величина выходного напряжения усилительного каскада.
Режим покоя усилительного каскада, при котором UВХ = 0, определяет положение рабочей точки на семействе выходных характеристик на рис. 6.17. Положение рабочей точки (точка А) определяется значениями сопротивлений базовых резисторов R1, R2, коллекторного резистора RK при заданном значении напряжения питания ЕК. Резисторы R1, R2 создают на входе усилительного каскада в режиме покоя эквивалентную ЭДС, равную
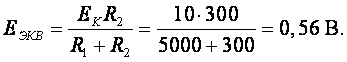
Эквивалентное базовое сопротивление каскада равно
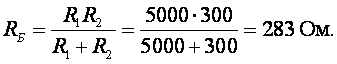
По второму закону Кирхгофа для входной цепи в режиме покоя имеем:
EЭКВ = IБRБ + UБЭ,
где UБЭ – напряжение между базой и эмиттером в режиме покоя.
Данное уравнение изображается на входной характеристике транзистора в виде прямой линии (линии нагрузки), построение которой проходит путем нахождения двух характерных точек: в режиме холостого хода, когда IБ = 0, имеем UБЭ = EЭКВ= 0,56 В; и в режиме короткого замыкания – UБЭ = 0, имеем IБ = EЭКВ/RБ = 0,56/283 = 0,00198 А = 1,98 mА. В результате пересечения линии нагрузки с входной характеристикой IБ = f(UБЭ), при UКЭ = – 5 В находим положение точки покоя (рабочей точки) IБ0 = 0,48 мА, UБЭ0 = 0,43 В.
Положение рабочей точки на коллекторных характеристиках получается при пересечении линии нагрузки с характеристикой IK = f(UКЭ), при IБ0 = 0,48 mА. Построение данной характеристики проводим приближенно, она лежит между характеристиками при IБ = 0,4 mА и IБ = 0,6 mА. Таким образом, в коллекторной цепи рабочая точка будет соответствовать значениям IK0 = 35 mА и UКЭ0 = 6,6 В.
При работе транзисторов в качестве усилителей малых электрических сигналов, свойства транзисторов определяются с помощью, так называемых, h – параметров. Всего h – параметров четыре: h11, h12, h21 и h22. Они связывают входные и выходные токи и напряжения транзистора и определяются для схемы ОЭ, рис.6.15, б, по следующим выражениям:
h11 = ∆UВХ/∆IВХ = ∆UБЭ/∆IБ при неизменном напряжении. UВЫХ = UКЭ = const.
Параметр h11 численно равен входному сопротивления схемы ОЭ. Знак ∆ обозначает приращение соответствующей величины тока или напряжения.
h12 = ∆UВХ/∆UВЫХ = ∆UБЭ/∆UКЭ при IБ = const.
Параметр h12 равен коэффициенту обратной связи по напряжению.
h21 = ∆IВЫХ/∆IВХ = ∆IК/∆IБ при UКЭ = const.
Параметр h21 равен коэффициенту прямой передачи по току.
h22 = ∆IВЫХ/ ∆UВЫХ = ∆IК/∆UКЭ при IБ = const.
Параметр h22 равен выходной проводимости транзистора.
Значения h – параметров можно найти с помощью входных и выходных характеристик транзистора. Параметры входной цепи h11 и h12 определяют по входным характеристикам транзистора, рис.6.16. Рабочая точка А определяется при пересечении линии нагрузки с входной характеристикой транзистора при UКЭ = – 5 В. В результате чего имеем UКЭ0 = 0,43 В, IБ0 = 0,48 mА. В данной рабочей точке задаем приращение тока базы ∆IБ при постоянном напряжении коллектора UКЭ = – 5 В и находим получающееся при этом приращение напряжения базы ∆UБЭ. Тогда входное сопротивление транзистора равно
h11 = ∆UБЭ/∆IБ = 0,1 В/ 0,3 mА = 333 Ом.
Затем при постоянном токе базы IБ = 0,48 mА задаем приращение напряжения коллектора ∆UКЭ = 5 В и определяем получающееся при этом приращение напряжения базы ∆UБЭ= 0,25 В. Тогда коэффициент обратной связи по напряжению равен
h12 = ∆UБЭ/∆UКЭ= 0,25 /5 = 0,05.
Параметры h21 и h22 определяют по выходным характеристикам транзистора, рис.6.17. В районе рабочей точки А (IБ = 0,48 mА, UКЭ = – 5 В) при постоянном токе базы IБ = 5 mА задаем приращение коллекторного напряжения ∆UКЭ = 5 В и находим при этом приращение тока коллектора ∆IК2 = 5 mА. Тогда выходная проводимость транзистора равна
h22 = ∆IК2/∆UКЭ = 5 mА /5 В = 1,0 мСм.
Далее при постоянном напряжении коллектора UКЭ= 5 В задаем приращение тока базы ∆IБ = 0,2 mА и определяем получающееся при этом приращение тока коллектора ∆IК1 = 20 mА. Тогда коэффициент передачи по току равен
h21 = ∆IК1/∆IБ = 20 mА / 0,2 mА = 100.
Входное сопротивление усилительного каскада равно:
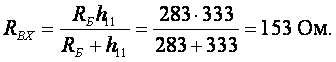
Выходное сопротивление усилительного каскада равно:
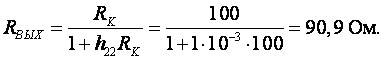
Коэффициент усиления по напряжению

Величина выходного напряжения усилительного каскада
UВЫХ = КUUВХ = 27,3·0,1 = 2,73 В.
Контрольные вопросы к зачету (экзамену) по разделу ” Основы электроники”.
1. Зонная структура собственного полупроводника. Что такое валентная зона? Что такое зона проводимости? Что такое запрещенная зона? Проводимость собственного полупроводника.
2. Зонная структура и проводимость акцепторного полупроводника..
3. Зонная структура и проводимость донорного полупроводника Что такое основные носители? Что такое не основные носители? Механизм генерации неосновных носителей заряда.
4. Технология изготовления p-n – перехода. Образование p-n – перехода. Основные параметры p-n – перехода.
5. P-n- переход в равновесном состоянии. Потенциальный барьер?
Токи через п-р переход?
6. P-n переход смещенный в прямом направлении? Потенциальный барьер? Токи через p-n – переход.
7. . P-n – переход смещенный в обратном направлении? Потенциальный барьер? Токи через п-р переход?
8. Идеальная характеристика p-n – перехода .
9. Диод. Типы диода. Условные обозначения. Рабочая схема диода. Вольт – амперная характеристика диода. Ее отличия от идеальной вольт – амперной характеристики.
10. Лавинный пробой. Механизм развития. Тепловой пробой. Емкости п-р – перехода.
11. Параметры и маркировка диода.
12. Биполярный транзистор .Типы транзистора. Схемы включения .
13. Принцип действия, токи транзистора.
14. Входные характеристики транзистора в схеме с ОЭ.
15. Выходные характеристики транзистора в схеме с ОЭ.
16. Предельно-допустимые параметры транзисторов. Маркировка.
17. Полевые транзисторы. Типы транзисторов . Устройство принцип действия. Назначение. Вольтамперная характеристика. Параметры. Маркировка
18. Тиристоры. Типы тиристоров . Устройство принцип действия. Назначение. Вольтамперная характеристика. Параметры. Маркировка.
19. Оптоэлектронные приборы. Фотоприемники.
20. Оптоэлектронные приборы. Светоизлучающие приборы
19. Микросхемы. Классификация , маркировка назначение.
20. Вторичные источники тока. Блок-схема, назначение.
21. Полупроводниковые выпрямители. Электрические схемы и принцип работы выпрямителя. Электрические фильтры.
22. Стабилизаторы напряжения и тока.
23. Тиристорные преобразователи.
24. Классификация и принцип действия усилителей переменного тока.
25. Анализ работы однокаскадного усилителя.
26. Обратные связи. Их влияние на параметры усиления.
27. Многокаскадные усилители.
28. Усилители постоянного тока . Операционный усилитель.
29. Автогенераторы , LC – типа и генераторы RC- типа.
30. Транзисторный ключ.
31. Логические операции и способы их аппаратной реализации.
32. Логические схемы.
33. Микропроцессор.
34. Электрические измерения.
35. Электрические приборы.
89
studfile.net
Выпрямители: Однофазный однополупериодный выпрямитель – Club155.ru
Простейшим выпрямителем является схема однофазного однополупериодного выпрямителя (рис. 3.4-1а). Графики, поясняющие его работу при синусоидальном входном напряжении \(U_{вх} = U_{вх max} \sin{\left( \omega t \right)}\) , представлены на рис. 3.4-1б.
Рис. 3.4-1. Однофазный однополупериодный выпрямитель (а) и временные диаграммы, поясняющие его работу (б)
На интервале времени \(\left[ {0;} T/2 \right]\) полупроводниковый диод выпрямителя смещен в прямом направлении и напряжение, а следовательно, и ток в нагрузочном резисторе повторяют форму входного сигнала. На интервале \(\left[ T/2 {;} T \right]\) диод смещен в обратном направлении и напряжение (ток) на нагрузке равно нулю. Таким образом, среднее значение напряжения на нагрузочном резисторе будет равно:
\(U_{н ср} = \cfrac{1}{T} {\huge \int \normalsize}_{0}^{T} U_н \operatorname{d}t = \cfrac{1}{T} {\huge \int \normalsize}_{0}^{T/2} U_{вх max} \sin{\left( \omega t \right)} \operatorname{d}t = \)
\(= – \cfrac{U_{вх max}}{T \omega} \cos{\left( \omega t \right)}{\huge \vert \normalsize}_{0}^{T/2} \approx \cfrac{U_{вх max}}{\pi} = \sqrt{2} \cfrac{U_{вх д}}{\pi}\),
где \(U_{вх д}\) — действующее значение переменного напряжения на входе выпрямителя.
Аналогично, для среднего тока нагрузки:
\(I_{н ср} = \cfrac{1}{2 \pi} {\huge \int \normalsize}_{0}^{\pi} I_{max} \sin{\left( \omega t \right)} \operatorname{d} t \approx \cfrac{I_{max}}{\pi} = {0,318} \cdot I_{max} \),
где \(I_{max}\) — максимальная амплитуда выпрямленного тока.
Действующее значение тока нагрузки \(I_{н д}\) (через диод протекает такой же ток):
\(I_{н д} = \sqrt{\cfrac{I_{max}^2}{2 \pi} {\huge \int \normalsize}_{0}^{\pi^{ }} \sin{\left( \omega t \right)}^2 \operatorname{d} t} = \cfrac{I_{max}}{2} = {0,5} \cdot I_{max} \)
Отношение среднего значения выпрямленного напряжения \(U_{н ср}\) к действующему значению входного переменного напряжения \(U_{вх д}\) называется коэффициентом выпрямления (\(K_{вып}\)). Для рассматриваемой схемы \(K_{вып} = {0,45}\).
Максимальное обратное напряжение на диоде \(U_{обр max} = U_{вх max} = \pi U_{н ср}\) , т.е. более чем в три раза превышает среднее выпрямленное напряжение (это следует учитывать при выборе диода для выпрямителя).
Спектральный состав выпрямленного напряжения имеет вид (разложение в ряд Фурье):
\(U_н = \cfrac{1}{\pi} U_{вх max} + \cfrac{1}{2} U_{вх max} \sin{\left( \omega t \right)} – \cfrac{2}{3 \pi} \cos{\left( 2 \omega t \right)} – \)
\( – \cfrac{2}{15 \pi} U_{вх max} \cos{\left( 4 \omega t \right)} – {…} \)
Коэффициент пульсаций, равный отношению амплитуды низшей (основной) гармоники пульсаций к среднему значению выпрямленного напряжения, для описываемой схемы однополупериодного выпрямителя равен:
\(K_п = \cfrac{U_{пульс max 01}}{U_{н ср}} = \cfrac{\pi}{2} = {1,57}\).
Как видно, однополупериодное выпрямление имеет низкую эффективность из-за высокой пульсации выпрямленного напряжения.
Еще один отрицательный аспект однополупериодного выпрямления связан с неэффективным использованием силового трансформатора, с которого берется переменное напряжение. Это обусловлено тем, что в токе вторичной обмотки трансформатора существует постоянная составляющая, равная среднему значению выпрямленного тока. Такая составляющая не трансформируется, т.е.:
\(I_1 \cdot w_1 = \left( I_2 – I_{н ср} \right) w_2\) ,
где \(I_1\), \(I_2\) — токи первичной и вторичной обмоток, а \(w_1\), \(w_2\) — число витков первичной и вторичной обмоток трансформатора.
Временнáя диаграмма тока первичной обмотки трансформатора (рис. 3.4-2) подобна диаграмме тока вторичной обмотки, но смещена на величину \(I_{н ср} \cfrac{w_2}{w_1}\).
Рис. 3.4-2. Временная диаграмма токов в первичной и вторичной обмотках силового трансформатора, нагруженного на схему однофазного однополупериодного выпрямителя
В сердечнике трансформатора за счет постоянной составляющей тока вторичной обмотки создается постоянный магнитный поток \(\Phi_0 = w_2 \cdot I_0\). Это явление принято называть вынужденным намагничиванием сердечника трансформатора. Оно может вызвать насыщение магнитной системы трансформатора, т.е. увеличение тока холостого хода, действующего значения первичного тока и следовательно, расчетной мощности первичной обмотки трансформатора, что обусловливает увеличение необходимых размеров трансформатора в целом.
Дополнительный минус однополупериодного выпрямления состоит в наличии участка стабильного тока, что также снижает эффективность использования трансформатора по мощности. Максимальный коэффициент использования трансформатора по мощности для такой схемы не превышает \(k_{тр P} \approx {0,48}\).
Для снижения уровня пульсаций на выходе выпрямителя включаются разнообразные индуктивно-емкостные фильтры. Наличие конденсаторов и индуктивностей в цепи нагрузки оказывает значительное влияние на работу выпрямителя.
В маломощных выпрямителях обычно применяют простейший емкостный фильтр, который представляет собой конденсатор, включенный параллельно нагрузке (рис. 3.4-3).
Рис. 3.4-3. Схема однофазного однополупериодного выпрямителя с емкостным фильтром (а) и временные диаграммы, поясняющие его работу (б)
В установившемся режиме работы, когда напряжение на входе выпрямителя \(U_{вх}\) больше напряжения на нагрузке \(U_н\) и диод выпрямителя открыт, конденсатор будет подзаряжаться, накапливая энергию, поступающую от внешнего источника. Когда же напряжение на входе выпрямителя упадет ниже уровня открывания диода и он закроется, конденсатор начнет разряжаться через \(R_н\), предотвращая при этом быстрое падение уровня напряжения на нагрузке. Таким образом, результирующее напряжение на выходе выпрямителя (на нагрузке) окажется уже не таким пульсирующим, а будет значительно сглажено, причем тем сильнее, чем большую емкость будет иметь применяемый конденсатор.
Обычно, емкость конденсатора фильтра выбирают такой, чтобы его реактивное сопротивление было намного меньше сопротивления нагрузки (\(1/ \omega C \ll R_н\)). В этом случае пульсации напряжения на нагрузке малы и допустимо предполагать, что это напряжение постоянно (\(U_н \approx {const}\)). Примем: \(U_н = U_{вх max} \cos{\beta}\), где \(\beta\) — некоторая константа, определяющая значение напряжения на нагрузке. Очевидно, что в общем случае \(\beta\) зависит от емкости конденсатора, сопротивления нагрузки, частоты входного напряжения и т.п. Физический смысл этой величины можно понять из временных диаграмм, приведенных на рис. 3.4-4. Как видно, \(\beta\) отражает длительность временного интервала в одном периоде колебаний внешнего напряжения, когда диод выпрямителя находится в открытом состоянии (\(\beta = \omega \cdot t_{откр}/2\)). Угол \( \beta\) принято называть углом отсечки.
Рис. 3.4-4. График зависимости \(A(\beta)\)
Для тока, протекающего через диод в открытом состоянии, можно записать:
\( I_д = \cfrac{U_{вх} – U_н}{r} \) ,
где \(r\) — активное сопротивление, обусловленное сопротивлением диода в открытом состоянии и сопротивлением вторичной обмотки трансформатора (иногда его называют сопротивлением фазы выпрямителя).
Учитывая, что \(U_{вх} = U_{вх max} \sin{\left( \omega t \right)} \):
\(I_д = \cfrac{U_{вх max}}{r} \left( \sin{\left( \omega t \right)} – \cos{\left( \beta \right)} \right) = \cfrac{U_{вх max}}{r} \left(\sin{\left(\varphi \right)} – \cos{\left( \beta \right)} \right)\) (3.4.1)
Среднее за период значение выпрямленного тока диода (учитывая, что диод открыт только на участке \(\varphi = \left[\pi/2 – \beta ; \pi/2 + \beta \right]\):
\(I_{д ср} =\cfrac{1}{2 \pi} {\huge \int \normalsize}_{\frac{\pi}{2} – \beta}^{\frac{\pi}{2} + \beta} \cfrac{U_{вх max}}{r} \left( \sin{ \left( \varphi \right)} – \cos{\left( \beta \right)} \right) \operatorname{d} \varphi =\)
\(= \cfrac{U_{вх max}}{\pi r} \left( \sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)} \right) \)
Поскольку \(U_{вх max} = \cfrac{U_н}{\cos{\left( \beta \right)}} \):
\(I_{д ср} =\cfrac{U_н}{\pi r} \cdot \cfrac{\sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)}}{\cos{\left( \beta \right)} } = \cfrac{U_н}{\pi r} A \left( \beta \right) \),
где \( A \left( \beta \right) = \cfrac{\sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)}}{\cos{\left( \beta \right)}} = \operatorname{tg} \left( \beta \right) – \beta \) (3.4.2)
Формула (3.4.2) очень важна при расчете выпрямителя. Ведь угол отсечки \(\beta\) не является заранее известным исходным параметром, как правило, его приходится вычислять на основании заданных выходного напряжения (\(U_н\)), сопротивления (\(R_н\)) или тока нагрузки (\(I_н\)), а также параметров применяемого диода и трансформатора (которые определяют сопротивление фазы \(r\)). Располагая этими данными и учитывая (3.4.2) можно определить значение коэффициента \(A\):
\(A \left( \beta \right) = \cfrac{I_{д ср} \pi r}{U_н} \)
Средний ток через диод \(I_{д ср}\) равен среднему току нагрузки \(I_{н ср}\), а учитывая, что напряжение на нагрузке предполагается неизменным, то и мгновенное значение тока через нагрузку равно току диода: \(I_н = I_{д ср}\). Таким образом:
\(A \left( \beta \right) = \cfrac{I_{н} \pi r}{U_н} = \cfrac{\pi r}{R_н} \)
Для нахождения угла отсечки \(\beta\) при известном коэффициенте \(A(\beta)\) на практике обычно пользуются графиком (рис. 3.4-4).
Максимальное значение тока диода достигается при \(U_{вх} = U_{вх max}\) в момент времени, когда \(\varphi = \pi/2 \), т.е. согласно выражения (3.4.1):
\( I_{д max} = \cfrac{U_{вх max}}{r} \left( 1 – \cos{\left( \beta \right)} \right) = \cfrac{U_н}{r} \cdot \cfrac{\pi \left( 1 – \cos{\left( \beta \right)} \right)}{\cos{\left( \beta \right)}} \)
И далее, учитывая (3.4.2) получим:
\( I_{д max} = \cfrac{I_{д ср} \cdot \pi}{A \left( \beta \right)} \cdot \cfrac{1- \cos{\left( \beta \right)}}{\cos{\left( \beta \right)}}\), где \(F \left( \beta \right) = \cfrac{\pi \cdot \left( 1 – \cos{\left( \beta \right)} \right)}{\sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)}}\)
График функции \(F(\beta)\) представлен на рис. 3.4-5. Из него видно, что с уменьшением угла отсечки \(\beta\) существенно увеличивается амплитуда тока через вентили.
Рис. 3.4-5. График зависимости \(F(\beta)\)
Таким образом, емкостный характер нагрузки выпрямителя приводит к тому, что выпрямительный диод оказывается открытым в течение меньшего промежутка времени, а амплитуда тока, проходящего в это время через диод, оказывается больше, чем в аналогичной схеме, работающей на чисто активную нагрузку. Этот факт необходимо учитывать при выборе диода, который должен выдерживать повторяющийся ток соответствующей амплитуды и более того, нормально переносить первоначальный всплеск тока при включении, когда происходит первоначальная зарядка конденсатора.
Указанная закономерность справедлива не только для описываемой схемы однофазного однополупериодного выпрямления. Аналогичным образом будет происходить работа и других рассматриваемых далее схем, имеющих нагрузку емкостного характера.
Требуемый коэффициент пульсаций на выходе однофазного однополупериодного выпрямителя с емкостным фильтром \(K_п\) может быть получен при правильном выборе емкости сглаживающего конденсатора. Для ее нахождения используется следующая формула:
\( С = \cfrac{H(\beta)}{r \cdot K_п}\),
где \(H(\beta)\) — это еще один вспомогательный коэффициент, значение которого находится по графику (рис. 3.4-6).
Рис. 3.4-6. График зависимости \(H(\beta)\)
Емкостный фильтр характерен для выпрямителей, рассчитанных на малые токи нагрузки. При больших токах обычно применяют индуктивные фильтры. Такой фильтр представляет собой катушку индуктивности (обычно с ферромагнитным сердечником), включенную последовательно с нагрузкой (рис. 3.4-7). Наличие индуктивности в цепи нагрузки также как и емкость оказывает значительное влияние на режим работы вентилей выпрямителя.
Рис. 3.4-7. Схема однофазного однополупериодного выпрямителя с индуктивным фильтром (а) и временные диаграммы, поясняющие его работу (б)
Работа схемы на рис. 3.4-7 описывается уравнением:
\( U_{вх max} \sin{\left( \omega t \right)} = L \cfrac{\operatorname{d} I_н}{\operatorname{d} t} + I_н R_н \)
Приняв ток в цепи в начальный момент времени \((t = 0)\) равным нулю, решив данное уравнение получим следующее выражение для тока в цепи нагрузки:
\(I_н(t) = \cfrac{U_{вх max}}{\sqrt{R_н^2 + {\left( \omega L \right)}^2}} \left( \sin{\left( \omega t – \theta \right)} + e^{- \cfrac{R_н t}{L}} \sin{( \theta )} \right) \),
где \( \theta = \operatorname{arctg} \left( \cfrac{\omega L}{R_н} \right) \)
Временная диаграмма, отражающая эту зависимость приведена на рис. 3.4-7(б). По ней хорошо виден физический смысл константы \(\theta\). Она представляет собой угол, на который запаздывает основной всплеск тока в нагрузке относительно инициирующего его всплеска напряжения на входе выпрямителя.
Если проанализировать зависимость тока нагрузки \(I_н(t)\), можно заметить, что его амплитуда с увеличением индуктивности катушки падает (соответственно падает и его среднее значение). Т.е. среднее значение напряжения на нагрузке оказывается меньшим, чем в случае отсутствия индуктивности, уменьшаются также пульсации выходного напряжения. Сами колебания тока оказываются сдвинутыми относительно колебаний входного напряжения на угол \(\theta\). Это является причиной скачкообразного приложения к диоду в момент его запирания отрицательного обратного напряжения величиною до \(U_{обр} = U_{вх max}\).
Описанный режим работы вентилей (затягивание тока, уменьшение его амплитуды, скачкообразное приложение обратного напряжения) при наличии индуктивного фильтра характерен для всех схем выпрямителей. Индуктивный фильтр обычно применяют в схемах мощных выпрямителей, поскольку в этом случае требуемая для существенного изменения параметров выходного напряжения индуктивность оказывается незначительной.
Наиболее эффективно сглаживание пульсаций выпрямленного напряжения осуществляется с помощью сложных многозвенных фильтров, в состав которых входят и катушки индуктивности и конденсаторы (основой таких фильтров являются т.н. Г- или П-образные звенья).
| < Предыдущая | Следующая > |
|---|
www.club155.ru
§ 5.2. Трансформаторы для выпрямительных установок
Во вторичные обмотки этих трансформаторов включены вентили — устройства, обладающие односторонней проводимостью.
Рассмотрим работу однофазного трансформатора в схеме однополупериодного выпрямления (рис. 5.3, а). Ток во вторичной обмотке этого трансформатора i2 является пульсирующим, так как он создается только положительными полуволнами вторичного напряженияU2 (рис. 5.3,б). Этот пульсирующий ток имеет две составляющие: постоянную
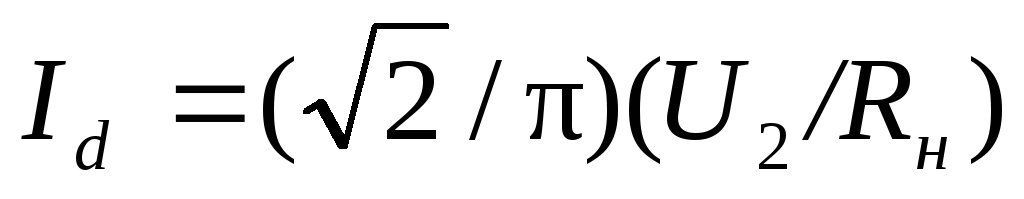 (5.2)
(5.2)
и переменную
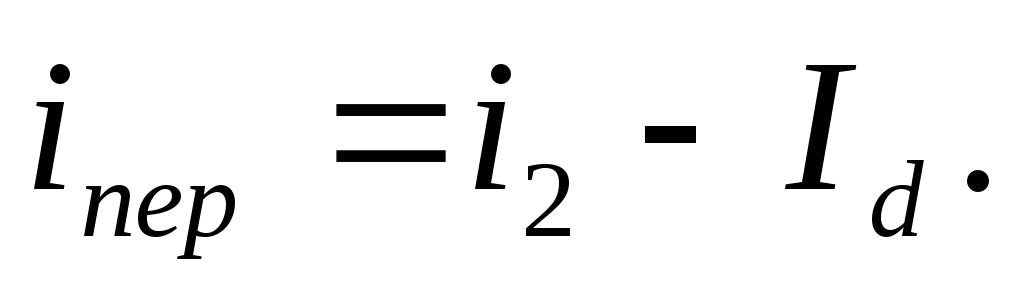 (5.3)
(5.3)
Пренебрегая током х.х. и учитывая (5.3), уравнение МДС рассматриваемого трансформатора можно записать в виде
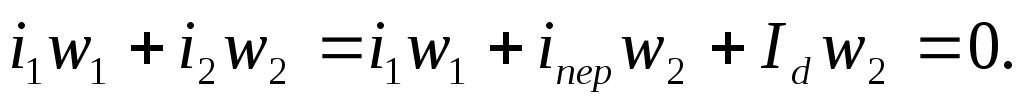 (5.4)
(5.4)
Рис. 5.3. Трансформатор в схеме выпрямления
В первичную обмотку трансформируется лишь переменная составляющая вторичного тока (5.3), поэтому МДСIdw2 остаетсянеуравновешенной и создает в магнитопроводе трансформатора постоянный магнитный поток Фd, называемый потоком вынужденного намагничивания. Этот поток вызывает дополнительное магнитное насыщение элементов магнитопровода; для того чтобы это насыщение не превышало допустимого значения, необходимо увеличить сечение сердечников и ярм. Эта мера приводит к увеличению расхода стали и меди, т. е. ведет к повышению габаритов, веса и стоимости трансформатора. Этот недостаток однофазной однополупериодной схемы распространяется и на трехфазную однополупериодную схему при соединении вторичной обмотки трансформатора по схеме «звезда—звезда с нулевым выводом» (рис. 5.3, в). В этом случае магнитный поток вынужденного намагничивания Фd значительно меньше, так как, действуя одновременно во всех трех стержнях магнитопровода, он замыкается вне магнитопровода — через медь, воздух, стенки бака — аналогично третьим гармоникам основного магнитного потока (см. рис. 1.26). Однофазную однополупериодную схему применяют лишь для маломощных выпрямителей, что объясняется не только недостатком, вызванным наличием потока Фd, но и значительными пульсациями выпрямленного тока. Трехфазная однополупериодная схема соединения вторичной обмотки в звезду с нулевым выводом также ограничивается выпрямителями небольшой мощности. Если же вторичную обмотку соединить в равноплечий зигзаг с нулевым выводом (см. рис. 1.22), то недостатки однополупериодной схемы выпрямления, обусловленные возникновением потока Фd, устраняются. Объясняется это тем, что при соединении в равноплечий зигзаг (см. § 1.8) на каждом стержне оказываются две вторичные катушки со встречным соединением. При трехфазной однополупериодной схеме ток Id проходя по всем фазам вторичной обмотки, создает в каждом стержне два потока Фd/2, но так как эти потоки направлены в разные стороны, то они взаимно уравновешиваются. Это достоинство схемы соединения обмоток в зигзаг позволяет применять трехфазную однополупериодную схему при значительных мощностях.
В двухполупериодных схемах, когда ток во вторичной цепи трансформатора создается в течение обоих полупериодов, условия работы трансформатора оказываются намного лучше и неуравновешенной МДС не возникает.
Другим обстоятельством, нежелательно влияющим на работу трансформаторов в схемах выпрямления, является несинусоидальная форма токов в обмотках. В результате в первичной и вторичной обмотках появляются токи высших гармоник, ухудшающие эксплуатационные показатели трансформатора, в частности снижающие его КПД.
Количественно влияние различных причин на работу трансформаторов в схемах выпрямления зависит от ряда факторов: схем выпрямления, наличия сглаживающего фильтра, характера нагрузки.
В связи с тем что первичный и вторичный токи трансформаторов имеют разные действующие значения (из-за их несинусоидальности), расчетные мощности первичной и вторичной обмоток одного и того же трансформатора неодинаковы (S1ном ≠ S2ном). Поэтому для оценки мощности трансформатора, работающего в выпрямительной схеме, вводятся понятия типовой мощности
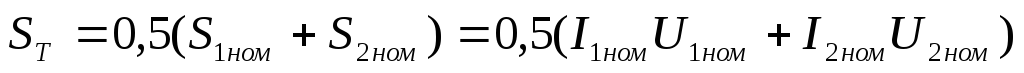 (5.5)
(5.5)
и коэффициента типовой мощности
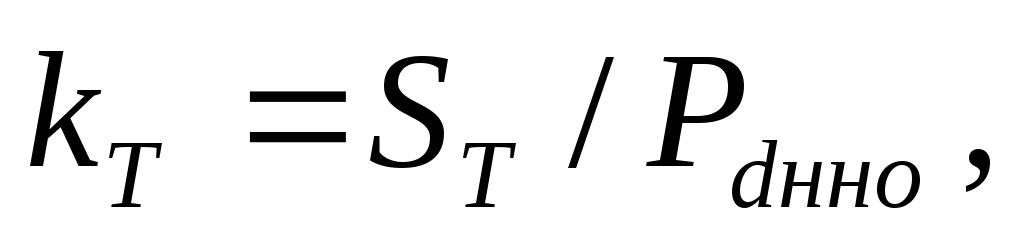 (5.6)
(5.6)
где выходная мощность, т. е. мощность, поступающая в потребитель постоянного тока,
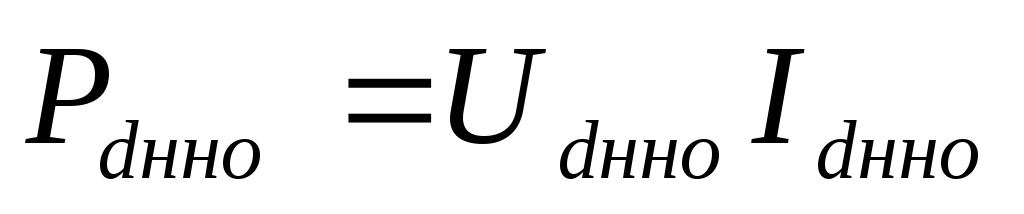 (5.7)‘
(5.7)‘
в номинальном режиме (при номинальных напряжениях UdномитокеId ном).
Типовая мощность трансформатора всегда больше его выходной мощности, т.е.kт>1. Объясняется это тем, что при любой схеме выпрямленияU2>Ud иI2>Id
Из этого следует, что габариты и вес трансформаторов для выпрямителей всегда больше, чем у трансформаторов такой же выходной мощности, но при синусоидальных токах в обмотках. Это объясняется тем, что в трансформаторах, работающих в выпрямительных схемах, полезная мощность определяется постоянной составляющей вторичного токаId а нагрев обмоток — полным вторичным I2 и первичным I1 токами, содержащими высшие гармонические.
При выборе трансформатора для выпрямительной установки или же при его проектировании необходимо знать значение коэффициента kТ.
Значение переменного напряжения на выходе вторичной обмотки трансформатора, необходимого для получения заданного номинального значения постоянного напряжения Udном, определяется выражением
 (5.8)
(5.8)
где kU— коэффициент напряжения.
Значения коэффициентов напряжения ku и типовой мощности kт для некоторых наиболее распространенных схем выпрямления приведены ниже.
Схемы выпрямляния | kU | kT |
Однофазная однополупериодная Однофазная двухполупериодная мостовая Однофазная двухполупериодная с нулевым выводом Трехфазная с нулевым выводом Трехфазная мостовая | 2,22 1,11 1,11 0,855 0,427 | 3,09 1,23 1,48 1,345 1,05 |
Сравнение различных схем выпрямления показывает, что лучшее использование трансформатора обеспечивается в мостовых схемах выпрямления, для которых коэффициент kT имеет минимальные значения.
studfile.net
5. Методика расчета однофазных выпрямителей переменного тока
Выпрямители являются вторичными источниками питания радиоэлектронной аппаратуры, для которых первичным источником электропитания является сеть переменного тока или выходная обмотка трансформатора. Выпрямители используются для преобразования переменного напряжения в постоянное. Выпрямители располагаются между трансформатором переменного напряжения и сглаживающим фильтром или стабилизатором напряжения и в основном работают на емкостную нагрузку.
Для выпрямления в настоящее время используются в основном полупроводниковые вентили (диоды). Существует три основных схемы однофазных выпрямителей: однополупериодная, двухполупериодная и мостовая (рис.6). Однополупериодную схему выпрямления применяют в основном при небольших мощностях нагрузки, когда не требуется малая амплитуда пульсаций выходного напряжения. Частота пульсаций выходного напряжения для этой схемы равна частоте питающей сети переменного тока. Двухполупериодную схему используют при выходных мощностях до 100 Вт и напряжениях до 500 В. Частота пульсаций выходного напряжения для этой схемы в два раза выше частоты питающей сети переменного тока. Недостатком такой схемы является необходимость иметь две одинаковые обмотки трансформатора, а достоинством – наличие только двух выпрямляющих вентилей. Мостовая схема выпрямления характеризуется хорошим использованием энергии трансформатора и используется при выпрямлении больших мощностей (до 1000 Вт). Обратное напряжение на выпрямляющих вентилях в этой схеме в 2 раза ниже, чем в предыдущих схемах выпрямления. Кроме того, для такой схемы необходима только одна обмотка трансформатор Частота пульсаций выходного напряжения для этой схемы в два раза выше частоты питающей сети переменного тока.
В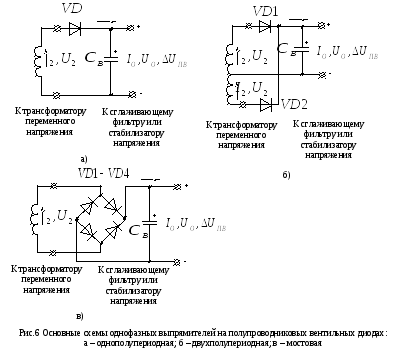 ходными
данными для расчета выпрямителя на
полупроводниковых вентилях, работающего
на емкостную нагрузку являются:
ходными
данными для расчета выпрямителя на
полупроводниковых вентилях, работающего
на емкостную нагрузку являются:
напряжение на выходе выпрямителя
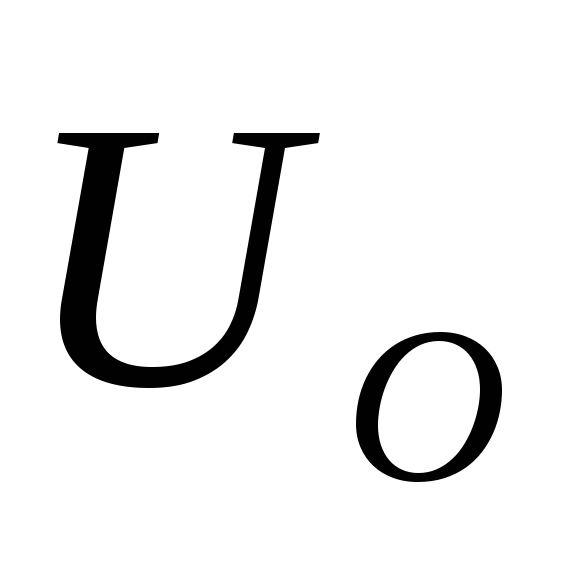 ;
;ток на выходе выпрямителя
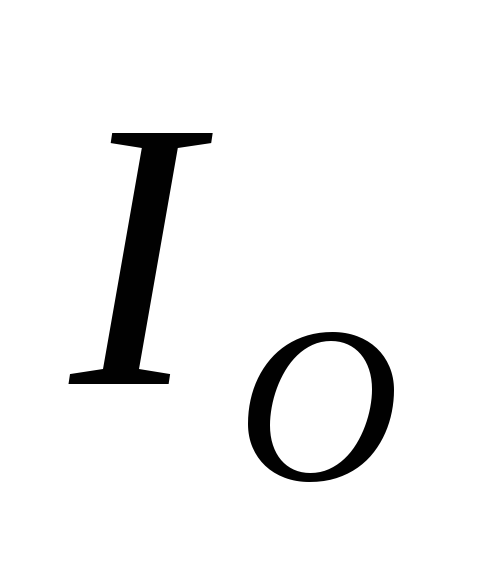 ;
;напряжение пульсаций на выходе выпрямителя
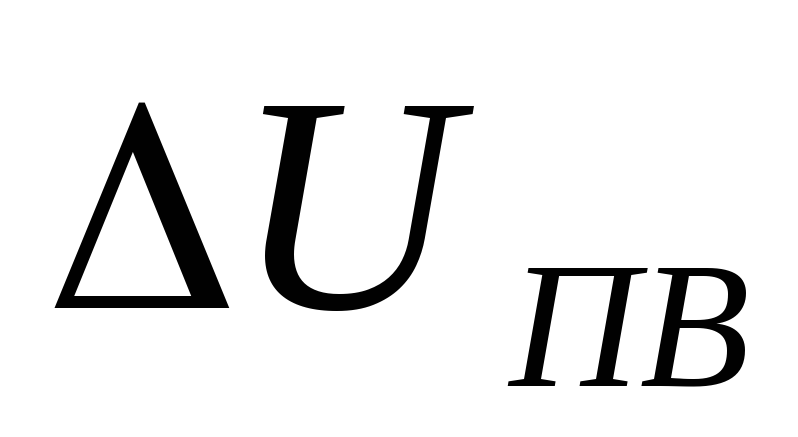 .
.
Эти данные были получены при расчете сглаживающего фильтра или стабилизатора напряжения.
После расчета элементов выпрямителя получим данные для расчета трансформатора:
напряжение на входе выпрямителя (напряжение вторичной обмотки трансформатора)
 ;
;ток на входе выпрямителя (ток вторичной обмотки трансформатора)
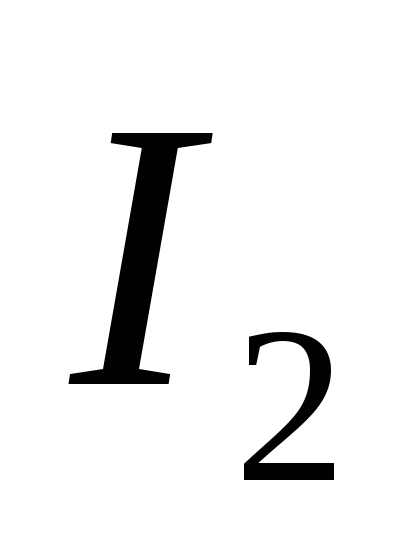 .
.
Методика расчета однофазного выпрямителя, работающего на емкостную нагрузку следующая.
Находим приблизительные значения обратного напряжения на вентиле
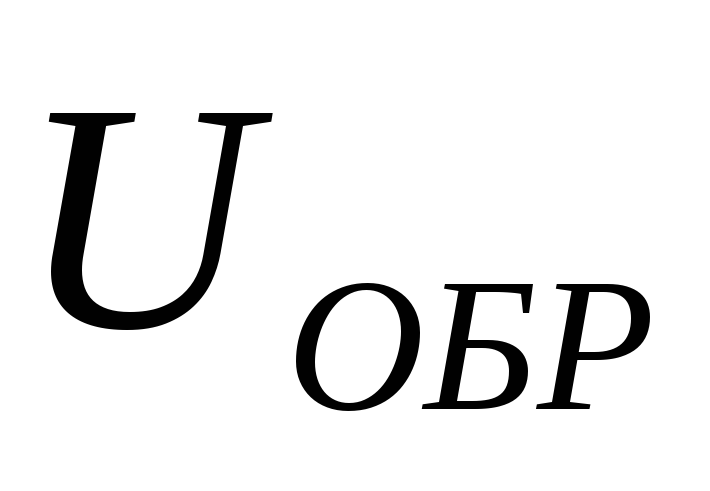 ,
среднего тока, протекающего через
вентиль
,
среднего тока, протекающего через
вентиль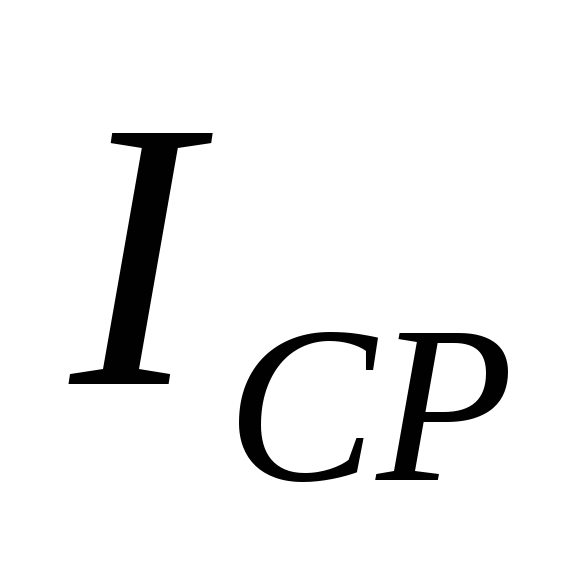 и амплитудного значения тока
и амплитудного значения тока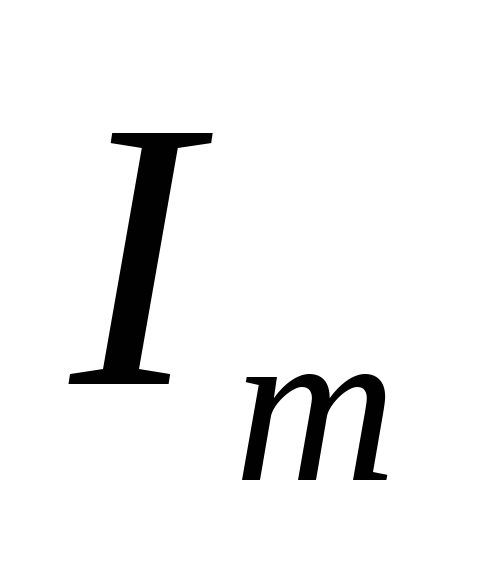 ,
протекающего через вентиль, из
приблизительных соотношений, которые
зависят от заданной схемы выпрямления:
,
протекающего через вентиль, из
приблизительных соотношений, которые
зависят от заданной схемы выпрямления:
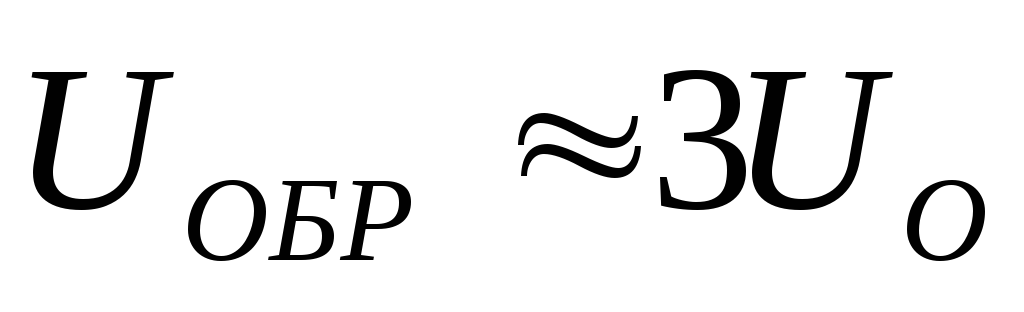 – для однополупериодной
или двухполупериодной схемы,
– для однополупериодной
или двухполупериодной схемы,
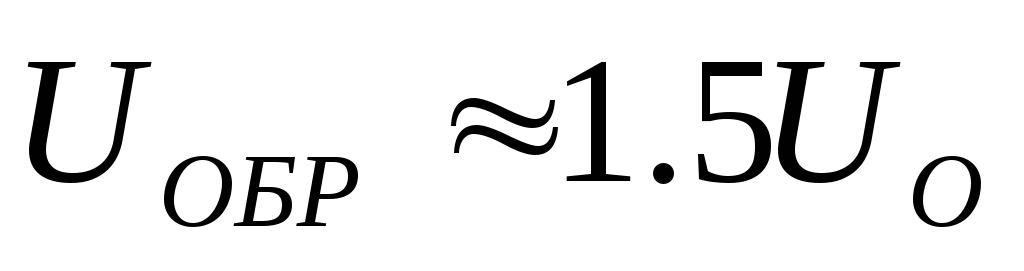 – для мостовой
схемы выпрямления. (5.1)
– для мостовой
схемы выпрямления. (5.1)
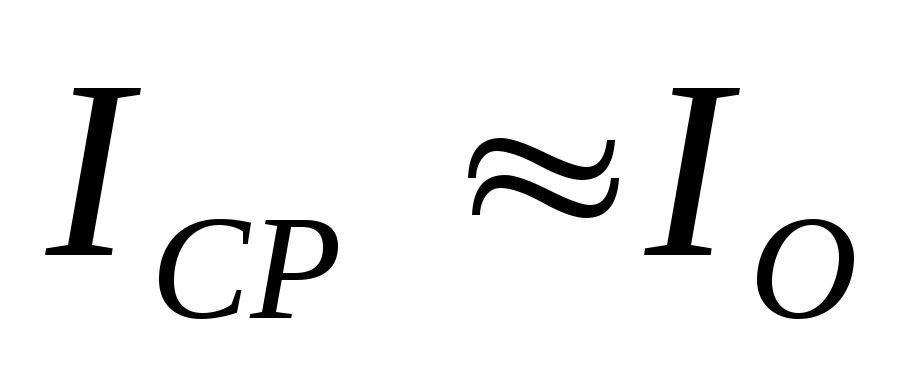 – для однополупериодной,
– для однополупериодной,
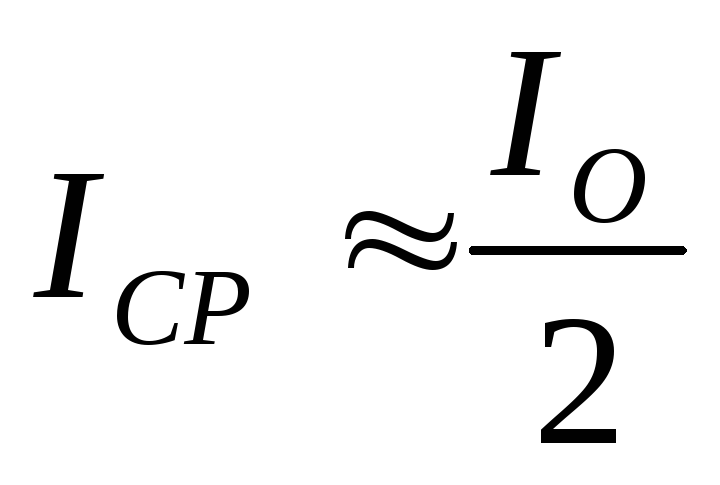 – для двухполупериодной
или мостовой схем выпрямления. (5.2)
– для двухполупериодной
или мостовой схем выпрямления. (5.2)
 – для однополупериодной,
– для однополупериодной,
 – для двухполупериодной
или мостовой схем выпрямления. (5.3)
– для двухполупериодной
или мостовой схем выпрямления. (5.3)
По
рассчитанным значениям 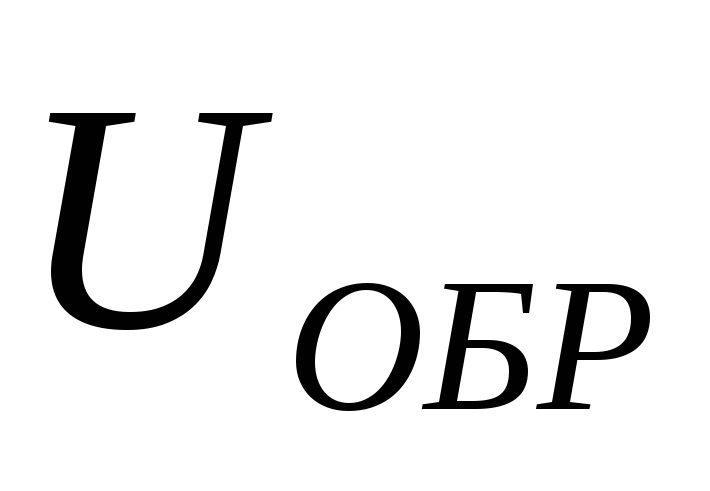 ,
,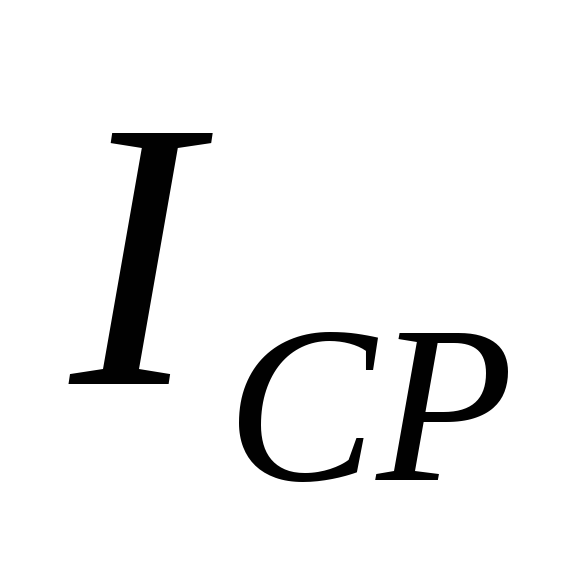 и
и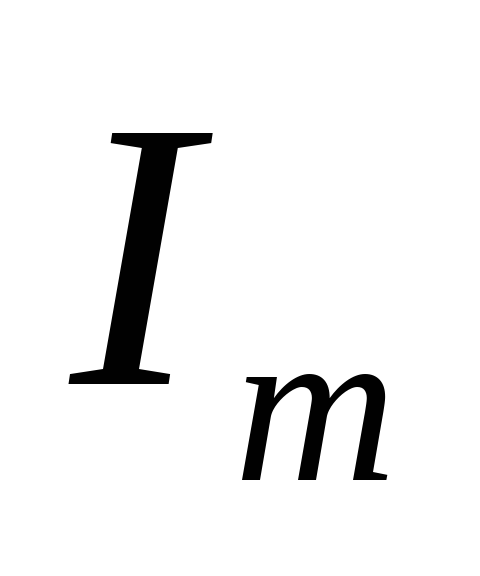 с помощью приложения 6 выбирают
выпрямительные диоды, так чтобы
максимально допустимые значения
обратного напряжения, среднего и
амплитудного тока выпрямительного
диода превышали рассчитанные значения.
с помощью приложения 6 выбирают
выпрямительные диоды, так чтобы
максимально допустимые значения
обратного напряжения, среднего и
амплитудного тока выпрямительного
диода превышали рассчитанные значения.
Находим сопротивление нагрузки выпрямителя
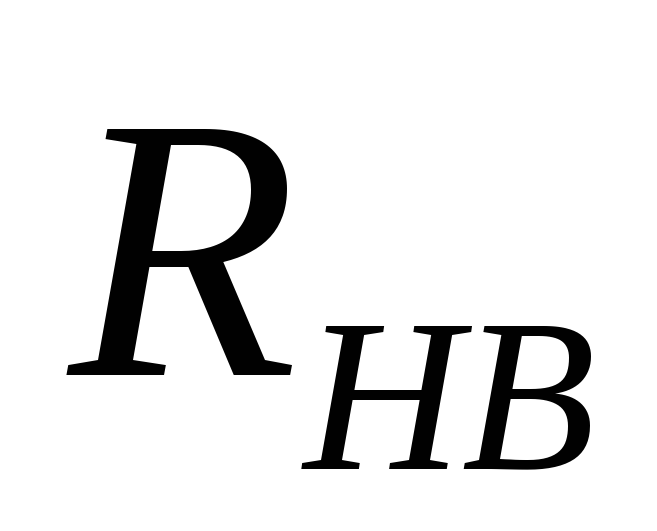 :
:
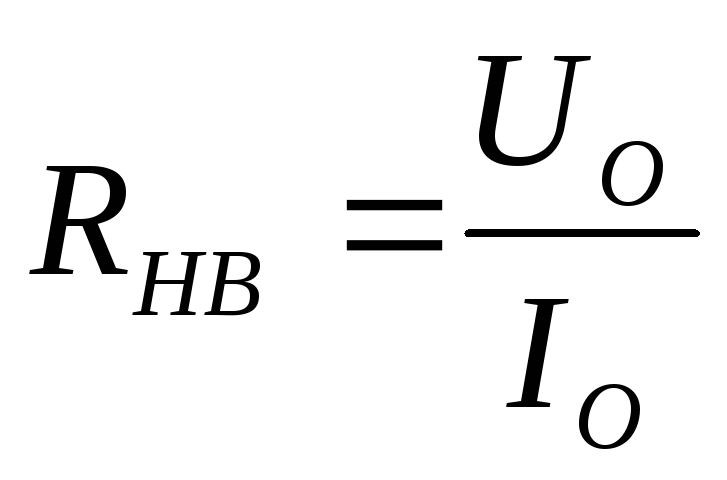 . (5.4)
. (5.4)
Находим сопротивление обмотки трансформатора

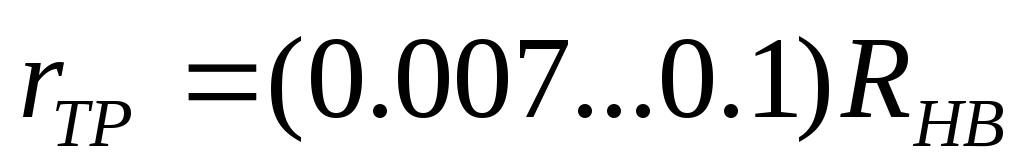 . (5.5)
. (5.5)
При этом большие значения относятся к менее мощным выпрямителям.
Находим приблизительное значение прямого сопротивления выпрямительного диода
 :
:
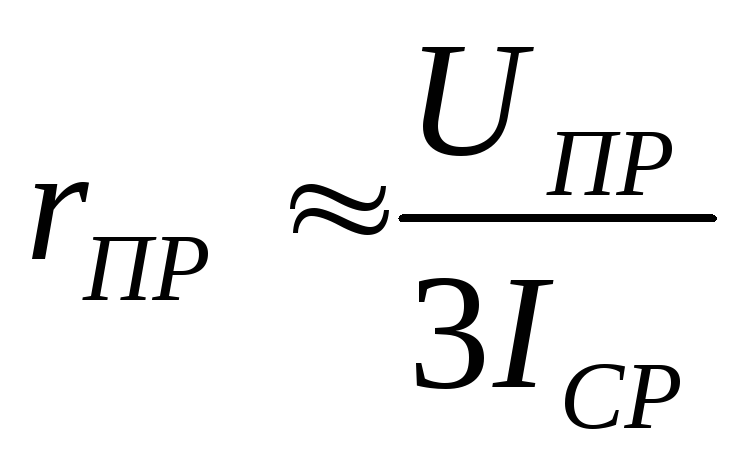 , (5.6)
, (5.6)
где  – постоянное прямое падение напряжения
на диоде, которое выбирается из приложения
6.
– постоянное прямое падение напряжения
на диоде, которое выбирается из приложения
6.
Определяем активное сопротивление фазы выпрямителя
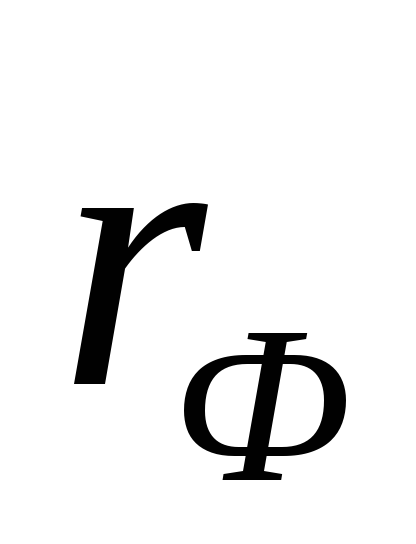 в зависимости от заданной схемы
выпрямления из соответствующих
выражений:
в зависимости от заданной схемы
выпрямления из соответствующих
выражений:
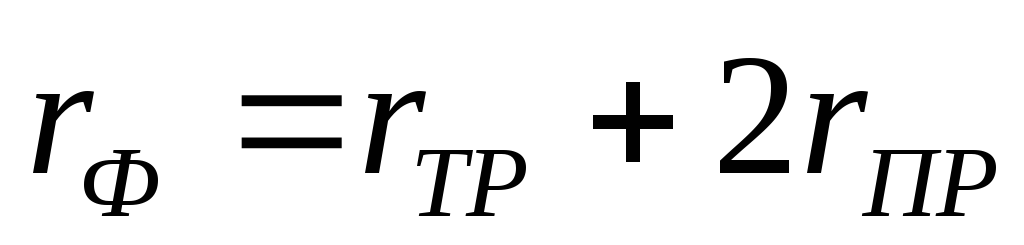 – для мостовой
схемы выпрямления,
– для мостовой
схемы выпрямления,
 – для одно- и
двухполупериодной схем выпрямления. (5.7)
– для одно- и
двухполупериодной схем выпрямления. (5.7)
Определяем значение вспомогательного коэффициента
 в зависимости от заданной схемы
выпрямления:
в зависимости от заданной схемы
выпрямления:
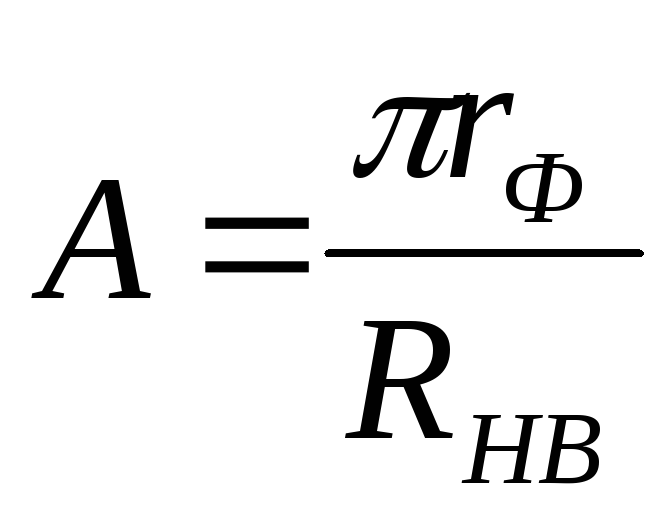 – для
однополупериодной схемы выпрямления,
– для
однополупериодной схемы выпрямления,
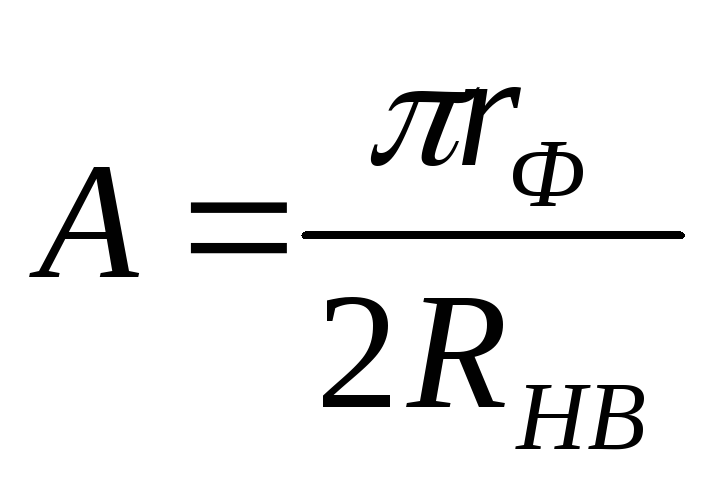 – для двухполупериодной
или мостовой схемы выпрямления. (5.8)
– для двухполупериодной
или мостовой схемы выпрямления. (5.8)
По графику рис.7а находим значения коэффициентов
 .
.Н
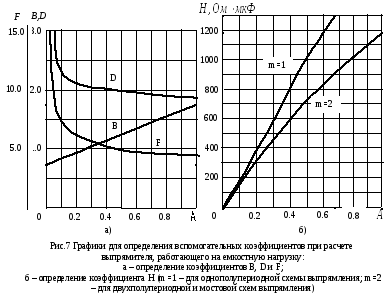 аходим
значение напряжения на входе выпрямителя
аходим
значение напряжения на входе выпрямителя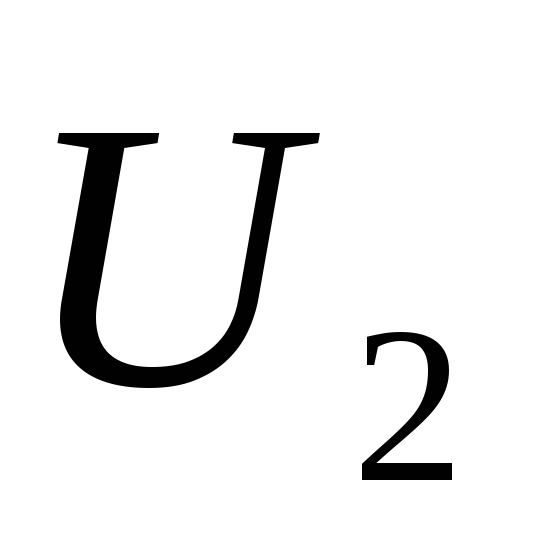 (напряжение
вторичной обмотки трансформатора) и
ток вторичной обмотки трансформатора
(напряжение
вторичной обмотки трансформатора) и
ток вторичной обмотки трансформатора в зависимости от заданной схемы
выпрямления:
в зависимости от заданной схемы
выпрямления:
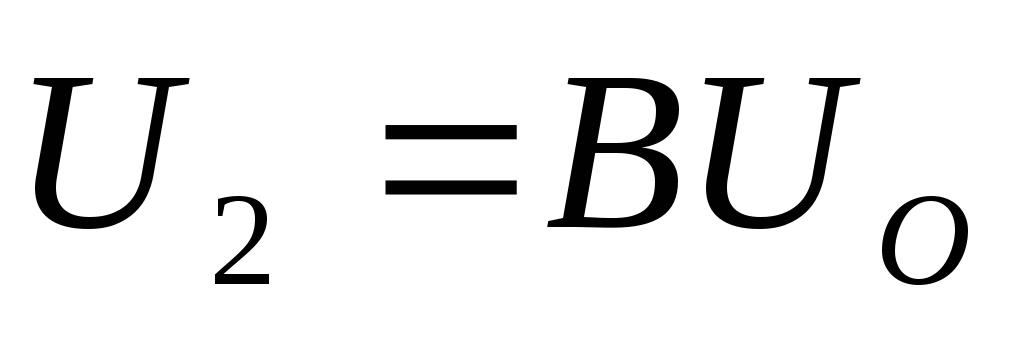 ,
,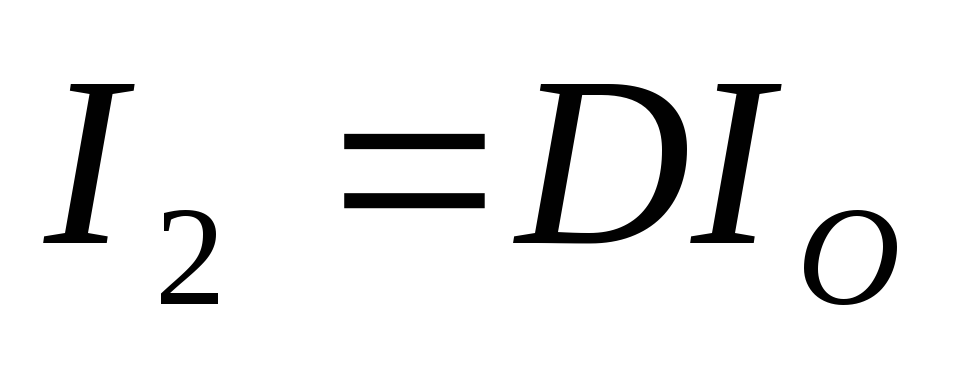 – для однополупериодной схемы выпрямления,
– для однополупериодной схемы выпрямления,
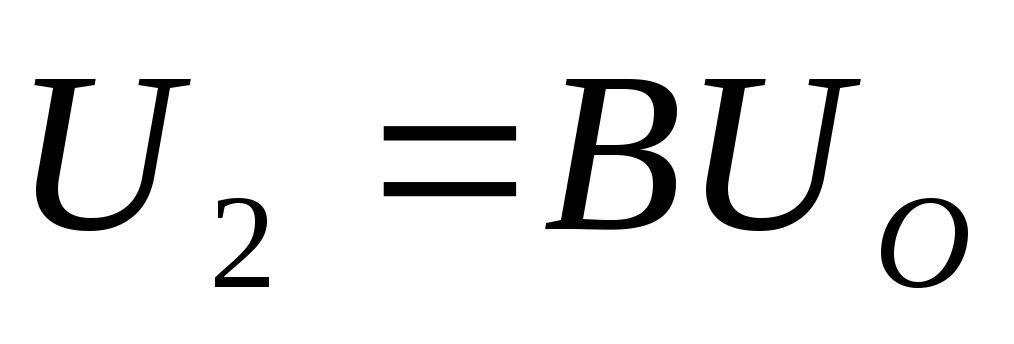 ,
,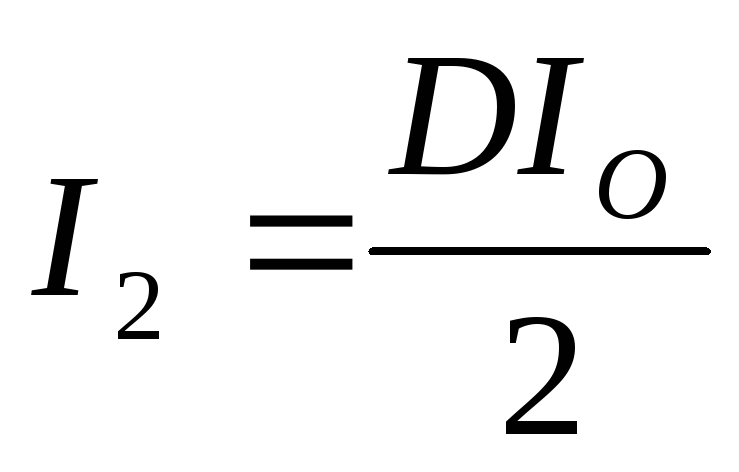 – для двухполупериодной схемы выпрямления,
– для двухполупериодной схемы выпрямления,
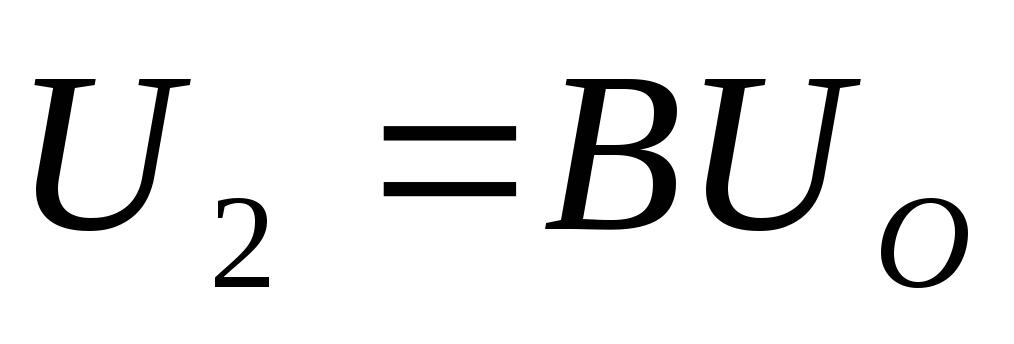 ,
,  – для мостовой схемы выпрямления.
(5.9)
– для мостовой схемы выпрямления.
(5.9)
Уточняем значение обратного напряжения
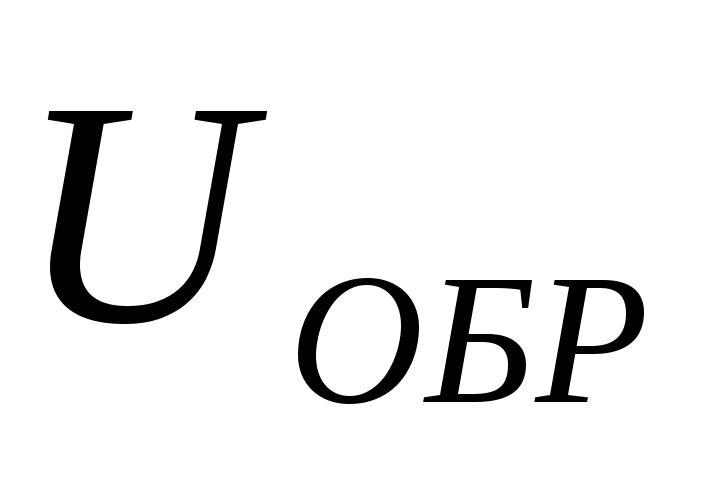 и амплитудного значения тока
и амплитудного значения тока 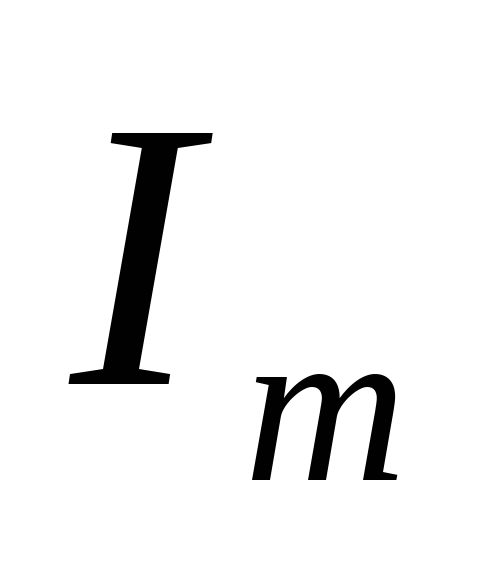 вентильного диода в зависимости от
заданной схемы выпрямления:
вентильного диода в зависимости от
заданной схемы выпрямления:
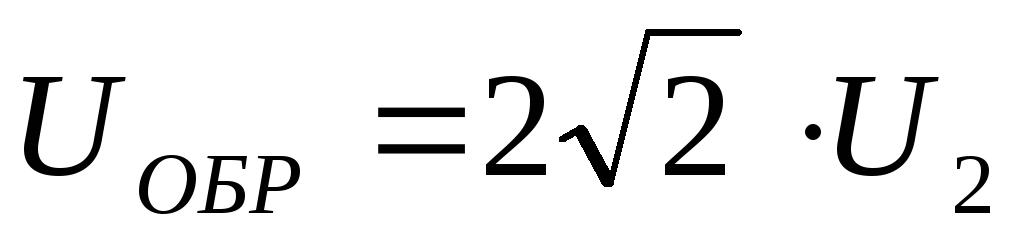 ,
, 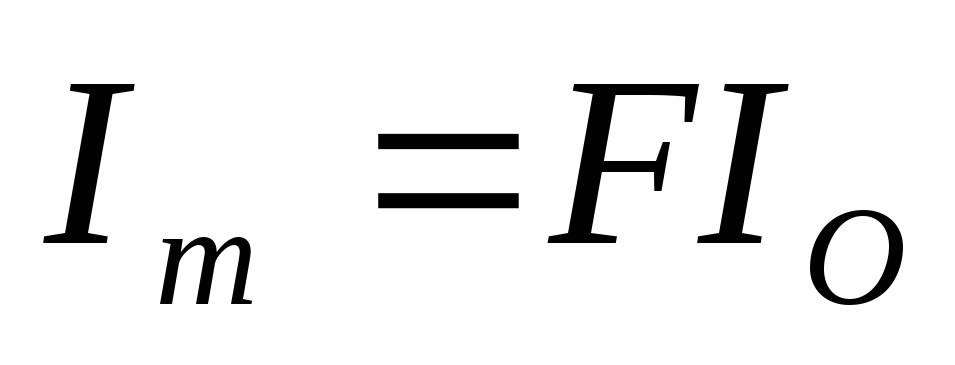 – для однополупериодной схемы выпрямления,
– для однополупериодной схемы выпрямления,
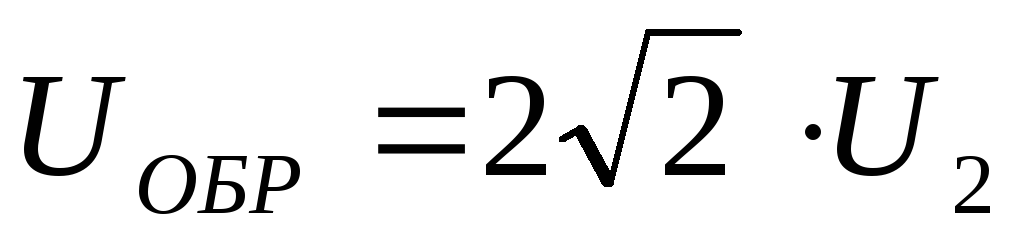 ,
, 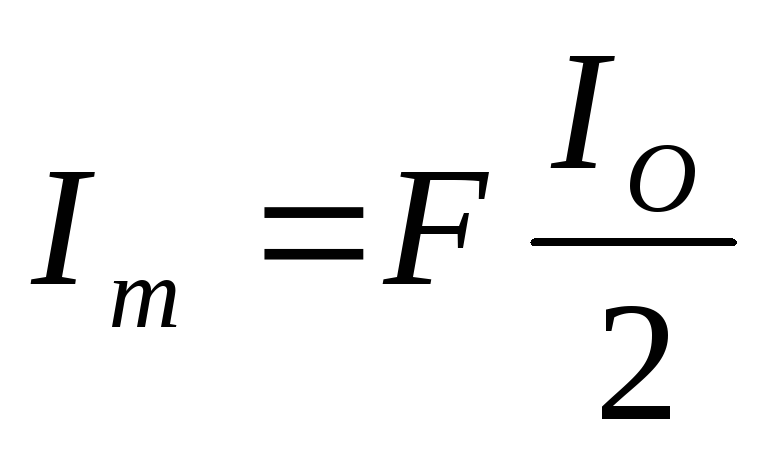 – для двухполупериодной схемы выпрямления,
– для двухполупериодной схемы выпрямления,
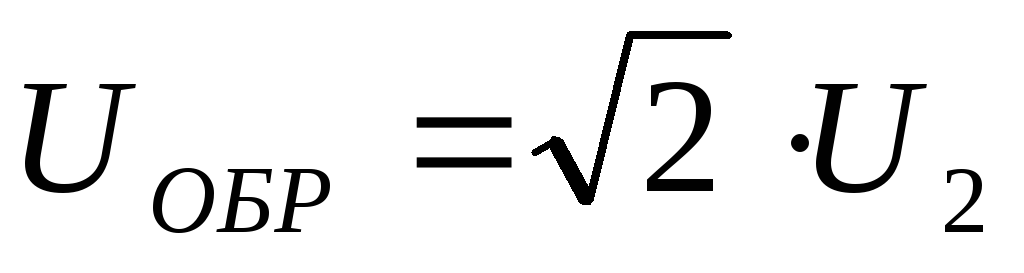 ,
,  – для мостовой схемы выпрямления.
(5.10)
– для мостовой схемы выпрямления.
(5.10)
Полученные значения обратного напряжения и амплитудного значения тока через выпрямительный диод не должны превышать соответствующих табличных параметров для выбранного диода, т.е.
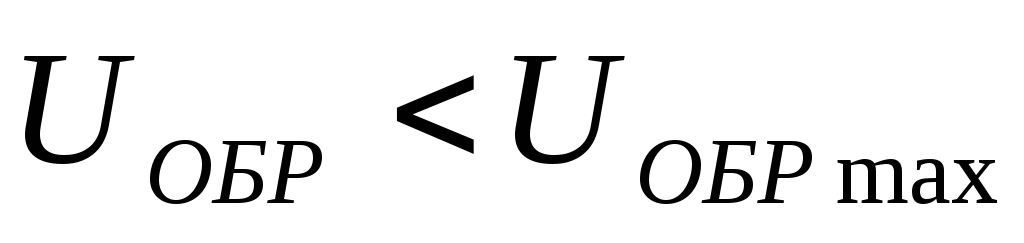 и
и 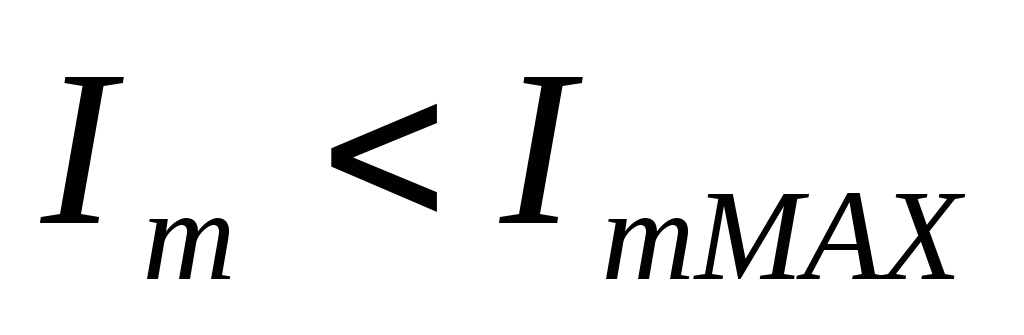 , (5.11)
, (5.11)
иначе необходимо выбрать более мощные диоды и провести расчет сначала.
Находим требуемый коэффициент пульсаций на выходе выпрямителя
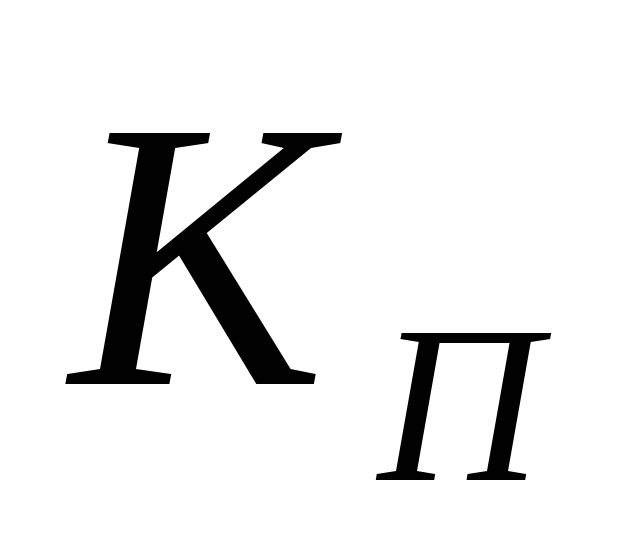 :
:
 . (5.12)
. (5.12)
Полученное значение коэффициента пульсаций не должно превышать (0.1…0.15), в противном случае его принимают равным 0.15.
По графику рис.7б находим вспомогательный коэффициент
 .
.Определяем необходимое значение емкости конденсатора выпрямителя в мкФ:
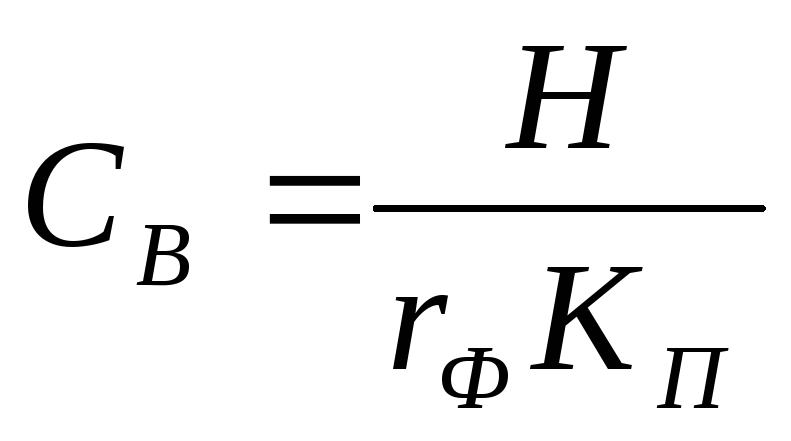 , (5.13)
, (5.13)
и согласно приложению 2 выбираем номинальное значение емкости конденсатора фильтра.
Находим рабочее напряжение конденсатора фильтра
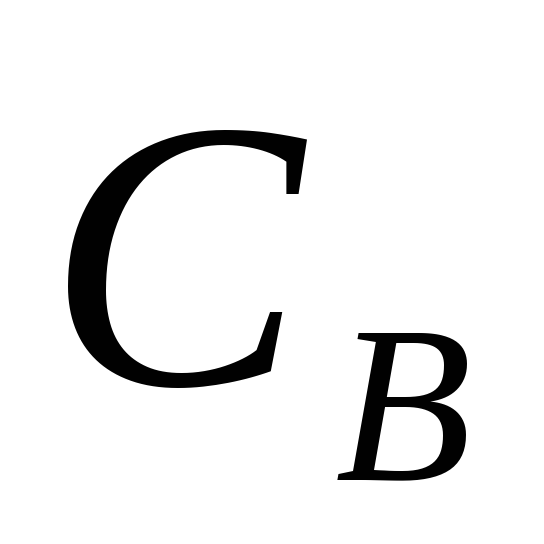 :
:
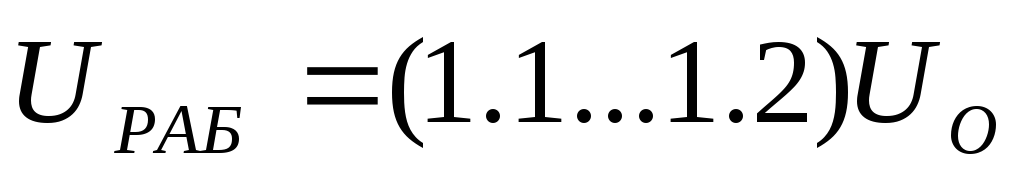 , (5.14)
, (5.14)
и выбираем требуемый тип конденсатора фильтра.
Для последующего расчета трансформатора используют следующие рассчитанные данные:
Далее переходят к расчету трансформатора согласно методике раздела 6.
studfile.net
Выпрямители тока
Существует два типа выпрямителей:
1. Однополупериодный выпрямитель, показан на рис. 29.1. Диод D1 в схеме на рис. 29.1 (а) проводит ток только в течение положительных полупериодов входного напряжения, обеспечивая формирование на выходе выпрямителя напряжение только положительной полярности. Если изменить полярность включения диода (рис. 29.1(б)), то на выходе выпрямителя будут воспроизводиться только отрицательные полупериоды входного напряжения. Выходное напряжение содержит постоянную составляющую (рис. 29.2), уровень которой приблизительно втрое ниже максимального (пикового) уровня напряжения (0,318Vp, где Vp – максимальное напряжение).
2. Двухполупериодный выпрямитель, показан на рис. 29.3. В этом случае используется трансформатор с отводом от средней точки вторичной обмотки. ЭДС, индуцируемые в каждой из половин вторичной обмотки, в любой момент времени равны по величине и противоположны по знаку.

Рис. 29.1. Однополупериодный выпрямитель с положительной (а)
и отрицательной (б) полярностью выходного напряжения.

| Рис. 29.2 | ||
|

Рис. 29.4. Уровень постоянной составляющей при двухполупериодном выпрямлении синусоидального тока вдвое выше (0,636Vр), чем при однополупериодном выпрямлении.
Для одного полупериода входного напряжения потенциал точки А положителен, а потенциал точки В отрицателен по отношению к среднему выводу вторичной обмотки, для другого полупериода ситуация изменяется на обратную. В первом случае открыт диод diи через этот диод и нагрузку RL протекает ток I1. Во втором случае открыт диод D1 и ток I2 протекает через нагрузку RL в том же направлении, что и ток I1. Форма выходного напряжения показана на рис. 29.4. В данном случае уровень постоянной составляющей на выходе выпрямителя вдвое выше, чем при однополупериодном выпрямлении тока (0,636Vp, или приблизительно две трети от максимального напряжения).
Мостовой выпрямитель
Еще одна схема, обеспечивающая двухполупериодное выпрямление тока, показана на рис. 29.5. Это так называемый мостовой выпрямитель. В течение положительного полупериода входного напряжения (рис. 29.6(а)) потенциал точки А положителен, а потенциал точки В отрицателен. Диоды D1и D3 открыты, и ток I1 протекает через нагрузку RLв направлений, указанном стрелкой (сверху вниз на рисунке). В течение отрицательного полупериода (рис. 29.6(б)), напротив, потенциал точки А отрицателен, а потенциал точки В положителен.

Рис. 29.5. Мостовой выпрямитель.

Рис. 29.6.
Теперь открыты диоды D2 и D4, и ток протекает через нагрузку RLв том же самом направлении.
Для мостового выпрямителя не нужен трансформатор с отводом от средней точки вторичной обмотки. Однако трансформатор может быть использован для изменения уровня переменного напряжения на входе этого выпрямителя.
Накопительный конденсатор
Для снижения уровня переменных составляющих выпрямленного тока используется накопительный конденсатор С1, включаемый параллельно нагрузке (рис. 29.7). Этот конденсатор заряжается до максимального входного напряжения и затем разряжается через нагрузку RL, предотвращая быстрый спад напряжения. На рис. 29.8 иллюстрируется влияние накопительного конденсатора на форму выходного напряжения однополупериодного и двухполупериодного выпрямителей. В обоих случаях выходное напряжение содержит значительную по величине постояннуюсоставляющую, на которую наложены малые пульсации напряжения. Амплитуда этих пульсаций определяется постоянной времени (RC-постоянной) для используемого накопительного конденсатора и нагрузочного резистора.

Рис. 29.7. Источник питания постоянного тока с накопительным конденсатором.

Рис. 29.8. Влияние накопительного конденсатора на форму выпрямленного
синусоидального напряжения.
Поэтому накопительный конденсатор должен иметь значительную емкость – от 100 до 5000 мкФ (и даже больше).
Сравнение двух временных диаграмм, представленных на рис. 29.8, показывает, что двухполупериодное выпрямление тока имеет следующие преимущества:
1. Время разряда накопительного конденсатора меньше, поэтому амплитуда пульсаций выходного напряжения тоже меньше.
2. Частота пульсаций вдвое превышает частоту входного питающего напряжения переменного тока, тогда как при однополупериодном выпрямлении частота пульсаций совпадает с частотой питающего напряжения. Например, если выпрямитель питается от бытовой электросети, то для двухполупериодного выпрямителя частота пульсаций будет равна 2 · 50 = 100 Гц, а для однополупериодного — только 50 Гц. Как будет показано далее, более высокочастотные пульсации отфильтровываются легче.
Напряжение холостого хода
Напряжением холостого хода называют величину выходного напряжений источника питания при нулевом токе нагрузки, т. е. при отключенной нагрузке.

Рис. 29.9. Напряжение холостого хода равно максимальному входному напряжению.
На рис 29.9 показан простой источник питания без нагрузочного резистора. Накопительный конденсатор заряжается, как обычно, до максимального значения входного напряжения. Однако, если нагрузка подключена (noload), этот конденсатор сохраняет свой заряд и обеспечивает тем самым постоянное значение выходного напряжения (равное максимальному входному напряжению) без каких-либо пульсаций. Таким образом, напряжение холостого хода Vnl – это максимально возможное выходное напряжение источника питания. При питании от бытовой электросети с напряжением Vср.кв. = 240 В (среднеквадратическое значение) напряжение холостого хода
Максимальное обратное напряжение
Важный фактор, который необходимо принимать во внимание при выборе диодов для источников питания постоянного тока, — максимальное напряжение, приложенное к диоду в «непроводящем» полупериоде. Эта величина называется максимальным обратным напряжением. Рассмотрим схему на рис. 29.9. Максимальное значение потенциала катода диода Dравно напряжению холостого хода 336 В. Потенциал катода изменяется от положительного максимума +336 В до отрицательного минимума -336 В. Максимальное обратное напряжение, которое должен выдерживать диод, достигается, когда потенциал анода отрицателен и максимален по абсолютной величине, то есть, равен -336 В. В этом случае на диоде падает напряжение 336 + 336 = 672 В. Таким образом, максимальное обратное напряжение вдвое больше напряжения холостого хода, т. е. вдвое больше максимального входного напряжения.
RC-сглаживание
Пульсации напряжения в выходном сигнале выпрямителя могут быть Уменьшены с помощью фильтра нижних частот (сглаживающего фильма). Резистор R1 и конденсатор С2 в схеме на рис. 29.10 образуют простейший RC-фильтр. Для эффективного ослабления пульсаций постоянная времени R1C2 должна быть очень велика по сравнению с периодом пульсаций.

Рис. 29.10. Источник питания с RC-фильтром.
При заданной постоянной времени, чем короче период пульсаций (т. е. чем выше их частота), тем эффективнее осуществляется сглаживание. Именно поэтому пульсации на выходе двухполупериодного выпрямителя сглаживаются лучше, чем пульсации на выходе однополупериодного выпрямителя.
Емкость конденсатора C2 сглаживающего фильтра должна быть большой — от 100 до 5000 мкФ, т. е. сравнима с емкостью накопительного конденсатора C1. Сопротивление резистора R1, наоборот, должно быть мало, в противном случае ток нагрузки будет создавать на нем большое падение напряжения и выходное напряжение источника питания уменьшится. Номинал этого резистора выбирается в диапазоне 1 – 100 Ом в зависимости от величины тока нагрузки.
LC-сглаживание
Более эффективная схема сглаживания пульсаций показана на рис. 29.11. Катушка индуктивности L1 и конденсатор C2 образуют фильтр нижних частот. Дроссель L1 сглаживающего фильтра имеет большую индуктивность (100 мГн — 10 Гн), благодаря чему сглаживаются изменения тока, протекающего через дроссель, и, как следствие, пульсации выходного напряжения. Низкое активное сопротивление дросселя — одно из его преимуществ, большие габариты — недостаток. Заметим, что в отличие от накопительного конденсатора, который повышает уровень постоянной составляющей выходного напряжения источника питания, сглаживающая цепь оставляет этот уровень практически неизменным. Она только ослабляет переменную составляющую на выходе источника питания.
Стабилизация
Увеличение тока, потребляемого от источника питания, приводит к уменьшению его выходного напряжения.

Рис. 29.11. Источник питания постоянного тока с LC-фильтром.

Рис. 29.12. Нагрузочная характеристика нестабилизированного источника питания.
Это связано с тем, что источник питания имеет свое внутреннее сопротивление, представляющее собой сумму сопротивлений обмотки трансформатора, выпрямительных диодов и резистора или дросселя сглаживающего фильтра. Рисунок 29.12 иллюстрирует изменение напряжения на выходе источника питания при изменении тока нагрузки. Представленная кривая называется нагрузочной характеристикой (кривой). Выходное напряжение максимально, когда ток нагрузки равен нулю, т. е. при холостом ходе. Напряжение на выходе источника питания, которое он обеспечивает при установленной полной нагрузке или номинальном (полном) токе нагрузки (fullload), называется номинальным выходным напряжением источника питания Vfl.
Изменение выходного напряжения при изменении тока нагрузки от нуля до номинального значения задается в процентах и определяется как
Напряжение холостого хода — Номинальное напряжение Vnl – Vfl
——————————————————————————— · 100% = ———— · 100%
Номинальное напряжение Vfl
В этом видео рассказывается о выпрямительных схемах:
Добавить комментарий
radiolubitel.net


