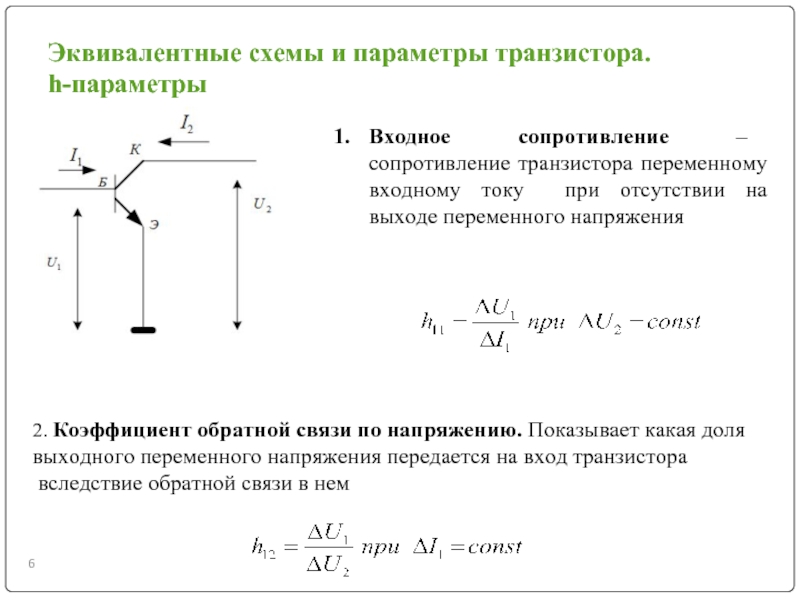
Входное и выходное сопротивления усилителя (БТ, BJT)
- Радиоэлектроника
- Схемотехника
- Основы электроники и схемотехники
- Том 3 – Полупроводниковые приборы
- Книги / руководства / серии статей
- Основы электроники и схемотехники. Том 3. Полупроводниковые приборы
Добавлено 26 января 2018 в 06:04
Входное сопротивление усилителя значительно варьируется в зависимости от конфигурации схемы, как показано на рисунке ниже. Оно также зависит от смещения. Здесь не учитывается, что входной импеданс является комплексной величиной и зависит от частоты. Для схем с общим эмиттером и общим коллектором он равен сопротивлению базы, умноженному на коэффициент β. Сопротивление базы по отношению к транзистору может быть как внутренним, так и внешним. Для схемы с общим коллектором:
\(R_{вх} = \beta R_Э\)
Для схемы с общим эмиттером немного сложнее. Нам необходимо знать внутреннее сопротивление эмиттера rЭ. Оно вычисляется по формуле:
\(r_Э = KT/I_Э m\)
где
- K=1.
 38×10-23 Дж·К−1 – постоянная Больцмана;
38×10-23 Дж·К−1 – постоянная Больцмана; - T – температура в Кельвинах, берем ≅300;
- IЭ – ток эмиттера;
- m – для кремния изменяется от 1 до 2.
\(r_Э = 0,026 В/I_Э = 26 мВ/I_Э\)
Таким образом, Rвх для схемы с общим эмиттером равно:
\(R_{вх} = \beta r_{Э}\)
Например, входное сопротивление усилителя на транзисторе с β = 100, на схеме с общим эмиттером и смещением 1 мА равно:
\(r_Э = 26 мВ/ 1 мА = 26 \;Ом\)
\(R_{вх} = \beta r_Э = 100 \cdot 26 = 2600 \;Ом\)
Для более точного определения Rвх для схемы с общим коллектором необходимо учитывать RЭ:
\(R_{вх} = \beta (R_Э + r_Э)\)
Формула выше также применима и для схемы с общим эмиттером с резистором эмиттера.
Входной импеданс схемы с общей базой равен Rвх = rЭ.
Высокий входной импеданс схемы с общим коллектором согласовывается с источниками с высоким выходным сопротивлением. Одним из таких источников с высоким импедансом является керамический микрофон. Схема с общей базой иногда используется в RF (радиочастотных) схемах для согласования с источником с низким импедансом, например, с коаксиальным кабелем 50 Ом. С источниками со средним импедансом хорошо согласуется схема с общим эмиттером. Примером может служить динамический микрофон.
Одним из таких источников с высоким импедансом является керамический микрофон. Схема с общей базой иногда используется в RF (радиочастотных) схемах для согласования с источником с низким импедансом, например, с коаксиальным кабелем 50 Ом. С источниками со средним импедансом хорошо согласуется схема с общим эмиттером. Примером может служить динамический микрофон.
Выходные сопротивления трех основных типов схем приведены на рисунке ниже. Средний выходной импеданс схемы с общим эмиттером сделал ее самой популярной в использовании. Низкое выходное сопротивление схемы с общим коллектором хорошо подходит для согласования, например, для бестрансформаторного соединения с 4-омным динамиком.
Характеристики схем усилителей на биполярных транзисторахПодведем итоги
Смотрите рисунок выше.
Оригинал статьи:
- Amplifier Impedances
Теги
Биполярный транзисторВходной импедансВыходной импедансКаскад с общей базойКаскад с общим коллекторомКаскад с общим эмиттеромКаскодный усилительКоэффициент усиления по напряжениюКоэффициент усиления по токуОбучениеЭлектроникаНазад
Оглавление
Вперед
На сайте работает сервис комментирования DISQUS, который позволяет вам оставлять
комментарии на множестве сайтов, имея лишь один аккаунт на Disqus. com.
com.
В случае комментирования в качестве гостя (без регистрации на disqus.com) для публикации комментария требуется время на премодерацию.
Расчет входного сопротивления транзистора со стороны базы
Входное сопротивление со стороны базы соответствует входному сопротивлению транзистора без учета шунтирующего действия резистивного делителя в цепи базы: .
Расчет резистивного делителя в цепи базы транзистора
Резистивный делитель R1, R2, формирует потенциал базы относительно земли. Уровень данного потенциала не должен зависеть от тока эмиттера , протекающего по резистору . Последний является датчиком температуры. Если ток делителя значительно превышает ток базы , то потенциал определяется напряжением питания и соотношением резисторов R1, R2. Поскольку коэффициент , а ток , то потенциал базы не зависит от тока при условии:
.
Потенциал базы определяется по второму закону Кирхгофа:
,
где d статический потенциал эмиттерного рn – перехода.
Резисторы R1, R2 рассчитываются по закону Ома:
; .
Определяются мощности , рассеиваемые на сопротивлениях R1, R2:
; .
Примечание. Для германиевых транзисторов ; для кремневых транзисторов [9].
В среде «CIRCUITMAKER» принимается .
Расчет эквивалентного сопротивления базового делителя
При
усилении сигналов переменного
тока с частотой шина источника питания заземлена через
внутренний конденсатор фильтра (на рисунке 1 не показан), т.к. емкостное
сопротивление .
Следовательно, по переменному току резисторы R1,
R2
соединены параллельно.
Эквивалентное сопротивление делителя .
Расчет активного входного сопротивления усилителя
На низких частотах, несоизмеримых с быстродействием выбранного транзистора, входное сопротивление усилителя является чисто активным и соответствует параллельному соединению сопротивлений и :
.
Примечание. В области высоких частот, соизмеримых с быстродействием выбранного транзистора, начинают влиять межэлектродные емкости: входное сопротивление (импеданс) транзистора является комплексной величиной
Расчет емкости разделительного конденсатора на входе усилителя
Разделительный конденсатор отделяет постоянный потенциал базы от источника информационного сигнала, подавляет низкие частоты и пропускает высокие частоты. Величина емкости рассчитывается на нижней частоте информационного сигнала по формуле:
.
Для уменьшения ослабления входного сигнала на низких частотах расчетное значение емкости увеличивается в 10-100 раз.
Расчет коэффициента усиления
Определяется емкость шунтирующего конденсатора в цепи эмиттера для заданного значения модуля коэффициента усиления
.
Определяется модуль коэффициента усиления для расчетного значения емкости
.
Расчет амплитуды входного напряжения и тока
Номинальная амплитуда входного напряжения
Амплитуда входного тока .
Расчет коэффициента усиления по току и по мощности
Коэффициент усиления по мощности .
Расчет номинальной мощности входного сигнала
Номинальная входная мощность определяется из тождества:
.
2.2 Расчет усилителя с общим коллектором
Исходными данными для расчета усилителя с общим коллектором (Рисунок 2) являются следующие параметры:
активное сопротивление нагрузки ;
активная мощность нагрузки ;
напряжение питания ;
коэффициент передачи тока базы транзистора;
рабочая частота (частотный диапазон) информационного сигнала .
Методика расчета
Расчет амплитуды выходного напряжения и тока нагрузки
Амплитуда выходного напряжения и ток нагрузки усилителя определяется в соответствии с разделом 2.1, п.1.
Выбор транзисторов
Выбор
транзисторов осуществляется в соответствии
с разделом 2. 1, п.2.
1, п.2.
Расчет емкости разделительного конденсатора на выходе усилителя
Расчет емкости разделительного конденсатора на выходе осуществляется в соответствии с разделом 2.1, п.3: .
Расчет резистора в цепи эмиттера и его мощности
Для исключения искажений информационного сигнала потенциал эмиттера и ток эмиттера в статическом режиме (при отсутствии входного сигнала) выбираются из условия: , .
Резистор в цепи эмиттера . Мощность , рассеиваемая на сопротивлении R3: .
Расчет эквивалентного сопротивления эмиттерной цепи
При
достаточно большой емкости разделительного конденсатора
С3 эквивалентное сопротивление эмиттерной
цепи соответствует параллельному соединению сопротивлений и :
.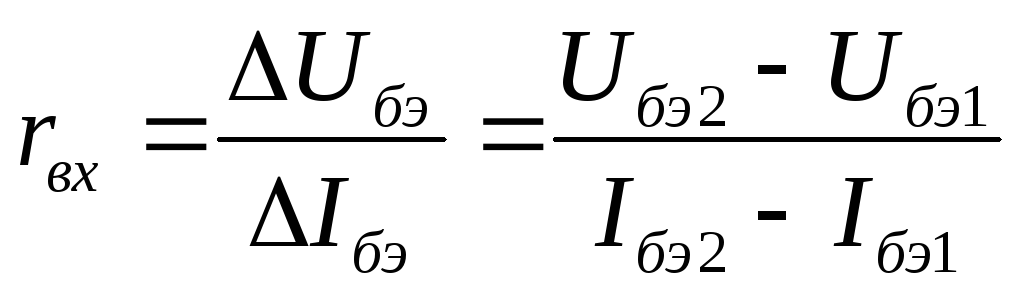
Расчет входного сопротивления транзистора
Для схемы с общим коллектором входное сопротивление транзистора определяется без учета шунтирующего действия резистивного делителя со стороны базы: .
Расчет тока базы в статическом режиме
При известном значении параметров и транзистора статический ток базы .
Расчет резистивного делителя в цепи базы транзистора
Резистивный
делитель R1,
R2,
формирует потенциал базы
относительно земли. Элементы делителя
выбираются таким образом, чтобы
минимизировать шунтирование входного сопротивления
.
По первому закону Кирхгофа в базовом
узле ток
растекается: по резистору R2
течет ток ,
а по резистору R1
– ток .
Для уменьшения шунтирующего действия
делителя R1,
R2
величина тока
выбирается из условия: .
Расчет сопротивлений делителя R1, R2:
расчет потенциала базы в статическом режиме:
расчет сопротивления R2 делителя: .
расчет сопротивления R1 делителя: .
расчет мощностей резисторов делителя: , .
Примечание. Для германиевых транзисторов ; для кремневых транзисторов . В среде «CIRCUITMAKER» принимается .
Расчет эквивалентного сопротивления делителя в цепи базы
При достаточно большой емкости фильтра эквивалентное сопротивление базового делителя на переменном токе соответствует параллельному соединению его элементов: .
Расчет активного входного сопротивления усилителя
На низких частотах, несоизмеримых с быстродействием выбранного транзистора, входное сопротивление усилителя является чисто активным и соответствует параллельному соединению сопротивлений и :
.
Расчет емкости разделительного конденсатора на входе усилителя
Расчет емкости разделительного конденсатора на входе осуществляется в соответствии с разделом 2.1, п.12: .
Расчет коэффициента усиления по напряжению
Модуль коэффициента усиления по напряжению зависит от коэффициента транзистора, а также от соотношения эквивалентных сопротивлений участка коллектор-эмиттер и цепи эмиттера : .
Входной и выходной сигналы ЭП формируются относительно коллектора, имеющего на переменном токе нулевой потенциал. Следовательно, эквивалентное сопротивление эмиттерной цепи подключено параллельно динамическому сопротивлению участка коллектор – эмиттер транзистора :
;
.
Расчет амплитуды входного напряжения и тока
Номинальная амплитуда входного напряжения
Амплитуда
входного тока .
Расчет коэффициента усиления по току и по мощности
Коэффициент усиления по току .
Коэффициент усиления по мощности .
Расчет номинальной мощности входного сигнала
Номинальная мощность информационного сигнала на входе усилителя определяется из тождества: .
Расчет транзисторного ключа
Исходными данными для расчета транзисторного ключа (Рисунок 3, 4) являются следующие параметры:
напряжение питания ;
абсолютная температура окружающей среды ;
коэффициент передачи тока базы транзистора ;
ток эмиттера транзистора ;
активное сопротивление коллекторной нагрузки ;
остаточное напряжение на коллекторе транзистора
Методика расчета
Выбор транзистора: (см.
 раздел 2.1, п. 2) .
раздел 2.1, п. 2) .Расчет тока коллектора (тока нагрузки): .
Расчет тока эмиттера: .
Расчет тока базы (тока управления): ..
Расчет температурного потенциала: .
Расчет активного сопротивления эмиттерного вывода: .
Расчет ограничивающего резистора в цепи базы: .
Расчет мощности ограничивающего резистора в цепи базы: .
Расчет входного сопротивления транзисторного ключа: .
Примечание. Уровень входного напряжения должен обеспечить насыщение транзистора: , где максимальное напряжение между базой и эмиттером транзистора. У биполярных транзисторов: – германий, – кремний, [9, 11].
В среде «CIRCUITMAKER» принимается
. При расчете ТК обычно выбирают напряжение .
При расчете ТК обычно выбирают напряжение .
2.4 Расчет инвертирующего усилителя
Исходными данными для расчета инвертирующего операционного усилителя (Рисунок 8, а) являются следующие параметры:
активное сопротивление нагрузки усилителя ;
амплитуда напряжения на нагрузке усилителя
активное входное сопротивление усилителя ;
коэффициент усиления по напряжению .
Методика расчета
Расчет амплитуды тока нагрузки
Амплитуда тока нагрузки .
Расчет сопротивления отрицательной обратной связи
Входное
сопротивление инвертирующего усилителя .
При заданных значениях параметров
и сопротивление отрицательной обратной
связи определяется из выражения для модуля
коэффициента усиления по напряжению , .
Расчет амплитуды входного напряжения
Амплитуда входного сигнала .
Расчет амплитуды входного тока
Амплитуда входного тока .
Расчет коэффициента усиления по току
Модуль коэффициента усиления по току .
Расчет коэффициента усиления по мощности
Модуль коэффициента усиления по мощности .
2.5 расчет неинвертирующего усилителя
Исходными данными для расчета неинвертирующего операционного усилителя (Рисунок 8, б) являются следующие параметры:
активное сопротивление нагрузки усилителя ;
амплитуда напряжения на нагрузке усилителя
активное входное сопротивление усилителя ;
коэффициент усиления по напряжению .

Методика расчета
Если заданный коэффициент усиления по напряжению , то при фиксированном значении параметра сопротивление обратной связи определяется из выражений: , .
Если параметр , то неинвертирующий ОУ вырождается в повторитель напряжения (ПН): сопротивление R1 в схеме отсутствует , сопротивление – короткое замыкание между выходом ОУ и его инвертирующим входом (Рисунок 8, в).
Входное сопротивление ПН соответствует сопротивлению утечки интегральной микросхемы ОУ по неинвертирующему входу [1, 4, 6, 11].
Примечание. Для компенсации напряжения смещения на выходе ПН при отсутствии входного сигнала между выходом и инвертирующим входом ОУ включают резистор обратной связи , где внутреннее сопротивление источника информационного сигнала.
Дальнейший
расчет неинвертирующего ОУ осуществляется
в соответствии с методикой, изложенной
в разделе 2. 4, п.п. 1, 3…6.
4, п.п. 1, 3…6.
Каково фактическое входное сопротивление транзистора BJT (особенно схемы усилителя)?
спросил
Изменено 7 месяцев назад
Просмотрено 2к раз
\$\начало группы\$Что означает входное сопротивление биполярного транзистора? Почему его значение равно отношению входного напряжения к току базы в схеме с общим эмиттером?
Насколько мне известно, в схеме усилителя трансформатор используется для возбуждения сигнала в цепи. Почему существует сопротивление, которое мы называем входным сопротивлением? Действительно ли это сопротивление проводов?
В моей школьной программе нас учат проводам без сопротивления, поэтому я думаю, что предыдущий вопрос не имеет смысла. Я мог понять, что выходное сопротивление может относиться к совершенно другой схеме, с помощью которой усиленный сигнал может использоваться, например, для усиления звука, но почему существует входное сопротивление?
Почему входное сопротивление равно отношению входного напряжения к базовому току? Если мы используем закон Кирхгофа в петле база-эмиттер, то не должно ли это быть похоже на $$I_B×R_{in}+V_{напряжение перехода база-эмиттер}=V_{BE}+V_{in}$$
Как \$R_{in}=V_{in}/I_B\$?
Если возможно, сообщите мне также, почему коэффициент усиления по току и коэффициент усиления по току транзистора считаются постоянными.
Почему входное сопротивление представляет собой отношение входного напряжения к базовому току?
Потому что именно так оно определено, а малосигнальное (приращение) входное сопротивление при рабочем напряжении представляет собой отношение небольшого изменения входного напряжения к рабочему напряжению, деленное на соответствующее изменение базового тока. Это комбинированный эффект \$R_{\rm IN}\$ и перехода база-эмиттер.
\$\конечная группа\$ 2 \$\начало группы\$Биполярные переходные транзисторы не имеют входного сопротивления.
Входное сопротивление может быть определено для портов n-портовых сетей, таких как конфигурация с общим эмиттером, которую вы показали, с двумя терминалами, подключенными к \$V_{in}\$, являющимися одним таким портом. Если к такому порту подключить идеальный источник напряжения \$V_{in}\$, что приведет к протеканию тока \$I_{in}\$, входное сопротивление составит определил как
$$ R_{in} := \frac{V_{in}}{I_{in}}. $$
$$
Применив к вашей схеме с общим эмиттером, мы получаем \$ R_{in} = V_{in} / I_B \$.
Для входов постоянного тока \$R_{in}\$ сильно зависит от \$V_{in}\$ (в данном случае) – входное сопротивление будет большим для напряжений ниже прямого напряжения BE-диода и очень низким для напряжения выше прямого напряжения. Вы называете это входным сопротивлением большого сигнала .
При использовании в качестве усилителя сместите биполярный транзистор соответствующим образом постоянным напряжением, чтобы перевести его в линейную область и наложить небольшой сигнал переменного тока, который необходимо усилить. В данном случае представляет интерес малосигнальное входное сопротивление \$r_{in}\$. Вы можете рассчитать \$r_{in}\$ из слабосигнальной модели биполярного транзистора и различных параметров транзистора, которые могут зависеть от условий смещения. Любой учебник по BJT или схемам усилителя должен охватывать это.
Что касается вашей электрической схемы: я думаю, что она вводит в заблуждение. \$R_{in}\$, вероятно, не должно быть там. Он зависит от напряжения и, следовательно, не является фактическим резистором, и если вы считаете его резистором, зависящим от напряжения, он также будет включать диод BE.
\$R_{in}\$, вероятно, не должно быть там. Он зависит от напряжения и, следовательно, не является фактическим резистором, и если вы считаете его резистором, зависящим от напряжения, он также будет включать диод BE.
Относительно коэффициента усиления по току (с общим эмиттером) \$\beta\$: он примерно постоянен только в линейной области биполярного транзистора. (Если бы это было не так, не было бы линейной области, так что это просто тавтология.)
\$\конечная группа\$ 2 \$\начало группы\$В техническом описании транзистора 2N3904 есть график его типичного входного импеданса в зависимости от тока коллектора:
\$\конечная группа\$ 1 \$\начало группы\$Существует путаница в отношении термина Рин.
Когда фиксированный резистор Rin, как показано на схеме, является частью вопроса, отношение Vin/In НЕ идентично этому резистору Rin.
1. ) Общее входное сопротивление цепи по постоянному току равно сумме Rin плюс отношение постоянного тока Vbe/Ib. Только последняя часть суммы представляет собой входное сопротивление постоянного тока «транзистора».
) Общее входное сопротивление цепи по постоянному току равно сумме Rin плюс отношение постоянного тока Vbe/Ib. Только последняя часть суммы представляет собой входное сопротивление постоянного тока «транзистора».
Комментарий : Когда мы говорим о входном сопротивлении транзистора (или полной схемы), в большинстве случаев мы имеем в виду входное сопротивление переменному току rin.
2.) Входное сопротивление переменного тока показанной схемы составляет rin=(Rin + hie) .
Термин hie представляет собой входное сопротивление переменного тока в базовом узле. Это сопротивление идентично наклону входной характеристики Ib=f(Vbe).
Этот наклон равен hie=Vt/Ib .
Также можно рассчитать по соотношению (коэффициент усиления по току)/(крутизна): hie=hfe/gm .
\$\конечная группа\$ 2 \$\начало группы\$ Входное сопротивление транзистора переменному току = dVbe/dIb = re(1 + beta), где re = dVbe/dIe = 25 мВ/Ie (при 25°C).
re — собственное сопротивление эмиттера, также известное как динамическое сопротивление эмиттера.
Входное сопротивление переменного тока всей цепи = Rin + re(1 + beta).
Beta = hFE, коэффициент усиления транзистора по току = Ic/Ib
\$\конечная группа\$ \$\начало группы\$Вот часть таблицы данных Fairchild 2N3904:
\$\конечная группа\$ 1Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и парольОпубликовать как гость
Электронная почтаТребуется, но никогда не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.
Как получить входное сопротивление транзистора?
Уметь находить \$Z_b\$, включающее выходное сопротивление транслятора \$r_o\$. В первую очередь нам нужно найти напряжение в узле \$V_e\$. Потому что я собираюсь использовать метод тестового напряжения, чтобы найти \$Z_b\$
$$ Z_b = \frac{V_{test}}{I_{test}} = \frac{V_{test}}{\frac{V_{test} – V_e}{r_{\pi}}}$$
Схема выглядит так:
смоделируйте эту схему – Схема создана с помощью CircuitLab
Я буду использовать грубую силу -> узловой анализ. А математическую часть за меня сделает математическая программа.
У нас есть два узла. Таким образом, первое уравнение:
$$\frac{V_e}{R_E} +\frac{V_e + V_{test}}{r_{\pi}} +\frac{V_e – V_o}{r_o} – \beta \times\frac{V_{test} – V_e}{r_{\pi}} = 0 $$
И уравнение второго узла:
$$\frac{V_o}{R_C} + \frac{V_o – V_e}{r_o} + \beta \times\frac{V_{test} – V_e}{r_{\ pi}} = 0 $$
И после того, как мы решим это
$$V_e = V_{test} *\frac{R_E (R_C +\left(\beta +1) r_o \right)}{r_o r_{\ pi} + R_C (R_E + r_{\pi}) + R_E ( r_{\pi} +(\beta +1) r_o)}$$
$$V_o = V_{test} \times\frac{R_C\ : R_E – R_C\: r_o \beta}{r_o\: r_{\pi} + R_C(R_E + r_{\pi}) + R_E ((\beta +1)r_o + r_{\pi})} $$
Подставляем \$V_e\$ к \$Z_b\$ и решаем.
$$Z_b = \frac{(R_C + R_E + r_o)r_{\pi} + R_C R_E + R_E \:r_o + R_E\: r_o \:\beta}{R_C + R_E + r_o}\tag{Уравнение 1}$$
И теперь мы можем еще больше упростить это, но мы должны сделать это вручную, потому что программа не может дать ответ в “разыскиваемой человеком форме”.
$$ = \frac{(R_C + R_E + r_o)r_{\pi} + R_C R_E + R_E \:r_o + R_E\: r_o \:\beta}{R_C + R_E + r_o} = r_{\pi } + \frac{R_C R_E + R_E \:r_o + R_E\: r_o \:\beta}{R_C + R_E + r_o} $$
$$= r_{\pi} + \frac{\frac{R_C R_E }{r_o} + R_E + R_E\:\beta}{\frac{R_C + R_E}{r_o} + 1}$$ $$ = r _ {\ pi} + \ frac {\ frac {R_C R_E} {r_o} + R_E \: (\ beta + 1)} {\ frac {R_C + R_E} {r_o} + 1} $ $ $$= r_{\pi} + \frac{R_E \left(\frac{R_C}{r_o}+(\beta + 1)\right)}{\frac{R_C + R_E}{r_o} + 1}$ $
И это конец. Также обратите внимание, что этот метод не дает нам никакой интуиции схемы.
Чтобы получить некоторую интуицию, мы могли бы попробовать применить теорему Миллера (очень сильное упрощение).
И рассматривать \$r_ o\$ как резистор с меньшим сопротивлением \$\frac{r_ o}{A_V}\$, подключенный параллельно с резистором \$R_E\$.


 38×10-23 Дж·К−1 – постоянная Больцмана;
38×10-23 Дж·К−1 – постоянная Больцмана;