Выведение формул по физике: Выражение неизвестной, учимся выражать

2\alpha=\dfrac{1+\cos{2\alpha}}2\\&&&\\ \hline \end{array}\]

$\blacktriangleright$ Формулы произведения функций: \[\begin{array}{|c|} \hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}-\cos{(\alpha+\beta)}\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}+\cos{(\alpha+\beta)}\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin{(\alpha-\beta)}+\sin{(\alpha+\beta)}\bigg)\\\\ \hline \end{array}\]

$\blacktriangleright$ Формулы суммы/разности функций: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin\alpha+\sin\beta=2\sin{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \sin\alpha-\sin\beta=2\sin{\dfrac{\alpha-\beta}2}\cos{\dfrac{\alpha+\beta}2}\\&&&\\ \cos\alpha+\cos\beta=2\cos{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \cos\alpha -\cos\beta=-2\sin{\dfrac{\alpha-\beta}2}\sin{\dfrac{\alpha+\beta}2}\\&&&\\ \mathrm{tg}\, \alpha \pm \mathrm{tg}\, \beta=\dfrac{\sin{(\alpha\pm\beta)}}{\cos\alpha\cos\beta} &&& \mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta= – \dfrac{\sin{(\alpha\pm \beta)}}{\sin\alpha\sin\beta}\\&&&\\ \hline \end{array}\]

$\blacktriangleright$ Выражение синуса и косинуса через тангенс половинного угла: \[\begin{array}{|l|r|} \hline &\\ \sin{2\alpha}=\dfrac{2\mathrm{tg}\, \alpha}{1+\mathrm{tg}^2\, \alpha} & \cos{2\alpha}=\dfrac{1-\mathrm{tg}^2\, \alpha}{1+\mathrm{tg}^2\, \alpha}\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end{array}\]

$\blacktriangleright$ Формула вспомогательного аргумента: \[\begin{array}{|c|} \hline \text{Частный случай}\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin{\left(\alpha\pm \dfrac{\pi}4\right)}\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin{\left(\alpha\pm \dfrac{\pi}6\right)}\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin{\left(x\pm \dfrac{\pi}3\right)}\\\\ \hline \text{Общий случай}\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt{a^2+b^2}\cdot \sin{(\alpha\pm \phi)}, \ \ \cos\phi=\dfrac a{\sqrt{a^2+b^2}}, \ \sin\phi=\dfrac b{\sqrt{a^2+b^2}}\\\\ \hline \end{array}\]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. \circ-\alpha)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)

3) $\sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos(-\beta)+\sin(-\beta)\cos\alpha=\sin\alpha\cos\beta-\sin\beta\cos\alpha$

4) $\mathrm{tg}\,(\alpha\pm\beta)=\dfrac{\sin (\alpha\pm\beta)}{\cos (\alpha\pm\beta)}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}=$

разделим числитель и знаменатель дроби на $\cos\alpha\cos\beta\ne 0$
(при $\cos\alpha=0 \Rightarrow \mathrm{tg}\,(\alpha\pm\beta)=\mp \mathrm{ctg}\,\beta$, при $\cos\beta=0 \Rightarrow \mathrm{tg}\,(\alpha\pm\beta)=\pm \mathrm{ctg}\,\alpha$):

$=\dfrac{\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta}{1\mp\mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta}$

Таким образом, данная формула верна только при $\cos\alpha\cos\beta\ne 0$.

5) Аналогично, только делением на $\sin\alpha\sin\beta\ne 0$, выводится формула котангенса суммы/разности двух углов. 2\alpha=\dfrac{1-\cos2\alpha}2\)

Заметим, что в данных формулах степень синуса/косинуса равна $2$ в левой части, а в правой части степень косинуса равна $1$.

$\blacktriangleright$ Вывод формул произведения функций:

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$

$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$

Получим: $\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)$

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

$\sin\alpha\sin\beta=\dfrac12\Big(\cos(\alpha-\beta)-\cos(\alpha+\beta)\Big)$

3) Сложим формулы синуса суммы и синуса разности двух углов:

$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha$

$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\sin\beta\cos\alpha$

Получим: $\sin\alpha\cos\beta=\dfrac12\Big(\sin(\alpha-\beta)+\sin(\alpha+\beta)\Big)$

$\blacktriangleright$ Вывод формул суммы/разности функций:

Обозначим $\alpha+\beta=x, \alpha-\beta=y$. Тогда: $\alpha=\dfrac{x+y}2, \ \beta=\dfrac{x-y}2$. Подставим эти значения в предыдущие три формулы:

1) $2\cos{\dfrac{x+y}2}\cos{\dfrac{x-y}2}=\cos x+\cos y$

Получили формулу суммы косинусов.

2) $2\sin {\dfrac{x+y}2}\sin {\dfrac{x-y}2}=\cos y-\cos x$

Получили формулу разности косинусов.

3) $2\sin {\dfrac{x+y}2}\cos {\dfrac{x-y}2}=\sin y+\sin x$

Получили формулу суммы синусов.

4) Формулу разности синусов можно вывести из формулы суммы синусов:

$\sin x-\sin y=\sin x+\sin(-y)=2\sin {\dfrac{x-y}2}\cos {\dfrac{x+y}2}$

5) $\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta=\dfrac{\sin\alpha}{\cos\alpha}\pm\dfrac{\sin\beta}{\cos\beta}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta}=\dfrac{\sin(\alpha\pm\beta)}{\cos\alpha\cos\beta}$

Аналогично выводится формула суммы котангенсов.

$\blacktriangleright$ Вывод формул выражения синуса и косинуса через тангенс половинного угла:

1) $\sin2\alpha=\dfrac{\sin2\alpha}1=\dfrac{2\sin\alpha\cos\alpha}{\sin^2\alpha+\cos^2\alpha}=$

(разделим числитель и знаменатель дроби на $\cos^2\alpha\ne 0$ (при $\cos\alpha=0$ и $\sin2\alpha=0$):)

$=\dfrac{2\mathrm{tg}\,\alpha}{1+\mathrm{tg}^2\,\alpha}$

2) Так же, только делением на $\sin^2\alpha$, выводится формула для косинуса. 2}\,\cos (x-\phi)\]

$\blacktriangleright$ Рассмотрим некоторые частные случаи формул вспомогательного угла:

$a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1{\sqrt2}\sin x\pm\dfrac1{\sqrt2}\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac{\pi}4\right)$

$b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac{\sqrt3}2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac{\pi}6\right)$

$c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac{\sqrt3}2\cos x\right)=2\,\sin\left(x\pm\dfrac{\pi}3\right)$

Содержание

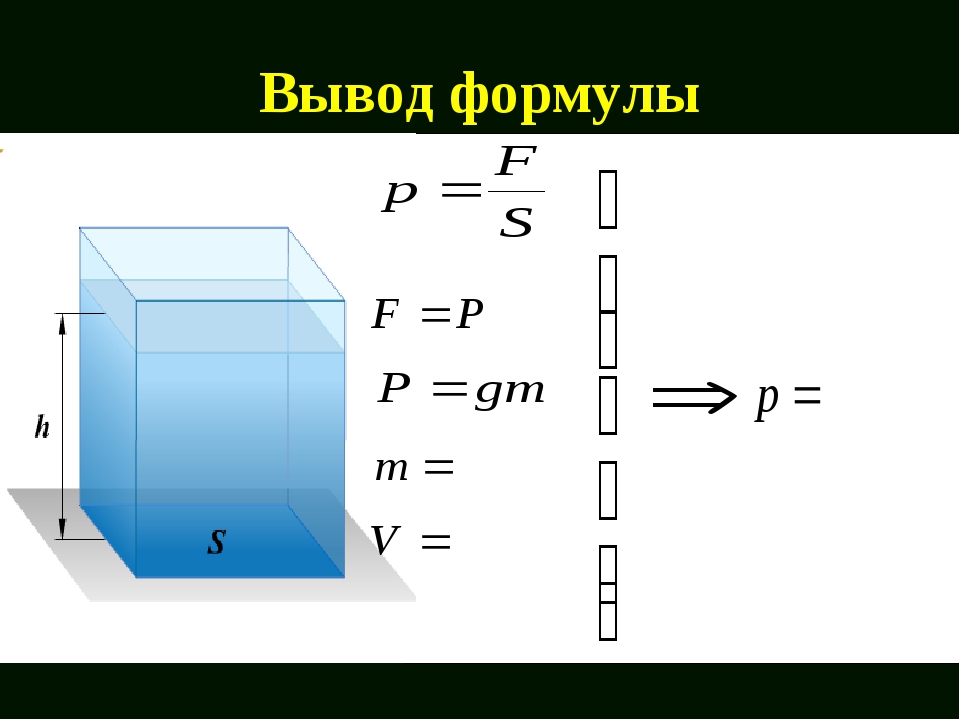
Формула работы в физике

Содержание:

Определение и формула работы

Определение

В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила совершает работу. Считают, что если скорость увеличивается, то работа является положительной, если скорость уменьшается, то работа, которую совершает сила – отрицательна. {2}}{2}(1)$$

Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи величины перемещения, которое совершает рассматриваемое тело под действием силы ($\bar{F}$).

Элементарная работа

Элментарная реабота $(\delta A)$ некоторой силы $\bar{F}$ определяется как скалярное произведение:

$$\delta A=\bar{F} \cdot d \bar{r}=F \cdot d s \cdot \cos \alpha(2)$$

$\bar{r}$ радиус – вектор точки, к которой приложена сила, $\bar{r}$ – элементарное перемещение точки по траектории, $\alpha$ – угол между векторами $d s=|d \bar{r}|$ и $d \bar{r}$. Если $\alpha$ является тупым углом работа меньше нуля, если угол $\alpha$ острый, то работа положительная, при $\alpha=\frac{\pi}{2} \delta A=0$

В декартовых координатах формула (2) имеет вид:

$$\delta A=F_{x} d x+F_{y} d y+F_{z} d z(3)$$

где F_x,F_y,F_z – проекции вектора $\bar{F}$ на декартовы оси.

При рассмотрении работы силы, приложенной к материальной точке можно использовать формулу:

$$\delta A=\bar{F} \bar{v} d t=\bar{v} d \bar{p}(4)$$

где $\bar{v}$ – скорость материальной точки, $\bar{p}$ – импульс материальной точки. р) Правой частью этого равенства является Интеграл, который окружает весь замкнутый контур (L),

окружающий границу области(/?), 262ЧАП. XXI. двойной Интеграл[346 Однако о т р и К а т е л ь н о м направлении. В соответствии с установленным нами соглашением о обозначении интеграла кривой в замкнутом контуре[n°332], мы можем переписать полученное уравнение следующим образом: (1)это уравнение выведено из предположения о правильном направлении оси, но, как можно легко видеть, предполагается, что это левое направление (только положительное направление оси). Ранее мы предполагали, что фигура

(О) является»изогнутой трапецией»типа, показанного на рисунке. 30, и справедливость Формулы (1) доказана только для таких областей. На практике это относится и к областям, ограниченным контурами более сложных форм. Достаточно предположить, что прямая фигура (о), параллельная оси Y, может быть разложена на ряд вышеупомянутых «трапеций кривой» (например, см. s G) (OK) -, x=X (y) 347]§3. Формула Грина 263 И два сегмента (RO) и (5/?), параллельно оси X. Эта формула обобщается в случае области, которая, как упоминалось выше, разложена линией, параллельной оси x, в трапецию такого рода

конечного числа кривых. Наконец, если область (O) удовлетворяет условиям обоих случаев одновременно, то есть она разлагается на трапецию конечного числа первого типа и (независимо) делится на конечное число второго типа. Ноль.-) (О) (3) Это формула Грина

). Z-это eqanie. Можно привести условия, при которых Формула (3) действительна в более обозримой форме. То есть, по формуле Грина, любые подопечные имеют кусочно-гладкий контур. Мы этого не докажем.

Смотрите также:

Решение задач по математическому анализу

формулы, определения, методы решения задач

Кинематика — это специальный раздел теоретической механики. Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.

Кинематика — описание

Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.

Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:

Путь, который преодолевает тело, существенно больше, чем его размеры.
Расстояние между телами значительно превышает их размеры.
Объект совершает поступательное движение.

Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.

Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.

Теория и формулы

Благодаря многолетним исследованиям в области кинематики ученым удалось вывести определенные закономерности движения тела. С помощью справедливых уравнений представляется возможным ответить на многие вопросы о разных характеристиках, которые изменяются либо остаются постоянными во время движения объектов.

Путь, время, скорость

Расстояние представляет собой удаленность одной точки положения тела от другой. Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.

Скорость представляет собой путь, который тело преодолело в течение единицы времени. В качестве единицы времени часто используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения.

В случае, когда в условиях задачи расстояние измеряется в метрах, а время пути — в секундах, то скорость следует рассчитывать в метрах в секунду (м/с). Для обозначения скорости используют латинскую букву $v$.

Нередко требуется определить время пути. Данный параметр обозначают с помощью латинской буквы $t$.

Важно отметить, что скорость, путь и время взаимосвязаны. При известных характеристиках скорости и времени можно определить расстояние, которое преодолело тело. Путь в данном случае равен произведению скорости и времени, рассчитывается по формуле:

$s=v\times t$

При известных величинах времени и расстояния достаточно просто определить скорость движения тела, руководствуясь следующим уравнением:

$v=\frac{s}{t}$

Равномерное движение

Равномерным движением называют движение тела, которое совершает равные перемещения в течение любых равных промежутков времени.

Источник: goodfon.ru

Скорость при равномерном движении определяется как отношение перемещения ко времени, в течение которого данное перемещение было совершено. Уравнение имеет следующий вид:

$\vec{v}=\frac{\vec{s}}{t}$

$\vec{v}=const$

Проекция вектора скорости на ось ОХ выглядит таким образом:

$v_{x}=\frac{s_{x}}{t}$

$v_{x}=const$

Если вектор скорости спроецировать на ось координат, то она будет равна быстроте изменения данной координаты:

$v_{x}=\frac{x-x_{0}}{t}$

Прямолинейное равноускоренное движение

Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.

Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:

$\vec{a}=const$

При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, необходимо выполнить следующий расчет:

$\vec{v}=\vec{v}_{0}+\vec{a}t$

Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:

$v_{x}=v_{0x}+a_{x}t$

a>0, движение является равноускоренным.

Источник: fizi4ka.ru

Во время торможения в проекции на ось ОХ скорость рассчитывают следующим образом:

$v_{x}=v_{0x}-a_{x}t$

а<0, движение является равнозамедленным.

Источник: fizi4ka.ru

Графически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:

Источник: fizi4ka.ru

График ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, которая параллельна оси времени:

график 1 находится над осью t, тело совершает разгон, ах>0;
график 2 размещен под осью t, тело тормозит, ах<0.

Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:

Источник: fizi4ka.ru

Графически скорость, характерная для равноускоренного движения тела, имеет вид прямой. График 1 направлен вверх, тело будет совершать равноускоренное движение в положительном направлении оси ОХ:

$v_{0x}>0$

$a_x>0$

$a_{1x} = tg α $

График 2 направлен вниз, тело будет двигаться равнозамедленно в положительном направлении оси ОХ:

$v_{0x}>0$

$a_x<0$

$a_{2x} = tg α $

График 3 направлен вниз, тело свершает равноускоренное движение против оси ОХ:

$v_{0x}<0$

$a_x<0$

Исходя из графика зависимости скорости от времени, определяют перемещение, которое тело преодолело в течение определенного промежутка времени $t_2-t_1$. {2}}{-2g}\)

В максимальной верхней точке тело, брошенное вверх, будет обладать нулевой скоростью, $v=0$. Для расчета времени подъема можно воспользоваться формулой:

$t=\frac{v_{0}}{g}$

Свободно падающее тело

Свободным падением называют движение тела в условиях безвоздушного пространства под действием силы тяжести.

В условиях свободного падения ускорения тел с разной массой будут равны. Данный параметр называют ускорением свободного падения. Оно всегда направлено к центру нашей планеты, то есть вертикально вниз. Величина обозначается латинской буквой g, а единицами измерения являются м/с².

Ускорение свободного падения равно 9,8 м/с². В задачах по физике допускается использовать значение g=10 м/с².

Движение по окружности с постоянной по модулю скоростью

Движением по окружности при постоянной по модулю скоростью называют простейшим видом криволинейного движения. {-1}\) (Гц).

$\nu=\frac{N}{t}$

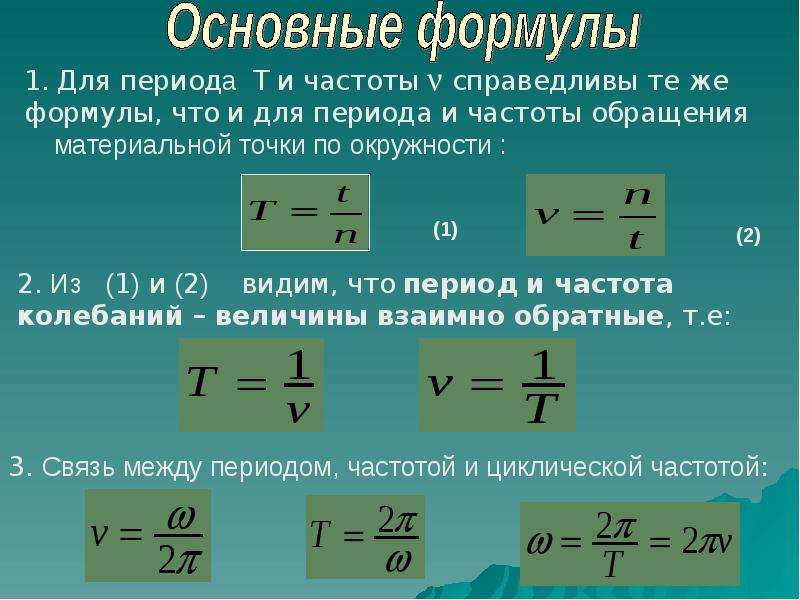
Период и частота являются взаимно обратными величинами:

$T=\frac{1}{\nu}$

$\nu =\frac{1}{T}$

Линейная скорость представляет собой скорость движения тела по окружности. Параметр обозначают латинской буквой v, единицами измерения являются м/с. Линейная скорость направлена по касательной к окружности и рассчитывается по формуле:

$v=\frac{2\pi \times R}{T}$

$R$ является радиусом окружности.

Угловой скоростью называют физическую величину, которая определяется как отношение угла поворота и времени, за которое тело совершает этот поворот. Обозначают параметр как ω. Единицами измерения угловой скорости являются рад/с. Угловая скорость определяется по формуле:

$\omega =\frac{\varphi }{t}$

$\varphi$ представляет собой угол поворота.

Источник: fizi4ka.ru

Направление угловой скорости определяют с помощью правила правого винта или буравчика. В случае, когда вращательное движение винта соотносится с направлением движения тела по окружности, то поступательное движение винта и направление угловой скорости совпадают. {2}R\)

$\omega = \frac{2\pi }{T}$

$\omega = 2\pi v$

Во время равномерного движения тела по окружности точки, расположенные на радиусе, перемещаются с равной угловой скоростью, так как радиус за одно и то же время поворачивается на одинаковый угол. В это время линейная скорость разных точек радиуса отличается в зависимости от того, насколько близко или далеко от центра они размещены:

$v_{1}=\omega r$

$v_{2}=\omega R$

$\frac{v_{1}}{v_{2}}=\frac{r}{R}$

Источник: fizi4ka.ru

При рассмотрении равномерного движения двух соединенных тел можно наблюдать отсутствие отличий в линейных скоростях, но при этом угловые скорости тел будут различны в зависимости от радиуса тела:

$\omega _{1}=\frac{v}{R_{1}}$

$\omega _{2}=\frac{v}{R_{2}}$

$\frac{\omega _{1}}{\omega _{2}}=\frac{R_{1}}{R_{2}}$

Источник: fizi4ka.ru

Движение тела, брошенного под углом к горизонту

Движение тела, которое бросили под углом к горизонту, можно представить в виде суперпозиции двух движений:

Равномерного горизонтального перемещения.

{2}}\)

Дальность полета тела соответствует уравнению:

$l=v_{0x}t=v_{0x}\sqrt{\frac{2h_{0}}{g}}$

Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:

$\tan \beta =\frac{v_{y}}{v_{x}}=\frac{-gt}{v_{0x}}$

Задачи по кинематике, их решение

Задача 1

Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч ($v_1$). Далее половину оставшегося времени он ехал со скоростью 6 км/ч ($v_2$). Остаток расстояния путник преодолел пешком со скоростью 4км/ч ($v_3$). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.

Решение

Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:

Источник: pandia.ru

$S = S_1 + S_2 + S_3$

$t = t_1 + t_2 + t_3$

На каждый отрезок пути необходимо составить уравнение движения:

$S_1 = v_1t_1$

$S_2 = v_2t_2$

$S_3 = v_3t_3$

Далее можно представить дополнительные условия задачи:

$S_1 = S_2 + S_3$

$t_2 = t_3$

$v_{sr}=\frac{S}{t}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}$

Следует преобразить формулу и подставить числовые значения:

$v_{sr}=\frac{2S_{1}}{\frac{S_{1}}{v_{1}}+\frac{2S_{1}}{v_{2}+v_{3}}}=\frac{2v_{1}\left(v_{2}+v_{3} \right)}{2v_{1}+v_{2}+v_{3}}$

$v_{sr}=\frac{2\times 12\left(6+4 \right)}{2\times 12+6+4}=7$

Ответ: средняя скорость составляет $7$ км/ч. {2}}=\frac{9,81}{0,17}=57,7\)

Ответ: камень упал с высоты $57,7$ м.

Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно применять справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.

5.4. Вывод формулы энергии связи атомных ядер

Структурную формулу связанной массы ядра преобразуем по законам комплексной алгебры, выделяя полевую массу и центральное ядро

Таким образом, ядро имеет массу

окруженную мнимой оболочкой

В мнимой оболочке движение энергетической массы происходит по циклической кривой С. В e -туннеле вихря происходит квантовый обмен между нуклонами. Согласно квантовой теории обменный квант движется со скоростью света, при этом согласно исследованиям главы 3, обменные частицы имеют общий e -туннель.

Таким образом, обменная масса мезонов квантов ядерного взаимодействия образует оболочку ядра, которая закручивается в циклонный вихрь С

₃ вокруг нуклонов и сжимает их до радиуса ядра

Согласно постулату теории относительности и аппарата комплексной алгебры обменные кванты взаимодействия находятся в пространство ядра в большей по величине размерности, чем сами нуклоны в ядре.

Создается в результате квантового обмена поле большой по величине размерности, чем то, в котором находились частицы до взаимодействия. Взаимодействие увеличивает размерность структуры.

При слиянии нуклонов в ядерную систему каждый из них выделяет в пространство сложной структуры обменную массу, образуя ядерную оболочку (с ядерными энергетическими туннелями. Обменные кванты в оболочке двигаются по простейшим пространственным траекториям типа С3 , охватывая тороидальную поверхность, и проходят e -туннель со скоростью света. Пространство нуклонов, таким образом, согласно выдвинутой гипотезе находится под давлением, создаваемым оболочкой.

В силу независимости поверхностного интеграла от аналитических функций от формы замкнутой поверхности, поверхность туннеля может быть деформирована во внутреннюю поверхность сферы. В этом случае создается оболочка толщиной d или

s. Это было обосновано в главе 1.

При взаимодействии, как уже отмечалось, пространства создают сложное образование, которое имеет свой туннель При этом туннели взаимодействующих пространств изменяют свои характеристики. При интенсивном взаимодействии туннель сложной частицы имеет меньший радиус.

На рис. 54 представлена модель взаимодействия двух нуклонных вихрей, которые образовали более сложное пространство со своей циклической кривой С3 и e -туннелем радиуса

Рис. 54. К выводу формулы “Энергия связи атомных ядер”

В результате слияния образуется кольцо взаимодействия площадью

Согласно комплексному анализу e -туннель сложной частицы с радиусом e

₂ выходит в пространство большей по величине размерности, чем размерность e -туннелей взаимодействующих пространств с туннелями e ₁, e -туннель является проекцией в пространство, в которое он вложен, что и обусловливает связность всей системы.

Кольцо S

_K находится под давлением массы обменных квантов, находящихся в оболочке сложной структуры.

Из соотношения Гейзенберга определяем максимальную толщину мнимой оболочки ядра

(5. 6.)

где

- усредненный обменный квант взаимодействия на один нуклон в ядре.

Предварительный энергетический расчет (пункт 3 табл. 2 ) обосновал введение величины усредненного обменного кванта на нуклон.

Далее объем пространства по модулю, в котором находятся нуклоны, равен

(5.7.)

где R_Я, – радиус ядра.

Объем ядра

Объем мнимой оболочки

(5.8.)

Плотность энергии в мнимой оболочке равна

(5. 9.)

Площадь сечения

циклонного e -туннеля ядра не может превышать площади сечения нуклона. Согласно модели ( рис.54) площадь , равная площади проекции нуклона, является предельной, обеспечивающей взаимодействие. В противном случае пространство разомкнется.

Таким образом, максимальная площадь кольца взаимодействия стремится к величине

где

- радиус протона.

Давление обменной массы через один e -туннель на пространство нуклонов выражается как произведение плотности энергии в оболочке

, площади кольца , высоты оболочки Н.

(5.10.)

В результате получена формула энергии связи одного циклонного вихря в ядре. За радиус нуклона

принимаем величину радиуса протона

В числителе и знаменателе формулы стоит квадрат длины, поэтому в дальнейшем коэффициент 10

^-13 опускаем.

В результате имеем

(5.11.)

Энергия связи ядра заряда Z будет равна

(5.12.)

Высота мнимой оболочки

H равна радиусу обменного кванта

Корректируем эту величину по радиусу протона

. Из ядерной физики известно

Из соотношения Гейзенберга эта величина равна

, радиус пиона , где за массу пиона на первом этапе приняли

Усредненная масса протона и нейтрона равна

Поэтому принимаем

см .

Радиус ядра

см , где -принимается равным 1.

Подставляя эти данные в формулу (5.12) получим

(5.13.)

Получили формулу энергии связи для атомных ядер элементов периодической системы как функцию массового числа А , заряда

Z ядра и величины периодичности Р. Результаты расчетов по этой формуле сведены в таблицу 1.Сходимость результатов расчета с эксперементальными данными позволяют продолжить исследования предложенной гипотезы.

Выведем формулу энергии связи атомных ядер как функцию большего количества

Параметров.

Высоту мнимой оболочки обменных квантов корректируем по радиусу нуклона

Коррекция законна, так как и нуклоны, и усредненная масса обменного кванта находятся в единой структуре взаимодействия, а согласно экспериментальным исследованиям радиус протона остается без изменения при больших энергиях взаимодействия. Формула преобразуется к виду

Формула, еще раз отметим, определяет энергию связи одного циклонного вихря. Энергия связи ядра будет иметь вид

(5.14.)

Исследуем выведенную формулу. Определим критическую величину усредненного обменного кванта на один нуклон из условия

которое после несложных преобразований дает уравнение

которое имеет один корень

Отсюда

и, следовательно, усредненная масса обменного кванта пропорциональна массе нуклона и обратно пропорциональна радиусу ядра.

Вторая производная

тождественно равна нулю,

поэтому величина

является стационарной.

Радиус атомного ядра выражается формулой

где

см.

В расчете берем r=1.4 -1.2, без коэффициента 10

^-13, как было оговорено выше. Коэффициент r₀ определен экспериментально. Радиус вихря в ядре равен

Таким образом, стационарная величина обменного кванта равна

(5.15.)

Подставим ее в формулу энергии связи

Окончательно будем иметь

Не ограничивая общности рассуждений за массу протона, примем усредненную массу протона и нейрона

Тогда

(5.16.)

Если принять

, как это рекомендует теоретическая физика, то и тогда

(5. 17.)

Откуда энергия связи одного вихря в ядре равна

.=192.2682 МэВ

Эта величина отличается от экспериментальной на 0.36282 МэВ, то есть на величину, меньшую чем масса электрона; =0,511 МэВ.

При обосновании циклонной модели атомного ядра было сделано заключение, что при распаде ядра урана происходит взрыв одного циклонного e -туннеля. Экспериментально известна энергия, которая выделяется при одном акте деления. Эта энергия, по разным источникам, заключена в интервале от 180 – 200 МэВ. Энергия связи одного циклонного вихря соответствует этому интервалу энергий. Это есть прямое доказательство выдвинутых гипотез и проведенных исследований.

Формула энергии связи (5.17) совпала с формулой, которая была выведена при обосновании циклонной структуры ядер. Поэтому табл. 2 служит одновременно экспериментальным подтверждением выведённой формулы.

В табл. 2 сведены результаты расчета по формуле (5.17.) энергии связи атомных ядер для устойчивых элементов. Из анализа таблицы следует вывод: величина периодичности формирования циклонных вихрей соответствует ранее установленной при исследовании системы элементов и составляет 9.2 - 9.9 единиц заряда, коэффициент при радиусе ядра равен рекомендуемому в физике ядра =1,25. С учетом влияния величины периодичности Р на радиус атомного ядра произведен расчет энергии связи легких ядер периодической системы элементов и их изотопов и сведен в табл. 3. Усредненная величина обменного кванта устойчиво колеблется в пределах 203 МэВ 214 МэВ. Если сопоставить эту величину с массой пиона 139,5669 МэВ, =134.9626 МэВ, то следует вывод, что три нуклона в ядре обмениваются двумя пионами.

Расчетные формулы дают достаточно стабильные результаты по энергии связи, радиусу ядра, величине обменного кванта. Ни одна из величин не выходит за пределы экспериментально установленных в ядерной физике.

Проведем исследования энергии связи ядер легких элементов от водорода до неона , где циклонный вихрь не вышел на энергию своего насыщения. Из формулы (5.14) произведем оценку радиусов ядер. Энергию связи ядер возьмем из таблицы 2 [12], определим радиус водорода в зависимости от периодичности системы, в которой он может находиться, при энергии связи, равной 2,2 МэВ

P	10	15	21	28	36	45	54	66	78
	2.57	2.25	2.0	1.83	1. 7	1.6	1.5	1.4	1.3
	107.49					108.12		108.15

Радиус ядра уменьшается с ростом величины периодичности. Величина обменного кванта остается постоянной. Произведем расчет для изотопа водорода

P	10	15	21
	1.64	1.43	1. 28
	147.37	147.39	147.5

Имеем уменьшение радиуса ядра с увеличением величины периодичности системы. Величина обменного кванта остается постоянной.

Изменение величины усредненного обменного кванта представлено ниже

Таким образом, величина усредненного обменного кванта выходит на продельную величину при окончательном формировании одного циклонного вихря в ядерной материи и составляет из расчета на три нуклона в ядре два пиона по энергетической массе.

Согласно проведенным исследованиям циклонный вихрь представляет результат разложения в пространстве энергии на два не суммируемых вектора, взаимно перпендикулярных и приложенных в разных окрестностях своего e -туннеля. Это разложение создает поле различной физической природы. В данном случае поле ядерных сил.

Так как величина обменного кванта совпала в пределе с величиной энергии связи одного циклонного вихря, то вихрь с энергией

имеет модуль, равный по величине энергии обменного кванта

200 МэВ

[Следующий параграф]

Мини оглавление:

[0], [1.1.1, 1.1.2, 1.1.3, 1.1.4, 1.1.5, 1.1.6, 1.1.7, 1.1.8, 1.2, 1.2.1, 1.2.2, 1.2.2.a, 1.2.2.b, 1.2.2.c, 1.2.2.d, 1.2.2.e, 1.2.2.f, 1.2.2.g, 1.2.2.h, 1.2.3, 1.3.1, 1.3.2, 1.3.3, 1.3.4, 1.3.5, 1.3.6, 1.4.1, 1.4.2, 1.5, 1.6, 1.7.1, 1.7.2, 1.7.3.1, 1.7.3.2, 1.7.3.3, 1.7.4.1, 1.7.4.2, 1.8.1], [2.1, 2.2],[3.1, 3.2, 3.3, 3.4.1, 3.4.2, 3.4.3, 3.4.4, 3.4.5],[4.1, 4.2, 4.3, 4.4],[5.1, 5.1.Рис.52, 5.2, 5.3, 5.4, 5.4.Т1, 5.4.Т2, 5.4.Т3, 5.5.1, 5.5.2, 5.5.3, 5.5.4],[6.1.1, 6.1.2, 6.2.1, 6.2.2, 6.2.3, 6.2. 4, 6.2.5, 6.3, 6.4.1, 6.4.2, 6.5.1, 6.5.2],[7.1, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7.1, 7.7.2, 7.8.1, 7.8.2, 7.8.3, 7.9],[8.1, 8.2.1, 8.2.2, 8.3, 8.4, 8.5, 8.6, 8.6.T1, 8.7, 8.8.1, 8.8.2, 8.8.3, 8.9.1, 8.9.2, 8.9.3, 8.10, 8.10.T2, 8.10.T3],[9.1, 9.2, 9.3, Рис.88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100],[10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, 10.11, 10.12, 10.13, 10.14, 10.15.1, 10.15.2, 10.16.1, 10.16.2, 10.17, 10.18],[11]

Размещенный материал является электронной версией книги: © В.И.Елисеев, “Введение в методы теории функций пространственного комплексного переменного”, изданной Центром научно-технического творчества молодежи Алгоритм. – М.:, НИАТ. – 1990. Шифр Д7-90/83308. в каталоге Государственной публичной научно-технической библиотеки. Сайт действует с 10 августа 1998.

E-mail: [email protected]

Движение по окружности-Теория.Скорость в физике

На главную Теория Задачи Учёные Интересные статьи Шкала скоростей

Kинематика равномерного вращения по окружности

При движении по окружности с постоянной по величине линейной скоростью v тело испытывает направленное к центру окружности постоянное центростремительное ускорение

a_ц = v²/R,

где R – радиус окружности.

Вывод формулы для центростремительного ускорения

По определению

На рисунке треугольники, образованные векторами перемещений и скоростей, подобны. Учитывая, что |r1| = |r2| = R и |v1| = |v2| = v, из подобия треугольников находим:

откуда

Поместим начало координат в центр окружности и выберем плоскость, в которой лежит окружность, за плоскость (x, y). Положение точки на окружности в любой момент времени однозначно определяется полярным углом j, измеряемым в радианах (рад), причем
x = R cos(j + j₀), y = R sin(j + j₀),

где j₀ определяет начальную фазу (начальное положение точки на окружности в нулевой момент времени).

В случае равномерного вращения угол j, измеряемый в радианах, линейно растет со временем:

j = wt,

где w называется циклической (круговой) частотой. Размерность циклической частоты: [w] = c^-1 = Гц.

Циклическая частота равна величине угла поворота (измеренном в рад) за единицу времени, так что иначе ее называют угловой скоростью.

Зависимость координат точки на окружности от времени в случае равномерного вращения с заданной частотой можно записать в виде:

x = R cos(wt + j₀),
y = R sin(wt + j₀).

Время, за которое совершается один оборот, называется периодом T.

Частота

n = 1/T.

Размерность частоты: [n] = с^-1 = Гц.

Связь циклической частоты с периодом и частотой: 2p = wT, откуда

w = 2p/T = 2pn.

Связь линейной скорости и угловой скорости находится из равенства: 2pR = vT, откуда

v = 2pR/T = wR.

Выражение для центростремительного ускорения можно записать разными способами, используя связи между скоростью, частотой и периодом:

a_ц = v2/R = w2R = 4p2n2R = 4p2R/T2.

Связь поступательного и вращательного движений

Основные кинематические характеристики движения по прямой с постоянным ускорением: перемещение s, скорость v и ускорение a. Соответствующие характеристики при движении по окружности радиусом R: угловое перемещение j, угловая скорость w и угловое ускорение a (в случае, если тело вращается с переменной скоростью). Из геометрических соображений вытекают следующие связи между этими характеристиками:

перемещение sугловое перемещение j = s/R;
скорость vугловая скорость w = v/R;
ускорение aугловое ускорение a = a/R.

Все формулы кинематики равноускоренного движения по прямой могут быть превращены в формулы кинематики вращения по окружности, если сделать указанные замены. Например:

s = vtj = wt,
v = v₀ + atw = w₀ + at.

Связь между линейной и угловой скоростями точки при вращении по окружности можно записать в векторной форме. Действительно, пусть окружность с центром в начале координат расположена в плоскости (x, y). В любой момент времени вектор R, проведенный из начала координат в точку на окружности, где находится тело, перпендикулярен вектору скорости тела v, направленному по касательной к окружности в этой точке. Определим вектор w, который по модулю равен угловой скорости w и направлен вдоль оси вращения в сторону, которая определяется правилом правого винта: если завинчивать винт так, чтобы направление его вращения совпадало с направлением вращения точки по окружности, то направление движения винта показывает направление вектора w. Тогда связь трех взаимно перпендикулярных векторов R, v и w можно записать с помощью векторного произведения векторов:

v = wR.

Задачи на эту тему

Центростремительное ускорение. Вывод формулы.

| by maxim | dx/dy

Движение по окружности часто встречается в природе и в деятельности человека. По окружности движутся спутники вокруг Земли (при упрощенном рассмотрении, на самом деле по эллиптической орбите), по окружности двигаются детали механизмов, ободы колес, шестерен, движение по окружности возникает при движении машин по закруглению дороги и так далее.

Рассмотрим равномерное движение тела по окружности.

Вектор скорости в таком случае направлен по касательной к окружности, и при движении не меняется по модулю, но, очевидно, изменяется по направлению.

Изобразим такое движение на схеме:

На схеме видно, как точка движется по окружности, из начального положения M переходит последовательно в положения М₁, М₂, М₃. Очевидно, что модуль вектора скорости в этих положениях не изменяется, а вектор всегда направлен по касательной окружности в этой точке.

Рассмотрим внимательнее перемещение точки из положения М в положение М₁ за интервал времени 𝛥t.

Отметим на рисунке векторы скоростей:

скорость точки в положении Мскорость точки в положении М₁

Эти скорости по модулю равны:

вектор изменения скорости.

Найдем изменение скорости. Для этого надо из конечного вектора скорости вычесть вектор скорости в начальной точке:

Среднее ускорение за время 𝛥t по определению (ускорение есть изменение скорости за промежуток времени) будет равно:

Найдем модуль и направление вектора ускорения.

Снова рассмотрим схему:

На схеме отмечены векторы:

вектор перемещения

И с помощью векторного вычитания отметим разность векторов скорости:

разность векторов (М₁АВ)

Для того, чтобы определить модуль среднего ускорения нам необходимо углубиться в геометрию.

Рассмотрим треугольники ОММ₁ и М₁АВ.

Это подобные треугольники. Докажем это:

во-первых, треугольники ОММ₁ и М₁АВ равнобедренные:

У треугольника ОММ₁ стороны ОМ = ОМ₁ (т. к. это радиусы окружности, по которой движется точка).

У треугольника М₁АВ стороны М₁А = АВ — так как это векторы скорости, их длина (модуль) не меняется во время движения.

Во-вторых, у треугольников ОММ₁ и М₁АВ равные углы при вершинах.

Докажем и это:

Эти углы равны, т.к. сторона ОМ треугольника ОММ₁ перпендикулярна стороне АВ треугольника М₁АВ, а сторона ОМ₁ треугольника ОММ₁ перпендикулярна стороне М₁А треугольника М₁АВ

(ведь ОМ и ОМ₁ — это радиусы окружности, а АВ и М₁А — это векторы скорости, направленные по касательной к окружности, а значит перпендикулярно радиусу).

Из курса геометрии вспомним теорему об углах с соответственно перпендикулярными сторонами: стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180º.

В нашем случае очевидно что оба угла острые, соответственно они равны.

Снова вспоминаем курс геометрии, а именно теорему о подобии треугольников: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

В нашем случае эти условия выполняются, стало быть треугольники ОММ₁ и М₁АВ подобны.

Для подобных треугольников мы можем составить пропорцию:

Вернемся из геометрии к физическому смыслу сторон наших треугольников, и запишем пропорцию в виде:

Разделим обе части равенства на промежуток времени 𝛥t:

Умножим обе части равенства на модуль скорости v:

Но ведь отношение разности скоростей к промежутку времени — это среднее ускорение:

а отношение вектора перемещения к промежутку времени — это средняя скорость:

Но нам необходимо найти модуль мгновенного ускорения. Для этого мы должны взять предельный случай, когда промежуток времени 𝛥t стремится к нулю.

В этом случае,

модуль ускорения точки в момент времени t

модуль вектора мгновенной скорости в момент времени t

Значит равенство:

мы можем записать в виде:

или:

Вот мы и вывели формулу вычисления центростремительного ускорения.

А так как в равномерном движении по окружности — радиус окружности и модуль скорости остаются постоянными, то и модуль центростремительного ускорения тоже остается постоянным.

Далее, определим направление вектора ускорения.

Из названия центростремительного ускорения очевидно, что вектор ускорения направлен к центру окружности, по которой движется точка. Но, докажем это. Снова рассмотрим схему:

Вектор ускорения будет направлен так, как направлен вектор

при приближении промежутка времени к нулю.

Если

то точка М₁ приближается к точке М, а угол 𝜑 стремится к нулю.

Это значит, что угол ВМ₁А стремится к 90°.

А это значит, что угол между вектором изменения скорости и радиусом окружности при приближении промежутка времени к нулю тоже стремится к нулю. Таким образом, вектор мгновенного ускорения стремится к центру окружности.

Для наглядности, изобразим это на схеме:

мы видим как при уменьшении промежутка времени 𝛥t направление разности векторов 𝛥v все ближе и ближе приближается к радиусу (отмечен пунктирной линией), и в конце концов совпадает с радиусом и в предельном случае, вектор изменения скорости направлен строго к центру. Соответственно, строго к центру направлен и вектор мгновенного ускорения.

Изобразим векторы ускорения на схеме:

Резюмируем: при равномерном движении точки по окружности (т.е. с постоянной линейной скоростью), модули скорости и ускорения остаются неизменными, вектор скорости постоянно направлен по касательной к окружности, а вектор центростремительного ускорения — к центру окружности.

Формула для определения центростремительного ускорения:

Вывод формулы по физике

Каковы выводы в физике?

В физике все сводится к лучшему пониманию основ. Вывод в физике определяет возникновение некоторого математического алгоритма на основе понимания любых физических явлений.

На этой странице мы узнаем о следующем:

Почему мы выводим формулы физики?
Как вывести формулы физики?
Как вывести уравнения в физике?
Вывод физических формул
Вывод физических уравнений

Почему мы выводим физические формулы?

За всем, что мы изучаем по физике, стоит определенная логика, а математика дает нам логику для понимания явлений, а когда мы видим связь между математикой и физикой, наше понимание значительно возрастает. Во время подачи заявления студенты могут столкнуться с множеством концепций, задач и математических формул. С помощью выводов учащиеся используют свои способности, творческий потенциал и хороший потенциал для поиска решений.

Как вывести уравнения физики?

Математические выводы важны при выводе физических уравнений, потому что они помогают нам понять, откуда пришло уравнение, почему это уравнение для конкретной задачи.

Как вывести физические формулы?

Физические формулы получены из наблюдений и экспериментов.

Ниже приводится несколько выводов, описывающих, как выводить физические формулы.

Вывод физических формул

Крутящий момент на стержневом магните

→

Однородное магнитное поле B представлено параллельными линиями.

NS – стержневой магнит длиной 2l и силой на каждом полюсе m.

→

Магнит удерживается под углом Ө к направлению B.

[Изображение будет загружено в ближайшее время]

→

Сила на северном полюсе = mB, вдоль B.

→

Сила на южном полюсе = mB, напротив B.

Силы равны, и они стремитесь повернуть магнит по часовой стрелке, чтобы выровнять его по

→

Следовательно, крутящий момент на стержневом магните определяется как

て = сила x перпендикулярное расстояние = mB x NA… (1)

Рассмотрим Δ NAS

SinӨ = NA / NS = NA / 2l => NA = 2lSinӨ… (2)

Подставляя значение (2) в (1)

て = mB x 2lSinӨ. Так как M = mx 2l

て = B x M sinӨ

В векторной форме уравнение (3) будет записано как

→ → →

て = B x M

→ →

Направление крутящего момента て ортогонально плоскости, содержащей M и B

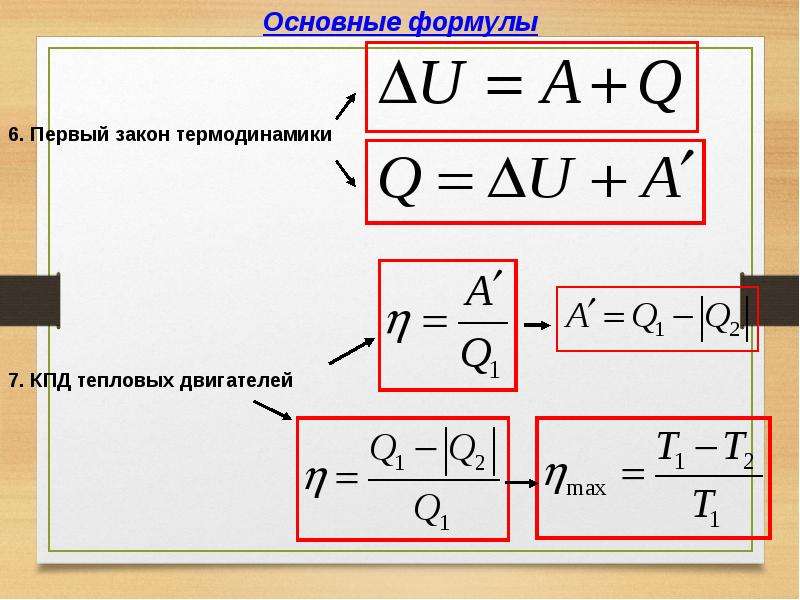
Тепловой двигатель

Тепловой двигатель – это устройство, которое без изменения преобразует тепловую энергию в механическую. во внутренней энергии системы.

Тепловая машина по существу состоит из следующих компонентов:

Предположим, Q1 = количество тепла, поглощенного рабочим телом от источника при T1 K,

Q2 = количество тепла, отведенного в сток при T2 K,

Вт – чистое количество внешней работы, выполняемой рабочим телом.

Следовательно, чистое количество поглощенного тепла,

dQ = Q1 – Q2

Поскольку рабочее вещество возвращается в исходное состояние, изменение его внутренней энергии dU будет равно нулю.

Согласно первому закону термодинамики,

dQ = dU + dW

Следовательно, dQ = dW… (1)

т.е. чистое количество поглощенного тепла = внешняя работа, выполняемая двигателем

Q1 – Q2 = W… (2)

Тепловой КПД (η)

Определяется как отношение работы, выполненной двигателем за цикл, к общему количеству тепла, поглощенного за цикл рабочим веществом от источника.

η = Чистая работа, выполненная за цикл (Вт) / Общее количество тепла, поглощенного за цикл (Q1)

= Q1- Q2 / Q1

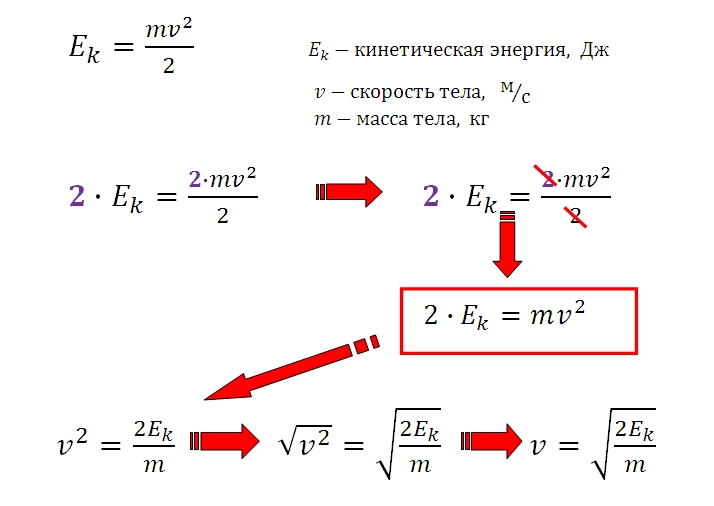
Общая энергия в S.H.M

Простое гармоническое движение – это движение, выполняемое точечной массой, на которую действует сила, пропорциональная перемещению частицы, но противоположная по знаку.

Частица, выполняющая Щ.М., обладает следующими характеристиками: потенциальная энергия и кинетическая энергия

потенциальная энергия.

Это связано с смещением частицы от ее среднего положения.

Рассмотрим частицу массы m, выполняющую S.H.M с амплитудой a и постоянной угловой частотой ω.Предположим, что через t секунд после начала из своего среднего положения смещение частицы равно y, что определяется выражением

Скорость частицы в момент t,

V = dy / dt = d (a Sin ωt) / dt = a xd (Sin ωt) / dt

Ускорение частицы в этот момент,

A = dV / dt = d (a ωCosωt) / dt = a ω d (Cosωt) / dt

A = – a ω ² Sin ωt = – ω ² y…. {y} \] hy dy = h [y ^{(1 + 1)} / (1 + 1) = hy ²/2]

Итак, проделанная работа отображается как потенциальная энергия в данный момент.Таким образом,

Kp = 1/2 hy ² (подставив значение ‘h’ из уравнения (4))

= 1/2 m ω ² y ² (положив значение ‘y’ из уравнения (1))

Kp = 1/2 м ω ² a ² Sin ² ωt…. (5)

Кинетическая энергия

Эта энергия зависит от скорости частицы.

Кинетическая энергия в момент времени t определяется как

Kk = 1/2 м V ² (Принимая значение ‘V’ из уравнения (2))

= 1/2 м (aωCosωt) ² = 1/2 га ² ω ² (1 – Sin ² ωt)

= 1/2 га ² (1 – y ² / a ²)

Kk = 1/2 м ω ² (a ² – 1 – y ²)

Общая энергия = Kp + Kp

= 1 / ky ² + 1/2 м ω ² (a ² – 1 – y ²) = 1/2 га ² = 1/2 м ω ² a ²

= 1/2 м (2 ሀ π) ² a ²

Список важных физических выводов в классе 12

Здесь

Тема	Формула	Описание
Скорость дрейфа	Vd = 1 / て = ½ (eE / m) (て)	Vd пропорционально электрическому полю E и столкновению. время て
Закон Био-Савара (Величина магнитного поля)	дБ = μo / 4π (idl Sinθ / r ²	Здесь θ – угол → → между dl и r
Закон Кулона в векторной форме	→ → F = kq1q2 r / r ³	Здесь q1 и q2 – заряды частиц, r – расстояние между → их, r – вектор положения испытывающей силу частицы
Циклотронная частота	ሀ = 1 / T = qB / 2 πm Ω = 2 πf = qB / m	Здесь f – циклотронная частота, T – период обращения.
Коэффициент добротности резонансного контура	Q = 1 / R ✓L / C Q принимается как умножение напряжения	Здесь Q – отношение напряжения, развиваемого на индуктивность или емкость в резонансе с приложенным напряжением, которое прикладывается к R.
Движущаяся или наведенная ЭДС	E = -vLB	ЭДС, индуцированная движением проводника по магнитному полю. поле – это двигательная электродвижущая сила.Это уравнение верно до тех пор, пока скорость, поле и длина взаимно перпендикулярны.
Волновое уравнение Шредингера	ih ძ Ψ / ძ t = – h ² / 2m ძ ² / ძ x ² + V (x). (X, t)	, Ψ = Ae ⁱ (kx-ωt) K = волновое число = 2π / λ Гамильтониан системы T = PE + К.Е. E = hω
Эксперимент Юнга с двойной щелью	Полоса пропускания, β = (D / d) λ	Расстояние между последовательными яркими полосами (n + 1) и n-го порядка. xn + 1 – xn = [(D / d) [(n + 1) λ] – (D / d) [(n) λ]]] = (D / d) λ

Вывод физических уравнений

Уравнение равноускоренного движения методом расчетов

Рассмотрим тело, совершающее линейное движение с равномерным ускорением a.

Пусть v и v2 – скорость тела в момент времени t1 и t2 соответственно.

Соотношение скорость-время

Пусть в момент времени t скорость равна v, а изменение скорости равно dv в интервале времени dt.{t} \] (v0 + at) dt

s – s0 = v0t + ½ at2

Список важных физических выводов в классе 11

Закон Сток9 = 6πηrv

vt = 2 a ² (ρ -σ) / 9η

Тема	Формула	Описание
Ускорение свободного падения и его изменение с глубиной	gd = g (1- d / R)	Это выражение для ускорения свободного падения на глубине ниже поверхности земли и в центре земли d = R.
Закон Гука	Fs = hx	Fs = усилие пружины h = постоянная пружины x = растяжение или сжатие струны
	Значение k для сферического тела = 6π F = Сила вязкости, действующая на сферическое тело, падающее через жидкость. vt = Конечная скорость.ρ и σ – массовые плотности шара и жидкости соответственно.
Уравнение траектории снаряда	Y = x tanθ −g × x ²/ 2u ² cos ² θ 3	Траектория

Резюме

Деривация означает действие по получению чего-либо из источника или происхождения.
Путем вывода мы находим логическую связь между природным явлением и математическим описанием этого явления.В целом это указывает на важный вывод о самой природе.

Как получить формулу

Решит ли искусственный интеллект все проблемы, сделав научные формулы излишними? Авторы этой книги утверждают, что их формулировка по-прежнему играет жизненно важную роль в понимании законов природы. Чтобы вывести формулу, нужно выполнить ряд шагов; наконец, проверьте правильность результата, прежде всего, путем анализа предельных случаев.Книга посвящена разгадке этого механизма.

Математика – «королева всех наук», но студенты сталкиваются с множеством препятствий в изучении предмета – знакомством с доказательствами сотен теорем, загадочными символами и техническими процедурами, полезность которых не очевидна заранее. Те, кто интересуется физическими науками, могут потерять мотивацию, не видя леса за деревьями.

Как вывести формулу – это попытка вовлечь этих учащихся, излагая математические методы простым языком, с упором на навыки, а не на технические знания.Основываясь на интуиции и здравом смысле, а не на математической строгости, он обучает студентов с нуля, используя подходящие примеры, многие из которых взяты из физических наук.

Эта книга предлагает новый интересный взгляд на то, каким может быть учебник математики, включая исторические факты и юмор в дополнение к материалу.

исправлений
исправлений (756 КБ)

Примеры глав
Предисловие
Глава 1: Основные функции

Запрос копии

Состав:

Предисловие
Введение
Из базового лагеря – понимание функций и переменных: первый этап:
- Основные функции
- Полиномиальные разложения: когда они работают, а когда нет
- Ограничения, дифференциация и интеграция
- Как проверить себя: анализ предельных случаев
- Определенные интегралы как функции
- Функции распределения вероятностей и функции фильтрации как предельные случаи
- Векторы и введение в векторное исчисление
- Понимание последовательностей и серий
- Комплексные числа
- Размерность и масштаб
- Заключительные замечания
- Проблемы
Из лагеря 1: более глубокое понимание функций и решение уравнений:
- Введение в функции двух или более переменных
- Ряды Фурье и интегралы
- Линейные уравнения и определители
- Матрицы и симметрия
- Решение нелинейных, алгебраических и трансцендентных уравнений
- Введение в обыкновенные дифференциальные уравнения
- Дополнительные методы оценки интегралов и гамма-функции
- Функции комплексной переменной
Заключительные замечания
Проблемы
Инструкции по доступу к наброскам решений

Читательская аудитория: Продвинутые школьники и школьники-энтузиасты, готовящиеся к поступлению в университеты, специализирующиеся на естественных науках – A-level (Великобритания), Abitur (Германия), Lycée (Франция), старшая школа (США) и тому подобное; учителя и воспитатели; студенты; преподаватели вузов.

«В этой книге авторы преподают искусство прикладной физико-математической математики на продвинутом уровне бакалавриата. В отличие от традиционных книг по математике, формальные выводы и теоремы заменяются отработанными примерами с интуитивными решениями и приближениями, учитывая некоторое знакомство с физикой и Таким образом, книга охватывает широкий круг тем, таких как векторное исчисление, дифференциальные и интегральные уравнения, линейная алгебра, вероятность и статистика, функции комплексных переменных, масштабирование и анализ размерностей.Систематические методы асимптотического приближения представлены в простых практических терминах, демонстрируя ценность анализа «предельных случаев». В отличие от большинства учебников по естествознанию или инженерии, примеры физических упражнений охватывают столь же широкий диапазон, позволяя сообразительному читателю оценить универсальную красоту прикладной математики, одновременно изучая полезные методы вывода формулы ».

Мартин З. Базант
Профессор математики и
Э.Г. Роос, профессор химической инженерии
Массачусетский технологический институт

«Для многих студентов естественных наук преподавание математики отделено от реального изучения науки.Для них математика – всего лишь умственное препятствие, которое нужно преодолевать на экзаменах. Напротив, эта книга показывает студенту, что математика является и всегда была языком науки, потому что только с помощью математического анализа модель явления или процесса может быть построена и проверена на эксперименте. Эта книга, объединяющая математические науки в науку, показывает студентам, как развивается понимание в науке и что это влечет за собой “.

Адриан Саттон FRS
Заслуженный профессор физики
Имперский колледж Лондона

«Самая большая проблема понимания научных и инженерных предметов для студентов – это отсутствие надлежащей математической подготовки.Мы учим их понимать науку, но проблема в том, что наш язык может быть для них слишком сложным, и сообщение часто теряется. У студентов и ученых раньше не было ресурсов для преодоления этой трудности. Эта книга очень элегантно и привлекательно восполняет этот пробел. Я настоятельно рекомендую эту книгу всем, кто заинтересован в понимании механизмов природных явлений, и считаю, что эта книга должна быть у каждого студента естественных наук и инженерного дела! »

Коломейский Анатолий Б
Университет Райса

исправлений
исправлений (756 КБ)

Примеры глав
Предисловие
Глава 1: Основные функции

Дополнительные материалы

Доступ к следующим материалам предоставляется при покупке этой книги.

Краткое изложение решений, часть 1.pdf (1 МБ)
Краткое изложение решений, часть 2.pdf (1 МБ)

Интернет-доступ предоставляется автоматически, если вы покупаете электронную книгу через Интернет на сайте www.worldscientific.com.

Если вы приобрели печатную копию этой книги или электронную книгу через другие каналы продаж, следуйте инструкциям, изложенным в книге, для доступа к дополнительным материалам.

Ваш токен доступа был бы активирован под вашим именем пользователя, когда вы купили электронную книгу непосредственно на веб-сайте WSPC ИЛИ когда вы щелкнули ссылку активации URL-адреса, предоставленную в печатной или электронной книге.Следовательно, для последующего доступа к дополнительным материалам, пожалуйста, просто войдите в систему с тем же именем пользователя, и вы получите доступ.

По любым вопросам, связанным с доступом, обращайтесь по электронной почте [адрес электронной почты защищен].

Equations of Motion – The Physics Hypertextbook

Обсуждение

постоянное ускорение

Для точности этот раздел следует называть «Одномерные уравнения движения для постоянного ускорения». Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки.Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.

Учитывая, что мы живем в трехмерной вселенной, в которой единственная константа – это изменение, у вас может возникнуть соблазн сразу отказаться от этого раздела. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время – ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Об этом я могу сказать с абсолютной метафизической уверенностью.

Так что же тогда хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект путешествовал или будет двигаться по прямому пути с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать фактически одномерным, если для задействованных объектов существует только одна степень свободы .Дорога может извиваться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы – свободу двигаться в одном или противоположном направлении. (Вы не можете ездить по дороге по диагонали и надеетесь остаться на ней надолго. ) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.

Наша цель в этом разделе – вывести новые уравнения, которые можно использовать для описания движения объекта в терминах его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ( т ). Их можно объединить в пары: скорость-время, положение-время и скорость-положение. В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.

Поскольку мы имеем дело с движением по прямой линии, направление будет обозначаться знаком – положительные величины указывают в одну сторону, а отрицательные величины указывают в противоположную сторону.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, если одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.

скорость-время

Связь между скоростью и временем проста при равномерно ускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, когда ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиваться вдвое на эту величину в два раза быстрее. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы должны быть в состоянии увидеть уравнение уже мысленным взором.

Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начнем с определения ускорения.

Расширьте ∆ v от до v – v ₀ и конденсируйте ∆ t до t .

Затем найдите v как функцию от t .

v = v ₀ + at [1]

Это первое уравнение движения . Он записывается как полином – постоянный член ( против ₀), за которым следует член первого порядка ( на ).Поскольку наивысший порядок равен 1, правильнее называть его линейной функцией .

Символ v ₀ [vee naught] называется начальной скоростью или скоростью a раз t = 0. Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшее определение было бы сказать, что начальная скорость – это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос “Какая начальная скорость?” “Это зависит от обстоятельств”. Это оказывается ответом на множество вопросов.

Символ v – это скорость через некоторое время t после начальной скорости. Его часто называют конечной скоростью , но это не делает его «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость обозначена символом v ? Если вы внимательно слушали, значит, вы должны были ожидать ответа. Это зависит. Это может быть скорость метеора, когда он проходит мимо Луны, входит в атмосферу Земли или ударяется о поверхность Земли. Это также может быть скорость метеорита, находящегося на дне кратера. (В этом случае v = 0 м / с.) Является ли какое-либо из этих значений конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из дыры в земле и уехать вместе с ним.Это актуально? Наверное, нет, но это зависит от обстоятельств. Для такого рода вещей нет правил. Вы должны проанализировать текст задачи на предмет физических величин, а затем присвоить значение математическим символам.

Последняя часть этого уравнения на – это изменение скорости по сравнению с начальным значением. Вспомните, что a – это скорость изменения скорости, а t – это время после некоторого начального события _{. Ставка раз время меняется. Учитывая, что объект ускоряется со скоростью 10 м / с ², через 5 с он будет двигаться на 50 м / с быстрее.Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…}

15 м / с + 50 м / с = 65 м / с

позиция-время

Смещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как и дольше). Иди дальше. Ускорение усугубляет эту простую ситуацию, поскольку скорость теперь также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит нелепо. «Смещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.”Время является двойным, поэтому смещение пропорционально квадрату времени. Автомобиль, разгоняющийся в течение двух секунд, преодолеет в четыре раза расстояние, превышающее расстояние автомобиля, ускоряющегося всего за одну секунду (2 ² = 4). Автомобиль, ускоряющийся в течение трех секунды покрыли бы расстояние в девять раз большее (3 ² = 9).

Если бы это было так просто. Этот пример работает, только когда начальная скорость равна нулю. Смещение пропорционально квадрату времени, когда ускорение постоянное, а начальная скорость равна нулю.Истинное общее утверждение должно учитывать любую начальную скорость и то, как она менялась. Это приводит к ужасно запутанному утверждению соразмерности. Смещение прямо пропорционально времени и пропорционально квадрату времени, когда ускорение постоянно. Функция, которая одновременно является линейной и квадратной, называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Смещение является квадратичной функцией времени при постоянном ускорении

Формулировки пропорциональности полезны, но не столь общие, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой проблемы. Один из способов понять их – использовать алгебру.

Начнем с определения средней скорости.

Увеличьте ∆ s от до s – s ₀ и конденсируйте ∆ t до t .

Определите позицию.

с = с ₀ + vt [a]

Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона .Я предпочитаю второй вариант, поскольку правило может применяться к любой величине, которая изменяется с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже, Оксфорд, английским философом, математиком, логиком и калькулятором Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится на полпути между ее конечным и начальным значениями.

v = ½ ( v + v ₀) [4]

Подставьте первое уравнение движения [1] в это уравнение [4] и упростите его, исключив v .

v = ½ [( v ₀ + при ) + v ₀]

v = ½ (2 v ₀ + 3 4) 9 v = v ₀ + ½ at [b]

Теперь замените [b] на [a], чтобы исключить v [vee bar].

с = с ₀ + ( v ₀ + ½ при ) t

И, наконец, найдите s как функцию от t .

s = s ₀ + v ₀ t + ½ при ² [2]

Это второе уравнение движения . Он записывается как полином – постоянный член ( s ₀), за которым следует член первого порядка ( v ₀ t ), за которым следует член второго порядка (½ at ² ). Поскольку наивысший порядок равен 2, правильнее называть его квадратичным .

Символ s ₀ [ess naught] часто рассматривается как начальная позиция . Символ s – это позиция t позже. Если хотите, вы можете назвать ее конечной позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.

∆ s = v ₀ t + ½ при ² [2]

скорость-позиция

Каждое из первых двух уравнений движения описывает одну кинематическую переменную как функцию времени.По сути…

Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
Смещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ т ²).

Объединение этих двух утверждений дает начало третьему, не зависящему от времени. При замене должно быть очевидно, что…

Смещение пропорционально квадрату скорости при постоянном ускорении (∆ s ∝ v ²).

Это утверждение особенно важно для безопасности вождения. Когда вы вдвое увеличиваете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить. Увеличьте скорость втрое, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.

Концептуальное введение выполнено. Пришло время вывести формальное уравнение.

метод 1

Объедините первые два уравнения таким образом, чтобы исключить время как переменную. Самый простой способ сделать это – начать с первого уравнения движения…

v = v ₀ + at [1]

решить на время…

и подставляем во второе уравнение движения…

s = s ₀ + v ₀ t + ½ при ² [2]

нравится…

с =	s ₀ + v ₀	⎛ ⎜ ⎝	v – v ₀	⎞ ⎟ ⎠	+ ½ a	⎛ ⎜ ⎝	v – v ₀	⎞ ² ⎟ ⎠

с – с ₀ =	vv ₀– v ₀ ²	+	v ²-2 vv ₀ + v ₀ ²
			2 а

2 a ( s – s ₀) = 2 ( vv ₀ – v ₀ ²) + (^{9 v 2} 8) + (^{9 v 2} 2 vv ₀ + v ₀ ²)

2 a ( s – s ₀) = v ²– v ₀ ²

Возведите объект в квадрат скорости, и все готово.

v ² = v ₀ ² + 2 a ( s – s ₀) [3]

Это третье уравнение движения . Еще раз, символ s ₀ [ess naught] – это начальная позиция , а s – это позиция через некоторое время t позже. Если хотите, вы можете написать уравнение, используя ∆ s – изменение положения на , смещение на или на расстояние в зависимости от ситуации.

v ² = v ₀ ² + 2 a ∆ s [3]

метод 2

Более сложный способ вывести это уравнение – начать со второго уравнения движения в этой форме…

∆ s = v ₀ t + ½ при ² [2]

и решите ее на время. Это непростая работа, поскольку уравнение квадратично. Переставьте термины следующим образом…

½ при ² + v ₀ t – ∆ s = 0

и сравните его с общей формой квадратичной.

топор ² + bx + c = 0

Решение этой задачи дает известное уравнение…

x =	– b ± √ ( b ² – 4 ac )
	2

Замените символы в общем уравнении эквивалентными символами из нашего преобразованного второго уравнения движения…

т =	– v ₀ ± √ [ v ₀ ² – 4 (½ a ) (- ∆ s )]
	2 (½ a )

почисти немного…

т =	– v ₀ ± √ ( v ₀ ² + 2 a ∆ s )

, а затем подставьте его обратно в первое уравнение движения.

v = v ₀ + at [1]

v = v ₀ + a	⎛ ⎜ ⎝	– v ₀ ± √ ( v ₀ ² + 2 a ∆ s )	⎞ ⎟ ⎠

Stuff отменяется, и мы получаем это…

v = ± √ ( v ₀ ² + 2 a ∆ s )

Выровняйте обе стороны, и все готово.

v ² = v ₀ ² + 2 a ∆ s [3]

Это было не так уж плохо, не так ли?

исчисления выводов

Исчисление – это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение – это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорости-времени. Если предположить, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].

	=
дв	=	a dt

	=
v – v ₀	=	при

v	=	v ₀ + at [1]

Опять же, по определению, скорость – это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].

v dt

( v ₀ + at ) dt

т
⌠ ⌡	( v ₀ + at ) dt
0

с – с ₀

v ₀ t + ½ при ²

s ₀ + v ₀ t + ½ at ² [2]

В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.

Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…

Второе уравнение движения связывает положение со временем. Это произошло от этой производной…

Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…

Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Он также равен самому себе, умноженному на 1. Мы будем использовать специальную версию 1 (^dt _dt) и специальную версию алгебры (алгебру с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению (^dv _dt), и другую производную, равную обратной скорости (^dt _ds).

дв	=	дв	1
DS		DS
дв	=	дв	дт
DS		DS	дт
дв	=	дв	дт
DS		дт	DS
дв	=		1
DS			в

Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем, когда ускорение постоянное…

		=
в дв		=	а DS

		=
½ ( v ²– v ₀ ²)		=	a ( s – s ₀)

	v ²	=	v ₀ ² + 2 a ( s – s ₀) [3]

Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.Однако на самом деле это сработало только потому, что ускорение было постоянным – постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.

v =	v ₀ + at	[1]
		+
с =	s ₀ + v ₀ t + ½ at ²	[2]
		=
v ² =	v ₀ ² + 2 a ( s – s ₀)	[3]

Математика кругового движения

Есть три математические величины, которые будут для нас в первую очередь интересны, когда мы будем анализировать движение объектов по кругу.Эти три величины – скорость, ускорение и сила. Скорость объекта, движущегося по кругу, определяется следующим уравнением.

Ускорение объекта, движущегося по кругу, можно определить с помощью одного из двух следующих уравнений.

Уравнение справа (вверху) получено из уравнения слева путем подстановки выражения для скорости.

Чистая сила ( F _net ), действующая на объект, движущийся по кругу, направлена внутрь.Хотя на объект может действовать более одной силы, их векторная сумма должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если таковая имеется), так что внешняя сила компенсируется, и неуравновешенная сила направлена в направлении центра круга. Чистая сила связана с ускорением объекта (как всегда) и, таким образом, определяется следующими тремя уравнениями:

Уравнения в середине (вверху) и справа (вверху) получены из уравнения слева путем подстановки выражений для ускорения.

Этот набор уравнений кругового движения можно использовать двумя способами:

Эти два способа показаны ниже.

Уравнения как руководство к мышлению

Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение второго закона Ньютона определяет, как ускорение связано с чистой силой и массой объекта.

Соотношение, выражаемое уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. Фактически, если бы чистая сила была увеличена в 2 раза, уравнение предсказало бы, что ускорение увеличится в 2 раза. Точно так же, если бы чистая сила была уменьшена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза.

Уравнение второго закона

Ньютона также показывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта. Другими словами, чем больше значение массы, тем меньше будет значение ускорения. По мере увеличения массы ускорение уменьшается. Фактически, если бы масса была увеличена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса была уменьшена в 2 раза, уравнение предсказало бы, что ускорение будет увеличиваются в 2 раза.

Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на вторую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Прогностическая способность уравнения усложняется, когда одна из величин, включенных в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее чистую силу ( F _net ) со скоростью ( v ) объекта, движущегося с равномерным круговым движением.

Это уравнение показывает, что чистая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. При постоянной массе и радиусе сеть F пропорциональна скорости ² .

Фактор, на который изменяется чистая сила, является квадратом фактора, на который изменяется скорость. Впоследствии, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза.И если скорость объекта уменьшается вдвое (уменьшается в 2 раза), требуемая полезная сила уменьшается в 4 раза.

Уравнения как рецепт решения проблем

Математические уравнения, представленные выше для движения объектов по кругу, могут использоваться для решения задач кругового движения, в которых должна быть определена неизвестная величина. Процесс решения задачи кругового движения очень похож на любую другую задачу в классе физики.Процесс включает в себя внимательное прочтение проблемы, идентификацию известной и требуемой информации в переменной форме, выбор соответствующего уравнения (й), замену известных значений в уравнение и, наконец, алгебраическое манипулирование уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам кругового движения.

Пример задачи № 1

Автомобиль массой 900 кг, движущийся со скоростью 10 м / с, совершает разворот по окружности с радиусом 25.0 мес. Определите ускорение и чистую силу, действующую на автомобиль.

Решение этой проблемы начинается с выявления известной и запрошенной информации.

Известная информация:

м = 900 кг
v = 10,0 м / с
R = 25,0 м

Запрошенная информация:

а = ????
F _net = ????

Чтобы определить ускорение автомобиля, используйте уравнение a = v ² / R.Решение выглядит следующим образом:

а = v ² / R

a = (10,0 м / с) ² / (25,0 м)

a = (100 м ² / с ²) / (25,0 м)

a = 4 м / с ²

Чтобы определить чистую силу, действующую на автомобиль, используйте уравнение F _net = m • a. Решение следующее.

F _net = m • a

F _нетто = (900 кг) • (4 м / с ²)

F _нетто = 3600 Н

Пример задачи № 2

Полузащитник весом 95 кг делает разворот на футбольном поле.Полузащитник прокладывает путь, который представляет собой часть круга радиусом 12 метров. Полузащитник делает четверть оборота по кругу за 2,1 секунды. Определите скорость, ускорение и чистую силу, действующую на полузащитника.

Решение этой проблемы начинается с выявления известной и запрошенной информации.

Известная информация:

м = 95.0 кг
R = 12,0 м
Пройдет 1/4 окружности за 2,1 с

Запрошенная информация:

v = ????
а = ????
F _net = ????

Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d составляет одну четвертую окружности, а время равно 2.1 с. Решение выглядит следующим образом:

v = d / t

v = (0,25 • 2 • pi • R) / т

v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)

v = 8,97 м / с

Чтобы определить ускорение полузащитника, используйте уравнение a = v ² / R. Решение следующее:

а = v ² / R

a = (8,97 м / с) ² / (12,0 м)

а = (80.5 м ² / с ²) / (12,0 м)

a = 6,71 м / с ²

Чтобы определить чистую силу, действующую на полузащитника, используйте уравнение F _net = m • a. Решение следующее.

F _нетто = м * а

F _нетто = (95,0 кг) * (6,71 м / с ²)

F _нетто = 637 N

В Уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных сценариев движения в реальном мире, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.

Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства однородного кругового движения. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся в интерактивном режиме исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу.

Проверьте свое понимание

1. Анна Литикал практикует демонстрацию центростремительной силы дома. Она наполняет ведро водой, привязывает его к прочной веревке и крутит по кругу. Анна вращает ведро, когда оно наполовину заполнено водой, а когда оно на четверть. В каком случае для вращения ведра по кругу требуется больше силы? Объясните, используя уравнение как «руководство к размышлениям».

2.Линкольн Континенталь и Юго делают поворот. Линкольн в четыре раза массивнее Юго. Если они совершают поворот с одинаковой скоростью, то как сравнить центростремительные силы, действующие на две машины? Объяснять.

3. Cajun Cliffhanger в Great America – это аттракцион, в котором пассажиры выстраиваются по периметру цилиндра и вращаются по кругу с высокой скоростью поворота. Когда цилиндр начинает очень быстро вращаться, пол убирается из-под ног гонщиков.Какое влияние удвоение скорости оказывает на центростремительную силу? Объяснять.

4. Определите центростремительную силу, действующую на ребенка весом 40 кг, который совершает 10 оборотов вокруг Cliffhanger за 29,3 секунды. Радиус ствола – 2,90 метра.

советов по запоминанию формул по химии, математике и физике

1.Просмотрите и ознакомьтесь с

В физике есть повторяющиеся переменные, например, «r» или «R» используется для радиуса, и это часто встречается в большинстве формул. Итак, сначала составьте список и изучите, какая переменная для чего предназначена, вот как вы с ними познакомитесь. Просто сначала просмотрите их и попытайтесь запомнить, какая формула относится к какой главе и что обозначают переменные. Не просто грабите. Вы должны учиться, записывая формулы по крайней мере 5 раз для каждой главы, и повторять это по крайней мере в течение недели, по одному часу в день.Это поможет вам привыкнуть к ним, и это будет менее сложно, поскольку наши глаза улавливают картину того, что мы видим, поэтому их написание может быть полезным.

2. Применяйте и практикуйтесь в решении

Практика поможет вам научиться применять формулы правильным образом и в правильной последовательности одновременно. Решая задачи на основе формулы, вы поймете, как ее использовать и где какую формулу использовать. Кроме того, по мере решения задач вы автоматически запоминаете формулы.

3. Научитесь выводить формулы

Ты не можешь все вспомнить. Следовательно, вам нужно уменьшить нагрузку на запоминание сотен формул вместе. Лучший способ сделать это – вывести формулу. Есть формулы, которые можно получить из других формул, и это очень упрощает процесс запоминания. Краткий список формул в главе “Круговое движение” или в любой другой главе физики поможет вам получить множество других формул, как показано ниже:

а. d (диаметр круга в метрах (м)) = 2r (радиус круга в м)
г. v (скорость движения в м / с) = ωr
г. a (величина ускорения движения в м / с2) = ωv
г. ω (угловая частота s ^-1) = 2πf
e. T (время оборота в секундах) = 1 / f (количество оборотов в единицу времени в с ^-1 / Гц)
ф. C (длина окружности в м) = 2πr

Например,
v = ωr и a = ωv
может дать вам соотношение между a и r
a = ω ² r , поэтому из двух основных формул вы можете получить другую формулу, которую вам не нужно запоминать .

4. Понимание структуры и единиц формулы

Структура:

Считай, а = Ф / м

Здесь сила находится на вершине, поскольку вам нужна сила, чтобы быстро переместить объект, чтобы он имел преимущество, в то время как масса должна перемещаться с силой, поэтому вам нужна сила для ускорения массы.

Принимая во внимание, что a = m / F имеет преимущество, но помните, что без силы объект не может двигаться, поэтому масса не может быть сверху. Так что здесь должно быть что-то не так в формуле.

Квартир:

Опять же, a = F / m

Единица ускорения: a = м / с ² (поскольку a = vω, ω = 1 / с и v = м / с ∴ a = м / с ²)

Итак, когда вы решаете единицы F и m, вы должны получить единицу ускорения.

Теперь F – сила, а m – масса объекта;

F = кг · м / с ² или Ньютон и м (масса) = кг

, поэтому, когда вы подставляете в,

a = (Ф / м) = (кг.м / кг.с ²) = м / с ²

5. Делайте заметки

Сделайте заметки с важными формулами и приклейте их на стену, в шкаф или рядом с зеркалом. Это поможет вам просмотреть и не забыть формулы.

6. Визуализируйте и проверьте себя

Выберите пару задач и напишите формулу, которую вы будете использовать для каждой из них. Если вы столкнулись с проблемой, при которой вы не помните формулу, отметьте ее красным в составленном вами списке, чтобы не забыть ее снова.Пройдите тест на Embibe и посмотрите, сможете ли вы применить формулы. Также не используйте список формул при решении задач.

3.4 Движение с постоянным ускорением – University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

Определите, какие уравнения движения следует использовать для решения неизвестных.
Используйте соответствующие уравнения движения, чтобы решить задачу о преследовании двух тел.

Вы можете догадаться, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.

Обозначение

Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, взятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 – это начальная позиция , а v0v0 – начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t – это последнее время , x – это конечное положение , а v – это конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,

Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,

, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.

Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть

a– = a = постоянная. a– = a = постоянная.

Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение является постоянным в большом количестве ситуаций.Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.

Смещение и положение от скорости

Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:

Подставляя упрощенные обозначения для ΔxΔx и ΔtΔt, получаем

v– = x − x0t.v– = x − x0t.

Решение относительно x дает нам

x = x0 + v – t, x = x0 + v – t,

3.10

, где средняя скорость

v– = v0 + v2.v– = v0 + v2.

3.11

Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой простое среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:

v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.

В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).

Фигура 3,18 (а) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч 22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.

Решение для окончательной скорости по ускорению и времени

Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:

Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает

а = v − v0t (константа). a = v − v0t (константа).

Решение для v дает

v = v0 + at (constanta). v = v0 + at (constanta).

3,12

Пример 3,7

Расчет конечной скорости

Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с ² за 40,0 с. Какова его конечная скорость?

Стратегия

Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.

Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.

Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.

Решение

Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.

Рисунок 3.19 представляет собой эскиз, на котором показаны векторы ускорения и скорости.

Фигура 3,19 Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.

Значение

Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.

Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что

Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v ₀), как и ожидалось (другими словами, скорость постоянна)
Если a отрицательное, то конечная скорость меньше начальной скорости

Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.

Решение для конечного положения с постоянным ускорением

Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с

Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает

v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.

Поскольку v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем

v– = v0 + 12at.v– = v0 + 12at.

Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает

х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).

3,13

Пример 3,8

Расчет смещения ускоряющегося объекта

Драгстеры могут развивать среднее ускорение 26,0 м / с ². Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?

Фигура 3.20 Пилот американской армии Top Fuel Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд.Фото любезно предоставлено Армией США.)

Стратегия

Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы примем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.

Фигура 3,21 Эскиз разгонного драгстера.

Решение

Во-первых, нам нужно определить известные. Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с ² и t задается как 5,56 с.

Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:

x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.

Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до

Подстановка идентифицированных значений на и t дает

х = 12 (26.0 м / с2) (5,56 с) 2 = 402 м. X = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.

Значение

Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.

Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:

Смещение зависит от квадрата истекшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.

Расчет конечной скорости по расстоянию и ускорению

Четвертое полезное уравнение может быть получено путем другой алгебраической манипуляции с предыдущими уравнениями. Если мы решим v = v0 + atv = v0 + at для t , мы получим

Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем

v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).

3,14

Пример 3.9

Расчет конечной скорости

Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.

Стратегия

Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.

Решение

Сначала мы идентифицируем известные значения. Мы знаем, что v ₀ = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x – x ₀ = 402 м (это был ответ в примере 3.8). Среднее ускорение было равно , а = 26.0 м / с ².

Во-вторых, мы подставляем известные значения в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :

v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).

Таким образом,

v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.

Значение

Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.

Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:

Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
При фиксированном ускорении машина, едущая вдвое быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)

Объединение уравнений

В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.

Сводка кинематических уравнений (константа

a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)

Прежде чем перейти к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем

Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.

Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:

а = v2-v022 (х-х0).а = v2-v022 (х-х0).

Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.

Пример 3.10

Как далеко уезжает машина?

На сухом бетоне автомобиль может ускоряться противоположно движению со скоростью 7,00 м / с ², тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5 м / с.00 м / с ². Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы он нажал ногу на тормоз.

Стратегия

Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.

Фигура 3,22 Образец эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.

Решение

Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v ₀ = 30,0 м / с, v = 0 и a = −7,00 м / с ² ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x ₀ равным нулю.Ищем смещение ΔxΔx, или x – x ₀.
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования – v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем.Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: x − 0 = 02− (30,0 м / с) 22 (−7,00 м / с2). x − 0 = 02− (30,0 м / с) 22 (−7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне.
Эта часть может быть решена точно так же, как (а). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с ². Результат xwet = 90,0 м по мокрому бетону. xwet = 90.0м по мокрому бетону.
Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы снова определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / св– = 30,0 м / с, treaction = 0.500streaction = 0.500s, а areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение – x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это означает, что автомобиль проезжает 15,0 м, пока водитель реагирует, создавая общие перемещения в двух случаях: сухой и мокрый бетон 15.На 0 м больше, чем если бы он среагировал мгновенно.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (а) равным 64,3 м + 15,0 м = 79,3 м в сухом состоянии и (б) равным 90,0 м + 15,0 м = 105 м во влажном состоянии.

Фигура 3,23 Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, едущего с начальной скоростью 30.0 м / с. Также показаны общие расстояния, пройденные от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.

Значение

Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля. Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение.Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.

Пример 3.11

Расчет времени

Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость составляет 10,0 м / с, а ускорение составляет 2,00 м / с ², сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)

Стратегия

Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t ).

Фигура 3,24 Эскиз автомобиля, ускоряющегося на съезде с автострады.

Решение

Опять же, мы идентифицируем то, что нам известно, и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,
v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2.00 м / с2 и x = 200 м.

Нам нужно найти т. . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.

Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:

200 м = 0 м + (10,0 м / с) t + 12 (2.00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.

Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t – величина времени, а s – единица измерения. Остается

Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,

t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,

, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,

Значение

Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.

Проверьте свое понимание 3.5

Ракета ускоряется со скоростью 20 м / с. ² во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?

Пример 3,12

Ускорение космического корабля

Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с ² за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?

Стратегия

Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.

Решение

Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.

Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:

v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.

Значение

Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.

Установив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .

Задачи преследования двух тел

До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на Рисунке 3.25.

Фигура 3,25 Сценарий преследования с двумя телами, когда автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.

Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.

Рассмотрим следующий пример.

Пример 3,13

Гепард ловит газель

Гепард прячется за кустом.Гепард замечает пробегающую мимо газель со скоростью 10 м / с. В тот момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с ², чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?

Стратегия

Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, – это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно рассмотрим проблему, становится ясно, что общим параметром для каждого животного является их положение x , в более позднее время t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем установить уравнения, равные друг другу, и решить для неизвестного, то есть времени.

Решение

Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда составляет 4 м / с ². Оценивая t , время, когда гепард достигнет газели, имеем t = 2v – a = 2 (10 м / с) 4m / s2 = 5s. t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.
Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. Водоизмещение газели: x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.

Значение

Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.

Проверьте свое понимание 3,6

Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и начинает бежать, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?

Формула науки – Как обсуждать

Научная формула

Какие полезные формулы физики?

Формула средней скорости: Средняя скорость – это средняя скорость движущегося тела на всем пройденном расстоянии.
Формула ускорения: Ускорение определяется как изменение скорости относительно изменения во времени. Он отмечен символом.
Формула плотности: Плотность материала указывает плотность в определенном диапазоне.

Какой пример таблицы формул?

Таблица физических формул. Пример описания формулы. s = d / t скорость = расстояние / время 10 м / с. v = d / t в одном направлении Скорость = расстояние / время в одном направлении.

Какова формула времени в науке?

Формула времени в физике. Вот простые формулы: 1) Для расчета скорости: Speed = \\ (\\ frac {Distance} {Time} \\) 2) Для расчета расстояния: Distance = Speed × Time.3) Вычислить время: Время = \\ (\\ frac {Distance} {Speed} \\) С математической точки зрения они имеют следующие формулы :.

Какова формула Мю в физике?

Вот также ваша формула для Mu: F = Mu (FN) они знают, что FN равно W, поэтому они могут вставить свои знания в формулу и получить: 34 N = Mu S (67 N) Разделить 34 на 67 и вы получите 0,507462, что округлено до 0,51.

Какое математическое уравнение является самым важным?

Самая известная формула во всей математике (величайшее уравнение всех времен) – это i.π + 1 = 0. Это тождество Эйлера известно как самая известная формула во всей математике и использует все основные математические константы.

Какое уравнение для физики?

Некоторые из наиболее распространенных физических уравнений используются для описания энергии, силы и скорости. Эти уравнения могут помочь ученым понять, как объекты реагируют в определенных условиях, без необходимости экспериментировать непосредственно с объектами. Пожалуй, самые известные физические уравнения относятся к энергии: E = mc 2.

Что такое уравнение физики?

Определение уравнений (физика) В физике определение уравнений – это уравнения, которые определяют новые величины относительно основных величин.

Что такое научное уравнение?

Уравнение – это математическое утверждение, что два выражения – это одна и та же математика, математика, математика, наука (или группа связанных наук), которая имеет дело с логикой количества, формы и местоположения.

Какие полезные формулы физики для начинающих?

Ответ: Советы по запоминанию формул в физике: 1 Просмотрите и прочтите.2 монополизируют большую часть ажиотажа, многие менее известные формулы овладели учеными. Live Science спросила физиков, астрономов и математиков, какие уравнения им больше всего нравятся, и получила следующие результаты:

Что вам нужно знать об основах физики?

Основная физическая формула. Физика – это формулировка вещей с реальными ценностями, а не их запоминание. В процессе подачи заявки вы можете столкнуться с различными математическими концепциями, задачами и формулами.Для поиска решений они должны использовать свои навыки, творческий потенциал и хороший потенциал.

Какова формула расстояния в физике?

Какая формула для расстояния в физике? Ответ: Используйте формулу расстояния d = st, чтобы решить все задачи о расстоянии. Скорость и скорость схожи в том, что они оба представляют расстояние в единице времени, например, мили в час или километры в час.

Какие полезные формулы физики для колледжа

Здесь все физические формулы представлены в простом формате для создания хранилища, где исследователь может иметь в руках все формулы, которые он ищет.Постоянная смещения Вина b = × 10−3 м K. волна = ∆x ∆t волна = средняя скорость ∆x = расстояние ∆t = затраченное время.

Какова правильная формула кинетической энергии?

KE = кинетическая энергия. «Энергия работы», которой их учили, – это утверждение, что работа всей силы над объектом равна изменению кинетической энергии объекта. вы можете записать это как E = KE + PE E = полная энергия.

Что лучше: физика или AP Physics?

Это также зависит от ваших математических и аналитических навыков решения проблем.Если вы хорошо разбираетесь в математике и имеете хорошие навыки решения проблем, я определенно рекомендую 1 AP Physics или, если вы посещали математический класс, C: Mech Physics.

Какова формула конечной скорости в физике?

Формула окончательной скорости: v_f = v_i + \\ Delta v Конечная скорость равна начальной скорости плюс изменение скорости.

Какие полезные формулы физики для написания?

Лучший способ использовать формулы физики – делать заметки из учебника.Примечания к каждой главе должны быть резюме на последней странице и записывать все важные интеллектуальные карты и формулы. Используйте предыдущий лист на этой странице для дополнительных формул на одной странице. Это отличный способ создать эффективный лист формул физики.

Почему важно знать формулы физики?

Студенты, которые хотят достичь больших высот в своей карьере, должны полностью овладеть физическими формулами, предложенными командой Entry, приобрести новые навыки и расширить свои мыслительные способности.Формулы физики, предоставленные командой, помогают студентам получить концептуальную ясность.

Где я могу найти список всех физических формул в Индии?

Да, можно собрать все основные физические формулы в одном месте, посетив веб-сайт Entranceis, одной из ведущих индийских компаний. На Entrancei вы найдете обзор всех важных физических формул на одной странице.

Какие полезные формулы физики для класса

Список физических формул.Формула челнока. Формула ускорения. Формула плотности. Формула скорости. Формула энергии. Формула числа Рейнольдса. Формула кинетической энергии. Формула Фаренгейта Цельсия.

Вы знаете формулу физики для 9 класса?

Девятиклассникам рекомендуется внимательно изучить списки физических формул, чтобы понять предмет. Без усвоения физических формул в девятом классе ученики столкнутся с большими трудностями при решении задач по физическим предметам, таким как оптика, электрический ток, электромагнетизм, законы движения, электромагнитное излучение и т. Д.

Хорошо ли иметь шпаргалку по физическим формулам?

Иногда бывает трудно запомнить физические формулы. Хорошая идея – всегда носить с собой шпаргалку по физике. Вот почему они составили впечатляющий список физических формул. Следующий список содержит все формулы от 5-го до 12-го класса CBSE. Эти формулы являются наиболее часто используемыми выражениями, уравнениями, правилами и утверждениями в физике.

Что такое научное уравнение?

Уравнение – это математическое утверждение, что два выражения равны.Математика, математика, математика – это наука (или группа смежных наук), которая занимается логикой количества, формы и местоположения.

Какие полезные физические формулы для статистики

Предположим, что для следующих формул Y является линейным преобразованием случайной величины X, определяемой уравнением: Y = aX + b. Среднее значение линейного преобразования = E (Y) = Y = a X + b. Дисперсия линейного преобразования = Var (Y) = a 2 * Var (X). Стандартизированная оценка = z = (x μ x) / σ x.

Какая формула является правильной для статистики?

Статистика таблицы формул. Важные статистические формулы показаны в следующей таблице: Среднее значение. x = данные наблюдения. n = общее количество наблюдений. Медиана. Если n нечетное, то. M = срок. Если даже тогда.

Что нужно знать о статистике?

Таким образом, статистика относится к сбору, классификации, упорядочиванию и представлению числовых данных. Это позволяет им интерпретировать разные результаты и предсказывать множество возможностей.Статистика относится к фактам, наблюдениям и информации, которые существуют только в форме числовых данных.

Какова формула физики?

Пожалуй, самые известные физические уравнения относятся к энергии: E = mc 2. В этом уравнении E означает энергию, m – массу, а c – скорость света в вакууме (около 186 000 миль / сек или 3×108. метров) .. / Second Это уравнение разработал ученый Альберт Эйнштейн.

Какое уравнение работы в физике?

Формула работы по физике.Рабочая формула w = F × d. ш = работа. F = сила. d = расстояние. Как видно из формулы, работа зависит от силы, приложенной к объекту, и расстояния от объекта. Другими словами, каждый раз, когда объект перемещается (или перемещается) из-за приложения силы к объекту, вы работаете с объектом.

Какова научная формула работы?

Работа имеет особое значение в науке. Это произведение силы, действующей на объект, и расстояния, которое объект прошел.Единица работы – джоуль (Дж). Формула для работы: W = F * d (работа = сила, умноженная на расстояние).

Какова формула физической науки в химии

Как правило, физическое состояние в химическом уравнении указывается в скобках и сокращении сразу после химической формулы. Это можно увидеть в следующем уравнении: 2 H 2 (г) + O 2 (г) → 2 H 2O (l) Водород и кислород обозначены (г), поэтому они являются газами.

Что такое эмпирическая химия?

В химии эмпирическая формула химического соединения представляет собой простейшее положительное целочисленное отношение атомов, присутствующих в соединении.Простым примером этой концепции является то, что молекулярная формула монооксида серы или SO – это просто SO, как и молекулярная формула диоксида серы S2O на 29 ноября 2019 года.

Какова формула на рабочем листе по физике

Дети будут оттачивать свои знания физики, классифицируя элементы в этой фитнес-таблице 4 класса на твердые или жидкие. Используйте этот вводный лист, чтобы научить вашего ребенка различать потенциальную и кинетическую энергию. Что такое солнечная энергия?

Что такое блок физики 1 в TCSS?

TCSS Physical Science Unit 1 – Вехи информации о материи Площадь / вес: химические реакции и свойства вещества 25% Стандарты деятельности штата Джорджия: SPS2.Студенты изучают природу материи, ее классификацию и систему обозначения типов материи.

Как рабочие листы используются только в фактах?

В «Just the Facts: Physical Science» студентам предоставляется основная фактическая информация, которая позволяет им проводить исследования, во многом аналогичные экспериментам, которые ученые проводят каждый день. Рабочие листы и задания в этой книге дополняют ваш ежедневный учебный процесс, и некоторые из них можно использовать.

Какая формула для определения скорости и расстояния является правильной?

Скорость = расстояние ÷ время v = d ÷ t единицы измерения: метры / секунды Изменено: расстояние = скорость x единицы времени: метры время = расстояние единицы скорости: секунды Импульс = масса x скорость p = m x v единицы: кг.м / с ускорение = (конечная скорость начальная скорость) ÷ время a = Δv ÷ t единицы: метры / (секунда) 2.

Какова формула физической науки в науке

Момент – это произведение массы и скорости тела. Импульс рассчитывается по формуле: P = m (масса) x v (скорость) Сила может быть определена как нечто, что вызывает изменение количества движения тела. Сила возникает из известного закона движения Ньютона: F = m (масса) x a (ускорение).

Какова формула работы по физике?

Общая формула для работы и определения объема работы, которая должна быть проделана с объектом: W = Сила 64 Н под углом 120 °, выполнение работы Джоуля по перемещению книги на 3 метра.Science Trends – популярный источник новостей науки и образования во всем мире.

Какие виды физических наук?

Естественные науки – это естественные науки, которые включают астрономию, физику, химию и науки о Земле. Физическая наука – это изучение, измерение и наблюдение неодушевленных объектов, а биологическая наука – это изучение живых объектов.

Какой пример физического поля?

Астрономия, физика, химия и науки о Земле являются основными областями естественных наук и состоят из нескольких разделов.Например, физика сосредотачивается на свойствах атомов, а химия фокусируется на том, как эти свойства меняются, когда атомы взаимодействуют друг с другом.

Как найти формулу давления?

Формула пресса. Давление – это сила, которую один объект оказывает на другой. Обозначается буквой P. A = общая площадь объекта. Формула давления используется для расчета давления, силы, площади, плотности, высоты и силы тяжести, если указаны некоторые из этих чисел. Давление выражается в паскалях (Па).

Какова формула определения физической науки

В науке формула – это краткий способ символического выражения информации, например, в математической формуле или химической формуле. Неформальное использование термина «формула» в науке относится к общему построению отношений между данными значениями.

Какова формула викторины по физике

GPE = mgh GPE = масса в кг (сила тяжести) Высота в м Сила гравитационного поля на Земле = ms2) Формула для потенциальной гравитационной энергии KE = 1 / 2mv2 KE = 1/2 массы в кг (квадрат скорости) Формула d ‘кинетическая энергия.

Что означает p в физической науке?

P означает мощность PE означает потенциальную энергию GPE означает гравитационную потенциальную энергию KE означает кинетическую энергию vw означает скорость волны V означает, что в V = IR разница в электрическом потенциале I означает ток R означает сопротивление D означает плотность V означает, что в D = M / В объем.

Что означает VF в физике?

Vf означает конечную скорость Vi означает начальную скорость F означает силу m означает массу g означает гравитацию W означает работу P означает мощность PE означает потенциальную энергию GPE означает потенциальную гравитационную энергию KE означает кинетическую энергию.

Что обозначают буквы в физике?

Vi означает начальную скорость F означает силу m означает массу g означает гравитацию W означает работу P означает мощность PE означает потенциальную энергию GPE означает потенциальную гравитационную энергию KE означает кинетическую энергию vw означает скорость волны V означает, что в V = IR разность электрических потенциалов Я имею в виду Текущий.

Как формулы используются в естествознании и математике?

Формулы, используемые в науке, почти всегда требуют выбора единиц.Формулы используются в физике для обозначения взаимосвязей между различными величинами, такими как температура, масса или заряд.

Что вы изучаете в курсе физики?

Этот курс охватывает основные понятия естественных наук, такие как органическая химия, атмосферные науки, типы горных пород, химические связи и стехиометрия. Уроки этого курса представляют собой короткие видеоуроки с привлекательными изображениями и иллюстрациями, которые помогут вам понять ключевые концепции и терминологию.

Почему физические формулы даны по порядку?

Физические формулы представлены в правильном порядке, чтобы учащиеся могли изучать предмет шаг за шагом. Студентам рекомендуется внимательно изучать формулы, чтобы получить хорошие оценки по важным физическим темам, таким как термодинамика, электрический ток, законы движения, оптика, преобразование энергии и т. Д.

Какое уравнение для расчета времени?

Уравнение времени получается путем подстановки результата вычисления прямого восхождения в формулу уравнения времени.Здесь используется Δ t (M) = M + λ p – α, отчасти потому, что незначительные корректировки (порядка 1 секунды), которые оправдывали бы использование E, не включены, а отчасти потому, что цель получает простое аналитическое выражение.

Как рассчитать расстояние, скорость и время?

Рассчитайте расстояние, скорость и время друг друга. Формулы: d = r * t, r = d / t, t = d / r. Где D – расстояние, R – скорость, а T – время.

Какое уравнение для времени?

Военно-морская обсерватория США утверждает, что уравнение времени – это разница между видимым солнечным временем и средним солнечным временем.Если солнце опережает часы, знак положительный, а если часы опережают солнце, знак отрицательный. Уравнение времени показано на диаграмме выше для периода чуть более года.

Какова физическая формула времени?

Формула времени в физике. Вот простые формулы: 1) Чтобы вычислить скорость: Speed = (frac {Distance} {Time}) 2) Чтобы вычислить расстояние: Distance = Speed × Time. 3) Вычислить время: Время = (frac {distance} {speed}) Математически они имеют следующие формулы: s = (frac {d} {t}) d = s × t.

Какова формула времени в научном проекте

За основу взята следующая формула: d = 1/2 gt 2. В этой формуле «d» – это расстояние, на которое упал объект, «g» – это ускорение свободного падения (м / с2), а «t» – момент падения объекта .. объект упал. Чтобы упростить процесс, они создали таблицу времени ответа с уже выполненными расчетами.

Как проверить гипотезу в эксперименте на время реакции?

Попросите учащегося придумать проверяемый вопрос (гипотезу).Пример: у людей разного возраста разное время реакции? Встаньте на объект с вытянутой рукой и возьмите линейку между большим и указательным пальцами. Поместите начало (конец начинается с нуля) линейки точно между раскрытыми пальцами испытуемого.

Как я могу использовать график времени реакции?

Используйте таблицу времени реакции, чтобы преобразовать расстояние во время реакции. Используйте график времени отклика, чтобы построить данные для измерения тенденций. Настройте различные переменные, чтобы увидеть, что может ускорить или замедлить время реакции.Может ли предупреждение о сбое правила изменить скорость ответа получателя?

Где проводится эксперимент в научном методе?

Хотя некоторые эксперименты проводятся в лабораториях, вы можете проводить их в любое время и в любом месте. Просмотрите этапы научного метода – сделайте наблюдения. Сформулируйте гипотезу. Разработайте и проведите эксперимент, чтобы проверить свою гипотезу. Оцените результаты эксперимента.

Какая формула для времени

Формула для времени получается из.Чтобы рассчитать расстояние, формула для времени может быть. Как рассчитать скорость по формуле времени? Формула для времени получается из.

Как рассчитать разницу во времени между двумя датами или временем?

Чтобы вычислить время между двумя датами и временем, вы можете просто вычесть одно из другого. Однако вы должны отформатировать каждую ячейку, чтобы Excel получил желаемый результат. 1. Введите две полные даты и время.

Как измерить время реакции вашего партнера на падение?

Попросите вашего партнера поймать вас как можно скорее, как только вы увидите, что он начинает падать.Бросьте веревку, не сказав партнеру. Отметьте, как далеко вы упали, прежде чем ваш партнер поймает вас. Обратитесь к таблице времени ответа, чтобы определить время ответа. Повторите это как минимум дважды.

Как в реальной жизни используется время реакции?

В спорте время реакции, интервал между стимуляцией и реакцией, часто определяет, кто победит, а кто проиграет. Что еще более важно, в реальных жизненных ситуациях, таких как вождение автомобиля, это может иметь значение между жизнью и смертью. Измерьте время отклика со следующим проектом.

Какое уравнение определяет скорость автомобиля?

Уравнение для быстрой машины: d = vf (t), где vf – скорость быстрой машины. Общее расстояние, пройденное каждым транспортным средством, одинаково.

Какая формула времени в теории науки

Формула времени в физике. Вот простые формулы: 1) Чтобы вычислить скорость: Speed = (frac {Distance} {Time}) 2) Чтобы вычислить расстояние: Distance = Speed × Time. 3) Чтобы вычислить время: Время = (frac {Distance} {Speed}) С математической точки зрения они имеют следующие формулы :.

Как рассчитать формулу времени?

Введите формулу времени в Excel. Чтобы рассчитать разницу между временем прибытия и временем отправления, введите знак равенства (=) в ячейку под «Общее количество часов (C2)», щелкните ячейку отправления слева, введите знак «минус» () и нажмите «Конвертировать часы». в ячейку слева и нажмите Enter.

Какое определение времени в физике?

Запасное время. Путешествие во времени. V.T.e. Маятник Фуко в Пантеоне в Париже может измерять время и показывать вращение Земли.2cos <2} theta} Это уравнение траектории движения снаряда, и оно доказывает, что снаряд движется. он всегда имеет параболическую природу.

Как время является фундаментальной величиной в физике?

Время в физике. В классической нерелятивистской физике это скалярная величина и, как и длина, масса и заряд, обычно описывается как фундаментальная величина. Время можно математически комбинировать с другими физическими величинами для получения других понятий, таких как движение, кинетическая энергия и изменяющиеся во времени поля.

Какова формула времени в научной фантастике

Тег «Формула фантастики» присуждается за повторное использование сюжета, сюжетные уловки и безвкусные персонажи. Такие жанры, как художественная космическая опера, запад и научная фантастика, часто имеют специфические настройки, такие как псевдосредневековые европейские пейзажи, дикий запад или космическое пространство.

Что делает научную фантастику научно-фантастической историей?

Научно-фантастический роман может быть о космосе, путешествиях во времени, пришельцах или пришельцах, путешествующих во времени в пространстве.Независимо от окружения и персонажей, все научно-фантастические рассказы сложны, содержат нюансы и исследуют более широкие, иногда сатирические темы и комментарии к оккультному обществу.

Как определяется формула рассказа?

Формула определяется предсказуемой повествовательной структурой. В артикулированном повествовании представлены истории, которые так много раз использовались повторно, что их легко обнаружить.

Когда был написан первый научно-фантастический рассказ?

История научной фантастики Жанр научной фантастики восходит ко второму веку.Правдивая история, написанная сирийским сатириком Лучианом, считается первой научной фантастикой о других вселенных и инопланетных формах жизни.

Какие единицы Мю в физике?

Единицы измерения в физике – это разные шкалы, используемые для измерения объекта. Многое измеряется в генри на метр, что составляет 2 ньютона на квадратный ампер (2).

Что означает Му в физике?

Коэффициент трения, отношение силы трения, противодействующей движению двух соприкасающихся поверхностей, к нормальной силе, толкающей две поверхности вместе.Обычно это обозначается греческой буквой мю (μ).

Что такое мю ноль?

Zero Mu Mught (µ 0), или абсолютная проницаемость свободного пространства, была точно определена до 20 мая 2019 г. Множественное число: µ = 4pi × 107 H / m.

Какова формула для mu в математике физики?

Определение и вычисление постоянной зависимости называется коэффициентом трения и обычно обозначается греческой буквой mu (μ). Математически = F / L. Поскольку трение и нагрузка измеряются в единицах силы (например, фунтах или ньютонах), коэффициент трения безразмерен.6 #) Обозначает коэффициент трения. Представьте себе уменьшенную массу в задаче двух тел. Представьте массу на единицу длины струн и других объектов, которые кажутся одномерными.

Что означает μ в физике?

Постоянная связь называется коэффициентом трения и обычно обозначается греческой буквой мю (μ). Математически = F / L. Поскольку трение и нагрузка измеряются в единицах силы (например, фунтах или ньютонах), коэффициент трения безразмерен.Что значит ?

Что означает Мю в термодинамике?

Представьте себе мюон () и антимюон (¯¯μ). В термодинамике – для представления химического потенциала системы или части системы.

Как в физике измеряется значение Mu naught?

Единицы измерения в физике – это разные шкалы, используемые для измерения объекта. Многое измеряется в генри на метр, что равно ньютону () на квадратный ампер (). Надеюсь, вы знаете значение му-нада, а также единицу измерения му-нада в системе СИ в физике.

Какова формула для mu в физике?

Коэффициент трения, отношение силы трения, противодействующей движению двух соприкасающихся поверхностей, к нормальной силе, толкающей эти две поверхности вместе. Обычно это обозначается греческой буквой мю (μ). Математически μ = F / N, где F – сила трения, а N – нормальная сила.

Какова формула для мю в физике 1

Греческая буква мю (μ) с нижним индексом s обозначает статический коэффициент трения.Максимальная сила статического трения в с, умноженная на нормальную силу, действующую на объект. Сила статического трения ≤ (статический коэффициент трения) (нормальная сила) максимальная сила статического трения = (статический коэффициент трения) (нормальная сила).

Какая формула для mu в физике химии

9 марта 2018 года. # \\ mu # можно описать по-разному. Иногда он используется в кинематике для коэффициентов трения или даже в физике частиц для приведенной массы частицы.

Как Mu используется в термодинамике и химии?

Mu имеет несколько применений: он используется для обозначения проницаемости материала, насколько хорошо он сопротивляется образованию магнитного поля. Представьте себе магнитный момент. В термодинамике укажите химический потенциал системы или части системы.

Когда использовать приставку mu в математике?

9 марта 2018 г. # Mu # используется в нескольких целях: В качестве префикса для представленных измерений (# 1 * 10 ^ 6 #) Представляет коэффициент трения.Представьте себе уменьшенную массу в задаче двух тел. Представьте массу на единицу длины струн и других объектов, которые кажутся одномерными.

Какая польза от μ в физике?

μ может описывать множество величин. Иногда он используется в кинематике для коэффициентов трения или даже в физике частиц для приведенной массы частицы. Му имеет несколько применений, он используется для представления массы на единицу длины в струнах и других объектах, которые кажутся одномерными.

Какова формула для мю в физическом калькуляторе?

Молекулярная масса (M) – это физическое свойство, определяемое как масса одного моля химического вещества или отношение между массой химического вещества и его количеством. Единица измерения молярной массы – кг / моль. Формула для вычисления массы: масса = × v.

Какова формула величины силы?

Величина силы F = qvB sinθ, где угол <180 градусов между скоростью и магнитным полем.

Как рассчитать ускорение по массе?

Перепишем уравнение F = ma, чтобы найти ускорение.Вы можете изменить эту формулу, чтобы найти ускорение, разделив обе стороны на массу, как показано ниже: a = F / m. Чтобы найти ускорение, просто разделите силу на массу ускоряющегося объекта.

Как рассчитать центростремительную силу?

Расчет центростремительной силы. Центростремительная сила = масса x скорость 2 / радиус. Обратите внимание, что условия здесь не имеют дополнительной силы, например: B. горизонтальный круг на поверхности без трения. Для вертикального круга скорость и натяжение должны меняться.

Какой лучший натуральный корм для собак?

Натуральная и недорогая еда, которую любят большинство собак, – сыр. Его можно легко включить в рацион вашей собаки в качестве вкусного лакомства, а также как хороший источник кальция и многих других важных питательных веществ. Овощи также могут быть хорошей заменой. Клетчатка, такая как овсяные отруби, может помочь предотвратить определенные проблемы с железами.

Каковы потребности в питании собак?

Пищевая потребность собаки в белках и аминокислотах.Собаки не могут выжить без белка в рационе. Жиры и жирные кислоты. Рекомендуемое ежедневное потребление белков и жиров. Энергетические требования. Минералы Рекомендуемая суточная доза минералов.

Какой самый полезный сухой корм для собак?

В целом, Natural Balance Original Ultra Whole Body Healthy Dry Dog Food – лучший корм для йорков, если ваша собака не чувствительна к курице. В отличие от других кормов, таких как Wellness CORE, этот корм можно давать вашей собаке независимо от возраста.

Какой корм для щенков лучше всего рекомендуют ветеринары?

10 лучших брендов кормов для собак, рекомендованных Hills Science Diet Vets.Во главе моего списка рекомендованных ветеринарами брендов кормов для собак стоит Hills Science Diet. Настоящая собака. План Purina Pro. Источник. Натуральный корм для собак, приятный на ощупь. Кастор и Поллукс. Iams / Eukanuba. Nutro Ultra.

Как изучать научные формулы по главам?

Научные формулы в главе содержат все важные моменты главы. Воспользуйтесь приведенными ниже советами и подсказками, которые помогут вам легко усвоить формулы. Ваш мозг и сосредоточьтесь на научных формулах. столько, сколько вы можете.все важные формулы на листе бумаги для практики.

Как лучше всего запоминать научные формулы?

лет Чтобы запоминать научные формулы, вы можете использовать следующие советы. и сначала напишите формулы при решении связанных вопросов. Формулы регулярно и просматривайте их. Используйте творческие и мнемонические средства, чтобы запоминать долгосрочные формулы.

Какая формула карбоната кальция правильная?

Химические формулы соединений Название соединения Молекулярный вес Молекулярная формула 9 Карбонат кальция г / моль CaCO 3 10 Сульфат аммония г / моль (NH 4) 2 SO 4 11 Угольная кислота г / моль H 2 CO 3 12 Бикарбонат натрия 84.