Закан ома – простое объяснение для чайников с формулой и понятиями

Закон Ома для полной цепи и для участка цепи: формулы, описание и объяснение

Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.

Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.

И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.

Содержание статьи:

Отдельный участок и полная электрическая цепь

Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.

Расчет тока участка электрической схемы

Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.

Поэтому расчетная формула, в данном случае, выглядит просто:

I = U/ R,

Где, соответственно:

• I – сила тока;
• U – приложенное напряжение;
• R – сопротивление.

Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.

Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор “P” – формулы мощности; сектор “U” – формулы напряжения; сектор “I” – формулы тока; сектор “R” – формулы сопротивления

Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.

Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.

Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 – определение тока; 2 – определение сопротивления; 3 – определение напряжения, где I – сила тока, U – напряжение, R – сопротивление

Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.

Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).

Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.

Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.

Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.

Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.

У нас на сайте есть подробная инструкция по по мощности и току.

Вариант расчета для полной цепи

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.

Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.

Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I – прохождение тока; R – резистивный элемент внешний; r – резистивный фактор ЭДС (источника энергии)

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.

Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Рассмотрение действия закона к переменной величине

Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса».  Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).

Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения – синусоидальной величине тока.

Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R – резистивная составляющая; С – емкостная составляющая; L – индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока

Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.

Расчёт подобных явлений ведётся при помощи формулы:

Z = U / I или Z = R + J * (X_L – X_C)

где: Z – импеданс; R – активная нагрузка; X_L , X_C – индуктивная и емкостная нагрузка; J – коэффициент.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I₁ = I₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение

Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I₁ + I₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ   

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Выводы и полезное видео по теме

Подробный разбор закона Ома в видеоролике, представленном ниже, поможет окончательно закрепить знания в этом направлении.

Своеобразный видеоурок качественно подкрепляет теоретическое письменное изложение:

Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.

Объёмных знаний по данному вопросу не требуется – достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.

Хотите дополнить изложенный выше материал ценными замечаниями или выразить свое мнение? Пишите, пожалуйста, комментарии в блоке под статьей. Если у вас остались вопросы, не стесняйтесь задавать их нашим экспертам.

sovet-ingenera.com

Закон Ома для неоднородного участка цепи

На практике видно, что для поддержания стабильного тока в замкнутой цепи необходимы силы принципиально иной природы, нежели кулоновские, тогда наблюдается случай, когда на участке цепи на свободные электрические заряды одновременно действуют как силы электрического поля, так и сторонние силы (любые неконсервативные силы, действующие на заряд, за исключением сил электрического сопротивления (кулоновских сил)). Такой участок называется неоднородным участком цепи. На рисунке ниже приведен пример такого участка.

Напряженность поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил:

Сформулируем закон Ома для неоднородного участка цепи – Сила тока прямо пропорциональна напряжению на этом участке и обратно пропорциональна его полному сопротивлению:

– формула закона Ома для неоднородного участка цепи.

Где

• I – сила тока,
• U12 – напряжение на участке,
• R – полное сопротивление цепи.

Работа на неоднородном участке цепи

Нужна помощь в написании работы?

Разность потенциалов характеризует работу силы электрического поля по переносу единичного положительного заряда (q) из точки 1 в точку 2:

– где φ1 и φ 2 – потенциалы на концах участка.

ЭДС характеризует работу сторонних сил по переносу единичного положительного заряда точки 1 в точку 2:

– где ε12 – ЭДС, действующая на данном участке, численно равна работе по перемещению единичного положительного заряда вдоль контура.

Напряжение на участке цепи представляет собой суммарную работу сил ЭП и сторонних сил:

Тогда закон Ома примет вид:

ЭДС может быть как положительной, так и отрицательной. Это зависит от полярности включения ЭДС в участок. Если внутри источника тока обход совершается от отрицательного полюса к положительному, то ЭДС положительная (см. рисунок). Сторонние силы при этом совершают положительную работу. Если же обход совершается от положительного полюса к отрицательному, то ЭДС отрицательная. Проще говоря, если ЭДС способствует движению положительных зарядов, то ε>0, иначе ε

Решение задач по закону ому для неоднородного участка цепи

Определить ток, идущий по изображенному на рисунке участку АВ. ЭДС источника 20 В, внутреннее сопротивление 1 Ом, потенциалы точек А и В соответственно 15 В и 5 В, сопротивление проводов 3 Ом.

Дано:	Решение:
ε = 20 В r = 1 Ом φ1 = 15 В φ2 = 5 В R = 3 Ом	Запишем закон Ома для неоднородного участка цепи – Считая, что точка А начало участка, а точка В – конец, возьмем ЭДС со знаком «минус» и, подставив исходные данные, получим Знак «минус» говорит о том, что ток идет от точки В к точке А, от точки с меньшим потенциалом к точке с большим, что обычно для источников тока. Ответ: –2,5 А

Два элемента соединены «навстречу» друг другу, как показано на рисунке. Определить разность потенциалов между точками А и В, если ε1 = 1,4 В, r1 = 0,4 Ом, ε2 = 1,8 В, r2 = 0,6 Ом.

Дано:	Решение:
ε1 = 1,4 В r1 = 0,4 Ом ε2 = 1,8 В r2 = 0,6 Ом	Запишем закон Ома для неоднородного участка цепи – Разобьём схему на два участка: АЕ2В и ВЕ1А. Тогда получим – для первого участка цепи, – для второго участка. Ток на участках один и тот же, то есть можем приравнять правые части уравнений. Знак «минус» показывает, что потенциал точки В выше, чем потенциал точки А. Ответ: -1,56 В.

Решим любые задачи

zakon-oma.ru

Закон Ома

В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.

Закон Ома – физическая закономерность, которая определяет взаимосвязь между током, напряжением и сопротивлением проводника. Он имеет две основные формы.

Закон Ома для участка цепи

Формулировка закона Ома для участка цепи – сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению.

Это простое выражение помогает на практике решать широчайший круг вопросов. Для лучшего запоминания решим задачу.

  Задача 1.1

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм², если к концам провода приложено напряжение 12 B.

Задача простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Закон Ома для полной цепи

Формулировка закона Ома для полной цепи – сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

Здесь могут возникнуть вопросы. Например, что такое ЭДС? Электродвижущая сила – это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электро

движущая говорит о том, что эта сила двигает электричество, то есть заряд.

В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.

Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.

  Задача 2.1

Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

 

Теперь решим задачу посложнее.

  Задача 2.2

Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм². Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.

Приступим.

Мнемоническая диаграмма

Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.

Успехов в изучении электричества! Рекомендуем прочесть статью – законы Кирхгофа.

Просмотров: 10743

electroandi.ru

2. Закон Ома для участка и полной цепи

Закон Ома для участка цепи: сила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

Формула закона: I=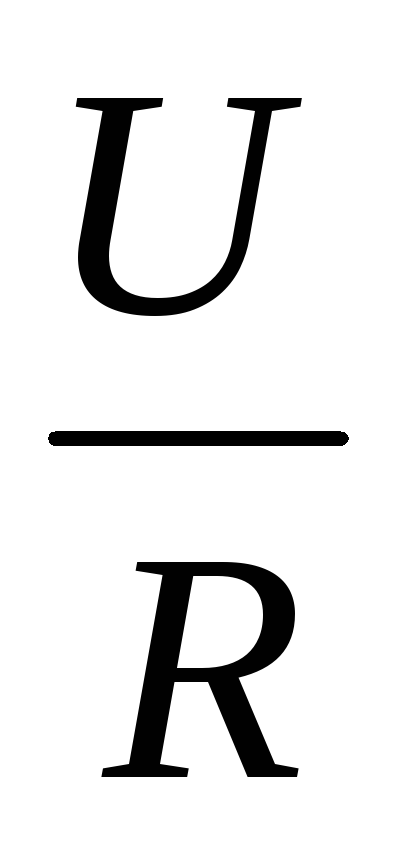. Отсюда запишем формулыU= IR и R =.

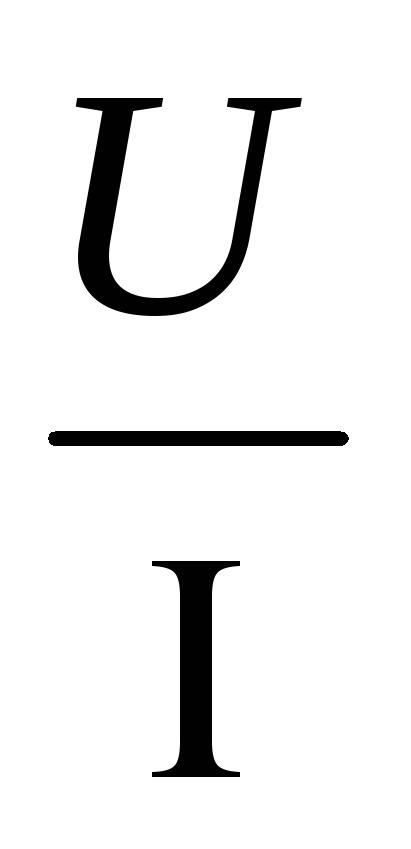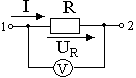Рис.1.Участок цепи 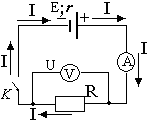Рис.2.Полная цепь

Закон Ома для полной цепи: сила тока I полной электрической цепи равна ЭДС (электродвижущей силе) источника тока Е, деленной на полное сопротивление цепи (R + r). Полное сопротивление цепи равно сумме сопротивлений внешней цепи R и внутреннего r источника тока. Формула закона I = 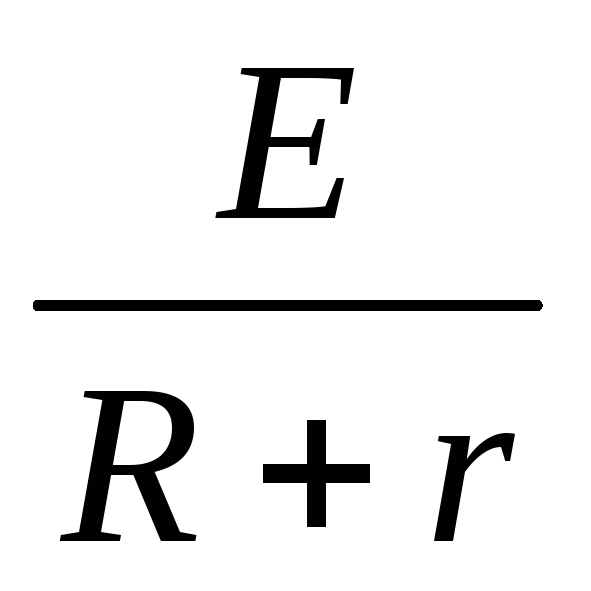. На рис. 1 и 2 приведены схемы электрических цепей.

3. Последовательное и параллельное соединение проводников

Проводники в электрических цепях могут соединяться последовательно и параллельно. Смешанное соединение сочетает оба эти соединения.

Сопротивление, при включении которого вместо всех других проводников, находящихся между двумя точками цепи, ток и напряжение остаются неизменными, называют эквивалентным сопротивлением этих проводников.

Последовательное соединение

Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.

Как следует из первого правила Кирхгофа, при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).

1. При последовательном соединении проводников (рис. 1) сила тока во всех проводниках одинакова: I₁ = I₂ =  I₃ = I

Рис. 1. Последовательное соединение двух проводников.

2. Согласно закону Ома, напряжения U₁ и U₂ на проводниках равны U₁ = IR₁,  U₂ = IR₂, U₃ = IR₃.

Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.

U = U₁ + U₂ + U₃

По закону Ома, напряжения U_1,U₂на проводниках равны U₁ = IR₁,  U₂ = IR₂, В соответствии вторым правилом Кирхгофа напряжение на всем участке:

U = U₁ + U₂ = IR₁+ IR₂ = I(R₁+ R₂)= I·R. Получаем: R = R₁ + R₂ 

Общее напряжение U на проводниках равно сумме напряжений U₁, U_{2 ,}U₃ равно: U = U₁ + U₂ + U₃ = I·(R₁ + R₂ + R₃)  = IR

где R_ЭКВ – эквивалентное сопротивление всей цепи. Отсюда: R_ЭКВ = R₁ + R₂ + R₃

При последовательном соединении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи: R _ЭКВ= R₁ + R₂ + R₃+…

Этот результат справедлив для любого числа последовательно соединенных проводников.

Из закона Ома следует: при равенстве сил тока при последовательном соединении:

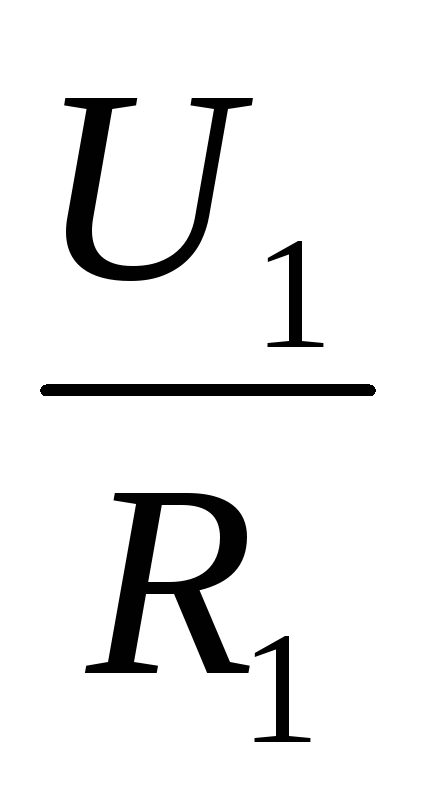I = ,I = 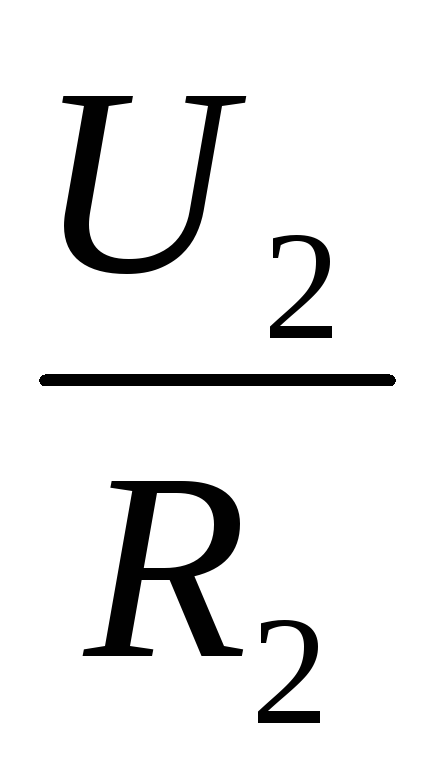. Отсюда 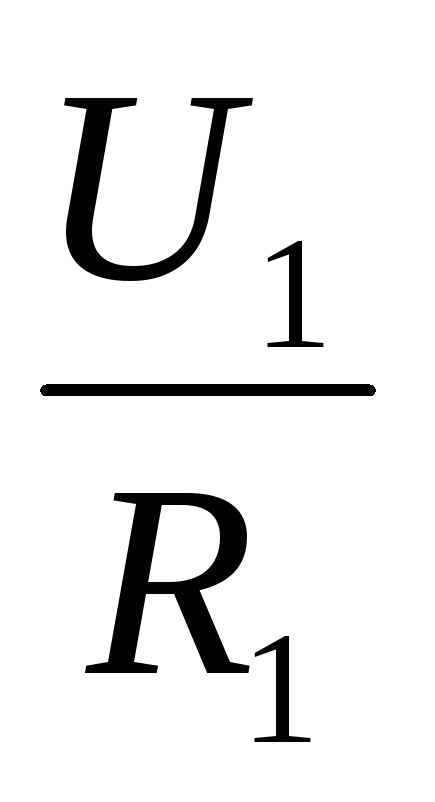= 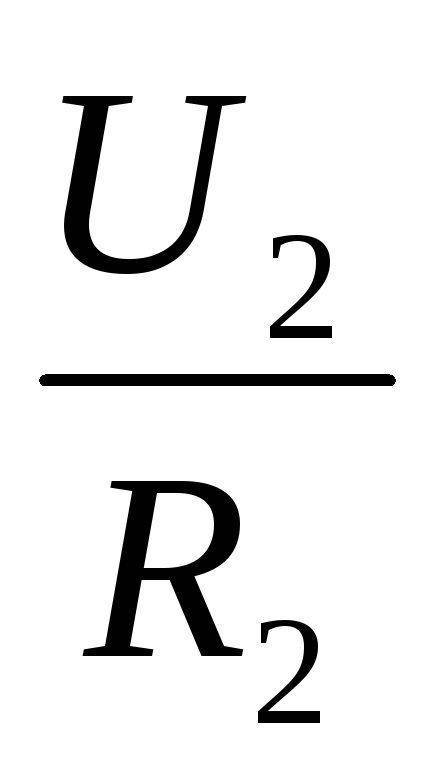или 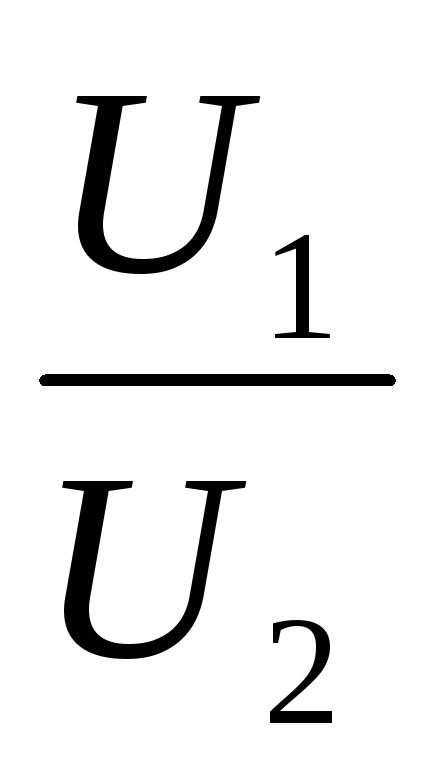=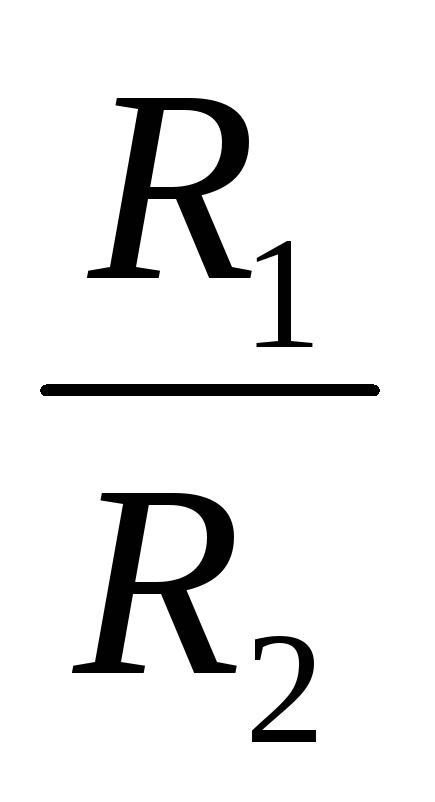, т. е. напряжения на отдельных участках цепи прямо пропорциональны сопротивлениям участков.

При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U₁ на их количество n:

U_ПОСЛЕД= n ·U₁. Аналогично для сопротивлений: R_ПОСЛЕД = n· R₁

При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.

studfile.net

Закон Ома для однородного участка цепи

Обязательным условием существования электрического тока является наличие электрического поля, для существования которого, в свою очередь, необходима разность потенциалов (напряжение). Ток будет направлен в сторону уменьшения потенциалов (на рисунке – влево), а свободные электроны будут двигаться в обратную сторону.

На концах участка проводника заданы потенциалы φ_1 и φ_2, причем φ_1>φ_2. Напряжение в таком случае можно найти по формуле:

В 1826 году Георг Ом, обобщив итоги опытов, показавших, что, чем больше напряжение на участке, тем больше сила тока, проходящего через него, получил зависимость, названную законом Ома. В ходе экспериментов Ом выявил, что различные проводники при одинаково заданном напряжении будут проводить ток по-разному, т.е., каждый проводник обладает различной мерой проводимости. Эту величину назвали электрическим сопротивлением.

Определеение Закона Ома для однородного участка цепи гласит: сила тока для однородного проводника на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению проводника.

Формула закона Ома для однородного участка цепи

• I [А] – сила тока,
• U [В] – напряжение,
• R [Ом] – электрическое сопротивление.

Сопротивление – главная характеристика проводника. В зависимости от строения проводника, в них существует различное количество узлов кристаллической решетки и атомов примесей, взаимодействуя с которыми электроны замедляются.

Сопротивление будет зависеть от рода и размеров проводника:

где:

• P – удельное сопротивление проводника (табличная величина, характеризующая способность материала к сопротивлению).
• l [м] – длина проводника,
• S [мм2] – площадь поперечного сечения проводника.

Нужна помощь в написании работы?

Решение задачи по теме Закон Ома для однородного участка цепи

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 1 мм2, если к концам провода приложено напряжение 8,5 В.

zakon-oma.ru

Закон Ома – это… Что такое Закон Ома?

V — напряжение,
I — сила тока,
R — сопротивление.

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

Из закона Ома для полной цепи вытекают следствия:

• При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
• При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Часто^[2] выражение:

(3)

(где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

(4)

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

(5)

Применима другая формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Выражение (5) можно переписать в виде:

(6)

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо^[3], впоследствии переименованный в Си́менс (обозначение: См, S).

Мнемоническая диаграмма для Закона

Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления

В соответствии с этой диаграммой формально может быть записано выражение:

(7)

Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

(8)

где:

•  — удельное сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

= (9)

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига.

Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U₀e^iωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re^−iδ — комплексное сопротивление (импеданс),
• R = (R_a² + R_r²)^1/2 — полное сопротивление,
• R_r = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
• R_а — активное (омическое) сопротивление, не зависящее от частоты,
• δ = − arctg (R_r/R_a) — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Трактовка закона Ома

Закон Ома можно просто объяснить при помощи теории Друде:

Здесь:

См. также

Примечания

Ссылки

dal.academic.ru

Закон Ома в комплексной форме

Для анализа электрических цепей синусоидального тока удобнее применять закон Ома в комплексной форме. Цепи синусоидального тока – линейные цепи с установившимся режимом работы, когда после окончания в них переходных процессов, падения напряжений на участках, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В обратном случае закон в такой форме неприменим.

В отличие от обычной формы закона Ома, в комплексной форме напряжение, токи, сопротивления и ЭДС записываются как комплексные числа. Данное нововведение основано на том, что в цепях переменного тока существуют активные и реактивные значения напряжений, токов и сопротивлений, что требует определенных корректив.

Итак, вместо активного сопротивления R, которое используется в основном в цепях постоянного тока, запишем полное (комплексное) сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже становятся комплексными величинами. При практических расчетах удобнее пользоваться действующими значениями. Запишем формулу закона Ома в комплексной форме:

где

• Z – комплексное (полное) сопротивление,
• Y – комплексная (полная) проводимость.

где

• r – активное сопротивление,
• x – реактивное сопротивление,
• z – полное сопротивление,
• g – активная проводимость,
• b – реактивная проводимость,
• y – полная проводимость,
• j – комплексная единица, j=√(-1).

Решение задач

По заданной схеме определить полное сопротивление цепи, токи (I_1 ) ̇, (I_2 ) ̇, (I_3 ) ̇. U = 120 В, xC1 = 100 Ом, xL2 = 50 Ом, xC3 = 50 Ом, r1 = 25 Ом, r2 = 20 Ом.

Дано:	Решение:
U = 120 В xC1 = 100 Ом xL2 = 50 Ом xC3 = 50 Ом r1 = 25 Ом r2 = 20 Ом Z – ? I_1 – ? I_2 – ? I_3 – ?	Запишем формулу закона Ома в комплексной форме: – Найдем полное сопротивление цепи по формуле: Примем начальную фазу напряжения за нуль, тогда: По следствию из закона Ома ток распределяется обратно пропорционально сопротивлению ветвей, а значит

zakon-oma.ru