Применение закона Ома на практике
Принцип работы одного из основополагающих законов электротехники хочется начать объяснять с аллегории — показа небольшого карикатурного изображения 1 из трех человечков под именами «Напряжение U», «Сопротивление R» и «Ток I».
На нем видно, что «Ток» пытается пролезть через сужение в трубе, которое «Сопротивление» усердно затягивает. В то же время «Напряжение» прилагает максимально возможное усилие для прохождения, проталкивания «Тока».
Этот рисунок напоминает, что электрический ток — это упорядоченное движение заряженных частиц в определенной среде. Передвижение их возможно под действием приложенной внешней энергии, создающей разность потенциалов — напряжение. Однако, внутренние силы проводников и элементов схемы уменьшают величину тока, оказывают сопротивление его перемещению.
Рассмотрим простую схему 2, поясняющую действие закона Ома для участка электрической цепи постоянного тока.
В качестве источника напряжения U используем аккумуляторную батарею, которую подключим к сопротивлению R толстыми и одновременно короткими проводами в точках А и В. Допустим, что провода не влияют на величину прохождения тока I к резистору R.
Формула (1) выражает соотношения между сопротивлением (омы), напряжением (вольты) и током (амперы). Ее называют законом Ома для участка цепи. Кружок под формулой облегчает ее запоминание и пользование для выражения каждого из составляющих параметров U, R или I (U расположено сверху над черточкой, а R и I — снизу).
Если надо определить один из них, то мысленно закрываем его и работаем с двумя оставшимися, выполняя арифметические действия. Когда величины расположены на одной строчке, то их перемножаем. А в случае расположения их на разных уровнях выполняем деление верхнего на нижний.
Эти соотношения показаны на формулах 2 и 3 рисунка 3 ниже.
В этой схеме для измерения тока используется амперметр, который соединен последовательно с нагрузкой R, а напряжения — вольтметр, подключенный параллельно точкам 1 и 2 резистора. Учитывая конструктивные особенности приборов, допустим, что амперметр не влияет на величину тока в схеме, а вольтметр — напряжения.
Определение сопротивления с помощью закона Ома
Пользуясь показаниями приборов (U=12 В, I=2,5 А) можно по формуле 1 определить величину сопротивления R=12/2,5=4,8 Ом.
На практике этот принцип заложен в работу измерительных приборов — омметров, определяющих активное сопротивление различных электрических устройств. Поскольку они могут быть настроены на замеры различных диапазонов величин, то их соответственно подразделяют на микроомметры и миллиомметры, работающие с малыми сопротивлениями и тера-, гиго- и мегаомметры — измеряющие очень большие значения.
Для конкретных условий эксплуатации их выпускают:
-
переносными;
-
щитовыми;
-
лабораторными моделями.
-
Принцип работы омметра
Для выполнения замеров обычно используются магнитоэлектрические приборы, хотя в последнее время широко внедряются электронные (как аналоговые, так и цифровые).
В омметре магнитоэлектрической системы используется токоограничивающий резистор R, пропускающий через себя только миллиамперы и чувствительная измерительная головка (миллиамперметр). Она реагирует на протекание малых токов через прибор за счет взаимодействия двух электромагнитных полей от постоянного магнита N-S и поля, создаваемого током, проходящим через обмотку катушки 1 с токопроводящей пружинкой 2.
В результате взаимодействия сил магнитных полей происходит отклонение стрелки прибора на определенный угол. Шкала головки для облегчения работы сразу проградуирована в омах. При этом используется выражение сопротивления через ток по формуле 3.
У омметра для обеспечения точных замеров должно поддерживаться стабилизированное значение подаваемого напряжения от батареи питания. С этой целью применяется калибровка посредством использования добавочного регулировочного резистора R рег. С его помощью до начала измерения на схему ограничивается подача излишнего напряжения от источника, выставляется строго стабильная, нормируемая величина.
Определение напряжения с помощью закона Ома
Во время работ с электрическими схемами бывают случаи, когда необходимо узнать падение напряжения на каком-то элементе, например, резисторе, а известно его сопротивление, которое обычно маркируется на корпусе, и проходящий сквозь него ток. Для этого не обязательно подключать вольтметр, а достаточно воспользоваться расчетами по формуле 2.
В нашем случае для рисунка 3 проведем расчеты: U=2,5·4,8 =12 В.
Определение тока с помощью закона Ома
Этот случай описывает формула 3.
Его используют для расчета нагрузок в электрических схемах, выбора сечений проводников, кабелей, предохранителей или защитных автоматов.В нашем примере расчет выглядит так: I=12/4,8=2,5 А.
Шунтирование
Этот способ в электротехнике используют для исключения работы определенных элементов из схемы без их демонтажа. Для этого на ненужном резисторе замыкают накоротко проводником входящую и отходящую клеммы (на рисунке 1 и 2) — шунтируют.
В результате ток схемы выбирает для себя путь с меньшим сопротивлением через шунт и резко возрастает, а напряжение зашунтированного элемента падает до нуля.
Короткое замыкание
Этот режим является частным случаем шунтирования и, в общем-то, показан на рисунке выше, когда закоротка устанавливается на выходные клеммы источника. При его возникновении создаются очень опасные большие токи, способные поражать людей и сжигать не защищенное электрооборудование.
Для борьбы со случайно возникающими замыканиями в электрической сети используют защиты. На них выставляют такие уставки, которые не мешают работать схеме в нормальном режиме. Они отключают питание только при аварийных случаях.
Например, если ребенок по неосторожности всунет в домашнюю розетку проволоку, то правильно настроенный автоматический выключатель вводного квартирного щита практически моментально отключит электроснабжение.
Все, что описано выше, относится к закону Ома для участка цепи постоянного тока, а не полной схемы, где процессов может быть значительно больше. Следует представлять, что это только небольшая часть применения его в электротехнике.
Закономерности, выявленные знаменитым ученым Георгом Симоном Омом между током, напряжением и сопротивлением по-разному описываются в различных средах и цепях переменного тока: однофазных и трехфазных.
Вот основные формулы, выражающие соотношения электрических параметров в металлических проводниках.
Более сложные формулы для проведения специальных расчетов закона Ома на практике.
Как видим, исследования, которые провел гениальный ученый Георг Симон Ом, имеют огромное значение даже в наше время бурного развития электротехники и автоматики.
Его используют для расчета нагрузок в электрических схемах, выбора сечений проводников, кабелей, предохранителей или защитных автоматов.
Закон ома и его практическое применение
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается в следующем виде:
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома.
Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
Где и когда можно применять закон Ома?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Принцип работы одного из основополагающих законов электротехники хочется начать объяснять с аллегории — показа небольшого карикатурного изображения 1 из трех человечков под именами «Напряжение U», «Сопротивление R» и «Ток I».
На нем видно, что «Ток» пытается пролезть через сужение в трубе, которое «Сопротивление» усердно затягивает.
В то же время «Напряжение» прилагает максимально возможное усилие для прохождения, проталкивания «Тока».
Этот рисунок напоминает, что электрический ток — это упорядоченное движение заряженных частиц в определенной среде. Передвижение их возможно под действием приложенной внешней энергии, создающей разность потенциалов — напряжение. Однако, внутренние силы проводников и элементов схемы уменьшают величину тока, оказывают сопротивление его перемещению.
Рассмотрим простую схему 2, поясняющую действие закона Ома для участка электрической цепи постоянного тока.
В качестве источника напряжения U используем аккумуляторную батарею, которую подключим к сопротивлению R толстыми и одновременно короткими проводами в точках А и В. Допустим, что провода не влияют на величину прохождения тока I к резистору R.
Формула (1) выражает соотношения между сопротивлением (омы), напряжением (вольты) и током (амперы). Ее называют законом Ома для участка цепи. Кружок под формулой облегчает ее запоминание и пользование для выражения каждого из составляющих параметров U, R или I (U расположено сверху над черточкой, а R и I — снизу).
Если надо определить один из них, то мысленно закрываем его и работаем с двумя оставшимися, выполняя арифметические действия. Когда величины расположены на одной строчке, то их перемножаем. А в случае расположения их на разных уровнях выполняем деление верхнего на нижний.
Эти соотношения показаны на формулах 2 и 3 рисунка 3 ниже.
В этой схеме для измерения тока используется амперметр, который соединен последовательно с нагрузкой R, а напряжения — вольтметр, подключенный параллельно точкам 1 и 2 резистора. Учитывая конструктивные особенности приборов, допустим, что амперметр не влияет на величину тока в схеме, а вольтметр — напряжения.
Определение сопротивления с помощью закона Ома
Пользуясь показаниями приборов (U=12 В, I=2,5 А) можно по формуле 1 определить величину сопротивления R=12/2,5=4,8 Ом.
На практике этот принцип заложен в работу измерительных приборов — омметров, определяющих активное сопротивление различных электрических устройств. Поскольку они могут быть настроены на замеры различных диапазонов величин, то их соответственно подразделяют на микроомметры и миллиомметры, работающие с малыми сопротивлениями и тера-, гиго- и мегаомметры — измеряющие очень большие значения.
Для конкретных условий эксплуатации их выпускают:
Принцип работы омметра
Для выполнения замеров обычно используются магнитоэлектрические приборы, хотя в последнее время широко внедряются электронные (как аналоговые, так и цифровые).
В омметре магнитоэлектрической системы используется токоограничивающий резистор R, пропускающий через себя только миллиамперы и чувствительная измерительная головка (миллиамперметр). Она реагирует на протекание малых токов через прибор за счет взаимодействия двух электромагнитных полей от постоянного магнита N-S и поля, создаваемого током, проходящим через обмотку катушки 1 с токопроводящей пружинкой 2.
В результате взаимодействия сил магнитных полей происходит отклонение стрелки прибора на определенный угол. Шкала головки для облегчения работы сразу проградуирована в омах. При этом используется выражение сопротивления через ток по формуле 3.
У омметра для обеспечения точных замеров должно поддерживаться стабилизированное значение подаваемого напряжения от батареи питания.
С этой целью применяется калибровка посредством использования добавочного регулировочного резистора R рег. С его помощью до начала измерения на схему ограничивается подача излишнего напряжения от источника, выставляется строго стабильная, нормируемая величина.
Определение напряжения с помощью закона Ома
Во время работ с электрическими схемами бывают случаи, когда необходимо узнать падение напряжения на каком-то элементе, например, резисторе, а известно его сопротивление, которое обычно маркируется на корпусе, и проходящий сквозь него ток. Для этого не обязательно подключать вольтметр, а достаточно воспользоваться расчетами по формуле 2.
В нашем случае для рисунка 3 проведем расчеты: U=2,5·4,8 =12 В.
Определение тока с помощью закона Ома
Этот случай описывает формула 3. Его используют для расчета нагрузок в электрических схемах, выбора сечений проводников, кабелей, предохранителей или защитных автоматов.
В нашем примере расчет выглядит так: I=12/4,8=2,5 А.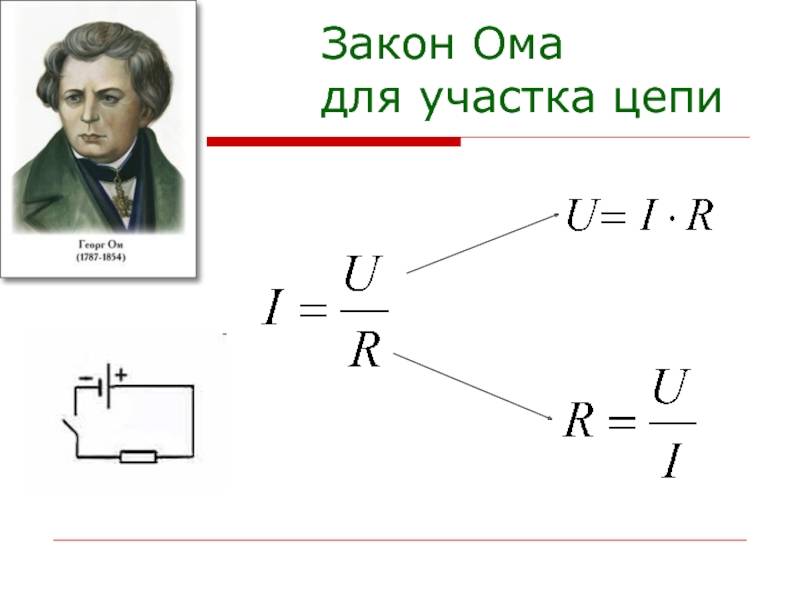
Этот способ в электротехнике используют для исключения работы определенных элементов из схемы без их демонтажа. Для этого на ненужном резисторе замыкают накоротко проводником входящую и отходящую клеммы (на рисунке 1 и 2) — шунтируют.
В результате ток схемы выбирает для себя путь с меньшим сопротивлением через шунт и резко возрастает, а напряжение зашунтированного элемента падает до нуля.
Этот режим является частным случаем шунтирования и, в общем-то, показан на рисунке выше, когда закоротка устанавливается на выходные клеммы источника. При его возникновении создаются очень опасные большие токи, способные поражать людей и сжигать не защищенное электрооборудование.
Для борьбы со случайно возникающими замыканиями в электрической сети используют защиты. На них выставляют такие уставки, которые не мешают работать схеме в нормальном режиме. Они отключают питание только при аварийных случаях.
Например, если ребенок по неосторожности всунет в домашнюю розетку проволоку, то правильно настроенный автоматический выключатель вводного квартирного щита практически моментально отключит электроснабжение.
Все, что описано выше, относится к закону Ома для участка цепи постоянного тока, а не полной схемы, где процессов может быть значительно больше. Следует представлять, что это только небольшая часть применения его в электротехнике.
Закономерности, выявленные знаменитым ученым Георгом Симоном Омом между током, напряжением и сопротивлением по-разному описываются в различных средах и цепях переменного тока: однофазных и трехфазных.
Вот основные формулы, выражающие соотношения электрических параметров в металлических проводниках.
Более сложные формулы для проведения специальных расчетов закона Ома на практике.
Как видим, исследования, которые провел гениальный ученый Георг Симон Ом, имеют огромное значение даже в наше время бурного развития электротехники и автоматики.
В природе существует два основных вида материалов, проводящие ток и непроводящие (диэлектрики). Отличаются эти материалы наличием условий для перемещения в них электрического тока (электронов).
Из токопроводящих материалов (медь, алюминий, графит, и многие другие), делают электрические проводники, в них электроны не связаны и могут свободно перемещаться.
В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может. Из них делают изоляцию для проводов, детали электроприборов.
Для того чтобы электроны начали перемещаться в проводнике (по участку цепи пошел ток), им нужно создать условия. Для этого в начале участка цепи должен быть избыток электронов, а в конце – недостаток. Для создания таких условий используют источники напряжения – аккумуляторы, батарейки, электростанции.
Формула Закона Ома
В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.
Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.
Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.
где I – сила тока, измеряется в амперах и обозначается буквой А; U – напряжение, измеряется в вольтах и обозначается буквой В; R – сопротивление, измеряется в омах и обозначается Oм.
Если известны напряжение питания U и сопротивление электроприбора R, то с помощью вышеприведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I.
| Онлайн калькулятор для определения силы тока | |
|---|---|
| Напряжение, В: | |
| Сопротивление, Ом: | |
С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I, а величину сопротивления R.
Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.
| Онлайн калькулятор для определения величины сопротивления | |
|---|---|
| Напряжение, В: | |
| Величина тока, А: | |
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика.
В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.
Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
где P – мощность, измеряется в ваттах и обозначается Вт; U – напряжение, измеряется в вольтах и обозначается буквой В; I – сила ток, измеряется в амперах и обозначается буквой А.
Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
| Онлайн калькулятор для определения потребляемой мощности | |
|---|---|
| Напряжение, В: | |
| Сила тока, А: | |
Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания.
Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.
| Онлайн калькулятор для определения силы тока в зависимости от потребляемой мощности | |
|---|---|
| Потребляемая мощность, Вт: | |
| Напряжение питания, В: | |
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В.
Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
Преобразованные формулы Закона Ома и Джоуля-Ленца
Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения
По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.
А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.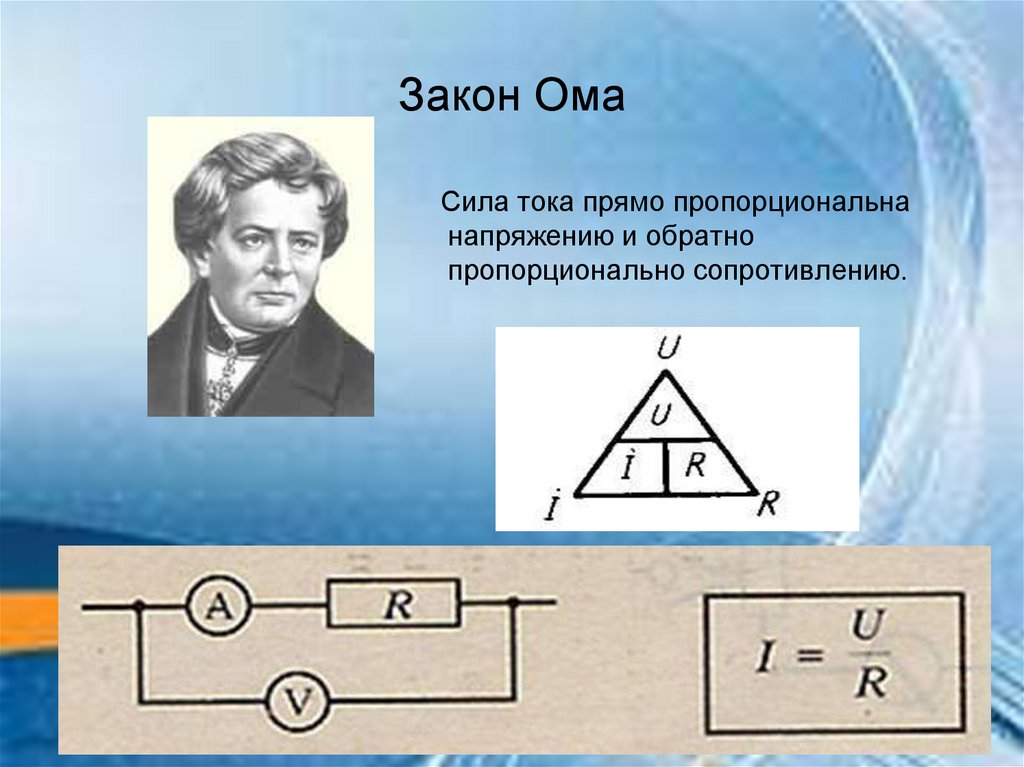
Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.
Закон Ома Практика Задачи Онлайн
На приведенном выше графике показан ток через нихромовую проволоку в зависимости от приложенного напряжения. Если i=200 мАi=\si{200\ \милли\ампер}i=200 мА и v=125 Vv=\si{125\ \volt}v=125 В,) каково сопротивление (в Ом\ОмегаОм) из нихромовой проволоки?
625 1600 250 25Показать объяснение
View wiki
Известно, что величина тока, необходимого для прохождения через человека, чтобы вызвать у него фибрилляцию желудочков (сердечный приступ), составляет около 100 мА.
При каком минимальном напряжении (в вольтах) у человека с сопротивлением тела 1723 Ом1723\ \Омега1723 Ом разовьется фибрилляция желудочков?
17.23 58.03 580,3 172,3Показать объяснение
View wiki
Если ток I=0,9 AI=0,9\text{ A}I=0,9 A протекает через резистор R=7 ΩR=7\ \OmegaR=7 Ω длины Δd=5 \Delta d=5 \ Δd=5 м, какова напряженность электрического поля внутри резистора?
3.16 Н/З 1,46 Н/З 1,26 Н/З 1,76 Н/ЗПоказать объяснение
Посмотреть вики
В приведенной выше схеме V=5 В, V=5\text{ V},V=5 В, R1=1 Ом, R_1=1\ \Omega,R1=1 Ом, R2=6 Ом, R_2=6 \\Omega,R2=6 Ом и R3=12 Ом.
R_3=12\ \Omega.R3=12 Ом. Найдите ток через R1.R_1.R1.
Показать объяснение
Посмотреть вики
Если I=1 AI=1\text{ A}I=1 A и R=8 Ом, R=8\ \Omega,R=8 Ом, каково напряжение батареи?
9 В9\текст{ В}9 В 8 В8\текст{ В}8 В 10 В10\текст{ В}10 В 11 В11\текст{ В}11 ВПоказать объяснение
View wiki
Учебное пособие по закону Ома с простыми практическими задачами -…
Опубликовано
Закон Ома является основополагающим уравнением в основных схемах и поражает своей простотой и использованием. В этом уроке мы узнаем, что такое закон Ома, где вы можете и не можете его использовать, и сделаем несколько примеров очень, очень простых схем.
Закон Ома устанавливает связь между напряжением и током через линейное сопротивление. В учебнике, определяющем и связывающем напряжение, ток, сопротивление и мощность, мы использовали воду в качестве примера. Размышляя об этой аналогии, неудивительно, что существует математическая зависимость между тем, сколько воды течет, в зависимости от высоты водяного столба и размера трубы. Для электричества это соотношение устанавливается как:
или
Несколько важных замечаний:
- Это означает, что напряжение, деленное на сопротивление, дает ток. Или высота воды, деленная на размер трубы, дает вам расход воды. Интуитивно это должно иметь смысл. По мере того, как вы переходите к более высокому потенциалу, больше тока будет течь. Если вы увеличите размер трубы, уменьшив сопротивление, будет течь больший ток. И обратное верно.
- Это линейное уравнение. Это не только означает, что зависимость представляет собой прямую линию, но если вы имеете дело с чем-то нелинейным, где сопротивление изменяется в зависимости от напряжения, это уравнение неприменимо. Это необычно, поэтому мы будем считать резисторы линейными, если явно не указано иное.
- Это верно, когда у вас есть напряжение и сопротивление (обычно это резистор), но когда мы узнаем о других компонентах и источниках питания, этот закон обычно не применяется к ним.
Интуитивно это должно иметь смысл. По мере того, как вы переходите к более высокому потенциалу, больше тока будет течь. Если вы увеличите размер трубы, уменьшив сопротивление, будет течь больший ток. И обратное верно. Напряжение и ток могут быть как положительными, так и отрицательными. Как упоминалось в предыдущем уроке, напряжение является относительным, поэтому отрицательное напряжение имеет более низкий потенциал, чем то, что (возможно, произвольно) установлено как ноль вольт или заземление.
Ток, будучи мерой потока, бывает положительным или отрицательным в зависимости от того, каким образом вы или проблема назначаете поток. Если вы говорите, что ток течет от А к В, а на самом деле ток течет от В к А, то этот ток отрицательный. Однако, если вы посмотрите на ту же ситуацию и определите, что ток течет от B к A, тогда, когда ток действительно течет от B к A, это положительный ток! Поначалу это может сбивать с толку, и оба они до сих пор сбивают меня с толку, если я какое-то время не решал никаких проблем со схемой. Самое главное, чтобы они были прямыми, — это сделать ваши предположения о потенциале напряжения и протекании тока и убедиться, что используемые вами уравнения соответствуют этим предположениям. Мы рассмотрим эту концепцию в некоторых практических задачах в конце этого урока.
Есть две распространенные крайности, которые вы можете увидеть в законе Ома в отношении сопротивления. Когда сопротивление равно нулю и когда сопротивление бесконечно. Когда сопротивление равно нулю, в основном, когда провод соединяет два разных потенциала напряжения, это называется коротким замыканием.
Это замыкает напряжения вместе. Глядя на закон Ома, когда сопротивление равно нулю, если у вас есть какое-либо конечное напряжение, вы получите бесконечный ток. Хотя в реальной жизни не существует такой вещи, как бесконечный ток, если это не запланировано, ток будет достаточно высоким, чтобы нанести некоторый ущерб!
Другая крайность — это когда сопротивление бесконечно, или когда два потенциала напряжения полностью и полностью разделены. В зависимости от обстоятельств иногда вы можете рассматривать чрезвычайно высокие сопротивления как бесконечно большие, но используйте это предположение с осторожностью. Когда сопротивление бесконечно, это означает, что при любом напряжении ток отсутствует. Если это желательно, то отлично. Если нет, это обычно означает, что то, что ожидает силы, не получает ее.
Заключительные пункты примечания
Иногда вы будете слышать о двух связанных, но разных терминах. Первым из этих терминов является удельное сопротивление.
Удельное сопротивление является свойством материала и является основой сопротивления. Материал с высокой проводимостью будет иметь очень низкое удельное сопротивление (например, медь), в то время как материал с высокой изоляцией будет иметь очень высокое удельное сопротивление (например, резина). Большинство материалов, используемых для резистора, будут где-то посередине. Зная длину и площадь поперечного сечения материала, можно умножить удельное сопротивление на длину и разделить на площадь поперечного сечения.
R – Сопротивление (Ом)
ρ – Удельное сопротивление (Ом-см или Ом-м)
l – Длина (см или м)
A – Площадь поперечного сечения (см 2 или m 2 )
Если вы на минутку посмотрите на это уравнение, оно должно быть интуитивно понятным. По мере увеличения длины сопротивление будет расти. Если увеличить площадь, через которую могут пройти электроны, сопротивление уменьшится.
Второй член — это проводимость, Г.
Это просто обратная величина сопротивления. Он используется в определенных случаях, но по сравнению с резистентностью встречается крайне редко. Единицы измерения иногда называют «мос» с перевернутым символом омега по сравнению с «омами» с перевернутым символом омега. Иногда их также называют Siemens.
Вы также получаете инвертированный закон Ома:
Пример / практические задачи
Задача 1. От узла A: 1000 В до узла B: 0 В, через резистор 100 Ом.
Решение:
В этой первой практической задаче мы определяем падение напряжения на резисторе и формулируем уравнение. Узел A — 1000 вольт, а узел B — 0 вольт, поэтому мы можем составить уравнение как 1000V — 0V, а затем разделить его на сопротивление, которое равно 100 Ом. Получаем:
Таким образом, мы получаем 10 А тока, протекающего от узла А к узлу Б.
Проблема 2. Узел А: 12 В к узлу Б: 3 В через резистор 200 Ом.
Решение:
В этой второй практической задаче мы выполняем те же шаги, что и в первой задаче, но с другими номерами.
Мы смотрим на падение напряжения от узла A к узлу B и устанавливаем первую часть уравнения, которая составляет 12–3 В. Разделив его на сопротивление, мы получим окончательное уравнение:
В этом случае мы получим 45 миллиампер, протекающих от узла А к узлу Б.
Проблема 3. От узла A: 16 В до узла B: 24 В через резистор 800 Ом.
Решение:
В этой третьей практической задаче, из-за того, что мы все еще используем термины «узел А» и «узел Б», мы по-прежнему установим уравнения относительно потока, идущего от узла А к узлу Б, даже хотя при осмотре мы можем сказать, что узел B имеет более высокий потенциал напряжения. Ничего страшного, потому что, пока мы все помечаем правильно, ответ все равно будет правильным. Итак, у нас есть 16 В – 24 В, а затем разделите это на 800 Ом.
Таким образом, мы получаем отрицательные 10 миллиампер от узла A к узлу B. Это имеет смысл, поскольку узел B находится под более высоким напряжением, поэтому, если мы определим ток, идущий от A к B, если ток равен , фактически , идущий от B к узлу B.
А, то ток отрицательный.
Проблема 4. Узел A: -7 В к узлу B: -13 В, через резистор 1,2 кОм.
Решение:
В этой четвертой и последней практической задаче, которую мы собираемся решить, мы по-прежнему определим задачу с точки зрения тока, протекающего от узла А к узлу Б. Итак, еще раз мы составляем уравнение. (-7 – (-13))/1200.
Обратите внимание: поскольку мы были последовательны в определении вещей, мы знаем, что единственное изменение этой задачи по сравнению с последними тремя задачами заключается в том, что мы вычитаем отрицательное число, таким образом, складывая его. Опять же, поскольку напряжения относительны, фактические напряжения не так важны, как разница между ними. Если вы хотите убедиться в этом сами, повторите эту задачу с узлом A на 6 В и узлом B на 0 В.
Резюме
Закон Ома лежит в основе большинства анализов цепей и довольно прост, если вы внимательно следите за тем, чтобы способ, которым вы устанавливаете свои уравнения, соответствовал тому, как вы назначили полярности и потоки в программа.
Короткие замыкания и разомкнутые цепи — чрезвычайно распространенные сценарии как в академических кругах, так и в реальной жизни, поэтому полезно сделать их второй натурой для вашего понимания цепей.
Далее мы узнаем о ветвях, узлах и циклах, а также о том, как можно последовательно и параллельно размещать компоненты. Это позволит нам применять закон Ома к значительно более широкому и более практичному набору практических цепей.
Чтобы узнать больше о резисторах, ознакомьтесь с этим руководством.
Чтобы узнать больше о переменных резисторах или потенциометрах, ознакомьтесь с этим руководством.
Автор:
Джош Бишоп
Интересуясь встраиваемыми системами, туризмом, кулинарией и чтением, Джош получил степень бакалавра электротехники в Университете штата Бойсе. Проработав несколько лет офицером CEC (Seabee) в ВМС США, Джош уволился и в конце концов начал работать над CircuitBread с кучей замечательных людей. В настоящее время Джош живет на юге Айдахо с женой и четырьмя детьми.
