Условное обозначение конденсаторов на схемах
Наряду с резисторами конденсаторы являются наиболее широко используемыми компонентами электрических цепей. Основные характеристики конденсатора — номинальная ёмкость и номинальное напряжение. Чаще всего в схемах используются постоянные конденсаторы, и гораздо реже — переменные и подстроенные. Отдельной группой стоят конденсаторы, изменяющие свою ёмкость под воздействием внешних факторов.
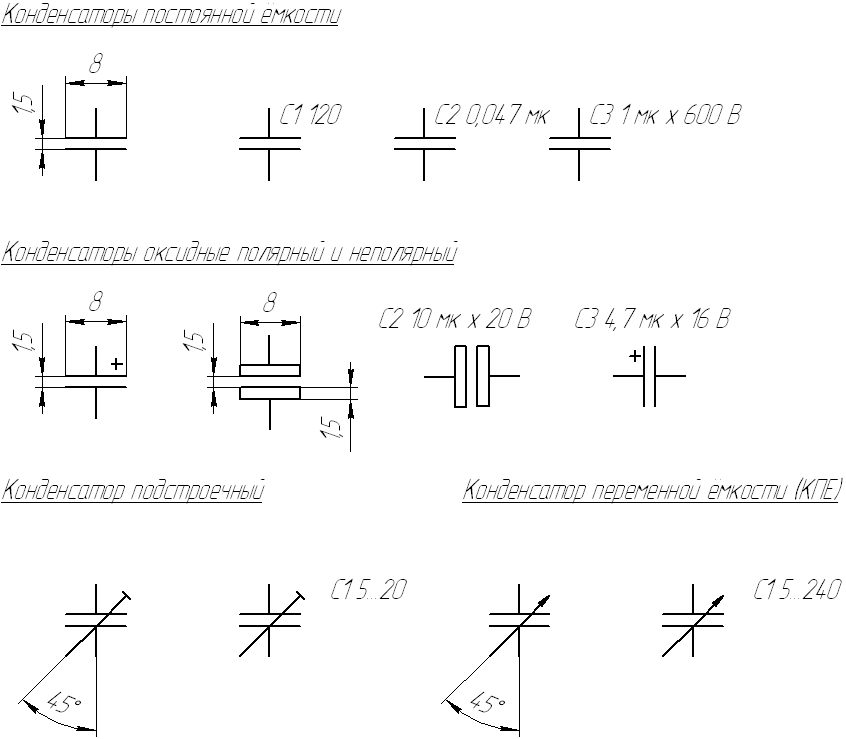
Общие условные графические обозначения конденсаторов постоянной ёмкости приведены на рис. 1 и их определяет соответствующий ГОСТ.
Рис.1. Условное обозначение конденсаторов
Номинальное напряжение конденсаторов (кроме так называемых оксидных) на схемах, как правило, не указывают. Только в некоторых случаях, например,
в схемах цепей высокого напряжения рядом с обозначением номинальной ёмкости можно указывать и номинальное напряжение (см.
Рис.2. Условное обозначение оксидных (электролитических) конденсаторов
Подавляющее большинство оксидных конденсаторов — полярные, поэтому включать их в электрическую цепь можно только с соблюдением полярности. Чтобы показать это на схеме, у символа положительной обкладки такого конденсатора ставят знак «+». Обозначение С1 на рис. 2 — общее обозначение поляризованного конденсатора. Иногда используется другое изображение обкладок конденсатора (см. рис.2, C2 и C3).
С технологическими целями или при необходимости уменьшения габаритов в некоторых случаях в один корпус помещают два конденсатора,
но выводов делают только три (один из них — общий). Условное графическое обозначение сдвоенного конденсатора наглядно передает эту идею (см.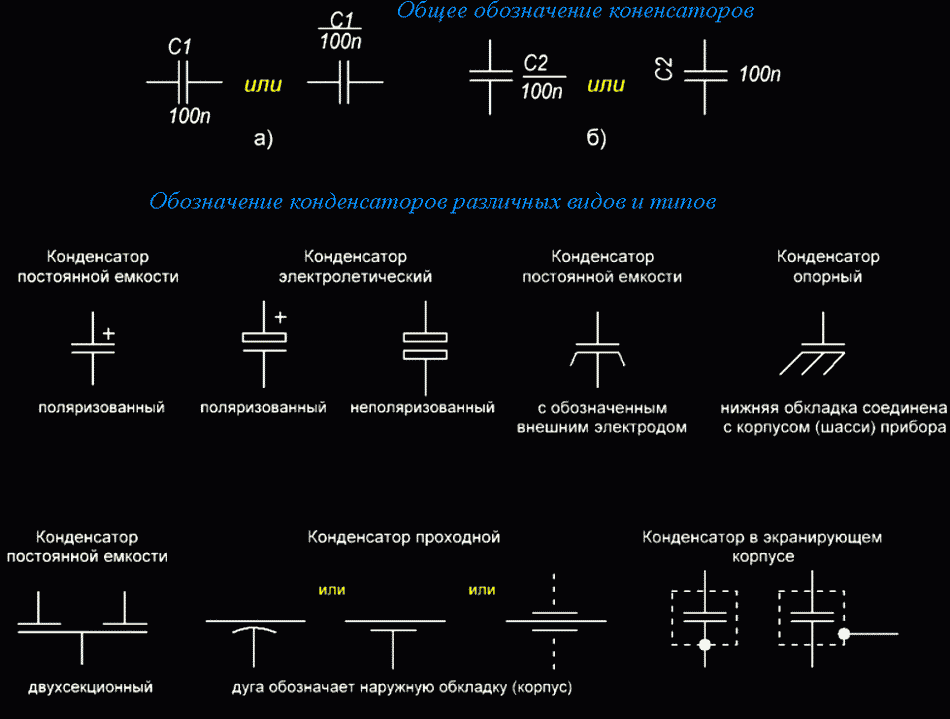
Для развязки цепей питания высокочастотных устройств по переменному току применяют так называемые проходные конденсаторы. У них тоже три вывода: два — от одной обкладки («вход» и «выход»), а третий (чаще в виде винта) — от другой, наружной, которую соединяют с экраном или завёртывают в шасси. Эту особенность конструкции отражает условное графическое обозначение такого конденсатора (рис. 3, С1). Наружную обкладку обозначают короткой дугой, а также одним (C2) или двумя (C3) отрезками прямых линий с выводами от середины. Условное графическое обозначение с позиционным обозначением С3 используют при изображении проходного конденсатора в стенке экрана. С той же целью, что и проходные, применяют опорные конденсаторы. Обкладку, соединяемую с корпусом (шасси), выделяют в обозначении такого конденсатора тремя наклонными линиями, символизирующими «заземление» (см. рис. 3, С4).
Рис.
3. Условное обозначение проходных конденсаторов
Конденсаторы переменной ёмкости (КПЕ) предназначены для оперативной регулировки и состоят обычно из статора и ротора. Такие конденсаторы широко использовались, например, для изменения частоты настройки радиовещательных приёмников. Как говорит само название, они допускают многократную регулировку ёмкости в определенных пределах. Это их свойство показывают на схемах знаком регулирования — наклонной стрелкой, пересекающей базовый символ под углом 45°, а возле него часто указывают минимальную и максимальную ёмкость конденсатора (рис. 4). Если необходимо обозначить ротор КПЕ, поступают так же, как и в случае проходного конденсатора (см. рис. 4, С2).
Рис.4. Условное обозначение переменных конденсаторов
Для одновременного изменения ёмкости в нескольких цепях (например, в колебательных контурах) используют блоки, состоящие из двух, грех и большего числе КПЕ.
Принадлежность КПЕ к одному блоку показывают на схемах штриховой линией механической связи, соединяющей знаки регулирования, и нумерацией секций
(через точку в позиционном обозначении, рис. 5). При изображении КПЕ блока в разных, далеко отстоящих одна от другой частях схемы механическую
связь не показывают, ограничиваясь только соответствующей нумерацией секций (см. рис. 5, С2.1, С2.2, С2.3).
Рис.5. Условное обозначение блочных переменных конденсаторов
Разновидность КПЕ —
Рис.6. Условное обозначение подстроечных конденсаторов
Саморегулирумые конденсаторы (или нелинейные) обладают способностью изменять ёмкость под действием внешних факторов.
В радиоэлектронных устройствах часто применяют вариконды (от английских слов vari(able) — переменный и cond(enser)—еще одно название конденсатора).
Их ёмкость зависит от приложенного к обкладкам напряжения. Буквенный код варикондов — CU (U— общепринятый символ напряжения), обозначаются в этом случае — базовый символ конденсатора,
перечеркнутый знаком нелинейного саморегулирования с латинской буквой U (рис. 7, конденсатор CU1).
Рис.7. Условное обозначение варикондов и термоконденсаторов
Аналогично построено обозначение термоконденсаторов. Буквенный код этой разновидности конденсаторов — СK (рис. 7, конденсатор СК2). Температура среды, естественно, обозначается символом t°.
Как определить конденсатор на схеме
2013, Апрель 1 , Понедельник
Домашняя старницаНемного электричестваКак определить конденсатор на схеме
Автор: Игорь Александрович Немного электричества 0 Комментариев
Мало кому известно, что работа двигателя внутреннего сгорания, каким бы модернизированным он не был, зависит от маленькой детальки, именуемой нами конденсатором.
Наверное, каждый замечал при расчёсывании своих волос прилипание на расчёску пуха или выпавшего волоса, треск синтетической одежды в сухую погоду. Возможно, кто-то получал лёгкий, но неприятный удар электрического заряда от дверцы при выходе из автомобиля. Да и каждый в своей жизни хоть раз, но видел разряд молнии. Что объединяет эти примеры?
На расчёске, одежде, кузове автомобиля, атмосферных слоях накапливается электрический заряд. Обратите внимание: накапливается до определённой величины и сила каждого заряда зависит от размера объекта, который его накапливает.
До XVII века разгадка электрических явлений не была найдена. Разными способами пытались ‘поймать электрическую жидкость’, используя для этого различные приспособления, именуемые накопителями. Первым конденсатором(от лат. condensare — ‘уплотнять’, ‘сгущать’) можно назвать Лейденскую банку — стеклянный сосуд, оклеенный внутри и снаружи листовым оловом и способным накапливать и хранить сравнительно большие электрические заряды.
Современная, обычная конструкция электрического конденсатора состоит, конечно же, не из листового олова, а из двух металлических пластин или поверхностей — обкладок, разделёнными между собой материалом, который не проводит электричество в естественных условиях — диэлектрик. К каждой обкладке присоединено по одному проводнику, которые служат для подключения конденсатора к электрической цепи. По геометрическому виду электрические конденсаторы бывают плоские, цилиндрические, сферические, трубчатые.
Конденсаторы с малой способностью накопления заряда — с малой электрической ёмкостью — имеют всего лишь две плоские обкладки с диэлектриком посередине, либо с двухсторонним напылением металла на керамическую плитку. В цилиндрических конденсаторах в роли обкладки выступает смотанный рулон металлизированной фольги — станиоль или алюминиевая фольга — с прослойкой диэлектрика. Трубчатые конденсаторы сочетают в себе тип конструкции плоских конденсаторов.
Для быстрого заряда и хранения накопленной электрической энергии используют ионисторы — суперконденсаторы, называемые ещё конденсатор-аккумулятор.
Вместо обкладок у них используется активированный уголь или вспененный металл с тонкой диэлектрической прослойкой.
Как различить конденсаторы на рисунке электросхемы.
В зависимости от типа используемых обкладок и используемого диэлектрика электрические конденсаторы по своему исполнению имеют различный вид: цилиндрические, сферические, плоские и имеют две группы использования: общего назначения — повсеместное использование, и специального назначения — импульсные, высоковольтные и др., и могут иметь два и более выводов для соединения.
Конденсаторы, не изменяющие своей ёмкости, кроме изменённой ёмкости по истечении гарантийного срока, называются постоянными — с постоянной ёмкостью, и имеют только два вывода для подключения к цепи. Бывают и исключения, когда при наличии двух выводов конденсатор является переменным — конденсатор переменной ёмкости. Такие электрические конденсаторы изменяют свою ёмкость под воздействием магнитного поля, приложенного напряжения, механического воздействия или от влияния ещё каких-либо внешних сил, известных современной физике.
К примеру: когда при настройке радиоприёмника Вы вращаете ручку управления для поиска новой радиостанции, то в процессе вращения ручки изменяется ёмкость конденсатора, управляющего обработкой частоты принимаемого радиоприёмником сигнала. Тут используется переменный конденсатор — конденсатор переменной ёмкости.
Когда производится настройка принимаемого телевизионного сигнала телевизором, так же происходит изменение ёмкости конденсатора, управляемого частотой обработки сигнала, но разница состоит в управлении изменением ёмкости. У приёмника — поворотом ручки — смещение обкладок конденсатора переменной ёмкости относительно друг-друга, а у телевизора — изменением напряжения, приложенного к управляющей обкладке элемента, называемого варикапом, в большей степени относящемуся к полупроводниковому диоду.
Как отличить на схеме конденсаторы?
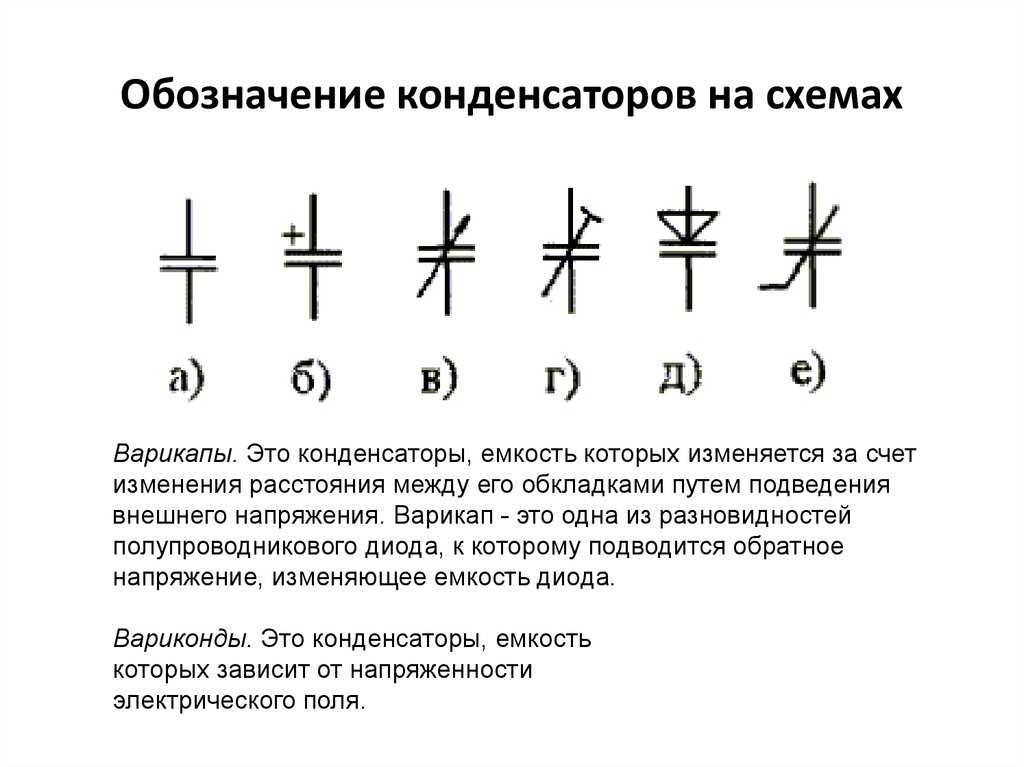
Конденсаторы постоянной ёмкости изображаются параллельными отрезками с отводными соединительными линиями от середины. У переменных конденсаторов — две и более параллельных линии или одна из них дугообразная, с пересекаемой линией со стрелкой на конце.
Варикапы имеют на рисунке так же два вывода, один из которых заменён на треугольничек, обращённый углом к обкладке и выводом на основании. Не путайте с варикондами, которые рисуются так же, как и постоянные конденсаторы, но имеют пересекаемую линию через обкладки со стрелкой на конце и изменяют свою ёмкость от приложенного к обкладкам напряжения. Ионисторы рисуются двумя параллельными, как конденсаторы постоянной ёмкости, но помещённые в окружность или с одинаково жирными обкладками.
В зависимости от типа напряжения все конденсаторы делятся на две группы: полярные — работающие в среде постоянного тока и неполярные — обеспечивающие свою работоспособность в среде переменного тока. Полярные конденсаторы изображаются параллельными прямыми, с указанием возле одной обкладки знака полярности приложенного напряжения — (+), или с обкладками, различающимися толщиной или формой.
Буквенное обозначение у всех конденсаторов одинаковое — С , за исключением ионисторов, обозначаемых буквой К и варикапов, обозначаемых КВ.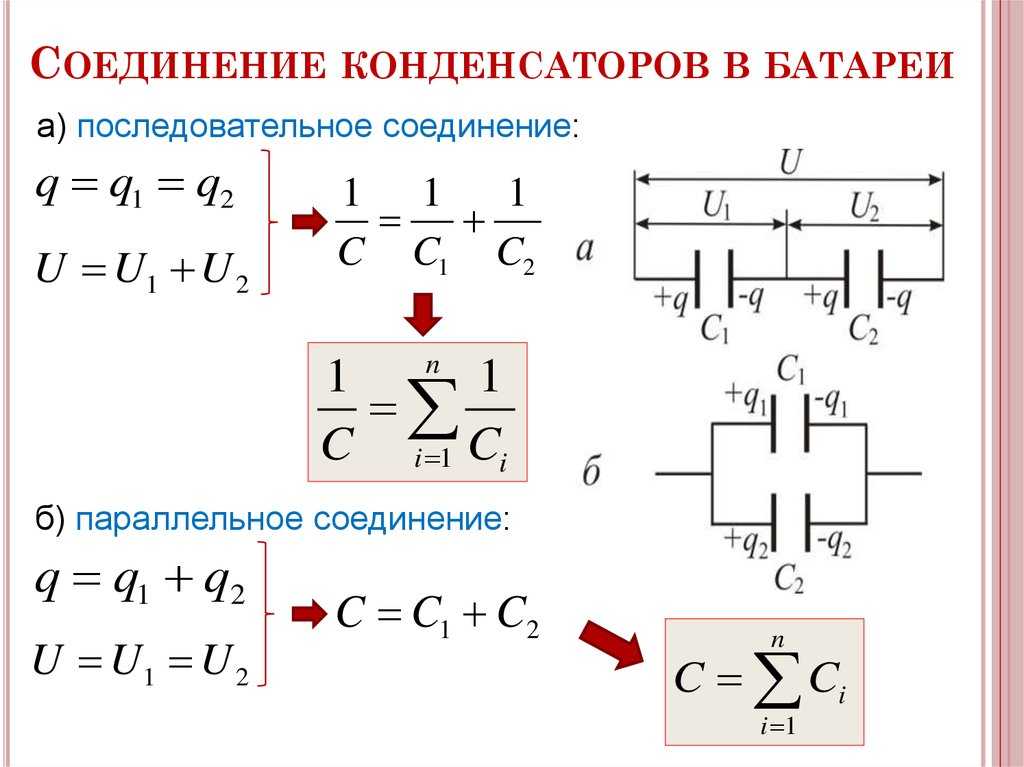
При использовании конденсаторов недавно бывших в работе в какой-либо электрической схеме обязательно перед тем, как Вы возьмёте его в руки, замкните накоротко его выводы изолированным инструментом для снятия электрического заряда. А вот с ионисторами так не поступайте, иначе его испортите, создав большой ток короткого замыкания.
Оцените публикацию !
[Всего: 4 Общая: 5]
◀ Как обозначаются сопротивления на электросхемах
Как узнать тип электролампы по её изображению на схеме ▶
Об Авторе
Игорь Александрович
Возможно, предоставляемые мною сведения не будут достаточно удовлетворять заинтересовавшегося гостя в поиске нужной для него информации. Не оставлю без внимания ни один комментарий, даже компрометирующий меня, но только по соответствующей теме. Обратиться ко мне лично по некоторым вопросам можно на странице Связь с администратором “Весёлый Карандашик” .
ОШИБКА – 404 – НЕ НАЙДЕНА
- Главная
- Э-э, мой плохой.
..
..Наши серверные гномы не смогли найти страницу, которую вы ищете.
Похоже, вы неправильно набрали URL-адрес в адресной строке или перешли по старой закладке.
Возможно, некоторые из них могут вас заинтересовать?
Набор бинарных бластеров SparkFun
В наличии КОМПЛЕКТ-12037
$29.50
5
Избранное Любимый 11
Список желаний
Футболка AVC 2017 – маленькая
16 в наличии SWG-14511
14,95 $
Избранное Любимый 0
Список желаний
Промежуточный комплект SparkFun Jetson с блоком питания
19 в наличии КОМПЛЕКТ-19409
129,95 $
Избранное Любимый 2
Список желаний
МИКРОЭ АЦП 16 Click
Нет в наличии DEV-20512
32,95 $
Избранное Любимый 0
Список желаний
Игра началась!
1 декабря 2020 г.
Оцените эти замечательные игровые контроллеры от 8Bitdo! Это отличная идея для подарка или чулок!
Избранное Любимый 2
Технология точного земледелия и мониторинга окружающей среды
6 апреля 2021 г.
Мы изучили, что сельскохозяйственные, сельскохозяйственные и аналогичные компании используют наши компоненты, и создали страницу ресурсов для всех, кто изучает технологии для повышения производительности, эффективности, безопасности и использования ресурсов в сельском хозяйстве.
Избранное Любимый 0
Электроэнергия
26 июня 2013 г.
Обзор электроэнергии, скорость передачи энергии. Мы поговорим об определении мощности, ваттах, уравнениях и номинальных мощностях. 1,21 гигаватт обучающего веселья!
Избранное Любимый 57
Руководство по графическому интерфейсу Python: введение в Tkinter
13 августа 2018 г.
Tkinter — это стандартный пакет графического интерфейса пользователя, поставляемый с Python. В этом руководстве показано, как создавать базовые оконные приложения, а также полные примеры полноэкранных информационных панелей с обновлениями графиков в реальном времени из matplotlib.
Избранное Любимый 24
Конденсатор в последовательных, параллельных цепях и цепях переменного тока
Конденсатор является одним из наиболее часто используемых электронных компонентов. Он обладает способностью накапливать внутри себя энергию в виде электрического заряда, создающего статическое напряжение (разность потенциалов) на его пластинах. Проще говоря, конденсатор похож на небольшую аккумуляторную батарею. Конденсатор представляет собой просто комбинацию двух проводящих или металлических пластин, расположенных параллельно и электрически разделенных хорошим изолирующим слоем (также называемым 9009).1 Диэлектрик) из вощеной бумаги, слюды, керамики, пластмассы и т.
д.
Существует много применений конденсатора в электронике, некоторые из них перечислены ниже:
- Аккумулирование энергии
- Система стабилизации питания
- Коррекция коэффициента мощности
- Фильтрация
- Осцилляторы
Теперь вопрос как работает конденсатор ? Когда вы подключаете источник питания к конденсатору, он блокирует постоянный ток из-за изолирующего слоя и позволяет напряжению присутствовать на пластинах в виде электрического заряда. Итак, вы знаете, как работает конденсатор и каковы его области применения или применения, но вы должны узнать, как использовать конденсатор в электронных схемах.
Как подключить конденсатор в электронной цепи?
Здесь мы собираемся продемонстрировать вам подключение конденсатора и эффект от него на примерах.
- Конденсатор серии
- Конденсатор параллельно
- Конденсатор в цепи переменного тока
Конденсатор в последовательной цепи
В цепи при последовательном соединении конденсаторов, как показано на рисунке выше, общая емкость уменьшается.
Ток через последовательно соединенные конденсаторы одинаков (т.е. i T = i 1 = i 2 = i 3 = i n ). Следовательно, заряд, накопленный конденсаторами, также одинаков (т. е. Q T = Q 1 = Q 2 = Q 3 ), потому что заряд, накопленный пластиной любого конденсатора, поступает от пластины соседнего конденсатора. конденсатор в цепи.
Применяя Закон Кирхгофа о напряжении (KVL) в цепи, мы имеем
В Т = В С1 + В С2 + V C3 … уравнение (1)
Как известно,
Q = CV Итак, V = Q / C
Где, V C1 = Q / C 1 ; V C2 = Q / C 2 ; V C3 = Q / C 3
Теперь, подставив вышеуказанные значения в уравнение (1)
(1/С Т ) = (1/С 1 ) + (1/С 2 ) + (1/С 3 )
Для n последовательных конденсаторов уравнение будет
(1/С Т ) = (1/С 1 ) + (1/С 2 ) + (1/С 3 ) + ….
+ (1 / Cn)
Следовательно, приведенное выше уравнение является уравнением для конденсаторов серии .
Где, C T = общая емкость цепи
C 1 …n = емкость конденсаторов
Емкость Уравнение для двух особых случаев определяется ниже:
Случай I: , если есть два последовательно соединенных конденсатора с разными значениями, емкость будет выражена как:
(1 / С Т ) = (С 1 + С 2 ) / (С 1 * С 2 ) Или, C T = (C 1 * C 2 ) / (C 1 + C 2 ) … уравнение (2)
(1/С Т ) = 2С/С 2 = 2/С Или, C T = C / 2
Пример для цепи последовательного конденсатора:
Теперь в приведенном ниже примере мы покажем вам, как рассчитать общую емкость и среднеквадратичное падение напряжения на каждом конденсаторе.
Как и на приведенной выше принципиальной схеме, два конденсатора соединены последовательно с разными номиналами. Значит, и падение напряжения на конденсаторах неодинаково. Если мы подключим два конденсатора с одинаковым значением, падение напряжения также будет одинаковым.
Теперь для общего значения емкости мы будем использовать формулу из уравнения (2)
Итак, С Т = (С 1 * С 2 ) / (С 1 + С 2 ) Здесь С 1 = 4,7 мкФ и С 2 = 1 мкФ C T = (4,7 мкФ * 1 мкФ) / (4,7 мкФ + 1 мкФ) C T = 4,7 мкФ / 5,7 мкФ C T = 0,824 мкФ
Теперь падение напряжения на конденсаторе C 1 это:
ВК 1 = (С Т / С 1 ) * В Т VC 1 = (0,824 мкФ / 4,7 мкФ) * 12 VC 1 = 2,103 В
Теперь падение напряжения на конденсаторе C 2 равно:
ВК 2 = (С Т / С 2 ) * В Т ВК 2 = (0,824 мкФ / 1 мкФ) * 12 ВК 2 = 9,88 В
Конденсатор в параллельной цепи
При параллельном соединении конденсаторов общая емкость будет равна сумме емкостей всех конденсаторов.
Потому что верхняя пластина всех конденсаторов соединена вместе, а нижняя пластина тоже. Таким образом, касаясь друг друга, эффективная площадь пластин также увеличивается. Следовательно, емкость пропорциональна отношению площади к расстоянию.
При подаче заявки Текущий закон Кирхгофа (KCL) в вышеуказанной схеме,
i T = i 1 +i 2 + i 3
Как мы знаем, ток через конденсатор выражается как;
i = C (dV / dt ) SO, I T = C 1 (DV / DT ) + C 2 (DV / DT ) + C 3(DT
) + C 3 9001 (D ) + C 3 (D ).0092 ) И, i T = (C 1 + C 2 + C 3 )* (dV /9 0
2
dt i T = C T (dV / dt ) … уравнение (3)
909010 Из уравнения (3) уравнение С Т = С 1 + С 2 + С 3
Для числа n конденсаторов, соединенных параллельно, приведенное выше уравнение выражается как:
C T = C 1 + C 2 + C 3 +… + CN
Пример.
параллельно . Поскольку эти конденсаторы соединены параллельно, эквивалентная или общая емкость будет равна сумме отдельных емкостей.
С Т = С 1 + С 2 + С 3 Где, С 1 = 4,7 мкФ; С 2 = 1 мкФ и С 3 = 0,1 мкФ Итак, С Т = (4,7 + 1 + 0,1) мкФ C T = 5,8 мкФ
Конденсатор в цепях переменного тока
Когда конденсатор подключен к источнику постоянного тока, он начинает медленно заряжаться. И когда напряжение зарядного тока конденсатора равно напряжению питания, говорят, что он полностью заряжен. Здесь, в этом состоянии, конденсатор работает как источник энергии, пока подается напряжение. Кроме того, конденсаторы не пропускают ток после полной зарядки.
Всякий раз, когда переменное напряжение подается на конденсатор, как показано в приведенной выше чисто емкостной цепи.
Затем конденсатор непрерывно заряжается и разряжается до каждого нового уровня напряжения (заряжается при положительном уровне напряжения и разряжается при отрицательном уровне напряжения). Емкость конденсатора в цепях переменного тока зависит от частоты входного напряжения, подаваемого в цепь. Ток прямо пропорционален скорости изменения напряжения, приложенного к цепи.
i = dQ / dt = C (dV / dt )
Phasor diagram for Capacitor in AC Circuit
As you see the phasor diagram for AC capacitor на изображении ниже ток и напряжение представлены синусоидой. При наблюдении при 0⁰ зарядный ток достигает своего пикового значения из-за постоянного увеличения напряжения в положительном направлении.
Теперь при 90⁰ ток через конденсатор не течет, так как напряжение питания достигает максимального значения.
При 180⁰ напряжение начинает медленно снижаться до нуля, а ток достигает максимального значения в отрицательном направлении. И снова зарядка достигает своего пикового значения в 360⁰, потому что напряжение питания находится на минимальном значении.
Таким образом, из приведенной выше формы сигнала видно, что ток опережает напряжение на 90⁰. Итак, мы можем сказать, что переменное напряжение отстает от тока на 90⁰ в идеальной конденсаторной цепи .
Реактивное сопротивление конденсатора (Xc) в цепи переменного тока
Рассмотрим приведенную выше принципиальную схему, поскольку мы знаем, что входное напряжение переменного тока выражается как
. V = V м Sin вес
А, заряд конденсатора Q = CV,
Итак, Q = CV m Sin wt
А, ток через конденсатор, i = dQ / dt
So,
i = d (CV m Sin wt ) / dt i = C * d (V m Sin wt ) / dt i = C*V m Cos вес *w i = w*C*V m Sin(wt + π/2) ат, мас = 0 sin(wt + π/2) = 1 , следовательно, i м = wCV м В м / i м = 1 / wC
Как мы знаем, w = 2πf
Итак,
Capacitive Reactance (Xc) = V m / i m = 1 / 2πfC
Example for Capacitive Reactance in AC Circuit
diagram
Let’s, consider the value of C = 2.
