Мощность резисторов на схеме: Мощность резистора

Мощность резистора

2 марта 2022 151

Сегодня поговорим о мощности резисторов. Это тоже очень важный параметр. Я уже рассказывал о том что такое резистор, и какие виды и типы резисторов бывают. Но подробно про мощность мы не говорили.

Мощность резистора — это максимально допустимое значение мощности электрического тока (единица измерения Ватт), которое резистор может пропустить через себя без перегрева и выхода из строя. Резистор в зависимости от своего сопротивления и тока проходящего через него превращает часть электрической энергии в тепло. Это и называется мощностью рассеивания резистора.

Какая мощность будет выделяться (рассеиваться) на резисторе

Как я уже написал чуть выше, мощность рассеивания резистора зависит от его сопротивления и силы тока, проходящего по нему. Для расчета мощности, которая будет рассеиваться в виде тепла на резисторе используется формула: P = I² * R

• P — мощность в Ватт
• I — Сила тока в Ампер
• R — Сопротивление в Ом

Для примера рассчитаем мощность которая будет рассеиваться на резисторе в схеме с подключением светодиода. Вот схема подключения:

Про то как рассчитать номинал резистора для подключения светодиода и силу тока в цепи, а так же как управлять светодиодом с помощью Ардуино я писал в этой статье. В нашем примере используется резистор на 150 Ом и сила тока в цепи составляет 20 миллиампер или 0.02 ампера. Теперь мы можем рассчитать мощность, которая будет рассеиваться на резисторе.

P = I² * R = 0.02² * 150 = 0.0004 * 150 = 0.06 Ватт

Это значит что на нашем резисторе будет рассеиваться 0.06 Ватт. Это совсем не много, поэтому подойдет практически любой резистор кроме самых маломощных SMD элементов.

Если фактическая рассеиваемая мощность превышает допустимую для резистора, то он будет перегреваться и в итоге сгорит. Это не только разорвет электрическую цепь, но и может стать причиной пожара. Поэтому старайтесь использовать резисторы с заявленной мощностью больше чем необходимая в 1.5-2 раза.

Как определить мощность резистора

Как я уже писал в других статьях, обычно резисторы — это мелкие элементы, поэтому на их корпусе сложно описать все их параметры.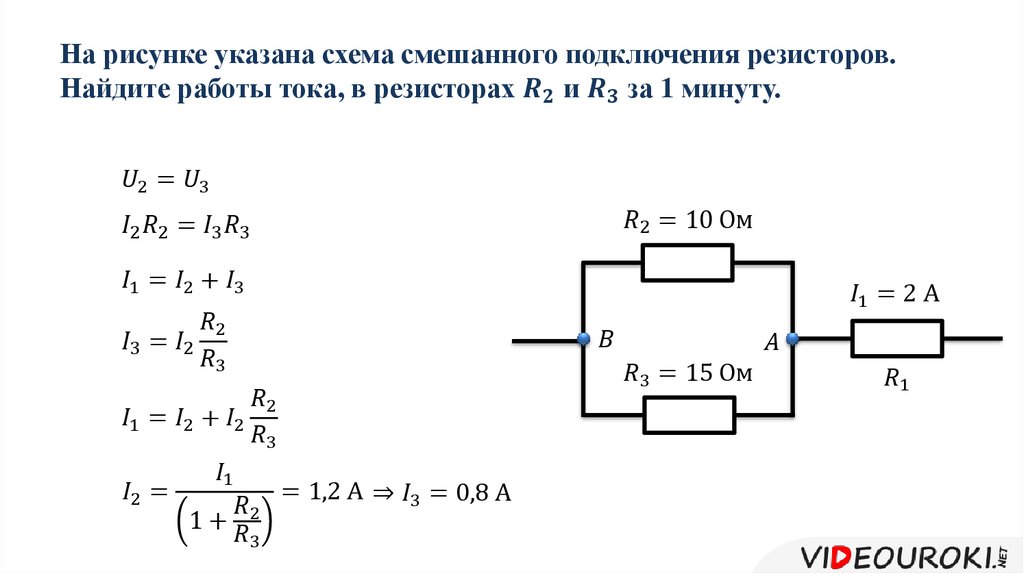 Для описания номинала и класса точности используется цветовая маркировка или специальная маркировка для SMD резисторов. А для того что бы понять какой мощности резистор нужно его измерить. Вот схема которая поможет узнать мощность резисторов в зависимости от их размера:

Мощность резисторов в зависимости от размера

Так же существуют резисторы рассчитанные и на более высокие мощности. Они уже крупнее, поэтому их мощность и номинал написаны на корпусе «человеческим языком». Вот керамические резисторы или даже высокомощные с радиатором для рассеивания тепла:

Керамические резисторы с сопротивлением 10 Ом и мощностью 10 ВаттРезистор с радиатором на 10 Ом и мощностью 50 Ватт

Мощность SMD резисторов

Показатель максимальной мощности в маркировку на таких маленьких корпусах поместить было просто не возможно. Но мы все равно можем определить максимальную мощность смд резистора при помощи штангенциркуля, ну или хотя бы обычной линейки. Дело в том что мощность зависит от размера корпуса smd резистора. Поэтому они делятся на типоразмеры и обозначаются цифрами, которые означают длину и ширину корпуса в дюймах. Вот таблица с помощью которой вы сможете определить допустимую мощность резистора в smd исполнении:

Размер в дюймах	Длинна в мм	Ширина в мм	Мощность при 70°C в Ватт
0075	0,3	0,15	0,02
01005	0,4	0,2	0,03
0201	0,6	0,3	0,05
0402	1	0,5	0,063
0603	1,6	0,8	0,1
0805	2,0	1,25	0,125
1206	3,2	1,6	0,25
1210	3,2	2,5	0,5
1218	3,2	4,8	1
1812	4,5	3,2	0,75
2010	5	2,5	0,75
2512	6,4	3,2	2

Таблица мощности SMD резисторов

Обратите внимание что при последовательном и параллельном подключении резисторов, рассеиваемая мощность рассчитывается для каждого резистора отдельно.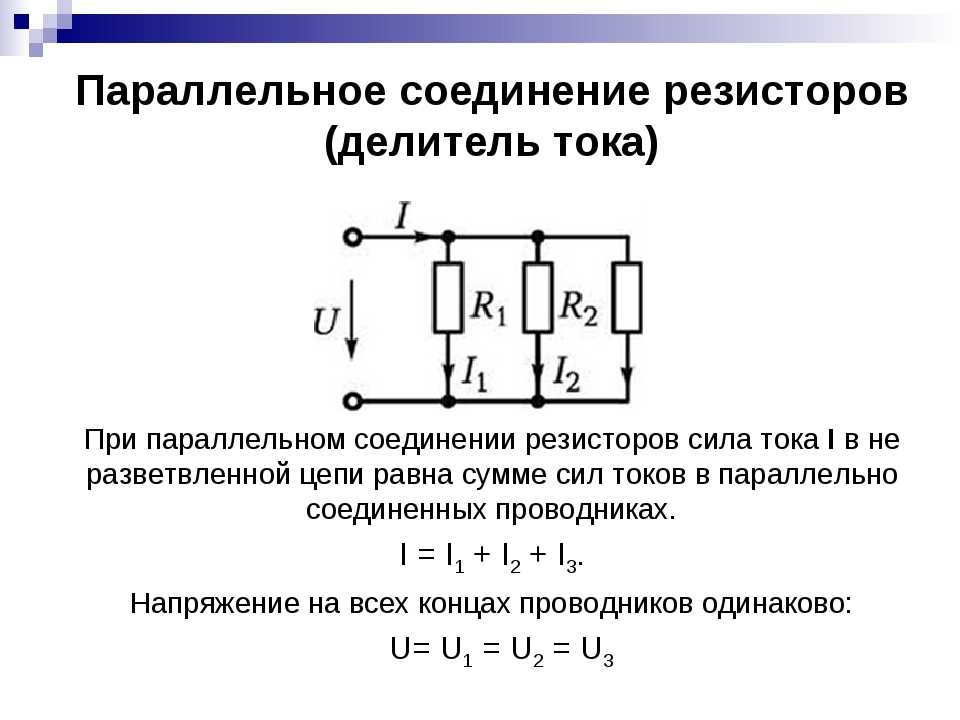

Резистор

16 декабря 2022 – Admin

Главная / Теория

Резистор — один из самых простых электронных компонентов. Вместе с тем, без резисторов не обходится практически ни одна схема. Казалось бы, что важного он делает — только сопротивляется току, и больше ничего? Но не всё так просто. В этой статье собраны все базовые знания о резисторах, необходимые электронщику.

Содержание статьи:

• Общие сведения о резисторах
• Закон Ома
• Как измерить сопротивление
• Параллельное и последовательное соединение резисторов
• Применение: делители напряжения и тока
• Рассеиваемая мощность
• Устройство резистора
• Паразитные характеристики
• Переменные и подстроечные резисторы
• Другие типы резисторов

Общие сведения

Резистор, или сопротивление, относятся к пассивным компонентам электрических цепей. Пассивный — значит, не привносящий в цепь дополнительную энергию. В отличие от, например, транзистора — который способен усиливать слабый сигнал, добавляя к нему энергию от более мощного источника питания.

Резистор оказывает сопротивление идущему через него току. В качестве механической аналогии можно представить трубу с водой. Резистор — сужение на этой трубе, замедляющее поток. Из-за сужения по трубе будет проходить меньше воды в единицу времени.

Сужение в трубе, замедляющее поток

Резистор обозначается на схеме вытянутым прямоугольником, с двумя выводами. Обычно каждому резистору присваивается буква R с порядковым номером. Иногда в зарубежной литературе можно встретить обозначение ломаной линией.

Два варианта обозначения резистора на схемах

Резистор и закон Ома

Главная характеристика резистора — его сопротивление. Оно измеряется в Омах. А ток, проходящий через резистор, зависит от приложенного напряжения. Перечисленные величины  связаны законом Ома. При этом в случае идеального резистора ток линейно зависит от напряжения, то есть резистор обладает линейной вольт-амперной характеристикой:

Вольт-амперные характеристики двух резисторов и закон Ома

Как измерить сопротивление резистора

В лаборатории радиолюбителя для измерения сопротивлений должен быть омметр. Обычно, эта функция входит в состав комбинированных приборов, мультиметров. Между тем, принцип измерения сопротивления основан всё на том же законе Ома: омметр прикладывает к тестируемому резистору небольшое напряжение и замеряет ток, после чего вычисляет сопротивление.

Измерение сопротивления с помощью мультиметра. В данном примере взят резистор 20 кОм.

Кстати, об этом нужно помнить, тыкая омметром в схемы: на схему попадает небольшое напряжение, которое для чувствительных деталей может оказаться фатальным.

Параллельное и последовательное соединение резисторов

Резисторы нужны в схеме, чтобы упрявлять токами и напряжениями. Но сначала нужно разобраться, как они взаимодействуют между собой и с другими элементами схемы.

Если соединить несколько резисторов последовательно, через каждый из них будет течь одинаковый ток. Это логично: сколько зарядов вошло в цепь, столько же должно выйти на другом конце, закон сохранения заряда. А вот напряжение (потенциал) распределяется по-разному.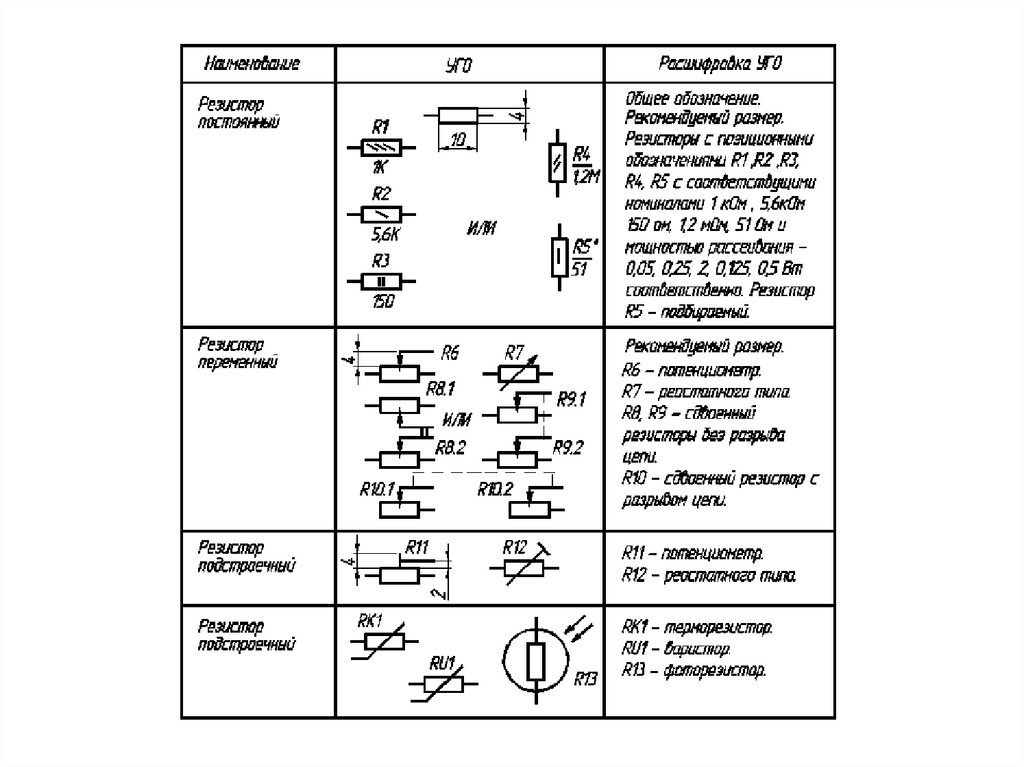 Чем выше сопротивление резистора, тем больше на нём падение напряжения — нужно большее усилие, чтобы протолкнуть через большое сопротивление заряды.

При этом, если просуммировать потенциал на всех резисторах, сумма будет равна напряжению, приложенному к концам цепи. Отсюда выводится формула суммарного сопротивления цепочки из последовательных резисторов: оно равно сумме сопротивлений всех резисторов.

Последовательное соединение резисторов

При параллельном соединении резисторов картина иная. Здесь фиксировано напряжение — оно одинаковое на каждом резисторе. А вот ток будет разный — он потечёт туда, где ему легче пройти. Опять же, применяя несложные рассуждения и используя закон Ома, выводится формула общего сопротивления параллельно соединённых резисторов.

Параллельное соединение резисторов

Более сложные, смешанные соединения резисторов разбиваются на небольшие блоки, и так последовательно, от меньших к большим блокам считается общее сопротивление:

Сложное соединение резисторов. Сначала считаем блок R1,R2 (параллельные), потом к этому блоку добавляем последовательно R3, наконец, считаем параллельно R1,R2,R3 и R4. Если каждое сопротивление по 10 Ом, общее сопротивление получается 6 Ом.

Нужно добавить, что иногда разбить на блоки невозможно. В этом случаи применяются более сложный метод расчёта — правила Кирхгофа.

Применение резисторов в схемах

Итак, как же с помощью резисторов управляют напряжениями и токами? Допустим, стоит задача ограничить напряжение на нагрузке. Под «нагрузкой» здесь может пониматься любой элемент или узел схемы, на котором мы хотим получить заданное напряжение или заданный ток.  Это могут быть и лампочка, и светодиод, и следующий каскад усилителя и т. д.

Самое простое — поставить последовательно с нагрузкой гасящий резистор. Как мы обсуждали выше, в этом случае напряжение распределится между элементами в соответствии с сопротивлением каждого. То есть, получается делитель напряжения.

Схема делителя напряжения, когда нагрузка является элементом делителя.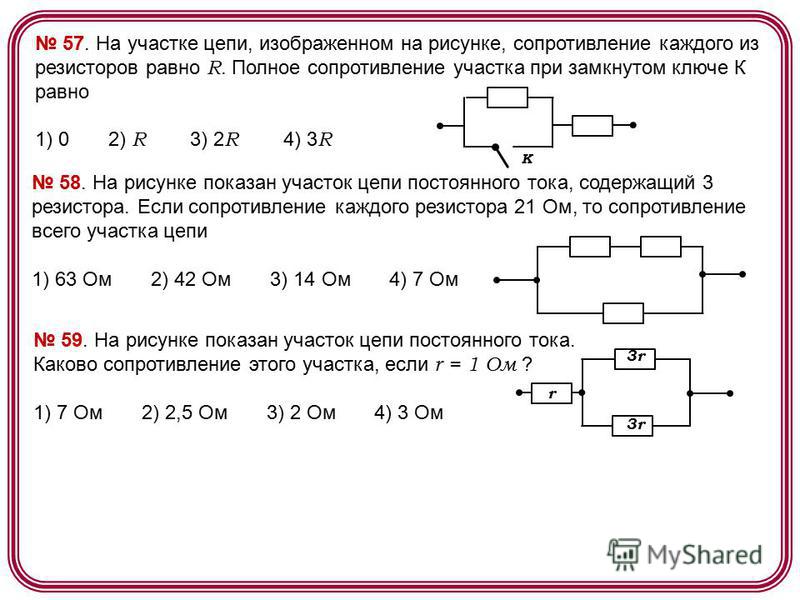

А что делать, если сопротивление нагрузки очень велико или не постоянно? В этом случае ставят два последовательных резистора, образующих плечи делителя. А нагрузка снимает напряжение с одного из них. Подчеркну, что всегда нужно помнить про сопротивление нагрузки. Оно должно быть достаточно большим, чтобы им можно было пренебречь при расчёте делителя.

Схема делителя напряжения, когда нагрузка подключена параллельно нижнему плечу делителя

Если последовательное соединение резисторов является делителем напряжения, нетрудно догадаться, что паралелльное соединение — делитель тока. На рисунке приведён способ ограничить ток через нагрузку — поставить параллельно ей резистор, так называемый шунт. Который будет отвевлять на себя часть тока, обратно пропорциональную его сопротивлению.

Схема делителя тока

Мощность резистора

Резистор сопротивляется проходящему току. Значит, он отбирает у тока часть энергии. И куда она девается? Переходит в тепло.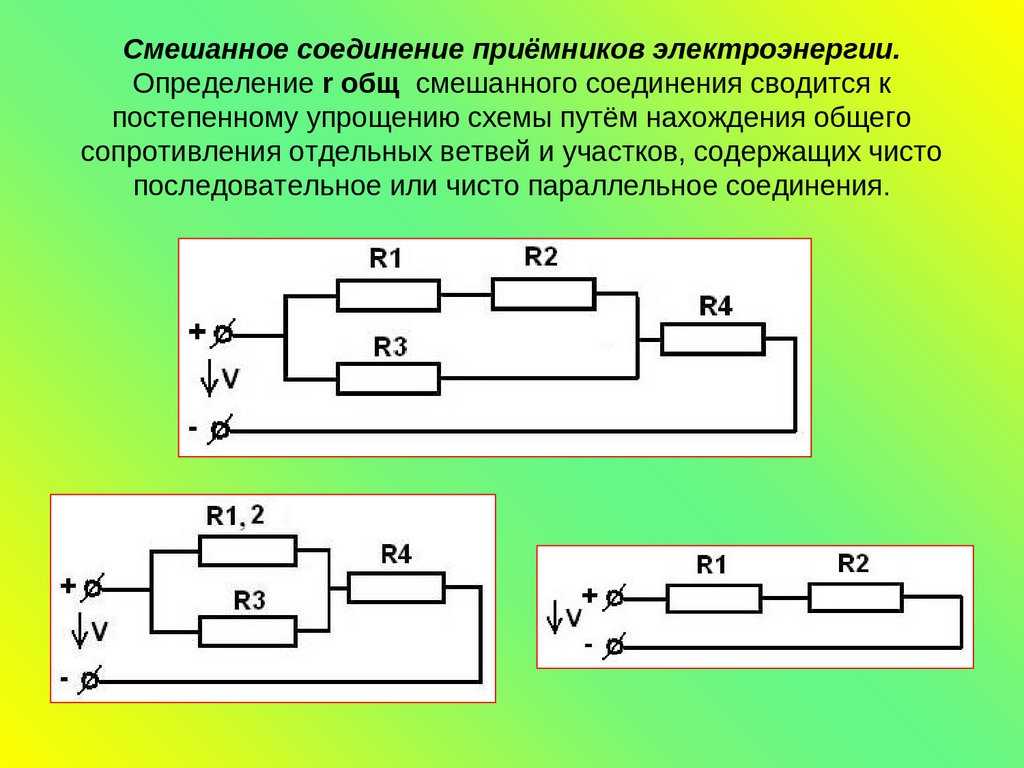 Мощность, рассеиваемая на резисторе, считается по формуле P = U*I. Поскольку U, I и R связаны законом Ома, можно записать несколько вариантов этой формулы, выражая мощность через U и R, или через R и I. Кстати, на сайте есть онлайн-калькулятор мощности и закона Ома.

Так вот, если ток через резистор слишком велик, из-за большой рассеиваемой мощности резистор перегреется и выйдет из строя, в буквальном смысле, сгорит. В этом случае нужно взять резистор такого же номинала, но рассчитанный на бОльшую мощность рассеивания. Более мощные резисторы и физически большего размера, чтобы увеличить площадь рассеивания тепловой энергии.

Там, где это важно (где ожидаются сравнительно большие токи), на схемах указывают, на какую мощность должен быть рассчитан резистор, с помощью следующих обозначений:

Допустимая мощность рассеивания резистора

Устройство резисторов

Из школьного курса физики мы знаем, что сопротивление проводника определяется его удельным сопротивлением, длинной и сечением.

Формула сопротивления проводника

В начале статьи приводилась механическая аналогия резистора, как сужения трубы. Это работает и в элекрике: если уменьшить сечение проводника, его сопротивление увеличится.

Поэтому, резисторы делают из тонкой проволоки, из тонких плёнок разных металлов и сплавов, из композитных материалов. При этом, чтобы увеличить эффективную длину, в резистивном слое нарезают различного вида спирали и канавки:

Очень условно показано устройство резистора. Слева: на поверхности цилиндрической основы резистора слой токопроводящего материала, в котором нарезаны канавки для увеличения сопротивления. Справа: плёночный вариант.

Паразитные характеристики

Но, такой подход, кроме плюсов, даёт ещё и некоторые минусы. Дело в том, что реальный резистор, в отличие от идеального, обладает не только сопротивлением, но и некоторой индуктивностью и ёмкостью. То есть схема реального резистора выглядит примерно так:

Схема замещения резистора

Ёмкость и индуктивность – паразитные характеристики резистора, они искажают его функции в схеме.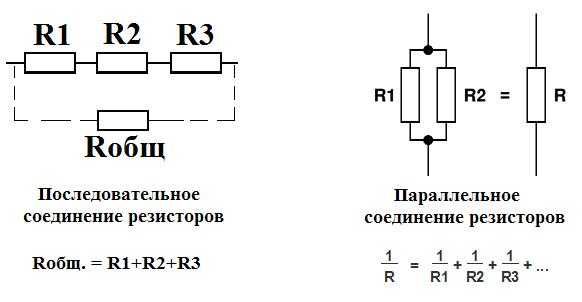 И само по себе устройство резистора может являться причиной этих паразитных свойств. Спиральные канавки в резистивном слое – чем не витки катушки индуктивности? А между близко расположенными участками проводящего слоя возникает ёмкость.

Хотя эти индуктивность и ёмкость небольшие по величине, но в некоторых ситуациях (например, на высоких частотах) способны вносить заметные искажения.

Поэтому, при изготовлении резисторов применяют различные ухищрения, чтобы снизить паразитные характеристики. Например, нарезают канавки хитрым рисунком. Впрочем, эта тема уже выходит за рамки данной статьи.

Переменные и подстроечные резисторы

Иногда в схеме необходимы резисторы с переменным сопротивлением. Они являются элементами настройки и управления.

Различают переменные резисторы (обычно их ручку выводят на панель управления) и подстроечные (которые регулируются отвёрткой на плате и к которым нет доступа, пока не разобрать корпус устройства). Вот как они выглядят:

Переменные и подстроечные резисторы

У них три вывода.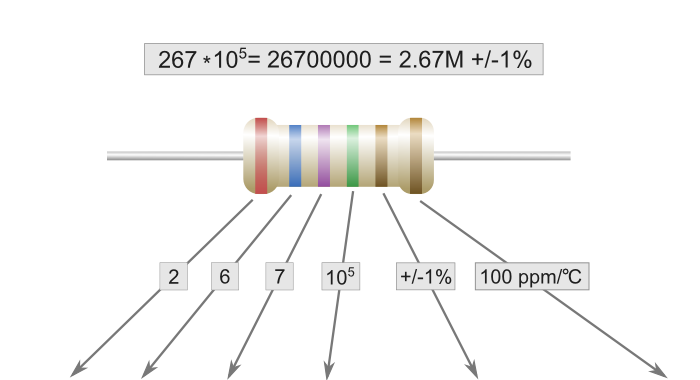 Между двумя крайними постоянное сопротивление. А средний “скользит” между ними. Таким образом, получается готовый делитель напряжения, с регулируемым сопротивлением плечей.

Если средний вывод соединить с одним из крайних – получится реостат, резистор с переменным сопротивлением.

Другие типы резисторов

В заключение остаётся упомянуть некоторые специфичные типы резисторов. Например, теримистор. Его сопротивление зависит от температуры, и этот тип резисторов широко используется в электронных термометрах и схемах контроля температуры.

Или, фоторезистор. Его сопротивление зависит от освещённости.

Варисторы – уменьшают своё сопротивление при росте приложенного напряжения. Могут использоваться в схемах защиты и стабилизаторах.

Поделиться в соцсетях:

Основы: Рассеиваемая мощность и электронные компоненты

 

Постоянной проблемой при проектировании электронных схем является выбор подходящих компонентов, которые не только выполняют предназначенную для них задачу, но и сохраняют работоспособность в прогнозируемых условиях эксплуатации. Большая часть этого процесса заключается в обеспечении того, чтобы ваши компоненты оставались в безопасных рабочих пределах с точки зрения тока, напряжения и мощности. Из этих трех «энергетическая» часть часто является самой сложной (как для новичков, так и для экспертов), потому что безопасная рабочая область может сильно зависеть от особенностей ситуации.

Далее мы представим некоторые из основных концепций рассеивания мощности в электронных компонентах, чтобы понять, как выбирать компоненты для простых схем с учетом ограничений по мощности.

— НАЧАЛО ПРОСТО —

Давайте начнем с одной из самых простых схем, которые только можно себе представить: Батарея, подключенная к одному резистору:

Здесь у нас есть одна батарея на 9 В и одна батарея на 100 Ом. Резистор (100 Ом), соединенный проводами в виде полной цепи.

Достаточно просто, правда? Но теперь вопрос: если вы действительно хотите построить эту схему, насколько «большой» из 100? резистор вам нужно использовать, чтобы убедиться, что он не перегревается? Другими словами, можем ли мы просто использовать «обычный» резистор ¼ Вт, как показано ниже, или нам нужно увеличить его?

 

Чтобы это выяснить, нам нужно рассчитать мощность, которую будет рассеивать резистор.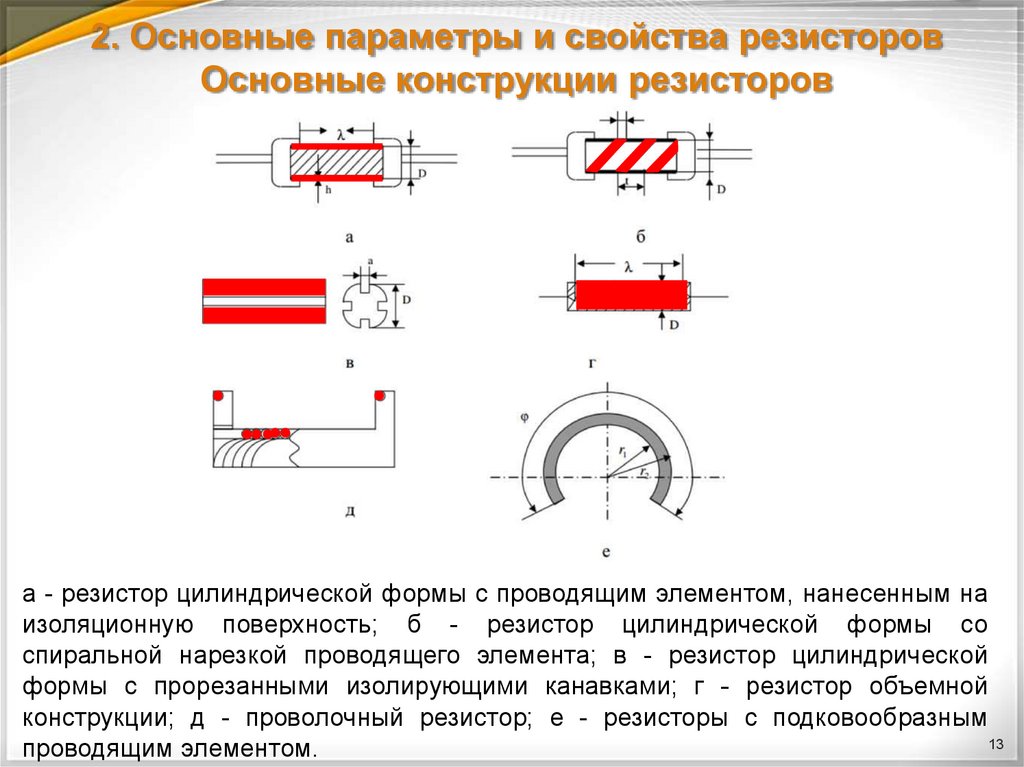
Вот общее правило расчета рассеиваемой мощности:

Правило мощности: P = I × В
Если ток I протекает через данный элемент в вашей цепи, теряя при этом напряжение В , то мощность, рассеиваемая этим элементом элемент цепи является произведением этого тока и напряжения: P = I × В .

 

Кроме :
Как ток, умноженный на напряжение, может дать нам измерение «мощности»?

Чтобы понять это, нам нужно вспомнить, что физически представляют ток и напряжение.

Электрический ток – это скорость прохождения электрического заряда по цепи, обычно выражаемая в амперах, где 1 ампер = 1 кулон в секунду. (Кулон — это единица измерения электрического заряда в системе СИ.)

Напряжение, или, более формально, электрический потенциал — это потенциальная энергия на единицу электрического заряда на рассматриваемом элементе цепи. В большинстве случаев вы можете думать об этом как о количестве энергии, которая «израсходована» в элементе на единицу прошедшего через него заряда. Электрический потенциал обычно измеряется в вольтах, где 1 вольт = 1 джоуль на кулон. (Джоуль — это единица измерения энергии в системе СИ.)

Таким образом, если мы возьмем ток, умноженный на напряжение, это даст нам количество энергии, которая «израсходована» в элементе на единицу заряда, умножить на количество этих единиц заряда, проходящих через элемент на единицу заряда. секунда:

1 ампер × 1 вольт =
1 (кулон/секунда) × 1 (джоуль/кулон) =
1 джоуль/секунда

Полученная величина выражается в единицах один джоуль в секунду: скорость потока энергии , более известный как власть. Единицей мощности в СИ является ватт, где 1 ватт = 1 джоуль в секунду.

Наконец, у нас есть

1 ампер × 1 вольт = 1 ватт

Вернемся к нашей схеме! Чтобы использовать правило мощности ( P = I × V ), нам нужно знать как ток через резистор, так и напряжение на резисторе.

Во-первых, мы используем закон Ома ( В = I × R ), чтобы найти ток через резистор.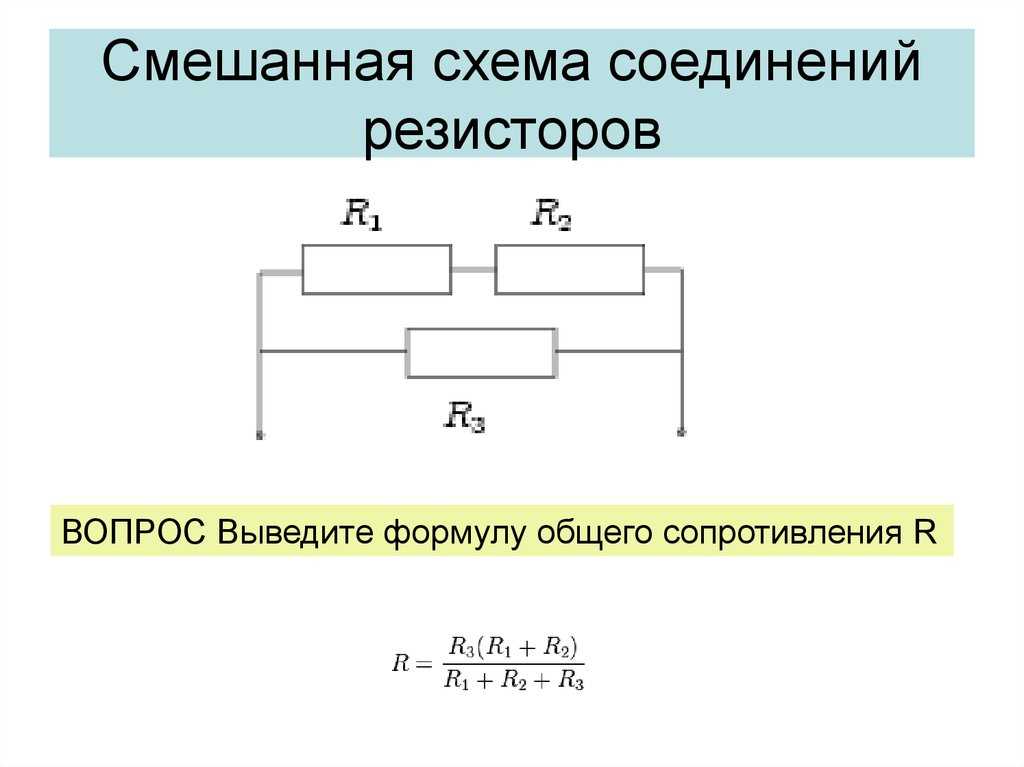
• Напряжение на резисторе В = 9 В.
• Сопротивление резистора 9 Ом.0031 Р = 100?.

Следовательно, ток через резистор равен:

I = В / R = 9 В / 100 ? = 90 мА

Затем мы можем использовать правило мощности ( P = I × В ), чтобы найти мощность, рассеиваемую резистором.
• Ток через резистор I = 90 мА.
• Напряжение на резисторе В = 9 В.

Следовательно, мощность, рассеиваемая на резисторе:

P = I × В = 90 мА × 9 В = 0,81 Вт

 

Итак, вы можете использовать этот резистор 1/4 Вт?

Нет, потому что он, скорее всего, выйдет из строя из-за перегрева.
100 ? Резистор в этой цепи должен быть рассчитан как минимум на 0,81 Вт. Как правило, выбирается следующий больший доступный размер, в данном случае 1 Вт.

Резистор мощностью 1 Вт обычно поставляется в гораздо большей физической упаковке, например, показанной здесь:

(резистор мощностью 1 Вт, 51 Ом, для сравнения размеров).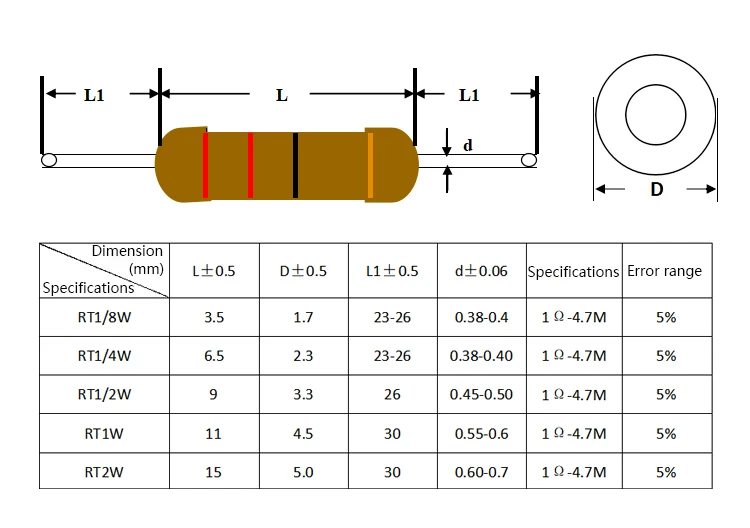

Поскольку резистор мощностью 1 Вт физически намного больше, он должен рассеивать большую мощность благодаря большей площади поверхности и более широким выводам. . (Он все еще может быть очень горячим на ощупь, но не должен нагреваться настолько, чтобы выйти из строя.) последовательно соединенные резисторы (все равно получается 100 Ом). В этом случае ток через каждый резистор по-прежнему равен 90 мА. Но, поскольку на каждом резисторе напряжение всего на одну четверть меньше, на каждом резисторе рассеивается только одна четверть мощности. Для этой схемы нужны только четыре резистора с номиналом 1/4 Вт.

Поскольку четыре резистора соединены последовательно, мы можем сложить их значения, чтобы получить их общее сопротивление, 100 Ом. Используя закон Ома с этим полным сопротивлением, мы снова получаем ток 90 мА. И опять же, так как резисторы включены последовательно, то одинаковый ток (90 мА) должен протекать через каждый обратно к аккумулятору. Напряжение на каждом 25 Ом.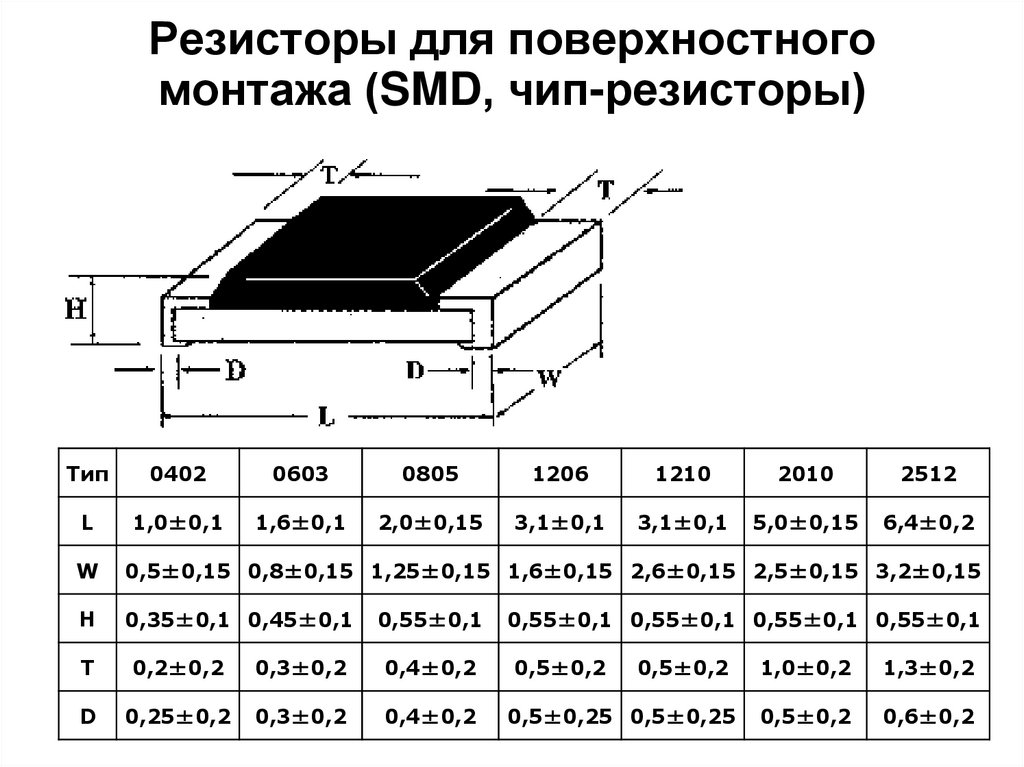 резистор В = I × R или 90 мА × 25 ? = 2,25 В. (Чтобы еще раз убедиться, что это разумно, обратите внимание, что напряжения на четырех резисторах в сумме составляют 4 × 2,25 В = 9 В.)

Мощность на каждом отдельном 25 ? резистор P = I × В = 90 мА × 2,25 В ? 0,20 Вт, безопасный уровень для использования с резистором 1/4 Вт. Интуитивно понятно, что если разделить 100 ? резистор на четыре равные части, каждая из которых должна рассеивать одну четверть общей мощности.

 

— НА ЗА РЕЗИСТОРАМИ —

Для нашего следующего примера давайте рассмотрим следующую ситуацию: Предположим, что у вас есть схема, которая получает вход от источника питания 9 В, и имеет встроенный линейный регулятор для шага. напряжение до 5 В, где все на самом деле работает. Ваша нагрузка на конце 5 В может достигать 1 А.

Как выглядит мощность в этой ситуации?

Регулятор действует как большой переменный резистор, который регулирует свое сопротивление по мере необходимости, чтобы поддерживать постоянное выходное напряжение 5 В. Когда выходная нагрузка составляет полный 1 А, выходная мощность, выдаваемая стабилизатором, составляет 5 В × 1 А = 5 Вт, а мощность, подводимая к цепи, составляет 9 В.V питания составляет 9 Вт. Падение напряжения на стабилизаторе составляет 4 В, а при 1 А это означает, что линейный стабилизатор рассеивает 4 Вт — также разница между входной и выходной мощностью.

В каждой части этой схемы соотношение мощностей определяется как P = I × В . Две части — регулятор и нагрузка — это места, где рассеивается мощность. А в части цепи по питанию P = I × В описывает мощность на входе в систему — напряжение увеличивается по мере прохождения тока через источник питания.

Кроме того, стоит отметить, что мы не сказали , какая нагрузка тянет этот 1 А. Мощность потребляется, но это не обязательно означает, что она преобразуется в (просто) тепловую энергию — она могла Например, для питания двигателя или набора зарядных устройств.

Сторона:
Несмотря на то, что установка линейного регулятора напряжения, подобная этой, является очень распространенной схемой для электроники, стоит отметить, что это также невероятно неэффективная схема : 4/9 входной мощности просто сгорает в виде тепла, даже при работе на меньших токах.

 

— ЕСЛИ НЕТ ПРОСТОЙ СПЕЦИФИКАЦИИ «МОЩНОСТЬ» —

Далее, немного более сложная часть: убедитесь, что ваш регулятор выдерживает мощность. В то время как на резисторах четко указана их мощность, на линейных регуляторах это не всегда так. В приведенном выше примере регулятора давайте также предположим, что мы используем регулятор L7805ABV от ST (техническое описание здесь).

 

(Фото: типичный корпус TO-220, который обычно используется для линейных стабилизаторов средней мощности) выше), который рассчитан на выходной ток 1,5 А и входное напряжение до 35 В.

Наивно предположить, что вы можете подключить это прямо к входному напряжению 35 В и получить 1,5 А на выходе, а это означает, что регулятор будет излучать 30 В * 1,5 А = 45 Вт мощности. Но это крошечный пластиковый пакет; на самом деле он не может справиться с такой большой мощностью. Если вы заглянете в таблицу данных в разделе «Абсолютные максимальные характеристики», чтобы попытаться определить, какую мощность он может выдержать, все, что там написано, это «Внутреннее ограничение», что само по себе далеко не ясно.

Оказывается, фактическая номинальная мощность есть, но обычно она несколько «спрятана» в техническом описании. Вы можете понять это, взглянув на пару связанных спецификаций:

• T _OP , Диапазон рабочих температур перехода: от -40 до 125 °C

• R _thJA , Тепловое сопротивление переход-окружающая среда: 50 °C /W

• R _thJC , Термическое сопротивление переход-корпус: 5 °C/W

Диапазон рабочих температур перехода, T _OP определяет, насколько горячим может быть «переход» — активная часть интегральной схемы регулятора — до того, как он перейдет в режим теплового отключения. (Температурное отключение — это внутренний предел, который делает мощность регулятора «внутренне ограниченной». ) Для нас это максимум 125 °C.

Тепловое сопротивление переход-окружающая среда R _thJA (часто пишется как ? _JA ) говорит нам, насколько нагревается переход, когда (1) регулятор рассеивает заданное количество энергии и (2) регулятор находится в режиме ожидания. на открытом воздухе при заданной температуре окружающей среды. Предположим, нам нужно спроектировать наш регулятор для работы только в умеренных коммерческих условиях, не превышающих 60 °C. Если нам нужно поддерживать температуру перехода ниже 125 °C, то максимальное повышение температуры, которое мы можем допустить, составляет 65 °C. Если у нас есть R _thJA 50 °C/Вт, то максимальная рассеиваемая мощность, которую мы можем допустить, составляет 65/50 = 1,3 Вт, если мы хотим предотвратить перегрев регулятора. Это значительно ниже 4 Вт, которые мы ожидаем при токе нагрузки 1 А. На самом деле мы можем допустить только 1,3 Вт / 4 В = 325 мА среднего выходного тока, не отправляя регулятор в режим теплового отключения.

Это, однако, для случая ТО-220, излучающего в окружающий воздух – почти наихудшая ситуация. Если мы сможем добавить радиатор или иным образом охладить регулятор, мы сможем добиться большего успеха.

Противоположный конец спектра соответствует другой тепловой спецификации: тепловое сопротивление переход-корпус, R _thJC . Это определяет ожидаемую разницу температур между спаем и внешней частью корпуса TO-220: всего 5 °C/Вт. Это актуальный номер , если вы можете быстро отвести тепло от корпуса, например, если у вас есть очень хороший теплоотвод, подключенный снаружи к корпусу ТО-220. С большим радиатором и идеальной связью с этим радиатором при 4 Вт температура перехода поднимется всего на 20 °C выше температуры вашего радиатора. Это представляет собой абсолютный минимум нагрева, который вы можете ожидать в идеальных условиях.

В зависимости от технических требований, вы можете начать с этого момента, чтобы построить полный бюджет мощности, чтобы учесть теплопроводность каждого элемента вашей системы, от самого регулятора до прокладки термоинтерфейса между ним и радиатором , к тепловой связи радиатора с окружающим воздухом. Затем вы можете проверить связи и относительные температуры каждого компонента с помощью точечного бесконтактного инфракрасного термометра. Но часто лучше переоценить ситуацию и посмотреть, есть ли лучший способ сделать это.

В данной ситуации можно было бы рассмотреть возможность перехода на стабилизатор для поверхностного монтажа, который предлагает лучшую мощность (за счет использования печатной платы в качестве радиатора), или, возможно, стоит рассмотреть возможность добавления мощного резистора (или стабилитрона). ) перед регулятором сбросить большую часть напряжения за пределы блока регулятора, снизив нагрузку на него. Или, что еще лучше, посмотрите, есть ли способ построить вашу схему без каскада линейного регулятора с потерями.

 

— ПОСЛЕСЛОВИЕ —

Мы рассмотрели основы понимания рассеяния мощности в нескольких простых цепях постоянного тока.

Принципы, которые мы рассмотрели, являются довольно общими и могут быть использованы для понимания энергопотребления в большинстве типов пассивных элементов и даже в большинстве типов интегральных схем. Однако существуют реальные ограничения, и можно потратить всю жизнь на изучение нюансов энергопотребления, особенно при более низких токах или высоких частотах, когда малые потери, которыми мы пренебрегли, становятся важными.

В цепях переменного тока многие элементы ведут себя по-разному, но правило мощности по-прежнему выполняется в большинстве случаев: P(t) = I(t) × V(t) для изменяющихся во времени тока и напряжения. И не все стабилизаторы имеют такие потери: импульсные источники питания могут преобразовывать (например) 9 В постоянного тока в 5 В постоянного тока с эффективностью 90% или выше, а это означает, что при хорошей конструкции для преобразования может потребоваться всего около 0,6 А при 9 В. производить 5 В на 1 А. Но это история в другой раз.

Эта запись была размещена в Основы, Электроника, Проекты EMSL, Инженерия и помечена как электроника. Добавьте постоянную ссылку в закладки.

3.5: Рассеиваемая мощность в резисторных цепях

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

1610

• Дон Х. Джонсон
• Rice University via Connections

Цели обучения

• Рассеивание мощности в резисторных цепях.

Мы можем найти напряжения и токи в простых цепях, содержащих резисторы и источники напряжения или тока. Мы должны проверить, подчиняются ли эти переменные цепи принципу сохранения мощности: поскольку цепь является замкнутой системой, она не должна рассеивать или создавать энергию. На данный момент наш подход состоит в том, чтобы сначала исследовать потребление/создание мощности резисторной цепи . Позже мы будем доказывают

, что благодаря КВЛ и ККЛ все цепи сохраняют мощность.

Как определено на [ссылка], мгновенная мощность, потребляемая/вырабатываемая каждым элементом цепи, равна произведению его напряжения и тока. Общая мощность, потребляемая/вырабатываемая схемой, равна сумме мощностей каждого элемента.

\[P=\sum_{k}v_{k}i_{k} \номер\]

Напомним, что ток и напряжение каждого элемента должны соответствовать соглашению о том, что положительный ток поступает на клемму положительного напряжения. При таком соглашении положительное значение v _k i _k соответствует потребляемой мощности, отрицательное значение – создаваемой мощности. Поскольку общая мощность в цепи должна быть равна нулю ( P = 0), одни элементы цепи должны создавать мощность, а другие ее потреблять.

Рассмотрим простую последовательную схему в [ссылка]. При выполнении наших расчетов мы определили ток i _out , протекающий через выводы положительного напряжения обоих резисторов, и нашли его равным: 9{2}R \номер\]

Поскольку резисторы имеют положительное значение, резисторы всегда рассеивают мощность . Но куда девается мощность резистора? По закону сохранения мощности рассеиваемая мощность должна где-то поглощаться. Ответ не предсказывается непосредственно теорией цепей, но физикой. Ток, протекающий через резистор, нагревает его; его мощность рассеивается за счет тепла.

Удельное сопротивление

Физический провод имеет сопротивление и, следовательно, рассеивает мощность (он нагревается так же, как резистор в цепи). В самом деле, сопротивление провода длиной L и площадь поперечного сечения

A определяется как:

\[R=\frac{\rho L}{A} \nonumber \]

Величина ρ известна как удельное сопротивление и представляет собой сопротивление материала единицы длины с единицей площади поперечного сечения, из которого состоит провод. Удельное сопротивление измеряется в ом-метрах. Большинство материалов имеют положительное значение ρ , что означает, что чем длиннее провод, тем больше сопротивление и, следовательно, рассеиваемая мощность. Чем толще провод, тем меньше сопротивление. Сверхпроводники имеют нулевое удельное сопротивление и, следовательно, не рассеивают мощность. Если бы удалось найти сверхпроводник при комнатной температуре, электроэнергию можно было бы передавать по линиям электропередач без потерь! 9{2} \nonumber \]

Этот результат достаточно общий: источники производят мощность, а элементы схемы, особенно резисторы, потребляют ее.