Найти ток через сопротивление r в схеме: Найти ток через сопротивление R в схеме… – Физика

Задачи по физике и математике с решениями и ответами

Задача по физике – 7478

На рис. показана схема потенциометра, с помощью которого можно менять напряжение $U$, подаваемое на некоторый прибор с сопротивлением $R$. Потенциометр имеет длину $l$, сопротивление $R_{0}$ и находится под напряжением $U_{0}$. Найти напряжение $U$, снимаемое на прибор, как функцию расстояния $x$. Исследовать отдельно случай $R \gg R_{0}$.
Подробнее

Задача по физике – 7479

Найти э. д. с. и внутреннее сопротивление источника, эквивалентного двум параллельно соединенным элементам с э. д. с. $\mathcal{E}_{1}$ и $\mathcal{E}_{2}$ и внутренними сопротивлениями $R_{1}$ и $R_{2}$. Подробнее

Задача по физике – 7480

Найти значение и направление тока через сопротивление $R$ в схеме (рис. ), если э. д. с. источников $\mathcal{E}_{1} = 1,5 В, \mathcal{E}_{2} = 3,7 В$ и сопротивления $R_{1} = 10 Ом, R_{2} = 20 Ом$ и $R = 5,0 Ом$. Внутренние сопротивления источников тока пренебрежимо малы.
Подробнее

Задача по физике – 7481

В схеме (рис.) э. д. с. источников $\mathcal{E}_{1} = 1,5 В, \mathcal{E}_{2} = 2,0 В, \mathcal{E}_{3} = 2,5 В$ и сопротивления $R_{1} = 10 Ом, R_{2} = 20 Ом, R_{3} = 30 Ом$. Внутренние сопротивления источников пренебрежимо малы. Найти:
а) ток через сопротивление $R_{1}$
б) разность потенциалов $\phi_{A} – \phi_{B}$ между точками А и В.
Подробнее

Задача по физике – 7483

Найти разность потенциалов $\phi_{A} – \phi_{B}$ между обкладками конденсатора $C$ схемы (рис. ), если э. д. с. источников $\mathcal{E}_{1} = 4,0 В, \mathcal{E}_{2} = 1,0 В$ и сопротивления $R_{1} = 10 Ом, R_{2} = 20 Ом, R_{3} = 30 Ом$. Внутренние сопротивления источников пренебрежимо малы.
Подробнее

Задача по физике – 7484

Найти ток, протекающий через сопротивление $R_{1}$ участка цепи (рис.), если сопротивления $R_{1} = 10 Ом, R_{2} = 20 Ом, R_{3} = 30 Ом$ и потенциалы точек 1,2 и 3 равны соответственно $\phi_{1} = 10 В, \phi_{2} = 6 В, \phi_{3} = 5 В$.
Подробнее

Задача по физике – 7485

Между точками А и В цепи (рис.) поддерживают постоянное напряжение $U = 25 В$. Найти значение и направление тока в участке СD, если сопротивления $R_{1} = 1,0 Ом, R_{2} = 2,0 Ом, R_{3} = 3,0 Ом$ и $R_{4} = 4,0 Ом$.
Подробнее

Задача по физике – 7488

Сколько тепла выделится в спирали сопротивлением $R$ при прохождении через нее количества электричества $q$, если ток в спирали:
а) равномерно убывал до нуля в течение времени $\Delta t$;
б) монотонно убывал до нуля так, что за каждые $\Delta t$ секунд он уменьшался вдвое? Подробнее

Задача по физике – 7489

К источнику постоянного тока с внутренним сопротивлением $R_{0}$ подключили три одинаковых сопротивления $R$, соединенных между собой, как показано на рис. При каком значении $R$ тепловая мощность, выделяемая на этом участке, будет максимальна?
Подробнее

Задача по физике – 7490

Убедиться, что распределение тока в параллельно соединенных сопротивлениях $R_{1}$ и $R_{2}$ соответствует минимуму выделяемой на этом участке тепловой мощности. Подробнее

Задача по физике – 7491

Аккумулятор с э. д. с. $\mathcal{E} = 2,6 В$, замкнутый на внешнее сопротивление, дает ток $I = 1,0 А$. При этом разность потенциалов между полюсами аккумулятора $U = 2,0 В$. Найти тепловую мощность, выделяемую в аккумуляторе, и мощность, которую развивают в нем электрические силы. Подробнее

Задача по физике – 7492

Электромотор постоянного тока подключили к напряжению $U$. Сопротивление обмотки якоря равно $R$. При каком значении тока через обмотку полезная мощность мотора будет максимальной? Чему она равна? Каков при этом к. п. д. мотора? Подробнее

Иродов – Страница 42

Раздел: Иродов, Решения задач, Физика

Иродов 3.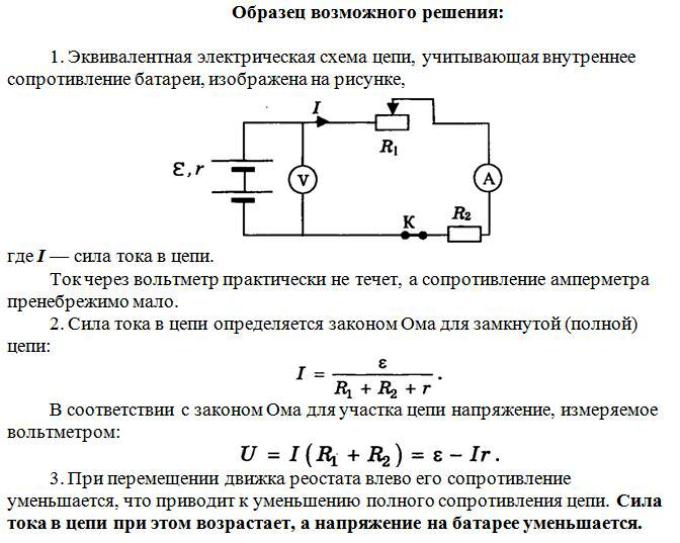 190. К источнику постоянного тока с внутренним сопротивлением R0 подключили три одинаковых сопротивления R, соединенных между собой, как показано на рис. 3.52. При каком значении R тепловая мощность, выделяемая на этом участке, будет максимальна? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.189. Сколько тепла выделится в спирали сопротивлением R при прохождении через нее количества электричества q, если ток в спирали: а) равномерно убывал до нуля в течение времени Δt; б) монотонно убывал до нуля так, что за каждые Δt секунд он уменьшался вдвое? Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.185. Найти ток, протекающий через сопротивление R1 участка цепи (рис. 3.48), если сопротивления R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом и потенциалы точек 1, 2 и 3 равны соответственно φ1 = 10 В, φ2 = 6 В, φ3 = 5 В.

Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.184. Найти разность потенциалов φA — φB между обкладками конденсатора С схемы (рис. 3.47), если э. д. с. источников ξ1 = 4,0 В, ξ2 = 1,0 В и сопротивления R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом. Внутренние сопротивления источников пренебрежимо малы. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.183. Найти ток через сопротивление R в схеме (рис. 3.46). Внутренние сопротивления обоих источников пренебрежимо малы. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.182. В схеме (рис. 3.45) э. д. с. источников ξ1 = 1,5 В, ξ2 = 2,0 В, ξ3 = 2,5 В и сопротивления R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом.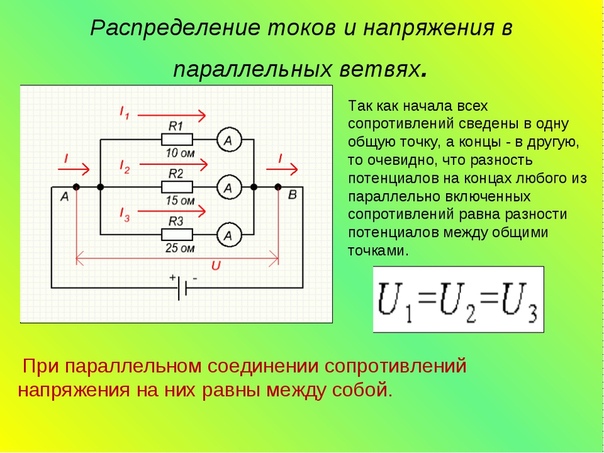

Внутренние сопротивления источников пренебрежимо малы. Найти: а) ток через сопротивление R1; б) разность потенциалов φA — φB между точками […]

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.181. Найти значение и направление тока через сопротивление R в схеме (рис. 3.44), если э. д. с. источников ξ1 = 1,5 В, ξ2 = 3,7 В и сопротивления R1 = 10 Ом, R2 = 20 Ом и R = 5,0 Ом. Внутренние сопротивления источников тока пренебрежимо малы. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.180. Найти э. д. с. и внутреннее сопротивление источника, эквивалентного двум параллельно соединенным элементам с э. д. с. ξ1 и ξ2 и внутренними сопротивлениями R1 и R2. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.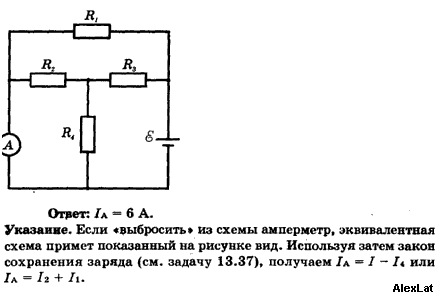 179. На рис. 3.43 показана схема потенциометра, с помощью которого можно менять напряжение U, подаваемое на некоторый прибор с сопротивлением R. Потенциометр имеет длину l, сопротивление R0 и находится под напряжением U0. Найти напряжение U, снимаемое на прибор, как функцию расстояния x. Исследовать отдельно случай R >> R0. Скачать решение: Скачать решение задачи

Смотреть материал

Раздел: Иродов, Решения задач, Физика

Иродов 3.178. В схеме (рис. 3.42) э. д. с. источника ξ = 5,0 В и сопротивления R1 = 4,0 Ом, R2 = 6,0 Ом. Внутреннее сопротивление источника R = 0,10 Ом. Найти токи, текущие через сопротивления R1 и R2. Скачать решение: Скачать решение задачи

Смотреть материал

Источники тока, имеющие одинаковые внутренние сопротивления r=0,5 Ом, подключены

Условие задачи:

Источники тока, имеющие одинаковые внутренние сопротивления \(r=0,5\) Ом, подключены к одинаковым резисторам \(R\).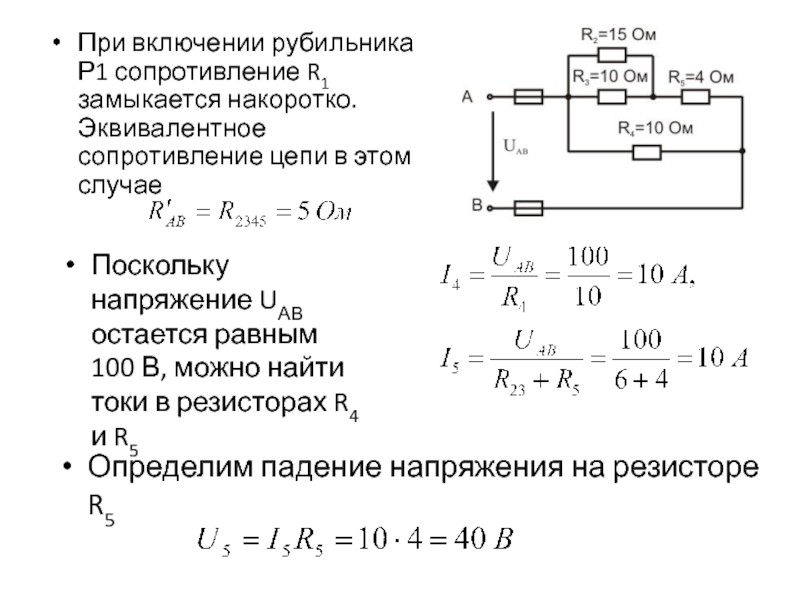 ЭДС источников тока \(\rm E_1=12\) В, \(\rm E_2=6\) В. Определите величину сопротивления \(R\), при котором ток, протекающий через источник \(\rm E_2\), равен нулю.

Задача №7.2.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(r=0,5\) Ом, \(\rm E_1=12\) В, \(\rm E_2=6\) В, \(I_2=0\), \(R-?\)

Решение задачи:

Приведенную в условии схему представим в измененном виде. Во-первых, покажем явно внутренние сопротивления источников, два параллельно соединенных сопротивления \(R\) представим в виде эквивалентного \(\frac{R}{2}\), также покажем потенциалы наиболее характерных точек.

Тогда можно три раза записать закон Ома для участка цепи и один раз первый закон Кирхгофа (сумма токов, входящих в узел, равна сумме токов, выходящих из него):

\[\left\{ \begin{gathered}
{{\rm E}_1} – \varphi = {I_1}r \hfill \\
{{\rm E}_2} – \varphi = {I_2}r \hfill \\
\varphi – 0 = I\frac{R}{2} \hfill \\
{I_1} + {I_2} = I \;\;\;\;(1)\hfill \\
\end{gathered} \right. \]

Так как по условию задачи ток \(I_2\), протекающий через источник \(\rm E_2\), равен нулю, то равенство (1) примет вид:

\[{I_1} = I\]

В таком случае система станет такой:

\[\left\{ \begin{gathered}
{{\rm E}_1} – \varphi = Ir \;\;\;\;(2)\hfill \\
{{\rm E}_2} = \varphi \;\;\;\;(3)\hfill \\
\varphi – 0 = I\frac{R}{2} \;\;\;\;(4)\hfill \\
\end{gathered} \right.\]

Из равенства (4) выразим искомое сопротивление \(R\):

\[R = \frac{{2\varphi }}{I}\]

Учитывая (3), имеем:

\[R = \frac{{2{{\rm E}_2}}}{I}\;\;\;\;(5)\]

Из равенств (2) и (3) получим:

\[{{\rm E}_1} – {{\rm E}_2} = Ir\]

Откуда ток \(I\) равен:

\[I = \frac{{{{\rm E}_1} – {{\rm E}_2}}}{r}\]

Полученное выражение подставим в (5), таким образом, мы получим решение этой задачи в общем виде:

\[R = \frac{{2{{\rm E}_2}r}}{{{{\rm E}_1} – {{\rm E}_2}}}\]

Посчитаем численный ответ:

\[R = \frac{{2 \cdot 6 \cdot 0,5}}{{12 – 6}} = 1\;Ом\]

Ответ: 1 Ом.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Работа и мощность тока. Закон Джоуля — Ленца

6 Дуговая печь потребляет ток I=200 А от сети с напряжением V=120B через ограничивающее сопротивление R = 0,2 Ом. Найти мощность, потребляемую печью.

Решение:
N=I(V-IR)=16 кВт.

7 Нагревательная спираль электроаппарата для испарения воды имеет при температуре t=100°С сопротивление R= 10 Ом. Какой ток I надо пропускать через эту спираль, чтобы аппарат испарял массу воды m=100г за время τ=1 мин? Удельная теплота парообразования воды λ = 2,3 МДж/кг.

Решение:
Считая, что вся электрическая энергия затрачивается на испарение воды, получим

8 Электропечь должна давать количество теплоты Q = 0,1 МДж за время τ = 10 мин. Какова должна быть длина нихромовой проволоки сечения S=0,5 мм², если печь предназначается для сети с напряжением V=36 В? Удельное сопротивление нихрома ρ=1,2мкОм⋅м.
Решение:
По закону Джоуля — Ленца
-сопротивление проволоки, l-ее длина; отсюда

9 Комната теряет в сутки количество теплоты Q = 87 МДж. Какой длины l надо взять нихромовую проволоку диаметра D = 1 мм для намотки электропечи, поддерживающей температуру комнаты неизменной? Печь включается в сеть с напряжением V=120В, удельное сопротивление нихрома ρ=1,2мкОм⋅м.

Решение:

10 В сосуд, содержащий массу воды m = 480 г, помещен электронагреватель мощности N=40 Вт. Насколько изменилась температура воды в сосуде, если ток через нагреватель проходил в течение времени τ = 21 мин? Удельная теплоемкость воды с=4,2 кДж/(кг·К), теплоемкость сосуда вместе с нагревателем С_с=100Дж/К.

Решение:
Полученное количество теплоты идет на нагревание воды и сосуда с нагревателем, поэтому

где t1 и t2-начальная и конечная температуры воды. Изменение температуры воды

11 Найти мощность N электронагревателя кастрюли, если в ней за время τ = 20 мин можно вскипятить объем воды V=2 л. К.п.д. электронагревателя η = 70%. Удельная теплоемкость воды с = 4,2 кДж/(кг·К), начальная температура воды t₁ = 20° С.

Решение:
Электрическая энергия, идущая на нагревание воды,

где

— масса воды, t2 = 100° С- конечная температура воды; отсюда

12 Сколько времени надо нагревать на электроплитке мощности N=600 Вт при к.п.д. η = 75% массу льда m_л = 2кг, взятого при температуре t₁ = —16° С, чтобы обратить его в воду, а воду нагреть до температуры t₂ = 100°C? Удельная теплоемкость льда с_л = 2,1 кДж/(кг·К), удельная теплота плавления льда r=0,33 МДж/кг, удельная теплоемкость воды с = 4,2 кДж/(кг·К).

Решение:
Время нагревания определяется из уравнения теплового баланса (tо=0°С):

13 Какова должна быть длина нихромовой проволоки диаметра D = 0,3 мм, чтобы при включении последовательно с 40-ваттной лампочкой, рассчитанной на 127 В, проволока давала нормальный накал при напряжении в сети V=220 В? Удельное сопротивление нихрома ρ = 1,2 мкОм⋅м.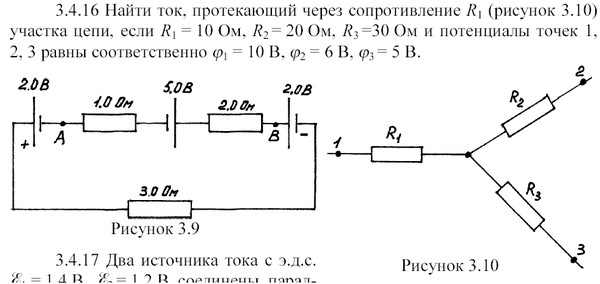

Решение:


14 Реостат с полным сопротивлением R подключен к сети с напряжением V (рис. 134). Во сколько раз изменится потребляемая от сети мощность, если движок реостата переместить на 1/4 длины от его конца?

Решение:
Отношение выделяемых на реостате мощностей N₀/N=4/3.

15 Найти к.п.д. насосной установки, которая подает в единицу времени объем воды V_τ = 75 л/с на высоту h = 4,7 м через трубу, имеющую сечение S=0,01 м², если мотор потребляет мощность N=10 кВт.

Решение:
Для подачи воды на высоту А необходима мощность

К. п. д. установки


16 Моторы электропоезда при движении со скоростью υ = 54 км/ч потребляют мощность N=900 кВт. К.п.д. моторов и передающих механизмов h = 80%. Найти силу тяги F, развиваемую моторами.
Решение:
Мощность, необходимая для движения поезда, равна

отсюда

17 Железная и медная проволоки одинаковых длин и сечений соединены последовательно и включены в сеть. Найти отношение количеств теплоты, выделившихся в каждой проволоке. Удельные сопротивления железа и меди равны ρ₁ =0,12 мкОм⋅м и ρ₂ = 0,017 мкОм⋅м. Решить эту же задачу для случая параллельного соединения проволок.

Решение:
Токи, идущие через обе проволоки, соединенные последовательно, одинаковы и равны I. При этом в проволоках за время t выделяются количества теплоты

-сопротивления железной и медной проволок, l и S-их длина и площадь сечения. Отношение количеств теплоты при последовательном соединении

При параллельном соединении токи в железной и медной проволоках

где V-напряжение в сети. В этом случае за время τ в проволоках выделяются количества теплоты
Их отношение


18 Железная и медная проволоки одинаковых длин и сечений включены в сеть на равные промежутки времени сначала последовательно, затем параллельно. Найти отношение количеств теплоты, выделившихся в проволоках в обоих случаях, если по железной проволоке тек один и тот же ток. Удельные сопротивления железа и меди ρ₁ =0,12 мкОм·м и ρ₂ = 0,017 мкОм·м.

Решение:


19 За время τ₁=40c в цепи из трех одинаковых проводников, соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты. За какое время τ₂ выделится такое же количество теплоты, если проводники соединить последовательно?

Решение:


20 Два одинаковых электронагревателя, потребляющих каждый мощность N = 200 Вт при напряжении V= 120 В, длинными и тонкими проводами подключены к источнику тока. Найти сопротивление проводов R, если при последовательном и при параллельном соединениях нагревателей они выделяют в единицу времени одно и то же количество теплоты.

Решение:


21 В электрочайнике с двумя нагревателями необходимо нагреть объем воды V=2 л от комнатной температуры (t₀ = 20° С) до температуры кипения. Каждый нагреватель, включенный в сеть отдельно, выделяет мощность N₁ = 250 Вт. Через какое время закипит вода, если ее подогревать одним нагревателем или двумя, включенными в ту же сеть последовательно или параллельно друг другу? К.п.д. нагревателя η = 80%. Удельная теплоемкость воды с = 4,2 кДж/(кг·К).

Решение:
Для нагревания воды до температуры кипения t=100° С необходимо количество теплоты
—
масса воды в чайнике. При включении одного нагревателя его мощность N₁=IV, где I-ток, текущий через него, и V-напряжение сети. В этом случае на нагревание воды идет часть теплоты, выделяемой нагревателем,

отсюда время нагревания воды одним нагревателем

При параллельном включении двух нагревателей, как и при включении одного из них, на каждом нагревателе будет напряжение сети V. Следовательно, в каждом из них будет выделяться та же мощность N₁ и общая мощность будет N₂ = 2N₁; отсюда время нагревания воды двумя нагревателями

При последовательном включении нагревателей общий ток через них будет равен 1/2. Поэтому общая мощность, выделяемая в них,

Следовательно, время нагревания воды в этом случае

22 Электрочайник имеет в нагревателе две секции. При включении первой секции вода в чайнике закипает за время τ₁ = 10 мин, а при включении второй секции — за время τ₂ = 40мин. Через какое время закипит вода, если включить обе секции параллельно или последовательно?

Решение:
При последовательном соединении секций

при параллельном соединении секций

23 Две лампы имеют одинаковые мощности. Одна из них рассчитана на напряжение V₁ = 120 В, другая—на напряжение V₂ = 220 В. Во сколько раз отличаются сопротивления ламп?

Решение:
Используя закон Джоуля-Ленца

находим

24 Какое сопротивление имеют 40- и 75-ваттные лампы, рассчитанные на включение в сеть с напряжением V=120 В? Какой ток течет через каждую лампу?

Решение:
Мощность лампы

где I-ток, текущий через лампу, R-ее сопротивление; отсюда для первой и второй ламп имеем

25 Какую мощность будет потреблять 25-ваттная лампочка, рассчитанная на напряжение V₁ = 120 В, если ее включить в сеть с напряжением V₂ = 220 В?

Решение:


26 100-ваттная лампа включена в сеть с напряжением V=120В. Сопротивление лампы в накаленном состоянии больше, чем в холодном (при температуре t₀ = 0° С), в 10 раз. Найти температурный коэффициент сопротивления материала нити и сопротивление лампы в холодном состоянии, если во время горения лампы температура нити t = 2000° С.

Решение:
Когда лампа включена,

-сопротивление нити горящей лампы и Ro=R/10-сопротивление нити лампы при температуре t0; отсюда

27 Найти сопротивление 100-ваттной лампы при комнатной температуре t₀ = 20° С, если при напряжении сети V=220 В температура нити t = 2800° С. Температурный коэффициент сопротивления материала нити .

Решение:


28 К источнику тока с э.д.с. ε = 140 В на расстоянии l=400 м от него подключена лампа, рассчитанная на напряжение V=120B и мощность N=100 Вт. Как изменится падение напряжения на лампе, если параллельно ей подключить вторую такую же лампу? Удельное сопротивление провода ρ = 0,028 мкОм⋅м, его сечение S=1 мм².

Решение:
Сопротивления лампы и проводов

Ток, текущий по линии, и падение напряжения на лампе равны

При подключении второй лампы сопротивление двух ламп равно R₁/2. Поэтому ток, текущий по линии, и падение напряжения на лампах равны

Изменение напряжения на лампе

Знак минус показывает, что при включении второй лампы падение напряжения на первой уменьшается.

29 На какое расстояние l можно передавать электроэнергию от источника тока с э.д.с. ε = 5 кВ так, чтобы на нагрузке с сопротивлением R=1,6 кОм выделялась мощность N=10 кВт? Удельное сопротивление провода ρ = 0,017 мкОм⋅м, его сечение S=1 мм².

Решение:


30 Под каким напряжением V нужно передавать электроэнергию на расстояние l=10 км, чтобы при плотности тока j = 0,5 А/мм² в стальных проводах двухпроводной линии электропередачи потери в линии составляли 1% передаваемой мощности? Удельное сопротивление стали ρ = 0,12 мкОм⋅м.

Решение:

31 Цепь состоит из двух параллельно включенных ламп мощности N=30 Вт каждая. Потери мощности в подводящих проводах составляют 10% полезной мощности. Найти напряжение на зажимах источника тока, если он обеспечивает в цепи ток I=2 A.

Решение:
Напряжение на зажимах источника тока

где V₁ и V₂ — падения напряжения на нагрузке и на проводах линии.
Мощность, выделяемая на нагрузке,

Потери мощности в линии

отсюда


32 От источника тока с напряжением V=750 В необходимо передать мощность N=5 кВт на некоторое расстояние. Какое наибольшее сопротивление R может иметь линия передачи, чтобы потери энергии в ней не превышали 10% передаваемой мощности?

Решение:

33 Какой наибольшей мощности электропечь можно установить в конце двухпроводной линии, имеющей сопротивление R=10 Ом, если источник тока развивает мощность N=6 кВт при напряжении V= 1 кВ?

Решение:
Ток в линии I=N/V. Потери мощности в линии

Мощность электропечи

34 Два параллельно соединенных резистора с сопротивлениями R₁=6 Ом и R₂ = 12 Ом подключены последовательно с резистором, имеющим сопротивление R= 15 Ом, к зажимам генератора с э.д.с. ε = 200 В и внутренним сопротивлением r=1 Ом. Найти мощность, выделяющуюся на резисторе R.

Решение:

35 Элемент с э.д.с. ε = 12 В и внутренним сопротивлением r = 4 Ом замкнут на сопротивление R = 8 Ом. Какое количество теплоты будет выделяться во внешней цепи в единицу времени?

Решение:
Ток в цепи I=ε/(R+r). Количество теплоты, выделяемое во внешней цепи в единицу времени,

36 Найти полную мощность элемента при сопротивлении внешней цепи R = 4 Ом, если внутреннее сопротивление элемента r = 2 Ом, а напряжение на его зажимах V=6 В.

Решение:
Полная мощность элемента

где I-ток в цепи. Так как

37 Батарея элементов, замкнутая на сопротивление R₁ = 2 Ом, дает ток I₁ = 1,6 А. Та же батарея, замкнутая на сопротивление R₂ = 1 Ом, дает ток I₂ = 2 А. Найти мощность, теряемую внутри батареи во втором случае.

Решение:
Внутри батареи теряется мощность

где r-внутреннее сопротивление батареи. Если ε — э. д. с. батареи, то по закону Ома для полной цепи в первом и втором случаях

отсюда


38 Найти э.д.с. ε и внутреннее сопротивление r аккумулятора, если при токе I₁ = 15 А он отдает во внешнюю цепь мощность N₁=135 Вт, а при токе I₂ = 6 А — мощность N₂ = 64,8 Вт.

Решение:


39 К источнику тока с э.д.с. ε = 8 В подключена нагрузка. Напряжение на зажимах источника V=6,4 В. Найти к.п.д. схемы.

Решение:
К. п. д.- это отношение полезной работы (мощности) ко всей затраченной работе (полной мощности). Полезной мощностью в данном случае является мощность, выделяемая на нагрузке, N₁=IV, где I-ток в цепи. Так как э. д. с. ε по определению представляет собой полную работу, совершаемую источником тока при перемещении по цепи единичного заряда, а в единицу времени через сечение проводника проходит заряд, численно равный I, то полная мощность источника тока равна

Таким образом, к.п.д. схемы

40 Найти к.п.д. схемы, изображенной на рис. 135. Сопротивления резисторов R₁ = 2 Ом и R₂ = 5 Ом, внутреннее сопротивление источника тока r = 0,5 Ом.

Задачи Для схемы (рис. 5) найти токи в ветвях и напряжения между узлами а и b. R

Задачи

1. Для схемы (рис.5) найти токи в ветвях и напряжения между узлами а и b. R₁= 1 кОм, R₂= 2 кОм, R₃= 3 кОм, R₄ =4 кОм, Е₁ =15 В, Е₂ =35 В, Е₃ =7 В, J₁ =4 мА.

Решение. Выбираем произвольно положительное направление токов и напряжений в ветвях. Для решения воспользуемся законами Ома и Кирхгофа. Имеем в схеме два независимых узла и два контура.

По первому закону Кирхгофа для первого и второго узла получим

Рис.5

для первого узла,

для второго узла.

Выбираем направления обхода контуров и, пользуясь вторым законом Кирхгофа и законом Ома, составим еще два уравнения:

Подставим числовые значения, получим систему четырех уравнений с четырьмя неизвестными, которая имеет однозначное решение:

Решая систему уравнений, получим I₁ =–5.57 мА, I₂ =7.22 мА, I₃ =1.65 мА, I₄ =5.65 мА.

Воспользовавшись законом Ома и вторым законом Кирхгофа, найдем Uab:

2. Для схемы (рис.6) найти все токи, если Е₁ =12 В, Е₂ =19 В, R₁ =4.7 кОм, R₂ =8.2 кОм, R₃ =2.2 кОм.

Рис.8

Рис.9

Рис.6

3. В неразветвленной цепи (рис.7) Е₁ =12 В, Е₂ =35 В, R₁ =12 кОм, R₂ =8.2 кОм. Определить напряжение между точками а и b.

4. В схеме моста (рис.8) известны сопротивления R₁ =1.3 кОм, R₂ =0.8 кОм, R₃ =0.4 кОм. Сопротивление гальванометра R_Г =0.6 кОм. Е =2.5 В, I₁ =1 мА. Найти сопротивление R₄.

5. В цепи (рис.9) найти Е₁ и R_Х, если Е₂ =3 В, R₁ =R₂ =1 кОм, R₃ =4 кОм, R₄ =2 кОм, R₅ =3 кОм. Амперметр А₁ показывает 4 мА, а А₂ – 3 мА; полярности приборов показаны на схеме, а их сопротивлениями можно пренебречь.

6

Рис.10

. Для цепи (рис.10) найти эквивалентные сопротивления между зажимами а и b, с , d и f, если R₁ =6 кОм, R₂ =5 кОм, R₃ =15 кОм, R₄ =30 кОм, R₅ =6 кОм.

Решение. 1) расчет сопротивления R_ab.

Эквивалентное сопротивление соединенных параллельно сопротивлений R₄ и R₅ найдем по формуле

кОм.

Оно соединено последовательно с R₂. Их общее сопротивление R’ =R₂+R₄₅ =5+5= =10 кОм.

Сопротивление цепи состоит из сопротивления R₁, последовательно с которым соединены два параллельных сопротивления R и R₃:

кОм.

2) расчет сопротивления R_cd.

Сопротивления R₄ и R₅ соединены параллельно; сопротивление R₃ включено последовательно с ними:

кОм.

Сопротивление R_cd состоит из двух параллельно включенных сопротивлений R₂ и R и равно

кОм.

3) расчет сопротивления R_df.

Эквивалентное сопротивление цепи между точками d и f состоит из трех параллельно включенных сопротивлений R₅, R₄ и R₂+R₃ и может быть определено из формулы:

,

откуда R_df. = 4 кОм.

7. Определить эквивалентное сопротивление цепи между точками а и b при разомкнутом и замкнутом ключе К (рис.11). Дано: R₁=R₂=R₃=R₄=R₅=R₆=R₇=10 кОм.

Рис.12

Рис.11

Рис.13

8. Определить токи в ветвях цепи (рис.12) и показание вольтметра, включенного между точками c и d , считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи. Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю? Сопротивления элементов цепи: R₁ =2.7 кОм, R₂ =R₃ =R₅ =2.5 кОм, R₄ =5.6 В, Е =70 В.

9. В схеме (рис.13) найти сопротивление R_x, если I₁ =2.6 мА, I₃ =0.6 мА, R₁ =0.5 кОм, R₂ =1.4 кОм, R₃ =3 кОм, R₄ =2.5 кОм; найти Е, если внутреннее сопротивление источника напряжения R_i равно 100 Ом.

10. Для цепей (рис.14,а,б) определить относительное напряжение на выходе U₂ (выходные зажимы цепи разомкнуты) к напряжению U₁ на входе цепи. Сопротивления отдельных ветвей цепи в килоомах указаны на схемах.

a)

б)

1

Рис.17

1. При заданных значениях R₁=4.3 кОм, R₂=7.5 кОм, R₃=5.1 кОм, R₄ =6.8 кОм, R =0…47 кОм, Е =9 В (рис.17) вычислить ток I₂ при максимальном R. Вычислить I₀. Найти величину R, при котором I₂=0. На сколько изменится при этом I₀?

Решение. Используя законы Кирхгофа, составляем систему уравнений, в которой переменными являются токи. Выразим все токи через I₁, I₂, I₃:



Решая систему методом Крамера, получаем =7976. 941, ₂=1894.14, ₃=6771.06; I₂=₂/=0.237 мА, I₃=0.849 мА, I₀=1.086 мА.

Ток I₂ равен нулю только в том случае, если напряжение на R₂ равно нулю. Тогда R₂= можно исключить из схемы. Получаем , , значит

, 5.73 (кОм).

При этом I₀ = E/(R₁ + R₃) = 0.957 мА.

Изменение I₀ равно I₀ = 0.957-1.086 = –0.129 мА.

12. Для измерения силы тока в линейной цепи были использованы разные милли-амперметры и шунт. Известно, что внутреннее сопротивление первого милли-амперметра R₁=115 Ом, второго R₂=47 Ом, сопротивление шунта R_ш=159 Ом. При подключении шунта к первому прибору его ток полного отклонения стал I_п1=10 мА, ко второму – I_п2=20  мА. При подключении в цепь первый прибор показал I₁=3.7 мА, второй – I₂=4.1 мА. Определить эквивалентное сопротивление цепи R_i и ток в цепи до подключения приборов.

Решение. Вычислим сопротивления приборов с подключенными шунтами. Сопротивление первого миллиамперметра равно

Ом,

второго

Ом.

Составим схему (рис.18). Токи I₁ и I₂ равны, соответственно:

Рис.18

Отсюда ,

,

Ом.

Но до подключения приборов в цепи протекал ток , , величиной , который определим, вычислив Е,

.

Получим

мА.

13. Найти коэффициент передачи по напряжению цепи (рис.19), если R₁=R₂ =R₄= R₇=2. 2 кОм, R₃= R₅= R₆= R₈ =4.7 кОм.

Рис.19

Рис.20

Рис.21

Подсказка. Сначала упростим схему, приведя её к виду (рис.20), заменив цепь, состоящую из R₄… R₈ на R_э.

14. Определить параметры генератора тока, эквивалентного цепи, показанной на рис.21. Параметры: R₁… R₆=6.2 кОм, E₁=E₂=10 В, I₁= I₂=1.5 мА.

Подсказка. Сначала преобразуем источники напряжения в эквивалентные источники тока.

Ответ: U_х.х.=6.783 В,

Рис.22

J_к.з.=0.938 мА.

15. Найти напряжение U_R7 (рис. 22) при данных значениях сопротивлений: R₁=R₂=R₃=2.2 кОм,

R₄=R₅ =R₆=R₇=4.3 кОм. E=6.3 В.

Ответ: =2.089 В.

Подсказка. Сначала преобразуем «звезды» R₁– R₂– R₃ и R₄–R₅–R₆ в «треугольники».

16. Методом контурных токов найти токи в цепи (рис.23). Дано: E₁=100 В, E₂=60 В, E₃=12 В, E₄=7 В, R₁=R₂=10 кОм, R₃=6 кОм, R₄=4.7 кОм, R₅=15 кОм.

Рис.23

Рис.24

17. Найти все токи в схеме (рис.24), а также отношение U₃ к I₄, если E₁=12 В, E₂=27 В, E₃=5 В, J₁=19 мА, R₁=5. 6 кОм, R₂=3.3 кОм, R₃=6.8 кОм, R₄=2.7 кОм, R₅=18.7 кОм, R₆=8.2 кОм, R₇=4.7 кОм.

Решение. Преобразуем источник тока с параллельно включенным сопротивлением в источник напряжения с последовательно включенным сопротивлением

, В.

Составим матрицы [U], [R] и [J]

,

,

J_I=–2.69 мА, J_II=–3.09 мА, J_III=–2.71 мА,

I₁=2.69 мА, I₂=3.09 мА, I₃=0.40 мА,

I₄=–22.09 мА, I₅=–0.02 мА, I₆=–0.38 мА, I₇=–2.71 мА, кОм.

Рис.25

Рис.26

18. Для схемы (рис.25) вычислить токи. Заданы токи и внутренние проводимости генераторов тока первого и второго, соответственно: J₁=50 мА, g₁=10^-4 Сим, J₂=60 мА, g₂=510^-4 Сим. E₃=270 В, R₃=1 кОм, R₄=2 кОм, R₅=7.5 кОм, R₆=3 кОм. Задачу решить методом контурных токов.

19. Для схемы (рис.26) составить матрицу сопротивлений и найти схемные функции I₄/J₁, U₃/E₁, U₃/J₁, I₄/U₂. Дано: J=20 мА, E₁=11 В, E₂=17 В, E₃=23 В, R₁=1 кОм, R₂=3 кОм, R₃=4.3 кОм, R₄=13 кОм, R₅=8.2 кОм, R₆=5.6 кОм,.

20. Для схемы (рис.27) составить матрицу сопротивлений и найти схемные функции E₁/U₅, J₂/U₅, U₇/U₃, U₅/J₁. Найти также токи в каждой ветви. Параметры элементов схемы: R₁=R₃=R₅=R₇=R₉=4.7 кОм, R₂=R₄=R₆=R₈=7.5 кОм,. J₁=10 мА, J₂=35 мА, J₃=7 мА, E₁=E₂=E₃=E₄=E₅=27 В.

Рис.27

Рис.28

21. Для схемы (рис.28) составить матрицу сопротивлений, вписав в неё зависимые источники напряжения. Найти схемную функцию U₂/U₁, если r₁=3 В/мА, r₂=5 В/мА, r₃=8 В/мА, R₁=R₃=R₅=4.3 кОм, R₂=R₄=12 кОм.

Решение. Введем обозначения:

,

,

Составим согласно МКТ систему уравнений

.

Поскольку напряжения зависимых источников напряжения матрицу сопротивлений E₁, E₂, E₃ зависят от величины неизвестных контурных токов, то множители при этих токах r₁, r₂, r₃ необходимо из столбца напряжений перенести в матрицу сопротивлений с противоположными знаками. При этом матрица сопротивлений будет иметь вид:

.

Теперь найдем схемную функцию U₂/U₁:

.

22. Для схемы (рис.29) составить матрицу сопротивлений, вписав в неё все зависимые источники. Найти следующие схемные функции U₃/I₅, I₅/U₃., U₅/U₁, если ₁=6, r₁=2 В/мА, r₂=7 В/мА, r₃=4.5 В/мА, R₁=7.5 кОм, R₂=12 кОм, R₃=1.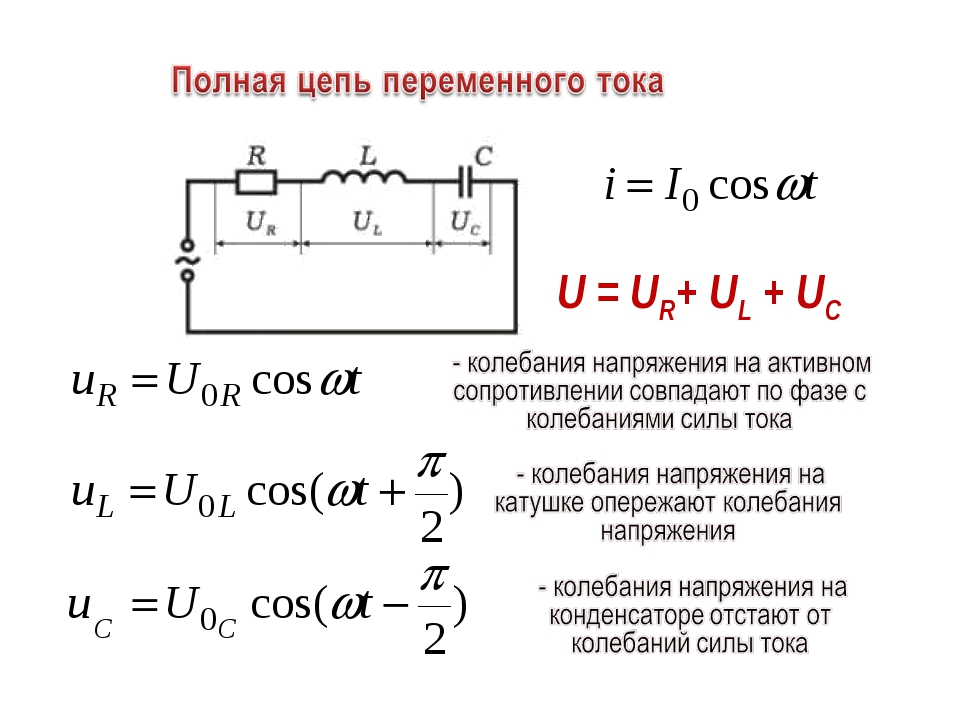 2 кОм, R₄=4.7 кОм, R₅=18 кОм.

23. Для схемы (рис.30) составить матрицу сопротивлений, вписав в неё все зависимые источники. Найти схемные функции U₂/U₁, I₃/U₁U₁/I₃, U₂/I₃, I₃/U₂, если r=11 В/мА, S₁=7 мА/В, S₂=19 мА/В R₁=R₂=R₃=6.8 кОм, R₄=R₅=7.5 кОм, R₆=12 кОм.

24. Для схемы (рис.31) составить матрицу сопротивлений, вписав в неё все зависи-мые источники. Найти схемную функцию U₂/U₁. Параметры схемы r₁=12 В/мА, r₂=3 В/мА, S=16 мА/В, R₁=R₂=3.3 кОм, R₃=1.2 кОм, R₄=0. 5 кОм, R₅=R₆=8.2 кОм.

Рис.29

Рис.30

Рис.31

Как найти силу тока на каждом резисторе

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.

Пример 1

Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R₁ = 20 и R₂ = 32 Ом.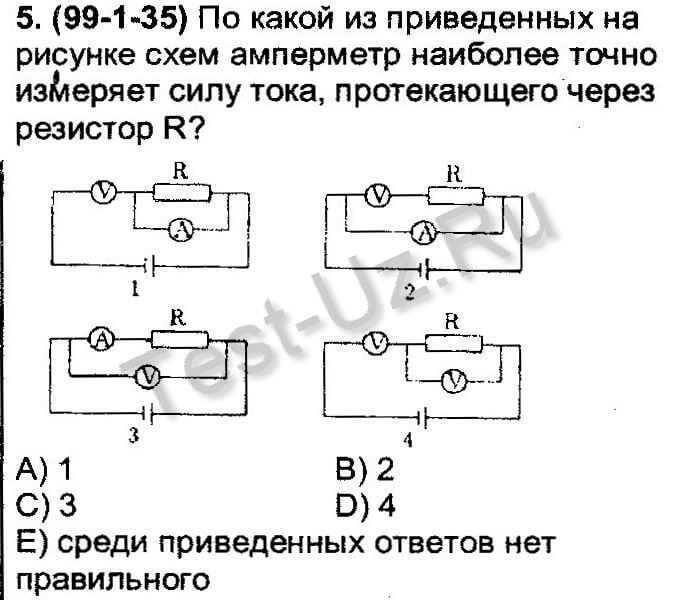 Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.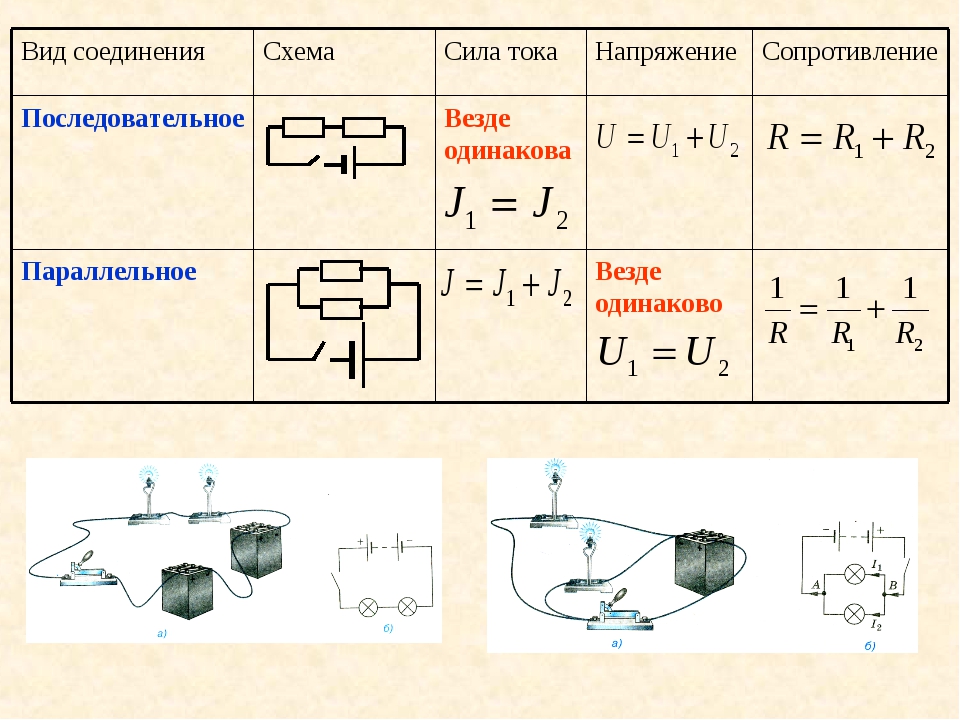

Пример 2

Общий ток цепи, содержащей два соединенных параллельно резистора R₁=70 Ом и R₂=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.

Токи в резисторах

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи

А затем напряжение

Зная напряжения, найдем токи, протекающие через резисторы

Как видите, токи получились теми же.

Пример 3

В электрической цепи, изображенной на схеме R₁=50 Ом, R₂=180 Ом, R₃=220 Ом. Найти мощность, выделяемую на резисторе R₁, ток через резистор R₂, напряжение на резисторе R₃, если известно, что напряжение на зажимах цепи 100 В.

Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R₁, необходимо определить ток I₁, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.

Эквивалентное сопротивление и ток в цепи

Отсюда мощность, выделяемая на R 1

Ток I₂ определим с помощью формулы делителя тока, учитывая, что ток I₁ для этого делителя является общим

Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U₃, как напряжение на резисторе R₂

Таким образом производится расчет простых цепей постоянного тока.

Резистор тока выполняет сразу несколько очень важных задач: служит ограничителем электрического тока в цепи, создает падение напряжения на отдельных ее участках и разделяет пульсирующий ток.

Помимо номинального сопротивления, одним из наиболее важных параметров резистора является рассеиваемая мощность. Она зависима от напряжения и тока. Мощность – это то тепло, которое выделяется на резисторе, когда под воздействием протекающего тока он нагревается. При пропуске тока, превышающего заданное значение мощности, резистор может сгореть.

Мощность постоянного тока может быть рассчитана по простой формуле P(Вт) = U(В) * I(А),

Чтобы избежать сгорания резистора тока, необходимо учитывать его мощность. Соответственно, если схема указывает на замену резистора с мощностью 0,5 Ватт – 0,5 Ватт в данном случае – минимум.

Мощность резистора может зависеть от его размеров. Как правило, чем меньше резистор – тем меньше мощность его рассеивания. Стандартный ряд мощностей резисторов тока состоит из значений:

Рассмотрим на примере: номинальное сопротивление нашего резистора тока – 100 Ом. Через него течет ток 0,1 Ампер. Чтобы узнать мощность, на которую рассчитан наш резистор тока, необходимо воспользоваться следующей формулой: P(Вт) = I2(А) * R(Ом),

• P(Вт) – мощность,
• R(Ом) – сопротивление цепи (в данном случае резистора),
• I(А) – ток, протекающий через резистор.

Внимание! При расчётах следует соблюдать размерность. Например, 1 кА= 1000 А . Это же касается и других величин.

Итак, рассчитаем мощность для нашего резистора тока: P(Вт) = 0,12(А) *100 (Ом)= 1(Вт)

Получилось, что минимальная мощность нашего резистора составляет 1 Ватт. Однако в схему следует установить резистор с мощностью в 1,5 – 2 раза выше рассчитанной. Соответственно идеальным для нас будет резистор тока мощностью 2 Вт.

Бывает, что ток, протекающий через резистор неизвестен. Для расчёта мощности в таком случае предусмотрена специальная формула:

Соединение цепи может быть последовательным и параллельным. Однако никакого труда не составляет рассчитать мощность резистора тока как в параллельной, так и в последовательной цепи. Следует учитывать лишь то, что в последовательно цепи через резисторы течет один ток.

Например, нам необходимо произвести замену резистора тока сопротивлением 100 Ом. Ток, протекающий через него – 0,1 Ампер. Соответственно, его мощность – 1 Ватт. Следует рассчитать мощность двух соединенных последовательно резисторов для его замены. Согласно формуле расчёта мощности, мощность рассеивания резистора на 20 Ом – 0,2 Вт, мощность резистора на 80 Ом – 0,8 Вт. Стандартный ряд мощностей поможет выбрать резисторы тока:

R1 – 20 Ом (0.5 Вт)

R2 – 80 Ом (1 Вт)

Из всего вышесказанного можно сделать вывод, что разное сопротивление резисторов гарантирует их разную выделяемую мощность, так как она распределяется между резисторами разных номиналов. Если не учитывать это обстоятельство, то можно столкнуться с большим количеством трудностей. Если один из резисторов выбран неправильно – второй работает в тяжелом температурном режиме. Также присутствует угроза возгорания резистора из-за несоблюдения правил мощности.

Для того, чтобы сэкономить время и не рассчитывать мощность каждого отдельного резистора тока нужно запомнить одно простое правило: мощность заменяемого резистора должна быть равна мощности каждого резистора, составляющего параллельную или последовательную цепь. То есть при замене резистора мощностью 0,5 Вт надо следить за тем, чтобы каждый из резисторов для замены имел мощность не менее 0,5 Вт.

При параллельном соединение резисторов важно помнить, что чем меньше сопротивление резистора, тем больший ток через него протекает, а значит на нем будет рассеяна большая мощность.

В упрощенном понимании электрическая цепь представляет собой совокупность элементов, реализующих определенные задачи при взаимодействии с электрическим током. При этом каждая из деталей выполняет свои функции при строго определенных параметрах. Они могут значительно отличаться от входящих значений. Одним из самых распространенных элементов электрической схемы является резистор.

Резистор выступает своеобразным ограничителем силы тока. По своей сути этот элемент является дополнительным сопротивлением, которое измеряется в омах. Собственно, зная это значение можно определить силу тока в резисторе, а также напряжение в цепи после него.

Определение силы тока на резисторе при разных типах соединения

Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.

Но данный вариант не всегда возможен. Под рукой может не оказаться тестера или технически невозможно разорвать цепь чтобы измерить силу тока на резисторе. В такой ситуации на помощь придет известный из школьной физики закон Ома, который выглядит следующим образом:

I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.

В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.

Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.

Последовательное соединение резисторов

Рассмотрим электрическую цепь, в которой три резистора расположены последовательно, т.е. друг за другом. Общее их сопротивление (R) будет рано сумме сопротивлений отдельного резистора (r).

Для наглядности примера, в качестве резисторов рассмотрим обычные 40 Вт лампы накаливании. В данном случае вольфрамовая нить обладает своим сопротивлением и ее вполне можно считать резистором. Также введем понятие мощности нагрузки или резистора (P), которая измеряется в ватах (Вт).

Она имеет прямолинейную зависимость от силы тока и напряжения и вычисляется по формуле: P=I х U. С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.

Сила тока (I) = Мощность лампы (Р) / Напряжение (U) = 40 Вт / 220 В = 0,1818 А.

Для последовательного соединения элементов в электрической цепи справедливо правило, что силы тока протекающие через все проводники одинакова. Таким образом сила тока в резисторе r2 или r3 также будет 0,1818 А. Но в нашем варианте с лампочками будет отмечена одна особенность – яркость свечения уменьшится. Это происходит из-за того, что резистор выступает в качестве делителя напряжения. Этот нюанс часто используют для продления срока службы не ответственных устройств. Например, впаяв сопротивление перед лампочкой можно продлить срок ее службы, но при этом придется смерится с недостатком освещенности.

Параллельное соединение резисторов

При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.

Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений. Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной. Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.

Смешанное соединение резисторов в цепи

В чистом виде параллельные и последовательные цепи в электротехнике встречаются крайне редко. Как правило, присутствует их совместная комбинация. Для того чтобы найти силу тока в каждом резисторе при смешанном соединении, необходимо цепь разбить на участки. Таким образом при расположении элементов друг после друга, т.н. «каскадом», применяются правила и формулы для последовательного соединения.

Результаты измерения силы тока в резисторе. Различные типы резисторов.

Необходимо отметить, что для упрощения расчетов параллельно расположенные резисторы можно группировать. При вычислении силы тока на определенном участке, они принимаются за самостоятельный элемент. Соответственно в этом случае формулы используются как для расчета параметров при параллельном соединении.

Обозначение мощности резистора на схеме, как её увеличить, что делать, если нет подходящего по мощности резистора

Обозначение мощности резистора на схеме, как её увеличить, что делать, если нет подходящего по мощности резистора

Резистор — пассивный элемент электрических цепей, обладающий определённым или переменным значением электрического сопротивления, предназначенный для линейного преобразования силы тока в напряжение и напряжения в силу тока, ограничения тока, поглощения электрической энергии и др. Весьма широко используемый компонент практически всех электрических и электронных устройств.

В схемах радиоэлектронной аппаратуры одним из наиболее часто встречающихся элементов является резистор, другое его название это сопротивление. У него есть целый ряд характеристик, среди которых есть мощность. В этой статье мы поговорим о резисторах, что делать, если у вас нет подходящего по мощности элемента, и почему они сгорают.

Характеристики резисторов

1. Основной параметр резистора – это номинальное сопротивление.

2. Второй параметр, по которому его выбирают – это максимальная (или предельная) рассеиваемая мощность.

3. Температурный коэффициент сопротивления – описывает, насколько изменяется сопротивление, при изменении его температуры на 1 градус Цельсия.

4. Допустимое отклонение от номинала. Обычно разброс параметров резистора от одного заявленного в пределах 5-10%, это зависит от ГОСТ или ТУ по которому он произведен, существуют и точные резисторы с отклонением до 1%, обычно стоят дороже.

5. Предельное рабочее напряжение, зависит от конструкции элемента, в бытовых электроприборах с напряжением питания 220В могут применяться практически любые резисторы.

6. Шумовые характеристики.

7. Максимальная температура окружающей среды. Это такая температура, которая может быть при достижении максимальной рассеиваемой мощности самого резистора. Об этом подробнее поговорим позже.

8. Влаго- и термоустойчивость.

Есть еще две характеристики, о которых начинающие чаще всего не знают, это:

1. Паразитная индуктивность.

2. Паразитная ёмкость.

Оба параметра зависят от типа и конструктивных особенностей резистора. Индуктивность имеет в любом проводнике, вопрос в её величины. Типовые величины паразитных индуктивностей и емкостей приводить бессмысленно. Паразитные составляющие следует учитывать при проектировании и ремонте высокочастотных приборах.

На низких частотах (например, в пределах звукового диапазона до 20 кГц), существенного влияния в работу схемы они не вносят. В высокочастотных приборах, с рабочими частотами в сотни тысяч и выше герц существенное влияние вносит даже расположение дорожек на плате и их форма.

Мощность резистора

Из курса физики многие отлично помнят формулу мощности для электричества, это: P=U*I

Отсюда следует, что она линейно зависит от тока и напряжения. Ток же через резистор зависит от его сопротивления и приложенного к нему напряжению, то есть:

I=U/R

Падение напряжения на резисторе (сколько на его выводах остаётся напряжения от приложенного к цепи, в которой он установлен), так же зависит от тока и сопротивления:

I=U/R

Теперь объясним простыми словами, что такое мощность у резистора и куда она выделяется.

У любого металла есть своё удельное сопротивление, это такая величина, которая зависит от структуры этого самого металла. Когда носители зарядов (в нашем случае электроны), под воздействием электрического тока протекают через проводник, они сталкиваются с частицами, из которого состоит металл.

В результате этих столкновений затрудняется движение тока. Если очень обобщенно сказать, то получается, так, что чем плотнее структура металла, тем сложнее протекать току (тем больше сопротивление).

На картинке пример кристаллической решетки, для наглядности.

Из-за этих столкновений выделяется тепло. Это можно представить, как если бы вы шли через толпу (большое сопротивление), где вас еще и толкают, или если бы шли по пустому коридору, где вы сильнее вспотеете?

То же самое происходит и с металлом. Мощность выделяется в виде тепла. В некоторых случаях это плохо, потому что так снижается коэффициент полезного действия прибора. В других ситуациях – это полезное свойство, например в работе ТЭНов. В лампах накаливания за счет своего сопротивления спираль раскаляется до яркого свечения.

Но как это относится к резисторам?

Дело в том, что резисторы применяют для ограничения тока при питании каких-либо устройств, или элементов цепи, или для задания режимов работы полупроводниковым приборам. Из формулы выше станет ясно, что ток снижается, за счет снижения напряжения. Лишнее напряжение можно сказать, что сгорает в виде тепла на резисторе, мощность при этом считается по той же формуле, что и общая мощность:

P=U*I

Здесь U – это количество вольт «сожженных» на резисторе, а I – это ток, который через него протекает.2/1=144/1=144 Вт.

Всё сходится. Резистор будет выделять тепло с мощностью в 144Вт. Это условные значения, взятые в качестве примера. На практике таких резисторов вы не встретите в радиоэлектронной аппаратуре, исключением являются большие сопротивления для регулирования двигателей постоянного тока или пуска мощных синхронных машин в асинхронном режиме.

Какие бывают резисторы и как они обозначаются на схеме

Ряд мощностей резисторов стандартен: 0.05 (0.62) – 0.125 – 0.25 – 0.5 – 1 – 2 – 5

Это типовые номиналы распространенных резисторов, бывают и большие значения, или другие величины. Но этот ряд наиболее распространен. При сборке электроники используют схему электрическую принципиальную, с порядкового номера элементов. Реже указываться номинальное сопротивление, еще реже указывается номинальное сопротивление и мощность.

Чтобы быстро определить мощность резистора на схеме были введены соответствующие УГО (условные графические обозначения) по ГОСТ. Внешний вид таких обозначений и их расшифровка представлены в таблице ниже.

Вообще эти данные, а также название конкретного типа резистора указываются в перечне элементов, там же указывается и разрешенный допуск в %.

Внешне, они отличаются размером, чем мощнее элемент, тем больше его размер. Больший размер увеличивает площадь теплообмена резистора с окружающей средой. Поэтому тепло, которое выделяется при прохождении тока через сопротивление, быстрее отдаётся воздуху (если окружающая среда воздух).

Это значит, что резистор может греться с большей мощностью (выделять определенное количество тепла в единицу времени). Когда температура сопротивления достигает определенного уровня, сначала начинает выгорать внешний слой с маркировкой, дальше сгорает резистивный слой (пленка, проволока или что-то другое).

Чтобы вы оценили, как сильно может греться резистор, взгляните на нагрев спирали разобранного мощного резистора (более 5 Вт) в керамическом корпусе.

В характеристиках был такой параметр, как допустимая температура окружающей среды. Она указывается, для правильного подбора элемента. Дело в том, что раз мощность резистора ограничена способностью отдать тепло и, при этом, не перегреться, а для отдачи тепла, т.е. охлаждения элемента путем конвекции или принудительным потоком воздуха должна быть как можно большая разница температур элемента и окружающей среды.

Поэтому если вокруг элемента слишком жарко он быстрее нагреется и сгорит, даже если электрическая мощность на нем ниже максимально рассеиваемой. Нормальной температурой является 20-25 градусов Цельсия.

Что делать, если нет резистора нужной мощности?

Частой проблемой радиолюбителей является отсутствия резистора нужной мощности. Если у вас есть резисторы мощнее, чем нужно – ничего страшного в этом нет, можно ставить не задумываясь. Лишь бы он влез по размеру. Если все имеющиеся резисторы по мощности меньше, чем нужно – это уже проблема.

На самом деле решить этот вопрос достаточно просто. Вспомните законы последовательного и параллельного соединения резисторов.

1. При последовательном соединении резисторов сумма падений напряжений на всей цепочке равняется сумме падений на каждом из них. А ток, протекающий через каждый резистор равен общему току, т.е. в цепи из последовательно соединенных элементов протекает ОДИН ток, но приложенные к каждому из них напряжения РАЗНЫЕ, определяются по закону Ома для участка цепи (см. выше) Uобщ=U1+U2+U3

2. При параллельном соединении резисторов падение на всех напряжения равны, а ток, протекающий в каждой из ветвей обратно пропорционален сопротивлению ветви. Общий ток цепочки из параллельно соединенных резисторов равен сумме токов каждой из ветвей.

На этой картинке изображено всё вышесказанное, в удобной для запоминания форме.

Так, как при последовательном соединении резисторов снизится напряжение на каждом из них, а при параллельном соединении ток, то если P=U*I

Мощность, выделяемая на каждом из них, снизится соответствующим образом.

Поэтому, если у вас нет резистора 100 Ом на 1 Вт, его можно почти всегда заменить 2 резисторами на 50 Ом и 0.5 Вт соединенными последовательно, или 2 резисторами на 200 Ом и 0.5 Вт соединенными параллельно.

Я не просто так написал «ПОЧТИ ВСЕГДА». Дело в том, что не все резисторы одинаково хорошо переносят ударные токи, в некоторых цепях, например связанные с зарядом конденсаторов большой ёмкости, в первоначальный момент времени переносят большую ударную нагрузку, которая может повредить его резистивный слой. Такие связки нужно проверять на практике или путем долгих расчетов и чтением технической документации и ТУ на резисторы, чем почти никогда и никто не занимается.

Заключение

Мощность резистора – это величина не менее важная, чем его номинальное сопротивление. Если не уделять внимания подбору сопротивлений нужно мощности, то они будут перегорать и сильно греться, что плохо в любой цепи.

При ремонте аппаратуры, особенно китайской, ни в коем случае не пытайтесь ставить резисторы меньшей мощности, лучше поставить с запасом, если есть такая возможность поместить его по габаритам на плате.

Для стабильной и надежной работы радиоэлектронного устройства нужно подбирать мощность, как минимум, с запасом в половину от предполагаемой, а лучше в 2 раза больше. Это значит, что если по расчетам на резисторе выделяется 0.9-1 Вт, то мощность резистора или их сборки должна быть не меньше, чем 1.5-2 Вт.

Ранее ЭлектроВести писали, что JinkoSolar объявила, что она установила новый рекорд эффективности для монокристаллических PERC-панелей, который составил 24,38%. Компания также разработала модуль мощностью 469,3 Вт. Кроме того, китайский производитель фотоэлектрических элементов поравнялся с фирмой Trina Solar, которая на прошлой неделе заявила о рекордном 24,58% показателе КПД монокристаллических панелей n-типа.

По материалам: electrik.info.

Резисторы

в схемах – Практика – Физический гипертекст

Давайте начнем процесс с комбинирования резисторов. В этой схеме четыре последовательных пары.

осталось

R с = 3 Ом + 1 Ом R с = 4 Ом R с = 4 Ом + 2 Ом R с = 6 Ом

правый

R с = 2 Ом + 3 Ом R с = 5 Ом R с = 1 Ом + 4 Ом R с = 5 Ом

Эти пары образуют две параллельные цепи, одну слева и одну справа.

осталось

1 = 1 + 1 R p 4 Ом 6 Ом

R p = 12 Ом = 2.4 Ом 5

правый

1 = 1 + 1 R p 5 Ом 5 Ом

R p = 5 Ом = 2.5 Ом 2

Каждый набор из четырех резисторов включен последовательно с другим.

осталось

R с = 2,4 Ом + 0,6 Ом R с = 3 Ом

правый

R с = 2,5 Ом + 0,5 Ом R с = 3 Ом

Левая и правая половины цепи параллельны друг другу и батарее.

1 = 1 + 1 = 2 R p 3 Ом 3 Ом 3 Ом

R p = 3 Ом = 1.5 Ом 2

Теперь, когда у нас есть эффективное сопротивление всей цепи, давайте определим ток источника питания по закону Ома.

I итого =	В всего	+	24 В	= 16 А
	R Всего		1.5 Ом

А теперь пройдемся по трассе (не в буквальном смысле конечно). На каждом соединении ток будет делиться: больше по пути с меньшим сопротивлением и меньше по пути с большим сопротивлением. Поскольку заряд не протекает нигде в полной цепи, ток будет одинаковым для всех элементов, последовательно соединенных друг с другом.

Левая и правая половины схемы идентичны по общему сопротивлению, что означает, что ток будет равномерно делиться между ними.

8 A для резистора 0,6 Ом на слева .

8 A для резистора 0,5 Ом на правом .

С каждой стороны ток снова делится на две параллельные ветви.

Ветви на слева имеют сопротивления в соотношении…

R 1 и 3 = 4 Ом + 2 R 2 и 4 6 Ом 3

то есть токи разделятся в соотношении…

для резисторов 1 Ом и 3 Ом на слева .

для резисторов 2 Ом и 4 Ом на слева .

Ветви на правом идентичны, поэтому ток разделяется на две равные половины.

28

28

☟

☟

28

для резисторов 2 Ом и 3 Ом на правой .

для резисторов 1 Ом и 4 Ом на правой стороне .

Закон Ома | Электрические цепи

Закон 11,2 Ома (ESBQ6)

Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Резюме:

1. Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.

2. Разность потенциалов или напряжение \ (В \) – это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.

3. Сопротивление, \ (R \), является мерой того, насколько “трудно” протолкнуть ток через элемент схемы.

Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.

Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .

Закон Ома

Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как

. \ (I = \ frac {V} {R} \)

где \ (I \) – ток через проводник, \ (V \) – напряжение на проводнике, а \ (R \) – сопротивление проводника. Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.

Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток – на ось y графика, мы получим прямую линию.

Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R}. \] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I}.\]

Закон Ома

Цель

Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.

Аппарат

4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода

Метод

Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное к резистору напряжение и измерять результирующий ток в цепи. Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе.После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.

1. Изменение напряжения:

   1. Установите схему в соответствии со схемой 1), начиная с одной ячейки.

   2. Нарисуйте следующую таблицу в своем лабораторном журнале.

      Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
      \ (\ text {1} \)
      \ (\ text {2} \)
      \ (\ text {3} \)
      \ (\ text {4} \)

   3. Попросите учителя проверить электрическую цепь перед включением питания.

   4. Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.

   5. Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.

   6. Повторяйте, пока не получите четыре ячейки и не заполните таблицу.

2. Изменение тока:

   1. Установите схему в соответствии со схемой 2), начиная с одного резистора в цепи.

   2. Нарисуйте следующую таблицу в своем лабораторном журнале.

      Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))

   3. Попросите учителя проверить вашу схему перед включением питания.

   4. Измерьте ток и напряжение на единственном резисторе.

   5. Теперь добавьте еще один резистор последовательно в схему и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.

Анализ и результаты

1. Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение – это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).

2. Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).

Выводы

1. Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?

2. Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?

3. Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Вопросы и обсуждение

1. Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?

2. Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?

Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.

Зарегистрируйтесь здесь

Закон Ома

Упражнение 11.1

Постройте график напряжения (по оси X) и тока (по оси Y).

Какой тип графика вы получите (прямолинейный, парабола, другая кривая)

прямая линия

Рассчитайте градиент графика.

Градиент графика (\ (m \)) – это изменение тока, деленное на изменение напряжения:

\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) – (\ text {0,4})} {(\ text {12}) – (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}

Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.

Как вы можете определить сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?

Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.

Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение для каждого из резисторов.

Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:

\ [V = IR \]

Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток одинаков во всей цепи, мы можем найти неизвестное сопротивление.

\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}

Омические и неомические проводники (ESBQ7)

Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток через них.Эти проводники называются омическими проводниками. График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторыми примерами омических проводников являются резисторы цепи и нихромовая проволока.

Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка – типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.

В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, возникающее в результате увеличение тока приведет к повышению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.

Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.

В общем, для неомических проводников график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.

Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка – нет.

Омические и неомические проводники

Aim

Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома

Аппарат

4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр

Метод

Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй – лампочка.Настройте обе схемы, указанные выше, начиная с 1 ячейки. Для каждой цепи:

1. Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.

2. Измерить ток в цепи с помощью амперметра.

3. Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.

Результаты

Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.

Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)

Анализ

Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) – ось) vs.\ (V \) (\ (x \) – ось), один для резистора и один для лампочки.

Вопросы и обсуждение

Внимательно изучите свои графики и ответьте на следующие вопросы:

1. Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?

2. Один или оба ваших графика выглядят так?

3. Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?

4. Имеет ли лампочка омический или неомический провод?

Использование закона Ома (ESBQ8)

Теперь мы готовы увидеть, как закон Ома используется для анализа схем.

Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача – нарисовать принципиальную схему. Решая любую проблему с электрическими цепями, очень важно составить схему схемы, прежде чем производить какие-либо расчеты. Принципиальная схема для этой проблемы выглядит следующим образом:

Уравнение закона Ома: \ [R = \ frac {V} {I} \]

, который можно преобразовать в: \ [I = \ frac {V} {R} \]

Ток, протекающий через резистор:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}

Рабочий пример 1: Закон Ома

Изучите принципиальную схему ниже:

Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?

Определите, как подойти к проблеме

Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]

Решить проблему

Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \). \ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}

Напишите окончательный ответ

Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).

Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.

Зарегистрируйтесь здесь

Закон Ома

Упражнение 11.2

Вычислите сопротивление резистора, разность потенциалов которого равна \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}

Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}

Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}

Переплет резисторов последовательно и параллельно (ESBQ9)

В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.

Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .

Эквивалентное последовательное сопротивление

В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление – это просто сумма сопротивлений всех резисторов.

Эквивалентное сопротивление в последовательной цепи,

Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]

Применим это к следующей схеме.

Резисторы включены последовательно, следовательно:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {align *}

Эквивалентное параллельное сопротивление

В схеме, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующим определением.

Эквивалентное сопротивление в параллельной цепи

Для параллельных резисторов \ (n \) эквивалентное сопротивление составляет:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]

Применим эту формулу к следующей схеме.

Какое полное (эквивалентное) сопротивление в цепи?

\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \верно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {align *}

Последовательное и параллельное сопротивление

Упражнение 11.3

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}

Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} – R_ {1} \\ & = \ text {100} \ text {Ω} – \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}

Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} – \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} – \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} – \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}

Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:

a) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}

b) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}

c) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}

d) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}

Использование закона Ома в последовательных и параллельных цепях (ESBQB)

Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.

Цепи серии

Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.

Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.

Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:

\ [I = I_ {1} = I_ {2} = I_ {3}. \]

Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:

\ [V = V_ {1} + V_ {2} + V_ {3} \]

Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления последовательно соединенных резисторов, мы можем решить некоторые проблемы схемы.

Рабочий пример 2: Закон Ома, последовательная цепь

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Нам необходимо рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.

Найти полное сопротивление в цепи

Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:

\ [R = R_ {1} + R_ {2} \]

Следовательно,

\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {align *}

Примените закон Ома

\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).

Рабочий пример 3: Закон Ома, последовательная цепь

Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).

Нарисуйте схему и введите все известные значения.

Определите, как подойти к проблеме.

Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:

\ [R = R_ {1} + R_ {2} \]

, потому что он находится в последовательной цепи.

Найдите полное сопротивление

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {align *}

Найдите неизвестное сопротивление

Мы знаем, что:

\ [R = \ text {6} \ text {Ω} \]

и что

\ [R_ {1} = \ text {1} \ text {Ω} \]

С

\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R – R_ {1} \]

Следовательно,

\ [R_ {1} = \ text {5} \ text {Ω} \]

Рабочий пример 4: Закон Ома, последовательная цепь

Для следующей схемы рассчитайте:

1. падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)

2. сопротивление \ (R_3 \).

Определите, как подойти к проблеме

Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).

Рассчитать падение напряжения на \ (R_1 \)

Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_2 \)

Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_3 \)

Поскольку падение напряжения на всех резисторах, вместе взятых, должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V – V_1 – V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}

Найдите сопротивление \ (R_3 \)

Нам известно напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома для вычисления значения сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}

Напишите окончательный ответ

\ (V_1 = \ text {2} \ text {V} \)

\ (V_2 = \ text {6} \ text {V} \)

\ (V_3 = \ text {10} \ text {V} \)

\ (R_1 = \ text {5} \ Omega \)

Параллельные цепи

Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.

Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Итак, для показанной схемы верно следующее:

\ [V = V_ {1} = V_ {2} = V_ {3}. \]

Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны в сумме равняться общему току в цепи:

\ [I = I_ {1} + I_ {2} + I_ {3}.\]

Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельных резисторов, мы теперь можем подойти к некоторым проблемам схемы, связанным с параллельными резисторами.

Рабочий пример 5: Закон Ома, параллельная цепь

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Нам необходимо рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома.Однако в цепи два резистора, и нам нужно найти полное сопротивление.

Найдите эквивалентное сопротивление в цепи

.

Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:

\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {align *}

Применить закон Ома

\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).

Рабочий пример 6: Закон Ома, параллельная цепь

Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найдите сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ текст {9} \) \ (\ text {V} \).

Определите, что требуется

Нам нужно рассчитать сопротивление \ (R_2 \).

Определите, как подойти к проблеме

Поскольку резисторы омические и нам даны напряжение на ячейке и ток в ячейке, мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи.\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}

Рассчитайте значение для \ (R_2 \)

Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для параллельных резисторов, чтобы найти сопротивление \ (R_2 \). \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \ end {выровнять *} Переставляем решение для \ (R_2 \): \ begin {align *} \ frac {1} {R_2} & = \ frac {1} {R} – \ frac {1} {R_1} \\ & = \ frac {1} {\ text {1,875}} – \ frac {1} {3} \\ & = \ текст {0,2} \\ R_2 & = \ frac {1} {\ text {0,2}} \\ & = \ текст {5} \ \ Omega \ end {align *}

Напишите окончательный ответ

Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)

Рабочий пример 7: Закон Ома, параллельная цепь

Ячейка на 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.

Сначала нарисуйте схему, прежде чем производить какие-либо вычисления

Определите, как подойти к проблеме

Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.

Рассчитать ток через ячейку

Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи.Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}

Теперь определите ток через один из параллельных резисторов

Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_1 = V_2 = \ text {18} \ text {V} \ end {выровнять *} Начнем с расчета тока через \ (R_1 \) по закону Ома: \ begin {align *} R_1 & = \ frac {V_1} {I_1} \\ I_1 & = \ frac {V_1} {R_1} \\ & = \ frac {18} {4} \\ I_1 & = \ text {4,5} \ text {A} \ end {align *}

Рассчитайте ток через другой параллельный резистор

Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \): \ begin {align *} R_2 & = \ frac {V_2} {I_2} \\ I_2 & = \ frac {V_2} {R_2} \\ & = \ frac {18} {12} \\ I_2 & = \ text {1,5} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через ячейку: \ begin {align *} I & = I_1 + I_2 \\ I_2 & = I – I_1 \\ & = 6 – 4.5 \\ I_2 & = \ text {1,5} \ text {A} \ end {align *}

Напишите окончательный ответ

Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).

Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).

Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).

Закон Ома в последовательной и параллельной цепях

Упражнение 11.4

Рассчитать номинал неизвестного резистора в цепи:

Сначала мы используем закон Ома для расчета полного последовательного сопротивления:

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}

Теперь мы можем найти неизвестное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} – R_ {1} – R_ {2} – R_ {3} \\ & = 9 – 3 – 3 – 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}

Рассчитайте значение тока в следующей цепи:

Сначала находим общее сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *}

Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены последовательно с батареей \ (\ text {12} \) \ (\ text {V} \).Рассчитайте значение тока в цепи.

Рисуем принципиальную схему:

Теперь мы находим общее сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {A} \ end {выровнять *}

Рассчитайте ток через ячейку, если оба резистора имеют омическую природу.

Сначала находим общее сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}

Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:

Сначала находим общее сопротивление:

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать неизвестное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} – \ frac {1} {R_ {1}} – \ frac {1} {R_ {2}} – \ гидроразрыв {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} – \ frac {1} {\ text {120}} – \ frac {1} {\ text {40}} – \ frac {1} {\ text { 60}} \\ & = \ frac {10 – 1 – 3 – 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}

значение тока через аккумулятор

Рисуем принципиальную схему:

Чтобы вычислить значение тока через батарею, нам сначала нужно вычислить эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}

Теперь можем посчитать ток через батарею:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *}

значение тока в каждом из трех резисторов.

Для параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из резисторов. Для этой схемы:

\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]

Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}

Далее мы вычисляем ток через \ (R_ {2} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}

И наконец вычисляем ток через \ (R_ {3} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *}

Вы можете проверить, что они в сумме составляют общий ток.

Последовательные и параллельные сети резисторов (ESBQC)

Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы заняться цепями, которые объединяют эти две схемы, например, следующей цепью:

Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.

Проработать такие схемы относительно легко, потому что вы используете все, что вы уже узнали о последовательных и параллельных схемах.Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из 2 параллельных частей, которые затем включены последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начинаете с вычисления общего сопротивления каждой из параллельных частей, а затем последовательно складываете эти сопротивления. Если бы все резисторы на рисунке 11.1 имели сопротивление \ (\ text {10} \) \ (\ text {Ω} \), мы можем вычислить эквивалентное сопротивление всей цепи.

Начнем с вычисления общего сопротивления параллельной цепи 1 .{-1} \\ & = \ текст {5} \, \ Omega \ end {align *}

Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:

Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}

Эквивалентное сопротивление цепи на рисунке 11.1 равно \ (\ text {10} \) \ (\ text {Ω} \).

Последовательные и параллельные сети

Упражнение 11.5

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}

ток \ (I \) через ячейку.

Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *}

ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).

Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ text {A} \). (Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):

\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторе \ (\ text {5} \) \ (\ text {Ω} \).

Итак, теперь мы можем рассчитать ток через резистор:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {A} \ end {выровнять *}

Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы омические, рассчитайте напряжение на ячейке и на каждом из резисторов, \ (R_1 \ ), \ (R_2 \) и \ (R_3 \) соответственно.

Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление.Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}

Итак, напряжение на ячейке:

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *}

Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с нахождения напряжения на \ (R_ {1} \):

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}

Теперь находим напряжение на параллельной комбинации:

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).

ток через ячейку

Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}

падение напряжения на \ (R_4 \)

Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через \ (R_ {4} \):

\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}

ток через \ (R_2 \)

Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти ток через \ (R_ {2} \).

Сначала нам нужно найти напряжение на параллельной комбинации:

\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}

Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение одинаково на всех резисторах в параллельной комбинации:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *}

Определение напряжения по закону Ома

Определение напряжения по закону Ома

Рисунок 1. А напряжение В падающий на резисторе R в цепи с током I .

В начале 1800-х годов Джордж Ом открыл математическую связь для электрических цепей с простыми резисторами. В цепи, имеющей ток I (в амперах), падение напряжения (В в вольтах) на сопротивлении (R в омах) составляет В = I x R .Эти отношения часто проявляются тремя способами:

Первая форма позволяет нам вычислить падение напряжения на резисторе для заданного тока в цепи. Предположим, амперметр измеряет ток I = 1,8 ампера через сопротивление R = 3,5 Ом. Тогда падение напряжения на сопротивлении составит:

Обратите внимание на единицы измерения. Помните: Ом – это единица измерения сопротивления, определяемая как такое сопротивление, при котором один вольт на нем создает ток в один ампер.

Вы должны быть осторожны при работе с агрегатами. Токи часто измеряются в миллиамперах (1/1 000 ампер) или даже в микроамперах (1/1 000 000 ампер). Сопротивление может выражаться в киломах (1000 Ом) или даже мегомах (1000000 Ом).

Предположим, что через резистор на 2,5 МОм проходит ток 3,9 мА. Напряжение на резисторе:

Часто бывает полезно преобразовать метрические префиксы в экспоненциальную нотацию.

микро- = 10 –6

милли- = 10 –3

килограмм – = 10 3

мега- = 10 6

Решение упражнений на странице 32

Решения упражнений

1.An электрическая схема проиллюстрирована ниже.

Какое эквивалентное сопротивление эта схема?

₂ + ₃ = _{рэндов экв.}

6 + 6 = 12 Вт

1 / Rp = 1 / R ₁ + 1 / R _экв

1 / Rp = 1/4 + 1/12

Rp = 3 Вт

Rt = 3 + 6 = 9 Вт

2.An электрическая схема проиллюстрирована ниже.

Какой номинал резистора R ₃ ?

Я ₁ = Я ₂ + Я ₃ потому что в этом случае I1 – это полный ток.

2 = 1,5 + я ₃

I ₃ = 0,5 А

Если V ₂ = 90 В, то V ₃ = 90 В, потому что параллельное напряжение постоянно.

R ₃ = V ₃ / I ₃ = 90 / 0,5 = 180 Вт

3. А последовательно-параллельная электрическая схема проиллюстрирована ниже.

Найдите R _t .

₄ и ₃ соединены последовательно, так что _{рэндов eq1} = ₄ рэндов + ₃ рэнд = 10 + 20 = 30Вт.

₂ и _экв1 работают параллельно, поэтому

1 / R _экв2 = 1/ ₂ + 1/ _экв1

1 / R _экв2 = 1 / 15+ 1/30

R _экв2 = 10 Вт.

Rt = ₅ руб. + R _eq2 + R ₁ = 10 + 10 + 10 = 30 Вт.

4. А последовательно-параллельная электрическая схема проиллюстрирована ниже.

Какая разница потенциалов на выводе резистора R ₁ ?

Первое обнаруженное общее сопротивление: 1 / R экв = 1 / R 1 + 1 / ( 2 + 3 ) 1 / R экв. = 1/30 + 1 / (5 + 10)

= 10 Вт.

_{рупий =} рупий = ₄ рупий + R _экв = 20 + 10 = 30 Вт.

I _т = V / R = 12/30 = 0,40 A

В ₄ = IR ₄ = 0,40 (20) = 8 В

В ₁ = В _т В ₄ = 12 8 = 4 В

5. А последовательно-параллельный электрический показан ниже.

Какая сила тока от источника питания, I _с ?

R ₂ и R ₃ испытывают одинаковое напряжение, поэтому V ₂ = I ₂ R ₂ = (0.5) 75 = 37,5 В и

I = V ₃ / R ₃ = 37,5 / 100 = 0,375 A

Так общий ток = 0,5 + 0,375 = 0,875 А

6. Следующая электрическая схема состоит из блока питания, пять резисторов (R ₁ , R ₂ , R ₃ , R ₄ и R ₅ ) и амперметр.

Амперметр показывает 0,25 А.

а.Какая разница потенциалов (напряжение), В _т , через клеммы блока питания?

1 / R _экв1 = 1 / ( ₁ + ₂ ) + 1/ ₃

1 / R _экв1 = 1 / (20 + 40) + 1/30

р _экв1 = 20 Вт.

1 / R _экв2 = 1/ ₄ + 1/ ₅

1 / R _экв2 = 1/40 + 1/120

R _экв2 = 30 Вт.

Rt = _{рэндов экв1} + R _экв2 = 20 + 30 = 50 Вт.

Вт = IRt = 0,25 (50) = 12,5 В

г. Какая разница потенциалов на R ₃ ?

Vp = V ₃ = I _t R _eq1 = 0,25 (20) = 5 В

г. Какие равна разности потенциалов на R ₁ ?

Я ₁ = Вп / ( ₁ + ₂ ) = 5 / (20 + 40) = 0.0833A

В ₁ = I ₁ R ₁ = 0,0833 (20) = 1,67 В

г. Какой ток протекает через R ₅ ?

В ₅ = Вт В ₃ = 12,5 – 5 = 7,5 В

Я ₅ = V ₅ / R ₅ = 7,5 / 120 = 0,0625 A

7. An электрическая схема проиллюстрирована ниже.

Какова сила тока, I , в резисторах R ₂ и R ₃ ?

R _экв. = 1 / R ₄ + 1 / ( ₂ + R ₃ )

R _экв = 1/10 + 1 / (3 + 7)

R _экв = 5 Вт.

РТ = R ₁ + R _экв = 7 + 5 = 12 Вт.

Это = Vt / Rt = 6/12 = 0,5 А

ток, протекающий через R ₂ и R ₃ , будет таким же, как и то, что сверху (поскольку R – то же самое), поэтому будет 0,5 / 2 = 0,25A

8. Следующая электрическая схема состоит из источника питания пять резисторов (R ₁ , R ₂ , R ₃ , R ₄ и R ₅ ) и два амперметра и.

Какая разница потенциалов (напряжение) на выводах резисторов R ₃ ?

₂ и ₃ получают 1,5 0,75 = 0,75 A. (тот же ток!) Это означает, что ₂ + ₃ = ₄ рэнд.

Так R ₃ = 20 10 = 10 W.

9.Следующая схема состоит из источник питания, два амперметра и, вольтметр и три резистора (R ₁ , ₂ и ₃ ).

Суммарная сила тока I _т составляет 20 А. Сила тока I ₃ составляет 12 А. разность потенциалов (напряжение) В ₁ на выводах резистора R ₁ напряжение 5 В.

Какое сопротивление резистора R ₃ ?

I ₁ = It- I ₃ = 20-12 = 8 A = I ₂

В ₂ = I ₂ R ₂ = 8 (5) = 40 В.

В ₁ + V ₂ = V ₃

5 + 40 = В ₃ = 45 В

Р ₃ = V ₃ / I ₃ = 45/12 = 3.75 Вт.

10. Источник с разностью потенциалов 30 В подключено к схеме, показанной ниже.

Какая сила тока I в цепи?

В ₂ = I ₂ R ₂ = 1 (10) = 10 В

В ₃ = Vt V ₂ = 30 10 = 20 V

Это = V ₃ / R ₃ = 20/10 = 2 A

11.Следующие электрические Схема состоит из источника питания, четырех резисторов ( R ₁ , R ₂ , R ₃ и R ₄ ) и вольтметр В ₄ ( В _с = В _итого ).

Какова сила тока ( I ₃ ) через R ₃ ?

В _{2 и 3} = 100 60 = 40 В

I ₃ = V _{2 и 3} / (R ₂ + R ₃ ) = 40 / (10 + 30) = 1.0 А

12. Как подключить резистор 25 Вт и два резистора по 100 Вт? чтобы их общее сопротивление было 75 Вт?

Поместите два резистора по 100 Вт параллельно. (поэтому Req = 50 Вт) и подключите новую ветвь к 25 Вт.

13. Как можно подключить четыре резистора 1,0 Вт и один резистор 2,0 Вт дать комбинированное сопротивление 1,5 Вт?

14.Четыре одинаковых резисторы подключены, как показано. Если общее напряжение составляет 12 В, найдите напряжение на каждом резисторе.

R ₁ имеет полное 12 В.Это ни с чем не связано.

R ₂ имеет вдвое больше сопротивление R ₃ и R ₄ комбинированные (запутались? Просто назначьте любое значение (например, 1 Ом на все 4 одинаковых резистора и разобраться), так что он будет иметь вдвое большее напряжение. 12 = 2х + х; х = 4 В.

Вывод В ₂ = 2х = 8В; V ₃ и V ₄ = 4 В.

19.3 Параллельные схемы | Texas Gateway

Робот

Роботы захватывают наше коллективное воображение уже более века.Теперь мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стала огромной областью исследований и разработок, причем некоторые технологии уже коммерциализированы. Подумайте, например, о небольших автономных пылесосах.

На рис. 19.21 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые роботы-гуманоиды могут ходить, наливать напитки и даже танцевать (хотя и не очень изящно).Другие роботы вдохновлены биологией, например, собачий робот , показанный на средней фотографии рис. 19.21. Этот робот может нести сотни фунтов груза по пересеченной местности. Фотография справа на рис. 19.21 показывает внутреннюю работу блока M, , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться, переворачиваться в воздух и соединяться друг с другом в самых разных формах. Обмениваясь беспроводной связью между собой, они самостоятельно собираются в различные формы, такие как столы, стулья и, возможно, когда-нибудь даже здания.

Все роботы включают в себя огромное количество физики и инженерии. Простое наливание напитка было освоено роботами совсем недавно, после более 30 лет исследований и разработок! Баланс и выбор времени, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложной задачей, требующей отличного баланса, ловкости и обратной связи. Чтобы справиться с этим, требуются датчики для обнаружения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсирующих действий, а также соединения и приводы для выполнения требуемых действий.

Помимо определения силы тяжести или ускорения, роботы могут содержать несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. Д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для машинного зрения, аналогична оптике, используемой в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы. Для определения температуры можно использовать простые термисторы, которые представляют собой резисторы, сопротивление которых изменяется в зависимости от температуры.

Построить робота сегодня намного проще, чем несколько лет назад. Многие компании сейчас предлагают комплекты для сборки роботов. Они варьируются по сложности от того, что подходит для детей младшего школьного возраста, до того, что бросает вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать создавать своего собственного робота уже сегодня.

Рис. 19.21 Роботы бывают разных форм и размеров, от классического гуманоида до собачьих роботов и маленьких кубиков, которые самостоятельно собираются для выполнения разнообразных задач.

РЕШЕНО: В схеме, показанной на \ textbf {Рис. E26.2…

Стенограмма видео

Считается, что щель

Это ток, проходящий через наш, я пишу. У меня есть. И если вы видите цифру, то великая выпивка с этим – это Х прямо и погашено. Шесть плохих ампер идут по этому пути, а оставшиеся должны идти по этому пути. Ну и что? Мы видим, что этот фиолетовый цвет на рисунке показывает, что цыплята должны быть в хорошем настроении. Ток, который проходит через их сестер, равен 2 м равным.Видишь, это так просто. Были сделаны. Уже готово с вечеринкой. Вопросы возникают, глядя на схему. Верно? Так что мне нужен дым для тела. Обратите внимание на сопротивление, чтобы найти сопротивление. Нарисуйте здесь петли. Так что сначала этого нет, на втором Этот взгляд. Хорошо. Теперь для первого цикла, чтобы поддержать тройки, и которые отдыхают в цепи, как враги. Так, значит, 28 минус, он увольняется? Итак, мы выходим из этого. Они уходят. Это место, правда? Итак, слева внутри, перезапись отснятого материала находится справа.Записываем, что внутри капли. Так как они оба смотрят на одни и те же кирпичи, и поэтому ток не может компенсировать друг друга, они оказываются противоположными друг другу. Итак, мы рассматриваем 28 как положительную сторону. Так что мы, потому что собираемся в сторону Итак, 28 минус. Итак, по мере того, как мы идем дальше, вставляем каплю через комнату, правильно. Это наша машина. 61 г. И величины в обратном направлении Итак, мы можем записать минус четыре из шести. Прямо сейчас По мере продвижения вперед есть еще одно потенциальное падение.То есть я раз так, что мы уже закончили. Я тоже. Так что вы можете ударить два раза, это личное. Теперь для второго цикла мы снова пишем с. Есть только одна страна, в которой мы сейчас, так как мы начинаем выпускной E. Так что это политика. Значит, он здесь размещен, верно? Итак, по мере того, как мы движемся сюда Итак, есть точка в центре этого потока, играющая от петли, есть один крендель, падающий близко через шесть длинных исследователей этой дисперсии тока. Итак, что мы можем исправить, так это то, что он равен двум, трижды шести, верно, перепад на три больше.Сестра. Благослови. Другой сформирован. Мне шесть. Это падение через шесть или твою сестру. Все нормально. Итак, это пещерная система. Я люблю его. Верно? Это была движущая цель. 18. То есть 42 голоса. Что ж, мы пытались сделать части миссии, и мы это уже сделали. Горшок. См. Вопрос здесь. Верно. Итак, что дальше? Мы все еще хотим. О, шоколад – все в порядке. Так что мы не можем просто использовать здесь для продолжения этого уравнения. 28 минус. Ему 42 года, верно? Мы продолжали бормотать, что часть C равна минус 24.Улицы такие, что получается почти 52 минус четыре градуса. Так что равны. Студент пришел к тому, что пять. Верно? Так что мы можем там пожадничать. Сопротивление. Это для вечеринки. Мы кабинет в год. Это для второй части. Видите, мы рассчитали ток, То есть для вечеринки. У нас снег. Мы все еще должны быть здесь, чтобы узнать. Итак, если цепь разорвана, это нормально, если поверхность разорвана в точке X, так что схема будет очень простой, как эта. Каждый B r здесь 28 мячей. Итак, поскольку цепь разорвана, у 61-го участника сопротивления нет, так что у него напрямую были три младшие сестры.Ага, скоро вернее станет швейцарец. Итак, для части вопроса, посмотрите на эту звезду здесь, на рисунке. Мы можем видеть сопротивление завету, на рисунке – наши последние три. Пять плюс три, это настоящая дверь, и сейчас будет 28, разделенные на восемь. Так что текущие его три целых и целых пять десятков лет протекают через него. Так что вы просто спросите хозяина тока через устойчивое Нет, поскольку исследователей трое в городах, поэтому они оба получат ток. И это то же самое. Это то же самое, что хитрость, которая проходит через звезду.Итак, мы закончили с вечеринкой по астме. Итак, это должно всплыть в этом вопросе. Спасибо за просмотр

Анализ цепей

Развитие понимания схем – это первый шаг в изучении современных электронных устройств, которые доминируют в том, что становится известным как «век информации». Основной тип цепи, последовательная цепь, представляет собой цепь, в которой есть только один путь тока. Законы Кирхгофа предоставляют нам инструменты для анализа цепей любого типа.

Законы Кирхгофа

Закон Кирхгофа (KCL), названный в честь немецкого физика Густава Кирхгофа, гласит, что сумма всего тока, входящего в любую точку цепи, должна равняться сумме всего тока, выходящего из любой точки в цепи. Проще говоря, это еще один способ взглянуть на закон сохранения заряда .

Закон Кирхгофа о напряжении (KVL) гласит, что сумма всех падений потенциала в любом замкнутом контуре цепи должна быть равна нулю.Проще говоря, KVL – это метод применения закона сохранения энергии к цепи.

Вопрос: Резистор сопротивлением 3,0 Ом и резистор 6,0 Ом соединены последовательно в рабочую электрическую цепь. Если ток через резистор сопротивлением 3,0 Ом составляет 4,0 ампера, какова разница потенциалов на резисторе сопротивлением 6,0 Ом?

Ответ: Для начала давайте нарисуем картину ситуации. Если через резистор сопротивлением 3 Ом протекает ток 4 ампера, то в соответствии с законом Кирхгофа через резистор 6 Ом должно протекать 4 ампера тока.Зная ток и сопротивление, мы можем рассчитать падение напряжения на 6-омном резисторе, используя закон Ома:

Резисторы

серии

Рассмотрим пример схемы, состоящей из трех резисторов сопротивлением 2000 Ом (2K):

В цепи есть только один путь тока, который проходит через все три резистора. Вместо использования трех отдельных резисторов 2K, мы могли бы заменить три резистора одним резистором с эквивалентным сопротивлением.Чтобы найти эквивалентное сопротивление любого количества последовательных резисторов, мы просто складываем их отдельные сопротивления:

Обратите внимание, что поскольку существует только один путь тока, одинаковый ток должен протекать через каждый из резисторов.

Таблицы VIRP

Простой и понятный метод анализа цепей включает создание таблицы VIRP для каждой обнаруженной цепи. Объединив свои знания о законе Ома, законе тока Кирхгофа, законе напряжения Кирхгофа и эквивалентном сопротивлении, вы можете использовать эту таблицу для определения деталей любой схемы.

Таблица VIRP описывает падение потенциала (V-напряжение), ток (I-ток), сопротивление (R) и рассеиваемую мощность (P-мощность) для каждого элемента в вашей цепи, а также для цепи в целом. . Давайте использовать нашу схему с тремя резисторами на 2000 Ом в качестве примера, чтобы продемонстрировать, как используется таблица VIRP. Чтобы создать таблицу VIRP, мы сначала перечисляем наши элементы схемы и итоги в строках таблицы, затем создаем столбцы для V, I, R и P:

Таблица VIRP

	V	я	R	P
R1
R2
R3
Всего

Далее мы заполняем информацию в таблице, которая нам известна.Например, нам известно общее напряжение в цепи (12 В), обеспечиваемое батареей, и нам известны значения сопротивления для каждого отдельного резистора:

Таблица VIRP

	V	я	R	P
R1			2000
R2			2000
R3			2000
Всего	12В

После ввода исходной информации мы можем также вычислить полное сопротивление или эквивалентное сопротивление всей цепи.В нашем случае это 6000 Ом:

Таблица VIRP

	V	я	R	P
R1			2000
R2			2000
R3			2000
Всего	12В		6000

Если я посмотрю на нижнюю (итоговую) строку своей таблицы, я знаю как падение напряжения (V), так и сопротивление (R).Зная эти два элемента, я могу рассчитать общий ток, протекающий в цепи, используя закон Ома, а также могу рассчитать общую мощность, рассеиваемую в цепи, используя свои формулы для электрической мощности:

Теперь я могу ввести дополнительную информацию в таблицу VIRP:

Таблица VIRP

	V	я	R	P
R1			2000
R2			2000
R3			2000
Всего	12В	0.002A	6000	0,024 Вт

Поскольку это последовательная схема, общий ток должен быть таким же, как ток через каждый отдельный элемент, поэтому я могу заполнить ток через каждый из отдельных резисторов:

Таблица VIRP

	V	я	R	P
R1		0.002A	2000
R2		0,002A	2000
R3		0,002A	2000
Всего	12В	0,002A	6000	0.024Вт

Наконец, для каждого элемента в цепи я теперь знаю ток и сопротивление. Используя эти знания, я могу применить закон Ома, чтобы получить падение напряжения (V = IR), и формулу для мощности (P = I2R), чтобы заполнить таблицу.

Таблица VIRP

	V	я	R	P
R1	4V	0.002A	2000	0,008 Вт
R2	4V	0,002A	2000	0,008 Вт
R3	4V	0,002A	2000	0,008 Вт
Всего	12В	0,002A	6000	0.024Вт

Итак, что на самом деле говорит нам эта таблица теперь, когда она полностью заполнена? Нам известны падение потенциала на каждом резисторе (4 В), ток через каждый резистор (2 мА) и мощность, рассеиваемая каждым резистором (8 мВт). Кроме того, мы знаем, что полное падение потенциала для всей цепи составляет 12 В, и вся схема рассеивает 24 мВт мощности. Обратите внимание, что для последовательной цепи сумма отдельных падений напряжения на каждом элементе равна общей разности потенциалов в цепи, ток одинаков во всей цепи, а значения сопротивления и рассеиваемой мощности также складываются в общее сопротивление и общая рассеиваемая мощность.Они кратко изложены для вас в справочной таблице следующим образом:

Пример задачи

Параллельные схемы

Другой базовый тип схемы – это параллельная цепь, в которой имеется более одного пути тока. Для анализа резисторов в последовательной цепи мы нашли эквивалентное сопротивление.Мы будем следовать той же стратегии при параллельном анализе резисторов.

Параллельные резисторы

Давайте посмотрим на схему, состоящую из тех же компонентов, которые мы использовали в нашем исследовании последовательных схем, но теперь мы соединим наши компоненты так, чтобы обеспечить несколько путей тока, создавая параллельную схему .

Обратите внимание, что в этой цепи электричество может проходить по одному из трех разных путей через каждый из резисторов. Во многом это похоже на реку, которая разветвляется на три разные более мелкие реки.Таким образом, каждый резистор вызывает падение потенциала (аналогично водопаду), затем три реки рекомбинируют, прежде чем вернуться к батарее, которую мы можем представить как насос, поднимая реку до более высокого потенциала, прежде чем отправить ее обратно. зацикленный путь.

Мы можем найти эквивалентное сопротивление резисторов, включенных параллельно, по формуле:

Будьте осторожны при использовании этого уравнения, так как при выполнении расчетов легко допустить ошибку. Посмотрим, сможем ли мы найти эквивалентное сопротивление для нашего образца схемы.

Анализ цепей

Мы снова можем использовать таблицу VIRP для анализа нашей схемы, начав с заполнения того, что мы знаем непосредственно из принципиальной схемы.

Таблица VIRP

	V	я	R	P
R1			2000
R2			2000
R3			2000
Всего	12В

Из принципиальной схемы также видно, что падение потенциала на каждом резисторе должно составлять 12 В, поскольку концы каждого резистора удерживаются аккумулятором с разницей в 12 В.

Таблица VIRP

	V	я	R	P
R1	12 В		2000
R2	12 В		2000
R3	12 В		2000
Всего	12В

Затем мы можем ввести ток через каждый из отдельных резисторов, так как мы знаем падение напряжения на каждом резисторе, используя закон Ома (I = V / R), чтобы найти I = 0.006A.

Таблица VIRP

	V	я	R	P
R1	12 В	0,006A	2000
R2	12 В	0,006A	2000
R3	12 В	0.006A	2000
Всего	12В

Используя закон Кирхгофа по току, мы можем увидеть, что если через каждый из резисторов протекает 0,006 А, все эти токи объединяются, образуя общий ток 0,018 А.

Таблица VIRP

	V	я	R	P
R1	12 В	0.006A	2000
R2	12 В	0,006A	2000
R3	12 В	0,006A	2000
Всего	12В	0,018A

Поскольку каждый из трех резисторов имеет одинаковое сопротивление, имеет смысл только то, что ток будет равномерно распределяться между ними.И мы можем подтвердить наш предыдущий расчет эквивалентного сопротивления, вычислив полное сопротивление цепи с помощью закона Ома:.

Таблица VIRP

	V	я	R	P
R1	12 В	0,006A	2000
R2	12 В	0.006A	2000
R3	12 В	0,006A	2000
Всего	12В	0,018A	667

Наконец, мы можем закончить нашу таблицу VIRP, используя любое из трех применимых уравнений для рассеяния мощности, чтобы найти:

Таблица VIRP

	V	я	R	P
R1	12 В	0.006A	2000	0,072 Вт
R2	12 В	0,006A	2000	0,072 Вт
R3	12 В	0,006A	2000	0,072 Вт
Всего	12В	0.018A	667	0,216 Вт

Обратите внимание, что для резисторов, включенных параллельно, эквивалентное сопротивление всегда меньше, чем сопротивление любого из отдельных резисторов. Разность потенциалов на каждом из резисторов, включенных параллельно, одинакова, а ток через каждый из резисторов складывается в общий ток. Это кратко изложено для вас в справочной таблице:

Примеры задач

Давайте посмотрим на базовую задачу анализа параллельной цепи:

Аналогичным образом мы также сможем построить принципиальные схемы из описаний схемы:

Давайте рассмотрим последний пример задачи, на этот раз связанный с использованием амперметров при анализе нашей параллельной цепи:

Комбинированные последовательно-параллельные схемы

Цепь не обязательно должна быть полностью последовательной или параллельной.Фактически, в большинстве схем есть элементы обоих типов. Анализ этих цепей может быть выполнен с использованием основ, которые вы изучили при анализе последовательных и параллельных цепей по отдельности и их применении в логической последовательности.

Во-первых, ищите части схемы с параллельными элементами. Поскольку напряжение на параллельных элементах должно быть одинаковым, замените параллельные резисторы на эквивалентный одиночный резистор, включенный последовательно, и нарисуйте новую схему.Теперь вы можете проанализировать эквивалентную последовательную схему с помощью таблицы VIRP. После того, как ваша таблица будет заполнена, вернитесь к исходной схеме, используя KCL и KVL, пока не узнаете ток, напряжение и сопротивление каждого отдельного элемента в вашей цепи.

Вопрос: Найдите ток через R ₂ в схеме ниже.

Ответ: Сначала найдите эквивалентное сопротивление для R ₂ и R ₃ , включенных параллельно.

Затем нарисуйте принципиальную электрическую схему как эквивалентную последовательную схему.

Теперь вы можете использовать свою таблицу VIRP для анализа цепи.

Таблица VIRP

	V	я	R	P
р 1	3.39 В	0,169A	20	0,57 Вт
р 23	3,22 В	0,169A	19	0,54 Вт
р 4	3,39 В	0,169A	20	0,57 Вт
Всего	10 В	0. Больше новостей Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт