Основы цифровой схемотехники: Новиков Ю.В. Основы цифровой схемотехники

Содержание

Новиков Ю.В. Основы цифровой схемотехники

Предисловие

Цель этой книги – помочь в изучении основ цифровой схемотехники любому желающему – от студента до профессионала. Причем речь в данном случае идет не о физических основах электроники, не о технологии производства электронных компонентов, не об электронике или схемотехнике вообще, а именно о цифровой схемотехнике с ее специфическими особенностями.

В книге рассмотрены многие важные вопросы цифровой схемотехники, которым в литературе обычно уделяется недостаточно внимания. Видимо, авторы книг счиrают их чем-то само собой разумеющимся или полагают, что читатели сами должны сформулировать эти вопросы и сами же найти на них ответы. В результате нередки случаи, когда даже выпускники институтов по специальностям, связанным с электроникой, не могут самостоятельно разработать более или менее сложное нестандартное цифровое устройство. После изучения данной книги читатель будет обладать необходимыми навыками для проектирования как простейших узлов, так и довольно сложных устройств.

Книга написана сжато, последовательно и доступно и требует минимального обращения к другим источникам. Часть материала, представленного в ней, написана на основе лекций, читаемых автором в МИФИ.

Конечно, в такой небольшой книге невозможно рассмотреть все компоненты цифровой электроники и все приемы проектирования цифровой схемотехники. Предполагается, что она станет первой в серии книг по цифровой схемотехнике. В последующих книгах серии будут рассмотрены, в частности, следующие темы:

схемотехника устройств на основе программируемой логики;
схемотехника микропроцессорных устройств;
схемотехника устройств на основе микроконтроллеров;
схемотехника персональных компьютеров;
схемотехника компьютерных систем измерения, контроля и управления;
аппаратно-программные средства отладки и контроля цифровых устройств;
программные средства проектирования цифровых устройств.

…

Основы цифровой схемотехники

ОГЛАВЛЕНИЕ

Введение

Глава 1. Философия цифровой электроники

1.1. Аналог или цифра?

1.2. Уровни представления цифровых устройств

1.3. Входы и выходы цифровых микросхем

1.4. Основные обозначения на схемах

1.5. Серии цифровых микросхем

1.6. Корпуса цифровых микросхем

1.7. Двоичное кодирование

1.8. Функции цифровых устройств

Глава 2. Применение логических элементов

2.1. Инверторы

2.2. Повторители и буферы

2.3. Элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ

2.4. Элементы Исключающее ИЛИ

2.5. Сложные логические элементы

2.6. Триггеры Шмитта

Глава 3. Применение комбинационных микросхем

3.1. Дешифраторы и шифраторы

3.2. Мультиплексоры

3.3. Компараторы кодов

3.4. Сумматоры

3.5. Преобразователи кодов

3.6. Одновибраторы и генераторы

Глава 4. Применение триггеров и регистров

4.1. Триггеры

4.1.1. Принцип работы и разновидности триггеров

4.1.2. Основные схемы включения триггеров

4.2. Регистры

4.2.1. Регистры, срабатывающие по фронту

4.2.2. Регистры, срабатывающие по уровню

4.2.3. Сдвиговые регистры

Глава 5. Применение счетчиков

5.1. Асинхронные счетчики

5.2. Синхронные счетчики с асинхронным переносом

5.3. Синхронные счетчики

Глава 6. Применение микросхем памяти

6.1. Постоянная память

6.1.1. ПЗУ как универсальная комбинационная микросхема

6.1.2. ПЗУ в генераторах импульсных последовательностей

6.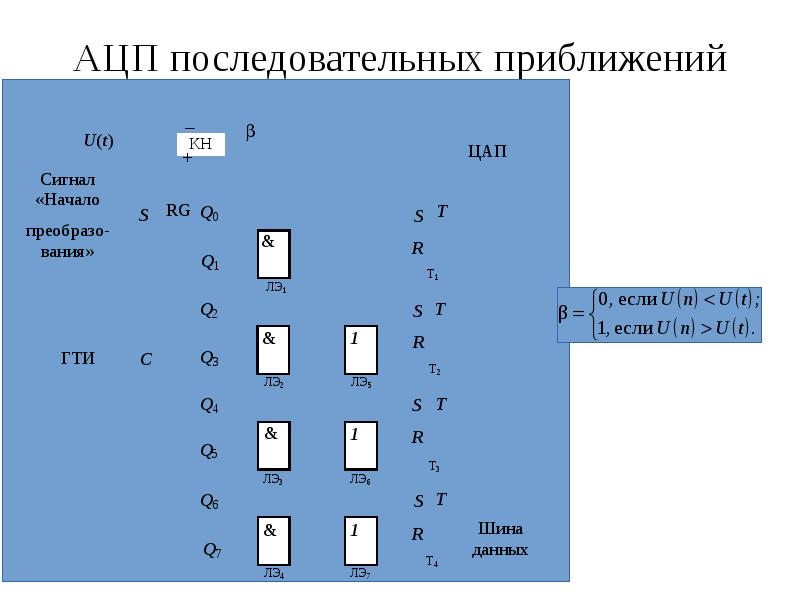 1.3. Микропрограммные автоматы на ПЗУ

6.2. Оперативная память

6.2.1. ОЗУ для временного хранения информации

6.2.2. ОЗУ как информационный буфер

6.2.3. Улучшение параметров ОЗУ

Глава 7. Применение микросхем ЦАП и АЦП

7.1. Применение ЦАП

7.2. Применение АЦП

Глава 8. Примеры разработки цифровых устройств

8.1. Разработка клавиатуры

8.2. Разработка вычислителя контрольной суммы

8.3. Разработка логического анализатора

8.4. Разработка генератора аналоговых сигналов

Приложение. Микросхемы, параметры, сигналы

Список литературы

Словарь терминов и сокращений

ВВЕДЕНИЕ

Цифровая электроника в настоящее время все более и более вытесняет традиционную аналоговую. Ведущие фирмы, производящие самую разную электронную аппаратуру, все чаще заявляют о полном переходе на цифровую технологию. Причем это относится как к бытовой технике (аудио-, видеоаппаратура, средства связи), так и к профессиональной технике (измерительная, управляющая аппаратура). Ставшие уже привычными персональные компьютеры также полностью реализованы на цифровой электронике. Видимо, в ближайшем будущем полностью аналоговые устройства будут применяться только в тех случаях, когда требуются уникальные, рекордные характеристики.

Между тем, литературы, позволяющей самостоятельно изучить основы и главные методы цифровой схемотехники, освоить основные практические приемы проектирования цифровых устройств, явно недостаточно. Книги, которые претендуют на освещение основ цифровой схемотехники, можно разделить на три большие группы.

К первой группе относятся книги, которые стремятся охватить всю электронику в целом (как цифровую, так и аналоговую).

Такой глобальный подход неизбежно приводит к тому, что цифровая схемотехника рассматривается чересчур кратко, поверхностно. Даже самые лучшие из книг этой группы уделяют цифровой электронике не более четверти своего объема. Между тем цифровая электроника существенно отличается от аналоговой не только видом используемых сигналов, но, что самое главное, приемами проектирования, требуемым стилем мышления разработчика, принципами построения сложных систем. Данные книги хороши в основном для повышения общего уровня образования читателя, для создания общего базиса, на котором только и может вырасти настоящий специалист, разработчик электронной аппаратуры.

Ко второй группе относятся книги, посвященные цифровым микросхемам и их применению. Эти книги стремятся описать как можно более подробно все имеющиеся микросхемы, поэтому обязательно содержат большой справочный материал. Однако в любом случае приводимые в них справочные данные далеко не полны и к тому же неизбежно содержат большое количество ошибок.

Справочников по микросхемам должно быть как можно меньше, и они должны быть очень подробными, иначе они просто не имеют смысла. В идеале справочники должны выпускаться только фирмами-изготовителями микросхем. А попытка ввести в книгу даже краткие справочные данные по всем существующим микросхемам не оставляет достаточно места для описания самого главного — разнообразных применений этих микросхем, методам проектирования цифровых узлов и устройств на их основе. Поэтому книги этой группы годятся обычно только для первичного знакомства с темой.

Наконец, третья группа книг описывает готовые цифровые устройства различного назначения. В основном такие книги рассчитаны на «радиолюбителей», хотя, что подразумевается под этим понятием, обычно не совсем понятно. Среди тех, кто называют себя радиолюбителями, немало прекрасных разработчиков, а среди дипломированных профессионалов встречаются те, кто не может разработать даже простейшей схемы.

Книги этой третьей группы, как правило, не говорят о том, как устройства разрабатывались, какие приемы проектирования применялись и почему. То есть они обычно подразумевают бездумное повторение готовых решений, использование шаблонов. Настоящую пользу данные книги могут принести только тому, у кого уже есть хороший базовый запас знаний и умений по проектированию цифровых устройств. Впрочем, для таких людей чужие схемы не слишком интересны, они могут проектировать свои.

К недостаткам многих существующих книг можно отнести также чрезмерное увлечение описание тонкостей физических процессов, лежащих в основе цифровой электроники, и подробное рассмотрение особенностей технологии микросхем. Конечно, все это тоже нужно, полезно, интересно, но с самой схемотехникой связано не жестко, не прямо и не слишком сильно. Разработчик цифровой аппаратуры в подавляющем большинстве случаев работает с микросхемами как с «черным ящиком», ему не слишком важно, что происходит внутри, как реализуется та или иная функция микросхемы.

Видимо, целесообразно физику полупроводников и технологию изучать отдельно от схемотехники, параллельно с ней, до нее или после нее, чтобы не смешивать две различные области знаний.

Наконец, еще одним недостатком книг о цифровой схемотехнике можно назвать стремление охватить в одной книге все области цифровой электроники: от логических элементов до компьютеров и других сложных электронных систем. В результате все вопросы рассматриваются недостаточно глубоко, и до практики разработки дело не доходит. К тому же проектирование интеллектуальных устройств довольно сильно отличается от проектирования устройств на жесткой логике, они порой требуют применения совершенно разных подходов. Поэтому их целесообразно рассматривать в различных книгах.

Данная книга посвящена самым основам цифровой схемотехники, ее азбуке, ее основным методам, подходам и приемам. Отличие ее состоит в том, что она может дать представление о цифровой схемотехнике даже тем читателям, которые имеют слабое представление об электронике вообще. Впрочем, это вовсе не означает, что книга посвящена только самым общим, неконкретным, отвлеченным вопросам. Наоборот, она призвана сформировать действительно хорошего проектировщика, способного строить высокоэффективные цифровые системы самой различной сложности и четко представляющего себе взаимосвязь всех процессов в этих системах сверху донизу. Конечно, чтобы стать таким классным специалистом, нужны определенные способности, даже талант, но строить простейшие цифровые устройства, пусть и не оптимальные, не уникальные, но полезные и вполне работоспособные, способен практически каждый человек. Хотелось бы надеяться, что данная книга окажет в этом деле действенную помощь.

Книга ни в коем случае не претендует на то, чтобы заменить собой справочники по микросхемам, хотя в ней и разъясняются функции многих микросхем. Главное, чему уделено внимание — это применение микросхем для различных задач (причем как стандартное применение, так и не стандартное), а также приемы объединения, комбинирования микросхем, позволяющие создавать разнообразные узлы, устройства и системы.

Материал данной книги представляет собой тот необходимый минимум знаний который должен иметь и которым должен свободно и активно пользоваться каждый профессиональный разработчик цифровой аппаратуры. Любые другие, дополнительные знания, конечно же, не повредят, но заменить собой то, что изложено здесь, они не смогут.

Возможно, подход, предлагаемый в данной книге, несколько отличается от общепринятого. Возможно также, что используемый набор терминов не полностью совпадает со стандартным (отечественные стандарты слишком часто меняются). Но главное — это научить проектировать цифровые устройства и системы, а какие для этого используются подходы и термины, наверное, не слишком принципиально.

Книга написана на основе многолетнего личного опыта автора по разработке цифровых устройств, а также на базе материала учебных курсов, читаемых автором, доцентом кафедры электроники Московского инженерно-физического института (МИФИ).

Несколько слов о структуре книги.

Первая глава рассматривает основополагающие принципы цифровой электроники, знакомит с терминологией и основными правилами оформления схем.

Главы со второй по шестую посвящены основным базовым элементам цифровых устройств, типовым и нестандартным схемам их включения. Практически все приведенные схемы проверялись автором на практике. Микросхемы описаны начиная с самых простейших логических элементов в порядке усложнения через комбинационные микросхемы, триггеры, регистры, счетчики до микросхем памяти. Каждая глава включает в себя множество примеров включений микросхем, как рассматриваемых в данной главе, так и рассмотренных в предыдущих главах.

Седьмая глава содержит краткие сведения о цифро-аналоговых и аналого-цифровых преобразователях и основных методах их включения в аналого-цифровых устройствах. Без этих сведений книга была бы неполна.

В восьмой главе приводятся примеры нескольких сравнительно сложных цифровых устройств с подробным описанием всех этапов проектирования и принципов работы и взаимодействия всех узлов и микросхем. Цель этого не в том, чтобы читатель повторил данные устройства, а в том, чтобы на практике показать приемы проектирования, которые затем позволят строить любые другие цифровые устройства.

В приложении приведены таблицы параметров микросхем, таблицы основных обозначений микросхем и сигналов, таблицы соответствия отечественных и зарубежных микросхем. В конце книги имеется подробный словарь терминов и сокращений цифровой схемотехники.

В книгу не вошли материалы по основам микропроцессорной техники, по принципам устройства и применения микроконтроллеров и персональных компьютеров, по основам работы с программируемыми микросхемами (ПЛИС), по методам контроля и отладки цифровых устройств, а также по программным средствам, предназначенным для проектирования цифровых устройств и систем. Все эти вопросы планируется рассмотреть в других книгах данной серии.

Новиков Ю. В. Основы цифровой схемотехники. Базовые элементы и схемы. Методы проектирования. — М.: Мир, 2001. — 379 с, ил. — (Современная схемотехника) :: Библиотека технической литературы

Книга представляет собой учебник по основам цифровой схемотехники. Рассматриваются основы схемотехники цифровых устройств, которыми должен свободно владеть и активно пользоваться каждый профессиональный разработчик цифровой аппаратуры. Обсуждается функционирование и взаимодействие всех основных типов цифровых микросхем — от самых простых до самых сложных. Описываются модели и уровни представления цифровых микросхем, используемых при проектировании цифровых электронных систем, способы оптимального построения высокоэффективных цифровых систем самой различной степени сложности. Книга позволяет освоить азбуку цифровой схемотехники даже читателям с начальным уровнем знаний по электронике. Усвоению материала помогает большое количество конкретных примеров построения самых различных цифровых устройств.
Для студентов, преподавателей и профессиональных разработчиков цифровых электронных систем.

ОГЛАВЛЕНИЕ
Предисловие …………………………………. 7
Введение ……………………………………. 8
Глава 1. Философия цифровой электроники…………… 13
1.1. Аналог или цифра?………………………… 13
1.2. Модели и уровни представления цифровых устройств 17
1.3. Входы и выходы цифровых микросхем…………. 24
1.4. Основные обозначения на схемах …………….. 32
1.5. Серии цифровых микросхем…………………. 37
1.6. Корпуса цифровых микросхем……………….. 43
1.7. Двоичное кодирование …………………….. 44
1.8. Функции цифровых устройств……………….. 50
Глава 2. Применение логических элементов…………… 53
2.1. Инверторы. ……………………………… 54
2.2. Повторители и буферы……………………… 58
2.3. Логические элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ—- 65
2.4. Логические элементы Исключающее ИЛИ……… 74
2.5. Сложные логические элементы ………………. 78
2.6. Триггеры Шмитта…………………………. 80
Глава 3. Применение комбинационных микросхем………. 87
3.1. Дешифраторы и шифраторы…………………. 88
3.2. Мультиплексоры………………………….. 97
3.3. Компараторы кодов ……………………….. 101
3.4. Сумматоры …………………………….. 105
3.5. Преобразователи кодов…………………….. 109
3.6. Одновибраторы и генераторы………………… 114
Глава 4. Применение триггеров и регистров…………… 123
4.1. Триггеры………………………………… 124
4.1.1. Принцип работы и разновидности триггеров….. 124
4.1.2. Основные схемы включения триггеров. ……… 131
4.2. Регистры………………………………… 142
4.2.1. Регистры, срабатывающие по фронту……….. 144
4.2.2. Регистры, срабатывающие по уровню……….. 153
4.2.3. Сдвиговые регистры…………………….. 157
Глава 5. Применение счетчиков …………………… 170
5.1. Асинхронные счетчики …………………….. 172
5.2. Синхронные счетчики с асинхронным переносом … 181
5.3. Синхронные счетчики……………………… 209
Глава 6. Применение микросхем памяти……………… 222
6.1. Постоянная память………………………… 225
6.1.1. ПЗУ как универсальная комбинационная микросхема …………………………………. 231
6.1.2. ПЗУ в генераторах импульсных последовательностей ………………………………….. 240
6.1.3. Микропрограммные автоматы на ПЗУ………. 245
6.2. Оперативная память………………………. 258
6.2.1. ОЗУ для временного хранения информации . …. 264
6.2.2. ОЗУ как информационный буфер………….. 272
6.2.3. Улучшение параметров ОЗУ………………. 280
Глава 7. Применение микросхем ЦДЛ и АЦП…………. 284
7.1. Применение ЦАП…………………………. 285
7.2. Применение АЦП…………………………. 295
Глава 8. Примеры разработки цифровых устройств……… 307
8.1. Разработка клавиатуры …………………….. 308
8.2. Разработка вычислителя контрольной суммы……. 316
8.3. Разработка логического анализатора ………….. 321
8.4. Разработка генератора аналоговых сигналов…….. 336
Приложение. Микросхемы, параметры, сигналы………… 351
Список литературы……………………………… 365
Словарь терминов и сокращений……………………. 368

…

Основы схемотехники для начинающих

У сегодняшних программистов нет необходимости знать устройство компьютера на самом низком уровне, и все же без этого чувствуешь, что упустил что-то важное. К сожалению, в одной статье я не смогу рассказать о том, как работает даже самый примитивный процессор, поэтому мы начнем с изучения сумматора — ключевого элемента арифметико-логического устройства (АЛУ). Немного поговорим по теории, потом перейдем к практике: познакомимся с микросхемой 74HC283 и попробуем собрать на макетной плате небольшой тестовый стенд.

Говорят, древние кодеры собирали свои компы самостоятельно, уверенно обращались с паяльником и знали ассемблер. Но потом эти умения были безвозвратно погребены под слоями абстракции, и теперь каждый — специалист в узкой области, который редко заглядывает дальше ее. Если вы не работаете с железом, то схемотехника вам вряд ли пригодится сама по себе. Так зачем ее учить? Попробую показать на примере.

Знаете, что изображено на этой картинке?

Так выглядит руль болида «Формулы-1». Нетрудно догадаться, что у пилота за таким штурвалом совершенно иной уровень подготовки. И речь не о скорости реакции или рефлексах: тут абсолютно другое, качественно более глубокое понимание принципов и особенностей работы машины.

Знания пилота «Формулы-1» — это и немного знаний конструктора, и инженера, и механика. Только так можно выжать из этого автомобиля максимум и нестись по трассе на огромной скорости под восхищенные крики болельщиц. Примерно то же и со схемотехникой: без нее ты просто скучный современный водитель, от которого скрыли устройство его машины.

РЕКОМЕНДУЕМ:
3D-сканер из смартфона или фотокамеры

Лично мне цифровая схемотехника дала многое. Я, например, узнал, что собой представляет конвейер в процессоре, почему его сброс дорого обходится для исполняемой программы и как выглядит компромисс времени и памяти на аппаратном уровне. Если мне удалось вас убедить и вы тоже хотите хоть немного овладеть этой наукой, то приступим!

Форма сигнала

Схемотехнику принято делить на две большие области: цифровую и аналоговую, по типу сигнала. Аналоговая оперирует такими параметрами, как сила тока, напряжение (иногда оно бывает отрицательным) и сопротивление. В цифровой все проще — в схеме есть только высокий и низкий логические уровни, даже без конкретных значений.

В С/С++ подобное отношение моделирует тип bool и два его состояния — true и false. Я и дальше буду использовать аналогии из языков программирования, где это уместно. Надеюсь, это поможет тебе лучше понять происходящее. Кроме того, это ярко показывает, насколько тесно все связано в цифровом мире.

Аналоговая схемотехника капризна и непредсказуема — на параметры сигнала могут влиять не только хорошо известные факторы вроде температуры и внешних наводок, но и даже такие неочевидные вещи, как вовремя не отмытый с платы флюс или окислившиеся контакты (без шуток). Цифровая схемотехника, напротив, слабо зависит от окружающих условий и вообще устойчива к шумам.

Фирма Sony удачно обыграла аналоговую и цифровую природу сигнала в названии своих ноутбуков VAIO. Если внимательно присмотреться к их логотипу, то первые его две буквы повторяют аналоговую форму синусоиды, тогда как последние две представляют пару дискретных состояний цифрового бита.

Так что нет ничего удивительного в том, что сегодня большая часть информации существует именно в цифровом виде, а компьютеры оперируют исключительно числами (если точнее, то их двоичным представлением). Для базового понимания цифровой схемотехники не требуется особых знаний — достаточно только уметь переводить числа из десятичной формы в двоичную и обратно.

Цифровая схема

Типичная цифровая схема состоит из входов, выходов и логических элементов, также называемых вентилями. Сигналы поступают на входы схемы, преобразуются по определенным правилам внутри вентилей (об этом чуть ниже) и подаются на выходы.

В комбинационных схемах состояние сигналов на выходе зависит только от состояния на входе. В последовательностных схемах выход зависит не только от входа, но еще и от внутреннего состояния схемы. В любом случае важно понимать, что сигналы на выходе зависят от входа, не наоборот.

РЕКОМЕНДУЕМ:
Как научиться электронике и схемотехнике

В этой статье мы будем рассматривать только комбинационные схемы. Они проще для понимания и наглядней. Кстати, в отечественной литературе нет устоявшегося перевода для последовательностных схем. Кто-то называет их последовательными, кто-то предпочитает кальку с английского языка и использует термин «секвенциальные схемы» (sequential). Разницы нет никакой, но все равно учти это, когда будешь читать дополнительные источники.

Базовые блоки

Все цифровые схемы сводятся к нескольким стандартным логическим элементам. Это примерно как кубики Lego в детском конструкторе. Их можно комбинировать, соединять друг с другом и получать новые схемы. Для каждого элемента я привел таблицу истинности — соответствие между входными и выходными сигналами.

Существуют еще диаграммы Венна, но, на мой взгляд, они совершенно лишние и только осложняют дело. Впрочем, если ты предпочитаешь графическое представление, то можешь ознакомиться и с ними.

NOT

Самый простой вентиль, представляет собой логическое отрицание и инвертирует сигнал на единственном входе. Так как у нас всего два возможных состояния, таблица истинности совсем крохотная. В С/C++ это оператор !, хотя там его действие распространяется на любые переменные с числовым значением, не только бинарные.

Обрати внимание, что на рисунке выше (и на всех последующих) приведены два символа для обозначения конкретного элемента на схемах. Слева — американский вариант (ANSI), справа — его европейский аналог (МЭК и ГОСТ). Второй стандарт сейчас уже редко где применяется, и даже в русскоязычной литературе почти всегда используется графически более наглядный стандарт ANSI.

AND

Сигнал на выходе этого вентиля равен логической единице только тогда, когда на всех входах присутствует высокий уровень. При этом количество входов может быть любым — таблица истинности изменится незначительно. Кроме того, ничто не мешает каскадировать такие элементы, подавая выход одного вентиля AND на вход другого.

Традиционно таблица рисуется именно таким образом: сперва все входы находятся в состоянии логического ноля, а затем последовательно инвертируется один из разрядов, начиная с младшего. Можно смотреть на это и с другой стороны — как будто все входы кодируют какое-то число (в двоичном представлении) и в каждой строке мы прибавляем к нему по единичке, проходя все возможные значения.

В С/С++ существует аж два аналога для этого вентиля: булево И (оператор &) и логическое И (оператор &&). Первый применяется для проверки флагов и других операций над отдельными битами числа, тогда как второй используется в логических выражениях.

OR

Здесь выход находится в состоянии логического ноля, только когда все входы равны нулю. Остальные комбинации приводят к высокому уровню на выходе.

Вместе AND и OR — это два основных строительных «кирпичика» цифровой логики. Сразу возникает вопрос, как их отличать друг от друга на схемах. Конечно, все решает практика, и со временем они запомнятся сами собой, но можно воспользоваться простым правилом: форма элемента со стороны входов соответствует первой букве в английском обозначении.= y;

Но вернемся к нашим вентилям. Иногда в их список добавляют также сочетания с NOT: NOT + AND = NAND, NOT + OR = NOR и NOT + XOR = XNOR. При желании можешь вывести их таблицы истинности самостоятельно, это не составляет никакого труда.

Пример

Настало время применить полученные знания и собрать что-то практически полезное. Логические операции — это, конечно, прекрасно, но хотелось бы и работать с числами, хотя бы для разнообразия!

Представим, что наши требования к безопасности таковы, что мы не можем доверять даже процессорам крупных компаний. Мы опасаемся возможных закладок, на уровне компании — разработчика схемы или на уровне компании — производителя кристалла, каких-либо гипотетических уязвимостей, которые могут эксплуатировать недоброжелатели, — словом, мы опасаемся всего и сразу. Значит, нужно собрать все самостоятельно, не доверяя никому!

РЕКОМЕНДУЕМ:
Перехват и анализ радиосигнала

Начинать стоит именно с процессора, а если еще конкретнее, то с сумматора в АЛУ. Это ключевой блок всего компьютера. Как если бы мы захотели приехать в Москву и очутились бы сразу на Красной площади.

Полусумматор

Конкретизируем задачу — пусть нам надо сложить два восьмибитных положительных значения друг с другом. Если использовать алгоритм сложения столбиком, то это будет выглядеть примерно так.

Мы последовательно складываем цифры в каждом разряде, справа налево, и получаем результат для этого разряда. При этом мы распространяем дальше перенос, если у нас возникло переполнение. Таким образом, у нас в схеме должно быть два входа (A и B) и два выхода (S и C). Составим таблицу истинности для всех возможных комбинаций А и В.

Рассматривая по отдельности получившиеся колонки S и C, легко заметить, каким логическим элементам они соответствуют. Теперь можно представить схему полностью.

Сумматор

Предыдущий блок носил несколько обидное название «полусумматора». Почему только половинка — догадаться нетрудно, ведь здесь мы никак не учитываем выход с предыдущего разряда. Логично предположить, что, комбинируя два таких блока, мы можем составить схему полного сумматора. Это как с Землей — есть Северное и Южное полушария. Хотя стоп, есть же еще Западное и Восточное…

Вопрос, куда девали вторую Землю, остается открытым

Теперь, когда мы получили возможность полноценно складывать биты из одного разряда, мы можем последовательно вычислить полную сумму нашего числа, каким бы большим оно ни было. Да, вот так все просто!

Важная характеристика цифровой схемы — задержка распространения. Схема реагирует на изменение входных сигналов не мгновенно, а с некоторым запаздыванием. То есть приходится ждать какое-то время, в течение которого сигнал на выходе тоже может меняться. Чем больше элементов в схеме, тем хуже ее быстродействие. На примере с сумматором в такой наивной реализации сигнал переноса должен последовательно пройти через все биты числа, прежде чем сформируется итоговая сумма. К счастью, есть хитрые способы обойти такие ограничения, и один из них мы разберем ниже.

Практика

До этого момента в статье была сплошь теория. Сейчас я предлагаю закрепить ее практической частью и собрать восьмибитный сумматор. Нам потребуется пара беспаечных макетных плат, несколько DIP-переключателей, светодиоды для индикации, токоограничивающие резисторы на 10 кОм и пара микросхем 74HC283.

Серия 74xx включает в себя микросхемы самого разного назначения. Это могут быть как сборки логических вентилей (например, 74HC04 — шесть инверторов в одном корпусе), так и полноценные АЛУ (74HC181). Помимо комбинационных схем, там есть и последовательностные: триггеры (74НС74), регистры (74НС373) и счетчики (74НС393).

Чтобы ориентироваться во всем этом номенклатурном разнообразии, я рекомендую не скачивать документацию на каждую микросхему в отдельности, а сразу найти целый справочник по всей серии. Например, есть справочник Texas Instruments в PDF.

В СССР и России существуют аналогичные микросхемы серий К155 и КР1564, для замены 74хх и 74НСхх соответственно. Большинство из них совместимы по корпусам и контактам с зарубежными, но из-за своей редкости и высокой цены они остаются скорее занятной диковинкой. Для этой статьи я пытался достать парочку интегральных схем (ИС) белорусского «Интеграла» (ЭКР5564ИМ6), но в наличии их не оказалось, поэтому пришлось ограничиться более массовыми SN74HC283 все той же Texas Instruments.

Расположение выводов у микросхемы 74HC283 можно найти на странице 176 справочника, принципиальную схему и таблицы истинности смотри на страницах 390–391. И хотя это сумматор всего лишь на четыре бита, тут есть функция ускоренного переноса, а сами микросхемы можно объединять, собирая сумматоры на 8, 16 или даже 32 бит.

Хорошо видно, что схема здесь несколько отличается от той, что мы вывели ранее. В этом нет ничего необычного, одну и ту же функцию можно реализовать несколькими способами, и в производстве зачастую используют тот, который дешевле (по элементам) и лучше подходит для техпроцесса.

При этом все равно осталось некоторое сходство — его можно заметить при внимательном изучении. Например, элементы XOR от полусумматоров располагаются непосредственно перед выходом для значений каждого из разрядов.

Кроме того, можно понять, что значение для переноса вычисляется параллельно со значениями разрядов — для этого в микросхеме и присутствуют «лишние» элементы. Пожалуй, это самая сложная часть в статье. Поэтому, если у тебя возникли трудности, попробуй рассмотреть схему ускоренного переноса отдельно — это ИС 74HC182 на с. 338 (вот она, польза от полноценного справочника).

Сложение

Теперь, когда принцип работы микросхемы и назначение каждого ее вывода для нас не составляет секрета, можно собирать рабочий сумматор на восемь бит на макетных платах. Потребуется целый ворох проводов и перемычек, чтобы соединить все компоненты, так что главное здесь — быть внимательным и не допускать ошибок.

Как правило, значения в АЛУ попадают из регистров — самого быстрого типа памяти в компьютере. Здесь же я для удобства использую пару DIP-переключателей (левый верхний угол), чтобы можно было легко задавать нужные значения. По сути, это регистры А и В нашего протокомпьютера.

К сожалению, производитель переключателей явно не рассчитывал на такое применение, поэтому нумерация битов в каждом регистре мало того что начинается с единицы, так еще и идет в «неправильном» порядке, слева направо! Учитывай это, когда будешь работать со схемой.

Пара 74НС283 располагается по центру на нижней макетке, а результат операции отображается на линии из светодиодов (правый верхний угол). В левом нижем углу роль источника питания выполняет преобразователь USB — UART (другого способа подать стабильные 5 В я в тот момент не нашел).

Если схема была собрана без ошибок, то, задавая двоичное представление чисел на переключателях, ты сможешь наблюдать значение суммы на светодиодах. Примерно как на картинке выше.

Вычитание

Удивительно, но такую схему без каких-либо изменений и доработок можно использовать и для вычитания. Да, раньше я не говорил об этом ни слова, но такое действительно возможно. Если использовать представление отрицательных чисел в дополнительном коде, нам никак не нужно переопределять операцию сложения — все будет работать на имеющемся железе.

Наверняка ты уже представляешь, как на уровне цифровой схемы из положительного числа можно сделать отрицательное (в дополнительном коде). Действительно, достаточно только к каждому биту применить операцию NOT, а затем подать на вход сумматора вместе с единицей. Как видишь, подобное представление неочевидно с точки зрения человека, но очень удобно для реализации из набора логических вентилей.

Заключение

Статья подошла к концу, но цифровая схемотехника на этом отнюдь не заканчивается. Скорее наоборот, только начинается! Мы рассмотрели лишь самые простые комбинационные схемы (за исключением, может быть, ускоренного переноса). За бортом оказались дешифраторы, мультиплексоры, буферы и все последовательностные схемы (они несколько сложнее для понимания).

Кроме того, можно было бы спуститься на уровень ниже и рассказать о том, как собирать логические вентили из дискретных элементов — транзисторов, диодов и резисторов. В разные времена для этого использовали разные технологии, в зависимости от развития промышленности — ТТЛ (транзисторно-транзисторная логика), КМОП (комплиментарный металл-оксид-полупроводник) и другие.

РЕКОМЕНДУЕМ:
Как сделать робота для сборки кубика Рубика

Конечно, собранная самостоятельно на макетке схема с точки зрения производительности навсегда останется на уровне решений семидесятых годов прошлого века. И она никогда не сможет соперничать с современными многоядерными процессорами, с их многоуровневым кешем, блоками спекулятивных вычислений и параллелизмом.

С другой стороны, важно понимать, что основные принципы работы компьютеров не сильно изменились с тех пор. За исключением разве что квантовых машин, но это совсем другая история. Интересно, сможем ли мы когда-нибудь собирать квантовые компьютеры так же просто, как сейчас на основе полупроводниковых микросхем?

Продолжение в статье «Логические элементы и биты памяти в компьютере».

Загрузка…

Основы цифровой схемотехники. 09. Умножители

${form_setting.title_name}

${form_setting.first_name_required}

* ${form_setting.first_name_required}

${form_setting.title_fam}

${form_setting.last_name_required}

* ${form_setting.last_name_required}

${form_setting.title_otchestvo}

Для преподавателей отчество обязательно

* Для преподавателей отчество обязательно

${form_setting.title_phone}

${country_title}

${phone.title} ${form_setting.phone_required} ${form_setting.country_required}

${form_setting.type_action}

${action.title}

${form_setting.type_action_required}

${form_setting.title_find_company}

* Выберите организацию Такой организации нет

${org.title}

Выберите организацию

Некорректный url сайта

${form_setting.title_no_company}

${form_setting.title_fac}

${form_setting.facultet_required}

${Data.select_facultet.title}

${faculty.title}

${form_setting.facultet_required}

Не нашел в списке Факультет

${form_setting.title_caf}

${form_setting.cafedra_required}

${Data.select_cafedra}

${cafedra.title}

${form_setting.cafedra_required}

Не нашел в списке Кафедру

${form_setting.title_position}

${form_setting.position_required}

* ${ error }

${form_setting.title_departament}

Открытое образование – Цифровая схемотехника

10 weeks
от 3 до 4 часов в неделю
2 credit points

About

Цифровая схемотехника – это курс, посвященный изучению методов и средств построения устройств для автоматической обработки информации представленной в цифровой форме.

В курсе рассматриваются основные принципы и приемы проектирования инвариантные к технологической реализации.

Course program

Темы 1. Введение. Краткая история развития цифровой схемотехнической базы различных поколений. Классификация элементной базы. Электрические характеристики элементов.

Тема 2. Представление информации в цифровой форме. Представление логических переменных электрическими сигналами в потенциальной и импульсной системе. Параметры элементов и их связь с характеристиками.

Тема 3. Элементная база. ГОСТы и ЕСКД в цифровой схемотехнике. Условные графические и условные буквенные обозначения. Типы логик и их связь с условными графическими изображениями. Прямые и инверсные входы и выходы.

Тема 4. Логические основы цифровой схемотехники. Функции Алгебры Логики (ФАЛ). Способы задания функций. Понятие Базиса. СДНФ, СКНФ. Переход из одного базиса в другой. Комбинационная Схема. Минимизация ФАЛ методом Квайна Мак-Класски. Графические методы минимизации ФАЛ. Не полностью определенные функции. Минимизация не полностью определенных функций.

Тема 5. Комбинационные схемы. Постановка задачи, этапы анализа и синтеза комбинационных схем на базе аппарата ФАЛ. Реализация булевых функций на элементах. Синтез и функциональные узлы комбинационных схем: исключающие ИЛИ, мультиплексор, дешифратор, Использование мультиплексоров и дешифраторов для реализации логических функций. Увеличение разрядности комбинационных схем. Классификация сумматоров. Построение комбинационных сумматоров, быстродействие сумматора. Увеличение разрядности сумматора, организация цепей ускоренного переноса.

Тема 6. Временные параметры. Модель логического элемента. Временные параметры. Построение временных диаграмм комбинационных схем методом ранжирования. Построение временных диаграмм схем с памятью событийным методом. Анализ критического пути.

Тема 7. Состязания сигналов. Состязания сигналов в цифровых схемах: причины появления состязаний, переходные процессы в цифровых схемах. Классификация состязаний сигналов: примеры статических и динамических состязаний. Анализ цифровых схем на состязания. Устранение состязаний сигналов в комбинационных схемах. Способы синтеза цифровых схем, свободных от состязаний.

Тема 8. Схемы с памятью. Элементарные триггерные схемы на элементах И-НЕ, ИЛИ-НЕ. Классификация триггерных схем. Таблицы внешних переходов. Асинхронные и синхронные триггерные схемы. Триггерные схемы со статическим и динамическим управлением записью, двухступенчатые триггерные схемы. Примеры двухступенчатых триггеров типа RS, JK, DV, D, T. Примеры триггеров с прямым и инверсным динамическим управлением записью типов RS, JK, DV, D, T.

Тема 9. Проектирование триггера. Проектирование триггера с заданной таблицей перехода. Построение временных диаграмм работы триггера, определение динамических параметров: время переключения, время предварительной установки, время удержания, длительность импульса.

Тема 10. Разработка произвольного счетчика. Классификация счетчиков. Синхронные и асинхронные счетчики. Двоично-десятичные счетчики. Реверсивные счетчики. Увеличение разрядности счетчиков и организация цепей переноса, динамические параметры. Счетчики по модулю М. Проектирование счетчиков с заданным модулем пересчета.

Тема 11. Проектирование многофункционального регистра. Классификация регистров. Регистры хранения и сдвига. Многофункциональные регистры. Организация цепей ввода и вывода информации. Основные принципы проектирования регистров. Примеры регистров. Динамические параметры регистров. Распределители сигналов, формирователи импульсов.

Тема 12. Запоминающие устройства. Схемотехника запоминающих устройств: параметры и классификация ЗУ, временные диаграммы работы и динамические параметры; статические, динамические и постоянные ЗУ. Двух портовая память. Организация буферной (FIFO) и стековой (LIFO) памяти.

Тема 13. Особенности передачи сигналов в цифровых схемах. Типы выходных каскадов: логический выход, элементы с тремя состояниями, выход с открытым коллектором. Элементы индикации, оптоэлектронные развязки, генераторы импульсов, элементы задержки. Организация цепей питания: фильтрация питающих напряжений. Линии передачи сигналов, длинные линии, отражения, согласованная нагрузка.

Тема 14. Программируемая логика. ПЛМ и ПЛИС FPGA. Программируемые логические матрицы (ПЛМ), программируемая матричная логика (ПМК), базовые матричные кристаллы (БМК): базовые структуры, схемные и конструктивные особенности, примеры реализации функций. Программируемые логические интегральные схемы (ПЛИС). Классификация ПЛИС (FPGA, CPLD, FLEX, SOC и др.). Архитектура и топология ПЛИС. Основные элементы: конфигурируемые логические элементы (логическая таблица, триггер, мультиплексор, схемы ускоренного переноса), блоки ввода-вывода, блоки линий межсоединений, «теневое ЗУ». ОЗУ в ПЛИС, шины с тремя состояниями, система синхронизации. Конфигурация ПЛИС. Примеры реализации функций и типовых цифровых узлов.

Тема 15. Средства автоматизации проектирования и отладки цифровых устройств. Этапы проектирования цифровых устройств. Методика и средства автоматизированного проектирования. Использование языков высокого уровня для описания цифровых устройств: проблемно-ориентированный язык VHDL. Примеры проектирования цифровых элементов с применением языка VHDL: описание проекта, компиляция, тестирование и реализация на кристалле FPGA. Тема 16. Заключение. Перспективы развития цифровой схемотехники

Райхлин, Вадим Абрамович – Основы цифровой схемотехники : учебное пособие для студентов вузов, обучающихся по направлению “Информатика и вычислительная техника”

Поиск по определенным полям

Чтобы сузить результаты поисковой выдачи, можно уточнить запрос, указав поля, по которым производить поиск. Список полей представлен выше. Например:

author:иванов

Можно искать по нескольким полям одновременно:

author:иванов title:исследование

Логически операторы

По умолчанию используется оператор AND.
Оператор AND означает, что документ должен соответствовать всем элементам в группе:

исследование разработка

author:иванов title:разработка

оператор OR означает, что документ должен соответствовать одному из значений в группе:

исследование OR разработка

author:иванов OR title:разработка

оператор NOT исключает документы, содержащие данный элемент:

исследование NOT разработка

author:иванов NOT title:разработка

Тип поиска

При написании запроса можно указывать способ, по которому фраза будет искаться. Поддерживается четыре метода: поиск с учетом морфологии, без морфологии, поиск префикса, поиск фразы.
По-умолчанию, поиск производится с учетом морфологии.
Для поиска без морфологии, перед словами в фразе достаточно поставить знак “доллар”:

$исследование $развития

Для поиска префикса нужно поставить звездочку после запроса:

исследование*

Для поиска фразы нужно заключить запрос в двойные кавычки:

“исследование и разработка“

Поиск по синонимам

Для включения в результаты поиска синонимов слова нужно поставить решётку “#” перед словом или перед выражением в скобках.
В применении к одному слову для него будет найдено до трёх синонимов.
В применении к выражению в скобках к каждому слову будет добавлен синоним, если он был найден.
Не сочетается с поиском без морфологии, поиском по префиксу или поиском по фразе.

#исследование

Группировка

Для того, чтобы сгруппировать поисковые фразы нужно использовать скобки. Это позволяет управлять булевой логикой запроса.
Например, нужно составить запрос: найти документы у которых автор Иванов или Петров, и заглавие содержит слова исследование или разработка:

author:(иванов OR петров) title:(исследование OR разработка)

Приблизительный поиск слова

Для приблизительного поиска нужно поставить тильду “~” в конце слова из фразы. Например:

бром~

При поиске будут найдены такие слова, как “бром”, “ром”, “пром” и т.д.
Можно дополнительно указать максимальное количество возможных правок: 0, 1 или 2.4 разработка

По умолчанию, уровень равен 1. Допустимые значения – положительное вещественное число.

Поиск в интервале

Для указания интервала, в котором должно находиться значение какого-то поля, следует указать в скобках граничные значения, разделенные оператором TO.
Будет произведена лексикографическая сортировка.

author:[Иванов TO Петров]

Будут возвращены результаты с автором, начиная от Иванова и заканчивая Петровым, Иванов и Петров будут включены в результат.

author:{Иванов TO Петров}

Такой запрос вернёт результаты с автором, начиная от Иванова и заканчивая Петровым, но Иванов и Петров не будут включены в результат.
Для того, чтобы включить значение в интервал, используйте квадратные скобки. Для исключения значения используйте фигурные скобки. Основы

, схемотехника, проблемы проектирования и их применения.

Цифровые схемы или цифровая электроника – это отрасль электроники, которая имеет дело с цифровыми сигналами для выполнения различных задач в соответствии с различными требованиями. Входной сигнал, подаваемый на эти схемы, имеет цифровую форму, которая представлена в двоичном языковом формате 0 и 1. Эти схемы разработаны с использованием логических элементов, таких как И, ИЛИ, НЕ, NANAD, NOR, XOR, которые выполняют логические операции. Это представление помогает схеме переключаться из одного состояния в другое для обеспечения точного вывода.Системы цифровых схем в основном предназначены для преодоления недостатка аналоговых систем, которые работают медленнее, и получаемые выходные данные могут содержать ошибку.

Что такое цифровая схема?

Определение : Цифровая схема разработана с использованием ряда логических вентилей на одной интегральной схеме – IC. Вход в любую цифровую схему имеет двоичную форму «0» и «1». Выходные данные, полученные при обработке необработанных цифровых данных, имеют точную ценность. Эти схемы могут быть представлены двумя способами: комбинационным или последовательным.

Основы цифровых схем

Проектирование цифровых схем сначала было начато с разработки реле, позднее – электронных ламп, транзисторно-транзисторной логики TTL, эмиттерно-связанной логики и логики CMOS. Эти конструкции используют большое количество логических вентилей, таких как И, ИЛИ, НЕ и т. Д., Интегрированных в одну ИС. Ввод и вывод цифровых данных представлены в логической таблице истинности и временной диаграмме.

Логический уровень

Цифровые данные представлены в логическом формате, то есть в формате «0» и «1».Где логический 0 означает низкий уровень сигнала или «GND», а логический 1 означает высокий уровень сигнала или подключение к источнику «VCC», как показано ниже.

Логический уровень

Таблица логической истины

Таблица логической истинности представляет собой математическое представление рабочих характеристик. цифрового сигнала при прохождении через цифровую схему. Таблица состоит из 3 столбцов: столбца часов, столбца ввода и столбца вывода. Например, логическая таблица логического элемента НЕ представлена следующим образом:

Тактовый сигнал	Входная логика	Выходная логика
High	0	1
High	1	0

Временная диаграмма

Поведение цифрового сигнала представлено во временной области, например, если мы рассматриваем НЕ таблицу истинности логического элемента, временная диаграмма представлена следующим образом, когда часы высокий, вход низкий, затем выход высокий.Точно так же, когда вход высокий, выход становится низким.

Временная диаграмма

Шлюз

Логический вентиль – это электронный компонент, который реализован с использованием логической функции. Затворы обычно реализуются с использованием диодов, транзисторов и реле. Существуют разные типы логических вентилей: AND, OR, NOT, NANAD, NOR, XOR. Среди которых AND, OR, NOT являются основными воротами, а NAND и NOR – универсальными воротами. Давайте рассмотрим представление логического элемента И, как показано ниже, которое имеет 2 входа и один выход.

AND Gate

Тактовый сигнал	Входная логика 1	Входная логика 2	Выходная логика
High	0	029
Высокий	0	1	0
Высокий	1	0	0
Высокий	1	1	1

Таблица истинности Логический элемент И

Временная диаграмма логического элемента И

Существует множество способов построения цифровой схемы, использующей логические элементы, путем создания комбинационной логики, последовательной логической схемы или с помощью программируемого логического устройства, которое использует таблицы поиска, или с помощью комбинации многих IC и т. д.Обычно они разрабатываются с использованием формата комбинационной и последовательной схемы, как показано ниже.

Комбинированная логическая схема

Это комбинация различных логических элементов, таких как И, ИЛИ, НЕ. Дизайн комбинационной логики сделан таким образом, что выход зависит от текущего входа, а логика не зависит от времени. Комбинационные логические схемы подразделяются на 3 типа, это

Комбинационная логическая схема

Последовательная схема

Конструкция последовательной схемы отличается от комбинационной схемы.В последовательной схеме логика вывода зависит как от текущих, так и от прошлых входных значений. Он также состоит из элемента памяти, в котором хранятся обработанные и обработанные данные. Последовательные схемы подразделяются на 2 типа:

Синхронная схема
Асинхронная схема

Некоторыми примерами последовательных схем являются триггеры, тактовые генераторы, счетчики и т. Д.

Схема последовательной схемы

Конструкция цифровой схемы

Цифровая схемы могут быть спроектированы следующими способами:

Использование последовательного представления системы и представления комбинационной системы
Использование математических методов путем сокращения алгоритмов логической избыточности, таких как K-Map, булева алгебра, алгоритм QM, диаграммы двоичных решений и т. д.
Использование машин потока данных, которые состоят из регистров и шин или проводов. Данные передаются между различными компонентами с помощью шин и регистров. Эти машины разработаны с использованием языков описания оборудования, таких как VHDL или Verilog.
Компьютер – это логическая машина общего назначения с переносом регистров, разработанная с использованием микропрограммы и процессора микропоследовательностей.

Проблемы проектирования цифровых схем

Поскольку цифровые схемы состоят из аналоговых компонентов, таких как резисторы, реле, транзисторы, диоды, триггеры и т. Д.Необходимо отметить, что эти компоненты не влияют на поведение сигнала или данных во время работы цифровой схемы. Ниже приведены проблемы проектирования, которые обычно наблюдаются:

Проблемы, такие как сбои, могут возникнуть из-за неправильной конструкции системы
Неправильная синхронизация другого тактового сигнала приводит к метастабильности в схеме
Расчет цифровых схем более многократно из-за высокой помехоустойчивости.

Примеры цифровых схем

Ниже приведены примеры цифровых схем

Мобильные телефоны
Радио
Калькуляторы и т. Д.

Преимущества

Ниже приведены преимущества

Высокая точность и программируемость
Простота сохранения цифровых данных
Устойчивость к шумам
Многие цифровые схемы могут быть интегрированы в одну микросхему
Высокая гибкость
Высокая надежность
Высокая скорость передачи
Высокая безопасность.

Недостатки

Ниже приведены недостатки

Они работают только с цифровыми сигналами
Потребляет больше энергии, чем аналоговые схемы
Рассеивание тепла больше
Высокая стоимость.

Приложения

Ниже приведены приложения

Часто задаваемые вопросы

1). Для чего используются цифровые схемы?

Цифровые схемы используются для выполнения логических операций.

2). Как работает цифровая схема?

Цифровая схема работает с дискретными сигналами, которые представлены в двоичной форме нулей и единиц.

3). Каковы основные компоненты цифровой схемы?

Основными компонентами цифровых схем являются триггеры, диоды, транзисторы, вентили и т. Д.

4). Из чего сделана схема?

Электронная схема состоит из ряда пассивных и активных компонентов, соединенных между собой проводящими проводами.

5). Назовите несколько примеров активных и пассивных компонентов?

Примерами активных компонентов являются диоды, ИС, триодные вакуумные лампы и т. Д.
Примерами пассивных компонентов являются резистор, конденсатор, катушка индуктивности, трансформатор и т. Д.

6). Почему мы используем резистор в схемах?

Мы используем резистор в цепи, чтобы контролировать ток.

Электронная схема состоит из ряда пассивных и активных компонентов, соединенных между собой проводящими проводами. Это два типа схем: аналоговая схема и цифровая схема. Входом в аналоговую схему является непрерывный переменный сигнал, который предоставляет информацию о сигнале, такую как ток, напряжение и т. Д. Входной сигнал цифровой схемы находится в дискретном формате временной области, который представлен в виде «0» и «1». Он обеспечивает уровень сигнала, коэффициент шума, затухание и т. Д. Характеристики цифрового сигнала.Основное преимущество использования цифровых схем в том, что их легко реализовать и понять.

4. Базовые цифровые схемы – Введение в цифровые схемы

Все логические схемы, которые мы обсуждали до сих пор, являются ациклическими , то есть они не образуют циклов или циклов, кроме как неявно через источник питания. Ациклические схемы имеют входы \ (A \) и выходы \ (Y, \) и реализовать логические функции входов, \ (Y = f (A). \) Когда входы изменяются, выходы принимают значения, определенные на \ (f \) после задержки распространения, характерной для схемы.Циклический схемы демонстрируют более сложное, зависящее от времени поведение, чем их ациклические кузены, потому что их выходы зависят от входной последовательности включая текущие и прошлые входные значения. Циклические схемы бывают Особый интерес представляет реализация элементов памяти. В В этом разделе мы обсудим два наиболее часто используемых типа памяти. элементы, D-защелка и D-триггер .

4.7.1. Циклические схемы

Циклическая схема имеет один или несколько контуров , не считая неявные контуры питания.Например, Рисунок 4.50. показаны две циклические схемы с одним контуром в каждой.

Рисунок 4.50: Циклические схемы с одним контуром из двух (слева) и трех (справа) инверторов.

Циклические схемы труднее анализировать, чем ациклические схемы. В частности, схемы, показанные на рисунке 4.50, не даже различают входные и выходные клеммы. Инверторная пара слева на рисунке 4.50 есть два провода: \ (Q_0 \) подключает выход инвертора 0 к входу инвертора 1, и \ (Q_1 \) соединяет выход инвертора 1 со входом инвертора. 0.Аналогично, цикл с тремя инверторами справа имеет три провода, \ (Q_0, \) \ (Q_1, \) и \ (Q_2. \)

Разберем функциональность двухинверторного контура. Выход каждого инвертора может быть 0 или 1. Сначала предположим, что \ (Q_0 = 0. \) Таким образом, вход инвертора 1 равен 0, следовательно, \ (Q_1 = 1. \) Поскольку \ (Q_1 \) – вход инвертора 0, выход инвертора 0 должен быть \ (Q_0 = 0. \) Это то же значение, с которого мы начали. Мы заключаем, что схема усиливает \ (Q_0 = 0 \) и, по симметрия, \ (Q_1 = 1.\) Во-вторых, предположим, что \ (Q_0 = 1. \) Тогда выход инвертора 1 равен \ (Q_1 = 0, \), что вызывает выход инвертора 0 должно быть \ (Q_0 = 1. \) Это также то же значение с началось с. Заметим, что петля с двумя инверторами усиливает его состояние в любом случае \ (Q_0 = 0 \) или \ (Q_0 = 1. \)

Цепь с тремя инверторами ведет себя совсем не так, как цепь с двумя инверторами. петля. Предположим, что \ (Q_0 = 0. \) Поскольку \ (Q_0 \) является входом инвертора 1, выход инвертора 1 должен быть \ (Q_1 = 1. \) Поскольку \ (Q_1 \) – вход инвертора 2, его выход должен быть \ (Q_2 = 0.\) Теперь вход \ (Q_2 \) является входом инвертора 0. Следовательно, выход инвертора 0 должен быть \ (Q_0 = 1, \), что является дополнение к предположению, с которого мы начали. Если мы пройдем по петле во второй раз находим \ (Q_0 = 0, \) то есть провод дополнил снова. Заметим, что схема не усиливает его состояние. Вместо этого значения проводов переключаются со скоростью определяется задержкой распространения инверторов.

Мы заключаем, что контур с двумя инверторами стабилен, тогда как трехинверторного шлейфа нет.Фактически, такое поведение можно наблюдать и в более крупные петли. Каждый контур инвертора с четным числом инверторы работает стабильно. В отличие от контуров инвертора с нечетным числом инверторы как нестабильные. Шлейфы инвертора с нечетными номерами называются кольцом . генераторы , и полезны для измерения средней задержки распространения инвертора в данном производственном процессе. Кольцевые генераторы не используются в качестве логических элементов в цифровых схемах. Напротив, петли с четным числом инверторов – полезные строительные блоки, потому что они бистабильные .Бистабильная схема – это схема с двумя стабильные состояния. Состояние стабильное , если схема не переход в другое состояние без внешнего раздражителя. Два стабильными состояниями бистабильного контура с двумя инверторами являются \ (S_0 = \ {Q_0 = 0, Q_1 = 1 \} \) и \ (S_1 = \ {Q_0 = 1, Q_1 = 0 \}. \) Когда цепь принимает стабильное состояние, инверторы обеспечивают выполнение \ (Q_0 \) и \ (Q_1 \) дополняют друг друга, \ (Q_0 = \ overline {Q_1}. \) Таким образом, на рис. 4.51 мы вызываем провода просто \ (Q \) и \ (\ overline {Q}.\)

Рисунок 4.51: Два состояния бистабильного контура инвертора.

Проблема с бистабильным контуром инвертора на рис. 4.51 заключается в том, что мы не можем контролировать его состояние. Поскольку схема стабильно и не имеет входов, не очевидно, как перейти на цепь из одного стабильного состояния в другое. D-защелка , которую мы обсуждается ниже, устраняет этот недостаток.

4.7.2. D-защелка

A D-latch – бистабильный элемент памяти с вводом данных \ (D, \) вход часов \ (\ phi, \) и выход \ (Q.\) Символ D-защелки показано справа. На рисунке 4.52 изображена D-образная защелка. реализация с бистабильным контуром инвертора и мультиплексором 2: 1 для направить входной сигнал данных в цикл.

Рисунок 4.52: D-защелка, реализованная как бистабильный инверторный контур с входом мультиплексор.

Вход часов \ (\ phi \) D-защелки служит входом выбора мультиплексор, и определяет, подтверждает ли ввод данных \ (D \) состояние бистабильного контура инвертора. Следовательно, мы различаем два режима операция:

\ (\ phi = 1 \): D-образная защелка прозрачная.

Контур инвертора разомкнут, и вход \ (D \) управляет инверторная пара. Поскольку вывод \ (Q \) следует за вводом \ (D, \) мы говорим, что D-защелка прозрачная .

\ (\ phi = 0 \): D-образная защелка непрозрачна.

Контур инвертора замкнут и сохраняет текущее состояние. Поскольку выход \ (Q \) сохраняет свое значение независимо от input \ (D, \) мы говорим, что D-защелка непрозрачна .

На рисунке 4.53 показана схема D-защелки с мультиплексором. заменен на его модель переключателя.Режим работы зависит от положение переключателя мультиплексора. Если \ (\ phi = 1, \) цикл открытый, а вход \ (D \) управляет как выходом \ (Q \), так и инверторная пара. В противном случае, если \ (\ phi = 0, \) замкнутый цикл отключен от входа \ (D, \) и сохраняет значение \ (Q \), потому что петля представляет собой бистабильную циклическую схему.

Рисунок 4.53: Режимы работы D-защелки. D-образная защелка либо (слева) прозрачный: вывод \ (Q \) следует за вводом \ (D, \) или (справа) непрозрачный: контур инвертора сохраняет значение \ (Q.\)

Диаграмма формы сигнала на рис. 4.54 иллюстрирует срабатывание D-защелки с течением времени. На схеме показано напряжение уровни входов часов и данных, а также выхода D-защелки. Первоначально D-защелка непрозрачна и хранит выходное значение \ (Q = 0. \) Вход \ (D \) переходит в 1 перед синхросигналом. Когда D-защелка становится прозрачной, вывод следует за вводом \ (D \) после задержки распространения, обозначенной изогнутой стрелкой от \ (\ phi \) to \ (Q. \) D-защелка остается прозрачной, пока тактовый сигнал равен \ (\ phi = 1.\) Выход \ (Q \) следует за входом \ (D \) после задержки распространения, обозначенной изогнутыми стрелками от переходов \ (D \) к \ (Q. \) Когда часы переходит на \ (\ phi = 0, \) D-защелка сохраняет последнее значение введите \ (D \) перед переходом часов и удерживает это значение для пока D-образная защелка остается непрозрачной. D-защелка называется чувствительный к уровню , потому что его два режима работы зависят от уровень тактового сигнала.

Рисунок 4.54: Диаграмма формы сигнала D-защелки.Когда D-образная защелка прозрачна, выход \ (Q \) следует за входом \ (D. \) В противном случае во время серые заштрихованные временные интервалы, D-защелка непрозрачна, т.е. удерживает вывод \ (Q \) без изменений и блокирует распространение \ (D \) на выход.

Далее мы выводим схему CMOS для D-защелки в Рисунок 4.52. Начнем с реализации Мультиплексор 2: 1 с двумя рычагами выбора, интегрирующий \ (\ overline {\ phi} \) – рычаг в контур инвертора, как показано на Рисунок 4.55. Поскольку эта схема мультиплексора инвертирует выход, мы добавляем инвертор для генерации незавершенного вывод \ (Q.\) На рис. 4.55 показан рычаги выбора мультиплексора трехсторонние инверторы в форме инвертора, который управляет передачей ворота.

Рисунок 4.55: Реализация D-защелки с рычагами выбора мультиплексора, показанными как трехпозиционные инверторы.

Функциональность схемы D-защелки существенно зависит от состояние внутреннего узла \ (X. \) Когда \ (\ phi \) – рука закрыто, он направляет вход \ (D \) в \ (X. \). плечо мультиплексора меняет полярность, мы имеем \ (X = \ overline {D}.\) выходной инвертор заставляет \ (X \) выводить \ (Q, \), так что \ (Q = \ overline {X} = D \), когда ввод часов \ (\ phi = 1, \) и D-защелка прозрачный. В противном случае, когда \ (\ phi = 0, \) \ (\ phi \) – рука открытый и \ (\ overline {\ phi} \) – рука закрыта, затем узел \ (X \) отключен от входа \ (D \) и контура инвертора усиливает \ (X = \ overline {Q}. \) D-образная защелка непрозрачна и выводит \ (Q \) сохраняет свое значение.

Компактная КМОП-реализация мультиплексоров показана на Рисунок 4.56. Мы используем эквивалентность схем в Рисунок 4.39 для реализации каждого плеча мультиплексора с четыре транзистора.

Рисунок 4.56: Реализация D-защелки с разнесенными рычагами выбора мультиплексора.

На рис. 4.57 показана полная 12-транзисторная схема. Схема CMOS для D-защелки, включая модель интерактивного переключателя. Обратите внимание, что выходной сигнал инвертора обратной связи равен \ (Y = \ overline {X}, \) и схема также применяет \ (X = \ overline {Q} \) и \ (Y = Q. \)

Временные характеристики D-защелки зависят от режима работы. Когда D-защелка прозрачна, критический путь простирается от данных вход \ (D \) в выход \ (Q.\) Сигнал распространяется через внутренний узел \ (X, \) и полностью обходит контур обратной связи. В задержка не зависит от тактового сигнала \ (\ phi. \) Когда D-защелка непрозрачный, вывод остается без изменений. Следовательно, это не делает есть смысл говорить о задержке распространения. Поэтому мы обсуждаем задержка распространения прозрачной D-защелки. В частности, мы проанализировать критический путь D-защелки с согласованным транзистором размеры указаны на рисунке 4.58.

Рисунок 4.58: Схема D-защелки с согласованными размерами транзисторов.

Задержка распространения прозрачной D-защелки – это задержка Мультиплексор 2: 1 плюс задержка выходного инвертора: \ (d_ {D \ rightarrow Q} = d_ {mux} + d_ {inv}. \) Предполагая, что вывод \ (Q \) управляет емкостной нагрузкой \ (C_L, \) выходной инвертор имеет электрическое усилие \ (h_ {inv} = C_L / C_ {inv} \) и паразитная задержка \ (p_ {inv} = 1, \) такое, что \ (d_ {inv} = C_L / 3 + 1 \) единиц времени. Далее мы анализируем мультиплексор. Логическое усилие – это ввод емкость \ (C_ {mux} (D) \) входа \ (D \), деленная на вход емкость опорного инвертора \ (C_ {inv} = 3.\) Вход \ (D \) управляет pMOS-транзистором шириной 4 и nMOS транзистор шириной 2 плеча \ (\ phi \). Таким образом, \ (C_ {mux} (D) = 6, \) и логическое усилие ввода \ (D \) из мультиплексор равен \ (g_ {mux} (D) = 6/3 = 2. \) Для определения электрического усилие мультиплексора, обратите внимание, что выход \ (X \) мультиплексора управляет двумя инверторы, инвертор обратной связи и выходной инвертор. Таким образом Емкость нагрузки мультиплексора равна \ (C_L (mux) = 2 C_ {inv} = 6. \) Следовательно, электрическое усилие входа \ (D \) мультиплексора равно \ (h_ {мультиплексор} (D) = C_L (мультиплексор) / C_ {мультиплексор} (D) = 6/6 = 1.\) Паразитический задержка мультиплексора 2: 1 равна \ (p_ {mux} = 4, \) см. мультиплексор. Мы обнаруживаем, что задержка мультиплексора равна \ (d_ {mux} = g_ {mux} (D) h_ {mux} (D) + p_ {mux} = 2 \ cdot 1 + 4 = 6, \) и задержка распространения D-образной защелки составляет

\ [d_ {D \ rightarrow Q} = d_ {mux} + d_ {inv} = 6 + \ frac {C_L} {3} + 1 = \ frac {C_L} {3} + 7 \,. \]

Эта задержка может служить точкой отсчета для цепи оптимизации. Например, мы наблюдаем, что инвертор обратной связи отводит ток с выхода мультиплексора.Если мы сжимаем pMOS транзистор инвертора обратной связи от 2 до 1 ед. нормированной ширины, уменьшаем емкость ответвления и задержку интересующего пути.

Задержка распространения \ (d_ {D \ rightarrow Q} \) – лишь одна из нескольких характерные величины временного поведения D-защелки. Возможно, даже более важным является временное поведение D-защелки. при изменении входа часов. Лаконичнее, если и часы, и входные данные меняются примерно одновременно, D-защелка может стать нестабильный.Цифровые схемы с D-защелками должны избегать этого сценария. во что бы то ни стало, потому что это может отрицательно повлиять на функциональность. Функциональные ошибки, вызванные неосторожным поведением по времени, особенно трудно раскрыть. Мы обсуждаем временные характеристики D-защелки. на рисунке 4.59, где ввод данных \ (D \) переходы в момент времени \ (t = 0 \) и ввод часов \ (\ phi \) в момент времени \ (t = 14. \)

Рисунок 4.59: Схема D-защелки и временной анализ. Входные переходы часов от 1 до 0 в момент времени \ (t = 14. \) D-защелка прозрачна для \ (t <14 \) и непрозрачным для \ (t> 14.\) Непрозрачная D-защелка сохраняет входное значение \ (D = 1. \)

Учитывая размеры транзисторов D-защелки на рис. 4.58 и ёмкость нагрузки \ (C_L = 12, \) задержки цепи элементами D-защелки являются:

\ (d_ {D \ rightarrow X} \): \ (\ quad \ phi \) – задержка руки; \ (d_ {D \ rightarrow X} = d_ {mux} = 6 \)
\ (d_ {X \ rightarrow Y} \): \ (\ quad \) задержка инвертора обратной связи; \ (d_ {X \ rightarrow Y} = 6/3 + 1 = 3 \)
\ (d_ {Y \ rightarrow X} \): \ (\ quad \ overline {\ phi} \) – задержка руки; \ (d_ {Y \ rightarrow X} = d_ {mux} = 6 \)
\ (d_ {X \ rightarrow Q} \): \ (\ quad \) задержка выходного инвертора; \ (d_ {X \ rightarrow Q} = d_ {inv} = C_L / 3 + 1 = 5 \)

С помощью этих задержек элементов мы можем выразить задержку распространения прозрачная D-защелка как \ (d_ {D \ rightarrow Q} = d_ {D \ rightarrow X}) + d_ {X \ rightarrow Q} = 11.\) Диаграмма формы сигнала показывает соответствующие переходы. Изначально D-образная защелка прозрачная. потому что \ (\ phi = 1, \) и \ (\ phi \) – рука закрыта, тогда как \ (\ overline {\ phi} \) – рука открыта. В момент \ (t = 0, \) \ (D \) – вход меняется с 0 на 1. Выход \ (Q \) будет следовать \ (D \) после того, как вход прошел через \ (\ phi \) – руку во внутренний узел \ (X \) в \ (t = 6, \), а затем через выходной инвертор в момент \ (t = 11. \) Изменение внутреннего узел \ (X \) также влияет на узел \ (Y, \), который изменяется со временем \ (t = 9 \) от 0 до 1 после задержки распространения \ (d_ {X \ rightarrow Y} \) инвертора обратной связи.

Когда D-защелка становится непрозрачной в момент времени \ (t = 14, \), она сохраняет значение \ (Q = 1. \) Сигнал часов \ (\ phi = 0 \) закрывается или поворачивается , кнопка \ (\ overline {\ phi} \) – и открывает или выключает \ (\ phi \) – рука. Таким образом, после часового перехода при \ (t = 14, \) сигнал \ (Y = 1 \) принимает задержку распространения \ (d_ {Y \ rightarrow X} = 6 \) единиц времени через инвертирующий \ (\ overline {\ phi} \) – руку на усилить внутренний узел \ (X = 0 \) в момент \ (t = 20. \) Это эта задержка переключения мультиплексора, которая может вызвать проблемы.В в частности, переход входа \ (D \) должен происходить достаточно длительный период времени до отрицательного перехода часов \ (\ phi \) для стабилизации внутреннего узла \ (Y \) через обратную связь инвертор, так как контур обратной связи бистабильный, только если \ (X = \ overline {Y}. \) Если мы заставим \ (X = Y, \), цикл обратной связи будет принять непредсказуемое состояние. Это может произойти, если временной интервал \ (d_ {D \ rightarrow \ phi} \) между переходами входов \ (D \) и \ (\ phi \) слишком малы. Рисунок 4.60 иллюстрирует проблемы синхронизации D-защелки.

Рисунок 4.60: Проблемы синхронизации D-защелки: (слева) в угловом корпусе \ (d_ {D \ rightarrow \ phi} = d_ {D \ rightarrow X} + d_ {X \ rightarrow Y} \) D-защелка сохраняет ввод после \ (d_ {D \ rightarrow Q} = d_ {D \ rightarrow X} + d_ {X \ rightarrow Q}, \) (в центре) \ (d_ {D \ rightarrow X}

На диаграмме осциллограмм слева на рис. 4.60 интервал между переходом входного сигнала \ (D \) и часы \ (\ phi \) – это \ (d_ {D \ rightarrow \ phi} = d_ {D \ rightarrow X} + d_ {X \ rightarrow Y}. \) В момент \ (t = 9, \) отрицательные часы край начинает закрывать \ (\ overline {\ phi} \) – плечо и открывать \ (\ phi \) – рука. Внутренний узел \ (Y \) следует за \ (D \) прямо в время в \ (t = 9 \) для усиления внутреннего узла \ (X \) после задержка мультиплексора \ (d_ {Y \ rightarrow X} = 6 \) единиц времени, поэтому что \ (X = 0 \) для \ (t> 15.\) Временной интервал \ (d_ {D \ rightarrow \ phi} = d_ {D \ rightarrow X} + d_ {X \ rightarrow Y} \) – это наименьший интервал для D-защелки для захвата ввода. \ (D \) безопасно.

Диаграмма формы сигнала в середине рисунка 4.60 предполагает, что интервал \ (d_ {D \ rightarrow \ phi} \) равен меньше, то есть \ (d_ {D \ rightarrow X} на узле \ (X \) распространяется через обратную связь и выходные инверторы. Поскольку инверторы ослабить такие сбои, петля обратной связи стабилизируется и восстанавливается \ (X = 0. \) Однако сбой появляется на выходе \ (Q \) после задержка распространения \ (d_ {glitch} = d_ {D \ rightarrow \ phi} + D_ {Y \ rightarrow X} + d_ {X \ rightarrow Q}, \), который больше, чем задержка распространения \ (d_ {D \ rightarrow X} + d_ {X \ rightarrow Q} \) прозрачная D-образная защелка.

Диаграмма формы сигнала справа на Рисунке 4.60 предполагает еще меньший интервал \ (d_ {D \ rightarrow \ phi} < d_ {D \ rightarrow X}. \) Отрицательный фронт часов открывает \ (\ phi \) - рука слишком рано, чтобы подтянуть внутренний узел \ (X \) к нулю. \ (\ phi \) - рука сражается закрывающей \ (\ overline {\ phi} \) - рукой, которая удается подтянуть \ (X \) к 1. Как следствие, D-защелка не работает. для захвата ввода \ (D = 1 \) и продолжает сохранять старое значение \ (Q = D = 0. \) Выходной инвертор распространяет сбой узла \ (X \) для вывода \ (Q \) перед восстановлением старого выходного значения \ (Q = 0.\)

Рисунок 4.61: Синхронизация D-защелки: чем меньше интервал между входными переходами \ (D \) и отрицательный фронт часов, \ (d_ {D \ rightarrow \ phi}, \) становится, чем больше задержка распространения от входа \ (D \) для вывода \ (Q, \) \ (d_ {D \ rightarrow Q}, \) становится. Когда интервал становится слишком маленьким, D-защелка не может захватить входной переход целиком, см. случай (4).

На рисунке 4.61 показаны временные характеристики D-защелки. в графе, который строит интервал \ (d_ {D \ rightarrow \ phi} \) на горизонтальная ось и задержка распространения \ (d_ {D \ rightarrow Q} \) на вертикальная ось.Случай (1) соответствует сценарию в Рисунок 4.59, где переход входа \ (D \) происходит достаточно рано до отрицательного фронта тактового сигнала для D-защелка для безопасного распространения изменения на выход \ (Q. \) задержка распространения – это сумма задержек \ (\ phi \) – плеча и выходной инвертор, \ (d_ {D \ rightarrow Q} = d_ {D \ rightarrow X} + d_ {X \ rightarrow Q}. \) Senarios (2), (3) и (4) соответствуют три случая, показанные на рис. 4.60. В ближе переход входа \ (D \) к отрицательным часам края, увеличивается задержка распространения \ (d_ {D \ rightarrow Q} \).Когда интервал \ (d_ {D \ rightarrow \ phi} \) становится слишком маленьким, D-защелка не может полностью захватить новый входной сигнал и сохраняет старое входное значение. Мы наблюдаем, что для безопасной работы D-защелка, нам нужно гарантировать, что input \ (D \) изменится достаточно рано до отрицательного фронта тактового сигнала, т.е. интервала \ (d_ {D \ rightarrow \ phi} \) должен быть достаточно большим.

Время установки \ (t_ {setup} \) – минимальное время ввода \ (D \) должен быть стабильным до отрицательного фронта тактового сигнала для захвата вводимое значение с разумной задержкой \ (d_ {D \ rightarrow Q}.\)

Например, разумные спецификации определяют \ (t_ {setup} \) как \ (5 \, \% \) больше, чем задержка распространения прозрачного D-защелка, \ (t_ {setup} = 1.05 \, (d_ {D \ rightarrow X} + d_ {X \ rightarrow Q}). \)

Рисунок 4.62: Время установки D-защелки и время удержания характеризуют временной интервал вокруг отрицательного фронта тактового сигнала, когда вход \ (D \) может безопасно измениться. Отрицательный фронт часов находится в \ (d_ {D \ rightarrow \ phi} = 0. \)

Проблемы синхронизации D-защелки возникают даже при переходе ввод \ (D \) происходит после отрицательного фронта тактового сигнала.Если ввод \ (D \) переходы до того, как \ (\ phi \) – рука будет полностью открыта, сбои могут распространяться на выход \ (Q. \). Рисунок 4.62 иллюстрирует задержку \ (d_ {D \ rightarrow Q} \) как функция интервала \ (d_ {D \ rightarrow \ phi}. \) Аналогично время установки, для бесперебойной работы D-защелки мы должны обеспечить этот вход \ (D \) не переходит до периода времени после отрицательный фронт часов прошел.

Время удержания \ (t_ {hold} \) – минимальное время на входе \ (D \) должен быть стабильным после отрицательного фронта тактового сигнала для захвата вводимое значение с разумной задержкой \ (d_ {D \ rightarrow Q}.\)

Время установки и время удержания характеризуют временное поведение D-защелка вокруг отрицательного фронта часов. Большинство производителей предлагают D-образные защелки в качестве основных элементов схемы и обеспечивают их питание в зависимости от процесса. настройте и удерживайте время в своих таблицах данных. Для проектировщика схем, важно убедиться, что ввод данных не меняется в интервал вокруг отрицательного тактового фронта D-защелки. Это причина, по которой тактовый вход D-защелки обычно подключается к регулярные биения тактового сигнала с четко определенным тактовым периодом.Такой тактовый сигнал ограничивает выбор конструкции, но дает разработчик эталон чистого времени для допустимого диапазона задержки схемы, управляющей вводом данных D-защелки.

4.7.3. D-триггер

A D-flipflop – бистабильный элемент памяти с вводом данных. \ (D, \) вход часов \ (\ phi, \) и выход \ (Q. \) A D-триггер – это элемент памяти , запускаемый по фронту, который активируется по краю часов. На фронте тактового сигнала срабатывания D-триггер сохраняет введите \ (D \), пока не появится следующий фронт синхронизации.Этот поведение отличается от D-защелки, которая чувствительна к уровню . В то время как D-защелка непрозрачна при низком уровне входного сигнала синхронизации, D-триггер всегда непрозрачен, за исключением короткого периода времени около синхронизирующий фронт часов. Тем не менее, D-триггер можно построить последовательной композицией из двух D-образных защелок с дополненными часами входы, как показано на рисунке 4.63. В Символ D-триггера справа имеет треугольник на входе часов для указывают, что триггер срабатывает по фронту.

Рисунок 4.63: D-триггер с положительным фронтом, реализованный с двумя вставные D-образные защелки и дополненные часы.

Первая D-защелка с входом \ (D \) и выходом \ (Q1 \) называется фиксатор master и отрицательно-чувствительный , потому что он прозрачный при вводе часов \ (\ phi = 0. \) Вторая D-защелка с входом \ (Q1 \) и выходом \ (Q \) – это защелка ведомого устройства , а положительно-чувствительный , потому что он прозрачен при вводе часов \ (\ phi = 1.\) D-триггер – это срабатывание по положительному фронту потому что он хранит ввод \ (D \) на переднем фронте тактового сигнала. Если мы инвертируем вход часов, триггер будет с отрицательным фронтом запускается, и сохраняет ввод \ (D \) по заднему фронту тактового сигнала. На рисунке 4.64 показана схема CMOS для положительного фронта. сработал D-триггер. Схема экономит четыре транзистора за счет удаления выходной инвертор мастер-защелки и входной инвертор рабская защелка.

Рисунок 4.64: 20-транзисторная КМОП-схема для срабатывания положительного фронта. D-триггер сохраняет выходной инвертор мастер-защелки и входной инвертор ведомой защелки.

Чтобы понять функциональность D-триггера, рассмотрим переключатель модели и соответствующие диаграммы форм сигналов на рисунках 4.65 и 4.66. Рисунок 4.65 иллюстрирует работу во время отрицательного полупериода часы. Основная защелка прозрачна, и ввод \ (D \) может распространяются на внутренний узел \ (Q1. \) Поскольку защелка подчиненного устройства непрозрачна, вход \ (D \) не может распространяться за пределы \ (Q1 \) для вывода \ (Q. \) Вместо этого защелка ведомого усиливает выходное значение \ (Q. \)

Рисунок 4.65: Модель переключения D-триггера и работа во время отрицательного полупериода часов. Основная защелка прозрачна, а вспомогательная защелка непрозрачный.

Во время положительного полупериода часов, показанного на На рис. 4.66 основная защелка непрозрачна, а отключает вход \ (D \) от внутреннего узла \ (Q1. \) Таким образом, главная защелка сохраняет последнее значение ввода \ (D \) перед положительный фронт часов. Защелка ведомого прозрачна, выдвигается значение \ (Q1 \) для вывода \ (Q, \), которое является последним значением входа \ (D \) до положительного фронта тактового сигнала.

Рисунок 4.66: Модель переключателя D-триггера и работа в течение положительного полупериода часов. Основная защелка непрозрачна, а вспомогательная защелка прозрачный.

Обратите внимание, что выход \ (Q \) остается неизменным после отрицательных часов. край, потому что непрозрачная защелка ведомого сохраняет во время отрицательного полупериод значения, сохраненного мастер-защелкой во время предыдущего положительный полупериод часов.

Синхронизирующий фронт синхросигнала является критическим по времени переходом D-триггер.В случае срабатывания D-триггера положительным фронтом, нарастающий фронт часов превращается в спадающий фронт часов мастера защелка. Это критический фронт часов, на котором время установки и удержания время основной D-защелки должно быть соблюдено. Таким образом, D-триггер – это подчиняется тем же временным ограничениям, что и D-защелка. Входной сигнал \ (D \) должен быть стабильным во время установки до положительного тактовый фронт и в течение времени удержания после положительного фронта тактового сигнала.

D-триггер также называется регистром и является одним из самых широко используемые элементы памяти в проектировании цифровых схем.Один D-триггер реализует 1-битный регистр. \ (N \) – битовый регистр состоит из \ (n \) D-триггеров, запускаемых одним и тем же тактовым сигналом. Каждый из \ (n \) D-триггеров имеет независимый D-вход и Q-выход. Символ регистра показан справа.

4.2

D-образная защелка прозрачна, когда часы \ (\ phi = 1 \) и непрозрачны. когда \ (\ phi = 0. \) D-триггер с положительным фронтом сохраняет вход \ (D \) на переднем фронте тактового сигнала \ (\ phi. \) Завершите приведенную ниже диаграмму формы сигнала с выходом D-защелки. \ (Q_ \ text {latch} \) и выход D-триггера \ (Q_ \ text {ff}, \) предполагая, что оба элемента памяти подключены к часам \ (\ phi \) и входной сигнал \ (D.\)

Выход D-защелки \ (Q_ \ text {latch} \) следует за входом \ (D \), в то время как clock \ (\ phi = 1. \) На отрицательном фронте, когда часы переходит с 1 на 0, D-защелка сохраняет введенное значение \ (D \) имеет при переходе.

Выход D-триггера \ (Q_ \ text {ff} \) изменяется при положительных часах только по краям, то есть там, где тактовый сигнал переходит с 0 на 1. Там он хранит значение input \ (D, \) и сохраняет это значение для всего тактового цикла до следующего положительного фронта тактового сигнала имеет место.

Решение

Руководство по цифровой электронике для новичков

УЗНАЙТЕ, КАК ЦИФРЫ «1» И «0» ИЗМЕНИЛИ МИР

Эта статья написана специально для новичков в области цифровой электроники. Если вы всегда хотели знать, как устроен цифровой мир, продолжайте читать. Чтобы закончить эту статью, вам не нужно знать математику, алгебру или какие-либо сложные формулы. Единственные требования – это интерес к цифровой электронике и желание учиться.Поскольку вы читаете этот абзац, очевидно, что вам хотя бы немного интересно узнать о цифровом мире. К счастью, любопытство – это полдела на пути к просветлению.

Сравнение аналоговых и цифровых

Мир электроники намного легче понять, если мы начнем с разделения его на две отдельные категории: «аналоговый» мир и «цифровой» мир. Аналоговый мир обычно относится к любому природному явлению, которое со временем меняет свои свойства. Возьмем, к примеру, температуру наружного воздуха.Мы замечаем, что она довольно медленно меняется в течение дня, и в любой момент мы можем измерить, насколько она горячая или холодная, с помощью простого термометра.

Те же самые изменяющиеся свойства можно наблюдать, измерять и записывать в других природных явлениях, таких как атмосферное давление, скорость ветра, солнечное излучение и т. Д. Если бы вы записывали и графически отображали каждое из вышеуказанных событий в течение 24 часов, вы обратите внимание на одну похожую характеристику: физические свойства каждого явления меняются со временем.

В каждом случае, если вы соедините все точки на графике, результаты всегда будут формировать некоторый тип «аналогового сигнала» (волны), как в следующих примерах:

Задача инженера-электронщика analog – иметь дело со многими из этих тепловых, магнитных, оптических, акустических, биологических, химических или электрических «сигналов» путем разработки соответствующих аналоговых датчиков и схем управления.

Цифровой мир

Цифровая электроника – это совсем другой вид животных.Чем цифровой мир отличается от аналогового? Что ж, в цифровой сфере (т.е. цифровых электронных схемах) важны только два «состояния»: ВКЛ или ВЫКЛ. Например, когда вы включаете выключатель света в ванной, вы знаете, что есть только два возможных положения, в которых он может находиться (да, ВКЛ или ВЫКЛ). Вас не беспокоит то, что через электрическую проводку, подключенную к переключателю света, может проходить 110, 113, 120 или 125 вольт (т. Е. Колеблющийся аналоговый «сигнал» ).

Важно помнить, что включение света не только выполняет некоторую полезную работу (освещает ванную комнату), но также передает некоторую реальную базовую цифровую информацию – что свет был включен, а не выключен. Этот код включения / выключения – это именно то, как работает мир цифровой электроники. Как вы увидите позже, это переключение ВКЛ / ВЫКЛ – это та же логика, которая используется для построения цифровых электронных схем внутри вашего портативного компьютера, устройства GPS и смартфона. Взгляните на Рис. 1 , чтобы вам было ясно различие между аналоговым и цифровым мирами.

РИСУНОК 1.

Рис. 1a – это график, показывающий, как электричество (уровень напряжения) в вашем доме изменяется в течение 12 часов. В какой-то момент в течение 12 часов мы видим, что уровень напряжения в 14:00 составлял 110 вольт. В 16:00 оно изменилось на 120 вольт. В Рис. 1b , с другой стороны, у нас есть выключатель света, который можно включать или выключать в течение дня. Обратите внимание, что на рис. 1b выключатель света был включен в 14:00, а затем выключен в 16:00.Затем он снова был включен в 19:00, а затем выключен в 21:00.

В этом примере не имеет большого значения, какой уровень напряжения присутствует во всей электрической цепи (105 В, 110 В, 115 В, 120 В). Здесь важна «информация», представленная на рис. 1b – независимо от того, был ли переключатель включен или выключен. Это «мгновенное» электрическое переключение ВКЛ / ВЫКЛ обычно называют «цифровым» сигналом.

[Примечание автора: чтобы не сбить вас с толку, но – и это очень важно – цифровые электронные схемы работают на 1.5-15 вольт постоянного тока ( DC ) – не 110 вольт переменного тока ( AC ), который выходит из сетевой розетки в вашем доме. Уровень напряжения переменного тока на рис. 1b использовался только для того, чтобы показать, как выглядит цифровой сигнал (прямоугольная волна) по сравнению с аналоговым сигналом (т. Е. Колеблющаяся волна на рис. , рис. 1а, ).]

Цифровой – Вкл. Или Выкл.

Чтобы увидеть, как выключатель света может передавать цифровую информацию, предположим, что вы сказали другу по телефону, что, если она случайно проезжает мимо вашего дома и замечает, что свет на вашем крыльце выключен, у вас есть компания – не делайте этого. приезжать.Однако, если свет на крыльце включен, она должна зайти. Как видите, этот небольшой «код» позволяет вам использовать один свет для передачи двух сообщений. А теперь давайте продолжим эту идею и воспользуемся двумя источниками света.

Если вы скажете своей подруге, когда она увидит, что свет в спальне выключен, а на крыльце выключен, это означает, что ваши родители все еще дома – так что, опять же, не приходите. Однако, если свет в спальне включен, а свет на крыльце выключен – остановитесь. Кроме того, если она видит, что свет в спальне выключен, а свет на крыльце включен, это означает, что вы встретите ее в магазине пиццы.

Тогда, наконец, если свет в спальне включен, а на крыльце включен, вы встретитесь с ней позже в доме Сью. Обратите внимание, что на этот раз с помощью только «двух» индикаторов (включенных или выключенных) вы передали «четыре» сообщения (см. , рис. 2, ).

РИСУНОК 2.

Здесь возникает вопрос: сколько сообщений вы можете передать своему другу, если вы использовали четыре лампы вместо двух? Посмотрите Рисунок 3 для ответа.

РИСУНОК 3.

Поскольку имеется четыре источника света и только два «состояния» или положения, в которых может находиться переключатель света (ВКЛ или ВЫКЛ), имеется максимум 16 сообщений (2 для 4 ^th power или 2 ⁴ = 2x2x2x2) что вы можете передать своему другу. Очевидно, что с 16 сообщениями вам и вашему другу понадобится список инструкций для декодирования каждой последовательности огней.

Обратите внимание в нашем предыдущем примере, как информация передавалась (передавалась) с помощью простого переключателя света, который был ограничен только двумя положениями или «логическими состояниями» (ВКЛ или ВЫКЛ).Опять же, не имело значения, сколько электричества протекает в цепях освещения крыльца, спальни, гаража или гостиной.

Здесь следует помнить два наиболее важных фактора: были ли огни включены или выключены, и в какой последовательности или позиции свет был включен.

Как видите, цифровая электроника основана на «логике переключения» (ВКЛ или ВЫКЛ). С другой стороны, аналоговая электроника больше связана с колебанием , (постоянно меняющейся) электрической величиной, такой как напряжение и / или ток.При необходимости снова обратитесь к , рис. 1 , чтобы вам было ясно различие между цифровыми и аналоговыми сигналами. Это очень важная концепция для понимания, поэтому не продолжайте читать, пока не проведете различие между аналоговой и цифровой информацией / сигналами.

Двоичная система

В наших предыдущих примерах мы видели, как работает мир цифровой электроники, ограничивая себя двумя состояниями. Двоичная (bi = two) система счисления также имеет дело с двумя состояниями или числами: 1 и 0.Как вы увидите, двоичные числа очень важны и полезны в области цифровой электроники.

Теперь предположим, что мы берем наш предыдущий пример с четырьмя источниками света (, рис. 3, ) и вместо использования кода включения или выключения мы заменяем «1» на «ВКЛ» и «0» на «ВЫКЛ». Рисунок 4 показывает, как выглядит наша диаграмма сообщений после этого изменения.

РИСУНОК 4.

Вам может показаться, что расположение ВКЛ и ВЫКЛ на рис. 3 и расположение 1 и 0 на рис. 4 было выбрано случайным образом.Дело в том, что единицы и нули, которые вы видите на , рис. 4, – это просто способ, которым вы считаете в «двоичном формате». ( Помните, двоичная система счисления основана на числе «два»: 2 ⁰ = 1, 2 ¹ = 2, 2 ² = 4, 2 ³ = 8, 2 ⁴ = 16 и т. Д., А наша десятичная система счисления основана на числе «десять»: 10 ⁰ = 1, 10 ¹ = 10, 10 ² = 100, 10 ³ = 1000, 10 ⁴ = 10000 и т. Д.)

Вот как работает двоичная система счисления:

Например, давайте преобразуем двоичное число 1101 из списка в рис. 4 в его десятичный (основание 10) эквивалент:

В этом примере двоичное число 1101 равно десятичному числу 13.

Из этого примера можно усвоить четыре ключевых момента:

Обратите внимание, как «десятичные» числа 1 , 2 , 4 и 8 «удваиваются» при каждом увеличении степени в двоичной системе счисления (т.е.е., двоичный 2 ⁰ = десятичный 1 ; Двоичный 2 ¹ = Десятичный 2 ; Двоичный 2 ² = Десятичный 4 ; Двоичное 2 ³ = Десятичное 8 и т. Д.).
Обратите внимание, что каждое двоичное число 1 или 0 содержит «позицию» или «вес» в двоичной системе счисления. Другими словами, в цифровом мире 0 так же важен, как и 1.
Обратите внимание, что каждая позиция в двоичной системе счисления равна точному десятичному значению числа (1, 2, 4, 8, 16, 32, 64 и т. Д.).
Обратите внимание, что вы складываете только десятичные числовые значения вместе, если в двоичном числе стоит 1.

Давайте преобразуем еще одно двоичное число в десятичное, прежде чем двигаться дальше. Преобразуйте 1010110 в десятичное число:

Еще раз обратите внимание, что хотя каждый ноль в двоичном числе 1010110 занимает определенное место и очень важен, его десятичное значение игнорируется, когда мы складываем все десятичные числа вместе (всего = 86).

Эти примеры должны дать вам представление о том, как был создан список двоичных чисел в , рис. 4 . Первоначально мы использовали выключатели света ON и OFF для передачи кодированных сообщений (, рис. 3, ). Теперь вместо сообщений мы можем преобразовывать двоичные числа в их десятичный эквивалент.

Если вы спрашиваете себя, какое отношение это имеет к цифровой электронике, вы задали очень важный вопрос. Если вы помните, что мы говорили о цифровой логике (что это логика переключения – ВКЛ или ВЫКЛ), вы, вероятно, увидите, что передача этих двоичных единиц и нулей по электрическому проводу – это просто вопрос «включения» электрического напряжения и ВЫКЛ (пять вольт = 1, ноль вольт = 0).Помните, что с электричеством можно делать только две вещи: можно включить или выключить.

Например, предположим, что мы хотели отправить десятичные числа 72, 69, 76 и 80 с компьютера в одном офисе на компьютер в другом офисе. Все, что нам нужно сделать, это преобразовать каждое десятичное число 72, 69, 76 и 80 в двоичное число, преобразовать эти двоичные единицы и нули в электрический сигнал (пять вольт = 1, ноль вольт = 0), а затем отправить это цифровое код над электрическим проводом (см. Рисунок 5 ).

РИСУНОК 5.

Если вы некоторое время изучите рис. 5 , ответ на ваш первоначальный вопрос (какое отношение имеет двоичная система счисления к цифровой электронике?) Станет очевидным. Рисунок 5 показывает, как десятичные числа 72, 69, 76 и 80 и их двоичный эквивалент преобразуются компьютером в цифровой сигнал (ноль вольт и пять вольт), а затем передаются по электрическому проводу. Цифровая электронная схема внутри компьютера №2 преобразует уровни напряжения (ноль вольт и пять вольт) в двоичные единицы и нули, а затем отображает (ЖК-монитор) эту информацию в буквенно-цифровых символах, чтобы мы могли понять исходное сообщение.

Как вы могли догадаться, числа 72, 69, 76 и 80 в приведенном выше примере были выбраны не с воздуха. Если вы посмотрите любую таблицу Американского стандартного кода обмена информацией (ASCII), вы увидите, что число 72 = H, 69 = E, 76 = L и 80 = P является кодом для слова HELP.

Что важно в этом примере, так это то, что мы можем преобразовать слово HELP в десятичные числа, затем в двоичный код единиц и нулей и, наконец, в цифровые уровни напряжения, которые могут передаваться по электрическому проводу.Просто подумай об этом. Все началось с того, что включил и выключил свет в ванной!

Теперь, когда вы знаете, что цифровой мир управляется двоичными числами (1 или 0), пришло время использовать эту двоичную систему для создания некоторых цифровых логических вентилей. Вы действительно увидите, насколько важны двоичные числа для цифровых схем, прочитав следующий раздел.

Цифровые логические ворота: строительные блоки всех цифровых электронных схем

Понимание цифровых логических вентилей – важная предпосылка для изучения того, как работают все цифровые электронные схемы.По сути, существует три типа электронных «логических вентилей»: вентиль И, вентиль ИЛИ и вентиль НЕ. (На самом деле существует еще несколько типов вентилей, которые мы рассмотрим позже в этой статье.) Просто помните, логические вентили являются основными строительными блоками всех цифровых логических схем.

Ворота И

Давайте сначала проанализируем логический элемент И на рис. 6 . Взгляните на логический символ логического элемента И на рис. 6а .

РИСУНОК 6.

Имеет два входа (A и B) и один выход (X). Элемент И работает (логически) следующим образом: если на входе A имеется двоичная 1, а на входе B – двоичная 1, двоичный выход (X) будет равен 1. Если на входе A есть 1, а на входе B – 0, выход (X) равен 0. В свою очередь, если вход B имеет 1, а вход A имеет 0, то выход (X) будет 0. Наконец, если вход A имеет 0, а вход B имеет 0, то output (X) также будет 0.

Хорошо, давайте построим электрическую схему, которая имитирует логику логического элемента И.Взгляните на электрическую схему Рисунок 6b . У нас есть батарея на девять вольт, лампочка и два переключателя. Обратите внимание, что если мы замкнем выключатель A, свет НЕ загорится, потому что выключатель B разомкнут (т.е. электрический свет не подключен к батарее).

Если переключатель B замкнут, а переключатель A разомкнут, свет остается выключенным. Обратите внимание, что свет загорается только тогда, когда переключатель A «И» B замкнут.

Теперь взгляните на , рис. 7b, , и вы должны увидеть, что наш старый друг логический вентиль И работает так же, как наша электрическая световая цепь на , рис. 7а, .Вы можете увидеть этот очень важный момент, посмотрев на две логические таблицы на рис. 7 .

Обратите внимание на рис. 7b , что единицы (1) в таблице логической истинности совпадают (в том же положении) с «замкнутыми» переключателями в таблице истинности схемы рис. 7a .

РИСУНОК 7.

Важно, чтобы вы понимали, как связаны логический символ логического элемента И на рис. 7b и электрическая схема на рис. 7а .Обратите внимание на Рисунок 7b , как двоичная система счисления играет здесь роль. Единственный выход времени (X), равный 1, – это когда оба входа A и B также равны 1. Единственный раз, когда свет включается в , рис. 7a , – это когда оба переключателя A и B замкнуты.

Хорошо, вопрос здесь в том, что произойдет, если мы заменим единицы и нули на рис. 7 на цифровые электронные сигналы (1 = пять вольт, 0 = ноль вольт)? Посмотрите на , рисунок 8, , и вы получите ответ на этот вопрос.

РИСУНОК 8.

Глядя на , рис. 8c , вы можете увидеть, что, хотя мы изменили двоичные единицы и нули на пять вольт и ноль вольт, таблицы истинности все те же. Это означает, что электрическая схема с двумя переключателями A и B (, рис. 8a, ) работает аналогично логической таблице истинности логического элемента И на рис. , рис. 8b, и , рис. 8c, .

Вы, вероятно, спрашиваете себя: «Нужны ли мне все эти таблицы истинности, логические элементы И и логика 1 и 0 для понимания цифровой электроники?» Ответ на этот вопрос – ДА! Весь цифровой мир основан на знании того, какими будут входные и выходные значения для любой цифровой логической схемы.

Например, посмотрите на интегральную схему (ИС) 7400 на рис. . Вы можете приобрести эту ИС в Интернете и убедиться, что она работает точно так же, как построенные нами таблицы истинности.

РИСУНОК 9.

В микросхему 7400 встроен тот же логический элемент И, о котором мы говорили в , рис. 7, и , рис. 8, .

Если вы подключите 7400 IC, как показано на рис. 9 , вы можете доказать себе, что таблица истинности для пяти и нулевого вольт на рис. 8c верна.Что еще более важно, вы увидите, как цифровые логические вентили и таблицы истинности используются для создания цифровых электронных схем.

Теперь, когда вы понимаете, как работает логический элемент И, давайте воспользуемся этим электронным логическим элементом И в реальном приложении. Допустим, у нас есть лифт с двумя дверями, которые обязательно нужно закрыть, прежде чем лифт начнет подниматься или опускаться. У каждой двери есть электрический выключатель (A и B), который подключен к логическому элементу AND.

Выход (X) логического элемента И подключен к электродвигателю, который перемещает лифт вверх или вниз.

Наша задача – убедиться, что лифт может двигаться только тогда, когда обе двери полностью закрыты. Давайте создадим таблицу истинности для того, что мы хотим, чтобы лифт делал (см. , рис. 10, ). Обратите внимание на то, как мы создали таблицу на рис. , рис. 10 . Мы определили, как должен реагировать выход (X) (двигатель включен или двигатель выключен) в зависимости от положения каждой двери (ОТКРЫТА или ЗАКРЫТА).

РИСУНОК 10.

Также обратите внимание (, рис. 11, ), что таблица истинности лифта такая же, как таблица истинности логического элемента И и наша логическая (двоичная) таблица истинности.

РИСУНОК 11.

К настоящему времени должно быть очевидно, что логический элемент И и его таблица истинности могут использоваться для проектирования и создания цифровых электронных схем, которые имеют практическое применение в реальном мире.

Теперь давайте посмотрим на наши следующие ворота: ворота «ИЛИ».

Ворота OR

Как упоминалось ранее, логический элемент И является одним из трех основных логических элементов (И, ИЛИ, НЕ). Давайте посмотрим, чем вентиль OR отличается от логического элемента AND.

Глядя на электрическую схему на рис. 12 , вы заметите, что два переключателя (A, B) соединены параллельно.Обратите внимание, что если переключатель A ЗАКРЫТ, он замкнет электрическую цепь и загорится свет (X).

РИСУНОК 12.

Теперь, если переключатель A ОТКРЫТ, а переключатель B ЗАКРЫТ, свет также включится. Если оба переключателя ЗАКРЫТЫ, свет также включен. Обратите внимание, что пока один переключатель (A ИЛИ B) ЗАКРЫТ, свет будет включаться.

Свет гаснет только тогда, когда оба переключателя ОТКРЫТЫ. Изучите , рис. 12, , пока не увидите, как таблица истинности ворот OR совпадает с таблицей истинности электрических цепей.

Давайте посмотрим на практическое применение ворот OR. Схема ворот OR может использоваться для защиты дома от грабителя. Рисунок 13 показывает простую систему сигнализации, основанную на вентиле OR.

РИСУНОК 13.

На рис. 13b легко увидеть, что если выключатель спальни (A) ЗАКРЫТ (окно открыто) «ИЛИ», выключатель окна подвала (B) закрыт, то сработает сигнал тревоги. Обратите внимание в таблице истинности логического элемента ИЛИ (, рис. 13b, ), что переключатель A OR B может включить сигнализацию.

Как видите, логическая таблица истинности логического элемента ИЛИ может использоваться для разработки системы охранной сигнализации точно так же, как логическая таблица истинности логического элемента И использовалась для запуска и остановки двигателя лифта.

Теперь взгляните на , рис. 14, , чтобы увидеть разницу между логическим элементом И и логическим элементом ИЛИ.

РИСУНОК 14.

Обратите внимание на основное различие между логическим элементом ИЛИ и логическим элементом И. Логический элемент ИЛИ будет выводить единицу (1), когда любой вход A ИЛИ B равен 1, тогда как логический элемент И будет выводить 1 только тогда, когда оба входа A И B равны 1.

Ворота НЕ (инвертор)

Давайте обратим наше внимание на последний из трех основных ворот: ворота НЕ (см. , рис. 15, ).

РИСУНОК 15.

Элемент НЕ обычно называют «инвертором». Он имеет один вход (A) и один выход (X). Если вход элемента НЕ (A) равен 1, на выходе будет 0. И наоборот, если вход элемента НЕ (A) равен 0, то на выходе будет 1. Теперь вы можете понять, почему они называют вентиль НЕ инвертором.”

Чтобы лучше понять, как работает вентиль НЕ, взгляните на электрическую схему на рис. 15 . Здесь, если переключатель A ЗАКРЫТ, электрический ток от батареи будет обходить свет; следовательно, свет не будет иметь достаточного тока для включения.

Однако, если переключатель (A) ОТКРЫТ, свет останется включенным, потому что электрический ток проходит мимо переключателя и направляется прямо к свету. Логический элемент НЕ широко используется в цифровых логических схемах.

Далее вы увидите, как он может изменить ворота И и ИЛИ на ворота И-НЕ и НЕ-ИЛИ.

Опись

Пришло время проанализировать, сколько мы уже узнали. Возможно, вы этого не осознавали, но некоторые очень важные концепции были затронуты. Вы начали с простого настенного выключателя в ванной, который включал или выключал свет. Вы преобразовали эти цифровые сигналы включения и выключения в двоичный код 1 и 0. Вы узнали о логических элементах И, ИЛИ и НЕ и связанных с ними таблицах истинности.

Наконец, вы преобразовали все эти единицы и нули в электрические схемы для реальных приложений. Хорошая работа!

Ворота NAND, NOR, EX-OR и EX-NOR

В предыдущем разделе я упоминал, насколько важен вентиль НЕ в цифровых электронных схемах. Теперь вы увидите, как вентиль НЕ используется для создания вентилей И-НЕ и ИЛИ-НЕ. Кроме того, мы рассмотрим два других специальных входа, используемых во всем мире цифровой электроники: ворота EX-OR и EX-NOR.

Ворота NAND

Начнем с логического элемента И-НЕ.Логический элемент И-НЕ ( N, или И ) представляет собой логический элемент И с логическим элементом НЕ (инвертор), подключенным к его выходу (см. , рис. 16, ).

РИСУНОК 16.

Обратите внимание на кружок на выходе (X) логического элемента И-НЕ в Рисунок 16 . Этот кружок является стандартным символом в цифровой электронике для обозначения инверсии (НЕ = ИНВЕРТОР). По логике он равен логическому элементу НЕ с его символами треугольника и круга.

Итак, с этого момента каждый раз, когда вы видите кружок на входе или выходе затвора, это означает, что вы должны инвертировать сигнал или логику (от 1 до 0, от 0 до 1, от нуля вольт до пяти вольт, пяти вольт до нуля. вольт, от высокого до низкого, от низкого до высокого).

Как вы можете видеть на рис. 16 , таблица истинности показывает, что единственный раз, когда выход логического элемента И-НЕ будет 0 (или НИЗКИЙ), – это когда оба входа A и B имеют значение 1 (ВЫСОКИЙ). Также обратите внимание на таблицу истинности, что любой 0 (LOW) на входе A или B сделает выход (X) равным 1. Другими словами, любой 0 (LOW) на входе логического элемента NAND даст 1 (HIGH). на выходе (X).

Так же, как вентили И и ИЛИ, рассмотренные ранее, давайте использовать вентиль И-НЕ в практических приложениях реального мира.Предположим, мы построили электрическую схему затвора И-НЕ, которая контролирует два наружных фонаря безопасности, так что если любой из них погаснет (ВЫКЛ), сработает сигнал тревоги. Еще раз, первое, что мы делаем, это настраиваем таблицу истинности для нашей световой цепи (см. Рисунок 17 ).

РИСУНОК 17.

Еще раз обратите внимание на таблицу истинности, что если «либо» индикатор A или индикатор B погаснет, включится сигнализация. Вы также должны увидеть, что будильник останется ВЫКЛЮЧЕННЫМ только до тех пор, пока горят оба индикатора.

Невозможно переоценить важность таблиц истинности при проектировании электронных схем. В любой цифровой электронной схеме, в которой используются логические элементы (И, НЕ, ИЛИ, И-НЕ и т. Д.), Вы должны определить, что должна делать схема. Очевидно, лучший способ увидеть, какой будет логика ввода и вывода вашей схемы, – это создать таблицу истинности.

Давайте перейдем к нашим следующим воротам: воротам NOR.

Ворота NOR

Еще раз, таблица истинности на рис. 18 говорит нам, как именно работает вентиль ИЛИ-НЕ.Единственный раз, когда выход (X) логического элемента ИЛИ-НЕ будет равен 1, – это когда «оба» входа A и B равны 0. Другой способ сказать, что это когда оба входа в вентиль ИЛИ-НЕ равны 0 (НИЗКИЙ), выход ворота NOR будут 1 (ВЫСОКИЙ).

РИСУНОК 18.

Конечно, как и другие наши врата, есть еще один способ взглянуть на таблицу истинности. Обратите внимание, что если «любой» вход A или B в вентиль ИЛИ-НЕ равен 1, выход (X) равен 0. Мы также можем сказать, что любая 1 на любом входе (A или B) вентиля ИЛИ-НЕ даст 0 (LOW) на его выходе (X).

Давайте перейдем к следующим воротам: EX-OR.

Ворота EX-OR

Посмотрите на , рис. 19c , и вы заметите, что свет загорается, когда переключатель A находится в положении 0, а переключатель B – в положении 1. Обратное также верно.

РИСУНОК 19.

Цепь замыкается (горит индикатор), когда переключатель B находится в положении 0, а переключатель A находится в положении 1. Свет никогда не загорится, если переключатель A или переключатель B находятся в одном и том же положении (1, 1 или 0, 0).

Можно сказать по-другому: либо 1, либо 0, но не оба сразу. А теперь поговорим о воротах EX-NOR.

Ворота EX-NOR

Как вы можете видеть на Рис. 20c , свет будет включаться только тогда, когда переключатель A и переключатель B находятся в положении 1 или 0.

РИСУНОК 20.

Другими словами, у вас есть выход (светится), когда «оба» переключателя A и переключатель B находятся в одном положении, но не когда A и B равны 1, 0 или 0, 1.

Можно сказать так: и то и другое, но не то и другое, или .

Вентили EX-OR и EX-NOR широко используются в цифровых схемах. Одно из применений EX-NOR, которое довольно часто используется в коммуникациях, – это проверка равенства двух двоичных чисел.

Помните, мы можем преобразовать двоичные числа в десятичные и с помощью вентилей EX-NOR сравнивать два десятичных числа, сравнивая их двоичный эквивалент.

Например, если нам нужно сравнить два двоичных числа, таких как 10 и 01, чтобы убедиться, что они равны, мы могли бы использовать схему затвора EX-NOR на , рис. 21, .

РИСУНОК 21.

Двоичные 1, 0 и 0, 1, представленные на входах обоих вентилей EX-NOR, создают 0 на выходе логического элемента AND. Следовательно, 1, 0 и 0, 1 не равны двоичным числам.

Теперь попробуйте 1, 0 и 1, 0 на входах обоих вентилей EX-NOR. Выходной сигнал логического элемента И будет равен 1, тем самым сигнализируя, что оба двоичных числа равны.

Ну вот и все. Надеюсь, вам понравилось узнавать о цифровом мире. NV

Цифровые схемы
– обзор
Цифровые схемы бывают нескольких разновидностей, но одним из самых основных и важных типов является вентиль , который используется для управления действиями, а не только для подсчета. Более чем за 100 лет до того, как была создана цифровая электроника, английский математик Джордж Буль доказал, что все утверждения человеческой логики могут быть выражены комбинациями трех правил, которые он назвал И, ИЛИ и НЕ.Эта логическая система теперь известна как Boolean logic . Позже мы увидим, как эти вентили также можно использовать для простых арифметических действий.
Определение
Затвор в цифровой электронике означает схему, выход которой равен 1 только для некоторой указанной комбинации входов. Этот тип схемы иногда называют комбинационной схемой .
Примечание
Не путайте это с аналоговой схемой затвора , которая включает или выключает аналоговую форму волны в зависимости от состояния стробирующего входного сигнала.
Важность всего этого заключается в том, что, если мы можем обеспечить действия цифрового логического элемента, соответствующие этим трем правилам И, ИЛИ и НЕ, мы сможем построить схему, которая будет выдавать 1 выход для любого набора логических правил. Например, если мы хотим, чтобы электродвигатель включался, когда крышка опущена, переключатель поднят, а таймер достиг нуля или когда нажат переключатель блокировки, то этот набор правил может быть выражен в терминах И, ИЛИ, и НЕ, и ворота или набор ворот могут выполнять действие.
На рисунке 10.1 показаны символы, которые используются для трех основных типов вентилей, вентилей И, ИЛИ и НЕ, с использованием вентилей с двумя входами в примере. Действие этих ворот будет подробно обсуждено в ближайшее время, но на данный момент обратите внимание, что маленький кружок, показанный в символе НЕ, используется для обозначения инверсии, преобразования 1 в 0 или 0 в 1. Мы можем комбинировать другие базовые символы с символом НЕ круговой символ для обозначения других действий ворот. Ранние цифровые интегральные схемы (ИС) обычно содержали четыре логических элемента одного типа на микросхему, но современное электронное оборудование с большей вероятностью будет использовать микросхемы, изготовленные на заказ, со всеми логическими элементами и их соединениями, сформированными в одном процессе с использованием тысяч или миллионов ворота на одной микросхеме.
Рисунок 10.1. Символы ворот для основных действий И, ИЛИ и НЕ. Эти символы используются во всем мире, и на этом чертеже показаны два варианта символа ИЛИ.
Еще раз, это делает более полезным отображение блок-схем, а не деталей схемы затвора. Схема схемы затвора будет состоять из большого количества символов затвора с соединительными линиями, так что выход затвора будет связан с одним или несколькими другими входами затвора. При условии, что мы знаем, что делает каждый базовый тип ворот, мы можем проанализировать действие полных схем ворот.В этой книге нас больше интересуют блок-схемы, чем схемы затворов, но некоторые знания схем затворов полезны, и в любом случае они по духу ближе к блок-схемам, чем к принципиальным схемам.
Сводка
Логические схемы существуют для выполнения набора логических действий, например, используемых для управления стиральными машинами, приводами магнитофонов, компьютерными дисководами, системами безопасности и множеством производственных контрольных действий. Простые арифметические действия также можно выполнять с помощью логических схем.Все логические действия, какими бы сложными они ни были, могут быть проанализированы в простые действия, которые называются И, ИЛИ и НЕ, так что схемы, называемые вентилями, которые выполняют такие действия, являются основой логических схем.
Примечание
Помните, что ИС классифицируются как интеграция среднего размера (MSI), интеграция большого размера (LSI), интеграция очень большого размера (VLSI) и т. Д. По количеству эквивалентных схем затвора на одном кристалле. .
Определение
Действие любого логического элемента может быть выражено в таблице истинности .Это просто таблица, в которой показаны все возможные входы для логического элемента и выход для каждого набора входов. Помните, что каждый вход может быть только 0 или 1, так что каждый вход дает два возможных выхода. Общее количество выходов равно 2 ⁿ , где n – количество входов.
Например, если у логического элемента четыре входа, то количество возможностей равно 2 ⁴ = 16, а его таблица истинности будет состоять из 16 строк. Для многих таблиц истинности существует только один результат, который отличается от остальных, и легче запомнить, какой именно, чем пытаться запомнить всю таблицу истинности.
Примечание
Таблицы истинности – это самый простой способ показать, что делает маломасштабный вентиль или вентильная схема, но они невероятно неуклюжи, когда мы пытаемся использовать их на сложных вентилях с большим количеством входов. Более полезный для профессионального использования метод называется Boolean algebra , но, как и другие математические методы, он выходит за рамки этой книги. Существуют компьютерные программы, которые анализируют действие схемы вентилей с помощью булевой алгебры.
Рисунок 10.2 показаны таблицы истинности для основных вентилей И, ИЛИ и НЕ с двумя входами. Из них вентиль НЕ является простым, с одним входом и одним выходом. Его действие аналогично логическому инвертору. Если вход равен 0, то выход не равен 0, а равен 1. Если вход равен 1, то выход не равен 1, что равно 0. Два других типа вентилей допускают более одного входа, и в примерах показаны два входа, самый распространенный номер. Действие логического элемента И состоит в том, чтобы выдавать 1 на выходе только тогда, когда оба входа равны 1, и 0 на выходе для любой другой комбинации.Действие логического элемента ИЛИ состоит в том, чтобы выдавать на выходе 0, когда каждый вход равен 0, и 1 для любой другой комбинации входов. Те же аргументы применимы к воротам с более чем двумя входами.
Рисунок 10.2. Таблицы правды для ворот. Логические элементы «И» и «ИЛИ» показаны в виде двух входов.
Сводка
Таблица истинности – это простой, но неуклюжий способ показать, каким будет выход логического элемента или логической схемы для каждой и каждой возможной комбинации входов. Альтернативой является использование булевой алгебры, процесса, который значительно упрощается компьютерными программами, выполняющими анализ схем вентилей.
Анализ вентильных систем
Схема, составленная путем соединения нескольких стандартных вентилей, имеющая несколько входов и выходов, может быть проанализирована, чтобы определить ее действие. Этот анализ может быть выполнен путем составления таблиц истинности или с помощью метода, называемого булевой алгеброй. Метод таблицы истинности проще, но утомительнее, чем метод булевой алгебры, который не рассматривается в этой книге. Метод анализа по таблице истинности можно свести к нескольким правилам.
1.
Обозначьте каждый вход схемы (A, B, C), а также каждую точку, где выход одного элемента соединен со входом другого элемента, используя разные буквы для каждой точки. Обозначьте окончательный результат как Q.
2.
Составьте пустую таблицу истинности, используя по одному столбцу для каждой выделенной буквы и с 2 строками ⁿ , где n – число сигнальных входов в схему.
3.
Запишите все возможные комбинации входов.Это проще всего сделать, начав с 0000 и продолжив в виде двоичного счета (0001, 0010, 0011, 0100, 0101) до входа, который полностью состоит из единиц.
4.
Зная таблицы истинности для стандартных вентилей, запишите логические состояния (0 или 1) для выходов вентилей на входах в каждой строке таблицы истинности.
5.
Первый набор выходов теперь будет входами для следующего набора вентилей, так что их выходы могут быть записаны в таблицу истинности.
6.
Продолжайте так, пока таблица истинности не будет заполнена.
В качестве примера на рисунке 10.6 показана логическая схема электронного кодового замка. Это простая конструкция с четырьмя основными входами и, следовательно, с 16 комбинациями, игнорируя вход разблокировки E. Замок устроен так, что только правильная комбинация входов открывает замок, а любая другая комбинация вызывает звуковой сигнал, так что ее нельзя решить, пробуя каждую возможную комбинацию.
Рисунок 10.6. Схема затвора, используемая в качестве примера для анализа с использованием таблиц истинности
Входы A, B, C и D поступают от переключателей, которые должны быть установлены в соответствии с шаблоном, необходимым для открытия замка. Когда эти переключатели установлены, нажатие кнопки E вызовет разблокировку двери (Q = 1), если комбинация правильная, или вызовет звуковой сигнал (X = 1), если комбинация неправильная. Чтобы проанализировать эту цифровую схему, пометьте входы, как показано на рисунке 10.7.
Рисунок 10.7. Таблица с заполненными входными данными и промежуточными значениями, предоставленными для
. Важными входными данными являются A, B, C и D, потому что E используется только после того, как все остальные были установлены в правильный образец. Промежуточные точки, где выход одного элемента управляет входом другого элемента, теперь можно обозначить буквами F, G, H, I и J, как показано на рисунке 10.7. Поскольку есть четыре основных входа, потребуется 16 строк таблицы истинности.
Для каждой использованной буквы будет по одному столбцу, но столбец для входа E можно разместить рядом с столбцом Q, потому что вход E используется только тогда, когда определяется выход Q (после того, как все остальные входы имеют был установлен).Логическое напряжение E можно записать как 1 в каждой строке, потому что блокировка сработает только тогда, когда E установлен в 1 (кнопка активации нажата). Все возможные входы A, B, C, D теперь могут быть записаны, начиная с 0000 и проходя двоичный счет до 1111, всего 16 строк в таблице истинности на рисунке 10.7.
Теперь мы можем проанализировать схему (рисунок 10.8). Входы A и B являются входами логического элемента И-НЕ. логика которого заключается в том, что выход равен 0 только тогда, когда оба входа равны 1. Столбец F, который является выходом этого элемента, поэтому имеет 0, введенный для последних четырех строк таблицы, когда оба A и B находятся на логической 1 , и 1, введенная для всех остальных строк. Столбец G является просто инверсией столбца C, поэтому теперь в него можно записывать значения.
Рисунок 10.8. Таблица заполнена с использованием таблиц истинности для вентилей для заполнения промежуточных значений
Значения в столбце H являются выходами другого логического элемента И-НЕ, входами которого являются G и D, так что выход равен 0 только при G = 1 и D = 1, как показано. Значения в столбцах F и H теперь являются входами логического элемента ИЛИ-НЕ, выходы которого записаны в столбец I.
Логика элемента ИЛИ-НЕ состоит в том, что выход равен 1 только тогда, когда оба выхода равны 0, и это происходит только в одна строка таблицы, когда A = 1, B = 1, C = 0, D = 1.Когда I = 1 и E = 1, выход логического элемента И дает Q = 1, так что замок открывается. Для любой другой комбинации входов в A, B, C и D значение Q равно 0, а значение в J равно 1 (из-за инвертора), а комбинация E = 1, J = 1 вызывает X = 1 , бить тревогу, но держать дверь запертой. Кроме того, нажатие переключателя E до того, как будут установлены какие-либо другие, также вызовет срабатывание будильника. Действие этого набора ворот – открывать замок только при правильной комбинации входов и подавать сигнал тревоги при неправильной комбинации.На рис. 10.8 показано окончательное состояние таблицы истинности.
Сводка
Любую схему логического элемента можно проанализировать, составив таблицу истинности или набор таблиц истинности. Хотя это может быть утомительно, когда схема имеет большое количество входов, это проще, чем альтернативный метод булевой алгебры (хотя это может быть выполнено с помощью компьютерного приложения). Этот метод основан на использовании буквенного обозначения для идентификации всех входов, выходов и промежуточных точек и поэтапного составления таблицы истинности, начиная со всех возможных комбинаций на входах.
Что такое цифровая логика? – Основы схемотехники
Цифровая логика или логическая логика представляет сигналы и последовательности в цифровой схеме посредством чисел. Это система правил, которая позволяет нам принимать сложные решения на основе простых вопросов «да / нет». Он становится основой цифровых вычислений и объясняет, как схемы и оборудование взаимодействуют внутри компьютера. Цифровая логика – это основа вычислений и многих других электронных устройств, а также систем управления в этом постоянно развивающемся цифровом мире.Он создает реализацию компьютерных операций, манипулируя двоичными значениями с помощью технологии печатных плат, которая использует схемы и логические вентили. Большинство электронных устройств, включая калькуляторы, компьютеры, видеоигры и часы, содержат эту функцию. Знание цифровой логики может быть преимуществом для многих людей, которые работают с компьютерами и технологиями, например, инженеров и техников.
Логические ворота
Логические вентили используются в компьютере для преобразования единиц и нулей из входных проводов.Он принимает входные данные, а выходными данными являются результаты, основанные на их состоянии. Логический вентиль – это небольшая транзисторная схема, которая является частью различных форм в интегральной схеме. Каждый тип ворот имеет один или обычно два входа и один выход.
Цифровая электроника зависит от работы всего семи типов логических вентилей, показанных в таблице ниже.
Семь типов логических вентилей
Таблица истинности
Таблица истинности используется в математическом представлении для представления всех комбинаций значений для входов и соответствующих им выходов.Он используется в логических задачах, таких как логическая алгебра и электронные схемы. Таблица истинности показывает все возможные результаты в данном сценарии, которые являются фактическими. Он также показывает результаты логического выражения с использованием отдельных столбцов для каждой переменной и соответствующего ей вывода. Столбцы для значений входов перечислены слева, а выходные данные – справа.
Таблица истинности для логического элемента И с 2 входами
Логические вентили на транзисторах
Логические вентили построены на транзисторах.Диод база-эмиттер должен включиться для достижения насыщения, в то время как напряжение коллектора относительно эмиттера может быть близким к нулю.
И Ворота
Схема логического элемента И на транзисторах
Транзисторы должны быть включены последовательно, и оба транзистора должны быть в проводящем состоянии, чтобы на выходе был высокий уровень.
OR Выход
Схема логического элемента ИЛИ на транзисторах
Транзисторы должны быть включены параллельно, потому что, если какой-либо из транзисторов является проводящим, на выходе будет высокий уровень.
NAND Gate
Схема затвора И-НЕ на транзисторах
Транзисторы должны быть включены последовательно, даже если выход выше них. Выход должен быть близок к потенциалу земли, поскольку он всегда высокий, если только входы A и B не имеют высокого уровня.
NOR Ворота
Схема двойного транзистора NOR Gate

Транзисторы должны быть параллельны выходу над ними, чтобы на выходе был низкий уровень, когда один или оба входа имеют высокий уровень.
Схема одиночного транзистора NOR Gate

Если один или оба входа имеют высокий уровень, выход будет низким; поэтому используется только один транзистор, а два входа подключены к его базе через резисторы.
Комбинационная логика
Комбинационная логика – это цифровая логика, реализующая логические схемы, в которых выход является функцией только текущего входа. Логическая функция текущего состояния входа, логический «0» или логическая «1», в любой данный момент времени определяет выходы комбинационной логики.
Способы определения функции комбинационной логической схемы
Логическое выражение
Это алгебраическое выражение, показывающее работу логической схемы для каждой входной переменной.
Логическая схема
Он показывает проводку и соединения каждого логического элемента, которые представлены определенным графическим символом.
Логическая диаграмма булевого уравнения
Таблица истинности
Он определяет функцию логического элемента, используя список, который показывает все выходные состояния в табличной форме для каждой возможной комбинации входной переменной.
Таблица истинности булевого уравнения
Что такое карта Карно?
Карта Карно используется для упрощения логических выражений. Он сообщает вам, какой выход ваша схема будет давать вашим входам. Карта Карно сочетает в себе иллюстрации с общими факторами и, следовательно, устраняет нежелательные переменные.
Карта Карно имеет правила, которым мы должны следовать для упрощения выражений путем группирования ячеек, содержащих логическую «1».
Группа не может иметь логический «0». Значит, это неправильно:
Вместо этого должно быть:
Группы не могут быть диагональными, но могут быть горизонтальными или вертикальными. Значит, это неправильно:
Вместо этого должно быть:
Группы должны содержать 1, 2, 4, 8 или в целом 2 ⁿ ячеек.
То есть, если n = 1, группа будет содержать две единицы, поскольку 2 ¹ = 2.
Если n = 2, группа будет содержать четыре единицы, поскольку 2 ² = 4.Следовательно, это неверно:
K-карта, показывающая группу из 3 K-карта, показывающая группу 5
Вместо этого они могут быть:
K-карта, показывающая группу 2 K-карта, показывающая группу 4
Убедитесь, что каждая группа должна быть как можно больше. Значит, это неправильно:
Примечание. Он не нарушил никаких логических законов, но он не является достаточно минимальным. Так и должно быть:
Убедитесь, что каждая ячейка, содержащая 1 , должна входить хотя бы в одну группу.
Группы могут перекрываться.
K-карта с перекрывающимися группами K-карта без перекрывающихся групп
Группы могут вращаться вокруг стола. Верхняя ячейка в столбце может быть сгруппирована с нижней ячейкой, а крайняя левая ячейка в строке может быть сгруппирована с самой правой ячейкой.
Убедитесь, что существует как можно меньше групп без нарушения каких-либо предыдущих правил. Следовательно, это неправильно:
Вместо этого должно быть:

Чтобы прояснить все, вот краткое изложение правил для карты Карно:
В группе нельзя использовать нули.
Никакие диагонали не допускаются.
Только мощность 2-х ячеек в каждой группе.
Группы должны быть максимально большими.
Каждая логическая «1» должна быть хотя бы в одной группе.
Перекрытие допускается.
Допускается наматывание.
Как можно меньше групп.

цифровых схем Elemental | Renesas
Введение в цифровые схемы: 1 из 3
В следующих трех сессиях мы рассмотрим цифровые схемы.Сегодня мы рассмотрим концепцию цифровых технологий и рассмотрим конструкцию некоторых основных цифровых схем.
Аналоговые и цифровые: в чем разница?
Температура воздуха, громкость звука, сила света – в природе все эти величины плавно и непрерывно изменяются в определенном диапазоне. Такая величина называется «аналоговой» величиной.
Сегодняшние компьютеры, напротив, работают с дискретными величинами. Эти дискретные величины называются «цифровыми» значениями.Если аналоговое измерение представляет собой плавную кривую, которая «выглядит как» измеряемое свойство, цифровые измерения представляют собой серию прерывистых уровней.
Можно сказать иначе: аналоговые значения – это действительные числа, а цифровые значения – целые. Вещественные числа могут представлять любую точку на числовой строке, тогда как целые числа ограничиваются выражением тех особых точек, равномерно расположенных на линии.
Аналоговая схема работает с аналоговыми сигналами, где значения изменяются непрерывно. Цифровая схема работает с цифровыми сигналами, где все значения дискретны.
Рисунок 1: Аналоговый и цифровой
Чтобы ввести аналоговую информацию природы в цифровые схемы, сначала необходимо оцифровать информацию, то есть преобразовать аналоговый сигнал в цифровой. Аналогово-цифровой (A / D) преобразователь дискретизирует аналоговый сигнал (считывает значение через заданный интервал времени) и преобразует каждое показание в соответствующее двоичное число (значение с основанием 2, выраженное в нулях и единицах).
Поскольку преобразователь преобразует аналоговый сигнал, который может принимать любое дробное значение, в цифровой сигнал, который может принимать только дискретные значения, некоторая информация будет потеряна.Каждое аналоговое показание должно быть округлено до ближайшего цифрового значения в большую или меньшую сторону. А поскольку преобразователь считывает аналоговый сигнал только с определенным интервалом, он теряет аналоговую информацию, которая существует между этими интервалами.
В результате цифровые значения являются только приближением аналогового сигнала и всегда содержат ошибку преобразования. Однако эту ошибку можно уменьшить, сократив интервал между измерениями и используя более точные (то есть с большей длиной в битах) цифровые значения.
Но какой смысл преобразовывать плавный аналоговый сигнал в прерывистый и неточный ряд чисел? Есть как минимум два преимущества: цифровые сигналы гораздо более устойчивы к шумам; и потому, что современные компьютеры работают только с цифровыми ценностями.
Современные мощные микроконтроллеры способны быстро обрабатывать большие объемы цифровой информации. Эти микроконтроллеры используют цифровые схемы, которые в полной мере используют тот факт, что, в отличие от аналоговых сигналов, цифровые сигналы не теряют информацию во время передачи и воспроизведения.
Двоичные числа
Цифровые сигналы обычно выражают значения с использованием двоичной (также называемой «основанием 2») нумерации, где каждое число записывается с использованием только нулей и единиц. В частности, крайняя правая цифра числа представляет 2 ⁰, следующая цифра слева представляет 2 ¹, затем 2 ² и т. Д. Таким образом, четырехзначное двоичное число может представлять 16 значений, начиная с 0 на 15, как вы можете видеть в Таблице 1. Значения выше 15 могут быть представлены путем добавления дополнительных цифр, если это необходимо.
Одним из преимуществ обработки цифровых сигналов как двоичных является то, что легко создавать логические схемы с двоичным выходом: схемы либо включены, либо выключены, что соответствует единицам и нулям числовых двоичных чисел. Состояния ВКЛ и ВЫКЛ физически реализуются как два состояния напряжения: высокое («H») и низкое («L»). В типичной КМОП ИС с источником питания 5 В, «L» обозначает напряжение от 0 до 1,35 В, а «H» обозначает напряжение от 3,15 В и выше. Поскольку 0 и 1 соответствуют этим относительно широким диапазонам напряжения, схема выдает правильный выходной сигнал даже при умеренном уровне шума в линии.
Десятичное двоичный
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
Таблица 1: Двоичное представление десятичных значений
Цифровые схемы = Логические схемы
Цифровая схема, также называемая логической схемой, выполняет логическую операцию.Три элементарные схемы – И, ИЛИ и НЕ – могут быть объединены для построения любой желаемой логической операции.
Логические схемы выражаются с помощью логических выражений и символов схем. (Здесь мы используем символы MIL, хотя вместо них могут использоваться символы JIS или другие символы.) Таблица истинности показывает, каким будет выход схемы для всех комбинаций входов.
Цепь И, Цепь последовательного соединения
Схема И, также называемая схемой логического произведения, принимает два входа и выводит 1, если оба входа равны 1, и 0 в противном случае.
Логическое выражение AND
Записывается с использованием оператора “・”. Пример: Y = A ・ B
И обозначение цепи
Таблица истинности
А B Y
0 0 0
0 1 0
1 0 0
1 1 1
Давайте посмотрим, как работает схема И.На рисунке 2 показана схема И, содержащая два переключателя (SW A и SW B) и светодиодный индикатор. Обратите внимание:
SW A включен, если вход A равен 1; SW A выключен, если вход A равен 0.
SW B включен, если вход B равен 1; SW B выключен, если вход B равен 0.
Светодиод Y горит (горит), если выход Y равен 1; Светодиод Y не горит (не горит), если выход Y равен 0
Рисунок 2: Схема AND
Эта схема AND работает следующим образом.
Если переключатели SW A и B включены, то светодиод Y горит (горит).
Если один переключатель включен, а другой выключен, светодиод Y не горит (темный).
Если оба переключателя выключены, светодиод Y выключен (темный).
Базовые логические схемы также называются вентилями. Обратите внимание, что вы можете контролировать значение выхода, оставив один переключатель замкнутым, одновременно управляя другим переключателем. Рисунок 2 иллюстрирует работу затвора логической схемы И.
Если для переключателя SW A или SW B установлено значение «Выкл.», Светодиод останется темным; то есть выход также будет зафиксирован на Off (ворота закрыты).
Если переключатель SW A или SW B зафиксирован на On, то шлюз будет выводить значение нефиксированного SW (шлюз открыт).
Цепь OR, параллельная цепь
Схема ИЛИ, также называемая «схемой логической суммы», выводит 1, если один или оба входа равны 1, и выводит 0, если оба входа равны 0. Пример: Y = A + B.
Логическое выражение OR
Записывается с использованием оператора “+”. Пример: Y = A + B
ИЛИ Обозначение цепи
Таблица истинности
А B Y
0 0 0
0 1 1
1 0 1
1 1 1
На рисунке 3 показана схема ИЛИ: параллельная схема с двумя переключателями и одним светодиодным индикатором.
Поскольку это параллельная схема, выход будет включен (светодиод Y загорится), если только SW A, только SW B или оба SW A и SW B включены.
Операция логического элемента в схеме ИЛИ является обратной по отношению к операции логической схемы И.
Если для переключателя SW A или SW B установлено значение «Вкл.», Загорится светодиодный индикатор; то есть выход также будет зафиксирован на On (ворота закрыты).
Если переключатель SW A или SW B зафиксирован на Off, гейт будет выводить значение нефиксированного SW (шлюз открыт)
Рисунок 3: Схема OR
Цепь НЕ, Цепь инвертора
Схема НЕ (также называемая «схемой инвертора») принимает только один вход и выводит инверсию входа.Если вход равен 1, выход равен 0. Если вход равен 0, выход равен 1.
Логическое выражение НЕ
Записывается с использованием оператора «¯». Пример: Y =
НЕ Обозначение цепи
В следующий раз мы посмотрим, как работают цифровые ИС.
Список модулей
Цифровые схемы Elemental
Цифровые ИС / Комбинационная логика
Последовательная логика
Проекты цифровых схем
: обзор цифровых схем посредством реализации интегральных схем
Отзыв Кевина Никелса, доцента Тринити-университета, 11.04.17
Полнота рейтинг: 4 видеть меньше
Базовое комбинаторное покрытие довольно прочное.Канн упоминает дизайн только NAND, но не только NOR, что также важно, и не показывает, как преобразовать минимизированную функцию в NAND. Я также хотел бы увидеть раздел о Куайне-МакКласки для ученых и / или раздел с рекомендациями (я обычно рекомендую LogicFriday) по бесплатным программам для минимизации для любителей. Последовательное покрытие менее развито. Основы здесь, но, на мой взгляд, Канн тратит слишком много времени на разработку DFF (D-защелка, затем D с включением, затем, наконец, D-триггер) и слишком мало на State Machines.Он показывает три способа реализации 2-битного счетчика (Gates / FF, ROM / FF и MUX / FF), но не распространяется на конечные автоматы с дополнительными входами (такими как, в случае счетчика, Enable вход или вход синхронного сброса). Это, наверное, самое серьезное упущение. Разработка ЦП в главе 11 происходит очень быстро и, на мой взгляд, не очень хорошо отличается от других глав. Чтобы по-настоящему понять эту конструкцию, необходимо больше информации о частях процессора.
Точность содержания рейтинг: 5
Содержание точное.Подход Канна очень прагматичен, поэтому он замалчивает некоторые причины, по которым вы делаете то или иное дело, но то, что он говорит, правильно, и он, очевидно, помог студентам провести все эти эксперименты, что еще раз доказывает это. Единственный сомнительный момент, который я обнаружил, это то, что он говорит, что LS и ALVC не будут работать – ALVC – несовместимая серия с низким напряжением, поэтому он не будет работать, но я смешал LS с CMOS и не-LS TTL. без проблем (надо смотреть разветвление). Не большая проблема.
Актуальность / долголетие рейтинг: 5
С точки зрения технологий, основы цифрового дизайна неподвластны времени.Дискретные микросхемы, такие как серия 74XX, уже несколько десятилетий являются устаревшими, за исключением обучения и некоторых хобби, но они очень полезны для изучения основ и будут использоваться для этого еще долгое время. Расположение разделов / глав должно упростить, например: добавить раздел о ПЛИС в каждый раздел, показывающий, как можно использовать современные инструменты EDA, чтобы сделать то же самое.
Ясность рейтинг: 5
Канн как относительный «аутсайдер» цифровой инженерии делает хорошую работу по введению технической терминологии перед ее использованием.Учитывая желаемую аудиторию любителей, он уделил этому больше внимания, чем большинство авторов.
Последовательность рейтинг: 5
Никаких несоответствий в терминологии не заметил.
Модульность рейтинг: 5
В этой книге эффективно используются разделы и подразделы. В самом деле, курс, для которого я это оцениваю, будет использовать главы 1, 2, 4, 5, 9 и 10, поскольку мы будем реализовывать все на ПЛИС. Легко прочитать текст, чтобы увидеть, что основано на другом материале, а что стоит особняком.
Организация / структура / поток рейтинг: 4
Ход тем ясен. Единственный реальный недостаток в этом – переход от Ch20 (последовательные схемы, представленные как 2-битный счетчик) к Ch21 (урезанный CPU). Бывают случаи, когда отступление в практические вопросы немного раздражает (например, 10.2 Debouncing), но оно служит для того, чтобы поместить нужные вам вещи в нужное место, так что это хороший компромисс.
Интерфейс рейтинг: 4
Последовательное использование пронумерованных заголовков и подзаголовков, а также пронумерованных рисунков / таблиц делает это несложным.Навигация довольно проста. Есть несколько таблиц, разбитых по страницам в неудачных местах, и несколько вдов / сирот, чего я не ожидал бы от действительно профессиональных публикаций.
Грамматические ошибки рейтинг: 5
Как правило, очень грамматический и легко читаемый, с несколькими нечетными фразами.
Культурная значимость рейтинг: 5
Трудно представить текст по этой теме, в котором были бы такие проблемы.
Комментарии
Текст читается в черно-белом режиме, но цвет значительно выигрывает.Например, использование тире или точек вместо кружков на K-картах может улучшить читаемость.

Десятичное	двоичный
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111