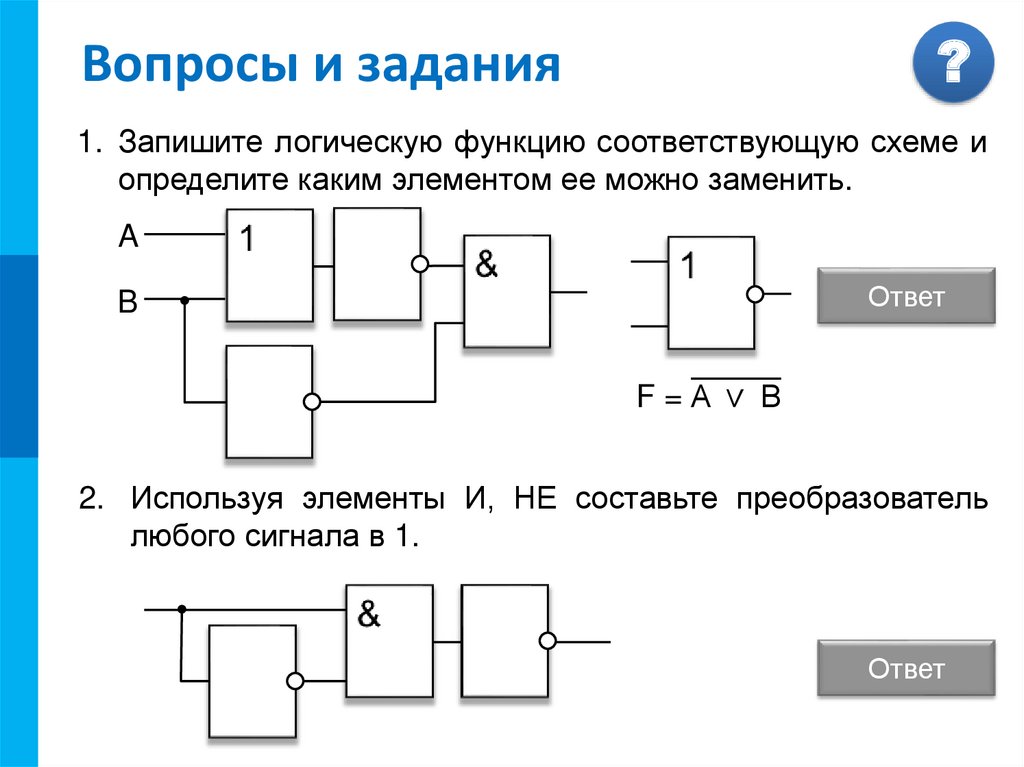
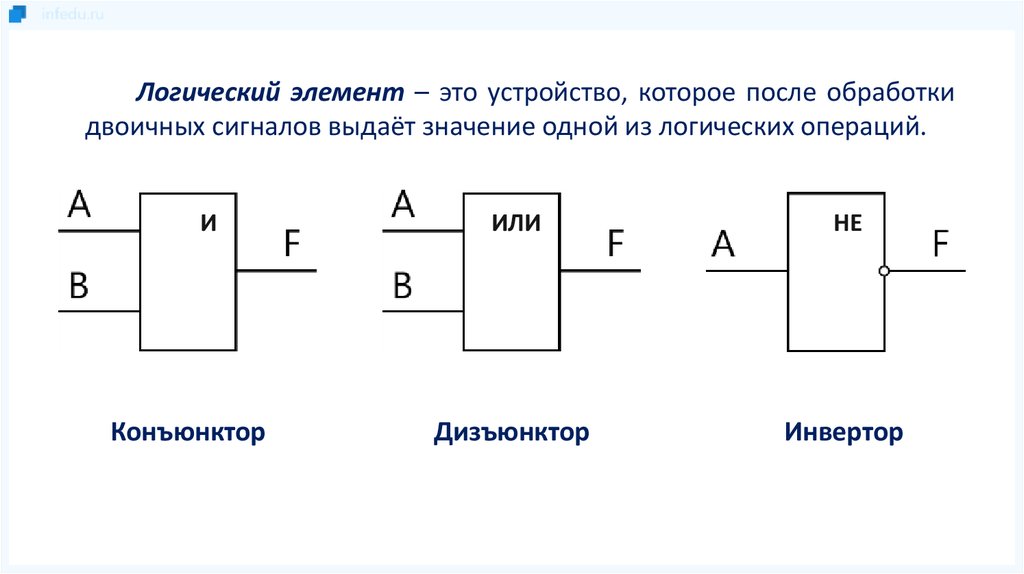
Логические элементы схемы: Логические схемы и таблицы истинности

Логические схемы – презентация онлайн

1. Логические схемы

Логические схемы нужны для того чтобы в наглядной графической форме
отобразить последовательность выполнения операций при вычислении логических
формул.
Входящие слева линии и цифры около них обозначают значения операндов, линия
справа и соответствующая цифра – результат операции (значение на выходе
логических элементов). 1 – это логическая единица (истина), 0 – логический ноль
(ложь).
Таблицы истинности в форме логических схем будут выглядеть т.о.

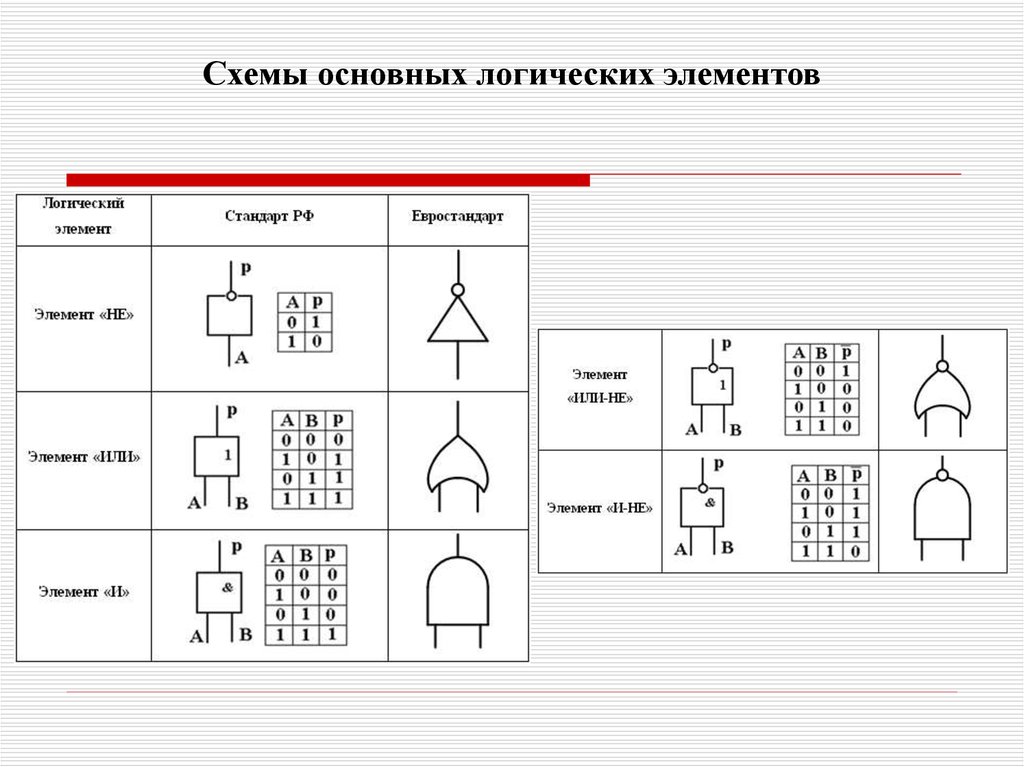
3.      Логический элемент НЕ (инвертор)

Логический элемент НЕ (инвертор)
Простейшим логическим элементом является инвертор,
выполняющий функцию отрицания (инверсию). У этого элемента один
вход и один выход. На функциональных схемах он обозначается:
Если на вход поступает сигнал, соответствующий 1, то на выходе
будет 0. И наоборот.
вход
выход
1
0
0
1

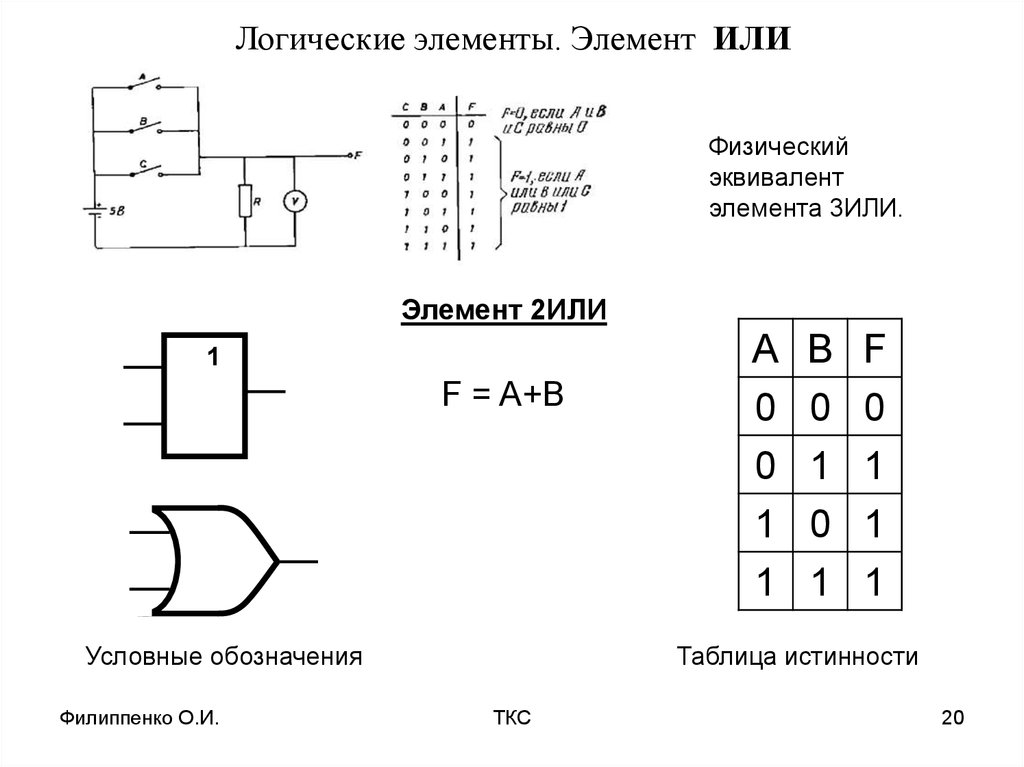
4. Логический элемент ИЛИ (дизъюнктор)

Логический элемент, выполняющий логическое сложение, называется
дизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах
он обозначается:
Если хотя бы на один вход поступает сигнал 1, то на выходе будет сигнал 1.
вход 1
вход 2
выход
0
0
0
0
1
1
1
0
1
1
1
1

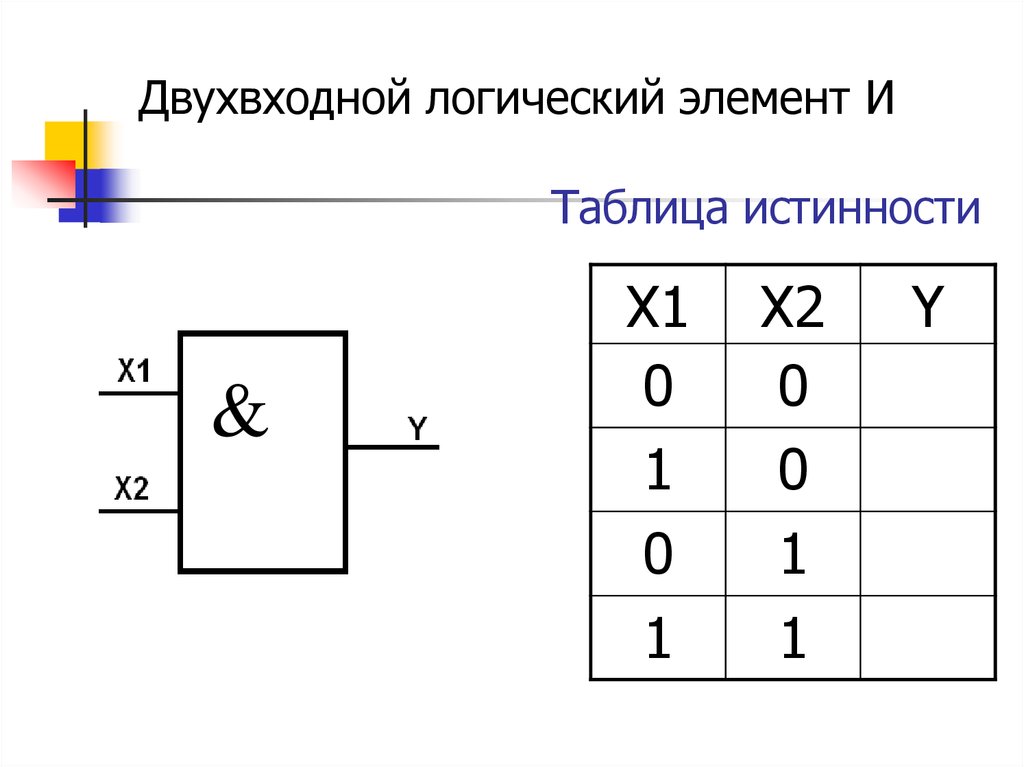
5. Логический элемент И (конъюнктор)

Логический элемент, выполняющий логическое умножение, называется
конъюнктор. Он имеет, как минимум, два входа. На функциональных
схемах он обозначается:
На выходе этого элемента будет сигнал 1 только в том случае,
когда на все входы поступает сигнал 1. Когда хотя бы на одном входе
будет ноль, на выходе также будет ноль.
вход 1
вход 2
выход
0
0
0
0
1
0
1
0
0
1
1
1
Другие логические элементы построены из трех простейших базовых
элементов и выполняют более сложные логические преобразования
информации.
Рассмотрим еще два логических элемента, которые играют роль
базовых при создании более сложных элементов и схем.
Логический элемент И-НЕ
Логический элемент И-НЕ выполняет логическую функцию штрих Шеффера (ИНЕ), он имеет, как минимум, два входа. На функциональных схемах он
обозначается:
вход 1
вход 2
выход
0
0
1
0
1
1
1
0
1
1
1
0
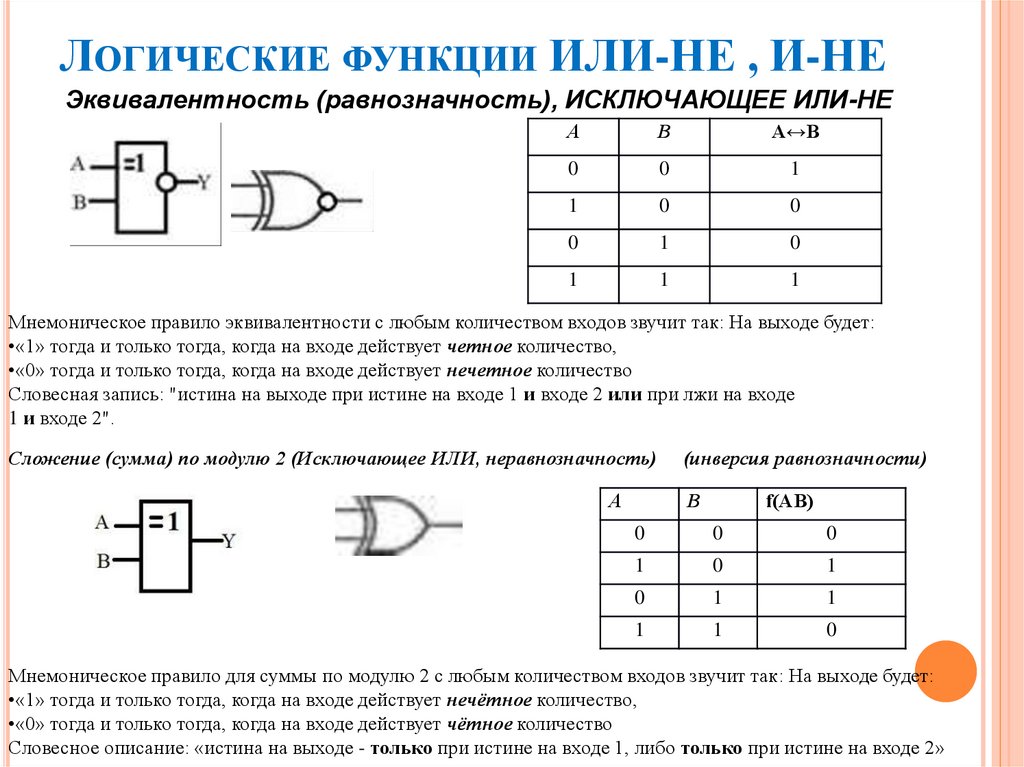
Логический элемент ИЛИ-НЕ
Логический элемент ИЛИ-НЕ выполняет логическую функцию стрелка Пирса (ИНЕ), он имеет, как минимум, два входа. На функциональных схемах он обозначается:
вход. 1
вход 2
выход
0
0
1
0
1
0
1
0
0
1
1
0
Логические основы компьютеров
7
значок инверсии
A
A
A
&
A
A B
B
НЕ
B
И
A
&
B
ИЛИ
A
1
B
И-НЕ
К. Поляков, 2007-2012
A B
1
ИЛИ-НЕ
A B
A B
Логические основы компьютеров
8
Любое логическое выражение можно реализовать на
элементах И-НЕ или ИЛИ-НЕ.
И: A B A B
НЕ: A A A A A
A
&
ИЛИ:
A
A
B
A
&
& A B
A
A B A B
&
B
&
B
К. Поляков, 2007-2012
&
A B
A B

9. Составление схем

Логические основы компьютеров
9
Составление схем
последняя операция – ИЛИ
X A B A B C
И
A
B
C
К. Поляков, 2007-2012
A
B
&
A
B
& A B
A B
A B C
C
&
1
X
Пример 1. Нарисовать схему для логического выражения: 1 ИЛИ 0 и 1.
Читать эту схему надо слева направо. Первой выполняется операция И (что
наглядно видно на схеме), затем ИЛИ.
Теперь в порядке слева направо припишем к выходящим линиям
результаты операций:
В результате получилась 1, т.е. “истина”.
Пример 2. Представить в виде логической схемы логическую формулу:
НЕ (А И (В ИЛИ С) И D)
Логическая схема будет выглядеть так:
Теперь с помощью схемы рассчитаем значение формулы при А=С=D=1,
B=0
В результате получится логический ноль, т.е. “ложно”.

12. Функциональные схемы

Сигнал, выработанный одним логическим элементом, можно
подавать на вход другого элемента, это дает возможность образовывать
цепочки из отдельных логических элементов — функциональные схемы.
Функциональная (логическая) схема – это схема, состоящая из
логических элементов, которая выполняет определённую функцию.
Анализируя функциональную схему, можно понять, как работает логическое
устройство, т.е. дать ответ на вопрос: какую функцию она выполняет.
Важной формой описания функциональных схем является структурная
формула. Покажем на примере, как выписывают формулу по заданной
функциональной схеме.
Ясно, что элемент “И” осуществляет логическое умножение значений ¬А и В.
Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е.
вычисляется значение выражения:
A&B
Таким образом структурной формулой данной функциональной
схемы является формула:
C A&B

13. Таблица истинности функциональной схемы

Для функциональной схемы можно составить таблицу истинности, то есть
таблицу значений сигналов на входах и выходах схемы, по которой можно
понять какую функцию выполняет данная схема. Таблица истинности это табличное представление логической (функциональной) схемы в
котором перечислены все возможные сочетания значений входных
сигналов вместе со значением выходного сигнала для каждого из этих
сочетаний. Составим таблицу истинности для данной логической схемы:
Начертим таблицу: количество столбцов = количество входов + количество
выходов, количество строк = 2 количество входов. В данной таблице 3 столбца и 4
строки. Заполним первые столбцы всеми возможными вариантами входных
А
В
С
сигналов
(вход 1)
(вход 2)
0
0
0
1
1
0
1
1
(выход)
Рассмотрим первый вариант входных сигналов: А=0, В=0. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
Рассмотрим второй вариант входных сигналов: А=0, В=1. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=0), запишем в таблицу.
Рассмотрим третий вариант входных сигналов: А=1, В=0. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
Рассмотрим четвёртый вариант входных сигналов: А=1, В=1. Проследим по схеме, как проходят
и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
В результате получаем таблицу истинности данной логической схемы:
А
(вход 1)
В
(вход 2)
С
(выход)
0
0
1
0
1
0
1
0
1
1
1
1
Задание. Построить таблицу истинности для данной логической схемы и записать формулу
для данной схемы:

16. Логическая реализация типовых устройств компьютера

Обработка любой информации на компьютере
сводится к выполнению процессором различных
арифметических и логических операций. Для этого в
состав процессора входит так называемое арифметикологическое устройство (АЛУ). Оно состоит из ряда
устройств, построенных на рассмотренных выше
логических элементах. Важнейшими из таких устройств
являются триггеры, полусумматоры, сумматоры,
шифраторы, дешифраторы, счетчики, регистры.
Выясним , как из логических элементов
разрабатываются логические устройства.
Логическая реализация типовых
устройств компьютера

17. Этапы конструирования логического устройства.

Конструирование логического устройства состоит из
следующих этапов:
1. Построение таблицы истинности по заданным
условиям работы проектируемого узла (т.е. по
соответствию его входных и выходных сигналов).
2. Конструирование логической функции данного узла
по таблице истинности, ее преобразование (упрощение),
если это возможно и необходимо.
3. Составление функциональной схемы проектируемого
узла по формуле логической функции.
После этого остается только реализовать полученную
схему.
Задание. Построить логическую схему для заданной таблицы истинности:
Запишем логическую функцию по данной таблице
истинности:
F A & B &C A& B &C
Упростим полученное логическое выражение:
F С & ( A & B A & B ) С & (( A B ) A & B )
Построим логическую схему для данного выражения:
А
В
С
F
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
Попробуем, действуя по этому плану, сконструировать устройство для
сложения двух двоичных чисел (одноразрядный полусумматор).
Пусть нам необходимо сложить двоичные числа А и В. Через P и S
обозначим первую и вторую цифру суммы: A + B = PS. Вспомните таблицу
сложения двоичных чисел.
1. Таблица истинности, определяющая результат сложения, имеет вид:
Слагаемые
Перенос
Сумма
А
В
Р
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
2. Сконструируем функции P(A,B) и S(A,B) по этой таблице:
Р( A, B) A & B
S ( A, B) A & B A & B
Преобразуем вторую формулу, пользуясь законами логики:
S ( A, B) A & B A & B A & B A & B A & A B & B ( A & A A & B) ( A & B B & B )
A & ( A B) B & ( A B) ( A B) & ( A & B ) ( A B) & ( A & B)
3. Теперь можно построить функциональную схему одноразрядного
полусумматора:
Р( A, B) A & B
S ( A, B) ( A B) & ( A & B)
Чтобы убедиться в том, как работает схема, проследите за прохождением
сигналов в каждом из четырёх случаев и составьте таблицу истинности
данной логической схемы.
Условное обозначение одноразрядного
сумматора:

21. Полусумматор

Логические основы компьютеров
21
Полусумматор
Полусумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа.
A
S сумма
A B
P
S
Σ
B
P перенос
P A B
S A B A B A B
A
B
A
B
К. Поляков, 2007-2012
& A B
& A B
& A B
1
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
S A B A B
P
?
Схема на 4-х
элементах?

22. Полный одноразрядный сумматор.

Одноразрядный двоичный сумматор на три входа и два выхода называется
полным одноразрядным сумматором.
Логика работы одноразрядного сумматора на три входа или полного
сумматора приведена в таблице, где А, В – суммируемые двоичные цифры
, Pо – перенос из младшего разряда, S – образующаяся сумма данного
разряда и осуществляет перенос P в следующий старший разряд.
Слагаемые
Перенос из
младшего
разряда
Сумма
Перенос
А
B
P0
S
P
0
0
0
0
0
.0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Формула переноса:P A & B & P0 A & B & P0 A & B & P0 A & B & P0
Формула для вычисления суммы: S A & B & P0 A & B & P0 A & B & P0 A & B & P0
После преобразования формулы переноса и суммы принимают вид:
P A & B A & P0 B & P0
S ( A B P0 ) & P0 ( A & B & P0 )
Теперь можно построить схему полного одноразрядного сумматора с
учётом переноса из младшего разряда.
Сумматор – это электронная логическая схема,
выполняющая суммирование двоичных чисел поразрядным
сложением. Сумматор является центральным узлом
арифметико-логического устройства процессора. Находит он
применение и в других устройствах компьютера. В реальных
электронных схемах сумматор изображается так:
Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой
последовательное соединение одноразрядных двоичных сумматоров, каждый из которых
осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то
перенос суммируется с содержимым старшего соседнего разряда.
На рисунке показано, как из N сумматоров можно составить устройство для сложения двух Nразрядных двоичных кодов, это схема многоразрядного сумматора.

25. Сумматор

Логические основы компьютеров
25
Сумматор
Сумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа с
переносом из предыдущего разряда.
перенос
A
B
C
Σ
К. Поляков, 2007-2012
A
B
C
P
S
0
0
0
0
0
S сумма
0
0
1
0
1
P перенос
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1

26.

Многоразрядный сумматорЛогические основы компьютеров
26
Многоразрядный сумматор
это логическая схема, способная складывать два
n-разрядных двоичных числа.
A
an an-1 a1
B
bn bn-1 b1
C p cn cn-1 c1
перенос
a1
b1
c1
Σ
0
К. Поляков, 2007-2012
p2
a2
b2
Σ
c2
p3
an
bn
pn
cn
Σ
p
перенос

27. ТРИГГЕР

Триггер – электронная схема, применяемая для хранения значения
одноразрядного двоичного кода.
Воздействуя на входы триггера, его переводят в одно из двух возможных
состояний (0 или 1). С поступлением сигналов на входы триггера в
зависимости от его состояния либо происходит переключение, либо
исходное состояние сохраняется. При отсутствии входных сигналов триггер
сохраняет свое состояние сколь угодно долго.
Термин триггер происходит от английского слова trigger – защёлка,
спусковой крючок. Для обозначения этой схемы в английском языке чаще
употребляется термин flip-flop, что в переводе означает “хлопанье”. Это
звукоподражательное название электронной схемы указывает на её
способность почти мгновенно переходить (“перебрасываться”) из одного
электрического состояния в другое.
Существуют разные варианты исполнения триггеров в зависимости от
элементной базы (И-НЕ, ИЛИ-НЕ) и функциональных связей между
сигналами на входах и выходах (RS, JK, T, D и другие).
Самый распространённый тип триггера – это RS-триггер (S и R
соответственно от английских set – установка, и reset – сброс). Условное
обозначение RS-триггера:

28. RS-триггер

RS-триггер построен на 2-х логических элементах: ИЛИ – НЕ либо И – НЕ.
Как, правило, триггер имеет 2 выхода: прямой и инверсный Q и
Как он работает?
Пусть на вход элемента №1 подан сигнал 1, а на вход элемента № 3 – 0. На выходе элемента №1
независимо от того, какой второй сигнал поступит на вход, будет 1, т.к. это элемент ИЛИ (по
свойствам дизъюнкции). Пройдя через элемент № 2 сигнал примет значение 0 (Q=0).
Следовательно, и на втором входе элемента № 3 установится сигнал 0. На выходе элемента №3
– 0. Пройдя через элемент № 4 сигнал изменится на 1. Следовательно,
= 1.
Убедимся, что данное устройство сохраняет информацию. Запомните, что S=0, R=1, Q=0,
=1.
В момент прекращения входных сигналов (S=0, R=0) на выходе =1. Это напряжение подается на
вход элемента № 1. На выходе элемента №1 сохраняется 1, и на Q – сигнал 0. На входах
элемента №3 – 0, следовательно
=1. Таким образом, при отсутствии на внешних входах
сигналов 1 триггер поддерживает постоянное напряжение на своих выходах. Чтобы изменить
напряжение на выходах триггера, надо подать сигнал 1 на вход элемента № 3. Тогда Q=1, =0.

29. Триггер (англ. trigger – защёлка)

Логические основы компьютеров
29
Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная хранить
1 бит информации (1 или 0). Строится на 2-х
элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
set, установка
S
1
1
R
reset, сброс
К. Поляков, 2007-2012
вспомогательный
выход
Q
S R Q Q
режим
0 0 Q Q
хранение
обратные связи
0 1
0
1
сброс
Q
1 0
1 1
1
0
0
0
установка 1
основной
выход
запрещен

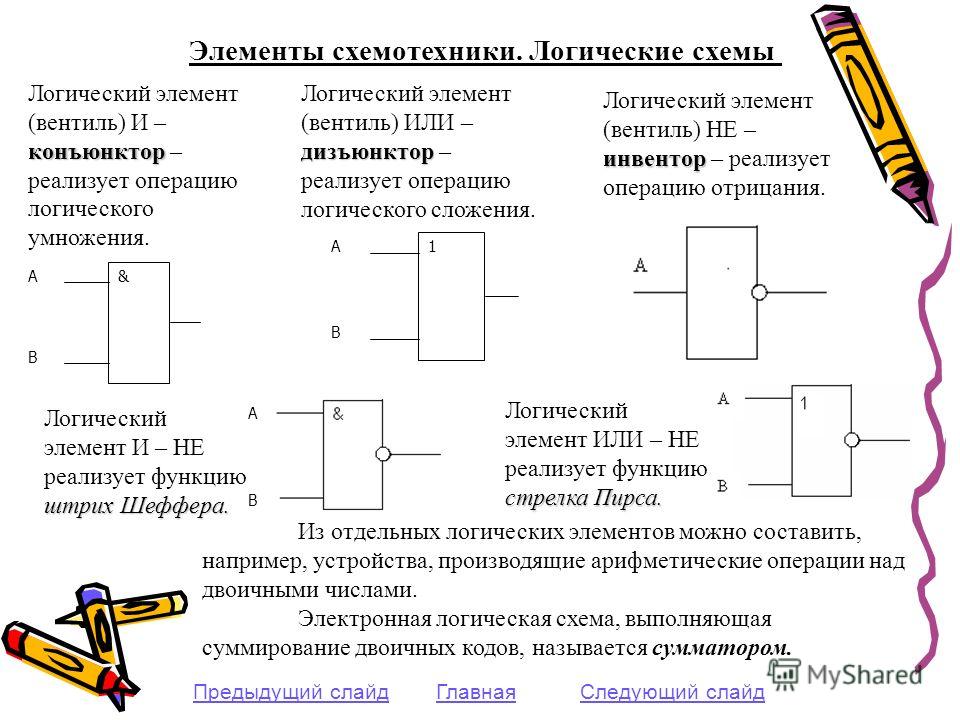
Элементы схемотехники. Логические схемы

Информатика. 10 класса. Босова Л.Л. Оглавление

§ 21. Элементы схемотехники. Логические схемы

---

Элементы схемотехники. Логические схемы

Любое устройство компьютера, выполняющее арифметические или логические операции, может рассматриваться как преобразователь двоичной информации: значения входных переменных для него — последовательность нулей и единиц, а значение выходной функции — новая двоичная последовательность. Необходимые преобразования информации в блоках компьютера производятся логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.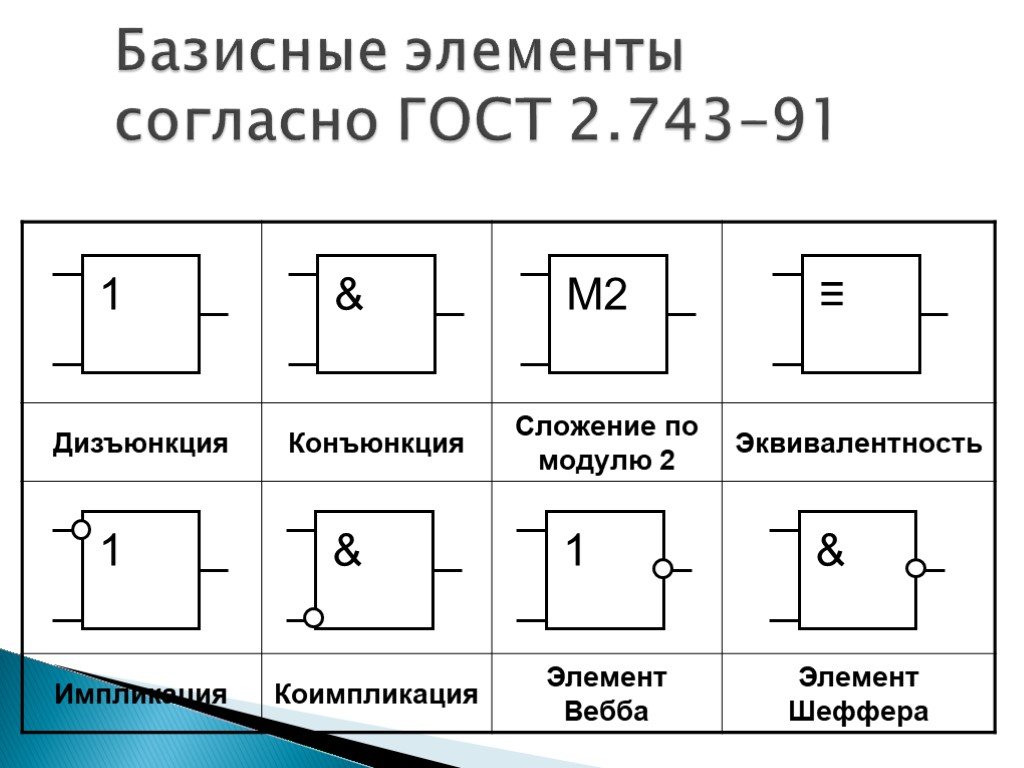

В комбинационной схеме набор выходных сигналов в любой момент времени полностью определяется набором входных сигналов.

В цифровых автоматах с памятью набор выходных сигналов зависит не только от набора входных сигналов, но и от внутреннего состояния данного устройства. Такие устройства всегда имеют память.

Схемотехника — научно-техническое направление, занимающееся проектированием, созданием и отладкой электронных схем и электронных устройств различного назначения.

---

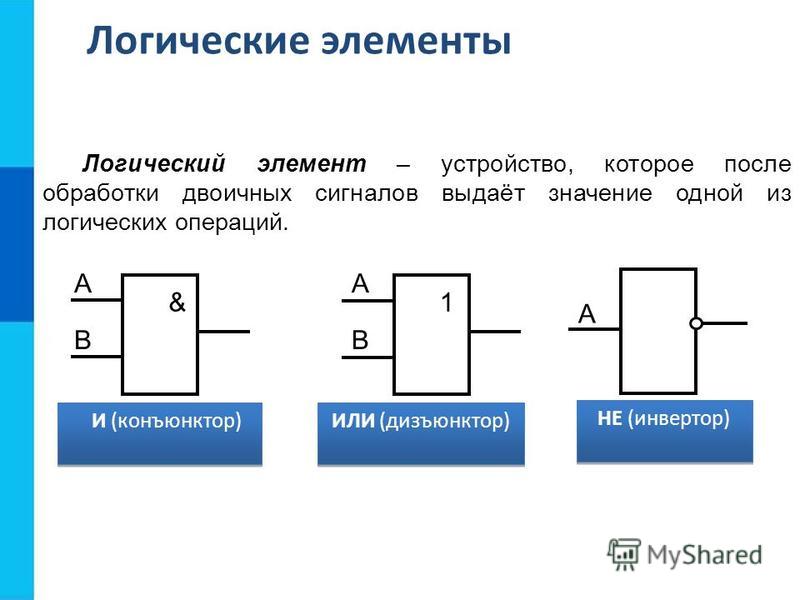
21.1. Логические элементы

Логический элемент — это устройство с л входами и одним выходом, которое преобразует входные двоичные сигналы в двоичный сигнал на выходе.

Работу любого логического элемента математически удобно описать как логическую функцию, которая упорядоченному набору из нулей и единиц ставит в соответствие значение, также равное нулю или единице.

В схемотехнике широко используются логические элементы, представленные в таблице 4.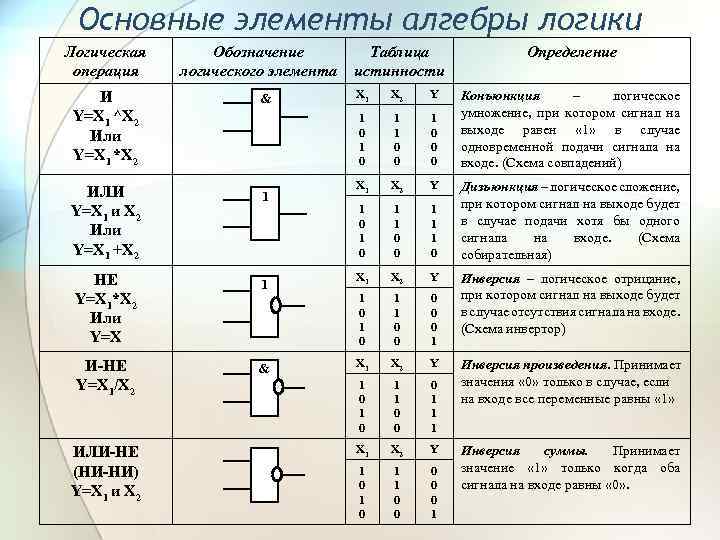 2.

Таблица 4.2

Условные обозначения типовых логических элементов

Логический элемент И (конъюнктор) реализует операцию логического умножения. Единица на выходе этого элемента появится тогда и только тогда, когда на всех входах будут единицы.

Опишите подобным образом логические элементы ИЛИ (дизъюнктор), НЕ (инвертор), И-НЕ, ИЛИ-НЕ.

Однотипность сигналов на входах и выходах позволяет подавать сигнал, вырабатываемый одним элементом, на вход другого элемента. Это позволяет из двухвходовых элементов «собирать» многовходовые элементы (рис 4.7), а также синтезировать произвольные комбинационные схемы, соединяя в цепочки отдельные логические элементы.

Рис. 4.7. Схема и обозначение четырёхвходового конъюнктора

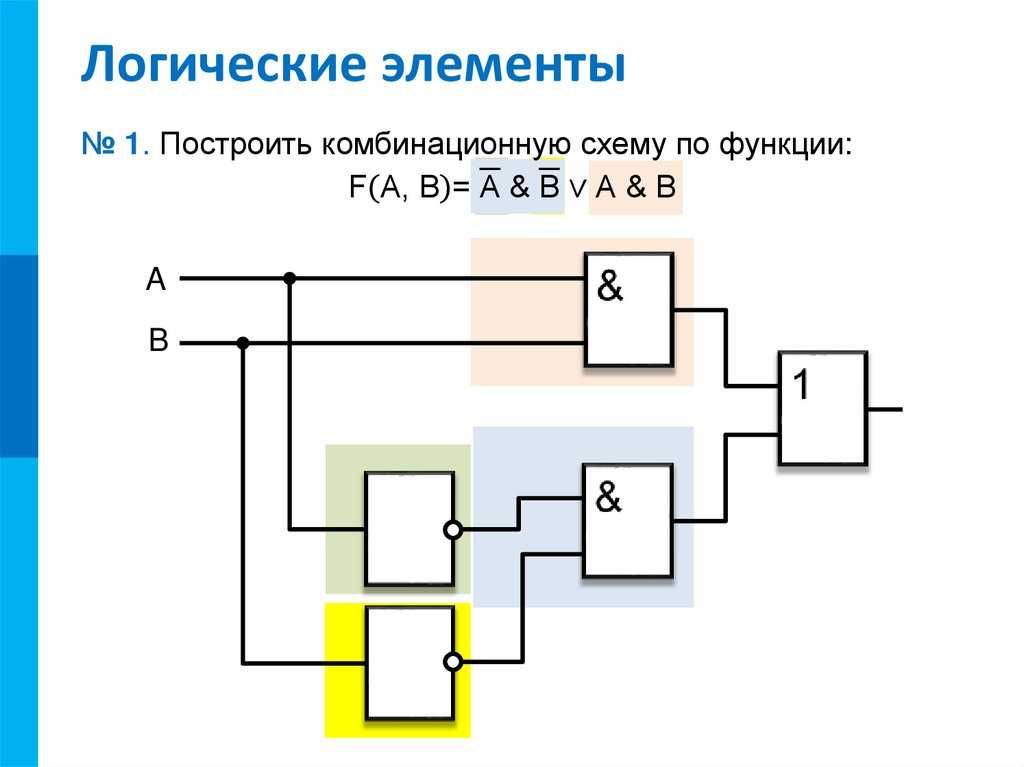
Пример. По заданной логической функции F(A, В) =  & В v А &  построим комбинационную схему (рис. 4.8).

Построение начнём с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Рис. 4.8. Комбинационная схема функции F(A, В) =  & В v А & 

21.2. Сумматор

Из отдельных логических элементов можно составить устройства, производящие арифметические операции над двоичными числами.

Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.

Вспомним схему сложения двух n-разрядных двоичных чисел (рис. 4.9).

Рис. 4.9. Схема сложения двух n-разрядных двоичных чисел

Заметим, что при сложении цифр в i-м разряде мы должны сложить цифру a_i числа а, цифру b_i числа b, а также р_i — перенос из (i — 1)-го разряда. В результате сложения должны получиться цифра результата s_i и цифра переноса (0 или 1) в следующий разряд p_i+1.

Основываясь на этих рассуждениях, построим таблицу истинности для функций, которые в зависимости от цифр a_i, b_i и p_i получают цифры s_i и p_i+l.

Вам известен алгоритм построения логического выражения по таблице истинности. Воспользуемся им и запишем выражение для функции p_i+1:

Попытаемся упростить это выражение, воспользовавшись тем, что A v А = А. Основываясь на этом законе, включим в имеющуюся дизъюнкцию ещё два слагаемых вида a_i & b_i & p_i, причём на основании коммутативного и ассоциативного законов преобразуем полученное выражение к виду:

Полученное выражение означает, что функция р_i+1 принимает значение 1 только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Обратите внимание на то, что такой вывод можно сделать и в результате анализа таблицы истинности.

По таблице истинности можем записать выражение для s_i:

Его также можно попытаться преобразовать к более короткому виду. Но можно пойти другим путём и провести более тщательный анализ таблицы истинности для функции s_i.

Из таблицы видно, что значение s_i равно 1, если все входные сигналы равны 1. Этому соответствует выражение a_i & b_i & p_i = 1.

Или значение s_i равно 1, если в комбинации входных сигналов есть единственная 1, т. е. единица среди переменных есть, но нет одновременно двух переменных, значения которых равны

1. Это можно записать так:

Следовательно, s,- можно записать так:

Можно попытаться самостоятельно провести преобразование логического выражения, полученного по таблице истинности для s_i к итоговому виду. Но, чтобы убедиться в равносильности этих двух выражений, достаточно построить таблицу истинности для второго из них.

Полученные выражения позволяют реализовать одноразрядный двоичный сумматор схемой, представленной на рисунке 4.10.

Рис. 4.10. Схема одноразрядного сумматора

Выразить s_i и p_i+1 можно и другими формулами.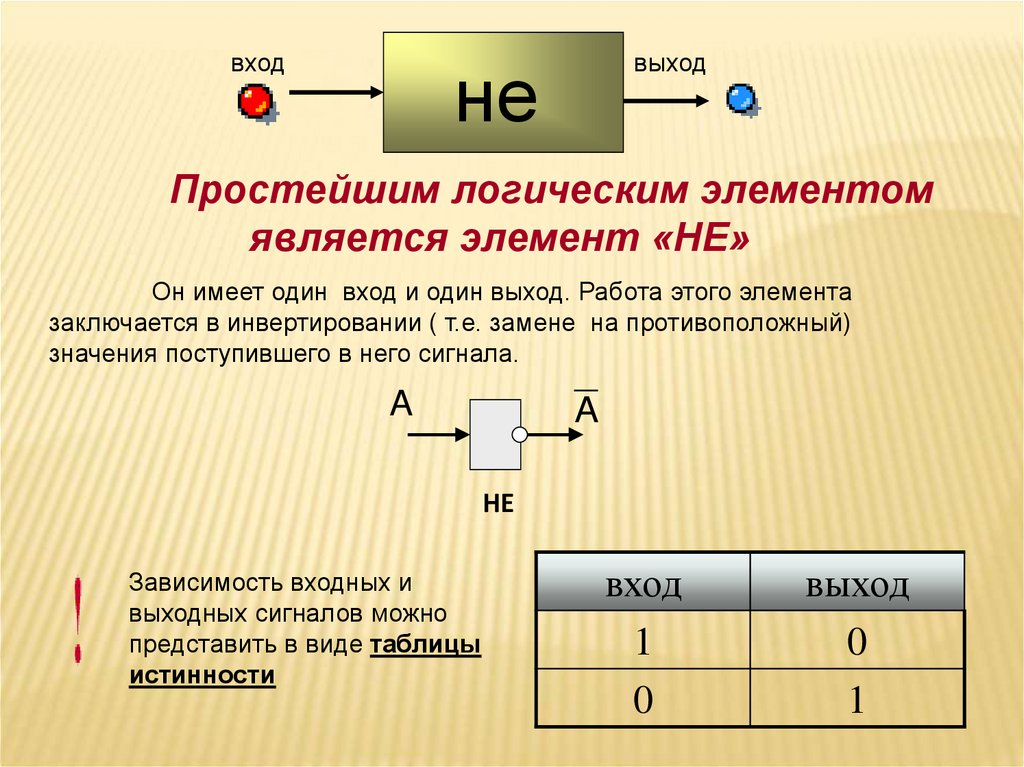 Например, самое короткое выражение для s_i имеет вид: s_i = a_i ? b_i ? p_i, что позволяет построить сумматор, используя другие логические элементы.

Сложение n-разрядных двоичных чисел осуществляется с помощью комбинации одноразрядных сумматоров (условное обозначение одноразрядных сумматоров приведено на рисунке слева).

---

21.3. Триггер

Триггер (от англ. trigger — защёлка, спусковой крючок) — логический элемент, способный хранить один разряд двоичного числа.

Триггер был изобретён в 1918 году М. А. Бонч-Бруевичем.

Михаил Александрович Бонч-Бруевич (1988-1940) — русский и советский радиотехник, основатель отечественной радиоламповой промышленности. Работал в области радиовещания и дальней связи на коротких волнах. В 1918 году М. А. Бонч-Бруевич предложил схему переключающего устройства, имеющего два устойчивых рабочих состояния, под названием «катодное реле». Это устройство впоследствии было названо триггером.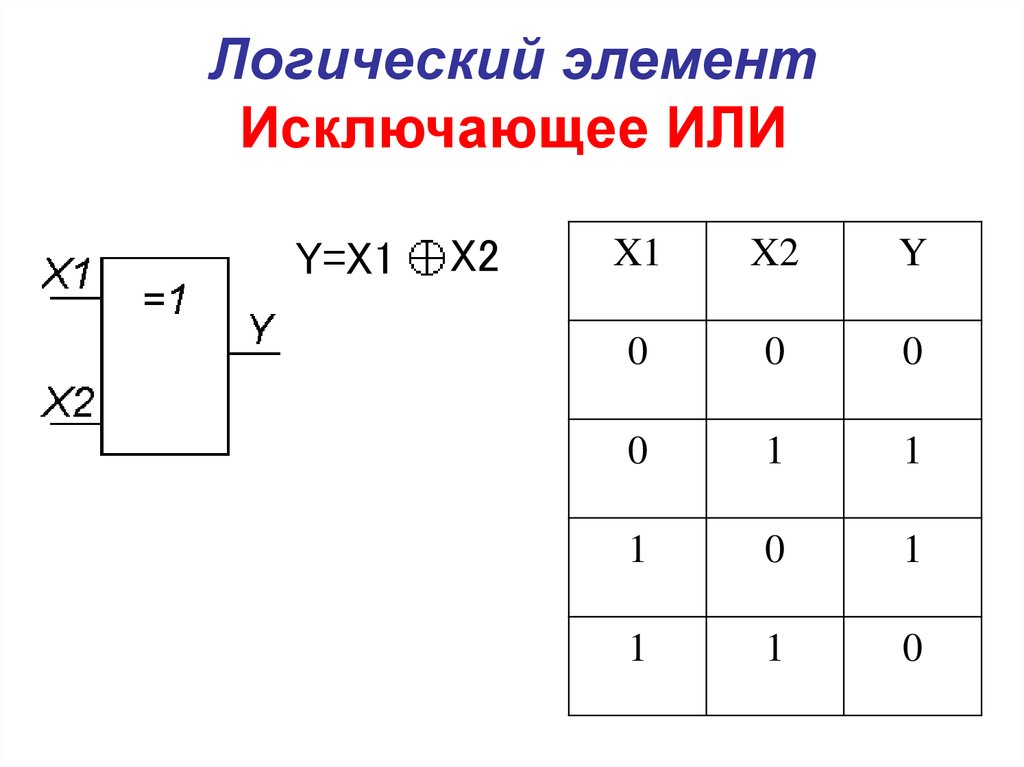

Самый простой триггер — RS. Он состоит из двух логических элементов ИЛИ-HE, входы и выходы которых соединены кольцом: выход первого соединён со входом второго и выход второго — со входом первого. Схема RS-триггера представлена на рисунке 4.11.

Рис. 4.11. Логическая схема RS-триггера

Триггер имеет два входа: S (от англ. set — установка) и R (от англ. reset — сброс) и два выхода: Q (прямой) и  (инверсный). Принцип его работы иллюстрирует следующая таблица истинности:

Если на входы поступают сигналы R = 0 и S = O, то триггер находится в режиме хранения — на выходах Q и  сохраняются установленные ранее значения.

Если на установочный вход S на короткое время поступает сигнал 1, то триггер переходит в состояние 1 и после того, как сигнал на входе S станет равен 0, триггер будет сохранять это состояние, т. е. будет хранить 1.

При подаче 1 на вход R триггер перейдёт в состояние 0.

Подача на оба входа S и R логической единицы может привести к неоднозначному результату, поэтому такая комбинация входных сигналов запрещена.

Триггер используется для хранения информации в оперативной памяти компьютера, а также во внутренних регистрах процессора. Для хранения одного байта информации необходимо 8 триггеров, для килобайта — 8 • 1024 триггеров. Оперативная память современных компьютеров содержит миллионы триггеров.

В целом же компьютер состоит из огромного числа логических устройств, образующих все его узлы и память.

---

САМОЕ ГЛАВНОЕ

Необходимые преобразования информации в блоках компьютера производятся логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.

В комбинационной схеме набор выходных сигналов в любой момент времени полностью определяется набором входных сигналов. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом. Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.

В цифровых автоматах с памятью набор выходных сигналов зависит не только от набора входных сигналов, но и от внутреннего состояния данного устройства. Такие устройства всегда имеют память. Триггер — логический элемент, способный хранить один разряд двоичного числа. Оперативная память современных компьютеров содержит миллионы триггеров.

В целом же компьютер состоит из огромного числа логических устройств, образующих все его узлы и память.

---

Вопросы и задания

1. Что такое логический элемент? Перечислите базовые логические элементы?

2. По логическому выражению  требуется разработать логическое устройство. Какие логические элементы необходимы для его создания?

3. Найдите значение выходного сигнала в приведенной схеме, если

4. Определите логическое выражение преобразования, выполняемого схемой:

5. Постройте логические схемы для следующих функций:

6. Постройте схему устройства, выполняющего преобразование информации в соответствии с данной таблицей истинности:

7. Пусть в некотором конкурсе вопрос о допуске того или иного участника к следующему туру решается тремя членами жюри: А, В и С.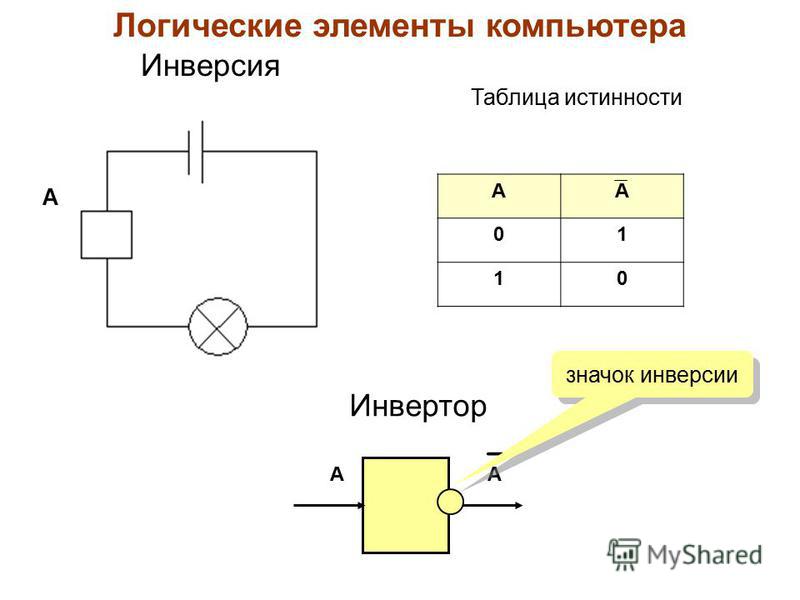 Решение положительно тогда и только тогда, когда хотя бы двое членов жюри высказываются за допуск, причём среди них обязательно должен быть председатель жюри А. Необходимо разработать устройство для голосования, в котором каждый член жюри нажимает на одну из двух кнопок — «За» или «Против», а результат голосования всех трёх членов жюри определяется по тому, загорится (участник допускается) или нет (участник не допускается) сигнальная лампочка. Составьте схему устройства, которое на выходе выдавало бы 1, если участник допускается к следующему туру, и 0, если не допускается.

8. Существует 16 логических устройств, имеющих два входа (16 логических функций от двух переменных). Реализуйте их комбинационные схемы с помощью логических элементов И, ИЛИ, НЕ.

9. Если при суммировании не учитывается признак переноса, то соответствующая логическая схема называется полусумматором. По имеющейся таблице истинности постройте логическую схему полусумматора.

10.  Что такое триггер? В чём основное отличие триггера от таких логических элементов, как инвертор или конъюнктор?

11. Подготовьте краткую биографическую справку о нашем выдающемся соотечественнике М. А. Бонч-Бруевиче. В чём заключается его вклад в развитие вычислительной техники?

---

§ 20. Преобразование логических выражений
§ 21. Элементы схемотехники. Логические схемы
§ 22. Логические задачи и способы их решения

---

логических схем

логических схем

Логические схемы

Логические схемы используют два разных значения физической величины, обычно напряжение, для представления логических значений true (или 1) и ложь (или 0). Логические схемы могут иметь входы и один или несколько выходов, которые хотя бы частично зависят от их вложений. В схемах логических цепей соединения от выхода одной схемы к вход другой схемы часто обозначается стрелкой на входе конец.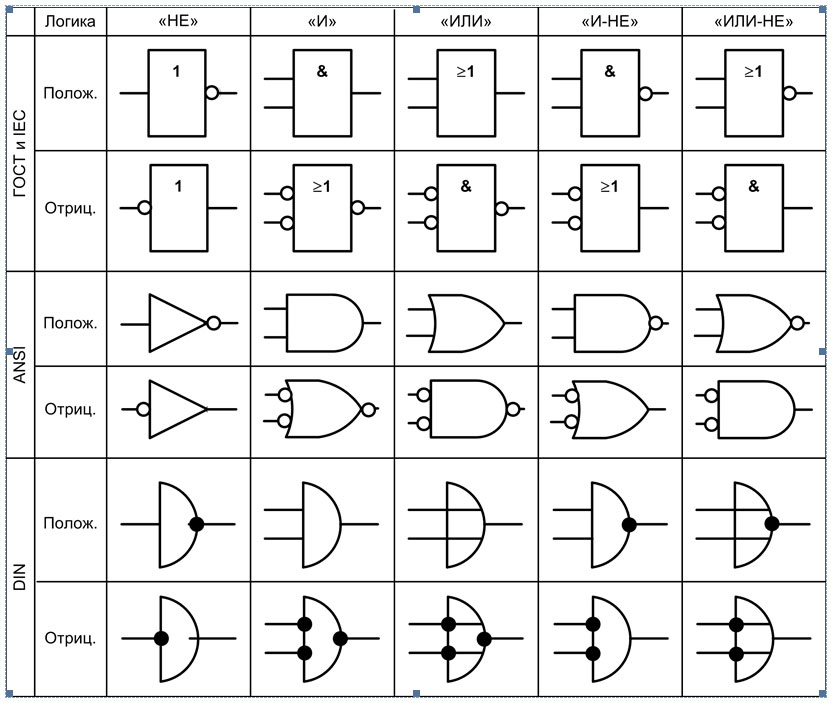

По своему поведению логические схемы очень похожи на программирование. языковые функции или методы. Их входы аналогичны параметрам функций, а их выходы аналогичны значениям, возвращаемым функцией. Однако логическая схема может иметь несколько выходов.

Существует два основных типа логических схем: комбинационные схемы и государственная схема.

• Комбинационная схема ведет себя как простая функция. Выход комбинационной схемы зависит только от тока значения его входа.
• Схема состояния ведет себя больше как объектный метод. Выход схемы состояния зависит не только от ее входов. — это также зависит от прошлой истории его входов. Другими словами, схема имеет память. Это очень похоже на метод объекта, значение которого зависит от состояние объекта: его переменные экземпляра.

Эти два типа схем работают вместе, чтобы составить процессор. путь к данным.

Процессор Datapath

Путь данных процессора концептуально состоит из двух частей:

• Элементы состояния содержат информацию о состоянии процессора. в течение текущего такта. Все регистры являются элементами состояния.
• Комбинационная логика определяет состояние процессора для следующий такт. АЛУ представляет собой комбинационную логику.

Эта диаграмма, как и большинство диаграмм на этом веб-сайте, соответствует следующие соглашения:

• Тактовые сигналы окрашены апельсин.
• Сигналы управления окрашены в синий цвет.

Комбинированная схема

Выход комбинационной схемы зависит только от тока значения его входа.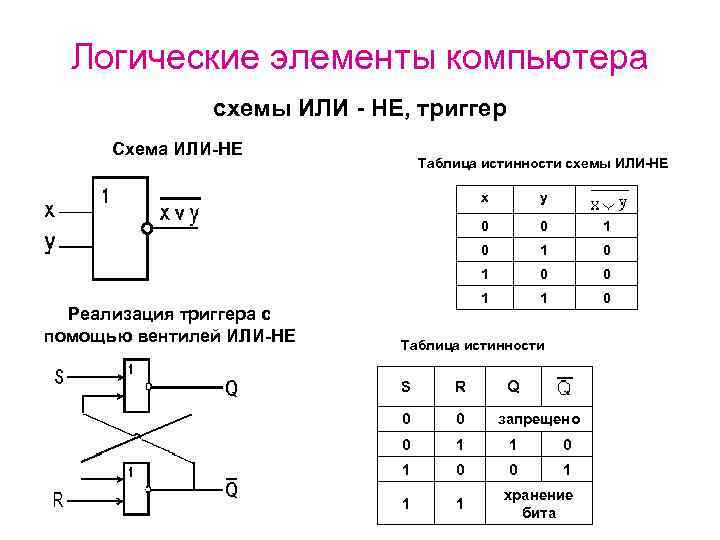 Комбинационная схема концептуально построена из базовой логики вентили: вентили И, вентили ИЛИ, вентили исключающее ИЛИ и инверторы. Выходы вентилей в комбинационной схеме никогда не возвращаются обратно. непосредственно к более ранним входам.

Базовые логические вентили можно комбинировать для формирования различных логических вентилей более высокого уровня. единицы измерения:

• Маршрутизация
  • мультиплексоры — имеют несколько входных сигналов данных и управляющий вход. Выход идентичен одному из входов. Значение управляющего сигнала определяет какой из них.
  • демультиплексоры — имеют один входной сигнал данных, управляющий входные и несколько выходных сигналов. Все выходные сигналы равны 0 (ложь), кроме одного выбирается управляющим входом.
    Выбранный выход идентичен вводу данных.
• Вычислительный
  • полные сумматоры — выполняют один столбец двоичного файла добавление. Они являются основным строительным блоком для многоразрядных сумматоров и вычитатели.
  • сумматоры и вычитатели — добавляют или вычитают два двоичных или числа с дополнением до двух. Вычитатель — это просто сумматор с дополнительной схемой для выполнения вычислений. операция дополнения до двух на одном из входов. Обычно они предназначены для сложения или вычитания. по указанию управляющего сигнала.
  • компараторы — сравнивают два двоичных файла или дополнение до двух числа.

Сумматоры, вычитатели и компараторы здесь не описываются.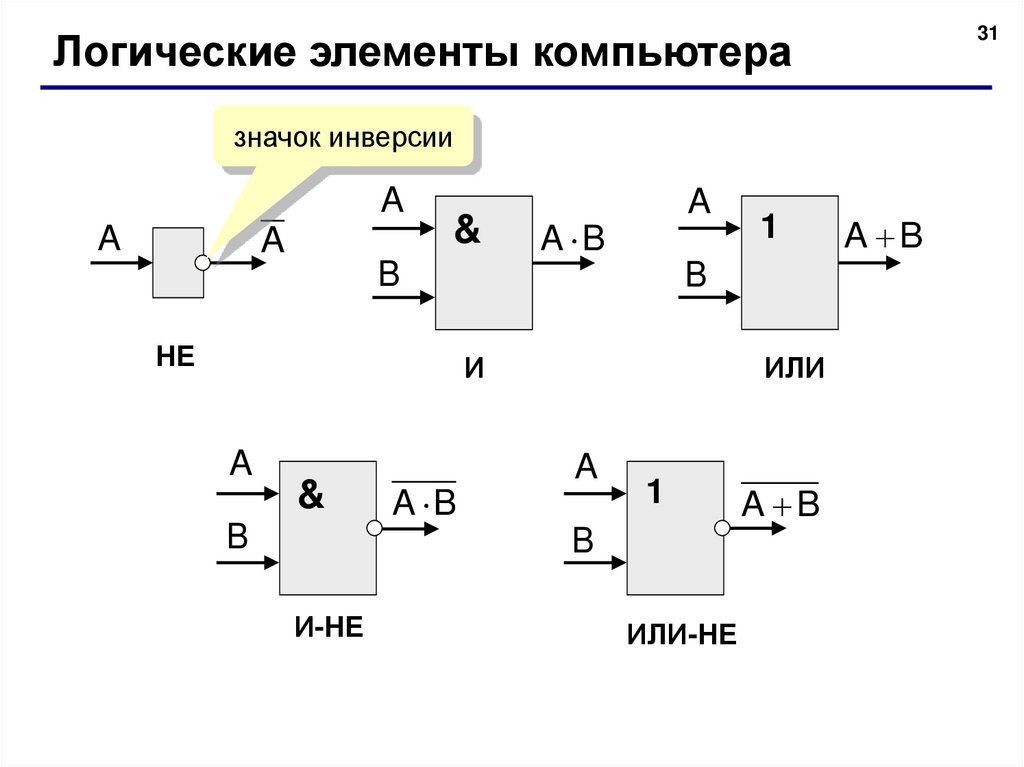 Они описаны в Целочисленное сложение и Вычитание.

Вьетнамки

Триггер является основным элементом схемы состояния. Он имеет три входа:

• D – данные для записи в триггер
• En – позволяет записывать данные в триггер
• Cl – часы, которые определяют, когда данные записываются в триггер

Триггер имеет один выход:

• Q – данные выводятся, самое последнее значение данных записывается в триггер.

Реализация триггера

Регистры

Регистр — это всего лишь многоразрядный аналог триггера. Он имеет три входа:

• D – данные для записи в регистр
• En – разрешает запись данных в регистр
• Cl — часы, определяющие, когда данные записываются в регистр

Регистр имеет один выход:

• Q – данные выводятся, самое последнее значение данных записывается в регистр

Это те же входы и выходы, что и у триггера.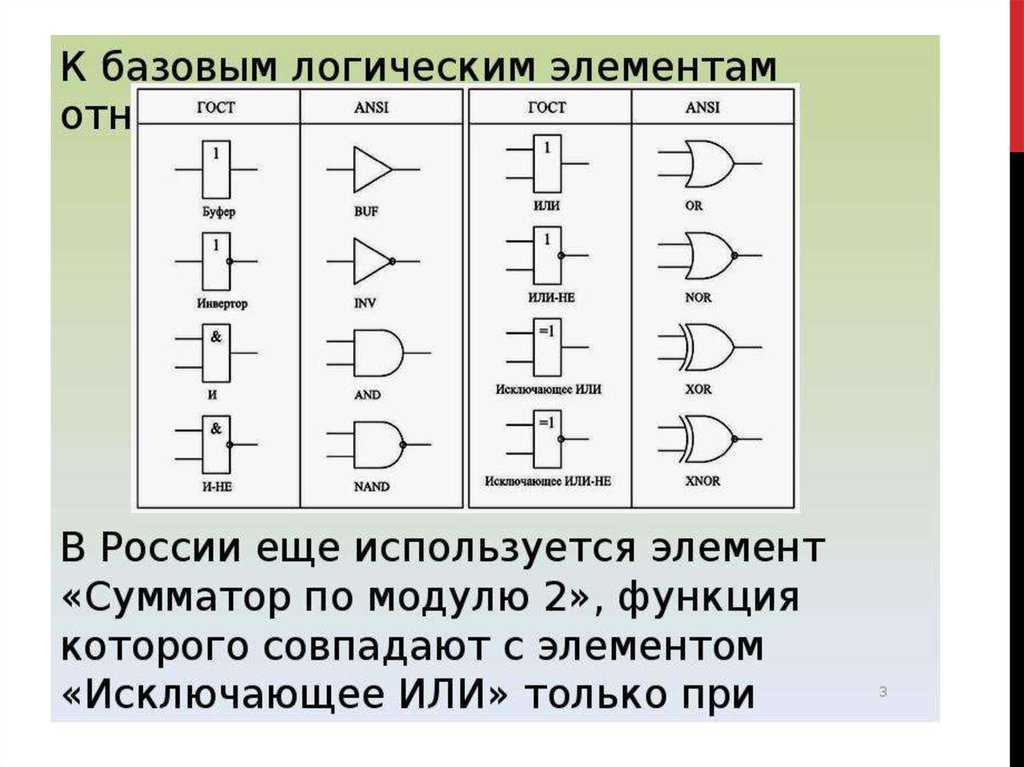 Разница лишь в том, что вход D и вход Q Выход – это многобитные сигналы.

Как показано слева, регистр реализован как группа триггеры, которые разделяют свои часы и разрешают сигналы.

Реализация регистра

Регистр реализован как группа триггеров, которые имеют общие часы и разрешающие сигналы.

Процессор Datapath Control

Сигналы управления трактом передачи данных процессора можно классифицировать по какую часть процессора они контролируют:

• Государственный контроль
• Комбинированные элементы управления

Комбинационное логическое управление

Сигналы управления для комбинационной логики часто просто контроль маршрутизации. Часто эти сигналы подаются на мультиплексоры.

Например, многие инструкции записывают результат в регистр.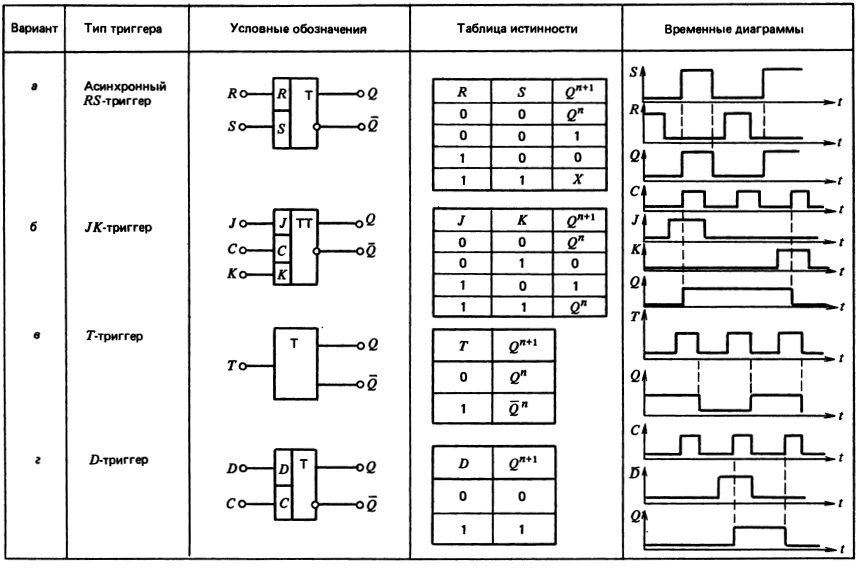 Мультиплексор необходим, чтобы выбрать, поступают ли эти данные из вычисления (арифметические и логические инструкции) или из памяти (загрузка инструкции).

MOSFET, затвор и логика

Дата: 15.12.2016

Этот модуль охватывает фундаментальные идеи, лежащие в основе проектирования современных цифровых систем. Этот модуль объясняет основы элементов схемы, как они взаимосвязаны для формирования цифровых схем, а также неидеальные эффекты дизайна.

Цифровые системы
Слово «цифровые» относится к представлению любой информации всего двумя уровнями напряжения [логический ноль (0) или высокий логический уровень (1)]. Логический ноль означает нулевое напряжение, логический высокий уровень означает некоторый уровень напряжения электрического потенциала, который обычно составляет 3,3 В или 5 В.

Цифровые системы более широко используются, чем аналоговые системы для обработки данных, по следующим причинам: Цифровые системы легче проектировать, поскольку цифровые системы используют цифровые сигналы, которые обеспечивают множество будущих возможностей, таких как очень меньшая подверженность шуму, сигнал может быть легко регенерирован и т.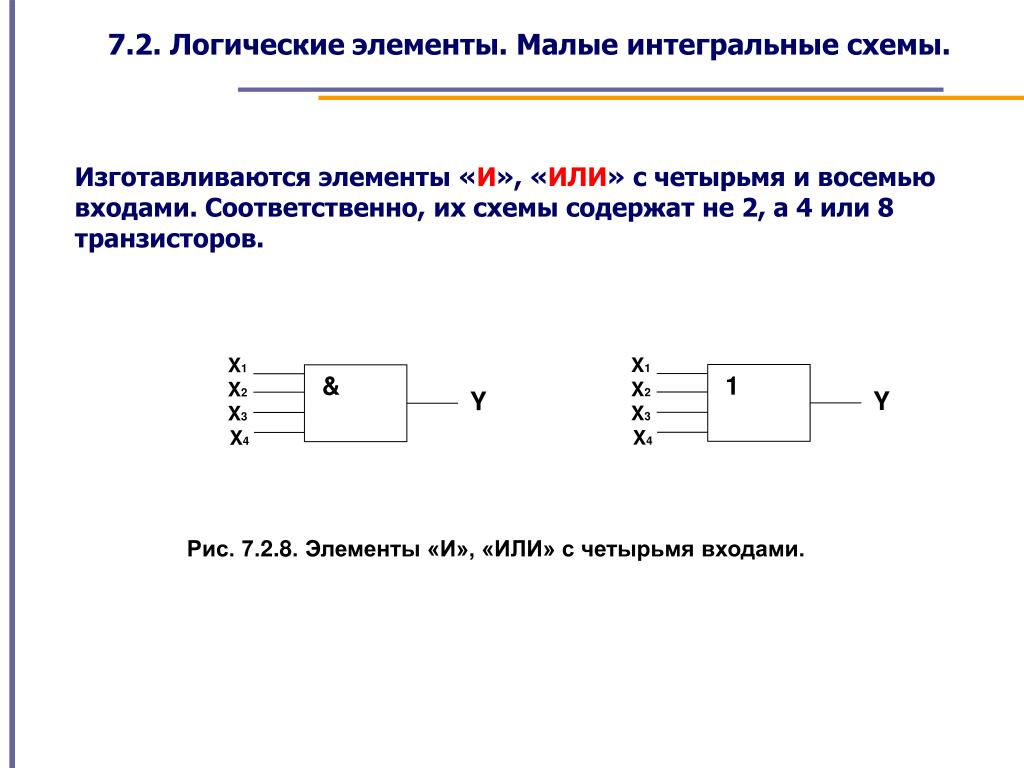

д. Термин «проектирование» относится к систематическому процессу разработки схем, отвечающих заданным требованиям, но при этом удовлетворяющих ограничениям по стоимости, производительности, энергопотреблению, размеру, высоте и другим свойствам.

Давайте начнем обсуждение логических вентилей, работающих с цифровым сигналом.
Существует три основных вентиля, а именно И, НЕ, ИЛИ, из которых получены вентили И-НЕ, ИЛИ-НЕ, Исключающее ИЛИ, Исключающее-ИЛИ. Ворота И-НЕ и ИЛИ-НЕ обычно называют универсальными воротами. Теперь давайте начнем обсуждать, как работают эти ворота.

Ворота НЕ:

В компьютерном мире символом, используемым для обозначения ворот НЕ, является “~” (или) (!) (отрицание). Когда какой-либо высокий логический сигнал входит в вентиль НЕ, выход не будет низким сигналом, и происходит обратная операция, когда низкий сигнал входит в вентиль НЕ. Символ ворот НЕ изображен на рисунке 1, а его работа представлена ​​в таблице истинности.

Рисунок 1: (a) символ инвертора (b) таблица истинности (c) ИС для не вентиля (d) схема инвертора
IC 7404 используется для вентиля НЕ, шесть вентилей НЕ встроены в IC 7404. Схематическая диаграмма для вентиля НЕ показан на рисунке1

Вентиль И
В отличие от вентиля НЕ, вентиль И имеет две входные клеммы. Символ для представления функции И — «&». Выход логического элемента И будет высоким только тогда, когда оба входа будут высокими. Символ вентиля И показан на рисунке 2 ниже.

Рисунок 2: Логический элемент И, таблица истинности и внутренний вид IC7408 и IC7411

IC 7408 используется для операции И. Он содержит 4 вентиля И, каждый из которых имеет по два входа. У нас может быть 3 входа И вентиль (IC7411). Конфигурация выводов IC 7408 и 7411 показана на рисунке 2.

Мы можем получить 4-х входные логические элементы И с помощью двух входных логических элементов И. Давайте посмотрим, как мы можем это сделать:

Рисунок 3: 4-х входные логические элементы И, полученные из двух входных логических элементов И и их истинности.

На рисунке ниже показана принципиальная схема двухвходового И-затвора, выполненного с использованием полевых МОП-транзисторов.

ИЛИ ворота:

Символ для представления или ворот “|”. Ворота ИЛИ выполняют сложение. когда любой из входов вентиля ИЛИ имеет высокий логический уровень, выход будет высоким. Таблица символов и истинности вентиля ИЛИ показана на рисунке 5. IC 7432 используется для операции ИЛИ. он содержит четыре, 2 входных элемента ИЛИ.

Рис. 5: Таблица символов и истинности вентиля ИЛИ.

Рис. 6: Схема вентиля ИЛИ
Примечание. Чтобы узнать больше о номерах микросхем для цифровых схем, посетите: https://en.wikipedia.org/wiki/List_of_7400_series_integrated_circuits

Включение света в комнате, когда в комнате темно, с помощью простого И-ворота :

Вот реальный пример, который всегда прост, И-ворота можно использовать для включения света в комнате, когда в комнате темно. Пожалуйста, смотрите рисунок 7. Это говорит о двух входных логических элементах И, где один вход подключен к переключателю, который либо подключен к +5 В высокого напряжения, либо заземлен к 0 напряжению.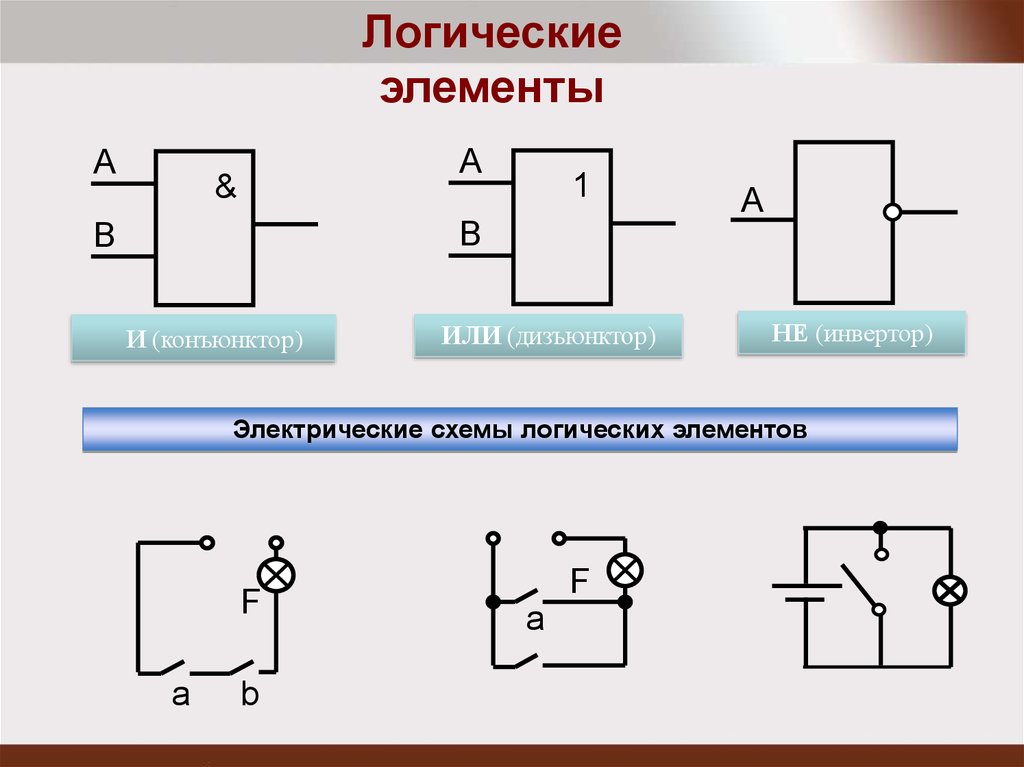 Чтобы заставить это устройство работать, вы должны держать переключатель таким образом, чтобы он был подключен к +5 В, чтобы вход на вентиль И всегда был высоким. Другой вход, верхний логический элемент И, подключен к датчику освещенности, который вырабатывает +5 В, когда темно или нет света, в противном случае нулевое напряжение низкого уровня, когда есть свет. Логический элемент И подключен к реле, которое может включать лампочку. Лампочка загорится только тогда, когда на обоих входах и будет высокий уровень. Так бывает только тогда, когда темно.

Рис. 7: Реальный пример с использованием вентиля И.

Приложения настолько просты, что логические вентили управляют современным миром в виде сложных процессорных чипов, которые имеют миллионы таких вентилей. В этом курсе мы познакомим вас с тем, как миллионы логических вентилей или проводных соединений выполняют сложную функцию для использования в режиме реального времени.
Мы начали с логических элементов в основном для того, чтобы объяснить с помощью приведенного выше приложения, где логические схемы могут использоваться для автоматизации многих наших потребностей.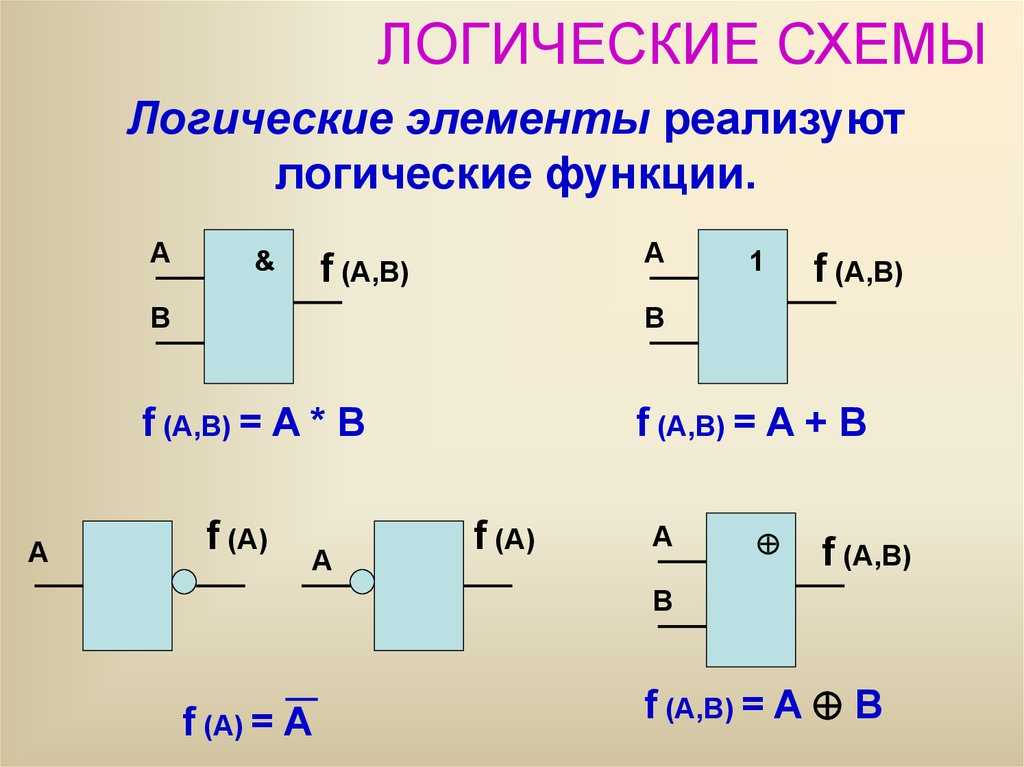

Пример 2:
Рассмотрим завод по производству пластмасс. Установка должна поддерживаться ниже с определенным порогом температуры и давления. Если температура или давление превышают предельные значения, установка должна быть остановлена.

Рисунок 8: реальный пример для вентиля ИЛИ

Пример 3
В реальных инверторах, соединенных встречно-параллельно с нечетными числами, обратная связь передается от выхода к входу для получения колебаний.

Рисунок 9: Кольцевой осциллятор

Примечание. Конструкция должна удовлетворять критериям Баркгаузена для цифровых и смешанных СБИС от Razavi.

Универсальные вентили (НЕ-И и ИЛИ-НЕ)

Вентиль-НЕ является обратным вентилю И. Символ логического элемента И-НЕ показан на рисунке 10. Работа логического элемента И объясняется в таблице истинности.

Рисунок 10: символ вентиля НЕ-И и его таблица истинности

Вентиль НЕ-ИЛИ является обратным вентилю ИЛИ. Символ вентиля ИЛИ-НЕ изображен на рисунке 11. Работа вентиля ИЛИ-ИЛИ объясняется в таблице истинности 9.0009

Рисунок 11: символ вентиля НЕ-ИЛИ и его таблица истинности

Из вентилей НЕ-И и НЕ-ИЛИ мы можем получить любые другие вентили, отсюда и название универсальных вентилей. Давайте посмотрим, как это сделано:

NAND как вентиль AND

NAND как вентиль OR

NOR как вентиль AND

вентиль XOR: Произносится как XOR-операция вентиля4 сумма 9000s OR: 9000s который не включает Carry. Он содержит два входа и один выход. Символ вентиля XOR показан на рисунке 12.

Рисунок 12: символ логического элемента исключающее ИЛИ и его таблица истинности универсальные ворота в реальном мире.

Пример 1: Рассмотрим сценарий Промышленные химикаты хранятся на складах, где происходят химические реакции, приводящие к образованию токсичных паров, которые выбрасываются в атмосферу через вытяжные вентиляторы. В складских помещениях необходимо установить три вытяжных вентилятора для отвода ядовитого воздуха в процессе их работы.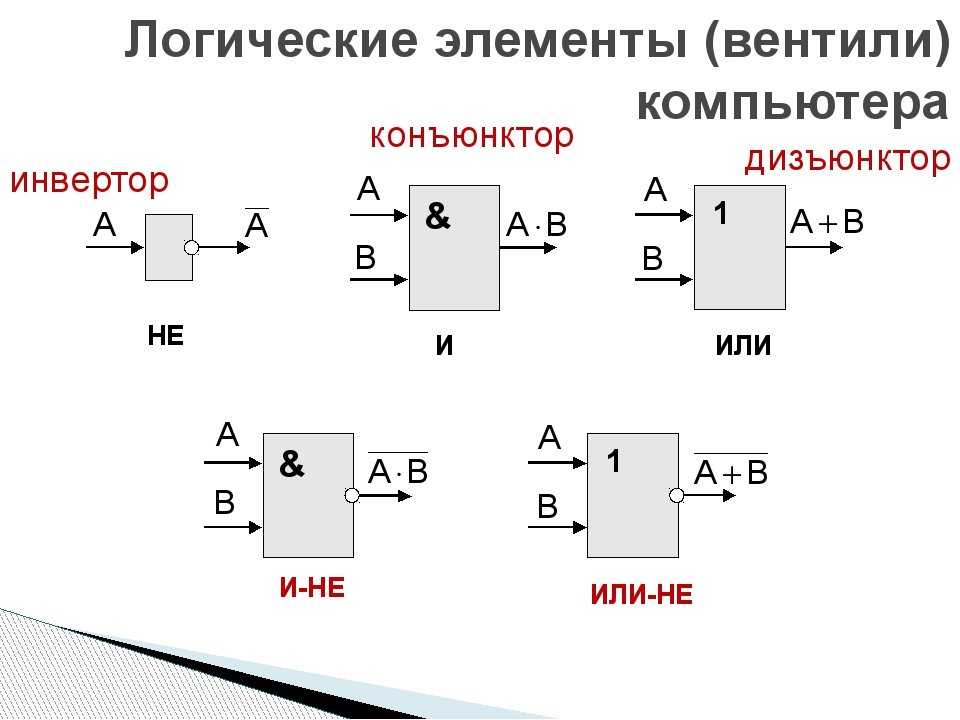 Если один или несколько вытяжных вентиляторов выходят из строя, активируется аварийный сигнал.

Рис. выше: Система обнаружения отказа вытяжного вентилятора на основе вентиля И-НЕ

Пример 2: Стиральная машина оснащена тремя датчиками для проверки ее работы. Первая операция — это функционирование двери, вторая — уровень воды, а третья — взвешивание одежды. Если одна из функций выходит из строя, например, открытие или закрытие двери, изменение уровня воды или перегрузка одежды, генерирует соответствующие выходы датчика на 1. Выходы 3 датчиков подключены к 3 входам вентиля ИЛИ-НЕ. Выходы датчиков будут равны 0 при нормальной работе стиральной машины. Выход вентиля ИЛИ-НЕ равен 0, если ошибочное состояние обнаружено любым одним или несколькими датчиками. Выход вентиля ИЛИ-ИЛИ подключен к выключателю стиральной машины.

Булева алгебра:

Булева алгебра используется в качестве основы для цифрового дизайна. Цифровые системы могут быть выражены в терминах логических выражений, которые содержат логические операторы, переменные и логические значения.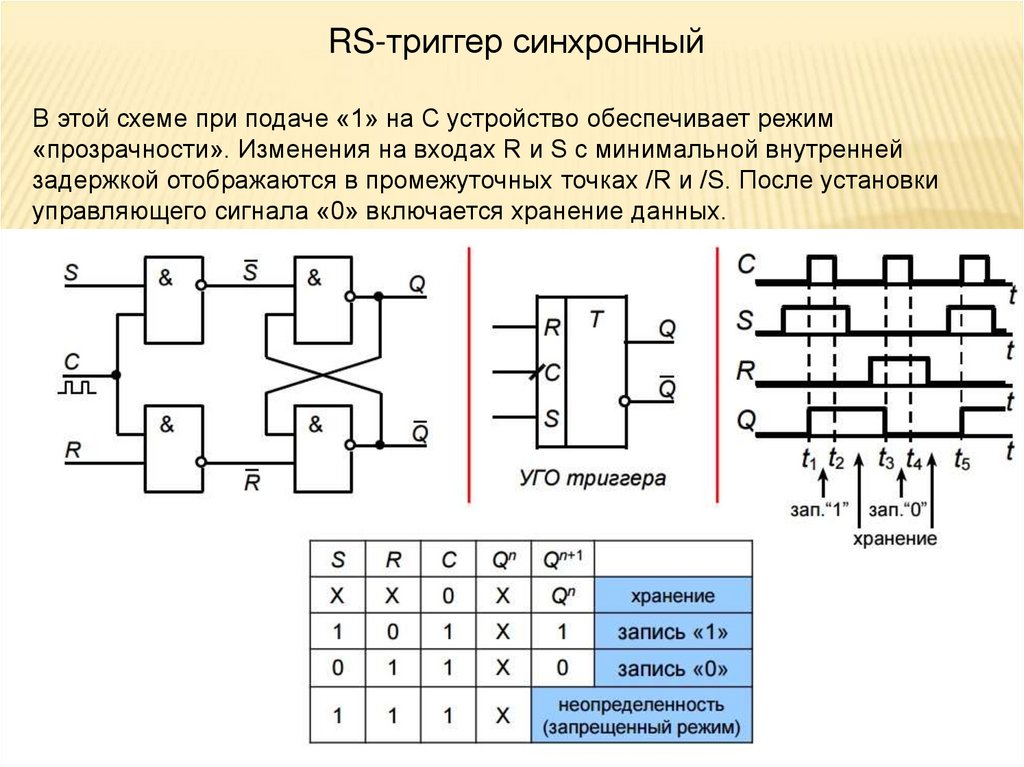
Булева алгебра имеет дело с логическим выражением
Пример логического выражения

В приведенном выше примере A, B, C являются переменными , +& . являются операторами, а 0 и 1 — логическими значениями. Аксиомы булевой алгебры перечислены ниже:

Законы тождества
X+0=X
X.1=X

Законы ассоциации
(X+Y)+Z= X+(Y+Z)
(X.Y).Z=X(Y.Z)

Законы коммутации
X+Y=Y+X
X.Y= Y.X

Законы распределения
X+ (Y.Z)= (X+Y).(X+Z)
X.(Y+Z)= (X.Y)+(X.Z)

Дополнительные законы

Ниже перечислены некоторые полезные теоремы, которые можно использовать при работе с булевыми выражениями.

Законы идемпотентности
X+X= X
X.X=X

Законы поглощения
X+(X.Y)=X
X.(X+Y)=X

Другие законы тождества
X+1=1
X.0=0

Законы Де Моргана

Здесь + представляет операцию ИЛИ
. представляет операцию умножения, т.е. операцию И

(2) f= AB+A(B+C)+B(B+C)

(3) f=A(B+CD)

Логические выражения может быть выражена в двух формах, а именно в виде суммы произведений (SOP) и произведения сумм (POS):
Сумма произведений: термины произведения логических выражений суммируются логическим сложением в форме SOP 9. 0143 Пример:- 1. AB+BC+CA
2. AB+B(C+D)
Произведение сумм: сумма переменных умножается на сумму других членов выражения.

(A+B+C)A (D+F)

Мы не можем преобразовать логическое выражение в SOP или POS. Давайте посмотрим, как мы можем этого добиться:

AB+B(CD+EF) преобразуется в SOP
Ans. AB+BCD+BEF
(A+B) (B+C+D) преобразовать в SOP
Ответ. AB+AC+AD

Примечание. Итак, мы уже видели выражения SOP и POS. Приведены примеры нестандартного способа выражения булевых выражений.
Стандартная СОП:
Рассмотрим пример f= AB+BC+CA, давайте преобразуем его в стандартную форму СОП:
>AB+BC+CA

Стандартное выражение СОП — это выражение, в котором все переменные домена появляются в каждом термине продукта в выражении.

Standard POS

Упрощение логических выражений с помощью булевой алгебры

AB+A(B+C)+B(B+C)
=AB+AB+AC+BB+BC
= AB+AC +BC+B
= B+ AC+AB
= B (1+A)+AC
=B+AC

Упрощение логического выражения упростит логику.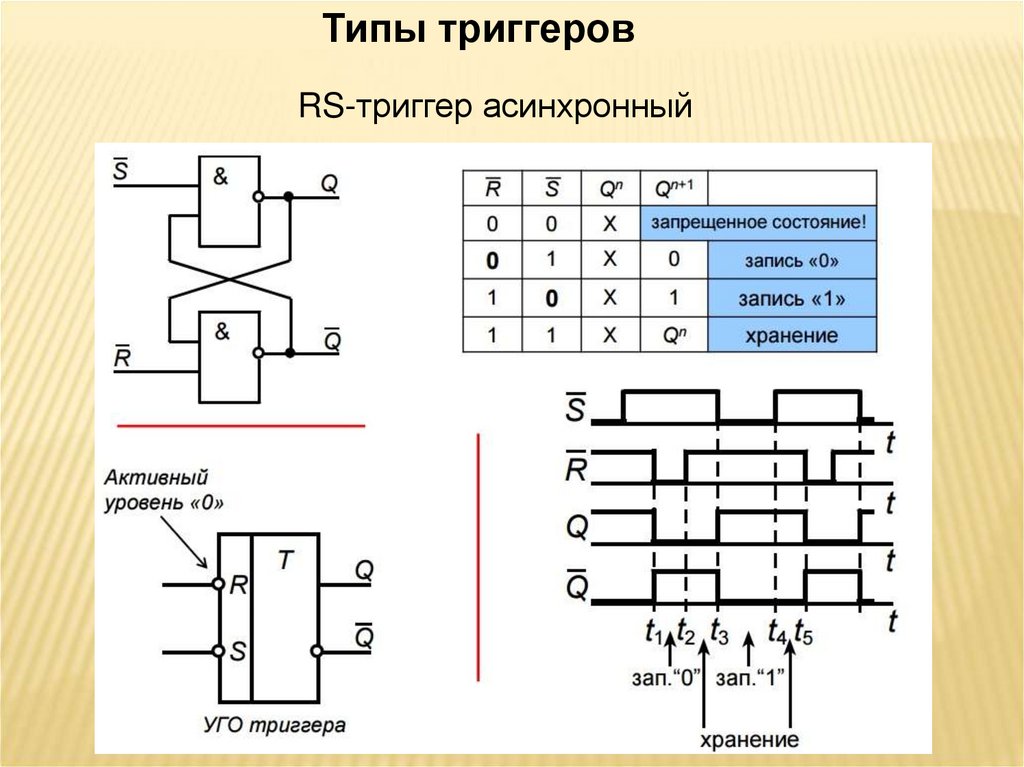
Рассмотрим выражение AB+A(B+C)+B(B+C), это эквивалентные логические схемы, а упрощенная принципиальная схема показана ниже и некоторые из них перечислены ниже:

1. Карта Карно
2. Алгоритм Куайна-Маккласки
3. Минимизация переменной состояния

Для получения дополнительной информации об упрощении логики см. приложения и разработки цифровой логики Джона М. Ярбро.

Неидеальные эффекты элементов схемы

(1) Задержка распространения: Задержка распространения обусловлена ​​внутренней коммутационной активностью (т. е. временем, необходимым для зарядки и разрядки паразитной емкости транзисторов)

Уровни сигналов не изменяются мгновенно из-за к переключению деятельности. Время, необходимое для повышения напряжения сигнала от низкого уровня до высокого уровня, называется временем нарастания. Время, необходимое для падения напряжения сигнала с высокого уровня на низкий, называется временем спада.

Рассмотрим схему, показанную на рисунке ниже.

Одним из способов уменьшения задержки распространения является уменьшение паразитной емкости. Если к выходу предыдущего блока подключено более одного логического блока, паразитная емкость суммируется, что приводит к чтобы больше задержка распространения, другими словами разветвление должно быть меньше.

(2)Задержка провода

Мы думаем, что провод ведет себя как чистый проводник без какого-либо сопротивления, но на самом деле провода будут иметь сопротивление, индуктивность и емкость. Когда длина провода слишком мала, этими значениями можно пренебречь. Когда длина проводов слишком велика, они становятся линией передачи с разумной задержкой распространения. Эти задержки следует учитывать при проектировании высокоскоростных систем.

(3)Глюки

Глитчи также известны как недействительные выходные данные, которые возникают из-за задержки распространения на входах, входящих в логический блок, например, возьмем электрическую схему, показанную ниже

В приведенном выше примере мы можем сказать, что неожиданный ноль на выходе схемы. Это называется сбоем, и он вызывает проблемы для остальных цепей, поскольку он распространяется на следующие цепи и приводит к большему количеству сбоев.

Решение этой проблемы: добавление буфера к пути с меньшими задержками распространения. Эти буферы компенсируют задержку, чтобы мы могли ожидать корректных результатов на выходе.

Комбинационные логические схемы и последовательные логические схемы
комбинационные логические схемы выполняют операции над входами, входящими в схему, и определяют выход как логическую функцию входа.
Другими словами, вывод является функцией только ввода. На рисунке ниже показана общая блок-схема комбинационной схемы.

Этим комбинационным логическим схемам не хватает сохранения каких-либо предыдущих выходов. Другими словами, у него нет памяти. Это можно преодолеть, используя последовательные схемы, в которых выход определяется как предыдущим, так и текущим входом. На рисунке ниже показана блок-схема последовательных логических схем.