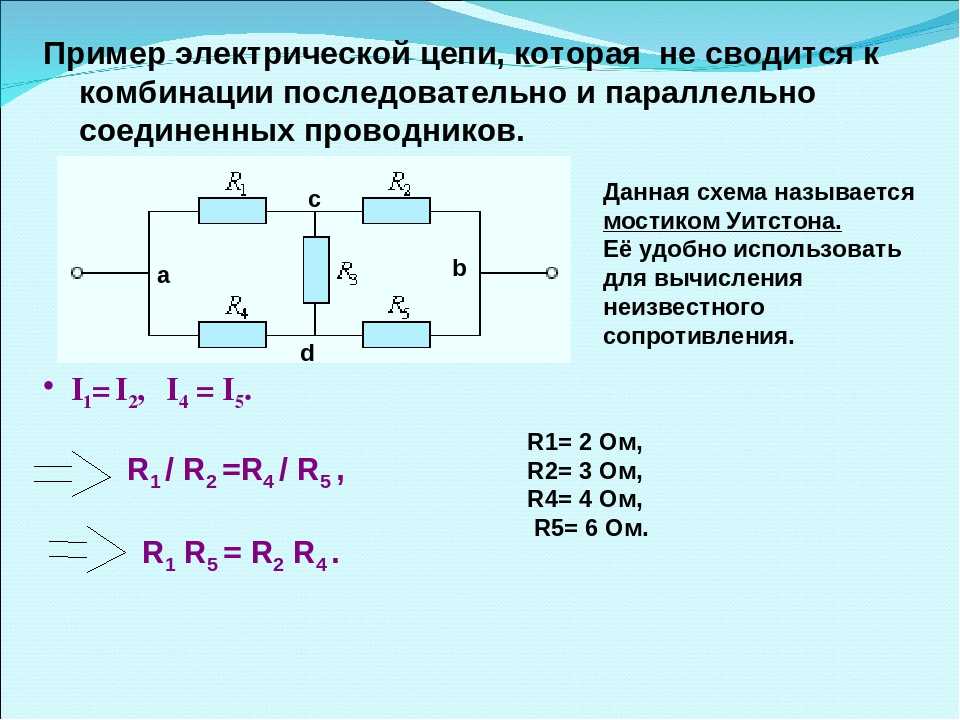
Схемы подключения резисторов: Параллельное включение резисторов – схема и расчет. Как отличается параллельное и последовательное соединение резисторов?

Содержание

Параллельное включение резисторов – схема и расчет. Как отличается параллельное и последовательное соединение резисторов?

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

Проводники (все металлы, ионизированный газ и электролитические растворы).
Полупроводники (Si, Ge, GaAs, InP и InSb).
Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда.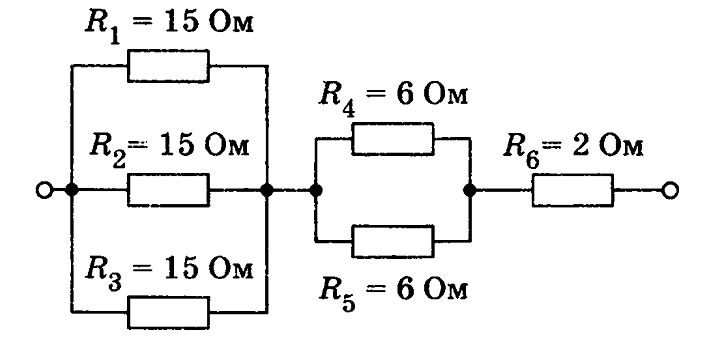 При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

С правого края – правый.
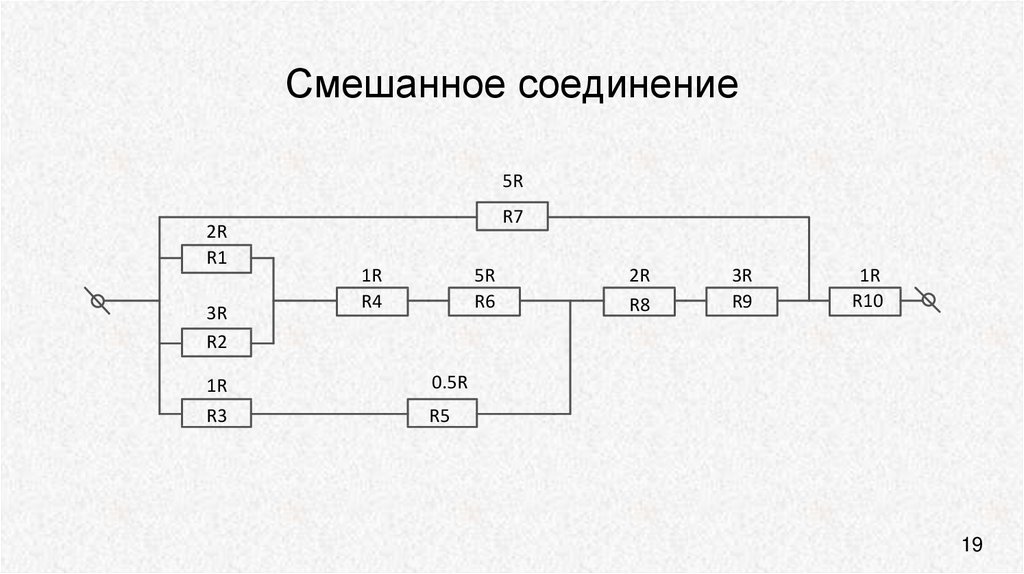
С левого края – левый.

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Общее сопротивление

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

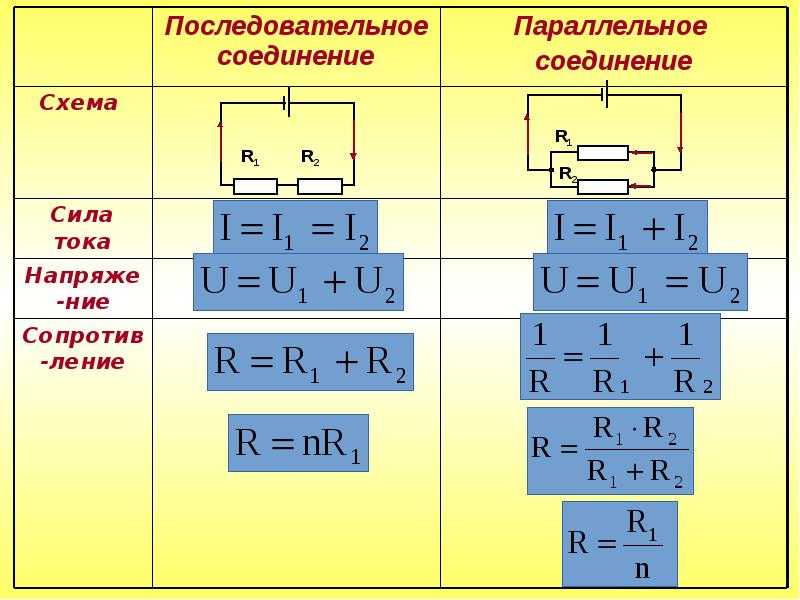
Схема

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.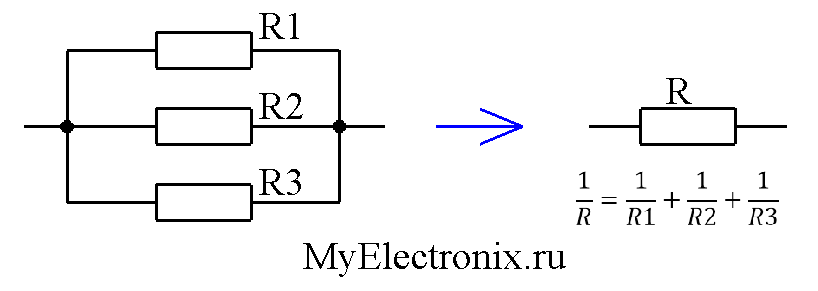

Будет интересно➡ Переменный резистор

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Как выглядит формула Георга Ома

Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.

Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:

U1 = U2 = U.

Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:

I = I1 + I2.

Расчет силы тока при помощи закона Ома записывается как:

I = U/R;

I1 = U1/R1;

I2 = U2/R2.

Из формулы следует:

U/R = U1/R1 + U2/R2;

U = U1 = U2;

1/R = 1/R1 + 1/R2.

Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.

Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.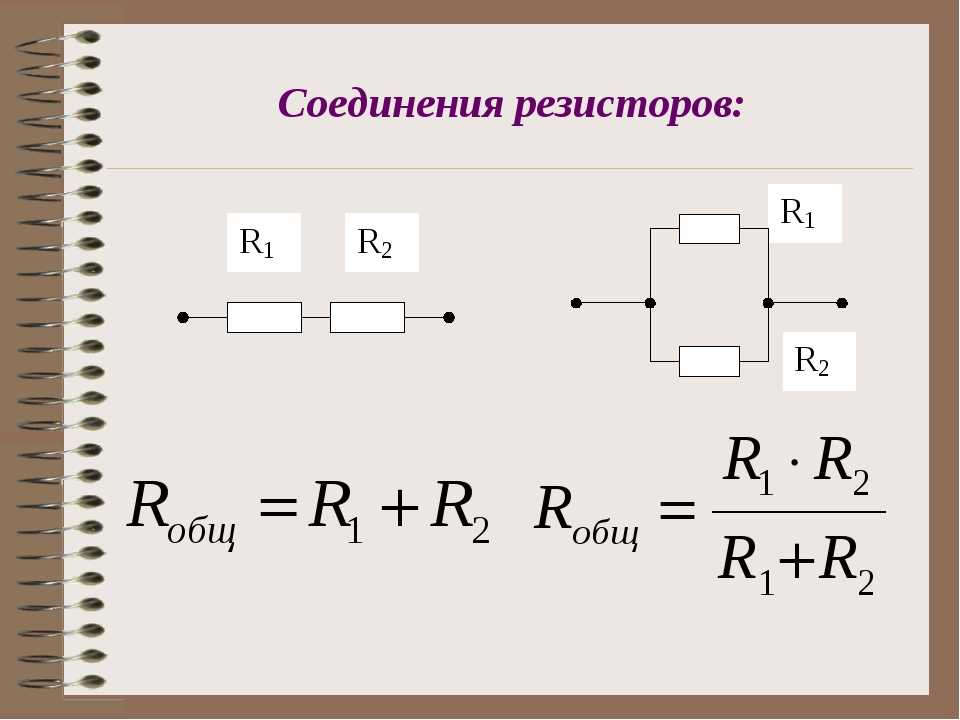

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока.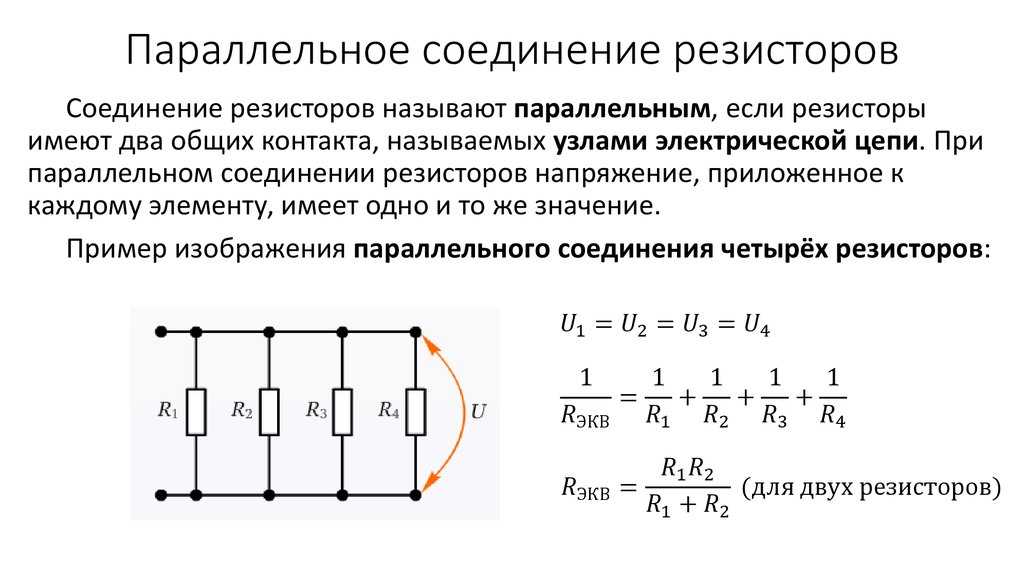 Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Следовательно,

UR1 = IR1 =1×2=2 Вольта

UR2 = IR2 = 1×3=3 Вольта

UR3 = IR3 =1×5=5 Вольт

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Получается

U=UR1+UR2+UR3

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Отличия от последовательного и смешанного подключений

Параллельное соединение проводников

Иные способы соединения понятны из показанных на картинке примеров. Без специальных вычислений понятно, что параллельное включение резисторов создает несколько путей прохождения тока. Следовательно, в отдельных цепях его сила будет меньше, по сравнению с контрольными точками на входе и выходе. Вместе с тем напряжение в отмеченных местах остается неизменным.

Последовательное соединение резисторов увеличивает общее электрическое сопротивление. Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.

Смешанный вариант – это объединение представленных выше соединений. Различные комбинации используют для деления напряжения, решения других задач. Для упрощения расчетов суммируют последовательность соединенных сопротивлений в отдельных цепях:

Rобщ = R1 + R2 + … + Rn.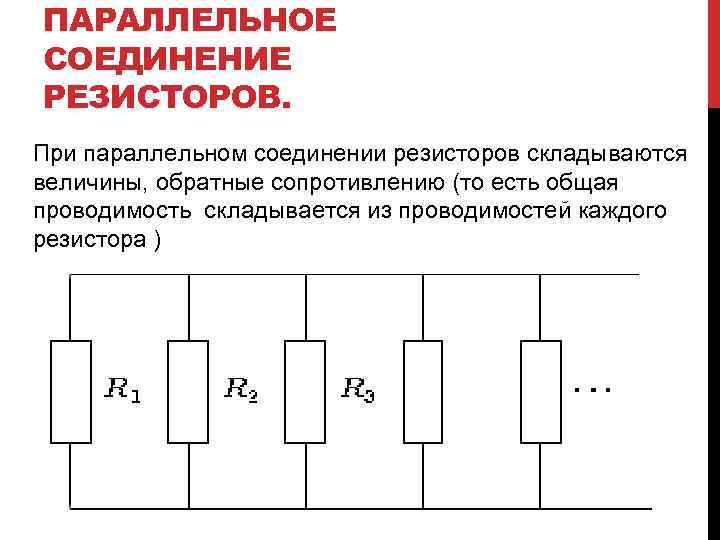

Вне зависимости от сложности схемы, на входе и выходе по первому закону Кирхгофа токи будут одинаковыми.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения.

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм.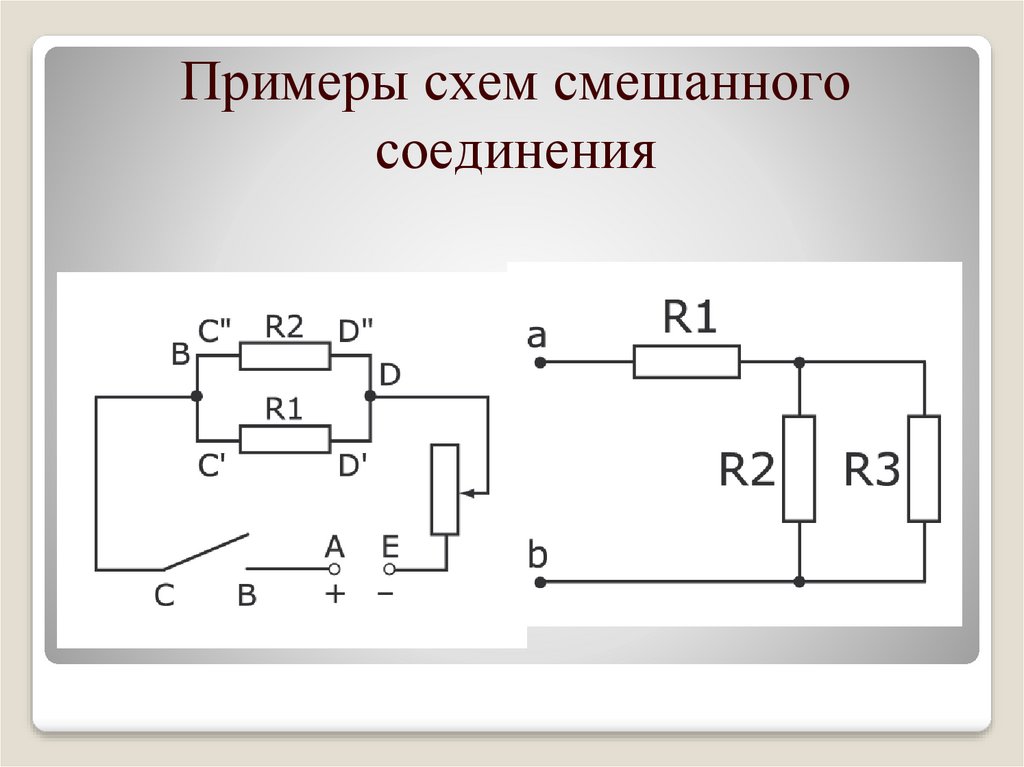 Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Источники

https://rusenergetics. ru/praktika/raschet-soprotivleniya-rezistorov
https://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html
https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
https://rusenergetics.ru/polezno-znat/parallelnoe-soedinenie
https://www.RusElectronic.com/serial-and-parallel/
https://amperof.ru/teoriya/parallelnoe-soedinenie-rezistorov.html
https://www.translatorscafe.com/unit-converter/ru-RU/calculator/parallel-resistance/
http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/

[свернуть]

Параллельное и смешанное соединение резисторов: разные способы подключения сопротивления

Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления. В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов. Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах.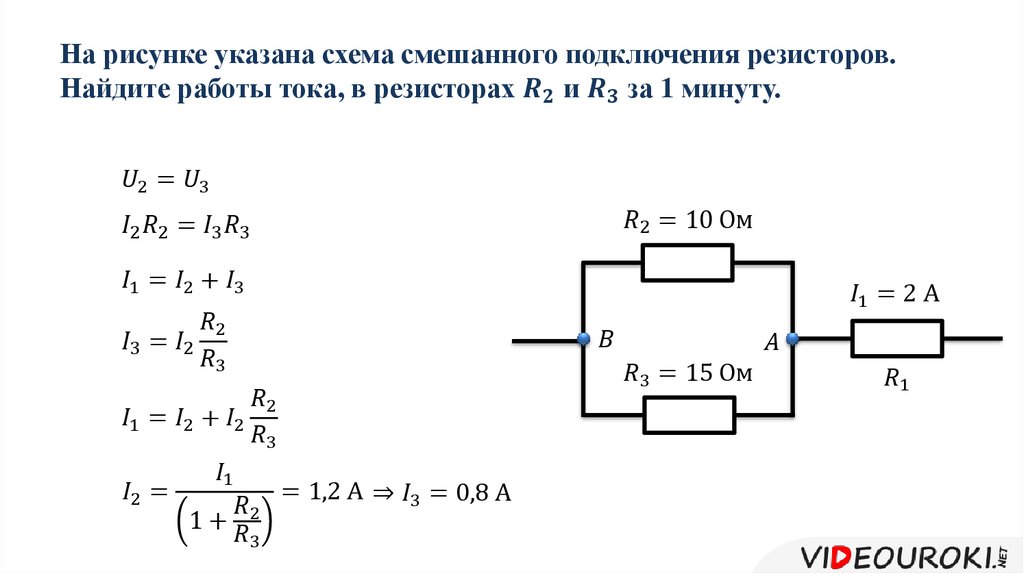 Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.

Последовательное соединение
Параллельное подключение
Смешанный вариант

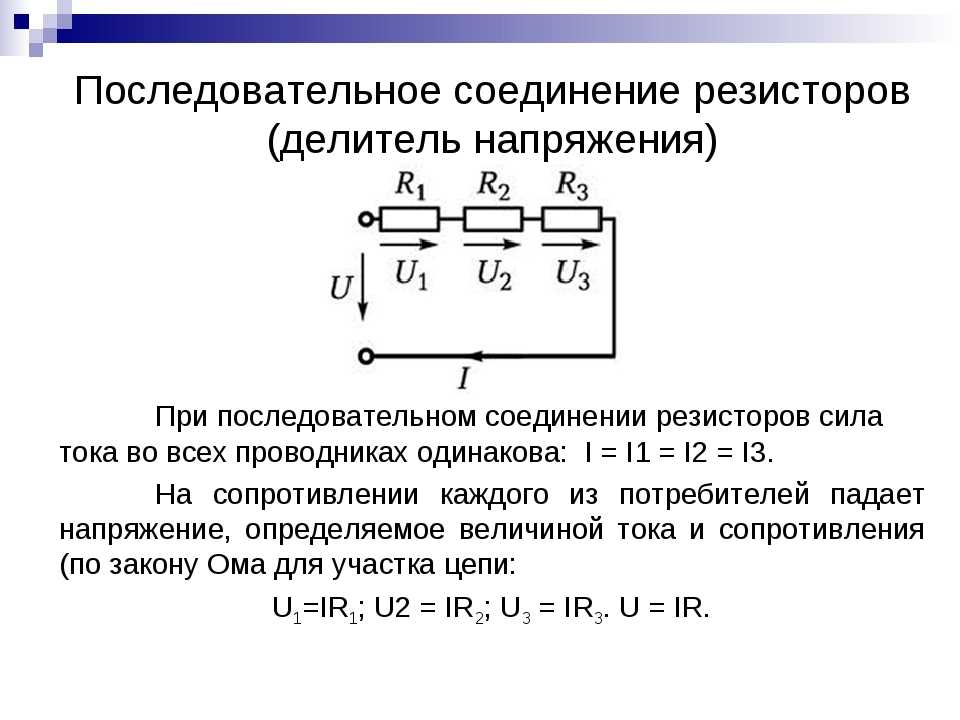
Последовательное соединение

Выделяют такие способы соединения резисторов: последовательное, параллельное и комбинированное. При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.

От количества подключённых резисторов зависит сопротивление протекающему электричеству. Чем больше составляющих, тем оно выше. Его рассчитывают по формуле: R общее = R1+R2+…+Rn, где:

R общее — это сумма всех сопротивлений;
R1 — первый резистор;
R2 — второй компонент;
Rn — последняя составляющая в цепи.

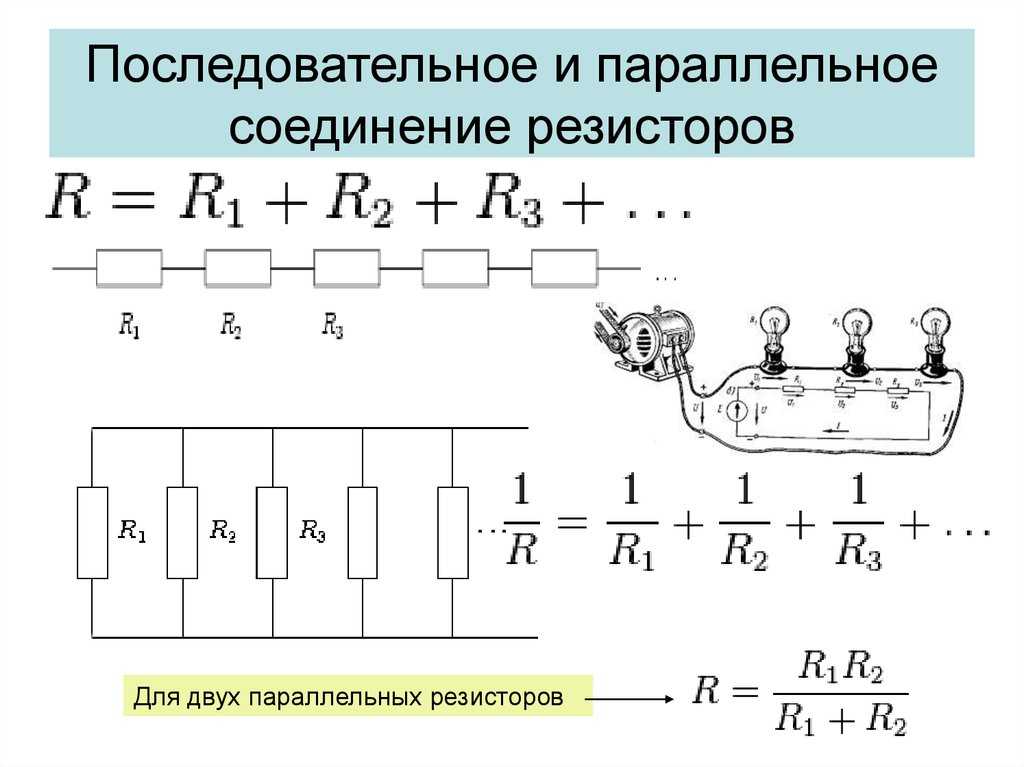
Параллельное подключение

Параллельное соединение подразумевает подключение начал резисторов к одной точке, а концов к другой. Сами компоненты при этом расположены на одинаковом расстоянии друг от друга, а их количество не ограничено. По каждой составляющей электричество протекает отдельно, выбирая один из нескольких путей.

Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.

В расчётах общее сопротивление всегда должно быть меньше любого из составляющих цепи. Способ вычисления суммы противостояния для схемы из двух резисторов немного отличается: 1/R общее = (R1 х R2)/(R1+R2). Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.

Смешанный вариант

В смешанном соединении сопротивлений комбинируют последовательную и параллельную схему подключений. В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.

Для вычисления суммы противостояния электричеству схему нужно разбить на мелкие участки, в которых резисторы подключены одинаковым способом. Затем расчёты проводят по алгоритму:

в цепи с параллельно соединёнными компонентами высчитывают эквивалентное сопротивление;
после этого высчитывают противостояние на последовательно подключённых участках схемы;
наглядную иллюстрацию нужно перерисовать, обычно получается цепь с последовательным соединением резисторов;
рассчитывают сопротивление в новой схеме по одной из двух формул.

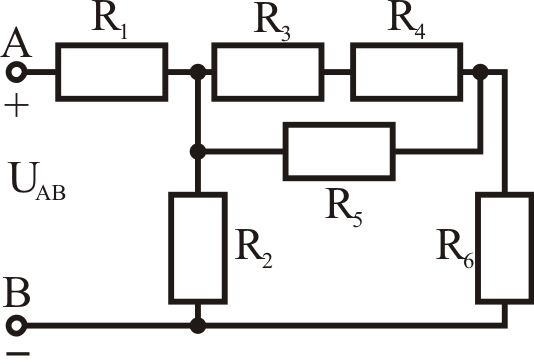
Лучше понять методы вычислений поможет пример. Если в схеме всего пять компонентов, они могут располагаться по-разному. Начало первого резистора подключено к точке А, конец — к В. От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.

Сначала высчитывают сумму сопротивления последовательного участка внутренней схемы: R2+R3. После этого цепь перерисовывают так, чтобы второй и третий компоненты были соединены в один. В результате внутренняя цепь имеет параллельное подключение. Теперь высчитывают её противостояние: (R2,3xR4)/(R2,3+R4). Можно второй раз изобразить полученную цепь.

В схеме будет три резистора, соединённые последовательным методов. Причём средний включает параметры второго, третьего и четвёртого компонента.

Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5. Можно сразу подставить в неё все параметры компонентов.

На практике последовательный и параллельный метод соединения используются редко, ведь в приборах схемы обычно сложные. Поэтому в цепях резисторы часто соединены комбинированным способом. Сопротивление в таких случаях высчитывают пошагово.

Если сразу выводить числа в общую формулу, то можно ошибиться и получить неверные результаты. А это может отрицательно сказаться на работе электрического прибора.

Схемы резисторов

: понимание соединений и функций

О схемах резисторов，Резисторы являются одним из наиболее важных электронных компонентов электронного устройства. Они являются пассивными компонентами, ограничивающими протекание тока, обеспечивающими определенное падение напряжения и действующими в качестве электрических нагрузок для цепей.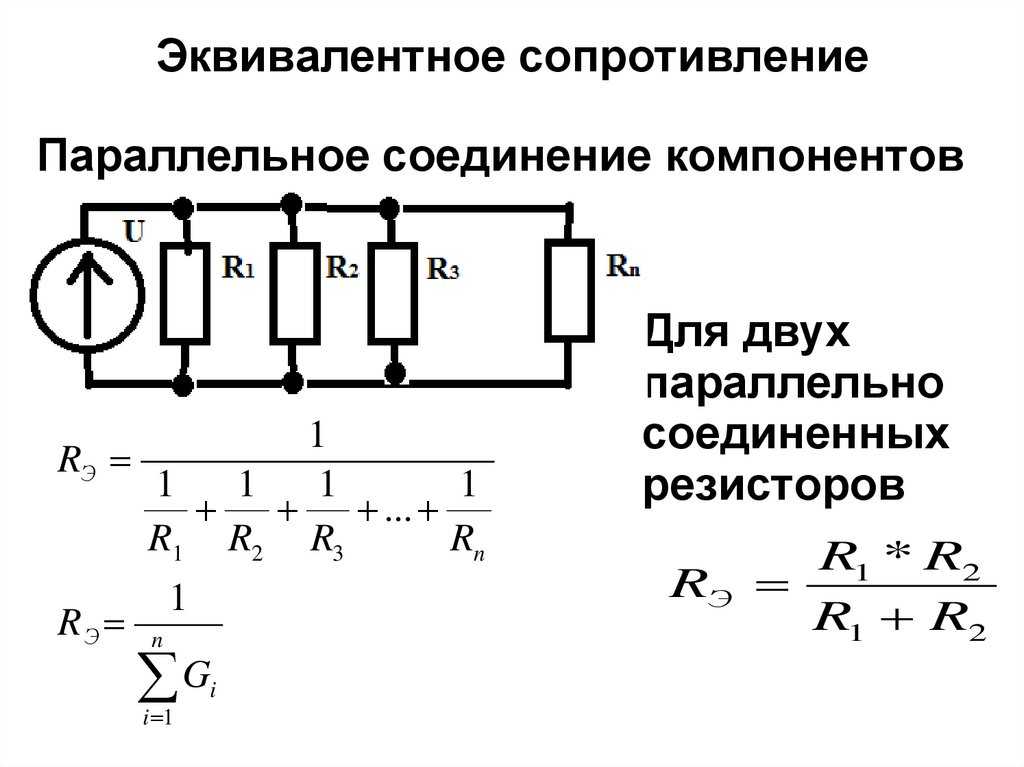

Вы можете сделать конфигурацию резисторов различными способами для достижения этих целей. Есть три первичных резистора в последовательном соединении, резисторы в параллельном соединении и комбинации резисторов в последовательном и параллельном соединении.

В этой статье будут рассмотрены все три типа со схемами, показывающими, как они работают! Давайте начнем!

Резисторы в последовательном соединении

Резисторы в последовательном соединении имеют два или более резистора, соединенных встык с одинаковым напряжением на всех них.

Как последовательно соединить резисторы

Подсоедините концы каждого резистора к источнику выходной мощности, предполагая, что провода имеют незначительное сопротивление. Резисторы соединены последовательно, поэтому, если один резистор имеет сопротивление R1, другой резистор также имеет сопротивление R2. Общее сопротивление равно сумме номинал отдельного резистора; в этом случае мы используем закон Ома для расчета.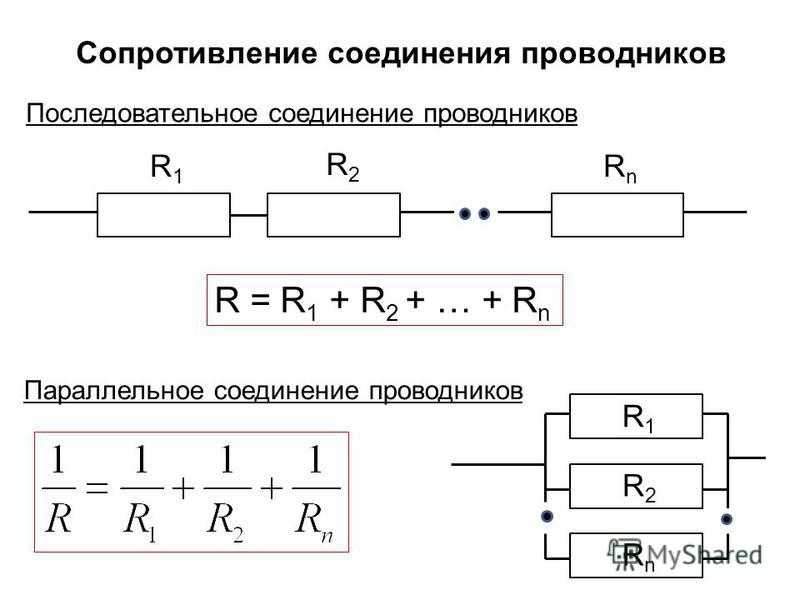

Закон Ома в цепях с последовательным сопротивлением

Закон Ома гласит, что ток прямо пропорционален напряжению в двух точках любого проводника. В нашем случае резисторы.

На приведенной ниже схеме показана простая схема с последовательностью соединений резисторов. Первый резистор имеет значение сопротивления R1, а второй резистор имеет значение сопротивления R2.

По закону Ома; В=ИК

В = I * R_t

Где R_t — эффективное сопротивление резисторов, включенных в цепь. Напряжение источника (В) в цепи резистора такое же, как и напряжение. Причем резисторы включены последовательно, поэтому падение потенциала на них одинаковое. Мы также можем использовать закон Ома, чтобы найти это значение.

Ток и мощность в последовательных цепях

(цепь с последовательным резистором)

В цепи с последовательным резистором общий ток (I) одинаков для всех резисторов. То есть ток, протекающий через резистор_1, является тем же током, который будет протекать через резистор_2.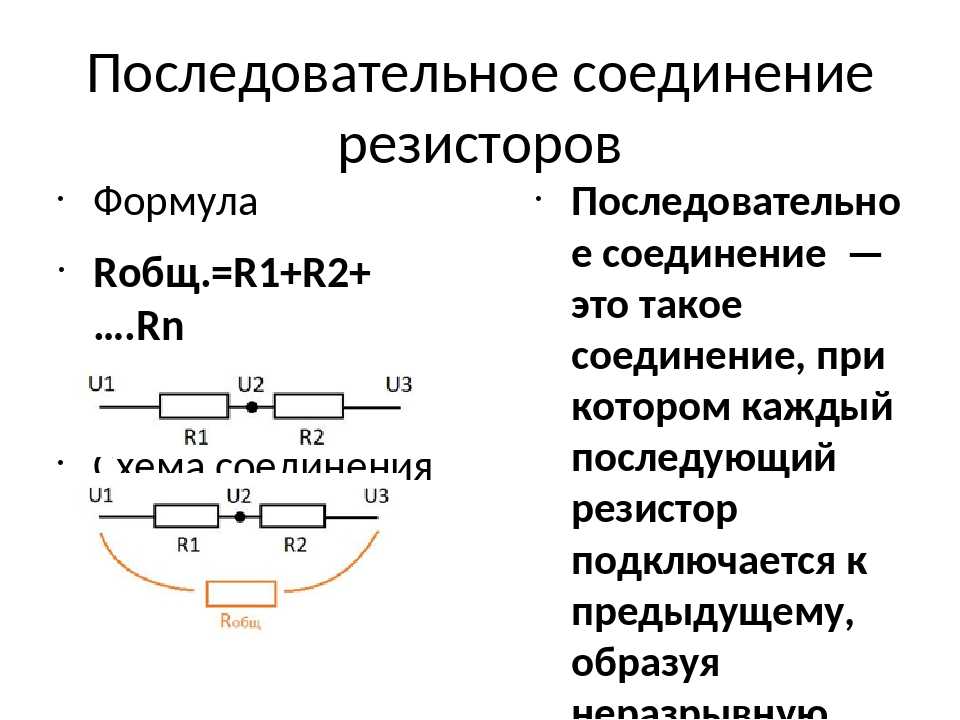 Кроме того, выходной ток равен тому, который обеспечивает батарея. Примечательно, что если вы добавите в цепь больше резисторов, текущее значение со временем уменьшится. Это связано с тем, что резисторы одинаково распределяют ток, несмотря на разницу в сопротивлении.

Итак, текущий; I_t = I_1=I_2.

Аналогично, Ток, я тоже =V/Rt

Другими словами, приложенное напряжение батареи (В), деленное на эффективное сопротивление (Rt).

Мощность определяется по формуле; P=V*I

В последовательной цепи приложенная разность потенциалов представляет собой общую сумму отдельных напряжений на каждом резисторе.

Следовательно, при расчете электроэнергии; P=V_total*I_total

Эффективное сопротивление в последовательной цепи

Эквивалентное сопротивление — это величина сопротивления, которая необходима одному резистору, чтобы сравняться с общим эффектом набора резисторов, присутствующих в трассе.

В простой последовательной цепи общее сопротивление равно сумме номиналов отдельных резисторов. Чтобы уточнить, сложите номиналы резисторов. Но резисторы также имеют такое же падение потенциала. Например, в приведенной выше схеме уравнение эффективного сопротивления имеет вид;

Rtotal = R1 + R2 + R3

R_t = 5 Ом + 10 Ом + 5 Ом = 20 Ом следовательно, каждому нужен ток, равный или меньший, чем его номинал. В противном случае они будут повреждены или разрушены, если через цепь будет протекать слишком большой ток. Это опасно и может привести к повреждению компонентов или, что еще хуже, к пожару! Поэтому лучше всего использовать последовательное соединение резисторов для защиты ваших электрических цепей. Последовательный резистор ограничивает максимальное падение напряжения на светодиоде, что позволяет ему работать в безопасных условиях!

Резисторы в параллельном соединении

Для резисторов в параллельном соединении один конец всех резисторов подключается через стандартный провод. Аналогично все остальные концы соединяются через стандартный провод.

Как соединить резисторы параллельно

(Схема параллельного соединения резисторов)

В приведенном выше примере у нас есть простая схема с параллельным соединением резисторов. Параллельное соединение резисторов отличается тем, что концы каждого резистора не подключены к источнику питания, а вместо этого они имеют одну общую точку в качестве общего соединения. Кроме того, предположим, что провода имеют незначительное сопротивление.

Схемы резисторов – Закон Ома в цепи параллельного сопротивления

Мы используем закон Ома, чтобы найти отдельный ток, который протекает через каждый резистор параллельно. Это связано с тем, что падение потенциала одинаково на каждом резисторе. В случае, когда выходное напряжение постоянно на каждом резисторе, ток I=V/R

Схемы цепей резисторов– Ток и мощность в параллельных цепях

Для резисторов в цепи с параллельной конфигурацией падение напряжения на параллельной ветки одинаковые. Кроме того, ток, протекающий по всей цепи, равен сумме индивидуальных токов, протекающих через каждый резистор. Однако, если вы добавите в цепь больше резисторов, общее сопротивление цепи уменьшится.

(Разделение тока при параллельном соединении)

Поскольку общий общий ток делится на каждый резистор.

Итак, применим уравнение для тока I_t=I_1+I_2

То есть общий ток, протекающий в цепи, равен добавленным разделенным токам, протекающим через резисторы.

Суммарная мощность, рассеиваемая резисторами, определяется с помощью P=VI. Где I — общий ток в амперах, а V — напряжение на каждом параллельном резисторе. Резисторы с самым значительным сопротивлением получают самый низкий ток, в то время как резисторы с самым маленьким индивидуальным сопротивлением получают самый высокий ток.

Поэтому; P=VI

P = (I_1 + I_2) * V

Итак, для каждого резистора, резистор R_1 I1= V1/R1. Резистор R_2 I2= V2/R2

Эффективное сопротивление в параллельной цепи

На приведенной ниже диаграмме показано, как найти эффективное сопротивление в параллельной цепи.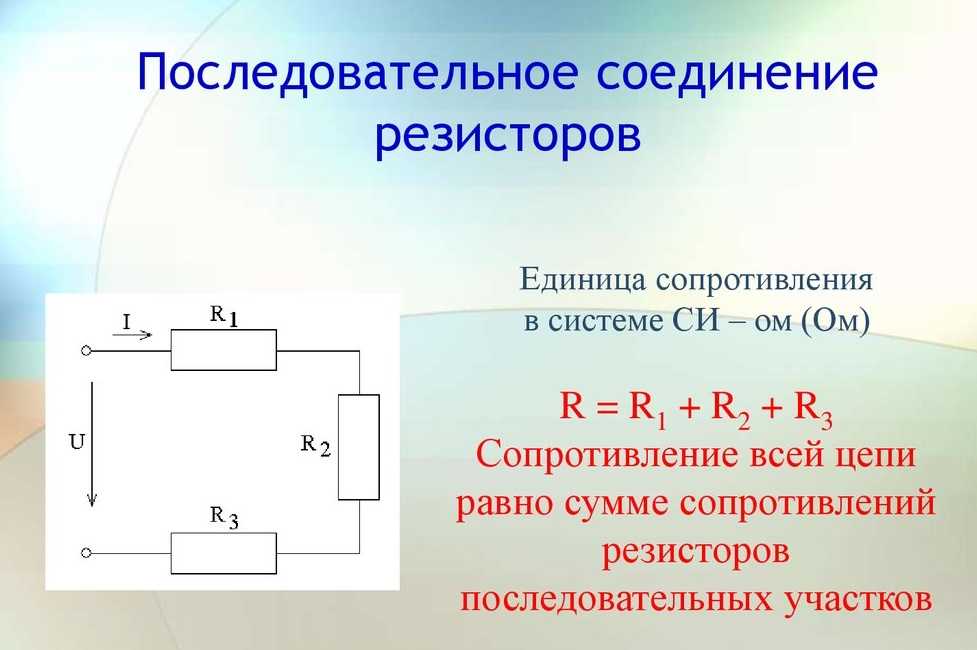

(схематическая диаграмма, объясняющая эффективное сопротивление)

Чтобы рассчитать эквивалентное сопротивление, нам нужно понять правило перехода в соответствии с петлевым законом Кирхгофа . Общее сопротивление в цепи с параллельной конфигурацией является обратной величиной суммы всех обратных сопротивлений. То есть; если у вас есть два резистора в параллельном соединении, практический расчет сопротивления становится;

Уравнения цепи следующие;

Так как ток разделяется в месте соединения, согласно правилу контура, то I=I1+I2

И, так как V=I1R1 и I1R1=I2R2

Тогда Ток, I =I_1+ I_2

Р2

, но V то же самое = V/R1+ V/R2

= V [1/R1+ 1/R2] = V/REQ

1/REQ = 1/R1+ 1/R2

Также, уравнение резистентности = [1/R1+ 1/R2]⁻¹

Комбинация резисторов в последовательном и параллельном соединении

В комбинации резисторов некоторые резисторы расположены последовательно, а другие — параллельно.

Самое главное, это больше сложных схем для понимания. Центральная концепция определения сопротивления в комбинированных цепях заключается в преобразовании всего курса в схему последовательного соединения. Это быстро делается путем применения понимания эквивалентного сопротивления в параллельной цепи ко всей комбинированной цепи.

Схемы резисторов – Как соединить резисторы последовательно и параллельно

(Схема комбинирования резисторов)

Соединение резисторов последовательно и параллельно довольно просто. Во-первых, все, что вам нужно сделать, это подключить R2 и R3 параллельно. Затем щелкните концы каждого резистора, чтобы создать узел. Теперь добавьте еще один резистор R1 к соединительному узлу, как показано на схеме выше. Наконец, подключите концы проводов к источнику питания. Общее сопротивление представляет собой сумму номиналов каждого резистора; в этом случае используйте для расчетов закон Ома.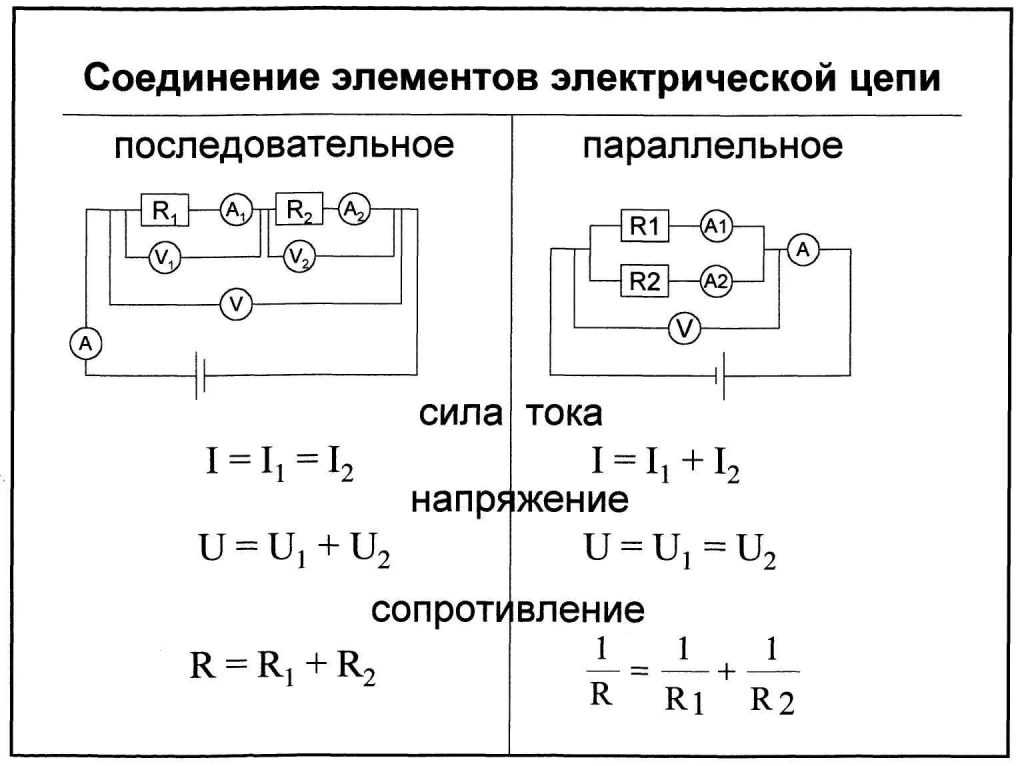

Схемы резисторных цепей – Ток и мощность в комбинации последовательных и параллельных цепей резисторов

Общий ток представляет собой сумму всех отдельных токов, как и мощность. Если несколько резисторов включены параллельно, то они будут иметь общий источник выходного напряжения. Важно отметить, что это при условии, что внутреннее сопротивление пренебрежимо мало. Это также означает, что напряжение на каждом резисторе будет меньше, чем если бы оно было последовательно.

(резисторы, подключенные последовательно и параллельно)

Если у вас есть комбинации резисторов, подключенных как последовательно, так и параллельно, вам придется использовать различные деления напряжения и тока. Помните, что это сложные связи для понимания.

Используйте комбинированную форму закона Ома, чтобы найти общий выходной ток, где I=V/R_total.

Это означает, что подключенные резисторы распределяют ток между собой.

Общая мощность такая же, как и при последовательном соединении, но каждый резистор рассеивает меньший ток и напряжение.

P=VI = (Vsource/R_total) * I

Схемы резисторов – Эффективное сопротивление в последовательных и параллельных цепях

(Сочетание последовательных и параллельных цепей резисторов) резисторов зависит от их номиналов и способа соединения. Следовательно, общее сопротивление в различных цепях последовательных и параллельных резисторов находится с использованием закона Ома.

Во-первых, R_total = Req(Series) + Req(Parallel)

Тогда Req parallel= Req₂₃=(1/R2+ 1/R3)⁻¹

= (1/10 Ом + 1/10 Ом)⁻¹ = 5 Ом, параллельные резисторы

теперь последовательно с R1.

Таким образом, R-total=Req(серия) +Req(Parallel)

Rt= 5 Ом + 5 Ом = 10 Ом.

Объединение резисторов последовательно и параллельно помогает контролировать токи, ограничивая падение потенциала на электрической нагрузке.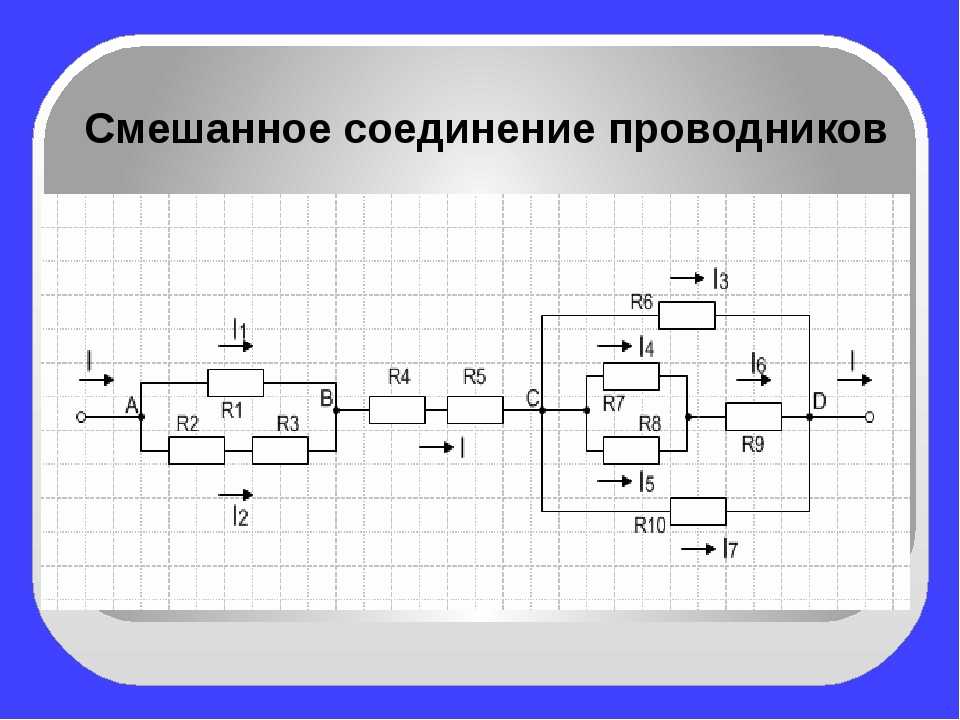

Схемы резисторов – пример применения

(Схема холодильника)

В цепях холодильника присутствует комбинация цепей резисторов. На приведенной выше диаграмме, когда дверца холодильника открывается, лампочка тускнеет. Это связано с тем, что двигатель холодильника потребляет большой ток. В результате лампочка получает низкую мощность и затемняется, так как R1 в цепи испытывает большие перепады напряжения. Комбинации резисторов помогают ограничить максимальную величину тока, проходящего через цепь. В то же время они обеспечивают определенное снижение потенциала электрических нагрузок.

Резюме

В заключение мы рассмотрели три наиболее распространенных типа схем резисторов. Мы надеемся, что теперь вы лучше понимаете различные типы подключения и то, как они работают.

Теперь вы можете создавать схемы резисторов! Если у вас есть дополнительные вопросы о том, как это сделать, пожалуйста, свяжитесь с нами.

Резисторы в цепях — Задачи — Гиперучебник по физике

[закрыть]

практика

Определите следующие величины для каждой из двух цепей, показанных ниже…
1. эквивалент сопротивления
2. ток от блока питания
3. ток через каждый резистор
4. падение напряжения на каждом резисторе
5. мощность, рассеиваемая на каждом резисторе
На кухне в Северной Америке есть три прибора, подключенных к сети 120 В с автоматическим выключателем на 15 А: кофеварка на 850 Вт, микроволновая печь на 1200 Вт и 900 Вт тостер.
1. Нарисуйте принципиальную схему этой цепи.
2. Какие из этих приборов могут работать одновременно без срабатывания автоматического выключателя?
На приведенной ниже схеме показана схема с одной батареей и 10 резисторами; 5 слева и 5 справа. Определять…
1. ток через
2. падение напряжения на
3. мощность, рассеиваемая каждым резистором
Учитывая схему ниже…
1. Рассчитайте эквивалентное сопротивление цепи.
2. Рассчитайте ток через батарею.
3. Нарисуйте график зависимости напряжения от положения в цепи, предполагая, что В _a = 0 В на отрицательной клемме аккумулятора.
4. График тока в зависимости от положения в цепи.

концептуальный

Что происходит с полным током, когда резисторы добавляются в цепь…
1. последовательно?
2. параллельно?
Укажите две причины, по которым бытовые розетки не соединены последовательно.
Что означает термин “короткое замыкание”? Чем опасно короткое замыкание?

Источник питания и четыре одинаковые пронумерованные лампочки соединены вместе, как показано на схеме справа.

Расположите лампочки в порядке яркости.
Одним словом опишите влияние удаления любой из лампочек на яркость трех других.
1. Снять лампу 1
2. Снять лампу 2
3. Снять лампу 3
4. Удалить лампу 4

Соберите свои ответы на этот вопрос в таблицу, подобную приведенной ниже.

	Р ₁	Р ₂	Р ₃	Р ₄
а.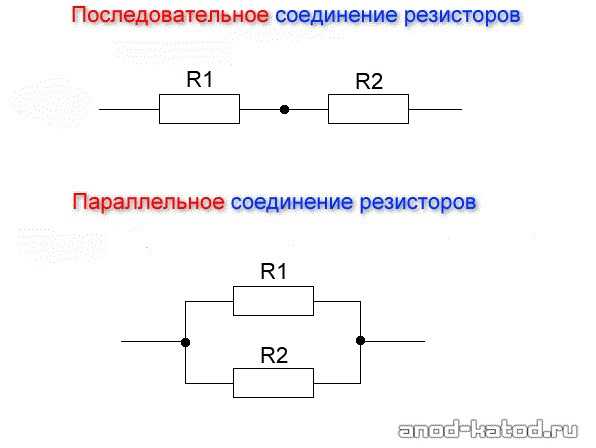
б. я.	×
б. II.		×
б. III.			×
б. IV.				×

Расположите лампочки в порядке яркости.
Одним словом опишите влияние удаления любой из лампочек на яркость трех других.
1. Снять лампу 1
2. Снять лампу 2
3. Снять лампу 3
4. Удалить лампу 4