3 закон ома: Закон Ома. Формула Закона Ома

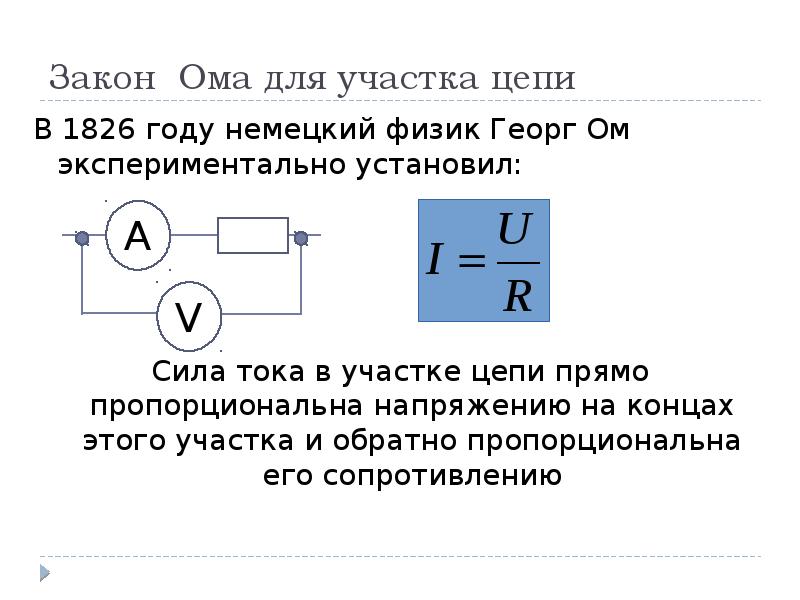
Закон Ома. Формула Закона Ома

Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.

Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.

Георг Симон Ом

Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.

Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

Формула закона Ома записывается в следующем виде:

где

I – сила тока в проводнике, единица измерения силы тока – ампер [А];

U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];

R – электрическое сопротивление проводника, единица измерения электрического сопротивления – ом [Ом].

Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза

И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.

Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:

Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника.

В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.

Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.

Где и когда можно применять закон Ома?

Нужна помощь в написании работы?

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.

Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

простое объяснение для чайников с формулой и понятиями

 

Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.

Основные понятия закона Ома

Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.

Сила тока I

Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10^-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.

Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в

Амперах.

Напряжение U, или разность потенциалов

Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.

Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.

Сопротивление R

Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в

Омах.

 

Памятник Георгу Симону Ому

 

Формулировка и объяснение закона Ома

Закон немецкого учителя Георга Ома очень прост. Он гласит:

Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.

Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.

Кстати! Для наших читателей сейчас действует скидка 10% на

любой вид работы

Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря “участок цепи” мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.

Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.

Пусть  у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон запишется в следующем виде:

Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.

Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.

Как понять закон Ома?

Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.

Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе.  Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.

Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)

Сила тока прямо пропорциональна напряжению.

Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.

Сила тока обратно пропорциональна сопротивлению.

Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.

В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.

 

Ток в проводнике

 

В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене.

Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.

Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!

Закон Ома ? для участка цепи, формула. Закон Ома ? в дифференциальной форме для полной цепи и её участка

Автор Даниил Леонидович На чтение 5 мин. Просмотров 6.1k. Опубликовано 18 ноября Обновлено 18 ноября

Физический закон ома получен путём экспериментов.

3 формулировки ома – одни из основополагающих в физике, устанавливающие связь между электротоком, сопротивлением и энергонапряжением. Год открытия – 1826. Впервые все 3 физических закона ома сформулировал физик-экспериментатор немецкого происхождения Георг Ом, с фамилией которого связано их определение.

Мнемоническая схема

Согласно мнемосхеме, чтобы высчитать электросопротивление по закону ома для участка цепи постоянного тока, необходимо комплексное напряжение на участке цепи разделить на силу тока для полной цепи. Однако, с физико-математической точки зрения, формулу ома для участка цепи для вычисления только по первому закону ома принято считать неполной.

Альтернативный способ вычислить токовое сопротивление по закону ома кратко подразумевает умножение электросопротивления материи, из которой выполнен проводник, на длину с последующим делением на площадь пересекающегося сечения.

Для выполнения вычислений сформулируйте по закону ома для участка цепи уравнение, исходя из имеющихся числовых данных:

Применение на линии электропередач

В процессе доставки на линию электропередач потери энергии должны быть минимизированы. Причиной энергетических потерь является нагрев провода, во время которого энергия электротока превращается в теплоэнергию.

Чтобы дать определение по закону ома потерянной мощности, необходимо показатель электрической мощности во второй степени умножить на внутреннее сопротивление источника напряжения и разделить на ЭДС в квадрате.

Из этого следует, что рост потери энергомощности осуществляется пропорционально протяжённости линии электропередач и квадрату электродвижущей силы.

Поскольку электродвижущую силу ограничивает прочность обмотки генератора, то повышение энергонапряжения возможно после того, как из генератора выйдет электроток, на участке входа линии.

Переменный ток легче всего распределяется по линии через трансформатор. Однако, поскольку следствием повышения энергонапряжения является потеря коронирования, а надёжность изоляции обеспечивается с трудом, напряжение на участке цепи протяжённой линии электропередач не превышает миллиона вольт.

Внимание!

Поведение линии электропередач в пространстве подобно антенне, ввиду чего берётся во внимание потеря на излучение.

Отображение в дифференциальной форме

На подсчёт сопротивления влияет тип материи, по которой протекает электроток, а также геометрические габариты проводника.

Дифференциальная форма формулировки Ома, записывающаяся достаточно кратко, отображает электропроводящие характеристики изотропных материалов и заключается в умножении удельной проводимости на вектор напряжённости электрополя с целью вычисления вектора плотности энерготока.

Для выполнения требуемых вычислений, уравнение сформулируйте по закону ома:

Интересно!

Если исходить из научных данных, следует сделать вывод о законе ома в дифференциальной форме об отсутствии зависимого соотношения геометрических габаритов.

При использовании анизотропеновых электроэлементов нередко встречается несовпадение вектора плотности токового энергонапряжения. Данное суждение справедливо для закона ома в интегральной и дифференциальной формах.

Переменный ток

Величины являются комплексными, если речь идёт о синусоидальных формах энерготока с циклической частотой, в цепях которых присутствуют активная ёмкость с индуктивностью.

В перечень комплексных величин входят:

• разность между потенциалами;
• сила тока;
• комплексное электросопротивление;
• модуль импеданса;
• разность индуктивного и ёмкостного сопротивлений;
• омическое электросопротивление;
• фаза импеданса.

Если несинусоидальный энерготок допустимо измерить временными показателями, закон ома для неполной электрической цепи может быть представлен в виде сложенных синусоидальных Фурье-компонентов. В линейной цепи составные элементы фурье-разложения являются независимо функционирующими. В нелинейных цепях образуются гармоники и множество колебаний. Таким образом, можно сделать вывод о невозможности выполнения правила Ома для нелинейной электроцепи.

Внимание!

Гармоника – это колебание, частота которого кратна частоте напряжения.

Как трактуется правило Ома

Так как обобщённая формула ома не считается основополагающей, правило применяется для описания разновидностей проводников в условиях приближения незначительной частоты, плотности тока и напряжения электрополя. Следует отметить, что в ряде случаев как первый закон, так и второй закон, применяемый для полной цепи, не соблюдаются.

Существует теория Друде, для выражения которой используются следующие величины:

• удельная электропроводимость;
• концентрированное размещение электронов;
• показатель элементарного заряда;
• время затихания по импульсам;
• эффективная масса электрона.

Внимание!

Все формулы Ома – первый, второй физический закон ома и третий распространяются на омические компоненты.

Перечень условий, при которых становится невозможным соблюдения правила Ома:

1. высокие частоты с чрезмерно большой скоростью изменения электротока;
2. пониженная температура сверхпроводимого вещества;
3. перегрев проводника проходящим электротоком;
4. в ситуации пробоя, возникшего в результате подсоединения к проводниковому элементу высокого напряжения;
5. в вакуумной или газонаполненной электролампе;
6. для гетерогенного полупроводникового прибора;
7. при образовании пространственного диэлектрического заряда в контакте металлического диэлектрика.

Интерпретация

Определяющаяся действием приложенного напряжения мощностная сила тока является пропорциональной показателю его напряжения. К примеру, при двойном увеличении приложенного напряжения, интенсивность постоянного тока также удваивается.

Интересно!

Наиболее часто правило Ома применяется для металла и керамики.

Методы запоминания формулы

Чтобы легче запомнить формулу расчёта напряжения на участке цепи, следует выписать на бумажном листе все величины, из которых она состоит, в которую также входит сопротивление и сила тока. Искомую величину закрыть пальцем, вследствие чего соотношение оставшихся величин будет отображать действие, которое необходимо совершить для её вычисления.

Ниже будет представлено видео с подробным объяснением всех правил и формул, относящихся к рассматриваемой теме.

Закон Ома – один из самых несложных для понимания, который входит в программу школьных учебников физики начального уровня. Пользуясь графическим приёмом расчёта величин – при необходимости или для самопроверки, можно получить безошибочные результаты вычислений.

Урок 31. закон ома для полной цепи – Физика – 10 класс

Физика, 10 класс

Урок 31. Закон Ома для полной цепи

Перечень вопросов, рассматриваемых на уроке:

1) закон Ома для полной цепи;

2) связь ЭДС с внутренним сопротивлением;

3) короткое замыкание;

4) различие между ЭДС, напряжением и разностью потенциалов.

Глоссарий по теме

Электрическая цепь – набор устройств, которые соединены проводниками, предназначенный для протекания тока.

Электродвижущая сила – это отношение работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда.

Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению:

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М. : Просвещение, 2017. С. 348 – 354.

2.Рымкевич А. П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2009. С. 106-108.

Теоретический материал для самостоятельного изучения

Любые силы, которые действуют на электрически заряженные частицы, кроме сил электростатического происхождения (т.е. кулоновских), называют сторонними силами. Сторонние силы приводят в движение заряженные частицы внутри всех источников тока.

Действие сторонних сил характеризуется важной физической величиной электродвижущей силой (ЭДС). Электродвижущая сила в замкнутом контуре – отношение работы сторонних сил при перемещении заряда вдоль контура к заряду.

В источнике тока из-за действием сторонних сил происходит разделение зарядов. Так как они движутся, они взаимодействуют с ионами кристаллов и электролитов и отдают им часть своей энергии. Это приводит к уменьшению силы тока, таким образом, источник тока обладает сопротивлением, которое называют внутренним r.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи:

Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению

Короткое замыкание

При коротком замыкании, когда внешнее сопротивление стремится к нулю , сила тока в цепи определяется именно внутренним сопротивлением и может оказаться очень большой . И тогда провода могут расплавиться, что может привести к опасным последствиям.

Примеры и разбор решения заданий:

1. К каждой позиции первого столбца подберите соответствующую позицию второго:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Электродвижущая сила
Сила тока
Сопротивление
Разность потенциалов

Решение.

Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.

Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.

ЭДС определяется по формуле:

Сила тока определяется по формуле:

Сопротивление определяется по формуле:

Разность потенциалов определяется по формуле:

Правильный ответ:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Электродвижущая сила
Сила тока
Сопротивление
Разность потенциалов

2. ЭДС батарейки карманного фонарика – 3,7 В, внутреннее сопротивление 1,5 Ом. Батарейка замкнута на сопротивление 11,7 Ом. Каково напряжение на зажимах батарейки?

Решение:

Напряжение рассчитывается по формуле:

Чтобы найти силу тока применим закон Ома для полной цепи:

Делаем расчёт:

Ответ: U = 3,28 В.

формулы и определения / Блог / Справочник :: Бингоскул

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

 

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

1. I — сила тока (в системе СИ измеряется — Ампер)
   • Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
   • Формула: I=\frac{U}{R}
2. U — напряжение (в системе СИ измеряется — Вольт)
   • Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
   • Формула: U=IR
3. R — электрическое сопротивление (в системе СИ измеряется — Ом).
   • Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
   • Формула R=\frac{U}{I}

 

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).

 

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

 

Формула I=\frac{\varepsilon}{R+r}

• \varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

 

Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

 

• U — электрическое напряжение;
• I — сила тока;
• P — электрическая мощность;
• R — электрическое сопротивление

---

 

Смотри также:

 

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

Закон Ома для полной (замкнутой) цепи

Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока. Другое название этого закона – закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.

Потребители электрического тока (например, электрические лампы) вместе с источником тока образуют замкнутую электрическую цепь. На рисунке 1 показана замкнутая электрическая цепь, состоящая из автомобильного аккумулятора и лампочки.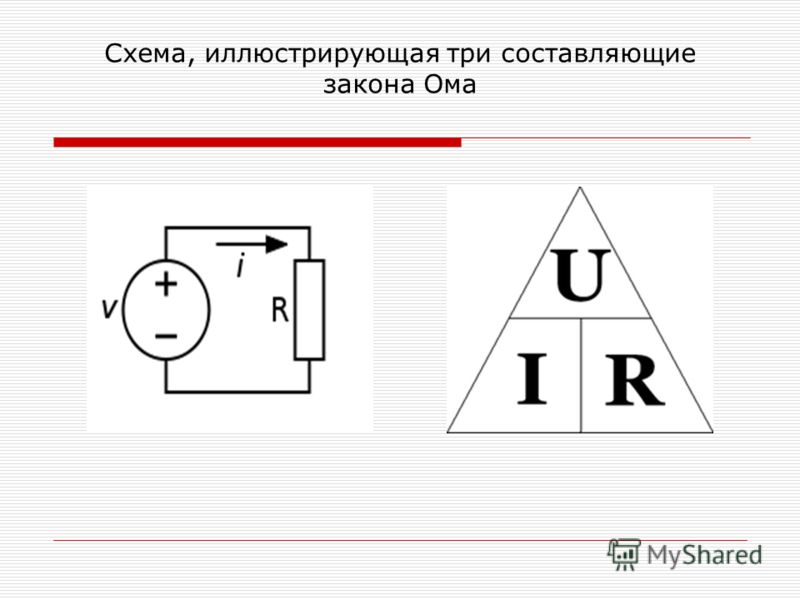

Рисунок 1. Замкнутая цепь, поясняющея закон Ома для полной цепи.

Ток, проходящий через лампочку, проходит также и через источник тока. Следовательно, проходя по цепи, ток кроме сопротивления проводника встретит еще и то сопротивление, которое ему будет оказывать сам источник тока (сопротивле­ние электролита между пластинами и сопротивление пограничных слоев электролита и пластин). Следовательно, общее сопротивление замкнутой цепи будет складываться из сопротивления лампочки и сопротивления источника тока.

Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а со­противление самого источника тока — внутренним со­противлением. Внутреннее сопротивление обозначается буквой r.

Если по цепи, изображенной на рисунке 1, протекает ток I, то для поддержания этого тока во внешней цепи согласно за­кону Ома между ее концами должна существовать раз­ность потенциалов, равная I*R. Но этот же ток I протекает и по внутренней цепи. Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.

Поэтому для поддержания тока в цепи электродвижущая сила (ЭДС) аккумулятора должна иметь величину:

E=I*r+I*R

Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:

E=I(r+R)

или

I=E/(r+R)

Две последние формулы выражают закона Ома для полной цепи.

Закон Ома для полной замкнутой цепи формулируется так: сила тока в замкнутой цепи прямо пропорциональ­на ЭДС в цепи и обратно пропорциональ­на общему сопротивлению цепи.

Под общим со­противлением подразумевается сумма внешнего и внутреннего сопротивлений.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Три закона Ома.

Отрывок из книги «Тонкая физика. Масса, эфир и объединение всемирных сил»

Недавно в издательстве «Питер» вышла на русском языке книга Фрэнка Вильчека (Frank Wilczek) «Тонкая физика. Масса, эфир и объединение всемирных сил». Автор, лауреат Нобелевской премии по физике, излагает современные взгляды на нашу невероятную Вселенную и прогнозирует новый золотой век фундаментальной физической науки. Мы уже публиковали один отрывок из этой замечательной книги, сегодня публикуем второй — о том, почему эквивалентные равенства могут поведать нам о разных явлениях.

Из третьей главы. Второй закон Ома

Второй закон Эйнштейна, m = E/c², поднимает вопрос о том, может ли масса быть понята более глубоко — как энергия. Можем ли мы создать, как выразился Уилер, «массу без массы»?

Когда я ещё только собирался начать преподавать в Принстоне, мой друг и наставник Сэм Трейман позвал меня в свой кабинет. Он хотел поделиться со мной своей мудростью. Сэм вытащил из ящика стола потрёпанное руководство в мягкой обложке и сказал мне: «Во время Второй мировой войны ВМС приходилось в спешке обучать новобранцев налаживанию и использованию радиосвязи. Многие из этих новобранцев прибывали прямо с ферм, так что быстро ввести их в курс дела было очень трудно. С помощью той великолепной книги командованию военно-морского флота это удалось. Это шедевр педагогики. Особенно первая глава. Взгляни».

Он вручил мне книгу, открытую на первой главе. Она называлась «Три закона Ома». Я был знаком с одним законом Ома, известным соотношением V = IR, который связывает напряжение (V), силу тока (I) и сопротивление (R) в электрической цепи.

Это оказалось первым законом Ома.

Мне было очень интересно узнать, каковы два других закона Ома. Перевернув несколько хрупких пожелтевших страниц, я обнаружил второй закон Ома: I = V/R. Я предположил, что третий закон Ома формулируется как R = I/V, и оказался прав.

Открывать новые законы легко

Тем, кто знаком с элементарной алгеброй, так очевидно, что эти три закона эквивалентны друг другу, что данная история воспринимается как шутка. Однако в ней заключён глубокий смысл. (Кроме того, в ней есть и неглубокий смысл, который, как мне кажется, Сэм хотел до меня донести. При обучении начинающих вы должны несколько раз сказать одно и то же, но по-разному. Соотношения, которые бесспорны для профессионала, могут не быть таковыми для новичка. Студенты не будут возражать против объяснения очевидного. Очень немногие люди обижаются, когда вы позволяете им почувствовать себя умными.)

Глубокий смысл содержит заявление великого физика-теоретика Поля Дирака. Когда его спросили, как он открывает новые законы природы, Дирак ответил: «Я играю с уравнениями». Суть в том, что различные способы написания одного и того же уравнения могут говорить о совершенно разных вещах, даже если они являются логически эквивалентными.

Второй закон Эйнштейна

Второй закон Эйнштейна формулируется следующим образом:

m = E/c².

Первый закон Эйнштейна — это, разумеется, E = mc². Здорово, что первый закон предполагает возможность получения большого количества энергии из небольшого количества массы. Он наводит на мысль о ядерных реакторах и ядерных бомбах.

Второй закон Эйнштейна предполагает нечто совершенно иное.

Он предполагает возможность объяснения того, как масса возникает из энергии.

На самом деле этот закон неправильно называть «вторым».

В оригинальной работе Эйнштейна 1905 года вы не найдёте уравнения E = mc². Вы встретите уравнение m = E/c². (Поэтому, возможно, нам следует назвать его нулевым законом Эйнштейна.)

На самом деле в качестве названия этой статьи используется вопрос: «Зависит ли инерция тела от содержащейся в нем энергии?»

Другими словами, может ли некоторое количество массы тела возникать из энергии содержащегося в нем вещества? С самого начала Эйнштейн размышлял о концептуальных основах физики, а не о возможности создания бомб или реакторов.

Понятие энергии играет гораздо более важную роль в современной физике, чем понятие массы. Это проявляется во многих отношениях. Сохраняется именно энергия, а не масса. Именно энергия фигурирует в таких фундаментальных уравнениях, как уравнение Больцмана для статистической механики, уравнения Шрёдингера для квантовой механики и уравнение Эйнштейна для гравитации. Масса в более техническом смысле проявляется в качестве метки для неприводимых представлений группы Пуанкаре.

(Я даже не буду пытаться объяснить, что означает предыдущее утверждение, к счастью, суть заключается в самом факте утверждения.)

Таким образом, вопрос Эйнштейна бросает вызов. Если мы сможем объяснить массу в терминах энергии, мы улучшим наше описание мира. В этом случае в нашем рецепте нам потребуется меньшее количество ингредиентов. Второй закон Эйнштейна позволяет дать хороший ответ на вопрос, который мы задали ранее. Откуда берётся масса? Может быть, из энергии. На самом деле, как мы увидим далее, в основном так и есть.

Закон Ома

Закон Ома

Национальная аэронавтика и Космическое управление Исследовательский центр Гленна

Образовательный продукт Учителя 9–12 классы

---

Где:




V = напряжение

I = ток

R = Сопротивление

---

Пример проблемы:

Батарея на девять вольт обеспечивает питание беспроводного плойка с сопротивлением 18 Ом. Насколько ток протекает через щипцы для завивки?


Эскиз:



---

Решение:


1.) Поскольку V (напряжение) и R (сопротивление) известны, решите для I (ток), разделив обе стороны уравнение Р.

2.) Буквы R в правой части уравнения Отмена.


3.) I остается в терминах V и R.


4.) Подставьте значения для V (напряжение) и R (Сопротивление).





5.) Решите относительно I (Текущий).


---


Проблема № 1



Настенная розетка на 110 В обеспечивает питание стробоскопа. свет с сопротивлением 2200 Ом. Сколько тока течет через стробоскоп?


Эскиз:

Выберите свой ответ ниже
1. 0.5 усилители
2. 2,0 усилители
3. 0,05 усилители
4. 1,0 усилители

---


Проблема № 2


Проигрыватель компакт-дисков с сопротивлением 40 Ом имеет через него протекает ток 0,1 ампер. Набросайте принципиальную схему и посчитайте, сколько вольт питает проигрыватель компакт-дисков?

Выберите свой ответ ниже
1. 0.0025 вольт
2. 4,0 вольт
3. 10,0 вольт
4. 400,0 вольт

---

Это задание было создано Стивеном Гутьерресом, для проекта “Технологии обучения”, в Исследовательском центре Гленна НАСА в 1996 году.

---


Веб-страница закона Ома

Навигация ..

Руководство для начинающих Домашняя страница

Любые комментарии направляйте по адресу:
Томас[email protected]


Закон Ома и соотношение V-I-R

В физике есть определенные формулы, которые настолько мощны и распространены, что достигают уровня общеизвестных знаний. Студент, изучающий физику, записывал такие формулы столько раз, что запоминал их, даже не пытаясь. Безусловно, для профессионалов в этой области такие формулы настолько важны, что остаются в их сознании.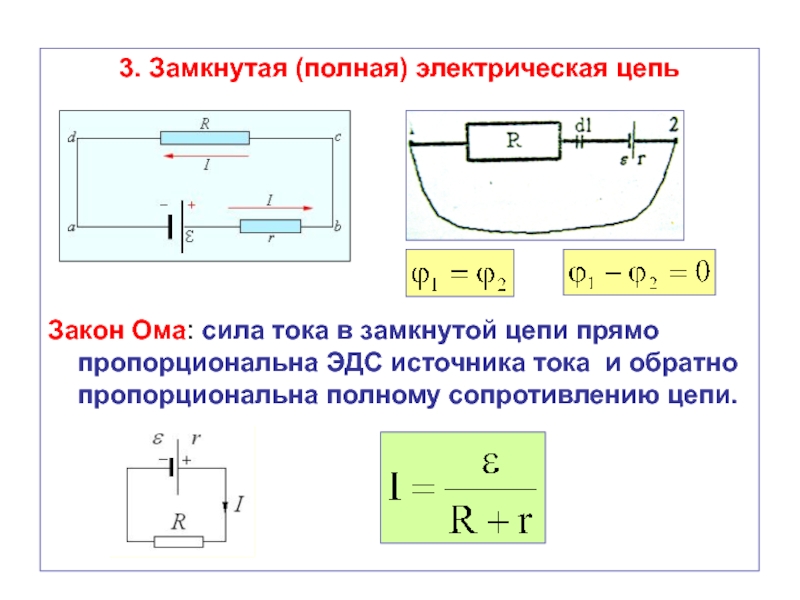 В области современной физики E = m • c ² .В области ньютоновской механики существует F _net = m • a. В области волновой механики v = f • λ. А в области текущего электричества ΔV = I • R.

Преобладающим уравнением, которое пронизывает изучение электрических цепей, является уравнение

ΔV = I • R

Другими словами, разность электрических потенциалов между двумя точками в цепи ( ΔV ) эквивалентна произведению тока между этими двумя точками ( I ) и общего сопротивления всех электрических устройств, присутствующих между этими двумя точками ( R ).В остальной части этого раздела Физического класса это уравнение станет самым распространенным уравнением, которое мы видим. Это уравнение, часто называемое уравнением закона Ома , является мощным предсказателем взаимосвязи между разностью потенциалов, током и сопротивлением.

Закон Ома как предсказатель тока

Уравнение закона Ома можно переформулировать и выразить как

В качестве уравнения это служит алгебраическим рецептом для вычисления тока, если известны разность электрических потенциалов и сопротивление.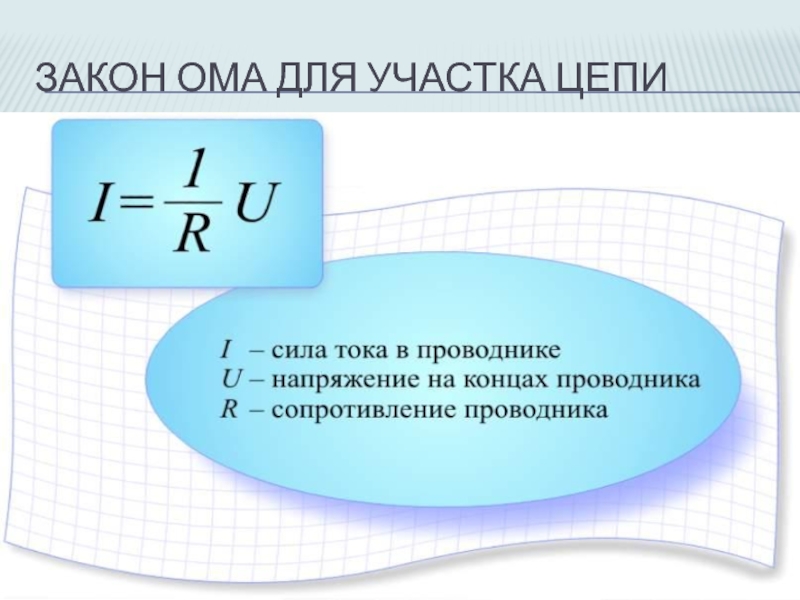 Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, это гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Ток в цепи прямо пропорционален разности электрических потенциалов, приложенной к ее концам, и обратно пропорционален общему сопротивлению внешней цепи. Чем больше напряжение аккумулятора (то есть разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток.Заряд идет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. Фактически, двукратное увеличение напряжения батареи привело бы к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.

Приведенная ниже таблица иллюстрирует эту взаимосвязь как качественно, так и количественно для нескольких цепей с различными напряжениями и сопротивлением батарей.


Строки 1, 2 и 3 показывают, что удвоение и утроение напряжения батареи приводит к удвоению и утроению тока в цепи. Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления служит для уменьшения вдвое тока в цепи.

Поскольку на ток в цепи влияет сопротивление, в цепях электроприборов часто используются резисторы, чтобы влиять на величину тока, присутствующего в ее различных компонентах.Увеличивая или уменьшая величину сопротивления в конкретной ветви схемы, производитель может увеличивать или уменьшать величину тока в этой ветви . Кухонные приборы, такие как электрические миксеры и переключатели света, работают, изменяя ток на нагрузке, увеличивая или уменьшая сопротивление цепи. Нажатие различных кнопок на электрическом микшере может изменить режим с микширования на взбивание, уменьшив сопротивление и позволив большему току присутствовать в миксере.Точно так же поворот ручки регулятора яркости может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.

На схеме ниже изображена пара цепей, содержащих источник напряжения (аккумуляторная батарея), резистор (лампочка) и амперметр (для измерения тока). В какой цепи у лампочки наибольшее сопротивление? Нажмите кнопку «Посмотреть ответ», чтобы убедиться, что вы правы.




Уравнение закона Ома часто исследуется в физических лабораториях с использованием резистора, аккумуляторной батареи, амперметра и вольтметра.Амперметр – это устройство, используемое для измерения силы тока в заданном месте. Вольтметр – это устройство, оснащенное датчиками, которых можно прикоснуться к двум точкам цепи, чтобы определить разность электрических потенциалов в этих местах. Изменяя количество ячеек в аккумуляторной батарее, можно изменять разность электрических потенциалов во внешней цепи. Вольтметр может использоваться для определения этой разности потенциалов, а амперметр может использоваться для определения тока, связанного с этим ΔV.К батарейному блоку можно добавить батарею, и процесс можно повторить несколько раз, чтобы получить набор данных I-ΔV.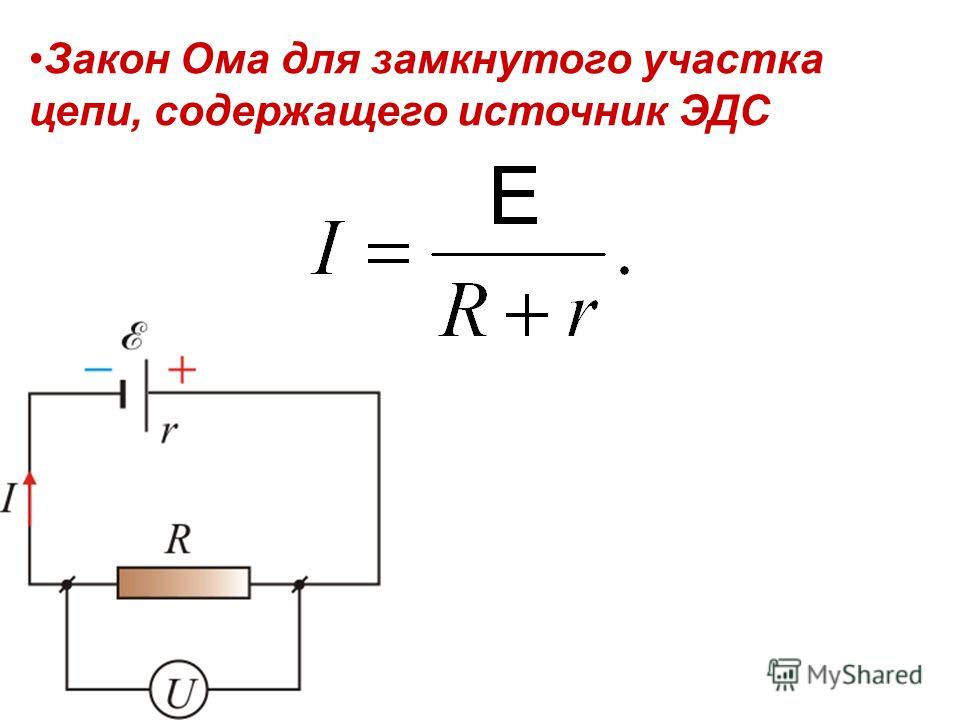 График зависимости I от ΔV даст линию с крутизной, эквивалентной обратной величине сопротивления резистора. Это значение можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и справедливость уравнения закона Ома.

Величины, символы, уравнения и единицы!

Тенденция уделять внимание единицам измерения – неотъемлемая черта любого хорошего студента-физика.Многие трудности, связанные с решением проблем, могут быть связаны с тем, что не уделялось внимания подразделениям. Поскольку все больше и больше электрических величин и их соответствующих метрических единиц вводится в этот раздел учебного пособия «Физический класс», становится все более важным систематизировать информацию в своей голове. В таблице ниже перечислены некоторые из введенных на данный момент количеств. Для каждой величины также указаны символ, уравнение и соответствующие метрические единицы.Было бы разумно часто обращаться к этому списку или даже делать свою копию и добавлять к ней по мере развития модуля. Некоторые студенты считают полезным составить пятый столбец, в котором приводится определение каждой величины.

Кол. Акций	Символ	Уравнение (я)	Стандартная метрическая единица	Другие единицы
Разность потенциалов (г.к.а. напряжение)	ΔV	ΔV = ΔPE / Q ΔV = I • R	Вольт (В)	J / C
Текущий	я	I = Q / т I = ΔV / R	Амперы (А)	Усилитель или К / с или В / Ом
Власть	п	P = ΔPE / т (еще впереди)	Ватт (Вт)	Дж / с
Сопротивление	р	R = ρ • L / A R = ΔV / I	Ом (Ом)	В / А
Энергия	E или ΔPE	ΔPE = ΔV • Q ΔPE = P • t	Джоуль (Дж)	V • C или Вт • с

(Обратите внимание, что символ C представляет собой кулоны. )

В следующем разделе Урока 3 мы еще раз рассмотрим количественную мощность. Новое уравнение мощности будет введено путем объединения двух (или более) уравнений в приведенной выше таблице.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие – это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Легко перетащите источник напряжения, резисторы и провода на рабочее место. Соедините их, и у вас будет схема. Добавьте амперметр для измерения тока и используйте датчики напряжения для определения падения напряжения.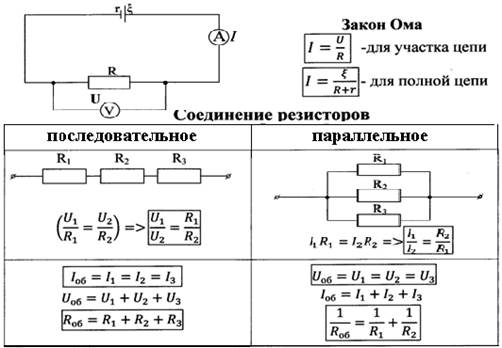 Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).




Проверьте свое понимание

1. Что из перечисленного ниже приведет к уменьшению тока в электрической цепи? Выберите все, что подходит.

а. уменьшить напряжение

г. уменьшить сопротивление

г. увеличить напряжение

г.увеличить сопротивление

2. Определенная электрическая цепь содержит батарею из трех элементов, провода и лампочку. Что из перечисленного может привести к тому, что лампа будет светить менее ярко? Выберите все, что подходит.

а. увеличить напряжение АКБ (добавить еще одну ячейку)

г. уменьшить напряжение аккумулятора (удалить элемент)

г.уменьшить сопротивление цепи

г. увеличить сопротивление цепи

3. Вероятно, вас предупредили, чтобы вы не прикасались к электроприборам или даже к электрическим розеткам мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.

а.напряжение цепи должно быть выше

г. напряжение в цепи должно быть ниже

г. ваше сопротивление будет выше

г. ваше сопротивление должно быть ниже

e. ток через тебя будет ниже

4. Если бы сопротивление цепи было утроено, то ток в цепи был бы ____.

а. треть от

г. втрое больше

г. без изменений

г. … ерунда! Сделать такой прогноз невозможно.

5. Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.

а.четверть от

г. в четыре раза больше

г. без изменений

г. … ерунда! Сделать такой прогноз невозможно.

6. В схему подключены блок питания, резистор и амперметр (для измерения тока). Амперметр показывает ток 24 мА (миллиампер). Определите новый ток, если напряжение источника питания было…

а. … увеличился в 2 раза, а сопротивление осталось постоянным.

г. … увеличилось в 3 раза, а сопротивление осталось постоянным.

г. … уменьшилось в 2 раза, а сопротивление осталось постоянным.

г. … оставалось постоянным, а сопротивление увеличивалось в 2 раза.

e. … оставалось постоянным, а сопротивление увеличивалось в 4 раза.

ф…. оставалось постоянным, а сопротивление уменьшалось в 2 раза.

г. … увеличилось в 2 раза, а сопротивление увеличилось в 2 раза.

ч. … увеличилось в 3 раза, а сопротивление уменьшилось в 2 раза.

и. … уменьшилось в 2 раза, а сопротивление увеличилось в 2 раза.

7.Используйте уравнение закона Ома, чтобы дать числовые ответы на следующие вопросы:

а. Электрическое устройство с сопротивлением 3,0 Ом позволит протекать через него току 4,0 А, если на устройстве наблюдается падение напряжения ________ Вольт.

г. Когда на электрический нагреватель подается напряжение 120 В, через нагреватель будет протекать ток 10,0 А, если сопротивление составляет ________ Ом.

г. Фонарик, который питается от 3 вольт и использует лампочку с сопротивлением 60 Ом, будет иметь ток ________ ампер.

8. Используйте уравнение закона Ома для определения недостающих значений в следующих схемах.

9. См. Вопрос 8 выше. В схемах схем A и B какой метод использовался для контроля тока в схемах? А в схемах схем C и D какой метод использовался для контроля тока в схемах?

Молекулярные выражения: электричество и магнетизм

Закон Ома

Георг Симон Ом (1787-1854) сформулировал отношения между напряжением, током и сопротивлением следующим образом:

Ток в цепи прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению цепи.

Схема ниже демонстрирует эти отношения.

• Щелкните ползунок сопротивления, чтобы изменить резисторы.
• Щелкните ползунок напряжения, чтобы отрегулировать напряжение регулируемого источника питания.

Математически закон Ома можно записать как:

I = E / R

, где I – ток в амперах, E – приложенное напряжение в вольтах, а R – сопротивление в омах.

Эта схема содержит амперметр, измеряющий ток в миллиамперах. Обратите внимание, что по мере увеличения напряжения увеличивается ток. По мере увеличения сопротивления ток уменьшается.

Важно отметить, что сопротивление не может быть изменено путем изменения напряжения или тока. Сопротивление в цепи – это физическая константа. Сопротивление в цепи можно изменить только путем замены компонентов или резисторов, рассчитанных на большее или меньшее сопротивление. Изменение сопротивления в этой цепи имитирует физическое изменение резисторов с разными номиналами.

Узнайте, как резисторы имеют цветовую маркировку, в нашем интерактивном руководстве по резисторам Java .

НАЗАД К РУКОВОДСТВАМ ПО ЭЛЕКТРИЧЕСТВЕ И МАГНИТИЗМУ

Вопросы или комментарии? Отправить нам письмо.

© 1995-2021, автор – Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения правообладателей.Использование этого веб-сайта означает, что вы соглашаетесь со всеми юридическими положениями и условиями, изложенными владельцами.

Этот веб-сайт поддерживается нашим


Команда графического и веб-программирования
в сотрудничестве с оптической микроскопией в Национальной лаборатории сильного магнитного поля
.

Последнее изменение: 7 июня 2017 г., 12:03

Счетчик доступа с 14 апреля 1999 г .: 548673

Что такое закон Ома и как он применим к тепловым системам?

Применение закона Ома к тепловым системам

Чтобы понять, как сопротивление электрической цепи влияет на вашу тепловую систему, просмотрите различные схемы и решения по обогреву.Эти знания помогут вам приобрести оптимальный электрический нагреватель и контроллер для вашего приложения.

Определение тока

Определение величины тока, который будет протекать в вашей системе, важно для обеспечения защиты компонентов системы с помощью соответствующих предохранителей или автоматических выключателей. Ток также можно определить по закону Ома. Ток I в амперах (A) равен напряжению E в вольтах (V), деленному на сопротивление R в омах (Ω).

• ● Ток = напряжение / сопротивление, поэтому I = E / R

Например, если нагреватель измеряет сопротивление 100 Ом, а напряжение, подаваемое в систему, составляет 240 вольт, каков ток в амперах? I = 240/100, поэтому I = 2.4 ампера.

Расчет сопротивления последовательной и параллельной цепей

Электрические цепи состоят из четырех основных компонентов. Эти четыре компонента могут быть включены в последовательную или параллельную цепь для питания ваших нагревательных приборов:

• ● Резистивное устройство (нагревательные элементы)
• ● Источник напряжения
• ● Текущий путь
• ● Переключатель

Последовательная цепь соединяет нагреватели встык.Сопротивление каждого нагревателя необходимо сложить, чтобы получить общее сопротивление цепи. Параллельные цепи открывают большие возможности для прохождения электричества, поэтому добавление нагревательных элементов в параллельную цепь снижает общее сопротивление. Просто установите постоянное напряжение закона Ома и рассчитайте сопротивление вашей системы.

Последовательная цепь характеризуется общим током, протекающим через все резисторы, так как ток может идти только по одному пути.Эквивалентное сопротивление для последовательной цепи – это сумма всех отдельных сопротивлений, поэтому R _всего = R₁ + R₂ +… + Rn. Между тем, параллельная цепь характеризуется общей разностью потенциалов (напряжением) на концах всех резисторов. Эквивалентное сопротивление для параллельной цепи рассчитывается по следующей формуле: 1 / R _всего = 1 / R₁ + 1 / R₂ + … + 1 / Rn.

Рис. 1. На схеме слева показана схема, состоящая из источника напряжения и трех резисторов серии .Правая диаграмма представляет собой схему с источником напряжения и 3 резисторами, включенными параллельно . Например, у вас есть три нагревателя с R1 = 10 Ом, R2 = 16 Ом и R3 = 5 Ом. Итак, рассчитав сопротивление для последовательной цепи, R _всего = 10 + 16 + 5 = 31 Ом. Расчет для параллельной схемы: 1 / R _всего = 1/10 + 1/16 + 1/5, поэтому 1 / R _всего = 0,3625 и R _всего = 2,76 Ом.

Обратите внимание, что при последовательном размещении резисторов общее сопротивление превышает сопротивление каждого отдельного нагревателя, а при параллельном размещении общее сопротивление уменьшается до уровня, меньшего, чем сопротивление каждого отдельного нагревателя.

В параллельных цепях все нагревательные элементы имеют одинаковое напряжение, а в последовательных цепях – одинаковый ток. По сути, последовательная проводка предназначена только для двух нагревателей одинаковой мощности и напряжения. В дополнение к уменьшенному сопротивлению параллельная схема не требует от каждого нагревателя постоянного тока электричества. Если один нагреватель выходит из строя последовательно, цепь разрывается, и вся линейка нагревателей перестает работать. Один поврежденный нагреватель в параллельной цепи влияет только на отдельный нагреватель, поэтому другие нагреватели могут продолжать работать.

Как улучшить тепловую систему Закон

Ома может помочь вам в поиске и устранении неисправностей в вашей тепловой системе. Если ваши контроллеры мощности и температуры показывают колебания электрического тока или тепловой мощности, вы можете использовать закон Ома для проверки статических значений компонентов схемы и определения измерений напряжения на компонентах.

Измерение большого тока в вашей цепи может быть вызвано увеличением напряжения или уменьшением сопротивления.Ваш испытательный прибор может идентифицировать любое изменение напряжения, что позволяет использовать закон Ома для расчета сопротивления, чтобы определить, вызвана ли проблема поврежденными компонентами или ослабленными электрическими соединениями. В этом случае это действительно вызовет увеличение сопротивления; низкий I и высокий W, при этом высокий W означает больший нагрев на концах.

Закон

Ома – важный инструмент, используемый инженерами-конструкторами для расчета взаимосвязи между напряжением, током и сопротивлением. Однако это не считается универсальным законом.Закон Ома не применяется в случаях, когда есть индуктивная нагрузка или когда сопротивление не является постоянным. Хотя большинство нагревателей имеют стабильное сопротивление при повышении температуры, некоторые – нет. Примеры этого включают вольфрамовые лампы и нагреватели из карбида кремния.

Существуют исключения схемы, особенно когда протекающий ток не прямо пропорционален разности потенциалов в проводнике. Закон Ома нельзя применять к устройствам с нелинейной зависимостью между напряжением и током, таким как термистор.Для получения дополнительной информации о законе Ома и его исключениях обратитесь к торговому представителю Watlow.

Что такое закон Ома – формульное уравнение »Электроника

Закон Ома – один из самых фундаментальных законов теории электричества. Формула или уравнение закона Ома связывает напряжение и ток со свойствами проводника, то есть его сопротивлением в цепи.

---

Resistance Tutorial:
Что такое сопротивление Закон Ома Омические и неомические проводники Сопротивление лампы накаливания Удельное сопротивление Таблица удельного сопротивления для распространенных материалов Температурный коэффициент сопротивления Электрическая проводимость Последовательные и параллельные резисторы Таблица параллельных резисторов

---

Закон Ома – один из самых фундаментальных и важных законов, регулирующих электрические и электронные схемы.Он связывает ток, напряжение и сопротивление для линейного устройства, так что, если известны два, можно вычислить третье.

Поскольку ток, напряжение и сопротивление являются тремя основными величинами цепи, это означает, что закон Ома также чрезвычайно важен.

Закон Ома используется во всех областях электротехники и электроники. Он используется для расчета номинала резисторов, необходимых в схемах, а также может использоваться для определения тока, протекающего в цепи, где напряжение можно легко измерить на известном резисторе, но более того, закон Ома используется в огромное количество вычислений во всех формах электрических и электронных схем – практически везде, где течет ток.

Открытие закона Ома

Существует математическая зависимость, связывающая ток, напряжение и сопротивление. Немецкий ученый по имени Георг Ом провел множество экспериментов, пытаясь показать связь между ними. В те дни, когда он проводил свои эксперименты, не было счетчиков в том виде, в каком мы их знаем сегодня.

Только после значительных усилий и со второй попытки ему удалось разработать то, что мы знаем сегодня как закон Ома.

Примечание Георга Ома:

Родившийся в Эрлангене, примерно в 50 милях к северу от Мюнхена в 1879 году, Георг Ом стал одним из тех, кто много исследовал новую науку, связанную с электричеством, обнаружив взаимосвязь между напряжением и током в проводнике – теперь этот закон действует. назвал Закон Ома, отдавая дань уважения проделанной им работе.

Подробнее о Георг Ом.

Что такое закон Ома?

Закон Ома описывает способ протекания тока через материал при приложении разных уровней напряжения. Некоторые материалы, такие как электрические провода, имеют небольшое сопротивление току, и этот тип материала называется проводником. Следовательно, если этот провод, например, проложить прямо через батарею, будет протекать большой ток.

В других случаях другой материал может препятствовать прохождению тока, но все же пропускать некоторые из них. В электрических схемах эти компоненты часто называют резисторами. Однако другие материалы практически не пропускают ток, и эти материалы называются изоляторами.


Посмотрите наше видео о законе Ома

Ом посмотрел на то, как ток течет в различных материалах, и смог разработать свой закон, который мы теперь называем законом Ома.

Чтобы получить первое представление о том, что происходит, можно сравнить электрическую ситуацию с потоком воды в трубе.Напряжение представлено давлением воды в трубе, ток представлен количеством воды, протекающей по трубе, и, наконец, сопротивление равно размеру трубы.

Можно представить, что чем шире труба, тем больше воды будет течь. Причина этого в том, что большему количеству воды легче течь по более широкой трубе, чем по более узкой – более узкая труба оказывает большее сопротивление потоку воды. Кроме того, если давление в электронной трубе больше, то по той же трубе будет течь больше воды.

Ом определил, что для обычных материалов удвоение напряжения удваивает ток, протекающий для данного компонента. Различные материалы или одни и те же материалы с разной формой будут иметь разные уровни сопротивления току.

Определение закона Ома

Закон Ома гласит, что ток, протекающий в цепи, прямо пропорционален приложенной разности потенциалов и обратно пропорционален сопротивлению в цепи.

Другими словами, удвоив напряжение в цепи, удвоится и ток. Однако, если сопротивление увеличено вдвое, ток упадет вдвое.

В этом математическом соотношении единица сопротивления измеряется в Омах.

Формула закона Ома

Формула или уравнение закона Ома очень проста.

Закон Ома можно выразить в математической форме:

Где:
V = напряжение, выраженное в вольтах
I = ток, выраженный в амперах
R = сопротивление, выраженное в омах

Формулой можно манипулировать так, чтобы, если известны любые две величины, можно было бы вычислить третью.

Треугольник закона Ома

Чтобы запомнить формулу, можно использовать треугольник, одна сторона которого горизонтальна, а вершина наверху напоминает пирамиду. Иногда это называют треугольником закона Ома.

В верхнем углу треугольника закона Ома находится буква V, в левом углу – буква I, а в правом нижнем углу – R.

Чтобы использовать треугольник, закройте неизвестное количество, а затем вычислите его из двух других. Если они выстроены в линию, они умножаются, но если один находится поверх другого, их следует разделить.Другими словами, если необходимо рассчитать ток, напряжение делится на сопротивление, то есть V / R и так далее.

Если необходимо рассчитать напряжение, оно определяется путем умножения силы тока на сопротивление, т. Е. I x R.

Пример расчета закона Ома

Если на резистор 500 Ом подается напряжение 10 В, определите величину тока, который будет протекать.

Глядя на треугольник закона Ома, ток неизвестен, а напряжение и сопротивление остаются известными значениями.

Таким образом, ток определяется делением напряжения на сопротивление.

I = VR = 10500 = 0,02 A = 20 мА

Пример 2
Аналогичным образом можно использовать закон Ома для определения сопротивления, если известны ток и напряжение. Возьмем, например, напряжение 10 вольт, а ток 0,1 А. Используя треугольник закона Ома, можно увидеть, что:

Пример 3
Наконец, другая комбинация состоит в том, что если сопротивление и ток известны, то можно рассчитать ожидаемое напряжение на сопротивлении.Возьмем, к примеру, расстояние 250 Ом, через которое протекает ток 0,1 А, тогда напряжение можно рассчитать следующим образом:

V = I R = 0,1 × 250 = 25 вольт

Проводники омические и неомические

Используя закон Ома, можно увидеть, что если бы напряжение и ток были нанесены на график для фиксированного резистора или отрезка провода и т. Д., То была бы прямая линия.

Видно, что удвоение напряжения удваивает ток, который проходит через конкретный элемент схемы.

График напряжения и тока для линейного сопротивления

На графике есть две линии, одна для более высокого сопротивления – эта требует приложения большего напряжения для данного протекающего тока. Соответственно, у него должно быть более высокое сопротивление. И наоборот, кривая для более низкого сопротивления показывает компонент, который требует приложения более низкого напряжения для данного тока.

Компоненты, имеющие прямую или прямую линию, подчиняются закону Ома и известны как омические проводники.Однако не все электрические электронные компоненты имеют прямолинейный график для напряжения и тока. По разным причинам они могут иметь разные вольт-амперные характеристики. Эти проводники часто называют неомическими.

Закон Ома – одно из самых основных понятий в электротехнике и электронной технике. Концепция элемента, имеющего определенное сопротивление, которое определяет количество тока, протекающего через него при определенном напряжении, является ключом к работе практически всех цепей.

Дополнительные концепции и руководства по основам электроники:
Напряжение Текущий Власть Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность Радиочастотный шум
Вернуться в меню «Основные понятия электроники». . .

Закон

Ом – обзор

8.2.2 Паразитная емкость

Закон Ома, как указано в уравнении. (8.1), не выполняется, если модель устройства включает реактивные (емкостные или индуктивные) компоненты и учитываются изменяющиеся во времени напряжения / токи. В таких случаях обобщенная форма закона Ома, показанная в формуле. (8.4) описывает взаимосвязь между напряжением и током через понятие электрического импеданса Z .

(8.4) V = ZIwithZ = R + jX

Электрический импеданс Z представлен комплексным числом, действительной частью которого является сопротивление R , как определено ранее, тогда как мнимая часть X , называемое реактивным сопротивлением, учитывает реактивные эффекты.

Некоторые датчики несут информацию, относящуюся к измеряемым величинам, как в резистивных, так и реактивных компонентах импеданса, поэтому интерфейсные схемы должны иметь возможность выполнять одновременную оценку R и X . С другой стороны, если полезная информация содержится только в резистивном компоненте, как это обычно бывает с резистивными датчиками, реактивный компонент считается паразитным элементом, влияние которого следует минимизировать.

При работе с резистивными датчиками обычно основной паразитный вклад имеет емкостный характер.В отличие от неидеальности большинства компонентов схемы, эти емкостные эффекты не могут быть компенсированы правильной калибровкой схемы, поскольку они зависят от конкретного датчика и условий эксплуатации. Если не принять во внимание надлежащим образом, такие эффекты могут вызвать ошибки в оценке сопротивления, как будет разъяснено в следующих разделах.

Одна из наиболее распространенных причин возникновения паразитных емкостных эффектов связана с производством датчиков. Если эффект обнаружения достигается определенными явлениями, происходящими на поверхности датчика (например,g., с фотодетекторами и датчиками газа), обычный способ улучшить чувствительность датчика – это максимизировать поверхностные эффекты за счет реализации метода, основанного на встречно-штыревых электродах, показанном на рис. 8.3. К сожалению, эта структура привносит повышенную паразитную емкость C _ee между электродами, как показано на рис. 8.3, которая становится еще более значительной по мере повторения встречно-штыревой структуры (Polese et al., 2017).

Рисунок 8.3. Паразитно-емкостный эффект в датчиках с встречно-штыревыми электродами.

Другая ситуация, в которой возникают паразитные емкостные эффекты, характерна для газовых датчиков. Некоторые устройства для измерения газа должны работать при гораздо более высокой температуре, чем температура окружающей среды, и по этой причине они обычно снабжены встроенной нитью накала R _h , которая действует как нагреватель (Samà et al. , 2017). Нить накала нагревателя представляет собой проводник, реализованный на той же подложке чувствительного компонента R _s и разделенный диэлектрическим материалом, который электрически изолирует два компонента датчика.Однако небольшой размер реализованных устройств заставляет эти два компонента взаимодействовать друг с другом из-за емкостных эффектов, как показано на рис. 8.4.

Рисунок 8.4. Паразитно-емкостный эффект в газовых сенсорах со встроенной нитью нагревателя.

В дополнение к этим возможным внутренним источникам емкостные эффекты могут возникать из-за внешних причин, таких как соединение между датчиком и измерительной системой, как показано на рис. 8.5. Фактически, разъемы и провода, используемые для соединения датчика с электронной схемой, демонстрируют распределенную емкостную характеристику C _c , которая, с точки зрения приборов, наблюдается параллельно датчику.

Рисунок 8.5. Паразитно-емкостный эффект из-за связи датчика с измерительной системой.

Расчет общего емкостного паразитного эффекта далеко не простой и часто требует полного понимания характеристик датчика, в том числе на микроскопическом уровне. По этой причине, когда необходимо учитывать паразитную емкость, обычно рассматривается упрощенная модель датчика, где паразитный конденсатор C _с представлен параллельно с сопротивлением датчика R _с , с учетом всех возможных емкостных паразитных эффектов.Упрощенная модель датчика, используемая в следующих разделах, показана на рис. 8.6.

Рисунок 8.6. Упрощенная модель резистивного датчика с учетом паразитно-емкостных эффектов.

Следует отметить, что, когда R _s очень большое (напоминающее поведение, связанное с разомкнутой цепью) C _s может преобладать, что приводит к значительным ошибкам в оценке сопротивления . В этих случаях (например,g., при работе с датчиками MOX), интерфейсные схемы должны быть спроектированы так, чтобы ограничить это явление.

11,2 Закон Ома | Электрические цепи

11,2 Закон Ома (ESBQ6)

Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление . Резюме:

1. Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.

2. Разность потенциалов или напряжение \ (В \) – это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.

3. Сопротивление, \ (R \), является мерой того, насколько “сложно” протолкнуть ток через элемент схемы.

Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.

Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .

Закон Ома

Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как

. \ (I = \ frac {V} {R} \)

где \ (I \) – ток через проводник, \ (V \) – напряжение на проводнике, а \ (R \) – сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.

Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток – на ось y графика, мы получим прямую линию.

Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R}.\] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I}. \]

Закон Ома

Цель

Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.

Аппарат

4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода

Метод

Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.

1. Изменение напряжения:

   1. Установите схему в соответствии со схемой 1), начиная с одной ячейки.

   2. Нарисуйте следующую таблицу в своем лабораторном журнале.

      Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
      \ (\ text {1} \)
      \ (\ text {2} \)
      \ (\ text {3} \)
      \ (\ text {4} \)

   3. Попросите учителя проверить электрическую цепь перед включением питания.

   4. Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.

   5. Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.

   6. Повторяйте, пока не получите четыре ячейки и не заполните таблицу.

2. Изменение тока:

   1. Установите схему в соответствии со схемой 2), начиная с одного резистора в цепи.

   2. Нарисуйте следующую таблицу в своем лабораторном журнале.

      Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))

   3. Попросите учителя проверить вашу схему перед включением питания.

   4. Измерьте ток и напряжение на единственном резисторе.

   5. Теперь добавьте еще один резистор последовательно в схему и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.

Анализ и результаты

1. Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение – это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).

2. Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).

Выводы

1. Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?

2. Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?

3. Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Вопросы и обсуждение

1. Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?

2. Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?

Высокие оценки в науке – залог вашего успеха и будущих планов.Проверьте себя и узнайте больше о практике Сиявулы.

Зарегистрируйтесь и проверьте себя

Закон Ома

Учебное пособие Упражнение 11.1

Постройте график напряжения (по оси X) и тока (по оси Y).

Какой тип графика вы получите (прямой, парабола, другая кривая)

прямая линия

Рассчитайте градиент графика.

Градиент графика (\ (m \)) – это изменение тока, деленное на изменение напряжения:

\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) – (\ text {0,4})} {(\ text {12}) – (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}

Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.

Как вы можете определить сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?

Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.

Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение для каждого из резисторов.

Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:

\ [V = IR \]

Итак, используя это и тот факт, что для резисторов, включенных последовательно, ток одинаков во всей цепи, мы можем найти неизвестное сопротивление.

\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}

Омические и неомические проводники (ESBQ7)

Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток, проходящий через них.Эти проводники называются омическими проводниками . График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторыми примерами омических проводников являются резисторы цепи и нихромовая проволока.

Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка – типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.

В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, то увеличение тока приведет к увеличению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.

Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых изготовлено большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.

В общем, для неомических проводов график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.

Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка – нет.

Омические и неомические проводники

Aim

Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома

Аппарат

4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр

Метод

Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй – лампочка.Настройте обе схемы, указанные выше, начиная с 1 ячейки. Для каждой цепи:

1. Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.

2. Измерить ток в цепи с помощью амперметра.

3. Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.

Результаты

Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.

Количество ячеек	Напряжение, В (\ (\ text {V} \))	Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)

Анализ

Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) – ось) vs.\ (V \) (\ (x \) – ось), один для резистора и один для лампочки.

Вопросы и обсуждение

Внимательно изучите свои графики и ответьте на следующие вопросы:

1. Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?

2. Один или оба ваших графика выглядят так?

3. Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?

4. Имеет ли лампочка омический или неомический провод?

Использование закона Ома (ESBQ8)

Теперь мы готовы посмотреть, как закон Ома используется для анализа схем.

Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача – нарисовать принципиальную схему. При решении любой проблемы с электрическими схемами очень важно составить схему схемы перед тем, как производить какие-либо расчеты. Принципиальная схема для этой проблемы выглядит следующим образом:

Уравнение закона Ома: \ [R = \ frac {V} {I} \]

, который можно преобразовать в: \ [I = \ frac {V} {R} \]

Ток, протекающий через резистор:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}

Рабочий пример 1: Закон Ома

Изучите принципиальную схему ниже:

Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?

Определите, как подойти к проблеме

Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]

Решаем проблему

Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \). \ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}

Напишите окончательный ответ

Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).

Высокие оценки в науке – залог вашего успеха и будущих планов. Проверьте себя и узнайте больше о практике Сиявулы.

Зарегистрируйтесь и проверьте себя

Закон Ома

Учебное пособие Упражнение 11.2

Рассчитайте сопротивление резистора, разность потенциалов которого составляет \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}

Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}

Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.

Сопротивление неизвестного резистора составляет:

. \ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}

Резисторы последовательно и параллельно (ESBQ9)

В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.

Когда в цепи более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .

Эквивалентное последовательное сопротивление

В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление – это просто сумма сопротивлений всех резисторов.

Эквивалентное сопротивление в последовательной цепи,

Для последовательно подключенных n резисторов эквивалентное сопротивление составляет:

. \ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]

Применим это к следующей схеме.

Резисторы включены последовательно, следовательно:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {align *}

Эквивалентное параллельное сопротивление

В схеме, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующим определением.

Эквивалентное сопротивление в параллельной цепи

Для резисторов \ (n \), включенных параллельно, эквивалентное сопротивление составляет:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]

Применим эту формулу к следующей схеме.

Какое полное (эквивалентное) сопротивление в цепи?

\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \Правильно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {align *}

Последовательное и параллельное сопротивление

Учебное пособие Упражнение 11.3

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}

Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.

Поскольку резисторы включены последовательно, мы можем использовать:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} – R_ {1} \\ & = \ text {100} \ text {Ω} – \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}

Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}

Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?

Поскольку резисторы включены параллельно, мы можем использовать:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} – \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} – \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} – \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}

Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:

a) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}

b) Резисторы включены параллельно, поэтому мы используем:

\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]

Эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}

c) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}

d) Резисторы включены последовательно, поэтому мы используем:

\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]

Эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}

Использование закона Ома в последовательных и параллельных цепях (ESBQB)

Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.

Последовательные цепи

Рассмотрим схему, состоящую из трех резисторов и одного одиночная ячейка соединена последовательно.

Первый принцип, который необходимо понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.

Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:

\ [I = I_ {1} = I_ {2} = I_ {3}. \]

Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:

\ [V = V_ {1} + V_ {2} + V_ {3} \]

Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления последовательно соединенных резисторов, мы можем решить некоторые проблемы схемы.

Рабочий пример 2: Закон Ома, последовательная цепь

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Нам необходимо рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.

Найти полное сопротивление в цепи

Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:

\ [R = R_ {1} + R_ {2} \]

Следовательно,

\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {align *}

Применить закон Ома

\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).

Рабочий пример 3: Закон Ома, последовательная цепь

Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).

Нарисуйте схему и введите все известные значения.

Определите, как подойти к проблеме.

Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:

\ [R = R_ {1} + R_ {2} \]

, потому что он находится в последовательной цепи.

Найдите полное сопротивление

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {align *}

Найдите неизвестное сопротивление

Мы знаем, что:

\ [R = \ text {6} \ text {Ω} \]

и что

\ [R_ {1} = \ text {1} \ text {Ω} \]

С

\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R – R_ {1} \]

Следовательно,

\ [R_ {1} = \ text {5} \ text {Ω} \]

Рабочий пример 4: Закон Ома, последовательная цепь

Для следующей схемы рассчитайте:

1. падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)

2. сопротивление \ (R_3 \).

Определите, как подойти к проблеме

Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).

Рассчитать падение напряжения на \ (R_1 \)

Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_2 \)

Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}

Рассчитать падение напряжения на \ (R_3 \)

Поскольку падение напряжения на всех резисторах вместе должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V – V_1 – V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}

Найдите сопротивление \ (R_3 \)

Нам известно напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома для вычисления значения сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}

Напишите окончательный ответ

\ (V_1 = \ text {2} \ text {V} \)

\ (V_2 = \ text {6} \ text {V} \)

\ (V_3 = \ text {10} \ text {V} \)

\ (R_1 = \ text {5} \ Omega \)

Параллельные цепи

Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.

Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Итак, для показанной схемы верно следующее:

\ [V = V_ {1} = V_ {2} = V_ {3}. \]

Второй принцип параллельной схемы заключается в том, что все токи, проходящие через каждый резистор, должны составлять общий ток в цепи:

\ [I = I_ {1} + I_ {2} + I_ {3}.\]

Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельных резисторов, мы теперь можем подойти к некоторым проблемам схемы, связанным с параллельными резисторами.

Рабочий пример 5: Закон Ома, параллельная цепь

Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.

Определите, что требуется

Нам необходимо рассчитать ток, протекающий в цепи.

Определите, как подойти к проблеме

Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома.Однако в цепи два резистора, и нам нужно найти полное сопротивление.

Найдите эквивалентное сопротивление в цепи

.

Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:

\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {align *}

Применить закон Ома

\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {align *}

Напишите окончательный ответ

В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).

Рабочий пример 6: Закон Ома, параллельная цепь

Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найдите сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ текст {9} \) \ (\ text {V} \).

Определите, что требуется

Нам нужно рассчитать сопротивление \ (R_2 \).

Определите, как подойти к проблеме

Поскольку резисторы омические, и нам даны напряжение на ячейке и ток в ячейке, мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи.\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}

Рассчитайте значение для \ (R_2 \)

Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для параллельных резисторов, чтобы найти сопротивление \ (R_2 \). \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \ end {выровнять *} Переставляем решение для \ (R_2 \): \ begin {align *} \ frac {1} {R_2} & = \ frac {1} {R} – \ frac {1} {R_1} \\ & = \ frac {1} {\ text {1,875}} – \ frac {1} {3} \\ & = \ текст {0,2} \\ R_2 & = \ frac {1} {\ text {0,2}} \\ & = \ текст {5} \ \ Omega \ end {align *}

Напишите окончательный ответ

Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)

Рабочий пример 7: Закон Ома, параллельная цепь

Ячейка на 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.

Сначала нарисуйте схему перед выполнением любых расчетов

Определите, как подойти к проблеме

Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.

Рассчитать ток через ячейку

Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи.Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}

Теперь определим ток через один из параллельных резисторов

Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_1 = V_2 = \ text {18} \ text {V} \ end {выровнять *} Начнем с расчета тока через \ (R_1 \) по закону Ома: \ begin {align *} R_1 & = \ frac {V_1} {I_1} \\ I_1 & = \ frac {V_1} {R_1} \\ & = \ frac {18} {4} \\ I_1 & = \ text {4,5} \ text {A} \ end {align *}

Рассчитайте ток через другой параллельный резистор

Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \): \ begin {align *} R_2 & = \ frac {V_2} {I_2} \\ I_2 & = \ frac {V_2} {R_2} \\ & = \ frac {18} {12} \\ I_2 & = \ text {1,5} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять суммарный ток через ячейку: \ begin {align *} I & = I_1 + I_2 \\ I_2 & = I – I_1 \\ & = 6 – 4.5 \\ I_2 & = \ text {1,5} \ text {A} \ end {align *}

Напишите окончательный ответ

Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).

Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).

Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).

Закон Ома в последовательной и параллельной цепях

Учебное упражнение 11.4

Рассчитать номинал неизвестного резистора в цепи:

Сначала мы используем закон Ома для расчета полного последовательного сопротивления:

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}

Теперь мы можем найти неизвестное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} – R_ {1} – R_ {2} – R_ {3} \\ & = 9 – 3 – 3 – 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}

Рассчитайте значение тока в следующей цепи:

Сначала находим общее сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *}

Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены последовательно с батареей \ (\ text {12} \) \ (\ text {V} \).Рассчитайте значение тока в цепи.

Рисуем принципиальную схему:

Теперь мы находим общее сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {A} \ end {выровнять *}

Рассчитайте ток через ячейку, если оба резистора омические по своей природе.

Сначала находим общее сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать текущую:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}

Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:

Сначала находим общее сопротивление:

\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}

Теперь мы можем рассчитать неизвестное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} – \ frac {1} {R_ {1}} – \ frac {1} {R_ {2}} – \ гидроразрыв {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} – \ frac {1} {\ text {120}} – \ frac {1} {\ text {40}} – \ frac {1} {\ text { 60}} \\ & = \ frac {10 – 1 – 3 – 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}

значение тока через аккумулятор

Рисуем принципиальную схему:

Чтобы вычислить значение тока через батарею, нам сначала нужно вычислить эквивалентное сопротивление:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}

Теперь можем посчитать ток через батарею:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *}

значение тока в каждом из трех резисторов.

Для параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из резисторов. Для этой схемы:

\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]

Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}

Затем мы вычисляем ток через \ (R_ {2} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}

И наконец вычисляем ток через \ (R_ {3} \):

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *}

Вы можете проверить, что они составляют в сумме общий ток.

Последовательные и параллельные сети резисторов (ESBQC)

Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы заняться цепями, в которых сочетаются эти две схемы, например следующей цепью:

Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.

Проработать такие схемы относительно легко, потому что вы используете все, что вы уже узнали о последовательных и параллельных схемах.Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из 2 параллельных частей, которые затем включены последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начинаете с вычисления общего сопротивления каждой из параллельных частей, а затем последовательно складываете эти сопротивления. Если бы все резисторы на рисунке 11.1 имели сопротивление \ (\ text {10} \) \ (\ text {Ω} \), мы можем вычислить эквивалентное сопротивление всей цепи.

Начнем с расчета общего сопротивления параллельной цепи 1 .{-1} \\ & = \ текст {5} \, \ Omega \ end {align *}

Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:

Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}

Эквивалентное сопротивление цепи на рисунке 11.1 равно \ (\ text {10} \) \ (\ text {Ω} \).

Последовательные и параллельные сети

Учебное пособие, упражнение 11.5

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}

Начнем с определения эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}

ток \ (I \) через ячейку.

Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *}

ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).

Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ text {A} \). (Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):

\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторе \ (\ text {5} \) \ (\ text {Ω} \).

Итак, теперь мы можем рассчитать ток через резистор:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {А} \ end {выровнять *}

Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы омические, рассчитайте напряжение на ячейке и на каждом из резисторов, \ (R_1 \ ), \ (R_2 \) и \ (R_3 \) соответственно.

Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление.Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}

Итак, напряжение на ячейке:

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *}

Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с определения напряжения на \ (R_ {1} \):

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}

Теперь находим напряжение на параллельной комбинации:

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *}

Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).

ток через ячейку

Чтобы найти ток, нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:

\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}

Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:

\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}

Итак, ток через ячейку:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}

падение напряжения на \ (R_4 \)

Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти напряжение через \ (R_ {4} \):

\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2,5}) (\ текст {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}

ток через \ (R_2 \)

Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)

Используя это, мы можем найти ток через \ (R_ {2} \).

Сначала нам нужно найти напряжение на параллельной комбинации:

\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}

Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение одинаково на всех резисторах в параллельной комбинации:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *} .