Ацп последовательного приближения: В чем разница между Δ∑-АЦП и АЦП последовательного приближения?

В чем разница между Δ∑-АЦП и АЦП последовательного приближения?

Выбирая между АЦП последовательного приближения и Δ∑-АЦП, разработчик, как правило, должен решить, что для него важнее в конкретном приложении – высокое разрешение или частота дискретизации.

Сегодня практически в каждом электронном устройстве используются аналого-цифровые преобразователи (АЦП). Одна из задач, стоящих перед разработчиком при создании нового устройства, заключается в выборе типа АЦП. Этот выбор во многом определяет эффективность конечного решения. В данной статье рассматриваются два наиболее популярных типа АЦП: АЦП последовательного приближения и Δ∑-АЦП. В заключении даются рекомендации, которые помогут разработчикам сделать грамотный выбор между этими архитектурами.

Для описания АЦП используются десятки различных параметров. Рассмотри наиболее важные из них.

Разрешение. Разрешение АЦП определяется его максимальной разрядностью. Разрешение также может выражаться как минимальное изменение входного аналогового сигнала, которое приводит к изменению выходного цифрового значения на 1 бит LSB (младший значащий разряд). Таким образом, аналоговое разрешение определяет минимальное изменение входного сигнала, которое может быть зафиксировано АЦП.

Точность. Точность АЦП характеризует, насколько реальный выходной цифровой сигнал отличается от идеального значения. Точность АЦП определяется шумом квантования, нелинейностями в передаточной характеристике и дополнительными источниками шума.

Частота дискретизации. Частота дискретизации – это наибольшее количество выборок, которое АЦП способен выполнить за одну секунду. Например, АЦП может делать 10 миллионов выборок в секунду (10 MSPS). Частота дискретизации связана со временем преобразования, то есть тем временем, которое требуется для выполнения одного преобразования. Для частоты дискретизации 10 MSPS время преобразования составляет 100 нс.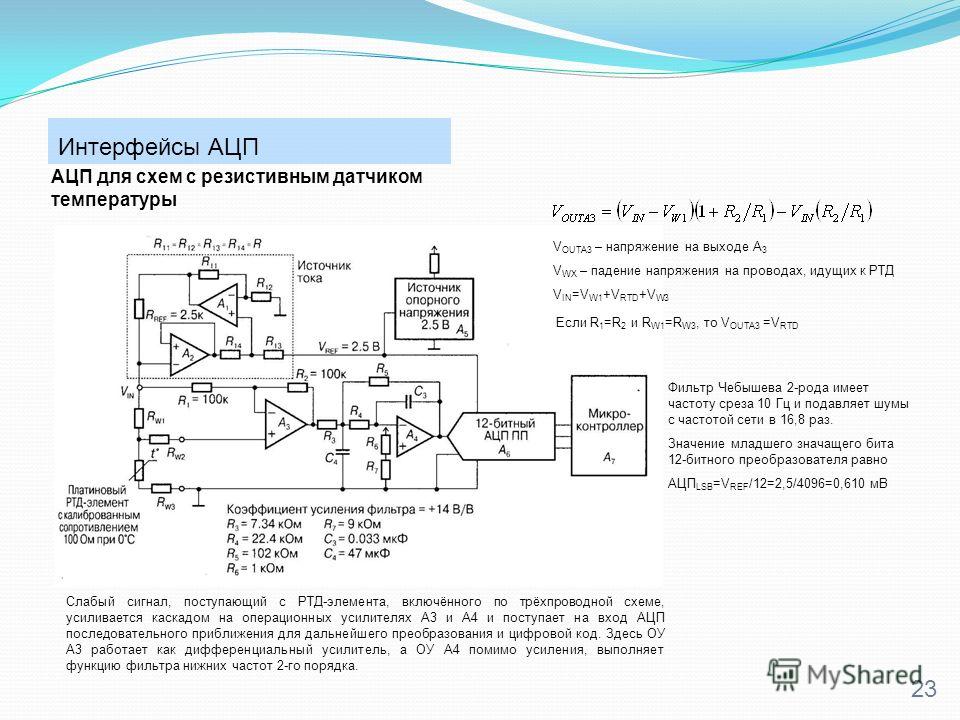

Шум квантования. Шум квантования представляет собой ошибку, возникающую при выполнении преобразования. Говоря конкретным языком, это разница между фактическим входным значением аналогового напряжения и выходным напряжением, представленным в цифровом виде. Пиковое значение шума квантования равно аналоговому разрешению, то есть напряжению, которое соответствует младшему значащему разряду LSB. Это значение определяется как V_R/ 2^N, где V_R – это опорное напряжение преобразователя, 2^N – это число битов разрешения. Шум квантования уменьшается с увеличением разрешения.

Есть и другие важные характеристики АЦП, но, к сожалению, они оказываются слишком сложными, чтобы их можно было рассмотреть в рамках данной короткой статьи. При необходимости с ними можно ознакомиться самостоятельно с помощью других публикаций.

Сравнение типов АЦП

Существует пять наиболее распространенных архитектур АЦП: АЦП двойного интегрирования (dual slope ADC), АЦП последовательного приближения (successive approximation ADC), АЦП прямого преобразования (flash ADC), АЦП конвейерного типа (pipelined ADC), дельта-сигма АЦП (delta-sigma ADC).

АЦП двойного интегрирования отличаются низкой частотой дискретизации и используются в основном в измерительных приборах, таких, например, как цифровые вольтметры. АЦП с последовательным приближением имеют хорошее разрешение и умеренно высокую частоту дискретизации, в то время как АЦП прямого преобразования предлагают самую высокую скорость преобразования, но характеризуются невысоким разрешением. Преобразователи конвейерного типа использует несколько АЦП прямого преобразования, что позволяет увеличить разрешение и сохранить высокую частоту дискретизации. Наконец, сигма-дельта АЦП (Δ∑) обеспечивают очень высокое разрешение, но отличаются самой низкой частотой дискретизации. В таблице 1 представлены характеристики всех перечисленных типов преобразователей.

Таблица 1. Характеристики различных типов АЦП

Тип АЦП	Разрешение, бит	Частота дискретизации
Двойного интегрирования	12-20	100 выборок в секунду
Последовательного приближения	8-18	10 миллионов выборок в секунду
Прямого преобразования	4-12	10 миллиардов выборок в секунду
Конвейерные	8-16	1 миллиард выборок в секунду
Дельта-сигма	8-32	1 миллион выборок в секунду

Самыми популярными типами АЦП являются АЦП последовательного приближения и Δ∑-АЦП.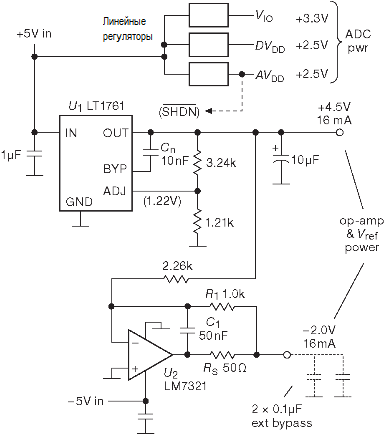 Оставшаяся часть статьи посвящена более детальному рассмотрению особенностей этих двух типов преобразователей.

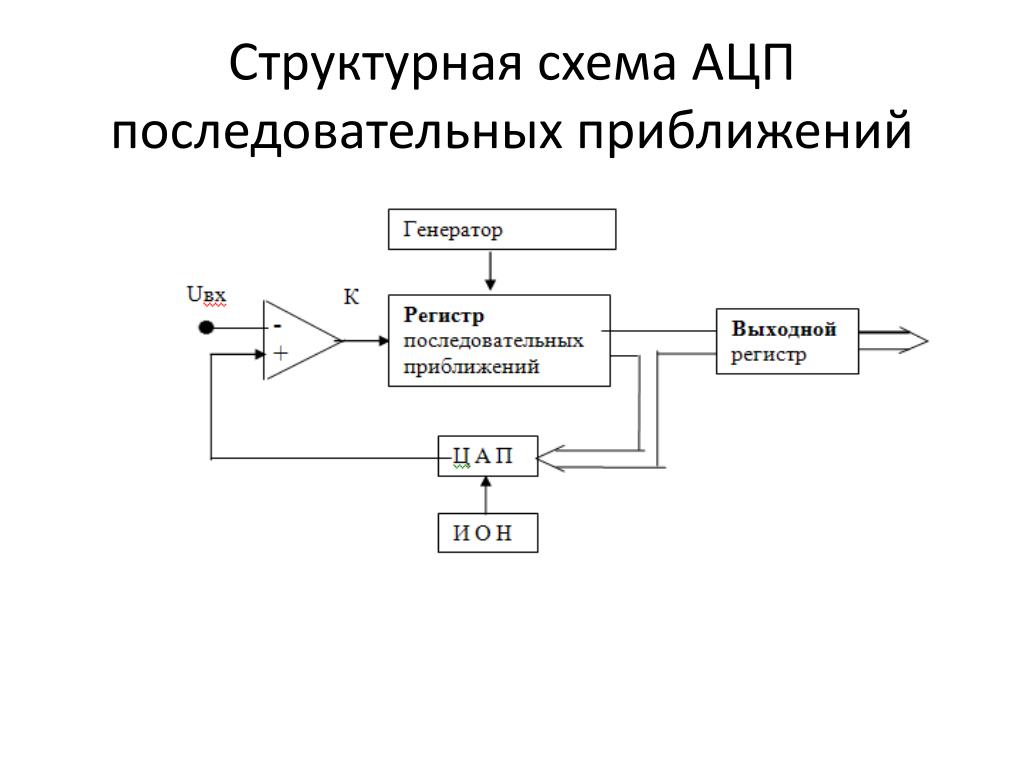
АЦП последовательного приближения

АЦП последовательного приближения является одним из старейших и наиболее популярных типов АЦП. Их обычно используют в приложениях сбора данных, в промышленной автоматике и в контрольно-измерительных приборах, то есть там, где сверхвысокая скорость не требуется.

На рис. 1 показана структурная схема АЦП последовательного приближения. В ее основе лежит регистр последовательного приближения. Результат, хранящийся в этом регистре, поступает на выход АЦП по параллельной шине. Эта же шина подключена к цифроаналоговому преобразователю (ЦАП), который формирует аналоговый сигнал в соответствии с содержимым регистра. Сигнал от источника опорного напряжения, подаваемого на вход ЦАП, определяет диапазон входных напряжений АЦП (например, от 0 до 5 В).

Рис. 1. В основе АЦП последовательного приближения лежит регистр последовательного приближения

Сигнал с выхода ЦАП поступает на вход компаратора.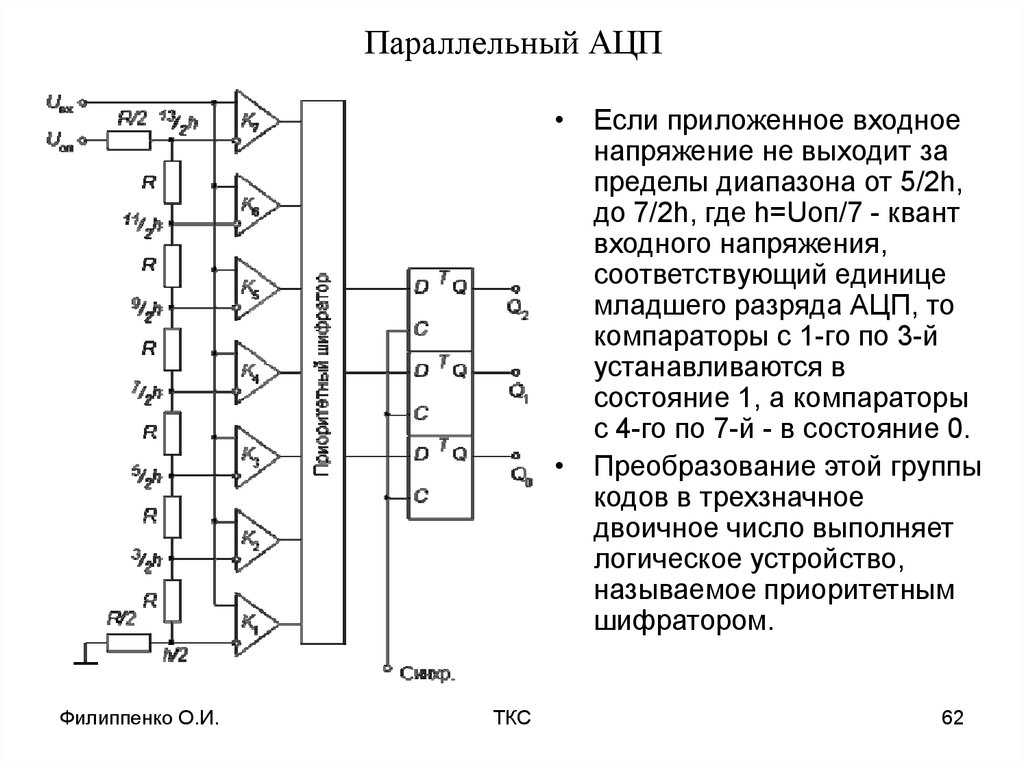

На другой вход компаратора подается аналоговый сигнал, который требуется оцифровать. Этот сигнал обычно предварительно нормализуется с помощью усилителя выборки хранения. Усилитель выборки хранения содержит ключ и конденсатор, который заряжает/ разряжается входным напряжением. Каждое преобразование начинается с выборки входного напряжения. Для этого ключ усилителя открывается, и входное напряжение заряжает конденсатор. Далее усилитель обеспечивает постоянство этого напряжения в течение всего процесса преобразования.

В некоторых случаях усилитель выборки-хранения может отсутствовать. Речь идет об АЦП с низким быстродействием и невысоким разрешением.

Разрешение АЦП последовательного приближения обычно находится в диапазоне от 8 до 18 бит и зависит от количества битов в регистре последовательного приближения. Чем больше количество битов, тем больше разрешение и точность. Например, для 12-разрядного АЦП с опорным 5 В ЦАП аналоговое разрешение составит V

R/ 2^N = 5/ 2¹² = 5/ 4096 = 1,22 мВ.

АЦП использует специальный алгоритм работы. Логика управления последовательно устанавливает или сбрасывает отдельные биты в регистре последовательного приближения в соответствии с состоянием выхода компаратора. Изначально все биты регистра сброшены. При запуске преобразования старший бит регистра (MSB) устанавливается в «1». Далее выполняется сравнение. Если входное напряжение АЦП оказывается больше, чем напряжение на выходе ЦАП, то бит регистра остается установленным, в противном случае сбрасывается.

Затем устанавливается следующий по старшинству бит и выполняется новое сравнение. Тактовый сигнал определяет скорость установки и сброса битов регистра. Процесс продолжается до тех пор, пока не будут оценены все биты. Общее время преобразования в таком случае определяется временем установки/ сброса одного бита, умноженным на количество битов в регистре последовательного приближения. Для 16-разрядного АЦП с тактовой частотой 2 МГц время преобразования составляет 16 x 0,5 мкс = 8 мкс.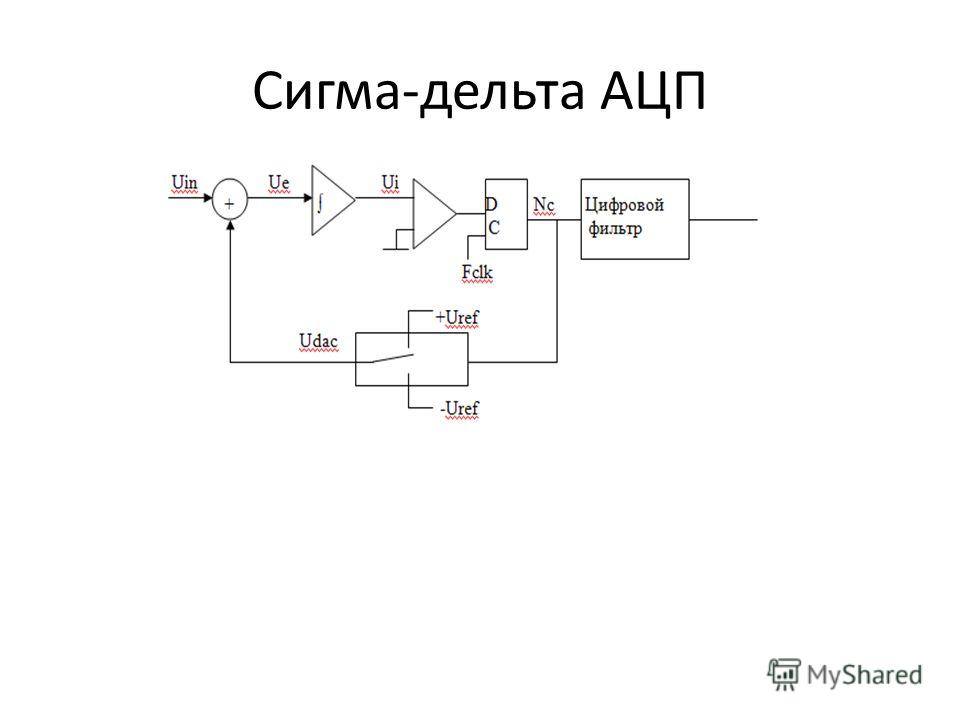

Время преобразования определяет частоту дискретизации АЦП.

После выполнения преобразования полученное цифровое значение входного напряжения может быть считано по параллельной шине напрямую из регистра последовательного приближения, либо в качестве альтернативного варианта содержимое регистра может быть перенесено в сдвиговый регистр, из которого результат считывается с помощью последовательного интерфейса. 

Дельта-сигма АЦП

??-АЦП используют более современную архитектуру, которая была разработана после создания эффективных механизмов цифровой обработки сигналов (DSP). Эта архитектура оказывается уникальной и сложной, но обеспечивает рекордное разрешение и минимальный уровень шума. В то же время, Δ∑-АЦП уступают остальным типам АЦП по частоте дискретизации, поэтому чаще всего их используют для работы с постоянными сигналами и низкочастотными сигналами аудиодиапазона. Типичными приложениями для Δ∑-АЦП являются измерительные приборы и цифровое аудио (например, CD, MP3 и т.

д.).

На рис. 2 показана структурная схема Δ∑-АЦП. В ее основе лежит Δ∑-модулятор. Входной сигнал АЦП подается на дифференциальный усилитель, где из него вычитается выходной сигнал встроенного 1-битного ЦАП. Затем результат интегрируется и поступает на компаратор, который сравнивает его с нулевым потенциалом. Далее выход компаратора устанавливает или сбрасывает D-триггер. Состояние D-триггера снова отправляется в ЦАП. Так как ЦАП имеет разрядность 1 бит, то на его выходе может присутствовать либо 0 В, либо напряжение опорного источника. В качестве альтернативного варианта ЦАП может формировать двухполярный сигнал, например ± 1 В.

Рис. 2. В основе ??-АЦП лежит схема модулятора

В результате на выходе D-триггера создается битовый поток. Плотность появления логических единиц «1» в этом потоке пропорциональна уровню входного напряжения. Каждый тактовый импульс генерирует один бит входного сигнала и один бит последовательного выходного сигнала.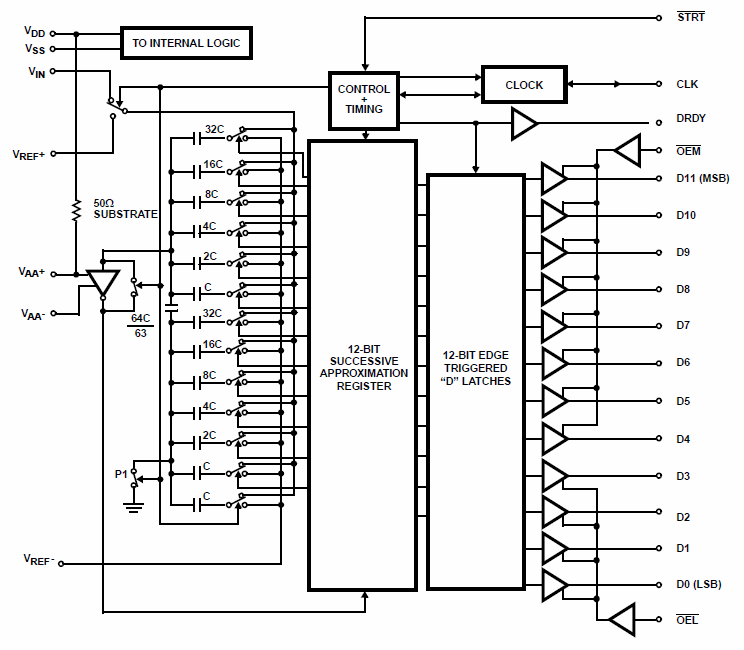 Тактовая частота обычно намного выше, чем частота входного сигнала, что необходимо для обеспечения передискретизации.

Сам по себе битовый поток оказывается не очень полезным. По этой причине в дальнейшем он обрабатывается низкочастотным DSP-фильтром и дециматором. Описание фактических процессов, происходящих в этих блоках, выходит за рамки данной статьи. Отметим лишь, что на выходе формируются цифровые битовые слова заданной длины. Цифровой фильтр и дециматор обычно входят в состав АЦП.

Ключевой особенностью Δ∑-АЦП является тот факт, что фильтр нижних частот удаляет большую часть высокочастотного шума, генерируемого в процессе измерений. Дециматор уменьшает количество выходных слов в соответствии с заданным коэффициентом прореживания. Коэффициент прореживания определяет, какое количество выборок будет усреднено для получения каждого выходного цифрового слова.

Итак, какие преобразователи лучше: Δ∑-АЦП или АЦП последовательного приближения?

Ответ зависит от конкретного приложения. Какой из параметров оказывается для Вас наиболее критичным: разрешение или частота дискретизации? Для получения максимального разрешения следует выбирать Δ∑-АЦП, для которых разрядность достигает 32 бит. Разрешение у АЦП последовательного приближения также весьма достойное, но, как правило, не превышает 18 бит.

Скорость выборки также имеет большое значение. АЦП должен быть достаточно быстрым, чтобы отрабатывать наиболее высокочастотные входные сигналы. В соответствии с теоремой Котельникова частота дискретизации должна превышать самую высокочастотную составляющую исследуемого сигнала как минимум в два раза. Так, например, если максимальная частота входного сигнала составляет 45 кГц, то частота дискретизации должна быть более 90 кГц. На практике для получения приемлемых результатов используют частоту дискретизации, превышающую частоту исследуемого сигнала в пять-десять раз.

Δ∑-АЦП и АЦП последовательного приближения имеют максимальную частоту дискретизации до 10 миллионов выборок в секунду (10 MSPS). Однако следует иметь в виду, что для Δ∑-АЦП частота обновления данных оказывается меньше из-за выполнения децимации и обычно находится в диапазоне тысяч выборок в секунду (kSPS). Вместе с тем ??-АЦП обеспечивают более качественное удаление шума, чем АЦП последовательного приближения.

Одно из преимуществ АЦП последовательного приближения заключается в том, что в них может использоваться мультиплексирование нескольких входов для получения многоканальных решений. Мультиплексор выполняет коммутацию каналов, подавая входные сигналы на усилитель выборки-хранения. Очевидно, что при последовательном опросе каналов частота дискретизации для каждого отдельного входа оказывается ниже. Например, четырехканальный АЦП с частотой дискретизации 5 MSPS обеспечивает частоту измерений для каждого канала 1,25 MSPS.

Таблица 2. Достоинства, недостатки и области применения ??-АЦП и АЦП последовательного приближения

Тип АЦП	Разрешение, бит	Частота дискрети- зации	Преимущества	Недостатки	Приложения
Последо- вательного приближения	8-18	10 млн выборок в секунду	скорость, низкое потребление, дешевизна, возможность мультиплек- сирования	низкое разрешение, значительный шум	сбор данных, промышленная автоматика, приложения с батарейным питанием
Дельта- сигма	8-32	1 млн выборок в секунду	низкий уровень шума, высокое разрешение, нет необходимости в устройстве выборки- хранения	низкая скорость, стоимость, потребление	Измерительные системы, аудиосистемы, медицинские системы

 

Автор: Лу Френцель Перевод: Гавриков Вячеслав (г.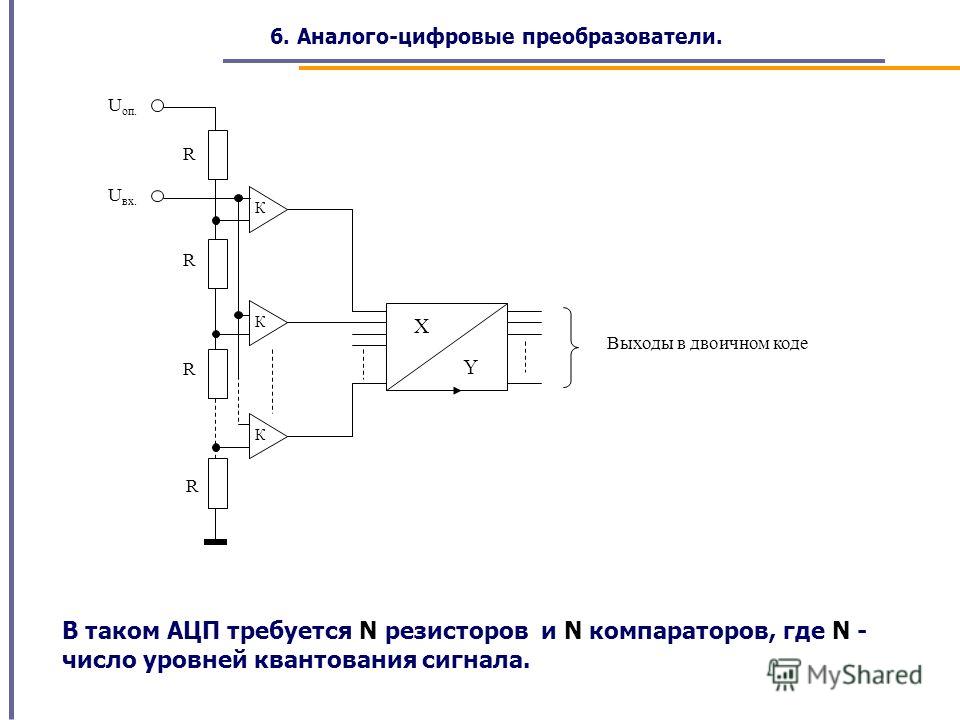 Смоленск)

Разделы: Аналого-цифровые преобразователи

Опубликовано: 04.09.2018

Как работают аналогово-цифровые преобразователи и что можно узнать из спецификации на АЦП

В статье рассказывается об устройстве и принципах действия аналогово-цифровых преобразователей различных типов, а также об их основных характеристиках, указываемых производителями в документации.

Аналогово-цифровой преобразователь (АЦП) — один из самых важных электронных компонентов в измерительном и тестовом оборудовании. АЦП преобразует напряжение (аналоговый сигнал) в код, над которым микропроцессор и программное обеспечение выполняют определенные действия. Даже если Вы работаете только с цифровыми сигналами, скорее всего Вы используете АЦП в составе осциллографа, чтобы узнать их аналоговые характеристики.

Существует несколько основных типов архитектуры АЦП, хотя в пределах каждого типа существует также множество вариаций. Различные типы измерительного оборудования используют различные типы АЦП. Например, в цифровом осциллографе используется высокая частота дискретизации, но не требуется высокое разрешение. В цифровых мультиметрах нужно большее разрешение, но можно пожертвовать скоростью измерения. Системы сбора данных общего назначения по скорости дискретизации и разрешающей способности обычно занимают место между осциллографами и цифровыми мультиметрами. В оборудовании такого типа используются АЦП последовательного приближения либо сигма-дельта АЦП. Существуют также параллельные АЦП для приложений, требующих скоростной обработки аналоговых сигналов, и интегрирующие АЦП с высокими разрешением и помехоподавлением.

На рис.1. показаны возможности основных архитектур АЦП в зависимости от разрешения и частоты дискретизации.

Рис. 1. Типы АЦП — разрешение в зависимости от частоты дискретизации

Параллельные АЦП

Большинство высокоскоростных осциллографов и некоторые высокочастотные измерительные приборы используют параллельные АЦП из-за их высокой скорости преобразования, которая может достигать 5Г (5х10
⁹) отсчетов/сек для стандартных устройств и 20Г отсчетов/сек для оригинальных разработок.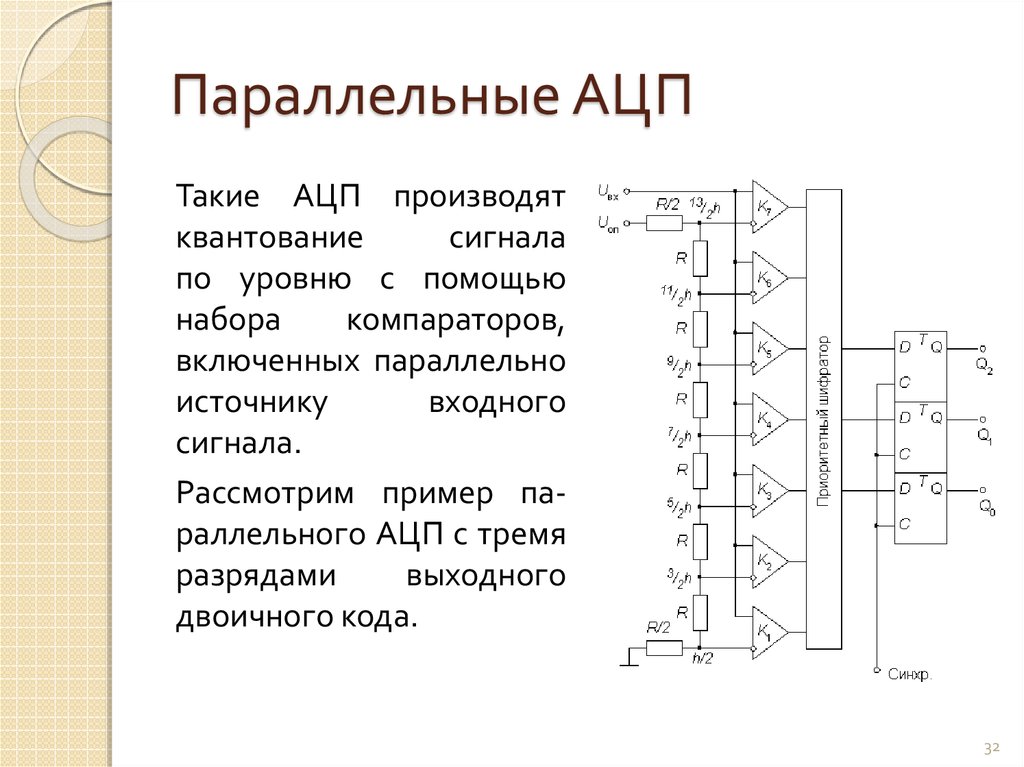 Обычно параллельные АЦП имеют разрешение до 8 разрядов, но встречаются также 10-ти разрядные версии.

Рис. 2. АЦП параллельного преобразования

Рис. 2 показывает упрощенную блок-схему 3-х разрядного параллельного АЦП (для преобразователей с большим разрешением принцип работы сохраняется). Здесь используется массив компараторов, каждый из которых сравнивает входное напряжение с индивидуальным опорным напряжением. Такое опорное напряжение для каждого компаратора формируется на встроенном прецизионном резистивном делителе. Значения опорных напряжений начинаются со значения, равного половине младшего значащего разряда (LSB), и увеличиваются при переходе к каждому следующему компаратору с шагом, равным V
_REF /2
³. В результате для 3-х разрядного АЦП требуется 2
³-1 или семь компараторов. А, например, для 8-разрядного параллельного АЦП потребуется уже 255 (или (2
⁸-1)) компараторов.

С увеличением входного напряжения компараторы последовательно устанавливают свои выходы в логическую единицу вместо логического нуля, начиная с компаратора, отвечающего за младший значащий разряд. Можно представить преобразователь как ртутный термометр: с ростом температуры столбик ртути поднимается. На рис. 2 входное напряжение попадает в интервал между V3 и V4, таким образом 4 нижних компаратора имеют на выходе «1», а верхние три компаратора — «0». Дешифратор преобразует (2
³-1) — разрядное цифровое слово с выходов компараторов в двоичный 3-х разрядный код.

Параллельные АЦП — достаточно быстрые устройства, но они имеют свои недостатки. Из-за необходимости использовать большое количество компараторов параллельные АЦП потребляют значительную мощность, и их нецелесообразно использовать в приложениях с батарейным питанием.

АЦП последовательного приближения

Когда необходимо разрешение 12, 14 или 16 разрядов и не требуется высокая скорость преобразования, а определяющими факторами являются невысокая цена и низкое энергопотребление, то обычно применяют АЦП последовательного приближения. Этот тип АЦП чаще всего используется в разнообразных измерительных приборах и в системах сбора данных. В настоящий момент АЦП последовательного приближения позволяют измерять напряжение с точностью до 16 разрядов с частотой дискретизации от 100К (1х10
³) до 1М (1х10
⁶) отсчетов/сек.

Рис. 3 показывает упрощенную блок-схему АЦП последовательного приближения. В основе АЦП данного типа лежит специальный регистр последовательного приближения. В начале цикла преобразования все выходы этого регистра устанавливаются в логический 0, за исключением первого (старшего) разряда. Это формирует на выходе внутреннего цифро-аналогового преобразователя (ЦАП) сигнал, значение которого равно половине входного диапазона АЦП. А выход компаратора переключается в состояние, определяющее разницу между сигналом на выходе ЦАП и измеряемым входным напряжением.

Рис. 3. АЦП последовательного приближения

Например, для 8-разрядного АЦП последовательного приближения (рис. 4) выходы регистра при этом устанавливаются в «10000000». Если входное напряжение меньше половины входного диапазона АЦП, тогда выход компаратора примет значение логического 0.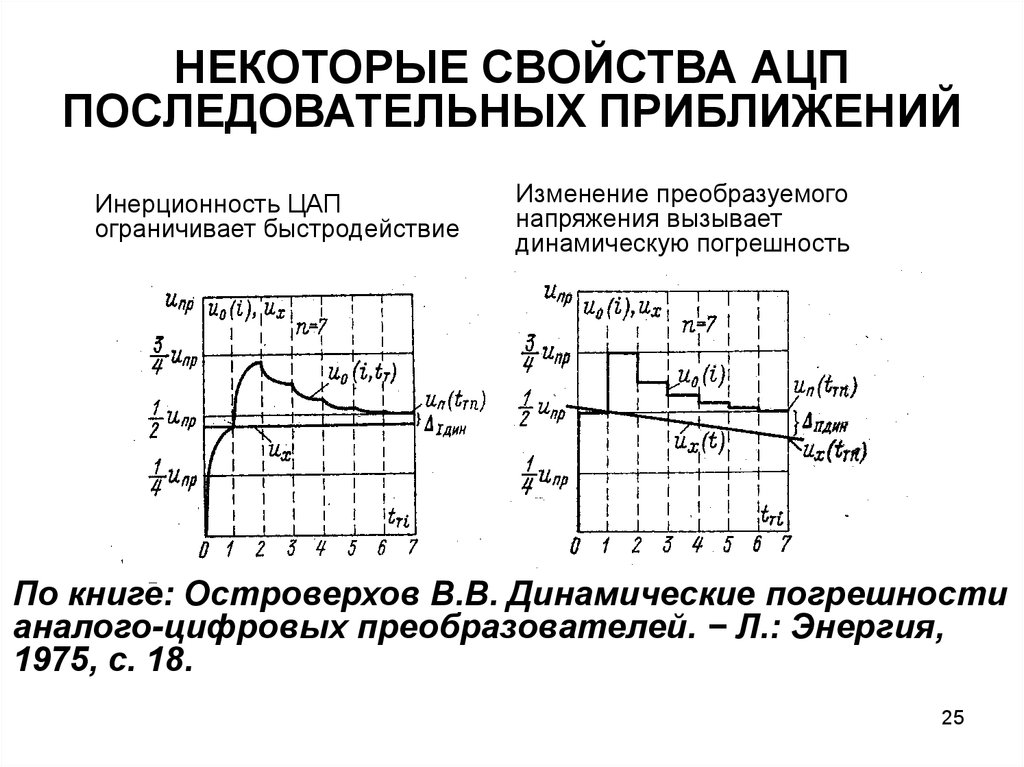 Это дает регистру последовательного приближения команду переключить свои выходы в состояние «01000000», что соответственно приведет к изменению выходного напряжения с ЦАП, подаваемого на компаратор. Если при этом выход компаратора по-прежнему оставался бы в «0», то выходы регистра переключились бы в состояние «00100000». Но на этом такте преобразования выходное напряжение ЦАП меньше, чем входное напряжение (рис. 4), и компаратор переключается в состояние логической 1. Это предписывает регистру последовательного приближения сохранить «1» во втором разряде и подать «1» на третий разряд. Описанный алгоритм работы затем вновь повторяется до последнего разряда. Таким образом, АЦП последовательного приближения требуется один внутренний такт преобразования для каждого разряда, или N тактов для N-разрядного преобразования.

Рис. 4. Преобразование в АЦП последовательных приближений

Тем не менее, работа АЦП последовательного приближения имеет особенность, связанную с переходными процессами во внутреннем ЦАП.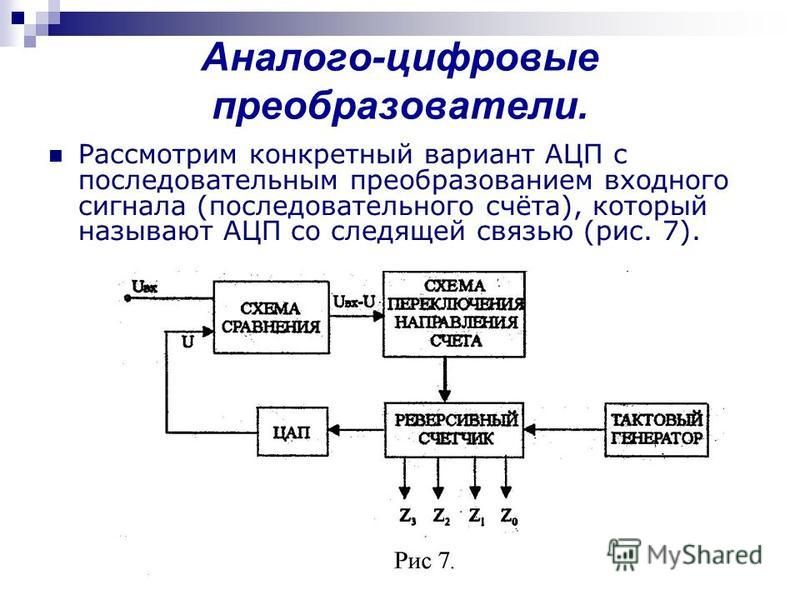 Теоретически, напряжение на выходе ЦАП для каждого из N внутренних тактов преобразования должно устанавливаться за одинаковый промежуток времени. Но на самом деле этот промежуток в первых тактах значительно больше, чем в последних. Поэтому время преобразования 16-разрядного АЦП последовательного приближения более, чем в два раза превышает время преобразования 8-разрядного АЦП данного типа.

Сигма-дельта АЦП

Для проведения большинства измерений часто не требуется АЦП со скоростью преобразования, которую даёт АЦП последовательного приближения, зато необходима большая разрешающая способность. Сигма-дельта АЦП могут обеспечивать разрешающую способность до 24 разрядов, но при этом уступают в скорости преобразования. Так, в сигма-дельта АЦП при 16 разрядах можно получить частоту дискретизации до 100К отсчетов/сек, а при 24 разрядах эта частота падает до 1К отсчетов/сек и менее, в зависимости от устройства.

Обычно сигма-дельта АЦП применяются в разнообразных системах сбора данных и в измерительном оборудовании (измерение давления, температуры, веса и т.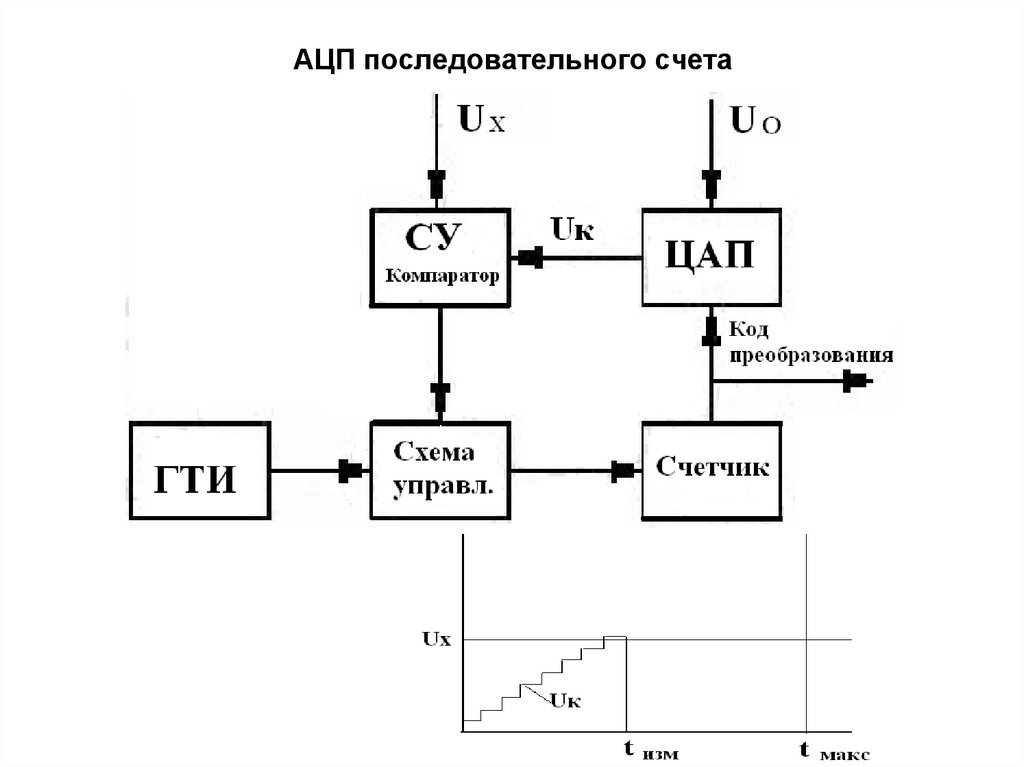 п.), когда не требуется высокая частота дискретизации и необходимо разрешение более 16 разрядов.

Принцип работы сигма-дельта АЦП сложнее для понимания. Эта архитектура относится к классу интегрирующих АЦП. Но основная особенность сигма-дельта АЦП состоит в том, что частота следования выборок, при которых собственно и происходит анализ уровня напряжения измеряемого сигнала, существенно превышает частоту появления отсчетов на выходе АЦП (частоту дискретизации). Эта частота следования выборок называется частотой передискретизации. Так, сигма-дельта АЦП со скоростью преобразования 100К отсчетов/сек, в котором используется частота передискретизации в 128 раз больше, будет производить выборку значений входного аналогового сигнала с частотой 12.8М отсчетов/сек.

Блок-схема сигма-дельта АЦП первого порядка приведена на рис. 5. Аналоговый сигнал подается на интегратор, выходы которого подсоединены к компаратору, который в свою очередь присоединен к 1-разрядному ЦАП в петле обратной связи.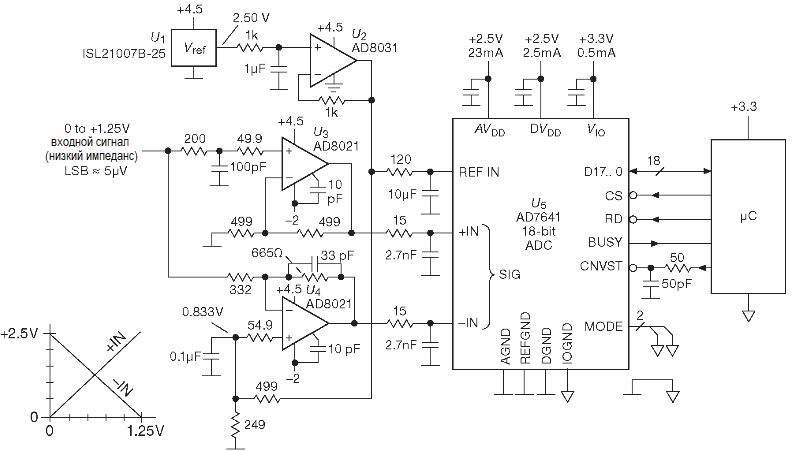 Путем серии последовательных итераций интегратор, компаратор, ЦАП и сумматор дают поток последовательных битов, в котором содержится информация о величине входного напряжения.

Рис. 5. Сигма-дельта АЦП

Результирующая цифровая последовательность затем подается на фильтр нижних частот для подавления компонентов с частотами выше частоты Котельникова (она составляет половину частоты дискретизации АЦП). После удаления высокочастотных составляющих следующий узел — дециматор — прореживает данные. В рассматриваемом нами АЦП дециматор будет оставлять 1 бит из каждых полученных 128 в выходной цифровой последовательности.

Так как внутренний цифровой ФНЧ в сигма-дельта АЦП представляет собой неотъемлемую часть для осуществления процесса преобразования, время установления ФНЧ становится фактором, который необходимо учитывать при скачкообразном изменении входного сигнала. Например, при переключении входного мультиплексора или при переключении предела измерения прибора необходимо подождать, пока пройдут несколько отсчетов АЦП, и лишь потом считывать корректные выходные данные.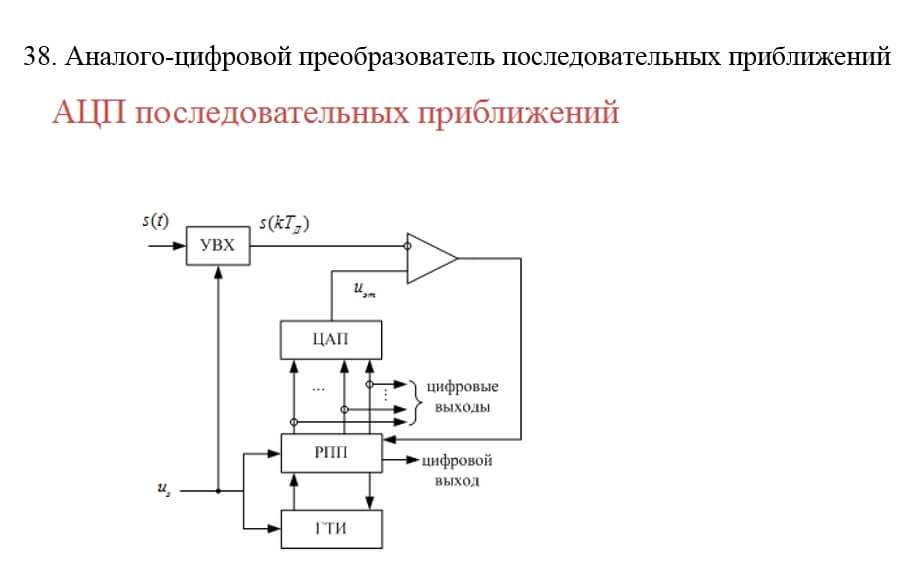

Дополнительным и очень важным достоинством сигма-дельта АЦП является то, что все его внутренние узлы могут быть выполнены интегральным способом на площади одного кремниевого кристалла. Это заметно снижает стоимость конечных устройств и повышает стабильность характеристик АЦП.

Интегрирующие АЦП

И последний тип АЦП, о котором пойдет здесь речь — АЦП двухтактного интегрирования. В цифровых мультиметрах, как правило, используются именно такие АЦП, т.к. в этих измерительных приборах необходимо сочетание высокого разрешения и высокого помехоподавления. Идея преобразования в таком интегрирующем АЦП гораздо менее сложна, чем в сигма-дельта АЦП.

На рисунке 6 показан принцип работы АЦП двухтактного интегрирования. Входной сигнал заряжает конденсатор в течение фиксированного периода времени, который обычно составляет один период частоты питающей сети (50 или 60Гц) или кратен ему. При интегрировании входного сигнала в течение промежутка времени такой длительности высокочастотные помехи подавляются.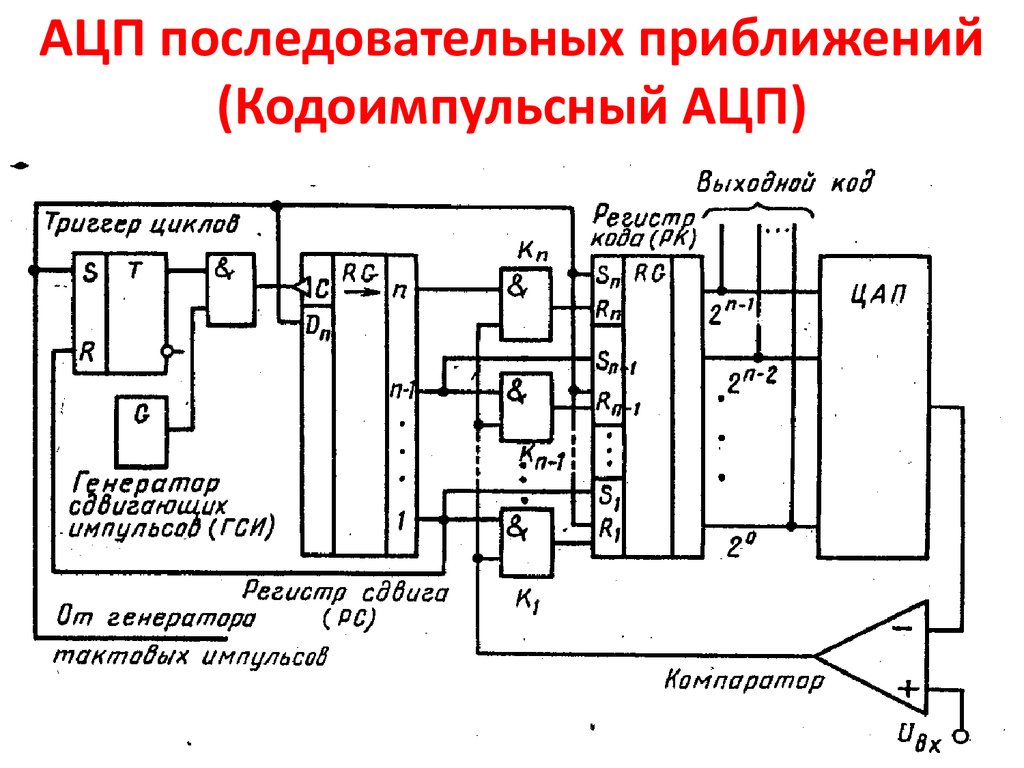 Одновременно исключается влияние нестабильности напряжения сетевого источника питания на точность преобразования. Это происходит потому, что значение интеграла от синусоидального сигнала равно нулю, если интегрирование осуществляется во временном интервале, кратном периоду изменения синусоиды.

Рис. 6. Интегрирующий АЦП. Зеленым цветом показана помеха от сети (1 период)

По окончании времени заряда АЦП разряжает конденсатор с фиксированной скоростью, в то время как внутренний счетчик подсчитывает количество тактовых импульсов за время разряда конденсатора. Большее время разряда, таким образом, соответствует большему значению показаний счетчика и большему измеряемому напряжению (рис. 6).

АЦП двухтактного интегрирования имеют высокую точность и высокую разрешающую способность, а также имеют сравнительно простую структуру. Это дает возможность выполнять их в виде интегральных микросхем. Основной недостаток таких АЦП — большое время преобразования, обусловленное привязкой периода интегрирования к длительности периода питающей сети.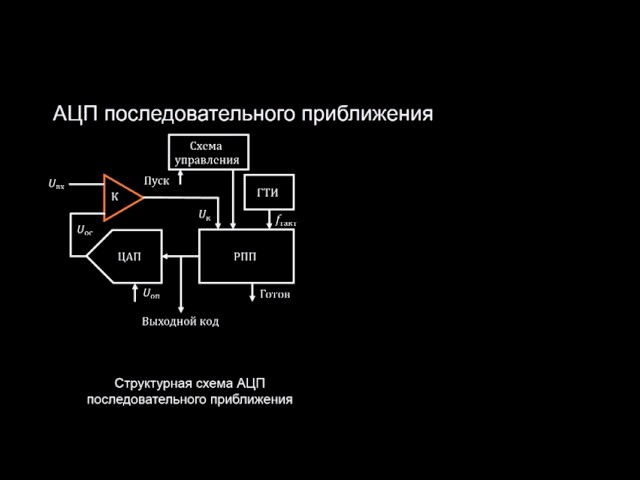 Например, для 50 Гц — оборудования частота дискретизации АЦП двухтактного интегрирования не превышает 25 отсчетов/сек. Конечно, такие АЦП могут работать и с большей частотой дискретизации, но при увеличении последней помехозащищенность падает.

Спецификация АЦП

Существуют общие определения, которые принято использовать в отношении аналого-цифровых преобразователей. Тем не менее, характеристики, приводимые в технической документации производителей АЦП, могут показаться довольно путаными. Правильный же выбор оптимального по сочетанию своих характеристик АЦП для конкретного приложения требует точной интерпретации данных, приводимых в технической документации.

Наиболее часто путаемыми параметрами являются разрешающая способность и точность, хотя эти две характеристики реального АЦП крайне слабо связаны между собой. Разрешение не идентично точности, 12-разрядный АЦП может иметь меньшую точность, чем 8-разрядный. Для АЦП разрешение представляет собой меру того, на какое количество сегментов может быть поделен входной диапазон измеряемого аналогового сигнала (например, для 8-разрядного АЦП это 28=256 сегментов).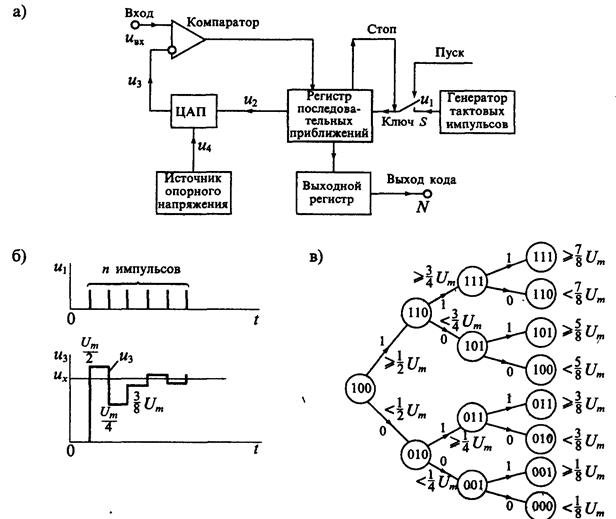 Точность же характеризует суммарное отклонение результата преобразования от своего идеального значения для данного входного напряжения. То есть, разрешающая способность характеризует потенциальные возможности АЦП, а совокупность точностных параметров определяет реализуемость такой потенциальной возможности.

АЦП преобразует входной аналоговый сигнал в выходной цифровой код. Для реальных преобразователей, изготавливаемых в виде интегральных микросхем, процесс преобразования не является идеальным: на него оказывают влияние как технологический разброс параметров при производстве, так и различные внешние помехи. Поэтому цифровой код на выходе АЦП определяется с погрешностью. В спецификации на АЦП указываются погрешности, которые дает сам преобразователь. Их обычно делят на статические и динамические. При этом именно конечное приложение определяет, какие характеристики АЦП будут считаться определяющими, самыми важными в каждом конкретном случае.

Статическая погрешность

В большинстве применений АЦП используют для измерения медленно изменяющегося, низкочастотного сигнала (например, от датчика температуры, давления, от тензодатчика и т. п.), когда входное напряжение пропорционально относительно постоянной физической величине. Здесь основную роль играет статическая погрешность измерения. В спецификации АЦП этот тип погрешности определяют аддитивная погрешность (Offset), мультипликативная погрешность (Full-Scale), дифференциальная нелинейность (DNL), интегральная нелинейность (INL) и погрешность квантования. Эти пять характеристик позволяют полностью описать статическую погрешность АЦП.

Идеальная передаточная характеристика АЦП

Передаточная характеристика АЦП — это функция зависимости кода на выходе АЦП от напряжения на его входе. Такой график представляет собой кусочно-линейную функцию из 2N «ступеней», где N — разрядность АЦП. Каждый горизонтальный отрезок этой функции соответствует одному из значений выходного кода АЦП (см. рис. 7). Если соединить линиями начала этих горизонтальных отрезков (на границах перехода от одного значения кода к другому), то идеальная передаточная характеристика будет представлять собой прямую линию, проходящую через начало координат.

Рис. 7. Идеальная передаточная характеристика 3-х разрядного АЦП

Рис. 7 иллюстрирует идеальную передаточную характеристику для 3-х разрядного АЦП с контрольными точками на границах перехода кода. Выходной код принимает наименьшее значение (000b) при значении входного сигнала от 0 до 1/8 полной шкалы (максимального значения кода этого АЦП). Также следует отметить, что АЦП достигнет значения кода полной шкалы (111b) при 7/8 полной шкалы, а не при значении полной шкалы. Т.о. переход в максимальное значение на выходе происходит не при напряжении полной шкалы, а при значении, меньшем на наименьший значащий разряд (LSB), чем входное напряжение полной шкалы. Передаточная характеристика может быть реализована со смещением -1/2 LSB. Это достигается смещением передаточной характеристики влево, что смещает погрешность квантования из диапазона -1… 0 LSB в диапазон -1/2 … +1/2 LSB.

Рис. 8. Передаточная характеристика 3-х разрядного АЦП со смещением на -1/2LSB

Из-за технологического разброса параметров при изготовлении интегральных микросхем реальные АЦП не имеют идеальной передаточной характеристики. Отклонения от идеальной передаточной характеристики определяют статическую погрешность АЦП и приводятся в технической документации.

Аддитивная погрешность

Идеальная передаточная характеристика АЦП пересекает начало координат, а первый переход кода происходит при достижении значения 1 LSB. Аддитивная погрешность (погрешность смещения) может быть определена как смещение всей передаточной характеристики влево или вправо относительно оси входного напряжения, как показано на рис.9. Таким образом, в определение аддитивной погрешности АЦП намеренно включено смещение 1/2 LSB.

Рис. 9. Аддитивная погрешность (Offset Error)

Мультипликативная погрешность

Мультипликативная погрешность (погрешность полной шкалы) представляет собой разность между идеальной и реальной передаточными характеристиками в точке максимального выходного значения при условии нулевой аддитивной погрешности (смещение отсутствует). Это проявляется как изменение наклона передаточной функции, что иллюстрирует рис. 10.

Рис. 10. Мультипликативная погрешность (Full-Scale Error)

Дифференциальная нелинейность

У идеальной передаточной характеристики АЦП ширина каждой «ступеньки» должна быть одинакова. Разница в длине горизонтальных отрезков этой кусочно-линейной функции из 2N «ступеней» представляет собой дифференциальную нелинейность (DNL).

Величина наименьшего значащего разряда у АЦП составляет Vref/2N, где Vref — опорное напряжение, N — разрешение АЦП. Разность напряжений между каждым кодовым переходом должна быть равна величине LSB. Отклонение этой разности от LSB определяются как дифференциальная нелинейность. На рисунке это показано как неравные промежутки между «шагами» кода или как «размытость» границ переходов на передаточной характеристике АЦП.

Рис. 11. Дифференциальная нелинейность (DNL)

Интегральная нелинейность

Интегральная нелинейность (INL) — это погрешность, которая вызывается отклонением линейной функции передаточной характеристики АЦП от прямой линии, как показано на рис. 12. Обычно передаточная функция с интегральной нелинейностью аппроксимируется прямой линией по методу наименьших квадратов. Часто аппроксимирующей прямой просто соединяют наименьшее и наибольшее значения. Интегральную нелинейность определяют путем сравнения напряжений, при которых происходят кодовые переходы. Для идеального АЦП эти переходы будут происходить при значениях входного напряжения, точно кратных LSB. А для реального преобразователя такое условие может выполняться с погрешностью. Разность между «идеальными» уровнями напряжения, при которых происходит кодовый переход, и их реальными значениями выражается в единицах LSB и называется интегральной нелинейностью.

Рис. 12. Интегральная нелинейность (INL)

Погрешность квантования

Одна из наиболее существенных составляющих ошибки при измерениях с помощью АЦП — погрешность квантования -является результатом самого процесса преобразования. Погрешность квантования — это погрешность, вызванная значением шага квантования и определяемая как ? величины наименьшего значащего разряда (LSB). Она не может быть исключена в аналого-цифровых преобразованиях, так как является неотъемлемой частью процесса преобразования, определяется разрешающей способностью АЦП и не меняется от АЦП к АЦП с равным разрешением.

Динамические характеристики

Динамические характеристики АЦП обычно определяют с помощью спектрального анализа, по результатам выполнения быстрого преобразования Фурье (БПФ) над массивом выходных значений АЦП, соответствующих некоторому тестовому входному сигналу.

На рис. 13 представлен пример частотного спектра измеряемого сигнала. Нулевая гармоника соответствует основной частоте входного сигнала. Все остальное представляет собой шум, который содержит гармонические искажения, тепловой шум, шум 1/f и шум квантования. Некоторые составляющие шума генерируются самим АЦП, некоторые могут поступать на вход АЦП из внешних цепей. Гармонические искажения, например, могут содержаться в измеряемом сигнале и одновременно генерироваться АЦП в процессе преобразования.

Рис. 13. Результат выполнения БПФ над выходными данными АЦП

Отношение «сигнал/шум»

Отношение «сигнал/шум» (SNR) — это отношение среднеквадратического значения величины входного сигнала к среднеквадратическому значению величины шума (за исключением гармонических искажений), выраженное в децибелах:

SNR(dB) = 20 log [ Vsignal(rms)/ Vnoise(rms) ]

Это значение позволяет определить долю шума в измеряемом сигнале по отношению к полезному сигналу.

Рис. 14. SNR — Отношение «сигнал/шум»

Рис. 15. БПФ отражает гармонические искажения

Шум, измеряемый при расчете SNR, не включает гармонические искажения, но включает шум квантования. Для АЦП с определенным разрешением именно шум квантования ограничивает возможности преобразователя теоретически лучшим значением отношения сигнал/шум, которое определяется как:

SNR(db) = 6.02 N + 1.76,

где N — разрешение АЦП.

Спектр шума квантования АЦП стандартных архитектур имеет равномерное распределение по частоте. Поэтому величина этого шума не может быть уменьшена путем увеличения времени преобразования и последующего усреднения результатов. Шум квантования может быть снижен только путем проведения измерений с помощью АЦП большей разрядности.

Особенность сигма-дельта АЦП состоит в том, что спектр шума квантования у него распределен по частоте неравномерно — он смещен в сторону высоких частот. Поэтому, увеличивая время измерения (и, соответственно, количество выборок измеряемого сигнала), накапливая и затем усредняя полученную выборку (фильтр нижних частот), можно получить результат измерений с более высокой точностью. Естественно, при этом общее время преобразования будет возрастать.

Другие источника шума АЦП включают тепловой шум, шум составляющей 1/f и джиттер опорной частоты.

Общие гармонические искажения

Нелинейность в результатах преобразования данных приводит к появлению гармонических искажений. Такие искажения наблюдаются как «выбросы» в спектре частот на четных и нечетных гармониках измеряемого сигнала (рис.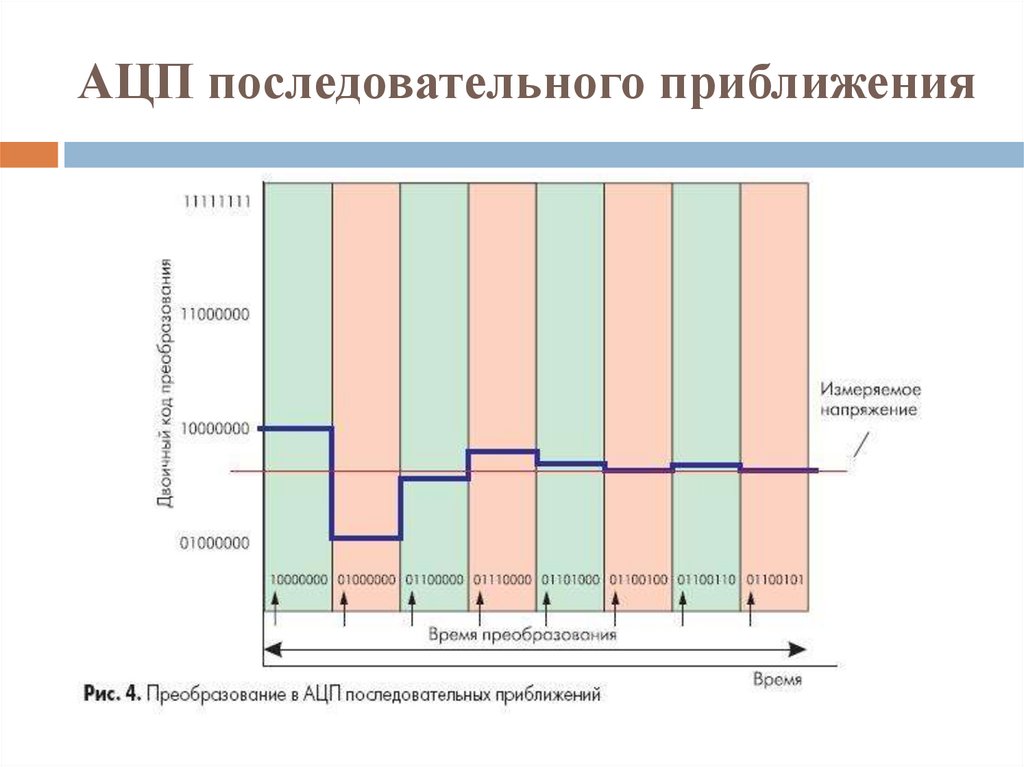 15).

Эти искажения определяют как общие гармонические искажения (THD). Они определяются как:

Величина гармонических искажений уменьшается на высоких частотах до точки, в которой амплитуда гармоник становится меньше, чем уровень шума. Таким образом, если мы анализируем вклад гармонических искажений в результаты преобразования, это можно делать либо во всем спектре частот, ограничивая при этом амплитуду гармоник уровнем шума, либо ограничивая полосу частот для анализа. Например, если в нашей системе стоит ФНЧ, то высокие частоты нам просто неинтересны и высокочастотные гармоники не подлежат учету.

Отношение «сигнал/шум и искажения»

Отношение «сигнал/шум и искажения» (SiNAD) более полно описывает шумовые характеристики АЦП. SiNAD учитывает величину как шума, так и гармонических искажений по отношению к полезному сигналу. SiNAD рассчитывается по следующей формуле:

Динамический диапазон, свободный от гармоник

Динамический диапазон, свободный от гармоник, представляет собой разницу между величиной измеряемого сигнала и наибольшим пиком искажений (см.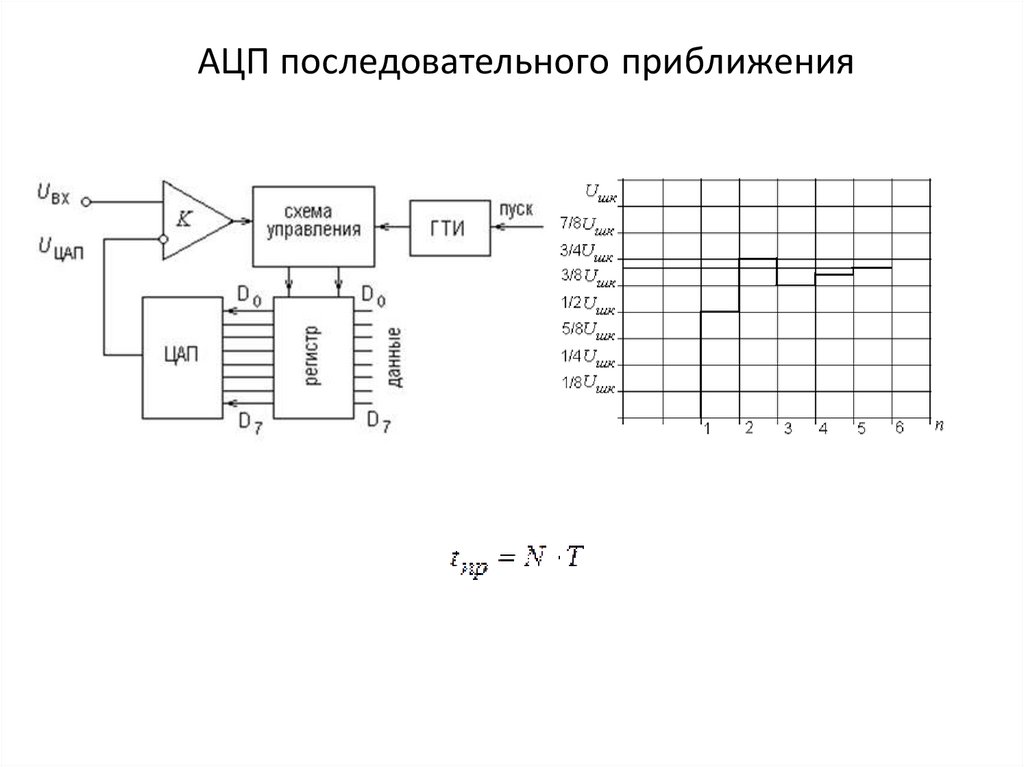 рис.16). Этот динамический диапазон обозначается как SFDR. Он ограничен снизу амплитудой максимальной гармоники паразитных выбросов на выходе АЦП в диапазоне его рабочих частот.

Рис. 16. Динамический диапазон, свободный от гармоник

Спецификация АЦП, приводимая в технической документации на микросхемы, помогает обоснованно выбрать преобразователь для конкретного применения. В качестве примера рассмотрим спецификацию АЦП, интегрированного в новый микроконтроллер C8051F064 производства фирмы Silicon Laboratories.

Микроконтроллер C8051F064

Кристалл C8051F064 представляет собой скоростной 8-разрядный микроконтроллер для совместной обработки аналоговых и цифровых сигналов с двумя интегрированными 16-разрядными АЦП последовательных приближений. Встроенные АЦП могут работать в однопроводном и дифференциальном режимах при максимальной производительности до 1М отсчетов/сек. В таблице приведены основные характеристики АЦП микроконтроллера C8051F064. Для самостоятельной оценки возможностей C8051F064 по цифровой и аналоговой обработке данных можно воспользоваться недорогим оценочным комплектом C8051F064EK (рис. 17). Комплект содержит оценочную плату на базе C8051F064, USB-кабель, документацию, а также программное обеспечение для тестирования аналоговых динамических и статических характеристик интегрированного высокоточного 16-разрядного АЦП.

Таблица. V
_DD= 3.0 V, AV+ = 3.0 V, AVDD = 3.0 V, V
_REF = 2.50 V (REFBE=0), -40 to +85°, если не указано иначе

;

Параметры	Условия	Типичное	Макс.	Единицы измерения
Характеристики на постоянном токе
Разрядность		16		бит
Интегральная нелинейность	Однопроводный	±0.75	±2	LSB
	Однопроводный	±0.5	±1	LSB
Дифференциальная нелинейность	Гарантированная монотонность	±+0.5		LSB
Аддитивная погрешность (смещение)		0,1		мВ
Мультипликативная погрешность		0,008		% F. S.
Температурный коэффициент усиления		0,5		ppm/°C
Динамические характеристики (Частота дискретизации 1 Msps, AVDD, AV+ = 3.3 В)
Сигнал/шум и искажения	Fin = 10 кГц, однопроводный	86		дБ
	Fin = 100 кГц, однопроводный	84		дБ
	Fin = 10 кГц, дифференциальный	89		дБ
	Fin = 100 кГц, дифференциальный	88		дБ
Общие гармонические искажения	Fin = 10 кГц, однопроводный	96		дБ
	Fin = 100 кГц, однопроводный	84		дБ
	Fin = 10 кГц, дифференциальный	103		дБ
	Fin = 100 кГц, дифференциальный	93		дБ
Динамический диапазон, свободный от гармоник	Fin = 10 кГц, однопроводный	97		дБ
	Fin = 100 кГц, однопроводный	88		дБ
	Fin = 10 кГц, дифференциальный	104		дБ
	Fin = 100 кГц, дифференциальный	99		дБ

Рис. 17. Оценочный комплект C8051F064EK

Литература

1. http://www.wbc-europe.com/en/services/pim_application_guide.html
2. www.silabs.com

АЦП последовательного приближения | Энциклопедия MDPI

АЦП последовательного приближения представляет собой тип аналого-цифрового преобразователя, который преобразует непрерывный аналоговый сигнал в дискретное цифровое представление посредством двоичного поиска по всем возможным уровням квантования, прежде чем окончательно сходится на цифровом выходе для каждого преобразования.

1. Блок-схема

Блок-схема АЦП последовательного приближения. https://handwiki.org/wiki/index.php?curid=1390932

Ключ

• ЦАП = цифро-аналоговый преобразователь
• EOC = конец преобразования
• SAR = регистр последовательного приближения
• S/H = схема выборки и удержания
• В _в = входное напряжение
• В _ref = опорное напряжение

2.

Алгоритм

Схема аналого-цифрового преобразователя последовательного приближения обычно состоит из четырех основных подсхем:

1. Схема выборки и хранения для получения входного напряжения ( В _в ).
2. Аналоговый компаратор напряжения, который сравнивает В _в с выходом внутреннего ЦАП и выводит результат сравнения в регистр последовательного приближения (SAR).
3. Подсхема регистра последовательного приближения, предназначенная для подачи приблизительного цифрового кода В _в на внутренний ЦАП.
4. Внутренний эталонный ЦАП, который для сравнения с В _REF подает на компаратор аналоговое напряжение, равное выходному цифровому коду SAR _в .

Анимация 4-битного АЦП последовательного приближения. https://handwiki.org/wiki/index.php?curid=1424719

Регистр последовательного приближения инициализируется таким образом, что старший бит (MSB) равен цифровой 1.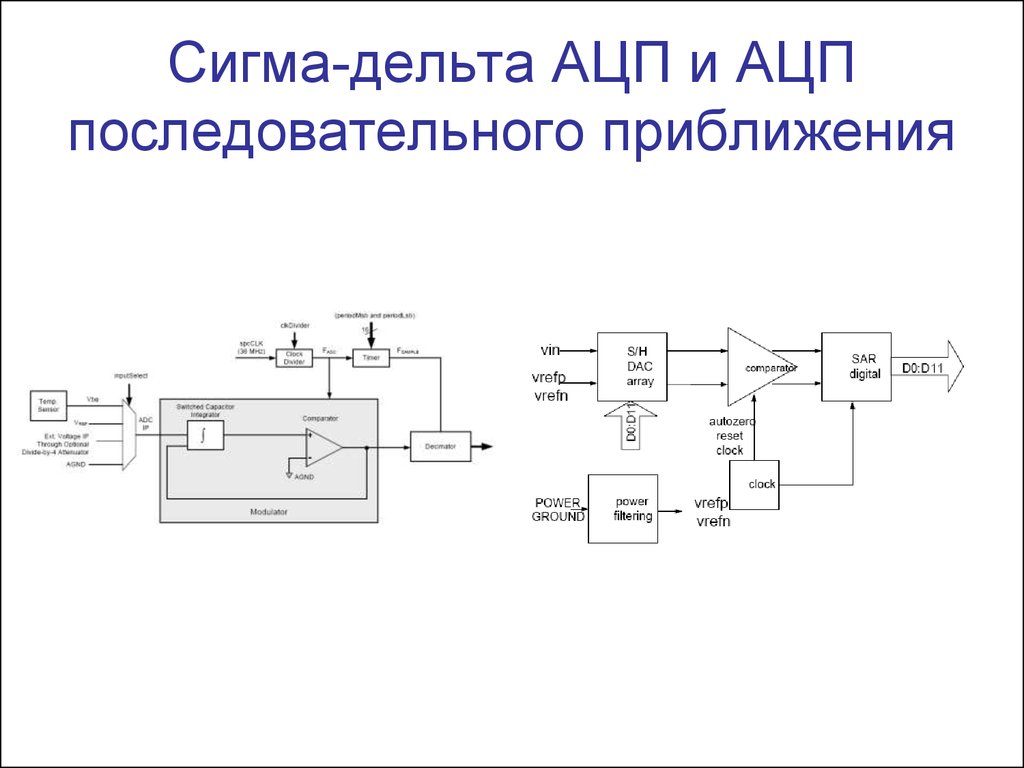 Этот код подается в ЦАП, который затем предоставляет аналоговый эквивалент этого цифрового кода ( В _исх. /2) в схему компаратора для сравнения с выбранным входным напряжением. Если это аналоговое напряжение превышает В _в , компаратор заставляет SAR сбросить этот бит; в противном случае бит остается равным 1. Затем следующий бит устанавливается в 1, и выполняется тот же тест, продолжая этот двоичный поиск до тех пор, пока не будет проверен каждый бит в SAR. Результирующий код представляет собой цифровую аппроксимацию выборочного входного напряжения и, наконец, выводится SAR в конце преобразования (EOC).

Математически пусть В _дюймов = x В _ref , поэтому x дюймов [−1, 1] — нормализованное входное напряжение. Цель состоит в том, чтобы примерно оцифровать x с точностью 1/2 ⁿ . Алгоритм работы следующий:

1. Начальное приближение x ₀ = 0,
2. i -е приближение x _i = x _{i -1} – с ( x _{i -1} – x )/2 ^{i 9,0023}

, где s ( x ) – сигнум-функция (sign( x )) (+1 для x ≥ 0, −1 для x < 0).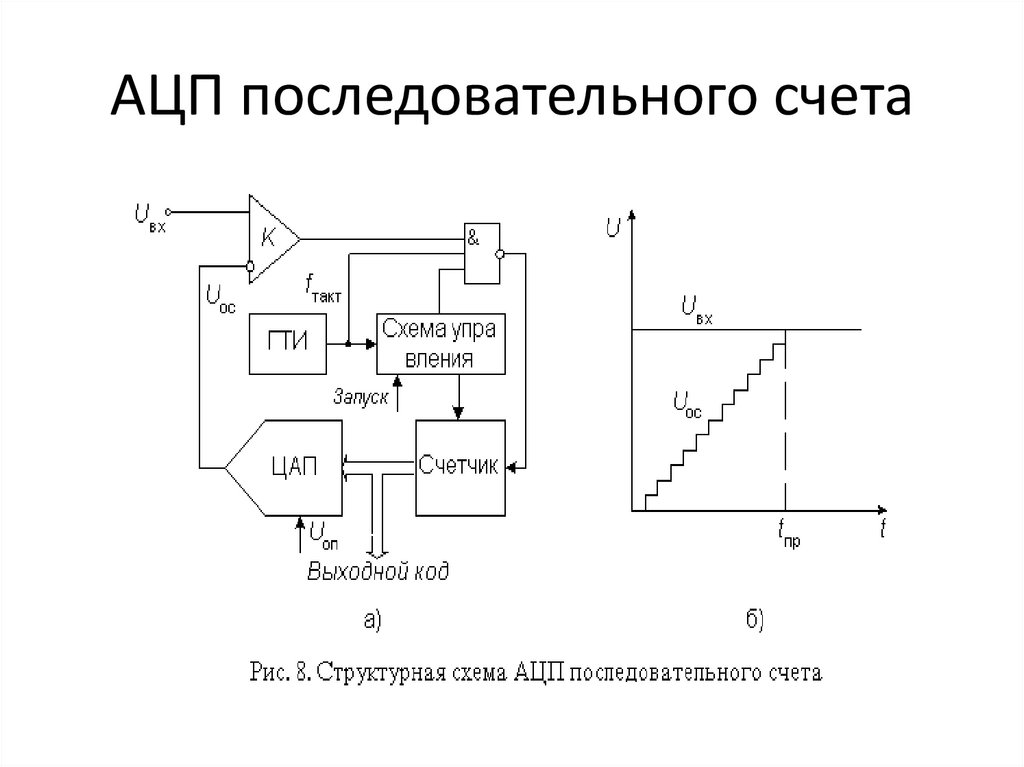 Используя математическую индукцию, следует, что | x _n − x | ≤ 1/2 ⁿ .

Как показано в приведенном выше алгоритме, АЦП последовательного поиска требует:

1. Источник входного напряжения В _в .
2. Источник опорного напряжения В _ref для нормализации входа.
3. ЦАП для преобразования i -го приближения x _i в напряжение.
4. Компаратор для выполнения функции s ( x _i − x ) путем сравнения напряжения ЦАП с входным напряжением.
5. Регистр для хранения вывода компаратора и применения x _{I −1} – S ( x _{I – 1} – x )/2 ..

Работа АЦП последовательного приближения при снижении входного напряжения от 5 до 0 В. Итерации по оси x. Приблизительное значение по оси Y. https://handwiki.org/wiki/index.php?curid=1586131

Пример: Здесь показаны десять шагов преобразования аналогового входа в 10-битный цифровой с использованием последовательного приближения для всех напряжений от 5 В до 0 В с шагом 0,1 В. Поскольку опорное напряжение равно 5 В, когда входное напряжение также равно 5 В, все биты установлены. Когда напряжение уменьшается до 4,9 В, очищаются только некоторые младшие значащие биты. Старший разряд будет оставаться установленным до тех пор, пока на входе не будет половина опорного напряжения, 2,5 В.

Двоичные веса, присвоенные каждому биту, начиная со старшего разряда, составляют 2,5, 1,25, 0,625, 0,3125, 0,15625, 0,078125, 0,039.0625, 0,01953125, 0,009765625, 0,0048828125. Все они в сумме дают 4,9951171875, что означает двоичное число 1111111111 или один младший бит меньше 5.

Когда аналоговый вход сравнивается с внутренним выходом ЦАП, он эффективно сравнивается с каждым из этих двоичных весов, начиная с 2,5. V и либо сохранить его, либо очистить в результате. Затем, добавляя следующий вес к предыдущему результату, снова сравнивая и повторяя это до тех пор, пока все биты и их веса не будут сравнены с входными данными, будет найден конечный результат, двоичное число, представляющее аналоговый вход.

3. АЦП последовательного приближения перераспределения заряда

ЦАП с масштабированием заряда. https://handwiki.org/wiki/index.php?curid=1326383

Одна из наиболее распространенных реализаций АЦП последовательного приближения, АЦП последовательного приближения с перераспределением заряда , использует ЦАП масштабирования заряда. ЦАП масштабирования заряда просто состоит из массива индивидуально переключаемых двоично-взвешенных конденсаторов. Количество заряда на каждом конденсаторе в массиве используется для выполнения вышеупомянутого двоичного поиска в сочетании с компаратором, встроенным в ЦАП, и регистром последовательного приближения.

1. Сначала конденсаторная решетка полностью разряжается до напряжения смещения компаратора, В _ОС . Этот шаг обеспечивает автоматическую компенсацию смещения (т. е. напряжение смещения представляет собой не что иное, как холостой заряд, которым не могут управлять конденсаторы).
2. Затем все конденсаторы массива переключаются на входной сигнал, v _IN . Конденсаторы теперь имеют заряд, равный их соответствующей емкости, умноженной на входное напряжение минус напряжение смещения на каждом из них.
3. На третьем этапе конденсаторы переключаются таким образом, что этот заряд поступает на вход компаратора, создавая входное напряжение компаратора, равное − v _IN .
4. Наконец, процесс преобразования продолжается. Сначала конденсатор MSB переключается на В _REF , что соответствует полному диапазону АЦП. Из-за двоичного взвешивания массива конденсатор MSB образует делитель заряда 1:1 с остальной частью массива. Таким образом, входное напряжение компаратора теперь составляет − В _IN плюс В _№ /2. Впоследствии, если v _IN больше, чем V _REF /2, тогда компаратор выдает цифровую 1 в качестве MSB, в противном случае он выводит цифровой 0 в качестве MSB. Каждый конденсатор испытывается одинаково до тех пор, пока входное напряжение компаратора не сравняется с напряжением смещения или, по крайней мере, не приблизится настолько, насколько это возможно с учетом разрешения ЦАП.

3-битное моделирование емкостного АЦП. https://handwiki.org/wiki/index.php?curid=1296064

3.1. Использование с неидеальными аналоговыми схемами

При реализации в виде аналоговой схемы, где значение каждого последующего бита не идеально 2 ^N (например, 1.1, 2.12, 4.05, 8.01 и т. д.) – метод последовательного приближения может не выводить идеальное значение, потому что алгоритм бинарного поиска неправильно удаляет то, что он считает половиной значений, которые не могут быть неизвестными входными данными.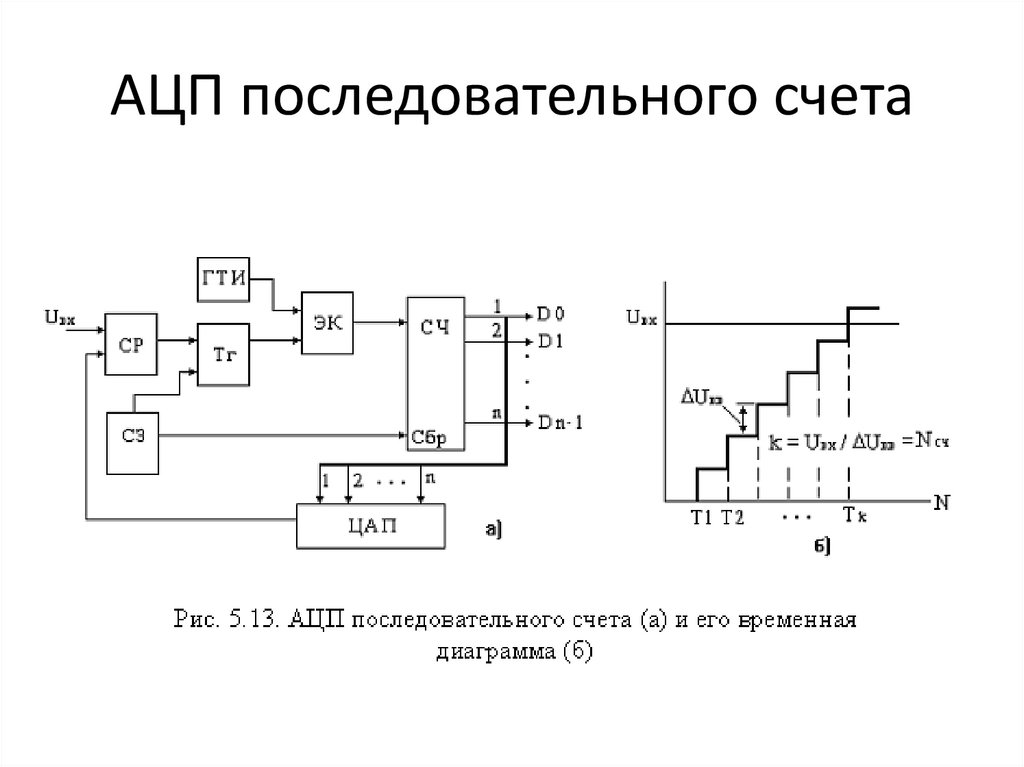 В зависимости от разницы между реальной и идеальной производительностью максимальная ошибка может легко превысить несколько младших разрядов, тем более, что ошибка между реальной и идеальной 2 ^N становится большим для одного или нескольких битов. Поскольку мы не знаем фактического неизвестного входа, поэтому очень важно, чтобы точность аналоговой схемы, используемой для реализации АЦП последовательного приближения, была очень близка к идеальным значениям; в противном случае мы не можем гарантировать поиск наилучшего соответствия.

Как работает АЦП последовательного приближения (SAR) и где его лучше всего использовать?

Аналого-цифровой преобразователь (АЦП) — это тип устройства, которое помогает нам обрабатывать хаотические данные реального мира с цифровой точки зрения. Чтобы понимать данные реального мира, такие как температура, влажность, давление, положение, нам нужны датчики, все они измеряют определенные параметры и возвращают нам электрический сигнал в виде напряжения и тока.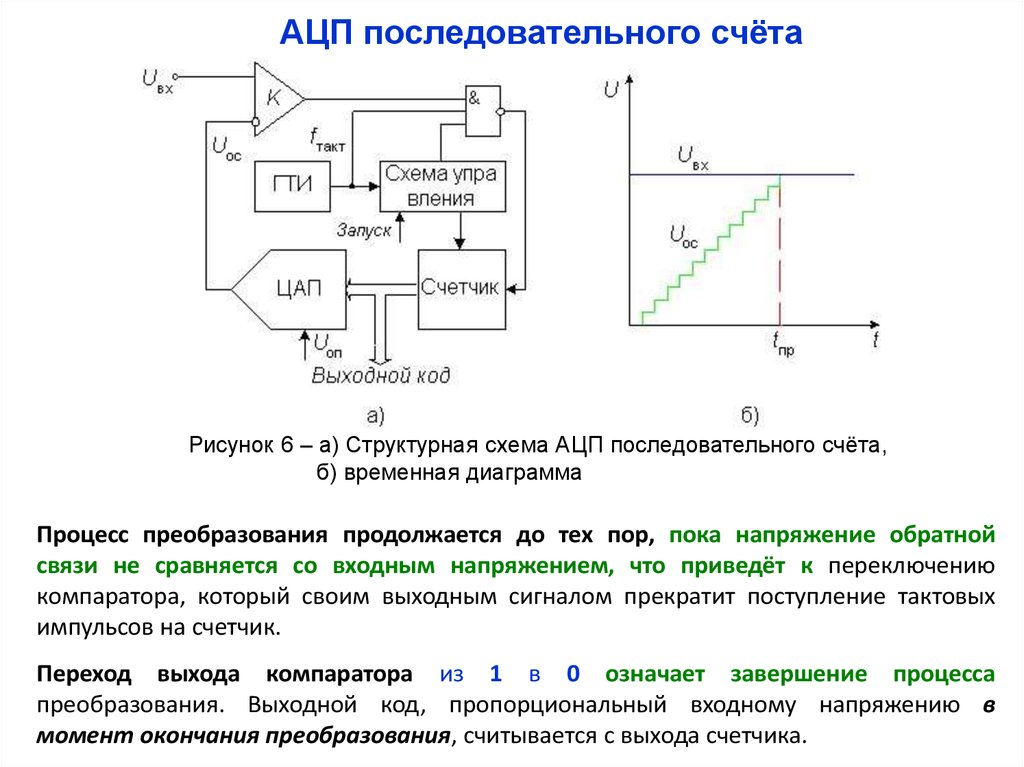 Поскольку большинство наших устройств в настоящее время являются цифровыми, становится необходимым преобразовать эти сигналы в цифровые сигналы. Вот где в дело вступает АЦП, хотя их много различных типов АЦП , но в этой статье мы поговорим об одном из наиболее часто используемых типов АЦП, который известен как АЦП последовательного приближения . В ранней статье мы говорили об основах АЦП с помощью Arduino, вы можете проверить это, если вы новичок в электронике и хотите узнать больше об АЦП.

Что такое АЦП последовательного приближения?

АЦП последовательного приближения АЦП — это предпочтительный АЦП для недорогих приложений со средним и высоким разрешением, 9Разрешение 0009 для АЦП последовательного приближения составляет от 8 до 18 бит со скоростью выборки до 5 мегавыборок в секунду (Мвыборок в секунду). Кроме того, он может быть выполнен в небольшом форм-факторе с низким энергопотреблением, поэтому этот тип АЦП используется для портативных приборов с батарейным питанием.

Как следует из названия, этот АЦП применяет алгоритм двоичного поиска для преобразования значений, поэтому внутренняя схема может работать на частоте в несколько МГц, но реальная частота дискретизации намного меньше из-за Алгоритм последовательного приближения . Подробнее об этом мы поговорим далее в этой статье.

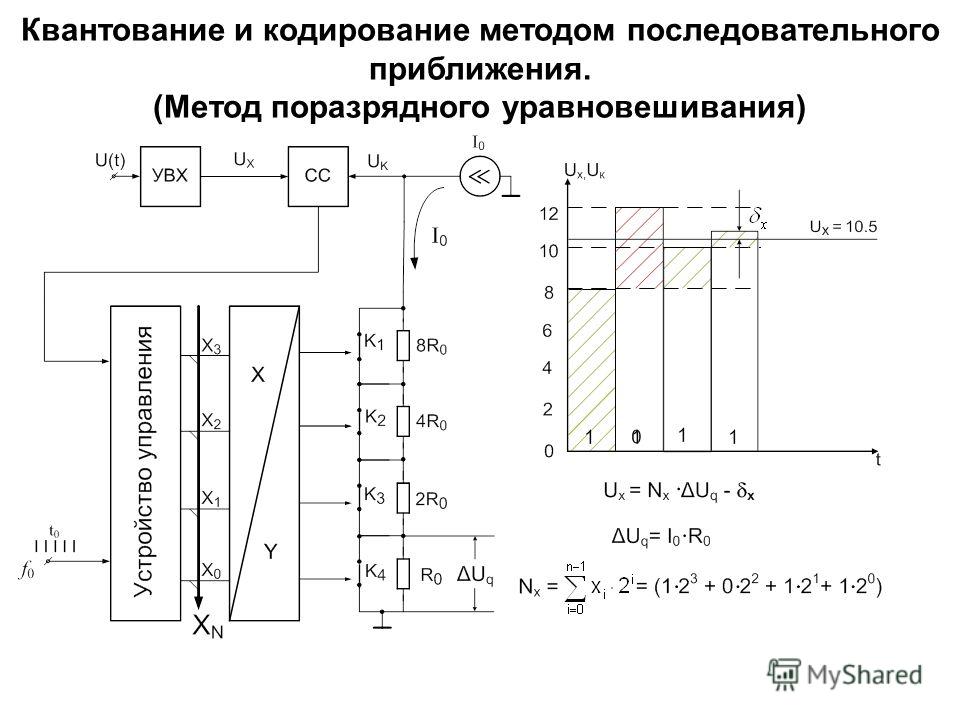
Работа АЦП последовательного приближения

На обложке показана базовая схема АЦП последовательного приближения . Но чтобы немного лучше понять принцип работы, мы собираемся использовать его 4-битную версию. Изображение ниже показывает именно это.

Как видите, этот АЦП состоит из компаратора, цифро-аналогового преобразователя и регистра последовательного приближения вместе со схемой управления. Теперь всякий раз, когда начинается новый разговор, схема выборки и удержания производит выборку входного сигнала. И этот сигнал сравнивается с конкретным выходным сигналом ЦАП.

Теперь предположим, что дискретизированный входной сигнал равен 5,8 В. Опорное значение АЦП составляет 10 В. Когда начинается преобразование, регистр последовательного приближения устанавливает старший бит в 1, а все остальные биты в ноль. Это означает, что значение становится равным 1, 0, 0, 0, что означает, что для опорного напряжения 10 В ЦАП выдаст значение 5 В, что составляет половину опорного напряжения. Теперь это напряжение будет сравниваться с входным напряжением и на основании выходного сигнала компаратора будет изменен выходной сигнал регистра последовательного приближения. Изображение ниже прояснит это больше. Кроме того, вы можете просмотреть общую справочную таблицу для получения более подробной информации о ЦАП. Ранее мы сделали много проектов по АЦП и ЦАП, вы можете ознакомиться с ними для получения дополнительной информации.

Это означает, что если Vin больше, чем выход ЦАП, старший бит останется прежним, а следующий бит будет установлен для нового сравнения. В противном случае, если входное напряжение меньше значения ЦАП, старший бит будет установлен в ноль, а следующий бит будет установлен в 1 для нового сравнения. Теперь, если вы видите изображение ниже, напряжение ЦАП составляет 5 В, и, поскольку оно меньше входного напряжения, следующий бит перед старшим битом будет установлен в единицу, а другие биты будут установлены в ноль, этот процесс будет продолжаться до тех пор, пока значение, наиболее близкое к входному напряжению.

Это то, как АЦП последовательного приближения изменяет 1 бит за раз, чтобы определить входное напряжение и получить выходное значение. И каким бы ни было значение за четыре итерации, мы получим выходной цифровой код из входного значения. Наконец, список всех возможных комбинаций для четырехбитного АЦП последовательного приближения показан ниже.

Время преобразования, скорость и разрешение АЦП последовательного приближения

Время преобразования:

В общем можно сказать, что для N битного АЦП потребуется N тактов, значит время преобразования этого АЦП станет –

Tc = N x Tclk 

*Tc — это сокращение от времени преобразования.

В отличие от других АЦП время преобразования этого АЦП не зависит от входного напряжения.

Поскольку мы используем 4-разрядный АЦП, чтобы избежать эффекта наложения спектров, нам необходимо брать выборку после 4 последовательных тактовых импульсов.

Скорость преобразования: 

Типичная скорость преобразования этого типа АЦП составляет около 2–5 мегавыборок в секунду (MSPS), но немногие могут достигать 10 (MSPS). Примером может служить LTC2378 от Linear Technologies.

Разрешение:

Разрешение АЦП этого типа может составлять около 8–16 бит, но некоторые типы могут достигать 20 бит, например, ADS8900B от Analog Devices.

Преимущества и недостатки АЦП последовательного приближения

Этот тип АЦП имеет много преимуществ перед другими. Он имеет высокую точность и низкое энергопотребление, в то же время прост в использовании и имеет малое время ожидания. Время задержки — это время начала сбора данных и время, когда данные доступны для выборки из АЦП, обычно это время задержки определяется в секундах. Но также в некоторых спецификациях этот параметр упоминается как циклов преобразования , в конкретном АЦП, если данные доступны для выборки в течение одного цикла преобразования, мы можем сказать, что он имеет задержку в один цикл обмена. И если данные доступны после N циклов, мы можем сказать, что они имеют задержку в один цикл преобразования. мажор Недостатком SAR ADC является сложность конструкции и стоимость производства.

Применение АЦП SAR

Поскольку это наиболее часто используемый АЦП, он используется во многих приложениях, таких как использование в биомедицинских устройствах, которые можно имплантировать пациенту, эти типы АЦП используются, поскольку они потребляют очень мало энергии. Кроме того, многие умные часы и датчики используют этот тип АЦП.

Подводя итог, можно сказать, что основными преимуществами этого типа АЦП являются низкое энергопотребление, высокое разрешение, малый форм-фактор и точность.