Активная и реактивная мощность что это такое: Полная, активная и реактивная мощность (PQS)

Что такое активная и реактивная электроэнергия?

Администрация2023-05-17T15:13:39+03:00

Статьи 0 Комментариев

Электроэнергия на сегодняшний день один из наиболее востребованных и распространенных энергоресурсов, потребляемых во всех сферах человеческой жизни. Тем не менее не каждому потребителю электроэнергии понятно что вместе с электрической энергией идущей на выполнение полезной работы (обогрев, освещение и пр.) коей является активная составляющая, он вынужден потреблять, а зачастую и оплачивать реактивную составляющую.

Реактивной составляющей считается электрическая мощность, которая накапливается в электрических цепях, однако в выполнении полезной работы не участвует. Как часть полной потребленной электроэнергии реактивная составляющая идет на разогрев проводников, а впоследствии возвращается в электрическую сеть.

Активную составляющую принято измерять в ваттах и киловаттах (Вт, кВт), в то время как для полной потребляемой электроэнергии с учетом реактивных мощностей существует своя единица измерения, именуемая вольт-амперами (ВА и кВА).

В качестве активных мощностей обычно рассматривают нагревательные приборы, лампы накаливания, утюги. Реактивная составляющая электроэнергии обычно присутствует в цепях индуктивных нагрузок, например содержащих электродвигатели (холодильники, стиральные машины, электроинструмент), дроссели, трансформаторы. Чем отличается активная и реактивная электроэнергия, попробуем разобраться.

Понятие трех типов мощностей

В принципе все три мощности, включая полную, представленную суммой активной и реактивной составляющих мы уже упомянули. Активная мощность, характерная для резистивной нагрузки полностью идет на выполнение полезной работы. Другим условием для потребления только активной мощности считаются цепи постоянного тока.

Совсем по-другому происходит энергопотребление в цепях переменного тока, реализованных на индуктивных и емкостных нагрузках.

В электрических цепях, содержащих реактивные элементы (емкости и индуктивность) происходит накопление электроэнергии. Причиной тому является несовпадение напряжения и тока по фазе:

• индуктивная составляющая вызывает отставание тока по фазе от напряжения;
• емкостная составляющая наоборот связана с опережением тока.

Фазовый сдвиг между ними определен углом ϕ. Таким образом, соотношения активной, реактивной и полной мощности определены формулой Пифагора, связанной с прямоугольным треугольником. Здесь активная (P) и реактивная (Q) мощности выступают в качестве катетов, а полная мощность (S) представлена гипотенузой:

S = √P²+Q²

Угол ϕ при этом будет находиться между гипотенузой (S) и катетом активной мощности (P), поэтому возвращаясь к той же геометрии можно представить себе и, так называемые коэффициенты мощности, определяемые соотношением активной мощности к полной выражением:

cos ϕ = P/S

Фактически если сравнивать с физикой в более широком понимании это коэффициенты полезного действия, поскольку вольт-амперы реактивные увеличивают потребления электроэнергии, при этом величина активной мощности меньше полной. Нетрудно догадаться, что величина cos ϕ = 1 соответствует исключительно активной нагрузке в этом случае потребляемая электроэнергия идет только на выполнение полезной работы.

Рассматривая присутствие емкостной или индуктивной составляющей в качестве паразитной нагрузки, компенсация реактивной мощности становится первоочередной задачей. Особенно это актуально для промышленных предприятий, где производственное оборудование имеет вполне весомую индуктивную составляющую. Как правило, здесь применяются емкостные компенсаторы реактивной мощности, позволяющие компенсировать реактивную электроэнергию.

В бытовых условиях величина потребленной реактивной мощности обычно невысока. Компенсаторы реактивной мощности, как правило, требуются, в случае если имеется электрический насос, либо хозяева часто пользуются электроинструментом.

Остались вопросы?

Заполните форму обратно связи ниже, наши специалисты свяжутся с Вами, проконсультируют, расскажут про возможные способы решения Вашей задачи.

заказать консультацию

Ваше имя (обязательно)

Ваш e-mail (обязательно)

Телефон

Сообщение

Прикрепить файл

Даю согласие на обработку данных

---

Реактивная и активная мощность – формула, как определить, коэффициент и баланс мощностей, потребление и нагрузка

Бытовая жизнь каждого из нас неразрывно связана с физикой, её остовыми законами и понятиями. Электронные приборы, без которых наша жизнь кажется невозможной, имеют определённую мощность. Именно понятие мощность, реактивная и активная, будет в дальнейшем рассмотрено для более глубокого понимания темы.

Содержание

Определения

Каждый электроприбор, который подключается к электрической сети, работает на базе переменного тока. Данное замечание важное, так как именно в таких условиях в дальнейшем будет разбираться «мощность».

Мощность — физическая величина, которая отображает скорость передачи или преобразования энергии электричества. По-другому данный термин объясняют как соотношение работы к определённому промежутку времени, за который работа была совершена.

Более подробно понятие «мощность» можно разобрать на примере обычной лампочки накаливания. Лампочка потребляет электричество и то, с какой скоростью оно будет преобразовано в свет или тепло — и есть мощность лампочки.

Также из этого можно сделать следующий вывод: чем больше у электроприбора изначальная мощность (в нашем случае лампочка), тем большее количество электроэнергии он будет потреблять, а следовательно, даст больше света.

Активная мощность

Активная мощность — мощность, характеризующая конкретно процесс видоизменения энергии электричества во что-то другое. Измеряется в Ваттах (Вт) и обозначается буквой P.

Активная мощность встречается на ТЭС, АЭС, так как именно там вырабатывается напряжение, ведь потом именно оно поступает для потребления в наши дома и позволяет питать электричеством все электроприборы.

Реактивная мощность

Реактивная мощность — физическая величина, которая является характеристикой нагрузки, появляющейся в приборах электрической цепи из-за колебаний энергии электромагнитного поля.

Возникает данный феномен в цепи с переменным током. Из этого также выведена определенная зависимость: мощность равна произведению среднеквадратичных значений силы тока и напряжения. Представленная формула в последствии будет рассмотрена более подробно.

Самым важным отличием реактивной нагрузки является наличие индуктивности и ёмкости. Иными словами – это способность запасать энергию, для того чтобы позже передавать её в электрическую сеть.

Энергия электротока, которую преобразует индукционная нагрузка, сперва превращается в магнитное поле, а уже после в электрический ток. Пример: электромагниты, трансформаторы, асинхронные двигатели.

Ёмкостная нагрузка, аналогично индукционной, также преобразует энергию тока, однако не в магнитное поле, а в электрическое.

Затем оно вновь превращается в электрический ток. Оба представленных процесса воспроизводятся за одну вторую полупериода. Примером могут послужить синхронные двигатели, батареи, конденсаторы.

По большей части, функция реактивной мощности заключается в блуждании от генератора электричества к потребителю и обратно. Однако, так как индуктивная нагрузка присутствует постоянно, то непременно появится и реактивный ток, который индукция потребляет.

По сути, данный процесс цикличен и, кажется, что бесконечен, но для того, чтобы электроны смогли постоянно двигаться по проводам – необходима активная энергия.

Физическое объединение реактивной и активной мощности

Существует такое понятие, как «полная мощность». Представленную величину можно вычислить геометрически — она равна корню суммы квадратов реактивной и активной мощностей. Обозначается такое понятие буквой S, а вычисляется она в Вольт-амперах (ВА).

В физике, для того чтобы зависимость между всеми мощностями была более понятна, существует «треугольник мощностей» ­­- соотношение активной, реактивной и полной мощности.

Сперва следует мысленно представить прямоугольный треугольник, где катеты – это активная и реактивная мощности, а гипотенуза – полная. Следуя геометрическим законам, косинус угла фи будет равен отношению реактивной и активной, другими словами – это коэффициент мощности.

Данный коэффициент исчисляется в пределе от нуля до единицы или же в процентах, от нуля процентов до ста. Чем больше активная мощность, тем больше коэффициент, а следовательно, лучше показатели электроприбора.

Формулы для нахождения мощностей

В большинстве случаев на электрических приборах указана активная мощность и числовое значение коэффициента косинуса фи. Когда есть подобные данные – далее рассчитать необходимые величины не представляет никакой сложности.

Расчётная формула полной мощности соответствует перемножению силы тока и напряжения:

• S = UxI, где
• S – полная мощность,
• U – электрическое напряжение,
• I – сила тока.

Реактивная мощность записывается буквой Р и исчисляется в Вольтах (Вт), и она вместе с активной при сложении образуют полную мощность:

S=P+Q

Однако на практике данная формула будет находится другим путём:

S= √(P2+Q2)

Порой, для нахождения мощностей могут понадобится емкостные и индуктивные нагрузки. Для этого важно помнить о том, что при работе с индуктивной кривая точка всегда будет дальше от кривой напряжения на одну вторую полупериода. В это же время, при работе ёмкостной нагрузки кривая точка будет опережать кривую напряжения на одну вторую полупериода.

На практике коэффициента косинуса фи чаще всего указывают в описании электроприбора, но, если появляется необходимость самостоятельно измерить данную величину используется фазометр или цифровой ваттметр. Оба прибора значительно упрощают различные вычисления, хотя и рекомендуется пользоваться формулами для более точного теоретического расчёта.

Вычисление коэффициента мощности необходимо для того, чтобы скомпенсировать его недостаток путём включения в цепь дополнительных элементов.

Порой, появляется необходимость скомпенсировать реактивную мощность. Для этого в электрическую цепь включают реактивный прибор, который выполняет противоположную функцию к уже действующему электрическому объекту. Например, чтобы скомпенсировать работу асинхронного двигателя — подключается в параллель конденсатор. Работа синхронного двигателя компенсируется электромагнитом.

Из изученного можно сделать вывод, что активная и реактивная мощность неразрывно связаны, однако не противоположны друг другу. Вместе они объединяются в другое понятие «полная мощность», а также позволяют вычислить коэффициент косинуса фи.

Мощность (активная, реактивная или полная) – наиважнейшее понятие в физике, как теоретической, так и практической. Знать, что эти величины обозначают, какими путями (через формулы или с помощью специальных приборов) их можно вычислить будет интересно и важно не только для обучающихся в школе или инженеров, но и для обычных людей, желающих развиваться всесторонне.

Фото реактивной и активной мощности

Автор статьи:

Активная и реактивная мощность – x-engineer.

org

Введение

В цепях переменного тока (AC) передача электрической энергии и поведение электрических машин часто легче понять, работая с мощностью, а не с напряжениями и токами. Мощность может быть определена различными способами, применимость определения зависит от типа цепи.

Наиболее распространенное определение мощности: энергия, затрачиваемая в единицу времени [Дж/с] .

P [Вт] = E [Дж] / время [с]

В цепях переменного тока понятие мощности немного отличается в том смысле, что существует три типа мощности:

• активная мощность
• реактивная мощность
• Полная мощность

Активная мощность

Для лучшего понимания концепции активной мощности мы будем использовать простую цепь переменного тока, состоящую из источника синусоидального напряжения и резистора.

Изображение: Источник переменного напряжения с резисторной цепью

В этой простой схеме мы видим, что ток протекает через резистор R = 2 Ом, меняя свое направление.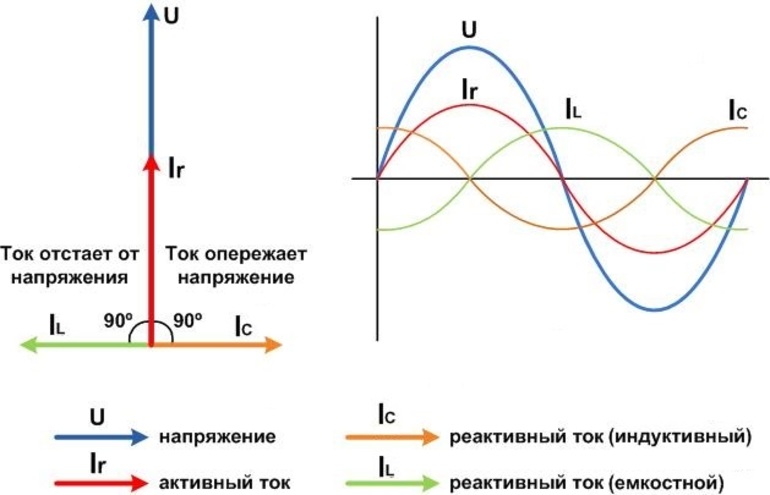 Если предположить, что напряжение переменного тока равно E [В], а ток равен I [А], мощность через резистор будет P [Вт] = EI.

Когда резистор включен в цепь переменного тока, он не изменит фазу (θ) между проходящим через него напряжением (E) и током (I). Другими словами, напряжение и ток, проходящие через резистор, находятся в фазе друг с другом . Если представить напряжение и ток, проходящие через резистор, в виде векторов (фазоров), они будут перекрываться.

Изображение: векторная диаграмма — резистор

Для лучшей визуализации этой концепции давайте создадим простую имитационную модель приведенной выше схемы с помощью Simetrix.

Изображение: Активная мощность – схема Simetrix

В этой имитационной модели у нас есть источник напряжения с амплитудой 162 В и частотой 60 Гц. Электрический ток будет течь через резистор сопротивлением 2 Ом. Измеряются напряжение, ток и мощность на резисторе, и результаты отображаются на изображении ниже.

Изображение: Активная мощность – график Simetrix

Как видно на верхнем графике, напряжение и ток совпадают по фазе, задержки между сигналами нет. Кроме того, мощность всегда положительна, будучи произведением напряжения и тока, которые имеют один и тот же знак, положительный или отрицательный. Мощность, которую мы измеряем на резисторе, равна активной мощности , потому что она всегда течет от источника (напряжение) к нагрузке (резистор). В чисто резистивной цепи вся мощность в цепи является активной мощностью.

В этом случае мощность преобразуется из одной формы в другую, например: из электричества в тепло, из механической в ​​электрическую и т. д. Это определение мощности обычно используется в физике и также известно как активная мощность или реальная мощность или реальная мощность .

В заключение, активная мощность P , также известная как истинная/реальная мощность , представляет собой мощность, которая преобразуется из одной формы в другую (например, электричество в тепло) и измеряется в Вт [Вт] . Мощность в чисто резистивной электрической цепи представляет собой полностью активную мощность.

Пример расчета активной мощности

Рассчитайте активную мощность, рассеиваемую на резисторе R = 2 Ом в цепи переменного тока при пиковом напряжении E _пик = 162 В и частоте f = 60 Гц. Визуализируйте функцию напряжения, тока и мощности от времени t [с] на графике вместе с их пиковыми и среднеквадратичными значениями.

Шаг 1 . Рассчитать E _{среднеквадратичное значение} = E _пик / √2 = 162 / √2 = 114,55 В

Шаг 2 . Рассчитать I _пик = E _пик / R = 162 / 2 = 81 A

Шаг 3 . Вычислить I _{среднеквадратичное значение} = I _{пиковое значение} / √2 = 81 / √2 = 57,28 А

Шаг 4 . Рассчитайте активную мощность P = E _{действ.} ⋅ I _{действ.} = 114,55 ⋅ 57,28 = 6,56 кВт

Шаг 5 . Визуализируйте функцию напряжения, тока и мощности от времени t [с] на графике.

Изображение: График напряжения, тока и активной мощности

Реактивная мощность

Когда электрическая цепь переменного тока содержит катушку индуктивности или конденсатор в дополнение к резистору, мощность, содержащаяся в этой цепи, не является полностью активной/истинной/реальной. Это связано с тем, что катушка индуктивности и конденсатор могут накапливать энергию в виде магнитных или электрических полей и возвращать ее обратно в цепь в виде электрической энергии.

В схеме ниже мы последовательно соединяем источник переменного напряжения, резистор и катушку индуктивности.

Изображение: источник переменного напряжения с цепью резистор-индуктор

Ток все еще проходит через компоненты, меняя свое направление, но в этом случае между напряжением и током имеется фазовая задержка 90º. Эта фазовая задержка возникает из-за индуктора, который преобразует энергию из электрической формы в магнитную и обратно. Если мы представим вектор напряжения и тока для приведенной выше схемы, мы получим следующее:

Изображение: векторная диаграмма — индуктор

Напряжение 0021 опережает ток с фазовой задержкой 90º.

Чтобы объяснить понятие реактивной мощности, мы будем использовать простую электрическую цепь переменного тока, которая содержит источник переменного напряжения с амплитудой 120 В и частотой 60 Гц, резистор 1 мкОм и катушку индуктивности 5 мГн (см. ниже). Сопротивление установлено очень низким, чтобы иметь «чисто» индуктивную цепь.

Изображение: Реактивная мощность — схема Simetrix

Мощность измеряется на выводе катушки индуктивности и напряжение на ней. Измерение тока выполняется перед резистором, но одинаково для обоих компонентов, соединенных последовательно. Эта схема смоделирована в Simetrix, и результаты показаны ниже.

Изображение: Реактивная мощность – график Simetrix

По результатам моделирования мало что можно заметить. Во-первых, мы видим, что ток отстает от напряжения с фазовой задержкой 90º. Кроме того, мощность на катушке индуктивности меняет знак, будучи либо положительной, либо отрицательной. Изменение знака означает, что мощность течет от источника напряжения к индуктору (положительная мощность) и от индуктора к источнику напряжения (отрицательная мощность). Мощность, отображаемая на графике, равна чисто 9.0021 реактивный , что означает, что он вообще не рассеивается в виде тепла. Реактивная мощность также известна как мнимая мощность .

Это изменение знака мощности связано с поведением индуктора, который заряжается энергией из цепи, а затем разряжает ту же энергию обратно в цепь. Можно сказать, что энергия «перерабатывается» и не используется для производства тепла или механической работы.

Изображение: источник переменного напряжения со схемой резистор-индуктор-переключатель

Схема выше помогает объяснить, как ведет себя индуктор и как энергия преобразуется из электрической формы в магнитную и обратно. Схема разделена на две части: цепь зарядки (слева) и цепь разряда (справа). Активация/деактивация каждой цепи осуществляется с помощью переключателя S. Действие зарядки/разрядки связано с катушкой индуктивности. При зарядке катушки индуктивности мощность от источника напряжения (12 В) разделяется на две части: активная/активная мощность, рассеиваемая резистором R ₁ = 140 Ом и реактивная/мнимая мощность, запасенная в катушке индуктивности L = 3H.

Когда переключатель S размыкает цепь зарядки, он также замыкает цепь разрядки. В этом состоянии запасенная в индукторе энергия разряжается через резистор R ₂ = 140 Ом. В фазе разряда вся электрическая мощность в цепи разряда представляет собой активную мощность из-за того, что она проходит через резистор, а катушка индуктивности теряет накопленную энергию.

Мощность, которая течет туда и обратно между источником и нагрузкой, называется реактивной или мнимой мощностью . Символ реактивной мощности — Q , и он также рассчитывается как произведение напряжения на ток, но единицей измерения является Вольт-ампер реактивный [ВАР] .

Из-за увеличения и уменьшения магнитного поля (катушка индуктивности) или электрического поля (конденсатор) реактивная мощность (Q) забирает мощность из цепи переменного тока, что затрудняет прямую подачу активной мощности (P) к цепи или нагрузке.

Пример расчета реактивной мощности

Рассчитайте реактивную мощность в катушке индуктивности L = 5 мГн в цепи переменного тока с пиковым напряжением E _пик = 162 В и частотой f = 60 Гц.

Шаг 1 . Рассчитать E _rms = E _пик / √2 = 162 / √2 = 114,55 В

Шаг 2 . Рассчитайте индуктивное сопротивление X _L = 2 ⋅ π ⋅ f ⋅ L = 2 ⋅ π ⋅ 60 ⋅ 5⋅10 ^-3 = 1,885 Ом

Шаг 3 . Вычислите I _пик = E _пик / X _L = 162 / 1,885 = 85,994 A

Шаг 4 . Вычислите I _rms = I _пик / √2 = 85,994 / √2 = 60,771 А

Шаг 5 .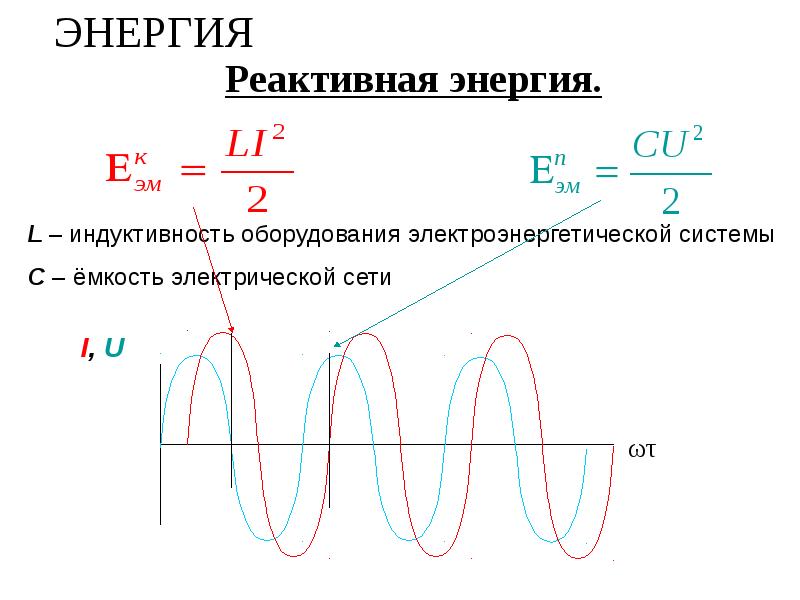 Расчет реактивной мощности Q = E _{действующее значение} ⋅ I _{действующее значение} = 114,55 ⋅ 60,771 = 6,9614 ВАР

Итог

Основные различия между активной и реактивной мощностью приведены в таблице ниже.

Активная мощность	Реактивная мощность
Реальная мощность, используемая/потребляемая/рассеиваемая цепью/нагрузкой	любая полезная работа
Всегда положительный, не меняет направление	Может быть положительным или отрицательным, периодически меняет направление
Поток только от источника к нагрузке/контуру	Потоки от источника к нагрузке или обратно, от нагрузки к источнику
Обозначается буквой P и измеряется в ваттах, P [Вт]	Обозначается буквой Q и измеряется в вольт-ампер-реактивных, Q [ VAR]
Измерено в реальной цепи с помощью ваттметра	Измерено в реальной цепи с помощью варметра
Вырабатывает полезную работу, например, механическую энергию, тепло или свет	Не производит полезную работу, только колеблется назад и далее между источником и нагрузкой/контуром
Зависит от рассеивающих элементов цепи (сопротивление)	Зависит от индуктивных или емкостных элементов цепи (реактивное сопротивление)
Максимум в чисто резистивной цепи	Это’ s максимум в чисто индуктивном или емкостная цепь

Ссылки

[1] Теодор Уилди, Электрические машины, приводы и энергосистемы, 6-е издание, Pearson, 2005.
[2] Стэн Гибилиско, Научитесь электричеству и электронике, 3-е издание, McGraw-Hill , 2001.

Что такое коэффициент мощности? Разница активной и реактивной мощности –

Посмотрим, какой коэффициент мощности? И, следовательно, мы увидим разницу между KVA и KW.

Сначала давайте посмотрим, что такое коэффициент мощности?

Говоря простыми словами, коэффициент мощности является мерой эффективного использования электроэнергии. Это означает, что чем больше коэффициент мощности, тем лучше использование энергии.

Коэффициент мощности — это не что иное, как угол между напряжением и током. Это разность фаз между напряжением и током. Следовательно, коэффициент мощности напрямую связан с разностью фаз между напряжением и током. Здесь мы можем видеть векторную диаграмму напряжения и тока источника переменного тока. Если мы рассмотрим напряжение как эталон, а Φ как угол между напряжением и током. Тогда коэффициент мощности равен cos Φ.

 

Теперь рассмотрим формы сигналов напряжения и тока. Это форма волны напряжения.

Уравнение напряжения:

V=VmsinωT

Где Vm=пиковое значение напряжения

ω=2πf, где f — частота, а T — время

Уравнения тока будут отличаться в зависимости от разности фаз между напряжением и током .

1. Ток в фазе с напряжением (Φ=0):

 

Это означает, что разность фаз между напряжением и током равна нулю. Это означает, что Φ равно нулю.

Следовательно, уравнение тока

I=ImsinωT

Аналогичное уравнение и векторная диаграмма, что и для напряжения.

Где

Im= Пиковое значение тока. ω=2πf. f – частота. Т – время.

Ток совпадает по фазе с напряжением.

2. Ток опережает напряжение (Φ+Ve):

Это означает, что Φ положителен.

Отсюда уравнение тока

I=Imsin(ωT+Φ)

Ток опережает напряжение в емкостной цепи или нагрузке.

Ток опережает напряжение.

3. Ток отстает от напряжения (Φ-Ve):

Это означает, что Φ отрицательно.

Отсюда уравнение тока

I=Imsin(ωT-Φ)

Ток отстает от напряжения в индуктивной цепи или нагрузке. Как правило, любая бытовая или промышленная нагрузка является индуктивной. Ток отстает от напряжения.

Теперь давайте посмотрим, почему существует разница фаз между напряжением и током сети переменного тока?

Как мы знаем, разность фаз есть не что иное, как разница во времени между распространением напряжения и тока. Разница фаз в основном связана с частотой источника питания переменного тока. Из-за своей переменной природы мощность переменного тока имеет частоту, которая вызывает разность фаз между напряжением и током как в индуктивных, так и в емкостных цепях. В силовой цепи постоянного тока нет частоты, следовательно, нет разности фаз между напряжением и током, и, следовательно, коэффициент мощности равен единице.

Что такое активная мощность? А что такое реактивная мощность?

Простыми словами, активная мощность полезна для мощности, за счет которой нагрузка выполняет свою функцию. Реактивная мощность существует в основном за счет индуктивных и емкостных свойств цепи или нагрузки, которая потребляется для зарядки цепей или нагрузок. Эта мощность перемещается между источником и нагрузкой. Следовательно, реактивная мощность не влияет непосредственно на функцию нагрузки.

Для лучшего понимания давайте посмотрим на треугольник мощности. В этом треугольнике мощности это активная мощность, обозначаемая как P, это реактивная мощность, обозначаемая как Q, и это векторное сложение активной и реактивной мощностей, называемое полной мощностью, обозначаемое как S. Как мы видели, только эта активная мощность полезна для мощности. . Опять же, эти три типа мощности существуют из-за фазового угла, который представляет собой разность фаз между напряжением и током. Следовательно, активная и реактивная мощности также напрямую связаны с коэффициентом мощности.

Теперь давайте посмотрим на соотношение между реактивной мощностью.

Как известно, активная мощность

P = VIcosΦ

И реактивная мощность

Q = VIsinΦ

Где

В — напряжение, I — ток, а Phi — разность фаз между напряжением и током.