Алгебра буля это: Булева алгебра (алгебра логики)

Булева алгебра (алгебра логики)

На этом уроке знакомимся с алгеброй логики (булевой алгеброй). Одним из её основателей стал английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том, что высказываниям можно присваивать значения 1 (“истина”) и 0 “ложь”.

Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.

Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Пусть функция от n переменных и любой из её аргументов могут принимать значения только из множества {0, 1}. Тогда эта функция называется логической, или булевой, или переключательной, или функцией алгебры логики. Описанную функцию часто называют также булевым вектором. Количество функций от n переменных равно 2 в степени n. То же самое можно сказать и иначе: число различных n-мерных булевых векторов равно 2 в степени n. А число различных функций алгебры логики от этих векторов равно уже .

Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая “1”) или сигнал отсутствует (логический “0”).

На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.

Законы булевой алгебры применяются и в программировании – при написании сложных логических условий и сложных запросов к базе данных. Один пример со скриптом на PHP приведён здесь (это статья о системе многокритериального поиска по сайту с базой данных). Ещё один пример – применение алгебры логики в создании многоуровневого меню сайта, в котором были бы открыты все пункты всех уровней, по которому пролегает путь к конечному открытому пункту меню.

Часто оказывается, что изначально построенное логическое выражение можно упростить, используя аксиомы, теоремы и законы алгебры логики.

Логические функции одной переменной

 

Переменная	Логические функции
x
0	0	0	1	1
1	0	1	0	1

 

Логические функции двух переменных

Ниже дана таблица истинности для логических функций от двух переменных.

В логических схемах функции могут быть реализованы с произвольных количеством входных переменных, примеры – в материале Логические схемы и таблицы истинности.

Ответить на контрольные вопросы, а затем посмотреть ответы

Контрольный вопрос 1.

Даны две переменные x1 и x2. Число различных булевых векторов и различных ФАЛ от полученных векторов равны соответственно:

• 8 и 16
• 8 и 32
• 4 и 8
• 4 и 16

Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной (и одна, и вторая в варианте ответа):

• отрицание и сложение по модулю два
• эквивалентность и повторение x
• отрицание и импликация
• функция Шеффера и эквивалентность
• запрет по x2 и отрицание

Правильные ответы на вопрос 1 и вопрос 2.

Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функции вместо аргументов (суперпозицию). Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.

Инверсия (логическое отрицание, “НЕ”)

.

0	1
1	0

Конъюнкция (логическое умножение, “И”)

.

Дизъюнкция (логическое сложение, “ИЛИ”)

.

В булевом базисе обычно строятся логические схемы, которые реализуют сколь угодно сложные логические функции, примеры – в материале Логические схемы и таблицы истинности.

В качестве исходного описания сложных логических функций обычно используется таблица истинности, однако упрощение функций удобнее производить в аналитической форме. При аналитической записи функция алгебры логики представляется либо в виде логической суммы элементарных логических произведений (дизъюнкции элементарных конъюнкций), либо в виде логического произведения элементарных логических сумм (конъюнкции элементарных дизъюнкций). Первая форма записи имеет название дизъюнктивной нормальной формы (ДНФ), вторая – конъюнктивной нормальной формы (КНФ). В этих названиях термин “нормальная” означает отсутствие общей инверсии (отрицания) над несколькими перемнными сразу.

Дизъюнктивная нормальная форма

.

Конъюнктивная нормальная форма

.

Применяются следующие способы описания логических функций:

• словесный;
• табличный;
• числовой;
• аналитический;
• координатный;
• графический.

Пример табличного описания функций алгебры логики. В верхней таблице под набором подразумевается набор значений логических переменных (1 или 0), а f – это значение функции алгебры логики, заданной определённой формулой. Нижняя таблица несёт в себе более подробную информацию о наборах, поскольку в ней указаны значения переменных.

Номер набора	f
0	0
1	1
2	0
3	0
4	1
5	1
6	0
7	1

 

X1	X2	X3	f
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

Приведённые выше таблицы имеют название таблиц истинности. Такие таблицы в практике необходимо строить для любой, сколь либо сложной булевой функции. Примеры таблиц истинности для булевых функций, реализованных в логических схемах – в материале Логические схемы и таблицы истинности.

Пример числового описания логических функций

или .

Пример аналитического описания логических функций

Пример координатного описания логических функций

Карта Карно

Пример графического описания логических функций

Аксиомы конъюнкции

.

Аксиомы дизъюнкции

.

Аксиомы отрицания

если , то ; если , то .

Теоремы исключения констант

.

Теоремы идемпотентности (тавтологии, повторения)

.

для n переменных

.

Теорема противоречия

.

Теорема “исключённого третьего”

.

Теорема двойного отрицания (инволюции)

.

Ассоциативный (сочетательный) закон

.

Коммутативный (переместительный) закон

.

Дистибутивный (распределительный) закон

.

.

Законы де Моргана (законы общей инверсии или дуальности)

.

.

Закон поглощения (элиминации)

.

Закон склеивания (исключения)

.

Джордж Буль Отец булевой алгебры. Архитекторы компьютерного мира

Джордж Буль

Отец булевой алгебры

Чистая математика была открыта Булем в работе, которую он назвал «Законы мышления».

Бертран Рассел

Джордж Буль

Все механизмы, шестеренки, вакуумные лампы и печатные платы — все это еще не компьютер.

Важны также разработки Паскаля и Лейбница, о которых мы вам уже рассказали, и Бэббиджа, о достижениях которого мы расскажем в следующей главе. Эти разработки требовали первоначальной теории логики для того, чтобы, в конечном счете, вдохнуть жизнь в машины, которые «думают».

Расширив общий метод Лейбница, сформулированный на 188 лет раньше, в котором все истинные причины были сведены к виду вычислений, английский математик Д. Буль в 1854 году заложил основу того, что мы сегодня знаем как математическую логику, опубликовав работу «Исследование законов мышления».

В этой работе, изданной, когда ему было 39 лет, Буль свел логику к чрезвычайно простому типу алгебры, алгебры логики высказываний, которая представляла собой систему символов и правил, применяемую к различным объектам (числам, буквам, предложениям).

Его теория логики, основанная на трех основных действиях — AND (и), OR (или), NOT (не), — должна была стать в XX веке основой для разработки переключающих телефонных линий и проекта ЭВМ. Так же, как и идеями Лейбница, булевой алгеброй пренебрегали в течение многих лет после того, как она была создана.

Важность работы, признанной логиком де Морганом, современником Буля, заключалась в следующем: «Символические процессы алгебры, созданные как инструменты числового вычисления, компетентно выражают каждый закон мысли и обладают грамматикой и словарем всего того, что содержит систему логики. Мы это и не предполагали, пока это не было доказано в „Законах мышления“».

Джордж Буль родился 2 ноября 1815 года в Линкольне (Англия), в семье бедного башмачника. Хотя он был современником Ч. Бэббиджа, но происходил не из привилегированного класса, как Бэббидж.

Выходец из слоя общества, дети которого фактически были лишены посещения университета, Джордж должен был заниматься самостоятельно.

Хотя промышленная революция уже произошла в Англии, знание древних языков было показателем уровня образования джентльмена. Конечно, никакой латинский или греческий не преподавали в школе, которую посещал Буль. Буль сам изучил греческий и латинский, пользуясь поддержкой малообразованного отца, и в возрасте 12 лет сумел перевести оду Хорейса на английский язык. Ничего не понимая в качестве техники перевода, гордый отец Буля все-таки напечатал его в местной газете. Некоторые специалисты заявляли, что 12-летний мальчик не мог сделать такой перевод, другие отмечали серьезные технические дефекты перевода. Решив совершенствовать свои знания латинского и греческого, Буль провел следующие два года в серьезном изучении этих языков, и снова без чьей-либо помощи.

Хотя этих знаний было недостаточно, чтобы превратиться в истинного джентльмена, такая тяжелая работа дисциплинировала его и способствовала классическому стилю созревавшей булевой прозы.

Известно, что его отец оставил школу после трех лет обучения, и в то же время удивительно, что Буль получил раннее математическое образование от своего отца, который был самоучкой в этой области.

В возрасте 16 лет для Буля стало необходимостью начать трудовую жизнь, чтобы помочь своим родителям. Получив работу «младшего учителя», или ассистента учителя в начальной школе, Буль должен был провести 4 года, преподавая в двух различных школах.

Всегда думая о перспективе занимаемого места в жизни, Буль начал рассматривать несколько путей, открытых для него. Его первоначальное преподавание было всегда на уровне, однако он не считал это профессией, хотя она и была почетна. Буль стал священнослужителем.

Когда он не преподавал, то проводил время в серьезном изучении французского, немецкого и итальянского языков, в подготовке к церковной жизни. Неудачи, бедность его семейства еще раз разрушили планы Буля; родители убеждали его отказаться от религиозной жизни ввиду их ухудшающегося финансового положения.

Отзывчивый, как всегда, к советам родителей, Буль решил открыть собственную школу. Ему было 20 лет. Преподавая, Буль считал себя также студентом и приступил к изучению полного курса высшей математики. Он проштудировал «Математические начала» Ньютона, «Аналитическую механику» Лагранжа, труды Лапласа и других авторов.

Свои математические исследования Буль начал с разработки операторных методов анализа и теории дифференциальных уравнений, а затем подобно де Моргану, с которым к этому времени подружился, занялся математической логикой.

В своей первой основной работе «Математический анализ логики, являющийся опытом исчисления дедуктивного рассуждения» 1847 года Буль отчетливо показал так называемое количественное истолкование объектов логики и необходимость нового подхода к решению проблем логики.

Этот подход требовал изменения и расширения символического языка алгебры: выбора символики, операций и законов, определяющих эти операции и отражающих специфику объектов исследования, — т.  е. по существу создания нового исчисления. Буль писал: «Те, кто знаком с настоящим состоянием символической алгебры, отдают себе отчет в том, что обоснованность процессов анализа зависит не от интерпретации используемых символов, а только от законов их комбинирования. Каждая интерпретация, сохраняющая предложенные отношения, равно допустима, и подобный процесс анализа может, таким образом, при одной интерпретации представлять решение вопроса, связанного со свойствами чисел, при другой — решение геометрической задачи и при третьей — решение проблемы динамики или статики. Необходимо подчеркнуть фундаментальность этого принципа».

С публикацией «Математического анализа…» взгляды и блестящая интуиция этого тихого, простого человека стали ясны его друзьям — математикам, которые советовали ему поступить в Кембридж, для получения общепринятого математического образования.

Буль неохотно отверг эти предложения, потому что его родные полностью существовали на его заработок. Не жалуясь на особенности своего обучения от случая к случаю, Буль, наконец, получил небольшой перерыв в 1849 году, когда его назначили профессором математики в недавно открытом Королевском колледже.

Это назначение позволило ему посвятить больше времени «Законам мышления…» — второй его основной работе, которую он непрерывно оттачивал и усовершенствовал в течение еще 5 лет, до публикации в 1854 году.

Как писал Буль в первом параграфе книги: «Цель данного трактата:

? исследовать фундаментальные законы тех действий разума, с помощью которых выполняются рассуждения;

? выразить их в символическом языке исчислений и на этой основе создать науку логики и построить метод;

? сделать этот метод непосредственно основой общего метода для выражения теории вероятностей;

? наконец, получить различные элементы истины;

? оценить в рамках решения этих вопросов некоторое вероятное сообщение».

И далее: «Теперь фактически исследования следующих страниц показывают логику, в практическом аспекте, как систему процессов, проведенных при помощи символов, имеющих определенную интерпретацию и подчиненных законам, основанным на этой единственной интерпретации. Но в то же самое время они показывают эти законы как идентичные по форме с законами общих символов алгебры, с одним единственным дополнением, viz».

Другими словами, в общей алгебре не выполняется, например: что каждый х тождественно равен своему квадрату — но это истина в булевой алгебре. Согласно Булю, х² = х для любого х в его системе. В числовой системе это уравнение имеет единственное решение «О» и «1». В этом заключается важность двоичной системы для современных компьютеров, логические части которых эффективно реализуют двоичные операции.

Кроме логики, булева алгебра имеет два других важных применения. Булева алгебра применяется в натуральной алгебре. Принимая также во внимание идею «количества элементов» в множестве, булева алгебра стала основой для теории вероятностей.

Несмотря на большое значение булевой алгебры во многих других областях математики, необычайная работа Буля в течение многих лет считалась странностью. Как и Бэббидж, Буль был человеком, опередившим свое время. Это произошло раньше, чем Альфред Уайтхед и Бертран Рассел опубликовали свой трехтомник «Принципы математики» (1910–1913), в котором рассматривались вопросы формальной логики.

Заслуживает внимания и то, что на достижения Буля частично опирались математические открытия, к тому времени появившиеся в Англии, в том числе и идеи Бэббиджа. Математики обратили внимание на идею Бэббиджа о математических операциях и величинах, использующихся в них. Идея стала возможной благодаря группе британских специалистов в области алгебры, к которым принадлежал и Буль.

Буль продемонстрировал, что логика может сводиться к очень простым алгебраическим системам, после чего для Бэббиджа и его последователей стало возможным создание механических устройств, которые могли решать необходимые логические задачи.

Через год после опубликования «Законов мышления…» Буль женился на Мэри Эверест, племяннице профессора греческого языка Королевского колледжа. Счастливый брак длился в течение девяти лет, вплоть до безвременной кончины Джорджа Буля. 8 декабря 1864 года, в возрасте 49 лет, почитаемый и известный, он умер от воспаления легких.

Буль был человеком последовательным и дисциплинированным, тем не менее, он широко демонстрировал собственное видение мира в своих утверждениях. Это мощное сочетание интеллекта и интуиции в Джордже Буле воплотилось в различных математических идеях. В заключение очерка об отце булевой алгебры хотелось бы коротко рассказать о семье Буля.

Как уже упоминалось, жена Буля была племянницей Джорджа Эвереста, в 1841 году завершившего в Индии грандиозные по масштабам работы.

В честь его заслуг высочайшая вершина мира Джомолунгма в Гималаях одно время даже именовалась Эверестом. Сама Мэри, в отличие от жен многих других математиков, понимала научные идеи своего мужа и своим вниманием и участием подвигала его на продолжение исследований. После его смерти она написала несколько сочинений и в последнем из них — «Философия и развлечения алгебры», — опубликованном в 1909 году, пропагандировала математические идеи Джорджа.

У четы Булей было пять дочерей. Старшая, Мэри, вышла замуж за Ч. Хинтона — математика, изобретателя и писателя-фантаста — автора широко известной повести «Случай в Флатландии», где описаны некие существа, живущие в плоском двухмерном мире. Из многочисленного потомства Хинтонов трое внуков стали учеными: Говард — энтомологом, а Вильям и Джоан — физиками. Последняя была одной из немногих женщин-физиков, принимавших участие в работе над атомным проектом в США.

Вторая дочь Булей, Маргарет, вошла в историю как мать крупнейшего английского механика и математика, иностранного члена Академии наук СССР Джеффри Тэйлора. Третья, Алисия, специализировалась в исследовании многомерных пространств и получила почетную ученую степень в Гронингенском университете. Четвертая, Люси, стала первой в Англии женщиной-профессором, возглавившей кафедру химии.

Но наиболее известной из всех дочерей Булей стала младшая, Этель Лилиан, вышедшая замуж за ученого — эмигранта из Польши Войнича. Войдя в революционную эмигрантскую среду, она написала прославивший ее на весь мир роман «Овод». За ним последовало еще несколько романов и музыкальных произведений, а также перевод на английский язык стихотворений Тараса Шевченко. Войнич скончалась в Нью-Йорке в возрасте 95 лет, немного не дожив до столетия со дня смерти своего знаменитого отца математика Джорджа Буля.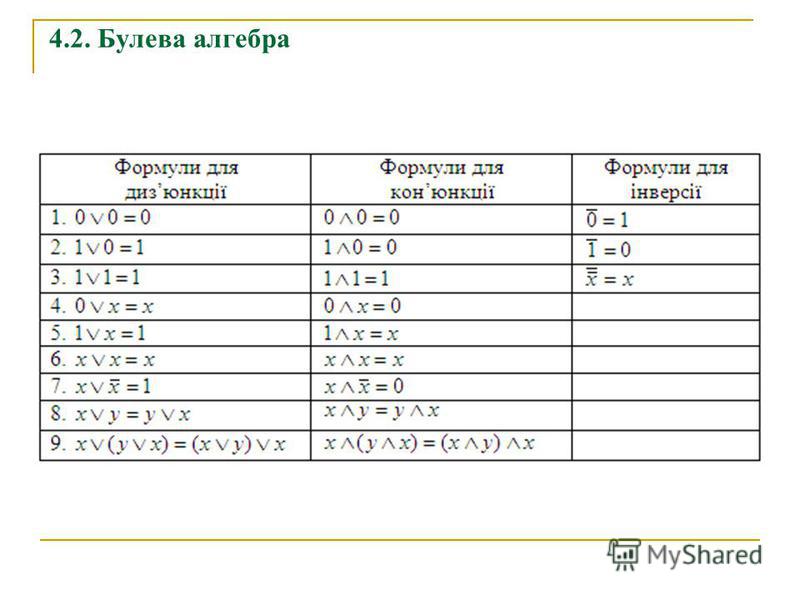

Математика и логика — Математическая составляющая

Математика и логика Поделиться    

Лев Дмитриевич Беклемишев

Логика как наука — предмет почти такой же древний, как и математика. В античное время и средние века она была составной частью тривиума (грамматика, риторика, логика/диалектика) — базового уровня образования; математические же предметы (арифметика, геометрия, астрономия и музыка) составляли следующий, более продвинутый, уровень, называемый квадривиум. (От слова «тривиум» происходит одно из любимых математиками выражений «тривиально».) Предметы тривиума понимались как науки о том, как правильно, без ошибок, писать, говорить и, соответственно, рассуждать.

Мы расскажем о том, как и почему возникла математическая логика, что она изучает, какие у неё есть достижения и современные применения.

От Аристотеля к Булю. Основы учения о правильных рассуждениях заложил Аристотель. Он заметил, что корректные умозаключения следуют определённым элементарным схемам, называемым силлогизмами, и перечислил ряд таких схем. (Классический пример силлогизма: «Все люди смертны. Сократ — человек. Следовательно, Сократ смертен».) Учение о силлогизмах в свою очередь опиралось на глубокий анализ понятий и их соединения в высказывания.

Силлогистика Аристотеля была не лишена недостатков, однако в целом была выдающейся теорией и стала основой изучения логики на протяжении античности и средних веков. В трудах античных стоиков и средневековых схоластов она была модифицирована и дополнена. В таком виде аристотелевская логика дошла вплоть до середины XIX века, где и встретила революцию, связанную с проникновением в логику математических методов.

Возникновение математической логики полностью изменило представления учёных как о методах исследования логики, так и о том, что составляет сам предмет её изучения.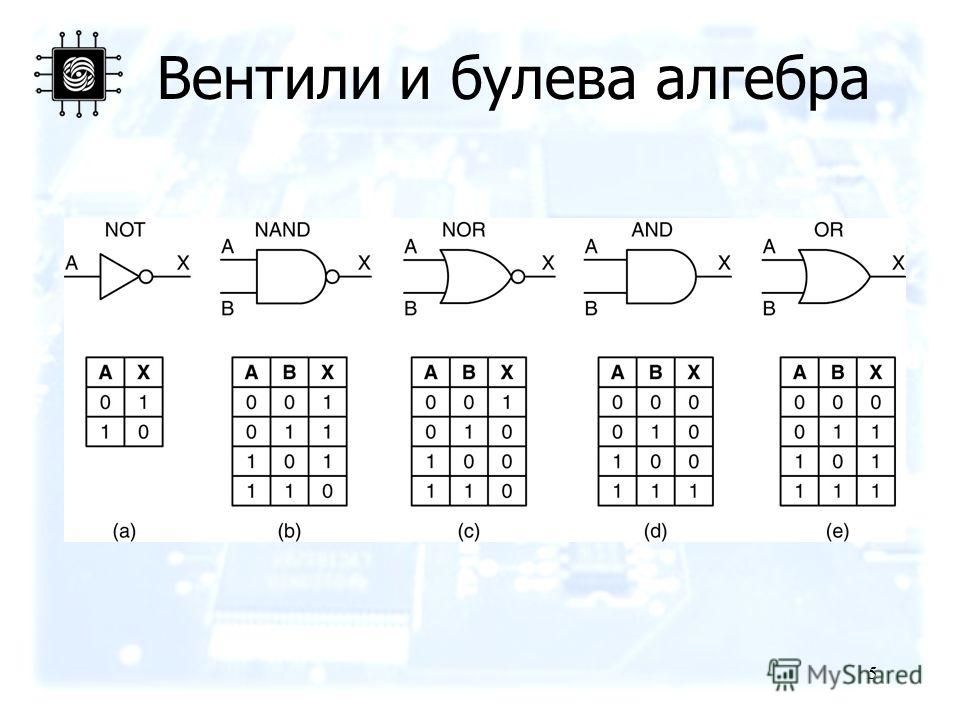 В наше время заявления, что логика есть наука о правильных рассуждениях, кажутся настолько же справедливыми, насколько утверждение «математика — это наука о правильных вычислениях».

Аналогия между рассуждениями и вычислениями несколько глубже, чем кажется на первый взгляд. Возникновение логики как математической науки было связано с работами британских учёных Джорджа Буля и Августа де Моргана, которые обнаружили, что с логическими высказываниями можно оперировать как с алгебраическими выражениями. Например, если сложение читать как логическую связку «или», умножение как «и», а равенство как «равносильно», то для любых высказываний $a$, $b$ выполняются законы
$$ a+b=b+a,\quad a\cdot(b+c)=a\cdot b+a\cdot c, $$

как и многие другие привычные нам законы арифметики. Но, помимо этого, в алгебре высказываний выполняется и кое‐что непривычное, например всегда
$$ a+a=a\quad \hbox{и}\quad a+(b\cdot c)=(a+b)\cdot (a+c). $$

Такой взгляд на логику высказываний и силлогистику оказался и неожиданным, и плодотворным. В наше время эту точку зрения разрабатывает область, называемая алгебраической логикой, а одним из её центральных понятий является понятие булевой алгебры, названной так в честь её первооткрывателя. Эта область исследований, через понятие реляционной алгебры, обобщающей булеву, привела в 1960‐х годах к теории реляционных баз данных, в наше время лежащей в основе самых распространённых языков запросов, таких как SQL.

Математизация логики и аксиоматизация математики. Движущей причиной процесса математизации логики был назревший в самой математике на рубеже XIX—XX веков кризис оснований. С одной стороны, во второй половине XIX века в математике получил распространение удобный язык теории множеств, созданной Георгом Кантором. Математики стали уверенно использовать в своих рассуждениях конструкции с бесконечными множествами. Математика, вооружённая теорией множеств, шла от успеха к успеху.

С другой стороны, в самой теории множеств Кантора обнаружились парадоксы, которые указывали на то, что с этой теорией не всё в порядке на самом базовом уровне. Простейший парадокс такого рода, в фольклорном варианте известный как парадокс брадобрея, был придуман Бертраном Расселом: рассмотрим множество $R$ всех тех множеств, которые не содержат сами себя в качестве элемента. Тогда $R\in R$ если и только если $R\notin R$, противоречие.

Такое положение дел заставило многих выдающихся математиков и философов той эпохи (Пеано, Фреге, Рассел, Гильберт, Пуанкаре, Брауэр, Вейль и др.) задуматься об основаниях математики. Их волновали такие фундаментальные вопросы как:

• Что означает доказать математическую теорему? Какие средства при этом законно использовать?
• Что значит выразить то или иное математическое понятие или утверждение на том или ином языке?
• Когда мы говорим об истинности и о доказуемости какого‐либо математического утверждения, имеется ли в виду одно и то же?

Параллельно в математике стали укореняться новые стандарты строгости. Основные области математики — анализ, алгебра, геометрия — были поставлены на аксиоматическую основу. Великий математик Давид Гильберт (1862—1943) был ярким сторонником и пропагандистом аксиоматического метода. Под его влиянием была построена и общепринятая в наше время система аксиом теории множеств, свободная от очевидных парадоксов. Эту аксиоматику предложил в 1908 году Э. Цермело и в дальнейшем дополнили Дж. фон Нейман и А. Френкель. Но где же настоящая гарантия, что полученная система не содержит противоречия? Каким образом это можно установить?

Эти вопросы оказались гораздо сложнее, чем представлялось тогда Гильберту. Они потребовали глубокого изучения аксиоматических систем и их формализации, привели к точному анализу структуры математического высказывания, первым формулировкам строгих математических моделей таких явлений, как доказуемость, выразимость, истинность, и сделали возможным их изучение математическими методами. Так возникла математическая логика — особая область исследований внутри математики. В рамках этой дисциплины был создан точный язык и математический аппарат для исследования целого пласта явлений, ранее относившихся к чисто гуманитарному знанию. (В этой роли математическую логику можно сравнить с такой областью современной математики, как теория вероятностей, которая ещё в начале XX века не была строго математической дисциплиной.)

Формальные языки. С современной точки зрения область интересов математической логики значительно шире, чем наука о правильных рассуждениях; её можно приблизительно описать, с оговорками и уточнениями, как построение и исследование формальных языков и систем математическими методами. Заметим, что если в этом определении отбросить слово «формальных», то вместо логики мы получим, по существу, математическую лингвистику — что указывает на определённое родство между этими двумя дисциплинами. Ключевое же отличие математической логики от логики в широком смысле слова — это именно использование математических методов, применяемых к точным формальным моделям.

Математическая логика по предмету сво-
ему есть логика, а по методу — математика.(П. С. Порецкий, 1884 год, Казань. )

Формальные и естественные языки имеют общие черты: у тех и у других есть синтаксис (то, как мы говорим или пишем), семантика (смысл того, что написано) и прагматика (то, как используется написанное). Основное отличие заключается в том, что — по крайней мере в идеале — синтаксис и семантика формальных языков могут быть определены на уровне математической строгости и поэтому в принципе поддаются анализу чисто математическими методами.

В наше время формальные языки встречаются в каждом доступном нам электронном устройстве, вроде мобильного телефона, а некоторые из них — языки программирования — даже изучают в школе. Поэтому за примерами далеко ходить не надо. Однако в середине XIX века, когда начался процесс математизации логики, формальных языков ещё не было, их только предстояло создать.

Логика предикатов. Разработчики первых формальных языков и систем, как правило, не думали о том, что эти системы могут быть реально использованы в вычислительных устройствах.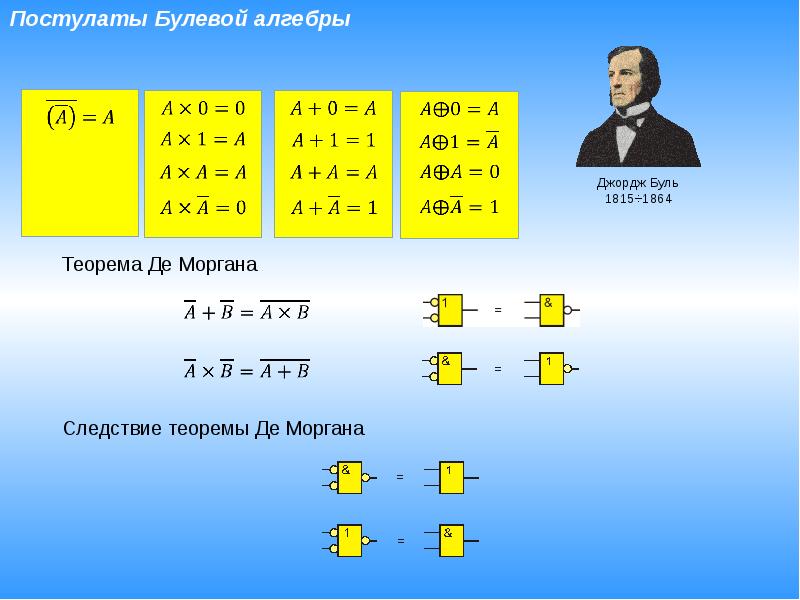 (Исключением, видимо, можно считать великого учёного Готфрида Вильгельма Лейбница (1646—1716), который почти за два века до Буля предвосхитил многие идеи математической логики, включая идею формализации языка математики, и даже построил механический арифмометр.)

Первые формальные языки и системы возникли как результат выделения фрагмента естественного языка, достаточного для передачи формулировок математических утверждений и их анализа. Процесс выработки основных категорий этого языка был продолжительным и шёл параллельно с выработкой некоторых ставших в наше время стандартными математических обозначений. (Одним из важных понятий, введённых в это время, стало понятие квантора, сформировавшееся в работах Г. Фреге и Ч. Пирса. Кванторы существования $\exists$ и всеобщности $\forall$ заменяют языковые конструкции «для некоторого» и «для всех». Первое из этих обозначений введено Дж. Пеано в 1897 году, второе — по аналогии — Г. Генценом в 1935 году, однако общеупотребительными эти обозначения стали лишь под влиянием Бурбаки во второй половине XX века. ) Этот процесс в основном завершился в 1920‐х годах, когда в качестве стандартного класса языков, предназначенных для формализации и анализа математических утверждений, стал рассматриваться язык логики предикатов (первого порядка).

Предикатом на множестве $M$ мы называем высказывание, зависящее от $n$ параметров из этого множества (например, «натуральное число $x$ чётно», «точки $x$, $y$ и $z$ плоскости лежат на одной прямой»). Как только фиксированы значения параметров, предикат принимает логическое значение ложь или истина. Таким образом, с формальной точки зрения предикат представляет собой функцию от $n$ аргументов из множества $M$ в $\{0,1\}$.

Не вдаваясь в технические подробности, можно приблизительно описать высказывания логики предикатов как такие, которые можно сформулировать (предполагая заранее заданными обозначения некоторых базовых предикатов) с помощью конструкций $\land$ «и», $\lor$ «или», $\neg$ «не», $\to$ «влечёт» и уже упомянутых кванторов. Например, текст $\forall{x} \exists{y} (y>x \land P(y))$ выражает неограниченность множества простых чисел, если договориться, что переменные пробегают множество натуральных чисел, «$>$» означает «больше», а $P(y)$ выражает простоту числа $y$. Эти договорённости составляют часть того, что мы назвали семантикой языка логики предикатов.

Удивительный факт, подтверждаемый всей существующей математической практикой, состоит в том, что выразительных средств языка логики предикатов — на первый взгляд очень скромных — достаточно для формулировки любых известных математических результатов. При этом может быть использовано всего лишь одно базовое понятие — предикат принадлежности $x\in y$ «множество $x$ есть элемент множества $y$». (В картине мира аксиоматической теории множеств все объекты, обозначаемые переменными, являются множествами.)

Доказуемость и вычислимость. Выразить в данном языке то или иное осмысленное утверждение — совсем не то же самое, что суметь его доказать. Следующий уровень языка логики предикатов состоит в описании таких текстов, которые следует признать корректными доказательствами. Традиционно этот уровень называется в математической логике исчислением предикатов. Формальное доказательство (в формате, который принято называть гильбертовским, но который существовал и до работ Давида Гильберта) представляет собой конечную цепочку высказываний логики предикатов, каждое из которых либо является аксиомой, либо получается из предшествующих высказываний по одному из постулируемых правил. Минимальный стандартный набор таких правил содержит лишь два: правило, позволяющее из высказываний $A$ и $A\to B$ вывести $B$, и правило, позволяющее из высказывания $A$ вывести $\forall x A$. (Если высказывание $A$ содержит параметр $x$, то формальное доказательство $A$ обосновывает его истинность при всех возможных значениях параметра.)

Таким образом, математическая доказуемость описывается двумя формальными языками — языком утверждений, описанным в предыдущем разделе, и языком доказательств — из которых второй является надстройкой над первым.

Похожая ситуация имеет место и с понятием вычислимости. Языки программирования предназначены для описания алгоритмов. Алгоритм при этом описывается программой — построенным по определённым правилам формальным текстом, который принято называть кодом. Таким образом, первый уровень языка программирования составляет язык текстов программ. Однако, процесс выполнения программы на данном компьютере на данном входе также может быть зафиксирован в виде текста (не важно, сохраняется ли этот текст в ходе работы программы или нет). В теории алгоритмов принято называть такой текст полным протоколом работы программы. То, каким образом порождается этот протокол, и составляет полное описание той или иной вычислительной модели. Для реальных языков программирования, разумеется, такое описание чрезвычайно сложно, однако для простейших моделей, таких как машина Тьюринга, оно гораздо проще.

Теория алгоритмов и создание компьютеров. Математическая логика сыграла важную роль в появлении компьютеров, хотя и не была единственной движущей силой в этом сложном процессе. Именно в математической логике, в попытке дать наиболее общее определение задачи, имеющей алгоритмическое решение, было осознано, что возможно построение универсального вычислительного устройства (машины), которое будет способно решать все теоретически разрешимые алгоритмические задачи.

Одним из первых, кто это понял, был Алан Тьюринг, давший точное определение и наиболее убедительный анализ понятия вычислимой функции в 1936 году. Другими учёными, которые наряду с Тьюрингом пришли к тем же идеям приблизительно в то же время, были Алонзо Чёрч и Эмиль Пост. Этими и другими исследователями в 1930‐х годах были созданы начала теории алгоритмов, которая стала основой понимания работы и построения вычислительных устройств в 40‐е и 50‐е годы. В частности, идея универсальной машины Тьюринга была в дальнейшем технически реализована в компьютерной архитектуре «по фон Нейману», в соответствии с которой программа хранится в памяти устройства и может быть модифицирована в ходе его работы. На основе этой идеи построены все операционные системы.

Задачей, которую стремились решить пионеры теории алгоритмов, был вопрос, поставленный Гильбертом и названный им по‐немецки Entscheidungsproblem, «проблема решения». Вопрос состоял в том, чтобы найти алгоритм, который по данному утверждению, записанному на языке логики предикатов, давал бы ответ, существует ли формальное доказательство этого утверждения или нет. Если бы такой алгоритм существовал, то все математические проблемы в некотором смысле имели бы чисто механическое решение: как уже упоминалось, на языке логики предикатов можно сформулировать практически любое математическое утверждение, например знаменитую гипотезу о бесконечности числа пар простых чисел‐близнецов. Тогда вопрос о том, выводима ли эта гипотеза из аксиом теории множеств, сводился бы к проверке доказуемости некоторого высказывания в исчислении предикатов. Неудивительно, что исследователи Entscheidungsproblem стремились показать, что требуемого алгоритма в принципе не может существовать.

Если доказать существование того или иного алгоритма можно, предъявив его явно, то для того, чтобы утверждать, что такого алгоритма не существует, необходимо располагать точным математическим описанием того класса задач, которые допускают алгоритмическое решение. Ответ на этот вопрос потребовал разработки формальных языков описания алгоритмов ещё до появления компьютеров. Причём, поскольку цель такой разработки была более теоретическая, чем практическая, исследователи стремились к формулировке наиболее простых для описания и в то же время универсальных вычислительных моделей. Первыми такими моделями были рекурсивные функции Гёделя—Эрбрана, лямбда‐исчисление Чёрча и машины Тьюринга.

Гёдель, хотя и был первым, кто фактически сформулировал универсальный язык программирования, не считал, что найденное им (и французским логиком Эрбраном) понятие является универсальным в смысле способности запрограммировать любой алгоритм. Первым, кто высказал тезис об универсальности своей вычислительной модели, был Алонзо Чёрч. Он также предъявил доказательство невозможности решения Entscheidungsproblem в рамках этой модели. Исчисление Чёрча было очень простым по форме, но больше напоминало формальное логическое исчисление, чем реальную вычислительную машину. Машины Тьюринга в этом смысле были ближе к будущей реальности, и поверить в тезис Тьюринга о том, что любая задача, имеющая алгоритмическое решение, может быть решена на машине Тьюринга, было намного легче, чем в аналогичный тезис Чёрча (известно, что именно работа Тьюринга смогла убедить Гёделя в справедливости этого тезиса). Тьюринг также показал, что его машины эквивалентны лямбда‐исчислению в смысле вычислительных возможностей, что стало косвенным свидетельством справедливости тезиса Чёрча—Тьюринга, как его теперь принято называть.

Впоследствии многие исследователи предлагали свои вычислительные модели в надежде расширить класс вычислимых функций, впервые описанный Чёрчем и Тьюрингом. Все такие попытки не привели к расширению этого класса, который оказался очень устойчивым. В настоящее время тезис Чёрча—Тьюринга — понимаемый в смысле любой из эквивалентных вычислительных моделей — является одним из краеугольных камней, на которых базируется теория алгоритмов.

Что касается лямбда‐исчисления, то оно долгое время пребывало на обочине математической логики, будучи вытеснено из теории алгоритмов более удобными и интуитивными моделями. Однако во второй половине XX века лямбда‐исчисление и системы на его основе нашли серьёзные практические применения. Лямбда‐исчисление Чёрча стало прообразом так называемых функциональных языков программирования (таких как современный язык Haskell), которые имеют ряд преимуществ по сравнению с традиционными императивными языками и в настоящее время очень активно развиваются.

Алгоритмически неразрешимые проблемы в математике. Вслед за Entscheidungsproblem с точки зрения теории алгоритмов были проанализированы и многие другие математические проблемы, поставленные как вопросы о построении того или иного алгоритма. Некоторые из таких трудных проблем, остававшихся открытыми десятилетиями, оказались алгоритмически неразрешимыми задачами.

Среди такого рода вопросов наиболее известна 10‐я проблема Гильберта о распознавании разрешимости диофантовых уравнений. Диофантово уравнение — это уравнение вида $P(x_1,…,x_n)=0$, где $P$ — многочлен с целыми коэффициентами от переменных $x_1$, …, $x_n$. Требуется узнать по заданному многочлену $P$, существуют ли целые числа $x_1$, …, $x_n$, удовлетворяющие такому уравнению.

Вопрос Гильберта о построении общего алгоритма, работающего для всех диофантовых уравнений, с самого начала выглядел безнадёжным. С появлением теории алгоритмов исследователи стали предпринимать усилия в попытке доказать неразрешимость этой задачи. Промежуточные результаты в этом направлении получили американские логики Дж. Робинсон, М. Дэвис и Х. Патнэм, на их основе окончательное решение задачи было получено лишь в 1970 году ленинградским математиком Ю. В. Матиясевичем.

В наше время в математике алгоритмические вопросы занимают подобающее им важное место. Математическая логика научила нас тому, что далеко не всякий такой вопрос является разрешимым. Кроме того, даже если алгоритм решения той или иной задачи существует в принципе, не всегда можно говорить о его применимости на практике. Например, выполнение алгоритма может потребовать слишком много времени или памяти компьютера. Такого рода вопросами занимается отдельная область теории алгоритмов — теория сложности вычислений, о которой подробно рассказано в другой статье этого сборника (см. «Теория сложности»).

Теоремы Гёделя и недоказуемые утверждения. Ещё одним открытием, сделанным гениальным австрийским логиком Куртом Гёделем в 1931 году, было явление непополняемости аксиоматических систем. Знаменитые теоремы Гёделя о неполноте не только оказали большое влияние на развитие математической логики и дали толчок к созданию теории алгоритмов, но и стали общекультурным явлением, затронувшим даже творчество писателей и художников. Гёдель был назван в числе ста наиболее влиятельных личностей XX века по версии журнала Тайм. Однако известность теорем Гёделя приводит и к тому, что часто они интерпретируются в слишком расширительном, метафорическом смысле.

Полными называют такие системы аксиом, в которых доказуемо или опровержимо любое утверждение того же языка (можно говорить о доказуемости в исчислении предикатов из данного множества аксиом). Понятно, что если мы хотим построить систему аксиом для той или иной области математики, нам бы хотелось, чтобы эта система была непротиворечивой и полной — неполнота означает, что мы «забыли» постулировать какие‐то принципы, касающиеся базовых понятий данного языка, и нужно их добавить к списку аксиом.

Теоремы Гёделя относятся к классу аксиоматических систем, удовлетворяющих двум естественным и широким требованиям. Во‐первых, необходимо, чтобы в рассматриваемом формальном языке по меньшей мере было выразимо понятие натурального числа и операции сложения и умножения. На первый взгляд это требование кажется весьма специальным, однако натуральные числа — один из базовых математических объектов, и языки, претендующие на формализацию значительной части математики, должны позволять о них говорить.

Целые числа создал Господь Бог,
всё остальное — дело рук человеческих. (Леопольд Кронекер, 1886 год, Берлин.)

Во‐вторых, должен существовать алгоритм, распознающий, является ли данный текст аксиомой рассматриваемой теории или нет. (Если аксиомы теории нераспознаваемы, то неясно, как можно строить доказательства в такой системе.)

Гёдель показал, что при выполнении этих требований любая система аксиом либо противоречива, либо неполна. Более того, для любой непротиворечивой системы можно явно указать предложение, касающееся арифметики натуральных чисел, которое нельзя ни доказать, ни опровергнуть в данной системе (такие утверждения принято называть независимыми от данной системы аксиом). В частности, это означает, что систему аксиом формальной арифметики нельзя никаким непротиворечивым образом «пополнить»: всегда найдутся независимые от неё арифметические утверждения. Это составляет содержание так называемой первой теоремы Гёделя.

Вторая теорема Гёделя говорит о том, что утверждение, выражающее непротиворечивость данной аксиоматической системы, не доказуемо в самой системе, если эта система и в самом деле непротиворечива. Если считать, что стандартные математические методы укладываются в рамки аксиоматической теории множеств, то из этой теоремы следует, например, что стандартными математическими методами нельзя установить непротиворечивость теории множеств (и, тем самым, их собственную непротиворечивость).

Теоремы Гёделя позволили построить первые примеры независимых утверждений для сильных систем аксиом, таких как арифметика или даже теория множеств. После работ Гёделя такие примеры были обнаружены среди открытых проблем в различных областях математики.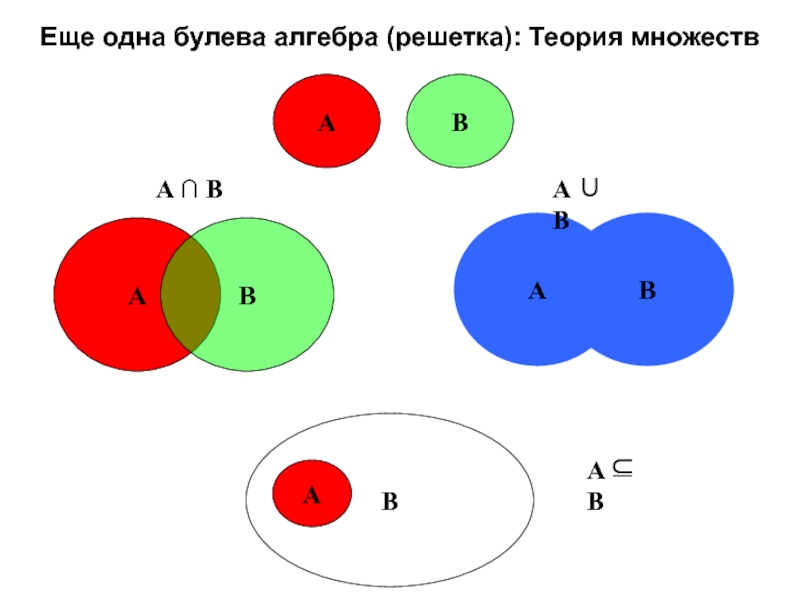 Одной из самых знаменитых открытых проблем в математике была континуум‐гипотеза Кантора, в соответствии с которой всякое бесконечное подмножество множества вещественных чисел либо счётно (равномощно множеству натуральных чисел), либо континуально (равномощно множеству вещественных чисел). В 1938 году Гёдель сумел доказать, что эту гипотезу невозможно опровергнуть в теории множеств, а в 1961 году американский математик Пол Коэн установил её недоказуемость.

Недоказуемые утверждения теоретико‐множественной природы впоследствии были обнаружены в самых разных частях математики — в анализе, алгебре, топологии и др. Сравнительно недавно, в конце 1970‐х годов, были найдены первые простые примеры утверждений из области конечной комбинаторики, независимые от аксиом формальной арифметики и даже от более сильных аксиоматических систем. Принципиальная разница с примерами типа континуум-гипотезы состоит в том, что комбинаторные примеры относятся к конечным и совершенно элементарным объектам, и их можно легко объяснить школьнику. Исследования в направлении поиска естественных примеров независимых утверждений активно ведутся и в наши дни.

Логика в других разделах математики. Наиболее впечатляющие достижения математической логики, описанные выше, так или иначе связаны с анализом трудных проблем, в том или ином смысле не имеющих решения. Такие проблемы в математике встречаются, по счастью, довольно редко. Для работающих математиков поэтому более ценным является вклад в копилку методов, годных для решения их собственных повседневных задач. Здесь мы упомянем некоторые известные приложения логики такого рода, хотя в целом следует признать, что их не слишком много.

Область математики, которая испытала на себе сильное влияние логических методов — это абстрактная алгебра. Соответствующее направление математической логики — теория моделей — возникло в 1940‐х годах в работах А. И. Мальцева в России и А. Тарского и А. Робинсона в США с прицелом на приложения в алгебре. Первые такие приложения были найдены в 1941 году А.  И. Мальцевым, который осмыслил доказанную им (а ранее в более слабой форме Гёделем) теорему о компактности для логики предикатов как общий метод получения локальных теорем в алгебре. Оказалось, что методы универсальной алгебры и методы теории моделей весьма близки и понимание взаимосвязей обогатило обе дисциплины. Некоторые конструкции, впервые найденные в математической логике, стали стандартными в алгебре и анализе, например так называемая конструкция ультрапроизведения, придуманная польским логиком Е. Лосем.

Одним из ярких достижений теории моделей 1960‐х годов стало создание нестандартного анализа Абрахамом Робинсоном. Он описал логическую конструкцию, которая позволила непротиворечиво рассматривать пополнение множества вещественных чисел бесконечно малыми и бесконечно большими числами. С помощью этой конструкции стало возможным дать объяснение исходной интуиции лейбницевских «бесконечно малых» и дать технически простое и интуитивное построение основных результатов математического анализа. n$ при $n>2$).

Методы теории доказательств — области математической логики, изучающей формальную доказуемость — также находят применения в «обычной» математике. Одним из успешных современных направлений является proof mining, извлечение конструктивных оценок из априори неконструктивных математических доказательств. Так называемые функциональные интерпретации, первоначально разработанные для анализа формальных систем, оказалось возможным применить и к конкретным содержательным математическим результатам (например, из области вещественного анализа, где интересен вопрос о скорости сходимости того или иного процесса к неподвижной точке и требуется явная оценка этой скорости). Результаты, полученные логическими методами, часто дают совершенно неочевидные усиления исходных теорем.

Логика в компьютерных науках. Если применения математической логики в «обычной» математике достаточно редки, то роль логических методов в информатике и компьютерных науках намного выше. Здесь математическая логика даёт подходящий язык для изучения возникающих задач и набор общих подходов к их решению. Удивительным образом, иногда оказывается, что концепции, сформулированные в математической логике очень давно и с другими целями, обретают новую жизнь в конкретных прикладных областях. Расскажем о некоторых направлениях, в которых логика доказала свою эффективность.

Реляционные базы данных и языки запросов. Многомиллиардная индустрия баз данных связана с технологией хранения больших объёмов структурированных данных, извлечением из них полезной информации и её обновлением. Поиск информации в базе данных осуществляется пользователем на языке запросов, который позволяет найти среди большого массива данных нужные сведения, потратив на это не слишком много времени. Поэтому языки запросов должны сочетать в себе достаточную гибкость для формулировки запросов и одновременно обеспечивать возможность эффективного поиска информации.

В 1960‐х годах американский учёный T.  Кодд понял, что самый обычный язык логики предикатов очень удобен для обеих целей, поскольку позволяет эффективно осуществлять поиск по запросу. Эффективность обеспечивается с помощью аппарата реляционной алгебры — языка операций над отношениями, разработанного до этого в математической логике (в школе Альфреда Тарского) как алгебраический эквивалент языка логики предикатов. Идея Кодда о том, что запросы на языке реляционной алгебры допускают эффективный поиск, была первоначальным стимулом в разработке реляционных баз данных и общеупотребительных в настоящее время языков запросов, таких как SQL. С тех пор теория баз данных и логических языков успешно развиваются рука об руку.

Верификация программ и протоколов. Задача верификации программ, протоколов, аппаратных средств является одной из наиболее трудных и практически важных в компьютерной индустрии. Под верификацией понимается доказательство корректности работы программы (протокола, процессорного чипа, и т. д.), т. е. соответствия того, что реально делает программа, тому, что нам хотелось бы, чтобы она делала. Поскольку программа работает с входными данными, а вариантов входных данных может быть бесконечно много, мы не можем протестировать работу программы на всех возможных входах. На практике применяют методы тестирования, которые увеличивают вероятность обнаружения ошибок, однако полной гарантии надёжности всё‐таки не дают.

Другой путь решения этой проблемы, также активно применяемый на практике, состоит в сведении рассматриваемой задачи к логическому вопросу о соответствии программы её формальной спецификации. Это предполагает формулировку требований к тому, что должна делать программа, на формальном языке спецификаций программ. (В качестве такого языка часто используется язык так называемой темпоральной, или временной, логики, одной из разновидностей модальных логик.)

Подход, называемый model checking, состоит в том, чтобы сопоставить программе граф, представляющий её возможные состояния и переходы между ними. Это позволяет свести задачу верификации программы к вопросу о выполнимости формулы, задающей спецификацию, в модели, представляющей программу. Для решения задачи проверки выполнимости формулы в данной модели разработаны эффективно работающие алгоритмы, что позволяет на практике верифицировать программы с большим числом состояний. Этот метод особенно хорошо себя зарекомендовал для верификации чипов.

Альтернативный подход, называемый theorem proving, состоит в том, чтобы сопоставить программе логическую формулу, выражающую её корректность, и искать формальное доказательство этой формулы — например, в исчислении предикатов. Этот подход на данный момент не так распространён на практике, как model checking, но продолжает развиваться. Успешность этого метода во многом зависит от эффективности работы пруверов — программ автоматического поиска формальных доказательств. Разработка такого рода систем активно ведётся в наши дни.

Теории типов и функциональное программирование. Парадигма функционального программирования сочетает в себе несколько базовых идей, первоначально возникших в математической логике.

Первая идея — это взгляд на функцию как на объект, к которому может применяться программа наряду с другими данными (аргументы функций в свою очередь могут быть функциями и т. д.). Функциональная программа в целом может рассматриваться как определение некоторой сложной функции, а исполнение программы — как процесс вычисления значения функции на данном аргументе, сводящийся к пошаговому упрощению (редукции) её определения.

Более привычный нам императивный стиль программирования, в традиции Тьюринга и фон Неймана, привязан к понятию состояния памяти компьютера, которое изменяется в результате применения команд, таких как присваивания переменным новых значений. Функциональные программы не предполагают явного хранения состояния вычисления, в них нет присваиваний, а функции больше соответствуют математическому пониманию функций, чем подпрограммы в императивном программировании, которые могут зависеть от внешних переменных и иметь побочные эффекты.

Эти особенности позволяют писать в функциональном стиле более прозрачный код, потенциально содержащий меньше ошибок. Кроме того, функциональные программы допускают хорошее распараллеливание, поскольку разные части определения функции могут быть вычислены независимо.

В последние годы функциональные языки занимают всё более важную нишу среди употребительных языков программирования и применяются в тех областях, где важно иметь надёжные программы, например, в банковской сфере. По существу, первым функциональным языком программирования было лямбда‐исчисление, придуманное Чёрчем как простейшая универсальная вычислительная модель. Идеи лямбда‐исчисления были затем воплощены в одном из первых действующих функциональных языков — языке LISP, а также во многих более современных языках вплоть до Ocaml и Haskell.

Другой ключевой идеей, идущей из математической логики, является идея типа данных, на которой основано подавляющее большинство языков программирования высокого уровня, не обязательно именно функциональных. Использование переменных и функций, которым приписан определённый тип (например, тип «число с плавающей точкой», или тип «массив целых чисел»), позволяет на уровне компиляции проводить контроль типов, что избавляет программы от значительного числа ошибок (связанных с несоответствием значения переменной типу). Развитие языков программирования идёт в сторону усовершенствования и усложнения системы типов, где контролю типов отводится всё большая роль.

Формальные языки с типами (в отличие от бестиповых языков, в которых все переменные имеют один и тот же тип) впервые возникли в фундаментальном труде Б. Рассела и А. Уайтхеда «Основания математики», целью которого было построение математики на основе непротиворечивой системы аксиом теории множеств. В математике эта система, однако, не прижилась и была заменена более простой бестиповой теорией множеств Цермело—Френкеля с аксиомой выбора.

В 1950‐е годы в логике было обнаружено, что в достаточно развитых системах на базе лямбда‐исчисления с типами последние ведут себя в точности как логические высказывания (языка интуиционистской логики), а функциональные программы — как формальные доказательства этих высказываний. Это явление, описанное здесь, разумеется, очень приблизительно, получило название соответствия Карри—Говарда. Через несколько десятков лет оно послужило основой для создания функциональных языков, в которых возможно написание программ с одновременной верификацией их кода. Наиболее известными языками такого рода являются Coq и Agda, созданные для формализации математических доказательств. В частности, именно на языке Coq удалось построить формальное доказательство гипотезы четырёх красок и ряда других трудных математических результатов. Эти же языки начинают применяться и для задач верификации программ, описанных в предыдущем пункте.

Этими тремя темами мы ограничим избранный список областей информатики, в которых на деле применяются результаты математической логики. Многие не менее важные темы при этом оказались не затронутыми: теория сложности вычислений, теория автоматов и монадическая логика, SAT‐solving, языки авторизации и контроля доступа к информации, логическое программирование и хорнова логика, онтологические базы данных и дескрипционная логика — перечисление можно очень долго продолжать.

Завершая обзор, посмотрим на отдельные области гуманитарных наук, испытавшие на себе влияние методов математической логики. Выбранные нами предметы касаются философии, языкознания и даже теории права. Эти разнообразные темы объединены в одну группу, поскольку связаны с изучением явлений, требующих модификации тех или иных аспектов классической логики.

Неклассические логики. Первые логические системы, отличные от традиционной двузначной, стали появляться ещё в то время, когда процесс формализации классической логики предикатов не был завершён. К настоящему времени неклассические логики представляют собой большое царство, населённое самыми разнообразными и экзотическими представителями (исчисляемое десятками семейств). Мотивации при рассмотрении неклассических логик могут быть самыми разными: попытки точнее передать те или иные свойства естественного языка; попытки построить систему, отвечающую тем или иным философским установкам; попытки расширить язык классической логики новыми выразительными возможностями или, наоборот, сузить выразительные возможности классической логики с тем, чтобы сделать её более эффективной для решения тех или иных задач. Проведём небольшую экскурсию по «зоопарку» неклассических логик.

Интуиционизм как философское течение возник в самом начале XX века в работах молодого нидерландского математика Л. Э. Я. Брауэра как реакция на кризис оснований математики и теории множеств. Характерной чертой философии Брауэра было желание избавить математику от неконструктивных теорем существования, т. е. утверждений о существовании тех или иных объектов, без возможности предъявить явно их конструкцию. Глубокий анализ привёл Брауэра к идее о том, что сама классическая логика, а именно закон исключённого третьего, является источником таких неконструктивных утверждений в математике. Это потребовало радикально пересмотреть традиционное понимание смысла математических утверждений, логических операций и кванторов.

Хотя сам Брауэр настаивал на неформальном характере своей философии математики — отсюда её название «интуиционизм» в противоположность гильбертовскому «формализму» — к началу 1930‐х годов возникла потребность в уточнении совокупности логических принципов, приемлемых с интуиционистской точки зрения. Решение этой задачи было дано учеником Брауэра А. Гейтингом, который сформулировал общепринятую в настоящее время интуиционистскую логику предикатов, опираясь на предшествовавшую работу А. Н. Колмогорова. Парадоксально, но в результате интуиционизм был также поставлен на прочную формальную основу.

Несмотря на поддержку ряда выдающихся математиков, одним из которых был Герман Вейль, интуиционизм не стал преобладающей философией математики. В настоящее время трудно найти подлинных сторонников этой философии даже среди логиков. Тем не менее, с точки зрения формальной логики, интуиционизм представляет собой стройную и богатую содержательными результатами систему. С течением времени было осознано, что интуиционистская логика скрывается во многих математических структурах, в частности в структурах топологической природы. Например, было обнаружено, что возникшее в работах А. Гротендика понятие топоса можно рассматривать как модель интуиционистской логики.

С другой стороны, интуиционистская логика часто возникает в различных приложениях в компьютерных науках. Это не случайно, поскольку интуиционистская логика теснее связана с понятием вычисления, чем логика классическая. Одним из важнейших проявлений этой связи является уже упомянутое соответствие Карри—Говарда.

Классическая логика допускает интерпретацию в логике интуиционистской, поэтому современная точка зрения на их соотношение состоит в том, что интуиционистская логика не ограничивает, а, наоборот, добавляет в классическую новые выразительные возможности — такие как различие между неконструктивным и конструктивным утверждением о существовании.

Модальная логика. Другим классом логик, обогащающих классическую новыми выразительными возможностями, являются так называемые модальные логики. Язык модальной логики, наряду с обычными связками, содержит новую одноместную логическую связку $ □\, $. Высказывание $□\, A$ в разных контекстах может пониматься совершенно по‐разному, что приводит к разным постулируемым принципам, т. е. разным модальным логикам. Стандартные логические связки, такие как импликация или отрицание, как правило, сохраняют в модальной логике классическую интерпретацию. (Разумеется, могут рассматриваться модальные логики и над другими логиками, например над интуиционистской, однако такие системы в целом сложнее и потому менее распространены.)

Исторически первым, идущим ещё от Аристотеля, прочтением формулы $□\, A$ было высказывание «$A$ необходимо». (Здесь мы говорим о языковой конструкции, присутствующей в нашем естественном языке, а не о каком‐либо математическом понимании того, что значит «необходимо».) Двойственное высказывание «не $A$ не является необходимым» обычно отождествляется с высказыванием «$A$ возможно» и обозначается $◇\, A$.

Перечислим некоторые известные интерпретации модальности, приводящие к интересным и полезным семействам логик.

Логика доказуемости: $□\, A$ означает «$A$ доказуемо» в данной аксиоматической теории, например в теории множеств. При этом высказывания понимаются как высказывания в языке теории множеств, каковым можно считать и само высказывание о доказуемости утверждения $A$. Эта логика интересна тем, что даёт точную математическую семантику модальности и применяется для исследования обычных классических аксиоматических теорий.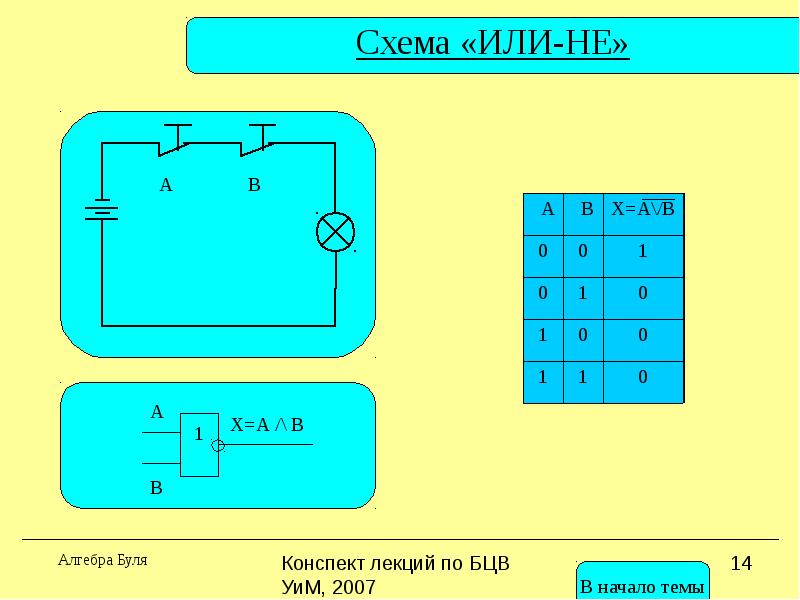

Временная логика, описывающая развитие некоторого процесса во времени: $□\, A$ означает «всегда в будущем будет верно $A$». Различные модели течения времени — непрерывное, дискретное или даже ветвящееся — приводят к разным временным логикам. Временные логики, применяемые на практике для верификации программ, используют и некоторые дополнительные связки, например двухместную связку, выражающую «$A$ имеет место до тех пор, пока $B$».

Эпистемическая логика, описывающая знания и обмен информации между несколькими агентами: $□\,_x A$ означает «агенту $x$ известно $A$» (в этой логике, как правило, описываются знания нескольких агентов $x$, $y$, … и каждому из них соответствует своя модальность $□\,_x$, $□\,_y$, …). Эпистемическая логика является частью (формальной) эпистемологии — обширного и важного раздела философии, занимающегося исследованием таких понятий, как знание и вера, того как знание возникает, как оно связано с понятием доказательства (обоснования).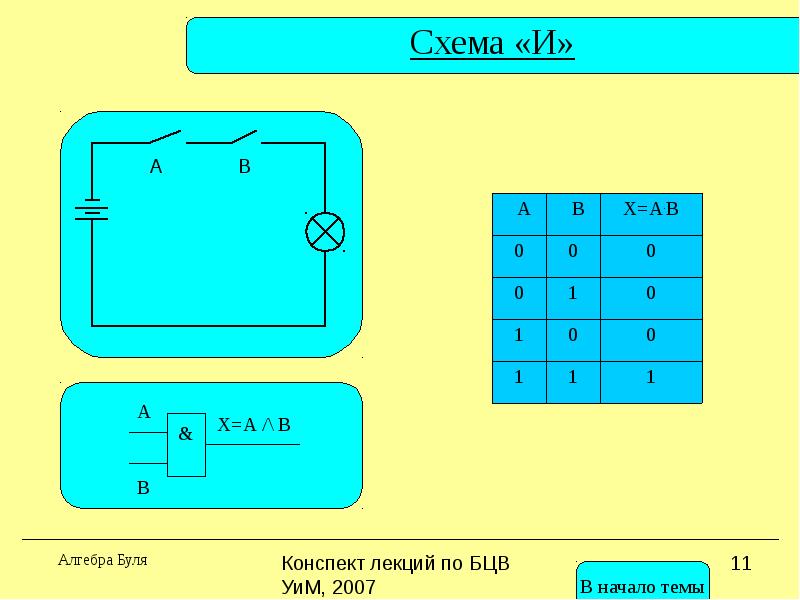 Формализм эпистемической логики позволяет построить модели различных аспектов этих явлений и использовать их для анализа тех или иных теоретических положений.

Эпистемическая логика также находит более конкретные применения в компьютерных науках и искусственном интеллекте для описания знания, возникающего в системах с несколькими агентами. Например, условие корректности протокола, связанного с обменом информацией, в котором не должна допускаться утечка информации третьим лицам, может быть сформулировано на языке эпистемической логики.

Деонтическая логика формализует модальности типа долженствования, например $□\, A$ можно понимать как «$A$ требуется» или «$A$ обязательно» (двойственную модальность можно понимать как «$A$ разрешено»). Такие логики впервые стали рассматриваться в философии и теории права для формализации и анализа различных аспектов правовых систем.

Многозначная логика и нечёткая логика. Многозначные логики возникают, если допускаются другие истинностные значения, помимо классических истины 1 и лжи 0.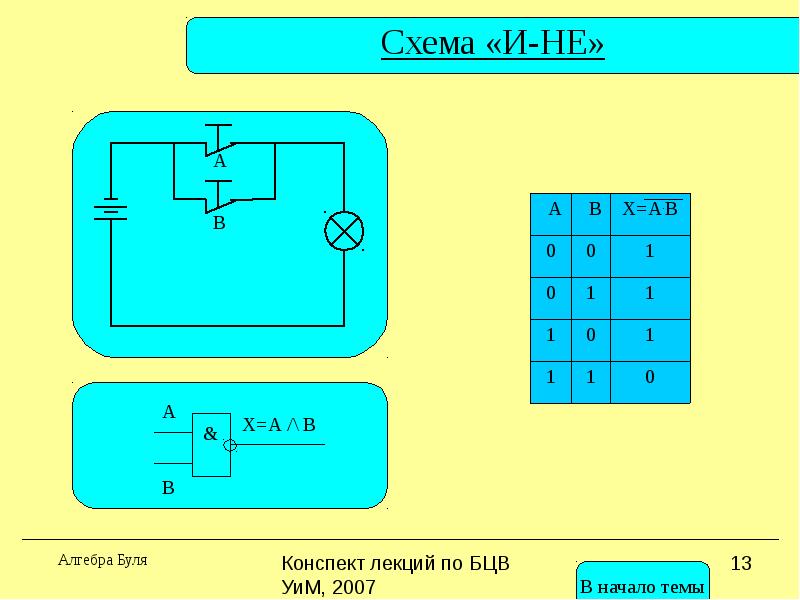 Например, можно рассматривать промежуточное значение 1/2 и интерпретировать его как «неизвестно». Следующий шаг требует определения того, каким образом вычисляются значения логических связок, и конкретное решение по этому поводу может привести к различным логикам.

Если пойти дальше по пути многозначности, то естественно возникает идея о том, что истинностным значением высказывания может быть любое вещественное число в интервале $[0,1]$ (например, это число может выражать степень нашей уверенности в справедливости высказывания). Такие логики часто называют «нечёткими» (fuzzy), поскольку предикаты в такой системе могут выглядеть как размытые, не имеющие чётких границ. Например, высказывание о том, что видимый цвет является красным, не является чётким в силу неопределённости самого понятия «красный».

Нечёткие логики призваны формализовать рассуждения в условиях неопределённости или неточности информации. Подлинным «отцом» нечёткой логики и теории нечётких множеств был Л. Заде. Он увидел потенциал этой логики для различных инженерных применений, например в такой области, как экспертные системы или теория управления, и сделал очень много для её популяризации.

Немонотонная логика. Классическая логика обладает очевидным свойством монотонности: добавление новых аксиом не отменяет никаких ранее доказанных теорем. В работе с базами данных, где не вся содержащаяся информация может быть верной, появление новой информации может привести к пересмотру уже известных фактов и их отмене. В этом случае свойство монотонности нарушается.

Аргументы и доказательства, приводимые в суде, могут быть оспорены или опровергнуты противной стороной. Процесс выстраивания аргументов, таким образом, на практике выглядит совершенно непохоже на привычные нам дедуктивные математические доказательства. Эти аспекты изучает теория аргументации — весьма развитая область исследований, связанная с философией, лингвистикой, теорией права и искусственным интеллектом. Формальные модели аргументации во многих случаях базируются на немонотонных логиках.

Паранепротиворечивая логика. Как известно, в классической логике действует закон ex contradictio quodlibet, т. е. из противоречия следует всё что угодно. Поэтому противоречивые классические системы все эквивалентны между собой и, по существу, бесполезны. На практике людям приходится рассуждать в не столь стерильных условиях: не всегда бывает известно, есть ли противоречие в имеющейся информации, на основании которой приходится делать выводы. Логики, приспособленные для рассуждений в условиях возможно противоречивых предположений, называются паранепротиворечивыми. В таких системах возникновение противоречия не приводит к доказуемости всех вообще утверждений.

Можно сказать, что наша обыденная логика (как способ умозаключений на основе имеющейся информации) является одновременно нечёткой, паранепротиворечивой и немонотонной. Разумеется, все эти формальные системы являются лишь приближёнными и грубыми моделями отдельных аспектов той самой «обыденной логики».

Грамматики Хомского и семантика Монтегю. Одной из теорий, соединивших в себе сразу несколько аспектов неклассических логик — кванторы, предикаты, модальности, модели Крипке и лямбда‐абстракцию — является семантика Монтегю. Эта теория, предложенная американским логиком Р. Монтегю в начале 1970‐х годов, представляет собой попытку применить идеи математической логики к трудной задаче описания семантики естественного языка. Она, по существу, положила начало целому направлению в математической лингвистике — формальной семантике. Ранее работы Н. Хомского, создавшего теорию формальных грамматик, произвели революцию в понимании синтаксиса естественных языков. Применения математической логики в лингвистике, из которых мы вскользь упомянули лишь два важных направления, безусловно заслуживают отдельного разговора.

Неужели это всё математика? — недоумённо воскликнет читатель. И да, и нет. Исследователи, применяющие методы математической логики в той или иной области знания, должны прежде всего быть компетентными специалистами именно в этой области и разбираться в постановках специфических для неё задач. Напомним, что многие создатели математической логики — Гёдель, Тьюринг, фон Нейман и др. — не были только лишь «чистыми» математиками.

Тем не менее, используемый в приложениях логический аппарат является самым настоящим математическим аппаратом, даже если он и совсем не похож на ту математику, которой традиционно обучают на математических факультетах университетов. Вопросы, связанные с неклассическими логиками — например, вопросы их полноты относительно семантики Крипке или топологической семантики, вопросы классификации различных семейств неклассических логик — имеют существенную математическую составляющую. Для успешной работы в философской логике, математической лингвистике, теории игр, теории баз данных и других областях приложений этой математикой также нужно овладеть. К счастью, порог входа здесь не так уж высок, и математическую логику с успехом преподают на факультетах компьютерных наук, философии и лингвистики.

Математически наиболее развитые части математической логики — такие, как теория множеств, теория алгоритмов и сложности вычислений, теория моделей или ординальный анализ формальных систем, содержат некоторые из наиболее сложных с математической точки зрения результатов и применяемых методов. Разумеется, современные исследования в этих давно сложившихся областях целиком и полностью лежат в области математики.

Кибернетический тузик, алгебра Буля, мультивибратор: как учили IT в СССР 40 лет назад

«Читатель! Если тебе никогда не приходилось знакомиться с устройством электронных вычислительных машин, если ты не в ладах с математикой, физикой и электроникой, а главное, если ты не привык докапываться до сути вещей, то лучше отложи эту книжку и займись чем-нибудь другим. Не нужно терять время зря».

Таким приветствием начинается книга «Что такое информатика», издания 1989 года. Мы прочитали несколько раритетных IT-учебников и спешим поделиться впечатлениями с вами.

Образный язык

Авторы советских учебников по кибернетике и информатике часто используют образы и аналогии, чтобы объяснить технические явления. Вот, например. О том, по какому принципу работает кибернетическая машина: «И в живых организмах, и в машинах-автоматах есть чувствительные органы. Это уши, глаза – у человека, микрофоны и фотоэлементы – у машины. Они осуществляют связь с внешним миром. Как у тех, так и у других есть центр управления, определяющий порядок действий в соответствии с полученными извне сведениями. Как те, так и другие имеют исполнительные механизмы, выполняющие указания, выработанные в «центре».

Липа никому не нужна.

«Компьютер, как и мясорубка, перерабатывает всё, что в него заложат. Если закладывают цифры «с потолка», то ЭВМ выдаёт «липу».

«Великий поэт Александр Блок ещё в начале века создал образ «стальных машин, где дышит интеграл». Вычислительная техника стала буквальным воплощением этих строк».

IT-сторителлинг – вот где ему можно поучиться

Советские технические книги богаты не только на образный язык и сравнения, но и на любопытные истории об изобретениях. Полистав «Юного кибернетика» вы найдёте отличные истории о пишущем мальчике швейцарского часовщика Пьера Дро и телеграфном будильнике Эдисона.

Истории не рассказывают развлечения ради – они подводят читателя к теме и помогают усваивать сложные понятия.

«На первый взгляд может показаться, что «игрушки» Пьера и Анри Дро не имеют никакого отношения к развитию техники и о них можно было бы не вспоминать. Но это не совсем так. Механические люди Дро сыграли очень важную роль в общем процессе человеческого познания природы и заложили основу автоматов с программным управлением. Уже в начале XIX века появляются прядильные и ткацкие станки-автоматы с программным управлением».

Авторы приводят любопытные исторические факты, помогающие лучше понять принципы теории вероятностей, распределения случайных числе и т.п. Вероятность выпадения орла и решки при подбрасывании семметричной монеты одинакова. Но как доказать это на практике? И есть ли достоверные «пруфы»? Есть.

Книга говорит о французском естествоиспытателе 18 века Жорже Бюффоне, который подбросил монету 4 040 раз, из которых 2 048 раз монета упала вверх орлом. Частота составила 0,50693.

А ещё более терпеливый учёный, математик и биолог Карл Пирсон (вы можете знать его по коэффициенту корреляции Пирсона) подбросил монету 24 000 раз (!), получив частоту выпадения орла, равную 0,5005.

Истории подкрепляются выводами, которые после такой наглядной иллюстрации должны усваиваться на «отлично»: «Случайные события не могут зависеть от предыдущих результатов […] Кубик или монета не имеют памяти».

Даже то, что люди забывают написать на конверте адрес получателя письма, подчиняется законам массовых явлений. По статистике почты, процент таких безадресных писем остаётся неизменным из года в год. Если бы почтовые сервисы позволяли отправить в никуда письмо без получателя, статистика, вероятно, была бы такой же.

Чтобы объяснить обратное явление – действительно случайные события – авторы снова обращаются к сторителлингу. А именно, к коротким рассказам о случайных открытиях.

Познакомьте детей с компьютерами, в которых дисковод был отдельным устройством!

ПО ССЫЛКЕ можно скачать отсканированную цветную книгу «А я был в компьютерном городе».

Что вызывает улыбку

Писатели-фантасты в своих прогнозах были куда смелее и оптимистичнее авторов советских учебников. Вот что косвенно говорит об искусственном интеллекте «Юный кибернетик»:

«Разве нельзя предусмотреть в программе машины заранее всё, вплоть до мелочей? Нет, всего не предусмотришь. Это было бы возможно, если бы речь шла о предмете, имеющим вполне определённое число признаков, каждый из которых можно моделировать и воспроизвести в машине. Но мозг человека обладает бесконечным количеством свойств. Создать его искусственно, воспроизведя в отдельности каждое из свойств, конечно, невозможно».

Прочитайте рассуждения советских авторов о жизни на Марсе. Сложно сказать, видел ли этот учебник Элон Маск.

«Недаром сейчас ученые полагают, что высадившиеся на Марс космонавты могут столкнуться с какими-нибудь дальними родственниками представителей нашей земной жизни. Пусть самыми простыми. Условия на Марсе особые, мало похожие на земные. Значит, нужно быть готовыми к тому, что и марсианские живые существа не такие, как на Земле».

Это сейчас IT-специалистам нужно постоянно шагать, чтобы оставаться на месте. И бежать, чтобы двигаться вперёд. Сорок лет назад программа обучения выглядела так:

«Для овладения языком общения с ЭВМ на хорошем уровне потребуется уже часов 40–50, а главное – практика. Итак, из символов – букв, цифр и математических знаков – складываются слова формального языка. А из слов – выражения и операторы».

Улыбаемся и рвению, с которым авторы призывают к экспериментам. Почти уверены, что сейчас этим никто не будет заниматься:

Так выглядит введение в тему «Генератор случайных чисел». А вы питаете странную склонность к начертанию восьмёрки?..

До появления Google оставалось 9 лет.

Что говорите, у вас ультратонкий ноутбук? А у нас дисплейный класс.

Siri, что такое компьютер-молчун?

Философские размышления

Советское образование хвалят за его фундаментальный подход, формирование базиса мышления. В старых учебниках мы нашли несколько полезных мыслей, справедливых и сейчас.

1. Там, где просто нет порядка, компьютеры пользы не принесут, они только поглотят ресурсы и останутся дорогостоящей управленческой забавой, памятниками бесхозяйственности – пирамидами из электроники.

2. Купит завод, институт или трест компьютер – отдачи не видно. Все идёт по старинке. В чем дело? Нет хороших, высококачественных программ решения нужных задач, никто не позаботился и о том, откуда будет поступать и кем готовиться исходная числовая или буквенная информация.

3. Возможности АСУ (автоматических систем управления) используются лишь в незначительной степени. Параллельно им «дедовскими» способами работают со старыми документами и по старым правилам управленцы, конструкторы, хозяйственники, снабженцы, кадровики. За последние полтора десятилетия резкого повышения эффективности аппарата управления и планирования не произошло, хотя расходы в сфере управления в связи с введением в строй АСУ заметно возросли.

4. (А этот абзац заставил задуматься о собственной лени. Три десятилетия назад добывать знания было труднее, но эта сложность стимулировала людей учиться. Делает ли это широкая доступность?..)

5. «Как далеко зайдет процесс интеллектуализации машин? Не получится ли так, как предсказывал чешский писатель Карел Чапек более пятидесяти лет назад: роботы окажутся умнее людей и возьмут власть над ними? Конечно, ничего подобного произойти не может. […] Так и с компьютерами. Человек в своём умственном развитии всегда шел и будет идти впереди машины, да иначе и быть не может».

Кстати, Стивен Хокинг придерживается иного мнения.

 

О тузике, Буле и мультивибраторе

В заголовок вынесены названия глав из книги «Юный кибернетик» 1978 г издания.

Кибернетический тузик – это простейшая собака-робот, представленная впервые в 1929 году на радиовыставке в Париже. Собака была сделана из фанеры и обклеена фетром. В глазные впадины были вставлены стеклянные шарики.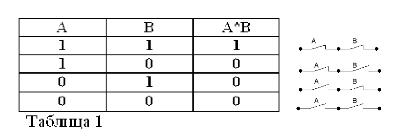 Когда собаку освещали, она начинала двигаться на свет и яростно лаяла.

Авторы объясняют принципы работы тузика и… подробно рассказывают, как его сделать. По книгам издательства «Детская литература» можно было спаять фоторобот, ориентирующийся на луч света. Это впечатляет.

В алгебре Буля элементы множества выражены не числами, а высказываниями. Эти высказывания рассматриваются не с точки зрения смысла, а в отношении того, истинны они или ложны. Учебник по кибернетике вводит понятия «логической суммы», «сомножителя», «логического уровнения».

Именно алгебра Буля отлично подошла для анализа и синтеза релейных схем. Её использовали для работы релейных и переключательных цепей с переменным сигналом. В основу её «преемницы» – релейной алгебры – легли операции И, ИЛИ, НЕ, условия для работы электрических схем. If…then…else!

С мультивибратором всё просто. Это генератор периодической последовательности импульсов прямоугольной формы. Как автоматический переключатель он используется в ёлочных гирляндах и в плате электронного волчка. А ещё мультивибратор может преобразовывать постоянный ток в колебательный.

***

Посмотрите отличное видео советских времён об информатике и компьютерах. Обволакивающий голос диктора, картинка в стиле «сепия» и та самая фоновая музыка прилагаются.

Смотришь и умиляешься: «Рисунок выполняется специальным устройством для ввода информации, так называемой мышью». Поностальгируйте!

Интересно? Поделитесь с друзьями!

Определение логической алгебры

Что такое булева алгебра?

Булева алгебра – это раздел математики, который занимается операциями с логическими значениями и включает двоичные переменные. Булева алгебра берет свое начало в книге математика Джорджа Буля 1854 года.

Отличительной чертой булевой алгебры является то, что она занимается только изучением двоичных переменных. Чаще всего логические переменные представлены с возможными значениями 1 («истина») или 0 («ложь»).Переменные также могут иметь более сложные интерпретации, например, в теории множеств. Булева алгебра также известна как бинарная алгебра.

Ключевые выводы

• Булева алгебра – это раздел математики, который имеет дело с операциями над логическими значениями с двоичными переменными.
• Логические переменные представлены в виде двоичных чисел для представления истин: 1 = истина и 0 = ложь.
• Элементарная алгебра занимается числовыми операциями, тогда как булева алгебра занимается логистическими операциями.
• Логическая алгебра использует соединение, дизъюнкцию и отрицание, в отличие от сложения, вычитания, умножения и деления.
• Основное современное использование булевой алгебры – это языки компьютерного программирования.
• В финансах в моделях биномиального ценообразования опционов используется булева алгебра, которая помогает определить, когда опцион должен быть исполнен.

Понимание булевой алгебры

Булева алгебра отличается от элементарной алгебры, поскольку последняя имеет дело с числовыми операциями, а первая – с логическими. Элементарная алгебра выражается с помощью основных математических функций, таких как сложение, вычитание, умножение и деление, тогда как булева алгебра имеет дело с конъюнкцией, дизъюнкцией и отрицанием.

Понятие булевой алгебры было впервые введено Джорджем Булем в его книге The Mathematical Analysis of Logic и далее расширено в его книге An Study of the Laws of Thought . Поскольку ее концепция была подробно описана, булевская алгебра в основном использовалась в языках программирования.Его математические цели используются в теории множеств и статистике.

Булева алгебра в финансах

Булева алгебра находит применение в финансах посредством математического моделирования рыночной деятельности. Например, исследованию цен на опционы на акции может помочь использование бинарного дерева для представления диапазона возможных результатов для базовой ценной бумаги. В этой биномиальной модели ценообразования опционов, где есть только два возможных результата, логическая переменная представляет увеличение или уменьшение цены ценной бумаги.

Этот тип моделирования необходим, потому что для американских опционов, которые могут быть исполнены в любое время, траектория цены ценной бумаги так же важна, как и ее окончательная цена. Модель ценообразования биномиальных опционов требует, чтобы траектория цены ценной бумаги была разбита на серию дискретных временных диапазонов.

Таким образом, модель ценообразования биномиальных опционов позволяет инвестору или трейдеру видеть изменение цены актива от одного периода к другому. Это позволяет им оценивать вариант на основе решений, принятых на разных этапах.Поскольку опцион в США может быть исполнен в любое время, это позволяет трейдеру определить, следует ли ему использовать опцион или удерживать его в течение более длительного периода. Анализ биномиального дерева позволит трейдеру заранее увидеть, следует ли исполнять опцион. Если есть положительное значение, то опцион должен быть исполнен, если значение отрицательное, то трейдер должен удерживать позицию.

математических единиц за минуту: логическая алгебра

A	B	A AND B
True	True	True
True	False	False
False	True	Ложь
Ложь	Ложь	Ложь

Простая таблица истинности, показывающая все
возможных значений « A И B ».

Каждый раз, когда вы пользуетесь компьютером, вы полагаетесь на логическую логику : систему логики, созданную задолго до появления компьютеров, названную в честь английского математика Джорджа Буля (1815–1864). В логической логике утверждения могут быть истинными или ложными (например, в данный момент «я хочу чашку чая» ложно, но «я хочу кусок торта» всегда верно), и вы можете связать их вместе, используя слова И , ИЛИ и НЕ. Чтобы установить, являются ли эти составные утверждения истинными или ложными, вы можете создать так называемую таблицу истинности , в которой перечислены все возможные значения, которые могут принимать базовые операторы, а затем все соответствующие значения, которые может принимать составной оператор.(Вы можете узнать больше в математике через минуту: таблицы истинности.)

Таблицы истинности полезны для простых логических утверждений, но быстро становятся утомительными и подверженными ошибкам для более сложных утверждений. Буль пришел на помощь, гениально осознав, что бинарные логические операции ведут себя поразительно похоже на наши обычные арифметические операции, с некоторыми особенностями.

В этом новом виде арифметики (называемом булевой алгеброй ) переменные представляют собой логические утверждения (грубо говоря, предложения, которые либо истинны, либо ложны).Поскольку они могут принимать только два значения, мы можем написать 0 для утверждения, которое, как мы знаем, ложно, и 1 для утверждения, которое, как мы знаем, истинно. Затем мы можем переписать OR как своего рода дополнение, используя только 0 и 1:

0 + 0 = 0 (поскольку «ложь ИЛИ ложь» – ложь)
1 + 0 = 0 + 1 = 1 (поскольку «истина ИЛИ ложь» и «ложь ИЛИ истина» оба истинны)
1 + 1 = 1 (поскольку “истина ИЛИ истина” верно).

Мы можем переписать AND как своего рода умножение:

0 x 1 = 1 x 0 = 0 (поскольку «ложь И истина» и «истина И ложь» оба ложны)
0 x 0 = 0 (поскольку «ложь И ложь» – ложь)
1 x 1 = 1 (поскольку “правда И правда” верно).

Поскольку переменные могут иметь только значения 0 и 1, мы можем определить операцию НЕ как дополнение, взяв число, противоположное ее значению:

Если A = 1, то НЕ A = 0
Если A = 0, то НЕ A = 1
A + НЕ A = 1 (поскольку «истина ИЛИ ложь» истинна)
A x НЕ A = 0 (поскольку «истина И ложь» – ложь).

Наша новая версия этих операций во многом похожа на наши более знакомые понятия сложения и умножения, но есть несколько ключевых отличий.Части уравнений могут удобно исчезать в булевой алгебре, что может быть очень удобно. Например, переменная B в

A + A x B

не имеет значения, независимо от того, какое значение имеет B или какое логическое утверждение оно представляет. Это потому, что если A истинно (или, что эквивалентно A = 1), то A OR ( A И B ) истинно независимо от того, истинно ли утверждение B или ложно. И если A ложно (то есть A = 0), то ( A AND B ) ложно независимо от значения B , и поэтому A OR ( A AND B ) неверно. Таким образом, логическая алгебра предоставляет нам исчезающий акт: выражение A + A x B равно простому маленькому A :

A + A x B = A .

Кроме того, в булевой алгебре существует своего рода обратная двойственность между сложением и умножением:

( A + B ) ‘= A ‘ x B ‘и ( A x B )’ = A ‘+ B ‘.

Эти два равенства известны как законы Де Моргана в честь британского математика Августа де Моргана (1806–1871). (Вы можете убедиться, что они верны, используя эквивалентные таблицы истинности.)

Это всего лишь два трюка, которые булева алгебра использует для упрощения сложных логических выражений – спасибо, Джордж!

Учебное пособие по таблице истинности булевой алгебры

– объяснение XOR, NOR и логических символов

Все мы любим компьютеры. Они могут делать так много удивительных вещей. За пару десятилетий компьютеры полностью изменили почти все аспекты человеческой жизни.

Они могут выполнять задачи разной степени сложности, просто переворачивая нули и единицы. Замечательно видеть, как такое простое действие может привести к такой сложности.

Но я уверен, что вы все знаете, что такая сложность не может быть достигнута (практически) простым случайным переворачиванием чисел. За этим действительно есть некоторые причины.Существуют правила, которые определяют, как это должно быть сделано. В этой статье мы обсудим эти правила и увидим, как они управляют “мышлением” компьютеров.

Что такое булева алгебра?

Правила, о которых я говорил выше, описываются в области математики, называемой булевой алгеброй.

В своей книге 1854 года британский математик Джордж Буль предложил систематический набор правил для манипулирования ценностями истины. Эти правила дали математическую основу для работы с логическими предложениями. Эти наборы основ привели к развитию булевой алгебры.

Чтобы лучше понять булеву алгебру, мы сначала должны понять сходства и различия между булевой алгеброй и другими формами алгебры.

Алгебра в целом занимается изучением математических символов и операций, которые могут быть выполнены с этими символами.

Эти символы не имеют самостоятельного значения. Они представляют собой какое-то другое количество. Именно эта величина придает некоторую ценность этим символам, и именно с этой величиной фактически выполняются операции.

Логическая алгебра также имеет дело с символами и правилами, которые управляют операциями с этими символами, но разница заключается в , что эти символы представляют .

В случае обычной алгебры символы представляют действительные числа, тогда как в булевой алгебре они представляют значения истины.

На изображении ниже показан весь набор вещественных чисел. Набор действительных чисел включает натуральные числа (1, 2, 3, 4 . …), целые числа (все натуральные числа и 0), целые числа (…..- 2, -1, 0, 1, 2, 3 …) и так далее. Обычная алгебра занимается всем этим набором чисел.

Значения «Истина» для сравнения состоят из набора только двух значений: «Ложь» и «Истина». Здесь я хотел бы отметить тот факт, что мы можем использовать любой другой символ для представления этих значений.

Например, в информатике мы чаще всего представляем эти значения, используя 0 и 1. 0 используется для False и 1 для True.

Вы также можете сделать это более изящными способами, представив значения истинности некоторыми другими символами, такими как Кошки и Собаки или Бананы и Апельсины.

Дело в том, что внутреннее значение этих символов останется неизменным независимо от того, какой символ вы используете. Но убедитесь, что вы не меняете символы при выполнении операций.

Теперь вопрос в том, что если (Истина и Ложь), (0 и 1) – это просто представления, то что они пытаются представить?

Значение, лежащее в основе значений истинности, исходит из области логики, где значения истинности используются, чтобы определить, является ли предложение «Истинным» или «Ложным». Здесь значения истинности представляют отношение предложения к истине, то есть, является ли предложение истинным или ложным.

Предложение – это просто утверждение вроде «Все кошки милые».

Если вышеприведенное утверждение верно, то мы присваиваем ему значение истинности «Истина» или «1», в противном случае мы присваиваем ему «Ложь» или «0».

В цифровой электронике истинные значения используются для представления состояний «включено» и «выключено» электронных схем. Мы обсудим это подробнее позже в этой статье.

Логические операции и таблицы истинности

Как и в обычной алгебре, в булевой алгебре есть операции, которые можно применять к значениям для получения некоторых результатов. Хотя эти операции не похожи на операции в обычной алгебре, потому что, как мы обсуждали ранее, булева алгебра работает со значениями истины, а не с действительными числами.

В логической алгебре есть три основных операции.

ИЛИ : Также известен как Disjunction . Эта операция выполняется с двумя логическими переменными.Результатом операции ИЛИ будет 0, когда оба операнда равны 0, в противном случае будет 1.

Чтобы получить более ясное представление о том, что делает эта операция, мы можем визуализировать ее с помощью приведенной ниже таблицы истинности .

  Таблицы истинности дают нам подробное представление о том, что делают булевы операции, а также служат удобным инструментом для выполнения логических операций.

ИЛИ Операция

Переменная-1 Переменная-2 Выход
  0 0 0
  0 1 1
  1 0 1
  1 1 1  

И : Также известна как Соединение .Эта операция выполняется с двумя логическими переменными. Результатом операции И будет 1, если оба операнда равны 1, в противном случае – 0. Таблица истинности представлена ​​следующим образом.

  И Работа

Переменная-1 Переменная-2 Выход
  0 0 0
  0 1 0
  1 0 0
  1 1 1  

НЕ : Также известно как Отрицание . Эта операция выполняется только с одной переменной. Если значение переменной равно 1, эта операция просто преобразует его в 0, а если значение переменной равно 0, то оно преобразует его в 1.

  Не работает

Выход переменной-1
  0 1
  1 0  

Булева алгебра и цифровые схемы

После своего первоначального развития булева алгебра в течение очень долгого времени оставалась одним из тех понятий в математике, которые не имели каких-либо значительных практических приложений.

В 1930-х годах американский математик Клод Шеннон понял, что булеву алгебру можно использовать в схемах, в которых двоичные переменные могут представлять сигналы «низкого» и «высокого» напряжения или состояния «включено» и «выключено».

Эта простая идея создания схем с помощью булевой алгебры привела к развитию цифровой электроники, которая внесла большой вклад в разработку схем для компьютеров.

Цифровые схемы реализуют логическую алгебру с помощью логических вентилей. Логические ворота – это схемы, которые представляют собой логическую операцию. Например, вентиль ИЛИ будет представлять операцию ИЛИ. То же самое касается ворот НЕ и И.

Наряду с основными логическими вентилями у нас также есть логические вентили, которые могут быть созданы с использованием комбинации базовых логических вентилей.

И-НЕ : вентиль И-НЕ образован комбинацией вентилей НЕ и И. Логический элемент И-НЕ дает на выходе 0, если оба входа равны 1, иначе 1.

Элемент И-НЕ содержит свойство функциональной полноты, что означает, что любая логическая функция может быть реализована только с использованием комбинации только элементов И-НЕ.

  Ворота NAND

Переменная-1 Переменная-2 Выход
  0 0 1
  0 1 1
  1 0 1
  1 1 0  

NOR : вентиль НЕ-НЕ образован комбинацией вентилей НЕ и ИЛИ.Элемент ИЛИ-НЕ дает на выходе 1, если оба входа равны 0, в противном случае – 0.

Элемент ИЛИ-НЕ, как и элемент И-НЕ, имеет свойство функциональной полноты, что означает, что любая логическая функция может быть реализована просто с помощью комбинации элементов ИЛИ-НЕ.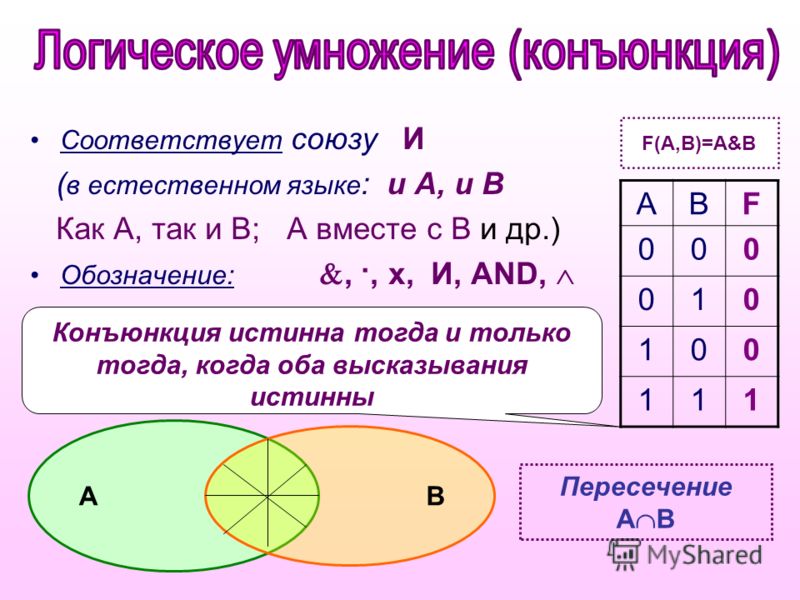 Только.

  NOR Ворота

Переменная-1 Переменная-2 Выход
  0 0 1
  0 1 0
  1 0 0
  1 1 0  

Большинство цифровых схем построено с использованием логических элементов И-НЕ или ИЛИ-ИЛИ из-за их функциональной полноты, а также из-за того, что их легко изготовить.

Помимо вышеупомянутых ворот, у нас также есть некоторые особые ворота, которые служат для определенной цели. Это следующие элементы:

XOR : вентиль XOR или вентиль Exclusive-OR – это особый тип логического элемента, который дает 0 на выходе, если оба входа равны 0 или 1, в противном случае он дает 1.

  XOR Ворота

Переменная-1 Переменная-2 Выход
  0 0 0
  0 1 1
  1 0 1
  1 1 0  

XNOR : вентиль XNOR или вентиль Exclusive-NOR – это особый тип логического элемента, который дает 1 на выходе, когда оба входа равны 0 или 1, в противном случае он дает 0.

  Ворота XNOR

Переменная-1 Переменная-2 Выход
  0 0 1
  0 1 0
  1 0 0
  1 1 1  

Заключение

Итак, со всем этим мы можем закончить здесь наше обсуждение булевой алгебры.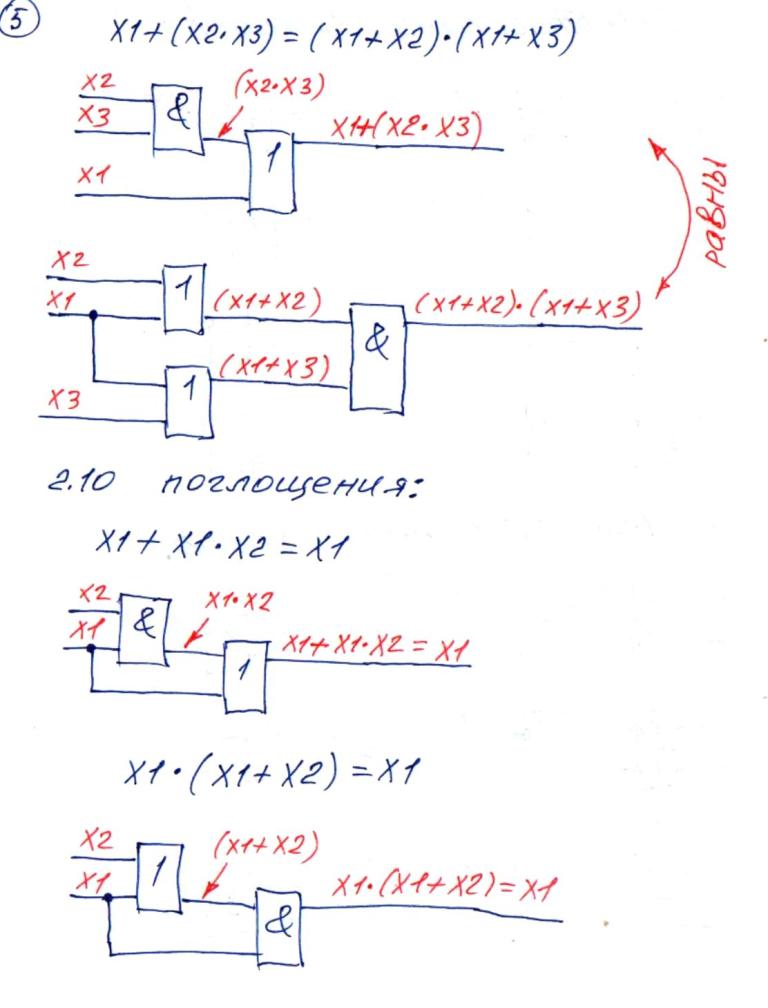 Я надеюсь, что теперь у вас есть достойное представление о том, что такое булева алгебра.

Это определенно не все, что вам нужно знать о булевой алгебре. Булева алгебра содержит множество концепций и деталей, которые мы не смогли обсудить в этой статье.

Логическая алгебра – курс цифровой электроники

Булева алгебра, логическая алгебра, позволяет применять правила, используемые в алгебре чисел, к логике.Он формализует правила логики. Булева алгебра используется для упрощения логических выражений которые представляют собой комбинационные логические схемы. Он сокращает исходное выражение до эквивалентного выражения с меньшим количеством терминов, что означает, что для реализации требуется меньше логических вентилей. комбинационная логическая схема.

Калькулятор логических выражений

Используйте калькулятор, чтобы найти сокращенное логическое выражение или проверить свои собственные ответы.

Ваш ответ

Примечания:
• Используйте ~ * + для обозначения НЕ И ИЛИ соответственно. Не пропускайте оператор * для операции И.
  • (~ AB) + (B ~ C) + (AB) вернет ошибку
  • (~ A * B) + (B * ~ C) + (A * B) в порядке
• Логические операции следуют порядку приоритета НЕ И ИЛИ. Выражения внутри квадратных скобок () всегда оцениваются первыми, имея приоритет над порядком приоритета.
• Пожалуйста, вводите только переменные, константы типа 0,1 не допускаются.
• Переменные E, I, N, O, Q, S не допускаются

Упрощение логических выражений

Ниже показан пример использования алгебраических методов для упрощения логического выражения

~ (A * B) * (~ A + B) * (~ B + B)
~ (A * B) * (~ A + B) * 1	6 – Закон дополнения
~ (A * B) * (~ A + B)	5 – Закон идентичности
(~ A + ~ B) * (~ A + B)	8 – Закон ДеМоргана
~ A + ~ B * B	4 – Закон распределения
~ A + 0	6 – Закон дополнения
~ A	5 – Закон идентичности

Каждая строка дает новое выражение и правило или правила, использованные для его вывода из предыдущего. Обычно есть несколько способов достичь результата.

Законы булевой алгебры

Законы логической алгебры используются для упрощения логических выражений.

Основные логические законы

1. Идемпотентный закон
2. Ассоциативный закон
   • (A * B) * C = A * (B * C)
   • (А + В) + С = А + (В + С)
3. Коммутативный закон
   • А * В = В * А
   • А + В = В + А
4. Распределительное право
   • А * (В + С) = А * В + А * С
   • А + (В * С) = (А + В) * (А + С)
5. Закон о личности
   • А * 0 = 0 А * 1 = А
   • А + 1 = 1 А + 0 = А
6. Закон о дополнении
7. Закон об инволюции
8. Закон ДеМоргана
   • ~ (A * B) = ~ A + ~ B
   • ~ (А + В) = ~ А * ~ В

   Законы о резервировании

9. Поглощение
   • А + (А * В) = А
   • А * (А + В) = А
10. • (А * В) + (А * ~ В) = А
    • (А + В) * (А + ~ В) = А
11. • А + (~ А * В) = А + В
    • А * (~ А + В) = А * В

Каждый закон описывается двумя частями, которые двойственны друг другу. Принцип двойственности

• Перестановка операций + (ИЛИ) и * (И) в выражении.
• Замена элементов 0 и 1 в выражении местами.
• Не меняет форму переменных.

Применение булевой алгебры

Разработка комбинационной логической схемы

включает следующие шаги

1. Из проектной спецификации найдите таблицу истинности
2. Из таблицы истинности выведите логическое выражение «Сумма произведений».
3. Используйте логическую алгебру, чтобы упростить логическое выражение. Чем проще логическое выражение, тем меньше логических элементов будет использоваться.
4. Используйте логические элементы для реализации упрощенного логического выражения.

Поскольку доходы от рекламы падают, несмотря на рост числа посетителей, нам нужна ваша помощь в поддержании и улучшении этого сайта, что требует времени, денег и тяжелого труда. Благодаря щедрости наших посетителей, которые давали раньше, вы можете использовать этот сайт бесплатно.

Если вы получили пользу от этого сайта и можете, пожалуйста, отдать 10 долларов через Paypal . Это позволит нам продолжаем в будущее. Это займет всего минуту. Спасибо!

Я хочу дать!

Щелкните Discussion , чтобы использовать наш новый форум Discourse. Снимок наших старых комментариев в Facebook приведен для справки

.

© 2021 Emant Pte Ltd Co., рег. № 200210155R | Условия использования | Конфиденциальность | О нас

Учебник по логической алгебре

Булева алгебра!

Это действительно логично.

Введение

Следующие страницы предназначены для того, чтобы дать вам прочную основу для работы с булевой алгеброй. Булеву алгебру также иногда называют булевой логикой или просто логикой. Этот метод представления выражений с использованием только двух значений (обычно True и False) был впервые предложен Джорджем Булем в 1847 году.

Наброски

Этот учебник по булевой алгебре разделен на 3 раздела. В общем, я рекомендую вам проработать их по порядку, но если вы пришли сюда только для того, чтобы узнать о конкретной теме, то кто я такой, чтобы замедлять вас, просто идите прямо вперед.

Продолжайте читать ниже, чтобы начать работу с булевой алгеброй, или перейдите к одному из следующих разделов.

1. Основы булева алгебры – Что такое булева алгебра и обзор основных операторов.
2. Законы булевой алгебры – Основной набор приложений и следствий операторов.
3. Выражения логической алгебры – Использование правил для управления и упрощения выражений булевой алгебры.

Так зачем мне изучать булеву алгебру?

Логическая алгебра является фундаментальной для работы программного и аппаратного обеспечения, которое мы используем каждый день. Если вы работаете в сфере информационных технологий, то понимание булевой алгебры полезно во многих отношениях.

Если вы не работаете в сфере информационных технологий, знание булевой алгебры может быть очень полезным. Даже если вы никогда не используете его формально, его изучение повлияет на то, как вы смотрите на мир и как вы видите и решаете проблемы.Это улучшит ваше мышление и сделает вас более сильным решателем проблем. Это также позволит вам представлять и думать о процессах альтернативными способами, чтобы лучше понять их, а затем потенциально упростить их.

Я считаю, что изучение булевой алгебры может быть полезным почти для всех и, что более важно, также весело.

Изучение логической алгебры

Основы булевой алгебры, как правило, довольно легко освоить.Тогда кривая обучения становится немного крутой. Во многом это потому, что это довольно абстрактно. Лучше всего выяснить, какие стратегии и подходы помогут вам лучше визуализировать и понять, что происходит. Вот несколько идей для начала, но все разные. Вам нужно будет выяснить, что лучше всего подходит для вас.

• Пройдите по вещи несколько раз с хорошим перерывом между ними. Вы будете удивлены, как что-то может иметь мало смысла в первый раз, когда вы это прочитаете, но если вы оставите это на некоторое время, чтобы позволить этому тушиться в вашей голове, а затем вернетесь к этому, это будет иметь больше смысла при втором чтении.
• Нарисуйте на бумаге. Я сталкиваюсь с множеством ленивых студентов, которые говорят: «Нет, все в порядке, я просто проработаю это в своей голове». Для абстрактных вещей, таких как логическая алгебра, это не работает, если вы достигли определенного уровня сложности. Немного времени и усилий, чтобы нарисовать это на бумаге, избавят вас от многих часов разочарования. Это также позволит очень легко повторить свои шаги, когда что-то пойдет не так.
• Произнесите это вслух , а не просто мысленно. Это может показаться глупым, но когда вы говорите это, а не просто думаете, вы увидите это с другой точки зрения, и это может помочь лучше понять, что происходит.
• Практика !! Чем больше вы практикуетесь, тем больше ваш ум будет складывать кусочки пазла из этих абстрактных понятий. Чем больше вещей начнут обретать смысл.

Если вы воспользуетесь этим подходом, то обнаружите, что это довольно приятный путь к овладению булевой алгеброй.Вы также можете найти наше руководство по решению проблем, которое стоит быстро прочитать.

Булева алгебра | Encyclopedia.com

Свойства множеств

Свойства булевой алгебры

Приложения

Ресурсы

Булеву алгебру часто называют алгеброй логики. Английский математик Джордж Буль (1815–1864), который в значительной степени ответственен за ее начало, был первым, кто применил алгебраические методы к логической методологии.Он показал, что логические предложения и их связки могут быть выражены на языке теории множеств. Таким образом, булева алгебра также является алгеброй множеств. Алгебра – это раздел математики, который занимается соотношением величин.

Начиная с элементов определенного набора (называемого универсальным набором), вместе с одной или несколькими двоичными операциями, определенными для этого набора, производятся процедуры для управления элементами набора с использованием определенных операций и комбинаций этих операций.И язык, и правила манипуляции меняются в зависимости от свойств элементов универсального набора. Например, алгебра действительных чисел отличается от алгебры комплексных чисел, потому что действительные числа и комплексные числа определяются по-разному, что приводит к разным определениям для двоичных операций сложения и умножения и приводит к различным правилам манипулирования двумя типами чисел. числа. Булева алгебра состоит из правил для управления подмножествами любого универсального набора, независимо от конкретных свойств, связанных с отдельными элементами этого набора. Напротив, это зависит от свойств множеств. Универсальным набором может быть любой набор, включая набор действительных чисел или набор комплексных чисел, поскольку интересующие элементы в булевой алгебре не являются отдельными членами универсального набора, а всеми возможными подмножествами универсального набора.

Набор – это набор объектов, называемых членами или элементами. Члены набора могут быть физическими объектами, такими как люди, звезды или розы, или они могут быть абстракциями, такими как числа или даже другими наборами.Набор называется универсальным набором (обычно называется I), если он содержит все рассматриваемые элементы. Множество S, не равное I, называется собственным подмножеством I, если каждый элемент S содержится в I. Это записывается и читается как «S содержится в I.» (см. рисунок 1)

Если S равно I, то S называется несобственным подмножеством I, то есть I является несобственным подмножеством самого себя (обратите внимание, что два множества равны тогда и только тогда, когда они оба содержат точно такие же элементы. ). Специальный символ дается набору без элементов, который называется пустым набором или нулевым набором.Нулевой набор – это подмножество каждого набора.

При работе с наборами необходимо выполнить три важных операции. Две из этих операций являются бинарными (то есть они включают объединение наборов по два за раз), а третья включает только один набор за раз. Две бинарные операции – это объединение и пересечение. Третья операция – дополнение. Объединение двух множеств S и T – это совокупность тех членов, которые принадлежат либо S, либо T, либо обоим. (см. рисунок 2)

Пересечение множеств S и T – это совокупность тех элементов, которые принадлежат как S, так и T.(см. рисунок 3)

Дополнение к подмножеству S – это та часть I, которая не содержится в S, и записывается как S ^’. (см. рисунок 4)

Свойства булевой алгебры можно свести к четырем основным правилам.

(1) Обе бинарные операции обладают свойством коммутативности, то есть порядок не имеет значения.

S∩T = T∩S и S∪T = T∪S.

(2) Каждая двоичная операция имеет связанный с ней элемент идентификации. Универсальный набор – это элемент идентичности для операции пересечения, а нулевой набор – это элемент идентичности для операции объединения.

S∩I = S и S ∪Ø = S.

(3) каждая операция является распределительной по отношению к другой.

S ∪ (T∩ V) = (S ∪ T) ∩ (S ∪ V) и S ∩ (T∪V) = (S ∩ T) U (S ∩ V).

Это отличается от алгебры действительных чисел, для которой умножение дистрибутивно по сравнению с сложением, a (b + c) = ab + ac, но сложение не является распределительным по умножению, a + (bc) не равно (a + b) (а + с).

(4) с каждым элементом связан второй элемент, так что объединение или пересечение двух приводит к идентичному элементу другой операции.

A ∪ ′ = I и A ∩ ′ = Ø.

Это также отличается от алгебры действительных чисел. С каждым действительным числом связаны два других, так что его сумма с одним из них является тождественным элементом для сложения, а его произведение с другим является тождественным элементом для умножения. То есть a + (-a) = 0 и a (1 / a) = 1.

Полезность булевой алгебры заключается в том, что ее правила можно показать применимыми к логическим операторам. Логическое утверждение или предложение может быть либо истинным, либо ложным, так же как уравнение с действительными числами

может быть истинным или ложным в зависимости от значения переменной.Однако в булевой алгебре переменные не представляют значения, которые делают утверждение истинным, вместо этого они представляют истинность или ложность утверждения. То есть логическая переменная может иметь только одно из двух значений. В контексте символической логики эти значения истинны и ложны.

Булева алгебра оказалась незаменимой в области компьютерной инженерии. Взяв двузначные переменные булевой алгебры для представления электронных состояний включения и выключения (или двоичных цифр 0 и 1), булеву алгебру можно использовать для разработки цифровых вычислительных схем.Таким образом, это основной язык дизайна всех современных компьютеров и других цифровых устройств.

См. Также Компьютер, цифровой.

КЛЮЧЕВЫЕ УСЛОВИЯ

Двоичная операция – Двоичная операция – это метод комбинирования элементов набора, по два за раз, таким образом, что их комбинация также является членом набора.

Дополнение – Дополнение набора S, записываемое как S ^’, – это набор, содержащий те элементы универсального набора, которые не содержатся в S.

Элемент – Любой элемент набора. Объект в комплекте.

Пересечение – Пересечение двух наборов само по себе является набором, состоящим из всех элементов, общих для обоих наборов.

Набор – Набор – это совокупность вещей, называемых членами или элементами набора. В математике членами множества часто являются числа.

Теория множеств – Теория множеств – это изучение свойств множеств и подмножеств, особенно тех свойств, которые не зависят от конкретных элементов в множестве.

Подмножество – Набор S называется подмножеством другого набора I, если каждый член S содержится в I.

Объединение – Объединение двух наборов – это набор, содержащий все элементы. можно найти в одном или другом из двух наборов.

Универсальный набор – Универсальный набор – это набор, содержащий все рассматриваемые элементы.

КНИГИ

Марковиц, Алан Б. Введение в логический дизайн. Нью-Йорк: Макгроу-Хилл, 2006.

Дж. Р. Мэддокс

Компьютеры с булевой алгеброй

Джордж Буль Wikimedia Commons Есть две основные причины, по которым математика очаровывает человечество на протяжении двух тысяч лет. Во-первых, математика дает нам инструменты, необходимые для понимания вселенной и построения вещей. Во-вторых, изучение самих математических объектов может быть красивым и интригующим, даже если у них нет очевидного практического применения.

Что действительно удивительно, так это то, что иногда отрасль математики начинается как нечто совершенно абстрактное, не имеющее непосредственных научных или инженерных приложений, а затем гораздо позже можно найти практическое применение.

«И», «Или», «Не»

Булева алгебра – это комбинация логики и алгебры, первоначально разработанная Джорджем Булем, в честь которого назван предмет, в 1840-х и 50-х годах, а затем усовершенствованная другими логиками. через остаток девятнадцатого и начала двадцатого веков.

Формальная логика занимается проверкой истинности или ложности утверждений или предложений. «Барак Обама – президент Соединенных Штатов» – верное утверждение. Утверждение «Google производит iPhone» – ложное утверждение.

Все становится интереснее, когда мы начинаем комбинировать простые предложения. «Барак Обама – президент Соединенных Штатов, а Джо Байден – вице-президент» верно, поскольку оба простых утверждения, соединенных «и» в середине, верны.«Либо в Техасе проживает 300 человек, либо телевидение было изобретено Исааком Ньютоном» – ложно, поскольку оба простых утверждения, соединенных «или» в середине, ложны.

Булева алгебра и другие формы абстрактной логики высказываний основаны на работе со сложными предложениями, состоящими из простых предложений, соединенных логическими связями, такими как «и», «или» и «не». Все, что имеет значение для определения истинности такого составного утверждения, – это абстрактные значения истинности компонентных предложений и формальные правила, основанные на том, какие логические соединители мы используем.

Например, если предложение X истинно, а предложение Y истинно, то составное предложение «X и Y» также верно. Если либо X, либо Y ложны, или оба ложны, тогда «X и Y» также ложны.

Boole признал, что этот вид логики, основанный на объединении символов для предложений с использованием таких соединителей, как «и», «или» и «не», имеет структуру, аналогичную нормальной алгебре и арифметике. В нормальной алгебре переменные, представляющие числа, объединяются в формулы и уравнения с помощью арифметических операций сложения, вычитания, умножения и деления.

В логической алгебре Буля переменные, представляющие логические предложения, объединяются в формулы и уравнения с помощью логических операций и, или, и not. Утверждение «X и Y истинно» преобразуется в уравнение X × Y = 1. Утверждение «X или Y ложно» преобразуется в X + Y = 0.

Булева алгебра позволяет использовать те же виды алгебраической методы, которые мы используем для решения обычных уравнений с использованием чисел, чтобы установить логические отношения. Решая булевы уравнения, логики могут легче увидеть, когда одна комбинация предложений логически ведет к другой.

Сто лет спустя

Если это кажется чрезвычайно абстрактным, то это так. Логика всегда находилась между философией и математикой, пытаясь рассуждать о том, как мы можем рассуждать, и достигая фундаментальных представлений о том, что такое истина и как быть уверенными в том, что мы знаем вещи. Хотя логика высказываний и булева алгебра были увлекательными, они изначально принадлежали исключительно к области чистой математики, с меньшим количеством приложений, чем такая отрасль математики, как дифференциальные уравнения и исчисление, которые лежат в основе нашего понимания физики.

Примечательно, что примерно через столетие после первых исследований Буля математики и ученые открыли чрезвычайно мощный набор приложений для формальной логики, и теперь этот явно абстрактный математический и логический инструмент лежит в основе глобальной экономики.

Wikimedia Commons Булева алгебра – получение истинных и ложных значений, манипулирование ими в соответствии с логическими правилами и получение соответствующих истинных и ложных результатов – является фундаментальной основой современного цифрового компьютера.

Одно из первых крупных приложений булевой алгебры пришло из магистерской диссертации 1937 года Клода Шеннона, одного из самых важных математиков и инженеров 20-го века. Шеннон понял, что переключатели в релейных сетях, таких как телефонная сеть или ранний протокомпьютер, можно легко описать, рассматривая «включенные» переключатели, имеющие логическое значение «истина», «выключенные» переключатели как имеющие логическое значение. со значением «false» и с различными шаблонами, в которых переключатели соединены друг с другом, соответствующими логическим операциям «and», «or» и «not».

Нововведение Шеннона значительно упростило проектирование коммутационных сетей: вместо того, чтобы экспериментировать с самими сетевыми соединениями, методы, разработанные Булем и его последователями, обеспечили математическую основу, позволяющую создавать более эффективные схемы сети.

Связь между электрическими переключателями и булевой алгеброй также идет в другом направлении. ЦП компьютера в значительной степени построен из логических вентилей: физических проявлений булевых операторов.Логические элементы принимают одно или несколько электрических логических значений: провод с высоким напряжением может представлять «истину», а провод с низким напряжением может представлять «ложь». Выход логического элемента, рассчитанный с использованием электронных свойств полупроводников, представляет собой соответствующее напряжение от желаемой булевой операции.

Элемент «and», например, принимает два входа. Если оба входа имеют высокое напряжение (представляющее «истину»), затвор «и» также имеет высокое напряжение на выходе, равное «истине», в то время как если один или оба входа имеют низкое напряжение или ложь, затвор будет иметь низкое напряжение. вывод false.

Правильное соединение этих ворот позволяет запускать компьютерные программы. Возможность выполнять логические операции с различными входами по существу позволяет ЦП решать, как обрабатывать эти входы.

Далее, эта булева алгебра, встроенная в компьютеры, возвращается к обычной математике. Логическая дихотомия истина и ложь прекрасно подходит для представления двоичных чисел: истина соответствует 1, а ложь – 0.В соответствии с этой интерпретацией можно собрать логические схемы, которые, просто правильно комбинируя два двоичных входных числа с использованием и или или, а не операций, могут складывать, вычитать, умножать или делить числа.

Иногда достижения в чистой математике спустя десятилетия или столетия могут иметь удивительное применение.

.